中考计算题专题复习
初中数学计算题复习大全附答案【中考必备】

初中数学计算题复习大全附答案【中考必备】2+33+2011=204223×1012-992×23=211π-2)-1-tan60-1/23=-(π/6+1/23)改写】计算以下表达式:8.(1)-2^-1+33+2011=20422)23×10^12-992×23=2112.4-(-9)-7-1=53.-14-(1+1/2)×(1/3)/(-4)=-7/84.(-3)-27+1-2+(1/3)+2=-236.64/125×(-2)^2=-32/1259.(1)-23+(-37)-(-12)+45=4710.(3/4+7/12-5)/(-1/60)=-36011.(1)(24-1/2)-((1/8)+6)=-82)(2/3-1/6-2/9)×(-6)^2=1212.43-12+18=4913.[(1)/(212-3/3)]×6=6/3514.(6x^4-2x^2)/3x=2x^2-2/315.(-3)^2+[(111/3)-2]/6=816.18-3+6-9+(5-2)+(1-2)^2=1617.(1)12-(27+(1/3))=-16⅓2)[(3-3)^2+(18-6)]/6^2=1/1818.-0.8-[(5/1)+(7/2)]/4+3/4=-3.319.12-(1/4)^-1-3/3+|3-2|=13.2520.(-1)^2013-(-2)+[(3-π)/4]×38/5=-2.521.(略)22.28-(11/2+6/3)=15.523.(3-2)^2+(5-3)×(5+3)=1616.解:原式=32-(3/3+6/3)-32+1+(2-1) = 23-33-4/3 = -3/3-5/3 = -8/3.解析】将分数化为通分后进行计算,注意符号的运用。
17.(1) -4/3 (2) 2.解析】(1) 将分数化为通分后进行计算。
初中数学计算题复习大全附答案【中考必备】

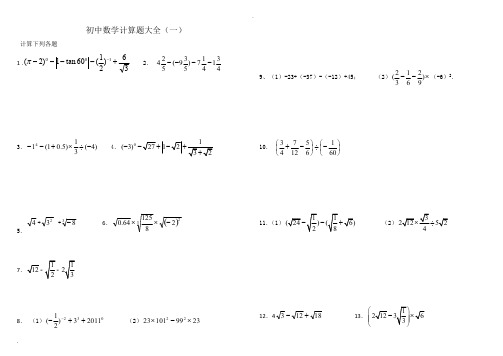
..初中数学计算题大全(一)计算下列各题1 .36)21(60tan 1)2(100+-----π 2. 431417)539(524----3.)4(31)5.01(14-÷⨯+-- 4.5.++ 6.7112238. (1)03220113)21(++-- (2)23991012322⨯-⨯10.11.(1)- (2)÷(3)1---+42338-()232812564.0-⨯⨯⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛-+601651274312.418123+- 13.⎛ ⎝ 14..x x x x 3)1246(÷- 15.61)2131()3(2÷-+-;16.20)21()25(2936318-+-+-+-17.(1))3127(12+- (2)()()6618332÷-+-18.()24335274158.0--+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛---1911()|2|4-+ 20. ())120131124π-⎛⎫---+ ⎪⎝⎭。
21.. 22.112812623-+23.2+参考答案1.解=1-|1-3|-2+23 =1+1-3-2+23 =3 【解析】略 2.5【解析】原式=14-9=53.87-【解析】解:)4(31)5.01(14-÷⨯+--⎪⎭⎫⎝⎛-⨯⨯--=4131231811+-=87-=先算乘方,再算乘除,最后算加减,有括号的先算括号里面的。
注意:41-底数是4,有小数又有分数时,一般都化成分数再进行计算。
4.==.【解析】略 5.3 6.4【解析】主要考查实数的运算,考查基本知识和基本的计算能力,题目简单,但易出错,计算需细心。
1、+ +=232=3+-252=42⨯⨯ 722【解析】试题分析:先化简,再合并同类二次根式即可计算出结果. 11223432223232332考点: 二次根式的运算.8.(1)32(2)9200 【解析】(1)原式=4+27+1 =32(2)原式=23(1012-992) (1分)=23(101+99)(101-99)(2分)=232200⨯⨯=9200 (1分) 利用幂的性质求值。
(完整版)初中数学中考计算题复习含答案
1 .23621601214314175395243 40431511454233862328125647--8123220113212399101232210601651274311121241318123214 1531246612131321620212529363181712312712661833218243352741581920112|4120131124212223231|1|3333325=14-9=5387431511441312318118741-44011536414233832527------813229200121012-992(101-99)21220091-3;210121-23+-37--12+45410-30=-45-606512743606560127604335+50=-3011121212121312131431323157.21113262969276161212233633231212122312231712233411851451424334155275424335274155424335274158019-2.+2-=-2.1. 2.201212352122232------------------------------------------------------------------63253--------71 220130 3|1|012013567 8 10 111213+|3|+1 151612120130+||222+412 17112013|7|+0121819122012302452211|3|+162320130222122312+124122512+12612272829201322012420113011一.解答题(共3011211+12121211101220130+1+13|1|01201312+1111212451141144362744421811139210+31111111212原式第一项利用立方根的定义化简,第二项利用负数的绝对值等于它的相反数计算法则计算,第四项利用负指数幂法则计算,第五项利用1181311321132132214 3.140+|3|+120131415221612120130+||222+412121122424242+4 17112013|7|+01211211115218原式第一项利用立方根的定义化简,第二项利用二次根式的化简公式化简,第三项利用零指数幂法则计算,1451912121114+1+|12|142121112012302452121222311416314211|3|+16232013021)原式第一项利用负数的绝对值等于它的相反数计算,第二项先计算乘方运算,再计算除法运算,第2131234622212121121313122312+11)原式第一项利用负数的绝对值等于它的相反数计算,第二项利用特殊角的三212172+1+324121)原式第一项利用绝对值的代数意义化简,第二项利用零指数幂法则计算,第三项利用负指数幂法则21+13+3213212512+112112+126121)原式第一项利用特殊角的三角函数值化简,第二项利用零指数幂法则计算,212211118272282129201322012420112011201122420112242011+522420110301819126-6 3020151351251513 223113415322 2215113656 709422023432852213222330 920121451012456011 ---3622337956347181213343144201232221113.解方程(本小题共61 2532436431.60.20.5140||6015 233218342101216241940 17582818 192221121276521223201120+|4|×0.5+21 21 49322922121212423424 25 0116033230148 31|4|201634232212117538131383171. 2. 3. 4. 5.62-36:-363-17.=-1+1-9-8=-174172312x-2=3x+5 2x-3x=2+5x=-7262(2x+1)-(5x-1)=6x=-354113【解析】先把第二个方程去分母得3x-4y=-2,4113622114211222212221117363236322182323931410123211212111-192-111=-9÷9-18=-1-18=-192753796418=-28+30-27+14=-111221311326313 1532436112171217129128122121543326452431.60.20.529362762732661361263616220561235414试题分析:原式第一项利用零指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用特殊角的三角函数值计算,最后一项利用立方根定义化简计算即可得到2. 3.153222123x-3+6≥2x332181-3x+3-8+x 0-23223421012122221161747 189190 2021-40--19-24=-40+19-24=-45 2-5-8--28 3-1256712=6+10-74-22--22-23-12011=-4-4+85-32+|-4|×0.52+2-12942912=-4+1+521 312124234 712166 102244124322421 1212423412166224001160341313200116034131322425 =2-1+230-76=-48+8-36=-76316412 95。
中考计算题专题一 解不等式

专题一:解不等式组本题是计算题的第一题,试卷中第19题,分值8分。
题目难度小,属常规题. 老师的叮嘱:不等式组要满分,解题规范、要记牢。
整理:去分母时要加括号,两边同乘最重要;去括号时要注意符号,防止漏乘最重要;移项:左侧未知项右侧常数项;求解:未知项系数化为1,同乘或同除负数系数要改变不等号方向;组解必是“四解之一”(同大取大、同小取小、大小小大,取之间、大大小小,是空集)(借助数轴最明晰,画图注意空心和实心,发展方向不能错,公共部分必是解;求特殊解时要注意,先组解集再求特殊,千万完整不要漏。
中考链接[2010·天津]解不等式组:⎩⎪⎨⎪⎧2x -1>x +1,x +8<4x -1. [2011·天津]解不等式组:⎩⎪⎨⎪⎧2x +1>x -5,4x ≤3x +2. [2014·天津]解不等式组 [2015·天津]36219x x +≥⎧⎨-≤⎩解不等式组:请结合题意填空,完成本小题的解答. (Ⅰ)解不等式①,得;(Ⅱ)解不等式②,得;(Ⅲ)把不等式①和②的解集在数轴上表示出来:(Ⅳ)原不等式组的解集为.[2017·天津]解不等式组 x +1≥2①5x≤4x +3②请结合题意填空,完成本题的解答.(1)解不等式①,得 ;(2)解不等式②,得 ;(3)把不等式①和②的解集在数轴上表示出来:⎩⎨⎧≤+-≥+②①312112x x(4)原不等式组的解集为.名师预测1、解不等式组2x−2≥3(x−2)2+x≤52、()315412123x xx x⎧++⎪⎨--≤⎪⎩解不等式组:3、解不等式组1252x xx+≤⎧⎨-⎩并写出它所有的整数解4、≤≤解不等式组:-83x-7115、2133212x yx y+=⎧⎨-=-⎩解方程组:6、解方程xx−1−1=3x−1(x+2)。
中考计算题复习

出厂日期
否要克服重力做功”这一问题 吗?如图11甲所示,小文同学对此进行了研究。有关测量数据 记录在下表中(表中的步距是指跨出每一步两脚之间的距离; 重心升降高度是指跨出每一步时,重心下降或升高的变化值): 1.站立时,小文双脚与地面的接触面积为400cm2,则行走时小 文对地面的压强是多少? 2.如图11乙所示时小文的脚跟提起后的姿势图。O点是脚尖与 地面的接触点,阻力F2的大小等于人的体重,其中 AO=16cm,AB=4cm,则排肠肌提起脚跟的动力F1为多大? 3.小文行走100m需要克服重力做的功多少?克服重力做功的功 率多大?
中考计算题
专题复习
计算题类型
双休目小明和爸爸自驾小轿车外出郊游,小轿车自重1.4吨,每个 轮胎与地面的接触面积是500 cm2:在行驶的过程中,善于观 察的小明看到汽车上有一个显示速度和路程的表盘,行驶到甲 地时,小明看到表盘的示数如图24甲所示,该车匀速行驶了一 段时间后到达乙地,表盘示数变为图24乙所示。(g取10N/kg) (1)该车静止在水平地面上时,对地面的压强是多大? (2)汽车从甲地到乙地行驶了多少时间? (3)若汽车行驶过程中受到的阻力是车重的0.2倍,则从甲地到乙地, 汽车的牵引力做了多少功?
如图2-13所示,某人用机械效率为80%的滑轮 组匀速提升重240N的物体,在2s内,绳的自由 端移动了6m。求: ⑴ 物体上升的高度和速度 ⑵ 人的拉力为多大? ⑶ 人所做的额外功是多大? (4)动滑轮重多少?
已知桑塔纳2000轿车的质量是1.6t,它以54 km/h的速度在水平路面上匀速行驶2min, 轿车受到的阻力是车重的0.1倍,求轿车 在这段时间内: ⑴通过的路程; ⑵发动机的牵引力; ⑶发动机的功率(g 取10N/kg)。
图26
初中数学中考计算题复习(最全)-含答案

--初中数学计算题大全(一)计算下列各题 1 .36)21(60tan 1)2(100+-----π 2. 431417)539(524----3.)4(31)5.01(14-÷⨯+-- 4.0(3)1---+5.4+23 +38- 6.()232812564.0-⨯⨯7112238. (1)03220113)21(++-- (2)23991012322⨯-⨯10. ⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛-+601651274311.(1)-(2)--12.418123+- 13.1212363⎛⎫-⨯ ⎪ ⎪⎝⎭ 14..x x x x 3)1246(÷- 15.61)2131()3(2÷-+-; 16.20)21()25(2936318-+-+-+-17.(1))3127(12+- (2)()()6618332÷-+-18.()24335274158.0--+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--- 19.1112()|32|43---+- 20.()()120133112384π-⎛⎫---+-⨯⨯ ⎪⎝⎭。
21.. 22.118122323.232)53)(53)+参考答案1.解=1-|1-3|-2+23 =1+1-3-2+23 =3 【解析】略 2.5【解析】原式=14-9=53.87-【解析】解:)4(31)5.01(14-÷⨯+--⎪⎭⎫⎝⎛-⨯⨯--=4131231811+-=87-=先算乘方,再算乘除,最后算加减,有括号的先算括号里面的。
注意:41-底数是4,有小数又有分数时,一般都化成分数再进行计算。
4.0(3)1-+=11--【解析】略 5.3 6.4【解析】主要考查实数的运算,考查基本知识和基本的计算能力,题目简单,但易出错,计算需细心。
1、4+23 +38-=232=3+-252=42⨯⨯2 【解析】试题分析:先化简,再合并同类二次根式即可计算出结果.1122343222323考点: 二次根式的运算.8.(1)32(2)9200 【解析】(1)原式=4+27+1 =32(2)原式=23(1012-992) (1分)=23(101+99)(101-99)(2分)=232200⨯⨯=9200 (1分) 利用幂的性质求值。
初中数学中考计算题复习(最全)-含答案

by by
4, 2
的解为
x
y
2, 1,
,则
2a-3b
的值为多少?
参考答案与试题解析
一.解答题(共 30 小题)
第 11 题 图
米的扇花台,那
a2 b2
.
2x y 5
3、已知 x 2 y 6 那么 x-y 的值是(
)
A. 1
B. ―1
C. 0
D. 2
4、若不等式组
x b
a2 2x 0
的解集是
1
x
1
,求
a
b
2010
的值
(1)23((xy12))5xy18
(5)
y 1 4
x
3
2
2x 3y 1
÷
+ ,其中 x=2 +1.
26.(1)计算:
;
(2)解方程:
.
27.计算:
.
28.计算:
.
29.计算:(1+ )2013﹣2(1+ )2012﹣4(1+ )2011.
30.计算:
.
1.化简求值:
,选择一个你喜欢且有意义的数代入求值.
2.先化简,再求值
,然后选取一个使原式有意义的 x 值代入求值.
一.解答题(共 30 小题)
1.计算题:
①
;
②解方程:
.
2.计算:
+(π﹣2013)0.
3.计算:|1﹣ |﹣2cos30°+(﹣ )0×(﹣1)2013.
4.计算:﹣
.
5.计算:
.
6.
.
7.计算:
.
8.计算: 9.计算:
中考化学计算题题复习专题

中考化学计算题题复习专题一、初中化学计算题1.有氯酸钾和二氧化锰混合物15g,加热使它完全反应,结果发现试管内固体物质为10.2g,试回答:可能用到的相对原子质量K:39,Cl:35.5,O:16,C:12,Mn;55(1)发生反应的化学方程式为:_______。
(2)生成氧气的质量是:_______。
(3)列出求解氯化钾质量(x)的比例式_______。
(4)原混合物中氯酸钾的质量是:_______。
(5)_______g二氧化碳中的氧元素质量与原混合物中氯酸钾的氧元素质量相同。
2.生铁和钢都是由铁和碳组成的合金,生铁中碳的含量为2%~4.3%,钢中碳的含量为0.03%~2%,为测定某种铁合金中碳的含量,小王同学取5.8g的合金样品盛放在烧杯中,并向其中逐滴加入100g稀盐酸至恰好完全反应,烧杯内剩余物的质量为105.6g。
请计算:(1)恰好完全反应时,生成氢气的质量为______g;(2)样品中碳的质量分数(计算结果保留到0.1%)。
3.某化学兴趣小组为了测定实验室用大理石和稀盐酸制备CO2后溶液的组成,取50g反应后的溶液,向其中加入10%的Na2CO3溶液,先出现气泡,后出现白色沉淀。
反应过程中加入Na2CO3溶液质量与生成的气体及沉淀质量关系如图。
(1)生成沉淀的质量是 g。
(2)50g溶液中CaCl2的质量分数是?(写出计算过程)(3)X=。
(4)C点对应的溶液的溶质是(填化学式)。
4.铜锌合金又称假黄金。
向盛有30 g铜锌合金粉末样品的烧杯中逐渐加入稀硫酸,生成氢气的质量与加入稀硫酸的质量关系如图所示。
计算:(1)充分反应后生成氢气的质量为_____g。
(2)合金样品中锌的质量。
(写计算过程,下同)(3)所用稀硫酸中硫酸的质量分数。
(结果精确到0.1%)5.某学习小组的同学取了当地的石灰石准备在实验室制取二氧化碳,采用了以下的办法:取用8g这种石灰石,把40g稀盐酸分四次加入,测量过程所得数据见下表(石灰石中杂质不溶于水,也不与盐酸反应)。
中考化学总复习《计算题》专项测试卷-带有答案

中考化学总复习《计算题》专项测试卷-带有答案学校:___________班级:___________姓名:___________考号:___________1.碳化铝(Al4C3)主要用作甲烷发生剂,在冷水中与水反应会产生甲烷,反应的化学方程式为:Al4C3+12H2O=4Al(OH)3+3CH4↑。
计算:(1)甲烷可用作燃料,点燃甲烷之前应。
(2)若产生9.6 kg甲烷,理论上需要消耗碳化铝的质量。
(写出计算过程)。
2.实验室中稀硫酸因标签破损,需测定其质量分数。
某化学兴趣小组的同学取该稀硫酸样品50g,逐滴加入质量分数为16%的NaOH溶液,溶液的pH随加入NaOH溶液质量的变化如图所示。
(1)图中A点时溶液中溶质的化学式是。
(2)求稀硫酸中溶质的质量分数(写出计算过程,计算结果精确到0.01%)3.化学就在我们身边,请从A或B两题中任选1个作答,若两题均作答,按A计分。
A B馒头,中国特色传统面食之一。
(1)蒸馒头的过程中常常需要加入发酵粉(主要成分是碳酸氢钠),使馒头更加松软。
碳酸氢钠的俗称是________________。
(2)碳酸氢钠(NaHCO3)中氢、氧元素的质量比为______________。
生活中将自来水煮沸会出现水垢,可以用白醋除掉水垢。
(1)自来水属于_________(填“纯净物”或“混合物”)(2)白醋中含有醋酸(CH3COOH),醋酸中氢元素质量分数的计算式为___________________。
4.某炼铁厂对本厂购进的赤铁矿样品(主要成分是氧化铁)进行分析。
取20g样品放入烧杯中,加入219g 稀盐酸时恰好完全反应,过滤后所得溶液的质量为235g;(假设杂质既不溶于酸,也不溶于水;不考虑实验中溶液的质量损失)。
请计算:(1)赤铁矿样品中铁元素的质量分数为%。
(2)所用稀盐酸中溶质的质量分数。
(结果精确到1%)5.黄铜是一种外观酷似黄金的铜锌合金。
某兴趣小组为测定某黄铜中锌的质量分数,进行如图1所示实验,测得实验数据并描绘成图2。
中考“计算题”专题复习

【 详解 】 ( )的 1
指 针 指 在 “0 的 位 9”
20 +0 N 7 0 ,则 p 面 0 =× a ( ) 0N 50 = 0 N = F=7 7 1 0N 2
.
0 m,O -. 。 在 A 端 挂 一 体 积 为 1 . 2 B Om 4 体, 曰端 施加 一竖 直 向下 、大 小为 1N的拉 力 ,杠 0 杆恰 能在 水平位 置平衡 。
【 知识点描述】本题涉及杠杆的平衡条件 F F l L
,密 度 的计 算公 式 P 和 G m 。 = g
()将 石蜡 块 浸 没在 酒精 中 ,石 蜡 块 受 到 的 3
浮力 ( - .x Ok / ) p ̄ O8 l 3gm
【 知识点描述 】本题涉及 密度的计算公式 p :
; 压强 的 计算 公 式 p F ;浮力 计 算公 式 F浮
下表 所示 :
【 知识点描述 】此题涉及速度表的读数 ,速度
表 的 单 位 是 k / :速 mh 度 单 位 的 换 算 :功 率 的计 算 公 式 尸 : 以 = 及 二力平衡 的知识
( )在 行驶过 程 中 ,车对地 面的压 强是多 大? 1 ( )该 同学 骑 车沿 直 线匀 速 行驶 1 mi 了 2 0 n做 多 少功 ?
1ri 同学骑 车行驶 的路程 为 S v- m/ lx 0= 0 n该 a - t4 s 0 6 s x 24 0 0 m。自行车 匀速 行驶 时f F 3 N.则 功 W= s - ==0 F=
中考数学专题复习《整式的运算》测试卷-附带答案

中考数学专题复习《整式的运算》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.计算(−x2)3的结果是()A.−x6B.x6C.−x5D.−x82.下列计算正确的是()A.x7÷x=x7B.(−3x2)2=−9x4C.x3•x3=2x6D.(x3)2=x63.下列计算正确的是()A.3x+3y=6xy B.a2•a3=a6C.b6÷b3=b2D.(m2)3=m6 4.下列计算正确的是()A.3a3⋅2a3=6a3B.(−4a3b)2=8a6b2C.(a+b)2=a2+b2D.−2a2+3a2=a25.下列运算正确的是()A.(x−1)(x+1)=x2−x−1B.x2−2x+3=(x−1)2+4C.(x−1)2=x2−2x−1D.(x−1)(−1−x)=1−x26.观察一列单项式:x−3x37x5−15x731x9⋯.则第n个单项式是()A.(−1)n+1(2n−1)x2n−1B.(−1)n(2n−1)x2n+1C.(−1)n+1(2n−1)x2n−1D.(−1)n(2n+1)x2n−17.若k为任意整数则(2k+3)2−4k2的值总能()A.被2整除B.被3整除C.被5整除D.被7整除8.已知10a=25,100b=40则a+2b的值是()A.1B.2C.3D.49.对于任意自然数n关于代数式(n+7)2﹣(n﹣5)2的值说法错误的是()A.总能被3整除B.总能被4整除C.总能被6整除D.总能被7整除10.若2a-3b=-1 则代数式4a2−12ab+9b2的值为()A.-1B.1C.2D.311.已知关于x的两个多项式A=x2−ax−2B=x2−2x−3.其中a为常数下列说法:①若A−B的值始终与x无关则a=−2②关于x的方程A+B=0始终有两个不相等的实数根③若A ⋅B 的结果不含x 2的项 则a =52④当a =1时 若A B 的值为整数 则x 的整数值只有2个.以上结论正确的个数有( ) A .4B .3C .2D .112.对于若干个单项式 我们先将任意两个单项式作差 再将这些差的绝对值进行求和并化简 这样的运算称为对这若干个单项式作“差绝对值运算”. 例如:对2,3,4作“差绝对值运算” 得到|2−3|+|2−4|+|3−4|=4 则①对1,3,4,7作“差绝对值运算”的结果是19 ②对x 2,x ,−3(x 2>x >−3)进行“差绝对值运算”的结果是38 则x =±4 ③对a ,b ,c (互不相等)进行“差绝对值运算”的结果一共有7种. 以上说法中正确的个数为( ) A .0B .1C .2D .3二 填空题13.已知3x+y=-3 xy=-6 则 xy 3+9x 3y = .14.若实数m 满足(m −2023)2+(2024−m)2=2025 则(m −2023)(2024−m)= .15. 已知 m +n +2m+n =4,则 (m +n )2+(2m+n )2的值为 . 16.小明在化简:(4x 2−6x +7)−(4x 2−□x +2)时发现系数“□”印刷不清楚 老师提示他:“此题的化简结果是常数” 则多项式中的“□”表示的数是 .17.如果一个三位自然数m =abc ̅̅̅̅̅的各数位上的数字互不相等且均不为0 满足a +c =b 那么称这个三位数为“中庸数”.将“中庸数”m =abc ̅̅̅̅̅的百位 个位数字交换位置 得到另一个“中庸数”m ′=cba ̅̅̅̅̅ 记F(m)=m−m ′99,T(m)=m+m ′121.例如:m =792,m ′=297.F(m)=792−29799=5 T(m)=792+297121=9.计算F(583)= 若“中庸数”m 满足2F(m)=s 2,2T(m)=t 2 其中s ,t 为自然数1 2 3…… 则该“中庸数”m 是 .18.一个四位自然数M 若它的千位数字与十位数字的差为3 百位数字与个位数字的差为2 则称M 为“接二连三数” 则最大的“接二连三数”为 已知“接二连三数”M 能被9整除 将其千位数字与百位数字之和记为P 十位数字与个位数字之差记为Q 当PQ 为整数时 满足条件的M 的最小值为 .三 计算题19.计算:(1)x(1−x)(2)(a−1)(2a+3)−2a(a−4)(3)x 2x−1−x−1.20.计算:(1)(−2xy2)2⋅3x2y.(2)(−2a2)(3ab2−5ab3).(3)(3m2n)2⋅(−2m2)3÷(−m2n)2.(4)(a−2b−3c)(a−2b+3c).21.(x+2)2+(2x+1)(2x﹣1)﹣4x(x+1)其中x=−12 ..22.−12(xy−x2)+3(y2−12x2)+2(14xy−12y2)其中x=−2y=12.23.先化简再求值:[(x+2y)2−(x+2y)(x−2y)]÷4y其中x=1y=−1.四解答题24.观察下面的等式:32−12=8×1,52−32=8×2,72−52=8×3,92−72=8×4,⋯(1)写出192−172的结果.(2)按上面的规律归纳出一个一般的结论(用含n的等式表示n为正整数)(3)请运用有关知识推理说明这个结论是正确的.25.尝试:①152=225=1×2×100+25.②252=625=2×3×100+25.③352=1225=_▲_...运用:小滨给出了猜想和证明请判断是否正确若有错误请给出正确解答.猜想:(10a+5)2=100a(a+1)+25.证明:(10a+5)2=100a(a+1)+25所以10a2+100a+5=100a2+100a+25.所以10a2=100a2.因为a≠0所以10a2≠100a2.所以等式不成立结论错误.26.已知实数a b满足(2a2+b2+1)(2a2+b2-1)=80 试求2a2+b2的值.解:设2a2+b2=m则原方程可化为(m+1)(m-1)=80 即m2=81 解得:m=±9 ∵2a2+b2≥0 ∴2a2+b2=9 上面的这种方法称为“换元法” 换元法是数学学习中最常用的一种思想方法在结构较复杂的数和式的运算中若把其中某些部分看成一个整体并用新字母代替(即换元)则能使复杂问题简单化.根据以上阅读材料解决下列问题:(1)已知实数x y满足(2x2+2y2-1)(x2+y2)=3 求3x2+3y2-2的值(2)若四个连续正整数的积为120 求这四个正整数.27.阅读下列材料:我们把多项式a2+2ab+b2及a2-2ab+b2叫做完全平方公式如果一个多项式不是完全平方公式我们常做如下变形:先添加一个适当的项使式子中出现完全平方式再减去这个项使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法可以求代数式的最大值或最小值.例如:求代数式x2+2x-3的最小值.解:x2+2x-3=x2+2x+12-12-3=(x2+2x+12)-4=(x+1)2-4.∵(x+1)2≥0 ∴(x+1)2-4≥-4∴当x=-1时x2+2x-3的最小值为-4.再例如:求代数式-x2+4x-1的最大值.解:-x2+4x-1=-(x2-4x+1)=-(x2-4x+22-22+1)=-[(x2-4x+22)-3]=-(x-2)2+3∵(x-2)2≥0 ∴-(x-2)2≤0 ∴-(x-2)2+3≤3.∴当x=2时-x2+4x-1的最大值为3.(1)【直接应用】代数式x2+4x+3的最小值为(2)【类比应用】若M=a2+b2-2a+4b+2023 试求M的最小值(3)【知识迁移】如图学校打算用长20m的篱笆围一个长方形菜地菜地的一面靠墙(墙足够长)求围成的菜地的最大面积.28.在学习《完全平方公式》时某数学学习小组发现:已知a+b=5 ab=3 可以在不求a b的值的情况下求出a2+b2的值.具体做法如下:a2+b2=a2+b2+2ab-2ab=(a+b)2-2ab=52-2×3=19.(1)若a+b=7 ab=6 则a2+b2=(2)若m满足(8-m)(m-3)=3 求(8-m)2+(m-3)2的值同样可以应用上述方法解决问题.具体操作如下:解:设8-m=a 8-m=a m-3=b则a+b=(8-m)+(m-3)=5 a+b=(8-m)+(m-3)=5 ab=(8-m)(m-3)=3所以(8-m)2+(m-3)2=a2+b2=(a+b)2-2ab=52-2×3=19.请参照上述方法解决下列问题:若(3x-2)(10-3x)=6 求(3x-2)2+(10-3x)2的值29.利用完全平方公式a2+2ab+b2=(a+b)2和a2−2ab+b=2(a−b)2的特点可以解决很多数学问题.下面给出两个例子:例1分解因式:x2+2x−3x2+2x−3=x2+2x+1−4=(x+1)2−4=(x+1+2)(x+1−2)=(x+3)(x−1)例2求代数式2x2−4x−6的最小值:2x2−4x−6=2(x2−2x)−6=2(x2−2x+1−1)−6=2[(x−1)2−1]−6=2(x−1)2−8又∵2(x−1)2≥0∴当x=1时代数式2x2−4x−6有最小值最小值是−8.仔细阅读上面例题模仿解决下列问题:(1)分解因式:m2−8m+12(2)代数式−x2+4x−2有最(大小)值当x=时最值是(3)当x y为何值时多项式2x2+y2−8x+6y+25有最小值?并求出这个最小值.30.发现:一个两位数的平方与其个位数字的平方的差一定是20的倍数.如:132−32=160160是20的8倍262−62=640640是20的32倍.(1)请你仿照上面的例子再举出一个例子:(⋅⋅⋅⋅)2−(⋅⋅⋅⋅⋅)2=(⋅⋅⋅⋅⋅)(2)十位数字为1 个位数字为a的两位数可表示为若该两位数的平方与a的平方的差是20的5倍则a=(3)设一个两位数的十位数字为m个位数字为n(0<m<100≤n<10且m n为正整数)请用含m n的式子论证“发现”的结论是否符合题意.31.灵活运用完全平方公式(a±b)2=a2±2ab+b2可以解决许多数学问题.例如:已知a−b=3,ab=1求a2+b2的值.解:∵a−b=3,ab=1∴(a−b)2=9,2ab=2,∴a2−2ab+b2=9∴a2−2+b2=9,∴a2+b2=9+2=11.请根据以上材料解答下列问题.(1)若a2+b2与2ab−4互为相反数求a+b的值.(2)如图矩形的长为a 宽为b 周长为14 面积为8 求a2+b2的值.32.定义:对于一个三位正整数如果十位数字恰好等于百位数字与个位数字之和的一半我们称这个三位正整数为“半和数”.例如三位正整数234 因为3=12×(2+4)所以234是“半和数”.(1)判断147是否为“半和数” 并说明理由(2)小林列举了几个“半和数”:111 123 234 840… 并且她发现:111÷3=37123÷3=41 234÷3=78840÷3=280… 所以她猜测任意一个“半和数”都能被3整除.小林的猜想正确吗?若正确请你帮小林说明该猜想的正确性若错误说明理由.答案解析部分1.【答案】A2.【答案】D3.【答案】D4.【答案】D5.【答案】D6.【答案】C7.【答案】B8.【答案】C9.【答案】D10.【答案】B11.【答案】B12.【答案】B13.【答案】-27014.【答案】−101215.【答案】1216.【答案】617.【答案】2 121或484或58318.【答案】9967 885619.【答案】(1)解:x(1−x)=x−x2(2)解:(a−1)(2a+3)−2a(a−4)=2a2+3a−2a−3−2a2+8a=9a−3(3)解:x 2x−1−x−1=x2x−1−(x+1)=x2−(x+1)(x−1)x−1=x2−x2+1x−1=1x−1.20.【答案】(1)解:(−2xy2)2⋅3x2y=4x2y4⋅3x2y=12x4y5(2)解:(−2a2)(3ab2−5ab3)=−6a3b2+10a3b3(3)解:(3m2n)2⋅(−2m2)3÷(−m2n)2=9m4n2⋅(−8m6)÷m4n2=−72m10n2÷m4n2=−72m6(4)解:(a−2b−3c)(a−2b+3c)=[(a−2b)−3c][(a−2b)+3c]=(a−2b)2−9c2=a2−4ab+4b2−9c2.21.【答案】解:原式=x2+4x+4+4x2﹣1﹣4x2﹣4x=x2+3当x=−1 2时∴原式=(−12)2+3=31 4.22.【答案】解:−12(xy−x2)+3(y2−12x2)+2(14xy−12y2)=−12xy+12x2+3y2−32x2+12xy−y2=−x2+2y2当x=−2y=1 2时原式=−(−2)2+2×(12)2=−4+2×1 4=−4+1 2=−72.23.【答案】解:化简方法一:[(x+2y)2−(x+2y)(x−2y)]÷4y=[(x+2y)(x+2y−x+2y)]÷4y=[(x+2y)·4y]÷4y=x+2y化简方法二:[(x+2y)2−(x+2y)(x−2y)]÷4y=[(x2+4xy+4y2)−(x2−4y2)]÷4y=(x2+4xy+4y2−x2+4y2)÷4y=(4xy+8y2)÷4y=4xy÷4y+8y2÷4y=x+2y当x=1y=−1时原式=1+2×(−1)=−1.24.【答案】(1)8×9(2)(2n+1)2−(2n−1)2=8n(3)(2n+1)2−(2n−1)2=(2n+1+2n−1)(2n+1−2n+1)=4n×2=8n。
初中数学中考计算题复习最全)-含答案

一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0.3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.4.计算:﹣.5.计算:.6..7.计算:.8.计算:.9.计算:.10.计算:.11.计算:.12..13.计算:.14.计算:﹣(π﹣3.14)0+|﹣3|+(﹣1)2013+tan45°.15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:.(1)19.(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°•tan60°+cos245°;(2).21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(1)计算:.22.(2)求不等式组的整数解.(1)计算:23.(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.1.化简求值:,选择一个你喜欢且有意义的数代入求值.2.先化简,再求值,然后选取一个使原式有意义的x值代入求值.3.先化简再求值:选一个使原代数式有意义的数代入中求值.4.先化简,再求值:,请选择一个你喜欢的数代入求值.5.(2010•红河州)先化简再求值:.选一个使原代数式有意义的数代入求值.6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值.7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值.8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值.9.化简求值(1)先化简,再求值,选择你喜欢的一个数代入求值.10.化简求值题:(1)先化简,再求值:,其中x=3.(2)先化简,再求值:,请选一个你喜欢且使式子有意义的数字代入求值.(3)先化简,再求值:,其中x=2.(4)先化简,再求值:,其中x=﹣1.11.(2006•巴中)化简求值:,其中a=.12.(2010•临沂)先化简,再求值:()÷,其中a=2.13.先化简:,再选一个恰当的x值代入求值.14.化简求值:(﹣1)÷,其中x=2.15.(2010•綦江县)先化简,再求值,,其中x=+1.16.(2009•随州)先化简,再求值:,其中x=+1.17.先化简,再求值:÷,其中x=tan45°.18.(2002•曲靖)化简,求值:(x+2)÷(x﹣),其中x=﹣1.19.先化简,再求值:(1+)÷,其中x=﹣3.20.先化简,再求值:,其中a=2.21.先化简,再求值÷(x﹣),其中x=2.22.先化简,再求值:,其中.23.先化简,再求值:(﹣1)÷,其中x—.25.(2011•新疆)先化简,再求值:(+1)÷,其中x=2.26.先化简,再求值:,其中x=2.27.(2011•南充)先化简,再求值:(﹣2),其中x=2.28.先化简,再求值:,其中a=﹣2.29.(2011•武汉)先化简,再求值:÷(x ﹣),其中x=3. 30.化简并求值:•,其中x=21.. 2。
初中数学中考计算题复习(最全)-含答案

一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0.3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.4.计算:﹣.5.计算:.6..7.计算:.8.计算:.9.计算:.10.计算:.11.计算:.12..13.计算:.14.计算:﹣(π﹣3.14)0+|﹣3|+(﹣1)2013+tan45°.15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:.(1)19.(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°•tan60°+cos245°;(2).21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(1)计算:.22.(2)求不等式组的整数解.(1)计算:23.(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.1.化简求值:,选择一个你喜欢且有意义的数代入求值.2.先化简,再求值,然后选取一个使原式有意义的x值代入求值.3.先化简再求值:选一个使原代数式有意义的数代入中求值.4.先化简,再求值:,请选择一个你喜欢的数代入求值.5.(2010•红河州)先化简再求值:.选一个使原代数式有意义的数代入求值.6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值.7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值.8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值.9.化简求值(1)先化简,再求值,选择你喜欢的一个数代入求值.(2)化简,其中m=5.10.化简求值题:(1)先化简,再求值:,其中x=3.(2)先化简,再求值:,请选一个你喜欢且使式子有意义的数字代入求值.(3)先化简,再求值:,其中x=2.(4)先化简,再求值:,其中x=﹣1.11.(2006•巴中)化简求值:,其中a=.12.(2010•临沂)先化简,再求值:()÷,其中a=2.13.先化简:,再选一个恰当的x值代入求值.14.化简求值:(﹣1)÷,其中x=2.15.(2010•綦江县)先化简,再求值,,其中x=+1.16.(2009•随州)先化简,再求值:,其中x=+1.17.先化简,再求值:÷,其中x=tan45°.18.(2002•曲靖)化简,求值:(x+2)÷(x﹣),其中x=﹣1.19.先化简,再求值:(1+)÷,其中x=﹣3.20.先化简,再求值:,其中a=2.21.先化简,再求值÷(x﹣),其中x=2.22.先化简,再求值:,其中.24.先化简代数式再求值,其中a=﹣2.25.(2011•新疆)先化简,再求值:(+1)÷,其中x=2.26.先化简,再求值:,其中x=2.27.(2011•南充)先化简,再求值:(﹣2),其中x=2.28.先化简,再求值:,其中a=﹣2.29.(2011•武汉)先化简,再求值:÷(x ﹣),其中x=3. 30.化简并求值:•,其中x=21. . 2。
2023年中考一轮复习—计算题专题(含答案)

中考数学一轮复习--解答题计算题专题一、一元一次方程(形如ax+b=0,a ≠0)一般的解题步骤:1、有括号的时候,先去括号。
2、有分式的时候,去分母(不等号两边同乘分母最小公倍数)3、移项,即单项式由等号左边移至等号右边,或由等号右边移至等号左边。
(注意:移项要变号,即+变-,-变+)4、合并同类项(加减运算中适用,所谓同类项是底数相同且底数相应的指数也相同的单项式。
),合并法则:底数与指数不变,系数相加减,如:a ²b-5a ²b=(1-4)a ²b=-3a ²b5、未知数系数化为1。
具体方法:方程两边同除以未知数的系数(系数要带符号)。
例题如下:例1:5x ﹣2(3﹣2x )=﹣3解:5x-6+4x=-3………………去括号(乘法分配率)5x+4x=-3+6………………移项(变号)9x=3……………………合并同类项9x 9 = 39…………………系数化为1 X = 13例2:5x+2(3x ﹣7)=9﹣4(2+x )解:5x+6x-14=9-8-4x …………去括号(乘法分配率)5x+6x+4x=9-8+14…………移项(变号) 15x=15…………………合并同类项15x 15=1515………………系数化为1 X=1二、一元一次不等式组(由两个及两个以上的一元一次不等式组成)1、不等式的一般解题步骤:①有括号的时候,先去括号。
②有分式的时候,去分母(不等号两边同乘分母最小公倍数)③移项,即单项式由不等号左边移至不等号右边,或由不等号右边移至不等号左边。
(注意:移项要变号,即+变-,-变+)④合并同类项(加减运算中适用,所谓同类项是底数相同且底数相应的指数也相同的单项式。
),合并法则:底数与指数不变,系数相加减,如:a²b-5a ²b=(1-4)a²b=-3a²b⑤未知数系数化为1。
具体方法:不等号两边同除以未知数的系数(系数要带符号),需特别注意:如果不等号两边同除或同乘负数,不等号要变号,如:-x≥1,则-x/-1≤1/-1,得:x≤-12、不等式组的解题步骤:①将不等式组中的每一个不等式单独求解。
中考:计算题专题(含答案)

专题(计算题)(30道)1.(2018·o 0113tan 30(4)()2π-+--【解析】()10133042tan π-⎛⎫-- ⎪⎝⎭+=1-2=+1-21. 2.(2019·江苏省中考模拟)先化简,再求值:221112a a a a a---÷+,其中1a =. 【解析】221112a a a a a---÷+,()()()21111a a a a a a +-=-⋅+-,21111a a a +=-=-++,当1a =时,原式=2=-.3.(2019·安徽省中考模拟)先化简,再求值:22231()111a a a a --÷+-+,其中1012cos30()(3)2a π-=︒+--【解析】原式=[2223(1)(1)(1)(1)a a a a a a ---+-+-]•(a+1)=1(1)(1)a a +-•(a+1)=11a -,当a=2cos30°+(12)-1-(π-3)0-+1时,原式3. 4.(2018·河南省中考模拟)请你先化简:2344111x x x x x ⎛⎫-+⎛⎫-+÷ ⎪ ⎪++⎝⎭⎝⎭,然后从12x -≤≤中选一个合适的整数作为x 的值代入求值.【解析】2344111x x x x x ⎛⎫-+⎛⎫-+÷ ⎪ ⎪++⎝⎭⎝⎭=()22231111x x x x x -⎛⎫--÷ ⎪+++⎝⎭=()()()222112x x x x x +-++-=22x x +-, 当0x =时,原式1=.5.(2018·湖北省中考模拟)计算:)2|﹣(12)﹣1. 【解析】原式22,==-=-6.(2018·河南省中考模拟)先化简,再求值:(223x y x y +-﹣222x xy -)÷22x yx y xy +-,其中+1,﹣1.【解析】解:原式=()()()xy x y 3x y 2x xy·x y xy x yx y -+-=+-++,当+1,1时,原式11==.7.(2019·辽宁省中考模拟)先化简,再求值:(2﹣11x x -+)÷22691x x x ++-,其中x 3. 【解析】原式=()()()211221·13x x x x x x +-+-+++=()()()2113·13x x x x x +-+++=13x x -+,当x ﹣31==-.8.(2019·广西壮族自治区中考模拟)(1)计算:|1(12)﹣1﹣2tan60°(2)先化简,再求值:22121()242x x x x x x -++÷-++,其中x ﹣1.【解析】(1)|1(12)﹣1﹣2tan60°﹣1+2﹣﹣1+2﹣; (2)22121()242x x x x x x -++÷-++=21(2)(21)222x x x x x x -+-+÷++()()=221222221x x x x x x -+++--()() =211211x x x -+-()()()=12(1)x x -+ ,当x 1=12.9.(2019·河南省中考模拟)先化简代数式:22321()393m m m m m m m --+-÷+-+ ,再从30≤≤m 的范围内选择一个合适的整数代入求值.【解析】解:原式23(1)3(3)(3)3m m m m m m m ⎡⎤--=-÷⎢⎥++-+⎣⎦ 2133(3)(1)m m m m m ⎡⎤+=-⋅⎢⎥++-⎣⎦ 2133(1)m m m m -+=⋅+-11m =-. 要使分式有意义,则3m ≠,一3,1.又∵30≤≤m 且为整数∵m 可取值0,2.选0m =,原式1=-.10.(2019·3tan60°+(2019﹣π)0﹣(12)﹣1【解析】原式=+1﹣2=﹣1.11.(2019·山东省中考模拟)先化简,再求值:(1﹣x+31x +)÷2441x x x +++,其中x=tan45°+(12)﹣1.【解析】原式=(21311x x x -+++)÷()221x x ++=()()()2221·12x x x x x +-+++=22x x -+,当x=tan45°+(12)﹣1=1+2=3时,原式=231235-=-+. 12.(2019·四川省中考模拟)化简:2416222a a a a -⎛⎫-+÷⎪--⎝⎭. 【解析】原式=()()()()()()2244222442444a a a a a a a a a a a a a -----⋅=⋅=-+--+-+.13.(2019·四川省中考模拟)(1)计算:3tan30°﹣12|﹣2﹣1+(π﹣2019)0;(2)解不等式组:2(1)3212223x x x x x +>-⎧⎪-⎨-≤-⎪⎩【解析】(1)原式=11-+122⎫⎪⎭11-+122 =1;(2)解不等式2(x+1)>3x ﹣2,得:x <4,解不等式12223x x -≤- ,得:x≥﹣95, 则不等式组的解集为﹣95≤x <4. 14.(2019·辽宁省中考模拟)先化简,再求值:22693111x x x x x x x -+-+÷--+,其中2sin 301x =-. 【解析】原式=2(3)11(1)(1)3x x x x x x x -++⋅-+--=311x x x x -+--=31x x x -+--=31x -,当2sin 301x =-=1212⨯-=0时,原式=3. 15.(2018·湖南省中考模拟)先化简,再求值:()22111a a a ⎛⎫-+÷+ ⎪+⎝⎭,其中1a =-.2【解析】(a -1+2a 1+)÷(a 2+1)=2a 12a 1-++·211a +=1a 1+当1a =时,原式2 16.(2018·重庆中考模拟)计算: (1)(y+2x )(y ﹣2x )﹣4x (2y ﹣x );(2)28163x x x -+-÷(x ﹣1633x x --)【解析】(1)原式=y 2﹣4x 2﹣8xy+4x 2=y 2﹣8xy ;(2)原式=()()()()22244316334333444x x x x x x x x x x x x x --⎛⎫--+--÷=⋅= ⎪---+-+⎝⎭. 17.(2019·陕西省中考模拟)先化简,再求值:22111·211x x x x x---++,其中x=2.【解析】原式=•﹣ =﹣ =﹣=,当x=2时,原式==.18.(2019·山东省中考模拟)先化简,再求值:1a a +÷(a ﹣1﹣211a a -+),并从﹣1,0,1,2四个数中,选一个合适的数代入求值【解析】原式=2121()111a a a a a a --÷-+++,=2211a a a a a -÷++=1·1(2)a a a a a ++-=12a -, ∵a≠﹣1且a≠0且a≠2,∵a=1,则原式=112-=﹣1.19.(2019·福建省中考模拟)先化简,再求值:2569122x x x x -+⎛⎫-÷⎪++⎝⎭,其中3x =. 【解析】解:原式=(22x x ++-52x +)•22(3)x x +-=32x x -+•22(3)x x +-=13x -,当x 时,原式.20.(2019·辽宁省中考模拟)计算:)2016tan3012π-⎛⎫-++ ⎪⎝⎭.【解析】原式=1-6×3-1=141-+=4.21.(2018·湖南省中考模拟)(1(﹣5)+(﹣3)2+20140; (2)化简:(a+1)2+2(1﹣a ).【解析】解:(1)原式 (2)原式=a 2+2a+1+2﹣2a=a 2+3.22.(2019·辽宁省中考模拟)化简分式:2222334424x x x x x x x ⎛⎫---÷ ⎪-+--⎝⎭,并从1,2,3,4这四个数中取一个合适的数作为x 的值代入求值.【解析】解:2222334424x x x x x x x ⎛⎫---÷ ⎪-+--⎝⎭22(2)33[](2)24x x x x x x --=-÷---233224x x x x x -⎛⎫=-÷ ⎪---⎝⎭ 3(2)(2)23x x x x x -+-=⨯--=x+2, ∵x 2-4≠0,x -3≠0,∵x≠2且x≠-2且x≠3,∵可取x=1代入,原式=3.23.(2019·北京中考模拟)计算:0(2019)4sin 45|2|︒--+-.【解析】解:原式=﹣4×2+2,=+1﹣+2,=3.24.(2019·辽宁省中考模拟)先化简代数式1﹣1x x -÷2212x x x-+,并从﹣1,0,1,3中选取一个合适的代入求值.【解析】原式=1﹣()()()21·11x x x x x x +-+- =1﹣21x x ++ =121x x x +--+=-11x +, 当x=3时,原式=﹣131+ =-14 .25.(2018·山东省中考模拟)解不等式组:3(2)21213x x xx +-≥⎧⎪+⎨-⎪⎩> 【解析】原不等式组为3(2)21213x x xx +-⎧⎪⎨+>-⎪⎩①② ∵解不等式∵,得x≥2,解不等式∵得,得x <4,∵原不等式组的解集是2≤x <4.26.(2019·北京中考模拟)解不等式组:()41710853x x x x ⎧+≤+⎪⎨--<⎪⎩,并写出它的所有非负整数解. 【解析】解:4(1)710{853x x x x +≤+--<①②由不等式∵得:x≥-2,由不等式∵得:,72x <, ∵不等式组的解集为:722x -<≤,∵x 的非负整数解为:0,1,2,3. 27.(2019·江西省中考模拟)解不等式组:31251422x x x x +>⎧⎪⎨+-≥⎪⎩,并把解集在数轴上表示出来.【解析】31251422x x x x +⎧⎪⎨+-≥⎪⎩>①②,解不等式∵,得x >﹣1,解不等式∵,得x ≤3,所以,原不等式组的解集为﹣1<x ≤3,在数轴上表示为:.28.(2018·陕西省中考模拟)解方程:28124x x x -=-- 【解析】解:方程两边乘(2)(2)x x +-,得()2(2)4=8x x x +--.解得2x =.检验:当2x =时,(2)(2)0x x +-=,因此2x =不是原分式方程的解,所以,原分式方程无解.29.(2018·江苏省中考模拟)解不等式组31234(1)9x x x +⎧≥+⎪⎨⎪+->-⎩,并把解集在数轴上表示出来.【解析】解:()3123419x x x +⎧≥+⎪⎨⎪+->-⎩①②, 解不等式∵得,x≤1;解不等式∵得,x>-2; ∵不等式组的解集为:-2<x≤1. 不等式组的解集在数轴上表示为:30.(2017·吉林省中考模拟)解方程:x 2﹣4x ﹣21=0. 【解析】解:x 2﹣4x ﹣21=0, (x ﹣7)(x+3)=0, x ﹣7=0,x+3=0, x 1=7,x 2=﹣3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.25.120015中考计算题专题复习可能用到的相对原子质量:Mn —55;Mg —24;Fe —56;Zn —65;Al —27;Ca —40;Cl —35.5;K —39;Cu —64;H —1;O —16;C —12;Na —23;S —32;N —14;Si —28;Ba —137一、 平均值型选择题混合物中确定各组分的有关计算是初中化学计算中难度较大的一种题型.如混合物中各组分均能与某一物质反应且得到的产物中有同一种物质或混合物中各组成成分均含有同一种元素,要确定其成分的有天计算可用平均值法求解。
解答此类题的关键是要先找出混合物中各成分的平均值(如平均二价相对原子质量、平均相对分子质量、平均质量、平均质量分数等),此平均值总是介于成分中对应值的最大值与最小值之间。
利用这些平均值解题的方法叫做平均值法。
有以下几类:(1)平均二价相对原子质量法 :由金属单质组成的混合物,要判断混合物的组成或计算某一成分的质量,利用平均二价相对原子质量法计算较为快捷、准确。
解题时先设该混合物为一种纯净的二价金属,利用化学方程式或其他方法求出平均二价相对原子质量,混合物各成分中一种金属的二价相对原子质量小于半均二价相对原子质量,则另一种金属的二价相对原子质量必须大于平均二价相对原子子质量,据此求出正确答案。
二价相对原子质量=×2 如:Na 的二价相对原子质量=×2=46Mg 的二价相对原子质量=×2=24 Al 的二价相对原子质量=×2=18(2相对分子质量平均值法:由化合物组成的混合物,要判断混合物中各物质是否存在或计算某成分的质量,可用相对分子质量平均值法解题。
解题时根据化学方程式和其他方法求出平均相对分子质量,混合物中一种物质的相对分子质量如果大于平均相对分子质量,则另一种物质的相对分子质量必小于平均相对分子质量,据此可求出正确答案。
(3)质量平均值法利用混合物中平均质量解题方法。
(4)质量分数平均值法混合物中某元素的质量分数总是介于混合物中一种成分该元素的质量分数与另一种成分中该元素的质量分数之间,据此可确定混合物的组成。
例:将13g 金属混合物粉末投入足量硫酸中,产生1g 氢气。
此金属混合物可能的组成是( )A 、Fe 和ZnB 、Mg 和ZnC 、Cu 和FeD 、Zn 和Cu 二、根据化学方程式计算1、不纯物的计算,应先把不纯物的质量换算成纯净物质量。
纯物质的质量==不纯物质的质量×纯度=不纯物质的质量×(1- 杂质的质量分数) 【例1】某班一次社会实践活动是到碱厂参观,该厂主要产品之一是小苏打(碳酸氢钠)。
参观结束,同学们带回一些化验室里废弃的小苏打样品,来测定其中碳酸氢钠的质量分数(假设该样品中只含有氯化钠一种杂质)。
取样品9.3 g逐滴加入稀盐酸,生成CO2气体的质量与滴加稀盐酸的质量关系如右图所示,求:(计算结果用百分数表示,保留到小数点后一位数字)(1)样品中碳酸氢钠的质量分数。
(2)恰好完全反应时,所得溶液中溶质的质量分数。
2、差量法计算:化学反应都必须遵循质量守恒定律,此定律是根据化学方程式进行计算的依据。
但有的化学反应在遵循质量守恒定律的同时,会出现固体、液体、气体质量在化学反应前后有所改变的现象,根据该变化的差值与化学方程式中反应物、生成物的质量成正比,可求出化学反应中反应物或生成物的质量,这一方法叫差量法。
此法解题的关键是分析物质变化的原因及规律,建立差量与所求量之间的对应关系。
如:①2KMnO4K2MnO4+MnO2+O2↑反应后固体质量减小,其差值为生成氧气的质量②H2+金属氧化物金属+水,该变化中固体质量减少量为生成水中氧元素的质量(或金属氧化物中氧元素的质量)③CO+金属氧化物金属+CO2,该变化中固体质量减少量为气体质量的增加量。
④C+金属氧化物金属+CO2,反应后固体质量减小,其差值为生成的二氧化碳的质量。
⑤2H2+O22H2O,反应后气体质量减小,其减小值为生成水的质量。
⑥金属+酸→盐+H2,该变化中金属质量减小,溶液质量增加,其增加值等于参加反应的金属质量与生成氢气质量的差值。
⑦金属+盐→盐+金属,该变化中金属质量若增加,溶液的质量则减小,否则相反。
其差值等于参加反应的金属质量与生成的金属质量的差值。
⑧难溶性碱金属氧化物+水,该变化中固体质量减小,其差值为生成的水的质量例:为了测定某些磁铁矿中四氧化三铁的质量,甲、乙两组同学根据磁铁矿与一氧化碳反应的原理,分别利用两种方法测定了磁铁矿中四氧化三铁的质量分数,已知磁铁矿与一氧化碳反应的化学方程式如下:Fe3O4+4CO3Fe+4CO2(1)甲组同学取该磁铁矿10g与足量的一氧化碳充分反应,并将产生的气体通入足量的氢氧化钠溶液中,溶液的质量增加了5.5g,请你根据甲组同学的实验数据,计算出磁铁矿样品中四氧化三铁的质量分数。
(2)乙组同学取该磁铁矿样品10g与足量的一氧化碳充分反应,测得反应后固体物质的质量为8g,请你根据乙组同学的实验数据,计算出磁铁矿样品中四氧化三铁的质量分数。
解析:(1)甲组同学的实验中被氢氧化钠溶液吸收的是CO还原Fe3O4生成的CO2,由5.5gCO2的质量作为已知条件,根据方程式可计算出Fe3O4的质量(2)乙组同学的实验中10g样品被CO充分还原后剩余8g固体,减少的质量为Fe3O4中氧元素的质量,利用产生的差量即可求出Fe3O4的质量。
也可以根据题中杂质不参加反应来建立等量关系,求出Fe3O4的质量。
答案:(1)Fe3O4+4CO3Fe+4CO2232176x 5.5g32/x=176/5.5g解得x=7.25g样品中Fe3O4的质量分数为7.25g/10g×100%=72.5%答:样品中Fe3O4的质量分数为72.5%(2)设样品中Fe3O4的质量分数为xFe3O4+4CO3Fe+4CO2△m232168232-168=64x10g-8g=2g32:64=x:2gx=7.25g样品中Fe3O4的质量分数为7.25g/10g×100%=72.5%答:样品中Fe3O4的质量分数为72.5%【实战演练】向一定质量的碳酸钙中加入100g稀盐酸,反应一段时间后,称得剩余溶液的质量为105.6g,求参加反应的碳酸钙质量。
【实战演练】将12gCO和CO2的混合气体通过灼热的氧化铜后,得到气体的总质量为18g,求混合气体中的CO的质量分数。
3、天平平衡化学计算中有关天平平衡问题的计算一般指反应前天平已处于平衡状态,当托盘两边烧杯中加入物质后,引起烧杯内物质净增量的变化,从而确定天平能否仍处于平衡的状态。
解此类题目必须理顺以下关系:烧杯内物质净增质量=加入物质质量一放出气体质量;当左边净增质量=右边净增质量时,天平仍处于平衡状念;当左边净增质量>右边净增质量时,天半指针向左偏转;当左边净增质量<右边净增质量时,天平指针向有偏转。
1、天平两端分别放置盛有足量稀盐酸的烧杯,把天平调到平衡,向其中一只烧杯中投入5.6g 氧化钙,向另一只烧杯中投入适量的镁片,要使天平最终保持平衡,需投入镁片的质量为()A.5.61g B.8.00g C.4.2g D.6.11g2、在天平的两盘分别放入质量相等的烧杯,烧杯中各盛100g9.8%的硫酸溶液,向两个烧中同时加入哪组金属,反应终止时天平仍保持平衡()A.锌、铁各7g B.锌、铁各5g C.锌、铁各4g D.锌、铁各3g 3、在天平的两个找盘里分别放上等重的两个烧杯,分别加入等质量的足量稀H2SO4,往左杯里放入0.44gCaO,要使天平重新达到平衡,可以往右边烧杯中加入的适宜物质是()A.100gCaCO3 B.0.48gMg粉C.0.924gMgCO3D.0.44gCu·Al 合金4、关系式法关系式法就是根据化学式、化学方程式和溶质质量分数等概念所包含的各种比例关系,找出已知量与未知量之间的比例关系式直接列比例式进行计算的方法。
它化繁为简,减少计算误差,是化学计算常用方法之一。
例:碳酸氢钠(NaHCO3)俗称小苏打,是一种白色固体,是焙制糕点的发酵粉的主要成分之一,它能与稀硫酸等酸反应生成CO2,试回答:(1)写出NaHCO3与稀硫酸反应的化学方程式(2)如何用98%的硫酸(密度为1.84g/mL)配制980g18.4%的硫酸溶液?(3)现将45gNaHCO3(混有KHCO3)固体粉末加入100mL稀硫酸,恰好完全反应后是气体全部逸出,固体粉末的质量与产生CO2的体积的关系如图(该状况下,CO2的密度为2g/L)所示,计算:①求100mL稀硫酸中硫酸的质量②若稀硫酸为120mL时,加入固体粉末为58.5g,求产生CO2的体积。
答案:(1)2NaHCO3+H2SO4==Na2SO4+2CO2↑+2H2O(2)将100ml98%的H2SO4沿着烧杯内壁慢慢倒入796ml水中,同时用玻璃棒不断搅拌。
(3)解:①45g固体完全反应时生成CO2的质量m(CO2)=11L×2g/L=22g设硫酸溶液中H2SO4的质量为x由(1)得H2SO4——2CO29888x22gx=(98×22g)/88=24.5g②设与120mL稀H2SO4完全反应的固体粉末的质量为y100mL/120mL=45g/yy=54g<58.5g所以固体粉末过量,以硫酸的量进行计算:V(CO2)=(11L×120mL)/100mL=13.2L答:100mL稀硫酸中硫酸的质量为24.5g,产生的CO2的体积为13.2L。
三、特殊规律型选择题例:某甲醛(HCHO)溶液中氢元素的质量分数为10%,则碳元素的质量分数正确的是()A.12% B.10% C.8% D.6%【讲解】:(甲醛)CH2O 水H2O 两种物质中氢氧的原子个数比均为2:1,整个混合物中除了氢氧,就是碳.因为氢元素的质量分数为10%,而氢、氧质量比为1:8,所以,氧的质量分数为80%,碳的质量分数为:1-10%-80%=10%知识迁移:已知NaHS、MgSO4、和NaHSO3由组成的混合物中硫元素的质量分数为20%,则氧元素的质量分数为()A.35%B.25%C.65%D.无法计算四、溶质的质量分数计算1、已知20℃硝酸钾的溶解度为31.6g。
在该温度下将20g硝酸钾放入50g水中,充分搅拌,则所得溶液中溶质的质量分数约为()A.24.0% B.28.6%C.31.6%D.40.0%2、对100g溶质质量分数为10%的某物质的溶液,分别进行如下操作:①蒸发掉10g水,无晶体析出②加入溶质质量分数为10%的同种溶质的溶液10g ③加入10g同种溶质,且完全溶解④加入10g水。
