2016年秋季新版苏科版七年级数学上学期4.2、解一元一次方程学案7
苏科版七年级上4.2解一元一次方程学案

4.2解一元一次方程(1)班级 姓名 学号 学习目标1. 了解方程的解和解方程的意义,养成检验的习惯。
2. 理解把握等式性质,并能用于解一元一次方程。
3. 了解解一元一次方程的目标——将一元一次方程变形成“x=a ”的形式。
学习难点等式性质的探索及应用。
教学过程 一、复习引入下列方程中是一元一次方程的有:232,0.31,51,2(1)22,43,20,20,1x x x x x x x x x x x y x -===---=-==+==二、探索新知 1.填表:当x= 时,方程2x+1=9成立。
2.分别把0、1、2、3、4代入下列方程,哪一个值能使方程成立: (1)2x-1=5; (2)3x-2=4x-33.方程的解:能使方程________________________________________叫做方程的解. 4.下列各未知数的值,哪个是方程5x-1=7x-2的解 x=0, x=-1, x=3, x=12.5.解方程:____________________________________________做解方程.6.①等式两边都_______________________________________,所得结果仍是等式; ②等式两边都_______________________________________,所得结果仍是等式。
三、例题教学 例 解下列方程:① x + 5 = 2 ② -2x = 4练习1.解下列方程:练习2.判断下列变形是否正确①由3x+1=5,得3x=4 ; ②由2y+a=b+2y ,得a=b ; ③由 12x=1,得x= 12; ④4由8x=16,得x=2。
练习3.如果ma=mb,那么下列变形不一定正确的是( )A.ma+1=mb+1 B.ma-3=mb-3 C.-0.5ma= -0.5mb D.a=b2234.(a 1)y 3y ,a 1-==--练习由得依据是什么?应受到什么限制,为什么。
苏科版数学七年级上册4.2《解一元一次方程》(第2课时)教学设计

苏科版数学七年级上册4.2《解一元一次方程》(第2课时)教学设计一. 教材分析《解一元一次方程》是苏科版数学七年级上册4.2节的内容,本节课的主要内容是一元一次方程的解法及应用。
通过本节课的学习,使学生掌握一元一次方程的解法,并能运用解方程的方法解决实际问题。
教材中通过丰富的例题和练习题,帮助学生巩固所学知识,提高解题能力。
二. 学情分析学生在学习本节课之前,已经学习了有理数的运算、方程的概念等知识,具备了一定的数学基础。
但部分学生在解方程时,仍存在运算错误、思路不清晰等问题。
因此,在教学过程中,要关注学生的学习情况,针对性地进行指导,提高学生的解题能力。
三. 教学目标1.理解一元一次方程的概念,掌握一元一次方程的解法。
2.能够运用解方程的方法解决实际问题。
3.培养学生的运算能力、逻辑思维能力及合作交流能力。
四. 教学重难点1.教学重点:一元一次方程的解法及应用。
2.教学难点:解方程时的运算规律及思路。
五. 教学方法1.情境教学法:通过生活实例引入方程,激发学生的学习兴趣。
2.引导发现法:引导学生发现解方程的规律,培养学生的自主学习能力。
3.合作交流法:分组讨论,引导学生相互学习、共同进步。
4.练习法:通过大量练习,巩固所学知识,提高解题能力。
六. 教学准备1.教学课件:制作课件,展示解方程的过程及方法。
2.练习题:准备适量练习题,巩固所学知识。
3.教学道具:准备一些教学道具,帮助学生直观地理解方程的解法。
七. 教学过程1.导入(5分钟)利用生活实例引入方程,激发学生的学习兴趣。
例如,讲述一个人在购物时,发现商品价格与数量之间的关系,从而引出一元一次方程。
2.呈现(10分钟)展示一元一次方程的定义及解法,引导学生理解方程的概念,掌握解方程的方法。
3.操练(10分钟)分组讨论,让学生互相交流解方程的方法。
每组选择一道练习题,共同解答,并总结解题规律。
4.巩固(10分钟)让学生独立解答一些练习题,巩固所学知识。
苏科版数学七年级上册4.2.1《解一元一次方程》教学设计

苏科版数学七年级上册4.2.1《解一元一次方程》教学设计一. 教材分析《解一元一次方程》是苏科版数学七年级上册4.2.1的内容,本节课主要让学生掌握一元一次方程的解法,理解方程解的概念,并能够运用解方程的方法解决实际问题。
教材通过引入未知数、列方程、解方程的过程,使学生掌握一元一次方程的解法,并能够运用到实际问题中。
二. 学情分析学生在学习本节课之前,已经学习了有理数、代数式等基础知识,对于未知数、列方程等概念有一定的了解。
但学生对于解方程的方法和技巧还不够熟练,需要通过本节课的学习,让学生掌握解一元一次方程的方法,并能够灵活运用。
三. 教学目标1.知识与技能:让学生掌握一元一次方程的解法,理解方程解的概念。
2.过程与方法:通过自主学习、合作探究的方式,培养学生解决实际问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的自信心和自主学习能力。
四. 教学重难点1.重点:一元一次方程的解法。
2.难点:解一元一次方程的技巧和应用。
五. 教学方法1.自主学习:让学生通过自学教材,了解一元一次方程的解法。
2.合作探究:学生分组讨论,共同解决实际问题。
3.案例分析:通过具体案例,让学生理解方程解的概念。
4.实践操作:让学生通过练习,巩固解一元一次方程的方法。
六. 教学准备1.教材:苏科版数学七年级上册。
2.课件:教学课件。
3.练习题:相关练习题。
4.教学工具:黑板、粉笔。
七. 教学过程1.导入(5分钟)教师通过引入未知数的概念,激发学生的好奇心,引导学生进入本节课的学习。
2.呈现(10分钟)教师通过讲解教材中的例题,让学生了解一元一次方程的解法,并引导学生思考解方程的步骤和技巧。
3.操练(10分钟)教师布置练习题,让学生独立完成,并及时给予指导和反馈。
4.巩固(10分钟)教师通过讲解练习题,让学生巩固解一元一次方程的方法,并引导学生总结解方程的步骤和技巧。
5.拓展(10分钟)教师通过布置综合练习题,让学生运用所学知识解决实际问题,提高学生的应用能力。
七年级数学上册 第四章 一元一次方程 4.2 解一元一次方程(第1课时)教案 (新版)苏科版

等式两边都乘(或除以)同一个不等于0的数,所得结果仍是等式.
对照天平、方程的变化,得出等式性质,为用等式性质解方程提供理论支撑.
三、根据等式性质解一元一次方程
例1解下列方程:
(1)x+5=2; (2)-2x=4.
求方程的解就是将方程变形为x=a的形式.
议一议:
若已知x=2是关于x的方程2x+3k=4的解,则k的值为多少?
解:(1)两边都减去5,得
x+5-5=2-5.
合并同类项,得
x=-3.(2)两边都除来自-2,得= ,即
x=-2.
因为x=2是关于x的方程2x+3k=4的解,
所以4+3k=4.
两边都减去4,得3k=0.
两边都除以3,得k=0.
根据等式性质解一元一次方程.体会解方程就是将方程变形为x=a的形式的转化思想.
(1)方程2x-1=-5的解为-2.
(2)方程 =1的解为3.
通过填表来找使方程两边相等的未知数的值,为引出方程的解和解方程的概念做准备.
二、等式的基本性质
方程2x+1=5可以变形如下:
方程3x=3+2x可以变形如下:
从以上的变形中,你发现等式具有怎样的性质?
结合天平,观察方程的变形,概括出等式的性质:
x-4= x-1,8+6(n-1)=140,5+x= (32+x)中未知数的值呢?
思考!
激发求知欲望.
一、方程的解和解方程
做一做:
填表:
x
1
2
3
4
5
2x+1
当x=_____时,方程2x+1=5两边相等.
试一试:
分别把0、1、2、3、4代入下列方程,哪一个值能使方程两边相等?
苏科版数学七年级上册4.2.2《解一元一次方程》教学设计

苏科版数学七年级上册4.2.2《解一元一次方程》教学设计一. 教材分析《苏科版数学七年级上册4.2.2》这一节主要让学生掌握一元一次方程的解法。
一元一次方程是数学中的一种基础方程,它具有广泛的应用。
本节课通过实例讲解,让学生了解一元一次方程的解法,并能够灵活运用。
教材从实际问题出发,引导学生认识一元一次方程,并通过自主探究、合作交流的方式,让学生掌握解方程的方法。
二. 学情分析七年级的学生已经具备了一定的数学基础,他们掌握了有理数的运算、方程的性质等知识。
但是,对于解一元一次方程,学生可能还存在着一些困惑,如:如何将实际问题转化为方程、如何选择合适的解方程方法等。
因此,在教学过程中,教师需要关注学生的认知基础,引导学生逐步掌握解方程的方法。
三. 教学目标1.知识与技能:使学生了解一元一次方程的概念,掌握一元一次方程的解法,能运用一元一次方程解决实际问题。
2.过程与方法:通过自主探究、合作交流,培养学生解决问题的能力。
3.情感态度与价值观:让学生感受数学与生活的密切联系,培养学生学习数学的兴趣。
四. 教学重难点1.重点:一元一次方程的解法。
2.难点:如何将实际问题转化为方程,并选择合适的解方程方法。
五. 教学方法1.情境教学法:通过生活实例,引导学生认识一元一次方程,激发学生的学习兴趣。
2.自主探究法:鼓励学生自主探究解方程的方法,培养学生的创新能力。
3.合作交流法:引导学生分组讨论,共同解决问题,提高学生的合作能力。
六. 教学准备1.课件:制作课件,展示一元一次方程的解法。
2.练习题:准备一些一元一次方程的练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)利用生活实例,引导学生认识一元一次方程,激发学生的学习兴趣。
例如:小明买了一些苹果,每斤的价格是5元,他一共花费了20元,请问他买了多少斤苹果?2.呈现(10分钟)展示一元一次方程的解法,引导学生了解解方程的步骤。
如:5x = 20,解得x = 4。
新苏科版七年级数学上册4.2 解一元一次方程(3)学案
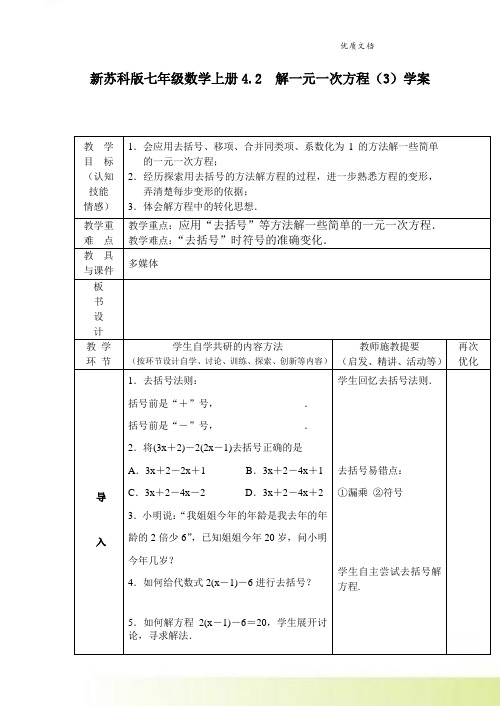
新苏科版七年级数学上册4.2 解一元一次方程(3)学案教学目标(认知技能情感)1.会应用去括号、移项、合并同类项、系数化为1的方法解一些简单的一元一次方程;2.经历探索用去括号的方法解方程的过程,进一步熟悉方程的变形,弄清楚每步变形的依据;3.体会解方程中的转化思想.教学重难点教学重点:应用“去括号”等方法解一些简单的一元一次方程.教学难点:“去括号”时符号的准确变化.教具与课件多媒体板书设计教学环节学生自学共研的内容方法(按环节设计自学、讨论、训练、探索、创新等内容)教师施教提要(启发、精讲、活动等)再次优化导入1.去括号法则:括号前是“+”号,_________________.括号前是“-”号,_________________.2.将(3x+2)-2(2x-1)去括号正确的是A.3x+2-2x+1 B.3x+2-4x+1C.3x+2-4x-2 D.3x+2-4x+23.小明说:“我姐姐今年的年龄是我去年的年龄的2倍少6”,已知姐姐今年20岁,问小明今年几岁?4.如何给代数式2(x-1)-6进行去括号?5.如何解方程2(x-1)-6=20,学生展开讨论,寻求解法.学生回忆去括号法则.去括号易错点:①漏乘②符号学生自主尝试去括号解方程.教学环节学生自学共研的内容方法(按环节设计自学、讨论、训练、探索、创新等内容)教师施教提要(启发、精讲、活动等)再次优化合作探究例1.解方程:(1)-3(x+1)=9;(2)2(2x+1)=1-5(x-2).例2.解方程:(1)6-3(x+23)=23;(2)12(x-1)-15(x+2)=13x+1.【教师强调】(1)去括号时“漏乘和符号”的问题;(2)移项要改变符号.例3.当x=2时,代数式2x2+3(3-c)x+c的值是10,求当x=-3时这个代数式的值?例4.当y取何值时,2(3y+4)的值比5(2y-7)的值大3?【思维拓展】解方程:32[2(x-12)+23]=5x.学生解答(要求学生检验).总结解方程的一般步骤:(1)去括号、(2)移项、(3)合并同类项、(4)系数化为1.熟悉去括号法则在解方程中的运用.注意解题步骤的规范化和检验的必要性.让学生注意解法的灵活性,不要过分按固定格式来解,可适当引导学生找出较好的解题方法进行转化.教学环节学生自学共研的内容方法(按环节设计自学、讨论、训练、探索、创新等内容)教师施教提要(启发、精讲、活动等)再次优化练习1.解方程:(1)-3(x -1)=9; (2)2(2x +1)=3-2(x -2). 2.解方程:(1)6-3(x -23 )=23 ;(2)32 [23 (14 x +1)+2]-212 =23 x .3.当x 取何值时,代数式3(2-x )和2(3+x )的值相等?4.小明今年6岁,他的爷爷62岁,几年后,小明的年龄是他爷爷年龄的31.布置 作业课堂作业 课本P102 练一练 课后作业 同步练习下节课预习内容教后感。
苏科初中数学七年级上册《4.2 解一元一次方程》教案 (7)【精品】.doc

1 解一元一次方程【教学目标】 1.了解与一元一次方程有关的概念,掌握等式的基本性质,能运用等式的基本性质解简单的一元一次方程.2.经历数值代入计算的过程,领会方程的解和解方程的意义.知道求方程的解就是将方程变形为x =a 的形式.3.强调检验的重要性,养成检验反思的好习惯 【教学重点】比较方程的解和解方程的异同;归纳等式的性质;【教学难点】利用性质解方程.【教学过程】一 、情境创设1.方程2x +1=5是什么方程? 2. 如何求方程2x +1=5中x 的值?二 、探索新知:1、做一做:填表 3 当 时,方程2、试一试:分别把0、1、2、3、4代入下列方程,哪一个值能使方程成立:(1) 2x -1=5;(2) 3x -2=4x -3由此得出方程的解和解方程的概念:能使方程两边的值相等的未知数的值叫做方程的解。
求方程的解的过程叫做解方程。
归纳出等式的基本性质:等式两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式。
等式两边都乘(或除以)同一个不等于0的数,所得的结果仍是等式。
三.例题分析例1、解下列方程:(1)x +5=2 (2)-2x =4练一练1、检验下列各题括号中的x 是否是前面方程的解.①825-=+x (x=-1) ②1253-=x x (x=6)2、解下列方程:(1)x +2=-6 (2)-3x =3-4x(3)21x =3 (4)-6x =2 3、在公元前1600年左右遗留下来的古埃及文献中,有这样一个问题:“它的全部,它的71,和等于19” .你能求出这个数吗?4、已知关于x 的方程12121=--n x 的解是1,求n 的值 四、展示交流1、用等式的基本性质解下列方程:(1)x +32=23 (2)-7x =632 (3)-2x +4=-3x (4)x +5x =-3 (5)-21x +1=-21 2、写出关于x 的形如ax +b =c(a ≠0)的一元一次方程,使它的解分别为:(1)-3 (2)310 3、当x 是什么数时,3x +2x 与1-x 的值相等?4、若方程3x +1=7的解也是关于x 的方程2x +a =7的解,则a 的值是多少?小明编了这样一道题“我们班有男生25人,比女生的2倍少15人,你猜我们班有多少名同学?”你会解这道题吗5、 你认为这节课你学到了什么?请你运用今天所学的知识看看老师的做法是否正确?解方程4x=2x解 两边都除以x,得4=2课堂练习1、解方程41x=31,正确的是 ( ) A .41x=31=x=34; B .41x=31, x=121 C .41x=31, x=34; D .41x=31, x= 43 2、下列变形是根据等式的性质的是 ( )A .由2x ﹣1=3得2x=4 B.由x 2=x 得 x=1C .由x 2=9得 x=3 D.由2x ﹣1=3x 得5x=﹣13、下列变形错误的是( )A.由x + 7= 5得x+7-7 = 5-7 ;B.由3x -2 =2x + 1得x= 3C.由4-3x = 4x -3得4+3 = 4x+3xD.由-2x= 3得x= -32 4、某数的4倍减去3比这个数的一半大4,则这个数为 __________.5、当m= __________时,方程2x+m=x+1的解为x=-4.当a= ____________时,方程3x 2a -2=4是一元一次方程.6、求作一个方程,使它的解为-5,这个方程为__________.三、拓展2a —3x=12是关于x 的方程.在解这个方程时,粗心的小虎误将-3x 看做3x ,得方程的解为x=3.请你帮助小虎求出原方程的解.【教学反思】。
苏科版-数学-七年级上册-4.2解一元一次方程 教案

解一元一次方程教学设计:1.了解与一元一次方程有关的概念,了解方程基本变形在方程中的应用。
2.掌握解一元一次方程的方法,了解解一元一次方程的一般步骤,能判别解的合理性。
3.经历和体会解一元一次方程中“转化”的思想方法。
重点:一元一次方程有关的概念,了解方程基本变形在方程中的应用。
难点:体会等式的性质及其应用。
一.创设情境1.创设情境一:计算并填表(同桌及前后4人一组)2.议一议:(1)从表中你能找出x =_____时,使方程2x + 1=5成立?(2)你能找出使下列方程成立的x的值吗?(a)2x - 1= 5 (b)3x - 2 = 4x -33.通过上述活动,给出方程的解、解方程的概念。
在填表中,全体同学都能正确写出,与备课时的准备是吻合的。
但是在讨论3x – 2 = 4x – 3 时,有些同学不太理解;有些小组的同学对表格中为什么x的取值是正整数提出了质疑,由于上述问题的提出是在前一课的小球的质量的问题中引出,所以同学们讨论后认为应该是正整数。
这在备课时未能想到,表格中的数给学生产生了一些错误的想法。
在有些小组的讨论中,学生发现了可以用枚举的方法找到方程的解,这是在正常教学中无法显现的。
2.创设情境二:天平称物(同桌二人一个小组,一架天平)工具:天平一架,100克质量的小球和50克砝码。
(1)问题:在天平的左右托盘内放入适量的小球和砝码(左边至少有一个小球,右边至少有一个砝码)使天平处于平衡状态;若设小球的质量为x ,你能列出相应的方程吗?(2)讲台上放有二架天平,其中一架的左边托盘内放有2个小球和一个砝码,右托盘内放有5个砝码(对应方程2x + 1 = 5);另一架天平的左托盘内放有3个小球,右托盘内放有4个砝码和1个小球(对应方程3x = x + 4)(3)教师演示天平中小球与砝码的增减过程写出方程2x + 1= 5的求解。
2x + 1 = 52x = 4x = 2(4)议一议:方程3x = x + 4 是怎么变形的?(5)通过上述活动,你发现了什么结论?与课本P153的叙述对照。
【最新苏科版精选】苏科初中数学七上《4.2 解一元一次方程》word教案 (2).doc

4、当y 取何值时,2(3y+4)的值比5(2y-7)的值大3?
四、课堂小结
通过这节课你学到了什么?
五、课堂作业 课本P102页练一 练T1
板书设计
教学反思
4.2解一元一次方程(3)
教学内容
年级学科
教学课时
共4课时第3课时
课型
教学目标
1.使学生进一步掌握解一元一次方程的移项规律。
2.掌握带有括号的 一元一次方程的解法
教学重点
带有括号的一元一次方程的解法
教学难点
解一元一次方程的移项规律
教学准备
多媒 体
教学过程
二次备课
一、知识回顾
1、用移项法解方程须注意点
去括号易错点:①漏乘②符号
4、如何给代数式-3(x+1)进行去括号?
5、如何解方程-3(x+1)=9,学生展开讨论,寻求解法.
二、引导探究:带括号的方程的解法。
例1.-3(x+1)=9
思考: 这样的题型首先该怎样处理 ?
解:
去括号,得
-3x-3 = 9
移项,得
-3x= 9 + 3
合并同 项,得
-3x = 12
-6x= -1 ,
X =
2、解方程:
(1)10y+7=12-5-3y; (2) 2.4x-9.8=1.4x-9
(3)3(y+ 4)12;(4)2-(1-z)=- 2
(5)2(3y-4)+7(4-y)=4y; (6)4x-3(20-x)=6x-7(9-x)
强调:(1)去括号时“漏乘和符号”的问题;
苏科版数学七年级上册4.2 解一元一次方程(第1课时)教教学设计

苏科版数学七年级上册4.2 解一元一次方程(第1课时)教教学设计一. 教材分析《苏科版数学七年级上册4.2 解一元一次方程(第1课时)》这一节内容,主要让学生掌握一元一次方程的解法。
一元一次方程是数学中的一种基础方程,也是解决实际问题的重要工具。
通过学习,学生将对一元一次方程有更深入的了解,并为后续学习更复杂的方程打下基础。
二. 学情分析学生在进入七年级之前,已经学习过一些关于代数的知识,对解方程有一定的了解。
但他们对一元一次方程的解法还没有系统的认识,需要通过本节课的学习,掌握解一元一次方程的方法和技巧。
此外,学生需要具备一定的逻辑思维能力和运算能力,以便能够灵活运用所学的知识解决实际问题。
三. 教学目标1.让学生掌握一元一次方程的解法,能够独立解出一元一次方程。
2.培养学生运用数学知识解决实际问题的能力。
3.提高学生的逻辑思维能力和运算能力。
四. 教学重难点1.教学重点:一元一次方程的解法。
2.教学难点:理解一元一次方程的解法,能够灵活运用解法解决实际问题。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过设置问题,引导学生思考和探索;通过案例分析,让学生了解一元一次方程在实际生活中的应用;通过小组合作学习,培养学生的团队协作能力和沟通能力。
六. 教学准备1.准备相关的一元一次方程案例,用于教学呈现。
2.准备解一元一次方程的练习题,用于课堂操练和巩固。
3.准备多媒体教学设备,用于展示和讲解。
七. 教学过程1.导入(5分钟)通过提问方式引导学生回顾已学的代数知识,为新课的学习做好铺垫。
例如:“你们还记得如何解方程吗?今天我们将学习一种新的方程,你们猜猜它是什么样的方程?”2.呈现(15分钟)利用多媒体展示一元一次方程的定义和性质,让学生了解一元一次方程的基本概念。
然后,呈现一些实际问题,让学生认识到一元一次方程在生活中的应用。
3.操练(20分钟)让学生分组合作,解决一些简单的一元一次方程。
苏科版七年级数学上册《4.2.1解一元一次方程》教学设计

苏科版七年级数学上册《4.2.1解一元一次方程》教学设计一. 教材分析《苏科版七年级数学上册》第四章第二节第一课时主要讲述了一元一次方程的解法。
本节课内容是学生在学习了代数基本概念、代数式的运算等知识的基础上进行学习的,是进一步学习更复杂方程的前提。
通过本节课的学习,学生需要掌握一元一次方程的解法,并能运用其解决实际问题。
二. 学情分析七年级的学生已经具备了一定的代数基础,对代数式、运算等概念有一定的了解。
但一部分学生在解决实际问题时,还不能很好地将数学知识与实际问题相结合。
因此,在教学过程中,需要关注这部分学生的学习情况,引导他们将理论知识与实际问题联系起来。
三. 教学目标1.知识与技能:掌握一元一次方程的解法,能够解简单的一元一次方程。
2.过程与方法:通过自主学习、合作交流的方式,提高学生解决问题的能力。
3.情感态度与价值观:培养学生对数学的兴趣,激发学生学习数学的积极性。
四. 教学重难点1.重点:一元一次方程的解法。
2.难点:如何将实际问题转化为方程,并运用解方程的方法解决问题。
五. 教学方法1.情境教学法:通过生活实例引入一元一次方程,使学生能够更好地理解方程的实际意义。
2.自主学习法:鼓励学生自主探索一元一次方程的解法,培养学生的独立思考能力。
3.合作交流法:在解决实际问题时,引导学生与他人合作,共同探讨问题的解决方法。
六. 教学准备1.准备一些实际问题,用于引导学生运用一元一次方程解决问题。
2.准备多媒体教学设备,用于展示和解题过程。
七. 教学过程1.导入(5分钟)通过一个生活实例,如购物问题,引导学生思考如何用数学方法表示问题,并引入一元一次方程的概念。
2.呈现(10分钟)呈现一些简单的一元一次方程,让学生观察并总结一元一次方程的特点。
同时,引导学生思考如何解决这些问题。
3.操练(10分钟)让学生独立解决一些简单的一元一次方程,教师巡回指导,解答学生的疑问。
4.巩固(10分钟)选取一些学生解决的实际问题,让学生运用一元一次方程进行解答,并讨论解题过程中的注意事项。
【最新】苏科版七年级上册数学《4.2 解一元一次方程》学案

新苏科版七年级上册数学《4.2 解一元一次方程》学案学习目标:1.会应用去括号、移项、合并同类项、系数化为1的方法解一些简单的一元一次方程;2.初步掌握解方程的一般步骤,培养学生的概括能力和耐心、细致的学习态度。
学习重点:应用“去括号”等方法解一些简单的一元一次方程;掌握解方程的一般步骤。
学习难点:正确使用去括号法则,把握解一元一次方程基本步骤,有效解方程。
一、知识回顾:1.什么叫做移项?移项的法则是什么?移项的依据是什么?移项时应注意什么?2.用移项法解一元一次方程的一般步骤怎样?3.用移项法解下列一元一次方程:(1)2y-1=5y+7 (2)31x-1=3x+31二、探索新知:情境:小明用50元钱购买了面值为1元和2元的邮票共30张,他买了多少张面值为1元的邮票?解:设他买了x 张面值为1元的邮票:x+2(30-x)=50问题:如何去掉方程中的括号?依据是什么?根据乘法分配律和去括号法则(括号前面是“+”号,把“+”号和括号去掉,括号内各项都不改变符号;括号前面是“-”号,把“-”号和括号去掉,括号内各项都要改变符号);去括号时要注意:(1)不要漏乘括号内的任何一项;(2)若括号前面是“-”号,记住去括号后括号内各项都变号。
三、例题评析:例1.解方程: -3(x+1)=9解:去括号,得: -3x -3=9 另解:方程两边同除以-3,得: x +1=-3移项,得: -3x=9+3 移项,得:x=-3-1合并同类项,得: -3x=12 合并同类项,得:x=-4 系数化为1,得: x= -4问题:1.你还有其他方法去掉方程中的括号吗?(见右上另解)2.观察上述两种解法,说出它们的区别归纳:解一元一次方程的步骤:(1)去括号;(2)移项;(2)合并同类项;(4)系数化为1(化成“x=a ”的形式);(5)检验(可在草稿纸上进行)。
例2. 解方程:(1)2(2x+1)=1-5(x-2); (2) 17(2-3y )-5(12-y )=8(1-7y ); (3)-51(x-15)= 21+31(7-x ); (4) 76[37(21x-51)-14]=3x -52练习:解下列方程:(1) ()612=-x ; (2)()x x -=-234; (3)5(x+2)=2(2x+7;(4)()()914322+-=-x x ; (5)()x x 2213=--; (6)5(x+1)=3(3x+1);(7)()()321210x x ---=;(8)()()()13153-=--+x x x ;(9)6-3(x+32)= -32x ; (10)x (71-14)= 41(x-20); (11)2[x 34-(32x-21)]=x 65; (12) 32[23(x-4) -6]=2x+1。
苏科版-数学-七年级上册-七上4.2 解一元一次方程(2)学案-

4.2 解一元一次方程(2)
【学习目标】了解方程的基本变形在解方程中的作用,掌握解一元一次方程的方法。
【学习重点】解一元一次方程的方法。
【学习过程】
『问题情境』
探索练习:
解下列方程:825=-x 467-=x x
方程两边都加上2,得 方程两边都减去6x ,得
28225+=+-x 46667--=-x x x x
即 285+=x 即 467-=-x x
比较这个方程与原方程,可以发现, 比较这个方程与原方程,可以发现,
-4
4
『例题讲评』
例1、解方程:(1)162=+x (2)7233+=+x x
例2、解方程:
32
141+-=x x
4.2 解一元一次方程(2)——随堂练习
评价_______________
1.判断下列移项是否正确:
(1)从6+x=9得到x=6+9; ( )
(2)从2x=x-5得到2x-x=-5;( )
(3)从4x+1=2x+3得到4x+2x=1+3; ( )
(4)从2x-1=3x+3得到2x-3x=3+1; ( )
2.填空,完成下列各题的移项、合并同类项的步骤。
(1)解方程6x=2+5x. (2)解方程-2x=4-3x 解:移项,得 解:移项,得
6x-________=2. -2x__________=______ 合并同类项,得
合并同类项,得 x=_________ x=_________
3.解方程:
(1)2
3x = 10- x
(2)13+2x = x-1
(3)21-3x
= 2x-2
(4)2-75.0x = 4
3。
苏科版七年级数学上册4-2解一元一次方程(7)教案

系数化为1,得依据
练习:解方程:
教
学
过
程
教学内容
个案调整
教师主导活动
学生主体活动
例4解方程:
【课堂练习】
1.小明是个“小马虎”下面是他做的题目,我们看看对不对?如果不对,请帮他改正。
(1)方程 去分母,得 ;
(2)方程 去分母,得 ;
(3)方程 去分母,得 ;
(4)方程 去分母,得 。
2、求下列各数的最小公倍数:
(1)2,3,4;
(2)3,6,8;
(3)3,4,18;
在上面的1、(2)中,可以保留分母,也可以去掉分母,得到整数系数,这样做比较简便。所以若方程中含有分母,则应先去掉分母,这样过程比较简便。
二、自主探究
1.解方程:
解:两边都乘以,去分母,得依据
去括号,得依据
移项,得依据
主备人
用案人
授课时间
月日
总第47课时课题课型来自新授课教学目标
会运用等式性质2正确去分母解一元一次方程。
重点
去分母时,不含分母的项会漏乘公分母,及没有对分子加括号
难点
去分母解方程
教法及教具
先学后教,当堂训练
教
学
过
程
教学内容
个案调整
教师主导活动
学生主体活动
【导学指导】
一、知识链接
1、解方程:
(1) 4-3(2-x)=5x (2) =3x-1
2.课本第101页练习
(1) ;(2) ;
【要点归纳】:
1、解一元一次方程的一般步骤为:
①去分母,②去括号,③移项,④合并同类项,⑤系数化为1。
2、去分母时要注意什么?(两点)
数学:4.2《解一元一次方程》学案(苏科版七年级上)

数学:4.2《解一元一次方程》学案(苏科版七年级上)【教材精讲】1、使方程左右两边的值相等的未知数的值叫方程的解。
如x=2是方程2x-4=0的解。
2、求方程解的过程叫解方程。
【例1】(2010·宿迁中考)已知5是关于x 的方程723=-a x 的解,则a 的值为________ [解析]由方程解的概念知:3×5-2a=7,可解得a=4。
1、用“=”表示相等关系的式子叫等式。
如a+b=c ,x(y+z)=xy+xz 等都是等式。
2、等式的基本性质:(1)等式基本性质1:同加(或同减)同一个整式,结果仍是等式。
(2)等式基本性质2:同乘(或同除以不为0)同一个的整式,结果仍是等式。
【例1】((2010·黄冈中考))通信市场竞争日益激烈,某通信公司的手机市话费标准按原标准每分钟降低a 元后,再次下调了20%,现在收费标准是每分钟b 元,求收费标准每分钟是多少元?(用等式的基本性质解方程)【解析】设原收费标准每分钟是x 元,根据题意得,(x-a )(1-20%)=b ,即54(x-a )=b. 两边同时乘以45,得:54(x-a )⨯45= b ⨯45,化简得x-a=54b 两边同时加a,得:x-a+a=54b+a知识点二 等式的基本性质(掌握)1、对等式的基本性质的理解强调两个“同”:一个是“等式两边同时”,另一个是“加上(或减或乘或除以不为0)同一个的整式”,有了这两手个词,才能保证变形前后仍是等式。
2、等式的基本性质可用字母表示:等式基本性质1:若a=b,则a+c=b+c,a-c=b-c; 等式基本性质2: 若a=b ,则ac=bc ,cbc a =(c ≠0) 名师指津知识点一 方程的解 (理解)1、方程解的作用?提示:把方程的解代入原方程,则原等式成立。
在以后的学习中你将体会到方程解的作用。
2、在求得方程的解之后,可以把解代入原方程,检验解方程是否正确。
名师指津移项得x=54b+a 。
苏科初中数学七年级上册《4.2 解一元一次方程》教案 (10)【精品】.doc

4.2 解一元一次方程学习目标:1.知道解一元一次方程的一般步骤,能灵活利用去分母、去括号、 移项、合并同类项、系数化为1等五大步骤解一元一次方程.2.巩固方程解法,经历求解过程,能体会到解法应根据具体方程本身特点而定.学习重点: 去分母的过程;解方程的一般步骤.学习难点: 利用“去分母”将方程作变形处理.一、自主预习:1.解下列方程:(1)64531-2+=x x ; (2)5-35512x =.2.①把-=10.30.6x x 分母化为整数为 . ②把20.25-0.1+=0.10.30.02x x 分母化为整数为 . 3.解一元一次方程的一般步骤是 .4、已知关于x 的方程324x m -=与21x m -=的解相同,求m 的值.二、合作探究:解方程:(1)11(+14)=(+20)74x x ; (2)1320-17-710=x x .(1)296182+=--x x x三、交流展示:例.解方程: (1)111+15=--7523t t ()(); (2)15.08402.01-3.0=--x x .四、课堂反馈:1. 解方程136221-=+--x x x 时,去分母去括号后正确的是哪一项 ( ) A. 1-22--3-3x x x = B. 1-2--1-x x x =C. 6-22--3-3x x x =D. 6-22-3-3x x x =+0.4 1.10.050.020.60.50.03x x ++=+2.解方程:(1)131225=--+x x ; (2)x x =+-515 ;(3)+1-2-=2-362x x x ; (4)0.1 1.7210.070.3x x --=.3.如果代数式43+a 比732-a 的值多1,求2-a 的值.五、拓展延伸:规定新运算符号“*”的运算规律为b a b a 41-31=* (1)求5*(-5)的值;(2)解方程:2*(2*x )=1*x.教学反思:。
七级数学上册第4章一元一次方程4.2解一元一次方程(1)教案苏科版

4.2 解一元一次方程课题§4.2 解一元一次方程课时4-1讲课时间班级课型新授讲课人知识与技术:认识与一元一次方程相关的观点,掌握等式的基天性质,能运用等式的基天性质解简单的一元一次方程.教课目的过程与方法:经历数值代入计算的过程,领悟方程的解和解方程的意义. 知道求方程的解就是将方程变形为x=a 的形式.感情、态度与价值观:重申查验的重要性,养成查验反省的好习惯.教学要点:比较方程的解和解方程的异同;重、难点难点:概括等式的性质;利用性质解方程。
教、学具投电影,小黑板1. 阅读课本P118- 119 的内容;预习要求2.达成课本 P118 的试一试。
教师活动内容、方式学生活动方式、内容旁注1.情形创建:(1)见课本 P118“如何解 2 x+ 1=5”. 经过填表试试,即采纳列举这一合情推理的方法找出知足方程的未知数的值,得出方程的解和解方程的概念.(2)见课本 P119由用天平测物,联想到等式的几种变形 . 探究得出:假如我们在两边盘内同时添学生感觉、议论回答上(或取下)同样质量的物体,能够看到天平依旧均衡,得 x+2=5→ x=5-2,3x=2x+2→3x-2x=2;假如我们将两边盘内物体的质量同时扩大到本来同样的倍数(或同时减小到本来的几分之一),也会看到天平依旧均衡,得 2x=6→x =6÷ 2. 学生概括等式的性质.2.学生活动、意义建构、数学理论:出示问题情形(1)后,学生考虑:如何求方程中的未知数的值?分别将1、2、3、4、5 代入方程,哪一个值能使方程建立?学生做课本P118试一试,教师讲解方程的解和解方程的观点 .引入问题情形(2)后,鼓舞学生说出各自不同的想法,互相沟通、增补,逐渐指引启迪学生教师活动内容、方式学生活动方式、内容旁注概括等式的性质 1:等式两边都加上或减去同一个数或同一个整式,所得结果还是等式;等式的性质 2:等式两边都乘以(或除以)同一个数(除数不为零),所得结果还是等式 . 等式的性质比较抽象,教课时不用在理论上作过多的睁开,重在问题情形②探究的过程,可多举例议论.3.数学运用:办理完问题情形(1)( 2),学生阅读课本P118— 119,进一步熟习学习内容,思虑:比较方程的解和解方程的异同?(方程的解是使方程建立的未知数的值;解方程是求方程解的过程,是一个等价变形过程,而求方程的解就是将方程变形为x=a 的形式).出示例 1解以下方程:(1)x+ 5=2;(2)- 2x=4.指引学生自己试试运用等式的基天性质解方程,求情楚每一步的依照,沟通解题方法 . 教师供给正确的解题格式 . 重申查验方法及查验的必需性.习题训练:( 1)以下变形能否正确?( 2)说明变形的依照?( 3)解方程,如课本 P120练一练 1,教师教课参照资料例题等.思想拓展:( 1)求作一个方程,使它的解为-1;( 2)简单应用题如课本P120练一练 2.4.回首反省:(1)小学阶段利用加减法、乘除法互为逆运算的方法解方程,学生印象深刻,教课时鼓舞学生运用等式的性质来求,但不强求.(2)解方程后,虽不要书面查验,但要修业生培育查验反省的好习惯 .(3)注意等式的性质中的“都”和“同”:“都”表示两边均要变形,“同”表示两边要作同样的变形.分小组议论,让学生充足议论,如何用一句话来表达这个变化,而后抽一名学生回答教师活动内容、方式学生活动方式、内容旁注(4)简单介绍等式的另两条性质:对称性与传达性 .5.实践应用解以下方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解一元一次方程
学习目标:
1.会应用去括号、移项、合并同类项、系数化为1的方法解一些简单的一元一次方程;
2.初步掌握解方程的一般步骤,培养学生的概括能力和耐心、细致的学习态度。
学习重点:应用“去括号”等方法解一些简单的一元一次方程;掌握解方程的一般步骤。
学习难点:正确使用去括号法则,把握解一元一次方程基本步骤,有效解方程。
一、知识回顾:
1.什么叫做移项?移项的法则是什么?移项的依据是什么?移项时应注意什么?
2.用移项法解一元一次方程的一般步骤怎样?
3.用移项法解下列一元一次方程:
(1)2y-1=5y+7 (2)31x-1=3x+3
1
二、探索新知:
情境:小明用50元钱购买了面值为1元和2元的邮票共30张,他买了多少张面值为1元的邮票?
解:设他买了x 张面值为1元的邮票:
x+2(30-x)=50
问题:如何去掉方程中的括号?依据是什么?
根据乘法分配律和去括号法则(括号前面是“+”号,把“+”号和括号去掉,括号内各项都不改变符号;括号前面是“-”号,把“-”号和括号去掉,括号内各项都要改变符号);去括号时要注意:(1)不要漏乘括号内的任何一项;(2)若括号前面是“-”号,记住去括号后括号内各项都变号。
三、例题评析:
例1.解方程: -3(x+1)=9
解:去括号,得: -3x -3=9 另解:方程两边同除以-3,得: x +1=-3 移项,得: -3x=9+3 移项,得:x=-3-1
合并同类项,得: -3x=12 合并同类项,得:x=-4 系数化为1,得: x= -4
问题:1.你还有其他方法去掉方程中的括号吗?(见右上另解)
2.观察上述两种解法,说出它们的区别
归纳:解一元一次方程的步骤:(1)去括号;(2)移项;(2)合并同类项;(4)系数化为1(化成“x=a ”的形式);(5)检验(可在草稿纸上进行)。
解方程:
(1)2(2x+1)=1-5(x-2); (2) 17(2-3y )-5(12-y )=8(1-7y ); (3)-51(x-15)= 21+31(7-x ); (4) 76[37(21x-51)-14]=3x -5
2
练习:解下列方程:
(1) ()612=-x ; (2)()x x -=-234; (3)5(x+2)=2(2x+7;
(4)()()914322+-=-x x ; (5)()x x 2213=--; (6)5(x+1)=3(3x+1);
(7)()()321210x x ---=;(8)()()()13153-=--+x x x ;(9)6-3(x+32)= -3
2x ; (10)x (71-14)= 41(x-20); (11)2[x 34-(32x-21)]=x 6
5; (12) 32[23(x-4) -6]=2x+1。
例3.当y 取何值时,2(3y+4)的值比5(2y-7)的值大3?
练习:1.当x 取何值时,代数式3(2-x )和-2(3+2x )的值相等?
2.当x 取何值时,代数式3(2-x )的值与-2(3+2x )的值互为相反数?
拓展提高:
已知a 是整数,且a 比0大,比10小。
请你设法找出a 的一些数值,使关于x 的方程 1―2
1ax= -5的解是偶数,看看你能找出几个.
四、课堂小结与反思:
1.去括号,一定要注意括号前的符号,特别是括号前是“-”时,括号内的每一项都要变号;
2.用分配律去括号时,不要漏乘括号中的项,并且不要搞错符号;
3.解一元一次方程的步骤。
五、课堂反馈:
1.方程7(2x-1)-3(4x-1)=11去括号后,正确的是( )
A .14x-7-12x+1=11 B. 14x-1-12x-3=11
C. 14x-7-12x+3=11
D. 14x-1-12x+3=11
2.如果代数式75-x 与94+x 的值互为相反数,则x 的值等于
3.方程12-(2x -4)= -(x -7)去括号得 .
4.若2(4a ﹣2)﹣6 = 3(4a ﹣2),则代数式a 2﹣3a + 4= .
5.解下列方程:
(1)4-3(x-3)=x+10 (2)7(a+2)= 12-5(a+2)
(3)2-3(m -1)= m +1; (4)3(2x+5)=2(4x+3)-3
(5) 4x + 3(2x –3)=12-(x +4) (6)6(x –4)+ 2x =7-(x –1)
(7) 2(10 - 0.5x)= -(1.5x-2); (8) 2(3-y)=-4(y –5);
(9)2(y -3)-3(2+y )=0; (10)3(2y+1)=2(1+y)-3(y+3)
6.若代数式3(2y-3)-y 的值与-7(1-y )互为相反数,求y 的值
课外练习:
1.方程3x+6=2x -8移项后,正确的是( )
A .3x+2x=6-8
B .3x -2x=-8+6
C .3x -2x=-6-8
D .3x -2x=8-6
2.方程7(2x-1)-3(4x-1)=11去括号后,正确的是( )
A .14x-7-12x+1=11 B. 14x-1-12x-3=11 C. 14x-7-12x+3=11 D. 14x-1-12x+3=11
3.如果代数式75-x 与94+x 的值互为相反数,则x 的值等于( ) A.29 B.29- C.92 D. 9
2- 4.如果123-n ab 与1+n ab 是同类项,则n 是( )
A.2
B.1
C.1-
D.0
5.已知矩形周长为20cm ,设长为x cm ,则宽为 ( )
A.x -20
B.x -10
C.x 220-
D. 2
20x - 6.方程2x-0.3=1.2+3x 移项得 .
7.若︱a ﹣1︱+(b+2)2=0,则a b = .
8.若3x+2与﹣2x+1互为相反数,则x-2的值是 .
9.方程2(1)6x -+=的解为 ;方程4(1)1x x -=-的解为 。
10.当x =_______时,代数式5(2)x +与2(27)x +的值相等;
11.若2x 与3(2)x -互为相反数,则x =________;
12.当x =_______时,代数式2(34)x +比5(72)x --的值大3.
13.若3(1)24x a b +与66x y a b +-是同类项,则x =_________,y =__________.
14.在公式1(1)n a a n d =+-中,已知13a =,2d =,n a =21,则n =________.
15.若x=4是关于x 的方程353(4)2a x x a -=++的解,则a =_________.
16.解下列方程
(1)3(12)2x x -+= (2) 3(1)2x x --=-
(3)3(2x+5)=2(4x+3)-3 (4)5X+2(3X-3)=11-(X+5)
(5)4y ﹣3(20﹣y)=6y ﹣7(9﹣y) (6)7(2x-1)-3(4x-1)=4(3x+2)-1
(9)[]2(34)265(7)y y +=-- (8) 111(9)(9)339x x x x ⎡⎤-
--=-⎢⎥⎣⎦
17.若
)6(243--m x 与)1(3-m x 是同类项,求m 的值。
18..在梯形面积公式1()2
S a b h =
+中,已知12a =,8h =,120S =,求b .
19..根据下图所示的程序计算代数式的值,输出的结果为17,列方程求x 的值.
2- +5
20.已知13y x =+,22y x =-.
当x 取何值时,1230y y -=? (2)当x 取何值时,1y 比22y 大5?
21..已知方程3(33)12x x +-=的解与关于x 的方程3274
m x m +=-的解相同,求m 的值.
22.将连续的偶数2,4,6,8,10,…,排成如下的数表.
回答下列问题: (1)十字框中的五个数的和与中间的数16有什么关系?
(2)设中间的数为a ,用代数式表示十字框中的五个数之和. (3)若将十字框上下左右平移,可框住另外五个数,试问这
五个数还有这种规律吗? (4)十字框的五个数之和能等于510吗?若能,写出这五个
数;若不能,说明理由.
23.有一张正方形纸片,第一次将它撕成4小片,第2次将其中的一小张又撕成4小片,以后每一次都将其中的一小张撕成4小片.那么:
(1)撕了5次后,一共有几张纸片?
(2)撕了n 次后, 一共有几张纸片?
(3)能否撕成2007张纸片? 能否撕成2008张纸片?。
