10,11,12北京考题选(立锥)
2023年高考北京卷物理真题(含解析)
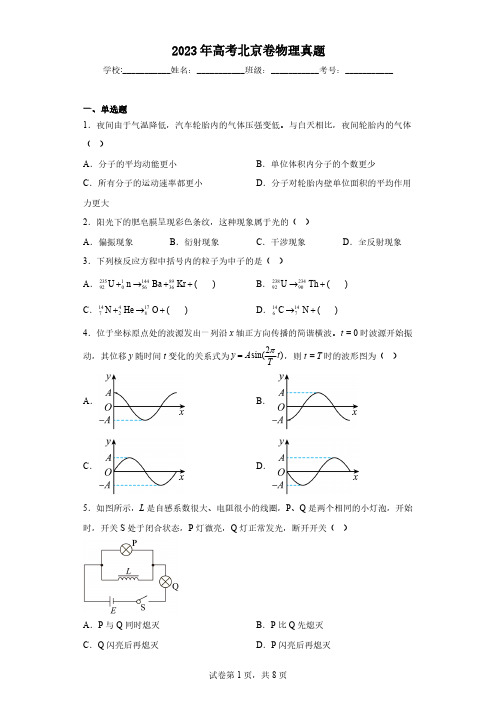
2023年高考北京卷物理真题学校:___________姓名:___________班级:___________考号:___________.....如图所示,L是自感系数很大、电阻很小的线圈,P、Q是两个相同的小灯泡,开始时,开关S处于闭合状态,灯正常发光,断开开关()A.P与Q同时熄灭C.Q闪亮后再熄灭6.如图所示,在光滑水平地面上,两相同物块用细线相连,两物块质量均为1kg,细线能承受的最大拉力为2N。
若在水平拉力F作用下,两物块一起向右做匀加速直线运动。
则F的最大值为()A.1N B.2N C.4N D.5N7.自制一个原、副线圈匝数分别为600匝和190匝的变压器,原线圈接12V的正弦交流电源,副线圈接额定电压为3.8V的小灯泡。
实际测得小灯泡两端电压为2.5V。
下列措施有可能使小灯泡正常发光的是()A.仅增加原线圈匝数B.仅增加副线圈匝数C.将原、副线圈匝数都增为原来的两倍D.将两个3.8V小灯泡并联起来接入副线圈8.如图所示,两个带等量正电的点电荷位于M、N两点上,E、F是MN连线中垂线上的两点,O为EF、MN的交点,EO=OF。
一带负电的点电荷在E点由静止释放后()A.做匀加速直线运动B.在O点所受静电力最大C.由E到O的时间等于由O到F的时间D.由E到F的过程中电势能先增大后减小9.如图所示,光滑水平面上的正方形导线框,以某一初速度进入竖直向下的匀强磁场并最终完全穿出。
线框的边长小于磁场宽度。
下列说法正确的是()A.线框进磁场的过程中电流方向为顺时针方向B.线框出磁场的过程中做匀减速直线运动C.线框在进和出的两过程中产生的焦耳热相等D.线框在进和出的两过程中通过导线横截面的电荷量相等A.圆周运动轨道可处于任意平面内B.小球的质量为222 4 FRtn πA.摩擦力做功大小与FC.F为水平方向时,F做功为12.2022年10月9日,我国综合性太阳探测卫星A.“夸父一号”的运行轨道平面平均每天转动的角度约为B.“夸父一号”绕地球做圆周运动的速度大于C.“夸父一号”绕地球做圆周运动的向心加速度大于地球表面的重力加速度D.由题干信息,根据开普勒第三定律,可求出日地间平均距离A.粒子在磁场中运动的圆弧半径为B.粒子质量为Bqa vC.管道内的等效电流为nq aπ二、填空题15.用油膜法估测油酸分子直径是一种通过测量宏观量来测量微观量的方法,已知1滴油酸酒精溶液中纯油酸的体积为V,在水面上形成的单分子油膜面积为S,则油酸分子的直径d ___________。
即兴评述模拟主持讲解

即兴评述示范:(1)阅读指定材料,在规定时间内做准备后发表评述:“我是一个不幸的孩子,我觉得自己支持部下去了……”所有亲人和医护人员都不愿意相信,这么沉重的话是一个六岁孩子说出来的。
在儿童医院的重症监护室里,可怜的小罗森在生死边缘徘徊者,六岁的呀已经两次被下达了病危通知单。
小罗森依靠着气管插管等仪器,在抱着最后一丝希望等待着一种救命药---复方磺胺甲而作注射针剂。
其实,这次临床紧缺的廉价老药就是复方新诺明,这是一种十几年前普遍应用于临床的特效药。
由于这种药平均只有2元多一支,价格与市场上大部分高昂的药品相比,实在低廉得让厂家无利可图,厂家已经停止生产,上海市场上根本买不到这种老药。
评述参考:看了这则报道之后,我的心久久不能平静,在深深地为这个孩子的病情、命运感到担忧的同时,我也想了很多。
廉价救命药为什么如此难寻呢,这种“求之不得”真让人感慨万千。
在患者和家属苦不堪言的同时,药厂却在大倒苦水,说这类药物利润太薄,生产实在难以继续,而有的医院也随声附和。
其实呢,作为企业,追求利润本是无可厚非的,但药品是用来救人的,如果厂家把钱看得太重了,是不是就会把病人之需看轻了呢?常言说得好,“医本仁术,德乃医本”。
我想这些药厂缺的就是为病人着想的这种“大德”,而这种大德恰恰是医药行业的立身之本。
市场上物美价廉的药消失了,那么药厂为什么不生产了呢?我想一来使因为药价太低、利润太薄,厂家实在觉得无利可图;另外,还因为在医院临床上,高价药备受亲眯,药厂自然就为了追逐厚利放弃了廉价药的生产;还有一个原因也不可忽视----有些药厂为了追逐利润,把原来的廉价老药换个包装,改个药名,这药品就价格倍增,这样也导致了药厂停产了廉价药。
总之,在利润的驱使下,廉价救命药自然就失去了立锥之地。
企业赚钱本是无可厚非,但,可千万别为了赚钱而丢了良心,还是要多为老百姓去着想。
(2)阅读指定材料,在规定时间内做准备后发表评述:未成年人“污点”可不入档案上海市人民检察院8日宣布,从即日起,上海市各级检查机关将全面推广试行未成年人刑事案件的污点限制公开制度,以及刑事案件和解制度。
09,10,11,12年北京高考圆锥曲线题选(文

09,10,11,12年北京高考圆锥曲线题选(文(2012北京文)(19).(本小题共14分)已知椭圆C:22xa+22yb=1(a>b>0)的一个顶点为A(2,0),离心率为22,直线y=k(x-1)与椭圆C交与不同的两点M,N(Ⅰ)求椭圆C的方程(Ⅱ)当△AMN的面积为103时,求k的值(2011北京文)19.(本小题共14分)已知椭圆2222:1(0)x yG a ba b+=>>的离心率为63,右焦点为(22,0),斜率为I的直线l与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).(I)求椭圆G的方程;(II)求P A B∆的面积.(2010北京文)(19)(本小题共14分)已知椭圆C的左、右焦点坐标分别是(2,0)-,(2,0),离心率是63,直线椭圆C交与不同的两点M,N,以线段为直径作圆P,圆心为P。
(Ⅰ)求椭圆C的方程;(Ⅱ)若圆P与x轴相切,求圆心P的坐标;(Ⅲ)设Q(x,y)是圆P上的动点,当变化时,求y的最大值。
解:(Ⅰ)因为63ca=,且2c=,所以223,1a b a c==-=所以椭圆C的方程为221 3xy+=(Ⅱ)由题意知(0,)(11)p t t-<<由2213y t x y =⎧⎪⎨+=⎪⎩ 得23(1)x t =±-所以圆P 的半径为23(1)t -解得32t =± 所以点P 的坐标是(0,32±)(Ⅲ)由(Ⅱ)知,圆P 的方程222()3(1)x y t t +-=-。
因为点(,)Q x y 在圆P 上。
所以2223(1)3(1)y t t x t t =±--≤+-设cos ,(0,)t θθπ=∈,则23(1)cos 3sin 2sin()6t t πθθθ+-=+=+当3πθ=,即12t =,且0x =,y 取最大值2.(2009北京文)19.(本小题共14分)已知双曲线2222:1(0,0)x y C a b ab-=>>的离心率为3,右准线方程为33x =。
2024北京高考真题物理汇编:力学选择

2024北京高考真题物理汇编力学选择一、单选题1.(2024北京高考真题)一辆汽车以10m/s的速度匀速行驶,制动后做匀减速直线运动,经2s停止,汽车的制动距离为()A.5m B.10m C.20m D.30m2.(2024北京高考真题)如图所示,飞船与空间站对接后,在推力F作用下一起向前运动。
飞船和空间站的质量分别为m和M,则飞船和空间站之间的作用力大小为()A.MFM m+B.mFM m+C.MFmD.mFM3.(2024北京高考真题)水平传送带匀速运动,将一物体无初速度地放置在传送带上,最终物体随传送带一起匀速运动。
下列说法正确的是()A.刚开始物体相对传送带向前运动B.物体匀速运动过程中,受到静摩擦力C.物体加速运动过程中,摩擦力对物体做负功D.传送带运动速度越大,物体加速运动的时间越长4.(2024北京高考真题)产生阿秒光脉冲的研究工作获得2023年的诺贝尔物理学奖,阿秒(as)是时间单位,1as = 1 × 10−18s,阿秒光脉冲是发光持续时间在阿秒量级的极短闪光,提供了阿秒量级的超快“光快门”,使探测原子内电子的动态过程成为可能。
设有一个持续时间为100as的阿秒光脉冲,持续时间内至少包含一个完整的光波周期。
取真空中光速c= 3.0 × 108m/s,普朗克常量h= 6.6 × 10−34J⋅s,下列说法正确的是()A.对于0.1mm宽的单缝,此阿秒光脉冲比波长为550nm的可见光的衍射现象更明显B.此阿秒光脉冲和波长为550nm的可见光束总能量相等时,阿秒光脉冲的光子数更多C.此阿秒光脉冲可以使能量为−13.6eV(−2.2 × 10−18J)的基态氢原子电离D.为了探测原子内电子的动态过程,阿秒光脉冲的持续时间应大于电子的运动周期5.(2024北京高考真题)将小球竖直向上抛出,小球从抛出到落回原处的过程中,若所受空气阻力大小与速度大小成正比,则下列说法正确的是()A.上升和下落两过程的时间相等B.上升和下落两过程损失的机械能相等C.上升过程合力的冲量大于下落过程合力的冲量D.上升过程的加速度始终小于下落过程的加速度6.(2024北京高考真题)如图所示,光滑水平轨道AB与竖直面内的光滑半圆形轨道BC在B点平滑连接。
2023年北京市R1快开门式压力容器操作考题(含答案)

2023年北京市R1快开门式压力容器操作考题(含答案)一、判断题(50题)1.如爆破片串联在安全阀出口时,爆破片的动作压力应低于安全阀整定压力。
A.正确B.错误2.《中华人民共和国特种设备安全法》规定:特种设备安全管理人员、检测人员和作业人员应当按照国家有关规定取得相应资格,方可从事相关工作。
A.正确B.错误3.压力容器投运前,应检查各有关阀门的开、闭情况。
A.正确B.错误4.安全阀是一种不可重复使用的安全泄放保护装置。
A.正确B.错误5.《特种设备安全监察条例》中,特种设备的事故的级别是完全按所造成的人员死亡人数确定的。
A.正确B.错误6.爆破片泄放装置适用于化学反应过程中导致容器快速升压时,需要快速泄压的压力容器。
A.正确B.错误7.O型橡胶圈是快开门式压力容器的常用密封材料。
A.正确B.错误8.压力容器的使用管理和操作不当是造成压力容器事故的主要原因。
A.正确B.错误9.压力容的韧性破坏一般不会产生塑性变形,但有碎片产生。
A.正确B.错误10.压力开关主要是判断容器内压力是否完全释放的元件。
A.正确B.错误11.快开门式压力容器使用前必须检查安全联锁装置是否在校验周期内。
A.正确B.错误12.《特种设备作业人员证》考试实行百分制,单科成绩达到70分为合格,实际操作技能考试合格,评定为考试合格。
A.正确B.错误13.工业生产和其他行业中常用蒸汽作为加热介质。
A.正确B.错误14.《特种设备使用管理规则》规定,特种设备使用单位应当按照特种设备的类型或型号批量建立特种设备安全与节能技术档案。
A.正确B.错误15.压力容器在运行中如发生介质泄漏,特别是易燃、有毒介质泄漏时,应迅速远离现场、防止人身伤害。
A.正确B.错误16.压力容器只要设计、制造、安装质量符合要求,运行中作业人员精心操作就不会发生事故。
A.正确B.错误17.《特种设备安全法》规定,特种设备行业协会应当加强行业自律,推进行业诚信体系建设,提高特种设备安全管理水平。
2025年北京市怀柔区高三下学期一调物理试题含解析

2025年北京市怀柔区高三下学期一调物理试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、一个质点做简谐运动的图象如图所示,下列说法不正确的是()A.质点振动的频率为4 HzB.在10s内质点经过的路程是20 cmC.在5s末,质点的速度为零,加速度最大D.t=1.5 s和t=4.5 s两时刻质点的位移大小相等,都是2cm2、关于近代物理学,下列说法正确的是A.光电效应现象揭示了光具有波动性B.—群氢原子从n=4的激发态跃迁时,最多能辐射6种不同频率的光子C.卢瑟福通过 粒子散射实验证实原子核由质子和中子组成D.氡的半衰期为3.8天,若取4个氡原子核,经过7.6天后一定剩下1个氡原子核3、一质点沿x轴正方向做直线运动,通过坐标原点时开始计时,其xt-t的图象如图所示,则A.质点做匀速直线运动,速度为0.5 m/sB.质点做匀加速直线运动,加速度为0.5 m/s2C.质点在1 s末速度为1.5 m/sD.质点在第1 s内的平均速度0.75 m/s4、如图所示,半径为R的光滑半圆形刚性细杆竖直固定,O点为其圆心,AB为水平直径,在细杆的A点固定一个光滑的小圆环,穿过小圆环的不可伸长的细线一端与质量为4m的重物相连,另一端与质量为m且套在细杆上的带孔小球相连。
开始时小球静止在细杆的C点,重物在A点正下方,细线恰好伸直,将重物由静止释放后,小球在重物拉动下沿细杆运动。
已知重力加速度为g,当小球运动到P点时,重物下落的速度为(OP、OC均与水平方向成60°角)()A.33-32gR B.33-15gRC.332gR D.(31)gR5、如图,工地上常用夹钳搬运砖块。
2022-2023学年北京市第二中学高一下学期期末物理试题(选考)

2022-2023学年北京市第二中学高一下学期期末物理试题(选考)1.下列物理量属于标量的是()A.动能B.动量C.速度D.冲量2.如图所示,一物体在与水平成角的拉力F作用下,匀速前进了时间t,则()A.摩擦力对物体的冲量大小为B.拉力对物体的冲量大小为FtC.重力对物体的冲量为零D.合外力对物体的冲量大小为Ft3.玻璃杯从同一高度落下,掉在水泥地上比掉在草地上容易碎,这是由于玻璃杯与水泥地面撞击的过程中( )A.玻璃杯的动量较大B.玻璃杯受到的冲量较大C.玻璃杯的动量变化较大D.玻璃杯的动量变化较快4.如图所示,用长为的轻绳悬挂一质量为的小球,对小球再施加一个力,使绳与竖直方向成角并绷紧,小球处于静止状态,此力最小为()A.B.C.D.5.某车队从同一地点先后从静止开出n辆汽车,在平直的公路上沿一直线行驶,各车均先做加速度为a的匀加速直线运动,达到速度v后做匀速直线运动,汽车都匀速行驶后,相邻两车距离均为s,则相邻两车启动的时间间隔为()A.B.C.D.6.质量为m速度为v的A球,跟质量为4m的静止B球发生正碰,碰撞可能是弹性,也可能是非弹性,则碰后B球的速度可能是()A.B.C.D.7.如图所示,一颗人造卫星原来在椭圆轨道1绕地球E运行,在P点变轨后进入轨道2做匀速圆周运动.下列说法正确的是:()A.不论在轨道1还是轨道2运行,卫星在P点的速度都相同B.不论在轨道1还是轨道2运行,卫星在P点的加速度都相同C.卫星在轨道1的任何位置都具有相同加速度D.卫星在轨道2的任何位置都具有相同动量(动量P = mv,v为瞬时速度)8.如图甲所示,两小球a,b在足够长的光滑水平面上发生正碰。
小球a、b质量分别为m1和m2,且m1=100g。
取水平向右为正方向,两小球碰撞前后位移随时间变化的x-t图像如图乙所示。
由此可以得出以下判断①碰撞前球a做匀速运动,球b静止;②碰撞后球a和球b都向右运动;③m2=300g;④碰撞前后两小球的机械能总量不变;则以上判断中正确的是()A.①③B.①②③C.①③④D.②④9.一物理学习小组在竖直电梯里研究超重失重现象:力传感器上端固定在铁架台上,下端悬挂一个质量为m的钩码。
【精品解析】北京市2012年高考数学最新联考试题分类大汇编(8)立体几何

精品解析:北京市2012年高考数学最新联考试题分类大汇编(8)立体几何试题解析一、选择题:(3)(北京市东城区2012年1月高三考试文科)一个几何体的三视图如图所示,则该几何体的体积为(A )32a (B ) 36a (C ) 312a (D )318a【答案】C【解析】该几何体为底面是直角边为a的等腰直角三角形,高为a 的直三棱柱,其体积为12a a a ⨯⨯⨯=32a 。
7.(北京市西城区2012年1月高三期末考试理科)某几何体的三视图如图所示,该几何体的体积是( ) (A )8 (B )83 (C )4 (D )43【答案】D正 ( 主 ) 视图俯视图侧 ( 左 ) 视图【解析】将三视图还原直观图,可知是一个底面为正方形(其对角线长为2),高为2的四棱锥,其体积为11142222.3323ABCD V S =⨯=⨯⨯⨯⨯=正方形A .βα//,//n m 且βα//,则n m //B .βα⊥⊥n m ,且βα⊥,则m //nC .βα//,n m ⊥且βα//,则n m ⊥D .βα⊥n m ,//且βα⊥,则n m //【答案】C 体的体积为 . 32(9)(北京市东城区2012年4月高考一模文科)已知一个四棱锥的三视图如图所示,则该四棱锥的体积是 . 4310. (2012年4月北京市房山区高三一模理科一个几何体的三视图如图所示,则这个几何体的体积为 .32正视图 侧视图F EDB A PC三、解答题:(17)(北京市东城区2012年1月高三考试文科)(本小题共14分)如图,在四棱锥ABCD P -中,底面ABCD 是正方形,PA ⊥平面ABCD , E 是PC 中点,F 为线段AC 上一点.(Ⅰ)求证:EF BD ⊥;(Ⅱ)试确定点F 在线段AC 上的位置,使EF //平面PBD ,并说明理由.【命题分析】本题考查线线垂直和线面探索性问题等综合问题。
考查学生的空间想象能力。
证明线线垂直的方法:(1)异面直线所成的角为直角;(2)线面垂直的性质定理;(3)面面垂直的性质定理;(4)三垂线定理和逆定理;(5)勾股定理;(6)向量垂直.要注意线面、面面垂直的性质定理的成立条件.解题过程中要特别体会平行关系性质的传递性,垂直关系的多样性.本题第一问利用方法二进行证明;探求某证明(Ⅰ)因为PA ⊥平面ABCD ,所以PA ⊥BD . 又四边形ABCD 是正方形, 所以BD AC ⊥,A AC PA = , 所以BD ⊥平面PAC , 又EF ⊂平面PAC ,所以EF BD ⊥. (7)分PBD . ………………14分(16) (2012年4月北京市海淀区高三一模理科)(本小题满分14分)在四棱锥P ABCD -中,AB //CD ,AB AD ^,4,2AB AD CD ===,PA ^平面ABCD ,4PA =.(Ⅰ)设平面PAB 平面PCD m =,求证:CD //m ; (Ⅱ)求证:BD ⊥平面PAC ;(Ⅲ)设点Q 为线段PB 上一点,且直线QC 与平面PAC 所成角PQ PB 的值.(16)(本小题满分14分)………………………………………5分PDCBA所以 (BD =- ,AC =, (0,0,4)AP =,所以(4)2000BD AC ⋅=-⨯+⨯=, (4)00040BD AP ⋅=-⨯++⨯=.所以 BD AC ⊥,BD AP ⊥.因为 AP AC A = ,AC ⊂平面PAC ,PA ⊂平面PAC ,所以 BD ⊥平面PAC .………………………………………9分由(Ⅱ)知平面PAC 的一个法向量为(BD =-.………………………………………12分17. (2012年3月北京市朝阳区高三一模文科)(本题满分13分)在如图所示的几何体中,四边形ABCD 为平行四边形,=90ABD ∠︒, EB ⊥平面ABCD ,EF//AB ,2AB=,=1EF ,BC ,且M 是BD 的中点. (Ⅰ)求证://EM 平面ADF ;FE D(Ⅱ)在EB 上是否存在一点P ,使得CPD ∠最大? 若存在,请求出CPD ∠的正切值;若不存在, 请说明理由. (17)(本小题满分13分)(Ⅱ)解:假设在EB 上存在一点P ,使得CPD ∠最大.因为EB ⊥平面ABD ,所以EB CD ⊥.又因为CD BD ⊥,所以CD ⊥平面EBD . ………………………8分 在Rt CPD ∆中,tan =CDCPD DP∠.17.(北京市西城区2012年4月高三第一次模拟文)(本小题满分14分)如图,矩形ABCD 中,3AB =,4=BC .E ,F 分别在线段BC 和AD 上,EF ∥AB ,将矩形ABEF 沿EF 折起.记折起后的矩形为MNEF ,且平面⊥MNEF 平面ECDF .(Ⅰ)求证:NC ∥平面MFD ; (Ⅱ)若3EC =,求证:FC ND ⊥; (Ⅲ)求四面体NFEC 体积的最大值.17.(本小题满分14分)(Ⅰ)证明:因为四边形MNEF ,EFDC 都是矩形, 所以 MN ∥EF ∥CD ,MN EF CD ==. 所以 四边形MNCD 是平行四边形,……………2分 所以 NC ∥MD , ………………3分 因为 NC ⊄平面MFD ,所以 NC ∥平面MFD . ………………4分(Ⅱ)证明:连接ED ,设ED FC O = .因为平面⊥MNEF 平面ECDF ,且EF NE ⊥, 所以 ⊥NE 平面ECDF , ……5分所以 FC NE ⊥. …………6分9分(Ⅲ)解:设x NE =,则x EC -=4,其中04x <<.由(Ⅰ)得⊥NE 平面FEC , 所以四面体NFEC 的体积为11(4)32NFEC EFC V S NE x x ∆=⋅=-. ………11分所以 21(4)[]222NFEC x x V +-≤=. ……………13分 当且仅当x x -=4,即2=x 时,四面体NFEC 的体积最大. ………………14分 (17)(北京市东城区2012年4月高考一模理科)(本小题共13分)图1 图2 (17)(共13分)(Ⅰ)证明:取BE 中点D ,连结DF .因为1AE CF ==,1DE =,所以2AF AD ==,而60A ∠=,即△ADF 是正三角形.又因为1AE ED ==, 所以EF AD ⊥. …………2分 所以在图2中有1A E EF ⊥,BE EF ⊥.…………3分 所以1A E B ∠为二面角1A E FB --的平面角.图1又二面角1A EF B --为直二面角,所以1A E BE ⊥. …………5分 又因为BE EF E = ,所以1A E ⊥平面BEF ,即1A E ⊥平面BEP . …………6分 (Ⅱ)解:由(Ⅰ)可知1A E ⊥平面BEP ,BE EF ⊥,如图,以E 为原点,建立空间直角坐标系E xyz -,则(0,0,0)E ,1(0,0,1)A ,(2,0,0)B,0)F .在图1中,连结DP . 因为12CF CP FA PB ==, 所以PF ∥BE ,且12PF BE DE ==. 所以四边形EFPD 为平行四边形. 所以EF ∥DP ,且EF DP =.故点P 的坐标为(10). 图2所以1(2,0,1)A B =- ,(1BP =-,1(0,0,1)EA = . …………8分不妨设平面1A BP 的法向量(,,)x y z =n ,则10,0.A B BP ⎧⋅=⎪⎨⋅=⎪⎩n n即20,0.x z x -=⎧⎪⎨-=⎪⎩令y =(3,,6)=n . …………10分 所以cos 〈1EA 〉n,11||||EA EA ⋅===n n . …………12分故直线1A E 与平面1A BP 所成角的大小为3π. …………13分 (17)(北京市东城区2012年4月高考一模文科)(本小题共14分)如图1,在边长为3的正三角形ABC 中,E ,F ,P 分别为AB ,AC ,BC 上的点,且满足1AE FC CP ===.将△AEF 沿EF 折起到△1A EF 的位置,使平面1A EF ⊥平面EFB ,连结1A B ,1A P .(如图2)(Ⅰ)若Q 为1A B 中点,求证:PQ ∥平面1A EF ; (Ⅱ)求证:1A E ⊥EP .图1 图2(17)(共14分)证明:(Ⅰ)取1A E 中点M ,连结,QM MF . 在△1A BE 中,,Q M 分别为11,A B A E 的中点,所以QM ∥BE ,且12QM BE =. 因为12CF CP FA PB ==, 所以PF ∥BE ,且12PF BE =, 所以QM ∥PF ,且QM PF =.所以四边形PQMF 为平行四边形.所以PQ ∥FM . …………5分 又因为FM ⊂平面1A EF ,且PQ ⊄平面1A EF ,所以PQ ∥平面1A EF . …………7分(Ⅱ) 取BE 中点D ,连结DF .因为1AE CF ==,1DE =,所以2AF AD ==,而60A ∠= ,即△ADF 是正三角形.又因为1AE ED ==, 所以EF AD ⊥.所以在图2中有1A E EF ⊥. …………9分因为平面1A EF ⊥平面EFB ,平面1A EF 平面EFB EF =, 所以1A E ⊥平面BEF . …………12分又EP ⊂平面BEF ,所以1A E ⊥EP . …………14分17. (2012年3月北京市丰台区高三一模文科)(本小题共14分)如图,四棱锥P-ABCD 中,底面ABCD 是菱形,PA =PD ,∠BAD =60º,E 是AD 的中点,点Q 在侧棱PC 上.(Ⅰ)求证:AD ⊥平面PBE ;(Ⅱ)若Q 是PC 的中点,求证:PA // 平面BDQ ;(Ⅲ)若V P-BCDE =2V Q - ABCD ,试求CP CQ的值. 17.证明:(Ⅰ)因为 E 是AD 的中点, PA =PD , 所以 AD ⊥PE. ……………………1分因为 底面ABCD 是菱形,∠BAD =60º,所以 AB =BD ,又因为E 是AD 的中点,所以 AD ⊥BE . (2)分因为 PE ∩BE =E , (3)分所以 AD ⊥平面PBE . (4)分(Ⅱ)连接AC 交BD 于点O ,连结OQ .……………………5分因为O 是AC 中点, Q 是PC 的中点,所以OQ 为△PAC 中位线.所以OQ //因为 12h CP h CQ=, 所以 83CP CQ =. ……………………14分 17. (2012年4月北京市房山区高三一模理科(本小题共14分)在直三棱柱111ABC A B C -中,1BC CC AB===2 ,BC AB ⊥.点N M ,分别是1CC ,C B 1的中点,G 是棱AB 上的动点.(I )求证:⊥C B 1平面BNG ;(II)若CG //平面M AB 1,试确定G 点的位置,并给出证明;(III)求二面角1M AB B --的余弦值.17.(本小题共14分)(I) 证明:∵在直三棱柱111ABC A B C -中,1CC BC =,点N 是C B 1的中点,∴C B BN 1⊥ …………………………1分BC AB ⊥,1BB AB ⊥,B BC BB = 1∴AB ⊥平面11BCC B ………………………2分⊂C B 1平面11BCC B∴AB C B ⊥1,即GB C B ⊥1 …………………3分又B BG BN =∴⊥C B 1平面BNG …………………………………4分(II )当G 是棱AB 的中点时,CG //平面M AB 1.……………………………5分 证明如下:连结1AB ,取1AB 的中点H ,连接GC HM HG ,,,则HG 为B AB 1∆的中位线∴GH ∥1BB ,121BB GH =…………………6分 ∵由已知条件,11BCC B 为正方形∴1CC ∥1BB ,11BB CC =∵M 为1CC 的中点,(III) ∵ 直三棱柱111ABC A B C -且BC AB ⊥又 平面1B AB 的法向量为11(2,0,0)BC = , ∴11cos ,BC n <> =1111B C n B C n ⋅⋅ =31, ……………………13分 设二面角1M AB B --的平面角为θ,且θ为锐角 ∴111cos cos ,3B C n θ=-= . ……………………14分。
北京市第十二中学2022-2022学年高一物理下学期五月测试选考试题(含解析)

B. 在小球运动半径相等的情况下,用质量不同的钢球做实验
C. 在小球运动半径不等的情况下,用质量不同的钢球做实验
D. 在小球运动半径不等的情况下,用质量相同的钢球做实验
【答案】A
【解析】
根据F=mrω2,知要研究小球受到的向心力大小与角速度的关系,需控制小球的质量和半径不变.故A正确
代入数据得 N.
15.恒星演化开展到一定阶段,可能成为恒星世界的“侏儒〞-中子星,中子星的半径较小,一般在7~20km,但它的密度大得惊人。假设中子星的半径为10km,密度为1.2×1017kg/m3。万有引力常量G=6.671011N m2/kg2,那么该中子星的第一宇宙速度约为多少?〔计算结果保存一位有效数字〕
10.如下列图,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内作圆周运动,关于小球在最高点的速度v0,以下说法中正确的选项是〔 〕
A.v0的最小值为
B.v0由零逐渐增大,向心力也逐渐增大
C. 当v0由 值逐渐增大时,杆对小球的弹力也逐渐增大
D. 当v0由 值逐渐增小时,杆对小球的弹力也仍然逐渐增大
应选B。
7.按照我国月球探测活动方案,在第一步“绕月〞工程圆满完成各工程标和科学探测任务后,第二步是“落月〞工程,该方案已在2021年之前完成。设月球半径为R,飞船沿距月球外表高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅰ绕月球做圆周运动.卫星在轨道ⅠA处的速度为 ,加速度为 ;在轨道ⅡA处的速度为 ,加速度为 ;在轨道ⅡB处的速度为 ,加速度为 ;在轨道ⅢB处的速度为 ,加速度为 。那么它们大小关系正确的有〔〕
2023-2024学年北京育才学校高一上学期期中物理试题含答案解析

北京育才学校2021-2022学年度高一年级期中考试物理试卷第I卷(共60分)一、单项选择题:本大题共15小题,每小题3分,共45分。
在每小题给出的四个选项中,只有一个选项是正确的,将正确的选项选出填在机读卡中。
1.下列物理量属于标量的是()A.速率B.位移C.力D.加速度2.在物理学中,突出问题的主要方面,忽略次要因素,建立理想化的“物理模型”,并将其作为研究对象,是经常采用的一种科学方法.质点就是这种物理模型之一.下列有关质点的说法正确的是A.只有细小的物体才能看成质点B.物体在任何情况下都能看成质点C.研究地球自转的规律时,可以把地球看成质点D.研究地球公转的规律时,可以把地球看成质点3.一位同学从操场A点出发,向西走了30m,到达B点,然后又向北走了40m,到达C 点。
在从A点到C点的过程中,该同学的位移大小是()A.70mB.50mC.40mD.30m4.下列各图象中,能够描述自由落体运动的是()A. B.C. D.5.一个加速直线运动的物体,其加速度是6m/s2,关于这个6m/s2理解正确的是()A.某1s末的速度比该1s初的速度大6m/sB.某1s末的速度比该1s初的速度大6倍C.某1s初的速度与前1s末的速度相差6m/sD.某1s末的速度与前1s初的速度总是相差6m/s6.如图所示,汽车向右沿直线运动,原来的速度是1v,经过一小段时间之后,速度变为2v,v∆表示速度的变化量,由图中所示信息可知()A.汽车在做加速直线运动B.汽车的加速度方向与1v的方向相同C.汽车的加速度方向与1v的方向相反D.汽车的加速度方向与v∆的方向相反7.如图所示,跳水运动员踩压跳板使跳板弯曲到最低点时,下列说法正确的是A.跳板发生形变,运动员的脚没有发生形变B.运动员受到的支持力,是跳板发生形变而产生的C.此时跳板对运动员的支持力和运动员的重力等大D.此时跳板对运动员的支持力大于运动员对跳板的压力8.下列情景中,两个物体a,b(a,b均处于静止状态,接触面光滑)间一定有弹力的是()A. B.C. D.9.2021年8月1日晚,东京奥林匹克体育场里,代表着“中国速度”的苏炳添在半决赛中跑出9秒83,成功晋级决赛!创造亚洲纪录!成为第一位闯入奥运百米决赛的黄种人!测得苏炳添在前60m跑了6.29s,后40米用时3秒54,最终以11.8m/s的速度冲过终点。
《化学实验基本操作训练》考题及要求(有答案)

《化学实验基本操作训练》考题及要求答案仅供参考一、说出下列化学实验仪器的名称1 干燥器2 电热套3 蒸发皿4洗瓶5 称量瓶6 试剂瓶7 锥形瓶8 抽滤瓶9滴瓶10 漏斗11 量筒12 1000 ml容量瓶13 量杯14分液漏斗15移液管16 酸式滴定管17碱式滴定管18刺形分馏柱19直形冷凝柱20球形冷凝柱21 布氏漏斗22 烧瓶23 蒸馏头24 接引管25滴管二、判断题1、洗净的玻璃仪器如烧杯、试剂瓶等不能倒扣在实验台上。
(V)2、洗瓶尖嘴不能接触容器内壁。
(V)3、铬酸洗液不能重复使用。
(X)4、量筒洗净后应放在烘箱中烘干.(X)5、用烘箱烘干玻璃仪器时,烘箱的温度可设定为105~110℃。
(V)6、化学实验操作过程中,头不可伸入到通风厨中.(V)7、分析纯、化学纯试剂的标签颜色分别为红色、蓝色。
(V)8、固体试剂装入广口试剂瓶,液体试剂装入细口试剂瓶。
(V)9、可以将鼻孔靠近试剂瓶口去感觉试剂的气味。
(X)10、在使用容量瓶、分液漏斗前,磨口玻璃塞要用橡皮筋系在瓶口。
(V)11、取用化学试剂时,若没有说明用量则应按照最少量取用:液体取l~2mL,固体只需盖满试管底部。
(V)12、实验过程中,未用完的化学药品不能放回原来的试剂瓶中,要将其丢弃。
(X)13、用胶头滴管往容器中加入较少量液体时,胶头滴管要垂直悬空.(V)14、采用倾倒法取用液体试剂时,试剂瓶的标签要靠在手心,试剂瓶口不能与承接试剂的容器口接触。
(X)15、为将粉末状固体试剂送入容器的底部,可以使用纸片折成的V型槽。
(V)16、用托盘天平称量固体试剂时,砝码应放在右盘。
(V)17、称量0。
1200~0.1300g药品时,要用加重法在分析天平上进行。
(X)18、带有刻度的烧杯可以作用量器使用。
(X)19、称量瓶不能用手直接接触,而要用纸带套住称量瓶。
(V)20、要待分析天平的零点显示稳定后方可进行称量操作。
(V)21、用移液管移取一定量的液体时,留在移液管尖嘴的少量液体要用洗耳球吹出。
北京市顺义一中2025届高三联合考试物理试题含解析

北京市顺义一中2025届高三联合考试物理试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、取一根长2m左右的细线,5个铁垫圈和一个金属盘,在线端系上第一个垫圈,隔12 cm再系一个,以后垫圈之间的距离分别是36 cm、60 cm、84 cm,如图所示.站在椅子上,向上提起线的上端,让线自由垂下,且第一个垫圈紧靠放在地上的金属盘,松手后开始计时,若不计空气阻力,则第2、3、4、5个垫圈()A.落到盘上的声音时间间隔越来越大B.落到盘上的声音时间间隔相等C.依次落到盘上的速率关系为2321:21:32:23D.依次落到盘上的时间关系为)(2、分子动理论较好地解释了物质的宏观热学性质。
据此可判断下列说法中正确的是()A.布朗运动是指液体分子的无规则运动B.分子间的相互作用力随着分子间距离的增大,先减小后增大C.气体从外界吸收热量,气体的内能一定增大D.若气体的温度不变,压强增大,说明每秒撞击单位面积器壁的分子数增多3、某移动电源上标志的4500mAh反映的物理量是()A.电压B.电量C.功率D.能量4、电梯在t=0时由静止开始上升,运动的a t-图像如图所示,电梯总质量m=2.0×103kg。
电梯内乘客的质量m0=50kg,忽略一切阻力,重力加速度g=10m/s2。
下列说法正确的是()A .第1s 内乘客处于超重状态,第9s 内乘客处于失重状态B .第2s 内乘客对电梯的压力大小为450NC .第2s 内钢索对电梯的拉力大小为2.2×104ND .第2s 内电梯对乘客的冲量大小为550N·s5、三根通电长直导线垂直纸面平行固定,其截面构成一正三角形,O 为三角形的重心,通过三根直导线的电流分别用I 1、I 2、I 3表示,方向如图。
2021年北京高三一模分类汇编立体几何(含解析)

2021北京高三一模数学汇编:立体几何一.选择题(共9小题)1.(2021•延庆区一模)某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是直角三角形,俯视图是直角梯形,则该四棱锥的体积是()A.1 B.2 C.3 D.42.(2021•西城区一模)某四棱锥的三视图如图所示,则该四棱锥的表面积为()A.12 B.C.16 D.3.(2021•东城区一模)某四棱锥的三视图如图所示,该四棱锥的体积为()A.B.9 C.D.274.(2021•怀柔区一模)某四棱柱的三视图如图所示,该几何体的体积为()A.2 B.4 C.6 D.85.(2021•石景山区一模)一几何体的直观图和主视图如图所示,下列给出的四个俯视图中正确的是()A.B.C.D.6.(2021•房山区一模)祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h(0<h<2)的平面截该几何体,则截面面积为()A.4πB.4πh2C.π(2﹣h2)D.π(4﹣h2)7.(2021•朝阳区一模)某三棱锥的三视图如图所示,已知网格纸上小正方形的边长为1,则该三棱锥最长的棱长为()A.2 B.C.D.8.(2021•门头沟区一模)某四棱锥的三视图如图所示,则此四棱锥最长的棱长为()A.2 B.C.4 D.9.(2021•丰台区一模)某三棱锥的三视图如图所示,该三棱锥中最长的棱长为()A.2 B.C.D.4二.填空题(共1小题)10.(2021•丰台区一模)如图,从长、宽、高分别为a,b,c的长方体AEBF﹣GCHD中截去部分几何体后,所得几何体为三棱锥A﹣BCD.下列四个结论中,所有正确结论的序号是.①三棱锥A﹣BCD的体积为;②三棱锥A﹣BCD的每个面都是锐角三角形;③三棱锥A﹣BCD中,二面角A﹣CD﹣B不会是直二面角;④三棱锥A﹣BCD中,三条侧棱与底面所成的角分别记为α,β,γ,则sin2α+sin2β+sin2γ≤2.三.解答题(共11小题)11.(2021•延庆区一模)如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是边长为2的正方形,侧面ADD1A1为矩形,且侧面ADD1A1⊥底面ABCD,AA1=4,E,M,N分别是BC,BB1,A1D的中点.(Ⅰ)求证:MN∥平面C1DE;(Ⅱ)求二面角D﹣C1E﹣B1的余弦值.12.(2021•西城区一模)如图,在正方体ABCD﹣A1B1C1D1中,E为DD1的中点.(Ⅰ)求证:BD∥平面ACE;(Ⅱ)求直线AD与平面ACE所成角的正弦值.13.(2021•东城区一模)如图,在长方体ABCD﹣A1B1C1D1中,四边形BCC1B1是边长为1的正方形,AB=2,M,N分别为AD,A1B1的中点.(Ⅰ)求证:MA1∥平面ANC;(Ⅱ)求直线CN与平面D1AC所成角的正弦值.14.(2021•海淀区一模)在如图所示的多面体中,AB∥CD,四边形ACFE为矩形,AB=AE=1,AD=CD=2.(Ⅰ)求证:平面ABE∥平面CDF;(Ⅱ)设平面BEF∩平面CDF=l,再从条件①、条件②、条件③这三个条件中选择若干个作为已知,使二面角B﹣l﹣C的大小确定,并求此二面角的余弦值.条件①:AB⊥AD;条件②:AE⊥平面ABCD;条件③:平面AED⊥平面ABCD.15.(2021•丰台区一模)如图,四棱锥P﹣ABCD中,底面ABCD是菱形,,M是棱PB上的点,O是AD 中点,且PO⊥底面ABCD,.(Ⅰ)求证:BC⊥OM;(Ⅱ)若,求二面角B﹣OM﹣C的余弦值.16.(2021•怀柔区一模)如图,在四棱柱ABCD﹣A1B1C1D1中,AB1⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2.(Ⅰ)求证:C1D∥平面ABB1A1;(Ⅱ)求证:AC⊥BC1;(Ⅲ)求二面角C1﹣BD﹣D1的余弦值.17.(2021•房山区一模)如图,在直三棱柱ABC﹣A1B1C1中,已知AB=BC=1,AC=,BB1=2,E为CC1上一点,且EC=.(Ⅰ)求证:平面ABE⊥平面B1BCC1;(Ⅱ)求直线A1C与平面ABE所成角的正弦值.18.(2021•石景山区一模)如图,在五面体ABCDEF中,面ABCD为正方形,面ABFE∩面CDEF=EF,AD⊥ED,CD ⊥EA.(Ⅰ)求证:CD∥平面ABFE;(Ⅱ)若EF=ED,CD=2EF=2,求平面ADE与平面BCF所成的锐二面角的大小.19.(2021•朝阳区一模)如图,在四棱锥P﹣ABCD中,O是AD边的中点,PO⊥底面ABCD,PO=1.在底面ABCD 中,BC∥AD,CD⊥AD,BC=CD=1,AD=2.(Ⅰ)求证:AB∥平面POC;(Ⅱ)求二面角B﹣AP﹣D的余弦值.20.(2021•门头沟区一模)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,AB=PA,PA⊥底面ABCD,∠ABC=,E是PC上任一点,AC∩BD=O.(Ⅰ)求证:平面EBD⊥平面PAC;(Ⅱ)若E是PC的中点,求ED与平面EBC所成角的正弦值.21.(2021•平谷区一模)如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,△PAB为正三角形,且侧面PAB⊥底面ABCD,PM=MD.(Ⅰ)求证:PB∥平面ACM;(Ⅱ)求二面角M﹣BC﹣D的余弦值.2021北京高三一模数学汇编:立体几何参考答案一.选择题(共9小题)1.【分析】由三视图还原原几何体,该几何体为四棱锥,底面ABCD为直角梯形,AD∥BC,AB⊥AD,PA⊥底面ABCD,且PA=AD=2,AB=BC=1,再由棱锥体积公式求解.【解答】解:由三视图还原原几何体如图,该几何体为四棱锥,底面ABCD为直角梯形,AB⊥AD,PA⊥底面ABCD,且PA=AD=2,则该几何体的体积为V=.故选:A.【点评】本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.2.【分析】由三视图知该四棱锥是底面为正方形,且一侧棱垂直于底面,由此求出四棱锥的表面积.【解答】解:由三视图知该四棱锥是底面为正方形,且一侧棱垂直于底面,画出四棱锥的直观图,如图所示:则该四棱锥的表面积为:S=S正方形ABCD+S△PAB+S△PAD+S△PBC+S△PCD=22+×2×3+×2×3.故选:D.【点评】本题考查了利用三视图求几何体表面积,是基础题.3.【分析】由三视图知该四棱锥底面为正方形,且一侧棱垂直于底面,结合图中数据求出四棱锥的体积.【解答】解:由三视图知该四棱锥是底面为正方形,且一侧棱垂直于底面,画出四棱锥的直观图,如图所示:则该四棱锥的体积为V=S正方形ABCD•PA=×36×3=9.故选:B.【点评】本题考查了利用三视图求几何体的体积,是基础题.4.【分析】首先把三视图转换为几何体的直观图,进一步求出几何体的体积.【解答】解:根据几何体的三视图转换为直观图为:该几何体为底面为直角梯形,高为2的直四棱柱;如图所示:故:V=.故选:C.【点评】本题考查的知识要点:三视图和几何体的直观图之间的转换,几何体的体积公式的应用,主要考查学生的运算能力和数学思维能力,属于基础题.5.【分析】通过几何体结合三视图的画图方法,判断选项即可.【解答】解:几何体的俯视图,轮廓是矩形,所以C;几何体的上部的棱与正视图方向垂直,所以A不正确.故选:B.【点评】本题考查三视图的画法,几何体的结构特征,属于基础题.6.【分析】根据三视图知该几何体为一个圆柱挖去一个圆锥,得到截面为圆环,根据圆环面积公式计算即可.【解答】解:由已知得到几何体为一个圆柱挖去一个圆锥,底面半径为2,截面为圆环,设小圆半径为r,则=,所以r=h,所以截面圆环的面积为4π﹣πh2=π(3﹣h2);故选:D.【点评】本题考查了几何体得到三视图以及截面面积的计算问题,也考查了空间几何体的结构特征,是基础题.7.【分析】首先把三视图转换为几何体的直观图,进一步求出几何体的个各棱长,从而确定结果.【解答】解:根据几何体的三视图转换为直观图为:该几何体为三棱锥A﹣BCD;如图所示:所以:AB=BC=,CD=BD=7,AC=,故选:C.【点评】本题考查的知识要点:三视图和几何体的直观图之间的转换,三棱锥的棱长的求法,主要考查学生的运算能力和数学思维能力,属于基础题.8.【分析】画出直观图,利用三视图的数据转化求解即可.【解答】解:根据直观图不难得出,PC是最长的棱长,长度为:.故选:D.【点评】本题考查三视图求解几何体的相关数据,最长棱长的求法,是基础题.9.【分析】首先把三视图转换为几何体的直观图,进一步求出最大棱长.【解答】解:根据几何体的三视图转换为直观图为:该几何体为三棱锥体;如图所示:最长的棱长为AB=.故选:C.【点评】本题考查的知识要点:三视图和几何体的直观图之间的转换,几何体的棱长的求法,主要考查学生的运算能力和数学思维能力,属于基础题.二.填空题(共1小题)10.【分析】求出三棱锥A﹣BCD的体积判断①;由余弦定理的推论判断②;利用空间向量判断③;直接证明sin2α+sin2β+sin2γ≤2判断④.【解答】解:对于①,长方体的体积为abc,三棱锥A﹣BCD的体积为abc﹣4×=,故①正确;对于②,三棱锥A﹣BCD的每一个面的三边长都可以用过一个顶点的三条侧棱表示,不妨以△ACD为例,AD2=a2+c2,AC2=b8+c2,CD2=a6+b2,∵AD2+AC5>CD2,AD2+CD3>AC2,AC2+CD3>AD2,∴△ACD一定是锐角三角形,同理可得△ABC,△BCD为锐角三角形,则三棱锥A﹣BCD的每个面都是锐角三角形,故②正确;对于③,如图,分别以FA、FD所在直线为x、y,则A(a,0,4),b,0),b,0),5,0),0,c),C(a,b,c),2,c),,,,设平面ACD的一个法向量为,由,取y=7,则,同理可得平面BCD的一个法向量为,,取a=b=,,可得二面角A﹣CD﹣B是直二面角;对于④,不妨设AB与底面所成角为α,AD与底面所成角为γ,由③可知,平面BCD的一个法向量为,,sinβ=,==.同理可得,,,则sin6α+sin2β+sin2γ,故④正确.故答案为:①②④.【点评】本题考查空间角与多面体体积的求法,考查空间想象能力与思维能力,考查运算求解能力,是中档题.三.解答题(共11小题)11.【分析】(Ⅰ)连结B1C,ME,利用中位线定理可证明四边形MNDE为平行四边形,从而得到MN∥ED,由线面平行的判定定理证明即可;(Ⅱ)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,利用待定系数法求出平面的法向量,然后由向量的夹角公式求解即可.【解答】(Ⅰ)证明:连结B1C,ME,E分别为BB1,BC的中点,所以ME∥B5C,且,又因为N为A1D的中点,所以,由题设知A1B7∥DC且A1B1=DC,可得B3C∥A1D且B1C=A8D,故ME∥ND且ME=ND,因此四边形MNDE为平行四边形,所以MN∥ED,又MN⊄平面C1DE,ED⊂平面C1DE,所以MN∥平面C8DE;(Ⅱ)因为底面ABCD是正方形,所以CD⊥AD,又因为侧面ADD1A1⊥底面ABCD,且侧面ADD2A1∩底面ABCD=AD,CD⊂平面ABCD,所以CD⊥平面ADD1A2,又DD1⊂平面ADD1A6,所以CD⊥DD1,又因为侧面ADD1A2为矩形,所以AD⊥DD1,以点D为坐标原点建立空间直角坐标系D﹣xyz如图所示,其中D(0,2,0),C1(7,2,4),4,0),2,3),所以,,因为CD⊥平面ADD1A4,所以DC⊥平面BCC1B1,故为平面C7EB1的一个法向量,设为平面DC1E面的法向量,则,即,令y=﹣2,可得,所以,因为二面角A﹣DE﹣B4的平面角是钝角,所以二面角A﹣DE﹣B1的余弦值.【点评】本题考查了立体几何的综合应用,涉及了线面平行的判定定理的应用,在求解有关空间角问题的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.12.【分析】(Ⅰ)连接BD交AC于点O,连接OE,证明OE∥BD1.然后证明BD1∥平面ACE.(Ⅱ)不妨设正方体的棱长为2,建立空间直角坐标系A﹣xyz.求出平面ACE的法向量,利用空间向量的数量积求解直线AD与平面ACE所成角的正弦值即可.【解答】(Ⅰ)证明:连接BD交AC于点O,连接OE,在正方形ABCD中,OB=OD.因为E为DD1的中点,所以OE∥BD1.………………(7分)因为BD1⊄平面ACE,OE⊂平面ACE,所以BD1∥平面ACE. ………………(8分)(Ⅱ)解:不妨设正方体的棱长为2,建立如图所示的空间直角坐标系A﹣xyz.则A(0,5,0),2,7),2,0),6,1),所以,,. ………………(8分)设平面ACE的法向量为=(x,y,所以所以即令y=﹣1,则x=7,于是=(1,2)设直线AD与平面ACE所成角为θ,则.………………(13分)所以直线AD与平面ACE所成角的正弦值为.【点评】本题考查直线与平面平行的判定定理的应用,直线与平面所成角的求法,考查空间想象能力,转化思想以及计算能力,是中档题.13.【分析】(Ⅰ)取AC的中点O,连结OM,ON,先证明OM∥CD,OM=CD,再证明NA1∥CD,NA1=CD,从而证明MA1∥ON,利用线面平行的判定定理证明即可;(Ⅱ)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,利用待定系数法求出平面D1AC的法向量,由向量的夹角公式求解即可.【解答】(Ⅰ)证明:取AC的中点O,连结OM,因为M是AD的中点,所以OM∥CD CD,在长方体ABCD﹣A6B1C1D5中,因为N是A1B1的中点,所以NA3∥CD,NA1=CD,所以NA1∥OM且NA1=OM,所以四边形NOMA3是平行四边形,所以MA1∥ON,又因为MA1⊄平面ANC,ON⊂平面ANC,所以MA8∥平面ANC;(Ⅱ)解:在长方体ABCD﹣A1B1C5D1中,以点B为坐标原点,则C(1,6,0),2,2),D1(1,7,1),1,6),所以,设平面D1AC的法向量为,则有,即,令y=1,则x=2,故,所以=,故直线CN与平面D1AC所成角的正弦值为.【点评】本题考查了线面平行的证明以及线面角的求解,在求解空间角的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.14.【分析】(Ⅰ)利用线面平行的判定定理分别证明CF∥平面ABE,CD∥平面ABE,再利用面面垂直的判定定理,即可证明面面平行;(Ⅱ)若选①②:建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,求出平面BEF和平面CDF的法向量,然后利用空间向量的夹角公式求解即可.若选①②③:建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,求出平面BEF和平面CDF的法向量,然后利用空间向量的夹角公式求解即可.若选①③:建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,求出平面BEF和平面CDF的法向量,然后利用空间向量的夹角公式求解即可.【解答】解:(Ⅰ)证明:因为四边形ACFE为矩形,所以CF∥AE,又AE⊂平面ABE,CF⊄平面ABE,又因为AB∥CD,又AB⊂平面ABE,所以CD∥平面ABE,又CD∩CF=C,CD,所以平面ABE∥平面CDF;(Ⅱ)选择①②:因为AE⊥平面ABCD,AB,所以AE⊥AB,AE⊥AD,所以AB,AE,以点A为坐标原点建立空间直角坐标系如图所示,则B(1,0,6),0,1),4,1),所以,设平面BEF的法向量为,则,即,令x=1,则y=﹣1,故,因为AD⊥平面ABE,又平面ABE∥平面CDF,所以AD⊥平面CDF,取平面CDF的一个法向量为,所以,故二面角B﹣l﹣C的余弦值为.选择①②③:因为AE⊥平面ABCD,AD⊂平面ABCD,因为平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,所以AB⊥平面ADE,又AE⊂平面ADE,所以AB⊥AE,又因为AB⊥AD,所以AB,AE,以点A为坐标原点建立空间直角坐标系如图所示,则B(1,0,3),0,1),7,1),所以,设平面BEF的法向量为,则,即,令x=1,则y=﹣1,故,因为AD⊥平面ABE,又平面ABE∥平面CDF,所以AD⊥平面CDF,取平面CDF的一个法向量为,所以,故二面角B﹣l﹣C的余弦值为.选择①③:因为平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,所以AB⊥平面ADE,又AE⊂平面ADE,所以AB⊥AE,在矩形ACFE中,AE⊥AC,又AC,AB⊂平面ABCD,所以AE⊥平面ABCD,又AD⊂平面ABCD,所以AE⊥AD,所以AB,AE,以点A为坐标原点建立空间直角坐标系如图所示,则B(1,0,5),0,1),4,1),所以,设平面BEF的法向量为,则,即,令x=1,则y=﹣1,故,因为AD⊥平面ABE,又平面ABE∥平面CDF,所以AD⊥平面CDF,取平面CDF的一个法向量为,所以,故二面角B﹣l﹣C的余弦值为.【点评】本题考查了立体几何的综合应用,涉及了面面平行的判定定理,在求解空间角的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.15.【分析】(Ⅰ)推导出OB⊥AD,由AD∥BC,得OB⊥BC,由PO⊥底面ABCD,得OP⊥BC,从而BC⊥平面POB,由此能证明BC⊥OM.(Ⅱ)由PO⊥底面ABCD,OB⊥AD,建立空间直角坐标系O﹣xyz,利用向量法能求出二面角B﹣OM﹣C的余弦值.【解答】解:(Ⅰ)证明:在菱形ABCD中,,△ABD为等边三角形,∵O为AD的中点,∴OB⊥AD,∵AD∥BC,∴OB⊥BC,∵PO⊥底面ABCD,BC⊂平面ABCD,∴OP⊥BC,∵OP∩OB=O,OP,∴BC⊥平面POB,∵M是棱PB上的点,∴OM⊂平面POB,∴BC⊥OM.(Ⅱ)∵PO⊥底面ABCD,OB⊥AD,建立如图所示的空间直角坐标系O﹣xyz,设OA=1,则OP=OB=,O(0,0,6),0,0),,0),,2),0,),∴=(﹣7,,由PM=,得==(6,,),设=(x,y,由,令y=2,得),∵平面POB的法向量为=(1,5,∴cos<>==.由题知二面角B﹣OM﹣C为锐二面角,∴二面角B﹣OM﹣C的余弦值为.【点评】本题考查线线垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.16.【分析】(Ⅰ)证明C1D平行于平面ABB1A1内的直线AB1即可;(Ⅱ)证明AC垂直于平面C1BD内两条相交直线,得到AC⊥平面C1BD,从而得到AC⊥BC1;(Ⅲ)先求二面角两面的法向量,再用夹角公式计算二面角的余弦值即可.【解答】解:(Ⅰ)证明:因为B1C1∥BC、B6C1=BC,AD∥BC,所以B1C2∥AD、B1C1=AD,所以四边形B5C1DA为平行四边形,所以C1D∥AB4,AB1⊂平面ABB1A7,C1D⊄平面ABB1A4,所以C1D∥平面ABB1A2;(Ⅱ)证明:因为AB1⊥平面ABCD,由(Ⅰ)知C1D∥AB8,所以C1D⊥平面ABCD,又因为AC⊂平面ABCD,所以AC⊥C1D,因为ABCD是正方形,所以AC⊥BD,又因为C6D∩BD=D,所以AC⊥平面C1BD,因为C1B⊂平面C6BD,所以AC⊥BC1;(Ⅲ)因为AB1⊥平面ABCD,所以AB5⊥AD,AB1⊥AB,又因为ABCD是正方形,所以AB⊥AD,于是AD、AB1两两垂直,建立如图所示的空间直角坐标系,平面C4BD的法向量为==(1,1,=(﹣4,1,0),,﹣1,),设平面BDD6的法向量为=(x,y,则,令y=,则,,1),所以二面角C2﹣BD﹣D1的余弦值为==.【点评】本题考查了直线与平面位置关系,线面垂直的判定定理和性质,考查了二面角的计算问题,属于中档题.17.【分析】(Ⅰ)由BB1⊥平面ABC,知BB1⊥AB,由勾股定理的逆定理证AB⊥BC,再结合线面垂直的判定定理、面面垂直的判定定理,即可证明平面ABE⊥平面B1BCC1;(Ⅱ)以B为原点建立空间直角坐标系,求得平面ABE的法向量,设直线A1C与平面ABE所成角为θ,由sin θ=|cos<,>|,求出直线A1C与平面ABE所成角的正弦值.【解答】解:(Ⅰ)证明:由直三棱柱的性质知,BB1⊥平面ABC,∵AB⊂平面ABC,∴BB1⊥AB,∵AB=BC=4,AC=,∴AB⊥BC,又BB1∩BC=B,BB2、BC⊂平面B1BCC1,∴AB⊥平面B4BCC1,∵AB⊂平面ABE,∴平面ABE⊥平面B1BCC6.(Ⅱ)以B为原点,BA,BB1所在直线分别为x,y,z轴,则A(1,3,0),0,3),1,0),8,),A7(1,0,4),∴=(﹣1,6,=(1,0,=(5,1,),设平面ABE的法向量为=(x,y,则,即,令z=2,则x=0,∴=(3,2),设直线A1C与平面ABE所成角为θ,则sinθ=|cos<,>|=||=,故直线A1C与平面ABE所成角的正弦值为.【点评】本题考查空间中线与面的垂直关系、线面角的求法,熟练掌握线面、面面垂直的判定定理或性质定理,以及利用空间向量处理线面角的方法是解题的关键,考查逻辑推理能力和运算能力,属于中档题.18.【分析】(Ⅰ)证明CD∥AB,然后证明CD∥平面ABFE.(Ⅱ)以点D为坐标原点,DA,DC,DE分别为x,y,z轴,建立空间直角坐标系.求出平面ADE的法向量,平面BCF的法向量,利用空间向量的数量积求解平面ADE与平面BCF所成锐二面角的大小即可.【解答】(Ⅰ)证明:在五面体ABCDEF中,因为面ABCD是正方形,所以CD∥AB.又因为AB⊂平面ABFE,CD⊄平面ABFE,所以CD∥平面ABFE.(Ⅱ)解:因为面ABCD是正方形,所以CD⊥AD.又因为CD⊥AE.又AD∩AE=A,所以CD⊥平面ADE又因为DE⊂平面ADE,所以CD⊥DE.因为面ABCD是正方形,所以CD⊥AD.又因为AD⊥DE,所以以点D为坐标原点,DA,DE分别为x,y,如图建立空间直角坐标系.因为CD=2EF=2,EF=ED,7,0),0,7),2,0),4,0),0,5).由(Ⅰ)CD∥平面ABFE,CD⊂平面CDEF,平面CDEF∩平面ABFE=EF,所以CD∥EF.所以.可得F(2,1,1).由题意知平面ADE的法向量为设平面BCF的法向量为.由得令y=1,得z=3,所以设平面ADE与平面BCF所成锐二面角为θ.cosθ=.所以平面ADE与平面BCF所成锐二面角为【点评】本题考查直线与平面平行的判断定理的应用,二面角的平面角的求法,考查空间想象能力,转化思想以及计算能力,是中档题.19.【分析】(Ⅰ)先证明四边形ABCO是平行四边形,即可得到AB∥OC,由线面平行的判定定理证明即可;(Ⅱ)建立空间直角坐标系,然后求出所需点的坐标,利用待定系数法求出平面BAP的法向量,由向量的夹角公式求解即可.【解答】(Ⅰ)证明:在四边形ABCD中,因为BC∥AD,,O是AD的中点,则BC∥AO,所以四边形ABCO是平行四边形,所以AB∥OC,又因为AB⊄平面POC,CO⊂平面POC,所以AB∥平面POC;(Ⅱ)连结OB,因为PO⊥平面ABCD,PO⊥OD,又因为点O时AD的中点,且,所以BC=OD,因为BC∥AD,CD⊥AD,所以四边形OBCD是正方形,所以BO⊥AD,建立空间直角坐标系如图所示,则A(0,﹣2,B(1,0,C(3,1,D(0,3,P(0,0,所以,设平面BAP的法向量为,则,即,令y=1,故,因为OB⊥平面PAD,所以是平面PAD的一个法向量,所以=,由图可知,二面角B﹣AP﹣D为锐角,所以二面角B﹣AP﹣D的余弦值为.【点评】本题考查了立体几何的综合应用,涉及了线面平行的判定定理的应用,在求解空间角的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.20.【分析】(Ⅰ)证明PA⊥BD,BD⊥AC,推出BD⊥平面PAC,即可证明平面EBD⊥平面PAC.(Ⅱ)E是PC的中点,连结OE,OB,OC,OE两两垂直,建立如图所示的坐标系,求出平面EBC的法向量,直线DE的方向向量,利用空间向量的数量积求解ED与平面EBC所成角的正弦值即可.【解答】解:(Ⅰ)PA⊥平面ABCD⇒PA⊥BD,…………………………………(1分)底面ABCD菱形,可得BD⊥AC又PA∩AC=A,又PA⊥BD,BD⊥AC,PA⊂平面PAC,AC⊂平面PAC,…………………………………………(2分)BD⊂平面EBD,平面EBD⊥平面PAC(Ⅱ)若E是PC的中点,连结OE,……(6分)所以,OB,OE两两垂直,………(1分)不妨设AB=2,则…(6分)设平面EBC的法向量为=(x,y,,取x=1,则y=z=,=(1,,),直线DE的方向向量为=(,0,cos==.ED与平面EBC所成角的正弦值为:.【点评】本题考查直线与平面垂直的判断定理的应用,直线与平面所成角的求法,是中档题.21.【分析】(Ⅰ)连接BD交AC于H点,连接MH,推导出MH∥BP,从而PB∥平面ACM;(Ⅱ)取AB中点O,连接PO,证明PO⊥平面ABCD,以O为原点,分别以OB,OH,OP所在直线为x,y,z轴建立空间直角坐标系,分别求出平面MBC与平面ABCD的一个法向量,由两法向量所成角的余弦值可得二面角M ﹣BC﹣D的余弦值.【解答】证明:(Ⅰ)连接BD交AC于H点,连接MH,∵四边形ABCD是菱形,∴点H为BD的中点.又∵M为PD的中点,∴MH∥BP,又∵BP⊄平面ACM,MH⊂平面ACM,∴PB∥平面ACM;解:(Ⅱ)取AB中点O,连接PO,∵△PAB为正三角形,且侧面PAB⊥底面ABCD,以O为原点,分别以OB,OP所在直线为x,y,则B(1,0,6),2,0),1,),=(0,2,0),,1,),设平面MBC的一个法向量为,由,取z=,得,平面ABCD的一个法向量为,∴cos<>==.由图可知,二面角M﹣BC﹣D为锐角.【点评】本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了利用空间向量求解空间角,是中档题.。
2021_2022学年北京市第十二中学高二(下)月考物理试卷(6月)(含答案解析)

C.如图丙所示,金属的遏制电压 与入射光的频率 的图像中,该直线的斜率为 ,纵截距的绝对值为
D.同一光电管在不同实验条件下得到了三条光电流与电压之间的关系曲线 甲光、乙光、丙光 ,如图丁所示。则可判断甲、乙、丙光的频率关系为
14.光电倍增管 是一种高灵敏度和超快时间响应光探测器,如图所示,它由光阴极K、倍增级和阳极A等组成,由玻璃封装,内部高真空,其倍增级又由一系列倍增极组成,每个倍增极工作在前级更高的电压下、当入射光照射光阴极,产生光电子,经电场加速聚焦后,带着更高的能量撞击第一级倍增管,发射更多的低能量的电子,这些电子依次被加速向下级倍增极撞击,导致一系列的几何级倍增,最后,在高电位的阳极收集到放大了的光电流。下列说法正确的是( )
A.少数 粒子穿过金箔后发生较大角度的偏转是由于其与电子发生了碰撞
B.绝大多数 粒子沿直线穿过,偏转角很小,说明原子内部大部分是中空的
C.极少数 粒子被弹回,说明原子中心是一个体积小、带正电且占有原子几乎全部质量的核
D.在 粒子散射实验中,当 粒子最接近原子核时,电势能最小
12.一定质量的理想气体从状态a经①②③过程再次回到状态a,气体压强和摄氏温度t的关系如图所示。下列说法正确的是( )
3.下列说法正确的是( )
A.竹筏漂浮在水面上,是分子表面张力作用的结果
B.液体表面层的分子比液体内部的分子有更小的分子势能
C.在夏季,人穿棉线衣服感觉舒适是因为汗水对棉线是浸润物体
D.布制的雨伞伞面能明显看到线的缝隙,但雨伞不漏雨水是因为水对伞面不浸润
4.下列关于固体的叙述,正确的是( )
A.晶体的各向异性是由于它的微粒按空间点阵排列
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10,11,12年北京高考题选
(2011北京文)17.(本小题共14分)
如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
(Ⅰ)求证:DE∥平面BCP;
(Ⅱ)求证:四边形DEFG为矩形;
(Ⅲ)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
(2011北京文)19.(本小题共14分)
已知椭圆
22
22
:1(0)
x y
G a b
a b
+=>>的离心率为
6
3
,右焦点为(22,0),斜率为I
的直线l与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
(I)求椭圆G的方程;
(II)求PAB
∆的面积.
(2012年)(7)某三棱锥的三视图如图所示,该三棱锥的表面积是
(A)28+65(B)30+65(C)56+125(D)60+125
(2012年北京文)(16)(本小题共14分)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2。
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由。
(2010北京文)(17)(本小题共13分)
如图,正方形ABCD和四边形ACEF所在的平面互相垂直。
EF//AC,AB=2,CE=EF=1
(Ⅰ)求证:AF//平面BDE;
(Ⅱ)求证:CF⊥平面BDF;
,(2,0),离心率是(2010年北京文)已知椭圆C的左、右焦点坐标分别是(2,0)
6
,直线y=t椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
3
(Ⅰ)求椭圆C的方程;
(Ⅱ)若圆P与x轴相切,求圆心P的坐标;
(Ⅲ)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值。
