数值线性代数第二版徐树方高立张平文上机习题第一章实验报告(供参考)
数值代数上机实验报告

数值代数上机实验报告试验项目名称:平方根法与改进平方根法实验内容:先用你熟悉的计算机语言将平方根法和改进平方根法编写成通用的子程序,然后用你编写的程序求解对称正定方程组Ax=b,其中,A=[101 10 1…1 10 11 10]100*100b随机生成,比较计算结果,评论方法优劣。
实验要求:平方根法与改进的平方根的解法步骤;存储单元,变量名称说明;系数矩阵与右端项的生成;结果分析。
实验报告姓名:罗胜利班级:信息与计算科学0802 学号:u200810087 实验一、平方根法与改进平方根法先用你所熟悉的计算机语言将平方根法和改进的平方根法编成通用的子程序,然后用你编写的程序求解对称正定方程组AX=b,其中系数矩阵为40阶Hilbert矩阵,即系数矩阵A的第i行第j列元素为=,向量b的第i个分量为=.平方根法函数程序如下:function [x,b]=pingfanggenfa(A,b)n=size(A);n=n(1);x=A^-1*b; %矩阵求解disp('Matlab自带解即为x');for k=1:nA(k,k)=sqrt(A(k,k));A(k+1:n,k)=A(k+1:n,k)/A(k,k);for j=k+1:n;A(j:n,j)=A(j:n,j)-A(j:n,k)*A(j,k);endend %Cholesky分解for j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j);endb(n)=b(n)/A(n,n); %前代法A=A';for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1); %回代法disp('平方根法的解即为b');endfunction [x]=ave(A,b,n) %用改进平方根法求解Ax=b L=zeros(n,n); %L为n*n矩阵D=diag(n,0); %D为n*n的主对角矩阵S=L*D;for i=1:n %L的主对角元素均为1L(i,i)=1;for i=1:nfor j=1:n %验证A是否为对称正定矩阵if (eig(A)<=0)|(A(i,j)~=A(j,i)) %A的特征值小于0或A非对称时,输出wrong disp('wrong');break;endendendD(1,1)=A(1,1); %将A分解使得A=LDL Tfor i=2:nfor j=1:i-1S(i,j)=A(i,j)-sum(S(i,1:j-1)*L(j,1:j-1)');L(i,1:i-1)=S(i,1:i-1)/D(1:i-1,1:i-1);endD(i,i)=A(i,i)-sum(S(i,1:i-1)*L(i,1:i-1)');endy=zeros(n,1); % x,y为n*1阶矩阵x=zeros(n,1);for i=1:ny(i)=(b(i)-sum(L(i,1:i-1)*D(1:i-1,1:i-1)*y(1:i-1)))/D(i,i); %通过LDy=b解得y的值endfor i=n:-1:1x(i)=y(i)-sum(L(i+1:n,i)'*x(i+1:n)); %通过L T x=y解得x的值改进平方根法函数程序如下:function b=gaijinpinfanggenfa(A,b)n=size(A);n=n(1);v=zeros(n,1);for j=1:nfor i=1:j-1v(i)=A(j,i)*A(i,i);endA(j,j)=A(j,j)-A(j,1:j-1)*v(1:j-1);A(j+1:n,j)=(A(j+1:n,j)-A(j+1:n,1:j-1)*v(1:j-1))/A(j,j);end %LDL'分解B=diag(A);D=zeros(n);for i=1:nD(i,i)=B(i);A(i,i)=1;EndA=tril(A); %得到L和Dfor j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j);endb(n)=b(n)/A(n,n); %前代法A=D*(A');for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1); %回代法disp('改进平方根法解得的解即为b');end调用函数解题:clear;clc;n=input('请输入矩阵维数:');b=zeros(n,1);A=zeros(n);for i=1:nfor j=1:nA(i,j)=1/(i+j-1);b(i)=b(i)+1/(i+j-1);endend %生成hilbert矩阵[x,b]=pingfanggenfa(A,b) b=gaijinpinfanggenfa(A,b)运行结果:请输入矩阵维数:40Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 6.570692e-020. > In pingfanggenfa at 4In qiujie at 10Matlab自带解即为x平方根法的解即为bx =1.60358.96850.85621.01950.9375-50.2500-3.0000-16.000024.0000-49.5000-30.000039.000022.0000-64.0000-12.00002.000010.2500-10.5000-1.0000-10.875083.000046.0000-98.0000-69.000068.000021.0000-50.7188-8.7500-8.0000 112.0000 6.0000 -68.7500 22.000044.0000 -28.0000 8.0000 -44.000012.0000b =1.0e+007 *0.0000-0.00000.0001-0.0004-0.00140.0424-0.29801.1419-2.73354.2539-4.30182.7733-1.19890.5406-0.36880.32850.4621-0.25130.05650.0000-0.00510.0071-0.0027-0.0031-0.00190.00090.0002-0.0002-0.00060.00040.0001-0.00020.00010.0000-0.00000.0000-0.0000-0.0000改进平方根法解得的解即为bb =1.0e+024 *0.0000-0.00000.0001-0.0012-0.0954 0.4208 -1.2101 2.0624 -1.0394 -3.3343 6.2567 -0.2463 -7.45942.80303.6990 0.7277 -1.7484 -0.4854 -3.6010 0.2532 5.1862 1.4410 0.8738 -4.5654 1.0422 4.0920 -2.7764 -2.2148 -0.8953 0.3665 4.8967 1.0416 0.1281-1.1902-2.83348.4610-3.6008实验二、利用QR分解解线性方程组:利用QR分解解线性方程组Ax=b,其中A=[16 4 8 4;4 10 8 4;8 8 12 10;4 4 10 12];b=[32 26 38 30];求解程序如下:定义house函数:function [v,B]=house(x)n=length(x);y=norm(x,inf);x=x/y;Q=x(2:n)'*x(2:n);v(1)=1;v(2:n)=x(2:n);if n==1B=0;elsea=sqrt(x(1)^2+Q);if x(1)<=0v(1)=x(1)-a;elsev(1)=-Q/(x(1)+a);endB=2*v(1)^2/(Q+v(1)^2);endend进行QR分解:clear;clc;A=[16 4 8 4;4 10 8 4;8 8 12 10;4 4 10 12]; b=[32 26 38 30];b=b';x=size(A);m=x(1);n=x(2);d=zeros(n,1);for j=1:n[v,B]=house(A(j:m,j));A(j:m,j:n)=(eye(m-j+1)-B*(v')*v)*A(j:m,j:n); d(j)=B;if j<m< p="">A(j+1:m,j)=v(2:m-j+1);endend %QR分解R=triu(A); %得到R D=A;I=eye(m,n);Q=I;for i=1:nD(i,i)=1;endH=tril(D);M=H';for i=1:nN=I-d(i)*H(1:m,i)*M(i,1:m);Q=Q*N;end %得到Qb=(Q')*b; %Q是正交阵for j=n:-1:2b(j)=b(j)/R(j,j);b(1:j-1)=b(1:j-1)-b(j)*R(1:j-1,j);endb(1)=b(1)/R(1,1); %回带法运行结果如下:R =18.7617 9.8072 15.7769 11.08640 9.9909 9.3358 7.53410 0 5.9945 9.80130 0 0 -0.5126Q =0.8528 -0.4368 -0.2297 -0.17090.2132 0.7916 -0.4594 -0.34170.4264 0.3822 0.2844 0.76890.2132 0.1911 0.8095 -0.5126b=1.000000000000001.000000000000010.9999999999999881.00000000000001实验三、Newton下山法解非线性方程组:3x-cos(yz)-=0,-81+sinz+1.06=0,exp(-xy)+20z+=0;要求满足数值解=满足或.定义所求方程组的函数:Newtonfun.mfunction F = Newtonfun(X)F(1,1)=3*X(1)-cos(X(2)*X(3))-1/2;F(2,1)=X(1)^2-81*(X(2)+0.1)^2+sin(X(3))+1.06;F(3,1)=exp(-X(1)*X(2))+20*X(3)+(10*pi-3)/3;End向量求导:Xiangliangqiudao.mfunction J=xiangliangqiudao()syms x y zX=[x,y,z];F=[3*X(1)-cos(X(2)*X(3))-1/2;X(1)^2-81*(X(2)+0.1)^2+sin(X(3))+1.06;exp(-X(1)*X(2))+20*X(3)+(10*pi-3)/3];J=jacobian(F,[x y z]);End代值函数:Jacobi.mfunction F=Jacobi(x)F=[ 3,x(3)*sin(x(2)*x(3)), x(2)*sin(x(2)*x(3));2*x(1), -162*x(2)-81/5,cos(x(3));-x(2)/exp(x(1)*x(2)),-x(1)/exp(x(1)*x(2)),20];End方程组求解:format long; %数据表示为双精度型X1=[0,0,0]';eps=10^(-8);k=1;i=1;X2=X1-Jacobi(X1)^(-1)*Newtonfun(X1);while (norm(subs(X2-X1,pi,3.1415926),2)>=eps)&&(norm(Newtonfun(X1),2)>=eps) if norm(Newtonfun(X2),2)<="" p="">X1=X2;B=inv(Jacobi(X2));C=Newtonfun(X2);X2=X2-B*C;i=i+1;elsev=1/(2^k); %引入下山因子X1=X2;B=inv(Jacobi(X2));C=Newtonfun(X2);X2=X2-v*B*C;k=k+1;endendj=i+k-1 %迭代次数X=X2 %输出结果运行结果如下:j =5X =0.500000000000000 -0.000000000000000 -0.523598775598299</m<>。
《数值计算方法》上机实验报告

《数值计算方法》上机实验报告华北电力大学实验名称数值il•算方法》上机实验课程名称数值计算方法专业班级:电力实08学生姓名:李超然学号:200801001008 成绩: 指导教师:郝育黔老师实验日期:2010年04月华北电力大学实验报告数值计算方法上机实验报吿一.各算法的算法原理及计算机程序框图1、牛顿法求解非线性方程*对于非线性方程,若已知根的一个近似值,将在处展开成一阶xxfx ()0, fx ()xkk泰勒公式"f 0 / 2 八八,fxfxfxxxxx 0 0 0 0 0 kkkk2!忽略高次项,有,fxfxfxxx 0 ()()(),,, kkk右端是直线方程,用这个直线方程来近似非线性方程。
将非线性方程的**根代入,即fx ()0, X ,* fxfxxx 0 0 0 0, ,, kkkfx 0 fx 0 0,解出fX 0 *k XX,, k' fx 0 k水将右端取为,则是比更接近于的近似值,即xxxxk, Ik, Ikfx ()k 八XX, Ikk* fx()k这就是牛顿迭代公式。
,2,计算机程序框图:,见,,3,输入变量、输出变量说明:X输入变量:迭代初值,迭代精度,迭代最大次数,\0输出变量:当前迭代次数,当前迭代值xkl,4,具体算例及求解结果:2/16华北电力大学实验报吿开始读入l>k/fx()0?,0fx 0 Oxx,,01* fx ()0XX,,,?10kk, ,1,kN, ?xx, 10输出迭代输出X输出奇异标志1失败标志,3,输入变量、输出变量说明: 结束例:导出计算的牛顿迭代公式,并il •算。
(课本P39例2-16) 115cc (0), 求解结果:10. 75000010.72383710. 72380510. 7238052、列主元素消去法求解线性方程组,1,算法原理:高斯消去法是利用现行方程组初等变换中的一种变换,即用一个不为零的数乘 -个 方程后加只另一个方程,使方程组变成同解的上三角方程组,然后再自下而上 对上三角3/16华北电力大学实验报告方程组求解。
数值代数上机实验报告

数值代数课程设计实验报告姓名: 班级: 学号: 实验日期:一、实验名称 代数的数值解法 二、实验环境 MATLAB7.0实验一、平方根法与改进平方根法一、实验要求:用熟悉的计算机语言将不选主元和列主元Gasuss 消元法编写成通用的子程序,然后用编写的程序求解下列方程组⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--⨯14151515157681681681681681612321n n n n n x x x x x x 用所编的程序分别求解40、84、120阶方程组的解。
二、算法描述及实验步骤GAuss 程序如下:(1)求A 的三角分解:LU A =;(2)求解b y =L 得y ; (3)求解y x =U 得x ;列主元Gasuss 消元法程序如下: 1求A 的列主元分解:LU PA =;2求解b y P L =得y ; 3求解y x =U 得x ;三、调试过程及实验结果:%----------------方程系数---------------->> A1=Sanduijiaozhen(8,6,1,40); >> A2=Sanduijiaozhen(8,6,1,84); >> A3=Sanduijiaozhen(8,6,1,120); >> b1(1)=7;b2(1)=7;b3(1)=7;>> for i=2:39b1(i)=15;end>> b1(40)=14;>> for i=2:83b2(i)=15;end>> b2(40)=14;>> for i=2:119b1(i)=15;end>> b3(120)=14;%----------------方程解---------------->> x11=GAuss(A1,b1')>> x12=GAuss Zhu(A1,b1')>> x21=GAuss(A2,b2')>> x22=GAuss Zhu(A3,b3')>> x31=GAuss(A3,b3')>> x32=GAuss Zhu(A3,b3')运行结果:(n=40)GAuss消元法的解即为x11 =1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000列主元GAuss消元法的解即为x12 =1 1 1 1 1 1 1 1 1 1 111111111111111111111111111111六、源程序:function A=Sanduijiaozhen(a,b,c,n)%生成n阶以a,b,c为元素的三对角阵A=diag(b*ones(1,n),0)+diag(c*ones(1,n-1),1)+diag(a*ones(1,n-1),-1);function x=GAuss(A,b)n=length(b);x=b;%-------分解---------------for i=1:n-1for j=i+1:nmi=A(j,i)/A(i,i);b(j)=b(j)-mi*b(i);for k=i:nA(j,k)=A(j,k)-mi*A(i,k);endAB=[A,b];endend%-----------回代------------------x(n)=b(n)/A(n,n);for i=n-1:-1:1s=0;for j=i+1:ns=s+A(i,j)*x(j);endx(i)=(b(i)-s)/A(i,i);endfunction x=GAussZhu(A,b)n=length(b);x=b;%----------------------选主元---------------------for k=1:n-1a_max=0;for i=k:nif abs(A(i,k))>a_maxa_max=abs(A(i,k));r=i;endendif r>kfor j=k:nz=A(k,j);A(k,j)=A(r,j);A(r,j)=z;endz=b(k);b(k)=b(r);b(r)=z;end%--------------消元-----------------for i=k+1:nm=A(i,k)/A(k,k);for j=k:nA(i,j)=A(i,j)-m*A(k,j);endb(i)=b(i)-m*b(k);endendif abs(A(n,n))==0return;endAbZhu=[A,b];%----------------回代-----------------------x(n)=b(n)/A(n,n);for i=n-1:-1:1for j=i+1:nb(i)=b(i)-A(i,j)*x(j);endx(i)=b(i)/A(i,i);end实验二、平方根法与改进平方根法一、实验要求:用计算机语言将平方根法和改进的平方根法编成通用的子程序,然后用编写的程序求解对称正定方程组100阶方程组AX=b,二、算法描述及实验步骤:平方根法函数程序如下:1、求A 的Cholesky 分解:L L A T=;2、求解b y =L 得y ;3、求解y x =TL 得x ; 改进平方根法函数程序如下:1、求A 的Cholesky 分解:T=LDL A ; 2、求解b y =L 得y ; 3、求解y x =TDL 得x ;三、调试过程及实验结果:clear;clc;%----------------方程系数---------------->> A=Sanduijiaozhen(1,10,1,100); >> b(1)=11; >> for i=2:99 b(i)=12; end>> b(100)=11;>> x1=Cholesky(A,b') >> x2=GJCholesky(A,b')运行结果:平方根法的解即为 x1 =1.0000 1.00001.0000 1.00001.0000 1.00001.0000 1.00001.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000改进平方根法解得的解即为x2 =1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00000.99991.00090.99081.09080.1010四、源程序:function x=Cholesky(A,b)n=size(A);n=n(1);% x=A^-1*b;% disp('Matlab自带解即为x');%-----------------Cholesky分解-------------------for k=1:nA(k,k)=sqrt(A(k,k));A(k+1:n,k)=A(k+1:n,k)/A(k,k);for j=k+1:n;A(j:n,j)=A(j:n,j)-A(j:n,k)*A(j,k);endend%------------------前代法求解Ly=b----------------------------for j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j);endb(n)=b(n)/A(n,n);%-----------------回代法求解L'x=y-----------------------------A=A';for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1);disp('平方根法的解即为');function b=GJCholesky(A,b)n=size(A);n=n(1);v=zeros(n,1);%----------------------LDL'分解-----------------------------for j=1:nfor i=1:j-1v(i)=A(j,i)*A(i,i);endA(j,j)=A(j,j)-A(j,1:j-1)*v(1:j-1);A(j+1:n,j)=(A(j+1:n,j)-A(j+1:n,1:j-1)*v(1:j-1))/A(j,j);endB=diag(A);D=zeros(n);for i=1:nD(i,i)=B(i);A(i,i)=1;end%-------------------前代法---------------------------A=tril(A); %得到L和Dfor j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j);endb(n)=b(n)/A(n,n);%-----------------回代法-----------------------------A=D*(A');for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1);disp('改进平方根法解得的解即为');实验三、二次多项式拟合一、实验要求:用计算机语言编制利用QR分解求解线性最小二乘问题的通用子程序,用编写的程序求解一个二次多项式使在残向量的范数最小的意义下拟合下面的数据t-1 -0.75 -0.5 0 0.25 0.5 0.75iy 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125i二、算法描述及实验步骤:QR分解求解程序如下:1、求A 的QR 分解;2、计算b c 11T =Q ;3、求解上三角方程1c x =R 得x ;三、调试过程及实验结果:>> t=[-1 -0.75 -0.5 0 0.25 0.5 0.75];>> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> plot(t,y,'r*');>> legend('实验数据(ti,yi)'); >> xlabel('t'), ylabel('y');>> title('二次多项式拟合的数据点(ti,yi)的散点图');运行后屏幕显示数据的散点图(略).(3)编写下列MATLAB 程序计算)(x f 在),(i i y x 处的函数值,即输入程序 >> syms a b c>> t=[-1 -0.75 -0.5 0 0.25 0.5 0.75]; >> fi=a.*t.^2+ b.*t+c%运行后屏幕显示关于 ,,a b c 的线性方程组fi =[a-b+c,9/16*a-3/4*b+c,1/4*a-1/2*b+c,c,1/16*a+1/4*b+c,1/4*a+1/2*b+c,9/16*a+3/4*b +c]编写构造残向量2范数的MATLAB 程序>> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> fy=fi-y; fy2=fy.^2; J=sum(fy.^2); 运行后屏幕显示误差平方和如下 J=(a-b+c-1)^2+(9/16*a-3/4*b+c-13/16)^2+(1/4*a-1/2*b+c-3/4)^2+(c-1)^2+(1/16*a+1/4*b+c-21/16)^2+(1/4*a+1/2*b+c-7/4)^2+(9/16*a+3/4*b+c-37/16)^2为求,,a b c 使J 达到最小,只需利用极值的必要条件0J a ∂=∂,0J b ∂=∂,0J c∂=∂,得到关于,,a b c 的线性方程组,这可以由下面的MATLAB 程序完成,即输入程序 >> Ja1=diff(J,a); Ja2=diff(J,b); Ja3=diff(J,c);>> Ja11=simple(Ja1), Ja21=simple(Ja2), Ja31=simple(Ja3) 运行后屏幕显示J 分别对,,a b c 的偏导数如下 Ja11 =451/128*a-63/32*b+43/8*c-887/128 Ja21 =-63/32*a+43/8*b-3/2*c-61/32Ja31 =43/8*a-3/2*b+14*c-143/8解线性方程组112131000Ja Ja Ja ===,,,输入下列程序 >> A=[451/128, -63/32, -3/2 ;-63/32,43/8,-3/2;43/8,-3/2,14]; >> B=[887/128,61/32,143/8]; >> C=B/A, f=poly2sym(C)运行后屏幕显示拟合函数f 及其系数C 如下 C =0.3081 0.8587 1.4018 f =924/2999*x^2+10301/11996*x+4204/2999 故所求的拟合曲线为2()0.30810.8581 1.4018f x x x =++四、源程序:>> t=[-1 -0.75 -0.5 0 0.25 0.5 0.75];>> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> plot(t,y,'r*');>> legend('实验数据(ti,yi)'); >> xlabel('t'), ylabel('y');>> title('二次多项式拟合的数据点(ti,yi)的散点图'); >> syms a b c>> t=[-1 -0.75 -0.5 0 0.25 0.5 0.75]; >> fi=a.*t.^2+ b.*t+c fi =[ a-b+c, 9/16*a-3/4*b+c, 1/4*a-1/2*b+c, c, 1/16*a+1/4*b+c, 1/4*a+1/2*b+c, 9/16*a+3/4*b+c]>> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> fy=fi-y; fy2=fy.^2; J=sum(fy.^2) J =(a-b+c-1)^2+(9/16*a-3/4*b+c-13/16)^2+(1/4*a-1/2*b+c-3/4)^2+(c-1)^2+(1/16*a+1/4*b+c-21/16)^2+(1/4*a+1/2*b+c-7/4)^2+(9/16*a+3/4*b+c-37/16)^2>> Ja1=diff(J,a); Ja2=diff(J,b); Ja3=diff(J,c);>> Ja11=simple(Ja1), Ja21=simple(Ja2), Ja31=simple(Ja3)Ja11 =451/128*a-63/32*b+43/8*c-887/128Ja21 =-63/32*a+43/8*b-3/2*c-61/32Ja31 =43/8*a-3/2*b+14*c-143/8>> A=[451/128, -63/32, -3/2 ;-63/32,43/8,-3/2;43/8,-3/2,14]; >> B=[887/128,61/32,143/8];>> C=B/A, f=poly2sym(C)C =0.3081 0.8587 1.4018f =924/2999*x^2+10301/11996*x+4204/2999>>。
(完整word版)数值线性代数第二版徐树方高立张平文上机习题第四章实验报告
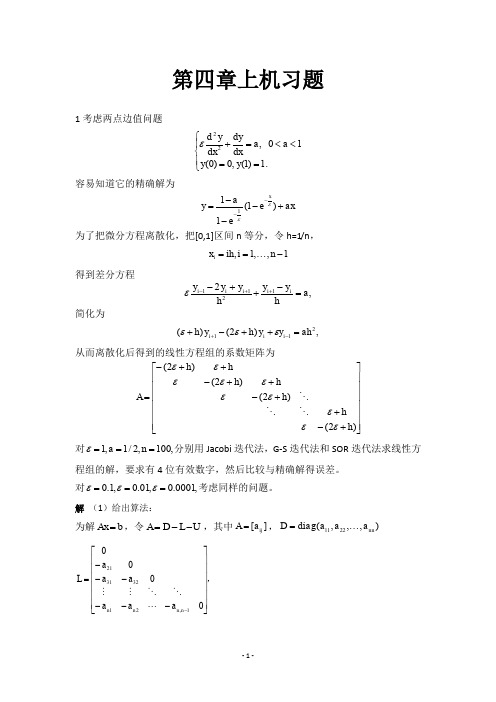
第四章上机习题1考虑两点边值问题⎪⎩⎪⎨⎧==<<=+.1)1(,0)0(10 ,22y y a a dx dy dx y d ε 容易知道它的精确解为ax e e ay x +---=--)1(111εε为了把微分方程离散化,把[0,1]区间n 等分,令h=1/n ,1,,1,-==n i ih x i得到差分方程,21211a hy y h y y y i i i i i =-++-++-ε简化为 ,)2()(211ah y y h y h i i i =++-+-+εεε从而离散化后得到的线性方程组的系数矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+-++-++-++-=)2()2()2()2(h h h h h h h A εεεεεεεεεε 对,100,2/1,1===n a ε分别用Jacobi 迭代法,G-S 迭代法和SOR 迭代法求线性方程组的解,要求有4位有效数字,然后比较与精确解得误差。
对,0001.0,01.0,1.0===εεε考虑同样的问题。
解 (1)给出算法:为解b Ax =,令U L D A --=,其中][ij a A =,),,,(2211nn a a a diag D = ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-00001,21323121n n n n a a a a a a L,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-0000,122311312 n n n n a a a a a a U 利用Jacobi 迭代法,G-S 迭代法,SOR 迭代法解线性方程组,均可以下步骤求解: step1给定初始向量x0=(0,0,...,0),最大迭代次数N ,精度要求c ,令k=1 step2令x=B*x0+gstep3若||x-x0||2<c ,算法停止,输出解和迭代次数k ,否则,转step4 step4若k>=N,算法停止,迭代失败,否则,令x0=x ,转step2在Jacobi 迭代法中,B=D -1*(L+U),g=D -1*b在G-S 迭代法中,B=D -1*(L+U),g=D -1*b在SOR 迭代法中,B=(D-w*L)-1*[(1-w)*D+w*U],g=w*(D-w*L)-1*b另外,在SOR 迭代法中,上面算法step1中要给定松弛因子w ,其中0<w<2 为计算结果,规定w=0.5。
数值分析上机实验指导书

“数值计算方法”上机实验指导书实验一 误差分析实验1.1(病态问题)实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。
对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。
通过本实验可获得一个初步体会。
数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。
病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。
问题提出:考虑一个高次的代数多项式)1.1()()20()2)(1()(201∏=−=−−−=k k x x x x x p显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。
现考虑该多项式的一个扰动)2.1(0)(19=+x x p ε其中ε是一个非常小的数。
这相当于是对(1.1)中19x 的系数作一个小的扰动。
我们希望比较(1.1)和(1.2)根的差别,从而分析方程(1.1)的解对扰动的敏感性。
实验内容:为了实现方便,我们先介绍两个MATLAB 函数:“roots ”和“poly ”。
roots(a)u =其中若变量a 存储n+1维的向量,则该函数的输出u 为一个n 维的向量。
设a 的元素依次为121,,,+n a a a ,则输出u 的各分量是多项式方程01121=+++++−n n n n a x a x a x a的全部根;而函数 poly(v)b =的输出b 是一个n+1维向量,它是以n 维向量v 的各分量为根的多项式的系数(从高到低排列)。
可见“roots ”和“poly ”是两个互逆的运算函数。
))20:1((;)2();21,1(;000000001.0ve poly roots ess ve zeros ve ess +===上述简单的MATLAB 程序便得到(1.2)的全部根,程序中的“ess ”即是(1.2)中的ε。
几份机械类专业课程习题答案

300份机械类专业课程习题答案电子版合集(共18页,myth920)材料力学第4版(刘鸿文)答案(有附件)【khdaw_cola】/bbs/viewthread.php?tid=1931&fromuid=9机械设计基础(第五版) 杨可桢程光蕴李仲生高教版课后答案【khdaw_cola】/bbs/viewthread.php?tid=2316&fromuid=9材料力学课后答案/bbs/viewthread.php?tid=96&fromuid=9材料力学(范钦珊主编著) 高等教育出版社课后答案/bbs/viewthread.php?tid=120&fromuid=9机械设计基础(第五版) 答案7-18章杨可桢程光蕴李仲生【khdaw_cola】/bbs/viewthread.php?tid=2570&fromuid=9材料力学第四版(刘鸿文著) 高等教育出版社课后答案/bbs/viewthread.php?tid=2461&fromuid=9《结构力学习题集》课后答案【khdaw】/bbs/viewthread.php?tid=3016&fromuid=9电工学第六版秦曾煌高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=2986&fromuid=9材料力学(I)第四版(孙训方)高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=5342&fromuid=9电力电子技术试题习题考题及答案题解【khdaw】/bbs/viewthread.php?tid=1169&fromuid=9机械工程控制基础(第四版第五版通用)杨叔子杨克冲华中科大课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10089&fromuid=9机械原理高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=664&fromuid=9机械原理学习指南(第二版)(孙恒著) 课后答案/bbs/viewthread.php?tid=569&fromuid=9机械原理习题+答案【khdaw_cola】/bbs/viewthread.php?tid=1210&fromuid=9机械设计及答案【khdaw_cola】/bbs/viewthread.php?tid=1172&fromuid=9机械设计第八版(濮良贵纪名刚著) 高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=7235&fromuid=9《机械工程测试技术基础》第三版(熊诗波黄长艺)机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=7488&fromuid=9材料力学第二版单辉祖高等教育出版课后答案【khdaw_cola】/bbs/viewthread.php?tid=7980&fromuid=9机械制图基本知识和技能课后答案/bbs/viewthread.php?tid=212&fromuid=9液压传动第二版习题答案【khdaw】/bbs/viewthread.php?tid=7046&fromuid=9电工学简明教程秦曾煌第二版高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=6764&fromuid=9机电传动控制答案邓星钟编第四版华中科技大学出版社【khdaw_cola】/bbs/viewthread.php?tid=5087&fromuid=9机械设计基础(第五版)杨可桢程光蕴李仲生高等教育出版课后答案【khdaw】/bbs/viewthread.php?tid=5570&fromuid=9机械设计基础考试样卷(4份,有答案)【khdaw_cola】/bbs/viewthread.php?tid=1168&fromuid=9机械原理第七版(孙恒陈作模葛文杰著) 高等教育出版社课后答案/bbs/viewthread.php?tid=7795&fromuid=9互换性与测量技术基础(王伯平著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=8360&fromuid=9结构力学教程高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=7111&fromuid=9电工学简明教程(第二版)秦曾煌主编/bbs/viewthread.php?tid=3403&fromuid=9水力学答案(李炜、徐孝平) 武汉水利电力大学出版社【khdaw_cola】/bbs/viewthread.php?tid=762&fromuid=9《机械设计》濮良贵第八版高等教育出版社课后答案_【khdaw_lxywyl】/bbs/viewthread.php?tid=9599&fromuid=9流体力学第二版上下册(张也影著) 高教版课后答案[khdaw]/bbs/viewthread.php?tid=7015&fromuid=9电工学第六版下电子技术(秦增煌著) 高等教育出版社课后答案/bbs/viewthread.php?tid=6191&fromuid=9电工学第六版(秦曾煌)上下册课件/bbs/viewthread.php?tid=5939&fromuid=9汽车标志大全/汽车驾驶图解教程/汽车构造图解说明【khdaw_cola】/bbs/viewthread.php?tid=1170&fromuid=9机械原理(七版)西工大课后答案/bbs/viewthread.php?tid=6003&fromuid=9汽车构造(刘玉梅高延龄著) 上海科学技术出版社课后答案/bbs/viewthread.php?tid=243&fromuid=9西北工大《机械原理》第六、七版(葛文杰,陈作模,著) 高等教育出版社完整答案【khdaw_cola】/bbs/viewthread.php?tid=7922&fromuid=9高分子化学、物理化工机械设计基础潘祖仁华幼卿课后答案全【khdaw_cola】/bbs/viewthread.php?tid=3980&fromuid=9几何量工差与检测第七版(课件和习题答案)【khdaw_cola】/bbs/viewthread.php?tid=532&fromuid=9机械原理同步辅导及习题全解西工大第七版孙恒陈作模葛文杰【khdaw】/bbs/viewthread.php?tid=6977&fromuid=9材料力学第4版刘鸿文课后答案【khdaw_cola】/bbs/viewthread.php?tid=6447&fromuid=9机械原理(第六版)答案,第七版适用(已上传)/bbs/viewthread.php?tid=6216&fromuid=9汽车构造(陈家瑞著) 机械工业出版社课后答案【khdaw_lxywy】/bbs/viewthread.php?tid=665&fromuid=9汽车构造(下)(第五版)陈家瑞机械工业出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=802&fromuid=9半导体物理学第7版刘恩科习题及答案【khdaw】/bbs/viewthread.php?tid=8740&fromuid=9机械工程英语第二版(叶邦彦陈统坚著) 机械工程出版社课文翻译【khdaw】/bbs/viewthread.php?tid=14459&fromuid=9机械制图答案/bbs/viewthread.php?tid=842&fromuid=9材料力学第三版(刘鸿文主编)课后答案【khdaw】/bbs/viewthread.php?tid=6252&fromuid=9模拟cmos集成电路设计毕查德·拉扎维(陈贵灿程军等译) 课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9777&fromuid=9《AutoCAD 2005 建筑设备线路设计》(胡仁喜)习题答案/bbs/viewthread.php?tid=248&fromuid=9材料科学基础复习题答案【khdaw】/bbs/viewthread.php?tid=5722&fromuid=9工程热力学(第三版)课后习题答案【khdaw】/bbs/viewthread.php?tid=5706&fromuid=9电工学第五版(上)秦曾煌高等教育出版社电子书/bbs/viewthread.php?tid=8706&fromuid=9工程热力学第三版沈维道高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=3220&fromuid=9机械设计第七版(5-8章)(濮良贵纪名刚著) 高等教育出版社课后答案/bbs/viewthread.php?tid=13555&fromuid=9材料力学第四版课件(刘鸿文著) 高等教育出版社课后答案/bbs/viewthread.php?tid=11243&fromuid=9高分子化学(第四版)潘祖仁化学工业出版社部分答案【khdaw_cola】/bbs/viewthread.php?tid=7234&fromuid=9工程力学静力学与材料力学(单辉祖谢传锋著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=16466&fromuid=9机械工程材料(哈尔滨工业大学)考试资料【khdaw_cola】/bbs/viewthread.php?tid=6592&fromuid=9工程力学(静力学与材料力学)(单辉祖谢传锋合著) 高等教育出版社课后答案【khdaw原创】/bbs/viewthread.php?tid=16614&fromuid=9测试技术(贾民平张洪亭著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=10863&fromuid=9工业工程专业英语翻译版王爱虎北京理工大学出版社部分章节/bbs/viewthread.php?tid=6582&fromuid=9工程材料及成型技术基础(吕广庶张元明著) 高等教育出版社课后答案/bbs/viewthread.php?tid=11017&fromuid=9液压与气压传动(姜继海宋锦春高常识著) 高等教育出版社参考习题及答案【khdaw】/bbs/viewthread.php?tid=13830&fromuid=9机械原理第七版(郑文纬吴克坚著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=14420&fromuid=9材料力学(1)第二版单辉祖高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=8311&fromuid=9微机原理部分作业与答案【khdaw_cola】/bbs/viewthread.php?tid=5711&fromuid=9材料力学1 第2版单辉祖高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=7596&fromuid=9江西工大的机械原理答案!!七版全有的/bbs/viewthread.php?tid=4051&fromuid=9金属热处理基础知识中南大学课后答案【khdaw_cola】/bbs/viewthread.php?tid=2140&fromuid=9液压传动第4版姜继海习题答案【khdaw_cola】/bbs/viewthread.php?tid=7554&fromuid=9机械工程测试技术基础(熊诗波黄长艺著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=14460&fromuid=9江西工大机械原理(第六版)课后答案【khdaw_cola】/bbs/viewthread.php?tid=4052&fromuid=9电工学(少学时)第三版张南主编高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=6477&fromuid=9汽车理论余志生机械工业出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=7696&fromuid=9机械设计基础2-11章王良才张文信黄阳北京大学出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=6973&fromuid=9自动控制理论第三版(翁贻方夏德钤著) 机械工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=13359&fromuid=9《机械工程控制基础:学习辅导与题解》熊良才华中科技大学出版社〖khdaw〗/bbs/viewthread.php?tid=7702&fromuid=9结构力学第二版(王焕定著) 高等教育出版社课后答案[khdaw]/bbs/viewthread.php?tid=7108&fromuid=9画法几何大连理工大学版/bbs/viewthread.php?tid=6661&fromuid=9c程序设计(第三版)程序版(谭浩强著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=17506&fromuid=9机械原理教材秦荣荣吉林大学高等教育出版课后答案【khdaw】/bbs/viewthread.php?tid=4417&fromuid=9液压传动与控制贾铭新第二版国防工业出版社部分习题解答【khdaw】/bbs/viewthread.php?tid=10075&fromuid=92007年造价师《造价案例分析》考试试题及答案【khdaw】/bbs/viewthread.php?tid=3537&fromuid=9机械原理第六版(陆品秦彦斌著) 高教版课后答案【khdaw_cola】/bbs/viewthread.php?tid=5707&fromuid=9常微分方程第三版部分(王高雄著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=17016&fromuid=9全国造价工程师职业资格考试试题及参考答案【khdaw】/bbs/viewthread.php?tid=3536&fromuid=9液压与气压传动技术张林人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9949&fromuid=9液压与气压传动(王守城容一鸣著) 北京出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=14621&fromuid=9机械控制工程基础(朱骥北著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=15501&fromuid=9机械设计第七版(11-15章)(西北工业大学机械原理及机械零件教研室濮良贵纪名刚著) 高等教育出版社课后答案【khdaw原创】/bbs/viewthread.php?tid=13566&fromuid=9几何量公差与检测(第7版)第4、7章(甘永立著) 上海科学技术出版社课后答案【khdaw原创】/bbs/viewthread.php?tid=13301&fromuid=9【真正】计算机网络第五版(谢希仁著) 电子工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=16443&fromuid=9工程材料与成形工艺基础苏德胜张丽敏化学工业出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=8084&fromuid=92007造价师《技术与计量(土建)》考试试题及答案【khdaw】/bbs/viewthread.php?tid=3534&fromuid=9机械工程基础第二版(张克猛赵玉成著) 西安交通大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=11010&fromuid=9机械原理复习精要与习题精解_【khdaw_lxywyl】/bbs/viewthread.php?tid=9566&fromuid=9汽车制造工艺学第四章(曾东建著)机械工业出版社课后答案【khdaw原创】/bbs/viewthread.php?tid=13380&fromuid=9流体输配管网第二版(付祥钊著) 中国建筑工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=14098&fromuid=9几何量公差与检测(第7版) 第2章(甘永立著) 上海科学技术出版社课后答案【khdaw原创】/bbs/viewthread.php?tid=13299&fromuid=9机械设计第七版(9-10章)(西北工业大学机械原理及机械零件教研室濮良贵纪名刚著) 高等教育出版社课后答案【khdaw原创】/bbs/viewthread.php?tid=13559&fromuid=9EDA技术实用教程第三版(潘松黄继业著) 科学出版社课后答案【khdaw】/bbs/viewthread.php?tid=16549&fromuid=9几何量公差与检测(第7版)第三章(甘永立著) 上海科学技术出版社课后答案【khdaw原创】/bbs/viewthread.php?tid=13300&fromuid=9大学课程《非开挖技术》复习题+答案【khdaw】/bbs/viewthread.php?tid=3531&fromuid=9高等数学(方明亮郭正光著) 广东科技出版社课后答案【khdaw】/bbs/viewthread.php?tid=17838&fromuid=9热处理工艺学中南大学(金属热处理)(试卷)【khdaw】/bbs/viewthread.php?tid=8459&fromuid=92007年造价师《工程造价计价与控制》试题及答案【khdaw】/bbs/viewthread.php?tid=3535&fromuid=92007造价答案【khdaw】/bbs/viewthread.php?tid=3529&fromuid=9(6140拨叉设计)机械制造及其工艺学课程设计赵家齐机械工业出版社【khdaw】/bbs/viewthread.php?tid=8505&fromuid=9材料科学基础(蔡珣戎咏华著) 上海交通大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=14163&fromuid=9材料力学II 第四版(孙训芳著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19236&fromuid=9数学物理方程第二版(谷超豪李大潜陈恕行郑颂穆谭永基著) 课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=18062&fromuid=9概率论与数理统计及其应用(详细版本)(盛骤谢式千著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=17480&fromuid=9《机械优化设计》孙靖民哈尔滨工业大学课后答案_【khdaw_lxywyl】/bbs/viewthread.php?tid=9600&fromuid=9计算机网络教程第五版(谢希仁著) 电子工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=16701&fromuid=9液压与气动技术马春峰人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9948&fromuid=9数学物理方法第三版(梁昆淼刘法缪国庆著) 高等教育出版社课后答案/bbs/viewthread.php?tid=16487&fromuid=9操作系统西电第三版(汤小丹梁红兵哲凤屏汤子瀛著) 西安电子科技大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=16725&fromuid=9《汽车理论》清华大学余志生主编第二版机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=9575&fromuid=9机械设计09年实训(二级直齿圆柱齿轮减速器)课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=16090&fromuid=9画法几何第三版习题集(缪临平著) 同济大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=17393&fromuid=9C++程序设计2008年版国家统编教材(刘振安著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=17670&fromuid=9VFP教程2008年版(严明单启成著) 苏州大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=17342&fromuid=9流体输配管网习题详解(重点)课后答案【khdaw】/bbs/viewthread.php?tid=16753&fromuid=9液压与气压传动第2版(1-4、6章)(王积伟章宏甲黄谊著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=20963&fromuid=9互换性与测量技术基础第3版(王伯平著) 机械工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=16050&fromuid=9微机原理及应用+期末复习题(含答案)(吴宁著) 电子工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=16569&fromuid=9机械制造工艺学第二版(王先逵著) 机械工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19530&fromuid=9软件工程第二版(张海蕃著) 人民邮电出版社课后答案【khdaw】/bbs/viewthread.php?tid=17633&fromuid=9冲压工艺与模具设计李大成人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9985&fromuid=93ds Max 9中文版基础教程詹翔王海英人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10007&fromuid=9计算方法复习与指导(不详著) 不详课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=16085&fromuid=9复变函数(第四版)(西安交大教研所著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=16697&fromuid=9汽车构造(6-11章)(鲁民巧著) 高等教育出版社课后答案【khdaw原创】/bbs/viewthread.php?tid=13297&fromuid=9极限配合与测量技术张林人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9999&fromuid=9《VB6.0程序设计教程第二版》(陈庆章,胡同森,罗朝盛等编著) 课后答案【khdaw】/bbs/viewthread.php?tid=17457&fromuid=9工程力学(范钦珊,王琪著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19402&fromuid=9土力学课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=16187&fromuid=9汽车构造(1-5章)(鲁民巧著) 高等教育出版社课后答案【khdaw原创】/bbs/viewthread.php?tid=13294&fromuid=9信息安全数学基础(陈恭亮著) 清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=16127&fromuid=9计算机体系结构量化研究方法第四版(John L.Hennessy 著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=17632&fromuid=9微型计算机原理与接口技术第4版(周荷琴吴秀清著) 中国科学技术大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=17756&fromuid=9中文AutoCAD 2005机械制图案例教程(刘璐著) 人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10594&fromuid=9汽车动力论课后答案【khdaw_cola】/bbs/viewthread.php?tid=6230&fromuid=980x96汇编语言程序设计(第二版) (王成耀著) 人民邮电出版社课后答案【khdaw】/bbs/viewthread.php?tid=17130&fromuid=9计算机组成原理(第二版)(石磊著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=16862&fromuid=9机械设计基础的几套题目以及参考答案【khdaw】/bbs/viewthread.php?tid=16917&fromuid=9组合数学西安电子科技大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=16883&fromuid=9机械制图与CAD技能训练曾令宜人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10048&fromuid=9《数控加工工艺设计与程序编制》周虹人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9762&fromuid=9集合论与图论(试题及答案著) 课后答案/bbs/viewthread.php?tid=16186&fromuid=9经济数学基础概率统计修订第四版(龚德恩著) 四川人民出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19034&fromuid=9机械制图第五版(钱可强著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=17588&fromuid=9机械设计作业集解题指南第三版(3-11章)(李育锡著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=20056&fromuid=9《模具制造技术》张信群人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9758&fromuid=9线性代数第二版(居余马著) 清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19403&fromuid=9AutoCAD 2006中文版建筑绘图基础教程(姜勇著) 化学工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10739&fromuid=9控制工程基础(王积伟吴振顺著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19033&fromuid=9复变函数及应用英文版第七版(布朗著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=17650&fromuid=9模具设计与制造(第2版) 李奇朱江峰人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9968&fromuid=9多媒体技术教程(林福宗著) 清华大学出版社练习与思考题参考答案【khdaw】/bbs/viewthread.php?tid=16822&fromuid=9VB程序设计(龚沛曾路慰民杨志强著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=17127&fromuid=9c++语言程序设计教程(吕凤翥著) 人民邮电出版社课后答案【khdaw】/bbs/viewthread.php?tid=17140&fromuid=9数字图像处理英文版各章要求+课后答案【khdaw】/bbs/viewthread.php?tid=17073&fromuid=9AutoCAD 2008中文版实例教程黄中友人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9908&fromuid=9近世代数(杨子胥著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=16775&fromuid=9液压技术与应用邱国庆人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9947&fromuid=9AutoCAD 2008机械绘图(林党养著) 人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10782&fromuid=9机械原理第二版(刘会英杨志强张明勤著) 机械工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19965&fromuid=9数学分析习题课教材(方企勤林源渠著) 北京大学课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=18158&fromuid=9AutoCAD2006中文版建筑绘图案例教程(马永志著) 课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9541&fromuid=9机械加工工艺与装备赵宏立人民邮电出版社课后答案【khdaw】/bbs/viewthread.php?tid=9810&fromuid=9《模具制造技术》张信群王雁彬人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9757&fromuid=9计算机系统结构(第三版)(部分)(张晨曦著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=20976&fromuid=9金属工艺学第五版(邓英文郭晓鹏著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=20489&fromuid=9电工电子技术(高蒙著) 中国铁道出版社课后答案【khdaw】/bbs/viewthread.php?tid=17450&fromuid=9计算机网络技术基础(尤峥徐楠刘辙著) 武汉大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=17447&fromuid=9计算机组成原理实用教程(王万生著) 清华大学出版社课后答案/bbs/viewthread.php?tid=18204&fromuid=9C++ primer 中文版(第四版)(Stanley B.Lippman 著) 人民邮电出版社课后答案【khdaw】/bbs/viewthread.php?tid=16771&fromuid=9Visual Basic程序设计教程(吴文斗周兵吴兴勇著) 湖南教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=17276&fromuid=9计算机科学概论第九版(J Glenn Brookshear 著) 人民邮电出版社课后答案【khdaw】/bbs/viewthread.php?tid=17830&fromuid=93ds Max 9中文版室内效果图制作实例教程黄喜云人民邮电课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9907&fromuid=9C#网络应用编程基础(马骏著) 人民邮电出版社课后答案/bbs/viewthread.php?tid=16892&fromuid=9数据结构实用教程(第二版) (徐孝凯著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=19612&fromuid=9机械加工方法与设备牛荣华人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9827&fromuid=9AutoCAD计算机辅助设计王茹雷光明人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9864&fromuid=9材料力学(范钦珊. 著) 人民出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19261&fromuid=9AutoCAD 2008中文版室内设计实例教程杨斌人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9903&fromuid=9机械设备维修技术吴先文人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9998&fromuid=9计算机组织与体系结构(第四版)(白中英戴志涛李贞著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=18899&fromuid=9操作系统操作精髓与设计原理第五版(William S talling 著) 电子工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19475&fromuid=9矩阵论(方保镕,周继东,李医民编著著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=18587&fromuid=9概率论与数理统计(龙永红著) 课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=20618&fromuid=9《智能楼宇技术》王用伦人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9951&fromuid=9实变函数论第二版(江泽坚吴智泉著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19158&fromuid=9机械精度设计基础及应用(俞立钧徐解民著) 上海大学出版社部分课后答案【khdaw】/bbs/viewthread.php?tid=17069&fromuid=9数据库系统原理及应用教程第三版(苗雪兰刘瑞新著) 机械工程出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=20843&fromuid=9概率论与数理统计(余长安著) 武汉大学课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=18233&fromuid=9模拟库管员岗位实训李洛嘉高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9747&fromuid=9密码编码学与网络安全:原理与实践+第四版习题解答(WILLIAM ST ALLINGS 著) 电子工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=20739&fromuid=9数学分析第三版上下册(欧阳光中朱学炎金福临陈传璋著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19330&fromuid=9机械工程设计(Mechanical Engineering Design)英文版原书第六版(Joseph E. Shigley; CharlesR. M/bbs/viewthread.php?tid=16485&fromuid=9数据与计算机通信第六版(中文版)(【美】William S tallings 著) 电子工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=16716&fromuid=9信号与系统(应自炉著) 国防工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19336&fromuid=9线性代数第二版(刘剑平施劲松著) 华东理工出版社课后答案【khdaw】/bbs/viewthread.php?tid=19424&fromuid=9画法几何与工程制图试卷(孙恒著) 机械工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19048&fromuid=9线性代数及其应用第三版(David C. Lay 著) 机械工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=18962&fromuid=9C++面向对象程序设计简明教程课后答案(康丽著) 中国电力出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19037&fromuid=9复变函数与积分变换第二版(李红谢松法著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=20115&fromuid=9计算机硬件技术基础第5章(韦大伟韩继红张杰张鲁国杨丽娜著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=16915&fromuid=9数值线性代数(徐树方,高立,张平文著) 北京大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=19533&fromuid=9微机原理与接口技术习题与答案(雷丽文著) 电子工业出版社【khdaw】/bbs/viewthread.php?tid=20345&fromuid=9数据结构(c++版)(王红梅胡明著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=19657&fromuid=9数学分析第二版全册(陈传璋著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=20859&fromuid=9c语言程序设计教程第2版(杨路明著) 北京邮电大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=20074&fromuid=9机械工程材料(王运炎著) 机械工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=20491&fromuid=9计算机操作系统教程(马海波王德广著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=20710&fromuid=9大学工程制图(钱自强林大均著) 华东理工大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=19425&fromuid=9应用近世代数第三版(部分)(胡冠章著) 清华大学出版社课后答案/习题解答【khdaw】/bbs/viewthread.php?tid=20065&fromuid=9高等数学第二版下册(11、12章)(童裕孙金路著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=20390&fromuid=9C语言程序设计第二版(丁亚涛著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19355&fromuid=9结构考研试题汇集(龙驭球著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=18287&fromuid=9信号与线性系统第二版(阎鸿森著) 西安交通大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19664&fromuid=9MATLAB数学实验答案(胡良剑著) 高等教育出版【khdaw】/bbs/viewthread.php?tid=20969&fromuid=9信号与信息处理基础第4章(彭军李宏著) 中国铁道出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19809&fromuid=9编译程序设计原理第二版(金成植金英著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=20797&fromuid=9机械原理(黄师予邹慧君著) 同济大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19646&fromuid=9概率论与数理统计习题册及参考答案(温广玉徐文科钟莉娜著) 哈工大版东北林业大学版【khdaw】/bbs/viewthread.php?tid=20058&fromuid=9数字逻辑第二版(毛法尧著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=20055&fromuid=9数据库系统概念第五版(杨冬青著) 机械工业出版社课后答案【khdaw】机械振动基础1-3章(胡海岩著) 北京航空航天大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19627&fromuid=9数据库系统教程第2版(施伯乐丁宝康汪卫著) 高等教育出版社参考答案及课件【khdaw】/bbs/viewthread.php?tid=20856&fromuid=9机械原理(4-13章)(谢进万朝燕等著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=20411&fromuid=9几何与代数导引(3-6章)(胡国权著) 科学出版社课后答案【khdaw】/bbs/viewthread.php?tid=21109&fromuid=9Power Builder (不详著) 不详课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=18687&fromuid=9信息论与编码技术(冯桂林其伟陈东华著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=19629&fromuid=9高等数学第六版(同济大学数学系著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=21247&fromuid=9微机原理与接口技术(基于32位机)(马春燕著) 电子工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19776&fromuid=9C语言程序设计学习指导实验指导与课程设计(盛夕清赵阳林科学徐大华著) 中国水利水电出版社课后答案【khdaw】/bbs/viewthread.php?tid=19543&fromuid=9数据结构教程第三版上机实验指导(李春葆尹为民李蓉蓉蒋晶珏喻丹丹安杨著) 清华大学出版社课后答案/bbs/viewthread.php?tid=21077&fromuid=9C语言程序设计基础(鲍广华著) 安徽大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19661&fromuid=9测量学(陈丽华著) 浙江大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=20213&fromuid=9点集拓补讲义第二版(熊金城著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19631&fromuid=9数据库原理编程与性能高等教育出版社课后答案【khdaw_lxywyl】。
数值线性代数第二版徐树方高立张平文上机习题第一章实验报告

@上机习题1.先用你所熟悉的的计算机语言将不选主元和列主元Gauss 消去法编写成通用的子程序;然后用你编写的程序求解84阶方程组;最后将你的计算结果与方程的精确解进行比较,并就此谈谈你对Gauss 消去法的看法。
Sol :(1)先用matlab 将不选主元和列主元Gauss 消去法编写成通用的子程序,得到P U L ,,: 不选主元Gauss 消去法:[])(,A GaussLA U L =得到U L ,满足LU A = 列主元Gauss 消去法:[])(,,A GaussCol P U L =得到P U L ,,满足LU PA = (2)用前代法解()Pb or b Ly =,得y用回代法解y Ux =,得x]求解程序为()P U L b A Gauss x ,,,,=(P 可缺省,缺省时默认为单位矩阵)(3)计算脚本为ex1_1 代码%算法(计算三角分解:Gauss 消去法) function [L,U]=GaussLA(A) n=length(A);—for k=1:n-1A(k+1:n,k)=A(k+1:n,k)/A(k,k);A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); endU=triu(A);L=tril(A);L=L-diag(diag(L))+diag(ones(1,n));end!%算法计算列主元三角分解:列主元Gauss消去法)function [L,U,P]=GaussCol(A)n=length(A);for k=1:n-1[s,t]=max(abs(A(k:n,k)));p=t+k-1;temp=A(k,1:n);¥A(k,1:n)=A(p,1:n);A(p,1:n)=temp;u(k)=p;if A(k,k)~=0A(k+1:n,k)=A(k+1:n,k)/A(k,k);A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); elsebreak;^endendL=tril(A);U=triu(A);L=L-diag(diag(L))+diag(ones(1,n)); P=eye(n);for i=1:n-1temp=P(i,:);P(i,:)=P(u(i),:);{P(u(i),:)=temp;endend%高斯消去法解线性方程组function x=Gauss(A,b,L,U,P)if nargin<5P=eye(length(A));¥endn=length(A);b=P*b;for j=1:n-1b(j)=b(j)/L(j,j);b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j);endb(n)=b(n)/L(n,n);<y=b;for j=n:-1:2y(j)=y(j)/U(j,j);y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);endy(1)=y(1)/U(1,1);x=y;|endex1_1clc;clear;%第一题A=6*eye(84)+diag(8*ones(1,83),-1)+diag(ones(1,83),1); b=[7;15*ones(82,1);14];%不选主元Gauss消去法)[L,U]=GaussLA(A);x1_1=Gauss(A,b,L,U);%列主元Gauss消去法[L,U,P]=GaussCol(A);x1_2=Gauss(A,b,L,U,P);%解的比较subplot(1,3,1);plot(1:84,x1_1,'o-');title('Gauss'); subplot(1,3,2);plot(1:84,x1_2,'.-');title('PGauss');(subplot(1,3,3);plot(1:84,ones(1,84),'*-');title('精确解');结果为(其中Gauss 表示不选主元的Gauss 消去法,PGauss 表示列主元Gauss消去法,精确解为[]'⨯8411,,1 ):8Gauss50100PGauss精确解由图,显然列主元消去法与精确解更为接近,不选主元的Gauss 消去法误差比列主元消去法大,且不如列主元消去法稳定。
数值线性代数第二版徐树方高立张平文上机习题第二章实验报告

(1)估计5到20阶Hilbert 矩阵的∞范数条件数(2)设n n R A ⨯∈⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=111111111011001ΛΛO O MM M O OΛ,先随机地选取n R x ∈,并计算出x A b n =;然后再用列主元Gauss 消去法求解该方程组,假定计算解为∧x 。
试对n 从5到30估计计算解∧x 的精度,并且与真实相对误差作比较。
解(1)分析:利用for 使n 从5循环到20,利用()hilb 函数得到Hilbert 矩阵A ;先将算法2、5、1编制成通用的子程序,利用算法2、5、1编成的子程序)(B opt v =,对TAB -=求解,得到∞-1A的一个估计值v v =~;再利用inf),(A norm 得到∞A ;则条件数inf),(1A norm v A A K *==∞∞-。
另,矩阵A 的∞范数条件数可由inf),(A cond 直接算出,两者可进行比较。
程序为1 算法2、5、1编成的子程序)(B opt v =function v=opt(B)k=1;n=length(B); x=1、/n*ones(n,1);while k==1 w=B*x;v=sign(w); z=B'*v;if norm(z,inf)<=z'*x v=norm(w,1); k=0; elsex=zeros(n,1);[s,t]=max(abs(z)); x(t)=1; k=1; end end end2 问题(1)求解 ex2_1for n=5:20A=hilb(n);B=inv(A、');v=opt(B);K1=v*norm(A,inf);K2=cond(A,inf);disp(['n=',num2str(n)])disp(['估计条件数为',num2str(K1)])disp(['实际条件数为',num2str(K2)])end计算结果为n=5估计条件数为943656实际条件数为943656n=6估计条件数为29070279、0028实际条件数为29070279、0028n=7估计条件数为985194887、5079实际条件数为985194887、5079n=8估计条件数为33872789099、7717实际条件数为33872789099、7717n=9估计条件数为16、422实际条件数为16、422n=10估计条件数为35353368771750、67实际条件数为35353368771750、67n=11估计条件数为1232433965549344实际条件数为1232433965549344Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、547634e-17、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、547634e-17、> In cond at 47In ex2_1 at 6n=12估计条件数为3、9245e+16实际条件数为3、9245e+16Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 7、847381e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 7、847381e-19、> In cond at 47In ex2_1 at 6n=13估计条件数为1、2727e+18实际条件数为1、2727e+18Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、246123e-18、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、246123e-18、> In cond at 47In ex2_1 at 6n=14估计条件数为4、8374e+17实际条件数为4、8374e+17Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 8、491876e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 8、491876e-19、> In cond at 47In ex2_1 at 6n=15估计条件数为4、6331e+17实际条件数为5、234289848563619e+17Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 9、137489e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 9、137489e-19、> In cond at 47In ex2_1 at 6n=16估计条件数为8、3166e+17实际条件数为8、3167e+17Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 6、244518e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 6、244518e-19、 > In cond at 47 In ex2_1 at 6 n=17估计条件数为1、43e+18 实际条件数为1、43e+18Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、693737e-19、 > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、693737e-19、 > In cond at 47 In ex2_1 at 6 n=18估计条件数为2、5551e+18 实际条件数为2、8893e+18Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、264685e-19、 > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、264685e-19、 > In cond at 47 In ex2_1 at 6 n=19估计条件数为2、411858563109357e+18 实际条件数为2、411858563109357e+18Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 1、351364e-19、 > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 1、351364e-19、 > In cond at 47 In ex2_1 at 6 n=20估计条件数为2、31633670586674e+18 实际条件数为6、37335273308473e+18结果分析随着矩阵阶数增加,估计值误差开始出现,20,17,16,15 n 时估计条件数与实际值存在误差;且条件数很大,Hilbert 矩阵为病态的。
段正敏主编《线性代数》习题解答

线性代数习题解答1张应应胡佩2013-3-1目录第一章行列式 (1)第二章矩阵 (22)第三章向量组的线性相关性 (50)第四章线性方程组 (69)第五章矩阵的相似对角化 (91)第六章二次型 (114)附录:习题参考答案 (129)1教材:段正敏,颜军,阴文革:《线性代数》,高等教育出版社,2010。
第一章 行列式1.填空题:(1)3421的逆序数为 5 ;解:该排列的逆序数为00235t =+++=. (2)517924的逆序数为 7 ;解:该排列的逆序数为0100337t =+++++=. (3)设有行列式2311187001234564021103152----=D =)(ij a ∆, 含因子543112a a a 的项为 -1440,0 ; 解:(23154)31223314554(1)(1)526831440t a a a a a -=-⋅⋅⋅⋅⋅=-(24153)41224314553(1)(1)506810t a a a a a -=-⋅⋅⋅⋅⋅=所以含因子543112a a a 的项为-1440和0.(4)若n 阶行列式=-∆==∆=)(,)(ij ij n a D a a D 则()1na-;解:Q 行列式中每一行可提出一个公因子,()()()1()1n nij ij D a a a ∴=∆-=-∆=-.(5)设328814412211111)(x x x x f --=,则0)(=x f 的根为 1,2,-2 ;解:是一个Vandermonde 行列式,()(1)(2)(2)(21)(22)(21)0f x x x x ∴=--+-----=的根为1,2,-2.(6)设321,,x x x 是方程03=++q px x 的三个根,则行列式=132213321x x x x x x x x x 0 ; 解:根据条件有332123123123()()()()x px q x x x x x x x x x x x ax x x x ++=---=-+++-比较系数可得:1230x x x ++=,123x x x q =-再根据条件得:311322333x px q x px q x px q⎧=--⎪=--⎨⎪=--⎩原行列式333123123123=3()33()0x x x x x x p x x x q q ++-=-++--⋅-=.(7)设有行列式10132x x x-=0,则x = 1,2 ; 解:2231032(1)(2)001xx x x x x x -=-+=--= 1,2x ∴=.(8)设=)(x f 444342343331242221131211a a a xa a x a a x a a x a a a ,则多项式中的系数为 0 ;解:按第一列展开11112121313141()f x a A a A a A xA =+++,Q 112131,,A A A 中最多只含有项,∴含有的项只可能是()()12134141222433343123413242233132234122433(1)a a x xA x a x a xa a x x a a a a a a x a a a a a a +=-⎡⎤ =-++-++⎣⎦Q 不含项,∴中的系数为0.(9)如果330020034564321x=0,则x = 2 ;解:12346543122(512)(63)000265330033xx x =⋅=--=2x ∴=.(10)00000000000dc b a = -abcd ;解:将行列式按第一行展开:1400000000(1)0000000000a b b a c abcd c dd+=⋅-=-. (11)如果121013c b a =1,则111425333---c b a = 1 ; 解:1323323133301302524121111111Tr r AA r r a a b c a b c b c -=+---=. (12)如333231232221131211a a a a a a a a a =2,则333232312322222113121211222222222222a a a a a a a a a a a a ---= -16 , 332313231332221222123121112111323232a a a a a a a a a a a a a a a ------= -4 ,3212000332313322212312111a a a a a a a a a = -4 ;解:1112131121312122231231222321233132331323332T a a a a a a A a a a A a a a a a a a a a αααβββ======()()1112121332122222312231223313232331221232222222222222222288016a a a a a a a a a a a a A αααααααααααααα--=-=-- =+-=-=-()1121112131122212223212123121231323132333122311232323232323232a a a a a a a a a a a a a a a ββββββββββββββββββ----=--=---- =-+-- =()1223122123224T A ββββββββββ-=- =-=-11213114122232132333000212423T a a a A a a a a a a + ⋅=-按第一行展开(-1).(13)设n 阶行列式=,且中的每列的元素之和为b ,则行列式中的第二行的代数余子式之和为=a b;解:11121111211112121222121212111=n n n n n n nn n n nn n n nna a a a a a a a a a a ab b b b a a a a a a a a a L L L L L LM M M M M M M M M L L L每行元素加到第二行 ()212220n b A A A a+++=≠L 按第二行展开∴212220,0n b A A A ≠+++≠L 且21222n aA A A b∴+++=L 实际上,由上述证明过程可知任意行代数余子式之和12,1,2,,i i in aA A A i n b+++==L K . (14)如果44434234333224232214131211000a a a a a a a a a a a a a =1,则24231211444342343332242322000a a a a a a a a a a a a a = -1 , 443424433323423222a a a a a a a a a =111a ;解:令222324323334424344a a a B a a a a a a =,则111213142223241111113233341142434401(1)10,000a a a a a a a a B a B a a a a a a a +=⋅-= ⇒ ≠=≠且 2223243233344111114243441112232400(1)10a a a a a a a B a B a a a a a a a +=⋅-=-=- 223242233343112434441T a a a a a a B B a a a a ===.(15)设有行列式101321x x -,则元素的余子式2的代数余子式(16)设3214214314324321=D =)(ij a ∆,ij ij a A 表示元素的代数余子式,则=+++44342414432A A A A 0 ;解:方法一:14243444234A A A A +++可看成中第一列各元素与第四列对应元素代数余子式乘积之和,故其值为0.方法二:11424344412312342234034134124A A A A +++=推论.(17)设cdb a ac bd a d b c d c b a D ==)(ij a ∆,ij ij a A 表示元素的代数余子式,则=+++44342414A A A A 0 ;解:1424344411011a bc c bd A A A A d b c a b d +++=推论4.(18)设6000000000000002000230023402345)(x x x x x x f --=,则的系数为 6 ;解:方法一:5425525432543243200432032000()66(1)(1)63200200002000000000006x x x x x f x x x x x x xx⨯--===⋅-⋅-⋅=--方法二:Q 只有一项非0()()54321615243342516610255543204320032000()12000000000006(1)(1)66t x x x f x a a a a a a x x x x -∴==-- =-⋅-⋅⋅=综上所述:的系数为6.(19)设1112121222121112111121212222122212120m m m m mm n m n m n n nnn n nma a a a a a a a a Db b bc c c b b b c c c b b b c c c =KK M M L M K K KK K MM LM MM LM KK, 且111212122212m mm m mma a a a a a a a a a =KK M M L M K111212122212n n n n nnb b b b b b b b b b =K K M M L M K,则=()1mnab - ; 解:方法一:令111212122212m m m m mm a a a a a a A a a a a ==L LM M M L,111212122212nnn n nnb b b b b b B b b b b ==L LM M M L则1A O D A B ab CB==⋅=,()()211mnmnO AD A B ab B C==-⋅=-证明:根据行列式性质2和5,将行列式变成下三角行列式,得到:11112121222212121212mm m m m mmm m ma a a a a a a a a A a a a a a a a a a a '====''LL L M MM M M O LL行列式、的变换和行列式的变换完全相同,得到:1212121111211112121222212221212m m m m n m n n n nm n n nna a a a a a D c c cb b bc c c b b b c c c b b b '''='''''''''M M O L L LL L M M M M M M LL1212122111211112121222212221212m m m nm n m n n nnn n nm a a a a a a D b b b c c c b b b c c c b b b c c c '''='''''''''MM O L LL L L M M M M M M LL分别将、第一次按第一行展开(变成第一行),第二次按第二行展开(变成第一行),……,总共进行m 次第一行展开,得到:112m D a a a B A B ab ==⋅=L ;()()()()()11111121211111n n n mn mnm D a a a B A B ab ++++++=-⋅--⋅=-⋅⋅=-L证毕.方法二:设()ij m m A a ⨯=,()pq n n B b ⨯=,()()()ij m n m n A O D d C B +⨯+⎛⎫== ⎪⎝⎭其中:(), 1:,1:, 1:,1:,, , 1:,1:, ij ij pq pja i m j m db i m m n j m m n p i m q j mc i m m n j m p i m ==⎧⎪==++=++=-=-*⎨⎪=++==-⎩那么:()(){}{}1111111,,,,1,,1m m m n m m m n m n t p p p pp mp m p m n p p p m n A O D d d d d C B +++++++=+==-∑L L L L L L ()()()()(){}{}{}{}()()()(){}{}{}{}()(){}{}()(){}11111111111111111111,,1,,,,1,,11,,1,,,,1,,11,,1,,,,11111m n m nm m n n m nmm n n m n m m t p p m l m l p mp l nl p p m l l n t p p t l l p mp l nl p p m l l n t p p t l l p mp l nl p p m l l a a b b a a b b a a b b *++=====-⎡⎤=-⋅-⎣⎦⎛⎫=-⋅- ⎪ ⎪⎝⎭∑∑∑L L L L L L L L L L L L L L L L L L L L L L L 由{}1,,n A B ab=⎛⎫ ⎪ ⎪⎝⎭=⋅=∑L1112121222122111211112121222212221212m m m m mmn m n m n n nn n n nma a a a a a a a a Db b bc c c b b b c c c b b b c c c =L L M M M L L L L L M M M M M M LL中依次与12,,,n b b b g g g L 对换,使得在下面;()1m a - g 依次与12,,,n b b b g g g L 对换,使得()1m a - g 在下面,在上面;……依次与12,,,n b b b g g g L 对换,使得在下面,在上面; 总共进行了mn 次对换。
线性代数 高教第二版 卢刚 第一章 课后答案

7
第一章《线性代数》习题解答
10 2 3 4
10 2 3 4
(6)原
第2,3,4行都加到第1行
10
3
4
1 0 第2,3,4行都减去第1行
10 4 1 2
0
1 1 -3 2 -2 -2
10 1 2 3
0 -1 -1 -1
1 1 3 10 2 2 2 160.
按第1列展开
14. A2 A [1 (B I )]2 1 (B I ) 1 (B 2 2BI I 2 ) 1 (B I )
2
2
4
2
(B 2 2B I ) 2(B I ) B 2 I.
n
n
n
15.(1) tr( A B) (aii bii ) aii bii tr( A) tr(B) .
第2列减去第1列 28092 1000
28092 1
5 -1 3 5 -1 3
第2行的( 98) 倍加到第3行
按第1行展开
(4) 原
2 2 2=2 1 1 1 = 8 .
0 73 0 73
(5)利用 P22 例 6 的结论.原 [5 (4 1) 1](5 1)3 512 .
第 7 页 共 20 页
0 1 0 0
0 0 1 0
0 0 0 1
(4)(直接计算即可)令
A
0 0 0
0 0 0
1 0 0
0 10
,则
A2
0
0 0
0 0 0
0 0 0
1
0 0
,
A3
0
0 0
0 0 0
0 0 0
0
0 0
,
0 0 0 0
数值线性代数大作业报告

数值线性代数实验大报告指导老师:赵国忠姓名:1108300001 刘帅1108300004 王敏1108300032 郭蒙一、实验名称:16题P75上机习题二、实验目的:编制通用的子程序,完成习题的计算任务三、实验内容与要求:P75上机习题先用熟悉的计算机语言将算法2.5.1编制成通用的子程序,然后再用所编制的子程序完成下面两个计算任务:(1) 估计5到20阶Hilbert 矩阵的无穷范数条件数。
(2) 设A n = 11...111................1-1 (01)-- 先随机地选取x ∈R n ,并计算出b=An x;然后再用列主元Gauss 消去法求解该方程组,假定计算解为∧x .试对n 从5到30估计计算解∧x 的精度,并且与真实的相对误差作比较。
四、 实验原理:(1)矩阵范数(martix norm )是数学上向量范数对矩阵的一个自然推广。
利用for循环和cond (a )Hilbert 求解Hilbert 矩阵的无穷范数,再利用norm(a,inf)求矩阵的无穷范数条件数。
(2)本题分为4步来求解。
先运用rand 随机选取x ∈R n,输入A n 矩阵,编制一个M 文件计算出b 。
第二步用列主元高斯消去法求解出方程的解X2。
第三步建立M 文件: soluerr.m 估计计算解∧x 的精度。
第四步, 建立M 文件: bijiao.m ,与真实相对误差作比较。
五、 实验过程:(1)程序:clearfor n=5:20for i=1:nfor j=1:na(i,j)=1/(i+j-1);endendc=cond(a);f=norm(c,inf);fprintf('n=%3.0f\nnorm(c,inf)%e\n',n,f) end运行结果:n= 5norm(c,inf)4.766073e+005n= 6norm(c,inf)1.495106e+007n= 7norm(c,inf)4.753674e+008n= 8norm(c,inf)1.525758e+010n= 9norm(c,inf)4.931542e+011n= 10norm(c,inf)1.602467e+013n= 11norm(c,inf)5.224376e+014n= 12norm(c,inf)1.698855e+016n= 13norm(c,inf)3.459404e+017n= 14norm(c,inf)4.696757e+017n= 15norm(c,inf)2.569881e+017n= 16norm(c,inf)7.356249e+017n= 17norm(c,inf)4.362844e+017n= 18norm(c,inf)1.229633e+018n= 19norm(c,inf)9.759023e+017n= 20norm(c,inf)1.644051e+018(2)程序:M文件:matrix1.mfunction [a,b,x1]=matrix1(n) format longA1=-1*ones(n,n)A2=tril(A1)for i=1:nA2(i,i)=1endA2(:,n)=1a=A2x1=rand(n,1)b=A2*x1end运行结果:>> A1 =-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1A2 =-1 0 0 0 0 -1 -1 0 0 0 -1 -1 -1 0 0 -1 -1 -1 -1 0 -1 -1 -1 -1 -1A2 =1 0 0 0 0 -1 -1 0 0 0 -1 -1 -1 0 0 -1 -1 -1 -1 0 -1 -1 -1 -1 -1A2 =1 0 0 0 0-1 -1 -1 0 0 -1 -1 -1 -1 0 -1 -1 -1 -1 -1A2 =1 0 0 0 0 -1 1 0 0 0 -1 -1 1 0 0 -1 -1 -1 -1 0 -1 -1 -1 -1 -1A2 =1 0 0 0 0 -1 1 0 0 0 -1 -1 1 0 0 -1 -1 -1 1 0 -1 -1 -1 -1 -1A2 =1 0 0 0 0 -1 1 0 0 0 -1 -1 1 0 0 -1 -1 -1 1 0 -1 -1 -1 -1 1A2 =1 0 0 0 1 -1 1 0 0 1 -1 -1 1 0 1 -1 -1 -1 1 1 -1 -1 -1 -1 1a =-1 1 0 0 1 -1 -1 1 0 1 -1 -1 -1 1 1 -1 -1 -1 -1 1x1 =0.8147236863931790.9057919370756190.1269868162935060.9133758561390190.632359246225410b =1.4470829326185890.723427496907850-0.961169560949882-0.301767337397875-2.128519049675914a =1 0 0 0 1 -1 1 0 0 1 -1 -1 1 0 1 -1 -1 -1 1 1 -1 -1 -1 -1 1b =1.4470829326185890.723427496907850-0.961169560949882-0.301767337397875-2.128519049675914x1 =0.8147236863931790.9057919370756190.1269868162935060.9133758561390190.632359246225410M文件:LZYgauss.mfunction[x2]=LZYgauss(a,b)format longn=length(a);x2=zeros(n,1);a=[a b];for k=1:n-1max=k;for i=k+1:nif a(i,k)>a(max,k)max=i;endendtemp=a(k,k:n+1);a(k,k:n+1)=a(max,k:n+1);a(max,k:n+1)=temp;for i=k+1:na(i,k)=-a(i,k)/a(k,k);a(i,k+1:n+1)=a(i,k+1:n+1)+a(i,k)*a(k,k+1:n+1);endendx2(n,1)=a(n,n+1)/a(n,n);for i=n-1:-1:1sum=0;for j=i+1:nsum=sum+x2(j,1)*a(i,j);endx2(i,1)=(a(i,n+1)-sum)/a(i,i);end运行结果:>> LZYgauss(a,b)ans =0.8147236863931790.9057919370756190.1269868162935060.913375856139020 0.632359246225410估计计算解x的精度:M文件: soluerr.mfunction [x,error]=soluerr(a,b)format long%估计计算解的精度% 算法:列主元Gauss消去法,其中% A --- 系数矩阵% b-右端项% index --- index=0表示计算成败;index=1表示计算成功%输出结果:error--本算法给出的计算解的估计% normA--逆矩阵无穷范数估计% rnorm--计算解的残量[n,m]=size(a); nb=length(b);if n~=merror('The rows and columns of matrix a must be equal!');return;endif m~=nberror('The columns of a must be equal the dimension of b!'); return;endindex=1;%列主元矩阵三角分解[L,U,u,index_col]=Gauss_col(a);%解下三角方程组Ly=Pb[y,index_low]=Gauss_low(L,b(u));%解上三角方程组Ux=y[x,index_upp]=Gauss_upp(U,y);%输出数值解xpause(0.3)%估计矩阵逆的无穷大范数normA=normAinv(L,U,u);%估计计算解的残量rnorm=norm(b-a*x,inf);%计算右端项bnorm=norm(b,inf);%计算矩阵A的范数Anorm=norm(a,inf);%计算解的精度error=normA*Anorm*rnorm/bnorm;运行结果:>> [x,error]=soluerr(a,b)x =0.8147236863931790.9057919370756190.1269868162935060.9133758561390200.632359246225410x =0.8147236863931790.9057919370756190.1269868162935060.9133758561390200.632359246225410error =5.215941218821592e-016X1与真实相对误差做比较M文件:bijiao.mfunction [x,x1,error,error1]=bijiao(a,b,n) [a,x1]=matrix1(n)[x,error]=soluerr(a,b)error1=abs((x-x1)/x1)运行结果:>>x =0.8147236863931790.9057919370756190.1269868162935060.9133758561390200.632359246225410x1 =0.9578935505663481.6132601689718680.629241553693582-0.799716694069468-1.770467991515150error =5.215941218821592e-016error1 =Columns 1 through 40 0 0 00 0 0 00 0 0 00 0 0 00 0 0 0Column 50.0808655478999350.3995939126190040.2836847318376260.9675930648949141.357170674226221六、结果分析:1、矩阵范数(martix norm)是数学上向量范数对矩阵的一个自然推广。
数值线性代数实验

数值线性代数实验题目:数值线性代数专业:信息与计算科学班级:班姓名:山东科技大学2013年 1 月16日实验报告说明学院:信息学院专业:信息班级10-2 姓名:一、主要参考资料:(1)《Matlab数值计算-案例分析》北京航空出版(2)《Matlab数值分析》机械工业出版二、课程设计应解决的主要问题:(1)平方根(2)QR方法(3)最小二乘法三、应用软件:(1)Matlab7.0(2)数学公式编辑器四、发出日期:课程设计完成日期:指导教师签字:系主任签字:指导教师对课程设计的评语指导教师签字:年月日一、问题描述先用你所熟悉的计算机语言将平方根和改进的平方根法编成写通用的子程序,然后用你编写的程序求解对称正定方程组b x =A ,其中 (1)b 随机的选取,系数矩阵位100阶矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1011101110111011101110(2)系数矩阵为40阶Hilbert 矩阵,即系数矩阵A 的第i 行第j 列元素为11-+=j i a ij ,向量b 的第i 个分量为∑=-+=nj i j i b 111。
二、分析与程序1. 平方根法函数程序如下:function [x,b]=pingfanggenfa(A,b) n=size(A); n=n(1);x=A^-1*b; disp('Matlab 自带解即为x'); for k=1:nA(k,k)=sqrt(A(k,k));A(k+1:n,k)=A(k+1:n,k)/A(k,k); for j=k+1:n;A(j:n,j)=A(j:n,j)-A(j:n,k)*A(j,k); endend for j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j);endb(n)=b(n)/A(n,n);A=A';for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1);disp('平方根法的解即为b');endfunction [x]=ave(A,b,n)求解Ax=bL=zeros(n,n);D=diag(n,0);S=L*D;for i=1:n %L的主对角元素均为1L(i,i)=1;endfor i=1:nfor j=1:nif (eig(A)<=0)|(A(i,j)~=A(j,i))disp('wrong');break;endendendD(1,1)=A(1,1);for i=2:nfor j=1:i-1S(i,j)=A(i,j)-sum(S(i,1:j-1)*L(j,1:j-1)');L(i,1:i-1)=S(i,1:i-1)/D(1:i-1,1:i-1);endD(i,i)=A(i,i)-sum(S(i,1:i-1)*L(i,1:i-1)');endy=zeros(n,1);x=zeros(n,1);for i=1:ny(i)=(b(i)-sum(L(i,1:i-1)*D(1:i-1,1:i-1)*y(1:i-1)))/D(i,i); endfor i=n:-1:1x(i)=y(i)-sum(L(i+1:n,i)'*x(i+1:n));end2.改进平方根法函数程序如下:function b=gaijinpinfanggenfa(A,b)n=size(A);n=n(1);v=zeros(n,1);for j=1:nfor i=1:j-1v(i)=A(j,i)*A(i,i);endA(j,j)=A(j,j)-A(j,1:j-1)*v(1:j-1);A(j+1:n,j)=(A(j+1:n,j)-A(j+1:n,1:j-1)*v(1:j-1))/A(j,j);end %LDL'分解B=diag(A);D=zeros(n);for i=1:nD(i,i)=B(i);A(i,i)=1;EndA=tril(A);for j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j); endb(n)=b(n)/A(n,n);A=D*(A');for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1);disp('改进平方根法解得的解即为b'); end3.调用函数解题:clear;clc;n=input('请输入矩阵维数:');b=zeros(n,1); A=zeros(n);for i=1:nfor j=1:nA(i,j)=1/(i+j-1);b(i)=b(i)+1/(i+j-1);endend[x,b]=pingfanggenfa(A,b)b=gaijinpinfanggenfa(A,b)4.运行结果:请输入矩阵维数:40Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 6.570692e-020. > In pingfanggenfa at 4In qiujie at 10Matlab自带解即为x平方根法的解即为bx =1.60358.96850.85621.01950.9375-50.2500-3.0000-16.000024.0000-49.5000-30.000039.000022.0000-64.0000 -12.00002.000010.2500 -10.5000-1.0000 -10.875083.000046.0000 -98.000012.0000 -69.000068.000021.000017.0000 -50.7188-8.7500-8.0000 112.00006.0000 -68.750022.000044.0000 -28.00008.0000 -44.000012.0000b =1.0e+007 *0.0000-0.00000.0001-0.0004-0.00140.0424-0.29801.1419-2.73354.2539-4.30182.7733-1.19890.5406-0.36880.3285-0.44380.4621-0.25130.05650.0000-0.00510.0071-0.0027-0.00310.0036-0.00190.00090.0002-0.0002-0.00060.00040.0001-0.00020.00010.0000-0.00000.0000-0.0000-0.0000改进平方根法解得的解即为bb =1.0e+024 *0.0000-0.00000.0001-0.00120.0139-0.09540.4208-1.21012.0624-1.0394-3.33436.2567-0.2463-7.45942.80303.69900.7277-1.7484-0.4854-3.60100.25325.1862-2.12991.44100.8738-4.56541.04224.0920-2.7764-2.2148-0.89530.36654.89671.04160.1281 -4.3387 -1.1902 -2.8334 8.4610 -3.6008一、问题描述先用你所熟悉的计算机语言将算法2.5.1编成写通用的子程序,然后用你编写的程序完成下面两个计算任务:(1) 估计5到20阶Hilbert 矩阵的∞范数条件数;(2)设n *n n R 11-1-1-111-1-101-1001A ∈⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=先随机的选取n R x ∈,并计算出x A b n =;然后再用列主元Gauss 消去法求解该方程组,假定计算解为xˆ。
数值计算基础实验指导+部分实验源代码+复习指导+三套试题及其答案

数值计算基础实验指导书2010 年目录实验一直接法解线性方程组的 (3)实验二插值方法 (12)实验三数值积分 (6)实验四常微分方程的数值解 (8)实验五迭代法解线性方程组与非线性方程 (10)b b ⎭ ⎭ 实验一 直接法解线性方程组一、实验目的掌握全选主元消去法与高斯-塞德尔法解线性方程组。
二、实验内容分别写出 Guass 列选主元消去法与追赶法的算法,编写程序上机调试出结果,要求所编 程序适用于任何一解线性方程组问题,即能解决这一类问题,而不是某一个问题。
实验中以 下列数据验证程序的正确性。
1、用 Guass 列选主元消去法求解方程组⎡2.52.3- 5.1⎤ ⎡ x 1 ⎤⎡3.7⎤⎢5.3 9.6 1.5 ⎥ ⎢ x ⎥ = ⎢3.8⎥ ⎢ ⎢⎣8.11.7 - 4.3 ⎥ ⎢ ⎥⎦ ⎢⎣ 2 ⎥ x 3 ⎥⎦ ⎢ ⎥⎢⎣5.5⎥⎦2、用追赶法求解方程组⎡- 2 0 0 00 ⎤ ⎡ x 1 ⎤⎡- 10⎤⎢ 1 - 2 0 0 0 ⎥ ⎢ x ⎥ ⎢ 0 ⎥ ⎢ ⎥ ⎢ 2 ⎥ ⎢ ⎥ ⎢ 0 1 - 2 0 0 ⎥ ⎢ x 3 ⎥ = ⎢ 0 ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ 0 0 1 - 2 0 ⎥ ⎢ x 4 ⎥ ⎢ 0 ⎥ 0 0 0 1 - 2 x 5 0三、实验仪器设备与材料主流微型计算机四、实验原理1、Guass 列选主元消去法 对于 AX =B~A B 是上三角矩阵。
即: 1)、消元过程:将(A|B )进行变换为 ( ~ | ~) ,其中 A⎛ a a a b ⎫ ⎛ 1 a a b ⎫ 11 12 1n 1 ⎪ 12 1n 1 ⎪a 21 a 22 a 2 nb 2 ⎪ 0 1 a 2 n b 2 ⎪⎪ → ⎪ ⎝ a n 1 a n 2 ⎪ a nn n⎪ ⎝ 0 0 ⎪ a nn n ⎪ k 从 1 到 n-1a 、 列选主元选取第 k 列中绝对值最大元素 max a ik k ≤i ≤n作为主元。
概率论与数理统计(茆诗松)第二版第一章课后习题1.5参考答案

习题1.51. 三人独立地破译一个密码,他们能单独译出的概率分别为1/5, 1/3, 1/4,求此密码被译出的概率. 解:设A , B , C 分别表示“第一、第二、第三人能单独译出”,有A , B , C 相互独立,即C B A ,,相互独立, 故所求概率为535214332541)()()(1)(1)(=−=××−=−=−=C P B P A P C B A P C B A P U U . 2. 有甲乙两批种子,发芽率分别为0.8和0.9,在两批种子中各任取一粒,求:(1)两粒种子都能发芽的概率;(2)至少有一粒种子能发芽的概率;(3)恰好有一粒种子能发芽的概率.解:设A , B 分别表示“甲批、乙批的种子能发芽”,有A , B 相互独立,(1)所求概率为P (AB ) = P (A ) P (B ) = 0.8 × 0.9 = 0.72;(2)所求概率为P (A ∪B ) = P (A ) + P (B ) − P (AB ) = 0.8 + 0.9 − 0.72 = 0.98;(3)所求概率为P (A ∪B − AB ) = P (A ∪B ) − P (AB ) = 0.98 − 0.72 = 0.26.3. 甲、乙两人独立地对同一目标射击一次,其命中率分别为0.8和0.7,现已知目标被击中,求它是甲射中的概率.解:设A , B 分别表示“甲、乙射击命中目标”,有A , B 相互独立, 故所求概率为)()()()()()()()()()()()|(B P A P B P A P A P AB P B P A P A P B A P A P B A A P −+=−+==U U 8511.0474094.08.07.08.07.08.08.0===×−+=. 4. 设电路由A , B , C 三个元件组成,若元件A , B , C 发生故障的概率分别是0.3, 0.2, 0.2,且各元件独立工作,试在以下情况下,求此电路发生故障的概率:(1)A , B , C 三个元件串联;(2)A , B , C 三个元件并联;(3)元件A 与两个并联的元件B 及C 串联而成.解:设A , B , C 分别表示“元件A , B , C 发生故障”,有A , B , C 相互独立, (1)所求概率为552.08.08.07.01()((1)(1)(=××−=−=−=P P P P C B A P U U ;(2)所求概率为P (ABC ) = P (A ) P (B ) P (C ) = 0.3 × 0.2 × 0.2 = 0.012;(3)所求概率为P (A ∪BC ) = P (A ) + P (BC ) − P (ABC ) = P (A ) + P (B ) P (C ) − P (A ) P (B ) P (C )= 0.3 + 0.2 × 0.2 − 0.3 × 0.2 × 0.2 = 0.328.5. 在一小时内甲、乙、丙三台机床需维修的概率分别是0.9、0.8和0.85,求一小时内(1)没有一台机床需要维修的概率;(2)至少有一台机床不需要维修的概率;(3)至多只有一台机床需要维修的概率.解:设A , B , C 分别表示“甲、乙、丙三台机床不需要维修”,有A , B , C 相互独立,(1)所求概率为P (ABC ) = P (A ) P (B ) P (C ) = 0.1 × 0.2 × 0.15 = 0.003;(2)所求概率为388.085.08.09.01()()(1)(1)(=××−=−=−=C P B P A P C B A P C B A P U U ;(3)所求概率为)()()()()(BC A P C B A P C AB P ABC P BC A C B A C AB ABC P +++=U U U)()()()()()()()()()()()(C P B P A P C P B P A P C P B P A P C P B P A P +++== 0.1 × 0.2 × 0.15 + 0.1 × 0.2 × 0.85 + 0.1 × 0.8 × 0.15 + 0.9 × 0.2 × 0.15 = 0.059.6. 设A 1 , A 2 , A 3相互独立,且P (A i ) = 2/3,i = 1, 2, 3.试求A 1 , A 2 , A 3中(1)至少出现一个的概率;(2)恰好出现一个的概率;(3)最多出现一个的概率.解:(1)所求概率为27263131311)()()(1)(1)(321321321=××−=−=−=A P A P A P A A A P A A A P U U ; (2)所求概率为)(321321321A A A A A A A A A P U U)()()()()()()()()(321321321A P A P A P A P A P A P A P A P A P ++=92323131313231313132=××+××+××=; (3)所求概率为)(321321321321A A A A A A A A A A A A P U U U)()()()()()()()()()()()(321321321321A P A P A P A P A P A P A P A P A P A P A P A P +++=277313131323131313231313132=××+××+××+××=. 7. 若事件A 与B 相互独立且互不相容,试求min{P (A ), P (B )}.解:因事件A 与B 相互独立且互不相容,有P (AB ) = P (A ) P (B ) 且AB = ∅,即P (AB ) = 0,则P (A ) P (B ) = 0,即P (A ) = 0或P (B ) = 0,故min{P (A ), P (B )} = 0.8. 假设P (A ) = 0.4,P (A ∪B ) = 0.9,在以下情况下求P (B ):(1)A , B 不相容;(2)A , B 独立;(3)A ⊂ B .解:(1)因A , B 不相容,有P (A ∪B ) = P (A ) + P (B ),故P (B ) = P (A ∪B ) − P (A ) = 0.9 − 0.4 = 0.5;(2)因A , B 独立,有P (A ∪B ) = P (A ) + P (B ) − P (AB ) = P (A ) + P (B ) − P (A ) P (B ), 故8333.06.05.04.014.09.0)(1)()()(==−−=−−=A P A P B A P B P U ; (3)因A ⊂ B ,有P (B ) = P (A ∪B ) = 0.9.9. 设A , B , C 两两独立,且ABC = ∅.(1)如果P (A ) = P (B ) = P (C ) = x ,试求x 的最大值;(2)如果P (A ) = P (B ) = P (C ) < 1/2,且P (A ∪B ∪C ) = 9/16,求P (A ).解:(1)因ABC = ∅,有P (AB ∪AC ) = P (AB ) + P (AC ) − P (ABC ) = P (A ) P (B ) + P (A ) P (C ) = 2 x 2,则2 x 2 = P (AB ∪AC ) ≤ P (A ) = x ,得x ≤ 0.5, 另一方面,x 可以取到0.5,若取P (A ) = P (B ) = 0.5,P (AB ) = 0.25,B A B A C U =, 则5.0)()()()()()()()(=−+−=+==AB P B P AB P A P B P A P A P C P U ,且P (AB ) = 0.25 = P (A ) P (B ),A , B 独立,)()(25.0)()()()(C P A P AB P A P B A P AC P ==−==,有A , C 独立,)()(25.0)()()()(C P B P AB P B P A P BC P ==−==,有B , C 独立,即P (A ) = P (B ) = P (C ) = 0.5,A , B , C 两两独立,且ABC = ∅,得x 可以取到0.5,故x 的最大值等于0.5;注:掷两次硬币,设A 表示“第一次出现正面”,B 表示“第二次出现正面”,C 表示“恰好出现一次正面”,有P (A ) = P (B ) = P (C ) = 0.5,ABC = ∅,且AB 表示“两次都出现正面”,P (AB ) = 0.25 = P (A )P (B ),有A , B 独立;AC 表示“第一次出现正面,第二次反面”,P (AC ) = 0.25 = P (A )P (C ),有A , C 独立;BC 表示“第一次出现反面,第二次正面”,P (BC ) = 0.25 = P (B )P (C ),有B , C 独立.(2)设P (A ) = P (B ) = P (C ) = x ,有21<x , 因P (A ∪B ∪C ) = P (A ) + P (B ) + P (C ) − P (AB ) − P (AC ) − P (BC ) + P (ABC )= P (A ) + P (B ) + P (C ) − P (A ) P (B ) − P (A ) P (C ) − P (B ) P (C ) = 3x − 3x 2, 则233169x x −=,即0)43)(41(1632=−−=+−x x x x ,得41=x 或43=x ,但21<x , 故41=x . 10.事件A , B 独立,两个事件仅A 发生的概率或仅B 发生的概率都是1/4,求P (A ) 及P (B ).解:因A , B 独立,且41)()(==B A P B A P ,有)()](1[)()()](1)[()()(B P A P B P A P B P A P B P A P −==−=, 则P (A ) = P (B ),得41)](1)[(=−A P A P ,即0]21)([41)()]([22=−=+−A P A P A P , 故21)(=A P ,21)(=B P . 11.一实习生用同一台机器接连独立地制造3个同种零件,第i 个零件是不合格品的概率为p i = 1/(i + 1),i = 1, 2, 3,以X 表示3个零件中合格品的个数,求P {X ≤ 2}.解:设A i 表示“第i 个零件是不合格品”,i = 1, 2, 3,有A 1 , A 2 , A 3相互独立, 故)1)(1)(1(1)()()(1)(1}3{1}2{321321321p p p A P A P A P A A A P X P X P −−−−=−=−==−=≤434332211=××−=. 12.每门高射炮击中飞机的概率为0.3,独立同时射击时,要以99%的把握击中飞机,需要几门高射炮? 解:设X n 表示n 门高射炮击中飞机的次数,且每门高射炮击中飞机的概率为p = 0.3,则至少命中一次的概率为P {X n ≥ 1} = 1 − P {X n = 0} = 1 − (1 − p ) n = 1 − 0.7 n ≥ 0.99,即0.7 n ≤ 0.01, 故9114.127.0ln 01.0ln =≥n ,即需要13门高射炮就能以99%的把握击中飞机. 13.投掷一枚骰子,问需要投掷多少次,才能保证至少有一次出现点数为6的概率大于1/2?解:设X n 表示投掷n 次骰子出现点数为6的次数,且每次投掷骰子出现点数为6的概率p = 1/6,则至少有一次出现点数为6的概率为P {X n ≥ 1} = 1 − P {X n = 0} = 1 − (5/6) n ≥ 1/2,即(5/6) n ≤ 1/2, 故8018.3)6/5ln()2/1ln(=≥n ,即需要投掷4次,才能保证至少有一次出现点数为6的概率大于1/2. 14.一射手对同一目标独立地进行四次射击,若至少命中一次的概率为80/81,试求该射手进行一次射击的命中率.解:设X 表示该射手四次射击的命中次数,且射手进行一次射击的命中率为p , 则至少命中一次的概率为8180)1(1}0{1}1{4=−−==−=≥p X P X P ,即811)1(4=−p , 故射手进行一次射击的命中率为32=p . 15.每次射击命中率为0.2,试求:射击多少次才能使至少击中一次的概率不小于0.9?解:设X n 表示n 次射击的命中次数,且每次射击命中率为p = 0.2,则至少命中一次的概率为P {X n ≥ 1} = 1 − P {X n = 0} = 1 − (1 − p ) n = 1 − 0.8 n ≥ 0.9,即0.8 n ≤ 0.1, 故3189.108.0ln 1.0ln =≥n ,即射击至少11次才能使至少击中一次的概率不小于0.9. 16.设猎人在猎物100米处对猎物打第一枪,命中猎物的概率为0.5.若第一枪未命中,则猎人继续打第二枪,此时猎物与猎人已相距150米.若第二枪仍未命中,则猎人继续打第三枪,此时猎物与猎人已相距200米.若第三枪仍未命中,则猎物逃逸.假如该猎人命中猎物的概率与距离成反比,试求该猎物被击中的概率.解:设A i 表示“第i 枪命中猎物”,i = 1, 2, 3,有A 1 , A 2 , A 3相互独立,则P (A 1) = 0.5,31)(150100)(12==A P A P ,41)(200100)(13==A P A P , 故所求概率为)()()()(321211321211A A A P A A P A P A A A A A A P ++=U U43129413221312121)()()()()()(321211==××+×+=++=A P A P A P A P A P A P . 17.某血库急需AB 型血,要从身体合格的献血者中获得,根据经验,每百名身体合格的献血者中只有2名是AB 型血的;(1)求在20名身体合格的献血者中至少有一人是AB 型血的概率;(2)若要以95%的把握至少能获得一份AB 型血,需要多少位身体合格的献血者.解:设X n 表示n 名身体合格的献血者中AB 型血的人数,且每名献血者是AB 型血的概率为p = 0.02,(1)P {X 20 ≥ 1} = 1 − P {X 20 = 0} = 1 − (1 − p )20 = 1 − 0.9820 = 0.3324;(2)因P {X n ≥ 1} = 1 − P {X n = 0} = 1 − (1 − p ) n = 1 − 0.98 n ≥ 0.95,即0.98 n ≤ 0.05, 故2837.14898.0ln 05.0ln =≥n ,即需要149位献血者才能以95%的把握至少能获得一份AB 型血. 18.一个人的血型为A , B , AB , O 型的概率分别为0.37, 0.21, 0.08, 0.34.现任意挑选四个人,试求:(1)此四人的血型全不相同的概率;(2)此四人的血型全部相同的概率.解:(1)所求概率为P (A 1) = 4! × 0.37 × 0.21 × 0.08 × 0.34 = 0.0507;(2)所求概率为P (A 2) = 0.374 + 0.214 + 0.084 + 0.344 = 0.0341.19.甲、乙两选手进行乒乓球单打比赛,已知在每局中甲胜的概率为0.6,乙胜的概率为0.4.比赛可采用三局两胜制或五局三胜制,问哪一种比赛制度对甲更有利?解:三局两胜制,甲2∶0胜乙的概率为0.6 2 = 0.36,甲2∶1胜乙的概率为2 × 0.6 2 × 0.4 = 0.288,则三局两胜制时,甲获胜的概率为P (A 1) = 0.36 + 0.288 = 0.648;五局三胜制,甲3∶0胜乙的概率为0.6 3 = 0.216,甲3∶1胜乙的概率为3 × 0.63 × 0.4 = 0.2592, 且甲3∶2胜乙的概率为20736.04.06.02423=××⎟⎟⎠⎞⎜⎜⎝⎛,则五局三胜制时,甲获胜的概率为P (A 2) = 0.216 + 0.2592 + 0.20736 = 0.68256;故P (A 1) < P (A 2),五局三胜制时对甲更有利.20.甲、乙、丙三人进行比赛,规定每局两个人比赛,胜者与第三人比赛,依次循环,直至有一人连胜两场为止,此人即为冠军.而每次比赛双方取胜的概率都是1/2,现假定甲、乙两人先比,试求各人得冠军的概率.解:设每局比赛中,甲胜乙、乙胜甲、甲胜丙、丙胜甲、乙胜丙、丙胜乙分别记为A b , B a , A c , C a , B c , C b ,则甲得冠军的情况有两类:① A b A c ,A b C a B c A b A c ,A b C a B c A b C a B c A b A c ,……,(A b C a B c )k A b A c ,……,② B a C b A c A b ,B a C b A c B a C b A c A b ,B a C b A c B a C b A c B a C b A c A b ,……,(B a C b A c )k A b ,……,故甲得冠军的概率为P (A ) = (0.5 2 + 0.5 5 + 0.5 8 + ……) + (0.5 4 + 0.5 7 + 0.5 10 + ……)145141725.015.05.015.03432=+=−+−=; 由对称性知乙得冠军的概率145)()(==A P B P ; 而丙得冠军的情况也有两类:① A b C a C b ,A b C a B c A b C a C b ,A b C a B c A b C a B c A b C a C b ,……,(A b C a B c )k A b C a C b ,……,② B a C b C a ,B a C b A c B a C b C a ,B a C b A c B a C b A c B a C b C a ,……,(B a C b A c )k B a C b C a ,……,故丙得冠军的概率为P (C ) = (0.5 3 + 0.5 6 + 0.5 9 + ……) + (0.5 3 + 0.5 6 + 0.5 9 + ……)725.015.0233=−×=. 21.甲、乙两个赌徒在每一局获胜的概率都是1/2.两人约定谁先赢得一定的局数就获得全部赌本.但赌博在中途被打断了,请问在以下各种情况下,应如何合理分配赌本:(1)甲、乙两个赌徒都各需赢k 局才能获胜;(2)甲赌徒还需赢2局才能获胜,乙赌徒还需赢3局才能获胜;(3)甲赌徒还需赢n 局才能获胜,乙赌徒还需赢m 局才能获胜.解:记每一局中甲赢的概率为p = 0.5,假设赌博继续下去,按甲、乙最终获胜的概率分配赌本,(1)由对称性知,甲、乙获胜的概率相等,则P (A 1) = P (B 1) = 0.5,故甲、乙应各得赌本的一半;(2)因甲获胜的概率为P (A 2) = p 2 + 2 (1 − p ) p 2 + 3 (1 − p ) 2 p 2 = 0.5 2 + 2 × 0.5 3 + 3 × 0.5 4 = 0.6875,则乙获胜的概率P (B 2) = 1 − P (A 2) = 0.3125,故甲应得赌本的68.75%,乙应得赌本的31.25%;(3)因甲获胜的概率为n m n n np p m m n p p n p p n p A P 123)1(12)1(21)1(1)(−−⎟⎟⎠⎞⎜⎜⎝⎛−−+++−⎟⎟⎠⎞⎜⎜⎝⎛++−⎟⎟⎠⎞⎜⎜⎝⎛+=L 1215.0125.0215.015.0−+++⎟⎟⎠⎞⎜⎜⎝⎛−−+++⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+=m n n n n m m n n n L , 则乙获胜的概率为P (B 3) = 1 − P (A 3)⎥⎦⎤⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−−+++⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+−=−+++1215.0125.0215.015.01m n n n n m m n n n L , 故甲应得赌本的1215.0125.0215.015.0−+++⎟⎟⎠⎞⎜⎜⎝⎛−−+++⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+m n n n n m m n n n L , 乙应得赌本的⎥⎦⎤⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−−+++⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+−−+++1215.0125.0215.015.01m n n n n m m n n n L . 注:也可假设无论结果如何,都要进行n + m 局比赛,甲获胜的条件是前n + m − 1局比赛中,甲至少赢得n 局比赛,故甲获胜的概率为1211311)1(11)1(1)(−+−+−⎟⎟⎠⎞⎜⎜⎝⎛−+−+++−⎟⎟⎠⎞⎜⎜⎝⎛+−++−⎟⎟⎠⎞⎜⎜⎝⎛−+=m n m n m n p m n m n p p n m n p p n m n A P L 15.011111−+⎥⎦⎤⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−+−+++⎟⎟⎠⎞⎜⎜⎝⎛+−++⎟⎟⎠⎞⎜⎜⎝⎛−+=m n m n m n n m n n m n L . 22.一辆重型货车去边远山区送货.修理工告诉司机,由于车上六个轮胎都是旧的,前面两个轮胎损坏的概率都是0.1,后面四个轮胎损坏的概率都是0.2.你能告诉司机,此车在途中因轮胎损坏而发生故障的概率是多少吗?解:设X 与Y 分别表示在途中损坏的前胎个数与后胎个数,A 与B 分别表示至少有一个前胎与后胎损坏,且每个前胎损坏的概率为p 1 = 0.1,每个后胎损坏的概率为p 2 = 0.2,A 与B 相互独立,则P (A ) = P {X ≥ 1} = 1 − P {X = 0} = 1 − (1 − p 1)2 = 1 − 0.92 = 0.19,P (B ) = P {Y ≥ 1} = 1 − P {Y = 0} = 1 − (1 − p 2)4 = 1 − 0.84 = 0.5904,故P (A ∪B ) = P (A ) + P (B ) − P (AB ) = 0.19 + 0.5904 − 0.19 × 0.5904 = 0.6682.23.设0 < P (B ) < 1,试证事件A 与B 独立的充要条件是)|()|(B A P B A P =.证:必要性,若事件A 与B 独立, 则)()()()()()()|(A P B P B P A P B P AB P B A P ===,)(()()(()()|(A P P B P A P P B A P B A P === 故)|()|(B A P B A P =; 充分性,若)|()|(B A P B A P =,有)(1)()()()()()(B P AB P A P P B A P B P AB P −−==, 则P (AB )[1 − P (B )] = P (B )[P (A ) − P (AB )],即P (AB ) − P (AB )P (B ) = P (A )P (B ) − P (B )P (AB ),故P (AB ) = P (A ) P (B ),即事件A 与B 独立.24.设0 < P (A ) < 1,0 < P (B ) < 1,1)|()|(=+B A P B A P ,试证A 与B 独立. 证:因)(1)(1)()(()()()()|()|(B P B A P B P AB P P B A P B P AB P B A P B A P −−+=+=+U , )(1)()()(1)()(B P AB P B P A P B P AB P −+−−+= )](1)[()]()()(1)[()](1)[(B P B P AB P B P A P B P B P AB P −+−−+−= )](1)[()()()]([)()()()()()(2B P B P B P AB P B P B P A P B P B P AB P AB P −+−−+−= 1)](1)[()()()()](1)[()]([)()()()(2+−−=−−+−=B P B P B P A P AB P B P B P B P B P B P A P AB P , 且1|()|(=+B A P B A P , 则0)](1)[()()()(=−−B P B P B P A P AB P , 故P (AB ) = P (A ) P (B ),即事件A 与B 独立.25.若P (A ) > 0,P (B ) > 0,如果A , B 相互独立,试证A , B 相容.证:因A , B 相互独立,有P (AB ) = P (A ) P (B ) > 0,故AB ≠ ∅,即A , B 相容.。
段正敏主编《线性代数》知识题解答

线性代数习题解答1张应应胡佩2013-3-1目录第一章行列式 (1)第二章矩阵 (22)第三章向量组的线性相关性 (50)第四章线性方程组 (69)第五章矩阵的相似对角化 (91)第六章二次型 (114)附录:习题参考答案 (129)1教材:段正敏,颜军,阴文革:《线性代数》,高等教育出版社,2010。
第一章 行列式1.填空题:(1)3421的逆序数为 5 ; 解:该排列的逆序数为00235t =+++=. (2)517924的逆序数为 7 ; 解:该排列的逆序数为0100337t =+++++=. (3)设有行列式2311187001234564021103152----=D =)(ij a ∆, 含因子543112a a a 的项为 -1440,0 ; 解:(23154)31223314554(1)(1)526831440t a a a a a -=-⋅⋅⋅⋅⋅=-(24153)41224314553(1)(1)506810t a a a a a -=-⋅⋅⋅⋅⋅=所以D 含因子543112a a a 的项为-1440和0.(4)若n 阶行列式=-∆==∆=)(,)(ij ij n a D a a D 则()1na-;解:行列式D 中每一行可提出一个公因子1-,()()()1()1nnij ij D a a a ∴=∆-=-∆=-.(5)设328814412211111)(x xx x f --=,则0)(=x f 的根为 1,2,-2 ;解:()f x 是一个Vandermonde 行列式,()(1)(2)(2)(21)(22)(21)0f x x x x ∴=--+-----=的根为1,2,-2.(6)设321,,x x x 是方程03=++q px x 的三个根,则行列式=132213321x x x x x x x x x 0 ; 解:根据条件有332123123123()()()()x px q x x x x x x x x x x x ax x x x ++=---=-+++-比较系数可得:1230x x x ++=,123x x x q =-再根据条件得:311322333x px q x px q x px q⎧=--⎪=--⎨⎪=--⎩原行列式333123123123=3()33()0x x x x x x p x x x q q ++-=-++--⋅-=.(7)设有行列式10132x x x-=0,则x = 1,2 ; 解:2231032(1)(2)001xx x x x x x -=-+=--= 1,2x ∴=.(8)设=)(x f 444342343331242221131211a a a xa a x a a x a a xa a a ,则多项式)(x f 中3x 的系数为 0 ; 解:按第一列展开11112121313141()f x a A a A a A xA =+++,112131,,A A A 中最多只含有2x 项,∴含有3x 的项只可能是41xA()()12134141222433343123413242233132234122433(1)a a x xA x a x a xa a x x a a a a a a x a a a a a a +=-⎡⎤ =-++-++⎣⎦41xA 不含3x 项,∴()f x 中3x 的系数为0.(9)如果330020034564321x =0,则x = 2 ;解:12346543122(512)(63)000265330033xx x =⋅=--= 2x ∴=.(10)00000000000dcb a= -abcd ;解:将行列式按第一行展开:1400000000(1)0000000000a b b a cabcd cdd+=⋅-=-.(11)如果121013c ba =1,则111425333---c b a = 1 ;解:1323323133301302524121111111Tr r AA r r a a b c a b c bc -=+---=.(12)如333231232221131211a a a a a a a a a =2,则333232312322222113121211222222222222a a a a a a a a a a a a ---= -16 ,332313231332221222123121112111323232a a a a a a a a a a a a a a a ------= -4 ,3212000332313322212312111a a a a a a a a a= -4 ; 解:1112131121312122231231222321233132331323332T a a a a a a A a a a A a a a a a a a a a αααβββ======()()1112121332122222312231223313232331221232222222222222222288016a a a a a a a a a a a a A αααααααααααααα--=-=-- =+-=-=-()1121112131122212223212123121231323132333122311232323232323232a a a a a a a a a a a a a a a ββββββββββββββββββ----=--=---- =-+-- =()1223122123224T A ββββββββββ-=- =-=-11213114122232132333000212423T a a a A a a a a a a + ⋅=-按第一行展开(-1).(13)设n 阶行列式D =0≠a ,且D 中的每列的元素之和为b ,则行列式D 中的第二行的代数余子式之和为=a b;解:11121111211112121222121212111=n n n n n n nnn n nnn n nna a a a a a a a a a a ab b b ba a a a a a a a a 每行元素加到第二行()212220n b A A A a+++=≠按第二行展开∴212220,0n b A A A ≠+++≠且21222n a A A A b∴+++=实际上,由上述证明过程可知任意行代数余子式之和12,1,2,,i i in aA A A i n b+++==.(14)如果44434234333224232214131211a a a a a a a a a a a a a =1,则2423121144434234333224232200a a a a a a a a a a a a a = -1 , 443424433323423222a a a a a a a a a =111a ;解:令222324323334424344a a a B a a a a a a =,则 111213142223241111113233341142434401(1)10,000a a a a a a a a B a B a a a a a a a +=⋅-= ⇒ ≠=≠且 2223243233344111114243441112232400(1)10a a a a a a a B a B a a a a a a a +=⋅-=-=-223242233343112434441T a a a a a a B B a a a a ===. (15)设有行列式101321x x -,则元素1-的余子式21M =231x ,元素2的代数余子式12A =()1210101+- - ;(16)设3214214314324321=D =)(ij a ∆,ij ij a A 表示元素的代数余子式,则=+++44342414432A A A A 0 ;解:方法一:14243444234A A A A +++可看成D 中第一列各元素与第四列对应元素代数余子式乘积之和,故其值为0.方法二:11424344412312342234034134124A A A A +++=推论.(17)设cdb a a cbda dbcd c ba D ==)(ij a ∆,ij ij a A 表示元素的代数余子式,则=+++44342414A A A A 0 ;解:1424344411011a bc c bd A A A A dbc a bd +++=推论4.(18)设600000000000200023002342345)(x x x x x x f --=,则5x 的系数为 6 ; 解:方法一:54255254320543243200432032000()66(1)(1)632002000020000000000006x x x xx f x x x x x x x x ⨯--===⋅-⋅-⋅=--方法二:()f x 只有一项非0.()()54321615243342516610255543204320032000()120000000000006(1)(1)66t x x x f x a a a a a a x x x x -∴==-- =-⋅-⋅⋅= 综上所述:5x 的系数为6.(19)设111212122212111211112121222212221212m m m m mm n m n m n n nnn n nma a a a a a a a a Db b bc c c b b b c c c b b b c c c =, 且111212122212m m m m mma a a a a a a a a a =111212122212n n n n nnb b b b b b b b b b =,则D =()1mnab - ;解:方法一:令111212122212m m m m mma a a a a a A a a a a ==,111212122212n n n n nnb b b b b b B b b b b ==则1A O D A B ab CB==⋅=,()()211mnmnO AD A B ab B C==-⋅=-证明:根据行列式性质2和5,将行列式A 变成下三角行列式,得到:11112121222212121212m m m m m mmm m ma a a a a a a a a A a a a a a a a a a a '====''行列式1D 、2D 的变换和行列式A 的变换完全相同,得到:.1212121111211112121222212221212m m m m n m n n n nm n n nna a a a a a D c c cb b bc c c b b b c c c b b b '''='''''''''1212122111211112121222212221212m m m n m n m n n nnn n nm a a a a a a D b b b c c c b b b c c c b b b c c c '''='''''''''分别将1D 、2D 第一次按第一行展开(2a 变成第一行),第二次按第二行展开(3a 变成第一行),……,总共进行m 次第一行展开,得到:112m D a a a B A B ab ==⋅=;()()()()()11111121211111n n n mn mnm D a a a B A B ab ++++++=-⋅--⋅=-⋅⋅=-证毕.方法二:设()ij m m A a ⨯=,()pq n n B b ⨯=,()()()ij m n m n A O D d C B +⨯+⎛⎫== ⎪⎝⎭其中:(), 1:,1:, 1:,1:,, , 1:,1:, ij ij pq pja i m j m db i m m n j m m n p i m q j mc i m m n j m p i m ==⎧⎪==++=++=-=-*⎨⎪=++==-⎩那么:()(){}{}1111111,,,,1,,1m m m n m m m n m n t p p p p p mp m p m n p p p m n A OD d d d d C B +++++++=+==-∑.()()()()(){}{}{}{}()()()(){}{}{}{}()(){}{}()(){}11111111111111111111,,1,,,,1,,11,,1,,,,1,,11,,1,,,,11111m n m n m m n n m n m m n n m n m m t p p m l m l p mp l nl p p m l l n t p p t l l p mp l nl p p m l l n t p p t l l p mp l nl p p m l l a a b b a a b b a a b b *++=====-⎡⎤=-⋅-⎣⎦⎛⎫=-⋅- ⎪ ⎪⎝⎭∑∑∑由{}1,,n A B ab=⎛⎫⎪ ⎪⎝⎭=⋅=∑1112121222122111211112121222212221212m m m m mmn m n m n n nnn n nma a a a a a a a a Db b bc c c b b b c c c b b b c c c =2D 中m a 依次与12,,,n b b b 对换,使得m a 在n b 下面;()1m a - 依次与12,,,n b b b 对换,使得()1m a - 在n b 下面,在m a 上面;……1a 依次与12,,,n b b b 对换,使得1a 在n b 下面,在a 2 上面;总共进行了mn 次对换。
线性代数简明教程-第二版-答案

1 2 3 1 (1) A 2 4 6 2
1 2 3 1
r2 2r1
r3 r1
1 2 3 1 0 0 0 0
0 0 0 0
3 1 4 2 2
(2) B
1 1 1
0 2 4
1 1 13 3 3
0
4 0
1 0 1 1 0
r2 r1
3
1 1
1 2 4
0 0 0 1
(3)
1 a1 方法一 1
1
1 1 a2
1
1 1 1 an
1 a1 1 1 ri r1 a1 a2 0
a1 0 an
1 1 a1
a1a2 an 1
1
11
a2
an
10
01
n
c1
i2
ci
1 1 1 1
a1 a2
an
a1a2 an
0
0
11
a2
an
10
01
5、已知两个线性变换
x2
x1 2 y1 y3 2 y1 3y2
2 y3
x3 4 y1 y2 5 y3
y1 3z1 z2 y2 2z1 z3
,
y3 z2 3z3
求从 z1, z2 , z3 到 x1, x2 , x3 的 线性变换
分析:X AY ,Y BZ ,
~r3
4r2
0
r4
3r2
0 0
1 0 0
2 1 0 0 0 1
1 2
1 1
3 0
0 1
1 0
4 2
1 2 3 2 1 0 0 0
~r4 2r3
0
0 0
1 0 0
数值线性代数第二版徐树方高立张平文上机习题第一章实验报告(供参考)

上机习题1.先用你所熟悉的的计算机语言将不选主元和列主元Gauss 消去法编写成通用的子程序;然后用你编写的程序求解84阶方程组;最后将你的计算结果与方程的精确解进行比较,并就此谈谈你对Gauss 消去法的看法。
Sol :(1)先用matlab 将不选主元和列主元Gauss 消去法编写成通用的子程序,得到P U L ,,: 不选主元Gauss 消去法:[])(,A GaussLA U L =得到U L ,满足LU A =列主元Gauss 消去法:[])(,,A GaussCol P U L =得到P U L ,,满足LU PA =(2)用前代法解()Pb or b Ly =,得y用回代法解y Ux =,得x求解程序为()P U L b A Gauss x ,,,,=(P 可缺省,缺省时默认为单位矩阵)(3)计算脚本为ex1_1代码%算法(计算三角分解:Gauss 消去法)function [L,U]=GaussLA(A)n=length(A);for k=1:n-1A(k+1:n,k)=A(k+1:n,k)/A(k,k);A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n);endU=triu(A);L=tril(A);L=L-diag(diag(L))+diag(ones(1,n));end%算法计算列主元三角分解:列主元Gauss消去法)function [L,U,P]=GaussCol(A)n=length(A);for k=1:n-1[s,t]=max(abs(A(k:n,k)));p=t+k-1;temp=A(k,1:n);A(k,1:n)=A(p,1:n);A(p,1:n)=temp;u(k)=p;if A(k,k)~=0A(k+1:n,k)=A(k+1:n,k)/A(k,k);A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); elsebreak;endendL=tril(A);U=triu(A);L=L-diag(diag(L))+diag(ones(1,n));P=eye(n);for i=1:n-1temp=P(i,:);P(i,:)=P(u(i),:);P(u(i),:)=temp;endend%高斯消去法解线性方程组function x=Gauss(A,b,L,U,P)if nargin<5P=eye(length(A));endn=length(A);b=P*b;for j=1:n-1b(j)=b(j)/L(j,j);b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j); endb(n)=b(n)/L(n,n);y=b;for j=n:-1:2y(j)=y(j)/U(j,j);y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);endy(1)=y(1)/U(1,1);x=y;endex1_1clc;clear;%第一题A=6*eye(84)+diag(8*ones(1,83),-1)+diag(ones(1,83),1);b=[7;15*ones(82,1);14];%不选主元Gauss消去法[L,U]=GaussLA(A);x1_1=Gauss(A,b,L,U);%列主元Gauss消去法[L,U,P]=GaussCol(A);x1_2=Gauss(A,b,L,U,P);%解的比较subplot(1,3,1);plot(1:84,x1_1,'o-');title('Gauss');subplot(1,3,2);plot(1:84,x1_2,'.-');title('PGauss');subplot(1,3,3);plot(1:84,ones(1,84),'*-');title('精确解');结果为(其中Gauss表示不选主元的Gauss消去法,PGauss表示列主元Gauss 消去法,精确解为[]'⨯8411,,1 ):-6-4-202468Gauss050100PGauss 00.20.40.60.811.21.41.61.82精确解由图,显然列主元消去法与精确解更为接近,不选主元的Gauss 消去法误差比列主元消去法大,且不如列主元消去法稳定。
2021年数值线性代数第二版徐树方高立张平文上机习题实验报告2

第四章上机习题1考虑两点边值问题⎪⎩⎪⎨⎧==<<=+.1)1(,0)0(10 ,22y y a a dx dy dx y d ε 轻易知道它正确解为ax e e ay x +---=--)1(111εε为了把微分方程离散化, 把[0,1]区间n 等分, 令h=1/n,1,,1,-==n i ih x i得到差分方程,21211a hy y h y y y i i i i i =-++-++-ε简化为 ,)2()(211ah y y h y h i i i =++-+-+εεε从而离散化后得到线性方程组系数矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+-++-++-++-=)2()2()2()2(h h h h h h h A εεεεεεεεεε 对,100,2/1,1===n a ε分别用Jacobi 迭代法, G-S 迭代法和SOR 迭代法求线性方程组解, 要求有4位有效数字, 然后比较与正确解得误差。
对,0001.0,01.0,1.0===εεε考虑一样问题。
解 (1)给出算法:为解b Ax =, 令U L D A --=, 其中][ij a A =, ),,,(2211nn a a a diag D = ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-00001,21323121n n n n a a a a a a L,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-0000,122311312 n n n n a a a a a a U 利用Jacobi 迭代法, G-S 迭代法, SOR 迭代法解线性方程组, 均能够下步骤求解: step1给定初始向量x0=(0,0,...,0), 最大迭代次数N, 精度要求c, 令k=1 step2令x=B*x0+gstep3若||x-x0||2<c, 算法停止, 输出解和迭代次数k, 不然, 转step4step4若k>=N,算法停止, 迭代失败, 不然, 令x0=x, 转step2在Jacobi 迭代法中, B=D -1*(L+U),g=D -1*b在G-S 迭代法中, B=D -1*(L+U),g=D -1*b在SOR 迭代法中, B=(D-w*L)-1*[(1-w)*D+w*U],g=w*(D-w*L)-1*b另外, 在SOR 迭代法中, 上面算法step1中要给定松弛因子w, 其中0<w<2 为计算结果, 要求w=0.5。
数值线性代数(徐树方)答案

便可求得2.设为两个上三角矩阵,而且线性方程组是非奇异的,试给出一种运算量为的算法,求解该方程组。
因,故为求解线性方程组,可先求得上三角矩阵T的逆矩阵,依照上题的思想我们很容易得到计算的算法。
于是对该问题我们有(1)计算上三角矩阵T的逆矩阵,算法如下:算法 1(求解上三角矩阵的逆矩阵,回代法。
该算法的的运算量为)(2)计算上三角矩阵。
运算量大约为.(3)用回代法求解方程组:.运算量为;(4)用回代法求解方程组:运算量为。
算法总运算量大约为:3.证明:如果是一个Gauss变换,则也是一个Gauss变换。
按Gauss变换矩阵的定义,易知矩阵是Gauss变换。
下面我们只需证明它是Gauss变换的逆矩阵。
事实上注意到,则显然有从而有比较比较向量和可以发现Gauss变换L应具有功能:使向量的第二行加上第一行的2倍;使向量的第三行加上第一行的2倍。
于是Gauss变换如下5.证明:如果有三角分解,并且是非奇异的,那么定理1,其中都是单位下三角阵,都是上三角阵。
因一个单位下三角阵与一个上三角阵相等,故此,它们都必是单位矩阵。
即,6.设的定义如下有满足的三角分解。
[证明] 令 是单位下三角阵,是上三角阵。
定义如下容易验证:7.设A对称且,并假定经过一步Gauss消去之后,证明仍是对称阵。
其中,将A分块为由A的对称性,对称性则是显而易见的。
8.设是严格对角占优阵,即试证:矩阵仍是严格对角占优阵。
由此推断:对于对称的严格对角占优矩阵来说,于是主对角线上的元素满足 (1)非主对角线上的元素满足由于A是严格对角占优的,即故 (2)即,矩阵仍是严格对角占优阵。
9.设有三角分解。
指出当把Gauss消去法应用于矩阵时,怎样才为上三角矩阵U。
而这一组的初等行变换对应的变换矩阵就是,即这就是说,方程组和是同解方程。
而后者是上三角形方程组,可运用本章2求解。
这样我们就不必存储L,通求解方程组,来求解原方程组(1)用初等变换化;(2)利用回代法求解方程组。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上机习题1.先用你所熟悉的的计算机语言将不选主元和列主元Gauss 消去法编写成通用的子程序;然后用你编写的程序求解84阶方程组;最后将你的计算结果与方程的精确解进行比较,并就此谈谈你对Gauss 消去法的看法。
Sol :(1)先用matlab 将不选主元和列主元Gauss 消去法编写成通用的子程序,得到P U L ,,: 不选主元Gauss 消去法:[])(,A GaussLA U L =得到U L ,满足LU A =列主元Gauss 消去法:[])(,,A GaussCol P U L =得到P U L ,,满足LU PA =(2)用前代法解()Pb or b Ly =,得y用回代法解y Ux =,得x求解程序为()P U L b A Gauss x ,,,,=(P 可缺省,缺省时默认为单位矩阵)(3)计算脚本为ex1_1代码%算法(计算三角分解:Gauss 消去法)function [L,U]=GaussLA(A)n=length(A);for k=1:n-1A(k+1:n,k)=A(k+1:n,k)/A(k,k);A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n);endU=triu(A);L=tril(A);L=L-diag(diag(L))+diag(ones(1,n));end%算法计算列主元三角分解:列主元Gauss消去法)function [L,U,P]=GaussCol(A)n=length(A);for k=1:n-1[s,t]=max(abs(A(k:n,k)));p=t+k-1;temp=A(k,1:n);A(k,1:n)=A(p,1:n);A(p,1:n)=temp;u(k)=p;if A(k,k)~=0A(k+1:n,k)=A(k+1:n,k)/A(k,k);A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); elsebreak;endendL=tril(A);U=triu(A);L=L-diag(diag(L))+diag(ones(1,n));P=eye(n);for i=1:n-1temp=P(i,:);P(i,:)=P(u(i),:);P(u(i),:)=temp;endend%高斯消去法解线性方程组function x=Gauss(A,b,L,U,P)if nargin<5P=eye(length(A));endn=length(A);b=P*b;for j=1:n-1b(j)=b(j)/L(j,j);b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j); endb(n)=b(n)/L(n,n);y=b;for j=n:-1:2y(j)=y(j)/U(j,j);y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);endy(1)=y(1)/U(1,1);x=y;endex1_1clc;clear;%第一题A=6*eye(84)+diag(8*ones(1,83),-1)+diag(ones(1,83),1);b=[7;15*ones(82,1);14];%不选主元Gauss消去法[L,U]=GaussLA(A);x1_1=Gauss(A,b,L,U);%列主元Gauss消去法[L,U,P]=GaussCol(A);x1_2=Gauss(A,b,L,U,P);%解的比较subplot(1,3,1);plot(1:84,x1_1,'o-');title('Gauss');subplot(1,3,2);plot(1:84,x1_2,'.-');title('PGauss');subplot(1,3,3);plot(1:84,ones(1,84),'*-');title('精确解');结果为(其中Gauss表示不选主元的Gauss消去法,PGauss表示列主元Gauss 消去法,精确解为[]'⨯8411,,1 ):-6-4-202468Gauss050100PGauss 00.20.40.60.811.21.41.61.82精确解由图,显然列主元消去法与精确解更为接近,不选主元的Gauss 消去法误差比列主元消去法大,且不如列主元消去法稳定。
Gauss 消去法重点在于A 的分解过程,无论A 如何分解,后面两步的运算过程不变。
2.先用你所熟悉的的计算机语言将平方根法和改进的平方根法编写成通用的子程序;然后用你编写的程序求解对称正定方程组Ax=b 。
Sol :(1)先用matlab 将平方根法和改进的平方根法编写成通用的子程序,得到L ,(D): 平方根法:L=Cholesky(A)改进的平方根法:[L,D]=LDLt(A)(2)求解得b Ly =求解得y x DL or y x L TT == 求解程序为x=Gauss(A,b,L,U,P)(TT DL U or L U == ,P 此时缺省,缺省时默认为单位矩阵)(3)计算脚本为ex1_2代码%算法(计算Cholesky分解:平方根法)function L=Cholesky(A)n=length(A);for k=1:nA(k,k)=sqrt(A(k,k));A(k+1:n,k)=A(k+1:n,k)/A(k,k);for j=k+1:nA(j:n,j)=A(j:n,j)-A(j:n,k)*A(j,k);endendL=tril(A);end%计算LDL‘分解:改进的平方根法function [L,D]=LDLt(A)n=length(A);for j=1:nfor i=1:nv(i,1)=A(j,i)*A(i,i);endA(j,j)=A(j,j)-A(j,1:j-1)*v(1:j-1,1);A(j+1:n,j)=(A(j+1:n,j)-A(j+1:n,1:j-1)*v(1:j-1,1))/A(j,j);endL=tril(A);D=diag(diag(A));L=L-diag(diag(L))+diag(ones(1,n));end%高斯消去法解线性方程组function x=Gauss(A,b,L,U,P)if nargin<5P=eye(length(A));endn=length(A);b=P*b;for j=1:n-1b(j)=b(j)/L(j,j);b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j); endb(n)=b(n)/L(n,n);y=b;for j=n:-1:2y(j)=y(j)/U(j,j);y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j); endy(1)=y(1)/U(1,1);x=y;endex1_2%第二题%第一问A=10*eye(100)+diag(ones(1,99),-1)+diag(ones(1,99),1); b=round(100*rand(100,1));%平方根法L=Cholesky(A);x1_2_1_1=Gauss(A,b,L,L');%改进的平方根法[L,D]=LDLt(A);x1_2_1_2=Gauss(A,b,L,D*L');%第二问A=hilb(40);b=sum(A);b=b';%平方根法L=Cholesky(A);x1_2_2_1=Gauss(A,b,L,L');%改进的平方根法[L,D]=LDLt(A);x1_2_2_2=Gauss(A,b,L,D*L');结果分别为x1_2_1_1 =x1_2_1_2 =x1_2_2_1 =+07 *x1_2_2_2 =3.用第1题的程序求解第2题的两个方程组并比较所有的计算结果,然后评价各个方法的优劣。
Sol:Gauss表示不选主元的Gauss消去法,PGauss表示列主元Gauss消去法。
计算脚本为:%第三题%第一问A=10*eye(100)+diag(ones(1,99),-1)+diag(ones(1,99),1);b=round(100*rand(100,1));%不选主元Gauss消去法[L,U]=GaussLA(A);x1_3_1_1=Gauss(A,b,L,U);%列主元Gauss消去法[L,U,P]=GaussCol(A);x1_3_1_2=Gauss(A,b,L,U,P);%第二问A=hilb(40);b=sum(A);b=b';%不选主元Gauss消去法[L,U]=GaussLA(A);x1_3_2_1=Gauss(A,b,L,U);%列主元Gauss消去法[L,U,P]=GaussCol(A);x1_3_2_2=Gauss(A,b,L,U,P);ex1_2;y1=1:100;y2=1:40;subplot(4,2,1);plot(y1,x1_2_1_1);title('平方根法1'); subplot(4,2,2);plot(y1,x1_2_1_2);title('改进的平方根法1'); subplot(4,2,3);plot(y1,x1_3_1_1);title('Gauss1');subplot(4,2,4);plot(y1,x1_3_1_2);title('PGauss1');subplot(4,2,5);plot(y2,x1_2_2_1);title('平方根法2'); subplot(4,2,6);plot(y2,x1_2_2_2);title('改进的平方根法2'); subplot(4,2,7);plot(y2,x1_3_2_1);title('Gauss2');subplot(4,2,8);plot(y2,x1_3_2_2);title('PGauss2');平方根法和改进的平法根法计算量更小,计算过程稳定,但使用范围窄; 不选主元和列主元的Gauss 消去法计算量较大,但适用范围广。
例题考虑对称正定线性方程组Ax=b ,其中向量b 是随机生成的,其元素是服从区间[0,1]上均匀分布的随机数,矩阵TLL A ,这里L 是随机生成的一个下三角矩阵,其元素是服从区间[1,2]上均匀分布的随机数。
对n=10,20,...,500分别应用Gauss 消去法、列主元Gauss 消去法和Cholesky 分解法求解该方程组,画出它们所用的CPU 时间,其中“Gauss ”表示Gauss 消去法、“PGauss ”表示列主元Gauss 消去法,“Cholesky ”表示Cholesky 分解法。
