【2014丰台一模】北京市丰台区2014届高三下学期期中练习 数学文 Word版含答案
【2014丰台一模】北京市丰台区2014届高三下学期期中练习 英语 Word版含答案

北京市丰台区2014届高三第二学期统一练习(一)英语试卷2014.3第一部分:听力理解(共三节,30分)第一节(共5小题;每小题l.5分,共7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话你将听一遍。
1. What will the man do tonight?A. Go to a movie.B. Read books.C. Watch TV.2. Where will the bookshelf probably be put?A. Near the window.B. In the bedroom.C. Beside the fireplace.3. What does the man want to be?A. A dancer.B. A singer.C. A waiter.4. Who is the man?A. A taxi driver.B. A policeman.C. A front desk clerk.5. Where are the two speakers?A. In a hospital.B. In a supermarket.C. In a post office.第二节(共10小题;每小题1.5分,共15分)听下面4段对话或独白。
每段对话或独白后有几道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有5秒钟的时间阅读每小题。
听完后,每小题将给出5秒钟的作答时间。
每段对话或独白你将听两遍。
听下面一段对话,回答第6至7两道小题。
6. What is the woman doing?A. Seeing a doctor.B. Doing a survey.C. Making an appointment.7. How does the man keep fit?A. By eating a healthy diet.B. By taking enough sleep.C. By riding the bike to work.听下面一段独白,回答第8至9两道小题。
2014北京市丰台区高考英语一模试题(附答案)

北京市丰台区2014届高三第二学期统一练习(一)英语试卷2014.3第一部分:听力理解(共三节,30分)第一节(共5小题;每小题l.5分,共7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话你将听一遍。
1. What will the man do tonight?A. Go to a movie.B. Read books.C. Watch TV.2. Where will the bookshelf probably be put?A. Near the window.B. In the bedroom.C. Beside the fireplace.3. What does the man want to be?A. A dancer.B. A singer.C. A waiter.4. Who is the man?A. A taxi driver.B. A policeman.C. A front desk clerk.5. Where are the two speakers?A. In a hospital.B. In a supermarket.C. In a post office.第二节(共10小题;每小题1.5分,共15分)听下面4段对话或独白。
每段对话或独白后有几道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有5秒钟的时间阅读每小题。
听完后,每小题将给出5秒钟的作答时间。
每段对话或独白你将听两遍。
听下面一段对话,回答第6至7两道小题。
6. What is the woman doing?A. Seeing a doctor.B. Doing a survey.C. Making an appointment.7. How does the man keep fit?A. By eating a healthy diet.B. By taking enough sleep.C. By riding the bike to work.听下面一段独白,回答第8至9两道小题。
2014高三文-一模汇总

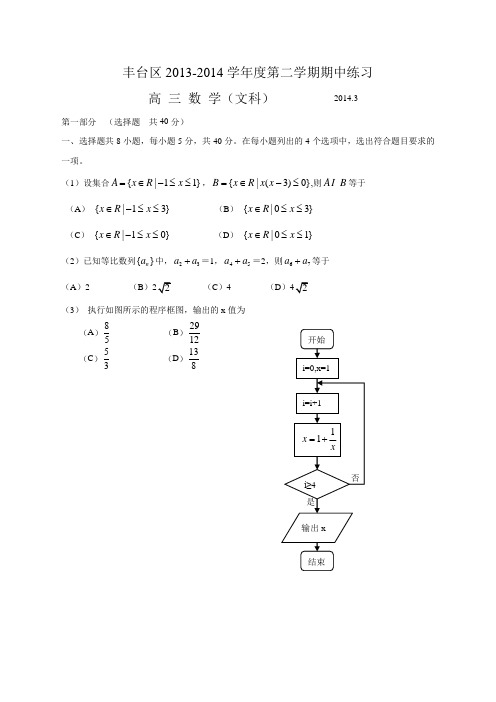
海淀区高三年级第二学期期中练习数 学 (文科) 2014.4一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.52i=-( ).A .2i - B .2i + C .12i + D . 12i - 2. 已知集合{}{}1,0,1,sin π,,A B y y x x A AB =-==∈=则( ).A .{}1-B .{}0C . {}1 D .Æ 3. 抛物线28y x =上到其焦点F 距离为5的点有( ). A .0个 B .1个 C . 2个 D . 4个4. 平面向量,a b 满足||2=a ,||1=b ,且,a b 的夹角为60︒,则()⋅+a a b =( ). A .1 B . 3 C .5 D . 75. 函数()2sin f x x x =+的部分图象可能是( ).A B C D6. 已知等比数列{}n a 的前n 项和为n S ,且1S ,22S a +,3S 成等差数列,则数列{}n a 的公比为( ). A .1 B .2 C .12D .3 7. 已知()x f x a =和()x g x b =是指数函数,则“(2)(2)f g >”是“a b >”的( ). A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D . 既不充分也不必要条件8. 已知(1,0)A ,点B 在曲线:G ln y x =上,若线段AB 与曲线:M 1y x=相交且交点恰为线段AB 的中点,则称B 为曲线G 关于曲线M 的一个关联点.那么曲线G 关于曲线M 的关联点的个数为( ). A .0 B .1 C .2 D .4OyxOyxOyxOyx二、填空题:本大题共6小题,每小题5分,共30分.9.双曲线221 3x y m -=的离心率为2,则m =__________.10. 李强用流程图把早上上班前需要做的事情做了如下几种方案,则所用时间最少的方案是_______ 方案一: 方案二: 方案三:11. 在ABC ∆中,3a =,5b =,120C =,则sin ______,_______.sin Ac B==12. 某商场2013年一月份到十二月份月销售额呈现先下降后上升的趋势,现有三种函数模型:①()x f x p q =⋅,(0,1)q q >≠;②()log (0,1)xp f x q p p =+>≠;③2()f x x px q =++.能较准确反映商场月销售额()f x 与月份x 关系的函数模型为 _________(填写相应函数的序号),若所选函数满足(1)10,(3)2f f ==,则()f x =_____________.13.一个空间几何体的三视图如图所示,该几何体的表面积为 __________.14. 设不等式组20,20x y x ay ++≥⎧⎨++≤⎩表示的区域为1Ω,不等式221x y +≤表示的平面区域为2Ω.(1)若1Ω与2Ω有且只有一个公共点,则a = ;(2)记()S a 为1Ω与2Ω公共部分的面积,则函数()S a 的取值范围是 .三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.33846俯视图主视图侧视图15.(本小题满分13分)已知函数π()sin sin()3f x x x =--.(Ⅰ)求π()6f ;(Ⅱ)求()f x 在ππ[,]22-上的取值范围.16.(本小题满分13分)某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查.调查问卷共10道题,答题情况如下表:答对题目数 [)0,88 9 10女 2 13 12 8 男337169(Ⅰ)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;(Ⅱ)从答对题目数少于8的出租车司机中任选出两人做进一步的调查,求选出的两人中至少有一名女出租车司机的概率.17. (本小题满分14分)如图1,在Rt △ABC 中,∠ABC =90°,D 为AC 中点,AE BD ⊥于E (不同于点D ),延长AE 交BC 于F ,将△ABD 沿BD 折起,得到三棱锥1A BCD -,如图2所示. (Ⅰ)若M 是FC 的中点,求证:直线DM //平面1A EF ; (Ⅱ)求证:BD ⊥1A F ;(Ⅲ)若平面1A BD ⊥平面BCD ,试判断直线1A B 与直线CD 能否垂直?并说明理由.FEDABC18. (本小题满分13分)1图 图 2E DA 1CBFM已知函数()ln f x x x =. (Ⅰ)求()f x 的单调区间;(Ⅱ)当1k ≤时,求证:()1f x kx ≥-恒成立.19. (本小题满分14分)已知1122(,),(,)A x y B x y 是椭圆22:24C x y +=上两点,点M 的坐标为(1,0). (Ⅰ)当,A B 关于点(1,0)M 对称时,求证:121x x ==;(Ⅱ)当直线AB 经过点(0,3) 时,求证:MAB ∆不可能为等边三角形.20. (本小题满分13分)在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)()A n :123,,,,n A A A A 与()B n :123,,,,n B B B B ,其中3n ≥,若同时满足:①两点列的起点和终点分别相同;②线段11i i i i A A B B ++⊥,其中1,2,3,,1i n =-,则称()A n 与()B n 互为正交点列.(Ⅰ)试判断(3)A :123(0,2),(3,0),(5,2)A A A 与(3)B :123(0,2),(2,5),(5,2)B B B 是否互为正交点列,并说明理由;(Ⅱ)求证:(4)A :12340,0),3,1),6,0)(((,9,1)(A A A A 不存在正交点列(4)B ; (Ⅲ)是否存在无正交点列(5)B 的有序整数点列(5)A ?并证明你的结论.2014年石景山区高三统一测试数学(文科)第Ⅰ卷(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.已知全集U =R ,集合{}2|20A x x x =-<,{}|10B x x =-≥,那么U AB =ð( )A .{}|01x x <<B .{}|0x x <C .{}|2x x >D .{}|12x x <<2.下列函数中,在(0)+∞,内单调递减,并且是偶函数的是( ) A .2y x = B .1y x =+ C .lg ||y x =-D .2x y =3.直线:340l x y +-=与圆22:+=4C x y 的位置关系是( )A .相交B .相切C .相离D .无法确定4.双曲线22221x y a b-=(00)a b >>,的渐近线方程是2y x =±,则其离心率为( ) A .5B .52C .3D .55.下列函数中周期为π且图象关于直线3x π=对称的函数是( ) A .2sin()23x y π=+B .2sin(2)6y x π=-C .2sin(2)6y x π=+D .2sin()23x y π=-6.正三棱柱的左视图如右图所示,则该正三棱柱的侧面积为( )7.阅读右面的程序框图,运行相应的程序,输出的结果为( )A .4B .12C .433 D .24 A .2- B .12 C .1- D .2否开始 1i i =+11A A=-2014i >是 输出A 结束02i A ==, 左视图 328.已知动点()P x y ,在椭圆22:12516x y C +=上,F 为椭圆C 的右焦点,若点M 满足||1MF =且0MP MF ⋅=,则||PM 的最小值为( )A .3B .3C .125D .1第Ⅱ卷(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.i 是虚数单位,计算41ii+=+_________.10.在等比数列}{n a 中,14=2=16a a ,,则数列}{n a 的通项公式=n a _____________,设2log n n b a =,则数列}{n b 的前n 项和=n S _____________.11.已知命题p :0x x e ∃∈<R ,,则p ⌝是____________________.12.已知变量x y ,满足约束条件20170x y x x y -+≤⎧⎪≥⎨⎪+-≤⎩,,,则2z x y =+的最大值是_________.13.一艘轮船在匀速行驶过程中每小时的燃料费与它速度的平方成正比,除燃料费外其它费用为每小时96元. 当速度为10海里/小时时,每小时的燃料费是6元. 若匀速行驶10海里,当这艘轮船的速度为___________海里/小时时,费用总和最小.14.若存在实常数k 和b ,使得函数()f x 和()g x 对其定义域内的任意实数x 分别满足:()f x kx b ≥+和()g x kx b ≤+,则称直线:l y kx b =+为()f x 和()g x 的“隔离直线”.已知函数2()1f x x =-和函数()2ln g x x =,那么函数()f x 和函数()g x 的隔离直线方程为_________.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)在△ABC 中,角A B C ,,的对边分别为a b c ,,,且a b c <<,32sin a b A =. (Ⅰ)求角B 的大小;(Ⅱ)若2a =,7b =,求c 边的长和△ABC 的面积.16.(本小题满分13分)分数频率组距0.0440.0280.0120.00810090807060500某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.(Ⅰ)求分数在[5060),的频率及全班人数; (Ⅱ)求分数在[8090),之间的频数,并计算频率分布直方图中[8090),间矩形的高; (Ⅲ)若要从分数在[80100),之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90100),之间的概率.17.(本小题满分14分)如图,已知四棱锥A BCDE -,1AB BC AC BE ====,2CD =,CD ⊥平面ABC ,BE ∥CD ,F 为AD 的中点.(Ⅰ)求证:EF ∥平面ABC ;(Ⅱ)求证:平面ADE ⊥平面ACD ; (Ⅲ)求四棱锥A BCDE -的体积.18.(本小题满分13分)已知函数22()2ln (0)f x x a x a =->.(Ⅰ)若()f x 在1x =处取得极值,求实数a 的值; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)若()f x 在[1]e ,上没有零点,求实数a 的取值范围. 19.(本小题满分14分)CD BAF E给定椭圆C :22221(0)x y a b a b+=>>,称圆心在原点O ,半径为22a b +的圆是椭圆C 的“准圆”.若椭圆C 的一个焦点为(20)F ,,其短轴上的一个端点到F 的距离为3. (Ⅰ)求椭圆C 的方程和其“准圆”方程;(Ⅱ)点P 是椭圆C 的“准圆”上的动点,过点P 作椭圆的切线12l l ,交“准圆”于点M N ,. (ⅰ)当点P 为“准圆”与y 轴正半轴的交点时,求直线12l l ,的方程并证明12l l ⊥; (ⅱ)求证:线段MN 的长为定值.20.(本小题满分13分)对于数列{}n a ,把1a 作为新数列{}n b 的第一项,把i a 或i a -(234i n =,,,,)作为新数列{}n b 的第i 项,数列{}n b 称为数列{}n a 的一个生成数列.例如,数列12345,,,,的一个生成数列是12345--,,,,.已知数列{}n b 为数列1{}()2n n *∈N 的生成数列,n S 为数列{}n b 的前n 项和. (Ⅰ)写出3S 的所有可能值;(Ⅱ)若生成数列{}n b 满足的通项公式为1312(1312nn n n k b k n k ⎧=+⎪⎪=∈⎨⎪-≠+⎪⎩N),,,,,求n S .xOyP1l2lMN开始 S =1,i =1 结束i =i +2i >7?输出S 是否S =S +i 北京市朝阳区高三年级第一次综合练习数学学科测试(文史类)2014.3一、选择题:本大题共8小题,每小题5分,共40分.(1)已知集合|03}A x x =∈<<N {,1|21}x B x -=>{,则A B =I ( ).A .∅B .{}1C .{}2D .{}1,2 (2)已知i 为虚数单位,复数2i1i-的值是( ). A .1i -- B .1i + C .1i -+ D .1i -(3)若,x y 满足约束条件,1,33,x y y x x y +⎧⎪+⎨⎪+⎩≤3≤≥则函数2z x y =-的最大值是( ).A .1-B .0C .3D .6(4)在索契冬奥会跳台滑雪空中技巧比赛赛前训练中,甲、乙两位队员各跳一次.设命题p 是“甲落地站稳”,q 是“乙落地站稳”,则命题“至少有一位队员落地没 有站稳”可表示为( ).A .p q ∨B .()p q ∨⌝C .()()p q ⌝∧⌝D .()()p q ⌝∨⌝(5)执行如右图所示的程序框图,则输出S 的值是( ).A .10B .17C .26D .28(6)函数2sin ()1xf x x =+的图象大致为( ).A .B .C .D .(7)已知AB uu u r和AC uuu r 是平面内两个单位向量,它们的夹角为60o ,则2AB AC -uu u r uuu r 与CA uu r 的夹角是 ( ).A .30oB .60oC .90oD .120o(8)如图,梯形ABCD 中,ADBC ,1AD AB ==,AD AB ⊥,45BCD ∠=o ,将ABD ∆沿对角线BDyxo-ππyxo-ππ-π2y xoπ2-π2yxoπ2折起.设折起后点A 的位置为A ',并且平面A BD '⊥平面BCD .给出下面四个命题: ①A D BC '⊥;②三棱锥A BCD '-的体积为22;③CD ⊥平面A BD ';④平面A BC '⊥平面A DC '. 其中正确命题的序号是( ).A .①②B .③④C .①③D .②④二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.(9)抛物线28y x =的准线方程是 .(10)在一次选秀比赛中,五位评委为一位表演者打分,若去掉一个最低分后平均分为90分,去掉一个最高分后平均分为86分.那么最高分比最低分高 分.(11)在ABC ∆中,,,a b c 分别是角,,A B C 的对边.已知4b =,2c =,60A ∠=o ,则a = ;C ∠= .(12)一个空间几何体的三视图如图所示,则这个几何体的体积为 ; 表面积为 .(13)已知直线y x m =+与曲线224x y +=交于不同的两点,A B ,若||AB ≥23,则实数m 的取值范围是 .(14)将1,2,3,…………,9这9个正整数分别写在三张卡片上,要求每一张卡片上的任意两数之差都不在这张卡片上.现在第一张卡片上已经写有1和5,第二张卡片上写有2,第三张卡片上写有3,则6应该写在第 张卡片上;第三张卡片上的所有数组成的集合是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题满分13分)已知函数()2sin cos 3cos 2f x x x x =-.(Ⅰ)求(0)f 的值及函数()f x 的单调递增区间;(Ⅱ)求函数()x f 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值.(16)(本小题满分13分)某单位从一所学校招收某类特殊人才.对20位已经选拔入围的学生进行运动协调能力和逻辑思维能力1 正视图侧视图11 俯视图 CBA D的测试,其测试结果如下表:一般 良好 优秀一般 2 21 良好 4b1优秀13 a 例如表中运动协调能力良好且逻辑思维能力一般的学生是4人.由于部分数据丢失,只知道从这20位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为15.(Ⅰ)求a ,ξ的值;(Ⅱ)从运动协调能力为优秀的学生中任意抽取2位,求其中至少有一位逻辑思维能力优秀的学生的概 率.(17)(本题满分14分)在四棱柱1111ABCD A B C D -中,1AA ⊥底面ABCD ,底面ABCD 为菱形,O 为11A C 与11B D 交点, 已知11AA AB ==,60BAD ∠=o . (Ⅰ)求证:11AC ⊥平面11B BDD ; (Ⅱ)求证:AO ∥平面1BC D ; (Ⅲ)设点M 在1BC D ∆内(含边界),且OM ⊥11B D ,说明满足条件的点M 的轨迹,并求OM 的最 小值.(18)(本小题满分13分)设函数()ln f x x =,()1g x ax =+,a ∈R ,记()()()F x f x g x =-. (Ⅰ)求曲线()y f x =在e x =处的切线方程; (Ⅱ)求函数()F x 的单调区间;(Ⅲ)当0a >时,若函数()F x 没有零点,求a 的取值范围.(19)(本小题满分14分)A B D 1 C 1D C O A 1 B 1运动 协调能力逻辑思维能力已知椭圆2222:1(0)x y C a b a b +=>>经过点3(1,)2,一个焦点为(3,0).(Ⅰ)求椭圆C 的方程;(Ⅱ)若直线(1)(0)y k x k =-≠与x 轴交于点P ,与椭圆C 交于,A B 两点,线段AB 的垂直平分线与x 轴交于点Q ,求||||AB PQ 的取值范围.(20)(本小题满分13分)已知{}n a 是公差不等于0的等差数列,{}n b 是等比数列(N )n *∈,且110a b =>.(Ⅰ)若33a b =,比较2a 与2b 的大小关系; (Ⅱ)若2244,a b a b ==.(ⅰ)判断10b 是否为数列{}n a 中的某一项,并请说明理由;(ⅱ)若m b 是数列{}n a 中的某一项,写出正整数m 的集合(不必说明理由).延庆县2013—2014学年度高考模拟检测试卷高三数学(文科) 2014.3一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1. 已知集合}3,2,1{=A ,}2|{≤=x x B ,则=⋂B AA .φB .}1{C .}2{D .}2,1{ 2. 复数ii i z )1)(1(-+=在复平面上所对应的点Z 位于A .实轴上B .虚轴上C .第一象限D .第二象限3. 设n S 是等差数列}{n a 的前n 项和,已知32=a ,116=a ,则=7S A .13 B .35 C .49 D .634. 执行右边的程序框图,则输出的S 值等于A . 91817161+++ B . 9181716151++++C . 10191817161++++D . 1019181716151+++++5. 下列函数中,既是偶函数,又是在区间(0,)+∞上单调递减的函数是 A . 1ln ||y x = B . 3y x = C . ||2x y = D . cos y x =6. 右图是一个几何体的三视图,则该几何体的体积是A . 3B . 34C . 1D . 327. 正三角形ABC 中,D 是边BC 上的点,若3,1AB BD ==,则AB AD ⋅= A . 221B .215C .213D .298. 对于函数x e x f xln )(-=,下列结论正确的一个是1i <是否0,0.5s i ==开始结束10.1s s i=+⨯输出 s 0.1i i =+121 2主视图左视图俯视图50%30%40岁以下20% 50岁以上40~50岁A . )(x f 有极小值,且极小值点)21,0(0∈xB . )(x f 有极大值,且极大值点)21,0(0∈xC . )(x f 有极小值,且极小值点)1,21(0∈xD . )(x f 有极大值,且极大值点)1,21(0∈x第Ⅱ卷(非选择题)二、填空题共6个小题,每小题5分,共30分.9. 设m 是常数,若点)5,0(F 是双曲线2219y x m -=的一个焦点,则m = . 10.圆034222=---+y x y x C :的圆心坐标为 ;直线l :0443=++y x 与圆C 位置关系是 .11.在相距2千米的,A B 两点处测量目标C ,若075,60CAB CBA ∠=∠=,则,A C 两点之间的距离是 千米.12.某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作为样本.用系统抽样的方法将全体职工随机按1~200编号,并按编号顺序分为40组(1~5号,6~10号,,,,,196~200号),若第5组抽出的号码为22,则第8组抽出的号码应是 ,若改用分层抽样的方法,则40岁以下年龄段应抽取 人.13. 若A 为不等式组⎪⎩⎪⎨⎧≤-≥≤200x y y x 表示的平面区域,则当a 的值从2-连续变化到1 时,动直线ay x l =+:扫过的A 中的那部分区域的面积为 .14.已知条件:p ABC ∆不是等边三角形,给出下列条件:① ABC ∆的三个内角不全是︒60 ② ABC ∆的三个内角全不是︒60 ③ ABC ∆至多有一个内角为︒60 ④ ABC ∆至少有两个内角不为︒60则其中是p 的充要条件的是 .(写出所有正确结论的序号)三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15. (本小题满分13分)0.020 0.0080.0240.048 频率/组距10 20 30 40 得分0 已知函数x x x x f 2sin cos sin )(+⋅=. (Ⅰ)求)(x f 的值域和最小正周期; (Ⅱ)设)2,0(πα∈,且1)(=αf ,求α的值.16.(本小题满分13分)如图,已知直三棱柱111C B A ABC -中,BC AC ⊥,D 为AB 的中点,1BB BC AC ==. (Ⅰ)求证://1BC 平面D CA 1; (Ⅱ)求证:11AB BC ⊥.17. (本小题满分13分)对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如右, 列出乙的得分统计表如下:(Ⅰ)估计甲在一场比赛中得分不低于20分的概率;(Ⅱ)判断甲、乙两名运动员哪个成绩更稳定;(结论不要求证明)(Ⅲ)在甲所进行的100场比赛中,以每场比赛得分所在区间中点的横坐标为这场比赛的得分,试计算甲每场比赛的平均得分.BC 1ADCB 1A 1分值 [ 0 , 10 ) [1 0 , 20 ) [ 20 , 30 ) [ 30 , 40 ) 场数 1020403018. (本小题满分13分)已知函数a ax x x f 23)(3+-=,)(R a ∈. (Ⅰ)求)(x f 的单调区间;(Ⅱ)曲线)(x f y =与x 轴有且只有一个公共点,求a 的取值范围.19. (本小题满分14分)已知直线022=+-y x 经过椭圆)0(1:2222>>=+b a by a x C 的左顶点A 和上顶点D ,椭圆C 的右顶点为B ,点S 是椭圆上位于x 轴上方的动点,直线AS ,BS 与直线4=x l :分别交于N M ,两点. (Ⅰ)求椭圆C 的方程;(Ⅱ)(ⅰ)设直线AS ,BS 的斜率分别为21,k k ,求证21k k ⋅为定值; (ⅱ)求线段MN 的长度的最小值.20. (本小题满分14分)在直角坐标系平面中,已知点)2,1(1P ,)2,2(22P ,)2,3(33P ,……,)2,(nn n P ,其中n 是正整数,对于平面上任意一点0A ,记1A 为0A 关于点1P 的对称点 ,2A 为1A 关于点2P 的对称点 ,……,n A 为1-n A 关于点n P 的对称点 . (Ⅰ)求向量20A A 的坐标;(Ⅱ)当点0A 在曲线C 上移动时,点2A 的轨迹是函数)(x f y =的图像,其中)(x f 是以3为周期的周期函数,且当]3,0(∈x 时,x x f lg )(=,求以曲线C 为图像的函数在]4,1(上的解析式; (Ⅲ)对任意偶数n ,用n 表示向量n A A 0的坐标.MY SD NlBxAO否是 开始i =0,x =1i =i+111x x=+i =0,x =1 输出x结束i ≥4 丰台区2013-2014学年度第二学期期中练习高 三 数 学(文科) 2014.3第一部分 (选择题 共40分)一、选择题共8小题,每小题5分,共40分。
丰台2014年北京中考一摸,各区试卷及答案

丰台区2014年初三毕业及统一练习语文试卷一、基础·运用(共24分)(一)选择题。
下面各题均有四个选项,其中只有一个..符合题意,选出答案后在答题卡上用铅笔把对应题目的选项字母涂黑涂满。
(共14分。
每小题2分)1.下列词语中加点字的读音完全正确的一项是A.庇.护(bì)谦逊.(xùn)翘.首(qiáo)称.心如意(chânɡ)B.剔.除(tī)炫.耀(xuàn)脂.肪(zhī)牵强.附会(qiǎnɡ)C.广袤.(mào)逃窜.(cuàn)逮.捕(dǎi)断壁残垣.(yuán)D.联袂.(mâi)憎.恶(zânɡ)妥帖.(tiē)万籁.俱寂(lài)2.下列句子中有错别字的一项是A.错落的灯笼、游弋的野鸭、静谧的垂柳,构成了什刹海傍晚时分特有的景象。
B.中华民族传统文化将竹子的自然属性拟人化,赋予其正直、虚心等品格。
C.以王羲之为代表的魏晋名家承前起后,在书法艺术发展史上占有重要地位。
D.北京丰台园博园于 4月1日重新开园,经过近半年的整修,面目焕然一新。
3.结合语境,在下列句子中的横线处填写词语正确的一项是①非物质文化遗产保护对于我国文化工作者来说是一项全新的课题。
,国外同行在这方面拥有很多可供我们学习借鉴的宝贵经验,我们可以从中受到启发。
②2014年2月,第22届冬季奥林匹克运动会在俄罗斯的索契召开。
来自88个国家或地区的5000多名运动员,向98枚金牌发起冲击,用他们的激情,诠释着“更快、更高、更强”的奥林匹克精神。
A.①句填“尺有所短,寸有所长”②句填“八仙过海,各显其能”B.①句填“尺有所短,寸有所长”②句填“各行其是”C.①句填“他山之石,可以攻玉”②句填“各行其是”D.①句填“他山之石,可以攻玉”②句填“八仙过海,各显其能”4.依据语段内容,对画线病句的修改最恰当的一项是剪纸是中华民族传统手工艺术中的瑰宝。
北京市丰台区2014届高三第二学期统一练习(一)

北京市丰台区2014届高三第二学期统一练习(一)英语试卷2014.3 第一部分:听力理解(共三节,30分)第一节(共5小题;每小题l.5分,共7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话你将听一遍。
1. What will the man do tonight?A. Go to a movie.B. Read books.C. Watch TV.2. Where will the bookshelf probably be put?A. Near the window.B. In the bedroom.C. Beside the fireplace.3. What does the man want to be?A. A dancer.B. A singer.C. A waiter.4. Who is the man?A. A taxi driver.B. A policeman.C. A front desk clerk.5. Where are the two speakers?A. In a hospital.B. In a supermarket.C. In a post office.第二节(共10小题;每小题1.5分,共15分)听下面4段对话或独白。
每段对话或独白后有几道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有5秒钟的时间阅读每小题。
听完后,每小题将给出5秒钟的作答时间。
每段对话或独白你将听两遍。
听下面一段对话,回答第6至7两道小题。
6. What is the woman doing?A. Seeing a doctor.B. Doing a survey.C. Making an appointment.7. How does the man keep fit?A. By eating a healthy diet.B. By taking enough sleep.C. By riding the bike to work.听下面一段独白,回答第8至9两道小题。
【2014丰台一模】北京市丰台区2014届高三下学期期中练习数学理Word版含答案

丰台区2013-2014学年度第二学期期中练习高 三 数 学(理科) 2014.3第一部分 (选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的4个选项中,选出符合题目要求的一项。
(1)设集合{|11}A x R x =∈-≤≤,{|(3)0}B x R x x =∈-≤,则A B 等于(A ) {|13}x R x ∈-≤≤ (B ) {|03}x R x ∈≤≤ (C ) {|10}x R x ∈-≤≤ (D ) {|01}x R x ∈≤≤ (2)在极坐标系中,点A (1,π)到直线cos 2=ρθ的距离是 (A )1 (B )2 (C )3 (D )4 (3)执行如图所示的程序框图,输出的x 值为 (A )85 (B )2912 (C )53(D )138(4)已知函数()f x 是定义在[6,6]-上的偶函数,且(3)(1)f f >,则下列各式中 一定成立的是(A )(0)(6)f f < (B )(-3)(-2)f f > (C )(1)(3)f f -< (D )(-2)(1)f f > (5) “1m n >>”是 “log 2log 2m n <”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 (6)某企业开展职工技能比赛,并从参赛职工中选1人参加该行业全国技能大 赛.经过6轮选拔,甲、乙两人成绩突出,得分情况如茎叶图所示.若甲乙两 人的平均成绩分别是x 甲,x 乙,则下列说法正确的是 (A )x x >甲乙,乙比甲成绩稳定,应该选乙参加比赛 (B )x x >甲乙,甲比乙成绩稳定,应该选甲参加比赛 (C )x x <甲乙,甲比乙成绩稳定,应该选甲参加比赛(D )x x <甲乙,乙比甲成绩稳定,应该选乙参加比赛(7)棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如 图所示,那么该几何体的体积是(A )143 (B )4 (C )103(D )3(8)如果某年年份的各位数字之和为7,我们称该年为“七巧年”.例如,今年 年份2014的各位数字之和为7,所以今年恰为“七巧年”.那么从2000年 到2999年中“七巧年”共有(A )24个 (B )21个 (C )19个 (D )18个侧视图俯视图主视图第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
北京市丰台区2014年高三5月统一练习(二模)数学(文)试题

丰台区2014年高三年级第二学期统一练习(二)数学(文科)2014.5第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)sin6000等于(A )12 (B )12- (C )(D )(2)已知数列{}n a 是等差数列,且394a a +=,那么数列{}n a 的前11项和等于(A )22 (B )24 (C )44 (D )48(3)将函数()sin f x x =图象所有的点向右移动3π个单位长度,再将所得各点的横坐标缩短到原来的12倍(纵坐标不变),所得图象的函数解析式为 (A )1sin()23y x =-π (B )1sin()26y x =-π (C )sin(2)3y x =-π (D )sin(2)6y x =-π (4)已知0.20.50.50.3,log 0.8,log 3a b c -===,那么,,a b c 的大小关系是(A ) a b c << (B ) c b a <<(C ) c a b << (D )a c b <<(5)圆C :(x +1)2+(y -3)2=9上有两点P ,Q 关于直线x +my +4=0对称,则m 等于(A )53- (B )53 (C )-1 (D ) 1 (6)已知实数0a ≠,函数22,1,(), 1.x a x f x x x ⎧+<=⎨-≥⎩若(1)(1)f a f a -≥+,则实数a 的取值范围是(A )[2,1](0,)--+∞ (B )[-2,-1] (C )(,0)-∞ (D )(0,)+∞(7)设m ,n 是两条不同的直线,α、β是两个不同的平面.则下列命题中正确的是(A )m ⊥α,n ⊂β,m ⊥n ⇒α⊥β(B )α⊥β,α∩β=m ,n ⊥m ⇒n ⊥β(C )α⊥β,m ⊥α,n ∥β⇒m ⊥n (D )α∥β,m ⊥α,n ∥β⇒m ⊥n(8)设函数()f x 的定义域为D ,如果x D y D ,∀∈∃∈,使得()()f x f y =-成立,则称函数()f x 为“Ω函数”. 给出下列四个函数:①y x =sin ;②2x y =;③11y x =-;④()ln f x x =, 则其中“Ω函数”共有 (A )1个 (B )2个 (C )3个 (D )4个二、填空题:本大题共6小题,每小题5分,共30分。
北京市丰台区2014届高三下学期期中考试[2014丰台一模]
![北京市丰台区2014届高三下学期期中考试[2014丰台一模]](https://img.taocdn.com/s3/m/692b751ded630b1c59eeb5f4.png)
北京市丰台区2014届高三第二学期统一练习(一)英语试卷 2014.3第一部分:听力理解(共三节,30分)第一节(共5小题;每小题l.5分,共7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话你将听一遍。
1. What will the man do tonight?A. Go to a movie.B. Read books.C. Watch TV.2. Where will the bookshelf probably be put?A. Near the window.B. In the bedroom.C. Beside the fireplace.3. What does the man want to be?A. A dancer.B. A singer.C. A waiter.4. Who is the man?A. A taxi driver.B. A policeman.C. A front desk clerk.5. Where are the two speakers?A. In a hospital.B. In a supermarket.C. In a post office.第二节(共10小题;每小题1.5分,共15分)听下面4段对话或独白。
每段对话或独白后有几道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有5秒钟的时间阅读每小题。
听完后,每小题将给出5秒钟的作答时间。
每段对话或独白你将听两遍。
听下面一段对话,回答第6至7两道小题。
6. What is the woman doing?A. Seeing a doctor.B. Doing a survey.C. Making an appointment.7. How does the man keep fit?A. By eating a healthy diet.B. By taking enough sleep.C. By riding the bike to work.听下面一段独白,回答第8至9两道小题。
2014届北京市丰台区高三下学期期中练习(一模)英语试题(含答案)(2014.03)(word版)

北京市丰台区2014届高三第二学期统一练习(一)英语试卷2014.3第一部分:听力理解(共三节,30分)第一节(共5小题;每小题l.5分,共7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话你将听一遍。
1. What will the man do tonight?A. Go to a movie.B. Read books.C. Watch TV.2. Where will the bookshelf probably be put?A. Near the window.B. In the bedroom.C. Beside the fireplace.3. What does the man want to be?A. A dancer.B. A singer.C. A waiter.4. Who is the man?A. A taxi driver.B. A policeman.C. A front desk clerk.5. Where are the two speakers?A. In a hospital.B. In a supermarket.C. In a post office.第二节(共10小题;每小题1.5分,共15分)听下面4段对话或独白。
每段对话或独白后有几道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有5秒钟的时间阅读每小题。
听完后,每小题将给出5秒钟的作答时间。
每段对话或独白你将听两遍。
听下面一段对话,回答第6至7两道小题。
6. What is the woman doing?A. Seeing a doctor.B. Doing a survey.C. Making an appointment.7. How does the man keep fit?A. By eating a healthy diet.B. By taking enough sleep.C. By riding the bike to work.听下面一段独白,回答第8至9两道小题。
北京市丰台区2014—2015学年度第二学期统一练习(一) (理科Word版含答案)

丰台区2014—2015学年度第二学期统一练习(一) 2015.3高三数学(理科)第一部分 (选择题 共40分)选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1. 在复平面内,复数734ii++对应的点的坐标为 (A) (1,1)-(B) (1,1)-(C) 17(,1)25- (D) 17(,1)5- 2.在等比数列}{n a 中,344a a +=,22a =,则公比q 等于(A) -2(B) 1或-2(C) 1(D)1或23.已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程是y =,它的一个焦点坐标为(2,0),则双曲线的方程为(A)22126x y -= (B)22162x y -= (C)2213y x -= (D) 2213x y -= 4.当n =5时,执行如图所示的程序框图,输出的S 值是(A) 7 (B)10 (C) 11(D) 16俯视图侧视图正视图5.在极坐标系中,曲线26cos 2sin 60ρρθρθ--+=与极轴交于A ,B 两点,则A ,B 两点间的距离等于(A)(B)(C) (D) 46.上图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是(A) 4 (B) 5(C)(D)7.将函数1cos()26y x π=-图象向左平移3π个长度单位,再把所得图象上各点的横坐标缩短到原来的一半(纵坐标不变),所得图象的函数解析式是 (A) cos(+)6y x π=(B) 1cos4y x = (C) cos y x =(D) 1cos()43y x π=-8.如图所示,在平面直角坐标系xOy 中,点B ,C 分别在x 轴和y 轴非负半轴上,点A 在第一象限,且90BAC ︒∠=,4AB AC ==,那么O ,A 两点间距离的(A) 最大值是,最小值是4 (B) 最大值是8,最小值是4(C) 最大值是,最小值是2 (D) 最大值是8,最小值是2第二部分 (非选择题 共110分)一、填空题共6小题,每小题5分,共30分. 9.定积分(cos )x x dx π+=⎰____.10.已知二项式2()nx x+的展开式中各项二项式系数和是16,则n =____,展开式中的常数项是____.11.若变量x ,y 满足约束条件40,40,0,y x y x y -≤⎧⎪+-≤⎨⎪-≤⎩则2z x y =+的最大值是____.12.已知函数()f x 是定义在R 上的偶函数,当x ≥0时, 2()2f x x x =-, 如果函数()()g x f x m =- ( m ∈R ) 恰有4个零点,则m 的取值范围 是____.13.如图,AB 是圆O 的直径,CD 与圆O 相切于点D ,AB =8,BC =1,则 CD=____;AD=____.14.已知平面上的点集A 及点P ,在集合A 内任取一点Q ,线段PQ 长度的最小值称为点P 到集合A 的距离,记作(,)d P A .如果集合={(,)|1(01)}A x y x y x +=≤≤,点P 的坐标为(2,0),那么(,)d P A =____;如果点集A 所表示的图形是边长为2的正三角形及其内部,那么点集{|0(,)1}D P d P A =<≤所表示的图形的面积为____.二、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)已知函数21()coscos2222xxx f x ωωω=-(0)ω>的最小正周期为π.(Ⅰ)求ω的值及函数()f x 的最大值和最小值; (Ⅱ)求函数()f x 的单调递增区间.16. (本小题共13分)甲、乙两人为了响应政府“节能减排”的号召,决定各购置一辆纯电动汽车.经了解目前市场上销售的主流纯电动汽车,按续驶里程数R (单位:公里)可分为三类车型,A :80≤R <150,B :150≤R <250, C :R ≥250.甲从A ,B ,C 三类车型中挑选,乙从B ,C 两类车型中挑选,甲、乙二人选择各类车型的概率如下表:若甲、乙都选C 类车型的概率为310. (Ⅰ)求p ,q 的值;(Ⅱ)求甲、乙选择不同车型的概率;记甲、乙两人购车所获得的财政补贴和.为X ,求X 的分布列.17. (本小题共14分)在如图所示的几何体中,四边形ABCD 为正方形,PA ⊥平面ABCD ,PA //BE ,AB =P A =4,BE =2.(Ⅰ)求证:CE //平面PAD ;(Ⅱ)求PD 与平面PCE 所成角的正弦值; (Ⅲ)在棱AB 上是否存在一点F ,使得平面DEF ⊥平面PCE ?如果存在,求AFAB的值; 如果不存在,说明理由.PEDCBA18.(本小题共13分)设函数()x f x e ax =-,x R ∈.(Ⅰ)当2a =时,求曲线()f x 在点(0,(0))f 处的切线方程; (Ⅱ)在(Ⅰ)的条件下,求证: ()0f x >; (Ⅲ)当1a >时,求函数()f x 在[0,]a 上的最大值.19.(本小题共14分)已知椭圆C :22221(0)x y a b a b+=>>的离心率为,右顶点A 是抛物线28y x =的焦点.直线l :(1)y k x =-与椭圆C 相交于P ,Q 两点.(Ⅰ)求椭圆C 的方程;(Ⅱ)如果AM AP AQ =+,点M 关于直线l 的对称点N 在y 轴上,求k 的值.20.(本小题共13分)如果数列A :1a ,2a ,…,m a (Z m ∈,且3)m ≥,满足:①Z i a ∈,22i m ma -≤≤(1,2,,)i m =; ②121m a a a +++=,那么称数列A 为“Ω”数列.(Ⅰ)已知数列M :-2,1,3,-1;数列N :0,1,0,-1,1.试判断数列M ,N 是否为“Ω”数列;(Ⅱ)是否存在一个等差数列是“Ω”数列?请证明你的结论;(Ⅲ)如果数列A 是“Ω”数列,求证:数列A 中必定存在若干项之和为0.(考生务必将答案答在答题卡上,在试卷上作答无效)丰台区2015年高三年级第二学期数学统一练习(一)数 学(理科)参考答案一、填空题:本大题共6小题,每小题5分,共30分.9.22π 10.4,24 11.612.(1,0)- 13.3 14.1,6π+ 注:第10,13,14题第一个空填对得3分,第二个空填对得2分.二、解答题:15.(本小题共13分)解:(Ⅰ)21()coscos2222xxx f x ωωω=+-21sin 232cos 1-++=x x ωω x x ωωc o s 21s i n 23+=)6s i n (πω+=x . 因为πωπ==2T ,0>ω,所以2=ω.因为)62sin()(π+=x x f ,R x ∈,所以1)62sin(1≤+≤-πx .所以函数()f x 的最大值为1,最小值为-1. ……………………8分(Ⅱ)令226222πππππ+≤+≤-k x k )(Z k ∈, 得322322ππππ+≤≤-k x k )(Z k ∈, 所以63ππππ+≤≤-k x k )(Z k ∈.所以函数()f x 的单调递增区间为3[ππ-k ,]6ππ+k )(Z k ∈.……………………13分16.(本小题共13分)解:(Ⅰ)因为33410115q p q =⎧⎪+=⎨+⎪⎪⎪⎩所以25p =,25q =. ……………………4分 (Ⅱ)设“甲、乙选择不同车型”为事件A ,则121233()554545P A ⨯+⨯=+=.答:所以甲、乙选择不同车型的概率是35. ……………………7分 (Ⅲ)X 可能取值为7,8,9,10.111(7)5420P X ==⨯=, 13211(8)54544P X ==⨯+⨯=, 21232(9)54545P X ==⨯+⨯=; 233(10)5410P X ==⨯=.……………………13分17.(本小题共14分) 解:(Ⅰ)设PA 中点为G ,连结EG ,DG .因为PA //BE ,且4PA =,2BE =, 所以BE //AG 且BE AG =,所以四边形BEGA 为平行四边形. 所以EG //AB ,且EG AB =.因为正方形ABCD ,所以CD //AB ,CD AB =所以EG //CD ,且EG CD =. 所以四边形CDGE 为平行四边形. 所以CE //DG .因为DG ⊂平面PAD ,CE ⊄平面PAD ,所以CE //平面PAD . ……………………4分(Ⅱ)如图建立空间坐标系,则(4,0,0)B ,(4,4,0)C ,(4,0,2)E ,(0,0,4)P ,(0,4,0)D ,所以(4,4,4)PC =-,(4,0,2)PE =-,(0,4,4)PD =-.设平面PCE 的一个法向量为(,,)m x y z =,所以00200m PC x y z x z m PE ⎧⋅=+-=⎧⎪⇒⎨⎨-=⋅=⎩⎪⎩.令1x =,则112x y z =⎧⎪=⎨⎪=⎩,所以(1,1,2)m =.设PD 与平面PCE 所成角为α,则sin cos ,6m PD m PD PD mα⋅=<>===. 所以PD与平面P C 所成角的正弦值是. ……………………9分 (Ⅲ)依题意,可设(,0,0)F a ,则(4,0,2)FE a =-,(4,4,2)DE =-.设平面DEF 的一个法向量为(,,)n x y z =,则0220(4)200n DE x y z a x z n FE ⎧⋅=-+=⎧⎪⇒⎨⎨-+=⋅=⎩⎪⎩.令2x =,则224x a y z a =⎧⎪⎪=⎨⎪=-⎪⎩,所以)4,2,2(-=a a n .因为平面DEF ⊥平面PCE ,所以0m n ⋅=,即08222=-++a a,所以4512<=a , 点12(,0,0)5F . 所以35AF AB =. ……………………14分18.(本小题共13分)解:(Ⅰ)当2a =时,()2x f x e x =-,(0)1f =,所以()2x f x e '=-.因为0(0)21f e '=-=-,即切线的斜率为1-, 所以切线方程为1(0)y x -=--,即10x y +-=. ……………………4分(Ⅱ)证明:由(Ⅰ)知()2x f x e '=-.令()0f x '=,则0ln 2x =.当(,ln 2)x ∈-∞时,0)('<x f ,()f x 在(,ln 2)-∞上单调递减, 当(ln 2,)x ∈+∞时,0)('>x f ,()f x 在(ln 2,)+∞上单调递增, 所以当ln 2x =时,函数最小值是ln 2(ln 2)2ln 222ln 20f e =-=->.命题得证. ……………………8分(Ⅲ)因为()x f x e ax =-,所以()x f x e a '=-.令()0f x '=,则ln 0x a =>.当1a >时,设()ln M a a a =-,因为11()10a M a a a-'=-=>, 所以()ln M a a a =-在(1,)+∞上单调递增,且(1)1ln11M =-=,所以()ln 0M a a a =->在(1,)+∞恒成立,即ln a a >. 所以当(0,ln )x a ∈,()0f x '<,()f x 在(0,ln )a 上单调递减;当(ln ,)x a a ∈,()0f x '>,()f x 在(ln ,)a a 上单调递增. 所以()f x 在[0,]a 上的最大值等于{(0),()}max f f a , 因为0(0)01f e a =-⋅=,2()a f a e a =-,不妨设2()()(0)1a h a f a f e a =-=--(1a >), 所以()2a h a e a '=-.由(Ⅱ)知()20a h a e a '=->在(1,)+∞恒成立,所以2()()(0)1a h a f a f e a =-=--在(1,)+∞上单调递增. 又因为12(1)1120h e e =--=->,所以2()()(0)10a h a f a f e a =-=-->在(1,)+∞恒成立,即()(0)f a f >. 所以当1a >时,()f x 在[0,]a 上的最大值为2()a f a e a =-. ……………………13分19.(本小题共14分)解:(Ⅰ)抛物线28y x =,所以焦点坐标为(2,0),即(2,0)A , 所以2a =.又因为c e a ==,所以c = 所以2221b a c =-=, 所以椭圆C的方程为2214x y +=. ……………………4分 (Ⅱ)设11(,)P x y ,22(,)Q x y ,因为AM AP AQ =+,(2,0)A ,所以11(2,)AP x y =-,22(2,)AQ x y =-,所以1212(4,+)AM AP AQ x x y y =+=+-, 所以()12122,M x x y y +-+.由2214(1)x y y k x ⎧+=⎪⎨⎪=-⎩,得2222(41)8440k x k x k +-+-=(判别式0∆>),得2122282224141k x x k k -+-=-=++,121222(2)4+1ky y k x x k -+=+-=, 即2222(,)4141k M k k --++. 设3(0,)N y , 则MN 中点坐标为3221(,)41412y kk k --+++,因为M ,N 关于直线l 对称,所以MN 的中点在直线l 上,所以3221(1)41241k y k k k --+=-++,解得32y k =-,即(0,2)N k -. 由于M ,N 关于直线l 对称,所以M ,N 所在直线与直线l 垂直,所以 222(2)4112041kk k k k ---+⋅=---+,解得2k =±. ……………………14分20.(本小题共13分)解:(Ⅰ)数列M 不是“Ω”数列;数列N 是“Ω”数列. ……………………2分(Ⅱ)不存在一个等差数列是“Ω”数列. 证明:假设存在等差数列是“Ω”数列,则由121m a a a +++= 得12m a a Z m+=∉,与i a Z ∈矛盾, 所以假设不成立,即不存在等差数列为“Ω”数列. ……………………7分 (Ⅲ)将数列A 按以下方法重新排列:设n S 为重新排列后所得数列的前n 项和(n Z ∈且1n m ≤≤),任取大于0的一项作为第一项,则满足1122m mS -+≤≤, 假设当2,n m n N ≤≤∈时,1122n m mS --+≤≤若10n S -=,则任取大于0的一项作为第n 项,可以保证122n m mS -+≤≤,若10n S -≠,则剩下的项必有0或与1n S -异号的一项,否则总和不是1, 所以取0或与1n S -异号的一项作为第n 项,可以保证122n m m S -+≤≤. 如果按上述排列后存在0n S =成立,那么命题得证;否则1S ,2S ,…,m S 这m 个整数只能取值区间[1,]22m m -+内的非0整数, 因为区间[1,]22m m -+内的非0整数至多m -1个,所以必存在i j S S =(1)i j m ≤<≤,那么从第1i +项到第j 项之和为0i j S S -=,命题得证.综上所述,数列A 中必存在若干项之和为0. ……………………13分(若用其他方法解题,请酌情给分)。
【2014丰台一模】北京市丰台区2014届高三下学期期中练习 数学文 Word版含答案
丰台区2013-2014学年度第二学期期中练习高 三 数 学(文科) 2014.3第一部分 (选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的4个选项中,选出符合题目要求的一项。
(1)设集合{|11}A x R x =∈-≤≤,{|(3)0}B x R x x =∈-≤,则A B 等于 (A ) {|13}x R x ∈-≤≤ (B ) {|03}x R x ∈≤≤ (C ) {|10}x R x ∈-≤≤ (D ) {|01}x R x ∈≤≤ (2)已知等比数列{}n a 中,23a a +=1,45a a +=2,则67a a +等于 (A )2 (B )(C )4 (D )(3) 执行如图所示的程序框图,输出的x 值为(A )85 (B )2912 (C )53 (D )138(4)已知函数()f x 是定义在R 上的偶函数,它在[0,)+∞上是减函数. 则下列各式一定成立的是 (A )(0)(6)f f < (B )(3)(2)f f -> (C )(1)(3)f f -> (D )(2)(3)f f -<-(5)设向量a =()21x ,-,b =()14x ,+,则“3x =”是“a //b”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 (6)某企业开展职工技能比赛,并从参赛职工中选1人参加该行业全国技能大 赛.经过6轮选拔,甲、乙两人成绩突出,得分情况如茎叶图所示.若甲乙两 人的平均成绩分别是x 甲,x 乙,则下列说法正确的是 (A )x x >甲乙,乙比甲成绩稳定,应该选乙参加比赛 (B )x x >甲乙,甲比乙成绩稳定,应该选甲参加比赛 (C )x x <甲乙,甲比乙成绩稳定,应该选甲参加比赛(D )x x <甲乙,乙比甲成绩稳定,应该选乙参加比赛 (7) 某三棱锥的三视图如图所示, 该三棱锥的体积是(A) (B) (C) (D)主视图侧视图俯视图(8)在同一直角坐标系中,方程22ax by ab +=与方程0ax by ab ++=表示的曲线可能是(C) (D)(A ) (B)第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
北京市丰台区高三数学下学期期中练习(丰台一模)文 新人教A版
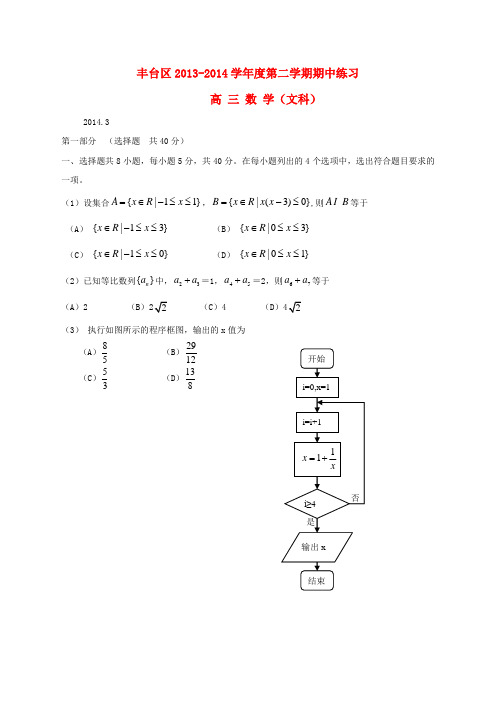
丰台区2013-2014学年度第二学期期中练习高 三 数 学(文科)2014.3第一部分 (选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的4个选项中,选出符合题目要求的一项。
(1)设集合{|11}A x R x =∈-≤≤,{|(3)0}B x R x x =∈-≤,则A B 等于(A ) {|13}x R x ∈-≤≤ (B ) {|03}x R x ∈≤≤ (C ) {|10}x R x ∈-≤≤ (D ) {|01}x R x ∈≤≤ (2)已知等比数列{}n a 中,23a a +=1,45a a +=2,则67a a +等于 (A )2 (B )(C )4 (D )(3) 执行如图所示的程序框图,输出的x 值为(A )85 (B )2912 (C )53 (D )138(4)已知函数()f x 是定义在R 上的偶函数,它在[0,)+∞上是减函数. 则下列各式一定成立的是 (A )(0)(6)f f < (B )(3)(2)f f -> (C )(1)(3)f f -> (D )(2)(3)f f -<-(5)设向量a =()21x ,-,b =()14x ,+,则“3x =”是“a //b ”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 (6)某企业开展职工技能比赛,并从参赛职工中选1人参加该行业全国技能大 赛.经过6轮选拔,甲、乙两人成绩突出,得分情况如茎叶图所示.若甲乙两 人的平均成绩分别是x 甲,x 乙,则下列说法正确的是 (A )x x >甲乙,乙比甲成绩稳定,应该选乙参加比赛 (B )x x >甲乙,甲比乙成绩稳定,应该选甲参加比赛 (C )x x <甲乙,甲比乙成绩稳定,应该选甲参加比赛(D )x x <甲乙,乙比甲成绩稳定,应该选乙参加比赛 (7) 某三棱锥的三视图如图所示, 该三棱锥的体积是(A)(B) (C)(D)主视图侧视图俯视图(8)在同一直角坐标系中,方程22ax by ab +=与方程0ax by ab ++=表示的曲线可能是(A ) (B) (C) (D)第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2014丰台一模北京市丰台区2014届高三第二学期统一练习(一) 理科4份

2014丰台一模语文试卷 (1)英语试卷 (17)高三数学(理科) (40)理科综合 (50)语文试卷2014.3本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分。
本试卷满分共150分。
考试时间150分钟。
第Ⅰ卷(共14分)一、本大题共7小题,每小题2分,共14分。
要研究江南的文化历史,就不能不读江南的古镇。
假若把整个江南比作一曲委婉柔丽、行云流水般的乐章,那么古镇就是一个非常精彩..的乐段。
当你参观了一座座江南的古镇后,就会惊异地发现:这些古镇的设置是那么的规整,(1)假如说长江黄河是孕育华夏文明的摇篮,那么一条条委婉曲流就是滋养古镇文明的清泉;(2)不绝如缕的舟舸,举帆落帆、扬桨收桨之间,就把一座古镇同整个江南人文大背景①得异常和谐熨帖....;(3)一条清流从远方飘逸而来,又从这里委婉流去,缠绵缱绻处就是一座古镇。
街道一律临河铺筑,两排挤挤的房屋把天空夹出细长一条,有一排房屋干脆就是半间建在河面上的吊脚楼,足见其对水的依傍。
青石板铺成的街面,被千万双脚板打磨得发亮,把一段缈远..的历史融凝进去,却不留一丝痕迹。
古街虽窄小,却并不失之于平直②,一条条幽深的小巷细弄,一头勾联着古街,一头曲曲折折地延伸过去,把整个一座古镇引宕得一波三折,有了音乐的节律。
小楼一夜听春雨,。
那绵长清丽....的诗意就该由古镇的小巷里③出来。
而夜卧古镇的吊脚楼上,听“乃”橹音从远处飘来,又从你枕下飘向远方,载去你的遐想和幢憬。
一座座“如虹饮水”的古拱桥,巧连妙构,宛若一帧行草书法,将笔墨酣畅淋漓地挥洒,而其间又有一缕墨韵衔接着,构成了整体的韵律和完美。
1. 文中加点词语有错别字的一项是(2分)A. 精彩B. 和谐熨帖C. 缈远D. 绵长清丽2. 将下列词语依次填入文中横线①②③处,最恰当的一组是(2分)A. 勾织简约演绎B. 勾织简短演绎C. 构画简约演化D. 构画简短演化3. 文中黑体字熟语,运用不当..的一项是(2分)A. 行云流水B. 不绝如缕C. 一波三折D. 酣畅淋漓4. 文中划横线的(1)(2)(3)句衔接不当,下列调整语序正确的一项是(2分)A. (1)(3)(2)B. (2)(1)(3)C. (2)(3)(1)D. (3)(1)(2)5. 将下列诗句填入文中波浪线处,与“小楼一夜听春雨”对仗最工整的一项是(2分)A. 多少楼台烟雨中B. 残花落尽见流莺C. 吹面不寒杨柳风D. 深巷明朝卖杏花6. 下列句中加点词的运用,不同于...其他三句的一项是(2分)A. 一条清流从远处飘逸..而来,又从这里委婉流去B. 那么一条条委婉曲流就是滋养..古镇文明的清泉C. 青石板铺成的街面,被千万双脚板打磨..得发亮D. 又从你枕下飘向远方,载.去你的遐想和憧憬7. 下列概括江南古镇特点的词语,最恰当的一项是(2分)A. 整洁B. 雄丽C. 幽美D. 空蒙第Ⅱ卷(136分)二、本大题共6小题,共20分。
北京市丰台区2014届高三年级第二学期统一练习二理科数学试卷(带解析)

北京市丰台区2014届高三年级第二学期统一练习二理科数学试卷(带解析)1.若复数(1)(2)m m -+-i (m ∈R )是纯虚数,则实数m 等于( ) (A )0 (B )1 (C )2 (D )1或2 【答案】B 【解析】试题分析:复数(1)(2)m m -+-i (m ∈R )是纯虚数,则1020m m -=⎧⎨-≠⎩,所以1m =.故B 正确.考点:纯虚数的定义.2.已知数列{}n a 是等差数列,且394a a +=,那么数列{}n a 的前11项和等于( ) (A )22 (B )24 (C )44 (D )48 【答案】A 【解析】试题分析:由等差数列的性质可知111394a a a a +=+=,则()11111111142222a a S +⨯===.故A 正确.考点:1等差数列的性质;2等差数列的前n 项和公式.3.直线1:0l x y +-=与直线2,2:(2x l t y ⎧=⎪⎪⎨⎪=⎪⎩为参数)的交点到原点O 的距离是( )(A )1 (B(C )2 (D )【答案】C 【解析】试题分析:将直线2l 化普通方程为y x =.解0y xx y =⎧⎪⎨+-=⎪⎩得两直线交点为,此交点到原点的距离为2d ==.故C 正确.考点:1参数方程和普通方程间的互化;2两点间的距离公式.4.将函数2()log (2)f x x =的图象向左平移1个单位长度,那么所得图象的函数解析式为( )(A )2log (21)y x =+ (B )2log (21)y x =- (C )2log (1)1y x =++ (D )2log (1)1y x =-+ 【答案】C 【解析】试题分析:因为2222()log (2)log 2log 1log f x x x x ==+=+,所以将其图象向左平移1个单位长度所得函数解析式为()21log 1y x =++.故C 正确. 考点:1对数函数的运算;2函数图像的平移.5.已知sin()cos2y x x π=+-,则y 的最小值和最大值分别为( ) (A )9,28- (B )-2,98 (C )3,24- (D )-2,34【答案】A 【解析】 试题分析:()22219sin()cos 2sin 12sin 2sin sin 12sin 48y x x x x x x x π⎛⎫=+-=---=--=-- ⎪⎝⎭,因为1sin 1x -≤≤,所以1sin 4x =,min 98y =-,当sin 1x =-时,max 2y =.故A 正确. 考点:1诱导公式、二倍角公式;2二次函数求最值.6.设m ,n 是两条不同的直线,α,β是两个不同的平面.则下列命题中正确的是( ) (A )m ⊥α,n ⊂β,m ⊥n ⇒α⊥β (B )α⊥β,α∩β=m ,n ⊥m ⇒n ⊥β(C )α⊥β,m ⊥α,n ∥β⇒m ⊥n (D )α∥β,m ⊥α,n ∥β⇒m ⊥n 【答案】D【解析】试题分析:试题分析:A 选项中α、β可能平行也可能相交,所以A 不正确;B 选项中n 和β可能平行、可能相交还可能线在面内,所以B 不正确;C 选项中,m n 两直线可能相交、平行或异面,所以C 不正确;D 选项中α∥β,m ⊥αm β⇒⊥,因为n ∥β,所以m n ⊥,故D 正确.考点:线线、线面、面面的位置关系.7.已知抛物线C :)0(22>=p px y 的焦点为F ,过点F 倾斜角为60°的直线l 与抛物线C在第一、四象限分别交于A 、B 两点,则||||BF AF 的值等于( ) (A )2 (B )3 (C )4 (D )5 【答案】B 【解析】试题分析:由抛物线的方程可知焦点,02p F ⎛⎫⎪⎝⎭,直线l 的斜率为tan603k ==l的方程为2p y x ⎫=-⎪⎭,设()()()112212,,,,0,0A x y B x yy y ><.将直线方程和抛物线方程联立削去x并整理可得220y py p -=,解得12,y y p ==.所以123AF y BF y ==.故B 正确. 考点:1直线与抛物线的位置关系;2数形结合思想.8.定义在R 上的函数()f x 和()g x 的导函数分别为'()f x ,'()g x ,则下面结论正确的是( )①若'()'()f x g x >,则函数()f x 的图象在函数()g x 的图象上方;②若函数'()f x 与'()g x 的图象关于直线x a =对称,则函数()f x 与()g x 的图象关于点(a ,0)对称;③函数()()f x f a x =-,则'()'()f x f a x =--; ④若'()f x 是增函数,则1212()()()22x x f x f x f ++≤. (A )①② (B )①②③ (C )③④ (D )②③④【答案】C 【解析】试题分析:①'()'()f x g x >时,说明函数()f x 比函数()g x 增加的快,但函数()f x 的图像不一定在函数()g x 图像的上方,故①不正确;②若函数'()f x 与'()g x 的图象关于直线x a =对称,则()()''2f x g a x =-.假设函数()f x 与()g x 的图像不于(),0a 对称,则()()2f x g a x ≠-,则有()()''2f x g a x ≠-,与()()''2f x g a x =-相矛盾,所以假设不成立,故②不正确;③因为()()f x f a x =-,所以()()'()'()'()''f x f a x f a x a x f a x =-=--=--,故③正确.④由导数的几何意义可知'()f x 是增函数即函数()f x 切线的斜率单调递增,所以函数()f x 是“凹型函数”,则必有1212()()()22x x f x f x f ++≤.故④正确. 综上可得结论正确的是③④.故C 正确.考点:函数的简单性质.9.已知数列{}n a 的前n 项和为31nn S =-,那么该数列的通项公式为n a =_______. 【答案】123n -⨯ 【解析】 试题分析:当1n =时,111312a S ==-=;当2n ≥时()()111313123n n n n n n a S S ---=-=---=⨯,将1n =代入上式可得111232a -=⨯=.综上可得123n n a -=⨯.考点:求数列的通项公式.10.已知一个样本容量为100的样本数据的频率分布直方图如图所示,那么样本数据落在[40,60)内的样本的频数为 ____ ;估计总体的众数为_________.【答案】15;75 【解析】试题分析:由图可知样本数据落在[40,60)内的频率为()0.010.005100.15+⨯=,所以样本数据落在[40,60)内的频数为1000.1515⨯=.频率分布直方图中最高的矩形的中点为75,所以估计总体的众数为75. 考点:频率分布直方图.11.已知圆C :(x+1)2+(y-3)2=9上的两点P ,Q 关于直线x+my+4=0对称,那么m=_________. 【答案】1- 【解析】试题分析:由题意分析可知圆心()1,3-在直线40x my ++=上.将点()1,3-代入直线方程可得1m =-.考点:1数形结合思想;2点关于直线的对称点问题.12.将6位志愿者分配到甲、已、丙3个志愿者工作站,每个工作站2人,由于志愿者特长不同,A 不能去甲工作站,B 只能去丙工作站,则不同的分配方法共有__________种. 【答案】18 【解析】试题分析:分析可知丙工作站除B 外还需要1人,当A 在丙工作站时不同的分配方法有2242431612C C ⨯=⨯=⨯;当A 不在丙工作站时又A 不能去甲工作站则说明A 只能在乙工作站,此时不同的分配方法有()224243121212C A ⨯=⨯⨯=⨯.综上可得不同的分配方法共有61218+=.考点:排列组合.13.已知向量(1,2)a =-,M 是平面区域0,010240x y x y x y ≥≥⎧⎪-+≥⎨⎪+-≤⎩内的动点,O 是坐标原点,则a OM ⋅ 的最小值是 .【答案】3- 【解析】试题分析:设(),M x y ,则(),O M x y =,所以2a OM x y ⋅=-.令2z x y =-.画出点M 所在的平面区域及目标函数线12y x =如图所示:平移目标函数线12y x =使之经过可行域,当目标函数线经过点()1,2B 时,z 取得最小值为min 1223z =-⨯=-.考点:1平面向量数量积公式;2线性规划.14.数列}{n a 的首项为1,其余各项为1或2,且在第k 个1和第1k +个1之间有21k -个2,即数列}{n a 为:1,2,1,2,2,2,1,2,2,2,2,2,1,…,记数列}{n a 的前n 项和为n S ,则20S = __ ;2014S ___ . 【答案】36;3983 【解析】试题分析:由数列可知前20项中有16个2,4个1,所以201624136S =⨯+⨯=.将第k 个1和它后边的21k -个2组成一组,记为第k 组.则第k 组中所含的元素个数为1212k b k k =+-=,所以()12324621k b b b b k k k ++++=++++=+L L ,当44k =时,44⨯=,所以()()19804418744121358744239162S +=⨯+++++=+⨯=L .因为2014198034-=,所以2014198013323916673983S S =++⨯=+=. 考点:等差数列的前n 项和公式.。
【丰台一模】北京市丰台区届高三下学期期中练习 语文 Word版含答案

北京市丰台区2014届高三第二学期统一练习(一) 语文试卷 2014.3 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分。
本试卷满分共150分。
考试时间150分钟。
第Ⅰ卷(共14分) 一、本大题共7小题,每小题2分,共14分。
要研究江南的文化历史,就不能不读江南的古镇。
假若把整个江南比作一曲委婉柔丽、行云流水般的乐章,那么古镇就是一个非常精彩的乐段。
当你参观了一座座江南的古镇后,就会惊异地发现:这些古镇的设置是那么的规整,(1)假如说长江黄河是孕育华夏文明的摇篮,那么一条条委婉曲流就是滋养古镇文明的清泉;(2)不绝如缕的舟舸,举帆落帆、扬桨收桨之间,就把一座古镇同整个江南人文大背景 ① 得异常和谐熨帖;(3)一条清流从远方飘逸而来,又从这里委婉流去,缠绵缱绻处就是一座古镇。
街道一律临河铺筑,两排挤挤的房屋把天空夹出细长一条,有一排房屋干脆就是半间建在河面上的吊脚楼,足见其对水的依傍。
青石板铺成的街面,被千万双脚板打磨得发亮,把一段缈远的历史融凝进去,却不留一丝痕迹。
古街虽窄小,却并不失之于平直 ② ,一条条幽深的小巷细弄,一头勾联着古街,一头曲曲折折地延伸过去,把整个一座古镇引宕得一波三折,有了音乐的节律。
小楼一夜听春雨, 。
那绵长清丽的诗意就该由古镇的小巷里 ③ 出来。
而夜卧古镇的吊脚楼上,听“乃”橹音从远处飘来,又从你枕下飘向远方,载去你的遐想和幢憬。
一座座“如虹饮水”的古拱桥,巧连妙构,宛若一帧行草书法,将笔墨酣畅淋漓地挥洒,而其间又有一缕墨韵衔接着,构成了整体的韵律和完美。
1. 文中加点词语有错别字的一项是(2分)A. 精彩B. 和谐熨帖C. 缈远D. 绵长清丽 2. 将下列词语依次填入文中横线①②③处,最恰当的一组是(2分)A. 勾织 简约 演绎B. 勾织 简短 演绎C. 构画 简约 演化D. 构画 简短 演化 3. 文中黑体字熟语,运用不当的一项是(2分)A. 行云流水B. 不绝如缕C. 一波三折D. 酣畅淋漓 4. 文中划横线的(1)(2)(3)句衔接不当,下列调整语序正确的一项是(2分)A. (1)(3)(2)B. (2)(1)(3)C. (2)(3)(1)D. (3)(1)(2) 5. 将下列诗句填入文中波浪线处,与“小楼一夜听春雨”对仗最工整的一项是(2分)A. 多少楼台烟雨中B. 残花落尽见流莺C. 吹面不寒杨柳风D. 深巷明朝卖杏花 6. 下列句中加点词的运用,不同于其他三句的一项是(2分) A. 一条清流从远处飘逸而来,又从这里委婉流去 B. 那么一条条委婉曲流就是滋养古镇文明的清泉 C. 青石板铺成的街面,被千万双脚板打磨得发亮 D. 又从你枕下飘向远方,载去你的遐想和憧憬 7. 下列概括江南古镇特点的词语,最恰当的一项是(2分)A. 整洁B. 雄丽C. 幽美D. 空蒙 第Ⅱ卷(136分) 二、本大题共6小题,共20分。
2014北京市丰台区高三(一模)数 学(文)

2014北京市丰台区高三(一模)数学(文)一、选择题共8小题,每小题5分,共40分.在每小题列出的4个选项中,选出符合题目要求的一项.1.(5分)设集合A={x∈R|﹣1≤x≤1},B={x∈R|x(x﹣3)≤0},则A∩B等于()A.{x∈R|﹣1≤x≤3} B.{x∈R|0≤x≤3} C.{x∈R|﹣1≤x≤0} D.{x∈R|0≤x≤1}2.(5分)已知等比数列{a n}中,a2+a3=1,a4+a5=2,则a6+a7等于()A.2 B.2 C.4 D.43.(5分)执行如图所示的程序框图,输出的x值为()A.B.C.D.4.(5分)已知函数f(x)是定义在R上的偶函数,它在[0,+∞)上是减函数.则下列各式一定成立的是()A.f(0)<f(6)B.f(﹣3)>f(2) C.f(﹣1)>f(3) D.f(﹣2)<f(﹣3)5.(5分)设向量=(2,x﹣1),=(x+1,4),则“x=3”是“∥”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件6.(5分)某企业开展职工技能比赛,并从参赛职工中选1人参加该行业全国技能大赛.经过6轮选拔,甲、乙两人成绩突出,得分情况如茎叶图所示.若甲乙两人的平均成绩分别是,,则下列说法正确的是()A.>,乙比甲成绩稳定,应该选乙参加比赛B.>,甲比乙成绩稳定,应该选甲参加比赛C.<,甲比乙成绩稳定,应该选甲参加比赛D.<,乙比甲成绩稳定,应该选乙参加比赛7.(5分)某三棱锥的三视图如图所示,该三棱锥的体积是()A.18B.36C.12D.248.(5分)在同一直角坐标系中,方程ax2+by2=ab与方程ax+by+ab=0表示的曲线可能是()A.B. C.D.二、填空题共6小题,每小题5分,共30分.9.(5分)已知tanα=2,则的值为.10.(5分)复数在复平面内对应的点的坐标是.11.(5分)以点(﹣1,1)为圆心且与直线x﹣y=0相切的圆的方程为.12.(5分)已知函数f(x)=2x,点P(a,b)在函数y=(x>0)图象上,那么f(a)•f(b)的最小值是.13.(5分)A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B 机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行公里.14.(5分)设不等式组表示的平面区域为M,不等式组(0≤t≤4)表示的平面区域为N.在M内随机取一个点,这个点在N内的概率为P.①当t=1时,P= ;②P的最大值是.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(13分)已知函数f(x)=2cos2x﹣sin(π+2x)﹣1.(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)求函数f(x)在区间[0,]上的最小值和最大值.16.(13分)年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:健康指数 2 1 0 ﹣160岁至79岁的人数120 133 34 1380岁及以上的人数9 18 14 9其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,﹣1代表“生活不能自理”.(Ⅰ)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是多少?(Ⅱ)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.17.(14分)如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.(Ⅰ)当E为线段BC中点时,求证:NC∥平面AEF;(Ⅱ)求证:平面AEF⊥BCMN平面;(Ⅲ)设=λ,写出λ为何值时MF⊥平面AEF(结论不要求证明).18.(13分)已知曲线f(x)=ax﹣e x(a>0).(Ⅰ)求曲线在点(0,f(0))处的切线;(Ⅱ)若存在实数x0使得f(x0)≥0,求a的取值范围.19.(14分)如图,已知椭圆E:+=1(a>b>0)的离心率为,过左焦点F(﹣,0)且斜率为k的直线交椭圆E于A,B两点,线段AB的中点为M,直线l:x+4ky=0交椭圆E于C,D两点.(Ⅰ)求椭圆E的方程;(Ⅱ)求证:点M在直线l上;(Ⅲ)是否存在实数k,使得四边形AOBC为平行四边形?若存在求出k的值,若不存在说明理由.20.(13分)从数列{a n}中抽出一些项,依原来的顺序组成的新数列叫数列{a n}的一个子列.(Ⅰ)写出数列{3n﹣1}的一个是等比数列的子列;(Ⅱ)设{a n}是无穷等比数列,首项a1=1,公比为q.求证:当0<q<1时,数列{a n}不存在是无穷等差数列的子列.数学试题答案一、选择题共8小题,每小题5分,共40分.在每小题列出的4个选项中,选出符合题目要求的一项.1.【解答】B={x∈R|x(x﹣3)≤0}={x∈R|0≤x≤3},则A∩B={x∈R|0≤x≤1},故选:D.2.【解答】设等比数列{a n}的公比为q,则q2==2,∴a6+a7=(a4+a5)q2=2×2=4故选:C3.【解答】由程序框图知:程序第一次运行i=0+1=1,x=1+=2;第二次运行i=1+1=2,x=1+=;第三次运行i=2+1=3,x=1+=;第四次运行i=3+1=4,x=1+=.满足条件i≥4,输出x=.故选:A.4.【解答】∵函数f(x)是定义在R上的偶函数,且在[0,+∞)上是减函数;∴当0<6时,f(0)>f(6),∴命题A错误;又∵f(﹣3)=f(3),且3>2,∴f(3)<f(2),命题B错误;又∵f(﹣1)=f(1),且1<3,∴f(1)>f(3),即f(﹣1)>f(3),∴命题C正确;又∵f(﹣2)=f(2),f(﹣3)=f(3),且2<3,∴f(2)>f(3),即f(﹣2)>f(﹣3),∴命题D错误;故选:C.5.【解答】当时,有2×4﹣(x﹣1)(x+1)=0,解得x=±3;因为集合{3}是集合{3,﹣3}的真子集,故“x=3”是“”的充分不必要条件.故选A6.【解答】有茎叶图中的数据可知,甲的数据主要集中85以下,乙的数据主要集中在86以上,∴根据数据分布可知<,乙比甲成绩稳定,故选:乙参加比较,故选:D.7.【解答】由三视图知:几何体是三棱锥,且三棱锥的高为6,底面三角形的底边长为3+3=6,高为3,∴几何体的体积V=××6××6=18.故选:A.8.【解答】方程ax2+by2=ab 即;方程ax+by+ab=0,即y=﹣x﹣a.考察A选项,椭圆的焦点在x轴上,即b>a>0,直线的斜率小于0,此时方程ax+by+ab=0的斜率﹣<0,符合题意;考察B选项,椭圆的焦点在y轴上,即a>b>0,直线的斜率大于0,但此时方程ax+by+ab=0的斜率﹣<0,不符合题意;考察C选项,双曲线的焦点在y轴上,则a>0,b<0,直线的斜率大于0,此时方程ax+by+ab=0的斜率﹣>0,但截距﹣a<0,不符合题意;考察D选项,双曲线的焦点在x轴上,则b>0,a<0,直线的斜率小于0,但此时方程ax+by+ab=0的斜率﹣>0,不符合题意;故选:A.二、填空题共6小题,每小题5分,共30分.9.【解答】∵tanα=2,∴===,故答案为:.10.【解答】=.∴复数在复平面内对应的点的坐标是.故答案为:.11.【解答】设点(﹣1,1)为圆心的圆的半径为r,依题意知,圆心(﹣1,1)到直线x﹣y=0的距离d=r==,∴所求的圆的方程为:(x+1)2+(y﹣1)2=2.故答案为:(x+1)2+(y﹣1)2=2.12.【解答】∵P(a,b)在函数y=(x>0)图象上,∴b=,即ab=1,∴f(a)•f(b)==22=4,即f(a)•f(b)的最小值是4,故答案为:413.【解答】设机场到甲地的距离为s,则A机的速度是(公里/小时),B机的速度是:(公里/小时),B机每小时比A机多飞行=20公里.故答案为:20.14.【解答】①不等式组表示的平面区域为M,则对应三角形的面积S M=.不等式组(0≤t≤4)表示的平面区域为矩形,则对应的矩形面积为2t(4﹣t)=﹣2t2+8t=﹣2(t﹣2)2+8,当t=1时,对应的面积S1=2×3=6,此时对应的概率P=.②当t=2时,区域N的面积最大为8,此时区域N的最大面积为8,则由几何概型的概率公式可知P的最大值是,故答案为:①,②.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.【解答】(Ⅰ)函数f(x)=2cos2x﹣sin(π+2x)﹣1=cos2x+sin2x=sin(2x+),∴函数的周期为T==π.(Ⅱ)∵x∈[0,],∴2x+∈[,],∴sin(2x+)∈[﹣,1],∴当2x+=时,函数f(x)取得最小值为﹣1,当2x+=时,函数f(x)取得最大值为.16.【解答】(Ⅰ)该小区80岁以下老龄人生活能够自理的频率为,所以该小区80岁以下老龄人生活能够自理的概率约为.(Ⅱ)该小区健康指数大于0的老龄人共有280人,健康指数不大于0的老龄人共有70人,由分层抽样可知,被抽取的5位老龄人中有4位健康指数大于0,有1位健康指数不大于0.设被抽取的4位健康指数大于0的老龄人为1,2,3,4,健康指数不大于0的老龄人为B.从这五人中抽取3人,结果有10种:(1,2,3),(1,2,4),(1,2,B),(1,3,4),(1,3,B),(1,4,B),(2,3,4),(2,3,B),(2,4,B),(3,4,B,),其中恰有一位老龄人健康指数不大于0的有6种:(1,2,B),(1,3,B),(1,4,B),(2,3,B),(2,4,B),(3,4,B,),∴被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率为.17.【解答】(Ⅰ)证明:∵F为线段NB的中点,E为线段BC中点,∴NC∥EF,又NC不包含平面AEF,EF⊂平面AEF,∴NC∥平面AEF.(4分)(Ⅱ)证明:四边形ABCD与四边形ADMN都为正方形,∴AD⊥NA,AD⊥AB,NA∩AB=A,∴AD⊥平面NAB,AF⊂平面NAB,故AD⊥AF,AD∥BC,∴BC⊥AF,由题意NA=AB,F为线段NB的中点,∴AF⊥NB,NB∩BC=B,∴AF⊥平面BCMN,∵AF⊂平面AEF,∴平面AEF⊥平面BCMN.(11分)(Ⅲ)解:λ=时,MF⊥平面AEF.(14分)18.【解答】(Ⅰ)∵f(x)=ax﹣e x(a>0),∴f(0)=﹣1,则切点为(0,﹣1).f′(x)=a﹣e x,f′(0)=a﹣1,∴曲线在点(0,f(0))处的切线方程为:y=(a﹣1)x﹣1;(Ⅱ)∵a>0,由f′(x)>0得,x<lna,由f′(x)<0得,x>lna,∴函数f(x)在(﹣∞,lna)上单调递增,在(lna,+∞)上单调递减,∴f(x)的最大值为f(lna)=alna﹣a.∵存在x0使得f(x0)≥0,∴alna﹣a≥0,∴a≥e.19.【解答】(Ⅰ)解:由题意可知,c=,于是a=2,∴.∴椭圆的标准方程为;(Ⅱ)证明:设A(x1,y1),B(x2,y1),M(x0,y0),由,即.,,,于是.∵,∴M在直线l上;(Ⅲ)设存在这样的平行四边形,则M为OC中点,设点C的坐标为(x3,y3),则.∵,解得.于是,解得,即.∴当时四边形AOBC的对角线互相平分,即当时四边形AOBC是平行四边形.20.【解答】(Ⅰ)解:数列{3n﹣1}中的2,8,32是一个等比数列,∵,,a3=32=22×3﹣1,由此猜想,∴数列{3n﹣1}的一个是等比数列的子列为{22n﹣1}.(若只写出2,8,32三项.给满分).(5分)(Ⅱ)证明:假设存在是等差数列的子列{b n},∵a1=1,0<q<1,∴,且数列{a n}是递减数列,∴{b n}也为递减数列且b n∈(0,1],d<0,令b1+(n﹣1)d<0,得n>1﹣,即存在n∈N*(n>1),使得b n<0,这与b n∈(0,1]矛盾.∴数列{a n}不存在是无穷等差数列的子列.(13分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
丰台区2013-2014学年度第二学期期中练习高 三 数 学(文科) 2014.3第一部分 (选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的4个选项中,选出符合题目要求的一项。
(1)设集合{|11}A x R x =∈-≤≤,{|(3)0}B x R x x =∈-≤,则A B 等于(A ) {|13}x R x ∈-≤≤ (B ) {|03}x R x ∈≤≤ (C ) {|10}x R x ∈-≤≤ (D ) {|01}x R x ∈≤≤ (2)已知等比数列{}n a 中,23a a +=1,45a a +=2,则67a a +等于 (A )2 (B )(C )4 (D )(3) 执行如图所示的程序框图,输出的x 值为 (A )85 (B )2912(C )53 (D )138(4)已知函数()f x 是定义在R 上的偶函数,它在[0,)+∞上是减函数. 则下列各式一定成立的是(A )(0)(6)f f < (B )(3)(2)f f -> (C )(1)(3)f f -> (D )(2)(3)f f -<-(5)设向量a =()21x ,-,b =()14x ,+,则“3x =”是“a //b ”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 (6)某企业开展职工技能比赛,并从参赛职工中选1人参加该行业全国技能大 赛.经过6轮选拔,甲、乙两人成绩突出,得分情况如茎叶图所示.若甲乙两 人的平均成绩分别是x 甲,x 乙,则下列说法正确的是 (A )x x >甲乙,乙比甲成绩稳定,应该选乙参加比赛 (B )x x >甲乙,甲比乙成绩稳定,应该选甲参加比赛 (C )x x <甲乙,甲比乙成绩稳定,应该选甲参加比赛(D )x x <甲乙,乙比甲成绩稳定,应该选乙参加比赛 (7) 某三棱锥的三视图如图所示, 该三棱锥的体积是(A) (B) (C) (D)主视图侧视图俯视图(8)在同一直角坐标系中,方程22ax by ab +=与方程0ax by ab ++=表示的曲线可能是(A ) (B) (C) (D)第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
(9)已知tan 2=α,则sin cos sin cos -+αααα的值为_______________.(10)复数2ii+在复平面内对应的点的坐标是____________. (11) 以点(-1,1)为圆心且与直线0x y -=相切的圆的方程为____________________. (12)已知函数()2x f x =,点P(,a b )在函数1(0)y x x=>图象上,那么()()f a f b ⋅ 的最小值是____________.(13) A ,B 两架直升机同时从机场出发,完成某项救灾物资空投任务.A 机到达甲地 完成任务后原路返回;B 机路过甲地,前往乙地完成任务后原路返回.图中折线分别表示A ,B 两架直升机离甲地的距离s 与时间t 之间的函数关系. 假设执行任务过程中A,B 均匀速直线飞行,则B 机每小时比A 机多飞行 公里.(14)设不等式组40,40,0x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩表示的平面区域为M ,不等式组,(04)04t x t t y t -≤≤⎧≤≤⎨≤≤-⎩表示的平面区域为N.在M 内随机取一个点,这个点在N 内的概率为P .①当1t =时,P=__________;② P 的最大值是_________.三、解答题共6小题,共80分。
解答应写出文字说明,演算步骤或证明过程。
(15)(本题共13分)已知函数2()2cos sin(2)1f x x x π=-+-. (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)求函数()f x 在区间[0,]2π上的最小值和最大值.(16)(本题共13分)年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人, 他们的健康状况如下表:其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”。
(Ⅰ)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是 多少?(Ⅱ)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5 位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的 健康指数不大于0的概率.(17)(本题共14分)如图,四边形ABCD 与四边形ADMN 都为正方形,AN AB ⊥,F 为线段BN 的中点,E 为线段BC 上的动点.(Ⅰ)当E 为线段BC 中点时,求证://NC 平面AEF ; (Ⅱ)求证:平面AEF ⊥BCMN 平面; (Ⅲ)设BEBC=λ,写出λ为何值时MF ⊥平面AEF(结论不要求证明).(18)(本题共13分)已知曲线()x f x ax e =-(0)a >. (Ⅰ)求曲线在点(0,(0)f )处的切线;(Ⅱ)若存在实数0x 使得0()0f x ≥,求a 的取值范围.(19)(本题共14分)如图,已知椭圆E: 22221(0)x y a b a b +=>>,过左焦点(F 且斜率为k的直线交椭圆E 于A,B 两点,线段AB 的中点为M,直线l :40x ky +=交椭圆E 于C,D 两点. (Ⅰ)求椭圆E 的方程;(Ⅱ)求证:点M 在直线l 上;(Ⅲ)是否存在实数k ,使得四边形AOBC 为平行四边形?若存在求出k 的值,若不存在说明理由.(20)(本题共13分)从数列{}n a 中抽出一些项,依原来的顺序组成的新数列叫数列{}n a 的一个子列. (Ⅰ)写出数列{31}n -的一个是等比数列的子列;(Ⅱ)设{}n a 是无穷等比数列,首项11a =,公比为q .求证:当01q <<时,数列{}n a 不存在是无穷等差数列的子列.丰台区2014年高三年级第二学期统一考试(一)数学(文科)答案 2014.3一、选择题二、填空题 9.13 10. 12,55⎛⎫ ⎪⎝⎭11. ()()22112x y ++-= 12. 4 13. 20 14. 38;12三、解答题 (15)解:(Ⅰ)()cos 2sin 2)4f x x x x π=+=+22T ππ∴==.---------------------------------------------------------------7分 (Ⅱ)0,2x π⎡⎤∈⎢⎥⎣⎦, 52,444x πππ⎡⎤∴+∈⎢⎥⎣⎦sin(2)4x π⎡⎤∴+∈⎢⎥⎣⎦5244x ∴+=ππ即2x π=时,()f x 的最小值为1-,242x +=ππ即8x π=时,()f x . -------------------------13分(16)解:(Ⅰ)该小区80岁以下老龄人生活能够自理的频率为120133342871201333413300++=+++,所以该小区80岁以下老龄人生活能够自理的概率约为287300.-----------5分(Ⅱ)该小区健康指数大于0的老龄人共有280人,健康指数不大于0的老龄人 共有70人,所以被抽取的5位老龄人中有4位健康指数大于0,有1位健康 指数不大于0.设被抽取的4位健康指数大于0的老龄人为, 健康指数不大于0的老龄人为B. 从这五人中抽取3人,结果有10种: ,,,,,,,,,其中恰有一位老龄人健康指数不大于0的有6种: ,,,,,所以被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率为. -----------------13分(17) (Ⅰ)证明:F 为线段NB 的中点, E 为线段BC 中点 所以又NC ⊄平面AEF, EF ⊆平面AEF 所以//NC 平面AEF-----------------------------------------------------------------4分 (Ⅱ)证明:四边形ABCD 与四边形ADMN 都为正方形 所以AD ⊥NA ,AD ⊥AB NAAB A =,所以AD ⊥平面NABAF ⊆平面NAB ,故AD ⊥AF //AD BC ,所以BC AF ⊥由题意NA =AB ,F 为线段NB 的中点 所以AF NB ⊥NB BC B =,所以AF ⊥平面BCMNAF ⊆平面AEF所以平面AEF ⊥平面BCMN .-------------------------------------------11分 (Ⅲ)12λ=--------------------------------------------------------------------14分 (18)解:(Ⅰ)因为(0)1f =-,所以切点为(0,-1). ()x f x a e '=-,(0)1f a '=-,所以曲线在点(0,(0)f )处的切线方程为:y=(a-1)x-1.---------------4分(Ⅱ)因为a>0,由()0f x '>得,ln x a <,由()0f x '<得,ln x a >,所以函数()f x 在(,ln )a -∞上单调递增,在(ln ,)a +∞上单调递减,所以()f x 的最大值为(ln )ln f a a a a =-.因为存在0x 使得0()0f x ≥,所以ln 0a a a -≥,所以a e ≥.----------13分 19. 解:(Ⅰ)由题意可知c e a ==c =2,1a b ==. 所以,椭圆的标准方程为2214x y +=程.---------------------------------3分(Ⅱ)设11(,)A x y ,22(,)B x y ,00(,)M x y ,22(14y k x x y ⎧=+⎪⎨+=⎪⎩即2222(41)1240k x x k +++-=.所以,12x x +=,1202x x x +==,00(y k x =+=,于是M ∴.40k +=,所以M 在直线l 上.---------------------------9分 (Ⅲ)设存在这样的平行四边形,则M 为OC 中点设点C 的坐标为33(,)x y ,则302y y =.因为22414x kyx y =-⎧⎪⎨+=⎪⎩,解得3y ==,解得218k =,即k =. 所以,当k =时四边形AOBC 的对角线互相平分,即当k =时四边形AOBC 是平行四边形.------------------------------------------------14分 (20)解: (Ⅰ)212n n a -=(若只写出2,8,32三项.给满分).----------------------------------5分(Ⅱ)证明:假设存在是等差数列的子列{}n b ,11,01a q =<<1(0,1]n n a q -∴=∈,且数列{}n a 是递减数列,所以{}n b 也为递减数列且n b ∈(0,1],0d <, 令1(1)0b n d +-<,得111b n d>->, 即存在*(1)n N n ∈>使得0n b <,这与n b ∈(0,1]矛盾.所以数列{}n a 不存在是无穷等差数列的子列.----------------------------13分。
