利用Matlab进行环肋肋效率数值计算
Matlab中常用的数值计算方法

Matlab中常用的数值计算方法数值计算是现代科学和工程领域中的一个重要问题。
Matlab是一种用于数值计算和科学计算的高级编程语言和环境,具有强大的数值计算功能。
本文将介绍Matlab中常用的数值计算方法,包括数值积分、数值解微分方程、非线性方程求解和线性方程组求解等。
一、数值积分数值积分是通过数值方法来近似计算函数的定积分。
在Matlab中,常用的数值积分函数是'quad'和'quadl'。
'quad'函数可以用于计算定积分,而'quadl'函数可以用于计算无穷积分。
下面是一个使用'quad'函数计算定积分的例子。
假设我们想计算函数f(x) = x^2在区间[0, 1]上的定积分。
我们可以使用如下的Matlab代码:```f = @(x) x^2;integral = quad(f, 0, 1);disp(integral);```运行这段代码后,我们可以得到定积分的近似值,即1/3。
二、数值解微分方程微分方程是描述自然界各种变化规律的数学方程。
在科学研究和工程应用中,常常需要求解微分方程的数值解。
在Matlab中,可以使用'ode45'函数来求解常微分方程的数值解。
'ode45'函数是采用基于Runge-Kutta方法的一种数值解法。
下面是一个使用'ode45'函数求解常微分方程的例子。
假设我们想求解一阶常微分方程dy/dx = 2*x,初始条件为y(0) = 1。
我们可以使用如下的Matlab代码:```fun = @(x, y) 2*x;[x, y] = ode45(fun, [0, 1], 1);plot(x, y);```运行这段代码后,我们可以得到微分方程的数值解,并绘制其图像。
三、非线性方程求解非线性方程是指方程中包含非线性项的方程。
在很多实际问题中,我们需要求解非线性方程的根。
MATLAB在导热问题中的应用

分类号密级U D C 编号本科毕业论文(设计) 题目MATLAB在导热问题中的运用所在院系数学与数量经济学院专业名称信息与计算科学年级 05级学生姓名朱赤学号 **********指导教师周瑾二00九年四月文献综述1、概述MATLAB是一个为科学和工程计算而专门设计的高级交互式的软件包。
它集数值分析、矩阵运算、信号处理和图形显示于一体,构成了一个方便的、界面友好的用户环境。
在这个环境下,对所要求解的问题,用户只需简单的列出数学表达式,其结果便以数值或图形方式显示出来。
MATLAB中有大量的命令和事先定义的可用函数集,也可通称为MATLAB的M文件,这就使得用它来求解问题通常比传统编程快得多;另外一点,也是它最重要的特点,易于扩展。
它允许用户自行建立完成指定功能的M文件。
从而构成适合于其它领域的工具箱。
MATLAB既是一种编程环境,又是一种程序设计语言。
它与其它高级程序设计语言C、Fortran等一样,也有其内定的规则,但其规则更接近于数学表示,使用起来更为方便,避免了诸如C、Fortran语言的许多限制,比方说,变量、矩阵无须事先定义;其次,它的语句功能之强大,是其它语言所无法比拟的,再者,MATLAB提供了良好的用户界面,许多函数本身会自动绘制出图形,而且会自动选取坐标刻度。
传热学是一门研究由温差引起的热能传递规律的科学,其理论和技术在生产、科学研究等领域得到了广泛的应用。
在能源动力、建筑建材及机械等传统工业部门中,传热学理论的应用解决了这些部门生产过程的热工艺技术,而在新能源利用、军事高科技等新技术领域中,它甚至对一些关键技术起到了决定性作用。
传热过程是传热学研究最基本的过程之一,传统的数学分析解法只能解决相对简单的传热问题,而在解决复杂的实际传热问题时,数学描述和求解都很困难。
随着计算机技术的兴起,解偏微分方程组等早期不能被很好解决或模拟的部分已逐渐被人们完成。
同时,计算机技术的发展,尤其是MATLAB的出现,不但解决了很多较复杂的问题,也大大促进了传热学理论的发展。
matlab中calculate的用法

MATLAB中calculate的用法1.介绍M A TL AB是一种强大的数值计算和科学编程环境,广泛应用于工程、科学和数学领域。
其中,c al cu la te(计算)是MA TL AB中最常用的功能之一。
本文将详细介绍M AT LA B中ca lc ul a te的用法,包括基本的计算操作、数学函数的应用等。
2.基本的计算操作在M AT LA B中,可以使用ca lc ul at e通过基本的算术运算符进行各种计算操作。
以下是一些常用的计算操作及其示例代码:2.1加法和减法加法和减法是最基本的计算操作之一。
可以使用加法运算符(+)进行两个数的相加,使用减法运算符(-)进行两个数的相减。
示例代码:```m at la ba=5;b=3;r e su lt_a dd it io n=a+b;%加法r e su lt_s ub tr ac tio n=a-b;%减法```2.2乘法和除法乘法和除法也是常用的计算操作之一。
可以使用乘法运算符(*)进行两个数的相乘,使用除法运算符(/)进行两个数的相除。
示例代码:```m at la ba=5;b=3;r e su lt_m ul ti pl ica t io n=a*b;%乘法r e su lt_d iv is io n=a/b;%除法```2.3幂运算幂运算可以使用乘方运算符(^)进行,可以计算一个数的任意次幂。
示例代码:```m at la ba=2;b=3;r e su lt_p ow er=a^b;%幂运算```2.4取余运算取余运算可以使用取余运算符(m od)进行,可以计算两个数相除后的余数。
示例代码:```m at la ba=7;b=3;r e su lt_r em ai nd er=m od(a,b);%取余运算```3.数学函数的应用除了基本的计算操作,M AT LA B还提供了许多强大的数学函数,可以实现更复杂的计算。
以下是一些常用的数学函数及其示例代码:3.1平方根可以使用sq rt函数来计算一个数的平方根。
基于BP-GA算法的环肋锥柱壳多目标优化设计

Vol. 43, No. 2Feb., 2021第43卷第2期2021年2月舰船科学技术SHIP SCIENCE AND TECHNOLOGY基于BP-GA 算法的环肋锥柱壳多目标优化设计李艳萍,黄小平(上海交通大学船舶海洋与建筑工程学院,上海200240)摘 要:本文以超大潜深的潜艇耐压壳结构为研究对象,利用排水量表达式估算潜艇主尺度。
通过Ansys 软件的Apdl 语言建立环肋锥柱壳的有限元模型,并分析计算耐压壳的强度及稳定性。
以肋骨间距、耐压壳厚度和肋骨尺寸作为离散设计变量,以结构重量、总体失稳临界压力作为优化目标,实现基于神经网络和遗传算法的环肋锥柱壳多目标优化设计。
在Matlab 平台上,首先用拉丁超立方体抽样,再用BP 神经网络建立起样本点和目标函数之 间的映射关系,构建神经网络代理模型,最后调用多目标优化函数gamultiobj 进行优化。
优化结果表明,利用BP 神经网络和遗传算法相结合进行复杂模型环肋锥柱壳的多目标优化,效率较高,精度较好,达到较理想的优化效果。
关键词:超大潜深;环肋锥柱壳;BP 神经网络;遗传算法;优化设计中图分类号:U674.76文献标识码:A文章编号:1672 - 7649(2021)02 - 0006 - 07 doi : 10.3404/j.issn,1672 - 7649.2021.02.002Multi-objective optimization design of ring-stiffenedcone-cylinder shell based on BP-GA algorithmLI Yan-ping, HUANG Xiao-ping(School of N aval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China)Abstract: In this paper, a ultra-deep submarine pressure shell is taken as the research object, and the main scales of thesubmarine are estimated by using the displacement expression. The finite element model of the ring stiffened cone shell was established by the APDL language of Ansys software, and the strength and stability of the pressure shell were analyzed. The stiffener spacing, the pressure shell thickness and the stiffener size are taken as discrete design variables. The structuralweight and the overall instability critical pressure are used as the optimization targets to realize the multi-objective optimiza tion design of the ring stiffened cone shell based on neural network and genetic algorithm. Using the Matlab, Latin hyper cube is firstly sampled, and then the BP neural network is used to establish the mapping relationship between the samplepoints and the objective function, and the neural network proxy model is constructed. Finally, the multi-objective optimiza tion function gamultiobj is called to optimize. The optimization results show that BP neural network cooperated with geneticalgorithm in solving the multi-objective optimization of complex ring stiffened cone shells are good in efficiency and preci sion.Key words: ultra deepth ; ring stiffened cone shell ; BP neural network ; genetic algorithm ; optimization design0引言潜艇具有侦察、攻击、掩护等多种功能,是大国海军不可或缺的战略性武器。
matlab数值计算()(PDF)

1.1 数值差分与差商 在MATLAB中,没有直接提供求数值导数的函数,只
有计算向前差分的函数diff,其调用格式为:
DX=diff(X):计算向量X的向前差分,即: DX(i)=X(i+1)-X(i),i=1,2,…,n-1。
注意:s1fft是关于N/2共轭对称的!
其中一组信号(蓝色曲线为滤波后的数据)
滤波用的matlab程序:
Flow=5; %不是5Hz Fhigh=500; sfft=fft(s);
sfftnew=sfft; sfftnew(1:Flow-1)=0;%:end-Mlow sfftnew(end-Flow+1:end)=0; sfftnew(Fhigh:end-Fhigh)=0; snew=ifft(sfftnew);
命令如下:
V=vander(1:6) DV=diff(V) %计算V的一阶差分
范得蒙(Vandermonde)矩阵最后一列全为1,倒数第二列为一个 指定的向量, 其他各列 是其后列与倒数第二列的点乘积。 可以用 一个指定向量生成一个范得蒙矩阵。 在 MATLAB中,函数vander(V)生成以向量 V 为基础向量的范得蒙矩阵 例如, A=vander([1;2;3;5])即可得到上述范得矩 阵。
例6-7 计算二重定积分 (1) 建立一个函数文件fxy.m: function f=fxy(x,y)
1 ∫
2 ∫
− e
x2 2
sin(x2 +
y)dxdy
−1−2
global ki;
ki=ki+1;
%ki用于统计被积函数的调用次数
f=exp(-x.^2/2).*sin(x.^2+y);
利用matlab求解机械设计优化问题-螺栓【整理版】

利用matlab求解机械设计优化问题-螺栓【整理版】3.机械优化设计应用实例机械优化设计把数学规划理论与数值方法应用于设计中,用计算机从大量可行方案中找出最优化设计方案,从而大大提高设计质量和设计效率。
MATLAB 具有解决线性规划和非线性规划、约束优化和无约束优化问题的内部函数,因而可以完成这一功能。
现举一例:螺栓组联结的优化设计 如图4所示的压力容器螺栓组联接中,已知D 1= 400mm,D 2 =250mm ,缸内工作压力为p=1.5 MPa ,螺栓材料为35号钢,σs =320Mpa,安全系数S=3,取残余预紧力Q ’p =1.6F,采用铜皮石棉密封垫片。
现从安全、可靠、经济的角度来选择螺栓的个数n 和螺栓的直径d 。
3.1 设计问题分析若从经济性考虑,螺栓数量尽量少些、尺寸小些,但这会使降低联结的强度和密封性,不能保证安全可靠的工作;若从安全、可靠度考虑,螺栓数量应多一些、尺寸大一些为好,显然经济性差,甚至造成安装扳手空间过小,操作困难。
为此,该问题的设计思想是:在追求螺栓组联结经济成本最小化的同时,还要保证联结工作安全、可靠。
3 .2 设计变量 目标函数 约束条件3.2 .1 设计变量 选取螺栓的个数n 和直径d(mm)为设计变量:T 21T ]x [x ]d [n X ==3.2 .2 目标函数 追求螺栓组联结经济成本C n 最小为目标。
而当螺栓的长度、材料和加工条件一定时,螺栓的总成本与nd 值成正比,所以本问题优化设计的目标函数为min F(X) = C n = n d = x 1x 2① 强度约束条件 为了保证安全可靠地工作,螺栓组联结必须满足强度条件][32.521σπσ≤=d Qca ; 其中Mpa S s 106.3320][===σσ; n n p n D F F F F Q Q p πππ6093742505.16.246.26.26.1222'=⨯=⨯==+=+=N ; 对于粗牙普通螺纹:由文献[3]推荐,小径 d 1=0.85d 所以,强度约束条件为:0106146192106146192106105624)(2212211≤-=-=-=x x nd nd X g ② 密封约束条件 为了保证密封安全,螺栓间距应小于10d ,所以,密封约束条件为:01040010)(2112≤-=-=x x d n D X g ππ③ 安装扳手空间约束条件 为了保证足够的扳手空间,螺栓间距应大于5d ,所以,安装约束条件为:040055)(1213≤-=-=x x n D d X g ππ ④ 边界约束条件 0)(14≤-=x X g ;0)(25≤-=x X g3.3 .3 建立数学模型综上所述,本问题的数学模型可表达为:设计变量:T 21]x [x X =目标函数:min F(X) = x 1x 2约束条件: s.t. 0)(≤X g i ( i = 1, 2, 3, 4, 5,)现运用MATLAB 的优化函数进行求解 :先编写M 文件function [c,ceq]=mynas(x)c(1)=146192/(x(1)*x(2)^2)-106; % 非线性不等式约束c(2)=400*pi/x(1)-10*x(2);c(3)=-400*pi/x(1)+5*x(2);ceq=[]; % 非线性等式约束在MATLAB 命令窗口输入:fun='x(1)*x(2)'; % 目标函数x0=[4,6]; % 设计变量初始值A=[-1,0;0,-1]; % 线性不等式约束矩阵b=[0;0];Aeq=[]; % 线性等式约束矩阵beq=[];lb=[]; % 边界约束矩阵ub=[];[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,@mynlsub) % 调用有约束优化函数运行结果如下:x = 11.4499 10.9751fval = 125.6637所以,该问题优化结果为:n =11.4499 ,d = 10.9751,目标函数最小值:F(X)= 125.6637。
MATLAB实验指导书(共5篇)

MATLAB实验指导书(共5篇)第一篇:MATLAB实验指导书MATLAB 实验指导书皖西学院信息工程学院实验一 MATLAB编程环境及简单命令的执行一、实验目的1.熟悉MATLAB编程环境二、实验环境1.计算机2.MATLAB7.0集成环境三、实验说明1.首先应熟悉MATLAB7.0运行环境,正确操作2.实验学时:2学时四、实验内容和步骤1.实验内容(1)命令窗口的使用。
(2)工作空间窗口的使用。
(3)工作目录、搜索路径的设置。
(4)命令历史记录窗口的使用。
(5)帮助系统的使用。
(6)了解各菜单的功能。
2.实验步骤(1)启动MATLAB,熟悉MATLAB的桌面。
(2)进入MATLAB7.0集成环境。
(3)在命令窗口执行命令完成以下运算,观察workspace的变化,记录运算结果。
1)(365-52⨯2-70)÷3 2)>>area=pi*2.5^2 3)已知x=3,y=4,在MATLAB中求z:x2y3 z=2(x-y)4)将下面的矩阵赋值给变量m1,在workspace中察看m1在内存中占用的字节数。
⎡162313⎤⎢511108⎥⎥m1=⎢⎢97612⎥⎢⎥414151⎣⎦执行以下命令>>m1(2 , 3)>>m1(11)>>m1(: , 3)>>m1(2 : 3 , 1 : 3)>>m1(1 ,4)+ m1(2 ,3)+ m1(3 ,2)+ m1(4 ,1)5)执行命令>>helpabs 查看函数abs的用法及用途,计算abs(3 + 4i)6)执行命令>>x=0:0.1:6*pi;>>y=5*sin(x);>>plot(x,y)7)运行MATLAB的演示程序,>>demo,以便对MATLAB有一个总体了解。
五、思考题1、以下变量名是否合法?为什么?(1)x2(2)3col(3)_row (4)for2、求以下变量的值,并在MATLAB中验证。
MATLAB优化工具箱的用法

MATLAB优化工具箱的用法MATLAB优化工具箱是一个用于求解优化问题的功能强大的工具。
它提供了各种求解优化问题的算法和工具函数,可以用于线性优化、非线性优化、整数优化等不同类型的问题。
下面将详细介绍MATLAB优化工具箱的使用方法。
1.线性优化问题求解线性优化问题是指目标函数和约束条件都是线性的优化问题。
MATLAB 优化工具箱中提供了'linprog'函数来求解线性优化问题。
其基本使用方法如下:[x,fval,exitflag,output,lambda] =linprog(f,A,b,Aeq,beq,lb,ub,options)其中,f是目标函数的系数向量,A和b是不等式约束矩阵和向量,Aeq和beq是等式约束矩阵和向量,lb和ub是变量的下界和上界,options是优化选项。
函数的返回值x是求解得到的优化变量的取值,fval是目标函数的取值,exitflag表示求解的结束状态,output是求解过程的详细信息,lambda是对偶变量。
2.非线性优化问题求解非线性优化问题是指目标函数和约束条件中至少有一个是非线性的优化问题。
MATLAB优化工具箱中提供了'fmincon'函数来求解非线性优化问题。
其基本使用方法如下:[x,fval,exitflag,output,lambda] =fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)其中,fun是目标函数的句柄或函数,x0是优化变量的初始值,A和b是不等式约束矩阵和向量,Aeq和beq是等式约束矩阵和向量,lb和ub 是变量的下界和上界,nonlcon是非线性约束函数句柄或函数,options 是优化选项。
函数的返回值x是求解得到的优化变量的取值,fval是目标函数的取值,exitflag表示求解的结束状态,output是求解过程的详细信息,lambda是对偶变量。
基于MATLAB的肋片传热特性分析与优化设计

适用于直角坐标即可适用于直肋 , a = 2 时适用
于柱坐标即可适用于环肋 ; h 为环境对流传热系 数 , W/ ( m2 ·℃) ; λ为肋片导热系数 , W/ ( m ·℃) ; δ为肋片厚度 , m ; 当肋片的纵向截面为 矩形时δ为常数 , 而肋片的纵向截面为梯形或三
角形时为肋高的函数 。
式 (1) 、 (2) 为矩形直肋在直角坐标系中 , 微分方
程 (1) 可以得到分析解 , 但是对非等截面肋片 ,
A C 为 x 的函数 , 在非直角坐标系中微分方程 (1)
则难以获得分析解甚至无法得到分析解[1] 。那么
其散热量通常利用肋效率曲线图[1]求解 , 计算繁
为自变量 , sol1y 为因变量值 , sol1y (1 , :) 则为
t1 值 , sol1y ( 2 , :) 则 为 t2 值 , 所 以 sol1y
(1 , :) 即为肋片上对应于不同肋片位置 x 的温度
分布 , sol1y (2 , :) 即为肋片上对应于不同肋片
位置 x 的温度梯度 ; 利用 plot (sol1x - x1 , sol1y
计算结果肋高 H 与散热量 q 的关系如图 2 所示 。
212 肋厚 肋片厚度减小 , 则在同样大小的基础面上所
拥有的肋片数目增加 , 传热面积增大从而散热量 增大 , 但是肋片厚度减小也使肋片导热阻力增 大 , 散热量增加幅度下降 。在肋高为 0101m 时 , 分 别 设 计 不 同 的 肋 厚 : 010001 、 010002 、 010003 、 010004 、 010005 、 010006 、 010008 、 010009 、 01001 、 010015 、 01002 、 010025 、 01003 、010035 、01004 、01005m 分析肋片散热 量的变化 , 如图 3 所示 。
MATLAB在导热问题中的应用

分类号密级U D C 编号本科毕业论文(设计) 题目MATLAB在导热问题中的运用所在院系数学与数量经济学院专业名称信息与计算科学年级 05级学生姓名朱赤学号 0515180004指导教师周瑾二00九年四月文献综述1、概述MATLAB是一个为科学和工程计算而专门设计的高级交互式的软件包。
它集数值分析、矩阵运算、信号处理和图形显示于一体,构成了一个方便的、界面友好的用户环境。
在这个环境下,对所要求解的问题,用户只需简单的列出数学表达式,其结果便以数值或图形方式显示出来。
MATLAB中有大量的命令和事先定义的可用函数集,也可通称为MATLAB的M文件,这就使得用它来求解问题通常比传统编程快得多;另外一点,也是它最重要的特点,易于扩展。
它允许用户自行建立完成指定功能的M文件。
从而构成适合于其它领域的工具箱。
MATLAB既是一种编程环境,又是一种程序设计语言。
它与其它高级程序设计语言C、Fortran等一样,也有其内定的规则,但其规则更接近于数学表示,使用起来更为方便,避免了诸如C、Fortran语言的许多限制,比方说,变量、矩阵无须事先定义;其次,它的语句功能之强大,是其它语言所无法比拟的,再者,MATLAB提供了良好的用户界面,许多函数本身会自动绘制出图形,而且会自动选取坐标刻度。
传热学是一门研究由温差引起的热能传递规律的科学,其理论和技术在生产、科学研究等领域得到了广泛的应用。
在能源动力、建筑建材及机械等传统工业部门中,传热学理论的应用解决了这些部门生产过程的热工艺技术,而在新能源利用、军事高科技等新技术领域中,它甚至对一些关键技术起到了决定性作用。
传热过程是传热学研究最基本的过程之一,传统的数学分析解法只能解决相对简单的传热问题,而在解决复杂的实际传热问题时,数学描述和求解都很困难。
随着计算机技术的兴起,解偏微分方程组等早期不能被很好解决或模拟的部分已逐渐被人们完成。
同时,计算机技术的发展,尤其是MATLAB的出现,不但解决了很多较复杂的问题,也大大促进了传热学理论的发展。
计算方法matlab实验报告

计算方法matlab实验报告计算方法MATLAB实验报告引言:计算方法是一门研究如何用计算机来解决数学问题的学科。
在计算方法的学习过程中,MATLAB作为一种强大的数值计算软件,被广泛应用于科学计算、工程计算、数据分析等领域。
本实验报告将介绍在计算方法课程中使用MATLAB 进行的实验内容和实验结果。
一、二分法求方程根在数值计算中,求解非线性方程是一个常见的问题。
二分法是一种简单而有效的求解非线性方程根的方法。
在MATLAB中,可以通过编写函数和使用循环结构来实现二分法求解方程根。
实验步骤:1. 编写函数f(x),表示待求解的非线性方程。
2. 设定初始区间[a, b],满足f(a) * f(b) < 0。
3. 利用二分法迭代求解方程根,直到满足精度要求或迭代次数达到预设值。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个非线性方程的根。
例如,对于方程f(x) = x^3 - 2x - 5,我们通过二分法迭代了5次,得到了方程的一个根x ≈ 2.0946。
二、高斯消元法解线性方程组线性方程组的求解是计算方法中的重要内容之一。
高斯消元法是一种常用的求解线性方程组的方法,它通过矩阵变换将线性方程组化为上三角矩阵,从而简化求解过程。
在MATLAB中,可以利用矩阵运算和循环结构来实现高斯消元法。
实验步骤:1. 构建线性方程组的系数矩阵A和常数向量b。
2. 利用高斯消元法将系数矩阵A化为上三角矩阵U,并相应地对常数向量b进行变换。
3. 利用回代法求解上三角矩阵U,得到线性方程组的解向量x。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个线性方程组。
例如,对于线性方程组:2x + 3y - z = 13x - 2y + 2z = -3-x + y + 3z = 7经过高斯消元法的计算,我们得到了方程组的解x = 1,y = -2,z = 3。
三、数值积分方法数值积分是计算方法中的重要内容之一,它用于计算函数在给定区间上的定积分。
用matlab求数值积分的方法

用matlab求数值积分的方法
数值积分是一种求解定积分近似值的方法。
在实际应用中,很多复杂函数难以通过解析方法求得定积分,因此需要借助数值积分方法来求解。
Matlab作为一种高效的数值计算软件,提供了多种数值积分方法,包括梯形法、辛普森法、高斯积分法等。
下面分别介绍这些方法的具体实现。
梯形法:将积分区间等分成若干个小区间,每个小区间内的积分近似用其两端点的函数值的平均值。
最终将所有小区间的积分结果相加即为整个积分的近似值。
辛普森法:同样将积分区间等分成若干个小区间,每三个小区间内的积分近似用一个二次函数来拟合。
最终将所有小区间的积分结果相加即为整个积分的近似值。
高斯积分法:通过将积分区间变换为[-1,1]区间上的积分,利用预先计算好的高斯积分点和权重,将原函数在[-1,1]区间上积分近似为高斯点的函数值和权重之积的加权和。
以上就是Matlab中求解数值积分的三种常用方法。
不同方法在精度和计算速度上也有所差别,具体使用时可以根据实际需求进行选择。
- 1 -。
第5讲 MATLAB数值计算

第五讲MATLAB数值计算数据处理与多项式计算数值微积分离散傅立叶变换线性方程组求解非线性方程与最优化问题求解常微分方程的数值求解一、数据处理与多项式计算(一)数据统计与分析1. 求矩阵最大元素和最小元素MATLAB提供的求数据序列的最大值和最小值的函数分别为max和min,两个函数的调用格式和操作过程类似。
(1)求向量的最大值和最小值y=max(X):返回向量X的最大值存入y,如果X中包含复数元素,则按模取最大值。
[y,I]=max(X):返回向量X的最大值存入y,最大值的序号存入I,如果X中包含复数元素,则按模取最大值。
求向量X的最小值的函数是min(X),用法和max(X)完全相同。
例1 求向量x的最大值。
命令如下:x=[-43,72,9,16,23,47];y=max(x) %求向量x中的最大值[y,l]=max(x) %求向量x中的最大值及其该元素的位置(2)求矩阵的最大值和最小值求矩阵A的最大值的函数有3种调用格式,分别是:max(A):返回一个行向量,向量的第i个元素是矩阵A的第i列上的最大值。
[Y,U]=max(A):返回行向量Y和U,Y向量记录A的每列的最大值,U向量记录每列最大值的行号。
max(A,[],dim):dim取1或2。
dim取1时,该函数和max(A)完全相同;dim取2时,该函数返回一个列向量,其第i个元素是A矩阵的第i行上的最大值。
求最小值的函数是min,其用法和max 完全相同。
例2 分别求矩阵A中各列和各行元素中的最大值,并求整个矩阵的最大值和最小值。
A=[17,0,1,0,15;23,5,7,14,16;4,0,13,0,22;10,12,19,21,3;... 11,18,25,2,19];(3)两个向量或矩阵对应元素的比较函数max和min还能对两个同型的向量或矩阵进行比较,调用格式为:U=max(A,B):A,B是两个同型的向量或矩阵,结果U是与A,B同型的向量或矩阵,U的每个元素等于A,B对应元素的较大者。
matlab拟合工具箱cftool及其统计指标公式计算
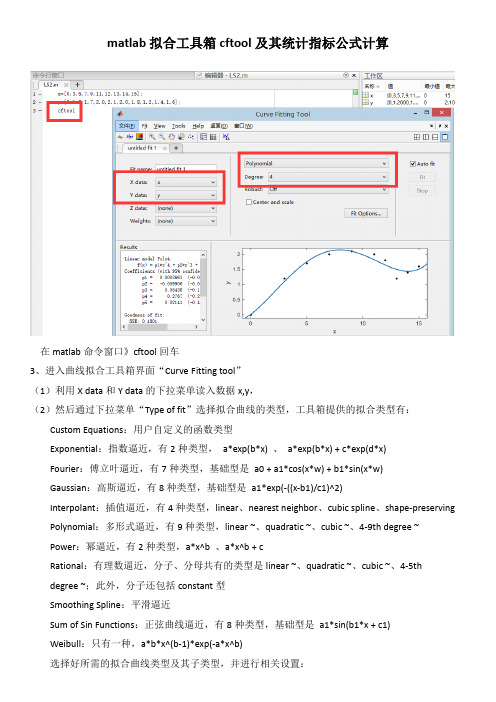
matlab拟合工具箱cftool及其统计指标公式计算在matlab命令窗口》cftool回车3、进入曲线拟合工具箱界面“Curve Fitting tool”(1)利用X data和Y data的下拉菜单读入数据x,y,(2)然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:Custom Equations:用户自定义的函数类型Exponential:指数逼近,有2种类型,a*exp(b*x) 、a*exp(b*x) + c*exp(d*x)Fourier:傅立叶逼近,有7种类型,基础型是a0 + a1*cos(x*w) + b1*sin(x*w)Gaussian:高斯逼近,有8种类型,基础型是a1*exp(-((x-b1)/c1)^2)Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~Power:幂逼近,有2种类型,a*x^b 、a*x^b + cRational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5thdegree ~;此外,分子还包括constant型Smoothing Spline:平滑逼近Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是a1*sin(b1*x + c1)Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations 线性等式”和“General Equations构造等式”两种标签。
matlab中evaluate函数

matlab中evaluate函数1. 引言1.1 概述本文将详细介绍Matlab中的evaluate函数。
该函数在Matlab中扮演着重要角色,可以用于数据分析、机器学习算法评估等应用场景。
通过对evaluate函数的使用方法、功能和特点进行探讨,并结合示例和应用场景的说明,我们将全面了解该函数的优势与不足。
1.2 文章结构本文共分为五个部分,即引言、Matlab中evaluate函数、示例与应用场景、优缺点分析以及结论与展望。
在引言部分,我们将对evaluate函数进行概述,并介绍本文的结构和目的。
随后,我们将深入研究evaluate函数在Matlab中的使用方法和其功能特点。
在示例与应用场景部分,我们将通过具体示例展示evaluate函数在数据分析和机器学习算法评估等领域的应用情景,并对其灵活性进行探讨。
进一步,在优缺点分析部分,我们将客观地评估evaluate函数的优劣,并与其他相关函数进行比较。
最后,在结论与展望部分,我们将总结主要结论并展望evaluate函数未来的发展前景。
1.3 目的本文旨在全面介绍Matlab中的evaluate函数,并针对其功能特点、使用方法和应用场景进行详细讨论。
通过对该函数的优缺点分析和与其他相关函数的比较,我们希望读者能够充分了解evaluate函数的优势和不足,并在实际应用中做出明智的选择。
同时,我们也将展望evaluate函数未来的发展前景,为读者提供更多参考和思考的空间。
2. Matlab中evaluate函数:2.1 函数概述:evaluate函数是Matlab中的一个内置函数,用于评估表达式的结果。
它可以将输入的字符串作为表达式进行求解,并返回计算结果。
该函数主要用于动态计算和求解需要改变的数学表达式,提供了一种灵活而方便的方式来进行数值运算和数学建模。
2.2 使用方法:evaluate函数的基本使用方法如下:matlabresult = evaluate(expression)其中,expression是一个表示数学表达式的字符串,可以包含变量、运算符和各种数学函数。
传热学
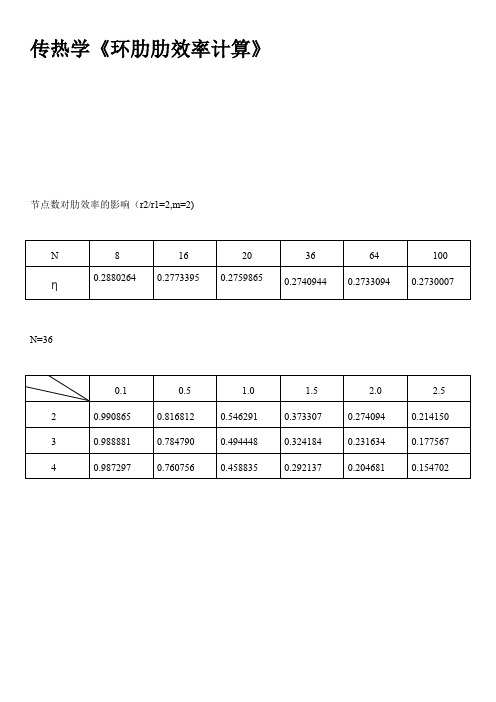
传热学《环肋肋效率计算》节点数对肋效率的影响(r2/r1=2,m=2)N=36MATLAB程序如下高斯-赛德尔迭代方法function [x] = crossover(A,b,x0)format long;D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);G=(D-L)\U;f=(D-L)\b;x=G*x0+f;n=1;while(n<100001)%此循环决定迭代次数,此处统一迭代了100000 次,方便满足取各节点值时的精度,x0=x;x=G*x0+f;n=n+1;end主函数clearformat;digits(30)disp('环肋肋效率matlab 程序.');k=input('请输入k=r2/r1 的值.');N=input('请输入节点数N 的值.');m=input('请输入参数m 的值.');DeltaR=1/(N-1);%定义步长R=[];%定义无量纲半径矩阵for i=1:1:NR(i)=(1/(k-1))+((i-1)/(N-1));%为无量纲半径赋值endb=zeros(N,1);%定义一个N 行1 列的零矩阵,作为右端项。
b(1)=1;%定义b 的第1 个值为1,以便表达出Θ1=1 这个条件。
theta0=ones(N,1);%设置Θ的迭代初值。
A=zeros(N,N);%定义一个系数矩阵A。
因为其中大部分元素为0,先使它成为一个零矩阵,再对特殊元A(1,1)=1;%定义A(1,1)的值为1,以便表达出Θ1=1 这个条件。
这个条件的表达必须将A(1,1)设for j=2:1:N-1A(j,j-1)=(1/(DeltaR^2))-(1/(2*DeltaR*R(j)));A(j,j)=-(2/(DeltaR^2))-2*m^2;A(j,j+1)=(1/(DeltaR^2))+(1/(2*DeltaR*R(j)));end%此循环为系数矩阵A 赋值。
matlab数值求解rayleigh--plesset 方程

Rayleigh-Plesset 方程描述了气泡在液体中的振动行为,通常用于描述超声波中的气泡动力学。
该方程的一般形式为:
RR+3
2
R2=
1
ρ
(P∞−P v−4μ
R
R
−2σ
1
R
)
其中:
•R是气泡半径,
•R是气泡半径的二阶时间导数(即加速度),
•R是气泡半径的一阶时间导数(即速度),
•ρ是液体的密度,
•P∞是无穷远处的压力,
•P v是气泡内的气体的压力,
•μ是液体的粘度,
•σ是液体和气泡之间的表面张力。
为了在 MATLAB 中求解这个微分方程,你可以使用 MATLAB 的 ODE 求解器。
以下是一个简单的例子:
这个例子中,bubble_dynamics函数定义了问题的参数和初始条件,然后调用ode45函数来求解微分方程。
bubble_eq函数定义了微分方程的右手边。
在主函数中,结果通过绘图显示了气泡半径随时间的演化。
你可以根据实际问题调整参数和初始条件。
MATLAB在导热问题中的应用

分类号密级2020-12-12【关键字】意见、情况、思路、方法、条件、动力、空间、领域、文件、质量、模式、监控、运行、传统、地方、问题、系统、有效、全力、整体、合理、良好、快速、执行、发展、建立、提出、发现、了解、研究、规律、特点、位置、关键、稳定、网络、基础、需要、环境、工程、途径、能力、方式、特色、作用、标准、结构、科学性、关系、设置、化解、分析、简化、丰富、推广、满足、指导、帮助、发挥、解决、优化、完善、方向、促进、实现、提高、深化、改进、中心、核心U D C 编号本科毕业论文(设计) 题目MATLAB在导热问题中的运用所在院系数学与数量经济学院专业名称信息与计算科学年级 05级学生姓名朱赤学号 04指导教师周瑾二00九年四月文献综述1、概述MATLAB是一个为科学和工程计算而专门设计的高级交互式的软件包。
它集数值分析、矩阵运算、信号处理和图形显示于一体,构成了一个方便的、界面友好的用户环境。
在这个环境下,对所要求解的问题,用户只需简单的列出数学表达式,其结果便以数值或图形方式显示出来。
MATLAB中有大量的命令和事先定义的可用函数集,也可通称为MATLAB的M文件,这就使得用它来求解问题通常比传统编程快得多;另外一点,也是它最重要的特点,易于扩展。
它允许用户自行建立完成指定功能的M文件。
从而构成适合于其它领域的工具箱。
MATLAB既是一种编程环境,又是一种程序设计语言。
它与其它高级程序设计语言C、Fortran等一样,也有其内定的规则,但其规则更接近于数学表示,使用起来更为方便,避免了诸如C、Fortran语言的许多限制,比方说,变量、矩阵无须事先定义;其次,它的语句功能之强大,是其它语言所无法比拟的,再者,MATLAB提供了良好的用户界面,许多函数本身会自动绘制出图形,而且会自动选取坐标刻度。
传热学是一门研究由温差引起的热能传递规律的科学,其理论和技术在生产、科学研究等领域得到了广泛的应用。
matlab中cvx牛顿法

MATLAB中CVX牛顿法
在MATLAB中使用CVX来求解优化问题时,牛顿法通常作为内嵌的优化算法。
CVX是一个用于解决凸优化问题的MATLAB包,支持多种内嵌算法,包括牛顿法。
在使用CVX进行优化时,你需要先定义问题(包括变量、约束和目标函数),然后选择一个求解器来求解该问题。
牛顿法通常作为求解器选项之一,可以通过设置选项来实现。
以下是一个使用CVX进行优化问题求解并使用牛顿法的示例代码:
在上述代码中,我们首先导入了CVX包,然后定义了一个变量x,目标函数
为f,约束条件为x >= 0。
接下来,我们通过cvx_solver('牛顿法')设置了求解器为牛顿法。
最后,我们调用cvx_solve(f, x)来求解优化问题,并使用disp(x)输出结果。
需要注意的是,CVX支持多种内嵌算法,包括牛顿法、梯度下降法、次梯度下降法等。
选择哪种算法取决于问题的性质和要求。
对于一些特殊问题或特定应用场景,可能需要对算法进行调整或定制化设置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
传热学课程项目研究报告
利用matlab 进行环肋肋效率数值计算
(精度极高!!)
学生姓名:储运16zyl 根据《传热学》中对导热方程的离散化,对离散方程进行进一步化简,可得:
)(1-4 0)211()22()21-1(122212=Θ∆+∆+Θ+∆-Θ∆∆+-n n n n n R
R R m R R R R )
(2-4 11=Θ)
(3-4 0-1=ΘΘ-N N 显然,可将离散方程表示为A Θ=b 的形式,其中A 为一个N ×N 的系数矩阵,Θ为一个1×N 的解矩阵,b 为一个1×N 的右端项矩阵。
这样做的目的是,利用矩阵的形式进行数值计算,较课本上的计算方法更有序,更容易从数值计算的角度理解。
以高斯-赛德尔迭代法为核心设计程序,程序设计框图如下:
高斯赛德尔迭代函数gaussseidel.m:
function[x]=gaussseidel(A,b,x0)
format;%四位精度
%至少输入方程组的系数矩阵,方程组右端项,以及初始解向量。
D=diag(diag(A));
L=-tril(A,-1);
U=-triu(A,1);
G=(D-L)\U;
f=(D-L)\b;
x=G*x0+f;
n=1;
while(n<100001)%此循环决定迭代次数,此处统一迭代了100000次,方便满足取各节点值时的精度,也可根据需要修改循环,以达到某允许误差值。
x0=x;
x=G*x0+f;
n=n+1;
End
主程序heat.m:
clear
clc
format;
disp('传热学.例题4-4.环肋肋效率matlab程序.储运实验1601.张颖龙.1601020125');
k=input('请输入k=r2/r1的值.');
k
N=input('请输入节点数N的值.');
N
m=input('请输入参数m的值.');
m
DeltaR=1/(N-1)%定义步长
R=[]%定义无量纲半径矩阵
for i=1:1:N
R(i)=(1/(k-1))+((i-1)/(N-1));%为无量纲半径赋值
end
b=zeros(N,1);%定义一个N行1列的零矩阵,作为右端项。
b(1)=1%定义b的第1个值为1,以便表达出Θ1=1这个条件。
theta0=ones(N,1)%设置Θ的迭代初值。
A=zeros(N,N)%定义一个系数矩阵A。
因为其中大部分元素为0,先使它成为一个零矩阵,再对特殊元素赋值。
A(1,1)=1;%定义A(1,1)的值为1,以便表达出Θ1=1这个条件。
这个条件的表达必须将A(1,1)设为1,否则在调用迭代函数时会因有一项对角元为0而出错。
for j=2:1:N-1
A(j,j-1)=(1/(DeltaR^2))-(1/(2*DeltaR*R(j)));
A(j,j)=-(2/(DeltaR^2))-2*m^2;
A(j,j+1)=(1/(DeltaR^2))+(1/(2*DeltaR*R(j)));
end%此循环为系数矩阵A赋值。
A(N,N-1)=-1;
A(N,N)=1;%这两个赋值是为了表达出ΘN-ΘN-1=0,即ΘN=ΘN-1这个顶端绝热条件。
theta=gaussseidel(A,b,theta0)%调用gauss-seidel函数。
%以下开始计算肋效率
s1=0;
s2=0;
for i=2:1:N-1
s1=s1+(R(i)-DeltaR/2)*DeltaR*theta(i);
s2=s2+(R(i)-DeltaR/2)*DeltaR;
end
s1=s1+R(1)*DeltaR/2*theta(1)+(R(N)-DeltaR/2)*DeltaR/2*theta(N);
s2=s2+R(1)*DeltaR/2+(R(N)-DeltaR/2)*DeltaR/2;
Fi=s1/s2;
disp('肋效率为:');
Fi
两个程序放在同一个文件夹内,运行主程序即可,分成两部分的原因在于迭代程序换成其他的迭代方法也未尝不可,故提供了再编辑的可能。
根据所设计的程序,可任意输入节点数,获得相应的肋效率。
表一列出了r2/r1=2,m=2,节点数N取16、20、36、64、100、150、200、250、300时肋效率的值。
表一节点数对肋效率的影响(r2/r1=2,m=2)
N16203664100150200250300
η0.27730.27600.27410.27330.27300.27280.27280.27270.2727由表一可知,在不同节点数下,肋效率可保证两位有效数字不再改变,特别是当节点数N取到150以上时,可使在三位有效数字下的解稳定。
根据网格无关性检验的结果,可取节点数N=150,分别计算当r2/r1=2、3、4,m 取0.1、0.5、1.0、1.5、2.0、2.5时肋效率η的值,列于表二中。
表二环肋肋效率随r2/r1及m的变化
m
0.10.51 1.52 2.5
r2/r1
20.99070.81410.54280.37100.27280.2135
30.98870.78160.49090.32220.23070.1773
40.98710.75730.45530.29040.20400.1547
(1)表一中数据与《传热学》教材表4-2进行对比分析,两表的最终结果都在三位有效数字要求下稳定到0.272;将表二中数据与《传热学》教材表4-3进行对比分析,两表中各对应数据之差不超过0.001。
(2)根据表二作出η-m曲线图(见附录),其中系列1为r2/r1=2的曲线,系列2为r2/r1=3的曲线,将其与《传热学》教材图2-20进行对比,两组曲线具有很高的拟合度。
实际上,《传热学》教材图2-20中环肋片效率曲线的绘制考虑了顶端换热的情况,会造成些许的误差,不过两者的高拟合度依然可以证明程序计算结果的可靠性。
(3)增大节点数N至200,重新计算表二中的数据,将计算结果列于表三中。
与表二进行对比,各数据在三位有效数字下的解稳定,可认为获得了与网格无关的解,节点数对计算结果的影响可忽略不计。
表三环肋肋效率随r2/r1及m的变化
m
0.10.51 1.52 2.5
r2/r1
20.99080.81440.54260.37090.27280.2134
30.98880.78260.49070.3220.23070.1773
40.98740.75910.45520.29030.20410.1547
首先对肋效率随m和r2/r1的变化进行定性分析:肋效率的物理意义为实际散热量与假设整个肋表面处于肋基温度下的散热量之比。
由它的物理意义可以看出,肋片表面的平均温度越接近肋基温度,则肋效率就会越大。
而要使肋片表面的平均温度接近肋基温度,则要求肋片导热系数 尽量大以及表面传热系数h尽量小(参数m的值小)、肋片尺寸尽量小(r2/r1小)。
由表二数据以及η-m曲线可以得出,环肋肋效率η随着m 的增大而减小、随着r2/r1的增大而减小。
这与定性分析的结果是相符的。
附录
图2-20:η-m曲线图:。
