dfgh
2021年江苏省常州市数学中考真题含答案解析

2021年江苏省常州市中考数学试卷一、选择题(每小题2分,共16分)1.(2分)(2015•潜江)﹣3的绝对值是( ) A.3B.﹣3C.D.2.(2分)(2015•常州)要使分式有意义,则x的取值范围是( ) A.x>2B.x<2C.x≠﹣2D.x≠23.(2分)(2015•常州)下列“慢行通过,注意危险,禁止行人通行,禁止非机动车通行”四个交通标志图(黑白阴影图片)中为轴对称图形的是( ) A.B.C.D.4.(2分)(2015•常州)如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( ) A.70°B.60°C.50°D.40°5.(2分)(2015•常州)如图,▱ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( ) A.AO=OD B.AO⊥OD C.AO=OC D.AO⊥AB6.(2分)(2015•常州)已知a=,b=,c=,则下列大小关系正确的是( ) A.a>b>c B.c>b>a C.b>a>c D.a>c>b7.(2分)(2015•常州)已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是( ) A.m=﹣1B.m=3C.m≤﹣1D.m≥﹣18.(2分)(2015•常州)将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是( ) A.cm2B.8cm2C.cm2D.16cm2二、填空题(每小题2分,共20分)9.(2分)(2015•常州)计算(π﹣1)0+2﹣1= .10.(2分)(2015•常州)太阳半径约为696 000千米,数字696 000用科学记数法表示为 .11.(2分)(2015•常州)分解因式:2x2﹣2y2= .12.(2分)(2015•常州)已知扇形的圆心角为120°,弧长为6π,则扇形的面积是 .13.(2分)(2015•常州)如图,在△ABC中,DE∥BC,AD:DB=1:2,DE=2,则BC的长是 .14.(2分)(2015•常州)已知x=2是关于x的方程a(x+1)=a+x的解,则a的值是 .15.(2分)(2015•常州)二次函数y=﹣x2+2x﹣3图象的顶点坐标是 .16.(2分)(2015•常州)如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是 .17.(2分)(2015•常州)数学家歌德巴赫通过研究下面一系列等式,作出了一个著名的猜想.4=2+2。
中考母题题源系列数学专题03新定义

【母题来源】2015扬州26【母题原题】平面直角坐标系中,点P (x ,y )的横坐标x 的绝对值表示为|x|,纵坐标y 的绝对值表示为|y|,我们把点P (x ,y )的横坐标与纵坐标的绝对值之和叫做点P (x ,y )的勾股值,记为「P 」,即「P 」=x +y .(其中的“+”是四则运算中的加法)(1)求点A (﹣1,3),B (32+,32-)的勾股值「A 」、「B 」;(2)点M 在反比例函数x y 3=的图象上,且「M 」=4,求点M 的坐标;(3)求满足条件「N 」=3的所有点N 围成的图形的面积.【答案】(1)「A 」=4,「B 」=4;(2)M (1,3)或M (﹣1,﹣3)或M (3,1)或M (﹣3,﹣1);(3)18.【考点定位】反比例函数综合题;新定义;阅读型;综合题.【试题解析】(1)∵A (﹣1,3),B (32+,32-),∴「A 」=|﹣1|+|3|=4,「B 」=2332++-=4;(2)设:点M 的坐标为(m ,n ),由题意得:由题意得43m n mn ⎧+=⎨=⎩,解得:13m n =⎧⎨=⎩或13m n =-⎧⎨=-⎩或31m n =⎧⎨=⎩或31m n =-⎧⎨=-⎩,∴M (1,3),(﹣1,﹣3),(3,1),(﹣3,﹣1);(3)设N 点的坐标为(x ,y ),∵「N 」=3,∴|x|+|y|=3,∴x+y=3,﹣x ﹣y=3,x ﹣y=3,﹣x+y=3,∴y=﹣x+3,y=﹣x ﹣3,y=x ﹣3,y=x+3,如图:所有点N 围成的图形的面积=3232⨯=18.【命题意图】本题主要考查如何用新定义解决数学问题.【方法、技巧、规律】解答新定义类型问题,一定要弄清楚概念的含义,然后根据概念解答相关问题.【探源、变式、扩展】新定义有些是课外的,有些是将来才学习的,有些是人为编撰的,无论哪一种,弄清楚概念是关键,然后尽量转化为我们熟悉的内容.【变式】(2015淮安,第27题,12分)阅读理解:如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.简单应用:(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是;(2)当图③中的∠BCD=120°时,∠AEB′= °;(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有个(包含四边形ABCD).拓展提升:(4)当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.【答案】(1)正方形;(2)80;(3)5;(4)45°.【考点】四边形综合题;新定义;阅读型;探究型;压轴题.【解析】(1)①∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠A=∠C≠90°,∠B=∠D≠90°,∴AB≠AD,BC≠CD,∴平行四边形不一定为“完美筝形”;②∵四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,∴AB≠AD,BC≠CD,∴矩形不一定为“完美筝形”;③∵四边形ABCD是菱形,∴AB=BC=CD=AD,∠A=∠C≠90°,∠B=∠D≠90°,∴菱形不一定为“完美筝形”;④∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,∴正方形一定为“完美筝形”;∴在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是正方形;故答案为:正方形;(2)根据题意得:∠B′=∠B=90°,∴在四边形CBEB′中,∠BEB′+∠BCB′=180°,∵∠AEB′+∠BEB′=180°,∴∠AEB′=∠BCB′,∵∠BCE=∠ECF=∠FCD ,∠BCD=120°,∴∠BCE=∠ECF=40°,∴∠AEB′=∠BCB′=40°+40°=80°;故答案为:80;(3)当图②中的四边形AECF 为菱形时,对应图③中的“完美筝形”有5个;理由如下;根据题意得:BE=B′E ,BC=B′C ,∠B=∠CB′E=90°,CD=CD′,FD=FD′,∠D=∠CD′F=90°,∴四边形EBCB′、四边形FDCD′是“完美筝形”;∵四边形ABCD 是“完美筝形”,∴AB=AD ,CB=CD ,∠B=∠D=90°,∴C D′=CB′,∠CD ′O=∠CB′O=90°,∴∠OD′E=∠OB′F=90°,∵四边形AECF 为菱形,∴AE=AF ,CE=CF ,AE ∥CF ,AF ∥CE ,∴D′E=B′F ,∠AEB′=∠CB′E=90°,∠AFD′=∠CD′F=90°,在△OED′和△OFB′中,∵∠OD ′E=∠OB ′F ,∠EOD ′=∠FOB ′,D ′E=B ′F ,∴△OED′≌△OFB′(AAS ),∴OD′=OB′,OE=OF ,∴四边形CD′OB′、四边形AEOF 是“完美筝形”;∴包含四边形ABCD ,对应图③中的“完美筝形”有5个;故答案为:5;(4)当图③中的∠BCD=90°时,如图所示:四边形ABCD 是正方形,∴∠A=90°,∵∠EB′F=90°,∴∠A+∠EB′F=180°,∴A 、E 、B′、F 四点共圆,∵AE=AF ,∴AE AF ,∴∠AB′E=∠AB ′F=12∠EB ′F=45°.1.(无锡市南长区)定义新运算:对于任意实数a ,b ,都有a ⊕b=23a a b -+,如3⊕5=23335-⨯+,若x ⊕1=11则实数x 的值 ……………………………………………………………………( )A .2或-5B .-2或5C .2或5D .-2或-5 2.(扬州市邗江区)记n n a a a s +++= 21,令n s s s T n n +++= 21,则称n T 为1a ,2a ,……,n a 这列数的“凯森和”.已知1a ,2a ,……,500a 的“凯森和”为2004,那么13,1a ,2a ,……,500a 的“凯森和”为( ) A .2013 B .2015 C .2017 D .20193.(南京市江宁区)如图,边长为a 的正方形发生形变后成为边长为a 的菱形,如果这个菱形的一组对边之间的距离为h ,记kh a =,我们把k 叫做这个菱形的“形变度”.若变形后的菱形有一个角是60°,则形变度k= .4.(2015常州,第26题,10分)设ω是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与ω的面积相等(简称等积),那么这样的等积转化称为ω的“化方”.(1)阅读填空如图①,已知矩形ABCD ,延长AD 到E ,使DE=DC ,以AE 为直径作半圆.延长CD 交半圆于点H ,以DH 为边作正方形DFGH ,则正方形DFGH 与矩形ABCD 等积.理由:连接AH ,EH .∵AE 为直径,∴∠AHE=90°,∴∠HAE+∠HEA=90°.∵DH ⊥AE ,∴∠ADH=∠EDH=90°∴∠HAD+∠AHD=90°∴∠AHD=∠HED ,∴△ADH ∽ .∴DE DH DHAD ,即DH2=AD×DE . 又∵DE=DC∴DH2= ,即正方形DFGH 与矩形ABCD 等积.(2)操作实践平行四边形的“化方”思路是,先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形. 如图②,请用尺规作图作出与▱ABCD 等积的矩形(不要求写具体作法,保留作图痕迹).(3)解决问题三角形的“化方”思路是:先把三角形转化为等积的 (填写图形名称),再转化为等积的正方形.如图③,△ABC 的顶点在正方形网格的格点上,请作出与△ABC 等积的正方形的一条边(不要求写具体作法,保留作图痕迹,不通过计算△ABC 面积作图).(4)拓展探究n 边形(n >3)的“化方”思路之一是:把n 边形转化为等积的n ﹣1边形,…,直至转化为等积的三角形,从而可以化方.如图④,四边形ABCD 的顶点在正方形网格的格点上,请作出与四边形ABCD 等积的三角形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD 面积作图).5.(2015盐城,第27题,12分)知识迁移我们知道,函数)(00,02>>≠+-=n ,m a n )m x (a y 的图像是由二次函数2ax y =的图像向右平移m 个单位,再向上平移n 个单位得到.类似地,函数)n m k (n m x k y 0,0,0>>≠+-=的图像是由反比例函数x k y =的图像向右平移m 个单位,再向上平移n 个单位得到,其对称中心坐标为(m ,n ).理解应用函数113+-=x y 的图像可以由函数x y 3=的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .灵活运用如图,在平面直角坐标系xOy 中,请根据所给的x y 4-=的图像画出函数224---=x y 的图像,并根据该图像指出,当x 在什么范围内变化时,y ≥1-?实际应用 某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x ,发现该生的记忆存留量随x 变化的函数关系为441+=x y ;若在t x =(t ≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x 变化的函数关系为a x y -=82.如果记忆存留量为21时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x 为何值时,是他第二次复习的“最佳时机点”?6.(南京市秦淮区)在一个三角形中,若一条边等于另一条边的两倍,则称这种三角形为“倍边三角形”.(1)下列三角形是倍边三角形的是( )A .顶角为30°的等腰三角形B .底角为30°的等腰三角形C .有一个角为30°的直角三角形D .有一个角为45°的直角三角形 (2)如图①,在△ABC 中,AB =AC ,延长AB 到D ,使BD =AB ,E 是AB 的中点.求证:△DCE 是倍边三角形;(3)如图②,Rt △ABC 中,∠C =90°,AC =3,BC =6,若点D 在边AB 上(点D 不与A 、B 重合),且△BCD 是倍边三角形,求BD 的长.7.(南京市溧水区)问题提出把多边形的任一边向两方延长,如果其它各边都在延长线的同一旁,则这样的多边形为凸多边形.如平行四边形、梯形等都是凸多边形.我们教材中所说的多边形如没作特别说明,一般都是指凸多边形.把多边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的多边形叫做凹多边形.凹多边形会有哪些性质呢?初步认识如图(1),四边形ABCD中,延长BC到M,则边AB、CD分别在直线BM的两旁,所以四边形ABCD 就是一个凹四边形.请你画一个凹五边形.(不要说明)性质探究请你完成凹四边形一个性质的证明:如图(2),在凹四边形ABCD中,求证:∠BCD=∠A+∠B+∠D.类比学习我们以前曾研究过凸四边形的中点四边形问题,如图(3),在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,则四边形EFGH是平行四边形.当四边形ABCD满足一定条件时,四边形EFGH还可能是矩形、菱形或正方形.如图(4),在凹四边形ABCD中,AB=AD,CB=CD,E、F、G、H分别是边AB、BC、CD、DA的中点,请判断四边形EFGH的形状,并证明你的结论.拓展延伸如图(5),在凹四边形ABCD的边上求作一点P,使得∠BPD=∠A+∠B+∠D.(不写作法、证明,保留作图痕迹)。
第九章 期末复习(1)
如图,□ABCD的对角线AC、BD相交于 点O,过点O的直线OM⊥AC.已知 ΔCDM的周长是22㎝.则□ABCD的周长 是 ㎝.
A
M
D
O
B
C
矩形的定义
有一个角是直角的平行四边形叫做矩形, 通常也叫长方形。 矩形的性质 ①矩形是特殊的平行四边形,它具有平行 四边形的一切性质; ②矩形既是轴对称图形也是中心对称图形, 对称轴是对边中点连线所在直线,有两条, 对称中心是对角线的交点。 ③矩形的对角线相等; ④矩形的四个角都是直角。
如图直角梯形ABCD中,AD∥BC, AB⊥BC,AD=2,BC=3,将腰CD以 D为中心逆时针旋转90°至ED,连AE、 CE,则△ADE的面积是 ( ) A.1 B.2 C.3 D.不能确定
E
A
D
G
B
F
C
Hale Waihona Puke 平行四边形性质 ①平行四边形的对边平行; ②平行四边形的对边相等; ① 2 组对边分别平行的四边形是平行四边形; ③平行四边形的对角相等; ② 2组对边分别相等的四边形是平行四边形; ④平行四边形的对角线互相平分。 ③2组对角分别相等的四边形是平行四边形; 判定 ④对角线互相平分的四边形是平行四边形; ⑤一组对边平行且相等的四边形是平行四边 形。
E
D
B
C
如图,在矩形ABCD中,点E在AD上,EC 平分∠BED。 (1)△BEC是否为等腰三角形?为什么? (2)若AB=1,∠ABE=45°,求BC的长
菱形的定义 有一组邻边相等的平行四边形叫做菱形。
菱形的性质 ①菱形是特殊的平行四边形,它具有平行四 边形的一切性质; ②菱形既是轴对称图形也是中心对称图形, 对称轴是两条对角线所在直线,对称中心是 对角线的交点。 ③菱形的四条边相等; ④菱形的对角线互相垂直,并且每一条对角 线平分一组对角
三角形全等几何模型5一线三等角专项练习20202021学年七年级数学下册基础知识专项讲练北师大版
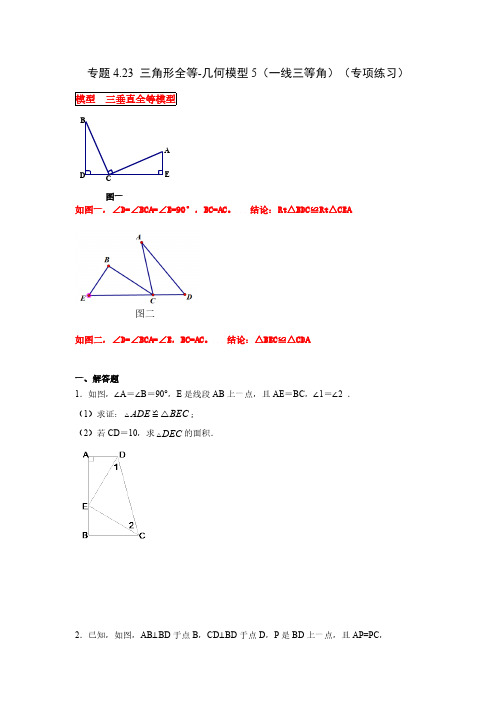
CD E BA专题4.23 三角形全等-几何模型5(一线三等角)(专项练习)模型 三垂直全等模型图一如图一,∠D=∠BCA=∠E=90°,BC=AC 。
结论:Rt △BDC ≌Rt △CEA图二如图二,∠D=∠BCA=∠E ,BC=AC 。
结论:△BEC ≌△CDA一、解答题1.如图,∠A =∠B =90°,E 是线段AB 上一点,且AE =BC ,∠1=∠2 .(1)求证:ADE V ≌BEC △;(2)若CD =10,求DEC V 的面积.2.已知,如图,AB ⊥BD 于点B ,CD ⊥BD 于点D,P 是BD 上一点,且AP=PC ,AP ⊥PC .(1)求证:△ABP ≌△PDC(2)若AB=3,CD=4,连接AC ,求AC 的长.3.如图,在ABC V 中,AB AC =,D 、A 、E 三点都在直线m 上,并且有BDA AEC BAC ÐÐÐ==,求证:DE BD CE =+.4.已知:如图,MS ⊥PS ,MN ⊥SN ,PQ ⊥SN ,垂足分别为S ,N ,Q ,MS =PS ,SN =4,MN =3.求NQ 的长.5.如图1,∠ACB =90°,AC =BC ,AD ⊥MN ,BE ⊥MN ,垂足分别为D 、E .(1)求证:△ADC ≌△CEB ;(2)猜想线段AD 、BE 、DE 之间具有怎样的数量关系,并说明理由;(3)题设条件不变,根据图2可得线段AD 、BE 、DE 之间的数量关系是 .6.如图,已知:ABC V 中,AB AC =,BAC 90Ð=°,分别过B ,C 向经过点A 的直线EF 作垂线,垂足为E ,F .(1)当EF 与斜边BC 不相交时,请证明EF BE CF(=+如图1);(2)如图2,当EF 与斜边BC 这样相交时,其他条件不变,证明:EF BE CF =-;7.如图,一条河流MN 旁边有两个村庄A ,B ,AD ⊥MN 于D .由于有山峰阻挡,村庄B 到河边MN 的距离不能直接测量,河边恰好有一个地点C 能到达A ,B 两个村庄,与A ,B 的连接夹角为90°,且与A ,B 的距离也相等,测量C ,D 的距离为150m ,请求出村庄B 到河边的距离.8.已知:AB BD ^,ED BD ^,AC CE =,BC DE =.(1)试猜想线段AC 与CE 的位置关系,并证明你的结论.(2)若将CD 沿CB 方向平移至图2情形,其余条件不变,结论12AC C E ^还成立吗?请说明理由.(3)若将CD 沿CB 方向平移至图3情形,其余条件不变,结论12AC C E ^还成立吗?请说明理由.9.如图,90ACB Ð=°,AC BC =,AD CE ^,BE CE ^,垂足分别为D ,E ,若9AD =,6DE =,求BE 的长.10.如图所示,A ,C ,E 三点在同一直线上,且ABC DAE △△≌.(1)求证:BC DE CE =+;(2)当ABC V 满足什么条件时,//BC DE ?11.已知:D ,A ,E 三点都在直线m 上,在直线m 的同一侧作ABC V ,使AB AC =,连接BD ,CE .(1)如图①,若90BAC Ð=°,BD m ^,CE m ^,求证ABD ACE @V V ;(2)如图②,若BDA AEC BAC Ð=Ð=Ð,请判断BD ,CE ,DE 三条线段之间的数量关系,并说明理由.12.如图,点C 在BE 上,AB ⊥BE ,DE ⊥BE ,且AB =CE ,AC =CD .判断AC 和CD 的关系并说明理由.13.直线CD 经过BCA Ð的顶点C ,CA=CB .E ,F 分别是直线CD 上两点,且BEC CFA a Ð=Ð=Ð.(1)(数学思考)若直线CD 经过BCA Ð的内部,且E ,F 在射线CD 上,请解决下面两个问题:①如图1,若90BCA Ð=°,90a Ð=°,求证:EF BE AF =-;②如图2,若090BCA °<Ð<°,当a Ð与BCA Ð之间满足________关系时,①中结论仍然成立,并给予证明.(2)(问题拓展)如图3,若直线CD 经过BCA Ð的外部,BCA a Ð=Ð,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.14.如图,已知在ABC V 中,AB AC =,90BAC Ð=°,别过B 、C 两点向过A 的直线作垂线,垂足分别为E 、F .求证:EF BE CF =+.15.在Rt ABC △中,90C Ð=°,8cm AC =,6cm BC =,点D 在AC 上,且6cm AD =,过点A 作射线AE AC ^(AE 与BC 在AC 同侧),若点P 从点A 出发,沿射线AE 匀速运动,运动速度为1cm/s ,设点P 运动时间为t 秒.连结PD 、BD .(1)如图①,当PD BD ^时,求证:PDA DBC △≌△;(2)如图②,当PD AB ^于点F 时,求此时t 的值.16.如图所示,△ABC 中,∠ACB=90°,AC=BC ,直线EF 经过点C ,BF ⊥EF 于点F ,AE ⊥EF于点E .(1)求证:△ACE ≌△CBF ;(2)如果AE 长12cm ,BF 长5cm ,求EF 的长.17.如图,90ACB Ð=°,AC BC =,AD CE ^,BE CE ^,垂足分别为D ,E ,2.5cm AD =,求1cm BE =,求DE 的长.18.已知AD ⊥AB 于A ,BE ⊥AB 于B ,点C 在线段AB 上,DC ⊥EC ,且DC=CE .(1)求证:AD+BE=AB ;(2)将△BEC 绕点C 逆时针旋转,使点B 落在AC 上,如图(2),试问:AD ,BE ,AB 又怎样的数量关系?说明理由.19.如图(1),已知ABC V 中,90BAC Ð=°,AB AC =;AE 是过A 的一条直线,且B ,C 在AE 的异侧,BD AE ^于D ,CE AE ^于E .(1)求证:BD DE CE =+;(2)若直线AE 绕A 点旋转到图(2)位置时(BD CE <),其余条件不变,问BD 与DE ,CE 的数量关系如何?请给予证明.(3)若直线AE 绕A 点旋转到图(3)位置时(BD CE >),其余条件不变,问BD 与DE ,CE 的数量关系如何?请直接写出结果,不需证明;(4)根据以上的讨论,请用简洁的语言表达直线AE 在不同位置时BD 与DE ,CE 的位置关系.20.如图,在ABC V 中,AB AC =,AB BC >,点D 在边BC 上,点E ,F 在线段AD 上,且2DF AF =,12BAC Ð=Ð=Ð.若BE 的长为5,求AD 的长.21.已知:如图,△ABC 中,∠BAC =90°,AB =AC ,l 是过点A 的一条直线,BD ⊥l ,CE ⊥l ,垂足分别为D 、E .(1) 如图(1),求证:DE =BD +CE ;(2) 若直线l 绕A 点旋转到图(2)位置时,其余条件不变,请把图形补充完整,写出BD 、CE 与DE 之间的数量关系,并证明你的结论.22.(1)如图1,已知OAB V 中,OA OB =,90AOB Ð=°,直线l 经过点O ,BC ⊥直线l ,AD ^ 直线l ,垂足分别为点C ,D .依题意补全图l ,并写出线段BC ,AD ,CD 之间的数量关系为______;(2)如图2,将(1)中的条件改为:在OAB V 中,OA OB =,C ,O ,D 三点都在直线l 上,并且有BCO ODA BOA Ð=Ð=Ð,请问(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,在ABC V 中,AB AC =,90CAB Ð=°,点A 的坐标为(0,1),点C 的坐标为()3,2,请直接写出点B 的坐标.23.在△ABC 中,AC=BC ,直线MN 经过点C ,AD ⊥MN 于点D ,BE ⊥MN 于点E ,且AD=CE ;(1)当直线MN 绕点C 旋转到如图1的位置时,求证:AC ⊥BC .(2)判断AD 、BE 、DE 这三条线段之间的数量关系,并说明理由.(3)当直线MN 绕点C 旋转到如图2的位置时,线段DE 、AD 、BE 之间又有什么样的数量关系?请你直接写出这个数量关系,不必证明.24.如图1所示,在△ABC 中,∠ACB=90°,AC= BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN 绕点C 旋转到图2(a)的位置,求证:①△ADC ≌△CEB;②DE=AD- BE .(2)当直线MN 绕点C 旋转到图2(b)的位置时,求证:DE= BE-AD .25.如图,90B C Ð=Ð=°,BAE CED Ð=Ð,且AB CE =.(1)试说明:ADE V 是等腰直角三角形;(2)若2CDE BAE Ð=Ð,求CDE Ð的度数.26.如图,已知在ABC V 中,AC BC AD ==,CDE B Ð=Ð,求证:ADE BCD △≌△.27.如图1,已知AB =AC ,AB ⊥AC .直线m 经过点A ,过点B 作BD ⊥m 于D , CE ⊥m 于E .我们把这种常见图形称为“K”字图.(1)悟空同学对图1进行一番探究后,得出结论:DE =BD +CE ,现请你替悟空同学完成证明过程.(2)悟空同学进一步对类似图形进行探究,在图2中,若AB =AC ,∠BAC =∠BDA =∠AEC ,则结论DE =BD +CE ,还成立吗?如果成立,请证明之.28.(1)如图①,已知:ABC V 中,90BAC Ð=°,AB AC =,直线m 经过点A ,BD m ^于D ,CE m ^于E ,请探索DE 、BD 、CE 三条线段之间的数量关系,直接写出结论;(2)拓展:如图2,将(1)中的条件改为:ABC V 中,AB AC =,D 、A 、E 三点都在直线m 上,并且BDA AEC BAC a Ð=Ð=Ð=,a 为任意锐角或钝角,请问(1)中结论是否还成立?如成立,请证明;若不成立,请说明理由;(3)应用:如图③,在ABC V 中,BAC Ð是钝角,AB AC =,BAD CAE ÐÐ>,BDA AEC BAC Ð=Ð=Ð,直线m 与BC 的延长线交于点F ,若2BC CF =,ABC V 的面积是16,求ABD △与CEF △的面积之和.29.如图(1)在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于点D ,BE ⊥MN 于点E .(1)求证:①△ADC ≌△CEB ;②DE =AD +BE .(2)当直线MN 绕点C 旋转到图(2)的位置时,DE 、AD 、BE 又怎样的关系?并加以证明.30.如图,在ABC V 中,90ACB Ð=°,AC BC =,直线MN 经过点C ,且AD MN ^于点D ,BE MN ^于点E .(1)当直线MN 绕点C 旋转到图1的位置时,求证:①ADC CEB △≌△;②DE AD BE =+;(2)当直线MN 绕点C 旋转到如图2所示的位置时,求证:DE AD BE =-;(3)当直线MN 绕点C 旋转到如图3所示的位置时,试问DE ,AD ,BE 具有怎样的数量关系?请直接写出这个等量关系,不需要证明.31.已知:如图,在ABC D 中,90C Ð=°,点E 在AC 上,且AE BC =,ED AB ^于点D ,过A 点作AC 的垂线,交ED 的延长线于点F .求证:AB EF =.32.如图,两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置,PA 、PB 与直线MN 重合,且三角板PAC 、三角板PBD 均可绕点P 逆时针旋转(1)试说明∠DPC=90°;(2)如图②,若三角板PBD 保持不动,三角板PAC 绕点P 逆时针旋转旋转一定角度,PF 平分∠APD ,PE 平分∠CPD ,求∠EPF ;(3)如图③.在图①基础上,若三角板PAC 开始绕点P 逆时针旋转,转速为5°/秒,同时三角板PBD 绕点P 逆时针旋转,转速为1°/秒,(当PA 转到与PM 重合时,两三角板都停止转动),在旋转过程中,PC 、PB 、PD 三条射线中,当其中一条射线平分另两条射线的夹角时,请求出旋转的时间.33.(1)如图1,∠MAN =90°,射线AE 在这个角的内部,点B 、C 在∠MAN 的边AM ,AN 上,且AB =AC ,CF ⊥AE 于点F ,BD ⊥AE 于点D .求证:ABD CAF @V V .(2)如图2,点B 、C 在∠MAN 的边AM 、AN 上,点E 、F 在∠MAN 内部射线AD 上,∠1,∠2分别是ABE △,CAF V 的外角,已知AB =AC ,∠1=∠2=∠BAC ,求证:ABE CAF @V V ;(3)如图3,在ABC V 中,AB =AC ,AB >BC ,点D 在边BC 上,CD =2BD ,点E 、F 在线段AD 上,12BAC Ð=Ð=Ð,若ABC V 的面积是15,则ACF V 与BDE V 的面积之和是_________.34.如图(1)AB=9cm ,AC ⊥AB ,AC=BD=7cm ,点P 在线段AB 上以2cm/s 的速度由点A 向点B 运动,同时,点Q 在线段BD 上由点B 向点D 运动,它们运动的时间为t (s ).(1)若点Q 的速度与点P 的速度相等,当t=1时.①求证:△ACP ≌△BPQ ;②判断此时PC 和PQ 的位置关系,并证明;(2)将图(1)中的“AC ⊥AB ,BD ⊥AB”,改为“∠CAB=∠DBA=70°”,得到图(2),其他条件不变.设点Q 的运动速度为x cm/s ,请问是否存在实数x ,使得△ACP 与△BPQ 全等?若存在,求出相应的x 和t 的值;若不存在,请说明理由.35.如图1,2OA =,4OB =,以A 点为顶点、AB 为腰在第三象限作等腰直角ABC D .(1)求点C 的坐标;(2)如图2,P 是y 轴负半轴上一个动点,当P 点向y 轴负半轴向下运动时,若以P 为直角顶点,PA 为腰作等腰直角APD D ,过点D 作DE x ^轴于点E ,求OP DE -的值;(3)如图3,已知点F 坐标为()3,3--,当G 在y 轴运动时,作等腰直角FGH D ,并始终保持90GFH Ð=°,FG 与y 轴交于点()0,G m ,FH 与x 轴交于点(),0H n ,求m 、n 满足的数量关系.36.已知:在ABC V 中,90BAC Ð=°,AB AC =,AE 是过点A 的一条直线,且BD AE ^于D ,CE AE ^于E .(1)当直线AE 处于如图①的位置时,有BD DE CE =+,请说明理由;(2)当直线AE 处于如图②的位置时,则BD 、DE 、CE 的关系如何?请说明理由.参考答案1.(1)证明见解析;(2)25【分析】(1)根据12Ð=Ð,∠A =∠B =90°,可得DE CE =,ADE V 和BEC △为直角三角形,利用“HL ”即可证明Rt ADE △≌Rt BEC △;(2)根据(1)中Rt ADE △≌Rt BEC △,则ADE BEC Ð=Ð,根据直角三角形的性质推出90AED BEC Ð+Ð=°,则可得DEC Ð为直角,又因为∠1=∠2,则可知DEC Ð为等腰直角三角形,进而通过等腰直角三角形的性质求出其面积.【详解】(1)∵12Ð=Ð,∴DE CE =,∵∠A =∠B =90°,在Rt ADE △和Rt BEC △中,DE EC AE BC =ìí=î,∴Rt ADE △≌Rt BEC △;(2)∵Rt ADE △≌Rt BEC △,∴ADE BEC Ð=Ð,∵90ADE AED Ð+Ð=°,∴90AED BEC Ð+Ð=°,∴90DEC Ð=°,∵12Ð=Ð,∴DE CE =,∴DEC V 为等腰直角三角形,∴其斜边CD 上的高为5,∴1105252DEC S =´´=△.【点拨】本题考查了直角三角形的判定和性质,全等三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题.2.(1)见解析;(2)【分析】(1)根据等角的余角相等证明BAP CPD Ð=Ð,继而证明()ABP PDC AAS @V V ;(2)根据全等三角形对应边相等性质及勾股定理解题.【详解】(1)证明:,AB BD CD BD^^Q 90B D \Ð=Ð=°90BAP APB \Ð+Ð=°AP PC^Q 90APB CPD \Ð+Ð=°BAP CPD\Ð=ÐAP PC=Q ()ABP PDC AAS \@V V ;(2)连接AC ,()ABP PDC AAS @QV V 3,4AB BP CD ===Q5AP \===在,5Rt APC AP PC ==VAC \==.【点拨】本题考查全等三角形的判定与性质、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.3.见解析【分析】首先根据等量代换得出CAE ABD Ð=Ð,从而可证ADB CEA △≌△,最后利用全等三角形的性质即可得出结论.【详解】证明:设BDA BAC a Ð=Ð=,∴180-DBA BAD BAD CAE a Ð+Ð=Ð+Ð=°,∴CAE ABD Ð=Ð,∵在ADB △和CEA V 中ABD CAE BDA CEA AB AC Ð=ÐìïÐ=Ðíï=î,∴()ADB CEA AAS ≌△△,∴AE BD =,AD CE =,∴DE AE AD BD CE =+=+.【点拨】本题主要考查全等三角形的判定及性质,掌握全等三角形判定方法和性质是解题的关键.4.NQ =1.【分析】首先求出∠M=∠PSQ ,进而利用AAS 证明△MNS ≌△SQP ,所以MN=SQ 问题可解.解:,MS ,PS MN SN PQ SN ^^^Q ,90MSP N SQP \Ð=Ð=Ð=°,M MSN MSN PSQ \Ð+Ð=Ð+Ð,M PSQ \Ð=Ð,在MNS △和SQP V 中,M PSQ MNS SQP MS PS Ð=ÐìïÐ=Ðíï=î,()MNS SQP AAS \△≌△,SQ MN \=,∵SN =4,MN =3,431NQ SN SQ SN MN \=-=-=-= .【点拨】本题考查了全等三角形的判定和性质,垂直定义,根据条件证MNS SQP △≌△是解此题的关键.5.(1)见解析;(2)AD =BE +DE ,见解析;(3)DE =AD +BE【分析】(1)由已知推出∠CDA=∠BEC=90°,因为∠ACD+∠BCE=90°,∠ACD +∠DAC =90°,推出∠DAC=∠ECB ,根据AAS 即可得到△ADC ≌△CEB ;(2)由(1)得到AD=CE ,CD=BE ,即可求出答案;(3)与(1)证法类似可证出∠ACD=∠CBE ,能推出△ADC ≌△CEB ,得到AD=CE ,CD=BE ,即可得到DE 、AD 、BE 之间的等量关系.(1)证明:∵AD ⊥MN ,BE ⊥MN ,∴∠CDA =∠BEC =90°.∴∠ACD +∠DAC =90°.∵∠ACB =90°,∴∠ACD +∠BCE =90°.∴∠DAC =∠ECB .在△ADC 和△CEB 中,CDA BEC DAC ECB AC CB ÐÐìïÐÐíïî===,∴△ADC ≌△CEB .(2)AD =BE +DE .理由如下:由(1)知△ADC ≌△CEB .∴AD =CE ,CD =BE .∴AD =CE =CD +DE =BE +DE .(3)DE =AD +BE .理由:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC=90°,∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB=90°,∴∠ECB+∠ACD=90°,∴∠ACD=∠CBE ,又∵∠ADC=∠CEB ,AC=CB ,∴△ADC ≌△CEB ,∴AD=CE ,CD=BE ,∵CD+CE=DE ,∴DE=AD+BE .【点拨】本题主要考查了余角的性质,直角三角形的两锐角互余,全等三角形的判定和性质等知识点,能根据已知证明△ADC ≌△CEBE 是解此题的关键,题型较好,综合性比较强.6.(1)见解析;(2)见解析.【分析】(1)根据已知条件容易证明△BEA ≌△AFC ,然后利用对应边相等就可以证明题目的结论;(2)根据(1)知道△BEA ≌△AFC 仍然成立,则BE=AF ,AE=CF ,就可以求出EF=BE-CF .解:(1)BE EA ^Q ,CF AF ^,BAC BEA CFE 90ÐÐÐ\===°,EAB CAF 90ÐÐ\+=°,EBA EAB 90ÐÐ+=°,CAF EBA ÐÐ\=,在ABE V 和CAF V 中,BEA AFC EBA FACAB AC Ð=ÐìïÐ=Ðíï=îBEA \V ≌()AFC AAS V ,EA FC \=,BE AF =,EF EA AF BE CF \=+=+.(2)BE EA ^Q ,CF AF ^,BAC BEA CFE 90ÐÐÐ\===°,EAB CAF 90ÐÐ\+=°,ABE EAB 90ÐÐ+=°,CAF ABE ÐÐ\=,在ABE V 和ACF V 中,EBA FAC BEA CFAAB AC Ð=ÐìïÐ=Ðíï=îBEA \V ≌()AFC AAS V ,EA FC \=,BE AF =,∵EF AF AE =-,∴EF BE CF=-【点拨】本题主要考查了全等三角形的性质与判定,利用它们解决问题,经常用全等来证线段和的问题.7.150米【分析】根据题意,判断出△ADC ≌△CEB 即可求解.解:如图,过点B 作BE ⊥MN 于点E ,∵∠ADC =∠ACB =90°,∴∠A =∠BCE (同角的余角相等).在△ADC 与△CEB 中,90ADC CEB A BCEAC CB Ð=Ð=°ìïÐ=Ðíï=î∴△ADC ≌△CEB (AAS ).∴BE =CD =150m .即村庄B 到河边的距离是150米.【点拨】本题主要考查的是全等三角形的实际应用,熟练掌握全等三角形的判定及性质是解答本题的关键.8.(1)AC CE ^,见解析;(2)成立,理由见解析;(3)成立,理由见解析【分析】(1)先用HL 判断出Rt Rt ABC CDE ≌△△,得出A DCE Ð=Ð,进而判断出90DCE ACB Ð+Ð=°,即可得出结论;(2)同(1)的方法,即可得出结论;(3)同(1)的方法,即可得出结论.【详解】解:(1)AC CE ^理由如下:∵AB BD ^,ED BD ^,∴90B D Ð=Ð=°在Rt ABC △和Rt CDE △中AC CE BC DE=ìí=î∴()Rt Rt HL ABC CDE △△≌,∴A DCEÐ=Ð∵90B Ð=°,∴90A ACB Ð+Ð=°,∴()18090ACE DCE ACB Ð=°-Ð+Ð=°,∴AC CE ^;(2)成立,理由如下:∵AB BD ^,ED BD ^,∴90B D Ð=Ð=°,在1Rt ABC V 和2Rt C DE △中121AC C E BC DE=ìí=î,∴()12Rt Rt HL ABC C DE ≌△△,∴2A C E D Ð=Ð,∵90B Ð=°,∴190B A AC Ð+Ð=°,∴2190DC E AC B Ð+Ð=°,在12C FC V 中,()122118090C FC DC E AC B Ð=°-Ð+Ð=°,∴12AC C E ^;(3)成立,理由如下:∵AB BD ^,ED BD ^,∴190ABC D Ð=Ð=°在1Rt ABC V 和2Rt C DE △中121AC C E BC DE =ìí=î,∴()12Rt Rt HL ABC C DE ≌△△,∴2A C E D Ð=Ð,∵190ABC Ð=°,∴190B A AC Ð+Ð=°,在12C FC V 中,()2112180=90C FC DC E AC B Ð=°-Ð+а,∴12AC C E ^.【点拨】此题是几何变换综合题,主要考查了全等三角形的判定和性质,直角三角形的性质,判断出12Rt Rt ABC C DE ≌△△是解本题的关键.9.3【分析】根据同角的余角相等可得EBC DCA Ð=Ð,根据“AAS”可证CEB △≌ADC V ,可得9AD CE ==,即可求BE 的长.解:∵BE CE ^,AD CE ^,∴90E ADC Ð=Ð=°,∴90EBC BCE Ð+Ð=°.∵90BCE ACD Ð+Ð=°,∴EBC DCA Ð=Ð.在CEB △和ADC V 中,E ADC EBC ACD BC AC Ð=ÐìïÐ=Ðíï=î,∴CEB △≌ADC V (AAS ),∴BE CD =,9AD CE ==,∴963BE CD CE DE ==-=-=.【点拨】本题考查了全等三角形的判定和性质,直角三角形的性质,熟练运用全等三角形的判定是本题的关键.10.(1)证明见解析;(2)ACB Ð为直角时,//BC DE【分析】(1)根据全等三角形的性质求出BD=AE ,AD=CE ,代入求出即可;2)根据全等三角形的性质求出∠E=∠BDA= 90°,推出∠BDE=90° ,根据平行线的判定求出即可.【详解】(1)证明:∵ABC DAE △△≌,∴AE=BC ,AC=DE ,又∵AE AC CE =+,∴BC DE CE =+.(2)若//BC DE ,则BCE E Ð=Ð,又∵ABC DAE △△≌,∴ACB E Ð=Ð,∴ACB BCE Ð=Ð,又∵180ACB BCE Ð+Ð=°,∴90ACB Ð=°,即当ABC V 满足ACB Ð为直角时,//BC DE .【点拨】本题考查全等三角形的性质和平行线的判定的应用,关键是通过三角形全等得出正确的结论.11.(1)见详解;(2)DE =BD +CE .理由见详解【分析】(1)根据BD ⊥直线m ,CE ⊥直线m 得∠BDA =∠CEA =90°,而∠BAC =90°,根据等角的余角相等,得∠CAE =∠ABD ,然后根据“AAS”可判断△ABD ≌△CAE ;(2)由∠BDA =∠AEC =∠BAC ,就可以求出∠BAD =∠ACE ,进而由ASA 就可以得出△ABD ≌△CAE ,就可以得出BD =AE ,DA =CE ,即可得出结论.【详解】(1)证明:如图①,∵D ,A ,E 三点都在直线m 上,∠BAC =90°,∴∠BAD +∠CAE =90°,∵BD ⊥m ,CE ⊥m ,∴∠ADB =∠CEA =90°,∴∠BAD +∠ABD =90°,∴∠ABD =∠CAE ,在△ABD 和△CAE 中,ADB AEC ABD CAE AB AC ÐÐìïÐÐíïî===,∴△ABD ≌△CAE (AAS );(2)DE =BD +CE .理由如下:如图②,∵∠BDA =∠AEC =∠BAC ,∴由三角形内角和及平角性质,得:∠BAD +∠ABD =∠BAD +∠CAE =∠CAE +∠ACE ,∴∠ABD =∠CAE ,∠BAD =∠ACE ,在△ABD 和△CAE 中,ABD CAE AB ACBAD ACE ÐÐìïíïÐÐî===,∴△ABD ≌△CAE (ASA ),∴BD =AE ,AD =CE ,∴DE =AD +AE =BD +CE .【点拨】本题考查了全等三角形的判定与性质以及三角形内角和定理的综合应用,解题的关键是熟练掌握全等三角形的判定方法,灵活运用所学知识解决问题.12.AC ⊥CD ,理由见解析【分析】根据条件证明△ABC ≌△CED 就得出∠ACD=90°,则可以得出AC ⊥CD .【详解】解:AC ⊥CD .理由:∵AB ⊥BE ,DE ⊥BE ,∴∠B =∠E =90°.在Rt △ABC 和Rt △CED 中,AB CE AC CD =ìí=î,∴Rt △ABC ≌Rt △CED (HL ),∴∠A =∠DCE ,∠ACB =∠D .∵∠A+∠ACB =90°,∴∠DCE+∠ACB =90°.∵∠DCE+∠ACB+∠ACD =180°,∴∠ACD =90°,∴AC ⊥CD .【点拨】本题考查了全等三角形的判定及性质的运用,垂直的判定及性质的运用,解答时证明三角形全等是关键.13.(1)证明见解析;(2)180ACB a Ð+Ð=°,证明见解析;(3)EF BE AF =+,证明见解析.【分析】(1)①求出∠BEC =∠AFC =90°,∠CBE =∠ACF ,根据AAS 证△BCE ≌△CAF ,推出BE =CF ,CE =AF 即可;②当∠α+∠ACB =180°,证明∠BEC =∠AFC ,∠CBE =∠ACF ,根据AAS 证△BCE ≌△CAF ,推出BE =CF ,CE =AF 即可;(2)求出∠BEC =∠AFC ,∠CBE =∠ACF ,根据AAS 证△BCE ≌△CAF ,推出BE =CF ,CE=AF 即可.【详解】(1)①在图1中,90BEC AFC Ð=Ð=°Q ,90ACB Ð=°,90BCE ACF Ð+Ð=°,90EBC BCE Ð+Ð=°,EBC ACF \Ð=Ð,在BCE V 和CAF V 中,EBC ACF BEC AFC BC AC Ð=ÐìïÐ=Ðíï=î,()BCE CAF AAS \@V V ,BE CF \=,CE AF =,EF CF CE BE AF \=-=-;②当180ACB a Ð+Ð=°时,①中结论仍然成立;证明:在图2中,BEC CFA a Ð=Ð=ÐQ ,180ACB a Ð+Ð=°,BCE ACF EBC BCE \Ð+Ð=Ð+Ð,EBC ACF \Ð=Ð,在BCE V 和CAF V 中,EBC ACF BEC AFC BC AC Ð=ÐìïÐ=Ðíï=î,()BCE CAF AAS \@V V ,BE CF \=,CE AF =,EF CF CE BE AF \=-=-.故答案为180ACB a Ð+Ð=°;(2)不成立,结论:EF BE AF =+.理由:在图3中,BEC CFA a Ð=Ð=ÐQ ,a BCA Ð=Ð,又180EBC BCE BEC +Ð+Ð=°Q ,180BCE ACF ACB Ð+Ð+Ð=°,EBC BCE BCE ACF \Ð+Ð=Ð+Ð,EBC ACF \Ð=Ð,在BEC △和CFA △中,EBC FCA BEC CFA BC CA Ð=ÐìïÐ=Ðíï=î,()BEC CFA AAS \@V V ,AF CE \=,BE CF =,EF CE CF =+Q ,EF BE AF \=+.【点拨】本题综合考查三角形综合题、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,注意这类题目图形发生变化,结论基本不变,证明方法完全类似,属于中考常考题型.14.见解析【分析】证明△BEA ≌△AFC ,得到AE=CF ,BE=AF ,即可得到结论.证明:BE EA ^Q ,CF AF ^,90BAC BEA AFC \Ð=Ð=Ð=°,90EAB CAF \Ð+Ð=°,90EBA EAB Ð+Ð=°,CAF EBA \Ð=Ð,在ABE △和AFC △中,BEA AFC EBA CAF AB AC Ð=ÐìïÐ=Ðíï=î,(AAS)BEA AFC \△≌△.AE CF ∴=,BE AF =.EF AF AE BE CF \=+=+..【点拨】此题考查全等三角形的判定及性质,熟记三角形的判定定理是解题的关键.15.(1)见解析;(2)8秒【分析】(1)根据垂直及角之间的关系证明出PDA CBD Ð=Ð,又有90PAD C Ð=Ð=°,=6AD BC =,根据三角形全等的判定定理则可证明PDA DBC △≌△.(2)根据垂直及角之间的关系证明APF DAF Ð=Ð,又因为90PAD C Ð=Ð=°,AD BC =,则可证明PAD ACB △≌△,所以8cm AP AC ==,即t=8秒.(1)证明:PD BD ^Q,90PDB \Ð=°,即90BDC PDA Ð+Ð=°又90C Ð=°Q ,90BDC CBD Ð+Ð=°PDA CBD\Ð=Ð又AE AC ^Q ,90PAD \Ð=°90PAD C \Ð=Ð=°又6cm BC =Q ,6cmAD =AD BC\=在PAD △和DCB V 中PAD C AD CBPDA DBC Ð=Ðìï=íïÐ=Ðî()PDA DBC ASA \△≌△(2)PD AB ^Q ,90AFD AFP \Ð=Ð=°,即90PAF APF Ð+Ð=°又AE AC ^Q ,90PAF DAF \Ð+Ð=°APF DAF\Ð=Ð又90PAD C Ð=Ð=°Q ,AD BC=在APD △和CAB △中APD CAB PAD CAD BC Ð=ÐìïÐ=Ðíï=î()PAD ACB AAS \△≌△8cmAP AC \==即8t =秒.【点拨】本题主要考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理,灵活运用角之间的关系是解题关键.16.(1)证明见解析;(2)EF=17cm .【分析】(1)根据垂直的定义可得∠AEC=∠CFB=90°,然后求出∠EAC=∠FCB ,再利用“角角边”证明即可;(2)由全等三角形的性质可得:AE=CF ,CE=BF ,再根据线段的和差求解即可.【详解】(1)证明:在Rt △ACB 中,∵∠ACB=90°,∴∠ACE+∠BCF=90°∵AE ⊥EF ,BF ⊥EF∴∠ACE+∠EAC=90°∴∠CAE=∠BCF又∵ AC=CB∴△ACE ≌△CBF(ASA)(2)由△ACE ≌△CBF 可得:AE=CF=12cm , EC=BF=5cm ,∴EF=EC+CF=12+5=17cm .【点拨】本题考查了全等三角形的判定与性质,同角的余角相等的性质,熟练掌握三角形全等的判断方法并找出全等的条件是解题的关键.17. 1.5cm DE =.【分析】根据垂直定义求出∠BEC =∠ACB =∠ADC ,根据等式性质求出∠ACD =∠CBE ,根据AAS 证明△BCE ≌△CAD ;根据全等三角形的对应边相等得到AD =CE ,BE =CD ,利用DE =CE−CD ,即可解答.【详解】AD CE ^Q ,BE CE^90ADC CEB \Ð=Ð=°90BCE CBE \Ð+Ð=°又90ACB Ð=°Q 90BCE ACD \Ð+Ð=°CBE ACD\=Ð在ACD △和CBE △中ADC CEB ACD CBEAC BC Ð=ÐìïÐ=Ðíï=î()AAS ACD CBE \△≌△CD BE \=,AD CE=又 2.5cm AD =Q ,1cmBE =2.5cm CE \=,1cm=CD 2.51 1.5cm DE CE CD \=-=-=.【点拨】本题考查了全等三角形的性质和判定,垂线的定义等知识点的应用,解此题的关键是推出证明ACD CBE \V V ≌的三个条件.18.(1)见解析;(2)BE= AB+AD ,理由见解析.【分析】(1)利用余角的性质得到∠ACD=∠BEC ,从而证明△ACD ≌△BEC ,得到AD=BC ,AC=BE ,从而得到结论;(2)根据△ACD ≌△BEC ,得到AD=BC ,AC=BE ,从而得到BE=AC=AB+BC=AB+AD .【详解】解:(1)∵BE ⊥AB ,∴∠BCE+∠BEC=90°,∵DC ⊥EC ,∴∠ACD+∠BCE=90°,∴∠ACD=∠BEC ,在△ACD 和△BEC 中,A B ACD BECCD CE Ð=ÐìïÐ=Ðíï=î∴△ACD ≌△BEC (AAS ),∴AD=BC ,AC=BE ,∴AD+BE=AC+BC=AB ;(2)由(1)可得:△ACD ≌△BEC ,∴AD=BC ,AC=BE ,∴BE=AC=AB+BC=AB+AD .【点拨】本题考查了全等三角形的判定与性质,找出条件,证明全等,利用全等的性质得到线段的数量关系是本题考查的内容.19.(1)见解析;(2)BD DE CE =-,见解析;(3)BD DE CE =-;(4)当B ,C 在AE 的同测时,BD DE CE =-;当B ,C 在AE 的异侧时,若BD CE >,则BD DE CE =+,若BD CE <,则BD CE DE=-【分析】(1)在直角三角形中,由题中条件可得∠ABD=EAC ,又有AB=AC ,则有一个角及斜边相等,则可判定△BAD ≌△AEC ,由三角形全等可得三角形对应边相等,进而通过线段之间的转化,可得出结论;(2)由题中条件同样可得出△BAD ≌△AEC ,得出对应线段相等,进而可得线段之间的关系;(3)同(2)的方法即可得出结论.(4)利用(1)(2)(3)即可得出结论.【详解】解:(1)∵BD ⊥AE ,CE ⊥AE∴∠ADB=∠CEA=90°∴∠ABD+∠BAD=90°又∵∠BAC=90°∴∠EAC+∠BAD=90°∴∠ABD=∠CAE在△ABD 与△ACE 中ADB CEA ABD CAEAB AC Ð=ÐìïÐ=Ðíï=î∴△ABD ≌△ACE∴BD=AE ,AD=EC ,∴BD=DE+CE(2)∵BD ⊥AE ,CE ⊥AE∴∠ADB=∠CEA=90°∴∠ABD+∠BAD=90°又∵∠BAC=90°∴∠EAC+∠BAD=90°∴∠ABD=∠CAE在△ABD 与△ACE 中ADB CEA ABD CAEAB AC Ð=ÐìïÐ=Ðíï=î∴△ABD ≌△ACE∴BD=AE ,AD=EC∴BD=DE-CE ,(3)∵∠BAC=90°,∴∠BAD+∠EAC=90°,又∵BD ⊥AE ,CE ⊥AE ,∴∠BDA=∠AEC=90°,∠BAD+∠ABD=90°,∴∠ABD=∠EAC ,在△ABD 与△CAE 中,BDA AEC ABD EACAB AC Ð=ÐìïÐ=Ðíï=î∴△ABD ≌△CAE ,∴BD=AE ,AD=CE ,∵DE=AD+AE=BD+CE ,∴BD=DE-CE .(4)归纳:由(1)(2)(3)可知:当B ,C 在AE 的同侧时,若BD> CE,则BD= DE +CE,若BD> CE,则BD= DE +CE,若BD< CE,则BD= CE- DE.【点拨】此题是几何变换综合题,主要考查了三角形全等的判定方法,余角的性质,线段的和差,熟练掌握全等三角形的判定和性质是解题的关键.20.15.【分析】解:由∠1=∠2=∠BAC ,得到∠BAE=∠ACF ,∠ABE=∠CAF 从而证明△ABE ≌△CAF(ASA).得到AF=BE ,再根据DF=2AF ,BE 的长为5,求得AD 的长.【详解】解:∵12BAC Ð=Ð=Ð,且1BAE ABE Ð=Ð+Ð,2CAF ACF Ð=Ð+Ð,∠BAC=∠BAE+∠CAF ,∴∠BAE=∠ACF ,∠ABE=∠CAF .在ABE △和CAF V 中,BAE ACF AB CAABE CAF Ð=Ðìï=íïÐ=Ðî∴()ABE CAF ASA ≌△△.∴AF BE=∵2DF AF =,BE 的长为5,∴10DF =,5AF BE ==,∴51015AD AF DF =+=+=.【点拨】本题考查了全等三角形的性质和判定,解题的关键是熟悉掌握全等三角形的性质和证明.21.(1)详见解析;(2)结论:DE =CE ﹣BD ,详见解析【分析】(1)利用已知得出∠CAE=∠ABD ,进而利用AAS 得出则△ABD ≌△CAE ,即可得出DE=BD+CE ;(2)利用已知得出∠CAE=∠ABD ,进而利用AAS 得出则△ABD ≌△CAE ,即可得出BD 、CE 与DE 之间的数量关系.【详解】解:(1)证明:∵BD ⊥l ,CE ⊥l ,∴∠BD A =∠AEC =90°又 ∵Rt ABC D ,∴∠BAD +∠CAE =90°,∠BAD +∠ABD =90°,∴∠CAE =∠ABD在△ABD 和△CAE 中=ABD CAE ADB CEAAB AC =ìïíï=î∠∠∠∠∴△ABD ≌ △CAE∴BD =AE ,AD =CE∵DE =AD +AE ,∴DE =CE +BD .(2) 如图②所示:结论:DE =CE ﹣BD证明:∵BD ⊥l ,CE ⊥l ,∴∠BD A =∠AEC = 90°∵∠BAD +∠CAE =90°,∠BAD +∠ABD =90°,∴∠CAE =∠ABD在△ABD 和△CAE 中==ABD CAE ADB CEAAB AC ìïíï=î∠∠∠∠∴△ABD ≌△CAE (AAS )∴BD =AE ,AD =CE∵DE =AD ﹣AE∴DE =CE ﹣BD【点拨】此题主要考查了全等三角形的判定与性质等知识,根据已知得出△ABD ≌△CAE 是解题关键.22.(1)补全如图所示见解析;CD BC AD =+;(2)成立,证明见解析;(3)点B 的坐标为()1,2-.【分析】(1)依题意补全图,易证△AOD ≌△OBC ,则有AD =CO ,OD =BC ,从而可得CD BC AD =+;(2)利用三角形内角和易证23ÐÐ=,再证明BCO ODA V V ≌,同(1)即可证明结论;(3)过B 、C 两点作y 轴垂线,构造如(1)图形,即可得三角形全等,再将线段关系即可求出点B 坐标.【详解】(1)补全图1如图所示,CD BC AD =+;证明:∵90AOB Ð=°,BC ⊥直线l ,AD ^ 直线l ,∴∠BCO =∠ODA =90°,∴∠BOC +∠OBC =90°,又∵90AOB Ð=°,∴∠BOC +∠AOD =90°,∴∠OBC =∠AOD ,在△AOD 和△OBC 中BCO ODA OBC AOD BO AO Ð=ÐìïÐ=Ðíï=î,∴△AOD ≌△OBC (AAS )∴AD =CO ,OD =BC ,∵CD OD CO =+,∴CD BC AD =+.(2)成立.证明:如图,∵12180BOA Ð+Ð=°-Ð,13180BOA Ð+Ð=°-Ð,BOA BCOÐ=Ð∴23ÐÐ=在BCO V 和ODA V中32BCO ODABO OA Ð=ÐìïÐ=Ðíï=î∴BCO ODA V V ≌(AAS )∴BC OD =,CO AD=∴CD CO OD AD BC=+=+(3)点B 的坐标为()1,2-.过程如下:过B 、C 两点作y 轴垂线,垂足分别为M 、N ,同理(1)可得,CN =AM ,AN =MB ,∵点A 的坐标为(0,1),点C 的坐标为()3,2,∴CN =AM =3,ON =2,OA =1,∴MB =AN =ON -OA =1,OM =AM -OA =2,∵点B 在第四象限,∴点B 坐标为:()1,2-.【点拨】主要考查了等腰直角三角形的性质,全等三角形的判定和性质、图形与坐标变换,构造出全等三角形是解本题的关键.23.(1)见解析;(2)DE =AD +BE ;见解析;(3)AD =DE +BE【分析】(1)利用垂直的定义得∠ADC =∠CEB =90°,再利用HL 证明Rt △ADC ≌Rt △CEB ,得到∠DAC =∠BCE ,再根据余角的定义得到∠ACD +∠BCE =∠ACB =90°,可得结论;(2)根据Rt △ADC ≌Rt △CEB 得到DC =BE ,从而利用等量代换得到DE =AD +BE ;(3)同理可证:Rt △ADC ≌Rt △CEB ,利用等量代换可得AD =DE +BE .【详解】解:(1)证明:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠CEB =90°,在Rt △ADC 和Rt △CEB 中,AC BC AD CE =ìí=î,∴Rt △ADC ≌Rt △CEB (HL ),∴∠DAC =∠BCE ,∵∠ADC =90°,即∠DAC +∠ACD =90°,∴∠ACD +∠BCE =90°,即∠ACB =90°,∴AC ⊥BC ;(2)DE =AD +BE ,理由如下:∵Rt △ADC ≌Rt △CEB ,∴DC =BE ,∵AD =CE ,∴DE =DC +CE =AD +BE ;(3)AD =DE +BE ,同理可证:Rt △ADC ≌Rt △CEB (HL ),∴CD =BE ,∴AD =CE =DE +CD =DE +BE ,∴即AD =DE +BE .【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”、“HL ”;全等三角形的对应边、对应角相等.24.(1)①见解析;②见解析;(2)见解析.【分析】(1)①根据已知可利用AAS 证明△ADC ≌△CEB ;②由①证得△ADC ≌△CEB ,得出对应边相等,CE =AD ,CD =BE 由此可证DE =AD−BE ;(2)根据已知可利用AAS 证明△ADC ≌△CEB ,得出对应边相等,AD =CE ,CD =BE ,由此可证DE =BE−AD .【详解】证明:(1)①∵∠ADC =∠ACB =∠BEC =90°,∴∠CAD +∠ACD =90°,∠BCE +∠CBE =90°,∠ACD +∠BCE =90°.∴∠CAD =∠BCE .∵AC =BC ,∴△ADC ≌△CEB .②由①证得△ACD ≌△CBE .∴CE =AD ,CD =BE .∴DE =CE−CD =AD−BE .(2)∵∠ADC =∠CEB =∠ACB =90°,∴∠ACD =∠CBE ,又∵AC =BC ,∴△ACD ≌△CBE ,∴AD =CE ,CD =BE ,∴DE =CD−CE =BE−AD .【点拨】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等,再根据全等三角形对应边相等得出结论.25.(1)见解析;(2)60°.【分析】(1)利用ASA 证明△BAE ≌△CED ,可证AE=DE ,后利用∠BAE+∠BEA=90°,证明∠BEA+∠CED=90°,问题得证;(2)利用直角三角形的两个锐角互余,求解即可.【详解】(1)∵90B C Ð=Ð=°,BAE CED Ð=Ð,且AB CE =,∴△BAE ≌△CED ,∴AE=DE ,∵∠BAE+∠BEA=90°,∴∠BEA+∠CED=90°,∴∠AED=90°,∴△AED 是等腰直角三角形;(2)∵2CDE BAE Ð=Ð,BAE CED Ð=Ð,∴2CDE CED Ð=Ð,∵∠CDE+∠CED=90°,∴∠CDE=60°.【点拨】本题考查了三角形的全等,等腰直角三角形的定义,直角三角形的锐角互余的性质,根据图形,结合条件选择对应判定方法,根据性质构造基本的计算等式是解题的关键.26.见解析.【分析】证明ADE BCD Ð=Ð,为三角形的全等提供条件即可.证明:ADE CDE B BCD Ð+Ð=Ð+ÐQ ,CDE B Ð=Ð,ADE BCD \Ð=Ð,AC BC =Q ,A B \Ð=Ð,在ADE V 和BCD △中A B AD BCADE BCD Ð=Ðìï=íïÐ=Ðî,ADE \V ≌BCD △(ASA) .【点拨】本题考查了ASA 证明三角形的全等,抓住题目的特点,补充全等需要的条件是解题的关键.27.(1)见解析;(2)成立,见解析【分析】(1)先证∠ABD=∠EAC ,再证△ABD ≌ △CAE (AAS )即可;(2)先证出∠ABD = ∠EAC ,再证△ABD ≌ △CAE (AAS )即可.证明:(1)∵AB ⊥AC,BD ⊥DE,CE ⊥DE,∴∠BDA=∠AEC=∠BAC=90°,∴∠DAB+∠ABD=∠EAC+∠DAB=90°,∴∠ABD=∠EAC,在△ABD 和 △CAE 中,ABD EAC BDA AEC AB AC Ð=ÐìïÐ=Ðíï=î,∴ △ABD ≌ △CAE (AAS ),∴ BD = AE ,AD = CE ,∴ DE = AE + DA ;(2)成立,理由如下:∵ ∠BAC + ∠BAD + ∠EAC = 180° ,∠ADB + ∠BAD + ∠ABD = 180°,∠BAC = ∠BDA ,∴∠ABD = ∠EAC ,在△ABD 和 △CAE 中,ABD EAC BDA AEC AB AC Ð=ÐìïÐ=Ðíï=î,∴ △ABD ≌ △CAE (AAS ),∴ BD = AE ,AD = CE ,∴ DE = AE + DA = BD + CE.【点拨】本题考查三角形全等的判定与性质,掌握三角形全等的判定与性质是解题关键.28.(1)DE BD CE =+;(2)成立,证明见详解;(3)8.【分析】(1)通过题中的直角和垂直条件,可得到CAE ABD Ð=Ð,然后证明△CAE ≌△ABD ,即得到BD AE =,AD CE =,然后通过等量代换即可得到结论;(2)同(1)中类似,先证明△CAE ≌△ABD 后得到对应边成比例即可;(3)证明△CAE ≌△ABD ,发现ABD △与CEF △的面积之和即为△ACF 的面积,然后根据2BC CF =即可得到答案.解:(1)DE BD CE =+,∵90BAC Ð=°,∴90BAD CAE Ð+Ð=°,∵BD m ^,CE m ^,∴90CEA BDA Ð=Ð=°,∴90BAD ABD Ð+Ð=°,∴CAE ABDÐ=Ð在△CAE 和△ABD 中,90CAE ABD AB ACCEA BDA Ð=Ð=Ð=Ð=°ìïíïî∴△CAE ≌△ABD ,∴BD AE =,AD CE =,∵DE AD AE =+,∴DE BD CE =+;(2)成立,∵BDA AEC BAC a Ð=Ð=Ð=,且180BAD BAC CAE Ð+Ð+Ð=°,∴180BAD CAE a Ð+Ð+=°,在△ABD 中,180BAD ABD BDA Ð+Ð+Ð=°,∴180BAD ABD a Ð+Ð+=°,∴CAE ABD Ð=Ð,在△CAE 和△ABD 中,。
5.2菱形(2)

B F C E D
DE,EF是△ABC的两条中位线,我们探究的问题是: (1)围成的四边形是否必定是平行四边形?
(2)在什么条件下,围成的四边形是菱形?
(3)在什么条件下,围成的四边形是矩形?
D
A
F
(4)你还能发现其他什么结论吗?
B
C E
例2、已知如图,在四边形ABCD中,E,F,G,H 依次是AB、BC、CD、DA的中点,请添一个 条件,使四边形DFGH为菱形。 解:添加的条件是: 理由是:
5.2菱形(2)
1、定义:一组邻边相等的平行四边形叫做菱形
边:对边平行且四边相等
2、性质
角: 对角相等
对角线: 互相平分且垂直, 每一条对角线平分一组对角.
3、判定
1、四边相等的四边形是平行四边形
2、对角线互相垂直的平行四边形是菱形
菱形的判定方法:
平行四边形
四边形
菱形
四边相等
辨一辨
(1)两条对角线互相垂直的四边形是菱形.
错
对
(2)两条对角线互相垂直平分的四边形是菱形.
(3)对角线互相垂直,且有一条对角线平分一组对 错 角的四边形是菱形; (3)对角线互相垂直,且每一条对角线平分一组对 每 角的四边形是菱形; 对
筝形是常用反例
例1、如图,在 矩形ABCD中,对角线AC的 垂直平分线与AD,BC分别交于E,F 求证:四边形AFCE是菱形
H
D
G
C
O
F
A
E
B
小结:
平行四边形
四边形
菱形
ቤተ መጻሕፍቲ ባይዱ
四边相等
正方形最小值问题-含答案

6
22.如图,在正方形 ABCD 中,已知 AB 2 ,点 E,G 分别是边 AD, CD 的中点,点 F 是 边 BC 上的动点,连接 EF ,将正方形 ABCD 沿 EF 折叠, A, B 的对应点分别为 A, B , 则线段 GB 的最小值是_____.
31.如图,正方形 ABCD 的边长为 4,点 E 为 CD 边上的一个动点,以 CE 为边向外作正 方形 ECFG ,连结 BG ,点 H 为 BG 中点,连结 EH ,则 EH 的最小值为______
32.如图,正方形 ABCD 的边长为 6,点 E 是正方形内部一点,连接 BE,CE,且∠ABE=∠BCE, 点 P 是边 AB 上一动点,连接 PD,PE,则 PD+PE 的最小值为_____.
9
35.如图,在正方形 ABCD 中,AB= 2 6 ,E 是对角线 AC 上的动点,以 DE 为边作正方形 DEFG,H 是 CD 的中点,连接 GH,则 GH 的最小值为____.
36.如图,正方形 ABCD 中,AB 4 ,O 是 BC 边的中点,点 E 是正方形内一动点,OE 2 , 连接 DE ,将线段 DE 绕点 D 逆时针旋转 90 得 DF ,连接 AE 、CF .则线段 OF 长的最
小值( )
2
A. 2 5
B. 5 2
C. 2 10-2
D. 5 2-2
8.如图,在正方形 ABCD 和正方形 CEFG 中,点 E 在边 BC 上的延长线上,点 G 在 CD 上,
若 AB 2 ,则线段 DF 的最小值为( )
A.1
B. 2
C. 3
D.2
9.如图,正方形 ABCD 的边长为 1,将其绕顶点 C 旋转,得到正方形 C 6 4 2
【备考2024】生物高考一轮复习:第21讲 染色体变异

【备考2024】生物高考一轮复习第21讲染色体变异[课标要求] 举例说明染色体结构和数量的变异都可能导致生物性状的改变甚至死亡。
[核心素养] (教师用书独具)1.通过染色体变异基本原理及其在生物学中意义的理解,建立起进化与适应的观点。
(生命观念)2.通过三种可遗传变异的比较及育种方法的比较,培养归纳与概括的能力。
(科学思维)3.通过低温诱导植物染色体数目的变化、生物变异类型的判断与实验探究以及育种方案的选择与设计,培养实验设计及结果分析的能力。
(科学探究)考点1染色体变异1.染色体数目的变异(1)染色体数目变异的类型①细胞内个别染色体的增加或减少。
②细胞内染色体数目以一套完整的非同源染色体为基数成倍地增加或成套地减少。
(2)染色体组①概念在大多数生物的体细胞中,染色体都是两两成对的,也就是说含有两套非同源染色体,其中每套非同源染色体称为一个染色体组。
②举例野生马铃薯的染色体组:12条形态和功能不同的非同源染色体(3)单倍体、二倍体和多倍体项目单倍体二倍体多倍体概念体细胞中含有本物种配子染色体数目的个体体细胞中含有两个染色体组的个体体细胞中含有三个或三个以上染色体组的个体发育起点配子受精卵(通常是)受精卵(通常是)植株特点①植株弱小;②高度不育正常可育①茎秆粗壮;②叶片、果实和种子较大;③营养物质含量都有所增加体细胞染色体组数≥1 2 ≥3三倍体和四倍体形成过程形成原因自然原因单性生殖正常的有性生殖外界环境条件剧变(如低温)人工诱导花药离体培养秋水仙素处理单倍体幼苗秋水仙素处理萌发的种子或幼苗(1)变异类型、图解及实例(连线)提示:①—c—Ⅰ②—d—Ⅱ③—a—Ⅳ④—b—Ⅲ(2)结果:使排列在染色体上的基因数目或排列顺序发生改变,导致性状的变异。
(3)对生物体的影响:大多数对生物体是不利的,有的甚至会导致生物体死亡。
1.DNA分子中发生三个碱基的缺失不会导致染色体结构变异。
(√) 2.染色体易位不改变基因数量,对个体性状不会产生影响。
dfgh

机械设计发展史摘要:本丈将机械设计发展的过程划分为四个阶段, 因社会进步,生产力的发展和对经典机械设计理论的深入研究与批判, 而建立的各种现代机械设计理论的基本观念、思路、原理和方法。
最后简述了我国机械设计的状况。
前言:设计一词的英语为Design,它源于拉丁语Designar,由De(记下)与Signare(符号,记号,图形等)两词组成。
因此,“设计"的最初含义是将符号,记号,图形之类高下来的意思。
随着生产的发展和科技的进步,设计的内涵不断向深度和广度发展,设计的含义愈来愈深刻和愈来愈先进。
设计是人类改造自然的基本的活动之一,设计是复杂的思维过程,设计过程蕴含着创新和发明的机会。
设计的目的是将预定的目标,经过一系列的规划与分析决策产生一定的信息(文字,数据,图形)形成设计,并通过制造,使设计成为产品,造福人类。
关健词:机械设计, 现代, 发展正文:随着人类文明的进步, 人们制作了各种各样的机械和机器, 并加以使用, 但专为工业生产所运用、具有明显的技术特征, 而又形成体系的机械设计, 则是在18 世纪工业革命以后的一段时间才被确立起来的。
在工业革命初期只有零散的工作, 谈不上系统研究, 其中较为重要的有英国人斯密顿对纽可门发明的各种功率的蒸汽机进行了系统分析, 写出许多实验报告, 并整理出一套计算公式, 瓦特就是在他工作的基础上, 先后于1756年和1782 年研制出新一代的蒸汽机。
此后, 机械设计经历了反复多次的失败, 才逐步积累了技术经验, 奠定了科学的基础, 形成完整的体系。
两百多年前的个体手工劳动的生产方式,现在已由大规模的机械化、自动化生产所代替。
过去, 产品的质量和性能, 完全依赖于劳动者个人的经验和手艺, 而现在已经可以做到由电子计算机对生产过程进行自动的适应性控制, 使得产品成量好、成本低。
人类在自己的生产活动中, 不断地总结经验和采用最新的科学技术来推动生产向前发展同时, 在发展生产的过程中, 又不断向科学技术提出新课题。
卡通清新淡雅唯美婚礼婚庆PPT模板

点击HGHDFGH内容点击
HGHDFGH内容
点击HGHDFGH内容
点此替换文本
我的爱人
点击HGHDFGH内容,点击HGHDFGH内容点击 HGHDFGH内容点击HGHDFGH内容点击HGHDFGH内 容点击HGHDFGH内容点击HGHDFGH内容
点击HGHDFGH内容点击HGHDFGH内容点击
点击HGHDFGH内容 点击HGHDFGH内容
点击HGHDFGH内容 点击HGHDFGH内容
点击HGHDFGH内容 点击HGHDFGH内容 点击HGHDFGH内容 点击HGHDFGH内容
Байду номын сангаас
OUR memory
My Love
ANGEL BABY
点击HGHDFGH内容,简要HGHDFGH 内容点击HGHDFGH内容,简要HGHDFGH 内容点击HGHDFGH内容, 简要HGHDFGH内容
点此替换文本
HGHDFGH内容 点击HGHDFGH内容
添加标题
HGHDFGH内容HGHDFGH
点击HGHDFGH内容, 简要HGHDFGH内容 点击HGHDFGH内容, 简要HGHDFGH内容 点击HGHDFGH内容, 简要HGHDFGH内容 点击HGHDFGH内容, 简要HGHDFGH内容
HGHDFGH内容点击HGHDFGH内容
点击HGHDFGH内容点击HGHDFGH内容点击 HGHDFGH内容点击HGHDFGH内容
点击HGHDFGH内容点击HGHDFGH内容点击HGHDFGH 内容点击HGHDFGH内容点击HGHDFGH内容点击 HGHDFGH内容
多一点内容,
点击HGHDFGH内容内容, 点击HGHDFGH内容, 多一点,多一点再多一点,
第一讲 列方程解应用题——典型题(教师版)

第一讲列方程解应用题——典型题(教师版)★1、一辆公共汽车上有乘客43人,在同志街站有7人下车,又上来一些人,这时车上有乘客52人,在同志街站上车多少人?解:设在同志街站上车x人43-7+x=52x=52-43+7x=16答:在同志站上车16人。
1、小华用二元五角钱买了面值二角和一角的邮票共17 张,问两种邮票各买多少张?答:二角8张,1角9张。
3、、某商店原有一些橘子,又购进120千克,卖出430千克后,还剩70千克。
商店原有橘子多少千克?解:设商店原有橘子x千克x+120-430=70x=70+430-120x=380答:商店有橘子380千克。
4、商店运来桃和梨两种水果,运来桃的重量是梨的3倍。
已知桃比梨多78千克,运来桃和梨一共多少千克?解:设运来梨x千克,则桃3x千克3x-x=782x=78x=393x=39×3=11739+117=156(棵)答:运来桃和梨一共156棵。
5、小刚和小华两人集邮,小刚的邮票数是小华的3倍,如果把小刚的邮票给小华45枚,那么两人邮票枚数相等。
求小刚和小华各有多少枚邮票?解:设小华有邮票x枚,则小刚有3 x枚3x-45=x+452x=90x=4545×3=135(枚)答:小华有邮票45枚,小刚有邮票135枚。
6、父亲今年的年龄是儿子年龄的4倍,8年后父子年龄的和是61,父亲和儿子今年各是多少岁?解:设儿子今年x岁,则父亲今年4 X岁(x+8)+(4x+8)=615x=61-16x=94x=4×9=36答:儿子今年9岁,父亲今年36岁.★ ★7、机器制造厂原来做一个零件用钢材2.2千克,为了增加它的耐久性,现在每个零件多用钢材0.3千克。
原来做600个零件的钢材现在可以做多少个?解:设原来做600个零件的钢材现在可以做X 个(2.2+0.3)x=2.2×6002.5x=1320 x=528答:原来做600个零件的钢材现在可以做528个.8、一车间加工一批零件,每人加工5个,还剩3个零件,如果其中2人各加工4个,其余人各加工6个,恰好完工,这批零件有多少个?解:设共有x 人5x+3=4×2+(x-2)×65x+3=8+6x-12 x=75x+3=5×7+3=38答:这批零件有38个.9、有三堆煤,甲堆比乙堆的3倍多30千克,丙堆比乙堆少15千克,三堆煤共240千克。
副高卫生职称《眼科学》(题库)考前点题卷二
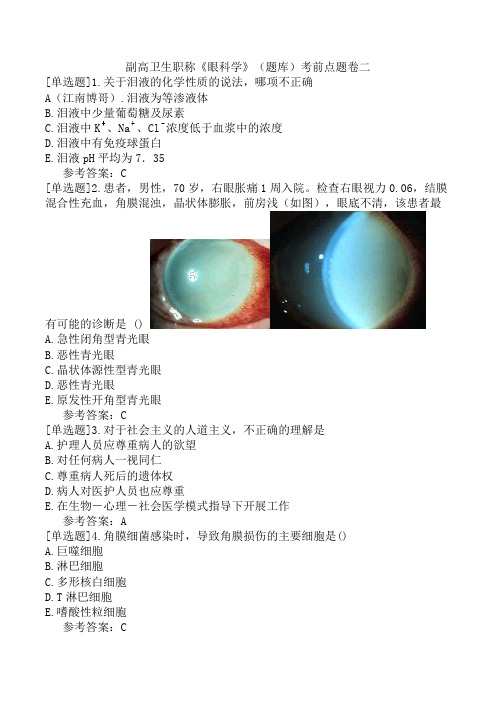
副高卫生职称《眼科学》(题库)考前点题卷二[单选题]1.关于泪液的化学性质的说法,哪项不正确A(江南博哥).泪液为等渗液体B.泪液中少量葡萄糖及尿素C.泪液中K、Na、Cl浓度低于血浆中的浓度D.泪液中有免疫球蛋白E.泪液pH平均为7.35参考答案:C[单选题]2.患者,男性,70岁,右眼胀痛1周入院。
检查右眼视力0.06,结膜混合性充血,角膜混浊,晶状体膨胀,前房浅(如图),眼底不清,该患者最有可能的诊断是 ()A.急性闭角型青光眼B.恶性青光眼C.晶状体源性型青光眼D.恶性青光眼E.原发性开角型青光眼参考答案:C[单选题]3.对于社会主义的人道主义,不正确的理解是A.护理人员应尊重病人的欲望B.对任何病人一视同仁C.尊重病人死后的遗体权D.病人对医护人员也应尊重E.在生物-心理-社会医学模式指导下开展工作参考答案:A[单选题]4.角膜细菌感染时,导致角膜损伤的主要细胞是()A.巨噬细胞B.淋巴细胞C.多形核白细胞D.T淋巴细胞E.嗜酸性粒细胞参考答案:C[单选题]5.该图最有可能是何种类型的白内障()A.中毒性白内障B.先天性白内障C.外伤性白内障D.后发性白内障E.以上都不是参考答案:C[单选题]6.下面哪项不属于眼的屈光系统A.角膜B.房水C.晶状体D.玻璃体E.视网膜参考答案:E参考解析:眼球主要有两部分,屈光传导系统和感光成像系统。
屈光系统包括角膜、晶状体和玻璃体。
感光成像系统是视网膜。
另外房水有一定的屈光指数,亦属屈光系统。
故本题答案为E。
[多选题]1.ERG的a波、b波均下降符合以下描述A.见于视网膜脱离B.反应视网膜内层损害C.反应视网膜外层损害D.反应眼的静息电位变化E.见于视网膜色素变性参考答案:ABCE[多选题]2.角膜的组织结构特点是 ()A.具有透明性B.由致密且相互交错的胶原纤维组成C.无血管D.角膜前面有泪膜E.含丰富的感觉神经参考答案:ACE[多选题]3.近视根据屈光成分分类为 ()A.病理性B.屈光性C.轴性D.良性E.恶性参考答案:BC[多选题]4.在前房角内可见到 ()A.Schwalbe线B.虹膜根C.巩膜突D.睫状带E.小梁网和Schlemm管参考答案:ABCDE[多选题]5.有晶状体眼人工晶状体植入术的并发症包括 ()A.角膜失代偿B.继发性青光眼C.白内障D.瞳孔阻滞E.视网膜脱离参考答案:ABCD[多选题]6.眼内注射的优点包括 ()A.将有效浓度药物释送到眼内作用部位B.适应各种眼病C.疗效较好D.是眼科给药的最佳途径E.所需药物的剂量和浓度均很小参考答案:ACE[多选题]7.不属于蚕蚀性角膜溃疡特征的有A.椭圆型、带匍行性边缘的中央基质溃疡B.溃疡起于周边部沿角膜缘环行发展,浸润缘呈潜掘状,略隆起C.慢性、疼痛性、周边性的角膜溃疡D.周边部角膜细小点状基质混浊,无充血,发展后角膜缘变薄扩张E.角膜病灶表面微隆起,溃疡周围有浅沟及卫星灶,进行性向周边角膜进展参考答案:ADE[多选题]8.有关对“病例报告”的叙述,正确的有A.它可描述所研究病例的发生和分布B.它可用来估计发生该病的危险C.无特设对照组D.优点是容易收集资料,所需人力、物力和时间较少E.它是一种描述性研究类型参考答案:CDE[多选题]9.患者女性,25岁。
菱形的定义

全课小结——菱形的判定 菱形的判定 全课小结
文字语言 判定 法一 判定 法二
四边相等的四边 形是菱形 对角线互相垂 直的平行四边 形是菱形 一组邻边相等 的平行四边形 是菱形
图形语言
A B A O C D
符号语言
∵AB=BC=CD=DA 四边形ABCD ABCD是菱形 ∴四边形ABCD是菱形 ∵□ABCD AC⊥BD 四边形ABCD ABCD是菱形 ∴四边形ABCD是菱形
做一做
1、如图,两张等宽的纸条交重叠在一起,重叠的部 如图,两张等宽的纸条交重叠在一起, 分ABCD是菱形吗?为什么? ABCD是菱形吗?为什么? 是菱形吗
A B C
D
做一做
2、如图,在平行四边形ABCD中,∠BAD的平分 如图,在平行四边形ABCD中 ABCD BAD的平分 线与BC交于点E 线与BC交于点E,∠ABC的平分线与AD交于点F, BC交于点 ABC的平分线与AD交于点F 的平分线与AD交于点 AE与BF相交于点O AE与BF相交于点O。 相交于点 求证:四边形ABEF是菱形 求证:四边形ABEF是菱形 ABEF
(3)判定一个四边形是不是菱形可根据什么? 判定一个四边形是不是菱形可根据什么?
定义法
(4)菱形还有其他判定方法吗? )菱形还有其他判定方法吗?
1.(1)已知菱形ABCD的边长为4, ∠DAB=60° 1.(1)已知菱形ABCD的边长为4, ∠DAB=60°,则对角线 已知菱形ABCD的边长为 AC=______,BD=____,面积S菱形ABCD 8 3 4 3 AC=______,BD=____,面积S菱形ABCD=________. 4 面积 (2)已知菱形ABCD的两条对角线长分别为2cm, (2)已知菱形ABCD的两条对角线长分别为2cm, 2 已知菱形ABCD的两条对角线长分别为 cm,则菱形ABCD的边长为_____cm. cm,则菱形ABCD的边长为_____cm. 则菱形ABCD的边长为 3 2.已知点E为菱形ABCD的一条对角线AC上的任意一点, 2.已知点E为菱形ABCD的一条对角线AC上的任意一点, 已知点 ABCD的一条对角线AC上的任意一点 连结BE并延长交AD于点F,连结DE. 连结BE并延长交AD于点F,连结DE. BE并延长交AD于点F,连结 求证:∠AFB=∠CDE. 求证:∠AFB=∠CDE.
经典初中数学题大全

一、填空题:1.一个正数a的平方根,用符号“________”表示,其中a叫做________,根指数是________.2.平方根等于它本身的数是________,算术平方根等于它本身的数是________.3.________的平方根有两个,________的平方根只有一个,并且________没有平方根.4.0.25的算术平方根是________.5.9的算术平方根是________,的算术平方根是________.6.36的平方根是________,若,则x=________.7.的平方根是________,的平方根是________,的算术平方根是________.8.81的平方根是________,算术平方根是________,算术平方根的相反数是________,平方根的倒数是________,平方根的绝对值是________.9.,则x=________.10.当 a________时,有意义.二、判断并加以说明.1.3 的平方是9;()2.1的平方根是1;()3.0的平方根是0;()4.无理数就是带根号的数;()5.的平方根是;()6.是25的一个平方根;()7.正数的平方根比它的平方小;()8.除零外,任何数都有两个平方根;()9.的平方根是;()10.没有平方根;()11.零是最小的实数;()12.23是的算术平方根.()三、选择题:1.下列说法正确的是().A.的算术平方根是 B.的平方根是C.的算术平方根是 D.的平方根是2.在四个数0,,2,中,有平方根的是().A.0与 B.0,与C.0与 D.0,2与3.若,则x为().A.1 B. C. D.4.的平方根是().A.3 B. C.9 D.5.的算术平方根是().A.16 B. C.4 D.6.如果有意义,则x的取值范围是().A.x≥0 B.x>0 C.x> D.x≥7.如果一个自然数的平方根是(a≥0),则下一个自然数的平方根为().A. B. C. D.8.下列叙述正确的是().A.是7的一个平方根 B.11的平方根是C.如果x有算术平方根,则x>0 D.9.计算的平方根,下列表达式正确的是().A. B.C. D.10.下列各式中正确的是().A. B.C. D.四、分别求出下列各数的平方根.1.36 2.0.0081 3.169 4.5. 6.40000 7. 8.五、分别求出下列各数的算术平方根.1.0.0169 2.225 3.1004. 5.16 6.25六、x为何值时,下列各式有意义?1. 2. 3. 4.5. 6. 7. 8.9. 10.参考答案一、1.;被开方数;2 2.0;0或1 3.正数;零;负数4.0.5 5.3;3(∵ ,∴ 的算术平方根即9的算术平方根)6.±6;±6 7.±2;±8;8 8.±9,9,-9,± ,9,9.0 10.a≥1二、1.√ 2.×(是±1) 3.√ 4.×() 5.×(-1没有平方根)6.√ 7.×(如0.1) 8.×(负数没有) 9.×(,-4没有平方根)10.×(有,是正数,结果为) 11.×(没有) 12.√三、1.D 2.D 3.C 4.B 5.C 6.D 7.C 8.A 9.B 10.D四、1.±6 2.±0.09 3.±13 4.± 5.±716.±200 7.± 8.±0.1五、1.0.13 2.15 3.10 4.12 5.4 6.5六、1.x≥0 2.x≥-1 3.x≥1 x为任意实数 5.x>-2 6.x>07.x为任意实数 8.x≥0 9.x≥ 10.x≥-2还有啊一、填空题:1.36的倒数的算术平方根的相反数是________.2.的最小值是________,此时a的取值是________.3.的算术平方根是2,x=________.4.已知正数a和b,有下列命题:(1)若,则≤(2)若,则≤(3)若,则≤根据以上三个命题所提供的规律猜想:若,则≤________.5.如果x的一个平方根是7.12,那么另一个平方根是________.6.一个正数的两个平方根的和是________.7.一个正数的两个平方根的商是________.8.如果,那么x=________;如果,那么 ________.9.当时, ________.10.一个数的平方根等于它本身,那么这个数是________.二、选择题:1.下列说法正确的是().A.的平方根是B.任何数的平方是非负数,因而任何数的平方根也是非负数C.任何一个非负数的平方根都不大于这个数D.2是4的平方根2.的平方根是().A. B.12 C D.3.下列各数没有平方根的是().A.18 B. C. D.11.14.如果有意义,则x可以取的最小整数为().A.0 B.1 C.2 D.35.的值是().A. B.3 C. D.96.下列说法不正确的是().A.表示两个数:或B.在数轴上表示正数的两个平方根的两个点,总是关于原点对称C.正数的两个平方根的积为负数D.的指数是2三、判断并加以说明.1.无理数没有平方根;()2.任何数的平方的算术平方根都存在,并且都是正数;()3.一定没有平方根;()4.2b是4 的算术平方根;()5.是1的算术平方根;()6.=1.()四、计算:1. 2. 3. 4.五、求下列各式中x的值.1. 2. 3. 4.六、下列各式中,哪些有意义?(1)(2)(3)(4)(5)拓展练习一、已知的平方根是,的平方根是,求的平方根.二、如图所示,已知正方形ABCD的面积是49平方厘米,正方形DFGH 的面积是25平方厘米,且AH=DG=CF=BE,BF=CG=DH=AE,求AD的长;EF的长;△AEH的面积.三、已知:,,且,求x.参考答案综合练习一、1. 2.2;a=-1 3. 4. 5.-7.12 6.0 7.-1 8.±9;±3 9.3 10.0二、1.D 2.D 3.B 4.C 5.B 6.D三、1.×(有平方根) 2.×(0) 3.√ 4.×(b=-1时,不成立)5.×(1是1的算术平方根) 6.√四、1. 2.28 3.-5 4.五、1.x=±5 2.或 3. 4.六、(1)、(2)、(4)、(5)拓展练习一、解:由题意知:,∴∴当a=5,b=2时,∴ a+2b的平方根是±3.二、解:∵ 正方形ABCD面积为AH=DG=CF=BEBF=CG=DH=AE∴ AD=7cm∵ 正方形EFGH的面积是∴ EF=5cm 又∵ 四边形ABCD是正方形AH=DG=CF=BEBF=CG=DH=AE∴ △AEH≌△DHG≌△CGF≌△BFE∴ S△AEH==∴ AD=7cmEF=5cm=三、x=±250。
中考数学专题训练第13讲轴对称与旋转1(解析版)

轴对称与旋转(压轴题组)1.综合与实践问题情境:数学活动课上.老师出示了一个问题:如图①.在平行四边形ABCD中.BE⊥AD.垂足为E.F为CD的中点.连接EF.BF.试猜想EF与BF的数量关系.并加以证明.独立思考:(1)请解答老师提出的问题.实践探究:(2)希望小组受此问题的启发.将平行四边形ABCD沿着BF(F为CD的中点)所在直线折叠.如图②.点C的对应点为C′.连接DC′并延长交AB于点G.请判断AG与BG的数量关系.并加以证明.问题解决:(3)智慧小组突发奇想.将▱ABCD沿过点B的直线折叠.如图③.点A的对应点为A′.使A′B⊥CD于点H.折痕交AD于点M.连接A′M.交CD于点N.该小组提出一个问题:若此平行四边形ABCD的面积为20.边长AB=5.BC=25.求图中阴影部分(四边形BHNM)的面积.请你思考此问题.直接写出结果.【答案】(1)EF=BF.理由见解析. (2)AG=BG.理由见解析. (3)223.【详解】解:(1)结论:EF=BF.理由如下:如图.过点F作FH∥AD交BE于点H.∵四边形ABCD是平行四边形.∴AD∥BC.∵FH∥AD.∴DE∥FH∥CB.∵F为CD的中点.即DF=CF.∴1EH DF HB FC== ∴EH =HB .∵BE ⊥AD .FH ∥AD .∴FH ⊥EB .∴EF =BF .(2)结论:AG =BG .理由如下:连接CC ' .由折叠知识得:BF CC '⊥ .FC FC '= .∵DF =FC .∴DF FC FC '==.∴,CC F C CF C DF DC F ''''∠=∠∠=∠ .∴CC D CC F DC F C CF C DF '''''∠=∠+∠=∠+∠.∴90CC D '∠=︒,∴CC GD '⊥ .∴DG ∥BF .∵DF ∥BG .∴四边形DFBG 是平行四边形.∴DF =BG .∵12AB CD DF CD ==, . ∴12BG AB = . ∴AG =GB .(3)如图.过点D 作DJ ⊥AB 于点J .过点M 作MT ⊥AB 于点T .∵S 平行四边形ABCD =AB ×DJ .∴DJ =20=45. ∵BC =5∴()222225-4=2AJ AD DJ =-= . 在平行四边形ABCD 中.AB ∥CD .∵A B CD '⊥ .∴A B AB '⊥ .∵DJ ⊥AB .∴∠DJB =∠JBH =∠DHB =90°.∴四边形DJBH 是矩形.∴BH =DJ =4.∴541A H A B BH ''=-=-= .∵MT ⊥AB .DJ ⊥AB .∴MT ∥DJ .∴ △ATM ∽△ADJ .∴MT AT DJ AJ = . ∴4=22MT DJ AT AJ ==. 设AT =x .则MT =2x .根据折叠得:45ABM MBA '∠=∠=︒ .∴MT =TB =2x .∴3x =5.解得:53x = . ∴103MT = . ∵,90A A AJD NHA ''∠=∠∠=∠=︒ .∴ △ADJ ∽△A 'NH .∴DJ AJ NH A H='.∴422NH DJA H AJ==='.∴NH=2.∴110255233 ABM A BMS S'==⨯⨯=.∴2512212323A BM NHABHNMS S S''=-=-⨯⨯=四边形.2.(2021·山东中区·九年级期末)定义:关于x轴对称且对称轴相同的两条抛物线叫作“同轴对称抛物线”.例如:y1=(x﹣1)2﹣2的“同轴对称抛物线”为y2=﹣(x﹣1)2+2.(1)请写出抛物线y1=(x﹣1)2﹣2的顶点坐标.及其“同轴对称抛物线”y2=﹣(x﹣1)2+2的顶点坐标.(2)求抛物线y=﹣2x2+4x+3的“同轴对称抛物线”的解析式.(3)如图.在平面直角坐标系中.点B是抛物线L:y=ax2﹣4ax+1上一点.点B的横坐标为1.过点B作x轴的垂线.交抛物线L的“同轴对称抛物线”于点C.分别作点B、C关于抛物线对称轴对称的点B'、C'.连接BC、CC'、B C''、BB'.①当四边形BB C C''为正方形时.求a的值.②当抛物线L与其“同轴对称抛物线”围成的封闭区域内(不包括边界)共有11个横、纵坐标均为整数的点时.直接写出a的取值范围.【答案】(1)(1.﹣2).(1.2).(2)y=2(x﹣1)2﹣5.(3)①a=23.②34≤a≤1或﹣14≤a<﹣15【详解】解:(1)由y1=(x﹣1)2﹣2知顶点坐标为(1.﹣2). 由y2=﹣(x﹣1)2+2知顶点坐标为(1.2).故答案为:(1.﹣2).(1.2).(2)∵y=﹣2x2+4x+3y=﹣2(x﹣1)2+5.∴“同轴对称抛物线”的解析式为:y=2(x﹣1)2﹣5.(3)①当x=1时.y=1﹣3a.∴B (1.1﹣3a ).∴C (1.3a ﹣1).∴BC =|1﹣3a ﹣(3a ﹣1)|=|2﹣6a |.∵抛物线L 的对称轴为直线x =42a a--=2. ∴点B '(3.1﹣3a ).∴BB '=3﹣1=2.∵四边形BB 'C 'C 是正方形.∴BC =BB '.即|2﹣6a |=2.解得:a =0(舍)或a =23. ②抛物线L 的对称轴为直线x =2.顶点坐标为(2.1﹣4a ).∵L 与“同轴对称抛物线”关于x 轴对称.∴整点数也是关于x 轴对称出现的.∴封闭区域内在x 轴上的整点可以是3个或5个.L 与x 轴围成的区域内整点个数为4个或3个.(i )当a >0时.∵L 开口向上.与y 轴交于点(0.1).∴封闭区域内在x 轴上只可能有3个整点.两个区域内各有4个整点.∴当x =1时.﹣2≤1﹣3a <﹣1.当x =2时.﹣3≤1﹣4a <﹣2. 解得:34≤a ≤1. (ii )当a <0时.∵L 开口向下.与y 轴交于点(0.1).∴封闭区域内在x 轴上只可能有5个整点.两个区域内各有3个整点.∴当x =2时.1<1﹣4a ≤2.当x =﹣1时.5a +1<0. 解得:1145a -≤<-. 综上所述:34≤a ≤1或﹣14≤a <﹣15. 3.(2021·江苏·苏州市景范中学校二模)如图1.在Rt ABC △中.90C ∠=︒.边6,8AC BC ==.点M N 、分别在线段AC BC 、上.将ABC 沿直线MN 翻折.点C 的对应点是点C '.(1)当M N 、分别是边AC BC 、的中点时.求出CC '的长度.(2)若2CN =.点C '到线段AB 的最短距离是________.(3)如图2.当点C '在落在边AB 上时.①点C '运动的路程长度是______.②当3611AM =时.求出CN 的长度. 【答案】(1)245.(2)85.(3)①4.② 6011. 【详解】 解:(1)设MN 交CC '于O∵M 、N 分别为AC 、BC 的中点∴AM =CM .CN =BN∴MN ∥AB (中位线定理).12MN AB =∵MC MC '=.NC NC '=∴MN 垂直平分CC '∴OC OC '=.12OC CC '= ∴CC AB '⊥且点C '落在AB 上∵∠C =90°∴2210AB AC BC =+=∵1122AC BC AB CC '= ∴245AC BC CC =AB '=(2)如图2中.过点N 作NH ⊥AB 与H∵2NC NC ='=.BC =8∴6BN BC CN =-= ∵sin NH AC B BN AB ==∠ ∴185AC BN NH AB == ∵点C '是在以N 为圆心.C N ' 长为半径的圆上.∴当点C '落在线段NH 上时.点C '到线段AB 的距离最短∴最短距离85NH NC '=-=.(3)①如图3-1所示.当点N 与B 重合时.BC '的值最大.最大值=BC =8. 如图3-2中.当M 与A 重合时.BC '的值最小.最小值=AB -AC '=AB -AC =4 观察图形可知.当点C '落在AB 上时.点C '的运动的路程长度为4②如图3-3中.过点M 作ME ⊥AB 于E .过点N 作NF ⊥AB 于F .设CN =x .则BN =8-x . ∵sin NF AC B BN AB ==∠.cos BF BC B BN AB ==∠ ∴()385AC BN NF x AB ==-.()485BC BN BF x AB ==- ∵A A ∠=∠.90AEM ACB ==∠∠∴MEA BCA △∽△∴AM AE EM AB AC BC== ∴10855AE =.1445ME =∵363061111MC MC AC AM '==-=-= ∴22223014442115555EC MC ME ⎛⎫⎛⎫''=-=-= ⎪ ⎪⎝⎭⎝⎭∴()()108424804108855555115C F AB AE EC BF x x ''=---=----=-- 由翻折的性质得:90ACB MC N '==∠∠∴90EC M FC N ''+=∠∠∵90EC M EMC ''+=∠∠∴EMC FC N ''=∠∠∴MEC C FN ''△∽△∴EM EC FC FN'=' ∴()()144425558043881155x x =--- 解得6011x = 经检验6011x =是分式方程的解 ∴6011CN =4.(2021·湖北当阳·一模)如图.在矩形ABCD 中.11AB =.6AD =.点E 是边AB 上的点(不与点A .B 重合).将A ∠沿DE 折叠.点1A 是点A 的对应点.点F 是边BC 上的点.将B 沿EF 折叠.点1B 是点B 的对应点.且点1B 在直线1EA 上.(1)若DE EF =.求CF 的长.(2)若点F 是BC 的中点.求tan ADE ∠的值.(3)当点1B 恰好落在边DC 上时.求四边形1DEBB 的面积.【答案】(1)1.(2)13或32.(3)44213+或44213- 【详解】解:(1)将A ∠沿DE 折叠.点1A 是点A 的对应点.∴△AED ≌△.∴1EDA DEA ∠=∠.∵将B 沿EF 折叠.点1B 是点B 的对应点.∴EFB △≌1EFB △.∴1BEF B EF ∠=∠.∴90DEF ∠=︒.∵90EDA DEA DEA FEB ∠+∠=∠+∠=°.∴DEA FEB ∠=∠.∵DE EF =.∴DAE △≌EBF △(AAS ).∴BF AE =.DA BE =.∵11AB =.6AD =.∴6EB =.5AE BF ==.∴1CF =.(2)由(1)知.DAE △∽EBF △.∴AE AD BF BE=. ∵点F 是BC 的中点.∴3BF =.∴6311AE AE=-. ∴2AE =或9AE =.在Rt ADE △中.1tan 3ADE ∠=或3tan 2ADE ∠=. (3)连接BB '.交EF 于M 点.∵点1B 恰好落在边DC 上.∴EF 是BB '的垂直平分线.∴BM EF ⊥.∴FEB FBB '∠=∠.∵ADE FEB ∠=∠.∴ADE CBB '∠=∠.∵AD BC =.90A C ∠=∠=︒.∴△AED ≌CBB '△(AAS ).∴AE B C '=.∴BE DB '=.∵//BE DB '.∴四边形DEBB '是平行四边形.设AE y =.BF x =.则B F x '=.6CF x =-.B C y '=.在Rt B CF '△中.()2226x y x =+-.∴21236x y =+.∵DAE △∽EBF △. ∴611y x y =-. ∴2611x y y =-.∴2236222y y y +=-. 解得11133y ±=. ∴四边形1DEBB 的面积44213=±,综上:四边形1DEBB 的面积为44+213或44213-.5.(2021·河北竞秀·一模)如图.平行四边形ABCD 中.AB =9.AD =13.tan A =125.点P 在射线AD 上运动.连接PB .沿PB 将△APB 折叠.得△A 'PB .(1)如图1.点P 在线段AD 上.当∠DP A'=20°时.∠APB = 度.(2)如图2.当P A '⊥BC 时.求线段P A 的长度.(3)当点A'落在平行四边形ABCD 的边所在的直线上时.求线段P A 的长度.(4)直接写出:在点P 沿射线AD 运动过程中.DA ′的最小值是多少?【答案】(1)80或100.(2)线段P A 的长度为15313.(3)线段P A 的长度为4513或9或1175.(4)DA ′的最小值是4109-.【详解】解:(1)当PA '在直线AD 的右侧时.△APB 折叠得到△A 'PB . 1=(18020)802APB A PB '∴∠=∠︒-︒=︒ 当PA '在直线AD 的左侧时.1=(18020)1002APB A PB '∴∠=∠︒+︒=︒. 故答案为:80或100.(2)如图.作BH AD ⊥于H .平行四边形ABCD 中.//,AD BC PA BC '⊥PA AD '∴⊥90APA '∴∠=︒45APB A PB '∴∠=∠=︒PH BH ∴=12tan 5A = 设12,5BH x AH x ==.22139AB AH BH x ∴=+==913x ∴=1081213BH x ∴== 45513AH x == 10813PH BH ∴== 10845153131313PA PH AH ∴=+=+=. (3)①当点A '在AD 上时.,AB A B PA PA ''==BP AD ∴⊥12tan 5A = 5451313AP AB ∴==. ②当点A '在BC 上时.由折叠可知.,AB A B AP A P ''==//AD BCAPB PBA ABP '∴∠=∠=∠AB PA ∴=∴四边形ABA P '是菱形.9AP ∴=.③当点A '在AB 的延长线上时.1902ABP ABA '∠=∠=︒1311755AP AB ∴== 综上所述.线段P A 的长度为4513或9或1175. (4)如图.作DH AB ⊥于H .连接,BD DA '.1213,tan 5DH AD A AH=== 12,5,954DH AH BH ∴===-=22410BD DH BH ∴+=DA BD BA ''≤-DA BD A B ''∴≤-9A B AB '==DA '∴的最小值是4109.6.(2021·四川·中江县凯江中学校九年级期中)在平面直角坐标系中.二次函数y =ax 2+bx+c 的图象与x 轴交于 A 、B 两点.与y 轴交于点C .过点D (53,24-)且顶点P 的坐标为(﹣1.3).(1)求二次函数的解析式.(2)如图1.若点M 是二次函数图象上的点.且在直线CD 的上方.连接MC .MD .求△MCD 面积的最大值及此时点M 的坐标.(3)如图2.设点Q 是抛物线对称轴上的一点.连接QC .将线段QC 绕点Q 逆时针旋转90°.点C 的对应点为F .连接PF 交抛物线于点E .求点E 的坐标.【答案】(1)222y x x -=-+.(2)△MCD 面积的最大值为12564.M 的坐标:547(,)416-(3)(2,2)E - 【详解】解:(1)二次函数y =ax 2+bx +c 的顶点P 的坐标为(﹣1.3).∴设二次函数的解析式为2(1)3y a x =++ 将点53(,)24D -代入.得 2351342a ⎛⎫=-++ ⎪⎝⎭解得1a =-∴二次函数的解析式为()213y x =-++222x x =--+∴222y x x -=-+ (2)如图.过点M 作MN y ∥轴.交直线DC 于点N .222y x x-=-+.令0x=.则2y=()0,2C∴53(,)24D-设直线CD的解析式为y kx b=+则53242k bb⎧-+=⎪⎨⎪=⎩解得122kb⎧=⎪⎨⎪=⎩∴直线CD的解析式为122y x=+点M是二次函数222y x x-=-+图象上的点.N是122y x=+上的点. 设()2,22M m m m--+.1(,2)2N m m+则12MCD C DS x x MN=⨯-⨯△2151(222)222m m m=⨯⨯--+--25542m m⎛⎫=-+⎪⎝⎭255125()4464m=-++当54m=-时.222m m--+=()213m-++25147(1)3341616=--++=-=547(,)416M∴-此时.△MCD 面积的最大值为12564 (3)设点(1,)Q n -.如图.当2n <时.过点Q 作HG x ∥轴.交y 轴于点G .过点F 作FH HG ⊥于点H .将线段QC 绕点Q 逆时针旋转90°.点C 的对应点为F . 90CQF ∴∠=︒.QC QF =.90CGQ FHQ FQC ∠=∠=∠=︒CQG FQH CQG QCG ∴∠+∠=∠+∠QCG FQH ∴∠=∠∴HQF GCQ △≌△,HQ CG FH QG ∴==(0,2)C ,(1,)Q n -1,2QG CG n ∴==-213,1HG n n FH ∴=-+=-=(3,1)F n n ∴-+(1,3)P -设直线PF 的解析式为y ax b =+.则31(3)a b n a n b =-+⎧⎨+=-+⎩解得14a b =⎧⎨=⎩∴直线PF 的解析式为4y x =+2422y x y x x =+⎧∴⎨=--+⎩解得1113x y =-⎧⎨=⎩.2222x y =-⎧⎨=⎩ (2,2)E ∴-②如图.当2n >时.过点C 作CK PQ ⊥于点K .过点F 作FL PQ ⊥于点L .同理可得.LQF KCQ △≌△2,211QK LF n LK n n ∴==-=-+=-(1,1),(3,1)L n F n n ∴-+--同理可得.直线PF 的解析式为4y x =+2422y x y x x =+⎧∴⎨=--+⎩解得1113x y =-⎧⎨=⎩.2222x y =-⎧⎨=⎩ (2,2)E ∴-③当2n =时.旋转后的C 点与F 点重合.此时过P 的点的直线由无数条.不能确定点E 的坐标.根据题意舍去.E .综上所述.(2,2)7.(2021·湖北新洲·九年级期中)问题背景:(1)如图1.等边△ABC.点P在△ABC左侧且∠APC=30°.将△APC绕点A顺时针旋转60°.画出图形.探究思考:(2)在(1)的条件下.求证:PB=AC.拓展创新:(3)如图2.等边△ABC.∠AMC=60°.AM=6.CM=4.直接写出BM的长.【答案】(1)见解析.(2)见解析.(3)192.【详解】(1)解:如图所示.(2)证明:如图2.连接PP'.由旋转得.AP'=AP.∠P AP'=60°.∠AP'B=∠APC=30°.∴△APP'是等边三角形.∴∠AP'P=60°.AP=AP'=PP'.∴∠PP'B=60°﹣30°=30°.∵AP'=PP'.∠PP'B=∠AP'B.BP'=BP'.∴△AP'B≌△PP'B(SAS).∴PB=AB.∵△ABC是等边三角形.∴AB=BC.∴PB=AC.(3)解:当点M在AC的右侧时.如图3.将△ACM绕点A顺时针旋转60°得到△ABG.连接CG.过点B作MH⊥BG.交BG的延长线于点H.设AG交BC于点T.由旋转得.AG=AM.∠MAG=60°.∠AGB=∠AMC=60°.BG=CM=4.∠ABG=∠ACM. ∵△ABC是等边三角形.∴∠ACB=∠ABC=60°.∴∠AGB=∠ACB=60°.∵∠BTG=∠ATC.∴△BTG∽△ATC.∴BT GT AT CT=.∵∠ATB=∠CTG.∴△ATB∽△CTG.∴∠BAT=∠BCG.∠AGC=∠ABC=60°.∵∠BAG+∠ABG+∠AGB=180°.∴∠BCG+∠ACM+∠ACB=180°.∴点G、C、M三点共线.∵AG=AM.∠MAG=60°.∴△AGM是等边三角形.∴GM=AM=6.∵∠AGM=∠AGB=60°.∴∠MGH=60°.∵MH⊥BG.∴GH=12GM=3.MH3=3∴BH=BG+GH=4+3=7.∴BM22227(33)BH MH+=+19当点M在AC的左侧时.如图4.将△ACM绕点A顺时针旋转60°得到△ABG.连接BM.同图3理可证.点G、B、M三点共线.GM=AM=6.BG=CM=4.∴BM=GM﹣BG=6﹣4=2.综上所述.BM的长为219或2.故答案为:219或2.8.(2021·重庆八中九年级期中)在△ABC中.CA=CB.CA⊥CB.点D是射线AC上一动点.连接BD.将BD绕点D逆时针旋转90°得ED.连接CE.(1)如图1.当点D在线段AC上时.若DE=10.BC=3.求△ABD的周长.(2)如图2.点D在AC延长线上.作点C关于AB边的对称点F.连接FE.FD.将FD绕点D 顺时针旋转90°得GD.连接AG.求证:AG=CE.(3)如图3.点D在AC延长线上运动过程中.延长EC交AG于H.当BH最大时.直接写出CD AB的值.【答案】(1)32102.(2)见解析.(3102+【详解】(1)解:如图1.在Rt△BCD中.BC=3.BD=DE=10.∴CD=1.∴AD=AC﹣CD=BC﹣AD=3﹣1=2.∵CA=CB.CA⊥CB.∴AB=22+=32.CA CB∴△ABD的周长是:3210++2.(2)证明:如图2.连接BG交EF于N.连接CF交AB于M.AB与EF交于点P.DF与BG交于O. ∵∠BDE=∠GDF=90°.∴∠BDE+∠ADF=∠GDF+∠ADF.即:∠BDG=∠FDE.∵DE=BD.DG=DF.∴△BDG≌△EDF(SAS).∴BG=EF.∴∠BGD=∠DFE.∵∠DOG=∠FOB.∴∠BNP=∠ONF=∠GDO=90°.∵∠BPN=∠MPF.∴∠CFE=∠ABG.∵CF=2CM=2AM=AB.∴△GAB≌△ECF(SAS).∴AG=CE.(3)如图3.由(2)得.△GAD≌△ECF.∴∠GAB=∠ECF.∴∠GAB﹣∠CAB=∠ECF﹣∠BCM. ∴∠CAB=∠BCM=45°.∴∠GAC=∠ECB.∵∠ACB=90°.∴∠ACH+∠ECB=90°.∴∠ACH+∠GAC=90°.∴∠AHC=90°.∴点H在以AC为直径的⊙I运动.如图4.当BH 过I 时.BH 最大.不妨设半径AI =CI =HI =1.∴BC =AC =2.∴IB 22IC BC +5作HT ⊥AC 于T .作EK ⊥AD 于K .∴∠HTI =∠ACB =90°.∴HT ∥BC .∴△HTI ∽△BCI . ∴HT BC =TI IC =HI IB . ∴2HT =1TI 5∴HT 25.TI 5∵∠BCD =∠BDE =∠K =90°.BD =DE .由“一线三等角”得.△BCD ≌△DKE .∴CD =EK .BC =DK =2.∵tan ∠KCE =tan ∠HCT . ∴EK CK =HT CT. ∴CD CD BC +25551+2555+∴CD BC 2555-2AB 2555-∴CD AB 102+ 9.(2021·河南汝阳·九年级期中)如图1.矩形AEGH 的顶点E 、H 在矩形ABCD 的边上.且AD :AB =AH :AE =1:2.(1)请直接写出HD :GC :EB 的结果(不必写计算过程).(2)如图2.矩形AEGH 绕点A 旋转一定角度.此时HD :GC :EB 的结果与(1)的结果有变化吗?如有变化.写出变化后结果并说明理由.若无变化.请说明理由.【答案】(1)HD :GC :EB =1:5:2.(2)无变化.见解析【详解】解:(1)如图1.作GF ⊥CD 于点F .连接AG .则∠DFG =∠GFC =90°.∵四边形AEGH 和四边形ABCD 都是矩形.∴∠D =∠AHG =∠EGH =90°.AB =DC .AE =HG .∴∠DHG =180°﹣∠AHG =90°. ∴四边形DFGH 是矩形.∴HG =DF .HD =GF .∠FGH =90°. ∴12AD AH AB AE ==. ∴G D DC A AH H =. ∴AH HD DF FC ++=AH HG . ∴AH GF HG FC ++=AH HG. 整理得GF AH=FC HG . ∵∠GFC =∠AHG .∴△GFC ∽△AHG .∴∠FGC =∠HAG .∴∠FGC +∠HGA =∠HAG +∠HGA =90°.∴∠FGC +∠HGA +∠FGH =180°.∴点A 、G 、C 在同一条直线上.∴点G 在矩形ABCD 的对角线AC 上.由GF AH =FC HG 得GF FC =AH HG =AH AE =12. ∴FC =2GF .∴GC =22(2)GF GF +=5GF .∴GF :GC :FC =GF :5GF :2GF =1:5:2.∵∠FGH +∠EGH =180°.∴点E 、G 、F 在同一条直线上.∵∠B =∠BCF =∠CFE =90°.∴FC =EB .∴HD :GC :EB =1:5:2.(2)无变化.理由:由(1)得:AH AD =AG AC =AE AB . ∴AH AG =AD AC .AG AE =AC AB. ∵AE =HG =2AH .∴AG =22(2)AH AH +=5AH .∴AH :AG :AE =AH :5AH :2AH =1:5:2.如图2.由旋转得.∠DAH =∠CAG =∠BAE .∴△DAH ∽△CAG ∽△BAE .∴HD GC =AH AG=15.GC EB =AG AE =52. ∴HD :GC :EB =1:5:2.∴HD :GC :EB 的结果无变化..10.(2021·湖北汉川·九年级期中)如图.若抛物线2y ax bx c =++(a 、b 、c 为常数.且0a ≠)与直线l 交于点()1,0A -.()2,3C -.与x 轴另一交点为()3,0B .(1)则抛物线的解析式为______.(2)若将直线AC 绕点A 逆时针旋转90°交抛物线于点P .①求点P 的坐标.此时AC AP的值为______. ②若M 是抛物线上一动点.过点M 作x 轴的垂线.垂足为N .连接BM .是否存在点M 使MN AC BN AP=若存在.请求出点M 的坐标.若不存在.请说明理由. 【答案】(1)223y x x =--.(2)①35.②存在.251,525⎛⎫-- ⎪⎝⎭.869,525⎛⎫- ⎪⎝⎭. 【详解】解:(1)将A 、B 、C 三个点的坐标代入可得:0930423a b c a b c a b C -+=⎧⎪++=⎨⎪++=-⎩. 解得:123a b c =⎧⎪=-⎨⎪=-⎩. ∴解析式为:223y x x =--.(2)①作点C 关于x 轴的对称点C '.交x 轴为点D .则()2,3C '.作直线AC '与抛物线交与点P .则点P 为所求.根据题意中可得:3CD =.3AD =. ∴45CAD ∠=︒.∴'90CAC ∠=︒.设直线AC '的解析式为y mx n =+.由题意得:032m n m n =-+⎧⎨=+⎩. 解得:11m n =⎧⎨=⎩. ∴直线AC '的解析式为1y x =+.将直线和抛物线的解析式联立得:2123y x y x x =+⎧⎨=--⎩. 解得1110x y =-⎧⎨=⎩(舍去)或2245x y =⎧⎨=⎩. ∴点P 的坐标为(4.5).根据图象可得:223332AC =+=225552AP +=∴此时35AC AP =. ②假设存在点M 使MN AC BN AP=. 设点()2,23M m m m --. ∵35AC AP =. ∴35MN BN =. ∴223335m m m --=-.解得25m=-或85m=-.3m=(舍去)当25m=-时.2512325m m--=-.∴251,525M⎛⎫--⎪⎝⎭.当85m=-.2692325m m--=.∴869,525M⎛⎫-⎪⎝⎭.∴存在符合条件的点M.M的坐标为251,525⎛⎫--⎪⎝⎭.869,525⎛⎫-⎪⎝⎭.。
植物雌激素对雄性生殖系统的影响

中图分类号:!""#文献标识码:$文章编号:%&&’()%’*(’&&))&#(&’+&(&)·综述·植物雌激素对雄性生殖系统的影响严继承,朱心强(浙江大学医学院卫生毒理学教研室,浙江杭州)%&&)%)关键词:植物雌激素;异黄酮;,-./012341;雄性生殖系统作者简介:严继承(%"*56),男,硕士研究生,研究方向:生殖毒理学。
植物雌激素是存在于天然植物中的一组化合物,能与雌激素受体(0127-8047090:2-7,;!)结合并诱导具有雌激素活性的非甾体类化合物的产生[%,’],因此在人体内能发挥雌激素样作用。
同时,它们具有弱雌激素活性以及通过其他途径减少体内雌激素的生成。
近年来随着对植物雌激素研究的逐渐深入,有证据表明雄性生殖系统疾患,如雄性生殖器官发育异常和精子数目减少等可能与这些物质密切接触有关[)]。
!植物雌激素的分类植物雌激素从结构上主要分为)类:异黄酮类、木酚素类和9-./012341,它们存在于植物及其种子中。
异黄酮类主要有染料木黄酮、黄豆苷原、染料木苷、黄豆苷、!6谷甾醇、<6=01/02>?@348-@041A4等;木酚素类常见的有肠内脂,肠二醇,去甲二氧愈创木酸、鸟台树脂酚、109-A1-@37A9A701A4-@等;9-./012341中最常见的是拟雌内醇。
此外,还有一类0B.-@,它是肠道内细菌降解刺芒柄花素或黄豆苷原的产物。
"植物雌激素的生物学作用体外实验证实,染料木黄酮对人体细胞有促进增生和抗增生作用,且这种双向作用主要取决于植物雌激素的浓度。
染料木黄酮、黄豆苷原、雌马酚和肠内酯的类雌激素样作用是由;!介导的,其标志是刺激肽合成酶’(CD’)/!E$的表达;而抗雌激素作用并不一定由;!介导,因为在;!阴性细胞中植物雌激素仍表现出抗增殖作用。
人教版九年级上册数学教材复习题24课件

x
y 6 O 6x
F
综合运用
16.如图,等腰三角形 ABC 的顶角∠A = 36°. ⊙O 和底边 BC 相切于 BC 的中点 D,并与两腰 AC,AB 分别相
交于 E,F,G,H 四点,其中 G,F 分别是两腰 AB,
∴
S阴影
=
π 0.52 360
+ π 0.52
360
+ π 0.52
360
=
0.25π (α + β + γ) = 0.125π (cm2),
360
即图中三个扇形的面积之和为 0.125π cm2.
综合运用
8. 估计图中三段弧的半径的大小关系,再用圆规 检验你的结论. 提示:分别找出三段弧所在圆的圆心,然后再 比较半径大小即可. 圆规检验略.
2
2
复习巩固
(4)以半径为 1 的圆的内接正三角形、正方形、 正六边形的边心距为三边作三角形,则( C ). A. 不能构成三角形 B. 这个三角形是等腰三角形 C. 这个三角形是直角三角形 D. 这个三角形是钝角三角形
复习巩固
(5)一个圆锥的侧面积是底面积的 2 倍,则圆 锥侧面展开图的扇形的圆心角是( B ). A. 120° B. 180° C. 240° D. 300°
AC 的中点. 求证:五边形 DEFGH 是正五边形.
证明:连接 AD,OD,DF,则 AD⊥BC. ∵ ⊙O 和 BC 相切于点 D, ∴ OD⊥BC,故 O,A,D 三点共线. ∵ G,F,D 分别为 AB,AC,BC 的中点, ∴ GF∥BC,GF = BD = CD.
dfgh htryrtsthj

百度文库 > 上传文档Checking file system on H:The type of the file system is FAT32.One of your disks needs to be checked for consistency. Youmay cancel the disk check, but it is strongly recommendedthat you continue.Windows will now check the disk. Checking file system on H: The type of the file system is FAT32.One of your disks needs to be checked for consistency. Youmay cancel the disk check, but it is strongly recommendedthat you continue.Windows wilChecking file system on H:The type of the file system is FAT32.One of your disks needs to be checked for consistency. Youmay cancel the disk check, but it is strongly recommendedthat you continue.Windows will now check the disk.Volume Serial Number is 3852-321BWindows has checked the file system and found no problems.4000825344 bytes total disk space.245760 bytes in 16 hidden files.4276224 bytes in 246 folders.1822916608 bytes in 9703 files.2173370368 bytes available on disk.16384 bytes in each allocation unit.244191 total allocation units on disk.132652 allocation units available on disk.l now check the disk.Volume Serial Number is 3852-321BWindows has checked the file system and found no problems.4000825344 bytes total disk space.245760 bytes in 16 hidden files.4276224 bytes in 246 folders.1822916608 bytes in 9703 files.2173370368 bytes available on disk.16384 bytes in each allocation unit.244191 total allocation units on disk.132652 allocation units available on disk.Volume Serial Number is 3852-321BWindows has checked the file system and found no problems.4000825344 bytes total disk space.245760 bytes in 16 hidden files.4276224 bytes in 246 folders.1822916608 bytes in 9703 files.2173370368 bytes available on disk.16384 bytes in each allocation unit.244191 total allocation units on disk.132652 allocation units available on disk.系统检测到您上传的文档中可能包含侵犯他人版权的内容。
post

语言职务结束日期开始日期工作职别OM 1531.12.199401.01.1900fasdfasdfs P 1531.12.999901.01.1995动力运行工P 12331.12.999917.01.2004ddd P 13331.12.999901.01.1900yreyrety P 15031.12.999901.01.1900r P 15131.12.999917.01.2004ddd P 16031.12.999917.01.2004rr P 124131.12.999917.01.2004rtyerty P 133031.12.999917.01.2004rwtr P 133531.12.999917.01.2004yuiytu P 139131.12.999917.01.2004hgjfgh P 139231.12.999917.01.2004dfghdfgh P 139931.12.999917.01.2004rwtwetr P 1505000031.12.999921.07.2000足球比赛者P 1505000131.12.999921.07.2000足球教练P 150********.12.999901.03.2000通过活动康复P 150********.12.999920.07.1999财务经理P 150********.12.999920.07.1999科目员P 150********.12.999920.07.1999人力资源部经理P 150********.12.999920.07.1999人事管理者P 150********.12.999920.07.1999工资核算管理员P 150********.12.999920.07.1999薪资发放管理员P 150********.12.999901.10.1995公司总经理P 150********.12.999901.10.1995公司副总经理P 150********.12.999901.10.1995公司总经理助理P 150********.12.999901.10.1995综合办公室主任P 150********.12.999901.10.1995综合办公室主任助理P 150********.12.999901.10.1995综合办公室副主任P 150********.12.999901.10.1995汽车工程研究院院长P 150********.12.999901.10.1995汽车工程研究院副院长P 150********.12.999901.10.1995汽车工程研究院院长助理P 150********.12.999901.10.1995部长P 150********.12.999901.10.1995副部长P 150********.12.999901.10.1995部长助理P 150********.12.999901.10.1995厂长P 150********.12.999901.10.1995副厂长P 150********.12.999901.10.1995厂长助理P 150********.12.999901.10.1995销售公司总经理P 150********.12.999901.10.1995销售公司副总经理P 150********.12.999901.10.1995销售公司总经理助理P 150********.12.999901.10.1995汽车工程研究院部长P 150********.12.999901.10.1995汽车工程研究院副部长P 150********.12.999901.10.1995销售公司部长P 150********.12.999901.10.1995车间主任P 150********.12.999901.10.1995车间主管P 150********.12.999901.10.1995科长P 150********.12.999901.10.1995主管P 150********.12.999901.10.1995室主任P 150********.12.999901.10.1995工段长P 150********.12.999901.10.1995班组长P 150********.12.999901.10.1995公司总工程师P150********.12.999901.10.1995公司副总工程师P 150********.12.999901.10.1995汽车工程研究院总工程师P 150********.12.999901.10.1995汽车工程研究院副总工程师P 150********.12.999901.10.1995部门总工程师P 150********.12.999901.10.1995部门副总工程师P 150********.12.999901.10.1995厂总工程师P 150********.12.999901.10.1995厂副总工程师P 150********.12.999901.10.1995项目经理P 150********.12.999901.10.1995区域经理P 150********.12.999901.10.1995安全管理员P 150********.12.999901.10.1995办事员P 150********.12.999901.10.1995备件管理员P 150********.12.999901.10.1995标准化管理P 150********.12.999901.10.1995仓库管理员P 150********.12.999901.10.1995产品认证管理P 150********.12.999901.10.1995刀具业务员P 150********.12.999901.10.1995服务管理员P 150********.12.999901.10.1995服务培训员P 150********.12.999901.10.1995工艺管理员P 150********.12.999901.10.1995工装管理员P 150********.12.999901.10.1995工资管理员P 150********.12.999901.10.1995供应商管理员P 150********.12.999901.10.1995计量管理员P 150********.12.999901.10.1995广告业务员P 150********.12.999901.10.1995工资员P 150********.12.999901.10.1995公共关系员P 150********.12.999901.10.1995公关业务员P 150********.12.999901.10.1995接待员P 150********.12.999901.10.1995客户代表P 150********.12.999901.10.1995客户管理员P 150********.12.999901.10.1995生产调度员P 150********.12.999901.10.1995生产服务员P 150********.12.999901.10.1995项目管理P 150********.12.999901.10.1995环境保护管理员P 150********.12.999901.10.1995总经理秘书P 150********.12.999901.10.1995计划设度员P 150********.12.999901.10.1995量检具管理员P 150********.12.999901.10.1995内审员P 150********.12.999901.10.1995培训管理员P 150********.12.999901.10.1995企业管理员P 150********.12.999901.10.1995区域管理员P 150********.12.999901.10.1995人事管理员P 150********.12.999901.10.1995设备管理员P 150********.12.999901.10.1995生活服务员P 150********.12.999901.10.1995市场调研员P 150********.12.999901.10.1995索赔员P 150********.12.999901.10.1995体系审核员P 150********.12.999901.10.1995网络管理员P 150********.12.999901.10.1995网络规划员P 150********.12.999901.10.1995网络建设员P 150********.12.999901.10.1995网站管理员P 150********.12.999901.10.1995物流管理员P150********.12.999901.10.1995物流规划员P 150********.12.999901.10.1995物资管理员P 150********.12.999901.10.1995行政管理员P 150********.12.999901.10.1995宣传员P 150********.12.999901.10.1995展示员P 150********.12.999901.10.1995政策研究员P 150********.12.999901.10.1995政工干事P 150********.12.999901.10.1995质量管理员P 150********.12.999901.10.1995中转库主任P 150********.12.999901.10.1995厂部秘书P 150********.12.999901.10.1995驻库员P 150********.12.999901.10.1995专利管理P 150********.12.999901.10.1995资料管理员P 150********.12.999901.10.1995人力资源专员P 150********.12.999901.10.1995综合管理员P 150********.12.999901.10.1995综合后勤员P 150********.12.999901.10.1995BOM管理P 150********.12.999901.10.1995情报资料管理P 150********.12.999901.10.1995文档员P 150********.12.999901.10.1995信息员P 150********.12.999901.10.1995设备员P 150********.12.999901.10.1995产品规划P 150********.12.999901.10.1995产品规划设计P 150********.12.999901.10.1995产品规划员P 150********.12.999901.10.1995产品审核员P 150********.12.999901.10.1995齿形测量员P 150********.12.999901.10.1995ERP数据员P 150********.12.999901.10.1995备件员P 150********.12.999901.10.1995电气工程师P 150********.12.999901.10.1995调查分析员P 150********.12.999901.10.1995动力员P 150********.12.999901.10.1995分析师P 150********.12.999901.10.1995分析员P 150********.12.999901.10.1995服务工程师P 150********.12.999901.10.1995高级试验师P 150********.12.999901.10.1995工厂设计师P 150********.12.999901.10.1995工程监理P 150********.12.999901.10.1995工具员P 150********.12.999901.10.1995工位器具设计P 150********.12.999901.10.1995工业工程师P 150********.12.999901.10.1995工艺师P 150********.12.999901.10.1995工艺员P 150********.12.999901.10.1995工艺装备设计P 150********.12.999901.10.1995工装员P 150********.12.999901.10.1995锅炉工程师P 150********.12.999901.10.1995合格证管理员P 150********.12.999901.10.1995机械工程师P 150********.12.999901.10.1995机械员P 150********.12.999901.10.1995计量工程师P 150********.12.999901.10.1995计量检定员P 150********.12.999901.10.1995计量员P 150********.12.999901.10.1995技术员P150********.12.999901.10.1995监控员P 150********.12.999901.10.1995精测工程师P 150********.12.999901.10.1995精密测量员P 150********.12.999901.10.1995模具工程师P 150********.12.999901.10.1995匹配工程师P 150********.12.999901.10.1995汽轮机工程师P 150********.12.999901.10.1995热控工程师P 150********.12.999901.10.1995软件工程师P 150********.12.999901.10.1995三坐标程序员P 150********.12.999901.10.1995设备员P 150********.12.999901.10.1995设备员P 150********.12.999901.10.1995设计师P 150********.12.999901.10.1995设计员P 150********.12.999901.10.1995施工员P 150********.12.999901.10.1995实验师P 150********.12.999901.10.1995实验员P 150********.12.999901.10.1995试验师P 150********.12.999901.10.1995试验员P 150********.12.999901.10.1995试制员P 150********.12.999901.10.1995维护工程师P 150********.12.999901.10.1995系统管理员P 150********.12.999901.10.1995信息系统管理P 150********.12.999901.10.1995质量工程师P 150********.12.999901.10.1995主管分析师P 150********.12.999901.10.1995主管工艺师P 150********.12.999901.10.1995主管规划设计P 150********.12.999901.10.1995主管设计师P 150********.12.999901.10.1995综合规划设计P 150********.12.999901.10.1995润滑员P 150********.12.999901.10.1995钣金工P 150********.12.999901.10.1995驳运员P 150********.12.999901.10.1995操作工P 150********.12.999901.10.1995物流工P 150********.12.999901.10.1995冲压工P 150********.12.999901.10.1995刀具调修工P 150********.12.999901.10.1995刀具磨锋工P 150********.12.999901.10.1995电焊工P 150********.12.999901.10.1995电仪维修工P 150********.12.999901.10.1995调试交检工P 150********.12.999901.10.1995调整工P 150********.12.999901.10.1995返修工P 150********.12.999901.10.1995服务工P 150********.12.999901.10.1995工装工P 150********.12.999901.10.1995管钳维修工P 150********.12.999901.10.1995焊接工P 150********.12.999901.10.1995化学分析工P 150********.12.999901.10.1995机床操作工P 150********.12.999901.10.1995机加工P 150********.12.999901.10.1995计划执行员P 150********.12.999901.10.1995驾驶员P 150********.12.999901.10.1995检测工P 150********.12.999901.10.1995库管工P150********.12.999901.10.1995开卷剪切工P 150********.12.999901.10.1995检验员P 150********.12.999901.10.1995冷作工P 150********.12.999901.10.1995量检具维修工P 150********.12.999901.10.1995密封工P 150********.12.999901.10.1995模修工P 150********.12.999901.10.1995喷涂工P 150********.12.999901.10.1995起重工P 150********.12.999901.10.1995气站操作工P 150********.12.999901.10.1995刃磨工P 150********.12.999901.10.1995润滑工P 150********.12.999901.10.1995三坐标操作员P 150********.12.999901.10.1995喷丸操作工P 150********.12.999901.10.1995上线调刀工P 150********.12.999901.10.1995上线调修工P 150********.12.999901.10.1995设备维修工P 150********.12.999901.10.1995试验工P 150********.12.999901.10.1995试制工P 150********.12.999901.10.1995水电维修工P 150********.12.999901.10.1995司炉工P 150********.12.999901.10.1995剃齿机调整工P 150********.12.999901.10.1995天车工P 150********.12.999901.10.1995涂装调整工P 150********.12.999901.10.1995外协检验员P 150********.12.999901.10.1995维修电工P 150********.12.999901.10.1995维修工P 150********.12.999901.10.1995维修钳工P 150********.12.999901.10.1995物流工P 150********.12.999901.10.1995校直操作工P 150********.12.999901.10.1995修磨工P 150********.12.999901.10.1995压合工P 150********.12.999901.10.1995油品化验工P 150********.12.999901.10.1995油漆返修工P 150********.12.999901.10.1995油漆工P 150********.12.999901.10.1995值班电工P 150********.12.999901.10.1995注塑工P 150********.12.999901.10.1995装配工P 150********.12.999901.10.1995采购工程师P 150********.12.999901.10.1995采购计划员P 150********.12.999901.10.1995采购员P 150********.12.999901.10.1995成本核算员P 150********.12.999901.10.1995成本控制员P 150********.12.999901.10.1995工程预算员P 150********.12.999901.10.1995会计核算员P 150********.12.999901.10.1995计划员P 150********.12.999901.10.1995经营计划员P 150********.12.999901.10.1995审计员P 150********.12.999901.10.1995生产计划员P 150********.12.999901.10.1995生产统计员P 150********.12.999901.10.1995数据员P 150********.12.999901.10.1995特销员P 150********.12.999901.10.1995统计员P150********.12.999901.10.1995投资管理员P 150********.12.999901.10.1995物流计划员P 150********.12.999901.10.1995物流统计员P 150********.12.999901.10.1995销售管理员P 150********.12.999901.10.1995信用控制员P 150********.12.999901.10.1995营销计划员P 150********.12.999901.10.1995综合统计员P 150********.12.999901.10.1995总帐管理员P 150********.12.999901.01.1999挪威上司P 150********.12.999901.01.2000工资核算计算P 150********.12.999901.01.2000薪资发放管理员P 150********.12.999901.01.2000HW 测试作业P 150********.12.999918.08.2000测试P 150********.12.999901.10.1995计划调度员P 150********.12.999901.10.1995设备规划设计P 150********.12.999901.10.1995冲压工艺员P 150********.12.999901.10.1995总装工艺员P 150********.12.999901.10.1995秘书P 150********.12.999901.10.1995焊装工艺员P 150********.12.999901.10.1995化验员P 150********.12.999901.10.1995外贸业务员P 150********.12.999901.10.1995驾驶员P 150********.12.999901.10.1995质检员P 150********.12.999901.10.1995分拣工P 150********.12.999901.10.1995汽车工程研究院部门总工程P 150********.12.999901.10.1995工位器具管理员P 150********.12.999901.10.1995新产品质量策划员P 150********.12.999901.10.1995ERP支持工程师P 150********.12.999901.10.1995工厂规划设计(土建)P 150********.12.999901.10.1995工厂规划设计(总图)P 150********.12.999901.10.1995工艺设备规划设计P 150********.12.999901.10.1995化学水处理工程师P 150********.12.999901.10.1995主管匹配工程师P 150********.12.999901.10.1995数控设备操作员P 150********.12.999901.10.1995控制员P 150********.12.999901.03.2004单元测试职务1P 150********.12.999901.03.2004单元测试职务2P 150********.12.999901.03.2004单元测试职务3P 150********.12.999901.10.1995顾问P 150********.12.999901.10.1995总经理办公室主任P 150********.12.999901.10.1995总经理办公室副主任P 150********.12.999901.10.1995总经理办公室主任助理P 150********.12.999901.10.1995综合服务科科长P 150********.12.999901.10.1995综合服务科主管P 150********.12.999901.10.1995人力资源部部长P 150********.12.999901.10.1995人力资源部副部长P 150********.12.999901.10.1995人力资源部部长助理P 150********.12.999901.10.1995企业管理部部长P 150********.12.999901.10.1995企业管理部副部长P 150********.12.999901.10.1995企业管理部部长助理P 150********.12.999901.10.1995财务部部长P 150********.12.999901.10.1995财务部副部长P150********.12.999901.10.1995财务部部长助理P 150********.12.999901.10.1995国际部部长P 150********.12.999901.10.1995国际部副部长P 150********.12.999901.10.1995国际部部长助理P 150********.12.999901.10.1995规划设计院院长P 150********.12.999901.01.1800规划设计院常务副院长P 150********.12.999901.10.1995规划设计院副院长P 150********.12.999901.10.1995规划设计院管理部部长P 150********.12.999901.10.1995规划设计院管理部副部长P 150********.12.999901.10.1995规划设计院管理部部长助理P 150********.12.999901.10.1995工厂规划部部长P 150********.12.999901.10.1995工厂规划部副部长P 150********.12.999901.10.1995工厂规划部部长助理P 150********.12.999901.10.1995工艺规划部部长P 150********.12.999901.10.1995工艺规划部副部长P 150********.12.999901.10.1995工艺规划部部长助理P 150********.12.999901.10.1995工程部部长P 150********.12.999901.10.1995工程部副部长P 150********.12.999901.10.1995工程部部长助理P 150********.12.999901.10.1995动能厂厂长P 150********.12.999901.10.1995动能厂副厂长P 150********.12.999901.10.1995动能厂厂长助理P 150********.12.999901.10.1995投资管理办公室主任P 150********.12.999901.10.1995发动机二厂厂长P 150********.12.999901.10.1995发动机二厂副厂长P 150********.12.999901.10.1995汽车工程研究院常务副院长P 150********.12.999901.10.1995汽车工程研究院院长P 150********.12.999901.10.1995汽车工程研究院副院长P 150********.12.999901.10.1995汽车工程研究院管理部部长P 150********.12.999901.10.1995汽车工程研究院管理部副部P 150********.12.999901.10.1995汽车工程研究院管理部部长P 150********.12.999901.10.1995发动机部部长P 150********.12.999901.10.1995发动机部副部长P 150********.12.999901.10.1995发动机部部长助理P 150********.12.999901.10.1995变速箱部部长P 150********.12.999901.10.1995变速箱部副部长P 150********.12.999901.10.1995变速箱部部长助理P 150********.12.999901.10.1995车型部部长P 150********.12.999901.10.1995车型部副部长P 150********.12.999901.10.1995车型部部长助理P 150********.12.999901.10.1995底盘部部长P 150********.12.999901.10.1995底盘部副部长P 150********.12.999901.10.1995底盘部部长助理P 150********.12.999901.10.1995电器电子部部长P 150********.12.999901.10.1995电器电子部副部长P 150********.12.999901.10.1995电器电子部部长助理P 150********.12.999901.10.1995车身部部长P 150********.12.999901.10.1995车身部副部长P 150********.12.999901.10.1995车身部部长助理P 150********.12.999901.10.1995CAE部部长P 150********.12.999901.10.1995CAE部副部长P 150********.12.999901.10.1995CAE部部长助理P150********.12.999901.10.1995试验部部长P 150********.12.999901.10.1995试验部副部长P 150********.12.999901.10.1995试验部部长助理P 150********.12.999901.10.1995质量保证部部长P 150********.12.999901.10.1995质量保证部副部长P 150********.12.999901.10.1995质量保证部部长助理P 150********.12.999901.10.1995生产管理部部长P 150********.12.999901.10.1995生产管理部副部长P 150********.12.999901.10.1995生产管理部部长助理P 150********.12.999901.10.1995变速箱厂厂长P 150********.12.999901.10.1995变速箱厂副厂长P 150********.12.999901.10.1995变速箱厂厂长助理P 150********.12.999901.10.1995发动机一厂厂长P 150********.12.999901.10.1995发动机一厂副厂长P 150********.12.999901.10.1995发动机一厂厂长助理P 150********.12.999901.10.1995轿车一厂厂长P 150********.12.999901.10.1995轿车一厂副厂长P 150********.12.999901.10.1995轿车一厂厂长助理P 150********.12.999901.10.1995轿车二厂厂长P 150********.12.999901.10.1995轿车二厂副厂长P 150********.12.999901.10.1995轿车二厂厂长助理P 150********.12.999901.10.1995部长秘书P 150********.12.999901.10.1995院长P 150********.12.999901.10.1995常务副院长P 150********.12.999901.10.1995副院长P 150********.12.999901.10.1995院长助理P 150********.12.999901.10.1995院副总工程师P 150********.12.999901.10.1995公司总管P 150********.12.999901.10.1995安全员P 150********.12.999901.10.1995项目管理员P 150********.12.999901.10.1995工艺路线规划员P 150********.12.999901.10.1995工厂规划员P 150********.12.999901.10.1995物流规划员P 150********.12.999901.10.1995设备规划员P 150********.12.999901.10.1995环保规划员P 150********.12.999901.10.1995物流规划员P 150********.12.999901.10.1995物流规划员P 150********.12.999901.10.1995工艺规划员P 150********.12.999901.10.1995主任P 150********.12.999901.10.1995工程造价师P 150********.12.999901.10.1995工程预算员P 150********.12.999901.10.1995动能计划员P 150********.12.999901.10.1995动能调度员P 150********.12.999901.10.1995汽机工程师P 150********.12.999901.10.1995锅炉工程师P 150********.12.999901.10.1995电气工程师P 150********.09.200501.10.1995化水工程师P 150********.12.999901.10.2005化学工程师P 150********.12.999901.10.1995热工工程师P 150********.12.999901.10.1995机务维修工P 150********.12.999901.10.1995机务维修工P 150********.12.999901.10.1995司炉运行工P150********.12.999901.10.1995司机P 150********.12.999901.10.1995电气运行工P 150********.12.999901.10.1995化水运行工P 150********.12.999901.10.1995辅机运行工P 150********.12.999901.10.1995化验工P 150********.12.999901.10.1995天车工P 150********.12.999901.10.1995值长P 150********.12.999901.10.1995管道工P 150********.12.999901.10.1995电仪工P 150********.12.999901.10.1995管理总监P 150********.12.999901.10.1995销售公司总监P 150********.12.999901.10.1995销售公司副总监P 150********.12.999901.10.1995销售公司总监助理P 150********.12.999901.10.1995部长/主管P 150********.12.999901.10.1995轿车厂总工程师P 150********.12.999901.10.1995轿车厂副总工程师P 150********.12.999901.10.1995工位器具设计员P 150********.12.999901.10.1995工艺装备设计员P 150********.12.999901.10.1995班组长P 150********.12.999901.10.1995库管工P 150********.12.999901.10.1995工段长P 150********.12.999901.10.1995P 150********.12.999901.10.1995钣金工P 150********.12.999901.10.1995工艺员P 150********.12.999901.10.1995工段长P 150********.12.999901.10.1995维修管理员P 150********.12.999901.10.1995施工员P 150********.12.999901.10.1995试验工P 150********.12.999901.10.1995车工P 150********.12.999901.10.1995动能调度员P 150********.12.999901.10.1995能源管理员P 150********.12.999901.10.1995办事员P 150********.12.999901.10.1995统计员P 150********.12.999901.10.1995办事员P 150********.12.999901.10.1995统计员P 150********.12.999901.10.1995动能厂顾问P 150********.12.999901.10.1995管理部顾问P 150********.12.999901.10.1995项目管理员P 150********.12.999901.10.1995项目管理员P 150********.12.999901.10.1995工厂规划部顾问P 150********.12.999905.04.2004质量管理员P 150********.12.999901.10.1995副总工程师P 150********.12.999901.10.1995规划师P 150********.12.999901.10.1995主任P 150********.12.999901.10.1995主管P 150********.12.999901.10.1995模具工程师P 150********.12.999901.10.1995工段长P 150********.12.999901.10.1995工艺员P 150********.12.999901.10.1995质量工程师P 150********.12.999901.10.1995设备员P 150********.12.999901.10.1995机械员P 150********.12.999901.10.1995动力员P150********.12.999901.10.1995计划调度员P 150********.12.999901.10.1995培训管理员P 150********.12.999901.10.1995培训管理员P 150********.12.999901.10.1995办事员P 150********.12.999901.10.1995钣金工P 150********.12.999901.10.1995模修工P 150********.12.999901.10.1995生产统计员P 150********.12.999901.10.1995成本核算员P 150********.12.999901.10.1995安全管理员P 150********.12.999901.10.1995检验员P 150********.12.999901.10.1995班组长P 150********.12.999901.10.1995物流工P 150********.12.999901.10.1995库管工P 150********.12.999901.10.1995维修电工P 150********.12.999901.10.1995设计师P 150********.12.999901.10.1995设计员P 150********.12.999901.10.1995注塑工P 150********.12.999901.10.1995调整工P 150********.12.999901.10.1995调整工P 150********.12.999901.10.1995化学分析工P 150********.12.999901.10.1995修磨工P 150********.12.999901.10.1995喷涂工P 150********.12.999901.10.1995操作工P 150********.12.999901.10.1995涂装项目指挥P 150********.12.999901.10.1995总经理助理P 150********.12.999901.10.1995总经理P 150********.12.999901.10.1995综合部部长P 150********.12.999901.10.1995总经理助理P 150********.12.999901.10.1995副总工程师P 150********.12.999901.10.1995注塑工程师P 150********.12.999901.10.1995技术顾问P 150********.12.999901.10.1995副总工程师P 150********.12.999901.10.1995副总经理P 150********.12.999901.10.1995电子电器工程师P 150********.12.999901.10.1995高级工程师P 150********.12.999901.10.1995锅炉技师P 150********.09.200501.10.1995水处理工P 150********.12.999901.10.2005废水处理工P 150********.12.999901.10.1995顾问P 150********.12.999901.10.1995油库工P 150********.12.999901.10.1995电器电子设计员P 150********.12.999901.10.1995钳工技师P 150********.12.999901.10.1995外贸业务员P 150********.12.999901.10.1995实习生(技术工人)P 150********.12.999901.10.1995培训讲师P 150********.12.999901.10.1995工艺规划师P 150********.12.999901.10.1995工艺规划师P 150********.12.999901.10.1995工艺规划师P 150********.12.999901.10.1995工艺规划师P 150********.12.999901.10.1995培训讲师P 150********.12.999901.10.1995培训讲师P 150********.12.999901.10.1995培训讲师P150********.12.999901.10.1995主任规划师P 150********.12.999901.10.1995培训讲师P 150********.12.999901.10.1995预算控制员P 150********.12.999901.01.1800凯越常务副总P 150********.12.999901.10.1995规划员P 150********.12.999901.10.1995科威常务副总P 150********.12.999901.10.1995副总经理P 150********.12.999901.10.1995科威常务副总P 150********.12.999901.10.1995电气规划P 150********.12.999901.10.1995综合计划员P 150********.12.999901.10.1995标准化员P 150********.12.999901.10.1995计量工P 150********.12.999901.10.1995工程师P 150********.12.999901.10.1995调查分析员P 150********.12.999901.10.1995经管会成员P 150********.12.999901.10.1995值班员P 150********.12.999901.10.1995销售负责人P 150********.12.999901.10.1995质量员P 150********.12.999901.10.1995经理P 150********.12.999901.10.1995P 150********.12.999901.10.1995副经理P 150********.12.999901.10.1995P 150********.12.999901.09.2004负责人P 150********.12.999901.10.1995P 150********.12.999901.10.1995翻译P 150********.12.999901.10.1995企划管理员P 150********.12.999901.10.1995单证管理员P 150********.12.999901.10.1995技术服务员P 150********.12.999901.10.1995档案管理员P 150********.12.999901.10.1995维修电工P 150********.12.999901.10.1995运行工P 150********.12.999901.10.1995包装工P 150********.12.999901.10.1995广告策划员P 150********.12.999913.10.2004法务政策员P 150********.12.999901.10.1995成本员P 150********.12.999901.01.2005总监P 150********.12.999901.01.2005总工程师P 150********.12.999901.10.1995科威常务副总P 150********.12.999901.01.2005市场分析员P 150********.12.999901.01.2005经理助理P 150********.12.999901.01.2005设备工程师P 150********.12.999901.01.2005业务员P 150********.12.999901.01.2005项目主管P 150********.12.999901.01.1995动力运行工P 150********.12.999901.01.1995动能工程师P 150********.12.999901.10.1995环保员P 150********.12.999901.10.1995审计师P 150********.12.999901.10.1995项目助理P 150********.12.999901.10.1995项目计划员P 150********.12.999901.04.2005夸克公司副总经理P 150********.12.999901.01.1800一车间主管P 150********.12.999901.01.1800审核员P150********.12.999901.01.1800调漆工P 150********.12.999901.01.1800工具钳工P 150********.12.999901.01.1800喷蜡工P 150********.12.999901.01.1800污水处理工P 150********.12.999901.01.1800瑞赛克临时负责人P 150********.12.999901.01.1800模具清洗工P 150********.12.999901.01.1800输煤运行工P 150********.12.999901.01.1800品牌管理员P 150********.12.999901.10.1995制图员P 150********.12.999901.10.1995档案员P 150********.12.999901.10.1995检验员P 150********.12.999901.01.2005模修钳工P 150********.12.999901.04.2005PBOM管理员P 150********.12.999901.07.2005见习生P 150********.12.999901.08.2005涂装工P 150********.12.999901.08.2005修磨工P 150********.12.999901.01.2005安全管理员P 150********.12.999901.01.2005化学分析工P 150********.12.999901.01.2005汽机运行工P 150********.12.999901.01.2005输煤工P 150********.12.999901.01.2005法务专员P 150********.12.999901.01.2005建模员P 150********.12.999901.01.2005培训专员P 150********.12.999901.01.2005品牌助理P 150********.12.999901.01.2005公务司机P 150********.12.999901.01.2005设计师P 150********.12.999901.01.2005库管员P 150********.12.999901.01.2005工厂后勤管理员P 150********.12.999901.01.2005涂装工P 150********.12.999901.01.2005项目管理员P 150********.12.999901.01.2005人力资源专员P 150********.12.999901.01.2005人事助理P 150********.12.999901.01.2005试验工P 150********.12.999901.01.2005党群管理员P 150********.12.999901.01.2005生活管理员P 150********.12.999901.01.2005BOM管理师P 150********.12.999901.01.2005BOM管理员P 150********.12.999901.01.2005安全技术工程师P 150********.12.999901.01.2005安全检查员P 150********.12.999901.01.2005安全值班员P 150********.12.999901.01.2005CO2维护工P 150********.12.999901.01.2005钣金成型师P 150********.12.999901.01.2005钣金成型设计员P 150********.12.999901.01.2005备件工程师P 150********.12.999901.01.2005备件计划员P 150********.12.999901.01.2005备件技术员P 150********.12.999901.01.2005变速箱厂副总工程师P 150********.12.999901.01.2005变速箱厂总工程师P 150********.12.999901.01.2005标准化师P 150********.12.999901.01.2005材料分析员P 150********.12.999901.01.2005材料工程师P 150********.12.999901.01.2005材料实验员P150********.12.999901.01.2005车型管理员P 150********.12.999901.01.2005成本会计P 150********.12.999901.01.2005单证业务员P 150********.12.999901.01.2005动能厂副总工程师P 150********.12.999901.01.2005动能厂总工程师P 150********.12.999901.01.2005发动机厂副总工程师P 150********.12.999901.01.2005发动机厂总工程师P 150********.12.999901.01.2005法律顾问P 150********.12.999901.01.2005分销处主任P 150********.12.999901.01.2005服务代表P 150********.12.999901.01.2005服务技术部副总工程师P 150********.12.999901.01.2005服务技术部总工程师P 150********.12.999901.01.2005服务经理P 150********.12.999901.01.2005高级培训专员P 150********.12.999901.01.2005高级人力资源专员P 150********.12.999901.01.2005高级薪酬专员P 150********.12.999901.01.2005高级员工关系专员P 150********.12.999901.01.2005高级招聘专员P 150********.12.999901.01.2005工厂规划师P 150********.12.999901.01.2005工程计划员P 150********.12.999901.01.2005工程监理师P 150********.12.999901.01.2005工程监理员P 150********.12.999901.01.2005工程造价员P 150********.12.999901.01.2005工具员P 150********.12.999901.01.2005工艺分析师P 150********.12.999901.01.2005工艺分析员P 150********.12.999901.01.2005公关策划员P 150********.12.999901.01.2005公司总工程师P 150********.12.999901.01.2005公用设计师P 150********.12.999901.01.2005公用设计员P 150********.12.999901.01.2005规划设计院副总工程师P 150********.12.999901.01.2005规划设计院总工程师P 150********.12.999901.01.2005核算会计P 150********.12.999901.01.2005化学工程师P 150********.12.999901.01.2005环保工程师P 150********.12.999901.01.2005计量工P 150********.12.999901.01.2005计量检验员P 150********.12.999901.01.2005技术服务工程师P 150********.12.999901.01.2005建筑设计师P 150********.12.999901.01.2005建筑设计员P 150********.12.999901.01.2005轿车厂副总工程师P 150********.12.999901.01.2005轿车厂总工程师P 150********.12.999901.01.2005金融会计P 150********.12.999901.01.2005开卷工P 150********.12.999901.01.2005客户代表P 150********.12.999901.01.2005库主任P 150********.12.999901.01.2005路线规划师P 150********.12.999901.01.2005路线规划员P 150********.12.999901.01.2005媒介策划员P 150********.12.999901.01.2005媒介购买员P 150********.12.999901.01.2005媒介关系员P 150********.12.999901.01.2005模具员P150********.12.999901.01.2005模型工P 150********.12.999901.01.2005模型师P 150********.12.999901.01.2005模型员P 150********.12.999901.01.2005能源管理员P 150********.12.999901.01.2005企业文化宣传员P 150********.12.999901.01.2005清洁度试验工P 150********.12.999901.01.2005热处理工P 150********.12.999901.01.2005认证管理员P 150********.12.999901.01.2005润滑工P 150********.12.999901.01.2005设备操作工P 150********.12.999901.01.2005审计师P 150********.12.999901.01.2005生产管理部副总工程师P 150********.12.999901.01.2005生产管理部总工程师P 150********.12.999901.01.2005实验工程师P 150********.12.999901.01.2005市场策划员P 150********.12.999901.01.2005市场研究员P 150********.12.999901.01.2005数据工程师P 150********.12.999901.01.2005机床操作工P 150********.12.999901.01.2005数控程序员P 150********.12.999901.01.2005司磅工P 150********.12.999901.01.2005特销代表P 150********.12.999901.01.2005特销项目经理P 150********.12.999901.01.2005投资控制师P 150********.12.999901.01.2005投资控制员P 150********.12.999901.01.2005外贸业务经理P 150********.12.999901.01.2005网络维护工程师P 150********.12.999901.01.2005维护员P 150********.12.999901.01.2005物流工艺员P 150********.12.999901.01.2005物流规划师P 150********.12.999901.01.2005物流司机P 150********.12.999901.01.2005系统工程师P 150********.12.999901.01.2005系统数据员P 150********.12.999901.01.2005现场工程师P 150********.12.999901.01.2005项目管理师P 150********.12.999901.01.2005项目协理P 150********.12.999901.01.2005销售促进员P 150********.12.999901.01.2005销售代表P 150********.12.999901.01.2005销售计划员P 150********.12.999901.01.2005销售经理P 150********.12.999901.01.2005薪酬专员P 150********.12.999901.01.2005信息情报员P 150********.12.999901.01.2005邮政收发员P 150********.12.999901.01.2005员工关系专员P 150********.12.999901.01.2005院部副总工程师P 150********.12.999901.01.2005院部总工程师P 150********.12.999901.01.2005院总工程师P 150********.12.999901.01.2005造型师P 150********.12.999901.01.2005造型员P 150********.12.999901.01.2005展示业务员P 150********.12.999901.01.2005招聘专员P 150********.12.999901.01.2005制造钳工P 150********.12.999901.01.2005主管材料工程师P150********.12.999901.01.2005主管分析师P 150********.12.999901.01.2005主管工艺规划师P 150********.12.999901.01.2005主管工艺师P 150********.12.999901.01.2005主管规划师P 150********.12.999901.01.2005主管监理师P 150********.12.999901.01.2005主管模型师P 150********.12.999901.01.2005主管匹配工程师P 150********.12.999901.01.2005主管设备工程师P 150********.12.999901.01.2005主管试验师P 150********.12.999901.01.2005主管造价师P 150********.12.999901.01.2005主管造型师P 150********.12.999901.01.2005主管质量工程师P 150********.12.999901.01.2005助理材料工程师P 150********.12.999901.01.2005专利顾问P 150********.12.999901.01.2005专利研究员P 150********.12.999901.01.2005总图规划师P 150********.12.999901.01.2005总图规划员P 150********.12.999901.01.2005总务管理员P 150********.12.999901.01.2005顾问P 150********.12.999901.01.2005值长P 150********.12.999901.10.2005驻点销售员P 150********.12.999901.10.1995董事长P 150********.12.999901.10.1995总经理P 150********.12.999901.10.1995金融管理员P 150********.12.999901.10.1995统计管理员P 150********.12.999901.01.1800所长P 150********.12.999901.01.1800主任助理P 150********.12.999901.01.1800助理P 150********.12.999901.01.1800高级人力资源专员P 150********.12.999901.01.1800试验技师P 150********.12.999901.05.2006科技项目管理员P 150********.12.999901.01.1800设备安调工P 150********.12.999901.05.2006尺寸技术员P 150********.12.999901.01.1800展示推广员P 150********.12.999901.01.2006培训业务经理P 150********.12.999901.01.2006P 150********.12.999901.01.1800数据员P 150********.12.999901.06.2006销售主管P 150********.12.999901.07.2006销售主任P 150********.12.999901.07.2006装配工P 150********.12.999901.01.2006试验工程师P 150********.12.999901.01.2006客服代表P 150********.12.999901.01.2006网络督导员P 150********.12.999901.01.1800BOM高级管理员P 150********.12.999901.10.1995铸造项目负责人P 150********.12.999901.07.2006培训助理P 150********.12.999901.07.2006材料核算员P 150********.12.999901.01.1800成本管理员P 150********.12.999901.01.1800班长P 150********.12.999901.01.1800三坐标测量员P 150********.12.999901.07.2006组长P 150********.12.999901.07.2006副组长P。
四年面积

十一、长方形和正方形的面积(一)一、习惯引导:粗心是办事不认真的表现。
做作业时粗,影响作业质量;考试时粗心,影响考试成绩;长大参加工作时粗心,会给工作带来损失,甚至严重损失。
毛主席说:“粗心大意,往往搞错。
”有粗心毛病的人,应坚决克服。
二、简要提示:在解答比较复杂的关于长方形、正方形的面积问题时,要用到割补、移动、代换和添辅助线的方法。
因此,解题时要仔细看图,把观察与思考结合起来。
三、例题探究:例1:下图的面积你能用几种方法求出来?请你把几种解题方法都写出来。
求下图的面积时,怎样割?有几种割法?怎样补?把割和补的图画出来。
例2:有两个相同的长方形是8厘米,宽是3厘米。
如果把它们按下图的样子叠放,这个图形的面是多少?想:有几种解答方法?最简的是哪一种?例3:一个长方形若长增加2厘米,面积就增加10平方厘米;若宽减少了3厘米,面积就减少了18平方厘米。
原来长方形的面积多少平方厘米?想:根据“长增加2厘米面积就增加10平方厘米”这条件可求什么?根据“宽减了3厘米,面积就减少了18平方厘米”这条件可求什么?例4:在一块长方形的地面,一头修一个少年活动中心,底层是一个正方形,余下部分修一个游泳池。
长方形地面的长150米,总面积为9000平方米。
游泳池的占地面积多少平方米?想:长方形地面的宽是多少米?少年活动中心占地面积是多少?四、课堂做做练习十一1、一个长方形,如果长不变,宽减少3厘米,那么它的面积就减少36平方厘米;如果宽不变,长增加6厘米,那么它的面积增加54平方厘米,这个长方形的面积是多少平方厘米?2、一块长方形铁板,长18分米,面积120平方分米,现在要截去一个最大的正方形,剩下的铁板是多少平方分米?3、有两个完全一样的长方形,长10厘米,宽4厘米。
如果把它们按下图的样子叠放,这个图形的面积是多少?4、图中小正方形的边长3厘米,用两种方法求出大正方形的面积。
五、回家练练1、复习练习(1)求下图的周长(单位:厘米)(2)求下图的周长(单位:厘米)2、重点练习(1)如图,明明用三个同样大小的长方形,拼成一个大长方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
库顶设有溢流式生料分配器。
NC型多料流式均化库
库顶多点下料,平铺生料。
4、磨机系统操作自动化;
5、各种新型优质研磨体、锁风装置、密封材料、大型专用驱动装置等的广泛应用,为主机安全、高效运转提供了保证。
5.3 生料粉磨细度及颗粒级配要求
控制生料粉磨细度的意义:生料细度影响熟料的煅烧速度,也影响熟料的质量。生料越细,熟料的形成越快,产量提高,且游离氧化钙下降。但过细后,对煅烧的影响不大,反而会使生料磨的产量下降,电耗明显升高。因此,细度须控制适当。
硅酸盐水泥配料及生料制备(III)【教学资料】
2007-1-4 作者:
四、 配料工艺
4.1 配料工艺及配料方式:
1、 配料工艺:根据配料计算结果,将各种原料经过计量按要求的配合比配合的过程。
2、配料方式:
磨头仓配料:原料在磨头设置的配料小仓备料,经配料小仓的仓底计量设备称量配合后直接喂入磨机内粉磨的工艺。常见的工艺流程如下图所示:
2、类型:
(1)、混合室或均化室均化库:
A 结构:如图
B特点:
a 兼备储存与均化功能。均化原料系采用库内“平铺直取”与混合室或均化室内空气搅拌相结合。
b 库顶中心设有生料分配器
c 库底部设置的混合室或均化室,其环形区呈圆锥形斜面,向库中心倾斜。环形区内分几个小区布置充气装置,并由空气分配阀轮流充气,使生料膨松活化,向中央的混合室或均化室流动。产生重力均化和径向混合均化,进入混合室或均化室的生料由空气进行搅拌均化。
5、均化工艺控制及应注意的问题
①、确保足够的充其量、充气压力
②、努力提高出磨生料的合格率
③、做好搅拌前入库生料的调配工作
④、入搅拌库生料水分在1.0%以下
⑤、搅拌库中生料料高不宜超过库直筒高度的75%
⑥、充气搅拌时间不宜过长。
(二)、连续式生料均化系统
1、均化原理:采用空气搅拌及重力作用下产生的“漏斗效应”(或称鼠穴效应),使生料粉向下落降时切割尽量多层料面予以混合。同时,在不同流化空气的作用下,使沿库内平行料面发生大小不同的流化膨胀作用,有的区域卸料,有的区域流化,从而使库内料面产生径向混合均化。简单讲即:空气搅拌、重力均化、径向混合均化。三种均化作用匹配完成整体均化。
5. 无法控制的其它因素,如库内贮量、出入库物料流量、进库物料成分波动周期等。
控制生料颗粒分布的意义:生料细度不均匀,反应不一致,尤其是粗颗粒,反应很慢,对熟料质量的影响很大,粗颗粒越多,同样煅烧条件下,熟料中游离氧化钙含量越高。因此要限制生料中粗颗粒的含量。
合理的粉磨细度包括两个含义:
1、使生料的平均细度控制在一定范围内:通常用0.08mm方孔筛筛余控制,一般8%~12%;
(9)、立式磨系统:
(10)、挤压粉磨系统:
A、混合粉磨系统:
B、预粉磨系统:
C、终粉磨系统
5.2 生料粉磨发展的特点
1、利用废气进行磨内物料的烘干;
2、粉磨设备日趋大型化;
3、新型磨机、高效选粉机等及其由它们组合成的各种新型闭路粉磨系统,使粉磨效率提高,粉磨功的有效利用率提高,水泥生产综合能耗下降;
5.1 生料粉磨流程(粉磨系统)及应用
1、分类:按生产方法不同分为湿法和干法两类。
按是否有选粉设备分为开路和闭路两类。
重点介绍干法生料粉磨系统
干法生料粉磨系统分类:
按是否有烘干功能分为:
普通干法粉磨;可以是开路或闭路。
烘干兼粉磨系统:属闭路系统。
按磨机类型分为:
钢球磨;
立式磨;
4、固定某些组分流量、调整个别原料流量
特点:只检测生料中CaO Fe2O3的含量,间接控制生料的三率值。据检测结果调整原料配比,但原料种类较多,固定其中一些成分,单独调整某些成分。具体方法很多,视实际情况定。
五、生料粉磨
粉磨:将小块状(粒状)物料破碎成细粉(100μm以下)的过程。
生料粉磨:将原料配合后粉磨成生料的工艺。
生料的均化包括生料浆的均化和生料粉的均化。
主要介绍生料粉的均化:
6.1 均化方式: 机械均化:包括机械均化库、多库搭配、机械倒库等
气力均化:间歇式均化、连续式均化。
(一)、间歇式均化系统
1、组成:生料搅拌库(一般设两个以上)、储存库(一般设一个,但容积较大)。
2、特点:均化效果(H)高,但耗电量大,多库间歇作业。
库内设有锥形中心室,库底分18个区,中心室内为1~10区,中心室与库壁的环形区为11~18区。生料从外环形区进入中心室,再从中心室卸入库下称重小仓。向中心室进料时,外环区充气箱仅对11~18区中的一个区充气。
物料进入中心仓后,在减压锥的减压作用下,中心区1~8区也轮流充气,并同外环区充气相对应,使进入中心区生料能迅速膨胀、活化及混合均化。9~10区一直充气,进行活化卸料。卸料主要通过一根溢流管进行,保证物料不会在中心仓短路。
恒速定量给料秤(悬臂式电子皮带称)
调速定量给料电子皮带称
失重称
核子称(需匹配给料机与输送设备)
4.3 影响配料准确性的因素
1、工艺设备不能满足要求
2、物料成分、水分、粒度波动过大
3、数据反馈与调整不及时、
4.4 配料的调整
大调整:当原、燃料成分变化时,应重新进行系统配料。
d 混合室库及均化室库的区别主要在于库下部设置的空气搅拌室的形状与容积大小。混合室为尖顶,容积较小,均化室为圆柱形,容积较大。均化室库均化效果好于混合室库,但电耗较高。
e 库内、多料流式均化库 目前使用最广泛
A 原理:侧重于库内的重力混合作用,基本不用或减小气力均化作用以简化设备和节省电力。多数库底增设一个小型搅拌仓。动力消耗小。
挤压粉磨技术。
2、几种粉磨流程:
闭路粉磨系统
(1)、开路粉磨系统:
(2)、闭路粉磨系统:
喂料
(3)、风扫磨系统:
(4)、尾卸提升循环磨系统:
(5)、中卸提升循环磨系统:
(6)、选粉烘干系统:
(7)、带有立式烘干塔的粉磨系统:
(8)、预破碎烘干系统:
(2)充气装置示意图:
其透气层材质:陶瓷多孔板、水泥多孔板、涤纶或尼龙等化纤织物。
(3)充气方式:
①、强气充气法:先在全区域同时低压充气10~15min,使库内生料膨胀,然后在充气区通入足够的压缩空气,其余区不充气,每隔10~15min轮换一次,如此重复,直至库内生料均匀性符合要求。
②、强弱充气法:先在全区域同时充入强气约15 min左右使物料流态化,然后改为一区充强气(约占总空气量的75%),其余区充弱气(约占25%),每隔10~20min依次轮换,循环一周或两周。
库底的42个三角形充气箱充气卸料由设定的计算机软件控制,使库内卸料形成的42个漏斗流,按不同流量卸料,以便使物料产生重力纵向均化的同时,产生径向混合均化。一般保持3个卸料区同时卸料,进入库下小型混合室后有搅拌混合作用。
库内结构较复杂,充气管路多,自动化水平高,维修较困难。
MF型多料流式均化库
库顶设有生料分配器及输送斜槽,库底为锥形,略向中心倾斜,库底设有一个容积较小的中心室,其上部与库底的连接处四周开有许多入料孔。
3、均化原理:压缩空气经库底充气装置的透气层进入库内的料层,使库内料粉松动并呈流态化。库底充气装置各区按一定规律改变进气压力或进气量,会使已呈流态化的粉料也按同样的规律产生上下翻滚和激烈搅拌,从而使全库生料得到充分混合,最终达到成分均匀一致的目的。
4、充气装置(充气箱):
(1)形式:扇形、环形、条形等,如图:
CF型控制流式均化库
CF库生料入库方式为单点进料
库底分为7个卸料区域,每区由6个三角形充气区组成,因而共有6×7=42个三角形充气区。每个三角形充气区的充气箱都是独立的。
每个卸料区中心有个出料孔,上边由减压锥覆盖。卸料孔下部与卸料阀及空气斜槽相联,将生料送到库底中央的小混合室中。
库下小混合室由负荷传感器支撑,以此控制料位及卸料的开停。
2、尽量避免粗颗粒:通常用0.2mm方孔筛筛余控制,一般小于1.0%~1.5%,当生料中含有石英、方解石时,或KH、n偏高时,控制小于0.5%~1.0%。
六、 生料的均化
概念:粉磨后的生料通过合理搭配或气力搅拌等方式,使其成分趋于均匀一致的过程。
意义:生料均化是生料均化链中的最后一环,担负着均化任务的40%。
特点:配置有多元素分析仪,如X荧光光谱仪、X荧光能谱仪、同位素多元素分析仪等。能快速、准确测定出四种氧化物。
根据熟料率值推出生料率值作为控制指标。
3、利用质量配料控制系统调整
特点:不配置分析仪器,靠人工设定的各种原料给料量和他们之间的比例,自动控制计量、给料设备保持这一喂料量和比例不变。
多数立窑厂采用。
库内中心仓未设料位计,而是通过充气管道上的压力测量反映中心仓内料位状况。
(三)、影响均化效果的常见因素
1. 充气装置发生漏泄、堵塞、配气不匀等;
2. 生料物性与设计不符,如含水量、颗粒大小发生变化等;
3. 压缩空气压力不足或含水量大等;
4. 机电故障;
4.2 配料过程中的计量
计量:对连续料流的称量,以确定某一量值为目的的一组操作。
计量、给料设备:多数计量设备具有计量与给料(喂料)的功能,少数计量设备只有计量功能,需配合给料(喂料)设备。
