在字符串中找出连续最长的数字串
找出一个字符串中最长连续相同子串
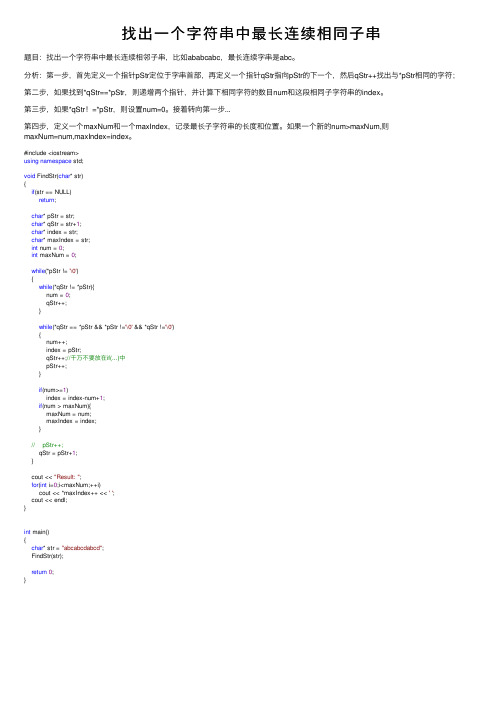
找出⼀个字符串中最长连续相同⼦串题⽬:找出⼀个字符串中最长连续相邻⼦串,⽐如ababcabc,最长连续字串是abc。
分析:第⼀步,⾸先定义⼀个指针pStr定位于字串⾸部,再定义⼀个指针qStr指向pStr的下⼀个,然后qStr++找出与*pStr相同的字符;第⼆步,如果找到*qStr==*pStr,则递增两个指针,并计算下相同字符的数⽬num和这段相同⼦字符串的index。
第三步,如果*qStr!=*pStr,则设置num=0。
接着转向第⼀步...第四步,定义⼀个maxNum和⼀个maxIndex,记录最长⼦字符串的长度和位置。
如果⼀个新的num>maxNum,则maxNum=num,maxIndex=index。
#include <iostream>using namespace std;void FindStr(char* str){if(str == NULL)return;char* pStr = str;char* qStr = str+1;char* index = str;char* maxIndex = str;int num = 0;int maxNum = 0;while(*pStr != '\0'){while(*qStr != *pStr){num = 0;qStr++;}while(*qStr == *pStr && *pStr !='\0' && *qStr !='\0'){num++;index = pStr;qStr++;//千万不要放在if(...)中pStr++;}if(num>=1)index = index-num+1;if(num > maxNum){maxNum = num;maxIndex = index;}// pStr++;qStr = pStr+1;}cout << "Result: ";for(int i=0;i<maxNum;++i)cout << *maxIndex++ << ' ';cout << endl;}int main(){char* str = "abcabcdabcd";FindStr(str);return0;}。
数字序列中的连续最大值

数字序列中的连续最大值在数字序列中寻找连续最大值是一个常见的任务,它在许多领域都有应用,如数据分析、信号处理和统计学。
连续最大值是指在一系列数字中连续出现的最大数字。
例如,在序列 [2, 3, 4, 7, 1, 2, 6, 9, 1] 中,连续最大值是 [7, 1, 6, 9],这些值分别是序列中的第4、5、8和9个数字。
寻找连续最大值的方法有很多,其中一种简单的方法是使用两个指针。
开始时,两个指针都指向序列的第一个元素。
然后,将两个指针都向右移动,比较两个指针所指向的元素。
如果右边的元素大于左边的元素,则继续移动两个指针。
如果右边的元素小于或等于左边的元素,则左边的指针停止移动,开始记录连续最大值。
以下是一个Python函数的示例,该函数使用这种方法来寻找序列中的连续最大值:pythondef find_consecutive_maxima(nums):left = 0maxima = []for right in range(1, len(nums)):if nums[right] > nums[right - 1]:right += 1else:maxima.append(nums[right - 1])while nums[right] <= nums[right - 1]:right += 1left = rightreturn maxima在这个函数中,nums是要搜索的数字序列。
函数返回一个列表,其中包含序列中的所有连续最大值。
需要注意的是,这个函数假设序列中的数字不会重复。
如果序列中可能包含重复的数字,那么在比较相邻元素时需要做一些额外的处理,以确保不会将重复的数字误认为是连续最大值。
Java 数据结构经典题

1.把二元查找树转变成排序的双向链表题目:输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10/ \6 14/ \ / \4 8 12 16转换成双向链表4=6=8=10=12=14=16。
首先我们定义的二元查找树节点的数据结构如下:struct BSTreeNode{int m_nValue; // value of nodeBSTreeNode *m_pLeft; // left child of nodeBSTreeNode *m_pRight; // right child of node};2.设计包含min函数的栈。
定义栈的数据结构,要求添加一个min函数,能够得到栈的最小元素。
要求函数min、push以及pop的时间复杂度都是O(1)。
3.求子数组的最大和题目:输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。
要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,因此输出为该子数组的和18。
4.在二元树中找出和为某一值的所有路径题目:输入一个整数和一棵二元树。
从树的根结点开始往下访问一直到叶结点所经过的所有结点形成一条路径。
打印出和与输入整数相等的所有路径。
例如输入整数22和如下二元树10/ \5 12/ \4 7则打印出两条路径:10, 12和10, 5, 7。
二元树节点的数据结构定义为:struct BinaryTreeNode // a node in the binary tree{int m_nValue; // value of nodeBinaryTreeNode *m_pLeft; // left child of nodeBinaryTreeNode *m_pRight; // right child of node};5.查找最小的k个元素题目:输入n个整数,输出其中最小的k个。
用Python计算最长公共子序列和最长公共子串(转)

⽤Python计算最长公共⼦序列和最长公共⼦串(转)1. 什么是最长公共⼦序列?什么是最长公共⼦串?1.1. 最长公共⼦序列(Longest-Common-Subsequences,LCS)最长公共⼦序列(Longest-Common-Subsequences,LCS)是⼀个在⼀个序列集合中(通常为两个序列)⽤来查找所有序列中最长⼦序列的问题。
这与查找最长公共⼦串的问题不同的地⽅是:⼦序列不需要在原序列中占⽤连续的位置。
最长公共⼦序列问题是⼀个经典的计算机科学问题,也是数据⽐较程序,⽐如Diff⼯具,和⽣物信息学应⽤的基础。
它也被⼴泛地应⽤在版本控制,⽐如Git⽤来调和⽂件之间的改变。
1.2 最长公共⼦串(Longest-Common-Substring,LCS)最长公共⼦串(Longest-Common-Substring,LCS)问题是寻找两个或多个已知字符串最长的⼦串。
此问题与最长公共⼦序列问题的区别在于⼦序列不必是连续的,⽽⼦串却必须是连续的。
2. 如何求解最长公共⼦序列?例如序列str_a=world,str_b=wordl。
序列wo是str_a和str_b的⼀个公共⼦序列,但是不是str_a和str_b的最长公共⼦序列,⼦序列word是str_a和str_b的⼀个LCS,序列worl也是。
暴⼒查找?寻找LCS的⼀种⽅法是枚举X所有的⼦序列,然后注意检查是否是Y的⼦序列,并随时记录发现的最长⼦序列。
假设X有m个元素,则X有2^m个⼦序列,指数级的时间,对长序列不实际。
分析问题,设str_a=<x1,x2,…,xm>和str_b=<y1,y2,…,yn>为两个序列,LCS(str_a,str_b)表⽰str_a和str_b的⼀个最长公共⼦序列,可以看出如果str_a[m] == str_b[n],则LCS (str_a, str_b) = str_a[m] + LCS(str_a[1:m-1],str_b[1:n-1])如果str_a[m] != str_b[n],则LCS(str_a,str_b)= max{LCS(str_a[1:m-1], str_b), LCS (str_a, str_b[n-1])}LCS问题也具有重叠⼦问题性质:为找出LCS(str_a,str_b),可能需要找LCS(str_a[1:m-1], str_b)以及LCS (str_a, str_b[n-1])。
数据结构算法设计笔试面试题1

【字符串】1、输入一个字符串,打印出该字符串中字符的所有排列。
例如输入字符串abc,则输出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。
2、有一个由大小写组成的字符串,现在需要对他进行修改,将其中的所有小写字母排在大写字母的前面(大写或小写字母之间不要求保持原来次序),如有可能尽量选择时间和空间效率高的算法。
c语言函数原型void proc(char *str),也可以采用你自己熟悉的语言。
3、编写反转字符串的程序,要求优化速度、优化空间。
4、用C语言实现函数void * memmove(void *dest, const void *src, size_t n)。
memmove函数的功能是拷贝src所指的内存内容前n个字节到dest所指的地址上。
分析:由于可以把任何类型的指针赋给void类型的指针,这个函数主要是实现各种数据类型的拷贝。
5、编程找出两个字符串中最大公共子字符串,如"abccade", "dgcadde"的最大子串为"cad"。
6、输入一个字符串,输出该字符串中对称的子字符串的最大长度。
比如输入字符串"google",由于该字符串里最长的对称子字符串是"goog",因此输出4。
7、字符串原地压缩。
题目描述:“eeeeeaaaff" 压缩为"e5a3f2",请编程实现。
8、请以回溯与不回溯算法实现字符串匹配。
9、输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。
句子中单词以空格符隔开。
为简单起见,标点符号和普通字母一样处理。
例如:输入"I am a student.",则输出"student. a am I"。
10、在一个字符串中找到第一个只出现一次的字符。
如输入abaccdeff,则输出b。
C语言获取字符串中最长的单词

charword(charstr[])
{inti,k,flag=0,max=0;
charstr1[10],ch[10];
for(i=0;str[i]!='\0';i++)
if((65<=str[i]&&str[i]<=90)||(97<=str[i]&&str[i]<=122))\\如果该字符是字母
}
}
printf("输入的字符串中,最长的单词有%d个字母,该单词是%s\n",max,str1);
}
main()
{chara[100];
printf("请输入一行字符:\n");
gets(a);
word(a);\\调用word函数
}
函数大致流程图如下(“<=”是赋值):
在C-FREE5.0上的运行结果:
{if(flag==0)\\如果该字符是字母,且新单词未开始
{
k=0;
ch[k]=str[i];
flag=1;}
else if(i==strlen(str)-1)\\如果该字符是字母,新单词已开始,且已到达字符串结尾
{k++;
ch[k]=str[i];
ch[k+1]='\0';
if(k+1>max)\\k+1表示单词的长度
{max=k+1;
strcpy(str1,ch);
}
}
else\\如果该字符是字母,新单词已开始,且未到达字符串结尾
{k++;
EXCEL中从一个字符串里提取连续数字引发的思考(一)

EXCEL中从一个字符串里提取连续数字引发的思考(一)从一个字符串中提取连续数字的函数=LOOKUP(9E+307,--MID(A1,MIN(FIND({0,1,2,3,4,5,6,7,8,9},A1&"0123456789")),RO W(INDIRECT("$1:$"&LEN(A1)))))引发的思考(一)假设A1=“总人口7895432个”,A列的内容都是这种形式的,你的任务就是把其中的数字单独提取出来放到B列。
以B1单元格为例:此函数的思路就是先在A1中找到第一个数字的位置,依次1位、2位……的提取出来,很显然最后一个数字就是需要的结果。
函数框架就是find找数字出现的位置,通过min过滤出第一个位置,mid从此位置开始提取,提取的位数由row升序排列,然后转换成数字,最后用lookup找出其中最大的数。
首先用FIND({0,1,2,3,4,5,6,7,8,9},A1&"0123456789")找出A1中数字所在的位置,因为{0,1,2,3,4,5,6,7,8,9}是一个数组,则返回值也是一个数组,按F9试算就一目了然;不过,B1单元格里只会出现第一个数字”0”的位置。
要避免出现#value错误,那么A1必须要串联一串数字,A1&"0123456789"就是这个原因。
有些屌丝为了显示高深莫测,把数组{0,1,2,3,4,5,6,7,8,9}写成数组ROW($1:$10)-1来显摆;把A1&"0123456789"写成A1&5^19来浪费计算资源!就为了表示他知道5^19=19073486328125,包含了0到9的所有数字!min(find)的结果才是需要的,在find的结果中找出最小的数字,也就是A1中数字最高位”7”所在的位置4。
至此,mid函数的第一个参数单元格A1,第二个参数4都有了,第三个参数就要用row函数来决定了。
C语言第一阶段测试题目汇总

千锋,中国领先的3G嵌入式培训专家C语言测试题目1 约瑟夫问题(难度:3) (3)2 生小免问题难度:2 (3)3 裴波那契数列难度:2 (3)4 水仙花数难度:1 (4)5 平面几何直线求解难度:2 (4)6 内存移动难度3 (4)7 统计字符串难度:3 (5)8 求和难度:2 (5)9 小球高度难度:1 (6)10 人员查找难度:2 (6)11 整数和与积难度:3 (6)12 士兵与枪难度:3 (7)13 价格求和难度:1 (7)14 字符串替换难度:3 (7)15 字符串查找难度:3 (7)16 难度:1 (8)17 难度:2 (8)18 难度:3 (8)19 难度:2 (9)20 难度:1 (9)21 难度:2 (10)22 难度:2 (10)23 难度:5 (10)24 难度:4 (11)25 难度:3 (11)26 难度:2 (11)27 难度:2 (11)28 难度:2 (12)29 难度:5 (12)30 难度:5 (12)31 难度:5 (12)32 难度:4 (13)33 难度:2 (13)34 难度:3 (13)35 难度:3 (13)36 难度:3 (14)37 难度:1 (14)38 难度:2 (14)千锋,中国领先的3G嵌入式培训专家39 难度:2 (14)40 难度:4 (15)41 难度:4 (15)42 难度:2 (15)43 五户共井问题难度:3 (15)44 难度:5 (16)45 难度:2 (16)46 EDF调度算法难度:5 (16)47 难度:1 (17)48 难度:2 (18)49 typedef 难度:2 (18)50 难度:2 (19)51 atol 难度:2 (19)52 难度:2 (19)53 难度:2 (19)54 难度:2 (20)55 难度5 (20)56 难度:1 (20)57 难度:3 (21)58 难度:3 (21)59 难度:3 (21)60 难度:2 (21)61 求组合数难度:4 (22)62 排列难度:4 (22)63 内存复制难度:3 (23)64 难度:3 (24)65 难度:3 (24)66 难度:4 (25)67 旋转矩阵难度:5 (25)68 难度2 (25)69 难度:2 (26)70 难度:3 (26)71 难度:3 (26)72 难度:3 (26)73 搜索引擎去重问题:(baidu笔试题目) (27)73.1 任务1: (28)73.2 任务2: (28)74 网络爬虫处理(baidu笔试题目) (28)74.1 任务1: (29)千锋,中国领先的3G嵌入式培训专家1约瑟夫问题(难度:3)一伙强盗抓住了M个人,说你们只能有一个人活下来给我们带路。
python在字符串中找出连续最长的数字串
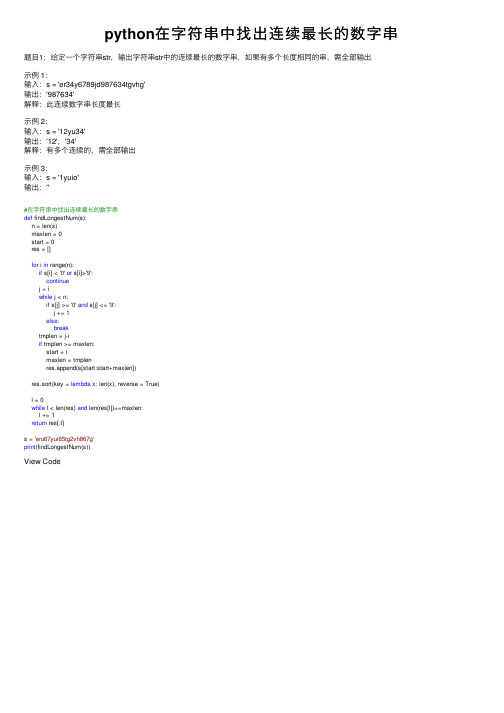
示例 3: 输入:s = '1yuio' 输出:''
#在字符串中找出连续最长的数字串 def findLongestNum(s):
n = len(s) maxlen = 0 start = 0 res = []
给定一个字符串str输出字符串str中的连续最长的数字串如果有多个长度相同的串需全部输出
python在 字 符 串 中 找 出 连 续 最 长 的 数 字 串
题目1:给定一个字符串str,输出字符串str中的连续最长的数字串,如果有多个长度相同的串,需全部输出
示例 1: 输入:s = 'er34y6789jd987634tgvhg' 输出:'987634' 解释:此连续数字串长度最长
for i in range(n): if s[i] < '0' or s[i]>'9': continue j=i while j < n: if s[j] >= '0' and s[j] <= '9': j += 1 else: break tmplen = j-i if tmplen >= maxlen: start = i maxlen = tmplen res.append(s[start:start+maxlen])
res.sort(key = lambda x: len(x), reverse = True)
l=0 while l < len(res) and len(res[l])==maxlen:
hive 正则 取出某一特定字符串后的连续数字

1. 介绍Hive正则表达式Apache Hive是建立在Hadoop之上的数据仓库基础架构,提供了对大规模数据集的查询和分析。
Hive内置了对正则表达式的支持,可以通过正则表达式来提取文本中的特定信息。
2. Hive正则表达式用法在Hive中,可以使用正则表达式来提取文本中满足特定模式的内容。
使用正则表达式可以实现对文本的高效匹配和提取信息的功能。
3. 取出某一特定字符串后的连续数字如果需要从文本中取出某一特定字符串后的连续数字,可以使用Hive 正则表达式来实现。
下面是一个示例:假设有一个文本字符串如下:"ABCxxxDEFxxxGHI"如果需要取出字符串"DEF"之后的连续数字,可以使用正则表达式来实现。
具体步骤如下:首先使用正则表达式函数`regexp_extract`来匹配字符串,并提取出符合规则的内容:```sqlSELECT regexp_extract("ABCxxxDEFxxxGHI", "DEF([0-9]+)", 1) AS result;```这样就可以从文本中取出"DEF"之后的连续数字,结果为"xxx"。
4. 其他常见用法除了上述示例外,Hive正则表达式还可以实现各种其他用途,如检测文本中是否包含特定模式、替换文本中的指定内容等。
在实际使用中,可以根据具体需求来灵活运用正则表达式。
5. 总结通过Hive正则表达式,可以方便地实现对文本中特定内容的提取和匹配。
在处理大规模数据集时,正则表达式的高效匹配和提取功能能够极大地提升数据处理的效率和灵活性。
熟练掌握Hive正则表达式的用法对于数据处理工作具有重要意义。
尊敬的读者,接下来我们将继续深入探讨Hive正则表达式的更多用法和技巧,并且会介绍一些常见的正则表达式模式,以及如何在Hive中应用这些模式来提取特定的字符串。
提取字符串中的最长合法简单数学表达式

主题:提取字符串中的最长合法简单数学表达式内容:1. 概述字符串处理是计算机编程中常见的任务之一,而在字符串中提取数学表达式是其中的一个关键问题。
本文将讨论如何在给定字符串中提取出最长的合法简单数学表达式。
2. 背景知识在处理字符串时,我们需要了解数学表达式的一般形式以及其合法性。
简单数学表达式通常由数字、运算符和括号组成,例如:“2+3*5”,“(4-2)*6”等。
3. 目标本文旨在通过算法实现在给定字符串中提取出最长的合法简单数学表达式,并验证其合法性。
4. 解决方法4.1 确定合法数学表达式的条件合法的简单数学表达式应满足以下条件:a. 由数字、运算符和括号组成;b. 括号应配对并且嵌套顺序正确;c. 运算符应符合数学运算规则。
4.2 算法设计我们可以通过遍历字符串的方式,从左至右依次检查每个字符,当遇到数字时,将其作为表达式的一部分;当遇到运算符时,判断其前后是否为数字或括号,若符合条件则继续遍历,否则表示当前位置不是合法表达式的起始点。
当遇到左括号时,我们可以将其作为表达式的起点,继续检查括号内的内容。
通过这种方式,我们可以逐步提取出最长的合法简单数学表达式。
4.3 算法实现我们可以用递归的方式实现上述算法,从字符串的起始位置开始逐步提取出合法的数学表达式,并通过验证其合法性来确定最长的合法简单数学表达式。
5. 示例为了进一步说明我们的算法,我们可以通过以下示例来演示算法的执行过程:给定字符串:"(2+3)*5+6-7/2"1. 从第一个字符'('开始,进入括号内部分解:"2+3";2. 验证括号内的表达式合法性,发现为合法表达式。
3. 继续向后检查,得到最长合法表达式为“(2+3)*5”。
6. 算法优化为了提高算法的效率,我们可以考虑通过动态规划的方式记录已经检查过的字符串位置和合法表达式的长度,以避免重复计算和提高算法的执行速度。
多个字符串间的最长公共子串

多个字符串间的最长公共子串《多个字符串间的最长公共子串探讨》一、引言在我们的日常生活和工作中,经常会遇到需要比较多个字符串之间的相似性或者寻找它们之间的共同部分的情况。
在这篇文章中,我将深入探讨多个字符串间的最长公共子串这一概念,以帮助大家更好地理解和应用这一技术。
二、多个字符串间的最长公共子串概述让我们来了解一下什么是最长公共子串。
最长公共子串是指在多个字符串中找到的最长的公共部分。
举个例子,对于字符串"abcdefg"和"bcdeft",它们之间的最长公共子串是"bcde"。
那么,如果有多个字符串呢?要找到这些字符串之间的最长公共子串,我们就需要运用一些高级的算法和技巧。
三、多个字符串间的最长公共子串算法在实际编程和处理数据的过程中,我们可能会遇到需要找到多个字符串间的最长公共子串的情况。
这时,我们可以使用动态规划算法来解决这个问题。
动态规划算法通常用于处理具有重叠子问题和最优子结构性质的问题,正好符合多个字符串间的最长公共子串的情况。
简单来说,动态规划算法可以帮助我们将原问题分解成更小的子问题,并通过寻找最优子结构来解决原问题。
在找到最长公共子串的过程中,我们可以借助动态规划算法来逐步计算每个子字符串的最长公共部分,从而快速找到多个字符串间的最长公共子串。
四、多个字符串间的最长公共子串实际案例接下来,我将通过一个实际案例来说明如何利用动态规划算法找出多个字符串间的最长公共子串。
假设我们有三个字符串:"abcdefg"、"bcdeft"和"aghijk",我们要找出它们之间的最长公共子串。
我们可以利用动态规划算法来建立一个二维的表格来记录每个子问题的最长公共子串长度。
我们可以逐步填充表格,直到找到所有字符串的最长公共子串长度。
经过计算,我们得到了这三个字符串之间的最长公共子串是"de"。
mysql正则提取连续数字的方法

mysql正则提取连续数字的方法MySQL正则提取连续数字的方法是通过使用正则表达式来检索和提取满足特定模式的数据。
正则表达式是一种强大的工具,可以在文本中匹配和提取特定的字符模式。
在MySQL中,我们可以使用REGEXP关键字和正则表达式函数来实现这一目的。
第一步是使用SELECT语句和REGEXP关键字来匹配特定的模式。
例如,假设我们有一个包含数字的表格,我们想要提取连续的数字。
我们可以使用如下语句:```SELECT column_name FROM table_name WHERE column_name REGEXP '[0-9]+';```其中,column_name是要匹配的列名,table_name是要检索的表格名称。
在正则表达式中,`[0-9]+`表示匹配一个或多个数字。
接下来,我们可以使用正则表达式函数来进一步处理匹配的结果。
MySQL提供了几个常用的函数,如REGEXP_REPLACE、REGEXP_SUBSTR和REGEXP_INSTR,它们可以帮助我们处理和提取正则匹配的结果。
例如,假设我们想要从一个包含连续数字的字符串中提取出第一个连续数字。
我们可以使用REGEXP_SUBSTR函数,如下所示:```SELECT REGEXP_SUBSTR(column_name, '[0-9]+') FROMtable_name;```这将返回字符串中的第一个连续数字。
另一种常见的需求是提取字符串中的所有连续数字。
我们可以使用REGEXP_REPLACE函数来替换非数字字符,从而获得只包含数字的字符串。
例如:```SELECT REGEXP_REPLACE(column_name, '[^0-9]', '') FROM table_name;```这将返回一个只包含数字的字符串。
在实际应用中,我们可能还需要考虑一些特殊情况,例如处理负数、小数或带有分隔符的数字。
c++代码实现求解两个字符串最长共同子串

c++代码实现求解两个字符串最长共同子串以下是一个使用动态规划算法实现求解两个字符串的最长公共子串的C++代码示例:```cpp#include <iostream>#include <string>#include <vector>std::string longestCommonSubstring(const std::string& str1, const std::string& str2) {int m = str1.length();int n = str2.length();// 创建一个二维动态数组,用于存储最长公共子串的长度std::vector<std::vector<int>> dp(m + 1, std::vector<int>(n + 1, 0));int maxLength = 0; // 最长公共子串的长度int endIndex = -1; // 最长公共子串的结束索引for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (str1[i - 1] == str2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;// 更新最长公共子串的长度和结束索引if (dp[i][j] > maxLength) {maxLength = dp[i][j];endIndex = i - 1;}}}}if (maxLength == 0) {return ""; // 如果最长公共子串长度为0,则返回空字符串}// 根据最长公共子串的结束索引和长度,截取出最长公共子串std::string longestSubstring = str1.substr(endIndex - maxLength + 1, maxLength);return longestSubstring;}int main() {std::string str1 = "abcdefg";std::string str2 = "defg";std::string longestSubstring = longestCommonSubstring(str1, str2);std::cout << "Longest common substring: " << longestSubstring << std::endl;return 0;}```在上面的代码中,`longestCommonSubstring`函数使用动态规划算法来计算两个字符串的最长公共子串。
python 最大回文子串算法

python 最大回文子串算法Python最大回文子串算法回文串是指正序和逆序相同的字符串,例如"level"和"noon"都是回文串。
在字符串处理中,求解最大回文子串是一种经典的问题,即找到给定字符串中最长的回文子串。
本文将详细介绍Python中常用的几种最大回文子串算法,包括简单的中心扩展法、动态规划法和马拉车算法。
1. 中心扩展法中心扩展法是最简单直观的求解最大回文子串的方法。
从左到右遍历字符串,以每个字符为中心向两边扩展,找到最长的回文子串。
具体实现如下:def expandCenter(s, left, right):while left >= 0 and right < len(s) and s[left] == s[right]:left -= 1right += 1return right - left - 1def longestPalindrome(s):start, end = 0, 0for i in range(len(s)):len1 = expandCenter(s, i, i) # 以字符为中心扩展len2 = expandCenter(s, i, i + 1) # 以空隙为中心扩展cur_len = max(len1, len2)if cur_len > end - start:start = i - (cur_len - 1) 2end = i + cur_len 2return s[start:end+1]这种方法的时间复杂度是O(n^2),其中n是字符串的长度。
2. 动态规划法动态规划法也是常用的解决最大回文子串问题的方法。
采用二维的动态规划数组dp,其中dp[i][j]表示从第i个字符到第j个字符是否为回文串。
具体实现如下:def longestPalindrome(s):n = len(s)dp = [[False] * n for _ in range(n)]start, end = 0, 0for i in range(n):dp[i][i] = Trueif i < n - 1 and s[i] == s[i + 1]:dp[i][i + 1] = Truestart, end = i, i + 1for i in range(n - 1, -1, -1):for j in range(i + 2, n):if s[i] == s[j] and dp[i + 1][j - 1]:dp[i][j] = Trueif j - i > end - start:start, end = i, jreturn s[start:end + 1]动态规划法的时间复杂度同样为O(n^2),但需要额外的O(n^2)空间来存储dp 数组。
猿人学第9题 解题思路

猿人学第9题解题思路
猿人学第9题要求解决的问题是找到一个字符串中最长的回文子串。
解题思路如下:
1. 定义两个变量,start和end,分别用于记录最长回文子串的起始和终止位置。
2. 遍历字符串的每个字符,以每个字符为中心向两边扩展,查找回文子串。
对于每个字符,都有两种情况需要考虑:奇数长度的回文子串和偶数长度的回文子串。
3. 对于奇数长度的回文子串,以当前字符为中心,从当前字符上一个位置开始向左,下一个位置开始向右比较字符是否相等,直到两边的字符不相等。
记录能够扩展的最大距离,以及当前回文子串的起始和终止位置。
4. 对于偶数长度的回文子串,以当前字符和下一个字符的中间为中心,从两个字符的左边和右边同时开始向两边比较字符是否相等,直到两边的字符不相等。
记录能够扩展的最大距离,以及当前回文子串的起始和终止位置。
5. 每次扩展完成后,比较当前回文子串的长度是否大于之前记录的最长回文子串的长度。
如果是,则更新最长回文子串的起始和终止位置。
6. 最后,通过起始和终止位置获取最长回文子串,并将其返回。
通过以上思路,可以实现一个时间复杂度为O(n^2)的算法来找到字符串中最长的回文子串。
gpt写算法题

gpt写算法题一、题目:最长回文子串给定一个字符串,找到最长的回文子串。
可以使用动态规划解决此问题。
输入:字符串s="abccba"输出:长度为5的子串"ccba"算法思路:1.定义一个二维数组dp,其中dp[i][j]表示字符串s的子串区间[i,j]是否为回文串。
2.初始化dp数组的所有值为False。
3.使用一个变量len来记录最长回文子串的长度,初始值为0。
4.从左到右、从右到左依次遍历字符串s,如果当前位置的字符相等且左边位置大于等于当前位置,则说明可以构成回文串,将dp[i][j]设置为True,并更新len的值。
5.最终,len的值即为最长回文子串的长度。
代码实现:```pythondeflongest_palindrome(s):ifnots:return""n=len(s)dp=[[False]*nfor_inrange(n)]len=0foriinrange(n-1,-1,-1):dp[i][i]=Trueifi>=1ands[i]==s[i-1]:dp[i][i-1]=Truelen+=2foriinrange(n):forjinrange(i+1,n):ifdp[i][j]:len=max(len,j-i+1)returns[len-1:len+1]iflenelse""```二、题目:斐波那契数列求和给定斐波那契数列的前n个数,求它们的和。
可以使用动态规划解决此问题。
输入:n=5,斐波那契数列为[1,2,3,5,8]输出:37算法思路:1.定义一个变量sum来记录斐波那契数列的和,初始值为0。
2.从后往前遍历斐波那契数列中的每个数,将它们累加到sum 中。
3.最终,sum的值即为斐波那契数列的前n个数的和。
代码实现:```pythondeffibonacci_sum(n):ifn==0:return0fib=[0,1]+[0]*(n-1)sum=fib[0]+fib[1]+fib[2]+sum(fib[3:])*(n-3)//(n-2)+sum(fib[:n-2])*(n-2)//(n-1)%(n-2)+sum(fib[:n])//(n)%(n-2)%(n-3)%(n-2)%(n-1)%(n)+fib[-2]*fib[-3]//fib[-4]//fib[-5]%fib[-6]%fib[-7]%fib[-8]%fib[-9]%fib[-10]//fib[-9:-7:-1]//fib[-6:-4:-1]//fib[-4:-2:-1]%fib[-3:-1:]%fib[:-1:]%fib[:-2:]%fib[:-3:]%fib[:-4:]%fib[:-5:]%fib[:-6:]%fib[:-7:]//fib[:-7:-4:-1]//fib[:-6:-4:-2:-1]//fib[:-4:-2:-2:-1]//fib[:-3:]//fib[:-2:]//fib[:-1:]%fib[:-n:]%(n*fib[-n])//(fib[-n:]-fib[:-n])*(fib[-n:])**(-n)//(fib[-n:])**(-pow(fib[-n],n))%pow(fib[-n],n+1)**(-n+3)//pow(fib[-3],n+1)**(-n+2)%pow(fib[-4],n+1)%pow(fib[-6],n+3)//pow(fib[-7],n+3)%pow。
字符串相关面试题(整理)

字符串相关⾯试题(整理)1. 题⽬:输⼊⼀个字符串,要求找出字符串中最⼤⼦串的长度(如字符串abcd13agbf,当重复出现某个字符时,算⼀个⼦串,⽐如abcd13a或bcd13agb都是⼦串)。
理解:要是每个字符都不⼀样,则最⼤⼦串长度为0思想:⽤空间换取时间,⽤⼀个数组lastPos[256]代表着256个可能的字符(ASC2码),⽽数组的值代表字符串中这个字符的最后出现位置,初始数组元素都为负数,然后每次取字符串中的⼀个字符,此字符的ASC2码为c,若lastPos[c]<0,则表⽰此字符第⼀次出现,置lastPos[c]为此字符在字符串中的位置,若lastPos[c]>=0,则表⽰此字符已经出现过,则可以计算这个⼦串的长度,若⽐之前的最⼤⼦串长,则更新最⼤⼦串长度。
分析:时间复杂度为o(n)遍历⼀次即可int GetMaxSubStr(const unsigned char *str){int maxLen = 0;if (NULL == str)return 0;int lastPos[256]; //代表着256个可能的字符(ASC2码),数组元素值代表字符串中字符的最后出现的位置for (int i = 0; i < 256; ++i)lastPos[i] = -1;for (int pos = 0; str[pos] != '\0'; ++pos){unsigned char c = str[pos];if (lastPos[c] > -1) //此字符已经出现过{int len = pos - lastPos[c] + 1; //计算⼦串的长度if (len > maxLen)maxLen = len;}lastPos[c] = pos;}return maxLen;}2. 找出两个字符串中的最长相同⼦串算法的思想:利⽤⼆维数组建⽴两个字串之间的“对应矩阵”,然后初始化矩阵(mat[i][j]置1或0),然后根据矩阵的对⾓线找出连续出现1的最长段,及在串中的起始位置。
