三角形中的边角关系(1)

13.1三角形中的边角关系(第一课时)说课课件

2.教学方法
根据教材分析和目标分析，贯彻新课程改革下的课堂教学方法，本节课我主要采用引导——发现式教学法和多媒体辅助教学。学生在教师营造的“可探索”环境里，积极参与，互相讨论，理解三角形的三边关系，再通过应用其解决相关问题，使学生得到更深刻的体会，从而实现教学目标。
3.学法指导
引导、观察、概括、总结是学法指导的重点。课堂教学中，我引导学生带着问题阅读教材，自己动手操作、合作探究来获取新知，培养他们学习的自主性。让学生通过对问题的讨论归纳,在与老师、同学的交流中学习知识。
从动手操作的结果中归纳概括出一般的结论对于初二的学生来说还有一定的困难。
难点：三角形三边关系的探索
知识技能
1、了解三角形的概念，会将三角形按边进行分类，并会用几何符号表示三角形; 2、理解三角形三边之间的关系.
过程与方法
一节课的教学目标准确与否，直接关系到这节课教学效果的好坏，因此预设教学目标时，我力求准确。依据新课程的要求，我将本节课的教学目标确定为以下三
LOGO
13.1三角形中的边角关系
池州市第十一中学王岩
三角形中的边角关系（第1课时）
1 2 3 4 5 6
教材分析
教学目标
教法学法
教学过程
教学设计说明
教后反思
1. 地位及作用
2. 教学重点、难点
1. 地位及作用
本节课是在学生初步了解三角形定义的基础上，进一步研究三角形的组成特征。三角形是研究其他图形的基础。三角形三边关系又是学习三角形知识的基础，且在之后的几何学习中有着重要的应用。通过对其规律的总结发现，可以很好地展示几何知识源于客观实际的特点，培养学生理论联系实际的能力。

三角形中的边角关系

三角形中的边角关系三角形，作为几何学中最基本且最古老的存在之一，是我们理解空间结构的重要元素。

在众多的几何图形中，三角形以其独特的性质和关系，展示了丰富多样的形态和功能。

其中，边角关系是三角形属性中的核心内容之一。

我们来看三角形中的边与角的关系。

在任意一个三角形中，任意两边之和大于第三边，任意两边之差小于第三边。

这是三角形边长关系的基本定理，它告诉我们三角形的三边长度之间是相互制约的。

同时，三角形的三个内角之和等于180度，这是三角形角的关系的基本定理。

我们来看三角形中的特殊边角关系。

等边三角形是三边长度相等的三角形，其三个内角都是60度。

这是三角形中一种简单而特殊的形式，其中所有的边都相等，所有的角也都相等。

等腰三角形是两边长度相等的三角形，其两个内角相等。

这是三角形中另一种常见的形式，其中两边的长度相等，相应的两个角也相等。

在等腰直角三角形中，两边的长度相等，一个角是直角。

这种三角形的特性是，其斜边的长度是直角的边的两倍。

这种关系在解决几何问题时非常重要，例如在勾股定理的应用中。

我们还可以看到，在直角三角形中，斜边的平方等于两直角边的平方和。

这是勾股定理的表现形式，它揭示了直角三角形中边与边之间的深刻关系。

三角形的边角关系是几何学中的基本概念，它反映了三角形的基本属性和结构。

对这些关系的理解和掌握，不仅可以帮助我们解决各种几何问题，还可以帮助我们理解更复杂的几何结构。

这些知识将贯穿我们在数学和其他科学领域的学习和应用中。

一、测试目的本单元测试旨在检验学生对三角形中边角关系的理解与运用。

三角形中的边角关系是几何学中最基本的概念之一，理解并掌握这些关系对于进一步学习和解决几何问题具有重要意义。

二、测试内容本单元测试主要包括以下几个方面的内容：1、三角形内角和定理及其应用2、三角形边角关系的应用3、特殊三角形的性质与判定三、测试形式本单元测试采用闭卷、笔试形式，考试时间为60分钟，满分为100分。

三角形边角关系-第3讲的角与边学

第三讲三角形的角与边一、基础知识本讲重点介绍三角形的边、角不等关系,包括同一个三角形中的边、角不等关系以及不同三角形中的边、角不等关系.1.边与边的关系(1)在同一个三角形中两边之和大于第三边,两边之差小于第三边（三边满足什么条件时，三角形必然存在？）；(2)勾股定理:即在直角三角形中两条直角边的平方和等于斜边的平方.2.角与角的关系(1)三角形的内角和为180︒；(2)直角三角形中两锐角互余;(3)三角形的一个外角大于任何一个与它不相邻的内角；(4)三角形的一个外角等于与它不相邻的两内角之和.3.边和角的关系(1)在同一个三角形中,大边对大角,大角对大边;(2)在两个三角形中,如果有两条边对应相等,那么夹角大的所对的边也大;反之也成立,即在两个三角形中,如果有两条边对应相等,那么第三边大,则所对的角也大.4.不等式变形时常用的性质(1)若a>b,c>d,则a+c>b+d;(2)若a>b,c>d,则a-d>b-c;(3)若a>b,c>0,则ac>bc;若a>b,c<0,则ac<bc;(4)若a>b>0,则11 a b <;(5)总量大于任何一个部分量.5.三角形中的不等关系根源:(1)两点之间线段最短;(2)垂线段最短.二、例题第一部分边的问题例1. (★★希望杯训练题)将三边长为a,b,c的三角形记作(a,b,c).写出周长为20,各边长为正整数的所有不同的三角形.例2. (★★★ 2000年希望杯竞赛题）一个三角形的三条边的长分别是a,b,c（a,b,c都是质数），且a+b+c=16，则这个三角形是（）A.直角三角形B.等腰三角形C.等边三角形D.直角三角形或等腰三角形例3. (★★★1998年江苏省竞赛题)在不等边三角形中,如果有一条边长等于另两条边长的平均值,那么最大边上的高与最小边上的高的比值的取值范围是( )A.31 4k<<B.113k<<C.12k<< D.112k<<例4. (★★★1997年北京市竞赛题)等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm 两部分,则这个等腰三角形的底边的长为( )A.17cmB.5cmC.17cm或5cmD.无法确定例5. (★★★)如图3-1,已知P为三角形ABC内一点,求证:1()2AB AC BC PA PB PC AB AC BC++<++<++.例6. (★★★第三十二届美国邀请赛试题)不等边三角形ABC的两条高长度为4和12,若第三条高的长也是整数,试求它的长.例7. (★★★)若三角形ABC 的三边长是a,b,c,且满足:444224442244422,,a b c b c b c a a c c a b a b =+-=+-=+-,则ABC ∆是( )A.钝角三角形B.直角三角形C.等腰直角三角形D.等边三角形第二部分角的问题例8. (★★)如图3-4,在三角形ABC 中,042A ∠= ,ABC ∠和ACB ∠的三等分线分别交于D,E,求BDC ∠的度数.例9. (★★★1999年重庆市竞赛题)三角形的三个内角分别为,,αβγ,且αβγ≥≥,2αγ=.则β的取值范围是( )A.003645β≤≤B.004560β≤≤C.006090β≤≤D.004572β≤≤例10. (★★★)如图3-7,延长四边形ABCD 对边AD,BC 交于F ；DC,AB 交于E,若AED ∠,AFB ∠平分线交于O,求证:1()2EOF EAF BCD ∠=∠+∠第三部分边角综合24,例11. (★★★ 2000年江苏省竞赛题)在锐角三角形ABC中,AB>BC>AC,且最大内角比最小内角大0 的取值范围是( ).则A例12. (★★★★)如图3-2,在三角形ABC中，AB>AC>BC,P为三角形内任意一点,连结AP并延长交BC于点D.求证:(1)AB+AC>AD+BC;(2)AB+AC>AP+BP+CP.例13. （★★★★）如图，在三角形ABC中，角A=90度，AD垂直于BC，求证：AB+AC<AD+BC例14.（★★★★）如图，在三角形ABC中，AC>AB,在CA上截取CD=AB,E,F分别是BC,AD的中点，连接EF 并延长交BA的延长线于G,求证：AF=AG例15. (★★★★★)设三角形的三个内角度数分别为A,B,C,相应的对边长分别为a,b,c,求证:60 aA bB cCa b c︒++≥++三、练习题1. (★★)设m,n,p均为自然数,满足m n p≤≤,且m+n+p=15,试问以m,n,p为边长的三角形有多少个?2.(★★ 1998年山东省竞赛题) 已知三角形三边的长均为整数,其中某两条边长之差为5,若此三角形周长为奇数,则第三边长的最小值为( )** B.7 C.6 D.43.(★★★)一个三角形的周长为偶数,其中的两条边长分别为4和2003,则满足上述条件的三角形的个数为( )A.1个B.3个C.5个D.7个4.（★ 2002，云南省中考题）两根木棒的长分别是7cm和10cm，要选择第三根木棒，将它们钉成一个三角形，若第三根木棒的长是acm，则a的取值范围是( ).5. (★)ABC 的一个内角的大小是040,且A B ∠=∠,那么C ∠的外角的大小是( )A.140︒B.80︒或100︒C.100︒或140︒D.80︒或140︒6. (★★★)如图3-5,在ABC ∆中,90ACB ︒∠=,D,E 为AB 上的两点,若AE=AC,45DCE ︒∠=则图中与BC 等长的线段是( ) A.CD B.BD C.CE D.AE-BE7. (★★★)如图3-6,在ABC ∆中,B ∠的平分线与C ∠的外角平分线相交于D,40D ︒∠=.则A ∠等于( )A.50︒B. 60︒C. 70︒D.80︒8. (★★ 第12届希望杯竞赛题)如图3-9,127.5︒∠=,295︒∠=,338.5︒∠=求4∠的大小.9. (★★★第5届希望杯竞赛题)如图3-8,BE 是ABD ∠的平分线,CF 是ACD ∠的平分线,BE 与CF 交于G,若140BDC ︒∠=,110BGC ︒∠=,求A ∠的度数.10. （★★★★）如图，三角形ABC 中，AB=BC=CA,AE=CD,AD,BE 相交于P,BQ 垂直于AD 于Q ，求证：BP=2PQ课外小故事五枚金币有个叫阿巴格的人生活在内蒙古草原上.有一次，年少的阿巴格和他爸爸在草原上迷了路，阿巴格又累又怕，到最后快走不动了.爸爸就从兜里掏出5枚硬币，把一枚硬币埋在草地里，把其余4枚放在阿巴格的手上，说：“人生有5枚金币，童年、少年、青年、中年、老年各有一枚，你现在才用了一枚，就是埋在草地里的那一枚，你不能把5枚都扔在草原里，你要一点点地用，每一次都用出不同来，这样才不枉人生一世.今天我们一定要走出草原，你将来也一定要走出草原.世界很大，人活着，就要多走些地方，多看看，不要让你的金币没有用就扔掉.”在父亲的鼓励下，那天阿巴格走出了草原.长大后，阿巴格离开了家乡，成了一名优秀的船长.珍惜生命，就能走出挫折的沼泽.。

三角形的边角关系

答：12
隨堂練習
（3）已知有一個等腰三角形，其三邊長分別為5、6、x，則 x ＝？
答：5，6
三角形任意兩邊差小於第三邊
c＋a＞b 移項 b－a＜c
a＋b＞c
c－b＜a
b＋c＞a
a－c＜b
A
c
b
B
C a
隨堂練習
（3）已知有長度分別為1、2、3、4、 5、6 的竹籤各一支，試問用這些竹籤可排出幾種不同形狀的三角形？
答：2、3、4；2、4、5；2、5、6； 3、4、5；3、4、6；3、5、6； 4、5、6 共 7 種
隨堂練習
（3）已知有長度分別為1、2、3、4、5、 6、7、8、9、10 的竹籤各一支，試問用這些竹籤可排出幾種不同形狀的三角形？
答：共 50 種
等腰三角形兩底角相等
【已知】等腰△ABC中，AB＝AC
§3-4三角形的邊角關係
重點：三角形邊角間的不等關係（1）三角形任意兩邊和大於第三邊（2）三角形任意兩邊差小於第三邊（3）三角形中若有兩邊不相等，則大邊對大角，
小邊對小角（4）等腰三角形兩底角相等（5）三角形中若有兩邊不相等，則大角對大邊，
小角對小邊（6）樞紐定理
三角形任意兩邊和大於第三邊
A
D
大
小
B 大 C E 小F
隨堂練習
已知△ABC與△DEF中，AB＝DE， AC＝DF （1）若∠A＝∠D，則BC EF
（填＞、＝、＜）（2）若∠A＞∠D，則BC EF
（填＞、＝、＜）答：（1）＝
（2）＞
隨堂練習
直角三角形中，哪一邊最長？為什麼？
答：斜邊因為直角為直角三角形的最大角，所以直角所對的邊（斜邊）為最大邊。

三角形的边角关系定理

三角形的边角关系定理三角形的边角关系定理是指在一个三角形中，三条边与三个内角之间存在一定的关系。

这个定理可以帮助我们解决与三角形相关的各种问题，例如求解缺失的边长或角度，判断三角形的类型等等。

在研究三角形的边角关系定理之前，我们首先需要了解一些基本的概念。

一个三角形由三条边和三个内角组成。

三角形的内角和为180度，即三个内角的度数之和为180度。

首先，我们来介绍三角形的最基本的边角关系定理——三角形内角和定理。

在任意三角形中，三个角的度数之和等于180度。

也就是说，对于一个三角形ABC来说，∠A + ∠B + ∠C = 180度。

在三角形的边角关系定理中，我们通常还会用到正弦定理和余弦定理。

正弦定理是指在任意三角形ABC中，三边的比值与其对应的角度正弦值的比值是相等的。

即对于一个三角形ABC来说，可以得到以下公式：a/sin∠A = b/sin∠B = c/sin∠C其中，a、b、c分别为三角形ABC的三条边的长度，∠A、∠B、∠C为三角形ABC的三个内角的度数。

余弦定理是指在任意三角形ABC中，任意两边的平方和减去它们的连乘积，再减去对应的两倍边长与夹角余弦值的乘积，等于第三边的平方。

即对于一个三角形ABC来说，可以得到以下公式：c² = a² + b² - 2abcos∠C这个公式在解决三角形相关问题时非常有用，可以帮助我们求解缺失的边长或角度。

三角形的边角关系定理还包括余弦定理的两个变形形式——正弦定理和弦定理。

正弦定理是余弦定理的一个变形形式，利用正弦定理可以帮助我们求解缺失的边长或角度。

正弦定理可以表示为：sin∠A/a = sin∠B/b = sin∠C/c弦定理是余弦定理的另一个变形形式，利用弦定理可以帮助我们求解缺失的边长或角度。

弦定理可以表示为：c/sin∠C = 2R （R为三角形的外接圆半径）在解决三角形问题时，我们可以根据具体情况选择使用三角形的边角关系定理中的哪个公式，以便更加准确地计算出所需要的结果。

三角形中的边角关系、命题与证明

高效学案4、三角形中的重要线段（1）三角形的角平分线：三角形的一个内角的平分线与它的对边相交，连接这个角的顶点和交点之间的线段.（2）三角形的中线：三角形中，连接一个顶点和它所对边的中点的线段叫做三角形的中线.（3）三角形的高：从三角形一个顶点向它的对边作一条垂线，三角形顶点和垂足之间的线段称三角形这条边上的高.三、经典例题【例1】以下列各组线段长为边，能组成三角形的是（）A ．1cm ，2cm ，4cmB ．8cm ，6cm ，4cmC ．12cm ，5cm ，6cmD ．2cm ，3cm ，6cm【变式1】两根木棒的长分别为7cm 和10cm ，要选择第三根棒，将它钉成一个三角形框架，那么第三根木棒长x cm 的范围是__________．【变式2】若a 、b 、c 是△ABC 的三边，化简c b a a c b c b a +--+--+--．【变式3】如图，已知P 是△ABC 内一点，连结AP ，PB ，PC ．求证：PA+PB+PC >21(AB+AC+BC)．【例2】等腰三角形的两边长分别为5 cm 和10 cm ，则此三角形的周长是（）A ．15cmB ．20cmC ．25 cmD ．20 cm 或25 cm【例3】已知△ABC 中：（1）∠A=20°，∠B ﹣∠C=40°，则∠B=______；（2）∠A=120°，2∠B+∠C=80°，则∠B=_______；（3）∠B=∠A+40°，∠C=∠B ﹣50°，则∠B=_______；（4）∠A ：∠B ：∠C=1：3：5，则∠B=_______．E DA 2 1 ABC 【变式】如图把△ABC 纸片沿DE 折叠，当点A 在四边形BCDE 的内部时，则∠A 与∠1、∠2之间有一种数量关系始终保持不变.请试着找出这个规律，你发现的规律是（）A.∠A=∠2＋∠1B.2∠A=∠2＋∠1C.3∠A=2∠1＋∠2D.3∠A=2∠1＋2∠2【例4】如图，α、β、γ分别是△ABC 的外角，且α：β：γ= 2：3：4，则α =__________．【变式1】如图，五角星ABCDE ，求E D C B A ∠+∠+∠+∠+∠的度数．【变式2】已知：如图1，线段AB 、CD 相交于点O ，连接AD 、CB ，我们把形如图1的图形称之为“8字形”．试解答下列问题：（1）在图1中，请直接写出∠A 、∠B 、∠C 、∠D 之间的数量关；（2）在图2中，若∠D=40°，∠B=36°，∠DAB 和∠BCD 的平分线AP 和CP 相交于点P ，并且与CD 、AB 分别相交于M 、N ．利用（1）的结论，试求∠P 的度数；（3）如果图2中∠D 和∠B 为任意角时，其他条件不变，试问∠P 与∠D 、∠B 之间存在着怎样的数量关系？【例5】如图，∆ABC 中，AD 是BC 上的中线，BE 是∆ABD 中AD 边上的中线，若∆ABC 的面积是24，则∆ABE 的面积是________．【例6】如图，在△ABC 中，BE ⊥AC ，BC=5cm ，AC=8cm ，BE=3cm .（1）求△ABC 的面积；（2）画出△ABC 中的BC 边上的高AD ，并求出AD 的值．【例7】已知：如图AB//CD 直线EF 分别交AB 、CD 于点E 、F ，BEF ∠的平分线与DFE ∠的平分线相交于P ，求证 90=∠P ．【变式】如图，∠MON=90°，点A ，B 分别在射线OM ，ON 上运动，BE 平分∠NBA ，BE 的反向延长线与∠BAO 的平分线交于点C ．∠BAO=45°则∠C 的度数是（）A ．30°B ．45°C ．55°D ．60°【例8】如图，△ABC 中，∠B 和∠C 的平分线交于点O ，若∠A=70°，则∠BOC= 度．【变式】认真阅读下面关于三角形内外角平分线所夹的探究片段，完成所提出的问题．探究1：如图1，在△ABC 中，O 是∠ABC 与∠ACB 的平分线BO 和CO 的交点，试分析∠BOC 与∠A 有怎样的关系？探究2：如图2中，O 是∠ABC 与外角∠ACD 的平分线BO 和CO 的交点，试分析∠BOC 与∠A 有怎样的关系？探究3：如图3中，O 是外角∠DBC 与外角∠ECB 的平分线BO 和CO 的交点，则∠BOC 与∠A 有怎样的关系？四、方法归纳1、三角形的边的关系，只需验证：两个较短的边之和大于第三边即可.2、三角形的两边长分别为b a ,，则第三边长c 的取值范围是：b a c b a +<<-.3、三角形的几种“心”.（1）重心：三条中线的交点.（2）外心：三边垂直平分线的交点.（3）内心：三条内角平分线的交点.（4）垂心：三条高线的交点.五、课后作业【作业1】1.如图所示，共有_______个三角形，以AD 为一边的三角形有___________________，∠C 是△ADC 的________边的对角，AE 是△ABE 中∠_____的对边.2.一个三角形周长为27cm ，三边长为2：3：4，则最长边为______cm.3.已知在△ABC 中，5=a ，3=b ，那么第三边c 的取值范围是_____________.4.在△ABC 中，2∠A=3∠B=6∠C ，则△ABC 是________三角形.5.在△ABC 中，已知∠B －∠A=5°，∠C －∠B=20°，则∠A=_______.6.如图，在△ABC 中，∠ACB=90°，∠ABC=25°，CD ⊥AB 于D ，则∠ACD =_________.7.等腰三角形周长为14，其中一边长为3，则腰长为________.8.一个三角形有两条边相等，一边长为4cm ，另一边长为9cm ，那么这个三角形的周长是__________.9.在△ABC 中，∠B ，∠C 的平分线交与点O ，若∠BOC=132°，则∠A=________.10.如图，在△ABC 中，D 、E 分别是AB 、AC 边上的点，DE ∥BC ，∠ADE=30°，∠C=120°，则∠A 等于（）A.60°B.45°C.30°D.20°11.如果三角形的一个角等于其他两个角的差，那么这个三角形一定是（）A.锐角三角形B.直角三角形C.钝角三角形D.不确定12.一个三角形的两边长分别为3和7，若第三边长为偶数，则第三边为（）A.4，6B.4，6，8C.6，8D.6，8，1013.能将三角形的面积分成相等的两部分的是（）A.三角形的角平分线B.三角形的中线C.三角形的高线D.以上都不对14.在△ABC 中，若∠A ：∠B ：∠C=1：2：3，则△ABC 是（）A.锐角三角形B.直角三角形C.钝角三角形D.正三角形15.如图，AD 、AF 分别是△ABC 的高和角平分线，已知∠B=36°，∠C=76°，求∠DAF 数.（提示：先证明∠DAF=21（∠C －∠B ））16.如图，已知I 为△ABC 的内角平分线的交点.求证：∠BIC=90°＋21∠A.17.如图，在△ABC 中，∠B = 60°，∠C = 50°，AD 是∠BAC 的平分线，DE 平分∠ADC 交AC 于E ，求∠BDE 的度数.18.如图，在△ABC 中，∠B=∠C ，FD ⊥BC ，DE ⊥AB ，垂足分别为D 、E ，已知∠AFD=150°，求∠EDF 等于多少度？【作业2】1.如图，AD ，BE ，CF 是△ABC 的中线、高、角平分线.则：BD=___=21___；∠___=∠___=90°；∠___=∠___=21∠___. 2.如图，在△ABC 中，AD ⊥BC ，CE ⊥AB ，已知AB=6，BC=4，AD=5，则CE=______.3.如图，AD 、AE 分别是△ABC 的中线、高，且AB=5，AC=3，则△ABD 与△ACD 的周长的差是_________，△ACD 与△ABD 的面积关系为__________.第1题第2题第3题第4题第5题4.如图，△ABC 的周长是21cm ，AB=AC ，中线BD 分△ABC 为两个三角形，且△ABD 的周长比△BCD 的周长大6cm ，则AB= ，BC=_________.5.如图，在△ABC 中，已知点D ，E ，F 分别为边BC ，AD ，CE 的中点，且2ABC cm 8=∆S ，则阴影部分的面积等于_________.6.在△ABC 中，若AB=5，AC=2，且三角形周长为偶数，则BC=________.7.△ABC 的三边长是a ，b ，c ，则c b a a c b c b a +++-----=________.第8题第9题第10题8.如图，在Rt △ABC 中，∠C=90°，点B 沿CB 所在直线远离C 点移动，下列说法不正确的是（）A.三角形面积随之增大B.∠CAB 的度数随之增大C.边AB 的长度随之增大D.BC 边上的高随之增大9.如图，在△ABC 中，∠B 、∠C 的平分线BE ，CD 相交于点F ，∠ABC=42°，∠A=60°，则∠BFC=（）A.118°B.119°C.120°D.121°10.如图，在△ABC 中，BO ，CO 分别平分∠ABC 和∠ACB ，则∠BOC 与∠A 的大小关系是（）A.∠BOC=2∠AB.∠BOC=90°+∠AC.∠BOC=90°+21∠A D.∠BOC=90°21-∠A11.如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论：①AD∥BC；②∠ACB=2∠ADB；③∠ADC=90°﹣∠ABD；④∠BDC=∠BAC.其中正确的结论有（）A.1个B.2个C.3个D.4个12.如图，在△ABC中，∠ABC与∠ACB的平分线相交于D，已知∠A=50°，求∠BDC的度数．13.如图，已知BD为∠ABC的平分线，CD为△ABC的外角∠ACE的平分线，CD与BD交于点D，试说明∠A=2∠D．14.如图，已知AB∥CD，EF与AB、CD分别相交于点E、F，∠BEF与∠EFD的平分线相交于点P，求证：EP⊥FP．15.如图所示，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数．16.已知：∠MON=40°，OE 平分∠MON ，点A 、B 、C 分别是射线OM 、OE 、ON 上的动点（A 、B 、C 不与点O 重合），连接AC 交射线OE 于点D ．设∠OAC x =°.21（1）如图1，若AB ∥ON ，则①∠ABO 的度数是；②当∠BAD=∠ABD 时，=x ；当∠BAD=∠BDA 时，=x ．（2）如图2，若AB ⊥OM ，则是否存在这样的x 的值，使得△ADB 中有两个相等的角？若存在，求出x 的值；若不存在，说明理由．第二节：命题与证明一、课堂导入有个学生请教爱因斯坦逻辑学有什么用。

直角三角形的边角关系

直角三角形的边角关系[知识链接]知识讲解:1．直角三角形中的边角关系(1)三边之间的关系：a 2＋b 2＝c 2 (2)锐角之间的关系：A ＋B ＝90°(3)边角之间的关系：sinA ＝cosB ＝c a ， cosA ＝sinB ＝c btanA ＝cotB ＝b a ， cotA ＝tanB ＝ab锐角三角函数的概念如图，在ABC 中，∠C 为直角，则锐角A 的各三角函数的定义如下：(1)角A 的正弦：锐角A 的对边与斜边的比叫做∠A 的正弦，记作sinA ，即sinA ＝ca(2)角A 的余弦：锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA ，即cosA ＝c b(3)角A 的正切：锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA ，即tanA ＝ba(4)角A 的余切：锐角A 的邻边与对边的比叫做∠A 的余切，记作cotA ，即cotA ＝ab2．三角函数的关系(1)同角的三角函数的关系1)平方关系：sinA 2＋cosA 2＝1 2)倒数关系：tanA·cotA ＝13)商的关系：tanA ＝A A cos sin ，cotA ＝AAsin cos(2)互为余角的函数之间的关系 sin(90°－A)＝cosA ， cos(90°－A)＝sinA tan(90°－A)＝cotA ， cot(90°－A)＝tanA 3．一些特殊角的三角函数值0°30°45°60°90°sinα0 1cosα 1 0tanα0 1 -----cotα----- 1 05．锐角α的三角函数值的符号及变化规律.(1)锐角α的三角函数值都是正值(2)若0＜α＜90° 则sinα，tanα随α的增大而增大，cosα，cotα随α的增大而减小.6．解直角三角形(1)直角三角形中的元素：除直角外，共有5个元素，即3条边和2个锐角.(2)解直角三角形：由直角三角形中除直角外的已知元素，求出所有未知的元素的过程叫做解直角三角形.7．解直角三角形的应用，解直角三角形的应用，主要是测量两点间的距离，测量物体的高度等，常用到下面几个概念：(1)仰角、俯角视线与水平线所成的角中，视线在水平线上方的叫做仰角，在水平线下方的叫做俯角(2)坡度．坡面的铅直高度h与水平宽度l的比叫做坡度，常用字母i表示，h即i＝l(3)坡角h 坡面与水平面的夹角叫做坡角，用字母α表示，则tanα＝i＝l(4)方位角从某点的指北方向线，按顺时针方向转到目标方向线所成的角.例题选讲：1、在Rt△ABC中，∠C=90°(1)已知∠A、c, 则a=__________;b=_________.(2)已知∠A、b, 则a=__________;c=_________.(3)已知∠A、a，则b=__________;c=_________.(4)已知a、b，则c=__________.(5)已知a、c，则b=__________.2、在下列直角三角形中，不能解的是（）A 、已知一直角边和所对的角B 、已知两个锐角C 、已知斜边和一个锐角D 、已知两直角边3、如图，在△ABC 中，已知AC=6，∠C=75°，∠B=45°，求△ABC 的面积.4、求证:平行四边形ABCD 的面积S=AB ·BC ·sinB(∠B 为锐角).5、山顶上有一旗杆，在地面上一点A 处测得杆顶B 的俯角α =600，杆底C 的俯角β =450，已知旗杆高BC=20米，求山高CD.课堂练习1、如图：P 是∠α的边OA 上一点，且P 点的坐标为（3，4），则sin （900 - α）＝_____________.2、下列说法正确的是( )A 、a 为锐角则 0≤sina ≤1B 、cos30°＋cos30°＝cos60°C 、若tanA ＝cot(90°－B), 则∠A 与∠B 互余D 、若α1，α2为锐角，且α1＜α2则c osα1＞c osα2 3、已知0°＜α＜45° 则s inα，c osα的大小关系为( )A 、s inα＞c osαB 、s inα＜c osαC 、s inα≥c osαD 、s inα≤c osα．4、∠C ＝90° 且tanA ＝31，则cosB 的值为( )A 、1013 B 、310 C 、1010 D 10103 5、直角梯形ABCD 中，AD ∥BC ，CD ＝10，∠B ＝90°，∠C ＝30°则AB ＝( )A 、53B 、5C 、25D 2356、一个三角形的一边长为2，这边上的中线长为1，另两边长之和为1＋，则这个三角形的面积为( )A. 1B.23C. D.437、外国船只，除特许外，不得进入我国海洋100海里以内的区域.如图，设A 、B 是我们的观察站，A 和B 之间的距离为160海里，海岸线是过A 、B 的一条直线.一外国船只在P 点，在A 点测得∠BAP=450，同时在B 点测得6BCACDABAB CDABP∠ABP=600，问此时是否要向外国船只发出警告，令其退出我国海域. 本课小结本章的重点是直角三角形中锐角三角函数的定义，特殊锐角的三角函数值，及互余两角的三角函数关系，运用这些知识解直角三角形的实际应用，既是重点也是难点.解直角三角形四类基本问题的方法是：(1)已知斜边和一直角边(如斜边c ，直角边a)：由sinA ＝ca，求A, B ＝90°－A ， b ＝(2)已知斜边和一锐角(如斜边c ，锐角A)； B ＝90°－A ， a ＝c·sinA ， b ＝c·cosA(3)已知一直角边和一锐角(如a ，A)： B ＝90°－A ，b ＝a·cotA ， c ＝Aasin(4)已知两直角边(如a ，b)： c ＝，由tanA ＝ba，求A, B ＝90°－A解直角三角形的思路是：(1)解直角三角形的方法可以概括为“有弦(斜边)用弦(正弦，余弦)，无弦用切(正切，余切)，取原避中”其意指：当已知或求解中有斜边时，可用正弦或余弦；既可由已知数据又可由中间数据求解时，取原始数据，忌用中间数据.(2)解含有非基本元素的直角三角形(即直角三角形的中线，高，角平分线，周长，面积等)一般将非基本元素转化为基本元素，或转化为基本元素间的关系式，再通过解方程组求解.解直角三角形在实际应用中的解题步骤如下：(1)审题：要弄清仰角，俯角，坡度，坡角，水平距离，垂直距离，水平等概念的意义，要审清题意.(2)画图并构造要求解的直角三角形，对于非直角三角形的图形可添加适当的辅助线把它们分割成一些直角三角形和矩形(包括正方形).(3)选择合适的边角关系式，使运算尽可能简便，不易出错.(4)按照题中已知数的精确度进行近似计算，并按照题目要求的精确度确定答案及注明单位.。

三角形边角关系-第3讲的角与边

第三讲三角形的角与边一、基础知识本讲重点介绍三角形的边、角不等关系,包括同一个三角形中的边、角不等关系以及不同三角形中的边、角不等关系.1.边与边的关系(1)在同一个三角形中两边之和大于第三边,两边之差小于第三边（三边满足什么条件时，三角形必然存在？）；(2)勾股定理:即在直角三角形中两条直角边的平方和等于斜边的平方.2.角与角的关系(1)三角形的内角和为180︒；(2)直角三角形中两锐角互余;(3)三角形的一个外角大于任何一个与它不相邻的内角；(4)三角形的一个外角等于与它不相邻的两内角之和.3.边和角的关系(1)在同一个三角形中,大边对大角,大角对大边;(2)在两个三角形中,如果有两条边对应相等,那么夹角大的所对的边也大;反之也成立,即在两个三角形中,如果有两条边对应相等,那么第三边大,则所对的角也大.4.不等式变形时常用的性质(1)若a>b,c>d,则a+c>b+d;(2)若a>b,c>d,则a-d>b-c;(3)若a>b,c>0,则ac>bc;若a>b,c<0,则ac<bc;(4)若a>b>0,则11 a b <;(5)总量大于任何一个部分量.5.三角形中的不等关系根源:(1)两点之间线段最短;(2)垂线段最短.二、例题第一部分边的问题例1. (★★希望杯训练题)将三边长为a,b,c的三角形记作(a,b,c).写出周长为20,各边长为正整数的所有不同的三角形.【分析与解答】:考点：三角形三边关系；周长等于20的三解形中,最长边小于10,且大于等于203,由于边长是整数,所以最长边可为9,8,7.用穷举法可以得下面8个三角形:(9,9,2)、(9,8,3)、(9,7,4)、 (9,6,5)、(8,8,4)、(8,7,5)、(8,6,6)、(7,7,6).例2. (★★★ 2000年希望杯竞赛题）一个三角形的三条边的长分别是a,b,c （a,b,c 都是质数），且a+b+c=16，则这个三角形是（）A.直角三角形B.等腰三角形C.等边三角形D.直角三角形或等腰三角形【分析与解答】:考点：特殊的质数2；“两边之差小于第三边”；因为a,b,c 均为质数且a+b+c=16,所以a,b,c 中有一数为2,设a=2,则b+c=14,所以||2b c -<.从而有b c -=或1b c -=.当1b c -=时,b,c 均不是整数,不合题意.因此,只有b c -=即a=2,b=c=7,所以三角形是等腰三角形.例3. (★★★1998年江苏省竞赛题)在不等边三角形中,如果有一条边长等于另两条边长的平均值,那么最大边上的高与最小边上的高的比值的取值范围是( )A.314k <<B.113k <<C.12k <<D.112k <<【分析与解答】:考点：在a>b>c 时，三边关系只需要满足a b c -<；题目可以转化为，已知02a b c a c b a b c>>>⎧⎪+⎪=⎨⎪-<⎪⎩，求c a 的范围；由已知条件易得3c a c <<，即113ca<<，选B例4. (★★★1997年北京市竞赛题)等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm两部分,则这个等腰三角形的底边的长为( )A.17cmB.5cmC.17cm 或5cmD.无法确定【分析与解答】:考点：特殊三角形的三边关系；分类讨论；设腰长为a ，底边长为b ，此题可分为两类，112212122a a b a a b ⎧+=⎪⎪⎪+=⎨⎪>⎪⎪⎩或121211222a a b a a b ⎧+=⎪⎪⎪+=⎨⎪>⎪⎪⎩，第一类无解；第二类解为145a b =⎧⎨=⎩，故选B.例5. (★★★)如图3-1,已知P 为三角形ABC 内一点, 求证:1()2AB AC BC PA PB PC AB AC BC ++<++<++.【分析与解答】:易证AB<PA+PB,BC<PB+PC,AC<PA+PC 相加除2得:1()2AB AC BC PA PB PC ++<++. 延长BP 交AC 于H.在ABH ∆中BP+PH<AB+AH ①在PHC ∆中,PC<PH+HC ② ①+②得,BP+PH+PC<AB+AH+PH+HC,BP+PH+PC<AB+AC+PH, BP+PC<AB+AC ④同理:BP+AP<BC+AC ⑤AP+PC<AB+BC ⑥ ④+⑤+⑥,得2(BP+AP+PC)<2(AB+AC+BC).∴ BP+AP+PC<AB+AC+BC 即:1()2AB AC BC PA PB PC AB AC BC ++<++<++.例6. (★★★ 第三十二届美国邀请赛试题)不等边三角形ABC 的两条高长度为4和12,若第三条高的长也是整数,试求它的长.【分析与解答】:考点：三边关系，面积的过渡作用；设第三边C 边上高为h,三角形面积为S,高为4,12的两边为a,b,则有111412222a b c h S⋅⋅=⋅⋅=⋅⋅=∴a=24S ,b=212S ,c=2S h 据三角形三边关系定理及推论,得22222412412S S S S S h -<<+,∴11163h <<h 为整数∴ h=4或5.又三角形为不等边三角形∴h=5.例7.(★★★)若三角形ABC 的三边长是a,b,c,且满足:444224442244422,,a b c b c b c a a c c a b a b =+-=+-=+-,则ABC ∆是( )A.钝角三角形B.直角三角形C.等腰直角三角形D.等边三角形【分析与解答】考点，三边关系之恒等变形；将三个方程叠加得到，222222444a b a c b c a b c ++=++，即222222222()()()0a b b c c a -+-+-=，则a b c ==，选D.第二部分角的问题例8.(★★)如图3-4,在三角形ABC中,042A ∠= ,ABC ∠和ACB ∠的三等分线分别交于D,E,求BDC ∠的度数.【分析与解答】: 考点，三角形内角和；简单，BDC ∠=88︒例9.(★★★1999年重庆市竞赛题)三角形的三个内角分别为,,αβγ,且αβγ≥≥,2αγ=.则β的取值范围是( )A.03645β≤≤ B.04560β≤≤ C.06090β≤≤ D.04572β≤≤ 【分析与解答】:考点：三角形内角和；由αβγ≥≥可得ααγβαγγαγ++≥++≥++,即21802αγαγ︒+≥≥+,又2αγ=,得51804γγ︒≥≥,解之,得3645γ︒︒≤≤,又180αβγ︒++=∴3180βγ︒+=∴1803βγ-=,∴18036453β︒︒-≤≤解这个不等式得4572β︒︒≤≤，选D例10. (★★★)如图3-7,延长四边形ABCD 对边AD,BC 交于F ；DC,AB 交于E,若AED ∠,AFB ∠平分线交于O,求证:1()2EOF EAF BCD ∠=∠+∠【分析与解答】:考点，角的关系；延长FO 交AE 于H 点，22()2()EOF FHE OEA FAE AFH OEA ∠=∠+∠=∠+∠+∠；222EAF BCD FBE OEA FAE FAE AFH OEA FAE ∠+∠=∠+∠+∠=∠+∠+∠+∠得证.第三部分边角综合例11. (★★★ 2000年江苏省竞赛题)在锐角三角形ABC 中,AB>BC>AC,且最大内角比最小内角大024,则A ∠的取值范围是( ).【分析与解答】:考点：角边对应关系；不等式推倒；易错点：三角形ABC 为“锐角三角形”；因为AB>BC>AC,所以C A B ∠>∠>∠.设B ∠=x,则C ∠=x+24︒,所以180(24)1562A x x x ︒︒︒∠=--+=-,从而有24156215622490x xx x x ︒︒︒︒︒⎧+>-⎪->⎨⎪+<⎩,所以4452,52156268x x ︒︒︒︒<<<-<.例12. (★★★★)如图3-2,在三角形ABC 中，AB>AC>BC,P 为三角形内任意一点,连结AP 并延长交BC 于点D.求证:(1)AB+AC>AD+BC; (2)AB+AC>AP+BP+CP.【分析与证明】:考点：边角对应关系； (1)AB>AC,∴ABD ACD ∠<∠.ADB ACD ∠>∠,∴ADB ABD ∠>∠.∴AB>AD.AC>BC,∴AB+AC>AD+BC.(2)过点P 作EFBC ,交AB,AC 于E,F,则AEF ABC ∠=∠,AFE ACB ∠=∠.由(1)知,AE+AF>AP+EF,BE+EP>BP,CF+FP>CP,∴(AE+BE)+(AF+CF)+(EP+FP)>AP+BP+CP+EF, 即AB+AC>AP+BP+CP.例13. （★★★★）如图，在三角形ABC 中，角A=90度，AD 垂直于BC 求证：AB+AC<AD+BC【分析与证明】：考点，特殊三角形的三边关系，恒等变形；过A 作AC ’垂直于AB 交BC 于C ’ 因为12AD*BC ’=12AB*AC ’，2,2,2AB AC BC += 所以AB^2+2AB*AC ’+AC ’^2=BC ’^2+2BC ’*AD<(BC ’+AD)^2 所以AB+AC ’<AD+BC ’ （1）又因为在三角形ACC ’中，AC-AC ’<CC ’（2）（1）+（2）得AB+AC<AD+(BC ’+CC ’) 即AB+AC<AD+BC例14. （★★★★）如图，在三角形ABC 中，AC>AB,在CA 上截取CD=AB,E,F 分别是BC,AD 的中点，连接EF 并延长交BA 的延长线于G ,求证：AF=AG【分析与证明】：考点，边角综合；取AC 中点N,连EN 所以EN//ABEN=1/2AB 因此角NEF=角G所以FN=FC-NC=1/2(AC+CD)-1/2AC=1/2CD=1/2AB 所以NE=FN 因此AF=AG例15. (★★★★★)设三角形的三个内角度数分别为A,B,C,相应的对边长分别为a,b,c,求证:60aA bB cCa b c ︒++≥++【分析与证明】:考点:边角关系；由"大边对大角"知,当a b ≥时,A ≥B;当a b ≤时,A B ≤所以总有a-b 与A-B 同号,由此得(a-b)(A-B)≥0.同理可得(b-c)⋅(B-C)≥0,(c-a)(C-A)≥0 即aA+bB ≥aB+bA,bB+cC ≥bC+cB,cC+aA≥cA+aC.以上三式相加得2(aA+bB+cC)≥a(B+C)+b(A+C)+c(A+B)=a(180︒-A)+b(180︒-B)+c(180︒-C)=180︒(a+b+c)-(aA+bB+cC)即3(aA+bB+cC)≥180︒(a+b+c).由此,得60aA bB cCa b c ︒++≥++.三、练习题1. (★★)设m,n,p 均为自然数,满足m n p ≤≤,且m+n+p=15,试问以m,n,p 为边长的三角形有多少个? 【分析与解答】:考点：三角形三边关系；提示,∴m+n+p=15,据三角形三边关系定理,可知p<m+n,即p+p<m+n+p,∴2p<15,p<152m n p ≤≤,∴153p ≥∴151532p ≤<p 为自然数∴p=5,6,7.若p=7,当n=7时,m=1;当n=6时,m=2;当n=5时,m=3;当n=4时,m=4;若p=6,当n=6时,m=3;当n=5时,m=4;若p=5,则m=n=5综上所述,以m,n,p 为三边长的三角形共有7个.2. (★★ 1998年山东省竞赛题) 已知三角形三边的长均为整数,其中某两条边长之差为5,若此三角形周长为奇数,则第三边长的最小值为( ) A.8 B.7 C.6 D.4 【分析与解答】:考点，三边关系；设a-b=5,由已知可得a+b+c 为奇数,所以c 为偶数,且c>a-b,所以c 的最小值为6.3. (★★★)一个三角形的周长为偶数,其中的两条边长分别为4和2003,则满足上述条件的三角形的个数为( )A.1个B.3个C.5个D.7个【分析与解答】:考点：三边关系，b c a b c -<<+；根据三角形三边关系定理,可求出三角形的第三边的取值范围是:大于1999而小于2007,再依其周长为偶数,可知第三边应为2000,2001,2002,2003,2004,2005,2006,这七个数中选出,而周长为偶数,已知一边长为偶数,一边长为奇数,由此可知,可第三边边长应为奇数.所以第三边边长为2001,或2003或2005.选B4. （★ 2002，云南省中考题）两根木棒的长分别是7cm 和10cm ，要选择第三根木棒，将它们钉成一个三角形，若第三根木棒的长是acm ，则a 的取值范围是( ). 【分析与解答】：3<a<17提示：根据三角形三边关系定理，可得10-7<a<10+7，解之即得.5. (★)ABC 的一个内角的大小是040,且A B ∠=∠,那么C ∠的外角的大小是( )A.140︒B.80︒或100︒C.100︒或140︒D.80︒或140︒【分析与解答】：简单，选D6. (★★★)如图3-5,在ABC ∆中,90ACB ︒∠=,D,E 为AB 上的两点,若AE=AC,45DCE ︒∠=则图中与BC 等长的线段是( )A.CDB.BDC.CED.AE-BE【分析与解答】:考点，角度变换；因为245︒∠=,AE=AC,所以523453︒∠=∠+∠=+∠.又因为4∠是ADC ∆的外角,5∠是BEC ∆的外角,所以:,15(453)(90)345445A B B A A ︒︒︒︒=∠+∠∠=∠-∠=+∠--∠=∠+∠-=∠-,由此得4145︒∠=∠+=BCD ∠,所以BC=BD.7. (★★★)如图3-6,在ABC ∆中,B ∠的平分线与C ∠的外角平分线相交于D,40D ︒∠=.则A ∠等于( D )A.50︒B. 60︒C. 70︒D.80︒【分析与解答】:考点，角度关系；依题意有21ABC ∠=∠,22ACE ∠=∠∴2(21)ACE ABC ∠-∠=∠-∠,根据三角形内角和定理的推论,有ACE ABC A ∠-∠=∠,21D ∠-∠=∠,所以:2A D∠=∠40D ︒∠=80A ︒∠=.8. (★★ 第12届希望杯竞赛题)如图3-9,127.5︒∠=,295︒∠=,338.5︒∠=求4∠的大小.【分析与解答】:4∠=19︒.23ADC ∠=∠+∠,14180ADC ︒∠+∠+∠= ∴2314180︒∠+∠+∠+∠=∴9538.527.54180︒︒︒︒+++∠= ∴419︒∠=9. (★★★第5届希望杯竞赛题)如图3-8,BE 是ABD ∠的平分线,CF 是ACD ∠的平分线,BE 与CF 交于G,若140BDC ︒∠=,110BGC ︒∠=,求A ∠的度数.【分析与解答】:延长BD 交AC 于H,则BDC HCD DHC ∠=∠+∠DHC A ABH ∠=∠+∠∴BDC A ABH HCD ∠=∠+∠+∠①,BGC GEC ECG GEC A ABE ∠=∠+∠∠=∠+∠∴BGC A ABE ECG ∠=∠+∠+∠ ∴2222BGC A ABE ECG ∠=∠+∠+∠即22BGC A ABH ACD ∠=∠+∠+∠②由②-①得2BGC BDC A ∠-∠=∠∴211014080A ︒︒︒∠=⨯-=10. （★★★★）如图，三角形ABC 中，AB=BC=CA,AE=CD,AD,BE 相交于P,BQ 垂直于AD 于Q ，求证：BP=2PQ【分析与证明】：考点，三角形其他；三角形ADC逆时针旋转120度即得三角形ABP所以AD于BE成120度角那么角BPQ=60度，角PBQ=30度，由BQ垂直于AD所以BP=2PQ课外小故事五枚金币有个叫阿巴格的人生活在内蒙古草原上.有一次，年少的阿巴格和他爸爸在草原上迷了路，阿巴格又累又怕，到最后快走不动了.爸爸就从兜里掏出5枚硬币，把一枚硬币埋在草地里，把其余4枚放在阿巴格的手上，说：“人生有5枚金币，童年、少年、青年、中年、老年各有一枚，你现在才用了一枚，就是埋在草地里的那一枚，你不能把5枚都扔在草原里，你要一点点地用，每一次都用出不同来，这样才不枉人生一世.今天我们一定要走出草原，你将来也一定要走出草原.世界很大，人活着，就要多走些地方，多看看，不要让你的金币没有用就扔掉.”在父亲的鼓励下，那天阿巴格走出了草原.长大后，阿巴格离开了家乡，成了一名优秀的船长.珍惜生命，就能走出挫折的沼泽.。

三角形中的边角关系--教学设计(车香)

三角形中的边角关系--教学设计（车香）13.1 三角形中的边角关系(第1课时）六安皋城中学车香一．教学背景本节课是沪科版教材八年级上册内容，研究三角形中边的关系。

学生在小学阶段已学习过三角形的有关内容，了解了三角形有关元素的名称，知道等腰三角形等的概念，并能对一些事物作简单的分类。

因此，本节课通过自主阅读教材中的相关内容完成对三角形有关元素及特殊三角形的认识，应符合八年级学生的数学现实。

但限于小学时的认知水平和教学要求，对三角形的概念表述还不够严谨。

因此，教师应通过必要的引导，让学生形成对三角形概念的准确理解。

学生在七年级已掌握了“两点之间，线段最短”的基本事实。

而“三角形的任何两边之和大于第三边”等结论可以认为是其推论，学生对结论的理解并不感到困难，因此不再设计对结论探究的活动。

而是引导学生将“两点之间，线段最短”的基本事实，通过提炼与概括，迁移得出三角形边的关系的新结论，从而在结论的形成过程中，加深对“任何”二字含义的理解，并感受数学结论的严谨性，感悟知识间的普遍联系。

二．教学目标1. 掌握三角形的概念；了解与三角形的有关元素及三角形的分类（按边）2. 经历探索三角形中的三条边之间的关系，感受几何学中基本图形的内涵。

3. 了解三条线段能组成三角形应满足的条件4. 让学生养成有条理的思考的习惯，以及说理有据的意识，体会三角形三边关系在现实生活中的实际价值。

三．教学重难点1.重点：三角形三边关系结论的形成及应用2.难点：三条线段能组成三角形应满足条件的探究四．教学过程（一）.创设情境，引入新课环节1. 由三角形→三条边应满足的关系；反之，三条线段应满足怎样的关系→三角形？引导学生猜想：如果三条线段，其中任何两条线段之和大于第三条线段，那么这三条线段能组成三角形。

环节2. 几何画板动态演示进行验证，以此得出结论：如果三条线段，其中任何两条线段之和大于第三条线段，那么这三条线段能组成三角形。

（三）.课堂练习，巩固新知1.下列长度的三条线段能否组成三角形？为什么？（1） 8，3，6 ( )（2） 5，10，3 ( )（3） 3，8，5 ( )说明：①让学生先做，并回答如何判断的，突出结论中的“任何”二字含义。

八年级数学上册 13.1 三角形中的边角关系

13.1 三角形中的边角关系第一课时三角形中的边角关系（一）教学目标1、了解三角形的概念，掌握分类思想2、经历探索三角形中的三条边之间的关系，感受几何学中基本图形的内涵3、让学生养成有条理的思考的习惯，以及说理有据的意识，体会三角形三边关系在现实生活中的实际价值重、难点与关键重点：了解三角形分类思想，弄清三角形三边关系难点：对两边之差小于第三边的领悟关键：从观察、联想入手，应用连结两点之间的线中，线段最短这一原理进行迁移教学过程一、情境合一，探究新知1、投影图片，把事先收集的与三角形有关系的生活图片，运用投影仪播放，让学生对三角形有一个感性认识.如下图：教师活动：通过播放图片，引导学生认识三角形，并提出图中能找出的几个三角形具有什么样的特性.学生讨论教师归纳，由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形.教师活动：给出一个三角形，如图，并标上字母，引导学生体会用符号来表示一个三角形的方法，认识三角形的基本元素：边、角、顶点等.学生活动：学会运用大小写字母来表示三角形的边与角，如图的三角形可记作⊿ABC，三边可记作AB、AC、CA；三个角可记作∠A、∠B、∠C，或可用三个字母表示为∠BAC、∠ABC、∠ACB.注意：表示边时要两个大写字母，或一个小写字母.注意小写字母标注的规律：通常顶点大写字母所对的变就是这个顶点的小写字母.2、教师给出不同类型的三角形，引导学生从边和角两种角度观察、分类.（1）从边的角度来分类有：不等边三角形等腰三角形（包括等边三角形）说明：对于等腰三角形来说，相等的两边称为腰，第三边称为底边。

两腰所夹的角称为顶角，腰与底边的夹角称为底角：而等边三角形的三边都相等，它是等腰三角形的特例.（2）从角的角度来分类有：锐角三角形（三个内角均为小于900的角）直角三角形（有一个角是900）钝角三角形（有一个内角大于900）二、联系实际，合作探究1、问题牵引1.国庆节的晚上，小明从甲地到乙地后再往丙地走，并到达丙地，小红从甲地直接到丙地，如图所示，请你谈谈小明和小红谁走的路程长？依据是什么？学生活动：发现小红走的路程短，小明走的路程长。

沪教版第十三章三角形中的边角关系

第十三章三角形中的边角关系一、三角形的分类1、按边分类：2、按角分类：不等边三角形直角三角形三角形三角形锐角三角形等腰三角形（等边三角形是特例）斜三角形钝角三角形二、三角形的边角性质1、三角形的三边关系：三角形中任何两边的和大于第三边；任何两边的差小于第三边。

2、三角形的三角关系：三角形内角和定理：三角形的三个内角的和等于180°。

三角形外角和定理：三角形的三个外角的和等于360°。

3、三角形的外角性质（1）三角形的一个外角等于与它不相邻的两个内角的和；（2）三角形的一个外角大于与它不相邻的任何一个内角。

三、三角形的角平分线、中线和高（说明：三角形的角平分线、中线和高都是线段）四、命题1、命题：凡是可以判断出真（正确）、假（错误）的语句叫做命题。

2、命题分类真命题：正确的命题命题假命题：错误的命题3、互逆命题4、反例：符合命题条件，但不满足命题结论的例子，称为反例。

原命题：如果p，那么q；逆命题：如果q，那么p。

（说明：交换一个命题的条件和结论就是它的逆命题。

）《三角形中的边角关系》测试卷一、选择题（每小题3分，共30分）1、下列长度的各组线段中，能组成三角形的是（）A．1，1，2 B．3，7，11 C．6，8，9 D．3，3，62、下列语句中，不是命题的是（）3、A．两点之间线段最短 B．对顶角相等C．不是对顶角不相等 D．过直线AB外一点P作直线AB的垂线3、下列命题中，假命题是（）A．如果|a|=a，则a≥0 B．如果，那么a=b或a=-bC．如果ab>0，则a>0，b>0 D．若，则a是一个负数4、若△ABC的三个内角满足关系式∠B＋∠C=3∠A，则这个三角形（）A．一定有一个内角为45° B．一定有一个内角为60°C．一定是直角三角形 D．一定是钝角三角形5、三角形的一个外角大于相邻的一个内角，则它是（）A.直角三角形B.锐角三角形C.钝角三角形D.不能确定6、下列命题中正确的是（）A．三角形可分为斜三角形、直角三角形和锐角三角形B．等腰三角形任一个内角都有可能是钝角或直角C．三角形外角一定是钝角D．△ABC中，如果∠A>∠B>∠C，那么∠A>60°，∠C<60°7、若一个三角形的三个内角的度数之比为1：2：3，那么相对应的三个外角的度数之比为（）A．3：2：1 B．5：4：3 C．3：4：5 D．1：2：38、设三角形三边之长分别为3，8，1－2a，则a的取值范围为（）A．－6<a<－3 B．－5<a<－2 C．－2<a<5 D．a<－5或a>29、如图9,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点, 且S △ABC=4cm2,则S阴影等于（） A.2cm2 B.1cm2 C.12cm2 D.14cm2图9 图1010、已知：如图10，在△ABC中，∠C=∠ABC=2∠A，BD是AC边的高，则∠DBC=（）A．10° B．18° C．20° D．30°二、填空题（每小题4分，共20分）11、已知三角形的周长为15cm，其中的两边长都等于第三边长的2倍，则这个三角形的最短边长是．12、已知一个等腰三角形两内角的度数之比为1∶4，则这个等腰三角形顶角的度数为．13、如下图，∠A＝70°，∠B＝30°，∠C＝20°，则∠BOC= ．14、如上图，AF、AD分别是△ABC的高和角平分线，且∠B=36°，∠C=76°，则∠DAF= ．15、如上图，D是△ABC的BC边上的一点，且∠1=∠2，∠3=∠4，∠BAC=63°，则∠DAC= ．16、如图，在△ABC中，AB=AC，AC上的中线把三角形的周长分为24cm和30cm的两个部分，求三角形各边的长．17、如图，已知∠1＋∠3＝180°，∠2＋∠3＝180°，求证AB∥OE∥CD.18、如图，已知DE∥BC，FG∥CD，求证：∠CDE＝∠BGF．19、已知△ABC，如图①，若P点是∠ABC和∠ACB的角平分线的交点，求证∠P=90°＋∠A；。

三角形的边角之间的关系

（1）三角形三内角和等于180°（在球面上，三角形内角之和大于180°）；（2）三角形的一个外角等于和它不相邻的两个内角之和；（3）三角形的一个外角大于任何一个和它不相邻的内角；（4）三角形两边之和大于第三边，两边之差小于第三边；（5）在同一个三角形内，大边对大角，大角对大边.（6）三角形中的四条特殊的线段：角平分线，中线，高，中位线.（7）三角形的角平分线的交点叫做三角形的内心，它是三角形内切圆的圆心，它到各边的距离相等.（8）三角形的外接圆圆心，即外心，是三角形三边的垂直平分线的交点，它到三个顶点的距离相等.（9）三角形的三条中线的交点叫三角形的重心，它到每个顶点的距离等于它到对边中点的距离的2倍。

（10）三角形的三条高的交点叫做三角形的垂心。

（11）三角形的中位线平行于第三边且等于第三边的1/2。

（12）三角形的一边与另一边延长线的夹角叫做三角形的外角。

注意: ①三角形的内心、重心都在三角形的内部. ②钝角三角形垂心、外心在三角形外部。

③直角三角形垂心、外心在三角形的边上。

（直角三角形的垂心为直角顶点，外心为斜边中点。

）④锐角三角形垂心、外心在三角形内部。

三角形相关定理重心定理三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍．上述交点叫做三角形的重心.外心定理三角形的三边的垂直平分线交于一点．这点叫做三角形的外心.垂心定理三角形的三条高交于一点．这点叫做三角形的垂心.内心定理三角形的三内角平分线交于一点．这点叫做三角形的内心.旁心定理三角形一内角平分线和另外两顶点处的外角平分线交于一点．这点叫做三角形的旁心．三角形有三个旁心．三角形的重心、外心、垂心、内心、旁心称为三角形的五心．它们都是三角形的重要相关点．中位线定理三角形的中位线平行于第三边且等于第三边的一半．三边关系定理三角形任意两边之和大于第三边，任意两边之差小于第三边．勾股定理在Rt三角形ABC中，A≤90度，则AB·AB+AC·AC=BC·BC梅涅劳斯定理梅涅劳斯（Menelaus）定理是由古希腊数学家梅涅劳斯首先证明的。

13.1 三角形中的边角关系第1课时三角形的三边关系教案沪科版数学八年级上册

13.1 三角形中的边角关系第1课时三角形的边关系教材分析:本节首先严格定义三角形的概念，强调“首尾顺次相接”。

为了加深理解这个条件，教学时可用图形说明定义中增加这几个字的必要性。

三角形的边、顶点、内角等概念，学生在小学已接触过，容易理解，只要学生理解它们的意义就可以了，不要求学生背它们的定义。

三角形任意两边的和大于第三边由两点之间，线段最短得到，可根据学生的实际情况，适当引导学生回忆七年级上册第四章中学过的这个基本事实。

本节的例题为巩固“三角形两边的和大于第三边”而设。

学生在前面学过线段、角以及相交线、平行线等知识，他们的空间观念得到了进一步的发展，现在继续学习三角形的有关知识，就有了更为充实的基础和准备。

通过本节的学习，可以丰富和加深学生对三角形的认识，同时为学习其他图形知识打好基础。

教学目标【知识与技能】1、认识三角形，理解三角形的边关系。

2、理解等腰三角形及其相关概念。

【过程与方法】1、经历三角形边长的数量关系的探索过程，理解三角形的三边关系。

2、掌握判断三条线段能否构成一个三角形的方法，并运用此方法解决有关问题。

【情感、态度与价值观】1、带领学生探究三角形的边角关系问题，引起学生的好奇心，激发学生的求知欲。

2、帮助学生树立几何知识源于生活并服务于生活的意识。

重点难点【教学重点】理解并掌握三角形的三边关系。

【教学难点】三角形三边关系的应用教学方法讲授与探究结合法教学准备直尺、三角板、小木棍、课件教学过程一、创设情境，导入新知教师活动:通过播放图片，引导学生认识三角形师：在我们的生活中几乎随处可见三角形。

它简单，有趣，也十分有用。

三角形可以帮助我们更好认识周围世界，解决很多的实际问题。

那什么样的图形是三角形呢？教师多媒体出示:通过播放图片，引导学生认识三角形学生讨论，教师归纳得出三角形定义，由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。

教师板书：1、三角形定义：由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形二、探究新知，了解三角形师：请同学们认真阅读课本第67页内容，完成下列学习任务：1、会用几何符号表示一个三角形2、知道三角形的顶点、角、边等概念3、会把三角形按边进行分类，知道每类三角形的特征4、知道等腰三角形的腰、底边、底角、顶角等概念教师多媒体出示:师：给出一个三角形，如图，并标上字母，引导学生体会用符号来表示一个三角形的方法，认识三角形的基本元素：边、角、顶点等。

直角三角形的边角关系(初中锐角三角函数)

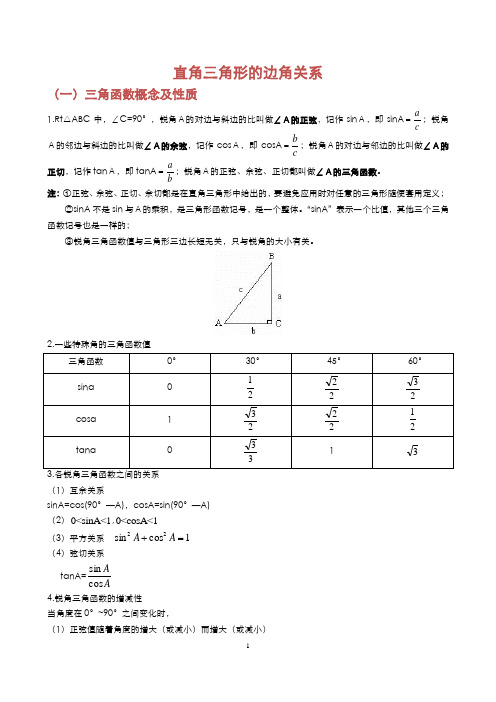
直角三角形的边角关系（一）三角函数概念及性质1.Rt △ABC 中，∠C=90°，锐角Ａ的对边与斜边的比叫做∠Ａ的正弦，记作sin Ａ，即sinA ＝；锐角Ａ的邻边与斜边的比叫做∠Ａ的余弦，记作cos Ａ，即cosA ＝；锐角Ａ的对边与邻边的比叫做∠Ａ的正切，记作tan Ａ，即tanA ＝；锐角Ａ的正弦、余弦、正切都叫做∠Ａ的三角函数。

注：①正弦、余弦、正切、余切都是在直角三角形中给出的，要避免应用时对任意的三角形随便套用定义；②sinA 不是sin 与Ａ的乘积，是三角形函数记号，是一个整体。

“sinA ”表示一个比值，其他三个三角函数记号也是一样的；③锐角三角函数值与三角形三边长短无关，只与锐角的大小有关。

2.一些特殊角的三角函数值（1）互余关系sinA=cos(90°—A)，cosA=sin(90°—A) （2）0<sinA<1,0<cosA<1 （3）平方关系 1cos sin 22=+A A（4）弦切关系 tanA=AAcos sin 4.锐角三角函数的增减性当角度在0°~90°之间变化时，（1）正弦值随着角度的增大（或减小）而增大（或减小）acbcab（2）余弦值随着角度的增大（或减小）而减小（或增大）（3）正切值随着角度的增大（或减小）而增大（或减小）【练习】练习1（求三角函数）1、在Rt △ABC 中，∠C=90°，a = 1 , c = 4 , 则sinA 的值是___A 、B 、C 、D 、 2、在△ABC 中，若三边BC ，CA ，AB 满足BC ：CA ：AB=5：12：13，则cosB=（）A 、512B 、125C 、513D 、12133、菱形的两条对角线分别是16和12.较长的一条对角线与菱形的一边的夹角为θ，则tan θ＝______.4、在Rt△ABC 中,∠C=90°,若AC=2BC,则sin A 的值是( )A ．12B ．2 CD5、直角三角形纸片的两直角边长分别为6，8，现将ABC △如图那样折叠，使点A 与点B 重合，折痕为DE ，则tan CBE 的值是（）A ．247BC ．724D ．136、如图，正方形ABCD 的边长为4，点M 在边DC 上，M 、N 两点关于对角线AC 对称，若DM=1，则tan ∠ADN= ．7、如图，在四边形ABCD 中，E 、F 分別是AB 、AD 的中点，若EF=2，BC=5，CD=3，则tanC 等于（）151541314158、如图，在△ABC 中，∠B=30°，P 为AB 上一点，BP AP =12，PQ ⊥BC 于Q ，连结AQ ，则cos ∠AQC=（）A 、217 B 、233 C 、277 D 、23219、如图所示，已知AD 是等腰△ABC 底边上的高，且tan ∠B= 34，AC 上有一点E ，满足AE ：CE=2：3，则tan ∠ADE 的值是（）A 、35 B 、8 9 C 、45D 、7910、如图，已知直线1l ∥2l ∥3l ∥4l ，相邻两条平行直线间的距离都是1，如果正方形ABCD 的四个顶点分别在四条直线上，则sin α= ．练习2（网格）1、如图，△ABC 的顶点都是正方形网格中的格点，则sin ∠ABC 等于_______________2、在正方形网格中，ABC △的位置如图所示，则cos B ∠的值为（）A ．12B ．2C D 3、如图，△ABC 的三个顶点在正方形网格的格点上，则tan ∠A 的值是___________4、如图，A 、B 、C 三点在正方形网格线的交点处，若将△ACB 绕着点A 逆时针旋转得到△AC’B’，则tanB’的值为_______。

(新)初一几何——三角形的边角关系(一)

泛美国际学校数学教研室数学的学习可以让我们理性面对生活，可以让我们学会坚持和变得坚强。

——吴老师第 1 页共 2 页初一几何——三角形的边角关系（一）【学习目标】1．根据三角形、多边形内角和定理计算较复杂图形中的相关角度。

2．充分利用三角形三边关系解决相关问题。

3．学会并掌握双垂直图形。

【知识库】1、三角形的边：三角形三边定理：三角形两边之和大于第三边即：△ABC 中，a+b>c,b+c>a,c+a>b （两点之间线段最短）由上式可变形得到： a>c －b ，b>a －c ，c>b －a 即有：三角形的两边之差小于第三边2、高：由三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫做三角形的高。

3、中线：连接三角形的顶点和它对边的中点的线段，称为三角形的中线【规律探索】（北京市竞赛题）如图，把△ABC 纸片沿DE 折叠，当点A 落在四边形BCDE 内部时，则∠A 与∠1＋∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，你发现的规律是（）．A ．∠A ＝∠1＋∠2B ．2∠A ＝∠1＋∠2C ．3∠A ＝2∠1＋∠2D ．3∠A ＝2（∠1＋∠2）变式：想一想，如果当点A 落在四边形BCDE 外部时，∠A 与∠1、∠2之间又有什么数量关系呢？试画出图形并说明。

【题型精讲】重难点一：三角形的面积。

例一：如图，△ACB 中，∠ACB =90°，∠1=∠B ．若AC =8，BC =6，AB =10，则CD 的长为．例二：如图，等腰三角形ABC 中，两腰AB =AC ，点P 在底边BC 上任意一点，求证：点P 到两腰的距离之和等于等腰三角形腰上的高。

（要求画出草图再求证）拓展延伸：已知等边△ABC 和点P ，设点P 到△ABC 三边的AB 、AC 、BC 的距离分别是h 1，h 2，h 3，△ABC 的高为h ，请你探索以下问题：（1）若点P 在一边BC 上（图1），此时h 3=0，问h 1、h 2与h 之间有怎样的数量关系？请说明理由；（2）若当点P 在△ABC 内（图2），此时h 1、h 2、h 3与h 之间有怎样的数量关系？请说明理由；（3）若点P 在△ABC 外（图3），此时h 1、h 2、h 3与h 之间有怎样的数量关系？请说明理由重难点二：三角形的三边关系例三：已知三角形三边分别为2，a -1，4，那么a 的取值范围是( )A.1<a <5B.2<a <6C.3<a <7D.4<a <6例四：已知△ABC 的周长是12，三边为a 、b 、c ，若b 是最大边，确定b 的取值范围。

三角形的边角性质

三角形的边角性质甲内容提要三角形边角性质主要的有：1. 边与边的关系是：任意两边和大于第三边，任意两边差小于第三边，反过来要使三条线段能组成一个三角形，必须任意两条线段的和都大于第三条线段，即最长边必须小于其他两边和。

用式子表示如下：a,b,c 是△ABC 的边长b a c b a b a c a c b c b a +<-⇔⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>+>+>+⇔＜推广到任意多边形：任意一边都小于其他各边的和2. 角与角的关系是：三角形三个内角和等于180 ；任意一个外角等于和它不相邻的两个内角和。

推广到任意多边形：四边形内角和=2×180 ，五边形内角和=3×180六边形内角和=4×180 n 边形内角和=(n －2) 1803. 边与角的关系① 在一个三角形中，等边对等角，等角对等边；大边对大角，大角对大边。

② 在直角三角形中，△ABC 中∠C=Rt ∠222c b a =+⇔(勾股定理及逆定理) △ABC 中⇔⎭⎬⎫=∠∠=∠ 30A Rt C a ：b ：c=1：3：2 △ABC 中⇔⎭⎬⎫=∠∠=∠ 45A Rt C a ：b ：c=1：1：2 乙例题例1.要使三条线段3a －1,4a+1,12－a 能组成一个三角形求a 的取值范围。

(1988年泉州市初二数学双基赛题)解：根据三角形任意两边和大于第三边，得不等式组 ⎪⎩⎪⎨⎧+>-+-->-++->++-141312131214121413a a a a a a a a a 解得⎪⎩⎪⎨⎧<->>51135.1a a ∴1.5<a<5答当1.5<a<5时，三条线段3a －1,4a+1,12－a 能组成一个三角形例2.如图A B C DAB=x ，AC=y, AD=z 若以AB 和CD 分别绕着点B 和点C 旋转，使点A 和D 重合组成三角形，下列不等式哪些必须满足？① x<2z , ②y<x+2z , ③y<2z 解由已知AB=x, BC=y －x, CD=z －x 要使AB ，BC ，CD 组成三角形，必须满足下列不等式组：⎪⎩⎪⎨⎧>-+-->-+->-+x y z x y x y y z x y z x y x 即⎪⎩⎪⎨⎧>>+>x z y z x z y 2222∴⎪⎪⎪⎩⎪⎪⎪⎨⎧<+<>222z x z x y z y 答y<x+2z 和y<2z 必须满足。

13.1三角形中的边角关系第1课时三角形中边的关系课件2024-2025学年沪科版数学八上册

新知讲解
三角形的构成要素：
点 A，B，C 叫做这个三角形的顶点；线段 AB，BC，CA 叫做这个三角形的边； ∠A，∠B，∠C 叫做这个三角形的内角，简称三角形角．
新知讲解
三角形的表示：我们把这个三角形记作“△ABC”，读作“三角形ABC”．
新知讲解
三角形边的表示：
三角形的三边有时用它所对角的相应小写字母表示：如边 BC 对着∠A，记作 A；边 CA 记作 B；边 AB 记作 C.
作业布置
【综合拓展类作业】 6.如图①,D为△ABC的边AC上任意一点，连接BD,E为BD上任意一点,连接CE.
(1)用不等号“>”或“<”填空: AB十AC ＞ DB十DC,DB十DC ＞
EB+ EC;
作业布置
【综合拓展类作业】 (2)如图②,M,N是△ABC内任意两点,试探索AB+AC与BM十 MN+NC之间的大小关系,并写出探究过程.
解：(2)延长BM交AC于点D,延长CN交BD于点E. 由(1)可得AB+AC> DB+DC> EB+ EC. ∵EB+EC=EM+BM+EN+NC=(EM+EN)+BM+NC, EM+EN>MN, ∴EB+ EC>MN+BM+NC, ∴AB+AC>BM+MN+NC.
新知讲解
任务二：三角形的分类三角形的分类：
三角形中，三条边互不相等的三角形叫做不等边三角形；有两条边相等的三角形叫做等腰三角形；三条边都相等的三角形叫做等边三角形，又叫做正三角形.
新知讲解
等腰三角形：

三角形中的边角关系

第13章三角形中的边角关系13.1三角形中的边角关系Ⅰ（预习学案）【学习目标】1、理解三角形概念及基本元素2、掌握三条边之间的关系，能按边的关系将三角形进行分类。

【学习重难点】1、重点：三角形的分类思想，三角形的三边关系。

2、难点：对三角形中两边之差小与第三边的领悟。

【预习内容】课本第67—69页【学习流程】一、基础达标，应知应会（一）旧知回顾1、请在右边空白处任意画一个三角形，并用a、b、c表示三边。

2、若三角形三边的长分别为a、b、c，则其周长L = _________________________3、若三角形的一边长为a，且这条边上的高为h，则其面积S = ________________4、请举出1—2个日常生活中形状为三角形的实例。

（二）新知探究1、三角形中的相关概念阅读课本第67页的内容后填空：（1）由______________________________________________叫做三角形。

（2）课本第67页图13—1中，三角形的三个顶点分别是__________；三条边分别是____________；∠A、∠B、∠C叫做三角形的________________，简称三角形的_____。

（3）如果一个三角形的三个顶点分别为A、B、C，则这个三角形可记为____，读作________。

（4）再看图13—1，三角形的三边也可以用小写字母来表示，通常情况下，∠A的对边BC，记作________；∠B的对边CA记作_________；∠C的对边AB记作__________。

小结：任何一个三角形都有_______条边，_______个顶点，_______个内角。

（5）在三角形中，三条边互不相等的三角形叫做________________；__________________叫做等腰三角形；____________________叫做等边三角形。

（6）在等腰三角形中，相等的两边叫做____，另一边叫做____，__ ____叫做顶角， _________________叫做底角。

三角形中的边角关系(1)

13.1三角形中的边角关系(第一课时)说课课件

三角形中的边角关系

三角形边角关系-第3讲的角与边学

三角形的边角关系

三角形的边角关系定理

三角形中的边角关系、命题与证明

直角三角形的边角关系

三角形边角关系-第3讲的角与边

三角形中的边角关系--教学设计(车香)

八年级数学上册 13.1 三角形中的边角关系

沪教版第十三章 三角形中的边角关系

三角形的边角之间的关系

13.1 三角形中的边角关系 第1课时 三角形的三边关系教案沪科版数学 八年级上册

直角三角形的边角关系(初中锐角三角函数)

(新)初一几何——三角形的边角关系(一)

三角形的边角性质

13.1三角形中的边角关系 第1课时 三角形中边的关系 课件2024-2025学年沪科版数学八上册

三角形中的边角关系

沪教版第十三章三角形中的边角关系

13.1 三角形中的边角关系第1课时三角形的三边关系教案沪科版数学八年级上册

13.1三角形中的边角关系第1课时三角形中边的关系课件2024-2025学年沪科版数学八上册