可变分区存储管理方式的内存分配和回收实验报告(最优算法)
可变分区存储管理的内存分配算法模拟实现----最佳适应算法

可变分区存储管理的内存分配算法模拟实现----最佳适应算法可变分区存储管理是一种内存管理技术,其通过将内存分割成不同大小的区域来存储进程。
每个进程被分配到与其大小最匹配的区域中。
内存分配算法的选择影响了系统的性能和资源利用率。
本文将介绍最佳适应算法,并模拟实现该算法。
一、什么是最佳适应算法?最佳适应算法是一种可变分区存储管理中的内存分配策略。
它的基本思想是在每次内存分配时选择最合适的空闲区域。
具体来说,它从可用的空闲区域中选择大小与需要分配给进程的内存最接近的区域。
二、算法实现思路最佳适应算法实现的关键是如何快速找到最合适的空闲区域。
下面给出一个模拟实现的思路:1. 初始化内存分区列表,首先将整个内存定义为一个大的空闲区域。
2. 当一个进程请求分配内存时,从列表中找到与所需内存最接近的空闲区域。
3. 将该空闲区域分割成两部分,一部分分配给进程,并将该部分标记为已分配,另一部分留作新的空闲区域。
4. 更新内存分区列表。
5. 当一个进程释放内存时,将其所占用的内存区域标记为空闲,然后尝试合并相邻的空闲区域。
三、算法模拟实现下面是一个简单的Python代码实现最佳适应算法:pythonclass MemoryPartition:def __init__(self, start_addr, end_addr, is_allocated=False): self.start_addr = start_addrself.end_addr = end_addrself.is_allocated = is_allocatedclass MemoryManager:def __init__(self, total_memory):self.total_memory = total_memoryself.partition_list = [MemoryPartition(0, total_memory)]def allocate_memory(self, process_size):best_fit_partition = Nonesmallest_size = float('inf')# 找到最佳适应的空闲区域for partition in self.partition_list:if not partition.is_allocated and partition.end_addr - partition.start_addr >= process_size:if partition.end_addr - partition.start_addr < smallest_size:best_fit_partition = partitionsmallest_size = partition.end_addr - partition.start_addrif best_fit_partition:# 将空闲区域分割,并标记为已分配new_partition =MemoryPartition(best_fit_partition.start_addr,best_fit_partition.start_addr + process_size, True)best_fit_partition.start_addr += process_sizeself.partition_list.append(new_partition)return new_partition.start_addr,new_partition.end_addrelse:return -1, -1def deallocate_memory(self, start_addr, end_addr):for partition in self.partition_list:if partition.start_addr == end_addr and not partition.is_allocated:# 标记空闲区域partition.is_allocated = False# 尝试合并相邻空闲区域for next_partition in self.partition_list:if not next_partition.is_allocated andnext_partition.start_addr == end_addr:end_addr = next_partition.end_addrself.partition_list.remove(next_partition)breakelse:breakdef print_partitions(self):for partition in self.partition_list:if partition.is_allocated:print(f"Allocated Partition: {partition.start_addr} - {partition.end_addr}")else:print(f"Free Partition: {partition.start_addr} - {partition.end_addr}")# 测试最佳适应算法if __name__ == "__main__":mm = MemoryManager(1024)start, end = mm.allocate_memory(256)print(f"Allocated memory: {start} - {end}")mm.print_partitions()mm.deallocate_memory(start, end)print("Memory deallocated:")mm.print_partitions()以上代码实现了一个简单的内存管理器类`MemoryManager`,它具有`allocate_memory`和`deallocate_memory`等方法。
在可变分区存储管理中,最优适应分配算法

在可变分区存储管理中,最优适应分配算法
最优适应分配算法(optimal fit algorithm)是可变分区存储管理中常用的算法,它是以一种有效而实用方式来利用磁盘存储空间的技术,目的是使用最小的空间来存放最多的文件。
一、算法简介
最优适应分配算法是在可变分区存储管理系统中应用最多的一种有效算法。
它通过寻找和利用未被利用的空间,有效地管理存储空间,减少内存的浪费。
此算法的基本原理是比较进程的内存空间需求和当前空闲分区的剩余空间,选择一个空闲分区分配给进程,使得分配的这块空间刚好能够满足进程的内存空间需求。
二、算法的优势
1、空间利用率高:最优适应分配算法做了色样的优化,通过对比空闲区和进程大小,可以在多个空闲区中选择一个最合适的空间来分配,这就有效地将空闲分区完全利用起来。
2、降低内存碎片:最优适应分配算法在进行存储空间的分配时,给每一个进程的存储空间要求满足有效利用完可用的空闲分区,这样就可以有效地降低内存碎片的影响。
3、处理时间短暂:最优适应分配算法虽然空间利用率高,但是相对地,其耗费的时间是少的,因此,这种算法可以满足时间要求,确保效率。
三、应用情况
最优适应分配算法主要用于可变分区存储管理技术,这种技术可以有效地管理大量文件,而不会浪费空间。
而且现在,这种算法已经被广泛应用于嵌入式系统中,专家们尤其是在嵌入式系统设计中广泛地使用最优适应分配算法,以在CPU装入的程序数量、运行程序数量不变的情况下,达到最大的利用空间效果。
内存的分配和回收分区链实验报告按照这个内容来完成

一、实验目的理解分区式存储管理的基本原理,熟悉分区分配和回收算法。
即理解在不同的存储管理方式下,如何实现主存空间的分配与回收;并掌握动态分区分配方式中的数据结构和分配算法及动态分区存储管理方式及其实现过程。
二、设备与环境1. 硬件设备:PC机一台2. 软件环境:安装Windows操作系统或者Linux操作系统,并安装相关的程序开发环境,如VC \VC++\Java 等编程语言环境。
三、实验原理实验要求使用可变分区存储管理方式,分区分配中所用的数据结构采用空闲分区表和空闲分区链来进行,分区分配中所用的算法采用首次适应算法、最佳适应算法、最差适应算法三种算法来实现主存的分配与回收。
同时,要求设计一个实用友好的用户界面,并显示分配与回收的过程。
同时要求设计一个实用友好的用户界面,并显示分配与回收的过程。
A、主存空间分配(1)首次适应算法在该算法中,把主存中所有空闲区按其起始地址递增的次序排列。
在为作业分配存储空间时,从上次找到的空闲分区的下一个空闲分区开始查找,直到找到第一个能满足要求的空闲区,从中划出与请求的大小相等的存储空间分配给作业,余下的空闲区仍留在空闲区链中。
(2)最佳适应算法在该算法中,把主存中所有空闲区按其起始地址递增的次序排列。
在为作业分配存储空间时,从上次找到的空闲分区的下一个空闲分区开始查找,直到找到一个能满足要求的空闲区且该空闲区的大小比其他满足要求的空闲区都小,从中划出与请求的大小相等的存储空间分配给作业,余下的空闲区仍留在空闲区链中(3)最坏适应算法在该算法中,把主存中所有空闲区按其起始地址递增的次序排列。
在为作业分配存储空间时,从上次找到的空闲分区的下一个空闲分区开始查找,直到找到一个能满足要求的空闲区且该空闲区的大小比其他满足要求的空闲区都大,从中划出与请求的大小相等的存储空间分配给作业,余下的空闲区仍留在空闲区链中。
B、主存空间回收当一个作业执行完成撤离时,作业所占的分区应该归还给系统。
可变分区存储管理实验报告
实验三可变分区存储管理
一、实验目的
通过编写可变分区存储模拟系统,掌握可变分区存储管理的基本原理,分区的分配与回收过程。
二、实验内容与步骤
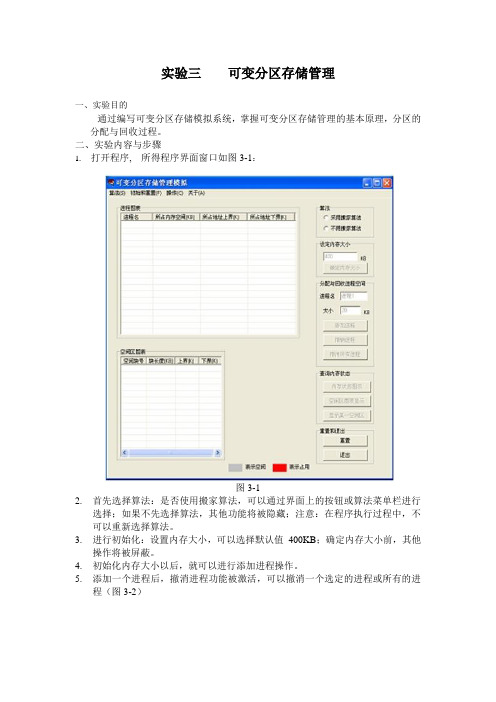
1.打开程序,所得程序界面窗口如图3-1:
图3-1
2.首先选择算法:是否使用搬家算法,可以通过界面上的按钮或算法菜单栏进行
选择;如果不先选择算法,其他功能将被隐藏;注意:在程序执行过程中,不可以重新选择算法。
3.进行初始化:设置内存大小,可以选择默认值400KB;确定内存大小前,其他
操作将被屏蔽。
4.初始化内存大小以后,就可以进行添加进程操作。
5.添加一个进程后,撤消进程功能被激活,可以撤消一个选定的进程或所有的进
程(图3-2)
图3-2
6.查询功能:可以通过按钮或菜单栏显示内存状态图形、空闲区图表,还可以在内存状态条里闪烁显示某一在空闲区图表选中的空闲区。
7.内存不足但经过搬家算法可以分配内存空间给进程,将有如下(图3-3)提示:
图3-3
8.内存空间不足也有相应提示。
9.重置或退出。
三、实验结果
第一至四组数据测试采用搬家算法,第二至八组数据测试不采用搬家算法。
第一组测试数据:(测试内存错误输入) 选择搬家算法,内存大小:0KB/-50KB/空
第二组测试数据:(测试内存空间不够)选择搬家算法,内存大小:400KB
第三组测试数据:(测试是否采用最佳适应法)选择搬家算法,内存大小:200KB 第四组数据:(测试搬家算法)选择搬家算法,内存大小:400KB
第五组数据至第八组数据:不采用搬家算法,内存大小:分别与第一至第四组数据相同,操作过程:分别与第一至第四组数据相同。
计算机操作系统内存管理系统可变分区存储管理方式的内存分配回收

计算机操作系统内存管理系统可变分区存储管理方式的内存分配回收内存管理是操作系统中非常重要的一个功能,它负责管理计算机内存资源的分配和回收。
内存分配是指在程序运行时,为进程分配适当大小的内存空间;内存回收是指当进程终止或不再需要分配的内存时,将它们释放回系统。
可变分区存储管理方式是一种常用的内存管理方式,它的特点是将内存分为若干个可变大小的分区。
下面将详细介绍可变分区存储管理方式的内存分配和回收。
一、内存分配:1. 首次适应算法(First Fit):从起始地址开始查找第一个满足分配要求的可用分区,分配其中一部分给进程,并将剩余部分作为新的可用分区。
2. 循环首次适应算法(Next Fit):与首次适应算法类似,但是从上一次分配的位置开始查找。
3. 最佳适应算法(Best Fit):在所有可用分区中找到最小且能满足分配要求的分区进行分配。
4. 最坏适应算法(Worst Fit):在所有可用分区中找到最大的空闲分区进行分配。
这种方法可能会造成大量外部碎片,但可以更好地支持大型进程。
二、内存回收:1.碎片整理:在每次回收内存时,可以通过将相邻的空闲分区合并为一个更大的分区来减少外部碎片。
这种方法需要考虑如何高效地查找相邻分区和合并它们。
2.分区分割:当一个进程释放内存时,生成的空闲分区可以进一步划分为更小的分区,并将其中一部分分配给新进程。
这样可以更好地利用内存空间,但会增加内存分配时的开销。
3.最佳合并:在每次回收内存时,可以选择将相邻的空闲分区按照最佳方式合并,以减少外部碎片。
4.分区回收:当一个进程终止时,可以将其所占用的分区标记为可用,以便其他进程使用。
三、优化技术:1.预分配内存池:为了避免频繁的内存分配和回收,可以预分配一定数量的内存作为内存池,由进程从内存池中直接分配和回收内存。
2.内存压缩:当内存不足时,可以通过将一部分进程的内存内容移动到磁盘等外部存储器中,释放出一定的内存空间。
3.页面替换算法:在虚拟内存系统中,当物理内存不足时使用页面替换算法,将不常用的页面淘汰出物理内存,以便为新页面分配内存。
内存分配回收实验报告

一、实验目的通过本次实验,加深对内存分配与回收机制的理解,掌握内存分配算法和回收策略,并能够运用所学知识解决实际内存管理问题。
二、实验内容1. 确定内存空间分配表;2. 采用首次适应算法实现内存分配;3. 采用最佳适应算法实现内存分配;4. 采用最坏适应算法实现内存分配;5. 实现内存回收功能;6. 对比分析不同内存分配算法的优缺点。
三、实验步骤1. 创建一个内存空间模拟程序,用于演示内存分配与回收过程;2. 定义内存空间分配表,记录内存块的起始地址、大小和状态(空闲或占用);3. 实现首次适应算法,在内存空间分配表中查找第一个满足条件的空闲内存块,分配给请求者;4. 实现最佳适应算法,在内存空间分配表中查找最接近请求大小的空闲内存块,分配给请求者;5. 实现最坏适应算法,在内存空间分配表中查找最大的空闲内存块,分配给请求者;6. 实现内存回收功能,当内存块释放时,将其状态更新为空闲,并合并相邻的空闲内存块;7. 对比分析不同内存分配算法的优缺点,包括分配时间、内存碎片和内存利用率等方面。
四、实验结果与分析1. 首次适应算法:该算法按照内存空间分配表的顺序查找空闲内存块,优点是分配速度快,缺点是容易产生内存碎片,且内存利用率较低;2. 最佳适应算法:该算法查找最接近请求大小的空闲内存块,优点是内存利用率较高,缺点是分配速度较慢,且内存碎片较多;3. 最坏适应算法:该算法查找最大的空闲内存块,优点是内存利用率较高,缺点是分配速度较慢,且内存碎片较多。
五、实验结论通过本次实验,我们掌握了内存分配与回收的基本原理和算法,了解了不同内存分配算法的优缺点。
在实际应用中,我们需要根据具体需求选择合适的内存分配算法,以优化内存管理,提高系统性能。
六、实验心得1. 内存分配与回收是计算机系统中重要的组成部分,对系统性能有着重要影响;2. 熟练掌握内存分配算法和回收策略,有助于解决实际内存管理问题;3. 在实际应用中,应根据具体需求选择合适的内存分配算法,以优化内存管理,提高系统性能。
操作系统-内存分配与回收实验报告

操作系统-内存分配与回收实验报告本次实验是关于内存管理的实验,主要涉及内存分配和回收的操作。
本文将对实验过程和结果进行详细介绍。
1. 实验目的本次实验的主要目的是熟悉内存管理的基本原理和机制,掌握内存分配和回收的方法,并且实现一个简单的内存管理器。
2. 实验原理内存管理是操作系统的重要组成部分,主要负责管理计算机的内存资源,并且协调进程对内存的访问。
在计算机工作过程中,内存扮演着重要的角色,因此内存管理的效率和稳定性对计算机的性能和稳定性有着重要影响。
内存管理包括内存分配和回收两个方面。
内存分配是指为进程分配空闲的内存空间,以便程序可以执行;内存回收是指将已经使用完成的内存空间还回给系统,以便其他进程使用。
3. 实验步骤为了实现一个简单的内存管理器,我们需要进行以下步骤:(1)定义内存块结构体首先,我们需要定义一个内存块结构体,用于描述内存块的基本信息。
内存块结构体可以包含以下信息:· 内存块的起始地址· 内存块是否被分配下面是一个内存块结构体定义的示例代码:typedef struct mem_block{void *start_address; // 内存块的起始地址size_t size; // 内存块的大小bool is_allocated; // 内存块是否已经分配}MemBlock;(3)实现内存分配函数现在,我们可以开始实现内存分配函数了。
内存分配函数需要完成以下工作:· 在内存管理器中寻找一个合适的内存块void *mem_alloc(MemManager *manager, size_t size){MemBlock *p = manager->block_list;while(p){if(p->size >= size && !p->is_allocated){p->is_allocated = true;return p->start_address;}p = p->next;}return NULL;}· 找到该内存块所在的位置· 将该内存块标记为未分配状态4. 实验结果本次实验实现了一个简单的内存管理器,通过该内存管理器可以实现内存分配和回收的操作。
可变分区存储管理方式的内存分配和回收

可变分区存储管理方式的内存分配和回收第一篇:可变分区存储管理方式的内存分配和回收#include//定义输入/输出函数#include//数据流输入/输出#include//字符串处理#include//参数化输入/输出const int MJ=10;//假定系统允许的最大作业数量为10typedef struct node{int address;int length;char tag[10];}job;job frees[MJ];int free_quantity;job occupys[MJ];int occupy_quantity;int read(){FILE *fp;char fn[10];cout<cin>>fn;if((fp=fopen(fn,“r”))==NULL){ 其意义是在当前目录下打开文件file a,只允许进行“读”操作,并使fp指向该文件cout<}else{while(!feof(fp)){fscanf(fp,“%d,%d”,&frees[free_quantity].address,&frees[free_quantity].length);free_quantity++;fscanf(文件指针,格式字符串,输入表列);}return 1;}return 0;}void sort(){int i,j,p;for(i=0;ip=i;for(j=i+1;jif(frees[j].addressp=j;}}if(p!=i){frees[free_quantity]=frees[i];frees[i]=frees[p];frees[p]=frees[free_quantity];}}}void view(){int i;cout<cout<for(i=0;icout.setf(2); cout.width(12); cout<cout.width(10); cout<cout.width(8); cout<}cout<cout<for(i=0;icout.setf(2); cout.width(12); cout<cout.width(10); cout<cout.width(8); cout<}}void ear(){char job_name[10]; int job_length;int i,j,flag,t;cout<cin>>job_name; cin>>job_length; flag=0;for(i=0;iif(frees[i].length>=job_length){flag=1;}}if(flag==0){//未找到空闲区,返回cout<}else{t=0;i=0;while(t==0){if(frees[i].length>=job_length){//找到可用空闲区,开始分配t=1;}i++;}i--;occupys[occupy_quantity].address=frees[i].address;//修改已分配区表strcpy(occupys[occupy_quantity].tag,job_name);occupys[occupy_quantity].length=job_length;occupy_quantity++;if(frees[i].length>job_length){frees[i].address+=job_length;frees[i].length-=job_length;}else{for(j=i;jfrees[j]=frees[j+1];}free_quantity--;cout<}}}void reclaim()//回收作业所占的内存空间{char job_name[20];int i,j,flag,p=0;int address;int length;//寻找已分分区表中对应的登记项cout<cin>>job_name;flag=-1;for(i=0;iif(!strcmp(occupys[i].tag,job_name)){flag=i;address=occupys[i].address;length=occupys[i].length;}}if(flag==-1){ //在已分分区表中找不到作业cout<}else{//修改空闲区表,加入空闲表for(i=0;iif((frees[i].address+frees[i].length)==address){ if(((i+1)for(j=i+1;jfrees[j]=frees[j+1];}free_quantity--;p=1;}else{frees[i].length+=length;p=1;}}if(frees[i].address==(address+length)){ frees[i].address=address;frees[i].length+=length;p=1;}}if(p==0){frees[free_quantity].address=address; frees[free_quantity].length=length; free_quantity++;}//删除分配表中的该作业for(i=flag;ioccupys[i]=occupys[i+1];}occupy_quantity--;}}void main(){int flag=0;int t=1;int chioce=0;int i;for(i=0;ifrees[i].address=-1;//空闲区表初始化frees[i].length=0;strcpy(frees[i].tag,“free”);occupys[i].address=-1;//已分分区表初始化occupys[i].length=0;strcpy(occupys[i].tag,“");}free_quantity=0;occupy_quantity=0;flag=read();while(flag==1){sort();cout<cin>>chioce;switch(chioce){case 0:flag=0;break;case 1:ear();break;case 2:reclaim();break;case 3:view();break;default:cout<}}}第二篇:可变分区存储管理方式的内存分配和回收实验报告一.实验目的通过编写和调试存储管理的模拟程序以加深对存储管理方案的理解,熟悉可变分区存储管理的内存分配和回收。
可变分区存储管理的内存分配算法模拟实现----最佳适应算法 -回复

可变分区存储管理的内存分配算法模拟实现----最佳适应算法-回复可变分区存储管理是一种常用的内存分配算法,用于管理计算机系统中的内存空间。
其中,最佳适应算法是其中一种经典的实现方式。
本文将围绕最佳适应算法展开,详细介绍其原理、实现方法以及优缺点。
首先,我们需要明确什么是可变分区存储管理。
在计算机系统中,内存是被划分为多个可用的分区,每个分区有不同的大小。
当一个程序需要内存时,系统会选择一个适合该程序大小的分区进行分配。
使用可变分区存储管理算法,系统可以灵活地分配和回收内存,并提高内存的利用率。
最佳适应算法是可变分区存储管理中的一种常用算法。
其核心思想是始终选择最小但足够容纳所需内存的分区进行分配。
这样可以最大程度地减少内存碎片的产生,提高系统内存利用率。
下面我们将一步一步来模拟实现最佳适应算法。
首先,我们需要创建一个数据结构来表示内存分区。
我们可以使用一个链表来存储每个分区的信息,每个节点包含分区的起始地址、结束地址和大小。
初始时,整个内存空间被视为一个大的可用分区。
接下来,当一个程序需要内存时,我们需要遍历整个分区链表,找到一个大小不小于所需内存的最小分区。
我们可以使用一个变量来记录当前找到的最小分区的大小,以及一个指针来指向该分区节点。
在遍历过程中,如果找到一个分区的大小恰好等于所需内存,那么直接分配给程序,并将该节点从链表中删除即可。
如果找到的分区的大小大于所需内存,我们需要进行分割操作。
即将该分区分成两个部分,一个部分分配给程序,另一个部分保留未分配状态,并将其添加到链表中。
同时,我们需要更新原有分区节点的起始地址和大小。
最后,当一个程序终止并释放内存时,我们需要将该内存块归还给系统,并进行合并操作。
即将释放的内存块与相邻的空闲内存块进行合并,以减少内存碎片。
通过以上步骤,我们可以实现最佳适应算法来管理内存分配。
但是,最佳适应算法也有其优缺点。
首先,最佳适应算法相对于其他算法来说,可以更好地减少内存碎片的产生。
可变分区存储管理实验报告

沈阳工程学院学生实验报告实验室名称:信息工程系信息安全实验室实验课程名称:操作系统实验项目名称:可变分区存储管理班级:计专本121 姓名:郑永凯学号:2012461127 实验日期:2013 年5 月27日实验台编号:F608指导教师:张楠批阅教师(签字):成绩:#include<stdio.h> #include<stdlib.h> #define NULL 0#define getjcb(type) (type*)malloc(sizeof(type))#define getsub(type) (type*)malloc(sizeof(type))int num,num2; //要调度的作业数和要回收的区域数int m=0; //已分配作业数int flag; //分配成功标志intisup,isdown; //回收区域存在上邻和下邻的标志int is=0;structjcb{char name[10];char state;intntime; //所需时间int size; //所需空间大小intaddr; //所分配分区的首地址structjcb *link;} *ready =NULL, *p,*q,*as=NULL;//作业队列ready,已分配作业队列as typedefstructjcb JCB;struct subarea{ //分区块char name[10];intaddr; //分区首地址int size; //分区大小char state;struct subarea *link;} *sub=NULL,*r,*s,*cur; //空闲分区队列sub,当前分区指针cur typedefstruct subarea SUB;void sort() /* 建立对作业按到达时间进行排列的函数,直接插在队列之尾*/ {JCB *first;if(ready==NULL) ready=p;else{first=ready;while(first->link!=NULL)first=first->link;first->link=p;p->link=NULL;}}void sort3() /*建立对已分配作业队列的排列函数,直接插在队列之尾*/ {JCB *fir;if(as==NULL) as=q;else{fir=as;while(fir->link!=NULL)fir=fir->link;fir->link=q;q->link=NULL;}m++;}void input() /* 建立作业控制块函数*/{int i;printf("\n请输入要调度的总作业数:");scanf("%d",&num);for(i=0;i<num;i++){printf("\n作业号No.%d:\n",i);p=getjcb(JCB);printf("\n输入作业名:");scanf("%s",&p->name);printf("\n输入作业的大小:");scanf("%d",&p->size);printf("\n输入作业所需运行时间:");scanf("%d",&p->ntime);p->state='w';p->link=NULL;sort(); /* 调用sort函数*/}printf("\n 按任一键继续......\n");getch();}void input2() /*建立要回收区域的函数*/{JCB *k;int has;q=getjcb(JCB);printf("\n输入区域名(作业名):");scanf("%s",&q->name);p=as;while(p!=NULL){if(strcmp(p->name,q->name)==0) /*在已分配作业队列中寻找*/{q->addr=p->addr;q->size=p->size;has=1; /*输入作业名存在标志位*/if(p==as) as=p->link; /*在已分配作业队列中删除该作业*/ else{k=as;while(k->link!=p) k=k->link;k->link=k->link->link; /*删除*/}printf("输出该作业首地址:%d\n",q->addr);printf("输出该作业大小:%d\n\n",q->size);q->link=NULL;break;}else{p=p->link; has=0;} /*输入作业名不存在标志*/}if(has==0){printf("\n输入作业名错误!请重新输入!\n");input2();}}void print(){printf("\n\n\n\n");printf("\t\t**************************************\n");printf("\t\t\t三.存储管理实验演示\n");printf("\t\t**************************************\n\n\n");printf("\t\t\t\t123456\n");printf("\t\t\t\t信自学院\n");printf("\t\t\t\t计专本121\n");printf("\t\t\t\t2012461119\n");printf("\t\t\t\t2013年5月\n");printf("\n\n\n");printf("\t\t\t按任意键进入演示");getch();system("cls");}void init_sub() /*初始化空闲分区表*/{r=getsub(SUB);strcpy(r->name,"0"); r->addr=5; r->size=10; r->state='F';sub=r;s=getsub(SUB);strcpy(s->name,"1"); s->addr=20; s->size=120; s->state='F';sub->link=s;r=s;s=getsub(SUB);strcpy(s->name,"2"); s->addr=160; s->size=40; s->state='F';r->link=s;r=s;s=getsub(SUB);strcpy(s->name,"3"); s->addr=220; s->size=10; s->state='F';r->link=s;r=s;s=getsub(SUB);strcpy(s->name,"4"); s->addr=250; s->size=20; s->state='F';r->link=s;r=s;s=getsub(SUB);strcpy(s->name,"5"); s->addr=300; s->size=80; s->state='F';r->link=s;s->link=0;}//--------------------------------------------------------------------------void disp() /*空闲分区表的显示函数*/{printf("\n\n");printf("\t\t 分区首地址长度状态\n");r=sub;while(r!=NULL){printf("\t\t %s\t\t%d\t\t%d\t\t%c\n",r->name,r->addr,r->size,r->state);r=r->link;}printf("\n");}void disp2() /*显示已分配内存的作业表函数*/{printf("\n\n");printf("\t\t 作业名首地址长度状态\n");p=as;while(p!=NULL){printf("\t\t %s\t\t%d\t\t%d\t\t%c\n",p->name,p->addr,p->size,p->state);p=p->link;}printf("\n\n");}void assign2(JCB *pr) /*首次适应作业分区*/{SUB *k;r=sub; /*从空闲表头开始寻找*/while(r!=NULL){if(((r->size)>(pr->size))&&(r->state=='F')) /*有空闲分区大于作业大小的情况*/ {pr->addr=r->addr;r->size-=pr->size;r->addr+=pr->size;flag=1; /*分配成功标志位置1*/q=pr;q->state='r';sort3(); /*插入已分配作业队列*/printf("作业%s的分区为[%s],首地址为%d.\n",p->name,r->name,pr->addr);break;}else if(((r->size)==(pr->size))&&(r->state=='F')) /*有空闲分区等于作业大小的情况*/ {pr->addr=r->addr;flag=1; /*分配成功标志位置1*/q=pr;sort3(); /*插入已分配作业队列*/s=sub; /*空闲分区已完成分配,应删除*/while(s->link!=r) s=s->link;s->link=s->link->link; /*删除空闲分区*/printf("作业%s的分区为[%s],首地址为%d.\n",p->name,r->name,pr->addr);break;}else{r=r->link; flag=0;}}if(flag==0) /*作业过大的情况*/{printf("作业%s长度过大,内存不足,分区分配出错!\n",p->name);is=1;}}void reclaim2(JCB *pr) /*首次适应与循环首次适应区域回收*/{SUB *k;r=sub;while(r!=NULL){if(r->addr==((pr->addr)+(pr->size))) /*回收区域有下邻*/{pr->size+=r->size;s=sub;isdown=1; /*下邻标志位置1*/while(s!=NULL){if(((s->addr)+(s->size))==(pr->addr)) /*有下邻又有上邻*/{s->size+=pr->size;k=sub;while(k->link!=r) k=k->link;k->link=k->link->link;isup=1; /*上邻标志位置1*/break;}else{s=s->link; isup=0;} /*上邻标志位置0*/}if(isup==0) /*有下邻无上邻*/{r->addr=pr->addr;r->size=pr->size;}break;}else{r=r->link; isdown=0;} /*下邻标志位置0*/}if(isdown==0) /*区域无下邻*/{s=sub;while(s!=NULL){if(((s->addr)+(s->size))==(pr->addr)) /*无下邻但有上邻*/{s->size+=pr->size;isup=1; /*上邻标志位置1*/break;}else{ s=s->link; isup=0;} /*上邻标志位置0*/}if(isup==0) /*无下邻且无上邻*/{k=getsub(SUB); /*重新生成一个新的分区结点*/strcpy(k->name,pr->name);k->addr=pr->addr;k->size=pr->size;k->state='n';r=sub;while(r!=NULL){if((r->addr)>(k->addr)) /*按分区首地址排列,回收区域插在合适的位置*/{if(r==sub) /*第一个空闲分区首址大于回收区域的情况*/ { k->link=r; sub->link=k; }else{s=sub;while(s->link!=r) s=s->link;k->link=r;s->link=k;}break;}else r=r->link;}if(r==NULL) /*所有空闲分区的首址都大于回收区域首址的情况*/ {s=sub;while(s->link!=NULL) s=s->link;s->link=k;k->link=NULL;}}}printf("\n区域%s己回收.",pr->name);}menu(){printf("\n\n\n\t\t**************************************\n");printf("\t\t\t存储管理实验演示\n");printf("\t\t**************************************\n\n\n");printf("\t\t\t 1. 显示空闲分区\n");printf("\t\t\t 2. 分配和回收作业\n");printf("\t\t\t 0. 退出\n");printf("\t\t\t请选择你要的操作:");switch(getchar()){case '1':system("cls");disp();getch();system("cls");menu();break;case '2':system("cls");printf("\n首次适应算法");input();printf("\n");while(num!=0){p=ready;ready=p->link;p->link=NULL;assign2(p);num--;}printf("\n显示回收后的空闲分区表和已分配作业表...");getch();printf("\n\t\t 完成分配后的空闲分区表\n"); disp();printf("\n\t\t 已分配作业表\n"); disp2();if(is==0)printf("\n 全部作业已经被分配内存.");else printf("\n 作业没有全部被分配内存.\n");printf("\n\n按任意键进行区域回收.");printf("\n");while(as!=NULL){getch();input2();printf("按任意键继续...");getch();printf("\n");reclaim2(q);printf("\n显示回收后的空闲分区表和已分配作业表...");getch();printf("\n\t\t 回收后的空闲分区表\n"); disp();printf("\n\t\t 已分配作业表\n"); disp2();printf("\n继续回收...(Enter)");}printf("\n所有已分配作业已完成!");printf("\nPress any key to return...");getch();system("cls");menu();break;case '0':system("cls");break;default:system("cls");menu();}}void main() /*主函数*/{init_sub();print();menu();}。
实验报告 可变分区 主存分配回收

printf("========================================\n");
printf("输入你的选择:\n");
scanf("%d",&j);
switch(j)
{
case 1:insertu(i);//为作业分配空间
//合并完之后的空闲分区的结束地址和相邻的空闲分区的起始地址也相连,则继续合并
{
fr[i].len=fr[i].len+fr[i+1].len;
for(k=i+1;k<m-1;k++)
{
fr[k].ad=fr[k+1].ad;
fr[k].len=fr[k+1].len;
fr[k].state=fr[k+1].state;
操作系统实验报告
设计题目
在可变分区管理方式下采用最先适应算法实现主存分配和实现主存回收
一、设计内容
主存储器空间的分配和回收。
二、设计目的
一个好的计算机系统不仅要有一个足够容量的、存取速度高的、稳定可靠的主存储器,而且要能合理地分配和使用这些存储空间。当用户提出申请存储器空间时,存储管理必须根据申请者的要求,按一定的策略分析主存空间的使用情况,找出足够的空闲区域分配给申请者。当作业撤离或主动归还主存资源时,则存储管理要收回作业占用的主存空间或归还部分主存空间。主存的分配和回收的实现虽与主存储器的管理方式有关的,通过本实习帮助学生理解在不同的存储管理方式下应怎样实现主存空间的分配和回收。
{
while(fr[i].state!='M')
内存的分配与回收实验报告

内存的分配与回收实验报告实验目的:了解计算机内存分配与回收的原理及实现方式,掌握最先适应算法的具体实现,加深对内存管理的理解。
实验原理:内存是计算机系统中的关键组成部分之一,它负责存储程序运行所需的数据和指令。
为了有效管理内存,将其划分为若干个固定大小的单元,称为分配单元。
内存分配与回收的基本原则是尽量高效地利用内存空间。
最先适应算法是一种常用的内存分配算法,它的基本思想是按照内存地址从小到大的顺序,依次寻找满足分配要求的第一个空闲分区。
因为每次分配都是从低地址开始,所以能够尽量填满被回收后的可用内存空间。
实验步骤:1.定义内存块的数据结构,包括起始地址、大小、状态等信息。
2.初始化内存,划分出若干个固定大小的内存块。
3.从给定的进程请求中获取进程需要的内存大小。
4.遍历内存块列表,寻找第一个满足分配要求的空闲分区,即大小大于等于进程需求的分区。
5.如果找到了满足要求的分区,则将其划分为两个分区,一个用于分配给进程,一个作为剩余的空闲分区。
6.更新内存块列表,记录分配给进程的内存块。
7.如果没有找到满足要求的分区,则返回分配失败的信息。
8.进程完成运行后,将其占用的内存块标记为空闲,并进行合并操作,合并相邻的空闲分区。
9.更新内存块列表,记录回收的内存块。
10.重复步骤3至步骤9,直到完成所有的进程请求。
实验结果:经过多次实验,使用最先适应算法进行内存分配与回收,可以有效地利用内存空间,提高内存利用率。
实验总结:通过本次实验,我深入理解了最先适应算法的实现原理和逻辑流程。
在实际的内存管理中,我们需要根据实际情况选择合适的内存分配策略,以避免出现内存碎片和浪费现象。
同时,回收后的内存块需要及时进行合并操作,以提高内存的利用率。
实验过程中还发现,在有大量并发的情况下,最先适应算法可能会产生较多的内存碎片,影响内存的使用效率,因此需要根据实际情况选择其他适合的内存分配算法。
总之,通过这次实验,我对内存分配与回收有了更深入的理解,对内存管理算法的选择和优化也更加清晰,为以后的实际应用打下了基础。
主存储器空间的分配和回收实验报告参考模板

主存储器空间的分配和回收一、实验题目:(1)在可变分区管理方式下采用最先适应算法实现主存分配和实现主存回收(2)在分页式管理方式下采用位示图来表示主存分配情况,实现主存空间的分配和回收二、实验目的:通过本实习帮助理解在不同的存储管理方式下应怎样实现主存空间的分配和回收。
三、实验原理:第一题:在可变分区管理方式下采用最先适应算法实现主存分配和实现主存回收(1)可变分区方式是按作业需要的主存空间大小来分割分区的。
当要装入一个作业时,根据作业需要的主存量查看是否有足够的空闲空间,若有,则按需要量分割一个分区分配给该作业;若无,则作业不能装入。
随着作业的装入、撤离,主存空间被分成许多个分区,有的分区被作业占用,而有的分区是空闲的。
例如:为了说明哪些区是空闲的,可以用来装入新作业,必须要有一张空闲区说明表,格式如下:(2)当有一个新作业要求装入主存时,必须查空闲区说明表,从中找出一个足够大的空闲区。
有时找到的空闲区可能大于作业需要量,这时应把原来的空闲区变成两部分:一部分分给作业占用;另一部分又成为一个较小的空闲区。
为了尽量减少由于分割造成的空闲区,而尽量保存高地址部分有较大的连续空闲区域,以利于大型作业的装入。
为此,在空闲区说明表中,把每个空闲区按其地址顺序登记,即每个后继的空闲区其起始地址总是比前者大。
为了方便查找还可使表格“紧缩”,总是让“空表目”栏集中在表格的后部。
(3)采用最先适应算法(顺序分配算法)分配主存空间。
按照作业的需要量,查空闲区说明表,顺序查看登记栏,找到第一个能满足要求的空闲区。
当空闲区大于需要量时,一部分用来装入作业,另一部分仍为空闲区登记在空闲区说明表中。
最先适应分配算法如图:(4)当一个作业执行结束撤离时,作业所占的区域应该归还,归还的区域如果与其它空闲区相邻,则应合成一个较大的空闲区,登记在空闲区说明表中。
例如,在提示(1)中列举的情况下,如果作业2撤离,归还所占主存区域时,应与上、下相邻的空闲区一起合成一个大的空闲区登记在空闲区说明表中。
内存管理实验报告-可变分区

沈阳工程学院
学生实验报告
实验室名称:计算机实验室实验课程名称:操作系统
实验项目名称:存储管理(1)实验日期:2016年月日
班级:姓名:学号:
指导教师:曲乐声批阅教师:成绩:
一.实验目的
通过编写和调试存储管理的模拟程序以加深对存储管理方案的理解,熟悉可变分区存储管理的内存分配和回收。
二.实验设备
PC机一台,WIN-TC软件。
三.实验项目
编写程序实现采用可变分区方法管理内存。
1、在该实验中,采用可变分区方式完成对存储空间的管理(即存储空间的分配与回收工作)。
2、设计用来记录主存使用情况的数据结构:已分区表和空闲分区表或链表。
3、在设计好的数据结构上设计一个主存分配算法。
4、在设计好的数据结构上设计一个主存回收算法。
其中,若回收的分区有上邻空闲分区和(或)下邻空闲分区,要求合并为一个空闲分区登记在空闲分区表的一个表项里。
5、(附加)若需要可以实现程序的浮动,对内存空间进行紧凑。
四.实验代码(附页)
五.实验结果
成绩评定
程序正确性 2.5 2 1.5 1 0.5 0
结果正确性 2.5 2 1.5 1 0.5 0
分析正确性 5 4 3 2 1 0
成绩
·1·。
可变分区的主存分配和回收的算法

可变分区的主存分配和回收的算法下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!1. 引言在操作系统中,可变分区的主存分配和回收是一个重要的主题。
《操作系统》实验报告2 可变分区存储管理方式的内存分配回收

scanf("%d",&a);
switch(a)
{case0;exit(0);
case1;
printf ("输º?入¨?作Á¡Â业°¦Ì名?J和¨ª作Á¡Â业°¦Ì所¨´需¨¨长¡è度¨¨xk:êo");
scanf("%*c%c%f",&J,&xk);
实验项目
名称
可变分区存储管理方式的内存分配回收
实验
目的及要求
1、深入了解采用可变分区存储管理方式的内存分配回收的实现
实验
内容
编写程序完成可变分区存储管理方式的内存分配回收
实验步骤
1、确定内存空间分配表
2、采用最优适应算法完成内存空间的分配和回收
3、编写主函数对所做工作进行测试
实验环境
Windows XP、visualstudio 2005
}
i++;
}
if(k!=-1)
if(j!=1)
{free_table[k].length=free_table[j].length+free_table[k].length+L;
free_table[j].flag=0;
}
else
free_table[k].length=free_table[k].length+L;
L=used_table[s].length;
j==1;k=-1;i=0;
while(i<m&&(j==-1||k==-1))
{
if(free_table[i].glag==0)
操作系统实验报告可变分区存储管理方式的内存分配回收

操作系统实验报告可变分区存储管理方式的内存分配回收集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY-实验三可变分区存储管理方式的内存分配回收一.实验目的(1)深入了解可变分区存储管理方式的内存分配回收的实现。
二.实验内容编写程序完成可变分区存储管理方式的内存分配回收,要求有内存空间分配表,并采用最优适应算法完成内存的分配与回收。
三.实验原理在可变分区模式下,在系统初启且用户作业尚未装入主存储器之前,整个用户区是一个大空闲分区,随着作业的装入和撤离,主存空间被分成许多分区,有的分区被占用,而有的分区时空闲的。
为了方便主存空间的分配和去配,用于管理的数据结构可由两张表组成:“已分配区表”和“未分配区表”。
在“未分配表中”将空闲区按长度递增顺序排列,当装入新作业时,从未分配区表中挑选一个能满足用户进程要求的最小分区进行分配。
这时从已分配表中找出一个空栏目登记新作业的起始地址和占用长度,同时修改未分配区表中空闲区的长度和起始地址。
当作业撤离时已分配区表中的相应状态变为“空”,而将收回的分区登记到未分配区表中,若有相邻空闲区再将其连接后登记。
可变分区的回收算法较为复杂,当一个作业撤离时,可分为4种情况:其临近都有作业(A和B),其一边有作业(A或B),其两边均为空闲区。
尤其重要的是,在程序中利用“new类型T(初值列表)”申请分配用于存放T类型数据的内存空间,利用“delete指针名”释放指针所指向的内存空间。
四.实验部分源程序#include<iostream>usingnamespacestd;typedefstructSNode{//SpaceNodeintstart,end;//起始,结束intlength;//长度大小structSNode*next;//指向下一结点的指针}*SP;SPHead=(SP)malloc(sizeof(SNode));//全局变量,内存空间头结voidDispSpace(){//显示内存空间分配情况SPp=Head->next;cout<<"\n空闲区说明表\n"<<"---地址--长度---\n";while(p){cout<<""<<p->start<<""<<p->length<<endl;p=p->next;}cout<<"----------------\n";}voidInitial(){//初始化说明表SPp,q;p=(SP)malloc(sizeof(SNode));q=(SP)malloc(sizeof(SNode));p->start=14;p->length=12;p->end=26;q->start=32;q->length=96;q->end=128;//指导书上的作业分配Head->next=p;//与头结点连接p->next=q;q->next=NULL;DispSpace();}voidAllocation(intlen){//分配内存给新作业SPp=Head->next,q;while(p){if(p->length<len)p=p->next;elseif(p->length>len){p->start=p->start+len;p->length=p->length-len;cout<<"分配成功!\n";DispSpace();return;}else{//当两者长度相等q=p->next;p->next=q->next;cout<<"分配成功!\n";DispSpace();return;}}cout<<"分配失败!\n";DispSpace();return;}voidCallBack(intsta,intlen){//回收内存SPp=Head,q=p->next,r;//开始地址和长度p->end=0;inten=sta+len;while(q){if(sta==0){//初始地址为0if(en==q->start){//正好回收q->start=0;q->length=q->end;return;}else{r=(SP)malloc(sizeof(SNode));r->start=sta;r->length=len;r->end=en; p->next=r;r->next=q;return;}}elseif((p->end<sta)&&(q->start>en)){//上邻区r=(SP)malloc(sizeof(SNode));r->start=sta;r->length=len;r->end=en;p->next=r;r->next=q;return;}elseif((p->end<sta)&&(q->start==en)){//邻区相接q->start=sta;q->length=q->end-sta;return;}elseif((p->end==sta)&&(q->start<en)){//下邻区p->end=en;p->length=en-p->start;return;}elseif(p->end==sta&&q->start==en){//邻区相接p->end=q->end;p->length=p->end-p->start;p->next=q->next;return;}else{p=p->next;q=q->next;}}}voidmain(){Initial();cout<<"现在分配大小为6K的作业4申请装入主存:"; Allocation(6);//分配时参数只有长度//--------指导书测试数据演示----------cout<<"现回收作业3(起址10,长度4)\n";CallBack(10,4);DispSpace();cout<<"现回收作业2(起址26,长度6)\n";CallBack(26,6);DispSpace();//---------------演示结束-------------system("pause");}五.实验结果与体会我的体会:。
计算机操作系统内存管理系统可变分区存储管理方式的内存分配回收

计算机操作系统内存管理系统可变分区存储管理方式的内存分配回收概述内存管理是操作系统中重要的一部分,它负责管理计算机内存的分配和回收。
可变分区存储管理方式是一种常用的内存管理方案,它将内存分为多个不同大小的分区,每个分区可以被分配给一个进程来使用。
本文将介绍可变分区存储管理方式的内存分配和回收过程。
内存分配可变分区存储管理方式的内存分配过程包括空闲分区的选择和分区的划分。
空闲分区的选择在可变分区存储管理方式中,操作系统需要选择一个合适的空闲分区来分配给进程。
常用的空闲分区选择算法有:•首次适应算法(First Fit):从头开始寻找满足进程需要的空闲分区。
•最佳适应算法(Best Fit):从所有满足进程需要的空闲分区中选择大小最接近的一个。
•最差适应算法(Worst Fit):选择能够满足进程需要且最大的空闲分区。
选择合适的空闲分区算法可以提高内存利用率和分配的效率。
分区的划分一旦选择了合适的空闲分区,操作系统需要对该分区进行划分,以满足进程的内存需求。
常用的分区划分方式包括:•等分划分:将空闲分区按照进程的内存需求进行等分划分。
•保留部分划分:只将进程需要的内存大小分配给进程,剩余的空闲分区保留。
分区的划分方式可以根据实际情况选择,以满足不同进程的内存需求。
内存回收可变分区存储管理方式的内存回收过程包括释放分区和合并分区两个步骤。
释放分区当一个进程终止或释放了分配给它的内存分区时,该分区将被标记为空闲,可以被其他进程使用。
合并分区在进行内存回收时,为了提高内存利用率,操作系统通常会进行分区的合并。
合并分区需要考虑到合并后的分区是否满足其他进程的内存需求。
常用的合并分区策略有:•相邻空闲分区合并:将相邻的两个空闲分区合并成一个更大的空闲分区。
•首次适应合并:从头开始寻找空闲分区,如果找到两个相邻的空闲分区,可以将它们合并起来。
通过合并分区,可以减少内存碎片,提高内存的利用率。
可变分区存储管理方式是一种常用的内存管理方案,在内存分配和回收过程中,通过选择合适的空闲分区和分区的划分以及合并分区,可以高效地管理计算机内存,提高内存利用率。
操作系统实验报告可变分区存储管理方式的内存分配回收

操作系统实验报告可变分区存储管理方式的内存分配回收可变分区存储管理方式是一种常见的内存分配和回收策略,通过将内存分成若干大小不等的分区,分配给不同大小的进程使用。
本文将对可变分区存储管理方式的内存分配和回收进行详细介绍。
首先,可变分区存储管理方式需要对内存进行划分,将内存分成若干个大小不等的分区。
这些分区可以是固定大小的,也可以是可变大小的。
当进程申请内存时,系统会根据申请内存的大小来选择一个合适大小的分区进行分配。
分配时分为两种情况:首次适应和最佳适应。
首次适应算法是指从内存的起始位置开始遍历分区,找到第一个能满足进程要求的分区进行分配。
这种算法的优点是找到满足条件的分区速度较快,缺点是容易造成较大的内存碎片。
最佳适应算法是指通过遍历整个内存,找到一个大小最接近进程要求的分区进行分配。
这种算法的优点是能够减小内存碎片的产生,但是分配速度较慢。
当进程结束时,需要回收其占用的内存。
对于可变分区存储管理方式,在回收内存时出现了两种情况:内部碎片和外部碎片。
内部碎片是指分配给进程的分区中,有一部分空闲内存无法被其他进程利用。
这是因为当一些进程需要分配内存时,分配的大小可能大于其实际需要的大小,导致分区中留下了空余空间。
解决内部碎片的方法是动态地调整分区的大小,使其能够更好地适应进程的大小需求。
外部碎片是指存储空闲的分区之间的一些不可利用的内存。
当进程需要分配内存时,可能没有一个分区能满足其大小需求,导致无法分配内存。
解决外部碎片的方法是内存紧缩和分区合并。
内存紧缩是指将内存中的进程向一端移动,使剩余的空闲内存空间连在一起。
这样可以使得所有的空闲内存空间都可以被利用,减少外部碎片的产生。
分区合并是指将不连续的空闲分区进行合并,形成更大的连续空闲分区。
这样可以提供给大型进程使用,减少外部碎片的产生。
综上所述,可变分区存储管理方式的内存分配和回收是一个动态的过程,需要根据进程的需求进行灵活地管理。
它可以通过首次适应或最佳适应算法选择合适的分区进行内存分配,通过动态调整分区大小解决内部碎片问题,并通过内存紧缩和分区合并减少外部碎片的产生。
可变分区存储管理方式的内存分配和

printf("%6.0f%9.0f%6c\n",used_table[i].address,used_table[i].length,used_table[i].flag);
break;
default:printf("没有该选项\n");
}
}
}
“已分分区表”的结构定义
#define n 10 0”0”1”0”0”1”ength>=xk&&free_table[i].flag==1)if(k==-1||free_table[i].length<free_table[k].length)
k=i;
if(k==-1) ength-xk<=min用来记录空间区和作业占用的区域。
由于可变分区的大小是由作业需求量决定的,故分区的长度是预先不固定的,且分区的个数也随内存分配和回收变动。总之,所有分区情况随时可能发生变化,数据表格的设计必须和这个特点相适应。由于分区长度不同,因此设计的表格应该包括分区在内存中的起始地址和长度。由于分配时空闲区有时会变成两个分区:空闲区和已分分区,回收内存分区时,可能会合并空闲分区,这样如果整个内存采用一张表格记录己分分区和空闲区,就会使表格操作繁琐。分配内存时查找空闲区进行分配,然后填写己分配区表,主要操作在空闲区;某个作业执行完后,将该分区变成空闲区,并将其与相邻的空闲区合并,主要操作也在空闲区。
{free_table[k].flag=0;
ad=free_table[k].address;
xk=free_table[k].length;
}
else
{free_table[k].length=free_table[k].length-xk;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.实验目的通过编写和调试存储管理的模拟程序以加深对存储管理方案的理解,熟悉可变分区存储管理的内存分配和回收。
二.实验内容1.确定内存空间分配表;2.采用最优适应算法完成内存空间的分配和回收;3.编写主函数对所做工作进行测试。
三.实验背景材料由于可变分区的大小是由作业需求量决定的,故分区的长度是预先不固定的,且分区的个数也随内存分配和回收变动。
总之,所有分区情况随时可能发生变化,数据表格的设计必须和这个特点相适应。
由于分区长度不同,因此设计的表格应该包括分区在内存中的起始地址和长度。
由于分配时空闲区有时会变成两个分区:空闲区和已分分区,回收内存分区时,可能会合并空闲分区,这样如果整个内存采用一张表格记录己分分区和空闲区,就会使表格操作繁琐。
分配内存时查找空闲区进行分配,然后填写己分配区表,主要操作在空闲区;某个作业执行完后,将该分区变成空闲区,并将其与相邻的空闲区合并,主要操作也在空闲区。
由此可见,内存的分配和回收主要是对空闲区的操作。
这样为了便于对内存空间的分配和回收,就建立两张分区表记录内存使用情况,一张表格记录作业占用分区的“己分分区表”;一张是记录空闲区的“空闲区表”。
这两张表的实现方法一般有两种:一种是链表形式,一种是顺序表形式。
在实验中,采用顺序表形式,用数组模拟。
由于顺序表的长度必须提前固定,所以无论是“已分分区表”还是“空闲区表”都必须事先确定长度。
它们的长度必须是系统可能的最大项数。
“已分分区表”的结构定义#define n 10 //假定系统允许的最大作业数量为nstruct{ float address; //已分分区起始地址float length; //已分分区长度、单位为字节int flag; //已分分区表登记栏标志,“0”表示空栏目,实验中只支持一个字符的作业名}used_table[n]; //已分分区表“空闲区表”的结构定义#define m 10 //假定系统允许的空闲区最大为mstruct{ float address; //空闲区起始地址float length; //空闲区长度、单位为字节int flag; //空闲区表登记栏标志,“0”表示空栏目,“1”表示未分配}used_table[n]; //空闲区表第二,在设计的数据表格基础上设计内存分配。
装入一个作业时,从空闲区表中查找满足作业长度的未分配区,如大于作业,空闲区划分成两个分区,一个给作业,一个成为小空闲分区。
实验中内存分配的算法采用“最优适应”算法,即选择一个能满足要求的最小空闲分区。
第三,在设计的数据表格基础上设计内存回收问题。
内存回收时若相邻有空闲分区则合并空闲区,修改空闲区表。
四、参考程序#define n 10 //假定系统允许的最大作业数量为n#define m 10 //假定系统允许的空闲区最大为m#define minisize 100struct{ float address; //已分分区起始地址float length; //已分分区长度、单位为字节int flag; //已分分区表登记栏标志,“0”表示空栏目,实验中只支持一个字符的作业名}used_table[n]; //已分分区表struct{ float address; //空闲区起始地址float length; //空闲区长度、单位为字节int flag; //空闲区表登记栏标志,“0”表示空栏目,“1”表示未分配}used_table[n]; //空闲区表allocate(J,xk) //采用最优分配算法分配xk大小的空间char J;float xk;{int i,k;float ad;k=-1;for(i=0;i<m;i++) //寻找空间大于xk的最小空闲区登记项if(free_table[i].length>=xk&&free_table[i].flag==1)if(k==-1||free_table[i].length<free_table[k].length)k=i;if(k==-1) //未找到空闲区,返回{printf("无可用的空闲区\n");return;}//找到可用空闲区,开始分配;若空闲区大小与要求分配的空间差小于minisize大小,则空闲区全部分配;//若空闲区大小与要求分配的空间差大于minisize大小,则从空闲区划分一部分分配if(free_table[k].length-xk<=minisize){free_table[k].flag=0;ad=free_table[k].address;xk=free_table[k].length;}else{free_table[k].length=free_table[k].length-xk;ad=free_table[k].address+free_table[k].length;}//修改已分配区表i=0;while(used_table[i].flag!=0&&i<n) //寻找空表目i++;if(i>=n) //无表目填写已分分区{printf("无表目填写以分分区,错误\n");if(free_table[k].flag==0) //前面找到的是整个空闲区free_table[k].flag=1;else //前面找到的是某个空闲区的一部分 free_table[k].length=free_table[k].length+xk;return;}else //修改已分配区表{used_table[i].address=ad;used_table[i].length=xk;used_table[i].flag=J;}return;}//内存分配函数结束reclaim(J) //回收作业名为J的作业所占的内存空间char J:{int i,k,j,s,t;float S,L;//寻找已分分区表中对应的登记项S=0;while((used_table[S].flag!=J||used_table[S].flag==0)&&S<n)S++;if(S>=n) //在已分分区表中找不到名字为J的作业{printf("找不到该作业\n");return;}//修改已分分区表used_table[S].flag=0;//取得归还分区的起始地址S和长度LS=used_table[S].address;L=used_table[S].length;j=-1;k=-1;i=0;//寻找回收分区的上下邻空闲区,上邻表目K,下邻表目Jwhile(i<m&&(j==-1||k==-1)){if(free_table[i].flag==0){if(free_table[i].address+free_table[i].length==0) k=i; //找到上邻 {if(free_table[i].address==S+L) j=1; //找到下邻 }i++;}if(k!=-1)if(j!=-1) //上邻空闲区,下邻空闲区,三项合并{free_table[k].length=free_table[j].length+free_table[k].length+L;free_table[j].flag+0;}else //上邻空闲区,下邻非空闲区,与上邻合并free_table[k].length=free_table[k].length+L;elseif(j!=-1) //上邻非空闲区,下邻空闲区,与下邻合并{free_table[j].address=S;free_table[j].length=free_table[j].length+L;}else{ //上下邻均为非空闲区,回收区域直接填入 t=0; //在空闲区表中寻找空栏目while(free_table[t].flag==1&&t<m)t++;if(t>=m) //空闲区表满,回收空间失败,将已分配分区表复原{printf("内存空闲表没有空间,回收空间失败\n");used_table[S].flag=J;return;}free_table[t].address=s;free_table[t].length=l;free_table[t].flag=1;}return(true);} //内存回收函数结束main(){ int i,a;float xk;char J;//空闲区表初始化free_table[0].address=10240;free_table[0].length=102400;free_table[0].flag=1;for(i=1;i<m;i++)free_table[i].flag=0;//已分分区表初始化for(i=1;i<n;i++)used_table[i].flag=0;while(1){printf("选择功能项(0—退出,1—分配内存,2-回收内存,3-显示内存)\n");printf("选择功项(0-3):");scanf("%d",&a);switch(a){case 0;exit(0); //a=0程序结束case 1; //a=1 分配内存空间printf("输入作业名J和作业所需长度XK:"); scanf("%c%c%f",&j,&xk);allocate(j,xk); //分配内存空间break;case 2; //a=2 回收内存空间printf("输入要回放分区的作业名");scanf("%c%c",&j);reclaim(j); //回收内存空间。
