14.1.1.直角三角形三边关系2
八年级数学上第14章勾股定理14.1勾股定理1直角三角形三边的关系目标二勾股定理与图形的面积华东师大

方法技巧练 1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月20日星期日下午2时52分39秒14:52:3922.3.20
2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那 些善于独立思考的人,给那些具有锲而不舍的人。2022年3月下午2时52分22.3.2014:52March 20, 2022
7 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边 分别为a,b,c,则a,b,c满足的关系为_a_2_+__b_2_=__c2. (1)分别以Rt△ABC的三边为边作正方形,如图①所示, 你能发现S1,S2,S3之间有什么关系吗? 解:由题意得S1=b2,S2=a2,S3=c2. 因为a2+b2=c2,所以S1+S2=S3.
(2)分别以Rt△ABC的三边为直径作半圆,如图②所示, (1)中的结论是否仍成立?请说明理由. 解:仍成立.理由如下: 由题意得 S1=π8·b2,S2=π8·a2,S3=π8·c2. 因为 a2+b2=c2,所以 S1+S2=S3. 即(1)中的结论仍成立.
(3)分别以Rt△ABC的三边为斜边作等腰直角三角形, 如图③所示,(1)中的结论仍成立吗(直接写出结论, 不需要证明)? 解:仍成立.
【点拨】
根据勾股定理可得a2+b2=13,由题意知四 个直角三角形的面积和是 1ab×4=13-1=12,
2 即2ab=12,则(a+b)2=a2+2ab+b2=13+12=
25.
6 如图是由两个直角三角形和三个正方形组成的图形,
其中阴影部分的面积( B )
A.16
核心素养导向下的数学教学设计——以14.1.“1_直角三角形三边的关系”为例

核心素养导向下的数学教学设计———————以14.1.1“直角三角形三边的关系”为例文|武旦珠核心素养导向下的数学教学是对传统教学的一次变革,摆脱了过去以课时为单位的传统范式,推崇以单元为整体的设计理念。
这种变革体现了对数学知识内在逻辑关系的深层次思考,教学设计应该体现单元整合教学内容。
这种教学设计旨在通过深入挖掘数学知识之间的关系,为学生提供更为系统和全面的学习体验。
教学设计要充分考虑核心素养的重要性,确保在整个教学过程中的指导作用。
教学目标应该是全面的、有层次的,可以涵盖知识、技能和态度的培养,以确保学生在学习过程中获得全面的发展。
教师要考虑学生的数学核心素养、创造力、批判性思维等方面的发展。
在每个课时中,结合教学内容和目标展开教学,能够更好地发展学生的核心素养。
【教材分析】北师大版数学八年级上册“直角三角形三边的关系”,是“勾股定理”章节的主要内容,重点讲解了勾股定理的证明过程。
教材通过两个例子“正方形的瓷砖”和“试一试”来发现直角三角形三边之间的关系。
接着,通过“做一做”的实践验证,学生先获得直接的经验,再进行总结和归纳,证明勾股定理。
勾股定理是几何学中最为重要的定理之一,它揭示了直角三角形中三边的数量关系。
直角三角形中斜边较长,而另外两条边较短,该定理证明它们之间有着精确的数量关系,为学生今后学习解直角三角形问题奠定基础。
因此,探索直角三角形三边的关系对学生来说非常重要,既能使学生更好地理解直角三角形,又能培养他们的逻辑思维能力。
【学情分析】八年级学生已经具备了一定的逻辑思维和抽象思维能力,并且掌握了学习数学的基本方法。
直角三角形是他们非常熟悉的图形,因此,通过自主探索、合作互助、交流分享的方式来验证和应用勾股定理是非常适合的。
通过这样的学习方式,学生能够轻松、愉快地完成本节课的学习目标。
【教学目标】1.育人目标(1)通过探究、验证、证明和应用勾股定理,培养学生对数学学习的意识和能力。
直角三角形三边的关系

解:如图,在Rt△ABC中, ∠ACB=90゜
AC=12, BC=5,
根据勾股定理得:
12
AB AC2BC2
5
122 52
13
答:要用13米长的直角钢三角丝形三边绳的关才系 能把电线杆固定.
例1如图14.1.4,将长为5.41米的梯子AC斜靠在墙上, BC长为2.16米,求梯子上端A到墙的底边的垂直 距离AB.(精确到0.01米)
(2)等腰直角三角形的三边关系:AC2 + BC2 =AB2
说明:在等腰直角三角形ABC中, 两直角边的平方和等于斜小
方
格 表 示
A
R c bQ
Sp 9
SQ 16
1 平 方
B aC
SR 25
Sp SQSR
厘
P
BC2 + AC2 =AB2
米
a2 b2 c2
直角三角形三边的关系
勾股定理: 对于任意的直角三角形,如果 它的两条直角边分别为a、 b,斜边为c, 那么一定有a2+b2=c2。
直角三角形两直角边的平方和等于斜边的平方
b
c
a
勾股定理揭示了直角三
角形三边之间的关系
直角三角形三边的关系
直角三角形两直角边的平方和 等于斜边的平方.
cb
┏
a
a2+b2=c2
直角三角形三边的关系
24m
9m
?
如图,大风将一根木制旗 杆吹裂,随时都可能倒下, 十分危急。接警后“119” 迅速赶到现场,并决定从 断裂处将旗杆折断。现在 需要划出一个安全警戒区 域,那么你能确定这个安 全区域的半径至少是多少 米吗?
2022秋八年级数学上册第14章勾股定理14.1勾股定理1直角三角形三边的关系__认识勾股定理授课课

解: 根据勾股定理, 可得
长度,可以求出第三 边的长度.
AB2 + BC2 = AC2. 所以 AC = A B 2 + B C 26 2 + 8 2 1 0 .
知1-讲
例2 在Rt△ABC中,∠A,∠B,∠C的对边分别是a, b,c, ∠C=90°. (1)已知a=3,b=,4,求c; (2)已知c=13,a=12,求b; (3)已知a∶b=2∶1,c=5,求b(结果保留根号).
知1-导
要点精析: (1)勾股定理揭示的是直角三 角形的三边的平方关系, 只有在直角三角形中才可 以使用勾股定理; (2)勾股定理的内容描述的是直角三角形三边之间的 数量关系,已知其中任意两边可以求出第三边; (3)勾股定理的变形公式:a2=c2-b2,b2=c2-a2; (4) 运用勾股定理,若分不清 哪条边是斜边时,则要 分 类讨论,写出所有可能的 情况,以免漏解或解 .
知1-讲
利用勾股定理求直角三角形边长的方法:一般 都要经过“一分二代三化简”这三步:即一分:分 清哪条边是斜边、哪些是直角边;二代:代入a2+b2 =c2及两边之间的关系式;三化简.
知1-讲
例1 在Rt△ABC中,已知∠B=90°, AB=6,BC=8.
求AC.
应用勾股定理,由直
角三角形任意两边的
知1-讲
例3 已知直角三角形的两边长分别为3,4,求第 三边的长.
错解:第三边的长为 32+ 42 255. 错解分析:由于习惯了“勾三股四弦五”的说法,因此
将题意理解为两直角边长分别为3和4,于是 斜边长为5.但这一理解的前提是3,4为直角 边长,而题中并没有任何说明,因而所求的 第三边长可能为斜边长,也可能为直角边 长.所以需要分情况求解.
正方形R的面积=
初中数学14.1.1直角三角形的三边关系(2)先进优质课课件

课堂小结: 通过本节课的学习你有什么收获?(从知识方面、能 力方面、解题技巧等方面进行总结)
运用勾股定理求三角形的边长时,还能运用方程解答。 在解决问题时,常把实际问题转化为数学问题,然后 运用数学知识解答。 运用勾股定理时要先构造直角三角形。 本节课运用的思想方法有:方程思想,转化思想,数 形结合思想。
设疑自探 勾股定理: 直角三角形两直角边的平方和等于斜边的平方 你能说说勾股定理的内容吗?公式又能如 若直角三角形的两条直角边分别为a,b, 何变形? 斜边为c,则 a2+b2=c2 .
A
c2=a2 + b2 a2=c2-b2 b2 =c2-a2
2
2
b
c
a c b
2
C
b= c2-a2
2
a
c a b B 在直角三角形中,知道任意两边长,利
展示点评分工表
题号 2 2 展示方式 板书 板书 展示组 4组3号 5组3号 评价组
1组2号 6组2号
展示要求:
1、展示要板书工整、规范、快速; 2、非展示同学结合展示仔细观察讨论或认真倾听,随时准备评 价,并做好变式编题 准备。
点评要求:
1、声音洪亮,言简意赅,思路清晰,点评出优、缺点及总结方法 规律。 2、非点评同学认真听讲,有疑问及时提出来,并设计变式训练。 3、注意教态端庄大方,身体与黑板成30°角。 4、对展示同学打分,每题满分10分。
质疑再探
通过刚才的学习,同学们还有哪些问题没 有解决,或又产生了哪些新的疑问,请大 胆提出来,大家共同解决。
拓展应用
1· 请你自编一道题,考考你的同桌,好的题 目不要忘了介绍给大家。
想一想:
14.1.1 直角三角形三边的关系 知识考点梳理(课件)华东师大版数学八年级上册

返回目录
解题通法
当题目中没有直角三角形时,往往先通过
重
难
题 作垂线(或作高)构造直角三角形,然后利用勾股定理求
型 得线段的长.
突
破
14.1.1 直角三角形三边的关系
返回目录
方 ■方法:利用分类讨论思想求直角三角形的边长
法
应用勾股定理时,若题目没有指明哪条边是斜边,哪些
技
巧 边是直角边时,应对未知边是直角边还是斜边进行分类讨
考
[解题思路] 图 1:∵S 梯形 ACED= ·(a+b)(a+b)
点
清
2
单 ,S梯形ACED= ab+ ab+ c ,∴ (a+b)(a+b)= ab+
解
读 ab+ c2,∴a2+2ab+b2=ab+ab+c2,∴a2+b2=c2,故图 1 可
以验证勾股定理;
图 2:图形的总面积可以表示为
∴S△ABC=
BC×AD= ×14×12=84(cm2).
返回目录
14.1.1 直角三角形三边的关系
返回目录
变式衍生
如图,一个直角三角形的两直角边长分别
重
难
题 为 6,8,分别以三边长为直径和一边作三个半圆和三个长
型 方形,则图中阴影部分的面积为 ________.
50
突
破
14.1.1 直角三角形三边的关系
续表
14.1.1 直角三角形三边的关系
考
点
清
单
解
读
华东师大版八年级数学上册14.1.1直角三角形三边的关系优秀教学案例

4.反思与评价:引导学生对自己的学习过程进行反思,总结学习方法和经验,提高他们的自我认知能力。组织学生进行评价,让他们学会欣赏他人,培养他们的公平竞争意识。通过评价,让学生了解自己的不足,激发他们的学习动力,促进他们的全面发展。
1.引导学生观察直角三角形模型,发现三边之间的关系。
2.通过讲解勾股定理的推导过程,使学生理解并掌握直角三角形三边的关系。
3.运用举例、讲解等方法,让学生明确直角三角形三边关系的应用。
(三)学生小组讨论
1.设计具有挑战性的问题,引导学生进行小组讨论,如:“你能用勾股定理解决实际问题吗?”
2.组织学生分享讨论成果,培养他们的合作意识和团队精神。
3.在讨论过程中,关注学生的个体差异,给予他们个性化的指导。
(四)总结归纳
1.引导学生总结直角三角形三边关系的知识点,加深他们对知识的理解。
2.总结本节课的学习方法,培养学生独立思考、合作交流的能力。
3.强调直角三角形三边关系在实际生活中的应用,提高学生的数学素养。
(五)作业小结
1.设计具有针对性的作业,让学生巩固直角三角形三边关系的知识。
五、案例亮点
1.生活情境的引入:通过房屋测量、篮球架高度等实际生活中的例子,引导学生关注直角三角形三边关系在现实生活中的应用,使学生认识到数学与生活的紧密联系,提高他们的学习兴趣。
2.问题导向:设计一系列具有启发性的问题,引导学生独立思考,发现直角三角形三边之间的关系。在解决问题的过程中,培养学生运用已学的知识解决实际问题的能力,提升他们的知识运用水平。
直角三角形三边关系教案_教案:《14.1.1直角三角形三边的关系》

直角三角形三边关系教案_教案:《14.1.1直角三角形三边的关系》教案原创教案:《14.1.1直角三角形三边的关系》一、教学内容华东师大版14.1.1直角三角形三边的关系二、教学目标1.知识与技能:体验勾股定理的探索过程,了解利用拼图验证勾股定理的方法,掌握勾股定理并会用它解决身边与实际生活相关的数学问题;2.思想与方法:在学生经历观察、归纳、猜想、探索勾股定理过程中,发展合情推理能力,体会数形结合思想,并在探索过程中,发展学生的归纳、概括能力;3.情感、态度、价值观:通过探索直角三角形的三边之间关系,培养学生积极参与、合作交流的意识,体验获得成功的喜悦,通过介绍勾股定理在中国古代的研究情况,提高学生民族自豪感,激发学生热爱祖国、奋发学习的热情.教学分析三、重点难点1.探索和验证勾股定理过程.2.通过面积计算探索勾股定理.四、教学方法及教学手段采用探究发现式的教学方法,通过计算面积为学生设计一个数学实验的平台,结合多媒体课件的演示,培养学生动手实践能力和合作交流的意识.五、教学过程(一)激趣导入多媒体演示勾股树图片,激发学生求知欲,成功导入本节课题.(二)合作互动1.小组讨论活动一:动脑想一想观察下图正方形大小,图中每一小方格表示,你能发现图中正方形P、Q、R的面积之间有什么关系?从中你发现了什么?(1)正方形P的面积为,正方形Q 的面积为,正方形R的面积为.(2)你能发现图中正方形P、Q、R的面积之间有什么关系?从中你发现了什么?活动二:其它一般的直角三角形,是否也有类似的性质呢?(你打算用什么方法来研究?共同讨论方法后再确立研究方向)(图中每一小方格表示)(1)正方形P的面积为,正方形Q的面积为,正方形R的面积为.(2)正方形P、Q、R的面积之间的关系是什么?(3)你能发现直角三角形三边长度之间存在什么关系吗?试一试:① 在方格图中,画出两条直角边分别为、的直角三角形.② 再用刻度尺量出斜边长.③ 验证刚才的结论对这个直角三角形是否成立?让学生自己总结,并用符号语言、文字语言表达勾股定理的内容.1.展示评价2.质疑解难勾股定理:直角三角形两直角边的平方和等于斜边的平方.注:(1)勾股定理揭示了直角三角形三边之间的关系.(2)在直角三角形中,任意已知其中的两边,就可以计算出第三边的长.C B A 例1 如图,在Rt△ABC中,已知∠B=90°,AB=6,BC=8,求AC. (三)拓展训练A c 1.如图,在Rt△ABC中,AB=c,BC=a ,AC=b,∠C=90°. b (1)已知a=6,c=10,求b; a C B (2)已知a=24,c=25,求b. 2.如果一个直角三角形的两边长分别是3厘米和4厘米,那么这个三角形的周长是多少?(精确到0.1厘米)3.小刚准备测量一条河的深度,他把一根竹竿插到离岸边2米远的水底,竹竿高出水面1米,把竹竿的顶端拉向岸边,竿顶刚好和水面相齐,这河水的深度为多少米? (四)课堂小结师生一起回顾本节知识,主要是让学生回忆学到了哪些知识和方法,教师最后再作补充.(1数学家大会所用标志.2勾股定理是宇宙语言.3利用勾股定理,可以解决“已知直角三角形的两边,求第三边”的问题)(五)作业布置:导学个性化增删部分:在情景引入中融入数学文化,展示国际数学大会的会标,向学生展示中华文化的博大深厚;知识结束后动态演示勾股树的形成,激发学生兴趣。
2勾股定理直角三角形三边的关系精品教案

第十四章勾股定理14.1.1 直角三角形三边的关系(1)教学目标:1.探索并掌握勾股定理:直角三角形两直角边的平方和等于斜边的平方.2.会应用勾股定理解决实际问题教学重点:探索勾股定理的证明过程教学难点:运用勾股定理解决实际问题教学过程:一。
探索勾股定理试一试测量你的两块直角三角尺的三边的长度,并将各边的长度填入下表:三角尺直角边a直角边b斜边c 关系12根据已经得到的数据,请猜想三边的长度a、b、c之间的关系.由图14.1.1得出等腰直角三角形的三边关系图14.1.1是正方形瓷砖拼成的地面,观察图中用阴影画出的三个正方形,很显然,两个小正方形P、Q的面积之和等于大正方形R的面积.即AC2+BC2=AB2,图14.1.1这说明,在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方.那么在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?试一试观察图14.1.2,如果每一小方格表示1平方厘米,那么可以得到:正方形P的面积=平方厘米;正方形Q的面积=平方厘米;(每一小方格表示1平方厘米)图14.1.2正方形R的面积=平方厘米.我们发现,正方形P、Q、R的面积之间的关系是.由此,我们得出直角三角形ABC的三边的长度之间存在关系.由图14.1.2得出一般直角三角形的三边关系.若∠C=90°,则222c b a =+勾股定理:直角三角形两直角边的平方和等于斜边的平方△ABC 中,∠C=90°, 则222c b a =+(a 、b 表示两直角边,c 表示斜边) 变式:222222,a c b b c a-=-=2.介绍勾股定理的历史背景。
二.例题分析:例1.Rt △ABC 中,AB=c,BC=a,AC=b,∠B=90° (1) 已知a=8,b=10,求c. (c=6) (2)已知a=5,c=12,求b (b=13)注意:“∠B 为直角”这个条件。
三、引申提高:例2如图14.1.4,将长为5.41米的梯子AC 斜靠在墙上,BC长为2.16米,求梯子上端A 到墙的底边的垂直距离AB.(精确到0.01米)解 如图14.1.4,在Rt △ABC中,BC=2.16米, AC=5.41米, 根据勾股定理可得AB=-BC AC 22=22 16.-2 41.5≈4.96(米).答: 梯子上端A 到墙的底边的垂直距离 AB 约为4.96米 四.巩固练习: 1.书本P51.1.2 五.课时小结: 1. 勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方2.已知直角三角形两边的长或知道两边关系和第三边的长,可以利用勾股定理求出三角形未知边长,并可运用面积关系式求斜边上的高。
直角三角形三边的关系导学课件华东师大版八年级数学上册

2 22
2
(a+b)2 c2+2ab
整个图形面积等于不
,
2
2
重叠、无空隙的各组
即a2+b2=c2.
成部分的面积的和.
感悟新知
3-1. 如图, 写出字母所代表的正方形的面积:SA= 625 ______1,44SB= ______.
感悟新知
3-2. (1)观察图① ②并填写下表(图中每个小方格的边长为1).
图① 图②
A的 面积
16 4
B的 面积
9 9
C的 面积
25 13
感悟新知
(2)三个正方形A,B,C的面积之间有什么关系? 解:三个正方形A,B,C的面积之间的关系为SA+SB=SC.
(3)三个正方形围成的一个直角三角形的三边长之间存在什 么关系? 三个正方形围成的一个直角三角形的三边长之间的关 系:直角三角形两直角边的平方和等于斜边的平方.
感悟新知
解题秘方:紧扣“总体面积等于各部分面积之和” 进行验证. 方法点拨:通过拼图,利用求面积来验证,这种方 法以数形转换为指导思想,以图形拼补为手段,以 各部分面积之间的关系为依据而达到目的.
感悟新知
证明:由题知C′D′=a,AD′=b.
∵四边形BCC′D′为直角梯形,
∴ S 梯形BCC′D′=
方法
加菲尔 德总 统拼图
毕达哥 拉斯 拼图
图形
证明
设梯形的面积为S,则S= 1
(a+b)(a+b)= 1 a2+ 1 b2+ab.2又
1
12
S= ∴
2 ab+ 2 ab+ a2+b2=c2
1 2
c22=
1 2
直角三角形三边的关系

实际应用 勾股定理
如图所示, 如图所示,一棵大树在一次强烈的地震 中于离地面10米处折断倒下 米处折断倒下, 中于离地面 米处折断倒下,树顶落在 离树根24米处 大树在折断之前高多少? 米处.大树在折断之前高多少 离树根 米处 大树在折断之前高多少?
10
解:如图,在Rt△ABC中,∠B=90°, 如图, 中 ° AB=10米,BC=24米, 米 利用勾股定理 勾股定理可以求出折断倒下部分的长度为 利用勾股定理可以求出折断倒下部分的长度为 26+10=36( AC + AB = 26+10=36(米). 所以,大树在折断之前高为36米 所以,大树在折断之前高为 米.
可要当心噢!
复习题 (P51) 勾股定理 A组 组 1. 求下列阴影部分的面积: 求下列阴影部分的面积: (1) 阴影部分是正方形; ) 阴影部分是正方形; (2) 阴影部分是长方形; ) 阴影部分是长方形; (3) 阴影部分是半圆. ) 阴影部分是半圆.
C A B C A A B C B
能力拓展题
每 一 小 方 格 表 示 1 平 方 厘 米
A
R
c
B
bQ
C
a
P
Sp + SQ = SR
BC2
2
Sp = 9 SQ = 16 SR = 25
AC2 =AB2 +
2 2
a +b = c
试一试 观察图,如果每一小方格表示 平方厘米, 观察图,如果每一小方格表示1平方厘米 平方厘米,
那么可以得到: 那么可以得到: 正方形P的面积 的面积= 9 平方厘米; 正方形 的面积=_________平方厘米; 平方厘米 正方形Q的面积 的面积= 16 平方厘米. 正方形 的面积=________平方厘米 平方厘米 正方形R的面积 ________平方厘米 的面积= 25 正方形R的面积=________平方厘米. 用等式的形式来 表示上面的结论
华师版八年级数学上册课件-14.1.1直角三角形三边的关系

A D
C
B
4.一高为2.5米的木梯,架在高为2.4米的墙上(如图), 这时梯脚与墙的距离是多少?
A
解:在Rt△ABC中,根据勾
股定理,得:
BC2=AB2-AC2
=2.52-2.42
优质 课件
优质八年级数学上(HS) 教学课件
第14章 勾股定理14.1 勾股定理1.直角三角形三边的关系
导入新课
讲授新课
当堂练习
课堂小结
学习目标
情境引入
1.掌握勾股定理及其简单应用,理解定理的一般探究方
法.(重点)
2.通过利用方格纸计算面积的方法探索勾股定理,经历
观察、归纳、猜想和验证的数学发现过程,发展数形结合
赵爽弦图
证明: S大正方形=c2
c b
a
b-a
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方
即形c2=4×12 ab+(b-a)2, c2=2ab+a2-2ab+b2
所以 a2+b2=c2
温馨提示:上述这种验证勾股定理的方法是用面积法
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明 才智,它是我国古代数学的骄傲.因为,这个图案被选为 2002年在北京召开的国际数学大会的会徽.
的数学思想.(难点)
导入新课
问题情境
某楼房三楼失火,消防队员赶来救火,了解到每层楼高 3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的 距离是2.5米,请问消防队员能否进入三楼灭火?
讲授新课
直角三角形三边的关系
八年级数学上第14章勾股定理14.1勾股定理2直角三角形三边的关系__验证勾股定理授课新华东师大1

知1-讲
3.用拼图法证明命题1的思路: (1)图形经过割补拼接后,只要没有重叠,没有空隙,面
积不会改变; (2)根据同一种图形的面积的不同表示方法列出等式; (3)利用等式性质变换证明结论成立,即拼出图形→写出
图形面积的表达式→找出等量关系→恒等变形→推出 命题1的结论.
知1-讲
例1 图14.1-1是用硬纸板做成的四个两直角边长分别 是a,b,斜边长为c的全等的直角三角形和一个 边长为c的正方形,请你将它们拼成一个能证明 命题1的图形. (1)画出拼成的这个图形的示意图; (2)证明命题1.
知2-讲
(2)已知直角三角形的一边确定另两边的关系; (3)证明含有平方关系的几何问题; (4)作长为n(n≥1,且n为整数)的线段; (5)一些非直角三角形的几何问题、日常生活中的
应用问题,对于这些问题,首先要将它们转化, 建立直角三角形模型,然后利用勾股定理构建方 程或方程组解决.
知2-讲
例2 如图,Rt △ABC的斜边AC比直角边 AB长 2cm,另一直角边BC长为6 cm.求AC的长.
知2-讲
本题运用建模思想解题,根据实际问题画出直 角三角形,再运用勾股定理解答.当图形不是直角 三角形时,常常通过作垂线构造直角三角形.
知2-讲
例5 如图,有一张直角三角形纸片,两直角边AC =6 cm,BC=8 cm,现将直角边AC沿AD折 叠,使点C落在斜边AB上的点E处,试求CD 的长.
导引:利用折叠前后重合的线段相等、重合的角相等, 通过勾股定理列方程,在Rt△BDE中求出线段 DE的长,从而得到CD的长.
解: 由已知AB=AC - 2, BC =6cm, 根据勾股定理,可得 AB2 + BC2 = (AC - 2)2 +62 = AC2, 解得AC= 10(cm).
14.1.1 直角三角形三边的关系(2)湘教版

4米
3米
应用知识回归生活 王子救公主的故事 y=0
营救方案
小船能漂多远?
应用知识回归生活 y=0
4. 如图,为了求出湖两岸的AB两点之间的距离, 一个观测者在点C设桩,使△ABC恰好为Rt△, 通过测量,得到AC长160米,BC长128米,问从A 点穿过湖到点B有多远?
解:Rt△ABC中,AC=160, BC=128, 根据勾股定理得:
c c
c
a
b
有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明, 就把这一证法称为“总统”证法。
C D c
c a
a
A b E
S 梯形 b
B
ABCD
1 ( a b( a b ) ) 2
1 2 2 ( a b 2 ab ) 2
北
东
C
练一练:
做一个长,宽,高分别为50厘米,40 厘米,30厘米的木箱,一根长为70厘米 的木棒能否放入,为什么?试用今天学 过的知识说明。
30cm 50cm
40cm
小 结:
1图形经过割补拼接后,只要没有空隙,没有 重叠,面积不会改变。
2构造直角三角形,将实际问题转化为数学问题, 运用勾股定理建立方程求解。
AB
2 2
x
AC
2
2
2
BC
2
2
2
x 160
128
x 96
x 160 128 答:从A点穿过湖到点B有96米。
应用知识回归生活 y=0
5. 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图 (如图),他们登陆后先往东走8千米,又往北走2千米,遇到 障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走 1千米就找到宝藏,问登陆点A到宝藏埋藏点B的直线距离是多 少千米?
14.1勾股定理1直角三角形三边的关系第2课时勾股定理的验证及简单应用作业新版华东师大版
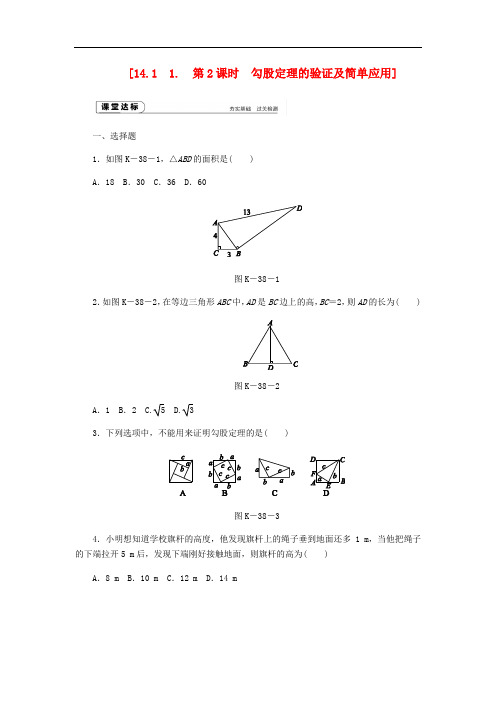
[14.1 1. 第2课时勾股定理的验证及简单应用]一、选择题1.如图K-38-1,△ABD的面积是( )A.18 B.30 C.36 D.60图K-38-12.如图K-38-2,在等边三角形ABC中,AD是BC边上的高,BC=2,则AD的长为( )图K-38-2A.1 B.2 C. 5 D. 33.下列选项中,不能用来证明勾股定理的是( )图K-38-34.小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,则旗杆的高为( )A.8 m B.10 m C.12 m D.14 m图K-38-45.如图K-38-4,在水塔O的东北方向32 m处有一抽水站A,在水塔的东南方向24 m 处有一建筑物工地B,在A,B之间建一条直水管,则水管的长为( )A.45 m B.40 mC.50 m D.56 m6.如图K-38-5,在△ABC中,AD⊥BC于点D,AB=3,BD=2,DC=1,则AC等于( )图K-38-5A.6 B. 6C. 5 D.4二、填空题7.如图K-38-6,为测量某池塘最宽处A,B两点间的距离,在池塘边定一点C,使∠BAC =90°,并测得AC的长为18 m,BC的长为30 m,则最宽处A,B两点间的距离为________.图K-38-68.在如图K-38-7所示的图形中,所有的三角形都是直角三角形,所有的四边形都是正方形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和是________.图K-38-79.如图K-38-8,学校有一块长方形草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“路”.他们仅仅少走了________步路(假设2步为1米),却踩伤了花草.图K-38-810.如图K-38-9,已知在Rt△ABC中,∠BCA=90°,AB=10,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2=________.图K-38-911.2017·丽水我国三国时期数学家赵爽为了证明勾股定理,绘制了一幅“弦图”,后人称其为“赵爽弦图”,如图K-38-10①所示.在图②中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,则正方形EFGH的边长为________.三、解答题12.如图K-38-11,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:(1)画线段AD∥BC,且使AD=BC,连结CD;(2)线段AC的长为______,CD的长为______,AD的长为________.图K-38-1113.在如图K-38-12所示的长方形零件示意图中,根据所给的部分尺寸,求两孔中心A和B的距离(单位:mm).图K-38-1214.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明灵感,他惊喜地发现,当四个全等的直角三角形如图K-38-13摆放时,可以用“面积法”来证明a2+b2=c2.请你写出证明过程.15.某市决定在相距10千米的A,B两地之间的E处修建一个土特产加工基地,A,E,B三点在同一条直线上,如图K-38-14所示,有C,D两个农庄,且DA⊥AB于点A,CB⊥AB于点B,已知AD=8千米,BC=2千米,要使C,D两农庄到基地的距离相等,那么基地E 应建在距离A地多远的位置?图K-38-14问题情境勾股定理是一条古老的数学定理,它有很多种证明方法.我国三国时期的数学家赵爽根据弦图,利用面积法进行证明.著名数学家华罗庚曾提出把“数形关系(勾股定理)”用探索飞船带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.定理表述请根据图K-38-15①中的直角三角形叙述勾股定理(用文字及符号语言叙述).图K-38-15尝试证明以图①中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图②),请你利用图②验证勾股定理.知识拓展利用图②中的直角梯形,我们可以证明a +bc<2,其证明如下: ∵BC =a +b ,AD =________.又∵在直角梯形ABCD 中,有BC ________AD (填“>”“<”或“=”),即______________,∴a +bc< 2.详解详析【课时作业】[课堂达标]1.B2.D3.D4.[解析] C设旗杆的高度为x m,则绳子的长为(x+1)m,由勾股定理,得(x+1)2=x2+52,解得x=12.5.[解析] B由题意知∠AOB=90°,由勾股定理得AB=OA2+OB2=322+242=40(m).6.[解析] B∵AD⊥BC,∴∠ADB=∠ADC=90°,∴由勾股定理,得AD=AB2-BD2=32-22= 5.又∵DC=1,∴AC=DC2+AD2= 6.7.24 m8.[答案] 49 cm2[解析] 如图,∵a2+b2=x2,c2+d2=y2,∴a2+b2+c2+d2=x2+y2=72=49(cm2).9.4 10. 12.5π11.10 [解析] 设直角三角形的勾(较短的直角边)为a ,股(较长的直角边)为b.根据题意,得⎩⎪⎨⎪⎧a +b =14,b -a =2,解得⎩⎪⎨⎪⎧a =6,b =8.由勾股定理得直角三角形的弦(斜边)为62+82=100=10, 即正方形EFGH 的边长为10.12.[解析] (1)根据AD =BC 和AD∥BC 即可确定点D ;(2)把AC ,CD ,AD 放在网格中的直角三角形中,用勾股定理分别求出AC ,CD ,AD 的长.解:(1)如图.(2)205 513.解:根据图中的数据得AC =90-40=50(mm ),BC =160-40=120(mm ),根据勾股定理,得AB =502+1202=130(mm ).即两孔中心A 和B 的距离为130 mm .14.证明:如图,∵S 五边形=S 左边梯形+S 右边梯形=S 大正方形+2S 直角三角形, ∴12(b +a +b)·b+12(a +a +b)·a=c 2+2×12ab ,即12ab+b2+a2+12ab=c2+ab,∴a2+b2=c2.15.解:∵C,D两农庄到基地E的距离相等,∴CE=DE.在Rt△CBE和Rt△DAE中,由勾股定理,得CE2=BE2+BC2,DE2=AD2+AE2,∴BE2+BC2=AD2+AE2.设AE=x千米,则BE=(10-x)千米,而BC=2千米,AD=8千米,所以(10-x)2+22=82+x2,解得x=2,即基地应建在距离A地2千米的位置.[素养提升]解:[定理表述]如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2. [尝试证明]∵Rt△ABE≌Rt△ECD,∴∠AEB=∠EDC.又∵∠EDC+∠DEC=90°,∴∠AEB+∠DEC=90°,∴∠AED=90°.∵S梯形ABCD=S Rt△ABE+S Rt△ECD+S Rt△AED,∴12(a+b)(a+b)=12ab+12ab+12c2,整理,得a2+b2=c2.[知识拓展]2c <a+b<2c。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
作者:李先贵(平昌县信义小学)
B
B
C
12
∠B=90°,AC=160,BC=128
根据勾股定理得
AB AC2 BC2
1602 1282
= 96(米) :课本112页练习1,2题
作者:李先贵(平昌县信义小学) 7
例题2:如图,将长为5.14米的梯子AC斜靠在墙上,BC长为2.16米,
求梯子上端A到墙的底端B的距离AB.(精确到0.01米)
解 在Rt△ABC中,
BC=2.16米,AC=5.14米,
根据勾股定理可得:
AB= AC 2 -BC2 = 5.142 -2.162 ≈4.96(米). 答:梯子上端A到墙的底边的垂直距离
2.16
?
AB约为4.96米.
作者:李先贵(平昌县信义小学)
8
变式:一个3m长的梯子AC,斜靠在一竖直的墙AB上,这时AB 的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么 梯子底端C向外移多少?(精确到0.01米) 解 在Rt△ABC中, ∴CE = BE-BC
2 2 2
S大正 c2
a b c
作者:李先贵(平昌县信义小学)
5
勾股定理的证明(三)
将上面弦图中的四个三角形 重新拼成右图形式。 你能用面积法证明勾股定理 吗?
2 证明: S大正方形 (a b)
4个
a 2 2ab b 2 2ab c 2
1 (a b) ab 4 c 2 2
2
S大正方形 1 ab 4 c 2 2
a b c
2 2
作者:李先贵(平昌县信义小学)
2
6
例1:如图,为了求出湖两岸的A、B 两点之间的距离,一个观测者在 点C设桩,使⊿ABC 恰好为直角三角形.通过测量,得到AC长160 米,BC长128米.问从点A穿过湖到点B 有多远?
解 在Rt△ABC中,
作者:李先贵(平昌县信义小学) 3
勾股定理的证明(二)
最早是由1700多年前三国 时期的数学家赵爽为《周髀算 经》作注时给出的,他用面积 法证明了勾股定理。 你能用面积法证明勾股定 理吗? 1 S大正 ab 4 b a 2 证明: 2
弦图
4个
1 2 ab 4 b a c 2 2 2ab b 2 2ab a 2 c 2
华东师大版八年级(上册)
第二课时
执教人:李先贵
作者:李先贵(平昌县信义小学) 1
复习:
1.什么叫勾股定理? 2.勾股定理有何作用?
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
3.已知:S1=1,S2=3,S3=2,S4=4.求S5,S6,S7.
S3
S4
分析:
S 1+S 2
SABC
1 1 AC BC AB CD 2 2
1 1 AC BC AB CD 2 2
12 5
10
1 1 3 4 5 CD 2 2
CD
作者:李先贵(平昌县信义小学)
例4:如图正△ ABC的边长为6cm.求: (1)高AD的长;(2)求△ABC的面积。
A
解 (1)过点A作AD垂直BC于D
∟
∵AB=AC,AD⊥BC ∴BD=1/2.BC 在Rt△ABD中, B AB=6,BD=1/2×6=3 根据勾股定理可得: AD= AB2 BD2 62 32 27 3 3 (2)∵AD⊥BC,BC=6, AD 3 3 1 1 S ABC BC AD 6 3 3 2 2
AC=3米,AB=2.5米, = 2.24-1.66 根据勾股定理可得: = 0.58 D 2 2 A C AB BC = ∴梯子底端C向外移0.58米. = 32 -2.52 ≈ 1.66 在Rt△DBE中, E DE=AC=3米, DB=AB-AD=2.5-0.5=2米, 根据勾股定理可得: 注意:此种类型梯子顶端下滑距离与 2 2 DE DB BE = 底端外移距离一般不相等. 2 2 3 - 2 = ≈2.24
D
C
9 3
B
练习:在Rt△ABC中,∠ACB=90°,∠A=30°, AB为6cm.求AC的长.
作者:李先贵(平昌县信义小学)
C
A
11
作 业
1.一个直角三角形的三边为三个连续偶数,则三边长为 . 一个直角三角形的三边为三个连续整数,则三边长为 . 2.已知:Rt△ABC中,AB=4,AC=3,则BC的长为 . 3.在Rt△ABC中,AB=c,BC=a,AC=b,∠B=90°. ①.已知a=6,b=10,求c; ②.已知a=24,c=25,求b. 4.如图,已知∠ACB=90°, CD⊥AB,AC=5,BC=12. 求CD的长. 5.如图,AB=AC,AB=13,BC=10.求△ABC的面积. A A D
S 3+S 4
S2 S1 S5
S6
S5
+
S7
S6
S7
作者:李先贵(平昌县信义小学)
2
勾股世界
两千多年前,古希腊有个毕达哥拉斯 学派,他们首先发现了勾股定理,因此在 国外人们通常称勾股定理为毕达哥拉斯定 理。为了纪念毕达哥拉斯学派,1955年希 腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的 国家之一。早在三千多年前,周 朝数学家商高就提出,将一根直 尺折成一个直角,如果勾等于三, 股等于四,那么弦就等于五,即 “勾三、股四、弦五”,它被记 载于我国古代著名的数学著作 《周髀算经》中。
9
作者:李先贵(平昌县信义小学)
例3.已知∠ACB=90°,CD⊥AB,AC=3, BC=4.求CD的长. 解 ∵∠ACB=90°,AC=3, BC=4
AB AC2 BC2
A 3 D
3 4 5
2
2
C
4
B
∵∠ACB=90°,CD⊥AB
注意:在直角三角形中两直角边的 积等于斜边与其高的积。
