第三章平面力系的平衡
第三章平面力系的合成与平衡

滑轮的受力图如图3.10(c)所示。
为了避免解联立方程,选直角坐标系如图所示,使x、 y轴分别与反力NBC、NAB垂直。
∑Fx=0,-NAB+Tcos60°-TBDcos30°=0 得 NAB=Tcos60°-TBDcos30°=-7.33kN NAB为负值,表示该力的实际指向与受力图中所假设 的指向相反。即杆AB受压力作用。再由
R Rx2 Ry2 ( Fx )2 ( Fy )2
tan Ry Fy
Rx
Fx
上式表明了合力在任一轴上的投影,等于各分 力在同一轴上投影的代数和。我们称之为合力投影 定理。
【例3.3】图3.7所示的吊环上作用有3个共面的拉力,各 力的大小分别是T1=3kN、T2=1kN、T3=1.5kN,方向如图
【解】绳AB作用于桩上的拉力是由绳BD传来的。因此先 取结点D为研究对象求出绳BD的拉力。
作用在结点D上的力有已知力F、绳DE的拉力TDE和 绳BD的拉力TDB,这三个力组成一平面汇交力系。结点D 的受力图如图3.11(b)所示。
选直角坐标系如图,使y轴与TDE垂直。列平衡方程
∑Fy=0,TDBsinα-Fcosα=0 得 TDB=Fcotα=4000N 再取结点B为研究对象。作用在结点B上的力有绳BC、 BD和BA的拉力TBC、TBD、TBA,绳BD给两结点D和B的 作用力应大小相等、方向相反,即有TBD=TDB=4000N。 力TBC、TBD、TBA组成一个平面汇交力系,结点B的受力 图如图3.11(c)所示。
3.1 平面汇交力系 3.1.1 力在坐标轴上的投影
设力F作用于物体的A点,如图3.4所示。
平面力系的平衡方程

平面力系的平衡方程平面力系是物理学中一个重要的概念,它描述了在平面内作用的多个力之间的关系。
平面力系的平衡方程是研究平面力系平衡状态的基本工具。
本文将从平面力系的定义、平衡条件以及平衡方程的推导和应用等方面进行论述。
一、平面力系的定义平面力系是指在平面内作用的多个力所构成的力系统。
这些力可以是来自不同方向的,也可以是来自同一方向的。
平面力系的特点是力的作用线都在同一平面内。
二、平衡条件平面力系的平衡条件是指力系中所有力的合力为零,力矩也为零。
力的合力为零意味着力系中所有力的矢量和为零,即ΣF=0。
力的合力为零是平衡的必要条件,但不是充分条件。
力矩为零意味着力系中所有力对某一点的力矩的矢量和为零,即ΣM=0。
力矩为零是平衡的充分条件。
三、平衡方程的推导平衡方程的推导基于牛顿第二定律和力矩的定义。
根据牛顿第二定律,物体的加速度与作用在其上的合外力成正比,反向相反。
对于平面力系,可以将合外力分解为水平方向和垂直方向的分力。
设水平方向的合外力为ΣFx,垂直方向的合外力为ΣFy。
根据牛顿第二定律,物体在水平方向和垂直方向的加速度分别为a_x和a_y,则有ΣFx=ma_x,ΣFy=ma_y。
对于力矩的定义,力矩等于力的大小与力臂的乘积。
力臂是指力作用线与某一点的垂直距离。
设力F_i的力臂为r_i,则力F_i对该点的力矩为M_i=F_i*r_i。
根据力矩的定义,平面力系中所有力对该点的力矩的矢量和为零,即ΣM=0。
四、平衡方程的应用平衡方程可以用于解决平面力系的平衡问题。
通过列写平衡方程,可以求解未知力的大小和方向。
在列写平衡方程时,需要选择合适的坐标系,并确定参考点。
参考点的选择应该便于计算力矩,通常选择力系中力的作用点或力的交点作为参考点。
在实际应用中,平衡方程可以用于解决各种平面力系的平衡问题。
例如,可以用平衡方程来分析悬挂物体的平衡状态,计算悬挂绳的张力和物体的重力。
还可以用平衡方程来分析桥梁、建筑物等结构的平衡状态,计算支撑力和应力分布等。
建筑力学第三章 平面力系的平衡方程
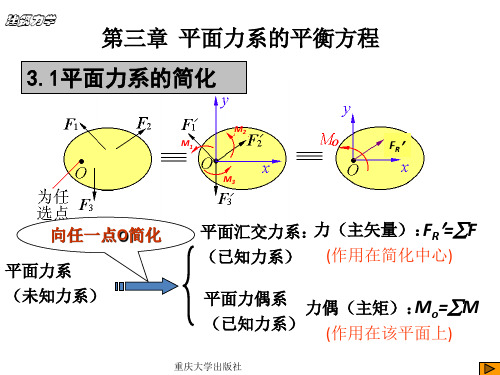
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时, 简化结果就是合力(这个力系的合力), FR FR'。(此时
与简化中心有关,换个简化中心,主矩不为零)
重庆大学出版社
建筑力学
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
重庆大学出版社
建筑力学
[例] 已知:Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求:
BC杆拉力和铰A处的支座反力?
解:(1)选AB梁为研究对象。
C
(2)画受力图
FAy
FBC
A
FAx
l/2 P
B Q
a
Байду номын сангаас
l
A
l/2 P
B Q
a
l
重庆大学出版社
建筑力学
(3)列平衡方程,求未知量。
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
重庆大学出版社
建筑力学
物系平衡问题的特点: ①物体系统平衡,物系中每个单体也是平衡的。 ②每个单体可列3个(平面任意力系)平衡方程,整个系统
可列3n个方程(设物系中有n个物体)。
解物系问题的一般方法:
机构问题: 个体 个体
个体
“各个击破”
力系中各力对于同一点之矩的代数和。
重庆大学出版社
建筑力学
3.2平面力系的平衡方程及应用
FR=0, MO =0,力系平衡
FR =0 为力平衡
MO =0 为力偶也平衡 平面力系平衡的充要条件为:
基础篇 单元三 平面力系的平衡

当物系平衡时,系统内的每一部分都是平衡的。既可以选 择整个物系为研究对象,也可以选择其中的某几个或某一个物 体作为研究对象。
单元三 平面力系的平衡
课题三 物体系统的平衡
对于一般的静定物系平衡问题,应首先画出整体、局部或单 个物体的受力图,再从有已知力且未知量数少于或等于独立平衡 方程数的物体着手分析,便可解除全部未知量。若物系内分离体 均不符合可解条件,必须寻找有局部可解条件的分离体。
课题一 平面任意力系的平衡
单元三 平面力系的平衡
课题一 平面任意力系的平衡
由平衡方程可知,平面任意力系平衡的解析条件为:力系 中各力在两个任选的坐标轴上投影的代数和等于零,各力对力 系作用面内任意一点之矩的代数和等于零。除基本形式之外, 平面任意力平衡方程还可表示为二力矩形式。
M M
座的约束力。
解 (1)取齿轮轴为研究对象,画其受力图,如图3-2b。
(2)建立直角坐标系Axy,如图3-2b所示,列平衡方程求解
单元三 平面力系的平衡
课题一 平面任意力系的平衡
Fx 0 F FBx 0
解得 FBx F
M A(F) 0 FA 3a F 2a 2Fa Fa 0 解得 FA F
3 kN 11.4kN 2
将FT代入式(b)得 FAy G1 G2 FT sin 2.1kN
本题也可用二力矩式求解。
单元三 平面力系的平衡
课题一 平面任意力系的平衡
例3-3 减速器中的齿轮轴B端可分别简化为固定铰支座,
A端可简化为可定铰支座,如图3-2a所示。已知F、a,求两支
解 取工件为研究对象。工件在水平面受三个力偶和两个螺 栓的水平约束力的作用,三个力偶合成后仍为一力偶,若工件 平衡,必有一约束力偶与它相平衡,因此螺栓A和B的水平力 FNA和FNB必组成一力偶,方向如图3-5b所示,且FNA=FNB 。列 平衡方程
理论力学第3章 力系的平衡条件与平衡方程

10
例题二的解答
解:选取研究对象:杆CE(带有销 钉D)以及滑轮、绳索、重物组成 的系统(小系统)受力分析如图, 列平衡方程:
M D (F ) 0 M C (F ) 0 M B (F ) 0
( F C cos ) CD F ( DE R ) PR 0 F Dx DC F ( CE R ) PR 0 F BD F ( DE R ) P ( DB R ) 0 Dy
2012年11月3日星期六
北京邮电大学自动化学院
29
滚动摩擦力偶的性质
滚动摩擦力偶M 具有如下性质(与滑动摩擦力性质类似): ◆ 其大小由平衡条件确定; ◆ 转向与滚动趋势相反; ◆ 当滚子处于将滚未滚的平衡临界状态时, M = M max =δFN
式中:δ —滚动摩擦系数,它的量纲为长度; FN —法向反力(一般由平衡条件确定)。
q (2a b) 2a
2
YA q (2a b)
16
2012年11月3日星期六
北京邮电大学自动化学院
课堂练习3
多跨静定梁由AB梁和BC梁用中间铰B连接而成,支撑和荷 载情况如图所示,已知P = 20kN,q=5kN⋅m,α = 45°。求 支座A、C的反力和中间铰B处的反力。
2012年11月3日星期六
x
xC
x
2012年11月3日星期六
北京邮电大学自动化学院
5
平行分布线载荷的简化
Q
q
1、均布荷载 Q=ql
l 2
l 2
Q
q
2、三角形荷载 Q=ql /2
2l 3
l 3
Q
3、梯形荷载 Q=(q1+q2)l /2 (自己求合力的位置)
《工程力学:第三章-力系的平衡条件和平衡方程》解析

工程力学 1. 选择研究对象。以吊车大梁 AB为研究对象,进行受力分析 (如图所示) 2.建立平衡方程
第三章 力系的平衡条件和平衡方程
FAX FTB cos 0 Fy 0
F
x
0
: (1)
M
FAy FQ FP FTB sin 0
A
(F ) 0
工程力学
第三章 力系的平衡条件和平衡方程
§3.3 考虑摩擦时的平衡问题
3.3.1 滑动摩擦定律
概念:
静摩擦力:F 最大静摩擦力:Fmax 滑动摩擦力: Fd
静摩擦因数:
水平拉力: Fp
Fmax f s FN
fs
工程力学
第三章 力系的平衡条件和平衡方程
3.3.2 考虑摩擦时构件的平衡问题
考虑摩擦力时与不考虑摩擦力时的平衡 解题方法和过程基本相同, 但是要注意摩擦力的方向与运动趋势方向相反;且在滑动之前摩擦 力不是一个定值,而是在一定范围内取值。
l l sin 0
(3)
工程力学
第三章 力系的平衡条件和平衡方程
• 联立方程(1)(2)(3)得:
FAX
FQ FP 3 l x 2
(2)由FTB结果可以看出,当x=L时,即当电动机移动到大梁右 端B点时,钢索所受的拉力最大,最大值为
非静定问题:未知数的数目多于等于独立的平衡方程的数目,不能 解出所有未知量。相应的结构为非静定结构或超静定结构。
会判断静定问题和非静定问题
工程力学
第三章 力系的平衡条件和平衡方程
工程力学
第三章 力系的平衡条件和平衡方程
3.2.2 刚体系统平衡问题的特点与解法
1.整体平衡与局部平衡的概念 系统如果整体是平衡的,则组成系统的每一个局部以及每一个 2.研究对象有多种选择 刚体也必然是平衡的。
平面力系的平衡

Fx F cosa
Fy F cos b F sina
即力在某个轴上的投影等于力的模乘以力与该轴的 正向间夹角的余弦。投影的符号规定为:由起点a 到终点b连线(或a/由b/到)的指向与坐标轴正向相 同时为正,反之为负。 故力在坐标轴上的投影是个代数量。
投影练习
【例1】 试分别求出图2-2中各力在x轴和y轴上投影。已知
二、力的平移定理
作用在物体上的力F可以平行移动到物体内任一点O,但 必须同时附加一个力偶,才能与原来的作用等效。其附加力 偶的力偶矩等于原力F对平移点O的力矩。这就是力的平移定 理。
F′ B F A
a)
F′ F A
b)
F′
M
B
Bቤተ መጻሕፍቲ ባይዱ
A
c)
图1-15
F
F
F’ = F’’=F
F’ F”
F
F’ M=Fh
F2 x F2 cos30 150N 0.866 = 129.9N
F3x F3 cos90 0
F3 y F3 sin90 200N 1.0 = 200N F4 x F4 cos60 200N 0.5 =100N
F4 y F4 sin 60 200N 0.866 = 173.2N
四、平面力系平衡的条件
平面 汇交力系 平面 平行力系 平面 力偶系 平面 任意力系
F F
F M M
x
y
0
0
0
两个独立方程,只能求两个独立未知数。
两个独立方程,只能求两个独立未知数。
y A
(F ) 0
i
0 一个独立方程,只能求一个独立未知数。
0
0
工程力学-平面任意力系平衡方程

4)FR=0 M0=0 力系处于平衡状态。
例3-1 图示物体平面A、B、C三点构成一等边三角形,三点分别作
用F力,试简化该力系。
解:1.求力系的主矢
F x F F cos60o F cos60o 0
Fy 0 F sin 60o F sin 60o 0
y
C
F M0 F
上作用F力,集中力偶M0=Fa,=45°,试求杆件AB的约束力。
A
M0=Fa
C
B
F
解:1.取AB杆为研究对象画受力图
2.列平衡方程求约束力
Da a
FAx
A
M0=Fa
C
FAy FC
B F
aa
M A (F ) 0 : FC sin 45 a F 2a M 0 0
FC
2Fa a
Fa 2/2
MC (F) 0:
FAx
2
3a 3
F
a
M0
0
FAy 0 FAx 3F
C aa
一 矩
MA(F) 0: Fx 0 :
二 矩
MA(F) 0: MB(F) 0:
三 矩
MA(F) 0: MB(F) 0:
2 3a
式 Fy 0 :
式 Fx 0 :
式 M C (F8) 0 :
3
本课节小结
A F
B x
FR ( Fx )2 ( Fy )2 0
2.选A点为简化中心,求力系的主矩
M0
M A (F)
F
sin 60
AB
F
AB 2
简化结果表明该力系是一平面力偶系。
4
二、平面任意力系的平衡方程
工程力学第三章-力系的平衡

将上式两边向x、y、z 轴投影,可得平衡方程
F F F
可以求解3个未知量。
x y
z
0 0 0
• 2.平面汇交力系
力系的平衡
• 力偶系的平衡方程 • 1.空间力偶系
平衡的充要条件(几何条件) M Mi 0 将上式两边向x、y、z 轴投影,可得平衡方程
M M M
可以求解3个未知量。
ix iy iz
0 0 0
• 2.平面力偶系
力系的平衡
• 平衡的充要条件:力偶系中各力偶矩的代数和等于零.
m 0
i
• 任意力系的平衡方程 空间任意力系: • 平衡的充要条件:力系的主矢和对任一点的主矩均为零。
FR 0
MO 0
G3 a
e
G 3(a b) FNAb G1e G 2L 0 G 3(a b) G1e G 2L FNA 2 b
由(1)、(2)式 得:
G1 G2 L
G1e G 2L G3 ab
3
A FN A b
B FN B
(2)空载时
不翻倒条件:FNB≥0 (4) 由 mA 0 得:
FAB = 45 kN
600
y B TBC 15 15 30 TBD
0 0 0
x
C
D
150
B
300
TBD=G E
A
E
FAB G
解题技巧及说明:
1、一般地,对于只受三个力作用的物体,且角度特殊时用 几 何法(解力三角形)比较简便。 2、一般对于受多个力作用的物体,且角度不特殊或特殊, 都用解析法。 3、投影轴常选择与未知力垂直,最好使每个方程中只有一 个未知数。
第三章.平面力系的合成与平衡

各力首尾相接
§3-1 平面汇交力系的合成与平衡
例4
已知:
系统如图,不计杆、轮自重,忽略滑轮大小,P=20kN; 求:系统平衡时,杆AB、BC受力。 解:AB、BC杆为二力杆, 取滑轮B(或点B),画受力图。
用解析法,建图示坐标系。
F
x
0
FBA F1 cos 60 F2 cos 30 0
Fy F cos F Fx Fy
Fx cos F
Fx
x
O
Fx
F Fx2 Fy2
cos
Fy F
§3-1 平面汇交力系的合成与平衡 3)合力投影定理 平面汇交力系,由三个力组成的力多边形 合力投影定理建立了合力投影与各分力投影的关系
FRx Fix
当 x轴与 y 轴不是正交轴时 :
F Fx Fy
力在坐标轴上的投影不等于力在这个轴上的分量。
§3-1 平面汇交力系的合成与平衡 2、平面汇交力系的解析法 2)力沿坐标轴的分解 当
Fx Fx
x y
y
Fy Fy
B
Fy
Fx F cos
Fy
A
β α
矢量和
θ
P
FNA 11.4kN FNB 10kN
F
FNB
F
θ P FNA
§3-1 平面汇交力系的合成与平衡 2、平面汇交力系的解析法 1)力在坐标轴上的投影 F力在 x 轴上的投影:
Fx F cosθ
Fy
Fx
F力在 y 轴上的投影:
Fy F cosβ
3 FR 2 FR1 F3 Fi i 1
理论力学第3章 力系的平衡

基础部分——静力学第3 章力系的平衡主要内容:§3-7 重心即:力系平衡的充分必要条件是,力系的主矢和对任一点3-2-1 平衡方程的一般形式∑=iF F R ∑=)(i O O F M M 已知∑=iF F R ∑=)(i O O F M M 投影式:平衡方程i即:力系中所有力在各坐标轴上投影的代数和分别等于零;所有力对各坐标轴之矩的代数和分别等于零。
说明:¾一般¾6个3个投影式,3个力矩式;¾一般形式基本形式3-2-2 平面一般力系的平衡方程xy zOF1F2Fn平面内,¾一般形式¾3个2个投影式,1个力矩式;¾ABAzzCC附加条件:不垂直附加条件:不共线Bx二矩式的证明必要性充分性合力平衡AA 点。
B 点。
过ABBx故必有合力为零,力系平衡证毕平面问题3个3个 解题思路BAMFo45l l[例3-1] 悬臂梁,2解:M A 校核:0)(=∑F MB满足!解题思路?AyF AxF[例3-2] 伸臂梁F AxF AyF BF q 解:0=∑x F 0)(=∑F AM3(F −+0=∑yF3(F −+(F −+0)(=∑F AM=∑yF0=∑x F F AxF AyF BF q 思考:如何用其他形式的平衡方程来求解?0=∑x F 3(F −+0)(=∑F AMF AxF F BF q 0)(=∑F BM(F −+二矩式思考练习][练习FFlll F ACB DlllACB DM=F l[思考][思考]lll F ACB DlllACB DF见书P54例3-1—约束lllACB DF—约束CBADEFM—约束—约束—整体平衡局部平衡CB ADEFM研究对象的选取原则¾仅取整体或某个局部,无法求解;¾一般先分析整体,后考虑局部;¾尽量做到一个方程解一个未知力。
qCBAm2m2m2m2MBCM[例3-3] 多跨梁,求:如何选取研究对象?F CqF CFAxF AyM ABAqF'BxF'ByM A F Ax F AyF Bx F By解:先将分布力用合力来代替。
第3章力系平衡方程

M M1 M 2 M n M
(2)平面力偶系的平衡 ∑M=0
2016/12/14
【例3-6】如图3-12所示,某物体受三个共面力偶作 用,已知F1=25kN,d1=2m,F2=50kN,d2=1.5m,M3=- 20kN·m,试求其合力偶。
【解】
M1=F1· d1=25×2=50kN· m
(3)求合力的方向
tan FRy FRx 112.35 0.869 129.25
α=40.99º 由于FRx和FRy均为正,故α应在第一象限,合力FR的 作用线通过力系的汇交点O,如图3-5所示。
2016/12/14
3.平面汇交力系的平衡方程
平面汇交力系平衡的必要和充分条件是:该力系的合 力FR等于零。即:
按其作用线所在的位置:平面力系和空间力系。 平面力系:力系中各力的作用线都在同一平面内。 空间力系:力系中各力的作用线不在同一平面内。 平面力系:平面汇交力系、平面平行力系和平面一般力系。 平面汇交力系:在平面力系中,各力的作用线均汇交于一 点的力系。
1.力在直角坐标轴上的投影
F在x轴上的投影,以Fx表示;F在y轴上的投影,以Fy表示。
作用在刚体上A点的力F,可以平移到同一刚体上的 任一点O,但必须附加一个力偶,其力偶矩等于原来的力 F对新作用点O之矩。
图3-16
力的平移定理
2016/12/14
【例3-8】如图3-17(a)所示,柱子的A点受到吊 车梁传来的集中力F=120kN。求将该力F平移到柱轴上O 点时应附加的力偶矩,其中e=0.4m。 【解】 M=MO(F)=-Fe =-120×0.4=48kN· m 负号表示该附加力 偶的转向是顺时针的。
arctan
工程力学 第3章 力系的平衡

6
解 :1. 受力分析, 确定平衡对象 圆弧杆两端 A 、 B 均为铰链,中间无外力作用,因此圆弧杆为二力杆。 A 、 B 二处的 约束力 FA 和 FB 大小相等、 方向相反并且作用线与 AB 连线重合。 其受力图如图 3-6b 所示。 若 以圆弧杆作为平衡对象,不能确定未知力的数值。所以,只能以折杆 BCD 作为平衡对象。 ' 折杆 BCD , 在 B 处的约束力 FB 与圆弧杆上 B 处的约束力 FB 互为作用与反作用力, 故 二者方向相反; C 处为固定铰支座,本有一个方向待定的约束力,但由于作用在折杆上的 ' 只有一个外加力偶,因此,为保持折杆平衡,约束力 FC 和 FB 必须组成一力偶,与外加力 偶平衡。于是折杆的受力如图 3-6c 所示。 2.应用平衡方程确定约束力 根据平面力偶系平衡方程(3-10) ,对于折杆有 M + M BC = 0 (a) 其中 M BC 为力偶( FB , FC )的力偶矩代数值
图 3-8 例 3-3 图
解 :1. 选择平衡对象 本例中只有平面刚架 ABCD 一个刚体(折杆) ,因而是唯一的平衡对象。 2 受力分析 刚架 A 处为固定端约束, 又因为是平面受力, 故有 3 个同处于刚架平面内的约束力 FAx、 FAy 和 MA 。 刚架的隔离体受力图如图 3-8b 所示。 其中作用在 CD 部分的均布荷载已简化为一集中 力 ql 作用在 CD 杆的中点。 3. 建立平衡方程求解未
习 题
本章正文 返回总目录
2
第 3 章 力系的平衡
§3-1 平衡与平衡条件
3-1-1 平衡的概念
物体静止或作等速直线运动,这种状态称为平衡。平衡是运动的一种特殊情形。
平衡是相对于确定的参考系而言的。例如,地球上平衡的物体是相对于地球上固定参 考系的, 相对于太阳系的参考系则是不平衡的。 本章所讨论的平衡问题都是以地球作为固定 参考系的。 工程静力学所讨论的平衡问题,可以是单个刚体,也可能是由若干个刚体组成的系统, 这种系统称为刚体系统。 刚体或刚体系统的平衡与否,取决于作用在其上的力系。
工程力学第3章

1第三章力系的平衡§3–1 平面力系的平衡方程§3–2 空间力系的平衡方程§3–3 物体系统的平衡方程§3–4 静定与静不定的基本概念§3-1 平面力系的平衡方程由于=0 为力平衡M O =0 为力偶也平衡所以平面任意力系平衡的充要条件为:力系的主矢F R 和主矩M O 都等于零,即:)()(22=+=∑∑Y X F R 0)(==∑i O O F m M 1、平面任意力系的平衡方程R F=∑X 0)(=∑i A F m 0)(=∑i B F m ②二矩式条件:x 轴不AB连线⊥0)(=∑i A F m 0)(=∑i B F m 0)(=∑i C F m ③三矩式条件:A ,B ,C 不在同一直线上上式有三个独立方程,只能求出三个未知数。
=∑X 0=∑Y 0)(=∑i O F m ①一矩式①平面汇交力系=∑xF 0=∑yF2、平面特殊力系的平衡方程②平面力偶系=∑M ③平面平行力系=∑y F 0)(=∑F M O 0)(=∑F MB0)(=∑F M A AB 不x 轴⊥[例] 已知:P , a , 求:A 、B 两点的支座反力?解:①选AB 梁研究②画受力图(以后注明解除约束,可把支反力直接画在整体结构的原图上))(=∑i A F m 由32 ,032PN a N a P B B =∴=⋅+⋅-0=∑X 0=A X 0=∑Y 3,0PY P N Y A B B =∴=-+解除约束,0==∑A X X 由022;0)(=⋅-+⋅⋅+⋅=∑a P m aa q a R F m B A 0=∑Y 0=--+∴P qa R Y B A )kN (122028.01628.02022=⨯+-⨯-=+--=P a m qa R B )kN (24128.02020=-⨯+=-+=B A R qa P Y [例] 已知:P =20kN, m =16kN·m, q =20kN/m, a =0.8m求:A 、B 的支反力。
建筑力学大纲 知识点第三章 平面力系得平衡条件
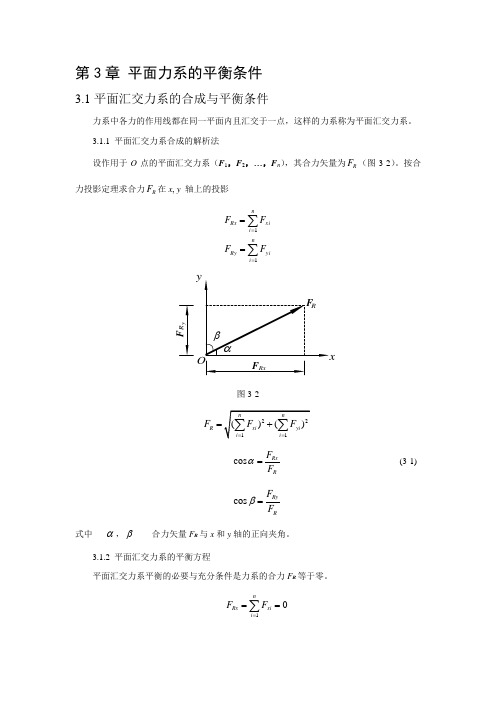
第3章 平面力系的平衡条件3.1平面汇交力系的合成与平衡条件力系中各力的作用线都在同一平面内且汇交于一点,这样的力系称为平面汇交力系。
3.1.1 平面汇交力系合成的解析法设作用于O 点的平面汇交力系(F 1,F 2,…,F n ),其合力矢量为R F (图3-2)。
按合力投影定理求合力R F 在x , y 轴上的投影∑∑====ni yiRy ni xiRx F F F F 11y图3-2R F = cos RxRF F α=(3-1) cos Ry RF F β=式中α,β------合力矢量F R 与x 和y 轴的正向夹角。
3.1.2 平面汇交力系的平衡方程平面汇交力系平衡的必要与充分条件是力系的合力F R 等于零。
10nRx xi i F F ===∑10nRy yii F F===∑ (3-2)于是,平面汇交力系平衡的必要与充分条件可解析地表达为:力系中所有各力在两个坐标轴上投影的代数和分别为零。
式(3-2)称为平面汇交力系的平衡方程。
3.2平面力偶系的合成与平衡条件3.2.1 平面力偶系的合成应用力偶的等效条件,可将n 个力偶合成为一合力偶,合力偶矩记为M 。
∑==ni i M M 1(3-3)3.2.2 平面力偶系的平衡条件平面力偶系平衡的必要与充分条件:力偶系中所有各力偶的力偶矩的代数和等于零,即 10nii M M===∑ (3-4)3.3平面任意力系的合成与平衡条件3.3.1工程中的平面任意力系问题力系中各力的作用线在同一平面内,且任意地分布,这样的力系称为平面任意力系。
3.3.2 平面任意力系向一点的简化 主矢和主矩如图3-7(a )所示。
在力系作用面内任选一点O ,将力系向O 点简化,并称O 点为简化中心。
i ′图3-7由力12,,,n F F F '''L 所组成的平面汇交力系,可简化为作用于简化中心O 的一个力RF ',该力矢量∑==ni i RF F 1'(3-5)R F '称作平面任意力系的主矢。
第3章 平面力系的合成与平衡

4、对力的方向判定不准的,一般用解析法。
5、解析法解题时,力的方向可以任意设,如果求出 负值,说明力方向与假设相反。对于二力构件,一般先 设为拉力,如果求出负值,说明物体受压力。
作业
习题3-5;
习题3-8。
第三章 目录
3.1 汇交力系的合成与平衡
3.2 力线的平移
3.3 平面一般力系的合成
3.4 平面一般力系的平衡方程和应用
平面力系的 第三章 合成与平衡
教学目标
了解平面力系的定义及其分类;
掌握平面力系平衡方程的求解;
理解力线平移原理,平面力系的简化。
第三章 目录
3.1 汇交力系的合成与平衡
3.2 力线的平移
3.3 平面一般力系的合成
3.4 平面一般力系的平衡方程和应用
3.5 平面平行力系的合成与平衡
• 力系的分类
• 【思考题】
1.力系的合力与主矢有什么区别?
2.力系的主矩与合力偶有什么不同?
• 主矢的确定
FR F F
2 Rx 2 Ry
F F
2 x y
2
Fx F Rx cos FR , i FR FR
FRy Fy cos FR , j FR FR
FR2
d
F4
e
F3
a
FR
FR F1 F2 F3 F4
• 1. 力多边形
c
F2
F3
d
F4
由各分力和合力构
成的多边形 abcde 称 为力多边形,这种作图
b
F1
e
a
FR
法称力多边形法则。
合力的作用线通过汇交点,大小和方向
理论力学第3章力系平衡方程及应用

a
分布力(均布载荷) 合力作用线位于AB
中点。
3.1 平面力系平衡方程
a
【解】
y M=qa2 a
2qa
F3
C
FAx
A
aFAy
45
B
D
x
2a FB a
F3 2qa
MA 0
q 2 2 a q a a F B 2 a 2 q sa 4 i 3 n a 5 0
FB 2qa
Fx 0 FAx2qcao4s50 FAx qa
C
【解】 F2
构件CGB( 图b)
F2
构件AED
(图c)
C
R
D
45
FC
FD
D
G
45
F1
E
a
F1
E
a
A
B
G 图b
FBy
图c A FAx
MA
FAy
构件CD(图a )
3个未知量 B FBx
4个未知量
F'C
3个独立方程
3个独立方程
【基本思路】
C R
杆CGB受力图计算FCAED受力图
计算A处的反力(偶);CGB受力图计算
3.2 平面物体系平衡问题
q
C
B
30
FC FBy
l
l
【解】 杆CB
FBx
MB 0
FCco3s0l qll/2 0
FC
3 ql 30.5kN/m 2m 0.577kN
3
3
3.2 平面物体系平衡问题
【解】整体
FAy
l
l
l
Fx 0
MA
A
FAx
平面力系的平衡及应用

平面力系的平衡及应用平面力系的平衡及应用平面力系是指在一个平面上作用的多个力的集合。
平面力系的平衡是指作用在物体上的力在该平面上的合力和合力矩都等于零。
平面力系的平衡是力学研究的基本内容,具有广泛的应用价值。
平面力系的平衡与力的平衡是密切相关的。
力的平衡是指作用在物体上的所有力之和等于零,即ΣF=0。
平面力系的平衡可以通过力的平衡方程和力的平衡图进行研究与分析。
力的平衡方程是指将力的平衡条件表示为方程的形式,通过对所有力在X轴和Y 轴上的分量进行求和得到。
对于平面力系,如果力系在X轴和Y轴上的合力都为零,则有ΣFx=0和ΣFy=0。
这两个方程可以帮助我们计算出力系中未知力的大小与方向。
力的平衡图是指将所有力按照其大小和方向画在一个平面上的图形。
通过绘制力的平衡图,可以直观地了解力的平衡情况,进而确定力系中未知力的大小与方向。
平面力系的平衡是力学的基本原理之一,具有广泛的应用。
下面介绍几个应用平面力系平衡原理的实例。
第一个应用是悬挂物体的平衡问题。
当一个物体悬挂在绳子上时,绳子所受的张力需要平衡物体的重力。
在该情况下,可以通过绘制力的平衡图,计算出绳子所受的张力大小。
第二个应用是斜面上物体的平衡问题。
当一个物体放置在斜面上时,斜面对物体的支持力需要平衡物体在斜面上的重力分量。
在该情况下,可以通过绘制力的平衡图,计算出斜面对物体的支持力大小。
第三个应用是平衡梁的问题。
平衡梁是指在一个平面上作用的多个力使得梁保持平衡的情况。
在平衡梁问题中,需要计算出每个支点所受的力大小和方向,以及梁的平衡条件。
第四个应用是静止摩擦力的计算。
在平面力系的平衡中,静止摩擦力是指使物体保持静止的摩擦力。
通过力的平衡图可以求解静止摩擦力的大小。
以上只是平面力系平衡原理的一些应用示例,实际应用中还有更多的情况。
平面力系的平衡原理对于工程设计、物体平衡、结构强度等领域都有重要作用。
总结起来,平面力系的平衡是指作用在物体上的力在该平面上的合力和合力矩都等于零。
-建筑力学第三章平面力系的合成与平衡

平面汇交力系合成与平衡的几何法小 结
几何法解题步骤:1. 取研究对象;2. 画受力图; 3. 作力多边形;4. 选比例尺; 5. 解出未知数。
几何法解题不足: 1. 精度不够,误差大; 2. 作图要求精度高; 3. 不能表达各个量之间的函数关系。
平面汇交力系合成与平衡的另一种方法: 解析法(重点掌 握)。
R0
Rx2
R
2 y
0
或:力系中所有力在各个坐标轴上投影的代
数和分别等于零。
Rx Fx 0 Ry Fy 0
为平衡的充要条件, 也叫平衡方程
解析法求解汇交力系平衡问题的一般步骤:
1.选-对像;即依需选分离体,分离体选取应最好含题设
的已知条件; 2.画-分离体受力图,作到准确无误;
应用力线平移定理,可将刚体上平面任意力系中各个力
的作用线全部平行移到作用面内某一给定点O 。从而这
力系被分解为平面汇交力系和平面力偶系。这种变换的
方法称为力系向给定点O 的简化。点O 称为简化中心。 R0 -----主矢,与简化中心选取无关; M0 ---主矩,与简化中心有关。
2、主矢和主矩 (1)主矢R0
F3 F2
D
C
F2 F4 F3
R
F4
R
F4
E
E
3、汇交力系的合成结果
汇交力系可以合成为一个力,合力作用在力系
的公共作用点,它等于这些力的矢量和,并可由这
力系的力多边形的封闭边表示。
矢量的表达式:R F1 F 2
F1
A F2
F4 F3
F1
A
B F2
R
C
F3
D
F4
n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
o
l
l
l
l
∑F = 0
y
FAy − 2ql + F sin 60o− F cos 30o = 0 B
MA
FAy
A
M
q
C B
30
o
F
FAx
60
o
D
∑M (F) = 0
A
FB
l l
l l
MA − M− 2ql ×2l + F sin 60o ×3l − F cos 30o ×4l = 0 B
解得: 解得: FAx = 32.89 kN, FAy = −2.32 kN, MA = 10.37 kN ⋅ m
★平面力系平衡方程讨论: 平面力系平衡方程讨论: 讨论
{
x
Σ Fx = 0 Σ Fy = 0 Σ MO= 0
x 思考:, y 的选择是否有一定任意性? 思考: 的选择是否有一定任意性?
x x
y
y
y
在图示刚架的点B 例1 在图示刚架的点B作 用一水平F 用一水平F,刚架重量略 去不计。 去不计。 求支座A 的反力。 求支座A、D的反力。 解:法1分析刚架
解:(b)情形 (b)情形
q
B
l
l
l
l
l
C
r
q
B
l
l
l
l
C
r
l
D
E FP
l
l
E
D
FP
1.5l 1.5l
.
A
1.5l 1.5l FA x
.
MA A
FA y
图示构架,由直杆BC, 思考图示构架,由直杆BC, CD及直角弯杆 AB组成 , CD 及直角弯杆 组成 及直角弯杆AB 组成, 各杆自重不计。 在销钉B 各杆自重不计 。 在销钉 B 上作用载荷P 已知: qa、 上作用载荷 P 。 已知 : qa 、 M=qa2、P=qa 如何求: 销钉B BC 作用 如何求 : 销钉 B 对 BC作用 力? 分析CD,不含 销钉的BC。 分析CD,不含B销钉的BC。 不含B
★平面任意力系向面内一点简化
固定端的约束力为何可表示 思考: 思考: 成两个力和一个力偶? 成两个力和一个力偶?
F F
MA FAx A FAy
A
★平面任意力系简化结果分析
主矢: F′ = ∑F 主矢: R i
i= 1 n
FR O Mo
主矩 : MO = ∑MO(F ) i
i=1
n
平面任意力系简化结果: 平面任意力系简化结果:
2 ∑Fx = 0, F − FA ⋅ =0 5 1 ∑Fy = 0, FD − FA ⋅ =0 5
故
5 FA = F = 1.12F 2
FA
FD
F = 0.5F D
解:法2几何法
F FD FA FA FD
解三角形得
5 FA = F = 1.12F 2
F = 0.5F D
方法比较:法2要求受力图中的反力方向必须 要求受力图中的反力方向必须 方法比较: 实际方向,要使用三力汇交 三力汇交; 实际方向,要使用三力汇交;法1对画受力图 适用面更广,但仍要用三力汇交表示A 三力汇交表示 宽,适用面更广,但仍要用三力汇交表示A处 反力,否则三个未知数。 反力,否则三个未知数。
超静定问题
思考: 思考: 指出下列问题属于静定问题还是超静定问题
静定问题
超静定问题
(a)
(c)
超静定问题
都不是
(b)
(d)
例 4 如图组合梁 , 已知 : 如图组合梁, 已知: F=20 kN , 均 布 载 荷 q=10 kN/m , M=20
A
M
q
C B
30
o
F
60
o
D
kN•m,l=1 m。 kN• 求:A处的约束力。 处的约束力。 解:1、取梁CD为研究对象 取梁CD为研究对象
FB D FC
解:法2分析BDC 分析BDC
∑MA = 0 , M- F y ⋅ 3r = 0 C
M Fy = C 3r 2 ∑Fy = 0 , 2 FB − FCy = 0
2M F = B 3r
FB FCx D FCy
∑F
x
=0 ,
2 F −F x =0 B C 2
A
M Fx = C 3r
例4 图 示 是 汽 车 制 动 机 构 的 一部分。踩到制动蹬上的力F 一部分 。 踩到制动蹬上的力 F, 方向与水平面成a 45° 方向与水平面成a = 45°角。图 示平衡不计自重。 平衡不计自重 不计自重。 求:C处和D处约束力。 处和D处约束力。 解:分析BC为二力杆 分析BC BC为二力杆 取整体研究
利用合力矩定理对线性分布力系简化 利用合力矩定理对线性分布力系简化
q
ql
l
l/2
q
ql 2
2l / 3
l
q2 q1 q1
q2
l
l
q1l
(q2 − q1 )l 2
2l / 3
q1l
(q2 − q1 )l 2
l/2
l/2
l /3
■ 平衡条件与平衡方程
★ 平面任意力系平衡的充要条件 ★ 平面任意力系平衡方程的形式 ★ 平面力系平衡方程讨论 ★ 平面力系平衡例题
★ 平面任意力系向面内一点简化
F2 O M2 Fn FR′ O Mo F2 O M1 Mn Fn F1
F1
★ 平面任意力系向面内一点简化
力系主矢: R 力系主矢:F′ = ∑F i
i= 1 n
FR′ O Mo
力系主矩 : MO = ∑MO(F ) i
i=1
n
点O ─简化中心 力系主矢和主矩是否与简化中心有关? 力系主矢和主矩是否与简化中心有关? 思考: 思考: 主矢与简化中心无关; 主矢与简化中心无关; 主矩一般与简化中心有关( 主矩一般与简化中心有关(除?外)。
{ {
★平衡方程其他形式: 平衡方程其他形式: 其他形式 Σ Fx = 0 Σ MA(F)= 0 Σ MB(F)= 0 Σ MA(F)= 0 Σ MB(F)= 0 Σ MC(F)= 0
A
B
x
(两矩式) 两矩式)
A、B 连线不垂直 于x 轴 C B A C
(三矩式) 三矩式)
A、B、C三点不 在同一条直线上
B FDx D FDy
A α
F
240 C FC 60
(a)
∑M = 0 , 150 2F−60F = 0 F − 2 F =0 ∑F = 0 , 2 2 ∑F = 0 , F + F − 2 F = 0
D
C
y
Dy
x
Dx
C
解:取整体研究
∑M = 0 , 150 2F −60F 2 ∑F = 0 , F − 2 F = 0
★ 工 程 实 例 与 理 想 桁 架
★桁架分类:平面桁架和空间桁架 桁架分类:平面桁架和空间桁架 2、空间桁架 ● 结构是空间的。 结构是空间的。 ● 结构是平面的, 结构是平面的, 载荷与结构不共面。 载荷与结构不共面。
★平面力系平衡方程求解: 平面力系平衡方程求解:
解:法3分析刚架
∑Fx = 0, F − FAx = 0
FAx = F
⋅ ∑MA = 0, 2a⋅ F −a⋅ F = 0 ⋅ D
F = 0.5F D
∑F
y
= 0, F y + F = 0 A D
FAy = −0.5F
FAx FAy
FD
综述: 综述:法3最好
物体系是指由几个物体通过约束组成的系统 物体系是指由几个物体通过约束组成的系统。 是指由几个物体通过约束组成的系统
特点:整体系统平衡,每个物体也平衡, 特点:整体系统平衡,每个物体也平衡,局 部也平衡。 部也平衡。可取整体或部分系统或单个物体 或局部为研究对象。
★ 静定与静不定问题
静定问题 (statically determinate problem) problem) —由平衡方程可解出全部未知数。 由平衡方程可解出全部未知数。 由平衡方程可解出全部未知数 problem) 静不定问题(statically indeterminate problem) — 由平衡方程无法求出全部未知数。 由平衡方程无法求出全部未知数。
★平面力系平衡方程讨论: 平面力系平衡方程讨论: 讨论
{
Σ Fx = 0 Σ Fy = 0 Σ MO= 0
平面任意力系: 平面任意力系: 三个独立的平衡方程,可解3 三个独立的平衡方程,可解3个未知量 平面汇交力系: 平面汇交力系: 二个独立的平衡方程,可解2 二个独立的平衡方程,可解2个未知量 平面平行力系: 二个独立的平衡方程, 平面平行力系: 二个独立的平衡方程,可2个未知量 平面力偶系: 一个独立的平衡方程,可解1 平面力偶系: 一个独立的平衡方程,可解1个未知量。
FC
y
l
l
l
o
l
30
q B
F
60
o
∑M (F) = 0
C
,
FCx C
D
FB l o o −ql× + F sin 60 ×l − F cos 30 ×2l = 0 × B 2 代入数据得 F = 45.77 kN B
解:2、取整体为研究对象
M
A
q
C B
30
o
F
60
o
D
∑F = 0
x
FAx − F cos 60 − F sin 30 = 0 B
■ 力系简化 ★ 力的平移定理 ★ 平面任意力系向面内一点简化 ★ 平面任意力系简化结果分析 ★ 合力矩定理 ★ 例题
