Ch24
调光台型号DISCO24016CH24DM512说明书

调光台型号DISCO240,16CH*24DM*512说明书一;电脑灯的程序场编辑1.按(BLACK)键使该LED指示灯熄灭2.按(DEIT\RUN)键使该LED指示灯亮,进入编程状态3.按数字键(P1—P12)中任意一次,选择要编程的程序场编号,显示在LED的CHASE括号中。
4.再按数字键(P1—P12)选择出受控的电脑灯,使之对应的LED灯亮,则表示该项灯未选中,不受第5步的影响。
电脑灯效果(如果以设置了X\Y运行方向扫描通道转移,则其中有两个直滑电位器不求作用,你可操纵右下角摇杆电位器获取数据)。
5.推动CH1—CH8调节电脑灯个通道数值,或按SA\SB键,推动CH9—CH16调光对应的6.重复4.5步调节其他电脑灯,使之所需电脑等场景达到预订效果。
7.推动SPEED CROSS电位器,调节好场景停留时间及场景过渡时间。
8.按(+ 三角行)记忆次步场景效果,并进入下一步编辑。
若按(三角形—)键可查看一步场景。
重复4567步修改,再按(+ 三角形)储存。
9.重复4~8步编辑其他场景(程序步)10.按(EDIT\RUN)键,使该对应指示灯熄灭,记忆并退出编程状态,进入运行状态。
11.重复2~10步编辑其它程序场。
二:特殊场景表现在运行程序状态下,即(RUN\EDIT)键对应指示灯熄灭,按(RUN\SCENE)J键,再按P1~P12中任意键可调出已编程中第一号程序中的前12个场景,所以我们建议第一号程序的前12个场景在编程时最好有特殊定义,可作一些特技表演效果。
三:如何设置取消摇杆电位器设置摇杆电位器设置,按RUN\EDIT键,使该指示灯亮紧接着按SET X\Y键,根据液晶屏显示从P1~P8或按SA\SB键从PCH9~PCH16中选取两个对应电脑灯XY运行方向的扫描通道,转移到摇杆电位器去控制绿色指示灯随即点亮,如果输入错误按DELETE消除输入数据,绿色指示灯熄灭再按SET X\Y键记忆退出。
ETAP帮助手册ch24动态模型

第24章动态模型(Dynamic Models)动态电动机起动、暂态稳定性和发电机起动分析中都要用到电动机动态模型。
发电机动态模型和一些控制单元(如励磁器和调速器等)只在暂态稳定分析中用到。
另外,电动机起动分析和暂态稳定分析也要求有负荷转矩特性。
ETAP为各种分析提供了各种感应电机和同步电机模型以及全面的励磁器和调速器库。
在动态电机加速分析中,只有加速的电动机需要动态模型,也就是说,发电机,励磁器和调速器都不需要动态模型。
在暂态稳定分析中,所有的发电机,励磁器和调速器都是动态模型的。
有动态模型的电动机和在分析案例中被设为动态模型的电动机都会被动态模拟。
在发电机起动和依赖于频率的暂态稳定分析中,所有的发电机、励磁器和调速器都必须是依赖于频率的模型。
本章描述了不同类型的电机模型,电机控制单元模型和负荷模型并解释了他们在电动机起动和暂态稳定性分析中的应用。
也介绍了在选择模型和设定模型参数时所用到的工具。
感应电机模型部分介绍了五种不同的感应电机模型和这些模型的依赖于频率形式,分别是电路模型 (Single1、Single2、DBL1、DBL2) 和特性曲线模型。
在同步电机模型部分,介绍了五种不同的同步电机模型和这些模型的依赖于频率形式。
这些模型分别是等值电路模型,隐极电机的暂态模型,隐极电机的次暂态模型,凸极电机的暂态模型和凸极电机的次暂态模型。
电动机起动分析和暂态稳定性分析也把等效电网系统模拟成一个等值电机。
在等效电网部分介绍了等效电网系统的模型。
在励磁器和自动电压调节器模型部分定义不同类型的励磁器和自动电压调节器模型,包括标准IEEE模型和商用特有模型。
在调速器-涡轮部分列举了以IEEE标准和商用产品手册为准的调速器-涡轮模型。
最后,在机械负荷部分介绍了不同类型的负荷模型。
24.1 感应电机模型(Induction Machine Models)ETAP提供了五种在感应电机设计中较常用的感应电机模型。
期权、期货及其他衍生产品第9版-赫尔】Ch(24)

h
4
Currency Swaps
In theory, a swap where LIBOR in one currency is exchanged for LIBOR in another currency is worth zero
In practice it is sometimes the case that LIBOR in currency A is exchanged for LIBOR plus a spread in currency B
These cannot be accurately valued by assuming that forward rates will be realized
h
6
LIBOR-in Arrears Swap (Equation 33.1,
page 764-765)
Rate is observed at time ti and paid at time ti rather than time ti+1 It is necessary to make a convexity adjustment to each forward rate underlying the swap
ch24-体气

三、鲜姜汁治狐臭 用料:鲜姜。 制法:将鲜姜洗净,捣碎,用纱布绞压取汁液。涂汁于腋 下,每日数次。 用法:涂汁于腋下,每日数次
四、泥鳅消炎治狐臭制法:将泥鳅(不洗,带黏液)捣烂 。 用法:涂敷腋下,直至治愈。
五、腋臭灵擦剂 富尔马林3ml,明矾2克,氯羟基铝2克,氯酮1克,香精 1ml,适量70%的乙醇混合,加水至100ml即可。明搽 或湿敷腋下。 功效:杀菌、收敛、止汗、留香
十、 1.简易治疗: 每日早上,洗净腋部擦干后,用一块普通香 皂,将皂面稍加湿润,轻轻涂抹患处,即可保证全天之内 无臭味。 2.治狐臭>特一方:碘酒300毫升,尖红干辣椒50克,剪 成碎片或研末,泡在碘酒内15天后,每天擦腋窝一次,连 擦50天即根除
2.湿热蕴阻 症状:常无家族史,好发于夏季,皮肤潮湿多汗 ,或身热不扬,口干而粘,四肢困重或关节肿痛 ,脘腹胀满,大便溏而不爽,小便短少不畅,女 子带下黄浊,舌红苔黄,脉滑数或濡数。 治则:清热利湿,芳香化浊 方药:甘露饮合连朴饮化裁。
二、外治
1.腋香散:密佗僧15 g,生龙骨30 g,红粉6 g,木香10 g,白芷10 g,甘松15 g,冰片3 g 。分别研细和匀,纱布包扑患处,每日1次。 2.治胡臭方:辛夷、川芎、细辛、杜蘅、藁本各 3 g。上5味,以醋渍一宿,煎取汁。临睡前洗净 腋下等处,敷上药汁,次晨洗去,以瘥为度。
总之,先天禀赋是本病发病的基础,嗜食肥甘, 湿热内蕴则是本病的重要诱因。
西医认为,本病是由于青年人性腺的发育成熟, 性激素分泌增加,促进了大汗腺的分泌,经过细 菌的分解作用,分泌物中的有机物被分解为具有 特殊臭味的不饱和脂肪酸等物质而成,多与遗传 有关。少数患者可在精神或神经系统损害时产生 ,如偏执症和精神分裂症等。
会计学原理23版 英文版教学书册Wild FAP 23e Ch24 IRM
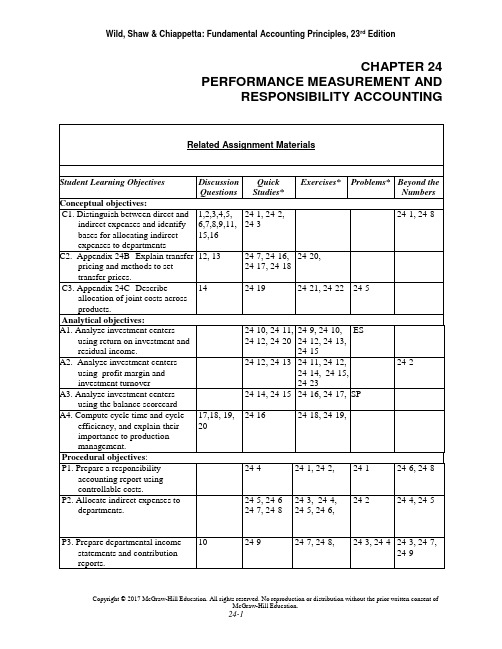
CHAPTER 24 PERFORMANCE MEASUREMENT AND RESPONSIBILITY ACCOUNTING*See additional information on next page that pertains to these quick studies, exercises and problems. SP refers to the Serial ProblemES refers to Excel SimulationsAdditional Information on Related Assignment MaterialConnectA vailable on the instructor’s course-specific website) repeats all numerical Quick Studies, all Exercises and Problems Set A. Connect also provides algorithmic versions for Quick Study, Exercises and Problems. It allows instructors to monitor, promote, and assess student learning. It can be used in practice, homework, or exam mode.Connect InsightThe first and only analytics tool of its kind, Connect Insight is a series of visual data displays that are each framed by an intuitive question and provide at-a-glance information regarding how an instructor’s class is performing. Connect Insight is available through Connect titles.The Serial Problem (SP) for Success Systems continues in this chapter.General LedgerAssignable within Connect, General Ledger (GL) problems offer students the ability to see how transactions post from the general journal all the way through the financial statements. Critical thinking and analysis components are added to each GL problem to ensure understanding of the entire process. GL problems are auto-graded and provide instant feedback to the student.Excel SimulationsAssignable within Connect, Excel Simulations allow students to practice their Excel skills—such as basic formulas and formatting—within the context of accounting. These questions feature animated, narrated Help and Show Me tutorials (when enabled). Excel Simulations are auto-graded and provide instant feedback to the student. Synopsis of Chapter RevisionsNEW opener—Ministry of Supply and entrepreneurial assignment.Reorganized chapter.Revised discussion of performance evaluation and decentralization.Revised discussion of Kraft Heinz responsibility centers.Revised exhibit on responsibility accounting.Revised discussion of responsibility accounting reports.Added NTKs on responsibility accounting, cost allocations, and balanced scorecard.Revised discussion of indirect expense allocations.New exhibit and discussion of general model of expense allocation.New exhibit on common allocation bases for indirect expenses.Revised discussion of preparing departmental income.New exhibit and formula for computing departmental income.Added short section on transfer pricing to the chapter.New Sustainability section with discussion of General Mills, Target and performance reporting, and Ministry of Supply example.Chapter OutlineNotes I.Responsibility AccountingA. Performance Evaluationrge companies are easier to manage if divided into smallerunits called divisions, segments, or departments.2.In decentralized organizations, decisions are made by unitmanagers rather than top management.3.In responsibility accounting, unit managers are evaluated onlyon what they are responsible for.4.The methods of performance evaluation vary for cost centers,profit centers and investment centers.a.Cost center−incurs cost or expenses without directlygenerating revenues (e.g. manufacturing department andservice department).b.Profit center−incurs costs and generates revenues (e.g.product centers).c.Investment center−incurs costs, generates revenues and isresponsible for effectively using center assets.5.Basis for evaluating performance:a.Cost center managers are evaluated on their success incontrolling costs compared to budgeted costs. Profit center:ability to generate more revenue than expenses.b.Profit center managers are evaluated on their success ingenerating income.c.Investment center managers are evaluated on their use ofinvestment-center assets to generate income.II.Controllable versus Uncontrollable CostsA.Controllable Costs -1.Those which a manager has the power to determine or at leastsignificantly affect the amount incurred.B. Uncontrollable costs –1.Are not within the manager’s control.2. A manager’s performance is evaluated using responsibilityreports that describe the department’s activities in terms ofcontrollable costs3.Distinguishing between controllable and uncontrollable costsdepends on the particular manager and the time period underanalysis.4.All costs are controllable at some level of management if the timeperiod is sufficiently long;5.Good judgment is required when identifying controllable costs.Chapter OutlineNotesC.Responsibility Accounting Performance Report1.Reports actual expenses that a manager is responsible for andtheir budgeted amounts.a.Management’s analysis of differences between actual andbudget often results in corrective actions.ed by upper management to evaluate effectiveness oflower-level managers in controlling costs.c.Recognizes that control over costs and expenses belongs toseveral layers of management.2.Responsibility Accounting Reporta.Provide relevant information for each management level.b.At lower levels, managers have limited responsibilities andtherefore fewer controllable costs.c.Responsibility and control broaden for higher-levelmanagers.III.Profit CentersA.The responsibility report focuses on how well each departmentcontrolled costs and generated revenues.B.The departmental income statement is a common way to reportprofit center performance.C.When computing department profits, two key accounting challengesinvolve allocating expenses:1.How to allocate indirect expenses, such as rent and utilities whichbenefit several departments.2.How to allocate service department expenses, such as payroll orpurchasing, that perform services that benefit severaldepartments.D.Direct and Indirect Expenses1.Direct Expenses are readily traced to a department.a.Incurred for sole benefit of that one department; no allocationrequired.b.Often, but not always, controllable costs.2.Indirect Expenses are incurred for joint benefit of more than onedepartment; can’t be readily traced to just one department.a.Allocated across departments benefiting from them.b.Ideally allocated using a cause-effect relation or, if cause-effect relation cannot be identified, allocated on a basisapproximating the benefit received by each department.c.Typically considered uncontrollable costs.Chapter OutlineNotesE.General Model – indirect and service department expenses areallocated across departments benefiting from them. Allocated using acause-effect relation. Sometimes hard to identify.1.Allocated Cost = Total Cost to Allocate x Percentage ofAllocation Base Used.F.Allocating Indirect Expenses – allocation bases vary acrossdepartments and organizations. Managers must use careful judgmentin developing allocation bases. Commonly used allocation bases:1.Wages and salaries –allocated using relative amount of hoursworked in each department.2.Rent and Utilities allocated based on portion of floor spaceoccupied. More valuable location may charge department higherrate.3.Advertising – allocated using a percentage of total sales.4.Depreciation – allocated using hours of depreciable asset used.G.Service Department expenses –provide support to an organization’soperating departments. Common allocation bases:1.Office, personnel, and payroll expenses – allocated based onnumber of employees in each department.2.Purchasing costs – allocated based on dollar amount of purchasesor number of purchase orders processed.3.Maintenance expenses – allocated based on square footage.H.Departmental Income Statements1.Departmental income is computed using the following formula:Departmental income = Dept. sales – Dept. direct expenses –Allocated indirect expenses – Allocated service dept. expenses.2.Four Steps for allocating costs and preparing departmentalincome statements:a.Step one – accumulate revenues and direct and indirectexpenses by department. Involves collecting the necessarydata from general company and departmental accounts.i.Direct and indirect expenses include salaries, depreciationand supplies expenses.b.Step two – allocate indirect expenses across both service andoperating departments.i. Uses a departmental expense allocation spreadsheetshown in Exhibit 24.10.ii.After selecting allocation bases, indirect expenses arerecorded in company accounts and allocated to bothoperating and service departments.Chapter OutlineNotesc.Step three – allocate service department expenses tooperating departments using a departmental expenseallocation spreadsheet. After service department costs areallocated, no expenses remain in the service departments.d.Step four – prepare departmental income statements using thedepartmental expense allocation spreadsheet.i. Actual service department expenses are compared withbudgeted amounts to help assess cost center performance.ii.Amounts in the operating department columns are used toprepare departmental income statements. (Exhibit 24.15)I.Departmental Contribution to Overhead (see Exhibit 24.12)1.Departmental income statements not always best for evaluatingeach profit center’s performance especially when indirectexpenses are a large portion of total expenses.2.Evaluate using departmental contributions to overhead a reportof the amount of sales less direct expenses.3.Behavioral Aspects of Departmental Performance Reports –a.Indirect expenses are typically uncontrollable, so a better wayto evaluate is using departmental contribution to overhead.b.Including indirect expenses in department manager’sperformance evaluation can lead to the manager being morecareful in using service departments.c.Some companies allocate budgeted service department costsso operating departments are not held responsible forexcessive costs from service departments.IV.Investment CenterA.Financial Performance Evaluation Measures include:1.Return on investment, return on assets, computed as investmentcenter income / by investment center average invested assets.2.Residual income – Expressed in dollars. Encourages divisionmanagers to accept all opportunities that return more than targetincome. Computed as investment center income – targetinvestment center income.3.Profit margin and investment turnover – split return oninvestment into two measures – profit margin and investmentturnover.a.Profit margin measures income earned per dollar of salescomputed as investment center income divided by investmentcenter sales. Usually use income before tax. Expressed as apercent.b.Investment turnover measures how efficiently an investmentcenter generates sales from its invested assets. Calculated asinvestment center sales divided by investment center averageassets. Expressed as the number of times assets wereconverted into sales.Chapter OutlineNotes4.Nonfinancial Performance Evaluation Measures –using solelyfinancial measures has limitations. Companies can considernonfinancial measures to help in evaluating division manager’sperformance.5.Balanced Scorecard: system of performance measures,including nonfinancial measures used to assess company anddivision manager performance. Requires managers to think oftheir company from four perspectives.a.Customer: what do they think of us?b.Internal process: which of our operations are critical?c.Innovation and learning: how can we improve?d.Financial: what do our owners think of us?V.Decision Analysis Cycle Time and Cycle EfficiencyA.As lean manufacturing practices help companies move toward justin time manufacturing it is important for companies to reduce thetime it takes to manufacture its products and improve efficiency.1.Cycle time measures the time element which describes the timeit takes to produce a product or service.Cycle time = Process + Inspection + Move + WaitTime Time Time Timea.Process time is considered value-added time – it is the onlyactivity in cycle time that adds value to the product from thecustomer’s perspective. The other three activities areconsidered non-value-added time: they add no value to thecustomer.2.Cycle Efficiency measures production efficiency. It is the ratioof value added time to total cycle time.Cycle Efficiency = Value added timecycle timea.If the cycle efficiency is low, the company should evaluatethe production process to see if it can identify ways toreduce the non-value added activities.VI.Appendix 24A – Cost Allocations uses the general model of costallocation to show how the cost allocations in Exhibits 24.10 and 24.11for A-1 Hardware. Rent expense, utilities expense, advertising expenseand insurance expense are allocated first. Then, the two servicedepartment’s expenses are allocated to the three operating departments.Chapter OutlineNotes VII.Appendix 24B – Transfer PricingThe price used to record transfers between divisions in the samecompany is called a transfer price. Can be used in cost, profit andinvestment centers.A.If there is no excess capacity, the internal supplier will not accept atransfer price less than the market price. This is called market basedtransfer pricing.B.If there is excess capacity, the internal supplier should accept a pricebetween the costs to manufacturer the part and the market price.This is called cost based transfer pricing.C.Other issues to consider in determining transfer prices include:1.Market price may not exist2.Cost controls3.Division managers’ negotiation4.Nonfinancial factors to consider include: quality control,reduced lead times and impact on employee morale.III.Appendix 24C – Joint CostsA.Joint Costs−the costs incurred to produce or purchase two or moreproducts at the same time; similar to indirect expense in that it’sshared across more than one cost object.1.Ignored when deciding to sell product as is or process further.2.Allocated to different products produced from it when total costof each product must be estimated (e.g., preparation of GAAPfinancial statements).3.Allocation basesa.Physical basis−allocates joint costs using physicalcharacteristics such as ratio of pounds, cubic feet or gallonsof each joint product to the total pounds, cubic feet orgallons of all joint products flowing from the cost; does notreflect the extra value flowing into some products or theinferior value flowing into others. Not the preferred method.b.Value basis−allocates joint cost in proportion to the salesvalue of the output produced by the process at the “split-offpoint”.Chapter 24 Alternate Demo ProblemJack and Susan Roberts own a farm that produces potatoes. Based on a review of the income statement shown below, Jack remarked that they should have fed the No. 3 potatoes to the pigs; then they would have avoided the loss from the sale of the those potatoes.JACK AND SUSAN ROBERTSIncome from the Production and Sale of PotatoesFor Year Ended December 31, 20xxResults by GradeSales by grades:No. 1, 300,000 lbs. $0.045 per lb.No. 2, 500,000 lbs. $0.04 per lb.No. 3, 200,000 lbs. $0.03 per lb.CombinedCosts:Land preparation, seed,planting,cultivating @ $0.01422 per lb.Harvesting, sorting, grading@ $0.01185 per lb.Marketing @ $0.00415 per lb.Total costsNet income (or loss)Jack and Susan divided their costs among the grades on a per pound basis, because their records do not show cost per grade. However, their records did show that $4,020 of the $4,150 of marketing costs represented the cost of placing the No. 1 and No. 2 potatoes in bags and hauling them to the warehouse of the produce buyer. Bagging and hauling costs were the same for both grades. The remaining $130 represented the cost of loading the No.3 potatoes into the trucks of the potato starch factory that bought these potatoes in bulk and picked them up at the farm.Required:Prepare an income statement that will better show the results of producing and marketing the each of the grades of potatoes.Chapter 24 Alternate Demo Problem: SolutionJACK AND SUSAN ROBERTSIncome from the Production and Sale of PotatoesFor Year Ended December 31, 20xxRevenue from sales:Costs:Land preparation, seed,planting, cultivatingHarvesting, sorting, gradingMarketingTotal costsNet incomeCOST ALLOCATIONSLand preparation, seed, planting, andcultivating:No. 1: $13,500 / $39,500 x $14,220 = No. 2: $20,000 / $39,500 x $14,220 = No. 3: $ 6,000 / $39,500 x $14,220 = $ 4,8607,2002,160 $14,220Harvesting, sorting, and grading:No. 1: $13,500 / $39,500 x $11,850 = No. 2: $20,000 / $39,500 x $11,850 = No. 3: $ 6,000 / $39,500 x $11,850 = $ 4,0506,0001,800 $11,850Marketing:No. 1: $13,500 / $33,500 x $4,020 = No. 2: $20,000 / $33,500 x $4,020 = $1,620 2,400Subtotal bagging and hauling costs 4,020 No. 3: Loading costs 130$4,150。
有机物的结构简式

有机物的结构简式编名称分子式结构,简,式号烷烃1甲烷ch42乙烷ch26ch—ch、chch、3333ch—ch—ch、chchch、3233233丙烷ch38、4正丁烷chch—ch—ch—ch、chchchch、41032233223 2—甲基丙烷5ch410,异丁烷,、ch,ch,、33ch—ch—ch—ch—ch、chchchchch、32223322236,正,戊烷ch512ch,ch,ch、32332—甲基丁烷7ch,异戊烷,5122,2—二甲基丙烷8ch512,新戊烷,、c,ch,34ch—ch—ch—ch—ch—ch、3222239正己烷ch614chchchchchch、ch,ch,ch、32222332432—甲基戊烷10ch614,异己烷,113—甲基戊烷ch6142,3—二甲基丁12ch614烷2,2—二甲基丁13ch614烷ch—ch—ch—ch—ch—ch—ch、322222314,正,庚烷ch716chchchchchchch、ch,ch,ch322222332532—甲基己烷15ch716,异庚烷,163—甲基己烷ch7162,2—二甲基戊17ch716烷3,3—二甲基戊18ch716烷2,3—二甲基戊19ch716烷2,4—二甲基戊20ch716烷2,2,3—三甲21ch716基丁烷3—乙基戊烷22ch7162,2,4,4—四甲23ch920基戊烷2,3—二甲基—24ch9203—乙基戊烷3,3,4—三甲基25ch920己烷2,2,4—三甲基26ch818戊烷2,3,3—三甲基27ch818戊烷2,2,3—三甲基28ch818戊烷2,3,4—三甲基29ch818戊烷环烷烃30环丙烷ch36、31环戊烷ch510 、32环己烷ch612、、33甲基环己烷ch714、34乙基环己烷ch816顺对二甲基环35ch816己烷反对二甲基环36ch816己烷烯烃37乙烯ch24ch,ch、2233丙烯chch—ch,ch、chch,ch363232341—丁烯chch,ch—ch—ch、48223352—丁烯chch—ch,ch—ch、chch,chch48333336甲基丙烯ch48ch,ch—ch—ch—ch、2223371—戊烯ch510ch,chchchch、ch,ch,ch,ch22232223ch—ch,ch—ch—ch、323382—戊烯ch510chch,chchch3232—甲基—1—39ch510丁烯3—甲基—1—40ch510丁烯2—甲基—2—41ch510丁烯421,3—丁二烯chch,ch—ch,ch、ch,chch,ch4622222—甲基—1,3—丁二烯43ch58,异戊二烯,2,2,5,5—四甲44ch1020基—3—己烯、,ch,h,chc,ch,33332,4,4—三甲基45ch816—1—戊烯2,4,4—三甲基46ch816—2—戊烯3—甲基—1,347ch814—己二烯2—甲基—483,2,2—乙基,—ch9161,3—丁二烯3,4—二甲基—492—乙基—1—ch918戊烯3—乙基—1,350ch712—戊二烯514—甲基环己烯ch712炔烃52乙炔chhc?ch、h—c?c—h22丙炔hc?c—ch、ch?h53ch3334541—丁炔chhc?c—ch—ch、ch?hch、462323552—丁炔chch—c?c—ch、chc?h463333561—戊炔chhc?c—ch—ch—ch、ch?hchch、58223223572—戊炔chch—c?c—ch—ch、chc?hch58323323 3—甲基—1—58ch58丁炔3—甲基己—359ch710—烯炔3—乙基戊—360ch710—烯炔芳香烃61苯ch66、、62甲苯ch78、、ch—ch65363乙苯ch810、、ch—ch652564邻二甲苯ch810间二甲苯65ch81066对二甲苯ch81067间甲乙苯ch912戊苯68ch1116chch、65511692—苯基戊烷ch11162—甲基—1—70ch1116苯基丁烷3—甲基—1—71ch1116苯基丁烷2—甲基—3—72ch1116苯基丁烷2,2—二甲基—73ch11161—苯基丙烷、chchc,ch,65233743—苯基戊烷ch1116、chch,chch,6523275苯乙烯ch88 、、chch,ch65276苯乙炔ch86、chc,ch6577联二苯ch1210、ch —ch、,ch,6565652二苯甲烷78ch1212、ch,ch,265279萘ch10880,—甲萘ch111081,—甲萘ch1110821,6—二甲萘ch1212831,5—二甲萘ch121284,—乙萘ch121285,—乙萘ch121286蒽ch141087菲ch141088并四苯ch181289并五苯ch2214 90ch161091ch2212卤代烃92一氯甲烷chclchcl3393二氯甲烷chclchcl222294三氯甲烷,氯仿,chclchcl3395四氯化碳ll4496三碘甲烷,碘仿,chichi3397四氟化碳cfcf4498四溴化碳cbrcbr4499四碘化碳cici44100氯乙烷chclchcl、chchcl252532101溴乙烷chbrchbr、chchbr252532102氯苯chcl65、chcl65103溴苯chbr65、、chbr65104四氟乙烯cfcf,cf24221,1,2,2—四溴105chbrchbr—chbr22422乙烷1061,2—二溴乙烯chbrbrch,chbr222107氯乙烯chclch,chcl2323,4—二溴—1108chbrch,ch—chbr—chbr46222—丁烯1,4—二溴—2109chbrchbr—ch,ch—chbr46222—丁烯110邻氯甲苯chcl77111间氯甲苯chcl77112对氯甲苯chcl772,4,6—三溴甲113chbr753苯114苄氯,苯甲氯,chcl771154—溴辛烷chbr817、ch,ch,chbr,ch,ch323223 醇116甲醇choch—oh、choh433117乙醇choch—oh、choh、chchoh262525321181—丙醇choch—oh、choh、chchchoh383737322 2—丙醇,异丙119cho38醇,1—丁醇h—oh、choh、ch,ch,ohc120cho4949323410,正丁醇, 2—丁醇121cho410,异丁醇,2—甲基—1—122cho410丙醇2—甲基—2—123cho410丙醇、2,2—二甲基—124cho5121—丙醇2—甲基—2—125cho512丁醇、、126乙二醇cho262、hohhoh、,choh,2222127丙三醇cho383 、ch,oh,3532—丁炔—1,4128cho462二醇129氨基乙醇chno272,2—二甲基—130cho6141—丁醇3—甲基—1—131cho512丁醇2—戊醇132cho512、1333—戊醇cho5121341,2—丁二醇cho411421352—氯乙醇chocl25136苯甲醇,苄醇,cho78137环丙醇cho36138对甲基环己醇cho714139邻甲基环己醇cho714醚140甲醚choch—o—ch、choch263333141甲乙醚choch—o—ch、choch、chochch38325325323h—o—ch、choch、c25252525142乙醚cho410chchochch、,ch,o3223252143甲正丙醚choch—o—ch、choch、chochchch4103373373223144甲异丙醚cho410choch,ch,、332145甲苯醚cho718146异丙醚cho614、,ch,choch,ch,3232环氧烷147环氧乙烷cho24148二氧杂环己烷cho48149甲基环氧乙烷cho36酚150苯酚cho66、1,2,3—苯三酚151cho663,邻苯三酚,1,3,5—苯三酚152cho663,间苯三酚,2,4,6—三溴苯153chobr633酚、154邻甲苯酚cho78155间甲酚cho78156对甲酚cho782,4,6—三硝基157chno6337苯酚醛和酮158甲醛cho2hcho、乙醛159cho24chcho、3160丙醛chochchcho、chcho363225161丁醛chochchchcho、chcho48322371622—甲基丙醛cho48、,ch,chcho321633—丁羟醛cho482164乙二醛cho222、、,cho,2165丙酮cho36、、,ch,co、chcoch3233166丁酮cho48、chcochch323167丙二烯酮co32o,c,c,c,o、邻乙酰基苯乙168醛羧酸169甲酸cho22hcooh、、170乙酸cho242chcooh、3171丙酸cho362chchcooh、chcooh、3225172丁酸chochchchcooh、chcooh48232237173甲基丙酸cho482、,ch,chcooh32174硬脂酸cho18362chcooh、1735175软脂酸cho16322chcooh、1531油酸176chochcooh183421733、、177苯甲酸cho762chcooh、65178苯正丙酸cho9102、chchchcooh6522179乙二酸cho224、、,cooh,、hooc—cooh2180丙二酸cho344、hooc—ch—cooh、ch,cooh,222181丁二酸cho464、hooc,ch,cooh、,chcooh,2222182顺丁烯二酸cho444183反丁烯二酸cho444184邻苯二甲酸cho864185间苯二甲酸cho864186对苯二甲酸cho864187甲,酸,酐cho,hco,o2232188乙酐cho463、,chco,o32乳酸189cho363,,—羟基丙酸,、,—羟基丙酸190cho3632,2—二甲基丙191cho4102酸、,ch,ooh333—甲基戊—4192cho6122—烯酸193邻羟基苯甲酸cho763194对羟基苯甲酸cho763、间羟基苯甲酸195cho763对羟基苯—2—196cho983丙烯酸间羟基羧基苯197cho884甲醇酯198甲酸甲酯chohcooch、2423199甲酸乙酯chohcooch、hcoochch3622523乙酸甲酯200cho362、chcooch33201乙酸乙酯cho、482chcooch、chcoochch325323202甲酸正丙酯chohcooch、hcoochchch48237223203甲酸异丙酯cho482、、hcooch,ch,32甲酸新戊酯、204甲酸,2,2—二甲cho6122基,丙酯、hcoochc,ch,233甲酸—2—甲基205cho6122丁酯206甲酸异戊酯cho6122、hcoo,ch,ch,ch,2232207对乙酸甲苯酯cho9102丙酸甲酯chchcooch、chcooch208cho323253482对羟基苯甲酸209cho883甲酯2,2—二甲基丙210酸甲酯、cho6122新戊酸甲酯、,ch,cooch333211硬脂酸甘油酯cho571106、,chcoo,ch173535212软脂酸甘油酯cho511706、,chcoo,ch153135213油脂酸甘油酯cho571046、,chcoo,ch173335214苯甲酸甲酯cho882、chcooch653215硝酸乙酯chnochono、chchono2532523223—羟基丙酸正216cho6123丙酯、ho,ch,coo,ch,ch22223 2—羟基丙酸正217cho6123丙酯218丙二酸二乙酯cho7124 、chooc—ch—cooch252252—丁酮酸异丁219cho8143酯220乙酸对甲酚酯cho9102221甲酸氯甲,醇,酯chocl232222异戊酸异戊酯cho10202、,ch,chcoo,ch,ch,ch,32232乙二酸乙二,醇,223cho444酯三硝酸甘油酯224chno3539,硝化甘油,硝基化合物225硝基苯chno652、、ch—no652226硝基甲烷chnoch—no、chno323232227硝基乙烷chnoch—no、chno、chchno252252252322 2,4,6—三硝基228chno7536甲苯,tnt,229,—硝基萘chno1072230,—硝基萘chno10721,8—二硝基萘231chno106242321,5—二硝基萘chno10624糖类233葡萄糖cho6126、choh,choh,cho24234果糖chochoh,choh,cochoh6126232235蔗糖chocho122211122211236麦芽糖chocho122211122211237淀粉,cho,,cho,6115n122211n238纤维素,cho,6115n、[cho,oh,]6723n氨基酸甘氨酸239chno252,氨基乙酸,丙氨酸240chno372,—氨基丙酸苯丙氨酸241,—氨基—,—chno8112苯基丙酸谷氨酸242chno594,—氨基戊二酸高分子化合物243聚乙烯,ch,24n244聚丙烯,ch,36n245聚氯乙烯,chcl,23n246聚苯乙烯,ch,88n、有机玻璃,聚甲247,cho,582n基丙烯酸甲酯,、聚丙烯腈248,ch,23n,人造羊毛,聚四氟乙烯249,cf,24n,塑料王,250酚醛塑料,电木,,cho,76n251脲醛塑料,电玉,,chno,42n252环氧树脂,cho,19203n聚对苯二甲酸253乙二醇酯,cho,10103n,涤纶、的确良,聚己内酰胺254,chno,611n,绵纶,聚乙烯醇缩甲255醛,cho,582n,维尼纶,256丁苯橡胶,ch,1214n257顺丁橡胶,ch,46n258氯丁橡胶,chcl,45n259丁腈橡胶,ch,79n260聚硫橡胶,chs,244n261硅橡胶,chsio,26n262丁基橡胶异戊橡胶263,ch,58n,合成天然橡胶,264聚乳酸,cho,332n265聚丙酸甲酯,cho,462n266聚丙酸正丁酯,cho,7122n267聚乙丙丁酯,ch,918n268人造象牙,cho,2n289聚环氧乙烷,cho,24n290聚乙炔,ch,22n291,ch,916n292戊苯橡胶,ch,1316n293,ch,1010n294,ch,1010n295nomex纤维,chno,141022n296,cho,15166n其它297二恶英,chocl,12424n298维生素c,cho,686n299立方烷,ch,88n2,3,4—三羟基苯甲酸—2,3—300,cho,14109n二羟基—5—羧基苯,酚,酯301苯磺酸chso663302对氨基苯磺酸chnso1093303吗啡chno17173304葡萄糖二酸cho6108三硝酸纤维素305,chno,6739n酯丙二酰氯306chocl3222307丙二酰胺chno36223,7—二甲基—308cho10162,6—辛二烯醛三聚甲醛309cho363310氨基树脂chn66621 / 21__来源网络整理,仅作为学习参考。
GP1I_Ch24_Electric Potential 电位势

Ch 24Electric PotentialOne goal of physics is to identify basic forces in ourworld, such as the electric force we discussed in Ch. 21.A related goal is to determine whether a force is conservative—that is, whether we can find a potential energy to be associated with the force.The motivation (動機) for associating a potentialenergy with a force is that we can then apply the principle of the conservation of mechanical energy to closed systems involving the force. This extremely powerful principle allows us to calculate the results of experiments for which force calculations alone would be very difficult.Experimentally, physicists and engineers discoveredthat the electric force is conservative and thus has an associated electric potential energy.When an electrostatic force acts between two or more charged particles within a system of particles, we can assign an electric potential energy U to the system. If the system changes its configuration(組態) from an initial state i to a final state f, the electrostatic force (帶電粒子之間)does work W (≡∫F•d S)on the particles. The resulting change in the potential energy of the system isΔU=U f-U i=-W(24-1) [保守力(重力、彈力、電力)作功(等速之下)造成系統位能變化(減少): W=-ΔU=-(U f-U i)]As with other conservative forces, the work done by the electrostatic force is path independent.Suppose a charged particle within the system moves from point i to point f while an electrostatic force between it and the rest of the system acts on it. Provided the rest of the system does not change, the work W done by the force on the particle is the same for all paths between points i and f.For convenience, we usually take the reference configuration of a system of charged particles to be that in which the particles are all infinitely separated from one another. Also, we usually set the corresponding reference potential energy to be zero(因為所有帶電粒子都相距無窮遠,當然之間電力為零,因此可設此時系統電位能為零).Suppose that several charged particles come together from initially infinite separations(initial state i) to form a system of neighboring particles (final state f).Let the initial potential energy U i=0, and let W∞representthe work done by the electrostatic forces between the particles during the move from initial state (相距∞)to final state (相距有限遠,此時之間電力≠0,可設系統位能≠0). Then from Eq. 24-1, the final potential energy U f≡U of the system isΔU = U f–U i= -W (24-1)U = -W∞(24-2)功的單位ΔU = U f–U i= -W (24-1)Adjacent points that have the same electric potential form an equipotential surface.No net work W is done on a charged particle by an electric field when the particle moves between two points i and f on the same equipotential surface. This follows from Eq. 24-7, which tells us that W must be zero if V f=V i.Because of the path independence of work(and thus of potential energy and potential), W=0 for any path connecting points i and f on a given equipotential surface regardless of whether that path lies entirely on that surface.1) The work done by the electric field on a charged particle as the particle moves from one end to the other of paths I and II is zero because each of these paths begins and ends on the same equipotentialsurface.2) The work done as the charged particle moves from one end to the other of paths III and IV is not zero but has the same value for both these paths because the initial and finalpotentials are identical for the two paths.e.g.DiscussionFrom symmetry, the equipotential surfaces produced by a point charge or a spherically symmetrical charge distribution are a family of concentric spheres.Equipotential surfaces are always perpendicular to electric field lines and thus to E, which is always tangent to these lines. If E were not perpendicular to an equipotential surface, it would have a component lying along that surface. This component would then do work on a charged particle as it moved along the surface.¨By Eq. 24-7 work cannot be done if the surface is truly an equipotential surface [V i=V f, W=0]; the only possible conclusion is that E must be everywhere perpendicular to the surface.perpendicularvf v可得(V=0, r=∞)∞單位正電荷q3q q21rO p = qd 其中p為電偶極矩22Many molecules, such as water, have permanent electric dipole moments. In other molecules (called nonpolar molecules) and in every isolated atom, the centers of the positive and negative charges coincide and thus no dipole moment is set up. If we place an atom or a nonpolar molecule in an external E-field, the field distorts the electron orbits and separates the centers of positive and negative charge. Because the electrons are negatively charged, they tend to be shifted in a direction opposite the field. This shift sets up a dipole moment that points in the direction of the field. This dipole moment p is said to be induced by the field, and the atom or molecule is then said to be polarized (極化) by the field. When the field is removed, the induced dipole moment pind and the polarization disappear.23Continuous distribution of charge (電荷連續分佈) → 將電荷 連 續 分 佈 源 切 割 成 無 數 細 小 微 分 電 荷 元 素 (dq) → dV dq=λds=σdA=ρdvPdV =1 4 πε0dq rdv dqr→ Use calculus (微積分) to calculate V已在§24-6假設無窮遠處之電位為024V=? λ dq=λdx假設2526取微分元素環dq27In Sec. 24-5, 已知 electric field 可求出 V In this section, 已知 electric potential 可求出E E=?A positive test charge q0 moves through a displacement ds from one equipotential surface to the adjacent surface.28(1) From Eq. 24-7, we see that the work the electric field does on the test charge during the move is dW=–q0dV. (2) From Eq. 24-16 and Fig. 24-14, we see that the work done by the electric field may also be written as the scalar product dW=(q0E)•ds, or q0E(cosθ)ds.Fig. 24-142930For any value of z, the direction of E must be along that axis because the disk has circular symmetry about that axis →只有E z≠0, E x=E y=0(1) 由q 1建立一電位雙點電荷粒子系統具有之電位能由q 1建立(2)<proof><example>(a) A plot of V(r) both inside and outside a charged spherical shell of radius 1.0 m. (b) A plot of E(r) for the same shell.On nonspherical conductors, a surface charge does not distribute itself uniformly over the surface of the conductor. At sharp points or sharp edges, the surface charge density—and thus the external electric field, which is proportional to it—may reach very high values (導體尖端處電荷分佈非常集中,使得電荷密度相當高,故電場於該尖端附近相當強).The air around such sharp points oredges may become ionized(離子化),producing the corona (冠狀) discharge.Such corona discharges, like hair thatstands on end, are often the precursors(前兆) of lightning strikes. In such circumstances, it is wise to encloseyourself in a cavity inside a conductingshell, where the electric field is guaranteedto be zero. A car is almost ideal.41HomeworksAns:Ans:Ans:Ans:Ans:Ans:Ans:Ans: -6.20 V.Ans: 3.24×10-2V。
K60(Rev6-Ch24-MCG)(中文)

第24章多用途时钟信号生成器(MCG)24.1 介绍多用途多用途时钟信号生成器(MCG)模块为MCU提供多种时钟源选项。
这个模块由一个频率环锁(FLL)和一个相位环锁(PLL)组成。
FLL可由一个内部或外部参考时钟控制,而PLL可由一个外部参考时钟控制。
这个模块要么在FLL或PLL输出时钟之间,要么在内部参考时钟或外部参考时钟之间选择一个时钟源以作为MCU系统时钟。
MCG操作与晶体振荡器有关,其中晶体振荡器允许一个外部晶体、陶瓷共振器或外部时钟源产生外部参考时钟。
24.1.1 特性MCG模块的关键特性:◆频率环锁(FLL)。
●数控石晶(DCO)。
●DCO可设置时钟范围有四个。
●低频率外部参考时钟源的编程选项和最大DCO输出频率。
●内外参考时钟可以作为FLL源。
●可以作为其他片上外设的时钟源。
◆相位环锁(PLL)●电压控制振荡器(VCO)●外部参考时钟作为PLL时钟源。
●VCO频分模块。
●相位/频率检测器。
●集成环过滤器。
●可以作为其他片上外设的时钟源。
◆内参考时钟生成器●9个微调位的精确慢时钟●4个微调位的快时钟●可以被用作FLL的时钟源。
在FEI模式下,只有慢内参考时钟(IRC)可以被用作FLL源。
●无论是快时钟还是慢时钟都不能用作MCU的时钟源●可以作为其他片上外设的时钟源。
◆低功耗的石晶时钟发生器位MCG外部参考提供控制信号:●HGO,RANGE,EREFS◆从晶振获得外部时钟●可被用作FLL或PLL的时钟源●可被用作MCU的时钟源◆从RTC获得外部时钟●只能作为FLL的时钟源●只能选择MCU的时钟源◆带有重置请求能力的外部时钟监视器,可以在FBE,PEE,BLPE或者FEE模式下对外部时钟进行监测◆在PLL中使用的有中断请求能力的锁检测器◆外时钟参考的内参考时钟自动裁切功能(ATM)。
◆FLL和PLL的参考分频。
◆为其他片上设备提供时钟源的MCG PLL 时钟(MCGPLLCLK)◆为其他片上设备提供时钟源的MCG FLL时钟(MCGPLLCLK)◆为其他片上设备提供时钟源的MCG Fixed Frequency时钟(MCGPLLCLK)◆为其他片上设备提供时钟源的MCG 内参考时钟(MCGPLLCLK)图24-1 多用途时钟生成器(MCG)框图24.1.2 运行模式MCG共有九中运行模式:FEI,FEE,FBI,FBE,PEE,BLPI,BLPE,和终止模式。
公司理财精要版原书第12版英文版最新精品课件Ross_12e_PPT_Ch24

OPTION VALUATION
Copyright © 2019 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
• Similar to paying an insurance premium to protect against potential loss
• Trade-off between the amount of protection and the price that you pay for the option
EXAMPLE: FINDING THE CALL PRICE
• You have looked in the financial press and found the following information:
▪ Current stock price = $50 ▪ Put price = $1.15 ▪ Exercise price = $45 ▪ Risk-free rate = 5% ▪ Expiration in 1 year
• Call + PV(E)
▪ PV(E) will be worth E at expiration of the option ▪ If S < E, let call expire and have investment, E ▪ If S ≥ E, exercise call using the investment and have S
▪ PV = 100e-0.08(3/12) = 98.02
24个声母的正确读法

24个声母的正确读法声母,是汉语拼音系统中的一个重要组成部分,它是识别汉字音节的基本元素之一。
汉语拼音共有24个声母,它们分别是b, p, m, f, d, t, n, l, g, k, h, j, q, x, zh, ch, sh, r, z, c, s, y, w。
正确掌握这24个声母的读音,对于学好汉语拼音和提高中文水平具有重要意义。
本文将详细介绍24个声母的正确读法。
1. b:发音时,嘴唇紧闭,气流从口腔中间猛地排出,发出一声短促的爆破音。
如“笔、报、八”。
2. p:发音时,与b类似,但唇部更紧闭,气流更猛烈,发出声音更清脆的爆破音。
如“批、披、盘”。
3. m:发音时,唇部紧闭,声音从鼻腔中发出,是唇鼻音。
如“妈、面、木”。
4. f:发音时,嘴唇稍微张开,舌头轻轻触到下齿,气流从口中排出,发出轻微摩擦声。
如“飞、非、凤”。
5. d:发音时,舌头抵住上牙龈,气流从口中猛烈排出,发出一个短促的爆破音。
如“的、大、地”。
6. t:与d类似,但舌头抵住上牙齿,气流更猛烈,发出声音更清脆的爆破音。
如“特、题、天”。
7. n:发音时,舌尖抵住上齿龈,气流从鼻腔中排出,是舌齿鼻音。
如“难、年、女”。
8. l:发音时,舌尖抵住上齿龈,舌面平铺,气流从舌面两侧排出,发出舌侧音。
如“路、来、绿”。
9. g:发音时,口腔中气流受到喉部的阻碍,压力逐渐增大,然后突然爆破,发出一个短促的声音。
如“狗、高、哥”。
10. k:与g类似,但口腔中的气流更猛烈,发出声音更清脆的爆破音。
如“卡、考、客”。
11. h:发音时,口腔中气流从喉部冲出,与声带摩擦,发出一个轻微的嘶声。
如“好、汉、红”。
12. j:发音时,舌尖先抵住上齿龈,然后突然离开,气流从口中排出,发出一个清脆的爆破音。
如“家、机、鸡”。
13. q:与j类似,但口腔中的气流更猛烈,发出声音更清脆的爆破音。
如“切、七、球”。
14. x:与q类似,但发音时舌头的位置稍微向后移动一点,舌尖抵住上腭,发出一个清脆的爆破音。
不等式高级水平必备

目录Ch1. 伯努利不等式Ch2. 均值不等式Ch3. 幂均不等式Ch4. 柯西不等式Ch5. 切比雪夫不等式Ch6. 排序不等式Ch7. 琴生不等式Ch8. 波波维奇亚不等式Ch9. 加权不等式Ch10. 赫尔德不等式Ch11. 闵可夫斯基不等式Ch12. 牛顿不等式Ch13. 麦克劳林不等式Ch14. 定义多项式Ch15. 舒尔不等式Ch16. 定义序列Ch17. 缪尔海德不等式Ch18. 卡拉玛塔不等式Ch19. 单调函数不等式Ch20. 3个对称变量pqr法Ch21. 3个对称变量uvw法Ch23. SOS 法 Ch24. SMV 法 Ch25. 拉格朗日乘数法 Ch26. 三角不等式 Ch27. 习题与习题解析Ch1. 伯努利不等式1.1若实数i x (i 12n ,,...,=)各项符号相同,且i x 1>-,则:12n 12n 1x 1x 1x 1x x x ()()...()...+++≥++++ 1()1()当12n x x x x ...====时,1()式变为:n 1x 1nx ()+≥+ 2() Ch2. 均值不等式2.1若12n a a a ,,...,为正实数,记:⑴n Q =,为平方平均数,简称平方均值;⑵ 12nn a a a A n...+++=,为算术平均数,简称算术均值;⑶n G =,为几何平均数,简称几何均值; ⑷ n 12nnH 111a a a ...=+++,为调和平均数,简称调和均值.则:n n n n Q A G H ≥≥≥ 3()iff 12n a a a ...===时,等号成立. (注:iff if and only if =当且仅当.)Ch3.幂均不等式3.1设12n a a a a (,,...,)=为正实数序列,实数r 0≠,则记:1r r rr12n r a a a M a n ...()⎛⎫+++= ⎪⎝⎭4()4()式的r M a ()称为幂平均函数.3.2若12n a a a a (,,...,)=为正实数序列,且实数r 0≠,则:r s M a M a ()()≤ 5()当r s ≤时,5()式对任何r 都成立,即r M a ()关于r 是单调递增函数.5()3.3设12n m m m m (,,...,)=为非负实数序列,且12n m m m 1...+++=,若12n a a a a (,,...,)=为正实数序列,且实数r 0≠,则:1m rrr rr1122n n M a m a m a m a ()(...)=+++ 6()6()式称为加权幂平均函数.3.4若12n a a a a (,,...,)=为正实数序列,且实数r 0≠,对m r M a ()则:m m r s M a M a ()()≤即:11rrr sss sr1122n n 1122n n m a m a m a m a m a m a (...)(...)+++≤+++ 7()当r s ≤时,7()式对任何r 都成立,即m r M a ()关于r 是单调递增函数.7()Ch4. 柯西不等式4.1若12n a a a ,,...,和12n b b b ,,...,均为实数,则:222222212n 12n 1122n n a a a b b b a b a b a b (...)(...)(...)++++++≥+++ 8()iffn 1212na a ab b b ...===时,等号成立.(注:iff if and only if =当且仅当.)4.2柯西不等式还可以表示为:222222212n 12n 1122n n a a a b b b a b a b a b n n n.........()()()+++++++++≥ 9()简称:“平方均值两乘积,大于积均值平方” 我们将1122n na b a b a b n...+++简称为积均值,记:n D =则:224n n n Q a Q b D ab [()][()][()]≥n D ab ()≥ 10() 4.3推论1:若a b c x y z ,,,,,为实数,x y z 0,,>,则:2222n 12n 1212n 12na a a a a ab b b b b b (...)......++++++≥+++ 11() iffn 1212na a ab b b ...===时,等号成立. 11()式是柯西不等式的推论,称权方和不等式4.4推论2:若12n a a a ,,...,和12n b b b ,,...,均为实数,则:...+≥12()iffn 1212na a ab b b ...===时,等号成立. 4.5推论3:若a bc x y z ,,,,,为正实数,则:x y zb c c a a b y z z x x y()()()+++++≥+++ 13() Ch5. 切比雪夫不等式5.1若12n a a a ...≤≤≤;12n b b b ...≤≤≤,且均为实数.则:12n 12n 1122n n a a a b b b n a b a b a b (...)(...)(...)++++++≤+++ 14()iff 12n a a a ...===或12n b b b ...===时,等号成立.12()由于有12n a a a ...≤≤≤,12n b b b ...≤≤≤条件,即序列同调, 所以使用时,常采用WLOG 12n a a a ...≤≤≤…… (注:WLOG Without Loss Of Generality =不失一般性) 5.2切比雪夫不等式常常表示为:12n 12n 1122n na a ab b b a b a b a b n n n.........()()()+++++++++≤ 15()简称:“切比雪夫同调数,均值积小积均值”.即:两个序列数的均值之积不大于两个序列数各积之均值. 则:2n n n A a A b D ab ()()[()]≤n D ab ()≤ 16() Ch6. 排序不等式6.1若12n a a a ...≤≤≤;12n b b b ...≤≤≤为实数,对于12n a a a (,,...,)的任何轮换12n x x x (,,...,),都有下列不等式:1122n n 1122n n n 1n 121n a b a b a b x b x b x b a b a b a b .........-+++≥+++≥+++ 17()17().其中,1122n n a b a b a b ...+++称正序和,n 1n 121n a b a b a b ...-+++称反序和,1122n n x b x b x b ...+++称乱序和. 故17()式可记为:18()6.2推论:若12n a a a ,,...,为实数,设12n x x x (,,...,)为12n a a a (,,...,)的一个排序,则:22212n 1122n n a a a a x a x a x ......+++≥+++ 19()Ch7. 琴生不等式7.1定义凸函数:对一切x y a b ,[,]∈,01(,)α∈,若函数f a b R :[,]→是向下凸函数,则:f x 1y f x 1f y (())()()()ααα+-≤+- 20()20()式是向下凸函数的定义式.注:f a b R :[,]→表示区间a b [,]和函数f x ()在a b [,]区间都是实数.7.2若f a b R :(,)→对任意x a b (,)∈,存在二次导数f x 0''()≥,则f x ()在a b (,)区间为向下凸函数;iff x a b (,)∈时,若f x 0''()>,则f x ()在a b (,)区间为严格向下凸函数. 7.3若12n f f f ,,...,在a b (,)区间为向下凸函数,则函数1122n n c f c f c f ...+++在在a b (,)区间对任何12n c c c 0,,...,(,)∈∞也是向下凸函数.7.4若f a b R :(,)→是一个在a b (,)区间的向下凸函数,设n N ∈,12n 01,,...,(,)ααα∈为实数,且12n 1...ααα+++=,则对任何12n x x x a b ,,...,(,)∈,有:1122n n 1122n n f x x x f x f x f x (...)()()...()αααααα+++≤+++ 21()21()简称:“对于向下凸函数,均值的函数值不大于函数的均值”. Ch8. 波波维奇亚不等式8.1若f a b R :[,]→是一个在a b [,]区间的向下凸函数,则对一切x y z a b ,,[,]∈,有:x y z f x f y f z 2x y y z z xf f f f 333222()()()()[()()()]++++++++≥++ 22() 22()8.2波波维奇亚不等式可以写成:x y z f x f y f z x y y z z xf f f f 3322223()()()()()()()++++++++++≥23() 简称:“对于向下凸函数的三点情况,三点均值的函数与函数的均值之平均值,不小于两点均值的函数值之平均值”.8.3若f a b R :[,]→是一个在a b [,]区间的向下凸函数,12n a a a a b ,,...,[,]∈,则:12n 12n f a f a f a n n 2f a n 1f b f b f b ()()...()()()()[()()...()]++++-≥-+++ 24()其中:12n a a a a n...+++=,i j i j 1b a n 1≠=-∑(对所有的i ) 24()当1a x =,2a y =,3a z =,n 3=时,x y z a 3++=,1y z b 2+=,2z x b 2+=,3x yb 2+= 代入23()式得:x y z y z z x x yf x f y f z 3f 2f f f 3222()()()()[()()()]++++++++≥++ 即:x y z f x f y f z 2x y y z z xf f f f 333222()()()()[()()()]++++++++≥++ 25() 25()式正是22()式.Ch9. 加权不等式9.1若i a 0(,)∈∞,i 01[,]α∈(i 12n ,,...,=),且12n 1...ααα+++=,则:n 1212n 1122n n a a a a a a ......αααααα≤+++ 26()26()26()式形式直接理解为:几何均值不大于算术均值.Ch10. 赫尔德不等式10.1若实数a b 0,>,实数p q 1,>且111p q+=,则:p q a b ab p q ≤+ 27() iff p q a b =时,等号成立.27()10.2若12n a a a ,,...和12n b b b ,,...为正实数,p q 1,>且111p q+=,则: 11p p p q q q pq1122n n 12n 12n a b a b a b a a a b b b ...(...)(...)+++≤++++++ 28()28()iff p p pn 12q q q 12na a ab b b ...===时,等号成立.10.3赫尔德不等式还可以写成:11p p p q q q p q1122n n 12n 12n a b a b a b a a a b b b n n n.........()()+++++++++≤ 29()即:2n p q D ab M a M b [()]()()≤n D ab ()≥ 30() 简称:“幂均值的几何均值不小于积均值”. (注:赫尔德与切比雪夫的不同点:赫尔德要求是111p q+=,切比雪夫要求是同调;赫尔德的积均值小,切比雪夫的积均值大.)10.4若12n a a a ,,...、12n b b b ,,...和12n m m m ,,...为三个正实数序列,p q 1,>且111p q+=,则: 11nnnpqp qi i i i i i i i 1i 1i 1a b m a m b m ===⎛⎫⎛⎫≤ ⎪ ⎪⎝⎭⎝⎭∑∑∑ 31() 31()iff p p pn 12q q q 12na a ab b b ...===时,等号成立.10.5若ij a (i 12m ,,...,=;j 12n ,,...,=),12n ,,...,ααα为正实数且...12n 1ααα+++=,则:()()jj m mnn ijij j 1j 1i 1i 1aa αα====≤∏∏∑∑ 32()32()10.6推论:若123a a a N ,,+∈,123b b b N ,,+∈,123c c c N ,,+∈,则:3333333333123123123111222333a a a b b b c c c a b c a b c a b c ()()()()++++++≥++ 33()简称:“立方和的乘积不小于乘积和的立方”. Ch11.闵可夫斯基不等式11.1若12n a a a ,,...,;12n b b b ,,...,为正实数,且p 1>,则:111nnnppppppi i i i i 1i 1i 1a b a b (())()()===+≤+∑∑∑ 34()iffn 1212na a ab b b ...===时,等号成立. 34()11.2若12n a a a ,,...,;12n b b b ,,...,为正实数,且p 1>,则:11nnn pp p p p pi i i i i 1i 1i 1a b a b ()()()===⎛⎫+≤+ ⎪⎝⎭∑∑∑ 35()iffn 1212na a ab b b ...===时,等号成立. 35()11.3若12n a a a ,,...,;12n b b b ,,...,;12n m m m ,,...,为三个正实数序列,且p 1>,则:111nnnp p p pppi i i i i i i i 1i 1i 1a b m a m b m (())()()===+≤+∑∑∑ 36()iffn 1212na a ab b b ...===时,等号成立. 36()Ch12.牛顿不等式12.1若12n a a a ,,...,为任意实数,考虑多项式:n n 112n 01n 1n P x x a x a x a c x c x c x c ()()()...()...--=+++=++++ 37()的系数01n c c c ,,...,作为12n a a a ,,...,的函数可表达为:0c 1=;112n c a a a ...=+++;21213n 1n i j c a a a a a a a a ...-=+++=∑;(i j n <≤) 3i j k c a a a =∑;(i j k n <<≤) ……n 12n c a a a ...=.对每个k 12n ,,...,=,我们定义k k k k n c k n k p c C n !()!!-== 38() 则37()式类似于二项式定理,系数为:kk nk c C p =. 12.2若12n a a a ,,...,为正实数,则对每个k 12n 1,,...,=-有:2k 1k 1k p p p -+≤ 39()iff 12k a a a ...===时,等号成立. 39()Ch13.麦克劳林不等式13.1若12n a a a ,,...,为正实数,按38()定义,则:111kn212k n p p p p ......≥≥≥≥ 40()iff 12k a a a ...===时,等号成立.40()Ch14.定义多项式14.1若12n x x x ,,...,为正实数序列,并设12n ,,...,ααα为任意实数.记:n 1212n 12n F x x x x x x (,,...,)...ααα=;12n T [,,...,]ααα为12n F x x x (,,...,)所有可能的积之和,遍及12n ,,...,ααα的所有轮换.14.2举例说明⑴ T 100[,,]:表示共有3个参数的所有积之和,共有36!=项.第1个参数的指数是1,第2和第3个参数的指数是0.故:[,,]()!()()100100100T 10031x y z y x z z y x 2x y z =-⋅++=++.⑵ T 11[,]:表示共有2个参数的所有积之和,共有22!=项.第1个和第2个参数的指数是1.故:[,]()!()11T 1121x y 2xy =-⋅=.⑶ T 12[,]:表示共有2个参数的所有积之和,共有22!=项.第1个参数的指数是1,第2个参数的指数是2.故:[,]()!()121222T 1221x y y x xy x y =-⋅+=+.⑷ T 121[,,]:表示共有3个参数的所有积之和,共有36!=项.第1个参数的指数是1,第2个参数的指数是2,第3个参数的指数是1.故:[,,]()222T 1212xy z x yz xyz =++.即:[,,][,,]T 121T 211=⑸ T 210[,,]:表示共有3个参数的所有积之和,共有36!=项.第1个参数的指数是2,第2个参数的指数是1,第3个参数的指数是0.故:222222T 210x y x z y x y z z x z y [,,]=+++++.⑹ T 300[,,]:表示共有3个参数的所有积之和,共有36!=项.第1个参数的指数是3,第2个和第3个参数的指数是0.故:333T 3002x y z [,,]()=++.⑺ [,,]T a b c :表示共有3个参数的所有积之和,共有36!=项.第1个参数的指数是a ,第2个参数的指数是b ,第3个参数的指数是c .故:[,,]a b c a c b b c a b a c c a b c b a T a b c x y z x y z x y z x y z x y z x y z =+++++.由于[,,][,,][,,][,,][,,]...T a b c T b c a T c a b T c b a T b a c =====表达式比较多,所以我们规定:[,,]T a b c (a b c ≥≥).Ch15.舒尔不等式15.1若R α∈,且0β>,则:[,,][,,][,,]T 200T 2T 0αβαββαββ++≥+ ()41()4115.2 解析()41式[,,]()222T 2002x y z αβαβαβαβ++++=++;[,,]()T 2x y z x y z x y z αβββαβββααββ=++;[,,]T 0x y x y y z y z x z x z αβββαβαβββαββαβαββαββ+++++++=+++++将上式代入()41式得:222x y z x y z x y z x y z αβαβαβαβββαβββα++++++++x y x y y z y z x z x z αβββαβαβββαββαβαββ++++++≥+++++即:222y x y z z x y x z x y z αβααββαβαβββββα++++++++y x y y z x y x z 0z x z βαβββααββαβββαβαββ++++++------≥即:()()22x x y z x y x z y y x z x y y z αβββββββαβββββββ++--+--()2z z x y y z x z 0αβββββββ++-≥-即:()()()()()()x x y x z y y z y x z z x z y 0αββββαββββαββββ--+--+--≥ ()42()42式与()4115.3若实数,,x y z 0>,设t R ∈,则:()()()()()()t t t x x y x z y y z y x z z x z y 0--+--+--≥ ()43iff x y z ==或,x y z 0==及轮换,等号成立.按照()41式写法,即:t α=,1β=,则:[,,][,,][,,]T t 200T t 112T t 110++≥+ ()44()43式是我们最常见的舒尔不等式形式.15.4推论:设实数,,x y z 0>,实数,,a b c 0>且a b c ≥≥或a b c ≤≤,则:()()()()()()a x y x z b y z y x c z x z y 0--+--+--≥ ()45()43式中,t x a =,t y b =,t z c =,就得到()45式.15.5推论:设实数,,x y z 0>,则:[()()()]3333332223xyz x y z 2xy yz zx +++≥++ ()4615.6推论:若(,]k 03∈,则对于一切,,a b c R +∈,有:()()()2222k 3k k abc a b c 2ab bc ca -++++≥++ ()47Ch16. 定义序列16.1设存在两个序列()(,,...,)n i i 112n ββββ==和()(,,...,)n i i 112n αααα==,当满足下列条件:⑴ ......12n 12n βββααα+++=+++ ①⑵ ...12n βββ≥≥≥且...12n ααα≥≥≥ ②⑶ ......12s 12s βββααα+++≤+++ ③对一切[,]s 1n ∈,③式都成立.则:()n i i 1β=就是()n i i 1α=的优化值,记作:()()i i βα<.注:这里的序列只有定性的比较,没有定量的比较.Ch17.缪尔海德不等式17.1若,,...,12n x x x 为非负实数序列,设()i α和()i β为正实数序列,且()()i i βα<,则:[][]i i T T βα≤ ()48iff ()()i i αβ=或...12n x x x ===时,等号成立.()4817.2解析()48式若实数123a a a 0≥≥≥,实数123b b b 0≥≥≥,且满足11a b ≥,1212a a b b +≥+,123123a a a b b b ++=++;设,,x y z 0>,则:满足序列(,,)(,,)123123b b b a a a <条件, 则:[,,]333333121221211221b b b b b b b b b b b b b b b b b b 123T b b b x y z x y z x y z x y z x y z x y z =+++++[,,]333333121221211221a a a a a a a a a a a a a a a a a a 123T a a a x y z x y z x y z x y z x y z x y z =+++++ 即()48式为: [,,][,,]123123T b b b T a a a ≤用通俗的方法表达即:331212a b a a b b sym sym x y z x y z ≥∑∑ ()4917.3例题:设(,,)x y z 为非负变量序列,考虑(,,)221和(,,)311.由16.1中的序列优化得:(,,)(,,)221311<由缪尔海德不等式()48式得:[,,][,,]T 221T 311< ①[,,]()222222T 2212x y z x yz xy z =++ ②[,,]()333T 3112x yz xy z xyz =++ ③将②③代入①得:222222333x y z x yz xy z x yz xy z xyz ++≤++即:222xy yz zx x y z ++≤++ ④由柯西不等式:()()()2222222x y z y z x xy yz zx ++++≥++即:()()22222x y z xy yz zx ++≥++即:222x y z xy yz zx ++≥++ ⑤⑤式④式等价,这就证明了④式是成立的,而缪尔海德不等式直接得到①式是成立的. ⑤式可以用[,,][,,]T 200T 110≥来表示,这正是缪尔海德不等式的()48式.Ch18.卡拉玛塔不等式18.1设在实数区间I R ∈的函数f 为向下凸函数,且当,i i a b I ∈(,,...,i 12n =)两个序列()n i i 1a =和()n i i 1b =满足()()i i a b >,则: ()()...()()()...()12n 12n f a f a f a f b f b f b +++≥+++ ()50()5018.2若函数f 为严格向下凸函数,即不等取等号,()()i i a b ≠,且()()i i a b >,则:()()...()()()...()12n 12n f a f a f a f b f b f b +++>+++ ()51 若函数f 为严格向上凸函数,则卡拉玛塔不等式反向.Ch19.单调函数不等式19.1若实数函数:(,)f a b R →在区间(,)a b 对一切,(,)x y a b ∈为单调增函数,则当x y ≥时,有()()f x f y ≥;若f 在区间(,)a b 对一切,(,)x y a b ∈为严格单调增函数,当x y >时,有()()f x f y >.19.2若实数函数:(,)f a b R →在区间(,)a b 对一切,(,)x y a b ∈为单调减函数,则当x y ≥时,有()()f x f y ≤;若f 在区间(,)a b 对一切,(,)x y a b ∈为严格单调减函数,当x y >时,有()()f x f y <.19.3若实数函数:(,)f a b R →在区间(,)a b 为可导函数,当对一切(,)x a b ∈,'()f x 0≥,则f 在区间(,)a b 为单调递增函数;当对一切(,)x a b ∈,'()f x 0≤,则f 在区间(,)a b 为单调递减函数.19.4设两个函数:[,]f a b R →和:[,]g a b R →满足下列条件:⑴ 函数f 和g 在[,]a b 区间是连续的,且()()f a g a =;⑵ 函数f 和g 在[,]a b 区间可导;⑶ 导数'()'()f x g x >对一切(,)x a b ∈成立,则对一切(,)x a b ∈有:()()f x g x > ()52()52Ch20.3个对称变量pqr 法20.1设,,x y z R +∈,对于具有变量对称形式的不等式,采用下列变量代换:p x y z =++;q xy yz zx =++;r xyz =,则,,p q r R +∈.代换后的不等式(,,)f p q r ,很容易看出其满足的不等式关系,这样证明不等式的方法称为pqr 法.20.2常用的代换如下:⑴22cyc x p 2q =-∑ ⑵ ()32cycx p p 3q 3r =-+∑⑶ 222cycx y q 2pr =-∑⑷ ()()()x y y z z x pq r +++=-⑸()()2cyc x y y z p q ++=+∑ ⑹ ()cycxy x y pq 3r +=-∑⑺ ()()()1x 1y 1z 1p q r +++=+++⑻ ()()cyc1x 1y 32p q ++=++∑⑼()()2cyc cycx y z xy x y pq 3r +=+=-∑∑20.3常用的pqr 法的不等式若,,x y z 0≥,则:⑴ 3p qr 4pq +≥⑵ pq 9r ≥⑶ 2p 3q ≥⑷ 3p 27r ≥⑸ 32q 27r ≥⑹ 2q 3pr ≥⑺ 32p 9r 7pq +≥⑻ 322p 9r 7pqr +≥⑼ 22p q 3pr 4q +≥Ch21.3个对称变量uvw 法21.1在,,a b c R ∈的不等式中,采用下列变量代换:3u a b c =++;23v ab bc ca =++;3w abc =.上述变换强烈含有“平均”的意味:u 对应“算术平均值”;v 对应“积均值”;w 对应“几何平均值”. 21.2当,,a b c 0≥时,则:u v w ≥≥ ()53()53即:“算术平均值”≥“积均值”≥“几何平均值”.21.3若,,a b c 0≥,则,,23u v w 0≥ ()54()5421.4若,,23u v w R ∈,任给,,a b c R ∈,则当且仅当22u v ≥,且[32323w 3uv 2u 3uv 2u ∈---+时, 则:3u a b c =++,23v ab bc ca =++,3w abc =等式成立.这称为uvw 定理.Ch22.ABC 法22.1 ABC 法即Abstract Concreteness Method设p x y z =++;q xy yz zx =++;r xyz =.则函数(,,)f x y z 变换为(,,)f r q p .这与Ch20.3个对称变量pqr 法类似.22.2若函数(,,)f r q p 是单调的,则当()()()x y y z z x 0---=时,(,,)f r q p 达到极值. 22.3若函数(,,)f r q p 是凸函数,则当()()()x y y z z x 0---=时,(,,)f r q p 达到极值. 22.4若函数(,,)f r q p 是r 的线性函数,则当()()()x y y z z x 0---=时,(,,)f r q p 达到极值. 22.5若函数(,,)f r q p 是r 的二次三项式,则当()()()x y y z z x 0---=时,(,,)f r q p 达到极值.Ch23.SOS 法23.1 SOS 法即Sum Of Squares23.2本法的全部思想是将给出的不等式改写成以下形式:()()()222a b c S S b c S a c S a b =-+-+- ()55其中,,,a b c S S S 分别都是,,a b c 的函数.⑴ 若,,a b c S S S 0≥,则S 0≥;⑵ 若a b c ≥≥或a b c ≤≤,且,,b b a b c S S S S S 0++≥,则S 0≥; ⑶ 若a b c ≥≥或a b c ≤≤,且,,,a c a b c b S S S 2S S 2S 0++≥,则S 0≥; ⑷ 若a b c ≥≥,且,,22b c b a S S a S b S 0+≥,则S 0≥;⑸ 若a b S S 0+≥或b c S S 0+≥或c a S S 0+≥,且a b b c c a S S S S S S 0++≥,则S 0≥. 23.3 常用的形式⑴ ()22cyc cyc cyc1a ab a b 2-=-∑∑∑ ⑵ ()32cyc cyc cyc1a 3abc a a b 2-=⋅-∑∑∑ ⑶ ()223cyc cyccyc 1a b ab a b 3-=-∑∑∑ ⑷ ()()322cyc cyc cyc1a a b 2a b a b 3-=+-∑∑∑ ⑸()333cyc cyccyc cyc 1a b ab a b a 3-=⋅-∑∑∑∑ ⑹ ()()42222cyc cyc cyca ab 2a b a b -=+-∑∑∑ Ch24.SMV 法24.1 SMV 法即Strong Mixing Variables Method本法对多于2个变量的对称不等式非常有用.24.2 设(,,...,)12n x x x 为任意实数序列,⑴ 选择,{,,...,}i j 12n ∈使min{,,...,}i 12n x x x x =,max{,,...,}j 12n x x x x =; ⑵ 用其平均数i j x x 2+代替i x 和j x ,经过多次代换后各项i x (,,...,i 12n =)都趋于相同的极限...12n x x x x n+++=. 24.3 设实数空间的函数F 是一个对称的连续函数,满足(,,...,)(,,...,)12n 12n F a a a F b b b ≥ ()56其中,(,,...,)12n b b b 序列是由(,,...,)12n a a a 序列经过预定义变换而得到的.预定义变换可根据当前的题目灵活采用,如a b 2+. 24.4 例题说明例题:设实数,,a b c 0>,证明:a b c 3b c c a a b 2++≥+++. 解析:采用SMV 法. 设:(,,)a b c f a b c b c c a a b =+++++ ① 则:(,,)t t c 2t c f t t c t c c t t t t c 2t =++=+++++ ② 其中,a b t 2+=. 由②得:(,,)()()2t c 112t c t 113f t t c 2t c 2t 22t c 2t 222+=++-=+-≥-=++ 由()56式得:(,,)(,,)3f a b c f t t c 2≥≥证毕. Ch25.拉格朗日乘数法 25.1 设函数(,,...,)12n f x x x 在实数空间的I R ∈连续可导,且(,,...,)i 12n g x x x 0=,其中(,,....i 12k =),即有k 个约束条件,则(,,...,)12n f x x x 的极值出现在I 区间的边界或偏导数(函数为ki i i 1L f g λ==-∑)全部为零的点上.Ch26.三角不等式26.1 设,,(,)0αβγπ∈,且αβγπ++=,则,,αβγ就是同一个三角形的内角. 26.2 若,,αβγ为同一个三角形的内角,则有下列不等式:⑴ sin sin sin 2αβγ++≤; ⑵ cos cos cos 32αβγ++≤;⑶ sin sin sin αβγ≤⑷ cos cos cos 18αβγ≤; ⑸ sin sin sin 22294αβγ++≤; ⑹ cos cos cos 22234αβγ++≥; ⑺ tan tan tan αβγ++≥;⑻ cot cot cot αβγ++≥;⑼ sinsin sin 32222αβγ++≤;⑽ coscos cos 222αβγ++≤; ⑾ sinsin sin 12228αβγ≤;⑿ cos cos cos 222αβγ≤; ⒀ sin sin sin 22232224αβγ++≥; ⒁ cos cos cos 22292224αβγ++≤;⒂tan tantan222αβγ++≥⒃cotcotcot222αβγ++≥Ch27.习题27.1 设,,...,(,]12n x x x 01∈,求证:()()...()321111x x x n 12n 1x 1x 1x 2+++≥.27.2 设,,...,12n x x x 0≥,且...12n 1x x x 2+++=,求证:()()...()12n 11x 1x 1x 2---≥. 27.3 设,,...,12n a a a R +∈,且...12n a a a 1=......12n a a a +≤+++. 27.4 设,,a b c 0>,且abc 1=,求证:333a b c ab bc ca ++≥++. 27.5 设,,,a b c d 0>,求证:a b c d 2b 2c 3d c 2d 3a d 2a 3b a 2b 3c 3+++≥++++++++.27.6 设,,a b c 0>,求证:222a bc b ca c aba b c b c c a a b+++++≥+++++. 27.7设,a b 0>,n N ∈,求证:()()n n n 1a b112b a++++≥.27.8 设,,...,12n x x x R +∈,且...22212n x x x 1+++=,若n N ∈,n 2≥,求(,,...,)...()()()555n 1212n nnni 1i 2i ni 1i 1i 1x x x f x x x x x x x x x ====+++---∑∑∑的最小值.27.9 设,,a b c R +∈,且a b c abc ++=32≤. 27.10 设,,a b c R ∈. 27.11设,,a b c R +∈,且ab bc ca 3++=,求证:()()()2221a 1b 1c 8+++≥.27.12设,,a b c 0>,且a b c 1++=,求证:()()3332226a b c 15a b c +++≥++. 27.13设,,a b c 0≥,且a b c 2++=,求证:444333a b c abc a b c +++≥++.27.14设,,a b c 0>,求证:()()()()3333338a b c a b b c c a ++≥+++++. 27.15设,,a b c 0≥,求证:()33331a b c abc a b c 7+++≥++. 27.16设,,a b c 0>,且a b c 1++=,求证:2224a b c 3abc 9+++≥. 27.17设,,...,12n a a a 0>,求证:()()...()()()...()222n 1212n 231a a a 1a 1a 1a 111a a a +++≤+++.27.18设,,,a b c d 0>,且abcd 1=,求证:()()()()2222111111a 1b 1c 1d +++≥++++.27.19设,,,a b c d 0≥,且a b c d 4+++=,求证:()()()()2222abc bcd cda dab abc bcd cda dab 8+++++++≤.27.20设,,a b c 0≥,且222a b c 3++=,求证:222222a b b c c d a b c ++≤++.27.21设,,a b c R ∈,求证:()()()2222223333333a ab b b bc c c ca a a b b c c a -+-+-+≥++.27.22设,,,a b c d 0>,且a b c d abcd 5++++=,求证:11114a b c d+++≥.27.23设不等式:()()()()2222222222ab a b bc b c ca c a M a b c -+-+-≤++对一切实数,,a b c 都成立,求M 的最小值.27.24设,,a b c 0≥,且a b c 3++=,求证:()()222a b b c c a ab bc ca 9++++≤.Ch27.习题解析27.1 设,,...,(,]12n x x x 01∈,求证:()()...()321111x x x n 12n 1x 1x 1x 2+++≥.解析:设:n 11x x +=,则:因为i x 01(,]∈,所以i11x [,)∈+∞ (i 12n ,,...,=) 由伯努利不等式2():当i x 1>-且i 1[,)α∈+∞时,i i i i 1x 1x ()αα+≥+ ①iff i x 0=或i 1α=时,①式等号成立.由均值不等式3():i i 1x α+≥ ②iff i i x 1α=时,②式等号成立.由①②式得:i i 1x ()α+≥ ③iff i i x 1α==时, ③式等号成立.设:i i 11x α+=,则由③式得:i 11x i 1x ()++≥ ④则:21x 11x ()+≥31x 21x ()+≥11x n 1x ()+≥上面各式相乘得:321111x x x n 12n 1x 1x 1x 22()()...()+++≥=. 证毕.27.2 设,,...,12n x x x 0≥,且...12n 1x x x 2+++=,求证:()()...()12n 11x 1x 1x 2---≥. 解析:因为i x 0≥,ni i 11x 2==∑,所以i 1x 02[,]∈ 设i i y x =-,则i 1y 012[,]∈->-由伯努利不等式1():12n 12n 1y 1y 1y 1y y y ()()...()(...)+++≥++++ ① 将i i y x =-代入①式,并代入...12n 1x x x 2+++=得: 12n 12n 111x 1x 1x 1x x x 122()()...()(...)---≥-+++=-=. 证毕.27.3 设12n a a a 0,,...,>,且...12n a a a 1=......12n a a a +≤+++. 解析:因为12n a a a 0,,...,>,且...12n a a a 1=,所以由均值不等式3()n ...+≥=1≥ ①iff 12n a a a 1...====时,①式等号成立.由柯西不等式8():2222222111...](...)...++++++≥+ 即:212n a a a n (...)...+++⋅≥即:12n a a a (...)...+++≥+ ②iff 12n a a a 1...====时,②式等号成立.将①式代入②式得:12n a a a ......+++≥+ ③iff 12n a a a 1...====时, ③式等号成立. 证毕.27.4 设,,a b c 0>,且abc 1=,求证:333a b c ab bc ca ++≥++. 解析:因为,,a b c 0>,且abc 1=,所以由均值不等式3():222222222a b b c c a a b c ab bc ca 222+++++=++≥++ ① iff a b c 1===时,①式等号成立.由均值不等式3():a b c 3++≥=,即:a b c13++≥ ② iff a b c 1===时,②式等号成立.WLOG ,设a b c ≤≤,则因为,,a b c 0>,所以222a b c ≤≤由切比雪夫不等式14():222222a b c a b c 3a a b b c c ()()()++++≤⋅+⋅+⋅ 即:333222a b ca b c a b c 3()++++≥⋅++ ③ iff a b c 1===时,③式等号成立.将①②代入③式得:333a b c ab bc ca ++≥++ ④iff a b c 1===时, ④式等号成立. 证毕.27.5 设,,,a b c d 0>,求证:a b c d 2b 2c 3d c 2d 3a d 2a 3b a 2b 3c 3+++≥++++++++.解析:记A b 2c 3d =++,B c 2d 3a =++,C d 2a 3b =++,D a 2b 3c =++则:aA bB cC dD 4ab ac ad bc bd cd ()+++=+++++ ① 待证式为:a b c d 2A B C D 3+++≥ ② 由柯西不等式8():2a b c daA bB cC dD a b c d A B C D()()()++++++≥+++ 即:2a b c d a b c d A B C D aA bB cC dD ()++++++≥+++ ③由②③式,只需证明2a b c d 2aA bB cC dD 3()+++≥+++ ④ 设多项式:P x x a x b x c x d ()()()()()=++++43201234c x c x c x c x c =++++则: 1c a b c d =+++ ⑤2c ab ac ad bc bd cd =+++++代入①式得:2aA bB cC dD 4c +++= ⑥ 根据定义38():k k k nc p C =得:11114c c p C 4==,即:11c 4p =;22224c c p C 6==,即:22c 6p = 则:2221112222c 16p p 24c a b cd aA bB cC 6p 3D p d 4()==⋅++⋅+++=+ ⑦ 由麦克劳林不等式40():1212p p ≥,即:212p 1p ≥代入⑦式得:2a b c d aA bB c dD 23C ()++++≥++,④式得证. iff a b c d ===时,等号成立. 证毕.27.6 设,,a b c 0>,求证:222a bc b ca c aba b c b c c a a b +++++≥+++++. 解析:不等式左边=222a b c b c c b c c b c a c a a b ba a ab +++++++++++ 不等式右边=()()()a c ab a bc b c a b c c a a b b c +++++=+++++222ab a ac b c c a b c c a a b b c ca b b =+++++++++++ 则不等式其实就是:222222a b c c a b b c c a a b b c c a a b++≥++++++++ ① 由于是对称不等式,WLOG ,假设a b c ≥≥,则222a b c ≥≥ ②且b c a c a b +≤+≤+,即:111b c c a a b ≥≥+++③ 则有排序不等式()18:222222a b c c a b b c c a a b b c c a a b ++≥++++++++ 其中,222a b c b c c a a b +++++为正序和;222c a b b c c a a b+++++为乱序和. iff a b c ==时,等号成立. 证毕.27.7设,a b 0>,n N ∈证:()()n n n 1a b112b a++++≥.解析:当n 0=时,()()00a b112b a+++=,0122+=,不等式成立;当n 1=时,()()11a b a b1124b a b a+++=++≥,1124+=,不等式成立;当n 2≥时,构建函数()n f x x =. 则函数的导数'()n 1f x nx -=;二次导数''()()n 2f x n n 1x 0-=-≥,故在x 0>时函数为向下凸函数. 由琴生不等式()20:()()()1212f x f x x x f 22++≥ ①将()()n 1a f x 1b =+,()()n 2bf x 1a=+ ,()()()[][()]n n n 12b a 11x x 1b a a b f 12222a b++++==++≥ 带入①式得:()()n nn a b11b a 22+++≥,即:()()n n n 1a b 112b a ++++≥ 综上,当n 0=、n 1=和n 2≥时, ()()n n n 1a b112b a ++++≥都成立,即n N ∈时,()()n n n 1a b112b a++++≥成立. 证毕.27.8 设,,...,12n x x x R +∈,且...22212n x x x 1+++=,若n N ∈,n 2≥,求(,,...,)...()()()555n 1212n nnni 1i 2i ni 1i 1i 1x x x f x x x x x x x x x ====+++---∑∑∑的最小值.解析:记ni i 1S x ==∑,(,,...,i 12n =).则(,,...,) (555)n 1212n 12nx x x f x x x S x S x S x =+++---①WLOG 假设...12n x x x ≥≥≥,则...44412n x x x ≥≥≥ ② 由于ni i 1S x ==∑,所以()nk i k i 1S x x x =-=-∑与k x 无关,则kkx S x -与k x 同单调性. 即:...n 1212nx x x S x S x S x ≥≥≥--- ③ 由切比雪夫不等式14():若(,,...,)12n a a a 与(,,...,)12n b b b 同单调性,则有:12n 12n 1122n n a a a b b b n a b a b a b (...)(...)(...)++++++≤+++ ④设:4i i a x =,ni nx b S x =-,(,,...,i 12n =),则满足{}i a 与{}i b 同单调性. 代入④式得:(...)(...)(...)4444n n 111n 1n 1n 1nx x x x x x n x x S x S x S x S x ++++≤⋅++⋅----即:......()(...)5445n 1n n 111n 1n x x x x x xf S x S x n S x S x ++=++≥⋅++---- ⑤由均值不等式()3:n n Q A ≥...221n x x 1n n ++=故:...441n 1x x n++≥ ⑥ 构建函数:()xg x S x=- ⑦ 则导函数:'()()2S g x S x =-,''()()32Sg x 0S x =>- 故()g x 为向下凸函数.由琴生不等式21():(...)()()...()1122n n 1122n n g x x x g x g x g x αααααα+++≤+++ 取加权i 1nα=(,,...,i 12n =)时,上式变为: ...()()...()()12n 12n x x x g x g x g x g n n++++++≤ ⑧即:...()()...()()12n12n x x x g x g x g x n g n++++++≥⋅即:.........12n n 112n 1nx x x Sx x n n n n n x x x S S x S x n 1S S n n +++++≥⋅=⋅=+++-----⑨ 将⑥和⑨式代入⑤式得:...()55n 11n x x 11n 1f S x S x n n n 1n n 1=++≥⋅⋅=---- 故:(,,...,)12n f x x x 的最小值是()1n n 1-.27.9 设,,a b c R +∈,且a b c abc ++=32≤. 解析:在圆锥曲线里,椭圆方程为:2222x y 1ab+=时,常常采用的参数方程是:cos x a θ=,sin y b θ=,因为将它带入方程时满足cos sin 221θθ+=,这个三角函数的基本关系. 对于三角形的内角,,A B C ,同样有关系A B C π++=和tan tan tan tan tan tan A B C A B C ++=. 而本题初始条件a b c abc ++=.设tan a A =.tan b B =,tan c C =,因为,,a b c R +∈,所以,,(,)A B C 02π∈ ①则当,,A B C 为三角形的内角时,A B C π++=, tan tan tan tan tan tan A B C A B C ++=满足条件. 带入不等式左边得:+=cos cos cos A B C =++ ②构建函数()cos f x x =-,则在(,)x 02π∈区间函数()f x 为向下凸函数,故由琴生不等式21()得:函数值的均值不小于均值的函数值.1122n n 1122n n f x x x f x f x f x (...)()()...()αααααα+++≤+++ ③当加权...12n 1nααα====时,③式变为: ()()...()...()12n 12nf x f x f x x x x f n n ++++++≥即:()()()()f A f B f C A B Cf 33++++≥ ④即:cos cos cos cos()cos A B C A B C 13332π++++-≥-=-=-即:cos cos cos 3A B C 2++≤ ⑤32+≤. 证毕.解析:因为,,a b c R ∈,由柯西不等式12()式...+≥=≥==.2≥. 证毕. 27.11设,,a b c R +∈,且ab bc ca 3++=,求证:()()()2221a 1b 1c 8+++≥. 解析:对赫尔德不等式32():jjm nn mijij i 1j 1j 1i 1aa ()()αα====≤∑∏∏∑ 32()当 n 4=,m 4=,123414αααα====时,32()式为: ()()()()1111444411121314212223243132333441424344a a a a a a a a a a a a a a a a +++[()()()()]1411213141122232421323334314243444a a a a a a a a a a a a a a a a ≤++++++++++++即:()()()()11213141122232421323334314243444a a a a a a a a a a a a a a a a ++++++++++++[()()()()]11114444411121314212223243132333441424344a a a a a a a a a a a a a a a a ≥+++ ①设:11a 1=,221a a =,231a b =,2241a a b =;12a 1=,2222a c a =,232a c =,242a a =;13a 1=,223a c =,2233a b c =,243a b =; 14a 1=,24a 1=,34a 1=,44a 1=.代入①式得:()()()()2222222222221a b a b 1c a c a 1c b c b 1111+++⋅+++⋅+++⋅+++[()()()()]1111222222222222444441111a c a c 1b c b c 1a b a b 1≥⋅⋅⋅+⋅⋅⋅+⋅⋅⋅+⋅⋅⋅ ()41ac bc ab =+++ ②②式就是赫尔德不等式.()()()2222221a 1b 1c +++()()()()()()2222221a 1b 1c 1a 1b 1c =++⋅++⋅++()()()2222222222221a b a b 1c a c a 1b c b c =+++⋅+++⋅+++()()()()222222222222222211a b a b 1c a c a 1b c b c 11114=+++⋅+++⋅+++⋅+++ ()()()()222222222222222211a b a b 1c a c a 1c b c b 11114=+++⋅+++⋅+++⋅+++ 将②式代入上式得:(())()()2222224111a 1b 1c 4ac bc ab ++++++≤开方出来即:()()()()222211a 1b 1c 21ac bc ab ++++++≤③ 将ab bc ca 3++=代入③式得:()()(())222211a 1b 1c 8213++++=≤. iff a b c 1===时等号成立. 证毕.27.12设,,a b c 0>,且a b c 1++=,求证:()()3332226a b c 15a b c +++≥++. 解析:采用pqr 法.设:p a b c =++,q ab bc ca =++,r abc =,则:p 1=⑴22cycx p 2q=-∑; ⑵ ()32cycx p p 3q 3r =-+∑则:2222a b c p 2q ++=-;()3332a b c p p 3q 3r 13q 3r ++=-+=-+于是,待证式变为:()()2613q 3r 15p 2q -++≥-即:28q 18r 0-+≥,即:14q 9r 0-+≥,即:3p 4pq 9r 0-+≥ ①⑴ 3p qr 4pq +≥,即:3p 4pq 9r 0-+≥ 故:①式成立,即待证式成立. 证毕.27.13设,,a b c 0≥,且a b c 2++=,求证:444333a b c abc a b c +++≥++. 解析:由舒尔不等式()43:()()()()()()t t t x x y x z y y z y x z z x z y 0--+--+--≥ ① 即:()()()t 2t 2t 2x x xy xz yz y y yz xy zx z z zx yz xy 0--++--++--+≥ 即:()()()()()()t 2t 2t 2t 1t 1t 1x x yz y y zx z z xy x y z y z x z x y ++++++++≥+++++ 即:()()()t 2t t 2t t 2t t 1t 1t 1x x yz y xy z z xyz x y z y z x z x y +++++++++++≥+++++ 即:()()()()t 2t 2t 2t 1t 1t 1t 1t 1t 1x y z x y z xyz x y z y z x z x y +++---++++++++≥+++++ 两边都加t 2t 2t 2x y z +++++得:()()()()t 2t 2t 2t 1t 1t 1t 1t 1t 12x y z x y z xyz x y z x y z +++---++++++++≥++++ ② ②式就是舒尔不等式.设t 2=,代入②式得:()()()()4443332x y z x y z xyz x y z x y z +++++≥++++ 将a b c 2++=代入上式得:()()4443332x y z 2xyz 2x y z +++≥++ 即:444333a b c abc a b c +++≥++ ③ ③式就是我们要证明的不等式. 证毕.27.14设,,a b c 0>,求证:()()()()3333338a b c a b b c c a ++≥+++++.。
衍生品市场课后习题答案-m48-ch24

(10)
Either way we lose .00003. This is a binomial version of the impossibility of a no arbitrage flat (stochastic) yield curve.
Question 24.5.
For this question, let P1 be the price of the 4 year, 5% coupon bond and let P2 be the price of the
V8.25% = e−.0825(3−1/365) − .63562e−.0825(6−1/365) = .39338.
(9)
If yields fall to 7.75%, the value will be
V7.75% = e−.0775(3−1/365) − .63562e−.0775(6−1/365) = .39338.
1.11BSP ut (.7722, .7653, .105, 0, 2, 0) = $0.0468.
(5)
304
Chapter 24 Interest Rate Mo must sum three caplets. The one year option has a value of .0248, the two year option has a value .0404, and the three year option has a value of .0483. The three caplets have a combined value of
(4)
d) The caplet is worth 1.11 two year put options with strike 1/1.11 = .9009. The no interest formula will use (.9009) (.8495) = .7653 as the strike. The caplet has a value of
ch24 移动网络(Network Mobility)Section 4.5 of RFC 3344 移动IP技术 教学课件

128.183.13.1 Internet WAN
Tunnel-1
Internet
Foreign Agent
139.88.112.1 Internet WAN
No Foreign Agent No Second Tunnel
Home Agent
128.184.25.1 HA Loopback Virtual Interface
Mobile-Router (IPv4) Foreign Agent Care-Of-Address
(Reverse Tunneling)
128.184.24.1 Virtual LAN Interface
128.184.24.2
10.2.2.1 Roaming Interface Tunnel-0
– The network prefix of the subnet delegated to a Mobile Router as the Mobile Network.
地址的网络前缀与它的家乡链路的网络前缀很可能相等。 • 当连接在家乡链路上时,移动路由器和家乡代理只是相邻的路由器。 • 当移动路由器连接在外地链路上时,路由器之间将仍然互相交换路由
更新信息,只是这时是通过一条双向的隧道。
11.2.1 家乡链路上的移动路由器
• 家乡链路的网络前缀为7. 7. 7,一个连接在这条链路上的主机具有IP 地址7.7.7.1
for Mobile IPv4 RFC5177
• This document describes network mobility extensions to the Mobile IPv4 protocol.
• The goal of introducing these extensions is to accommodate mobility scenarios where groups of hosts and routers move homogeneously (as a whole).
24声母字母表

24声母字母表声母、韵母和整体认读音节是汉语拼音的三大要素,其中声母指的是以元音和辅音开头的音节,是汉语拼音的重要组成部分。
中国的汉语拼音制度规定了有24个声母字母,它们分别是:b、p、m、f、d、t、n、l、g、k、h、j、q、x、zh、ch、sh、r、z、c、s、y、w、yi 。
一、声母:1、辅音b、p、m、f、d、t、n、l:b:表示清爆音,发音时双唇分开,上下齿略有发出爆音时的尖端,舌位在双齿之间,声带震动。
如:ban(班),bi(比)。
p:表示清爆音,发音时双唇尽量接近,上下齿接近,舌位在上下齿之间,声带震动。
如:pan(叛),pi(皮)。
m:表示清合音,发音时双唇尽量接近,上唇显眉,下唇收起,舌位在双齿之间,唇齿表达音,声带震动。
如:man(满),mi(米)。
f:表示清爆音,发音时双唇稍微接近,上下唇稍微分开,舌位在上下齿之间,唇齿表达浊音,声带震动。
如:fan(番),fu(服)。
d:表示清爆音,发音时双唇尽量接近,上下齿略有发出爆音时的尖端,舌位在双齿之间,唇齿表达浊音,声带震动。
如:dan(但),di(底)。
t:表示清爆音,发音时双唇稍微接近,上下齿分开,舌位在上下齿之间,唇齿表达浊音,声带震动。
如:tan(叹),ti(体)。
n:表示清合音,发音时双唇尽量接近,上唇显眉,下唇收起,舌位在双齿之间,唇齿表达音,声带震动。
如:nan(难),ni(尼)。
l:表示清合音,发音时唇张得略宽,舌位在双齿之间,唇齿表达音,声带震动,发出混合清音。
如:lan(烂),li(里)。
2、辅音g、k、h、j、q、x:g:表示音,发音时双唇略张,上下齿靠的很近,舌位在双齿之间,唇齿表达浊音,舌头稍稍向上拱形,声带震动。
如:gan(赶),gu估)。
k:表示音,发音时双唇略张,上下齿略有间隔,舌位在上下齿之间,唇齿表达浊音,舌头稍稍向上拱形,声带震动。
如:kan(看),ku裤)。
h:表示音,发音时双唇几乎接触,上下齿间隔不大,舌位在上下齿之间,唇齿表达浊音,舌头稍稍向上拱形,声带震动。
