2017-2018学年北京市怀柔区九年级(上)期末数学试卷含答案解析
北京市怀柔区九年级数学上册期末质量试题有答案【最新】

怀柔区第一学期初三期末质量检测数 学 试 卷第1-8题均有四个选项,符合题意的选项只有一个1. 北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用. 将178800用科学记数法表示应为A .1.788×104B .1.788×105C .1.788×106D .1.788×107 2.若将抛物线y = -122先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是 A .2)3(212-+-=x y B .2)3(212---=x y C .2)3(2-+=x y D. 2)3(212++-=x y 3.在Rt △ABC 中,∠C =90°,AC =4,BC =3,则tan A 的值为 A .34B .43C .53D .54 4. 如图,在△ABC 中,点D ,E 分别为边AB,AC 上的点,且DE ∥BC ,若AD =4,BD =8,AE =2,则CE 的长为A .2B .4C .6D .85. 如图,⊙O 是△ABC 的外接圆,∠BOC =100° )A .40︒B .50︒C .80︒D .100︒6. 网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB 的高度).中网比赛中,某运动员退出场地在距球网14米的D 点处接球,设计打出直线..穿越球,使球落在对方底线上C 处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为EDC BA第4题图 第5题图A. 1.65米B. 1.75米C.1.85米D. 1.95米 7. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O ,再任意找出圆O 的一条直径标记为AB (如图1),测量出AB =4分米;②将圆环进行翻折使点B 落在圆心O 的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C 、D (如图2);③用一细橡胶棒连接C 、D 两点(如图3); ④计算出橡胶棒CD 的长度.A .22 分米B .23分米C .32 分米D .33分米8.如图1,⊙O 过正方形ABCD 的顶点A 、D 且与边BC 相切于点E ,分别交AB 、DC 于点M 、N .动点P 在⊙O 或正方形ABCD 的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为,圆心O 与P 点的距离为y ,图2记录了一段时间里y 与的函数关系,在这段时间里P 点的运动路径为 A.从D点出发,沿弧DA →弧AM →线段BM →线段BC B.从B 点出发,沿线段BC →线段CN →弧ND →弧DAC.从A 点出发,沿弧AM →线段BM →线段BC →线段CND.从C 点出发,沿线段CN →弧ND →弧DA →线段AB二、填空题(本题共16分,每小题2分)9.分解因式:33-62+3=_________.第8题图1第8题图210.若△ABC ∽△DEF ,且对应边BC 与EF 的比为1∶3,则△ABC 与△DEF 的面积比等于 . 11. 有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可): .12.抛物线y =2(+1)2+3 的顶点坐标是 .13.把二次函数y =2-4+5化成y=a (-h )2+的形式为__________________.14. 数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组到教室内窗台旁,在点E 处测得旗杆顶部A 的仰角α为45°,旗杆底部B 的俯角β为60°. 室外测量组测得BF 的长度为5米.则旗杆AB =______米.15.1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为米2.16. 阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程.17.计算:4sin45°-8+(3-1)0+|-2|.18.如图,在△ABC 中,D 为AC 边上一点,BC =4,AC =8,CD=2.求证:△BCD ∽△ACB .19. 如图,在△ABC 中,tan A =4,∠B =45°,AB =14. 求BC 的长. 20.在平面直角坐标系Oy 中,直线3+-=x y 与双曲线ky =相交于点A (m ,2). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图;(3)若P 是坐标轴上一点,且满足P A =OA . 直接写出点P 的坐标.21.一个二次函数图象上部分点的横坐标,纵坐标y (2)求m 的值;(3)在给定的直角坐标系中,画出这个函数的图象; (4)根据图象,写出当y <0时,的取值范围.22. 如图,已知AB 是⊙O 的直径,点M 在BA 的延长线上,MD切⊙O 于点D ,过点B 作BN ⊥MD 于点C ,连接AD 并延长,交BN 于点N . (1)求证:AB =BN ;(2)若⊙O 半径的长为3,cosB =52,求MA 的长.第18题图 第19题图DB23.数学课上老师提出了下面的问题: 在正方形ABCD 对角线BD 上取一点F ,使51=D B DF . 小明的做法如下:如图① 应用尺规作图作出边AD 的中点M ; ② 应用尺规作图作出MD 的中点E ; ③ 连接EC ,交BD 于点F . 所以F 点就是所求作的点.请你判断小明的做法是否正确,并说明理由.24. 已知:如图,在四边形ABCD 中,BD 是一条对角线,∠DBC =30°, ∠DBA =45°,∠C =70°.若DC =a ,AB=b , 请写出求tan ∠ADB 的思路. (不用写出计算结果........)25.如图,在四边形ABCD 中,AD ∥BC ,∠ADC =90°,点E 是BC ,过点E 作AE 的垂线交直线CD 于点F .已知AD =4cm ,CD =2cm ,BC =5cm ,设BE 的长为 cm ,CF 的长为y cm.小东根据学习函数的经验,对函数y 随自变量的变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了与y 的几组值,如下表:((2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题 当BE =CF 时,BE 的长度约为 cm.B 26.在平面直角坐标系Oy 中,直线l n x y +-=2与抛物线3242---=m mx mx y 相交于点A(2-,7). (1)求m 、n 的值;(2)过点A 作AB ∥轴交抛物线于点B ,设抛物线 与轴交于点C 、D (点C 在点D 的左侧),求△BCD 的面积;(3)点E (t ,0)为轴上一个动点,过点E 作平行于y 轴的直线与直线l 和抛物线分别交于点P 、Q .当点P 在点Q 上方时,求线段PQ 的最大值.27. 在等腰△ABC 中,AB =AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P . (1)依题意补全图形;(2)若∠BAC =2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.28.在平面直角坐标系Oy 中,点P 的横坐标为,纵坐标为2,满足这样条件的点称为“关系点”.(1)在点A (1,2)、B (2,1)、M (21,1)、N (1,21)中, 是“关系点”的 ;(2)⊙O 的半径为1,若在⊙O 上存在“关系点”P , 求点P 坐标;(3)点C 的坐标为(3,0),若在⊙C 上有且只有....一个..“关系点”P ,且“关系点”P 的横坐标满足-2≤≤2.请直接写出⊙C 的半径r 的取值范围.第一学期期末初三质量检测数学试卷评分标准一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个9.3(-1)2. 10.19. 11.答案不唯一,<0即可. 12.(﹣1,3). 13.y =(-2)2+1. 14. 5+53. 15. 16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程.17. 解原式=4×22-22+1+2 …………………………………………………………………… 4分 =3 ………………………………………………………………………………………5分18.证明:∵BC =4,AC =8,CD =2.…………………………1分∴BC CD AC BC =………………………………………3分 又∵∠C =∠C …………………………………………………………………………4分∴ △BCD ∽△ACB ……………………………………………………………………5分19.解:过点C 作CD ⊥AB 于点D ,如图. ………………………………………………1分 ∵在Rt △CDA 中,tan A =AD CD = 43设CD =3,AD =4. ……………………………………………………………………………2分 ∵在Rt △CDB 中,∠B =45°π25∴tan B =DB CD = 1,sin B =BCCD =22,……………………………………………………………3分∵CD =3. ∴BD =3,BC =2·3=32. 又∵AB =AD+BD =14, ∴4+3=14,解得=2.…………………………………………………………………………4分∴BC =62. ……………………………………………………………………………………5分 20.解:(1)∵直线3+-=x y 与双曲线xky =相交于点A (m ,2). ∴ A (1,2)………………………………………1分∴xy 2=…………………………………………2分 (2)如图…………………………………………………………4分(3)P (0,4)或P (2,0) …………………………………………6分 21.解:(1)设这个二次函数的表达式为2()y a x h k =-+. 依题意可知,顶点为(-1,2),………………………1分 ∴ ()212++=x a y .∵图象过点(1,0), ∴()21102++=a .∴12a =-. ∴这个二次函数的表达式为()21212++-=x y …………2分 (2)25-=m .………………………………………………3分 (3)如图…………………………………………………………………………………………5分 (4)<-3或>1..…………………………………………………………………………………6分 22.(1)证明:连接OD ,…………………………1分 ∵MD 切⊙O 于点D ,∴OD ⊥MD , ∵BN ⊥MC ,D∴OD ∥BN ,…………………………………2分 ∴∠ADO =∠N ,∵OA =OD ,∴∠OAD =∠ADO ,∴∠OAD =∠N ,∴AB =BN ;………………………………………………………………………………………3分 (2)解:由(1)OD ∥BN ,∴∠MOD =∠B ,………………………………………………………………………………4分 ∴cos ∠MOD =cosB =52, 在Rt △MOD 中,cos ∠MOD ==OMOD, ∵OD =OA ,MO =MA +OA =3+MA ,∴AM 33=52,∴MA =4.5………………………………………………………………………………………5分 23.解:正确. ………………………………………………………………………………………1分 理由如下: 由做法可知M 为AD 的中点,E 为MD 的中点, ∴AD DE =41. …………………………………………………………2分 ∵四边形ABCD 是正方形,∴AD=BC ,ED ∥BC . ………………………………………………3分 ∴△DEF ∽△BFC ∴BC DE =BF DF ………………………………………………………..4分 ∵AD =BC ∴BF DF =BC DE =41∴BD DF =51………………………………………………………………………………………5分 24.解 (1)过D 点作DE ⊥BC 于点E ,可知△CDE 和△DEB 都是直角三角形;……………1分 (2)由∠C =70°,可知sin ∠C 的值,在Rt △CDE 中,由sin ∠C 和DC =a ,可求DE 的长;……………………………………………………………………………………………2分 (3)在Rt △DEB 中,由∠DBC =30°,DE 的长,可求BD 的长………………………………3分 (4)过A 点作AF ⊥BD 于点F , 可知△DF A 和△AFB 都是直角三角形; ………………4分(5)在Rt△AFB中,由∠DBA=45°,AB=b,可求AF和BF的长;(6)由DB、BF的长,可知DF的长;(7)在Rt△DF A中,由DFFA,可求tan∠ADB. ………………5分25.解:(1)1.5……………………………………… ..1分(2)如图……………………………………………4分(3)0.7(0.6~0.8均可以) .………………………….5分.26.解:(1)m=1………………………………………………………………………………………1分n=3………………………………………………………………………………………………2分(2)由(1)知抛物线表达式为y=2-4-5令y=0得,2-4-5=0.解得1=-1,2=5,……………………………………………………………………………3分∴抛物线y=2-4-5与轴得两个交点C、D的坐标分别为C(-1,0),D(5,0)∴CD=6.∵A(2-,7),AB∥轴交抛物线于点B,根据抛物线的轴对称性,可知B(6,7)………4分∴S△BCD=21.……………………………………………………………………………………5分(3) 据题意,可知P(t,-2 t+3),Q( t,t2-4 t-5),由2-4-5=-2+3得直线y=-2+3与抛物线y= 2-4-5的两个交点坐标分别为(-2,7)和(4,-5) ……………………………………………………………………………………………6分∵点P在点Q上方∴-2<t<5, ∴PQ= -t2+2 t+8=-( t-2) 2+9∵a=-1∴PQ的最大值为9.……………………………………………………………………………7分27.解:(1)如图……………………………………………1分(2) ∵∠BAC=2α,∠AHB=90°∴∠ABH=90°-2α…………………………………………………………………………… 2分∵BA=BD∴∠BDA=45°+α………………………………………………………………………………3分(3)补全图形,如图………………4分证明过程如下:∵D 关于BC 的对称点为E ,且DE 交BP 于G∴DE ⊥BP ,DG =GE ,∠DBP =∠EBP ,BD =BE ;…………………………………………5分 ∵AB=AC ,∠BAC=2α∴∠ABC=90°-α由(2)知∠ABH =90°-2α∠DBP =90°-α-(90°-2α)=α∴∠DBP =∠EBP =α∴∠BDE =2α∵AB =BD ∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45°∴DP DG =21, ∴DPDE =2, ∴DP BC =2, ∴BC =2DP .………………………………………………………………………………7分 28.解:(1)A 、M . ……………………………………………………………………………………2分(2)过点P 作PG ⊥轴于点G …………………………………………………………………3分 设P (,2)∵OG 2+PG 2=OP 2 ………………………………………………………………………………4分 ∴2+42=1∴52=1∴2=51 ∴=55∴P (55,552)或P (55-,552-)……………………………………………………5分 (3)r =556或 4117≤<r …………………………………………………………7分。
北京市怀柔区2017届九年级上期末质量检测数学试题含答案

11.分解因式: a2b b3
.
12.请写出一个开口向下,且通过( 0,3)的抛物线的表达式
.
13.农业部门引进一批新麦种 ,在播种前做了五次发芽试验 , 目的是想了
解一粒如此的麦种发芽情形
实验的麦种数 / 粒 500
发芽的麦种数 / 粒 492
发芽率 /%
98.40
,实验统计数据如下 :
500
500
题
1
2
3
4
5
6
7
8
9 10
号
答 (B) (C) (B) (D) (B) (C) (D) (A) (B) (C)
知 5. 字迹要工整 , 卷面要整洁。
一、选择题 (本题共 30 分,每小题 3 分)
第 1-10 题均有四个选项,符合题意的选项只有一个
1.2016 年 9 月 15 日 22 时 04 分 09 秒 “天宫二号”在酒泉卫星发射中
心成功发射,为祖国的航天历史打开新的历程 .“天宫二号”全长 10.4 米,
过点 A 作 AB ⊥y 轴于点 B,作正方形 ABCD(点 A、B、C、D 顺时针排列),
即称正方形 ABCD 为以 A 为圆心, OA 为半径的⊙ A 的“友好正方形” .
(1)如图 1,若点 A 的坐标为 (1,1),则⊙ A 的半径为
.
(2)如图 2,点 A 在双曲线 y= 1 (x>0)上,它的横坐标是 2,正方
北京市怀柔区 2017 届九年级上期末质量检测数 学试题含答案
数学试卷
2017.1
考 1. 本试卷共 8 页,三道大题 ,29 道小题;满分 120 分。考试时刻 120 分钟。
生 2. 认真填写第 1、 5 页密封线内的学校、姓名、考号。 3. 考生将选择题答案一律填在选择题答案表内。
2019年秋北京市怀柔区九年级上册数学期末质量试题有答案【精选】.doc

1怀柔区2017—2018学年度第一学期初三期末质量检测数 学 试 卷 2018.1第1-8题均有四个选项,符合题意的选项只有一个1. 北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用. 将178800用科学记数法表示应为A .1.788×104B .1.788×105C .1.788×106D .1.788×107 2.若将抛物线y = -12x 2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是 A .2)3(212-+-=x y B .2)3(212---=x y C .2)3(2-+=x y D. 2)3(212++-=x y 3.在Rt △ABC 中,∠C =90°,AC =4,BC =3,则tan A 的值为 A .34B .43C .53D .54 4. 如图,在△ABC 中,点D ,E 分别为边AB,AC 上的点,且DE ∥BC ,若AD =4,BD =8,AE =2,则CE 的长为A .2B .4C .6D .85. 如图,⊙O 是△ABC 的外接圆,∠BOC =100°)A .40︒B .50︒C .80︒D .100︒6. 网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB 的高度).中网比赛中,某运动员退出场地在距球网14米的D 点处接球,设计打出直线..穿越球,使球落在对方EDC A第4题图 第5题图E2底线上C 处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为A. 1.65米B. 1.75米C.1.85米D. 1.95米 7. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O ,再任意找出圆O 的一条直径标记为AB (如图1),测量出AB =4分米;②将圆环进行翻折使点B 落在圆心O 的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C 、D (如图2);③用一细橡胶棒连接C 、D 两点(如图3); ④计算出橡胶棒CD 的长度.A .22 分米B .23分米C .32 分米D .33分米8.如图1,⊙O 过正方形ABCD 的顶点A 、D 且与边BC 相切于点E ,分别交AB 、DC 于点M 、N .动点P 在⊙O 或正方形ABCD 的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O 与P 点的距离为y ,图2记录了一段时间里y 与x 的函数关系,在这段时间里P 点的运动路径为 A.从D点出发,沿弧DA →弧AM →线段BM →线段BC B.从B 点出发,沿线段BC →线段CN →弧ND →弧DAC.从A 点出发,沿弧AM →线段BM →线段BC →线段CN第8题图1第8题图2D.从C 点出发,沿线段CN →弧ND →弧DA →线段AB二、填空题(本题共16分,每小题2分)9.分解因式:3x 3-6x 2+3x =_________.10.若△ABC ∽△DEF ,且对应边BC 与EF 的比为1∶3,则△ABC 与△DEF 的面积比等于 . 11. 有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可): .12.抛物线y =2(x +1)2+3 的顶点坐标是 .13.把二次函数y =x 2-4x +5化成y=a (x -h )2+k 的形式为__________________.14. 数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E 处测得旗杆顶部A 的仰角α为45°,旗杆底部B 的俯角β为60°. 室外测量组测得BF 的长度为5米.则旗杆AB =______米.15.1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为米2.16. 阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:4请回答:这样做的依据是 .三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程.17.计算:4sin45°-8+(3-1)0+|-2|.18.如图,在△ABC 中,D 为AC 边上一点,BC =4,AC =8,CD=2.求证:△BCD ∽△ACB .19. 如图,在△ABC 中,tan A =4,∠B =45°,AB =14. 求BC 的长. 20.在平面直角坐标系xOy 中,直线3+-=x y 与双曲线ky =相交于点A (m ,2). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图;(3)若P 是坐标轴上一点,且满足P A =OA . 直接写出点P 的坐标.21.一个二次函数图象上部分点的横坐标x ,纵坐标y (2)求m 的值;(3)在给定的直角坐标系中,画出这个函数的图象; (4)根据图象,写出当y <0时,x 的取值范围.22. 如图,已知AB 是⊙O 的直径,点M 在BA 的延长线上,MD 切⊙O 于点D ,过点B 作BN ⊥MD 于点于点N .(1)求证:AB =BN ;第18题图 第19题图5DB(2)若⊙O 半径的长为3,cosB =52,求MA 的长.23.数学课上老师提出了下面的问题: 在正方形ABCD 对角线BD 上取一点F ,使51=D B DF . 小明的做法如下:如图① 应用尺规作图作出边AD 的中点M ; ② 应用尺规作图作出MD 的中点E ; ③ 连接EC ,交BD 于点F . 所以F 点就是所求作的点.请你判断小明的做法是否正确,并说明理由.24. 已知:如图,在四边形ABCD 中,BD 是一条对角线,∠DBC =30°, ∠DBA =45°,∠C =70°.若DC =a ,AB=b , 请写出求tan ∠ADB 的思路. (不用写出计算结果........)25.如图,在四边形ABCD 中,AD ∥BC ,∠ADC =90°,点E 是BC ,过点E 作AE 的垂线交直线CD 于点F .已知AD =4cm ,CD =2cm ,BC =5cm ,设BE 的长为x cm ,CF 的长为y cm.的变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:((2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;6CB(3)结合画出的函数图象,解决问题: 当BE =CF 时,BE 的长度约为 cm.26.在平面直角坐标系xOy 中,直线l : n x y +-=2与抛物线3242---=m mx mx y 相交于点A(2-,7). (1)求m 、n 的值;(2)过点A 作AB ∥x 轴交抛物线于点B ,设抛物线 与x 轴交于点C 、D (点C 在点D 的左侧),求△BCD 的面积;(3)点E (t ,0)为x 轴上一个动点,过点E 作平行于y轴的直线与直线l 和抛物线分别交于点P 、Q .当点P 在点Q 上方时,求线段PQ 的最大值.27. 在等腰△ABC 中,AB =AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P . (1)依题意补全图形;(2)若∠BAC =2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.28.在平面直角坐标系xOy 中,点P 的横坐标为x ,纵坐标为2x ,满足这样条件的点称为“关系点”.7(1)在点A (1,2)、B (2,1)、M (21,1)、N (1,21)中, 是“关系点”的 ;(2)⊙O 的半径为1,若在⊙O 上存在“关系点”P , 求点P 坐标;(3)点C 的坐标为(3,0),若在⊙C 上有且只有....一个..“关系点”P ,且“关系点”P 的横坐标满足 -2≤x≤2.请直接写出⊙C 的半径r 的取值范围.2019-2020学年度第一学期期末初三质量检测数学试卷评分标准一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一9.3x (x -1)2. 10.1:9. 11.答案不唯一,k <0即可. 12.(﹣1,3). 13.y =(x -2)2+1. 14. 5+53. 15. 16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程.17. 解:原式=4×22-22+1+2 …………………………………………………………………… 4分 =3 ………………………………………………………………………………………5分18.证明:∵BC =4,AC =8,CD =2.…………………………1分∴BC CD AC BC =………………………………………3分 又∵∠C =∠C …………………………………………………………………………4分∴ △BCD ∽△ACB ……………………………………………………………………5分π25819.解:过点C 作CD ⊥AB 于点D ,如图. ………………………………………………1分 ∵在Rt △CDA 中,tan A =AD CD = 43设CD =3x ,AD =4x . ……………………………………………………………………………2分 ∵在Rt △CDB 中,∠B =45° ∴tan B =DB CD = 1,sin B =BC CD =22,……………………………………………………………3分 ∵CD =3x . ∴BD =3x ,BC =2·3x =32x . 又∵AB =AD+BD =14, ∴4x +3x =14,解得x =2.…………………………………………………………………………4分∴BC =62. ……………………………………………………………………………………5分 20.解:(1)∵直线3+-=x y 与双曲线xky =相交于点A (m ,2). ∴ A (1,2)………………………………………1分 ∴xy 2=…………………………………………2分 (2)如图…………………………………………………………4分(3)P (0,4)或P (2,0) …………………………………………6分 21.解:(1)设这个二次函数的表达式为2()y a x h k =-+. 依题意可知,顶点为(-1,2),………………………1分 ∴ ()212++=x a y .∵图象过点(1,0), ∴()21102++=a .∴12a =-.∴这个二次函数的表达式为()21212++-=x y …………2分 (2)25-=m .………………………………………………3分(3)如图…………………………………………………………………………………………5分9(4)x <-3或x >1..…………………………………………………………………………………6分 22.(1)证明:连接OD ,…………………………1分 ∵MD 切⊙O 于点D ,∴OD ⊥MD , ∵BN ⊥MC ,∴OD ∥BN ,…………………………………2分 ∴∠ADO =∠N ,∵OA =OD ,∴∠OAD =∠ADO ,∴∠OAD =∠N ,∴AB =BN ;………………………………………………………………………………………3分 (2)解:由(1)OD ∥BN ,∴∠MOD =∠B ,………………………………………………………………………………4分 ∴cos ∠MOD =cosB =52, 在Rt △MOD 中,cos ∠MOD ==OMOD, ∵OD =OA ,MO =MA +OA =3+MA ,∴AM 33=52,∴MA =4.5………………………………………………………………………………………5分 23.解:正确. ………………………………………………………………………………………1分 理由如下: 由做法可知M 为AD 的中点,E 为MD 的中点, ∴AD DE =41. …………………………………………………………2分 ∵四边形ABCD 是正方形,∴AD=BC ,ED ∥BC . ………………………………………………3分 ∴△DEF ∽△BFC ∴BC DE =BF DF ………………………………………………………..4分 ∵AD =BC ∴BF DF =BC DE =41∴BD DF =51………………………………………………………………………………………5分 24.解: (1)过D 点作DE ⊥BC 于点E ,可知△CDE 和△DEB 都是直角三角形;……………1分 (2)由∠C =70°,可知sin ∠C 的值,在Rt △CDE 中,由sin ∠C 和DC =a ,可求DE 的长;10D……………………………………………………………………………………………2分 (3)在Rt △DEB 中,由∠DBC =30°,DE 的长,可求BD 的长………………………………3分 (4)过A 点作AF ⊥BD 于点F , 可知△DF A 和△AFB 都是直角三角形; ………………4分 (5)在Rt △AFB 中,由∠DBA =45°,AB =b ,可求AF 和BF 的长;(6)由DB 、BF 的长,可知DF 的长;(7)在Rt △DF A 中,由DF F A ,可求tan ∠ADB . ………………5分 25.解:(1)1.5……………………………………… ..1分 (2)如图……………………………………………4分(3)0.7(0.6~0.8均可以) .………………………….5分 . 26. 解:(1)m =1………………………………………………………………………………………1分 n =3………………………………………………………………………………………………2分 (2)由(1)知抛物线表达式为y =x 2-4x -5 令y =0得,x 2-4x -5=0.解得x 1=-1,x 2=5,……………………………………………………………………………3分 ∴抛物线y =x 2-4x -5与x 轴得两个交点C 、D 的坐标分别为C (-1,0),D (5,0) ∴CD =6.∵A (2-,7),AB ∥x 轴交抛物线于点B ,根据抛物线的轴对称性,可知B (6,7)………4分∴S △BCD =21.……………………………………………………………………………………5分(3) 据题意,可知P (t ,-2 t +3),Q ( t ,t 2-4 t -5),由x 2-4x -5=-2x +3得直线y =-2x +3与抛物线y = x 2-4x -5的两个交点坐标分别为(-2,7)和(4,-5) ……………………………………………………………………………………………6分 ∵点P 在点Q 上方∴-2<t <5, ∴PQ = -t 2+2 t +8=-( t -2) 2+9 ∵a =-1∴PQ 的最大值为9.……………………………………………………………………………7分27. 解:(1)如图……………………………………………1分(2) ∵∠BAC =2α,∠AHB =90°∴∠ABH =90°-2α …………………………………………………………………………… 2分 ∵BA =BD ∴∠BDA =45°+α………………………………………………………………………………3分11(3)补全图形,如图………………4分证明过程如下:∵D 关于BC 的对称点为E ,且DE 交BP 于G∴DE ⊥BP ,DG =GE ,∠DBP =∠EBP ,BD =BE ;…………………………………………5分 ∵AB=AC ,∠BAC=2α∴∠ABC=90°-α由(2)知∠ABH =90°-2α∠DBP =90°-α-(90°-2α)=α∴∠DBP =∠EBP =α∴∠BDE =2α∵AB =BD ∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45°∴DP DG =21, ∴DPDE =2, ∴DP BC =2, ∴BC =2DP .………………………………………………………………………………7分 28.解:(1)A 、M . ……………………………………………………………………………………2分(2)过点P 作PG ⊥x 轴于点G …………………………………………………………………3分 设P (x ,2x )∵OG 2+PG 2=OP 2 ………………………………………………………………………………4分 ∴x 2+4x 2=1∴5x 2=1∴x 2=51 ∴x =55± ∴P (55,552)或P (55-,552-)……………………………………………………5分12(3)r =556或 4117≤<r …………………………………………………………7分。
北京市怀柔区2017届九年级上学期期末考试数学试题

怀柔区2018——2018学年度第一学期期末九年级教学质量检测数 学 试 卷 2018.1一、选择题<共8道小题,每小题4分,共32分)下面各题均有四个选项,其中只有一个是符合题意的.1.13-的相反数是 < )YIsT09cCIN A .3- B .3 C .13- D .132.已知,ABC △中,∠C=90°,sin ∠ A 的度数是 < )A .30°B .45°C .60°D . 90°YIsT09cCIN 3.若反比例函数2k y x+=的图象位于第二、四象限内,则k 的取值范围是 < )A .2k >-B .2k <-C .0k >D .0k < 4.如图,⊙O 的半径为5,AB 为弦,OC ⊥AB ,垂足为C ,若OC =3,则弦AB 的长为< ). A . 8B .6C .4D .105.如图,D 是ABC △边AB 上一点,则下列四个条件不能单独判定ABC ACD △∽△的是( >A .B ACD ∠=∠ B .ADC ACB ∠=∠ C .AC ABCD BC= D .2AC AD AB =⋅7题图6题图5题图4题图6.如图,若将飞镖投中一个被平均分成6份的圆形靶子,则落在阴影部分的概率是 ( >A .12B .56C .13D .237.如图,BC 是⊙O 的直径,A 、D 是⊙O 上两点,若∠D = 35°,则∠OAC 的度数是 ( >YIsT09cCIN A .35° B .55° C .65° D .70° YIsT09cCIN 8.如图,在Rt △ABC 中,∠ACB =90°,∠BAC =30°,AB=2,D 是AB边上的一个动点<不与点A 、B 重合),过点D 作CD 的垂线交射线CA 于点E .设AD=x ,CE=y ,则下列图象中,能表示y 与x 的函数关系的图象大致是 ( >YIsT09cCIN二、填空题<共4道小题,每小题4分,共16分)9.如图,在△ABC 中,DE ∥BC ,若DE=1,BC=3,那么△ADE 与△ABC 面积的比为 .10.如图,点A 、B 、C 是半径为3cm 的⊙O 上三个点,且︒=∠30ABC , 则劣弧 AC 的长是 .11.如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O 的圆心O 在格点上,则∠AED 的正弦值等于 .12.如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第99个格子中的数为 ,2018个格子中的数为 . YIsT09cCIN 三、解答题<本题共30分,每小题5分)13.计算:2sin 452cos 6060︒+︒-︒14.已知抛物线228y x x =--.<1)用配方法把228y x x =--化为2()y x h k =-+形式;<2)并指出:抛物线的顶点坐标是 ,抛物线的对称轴方程是 ,YIsT09cCIN 抛物线与x 轴交点坐标是 ,当x 时,y 随x 的增大而增大.YIsT09cCIN 解15.解不等式: 4(x +1>≤5x +8,并把它的解集在数轴上表示出来.解:16.如图:已知,梯形ABCD 中,∠B=90°,AD ∥BC ,AB ⊥BC ,AB=AD=3,BC=7. 求cos ∠C. 解:A17. 以直线1x =为对称轴的抛物线过点A<3,0)和点B(0,3>,求此抛物线的解读式. 解:18.如图,在ABC △中,90C =∠,在AB 边上取一点D ,使BD BC =,过D 作DE AB ⊥交AC 于E ,AC=8,BC=6解:四、解答题<本题共20分,每小题5分)19.如图,小明在十月一日到公园放风筝,风筝飞到C 处时的线长为20M ,此时小明正好站在A 处,并测得60CBD ∠=,牵引底端B 离地面1.5M ,求此时风筝离地面的高度. 解:20.甲、乙两大型超市为了吸引顾客,都举行有奖酬宾活动,凡购物满200元,均可得到一次抽奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,抽奖者一次从中摸出两个球,根据球的颜色决定送礼金券<在他们超市使用时,与人民币等值)的多少<如下表).YIsT09cCIN 甲超市.乙超市:<1)用树状图表示得到一次摸奖机会时中礼金券的所有情况; <2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.解:21. 如图,AB 是⊙O 的直径,AD 是弦,22.5A ∠=,延长AB 到点C ,使得∠ACD=45°.<1)求证:CD 是⊙O 的切线; <2)若AB =OC 的长. 证明:22.在△ABC 中,∠C=120°,AC=BC ,AB=4,半圆的圆心O 在AB上,且与AC ,BC 分别相切于点D ,E.YIsT09cCIN <1)求半圆O 的半径; <2)求图中阴影部分的面积. 解:五、解答题<本题共22分,23题7分,24题7分,25题8分) 23.如图所示,在直角坐标系中,点A 是反比例函数1ky x=的图象上一点,AB x ⊥轴的正半轴于B 点,C 是OB 的中点;一次函数2y ax b =+的图象经过A 、C 两点,并交y轴于点()02D -,,若4AOD S=△.YIsT09cCIN <1)求反比例函数和一次函数的解读式;AC<2)观察图象,请指出在y轴的右侧,当12y y>时x的取值范围,当1y<2y时x的取值范围.解:24. 把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中,将它绕点C顺时针旋转α角,旋转后的矩形记为矩形EDCF.在旋转过程中,<1)如图①,当点E在射线CB上时,E点坐标为;<2)当CBD∆是等边三角形时,旋转角α的度数是<α为锐角时);<3)如图②,设EF与BC交于点G,当EG=CG时,求点G的坐标.(4> 如图③,当旋转角90α=时,请判断矩形EDCF的对称中心A图②25.如图,在平面直角坐标系中,顶点为<4,1-)的抛物线交y轴于A点,交x轴于B,C两点<点B在点C的左侧). 已知A点坐标为<0,3). YIsT09cCIN<1)求此抛物线的解读式;x<2)过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;YIsT09cCIN <3)已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC ∆的面积最大?并求出此时P 点的坐标和PAC ∆的最大面积. YIsT09cCIN题号 9 10 1112 答案 91 π 552; -1三、解答题<本题共30分,每小题5分) 13.计算:2sin 452cos 6060︒+︒-︒解: 原式=122⋅4分 =………………………………………………5分 14.已知抛物线228y x x =--.<1)用配方法把228y x x =--化为2()y x h k =-+形式;<2)并指出:抛物线的顶点坐标是 ,抛物线的对称轴方程是 ,YIsT09cCIN抛物线与x 轴交点坐标是 ,当x 时,y 随x 的增大而增大.YIsT09cCIN 解<1)228y x x =-- =x2-2x+1-1-8 =(x -1>2 -9.………………………………………………3分(2>抛物线的顶点坐标是 (1,-9> 抛物线的对称轴方程是 x=1 ……………………………4分抛物线与x 轴交点坐标是<-2,0)<4,0); 当x >1 时,y 随x 的增大而增大. ………………………………5分15.解不等式: 4(x +1>≤5x +8,并把它的解集在数轴上表示出来.解: 去括号,得 4x +4≤5x +8 ……………………………… 1分移项、合并同类项,得-x ≤4……………………………… 3分系数化为1,得 x ≥4- ……………………………… 4分 不等式的解集在数轴上表示如下: (5)分16.如图:已知,梯形ABCD 中,∠B=90°,AD ∥BC ,AB ⊥BC ,AB=AD=3,BC=7.求cos ∠C.解:方法一、作DE ⊥BC ,如图1所示,…………1分 ∵AD ∥BC ,AB ⊥BC ,AB=AD=3,∴四边形ABED 是正方形 (2)∴DE=BE=AB=3. 又∵BC=7,∴EC=4,……………………………………3分 由勾股定理得CD=5.…………………………4分 ∴ cos ∠C=45EC CD =.…………………………5分 方法二、作AE ∥CD ,如图2所示,……………1分 ∴∠1=∠C ,∵AD ∥BC ,∴四边形AECD 是平行四边形.………………2分 ∵AB=AD=3,∴EC=AD=3, 又∵BC=7,∴BE=4,……………………………………3分 ∵ AB ⊥BC ,由勾股定理得AE=5. ………………4分 ∴ cos ∠C= cos ∠1=45BE AE =. …………………………5分 17. 以直线1x =为对称轴的抛物线过点A<3,0)和点B(0,3>,求此抛物线的解读式.A解:设抛物线的解读式为2(1)y a x b =-+, ………………………………………1分抛物线过点A<3,0)和B(0,3>. ∴40,3.a b a b +=⎧⎨+=⎩解得1,4.a b =-⎧⎨=⎩ … ………4分 ∴抛物线的解读式为223y x x =-++. ……………………………………5分18.如图,在ABC △中,90C =∠,在AB 边上取一点D ,使BD BC =,过D 作DE AB ⊥交AC 于E ,86AC BC ==,.求DE 的长.解:在ABC △中,9086C AC BC ===,,∠, 10AB ∴==.…………………2分又6BD BC ==,4AD AB BD ∴=-=. DE AB ⊥,90ADE C ∴==∠∠. 又A A =∠∠,AED ABC ∴△∽△.………………………………4分DE ADBC AC∴=. .3684=⨯=⋅=BC AC AD DE ………………………5分 四、解答题<本题共20分,每小题5分)19.如图,小明在十月一日到公园放风筝,风筝飞到C 处时的线长为20M ,此时小明正好站在A 处,并测得60CBD ∠=,牵引底端B 离地面 1.5M ,求此时风筝离地面的高度.解:依题意得,90CDB BAE ABD AED ∠=∠=∠=∠=︒, ∴四边形ABDE 是矩形 ,…………1分1.5.DE AB ∴== ……………2分在Rt BCD △中,sin ,CDCBD BC∠=……………3分 又∵ 20BC = ,60CBD ∠=,由BCCD= 60sin∴sin 60202CD BC =⋅︒=⨯= .……………4分1.5CE ∴= .………………………………………5分即此时风筝离地面的高度为()1.5M .20.甲、乙两大型超市为了吸引顾客,都举行有奖酬宾活动,凡购物满200元,均可得到一次抽奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,抽奖者一次从中摸出两个球,根据球的颜色决定送礼金券<在他们超市使用时,与人民币等值)的多少<如下表).YIsT09cCIN 甲超市.乙超市:<1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;<2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.解:<1)树状图为:…………2分<2)∵去甲超市购物摸一次奖获50元礼金券的概率是P<甲)=64=32,…………3分去乙超市购物摸一次奖获50元礼金券的概率是P<乙)=62=31……………………4分 ∴我选择去甲超市购物……………………………………………………………………5分 21. 如图,AB 是⊙O 的直径,AD 是弦,22.5A ∠=,延长AB 到点C ,使得∠ACD=45°.<1)求证:CD 是⊙O 的切线; <2)若AB =OC 的长.<1)证明:连接OD .∵OA OD =,22.5A ∠=,22.5ODA A ∴∠=∠=︒,45DOC ∴∠=︒ . ……………………1分∵45ACD ∠=,90ODC ∴∠=︒ , OD CD ∴⊥ . ……………………2分又∵点D 在⊙O 上,∴CD 是⊙O 的切线 .……………………3分 <2)∵直径AB =12OD AB ∴== . …………… 4分AC在Rt OCD △中,sin ODC OC= , ∴sin 45OC ︒=, ∵sin 45︒=,2OC ∴= .……………………5分22.在△ABC 中,∠C=120°,AC=BC ,AB=4,半圆的圆心O 在AB上,且与AC ,BC 分别相切于点D ,E.YIsT09cCIN <1)求半圆O 的半径; <2)求图中阴影部分的面积. 解:<1)解:连结OD ,OC ,∵半圆与AC ,BC 分别相切于点D ,E.∴DCO ECO ∠=∠,且OD AC ⊥.∵AC BC =,∴CO AB ⊥且O 是AB 的中点. ∴122AO AB ==.∵120C ∠=︒,∴60DCO ∠=︒. ∴30A ∠=︒.∴在R t AOD △中,112OD AO ==.即半圆的半径为1. (3)分<2)设CO=x ,则在R t AOC △中,因为30A ∠=︒,所以AC=2x ,由勾股定理得:222AC OC AO -= 即 222(2)2x x -=解得 x =<x =舍去)∴ 11422ABC S AB OC =⋅=⨯=△. …………………….4分∵ 半圆的半径为1, ∴ 半圆的面积为2π,∴ 3326S ππ=-=阴影. ….…………………………….5分五、解答题<本题共22分,23题7分,24题7分,25题8分) 23.如图所示,在直角坐标系中,点A 是反比例函数1ky x=的图象上一点,AB x ⊥轴的正半轴于B 点,C 是OB 的中点;一次函数2y ax b =+的图象经过A 、C 两点,并交y 轴于点()02D -,,若4AOD S =△.YIsT09cCIN <1)求反比例函数和一次函数的解读式;<2)观察图象,请指出在y 轴的右侧,当12y y >时x 的取值范围,当1y <2y 时x 的取值范围.解:作AE y ⊥轴于E ∵42AOD S OD ==△, ∴.421=⋅AE OD∴4AE =. ………………………………………1分 ∵AB OB C ⊥,为OB 的中点,∴90DOC ABC OC BC OCD BCA ==︒==∠∠,,∠∠.∴Rt Rt DOC ABC △≌△.…………………………………3分 ∴2AB OD ==. ∴A<4,2).将A<4,2)代入1ky x=中,得8k =. 18y x∴=. ……………4分将()42A ,和()02D ,-代入2y ax b =+,得422a b b +=⎧⎨=-⎩解之得:12a b =⎧⎨=-⎩∴22y x =-.…………………………………………………………………5分<2)在y 轴的右侧,当12y y >时,04x <<.………………………6分 当1y <2y 时x >4. ……………………………………………………7分24. 把边长分别为4和6的矩形ABCO 如图放在平面直角坐标系中,将它绕点C 顺时针旋转α角,旋转后的矩形记为矩形EDCF .在旋转过程中, <1)如图①,当点E 在射线CB 上时,E 点坐标为 ;<2)当CBD ∆是等边三角形时,旋转角α的度数是 <α为锐角时);<3)如图②,设EF 与BC 交于点G ,当EG=CG 时,求点G 的坐标.(4> 如图③,当旋转角90α=时,请判断矩形EDCF 的对称中心H 是否在以C 为顶点,且经过点A图① 图②图③YIsT09cCIN 解:<1)E <4,132) ………………………………………………1分<2)︒60 …………………………………………………………………2分<3)设x CG =,则x EG =,x FG -=6,在Rt △FGC 中,∵222CG FG CF =+,∴222)6(4x x =-+, 解得 313=x ,即313=CG . ∴G <4,313). …………………………………………………………4分 <4)设以点C 为顶点的抛物线的解读式为2)4(-=x a y . 把A <0,6)代入得,2)40(6-=a . 解得, 83=a . ∴此抛物线的解读式为2)4(83-=x y .……………………………………6分 ∵矩形EDCF 的对称中心为对角线FD 、CE 的交点H , ∴由题意可知H 的坐标为<7,2). 当7=x 时,2827)47(832≠=-=y , ∴点H 不在此抛物线上. ………………………………………………7分x(第25题>x25.如图,在平面直角坐标系中,顶点为<4,1-)的抛物线交y 轴于A 点,交x 轴于B ,C 两点<点B 在点C 的左侧). 已知A 点坐标为<0,3). YIsT09cCIN <1)求此抛物线的解读式;<2)过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;YIsT09cCIN <3)已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC ∆点的坐标和PAC ∆的最大面积. YIsT09cCIN 解:<1)设抛物线为2(4)1y a x =--.∵抛物线经过点A <0,3),∴23(04)1a =--∴抛物线为2211(4)12344y x x x =--=-+. (2> 答:l 与⊙C 相交. ……………………………………3分 证明:当21(4)104x --=时,12x =,26x =. ∴B 为<2,0),C 为<6,0). ∴AB设⊙C 与BD 相切于点E ,连接CE , 则90BEC AOB ∠=︒=∠.∵90ABD ∠=︒,∴∠ABO +∠CBE =90°. 又∵∠ABO +∠BAO =90°, ∴BAO CBE ∠=∠.∴AOB ∆∽BEC ∆.∴CE BCOB AB =.∴2CE =∴2CE =>.…………4分 ∵抛物线的对称轴l 为4x =,∴C 点到l 的距离为2. ∴抛物线的对称轴l 与⊙C 相交. …………………5分 (3> 解:如图,过点P 作平行于y 轴的直线交AC 于点Q . 由点A<0,3)点C<6,0)可求出直线AC 的解读式为132y x =-+.………………6分设P 点的坐标为<m ,21234m m -+),则Q 点的坐标为<m ,132m -+). ∴2211133(23)2442PQ m m m m m =-+--+=-+.∵22113327()6(3)24244PAC PAQ PCQ S S S m m m ∆∆∆=+=⨯-+⨯=--+,∴当3m =时,PAC ∆的面积最大为274.此时,P 点的坐标为<3,34-). …………………8分解答(3>的关键是作PQ ∥y 轴交AC 于Q ,以PQ 为公共底,OC 就是高,用抛物线、直线解读式表示P 、Q 两点的纵坐标,利用三角形的面积推导出面积与P 点横坐标m 的函数关系式,YIsT09cCIN 即:2327(3)44PAC S m ∆=--+. 评分说明:部分解答题有多种解法,以上各题只给出了部分解法,学生的其他解法可参照评分标准给分. 申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
2017-2018北京初三(上)期末数学各区试题汇总-反比例函数及反比例函数与一次函数综合问题

●知识模块1:反比例函数图像与性质★图像特点与增减性1.(东城18期末4)点()11,y A x ,()22,y B x 都在反比例函数2y x=的图象上,若120x x <<,则( )A .210y y >>B .120y y >>C .210y y <<D .120y y <<2.(平谷18期末7)反比例函数2y x=的图象上有两点()11A x ,y ,()22B x ,y ,若x 1>x 2, x 1x 2>0,则y 1-y 2的值是( )A .正数B .负数C .0D .非负数3.(西城18期末2)点1(1,)A y ,2(3,)B y 是反比例函数6y x=-图象上的两点,那么1y ,2y 的大小关系是( ).A .12y y >B .12y y =C .12y y <D .不能确定4.(密云18期末3)已知点(1,m),(2,n)A B 在反比例函数(0)ky k x=<的图象上,则( ) A .0m n << B .0n m << C .0m n >> D .0n m >>5.(燕山18期末4)若点 (x 1,y 1),(x 2,y 2) 都是反比例函数6y x=图象上的点,并且y 1<0<y 2,则下列结论中正确的是( )A .x 1> x 2B .x 1 <x 2C .y 随 x 的增大而减小D .两点有可能在同一象限6.(通州18期末10)已知点()11,y x ,()22,y x 在反比例函数xy 2=上,当021<<y y 时,1x ,2x 的大小关系是____________.7.(大兴18期末3)已知反比例函数2m y x-=,当x >0时,y 随x 的增大而增大,则m 的取值范围是( )A .m <2B .m >2C .m ≤2D .m ≥28.(海淀18期末11)若一个反比例函数图象的每一支上,y 随x 的增大而减小,则此反比例函数表达式可以是 .(写出一个即可)9.(海淀18期末7)如图,反比例函数k y x=的图象经过点A (4,1),当1y <时,x 的取值范围是( )A .0x <或4x >B .04x <<C .4x <D .4x >10.(昌平18期末9)请写出一个图象在第二,四象限的反比例函数的表达式 . 11.(密云18期末13)请写出一个图象在第一、第三象限的反比例函数的表达式_________. 12.(怀柔18期末11)有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可): .13.(平谷18期末11)请写出一个过点(1,1),且与x 轴无交点的函数表达式 . 14.(顺义18期末14)已知y 与x 的函数满足下列条件:①它的图象经过(1,1)点;②当1x >时,y 随x 的增大而减小. 写出一个符合条件的函数: . 15.(丰台18期末13)已知函数的图象经过点(2,1),且与x 轴没有交点,写出一个满足题意的函数的表达式 .16.(朝阳18期末11)11. 在反比例函数xmy 23-=的图象上有两点A (x 1,y 1),B (x 2,y 2),x 1< x 2<0,y 1> y 2,则m 的取值范围是 .★k 与面积17.(燕山18期末6)如图,已知点 P 为反比例函数6y x =-上一点,过点 P 向坐标轴引垂线,垂足分别为 M ,N ,那么四边形 MONP的面积为( )A .- 6B .3C .6D .12 18.(昌平18期末3)如图,点B 是反比例函数(0)ky x k =≠在第一象限内图象上的一点,过点B 作BA ⊥x 轴于点A ,BC ⊥y 轴于点C ,矩形AOCB 的面积为6,则k 的值为( )A .3B .6C .-3D .-619.(西城18期末11)如图,在平面直角坐标系xOy 中,第一象限内的点(,)P x y 与点(2,2)A 在同一个反比例函数的图象上,PC ⊥y 轴于点C ,PD ⊥x 轴于点D ,那么矩形ODPC 的面积等于 .20.(丰台18期末5)如图,点A 为函数ky x=(x > 0)图象上的一点,过点A 作x 轴的平行线交y 轴于点B ,连接OA ,如果△AOB 的面积为2,那么k 的值为( )A .1B .2C .3D .4★待定系数法21.(顺义18期末4)已知蓄电池的电压为定值,使用蓄电池时,电流I (单位:A)与电阻R (单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R 表示电流I 的函数表达式为( )A .3I R = B .I R =-6 C .3I R=- D .I R =622.(通州18期末1)若反比例函数的图象经过点()2,3-,则该反比例函数的表达式为( )A. xy 6=B. xy 6-=C. x y 3=D. xy 3-=23.(燕山18期末10)点A (-2,5) 在反比例函数(0)ky xk =≠的图象上,则k 的值是_____.24.(门头沟18期末11)如图,在平面直角坐标系xOy 中有一矩形,顶点坐标分别为(1,1)、(4,1)、(4,3)、(1,3),有一反比例函数(0)k y k x=≠它的图象与此矩形没有交点,该表达式可以为_______.25.(燕山18期末8)如图,△ ABC 的三个顶点分别为 A (1,2),B (5,2),C (5,5).若反比例函数ky x=在第一象限内的图象与△ ABC 有交点,则 k 的取值范围是 A .2 ≤ k ≤ 25 B .2 ≤ k ≤ 10C .1 ≤ k ≤ 5D .10 ≤ k ≤ 2526.(东城18期末16)如图,在平面直角坐标系xOy 中,已知()8,0A ,()0,6C ,矩形OABC 的对角线交于点P ,点M 在经过点P 的函数()0ky x x=>的图象上运动,k 的值为 ,OM 长的最小值为 .27.(海淀18期末20)码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.轮船到达目的地后开始卸货,记平均卸货速度为v (单位:吨/天),卸货天数为t . (1)直接写出v 关于t 的函数表达式:v = ;(不需写自变量的取值范围) (2)如果船上的货物5天卸载完毕,那么平均每天要卸载多少吨?●知识模块2:反比例函数综合1.(石景山18期末13)如图,一次函数b kx y +=1的图象与反比例函数()02<=x xmy 的图象相交于点A 和点B .当021>>y y 时,x 的取值 范围是_______.2.(大兴18期末17)如图,在平面直角坐标系xOy 中,一次函数2y x=-的图象与反比例函数ky x=的图象的一个交点为A (-1,n ).求反比例函数ky x=的表达式. 3.(通州18期末18)如图,在平面直角坐标系xOy 中.一次函数()0≠+=k b kx y 与反比例函数()0≠=m x m y 交于点⎪⎭⎫⎝⎛--2,23A ,()a B ,1.(1)分别求出反比例函数和一次函数的表达式;(2)根据函数图象,直接写出不等式x mb kx >+的解集.4.(朝阳18期末22)22. 如图,在平面直角坐标系xOy 中,直线32--=x y 与双曲线xky =交于M (a ,2),N (1,b )两点. (1)求k ,a ,b 的值;(2)若P 是y 轴上一点,且△MPN 的面积是7,直接写出 点P 的坐标 .5.(丰台18期末21)平面直角坐标系xOy 中直线1y x =+与双曲线k y x=一个交点为P (m ,2).(1)求k 的值;(2)M (2,a ),N (n ,b )是双曲线上的两点,直接写出当a > b 时,n 的取值范围. 6.(东城18期末24)24.在平面直角坐标系xOy 中,直线24y x =+与反比例函数ky x=(k ≠0)的图象交于点()3,A a -和点B . (1)求反比例函数的表达式和点B 的坐标;(2)直接写出不等式24kx x+<的解集.7.(海淀18期末23)23.如图,函数ky x=(0x <)与y ax b =+的图象交于点A (-1,n )和点B (-2,1). (1)求k ,a ,b 的值;(2)直线x m =与ky x=(0x <)的图象交于点P ,与1y x =-+的图象交于点Q ,当90PAQ ∠>︒时,直接写出m 的取值范围.8.(怀柔18期末20)在平面直角坐标系xOy 中,直线3+-=x y 与双曲线xky =相交于点A (m ,2). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图;(3)若P 是坐标轴上一点,且满足P A =OA .直接写出点P 的坐标.9.(石景山18期末22)在平面直角坐标系xOy 中,一次函数y=x+b 的图象与x 轴交于点)0,2(A ,与反比例函数xky =的图象交于点),3(n B . (1)求一次函数与反比例函数的表达式;(2)若点P 为x 轴上的点,且△P AB 的面积是2,则点P 的坐标是 . 10.(西城18期末22)如图,在平面直角坐标系xOy 中,双曲线ky x =(k ≠0)与直线12y x =的交点为(,1)A a -,(2,)B b 两点,双曲线上一点P 的横坐标为1,直线P A ,PB 与x 轴的交点分别为点M ,N ,连接AN . (1)直接写出a ,k 的值;(2)求证:PM=PN ,PM PN ⊥.11.(平谷18期末22)如图,在平面直角坐标系xOy 中,函数y =kx(k >0,x >0)的图象与直线y =2x ﹣2交于点Q (2,m ). (1)求m ,k 的值; (2)已知点P (a ,0)(a >0)是x 轴上一动点,过点P 作平行于y 轴的直线,交直线y =2x ﹣2于点M ,交函数y =kx的图象于点N .①当a =4时,求MN 的长; ②若PM >PN ,结合图象,直接写出a 的取值范围.12.(密云18期末22)点P (1,4),Q (2,m )是双曲线ky x=图象上一点.(1)求k 值和m 值. (2)O 为坐标原点.过x 轴上的动点R 作x 轴的垂线,交双曲线于点S ,交直线OQ 于点T ,且点S 在点T 的上方.结合函数图象,直接写出R 的横坐标n 的取值范围.13.(顺义18期末25)如图,在平面直角坐标系xOy 中,直线2y x =-与双曲线ky x=(k ≠0)相交于A ,B 两点,且点A 的横坐标是3.(1)求k 的值;(2)过点P (0,n )作直线l ,使直线l 与x 轴平行,直线l 与直线2y x =-交于点M ,与双曲线ky x=(k ≠0)交于点N ,若点M 在N 右边,求n 的取值范围.14.(门头沟18期末21)在平面直角坐标xOy 中的第一象限内,直线10y kx k =≠()与双曲20my m x =≠()的一个交点为A (2,2).(1) 求k 、m 的值;(2) 过点(0)P x ,且垂直于x 轴的直线与1y kx =、2m y x =的图象分别相交于点M 、N ,点M 、N 的距离为1d ,点M 、N 中的某一点与点P 的距离为2d ,如果12d d =,在下图中画出示意图.....并且直接写出点P 的坐标.15.(燕山18期末25)如图,在平面直角坐标系 xOy 中,函数(0)ky x x=<时图象与直线 y=x+2 交于点A (-3,m ). (1)求 k ,m 的值; (2)已知点 P (a ,b) 是直线 y=x 上,位于第三象限的点,过点P 作平行于x 轴的直线,直线y=x+2于点M ,过点P 作平行于y 轴的直线,交函数(0)ky x x=<的图象于点N .①当 a=- 1时,判断线段PM 与PN 的数量关系,并说明理由; ②若PN ≥ P M 结合函数的图象,直接写出b 的取值范围.。
北京市怀柔区2017届九年级数学上学期期末考试试题20171019379

怀柔区 2016—2017学年度第一学期九年级期末质量检测数 学 试 卷一、选择题(本题共 30分,每小题 3分)第 1-10题均有四个选项,符合题意的选项只有一个1.2016年 9月 15日 22时 04分 09秒 “天宫二号”在酒泉卫星发射中心成功发射,为祖国的 航天历史打开新的历程.“天宫二号”全长 10.4米,总重量达 8600公斤,将 8600用科学记 数法表示应为 (A)86×102(B)8.6×103(C)86×103(D)0.86×1032.实数 a ,b ,c ,d 在数轴上对应点的位置如图所示,这四个数中,绝对值最小的是 (A)a(B)b–4b cad–3 –2 –1 0 12345(C)c (D)d3.已知5x 6y (y 0) ,那么下列比例式中正确的是(A)xy(B) 5 6xy (C)5 xx(D)6 6 5y 65y4.已知△ABC ∽△ A B C,如果它们的相似比为 3∶2,那么它们的面积比应是(A)3:2(B) 2:3(C)4:9(D)9:45.如图,在△ABC 中,DE ∥BC ,分别交 AB ,AC 于点 D ,E .若 AE =3,EC =6,则ADAB 的值为 1 2 (B) 1 3 (C)14 (D) 16DA (A)EB C6.一枚质地均匀的正方体骰子,其六个面上分别刻有 1、2、3、4、5、6的点数,掷这 个骰子一次,则掷得面朝上的点数为偶数的概率是 (A)14 (B) 16 (C) 12 (D) 137.将抛物线 y =-x 2 +1向上平移 2个单位,得到的抛物线表达式为 B(A)y=-(x+2)2(B)y=-(x-2)2 (C)y=-x 2 -1(D)y=-x 2 +38. 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为CA1(A)3 4 (B) 43 (C) 35 (D) 459.象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种.由于用具简单,趣味性强, 成为流行极为广泛的棋艺活动.如图是一方的棋盘,如果“马”的坐标是(-2,2),它是抛 物线 y ax 2 (a0) 上的一个点,那么下面哪个棋子在该抛物线上(A)帥(B)卒(C)炮(D)仕y/万10 9 8 7 65 43万 万 万 万 万2 1 万 万 万 万 万O 1 2 3 4 5 6 7 8 9x/万万 第 9 题 图第 10 题 图10.在 1: 7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬 菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能 是 (A)1月份(B)2月份(C)5月份(D)7月份二、填空题(本题共 18分,每小题 3分) 11.分解因式: a 2bb3.12.请写出一个开口向下,且经过(0,3)的抛物线的表达式.13.农业部门引进一批新麦种,在播种前做了五次发芽试验, 目的是想了解一粒这样的麦种发芽情况,实验统计数据如下: 实验的麦种数/粒5005005005005002发芽的麦种数/粒492 487 491 493 489发芽率/% 98.40 97.40 98.20 98.60 97.80估计在与实验条件相同的情况下,种一粒这样的麦种发芽的概率约为.14.已知扇形的圆心角是1200,半径是6,则它的面积是.15.有两棵树,一棵高15米,另一棵高7米,两树相距6米,一只鸟从一棵树的树梢飞到另一棵树的树梢.问小鸟至少飞行米.16. 阅读下面材料:在数学课上,老师给同学们布置了一道尺规作图题:已知:如图,正比例函数和反比例函数的y图象分别交于M、N两点.要求:在y轴上求作点P,使得∠MPN为直角.MOxN小丽的作法如下:y如图,以点O为圆心,以OM 长为半径作⊙O,⊙O 与y 轴交于P1、P2 两点,则点P1、P2 即为所求. P1MOxNP2老师说:“小丽的作法正确.”3请回答:小丽这样作图的依据是.三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)解答应写出文字说明、演算步骤或证明过程17.计算:8 (2)0 2 2 cos 45.18.已知x2 x 5 0,求代数式(x+1)2﹣x(2x+1)的值.19.如图,⊙O的半径为5,AB为弦,OC⊥AB,交AB于点D,O交⊙O于点C,CD=2.求弦AB的长.A BDC20.已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2 .求BC的长.AB C21.如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E, AB=3,EF=0.8,AF=2.4.求AD的长.A DFB CE22.如图,直线L1:y=b x+c与抛物线L2:y ax2 的两个交点坐标分别为A m, 4,1,1B.4(1)求 m 的值;(2)过动点 P(n ,0)且垂直于 x 轴的直线与 L1,L2的交点分别为 C ,D ,当点 C 位于点 D 上方时,请直接写出 n 的取值范围.23.《雁栖塔》位于怀柔“北京雁栖湖国际会都中心”所处大岛西南部突出部位的半岛上,是“北 京雁栖湖国际会都中心”的标志性建筑,也是整个雁栖湖风景区的标志性建筑.某校数学课外小组为了测量《雁栖塔》(底部可到达)的高度,准备了如下的测量工具:① 平面镜,②皮尺,③长为 1米的标杆,④高为 1.5m 的测角仪(测量仰角、俯角的仪器).第一 组选择用②④做测量工具;第二组选用②③做测量工具;第三组利用自身的高度并选用①② 做测量工具,分别画出如下三种测量方案示意图.(1)请你判断如下测量方案示意图各是哪个小组的,在测量方案示意图下方的括号内填上小组名称.(2)选择其中一个测量方案示意图,写出求《雁栖塔》高度的思路.AAAE ECBDF C B D EF CB( )()()24.阅读下列材料:“怀山俊秀,柔水有情”—怀柔,一直受到世人的青睐.早在上世纪 90年代,联合国第 4 届世界妇女大会 NGO 论坛的举办使怀柔蜚声海内外,此后,随着世界养生大会、国际青少年嘉5年华、全国汽车拉力赛等一系列活动赛事的成功举办,为这座国际交往新城聚集了庞大的人气.2014年11月11日,全世界的眼光再次聚焦在北京怀柔雁栖湖,这里成功举办了第22次APEC领导人峰会.现如今怀柔已成为以自然风光游为基础,休闲度假游、乡村美食游、满族风情游为特色,影视文化游、健身养生游、竞技赛事游为时尚的多元化旅游胜地.随着怀柔旅游业的迅速发展,也带动了怀柔的经济收入.据统计,2011年全年接待游客1047万人次,比上一年增长5.3%;2012年全年接待游客1085万人次,比上一年增长3.7%;2013年全年接待游客1107.6万人次,比上一年增长2%;2014年全年接待游客1135万人次,比上一年增长2.4%;2015年全年接待游客1297.4万人次,比上一年增长14.3%.(以上数据来源于怀柔信息网)根据以上材料解答下列问题:(1)用折线图将2011-2015年怀柔区全年接待游客量表示出来,并在图中标明相应数据;(2)根据绘制的折线图中提供的信息,预估2016年怀柔区全年接待游览客量约万人次,你的预估理由是.25.如图,AB是⊙O的直径,AE是弦,直线CG与⊙O相切于点C,CG∥AE,CG与BA的延长线交于点G,过点C作CD⊥AB于点D,交AE于点F.(1)求证::A C C:E;C E(2)若∠EAB=30°,CF=a,写出求四边形GAFC周长的思路. G AFD O B26.函数y x 2 3x 2 的图象如图所示,根据图象回答问题:4y (1)当x 时,x 2 3x 2 0 ;32(2)在上述问题的基础上,探究解决新问题:1①函数y (x 1)(x 2) 的自变量x的取值范围是___________;O–3 –2 –1 1–1x6②下表是函数y(x1)(x2) 的几组y与x的对应值.x …-7 -6 -4 -3 -2 -1 0 1 3 4 …5.477 4.472 2.449 1.414 1.414 2.449 4.472 5.477y …0 0 ………………………如下图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点的大概位置,请你根据描出的点,画出该函数的图象:③写出该函数的一条性质:.27.已知:关于x的方程x2-(m+2)x+m+1=0.(1)求证:该方程总有实数根;(2)若二次函数y= x2-(m+2)x+m+1(m>0)与x轴交点为A,B(点A在点B的左边),且两交点间的距离是2,求二次函数的表达式;(3)横、纵坐标都是整数的点叫做整点.在(2)的条件下,垂直于y轴的直线y=n与抛物线交于点E,F.若抛物线在点E,F之间的部分与线段EF所围成的区域内(包括边界)恰有7个整点,结合函数的图象,直接写出n的取值范围.y y5 54 43 32 21 1O–2 –1 1 2 3 4 5 –1 x O–2 –1 1 2 3 4 5–1x–2 –27 备用图1 备用图228.在等边△ABC中,E为BC边上一点,G为BC延长线上一点,过点E作∠AEM=60°,交∠AC G 的平分线于点M.(1)如图(1),当点E在BC边的中点位置时,通过测量AE,EM的长度,猜想AE与EM满足的数量关系是;(2) 如图(2),小晏通过观察、实验,提出猜想:当点E在BC边的任意位置时,始终有AE=EM.小晏把这个猜想与同学进行交流,通过讨论,形成了证明该猜想的几种想法:想法1:在BA上取一点H使AH=CE,连接EH,要证AE=EM,只需证△AHE≌△ECM.想法2:找点A关于直线BC的对称点F,连接AF,CF,EF.(易证∠BCF+∠BCA+ACM=180°,所以M,C,F三点在同一直线上)要证AE=EM,只需证ΔMEF为等腰三角形.想法3:将线段BE绕点B顺时针旋转60°,得到线段BF,连接CF,EF,要证AE=EM,只需证四边形MCFE为平行四边形.请你参考上面的想法,帮助小晏证明AE=EM.(一种方法即可)AAMMBE C G BE C G(1)(2)29.在平面直角坐标系xOy中,点A为平面内一点,给出如下定义:过点A作AB⊥y轴于点B,作正方形ABCD(点A、B、C、D顺时针排列),即称正方形ABCD为以A为圆心,OA为8半径的⊙A的“友好正方形”.(1)如图1,若点A的坐标为(1,1),则⊙A的半径为.(2)如图2,点A在双曲线y= 1x(x>0)上,它的横坐标是2,正方形ABCD是⊙A的“友好正方形”,试判断点C与⊙A的位置关系,并说明理由.(3)如图3,若点A是直线y=-x+2上一动点,正方形ABCD为⊙A的“友好正方形”,且正方形ABCD在⊙A的内部时,请直接写出点A的横坐标m的取值范围.yy yC D 43432B A2O万1 x11–3 –2 –1–1 1 2 3 4O–1万2x O–1–2–31 2 3 45x万39怀柔区2016—2017学年度第一学期初三期末质量检测数学试卷答案及评分参考一、选择题(本题共30分,每小题3分)第1-10题均有四个选项,符合题意的选项只有一个题 1 2 3 4 5 6 7 8 9 10号答(B) (C) (B) (D) (B) (C) (D) (A) (B) (C)案二、填空题(本题共18分,每小题3分)题11 12 13 14 15 16 号答b(a b)(a b) y=-x2+3等(满足约1210 半圆(或直径)案a〈0,c=3即可) 0.98 所对的圆周角是直角三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)217.解:原式=2 2 1 2 2………………………………4分2= 2 1 ………………………………5分18.解:原式=x2 2x12x2 x. ………………………………2分=x2 x1.………………………………3分∵x2 x 5 0,∴x2 x5.………………………………4分∴原式=x2 x1(x2 x) 1514.………………………………5分19.解:∵OC是⊙O的半径,OC⊥AB于点D,O10A BDC∴AD=BD=12AB. (1)分∵OC=5,CD=2,∴OD=OC-CD=3.………………………………2分在Rt△AOD中,OA=5,OD=3,∴AD=OA 2 OD2 =52 32 =4,………………………………4分∴AB=2AD=8.………………………………5分20.解:∵∠A=105°,∠B=30°.∴∠C=45°.……………………………… 1分过点A作AD⊥BC于点D,∴∠ADB=∠ADC=90°在Rt△ADC中,∠ADC=90°,∠C=45°,AC=2.∴∠DAC==∠C =45°.∵sinC=A DAC,∴AD= 2 .…………………2分A∴AD=CD= 2 .…………………………3分B CD在Rt△ADB中,∠ADB=90°,∠B=30°.∵AD= 2 , ∴AB=2 2 .∴由勾股定理得:BD= A B 2 AD 2 6 . (4)分∴BC=BD+CD= 6 2 . ………………………………5分21.解:∵四边形ABCD为平行四边形,∴AB=DC=3,AB∥DE. ………………………………1分∴AF DC.FE CEA D3∵AB=3,EF=0.8,AF=2.4,2.4 3∴.……………………………3分0.8 CE∴CE=1. ……………………………… 4分B2.40.8FEC∴DE=DC+CE=3+1=4.∵AB∥DE,∴∠BAE=∠E.∵AE平分∠BAD,∴∠BAE=∠DAE.∴∠E=∠DAE.∴AD=DE=4.∴AD的长为4. …………………………… 5分1122.解:(1)把B1, 1代入y ax得:a=1,∴y x2 (1)分2把A m,4代入y x得4=m2 .∴m=2 (2)分2∵点A在二象限,∴m=-2. ………………………………3分(2)-2〈n〈1. ………………………………5分23.解:(1)二组一组三组………………………………3分(2)一图思路:①分别测出在同一时刻标杆EF和《雁栖塔》AB的影长DF,CB;②由△ABC∽△EFD,利用AB CB求出AB的值. ………………………5分EF DF二图思路:①用测角仪测出∠ACB的角度; ②用皮尺测量CB的长;③AB=CBtan∠ACB; ④AE=AB+1.5………………………………5分三图思路:①用皮尺分别测量DF、CF、CB的长;②由△ABC∽△DFE , 利用AB CB求出AB的值.……………………………5分DF CF24.解:(1)如下图:………………………………3分2011-2015年怀柔区全年接待游客量统计图万万万200015001297.411351107.61047 10851000500万万2011 2012 2013 2014 2015(2)1375(预估值在1323:1483之间都可以),预估理由须包含折线图中提供的信息且支撑预估的数据. 如由前几年平均数得到等.………………………………5分EC25.证明:(1)连接OC,如图.∵直线CG与⊙O相切于点C,∴CG⊥OC. ∵CG∥AE,∴AE⊥OC. GFBA OD12又∵OC 为⊙O 的半径,∴ :A C C :E .…………………2分(2)连接 AC ,如图.由∠EAB=30°,CG ∥AE,可得∠CGB=30°,EC 又由直线 CG 与⊙O 相切于点 C ,∠AOC=60°, 可推出△AOC 是等边三角形. ………………………3分 由△AOC 是等边三角形,∠EAB=30°,CF=a ,GFBAOD可得∠CAF=∠ACF=30°,CF=AF=a ,DF=1 2a ,AD= 3 2a .…………………4分利用 CG ∥AE ,可得到△ADF ∽△GDC ,从而推出 AG= 3a ,GC=3a .④计算出四边形 GAFC 的周长为5a + 3a .(每一步没有写出结果,只要写出思路就可得满 分)………………………………5分 26.解:(1) x2或x1.………2分(2)① x2或x1………………3分②如图: ………………………………4分 ③关于直线 x=-1.5对称或增减性等. ……………………5分27.解:(1)△=(m+2)2-4(m+1)= m 2≥0y∴不论 m 取何值,该方程总有实数根. …………2分 (2)由题意可知:y=2x 1=1,x 2=m+1,(0,1)y=1∴A (1,0) B (m+1,0). ……………………3分O A(1,0)B (3,0)x∵两交点间距离为 2,y=-1C(2,-1)∴m+1-1=2.∴m=2. ……………………4分 ∴y= x 2-4x+3. …………5分13(3)1≤n<2. …………7分28.(1)相等;…………1分A1 (2)想法一:∵△A BC是等边三角形,∴AB=BC, ∠B=60°. …………2分B H2O3MC GE∵AH=CE,∴BH=BE. (2)∴∠BHE=60°.∴AC//HE.∴∠1=∠2. ……………………………3分A在△A OE和△CO M中,∠ACM=∠AEM=60°,∠AOE=MOE,1∴∠1=∠3.∴∠2=∠3. ……………………………5分OM∵∠BHE=60°,∴∠AHE=120°.B∵∠ECM=120°.∴∠AHE=∠2E C G ECM. ……………………………6分FA∵AH=CE,∴△AHE≌△ECM(AAS).∴AE=EM. ……………………………7分OMB(或根据一线三等角证△ABE∽△ECO,得∠BAE=∠CEM,E C G 再证∠AHE=∠ECM,得△AHE≌△ECM(ASA))想法二:F∵在△A OE和△CO M中,∠ACM=∠AEM=60°,∠AOE=∠COM,∴∠EAC=∠EMC. ……………………………3分又∵对称△ACE≌△FCE,∴∠EAC=∠EFC, AE=EF. …………5分∴∠EMC=∠EFC.∴EF=EM.∴AE=EM. …………7分想法三:∵将线段BE绕点B顺时针旋转60°,∴可证△ABE≌△CBF(SAS). …………………2分14∴∠1=∠2 AE=CF. …………………3分 ∵∠AEM=∠CBA=60°,∴∠1=∠CEM.∴∠2=∠CEM.∴EM//CF. …………4分 ∵∠CBF=60°,BE=BF,∴∠BEF=60°,∴∠MCE=∠CEF=1200.∴CM//EF. …………………5分 ∴四边形 MCFE 为平行四边形.∴CF=EM.∴AE=EM. …………………7分y29.解:(1) 2 ;…………………2分4(2)∵A (2,1 2 ), ∴O A= 1441723C2 D4 2 2 =3221 BA –1 O1234 –1∵AC=2 2=x∴O A<A C , ∴点 C 在⊙A 外. (或如图,利用勾股定理直观分析:∵OB<BC,AB=AB, ∴O A<A C 也可以) …………6分 (3) m<1且 m ≠0.…………8分15。
北京市怀柔区九年级数学上册期末质量试题有答案【精选】.doc

1怀柔区第一学期初三期末质量检测数 学 试 卷第1-8题均有四个选项,符合题意的选项只有一个1. 北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用. 将178800用科学记数法表示应为A .1.788×104B .1.788×105C .1.788×106D .1.788×107 2.若将抛物线y = -122先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是 A .2)3(212-+-=x y B .2)3(212---=x y C .2)3(2-+=x y D. 2)3(212++-=x y 3.在Rt △ABC 中,∠C =90°,AC =4,BC =3,则tan A 的值为 A .34B .43C .53D .54 4. 如图,在△ABC 中,点D ,E 分别为边AB,AC 上的点,且DE ∥BC ,若AD =4,BD =8,AE =2,则CE 的长为A .2B .4C .6D .85. 如图,⊙O 是△ABC 的外接圆,∠BOC =100°)A .40︒B .50︒C .80︒D .100︒6. 网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB 的高度).中网比赛中,某运动员退出场地在距球网14米的D 点处接球,设计打出直线..穿越球,使球落在对方底线上C 处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至EDC BA第4题图 第5题图2少为A. 1.65米B. 1.75米C.1.85米D. 1.95米 7. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O ,再任意找出圆O 的一条直径标记为AB (如图1),测量出AB =4分米;②将圆环进行翻折使点B 落在圆心O 的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C 、D (如图2);③用一细橡胶棒连接C 、D 两点(如图3); ④计算出橡胶棒CD 的长度.A .22 分米B .23分米C .32 分米D .33分米8.如图1,⊙O 过正方形ABCD 的顶点A 、D 且与边BC 相切于点E ,分别交AB 、DC 于点M 、N .动点P 在⊙O 或正方形ABCD 的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为,圆心O与P 点的距离为y ,图2记录了一段时间里y 与的函数关系,在这段时间里P 点的运动路径为 A.从D点出发,沿弧DA →弧AM →线段BM →线段BC B.从B 点出发,沿线段BC →线段CN →弧ND →弧DAC.从A 点出发,沿弧AM →线段BM →线段BC →线段CND.从C 点出发,沿线段CN →弧ND →弧DA →线段AB第8题图1第8题图2二、填空题(本题共16分,每小题2分)9.分解因式:33-62+3=_________.10.若△ABC ∽△DEF ,且对应边BC 与EF 的比为1∶3,则△ABC 与△DEF 的面积比等于 . 11. 有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可): .12.抛物线y =2(+1)2+3 的顶点坐标是 .13.把二次函数y =2-4+5化成y=a (-h )2+的形式为__________________.14. 数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组到教室内窗台旁,在点E 处测得旗杆顶部A 的仰角α为45°,旗杆底部B 的俯角β为60°. 室外测量组测得BF 的长度为5米.则旗杆AB =______米.15.1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为米2.16. 阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:4请回答:这样做的依据是 .三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程.17.计算:4sin45°-8+(3-1)0+|-2|.18.如图,在△ABC 中,D 为AC 边上一点,BC =4,AC =8,CD=2.求证:△BCD ∽△ACB .19. 如图,在△ABC 中,tan A =4,∠B =45°,AB =14. 求BC 的长. 20.在平面直角坐标系Oy中,直线3+-=x y 与双曲线ky =相交于点A (m ,2). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图;(3)若P 是坐标轴上一点,且满足P A =OA . 直接写出点P 的坐标.21.一个二次函数图象上部分点的横坐标,纵坐标y (2)求m 的值;(3)在给定的直角坐标系中,画出这个函数的图象; (4)根据图象,写出当y <0时,的取值范围.22. 如图,已知AB 是⊙O 的直径,点M 在BA 的延长线上,MD 切⊙O 于点D ,过点B 作BN ⊥MD 于点C ,连接AD 并延长,交BN 于点N . (1)求证:AB =BN ;(2)若⊙O 半径的长为3,cosB =52,求MA 的长. 第18题图 第19题图5DB23.数学课上老师提出了下面的问题: 在正方形ABCD 对角线BD 上取一点F ,使51=D B DF . 小明的做法如下:如图① 应用尺规作图作出边AD 的中点M ; ② 应用尺规作图作出MD 的中点E ; ③ 连接EC ,交BD 于点F . 所以F 点就是所求作的点.请你判断小明的做法是否正确,并说明理由.24. 已知:如图,在四边形ABCD 中,BD 是一条对角线,∠DBC =30°, ∠DBA =45°,∠C =70°.若DC =a ,AB=b , 请写出求tan ∠ADB 的思路. (不用写出计算结果........)25.如图,在四边形ABCD 中,AD ∥BC ,∠ADC =90°,点E 是BC ,过点E 作AE 的垂线交直线CD 于点F .已知AD =4cm ,CD =2cm ,BC =5cm ,设BE 的长为 cm ,CF 的长为y cm.变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了与y 的几组值,如下表:((2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;6CB(3)结合画出的函数图象,解决问题 当BE =CF 时,BE 的长度约为 cm.26.在平面直角坐标系Oy 中,直线l n x y +-=2与抛物线3242---=m mx mx y 相交于点A(2-,7). (1)求m 、n 的值;(2)过点A 作AB ∥轴交抛物线于点B ,设抛物线 与轴交于点C 、D (点C 在点D 的左侧),求△BCD 的面积;(3)点E (t ,0)为轴上一个动点,过点E 作平行于y 轴的直线与直线l 和抛物线分别交于点P 、Q .当点P 在点Q 上方时,求线段PQ 的最大值.27. 在等腰△ABC 中,AB =AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P . (1)依题意补全图形;(2)若∠BAC =2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.28.在平面直角坐标系Oy 中,点P 的横坐标为,纵坐标为2,满足这样条件的点称为“关系点”.7(1)在点A (1,2)、B (2,1)、M (21,1)、N (1,21)中, 是“关系点”的 ;(2)⊙O 的半径为1,若在⊙O 上存在“关系点”P , 求点P 坐标;(3)点C 的坐标为(3,0),若在⊙C 上有且只有....一个..“关系点”P ,且“关系点”P 的横坐标满足 -2≤≤2.请直接写出⊙C 的半径r 的取值范围.第一学期期末初三质量检测数学试卷评分标准一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一9.3(-1)2. 10.19. 11.答案不唯一,<0即可. 12.(﹣1,3). 13.y =(-2)2+1. 14. 5+53. 15. 16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程.17. 解原式=4×22-22+1+2 …………………………………………………………………… 4分 =3 ………………………………………………………………………………………5分18.证明:∵BC =4,AC =8,CD =2.…………………………1分∴BC CD AC BC =………………………………………3分 又∵∠C =∠π258C …………………………………………………………………………4分∴ △BCD ∽△ACB ……………………………………………………………………5分19.解:过点C 作CD ⊥AB 于点D ,如图. ………………………………………………1分 ∵在Rt △CDA 中,tan A =AD CD = 43设CD =3,AD =4. ……………………………………………………………………………2分 ∵在Rt △CDB 中,∠B =45° ∴tan B =DB CD = 1,sin B =BC CD =22,……………………………………………………………3分 ∵CD =3. ∴BD =3,BC =2·3=32. 又∵AB =AD+BD =14, ∴4+3=14,解得=2.…………………………………………………………………………4分∴BC =62. ……………………………………………………………………………………5分 20.解:(1)∵直线3+-=x y 与双曲线xky =相交于点A (m ,2). ∴ A (1,2)………………………………………1分 ∴xy 2=…………………………………………2分 (2)如图…………………………………………………………4分(3)P (0,4)或P (2,0) …………………………………………6分 21.解:(1)设这个二次函数的表达式为2()y a x h k =-+. 依题意可知,顶点为(-1,2),………………………1分 ∴ ()212++=x a y .∵图象过点(1,0), ∴()21102++=a .∴12a =-. ∴这个二次函数的表达式为9()21212++-=x y …………2分 (2)25-=m .………………………………………………3分 (3)如图…………………………………………………………………………………………5分 (4)<-3或>1..…………………………………………………………………………………6分 22.(1)证明:连接OD ,…………………………1分 ∵MD 切⊙O 于点D ,∴OD ⊥MD , ∵BN ⊥MC ,∴OD ∥BN ,…………………………………2分 ∴∠ADO =∠N ,∵OA =OD ,∴∠OAD =∠ADO ,∴∠OAD =∠N , ∴AB =BN ;………………………………………………………………………………………3分 (2)解:由(1)OD ∥BN ,∴∠MOD =∠B ,………………………………………………………………………………4分 ∴cos ∠MOD =cosB =52, 在Rt △MOD 中,cos ∠MOD ==OMOD, ∵OD =OA ,MO =MA +OA =3+MA ,∴AM +33=52,∴MA =4.5………………………………………………………………………………………5分 23.解:正确. ………………………………………………………………………………………1分 理由如下: 由做法可知M 为AD 的中点,E 为MD 的中点, ∴AD DE =41. …………………………………………………………2分 ∵四边形ABCD 是正方形,∴AD=BC ,ED ∥BC . ………………………………………………3分 ∴△DEF ∽△BFC ∴BC DE =BFDF ………………………………………………………..4分 ∵AD =BC10D∴BF DF =BC DE =41∴BD DF =51………………………………………………………………………………………5分 24.解 (1)过D 点作DE ⊥BC 于点E ,可知△CDE 和△DEB 都是直角三角形;……………1分 (2)由∠C =70°,可知sin ∠C 的值,在Rt △CDE 中,由sin ∠C 和DC =a ,可求DE 的长;……………………………………………………………………………………………2分 (3)在Rt △DEB 中,由∠DBC =30°,DE 的长,可求BD 的长………………………………3分 (4)过A 点作AF ⊥BD 于点F , 可知△DF A 和△AFB 都是直角三角形; ………………4分(5)在Rt △AFB 中,由∠DBA =45°,AB =b ,可求AF 和BF 的长; (6)由DB 、BF 的长,可知DF 的长; (7)在Rt △DF A 中,由DFFA ,可求tan ∠ADB . ………………5分 25.解:(1)1.5……………………………………… ..1分 (2)如图……………………………………………4分(3)0.7(0.6~0.8均可以) .………………………….5分 . 26. 解:(1)m =1………………………………………………………………………………………1分 n =3………………………………………………………………………………………………2分 (2)由(1)知抛物线表达式为y =2-4-5 令y =0得,2-4-5=0.解得1=-1,2=5,……………………………………………………………………………3分∴抛物线y =2-4-5与轴得两个交点C 、D 的坐标分别为C (-1,0),D (5,0) ∴CD =6.∵A (2-,7),AB ∥轴交抛物线于点B ,根据抛物线的轴对称性,可知B (6,7)………4分∴S △BCD =21.……………………………………………………………………………………5分(3) 据题意,可知P (t ,-2 t +3),Q ( t ,t 2-4 t -5), 由2-4-5=-2+3得直线y =-2+3与抛物线y = 2-4-5的两个交点坐标分别为(-2,7)和(4,-5) ……………………………………………………………………………………………6分11∵点P 在点Q 上方∴-2<t <5, ∴PQ = -t 2+2 t +8=-( t -2) 2+9∵a =-1∴PQ 的最大值为9.……………………………………………………………………………7分 27.解:(1)如图……………………………………………1分 (2) ∵∠BAC =2α,∠AHB =90°∴∠ABH =90°-2α …………………………………………………………………………… 2分 ∵BA =BD∴∠BDA =45°+α………………………………………………………………………………3分(3)补全图形,如图………………4分证明过程如下:∵D 关于BC 的对称点为E ,且DE 交BP 于G∴DE ⊥BP ,DG =GE ,∠DBP =∠EBP ,BD =BE ;…………………………………………5分 ∵AB=AC ,∠BAC=2α∴∠ABC=90°-α由(2)知∠ABH =90°-2α∠DBP =90°-α-(90°-2α)=α∴∠DBP =∠EBP =α∴∠BDE =2α∵AB =BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45°∴DP DG =21, ∴DPDE =2, ∴DP BC =2,12∴BC =2DP .………………………………………………………………………………7分 28.解:(1)A 、M . ……………………………………………………………………………………2分(2)过点P 作PG ⊥轴于点G …………………………………………………………………3分 设P (,2)∵OG 2+PG 2=OP 2 ………………………………………………………………………………4分 ∴2+42=1∴52=1 ∴2=51∴=55± ∴P (55,552)或P (55-,552-)……………………………………………………5分(3)r =556或 4117≤<r …………………………………………………………7分。
2017-2018北京初三(上)期末数学各区试题汇-解三角形
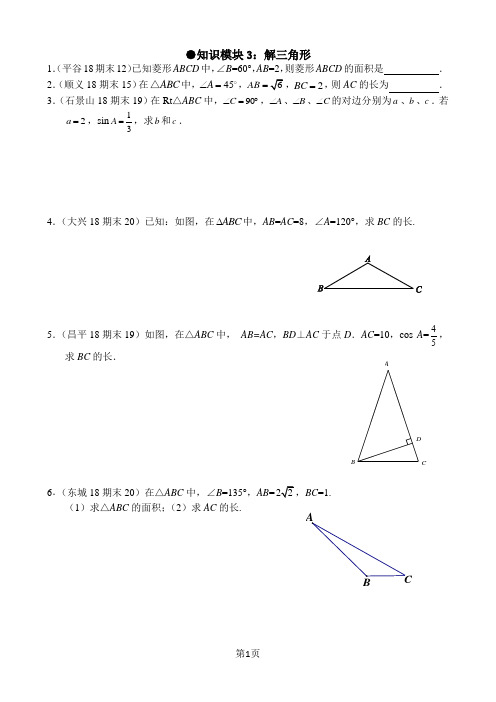
●知识模块3:解三角形1.(平谷18期末12)已知菱形ABCD 中,∠B =60°,AB =2,则菱形ABCD 的面积是 . 2.(顺义18期末15)在ABC △中,45A ∠=,AB ,2BC =,则AC 的长为 . 3.(石景山18期末19)在Rt △ABC 中,︒=∠90C ,A ∠、B ∠、C ∠的对边分别为a 、b 、c .若2=a ,sin 31=A ,求b 和c . 4.(大兴18期末20)已知:如图,在∆ABC 中,AB =AC =8,∠A =120°,求BC 的长.5.(昌平18期末19)如图,在△ABC 中, AB=AC ,BD ⊥AC 于点D .AC =10,cos A =45,求BC 的长.6.(东城18期末20)在△ABC 中,∠B =135°,AB=BC =1. (1)求△ABC 的面积;(2)求AC 的长.D C BA7.(海淀18期末19)如图,在△ABC 中,∠B 为锐角, AB=,AC =5,sin 35C =, 求BC 的长.8.(怀柔18期末19)如图,在△ABC 中,tan A =43,∠B =45°,AB =14. 求BC 的长.9.(密云18期末18)如图,ABC ∆中,60ABC ∠=︒,AB=2,BC=3,AD BC ⊥垂足为D.求AC 长.10.(燕山18期末23)如图,在 Rt △ ABC 中,∠ C=90°,点 D 是 BC 边的中点,BD =2,tan B =34(1)求 AD 和 AB 的长;(2)求 sin ∠ BAD 的值.DC B A B AD11.(西城18期末23)23.如图,线段BC 长为13,以C 为顶点,CB 为一边的α∠满足5cos 13α=.锐角△ABC 的顶点A 落在α∠的另一边l 上,且满足4sin 5A =.求△ABC 的高BD 及AB 边的长,并结合你的计算过程画出高BD 及AB 边.(图中提供的单位长度供补全图形使用) 12.(怀柔18期末24)已知:如图,在四边形ABCD 中,BD 是一条对角线,∠DBC =30°,∠DBA =45°,∠C =70°.若DC =a ,AB=b , 请写出求tan ∠ADB 的思路.(不用写出计算结果........)。
2017-2018学年北京市怀柔区初三上学期期末数学试卷(含答案)

1北京市怀柔区2017-2018学年度第一学期初三期末数学试卷及参考答案2018.1一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个1. 北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用. 将178800用科学记数法表示应为A .1.788×104B .1.788×105C .1.788×106D .1.788×107 2.若将抛物线y = -12x 2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是A .2)3(212-+-=x y B .2)3(212---=x y C .2)3(2-+=x y D. 2)3(212++-=x y3.在Rt △ABC 中,∠C =90°,AC =4,BC =3,则tan A 错误!未找到引用源。
的值为 A .34B .43C .53D .54 4. 如图,在△ABC 中,点D ,E 分别为边AB,AC 上的点,且DE ∥BC ,若AD =4,BD =8,AE =2,则CE 的长为A .2B .4C .6D .8 5. 如图,⊙O 是△ABC 的外接圆,∠BOC =100°) A .40︒B.50︒ D .100︒6. 网球单打比赛场地宽度为80.9米(如图AB 的高度)...E DC BA 第4题图 第5题图C穿越球,使球落在对方底线上C处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为A. 1.65米B. 1.75米C.1.85米D. 1.95米7. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);③用一细橡胶棒连接C、D两点(如图3);④计算出橡胶棒CD的长度.小明计算橡胶棒CD的长度为A.22分米B.23分米C.32分米D.33分米8.如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为第8题图1第8题图23A.从D点出发,沿弧DA→弧AM→线段BM→线段BCB.从B点出发,沿线段BC→线段CN→弧ND→弧DAC.从A点出发,沿弧AM→线段BM→线段BC→线段CND.从C点出发,沿线段CN→弧ND→弧DA→线段AB二、填空题(本题共16分,每小题2分)9.分解因式:3x3-6x2+3x=_________.10.若△ABC∽△DEF,且对应边BC与EF的比为1∶3,则△ABC与△DEF的面积比等于.11. 有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可):.12.抛物线y=2(x+1)2+3 的顶点坐标是.13.把二次函数y=x2-4x+5化成y=a(x-h)2+k的形式为__________________.14.数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B 的俯角β为60°. 室外测量组测得BF的长度为5米.则旗杆AB=______米.415.它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为 米2.16. 阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题: 请回答:这样做的依据是 . 三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程. 17.计算:4sin45°-8+(3-1)0+|-2|.18.如图,在△ABC 中,D 为AC 边上一点,BC =4,AC =8,CD=2.求证:△BCD ∽△ACB .第18题图第15题图519. 如图,在△ABC 中,tan A =43,∠B =45°,AB =14. 求BC 的长.20.在平面直角坐标系xOy 中,直线3+-=x y 与双曲线ky =相交于点A (m ,2). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图;(3)若P 是坐标轴上一点,且满足P A =OA . 直接写出点P 的坐标.21.一个二次函数图象上部分点的横坐标x ,纵坐标y 的对应值如下表:第19题图6(2)求m 的值;(3)在给定的直角坐标系中,画出这个函数的图象; (4)根据图象,写出当y <0时,x 的取值范围.22. 如图,已知AB 是⊙O 的直径,点M 在BA 的延长线上,MD 切⊙O 于点D ,过点B 作BN ⊥MD 于点C ,连接AD 并延长,交BN 于点N . (1)求证:AB =BN ;(2)若⊙O 半径的长为3,cosB =52,求MA 的长.7D23.数学课上老师提出了下面的问题: 在正方形ABCD 对角线BD 上取一点F ,使51=D B DF . 小明的做法如下:如图① 应用尺规作图作出边AD 的中点M ; ② 应用尺规作图作出MD 的中点E ; ③ 连接EC ,交BD 于点F . 所以F 点就是所求作的点.请你判断小明的做法是否正确,并说明理由.24. 已知:如图,在四边形ABCD 中,BD 是一条对角线,∠DBC =30°, ∠DBA =45°,∠C =70°.若DC =a ,AB=b , 请写出求tan ∠ADB 的思路. (不用写出计算结果........)25.如图,在四边形ABCD 中,AD ∥BC ,∠ADC =90°,点E 是BC 边上一动点,联结AE ,过点E 作AE 的垂线交直线=2cm ,BC =5cm ,设BE 的长为x cm ,CF 的长为y cm.8小东根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行探究. 下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(说明:补全表格时相关数据保留一位小数)(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题: 当BE =CF 时,BE 的长度约为 cm.26.在平面直角坐标系xOy 中,直线l : n x y +-=2与抛物线3242---=m mx mx y 相交于点A (2-,7). (1)求m 、n 的值;(2)过点A 作AB ∥x 轴交抛物线于点B ,设抛物线 与x 轴交于点C 、D (点C 在点D 的左侧),求△BCD 的面积;(3)点E (t ,0)为x 轴上一个动点,过点E 作平行于y 轴的直线与直线l 和抛物线分别交于点P 、Q .当点P 在点Q 上方时,求线段PQ 的最大值.9B27. 在等腰△ABC 中,AB =AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P . (1)依题意补全图形;(2)若∠BAC =2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.28.在平面直角坐标系xOy 中,点P 的横坐标为x ,纵坐标为2x ,满足这样条件的点称为“关系点”.(1)在点A (1,2)、B (2,1)、M (21,1)、N (1,21)中,是“关系点”的 ; (2)⊙O 的半径为1,若在⊙O 上存在“关系点”P ,求点P 坐标;(3)点C 的坐标为(3,0),若在⊙C 上有且只有一个......“关系点”P ,且“关系点”P 的横坐标满足-2≤x≤2.请直接写出⊙C 的半径r 的取值范围.102017-2018学年度第一学期期末初三质量检测数学试卷评分标准一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个二、填空题(本题共16分,每小题2分)9.3x (x -1)2. 10.1:9. 11.答案不唯一,k <0即可. 12.(﹣1,3). 13.y =(x -2)2+1. 14. 5+53. 15.16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程.2511A17. 解:原式=4×22-22+1+2 …………………………………………………… 4分 =3 ………………………………………………………………………………………5分18.证明:∵BC =4,AC =8,CD =2.…………………………1分∴BC CD AC BC =………………………………………3分 又∵∠C =∠C ……………………………………4分∴ △BCD ∽△ACB ……………………………………………………………………5分19. 解:过点C 作CD ⊥AB 于点D ,如图. …………………………1分 ∵在Rt △CDA 中,tan A =AD CD = 43设CD =3x ,AD =4x . ……………………………………………………………………………2分 ∵在Rt △CDB 中,∠B =45° ∴tan B =DB CD = 1,sin B =BCCD =22,……………………………………………………………3分∵CD =3x . ∴BD =3x ,BC =2·3x =32x . 又∵AB =AD+BD =14,∴4x +3x =14,解得x =2.…………………………………………………………………………4分 ∴BC =62. ……………………………………………………………………………………5分 20.解:(1)∵直线3+-=x y 与双曲线xky =相交于点A (m ,2). ∴ A (1,2)………………………………………1分 ∴xy 2=…………………………………………2分 (2)如图…………………………………………………………4分 (3)P (0,4)或P (2,0) …………………………………………6分1221.解:(1)设这个二次函数的表达式为2()y a x h k =-+. 依题意可知,顶点为(-1,2),………………………1分 ∴ ()212++=x a y .∵图象过点(1,0), ∴()21102++=a .∴12a =-. ∴这个二次函数的表达式为()21212++-=x y ………2分(2)25-=m .………………………………………………3分 (3)如图…………………………………………………………………………………………5分 (4)x <-3或x >1..…………………………………………………………………………………6分 22.(1)证明:连接OD ,…………………………1分 ∵MD 切⊙O 于点D ,∴OD ⊥MD , ∵BN ⊥MC ,∴OD ∥BN ,…………………………………2分 ∴∠ADO =∠N ,∵OA =OD ,∴∠OAD =∠ADO ,∴∠OAD =∠N ,∴AB =BN ;………………………………………………………………………………………3分 (2)解:由(1)OD ∥BN ,∴∠MOD =∠B ,………………………………………………………………………………4分 ∴cos ∠MOD =cosB =52, 在Rt △MOD 中,cos ∠MOD ==OMOD, ∵OD =OA ,MO =MA +OA =3+MA ,∴AM +33=52,∴MA =4.5………………………………………………………………………………………5分13D23.解:正确. ………………………………………………………………1分 理由如下: 由做法可知M 为AD 的中点,E 为MD 的中点, ∴AD DE =41. …………………………………………………………2分 ∵四边形ABCD 是正方形,∴AD=BC ,ED ∥BC . ………………………………………………3分 ∴△DEF ∽△BFC ∴BC DE =BF DF ………………………………………………………..4分 ∵AD =BC ∴BF DF =BC DE =41∴BD DF =51………………………………………………………………………………………5分 24. 解: (1)过D 点作DE ⊥BC 于点E ,可知△CDE 和△DEB 都是直角三角形;…………1分 (2)由∠C =70°,可知sin ∠C 的值,在Rt △CDE 中,由sin ∠C 和DC =a ,可求DE 的长;2分 (3)在Rt △DEB 中,由∠DBC =30°,DE 的长,可求BD 的长………………………………3分 (4)过A 点作AF ⊥BD 于点F , 可知△DF A 和△AFB 都是直角三角形; …………4分 (5)在Rt △AFB 中,由∠DBA =45°,AB =b ,可求AF 和BF 的长; (6)由DB 、BF 的长,可知DF 的长; (7)在Rt △DF A 中,由DFFA ,可求tan ∠ADB . ………………5分 25.解:(1)1.5……………………………………… ..1分 (2)如图……………………………………………4分 (3)0.7(0.6~0.8均可以) .………………………….5分 . 26. 解:(1)m =1………………………………………………………………………………………1分 n =3………………………………………………………………………………………………2分 (2)由(1)知抛物线表达式为y =x 2-4x -5 令y =0得,x 2-4x -5=0.14解得x 1=-1,x 2=5,……………………………………………………………………………3分 ∴抛物线y =x 2-4x -5与x 轴得两个交点C 、D 的坐标分别为C (-1,0),D (5,0) ∴CD =6.∵A (2-,7),AB ∥x 轴交抛物线于点B ,根据抛物线的轴对称性,可知B (6,7)………4分∴S △BCD =21.……………………………………………………………………………………5分(3) 据题意,可知P (t ,-2 t +3),Q ( t ,t 2-4 t -5),由x 2-4x -5=-2x +3得直线y =-2x +3与抛物线y = x 2-4x -5的两个交点坐标分别为(-2,7)和(4,-5) ……………………………………………………………………………………………6分 ∵点P 在点Q 上方∴-2<t <5, ∴PQ = -t 2+2 t +8=-( t -2) 2+9 ∵a =-1∴PQ 的最大值为9.……………………………………………………………………………7分27.解:(1)如图……………………………………………1分(2) ∵∠BAC =2α,∠AHB =90° ∴∠ABH =90°-2α …………………………………………………………………………… 2分 ∵BA =BD ∴∠BDA =45°+α………………………………………………………………………………3分(3)补全图形,如图………………4分证明过程如下:∵D 关于BC 的对称点为E ,且DE 交BP 于G∴DE ⊥BP ,DG =GE ,∠DBP =∠EBP ,BD =BE ;…………………………………………5分 ∵AB=AC ,∠BAC=2α ∴∠ABC=90°-α 由(2)知∠ABH =90°-2α ∠DBP =90°-α-(90°-2α)=α15∴∠DBP =∠EBP =α ∴∠BDE =2α ∵AB =BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DP DE=2, ∴DPBC=2, ∴BC =2DP .………………………………………………………………………………7分 28.解:(1)A 、M . ……………………………………………………………………………………2分 (2)过点P 作PG ⊥x 轴于点G …………………………………………………………………3分 设P (x ,2x )∵OG 2+PG 2=OP 2 ………………………………………………………………………………4分 ∴x 2+4x 2=1 ∴5x 2=1∴x 2=51∴x =55±∴P (55,552)或P (55-,552-)……………………………………………………5分 (3)r =556或 4117≤<r …………………………………………………………7分更多初中数学资料,初中数学试题精解请微信关注16。
15.怀柔区答案

初三数学答案1(共6页)2017-2018学年度初三一模怀柔数学试卷评分标准一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个二、填空题(本题共16分,每小题2分)9.311>.10. 6. 11. 1. 12.51. 13. (1,-3). 14. ①③. 15. ⎩⎨⎧=++=+.165,54y x x y y x16. 到角两边距离相等的点在角平分上;两点确定一条直线;角平分上的点到角两边的距离相等;圆的定义;经过半径的外端,并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第17—23、25每题5分,第24题6分,第26、27每题7分,第28题8分)解答应写出文字说明、演算步骤或证明过程. 17.解:原式1132=-+…………………………………………………4分 .…………………………………………………………………5分18.解:由①得:3x < . ………………………………………………………………………2分由②得:9x >- …………………………………………………………………………4分 原不等式组的解集为93x -<< 19. (1)答案不唯一.例如:先沿y 轴翻折,再向右平移1个单位,向下平移3个单位;先向左平移1个单位,向下平移3个单位,再沿y 轴翻折. ……………3分(2)如图所示………………………………………4分(3)π .………………………………………………5分4=初三数学答案2(共6页)20.(1)∵△=(-6m)2-4(9m 2-9) ……………………………………………………………………1分=36m 2-36m 2+36 =36>0. ∴方程有两个不相等的实数根……………………………………………………………2分 (2)66332m x m ±===±.……………………………………………………3分 ∵3m+3>3m-3,∴x 1=3m+3,x 2=3m-3, …………………………………………………………………………4分 ∴3m+3=2(3m-3) .∴m=3. …………………………………………………………………………………………5分21.(1)∵AB=AD ,∴∠ABD=∠ADB ,………………………………1分 ∵∠ADB=∠CDE ,∴∠ABD=∠CDE. ∵∠BAC=90°,∴∠ABD+∠ACB=90°.∵CE ⊥AE ,∴∠DCE+∠CDE=90°. ∴∠ACB=∠DCE. …………………………………2分 (2)补全图形,如图所示: …………………………3分 ∵∠BAD=45°, ∠BAC=90°,∴∠BAE=∠CAE=45°, ∠F=∠ACF=45°, ∵AE ⊥CF, BG ⊥CF,∴AD ∥BG . ∵BG ⊥CF, ∠BAC=90°,且∠ACB=∠DCE, ∴AB=BG.∵AB=AD ,∴BG=AD. ∴四边形ABGD 是平行四边形.∵AB=AD∴平行四边形ABGD 是菱形.…………………………………………………………………4分设AB=BG=GD=AD=x ,∴BF=2BG=2x.∴AB+BF=x+2x=2+2. ∴x=2, 过点B 作BH ⊥AD 于H.∴BH=22AB=1. ∴S 四边形ABDG =AD×BH=2. ……………………………………………………………………5分初三数学答案3(共6页)(1)∵双曲线x m y =过A (3,-2),将A (3,-2)代入xm y =, 解得:m= -6.∴所求反比例函数表达式为: y=x6-. …………………………………1分 ∵点A (3,-2)点B (0,1)在直线y=kx+b 上,∴-2=3k+1. …………………………………………………………………………………2分 ∴k=-1.∴所求一次函数表达式为y=-x+1. …………………………………………………………3分 (2)C(0,123+ )或 C(0,231- ). ……………………………………………………5分 23.(1)∵BA=BC ,AO=CO, ∴BD ⊥AC.∵CE 是⊙O 的切线, ∴CE ⊥AC.∴CE ∥BD. ……………………………………1分 ∴∠ECB=∠CBD. ∵BC 平分∠DBE, ∴∠CBE=∠CBD. ∴∠ECB=∠CBE.∴BE=CE. …………………………………………2分 (2)解:作EF ⊥BC 于F. …………………………3分 ∵⊙O 的直径长8, ∴CO=4.∴sin ∠CBD= sin ∠BCE= 45=OC BC. …………………………………………………………4分 ∴BC=5,OB=3. ∵BE=CE, ∴BF=1522BC =. ∵∠BOC=∠BFE=90°,∠CBO=∠EBF, ∴△CBO ∽△EBF.∴BE BF BC OB=. ∴BE=256. ……………………………………………………………………………………5分E初三数学答案4(共6页)xy–1123456–1123456O 补全表格:分 (1)130;…………………………………………………………………………………………4分 (2)答案不唯一,理由需支持判断结论. ………………………………………………………6分 25.(1)约1.1; ………………………………………………………………………………………1分 (2)如图:…………………………………………………………………………………………………4分(3)约1.7. ………………………………………………………………………………………5分 26.(1)M(2,-1); ………………………………………………………………………………2分 (2)B(4,3); …………………………………………………………………………………3分 (3)∵抛物线y=mx 2-4mx+4m-1(m ≠0)与y 轴交于点A (0,3), ∴4n-1=3.∴n=1. ……………………………………………………………………………………4分 ∴抛物线的表达式为342+-=x x y .由34212++=+x x m x . 由△=0,得: 161-=m ……………………………………………………………………5分初三数学答案5(共6页)B∵抛物线342+-=x x y 与x 轴的交点C 的坐标为(1,0), ∴点C 关于y 轴的对称点C 1的坐标为(-1,0).把(-1,0)代入m x y +=21,得:21=m .……………………………………………6分 把(-4,3)代入m x y +=21,得:5=m .∴所求m 的取值范围是161-=m 或21<m ≤ 5. …………………………………………7分27.(1)如图 …………………………………………………………………………………………1分 (2) ∵线段AD 绕点A 逆时针方向旋转90°,得到线段∴∠DAE=90°,AD=AE.∴∠DAC+∠CAE =90°. ∵∠BAC=90°, ∴∠BAD+∠DAC =90°.∴∠BAD=∠CAE . …………………………………………………………………………2分 又∵AB=AC,∴△ABD ≌△ACE. ∴∠B=∠ACE.∵△ABC 中,∠A=90°,AB=AC,∴∠B=∠ACB=∠ACE=45°.∴∠ECD=∠ACB+∠ACE=90°. ……………………………………………………………4分 (3)Ⅰ.连接DE,由于△ADE 为等腰直角三角形,所以可求DE=2;……………………5分 Ⅱ.由∠ADF=60°,∠CAE=7.5°,可求∠EDC 的度数和∠CDF 的度数,从而可知DF 的长; …………………………………………………………………………………………………6分 Ⅲ.过点A 作AH ⊥DF 于点H ,在Rt △ADH 中, 由∠ADF=60°,AD=1可求AH 、DH 的长; Ⅳ. 由DF 、DH 的长可求HF 的长;Ⅴ. 在Rt △AHF 中, 由AH 和HF,利用勾股定理可求AF 的长.…………………………7分初三数学答案6(共6页)28.(1)①P 1(2,0)、P 2(0,2)…………………………………………………………………2分 ②如图, 在y=x+b 上,若存在⊙O 的“特征点”点P ,点O 到直线y=x+b 的距离m ≤2. 直线y=x+b 1交y 轴于点E ,过O 作OH ⊥直线y=x+b 1于点H. 因为OH=2,在Rt △DOE 中,可知OE=22. 可得b 1=22.同理可得b 2=-22.∴b 的取值范围是:22-≤b ≤22. …………………………………………………6分 (2)x>3或 3-<x . …………………………………………………………………………8分。
北京市怀柔区九年级上数学期末试卷及答案

怀柔区—第一学期初三期末质量检测数 学 试 卷 .1一、选择题(本题共16分,每小题2分)下列各题均有四个选项,符合题意的选项只有..一个 1.已知∠A 为锐角,且sin A =12,那么∠A 等于 A .15° B .30° C .45° D .60° 2.如图,⊙O 是△ABC 的外接圆,∠A =50︒,则∠BOC 的大小为A .40°B .30°C .80°D .100°3.已知△ABC ∽△'''A B C ,如果它们的相似比为2∶3,那么它们的面积比是A .3:2B . 2:3C .4:9D .9:4 4.下面是一个反比例函数的图象,它的表达式可能是 A .2y x = B .4y x=C .3y x =-D . 12y x =5.正方形ABCD 内接于O ,若O 的半径是2,则正方形的边长是A .1B .2C .2D .226.如图,线段BD ,CE 相交于点A ,DE ∥BC .若BC =3,DE =1.5,AD =2,则AB 的长为 A .2 B .3 C .4 D .5D EC BA第6题图 y x P N M B A O 第8题图第2题图yxO第4题图DCBAO第5题图7.若要得到函数()21+2y x =-的图象,只需将函数2y x =的图象A .先向右平移1个单位长度,再向上平移2个单位长度B .先向左平移1个单位长度,再向上平移2个单位长度C .先向左平移1个单位长度,再向下平移2个单位长度D .先向右平移1个单位长度,再向下平移2个单位长度8. 如图,一条抛物线与x 轴相交于M ,N 两点(点M 在点N 的左侧),其顶点P 在线段AB 上移动,点A ,B 的坐标分别为(-2,-3),(1,-3),点N 的横坐标的最大值为4,则点M 的横坐标的最小值为 A.-1 B.-3 C.-5 D.-7 二、填空题(本题共16分,每小题2分)9.二次函数241y x x =++-2图象的开口方向是__________. 10.Rt△ABC 中,∠C=90°,AC=4,BC=3,则tanA的值为 .11. 如图,为了测量某棵树的高度,小颖用长为2m 的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点. 此时竹竿与这一点距离相距6m ,与树相距15m ,那么这棵树的高度为 .12.已知一个扇形的半径是1,圆心角是120°,则这个扇形的弧长是 . 13.如图所示的网格是正方形网格,则sin ∠BAC 与sin ∠DAE 的大小关系是 .14.写出抛物线y=2(x-1)2图象上一对对称点的坐标,这对对称点的坐标 可以是 和 .15.如图,为测量河内小岛B 到河边公路l 的距离,在l 上顺次取A ,C ,D 三点,在A 点测得∠BAD=30°,在C 点测得∠BCD=60°,又测得AC=50米,则小岛B 到公路l 的距离为 米.16.在平面直角坐标系xOy 内有三点:(0,-2),(1,-1),(2.17,0.37).则过这三个点 (填“能”或“不能”)画一个圆,理由是 .三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.17.已知:53a b =. 求:a bb+.11题图13题图CB A18.计算:2cos30-4sin 45+8︒︒ 19.已知二次函数 y = x 2-2x -3.(1)将y = x 2-2x -3化成y = a (x -h )2 + k 的形式; (2)求该二次函数图象的顶点坐标.20.如图,在△ABC 中,∠B 为锐角, AB =32BC =7,sin 2B =AC 的长.21. 如图,在四边形ABCD 中,AD ∥BC ,AB ⊥BC ,点E 在AB 上,AD =1,AE =2,BC =3,BE =1.5. 求证:∠DEC =90°.22.下面是小东设计的“在三角形一边上求作一个点,使这点和三角形的两个顶点构成的三角形与原三角形相似”的尺规作图过程. 已知: △ABC .求作: 在BC 边上求作一点P, 使得△P AC ∽△ABC . 作法:如图,①作线段AC 的垂直平分线GH ;②作线段AB 的垂直平分线EF,交GH 于点O ; ③以点O 为圆心,以OA 为半径作圆;④以点C 为圆心,CA 为半径画弧,交⊙O 于点D(与点A 不重合);HGAB E DCBA AB C⑤连接线段AD 交BC 于点P. 所以点P 就是所求作的点. 根据小东设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹) (2)完成下面的证明.证明: ∵CD=AC , ∴CD = . ∴∠ =∠ . 又∵∠ =∠ ,∴△P AC ∽△ABC ( )(填推理的依据).23.在平面直角坐标系xOy 中,直线y=x+2 与双曲线ky x相交于点A (m ,3). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图;(3)若P 是坐标轴上一点,当OA =P A 时.直接写出点P 的坐标.24. 如图,AB 是O 的直径,过点B 作O 的切线BM ,点A ,C ,D 分别为O 的三等分点,连接AC ,AD ,DC ,延长AD 交BM 于点E , CD 交AB 于点F. (1)求证://CD BM ;(2) 连接OE ,若DE=m ,求△OBE 的周长.yx–1–2–3–4–5–6123456–1–2–3–41234OO M F DCBA25. 在如图所示的半圆中,P是直径AB上一动点,过点P作PC⊥AB于点P,交半圆于点C,连接AC.已知AB=6cm,设A,P两点间的距离为x cm,P,C两点间的距离为y1cm,A,C两点间的距离为y2cm.小聪根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小聪的探究过程,请补充完整:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;x/cm0123456y1/cm0 2.24 2.83 2.83 2.240y2/cm0 2.45 3.46 4.24 4.90 5.486(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;(3)结合函数图象,解决问题:当△APC有一个角是30°时,AP的长度约为cm.26. 在平面直角坐标系xOy 中,抛物线22y ax ax c =++(其中a 、c 为常数,且a <0)与x 轴交于点A ()3,0-,与y 轴交于点B ,此抛物线顶点C 到x 轴的距离为4. (1)求抛物线的表达式; (2)求CAB ∠的正切值;(3)如果点P 是x 轴上的一点,且ABP CAO ∠=∠,直接写出点P 的坐标.27. 在菱形ABCD 中,∠ADC=60°,BD 是一条对角线,点P 在边CD 上(与点C ,D 不重合),连接AP ,平移ADP ∆,使点D 移动到点C ,得到BCQ ∆,在BD 上取一点H ,使HQ=HD ,连接HQ ,AH ,PH . (1) 依题意补全图1;(2)判断AH 与PH 的数量关系及∠AHP 的度数,并加以证明;(3)若141AHQ ∠=︒,菱形ABCD 的边长为1,请写出求DP 长的思路. (可以不写出计算结果.........)A BCDP图1A BCD备用图y x–1–2–31234–1–2–3–41234O28.在平面直角坐标系xOy中,点A(x,0),B(x,y),若线段AB上存在一点Q满足12QAQB=,则称点Q是线段AB的“倍分点”.(1)若点A(1,0),AB=3,点Q是线段AB的“倍分点”.①求点Q的坐标;②若点A关于直线y= x的对称点为A′,当点B在第一象限时,求' QA QB;(2)⊙T的圆心T(0,t),半径为2,点Q在直线3y x=上,⊙T上存在点B,使点Q是线段AB的“倍分点”,直接写出t的取值范围.yxO12022-2023第一学期期末初三质量检测数学试卷评分标准一、选择题(本题共16分,每小题2分)下列各题均有四个选项,符合题意的选项只有..一个题号12345678答案B D C B B C A C 二、填空题(本题共16分,每小题2分)9.下10.3411. m712.32π13.sin∠BAC>sin∠DAE14.(2,2),(0,2)(答案不唯一)15.253能,因为这三点不在一条直线上.三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分)17.解:∵53ab=,∴1a b ab b+=+=53+1=83.………………………5分32=2-4+2222⨯⨯18.解:原式………………………3分=3-22+22………………………4分35分19.解:(1)y=x2-2x-3=x2-2x+1-1-3……………………………2分=(x-1)2-4.……………………3分(2)∵y=(x-1)2-4,∴该二次函数图象的顶点坐标是(1,-4).………………………5分20.解:作AD⊥BC于点D,∴∠ADB=∠ADC=90°.∵sin2 B=∴∠B=∠BAD=45°.………………2分∵AB=32B∴AD=BD=3.…………………………3分 ∵BC =7,∴DC=4. ∴在Rt △ACD 中,225AC AD DC +=.…………………………5分21.(1)证明:∵AB ⊥BC ,∴∠B =90°.∵AD ∥BC ,∴∠A =90°.∴∠A =∠B .………………2分 ∵AD =1,AE =2,BC =3,BE =1.5, ∴121.53=.∴AD AEBE BC=∴△ADE ∽△BEC .∴∠3=∠2.………………3分 ∵∠1+∠3=90°,∴∠1+∠2=90°. ∴∠DEC =90°.………………5分22.(1)补全图形如图所示:………………2分 (2)AC ,∠CAP=∠B ,∠A CP=∠A CB ,有两组角对应相等的两个三角形相似.………………5分23.解:(1)∵直线y=x+2与双曲线ky x=相交于点A (m ,3).∴3=m+2,解得m=1.∴A (1,3)……………………………………1分 把A (1,3)代入ky x=解得k=3, 3y x=……………………………………2分(2)如图……………………………………4分(3)P (0,6)或P (2,0) ……………………………………6分 24.证明:(1)∵点A 、C 、D 为O 的三等分点,∴AD DC AC == , ∴AD=DC=AC. ∵AB 是O 的直径,∴AB ⊥CD.∵过点B 作O 的切线BM , ∴BE ⊥AB.∴//CD BM .…………………………3分(2) 连接DB.①由双垂直图形容易得出∠DBE=30°,在Rt △DBE 中,由DE=m ,解得BE=2m ,3m. ②在Rt △ADB 中利用30°角,解得3m ,3…………………4分∴CB AEFGHOPD yx–1–2–3–4–5–6–71234567–1–2–3–4–51234AOACDFM O在Rt △OBE 中,由勾股定理得出7m.………………………………5分 ④计算出△OB E 周长为237m.………………………………6分25.(1)3.00…………………………………1分(2)…………………………………………4分 (3)1.50或4.50……………………………2分26.解:(1)由题意得,抛物线22y ax ax c =++的对称轴是直线212ax a=-=-.………1分 ∵a <0,抛物线开口向下,又与x 轴有交点,∴抛物线的顶点C 在x 轴的上方. 由于抛物线顶点C 到x 轴的距离为4,因此顶点C 的坐标是()1,4-. 可设此抛物线的表达式是()214y a x =++,由于此抛物线与x 轴的交点A 的坐标是()3,0-,可得1a =-. 因此,抛物线的表达式是223y x x =--+.………………………2分 (2)点B 的坐标是()0,3.联结BC .∵218AB =,22BC =,220AC =,得222AB BC AC +=. ∴△ABC 为直角三角形,90ABC ∠=.所以1tan 3BC CAB AB ∠==. 即CAB ∠的正切值等于13.………………4分(3)点p 的坐标是(1,0).………………6分 27.(1)补全图形,如图所示.………………2分 (2)AH 与PH 的数量关系:AH =PH ,∠AHP =120°. 证明:如图,由平移可知,PQ=DC.A BCD P HQ∵四边形ABCD是菱形,∠ADC=60°,∴AD=DC,∠ADB=∠BDQ=30°.∴AD=PQ.∵HQ=HD,∴∠HQD=∠HDQ=30°.∴∠ADB=∠DQH,∠D HQ=120°.∴△ADH≌△PQH.∴AH=PH,∠A HD=∠P HQ.∴∠A HD+∠DHP =∠P HQ+∠DHP.∴∠A HP=∠D HQ. ∵∠D HQ=120°,∴∠A HP=120°.………………5分(3)求解思路如下:由∠A HQ=141°,∠B HQ=60°解得∠A HB=81°.a.在△ABH中,由∠A HB=81°,∠A BD=30°,解得∠BA H=69°.b.在△AHP中,由∠A HP=120°,AH=PH,解得∠PA H=30°.c.在△ADB中,由∠A DB=∠A BD= 30°,解得∠BAD=120°.由a、b、c可得∠DAP=21°.在△DAP中,由∠A DP= 60°,∠DAP=21°,AD=1,可解△DAP,从而求得DP长.…………………………………7分28.解:(1)∵A(1,0),AB=3∴B(1,3)或B(1,-3)∵12 QA QB=∴Q(1,1)或Q(1,-1)………………3分(2)点A(1,0)关于直线y= x的对称点为A′(0,1)∴Q A =Q A′∴QBA Q'21=………………5分(3)-4≤t≤4………………7分x(0,1)(1,3(1,0)QBA'AO11/ 11。
北京市怀柔区2018届九年级数学上学期期末考试试题 新人教版

北京市怀柔区2018届九年级数学上学期期末考试试题一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个1. 北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用. 将178800用科学记数法表示应为A .1.788×104B .1.788×105C .1.788×106D .1.788×107 2.若将抛物线y = -12x 2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是A .2)3(212-+-=x y B .2)3(212---=x y C .2)3(2-+=x y D. 2)3(212++-=x y3.在Rt △ABC 中,∠C =90°,AC =4,BC =3,则tan A 的值为 A .34 B .43C .53D .54 4. 如图,在△ABC 中,点D ,E 分别为边AB,AC 上的点,且DE ∥BC ,若AD =4,BD =8,AE =2,则CE 的长为A.2 B .4 C .6 D .85. 如图,⊙O 是△ABC 的外接圆,∠BOC =100°,则∠A 的大小为 ( )E DCA第4题图 第5题图A .40︒B .50︒C .80︒D .100︒6. 网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB 的高度).中网比赛中,某运动员退出场地在距球网14米的D 点处接球,设计打出直线..穿越球,使球落在对方底线上C 处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为A. 1.65米B. 1.75米C.1.85米D. 1.95米 7. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O ,再任意找出圆O 的一条直径标记为AB (如图1),测量出AB =4分米;②将圆环进行翻折使点B 落在圆心O 的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C 、D (如图2);③用一细橡胶棒连接C 、D 两点(如图3); ④计算出橡胶棒CD 的长度.小明计算橡胶棒CD 的长度为 A .22 分米B . 23分米C .32 分米D .33分米8.如图1,⊙O 过正方形ABCD 的顶点A 、D 且与边BC 相切于点E ,分别交AB 、DC 于点M 、N .动点P 在⊙O 或正方形ABCD 的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x ,圆心O 与P 点的距离为y ,图2记录了一段时间里y 与x 的函数关系,在这段时间里P第6题图C3点的运动路径为A.从D 点出发,沿弧DA →弧AM →线段BM →线段BCB.从B 点出发,沿线段BC →线段CN →弧ND →弧DAC.从A 点出发,沿弧AM →线段BM →线段BC →线段CND.从C 点出发,沿线段CN →弧ND →弧DA →线段AB 二、填空题(本题共16分,每小题2分) 9.分解因式:3x 3-6x 2+3x =_________.10.若△ABC ∽△DEF ,且对应边BC 与EF 的比为1∶3,则△ABC 与△DEF 的面积比等于 . 11. 有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可): .12.抛物线y =2(x +1)2+3 的顶点坐标是 .13.把二次函数y =x 2-4x +5化成y=a (x -h )2+k 的形式为__________________.14. 数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E 处测得旗杆顶部A 的仰角α为45°,旗杆底部B 的俯角β为60°. 室外测量组测得BF 的长度为5米.则旗杆AB =______米.第15题图15.在学校的花园里有一如图所示的花坛,它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为 米2. 16. 阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:小明的作法如下:请回答:这样做的依据是 .三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程. 17.计算:4si n45°-8+(3-1)0+|-2|.18.如图,在△ABC 中,D 为AC 边上一点,BC =4,AC =8,CD=2.求证:△BCD ∽△ACB .第18题图第19题图519. 如图,在△ABC 中,tan A =43,∠B =45°,AB =14. 求BC 的长. 20.在平面直角坐标系xOy 中,直线3+-=x y 与双曲线xky =相交于点A (m ,2). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图; (3)若P 是坐标轴上一点,且满足PA =OA . 直接写出点P 的坐标.21.一个二次函数图象上部分点的横坐标x ,纵坐标y 的对应值如下表:(2)求m 的值;(3)在给定的直角坐标系中,画出这个函数的图象; (4)根据图象,写出当y <0时,x 的取值范围.22. 如图,已知AB 是⊙O 的直径,点M 在BA 的延长线上,MD 切⊙O 于点D ,过点B 作BN ⊥MD 于点C ,连接AD 并延长,交BN 于点N . (1)求证:AB =BN ;(2)若⊙O 半径的长为3,cosB =52,求MA 的长.23.数学课上老师提出了下面的问题: 在正方形ABCD 对角线BD 上取一点F ,使51=D B DF . 小明的做法如下:如图D① 应用尺规作图作出边AD 的中点M ; ② 应用尺规作图作出MD 的中点E ; ③ 连接EC ,交BD 于点F . 所以F 点就是所求作的点.请你判断小明的做法是否正确,并说明理由.24. 已知:如图,在四边形ABCD 中,BD 是一条对角线,∠DBC =30°, ∠DBA =45°,∠C =70°.若DC =a ,AB=b , 请写出求tan ∠ADB 的思路. (不用写出计算结果........)25.如图,在四边形ABCD 中,AD ∥BC ,∠ADC =90°,点E 是BC 边上一动点,联结AE ,过点E 作AE 的垂线交直线CD 于点F .已知AD =4cm ,CD =2cm ,BC =5cm ,设BE 的长为x cm ,CF 的长为y cm.变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(说明:补全表格时相关数据保留一位小数)(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题: 当BE =CF 时,BE 的长度约为 cm.7CB26.在平面直角坐标系xOy 中,直线l :n x y +-=2与抛物线3242---=m mx mx y 相交于点A (2-,7).(1)求m 、n 的值;(2)过点A 作AB ∥x 轴交抛物线于点B ,设抛物线 与x 轴交于点C 、D (点C 在点D 的左侧),求△BCD 的面积;(3)点E (t ,0)为x 轴上一个动点,过点E 作平行于y 轴的直线与直线l 和抛物线分别交于点P 、Q .当点P 在点Q 上方时,求线段PQ 的最大值.27. 在等腰△ABC 中,AB =AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P . (1)依题意补全图形;(2)若∠BAC =2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.28.在平面直角坐标系xOy 中,点P 的横坐标为x ,纵坐标为2x ,满足这样条件的点称为“关系点”.(1)在点A (1,2)、B (2,1)、M (21,1)、N (1,21)中, 是“关系点”的 ;(2)⊙O 的半径为1,若在⊙O 上存在“关系点”P , 求点P 坐标;(3)点C 的坐标为(3,0),若在⊙C 上有且只有.... 一个..“关系点”P ,且“关系点”P 的横坐标满足 -2≤x≤2.请直接写出⊙C 的半径r 的取值范围.2017-2018学年度第一学期期末初三质量检测数学试卷评分标准一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个二、填空题(本题共16分,每小题2分)9.3x (x -1)2. 10.1:9. 11.答案不唯一,k <0即可.12.(﹣1,3). 13.y =(x -2)2+1. 14. 5+53. 15.16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程. 17.259A解:原式=4×22-22+1+2 …………………………………………………………………… 4分 =3 ………………………………………………………………………………………5分18.证明:∵BC =4,AC =8,CD =2.…………………………1分∴BC CDAC BC=………………………………………3分 又∵∠C =∠C …………………………………………………………………………4分 ∴ △BCD ∽△ACB ……………………………………………………………………5分19.解:过点C 作CD ⊥AB 于点D ,如图. ………………………………………………1分 ∵在Rt △CDA 中,tan A =AD CD = 43设CD =3x ,AD =4x . ……………………………………………………………………………2分 ∵在Rt △CDB 中,∠B =45° ∴tan B =DB CD = 1,sin B =BC CD =22,……………………………………………………………3分 ∵CD =3x . ∴BD =3x ,BC =2·3x =32x . 又∵AB =AD+BD =14, ∴4x +3x =14,解得x =2 (4)分∴BC =62. ……………………………………………………………………………………5分 20.解:(1)∵直线3+-=x y 与双曲线xky =相交于点A (m ,2). ∴ A (1,2)………………………………………1分 ∴xy 2=................................................2分 (2)如图 (4)分(3)P (0,4)或P (2,0) …………………………………………6分 21.解:(1)设这个二次函数的表达式为2()y a x h k =-+.依题意可知,顶点为(-1,2),………………………1分∴ ()212++=x a y . ∵图象过点(1,0), ∴()21102++=a .∴12a =-. ∴这个二次函数的表达式为()21212++-=x y …………2分 (2)25-=m .………………………………………………3分 (3)如图…………………………………………………………………………………………5分 (4)x <-3或x >1..…………………………………………………………………………………6分 22.(1)证明:连接OD ,…………………………1分 ∵MD 切⊙O 于点D ,∴OD ⊥MD ,∵BN ⊥MC ,∴OD ∥BN ,…………………………………2分 ∴∠ADO =∠N ,∵OA =OD ,∴∠OAD =∠ADO ,∴∠OAD =∠N ,∴AB =BN ;………………………………………………………………………………………3分 (2)解:由(1)OD ∥BN ,∴∠MOD =∠B ,………………………………………………………………………………4分 ∴cos ∠MOD =cosB =52, 在Rt △MOD 中,cos ∠MOD ==OMOD,11D∵OD =OA ,MO =MA +OA =3+MA ,∴AM 33=52,∴MA =4.5………………………………………………………………………………………5分 23.解:正确. ………………………………………………………………………………………1分 理由如下: 由做法可知M 为AD 的中点,E 为MD 的中点, ∴AD DE =41. …………………………………………………………2分 ∵四边形ABCD 是正方形,∴AD=BC ,ED ∥BC . ………………………………………………3分 ∴△DEF ∽△BFC ∴BC DE =BF DF ………………………………………………………..4分 ∵AD =BC ∴BF DF =BC DE =41∴BD DF =51………………………………………………………………………………………5分 24.解: (1)过D 点作DE ⊥BC 于点E ,可知△CDE 和△DEB 都是直角三角形;……………1分 (2)由∠C =70°,可知sin ∠C 的值,在Rt △CDE 中,由sin ∠C 和DC =a ,可求DE 的长;……………………………………………………………………………………………2分 (3)在Rt △DEB 中,由∠DBC =30°,DE 的长,可求BD 的长………………………………3分 (4)过A 点作AF ⊥BD 于点F , 可知△DFA 和△AFB 都是直角三角形; ………………4分(5)在Rt △AFB 中,由∠DBA =45°,AB =b ,可求AF 和BF 的长; (6)由DB 、BF 的长,可知DF 的长; (7)在Rt △DFA 中,由DFFA ,可求tan ∠ADB . ………………5分 25.解:(1)1.5............................................. ..1分 (2)如图 (4)分(3)0.7(0.6~0.8均可以) .………………………….5分 . 26.解:(1)m =1………………………………………………………………………………………1分n =3………………………………………………………………………………………………2分(2)由(1)知抛物线表达式为y =x 2-4x -5 令y =0得,x 2-4x -5=0.解得x 1=-1,x 2=5,……………………………………………………………………………3分∴抛物线y =x 2-4x -5与x 轴得两个交点C 、D 的坐标分别为C (-1,0),D (5,0) ∴CD =6.∵A (2-,7),AB ∥x 轴交抛物线于点B ,根据抛物线的轴对称性,可知B (6,7)………4分∴S △BCD =21.……………………………………………………………………………………5分(3) 据题意,可知P (t ,-2 t +3),Q ( t ,t 2-4 t -5),由x 2-4x -5=-2x +3得直线y =-2x +3与抛物线y = x 2-4x -5的两个交点坐标分别为(-2,7)和(4,-5) ……………………………………………………………………………………………6分 ∵点P 在点Q 上方∴-2<t <5, ∴PQ = -t 2+2 t +8=-( t -2) 2+9 ∵a =-1∴PQ 的最大值为9.……………………………………………………………………………7分27.解:(1)如图……………………………………………1分(2) ∵∠BAC =2α,∠AHB =90°∴∠ABH =90°-2α …………………………………………………………………………… 2分 ∵BA =BD∴∠BDA =45°+α………………………………………………………………………………3分 (3)补全图形,如图13………………4分证明过程如下:∵D 关于BC 的对称点为E ,且DE 交BP 于G∴DE ⊥BP ,DG =GE ,∠DBP =∠EBP ,BD =BE ;…………………………………………5分 ∵AB=AC ,∠BAC=2α ∴∠ABC=90°-α 由(2)知∠ABH =90°-2α ∠DBP =90°-α-(90°-2α)=α ∴∠DBP =∠EBP =α ∴∠BDE =2α ∵AB =BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DP DE=2, ∴DPBC=2, ∴BC =2DP.………………………………………………………………………………7分 28.解:(1)A 、M . ……………………………………………………………………………………2分 (2)过点P 作PG ⊥x 轴于点G …………………………………………………………………3分 设P (x ,2x )∵OG 2+PG 2=OP 2 ………………………………………………………………………………4分∴x 2+4x 2=1 ∴5x 2=1∴x 2=51∴x =55±∴P (55,552)或P (55-,552-)……………………………………………………5分 (3)r =556或4117≤<r …………………………………………………………7分。
北京市怀柔区2018届九年级数学上学期期末考试试题 新人教版

北京市怀柔区2018届九年级数学上学期期末考试试题一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个1. 北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用. 将178800用科学记数法表示应为A .1.788×104B .1.788×105C .1.788×106D .1.788×107 2.若将抛物线y = -12x 2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是A .2)3(212-+-=x y B .2)3(212---=x y C .2)3(2-+=x y D. 2)3(212++-=x y3.在Rt △ABC 中,∠C =90°,AC =4,BC =3,则tan A 的值为 A .34 B .43C .53D .54 4. 如图,在△ABC 中,点D ,E 分别为边AB,AC 上的点,且DE ∥BC ,若AD =4,BD =8,AE =2,则CE 的长为A.2 B .4 C .6 D .85. 如图,⊙O 是△ABC 的外接圆,∠BOC =100°,则∠A 的大小为 ( )E DCA第4题图 第5题图A .40︒B .50︒C .80︒D .100︒6. 网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB 的高度).中网比赛中,某运动员退出场地在距球网14米的D 点处接球,设计打出直线..穿越球,使球落在对方底线上C 处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为A. 1.65米B. 1.75米C.1.85米D. 1.95米 7. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O ,再任意找出圆O 的一条直径标记为AB (如图1),测量出AB =4分米;②将圆环进行翻折使点B 落在圆心O 的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C 、D (如图2);③用一细橡胶棒连接C 、D 两点(如图3); ④计算出橡胶棒CD 的长度.小明计算橡胶棒CD 的长度为 A .22 分米B . 23分米C .32 分米D .33分米8.如图1,⊙O 过正方形ABCD 的顶点A 、D 且与边BC 相切于点E ,分别交AB 、DC 于点M 、N .动点P 在⊙O 或正方形ABCD 的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x ,圆心O 与P 点的距离为y ,图2记录了一段时间里y 与x 的函数关系,在这段时间里P第6题图C3点的运动路径为A.从D 点出发,沿弧DA →弧AM →线段BM →线段BCB.从B 点出发,沿线段BC →线段CN →弧ND →弧DAC.从A 点出发,沿弧AM →线段BM →线段BC →线段CND.从C 点出发,沿线段CN →弧ND →弧DA →线段AB 二、填空题(本题共16分,每小题2分) 9.分解因式:3x 3-6x 2+3x =_________.10.若△ABC ∽△DEF ,且对应边BC 与EF 的比为1∶3,则△ABC 与△DEF 的面积比等于 . 11. 有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可): .12.抛物线y =2(x +1)2+3 的顶点坐标是 .13.把二次函数y =x 2-4x +5化成y=a (x -h )2+k 的形式为__________________.14. 数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E 处测得旗杆顶部A 的仰角α为45°,旗杆底部B 的俯角β为60°. 室外测量组测得BF 的长度为5米.则旗杆AB =______米.第15题图15.在学校的花园里有一如图所示的花坛,它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为 米2. 16. 阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:小明的作法如下:请回答:这样做的依据是 .三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程. 17.计算:4si n45°-8+(3-1)0+|-2|.18.如图,在△ABC 中,D 为AC 边上一点,BC =4,AC =8,CD=2.求证:△BCD ∽△ACB .第18题图第19题图519. 如图,在△ABC 中,tan A =43,∠B =45°,AB =14. 求BC 的长. 20.在平面直角坐标系xOy 中,直线3+-=x y 与双曲线ky =相交于点A (m ,2). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图; (3)若P 是坐标轴上一点,且满足PA =OA . 直接写出点P 的坐标.21.一个二次函数图象上部分点的横坐标x ,纵坐标y 的对应值如下表:(2)求m 的值;(3)在给定的直角坐标系中,画出这个函数的图象; (4)根据图象,写出当y <0时,x 的取值范围.22. 如图,已知AB 是⊙O 的直径,点M 在BA 的延长线上,MD 切⊙O 于点D ,过点B 作BN ⊥MD 于点C ,连接AD 并延长,交BN 于点N . (1)求证:AB =BN ;(2)若⊙O 半径的长为3,cosB =52,求MA 的长.23.数学课上老师提出了下面的问题: 在正方形ABCD 对角线BD 上取一点F ,使51=D B DF . 小明的做法如下:如图D① 应用尺规作图作出边AD 的中点M ; ② 应用尺规作图作出MD 的中点E ; ③ 连接EC ,交BD 于点F . 所以F 点就是所求作的点.请你判断小明的做法是否正确,并说明理由.24. 已知:如图,在四边形ABCD 中,BD 是一条对角线,∠DBC =30°, ∠DBA =45°,∠C =70°.若DC =a ,AB=b , 请写出求tan ∠ADB 的思路. (不用写出计算结果........)25.如图,在四边形ABCD 中,AD ∥BC ,∠ADC =90°,点E 是BC 边上一动点,联结AE ,过点E 作AE 的垂线交直线CD 于点F .已知AD =4cm ,CD =2cm ,BC =5cm ,设BE 的长为x cm ,CF 的长为y cm.变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(说明:补全表格时相关数据保留一位小数)(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题: 当BE =CF 时,BE 的长度约为 cm.7CB26.在平面直角坐标系xOy 中,直线l :n x y +-=2与抛物线3242---=m mx mx y 相交于点A (2-,7).(1)求m 、n 的值;(2)过点A 作AB ∥x 轴交抛物线于点B ,设抛物线 与x 轴交于点C 、D (点C 在点D 的左侧),求△BCD 的面积;(3)点E (t ,0)为x 轴上一个动点,过点E 作平行于y 轴的直线与直线l 和抛物线分别交于点P 、Q .当点P 在点Q 上方时,求线段PQ 的最大值.27. 在等腰△ABC 中,AB =AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P . (1)依题意补全图形;(2)若∠BAC =2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.28.在平面直角坐标系xOy 中,点P 的横坐标为x ,纵坐标为2x ,满足这样条件的点称为“关系点”.(1)在点A (1,2)、B (2,1)、M (21,1)、N (1,21)中, 是“关系点”的 ;(2)⊙O 的半径为1,若在⊙O 上存在“关系点”P , 求点P 坐标;(3)点C 的坐标为(3,0),若在⊙C 上有且只有.... 一个..“关系点”P ,且“关系点”P 的横坐标满足 -2≤x≤2.请直接写出⊙C 的半径r 的取值范围.2017-2018学年度第一学期期末初三质量检测数学试卷评分标准一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个二、填空题(本题共16分,每小题2分)9.3x (x -1)2. 10.1:9. 11.答案不唯一,k <0即可. 12.(﹣1,3). 13.y =(x -2)2+1. 14. 5+53. 15.16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程. 17.259A解:原式=4×22-22+1+2 …………………………………………………………………… 4分 =3 ………………………………………………………………………………………5分18.证明:∵BC =4,AC =8,CD =2.…………………………1分∴BC CDAC BC=………………………………………3分 又∵∠C =∠C …………………………………………………………………………4分 ∴ △BCD ∽△ACB ……………………………………………………………………5分19.解:过点C 作CD ⊥AB 于点D ,如图. ………………………………………………1分 ∵在Rt △CDA 中,tan A =AD CD = 43设CD =3x ,AD =4x . ……………………………………………………………………………2分 ∵在Rt △CDB 中,∠B =45° ∴tan B =DB CD = 1,sin B =BC CD =22,……………………………………………………………3分 ∵CD =3x . ∴BD =3x ,BC =2·3x =32x . 又∵AB =AD+BD =14, ∴4x +3x =14,解得x =2 (4)分∴BC =62. ……………………………………………………………………………………5分 20.解:(1)∵直线3+-=x y 与双曲线xky =相交于点A (m ,2). ∴ A (1,2)………………………………………1分 ∴xy 2=................................................2分 (2)如图 (4)分(3)P (0,4)或P (2,0) …………………………………………6分 21.解:(1)设这个二次函数的表达式为2()y a x h k =-+.依题意可知,顶点为(-1,2),………………………1分∴ ()212++=x a y . ∵图象过点(1,0), ∴()21102++=a .∴12a =-. ∴这个二次函数的表达式为()21212++-=x y …………2分 (2)25-=m .………………………………………………3分 (3)如图…………………………………………………………………………………………5分 (4)x <-3或x >1..…………………………………………………………………………………6分 22.(1)证明:连接OD ,…………………………1分 ∵MD 切⊙O 于点D ,∴OD ⊥MD ,∵BN ⊥MC ,∴OD ∥BN ,…………………………………2分 ∴∠ADO =∠N ,∵OA =OD ,∴∠OAD =∠ADO ,∴∠OAD =∠N ,∴AB =BN ;………………………………………………………………………………………3分 (2)解:由(1)OD ∥BN ,∴∠MOD =∠B ,………………………………………………………………………………4分 ∴cos ∠MOD =cosB =52, 在Rt △MOD 中,cos ∠MOD ==OMOD,11D∵OD =OA ,MO =MA +OA =3+MA ,∴AM 33=52,∴MA =4.5………………………………………………………………………………………5分 23.解:正确. ………………………………………………………………………………………1分 理由如下: 由做法可知M 为AD 的中点,E 为MD 的中点, ∴AD DE =41. …………………………………………………………2分 ∵四边形ABCD 是正方形,∴AD=BC ,ED ∥BC . ………………………………………………3分 ∴△DEF ∽△BFC ∴BC DE =BF DF ………………………………………………………..4分 ∵AD =BC ∴BF DF =BC DE =41∴BD DF =51………………………………………………………………………………………5分 24.解: (1)过D 点作DE ⊥BC 于点E ,可知△CDE 和△DEB 都是直角三角形;……………1分 (2)由∠C =70°,可知sin ∠C 的值,在Rt △CDE 中,由sin ∠C 和DC =a ,可求DE 的长;……………………………………………………………………………………………2分 (3)在Rt △DEB 中,由∠DBC =30°,DE 的长,可求BD 的长………………………………3分 (4)过A 点作AF ⊥BD 于点F , 可知△DFA 和△AFB 都是直角三角形; ………………4分(5)在Rt △AFB 中,由∠DBA =45°,AB =b ,可求AF 和BF 的长; (6)由DB 、BF 的长,可知DF 的长; (7)在Rt △DFA 中,由DFFA ,可求tan ∠ADB . ………………5分 25.解:(1)1.5............................................. ..1分 (2)如图 (4)分(3)0.7(0.6~0.8均可以) .………………………….5分 . 26.解:(1)m =1………………………………………………………………………………………1分n =3………………………………………………………………………………………………2分(2)由(1)知抛物线表达式为y =x 2-4x -5 令y =0得,x 2-4x -5=0.解得x 1=-1,x 2=5,……………………………………………………………………………3分∴抛物线y =x 2-4x -5与x 轴得两个交点C 、D 的坐标分别为C (-1,0),D (5,0) ∴CD =6.∵A (2-,7),AB ∥x 轴交抛物线于点B ,根据抛物线的轴对称性,可知B (6,7)………4分∴S △BCD =21.……………………………………………………………………………………5分(3) 据题意,可知P (t ,-2 t +3),Q ( t ,t 2-4 t -5),由x 2-4x -5=-2x +3得直线y =-2x +3与抛物线y = x 2-4x -5的两个交点坐标分别为(-2,7)和(4,-5) ……………………………………………………………………………………………6分 ∵点P 在点Q 上方∴-2<t <5, ∴PQ = -t 2+2 t +8=-( t -2) 2+9 ∵a =-1∴PQ 的最大值为9.……………………………………………………………………………7分27.解:(1)如图……………………………………………1分(2) ∵∠BAC =2α,∠AHB =90°∴∠ABH =90°-2α …………………………………………………………………………… 2分 ∵BA =BD∴∠BDA =45°+α………………………………………………………………………………3分 (3)补全图形,如图13………………4分证明过程如下:∵D 关于BC 的对称点为E ,且DE 交BP 于G∴DE ⊥BP ,DG =GE ,∠DBP =∠EBP ,BD =BE ;…………………………………………5分 ∵AB=AC ,∠BAC=2α ∴∠ABC=90°-α 由(2)知∠ABH =90°-2α ∠DBP =90°-α-(90°-2α)=α ∴∠DBP =∠EBP =α ∴∠BDE =2α ∵AB =BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DP DE=2, ∴DPBC=2, ∴BC =2DP.………………………………………………………………………………7分 28.解:(1)A 、M . ……………………………………………………………………………………2分 (2)过点P 作PG ⊥x 轴于点G …………………………………………………………………3分 设P (x ,2x )∵OG 2+PG 2=OP 2 ………………………………………………………………………………4分∴x 2+4x 2=1 ∴5x 2=1∴x 2=51∴x =55±∴P (55,552)或P (55-,552-)……………………………………………………5分 (3)r =556或 4117≤<r …………………………………………………………7分。
北京市怀柔区2018届九年级数学上学期期末考试试题新人教版

北京市怀柔区2018届九年级数学上学期期末考试试题一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个1.北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用. 将178800用科学记数法表示应为A .1.788×104B .1.788×105C .1.788×106D .1.788×107 2.若将抛物线y = -12x 2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是A .2)3(212-+-=x y B .2)3(212---=x y C .2)3(2-+=x y D. 2)3(212++-=x y3.在Rt △ABC 中,∠C =90°,AC =4,BC =3,则tan A 的值为 A .34 B .43 C .53 D .54 4.如图,在△ABC 中,点D ,E 分别为边AB,AC 上的点,且DE ∥BC ,若AD =4,BD =8,AE =2,则CE 的长为A.2 B .4 C .6 D .85. 如图,⊙O 是△ABC 的外接圆,∠BOC =100°,则∠A 的大小为 ( )E DCA第4题图 第5题图A .40︒B .50︒C .80︒D .100︒6. 网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB 的高度).中网比赛中,某运动员退出场地在距球网14米的D 点处接球,设计打出直线..穿越球,使球落在对方底线上C 处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为A. 1.65米B. 1.75米C.1.85米D. 1.95米 7. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O ,再任意找出圆O 的一条直径标记为AB (如图1),测量出AB =4分米;②将圆环进行翻折使点B 落在圆心O 的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C 、D (如图2);③用一细橡胶棒连接C 、D 两点(如图3); ④计算出橡胶棒CD 的长度.小明计算橡胶棒CD 的长度为 A .22 分米B . 23分米C .32 分米D .33分米8.如图1,⊙O 过正方形ABCD 的顶点A 、D 且与边BC 相切于点E ,分别交AB 、DC 于点M 、N .动点P 在⊙O 或正方形ABCD 的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x ,圆心O 与P 点的距离为y ,图2记录了一段时间里y 与x 的函数关系,在这段时间里P第6题图C点的运动路径为A.从D 点出发,沿弧DA →弧AM →线段BM →线段BCB.从B 点出发,沿线段BC →线段CN →弧ND →弧DAC.从A 点出发,沿弧AM →线段BM →线段BC →线段CND.从C 点出发,沿线段CN →弧ND →弧DA →线段AB 二、填空题(本题共16分,每小题2分) 9.分解因式:3x 3-6x 2+3x =_________.10.若△ABC ∽△DEF ,且对应边BC 与EF 的比为1∶3,则△ABC 与△DEF 的面积比等于.11. 有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可):. 12.抛物线y =2(x +1)2+3 的顶点坐标是.13.把二次函数y =x 2-4x +5化成y=a (x -h )2+k 的形式为__________________.14. 数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E 处测得旗杆顶部A 的仰角α为45°,旗杆底部B 的俯角β为60°. 室外测量组测得BF 的长度为5米.则旗杆AB =______米.第15题图15.在学校的花园里有一如图所示的花坛,它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为米2.16. 阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:小明的作法如下:请回答:这样做的依据是.三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程. 17.计算:4sin45°-8+(3-1)0+|-2|.18.如图,在△ABC 中,D 为AC 边上一点,BC =4,AC =8,CD=2.求证:△BCD ∽△ACB .第18题图第19题图19. 如图,在△ABC 中,tan A =43,∠B =45°,AB =14. 求BC 的长. 20.在平面直角坐标系xOy 中,直线3+-=x y 与双曲线xky =相交于点A (m ,2). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图; (3)若P 是坐标轴上一点,且满足PA =OA . 直接写出点P 的坐标.21.一个二次函数图象上部分点的横坐标x ,纵坐标y 的对应值如下表:(2)求m 的值;(3)在给定的直角坐标系中,画出这个函数的图象; (4)根据图象,写出当y <0时,x 的取值范围.22.如图,已知AB 是⊙O 的直径,点M 在BA 的延长线上,MD 切⊙O 于点D ,过点B 作BN ⊥MD 于点C ,连接AD 并延长,交BN 于点N .(1)求证:AB =BN ;(2)若⊙O 半径的长为3,cosB =52,求MA 的长.23.数学课上老师提出了下面的问题: 在正方形ABCD 对角线BD 上取一点F ,使51=D B DF . 小明的做法如下:如图D① 应用尺规作图作出边AD 的中点M ; ② 应用尺规作图作出MD 的中点E ; ③ 连接EC ,交BD 于点F . 所以F 点就是所求作的点.请你判断小明的做法是否正确,并说明理由.24. 已知:如图,在四边形ABCD 中,BD 是一条对角线,∠DBC =30°, ∠DBA =45°,∠C =70°.若DC =a ,AB=b , 请写出求tan ∠ADB 的思路. (不用写出计算结果........)25.如图,在四边形ABCD 中,AD ∥BC ,∠ADC =90°,点E 是BC 边上一动点,联结AE ,过点E 作AE 的垂线交直线CD 于点F .已知AD =4cm ,CD =2cm ,BC =5cm ,设BE 的长为x cm ,CF 的长为y cm.变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(说明:补全表格时相关数据保留一位小数)(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题: 当BE =CF 时,BE 的长度约为cm.CB26.在平面直角坐标系xOy 中,直线l :n x y +-=2与抛物线3242---=m mx mx y 相交于点A (2-,7).(1)求m 、n 的值;(2)过点A 作AB ∥x 轴交抛物线于点B ,设抛物线 与x 轴交于点C 、D (点C 在点D 的左侧),求△BCD 的面积;(3)点E (t ,0)为x 轴上一个动点,过点E 作平行于y 轴的直线与直线l 和抛物线分别交于点P 、Q .当点P 在点Q 上方时,求线段PQ 的最大值.27. 在等腰△ABC 中,AB =AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P . (1)依题意补全图形;(2)若∠BAC =2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.28.在平面直角坐标系xOy 中,点P 的横坐标为x ,纵坐标为2x ,满足这样条件的点称为“关系点”.(1)在点A (1,2)、B (2,1)、M (21,1)、N (1,21)中, 是“关系点”的;(2)⊙O 的半径为1,若在⊙O 上存在“关系点”P , 求点P 坐标;(3)点C 的坐标为(3,0),若在⊙C 上有且只有.... 一个..“关系点”P ,且“关系点”P 的横坐标满足 -2≤x≤2.请直接写出⊙C 的半径r 的取值范围.2017-2018学年度第一学期期末初三质量检测数学试卷评分标准一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个二、填空题(本题共16分,每小题2分) 9.3x (x -1)2.10.1:9.11.答案不唯一,k <0即可. 12.(﹣1,3).13.y =(x -2)2+1.14. 5+53.15.16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程. 17.25A解:原式=4×22-22+1+2 …………………………………………………………………… 4分 =3 ………………………………………………………………………………………5分18.证明:∵BC =4,AC =8,CD =2.…………………………1分∴BC CDAC BC=………………………………………3分 又∵∠C =∠C …………………………………………………………………………4分 ∴△BCD ∽△ACB ……………………………………………………………………5分19.解:过点C 作CD ⊥AB 于点D ,如图. ………………………………………………1分 ∵在Rt △CDA 中,tan A =AD CD = 43设CD =3x ,AD =4x . ……………………………………………………………………………2分 ∵在Rt △CDB 中,∠B =45° ∴tan B =DB CD = 1,sin B =BC CD =22,……………………………………………………………3分 ∵CD =3x . ∴BD =3x ,BC =2·3x =32x . 又∵AB =AD+BD =14, ∴4x +3x =14,解得x =2 (4)分∴BC =62. ……………………………………………………………………………………5分 20.解:(1)∵直线3+-=x y 与双曲线xky =相交于点A (m ,2). ∴ A (1,2)………………………………………1分 ∴xy 2=................................................2分 (2)如图 (4)分(3)P (0,4)或P (2,0) …………………………………………6分 21.解:(1)设这个二次函数的表达式为2()y a x h k =-+. 依题意可知,顶点为(-1,2),………………………1分∴()212++=x a y .∵图象过点(1,0), ∴()21102++=a .∴12a =-. ∴这个二次函数的表达式为()21212++-=x y …………2分 (2)25-=m .………………………………………………3分 (3)如图…………………………………………………………………………………………5分 (4)x <-3或x >1..…………………………………………………………………………………6分 22.(1)证明:连接OD ,…………………………1分 ∵MD 切⊙O 于点D ,∴OD ⊥MD ,∵BN ⊥MC ,∴OD ∥BN ,…………………………………2分 ∴∠ADO =∠N ,∵OA =OD ,∴∠OAD =∠ADO ,∴∠OAD =∠N ,∴AB =BN ;………………………………………………………………………………………3分 (2)解:由(1)OD ∥BN ,∴∠MOD =∠B ,………………………………………………………………………………4分 ∴cos ∠MOD =cosB =52, 在Rt △MOD 中,cos ∠MOD ==OMOD,D∵OD =OA ,MO =MA +OA =3+MA ,∴AM 33=52,∴MA =4.5………………………………………………………………………………………5分 23.解:正确. ………………………………………………………………………………………1分 理由如下: 由做法可知M 为AD 的中点,E 为MD 的中点, ∴AD DE =41. …………………………………………………………2分 ∵四边形ABCD 是正方形,∴AD=BC ,ED ∥BC . ………………………………………………3分 ∴△DEF ∽△BFC ∴BC DE =BFDF ………………………………………………………..4分∵AD =BC ∴BF DF =BC DE =41 ∴BD DF =51………………………………………………………………………………………5分 24.解: (1)过D 点作DE ⊥BC 于点E ,可知△CDE 和△DEB 都是直角三角形;……………1分 (2)由∠C =70°,可知sin ∠C 的值,在Rt △CDE 中,由sin ∠C 和DC =a ,可求DE 的长;……………………………………………………………………………………………2分 (3)在Rt △DEB 中,由∠DBC =30°,DE 的长,可求BD 的长………………………………3分 (4)过A 点作AF ⊥BD 于点F , 可知△DFA 和△AFB 都是直角三角形;………………4分(5)在Rt △AFB 中,由∠DBA =45°,AB =b ,可求AF 和BF 的长; (6)由DB 、BF 的长,可知DF 的长; (7)在Rt △DFA 中,由DFFA ,可求tan ∠ADB . ………………5分 25.解:(1)1.5............................................. ..1分 (2)如图 (4)分(3)0.7(0.6~0.8均可以) .………………………….5分 . 26.解:(1)m =1………………………………………………………………………………………1分n =3………………………………………………………………………………………………2分(2)由(1)知抛物线表达式为y =x 2-4x -5 令y =0得,x 2-4x -5=0.解得x 1=-1,x 2=5,……………………………………………………………………………3分∴抛物线y =x 2-4x -5与x 轴得两个交点C 、D 的坐标分别为C (-1,0),D (5,0) ∴CD =6.∵A (2-,7),AB ∥x 轴交抛物线于点B ,根据抛物线的轴对称性,可知B (6,7)………4分∴S △BCD =21.……………………………………………………………………………………5分(3)据题意,可知P (t ,-2 t +3),Q ( t ,t 2-4 t -5),由x 2-4x -5=-2x +3得直线y =-2x +3与抛物线y = x 2-4x -5的两个交点坐标分别为(-2,7)和(4,-5) ……………………………………………………………………………………………6分 ∵点P 在点Q 上方∴-2<t <5, ∴PQ = -t 2+2 t +8=-( t -2)2+9 ∵a =-1∴PQ 的最大值为9.……………………………………………………………………………7分27.解:(1)如图……………………………………………1分(2) ∵∠BAC =2α,∠AHB =90°∴∠ABH =90°-2α…………………………………………………………………………… 2分 ∵BA =BD∴∠BDA =45°+α………………………………………………………………………………3分 (3)补全图形,如图………………4分证明过程如下:∵D 关于BC 的对称点为E ,且DE 交BP 于G∴DE ⊥BP ,DG =GE ,∠DBP =∠EBP ,BD =BE ;…………………………………………5分 ∵AB=AC ,∠BAC=2α ∴∠ABC=90°-α 由(2)知∠ABH =90°-2α ∠DBP =90°-α-(90°-2α)=α ∴∠DBP =∠EBP =α ∴∠BDE =2α ∵AB =BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DP DE=2, ∴DPBC=2, ∴BC =2DP.………………………………………………………………………………7分 28.解:(1)A 、M . ……………………………………………………………………………………2分 (2)过点P 作PG ⊥x 轴于点G …………………………………………………………………3分 设P (x ,2x )∵OG 2+PG 2=OP 2………………………………………………………………………………4分∴x 2+4x 2=1 ∴5x 2=1∴x 2=51∴x =55±∴P (55,552)或P (55-,552-)……………………………………………………5分 (3)r =556或4117≤<r …………………………………………………………7分。
北京市怀柔区2018届九年级数学上学期期末考试试题 新人教版

北京市怀柔区2018届九年级数学上学期期末考试试题一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个1. 北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用. 将178800用科学记数法表示应为A .1.788×104B .1.788×105C .1.788×106D .1.788×107 2.若将抛物线y = -12x 2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是A .2)3(212-+-=x y B .2)3(212---=x y C .2)3(2-+=x y D. 2)3(212++-=x y3.在Rt △ABC 中,∠C =90°,AC =4,BC =3,则tan A 的值为 A .34 B .43C .53D .54 4. 如图,在△ABC 中,点D ,E 分别为边AB,AC 上的点,且DE ∥BC ,若AD =4,BD =8,AE =2,则CE 的长为A.2 B .4 C .6 D .85. 如图,⊙O 是△ABC 的外接圆,∠BOC =100°,则∠A 的大小为 ( )E DCA第4题图 第5题图A .40︒B .50︒C .80︒D .100︒6. 网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB 的高度).中网比赛中,某运动员退出场地在距球网14米的D 点处接球,设计打出直线..穿越球,使球落在对方底线上C 处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为A. 1.65米B. 1.75米C.1.85米D. 1.95米 7. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O ,再任意找出圆O 的一条直径标记为AB (如图1),测量出AB =4分米;②将圆环进行翻折使点B 落在圆心O 的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C 、D (如图2);③用一细橡胶棒连接C 、D 两点(如图3); ④计算出橡胶棒CD 的长度.小明计算橡胶棒CD 的长度为 A .22 分米B . 23分米C .32 分米D .33分米8.如图1,⊙O 过正方形ABCD 的顶点A 、D 且与边BC 相切于点E ,分别交AB 、DC 于点M 、N .动点P 在⊙O 或正方形ABCD 的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x ,圆心O 与P 点的距离为y ,图2记录了一段时间里y 与x 的函数关系,在这段时间里P第6题图C3点的运动路径为A.从D 点出发,沿弧DA →弧AM →线段BM →线段BCB.从B 点出发,沿线段BC →线段CN →弧ND →弧DAC.从A 点出发,沿弧AM →线段BM →线段BC →线段CND.从C 点出发,沿线段CN →弧ND →弧DA →线段AB 二、填空题(本题共16分,每小题2分) 9.分解因式:3x 3-6x 2+3x =_________.10.若△ABC ∽△DEF ,且对应边BC 与EF 的比为1∶3,则△ABC 与△DEF 的面积比等于 . 11. 有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可): .12.抛物线y =2(x +1)2+3 的顶点坐标是 .13.把二次函数y =x 2-4x +5化成y=a (x -h )2+k 的形式为__________________.14. 数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E 处测得旗杆顶部A 的仰角α为45°,旗杆底部B 的俯角β为60°. 室外测量组测得BF 的长度为5米.则旗杆AB =______米.第15题图15.在学校的花园里有一如图所示的花坛,它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为 米2. 16. 阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:小明的作法如下:请回答:这样做的依据是 .三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程. 17.计算:4si n45°-8+(3-1)0+|-2|.18.如图,在△ABC 中,D 为AC 边上一点,BC =4,AC =8,CD=2.求证:△BCD ∽△ACB .第18题图第19题图519. 如图,在△ABC 中,tan A =43,∠B =45°,AB =14. 求BC 的长. 20.在平面直角坐标系xOy 中,直线3+-=x y 与双曲线xky =相交于点A (m ,2). (1)求反比例函数的表达式; (2)画出直线和双曲线的示意图; (3)若P 是坐标轴上一点,且满足PA =OA . 直接写出点P 的坐标.21.一个二次函数图象上部分点的横坐标x ,纵坐标y 的对应值如下表:(2)求m 的值;(3)在给定的直角坐标系中,画出这个函数的图象; (4)根据图象,写出当y <0时,x 的取值范围.22. 如图,已知AB 是⊙O 的直径,点M 在BA 的延长线上,MD 切⊙O 于点D ,过点B 作BN ⊥MD 于点C ,连接AD 并延长,交BN 于点N . (1)求证:AB =BN ;(2)若⊙O 半径的长为3,cosB =52,求MA 的长.23.数学课上老师提出了下面的问题: 在正方形ABCD 对角线BD 上取一点F ,使51=D B DF . 小明的做法如下:如图D① 应用尺规作图作出边AD 的中点M ; ② 应用尺规作图作出MD 的中点E ; ③ 连接EC ,交BD 于点F . 所以F 点就是所求作的点.请你判断小明的做法是否正确,并说明理由.24. 已知:如图,在四边形ABCD 中,BD 是一条对角线,∠DBC =30°, ∠DBA =45°,∠C =70°.若DC =a ,AB=b , 请写出求tan ∠ADB 的思路. (不用写出计算结果........)25.如图,在四边形ABCD 中,AD ∥BC ,∠ADC =90°,点E 是BC 边上一动点,联结AE ,过点E 作AE 的垂线交直线CD 于点F .已知AD =4cm ,CD =2cm ,BC =5cm ,设BE 的长为x cm ,CF 的长为y cm.变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(说明:补全表格时相关数据保留一位小数)(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题: 当BE =CF 时,BE 的长度约为 cm.7CB26.在平面直角坐标系xOy 中,直线l :n x y +-=2与抛物线3242---=m mx mx y 相交于点A (2-,7).(1)求m 、n 的值;(2)过点A 作AB ∥x 轴交抛物线于点B ,设抛物线 与x 轴交于点C 、D (点C 在点D 的左侧),求△BCD 的面积;(3)点E (t ,0)为x 轴上一个动点,过点E 作平行于y 轴的直线与直线l 和抛物线分别交于点P 、Q .当点P 在点Q 上方时,求线段PQ 的最大值.27. 在等腰△ABC 中,AB =AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P . (1)依题意补全图形;(2)若∠BAC =2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.28.在平面直角坐标系xOy 中,点P 的横坐标为x ,纵坐标为2x ,满足这样条件的点称为“关系点”.(1)在点A (1,2)、B (2,1)、M (21,1)、N (1,21)中, 是“关系点”的 ;(2)⊙O 的半径为1,若在⊙O 上存在“关系点”P , 求点P 坐标;(3)点C 的坐标为(3,0),若在⊙C 上有且只有.... 一个..“关系点”P ,且“关系点”P 的横坐标满足 -2≤x≤2.请直接写出⊙C 的半径r 的取值范围.2017-2018学年度第一学期期末初三质量检测数学试卷评分标准一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个二、填空题(本题共16分,每小题2分)9.3x (x -1)2. 10.1:9. 11.答案不唯一,k <0即可.12.(﹣1,3). 13.y =(x -2)2+1. 14. 5+53. 15.16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第20、21题每小题6分,第26-28题每小题7分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程. 17.259A解:原式=4×22-22+1+2 …………………………………………………………………… 4分 =3 ………………………………………………………………………………………5分18.证明:∵BC =4,AC =8,CD =2.…………………………1分∴BC CDAC BC=………………………………………3分 又∵∠C =∠C …………………………………………………………………………4分 ∴ △BCD ∽△ACB ……………………………………………………………………5分19.解:过点C 作CD ⊥AB 于点D ,如图. ………………………………………………1分 ∵在Rt △CDA 中,tan A =AD CD = 43设CD =3x ,AD =4x . ……………………………………………………………………………2分 ∵在Rt △CDB 中,∠B =45° ∴tan B =DB CD = 1,sin B =BC CD =22,……………………………………………………………3分 ∵CD =3x . ∴BD =3x ,BC =2·3x =32x . 又∵AB =AD+BD =14, ∴4x +3x =14,解得x =2 (4)分∴BC =62. ……………………………………………………………………………………5分 20.解:(1)∵直线3+-=x y 与双曲线xky =相交于点A (m ,2). ∴ A (1,2)………………………………………1分 ∴xy 2=................................................2分 (2)如图 (4)分(3)P (0,4)或P (2,0) …………………………………………6分 21.解:(1)设这个二次函数的表达式为2()y a x h k =-+.依题意可知,顶点为(-1,2),………………………1分∴ ()212++=x a y . ∵图象过点(1,0), ∴()21102++=a .∴12a =-. ∴这个二次函数的表达式为()21212++-=x y …………2分 (2)25-=m .………………………………………………3分 (3)如图…………………………………………………………………………………………5分 (4)x <-3或x >1..…………………………………………………………………………………6分 22.(1)证明:连接OD ,…………………………1分 ∵MD 切⊙O 于点D ,∴OD ⊥MD ,∵BN ⊥MC ,∴OD ∥BN ,…………………………………2分 ∴∠ADO =∠N ,∵OA =OD ,∴∠OAD =∠ADO ,∴∠OAD =∠N ,∴AB =BN ;………………………………………………………………………………………3分 (2)解:由(1)OD ∥BN ,∴∠MOD =∠B ,………………………………………………………………………………4分 ∴cos ∠MOD =cosB =52, 在Rt △MOD 中,cos ∠MOD ==OMOD,11D∵OD =OA ,MO =MA +OA =3+MA ,∴AM 33=52,∴MA =4.5………………………………………………………………………………………5分 23.解:正确. ………………………………………………………………………………………1分 理由如下: 由做法可知M 为AD 的中点,E 为MD 的中点, ∴AD DE =41. …………………………………………………………2分 ∵四边形ABCD 是正方形,∴AD=BC ,ED ∥BC . ………………………………………………3分 ∴△DEF ∽△BFC ∴BC DE =BF DF ………………………………………………………..4分 ∵AD =BC ∴BF DF =BC DE =41∴BD DF =51………………………………………………………………………………………5分 24.解: (1)过D 点作DE ⊥BC 于点E ,可知△CDE 和△DEB 都是直角三角形;……………1分 (2)由∠C =70°,可知sin ∠C 的值,在Rt △CDE 中,由sin ∠C 和DC =a ,可求DE 的长;……………………………………………………………………………………………2分 (3)在Rt △DEB 中,由∠DBC =30°,DE 的长,可求BD 的长………………………………3分 (4)过A 点作AF ⊥BD 于点F , 可知△DFA 和△AFB 都是直角三角形; ………………4分(5)在Rt △AFB 中,由∠DBA =45°,AB =b ,可求AF 和BF 的长; (6)由DB 、BF 的长,可知DF 的长; (7)在Rt △DFA 中,由DFFA ,可求tan ∠ADB . ………………5分 25.解:(1)1.5............................................. ..1分 (2)如图 (4)分(3)0.7(0.6~0.8均可以) .………………………….5分 . 26.解:(1)m =1………………………………………………………………………………………1分n =3………………………………………………………………………………………………2分(2)由(1)知抛物线表达式为y =x 2-4x -5 令y =0得,x 2-4x -5=0.解得x 1=-1,x 2=5,……………………………………………………………………………3分∴抛物线y =x 2-4x -5与x 轴得两个交点C 、D 的坐标分别为C (-1,0),D (5,0) ∴CD =6.∵A (2-,7),AB ∥x 轴交抛物线于点B ,根据抛物线的轴对称性,可知B (6,7)………4分∴S △BCD =21.……………………………………………………………………………………5分(3) 据题意,可知P (t ,-2 t +3),Q ( t ,t 2-4 t -5),由x 2-4x -5=-2x +3得直线y =-2x +3与抛物线y = x 2-4x -5的两个交点坐标分别为(-2,7)和(4,-5) ……………………………………………………………………………………………6分 ∵点P 在点Q 上方∴-2<t <5, ∴PQ = -t 2+2 t +8=-( t -2) 2+9 ∵a =-1∴PQ 的最大值为9.……………………………………………………………………………7分27.解:(1)如图……………………………………………1分(2) ∵∠BAC =2α,∠AHB =90°∴∠ABH =90°-2α …………………………………………………………………………… 2分 ∵BA =BD∴∠BDA =45°+α………………………………………………………………………………3分 (3)补全图形,如图13………………4分证明过程如下:∵D 关于BC 的对称点为E ,且DE 交BP 于G∴DE ⊥BP ,DG =GE ,∠DBP =∠EBP ,BD =BE ;…………………………………………5分 ∵AB=AC ,∠BAC=2α ∴∠ABC=90°-α 由(2)知∠ABH =90°-2α ∠DBP =90°-α-(90°-2α)=α ∴∠DBP =∠EBP =α ∴∠BDE =2α ∵AB =BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DP DE=2, ∴DPBC=2, ∴BC =2DP.………………………………………………………………………………7分 28.解:(1)A 、M . ……………………………………………………………………………………2分 (2)过点P 作PG ⊥x 轴于点G …………………………………………………………………3分 设P (x ,2x )∵OG 2+PG 2=OP 2 ………………………………………………………………………………4分∴x 2+4x 2=1 ∴5x 2=1∴x 2=51∴x =55±∴P (55,552)或P (55-,552-)……………………………………………………5分 (3)r =556或4117≤<r …………………………………………………………7分。
北京市怀柔区届九级上学期期末考试数学试题(含答案)

怀柔区2018—2018学年第一学期初三期末质量检测数学试卷考生须知1.本试卷共6页,共五道大题,29道小题,满分120分。
考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B铅笔作答,其他试卷用黑色字迹签字笔作答。
5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一.选择题(共有10个小题,每小题3分,共30分)下面各题均有四个选项,其中只有一个..是符合题意的.1.我市南水北调配套工程建设进展顺利,工程运行调度有序.截止2018年12月底,已累计接收南水北调来水812000000立方M.使1100余万市民喝上了南水;通过“存水”增加了约550公顷水面,密云水库蓄水量稳定在10亿立方M左右,有效减缓了地下水位下降速率. 将812000000用科学记数法表示应为A.812×106 B.81.2×107 C.8.12×108 D.8.12×1092.实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大是A.a B.bC.cD.d3. 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=2,DB=4,则AEAC的值为A.12B.13C.14D.164. 若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为A.1:2 B.2:1 C.1:4 D.4:15.二次函数y=(x﹣1)2+2的最小值为()A.1 B.-1 C.2 D.-26.将抛物线2=-y x向上平移2个单位,则得到的抛物线表达式为A.2y=-(x+2) B.2y=-(x-2) C.2y=-x-2 D.2y=-x+27. 已知Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为()A.34B.43C.35D.458.如图是拦水坝的横断面,斜坡AB的水平宽度为12M,斜面坡度为1:2,则斜坡AB的长为–3–2–1012345–4cba d2题图EDCBA3题图宽:A.43M B.65M C.125M D.24M9.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B. 35°C. 40°D. 45°10.小刚在实践课上要做一个如图1所示的折扇,折扇扇面的宽度AB是骨柄长OA的34,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为243cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为()A. 21cm B.20 cm C.19cm D.18cm二、填空题(本题共6个小题,每小题3分,共18分)11.4的平方根是.12.不等式组⎪⎩⎪⎨⎧->+≥-123211xx的正整数解是.13.如图,tan∠ABC=.14.写出一个抛物线开口向上,与y轴交于(0,2)点的函数表达式.15.已知⊙O的半径2,则其内接正三角形的面积为.16.学校组织社会大课堂活动去首都博物馆参观,明明提前上网做了功课,查到了下面的一段文字:首都博物馆建筑本身是一座融古典美和现代美于一体的建筑艺术品,既具有浓郁的民族特色,又呈现鲜明的现代感.首都博物馆建筑物(地面以上)东西长152M、南北宽66M左右,建筑高度CBA30︒10题图1青铜展馆 41M.建筑内部分为三栋独立的建筑,即:矩形展馆,椭圆形专题展馆,条形的办公科研楼.椭圆形的青铜展馆斜出墙面寓意古代文物破土而出,散发着浓郁的历史气息.明明对首都博物馆建筑物产生了浓厚的兴趣,站到首都博物馆北广场,他被眼前这座建筑物震撼了.整个建筑宏大壮观,斜出的青铜展馆和北墙面交出一条抛物线,抛物线与外立面之间和谐、统一,明明走到过街天桥上照了一张照片(如图所示).明明想了想,算了算,对旁边的文文说:“我猜想这条抛物线的顶点到地面的距离应是15.7M 左右.” 文文反问:“你猜想的理由是什么”?明明说:“我的理由是”. 明明又说:“不过这只是我的猜想,这次准备不充分,下次来我要用学过的数学知识准确的测测这个高度,我想用学到的知识, 我要带等测量工具”.三、解答题(本题共72分,第17—25题,每小题5分,第26题8分,第27题6分,第28题6分,第29题7分) 17. 计算:2012(3)3cos602π---+--︒.18. 已知0362=--x x ,求代数式()()311)3(2+-+--x x x x 的值.19.已知如图,△ABC 中,AE 交BC 于点D ,∠C=∠E ,AD :DE=3:5,AE=8,BD=4,求DC 的长.20.如图,一次函数y =﹣x +2的图象与反比例函数y 2=xk的图象相交于A ,B 两点,点B 的坐标为(2m ,-m ).(1)求出m 值并确定反比例函数的表达式; (2)请直接写出当x <m 时,y 2的取值范围.21.已知如图,在△ABC 中,∠A=30°,∠C=105°,AC=32,求AB 的长.19题图22. 已知如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,连接A C .若∠A =22.5°,CD =8cm ,求⊙O 的半径.23. 如图,在数学实践课中,小明为了测量学校旗杆CD 的高度,在地面A 处放置高度为1.5M 的测角仪AB ,测得旗杆顶端D 的仰角为32°,AC 为22M ,求旗杆CD 的高度.(结果精确到0.1M.参考数据:sin 32°= 0.53,cos 32°= 0.85,tan 32°= 0.62)24. 如图,已知AB 是⊙O 的直径,点P 在BA 的延长线上,PD 切⊙O 于点D ,过点B 作BE 垂直于PD ,交PD 的延长线于点C ,连接AD 并延长,交BE 于点E . (1)求证:AB =BE ;(2)若PA =2,cosB =,求⊙O 半径的长.25.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m 长的篱笆围成一个矩形花园ABCD (篱笆只围AB ,BC 两边),设AB=xm .21题图 22题图23题图(1)若花园的面积为192m2,求x的值;(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求x取何值时,花园面积S最大,并求出花园面积S的最大值.26.在“解直角三角形”一章我们学习到“锐角的正弦、余弦、正切都是锐角的函数,统称为锐角三角函数” .小力根据学习函数的经验,对锐角的正弦函数进行了探究. 下面是小力的探究过程,请补充完成:(1)函数的定义是:“一般地,在一个变化的过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y是x的函数”.由函数定义可知,锐角的正弦函数的自变量是,因变量是,自变量的取值范围是___________.(2)利用描点法画函数的图象.小力先上网查到了整锐角的正弦值,如下:sin1°=0.01745240643728351 sin2°=0.03489949670250097 sin3°=0.05233595624294383sin4°=0.0697564737441253 sin5°=0.087816 sin6°=0.10452846326765346sin7°=0.124747 sin8°=0.006544 sin9°=0.023087sin10°=0.17364817766693033 sin11°=0.1908089953765448 sin12°=0.20791169081775931sin13°=0.22495105434386497 sin14°=0.241923 sin15°=0.25881904510252074sin16°=0.27563735581699916 sin17°=0.2923717047227367 sin18°=0.3090169943749474sin19°=0.3255681544571567 sin20°=0.3420201833256687 sin21°=0.35836794954530027sin22°=0.374606593415912 sin23°=0.3907311284892737 sin24°=0.40673664307580015sin25°=0.422644 sin26°=0.4383711467890774 sin27°=0.45399049973954675sin28°=0.46947 sin29°=0.48480962024633706 sin30°=0.5000000000000000sin31°=0.50542 sin32°=0.5299192642332049 sin33°=0.544639035015027sin34°=0.5591929034707468 sin35°=0.573576436351046 sin36°=0.5877852522924731sin37°=0.60183 sin38°=0.66583 sin39°=0.6293203910498375sin40°=0.6427876096865392 sin41°=0.6560590289905073 sin42°=0.66982sin43°=0.6819983600624985 sin44°=0.6946583704589972 sin45°=0.7071067811865475sin46°=0.7193398003386511 sin47°=0.73705 sin48°=0.7431448254773941sin49°=0.7547095802227719 sin50°=0.766044443118978 sin51°=0.77708sin52°=0.7880107536067219 sin53°=0.7986355100472928 sin54°=0.8090169943749474sin55°=0.81918 sin56°=0.8290375725550417 sin57°=0.8386705679454239sin58°=0.848048096156426 sin59°=0.8571673007021122 sin60°=0.8660254037844386sin61°=0.8746197071393957 sin62°=0.8829475928589269 sin63°=0.8910065241883678sin64°=0.898794046299167 sin65°=0.9063077870366499 sin66°=0.96009sin67°=0.9205048534524404 sin68°=0.92773 sin69°=0.9335804264972018sin70°=0.9396926207859083 sin71°=0.9455185755993167 sin72°=0.9510565162951535sin73°=0.9563047559630354 sin74°=0.9612616959383189 sin75°=0.9659258262890683sin76°=0.9702957262759965 sin77°=0.9743700647852352 sin78°=0.97857sin79°=0.981627183447664 sin80°=0.984807753012208 sin81°=0.9876883405951378sin82°=0.9902680687415704 sin83°=0.992546151641322 sin84°=0.99452sin85°=0.9961946980917455 sin86°=0.9975640502598242 sin87°=0.9986295347545738sin88°=0.9993908270190958 sin89°=0.9998476951563913②建立平面直角坐标系(两坐标轴可视数值需要分别选取不同长度做为单位长度)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年北京市怀柔区九年级(上)期末数学试卷一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一1.(2分)(2017秋•怀柔区期末)北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用.将178800用科学记数法表示应为()A.1.788×104B.1.788×105C.1.788×106D.1.788×107 2.(2分)(2019•金乡县模拟)若将抛物线y x2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是()A.y(x+3)2﹣2B.y(x﹣3)2﹣2C.y=(x+3)2﹣2D.y(x+3)2+23.(2分)(2017秋•怀柔区期末)在Rt△ABC中,∠C=90°,AC=4,BC=3,则tan A的值为()A.B.C.D.4.(2分)(2017秋•怀柔区期末)如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=4,BD=8,AE=2,则CE的长为()A.2B.4C.6D.85.(2分)(2012•中山区一模)如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数为()A.40°B.50°C.80°D.100°6.(2分)(2017秋•怀柔区期末)网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB的高度).中网比赛中,某运动员退出场地在距球网14米的D点处接球,设计打出直线穿越球,使球落在对方底线上C处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为()A.1.65米B.1.75米C.1.85米D.1.95米7.(2分)(2017秋•怀柔区期末)某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);③用一细橡胶棒连接C、D两点(如图3);④计算出橡胶棒CD的长度.小明计算橡胶棒CD的长度为()A.2分米B.2分米C.3分米D.3分米8.(2分)(2017秋•怀柔区期末)如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为()A.从D点出发,沿弧DA→弧AM→线段BM→线段BCB.从B点出发,沿线段BC→线段CN→弧ND→弧DAC.从A点出发,沿弧AM→线段BM→线段BC→线段CND.从C点出发,沿线段CN→弧ND→弧DA→线段AB二、填空题(本题共16分,每小题2分)9.(2分)(2009•赤峰)分解因式:3x3﹣6x2+3x=.10.(2分)(2017秋•怀柔区期末)若△ABC∽△DEF,且对应边BC与EF的比为1:3,则△ABC与△DEF的面积比等于.11.(2分)(2019•南开区一模)有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可):.12.(2分)(2012•虹口区一模)抛物线y=2(x+1)2+3的顶点坐标为.13.(2分)(2017秋•怀柔区期末)将y=x2﹣4x+5化成y=a(x﹣h)2+k的形式.14.(2分)(2017秋•怀柔区期末)数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°.室外测量组测得BF的长度为5米.则旗杆AB=米.15.(2分)(2017秋•怀柔区期末)在学校的花园里有一如图所示的花坛,它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为米2.16.(2分)(2017秋•怀柔区期末)阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:已知:如图1,△OAB.求作:⊙O,使⊙O与△OAB的边AB相切.小明的作法如下:如图2,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;②以O为圆心,OC为半径作⊙O;所以,⊙O就是所求作的圆.请回答:这样做的依据是.三、解答题(本题共68分,第20、21题每小题5分,第26-28题每小题5分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程.17.(5分)(2017秋•怀柔区期末)计算:4sin45°(1)0+|﹣2|.18.(5分)(2017秋•怀柔区期末)如图,在△ABC中,D为AC边上一点,BC=4,AC=8,CD=2.求证:△BCD∽△ACB.19.(5分)(2017秋•怀柔区期末)如图,在△ABC中,tan A,∠B=45°,AB=14.求BC的长.20.(6分)(2017秋•怀柔区期末)在平面直角坐标系xOy中,直线y=x+3与双曲线y相交于点A(m,2).(1)求反比例函数的表达式;(2)画出直线和双曲线的示意图;(3)若P是坐标轴上一点,且满足P A=OA.直接写出点P的坐标.21.(6分)(2017秋•怀柔区期末)一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:(1)求这个二次函数的表达式;(2)求m的值;(3)在给定的直角坐标系中,画出这个函数的图象;(4)根据图象,写出当y<0时,x的取值范围.22.(5分)(2017秋•怀柔区期末)如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.(1)求证:AB=BN;(2)若⊙O半径的长为3,cos B,求MA的长.23.(5分)(2017秋•怀柔区期末)数学课上老师提出了下面的问题:在正方形ABCD对角线BD上取一点F,使.小明的作法如下:如图①应用尺规作图作出边AD的中点M;②应用尺规作图作出MD的中点E;③连接EC,交BD于点F.所以F点就是所求作的点.请你判断小明的作法是否正确,并说明理由.24.(5分)(2017秋•怀柔区期末)已知:如图,在四边形ABCD中,BD是一条对角线,∠DBC=30°,∠DBA=45°,∠C=70°.若DC=a,AB=b,请写出求tan∠ADB的思路.(不用写出计算结果)25.(5分)(2017秋•怀柔区期末)如图,在四边形ABCD中,AD∥BC,∠ADC=90°,点E是BC边上一动点,联结AE,过点E作AE的垂线交直线CD于点F.已知AD=4cm,CD=2cm,BC=5cm,设BE的长为xcm,CF的长为ycm.小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数据保留一位小数)(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当BE=CF时,BE的长度约为cm.26.(7分)(2017秋•怀柔区期末)在平面直角坐标系xOy中,直线l:y=﹣2x+n与抛物线y=mx2﹣4mx﹣2m﹣3相交于点A(﹣2,7).(1)求m、n的值;(2)过点A作AB∥x轴交抛物线于点B,设抛物线与x轴交于点C、D(点C在点D的左侧),求△BCD的面积;(3)点E(t,0)为x轴上一个动点,过点E作平行于y轴的直线与直线l和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值.27.(7分)(2017秋•怀柔区期末)在等腰△ABC中,AB=AC,将线段BA绕点B顺时针旋转到BD,使BD⊥AC于H,连结AD并延长交BC的延长线于点P.(1)依题意补全图形;(2)若∠BAC=2α,求∠BDA的大小(用含α的式子表示);(3)小明作了点D关于直线BC的对称点点E,从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.28.(7分)(2017秋•怀柔区期末)在平面直角坐标系xOy中,点P的横坐标为x,纵坐标为2x,满足这样条件的点称为“关系点”.(1)在点A(1,2)、B(2,1)、M(,1)、N(1,)中,是“关系点”的;(2)⊙O的半径为1,若在⊙O上存在“关系点”P,求点P坐标;(3)点C的坐标为(3,0),若在⊙C上有且只有一个“关系点”P,且“关系点”P的横坐标满足﹣2≤x≤2.请直接写出⊙C的半径r的取值范围.2017-2018学年北京市怀柔区九年级(上)期末数学试卷参考答案与试题解析一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一1.(2分)(2017秋•怀柔区期末)北京电影学院落户,怀柔一期工程建设进展顺利,一期工程建筑面积为178800平方米,建设内容有教学行政办公、图书馆、各类实习用房、学生及教工宿舍、食堂用房等,预计将于2019年投入使用.将178800用科学记数法表示应为()A.1.788×104B.1.788×105C.1.788×106D.1.788×107【解答】解:178800用科学记数法表示应为1.788×105,故选:B.2.(2分)(2019•金乡县模拟)若将抛物线y x2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是()A.y(x+3)2﹣2B.y(x﹣3)2﹣2C.y=(x+3)2﹣2D.y(x+3)2+2【解答】解:抛物线y x2的顶点坐标为(0,0),先向左平移3个单位,再向下平移2个单位后的抛物线的顶点坐标为(﹣3,﹣2),所以,平移后的抛物线的解析式为y(x+3)2﹣2.故选:A.3.(2分)(2017秋•怀柔区期末)在Rt△ABC中,∠C=90°,AC=4,BC=3,则tan A的值为()A.B.C.D.【解答】解:如图,tan A.故选B.4.(2分)(2017秋•怀柔区期末)如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=4,BD=8,AE=2,则CE的长为()A.2B.4C.6D.8【解答】解:∵DE∥BC,∴,∴,∴EC=4,故选:B.5.(2分)(2012•中山区一模)如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数为()A.40°B.50°C.80°D.100°【解答】解:∵⊙O是△ABC的外接圆,∠BOC=100°,∴∠A∠B0C=50°.故选:B.6.(2分)(2017秋•怀柔区期末)网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB的高度).中网比赛中,某运动员退出场地在距球网14米的D点处接球,设计打出直线穿越球,使球落在对方底线上C处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为()A.1.65米B.1.75米C.1.85米D.1.95米【解答】解:由题意知AB∥DE,则△ABC∽△EDC,∴,即,解得:ED=1.95,故选:D.7.(2分)(2017秋•怀柔区期末)某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);③用一细橡胶棒连接C、D两点(如图3);④计算出橡胶棒CD的长度.小明计算橡胶棒CD的长度为()A.2分米B.2分米C.3分米D.3分米【解答】解:连接OC,作OE⊥CD,如图3,∵AB=4分米,∴OC=2分米,∵将圆环进行翻折使点B落在圆心O的位置,∴OE分米,在Rt△OCE中,CE分米,∴CD=2分米;故选:B.8.(2分)(2017秋•怀柔区期末)如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为()A.从D点出发,沿弧DA→弧AM→线段BM→线段BCB.从B点出发,沿线段BC→线段CN→弧ND→弧DAC.从A点出发,沿弧AM→线段BM→线段BC→线段CND.从C点出发,沿线段CN→弧ND→弧DA→线段AB【解答】解:根据画出的函数的图象,C符合,故选:C.二、填空题(本题共16分,每小题2分)9.(2分)(2009•赤峰)分解因式:3x3﹣6x2+3x=3x(x﹣1)2.【解答】解:3x3﹣6x2+3x,=3x•x2﹣3x•2x+3x,=3x(x2﹣2x+1),=3x(x﹣1)2.10.(2分)(2017秋•怀柔区期末)若△ABC∽△DEF,且对应边BC与EF的比为1:3,则△ABC与△DEF的面积比等于1:9.【解答】解:∵△ABC与△DEF的相似比是1:3,∴△ABC与△DEF的面积比等于12:32=1:9.故答案为1:9.11.(2分)(2019•南开区一模)有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可):y.【解答】解:∵反比例函数y(k是常数,k≠0),在其图象所在的每一个象限内,y 的值随着x的值的增大而增大,∴k<0,∴y.故答案为:y.12.(2分)(2012•虹口区一模)抛物线y=2(x+1)2+3的顶点坐标为(﹣1,3).【解答】解:顶点坐标是(﹣1,3).13.(2分)(2017秋•怀柔区期末)将y=x2﹣4x+5化成y=a(x﹣h)2+k的形式y=(x ﹣2)2+1.【解答】解:∵y=x2﹣4x+5,∴y=x2﹣4x+4+1,∴y=(x﹣2)2+1.故答案为y=(x﹣2)2+1.14.(2分)(2017秋•怀柔区期末)数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°.室外测量组测得BF的长度为5米.则旗杆AB=(5+5)米.【解答】解:如图所示:由题意可得,EN=BF=5m,∵α为45°,∴AN=EN=5m,tan60°,解得:BN=5,则旗杆AB=AN+BN=(5+5)m.故答案为:(5+5).15.(2分)(2017秋•怀柔区期末)在学校的花园里有一如图所示的花坛,它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为米2.【解答】解:草皮种植面积πm2,故答案为:π.16.(2分)(2017秋•怀柔区期末)阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:已知:如图1,△OAB.求作:⊙O,使⊙O与△OAB的边AB相切.小明的作法如下:如图2,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;②以O为圆心,OC为半径作⊙O;所以,⊙O就是所求作的圆.请回答:这样做的依据是圆的定义、直径所对的圆周角为90°,经过半径的外端并且垂直于这条半径的直线是圆的切线.【解答】解:①取线段OB的中点M;以M为圆心,MO为半径作⊙M,则根据圆的定义知OB为⊙M的直径;由直径所对圆周角为直角知OC⊥AB;②以O为圆心,OC为半径作⊙O;由经过半径的外端并且垂直于这条半径的直线是圆的切线知⊙O就是所求作的圆;综上,这样做的依据是:圆的定义、直径所对的圆周角为90°,经过半径的外端并且垂直于这条半径的直线是圆的切线.故答案为:圆的定义、直径所对的圆周角为90°,经过半径的外端并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第20、21题每小题5分,第26-28题每小题5分,其余每小题5分)解答应写出文字说明、演算步骤或证明过程.17.(5分)(2017秋•怀柔区期末)计算:4sin45°(1)0+|﹣2|.【解答】解:原式=421+2=223=3.18.(5分)(2017秋•怀柔区期末)如图,在△ABC中,D为AC边上一点,BC=4,AC=8,CD=2.求证:△BCD∽△ACB.【解答】证明:∵BC=4,AC=8,CD=2,∴,又∵∠C=∠C,∴△BCD∽△ACB.19.(5分)(2017秋•怀柔区期末)如图,在△ABC中,tan A,∠B=45°,AB=14.求BC的长.【解答】解:过点C作CD⊥AB于点D,如图,∵在Rt△CDA中,tan A,设CD=3x,AD=4x,∵在Rt△CDB中,∠B=45°∴tan B1,sin B,∵CD=3x.∴BD=3x,BC•3x=3x.又∵AB=AD+BD=14,∴4x+3x=14,解得x=2,∴BC=6.20.(6分)(2017秋•怀柔区期末)在平面直角坐标系xOy中,直线y=x+3与双曲线y相交于点A(m,2).(1)求反比例函数的表达式;(2)画出直线和双曲线的示意图;(3)若P是坐标轴上一点,且满足P A=OA.直接写出点P的坐标.【解答】解:(1)∵直线y=x+3与双曲线y相交于点A(m,2).∴A(﹣1,2),y.(2)函数图象如图所示.(3)观察图象可知满足条件的点P坐标为(0,4)或(﹣2,0).21.(6分)(2017秋•怀柔区期末)一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:(1)求这个二次函数的表达式;(2)求m的值;(3)在给定的直角坐标系中,画出这个函数的图象;(4)根据图象,写出当y<0时,x的取值范围.【解答】解:(1)由图表可知抛物线的顶点坐标为(﹣1,2),所以,设这个二次函数的表达式为y=a(x+1)2+2,∵图象过点(1,0),∴a(1+1)2+2=0,∴a,∴这个二次函数的表达式为y(x+1)2+2;(2)x=2时,m(2+1)2+2;(3)函数图象如图所示;(4)y<0时,x<﹣3或x>1.22.(5分)(2017秋•怀柔区期末)如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.(1)求证:AB=BN;(2)若⊙O半径的长为3,cos B,求MA的长.【解答】(1)证明:连接OD,∵MD切⊙O于点D,∴OD⊥MD,∵BN⊥MC,∴OD∥BN,∴∠ADO=∠N,∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠N,∴AB=BN;(2)由(1)OD∥BN,∴∠MOD=∠B,∴cos∠MOD=cos B,在Rt△MOD中,cos∠MOD═,∵OD=OA,MO=MA+OA=3+MA,∴,∴MA=4.5.23.(5分)(2017秋•怀柔区期末)数学课上老师提出了下面的问题:在正方形ABCD对角线BD上取一点F,使.小明的作法如下:如图①应用尺规作图作出边AD的中点M;②应用尺规作图作出MD的中点E;③连接EC,交BD于点F.所以F点就是所求作的点.请你判断小明的作法是否正确,并说明理由.【解答】解:正确.理由如下:由做法可知M为AD的中点,E为MD的中点,∴∵四边形ABCD是正方形,∴AD=BC,ED∥BC,∴△DEF∽△BFC∴∵AD=BC∴∴.24.(5分)(2017秋•怀柔区期末)已知:如图,在四边形ABCD中,BD是一条对角线,∠DBC=30°,∠DBA=45°,∠C=70°.若DC=a,AB=b,请写出求tan∠ADB的思路.(不用写出计算结果)【解答】解:如图,(1)过D点作DE⊥BC于点E,可知△CDE和△DEB都是直角三角形;(2)由∠C=70°,可知sin∠C的值,在Rt△CDE中,由sin∠C和DC=a,可求DE 的长;(3)在Rt△DEB中,由∠DBC=30°,DE的长,可求BD的长;(4)过A点作AF⊥BD于点F,可知△DF A和△AFB都是直角三角形;(5)在Rt△AFB中,由∠DBA=45°,AB=b,可求AF和BF的长;(6)由DB、BF的长,可知DF的长;(7)在Rt△DF A中,由可求tan∠ADB.25.(5分)(2017秋•怀柔区期末)如图,在四边形ABCD中,AD∥BC,∠ADC=90°,点E是BC边上一动点,联结AE,过点E作AE的垂线交直线CD于点F.已知AD=4cm,CD=2cm,BC=5cm,设BE的长为xcm,CF的长为ycm.小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数据保留一位小数)(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当BE=CF时,BE的长度约为0.6~0.8cm.【解答】解:(1)根据题意作图测量可得y=1.5故答案为:1.5(2)根据题意作图得(3)根据题意,所画图象于直线y=x交点即为所求数值.故测量数据在0.6~0.8之间.故答案为:0.6~0.826.(7分)(2017秋•怀柔区期末)在平面直角坐标系xOy中,直线l:y=﹣2x+n与抛物线y=mx2﹣4mx﹣2m﹣3相交于点A(﹣2,7).(1)求m、n的值;(2)过点A作AB∥x轴交抛物线于点B,设抛物线与x轴交于点C、D(点C在点D的左侧),求△BCD的面积;(3)点E(t,0)为x轴上一个动点,过点E作平行于y轴的直线与直线l和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值.【解答】解:(1)把A(﹣2,7)代入y=﹣2x+n,得7=4+n,解得n=3.把把A(﹣2,7)代入y=mx2﹣4mx﹣2m﹣3,得7=4m+8m﹣2m﹣3,解得m=1.综上所述,m=1,n=3;(2)由(1)知抛物线表达式为y=x2﹣4x﹣5令y=0得,x2﹣4x﹣5=0.解得x1=﹣1,x2=5,∴抛物线y=x2﹣4x﹣5与x轴得两个交点C、D的坐标分别为C(﹣1,0),D(5,0)∴CD=6.∵A(﹣2,7),AB∥x轴交抛物线于点B,根据抛物线的轴对称性,可知B(6,7)∵S△BCD=21;(3)据题意,可知P(t,﹣2t+3),Q(t,t2﹣4t﹣5),由x2﹣4x﹣5=﹣2x+3得直线y=﹣2x+3与抛物线y=x2﹣4x﹣5的两个交点坐标分别为(﹣2,7)和(4,﹣5)∵点P在点Q上方∴﹣2<t<4,∴PQ=﹣t2+2t+8=﹣(t﹣1)2+9∵a=﹣1∴PQ的最大值为9.27.(7分)(2017秋•怀柔区期末)在等腰△ABC中,AB=AC,将线段BA绕点B顺时针旋转到BD,使BD⊥AC于H,连结AD并延长交BC的延长线于点P.(1)依题意补全图形;(2)若∠BAC=2α,求∠BDA的大小(用含α的式子表示);(3)小明作了点D关于直线BC的对称点点E,从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.【解答】解:(1)如图:(2)∵∠BAC=2α,∠AHB=90°,∴∠ABH=90°﹣2α,∵BA=BD,∴∠BDA=45°+α;(3)补全图形,如图:证明过程如下:∵D关于BC的对称点为E,且DE交BP于G,∴DE⊥BP,DG=GE,∠DBP=∠EBP,BD=BE,∵AB=AC,∠BAC=2α,∴∠ABC=90°﹣α,由(2)知∠ABH=90°﹣2α,∠DBP=90°﹣α﹣(90°﹣2α)=α,∴∠DBP=∠EBP=α,∴∠BDE=2α,∵AB=BD,∴△ABC≌△BDE,∴BC=DE,∴∠DPB=∠ADB﹣∠DBP=45°+α﹣α=45°,∴,∴,∴,∴BC DP.28.(7分)(2017秋•怀柔区期末)在平面直角坐标系xOy中,点P的横坐标为x,纵坐标为2x,满足这样条件的点称为“关系点”.(1)在点A(1,2)、B(2,1)、M(,1)、N(1,)中,是“关系点”的A,M;(2)⊙O的半径为1,若在⊙O上存在“关系点”P,求点P坐标;(3)点C的坐标为(3,0),若在⊙C上有且只有一个“关系点”P,且“关系点”P的横坐标满足﹣2≤x≤2.请直接写出⊙C的半径r的取值范围.【解答】解:(1)设点P的纵坐标为y,则y=2x,∴点P在直线y=2x上,即:直线y=2x上的点称为“关系点”,当x=1时,y=2×1=1,∴点A是“关系点”,当x=2时,y=2×2=4≠1,∴点B不是“关系点”,当x时,y=21,∴点M是“关系点”,∴点A,M是“关系点”,故答案为:A,M;(2)如图1,过点P作PG⊥x轴于点G,设P(x,2x)∵OG2+PG2=OP2∴x2+4x2=1∴5x2=1∴x2∴x∴P(,)或P(,);(3)如图2,由(1)知,点P在直线y=2x上,∵﹣2≤x≤2,即:点(2,4)为B,(﹣2,﹣4)为A,过B作BE⊥x轴于E,∴OE=2,BE=4,在Rt△BOE中,根据勾股定理得,OB2,∴sin∠BOE,①当⊙C与线段AB相切时,切点记作D,连接CD,∵C(3,0),∴OC=3,在Rt△COD中,sin∠COD,∴,∴CD,②当以点C为圆心的圆刚好过点B时,与线段的另一个交点记作F,⊙C的半径BC,当以点C为圆心的圆刚好过点A时,⊙C的半径AC,∵在⊙C上有且只有一个“关系点”P,∴点P和点D重合时,满足条件,点P在线段AF上时,满足条件(包括点A,不包括点F),∴t或<r.。
