四边形专题复习
四边形复习(一)

两组对边分 四个角都 别平行且相 是直角 等
对角线互相平分且 中心对称、
相等
轴对称
菱
A
形
B
O
C
有一组邻边 相等的平行
D
四边形
四条边都相等
两组对角 分别相等
对角线互相垂直平分 且每一条对角线平分 一组对角
中心对称、 轴对称
B
正
方
形
O
A
有一个角是直 角且有一组邻 边相等的平行
四条边都相等 四个角都 是直角
两组对角分别相等 平行四边形
两条对角线互相平分
四条边相等
矩形
一组邻边相等、一个角是直角 对角线互相垂直且相等
正方形
菱形
四、关系
四边形 平行四边形 矩形 菱形
正方形
五、其他重点知识回顾
1、直角三角形斜边上的中线的性质:
A
直角三角形斜边上的中线等于斜边的一半。
符号语言:
在RtABC中,B 90,D为AC的中点
变式3:如图,四边形 ABCD中,点E, F,G, H分别是AD, BD, BC, AC的中点, 顺次连接 E,F,G,H,判断四边形 EFGH的形状。
D E A
F H
B
G
C
变式3:如图,四边形ABCD中,点E, F,G, H分别是AD, BD, BC,
AC的中点,顺次连接E,F,G,H, (1)若AB CD,则四边形EFGH的形状是________________。 (2)若AB CD,则四边形EFGH的形状是________________。
(3)若AB CD, AB CD,则四边形EFGH的形状是___________。
AE
D
2022年中考数学专题复习:四边形
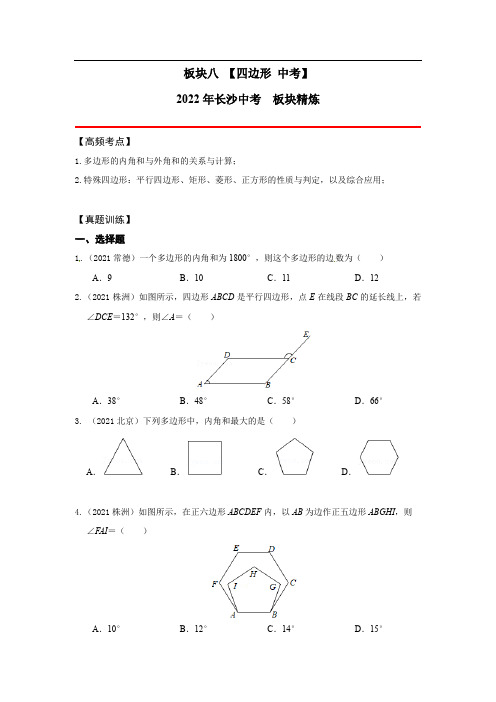
板块八【四边形中考】2022年长沙中考板块精炼【高频考点】1.多边形的内角和与外角和的关系与计算;2.特殊四边形:平行四边形、矩形、菱形、正方形的性质与判定,以及综合应用;【真题训练】一、选择题1.(2021常德)一个多边形的内角和为1800°,则这个多边形的边数为()A.9B.10C.11D.122.(2021株洲)如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=132°,则∠A=()A.38°B.48°C.58°D.66°3. (2021北京)下列多边形中,内角和最大的是()A.B.C.D.4.(2021株洲)如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠F AI=()A.10°B.12°C.14°D.15°5.(2021娄底)如图,点E、F在矩形ABCD的对角线BD所在的直线上,BE=DF,则四边形AECF是()A.平行四边形B.矩形C.菱形D.正方形6. (2021福建)如图,点F在正五边形ABCDE的内部,△ABF为等边三角形,则∠AFC等于()A.108°B.120°C.126°D.132°7.(2021湘西)如图,在菱形ABCD中,E是AC的中点,EF∥CD,交AD于点F,如果EF=5.5,那么菱形ABCD的周长是()A.11B.22C.33D.448. (2021安徽)如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为()A.3B.2+23C.3D.1+239.(2021常德)如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于P.则下列结论成立的是()A.BE=12AE B.PC=PD C.∠EAF+∠AFD=90°D.PE=EC10.(2021怀化)如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,AE⊥BC于E点,交BD于M点,反比例函数33yx(x>0)的图象经过线段DC的中点N,若BD=4,则ME的长为()A.ME=53B.ME=43C.ME=1D.ME=2311.(2021郴州)如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是()A.B.C.D.12.(2021衡阳)如图,矩形纸片ABCD,AB=4,BC=8,点M、N分别在矩形的边AD、BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN于点Q,连接CM.下列结论:①四边形CMPN是菱形;②点P与点A重合时,MN=5;③△PQM的面积S的取值范围是4≤S≤5.其中所有正确结论的序号是()A.①②③B.①②C.①③D.②③二、填空题13.(2021益阳)如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是(限填序号).14.(2021长沙)如图,菱形ABCD的对角线AC,BD相交于点O,点E是边AB的中点,若OE=6,则BC的长为.15. (2021邵阳)如图,在矩形ABCD中,DE⊥AC,垂足为点E.若sin∠ADE=45,AD=4,则AB的长为.16.(2021衡阳)如图1,菱形ABCD的对角线AC与BD相交于点O,P、Q两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为O—A—D —O,点Q的运动路线为O—C—B—O.设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在A—D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为厘米.17.(2021张家界)如图,在正方形ABCD外取一点E,连接DE,AE,CE,过点D作DE的垂线交AE于点P,若DE=DP=1,PC=6.下列结论:①△APD≌△CED;②AE⊥CE;③点C到直线DE的距离为6;④S正方形ABCD=5+22,其中正确结论的序号为.18.(2021北京)如图,在矩形ABCD中,点E,F分别在BC,AD上,AF=EC.只需添加一个条件即可证明四边形AECF是菱形,这个条件可以是(写出一个即可).19.(2021湘潭)如图,在▱ABCD 中,对角线AC ,BD 相交于点O ,点E 是边AB 的中点.已知BC =10,则OE = .20.(2021兰州)如图,在矩形ABCD 中,AB =1,AD =3.①以点A 为圆心,以不大于AB 长为半径作弧,分别交边AD ,AB 于点E ,F ,再分别以点E ,F 为圆心,以大于12EF 长为半径作弧,两弧交于点P ,作射线AP 分别交BD ,BC 于点O ,Q ;②分别以点C ,Q 为圆心,以大于12CQ 长为半径作弧,两弧交于点M ,N ,作直线MN 交AP 于点G ,则OG 长为 .三、解答题21.(2021长沙)如图,□ABCD 的对角线AC ,BD 相交于点O ,△OAB 是等边三角形,AB =4.(1)求证:□ABCD 是矩形; (2)求AD 的长.O QP E D22.(2021怀化)已知:如图,四边形ABCD为平行四边形,点E、A、C、F在同一直线上,AE=CF.求证:(1)△ADE≌△CBF;(2)ED∥BF.23. (2021湘潭)如图,矩形ABCD中,E为边BC上一点,将△ABE沿AE翻折后,点B 恰好落在对角线AC的中点F上.(1)证明:△AEF≌△CEF;(2)若AB=3,求折痕AE的长度.23.(2021株洲)如图所示,在矩形ABCD中,点E在线段CD上,点F在线段AB的延长线上,连接EF交线段BC于点G,连接BD,若DE=BF=2.(1)求证:四边形BFED是平行四边形;(2)若tan∠ABD=23,求线段BG的长度.24.(2021郴州)如图,四边形ABCD中,AB=DC,将对角线AC向两端分别延长至点E,F,使AE=CF.连接BE,DF,若BE=DF.证明:四边形ABCD是平行四边形.25. (2021衡阳)如图,点E为正方形ABCD外一点,∠AEB=90°,将Rt△ABE绕A点逆时针方向旋转90°得到△ADF,DF的延长线交BE于H点.(1)试判定四边形AFHE的形状,并说明理由;(2)已知BH=7,BC=13,求DH的长.26.(2021邵阳)如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.(1)证明:△ADE≌△CBF.(2)若AB=4,AE=2,求四边形BEDF的周长.27.(2021岳阳)如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F.(1)请你只添加一个条件(不另加辅助线),使得四边形AECF为平行四边形,你添加的条件是;(2)添加了条件后,证明四边形AECF为平行四边形.28.(2021张家界)如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,对角线AC所在的直线绕点O顺时针旋转角α(0°<α <120°),所得的直线l分别交AD,BC于点E,F.(1)求证:△AOE≌△COF;(2)当旋转角α为多少度时,四边形AFCE为菱形?试说明理由.29.(2020长沙)在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.(1)求证:△ABF∽△FCE;(2)若AB=23,AD=4,求EC的长;(3)若AE-DE=2EC,记∠BAF=α,∠F AE=β.求tanα+tanβ的值.板块八【四边形中考】2022年长沙中考板块精炼【答案或简析】【高频考点】1.多边形的内角和与外角和的关系与计算;2.特殊四边形:平行四边形、矩形、菱形、正方形的性质与判定,以及综合应用;【真题训练】一、选择题1.(2021常德)一个多边形的内角和为1800°,则这个多边形的边数为()A.9B.10C.11D.12【答案或简析】D.2.(2021株洲)如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=132°,则∠A=()A.38°B.48°C.58°D.66°【答案或简析】B.3. (2021北京)下列多边形中,内角和最大的是()A.B.C.D.【答案或简析】D.4.(2021株洲)如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠F AI=()A.10°B.12°C.14°D.15°【答案或简析】B.5.(2021娄底)如图,点E、F在矩形ABCD的对角线BD所在的直线上,BE=DF,则四边形AECF是()A.平行四边形B.矩形C.菱形D.正方形【答案或简析】A.6. (2021福建)如图,点F在正五边形ABCDE的内部,△ABF为等边三角形,则∠AFC等于()A.108°B.120°C.126°D.132°【答案或简析】C.7.(2021湘西)如图,在菱形ABCD中,E是AC的中点,EF∥CD,交AD于点F,如果EF=5.5,那么菱形ABCD的周长是()A.11B.22C.33D.44【答案或简析】D.8. (2021安徽)如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为()A.3+3B.2+23C.2+3D.1+23【答案或简析】B.9.(2021常德)如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于P.则下列结论成立的是()A.BE=12AE B.PC=PD C.∠EAF+∠AFD=90°D.PE=EC【答案或简析】C.10.(2021怀化)如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,AE⊥BC于E点,交BD于M点,反比例函数33yx(x>0)的图象经过线段DC的中点N,若BD=4,则ME的长为()A.ME=53B.ME=43C.ME=1D.ME=23【答案或简析】D.解:过N作y轴和x轴的垂线NG,NH,设N(b,a),∵反比例函数y=33x(x>0)的图象经过点N,∴ab 3,∵四边形ABCD是菱形,∴BD⊥AC,DO=12BD=2,∵NH⊥x轴,NG⊥y轴,∴四边形NGOH是矩形,∴NG∥x轴,NH∥y轴,∵N为CD的中点,∴DO•CO=2a•2b=4ab43∴CO23∴tan∠CDO=33 OCDO.∴∠CDO=30°,∴∠DCO=60°,∵四边形ABCD是菱形,∴∠ADC=∠ABC=2∠CDO=60°,∠ACB=∠DCO=60°,∴△ABC是等边三角形,∵AE⊥BC,BO⊥AC,∴AE=BO=2,∠BAE=30°=∠ABO,∴AM=BM,∴OM=EM,∵∠MBE=30°,∴BM=2EM=2OM,∴3EM=OB=2,∴ME=23,故选:D.11.(2021郴州)如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是()A.B.C.D.【答案或简析】A.12.(2021衡阳)如图,矩形纸片ABCD,AB=4,BC=8,点M、N分别在矩形的边AD、BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN于点Q,连接CM.下列结论:①四边形CMPN是菱形;②点P与点A重合时,MN=5;③△PQM的面积S的取值范围是4≤S≤5.其中所有正确结论的序号是()A.①②③B.①②C.①③D.②③【答案或简析】C.二、填空题13.(2021益阳)如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是(限填序号).【答案或简析】①.14.(2021长沙)如图,菱形ABCD的对角线AC,BD相交于点O,点E是边AB的中点,若OE=6,则BC的长为.【答案或简析】12.15. (2021邵阳)如图,在矩形ABCD中,DE⊥AC,垂足为点E.若sin∠ADE=45,AD=4,则AB的长为.【答案或简析】3.16.(2021衡阳)如图1,菱形ABCD的对角线AC与BD相交于点O,P、Q两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为O—A—D —O,点Q的运动路线为O—C—B—O.设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在A—D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为厘米.【答案或简析】23317.(2021张家界)如图,在正方形ABCD外取一点E,连接DE,AE,CE,过点D作DE的垂线交AE于点P,若DE=DP=1,PC=6.下列结论:①△APD≌△CED;②AE⊥CE;③点C到直线DE的距离为6;④S正方形ABCD=5+22,其中正确结论的序号为.【答案或简析】B.18.(2021北京)如图,在矩形ABCD中,点E,F分别在BC,AD上,AF=EC.只需添加一个条件即可证明四边形AECF是菱形,这个条件可以是(写出一个即可).【答案或简析】例如AE=EC.19.(2021湘潭)如图,在▱ABCD中,对角线AC,BD相交于点O,点E是边AB的中点.已知BC=10,则OE=.【答案或简析】5.20.(2021兰州)如图,在矩形ABCD中,AB=1,AD=3.①以点A为圆心,以不大于AB长为半径作弧,分别交边AD,AB于点E,F,再分别以点E,F为圆心,以大于12EF 长为半径作弧,两弧交于点P,作射线AP分别交BD,BC于点O,Q;②分别以点C,Q为圆心,以大于12CQ长为半径作弧,两弧交于点M,N,作直线MN交AP于点G,则OG长为.【答案或简析】524三、解答题21.(2021长沙)如图,□ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.(1)求证:□ABCD是矩形;(2)求AD的长.【答案或简析】(1)证明:∵△AOB为等边三角形,OQPE D∴∠BAO =∠AOB =60°,OA =OB , ∵四边形ABCD 是平行四边形 ∴OB =OD =12BD ,OA =OC =12AC , ∴BD =AC ,∴▱ABCD 是矩形;(2)解:∵▱ABCD 是矩形, ∴∠BAD =90°, ∵∠ABO =60°,∴∠ADB =90°﹣60°=30°, ∴AD =3AB =43.22. (2021怀化)已知:如图,四边形ABCD 为平行四边形,点E 、A 、C 、F 在同一直线上,AE =CF .求证:(1)△ADE ≌△CBF ;(2)ED ∥BF .【答案或简析】证明:(1)∵四边形ABCD 为平行四边形, ∴DA =BC ,DA ∥BC , ∴∠DAC =∠BCA ,∵∠DAC +∠EAD =180°,∠BCA +∠FCB =180°, ∴∠EAD =∠FCB , 在△ADE 和△CBF 中,,,,AE CF EAD FCB AD CB , ∴△ADE ≌△CBF (SAS );(2)由(1)知,△ADE ≌△CBF , ∴∠E =∠F , ∴ED ∥BF .23. (2021湘潭)如图,矩形ABCD 中,E 为边BC 上一点,将△ABE 沿AE 翻折后,点B恰好落在对角线AC 的中点F 上. (1)证明:△AEF ≌△CEF ;(2)若AB =3,求折痕AE 的长度. 【答案或简析】(1)证明:∵四边形ABCD 是矩形,∴∠B =90°,∵将△ABE 沿AE 翻折后,点B 恰好落在对角线AC 的中点F 上,∴∠AFE =∠B =90°,AF =CF , ∵∠AFE +∠CFE =180°,∴∠CFE =180°﹣∠AFE =90°, 在△AEF 和△CEF 中,,,,AF CF AFE CFE EF EF ∠∠, ∴△AEF ≌△CEF (SAS ).(2)解:由(1)知,△AEF ≌△CEF , ∴∠EAF =∠ECF ,由折叠性质得,∠BAE =∠EAF , ∴∠BAE =∠EAF =∠ECF , ∵∠B =90°,∴∠BAC +∠BCA =90°, ∴3∠BAE =90°, ∴∠BAE =30°,在Rt △ABE 中,AB =3,∠B =90°,∴AE =32cos3032AB .23.(2021株洲)如图所示,在矩形ABCD 中,点E 在线段CD 上,点F 在线段AB 的延长线上,连接EF 交线段BC 于点G ,连接BD ,若DE =BF =2. (1)求证:四边形BFED 是平行四边形; (2)若tan ∠ABD =23,求线段BG 的长度.【答案或简析】证明:(1)∵四边形ABCD 是矩形, ∴DC ∥AB , 又∵DE =BF ,∴四边形DEFB 是平行四边形; (2)∵四边形DEFB 是平行四边形, ∴DB ∥EF , ∴∠ABD =∠F ,∴tan ∠ABD =tan F =23, ∴23BG BF , 又∵BF =2, ∴BG =43.24.(2021郴州)如图,四边形ABCD 中,AB =DC ,将对角线AC 向两端分别延长至点E ,F ,使AE =CF .连接BE ,DF ,若BE =DF .证明:四边形ABCD 是平行四边形.【答案或简析】证明:在△BEA 和△DFC 中,,,,AB DC AE CF BE DF ∴△BEA ≌△DFC (SSS ), ∴∠EAB =∠FCD , ∴∠BAC =∠DCA , ∴AB ∥DC , ∵AB =DC ,∴四边形ABCD 是平行四边形.25. (2021衡阳)如图,点E 为正方形ABCD 外一点,∠AEB =90°,将Rt △ABE 绕A 点逆时针方向旋转90°得到△ADF ,DF 的延长线交BE 于H 点. (1)试判定四边形AFHE 的形状,并说明理由; (2)已知BH =7,BC =13,求DH 的长.【答案或简析】(1)四边形AFHE 是正方形,理由如下:由旋转得∠AEB =∠AED =90°,AE =AF ,∠DAF =∠EAB. ∴∠AFH =90°.∵四边形ABCD 是正方形, ∴∠DAB =90°,∴∠F AE =∠F AB +∠BAE =∠F AB +∠DAF =∠DAB =90°, ∴∠AEB =∠AFB =∠F AE =90°,∴四边形AFHE 是矩形. 又∵AE =AF ,∴四边形AFHE 是正方形. (2)连接BD ,由题意得,BC =CD =13, ∴在Rt △BCD 中,BD =22132CD CB .∵四边形AFHE 是正方形, ∴∠EHD =90°,∴∠DHB =90°, 在Rt △DHB 中,DH =22,BD BH又∵BH =7,∴DH =17.26.(2021邵阳)如图,在正方形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 是对角线AC 上的两点,且AE =CF .连接DE ,DF ,BE ,BF . (1)证明:△ADE ≌△CBF . (2)若AB =4,AE =2,求四边形BEDF 的周长.【答案或简析】(1)证明:由正方形对角线平分每一组对角可知:∠DAE =∠BCF =45°, 在△ADE 和△CBF 中,,,,AD BC DAE BCF AE CF ∠∠ ∴△ADE ≌△CBF (SAS ). (2)解:∵AB =AD =42, ∴BD =228AB AD ,由正方形对角线相等且互相垂直平分可得:AC =BD =8,DO =BO =4,OA =OC =4, 又AE =CF =2,∴OA ﹣AE =OC ﹣CF , 即OE =OF =4﹣2=2, 故四边形BEDF 为菱形. ∵∠DOE =90°, ∴DE =22224225DO EO .∴4DE =85,故四边形BEDF 的周长为85.27.(2021岳阳)如图,在四边形ABCD 中,AE ⊥BD ,CF ⊥BD ,垂足分别为点E ,F . (1)请你只添加一个条件(不另加辅助线),使得四边形AECF 为平行四边形,你添加的条件是 ;(2)添加了条件后,证明四边形AECF 为平行四边形.【答案或简析】解:(1)添加条件为:AE =CF , 故答案为:AE =CF ;(2)证明:∵AE ⊥BD ,CF ⊥BD , ∴AE ∥CF , ∵AE =CF ,∴四边形AECF 为平行四边形.28.(2021张家界)如图,在矩形ABCD 中,对角线AC 与BD 相交于点O ,∠AOB =60°,对角线AC 所在的直线绕点O 顺时针旋转角α(0°< α <120°),所得的直线l 分别交AD ,BC 于点E ,F . (1)求证:△AOE ≌△COF ;(2)当旋转角α为多少度时,四边形AFCE 为菱形?试说明理由.【答案或简析】 证明:(1)∵四边形ABCD 是矩形, ∴AD ∥BC ,AO =CO , ∴∠AEO =∠CFO , 在△AOE 和△COF 中,,,,AEO CFO AOE COF AO CO ∠∠∠∠, ∴△AOE ≌△COF (AAS );(2)当α=90°时,四边形AFCE 为菱形, 理由:∵△AOE ≌△COF , ∴OE =OF , 又∵AO =CO ,∴四边形AFCE 为平行四边形, 又∵∠AOE =90°,∴四边形AFCE 为菱形.29.(2020长沙)在矩形ABCD 中,E 为DC 边上一点,把△ADE 沿AE 翻折,使点D 恰好落在BC 边上的点F . (1)求证:△ABF ∽△FCE ;(2)若AB =23,AD =4,求EC 的长;(3)若AE -DE =2EC ,记∠BAF =α,∠F AE =β.求tan α+tan β的值.【答案或简析】(1)证明:∵四边形ABCD 是矩形, ∴∠B =∠C =∠D =90°, ∴∠CEF +∠EFC =90°, ∵△AEF 由△AED 翻折得到, ∴∠AFE =∠D =90°, ∴∠AFB +∠EFC =90°, ∴∠CEF =∠AFB , ∴△ABF ∽△FCE ; (2)∵四边形ABCD 是矩形, ∴AB =CD =23,AD =BC =4,设CE =x ,则DE =23-x , ∵△AEF 由△AED 翻折得到, ∴AD =AF =4,DE =EF =23-x ,在Rt △ABF 中,BF =AF 2-AB 2=42-(23)2=2, ∴CF =BC -BF =4-2=2,在Rt △CEF 中,EF 2=CE 2+CF 2,即(23-x )2=x 2+22, 解得x =233,即EC =233;(3)如解图,设EC =x ,DE =a ,则易得EF =a ,AB =a +x , ∵AE -DE =2EC ,∴AE -a =2x ,即AE =2x +a ,由勾股定理得:AF =AE 2-EF 2=(2x +a )2-a 2=4ax +4x 2, CF =EF 2-CE 2=a 2-x 2,由(1)知∠CEF =∠AFB ,∴∠BAF =∠CFE =α,∴cos ∠BAF =AB AF =a +x 4ax +4x 2,cos ∠CFE =CFEF =a 2-x 2a ,∴a +x 4ax +4x2=a 2-x 2a , a +x4x (a +x )=(a +x )(a -x )a,a (a +x )=(a +x )4x (a -x ), a =4ax -4x 2, 整理得(a -2x )2=0, ∴a =2x ,∴sin ∠CFE =CE EF =x a =x 2x =12,即∠CFE =∠BAF =α=30°,∴∠DAF =60°, ∴∠EAF =β=30°.∴tan α+tan β=tan 30°+tan 30°=233.。
九年级数学中考复习专题:四边形综合(考察全等证明、长度与面积计算等)

九年级数学中考复习专题:四边形综合(考察全等证明、长度与面积计算等)(一)1.综合与实践问题情境在数学活动课上,老师提出了这样一个问题:如图①,已知正方形ABCD,点E是边上一点,连接AE,以AE为边在BC的上方作正方形AEFG.数学思考(1)连接GD,求证:△ABE≌△ADG;(2)连接FC,求∠FCD的度数;实践探究(3)如图②,当点E在BC的延长线上时,连接AE,以AE为边在BC的上方作正方形AEFG,连接FC,若正方形ABCD的边长为4,CE=2,则CF的长是.2.如图,正方形ABCD的边长是2厘米,E为CD的中点,Q为正方形ABCD边上的一个动点,动点Q以每秒1厘米的速度从A出发沿A→B→C→D运动,最终到达点D,若点Q运动时间为x秒.(1)当x=1时,S△AQE=平方厘米;当x=时,S△AQE=平方厘米.(2)在点Q的运动路线上,当点Q与点E相距的路程不超过厘米时,求x的取值范围.(3)若△AQE的面积为平方厘米,直接写出x值.3.如图,在平行四边形ABCD中,∠BAD的平分线交C于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG.(1)求证:四边形ECFG是菱形;(2)连结BD、CG,若∠ABC=120°,则△BDG是等边三角形吗?为什么?(3)若∠ABC=90°,AB=10,AD=24,M是EF的中点,求DM的长.4.如图1,正方形ABCD沿GF折叠,使B落在CD边上点E处,连接BE,BH.(1)求∠HBE的度數;(2)若BH与GF交于点O,连接OE,判断△BOE的形状,说明理由;(3)在(2)的条件下,作EQ⊥AB于点Q,连接OQ,若AG=2,CE=3,求△OQR 的面积.5.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.(1)求证:BD、EF互相平分;(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.6.如图,已知正方形ABCD的面积是8,连接AC、BD交于点O,CM平分∠ACD交BD于点M,MN⊥CM,交AB于点N,(1)求∠BMN的度数;(2)求BN的长.7.如图,四边形OABC为矩形,其中O为原点,A、C两点分别在x轴和y轴上,B点的坐标是(4,6),将矩形沿直线DE折叠,使点C落在AB边上点F处,折痕分别交OC,BC于点E、D,且D点坐标是(,6).(1)求F点的坐标;(2)如图2,P点在第二象限,且△PDE≌△CED,求P点的坐标;(3)若M点为x轴上一动点,N点为直线DE上一动点,△FMN为以FN为底边的等腰直角三角形,求N点的坐标.8.已知,在平行四边形ABCD中,点F是AB上一点,连接DF交对角线AC于E,连接BE.(1)如图1,若∠EBC=∠EFA,EC平分∠DEB,求证:平行四边形ABCD是菱形;(2)如图2,对角线AC与BD相交于点O,当点F是AB的中点时,直接写出与△ADF 面积相等的三角形(不包括以AD为边的三角形).9.如图,四边形ABCD是平行四边形,∠BAC=90°,AB=AC,点H为边AB的中点,点E在CH的延长线上,且AE⊥BE.点F在线段AE上,且BF⊥CE,垂足为G.(1)若BF=AF,且EF=3,BE=4,求AD的长;(2)求证:BF+2EH=CE.10.在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,则线段AE与DF的关系是;(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;(3)如图2,连接AC,当△ACE为等腰三角形时,请你求出CE:CD的值.参考答案1.(1)证明:∵四边形ABCD和四边形AEFG是正方形,∴AB=AD,AE=AG,∠ABE=∠ADG=90°,∴∠BAE+∠EAD=∠DAG+∠EAD,∴∠BAE=∠DAG,在△ABE和△ADG中,,∴△ABE≌△ADG(SAS);(2)解:如图①,过点F作FH⊥BC,交BC的延长线于点H,∵∠AEF=∠ABE=90°,∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,∴∠FEH=∠BAE,又∵AE=EF,∠EHF=∠ABE=90°,∴△EHF≌△ABE(SAS),∴FH=EB,EH=AB=BC,∴CH=BE,∴CH=FH,∴∠FCH=45°,∴∠FCD=45°;(3)解:过点F作FH⊥BC,交BC的延长线于点H,如图②,由(2)知△EHF≌△ABE,∴EH=AB,FH=BE,∵AB=BC=4,CE=2,∴BE=FH=6,CH=CE+EH=6,∴CF==6.故答案为:6.2.解:(1)①∵E为CD的中点,∴DE=1,∵动点Q以每秒1厘米的速度从A出发沿A→B→C→D运动,∴当x=1时,AQ=1,∴S△AQE=×AQ×AD=×1×2=1,②∵AQ=,∴点Q在AB上,∴S△AQE=×AQ×AD=;故答案为:①1;②.(2)根据题意,得,解得:.∴x的取值范围是.(3)①当点Q在AB上,∵S△AQE=×x×2=,∴x=,②当点Q在BC上时,∵S△AQE=S梯形ABCE﹣S△ABQ﹣S△CQE=×2×(x﹣2)﹣×1×(4﹣x)=.∴x=,③当点Q在CD上时,∵S△AQE=,∴x=.综合以上可得x=或或.3.证明:(1)∵AF平分∠BAD,∴∠BAF=∠DAF,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAF=∠CEF,∠BAF=∠CFE,∴∠CEF=∠CFE,∴CE=CF,又∵四边形ECFG是平行四边形,∴四边形ECFG为菱形;(2)△BDG是等边三角形,理由如下:∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,AD∥BC,∵∠ABC=120°,∴∠BCD=60°,∠BCF=120°,由(1)知,四边形CEGF是菱形,∴CE=GE,∠BCG=∠BCF=60°,∴CG=GE=CE,∠DCG=120°,∵EG∥DF,∴∠BEG=120°=∠DCG,∵AE是∠BAD的平分线,∴∠DAE=∠BAE,∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE,∴BE=CD,∴△BEG≌△DCG(SAS),∴BG=DG,∠BGE=∠DGC,∴∠BGD=∠CGE,∵CG=GE=CE,∴△CEG是等边三角形,∴∠CGE=60°,∴∠BGD=60°,∵BG=DG,∴△BDG是等边三角形;(3)如图2中,连接BM,MC,∵∠ABC=90°,四边形ABCD是平行四边形,∴四边形ABCD是矩形,又由(1)可知四边形ECFG为菱形,∠ECF=90°,∴四边形ECFG为正方形.∵∠BAF=∠DAF,∴BE=AB=DC,∵M为EF中点,∴∠CEM=∠ECM=45°,∴∠BEM=∠DCM=135°,在△BME和△DMC中,∵,∴△BME≌△DMC(SAS),∴MB=MD,∠DMC=∠BME.∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,∴△BMD是等腰直角三角形.∵AB=10,AD=24,∴BD===26,∴DM=BD=13.4.解:(1)如图1中,过点E作EN⊥AB于N,过点B作BM⊥EA′于M.由翻折可知,∠ABF=∠FEA′=90°,FB=FE,∴∠FBE=∠FEB,∴∠EBN=∠BEM,∵∠ENB=∠BME=90°,BE=EB,∴△ENB≌△BME(AAS),∴EN=BM,∵四边形ABCD是正方形,∴∠NBC=∠C=∠A=∠ENB=90°,AB=BC,∴AB=BM=BC,∵BH=BH,BE=BE,∴Rt△BAH≌Rt△BMH(HL),Rt△BME≌Rt△BCE,∴∠ABH=∠MBH,∠EBM=∠EBC,∴∠HBE=∠MBH+∠EBM=∠ABC=45°.(2)结论:△BOE是等腰直角三角形.理由:如图2中,由翻折的旋转可知,FG垂直平分线段BE,∴∠OBE=∠OEB=45°,∴OB=OE,∠BOE=90°,∴△BOE是等腰直角三角形.(3)如图3中,过点O作OM⊥EQ于M,ON⊥AB于N,过点G作GJ⊥BC于J.∵∠A=∠ABJ=∠BJG=90°,∴四边形ABJG是矩形,∴AG=BJ=2,AB=GJ=BC,∵FG⊥BE,∴∠EBC+∠BFG=90°,∠BFG+∠JGF=90°,∴∠CBE=∠JGF,∵∠C=∠GJF=90°,BC=GJ,∴△GJF≌△BCE(AAS),∴FJ=CE=3,∴BF=EF=5,CF==4,∴BC=BF+CF=9,∴BE===3,∴OB=OE=3,∵EQ⊥AB,∴∠ONB=∠OME=∠OMQ=∠MQN=90°,∴四边形MQNO是矩形,∴∠MON=∠BOE=90°,∴∠BON=∠EOM,∴△ONB≌△OME(AAS),∴ON=OM,∴四边形MQNO是正方形,设OM=OM=NQ=MQ=x,∵∠C=∠CBQ=∠BQE=90°,∴四边形BCEQ是矩形,∴BQ=EC=3,EQ=BC=9,在Rt△BON中,则有x2+(x+3)2=(3)2,解得x=3或﹣6(舍弃),∴OM=QM=3,EM=BN=6,∵∠BQR=∠OMR=90°,∠BRQ=∠ORM,BQ=OM=3,∴△BQR≌△OMR(AAS),∴QR=MR=∴S△OQR=•QR•OM=××3=.5.(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,AD=BC,∵DE、BF分别是∠ADC和∠ABC的角平分线,∴∠ADE=∠CDE,∠CBF=∠ABF,∵CD∥AB,∴∠AED=∠CDE,∠CFB=∠ABF,∴∠AED=∠ADE,∠CFB=∠CBF,∴AE=AD,CF=CB,∴AE=CF,∴AB﹣AE=CD﹣CF即BE=DF,∵DF∥BE,∴四边形DEBF是平行四边形.∴BD、EF互相平分;(2)∵∠A=60°,AE=AD,∴△ADE是等边三角形,∵AD=4,∴DE=AE=4,∵AE=2EB,∴BE=GE=2,∴BG=4,过D点作DG⊥AB于点G,在Rt△ADG中,AD=4,∠A=60°,∴DG=AD cos∠A=4×=2,∴BD===2.6.解:(1)∵正方形ABCD的面积是8,∴BC=CD==2,∴BD=×2=4.∵四边形ABCD为正方形,∴∠DCO=∠BCO=∠CDO=∠MBN=45°,∵CM平分∠ACD,∴∠DCM=∠MCO=22.5°,∴∠BMC=∠CDO+∠DCM=45°+22.5°=67.5°.∵MN⊥CM,∴∠CMN=90°,∴∠BMN=90°﹣67.5°=22.5°,∴∠BMN的度数为22..5°.(2)∵∠MCO=22.5°,∠BCO=45°,∴∠BCM=∠BCO+∠MCO=67.5°,又∵∠BMC=67.5°,∴∠BCM=∠BMC,∴BM=BC=CD=2,∴DM=BD﹣BM=4﹣2.∵∠DCM=22.5°,∠BMN=22.5°,∴∠DCM=∠BMN.∴在△DCM和△BMN中,,∴△DCM≌△BMN(ASA),∴BN=DM=4﹣2,∴BN的长为4﹣2.7.解:(1)∵点D坐标是(,6),B点的坐标是(4,6),四边形OABC为矩形,∴BC=AO=4,OC=AB=6,CD=,BD=BC﹣CD=,∵将矩形沿直线DE折叠,∴DF=CD=,∴BF===2,∴AF=6﹣2=4,∴点F(4,4).(2)如图2中,连接PF交DE于J.当四边形EFDP是矩形时,△PDE≌△FED≌△CED,∵C(0,6),F(4,4),∴直线CF的解析式为y=﹣x+6,∵DE垂直平分线段CF,∴直线DE的解析式为y=2x+1,∴E(0,1),D(,6),∵DJ=JE,∴J(,),∵PJ=JF,∴P(﹣,3).(3)如图3中,连接FN,以FN为对角线构造正方形NMFM′,连接MM′交FN于K.设N(m,2m+1),则K(,),M(,),M′(,),当点M落在x轴上时,=0,解得m=﹣,当点M′落在X轴上时,=0,解得m=﹣9,∴满足条件的点N的坐标为(﹣,)或(﹣9,﹣17).8.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠EDC=∠EFA,∵∠EBC=∠EFA,∴∠EBC=∠EDC,∵EC平分∠DEB,∴∠DCE=∠BCE,在△CED和△CEB中,,∴△CED≌△CEB(AAS),∴CD=CB,∵四边形ABCD为平行四边形,∴平行四边形ABCD为菱形;(2)解:与△ADF面积相等的三角形(不包括以AD为边的三角形)为△AOB、△BOC、△COD、△DFB;理由如下:∵四边形ABCD是平行四边形,∴OA=OB,OC=OD,∴△AOB的面积=△BOC的面积=△COD的面积=△ABD的面积,∵点F是AB的中点,∴△ADF的面积=△DFB的面积=△ABD的面积,∴△AOB的面积=△BOC的面积=△COD的面积=△DFB的面积=△ADF的面积.9.解:(1)∵AE⊥BE.EF=3,BE=4,∴BF=,∵BF=AF,∴AF=5,∴AE=3+5=8,∴AB,∵∠BAC=90°,AB=AC,∴BC=,∵四边形ABCD是平行四边形,∴AD=BC=4;(2)在CH上截取HM=HE,连接BM和AM,如图,∵BE⊥AE,∴∠AEB=90°,∵点H为边AB的中点,∴EH=AH=BH=MH,∴四边形AEBM是矩形,∴∠EAM=90°,∵∠BAC=90°,∴∠BAF=∠CAM,∵BF⊥CE,∴∠EGB=90°,∴∠EBG+∠BEG=90°,∵∠EBG+∠BFE=90°,∴∠BEG=∠BFE,∵矩形AEBM中,BE∥AM,∴∠BEG=∠AMH,∴∠BFE=∠AMH,∴∠AFB=∠AMC,∵AB=AC,∴△ABF≌△ACM(AAS),∴BF=CM,∵CM+EM=CE,EM=EH+MH=2EH,∴BF+2EH=CE.10.解:(1)结论:AE=DF,AE⊥DF,理由:如图1中,∵四边形ABCD是正方形,∴AD=DC,∠ADE=∠DCF=90°,∵动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,∴DE=CF,在△ADE和△DCF中,,∴△ADE≌△DCF(SAS),∴AE=DF,∠DAE=∠FDC,∵∠ADE=90°,∴∠ADP+∠CDF=90°,∴∠ADP+∠DAE=90°,∴∠APD=180°﹣90°=90°,∴AE⊥DF;故答案为:AE=DF,AE⊥DF.(2)成立.理由如下:如图2中,∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠DCF=90°,∵动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,∴DE=CF,在△ADE和△DCF中,,∴△ADE≌△DCF(SAS),∴AE=DF,∠DAE=∠CDF,由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°,∴AE⊥DF.(3)有两种情况:①如图3﹣1中,当AC=CE时,设正方形ABCD的边长为a,由勾股定理得:AC=CE==a,则CE:CD=a:a=.②如图3﹣2中,当AE=AC时,设正方形ABCD的边长为a,由勾股定理得:AC=AE==a,∵四边形ABCD是正方形,∴∠ADC=90°,即AD⊥CE,∴DE=CD=a,∴CE:CD=2a:a=2,即CE:CD=或2.。
2023中考数学复习-专题22 四边形(讲通)(学生版)

专题22 四边形1.掌握平行四边形、菱形、矩形、梯形的概念和性质,了解它们之间的关系;了解四边形的不稳定性.2.探索并掌握平行四边形的有关性质和四边形是平行四边形的条件.3.探索并了解等腰梯形的有关性质和四边形是等腰梯形的条件.一、四边形的相关概念1.多边形的定义:在平面内,由不在同一直线上的一些线段首尾顺次相接组成的封闭图形叫做多边形.2.多边形的性质:(1)多边形的内角和定理:n边形的内角和等于(n-2)·180°;(2)推论:多边形的外角和是360°;(3)对角线条数公式:n边形的对角线有条;(4)正多边形定义:各边相等,各角也相等的多边形是正多边形.3.四边形的定义:同一平面内,由不在同一条直线上的四条线段首尾顺次相接组成的图形叫做四边形.4.四边形的性质:(1)定理:四边形的内角和是360°;(2)推论:四边形的外角和是360°.例1.一个多边形的外角和是内角和的,这个多边形的边数为()A.5B.6C.7D.8二、平行四边形的定义、性质与判定1.定义:两组对边分别平行的四边形是平行四边形.2.性质:(1)平行四边形的对边平行且相等;(2)平行四边形的对角相等,邻角互补;(3)平行四边形的对角线互相平分;(4)平行四边形是中心对称图形,对角线的交点是它的对称中心.3.判定:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.4.两条平行线间的距离:定义:夹在两条平行线间最短的线段的长度叫做两条平行线间的距离.性质:夹在两条平行线间的平行线段相等.5.平行四边形的面积:1.平行四边形的面积=底×高;2.同底(等底)同高(等高)的平行四边形面积相等.例2.如图,已知在▭ABCD中,对角线AC、BD相交于点O,AE▭BD,BM▭AC、DN▭AC,CF▭BD垂足分别是E、M、N、F,求证:EN▭MF.三、矩形的定义、性质与判定1.矩形的定义:有一个角是直角的平行四边形叫做矩形.2.矩形的性质矩形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质:①边的性质:对边平行且相等.②角的性质:四个角都是直角.③对角线性质:对角线互相平分且相等.④对称性:矩形是中心对称图形,也是轴对称图形.直角三角形斜边上的中线等于斜边的一半.直角三角形中,角所对的边等于斜边的一半.点评:这两条直角三角形的性质在教材上是应用矩形的对角线推得,用三角形知识也可推得.3.矩形的判定判定①:有一个角是直角的平行四边形是矩形.判定②:对角线相等的平行四边形是矩形.判定③:有三个角是直角的四边形是矩形.四、菱形的定义、性质与判定1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.2.菱形的性质①菱形的四条边都相等;②菱形的对角线互相垂直,并且每一条对角线平分一组对角.注意:菱形也具有平行四边形的一切性质.3.菱形的判定①有一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形④有一条对角线平分一组对角的平行四边形是菱形⑤对角线互相垂直且平分的四边形是菱形4.菱形的面积①对角线乘积的一半(只要是对角线互相垂直的四边形都可用);②设菱形的边长为a,一个夹角为x°,则面积公式是:S=a²·sinx5.菱形的周长菱形周长=边长×4用“a”表示菱形的边长,“C”表示菱形的周长,则C=4a例3.如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,CE与BF相交于点H.(1)判断四边形EHFG的形状;(2)在什么情况下,四边形EHFG为菱形?五、梯形1.梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.(1)互相平行的两边叫做梯形的底;较短的底叫做上底,较长的底叫做下底.(2)不平行的两边叫做梯形的腰.(3)梯形的四个角都叫做底角.2.直角梯形:一腰垂直于底的梯形叫做直角梯形.3.等腰梯形:两腰相等的梯形叫做等腰梯形.4.等腰梯形的性质:(1)等腰梯形的两腰相等;(2)等腰梯形同一底上的两个底角相等. (3)等腰梯形的对角线相等.5.等腰梯形的判定方法:(1)两腰相等的梯形是等腰梯形(定义);(2)同一底上的两个角相等的梯形是等腰梯形;(3)对角线相等的梯形是等腰梯形.6.梯形中位线:连接梯形两腰中点的线段叫梯形的中位线.7.面积公式:S=(a+b)h(a、b是梯形的上、下底,h是梯形的高).六、平面图形1.平面图形的镶嵌的定义:用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地铺成一片,这就是平面图形的镶嵌,又称做平面图形的密铺.2.平面图形镶嵌的条件:(1)同种正多边形镶嵌成一个平面的条件:周角是否是这种正多边形的一个内角的整倍数.在正多边形里只有正三角形、正四边形、正六边形可以镶嵌.(2)n种正多边形组合起来镶嵌成一个平面的条件:▭n个正多边形中的一个内角的和的倍数是360°;▭n个正多边形的边长相等,或其中一个或n个正多边形的边长是另一个或n个正多边形的边长的整数倍.1.(2022·泉州市东海中学)在四边形ABCD中,E,F,G,H分别为各边的中点,顺次连结E,F,G,H,得到中点四边形EFGH.当AC=BD时,则四边形EFGH是()A.平行四边形B.矩形C.菱形D.正方形2.(2022·黑龙江九年级期末)如图,矩形ABCD中8AB=把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.若254AF=,则AD的长为()A.4B.5C.6D.7 3.(2022·重庆实验外国语学校九年级月考)下列命题中,真命题是()A.对角线互相垂直的四边形是菱形B.对角线互相垂直平分的四边形是正方形C.四条边相等的四边形是矩形D.有一组对边平行且相等的四边形是平行四边形4.(2022·深圳市罗湖区翠园初级中学)如图,平行四边形ABCD中,对角线AC、BD相交于点O,则下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC▭BD时,它是菱形C.当AC=BD时,它是矩形D.当AC垂直平分BD时,它是正方形5.(2022·沙坪坝·重庆八中九年级月考)如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定ABE ADF≌的是()A.BE DF∠=∠∠=∠C.AE AF=B.BAF DAE=D.AEB AFD 6.(2022·重庆实验外国语学校九年级开学考试)下列说法不正确的是()A.平行四边形两组对边分别平行B.平行四边形的对角线互相平分C.平行四边形的对角互补,邻角相等D.平行四边形的两组对边分别平行且相等7.(2020·浙江杭州市·九年级)若一个梯形的中位线长为15,一条对角线把中位线分成两条线段.这两条线段的比是3:2,则梯形的上、下底长分别________.8.(2022·沈阳市第四十三中学九年级月考)如图,在▭ABC中,▭A=50°,AB=AC,点D 在AC边上,以CB、CD为边作平行四边形BCDE,则▭E的度数为_____.9.(2022·济南市章丘区实验中学九年级月考)已知:如图,平行四边形ABCD中,AC,BD⊥于点F.交于点O,AE BD⊥于点E,CF BD求证:OE OF=.10.(2019·宁波市慈湖中学九年级)如图,在梯形ABCD中,AD▭BC,AB=DC,若点M为线段AD上任意一点(M与A、D不重合).问:当点M在什么位置时,MB=MC,请说明理由.。
八年级下学期数学四边形专题复习试卷一(含答案)

八年级下学期数学四边形专题复习试卷一班级: 姓名: 学号:一、判断题:(每小题3分,共15分)1、n 边形的n 个外角中最多有三个钝角。
( )2、一组对边相等,另一组对边平行的四边形是平行四边形。
( )3、对角线平分相应的一组对角的平行四边形是菱形。
( )4、对角线垂直且相等的四边形是正方形。
( )5、菱形对角线交点到各边的距离相等。
( )二、填空题:(每小题3分,共18分)6、若n 边形的每个外角都等于200,则边数n = 。
7、平行四边形ABCD 的周长为20cm ,对角线AC 、BD 相交于点O ,若△BOC 的周长比△AOB 的周长大2cm ,则CD = cm 。
8、若矩形的对角线长为8,两条对角线的一个交角为600,则该矩形的面积为 。
9、若边长为4cm 的菱形的两邻角度数之比为1∶2,则该菱形的面积为 cm 2。
10、若菱形的两对角线之比为3∶4,对角线之差为2cm ,则该菱形的周长为 cm 。
11、梯形ABCD 中,AD ∥BC ,若∠A ∶∠B ∶∠C =2∶7∶3,则∠D = 度。
三、选择题:(每小题3分,共27分)12、n 边形的对角线总条数是( )A 、2n B 、)2(-n n C 、2)3(-n n D 、)3(-n n 13、矩形、菱形、正方形都具有的性质是( )A 、对角线相等B 、对角线互相平分C 、对角线互相垂直D 、对角线平分对角14、四边形ABCD 的对角线相交于点O ,能判定该四边形是正方形的题设是( )A 、AB =CD ,AB ∥CD ,AC =BD B 、AB =CD ,BC =ADC 、OA =OB =OC =OD ,AB =BC D 、AC =BD ,AC ⊥BD15、已知一个四边形ABCD 的边长分别为a 、b 、c 、d ,其中a 、c 为对边,且 满足条件bd ac d c b a 222222+=+++,则该四边形ABCD 的对角线( )A 、相等B 、相互平分C 、相互垂直D 、垂直且相等16、正方形的边长是2cm ,则它的一个顶点和另两边中点所构成三角形的面积为( )A 、21cm 2 B 、1cm 2 C 、23cm 2 D 、2cm 2 17、一个正方形的边长为4cm ,顺次连结它的各边中点所得的四边形的面积是( ) A 、4cm 2 B 、8cm 2 C 、12cm 2 D 、16cm 218、若顺次连结四边形ABCD 各边中点所得四边形是矩形,则四边形ABCD 必然是( )A 、菱形B 、对角线相互垂直的四边形C 、正方形D 、对角线相等的四边形19、以下图形中,是轴对称图形,但不是中心对称图形的是( )A 、平行四边形B 、矩形C 、菱形D 、等腰梯形20、如果矩形的四个内角的平分线能够围成一个四边形,那么这个四边形是( )A 、平行四边形B 、矩形C 、菱形D 、正方形四、解答题:(每小题10分,共60分)21、如图,E 、F 为平行四边形ABCD 对角线AC 延长线上的点,且AE =CF ,连结BF 、BE 、DF 、DE 。
2023中考数学专题复习——第七章 四边形

2023中考专题复习——第七章四边形时间:45分钟满分:80分一、选择题(每题4分,共32分)1.下列各组条件中,不能判断一个四边形是平行四边形的是() A.两组对边分别平行的四边形B.两组对角分别相等的四边形C.两条对角线互相平分的四边形D.一组对边平行另一组对边相等的四边形2.如图,在△ABC中,∠A=90°,点M,N分别为边AB和AC的中点,若AB =2,AC=4,则MN的长度为()A.2 3 B. 3 C.2 5 D. 5(第2题)(第3题)3.如图,在▱ABCD中,连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=()A.80°B.100°C.120°D.140°4.如图,四边形ABCD是菱形,其中A,B两点的坐标分别为A(0,3),B(4,0),则点D的坐标为()A.(0,1) B.(0,-1)C.(0,2) D.(0,-2)(第4题)(第5题)5.如图,在正方形ABCD的外侧作等边三角形CDE,连接AE,则∠DAE的度数是()A.15°B.20°C.12.5°D.10°6.如图,在矩形ABCD中,AB=4,BC=8,对角线AC,BD相交于点O,过点O作OE⊥AC交AD于点E,则DE的长是()A.3 B.5 C.2.4 D.2.5(第6题)(第7题)7.如图,在▱ABCD中,AB=BC=5,对角线BD=8,则▱ABCD的面积为() A.20 B.24 C.40 D.488.将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出()A.正方形纸片的面积B.四边形EFGH的面积C. △BEF的面积D. △AEH的面积(第8题)(第9题)二、填空题(每题4分,共16分)9.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有________条.10.在平面直角坐标系xOy中,已知点A(2,0),B(5,4),若四边形OABC是平行四边形,则▱OABC的周长等于________.11.如图,在Rt△ABC中,AC=3,BC=4,点D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E,F,则线段EF的最小值为________.(第11题)(第12题)12.如图,四边形ABCD是菱形,点E,F分别在边AB,AD上,且AE=DF,连接BF与DE相交于点G,已知AF=2DF,若FG =3,则GB=________.三、解答题(共32分)13.(8分)如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,且BE=DF,AF=CE.求证:四边形ABCD为平行四边形.(第13题)14.(24分)如图,已知在矩形ABCD中,点M,N分别是边AD,BC的中点,点P,Q分别是边BM,DN的中点.(1)求证:BM∥DN;(2)求证:四边形MPNQ是菱形;(3)当矩形ABCD的边AB与AD满足什么数量关系时,四边形MPNQ为正方形?请说明理由.3(第14题)答案一、1.D 2.D 3.C 4.D 5.A 6.A7.B8.C二、9.410.1411.12 512. 63点拨:如图,过点F作FP∥AB,交DE于点P,则△DFP∽△DAE.∵AF=2DF,∴FPAE=DFDA=13.∵四边形ABCD是菱形,∴AB=AD.∵AE=DF,∴BE=AF,∴BE=2AE,∴FPBE=FP2AE=16.∵FP∥AB,∴△FPG∽△BEG,∴GFGB=FPBE=16,∴GB=6GF=6 3.(第12题)三、13.证明:∵AF=CE,∴AF-EF=CE-EF,即AE=CF.∵BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°.∵BE=DF,∴△ABE≌△CDF.∴AB=CD,∠BAE=∠DCF.∴AB∥CD.∴四边形ABCD为平行四边形.14.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,AD=BC.∵点M,N分别为边AD,BC的中点,∴DM=BN,∴四边形DMBN是平行四边形.∴BM∥DN.(2)证明:由(1)可知四边形DMBN是平行四边形,∴BM=DN,BM∥DN.5∵点P,Q分别为边BM,DN的中点,∴MP=NQ.∴四边形MPNQ是平行四边形.如图,连接MN.(第14题)由(1)可知AD∥BC,AD=BC.∵点M,N分别为边AD,BC的中点,∴DM=CN,∴四边形DMNC是平行四边形.由题可知∠C=90°,∴四边形DMNC是矩形,∴∠DMN=∠C=90°.∵点Q是边DN的中点,∴MQ=NQ,∴四边形MPNQ是菱形.(3)解:当矩形ABCD的边AB与AD满足AB=12AD时,四边形MPNQ为正方形.理由:∵AB=12AD,点M是边AD的中点,∴AB=AM.易得矩形ABNM是正方形.∵P为正方形ABNM对角线BM的中点,∴∠NPM=90°.由(2)知四边形MPNQ是菱形,∴四边形MPNQ是正方形.。
初中数学四边形复习教案

初中数学四边形复习教案1. 知识与技能目标:使学生掌握四边形的定义和性质,能够识别和判断各种四边形,了解四边形在实际生活中的应用,提高学生的空间想象能力和抽象思维能力。
2. 过程与方法目标:通过观察、操作、猜想、验证等数学活动,培养学生的探究能力和合作能力,使学生在解决实际问题中能够灵活运用四边形的性质。
3. 情感、态度与价值观目标:学生在学习过程中能够积极参与,勇于尝试,体验数学学习的乐趣,增强自信心,培养克服困难的勇气和信心。
二、教学内容1. 四边形的定义和性质2. 四边形的分类和特点3. 四边形在实际生活中的应用三、教学重点与难点1. 教学重点:四边形的定义和性质,四边形的分类和特点。
2. 教学难点:四边形性质的探究和应用。
四、教学过程1. 导入新课通过展示一些生活中的四边形物体,如梯子、窗户、自行车等,引导学生关注四边形,激发学生学习四边形的兴趣。
然后提出问题:“你们知道四边形有哪些性质吗?”从而导入新课。
2. 探究四边形的性质(1)小组合作,观察探究将学生分成若干小组,每组发一些四边形的图片,让学生观察四边形的特点,探讨四边形的性质。
(2)汇报交流各小组汇报探究成果,教师引导学生总结四边形的性质,如对边相等、对角相等、对边平行等。
3. 四边形的分类和特点(1)长方形、正方形、梯形的定义和性质引导学生了解长方形、正方形、梯形是特殊的四边形,掌握它们的定义和性质。
(2)四边形的分类根据四边形的性质,引导学生对四边形进行分类,了解各种四边形的特点。
4. 四边形在实际生活中的应用通过一些实际问题,让学生运用四边形的性质解决问题,提高学生运用数学知识解决实际问题的能力。
5. 总结与反思本节课我们学习了四边形的定义、性质和分类,以及四边形在实际生活中的应用。
请大家回顾一下,我们是如何得出四边形的性质的?这个过程中,我们运用了哪些数学方法?通过这个问题,引导学生总结本节课的学习内容,提高学生的反思能力。
中考专题复习:中点四边形

3、连接对角线互相垂直的四边形四条边中点 得到的四边形是矩形
试一试
1、如图,四边形ABCD中,E,F,G,H分别是AB,
BC,CD,DA边上的中点,请你添加一个条件使四边
形EFGH是菱形,应添加的条件是
。
使四边形EFGH是矩形,应添加的条件是
四边形EFGH,四边形MNPQ的形状是( A )
A)矩形,菱形
B)菱形,矩形
C)矩形,矩形
D)矩形,正方形
4、如图,四边形ABCD中,AC=12,BD=8,面积 为40,点E、F、G、H分别是边AB、BC、CD、DA 中点,求:四边形 EFGH的周长是多少
D H A E
B
解:∵E、F分别是AB、BC中点
腰梯形中的哪一种,并写出证明过程。
A
DA
DA
D AQ D
F
B
E CB E
F CE B
M P
CE B N F
C F
小结:
本节课你学到了哪些知识?还有需要老师帮 你解决的难题吗?
D
D1
C3
C2
C1
B3 B2
C
A D2 O
D3
A1
A3
A2
B1
B
3、如图,在正方形ABCD中,点E,F分别是BC,CD的中点,AF,DE
相交于点G,则可得结论:
①AF=DE ②AF⊥DE(不须证明)
⑴如图②,若点E,F不是正方形ABCD的边BC,CD的中点,但满足
CE=DF则上面的结论①②是否仍然成立?(请直接回答“成立”
。
D
H A
G C
F E
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明:连接CD和BE,则HI=FG=BE,且 HI∥BE∥FG,GH=FI=CD,且 GH=FI=CD (三角形的中位线平行于底边且等于 D 底边的一半),在⊿ADE和⊿AB E中,AD=AB AC=AE,且∠DAB+∠BAC =∠EAC+∠BAC ,既∠DA I C=∠BAE ∴⊿DAE≌⊿BAE,由此得 ∠ADC=∠ABE,∴∠CDB+ ∠DBE=∠ADB+∠DBA= 90°,CD=BE既 FG=GH=HI=IF∴CD⊥BE, 既FG⊥GH,∴四边形FGHI是正方形
D E G
A
B
8.如图过正方形ABCD的A点 AM∥BD且DM=DB,求AM的长 解:设D坐标为(a,a)则直线BD为 y=x,AM为y=x+a,又设坐标M为 (x,y),MD 2=(x-a)2+(y-a)2=(xa)2+(x+a-a)2=2x2-2ax+a2=2a2 解得x=(1-√3) ÷2 M AM2=(0-x)2+(a-y)2 = (√6-√2)a/2
14.如果四边形两条AB与CD对边中点 的连线等于另两条对边AD与BC是和的 一半,试证此四边形是梯形
证明:作DH∥EF ,NH∥AB,则GF是 ∥ ⊿NDH和⊿DNC中位线,NC∥FG, 连接DE并延长CB与CB的延长线 交于I,则EG是⊿DIN的中位线, ∴EG∥NI,在⊿DAE和⊿IBE中, I AE=BE,DE=IE,∠D AE=∠IEB,∴⊿DAE ≌⊿IBE,∴∠DAE=∠I BE,∴DA∥IB,∴AD∥ BC,∴四边形ABCD是梯形, 此题得证。
A E D F C H
G N
B
15.如图所示,梯形ABCD的对角线AC、BD交于 O,⊿AOD的面积为S1,⊿BOC的面积为S2,求 证,梯形ABCD的面积S=(S1)1/2 + (S2) 1/2 证明:要证S= = (S1)1/2 +(S2) 1/2 ,只需证⊿A OB的面积+⊿COD面积等于2 (S1)1/2 ×(S2) 1/2 而⊿AOB面积+⊿COD面积=S -S1- S2=1/2(AD+BC)PQ—1/2AD h1-1/2BCh2=(ADh2+BC h1),因为 ⊿AOD∽⊿BOC∴AD×OQ=BD×OP,既AD h2=BCh1,既证,而⊿AOB面积+⊿COD面 积= 1/2(AD+BC)PQ—1/2ADh1-1 /2BCh2 = 1/2 (AD+BC)PQ—ADh P A 1-BCh2=(ADh2+BC h1)=BCh1,而 2 (S1)1/2 ×(S2) 1/2 =2×1/2(AD× OP) 1/2 O 1/2 =BCh1 (BC×OQ) Q B ∴⊿AOB面积+⊿COD面积= 2 (S1)1/2
D H E
FJ k I G
C
A
B
7.如图所示,在正方形ABCD中,E、 F分别是AD和CD的中点BF和CE交 于G,求证AG=AB
证明:设点A坐标为(0,0),B(2,0),C (2,2)直线BF为y=-2x+4,直线CE为 y=x/2+1由此得交点G坐标为(1.2,1.6)则 AG2=X2+Y2=(1.2)2+(1.6) 2=4∴AG=2=AB F C
A
D
B
C
9.如图过正方形ABCD的A点 AM∥BD且DM=DB,求AM的长
解:设AP=x,MP=y,由于AM∥BD, BD⊥AC,∴AM⊥AC, ∴⊿AMP是直角三角形,因此 ⊿AMP∽⊿ODP,∴AP/ OP=MP/DP, M ∴x/(√2/2-x)=y/(√2y),∴y=2x, 由于PD2= OP2+OD2 ∴(√2/2)2=(√2/2-x) 2+(√2-y)2∴x=√2/2-1/√6,由于 AM2=y2-x2=(2x)2-x2=3x2 ∴AM=√3(√2/2-1/√6)=(√6-√2)
C
A
E F
D
3.如图所示,在正方形ABCD中E为正方形CD 边的中点,F为EC的中点, 求证:∠DAE=1/2∠BAF 证明取BC的中点J连接AJ并延长且与DC 的延 长线交于G,则⊿ABJ≌⊿GCH,∠G=∠BAG, DE=3/4CD则AF=5/4CD而 FG=AF∠G=∠GAF,而 ∠DAE=∠BAH∴∠DAE=2∠BAF此题得证
D E F C G
H
A
B
4.如图,以⊿ABC的AB和AC边源自外 做正方形ABEF和ACGH,点I是BC 的中点, 求证:FH=2AI
F
J
H G
证明:延长AI至D,使DI=AI E 则四边形ABDC是平行四边形, 在 ⊿AFH和⊿BDA中, AF= AB,AH=AC= BD,∠FAH+∠BAC= 180°∠DBA+∠BAC=180° 所以∠FAH=∠ABD,因此 ⊿AFH≌⊿BDA,由此得证 FH=AD=2AI
A C I B D
5.如图 在平行四边形ABCD中 若AC2 ·BD2=AB4+AD4 求证∠DAB=45°
A
D
C
F E B
证明:设AB=a,AD=b,AC=p,BD=q则有 p2q2=a4+b4,又p2+q2=2(a4+b4)(定理126), 根据韦达定理得:x2-2(a2+b2)x+a4+b4=0 解得:x=a2+b2+√2ab(根下2乘以 ab),q2=a2+b2-√2ab,设 AE=b‘则q2=a2+b2-2ab’,由此得b=√2b‘既AD /AE=√2由此∠A=45°此题得证
E
11.如图,正方形ABCD中, ∠EAF=45°,那么EF和 BE+DF是否相等?请说明理 由.
证明:延长EB到G,使BG=DF,则 ⊿ABG≌⊿ADF由此可证⊿AGE≌⊿AEF则 EF=GB+BE=BE+DF
A D F
G
B
E
C
12.如图所示ABCD为矩形AP⊥BD,PM⊥BC, PN⊥CD求证PM2/3+PN2/3=BD2/3 证明:设∠ABD=θ,BD =a,在直角⊿ABD中, PM⊥BC, ∴∠BPM=∠ABD=θ,∴PM=PBcosθ 在直角⊿APB中PB=ABcosθ ∴PM=ABcos2θ,――(2)在直角⊿BAD中 A AB=BDcosθ,带入(2)中得: D PM=BDcos3θ=acos3θ,同理可得: P N 2θ=asin3θ PN=PDsinθ=ADsin B M C ∴PM2/3+PN2/3 =(acos3θ) 2/3 +(asin3θ) 2/3 = a 2/3 (sin2θ+cos2θ)= a2/3=BD2/3
平行 四边 形
①对边平行且相等 ②对角相等
③两条对角线互相平分
矩 形 菱 形
①对边平行且相等 ②四个角都是直角 ③对角线互相平分且相等 ①对边平行且四条边相等 ②对角相等 ③两条对角线互相垂直平
分且对角线平分对角
①有三个角是直角的四边形 ②是平行四边形且有一个角是直角 ③是平行四边形且两条对角线相等 ①四条边都相等 ②是平行四边形且有一组邻边相等 ③是平行四边形,且两条对角线互相垂
13.在正方形ABCD中过A作BD的平行线 AE且使BE=BD,求证DE=DF
证明:作垂线BG 与EA的延长线相交于G,∵E G∥BD∴AC⊥EG ∴∠BAG =ABG=45°∵AG=BG,由 于BE2=BD2= E 2AB2=4BG2∴EB=2BE A D ∴∠BEG=DBE=30° F ∴∠DFE=∠FEA+∠FAE G =45°+30°=75°, C ∠BED=(180°-30°) B =75°∴∠DEF=DFE=75° ∴DE=EF,此题得证
O E G B C
19.如图所示,在等腰梯形ABCD中,AD∥BC,对 角线AC和BD交于O,且∠BOC=60°点E、F、G 分别是 CD、OA、OB的中点,求证:⊿EFG是正三角形
直
转下页
二:特殊四边形的性质和判定
类别
正 方 形
性
质
判
定
①对边平行,四条边都相等 ②对角相等 ③两条对角线互相垂直平分
①是矩形,且有一组邻 边相等 ②是菱形,且一角是直 角
梯 形 等腰 梯形
①两底平行 ①有一组对边平行的四 边形是梯形 梯形的中位线平行两底且等于两 底和的一半 ①两底平行两腰相等 ②两条对角线相等 ③同底上的两角相等 ①是梯形,且两腰相等 ②是梯形,且同底上的 两底角相等
三:四 边 形 的 面 积
长为b,高为h,面 积为S 长为a,宽为b,面 积为S S=bh
平行四边形
S=ab
矩形
菱形 正方形 梯形
长对角线为L1,短对 S=1/2L1L2 角线为L2 面积为S
边长为a,面积为S S=a2 上底长为a,下底
S=1/2(a+b)h
1如图所示 ,以⊿ABC的AB和AC边为腰,向外作等腰 直角三角形ABD和ACE,取BC、CE、ED、DB的中点 F、G、H、I,求证四边形FGHI是正方形
D
C
16.在正方形ABCD中,CE∥BD, BE=BD,求证:DH=DE
证明:设BC=1,则BE=BD =( 2)1 /2 ,在⊿BCE中,BE/ sin135°=BC/sin∠BEC,既 ( 2)1/2 /sin135°= 1/ sin∠BEC A ∴sin∠BEC=1/2∴∠BEC =30° ∴∠DHE=(45+30)°=75°=∠D EH∴DE=DH,此得证题
6.如图所示,在正方形ABCD中,E、F分别是AD 和CD的中点BF和CE交于G,求证AI=AB
证明:作FI∥BC交CE于I, GJ⊥CD,GH与FI相较于K, BC=2ED =4FI,⊿FIG∽⊿ BCG, JG:FI=4:5,KI=FI﹣GJ=1 /4 BC ﹣ 1/4BC× 4/5= 1/20BC, KG= 1/10CD,HG= 1/2BC+ 1/10BC= 3/5BC, AH= 1/2BC + 1/4 BC+ 1/20BC=4/5BC ,所以 AI2=(4/5BC)2+( 3/5BC)2 AI=BC此题得证,
