16-17工科数学分析第一学期期末试题

合集下载

高三数学上学期期末考试试题理5

2016-2017学年度高三级第一学期期末试题（卷）数学（理科）一、选择题（本大题共12小题，每小题分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项填在试卷的答题卡中） 1 •已知集合A = {123},B = {xl ，＜9},则AcB = （） A. （-2,-1,0,123}B ・{ 一2,-1,0,1,2}C. {1,2}D. {123}2_i2 •复数z =— 在复平而上对应的点位于（）1 + z 扎第一象限B.第二象限C.第三象限D.第四象限3.用数字1, 2, 3, 4, 5组成没有重复数字的五位数，英中奇数的个数为（）A. 72B. 60C. 48D. 244. 钝角三角形ABC 的而积是丄，AB=1, BC=V2,则AC=（）2 A. 5B. y/sC r . r 2 D. 15•设a. 〃是实数，则“a ＞方”是"a 2＞ b 2 99的（）6. 圆（对1） 2+?=2的圆心到直线产对3的距离为（）扎 1B.2C. y/2D. 2 血7. 右图中的三个直角三角形是一个体积为2Qcm 3几何体的三视图，则/? = （） A. 4B. 5C. 6- D. 38•函数严竺空的图彖是（）A.充分而不必要条件 C.充分必要条件B.必要而不必要条件D.既不充分也不必要条件1x1文档从网络中收集，已重新整理排版.word 版本可编借•欢迎下载支持.x9•已知双曲线--4=1（b 〉0）,以原点为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条4 少渐近线相交于月，B, G Q 四点，四边形如?的而积为2b,则双曲线的方程为（）■厂 3）广t 戸& 4）厂’厂x ・〉广（“对 y" tA. —一^二1B. —-^―=1C. —- —=1D. —=14 44 34 44 1210. 已知函数f （x ） = sin2竺+丄sins:-丄（血>0）, xeR.若/（x ）在区间3,2龙）内没有零点，2 2 2 则e 的取值范围是（）A. （0,1]B. （0,；]U[：|]C. （0,|]D. （01]U[j,l ）8 8 4 8 8 4 8一 — -一 -— f -* 1 711. 已知向軽，b 是两个互相垂直的单位向量，且cy = cb = \，则对任意的正实数7, c + ta + -b 的最小值是（）A. 2^2B. 2C. 4近D. 412. 设函数/（X ）在7?上的导函数为/（X ）,且2f （x ） + xf （x ）>x\下而的不等式在/?上恒成立的是（）A ・ /（x ） > 0B ・ f （x ） <0C ・ f （x ）>xD ・ f （x ） < x 二、填空题：（本大题共4小题，每小题5分，共20分）.13. （x 2-!）8的展开式中中的系数为 _____________ ・（用数字作答）X<2914.若满足<兀一），+ 1»0,则z = 2x + y的最大值x+y-2>0,为 _________15.右边程序框图的算法思路源于我国古代数学需著《九章算术》中的“更相减损术” •执行该程序框图，若输入的“，方分别为14, 20.则输岀的"= ___________ •16.在AABC中，内角A,B,C的对边分别为a、b、c,已知a = Z?cos C + csin B, b=2,则AABC而积的最大值为 _______ •三、解答题：（本大题共5小题，共70分，解答应写出文字说明，证明过程或演第步骤.）17.（本小题满分12分）已知在递增等差数列｛©｝中，少=2, $是勺和坷的等比中项.（1）求数列｛色｝的通项公式；（2）若仇= 一，S“为数列｛仇｝的前"项和，是否存在实数川，使得< m ,对于任意的7?e/V*恒成立？若存在，请求实数川的取值范囤，若不存在，试说明理由.18.（本小题满分12分）某中•学高一年级共8个班，现从髙一年级选10名同学组成社区服务小组，其中高一（1）班选取3 名同学，其它各班各选取1划同学.现从这10名同学中随机选取3名同学，到社区老年中心参加“尊老爱老”活动（每位同学被选到的可能性相同）.（I）求选出的3爼同学来自不同班级的概率；（II）设X为选岀同学中髙一（1）班同学的人数，求随机变量X的分布列和数学期望・19.（本小题满分12分）在四棱锥P-ABCD中，平而P4Q丄平而ABCD,为等边三角形,AB = AD = -CD. AB 丄ABH CD、点M 是PC 的中点・2（I）求证：M8〃平而PAD；（II）求二而角P-BC-D的余弦值20.（本小题满分12分）已知椭圆G W+首=l（a>b>0）的一个顶点为月（2,0）,离心率为半，直线尸血一1）与椭圆C交于5 b Z不同的两点M挖（I）求椭圆Q的方程；⑵当△AKV的而积为零时，求&的值.21.（本小题满分12分）已知函数/（x） = In x - .（I ）若m = 2,求曲线y = f（x）在（1,/（1））处的切线方程;（II）若/（x） + m<0在"（0,+s）上恒成立,求实数加的值.请考生在［22］、［23］题中任逸一题作答。

工科数学分析试卷+答案

工科数学分析试题卷及答案考试形式（闭卷）：闭答题时间：150 （分钟）本卷面成绩占课程成绩 80 %一、填空题（每题2分，共20分）1．---→xx x x sin 11lim 30 3-2．若⎪⎩⎪⎨⎧=≠-+=0,0,13sin )(2x a x xe x xf ax 在0=x 处连续，则a 3- 3．设01lim 23=⎪⎪⎭⎫⎝⎛--++∞→b ax x x x ，则 =a 1 ， =b 0 4．用《δε-》语言叙述函数极限R U ⊂∈=→)(,)(lim 0x x A x f x x 的定义： εδδε)()()(:000A x f x x ∈→∈∀>∍>∀U 5．若当)1(,023+++-→cx bx ax e x x是3x 的高阶无穷小，则=a61=b21=c 1 6．设N ∈=--→n x x x f x f nx x ,1)()()(lim2000，则在0x x =处函数)(x f 取得何种极值？答：极小值姓名: 班级：学号：遵守考试纪律注意行为规范7．设x x y +=，则dydx x)211(+⋅8．设x x y sin =，则=dy dx xxx x xx)sin ln (cos sin +9．⎰=+dx x x 21arctan C x +2arctan 21 10．⎰=+dx ee xx12 C e e x x ++-)1l n ( 二、选择题：（每题2分，共20分）1．设0,2)1()1l n (2s i n2t a n li m 2222≠+=-+-+-→c a e d x c xb x a x x ，则必有（ D ）（A ）d b 4=；（B ）c a 4-=；（C ）d b 4-=；（D ）c a 2-= 2．设9320:0<<>k x ，则方程112=+x kx 的根的个数为（ B ）（A ）1 ；（B ） 2 ；（C ） 3 ；（D ）03．设)(x f 连续，且0)0(>'f ，则存在0>δ使得（ A ）（A ）)(x f 在),0(δ内单增；（B ）对),0(δ∈∀x 有)0()(f x f >；（C ）对)0,(δ-∈∀有)0()(f x f >；（D ）)(x f 在)0,(δ-内单减。

重庆市2016—2017学年高一上学期期末数学试卷 Word版含解析

重庆市2016—2017学年年高一上学期期末数学试卷一.选择题.（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．（5分）设集合A={x|x+2=0}，集合B={x|x2﹣4=0}，则A∩B=（）A．{﹣2} B．{2} C．{﹣2，2} D．∅2．（5分）已知函数f（x）为奇函数，且当x＞0时，，则f（﹣1）=（）A．﹣2 B．0 C．1 D．2 3．（5分）已知α是第四象限的角，若cosα=，则tanα=（）A．B．﹣C．D．﹣4．（5分）如图，在正六边形ABCDEF中，++等于（）A．0 B．C．D．5．（5分）函数f（x）=3x+x﹣3在区间（0，1）内的零点个数是（）A．3 B．2 C．1 D．0 6．（5分）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜）的部分图象如图所示，则f（x）的解析式是（）A．f（x）=2sin（2x+）B．f（x）=2sin（x+）C．f（x）=2sin（2x+）D．f（x）=2sin（x+）7．（5分）下列函数中，既是偶函数，又在区间（1，2）内是增函数的为（）A．y=cosx B．y=ln|x| C．y=D．y=tan2x8．（5分）设a=tan35°，b=cos55°，c=sin23°，则（）A．a＞b＞c B．b＞c＞a C．c＞b＞a D．c＞a＞b9．（5分）定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈B．C．D．二.填空题.（本大题共5小题，每小题5分，共25分.）11．（5分）tan=．12．（5分）如图所示，平行四边形ABCD的对角线AC与BD相交于点O，点M是线段OD的中点，设=，=，则=．（结果用，表示）13．（5分）（lg25﹣lg）÷100=．14．（5分）求值：=．15．（5分）设g（x）=x﹣1，已知f（x）=，若关于x的方程f（x）=m恰有三个互不相等的实根x1，x2，x3，则x12+x22+x32的取值范围是．三.解答题.（本大题共6小题，共75分.解答须写出文字说明、证明过程和演算步骤.）16．（13分）已知＜α＜π，tanα﹣=﹣．（Ⅰ）求tana的值；（Ⅱ）求的值．17．（13分）平面内给定三个向量=（3，2），=（﹣1，2），=（4，1）．（Ⅰ）设向量=+，且||=，求向量的坐标；（Ⅱ）若（+k）∥（2﹣），求实数k的值．18．（13分）已知函数f（x）=a x（a＞0，a≠1）在区间上的最大值是最小值的8倍．（Ⅰ）求a的值；（Ⅱ）当a＞1时，解不等式log a（2a+2x）＜log a（x2+1）．19．（12分）已知函数g（x）=4sin（ωx+），h（x）=cos（ωx+π）（ω＞0）．（Ⅰ）当ω=2时，把y=g（x）的图象向右平移个单位得到函数y=p（x）的图象，求函数y=p（x）的图象的对称中心坐标；（Ⅱ）设f（x）=g（x）h（x），若f（x）的图象与直线y=2﹣的相邻两个交点之间的距离为π，求ω的值，并求函数f（x）的单调递增区间．20．（12分）已知函数f（x）=log2（4x+1）+mx．（Ⅰ）若f（x）是偶函数，求实数m的值；（Ⅱ）当m＞0时，关于x的方程f（8（log4x）2+2log2+﹣4）=1在区间上恰有两个不同的实数解，求m的范围．21．（12分）已知定义在（﹣∞，﹣1）∪（1，+∞）函数满足：①f（4）=1；②对任意x ＞2均有f（x）＞0；③对任意x＞1，y＞1，均有f（x）+f（y）=f（xy﹣x﹣y+2）．（Ⅰ）求f（2）的值；（Ⅱ）证明：f（x）在（1，+∞）上为增函数；（Ⅲ）是否存在实数k，使得f（sin2θ﹣（k﹣4）（sinθ+cosθ）+k）＜2对任意的θ∈恒成立？若存在，求出k的范围；若不存在说明理由．重庆市2016—2017学年年高一上学期期末数学试卷参考答案与试题解析一.选择题.（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．（5分）设集合A={x|x+2=0}，集合B={x|x2﹣4=0}，则A∩B=（）A．{﹣2} B．{2} C．{﹣2，2} D．∅考点：交集及其运算．专题：计算题．分析：分别求出两集合中方程的解，确定出A与B，找出A与B的公共元素即可求出交集．解答：解：由A中的方程x+2=0，解得x=﹣2，即A={﹣2}；由B中的方程x2﹣4=0，解得x=2或﹣2，即B={﹣2，2}，则A∩B={﹣2}．故选A点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．（5分）已知函数f（x）为奇函数，且当x＞0时，，则f（﹣1）=（）A．﹣2 B．0 C．1 D．2考点：函数的值．专题：函数的性质及应用．分析：利用奇函数的性质，f（﹣1）=﹣f（1），即可求得答案．解答：解：∵函数f（x）为奇函数，x＞0时，f（x）=x2+，∴f（﹣1）=﹣f（1）=﹣2，故选A．点评：本题考查奇函数的性质，考查函数的求值，属于基础题．3．（5分）已知α是第四象限的角，若cosα=，则tanα=（）A．B．﹣C．D．﹣考点：同角三角函数基本关系的运用．专题：三角函数的求值．分析：由α为第四象限角，以及cosα的值，利用同角三角函数间的基本关系求出s inα的值，即可确定出tanα的值．解答：解：∵α是第四象限的角，若cosα=，∴sinα=﹣=﹣，则tanα==﹣，故选：D．点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．4．（5分）如图，在正六边形ABCDEF中，++等于（）A．0 B．C．D．考点：向量的加法及其几何意义．专题：平面向量及应用．分析：利用正六边形ABCDEF的性质，对边平行且相等得到向量相等或者相反，得到所求为0向量．解答：解：因为正六边形ABCDEF中，CD∥AF，CD=AF，所以++=++=；故选A．点评：本题考查了向量相等以及向量加法的三角形法则，属于基础题．5．（5分）函数f（x）=3x+x﹣3在区间（0，1）内的零点个数是（）A．3 B．2 C．1 D．0考点：函数零点的判定定理．专题：计算题；函数的性质及应用．分析：函数f（x）=3x+x﹣3在区间（0，1）上连续且单调递增，利用函数零点的判定定理求解即可．解答：解：函数f（x）=3x+x﹣3在区间（0，1）上连续且单调递增，又∵f（0）=1+0﹣3=﹣2＜0，f（1）=3+1﹣3=1＞0；∴f（0）•f（1）＜0；故函数f（x）=3x+x﹣3在区间（0，1）内有一个零点，故选C．点评：本题考查了函数零点的判定定理的应用及函数的单调性的应用，属于基础题．6．（5分）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜）的部分图象如图所示，则f（x）的解析式是（）A．f（x）=2sin（2x+）B．f（x）=2sin（x+）C．f（x）=2sin（2x+）D．f（x）=2sin（x+）考点：正弦函数的图象．专题：三角函数的图像与性质．分析：根据图象确定A，ω和φ的值即可求函数的解析式解答：解：由图象知函数的最大值为2，即A=2，函数的周期T=4（）=2，解得ω=1，即f（x）=2sin（x+φ），由五点对应法知+φ=π，解得φ=，故f（x）=2sin（x+），故选：B点评：本题主要考查函数解析式的求解，根据条件确定A，ω和φ的值是解决本题的关键．要要求熟练掌握五点对应法．7．（5分）下列函数中，既是偶函数，又在区间（1，2）内是增函数的为（）A．y=cosx B．y=ln|x| C．y=D．y=tan2x考点：函数单调性的判断与证明；函数奇偶性的判断．专题：函数的性质及应用．分析：根据余弦函数的单调性，对数函数的单调性，偶函数、奇函数的定义即可判断每个选项的正误．解答：解：A．y=cosx在（1，2）是减函数，所以A错误；B．显然y=ln|x|是偶函数，且在（1，2）内是增函数，所以B正确；C．显然函数是奇函数，所以该选项错误；D．tan﹣2x=﹣tan2x，所以该函数是奇函数，所以该选项错误．故选B．点评：考查余弦函数的单调性，对数函数的单调性，以及奇函数、偶函数的定义．8．（5分）设a=tan35°，b=cos55°，c=sin23°，则（）A．a＞b＞c B．b＞c＞a C．c＞b＞a D．c＞a＞b考点：正弦函数的图象．专题：三角函数的求值．分析：利用三角函数的诱导公式结合三角函数的单调性即可得到结论．解答：解：由诱导公式可得b=cos55°=cos（90°﹣35°）=sin35°，由正弦函数的单调性可知sin35°＞sin23°，即b＞c，而a=tan35°=＞sin35°=b，∴a＞b＞c，故选：A点评：本题考查三角函数值大小的比较，涉及诱导公式和三角函数的单调性，属基础题．9．（5分）定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈B． C．D．考点：函数的值域．专题：函数的性质及应用．分析：化简得出令=m，则1+sinx=2m﹣mcosx，sinx+mcosx=2m﹣1，φ）=2m﹣1得sin（x+φ）=，由≤1，解得0，利用函数性质求解f（m）=单增，解答：解：f（x）==﹣==﹣=令=m，则1+sinx=2m﹣mcosx，sinx+mcosx=2m﹣1，φ）=2m﹣1得sin（x+φ）=，由≤1，解得0，f（m）=单增，值域为点评：本题考察了函数的性质，换元法求解问题，属于难题，计算量较大．二.填空题.（本大题共5小题，每小题5分，共25分.）11．（5分）tan=﹣．考点：运用诱导公式化简求值．专题：三角函数的求值．分析：原式中的角度变形后，利用诱导公式及特殊角的三角函数值计算即可得到结果．解答：解：tan=tan（π﹣）=﹣tan=﹣．故答案为：﹣点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．12．（5分）如图所示，平行四边形ABCD的对角线AC与BD相交于点O，点M是线段OD的中点，设=，=，则=．（结果用，表示）考点：向量的三角形法则．专题：平面向量及应用．分析：利用向量的三角形法则、向量共线定理可得+==，即可得出．解答：解：+===．故答案为：．点评：本题考查了向量的三角形法则、向量共线定理，属于基础题．13．（5分）（lg25﹣lg）÷100=20．考点：有理数指数幂的化简求值．专题：函数的性质及应用．分析：根据对数的运算法则和有理数的公式进行化简即可．解答：解：（lg25﹣lg）÷100=（lg100）×=2×10=20，故答案为：20．点评：本题主要考查有理数的化简，比较基础．14．（5分）求值：=1．考点：三角函数的恒等变换及化简求值．专题：计算题．分析：先把原式中切转化成弦，利用两角和公式和整理后，运用诱导公式和二倍角公式化简整理求得答案．解答：解：原式=sin50°•=cos40°===1故答案为：1点评：本题主要考查了三角函数的恒等变换及其化简求值，以及两角和公式，诱导公式和二倍角公式的化简求值．考查了学生对三角函数基础知识的综合运用．15．（5分）设g（x）=x﹣1，已知f（x）=，若关于x的方程f（x）=m恰有三个互不相等的实根x1，x2，x3，则x12+x22+x32的取值范围是（，1）．考点：根的存在性及根的个数判断；分段函数的应用．专题：计算题；作图题；函数的性质及应用．分析：化简f（x）=，从而作出其图象，结合图象可得0＜m＜，从而分别讨论x1，x2，x3，再令y=x12+x22+x32=+1﹣2m，化简并利用换元法求取值范围即可．解答：解：∵g（x）=x﹣1，f（x）=，f（x）=；即f（x）=；作出其图象如下，若方程f（x）=m有三个根，则0＜m＜，且当x＞0时，方程可化为﹣x2+x﹣m=0，易知，x2+x3=1，x2x3=m；当x≤0时，方程可化为x2﹣x﹣m=0，可解得x1=；记y=x12+x22+x32=+1﹣2m=﹣m﹣+；令t=∈（1，），则y=﹣t2﹣t+，解得，y∈（，1）．故答案为：（，1）．点评：本题考查了分段函数的应用及数形结合的思想应用，同时考查了换元法的应用及方程的根与函数的图象的交点的关系应用，属于中档题．三.解答题.（本大题共6小题，共75分.解答须写出文字说明、证明过程和演算步骤.）16．（13分）已知＜α＜π，tanα﹣=﹣．（Ⅰ）求tana的值；（Ⅱ）求的值．考点：同角三角函数基本关系的运用；运用诱导公式化简求值．专题：三角函数的求值．分析：（Ⅰ）设tanα=x，已知等式变形后求出方程的解确定出x的值，即可求出tana 的值；（Ⅱ）原式利用诱导公式化简，再利用同角三角函数间基本关系变形，将tanα的值代入计算即可求出值．解答：解：（Ⅰ）令tanα=x，则x﹣=﹣，即2x2+3x﹣2=0，解得：x=或x=﹣2，∵＜α＜π，∴tanα＜0，则tanα=﹣2；（Ⅱ）原式==tanα+1=﹣2+1=﹣1．点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．17．（13分）平面内给定三个向量=（3，2），=（﹣1，2），=（4，1）．（Ⅰ）设向量=+，且||=，求向量的坐标；（Ⅱ）若（+k）∥（2﹣），求实数k的值．考点：平面向量共线（平行）的坐标表示；平面向量的坐标运算．专题：平面向量及应用．分析：（Ⅰ）根据向量的坐标运算以及模长公式，求出λ的值即可；（Ⅱ）根据向量平行的坐标表示，列出方程，即可求出k的值．解答：解：（Ⅰ）∵向量=（3，2），=（﹣1，2），∴=+=（，）+（﹣，）=（λ，3λ）；又||=，∴=，解得λ=±1，∴=（1，3）或=（﹣1，﹣3）；（Ⅱ）∵+k=（3，2）+k（4，1）=（3+4k，2+k），2﹣=2（﹣1，2）﹣（3，2）=（﹣5，2）；且（+k）∥（2﹣），∴2×（3+4k）﹣（﹣5）×（2+k）=0，解得k=﹣．点评：本题考查了平面向量的坐标运算问题，也考查了向量平行与求向量模长的问题，是基础题目．18．（13分）已知函数f（x）=a x（a＞0，a≠1）在区间上的最大值是最小值的8倍．（Ⅰ）求a的值；（Ⅱ）当a＞1时，解不等式log a（2a+2x）＜log a（x2+1）．考点：指数函数的图像与性质．专题：函数的性质及应用．分析：（Ⅰ）分类讨论当a＞1时，当0＜a＜1时，求出最大值，最小值，即可求解答案．（Ⅱ）转化log2（4+2x）＜log2（x2+1）得出得出不等式组，求解即可解答：解：f（x）max=a2，f（x）min=a﹣1，则=a2=8，解得a=2；当0＜a＜1时，f（x）=max=a﹣1，f（x）min=a2，则=a﹣3=8，解得a=；故a=2或a=（Ⅱ）当a＞1时，由前知a=2，不等式log a（2a+2x）＜log a（x2+1）即得解集为（﹣2，﹣1）∪（3，+∞）．点评：本题考察了指数函数的性质，分类讨论的思想，属于中档题，关键是分类得出方程，不等式组．19．（12分）已知函数g（x）=4sin（ωx+），h（x）=cos（ωx+π）（ω＞0）．（Ⅰ）当ω=2时，把y=g（x）的图象向右平移个单位得到函数y=p（x）的图象，求函数y=p（x）的图象的对称中心坐标；（Ⅱ）设f（x）=g（x）h（x），若f（x）的图象与直线y=2﹣的相邻两个交点之间的距离为π，求ω的值，并求函数f（x）的单调递增区间．考点：函数y=Asin（ωx+φ）的图象变换；正弦函数的图象；余弦函数的图象．专题：三角函数的求值；三角函数的图像与性质．分析：（Ⅰ）由题意，先求得：p（x）=4sin（2x+），令2x+=kπ，即可求得函数y=p（x）的图象的对称中心坐标；（Ⅱ）先求得解析式f（x）=2sin（2ωx﹣）﹣，由题意T=π，可解得ω的值，令t=2x﹣是x的增函数，则需y=2sint﹣是t的增函数，由2k≤2x﹣≤2k，可解得函数f（x）的单增区间．解答：解：（Ⅰ）当ω=2时，g（x）=4sin（2x+），g（x﹣）=4sin（2x﹣+）=4sin（2x+），p（x）=4sin（2x+），令2x+=kπ，得x=﹣+，中心为（﹣+，0）（k∈Z）；（Ⅱ）f（x）=4sin（ωx+）（﹣cosωx）=﹣4cosωx=2sinωxcosωx﹣2cos2ωx=sin2ωx﹣（1+cos2ωx）=2sin（2ωx﹣）﹣由题意，T=π，∴=π，ω=1令t=2x﹣是x的增函数，则需y=2sint﹣是t的增函数故2k≤2x﹣≤2k，2k≤2x≤2kπ+，k≤x≤kπ+函数f（x）的单增区间是（k∈Z）．点评：本题主要考查了函数y=Asin（ωx+φ）的图象变换，三角函数的图象和性质，属于基础题．20．（12分）已知函数f（x）=log2（4x+1）+mx．（Ⅰ）若f（x）是偶函数，求实数m的值；（Ⅱ）当m＞0时，关于x的方程f（8（log4x）2+2log2+﹣4）=1在区间上恰有两个不同的实数解，求m的范围．考点：对数函数的图像与性质；指数函数综合题．专题：函数的性质及应用．分析：（Ⅰ）根据f（x）是偶函数，建立方程关系即可求实数m的值；（Ⅱ）利用对数函数的性质，利用换元法，转化为两个函数的交点问题即可得到结论．解答：解：（Ⅰ）若f（x）是偶函数，则有f（﹣x）=f（x）恒成立，即：log2（4﹣x+1）﹣mx=log2（4x+1）+mx．于是2mx=log2（4﹣x+1）﹣log2（4x+1）=log2（）﹣log2（4x+1）=﹣2x，即是2mx=﹣2x对x∈R恒成立，故m=﹣1．（Ⅱ）当m＞0时，y=log2（4x+1），在R上单增，y=mx在R上也单增所以f（x）=log2（4x+1）+mx在R上单增，且f（0）=1，则f（8（log4x）2+2log2+﹣4）=1可化为f（8（log4x）2+2log2+﹣4）=f（0），又f（x）单增，得8（log4x）2+2log2+﹣4=0，换底得8（）2﹣2log2x+﹣4=0，即2（log2x）2﹣2log2x+﹣4=0，令t=log2x，则t∈，问题转换化为2t2﹣2t+﹣4=0在t∈，有两解，即=﹣2t2+2t+4，令y=﹣2t2+2t+4，则y=﹣2t2+2t+4=﹣2（t﹣）2+，∴当t=时，函数取得最大值，当t=0时，函数y=4，当t=时，函数取得最小值，若方程f（8（log4x）2+2log2+﹣4）=1在区间上恰有两个不同的实数解，则等价为4≤＜，解得＜m≤1，故求m的范围为＜m≤1．点评：本题主要考查函数奇偶性的应用，以及对数函数的应用，利用方程和函数之间的关系，转化为两个函数的交点问题是解决本题的关键．21．（12分）已知定义在（﹣∞，﹣1）∪（1，+∞）函数满足：①f（4）=1；②对任意x ＞2均有f（x）＞0；③对任意x＞1，y＞1，均有f（x）+f（y）=f（xy﹣x﹣y+2）．（Ⅰ）求f（2）的值；（Ⅱ）证明：f（x）在（1，+∞）上为增函数；（Ⅲ）是否存在实数k，使得f（sin2θ﹣（k﹣4）（sinθ+cosθ）+k）＜2对任意的θ∈恒成立？若存在，求出k的范围；若不存在说明理由．考点：函数恒成立问题；抽象函数及其应用．专题：函数的性质及应用；三角函数的图像与性质．分析：（Ⅰ）将条件③变形得到f（m+1）+f（n+1）=f（mn+1）对任意m，n＞0均成立，其中m=x﹣1，n=y﹣1，令m=n=1，即可解得f（2）=0；（Ⅱ）由（Ⅰ），将f（m+1）+f（n+1）=f（mn+1）变形得f（mn+1）﹣f（n+1）=f（m+1），则要证明f（x）在（1，+∞）上为增函数，只需m＞1即可．显然当m＞1即m+1＞2时f（m+1）＞0；（Ⅲ）利用条件①②将问题转化为是否存在实数k使得sin2θ﹣（k﹣4）（sinθ+cosθ）+k＜或1＜sin2θ﹣（k﹣4）（sinθ+cosθ）+k＜10对任意的θ∈恒成立．再令t=sinθ+cosθ，，则问题等价于t2﹣（k﹣4）t+k﹣1＜或1＜t2﹣（k﹣4）t+k﹣1＜10对恒成立．分情况讨论，利用二次函数的性质即可解题．解答：解：（Ⅰ）由条件③可知f（x）+f（y）=f（xy﹣x﹣y+2）=f=f，令m=x﹣1，n=y﹣1，则由x＞1，y＞1知m，n＞0，并且f（m+1）+f（n+1）=f（mn+1）对任意m，n＞0均成立．令m=n=1，即有f（2）+f（2）=f（2），故得f（2）=0．（Ⅱ）由（Ⅰ），将f（m+1）+f（n+1）=f（mn+1）变形得：f（mn+1）﹣f（n+1）=f（m+1），要证明f（x）在（1，+∞）上为增函数，只需m＞1即可．设x2=mn+1，x1=n+1，其中m，n＞0，m＞1，则x2﹣x1=n（m﹣1）＞0，故x2＞x1，则f（x2）﹣f（x1）=f（mn+1）﹣f（n+1）=f（m+1），m＞1，m+1＞2，所以f（m+1）＞0，即f（x2）﹣f（x1）＞0，所以f（x2）＞f（x1），即f（x）在（1，+∞）上为增函数；（Ⅲ）∵由f（m+1）+f（n+1）=f（mn+1）对任意m，n＞0均成立，及f（4）=1∴令m=n=3，有f（4）+f（4）=f（10），即f（10）=2．令m=9，n=，则f（9+1）+f（+1）=f（9×+1）=f（2），故f（）=f（2）﹣f（10）=﹣2，由奇偶性得f（﹣）=﹣2，则f（x）＜2的解集是．于是问题等价于是否存在实数k使得sin2θ﹣（k﹣4）（sinθ+cosθ）+k＜或1＜sin2θ﹣（k﹣4）（sinθ+cosθ）+k＜10对任意的θ∈恒成立．令t=sinθ+cosθ，，问题等价于t2﹣（k﹣4）t+k﹣1＜或1＜t2﹣（k﹣4）t+k﹣1＜10对恒成立．令g（t）=t2﹣（k﹣4）t+k﹣1，则g（t）对恒成立的必要条件是，即解得，此时无解；同理1＜g（t）＜10恒成立的必要条件是，即解得，即；当时，g（t）=t2﹣（k﹣4）t+k﹣1的对称轴．下面分两种情况讨论：（1）当时，对称轴在区间的右侧，此时g（t）=t2﹣（k﹣4）t+k﹣1在区间上单调递减，1＜g（t）＜10恒成立等价于恒成立，故当时，1＜g（t）＜10恒成立；（2）当时，对称轴在区间内，此时g（t）=t2﹣（k﹣4）t+k﹣1在区间上先单调递减后单调递增，1＜g（t）＜10恒成立还需，即，化简为k2﹣12k+24＜0，解得，从而，解得；综上所述，存在，使得f（sin2θ﹣（k﹣4）（sinθ+cosθ）+k）＜2对任意的θ∈恒成立．点评：本题考查了抽象函数的运算，单调性，以及函数恒成立问题，需要较强的分析、计算能力，属于难题．。

20162017学第一学期期末质量检测

绝密★启用前2016—2017学年度第一学期期末质量检测高三数学（理科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分全卷满分150分，考试时间120分钟。

注意：1. 考生在答题前，请务必将自己的姓名、准考证号等信息填在答题卡上．2. 选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，答在试卷上无效。

3. 填空题和解答题用毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内。

答在试题卷上无效。

第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

把答案填在答题卡上对应题号后的框内，答在试卷上无效。

1．已知集合2{|230}A x x x =--≥，{|22}B x x =-≤≤，则A B =IA ． [-2，-1]B ．[-1，2]C ．[-1，1]D ．[1，2]2. 设i 为虚数单位，z 表示复数z 的共轭复数，若1i z =+，则i i z z -+g g 等于A ．-2B ．-2iC ．2D ．2i3．定义在R 上的偶函数()f x 满足：对于任意的12,(,0]x x ∈-∞12()x x ≠，有2121()[()()]0x x f x f x -->，则当n *∈N 时，有A ．()(1)(1)f n f n f n -<-<+B ．(1)()(1)f n f n f n -<-<+C ．(1)()(1)f n f n f n +<-<-D ．(1)(1)()f n f n f n +<-<-试卷类型：A4．已知F为双曲线22:1(0)33x yCaa-=>的一个焦点，则点F到C的一条渐近线的距离为A．3B．3 C．3a D．3a5．高考后，4位考生各自在甲、乙两所大学中任选一所参观，则甲、乙两所大学都有考生参观的概率为A．18B．38C．58D．786．已知图甲是函数()y f x=的图象，图乙由图甲变换所得，则图乙中的图象对应的函数可能是A．(||)y f x=B．|()|y f x=C．(||)y f x=-D．(||)y f x=--7．如图所示，程序框图（算法流程图）的输出结果是A．34 B．55C．78 D．898．已知1tan()42πα+=，且02πα-<<，则22sin sin2cos()4ααπα+-等于A．25B．35C．310D259．若实数x，y满足不等式组33023010x yx yx my+-≥⎧⎪--≤⎨⎪-+≥⎩，且x y+的最大值为9，则实数m等于A．-2 B．-1 C．1 D．210．已知直线1:4360l x y-+=和直线2:1l x=-，抛物线24y x=上一点P到直线12l l和的距离之和的最小值是A35B．2 C．115D．311．一只蚂蚁从正方体1111ABCD A B C D-的顶点A处出发，经过正方体的表面，按最短路线爬行到达顶点1C 的位置，则下列图中可以表示正方体及蚂蚁最短爬行路线的正视图是A ．①②B ．①③C ．②④D ．③④12．定义在(0,)2π上的函数()f x ，()f x '是它的导函数，且恒有()tan ()0f x x f x '+<g成立，则 A ．2()()34f f ππ>B ．3()2()46f f ππ>C ．()3()36f f ππ>D ．3()()36f f ππ<第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分。

高等数学上试题与标准答案分析.doc

精品文档华南农业大学期末考试试卷（A 卷）2016~2017学年第 1 学期考试科目：高等数学 A Ⅰ考试类型：（闭卷）考试考试时间：120 分钟学号姓名年级专业题号一二三四总分得分评阅人得分一、填空题（本大题共 5小题，每小题 3分，共 15分）1．函数 yln1x 1 x 2 的定义域是。

1 x2．设 y arcsin x ，则 dy = 。

3． lim(xa ) x。

xx a4．不定积分e xdx =。

e 2x15．反常积分1dx = 。

1x(x 1)得分二、单项选择题（本大题共 5小题，每小题 3分，共 15分）sin 1, x1．设 f (x)x，那么 lim f ( x) 不存在的原因是（）x sin 1,xx 0xA ． f (0) 无定义B． lim f (x) 不存在x 0C ． lim f ( x) 不存在D ． lim f ( x) 和 lim f (x) 都存在但不相等x 0x 0x 02．设偶函数 f ( x) 二阶可导，且 f ''(0)0 ，那么 x 0（）.精品文档A ．不是 f ( x) 的驻点B．是 f (x) 的不可导点C ．是 f ( x) 的极小值点D．是 f (x) 的极大值点3．设 (x) x 2 sin t2dt ，则 '( x)（）A ． 2xsin x 4B． 2x sin x 2C． 2x sin x 2D． 2 x sin x 44．下列函数中不是函数 sin 2x 的原函数的有．1（） A ． 2 x B ． 2x C D．1cos2xsin cos sin 2x2 25．求由曲线 xy a 与直线 x a ， x 2a （ a0 ）及 y0 所围成的图形绕 y轴旋转一周所生成的旋转体的体积。

（）A ． 1aB． aC． 1 a 2D． 2 a 222得分三、计算题（本大题共 7小题，每小题 7分，共 49分）1. 求极限 limcos(sinx) 1 。

工科数学分析试卷1(含答案)

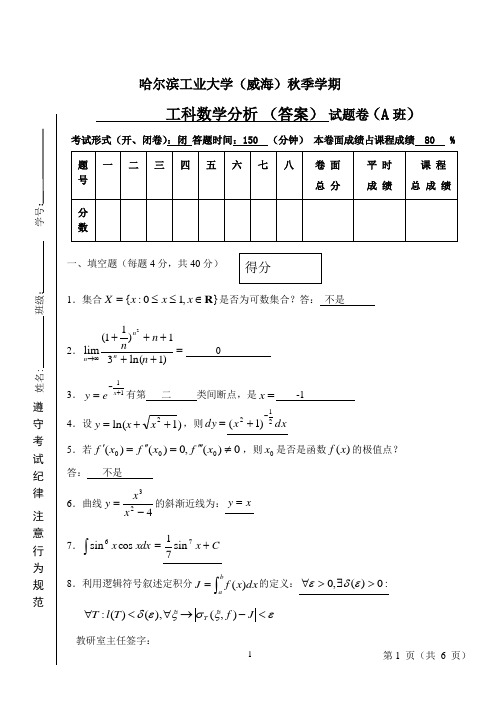
哈尔滨工业大学（威海）秋季学期工科数学分析（答案）试题卷（A 班）考试形式（开、闭卷）：闭答题时间：150 （分钟）本卷面成绩占课程成绩 80 %一、填空题（每题4分，共40分）1．集合},10:{R ∈≤≤=x x x X 是否为可数集合？答：不是2．=+++++∞→)1ln(31)11(lim 2n n nn n n 0 3．11+-=x ey 有第二类间断点，是=x -14．设)1ln(2++=x x y ，则=dy dx x 212)1(-+5．若0)(,0)()(000≠'''=''='x f x f x f ，则0x 是否是函数)(x f 的极值点？答：不是6．曲线423-=x x y 的斜渐近线为：x y =7．⎰=xdx x cos sin 6C x +7sin 718．利用逻辑符号叙述定积分⎰=badx x f J )(的定义：:0)(,0>∃>∀εδεεξσξεδ<-→∀<∀J f T l T T ),(),()(:遵守考试纪律注意行为规范教研室主任签字：姓名: 班级：学号：9．⎰+∞-=022dx xex 110．⎰-=-++222)33ln 1(sin ππdx xxx 2π二、试解答下列各题：（每题5分，共20分）1．设⎩⎨⎧=-=2)1ln(ty t x ，求22dx y d 解：t t x y dx dy t t222-=''= （2分）)1)(12(2122--='⋅'⎪⎭⎫ ⎝⎛=t t x dx dy dx y d t t（2分）（1分）2．设⎪⎩⎪⎨⎧=≠=⎰0,00,)(1)(02x x dt t tf x x F x，其中)(x f 在)0(δU 上连续且0)0(=f ，存在)0(f '，求)0(F '。

2016-2017第一学期考题答案(1)

2016-2017高数试题答案一、1. 设11ln(1)10()0x x x f x ex -+-<≤⎧⎪=⎨⎪>⎩，求()f x 的间断点，并指出间断点的类型。

解 0lim ()lim ln(1)0x x f x x --→→=+= 1110lim ()lim x x x f x e e ++--→→==所以0x =为跳跃间断点； ……………………..3分 1111lim ()lim 0x x x f x e ---→→==1111lim ()lim x x x f x e++-→→==∞所以1x =为第二类间断点。

………………………….6分 2.求,a b 的值，使点（1,3）为曲线32y ax bx =+的拐点解 232,62y a x b x y a x b '''=+=+， ………………………………..3分则 6203a b a b +=⎧⎨+=⎩，解得 39,22a b =-=。

…………………….6分 3.已知两曲线()y f x =与2arctan 0xt y e dt -=⎰在点(0, 0)处的切线相同，写出此切线方程，并求极限2lim ()n nf n→∞解 2(a r c t a n)21,(0)11x y e y x-''=⋅=+ 切线方程为 y x =， …………………………………3分2()(0)2lim ()lim 2(0)21n n f f n nf f nn→∞→∞-'=== …………………..6分 4.求定积分1解换元tan x t =23322144sec cos tan sec sin tdt tdt t t tππππ==⋅⎰⎰ ………………………3分341sin tππ=-=…………………………………6分或换元1x u=11==………………….3分=…………………………..6分5. 求不定积分2x xe dx -⎰解2221122xx x xe dx e x e dx ---=-+⎰⎰ ………………..3分 221124x x e x e C --=--+。

工科数学分析试题及答案

A一、求解下面问题（每小题6分，满分48分）1.设),(y x f 为一连续函数，求极限.),(122220lim dxdy y x f rr y x r ⎰⎰≤+→+π解 (0,0)),(12222limf dxdy y x f r r y x r =⎰⎰≤+→+π建议：中间过程4分2. 改变累次积分的积分顺序：dy y x f dx x x ),(-21-426-2⎰⎰0820-1(,)(,)ydy f x y dx dy f x y dx---=+⎰⎰⎰⎰3. 计算二重积分dxdy y x D22sin +⎰⎰，其中积分区域为}.4|),{(2222ππ≤+≤=y x y x D解：D⎰⎰4. 计算三重积分dxdydz x y V⎰⎰⎰+)1(2012，其中V 由22--4y x z =与223y x z +=所成的立体.解：由于V 是关于yoz 平面对称的，且x y 2012是关于x 的奇函数，所以02012=⎰⎰⎰d x d y d z x yV，于是23220121()r VVyx dxdydz dxdydz d πθ+==⎰⎰⎰⎰⎰⎰⎰⎰223)r d rdr πθ=⎰2223001)()2r d d r πθ=⎰22220012(4)()62r d r d r πθ⎤=--⎢⎥⎣⎦⎰34222001219(4)6236r d r πθπ⎡=⋅---=⎢⎥⎣⎦⎰ （写出对称性给2分，计算过程适当给分）2204sin 6d r rdr πππθπ==-⎰⎰5. 计算积分2(2)I x z ds Γ=+⎰，其中曲线Γ为2222,0.x y z a x y z ⎧++=⎨++=⎩（利用对称性）解：利用轮换对称性知2322222212()333a a x ds y ds z ds x y z ds ds πΓΓΓΓΓ===++==⎰⎰⎰⎰⎰1()03zds xds yds x y z ds ΓΓΓΓ===++=⎰⎰⎰⎰ 所以322(2)3a x z ds πΓ+=⎰（建议：两个对称性各3分，写出参数方程直接计算适当给分）6. 计算第一型曲面积分()x y z dS ∑++⎰⎰，其中∑为球面2222x y z a ++=上z h ≥)0(a h <<的部分. （可利用对称性）解：利用对称性知0xdS ydS ∑∑==⎰⎰⎰⎰设xy D ={|),(y x 2222x y a h +≤-} 则()x y z dS ∑++⎰⎰=zdS ∑⎰⎰=⎰⎰=aDxydxdy ⎰⎰=22()a a h π-（建议：对称性0xdS ydS∑∑==⎰⎰⎰⎰2分，= 1分，zdS ∑⎰⎰计算过程3分）7. 证明向量场))2(),2(),2((z y x xy z y x xz z y x yz F ++++++= 是有势场，并求其势函数.解：先验证有势场0)2()2()2(=++++++=∂∂∂∂∂∂z y x xy z y x xz z y x yz F rot zyxk j故是有势场. ---------3分.)2()2()2(.),,222000000),,(),,(),,(),,(0000000C xyz z xy yz x dz z y x xy dy z y x xz dx z y x z y RdzQdy Pdx s d F z y x zzyy xx z y x z y x z y x z y x +++=++++++++=++==⎰⎰⎰⎰⎰（φ（另一种方法也可（这里略），请判卷的时候注意。

广东省珠海市2017届高三上学期期末考试数学理试题Word版含答案

米．
三、解答题 : 解答应写出文字说明，证明过程或演算步骤 17．（本小题满分 12 分）
.请在答题卡上做答 .
已知 { an }为等比数列， a1 1 ， a4 27； Sn 为等差数列 { bn } 的前 n 项和， b1 3，
S5 35.
Байду номын сангаас
(1)求 { a n }和{ bn } 的通项公式；
(2)设数列 { cn } 满足 cn anbn (n N *) ，求数列 { cn } 的前 n 项和 Tn .
如图，四边形 ABCD与 BDEF 均为菱形， FA＝FC 且 ∠ DAB＝∠ DBF＝60° ． (1)求证： AC ⊥平面 BDEF ； (2)求证： FC// 平面 EAD； (3)求二面角 A － FC －B的余弦值．
20．（本小题满分 12 分）
在平面直角坐标系 xOy 中，椭圆 G的中心为坐标原点，左焦点为 F1(－1，0)，离心率 e＝ 2. 2
B． 2 1 17
C． 2 2 17
D．
1 2
9
7.某城市有 3 个演习点同时进行消防演习，现将 5 个消防队分配到这 3 个演习点，若每个演
习点至少安排 1 个消防队，则不同的分配方案种数为（
）
A．150 B．240 C． 360 D． 540
8．某几何体的三视图如图所示（图中每个小网格的边长为
1 个单位），其中俯视图为扇形，
则该几何体的体积为（）
2
A．
3
4
B．
3
14
C．
3
9．已知函数 f ( x) Asin( x )( A 0,
(x)的说法中正确的是
16
D．

大一工科数学分析试卷及答案

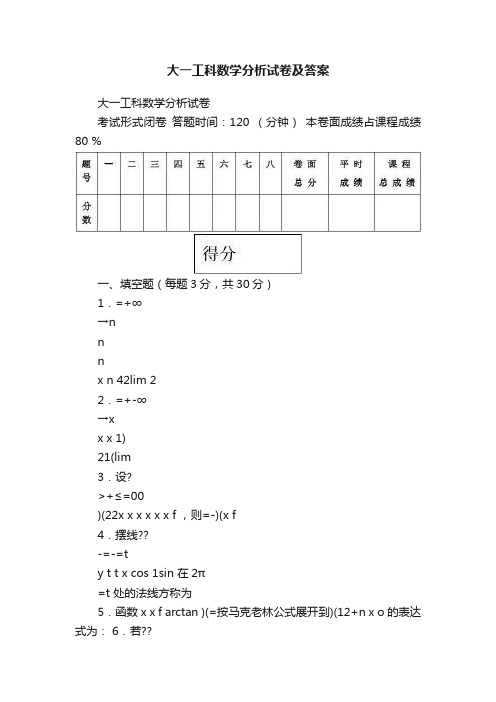
大一工科数学分析试卷及答案大一工科数学分析试卷考试形式闭卷答题时间：120 （分钟）本卷面成绩占课程成绩80 %一、填空题（每题3分，共30分）1．=+∞→nnnx n 42lim 22．=+-∞→xx x 1)21(lim3．设?>+≤=00)(22x x x x x x f ，则=-)(x f4．摆线??-=-=ty t t x cos 1sin 在2π=t 处的法线方称为5．函数x x f arctan )(=按马克老林公式展开到)(12+n x ο的表达式为： 6．若??x t dt t f dt e 11)(32，则=)(x f7．若?++=c x dx x f 2cos sin )(（其中c 时任意常数），则 =)(x f8．?-=-+112)1cos (dx x x x9．设)100()2)(1()(---=x x x x f ，则=')1(f姓名: 班级：学号：遵守考试纪律注意行为规范10．若-ba xb dxα)(收敛（其中0>α），则α的取值范围是二、试解答下列各题：（每题5分，共50分）1．求极限)2122321(lim 2nn n -+++∞2．已知0)11(lim 2=--++∞→b ax x x x ，求b a ,。

遵守考试纪律注意行为规范3．设1lim )()1()1(2+++=--∞→x n x m n e bax e x x f ，求b a ,使)(x f 可导。

4．求由等式0333=-+xy y x 确定的)(x f y =在0>x 范围内的极限点。

5．设ttte y e x ==-,，求22,dx y d dx dy 。

6．求曲线)1ln()(2++=x x x f 在1=x 时的曲率。

7．计算不定积分?-dx e x11。

8．计算定积分?20xdx x 。

9．设?<+≥+=011011)(x e x xx f x，求-2)1(dx x f 。

2021-2022学年工科数学分析期末试题

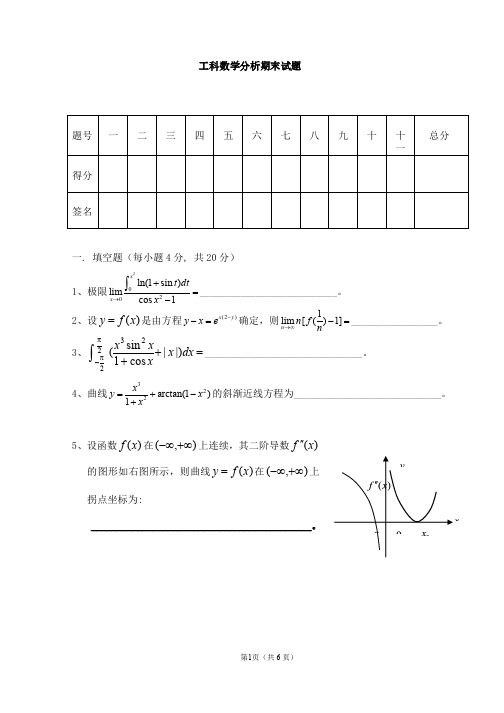
工科数学分析期末试题题号一二三四五六七八九十十一总分得分签名一. 填空题（每小题4分, 共20分）1、极限___________________________。

2、设是由方程确定，则_________________。

3、_______________________________。

4、曲线的斜渐近线方程为_____________________________。

5、设函数在上连续，其二阶导数的图形如右图所示，则曲线在上拐点坐标为:___________________________________________。

22ln(1sin )limcos 1x x t dt x ®+=-ò)(x f y =(2)x y y x e --=1lim [()1]n n f n ®¥-==++òpp -dx x xx x |)|cos 1sin (2223322arctan(1)1x y x x =+-+)(x f ),(+¥-¥)(x f ¢¢)(x f y =),(+¥-¥二、（8分）设。

（1）当时，求；（2）证明当时，恒等于常数，并确定此常数值。

三. (8分) 已知，求在上的表达式，并讨论在上的连续性。

22()2arctan arcsin1xf x x x=++0x >()f x ¢1³x ()f x 10()0x x f x x x +<ì=í³î1()()x F x f x dx -=ò[1,1]-()F x [1,1]-四. (8分) (1)求不定积分；(2)求广义积分五、（8分）设曲线方程为。

（1）求曲线在处的切线方程；（2）求曲线在处的曲率。

ò+dx e e x x )1ln(ò¥++1)1(xx dx 1cos r q =+2p q =2p q =六. (8分) 求微分方程满足条件的解。

2016-2017学年高二上学期数学(理)期末试题及答案

2016-2017学年高二上学期数学(理)期末试题及答案2016-2017学年度上学期期末考试高二理科数学试卷考试说明：本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分，考试时间120分钟。

1.答题前，请填写姓名和准考证号码。

2.选择题必须使用2B铅笔填涂，非选择题必须使用0.5毫米黑色签字笔书写，字迹清楚。

3.请在各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿纸上答题无效。

4.保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀。

第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一个是符合题目要求的。

1.某中学有3500名高中生和1500名初中生。

为了解学生的研究情况，从该校学生中采用分层抽样的方法抽取一个容量为n的样本。

已知从高中生中抽取了70人，则n的值为（）。

A。

100B。

150C。

200D。

2502.如图所示，将图（1）中的正方体截去两个三棱锥，得到图（2）中的几何体，则该几何体的侧视图为（）。

无法提供图像）3.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点为F，点F到渐近线的距离等于2a，则该双曲线的离心率等于（）。

A。

2B。

3C。

5D。

3/44.已知两条直线a,b，两个平面$\alpha,\beta$，下面四个命题中不正确的是（）。

A。

$a\perp\alpha,\alpha//\beta,b\parallel\beta\iff a\perp b$B。

$\alpha//\beta,a//b,a\perp\alpha\implies b\perp\beta$C。

$m//\alpha,m\perp\beta\implies\alpha\perp\beta$D。

$a//b,a//\alpha\implies b//\alpha$5.下列命题中，说法正确的是（）。

2016-2017学年高三上学期期末数学试卷(理科) Word版含解析

2016-2017学年高三上学期期末试卷（理科数学）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）抛物线x2=﹣2y的焦点坐标是（）A．（﹣1，0）B．（1，0）C．D．2．（5分）如图所示，在复平面内，点A对应的复数为z，则复数z2=（）A．﹣3﹣4i B．5+4i C．5﹣4i D．3﹣4i3．（5分）当向量=c=（﹣2，2），=（1，0）时，执行如图所示的程序框图，输出的i值为（）A．5 B．4 C．3 D．24．（5分）已知直线l1：ax+（a+2）y+1=0，l2：x+ay+2=0．若l1⊥l2，则实数a的值是（）A．0 B．2或﹣1 C．0或﹣3 D．﹣35．（5分）设不等式组表示的平面区域为D．则区域D上的点到坐标原点的距离的最小值是（）A．1 B．C．D．56．（5分）某三棱锥的三视图如图所示，该三棱锥四个面的面积中最大的是（）A．B．12 C．D．7．（5分）某堆雪在融化过程中，其体积V（单位：m3）与融化时间t（单位：h）近似满足函数关系：（H为常数），其图象如图所示．记此堆雪从融化开始到结束的平均融化速度为．那么瞬时融化速度等于的时刻是图中的（）A．t1B．t2C．t3D．t48．（5分）已知点A在曲线P：y=x2（x＞0）上，⊙A过原点O，且与y轴的另一个交点为M．若线段OM，⊙A 和曲线P上分别存在点B、点C和点D，使得四边形ABCD（点A，B，C，D顺时针排列）是正方形，则称点A为曲线P的“完美点”．那么下列结论中正确的是（）A．曲线P上不存在“完美点”B．曲线P上只存在一个“完美点”，其横坐标大于1C．曲线P上只存在一个“完美点”，其横坐标大于且小于1D．曲线P上存在两个“完美点”，其横坐标均大于二、填空题共6小题，每小题5分，共30分．9．（5分）在的展开式中，常数项是．（用数字作答）10．（5分）在极坐标系中，直线ρsinθ=3被圆ρ=4sinθ截得的弦长为．11．（5分）若双曲线的一条渐近线的倾斜角为60°，则m=．12．（5分）如图所示，AD是⊙O的切线，AB=，∠ACB=，那么∠CAD=．13．（5分）在等比数列{a n}中，若a1=﹣24，a4=﹣，则公比q=；当n=时，{a n}的前n项积最大．14．（5分）如图所示，在正方体ABCD﹣A1B1C1D1中，点E是边BC的中点．动点P在直线BD1（除B，D1两点）上运动的过程中，平面DEP可能经过的该正方体的顶点是．（写出满足条件的所有顶点）三、解答题共6小题，共80分．解答应写出文字说明、演算步骤或证明过程．15．（13分）函数f（x）=cos（πx+φ）（0＜φ＜）的部分图象如图所示．（Ⅰ）写出φ及图中x0的值；（Ⅱ）设g（x）=f（x）+f（x+），求函数g（x）在区间上的最大值和最小值．16．（13分）某中学在2014-2015学年高二年级开设大学先修课程《线性代数》，共有50名同学选修，其中男同学30名，女同学20名．为了对这门课程的教学效果进行评估，学校按性别采用分层抽样的方法抽取5人进行考核．（Ⅰ）求抽取的5人中男、女同学的人数；（Ⅱ）考核的第一轮是答辩，顺序由已抽取的甲、乙等5位同学按抽签方式决定．设甲、乙两位同学间隔的人数为X，X的分布列为X 3 2 1 0P a b求数学期望EX；（Ⅲ）考核的第二轮是笔试：5位同学的笔试成绩分别为115，122，105，111，109；结合第一轮的答辩情况，他们的考核成绩分别为125，132，115，121，119．这5位同学笔试成绩与考核成绩的方差分别记为s12，s22，试比较s12与s22的大小．（只需写出结论）17．（14分）如图所示，在三棱柱ABC﹣A1B1C1中，AA1B1B为正方形，BB1C1C为菱形，∠BB1C1=60°，平面AA1B1B⊥平面BB1C1C．（Ⅰ）求证：B1C⊥AC1；（Ⅱ）设点E，F分别是B1C，AA1的中点，试判断直线EF与平面ABC的位置关系，并说明理由；（Ⅲ）求二面角B﹣AC1﹣C的余弦值．18．（13分）已知椭圆M：=1，点F1，C分别是椭圆M的左焦点、左顶点，过点F1的直线l（不与x轴重合）交M于A，B两点．（Ⅰ）求M的离心率及短轴长；（Ⅱ）是否存在直线l，使得点B在以线段AC为直径的圆上，若存在，求出直线l的方程；若不存在，说明理由．19．（13分）已知函数f（x）=acosx+xsinx，．（Ⅰ）判断函数f（x）的奇偶性，并证明你的结论；（Ⅱ）求集合A={x|f（x）=0}中元素的个数；（Ⅲ）当1＜a＜2时，问函数f（x）有多少个极值点？（只需写出结论）20．（14分）已知集合S={a1，a2，a3，…，a n}（n≥3），集合T⊆{（x，y）|x∈S，y∈S，x≠y}且满足：∀a i，a j∈S（i，j=1，2，3，…，n，i≠j），（a i，a j）∈T与（a j，a i）∈T恰有一个成立．对于T定义d T（a，b）=l T（a i）=d T（a i，a1）+d T（a i，a2）+…+d T（a i，a i﹣1）+d T（a i，a i+1）+…+d T（a i，a n）（i=1，2，3，…，n）．（Ⅰ）若n=4，（a1，a2），（a3，a2），（a2，a4）∈T，求l T（a2）的值及l T（a4）的最大值；（Ⅱ）从l T（a1），l T（a2），…，l T（a n）中任意删去两个数，记剩下的n﹣2个数的和为M．求证：M≥n（n﹣5）+3；（Ⅲ）对于满足l T（a i）＜n﹣1（i=1，2，3，…，n）的每一个集合T，集合S中是否都存在三个不同的元素e，f，g，使得d T（e，f）+d T（f，g）+d T（g，e）=3恒成立，并说明理由．2016-2017学年高三上学期期末数学试卷（理科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）抛物线x2=﹣2y的焦点坐标是（）A．（﹣1，0）B．（1，0）C．D．考点：抛物线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：由x2=﹣2py（p＞0）的焦点坐标为（0，﹣），则抛物线x2=﹣2y的焦点坐标即可得到．解答：解：由x2=﹣2py（p＞0）的焦点坐标为（0，﹣），则抛物线x2=﹣2y的焦点坐标是（0，﹣），故选C．点评：本题考查抛物线的方程和性质，主要考查抛物线的焦点坐标，属于基础题．2．（5分）如图所示，在复平面内，点A对应的复数为z，则复数z2=（）A．﹣3﹣4i B．5+4i C．5﹣4i D．3﹣4i考点：复数代数形式的乘除运算；复数的基本概念．专题：数系的扩充和复数．分析：在复平面内，点A对应的复数为z=﹣2+i，再利用复数的运算法则即可得出．解答：解：在复平面内，点A对应的复数为z=﹣2+i，则复数z2=（﹣2+i）2=3﹣4i．故选：D．点评：本题考查了复数的运算法则、几何意义，属于基础题．3．（5分）当向量=c=（﹣2，2），=（1，0）时，执行如图所示的程序框图，输出的i值为（）A．5 B．4 C．3 D．2考点：程序框图．专题：算法和程序框图．分析：模拟程序运行，依次写出每次循环得到的的值，当=（﹣2，2），满足条件a•c=0，退出循环，输出i的值为4．解答：解：模拟程序运行，有i=1时，=（﹣1，2），不满足条件a•c=0i=2时，=（0，2），不满足条件a•c=0i=3时，=（1，2），不满足条件a•c=0i=4时，=（﹣2，2），满足条件a•c=0退出循环，输出i的值为4．故选：B．点评：本题主要考察了程序框图和算法，正确理解循环结构的功能是解题的关键，属于基本知识的考查．4．（5分）已知直线l1：ax+（a+2）y+1=0，l2：x+ay+2=0．若l1⊥l2，则实数a的值是（）A．0 B．2或﹣1 C．0或﹣3 D．﹣3考点：直线的一般式方程与直线的垂直关系．专题：直线与圆．分析：由垂直可得a+a（a+2）=0，解方程可得．解答：解：∵直线l1：ax+（a+2）y+1=0，l2：x+ay+2=0，且l1⊥l2，∴a+a（a+2）=0，解得a=0或a=﹣3故选：C点评：本题考查直线的一般式方程和垂直关系，属基础题．5．（5分）设不等式组表示的平面区域为D．则区域D上的点到坐标原点的距离的最小值是（）A．1 B．C．D．5考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用数形结合即可得到结论．解答：解：作出不等式组对应的平面区域如图：由图象可知，当OQ垂直直线x+y﹣1=0时，此时区域D上的点到坐标原点的距离的最小，最小值为圆心到直线x+y﹣1=0的距离d=故选：B点评：本题主要考查两点间距离的应用，利用数形结合以及点到直线的距离公式是解决本题的关键．6．（5分）某三棱锥的三视图如图所示，该三棱锥四个面的面积中最大的是（）A．B．12 C．D．考点：由三视图求面积、体积．专题：计算题；空间位置关系与距离．分析：由题意和三视图知，需要从对应的长方体中确定三棱锥，根据三视图的数据和几何体的垂直关系，求出四面体四个面的面积，再确定出它们的最大值．解答：解：将该几何体放入在长方体中，且长、宽、高为4、3、4，由三视图可知该三棱锥为B﹣A1D1C1，由三视图可得，A1D1=CC1=4、D1C1=3，所以BA1=A1C1=5，BC1==4，则三角形BA1C1的面积S=×BC1×h==，因为A1D1⊥平面ABA1B1，所以A1D1⊥A1B，则三角形BA1D1的面积S=×BA1×A1D1==10，同理可得，三角形BD1C1的面积S=×BC1×D1C1==6，又三角形A1D1C1的面积S=×D1C1×A1D1=3=6，所以最大的面为A1BC1，且面积为，故选：A．点评：本题考查由三视图还原几何体，以及线面垂直关系，将几何体放入正方体中去研究是解决本题的关键，考查了空间想象能力和转化能力．7．（5分）某堆雪在融化过程中，其体积V（单位：m3）与融化时间t（单位：h）近似满足函数关系：（H为常数），其图象如图所示．记此堆雪从融化开始到结束的平均融化速度为．那么瞬时融化速度等于的时刻是图中的（）A．t1B．t2C．t3D．t4考点：函数的图象．专题：函数的性质及应用．分析：根据题意可知，平均融化速度为=，反映的是V（t）图象与坐标轴交点连线的斜率，通过观察某一时刻处瞬时速度（即切线的斜率），即可得到答案解答：解：平均融化速度为=，反映的是V（t）图象与坐标轴交点连线的斜率，观察可知t3处瞬时速度（即切线的斜率）为平均速速一致，故选：C点评：本题考查了图象的识别，关键理解平均速度表示的几何意义（即斜率），属于基础题8．（5分）已知点A在曲线P：y=x2（x＞0）上，⊙A过原点O，且与y轴的另一个交点为M．若线段OM，⊙A 和曲线P上分别存在点B、点C和点D，使得四边形ABCD（点A，B，C，D顺时针排列）是正方形，则称点A为曲线P的“完美点”．那么下列结论中正确的是（）A．曲线P上不存在“完美点”B．曲线P上只存在一个“完美点”，其横坐标大于1C．曲线P上只存在一个“完美点”，其横坐标大于且小于1D．曲线P上存在两个“完美点”，其横坐标均大于考点：二次函数的性质．专题：新定义．分析：假设点A为“完美点”，画出图象，设A（m，m2），通过讨论m＜1时，m≥1时的情况从而得到答案．解答：解：如下图左，如果点A为“完美点”，则AB=AD=AC=OA，以A为圆心，OA为半径作圆T（如下图右中虚线圆），交y轴于点B，B′（可重合），交抛物线于点D，D′，点A为“完美点”当且仅当AB⊥AD，若下图右，（结合图象知，B点一定是上方的交点，否则在抛物线上不存在D点使得AB⊥AD；D也一定是上方的交点，否则A，B，C，D不是顺时针），，，下面考虑当点A的横坐标越来越大时∠BAD的变化情况，设A（m，m2），当m＜1时，∠AOY=45°，此时圆T与y轴相离或相切时，此时A不是完美点，故只需考虑m≥1，当m增加时，∠BAD越来越小，且趋近于0，（推理在后面），而当m=1时，∠BAD＞90°，故曲线P上存在唯一一个完美点，其横坐标大于1，当m增加时，∠BAD越来越小，且趋近于0°的推理：过A作AH⊥y轴于点H，分别过点A，D作x轴，y轴的平行线交于N，先考虑∠BAH：cos∠BAH==，于是m增大时，cos∠BAH减小且趋于0，从而∠BAH增大，且趋于90°，再考虑∠DAN，记D（n，n2），则tan∠DAN==n+m，随着m的增大，OA的长增大，AD=OA也增大，于是m+n增大，从而tan∠DAN增大，∠DAN增大且趋近于90°，∴∠BAD=π﹣∠BAH﹣∠DAN随着m的增大而减小，且趋于0°，故选：B．点评：本题考查了新定义问题，考查了二次函数的性质，考查了数形结合思想，本题有一定难度．二、填空题共6小题，每小题5分，共30分．9．（5分）在的展开式中，常数项是15．（用数字作答）考点：二项式系数的性质．专题：计算题；二项式定理．分析：先求出二项式展开式的通项公式，再令x的幂指数等于0，求得r的值，即可求得展开式中的常数项．解答：解：∵在的展开式的通项公式为T r+1=•（﹣1）r•，令r﹣6=0，求得r=4，故的展开式中的常数项是5．故答案为：15．点评：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．10．（5分）在极坐标系中，直线ρsinθ=3被圆ρ=4sinθ截得的弦长为．考点：简单曲线的极坐标方程．专题：坐标系和参数方程．分析：把极坐标方程化为直角坐标方程、再利用点到直线的距离公式、弦长公式即可得出．解答：解：直线ρsinθ=3即y=3．ρ=4sinθ化为ρ2=4ρsinθ，∴x2+y2=4y，化为x2+（y﹣2）2=4．可得圆心C（0，2），半径r=2．∴圆心到直线的距离d=1，∴直线ρsinθ=3被圆ρ=4sinθ截得的弦长=2=2．故答案为：2．点评：本题考查了把极坐标方程化为直角坐标方程、再利用点到直线的距离公式、弦长公式，属于基础题．11．（5分）若双曲线的一条渐近线的倾斜角为60°，则m=3．考点：双曲线的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．分析：求出双曲线的渐近线方程，由题意可得，tan60°=，计算即可得到m．解答：解：双曲线（m＞0）的渐近线方程为y=x，则有tan60°=，即有=，即为m=3．故答案为：3．点评：本题考查双曲线的方程和性质，考查渐近线方程的运用，考查运算能力，属于基础题．12．（5分）如图所示，AD是⊙O的切线，AB=，∠ACB=，那么∠CAD=120°或60°．考点：弦切角．专题：立体几何．分析：首先根据正弦定理求出∠B的大小，进一步利用弦切角定理和三角形内角和定理求出结果．解答：解：AD是⊙O的切线，AB=，∠ACB=，所以：在△ABC中，利用正弦定理得：，解得：sin∠B=，所以：∠B=60°或120°．利用三角形内角和定理得：∠CAB=75°或15°根据弦切角定理得：∠BAD=∠C，所以：∠CAD=120°或60°，故答案为：120°或60°．点评：本题考查的知识要点：正弦定理得应用，弦切角定理的应用．三角形内角和定理的应用．属于基础题型．13．（5分）在等比数列{a n}中，若a1=﹣24，a4=﹣，则公比q=；当n=4时，{a n}的前n项积最大．考点：等比数列的前n项和．专题：等差数列与等比数列．分析：直接由已知及等比数列的通项公式求得公比；写出等比数列的通项公式，得到前n项积，然后根据奇数项积为负值，分析偶数项乘积得答案．解答：解：在等比数列{a n}中，由a1=﹣24，a4=﹣，得，∴q=；∴．则{a n}的前n项积：=．当n为奇数时T n＜0，∴当n为偶数时T n有最大值．又，且当n为大于等于4的偶数时，T n+2＜T n，∴当n=4时，{a n}的前n项积最大．故答案为：；4．点评：本题考查了等比数列的通项公式，考查了等比数列的性质，是中档题．14．（5分）如图所示，在正方体ABCD﹣A1B1C1D1中，点E是边BC的中点．动点P在直线BD1（除B，D1两点）上运动的过程中，平面DEP可能经过的该正方体的顶点是A1，B1，D．（写出满足条件的所有顶点）考点：棱柱的结构特征．专题：作图题；空间位置关系与距离．分析：取BB1的中点F，取A1D1的中点M，D1，B在平面MDEB1的两侧，可得结论．解答：解：取BB1的中点F，则A，D，E，F四点共面，D1，B在平面ADEF的两侧，故D1B与平面相交，满足题意；取A1D1的中点M，则M，D，E，B1四点共面，D1，B在平面MDEB1的两侧，故D1B与平面相交，满足题意；D显然满足．动点P在直线BD1（除B，D1两点）上运动的过程中，平面DEP可能经过的该正方体的顶点是A1，B1，D．故答案为：A1，B1，D．点评：本题考查棱柱的结构特征，考查共面问题，比较基础．三、解答题共6小题，共80分．解答应写出文字说明、演算步骤或证明过程．15．（13分）函数f（x）=cos（πx+φ）（0＜φ＜）的部分图象如图所示．（Ⅰ）写出φ及图中x0的值；（Ⅱ）设g（x）=f（x）+f（x+），求函数g（x）在区间上的最大值和最小值．考点：余弦函数的图象．专题：三角函数的求值；三角函数的图像与性质．分析：（Ⅰ）由题意可得=cos（0+φ），可得φ的值．由=cos（πx0+），可得x0的值．（Ⅱ）先求得g（x）的函数解析式，由，可得，从而可求函数g （x）在区间上的最大值和最小值．解答：（共13分）解：（Ⅰ）∵=cos（0+φ）∴φ的值是．…（2分）∵=cos（πx0+）∴2π﹣=πx0+，可得x0的值是．…（5分）（Ⅱ）由题意可得：．…（7分）所以=…（8分）==．…（10分）因为，所以．所以当，即时，g（x）取得最大值；当，即时，g（x）取得最小值．…（13分）点评：本题主要考察了，三角函数化简求值，三角函数的图象与性质，三角函数最值的解法，属于中档题．16．（13分）某中学在2014-2015学年高二年级开设大学先修课程《线性代数》，共有50名同学选修，其中男同学30名，女同学20名．为了对这门课程的教学效果进行评估，学校按性别采用分层抽样的方法抽取5人进行考核．（Ⅰ）求抽取的5人中男、女同学的人数；（Ⅱ）考核的第一轮是答辩，顺序由已抽取的甲、乙等5位同学按抽签方式决定．设甲、乙两位同学间隔的人数为X，X的分布列为X 3 2 1 0P a b求数学期望EX；（Ⅲ）考核的第二轮是笔试：5位同学的笔试成绩分别为115，122，105，111，109；结合第一轮的答辩情况，他们的考核成绩分别为125，132，115，121，119．这5位同学笔试成绩与考核成绩的方差分别记为s12，s22，试比较s12与s22的大小．（只需写出结论）考点：离散型随机变量的期望与方差；离散型随机变量及其分布列．专题：概率与统计．分析：（Ⅰ）由分层抽样的性质，能求出抽取的5人中男、女同学的人数．（Ⅱ）由题意可得a=，从而，由此能求出数学期望EX．（Ⅲ）由两组数据中相对应的数字之差均为10，得到．解答：解：（Ⅰ）由分层抽样的性质得：抽取的5人中男同学的人数为，女同学的人数为．…（4分）（Ⅱ）由题意可得：．即a=，…（6分）因为，所以．…（8分）所以．…（10分）（Ⅲ）．…（13分）点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，在历年2015届高考中都是必考题型之一．17．（14分）如图所示，在三棱柱ABC﹣A1B1C1中，AA1B1B为正方形，BB1C1C为菱形，∠BB1C1=60°，平面AA1B1B⊥平面BB1C1C．（Ⅰ）求证：B1C⊥AC1；（Ⅱ）设点E，F分别是B1C，AA1的中点，试判断直线EF与平面ABC的位置关系，并说明理由；（Ⅲ）求二面角B﹣AC1﹣C的余弦值．考点：二面角的平面角及求法；空间中直线与平面之间的位置关系．专题：空间位置关系与距离；空间角．分析：（Ⅰ）根据线面垂直的性质定理即可证明B1C⊥AC1；（Ⅱ）根据线面平行的判定定理即可判断直线EF与平面ABC的位置关系；（Ⅲ）建立空间坐标系，求出平面的法向量，利用向量法进行求解即可．解答：证明：（Ⅰ）连接BC1．在正方形ABB1A1中，AB⊥BB1．因为平面AA1B1B⊥平面BB1C1C，平面AA1B1B∩平面BB1C1C=BB1，AB⊂平面ABB1A1，所以AB⊥平面BB1C1C．…（1分）因为 B1C⊂平面BB1C1C，所以AB⊥B1C．…（2分）在菱形BB1C1C中，BC1⊥B1C．因为 BC1⊂平面ABC1，AB⊂平面ABC1，BC1∩AB=B，所以 B1C⊥平面ABC1．…（4分）因为 AC1⊂平面ABC1，所以 B1C⊥AC1．…（5分）（Ⅱ）EF∥平面ABC，理由如下：…（6分）取BC的中点G，连接GE，GA．因为 E是B1C的中点，所以GE∥BB1，且GE=．因为 F是AA1的中点，所以 AF=．在正方形ABB1A1中，AA1∥BB1，AA1=BB1．所以GE∥AF，且GE=AF．所以四边形GEFA为平行四边形．所以EF∥GA．…（8分）因为 EF⊄平面ABC，GA⊂平面ABC，所以EF∥平面ABC．…（9分）（Ⅲ）在平面BB1C1C内过点B作Bz⊥BB1．由（Ⅰ）可知：AB⊥平面BB1C1C．以点B为坐标原点，分别以BA，BB1所在的直线为x，y轴，建立如图所示的空间直角坐标系B﹣xyz，设A（2，0，0），则B1（0，2，0）．在菱形BBC1C中，∠BB1C1=60°，所以，．设平面ACC1的一个法向量为n=（x，y，1）．因为即所以即．…（11分）由（Ⅰ）可知：是平面ABC1的一个法向量．…（12分）所以．所以二面角B﹣AC1﹣C的余弦值为．…（14分）点评：本题主要考查空间直线和平面之间的位置关系的判断，以及二面角的求解，要求熟练掌握相应的判定定理，利用向量法是解决二面角的常用方法，考查学生的运算和推理能力．18．（13分）已知椭圆M：=1，点F1，C分别是椭圆M的左焦点、左顶点，过点F1的直线l（不与x轴重合）交M于A，B两点．（Ⅰ）求M的离心率及短轴长；（Ⅱ）是否存在直线l，使得点B在以线段AC为直径的圆上，若存在，求出直线l的方程；若不存在，说明理由．考点：直线与圆锥曲线的综合问题．专题：圆锥曲线的定义、性质与方程．分析：（Ⅰ）通过椭圆M方程：，直接计算即可；（Ⅱ）通过设B（x0，y0）（﹣2＜x0＜2），利用•＞0可得，进而可得结论．解答：解：（Ⅰ）由，得：，∴椭圆M的短轴长为，∴，∴，即M的离心率为；（Ⅱ）结论：不存在直线l，使得点B在以AC为直径的圆上．理由如下：由题意知：C（﹣2，0），F1（﹣1，0），设B（x0，y0）（﹣2＜x0＜2），则．∵==，∴．∴点B不在以AC为直径的圆上，即：不存在直线l，使得点B在以AC为直径的圆上．点评：本题是一道直线与圆锥曲线的综合题，考查运算求解能力，考查分析问题、解决问题的能力，注意解题方法的积累，属于中档题．19．（13分）已知函数f（x）=acosx+xsinx，．（Ⅰ）判断函数f（x）的奇偶性，并证明你的结论；（Ⅱ）求集合A={x|f（x）=0}中元素的个数；（Ⅲ）当1＜a＜2时，问函数f（x）有多少个极值点？（只需写出结论）考点：三角函数中的恒等变换应用；正弦函数的图象．专题：综合题；函数的性质及应用；三角函数的图像与性质．分析：（Ⅰ）证明f（﹣x）=f（x），即可证明f（x）是偶函数．（Ⅱ）分情况讨论：当a＞0时，因为 f（x）=acosx+xsinx＞0，恒成立，当a=0时，令f（x）=xsinx=0，得 x=0．当a＜0时，函数f（x）是上的增函数．由，可得f（x）在上只有一个零点．综上所述，即可求出集合A={x|f（x）=0}中元素的个数；（Ⅲ）函数f（x）有3个极值点．解答：（共13分）解：（Ⅰ）函数f（x）是偶函数，证明如下：…（1分）对于，则．…（2分）因为 f（﹣x）=acos（﹣x）﹣xsin（﹣x）=acosx+xsinx=f（x），所以 f（x）是偶函数．…（4分）（Ⅱ）当a＞0时，因为 f（x）=acosx+xsinx＞0，恒成立，所以集合A={x|f（x）=0}中元素的个数为0．…（5分）当a=0时，令f（x）=xsinx=0，由，得 x=0．所以集合A={x|f（x）=0}中元素的个数为1．…（6分）当a＜0时，因为，所以函数f（x）是上的增函数．…（8分）因为，所以 f（x）在上只有一个零点．由f（x）是偶函数可知，集合A={x|f（x）=0}中元素的个数为2．…（10分）综上所述，当a＞0时，集合A={x|f（x）=0}中元素的个数为0；当a=0时，集合A={x|f（x）=0}中元素的个数为1；当a＜0时，集合A={x|f（x）=0}中元素的个数为2．（Ⅲ）函数f（x）有3个极值点．…（13分）点评：本题主要考察了三角函数中的恒等变换应用，三角函数的图象与性质，函数的性质及应用，属于中档题．20．（14分）已知集合S={a1，a2，a3，…，a n}（n≥3），集合T⊆{（x，y）|x∈S，y∈S，x≠y}且满足：∀a i，a j∈S（i，j=1，2，3，…，n，i≠j），（a i，a j）∈T与（a j，a i）∈T恰有一个成立．对于T定义d T（a，b）=l T（a i）=d T（a i，a1）+d T（a i，a2）+…+d T（a i，a i﹣1）+d T（a i，a i+1）+…+d T（a i，a n）（i=1，2，3，…，n）．（Ⅰ）若n=4，（a1，a2），（a3，a2），（a2，a4）∈T，求l T（a2）的值及l T（a4）的最大值；（Ⅱ）从l T（a1），l T（a2），…，l T（a n）中任意删去两个数，记剩下的n﹣2个数的和为M．求证：M≥n（n﹣5）+3；（Ⅲ）对于满足l T（a i）＜n﹣1（i=1，2，3，…，n）的每一个集合T，集合S中是否都存在三个不同的元素e，f，g，使得d T（e，f）+d T（f，g）+d T（g，e）=3恒成立，并说明理由．考点：进行简单的合情推理．专题：综合题；推理和证明．分析：（Ⅰ）利用d T（a2，a1）=0，d T（a2，a3）=0，d T（a2，a4）=1，可得l T（a2）=1；利用l T（a4）=d T （a4，a1）+d T（a4，a2）+d T（a4，a3）≤1+0+1=2，可得l T（a4）取得最大值2；（Ⅱ）由d T（a，b）的定义可知：d T（a，b）+d T（b，a）=1，设删去的两个数为l T（a k），l T（a m），则．由题意可知：l T（a k）≤n﹣1，l T（a m）≤n﹣1，且当其中一个不等式中等号成立，即可得出结论；（Ⅲ）对于满足l T（a i）＜n﹣1（i=1，2，3，…，n）的每一个集合T，集合S中都存在三个不同的元素e，f，g，使得d T（e，f）+d T（f，g）+d T（g， e）=3恒成立．解答：解：（Ⅰ）因为（a1，a2），（a3，a2），（a2，a4）∈T，所以 d T（a2，a1）=0，d T（a2，a3）=0，d T（a2，a4）=1，故l T（a2）=1．…（1分）因为（a2，a4）∈T，所以 d T（a4，a2）=0．所以 l T（a4）=d T（a4，a1）+d T（a4，a2）+d T（a4，a3）≤1+0+1=2．所以当（a2，a4），（a4，a1），（a4，a3）∈T时，l T（a4）取得最大值2．…（3分）（Ⅱ）由d T（a，b）的定义可知：d T（a，b）+d T（b，a）=1．所以=．…（6分）设删去的两个数为l T（a k），l T（a m），则．由题意可知：l T（a k）≤n﹣1，l T（a m）≤n﹣1，且当其中一个不等式中等号成立，不放设l T（a k）=n﹣1时，d T（a k，a m）=1，d T（a m，a k）=0．所以 l T（a m）≤n﹣2．…（7分）所以l T（a k）+l T（a m）≤n﹣1+n﹣2=2n﹣3．所以，即．…（8分）（Ⅲ）对于满足l T（a i）＜n﹣1（i=1，2，3，…，n）的每一个集合T，集合S中都存在三个不同的元素e，f，g，使得d T（e，f）+d T（f，g）+d T（g，e）=3恒成立，理由如下：任取集合T，由l T（a i）＜n﹣1（i=1，2，3，…，n）可知，l T（a1），l T（a2），…，l T（a n）中存在最大数，不妨记为l T（f）（若最大数不唯一，任取一个）．因为 l T（f）＜n﹣1，所以存在e∈S，使得d T（f，e）=0，即（e，f）∈T．由l T（f）≥1可设集合G={x∈S|（f，x）∈T}≠∅．则G中一定存在元素g使得d T（g，e）=1．否则，l T（e）≥l T（f）+1，与l T（f）是最大数矛盾．所以d T（f，g）=1，d T（g，e）=1，即d T（e，f）+d T（f，g）+d T（g，e）=3．…（14分）点评：本题考查进行简单的合情推理，考查新定义，考查学生分析解决问题的能力，难度大．。