ACM二分图基础

合集下载

ACM培训——图论(一)

设x[i]等于1或0, 表示边e[i]是否属于生成树. 则比率 r = ∑(benifit[i] * x[i]) / ∑(cost[i] * x[i]), 0≤i<m . 令： z = ∑(benifit[i] * x[i]) - l * ∑(cost[i] * x[i]) 两个性质: 1. z单调递减证明: 因为cost为正数, 所以z随l的减小而增大. 2. z( max(r) ) = 0 证明: 若z( max(r) ) < 0, ∑(benifit[i] * x[i]) - max(r) * ∑(cost[i] * x[i]) < 0, 可化为 max(r) < max(r). 矛盾; 若z( max(r) ) >= 0, 根据性质1, 当z = 0 时r最大.
Prim算法
• 贪心准则
– 加入后仍形成树，且耗费最小 – 始终保持树的结构——Kruskal算法是森林
• 算法过程
– 从单一顶点的树T开始 – 不断加入耗费最小的边(u, v)，使T∪{(u, v)}仍为树 ——u、v中有一个已经在T中，另一个不在T中
Prim 算法过程
8 4 a 8 h 1 g 2 f b 2 i 7 6 10 c 7
一、图的BFS遍历
算法步骤： 1、用dis[]数组表示各点距离起点S的距离。dis[i]=-1表示i点还未被访问。用map[i][j]表示i点和j点之间是否有边。 2、将dis[s]初始化为0，将其它点的dis初始化为-1。将S点入队 3、while（队列非空） { 从队首出队一个元素u { 对于所有跟u有边相连的点v: if(dis[v]==-1) { dis[v]=dis[u]+1; v入队 } } }
int findp (int x) { return p[x]==-1?x:p[x]=findp(p[x]); } bool reunion (int x, int y) { int px=findp(x); int py=findp(y); if(px==py) { return false; } p[px]=py; return true; }

铁碳合金相图中每条线的含义AC、Acm、AC3、还有A点F点P点、Ld表示什么

铁碳合⾦相图中每条线的含义AC、Acm、AC3、还有A点F点P点、Ld表⽰什么在Fe-Fe3C相图中，230C有⼀根⽔平线代表什么意义？Fe-C平衡图中的特性线 AB—δ相的液相线 BC—γ相的液相线 CD— Fe3C的液相线 AH—δ相的固相线 JE—γ相的固相线 HN—碳在δ相中的溶解度线 JN—（δ+γ）相区与γ相区分界线 GP—⾼于A1时，碳在α相中的溶解度线 GOS—亚共析Fe-C合⾦的上临界点（A3） ES—碳在γ相中的溶解度线，过共析Fe-C合⾦的上临界点（Acm） PQ—低于A1时，碳在α相中的溶解度线HJB—γJ→LB+δH包晶转变线（δ0.09+L0.53 → A0.17） ECF—LC→γE+Fe3C共晶转变线（L4.30 → A2.11+Fe3C） MO—α- Fe磁性转变线（A2） PSK—γS→γF+Fe3C共析转变线（A0.77 → F0.0218+Fe3C），Fe-C合⾦的下临界点（A1） 230℃线—Fe3C磁性转变线（Ao）查看更多答案>>⼀⼂铁碳合⾦相图分析如下：Fe—Fe3C相图看起来⽐较复杂,但它仍然是由⼀些基本相图组成的,我们可以将Fe—Fe3C相图分成上下两个部分来分析.1.【共晶转变】（1）在1148℃,2.11%C的液相发⽣共晶转变:Lc (AE+Fe3C),（2）转变的产物称为莱⽒体,⽤符号Ld表⽰.（3）存在于1148℃~727℃之间的莱⽒体称为⾼温莱⽒体,⽤符号Ld表⽰,组织由奥⽒体和渗碳体组成;存在于727℃以下的莱⽒体称为变态莱⽒体或称低温莱⽒体,⽤符号Ldˊ表⽰,组织由渗碳体和珠光体组成.（4）低温莱⽒体是由珠光体,Fe3CⅡ和共晶Fe3C组成的机械混合物.经4%硝酸酒精溶液浸蚀后在显微镜下观察,其中珠光体呈⿊⾊颗粒状或短棒状分布在Fe3C基体上,Fe3CⅡ和共晶Fe3C交织在⼀起,⼀般⽆法分辨.2.【共析转变】（1）在727℃,0.77%的奥⽒体发⽣共析转变:AS (F+Fe3C),转变的产物称为珠光体.（2）共析转变与共晶转变的区别是转变物是固体⽽⾮液体.3.【特征点】（1）相图中应该掌握的特征点有:A,D,E,C,G(A3点),S(A1点),它们的含义⼀定要搞清楚.根据相图分析如下点：（2）相图中重要的点(14个)：1.组元的熔点: A (0, 1538) 铁的熔点;D (6.69, 1227) Fe3C的熔点2.同素异构转变点:N(0, 1394)δ-Fe γ-Fe;G(0, 912)γ-Fe α-Fe相图3.碳在铁中最⼤溶解度点:P(0.0218,727),碳在α-Fe 中的最⼤溶解度；E(2.11,1148),碳在γ-Fe 中的最⼤溶解度H (0.09,1495),碳在δ-Fe中的最⼤溶解度；Q(0.0008,RT),室温下碳在α-Fe 中的溶解度4.【三相共存点】S(共析点,0.77,727),(A+F +Fe3C)；C(共晶点,4.3,1148),( A+L +Fe3C)J(包晶点,0.17,1495)( δ+ A+L )5.【其它点】B(0.53,1495),发⽣包晶反应时液相的成分；F(6.69,1148 ) , 渗碳体；K (6.69,727 ) , 渗碳体6.【特性线】（1）相图中的⼀些线应该掌握的线有:ECF线,PSK线(A1线),GS线(A3线),ES线(ACM线)（2）⽔平线ECF为共晶反应线.（3）碳质量分数在2.11%～6.69%之间的铁碳合⾦, 在平衡结晶过程中均发⽣共晶反应.（4）⽔平线PSK为共析反应线（5）碳质量分数为0.0218%～6.69%的铁碳合⾦, 在平衡结晶过程中均发⽣共析反应.PSK线亦称A1线.（6）GS线是合⾦冷却时⾃A中开始析出F的临界温度线, 通常称A3线.（7）ES线是碳在A中的固溶线, 通常叫做Acm线.由于在1148℃时A中溶碳量最⼤可达2.11%,⽽在727℃时仅为0.77%, 因此碳质量分数⼤于0.77%的铁碳合⾦⾃1148℃冷⾄727℃的过程中,将从A中析出Fe3C.析出的渗碳体称为⼆次渗碳体(Fe3CII). Acm线亦为从A中开始析出Fe3CII的临界温度线.（8）PQ线是碳在F中固溶线.在727℃时F中溶碳量最⼤可达0.0218%, 室温时仅为0.0008%, 因此碳质量分数⼤于0.0008%的铁碳合⾦⾃727℃冷⾄室温的过程中, 将从F中析出Fe3C.析出的渗碳体称为三次渗碳体(Fe3CIII).PQ线亦为从F中开始析出Fe3CIII的临界温度线.Fe3CIII数量极少,往往予以忽略.（9）Ac1— 在加热过程中，奥⽒体开始形成的温度。

ACM软件配置

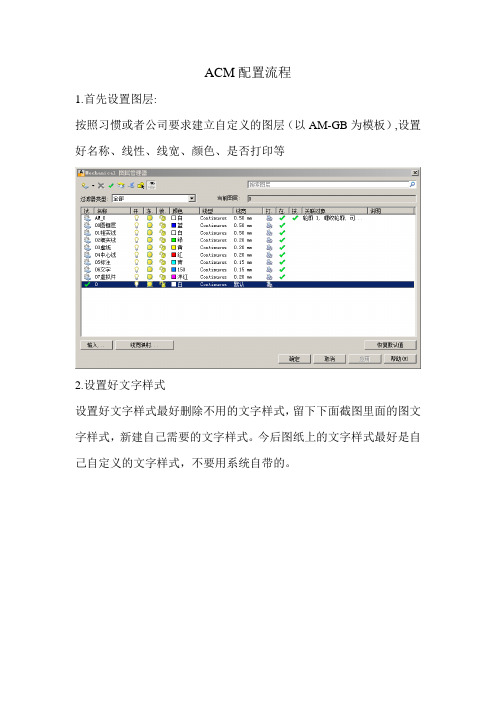
ACM配置流程1.首先设置图层:按照习惯或者公司要求建立自定义的图层（以AM-GB为模板）,设置好名称、线性、线宽、颜色、是否打印等2.设置好文字样式设置好文字样式最好删除不用的文字样式，留下下面截图里面的图文字样式，新建自己需要的文字样式。

今后图纸上的文字样式最好是自己自定义的文字样式，不要用系统自带的。

3.设置标注样式（最好新建），标注里面的文字样式选择自定义的文字样式4.设置AM标注4.1 进入进入工具-选项-AM标准选项卡，选择标准为国标双击右侧GB然后点击“设置”进行第一步自定义的图层与关联对象的映射设置，包括图层颜色、线性、线宽颜色、线性、线宽一般采用随层的样式4.2以上设置好后进入标注按照公司或者国标要求设置标注的表示法设置4.3设置工程图红框里面的是需要设置好自定义的标题栏，红线的图纸效果是4.4中心线设置4.5明细表设置4.5.1设置宽度4.5.2设置表头，文字高度等4.6BOM表设置4.7引出序号至于其余选项，根据自己的情况自己设定吧保存以上图纸为DWT模板，尽量不要覆盖软件自带模板5.自定义公司图框以刚才保存的模板新建图纸，绘制公司图框图框层为单独的层，不要使用图形的层（我的是00图框层）线宽这些自定义，不要随层所有的都在图框层上包括文字，文字采用第二步设置好的文字样式新建单行文字，对正方式为左对齐!GENTITLE-INSERT为图框插入点!GENTITLE-LL为图形左下边界!GENTITLE-LU为图形左上边界!GENTITLE-RU为图形右上边界!GENTITLE-MAX图纸最大边界设置好后坐标原点定义到图框左下角，然后定义图纸基点输入base 命令，选择左下角即可参照我的图形设置好久可以了自定义好A0-A4以及加长图纸后放到文件夹C:\Users\Public\Documents\Autodesk\AutoCAD Mechanical 2013\Acadm\Gen\Dwg（WIN7）系统自带文件可以新建个文件夹保存起来5.自定义公司标题栏以刚才保存的模板新建图纸，绘制公司标题栏图框层为单独的层，不要使用图形的层（我的是00图框层）线宽这些自定义，不要随层所有的都在图框层上包括文字，青色部分是需要填写的内容这部分采用定义属性的方式采用GEN-TITLE-NR{10}是图号，GEN-TITLE-DWG{7.14}名称GEN-TITLE-MAT1{10}是材料GEN-TITLE-SCA{4.8}是比例，当我们采用ACM自动调入图框是这是自动填写的。

ACM必须掌握的算法

ACM必须的算法1.最短路(Floyd、Dijstra,BellmanFord)2.最小生成树(先写个prim,kruscal要用并查集，不好写)3.大数（高精度）加减乘除4.二分查找. (代码可在五行以内)5.叉乘、判线段相交、然后写个凸包.6.BFS、DFS,同时熟练hash表(要熟，要灵活,代码要简)7.数学上的有：辗转相除（两行内），线段交点、多角形面积公式.8. 调用系统的qsort, 技巧很多，慢慢掌握.9. 任意进制间的转换第二阶段：练习复杂一点，但也较常用的算法。

：1. 二分图匹配（匈牙利），最小路径覆盖2. 网络流，最小费用流。

3. 线段树.4. 并查集。

5. 熟悉动态规划的各个典型：LCS、最长递增子串、三角剖分、记忆化dp6.博弈类算法。

博弈树，二进制法等。

7.最大团，最大独立集。

8.判断点在多边形内。

9. 差分约束系统. 10. 双向广度搜索、A*算法，最小耗散优先.相关的知识图论：路径问题 0/1边权最短路径 BFS 非负边权最短路径（Dijkstra）可以用Dijkstra解决问题的特征负边权最短路径Bellman-Ford Bellman-Ford的Yen-氏优化差分约束系统 Floyd 广义路径问题传递闭包极小极大距离 / 极大极小距离 EulerPath / Tour 圈套圈算法混合图的 Euler Path / TourHamilton Path / Tour 特殊图的Hamilton Path / Tour 构造生成树问题最小生成树第k小生成树最优比率生成树 0/1分数规划度限制生成树连通性问题强大的DFS算法无向图连通性割点割边二连通分支有向图连通性强连通分支 2-SAT最小点基有向无环图拓扑排序有向无环图与动态规划的关系二分图匹配问题一般图问题与二分图问题的转换思路最大匹配有向图的最小路径覆盖0 / 1矩阵的最小覆盖完备匹配最优匹配稳定婚姻网络流问题网络流模型的简单特征和与线性规划的关系最大流最小割定理最大流问题有上下界的最大流问题循环流最小费用最大流 / 最大费用最大流弦图的性质和判定组合数学解决组合数学问题时常用的思想逼近递推 / 动态规划概率问题Polya定理计算几何 / 解析几何计算几何的核心：叉积 / 面积解析几何的主力：复数基本形点直线，线段多边形凸多边形 / 凸包凸包算法的引进，卷包裹法Graham扫描法水平序的引进，共线凸包的补丁完美凸包算法相关判定两直线相交两线段相交点在任意多边形内的判定点在凸多边形内的判定经典问题最小外接圆近似O(n)的最小外接圆算法点集直径旋转卡壳，对踵点多边形的三角剖分数学 / 数论最大公约数Euclid算法扩展的Euclid算法同余方程 / 二元一次不定方程同余方程组线性方程组高斯消元法解mod 2域上的线性方程组整系数方程组的精确解法矩阵行列式的计算利用矩阵乘法快速计算递推关系分数分数树连分数逼近数论计算求N的约数个数求phi(N)求约数和快速数论变换……素数问题概率判素算法概率因子分解数据结构组织结构二叉堆左偏树二项树胜者树跳跃表样式图标斜堆reap统计结构树状数组虚二叉树线段树矩形面积并圆形面积并关系结构Hash表并查集路径压缩思想的应用 STL中的数据结构vectordequeset / map动态规划 / 记忆化搜索动态规划和记忆化搜索在思考方式上的区别最长子序列系列问题最长不下降子序列最长公共子序列最长公共不下降子序列一类NP问题的动态规划解法树型动态规划背包问题动态规划的优化四边形不等式函数的凸凹性状态设计规划方向线性规划常用思想二分最小表示法串KMPTrie结构后缀树/后缀数组 LCA/RMQ有限状态自动机理论排序选择/冒泡快速排序堆排序归并排序基数排序拓扑排序排序网络中级:一.基本算法:(1)C++的标准模版库的应用. (poj3096,poj3007)(2)较为复杂的模拟题的训练(poj3393,poj1472,poj3371,poj1027,poj2706)二.图算法:(1)差分约束系统的建立和求解. (poj1201,poj2983)(2)最小费用最大流(poj2516,poj2516,poj2195)(3)双连通分量(poj2942)(4)强连通分支及其缩点.(poj2186)(5)图的割边和割点(poj3352)(6)最小割模型、网络流规约(poj3308, )三.数据结构.(1)线段树. (poj2528,poj2828,poj2777,poj2886,poj2750)(2)静态二叉检索树. (poj2482,poj2352)(3)树状树组(poj1195,poj3321)(4)RMQ. (poj3264,poj3368)(5)并查集的高级应用. (poj1703,2492)(6)KMP算法. (poj1961,poj2406)四.搜索(1)最优化剪枝和可行性剪枝(2)搜索的技巧和优化 (poj3411,poj1724)(3)记忆化搜索(poj3373,poj1691)五.动态规划(1)较为复杂的动态规划(如动态规划解特别的施行商问题等)(poj1191,poj1054,poj3280,poj2029,poj2948,poj1925,poj3034)(2)记录状态的动态规划. (POJ3254,poj2411,poj1185)(3)树型动态规划(poj2057,poj1947,poj2486,poj3140)六.数学(1)组合数学:1.容斥原理.2.抽屉原理.3.置换群与Polya定理(poj1286,poj2409,poj3270,poj1026).4.递推关系和母函数.(2)数学.1.高斯消元法(poj2947,poj1487,poj2065,poj1166,poj1222)2.概率问题. (poj3071,poj3440)3.GCD、扩展的欧几里德(中国剩余定理) (poj3101)(3)计算方法.1.0/1分数规划. (poj2976)2.三分法求解单峰(单谷)的极值.3.矩阵法(poj3150,poj3422,poj3070)4.迭代逼近(poj3301)(4)随机化算法(poj3318,poj2454)(5)杂题.(poj1870,poj3296,poj3286,poj1095)七.计算几何学.(1)坐标离散化.(2)扫描线算法(例如求矩形的面积和周长并,常和线段树或堆一起使用).(poj1765,poj1177,poj1151,poj3277,po j2280,poj3004)(3)多边形的内核(半平面交)(poj3130,poj3335)(4)几何工具的综合应用.(poj1819,poj1066,poj2043,poj3227,poj2165,poj3429)高级:一.基本算法要求:(1)代码快速写成,精简但不失风格(poj2525,poj1684,poj1421,poj1048,poj2050,poj3306)(2)保证正确性和高效性. poj3434二.图算法:(1)度限制最小生成树和第K最短路. (poj1639)(2)最短路,最小生成树,二分图,最大流问题的相关理论(主要是模型建立和求解)(poj3155,poj2112,poj1966,poj3281,poj1087,poj2289,poj3216,poj2446(3)最优比率生成树. (poj2728)(4)最小树形图(poj3164)(5)次小生成树.(6)无向图、有向图的最小环三.数据结构.(1)trie图的建立和应用. (poj2778)(2)LCA和RMQ问题(LCA(最近公共祖先问题) 有离线算法(并查集+dfs) 和在线算法(RMQ+dfs)).(poj1330)(3)双端队列和它的应用(维护一个单调的队列,常常在动态规划中起到优化状态转移的目的). (poj2823)(4)左偏树(可合并堆).(5)后缀树(非常有用的数据结构,也是赛区考题的热点).(poj3415,poj3294)四.搜索(1)较麻烦的搜索题目训练(poj1069,poj3322,poj1475,poj1924,poj2049,poj3426)(2)广搜的状态优化:利用M进制数存储状态、转化为串用hash表判重、按位压缩存储状态、双向广搜、A*算法.(poj1768,poj1184,poj1872,poj1324,poj2046,poj1482)(3)深搜的优化:尽量用位运算、一定要加剪枝、函数参数尽可能少、层数不易过大、可以考虑双向搜索或者是轮换搜索、IDA*算法. (poj3131,poj2870,poj2286)五.动态规划(1)需要用数据结构优化的动态规划.(poj2754,poj3378,poj3017)(2)四边形不等式理论.(3)较难的状态DP(poj3133)六.数学(1)组合数学.1.MoBius反演(poj2888,poj2154)2.偏序关系理论.(2)博奕论.1.极大极小过程(poj3317,poj1085)2.Nim问题.七.计算几何学.(1)半平面求交(poj3384,poj2540)(2)可视图的建立(poj2966)(3)点集最小圆覆盖.(4)对踵点(poj2079)八.综合题.(poj3109,poj1478,poj1462,poj2729,poj2048,poj333 6,poj3315,poj2148,poj1263)初期:一.基本算法:(1)枚举. (poj1753,poj2965) (2)贪心(poj1328,poj2109,poj2586)(3)递归和分治法. (4)递推.(5)构造法.(poj3295) (6)模拟法.(poj1068,poj2632,poj1573,poj2993,poj2996)二.图算法:(1)图的深度优先遍历和广度优先遍历.(2)最短路径算法(dijkstra,bellman-ford,floyd,heap+dijkstra)(poj1860,poj3259,poj1062,poj2253,poj1125,po j2240)(3)最小生成树算法(prim,kruskal)(poj1789,poj2485,poj1258,poj3026)(4)拓扑排序 (poj1094)(5)二分图的最大匹配 (匈牙利算法) (poj3041,poj3020)(6)最大流的增广路算法(KM算法). (poj1459,poj3436)三.数据结构.(1)串 (poj1035,poj3080,poj1936)(2)排序(快排、归并排(与逆序数有关)、堆排)(poj2388,poj2299)(3)简单并查集的应用.(4)哈希表和二分查找等高效查找法(数的Hash,串的Hash)(poj3349,poj3274,POJ2151,poj1840,poj2002,po j2503)(5)哈夫曼树(poj3253)(6)堆(7)trie树(静态建树、动态建树) (poj2513)四.简单搜索(1)深度优先搜索(poj2488,poj3083,poj3009,poj1321,poj2251)(2)广度优先搜索(poj3278,poj1426,poj3126,poj3087.poj3414)(3)简单搜索技巧和剪枝(poj2531,poj1416,poj2676,1129)五.动态规划(1)背包问题. (poj1837,poj1276)(2)型如下表的简单DP(可参考lrj的书 page149):1.E[j]=opt{D+w(i,j)}(poj3267,poj1836,poj1260,poj2533)2.E[i,j]=opt{D[i-1,j]+xi,D[i,j-1]+yj,D[i-1][j-1 ]+zij} (最长公共子序列)(poj3176,poj1080,poj1159)3.C[i,j]=w[i,j]+opt{C[i,k-1]+C[k,j]}.(最优二分检索树问题)六.数学(1)组合数学:1.加法原理和乘法原理.2.排列组合.3.递推关系.(POJ3252,poj1850,poj1019,poj1942)(2)数论.1.素数与整除问题2.进制位.3.同余模运算.(poj2635, poj3292,poj1845,poj2115)(3)计算方法.1.二分法求解单调函数相关知识.(poj3273,poj3258,poj1905,poj3122)七.计算几何学.(1)几何公式.(2)叉积和点积的运用(如线段相交的判定,点到线段的距离等). (poj2031,poj1039)(3)多边型的简单算法(求面积)和相关判定(点在多边型内,多边型是否相交)(poj1408,poj1584)(4)凸包. (poj2187,poj1113)。

ACM算法模板(吉林大学)

目录目录 (1)Graph 图论 (3)|DAG的深度优先搜索标记 (3)|无向图找桥 (3)|无向图连通度(割) (3)|最大团问题DP+DFS (3)|欧拉路径O(E) (3)|D IJKSTRA数组实现O（N^2） (3)|D IJKSTRA O(E* LOG E) (4)|B ELLMAN F ORD单源最短路O(VE) (4)|SPFA(S HORTEST P ATH F ASTER A LGORITHM) (4)|第K短路（D IJKSTRA） (5)|第K短路（A*） (5)|P RIM求MST (6)|次小生成树O(V^2) (6)|最小生成森林问题(K颗树)O(MLOGM) (6)|有向图最小树形图 (6)|M INIMAL S TEINER T REE (6)|T ARJAN强连通分量 (7)|弦图判断 (7)|弦图的PERFECT ELIMINATION点排列 (7)|稳定婚姻问题O(N^2) (7)|拓扑排序 (8)|无向图连通分支(DFS/BFS邻接阵) (8)|有向图强连通分支(DFS/BFS邻接阵)O(N^2) (8)|有向图最小点基(邻接阵)O(N^2) (9)|F LOYD求最小环 (9)|2-SAT问题 (9)Network 网络流 (11)|二分图匹配（匈牙利算法DFS实现） (11)|二分图匹配（匈牙利算法BFS实现） (11)|二分图匹配（H OPCROFT－C ARP的算法） (11)|二分图最佳匹配（KUHN MUNKRAS算法O(M*M*N)）..11 |无向图最小割O(N^3) (12)|有上下界的最小(最大)流 (12)|D INIC最大流O(V^2*E) (12)|HLPP最大流O(V^3) (13)|最小费用流O(V*E* F).......................................13|最小费用流O(V^2* F). (14)|最佳边割集 (15)|最佳点割集 (15)|最小边割集 (15)|最小点割集（点连通度） (16)|最小路径覆盖O(N^3) (16)|最小点集覆盖 (16)Structure 数据结构 (17)|求某天是星期几 (17)|左偏树合并复杂度O(LOG N) (17)|树状数组 (17)|二维树状数组 (17)|T RIE树(K叉) (17)|T RIE树(左儿子又兄弟) (18)|后缀数组O(N* LOG N) (18)|后缀数组O(N) (18)|RMQ离线算法O(N*LOG N)+O(1) (19)|RMQ(R ANGE M INIMUM/M AXIMUM Q UERY)-ST算法(O(NLOGN +Q)) (19)|RMQ离线算法O(N*LOG N)+O(1)求解LCA (19)|LCA离线算法O(E)+O(1) (20)|带权值的并查集 (20)|快速排序 (20)|2台机器工作调度 (20)|比较高效的大数 (20)|普通的大数运算 (21)|最长公共递增子序列O(N^2) (22)|0-1分数规划 (22)|最长有序子序列（递增/递减/非递增/非递减） (22)|最长公共子序列 (23)|最少找硬币问题（贪心策略-深搜实现） (23)|棋盘分割 (23)|汉诺塔 (23)|STL中的PRIORITY_QUEUE (24)|堆栈 (24)|区间最大频率 (24)|取第K个元素 (25)|归并排序求逆序数 (25)|逆序数推排列数 (25)|二分查找 (25)|二分查找（大于等于V的第一个值） (25)|所有数位相加 (25)Number 数论 (26)|递推求欧拉函数PHI(I) (26)|单独求欧拉函数PHI(X) (26)|GCD最大公约数 (26)|快速GCD (26)|扩展GCD (26)|模线性方程 A * X = B (% N) (26)|模线性方程组 (26)|筛素数[1..N] (26)|高效求小范围素数[1..N] (26)|随机素数测试(伪素数原理) (26)|组合数学相关 (26)|P OLYA计数 (27)|组合数C(N, R) (27)|最大1矩阵 (27)|约瑟夫环问题（数学方法） (27)|约瑟夫环问题（数组模拟） (27)|取石子游戏1 (27)|集合划分问题 (27)|大数平方根（字符串数组表示） (28)|大数取模的二进制方法 (28)|线性方程组A[][]X[]=B[] (28)|追赶法解周期性方程 (28)|阶乘最后非零位,复杂度O(NLOGN) (29)递归方法求解排列组合问题 (30)|类循环排列 (30)|全排列 (30)|不重复排列 (30)|全组合 (31)|不重复组合 (31)|应用 (31)模式串匹配问题总结 (32)|字符串H ASH (32)|KMP匹配算法O(M+N) (32)|K ARP-R ABIN字符串匹配 (32)|基于K ARP-R ABIN的字符块匹配 (32)|函数名: STRSTR (32)|BM算法的改进的算法S UNDAY A LGORITHM (32)|最短公共祖先（两个长字符串） (33)|最短公共祖先（多个短字符串）...............................33Geometry 计算几何.. (34)|G RAHAM求凸包O(N* LOG N) (34)|判断线段相交 (34)|求多边形重心 (34)|三角形几个重要的点 (34)|平面最近点对O(N* LOG N) (34)|L IUCTIC的计算几何库 (35)|求平面上两点之间的距离 (35)|(P1-P0)*(P2-P0)的叉积 (35)|确定两条线段是否相交 (35)|判断点P是否在线段L上 (35)|判断两个点是否相等 (35)|线段相交判断函数 (35)|判断点Q是否在多边形内 (35)|计算多边形的面积 (35)|解二次方程A X^2+B X+C=0 (36)|计算直线的一般式A X+B Y+C=0 (36)|点到直线距离 (36)|直线与圆的交点，已知直线与圆相交 (36)|点是否在射线的正向 (36)|射线与圆的第一个交点 (36)|求点P1关于直线LN的对称点P2 (36)|两直线夹角（弧度） (36)ACM/ICPC竞赛之STL (37)ACM/ICPC竞赛之STL简介 (37)ACM/ICPC竞赛之STL--PAIR (37)ACM/ICPC竞赛之STL--VECTOR (37)ACM/ICPC竞赛之STL--ITERATOR简介 (38)ACM/ICPC竞赛之STL--STRING (38)ACM/ICPC竞赛之STL--STACK/QUEUE (38)ACM/ICPC竞赛之STL--MAP (40)ACM/ICPC竞赛之STL--ALGORITHM (40)STL IN ACM (41)头文件 (42)线段树 (43)求矩形并的面积（线段树+离散化+扫描线） (43)求矩形并的周长（线段树+离散化+扫描线） (44)Graph 图论/*==================================================*\| DAG的深度优先搜索标记| INIT: edge[][]邻接矩阵; pre[], post[], tag全置0;| CALL: dfstag(i, n); pre/post:开始/结束时间\*==================================================*/int edge[V][V], pre[V], post[V], tag;void dfstag(int cur, int n){ // vertex: 0 ~ n-1pre[cur] = ++tag;for (int i=0; i<n; ++i) if (edge[cur][i]) {if (0 == pre[i]) {printf("Tree Edge!\n");dfstag(i,n);} else {if (0 == post[i]) printf("Back Edge!\n");else if (pre[i] > pre[cur])printf("Down Edge!\n");else printf("Cross Edge!\n");}}post[cur] = ++tag;}/*==================================================*\| 无向图找桥| INIT: edge[][]邻接矩阵;vis[],pre[],anc[],bridge 置0;| CALL: dfs(0, -1, 1, n);\*==================================================*/int bridge, edge[V][V], anc[V], pre[V], vis[V];void dfs(int cur, int father, int dep, int n){ // vertex: 0 ~ n-1if (bridge) return;vis[cur] = 1; pre[cur] = anc[cur] = dep;for (int i=0; i<n; ++i) if (edge[cur][i]) {if (i != father && 1 == vis[i]) {if (pre[i] < anc[cur])anc[cur] = pre[i];//back edge}if (0 == vis[i]) { //tree edgedfs(i,cur,dep+1,n);if (bridge) return;if (anc[i] < anc[cur]) anc[cur] = anc[i];if (anc[i] > pre[cur]) { bridge = 1; return; } }}vis[cur] = 2;}/*==================================================*\| 无向图连通度(割)| INIT: edge[][]邻接矩阵;vis[],pre[],anc[],deg[]置为0;| CALL: dfs(0, -1, 1, n);| k=deg[0], deg[i]+1(i=1…n-1)为删除该节点后得到的连通图个数| 注意:0作为根比较特殊!\*==================================================*/int edge[V][V], anc[V], pre[V], vis[V], deg[V];void dfs(int cur, int father, int dep, int n){// vertex: 0 ~ n-1int cnt = 0;vis[cur] = 1; pre[cur] = anc[cur] = dep;for (int i=0; i<n; ++i) if (edge[cur][i]) {if (i != father && 1 == vis[i]) {if (pre[i] < anc[cur])anc[cur] = pre[i];//back edge}if (0 == vis[i]) { //tree edgedfs(i,cur,dep+1,n);++cnt; // 分支个数if (anc[i] < anc[cur]) anc[cur] = anc[i];if ((cur==0 && cnt>1) ||(cnt!=0 && anc[i]>=pre[cur]))++deg[cur];// link degree of a vertex }}vis[cur] = 2;} /*==================================================*\| 最大团问题 DP + DFS| INIT: g[][]邻接矩阵;| CALL: res = clique(n);\*==================================================*/int g[V][V], dp[V], stk[V][V], mx;int dfs(int n, int ns, int dep){if (0 == ns) {if (dep > mx) mx = dep;return 1;}int i, j, k, p, cnt;for (i = 0; i < ns; i++) {k = stk[dep][i]; cnt = 0;if (dep + n - k <= mx) return 0;if (dep + dp[k] <= mx) return 0;for (j = i + 1; j < ns; j++) {p=stk[dep][j];if (g[k][p]) stk[dep + 1][cnt++] = p;}dfs(n, cnt, dep + 1);}return 1;}int clique(int n){int i, j, ns;for (mx = 0, i = n - 1; i >= 0; i--) {// vertex: 0 ~ n-1for (ns = 0, j = i + 1; j < n; j++)if (g[i][j]) stk[1][ ns++ ] = j;dfs(n, ns, 1); dp[i] = mx;}return mx;}/*==================================================*\| 欧拉路径O(E)| INIT: adj[][]置为图的邻接表; cnt[a]为a点的邻接点个数;| CALL: elpath(0); 注意:不要有自向边\*==================================================*/int adj[V][V], idx[V][V], cnt[V], stk[V], top;int path(int v){for (int w ; cnt[v] > 0; v = w) {stk[ top++ ] = v;w = adj[v][ --cnt[v] ];adj[w][ idx[w][v] ] = adj[w][ --cnt[w] ];// 处理的是无向图—-边是双向的，删除v->w后，还要处理删除w->v}return v;}void elpath (int b, int n){ // begin from b int i, j;for (i = 0; i < n; ++i) // vertex: 0 ~ n-1 for (j = 0; j < cnt[i]; ++j)idx[i][ adj[i][j] ] = j;printf("%d", b);for (top = 0; path(b) == b && top != 0; ) {b = stk[ --top ];printf("-%d", b);}printf("\n");}/*==================================================*\| Dijkstra数组实现O（N^2）| Dijkstra --- 数组实现(在此基础上可直接改为STL的Queue实现)| lowcost[] --- beg到其他点的最近距离| path[] -- beg为根展开的树，记录父亲结点\*==================================================*/#define INF 0x03F3F3F3Fconst int N;int path[N], vis[N];void Dijkstra(int cost[][N], int lowcost[N], int n, int beg){ int i, j, min;memset(vis, 0, sizeof(vis));vis[beg] = 1;for (i=0; i<n; i++){lowcost[i] = cost[beg][i]; path[i] = beg;}lowcost[beg] = 0;path[beg] = -1; // 树根的标记int pre = beg;for (i=1; i<n; i++){min = INF;dist[v] = dist[u] + c;for (j=0; j<n; j++)// 下面的加法可能导致溢出,INF 不能取太大if (vis[j]==0 &&lowcost[pre]+cost[pre][j]<lowcost[j]){lowcost[j] =lowcost[pre] + cost[pre][j]; path[j] = pre; } for (j=0; j<n; j++) if (vis[j] == 0 && lowcost[j] < min){ min = lowcost[j]; pre = j; } vis[pre] = 1; } } /*==================================================*\ | Dijkstra O(E * log E) | INIT: 调用init(nv, ne)读入边并初始化; | CALL: dijkstra(n, src); dist[i]为src 到i 的最短距离 \*==================================================*/ #define typec int // type of cost const typec inf = 0x3f3f3f3f; // max of cost typec cost[E], dist[V]; int e, pnt[E], nxt[E], head[V], prev[V], vis[V]; struct qnode { int v; typec c; qnode (int vv = 0, typec cc = 0) : v(vv), c(cc) {} bool operator < (const qnode& r) const { return c>r.c; } }; void dijkstra(int n, const int src){ qnode mv; int i, j, k, pre; priority_queue<qnode> que; vis[src] = 1; dist[src] = 0; que.push(qnode(src, 0)); for (pre = src, i=1; i<n; i++) { for (j = head[pre]; j != -1; j = nxt[j]) { k = pnt[j]; if (vis[k] == 0 && dist[pre] + cost[j] < dist[k]){ dist[k] =dist[pre] + cost[j]; que.push(qnode(pnt[j], dist[k])); prev[k] = pre; } } while (!que.empty() && vis[que.top().v] == 1) que.pop(); if (que.empty()) break ; mv = que.top(); que.pop(); vis[pre = mv.v] = 1; } } inline void addedge(int u, int v, typec c){ pnt[e] = v; cost[e] = c; nxt[e] = head[u]; head[u] = e++; } void init(int nv, int ne){ int i, u, v; typec c; e = 0;memset(head, -1, sizeof (head));memset(vis, 0, sizeof (vis));memset(prev, -1, sizeof (prev));for (i = 0; i < nv; i++) dist[i] = inf;for (i = 0; i < ne; ++i) {scanf("%d%d%d", &u, &v, &c);// %d: type of cost addedge(u, v, c); // vertex: 0 ~ n-1, 单向边 }}/*==================================================*\| BellmanFord 单源最短路O(VE)| 能在一般情况下，包括存在负权边的情况下，解决单源最短路径问题| INIT: edge[E][3]为边表| CALL: bellman(src);有负环返回0;dist[i]为src 到i 的最短距| 可以解决差分约束系统: 需要首先构造约束图，构造不等式时>=表示求最小值, 作为最长路，<=表示求最大值, 作为最短路（v-u <= c:a[u][v] = c ）\*==================================================*/#define typec int // type of costconst typec inf=0x3f3f3f3f; // max of costint n, m, pre[V], edge[E][3];typec dist[V];int relax (int u, int v, typec c){if (dist[v] > dist[u] + c) {pre[v] = u; return 1; } return 0; } int bellman (int src){ int i, j;for (i=0; i<n; ++i) { dist[i] = inf; pre[i] = -1; } dist[src] = 0; bool flag; for (i=1; i<n; ++i){ flag = false; // 优化 for (j=0; j<m; ++j) { if( 1 == relax(edge[j][0], edge[j][1], edge[j][2]) ) flag = true; } if( !flag ) break; } for (j=0; j<m; ++j) { if (1 == relax(edge[j][0], edge[j][1], edge[j][2])) return 0; // 有负圈 } return 1; } /*==================================================*\ | SPFA(Shortest Path Faster Algorithm) Bellman-Ford 算法的一种队列实现，减少了不必要的冗余计算。

ACM基础——图

Status CreateMG(MGraph &G){ //无向图的构造 int i,j,k,v1,v2; scanf("%d%d",&G.vexnum,&G.arcnum); for(i=0;i<G.vexnum;i++) scanf(“%d”,&G.vexs[i]); //输入顶点数据 for(i=0;i<G.vexnum;i++) for(j=0;j<G.vexnum;j++) G.arcs[i][j].adj = 0; //初始化结束 for(k=0;k<G.arcnum;k++){ scanf("%d%d",&v1,&v2); i=LocateVex(G,v1); j=LocateVex(G,v2); G.arcs[i][j].adj=1; G.arcs[j][i].adj=G.arcs[i][j].adj; //创建有向图屏蔽此句 } return OK; }
0 0 0
1
1 0 0
Байду номын сангаас
3
2 1 2
V2
V4
V3 V4
图的邻接矩阵表示
# define INFINITY INT_MAX //表示不可达 # define MAX_VERTEX_NUM 20 //最大顶点个数
typedef int VRType;
//顶点关系类型
typedef int VertexType; //顶点数据类型
图
• 图的基本概念 • 图的存储 • 图的遍历
图(Graph)是由有穷非空的顶点集合和一个描述顶点之间关系的边（或者弧）的集合组成。

网络流题目集锦

(2010-02-07 18:00:40)转载分类：ACM标签：杂谈最大流POJ 1273 Drainage DitchesPOJ 1274 The Perfect Stall (二分图匹配)POJ 1698 Alice's ChancePOJ 1459 Power NetworkPOJ 2112 Optimal Milking (二分)POJ 2455 Secret Milking Machine (二分)POJ 3189 Steady Cow Assignment (枚举)POJ 1637 Sightseeing tour (混合图欧拉回路)POJ 3498 March of the Penguins (枚举汇点)POJ 1087 A Plug for UNIXPOJ 1149 Pigs (构图题)ZOJ 2760 How Many Shortest Path (边不相交最短路的条数)POJ 2391 Ombrophobic Bovines (必须拆点，否则有BUG)WHU 1124 Football Coach (构图题)SGU 326 Perspective (构图题，类似于 WHU 1124)UVa 563 CrimewaveUVa 820 Internet BandwidthPOJ 3281 Dining (构图题)POJ 3436 ACM Computer FactoryPOJ 2289 Jamie's Contact Groups (二分)SGU 438 The Glorious Karlutka River =) (按时间拆点)SGU 242 Student's Morning (输出一组解)SGU 185 Two shortest (Dijkstra 预处理，两次增广，必须用邻接阵实现，否则 MLE) HOJ 2816 Power LinePOJ 2699 The Maximum Number of Strong Kings (枚举+构图)ZOJ 2332 GemsJOJ 2453 Candy (构图题)SOJ3312 Stockholm KnightsSOJ3353 Total FlowSOJ2414 Leapin' Lizards最小割SOJ3106 Dual Core CPUSOJ3109 Space flightSOJ3107 SelectSOJ3185 Black and whiteSOJ3254 Rain and FgjSOJ3134 windy和水星 -- 水星交通HOJ 2634 How to earn moreZOJ 2071 Technology Trader (找割边)HNU 10940 CoconutsZOJ 2532 Internship (找关键割边)POJ 1815 Friendship (字典序最小的点割集)POJ 3204 Ikki's Story I - Road Reconstruction (找关键割边) POJ 3308 ParatroopersPOJ 3084 Panic RoomPOJ 3469 Dual Core CPUZOJ 2587 Unique Attack (最小割的唯一性判定)POJ 2125 Destroying The Graph (找割边)ZOJ 2539 Energy MinimizationTJU 2944 Mussy Paper (最大权闭合子图)POJ 1966 Cable TV Network (无向图点连通度)HDU 1565 方格取数(1) (最大点权独立集)HDU 1569 方格取数(2) (最大点权独立集)POJ 2987 Firing (最大权闭合子图)SPOJ 839 Optimal Marks (将异或操作转化为对每一位求最小割)HOJ 2811 Earthquake Damage (最小点割集)2008 Beijing Regional Contest Problem A Destroying the bus stations ( BFS 预处理 )( ZOJ 2676 Network Wars (参数搜索)POJ 3155 Hard Life (参数搜索)ZOJ 3241 Being a Hero有上下界ZOJ 2314 Reactor Cooling (无源汇可行流)POJ 2396 Budget (有源汇可行流)SGU 176 Flow Construction (有源汇最小流)ZOJ 3229 Shoot the Bullet (有源汇最大流)HDU 3157 Crazy Circuits (有源汇最小流)最小费用流HOJ 2715 Matrix3HOJ 2739 The Chinese Postman ProblemPOJ 2175 Evacuation Plan (消一次负圈)POJ 3422 Kaka's Matrix Travels (与 Matrix3 类似)POJ 2516 Minimum Cost (按物品种类多次建图)POJ 2195 Going HomeBUAA 1032 Destroying a PaintingPOJ 2400 Supervisor, Supervisee (输出所有最小权匹配)POJ 3680 IntervalsHOJ 2543 Stone IVPOJ 2135 Farm TourBASHU2445 餐巾问题---------------------------------------------onmylove原创最大流题目：TC：Single Round Match 200 Round 1 – Division I, Level Three Single Round Match 236 Round 1 – Division I, Level ThreeSingle Round Match 399 Round 1 – Division I, Level Three 同Hoj1024:2003 TCO Semifinal Round 4 – Division I, Level Three 2004 TCCC Championship Round – Division I, Level Three 2005 TCO Sponsor Track Round 3 – Division I, Level One混合图的欧拉回路Poj1637: ：求增广边：Poj3204：类似：Hoj1082: &pid=6pku图论、网络流入门题总结、汇总(2009-10-07 23:25:25)转载分类：acm_图论题标签：杂谈POJ 2449 Remmarguts' Date(中等)题意：经典问题：K短路解法：dijkstra+A*(rec)，方法很多相关：该题亦放在搜索推荐题中POJ 3013 - Big Christmas Tree(基础)题意：最简单最短路，但此题要过，需要较好的程序速度和，还要注意精度解法：DijkstraPOJ 3463 - Sightseeing(中等)题意：最短路和比最短路大1的路的数量解法：需要真正理解dijkstraPOJ 3613 - Cow Relays(较难)题意：求经过N条边的最短路解法：floyd + 倍增，贪心POJ 3621 - Sightseeing Cows(中等)题意：求一个环路，欢乐值 / 总路径最大解法：参数搜索 + 最短路(ms 原始的bellman tle, 用spfa才过) POJ 3635 - full tank?(中等)题意：最短路变形解法：广搜相关：生成树问题基本的生成树就不放上来了POJ 1639 - Picnic Planning(较难)题意：顶点度数有限制的最小生成树解法：贪心 + prim/kruskalPOJ 1679 - The Unique MST(基础)题意：判断MST是否唯一解法：prim就行，不过还是易错的题POJ 2728 - Desert King(中等)题意：所谓最优比率生成树解法：参数搜索 + primPOJ 3164 - Command Network(难)题意：最小树形图解法：刘朱算法，这个考到的可能性比较小吧？POJ 3522 - Slim Span(基础)题意：求一颗生成树，让最大边最小边差值最小解法：kruskal活用连通性，度数，拓扑问题此类问题主要牵扯到DFS，缩点等技巧POJ 1236 - Network of Schools(基础)题意：问添加多少边可成为完全连通图解法：缩点，看度数POJ 1659 - Frogs' Neighborhood(基础)题意：根据度序列构造图解法：贪心，详细证明参见havel定理POJ 2553 - The Bottom of a Graph(基础)POJ 2186 - Popular Cows(基础)题意：强连通分量缩点图出度为0的点POJ 2762 - Going from u to v or from v to u?(中等)题意：单向连通图判定解法：缩点 + dp找最长链POJ 2914 - Minimum Cut(难)题意：无向图最小割解法：Stoer-Wagner算法，用网络流加枚举判定会挂POJ 2942 - Knights of the Round Table(难)题意：求双联通分量(或称块)中是否含奇圈解法：求出双连通分量后做黑白染色进行二分图图判定相关： 3177 - Redundant Paths(中等)POJ 3352 - Road Construction(中等)题意：添加多少条边可成为双向连通图解法：把割边分开的不同分量缩点构树，看入度建议对比下1236，有向图添加多少条边变成强连通图POJ 3249 - Test for Job(基础)解法：bfs / dfs + dpPOJ 3592 - Instantaneous Transference(基础)解法：缩点，最长路，少人做的水题，注意细节POJ 3687 - Labeling Balls(中等)解法：拓扑排序POJ 3694 - Network(中等)解法：双连通分量+并查集2-SAT问题此类问题理解合取式的含义就不难POJ 2723 - Get Luffy Out(中等)POJ 2749 - Building roads(较难)解法：二分 + 2-SAT判定POJ 3207 - Ikki's Story IV - Panda's Trick(基础) 解法：简单的2-sat，不过其他方法更快POJ 3648- Wedding(中等)解法：用2-sat做会比较有意思，但是暴搜照样0ms POJ 3678 - Katu Puzzle(基础)解法：直接按合取式构图验证就行了POJ 3683 - Priest John's Busiest Day(中等)解法：n^2枚举点之间的相容性构图，求解2-SAT最大流问题变形很多，最小割最大流定理的理解是关键POJ 1149 - PIGS(较难)绝对经典的构图题POJ 1273 - Drainage Ditches(基础)最大流入门POJ 1459 - Power Network(基础)基本构图POJ 1637 - Sightseeing tour(Crazy)题意：求混合图的欧拉迹是否存在解法：无向边任意定向，构图，详建黑书P324POJ 1815 - Friendship(中等)题意：求最小点割解法：拆点转换为边割相关： 1966 - Cable TV Network(中等)题意：去掉多少点让图不连通解法：任定一源点，枚举汇点求点割集(转换到求边割)，求其中最小的点割POJ 2112 - Optimal Milking(基础)二分枚举，最大流POJ 2391 - Ombrophobic Bovines(中等)题意：floyd, 拆点，二分枚举相关： 2396 - Budget(中等)题意：有源汇的上下界可行流解法：用矩阵-网络流模型构图，然后拆边相关：，最小割模型在竞赛中的应用POJ 2455 - Secret Milking Machine(基础)二分枚举，一般来说需要写对边容量的更新操作而不是每次全部重新构图POJ 2699 - The Maximum Number of Strong Kings(较难)解法：枚举人数 + 最大流(感谢xpcnq_71大牛的建图的提示)POJ 2987 - Firing(较难)题意：最大权闭包解法：先边权放大，第一问总量-最大流，第二问求最小割相关：&_c02_owner=1Profit(中等)最大权闭包图的特殊情况ZOJ 2071 - Technology Trader 也是此类型，懒了没做3084 - Panic Room(中等，好题)题意：略解法：根据最小割建模POJ 3155 - Hard Life(很挑战一题)题意：最大密度子图解法：参数搜索 + 最大权闭合图，的论文(nb解法)最小割模型在信息学竞赛中的应用一文中也有讲POJ 3189 - Steady Cow Assignment(中等)题意：寻找最小的区间完成匹配解法：这题充分说明SAP的强大，纯暴力可过。

acm竞赛知识点

acm竞赛知识点
以下是ACM竞赛的主要知识点：
1、基础算法：
排序算法（如快速排序、归并排序）
搜索算法（如二分搜索）
递归与分治算法
2、图论：
最短路径算法（如Dijkstra算法、Bellman-Ford算法）最小生成树算法（如Prim算法、Kruskal算法）
拓扑排序
图的遍历（深度优先搜索DFS、广度优先搜索BFS）
3、动态规划：
背包问题
最长公共子序列（LCS）
最长递增子序列（LIS）
矩阵链乘法
4、数据结构：
栈和队列
链表和树的基本操作
哈希表
并查集
5、计算几何：
点和向量的基本运算
线段相交判定
凸包算法
6、字符串处理：
字符串匹配算法（如KMP、Boyer-Moore）后缀数组
字符串编辑距离
7、数论：
质数判定
最大公约数和最小公倍数
快速幂
8、图的高级算法：
最大流算法（如Ford-Fulkerson算法）二分图匹配
最小割算法
9、动态规划优化：状态压缩
斜率优化
记忆化搜索
10、其他：
模拟和贪心算法
数学问题
网络流问题。

ACMer需要掌握的算法讲解

ACM主要算法介绍初期篇一、基本算法(1)枚举(poj1753, poj2965)(2)贪心(poj1328, poj2109, poj2586)(3)递归和分治法(4)递推(5)构造法(poj3295)(6)模拟法(poj1068, poj2632, poj1573, poj2993, poj2996)二、图算法(1)图的深度优先遍历和广度优先遍历(2)最短路径算法(dijkstra, bellman-ford, floyd, heap+dijkstra)(poj1860, poj3259, poj1062, poj2253, poj1125, poj2240)(3)最小生成树算法(prim, kruskal)(poj1789, poj2485, poj1258, poj3026)(4)拓扑排序(poj1094)(5)二分图的最大匹配(匈牙利算法)(poj3041, poj3020)(6)最大流的增广路算法(KM算法)(poj1459, poj3436)三、数据结构(1)串(poj1035, poj3080, poj1936)(2)排序(快排、归并排(与逆序数有关)、堆排)(poj2388, poj2299)(3)简单并查集的应用(4)哈希表和二分查找等高效查找法(数的Hash, 串的Hash)(poj3349, poj3274, POJ2151, poj1840, poj2002, poj2503)(5)哈夫曼树(poj3253)(6)堆(7)trie树(静态建树、动态建树)(poj2513)四、简单搜索(1)深度优先搜索(poj2488, poj3083, poj3009, poj1321, poj2251)(2)广度优先搜索(poj3278, poj1426, poj3126, poj3087, poj3414)(3)简单搜索技巧和剪枝(poj2531, poj1416, poj2676, 1129)五、动态规划(1)背包问题(poj1837, poj1276)(2)型如下表的简单DP(可参考lrj的书page149)：1.E[j]=opt{D+w(i,j)} (poj3267, poj1836, poj1260, poj2533)2.E[i,j]=opt{D[i-1,j]+xi,D[i,j-1]+yj,D[i-1][j-1]+zij} (最长公共子序列)(poj3176, poj1080, poj1159)3.C[i,j]=w[i,j]+opt{C[i,k-1]+C[k,j]} (最优二分检索树问题)六、数学(1)组合数学1.加法原理和乘法原理2.排列组合3.递推关系(poj3252, poj1850, poj1019, poj1942)(2)数论1.素数与整除问题2.进制位3.同余模运算(poj2635, poj3292, poj1845, poj2115)(3)计算方法1.二分法求解单调函数相关知识(poj3273, poj3258, poj1905, poj3122)七、计算几何学(1)几何公式(2)叉积和点积的运用(如线段相交的判定，点到线段的距离等)(poj2031, poj1039)(3)多边型的简单算法(求面积)和相关判定(点在多边型内，多边型是否相交)(poj1408, poj1584)(4)凸包(poj2187, poj1113)中级篇一、基本算法(1)C++的标准模版库的应用(poj3096, poj3007)(2)较为复杂的模拟题的训练(poj3393, poj1472, poj3371, poj1027,poj2706)二、图算法(1)差分约束系统的建立和求解(poj1201, poj2983)(2)最小费用最大流(poj2516, poj2195)(3)双连通分量(poj2942)(4)强连通分支及其缩点(poj2186)(5)图的割边和割点(poj3352)(6)最小割模型、网络流规约(poj3308)三、数据结构(1)线段树(poj2528, poj2828, poj2777, poj2886, poj2750)(2)静态二叉检索树(poj2482, poj2352)(3)树状树组(poj1195, poj3321)(4)RMQ(poj3264, poj3368)(5)并查集的高级应用(poj1703, 2492)(6)KMP算法(poj1961, poj2406)四、搜索(1)最优化剪枝和可行性剪枝(2)搜索的技巧和优化(poj3411, poj1724)(3)记忆化搜索(poj3373, poj1691)五、动态规划(1)较为复杂的动态规划(如动态规划解特别的施行商问题等)(poj1191, poj1054, poj3280, poj2029, poj2948, poj1925, poj3034)(2)记录状态的动态规划(poj3254, poj2411, poj1185)(3)树型动态规划(poj2057, poj1947, poj2486, poj3140)六、数学(1)组合数学1.容斥原理2.抽屉原理3.置换群与Polya定理(poj1286, poj2409, poj3270, poj1026)4.递推关系和母函数(2)数学1.高斯消元法(poj2947, poj1487, poj2065, poj1166, poj1222)2.概率问题(poj3071, poj3440)3.GCD、扩展的欧几里德(中国剩余定理)(poj3101)(3)计算方法1.0/1分数规划(poj2976)2.三分法求解单峰(单谷)的极值3.矩阵法(poj3150, poj3422, poj3070)4.迭代逼近(poj3301)(4)随机化算法(poj3318, poj2454)(5)杂题(poj1870, poj3296, poj3286, poj1095)七、计算几何学(1)坐标离散化(2)扫描线算法(例如求矩形的面积和周长，并常和线段树或堆一起使用)(poj1765, poj1177, poj1151, poj3277, poj2280, poj3004)(3)多边形的内核(半平面交)(poj3130, poj3335)(4)几何工具的综合应用(poj1819, poj1066, poj2043, poj3227, poj2165, poj3429)高级篇一、基本算法要求(1)代码快速写成，精简但不失风格(poj2525, poj1684, poj1421,poj1048, poj2050, poj3306)(2)保证正确性和高效性(poj3434)二、图算法(1)度限制最小生成树和第K最短路(poj1639)(2)最短路，最小生成树，二分图，最大流问题的相关理论(主要是模型建立和求解)(poj3155, poj2112, poj1966, poj3281, poj1087, poj2289, poj3216, poj2446)(3)最优比率生成树(poj2728)(4)最小树形图(poj3164)(5)次小生成树(6)无向图、有向图的最小环三、数据结构(1)trie图的建立和应用(poj2778)(2)LCA和RMQ问题(LCA(最近公共祖先问题)，有离线算法(并查集+dfs)和在线算法(RMQ+dfs))(poj1330)(3)双端队列和它的应用(维护一个单调的队列，常常在动态规划中起到优化状态转移的目的)(poj2823)(4)左偏树(可合并堆)(5)后缀树(非常有用的数据结构，也是赛区考题的热点)(poj3415,poj3294)四、搜索(1)较麻烦的搜索题目训练(poj1069, poj3322, poj1475, poj1924,poj2049, poj3426)(2)广搜的状态优化：利用M进制数存储状态、转化为串用hash表判重、按位压缩存储状态、双向广搜、A*算法(poj1768, poj1184, poj1872, poj1324, poj2046, poj1482)(3)深搜的优化：尽量用位运算、一定要加剪枝、函数参数尽可能少、层数不易过大、可以考虑双向搜索或者是轮换搜索、IDA*算法(poj3131, poj2870, poj2286)五、动态规划(1)需要用数据结构优化的动态规划(poj2754, poj3378, poj3017)(2)四边形不等式理论(3)较难的状态DP(poj3133)六、数学(1)组合数学1.MoBius反演(poj2888, poj2154)2.偏序关系理论(2)博奕论1.极大极小过程(poj3317, poj1085)2.Nim问题七、计算几何学(1)半平面求交(poj3384, poj2540)(2)可视图的建立(poj2966)(3)点集最小圆覆盖(4)对踵点(poj2079)八、综合题(poj3109, poj1478, poj1462, poj2729, poj2048, poj3336, poj3315, poj2148, poj1263)附录：POJ是“北京大学程序在线评测系统”（Peking University Online Judge）的缩写，是个提供编程题目的网站，兼容Pascal、C、C＋＋、Java、Fortran等多种语言。

ACM题目分类

三.数据结构.
(1)串 (poj1035,poj3080,poj1936)
(2)排序(快排、归并排(与逆序数有关)、堆排) (poj2388,poj2299)
(3)简单并查集的应用.
(4)哈希表和二分查找等高效查找法(数的Hash,串的Hash)
(3)点集最小圆覆盖.
(4)对踵点(poj2079)
八.综合题.
(poj3109,poj1478,poj1462,poj2729,poj2048,poj3336,poj3315,poj2148,poj1263)
同时由于个人练习的时候可能有些偏向性,可能上面的总结不是很全,还请大家提出和指正,而且由于ACM的题目中专门针对某个算法的题目可能比较少出现,所以上面的分类中的题有可能有多种解法或者是一些算法的综合,这都不会影响大家做题,希望练习的同学能够认真,扎实地训练,做到真正的理解算法,掌握算法. 同时在论坛上还有许多前辈的分类,总结,大家也可以按自己的情况采用.注意FTP上有很多的资料,希望大家好好地利用.
目的). (poj2823)
(4)左偏树(可合并堆).
(5)后缀树(非常有用的数据结构,也是赛区考题的热点).
(poj3415,poj3294)
四.搜索
(1)较麻烦的搜索题目训练(poj1069,poj3322,poj1475,poj1924,poj2049,poj3426)
(5)杂题.
(poj1870,poj3296,poj3286,poj1095)
七.计算几何学.
(1)坐标离散化.
(2)扫描线算法(例如求矩形的面积和周长并,常和线段树或堆一起使用).
(poj1765,poj1177,poj1151,poj3277,poj2280,poj3004)

ACM培训大纲

实用标准文案ACM培训大纲基础内容：数据结构——》搜索——》图论DP数论博弈中级内容数据结构网络流第一章搜索1.二分搜索三分搜索2.栈3.队列4.深搜5,广搜6.第二章数据结构1.优先队列并查集2.二叉搜索树3.线段树（单点更新）4.5.精彩文档.实用标准文案第三章图论1.图的表示1.1二维数组1.2邻接表1.3前向星2.图的遍历2.1双连通分量2. 2拓扑排序3.最短路3.1迪杰斯特拉3. 2弗洛伊德4. 3 SPFA5.匹配匈牙利算法6.生成树7.网络流简介第四章动态规划1.状态转移方程2.引入3. 1 0-1背包4.2硬币问题5. 3矩阵链乘6.区间DP7.按位DP8.树形DP9.状压DP第五章数论1.欧几里得扩展欧几里得2.因数分解3. 费马小定理4.欧拉定理5.6.1筛法6. 2素数判定6. 2,1 0(Jn)方法精彩文档.实用标准文案6. 2. 2 Mi I ler-rabin 测试第六章博弈1.Nim 和2.SG函数第七章中级数据结构1.树状数组RMO 2.KMP3.AC自动机4.线段树（区间更新）5.第八章图论进阶1.网络流问题精彩文档.实用标准文案综述在很多人眼里，东北大学秦皇岛分校不算是985高校。

所以我们要用自己的能力证明我们有985 的实力。

ACM是计算机界认可度最高的一个比赛，可以说只要区域赛有过奖牌，国内任何IT公司没有理由不要。

同时，在高校之中，对一个大学计算机专业的评价，大部分人也会首先看ACM 的水平。

将ACM打出学校，在国内打出一定成绩，对扩大我校影响力很有帮助。

考虑到本校暂时没有进行专题训练的出题能力，专题训练的题目主要从UESTC 2014年集训队专题训练中获取，再加上从别的0J上找一些题目。

训练的平台设置在华中科技大学的vertual judge上面。

本人将在毕业之前承担培训任务。

在2015学年开始之前，培训计划为每两周一次，中间空闲的时间由大二或者大一熟悉C++的同学给不熟悉C++的同学进行基础的讲解。

二级密勒补偿运算放大器设计(西安邮电大学)

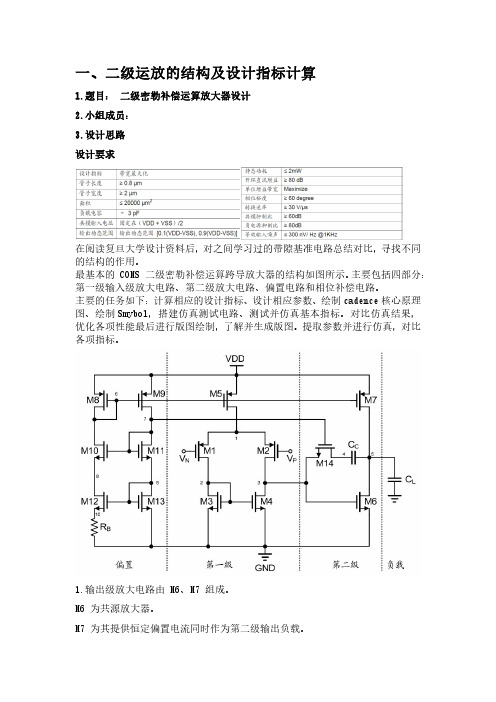
一、二级运放的结构及设计指标计算1.题目：二级密勒补偿运算放大器设计2.小组成员：3.设计思路设计要求在阅读复旦大学设计资料后，对之间学习过的带隙基准电路总结对比，寻找不同的结构的作用。

最基本的COMS二级密勒补偿运算跨导放大器的结构如图所示。

主要包括四部分：第一级输入级放大电路、第二级放大电路、偏置电路和相位补偿电路。

主要的任务如下：计算相应的设计指标、设计相应参数、绘制cadence核心原理图、绘制Smybol，搭建仿真测试电路、测试并仿真基本指标。

对比仿真结果，优化各项性能最后进行版图绘制，了解并生成版图。

提取参数并进行仿真，对比各项指标。

1.输出级放大电路由M6、M7组成。

M6为共源放大器。

M7为其提供恒定偏置电流同时作为第二级输出负载。

M14和Cc构成相位补偿电路。

因为M14工作在线性区，通过m14的直流电流为0，所以M14可等效为一个电阻，m14与电容Cc构成RC密勒补偿2.输出级放大电路由M6、M7组成。

M6为共源放大器。

M7为其提供恒定偏置电流同时作为第二级输出负载。

M14和Cc构成相位补偿电路。

因为M14工作在线性区，通过m14的直流电流为0，所以M14可等效为一个电阻，m14与电容Cc构成RC密勒补偿3.偏置电路由M8～M13和RB组成。

M8和M9宽长比相同。

M12与M13相比，源极加入了电阻RB，组成微电流源，产生电流IB。

对称的M11和M12构成共源共栅结构，减小沟道长度调制效应造成的电流误差。

在提供偏置电流的同时，还为M14栅极提供偏置电压。

M1和M2为第一级差分输入跨导级，将差分输入电压转换为差分电流；M3和M4为第一级负载，将差模电流恢复为差模电压；M6为第二级跨导级，将差分电压信号转换为电流；M7再将此电流信号转换为电压输出。

4.等效电路图5.静态功耗一旦电源电压确定，静态功耗取决于各支路静态电流总和。

考察各路电路，可以知道，此运放的静态功耗为6.单位增益带宽单位增益带宽是运放最重要的指标之一，它定义为当运放增益为1时，所加输入信号的频率，7.共模抑制比共模抑制比的定义为其中Adm是差模增益，Acm是共模增益。

ACM常见算法

ACM常见算法ACM算法⼀、数论算法 1．求两数的最⼤公约数 2．求两数的最⼩公倍数 3．素数的求法 A.⼩范围内判断⼀个数是否为质数： B.判断longint范围内的数是否为素数（包含求50000以内的素数表）：⼆、图论算法1．最⼩⽣成树A.Prim算法：B.Kruskal算法：(贪⼼) 按权值递增顺序删去图中的边，若不形成回路则将此边加⼊最⼩⽣成树。

2.最短路径 A.标号法求解单源点最短路径： B.Floyed算法求解所有顶点对之间的最短路径： C. Dijkstra 算法：3.计算图的传递闭包4．⽆向图的连通分量 A.深度优先 B 宽度优先（种⼦染⾊法）5．关键路径⼏个定义：顶点1为源点，n为汇点。

a. 顶点事件最早发⽣时间Ve[j], Ve [j] = max{ Ve [j] + w[I,j] },其中Ve (1) = 0; b. 顶点事件最晚发⽣时间 Vl[j], Vl [j] = min{ Vl[j] – w[I,j] },其中 Vl(n) = Ve(n); c. 边活动最早开始时间 Ee[I], 若边I由<j,k>表⽰，则Ee[I] = Ve[j]; d. 边活动最晚开始时间 El[I], 若边I由<j,k>表⽰，则El[I] = Vl[k] – w[j,k]; 若 Ee[j] = El[j] ，则活动j为关键活动，由关键活动组成的路径为关键路径。

求解⽅法： a. 从源点起topsort,判断是否有回路并计算Ve; b. 从汇点起topsort,求Vl; c. 算Ee 和 El;6．拓扑排序找⼊度为0的点，删去与其相连的所有边，不断重复这⼀过程。

例寻找⼀数列，其中任意连续p项之和为正，任意q 项之和为负，若不存在则输出NO.7.回路问题 Euler回路(DFS) 定义：经过图的每条边仅⼀次的回路。

（充要条件：图连同且⽆奇点） Hamilton回路定义：经过图的每个顶点仅⼀次的回路。

acm程序设计竞赛数学基础刘汝佳

数学基础(版本2009)刘汝佳例1. 同构计数•一个竞赛图是这样的有向图–任两个不同的点u、v之间有且只有一条边–不存在自环•用P表示对竞赛图顶点的一个置换。

当任两个不同顶点u、v间直接相连的边的方向与顶点P(u)、P(v)间的一样时，称该图在置换P下同构•对给定的置换P，我们想知道对多少种竞赛图在置换P下同构分析•先把置换它分解成为循环, 首先证明长度为L的偶循环将导致无解–对于点i1, 记P(i k)=i k+1, 假设i1和i L/2+1的边方向为i1->i L/2+1, 那么有i2->i L/2+2, i3->i L/2+3, …, i L/2+1->i1, 和假设矛盾!•假设确定其中k条独立边后其他边也会确定, 则答案为2k•考虑两类边: 循环内边和循环间边.分析•循环内顶点的关系–定了i 1和i j 之间的关系, i k 与i (k+j-2) mod n+1之间的关系也被确定下来了, 因此只需要确定i 1和i 2, i 3, …, i (L-1)/2+1这(L-1)/2对顶点的关系•不同循环间顶点的关系–设循环为(i 1,i 2,…,i L1)和(j 1,j 2,…,j L2), 通过类似分析得只需要确定gcd(L1, L2)对关系即可分析•最后答案为2k1+k2•其中k1=sum{(L-1)/2}, k2=sum{gcd(L1, L2)}•可以用二分法加速求幂例2. 图形变换•平面上有n个点需要依次进行m个变换处理•规则有4种, 分别把(x0,y)变为–平移M(x, y): (x0+x, y0+y)–缩放Z(L): (Lx0, Ly0)–翻转F(0): (x0, -y0); F(1): (-x0, y0)–旋转R(a): a为正时逆时针, 离原点距离不变, 旋转a度•给n(<=106)个点和m(<=106)条指令•求所有指令完成后每个点的坐标分析•如果直接模拟, 每次需要O(n)的时间, 一共O(nm), 无法承受•把点(x0, y)写成列向量[x, y]T, 则后3种变换可以都可以写成矩阵–缩放P’= Z * P, Z = [L 0; 0 L]–翻转P’= F * P, F = [1 0; 0 -1]或[-1 0; 0 1]–旋转P’= R * P, R = [cosa–sina; sina cosa]•可是无法实现平移, 怎么办呢?分析•修改表达方式, 令P = [x 0, y 0, 1]T , 则四种变换的矩阵M, Z, F, R 分别为100001,00001001x L M y Z L ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦100100010010001001F −⎡⎤⎡⎤⎢⎥⎢⎥=−⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦或cos sin 0,sin cos 0001a a R a a −⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦分析•只需要先计算所有变换矩阵的乘积A, 然后对于每个点, P’= A * P•注意: 矩阵乘法不满足交换律, 因此需要按照输入顺序进行乘法•每次矩阵乘法需要33=27次乘法, 则计算A一共需要27m次乘法, 对所有点变换需要27n 次乘法, 一共27(n+m)次例3. 染色方案•N*M(N<=10100, M<=5)的格子纸，每个格子被填上黑色或者白色。

ACM资料

最优比率生成树
0/1分数规划
度限制生成树
连通性问题
强大的DFS算法
无向图连通性
割点
割边
二连通分支
有向图连通性
强连通分支
2-SAT
最小点基
有向无环图
拓扑排序
有向无环图与动态规划的关系
二分图匹配问题
一般图问题与二分图问题的转换思路
组合数学
解决组合数学问题时常用的思想
逼近
递推 / 动态规划
概率问题
Polya定理
计算几何 / 解析几何
计算几何的核心：叉积 / 面积
解析几何的主力：复数
基本形
点
直线，线段
多边形
凸多边形 / 凸包
凸包算法的引进，卷包裹法
数论计算
求N的约数个数
求phi(N)
求约数和
快速数论变换
……
素数问题
概率判素算法
概率因子分解
数据结构
组织结构
二叉堆
左偏树
二项树
胜者树
跳跃表
样式图标
斜堆
reap
统计结构
树状数组
虚二叉树
线段树
8. 调用系统的qsort, 技巧很多，慢慢掌握.
9. 任意进制间的转换
第二阶段：
练习复杂一点，但也较常用的算法。
如：
1. 二分图匹配（匈牙利），最小路径覆盖
2. 网络流，最小费用流。
3. 线段树.
4. 并查集。
5. 熟悉动态规划的各个典型：LCS、最长递增子串、三角剖分、记忆化dp

【2016ACMICPC亚洲区大连站A】HDU-5971WrestlingMatch二分图染色

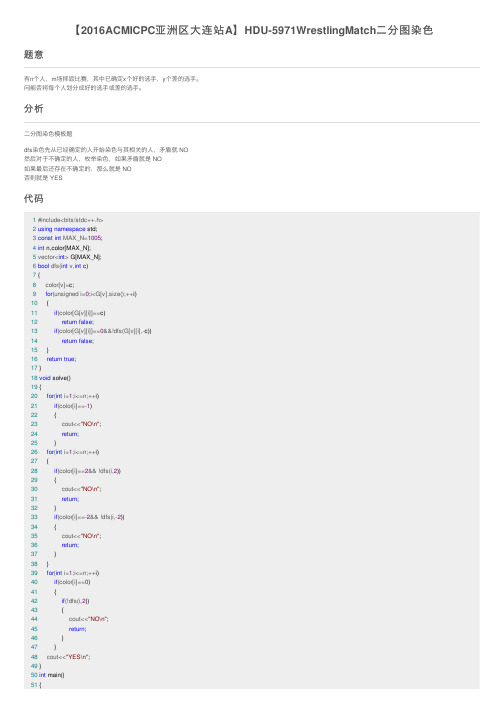
【2016ACMICPC亚洲区⼤连站A】HDU-5971WrestlingMatch⼆分图染⾊题意有n个⼈，m场摔跤⽐赛，其中已确定x个好的选⼿，y个差的选⼿。

问能否将每个⼈划分成好的选⼿或差的选⼿。

分析⼆分图染⾊模板题dfs染⾊先从已经确定的⼈开始染⾊与其相关的⼈，⽭盾就 NO然后对于不确定的⼈，枚举染⾊，如果⽭盾就是 NO如果最后还存在不确定的，那么就是 NO否则就是 YES代码1 #include<bits/stdc++.h>2using namespace std;3const int MAX_N=1005;4int n,color[MAX_N];5 vector<int> G[MAX_N];6bool dfs(int v,int c)7{8 color[v]=c;9for(unsigned i=0;i<G[v].size();++i)10 {11if(color[G[v][i]]==c)12return false;13if(color[G[v][i]]==0&&!dfs(G[v][i],-c))14return false;15 }16return true;17}18void solve()19{20for(int i=1;i<=n;++i)21if(color[i]==-1)22 {23 cout<<"NO\n";24return;25 }26for(int i=1;i<=n;++i)27 {28if(color[i]==2&& !dfs(i,2))29 {30 cout<<"NO\n";31return;32 }33if(color[i]==-2&& !dfs(i,-2))34 {35 cout<<"NO\n";36return;37 }38 }39for(int i=1;i<=n;++i)40if(color[i]==0)41 {42if(!dfs(i,2))43 {44 cout<<"NO\n";45return;46 }47 }48 cout<<"YES\n";49}50int main()51{52 ios::sync_with_stdio(false);53int m,x,y;54while(cin>>n>>m>>x>>y)55 {56int a,b;5758for(int i=1;i<=n;++i)//清空数据59 G[i].clear();60 memset(color,-1,sizeof(color)); 6162for(int i=1;i<=m;++i)63 {64 cin>>a>>b;65 color[a]=0;66 color[b]=0;67 G[a].push_back(b);68 G[b].push_back(a);69 }70for(int i=1;i<=x;++i)71 {72 cin>>a;73 color[a]=2;74 }75for(int i=1;i<=y;++i)76 {77 cin>>b;78 color[b]=-2;79 }80 solve();81 }82return0;83 }。

二部图

}
总结
从匈牙利算法中我们不难发现以下规律: 1.增广路的长度必定是奇数，第一条边和最后一条边均为
未匹配边 2.每次增广路的匹配边和为匹配边取反均会使最大匹配数
加一以上便是匈牙利算法的精髓所在，它的复杂度是O(n^3) 当然也可以用bfs来实现，复杂度相当
还有更快的一种叫Hopcroft算法，复杂度为 O( nm)
匈牙利算法
访问x6,找不到增广路算法结束，最大匹配数是5
x1 x2 x3 x4 x5 x6
y1( y2( y3( y4( y5( y6( y7( x3) x1) x4) x5) x2) -1) -1)
相关的代码
bool map[N][N];//邻接矩阵 int nx,ny;//x,y点集的个数 bool vis[N];//记录点有无被访问过 int link[N];//记录y集合到x集合映射关系 int dfs(int u){
匹配仍合法，但基数加一
匈牙利算法
主要算法框架： 1.初始化最大匹配数为0 2.每次从一个未盖点找一条增广路，若找到，最大匹配数加
1，并把找到的增广路上的所有匹配边和未匹配边取反 3.若所找的点集全部遍历完，算法结束
匹配数为0,所有y的link值为-1
x1 x2 x3 x4 x5 x6
匈牙利算法
y1( y2( y3( y4( y5( y6( y7(
x1 x2 x3 x4 x5 x6
y1( y2( y3( y4( y5( y6( y7( x1) -1) -1) -1) -1) -1) -1)
访问x2,和x1类似
x1 x2 x3 x4 x5 x6
匈牙利算法
y1( y2( y3( y4( y5( y6( y7( x1) x2) -1) -1) -1) -1) -1)

ACM讲课之二分图匹配(匈牙利算法)ppt课件

1
1
1
2
2
3
323Fra bibliotek44
5
可编辑课件PPT
5
11
i = 3时： Pre[1] = 3;
1 2 3 4 5
可编辑课件PPT
1 1
2
3
4
5
12
i = 4时： Pre[3] = 2; Pre[2] = 1; Pre[5] = 3; Pre[1] = 4;
1 2 3 4 5
可编辑课件PPT
1 2 3 4
匹配1
v1
v2
v3
匹配2
v1
v2
v3
v4
v5
v4
v5
可编辑课件PPT
3
二分图的最大匹配
最大匹配：图中包含边数最多的匹配称为图的最大匹配。
今天我要讲的是无权二分图的最大匹配问题，采用匈牙利算法。
可编辑课件PPT
4
匈牙利算法必备知识：
1.盖点：有被M中的边关联到的节点，未盖点则相反。
2.增广路径：若二分图中有一条路径p，其起始点和结束点都是未盖点，其间属于M的边和不属于M的边交替出现，则称路径p是一条关于 M的增广路径。
5
13
二分图最大匹配延伸
最小点覆盖最小边覆盖最大独立集有向图最小路径覆盖最优匹配（KM算法）
可编辑课件PPT
14
此课件下载可自行编辑修改，此课件供参考！部分内容来源于网络，如有侵权请与我联系删除！感谢你的观看！
匈牙利算法：计算二分图最大匹配就是应用增广路径的概念，每次寻找一条关于M 的增广路径p，通过M和增广路径进行异或，使得M中的匹配数增加1 。以此类推，直至二分图中不存在关于M的增广路径为止。此时得到匹配M就是图G的一个最大匹配。

北京大学 acm程序设计图论讲义

22
for (w=G->first(v); w<G->n(); w = G>next(v,w))
if (G->getMark(w) == UNVISITED) { G->setMark(w, VISITED); Q->enqueue(w); }
PostVisit(G, v); // Take action }}
Q Q
31
() ((1,1)) ((1,1) (2,3)) ((1,1) (2,4)) ((1,1) (2,4) (3.2))
Q Q
Q
32
() ((1,1)) ((1,1) (2,3)) ((1,1) (2,4)) ((1,1) (2,4) (3.2))
Q Q
33
Q () ((1,1)) ((1,1) (2,3)) ((1,1) (2,4)) ((1,1) (2,4) (3.2))
求解算法
穷举法贪心法深度/广度优先搜索
图和树的搜索回溯法（深度优先）
递归
分治
动态规划法
55
谢谢！
56
49
动态规划法的思想
自底向上构造在原问题的小子集中计算每一步列出局部最优解，并用一张
表保留这些局部最优解，以避免重复计算子集越来越大，最终在问题的全集上计算，所得出的就是整体最优解。
50
Fib(1)=Fib(2)=1
Fibonacci数列 Fib(n)=Fib(n-1) + Fib (n-2)
23
八数码深度优先搜索
1
23 184 765
2
c
3
283 164 75
283 14 765