2014年AP微积分考试综合评析及2015年展望

合集下载

2015年AP微积分BCfree-response-questions

f x be the particular solution to the differential equation with the initial condition f 2 (c) Let y Does f have a relative minimum, a relative maximum, or neither at x 2 ? Justify your answer.
(d) Find the values of the constants m and b for which y
3.
mx b is a solution to the differential equation.
© 2015 The College Board. Visit the College Board on the Web: .
4, so that f x
neither at x
1 . Determine whether f has a relative minimum, a relative maximum, or x 4x 2. Justify your answer.
2
(c) Find the value of k for which f has a critical point at x (d) Let k Find
2
x 2 kx
2
.
(a) Let k
3, so that f x
1 . Write an equation for the line tangent to the graph of f at the point x 3x
2
whose x-coordinate is 4. (b) Let k

2014年AP宏观经济学考试综合评析及2015年展望

2014年AP宏观经济学考试综合评析及2015年AP考试展望--北京新东方北美美本本地AP&SATII项目吴振媛AP宏观经济学考试自开展以来，在试题内容的侧重及试题形式方面呈现较强的变动性，以每年的考试试题作为研究样本对其综合解析，不仅有助于理解College Board出题人的焦点动向，同时可提升广大考生的复习效率，提高相关教研人员的教授效果。

结合AP宏观经济学课程的教研成果，以及对历年考试试题的分析与总结，我们发现2013年的考试呈现以下特征：一、考生时间管理难度加大基于宏观经济学考试的时间分布及安排，其中70分钟60道选择题的分配本身对考生的知识点掌握与答题“质”“量”的要求较高，加之考场气氛紧张，对于考生的心理素质也是一种考验。

因此，快速解析考点、熟练掌握分析工具并迅速完成试题是较好地完成选择题部分的关键。

针对考试时间有限性的问题，广大考生利用题海战术可以一定程度上解决这一矛盾，而官方给出的真题数目有限极大程度上限制了考生的复习效率。

另一方面，近十年内试题对各模块知识点的侧重及考核比例调整频率明显加快，因此凭借复习资料的“刷题”工作无法准确保证考生对复习重点的把握。

60分钟对于解答三道宏观经济学简答题而言相对比较宽松，尤其简答题的考点集中性强，同一知识点的试题规律性强，考生能够结合官方给出的历年真题进行重点复习。

2014年的考题现状表明：选择题在2013年考题难度基础上略有增加，简答题结构清晰、难度调整不大。

前者主要体现在：试题选项的文字长度有所增加，题目解答过程的平均思考步骤较之前年份更多，知识点综合性较之前年份显著增强。

这对考生的复习能力提出了极高的要求，同时考场时间安排等应试技巧的掌握，成为决定考试成败的另一重要因素。

复习资料的使用能够帮助考生扩充答题速度练习题库，而解决试题中的“疑难杂症”必须借助于平时课程中逐渐养成的经济分析思维，以及对知识点构建关系网络来触发答题思路。

2014年AP微观经济学考试综合评析及2015年AP考试展望

2014年AP微观经济学考试综合评析及2015年AP考试展望--北京新东方北美美本本地AP&SATII项目黄涓 2014年AP微观经济学考试整体分析一Free response 的题型趋于稳定，没有比较大的创新空间。

历来free response 考察的几个模型都很稳定。

这次考察了产品市场垄断模型，完全竞争劳动力市场模型和单位税收模型。

总体题目跟往年都很类似，其中第一题与之前题目基本完全一模一样。

在free response里college board喜欢常考的模型有完全竞争市场模型，垄断模型，税收模型，外部性模型，完全竞争劳动力市场模型，垄断劳动力市场。

偶尔几个年份会出现一些比较冷的模型，如关税模型和补助模型，包括考一些消费者理论和成本理论。

从这一点来看，考试题型基本是在经典模型上的创新是越来越少了，包括跨模型的综合考察也不常见了。

二free response考察的重点难点仍然是分配效率分配效率是每年free response 必考的知识点，也是比较抽象，可以灵活出题的知识点。

每个模型都可以涉及到这个知识点。

对于分配效率，大部分学生的理解或多或少都会有点偏差，导致模型稍微一变形，就容易做错，或者不会做。

所以在考试前有必要把这个概念强化理解。

它是指的一个行业的产量是否符合社会利益最大化，是生产太多了呢，还是生产太少了呢，那怎么衡量这个产量是否达到了社会福利最大化呢。

那就是在这个产量上，消费者愿意为最后一单位付的钱等于生产最后一单位给厂商增加的成本的时候及P=MC时，该产量为最优化。

因为在我们的理论假设里，消费者愿意为每增加一单位同样商品的消费所付的钱是越来越少的，而多生产一单位给厂商增加的成本是越来越多的。

所以如果生产超过了最优的产量，则多生产一单位给厂商增加的成本是大于消费者愿意为这单位付的钱的，所以给社会造成了损失。

相反如果厂商生产的太少了，则厂商每多生产一单位，消费者愿意为它付的钱大于给厂商增加的成本，社会可以从这个额外一单位得到正的净福利。

ap微积分真题答案

ap微积分真题答案【篇一：ap 微积分bc 选择题样卷一】version - section i - part a calculators are not permitted on this portion of the exam28 questions - 55 minutes1) givenfind dy/dx. a) b) c) d) e)2) give the volume of the solid generated by revolving the region bounded by the graph of y = ln(x), the x-axis, the lines x = 1 and x = e, about the y-axis. a) b) c) d)e)3) the graph of the derivative of fis shown below.find the area bounded between the graph of f and the x-axis over the interval [-2,1], given that f(0) = 1. a) b) c) d) e)4) determine dy/dt, given thatanda)b)c)d)e)5) the function-1is invertible. give the slope of the normal line to the graph of f atx = 3.a) b) c)d)e)6) determinea) b)c) d) e)7) give the polar representation for the circle of radius 2 centered at ( 0 , 2 ). a)b)c)d)e)8) determinea)b)c) d)e)9) determinea) b) c) d) e)10) give the radius of convergence for the seriesa)b)c) d)e)11) determinea)b)【篇二：ap 微积分bc选择题样卷二】17 questions - 50 minutes1) the limit of the sequenceas n approaches is -3. what is the value of c? a)b)c)d)e)2) ifand y = 3 when x = -2, then what is y? a) b) c)d) e)3) the graph of the derivative of fis given below.which of the following is false about the function f?a) f is increasing on [1,4].b) f is concave down on [1,5/2].c) f is concave down on [-3,0).d) f is not differentiable at 0. e) the funciton is constant on (-,-3].4) determinea)b)c) d) e)5) give the area that lies below the x-axis and is contained within theregion bounded by the polar curvea) b) c) d) e)6) give the error that occurs when the area between the curve and the x-axis over the interval [0,1] is approximated by the trapezoid rule with n = 4. a)b)c)d)e)7) letdetermine f(2/3). a)b)c) d) e)8) give the length of the curve determined byfor t from 0 to 2. a)b)c)d)e)9) particles a and b leave the origin at the same time and move along the y-axis. their positions are determined by the functionsfor t between 0 and 8. what is the velocity of particle b when particlea stops for the first time? a) b)c)d) e)10) the base of a solid is the region in the xy plane enclosed by thecurvesover the interval[0,/4]. cross sections of the solid perpendicular to the x-axis are squares. determine the volume of the solid. a)b)c)d)e)11) give the minimum value of the functionfor x 0. a)b)c)d)e)12) select the true statement associated with the function【篇三：ap微积分考试详解】>微积分ap课程包括微积分ab (calculus ab) 和微积分bc(calculus bc)两门课。

2014—2015学年度第二学期期末考试

2014—2015学年度第二学期期末考试五年级数学试题（时间：90分钟）等级：一、认真思考，填一填。

1．如果电梯上升15层记作+15，那么它下降2层应记作（）。

2．把5米长的木料平均截成8段，每段占这根木料的（）（）,每段长（）米。

3．23 =（）÷（）=（）15 5÷8=（）（）=30（）4．用分数表示下面各图中的阴影部分。

5．在里填上“＞”、“＜”或“=”。

59 58 53 35 78 91013 0.33 2.25 214 0.83 566．在括号里填上合适的容积或体积单位。

一个热水瓶的容积约是2（）。

一间教室的体积约是144（）。

一本词典的体积大约是900（）。

一个墨水瓶的容积约是60（）。

7．用棱长1厘米的小正方体木块拼成一个正方体模型，至少要用（）块小正方体木块，这个正方体模型的表面积是（）平方厘米，体积是（）立方厘米。

8．一个长方体的底面积是18平方厘米，体积是45立方厘米。

它的高是（）厘米。

9．从第1盒中任意摸出一个球，摸出白球的可能性是（），从第2盒中任意摸出一个球，摸出白球的可能性是（）。

二、火眼金睛，判一判。

1．0既不是正数也不是负数。

（）2．北偏东30°，也可以说成东偏北30°。

（）3．真分数都小于1，假分数都大于1。

（）4．如果甲、乙两数的最大公因数是1，那么这两个数的最小公倍数就是它们的积。

（）5．长方体有12条棱，8个顶点，6个面，相对面的面积相等。

（）三、开动脑筋，选一选。

1．某一天白天的最高气温是9℃，夜晚最低气温－3℃。

白天和夜晚气温相差（）℃。

A．6 B．12 C．－122．分子与分母相差1的分数一定是（）。

A．真分数B．假分数C．最简分数3．如果a=2×3×5，b=2×2×3，那么a和b的最大公因数和最小公倍数分别是（）。

A．4和60 B．6和60 C．6和3604．右面的两个长方体是由一样的小正方体拼成的，这两个长方体（）。

2014级微积分1答案

华东交通大学2014—2015学年第一学期考试卷《微积分Ⅰ》答案及评分标准一、填空题(每题3分，共15分) 41 1、；)1(102 2--=-=-+x y y x 或、；1,2)( 3、；1112 4、；41 5π-、二、选择题(每题2分，共10分) A 1、；C 2、；B 3、；D 4、；B 5、三、计算题(每题 12分，共48分)n n n n n n n n n 1112111111+<++++++<+ 1 ）解：（、 11lim ,11lim =+=+∞→∞→nn nn n n n 又1=∴原式x x x x cos 12e e lim )2(0--+=-→解：原式xx x x sin e e lim 0-→-=x x x x cos e e lim 0-→+=2=e 0 (1) 2==y x 时，当解：、，1111)(e ='⋅-++'+⋅y yx y x y x xy 求导得方程两边对 1e)0(1e e 0='-+==y y x 代入上式得：，把， 2e )0(='y 故 )11()11(11)2(2'-+⋅-++='x x x x y 解：222)1()1()1(22)1(-+--⋅+-=x x x x x 112+-=x ，x y y d d '=∴x x d 112+-= t t x t x d sec d tan )1(32==，则解：令、　⎰⎰=⋅⋅=t tt t t t t d sin cos d sec sec tan 1222原式C t +-=sin 1C x x ++-=12 3d ln 31)2(x x ⎰=解：原式⎰-=x x x x dln 31ln 3133⎰-=x x x x d 31ln 3123C x x x +-=3391ln 31 ⎰=πd cos 2(1)4x x 解：原式、　⎰=2d cos (2πx x )d cos 2⎰-ππx x )sin (sin 2220πππxx-=22=t t t x t x d tan sec d sec )2(==则，令解：， 0 1；时，当==t x 32π==t x 时，当⎰=⇒3d tan sec sec tan πt t t tt原式⎰-=32d )1(sec πt t 30)(tan πt t -=33π-=四、综合题 (共2题，每题10分，共20分)2d )48.0()()1(10++=⎰xt t x C 成本函数、解：　244.02)44.0(202++=++=x x t t xx x R 20)()2(=因为收益函数，2164.0)()()(2-+-=-=x x x C x R x L 所以利润函数 168.0)(+-='x x L ，200)(=='x x L 得唯一驻点令百台时利润最大，故当产量为又2008.0)(=<-=''x x L ，万元且最大利润为158)20(=L⎰--=1d )e e ((1) 2x S x x 面积解：、10)e e (x x -+=2ee 1-+=- ⎰--=10 22]d )e ()e [()2(x V x x π体积1022)e 21e 21(x x -+=π)2e e (222-+=-π 五、证明题(7分)x x x f 132)( +-=令证：，211)(xx x f -='则单调增加，故时，当)(0)(1x f x f x >'⇒>0)0(=f 又，0)(1>>x f x 时，有当所以， xx 132->即。

2014年高考数学试卷分析与2015年复习展望 PPT

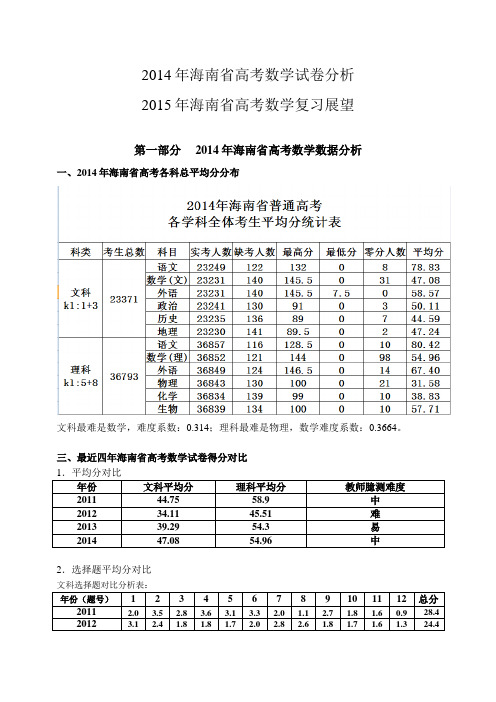
2014年海南省高考数学试卷分析2015年海南省高考数学复习展望第一部分 2014年海南省高考数学数据分析一、2014年海南省高考各科总平均分分布文科最难是数学，难度系数：0.314；理科最难是物理，数学难度系数：0.3664。

三、最近四年海南省高考数学试卷得分对比2．选择题平均分对比文科选择题对比分析表：理科选择题对比分析表：3．填空题平均分对比文科填空题对比分析理科填空题对比分析4．解答题平均分对比文科解答题对比分析理科解答题对比分析四、2014年海南省高考数学试卷内容、能力分项平均分情况高考数学（理）内容、能力分项平均分统计表高考数学（文）内容、能力分项平均分统计表五、2014年海南省高考语文、数学、英语分数段人数统计2014年海南省普通高考语、数、外分数段人数统计表第二部分 2014年海南省高考数学试题分析六、2014年海南省高考数学试题分析对于高考试卷的总体分析，我们可以从高考试卷结构及分值分布表以及高考试卷知识分布表中直观看出端倪。

1.海南省2014年文理科数学高考试卷考点分布：3.2011—2014年数学高考试卷知识比重理科文科从上表中可以看出，代数（集合、函数、三角、导数与定积分、数列、不等式、向量、算法、复数）、几何（立体几何与平面解析几何）、概率统计既是新课程中的主干知识块，又始终是历年以来知识考查的主线.我们以理科几何在试卷中所占有的为例，自2007年至2014年以来，一直是44分，一直占有的比例是29%，如果再仔细研究，会发现一直是“4小”（两道立体几何选填题和两道解析几何选填题）“两大”（一道立体几何简答题和一道解析几何简答题），这些都说明了试卷内容结构稳定，其比例也与《课标》中课时基本吻合。

七、2014年海南省高考数学试题试题特点：1、主干考点相对稳定，局部有变化数学试题围绕着主干知识、重点方法和主要数学思想展开，没有偏题怪题。

与去年相比，文科数学解答题依然考查了立体几何、概率、解析几何和导数等重点内容，试题的难度和相对位置保持稳定，考查方式和考查角度有所改变。

2014年江苏高考真题——数学试题1部分试题解析及2015届高三复习教学建议何睦含解析

2014年普通高等学校招生全国统一考试（江苏卷）数学Ⅰ部分试题解析及2015届高三教学建议江苏省张家港市常青藤实验中学何睦（感谢苏州松陵金晔老师提供如此精美的试卷word 版）（2014年高考江苏卷第10题）已知函数,1)(2-+=mx x x f 若对于任意]1,[+∈m m x ,都有0)(<x f 成立,则实数m 的取值范围是 ▲ .【思路探究】画出二次函数的分析简图：由图象分析可得结论：开口向上的二次函数()f x 在[],m n 上恒小于0的充要条件为()0,()0.f m f n <⎧⎨<⎩ ，开口向下的二次函数()f x 在[],m n 上恒大于0的充要条件为()0,()0.f m f n >⎧⎨>⎩【解法探究】()0,(1)0.30.2m f m m f m m ⎧<<⎪⎛⎫<⎧⎪⇒⇒∈ ⎪⎨⎨ ⎪+<⎩⎝⎭⎪-<<⎪⎩. 【教学建议】（1）一元二次不等式作为江苏高考考试说明的C 级要求，在教学中应突出和加强二次函数、二次方程的零点、一元二次不等式的研究性教学，由于三次函数求导后仍为二次函数问题，所以可考虑多渗透一些含参数问题的讨论，适时和．．．适当．．加大二次问题的教学难度. （2）多引导学生利用数形结合的方法研究函数问题.（2014年高考江苏卷第12题）如图，在平行四边形ABCD 中，已知8=AB ，5=AD ，PD CP 3=，2=⋅BP AP ，则 AD AB ⋅的值是 ▲ .【思路探究】向量是高中阶段数与形结合的完美典范，向量教学中尽可能的引导学生从代数和几何两个角度审视和考查向量问题，数一般指向量的坐标法，形一般指向量的基底法. 【解法探究】解法1：基底法，考虑将条件中涉及的,AP BP 向量用基底,AB AD 表示，而后实施计算.41+=+=，43-=+= 则)43()41(2AB AD AB AD BP AP -⋅+==⋅2216321AB AB AD AD -⋅-= 因为5,8==AD AB 则⋅-⋅-=2164163252，故22=⋅ 解法2：坐标法，不妨以A 点为坐标原点，AB 所在直线作为x 轴建立平面直角坐标系，可设(0,0),(8,0),(.).(2,),(8,)A B D a t P a t C a t ++，则(2,),(6,)AP a t BP a t =+=- 由2=⋅，得22414a t a +-=，由5=AD ，得2225a t +=，则411a =, 所求822AB AD a ⋅==. 【教学建议】（1）向量是高中阶段数与形结合的完美典范，在向量教学中尽可能的引导学生从代数和几何两个角度审视和考查向量问题，数一般指向量的坐标方法，形一般指向量的基底方法. （2）平面向量的数量积作为江苏高考考试说明的C 级要求，在教学中应重点加强. 此外，向量作为良好载体可与很多其他知识进行结合（如数列、函数、解析几何等等），这一点在其他省份的高考题中有所体现，江苏在这方面未有尝试，不妨关注一下. （2014年高考江苏卷第13题）已知)(x f 是定义在R 上且周期为3的函数,当)3,0[∈x 时,|212|)(2+-=x x x f .若函数 a x f y -=)(在区间]4,3[-上有10个零点(互不相同),则实数a 的取值范围是 ▲ .【解法探究】作出函数的简图，由图象分析可得10,2a ⎛⎫∈ ⎪⎝⎭.【教学建议】含绝对值的函数和分段函数是江苏省高考命题最为亲睐的考查内容之一，可以说每年高考填空题必考题型. 在教学中，应多让学生自己动手作图，不断提升“依性作图”和“以图识性”的能力.（2014年高考江苏卷第14题）若△ABC 的内角满足C B A sin 2sin 2sin =+,则C cos 的最小值是 ▲ . 【思路探究】多元函数的最值问题研究，考察正余弦定理和基本不等式.【类题链接】（2008年江苏高考）2,,,230,y x y z R x y z xz*∈-+=的最小值为 .【解法探究】由正弦定理得c b a 22=+，由余弦定理结合基本不等式有：422214322221432)22(2cos 2222222222-+=-+=+-+=-+=ab b a ab ab b a ab b a b a abcb a C4264222143222-=-≥ab ba ,当且仅当a =时等号成立. 【教学建议】多元函数最值问题的研究，应始终引导学生树立减元消参的意识，减元消参是数学求简的必然要求，是“简中求道”精神的体现.（2014年高考江苏卷第17题）如图,在平面直角坐标系xOy 中,21,F F 分别是椭圆22221(0)x y a b a b+=>>的左、右焦点，顶点B 的坐标为),0(b ，连结2BF 并延长交椭圆于点A ，过点A 作x 轴的垂线交椭圆于另一点C ，连结C F 1.（1）若点C 的坐标为)31,34(,且22=BF ,求椭圆的方程；（2）若,1AB C F ⊥求椭圆离心率e 的值.【解法探究】（1）由题意知2(0,),(,0)B b F c，则2BF a ===则椭圆方程为22212x y b +=. 点C )31,34(在椭圆上，故211611299b ⋅+=，解得21b =；所求椭圆方程为2212x y +=.（2）解法1：（垂直关系的先行表征）设000012(,),(.),(,0),(,0)C x y A x y F c F c --，由,1AB C F ⊥得001y b x c c ⋅=-+-，由A 在2BF 上，则001x y c b -+=；联立20000,.cx by c bx cy bc ⎧-=-⎪⎨-=⎪⎩ 解得：20222022,2.ca x b c bc y b c ⎧=⎪⎪-⎨⎪=⎪-⎩，00(,)C x y 在椭圆上，代入椭圆方程整理得2242224(2)c a c a c +=-，即225a c =，所以椭圆的离心率为5e =解法2：（垂直关系的最后表征）由题意知直线2BF 方程：()by x c c=--，与椭圆联立方程组得: 2222()1b y xc cx y a b ⎧=--⎪⎪⎨⎪+=⎪⎩得到222112()0x x a c c +-=，解得0B x =，2222A a c x a c =+；则2222(3)()A b b a c y x c c a c -+=--=+；又由12FC BF ⊥可知：2A A cx c y b+=-，代入化简有222222()(3)b a c c a c -=+，将222b a c =-代入化简得4225a a c =，即215e =，e =【教学建议】（1）解析几何的教学要注重“算理”的积累和表征，教会学生从不同的角度对问题进行表征，也符合江苏省对解析几何问题“多考一点想，少考一点算”的命题方向；（2）定点定值问题仍然是解析几何问题的命题热点、重点和难点，在教学中仍应引起足够重视，但江苏卷这两年解析几何的命题告诉我们：教学时也很有必要回归解析几何最最基本的运算（抛除一切所谓的运算技巧），我想这应该是这两年命题组老师的良苦用心吧；（3）加强解析几何的运算能力，如何提高？无它，算必躬亲耳.（2014年高考江苏卷第18题）如图,为了保护河上古桥OA ,规划建一座新桥BC ,同时设立一个圆形保护区.规划要求: 新桥BC 与河岸AB 垂直; 保护区的边界为圆心M 在线段OA 上并与BC 相切的圆.且古桥两端O 和A 到该圆上任意一点的距离均不少于80m. 经测量，点A 位于点O 正北方向60m 处, 点C 位于点O 正东方向170m 处(OC 为河岸),34tan =∠BCO . （1）求新桥BC 的长；（2）当OM 多长时,圆形保护区的面积最大？【解法探究】（1）解法1：（两角差的正切）连结AC ，由题意知6tan 17ACO ∠=，则由两角差的正切公式可得：2tan tan()3ACB BCO ACO ∠=∠-∠=，故cos 150BC ACB AC m =∠⋅= 答：新桥BC 的长度为150m.解法2：（解析法）由题意可知(0,60),(170,0)A B ；由 34tan =∠BCO 可知直线BC 的斜率43k =-，则直线BC 所在直线的方程为4(170)3y x =--；又由AB BC ⊥可知，AB 所在的直线方程为3604y x =+；联立方程组4(170)33604y x y x ⎧=--⎪⎪⎨⎪=+⎪⎩，解得80,120x y ==；即点(80,120)B，那么150BC ==. 答：新桥BC 的长度为150m.解法3：（初中解法）延长CB 交OA 所在直线于点G ，由34tan =∠BCO 可得6803OG =，8503CG =，5003AG =，4cos sin 5CGO GCO ∠=∠=，故 400cos 3BG CGO AG =∠⋅=，在OCG ∆中，由勾股定理得8503CG =，故150BC m =答：新桥BC 的长度为150m.（2）解法1：（解析法）由题意设(0,)M a (060)a ≤≤，圆M 的方程为222()x y a r +-=，且由题意可知68035a r -==. 又古桥两端O 和A 到该圆上任意一点的距离均不少于80m ，那么80(60)80r a r a -≥⎧⎨--≥⎩，解得1035a ≤≤；由函数68035ar -=为区间[10,35]上的减函数，故当10a =时，半径取到最大值为130.综上可知，当10OM m =时，圆形保护区的面积最大，且最大值为16900π. 解法2：（初中解法）（兴化顾卫老师）设BC 与圆切于点N ，连接MN ，过点A 作//AH BC 交MN 于点H .设OM a =，则60AM a =-，由古桥两端O 和A 到该圆上任意一点的距离均不少于80 m ，那么80(60)80r a r a -≥⎧⎨--≥⎩，解得1035a ≤≤. 由4tan tan 3AMH OCN ∠=∠=，可得3(60)5MH a =-，由（1）解法3可得100AB =，所以33100(60)13655MN x x =+-=-+，故MN 即圆的半径的最大值为130，当且仅当10a =时取得半径的最大值. 综上可知，当10OM m =时，圆形保护区的面积最大.【教学建议】（1）应用题从考试角度来说主要考查学生两个方面的能力：建立数学模型的能力（简称“建模”能力）、解决数学模型的能力（简称“解模”能力），从应试方法上如何突破呢？首先要系统研究所有可能出现的应用题并做到能对症下药，常考查的应用题类型有：函数应用题（以分式函数为载体的函数应用题、以分段函数为载体的函数应用题、以二次函数为载体的函数应用题）；三角测量应用题（以三角函数的定义为载体的三角应用题、以三角函数的图象为载体的三角应用题、以解三角形为载体的三角应用题、以立体几何为载体的三角应用题、以追击问题为载体的三角应用题、以米勒问题为载体的三角应用题）；数列应用题；线性规划应用题；解析几何应用题.（可参考何睦老师编写的《高考数学应用题复习题型归类解析讲义》）；其次是解模工具的积累，例如基本不等式、导数研究函数单调性等等.（2）本题的难点在于求出a 的取值范围，在教学中教师应注意多参数的参数范围问题注意目标意识的应用，注意减元意识的渗透．提供两个典型问题供各位练习：（Ex.1）（湖北高考题改编）锐角ABC ∆中，B A 2=，则A ∠的取值范围是___________. （Ex.2）（2014南通四模）图1是某种称为“凹槽”的机械部件的示意图，图2是凹槽的横截面（阴影部分）示意图，其中四边形ABCD 是矩形，弧CmD 是半圆，凹槽的横截面的周长为4．若凹槽的强度T 等于横截面的面积S 与边AB 的乘积，设AB =2x ，BC =y ．（1）写出y 关于x 函数表达式，并指出x 的取值范围；（2）求当x 取何值时，凹槽的强度T 最大．（Ex.3）（2014南通四模）设各项均为正整数的无穷等差数列{a n }，满足a 54=2014，且存在正整数k ，使a 1，a 54，a k 成等比数列，则公差d 的所有可能取值之和为．图1图2（2014年高考江苏卷第19题）已知函数x x x f -+=e e )(,其中e 是自然对数的底数. （1）证明:)(x f 是R 上的偶函数；（2）若关于x 的不等式)(x mf ≤1e -+-m x 在),0(+∞上恒成立，求实数m 的取值范围；（3）已知正数a 满足：存在),1[0+∞∈x ，使得)3()(0300x x a x f +-<成立.试比较1e -a 与1e -a 的大小，并证明你的结论. 【解法探究】（1）函数)(x f 的定义域为R ，关于原点对称；又因为()()xx f x e e f x --=+=，所以函数)(x f 是R 上的偶函数；（2）)(x mf ≤1e -+-m x ()e1xxxm e e m --⇔+≤+-，即(1)e 1x x xm e e --+-≤-；令(0)x t e t -=>；因为111211x x e e t t-+-=+-≥-=，当且仅当1t =时，等号成立；故2111111tt m t t t t--≤=-++-，令21()1t h t t t -=-+，下只要求min ()m h t ≤.2(2)'()(1)t t h t t t -=-+；则当2t >时，'()0h t >；则当02t <<时，'()0h t <；因此可知当2t =时，min 1()(2)3h t h ==-；则13m ≤-. 综上可知，实数m 的取值范围为1(,]3-∞-.（3）难题分解1：如何根据条件求出参数a 的取值范围？问题呈现：0[1,)x ∃∈+∞，使得)3()(0300x x a x f +-<成立”，求参数a 的取值范围.认知过程1：这是什么问题？（不等式的有解问题）认知过程2：怎么处理这类问题？（参数分离或者直接求函数的最值，选用哪种呢？管它呢，都试试吧！）分解路径1：直接求函数的最值（笔者称其为“单刀直入”法）解：令30000()()(3)g x f x a x x =--+，只要在0[1,)x ∈+∞上，0)(min 0<x g 即可.002200()1'()3(1)x x e g x a x e-=+-. 且当01x =时，0'()0g x =；当01x >时，2010x ->，02()10x e ->，则0'()0g x >. 故在区间[1,)+∞上，0'()0g x ≥，即函数0()g x 为[1,)+∞的增函数，则1min 0()(1)20g x g e e a -==+-<，解得12e e a -+>.分解路径2：参数分离可以吗？（of course!）解：欲使条件满足，则[)3,10∈x （想想这是为什么？留给大家思考.）此时03030>+-x x ，则03003)(x x x f a +->，构造函数030003)()(x x x f x g +-=，即求此函数在 [)3,10∈x 上的最小值.（编者按：可能会有同学一阵眩晕，别怕，你要有个信念：要研究这么复杂的函数的单调性，可能只是DDN （逗逗你），单调的！不妨先用直觉感知一下：在定义域上，分子是单调递增的函数，分母是单调递减的函数，且分子和分母均大于0恒成立，还不是单调递增吗？有了这个目标. 对接下去的证明工作起了很好的导向作用）.2030200300)3()33)(()3)(()(000x x x e e x x e e x g o x x x x +-+-+-+--='-- （编者按：又有同学说：My faint!（我晕），这么复杂的分子怎么办！你说咋办！刚才的直觉已经告诉你是单调递增了，那还不应该大于0恒成立吗？要因式分解吗？大可不必，先观察观察，然后再决定怎么办！）因为[)3,10∈x ，033,0,03,0200300000<+->+>+->---x e e x x e e x x x x ，（嘿嘿，出来了！），则0)33)(()3)((200300000>+-+-+----x e e x x e ex x x x . 则0)(0>'x g 在[)3,10∈x 上恒成立，故2)1()(1min0-+==e e g x g ，故12e e a -+>.难题分解2：如何根据求得的参数a 的取值范围比较1e -a 与1e -a 的大小？认知过程1：这是什么问题？（比大小问题）认知过程2：之前有没有见过类似的问题（见过，比如比较ba 和ab 的大小）材料重现：案例：取对数运算在数学解题中的应用（来源于教材习题）引例：设10<<<b a ，比较b a 和ab 的大小。

2014年AP统计学考试综合评析及2015年AP统计学考试展望

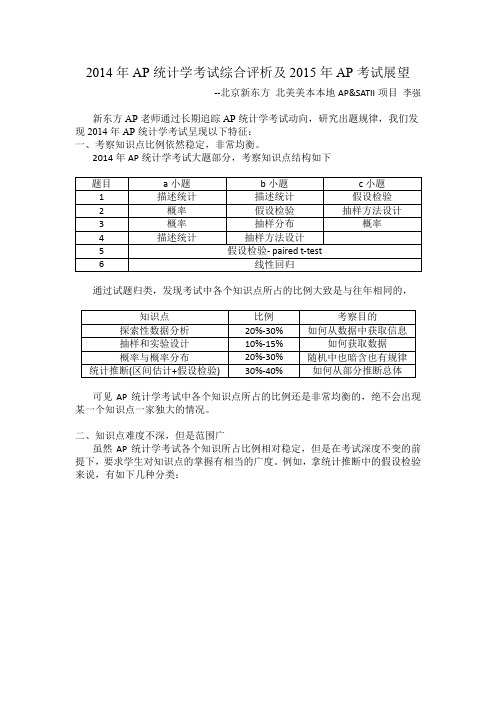
2014年AP统计学考试综合评析及2015年AP考试展望--北京新东方北美美本本地AP&SATII项目李强新东方AP老师通过长期追踪AP统计学考试动向，研究出题规律，我们发现2014 年AP统计学考试呈现以下特征：一、考察知识点比例依然稳定，非常均衡。

2014年AP统计学考试大题部分，考察知识点结构如下通过试题归类，发现考试中各个知识点所占的比例大致是与往年相同的，可见AP统计学考试中各个知识点所占的比例还是非常均衡的，绝不会出现某一个知识点一家独大的情况。

二、知识点难度不深，但是范围广虽然AP统计学考试各个知识所占比例相对稳定，但是在考试深度不变的前提下，要求学生对知识点的掌握有相当的广度。

例如，拿统计推断中的假设检验来说，有如下几种分类：其中χ2-test和pair-test相对于其他检验来说，是属于略微冷门的知识点，很对同学在复习的时候以为考的可能性很低，就战略性放弃了，这是绝对不可取的。

调查AP统计学以往出题，发现2013年AP统计学考试考查了χ2-test，2014年考查了pair-test，试题本身都不难，属于常规题型，套用答题模版即可轻松解决。

由此可见，AP统计学是实用型学科，并不考查学术本身，但是要求学生在各种真实背景下（题目中所描述的背景）解决实际问题，这时候知识点的广度就变得尤为重要，同学们在复习的时候，对于那些可以出大题，但又不常考的知识点，要格外小心。

三、考试7大黄金原则须谨记AP统计学考试不同于其他学科，擅长理科的同学非常惧怕文字阐述题目，擅长文科的同学又非常头疼各种公式计算。

而这些都是小问题，只要闹闹掌握住基本原理，就会发现AP考试题目本身是很简单的，它最要命的地方是读完题目感觉都会做，答完题目发现只有一半不到的分数，这才是AP统计真正的恐怖之处。

同学在考试过程中经常出现下面2种情况：1. 明明都会，但不知道从哪里开始下笔；2. 答题抓不住重点，密密麻麻写了半页纸，但只有一半甚至更少的分数。

2014年试题评析与2015年备考建议(数学)

是对“阿波罗尼斯圆”（平面内到两点距离之比等于不为1定值的点的轨迹）的逆向考查.
匠心独运体现导向
强化了试题与课本的联系，着力考查考生对数学本质的理解，理性回归学科本体. 避免“题海战术”的干扰，深化“依纲靠本”的备考导向.
1
2
3
特别建议：
1 2 3

年份
考察内容
涉及到知识点和方法
2014
求与抛物线有关的轨迹方程，直线与抛物线公共点个数的讨论直线与椭圆相交问题，动态探究型（存在性）问题
轨迹方程的求法（直接法、定义法），直线与曲线公共点个数的讨论，分类讨论思想，数形结合思想求直线与曲线交点坐标，解一元二次不等式转化思想（二维与一维转化—— 面积与坐标），数形结合
数学思想常考不懈
数学思想数形结合思想理科 3,4,5,6,7,10,14,15,19,22 文科 4,6,7,8,15,21,22
函数与方程思想 2,8,9,11,12,16,17,18,21,22 8,9,10,13,16,17,18,19,21,22 分类与整合思想 10,13,18,20,21,22 化归与转化思想 3,6,9,10,11,17,22 5,9,13,19,21,22 10,15,16,17,18,21,22
注重应用彰显价值
理科：8，17，20题，文科：10，11，16，18题
稳中求变适度创新
1.题型和难度的调整创新. 2.题目结构和问题情境设计的创新.
3.新定义题.理科第6题,正交函数对.
动态开放考查探究
加大直观与抽象、静态与动态、开放与探究的考查力度.理科试卷更明显. 18（2），19（2）以“是否存在” 切入问题，突出题目的开放性，考查探究能力.

2014广东高考数学评价及2015年复习建议116张ppt

• 理科包括：集合、复数、线性规划、向量、圆锥曲线、抽样、线线关系与命题、绝对值不等式、导数的基本应用、概率、三角函数、等比数列、坐标互化、三角形相似、三角函数计算、频率、直方图、线面垂直、数学归纳法、圆锥曲线、函数导数应用。
• 注重数学基本技能的评价数学技能主要包括：运算、几何技能（识图和作图）、基本的推理技能、数据处理、数学表达技能。
（1）具有熟练的运算技能
（2）能够识图、作图的几何技能几何技能就是，能够区别基本几何图形；能使用圆规、直尺绘制形体的直观图和截面图；能利用各种公式计算几何图形的面积、体积并简单的进行比较等等．几何技能或者称之为“图形处理技能”，包括两方面：识图技能和作图技能．识图技能是借助直观图形辅助学习数学知识、解决问题时所必备的识别图形各要素特点及关系的技能。
（4）数据处理技能 • 这个技能主要体现在概率统计问题中，考生要掌握基本的数据统计和处理技能。让学生经历收集数据、处理数据、分析数据、从数据中提取信息作出判断的全过程，并在经历过程中学会运用所学知识、方法去解决实际问题。 • 例6. 从0，1,2,3,4,5,6,7,8,9中任取七个不同的数，则这七个数的中位数是的概率为 .
•
突出重要的数学思想方法
• 2014年文科试题中的数学思想方法包括：方程（2，8， 14，19，20题）；函数（5，11，16，21题）；微积分思想（11,21题）；概率统计（12,17题）；转化的思想（13,15,19题）；放缩的思想方法（19题），分类讨论的思想方法（20,21题），数形结合的思想方法（4，8， 20）；数学模型（17）。 • 2014年理科试题中的数学思想方法包括：方程（2，,4， 14，20题）；函数（10，16，21题）；微积分思想（10,21题）；概率统计（6,17题）；转化的思想（9,13,15,19题）；归纳猜想（19题），分类讨论的思想方法（11，20,21题），数形结合的思想方法（3，20 题）；数学模型（17题）。

2014江苏高考试题1部分试题解析及2015届高三复习教学建议何睦

2014年普通高等学校招生全国统一考试（江苏卷）数学Ⅰ部分试题解析及2015届高三教学建议江苏省张家港市常青藤实验中学何睦（感谢苏州松陵金晔老师提供如此精美的试卷word 版）（2014年高考江苏卷第10题）已知函数,1)(2-+=mx x x f 若对于任意]1,[+∈m m x ,都有0)(<x f 成立,则实数m 的取值范围是 ▲ .【思路探究】画出二次函数的分析简图：由图象分析可得结论：开口向上的二次函数()f x 在[],m n 上恒小于0的充要条件为()0,()0.f m f n <⎧⎨<⎩ ，开口向下的二次函数()f x 在[],m n 上恒大于0的充要条件为()0,()0.f m f n >⎧⎨>⎩【解法探究】()0,22(1)0.230.2m f m m f m m ⎧-<<⎪⎛⎫<⎧⎪⇒⇒∈- ⎪⎨⎨ ⎪+<⎩⎝⎭⎪-<<⎪⎩. 【教学建议】（1）一元二次不等式作为江苏高考考试说明的C 级要求，在教学中应突出和加强二次函数、二次方程的零点、一元二次不等式的研究性教学，由于三次函数求导后仍为二次函数问题，所以可考虑多渗透一些含参数问题的讨论，适时和．．．适当．．加大二次问题的教学难度. （2）多引导学生利用数形结合的方法研究函数问题.如图，在平行四边形ABCD 中，已知8=AB ，5=AD ，PD CP 3=，2=⋅BP AP ，则 ⋅的值是 ▲ .【思路探究】向量是高中阶段数与形结合的完美典范，向量教学中尽可能的引导学生从代数和几何两个角度审视和考查向量问题，数一般指向量的坐标法，形一般指向量的基底法. 【解法探究】解法1：基底法，考虑将条件中涉及的,AP BP 向量用基底,AB AD 表示，而后实施计算.AB AD DP AD AP 41+=+=，AB AD CP BC BP 43-=+= 则)43()41(2AB AD AB AD BP AP -⋅+==⋅2216321AB AB AD AD -⋅-= 因为5,8==AD AB 则⋅-⋅-=2164163252，故22=⋅ 解法2：坐标法，不妨以A 点为坐标原点，AB 所在直线作为x 轴建立平面直角坐标系，可设(0,0),(8,0),(.).(2,),(8,)A B D a t P a t C a t ++，则(2,),(6,)AP a t BP a t =+=- 由2=⋅BP AP ，得22414a t a +-=，由5=AD ，得2225a t +=，则411a =, 所求822AB AD a ⋅==. 【教学建议】（1）向量是高中阶段数与形结合的完美典范，在向量教学中尽可能的引导学生从代数和几何两个角度审视和考查向量问题，数一般指向量的坐标方法，形一般指向量的基底方法. （2）平面向量的数量积作为江苏高考考试说明的C 级要求，在教学中应重点加强. 此外，向量作为良好载体可与很多其他知识进行结合（如数列、函数、解析几何等等），这一点在其他省份的高考题中有所体现，江苏在这方面未有尝试，不妨关注一下.已知)(x f 是定义在R 上且周期为3的函数,当)3,0[∈x 时,|212|)(2+-=x x x f .若函数 a x f y -=)(在区间]4,3[-上有10个零点(互不相同),则实数a 的取值范围是 ▲ .【解法探究】作出函数的简图，由图象分析可得10,2a ⎛⎫∈ ⎪⎝⎭.【教学建议】含绝对值的函数和分段函数是江苏省高考命题最为亲睐的考查内容之一，可以说每年高考填空题必考题型. 在教学中，应多让学生自己动手作图，不断提升“依性作图”和“以图识性”的能力.（2014年高考江苏卷第14题）若△ABC 的内角满足C B A sin 2sin 2sin =+,则C cos 的最小值是 ▲ . 【思路探究】多元函数的最值问题研究，考察正余弦定理和基本不等式.【类题链接】（2008年江苏高考）2,,,230,y x y z R x y z xz*∈-+=的最小值为 .【解法探究】由正弦定理得c b a 22=+，由余弦定理结合基本不等式有：422214322221432)22(2cos 2222222222-+=-+=+-+=-+=ab b a ab ab b a ab b a b a abcb a C4264222143222-=-≥ab ba ,当且仅当a =时等号成立. 【教学建议】多元函数最值问题的研究，应始终引导学生树立减元消参的意识，减元消参是数学求简的必然要求，是“简中求道”精神的体现.（2014年高考江苏卷第17题）如图,在平面直角坐标系xOy 中,21,F F 分别是椭圆22221(0)x y a b a b+=>>的左、右焦点，顶点B 的坐标为),0(b ，连结2BF 并延长交椭圆于点A ，过点A 作x 轴的垂线交椭圆于另一点C ，连结C F 1.（1）若点C 的坐标为)31,34(,且22=BF ,求椭圆的方程；（2）若,1AB C F ⊥求椭圆离心率e 的值.【解法探究】（1）由题意知2(0,),(,0)B b F c，则2BF a ===则椭圆方程为22212x y b +=. 点C )31,34(在椭圆上，故211611299b ⋅+=，解得21b =；所求椭圆方程为2212x y +=.（2）解法1：（垂直关系的先行表征）设000012(,),(.),(,0),(,0)C x y A x y F c F c --，由,1AB C F ⊥得001y b x c c ⋅=-+-，由A 在2BF 上，则001x y c b -+=；联立20000,.cx by c bx cy bc ⎧-=-⎪⎨-=⎪⎩ 解得：20222022,2.ca x b c bc y b c ⎧=⎪⎪-⎨⎪=⎪-⎩，00(,)C x y 在椭圆上，代入椭圆方程整理得2242224(2)c a c a c +=-，即225a c =，所以椭圆的离心率为5e =解法2：（垂直关系的最后表征）由题意知直线2BF 方程：()by x c c=--，与椭圆联立方程组得: 2222()1b y xc cx y a b ⎧=--⎪⎪⎨⎪+=⎪⎩得到222112()0x x a c c +-=，解得0B x =，2222A a c x a c =+；则2222(3)()A b b a c y x c c a c -+=--=+；又由12FC BF ⊥可知：2A A cx c y b+=-，代入化简有222222()(3)b a c c a c -=+，将222b a c =-代入化简得4225a a c =，即215e =，e =【教学建议】（1）解析几何的教学要注重“算理”的积累和表征，教会学生从不同的角度对问题进行表征，也符合江苏省对解析几何问题“多考一点想，少考一点算”的命题方向；（2）定点定值问题仍然是解析几何问题的命题热点、重点和难点，在教学中仍应引起足够重视，但江苏卷这两年解析几何的命题告诉我们：教学时也很有必要回归解析几何最最基本的运算（抛除一切所谓的运算技巧），我想这应该是这两年命题组老师的良苦用心吧；（3）加强解析几何的运算能力，如何提高？无它，算必躬亲耳.（2014年高考江苏卷第18题）如图,为了保护河上古桥OA ,规划建一座新桥BC ,同时设立一个圆形保护区.规划要求: 新桥BC 与河岸AB 垂直; 保护区的边界为圆心M 在线段OA 上并与BC 相切的圆.且古桥两端O 和A 到该圆上任意一点的距离均不少于80m. 经测量，点A 位于点O 正北方向60m 处, 点C 位于点O 正东方向170m 处(OC 为河岸),34tan =∠BCO . （1）求新桥BC 的长；（2）当OM 多长时,圆形保护区的面积最大？【解法探究】（1）解法1：（两角差的正切）连结AC ，由题意知6tan 17ACO ∠=，则由两角差的正切公式可得：2tan tan()3ACB BCO ACO ∠=∠-∠=，故cos 150BC ACB AC m =∠⋅= 答：新桥BC 的长度为150m.解法2：（解析法）由题意可知(0,60),(170,0)A B ；由 34tan =∠BCO 可知直线BC 的斜率43k =-，则直线BC 所在直线的方程为4(170)3y x =--；又由AB BC ⊥可知，AB 所在的直线方程为3604y x =+；联立方程组4(170)33604y x y x ⎧=--⎪⎪⎨⎪=+⎪⎩，解得80,120x y ==；即点(80,120)B，那么150BC ==. 答：新桥BC 的长度为150m.解法3：（初中解法）延长CB 交OA 所在直线于点G ，由34tan =∠BCO 可得6803OG =，8503CG =，5003AG =，4cos sin 5CGO GCO ∠=∠=，故 400cos 3BG CGO AG =∠⋅=，在OCG ∆中，由勾股定理得8503CG =，故150BC m =答：新桥BC 的长度为150m.（2）解法1：（解析法）由题意设(0,)M a (060)a ≤≤，圆M 的方程为222()x y a r +-=，且由题意可知68035a r -==. 又古桥两端O 和A 到该圆上任意一点的距离均不少于80m ，那么80(60)80r a r a -≥⎧⎨--≥⎩，解得1035a ≤≤；由函数68035ar -=为区间[10,35]上的减函数，故当10a =时，半径取到最大值为130.综上可知，当10OM m =时，圆形保护区的面积最大，且最大值为16900π. 解法2：（初中解法）（兴化顾卫老师）设BC 与圆切于点N ，连接MN ，过点A 作//AH BC 交MN 于点H .设OM a =，则60AM a =-，由古桥两端O 和A 到该圆上任意一点的距离均不少于80 m ，那么80(60)80r a r a -≥⎧⎨--≥⎩，解得1035a ≤≤. 由4tan tan 3AMH OCN ∠=∠=，可得3(60)5MH a =-，由（1）解法3可得100AB =，所以33100(60)13655MN x x =+-=-+，故MN 即圆的半径的最大值为130，当且仅当10a =时取得半径的最大值. 综上可知，当10OM m =时，圆形保护区的面积最大.【教学建议】（1）应用题从考试角度来说主要考查学生两个方面的能力：建立数学模型的能力（简称“建模”能力）、解决数学模型的能力（简称“解模”能力），从应试方法上如何突破呢？首先要系统研究所有可能出现的应用题并做到能对症下药，常考查的应用题类型有：函数应用题（以分式函数为载体的函数应用题、以分段函数为载体的函数应用题、以二次函数为载体的函数应用题）；三角测量应用题（以三角函数的定义为载体的三角应用题、以三角函数的图象为载体的三角应用题、以解三角形为载体的三角应用题、以立体几何为载体的三角应用题、以追击问题为载体的三角应用题、以米勒问题为载体的三角应用题）；数列应用题；线性规划应用题；解析几何应用题.（可参考何睦老师编写的《高考数学应用题复习题型归类解析讲义》）；其次是解模工具的积累，例如基本不等式、导数研究函数单调性等等.（2）本题的难点在于求出a 的取值范围，在教学中教师应注意多参数的参数范围问题注意目标意识的应用，注意减元意识的渗透．提供两个典型问题供各位练习：（Ex.1）（湖北高考题改编）锐角ABC ∆中，B A 2=，则A ∠的取值范围是___________. （Ex.2）（2014南通四模）图1是某种称为“凹槽”的机械部件的示意图，图2是凹槽的横截面（阴影部分）示意图，其中四边形ABCD 是矩形，弧CmD 是半圆，凹槽的横截面的周长为4．若凹槽的强度T 等于横截面的面积S 与边AB 的乘积，设AB =2x ，BC =y ．（1）写出y 关于x 函数表达式，并指出x 的取值范围；（2）求当x 取何值时，凹槽的强度T 最大．（Ex.3）（2014南通四模）设各项均为正整数的无穷等差数列{a n }，满足a 54=2014，且存在正整数k ，使a 1，a 54，a k 成等比数列，则公差d 的所有可能取值之和为．图1图2（2014年高考江苏卷第19题）已知函数x x x f -+=e e )(,其中e 是自然对数的底数. （1）证明:)(x f 是R 上的偶函数；（2）若关于x 的不等式)(x mf ≤1e -+-m x 在),0(+∞上恒成立，求实数m 的取值范围；（3）已知正数a 满足：存在),1[0+∞∈x ，使得)3()(0300x x a x f +-<成立.试比较1e -a 与1e -a 的大小，并证明你的结论. 【解法探究】（1）函数)(x f 的定义域为R ，关于原点对称；又因为()()xx f x e e f x --=+=，所以函数)(x f 是R 上的偶函数；（2）)(x mf ≤1e -+-m x ()e1xxxm e e m --⇔+≤+-，即(1)e1x x xm e e --+-≤-；令(0)x t e t -=>；因为111211x x e e t t-+-=+-≥-=，当且仅当1t =时，等号成立；故2111111tt m t t t t--≤=-++-，令21()1t h t t t -=-+，下只要求min ()m h t ≤.2(2)'()(1)t t h t t t -=-+；则当2t >时，'()0h t >；则当02t <<时，'()0h t <；因此可知当2t =时，min 1()(2)3h t h ==-；则13m ≤-. 综上可知，实数m 的取值范围为1(,]3-∞-.（3）难题分解1：如何根据条件求出参数a 的取值范围？问题呈现：0[1,)x ∃∈+∞，使得)3()(0300x x a x f +-<成立”，求参数a 的取值范围.认知过程1：这是什么问题？（不等式的有解问题）认知过程2：怎么处理这类问题？（参数分离或者直接求函数的最值，选用哪种呢？管它呢，都试试吧！）分解路径1：直接求函数的最值（笔者称其为“单刀直入”法）解：令30000()()(3)g x f x a x x =--+，只要在0[1,)x ∈+∞上，0)(min 0<x g 即可.002200()1'()3(1)x x e g x a x e-=+-. 且当01x =时，0'()0g x =；当01x >时，2010x ->，02()10x e ->，则0'()0g x >. 故在区间[1,)+∞上，0'()0g x ≥，即函数0()g x 为[1,)+∞的增函数，则1min 0()(1)20g x g e e a -==+-<，解得12e e a -+>.分解路径2：参数分离可以吗？（of course!）解：欲使条件满足，则[)3,10∈x （想想这是为什么？留给大家思考.）此时03030>+-x x ，则03003)(x x x f a +->，构造函数030003)()(x x x f x g +-=，即求此函数在 [)3,10∈x 上的最小值.（编者按：可能会有同学一阵眩晕，别怕，你要有个信念：要研究这么复杂的函数的单调性，可能只是DDN （逗逗你），单调的！不妨先用直觉感知一下：在定义域上，分子是单调递增的函数，分母是单调递减的函数，且分子和分母均大于0恒成立，还不是单调递增吗？有了这个目标. 对接下去的证明工作起了很好的导向作用）.2030200300)3()33)(()3)(()(000x x x e e x x e e x g o x x x x +-+-+-+--='-- （编者按：又有同学说：My faint!（我晕），这么复杂的分子怎么办！你说咋办！刚才的直觉已经告诉你是单调递增了，那还不应该大于0恒成立吗？要因式分解吗？大可不必，先观察观察，然后再决定怎么办！）因为[)3,10∈x ，033,0,03,0200300000<+->+>+->---x e e x x e e x x x x ，（嘿嘿，出来了！），则0)33)(()3)((200300000>+-+-+----x e e x x e ex x x x . 则0)(0>'x g 在[)3,10∈x 上恒成立，故2)1()(1min0-+==e e g x g ，故12e e a -+>.难题分解2：如何根据求得的参数a 的取值范围比较1e -a 与1e -a 的大小？认知过程1：这是什么问题？（比大小问题）认知过程2：之前有没有见过类似的问题（见过，比如比较ba 和ab 的大小）材料重现：案例：取对数运算在数学解题中的应用（来源于教材习题）引例：设10<<<b a ，比较b a 和ab 的大小。

2014级《微积分B(二)》A卷及解答

4.二次积分

2 d
cos f (r cos , r sin )rdr 可以写成
0
0
(D)一定有极值（D）
1
yy2
(A) dy
f (x, y)dx
0
0
1
1 y2
(B) dy
f (x, y)dx
0
0
1
1
(C) dx f (x, y)dy
0
0
1
xx2
(D) dx
2x3ex2
2.
1 －1
x2
tan
x

1
1 x
2

dx

2
3.设 z f (x ln y, y x) ，且 f 具有一阶连续偏导数，则全微分 dz
( f1ln
y
f
2)dx

(
x y
f1
f2)dy
第1页共3页
4.若 D 是由 x 1, y 1 围成的正方形区域，则 x2dxdy _____________
上海立信会计学院 2014～2015 学年第二学期
2014 级本科《微积分 B（二）》期终考试试卷（A）答案
（本场考试属闭卷考试，考试时间 120 分钟，禁止使用计算器）共 4 页
学院：
班级
学号
姓名
题号一
二
三
四
五总分
得分
一、单项选择题（本大题共 6 小题，每小题 2 分，共 12 分）
1.下列不等式中，成立的是

0 0
，解得唯一驻点：

x0

3a 2b 2a2 b2

2014年AP物理C考试综合评析及2015年展望

2014AP物理C考试综合评析及2015年AP物理C考试展望--北京新东方北美美本本地AP&SATII项目石晔AP考试作为一门标准化考试，强调的是试题难度的“稳定性”，也就是每年成绩的“可互相参考性”。

虽然随着中国考生大量进入AP考试领域，使得AP考试的平均分大幅度上浮，最后一定会导致Collegeboard提高AP考试的难度，但是就2015年来说，AP物理C考试的难度预计不会有太大幅度的变化，应当与往年的难度处于均衡或略微偏高的位置。

一、继续强调实验分析2014年物理C的力学和电磁学考试的解答题中，各出现了一道实验题，使得实验分析在解答题分值中占到了大约25%的比例，也即在全部考试中，占有12.5%的比例。

能否答对实验题，直接决定了考生是否能够将自己的分数提高一个档次。

在中国高中物理教学之中，教师总是过分强掉计算的重要性，而常常忽视对于设计实验、实验过程描述以及实验结果分析的训练，这也使得在中国教育体系甚至中国的国际学生，也常常会在实验问题上马失前蹄。

近几次AP考试给我们的启示是，在准备AP物理C的考试中必须加强对学生关于常见实验设计和分析手段的训练。

AP物理C中最为常见的实验分析手段就是描点和进行回归分析，在2014年的考试中这样的题目出现了两次。

考生需要具备将题目所给出的数据点在表格上表示出来，并且找到最为符合这些数据点的近似图像的能力。

学生需要考察所得出的图像是线性的还是非线性的。

一般来说，线性近似图像的斜率、横截距以及纵截距都是考察的重点，考生需要能够用简洁的语言正确的表示出斜率所蕴含的物理意义。

另外，对于图像整体所蕴含的意义，以及图像所表示的物理趋势，也是AP物理C考试的重点，以及学生最为头疼的难点。

这样的题目，其难度在于如何运用简洁的语言把握真正的物理意义，而不是单单用语言复述一遍题目的数学表达式。

例如在力学第一题中，题目先要求学生画出速度V与位移x之间的关系，这对于很多学生来说就是一大难点，因为一般对于学生的要求是掌握速度v和时间t之间的图像（简称v-t图像），而对于v-x图像学生却基本上从未见过，更别提如何归纳v-x图像的意义了。

2014年AP美国历史考试综合评析及2015年展望

2014年AP美国历史考试综合评析及2015年AP考试展望--北京新东方北美美本本地AP&SATII项目刘昱伶通过对2014年AP美国历史试题的分析研究，我们发现此次考试仍然沿用之前的形式，题型中规中矩，但在考点上有一定的创新之处。

其中，Document-based Question第一次提及美国的外交政策对一战及朝鲜战争结局的影响，Free-response Question考察了美国主要的党派和第三党派在经济、社会改良及西进运动中的不同做法，而在之前的考试汇中第三党派的考察比较少且没有这么细致。

但鉴于Collegeboard将于2015年对AP美国历史考试进行全方位改革，所以我们重点分析一下新的考试大纲，主要的变化有：第一大变化：课程结构更简洁，考察内容更明确。

现行的课程结构涵盖了28个历史时期、12个主题。

但是只是泛泛地列出了可能要考的主题，并没有明确说明要考察的内容。

改革后的课程结构精简为9个历史时期、7大主题，并在每一个章节中列出了需要掌握的三个主要概念、重要的历史事件及历史结构。

同时，新增一项考察技能——历史的思维方式，这要求考生不仅仅掌握某个知识点，而要更加全面地评判历史人物和事件。

当然，这离不开大量相关史料的阅读和辩证的思考。

第二大变化：主题划分明确，考察方式更开放。

现行的课程结构可能考察的主题有美国的多元化、美国的身份认同、美国文化、人口变化、经济转型、环境问题、全球化问题、政治和公民问题、改革问题、宗教问题、奴隶制在北美的遗留问题、战争和外交问题等，但是在之前的考试中很多主题并没有考察过。

新的课程结构主题紧扣美国历史主题中的重中之重，压缩为7大主题，如美国的身份认同问题、移民问题、工作交流和技术问题、政治和权力问题、环境地理问题、美国在世界的地位问题、观点、信仰及文化方面的问题等，新增简答题的形式对以上主题进行考察。

第三大变化：轻记忆重能力，考试题型更新颖。

现行的考试设计着重考察分散的历史知识，主要集中在课程内容方面，包括55分钟作答80道单选题；60分钟作答1道材料题；70分钟作答2道论述题。

15试卷综合分析

上海应用技术学院2014—2015学年第二学期《高等数学（工）2》期末试卷A （综合分析）一、解析几何知识概要：一、向量(,,),(,,)x y z x y z a a a a b b b b ==，则 ..cos(,)x x y y z z xy z xyza b a b a b a b a b a b ij k a b a a a b b b ==++⨯=注：0x x y y z z a b a b a b a b a b ⊥⇔=++= 二、直线与平面平面方程（1）点法式：0)()()(000=-+-+-z z C y y B x x A其中{}C B A n ,,=为平面法向量，),,(000z y x 为平面上一点。

（2）一般式：0=+++D Cz By Ax ，其中{}C B A n ,,=为平面法向量。

(3) 三点式：平面过三点111222333(,,),(,,),(,,)x y z x y z x y z ，则平面方程为：法向量n AB AC →→=⨯平面方程为： 1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 直线方程：（1）对称式（标准式、点向式）：pz z n y y m x x 000-=-=- 其中直线的方向向量为{}p n m s ,,=，),,(000z y x 为直线上一点。

（2）两点式：121121121z z z z y y y y x x x x --=--=--（3）参数式：⎪⎩⎪⎨⎧+=+=+=ptz z nt y y mt x x 000（4）一般式：⎩⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A ，其方向向量{}{}222111,,,,C B A C B A s ⨯=考试题：1．已知点(1,2,3)A ，(3,5,3)B -与(3,5,4)C -，则ABC ∆的面积为()．A ．52 BC ．72 D ．12.已知直线235235x y z ---==与平面370x ky z +++=平行，则k =．17．求点(4,1,3)M -在直线235:112x y z L ---==上的投影．关联考题11．曲面2210x y z +--=在点(2,1,4)处的切平面方程为. 16．设L 为从(0,0,0)到(1,1,1)的直线段，则Lzdx xdy ydz ++=⎰．13．u xy =在点(1,2)处沿方向2(,22l =的方向导数为．要提醒的题目例1、求过点A （1，2，3）和直线11211x y z -+==- 的平面方程。

2015年AP考试真题解析（宏观。微观经济学FR部分）解读

2015年AP考试真题解析(宏观经济学FR部分)AP宏观经济学的FR题目每年都是三道题，其中第一题问到的内容也相对较多，所占比重比较高，总分30分的简答题中，第一题占到了将近一半的分值。

AP宏观经济学的FR真题每年涉及的知识点大同小异，包括AD-AS、菲利普斯曲线、货币市场、可贷资金市场、外汇市场等模型，同时会涉及到财政政策、货币政策和国际贸易等政策性内容。

“2015年AP宏观经济学考试涉及的考点还是基本沿袭了之前的风格，AD-AS模型、可贷资金市场、货币市场、外汇市场都有所涉及，重要的图形中唯一没有考到的是菲利普斯曲线，财政政策和货币政策也都考到了，相对冷门的考点是第二题中的国际贸易。

另外，三道题中都可以看出每一小问之间的连带性，很多时候某一问做错了，后面连续就都做错了，这也是让考生们头疼的地方。

大家在2016年的AP宏观经济学考试中，一定要特别注意这种题目之间的连带性，每问得出结论是都要格外仔细。

第一题这是一道非常非常典型的AP宏观经济学FR第一题，涉及到了一个国家的运行以及如何使用政策改变现在的运行状态。

第一问：几乎每年都会让考生用AD-AS模型画出一个国家的运行状态。

题目中说到美国的经济正运行在充分就业以下，说明国家正处在衰退状态，这时在AD-AS模型中，我们要把长期AS曲线画在短期AS与AD曲线交点的右方，如下图：*注意横纵轴要写实际GDP和价格水平，短期均衡点对应Y1，而长期AS对应Yf第二问：说到美联储想要让经济回到充分就业，也就是经济不要继续衰退，那么它应该使用扩张型的货币政策，让利率下降，从而使得投资增加，达到扩张经济的效果。

（这里要强调的是，题目中提到的federal funds rate是指美国商业银行间的同业借贷利率，在题目中如果没有特意提到这个意思，考生们只要理解成美国最基准的利率就可以了。

所以在这道题中，只要回答应该以低的federal funds rate 为目标就可以了。