SPSS因子分析法-例子解释
spss因子分析案例

spss因子分析案例在进行SPSS因子分析时,我们通常遵循以下步骤:数据准备、因子提取、因子旋转、因子得分和结果解释。
下面是一个因子分析的案例,展示了如何使用SPSS软件进行这一统计分析。
首先,我们需要准备数据。
这通常涉及收集问卷调查数据,其中包含多个项目或变量,这些变量被认为是潜在因子的指标。
在SPSS中,数据应该以数据集的形式输入,每个变量代表一个问卷项目,每个案例代表一个受访者的回答。
接下来,我们进行因子提取。
在SPSS中,我们可以通过“分析”菜单选择“降维”然后选择“因子”来开始因子分析。
在因子分析对话框中,我们需要指定分析的变量,并决定提取因子的方法。
常见的提取方法包括主成分分析和最大似然法。
此外,我们还需要决定因子提取的标准,如特征值大于1的规则或基于特定比例的方差提取。
因子提取后,我们通常需要进行因子旋转。
旋转的目的是使因子结构更加清晰,便于解释。
SPSS提供了多种旋转方法,如正交旋转(如Varimax)和斜交旋转(如Promax)。
旋转后,每个变量的因子载荷(即变量与因子的相关系数)将被重新估计。
然后,我们可以计算因子得分。
因子得分是每个受访者在每个因子上的估计得分,它可以帮助我们了解每个受访者在潜在因子上的位置。
在SPSS中,可以通过“保存”选项来保存因子得分,以便进一步分析。
最后,我们需要解释因子分析的结果。
这包括解释每个因子的含义,以及哪些变量与每个因子最相关。
我们可以通过查看因子载荷矩阵来完成这一步骤。
通常,载荷值较高的变量被认为是该因子的良好指标。
在实际应用中,因子分析可以帮助我们识别数据中的潜在结构,简化数据集,并为进一步的分析提供基础。
例如,在市场研究中,因子分析可以用来识别消费者行为的潜在维度,从而帮助企业更好地理解其客户群体。
通过上述步骤,我们可以使用SPSS软件有效地进行因子分析,从而揭示数据背后的潜在结构,并为决策提供支持。
SPSS因子分析经典案例分享

SPSS因⼦分析经典案例分享因⼦分析已经被各⾏业⼴泛应⽤,各种案例琳琅满⽬,今天再次发布这⼀经典案例以飨读者。
什么是因⼦分析?因⼦分析⼜称因素分析,传统的因⼦分析是探索性的因⼦分析,即因⼦分析是基于相关关系⽽进⾏的数据分析技术,是⼀种建⽴在众多的观测数据的基础上的降维处理⽅法。
其主要⽬的是探索隐藏在⼤量观测数据背后的某种结构,寻找⼀组变量变化的共同因⼦。
因⼦分析能做什么?⼈的⼼理结构具有层次性,即分为外显和内隐。
但是作为具有同⼀性的个体来说,内隐的⽅⾯总是和外显的⽅⾯相互作⽤,内隐⽅⾯制约着外显特征。
所以我们经常说,⼀个⼈的内在⾃我会在相当程度上决定他的外在⾏为特征,表现为某些⾏为倾向具有⾼度的⼀致性或相关性。
反过来说,我们可以通过对个体进⾏系统的观察和测量,从⼀组⾼度相关的⾏为倾向(可观测)中,探索到某种稳定的内在⼼理结构(潜存在),这就是因⼦分析所能做的。
具体来说主要应⽤于:(1)个体的综合评价:按照综合因⼦得分对case进⾏排序;(2)调查问卷效度分析:问卷所列问题作为输⼊变量,通过KMO、因⼦特征值贡献率、因⼦命名等判断调查问卷架构质量;(3)降维处理,结果再利⽤:因⼦得分作为变量,进⾏聚类或其他分析。
案例描述:⾼中⼤家都读过吧,那是⼀个以成绩论英雄的时代,理科王⼦、⽂科⼩⽣是时代标签。
为什么我们会将数学、物理、化学归并为理科,其他的归并为⽂科,有没有数据⽀持?今天我们将⽤科学的⽅法找到答案。
100个学⽣数学、物理、化学、语⽂、历史、英语成绩如下表(部分),请你来评价他们。
这是⼀个有趣的案例,你可以客观的观测到每⼀科⽬的成绩,但你可以直接看到理科、⽂科的情况吗?6个科⽬的成绩是我们观测到的外在表现,隐藏在其中的公共因⼦你找到了吗?如果我们针对6科⽬做降维处理,会得到什么结果,拭⽬以待。
SPSS分析过程6科⽬成绩作为6个原始变量,利⽤SPSS进⾏因⼦分析,具体步骤请参照各因⼦分析教程,默认亦可,不在讨论范围之内。
如何利用SPSS做因子分析等分析(仅供参考)
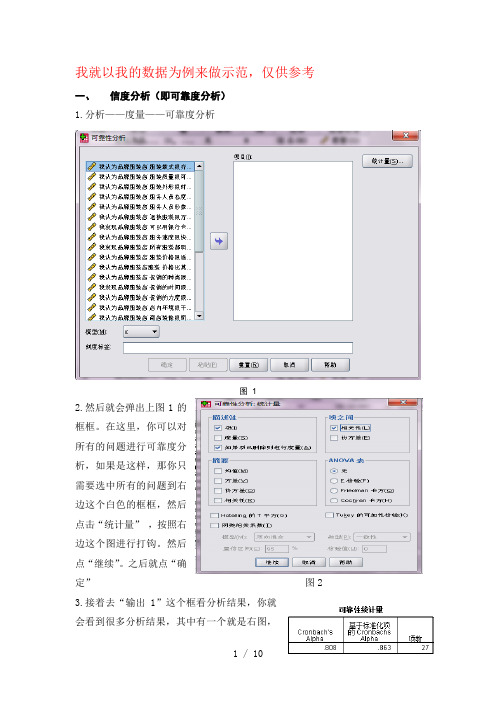
我就以我的数据为例来做示范,仅供参考一、信度分析(即可靠度分析)1.分析——度量——可靠度分析图 12.然后就会弹出上图1的框框。
在这里,你可以对所有的问题进行可靠度分析,如果是这样,那你只需要选中所有的问题到右边这个白色的框框,然后点击“统计量”,按照右边这个图进行打钩。
然后点“继续”。
之后就点“确定”图2 3.接着去“输出1”这个框看分析结果,你就会看到很多分析结果,其中有一个就是右图,那第一个0.808就是你所选择进行分析的数据的信度。
如果你想把每一个维度的数据进行独立的信度分析,那道理也是一样的。
二、因子分析在做因子分析之前首先要判断这些数据是否适合做因子分析,那这里就需要进行效度检验,不过总共效度检验是和因子分析的操作同步的,意思就是说你在做因子分析的时候也可以做效度检验。
具体示范如下:1.分析——降维——因子分析图 2一般来说,咱们做因子分析的时候是为了把那些具有共同属性的因子归类成一类,说的简单点就是要验证咱们所选取的每一个维度下面的题目是属于这个维度,而非其他维度的。
那一般来说,因子分析做出来的结果就是你原本有几个维度,最终分析结果就会归类成几个公因子。
2.一般来说,自变量的题目和因变量的题目是要独立分析的。
我的课题是“店面形象对顾客购买意愿的影响”那自变量就是店面形象的那些维度,因变量就是顾客购买意愿。
3.将要做分析的题目选择到右边的白框之后,就如下图打钩:“抽取”和“选项”两个不用管他。
然后就点“确定”4.按照上述步骤操作下来之后,就可以去“输出1”看分析结果。
首先看效度检验的结果:这里要看第一行和最后一行的数据,第一行数据为0.756,表明效度较高,sig为0.000,这两个结果显示这份数据完全可以做因子分析。
那就去看因子分析的结果。
5.看下面这张图,看“初始特征值”这一项下面的“合计”的数值,有几个数据是>1,那就表明此次因子分析共提取了几个公因子。
下图所示,有5个数据是>1,这表明可以提取5个公因子。
因子分析spss

因子分析spss因子分析是一种常用的统计方法,用于分析多个变量之间的关系。
在实际应用中,因子分析可以用于降维、构建变量、发现潜在结构等方面。
在本文中,将介绍因子分析的概念、原理和应用,并举例说明其具体操作步骤。
一、概念因子分析(Factor Analysis)是一种多变量统计方法,旨在识别一组观测变量中的潜在结构或因素。
它假设这些观测变量可以由几个潜在因素解释,每个观测变量与这些因素之间存在某种关系。
二、原理因子分析的基本原理是将多个相关变量转化为少数几个无关变量(即因子)。
在因子分析中,变量之间的相关性通过计算相关系数或协方差矩阵来衡量。
接下来,通过特征值分解或最大似然法等方法,将相关系数矩阵转化为因子载荷矩阵和因子得分矩阵。
因子载荷矩阵衡量了每个变量与每个因子之间的关系强度,而因子得分矩阵表示每个样本在每个因子上的得分。
三、步骤1. 确定研究目的和问题,构建研究假设。
2. 收集相关数据,并进行数据预处理,例如去除异常值、缺失值处理等。
3. 计算相关系数矩阵或协方差矩阵,以衡量变量之间的关系。
4. 进行因子提取,常用的方法有主成分分析和最大似然法。
5. 判断因子数目,可以采用特征值大于1、平行分析、因子解释度等方法。
6. 进行因子旋转,常用的方法有方差最大化旋转和直角旋转。
7. 解释因子载荷矩阵和因子得分矩阵,了解每个因子的意义和作用。
8. 进行因子得分的计算和解释,用于后续的数据分析和决策。
四、应用因子分析在实际应用中具有广泛的应用价值。
以下是一些常见的应用领域:1. 心理学:通过因子分析可以分析心理量表中的各项指标是否能够归纳到几个内在的心理因素上,从而简化研究和测量。
2. 经济学:通过因子分析可以将多个经济指标进行降维处理,方便经济发展的研究和分析。
3. 市场调研:通过因子分析可以对市场研究中的多个变量进行整合和分析,从而了解消费者的需求和市场趋势。
4. 教育评估:通过因子分析可以对学生的学业状况进行评估,从而提供有针对性的教育干预和指导。
SPSS因子分析法内容与案例

SPSS因子分析法内容与案例实验课:因子分析实验目的理解主成分(因子)分析的根本原理,熟悉并掌握SPSS中的主成分(因子)分析方法及其主要应用.因子分析、根底理论知识1概念因子分析(Factor analysis):就就是用少数几个因子来描述许多指标或因素之间的联系,以较少几个因子来反映原资料的大局部信息的统计学分析方法.从数学角度来瞧,主成分分析就是一种化繁为简的降维处理技术.主成分分析(Principal component analysis):就是因子分析的一个特例,就是使用最多的因子提取方法.它通过坐标变换手段,将原有的多个相关变量,做线性变化,转换为另外一组不相关的变量.选取前面几个方差最大的主成分,这样到达了因子分析较少变量个数的目的,同时又能与较少的变量反映原有变量的绝大局部的信息.两者关系:主成分分析(PCA)与因子分析(FA)就是两种把变量维数降低以便于描述、理解与分析的方法,而实际上主成分分析可以说就是因子分析的一个特例.2特点(1)因子变量的数量远少于原有的指标变量的数量,因而对因子变量的分析能够减少分析中的工作量.(2)因子变量不就是对原始变量的取舍,而就是根据原始变量的信息进行重新组构,它能够反映原有变量大局部的信息.(3)因子变量之间不存在显著的线性相关关系,对变量的分析比拟方便,但原始局部变量之间多存在较显著的相关关系.(4)因子变量具有命名解释性,即该变量就是对某些原始变量信息的综合与反映.在保证数据信息丧失最少的原那么下,对高维变量空间进行降维处理(即通过因子分析或主成分分析).显然,在一个低维空间解释系统要比在高维系统容易的多.SPSS因子分析法内容与案例3类型根据研究对象的不同,把因子分析分为R型与Q型两种.当研究对象就是变量时,属于R型因子分析;当研究对象就是样品时,属于Q型因子分析.但有的因子分析方法兼有R型与Q型因子分析的一些特点,如因子分析中的对应分析方法,有的学者称之为双重型因子分析 ,以示与其她两类的区别.4分析原理假定:有n个地理样本,每个样本共有p个变量,构成一个n x p阶的地理数据矩阵:X ii X12 X ip当p较大时,在p维空间中韦•察问磐比拟麻烦%这就需要进行降维处理,即用较少几个综X2i X22 X2 p合指标代替原来指标,而总使这些综合指标既能尽量多地反映原来指标所反映的信息,同时它们之间又就是彼此独立的.线性组合:记x1,x2,…,xP 肺变标标,z1,x2p…,zm(mw p)为新变量指标(主成分,那么其线性组合为:z1 l11 x1 l 12 x2 l1 p x pLij就是原变量在各主成@上l呼荷l Yz2 21 x1 22 x2 l2p x pzi 111x1 112x2 l1 p x p无论就是哪一种因子分析方法#相昌的因子解用不就是唯一的l因子解中之一. 舍瞌攵2m2% 21mp>pp,主因子解仅仅就是无数zi与zj相互无关;z1就是x1,x2,…,xp的4切㈣mOl合+2^21最大者1mp x z2就是与zi不相关的x1,x2,…的所有线性组合中方差最大者.那么 ,新变量指标z1,z2,…分别称为原变量指标的第一 ,第二,…主成分.Z为因子变量或公共因子,可以理解为在高维空间中互相垂直的m个坐标轴.主成分分析实质就就是确定原来变量xj(j=1,2 ,…,p)在各主成分zi(i=1,2,…,m)上的荷载lij.从数学上容易知道,从数学上也可以证实,它们分别就是相关矩阵的m个较大的特征值所对应的特征向量.5分析步骤5、1确定待分析的原有假设干变量就是否适合进行因子分析(第一步)因子分析就是从众多的原始变量中重构少数几个具有代表意义的因子变量的过程. 其潜在的要求:原有变量之间要具有比拟强的相关性. 因此,因子分析需要先进行相关分析,计算原始变量之间的相关系数矩阵.如果相关系数矩阵在进行统计检验时,大局部相关系数均小于0、3且未通过检验,那么这些原始变量就不太适合进行因子分析.SPSS因子分析法内容与案例差标准化方法,标准化后的数据均值为0,方差为1).SPSS在因子分析中还提供了几种判定就是否适合因子分析的检验方法.主要有以下3种:巴特利特球形检验(Bartlett Test of Sphericity)反映象相关矩阵检验(Anti-image correlation matriX)KMO(Kaiser-Meyer-Olkin)检验(1)巴特利特球形检验该检验以变量的相关系数矩阵作为出发点,它的零假设H0为相关系数矩阵就是一个单位阵,即相关系数矩阵对角线上的所有元素都为1,而所有非对角线上的元素都为0,也即原始变量两两之间不相关.巴特利特球形检验的统计量就是根据相关系数矩阵的行列式得到.如果该值较大,且其对应的相伴概率值小于用户指定的显著性水平,那么就应拒绝零假设H0,认为相关系数不可能就是单位阵,也即原始变量间存在相关性.(2)反映象相关矩阵检验该检验以变量的偏相关系数矩阵作为出发点,将偏相关系数矩阵的每个元素取反,得到反映象相关矩阵.偏相关系数就是在限制了其她变量影响的条件下计算出来的相关系数,如果变量之间存在较多的重叠影响,那么偏相关系数就会较小,这些变量越适合进行因子分析.(3)KMO(Kaiser-Meyer-Olkin)检验该检验的统计量用于比拟变量之间的简单相关与偏相关系数.KMO值介于0-1,越接近1,说明所有变量之间简单相关系数平方与远大于偏相关系数平方与,越适合因子分析.其中,Kaiser给出一个KMO 检验标准:KMO>0、9,非常适合;0、8<KMO<0、9适合;0、7<KMO<0、8,一般;0、6<KMO<0、7,不太适合;KMO<0、5,不适合.5、2构造因子变量因子分析中有很多确定因子变量的方法,如基于主成分模型的主成分分析与基于因子分析模型的主轴因子法、极大似然法、最小二乘法等.前者应用最为广泛.主成分分析法(Principal component analysis):该方法通过坐标变换,将原有变量作线性变化,转换为另外一组不相关的变量Zi(主成分).求相关系数矩阵的特征根入i (入1,入2,…,入p>0)与相应的标准正交的特征向量li;根据相SPSS 因子分析法内容与案例公共因子个数确实定准那么:1〕根据特征值的大小来确定,一般取大于1的特征值对应的几 个公共因子/主成分.2〕根据因子的累积方差奉献率来确定,一般取累计奉献率达 85-95%的特 征值所对应的第一、第二、…、第 m 〔mwp 〕个主成分.也有学者认为累积方差奉献率应在 80%以上.5、3因子变量的命名解释因子变量的命名解释就是因子分析的另一个核心问题.经过主成分分析得到的公共因子/主成分Z1,Z2,…,Zm 就是对原有变量的综合.原有变量就是有物理含义的变量 ,对它们进行线性变换后得到的新的综合变量的物理含义到底就是什么?在实际的应用分析中,主要通过对载荷矩阵进行分析 得到因子变量与原有变量之间的关 系,从而对新的因子变量进行命名.利用因子旋转方法能使因子变量更具有可解释性.计算主成分载荷,构建载荷矩阵A .正交旋转与斜通!转堤是因子旋裂的两类加l 1籍向于保持喻^汕的正交性,因此 使用最多.正本噂翎罚T 渊21多…,典21m 以方假设最历法最内常用.…bmjT方差最大令交旋转〔varimax . orthogonal rotation 〕 ----------------- 根本思想:使公共因子的相对负荷的■ ■■... ... ...方差之与最大,且彳柑寺原劄因子的指交性与今共方差总节不变:可使每l 个因子上的具有最 a p1 Pp1 ... Ppm p1 1 l p1 2... l pm* m大载荷的变量数最小,因此可以简化对因子的解释.斜交旋转〔oblique rotation 〕 ------------ 因子斜交旋转后,各因子负荷发生了变化,出现了两极分 化.各因子间不再相互独立,而就是彼此相关.各因子对各变量的奉献的总与也发生了改变.斜交旋转由于因子间的相关性而不受欢送. 但如果总体中各因子间存在明显的相关关系那么应该考虑斜交旋转.适用于大数据集的因子分析.无论就是正交旋转还就是斜交旋转,因子旋转的目的:就是使因子负荷两极分化 ,要么接近于0,要么接近于1.从而使原有因子变量更具有可解释性.5、4计算因子变量得分因子变量确定以后,对于每一个样本数据,我们希望得到它们在不同因子上的具体数据值 即因子得分.估计因子得分的方法主要有:回归法、Bartlette 法等.计算因子得分应首先将因关系数矩阵的特征根,即公共因子Zj 的方差奉献与〕,计算公共因子Zj 的方差奉献率与累积奉献率.〔等于因子载荷矩阵 L 中第j 列各元素的平方主成分分析I坐标原点与数据^M:心■合.一 〔方差奉献〕与方〔主成分〕所能代表的原始变量信息.,将原始变看 ;第一轴与数与等指标,,使得新的,化最大■向对■. ■!过计算特征根 来判断选取公共因子的数量 k 1 与公共因子SPSS因子分析法内容与案例子变量表示为原始变量的线性组合.即Bartlett 法:Bartlett 因子得分就是无偏的,但计算结果误差*因子得分可用于模型诊断,也可用作进一步分析如聚类分析、回归分析等的原始资料. 关于因子得分的进一步应用将在案例介绍一节分析.5、5结果的分析解释此局部详细见案例分析、案例分析1研究问题石家庄18个县市14个指标因子,具体来说有人均GDP〔元/人/人均全社会固定资产投资额、人均城镇固定资产投资额、人均一般预算性财政收入、第三产业占GDP比重〔%〕、人均社会消费品零售额、人均实际利用外资额〔万美元/人〕、人均城乡居民储蓄存款、农民人均纯收入、在岗职工平均工资、人才密度指数、科技支出占财政支出比重〔%〕、每万人拥有执业医师数量、每千人拥有病床数.要求根据这14项内容进行因子分析,得到维度较少的几个因子.2实现步骤【1】在"Analyze〞菜单“ Data Reduction〞中选择“Factor〞命令,如下列图所示[2]在弹出的下列图所示的Factor Analysis对话框中,从对话框左侧的变量列表中 选择这14个变量,使之添加到Variables 框中.[3]点击 “ Descriptives 〞 按钮,弹出 “Factor Analysis:Descriptives 〞 对木舌框,如图Value..OK Pasie1 r 1 rReset Cancel HelpFactor Analysis人均里枢经囱定奂… 人西城槽固定饶产… 人均一服限篡住附… 第三产业占GDP 出■.. 人均社会清费品零… 人均空布■利用外袋…Seierfion Vsrisble.Statistics框用于选择哪些相关的统计量,其中:Univariate descriptives傥量描述〕:输出变量均值、标准差;Initial solution 〔初始结果〕Correlation Matrix框中提供了几种检验变量就是否适合做引子分析的检验方法其中:Coefficients 〔相关系数矩阵〕Significance leves 一著性水平〕Determinant 〔相关系数矩P$的行列式〕Inverse 〔相关系数矩P$的逆矩阵〕Reproduced再生相关矩阵,原始相关与再生相关的差值〕Anti-image 〔反影像相关矩阵检验〕KMO and Bartlett' s test of sphericity 〔KMO 检验与巴特利特球形检验〕本例中,选中该对话框中所有选项,单击Continue按钮返回Factor Analysis对【4】单击"Extraction〞按钮,弹出“Factor Analysis:Extraction〞对话框,选择因子提取方法,如下列图所示:SPSS因子分析法内容与案例因子提取方法在Method下拉框中选取,SPSS共提供了7种方法:Principle Components Analysis 住成分分析〕Unweighted least square哧力口权最小平方法〕Generalized least square磔合最小平方法〕Maximum likelihood 〔最大似然估价法〕Principal axis factoring 〔主轴因子法〕Alpha factoring 〔〕因子〕Image factoring 〔影像因子〕Analyze框中用于选择提取变量依据,其中:Correlation matrix 〔相关系数矩阵〕Covariance matrix 的方差矩阵〕Extract框用于指定因子个数的标准,其中:Eigenvaluse over 大于特征值〕Number of factors 〔因子个数〕Display框用于选择输出哪些与因子提取有关的信息,其中:Unrotated factor solution 〔未经旋转的因子载荷矩阵〕Screen plot特征值排列图〕Maximun interations for Convergence框用于指定因子分析收敛的最大迭代次数, 系统默认的最大迭代次数为25.本例选用Principal components方法,选择相关系数矩阵作为提取因子变量的依据, 选中Unrotated factor solution与Scree plot项,输出未经过旋转的因子载荷矩阵与其特征值的碎石图;选择Eigenvaluse over®,在该选项后面可以输入1,指定提取特征值大于1的因子.单击Continue按钮返回Factor Analysis对话框.【5】单击Factor Analysis对话框中的Rotation 按钮,弹出Factor Analysis: Rotation 对话框,如下列图所示:SPSS因子分析法内容与案例该对话框用于选择因子载荷矩阵的旋转方法.旋转目的就是为了简化结构以帮助我们解释因子.SPSS默认不进行旋转〔None〕oMethod框用于选择因子旋转方法,其中:None3旋转〕Varimax〔正交旋转〕Direct Oblimin〔直接斜交旋转〕Quanlimax〔四分最大正交旋转〕Equamax〞均正交旋转〕Promax〔M交旋转〕Display框用于选择输出哪些与因子旋转有关的信息,其中:Rotated solution^俞出旋转后的因子载荷矩阵〕Loading plots〔输出载荷散点图〕本例选择方差极大法旋转Varimax,并选中Rotated solution与Loading plot项, 表示输出旋转后的因子载荷矩阵与载荷散点图 ,单击Continue按钮返回Factor Analysis对话框.【6】单击Factor Analysis对话框中的Scores按钮,弹出Factor Analysis: Scores^ 话框,如下列图所示:ED Fjctor Analysis: Factor Store-;回S.ava as variablesrMethod -----------------------------------------G f RegressionQ|国rtl曲匚〕Anderson-RubinH display 伯cttM n心nr外心ceHicient matrixCancel H*ContinueSPSS因子分析法内容与案例该对话框用以选择对因子得分进行设置,其中:Regression回归法〕:因子得分均值为0,采用多元相关平方;Bartlett 〔巴特利法〕:因子得分均值为0,采用超出变量范围各因子平方与被最小化;Anderson-Rubin 〔安德森-洛宾法〕:因子得分均值为0,标准差1,彼此不相关;Display factor score coefficient matrix:选择此项将在输出窗口中显示因子得分系数矩阵.【7】单击Factor Analysis 对话框中的Options 按钮,弹出Factor Analysis: Options 对话框,如下列图所示:该对话框可以指定其她因子分析的结果,并选择对缺失数据的处理方法,其中:Missing Values框用于选择缺失值处理方法:Exclude cases listwise去除所有缺失值的个案Exclude cases pairwis哈有缺失值的变量,去掉该案例Replace with mean用平均值代替缺失值Cofficient Display Format框用于选择载荷系数的显示格式:Sorted by size载荷系数根据数值大小排列Suppress absolute values less thaffi显示绝对值小于指定值的载荷量本例选中Exclude cases listwise项,单击Continue 按钮返回Factor Analysis对话框,完成设置.单击OK,完成计算.3结果与讨论〔1〕SPSS输出的第一局部如下:第一个表格中列出了18个原始变量的统计结果,包括平均值、标准差与分析的个案数.这个就是步骤3中选中Univariate descriptives项的输出结果.〔2〕SPSS输出结果文件中的第二局部如下:该表格给出的就是18个原始变量的相关矩阵Correlation Matrix⑶SPSS输出结果的第四局部如下该局部2&出了KMO检验与Bartlett球度检验结果.其中KMO值为0、551, 根据统计学家Kaiser给出的标准,KMO取值小于0、6,不太适合因子分析.Bartlett球度检验给出白相伴概率为0、00,小于显著性水平0、05,因此才!绝Bartlett 球度检验的零假设,认为适合于因子分析.〔4〕SPSS输出结果文件中的第六局部如下:CommunalitiesExtraction Method: Principal Component Analysis 、这就是因子分析初始结果,该表格的第一列列出了14个原始变量名;第二列就是根据因子分析初始解计算出的变量共同度.利用主成分分析方法得到14个特征值,它们就是因子分析的初始解,可利用这14个初始解与对应的特征向量计算出因子载荷矩阵.由于每个原始变量的所有方差都能被因子变量解释掉,因此每个变量的共同度为1;第三列就是根据因子分析最终解计算出的变量共同度. 根据最终提取的m个特征值与对应的特征向量计算出因子载荷矩阵. (此处由于软件的原因有点小问题)这时由于因子变量个数少于原始变量的个数,因此每个变量的共同度必然小于1. (5)输出结果第六局部为Total Variance Explained表格Extraction Method: Principal Component Analysis 、Total Variance ExplainedExtraction Method: Principal Component Analysis 、该表格就是因子分析后因子提取与因子旋转的结果. 其中,Component列与Initial Eigenvalues歹!J〔第一歹!J至U第四歹U 〕描述了因子分析初始解对原有变量总体描述情况.第一列就是因子分析13个初始解序号.第二列就是因子变量的方差贡献〔特征值〕,它就是衡量因子重要程度的指标,例如第一行的特征值为9、139,后面描述因子的方差依次减少.第三列就是各因子变量的方差奉献率〔% of Variance〕,表示该因子描述的方差占原有变量总方差的比例. 第四列就是因子变量的累计方差奉献率,表示前m个因子描述的总方差占原有变量的总方差的比例.第五列与第七列那么就是从初始解中根据一定标准〔在前面的分析中就是设定了提取因子的标准就是特征值大于1〕提取了3个公共因子后对原变量总体的描述情况.各列数据的含义与前面第二列到第四列相同,可见提取了5个因子后,它们反映了原变量的大局部信息.第八列到第十列就是旋转以后得到的因子对原变量总体的刻画情况.各列的含义与第五列到第七列就是一样的.〔6〕SPSS输出的该局部的结果如下Extraction Method: Principal Component Analysis 、a、13 components extracted 、该表格就是最终的因子载荷矩阵A,对应前面的因子分析的数学模型局部.根据该表格可以得到如下因子模型:X=AF+a &X I=0、959F1-0、075F2+0、015F3+0、158 F4-0、140F5-0、023F6-0、096F7+0、017F8-0、117F9+0、004F10-0、062F11-0、040 F12+0、021 F13aSPSS 因子分析法内容与案例-、116 、046 -、042 、036、044-、005 -、005 -、032 -、006、006 -、101 、023 、110 、039 、055、094 -、059 -、058 、053 -、045、081 、014 、000-、030、050Extraction Method: Principal Component Analysis a. 13 components extracted 、 Component Matrix aExtraction Method: Principal Component Analysis a 、 13 components extracted 、〔7〕SPSS输出的该局部的结果如下:该表格就是根据前面设定的方差极大法对因子载荷矩阵旋转后的结果.未经过旋转的载荷矩阵中,因子变量在许多变量上都有较高的载荷.经过旋转之后,第一个因子含义略加清楚,根本上放映了 “每万人拥有执业医师数量〞、“第三产业占GDP 比重〔%〕〞、“人均实际利用外资额〔万美元/人〕〞;第二个因子根本上反映了 “人 均全社会固定资产投资额〞、“人均城镇固定资产投资额〞 ;第三个因子反映了 “在岗职工平 均工资〞a 人均GDP 〔元/人〕 科技支出占财政支出比重〔%〕在岗职工平均工资农民人均纯收入SPSS因子分析法内容与案例Rotation Method: Varimax with Kaiser Normalizationa、Rotation converged in 7 iterations 、SPSS因子分析法内容与案例Extraction Method: Principal Component AnalysisRotation Method: Varimax with Kaiser Normalizationa、Rotation converged in 7 iterations 、Extraction Method: Principal Component Analysis 、Rotation Method: Varimax with Kaiser Normalization 、a、Rotation converged in 7 iterations 、〔8〕SPSS输出的该局部的结果如下:该局部输出的就是因子转换矩阵,说明了因子提取的方法就是主成分分析,旋转的方法就是方法极大法.Extraction Method: Prin( :ipal Compone snt Analysis 、Rotation Method: Varimax with Kaiser Normalization 、Component Transformation MatrixExtraction Method: Principal Component AnalysisRotation Method: Varimax with Kaiser Normalization(9)SPSS输出的该局部的结果如下Component Plot in Rotated Space该局部就是载荷散点图,这里为3个因子的三维因子载荷散点图,以三个因子为坐 标,给出各原始变量在该坐标中的载荷散点图,该图就是旋转后因子载荷矩阵的图 形化表示方式.如果因子载荷比拟复杂,那么通过该图那么较容易解释. 〔10〕SPSS 输出的该局部的结果如下:Component Score Coefficient MatrixComponent123456人均GDP 〔元/人〕 -、054 、003 、100 -、090 、046-、083 人均全社会固定资产投资额 -、237 、814 -、049 、044 -、064、141 人均城镇固定资产投资额 -、115 、520 -、158 -、164 、205、065 人均一般预算性财政收入 、045 -、143 、164 、148 -、191-、083 第三产业占GDP 比重〔%〕 、522-、062 -、111 -、161 、088-、193人均社会消费品零售额 -、217、017 -、092 、033 -、1942、033人均实际利用外资额〔万美元/ 、198 -、063-、026-、105、057-、231人〕人均城乡居民储蓄存款 、251 -、056 -、057 -、091 、018-、055 农民人均纯收入 、125、045 -、251-、036 1、119 -、657 在岗职工平均工资-、197 -、079 1、205-、096 -、183 -、179 人才密度指数-、099-、088-、021-、051-、068-、4171 .cr£ 0 5-c利打上出占时出点2止中 口 c.tr d E jGDP 〕人均一醺稹以性明 在岗朗「平均■ i ;i理千人相有病底数 士 人北 带度指我人均地; 赢人f 电0 第三产业叶GDP 比Jfi o O O幅i t 心—山 u 人均牡殳消费品单唐璇力美无人〕…邛、社或内泥诧桂箕相 o口人均城相固定镜产出 2收入人均实际利用外便领我民人上 poneni1Extraction Method: Principal Component Analysis 、Rotation Method: Varimax with Kaiser NormalizationComponent Scores 、Rotation Method: Varimax with Kaiser Normalization Component Scores 、Extraction Method: Principal Component Analysis 、Rotation Method: Varimax with Kaiser Normalization 、Component Scores 、该表格就是因子得分矩阵.这就是根据回归算法计算出来的因子得分函数的系数根据这个表格可以瞧出下面的因子得分函数.F I=-0、054x1+0、003x2+0、100x3-0、090X4+0、046x5-0、083x6-0、068x7+0、000x8+3、170x9+ 0、495x10-2、090x11-0、549x12+1、365x13[工定一E_上市H制* 「:事守■SPSS根据这13个因子的得分函数,自动计算2-个样本的3个因子得分,并且将3个引子得分作为新变量,保存在SPSS数据编辑窗口中〔分别为FAC1_1、FAC2_1、FAC3_1、FAC4_1、FAC5_1、FAC6_1、FAC7_1、FAC8_1、FAC9_1、FAC10_1、FAC11_1、FAC12_1、FAC13_1〕〔11〕SPSS输出的该局部的结果如下Extraction Method: Principal Component AnalysisRotation Method: Varimax with Kaiser Normalization Component Scores 、Extraction Method: Principal Component Analysis 、Rotation Method: Varimax with Kaiser Normalization 、Component Scores 、该输出局部就是因子变量的协方差矩阵. 在前面已经说明,所得到的因子变量应该就是正交、不相关的.从协方差矩阵瞧,不同因子之间的数据为0,因而也证实了因子之间就是不相关的.课程作业选择自己感兴趣的数据〔自己建立亦可〕,进行主成分分析,并对结果进行简要SPSS因子分析法内容与案例解释,可将结果与上次课中聚类分析结果进行比照.。
SPSS因子分析法例子解释

因子分析的基本概念与步骤一、因子分析的意义在研究实际问题时往往希望尽可能多地收集相关变量,以期望能对问题有比较全面、完整的把握与认识。
例如,对高等学校科研状况的评价研究,可能会搜集诸如投入科研活动的人数、立项课题数、项目经费、经费支出、结项课题数、发表论文数、发表专著数、获得奖励数等多项指标;再例如,学生综合评价研究中,可能会搜集诸如基础课成绩、专业基础课成绩、专业课成绩、体育等各类课程的成绩以及累计获得各项奖学金的次数等。
虽然收集这些数据需要投入许多精力,虽然它们能够较为全面精确地描述事物,但在实际数据建模时,这些变量未必能真正发挥预期的作用,“投入”与“产出”并非呈合理的正比,反而会给统计分析带来很多问题,可以表现在:计算量的问题由于收集的变量较多,如果这些变量都参与数据建模,无疑会增加分析过程中的计算工作量。
虽然,现在的计算技术已得到了迅猛发展,但高维变量与海量数据仍就是不容忽视的。
变量间的相关性问题收集到的诸多变量之间通常都会存在或多或少的相关性。
例如,高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性;学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。
而变量之间信息的高度重叠与高度相关会给统计方法的应用带来许多障碍。
例如,多元线性回归分析中,如果众多解释变量之间存在较强的相关性,即存在高度的多重共线性,那么会给回归方程的参数估计带来许多麻烦,致使回归方程参数不准确甚至模型不可用等。
类似的问题还有很多。
为了解决这些问题,最简单与最直接的解决方案就是削减变量的个数,但这必然又会导致信息丢失与信息不完整等问题的产生。
为此,人们希望探索一种更为有效的解决方法,它既能大大减少参与数据建模的变量个数,同时也不会造成信息的大量丢失。
因子分析正式这样一种能够有效降低变量维数,并已得到广泛应用的分析方法。
因子分析的概念起源于20世纪初Karl Pearson与Charles Spearmen等人关于智力测验的统计分析。
SPSS因子分析(因素分析)——实例分析

SPSS因子分析(因素分析)——实例分析提起因子分析那是老生常谈,分析人士大都喜欢讨论主成分与因子分析。
我也凑个热闹,顺便温习温习,时间长了就会很模糊。
一、概念探讨存在相关关系的变量之间,是否存在不能直接观察到的但对可观测变量的变化其支配作用的潜在因子的分析方法就是因子分析,也叫因素分析。
通俗点:原始变量是共性因子的线性组合。
二、简单实例现在有12个地区的5个经济指标调查数据(总人口、学校校龄、总雇员、专业服务、中等房价),为对这12个地区进行综合评价,请确定出这12 个地区的综合评价指标。
点击下载三、解决方案1、不同地区的不同指标不同,这导致目前我们拥有的5个指标数据很难对这12个地区给一个明确的评价。
所以,有必要确定综合评价指标,便于对比。
因子分析是一种选择,当然还有其他的方法。
5个指标即为我们分析的对象,直接选入。
2、描述统计选项卡。
我们要对比因子提取前后的方差变化,所以选定“初始分析结果”;现在是基于相关矩阵提取因子,所以,选定相关矩阵的“系数”;比较重要的还有KMO和球形检验,它告诉我们数据是不是适合做因子分析。
选定。
其他选择自定。
3、抽取选项卡。
提取因子的方法有很多,最常用的就是主成分法。
这里选主成分。
关于特征值,不想解释太多,这和显著性水平一样,都是统计学的一个基本概念。
因为参与分析的变量测度单位不同,所以选择“相关矩阵”,如果参与分析的变量测度单位相同,则考虑选用协方差矩阵。
4、是否需要旋转?因子分析要求对因子给予命名和解释,对因子旋转与否取决于因子的解释。
如果不经旋转因子已经很好解释,那么没有必要旋转,否则,应该旋转。
这里直接旋转,便于解释。
至于旋转就是坐标变换,使得因子系数向1和0靠近,对公因子的命名和解释更加容易。
5、要计算因子得分,就必须先写出因子的表达式。
而因子是不能直接观察到的,是潜在的。
但是可以通过可观测到的变量获得。
前面说到,因子分析模型是原始变量为因子的线性组合,现在我们可以根据回归的方法将模型倒过来,用原始变量也就是参与分析的变量来表示因子。
spss数据分析因子分析法

spss数据分析因子分析法
随着硬件技术的发展,每年被记录和存储下来的数据是非常庞大的,如何从庞大的数据堆中筛选出目标数据并分析得到有用的结论是现今重要的领域---数据挖掘。
为了能够充分有效的利用数据,化繁为简是一项必做的工作,希望将原来繁多的描述变量浓缩成少数几个新指标,同时尽可能多的保存旧变量的信息,这些分析过程被称为数据降维。
主成分分析和因子分析是数据降维分析的主要手段。
因子分析:
因子分析模型中,假定每个原始变量由两部分组成:共同因子和唯一因子。
共同因子是各个原始变量所共有的因子,解释变量之间的相关关系。
唯一因子顾名思义是每个原始变量所特有的因子,表示该变量不能被共同因子解释的部分。
举个例子:现在一个数据表有10个变量,因子分析可以将这10个变量通过特定的算法变为3个,4个,5个等等因子,而每个因子都能表达一种涵义,从而达到了降维的效果,方便接下来的数据分析。
SPSS因子分析法-内容及案例

实验课:因子分析实验目的理解主成分〔因子〕分析的根本原理,熟悉并掌握SPSS中的主成分〔因子〕分析方法及其主要应用。
因子分析一、根底理论知识1 概念因子分析〔Factor analysis〕:就是用少数几个因子来描述许多指标或因素之间的联系,以较少几个因子来反映原资料的大局部信息的统计学分析方法。
从数学角度来看,主成分分析是一种化繁为简的降维处理技术。
主成分分析〔Principal ponent analysis〕:是因子分析的一个特例,是使用最多的因子提取方法。
它通过坐标变换手段,将原有的多个相关变量,做线性变化,转换为另外一组不相关的变量。
选取前面几个方差最大的主成分,这样到达了因子分析较少变量个数的目的,同时又能与较少的变量反映原有变量的绝大局部的信息。
两者关系:主成分分析〔PCA〕和因子分析〔FA〕是两种把变量维数降低以便于描述、理解和分析的方法,而实际上主成分分析可以说是因子分析的一个特例。
2 特点〔1〕因子变量的数量远少于原有的指标变量的数量,因而对因子变量的分析能够减少分析中的工作量。
〔2〕因子变量不是对原始变量的取舍,而是根据原始变量的信息进展重新组构,它能够反映原有变量大局部的信息。
〔3〕因子变量之间不存在显著的线性相关关系,对变量的分析比拟方便,但原始局部变量之间多存在较显著的相关关系。
〔4〕因子变量具有命名解释性,即该变量是对某些原始变量信息的综合和反映。
在保证数据信息丧失最少的原那么下,对高维变量空间进展降维处理〔即通过因子分析或主成分分析〕。
显然,在一个低维空间解释系统要比在高维系统容易的多。
3 类型根据研究对象的不同,把因子分析分为R 型和Q 型两种。
当研究对象是变量时,属于R 型因子分析;当研究对象是样品时,属于Q 型因子分析。
但有的因子分析方法兼有R 型和Q 型因子分析的一些特点,如因子分析中的对应分析方法,有的学者称之为双重型因子分析,以示与其他两类的区别。
4分析原理假定:有n 个地理样本,每个样本共有p 个变量,构成一个n ×p 阶的地理数据矩阵 :当p 较大时,在p 维空间中考察问题比拟麻烦。
SPSS验证性因子怎么做?附案例讲解一文搞懂
验证性因子分析1、作用验证性因子分析(confirmatory factor analysis, CFA)是用于测试一个因子与相对应的测度项之间的关系是否符合研究者所设计的理论关系的一种研究方法,可用于调查问卷的量表分析。
2、输入输出描述输入:至少两项或以上的定量变量或有序的定类变量。
输出:测量因子与变量之间的对应关系是否符合研究者所设计的理论关系。
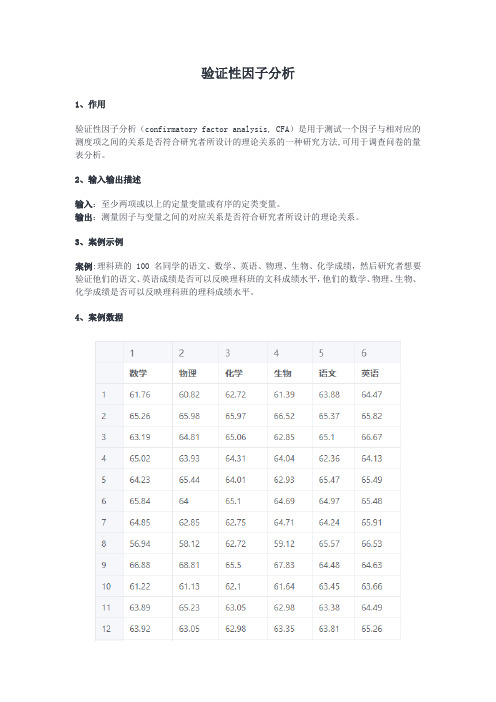
3、案例示例案例:理科班的 100 名同学的语文、数学、英语、物理、生物、化学成绩,然后研究者想要验证他们的语文、英语成绩是否可以反映理科班的文科成绩水平,他们的数学、物理、生物、化学成绩是否可以反映理科班的理科成绩水平。
4、案例数据验证性因子分析案例数据模型要求为至少两项或以上的定量变量或有序的定类变量,其中数学、物理、化学、生物为一个因子,语文和英语为一个因子。
5、案例操作Step1:新建分析;Step2:上传数据;Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;Step4:选择【验证性因子分析】;Step5:查看对应的数据数据格式,【验证性因子分析】要求特征序列至少两项或以上的定量变量或有序的定类变量。
在因子 1 拖入需验证的变量。
Step6:当涉及到多个因子时,点击【创建因子】.Step7:在因子 2 拖入需验证的变量。
Step8: 点击【开始分析】,完成全部操作6、输出结果分析输出结果 1:因子基本汇总表图表说明: 上表展示了样本频数的统计情况,包括样本中各个因子的字段频数、总计、总样本频数,CFA分析要求总样本数据最少要是因子内个别量表的5倍以上,且一般情况下至少需要200个样本。
结果分析:样本数据集共有因子数量 2 个,变量数 6 个,样本数 200 满足验证性因子分析基本数据要求。
输出结果 2:因子载荷系数表图表说明:上表为模型的因子载荷系数表格,包括潜变量、分析项、非标准载荷系数、z检验结果等。
测量关系时第一项会被作为参照项,因此不会呈现P值等统计量。
SPSS因子分析法-例子解释PDF

m
总和。变量 Z
j 的共同度 h 2 的数学定义为�h 2
�
�
2
a ji
�该式表明变量 Z
的共同度是因子
j
i�1
载荷矩阵 A 中第 j 行元素的平方和。由于变量 Z j 的方差可以表示成 h 2 � u 2 � 1 �因此变
量 Z j 的方差可由两个部分解释�第一部分为共同度 h 2 �是全部因子对变量 Z j 方差解释说
�因子的方差贡献�特征值 eigenvalue�
n
2
因子的方差贡献�特征值�的数学定义为� S i 2 � � a ji �该式表明�因子 F i 的方差
j�1
贡献是因子载荷矩阵 A 中第 i 列元素的平方和。因子 F i 的方差贡献反映了因子 F i 对原有
变量总方差的解释能力。该值越高�说明相应因子的重要性越高。因此�因子的方差贡 献和方差贡献率是衡量因子重要性的关键指标。
释性有助于对因子分析结果的解释评价�对因子的进一步应用有重要意义。例如�对高 校科研情况的因子分析中�如果能够得到两个因子�其中一个因子是对科研人力投入、 经费投入、立项项目数等变量的综合�而另一个是对结项项目数、发表论文数、获奖成 果数等变量的综合�那么�该因子分析就是较为理想的。因为这两个因子均有命名可解 释性�其中一个反映了科研投入方面的情况�可命名为科研投入因子�另一个反映了科 研产出方面的情况�可命名为科研产出因子。
Z j � a j1 F 1 � a j 2 F 2 � a j 3 F 3 � � � � � a jm F m � U j �j=1,2,3…,n�n 为原始变量总数�
可以用矩阵的形式表示为 Z � AF � U 。其中 F 称为因子�由于它们出现在每个原始
SPSS因子分析(因素分析)——实例分析

SPSS因子分析(因素分析)——实例分析SPSS因子分析(因素分析)——实例分析SPSS(Statistical Package for the Social Sciences)是一种广泛应用于数据分析的软件工具,其中的因子分析(Factor Analysis)被广泛用于统计学和社会科学领域的研究。
本文将通过一个实例分析来介绍SPSS因子分析的基本原理和步骤。
1.研究背景在实施因子分析之前,首先需要明确研究背景和目的。
假设我们正在研究消费者购物行为,并希望确定出不同因素对于购物偏好的影响。
2.数据收集和准备在进行因子分析前,需要收集并准备相关数据。
假设我们已经收集到了100位消费者的关于购物行为的调查问卷数据,包括10个关于购物偏好的变量。
在SPSS中,我们可以将这些数据输入到一个数据矩阵中,每一行代表一个消费者,每一列代表一个变量。
3.因子分析设置在SPSS中,通过导航菜单选择适当的分析工具来进行因子分析。
在设置选项中,我们可以选择因子提取方法(如主成分分析、极大似然法等)和旋转方法(如方差最大旋转、斜交旋转等)等。
根据实际情况,我们可以调整这些参数以获得最佳结果。
4.因子提取在因子分析的第一步中,SPSS会计算每个变量的因子载荷矩阵,并根据设定的准则提取出主要因子。
因子载荷表示了每个变量与每个因子之间的关联程度,值越大表示关联程度越高。
通过因子载荷矩阵,我们可以判断每个变量对于哪个因子具有较高的影响。
5.因子旋转因子旋转可用于调整因子载荷矩阵,以使其更易于解释。
旋转后的因子载荷矩阵通常会呈现出更简洁、更有意义的结果。
在SPSS中,我们可以选择合适的旋转方法并进行旋转操作。
6.因子解释和命名在完成因子分析后,我们需要对结果进行解释和命名。
根据因子载荷矩阵和旋转结果,我们可以确定每个因子代表了哪些变量,并为每个因子赋予一个描述性的名称,以便于后续的数据分析和报告撰写。
7.结果解读最后,根据因子分析的结果,我们可以进行一系列的统计推断和解读。
SPSS因子分析报告法-例子解释

因子分析的基本概念和步骤一、因子分析的意义在研究实际问题时往往希望尽可能多地收集相关变量,以期望能对问题有比较全面、完整的把握和认识。
例如,对高等学校科研状况的评价研究,可能会搜集诸如投入科研活动的人数、立项课题数、项目经费、经费支出、结项课题数、发表论文数、发表专著数、获得奖励数等多项指标;再例如,学生综合评价研究中,可能会搜集诸如基础课成绩、专业基础课成绩、专业课成绩、体育等各类课程的成绩以及累计获得各项奖学金的次数等。
虽然收集这些数据需要投入许多精力,虽然它们能够较为全面精确地描述事物,但在实际数据建模时,这些变量未必能真正发挥预期的作用,“投入”和“产出”并非呈合理的正比,反而会给统计分析带来很多问题,可以表现在:计算量的问题由于收集的变量较多,如果这些变量都参与数据建模,无疑会增加分析过程中的计算工作量。
虽然,现在的计算技术已得到了迅猛发展,但高维变量和海量数据仍是不容忽视的。
变量间的相关性问题收集到的诸多变量之间通常都会存在或多或少的相关性。
例如,高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性;学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。
而变量之间信息的高度重叠和高度相关会给统计方法的应用带来许多障碍。
例如,多元线性回归分析中,如果众多解释变量之间存在较强的相关性,即存在高度的多重共线性,那么会给回归方程的参数估计带来许多麻烦,致使回归方程参数不准确甚至模型不可用等。
类似的问题还有很多。
为了解决这些问题,最简单和最直接的解决方案是削减变量的个数,但这必然又会导致信息丢失和信息不完整等问题的产生。
为此,人们希望探索一种更为有效的解决方法,它既能大大减少参与数据建模的变量个数,同时也不会造成信息的大量丢失。
因子分析正式这样一种能够有效降低变量维数,并已得到广泛应用的分析方法。
因子分析的概念起源于20世纪初Karl Pearson和Charles Spearmen等人关于智力测验的统计分析。
SPSS因子分析——实例分析

SPSS因子分析——实例分析SPSS因子分析是一种统计方法,用于探索多个变量之间的相关性和结构。
它可以帮助研究者发现潜在的因素或维度,简化数据分析,并揭示变量之间的潜在关系。
本文将通过一个实例来介绍如何使用SPSS进行因子分析。
假设我们有一个关于消费者购买行为的调查问卷,包含了多个变量,如购买频率、购买金额、购买渠道等。
我们想要通过因子分析来探索这些变量之间的潜在结构,并识别出潜在的因素。
首先,我们需要将原始数据导入SPSS软件。
在SPSS的"变量视图"中,我们可以将每个变量名称输入到空白单元格中,并为每个变量选择适当的测量尺度(如定类尺度、定序尺度、定距尺度)。
然后,切换到"数据视图",在每一行中输入被调查者的数据。
接下来,我们需要进行因子分析的前提检测。
在SPSS的"分析"菜单中,选择"数据采样"并点击"样本界限",以确保我们选择的样本大小是否足够。
然后,我们选择"统计"中的"相关性",点击"双变量"并检查变量之间是否存在显著的相关性。
如果我们的数据满足以上要求,我们可以继续进行因子分析。
在SPSS的"分析"菜单中,选择"数据准备",点击"描述统计"并选择"频数",以检查每个变量的分布情况。
然后,我们再次选择"分析"中的"数据准备",点击"因子"并选择"提取方法"。
在弹出的对话框中,我们可以选择合适的提取方法,如主成分分析、极大似然估计等。
这些方法之间的选择要根据具体情况而定。
接下来,我们需要选择合适的因子数。
在"因子提取"对话框中,点击"因子"并输入我们认为合适的因子数。
(完整版)SPSS因子分析法-例子解释

因子分析的基本概念和步骤一、因子分析的意义在研究实际问题时往往希望尽可能多地收集相关变量,以期望能对问题有比较全面、完整的把握和认识。
例如,对高等学校科研状况的评价研究,可能会搜集诸如投入科研活动的人数、立项课题数、项目经费、经费支出、结项课题数、发表论文数、发表专著数、获得奖励数等多项指标;再例如,学生综合评价研究中,可能会搜集诸如基础课成绩、专业基础课成绩、专业课成绩、体育等各类课程的成绩以及累计获得各项奖学金的次数等。
虽然收集这些数据需要投入许多精力,虽然它们能够较为全面精确地描述事物,但在实际数据建模时,这些变量未必能真正发挥预期的作用,“投入”和“产出”并非呈合理的正比,反而会给统计分析带来很多问题,可以表现在:计算量的问题由于收集的变量较多,如果这些变量都参与数据建模,无疑会增加分析过程中的计算工作量。
虽然,现在的计算技术已得到了迅猛发展,但高维变量和海量数据仍是不容忽视的。
变量间的相关性问题收集到的诸多变量之间通常都会存在或多或少的相关性。
例如,高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性;学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。
而变量之间信息的高度重叠和高度相关会给统计方法的应用带来许多障碍。
例如,多元线性回归分析中,如果众多解释变量之间存在较强的相关性,即存在高度的多重共线性,那么会给回归方程的参数估计带来许多麻烦,致使回归方程参数不准确甚至模型不可用等。
类似的问题还有很多。
为了解决这些问题,最简单和最直接的解决方案是削减变量的个数,但这必然又会导致信息丢失和信息不完整等问题的产生。
为此,人们希望探索一种更为有效的解决方法,它既能大大减少参与数据建模的变量个数,同时也不会造成信息的大量丢失。
因子分析正式这样一种能够有效降低变量维数,并已得到广泛应用的分析方法。
因子分析的概念起源于20世纪初Karl Pearson和Charles Spearmen等人关于智力测验的统计分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因子分析的基本概念和步骤一、因子分析的意义在研究实际问题时往往希望尽可能多地收集相关变量,以期望能对问题有比较全面、完整的把握和认识。
例如,对高等学校科研状况的评价研究,可能会搜集诸如投入科研活动的人数、立项课题数、项目经费、经费支出、结项课题数、发表论文数、发表专著数、获得奖励数等多项指标;再例如,学生综合评价研究中,可能会搜集诸如基础课成绩、专业基础课成绩、专业课成绩、体育等各类课程的成绩以及累计获得各项奖学金的次数等。
虽然收集这些数据需要投入许多精力,虽然它们能够较为全面精确地描述事物,但在实际数据建模时,这些变量未必能真正发挥预期的作用,“投入”和“产出”并非呈合理的正比,反而会给统计分析带来很多问题,可以表现在:计算量的问题由于收集的变量较多,如果这些变量都参与数据建模,无疑会增加分析过程中的计算工作量。
虽然,现在的计算技术已得到了迅猛发展,但高维变量和海量数据仍是不容忽视的。
变量间的相关性问题收集到的诸多变量之间通常都会存在或多或少的相关性。
例如,高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性;学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。
而变量之间信息的高度重叠和高度相关会给统计方法的应用带来许多障碍。
例如,多元线性回归分析中,如果众多解释变量之间存在较强的相关性,即存在高度的多重共线性,那么会给回归方程的参数估计带来许多麻烦,致使回归方程参数不准确甚至模型不可用等。
类似的问题还有很多。
为了解决这些问题,最简单和最直接的解决方案是削减变量的个数,但这必然又会导致信息丢失和信息不完整等问题的产生。
为此,人们希望探索一种更为有效的解决方法,它既能大大减少参与数据建模的变量个数,同时也不会造成信息的大量丢失。
因子分析正式这样一种能够有效降低变量维数,并已得到广泛应用的分析方法。
因子分析的概念起源于20世纪初Karl Pearson和Charles Spearmen等人关于智力测验的统计分析。
目前,因子分析已成功应用于心理学、医学、气象、地址、经济学等领域,并因此促进了理论的不断丰富和完善。
因子分析以最少的信息丢失为前提,将众多的原有变量综合成较少几个综合指标,名为因子。
通常,因子有以下几个特点:↓因子个数远远少于原有变量的个数原有变量综合成少数几个因子之后,因子将可以替代原有变量参与数据建模,这将大大减少分析过程中的计算工作量。
↓因子能够反映原有变量的绝大部分信息因子并不是原有变量的简单取舍,而是原有变量重组后的结果,因此不会造成原有变量信息的大量丢失,并能够代表原有变量的绝大部分信息。
↓因子之间的线性关系并不显著由原有变量重组出来的因子之间的线性关系较弱,因子参与数据建模能够有效地解决变量多重共线性等给分析应用带来的诸多问题。
↓因子具有命名解释性通常,因子分析产生的因子能够通过各种方式最终获得命名解释性。
因子的命名解释性有助于对因子分析结果的解释评价,对因子的进一步应用有重要意义。
例如,对高校科研情况的因子分析中,如果能够得到两个因子,其中一个因子是对科研人力投入、经费投入、立项项目数等变量的综合,而另一个是对结项项目数、发表论文数、获奖成果数等变量的综合,那么,该因子分析就是较为理想的。
因为这两个因子均有命名可解释性,其中一个反映了科研投入方面的情况,可命名为科研投入因子,另一个反映了科研产出方面的情况,可命名为科研产出因子。
总之,因子分析是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个因子,如何使因子具有一定的命名解释性的多元统计分析方法。
二、因子分析的基本概念1、因子分析模型因子分析模型中,假定每个原始变量由两部分组成:共同因子(common factors )和唯一因子(unique factors )。
共同因子是各个原始变量所共有的因子,解释变量之间的相关关系。
唯一因子顾名思义是每个原始变量所特有的因子,表示该变量不能被共同因子解释的部分。
原始变量与因子分析时抽出的共同因子的相关关系用因子负荷(factor loadings )表示。
因子分析最常用的理论模式如下:j m jm j j j j U F a F a F a F a Z ++⋅⋅⋅+++=332211(j=1,2,3…,n ,n 为原始变量总数)可以用矩阵的形式表示为U AF Z +=。
其中F 称为因子,由于它们出现在每个原始变量的线性表达式中(原始变量可以用j X 表示,这里模型中实际上是以F 线性表示各个原始变量的标准化分数j Z ),因此又称为公共因子。
因子可理解为高维空间中互相垂直的m 个坐标轴,A 称为因子载荷矩阵,)...3,2,1,...3,2,1(m i n j a ji ==称为因子载荷,是第j 个原始变量在第i 个因子上的负荷。
如果把变量j Z 看成m 维因子空间中的一个向量,则ji a 表示j Z 在坐标轴i F 上的投影,相当于多元线性回归模型中的标准化回归系数;U 称为特殊因子,表示了原有变量不能被因子解释的部分,其均值为0,相当于多元线性回归模型中的残差。
其中,(1)j Z 为第j 个变量的标准化分数;(2)i F (i=1,2,…,m )为共同因素;(3)m 为所有变量共同因素的数目;(4)j U 为变量j Z 的唯一因素;(5)ji a 为因素负荷量。
2、因子分析数学模型中的几个相关概念因子载荷(因素负荷量factor loadings )所谓的因子载荷就是因素结构中,原始变量与因素分析时抽取出共同因素的相关。
可以证明,在因子不相关的前提下,因子载荷ji a 是变量j Z 和因子i F 的相关系数,反映了变量j Z 与因子i F 的相关程度。
因子载荷ji a 值小于等于1,绝对值越接近1,表明因子i F 与变量j Z 的相关性越强。
同时,因子载荷ji a 也反映了因子i F 对解释变量j Z 的重要作用和程度。
因子载荷作为因子分析模型中的重要统计量,表明了原始变量和共同因子之间的相关关系。
因素分析的理想情况,在于个别因素负荷量ji a 不是很大就是很小,这样每个变量才能与较少的共同因素产生密切关联,如果想要以最少的共同因素数来解释变量间的关系程度,则j U 彼此间或与共同因素间就不能有关联存在。
一般说来,负荷量为0.3或更大被认为有意义。
所以,当要判断一个因子的意义时,需要查看哪些变量的负荷达到了0.3或0.3以上。
↓变量共同度(共同性,Communality )变量共同度也就是变量方差,就是指每个原始变量在每个共同因子的负荷量的平方和,也就是指原始变量方差中由共同因子所决定的比率。
变量的方差由共同因子和唯一因子组成。
共同性表明了原始变量方差中能被共同因子解释的部分,共同性越大,变量能被因子说明的程度越高,即因子可解释该变量的方差越多。
共同性的意义在于说明如果用共同因子替代原始变量后,原始变量的信息被保留的程度。
因子分析通过简化相关矩阵,提取可解释相关的少数因子。
一个因子解释的是相关矩阵中的方差,而解释方差的大小称为因子的特征值。
一个因子的特征值等于所有变量在该因子上的负荷值的平方总和。
变量j Z 的共同度2h 的数学定义为:∑==mi ji a h 122,该式表明变量j Z 的共同度是因子载荷矩阵A 中第j 行元素的平方和。
由于变量j Z 的方差可以表示成122=+u h ,因此变量j Z 的方差可由两个部分解释:第一部分为共同度2h ,是全部因子对变量j Z 方差解释说明的比例,体现了因子全体对变量j Z 的解释贡献程度。
变量共同度2h 越接近1,说明因子全体解释说明了变量j Z 的较大部分方差,如果用因子全体刻画变量j Z ,则变量j Z 的信息丢失较少;第二部分为特殊因子U 的平方,反应了变量j Z 方差中不能由因子全体解释说明的比例,2u 越小则说明变量j Z 的信息丢失越少。
总之,变量d 共同度刻画了因子全体对变量j Z 信息解释的程度,是评价变量j Z 信息丢失程度的重要指标。
如果大多数原有变量的变量共同度均较高(如高于0.8),则说明提取的因子能够反映原有变量的大部分信息(80%以上)信息,仅有较少的信息丢失,因子分析的效果较好。
因子,变量共同度是衡量因子分析效果的重要依据。
↓因子的方差贡献(特征值eigenvalue )因子的方差贡献(特征值)的数学定义为:212∑==n j ji i a S ,该式表明,因子i F 的方差贡献是因子载荷矩阵A 中第i 列元素的平方和。
因子i F 的方差贡献反映了因子i F 对原有变量总方差的解释能力。
该值越高,说明相应因子的重要性越高。
因此,因子的方差贡献和方差贡献率是衡量因子重要性的关键指标。
为了便于说明,以三个变量抽取两个共同因素为例,三个变量的线性组合分别为:12121111U F a F a Z ++=22221212U F a F a Z ++=32321313U F a F a Z ++=素负荷量的平方和),也就是个别变量可以被共同因素解释的变异量百分比,这个值是个别变量与共同因素间多元相关的平方。
从共同性的大小可以判断这个原始变量与共同因素之间关系程度。
而各变量的唯一因素大小就是1减掉该变量共同性的值。
(在主成分分析中,有多少个原始变量便有多少个“component ”成分,所以共同性会等于1,没有唯一因素)。
至于特征值是每个变量在某一共同因素之因素负荷量的平方总和(一直行所有因素负荷量的平方和)。
在因素分析之共同因素抽取中,特征值大的共同因素会最先被抽取,其次是次大者,最后抽取的共同因素之特征值最小,通常会接近0(在主成分分析中,有几个题项,便有几个成分,因而特征值的总和刚好等于变量的总数)。
将每个共同因素的特征值除以总题数,为此共同因素可以解释的变异量,因素分析的目的,即在因素结构的简单化,希望以最少的共同因素,能对总变异量作最大的解释,因而抽取的因素越少越好,但抽取因素之累积解释的变异量则越大越好。
3、社会科学中因素分析通常应用在三个层面:(1)显示变量间因素分析的组型(pattern )(2)侦测变量间之群组(clusters ),每个群组所包括的变量彼此相关很高,同构型较大,亦即将关系密切的个别变量合并为一个子群。
(3)减少大量变量数目,使之称为一组涵括变量较少的统计自变量(称为因素),每个因素与原始变量间有某种线性关系存在,而以少数因素层面来代表多数、个别、独立的变量。
因素分析具有简化数据变量的功能,以较少层面来表示原来的数据结构,它根据变量间彼此的相关,找出变量间潜在的关系结构,变量间简单的结构关系称为“成份”(components )或“因素”(factors ).三、因素分析的主要方式围绕浓缩原有变量提取因子的核心目标,因子分析主要涉及以下五大基本步骤:1、因子分析的前提条件由于因子分析的主要任务之一是对原有变量进行浓缩,即将原有变量中的信息重叠部分提取和综合成因子,进而最终实现减少变量个数的目的。
