北京市各区2018届中考一模数学试卷精选汇编：几何综合(含答案)

合集下载

北京市各区2018届中考一模数学试卷精选汇编：几何综合(含答案)

几何综合东城区27. 已知△ABC 中，AD 是BAC ∠的平分线，且AD =AB ，过点C 作AD 的垂线，交 AD 的延长线于点H ．（1）如图1，若60BAC ∠=︒①直接写出B ∠和ACB ∠的度数； ②若AB =2，求AC 和AH 的长；（2）如图2，用等式表示线段AH 与AB +AC 之间的数量关系，并证明．27. （1）①75B ∠=︒，45ACB ∠=︒；--------------------2分②作DE ⊥AC 交AC 于点E .Rt △ADE 中，由30DAC ∠=︒，AD=2可得DE =1，AE 3. Rt △CDE 中，由45ACD ∠=︒，DE=1，可得EC =1. ∴AC 31=.Rt △ACH 中，由30DAC ∠=︒，可得AH 33+； --------------4分（2）线段AH 与AB +AC 之间的数量关系：2AH =AB +AC证明：延长AB 和CH 交于点F ，取BF 中点G ，连接GH . 易证△ACH ≌△AFH .∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =， ∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =.∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==. --------------7分西城区27．正方形ABCD 的边长为2，将射线AB 绕点A 顺时针旋转α，所得射线与线段BD 交于点M ，作CE AM ⊥于点E ，点N 与点M 关于直线CE 对称，连接CN ．（1）如图，当045α︒<<︒时， ①依题意补全图．②用等式表示NCE ∠与BAM ∠之间的数量关系：__________．（2）当4590α︒<<︒时，探究NCE ∠与BAM ∠之间的数量关系并加以证明．（3）当090α︒<<︒时，若边AD 的中点为F ，直接写出线段EF 长的最大值．CDBA图1备用图C DBAM【解析】（1）①补全的图形如图所示：NEMABDC②2NCE BAM ∠=∠．（2）1902MCE BAM ∠+∠=︒，连接CM ，NQM ABDC EDAM DCM ∠=∠，DAQ ECQ ∠=∠，∴2NCE MCE DAQ ∠=∠=∠，∴12DCM NCE ∠=∠，∵BAM BCM ∠=∠，90BCM DCM ∠+∠=︒，∴1902NCE BAM ∠+∠=︒．（3）∵90CEA ∠=︒， ∴点E 在以AC 为直径的圆上，E∴max 1EF FO r =+=+海淀区27（（27．.解：（1）作PF ⊥DE 交DE 于F .∵PE ⊥BO ，60AOB ∠=， ∴30OPE ∠=.∴30DPA OPE ∠=∠=.∴120EPD ∠=. ……………1分 ∵DP PE =,6DP PE +=, ∴30PDE ∠=,3PD PE ==.∴cos30DF PD =⋅︒=∴2DE DF == ………………3分（2）当M 点在射线OA上且满足OM =DMME的值不变，始终为1.理由如下： ………………4分当点P 与点M 不重合时，延长EP 到K 使得PK PD =. ∵,DPA OPE OPE KPA ∠=∠∠=∠, ∴KPA DPA ∠=∠. ∴KPM DPM ∠=∠. ∵PK PD =,PM 是公共边, ∴KPM △≌DPM △. ∴MKMD =. ………………5分作ML ⊥OE 于L ,MN ⊥EK 于N .∵60MO MOL =∠=， ∴sin 603ML MO =⋅=. ………………6分∵PE ⊥BO ,ML ⊥OE ,MN ⊥EK ， ∴四边形MNEL 为矩形. ∴3EN ML ==.∵6EK PE PK PE PD =+=+=, ∴EN NK =. ∵MN ⊥EK , ∴MKME =.∴ME MKMD ==,即1DMME=. 当点P 与点M 重合时，由上过程可知结论成立. ……………7分丰台区27．如图，Rt △ABC 中，∠ACB = 90°，CA = CB ，过点C 在△ABC 外作射线CE ，且∠BCE = α，点B 关于CE 的对称点为点D ，连接AD ，BD ，CD ，其中AD ，BD 分别交射线CE 于点M ，N .（1）依题意补全图形；（2）当α= 30°时，直接写出∠CMA 的度数；（3）当0°<α< 45°时，用等式表示线段AM ，CN 之间的数量关系，并证明．ABCE27．解：（1）如图； …………………1分（2）45°； …………………2分（3）结论：AM CN ． …………………3分证明：作AG ⊥EC 的延长线于点G ．∵点B 与点D 关于CE 对称， ∴CE 是BD 的垂直平分线． ∴CB =CD ． ∴∠1=∠2=α．∵CA =CB ，∴CA =CD ．∴∠3=∠CAD ． ∵∠4=90°， ∴∠3=12（180°-∠ACD ）=12（180°-90°-α-α）=45°-α． ∴∠5=∠2+∠3=α+45°-α=45°．…………………5分 ∵∠4=90°，CE 是BD 的垂直平分线， ∴∠1+∠7=90°，∠1+∠6=90°． ∴∠6=∠7． ∵AG ⊥EC ， ∴∠G =90°=∠8．∴在△BCN 和△CAG 中， ∠8=∠G ， ∠7=∠6， BC =CA ， ∴△BCN ≌△CAG ．∴CN =AG ． ∵Rt △AMG 中，∠G =90°，∠5=45°， ∴AM =2AG ．∴AM =2CN ． …………………7分（其他证法相应给分.）石景山区27．在正方形ABCD 中，M 是BC 边上一点，点P 在射线AM 上，将线段AP 绕点A 顺时针旋转90°得到线段AQ ，连接BP ，DQ ．（1）依题意补全图1；（2）①连接DP ，若点P ，Q ，D 恰好在同一条直线上，求证：2222DP DQ AB +=； ②若点P ，Q ，C 恰好在同一条直线上，则BP 与AB 的数量关系为：．27．（1）补全图形如图1. ………………… 1分（2）①证明：连接BD ，如图2，∵线段AP 绕点A 顺时针旋转90°得到线段AQ ， ∴AQ AP =，90QAP ∠=°． ∵四边形ABCD 是正方形， ∴AD AB =，90DAB ∠=°． ∴12∠=∠．∴△ADQ ≌△ABP ． ………………… 3分 ∴DQ BP =，3Q ∠=∠．∵在Rt QAP ∆中，90Q QPA ∠+∠=°， ∴390BPD QPA ∠=∠+∠=°． ∵在Rt BPD ∆中，222DP BP BD +=，又∵DQ BP =，222BD AB =，∴2222DP DQ AB +=． ………………… 5分 ②BP AB =． ………………… 7分证明：过点A 作AE ⊥PQ 于E ，连接BE ACC图1∴AE是△PAQ的垂线∵三△PAQ是等腰直角三角形（已证）∴AE是等腰直角三角形PAQ的垂线，角平分线∴∠AEP=90°，AE=PE∵正方形ABCD∴∠ABC=90°∠ACB=∠BAC=45°∠AEP+∠ABC=180°∴A ，B，C，E四点共圆∴∠AEB=∠ACB=45°，∠CEB=∠BAC=45°∴∠AEB=∠CEB=45°∵BE=BE∴△ABE≌△PBE (SAS)∴BP=AB朝阳区27. 如图，在菱形ABCD中，∠DAB=60°，点E为AB边上一动点（与点A，B不重合），连接CE，将∠ACE的两边所在射线CE，CA以点C为中心，顺时针旋转120°，分别交射线AD于点F，G.（1）依题意补全图形；（2）若∠ACE=α，求∠AFC的大小（用含α的式子表示）；（3）用等式表示线段AE、AF与CG之间的数量关系，并证明．27.（1）补全的图形如图所示.……………………………………1分（2）解：由题意可知，∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD 是菱形，∠DAB=60°，∴∠DAC=∠BAC= 30°. ……………………………………………2分 ∴∠AGC=30°.∴∠AFC =α+30°. …………………………3分（3）用等式表示线段AE 、AF 与CG 之间的数量关系为CG AF AE 3=+错误!未找到引用源。

2018北京市各区初三数学一模试题分类——四边形

目录类型1：多边形内角、外角 (2)类型2：平四与特殊平四的性质与判定（解答题） (3)类型3：几何综合 (9)类型1：多边形内角、外角1.（18平谷一模6）一个正多边形的每个内角的度数都等于相邻外角的度数，则该正多边形的边数是（）A．3 B．4 C．6 D．122.（18西城一模6）如果一个正多边形的内角和等于720︒，那么该正多边形的一个外角等于（）．A．45︒B．60︒C．72︒D．90︒3.（18大兴一模3）已知一个多边形的内角和是它的外角和的2倍，那么这个多边形的边数是（）A. 3B. 4 C．5 D． 64.（18海淀一模3）．若正多边形的一个外角是120°，则该正多边形的边数是A.6B. 5C. 4D.35.（18怀柔一模10）若正多边形的内角和为720°，则它的边数为______.6.（18延庆一模10）右图是一个正五边形，则∠1的度数是．7.（18石景山一模10）若正多边形的一个外角是45°，则该正多边形的边1数是_______．8. （18东城一模11）若多边形的内角和为其外角和的3倍，则该多边形的边数为_______.9. （18房山一模13）一个正方形和两个等边三角形的位置如图所示，则∠1+∠2+∠3 的度数为_________．类型2：平四与特殊平四的性质与判定（解答题）1.（18石景山一模19）问题:将菱形的面积五等分．小红发现只要将菱形周长五等分，再将各分点与菱形的对角线交点连接即可解决问题．如图，点O是菱形ABCD的对角线交点，5AB=，下面是小红将菱形ABCD面积五等分的操作与证明思路，请补充完整.（1）在AB边上取点E，使4AE=，连接OA，OE；（2）在BC边上取点F，使BF=，连接OF；（3）在CD边上取点G，使CG=，连接OG；（4）在DA边上取点H，使DH=，连接OH．由于AE=＋=＋=＋=.可证S△AOE==EOFB FOGC GOHDS S S==四边形四边形四边形S△HOA.2.（18平谷一模22）如图，在□ABCD中，BF平分∠ABC交AD于点F，AE⊥BF于点O，交BC于点E，连接EF．（1）求证：四边形ABEF是菱形；（2）连接CF，若∠ABC=60°，AB= 4，AF =2DF，求CF的长．3.（18延庆一模21）如图，Rt△ABC中，∠ABC=90°，点D，F分别是AC，AB的中点，CE∥DB，BE∥DC．（1）求证：四边形DBEC是菱形；（2）若AD=3，DF=1，求四边形DBEC面积.F EDCB A OHG F ED C BAFA B 3. （18石景山一模21）如图，在四边形ABCD 中，90A BCD ∠=∠=°，BC CD ==，CE AD⊥于点E ．（1）求证：AE CE =；（2）若tan 3D =，求AB 的长．4.（18房山一模21）如图，在ABC ∆中，90ACB ∠=，点,D E 分别是,BC AB 上的中点，连接DE 并延长至点F ，使EF =2DE ，连接,CE AF .（1）证明：AF CE =；（2）若30B ∠=，AC =2，连接BF ，求BF 的长5.（18西城一模21）如图，在ABD △中，ABD ADB ∠=∠，分别以点B ，D 为圆心，AB 长为半径在BD 的右侧作弧，两弧交于点C ，分别连接BC ，DC ，AC ，记AC 与BD 的交点为O ．（1）补全图形，求AOB ∠的度数并说明理由;（2）若5AB =，3cos 5ABD ∠=，求BD 的长．BDA6.（18朝阳毕业23）如图，在菱形ABCD 中，AC 和BD 相交于点O ，过点O 的线段EF 与一组对边AB ， CD 分别相交于点E ，F ．（1）求证：AE =CF ；（2）若AB=2，点E 是AB 中点，求EF 的长．7.（18怀柔一模21）直角三角形ABC 中，∠BAC=90°，D 是斜边BC 上一点，且AB=AD ，过点C 作CE ⊥AD ，交AD 的延长线于点E ，交AB 延长线于点F. （1）求证：∠ACB=∠DCE ；（2）若∠BAD=45°，B 作BG ⊥FC 于点G ，连接DG ．依题意补全图形，并求四边形ABGD 的面积8.（18海淀一模21）如图，□ABCD 的对角线,AC BD 相交于点O ，且AE ∥BD ，BE ∥AC ，OE = CD .（1）求证：四边形ABCD 是菱形；（2）若AD = 2，则当四边形ABCD 的形状是_______________时，四边形AOBE 的面积取得最大值是_________________.2+2AF C B EO AD D EB C9.（18朝阳一模21）如图，在△ABC 中，D 是AB 边上任意一点，E 是BC 边中点，过点C作AB 的平行线，交DE 的延长线于点F ，连接BF ，CD ．（1）求证：四边形CDBF 是平行四边形；（2）若∠FDB =30°，∠ABC =45°，BC =4√2，求DF 的长．10.（18东城一模21）如图，已知四边形ABCD 是平行四边形，延长BA 至点E ，使AE = AB ，连接DE ，AC .（1）求证：四边形ACDE 为平行四边形;（2）连接CE 交AD 于点O . 若AC=AB =3，1cos 3B ，求线段CE 的长.11.（18丰台一模21）已知：如图，菱形ABCD ，分别延长AB ，CB 到点F ，E ，使得BF = BA ，BE = BC ，连接AE ，EF ，FC ，CA ．（1）求证：四边形AEFC 为矩形；（2）连接DE 交AB 于点O ，如果DE ⊥AB ，AB = 4，求DE 的长．A B CE D F12.（18门头沟一模21）在矩形ABCD 中，连接AC ,AC 的垂直平分线交AC 于点O ,分别交AD 、BC 于点E 、F ，连接CE 和AF ．（1）求证：四边形AECF 为菱形；（2）若AB =4，BC =8，求菱形AECF 的周长．13.（18大兴一模21）如图，矩形ABCD 的对角线AC 、BD 交于点O ，且DE=O C ，CE=O D ．（1）求证：四边形OCED 是菱形；（2）若∠BAC ＝30°，AC ＝4，求菱形OCED 的面积．14.（18顺义一模21）如图，四边形ABCD 中，AD ∥BC ，∠A =90°，BD =BC ，点E 为CD 的中点，射线BE 交AD 的延长线于点F ，连接CF ．（1）求证：四边形BCFD 是菱形；（2）若AD =1，BC =2，求BF 的长．A BF E A B C D15.（18通州一模22）如图，在平行四边形ABCD中，DB⊥AB，点E是BC边中点，过点E作EF⊥CD，垂足为F，交AB的延长线于点G.（1）求证：四边形BDFG是矩形；（2）若AE平分∠BAD，求tan∠BAE的值.16.（18燕山一模23）如图，在△ABC中，D,E分别是AB,AC的中点，BE=2DE,延长DE到点F，使得EF=BE，连接CF．（1）求证：四边形BCFE是菱形；（2）若∠BCF=120°，CE=4，求菱形BCFE的面积．AD E FB C类型3：几何综合1.（28延庆一模27）如图1，正方形ABCD 中，点E 是BC 延长线上一点，连接DE ，过点B作BF ⊥DE 于点F ，连接FC ．（1）求证：∠FBC =∠CDF ．（2）作点C 关于直线DE 的对称点G ，连接CG ，FG ．①依据题意补全图形；②用等式表示线段DF ，BF ，CG 之间的数量关系并加以证明．图1 备用图FDEC BAFDEC BA3.（18西城一模27）正方形ABCD 的边长为2，将射线AB 绕点A 顺时针旋转α，所得射线与线段BD 交于点M ，作CE AM ⊥于点E ，点N 与点M 关于直线CE 对称，连接CN ．（1）如图1，当045α︒<<︒时，①依题意补全图1．②用等式表示NCE ∠与BAM ∠之间的数量关系：__________．（2）当4590α︒<<︒时，探究NCE ∠与BAM ∠之间的数量关系并加以证明．（3）当090α︒<<︒时，若边AD 的中点为F ，直接写出线段EF 长的最大值．4.（18平谷一模27）在△ABC 中，AB=AC ，CD ⊥BC 于点C ，交∠ABC 的平分线于点D ，AE平分∠BAC 交BD 于点E ，过点E 作EF ∥BC 交AC 于点F ，连接DF ．（1）补全图1；（2）如图1，当∠BAC =90°时，①求证：BE=DE ；②写出判断DF 与AB 的位置关系的思路（不用写出证明过程）；（3）如图2，当∠BAC=α时，直接写出α，DF ，AE 的关系．CDBA图1备用图C DBAMB图2图1B5.（18房山一模27）如图，已知Rt △ABC 中，∠C =90°，∠BAC =30°，点D 为边BC 上的点，连接AD ，∠BAD =α，点D 关于AB 的对称点为E ，点E 关于AC 的对称点为G ，线段EG 交AB 于点F ，连接AE ，DE ，DG ，AG .（1）依题意补全图形；（2）求∠AGE 的度数（用含α的式子表示）；（3）用等式表示线段EG 与EF ，AF 之间的数量关系，并说明理由.6.（18怀柔一模27）如图，在△ABC 中，∠A=90°，AB=AC ，点D 是BC 上任意一点，将线段AD 绕点A 逆时针方向旋转90°，得到线段AE ，连结EC.（1）依题意补全图形；（2）求∠ECD 的度数；（3）若∠CAE=7.5°，AD=1，将射线DA 绕点D 顺时针旋转60°交EC 的延长线于点F ，请写出求AF 长的思路．αD C B A7.（18海淀一模27）如图，已知60AOB ∠=︒，点P交OB 于点E ，点D 在AOB ∠内，且满足∠（1）当DP PE =时，求DE 的长；（2）在点P 你的判断.8.（18朝阳一模27）如图，在菱形ABCD 中，∠DAB =60°，点E 为AB 边上一动点（与点A ，B 不重合），连接CE ，将∠ACE 的两边所在射线CE ，CA 以点C 为中心，顺时针旋转120°，分别交射线AD 于点F ，G.（1）依题意补全图形；（2）若∠ACE=α，求∠AFC 的大小（用含α的式子表示）；（3）用等式表示线段AE 、AF 与CG 之间的数量关系，并证明．9.（18东城一模27）已知△ABC 中，AD 是BAC ∠的平分线，且AD =AB ，过点C 作AD 的垂线，交 AD 的延长线于点H ．（1）如图1，若60BAC =︒∠①直接写出B ∠和ACB ∠的度数； ②若AB =2，求AC 和AH 的长；（2）如图2，用等式表示线段AH 与AB +AC 之间的数量关系，并证明．10.（18丰台一模27）如图，Rt △ABC 中，∠ACB = 90°，CA = CB ，过点C 在△ABC 外作射线CE ，且∠BCE = α，点B 关于CE 的对称点为点D ，连接AD ，BD ，CD ，其中AD ，BD 分别交射线CE 于点M ，N .（1）依题意补全图形；（2）当α= 30°时，直接写出∠CMA 的度数；（3）当0°<α< 45°时，用等式表示线段AM ，CN 之间的数量关系，并证明．A B C E11.（18门头沟一模27）如图，在△ABC 中，AB =AC ，2A α∠=，点D 是BC 的中点，DE AB E ⊥于点，DF AC F ⊥于点.（1）EDB ∠=_________°；（用含α的式子表示）（2）作射线DM 与边AB 交于点M ，射线DM 绕点D 顺时针旋转1802α︒-，与AC 边交于点N ．①根据条件补全图形；②写出DM 与DN 的数量关系并证明；③用等式表示线段BM CN 、与BC 之间的数量关系，（用含α的锐角三角函数表示）并写出解题思路.12.（18大兴一模27）如图，在等腰直角△ABC 中，∠CAB=90°，F 是AB 边上一点，作射线CF ，过点B 作BG ⊥C F 于点G ，连接AG ．（1）求证：∠ABG =∠ACF ；（2）用等式表示线段CG ，AG ，BG 之间的等量关系，并证明．B13.（18顺义一模27）如图，在正方形ABCD 中，E 是BC 边上一点，连接AE ，延长CB 至点F ，使BF=BE ，过点F 作FH ⊥AE 于点H ，射线FH 分别交AB 、CD 于点M 、N ，交对角线AC 于点P ，连接AF ．（1）依题意补全图形；（2）求证：∠F AC =∠APF ；（3）判断线段FM 与PN 的数量关系，并加以证明．14.（18通州一模27）如图，直线l 是线段MN 的垂直平分线，交线段MN 于点O ，在MN 下方的直线l 上取点P ，连接PN .以线段PN 为边，在PN 上方作正方形NPAB .射线MA 交直线l 于点C ，连接BC .（1）设=ONP ∠，求AMN ∠的度数；（2）写出线段AM ，BC 之间的等量关系，并证明.E D C B A15.（18燕山一模28）在Rt△ABC中, ∠ACB=90°,CD是AB边的中线，DE⊥BC于E, 连结CD，点P在射线CB上（与B，C不重合）．（1）如果∠A=30°①如图1，∠DCB= °②如图2，点P在线段CB上，连结DP，将线段DP绕点D逆时针旋转60°，得到线段DF,连结BF，补全图2猜想CP、BF之间的数量关系，并证明你的结论；（2）如图3，若点P在线段CB的延长线上，且∠A=α（0°<α<90°），连结DP, 将线段DP绕点逆时针旋转α2得到线段DF，连结BF，请直接写出DE、BF、BP三者的数量关系（不需证明）．。

【中考汇编】北京市各区2018届中考一模数学试卷精选汇编88页含答案

北京市各区2018届中考一模数学试卷精选汇编目录北京市各区2018届中考一模数学试卷精选汇编：解不等式组（含答案）北京市各区2018届中考一模数学试卷精选汇编：计算题（含答案）北京市各区2018届中考一模数学试卷精选汇编：解四边形（含答案）北京市各区2018届中考一模数学试卷精选汇编：几何证明（含答案）北京市各区2018届中考一模数学试卷精选汇编：几何综合（含答案）北京市各区2018届中考一模数学试卷精选汇编：函数计算及运用（含答案）北京市各区2018届中考一模数学试卷精选汇编：二次函数综合（含答案）北京市各区2018届中考一模数学试卷精选汇编：统计（含答案）解不等式组专题东城区18．解不等式组4+6,23x x x x ⎧⎪+⎨⎪⎩＞≥，并写出它的所有整数解. 18. 解：4+6,23x x x x ⎧⎪⎨+⎪⎩①②＞≥，由①得，-x ＞2，------------------1分由②得，1x ≤， ------------------2分∴不等式组的解集为-1x 2＜≤.所有整数解为-1, 0, 1. ---------------------5分西城区18．解不等式组3(2)4112x x x ++⎧⎪⎨-<⎪⎩≥，并求该不等式组的非负整数解．【解析】解①得，364x x ++≥，22x -≥，1x -≥，解②得，12x -<，3x <，∴原不等式解集为13x -<≤，∴原不等式的非负整数解为0，，2．海淀区18．解不等式组：()5331,263.2x x x x +>-⎧⎪⎨-<-⎪⎩ 18.解：() 5331, 263. 2x x x x +>-⎧⎪⎨-<-⎪⎩①② 解不等式①，得3x >-. …2分解不等式②，得2x <. ………4分所以原不等式组的解集为32x -<<. ………5分18．解不等式组：341,51 2.2x x x x ≥-⎧⎪⎨->-⎪⎩ 18．解：解不等式①，得1x ≤， ……………………2分解不等式②，得1x >-. ……………………4分∴原不等式组的解集是11x -<≤．………5分石景山区18．解不等式组：3(1)45622x x x x +>++<⎧⎪⎨⎪⎩，． 18．解：原不等式组为3(1)45,62.2x x x x +>++<⎧⎪⎨⎪⎩ 解不等式①，得2x <-． ………………2分解不等式②，得2x <． ………………4分 ∴原不等式组的解集为<2x -． ………………5分朝阳区18. 解不等式组：⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x18. 解：原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式①，得 5<x . ………………………………………2分解不等式②，得 21>x .………………………………………………4分 ∴ 原不等式组的解集为521<<x . …………………………………5分① ②18．解不等式组：⎩⎪⎨⎪⎧x －32<1，2（x ＋1）≥x －1.18．解：由（1）得，x-3<2X<5 ……………………….2′（2）得 2x+2≥x-1x ≥-3 ……………………….4′所以不等式组的解是-3≤x ＜5……………………….5′ 门头沟区18. 解不等式组：1031+1.x x x ⎧-<⎪⎨⎪-⎩，≤3(）18．（本小题满分5分）解不等式①得，x ＜3， …………………………………………2分解不等式②得，x ≥﹣2， ………………………………4分所以，不等式组的解集是﹣2≤x ＜3． ………………5分大兴区17.解不等式组：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 并写出它的所有整数解. 17. 解：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 由①，得21-≥x . ………………………………………………………1分由②，得2<x . …………………………………………………………2分 ∴原不等式组的解集为221<≤-x . ………………………………………4分它的所有整数解为0，1. …………………………………………………5分① ②18．解不等式组3(1)45,513x x x x -≥-⎧⎪-⎨->⎪⎩，并写出它的所有整数解．．．． 18．解：3(1)455 3 1x x x x -≥-⎧⎪⎨-->⎪⎩①② 解不等式①，得 x ≤2． ·········································································1 解不等式②，得 x ＞-1． ·······································································3 ∴原不等式组的解集为12x -<≤． ························································4 ∴适合原不等式组的整数解为0,1,2． ·······················································5 怀柔区18.解不等式组:()⎪⎩⎪⎨⎧<+-<-.1213,213x x x x 18.解：由①得：3x < . ………………………………………………………………………2分由②得：9x >- …………………………………………………………………………4分原不等式组的解集为93x -<< ………………………………………………………5分延庆区18．解不等式组：523(2)53.2x x x x -<+⎧⎪⎨+≤⎪⎩，并写出它的所有整数解． 18．解：由①得，x <4． ……1分由②得，x ≥1 ． ……3分∴ 原不等式组的解集为1≤x <4． ……4分∴ 原不等式组的所有整数解为1，2，3． ……5分18．解不等式组：()7+1,2315 1.x x x x +⎧≥-⎪⎨⎪+<-⎩18．解不等式组：()7+12315x x x x +⎧≥-⎪⎨⎪+<-⎩解：解不等式①得 x ≥3- ……………………………………………………………2分解不等式②得 2x > ………………………………………………………………4分不等式组的解集是 2x > …………………………………………………………5分计算题专题东城区17．计算：()2012sin 60-π-2++1-3-⎛⎫︒ ⎪⎝⎭. =217.解：原式分分西城区17114sin 3015-⎛⎫+︒- ⎪⎝⎭．【解析】原式1541)52122=+⨯-=+=．海淀区17．计算：11()3tan 302|3-︒+． 17.解：原式=3323-⨯+- ………………4分=5- ………………5分丰台区1702cos 45(3π)|1-︒+-+-．1702cos 45(3π)|1︒+-+．=211++ ……………………4分= ……………………5分石景山区17．计算：012sin 455(3--++° 17．解：原式=2512⨯-+- ………………4分4=-- ………………5分朝阳区17. 计算：2sin30°+ .8)4()31(01+-+-π17. 解：原式 2213212+++⨯= …………………………………………………4分 225+=. ……………………………………………………………5分燕山区17．计算：4cos30°－12 + 20180 + ||1－317．4cos30°－12 + 20180 + ||1－3 =13132234-++-⨯=3 门头沟区17．计算：()201254sin 603π-⎛⎫--++-︒ ⎪⎝⎭．平谷区17．计算：(1013132sin 603-⎛⎫-+-︒ ⎪⎝⎭π.17．解：(1013132sin 603-⎛⎫-+--︒ ⎪⎝⎭π=331312-- ···········································································4 =1 ····································································································5 怀柔区17.计算：102130tan 3)3(31-︒⎪⎭⎫ ⎝⎛-+---π. 17.解：原式331132=--+ …………………………………………………4分.…………………………………………………………………5分延庆区17．计算：0113tan 301(2)()3π-︒+---．17．原式=3⨯33+3-1+1-3 ……4分=23-3 ……5分顺义区17．计算：()01312sin 452π--︒+-．17．解：()01312sin 452π--︒+-112132=-⨯+ (4)分13= ……………………………………………………………………………… 5分4=-解四边形专题东城区21．如图，已知四边形ABCD 是平行四边形，延长BA 至点E ，使AE = AB ，连接DE ，AC .（1）求证：四边形ACDE 为平行四边形;（2）连接CE 交AD 于点O . 若AC=AB =3，1cos 3B =，求线段CE 的长.21.(1) 证明：∵平行四边形ABCD ，∴=AB DC ，AB DC ∥.∵AB =AE ，∴=AE DC ，AE DC ∥.∴四边形ACDE 为平行四边形. -------------------2分(2) ∵=AB AC ，∴=AE AC .∴平行四边形ACDE 为菱形.∴AD ⊥CE .∵AD BC ∥，∴BC ⊥CE.在Rt △EBC 中，BE =6, 1cos 3BC B BE ==, ∴=2BC . 根据勾股定理，求得=42BC 分西城区21．如图，在ABD △中，ABD ADB ∠=∠，分别以点B ，D 为圆心，AB 长为半径在BD 的右侧作弧，两弧交于点C ，分别连接BC ，DC ，AC ，记AC 与BD 的交点为O ．（1）补全图形，求AOB ∠的度数并说明理由;（2）若5AB =，3cos 5ABD ∠=，求BD 的长．BDA【解析】（1）补全的图形如图所示．90AOB ∠=︒．证明：由题意可知BC AB =，DC AB =， ∵在ABD △中，ABD ADB ∠=∠， ∴AB AD =，∴BC DC AD AB ===， ∴四边形ABCD 为菱形， ∴AC BD ⊥， ∴90AOB ∠=︒．（2）∵四边形ABCD 为菱形， ∴OB OD =．在Rt ABO △中，90AOB ∠=︒，5AB =，3cos 5ABD ∠=，∴cos 3OB AB ABD =⋅∠=， ∴26BD OB ==．ABCDO海淀区21．如图，□ABCD 的对角线,AC BD 相交于点O ，且AE ∥BD ，BE ∥AC ，OE = CD . （1）求证：四边形ABCD 是菱形；（2）若AD = 2，则当四边形ABCD 的形状是__________时，四边形AOBE 的面积取得最大值是_______.C B EOAD21．（1）证明：∵AE BD ∥，BE AC ∥，∴四边形AEBO 是平行四边形. ………………1分 ∵四边形ABCD 是平行四边形，∴DC AB =. ∵OE CD =, ∴OE AB =.∴平行四边形AEBO 是矩形. ………………2分 ∴90BOA ∠=︒. ∴AC BD ⊥.∴平行四边形ABCD 是菱形. ………………3分 (2) 正方形； ………………4分2. ………………5分丰台区21．已知：如图，菱形ABCD ，分别延长AB ，CB 到点F ，E ，使得BF = BA ，BE = BC ，连接AE ，EF ，FC ，CA ．（1）求证：四边形AEFC 为矩形；（2）连接DE 交AB 于点O ，如果DE ⊥AB ，AB = 4，求DE 的长．ABCEDF21．（1）证明：∵BF =BA ，BE =BC ，∴四边形AEFC 为平行四边形. ………………………1分 ∵四边形ABCD 为菱形， ∴BA =BC .∴BE =BF .∴BA + BF = BC + BE ，即AF =EC .∴四边形AEFC 为矩形. ………………………2分（2）解：连接DB .由（1）知，AD ∥EB ，且AD =EB . ∴四边形AEBD 为平行四边形 ∵DE ⊥AB ，∴四边形AEBD 为菱形.∴AE =EB ，AB =2AG ，ED =2EG . ………………………4分 ∵矩形ABCD 中，EB =AB ，AB=4， ∴AG =2，AE =4.∴Rt △AEG 中，EG=23.∴ED=43. ………………………5分（其他证法相应给分）石景山区21．如图，在四边形ABCD 中，90A BCD ∠=∠=°，210BC CD ==，CE AD ⊥于点E ．（1）求证：AE CE =；（2）若tan 3D =，求AB 的长．BA CE D21．（1）证明：（法一）过点B 作BH ⊥CE 于H ，如图1． ∵CE ⊥AD ，∴∠BHC ＝∠CED ＝90°，190D ∠+∠=︒． ∵∠BCD ＝90°， ∴1290∠+∠=︒， ∴2D ∠=∠．又BC ＝CD∴BHC △≌CED △． ∴BH CE =．∵BH ⊥CE ，CE ⊥AD ，∠A ＝90°， ∴四边形ABHE 是矩形， ∴AE BH =．∴AE CE =． ………………3分（法二）过点C 作CH ⊥AB 交AB 的延长线于H ．图略，证明略．（2）解： ∵四边形ABHE 是矩形， ∴AB HE =．∵在Rt CED △中，tan 3CE D DE==,设,3DE x CE x ==，∴10210CD x ==． ∴2x =．∴2DE =,6CE =． ………………4分 ∵2CH DE ==．∴624AB HE ==-=． ………………5分朝阳区21. 如图，在△ABC 中，D 是AB 边上任意一点，E 是BC 边中点，过点C作AB 的平行线，交DE 的延长线于点F ，连接BF ，CD ．（1）求证：四边形CDBF 是平行四边形；（2）若∠FDB =30°，∠ABC =45°，BC =，求DF 的长．21.（1）证明：∵CF ∥AB ，∴∠ECF ＝∠EBD . ∵E 是BC 中点， ∴CE ＝BE .∵∠CEF ＝∠BED ， ∴△CEF ≌△BED . ∴CF ＝BD .∴四边形CDBF 是平行四边形. ………………………2分（2）解：如图，作EM ⊥DB 于点M ，∵四边形CDBF 是平行四边形，BC ＝24，∴2221==BC BE ，DE DF 2=. 在Rt △EMB 中，2sin =∠⋅=ABC BE EM . ……………………3分在Rt △EMD 中，42==EM DE . …………………4分∴DF ＝8. ………………………………………………………5分燕山区23．如图，在△ABC 错误!未找到引用源。

北京市各区2018届中考数学一模试卷精选汇编压轴题专题(附答案)

压轴题专题东城区28．给出如下定义：对于⊙O的弦MN和⊙O外一点P（M，O，N三点不共线，且P，O在直线MN的异侧），当∠MPN ＋∠MON=180°时，则称点 P是线段MN关于点O的关联点．图1是点P为线段MN关于点O的关联点的示意图.在平面直角坐标系xOy中，⊙O的半径为1.（1）如图2，2222M⎛⎫⎪⎪⎝⎭，2222N⎛-⎝⎭.在A（1，0），B（1，1），)2,0C三点中, 是线段MN关于点O的关联点的是；（2）如图3， M（0，1），N312⎫-⎪⎪⎝⎭，点D是线段MN关于点O的关联点.①∠MDN的大小为°；②在第一象限内有一点E)3,m m，点E是线段MN关于点O的关联点，判断△MNE的形状，并直接写出点E的坐标；③点F在直线323y x=-+上，当∠MFN≥∠MDN时，求点F的横坐标Fx的取值范围．28. 解：（1）C ； --------------2分（2）① 60°；② △MNE 是等边三角形，点E 的坐标为)；--------------5分③ 直线32y x =+交 y 轴于点K （0，2），交x 轴于点()3T ，0. ∴2OK =，23OT =. ∴60OKT ∠=︒.作OG ⊥KT 于点G ,连接MG . ∵()M 0，1， ∴OM =1. ∴M 为OK 中点 . ∴ MG =MK =OM =1.∴∠MGO =∠MOG =30°，OG 3∴33.2G ⎫⎪⎪⎝⎭， ∵120MON ∠=︒, ∴ 90GON ∠=︒. 又3OG 1ON =， ∴30OGN ∠=︒. ∴60MGN ∠=︒.∴G 是线段MN 关于点O 的关联点. 经验证，点)31E，在直线32y =+上. 结合图象可知，当点F 在线段GE 上时，符合题意. ∵G F E x x x ≤≤， ∴33F x ≤分西城区28．对于平面内的⊙C 和⊙C 外一点Q ，给出如下定义：若过点Q 的直线与⊙C 存在公共点，记为点A ，B ，设AQ BQk CQ+=，则称点A （或点B ）是⊙C 的“k 相关依附点”，特别地，当点A 和点B 重合时，规定AQ BQ =，2AQ k CQ =（或2BQCQ）．已知在平面直角坐标系xOy 中，(1,0)Q -，(1,0)C ，⊙C 的半径为r ．（1）如图，当r =①若1(0,1)A 是⊙C 的“k 相关依附点”，则k 的值为__________．②2(1A 是否为⊙C 的“2相关依附点”．答：__________（填“是”或“否”）．（2）若⊙C 上存在“k 相关依附点”点M ， ①当1r =，直线QM 与⊙C 相切时，求k 的值．②当k r 的取值范围．（3）若存在r 的值使得直线3y x b =-+与⊙C 有公共点，且公共点时⊙C 3b 的取值范围．图1CyxO A 1A 2Q【解析】（12（2）①如图，当1r =时，不妨设直线QM 与⊙C 相切的切点M 在x 轴上方（切点M 在x 轴下方时同理），连接CM ，则QM CM ⊥，x∵(1,0)Q -，(1,0)C ，1r =， ∴2CQ =，1CM =，∴MQ = 此时23MQk CQ== ②如图，若直线QM 与⊙C 不相切，设直线QM 与⊙C 的另一个交点为N （不妨设QN QM <，点N ，M 在x 轴下方时同理），作CD QM ⊥于点D ，则MD ND =，x∴()222MQ NQ MN NQ NQ ND NQ DQ +=++=+=， ∵2CQ =， ∴2MQ NQ DQk DQ CQ CQ+===，∴当k 3DQ = 此时221CD CQ DQ -，假设⊙C 经过点Q ，此时2r =， ∵点Q 早⊙C 外，∴r 的取值范围是12r <≤．（3）33b <．海淀区28．在平面直角坐标系xOy 中，对于点P 和C ，给出如下定义：若C 上存在一点T 不与O 重合，使点P 关于直线OT 的对称点'P 在C 上，则称P 为C 的反射点．下图为C 的反射点P 的示意图．（1）已知点A 的坐标为(1,0)，A 的半径为2，①在点(0,0)O ，(1,2)M ，(0,3)N -中，A 的反射点是____________；②点P 在直线y x =-上，若P 为A 的反射点，求点P 的横坐标的取值范围；（2）C 的圆心在x 轴上，半径为2，y 轴上存在点P 是C 的反射点，直接写出圆心C 的横坐标x 的取值范围．28．解（1）①A 的反射点是M ，N ． ………………1分②设直线y x =-与以原点为圆心，半径为1和3的两个圆的交点从左至右依次为D ，E ，F ，G ，过点D 作⊥DH x 轴于点H ，如图．可求得点D 的横坐标为32．同理可求得点E ，F ，G 的横坐标分别为2232 点P 是A 的反射点，则A 上存在一点T ，使点P 关于直线OT 的对称点'P 在A 上，则'OP OP =.∵1'3≤≤OP ，∴13≤≤OP ．反之，若13≤≤OP ，A 上存在点Q ，使得OP OQ =，故线段PQ 的垂直平分线经过原点，且与A 相交．因此点P 是A 的反射点．∴点P 的横坐标x的取值范围是≤xx ．………………4分（2）圆心C 的横坐标x 的取值范围是44≤≤x -． ………………7分丰台区28．对于平面直角坐标系xOy 中的点M 和图形1W ，2W 给出如下定义：点P 为图形1W 上一点，点Q 为图形2W 上一点，当点M 是线段PQ 的中点时，称点M 是图形1W ，2W 的“中立点”．如果点P (x 1，y 1)，Q (x 2，y 2)，那么“中立点”M 的坐标为⎪⎭⎫⎝⎛++2,22121y y x x ．已知，点A (-3，0)，B (0，4)，C (4，0)．（1）连接BC ，在点D (12，0)，E (0，1)，F (0，12)中，可以成为点A 和线段BC 的“中立点”的是____________；（2）已知点G (3，0)，⊙G 的半径为2．如果直线y = - x + 1上存在点K 可以成为点A 和⊙G 的“中立点”，求点K 的坐标；（3）以点C 为圆心，半径为2作圆．点N 为直线y = 2x + 4上的一点，如果存在点N ，使得y 轴上的一点可以成为点N 与⊙C 的“中立点”，直接写出点N 的横坐标的取值范围．54411231213xOy6654327654326528．解：（1）点A 和线段BC（2）点A 和⊙G 的“中立点”在以点O 为圆心、半径为1的圆上运动. 因为点K 在直线y =- x +1上，设点K 的坐标为（x ，- x +1），则x 2+（- x +1）2=12，解得x 1=0，x 2=1.所以点K 的坐标为（0，1）或（1，0）. ………5分（3）（说明：点N 与⊙C 的“中立点”在以线段NC 的中点P 为圆心、半径为1的圆上运动.圆P 与y 轴相切时，符合题意.）所以点N 的横坐标的取值范围为-6≤x N ≤-2. ………8分石景山区28．对于平面上两点A ，B ，给出如下定义：以点A 或B 为圆心，AB 长为半径的圆称为点A ，B 的“确定圆”．如图为点A ，B 的“确定圆”的示意图．．．． AB（1）已知点A 的坐标为(1,0)-，点B 的坐标为(3,3)，则点A ，B 的“确定圆”的面积为_________；（2）已知点A 的坐标为(0,0)，若直线y x b =+上只存在一个点B ，使得点A ，B 的“确定圆”的面积为9π，求点B 的坐标；（3）已知点A 在以(0)P m ，为圆心，以1为半径的圆上，点B 在直线33y =+ 若要使所有点A ，B 的“确定圆”的面积都不小于9π，直接写出m 的取值范围．28．解：（1）25π； ………………… 2分（2）∵直线y x b =+上只存在一个点B ，使得点,A B 的“确定圆”的面积为9π，∴⊙A 的半径3AB =且直线y x b =+与⊙A 相切于点B ，如图， ∴AB CD ⊥，45DCA ∠=°．xy xy①当0b >时，则点B 在第二象限．过点B 作BE x ⊥轴于点E ，∵在Rt BEA ∆中，45BAE ∠=°，3AB =， ∴322BE AE ==．∴323222B -（，． ②当0b <时，则点'B 在第四象限．同理可得3232'22B -（．综上所述，点B 的坐标为323222-（，或323222-（． ………………… 6分（3）5m -≤或11m ≥． ………………… 8分朝阳区28. 对于平面直角坐标系xOy 中的点P 和线段AB ，其中A (t ，0)、B (t +2，0)两点，给出如下定义：若在线段AB 上存在一点Q ，使得P ，Q 两点间的距离小于或等于1，则称P 为线段AB 的伴随点．（1）当t =-3时，①在点P 1（1，1），P 2（0，0），P 3（-2，-1）中，线段AB 的伴随点是；②在直线y =2x +b 上存在线段AB 的伴随点M 、N ，且MN =b 的取值范围；（2）线段AB 的中点关于点（2，0）的对称点是C ，将射线CO 以点C 为中心，顺时针旋转30°得到射线l ，若射线l 上存在线段AB 的伴随点，直接写出t 的取值范围．28. 解：（1）①线段AB的伴随点是:23,P P. …………………2分②如图1，当直线y=2x+b经过点（-3，-1）时，b=5，此时b取得最大值.…………………………………………4分如图2，当直线y=2x+b经过点（-1，1）时，b=3，此时b取得最小值.……………………………………………5分∴b的取值范围是3≤b≤5. ……………………………………6分（2）t的取值范围是-12.2t≤≤…………………………………………8分燕山区28．在Rt△ABC中, ∠ACB=90°,CD是AB边的中线，DE⊥BC于E, 连结CD，点P在射线CB上（与B，C不重合）．（1）如果∠A=30°①如图1，∠DCB= °②如图2，点P在线段CB上，连结DP，将线段DP绕点D逆时针旋转60°，得到线段DF,连结BF，补全图2猜想CP、BF之间的数量关系，并证明你的结论；( 2 )如图3，若点P在线段CB的延长线上，且∠A=α（0°<α<90°），连结DP, 将线段DP绕点逆时针旋转α2得到线段DF,连结BF, 请直接写出DE、BF、BP三者的数量关系（不需证明）．图1图228.解：(1) ①∠DCB=60°…………………………………1′②补全图形CP=BF …………………………………3′△ DCP ≌△ DBF …………………………………6′（2）BF-BP=2DE ⋅tan α…………………………………8′门头沟区28. 在平面直角坐标系xOy 中，点M 的坐标为11(,)x y ，点N 的坐标为22(,)x y ，且12x x ≠，12y y =,我们规定：如果存在点P ，使MNP ∆是以线段MN 为直角边的等腰直角三角形，那么称点P 为点M 、N 的 “和谐点”. （1）已知点A 的坐标为)3,1(，①若点B 的坐标为)3,3(，在直线AB 的上方，存在点A ，B 的“和谐点”C ，直接写出点C 的坐标； ②点C 在直线x =5上，且点C 为点A ，B 的“和谐点”，求直线AC 的表达式.（2）⊙O 的半径为r ，点D (1,4)为点E (1,2)、F ),(n m 的“和谐点”，若使得△DEF 与⊙O 有交点，画出示意．．图直接．．．写出半径r 的取值范围.备用图1 备用图228．（本小题满分8分）解： (1)①)5,3()5,1(21C C 或. ……………………………………………2分②由图可知，B )3,5( ∵A (1,3) ∴AB =4∵ABC ∆为等腰直角三角形 ∴BC =4∴)1,5()7,5(21-C C 或设直线AC 的表达式为(0)y kx b k =+≠ 当)7,5(1C 时，⎩⎨⎧=+=+753b k b k ⎩⎨⎧==∴21b k2+=∴x y …………………………………3分当)1,5(2-C 时，⎩⎨⎧-=+=+153b k b k ⎩⎨⎧=-=∴41b k4+-=∴x y …………………………………4分 ∴综上所述，直线AC 的表达式是2+=x y 或4+-=x y(2)当点F 在点E 左侧时：大兴区28.在平面直角坐标系xOy 中，过y 轴上一点A 作平行于x 轴的直线交某函数图象于点D ，点P 是x 轴上一动点，连接D P ，过点P 作DP 的垂线交y 轴于点E （E 在线段OA 上，E 不与点O 重合），则称∠DPE 为点D ，P ,E 的“平横纵直角”.图1为点D ，P ,E 的“平横纵直角”的示意图.图图2如图2，在平面直角坐标系xOy 中，已知二次函数图象与y 轴交于点与x 轴分别交于点B （3-，(0,)F m ，0），C （12，0）. 若过点F 作平行于x 轴的直线交抛物线于点N .（1）点N 的横坐标为；（2）已知一直角为点,,N M K 的“平横纵直角”，若在线段OC 上存在不同的两点1M 、2M ，使相应的点1K 、2K 都与点F 重合，试求m 的取值范围；（3）设抛物线的顶点为点Q ，连接BQ 与FN 交于点H ,当4560QHN ︒≤≤︒∠时，求m 的取值范围． 28.（1）9 ………………………………………………………………… 1分（2）方法一:MK ⊥MN ，∴要使线段OC 上存在不同的两点M 1、M 2，使相应的点K 1、K 2都与点F 重合，也就是使以FN 为直径的圆与OC 有两个交点，即m r >．29=r ，29<∴m ．又0>m ， 290<<∴m ． ………………………………………………4分方法二：0>m ，∴点K 在x 轴的上方．过N 作NW ⊥OC 于点W ，设OM x =，OK y =，则 CW ＝OC －OW ＝3，WM ＝9x -．由△MOK ∽△NWM ，得，∴9y x x m=-． ∴x mx m y 912+-=．当m y =时，219m x x m m=-+，化为0922=+-m x x ．当△=0，即22940m -=，解得92m =时，线段OC 上有且只有一点M ，使相应的点K 与点F 重合．0>m ，∴ 线段OC 上存在不同的两点M 1、M 2，使相应的点K 1、K 2都与点F 重合时，m 的取值范围为290<<m ． ………………………………………………………………………………4分（3）设抛物线的表达式为：)12)(3(-+=x x a y (a ≠0)，又抛物线过点F （0，m ），a m 36-=∴．m a 361-=∴．m x m x x m y 1625)29(361)12)(3(3612+--=-+-=∴． …………………………………5分过点Q 做QG ⊥x 轴与FN 交于点RFN ∥x 轴∴∠QRH =90°tan BG BQG QG∠=，2516QG m =，152BG =∴，又4560QHN ︒≤∠≤︒，∴3045BQG ︒≤∠≤︒∴当30BQG ∠=︒时，可求出3524=m ，………………………………… 6分当45BQG ∠=︒时，可求出524=m ． ……………………………………7分m ∴的取值范围为2424355m ≤≤…………………………………8分平谷区28. 在平面直角坐标系xOy 中，点M 的坐标为()11,x y ，点N 的坐标为()22,x y ，且12x x ≠，12y y ≠，以MN 为边构造菱形，若该菱形的两条对角线分别平行于x 轴，y 轴，则称该菱形为边的“坐标菱形”. （1）已知点A （2,0），B （3，则以AB 为边的“坐标菱形”的最小内角为_______；（2）若点C （1,2），点D 在直线y =5上，以CD 为边的“坐标菱形”为正方形，求直线CD 表达式；（3）⊙O 2P 的坐标为(3,m ) .若在⊙O 上存在一点Q ，使得以QP 为边的“坐标菱形”为正方形，求m 的取值范围．28．解：（1）60； ····························· 1 （2）∵以CD 为边的“坐标菱形”为正方形， ∴直线CD 与直线y =5的夹角是45°．过点C 作CE ⊥DE 于E ．∴D （4,5）或()2,5-． ............. 3 ∴直线CD 的表达式为1y x =+或3y x =-+． (5)（3）15m ≤≤或51m -≤≤-． ···················7怀柔区28. P 是⊙C 外一点，若射线．．PC 交⊙C 于点A ，B 两点，则给出如下定义：若0＜PAPB≤3，则点P 为⊙C 的“特征点”．(1)当⊙O 的半径为1时．①在点P 1（2,0）、P 2（0,2）、P 3（4，0）中，⊙O 的“特征点”是； ②点P 在直线y=x+b 上，若点P 为⊙O 的“特征点”．求b 的取值范围；(2)⊙C 的圆心在x 轴上，半径为1，直线y=x+1与x 轴，y 轴分别交于点M ，N ，若线段MN 上的所有点都不是．．．⊙C 的“特征点”，直接写出点C 的横坐标的取值范围．yx–1–2–3–4–512345–1–2–3–4–512345O28.(1)①P 1（2,0）、P 2（0,2）…………………………………………………………………2分yxE Hy=x+b 2y=x+b1–1–2–3–41234–1–2–3–41234OD②如图，在y=x+b 上，若存在⊙O 的“特征点”点P ，点O 到直线y=x+b 的距离m≤2. 直线y=x+b 1交y 轴于点E ，过O 作OH ⊥直线y=x+b 1于点H. 因为OH=2，在Rt△DOE 中，可知OE=22. 可得b 1=22.同理可得b 2=-22.∴b 的取值范围是:22-≤b ≤22. …………………………………………………6分 (2)x>3或 3-<x . …………………………………………………………………………8分延庆区28．平面直角坐标系xOy 中，点1(A x ，1)y 与2(B x ，2)y ，如果满足120x x +=，120y y -=，其中12x x ≠，则称点A 与点B 互为反等点．已知：点C (3，4)（1）下列各点中，与点C 互为反等点； D (-3，-4)，E （3，4），F （-3，4）（2）已知点G （-5，4），连接线段CG ，若在线段CG 上存在两点P ，Q 互为反等点，求点P 的横坐标p x 的取值范围；（3）已知⊙O 的半径为r ，若⊙O 与（2）中线段CG 的两个交点互为反等点，求r 的取值范围．28．(1)F ……1分(2) -3≤p x ≤3 且p x ≠0 ……4分(3)4 < r≤5 ……7分顺义区点P 任意引出一条射线分别与1L 、2L 交于1Q 、2Q ，总有12PQ PQ 是定值，我们称曲线1L 与2L “曲似”，定值12PQ PQ 为“曲似比”，点P 为“曲心”．例如：如图2，以点O'为圆心，半径分别为1r 、2r （都是常数）的两个同心圆1C 、2C ，从点O'任意引出一条射线分别与两圆交于点M 、N ，因为总有12''r O M O N r =是定值，所以同心圆1C 与2C 曲似，曲似比为12r r ，“曲心”为O'．（1）在平面直角坐标系xOy 中，直线y kx =与抛物线2y x =、212y x =分别交于点A 、B ，如图3所示，试判断两抛物线是否曲似，并说明理由；（2）在（1）的条件下，以O 为圆心，OA 为半径作圆，过点B 作x 轴的垂线，垂足为C ，是否存在k 值，使⊙O 与图2C 2C 1N MO'直线BC 相切？若存在，求出k 的值；若不存在，说明理由；（3）在（1）、（2）的条件下，若将“212y x =”改为“21y x m=”，其他条件不变，当存在⊙O 与直线BC 相切时，直接写出m 的取值范围及k 与m 之间的关系式．28．（1）是．。

北京市各区2018届中考数学一模试卷精选汇编解不等式组专题(附答案)

解不等式组专题东城区18．解不等式组4+6,23x x x x ⎧⎪+⎨⎪⎩＞≥，并写出它的所有整数解. 18. 解：4+6,23x x x x ⎧⎪⎨+⎪⎩①②＞≥，由①得，-x ＞2，------------------1分由②得，1x ≤， ------------------2分∴不等式组的解集为-1x 2＜≤.所有整数解为-1, 0, 1. ---------------------5分西城区18．解不等式组3(2)4112x x x ++⎧⎪⎨-<⎪⎩≥，并求该不等式组的非负整数解．【解析】解①得，364x x ++≥，22x -≥，1x -≥，解②得，12x -<，3x <，∴原不等式解集为13x -<≤，∴原不等式的非负整数解为0，，2．海淀区18．解不等式组：()5331,263.2x x x x +>-⎧⎪⎨-<-⎪⎩ 18.解：() 5331, 263. 2x x x x +>-⎧⎪⎨-<-⎪⎩①② 解不等式①，得3x >-. …2分解不等式②，得2x <. ………4分所以原不等式组的解集为32x -<<. ………5分丰台区18．解不等式组：341,51 2.2x x x x ≥-⎧⎪⎨->-⎪⎩ 18．解：解不等式①，得1x ≤， ……………………2分解不等式②，得1x >-. ……………………4分∴原不等式组的解集是11x -<≤．………5分石景山区18．解不等式组：3(1)45622x x x x +>++<⎧⎪⎨⎪⎩，． 18．解：原不等式组为3(1)45,62.2x x x x +>++<⎧⎪⎨⎪⎩ 解不等式①，得2x <-． ………………2分解不等式②，得2x <． ………………4分 ∴原不等式组的解集为<2x -． ………………5分朝阳区18. 解不等式组：⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x18. 解：原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式①，得 5<x . ………………………………………2分解不等式②，得 21>x .………………………………………………4分 ∴ 原不等式组的解集为521<<x . …………………………………5分燕山区① ②18．解不等式组：⎩⎪⎨⎪⎧x －32<1，2（x ＋1）≥x－1.18．解：由（1）得，x-3<2X<5 ……………………….2′（2）得 2x+2≥x-1x ≥-3 ……………………….4′所以不等式组的解是-3≤x ＜5……………………….5′门头沟区 18. 解不等式组：1031+1.x x x ⎧-<⎪⎨⎪-⎩，≤3(）18．（本小题满分5分）解不等式①得，x ＜3， …………………………………………2分解不等式②得，x ≥﹣2， ………………………………4分所以，不等式组的解集是﹣2≤x ＜3． ………………5分大兴区17.解不等式组：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 并写出它的所有整数解. 17. 解：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 由①，得21-≥x . ………………………………………………………1分由②，得2<x . …………………………………………………………2分 ∴原不等式组的解集为221<≤-x . ………………………………………4分它的所有整数解为0，1. …………………………………………………5分① ②平谷区18．解不等式组3(1)45,513x x x x -≥-⎧⎪-⎨->⎪⎩，并写出它的所有整数解．．．． 18．解：3(1)455 3 1x x x x -≥-⎧⎪⎨-->⎪⎩①② 解不等式①，得 x ≤2． ······················· 1 解不等式②，得 x ＞-1． ······················· 3 ∴原不等式组的解集为12x -<≤． ·················· 4 ∴适合原不等式组的整数解为0,1,2． ················· 5 怀柔区18.解不等式组:()⎪⎩⎪⎨⎧<+-<-.1213,213x x x x 18.解：由①得：3x < . ………………………………………………………………………2分由②得：9x >- …………………………………………………………………………4分原不等式组的解集为93x -<< ………………………………………………………5分延庆区18．解不等式组：523(2)53.2x x x x -<+⎧⎪⎨+≤⎪⎩，并写出它的所有整数解． 18．解：由①得，x <4． ……1分由②得，x ≥1 ． ……3分∴ 原不等式组的解集为1≤x <4． ……4分∴ 原不等式组的所有整数解为1，2，3． ……5分顺义区18．解不等式组：()7+1,2315 1.x x x x +⎧≥-⎪⎨⎪+<-⎩18．解不等式组：()7+12315x x x x +⎧≥-⎪⎨⎪+<-⎩解：解不等式①得 x ≥3- ……………………………………………………………2分解不等式②得 2x > ………………………………………………………………4分不等式组的解集是 2x > …………………………………………………………5分。

北京市朝阳区2018年中考一模数学试卷(含答案)

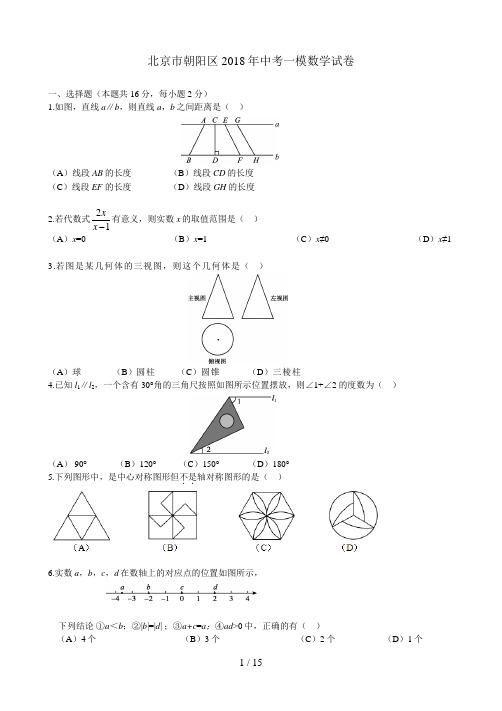
北京市朝阳区2018年中考一模数学试卷一、选择题（本题共16分，每小题2分）1.如图，直线a ∥b ，则直线a ，b 之间距离是（）（A ）线段AB 的长度（B ）线段CD 的长度（C ）线段EF 的长度（D ）线段GH 的长度2.若代数式12 x x有意义，则实数x 的取值范围是（）（A ）x =0 （B ）x =1 （C ）x ≠0（D ）x ≠13.若图是某几何体的三视图，则这个几何体是（）（A ）球（B ）圆柱（C ）圆锥（D ）三棱柱 4.已知 l 1∥l 2，一个含有30°角的三角尺按照如图所示位置摆放，则∠1+∠2的度数为（）（A ） 90° （B ）120° （C ）150° （D ）180° 5.下列图形中，是中心对称图形但不是．．轴对称图形的是（）6.实数a ，b ，c ，d 在数轴上的对应点的位置如图所示，下列结论 ①a ＜b ；②|b |=|d | ；③a+c =a ；④ad >0中，正确的有（）（A ）4个（B ）3个（C ）2个（D ）1个7. “享受光影文化，感受城市魅力”，2018年4月15-22日第八届北京国际电影节顺利举办.下面的统计图反映了北京国际电影节﹒电影市场的有关情况．根据统计图提供的信息，下列推断合理．．的是（）（A ）两届相比较，所占比例最稳定的是动作冒险（含战争）类（B ）两届相比较，所占比例增长最多的是剧情类（C ）第八届悬疑惊悚犯罪类申报数量比第六届2倍还多（D ）在第六届中，所占比例居前三位的类型是悬疑惊悚犯罪类、剧情类和爱情类8. 如图，△ABC 是等腰直角三角形，∠A =90°，AB =6，点P 是AB 边上一动点（点P 与点A 不重合），以AP 为边作正方形APDE ，设AP =x ，正方形APDE 与△ABC 重合部分（阴影部分）的面积为y ，则下列能大致反映y 与x 的函数关系的图象是（）二、填空题（本题共16分，每小题2分） 9. 赋予式子“ab ”一个实际意义：． 10.如果023≠=n m ，那么代数式)2(4322n m nm n m +⋅--的值是． 11.足球、篮球、排球已经成为北京体育的三张名片，越来越受到广大市民的关注. 下表是北京两支篮球队在2017-2018赛季CBA 常规赛的比赛成绩：设胜一场积x 分，负一场积y 分，依题意，可列二元一次方程组为． 12. 如图，AB ∥CD ，AB=21CD ，S △ABO ：S △CDO = ．13. 如图，点A，B，C在⊙O上，四边形OABC是平行四边形，OD⊥AB于点E，交⊙O于点D，则∠BAD= 度.14. 如图，在平面直角坐标系xOy中，△O'A'B'可以看作是△OAB经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△OAB得到△O'A'B'的过程： .15.下列随机事件的概率：①投掷一枚均匀的骰子，朝上一面为偶数的概率；②同时抛掷两枚质地均匀的硬币，两枚硬币全部正面朝上的概率；③抛一枚图钉，“钉尖向下”的概率；④某作物的种子在一定条件下的发芽率.既可以用列举法求得又可以用频率估计获得的是（只填写序号）.16.下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.三、解答题（本题共68分，第17-24题，每小题5分，第25题6分，第26-27题，每小题7分，第28题8分）17. 计算：2sin30°+ .8)4()31(01+-+-π18. 解不等式组：⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x19. 如图，在△ACB 中，AC =BC ，AD 为△ACB 的高线，CE 为△ACB 的中线.求证：∠DAB =∠ACE.20. 已知关于x 的一元二次方程0)1(2=+++k x k x ．（1）求证：方程总有两个实数根；（2）若该方程有一个根是正数，求k 的取值范围.21. 如图，在△ABC 中，D 是AB 边上任意一点，E 是BC 边中点，过点C 作AB 的平行线，交DE 的延长线于点F ，连接BF ，CD ．（1）求证：四边形CDBF 是平行四边形；（2）若∠FDB =30°，∠ABC =45°，BC =，求DF 的长．22. 如图，在平面直角坐标系xOy 中，直线AB 与x 轴、y 轴分别交于点A 、B ，与反比例函数xky 的图象在第四象限交于点C ，CD ⊥x 轴于点D ，tan ∠OAB ＝2，OA ＝2，OD ＝1．（1）求该反比例函数的表达式；（2）点M 是这个反比例函数图象上的点，过点M 作MN ⊥y 轴，垂足为点N ，连接OM 、AN ，如果S △ABN ＝2S △OMN ，直接写出点M 的坐标.23. 如图，在⊙O 中，C ，D 分别为半径OB ，弦AB 的中点，连接CD 并延长，交过点A 的切线于点E ．（1）求证：AE ⊥CE ．（2）若AE =，sin ∠ADE =31，求⊙O 半径的长．24. 水果基地为了选出适应市场需求的小西红柿秧苗，在条件基本相同的情况下，把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性，进行了抽样调查，过程如下，请补充完整．收集数据从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数：整理、描述数据按如下分组整理、描述这两组样本数据（说明：45个以下为产量不合格，45个及以上为产量合格，其中45~65个为产量良好，65~85个为产量优秀）分析数据两组样本数据的平均数、众数和方差如下表所示：a．估计乙大棚产量优秀的秧苗数为株；b．可以推断出大棚的小西红柿秧苗品种更适应市场需求，理由为．（至少从两个不同的角度说明推断的合理性）25.如图，AB是⊙O的直径，AB=4cm，C为AB上一动点，过点C的直线交⊙O于D、E两点，且∠ACD=60°，DF⊥AB于点F，EG⊥AB于点G，当点C在AB上运动时，设AF=x cm，DE=y cm（当x 的值为0或3时，y的值为2），探究函数y随自变量x的变化而变化的规律.（1）通过取点、画图、测量，得到了x与y的几组对应值，如下表：（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：点F与点O重合时，DE长度约为cm（结果保留一位小数）．26. 在平面直角坐标系xOy 中，抛物线()2440y ax ax a =--≠与y 轴交于点A ，其对称轴与x 轴交于点B .（1）求点A ，B 的坐标；（2）若方程()244=00ax ax a --≠有两个不相等的实数根，且两根都在1，3之间（包括1，3），结合函数的图象，求a 的取值范围.27. 如图，在菱形ABCD 中，∠DAB =60°，点E 为AB 边上一动点（与点A ，B 不重合），连接CE ，将∠ACE 的两边所在射线CE ，CA 以点C 为中心，顺时针旋转120°，分别交射线AD 于点F ，G. （1）依题意补全图形；（2）若∠ACE=α，求∠AFC 的大小（用含α的式子表示）；（3）用等式表示线段AE 、AF 与CG 之间的数量关系，并证明．28. 对于平面直角坐标系xOy中的点P和线段AB，其中A(t，0)、B(t+2，0)两点，给出如下定义：若在线段AB上存在一点Q，使得P，Q两点间的距离小于或等于1，则称P为线段AB的伴随点．（1）当t=-3时，①在点P1（1，1），P2（0，0），P3（-2，-1）中，线段AB的伴随点是；②在直线y=2x+b上存在线段AB的伴随点M、N，且MN=b的取值范围；（2）线段AB的中点关于点（2，0）的对称点是C，将射线CO以点C为中心，顺时针旋转30°得到射线l，若射线l上存在线段AB的伴随点，直接写出t的取值范围．北京市朝阳区2018年中考一模数学试卷参考答案及评分标准一、选择题（本题共16分，每小题2分）二、填空题（本题共16分，每小题2分）9. 答案不惟一，如：边长分别为a ，b 的矩形面积 10.4711. ⎩⎨⎧=+=+.562018,631325y x y x 12. 1:4 13. 1514. 答案不唯一，如：以x 轴为对称轴，作△OAB 的轴对称图形，再将得到三角形沿向右平移4个单位长度 15. ①②16. 与一条线段两个端点距离相等的点，在这条线段的垂直平分线上；直径所对的圆周角是直角三、解答题（本题共68分，第17-24题，每小题5分，第25题6分，第26-27题，每小题7分，第28题8分） 17. 解：原式 2213212+++⨯= …………………………………………………………………4分 225+=. ……………………………………………………………………………5分18. 解：原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式①，得 5<x . ………………………………………………………………………2分解不等式②，得 21>x .………………………………………………………………………4分 ∴ 原不等式组的解集为521<<x . …………………………………………………………5分19. 证明：∵AC ＝BC ，CE 为△ACB 的中线，∴∠CAB ＝∠B ，CE ⊥AB . ………………………………………………………………2分 ∴∠CAB ＋∠ACE ＝90°. …………………………………………………………………3分 ∵AD 为△ACB 的高线， ∴∠D ＝90°.∴∠DAB ＋∠B ＝90°. ……………………………………………………………………4分∴∠DAB ＝∠ACE . ………………………………………………………………………5分20. （1）证明：依题意，得k k 4)1(2-+=∆ ……………………………………………………1分 .)1(2-=k ……………………………………………………………2分∵0)1(2≥-k ，∴方程总有两个实数根. ……………………………………………………………3分（2）解：由求根公式，得11-=x ，k x -=2. …………………………………………………4分∵方程有一个根是正数， ∴0>-k .∴0<k .…………………………………………………………………………………5分21.（1）证明：∵CF ∥AB ，∴∠ECF ＝∠EBD . ∵E 是BC 中点， ∴CE ＝BE .∵∠CEF ＝∠BED ， ∴△CEF ≌△BED . ∴CF ＝BD .∴四边形CDBF 是平行四边形. ……………………………………………………2分（2）解：如图，作EM ⊥DB 于点M ，∵四边形CDBF 是平行四边形，BC ＝24， ∴2221==BC BE ，DE DF 2=.在Rt △EMB 中，2sin =∠⋅=ABC BE EM . …………………………………………3分在Rt △EMD 中，42==EM DE . ……………………………………………………4分∴DF ＝8. ……………………………………………………………………………………5分22. 解：（1）∵AO ＝2，OD ＝1，∴AD ＝AO+ OD ＝3. ……………………………………………………………………1分 ∵CD ⊥x 轴于点D ， ∴∠ADC ＝90°.在Rt △ADC 中，6tan =∠⋅=OAB AD CD ..∴C （1，－6）. ……………………………………………………………………………2分∴该反比例函数的表达式是xy 6-=. …………………………………………………3分A（2）点M 的坐标为（－3,2）或（53，－10）. ……………………………………………5分23. （1）证明：连接OA ，∵OA 是⊙O 的切线， ∴∠OAE ＝90º. ………………………………1分 ∵ C ，D 分别为半径OB ，弦AB 的中点，∴CD 为△AOB 的中位线.∴CD ∥OA ． ∴∠E ＝90º. ∴AE ⊥CE . …………………………………2分（2）解：连接OD ，∴∠ODB ＝90º. ………………………………………………………………………3分∵AE =，sin ∠ADE =31，在Rt △AED 中，23sin =∠=ADEAEAD .∵CD ∥OA ， ∴∠1＝∠ADE .在Rt △OAD 中，311sin ==∠OA OD .………………………………………………4分设OD ＝x ，则OA ＝3x ， ∵222OA AD OD =+， ∴()()222323x x =+.解得 231=x ，232-=x （舍）. ∴293==x OA . ……………………………………………………………………5分即⊙O 的半径长为29.24. 解：整理、描述数据按如下分组整理、描述这两组样本数据…………………………………………………………………………………………………2分25≤x <35 35≤x <45 45≤x <55 55≤x <65 65≤x <75 75≤x <85甲 5 5 5 5 4 1 乙24665212E CB O D x 大棚个数株数得出结论 a ．估计乙大棚产量优秀的秧苗数为 84 株； …………………………3分b ．答案不唯一，理由须支撑推断的合理性. ………………………………5分25. 解：本题答案不唯一，如：x /cm 0 0.400.55 1.00 1.80 2.29 2.61 3 y /cm23.683.844.003.653.132.702…………………………………………………………………………………………………1分（2）…………………………………………………………………………………………………4分（3）3.5．…………………………………………………………………………………………6分26.解：（1）44)2(4422---=--=a x a ax ax y ．∴A （0，－4），B （2，0）．…………………………………………………………2分（2）当抛物线经过点（1，0）时，34-=a ．……………………………………………4分当抛物线经过点（2，0）时，1-=a ． ……………………………………………6分结合函数图象可知，a 的取值范围为134<≤-a ．…………………………………7分27.（1）补全的图形如图所示.…………………………………………………………………………………………………1分（2）解：由题意可知，∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD 是菱形，∠DAB=60°， ∴∠DAC=∠BAC= 30°. ………………………………………………………………2分 ∴∠AGC=30°. ∴∠AFC =α+30°. ………………………………………………………………………3分（3）用等式表示线段AE 、AF 与CG 之间的数量关系为CG AF AE 3=+.证明：作CH ⊥AG 于点H.由（2）可知∠BAC=∠DAC=∠AGC=30°.∴CA=CG. ………………………………………………………………………………………5分 ∴HG =21AG. ∵∠ACE =∠GCF ，∠CAE =∠CGF ，∴△ACE ≌△GCF. ……………………………………………………………………………6分 ∴AE =FG .在Rt △HCG 中， .23cos CG CGH CG HG =∠⋅= ∴AG =3CG . …………………………………………………………………………………7分即AF+AE =3CG .28. 解：（1）①线段AB 的伴随点是: 23,P P . ………………………………………………2分②如图1，当直线y =2x +b 经过点（-3，-1）时，b =5，此时b 取得最大值.………………………………………………………………………………4分如图2，当直线y =2x +b 经过点（-1，1）时，b =3，此时b 取得最小值. ………………………………………………………………………………5分 ∴ b 的取值范围是3≤b ≤5. ……………………………………………………6分（2）t 的取值范围是-12.2t ≤≤………………………………………………………………8分图1 图2。

2018北京初三一模数学16区分类汇编--28题几何综合

BAC（2018燕山一模）△ABC 中，∠ABC ＝45°，AH ⊥BC 于点H ，将△AHC 绕点H 逆时针旋转90°后，点C 的对应点为点D ，直线BD 与直线AC 交于点E ，连接EH ．（1）如图1，当∠BAC 为锐角时，①求证：BE ⊥AC ； ②求∠BEH 的度数；（2）当∠BAC 为钝角时，请依题意用实线补全图2，并用等式表示出线段EC ，ED ，EH 之间的数量关系．（2018东城一模）已知：Rt△A′BC′和Rt△ABC 重合，∠A′C′B =∠ACB =90°，∠BA′C ′=∠BAC =30°，现将Rt△A′BC′绕点B 按逆时针方向旋转角α（60°≤α≤90°），设旋转过程中射线C′C 和线段AA′相交于点D ,连接BD ．（1）当α=60°时，A ’B 过点C ，如图1所示，判断BD 和A′A 之间的位置关系，不必证明；（2）当α=90°时，在图2中依题意补全图形，并猜想（1）中的结论是否仍然成立，不必证明；（3）如图3，对旋转角α（60°＜α＜90°），猜想（1）中的结论是否仍然成立；若成立，请证明你的结论；若不成立，请说明理由.A BHCEDAB H C图1图22018房山一模）如图1，已知线段BC=2，点B关于直线AC的对称点是点D，点E为射线CA上一点，且ED=BD，连接DE，BE.(1)依题意补全图1，并证明：△BDE为等边三角形；(2)若∠ACB=45°，点C关于直线BD的对称点为点F，连接FD、FB.将△CDE 绕点D顺时针旋转α度（0°＜α＜360°）得到△''C DE，点E的对应点为E′，点C的对应点为点C′.①如图2，当α=30°时，连接'BC．证明：EF='BC；②如图3，点M为DC中点，点P为线段''C E上的任意一点，试探究：在此旋转过程中，线段PM长度的取值范围？2018海淀一模）在菱形ABCD中，120ADC∠=︒，点E是对角线AC上一点，连接DE，50DEC∠=︒，将线段BC绕点B逆时针旋转50︒并延长得到射线BF，交ED的延长线于点G．（1）依题意补全图形；备用图（2）求证：EG BC=；（3）用等式表示线段AE，EG，BG之间的数量关系：_____________________________．EDCBAEDCBA图1 图2 图3图1 图2 图32018门头沟一模）在Rt △ABC 中，∠ACB =90°，D 是AB 的中点，DE ⊥BC 于E ，连接CD ．（1）如图1，如果∠A =30°，那么DE 与CE 之间的数量关系是．（2）如图2，在（1）的条件下，P 是线段CB 上一点，连接DP ，将线段DP绕点D 逆时针旋转60°，得到线段DF ，连接BF ，请猜想DE 、BF 、BP 三者之间的数量关系，并证明你的结论．（3）如图3，如果∠A =α（0°＜α＜90°），P 是射线CB 上一动点（不与B 、C 重合），连接DP ，将线段DP 绕点D 逆时针旋转2α，得到线段DF ，连接BF ，请直接写出DE 、BF 、BP 三者之间的数量关系（不需证明）．图1 图2 图32018通州一模）在菱形ABCD 中，∠ABC =60°，E 是对角线AC 上任意一点，F 是线段BC 延长线上一点，且CF =AE ，连接BE 、EF ．（1）如图1，当E 是线段AC 的中点时，易证BE =EF .（2）如图2，当点E 不是线段AC 的中点，其它条件不变时，请你判断（1）中的结论：.（填“成立”或“不成立”）（3）如图3，当点E 是线段AC 延长线上的任意一点，其它条件不变时，（1）中的结论是否成立？若成立，请给予证明；若不成立，请说明理由．)DBFE DAB E DAB C C CP AE2018丰台一模）在△ABC 中，CA =CB ，CD 为AB 边的中线，点P 是线段AC 上任意一点（不与点C重合），过点P 作PE 交CD 于点E ，使∠CPE =12∠CAB ，过点C 作CF ⊥PE 交PE 的延长线于点F ，交AB 于点G. （1）如果∠ACB =90°，①如图1，当点P 与点A 重合时，依题意补全图形，并指出与△CDG 全等的一个三角形；②如图2，当点P 不与点A 重合时，求CFPE 的值；（2）如果∠CAB =a ，如图3，请直接写出CFPE的值.（用含a 的式子表示）2018西城一模）27． △ABC 中，AB=AC ．取BC 边的中点D ，作DE ⊥AC 于点E ，取DE 的中点F ，连接BE ，AF 交于点H ．（1）如图1，如果90BAC ∠=︒，那么AHB ∠=︒，AFBE =；（2）如图2，如果60BAC ∠=︒，猜想AHB ∠的度数和AFBE的值，并证明你的结论；（3）如果BAC α∠=，那么AFBE=．（用含α的表达式表示）图1图2图32018平谷一模）（1）如图1，在四边形ABCD 中，AB=BC，∠ABC =80°，∠A +∠C =180°，点M 是AD 边上一点，把射线BM 绕点B 顺时针旋转40°，与CD 边交于点N ，请你补全图形，求MN ，AM ，CN 的数量关系；（2）如图2，在菱形ABCD 中，点M 是AD 边上任意一点，把射线BM 绕点B顺时针旋12ABC ，与CD 边交于点N ，连结MN ，请你补全图形并画出辅助线，直接写出AM ，CN ，MN 的数量关系是；（3）如图3，正方形ABCD 的边长是1，点M ，N 分别在AD ，CD 上，若△DMN 的周长为2，则△MBN 的面积最小值为．2018怀柔一模）在等边△ABC 外侧作直线AP ，点B 关于直线AP 的对称点为D ，连接BD,CD ，其中CD 交直线AP 于点E ．（1）依题意补全图1；（2）若∠PAB=30°，求∠ACE 的度数；（3）如图2，若60°<∠PAB<120°，判断由线段AB,CE,ED 可以构成一个含有多少度角的三角形，并证明.图2 图3 图1A BCPABCP2018朝阳一模）在△ABC 中，∠C =90°，AC =BC ，点D 在射线BC 上（不与点B 、C 重合），连接AD ，将AD 绕点D 顺时针旋转90°得到DE ，连接BE . （1）如图1，点D 在BC 边上.①依题意补全图1；②作DF ⊥BC 交AB 于点F ，若AC =8，DF =3，求BE 的长；（2）如图2，点D 在BC 边的延长线上，用等式表示线段AB 、BD 、BE 之间的数量关系（直接写出结论）.2018大兴一模）已知：如图，在四边形ABCD 中，AD ∥BC ， ABC=90°.点E 为边AD 上一点，将△ABE 沿直线BE 折叠，使点A 落在四边形对角线BD 上的点G 处，EG 的延长线交直线BC 于点F.（1）点E 可以是AD 的中点吗？请说明理由；（2）求证△ABG ∽△BFE ；（3）设AD=a ，AB=b ，BC=c.当四边形EFCD 为平行四边形时，求a ，b ，c 应满足的关系.图1 图22018石景山一模）在△ABC 中，90BAC ∠=︒．（1）如图1，直线l 是BC 的垂直平分线，请在图1中画出点A 关于直线l 的对称点'A ，连接'A C ，B A '，'A C 与AB 交于点E ；（2）将图1中的直线B A '沿着EC 方向平移，与直线EC 交于点D ，与直线BC交于点F ，过点F 作直线AB 的垂线，垂足为点H ．①如图2，若点D 在线段EC 上，请猜想线段FH ，DF ，AC 之间的数量关系，并证明；②若点D 在线段EC 的延长线上，直接写出线段FH ，DF ，AC 之间的数量关系．（2018顺义一模）28．如图，△ABC 中，AB =AC ，点P 是三角形右外一点，且∠APB =∠ABC ．（1）如图1，若∠BAC =60°，点P 恰巧在∠ABC 的平分线上，PA =2，求PB 的长；（2）如图2，若∠BAC =60°，探究PA ，PB ，PC 的数量关系，并证明；（3）如图3，若∠BAC =120°，请直接写出PA ，PB ，PC 的数量关系．GFE DCBAB E FQQ FE CB AP（2018延庆一模）28. 已知，点P 是△ABC 边AB 上一动点（不与A ，B 重合）分别过点A ，B 向直线CP 作垂线，垂足分别为E ，F ，Q 为边AB 的中点.（1）如图1，当点P 与点Q 重合时，AE 与BF 的位置关系是，QE 与QF 的数量关系是；（2）如图2，当点P 在线段AB 上不与点Q 重合时，试判断QE 与QF 的数量关系，并给予证明；（3）如图3，当点P 在线段BA 的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明.图3图1图2ABCPABPABC P图1图2图3。

北京市各区2018届中考一模数学试卷精选汇编 8套全集合(解析版)

北京市各区2018届中考一模数学试卷精选汇编8套全集合（解析版）计算题专题东城区17．计算：()2012sin 60-π-2++1-3-⎛⎫︒ ⎪⎝⎭. =22⨯17.解：原式分分西城区17114sin 3015-⎛⎫+︒ ⎪⎝⎭．【解析】原式1541)52122=+⨯-=+-=．海淀区17．计算：11()3tan 30|2|3-︒+． 17.解：原式=332-+ ………………4分=5- ………………5分丰台区1702cos 45(3π)|1︒+-+-．1702cos 45(3π)|1︒+-+-．=211++ ……………………4分= ……………………5分石景山区17．计算：012sin 455(3---++°17．解：原式=2512⨯-+- ………………4分4=-- ………………5分朝阳区17. 计算：2sin30°+ .8)4()31(01+-+-π17. 解：原式 2213212+++⨯= …………………………………………………4分 225+=. ……………………………………………………………5分燕山区17．计算：4cos30°－12 + 20180 + ||1－317．4cos30°－12 + 20180 + ||1－3 =13132234-++-⨯=3 门头沟区 17．计算：()201254sin 603π-⎛⎫--++-︒ ⎪⎝⎭．平谷区17．计算：(10112sin 603-⎛⎫-+-︒ ⎪⎝⎭π.17．解：(10112sin 603-⎛⎫-+-︒ ⎪⎝⎭π=3112-- (4)=1 (5)怀柔区17.计算：12130tan3)3(31-︒⎪⎭⎫⎝⎛-+---π.17.解：原式1132=-+…………………………………………………4分.…………………………………………………………………5分延庆区17．计算：0113tan301)()3π-︒+---．17．原式=3⨯33+3-1+1-3 ……4分=23-3……5分顺义区17．计算：()01312sin452π-+-︒+-．17．解：()01312sin452π-+-︒+-112132=-⨯+………………………………………………………4分13=……………………………………………………………………………… 5分4=解不等式组专题东城区18．解不等式组4+6,23x x x x ⎧⎪+⎨⎪⎩＞≥，并写出它的所有整数解. 18. 解：4+6,23x x x x ⎧⎪⎨+⎪⎩①②＞≥，由①得，-x ＞2，------------------1分由②得，1x ≤， ------------------2分∴不等式组的解集为-1x 2＜≤.所有整数解为-1, 0, 1. ---------------------5分西城区18．解不等式组3(2)4112x x x ++⎧⎪⎨-<⎪⎩≥，并求该不等式组的非负整数解．【解析】解①得，364x x ++≥，22x -≥，1x -≥，解②得，12x -<，3x <，∴原不等式解集为13x -<≤，∴原不等式的非负整数解为0，，2．海淀区18．解不等式组：()5331,263.2x x x x +>-⎧⎪⎨-<-⎪⎩ 18.解：() 5331, 263. 2x x x x +>-⎧⎪⎨-<-⎪⎩①② 解不等式①，得3x >-. …2分解不等式②，得2x <. ………4分所以原不等式组的解集为32x -<<. ………5分丰台区18．解不等式组：341,51 2.2x x x x ≥-⎧⎪⎨->-⎪⎩ 18．解：解不等式①，得1x ≤， ……………………2分解不等式②，得1x >-. ……………………4分∴原不等式组的解集是11x -<≤．………5分石景山区18．解不等式组：3(1)45622x x x x +>++<⎧⎪⎨⎪⎩，． 18．解：原不等式组为3(1)45,62.2x x x x +>++<⎧⎪⎨⎪⎩ 解不等式①，得2x <-． ………………2分解不等式②，得2x <． ………………4分 ∴原不等式组的解集为<2x -． ………………5分朝阳区18. 解不等式组：⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x18. 解：原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式①，得 5<x . ………………………………………2分① ②解不等式②，得 21>x .………………………………………………4分 ∴ 原不等式组的解集为521<<x . …………………………………5分燕山区18．解不等式组：⎩⎪⎨⎪⎧x －32<1，2（x ＋1）≥x －1.18．解：由（1）得，x-3<2X<5 ……………………….2′（2）得 2x+2≥x-1x ≥-3 ……………………….4′所以不等式组的解是-3≤x ＜5 ……………………….5′ 门头沟区18. 解不等式组：1031+1.x x x ⎧-<⎪⎨⎪-⎩，≤3(）18．（本小题满分5分）解不等式①得，x ＜3， …………………………………………2分解不等式②得，x ≥﹣2， ………………………………4分所以，不等式组的解集是﹣2≤x ＜3． ………………5分大兴区17.解不等式组：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 并写出它的所有整数解. 17. 解：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 ① ②由①，得21-≥x . ………………………………………………………1分由②，得2<x . …………………………………………………………2分 ∴原不等式组的解集为221<≤-x . ………………………………………4分它的所有整数解为0，1. …………………………………………………5分平谷区18．解不等式组3(1)45,513x x x x -≥-⎧⎪-⎨->⎪⎩，并写出它的所有整数解．．．． 18．解：3(1)455 3 1x x x x -≥-⎧⎪⎨-->⎪⎩①② 解不等式①，得 x ≤2． ································································································· 1 解不等式②，得 x ＞-1． ······························································································ 3 ∴原不等式组的解集为12x -<≤． ········································································· 4 ∴适合原不等式组的整数解为0,1,2． ········································································ 5 怀柔区18.解不等式组:()⎪⎩⎪⎨⎧<+-<-.1213,213x x x x 18.解：由①得：3x < . ………………………………………………………………………2分由②得：9x >- …………………………………………………………………………4分原不等式组的解集为93x -<< ………………………………………………………5分延庆区18．解不等式组：523(2)53.2x x x x -<+⎧⎪⎨+≤⎪⎩，并写出它的所有整数解．18．解：由①得，x <4． ……1分由②得，x ≥1 ． ……3分∴ 原不等式组的解集为1≤x <4． ……4分∴ 原不等式组的所有整数解为1，2，3． ……5分顺义区18．解不等式组：()7+1,2315 1.x x x x +⎧≥-⎪⎨⎪+<-⎩18．解不等式组：()7+12315x x x x +⎧≥-⎪⎨⎪+<-⎩解：解不等式①得 x ≥3- ……………………………………………………………2分解不等式②得 2x > ………………………………………………………………4分不等式组的解集是 2x > …………………………………………………………5分函数计算及运用专题东城区22. 已知函数()30y x x=＞的图象与一次函数()20y ax a =-≠的图象交于点A ()3,n . （1）求实数a 的值；(2) 设一次函数()20y ax a =-≠的图象与y 轴交于点B .若点C 在y 轴上，且=2ABC AOB S S △△，求点C 的坐标.22.解：（1）∵点()3,A n 在函数()30y xx=＞的图象上， ∴=1n ，点()3,1A .∵直线()20y ax a =-≠过点()3,1A ，∴ 321a -= .解得 1a =. ----------------------2分(2)易求得()0,2B -. 如图，12AOB A S OB x =⋅△，1=2ABC A S BC x ⋅△ ∵=2ABC AOB S S △△，∴=24BC OB =.∴()10,2C ,或()20,6C -. ----------------------5分西城区22．如图，在平面直角坐标系xOy 中，直线y x m =+与x 轴的交点为0()4,A -，与y 轴的交点为B ，线段AB 的中点M 在函数k y x=（0k ≠）的图象上（1）求m ，k 的值;（2）将线段AB 向左平移n 个单位长度（0n >）得到线段CD ，A ，MB 的对应点分别为C ，N ，D ．①当点D 落在函数k y x=（0x <）的图象上时，求n 的值． ②当MD MN ≤时，结合函数的图象，直接写出n 的取值范围．【解析】（1）如图．∵直线y x m =+与x 轴的交点为0()4,A -，∴4m =．∵直线y x m =+与y 轴的交点为B ，∴点B 的坐标为(0,4)B ．∵线段AB 的中点为M ，∴可得点M 的坐标为(2,2)M -．∵点M 在函数k y x =（0k ≠）的图象上， ∴4k =-．（2）①由题意得点D 的坐标为(,4)D n -，∵点D 落在函数k y x=（0k ≠）的图象上， ∴44n -=-，解得1n =．②n 的取值范围是2n ≥．海淀区22．在平面直角坐标系xOy 中，已知点P （2，2），Q （－1，2），函数m y x =.（1）当函数my x=的图象经过点P 时，求m 的值并画出直线y x m =+．（2）若P ，Q 两点中恰有一个点的坐标（x ，y ）满足不等式组,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0），求m 的取值范围．22．解：（1）∵函数my x=的图象经过点()22P ，， ∴2=2m，即4m =． ………………1分图象如图所示. ………………2分（2）当点()22P ，满足,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0）时，解不等式组2222m m⎧>⎪⎨⎪<+⎩，得04m <<． ………………3分当点()12Q -，满足,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0）时，解不等式组221m m>-⎧⎨<-+⎩，得3m >． ………………4分∵P Q ，两点中恰有一个点的坐标满足,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0）， ∴m 的取值范围是：03m <≤，或4m ≥． ………………5分丰台区22．在平面直角坐标系xOy 中，反比例函数2y x=的图象与一次函数y kx b =+的图象的交点分别为P (m ，2)，Q (-2，n ). （1）求一次函数的表达式；（2）过点Q 作平行于y 轴的直线，点M 为此直线上的一点，当MQ = PQ 时，直接写出点M 的坐标.22．（1）解： ∵反比例函数2y x=的图象经过点(,2)P m ，Q (-2，n )， ∴1m =，1n =-．∴点P ，Q 的坐标分别为(1，2)，(-2，-1). …….…….…….……2分 ∵一次函数y kx b =+的图象经过点P (1，2)，Q (-2，-1)，∴2,2 1.k b k b +=⎧⎨-+=-⎩ 解得1,1.k b =⎧⎨=⎩∴一次函数的表达式为1y x =+． .…….…….…….……3分（2）点M 的坐标为（-2，-2，……………5分石景山区22．在平面直角坐标系xOy 中，函数a y x=（0x >）的图象与直线1l y x b =+：交于点(3,2)A a -．（1）求a ，b 的值；（2）直线2l y x m =-+：与x 轴交于点B ，与直线1l 交于点C ，若S △ABC 6≥，求m 的取值范围．22．解：（1）∵函数()0a y x x=>的图象过点()3,2A a -，∴23a a -=，解得3a =． ………………1分∵直线1l y x b =+：过点()3,1A ,∴2b =-． ………………2分（2）设直线2y x =-与x 轴交于点D ，则(2,0)D ，直线y x m =-+与x 轴交于点(,0)B m ，与直线y x b =+交于点22(,)22m m C +-． ①当S △ABC =S △BCD +S △ABD =6时，如图1. 可得211(2)(242m m -+- 解得2m =-，8m =②当S △ABC =S △BCD -S △ABD =6时，如图2. 可得211(2)(2)1642m m ---⨯=，解得8m =，2m =-（舍）. 综上所述，当8m ≥或2m -≤时，S△ABC 6≥. ………………5分朝阳区22. 如图，在平面直角坐标系xOy 中，直线AB 与x 轴、y 轴分别交于点A 、B ，与反比例函数xky =的图象在第四象限交于点C ，CD ⊥x 轴于点D ，tan ∠OAB ＝2，OA ＝2，OD ＝1．（1）求该反比例函数的表达式；（2）点M 是这个反比例函数图象上的点，过点M作MN ⊥y 轴，垂足为点N ，连接OM 、AN ，如果 S △ABN ＝2S △OMN ，直接写出点M 的坐标.22. 解：（1）∵AO ＝2，OD ＝1，∴AD ＝AO+ OD ＝3. ………………………………………………1分 ∵CD ⊥x 轴于点D ， ∴∠ADC ＝90°.在Rt △ADC 中，6tan =∠⋅=OAB AD CD ..∴C （1，－6）. ……………………………………………………2分 ∴该反比例函数的表达式是xy 6-=. ……………………………………3分（2）点M 的坐标为（－3,2）或（53，－10）. ……………………5分 ∴OM 27=215 OM=715∴⊙O 的半径是715…………………………………6′ 门头沟区20. 如图，在平面直角坐标系xOy 中，一次函数y x =与反比例函数ky x=（k ≠0）的图象相交于点)A a . （1）求a 、k 的值；（2）直线x =b （0b >）分别与一次函数y x =、反比例函数ky x=的图象相交于点M 、N ，当MN =2时,画出示意图并直接写出b 的值.20．（本小题满分5分）（1）∵直线y x =与双曲线ky x=（k ≠0）相交于点)A a .∴a =1分∴A3k =………………………2分（2）示意图正确………………………………3分 3b =或1 ………………………………5分大兴区22．如图，点A 是直线2y x =与反比例函数1m y x-=（m 为常数）的图象的交点．过点A 作x 轴的垂线，垂足为B ，且OB =2．（1）求点A 的坐标及m 的值；(2)已知点P (0，n) (0＜n ≤8) ，过点P 作平行于x 轴的直线，交直线2y x =于点C 11(,)x y , 交反比例函数1m y x-=（m 为常数）的图象于点D 22(,)x y ,交垂线AB 于点E 33(,)x y , 若231x x x <<，结合函数的图象，直接写出123++x x x 的取值范围．22．（1）解：由题意得，可知点A 的横坐标是2，……………………1分由点A 在正比例函数2y x =的图象上，∴点A 的坐标为（2，4）……………………………………2分又点A 在反比例函数1m y x-=的图象上，142m -∴=，即9m =．……………………………………… 3分（2）6<x 1+x 2+x 3≤7 ……………………………………………… 5分平谷区22．如图，在□ABCD 中，BF 平分∠ABC 交AD 于点F ，AE ⊥BF 于点O ，交BC 于点E ，连接EF ．（1）求证：四边形ABEF 是菱形；（2）连接CF ，若∠ABC=60°， AB= 4，AF =2DF ，求CF 的长．22．（1）证明：∵BF平分∠ABC，∴∠ABF=∠CBF． (1)∵□ABCD，∴AD∥BC．∴∠AFB=∠CBF．∴∠ABF=∠AFB．∴AB=AF．∵AE⊥BF，∴∠ABF+∠BAO=∠CBF+∠BEO=90°．∴∠BAO=∠BEO．∴AB=BE．∴AF=BE．∴四边形ABEF是平行四边形．∴□ABEF是菱形． (2)（2）解：∵AD=BC，AF=BE，∴DF=CE．∴BE=2CE．∵AB=4，∴BE=4．∴CE=2．过点A作AG⊥BC于点G． (3)∵∠ABC=60°，AB=BE，∴△ABE是等边三角形．∴BG=GE=2．∴AF=CG=4． (4)∴四边形AGCF是平行四边形．∴□AGCF是矩形．∴AG=CF．在△ABG中，∠ABC=60°，AB=4，∴AG=∴CF=怀柔区22．在平面直角坐标系xOy 中,一次函数y=kx+b 的图象与y 轴交于点B （0,1），与反比例函数xmy =的图象交于点A(3，-2). (1)求反比例函数的表达式和一次函数表达式；(2)若点C 是y 轴上一点，且BC=BA ，直接写出点C 的坐标.y x–1–2–3–4–512345–1–2–3–4–512345O22．(1)∵双曲线x m y =过A （3，-2），将A （3，-2）代入xmy =，解得：m= -6.∴所求反比例函数表达式为: y=x6-. …………………………………1分 ∵点A （3，-2）点B （0,1）在直线y=kx+b 上，∴-2=3k+1. …………………………………………………………………………………2分 ∴k=-1.∴所求一次函数表达式为y=-x+1. …………………………………………………………3分 (2)C(0，123+ )或 C(0，231- ). ……………………………………………………5分延庆区22．在平面直角坐标系xOy 中，直(0)y kx b k =+≠ 与x 轴交于点A ，与y 轴交于点B ，与反比例函数(0)my m x=≠的图象在第一象限交于点P （1，3），连接OP ．（1）求反比例函数(0)my m x=≠的表达式；（2）若△AOB 的面积是△POB 的面积的2倍，求直线y kx b =+的表达式．22．（1）3y x……1分（2）如图22（1）：∵∴OA =2PE =2∴A （2,0） ……2分将A （2,0），P （1,3）代入y =kx +b 可得∴……3分图22（1）∴直线AB 的表达式为：y =-3x +6同理：如图22（2）直线AB 的表达式为：y =x +2 ……4分综上：直线AB 的表达式为y =-3x+6或y =x +2 ……5分图22（2）顺义区22．如图，在平面直角坐标系xOy 中，直线24y x =+与双曲线ky x=（k ≠0）相交于A （-3，a ），B 两点．（1）求k 的值；（2）过点P （0，m ）作直线l ，使直线l 与y 轴垂直，直线l 与直线AB 交于点M ，与双曲线ky x=交于点N ，若点P 在点M 与点N 之间，直接写出m 的取值范围．22．解：（1）∵点A （-3，a ）在直线24y x =+上，∴2(3)42a =⨯-+=-．∴点A 的坐标为（-3，-2）． …………………………………… 1分 ∵点A （-3，-2）在双曲线ky x=上， ∴23k-=-， ∴6k =． …………………………………… 3分（2）m 的取值范围是 04m <<． ……………………………… 5分二次函数综合专题东城区26．在平面直角坐标系xOy 中，抛物线()02342≠-+-=a a ax ax y 与x 轴交于A ，B 两点（点A 在点B 左侧）．（1）当抛物线过原点时，求实数a 的值；（2）①求抛物线的对称轴；②求抛物线的顶点的纵坐标（用含a 的代数式表示）；（3）当AB ≤4时，求实数a 的取值范围．26.解：(1) ∵点()0,0O 在抛物线上，∴320a -=，23a =.--------------------2分(2)①对称轴为直线2x =；②顶点的纵坐标为 2a --.--------------------4分 (3) （i ）当0a ＞时，依题意，-20320.a a -⎧⎨-⎩＜，≥解得2.3a ≥（ii ）当0a ＜时，依题意，-20320.a a -⎧⎨-⎩＞，≤解得a ＜-2.综上，2a -＜，或23a ≥. --------------------7分西城区26.在平面直角坐标系xOy 中，抛物线G ：221(0)y mx mx m m =++-≠与y 轴交于点C ，抛物线G 的顶点为D ，直线：1(0)y mx m m =+-≠．（1）当1m =时，画出直线和抛物线G ，并直接写出直线被抛物线G 截得的线段长．（2）随着m 取值的变化，判断点C ，D 是否都在直线上并说明理由．（3）若直线被抛物线G 截得的线段长不小于2，结合函数的图象，直接写出m 的取值范围．x【解析】（1）当1m =时，抛物线G 的函数表达式为22y x x =+，直线的函数表达式为y x =，直线被抛物线Gx（2）∵抛物线G ：221(0)y mx mx m m =++-≠与y 轴交于点C ， ∴点C 的坐标为(0,1)C m -，∵2221(1)1y mx mx m m x =++-=+-， ∴抛物线G 的顶点D 的坐标为(1,1)--，对于直线：1(0)y mx m m =+-≠，当0x =时，1y m =-，当1x =-时，(1)11y m m =⨯-+-=-， ∴无论m 取何值，点C ，D 都在直线上．（3）m的取值范围是m ≤m海淀区26．在平面直角坐标系xOy 中，已知抛物线22y x ax b =-+的顶点在 x 轴上，1(,)P x m ，2(,)Q x m （12x x <）是此抛物线上的两点．（1）若1a =，①当m b =时，求1x ，2x 的值；②将抛物线沿y 轴平移，使得它与x 轴的两个交点间的距离为4，试描述出这一变化过程；（2）若存在实数c ，使得11x c ≤-，且27x c ≥+成立，则m 的取值范围是．26．解：抛物线22y x ax b =-+的顶点在x 轴上，24(2)04b a --∴=.2b a ∴=. ………………1分（1）1a = ，1b ∴=.∴抛物线的解析式为221y x x =-+.① 1m b == ，2211x x ∴-+=，解得10x =，22x =. ………………2分 ②依题意，设平移后的抛物线为2(1)y x k =-+.抛物线的对称轴是1x =，平移后与x 轴的两个交点之间的距离是4，∴(3,0)是平移后的抛物线与x 轴的一个交点.2(31)0k ∴-+=，即4k =-.∴变化过程是：将原抛物线向下平移4个单位. ………………4分（2）16m ≥. ………………6分丰台区26．在平面直角坐标系xOy 中，抛物线243y ax ax a =-+的最高点的纵坐标是2．（1）求抛物线的对称轴及抛物线的表达式；（2）将抛物线在1≤x ≤4之间的部分记为图象G 1，将图象G 1沿直线x = 1翻折，翻折后的图象记为G 2，图象G 1和G 2组成图象G ．过(0，b )作与y 轴垂直的直线l ，当直线l 和图象G 只有两个公共点时，将这两个公共点分别记为P 1(x 1，y 1)，P 2(x 2，y 2)，求b 的取值范围和x 1 + x 2的值．)22a -，∴对称轴为x = 2．………………………………………1分 ∵抛物线最高点的纵坐标是2，∴a = -2． ………………………………………2分 ∴抛物线的表达式为2286y x x =-+-. ……………3分（2）由图象可知，2b = 或-6≤b <0.………………6分由图象的对称性可得：x 1+x 2=2． (7)分石景山区26．在平面直角坐标系xOy 中，将抛物线21G y mx =+：（0m ≠）向右平移位长度后得到抛物线2G ，点A 是抛物线2G 的顶点．xy（1）直接写出点A 的坐标；（2）过点0（且平行于x 轴的直线l 与抛物线2G 交于B ，C 两点． ①当=90BAC ∠°时，求抛物线2G 的表达式；②若60120BAC <∠<°°，直接写出m 的取值范围．26．解:（1）()A. ………………………………… 2分（2）①设抛物线2G的表达式为2(y m x =+如图所示，由题意可得AD ==∵=90BAC ∠°，AB AC =， ∴=45ABD ∠︒.∴BD AD ==∴点B的坐标为. ∵点B 在抛物线2G 上，可得3m =-.∴抛物线2G的表达式为23y x =-+，即223y x x =+ ………………… 5分②m <<-. ………………… 7分朝阳区26. 在平面直角坐标系xOy 中，抛物线()2440y ax ax a =--≠与y 轴交于点A ，其对称轴与x 轴交于点B . （1）求点A ，B 的坐标；（2）若方程()244=00ax ax a --≠有两个不相等的实数根，且两根都在1，3之间（包括1，3），结合函数的图象，求a 的取值范围.26.解：（1）44)2(4422---=--=a x a ax ax y ．∴A （0，－4），B （2，0）．……………………………………2分（2）当抛物线经过点（1，0）时，34-=a ．…………………… 4分当抛物线经过点（2，0）时，1-=a ． …………………………6分结合函数图象可知，a 的取值范围为134<≤-a ．……………… 7分燕山区24．如图，在平面直角坐标系中，直线l : y=kx+k (k ≠0)与x 轴,y 轴分别交于A,B 两点，且点B(0,2)，点P 在y 轴正半轴上运动，过点P 作平行于x 轴的直线y=t ．（1）求 k 的值和点A 的坐标；（2）当t=4时，直线y=t 与直线l 交于点M ，反比例函数xny =（n ≠0）的图象经过点M ，求反比例函数的解析式； (3)当t<4时，若直线y=t 与直线l 和（2）反比例函数的图象分别交于点C ，D ，当CD 间距离大于等于2时，求t 的取值范围.24.解：（1）∵直线l :y=kx+k 经过点B(0,2)，∴k=2∴ y=2x+2∴A(-1,0) ……………………….2′（2）当t=4时，将y=4代入y=2x+2得，x=1∴M(1,4)代入xny =得，n=4 ∴xy 4=……………………….2′ （3）当t=2时，B(0,2) 即C(0,2)，而D(2,2)如图，CD=2，当y=t 向下运动但是不超过x 轴时，符合要求∴ t 的取值范围是 0 <t ≤2 ……………………….5′门头沟区26.有一个二次函数满足以下条件：①函数图象与x 轴的交点坐标分别为(1,0)A ，22(,)B x y (点B 在点A 的右侧)； ②对称轴是3x =； ③该函数有最小值是-2.（1）请根据以上信息求出二次函数表达式；（2）将该函数图象2x x ＞的部分图象向下翻折与原图象未翻折的部分组成图象“G ”，平行于x 轴的直线与图象“G ”相交于点33(,)C x y 、44(,)D x y 、55(,)E x y （345x x x <<），结合画出的函数图象求345x x x ++的取值范围.26. （本小题满分7分）（1）解：有上述信息可知该函数图象的顶点坐标为: (3,2)- 设二次函数表达式为：2(3)2y a x =-- ……………1分 ∵该图象过(1,0)A∴20(13)2a =--，解得12a =……………2分 ∴表达式为21(3)22y x =-- （2）图象正确………………………………………………………3分由已知条件可知直线与图形“G ”要有三个交点① 当直线与x 轴重合时，有2个交点,由二次函数的轴对称性可求 346x x += ……………………………………4分 ∴34511x x x ++＞ ……………………………………5分 ②当直线过21(3)22y x =--的图象顶点时，有2个交点，由翻折可以得到翻折后的函数图象为21(3)22y x =--+ ∴令21(3)222x --+=-时，解得3x =±3x =-6分∴3459x x x +++＜综上所述345x x x ++11＜＜…………7分大兴区26. 在平面直角坐标系xOy 中,抛物线22(31)2(0)y x m x m m m =-+++>，与y 轴交于点C ，与x 轴交于点A 1(,0)x ,B 2(,0)x ，且12x x <.（1）求1223-+x x 的值；（2）当m=1223-+x x 时，将此抛物线沿对称轴向上平移n 个单位，使平移后得到的抛物线顶点落在△ABC 的内部（不包括△ABC 的边），求n 的取值范围（直接写出答案即可）．26.（1）解关于x 的一元二次方程，()223120x m x m m -+++=得x =2m +1, x =m ………………………………………………………2分 ∵m ＞0, x 1＜x 2∴x 1=m , x 2=2m+1. …………………………………………………… 3分 2x 1-x 2+3=2m -2m -1+3=2 …………………………………………… 4分（2）符合题意的n 的取值范围是. …………………………………7分平谷区26．在平面直角坐标系xOy 中，抛物线223y x bx =-+-的对称轴为直线x =2．（1）求b 的值；（2）在y 轴上有一动点P （0，m ），过点P 作垂直y 轴的直线交抛物线于点A （x 1，y 1），B （x 2 ，y 2），其中 12x x <．①当213x x -=时，结合函数图象，求出m 的值；②把直线PB 下方的函数图象，沿直线PB 向上翻折，图象的其余部分保持不变，得到一个新的图象W ，新图象W 在0≤x ≤5 时，44y -≤≤，求m 的取值范围．26．解：（1）∵抛物线223y x bx =-+-的对称轴为直线x =2，∴b =2． ································································· 1 （2）①∴抛物线的表达式为243y x x =-+-． ∵A （x 1，y ），B （x 2 ，y ）， ∴直线AB 平行x 轴．∵213x x -=， ∴AB =3． ∵对称轴为x =2， ∴AC =12． ···························································· 2 ∴当12x =时，54y m ==-． ......................... 3 ②当y =m =-4时，0≤x ≤5时，41y -≤≤； (4)当y =m =-2时，0≤x ≤5 时，24y -≤≤； ....... 5 ∴m 的取值范围为42m -≤≤-． .. (6)怀柔区26.在平面直角坐标系xOy 中，抛物线y=nx 2-4nx+4n-1(n ≠0)，与x 轴交于点C ，D(点C 在点D 的左侧)，与y 轴交于点A ． (1)求抛物线顶点M 的坐标；(2)若点A 的坐标为（0，3），AB ∥x 轴，交抛物线于点B ，求点B 的坐标；(3)在(2)的条件下，将抛物线在B ，C 两点之间的部分沿y 轴翻折，翻折后的图象记为G ，若直线m x y +=21与图象G 有一个交点，结合函数的图象，求m 的取值范围．y x–1–2–3–4–512345–1–2–3–4–512345O26.(1)M(2，-1)； ………………………………………………………………………………2分 (2)B(4，3)； …………………………………………………………………………………3分 (3)∵抛物线y=mx 2-4mx+4m-1(m ≠0)与y 轴交于点A （0,3）, ∴4n-1=3.∴n=1. ……………………………………………………………………………………4分 ∴抛物线的表达式为342+-=x x y .由34212++=+x x m x . 由△=0，得: 161-=m ……………………………………………………………………5分∵抛物线342+-=x x y 与x 轴的交点C 的坐标为（1,0），∴点C 关于y 轴的对称点C 1的坐标为（-1,0）.把（-1,0）代入m x y +=21，得：21=m .……………………………………………6分把（-4,3）代入m x y +=21，得：5=m .∴所求m 的取值范围是161-=m 或21＜m ≤ 5. …………………………………………7分延庆区26．在平面直角坐标系xOy 中，抛物线y =ax 2-4ax +3a (a ＞0)与x 轴交于A ，B 两点（A 在B 的左侧）．（1）求抛物线的对称轴及点A ，B 的坐标；（2）点C （t ，3）是抛物线243(0)y ax ax a a =-+>上一点，（点C 在对称轴的右侧），过点C 作x 轴的垂线，垂足为点D ．①当CD AD =时，求此时抛物线的表达式； ②当CD AD >时，求t 的取值范围．26．（1）对称轴：x =2 ……1分A （1，0）或B （3，0） ……1分（2）①如图1，∵AD =CD∴AD =3∴C 点坐标为（4，3） ……3分将C （4，3）代入243y ax ax a =-+∴316163a a a =-+∴a =1∴抛物线的表达式为：243y x x =-+ ……4分 ②34t << ……6分过程略顺义区26．在平面直角坐标系xOy 中，若抛物线2y x bx c =++顶点A 的横坐标是-1，且与y 轴交于点B （0，-1），点P 为抛物线上一点．（1）求抛物线的表达式；（2）若将抛物线2y x bx c =++向下平移4个单位，点P 平移后的对应点为Q ．如果OP =OQ ，求点Q 的坐标．26．解：（1）依题意12-=-b，b =2, 由B （0，-1），得c=-1,∴抛物线的表达式是221=+-y x x ．…………………… 2分4（2）向下平移4个单位得到225=+-y x x ，……………………… 3分 ∵OP =OQ ，∴P 、Q 两点横坐标相同，纵坐标互为相反数．∴2221250+-++-=x x x x ．∴13=-x ，21=x ．………………………………………………… 5分把13=-x ，21=x 分别代入225=+-y x x ．得出Q 1（-3，-2），Q 2（1，-2）．………………………………… 7分统计专题东城区24．随着高铁的建设，春运期间动车组发送旅客量越来越大.相关部门为了进一步了解春运期间动车组发送旅客量的变化情况，针对2014年至2018年春运期间铁路发送旅客量情况进行了调查，具体过程如下.(I)收集、整理数据请将表格补充完整：（II）描述数据为了更直观地显示春运期间动车组发送旅客量占比的变化趋势，需要用___________(填“折线图”或“扇形图”)进行描述；（III）分析数据、做出推测预计2019年春运期间动车组发送旅客量占比约为___________，你的预估理由是_________________________________________ .24. 解：(I)：56.8%；----------------------1分(II)折线图；----------------------3分(III)答案不唯一，预估的理由须支撑预估的数据，参考数据61%左右.--------5分西城区23．某同学所在年级的500名学生参加“志愿北京”活动，现有以下5个志愿服务项目：A．纪念馆志愿讲解员．B．书香社区图书整理．C．学编中国结及义卖．D．家风讲解员．E．校内志愿服务．要求：每位学生都从中选择一个项目参加，为了了解同学们选择这个5个项目的情况，该同学随机对年级中的40名同学选择的志愿服务项目进行了调查，过程如下：收集数据：设计调查问卷，收集到如下数据（志愿服务项目的编号，用字母代号表示）．B，E，B，A，E，C，C，C，B，B，A，C，E，D，B，A，B，E，C，A，D，D，B，B，C，C，A，A，E，B，C，B，D，C，A，C，C，A，C，E，整理、描述诗句：划记、整理、描述样本数据，绘制统计图如下，请补全统计表和统计图．选择各志愿服务项目的人数统计表分析数据、推断结论：a：抽样的40个样本数据（志愿服务项目的编号）的众数是__________．（填A E-的字母代号）b：请你任选A E-中的两个志愿服务项目，根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目．【解析】B项有10人，D项有4人．选择各志愿服务项目的人数比例统计图中，B占25%，D占10%．分析数据、推断结论：a．抽样的40个样本数据（志愿服务项目的编号）的众数是C．b：根据学生选择情况答案分别如下（写出任意两个即可）．⨯=（人）．A：50020%100⨯=（人）．B：50025%125C：50030%150⨯=（人）．⨯=（人）．D：50010%50⨯=（人）．E：50015%75海淀区24．某校九年级八个班共有280名学生，男女生人数大致相同，调查小组为调查学生的体质健康水平，开展了一次调查研究，请将下面的过程补全.收集数据调查小组计划选取40名学生的体质健康测试成绩作为样本，下面的取样方法中，合理的是___________（填字母）；A．抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本B．抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本C．从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本整理、描述数据抽样方法确定后，调查小组获得了40名学生的体质健康测试成绩如下：整理数据，如下表所示：分析数据、得出结论调查小组将统计后的数据与去年同期九年级的学生的体质健康测试成绩（直方图）进行了对比，2017年九年级部分学生体质健康成绩直方图你能从中得到的结论是_____________，你的理由是________________________________. 体育老师计划根据2018年的统计数据安排75分以下的同学参加体质加强训练项目，则全年级约有________名同学参加此项目.24．C ………………1分≤<x8085x≤<85908 10………………2分（2）去年的体质健康测试成绩比今年好．（答案不唯一，合理即可） (3)分去年较今年低分更少，高分更多，平均分更大．（答案不唯一，合理即可）………………4分（3）70．………………6分丰台区24．第二十四届冬季奥林匹克运动会将于2022年2月4日至2月20日在北京举行，北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市．某区举办了一次冬奥知识网上答题竞赛，甲、乙两校各有400名学生参加活动，为了解这两所学校的成绩情况，进行了抽样调查，过程如下，请补充完整．【收集数据】从甲、乙两校各随机抽取20名学生，在这次竞赛中他们的成绩如下：【整理、描述数据】按如下分数段整理、描述这两组样本数据：（说明：优秀成绩为80＜x≤100，良好成绩为50＜x≤80，合格成绩为30≤x≤50．）【分析数据】两组样本数据的平均分、中位数、众数如下表所示：其中a =__________.【得出结论】（1）小明同学说：“这次竞赛我得了70分，在我们学校排名属中游略偏上！”由表中数据可知小明是________校的学生；（填“甲”或“乙”）（2）张老师从乙校随机抽取一名学生的竞赛成绩，试估计这名学生的竞赛成绩为优秀的概率为________；（3）根据以上数据推断一所你认为竞赛成绩较好的学校，并说明理由．（至少从两个不同的角度说明推断的合理性）24．解：a=80；………………………1分（1）甲；………………………2分（2）110；………………………3分（3）答案不唯一，理由需支持推断结论.如：乙校竞赛成绩较好，因为乙校的平均分高于甲校的平均分说明平均水平高，乙校的中位数75高于甲校的中位数65，说明乙校分数不低于70分的学生比甲校多. ………………………5分石景山区24．某校诗词知识竞赛培训活动中，在相同条件下对甲、乙两名学生进行了10次测验，他们的10次成绩如下（单位：分）：整理、分析过程如下，请补充完整．（1）按如下分数段整理、描述这两组数据：（2）两组数据的极差、平均数、中位数、众数、方差如下表所示：24．解:（1）0，1，4，5，0，0 ………………1分（2）14，84.5，81 ………………4分（3）甲，理由：两人的平均数相同且甲的方差小于乙,说明甲成绩稳定;两人的平均数相同且甲的极差小于乙,说明甲成绩变化范围小.（写出其中一条即可）或：乙，理由：在90≤x≤100的分数段中，乙的次数大于甲.………………6分（答案不唯一，理由须支撑推断结论）朝阳区24. 水果基地为了选出适应市场需求的小西红柿秧苗，在条件基本相同的情况下，把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性，进行了抽样调查，过程如下，请补充完整．收集数据从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数：甲26 32 40 51 44 74 44 63 73 74 81 546241 33 54 43 34 51 63 64 73 64 54 33乙27 35 46 55 48 36 47 68 82 48 57 667527 36 57 57 66 58 61 71 38 47 46 71整理、描述数据按如下分组整理、描述这两组样本数据（说明：45个以下为产量不合格，45个及以上为产量合格，其中45~65个为产量良好，65~85个为产量优秀）分析数据两组样本数据的平均数、众数和方差如下表所示：得出结论a．估计乙大棚产量优秀的秧苗数为株；b．可以推断出大棚的小西红柿秧苗品种更适应市场需求，理由为．（至少从两个不同的角度说明推断的合理性）24. 解：整理、描述数据按如下分组整理、描述这两组样本数据分得出结论a．估计乙大棚产量优秀的秧苗数为84 株；…………………………3分b．答案不唯一，理由须支撑推断的合理性.………………………………5分燕山区22．豆豆妈妈用小米运动手环记录每天的运动情况，下面是她6天的（1）4月5日,4月6日，豆豆妈妈没来得及作记录，只有手机图片，请你根据图片数据，帮她补全表格．(2)豆豆利用自己学习的统计知识，把妈妈步行距离与燃烧脂肪情况用如下统计图表示出来，请你根据图中提供的信息写出结论：．（写一条即可）步行距离燃烧脂肪4月1日－6日妈妈步行距离与燃烧脂肪情况统计图（3）豆豆还帮妈妈分析出步行距离和卡路里消耗数近似成正比例关系，豆豆妈妈想使自己的卡路里消耗数达到250千卡，预估她一天步行距离为__________公里．（直接写出结果，精确到个位）22. （1）填数据 ……………………….2′(2)写出一条结论: ……………………….4′（3）预估她一天步行约为__________公里．（直接写出结果，精确到个位）门头沟区24.地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识，提高学生生态坏境保护意识，举办了“我参与，我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析，成绩如下：初一：76 88 93 65 78 94 89 68 95 5089 88 89 89 77 94 87 88 92 91初二：74 97 96 89 98 74 69 76 72 7899 72 97 76 99 74 99 73 98 74（1）根据上表中的数据，将下列表格补充完整；整理、描述数据：908090608060格）分析数据：（2）得出结论：你认为哪个年级掌握生态环保知识水平较好并说明理由.（至少从两个不同的角度说明推断的合理性）.24.（1）补全表格正确：初一：8 …………………………………………1分众数：89 …………………………………………2分中位数：77 …………………………………………3分（2）可以从给出的三个统计量去判断如果利用其它标准推断要有数据说明合理才能得分………………5分大兴区24.甲乙两组各有10名学生，进行电脑汉字输入速度比赛，现将他们的成绩进行统计，过程如下：收集数据各组参赛学生每分钟输入汉字个数统计如下表：分析数据两组数据的众数、中位数、平均数、方差如下表所示：得出结论(1)若每分钟输入汉字个数136及以上为优秀，则从优秀人数的角度评价甲、乙两组哪个成绩更好一些？(2)请你根据所学的统计知识，从不同角度评价甲、乙两组学生的比赛成绩（至少从两个角度进行评价）.24. （1）乙组成绩更好一些 (2)分（2）答案不唯一，评价需支撑推断结论…………………………………………………6分（说明：评价中只要说对2条即可，每条给2分，共4分）平谷区23．为了解某区初二年级数学学科期末质量监控情况，进行了抽样调查，过程如下，请将有关问题补充完整.收集数据随机抽取甲乙两所学校的20名学生的数学成绩进行分析：甲91 89 77 86 71 31 97 93 72 9181 92 85 85 95 88 88 90 44 91 乙84 93 66 69 76 87 77 82 85 8890 88 67 88 91 96 68 97 59 88 整理、描述数据分析数据两组数据的平均数、中位数、众数、方差如下表：的值是．得出结论a若甲学校有400名初二学生，估计这次考试成绩80分以上人数为 .b可以推断出学校学生的数学水平较高，理由为 . （至少从两个不同的角度说明推断的合理性） (2)分析数据经统计，表格中m的值是88 ． (3)得出结论a若甲学校有400名初二学生，估计这次考试成绩80分以上人数为300 . (4)b 答案不唯一，理由须支撑推断结论. (7)怀柔区24.某校初三体育考试选择项目中，选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况，进行了抽样调查，过程如下，请补充完整.收集数据从选择篮球和排球的学生中各随机抽取16人，进行了体育测试，测试成绩（十分制）如下：整理、描述数据按如下分数段整理、描述这两组样本数据：（说明：成绩8.5分及以上为优秀，6分及以上为合格，6分以下为不合格.）分析数据两组样本数据的平均数、中位数、众数如下表所示：得出结论(1)如果全校有160人选择篮球项目，达到优秀的人数约为人；(2)初二年级的小明和小军看到上面数据后，小明说：排球项目整体水平较高.小军说：篮球。

北京市各区2018届中考数学一模试卷精选汇编统计专题(附答案)

统计专题东城区24．随着高铁的建设，春运期间动车组发送旅客量越来越大.相关部门为了进一步了解春运期间动车组发送旅客量的变化情况，针对2014年至2018年春运期间铁路发送旅客量情况进行了调查，具体过程如下.(I)收集、整理数据请将表格补充完整：（II）描述数据为了更直观地显示春运期间动车组发送旅客量占比的变化趋势，需要用 ___________(填“折线图”或“扇形图”)进行描述；（III）分析数据、做出推测预计2019年春运期间动车组发送旅客量占比约为___________，你的预估理由是_________________________________________ .24. 解：(I)：56.8%；----------------------1分(II)折线图； ----------------------3分(III)答案不唯一，预估的理由须支撑预估的数据，参考数据61%左右.--------5分西城区23．某同学所在年级的500名学生参加“志愿北京”活动，现有以下5个志愿服务项目：A．纪念馆志愿讲解员．B．书香社区图书整理．C．学编中国结及义卖．D．家风讲解员．E．校内志愿服务．要求：每位学生都从中选择一个项目参加，为了了解同学们选择这个5个项目的情况，该同学随机对年级中的40名同学选择的志愿服务项目进行了调查，过程如下：收集数据：设计调查问卷，收集到如下数据（志愿服务项目的编号，用字母代号表示）．B，E，B，A，E，C，C，C，B，B，A，C，E，D，B，A，B，E，C，A，D，D，B，B，C，C，A，A，E，B，C，B，D，C，A，C，C，A，C，E，整理、描述诗句：划记、整理、描述样本数据，绘制统计图如下，请补全统计表和统计图．选择各志愿服务项目的人数统计表分析数据、推断结论：a：抽样的40个样本数据（志愿服务项目的编号）的众数是__________．（填A E-的字母代号）b：请你任选A E-中的两个志愿服务项目，根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目．【解析】B项有10人，D项有4人．选择各志愿服务项目的人数比例统计图中，B占25%，D占10%．分析数据、推断结论：a．抽样的40个样本数据（志愿服务项目的编号）的众数是C．b：根据学生选择情况答案分别如下（写出任意两个即可）．⨯=（人）．A：50020%100⨯=（人）．B：50025%125⨯=（人）．C：50030%150⨯=（人）．D：50010%50⨯=（人）．E：50015%75海淀区24．某校九年级八个班共有280名学生，男女生人数大致相同，调查小组为调查学生的体质健康水平，开展了一次调查研究，请将下面的过程补全. 收集数据调查小组计划选取40名学生的体质健康测试成绩作为样本，下面的取样方法中，合理的是___________（填字母）；A ．抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本B ．抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本C ．从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本整理、描述数据抽样方法确定后，调查小组获得了40名学生的体质健康测试成绩如下：整理数据，如下表所示：分析数据、得出结论调查小组将统计后的数据与去年同期九年级的学生的体质健康测试成绩（直方图）进行了对比，分频数2017年九年级部分学生体质健康成绩直方图0864210095908580757065605550你能从中得到的结论是_____________，你的理由是________________________________.体育老师计划根据2018年的统计数据安排75分以下的同学参加体质加强训练项目，则全年级约有________名同学参加此项目.24．………………1分………………2分（2）去年的体质健康测试成绩比今年好．（答案不唯一，合理即可） ………………3分去年较今年低分更少，高分更多，平均分更大．（答案不唯一，合理即可）………………4分（3）70． ………………6分丰台区24．第二十四届冬季奥林匹克运动会将于2022年2月4日至2月20日在北京举行，北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市．某区举办了一次冬奥知识网上答题竞赛，甲、乙两校各有400名学生参加活动，为了解这两所学校的成绩情况，进行了抽样调查，过程如下，请补充完整．【收集数据】从甲、乙两校各随机抽取20名学生，在这次竞赛中他们的成绩如下：【整理、描述数据】按如下分数段整理、描述这两组样本数据：（说明：优秀成绩为80＜x≤100，良好成绩为50＜x≤80，合格成绩为30≤x≤50．）【分析数据】两组样本数据的平均分、中位数、众数如下表所示：其中a =__________.【得出结论】（1）小明同学说：“这次竞赛我得了70分，在我们学校排名属中游略偏上！”由表中数据可知小明是________校的学生；（填“甲”或“乙”）（2）张老师从乙校随机抽取一名学生的竞赛成绩，试估计这名学生的竞赛成绩为优秀的概率为________；（3）根据以上数据推断一所你认为竞赛成绩较好的学校，并说明理由．（至少从两个不同的角度说明推断的合理性）24．解：a=80；………………………1分（1）甲；………………………2分（2）110；………………………3分（3）答案不唯一，理由需支持推断结论.如：乙校竞赛成绩较好，因为乙校的平均分高于甲校的平均分说明平均水平高，乙校的中位数75高于甲校的中位数65，说明乙校分数不低于70分的学生比甲校多. ………………………5分石景山区24．某校诗词知识竞赛培训活动中，在相同条件下对甲、乙两名学生进行了10次测验，他们的10次成绩如下（单位：分）：整理、分析过程如下，请补充完整．（1）按如下分数段整理、描述这两组数据：（2）两组数据的极差、平均数、中位数、众数、方差如下表所示：24．解:（1） 0，1，4，5，0，0 ………………1分（2） 14，84.5，81 ………………4分（3）甲，理由：两人的平均数相同且甲的方差小于乙,说明甲成绩稳定;两人的平均数相同且甲的极差小于乙,说明甲成绩变化范围小.（写出其中一条即可）或：乙，理由：在90≤x≤100的分数段中，乙的次数大于甲.………………6分（答案不唯一，理由须支撑推断结论）朝阳区24. 水果基地为了选出适应市场需求的小西红柿秧苗，在条件基本相同的情况下，把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性，进行了抽样调查，过程如下，请补充完整．收集数据从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数：甲 26 32 40 51 44 74 44 63 73 74 81 54 6241 33 54 43 34 51 63 64 73 64 54 33 乙 27 35 46 55 48 36 47 68 82 48 57 66 7527 36 57 57 66 58 61 71 38 47 46 71整理、描述数据按如下分组整理、描述这两组样本数据（说明：45个以下为产量不合格，45个及以上为产量合格，其中45~65个为产量良好，65~85个为产量优秀）分析数据两组样本数据的平均数、众数和方差如下表所示：得出结论 a ．估计乙大棚产量优秀的秧苗数为株；b ．可以推断出大棚的小西红柿秧苗品种更适应市场需求，理由为．（至少从两个不同的角度说明推断的合理性）24. 解：整理、描述数据按如下分组整理、描述这两组样本数据2分得出结论 a ．估计乙大棚产量优秀的秧苗数为 84 株； …………………………3分b ．答案不唯一，理由须支撑推断的合理性. ………………………………5分燕山区：（1）4月5日,4月6日，豆豆妈妈没来得及作记录，只有手机图片，请你根据图片数据，帮她补全表格． (2)豆豆利用自己学习的统计知识，把妈妈步行距离与燃烧脂肪情况用如下统计图表示出来，请你根据图中提供的信息写出结论：．（写一条即可）步行距离燃烧脂肪4月1日－6日妈妈步行距离与燃烧脂肪情况统计图（3）豆豆还帮妈妈分析出步行距离和卡路里消耗数近似成正比例关系，豆豆妈妈想使自己的卡路里消耗数达到250千卡，预估她一天步行距离为__________公里．（直接写出结果，精确到个位）22. （1）填数据……………………….2′(2)写出一条结论:……………………….4′（3）预估她一天步行约为__________公里．（直接写出结果，精确到个位）门头沟区24.地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识，提高学生生态坏境保护意识，举办了“我参与，我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析，成绩如下：初一： 76 88 93 65 78 94 89 68 95 5089 88 89 89 77 94 87 88 92 91初二： 74 97 96 89 98 74 69 76 72 7899 72 97 76 99 74 99 73 98 74（1）根据上表中的数据，将下列表格补充完整；整理、描述数据：（说明：成绩90分及以上为优秀，80~90分为良好，60~80分为合格，60分以下为不合格）（2）得出结论：你认为哪个年级掌握生态环保知识水平较好并说明理由.（至少从两个不同的角度说明推断的合理性）.24.（1）补全表格正确：初一： 8 …………………………………………1分众数：89 …………………………………………2分中位数：77 …………………………………………3分（2）可以从给出的三个统计量去判断如果利用其它标准推断要有数据说明合理才能得分………………5分大兴区24.甲乙两组各有10名学生，进行电脑汉字输入速度比赛，现将他们的成绩进行统计，过程如下：收集数据各组参赛学生每分钟输入汉字个数统计如下表：分析数据两组数据的众数、中位数、平均数、方差如下表所示：得出结论(1)若每分钟输入汉字个数136及以上为优秀，则从优秀人数的角度评价甲、乙两组哪个成绩更好一些？(2)请你根据所学的统计知识，从不同角度评价甲、乙两组学生的比赛成绩（至少从两个角度进行评价）. 24. （1）乙组成绩更好一些…………………………………………………………………2分（2）答案不唯一，评价需支撑推断结论…………………………………………………6分（说明：评价中只要说对2条即可，每条给2分，共4分）平谷区23．为了解某区初二年级数学学科期末质量监控情况，进行了抽样调查，过程如下，请将有关问题补充完整. 收集数据随机抽取甲乙两所学校的20名学生的数学成绩进行分析：甲91 89 77 86 71 31 97 93 72 9181 92 85 85 95 88 88 90 44 91乙84 93 66 69 76 87 77 82 85 8890 88 67 88 91 96 68 97 59 88整理、描述数据分析数据两组数据的平均数、中位数、众数、方差如下表：统计量平均数中位数众数方差学校甲81.85 88 91 268.43乙81.95 86 m 115.25经统计，表格中m的值是．得出结论a若甲学校有400名初二学生，估计这次考试成绩80分以上人数为 .b可以推断出学校学生的数学水平较高，理由为 . （至少从两个不同的角度说明推断的合理性）分析数据经统计，表格中m的值是 88 ． (3)得出结论a若甲学校有400名初二学生，估计这次考试成绩80分以上人数为 300 . (4)b 答案不唯一，理由须支撑推断结论. (7)怀柔区24.某校初三体育考试选择项目中，选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况，进行了抽样调查，过程如下，请补充完整.收集数据从选择篮球和排球的学生中各随机抽取16人，进行了体育测试，测试成绩（十分制）如下：整理、描述数据按如下分数段整理、描述这两组样本数据：（说明：成绩8.5分及以上为优秀，6分及以上为合格，6分以下为不合格.）分析数据两组样本数据的平均数、中位数、众数如下表所示：得出结论(1)如果全校有160人选择篮球项目，达到优秀的人数约为人；(2)初二年级的小明和小军看到上面数据后，小明说：排球项目整体水平较高.小军说：篮球项目整体水平较高.你同意的看法，理由为.（至少从两个不同的角度说明推断的合理性）24.补全表格：成绩x…………………………………………………………………………………………………2分(1)130；…………………………………………………………………………………………4分(2)答案不唯一，理由需支持判断结论. ………………………………………………………6分延庆区24．从北京市环保局证实，为满足2022年冬奥会对环境质量的要求，北京延庆正在对其周边的环境污染进行综合治理，率先在部分村镇进行“煤改电”改造．在治理的过程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测．过程如下，请补充完整.请将以上两个表格补充完整；得出结论：可以推断出______镇这一年中环境状况比较好，理由为_____________.（至少从两个不同的角度说明推断的合理性）24．（1）1，9，2．……1分（2） 82.5，90．……3分（3）千家店镇……4分理由：千家店镇污染指数平均数为80，永宁镇污染指数平均数为81.3，所以千家店镇污染指数平均数较低，空气质量较好；千家店镇空气质量为优的天数是4天，永宁镇空气质量为优的天数是1天，所以千家店镇空气质量为优的天数多，空气质量较好．…6分顺义区23．中华文明，源远流长，中华汉字，寓意深广，为了传承优秀传统文化，某校九年级组织600名学生参加了一次“汉字听写”大赛．赛后发现所有参赛学生的成绩均不低于60分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩作为样本，成绩如下：频数成绩x /分12108640100908070602141690，92，81，82，78，95，86，88，72，66， 62，68，89，86，93，97，100，73，76，80， 77，81，86，89，82，85，71，68，74，98， 90，97，100，84，87，73，65，92，96，60.对上述成绩（成绩x 取整数，总分100分）进行了整理，得到下列不完整的统计图表：请根据所给信息，解答下列问题：（1）a = ，b = ， c = ，d = ；（2）请补全频数分布直方图；（3）若成绩在90分以上（包括90分）的为“优”等，请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人？23．解：（1）a = 14 ，b = 0.35 ， c = 12 ，d = 0.3 ；………… 2分（2）补全频数分布直方图如下：…………………… 4分（3）估计参加这次比赛的600名学生中成绩“优”等的约有180人．……… 5分161426070809010004681012成绩x /分频数。

北京市各区2018届中考一模数学试卷精选汇编：几何证明(含答案)

几何证明东城区19. 如图，在△ABC中，∠BAC=90°，AD⊥BC于点D. BF平分∠ABC交AD于点E，交AC于点F. 求证：AE=AF.19.证明：∵∠BAC=90°，∴∠FBA+∠AFB=90°.-------------------1分∵AD⊥BC，∴∠DBE+∠DEB=90°．---------------- 2分∵BE平分∠ABC,∴∠DBE=∠FBA. -------------------3分∴∠AFB=∠DEB.-------------------4分∵∠DEB=∠FEA，∴∠AFB=∠FEA.∴AE=AF.-------------------5分西城区19．如图，AD平分BAC<．∠，BD AD⊥于点D，AB的中点为E，AE AC∥．（1）求证：DE AC（2）点F在线段AC上运动，当AF AE△全等的三角形是__________．=时，图中与ADFECBA【解析】（1）证明：∵AD 平分BAC ∠， ∴12∠=∠， ∵BD AD ⊥于点D ， ∴90ADB ∠=︒， ∴ABD △为直角三角形． ∵AB 的中点为E ， ∴2AB AE =，2ABDE =， ∴DE AE =， ∴13∠=∠， ∴23∠=∠， ∴DE AC ∥．（2）ADE △．321ECBA海淀区19．如图，△ABC 中，90ACB ∠=︒，D 为AB 的中点，连接CD ，过点B 作CD 的平行线EF ，求证：BC 平分ABF ∠．FE DCB A19. 证明：∵90ACB ∠=︒，D 为AB 的中点， ∴12CD AB BD ==. ∴ABC DCB ∠=∠. …………… ∵DC EF ∥，∴CBF DCB ∠=∠.∴CBF ABC ∠=∠. ∴BC 平分ABF ∠.丰台区19．如图，在△ABC 中，AB = AC ，D 是BC 边上的中点，DE ⊥AB 于点E ，DF ⊥AC 于点F ．求证：DE = DF ．F E CBA19．证明：连接AD .∵AB ＝BC ，D 是BC 边上的中点，∴∠BAD =∠CAD . ………………………3分 ∵DE ⊥AB 于点E ，DF ⊥AC 于点F ，∴DE ＝DF ． ………………………5分（其他证法相应给分）石景山区19．问题:将菱形的面积五等分．小红发现只要将菱形周长五等分，再将各分点与菱形的对角线交点连接即可解决问题．如图，点O 是菱形ABCD 的对角线交点，5AB =，下面是小红将菱形ABCD 面积五等分的操作与证明思路，请补充完整.O H GFE DCB A（1）在AB 边上取点E ，使4AE =，连接OA ，OE ；（2）在BC 边上取点F ，使BF = ，连接OF ；（3）在CD 边上取点G ，使CG = ，连接OG ；（4）在DA 边上取点H ，使D H = ，连接OH ．由于AE = ＋ = ＋ = ＋ = . 可证S △AOE ==EOFB FOGC GOHD S S S ==四边形四边形四边形S △HOA .19．解：3，2，1； ………………2分ABCEFEB 、BF ；FC 、CG ；GD 、DH ；HA. ………………4分朝阳区19. 如图，在△ACB 中，AC =BC ，AD 为△ACB 的高线，CE 为△ACB 的中线.求证：∠DAB =∠ACE.19. 证明：∵AC ＝BC ，CE 为△ACB 的中线，∴∠CAB ＝∠B ，CE ⊥AB . ……………………………………………2分 ∴∠CAB ＋∠ACE ＝90°. ………………………………………………3分 ∵AD 为△ACB 的高线， ∴∠D ＝90°.∴∠DAB ＋∠B ＝90°. ……………………………………………………4分 ∴∠DAB ＝∠ACE . ………………………………………………………5分燕山区19．文艺复兴时期，意大利艺术大师达．芬奇研究过用圆弧围成的部分图形的面积问题。

北京市各区2018届中考数学一模试卷精选汇编解不等式组专题

解不等式组专题东城区18．解不等式组4+6,23x x x x ⎧⎪+⎨⎪⎩＞，并写出它的所有整数解. 18. 解：4+6,23x x x x ⎧⎪⎨+⎪⎩①②＞≥，由①得，-x ＞2，------------------1分由②得，1x ≤， ------------------2分∴不等式组的解集为-1x 2＜≤.所有整数解为-1, 0, 1. ---------------------5分西城区18．解不等式组3(2)4112x x x ++⎧⎪⎨-<⎪⎩≥，并求该不等式组的非负整数解．【解析】解①得，364x x ++≥，22x -≥，1x -≥，解②得，12x -<，3x <，∴原不等式解集为13x -<≤，∴原不等式的非负整数解为0，，2．海淀区18．解不等式组：()5331,263.2x x x x +>-⎧⎪⎨-<-⎪⎩ 18.解：() 5331, 263. 2x x x x +>-⎧⎪⎨-<-⎪⎩①② 解不等式①，得3x >-. …2分解不等式②，得2x <. ………4分所以原不等式组的解集为32x -<<. ………5分丰台区18．解不等式组：341,51 2.2x x x x ≥-⎧⎪⎨->-⎪⎩ 18．解：解不等式①，得1x ≤， ……………………2分解不等式②，得1x >-. ……………………4分∴原不等式组的解集是11x -<≤．………5分石景山区18．解不等式组：3(1)45622x x x x +>++<⎧⎪⎨⎪⎩，． 18．解：原不等式组为3(1)45,62.2x x x x +>++<⎧⎪⎨⎪⎩ 解不等式①，得2x <-． ………………2分解不等式②，得2x <． ………………4分 ∴原不等式组的解集为<2x -． ………………5分朝阳区18. 解不等式组：⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x18. 解：原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式①，得 5<x . ………………………………………2分解不等式②，得 21>x .………………………………………………4分① ②∴ 原不等式组的解集为521<<x . …………………………………5分燕山区18．解不等式组：⎩⎪⎨⎪⎧x －32<1，2（x ＋1）≥x－1.18．解：由（1）得，x-3<2X<5 ……………………….2′（2）得 2x+2≥x-1x ≥-3 ……………………….4′所以不等式组的解是-3≤x＜5……………………….5′门头沟区18. 解不等式组：1031+1.xx x ⎧-<⎪⎨⎪-⎩，≤3(）18．（本小题满分5分）解不等式①得，x ＜3， …………………………………………2分解不等式②得，x ≥﹣2， ………………………………4分所以，不等式组的解集是﹣2≤x ＜3． ………………5分大兴区17.解不等式组：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2并写出它的所有整数解.17. 解：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 由①，得21-≥x . ………………………………………………………1分由②，得2<x . …………………………………………………………2分①②∴原不等式组的解集为221<≤-x . ………………………………………4分它的所有整数解为0，1. …………………………………………………5分平谷区18．解不等式组3(1)45,513x x x x -≥-⎧⎪-⎨->⎪⎩，并写出它的所有整数解．．．． 18．解：3(1)455 3 1x x x x -≥-⎧⎪⎨-->⎪⎩①② 解不等式①，得 x ≤2． ······················· 1 解不等式②，得 x ＞-1． ······················· 3 ∴原不等式组的解集为12x -<≤． ·················· 4 ∴适合原不等式组的整数解为0,1,2． ················· 5 怀柔区18.解不等式组:()⎪⎩⎪⎨⎧<+-<-.1213,213x x x x 18.解：由①得：3x < . ………………………………………………………………………2分由②得：9x >- …………………………………………………………………………4分原不等式组的解集为93x -<< ………………………………………………………5分延庆区18．解不等式组：523(2)53.2x x x x -<+⎧⎪⎨+≤⎪⎩，并写出它的所有整数解． 18．解：由①得，x <4． ……1分由②得，x ≥1 ． ……3分∴ 原不等式组的解集为1≤x <4． ……4分∴ 原不等式组的所有整数解为1，2，3． ……5分顺义区18．解不等式组：()7+1,2315 1.x x x x +⎧≥-⎪⎨⎪+<-⎩18．解不等式组：()7+12315x x x x +⎧≥-⎪⎨⎪+<-⎩解：解不等式①得 x ≥3- ……………………………………………………………2分解不等式②得 2x > ………………………………………………………………4分不等式组的解集是 2x > …………………………………………………………5分。