数字电子技术基础简明教程第三版课后第3章习题解答
数字电子技术基本第三版第三章答案解析

章组合逻辑电路第一节重点与难点一、重点:1.组合电路的基本概念组合电路的信号特点、电路结构特点以及逻辑功能特点。
2.组合电路的分析与设计组合电路分析是根据已知逻辑图说明电路实现的逻辑功能。
组合电路设计是根据给定设计要求及选用的器件进行设计,画出逻辑图。
如果选用小规模集成电路SSI,设计方法比较规范且容易理解,用SSI设计是读者应掌握的最基本设计方法。
由于设计电路由门电路组成,所以使用门的数量较多,集成度低。
若用中规模集成电路MSI进行设计,没有固定的规则,方法较灵活。
无论是用SSI或MSI设计电路,关键是将实际的设计要求转换为一个逻辑问题, 的要求即将文字描述变成一个逻辑函数表达式。
3.常用中规模集成电路的应用常用中规模集成电路有加法器、比较器、编码器、译码器、数据选择器和数据分配器等,重要的是理解外部引脚功能,能在电路设计时灵活应用。
4.竞争冒险现象竞争冒险现象的产生原因、判断是否存在竞争冒险现象以及如何消除。
二、难点:1.组合电路设计无论是用SSI还是用MSI设计电路,首先碰到的是如何将设计要求转换为逻辑问题,的真值表,这一步既是重点又是难点。
总结解决这一难点的方法如下:(1)分析设计问题的因果关系,分别确定输入变量、输出变量的个数及其名称。
(2)定义逻辑变量0、1信号的含义。
无论输入变量、输出变量均有两个状态状态代表的含义由设计者自己定义。
(3)再根据设计问题的因果关系以及变量定义,列出真值表。
2.常用组合电路模块的灵活应用同样的设计要求,用MSI设计完成后,所得的逻辑电路不仅与所选芯片有关,而且还与设计者对芯片的理解及灵活应用能力有关。
读者可在下面的例题和习题中体会。
3.硬件描述语言VHDL的应用VHDL的应用非常灵活,同一个电路问题可以有不同的描述方法,初学者可以先仔细阅读已有的程序实例,再自行设计。
三、考核题型与考核重点1.概念与简答题型1为填空、判断和选择;题型2为叙述基本概念与特点。
数字电子技术基础第三版课后习题解答与第章

【题3-2】 解:),=(A田B) C=A⑥B+C}、=AB+(AB)C=AB+(AB+AB)C=AB+ABC+ABC=AB+BC+AC)=A B CY,=AB+(A B)C=AB+BC+AC两个电路功能相同,均为全加器。
14
(2) CDAB 00 01 11o0[ X0111 1 1 X10 1 1
A₃B₃…A₀B₀ 91A₃B₃…A₀B₀A<B.A>R低位 A=B74LS85Fg FxBF,A>B
A₂B₇…A₄B₄A=B74LS85FAn FxnF
【题3-9】 解:连线图如图3-26所示。
图3 - 26
27
【题3-10】 解:A=A₃A₂A₁A₀ 8421BCD 码 B=B₃B₂B₁B₀ 余3 BCD 码C=C₃C₂C₁C₀ 2421BCD 码 D=D₃D₂D₁D₀ 余 3 循环码(1)卡诺图如图3 - 27所示。B₃=A₃+A₂A₁+A₂A₀=A₂A₂A₁A₂A₀
2
A
B
A
Y'
2
0
0
0
1
0
0
1
1
0
0
1
0
0
0
1
1
1
0
1
)
3-2 解:(1)X=AB;Y=AB+AB=AB+AB;Z=AB。真值表如表3-10所示。表3-10
(2)实现1 位数值比较功能。
3
Y₀=X,④X 。 Y₀=Y₁X₀=X₂X₇X。若令 X₂=B₂ 、X₁=B₁ 、λ₀=B, 则当 K=1 时电路可正确地实现3位二进制码到3位循环码的转换,即有 Y₂=G₂ 、Y,=G₁ 、Y₀=G₀ 。 若 令X₂=G₂ 、X,=G₁、X₀=G₀, 则当 K=0 时,通过比较可明显看出,只要去掉一个反相器便可实现3位循环码到3位二进制码的转换,即有 Y₂=B₂ 、Y₁=B₁ 、Y₀=B₀。
数字电子技术基础简明教程(第三版)作业第三章作业

文档收集于互联网,已重新整理排版.word 版本可编辑.欢迎下载支持.【题3.5】分别用与非门设计能够实现下列功能的组合电路。
(1) 四变量表决电路——输出与多数变量的状态一致。
解:输入信号用 A 、B 、C 、D 表示,输出信号用Y 表示,并且用卡诺图表示有关逻辑关系。
00 01 10 11 1Y 1=ABC+ABD+ACD+BCD=(2) 四变量不一致电路--------四个变量状态不相同时输出为1,相同时输出为0。
图2Y 2=AD+AB+BC+CD=A D A B C C 实现(1)(2)的电路图如下图所示【题3.8】 设计一个组合电路,其输入是四位二进制数D=D 3D 2D 1D 0 ,要求能判断下列三种情况:(1) D 中没有1. (2) D 中有两个1. (3) D 中有奇数个1.第三章作业解:表达式(1)Y1=D3 D2 D1 D0=D3+D2 +D1 +D0(2)Y2如下图a所示。
(3)Y3如下图b所示。
Y2=D3 D2 D1 D0+D3 D2 D1 D0+D3 D2 D1 D0+D3 D2 D1 D0+D3 D2 D1 D0+D3 D2 D1 D0+D3 D2 D1 D0+ D3 D2 D1 D0=(D 3+D2 )( D1+D0)+( D3+D1)( D2+D0)Y2=D3+D2 +D1+0逻辑图如下图所示【题3.10】用与非门分别设计能实现下列代码转换的组合电路:(1)将8421 BCD码转换为余3码。
(2)将8421 BCD码转换为2421码。
(3)将8421 BCD码转换为余3循环码。
(4)将余3码转换成为余3循环码。
解:A=A3 A2 A1 A08421 BCD码B=B3 B2 B1 B0余3BCD码C=C3 C2 C1 C02421 BCD码D=D3 D2 D1 D0余3循环码(1)卡诺图如下图所示B3=A3+A2 A1+A2 A0=A3 A2 A1A2 A0B2=A2 A0+A2 A1+A2 A1 A0=A2 A0 A2 A1 A2 A1 A0B1=A1 A0+A1 A0=A1 A0 A1A0B0= A0(2)卡诺图如下图所示C3=A3C2 =A3+A2 =A3 A2C1=A3+A1 =A3 A1C0=A0(3)卡诺图如下图所示D3=A3+A2 A1+A2 A0=A3A2 A1A2 A0D2 =A2 +A1+A3A0+A3A0=A2 A1 A3A0A3A0D1=A2 A1+A2 A0+A2 A1A0=A2 A1A2 A0A2 A1A0 D0=A1(4)卡诺图如下图所示D3=B3D 2 =B 3 B 2 +B 3 B 2 =B 3 B 2 B 3 B 2 D 1=B 2 B 1 +B 2 B 1 =B 2 B 1 B 2 B 1 D 0=B 2 B 1 +B 2 B 1 =B 2 B 1 B 2 B 1上述的逻辑电路图分别如下图1、2所示:【题3.12】 用集成二进制译码器74LS138和与非门构成全加器和全减器。
数字电子技术基础-第3章课后习题答案
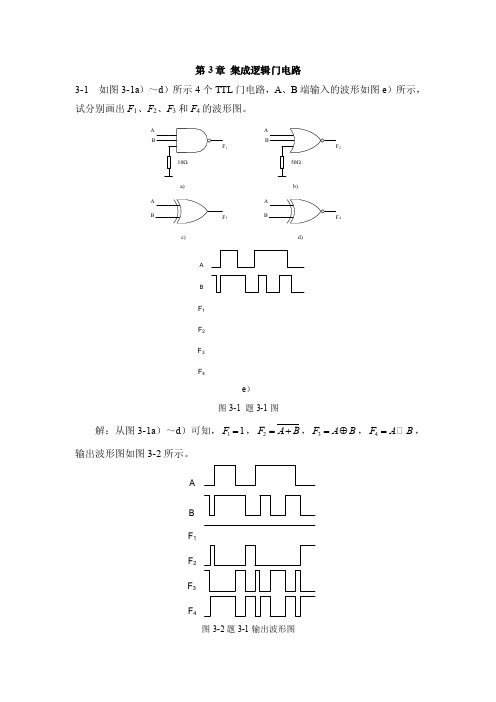
第3章集成逻辑门电路3-1 如图3-1a)~d)所示4个TTL门电路,A、B端输入的波形如图e)所示,试分别画出F1、F2、F3和F4的波形图。
A1A234a)b)c)d)F1F2F3F4BAe)图3-1 题3-1图解:从图3-1a)~d)可知,11F=,2F A B=+,3F A B=⊕,4F A B= ,输出波形图如图3-2所示。
F1F2F3F4AB图3-2题3-1输出波形图3-2 电路如图3-3a )所示,输入A 、B 的电压波形如图3-3b )所示,试画出各个门电路输出端的电压波形。
1A 23b)a)AB图3-3 题3-2图解:从图3-3a )可知,1F AB =,2F A B =+,3F A B =⊕,输出波形如图3-4所示。
F 1F 2F 3AB图3-4 题3-2输出波形3-3在图3-5a )所示的正逻辑与门和图b )所示的正逻辑或门电路中,若改用负逻辑,试列出它们的逻辑真值表,并说明F 和A 、B 之间是什么逻辑关系。
b)a)图3-5 题3-3图解:(1)图3-5a )负逻辑真值表如表3-1所示。
表3-1 与门负逻辑真值表F 与A 、B 之间相当于正逻辑的“或”操作。
(2)图3-5b )负逻辑真值表如表3-2所示。
表3-2 或门负逻辑真值表F 与A 、B 之间相当于正逻辑的“与”操作。
3-4试说明能否将与非门、或非门和异或门当做反相器使用?如果可以,各输入端应如何连接?解:与非门、或非门和异或门经过处理以后均可以实现反相器功能。
1)与非门:将多余输入端接至高电平或与另一端并联; 2)或非门:将多余输入端接至低电平或与另一端并联;3) 异或门:将另一个输入端接高电平。
3-5为了实现图3-6所示的各TTL 门电路输出端所示的逻辑关系,请合理地将多余的输入端进行处理。
b)a)AB=A B=+A BC DABC D图3-6 题3-5图解:a )多余输入端可以悬空,但建议接高电平或与另两个输入端的一端相连;b )多余输入端接低电平或与另两个输入端的一端相连;c) 未用与门的两个输入端至少一端接低电平,另一端可以悬空、接高电平或接低电平;d )未用或门的两个输入端悬空或都接高电平。
数字电子技术基础简明教程(第三版)余孟尝第三章-完成ok

第三章 组合逻辑电路【】 分析图P3.1电路的逻辑功能,写出Y 1、Y 2的逻辑函数式,列出真值表,指出电路完成了什么逻辑功能.Y 1【解】1()Y ABC A B C AB AC BC ABC ABC ABC ABC=+++•++=+++2Y AB BC AC =++由真值表可见,这是一个全加器电路。
A 、B 、C 为加数、被加数和来自低位的进位,Y 1是和,Y 2是进位输出。
【】 图3.2是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1;Z=0和COMP=0,Z=0时Y 1,Y 2,Y 3,Y 4的逻辑式,列出真值表。
Y 1Y 2Y 3Y 4A 1A 2A 3A 4Z【解】(1)COMP=1、Z=0时输出的逻辑式为11223234234Y A Y A Y A A Y A A A⎧=⎪=⎪⎨=⊕⎪⎪=++⎩ 〔2〕COMP=0、Z=0时输出的逻辑式为11223344Y A Y A Y A Y A =⎧⎪=⎪⎨=⎪⎪=⎩〔即不变换,真值表从略〕3个或3个以上为1时输出1,输入为其他状态时输出0。
【解】Y ABCD ABCD ABCD ABCD ABCD ABC ABD ACD BCD ABC ABD ACD BCD=++++=+++=•••B D Y【】 有一水箱由大、小两台水泵M L 、M S 供水,如图P3.4所示.水箱中设置了3个水位检测元件A、B 、C 。
水面低于检测元件时,检测元件给出高电平;水面高于检测元件时,检测元件给出低电平。
现要求当水位超过C 点时水泵停止工作;水位低于C 点高于B 点时M S 单独工作;水位低于B 点而高于A 点时M L 单独工作;水位低于A 点时M L 、M S 同时工作。
试用门电路设计一个控制两台水泵的逻辑电路,要求电路尽量简单。
【解】图P3.4M L真值表中的ABC 、ABC 、ABC 、ABC 为约束项,利用卡诺图【图A3.4(a)】化简后得到S L M A BCM B⎧=+⎪⎨=⎪⎩ 〔M S 、M L 的1状态表示工作,0状态表示停止〕 逻辑图如图A3.4(b).S M A BC =+L M B =〔a 〕(b)A B CM SM L【】。
(第三版)数字电子技术练习题答案(第三章)(江晓安编)

= =!第三章布尔代数与逻辑函数化简1.解:真值表如表3-1所示。
将F=1的与项相或即得F的逻辑表达式。
2.3.解对偶法则:将原式+→·,·→+,1→0,0→1并保持原来的优先级别,即得原函数对偶式。
反演法则;将原函数中+→·;·→+;0→1,1→0;原变量→反变量;反变量→原变量,两个或两个以上变量的非号不变,并保持原来的优先级别,得原函数的反函数。
4.5.解:6.解:(1)DF+A++=的卡诺图简化过程如图(a)+CABABBCCBCA所示。
简化结果为C=,将其二次反求,用求反律运算一次即F+BBA得与非式CF•==,其逻辑图如图(b)所示。
B+ABABCB++=的卡诺图简化过程如图(a)所示。
简化结F+AABCBCDABD果为C=+F•+=,,其逻辑图如图(b)所示。
AB=AABAACCABAF+C+=的卡诺图简化过程如图(a)所示。
简D+++CACBBABDBC化结果为D++F=B=++=,,其逻辑图如图(b)所CDBCACAADB示。
(2)卡诺图简化过程如图(a)所示。
简化结果为F=+=B=,其逻辑图如图(b)所示。
+CCBCB(3)卡诺图简化过程如图(a)所示。
简化结果为CF=,其逻辑图如图(b)所示。
(4) 卡诺图简化过程如图(a)所示。
简化结果为DF==,其BDB逻辑图如图(b)所示。
(5) 卡诺图简化过程如图(a)所示。
简化结果为CD D B BD CD D B BD CDD B BD F ••=++=++=,其逻辑图如图(b )所示。
(6) 卡诺图简化过程如图(a)所示。
简化结果为BCD C B A D C B C B A BCDC B AD C B C B A F •••=+++=,其逻辑图如图(b )所示。
(7) 卡诺图简化过程如图(a)所示。
简化结果为E C B BCD E D B E D B CE EC B BCDE D B E D B CEF ••••=++++=,其逻辑图如图(b )所示。
