分数乘法知识点和题型(全面)复习课程
分数乘法专题复习

分数乘法专题复习
介绍
本文档将为大家简要复分数乘法的相关知识点和技巧。
分数乘
法是数学中的重要概念之一,掌握好这个内容对于解决各种数学问
题非常有帮助。
在复过程中,请确保您已经熟悉了分数的基本概念。
内容
分数乘法的定义
分数乘法是指两个或多个分数相乘的操作。
在分数乘法中,我
们需要将分子与分子相乘,分母与分母相乘。
例如,对于分数a/b和c/d的乘法,结果可以表示为(a * c) / (b
* d)。
分数乘法的规则
1. 分数与整数相乘:将整数转化为分数,然后按照分数乘法的规则进行计算。
2. 分数与分数相乘:将两个分数的分子相乘,分母相乘,然后化简到最简形式。
分数乘法的技巧
1. 化简分数:在进行分数乘法时,可以先将分数化简到最简形式,这样有助于减少计算错误的概率。
2. 转化为小数:为了更好地理解分数乘法,有时可以将分数转化为小数进行计算,然后再转回分数形式。
3. 独立计算:将分数乘法问题分解成独立的计算步骤,分别计算分子和分母的乘积,最后将结果合并。
总结
分数乘法是数学中的重要概念。
通过掌握分数乘法的定义、规则和技巧,我们能够更加熟练地进行分数乘法计算,进而提高解决数学问题的能力。
在实践中,我们还应该不断练分数乘法,以加强对该内容的掌握和运用能力。
祝大家学习进步!。
人教版数学六年级上册分数乘法知识点和题型(全面)

2020年~2021年最新《分数的乘法》一、分数乘法 (一)分数乘法的意义:1.分数乘整数与整数乘法的意义相同。
都是求几个相同加数的和的简便运算。
例如: 1.98×5表示( )。
2.83+83+83=( )×( )=( ) 83+83+83+83=( )×( )=( )=( ) 3.24个32是多少? 145吨的7倍是多少吨?2.分数乘分数是求一个数的几分之几是多少。
例如: 1.98×43表示的意义是( )。
2.125吨的32是多少吨?3.一根绳子长109米,3根这样的绳子共长( )米;这根绳子的31长( )米。
(二)分数乘法的计算法则:1.分数与整数相乘:分子与整数相乘的积做分子,分母不变。
(整数和分母约分)例如:1.72×3 53×6 214×9 103×5 1611×12 2.52米=( )厘米 32时=( )分 107千克=( )克 算式: 2.分数与分数相乘:用分子相乘的积做分子,分母相乘的积做分母。
例如:152×85 3914×2813 4532×281565×25122110×533.为了计算简便,能约分的要先约分,再计算。
注意:当带分数进行乘法计算时,要先把带分数化成假分数再进行计算。
例如:32×143 83×154 2625×1513 6313×3914 85×52(三)规律:(乘法中比较大小时)一个数(0除外)乘大于1的数,积大于这个数。
一个数(0除外)乘小于1的数(0除外),积小于这个数。
一个数(0除外)乘1,积等于这个数。
例如:65×2 ○65 8×117○8 54×1 ○54 43×53 ○53 87×56 ○87×65 (五)整数乘法的交换律、结合律和分配律,对于分数乘法也同样适用。
分数乘法复习课课件

2、光明小学六年级有学生360人,五年级比六年级的 人数少 1 ,五年级比六年级少多少人?
5
3、六年级同学给灾区的小朋友捐款,一班捐了500元,
二班捐的是一班的 ,三4 班捐的是一班的 ,六9 三班
捐款多少元?
5
10
分数乘法复习课
22
4、果园有桃树120棵,梨树是桃树的 5,杏树是
梨树的 3 ,杏树有多少棵?
4、客车的速度是货车速度的
74C、,16(3 ×5
)是单位“1”。
5、AA、6、×货乘(车法2速+交度换32 律)=B1、B2+、客4乘车=1法速6结,度合这律是根C据、C(无、法乘确法定)分计3 ×12=
4
2 7
+2
7
+1=
3 5
×1
3
=
7 -1 =
93
数
到分数
法
第二单元
分数乘法复习课
2
一.复习分数乘法的意义和 计算法则
分数乘法复习课
3
复习分数乘法的意义
1、说出下列各式意义,再计算。
﹙1﹚
1 5 = 5
9
9
1
5个 的和是多少?
9 215 = 10
9
3
2
15个 的和是多少?
9
2 13 2
15
=
2
3个 2 1 的和是多少? 2
112 = 4
3
12个1 的和是多少? 3
1、新建一栋教学楼,原计划投资30万元, 实际节约了1/6。实际投资多少万元?
分数乘法复习课
25
已知:这个数 求:比这数多几分之几的数是多 少
比单位”1”多几分之几是多少
• 我市去年小学毕业生有6000人,今年 比去年多1/20。今年小学毕业生有多少 人?
分数乘法知识点归类与题型

分数乘法知识点归类与题型
知识点1 分数乘整数的意义和计算方法(重点)
分数乘整数的意义:求几个相同分数的和的简便运算。
(提示:分数乘整数的意义与整数乘法的意义相同,都是求几个相同加数的和的简便运算,只是这里的相同加数变成了分数。
)
分数乘整数的计算方法:分数与整数相乘,用分数的分子和整数相乘的积做分子,分母不变。
例1:3169
67⨯ 点拨:在计算分数乘整数时或整数乘分数时,先约分化简,然后利用法则相乘,计算结果要化为最简分数。
练习1:48
9623⨯
知识点2:一个数乘分数的意义和计算方法(重点、难点)
一个数乘分数的意义:一个数与分数相乘,可以看做是求这个数的几分之几是多少? 分数乘分数的计算方法:分数乘分数,用分子相乘的积做分子,分母相乘的积做分母。
知识点3:分数混合运算及运算定律(重点、难点)
分数混合运算的顺序:与整数的运算顺序相同,先算乘除,再算加减,有括号时要先算括号里的。
运算定律:交换律、结合律和分配律。
小学六年级上册数学知识点和题型

小学六年级上册数学知识点和题型第一单元分数乘法(一)分数乘法意义:1、分数乘整数的意义与整数乘法的意义相同,就是求几个相同加数的和的简便运算。
注:“分数乘整数”指的是第二个因数必须是整数,不能是分数。
2、一个数乘分数的意义就是求一个数的几分之几是多少。
(二)分数乘法计算法则:1、分数乘整数的运算法则是:分子与整数相乘的积作分子,分母不变。
注:(1)为了计算简便能约分的可先约分再计算。
(整数和分母约分)(2)约分是用整数和下面的分母约掉最大公因数。
(整数千万不能与分母相乘,计算结果必须是最简分数)2、分数乘分数的运算法则是:用分子相乘的积做分子,分母相乘的积做分母。
(分子乘分子,分母乘分母)注:①如果分数乘法算式中含有带分数,要先把带分数化成假分数再计算。
②分数化简的方法是:分子、分母同时除以它们的最大公因数。
③在乘的过程中约分,是把分子、分母中,两个可以约分的数先划去,再分别在它们的上、下方写出约分后的数。
(约分后分子和分母必须不再含有公因数,这样计算后的结果才是最简单分数)④分数的基本性质:分子、分母同时乘或者除以一个相同的数(0除外),分数的大小不变。
3、小数乘分数的运算法则是:(1)把小数化成分数计算;(2)如果所乘分数可以化成有限小数,也可以把分数化成小数计算;(3)小数和分母能约分的,先约分在计算比较方便。
(三)积与因数的关系:一个数(0除外)乘大于1的数,积大于这个数。
a×b=c,当b >1时,c>a. 一个数(0除外)乘小于1的数,积小于这个数。
a×b=c,当b <1时,c<a (b≠0). 一个数(0除外)乘等于1的数,积等于这个数。
a×b=c,当b =1时,c=a .注:在进行因数与积的大小比较时,要注意因数为0时的特殊情况。
(四)分数乘法混合运算1、分数乘法混合运算顺序与整数相同,先乘、除后加、减,有括号的先算括号里面的,再算括号外面的。
小学六年级数学(上册)知识点及题型总结

小学六年级上册数学知识点和题型第一单元分数乘法(一)分数乘法意义:1、分数乘整数的意义与整数乘法的意义相同,就是求几个相同加数的和的简便运算。
注:“分数乘整数”指的是第二个因数必须是整数,不能是分数。
2、一个数乘分数的意义就是求一个数的几分之几是多少。
(二)分数乘法计算法则:1、分数乘整数的运算法则是:分子与整数相乘的积作分子,分母不变。
注:(1)为了计算简便能约分的可先约分再计算。
(整数和分母约分)(2)约分是用整数和下面的分母约掉最大公因数。
(整数千万不能与分母相乘,计算结果必须是最简分数)2、分数乘分数的运算法则是:用分子相乘的积做分子,分母相乘的积做分母。
(分子乘分子,分母乘分母)注:①如果分数乘法算式中含有带分数,要先把带分数化成假分数再计算。
②分数化简的方法是:分子、分母同时除以它们的最大公因数。
③在乘的过程中约分,是把分子、分母中,两个可以约分的数先划去,再分别在它们的上、下方写出约分后的数。
(约分后分子和分母必须不再含有公因数,这样计算后的结果才是最简单分数)④分数的基本性质:分子、分母同时乘或者除以一个相同的数(0除外),分数的大小不变。
3、小数乘分数的运算法则是:(1)把小数化成分数计算;(2)如果所乘分数可以化成有限小数,也可以把分数化成小数计算;(3)小数和分母能约分的,先约分在计算比较方便。
(三)积与因数的关系:一个数(0除外)乘大于1的数,积大于这个数。
a×b=c,当b >1时,c>a. 一个数(0除外)乘小于1的数,积小于这个数。
a×b=c,当b <1时,c<a (b≠0).一个数(0除外)乘等于1的数,积等于这个数。
a×b=c,当b =1时,c=a . 注:在进行因数与积的大小比较时,要注意因数为0时的特殊情况。
(四)分数乘法混合运算1、分数乘法混合运算顺序与整数相同,先乘、除后加、减,有括号的先算括号里面的,再算括号外面的。
《分数乘法复习课》课件

分数乘法的运算顺序:先进行括号内的运算,再进行乘法运算,最后进 行加法运算。
分数乘法的运算性质:分数乘法具有交换律和结合律,即a×b=b×a和 (a×b)×c=a×(b×c)。
分数乘法的运算技巧:在计算分数乘法时,可以将分子和分母分别相乘, 然后再约分,以简化计算过程。
分数乘法在生活实践中的应用案例
分数乘法在购物中的应用:例如,计算打折后的价格,或者计算分摊费用等。
单击此处添加正文,文字是您思想的提炼,请言简意赅的阐述您的观点。单击此处添加正文, 文字是您思想的提炼,请言简意赅的阐述您的观点。
分数乘法在时间管理中的应用:例如,计算完成某项任务所需的时间,或者计算工作效率等。
分数乘法的基本概念与 法则
分数乘法的基本定义
分数乘法的定义:两个分数相乘,分子乘以分子,分母乘以分母 分数乘法的意义:表示一个数的几分之几 分数乘法与整数乘法的联系:可以看作是整数乘法在分数的扩展 分数乘法与加法的联系:可以看作是加法在分数的扩展
分数乘法的运算法则
分数乘法的基本概念:分数乘法是将两个分数相乘,得到它们的积。
分数乘法在面积计算中的应用:例如,计算某个图形的面积,或者计算某个物体的体积等。 这些 应用案例可以帮助学生更好地理解分数乘法的实际应用,提高他们的数学素养和解决问题的能力。
这些应用案例可以帮助学生更好地理解分数乘法的实际应用,提高他们的数学素养和解决问题 的能力。
拓展知识:分数的其他运算方法介绍
分数乘法的运算性质
分数乘法的基本 概念与法则
分数乘法的运算 性质
分数乘法的运算 性质的应用
分数乘法与加减 法的联系与区别
分数乘法的运算技巧与 实例
分数的乘除知识点总结

分数的乘除知识点总结一、分数的乘法基本概念1. 分数的乘法是指两个分数相乘的运算。
如:(1/2) × (2/3)2. 分数的乘法还可以与整数相乘。
如:(3/5) × 23. 分数的乘法可以看作是分子相乘得到新的分子,分母相乘得到新的分母。
如:a/b × c/d = (a×c)/(b×d)二、分数的乘法运算规则1. 分数的乘法满足交换律和结合律。
即,对于任意的分数a/b和c/d,有:a/b × c/d = c/d × a/b(a/b × c/d) × e/f = a/b × (c/d × e/f)2. 分数的乘法可以转化为通分的分数相乘。
当两个分数的分母不相同时,可以通过通分的方法将分母转化为相同的数,再进行乘法运算。
3. 分数的乘法还可以化简。
在运算过程中,我们可以化简分数,使分子和分母互质。
三、分数的乘法常见错误分析1. 错误:未进行通分运算就进行分数相乘。
如:(1/3) × (2/5) = 2/15正确的做法是先通分,然后再进行相乘:(1/3) × (2/5) = (1×2)/(3×5) = 2/152. 错误:运算过程中忽略了化简。
如:(5/10) × (3/5) = (5×3)/(10×5) = 15/50正确的做法是先化简,然后再进行相乘:(5/10) × (3/5) = (1/2) × (3/5) = (1×3)/(2×5) = 3/10四、分数的除法基本概念1. 分数的除法是指两个分数相除的运算。
如:(1/2) ÷ (2/3)2. 分数的除法还可以与整数相除。
如:(3/5) ÷ 23. 分数的除法可以看作是分子相乘得到新的分子,分母相乘得到新的分母。
第一单元:分数乘法(讲义)-2024-2025学年人教版六年级数学上册

分数乘法(思维导图+知识梳理+典例分析+高频真题+答案解析)【分数乘法-知识点归纳】1、分数乘法的意义:分数乘法的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算.2、乘积是1的两个数叫做互为倒数.3、分数乘法法则:(1)带分数乘法:先把带分数化成假分数,然后再乘.结果是假分数时,要把假分数化成带分数或整数.(2)(2)分数乘以分数:用分子相乘的积作为分子,用分母相乘的积作为分母.为了使计算简便,在计算的过程中,能够约分的,要约分.(3)分数乘以整数或整数乘以分数:由于任何整数(0除外)都可以化成分母是1的假分数,分数乘以整数或整数乘以分数,都可以转化成分数乘以分数的形式.因此,在计算中,是用分数的分子和整数相乘的积作为分子,分母不变.在乘的过程中,如果有可以约分的数,可以先约分,这样,可以使计算的数字缩小,从而使计算变得简便.【分数乘整数-知识点归纳】1、分子乘整数,可以求出一共有多少个这样的分数单位,而分数单位的个数其实就是分子乘整数的积,因此整数乘分子作分子。
求几个分数单位的和,分数单位不变,也就是分母不变。
2、分数乘整数的意义:分数乘整数,也是表示几个相同加数相加,与整数乘法的意义相同。
3、分数乘整数的计算方法:分数乘整数,用分子乘整数的积作分子,分母不变。
其实就是计算分数单位的个数。
【整数乘分数-知识点归纳】1、一个数乘分数的意义就是求一个数的几分之几是多少。
2、“一个数乘分数”指的是第二个因数必须是分数,不能是整数。
(第一个因数是什么都可以)3、方法总结;(1)、整数与分数相乘,用分数的分子与整数相乘,分母不变;(2)、计算时能约分的可以先约分再计算出结果。
【分数乘分数-知识点归纳】分数乘法的计算法则1、整数和分数相乘:整数和分子相乘的积作分子,分母不变。
2、分数和分数相乘:分子相乘的积作分子,分母相乘的积作分母。
【典例1】在“世界无烟日”健康知识竞赛中,小星答对了50道题,小铭答对的题数比小星少15。
分数乘法知识点

《分数乘法》分数乘法(一)知识点:1、理解分数乘整数的意义:数乘整数的意义同整数乘法的意义相同,就是求几个相同加数的和的简便运算。
2、分数乘整数的计算方法:分母不变,分子和整数相乘的积作分子。
能约分的要约成最简分数。
如:a ×=m n mn a 3、计算时,应该先约分再计算。
要简便一些补充知识点1、两个数相乘,其中一个乘数不变,另一个剩数扩大到原来的几倍(或缩小到原来的几分之几),积也相应地扩大到原来的几倍(或缩小到原来的几分之几)。
分数乘法(二)知识点 : 1、分数乘整数的意义:与整数乘法的意义相同,就是求几个相同加数的和的简便运算。
如:×5表示求5个的和是多1212少,或者表示的5倍是多少。
122、一个数乘分数的意义:就是求这个数的几分之几是多少。
如:4×表示求4的是多少。
3×表示3的是多少。
13131313 3、理解打折的含义。
例如:九折,是指现价是原价的十分之九。
现价=原价×109补充知识点1、在解决实际问题时,要找准把谁看作一个整体。
找准单位“1”并弄清所求问题与单位“1”的关系是解决问题的关键。
2、打折问题的公式:现价=原价×折扣原价=现价÷折扣折扣=现价÷原价2、打几折就是指现价是原价的百分之几,例如八五折,是指现85价是原价的百分之八十五。
现价=原价×1003、买一赠一打几折:出一份的钱拿两个货品,即1除以2等于零点五五折买三赠一打几折:出三份的钱拿四个货品,即3除以4等于零点七五七五折分数乘法(三)知识点:1、分数乘分数的计算方法:分子相乘做分子,分母相乘做分母,能约分的可以先约分,再计算。
(计算结果要求是最简分数。
)如:mb na m nb a ⨯⨯=⨯2、分数乘分数的意义:求一个分数的几分之几是多少。
3、比较分数相乘的积与每一个乘数的大小:真分数相乘积小于任何一个乘数;真分数与假分数相乘积大于真分数小于假分数。
《分数乘法复习课》课件

在进行分数乘法混合运算时,首先需要将带分数转化为假分数,然后进行计算。例如,计算$frac{3}{4} times frac{7}{2}$时,可以将带分数$frac{7}{2}$转化为假分数$frac{14}{4}$,然后进行计算得到$frac{21}{8}$。
Part
03
分数乘法的易错点解析
用符号“×”表示分数乘法,例如,将分数a/b与c/d相乘, 表示为(a/b) × (c/d)。
分数乘法的运算规则
分数乘法的交换律
交换两个分数的位置,其乘积不变, 即(a/b) × (c/d) = (c/d) × (a/b)。
分数乘法的结合律
分数乘法的分配律
一个分数与两个分数的和或差相乘, 等于这个分数分别与两个分数相乘的 和或差,即(a/b) × (c+d/e) = (a/b) × (c/e) + (a/b) × (d/e)。
在进行分数乘法时,首先观察分子和分母是否有公因数,如果有,则约去公因 数,使分数简化。例如,计算$frac{4}{5} times frac{3}{6}$时,可以约去公因 数$frac{1}{5}$,得到$frac{2}{3}$。
分数乘法的约分技巧
总结词
约分是简化分数乘法运算的另一种方法,通过约分可以快速找到分子和分母的最 大公约数,从而简化分数。
Part
05
分数乘法的练习题与答案
基础练习题
总结词:巩固基础
详细描述:这些题目主要针对分数乘法的基础知识,包括分数的乘法法则、约分 等。适合所有学生练习,帮助他们掌握分数乘法的基本概念和运算方法。
进阶练习题
总结词
提高解题能力
详细描述
这些题目难度稍大,需要学生具备一 定的解题技巧和思维能力。题目涉及 分数乘法的灵活运用,如解决实际问 题、进行复杂运算等。
小学六年级数学(上册)知识点及题型总结

小学六年级上册数学知识点和题型第一单元分数乘法(一)分数乘法意义:1、分数乘整数的意义与整数乘法的意义相同,就是求几个相同加数的和的简便运算。
注:“分数乘整数”指的是第二个因数必须是整数,不能是分数。
2、一个数乘分数的意义就是求一个数的几分之几是多少。
(二)分数乘法计算法则:1、分数乘整数的运算法则是:分子与整数相乘的积作分子,分母不变。
注:(1)为了计算简便能约分的可先约分再计算。
(整数和分母约分)(2)约分是用整数和下面的分母约掉最大公因数。
(整数千万不能与分母相乘,计算结果必须是最简分数)2、分数乘分数的运算法则是:用分子相乘的积做分子,分母相乘的积做分母。
(分子乘分子,分母乘分母)注:①如果分数乘法算式中含有带分数,要先把带分数化成假分数再计算。
②分数化简的方法是:分子、分母同时除以它们的最大公因数。
③在乘的过程中约分,是把分子、分母中,两个可以约分的数先划去,再分别在它们的上、下方写出约分后的数。
(约分后分子和分母必须不再含有公因数,这样计算后的结果才是最简单分数)④分数的基本性质:分子、分母同时乘或者除以一个相同的数(0除外),分数的大小不变。
3、小数乘分数的运算法则是:(1)把小数化成分数计算;(2)如果所乘分数可以化成有限小数,也可以把分数化成小数计算;(3)小数和分母能约分的,先约分在计算比较方便。
(三)积与因数的关系:一个数(0除外)乘大于1的数,积大于这个数。
a×b=c,当b >1时,c>a. 一个数(0除外)乘小于1的数,积小于这个数。
a×b=c,当b <1时,c<a (b≠0).一个数(0除外)乘等于1的数,积等于这个数。
a×b=c,当b =1时,c=a . 注:在进行因数与积的大小比较时,要注意因数为0时的特殊情况。
(四)分数乘法混合运算1、分数乘法混合运算顺序与整数相同,先乘、除后加、减,有括号的先算括号里面的,再算括号外面的。
第二单元分数乘法(复习课件)六年级数学上册
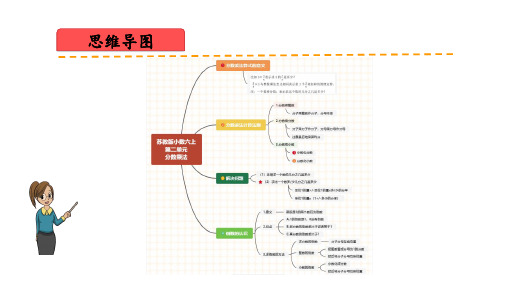
知识盘点
知识点二:分数乘分数及分数连乘 1、分数乘分数的意义。 分数乘分数的意义:求一个数的几分之几是多少。 2、分数乘分数的计算方法。 分数和分数相乘,用分子相乘的积做分子,分母相乘的积做分母。 3、连续求一个数的几分之几是多少的实际问题。 连续求一个数的几分之几是多少的解题关键是要找到每一步的单 位“1”,确定等量关系。
知识盘点
3、分数与整数相乘的简便算法。 分数乘整数的简便算法就是能约分的先约分,再计算,计算结果 一定是最简分数。约分时用整数和分母进行约分,然后将约分后 的整数与分子相乘。 4、求一个数的几分之几是多少用乘法计算。 求一个数的几分之几是多少,用乘法计算。 5、求一个数的几分之几是多少的简单实际问题 甲数比乙数多几分之几,其单位“1”就是乙数,乙数*几分之几 =甲数比乙数多的数。
易错攻略
1、分数和整数相乘的意义和计算方法。 (1)分数乘整数的意义。 分数乘整数的意义与整数乘法的意义相同,表示求几个相同加数 的和的简便运算。 分数乘整数表示求几个几分之几相加,不是表示求几分之几个几 相加。 (2)分数和整数相乘的计算方法。 整数和分母约分后,要把整数约分后的结果和原来的分子相乘。
易错攻略
2、求一个数的几分之几是多少,用乘法计算。 3、计算分数乘分数时,不能忘记分子与分子相乘,同时也不能 忘记分母与分母相乘。 4、在已知条件较多的情况下,一定要分清哪些条件与所求问题 有关,找准所乘分数对应的单位“1”。 5、计算分数乘法时,计算结果能约分的一定要约成最简分数。
易错攻略
6、互为倒数的两个数相互依存,不能单独存在,即2是倒数这种 说法是错误的。 7、非0自然数都有倒数,即0没有倒数。 8、不能将互为倒数的两个数用等号连接。 9、因为假分数大于或等于1,所以它的倒数小于或等于1。
小学数学分数乘法知识点

小学数学分数乘法知识点
小学数学分数乘法的知识点主要包括以下几个方面:
1. 分数的乘法规则:分数乘法是指将两个分数相乘的运算。
乘法的规则是分子相乘得到新的分子,分母相乘得到新的分母。
即,a/b * c/d = (a * c)/(b * d)。
2. 约分:在分数乘法时,可以对乘积进行约分,将分子和分母的公约数约掉,使分数变为最简形式。
约分可以使计算过程更简化。
3. 分数乘法的应用:分数乘法在实际生活中有广泛的应用,比如:分数乘法可以用来计算物品的总价、计算比例关系、计算速度、计算百分比等。
4. 分数乘法和整数乘法的关系:整数也可以看作是分母为1的分数,所以整数乘法可以看做是分数乘法的特殊情况。
5. 分数乘法的综合应用:分数乘法在解决问题时常常需要结合其他的数学知识,如加法、减法、比较大小等。
以上就是小学数学分数乘法的主要知识点,希望能对你有所帮助。
如有问题请继续追问。
第2讲 分数乘法+知识梳理

第2讲分数乘法(思维导图+知识梳理+典型精讲+易错专练)一、思维导图二、知识点梳理知识点一:分数与整数的乘法(一)分数与整数相乘的意义和计算方法1.整数乘法的意义。
求几个相同加数的和的简便运算。
2.(1)分数乘整数的意义与整数乘法的意义相同,都是求几个相同加数的和的简便运算。
(2)分数与整数相乘的计算方法:用分数的分子和整数相乘的积作分子,分母不变。
能约分的要先约分,再计算。
(二)求一个数的几分之几是多少1.求一个数的几分之几是多少,用乘法计算。
2.求比一个数多(少)几分之几的部分是多少解决求比一个数多(少)几分之几的部分是多少的问题,关键是找准单位“1”的量,单位“1”的量×比一个数多(少)的几分之几=比一个数多(少)的几分之几的量。
知识点二:分数与分数的乘法(一)分数乘分数的意义和计算方法1.分数乘分数的意义就是求一个数的几分之几是多少。
2.分数和分数相乘,用分子相乘的积作分子,分母相乘的积作分母。
能约分的要先约分,再计算。
3.整数可以看成分母是1的分数,所以分数与整数相乘,也可以看成是分数与分数相乘,即分数与分数相乘的计算方法适用于分数与整数相乘。
(二)连续求一个数的几分之几是多少的解题方法及分数连乘的计算方法1.连续求一个数的几分之几是多少的解题方法:先求出中间的间接量,再求出最后要求的量。
2.分数连乘的计算方法:分子和分子相乘的积作分子,分母和分母相乘的积作分母。
能约分的要先约分,再计算。
知识点三:倒数(一)倒数的意义及求法1.意义:乘积是1的两个数互为倒数。
2.理解“互为倒数”。
“互为倒数”是对两个数来说的,它们是相互依存的,不能单独说某个数是倒数。
3.求一个数的倒数的方法。
(1)求真分数、假分数的倒数,可以直接调换这个分数的分子、分母的位置。
(2)求一个整数(0除外)的倒数,先把整数看作分母是1的假分数,再调换这个分数分子、分母的位置。
(3)求小数的倒数,先把小数化成最简分数,再调换分子、分母的位置,也可以根据倒数的意义来找。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《分数的乘法》一、分数乘法(一)分数乘法的意义:1、分数乘整数与整数乘法的意义相同。
都是求几个相同加数的和的简便运算。
例如: 1、 98×5表示( )。
2、83+83+83=( )×( )=( ) 83+83+83+83=( )×( )=( )=( ) 3、24个32是多少? 145吨的7倍是多少吨? 2、分数乘分数是求一个数的几分之几是多少。
例如: 1、98×43表示的意义是( )。
2、125吨的32是多少吨? 3、一根绳子长109米,3根这样的绳子共长( )米;这根绳子的31长( )米。
(二)分数乘法的计算法则:1、分数与整数相乘:分子与整数相乘的积做分子,分母不变。
(整数和分母约分)例如:1、72×3 53×6 214×9 103×5 1611×12 2、52米=( )厘米 32时=( )分 107千克=( )克 算式:2、分数与分数相乘:用分子相乘的积做分子,分母相乘的积做分母。
例如:152×85 3914×2813 4532×2815 65×2512 2110×533、为了计算简便,能约分的要先约分,再计算。
注意:当带分数进行乘法计算时,要先把带分数化成假分数再进行计算。
例如:32×143 83×154 2625×1513 6313×3914 85×52(三)规律:(乘法中比较大小时)一个数(0除外)乘大于1的数,积大于这个数。
一个数(0除外)乘小于1的数(0除外),积小于这个数。
一个数(0除外)乘1,积等于这个数。
例如:65×2 ○65 8×117○8 54×1 ○54 43×53 ○53 87×56 ○87×65 (五)整数乘法的交换律、结合律和分配律,对于分数乘法也同样适用。
乘法交换律: a × b = b × a乘法结合律: ( a × b )×c = a × ( b × c )乘法分配律: ( a + b )×c = a c + b c例如:1、53×61×5 32×41×3 94×5×18 54×97×85 75×16×5212、(924 + 83 )× 124 ( 56 - 59 )×18 47 ×613 +37 ×613 56 ×59 + 59 × 163、10063×101 677 × 78 12×613 + 613 14×137-137二、分数乘法的解决问题(已知单位“1”的量(用乘法),求单位“1”的几分之几是多少)1、画线段图:(1)两个量的关系:画两条线段图; (2)部分和整体的关系:画一条线段图。
2、找单位“1”: 在分率句中分率的前面; 或 “占”、“是”、“比”的后面2、先用直线划出单位“1”的量,再把数量关系式补充完整。
例如:(1)皮球的个数比足球多52。
(2)实际用水量比原计划节约91。
( )的个数×52=( )的个数 ( )用水量×91=( )用水量 (3)一桶油用去53,正好用去12千克。
这桶油重多少千克?( )的千克数×53=( )的千克数(4)学校饲养组养黑兔12只,是白兔只数的32。
饲养组养白兔多少只?( )的只数×32=( )的只数 3、求一个数的几倍:一个数×几倍; 求一个数的几分之几是多少:一个数×几几。
4、写数量关系式技巧:(1)“的” 相当于 “×” “占”、“是”、“比”相当于“ ÷ ”(2)分率前是“的”: 单位“1”的量×分率=分率对应量(3)分率前是“多或少”的意思: 单位“1”的量×(1 分率)=分率对应量例如:1、育才小学有男生120人。
(1)男生是女生的35 ,女生有多少人? (2)女生是男生的35,女生有多少人?(3)女生比男生多35 ,女生有多少人?(4)男生比女生少35,女生有多少人?(5)男生占全校的35 ,女生有多少人?(6)女生占总数的35,全校有多少人?2、要一条路长100米,已经修了5037米,还有多少米没修? 3、要一条路长100米,已经修了5037,修了多少米?4、一段长3米的布,第一次剪去它的31,第二次又剪去31米,两次一共剪去多少米?还剩多少米?5、周大婶收了532吨南瓜,收的冬瓜比南瓜多815。
收的冬瓜比南瓜多多少吨?6、一本书450页,第一天看了全书的15,第二天看了65页,第三天应该从第几页看起?7、一根铁丝长12米,第一次用去了全长的14,第二次用去了全长的13,两次一共用去了多少米?8、学校一月份用电800度,二月份比一月份节约了15,二月少用电多少度?三、倒数(一)倒数的意义:乘积为1的两个数互为倒数。
1、倒数是两个数的关系,它们互相依存,不能单独存在。
单独一个数不能称为倒数。
(必须说清谁是谁的倒数)2、判断两个数是否互为倒数的唯一标准是:两数相乘的积是否为“1”。
例如:a ×b=1则a 、b 互为倒数。
(二)求倒数的方法:1、求分数的倒数:交换分子、分母的位置。
2、求整数的倒数:整数分之1。
3、求带分数的倒数:先化成假分数,再求倒数。
4、求小数的倒数:先化成分数再求倒数。
5、1的倒数是它本身,因为1×1=1。
0没有倒数,因为任何数乘0积都是0,且0不能作分母。
6、任意数a(a ≠0),它的倒数为 ;非零整数a 的倒数为 ;分数 的倒数是 。
7、真分数的倒数是假分数,真分数的倒数大于1,也大于它本身。
假分数的倒数小于或等于1。
带分数的倒数小于1。
例如:1、( )的两个数叫做互为倒数。
2、35 的倒数是( )94的倒数是( ) 3、23 的倒数是( ),7的倒数是( ),434 的倒数是( ),756的倒数是( ) 4、( )没有倒数,1的倒数是( )。
5、 89 的倒数与56 的积是多少?6、 100的倒数的19倍 是多少?7、1.4加上它的倒数,再减去57 ,结果是多少?8、有两个不同的质数,它们积的倒数是110,求这两个质数是多少?9、 45 与它的倒数的和是多少? 10、 一个数的倒数是35 ,这个数的45是多少?分数乘法综合练习题一、 填空题:1、15个53是多少?列式是 ;32的53是多少,列式是 ; 2、25的54是( );53的43是( );12个94相加的和是( );3、53千米=( )米;65时=( )分;4、10×( )=53×( )=173×( )=0.25×( )=1 5、2米的31和1米的( ) 相等,就是( )米。
6、5的倒数与10的倒数比较,( )的倒数>( )的倒数。
7、 当a=( )时,a 的倒数与a 的值相等。
二、判断1、分数乘整数的意义与整数乘法的意义相同。
( )2、2千克的31和1千克的32同样重。
( ) 3、36×94和94×36结果相等。
( ) 4、一个数乘假分数,积一定大于这个数。
( ) 5、一根长12米的钢管,截去了31,就是短了31米。
( ) 6、 任意一个数都有倒数。
( ) 7、 假分数的倒数是真分数。
( ) 8、 a 是个自然数,它的倒数是。
( )9、 因为13 +23 =1所以13 和23 互为倒数。
( ) 10、 0.3的倒数是3( )三、列式计算:(1)120千米的457是多少千米? (2)457的120倍是多少?(3)25是125的几分之几? (4)125是25的几倍?四、计算:2518×95 275×120 3916×3213 3415×3017514 × 2125 ×75 (124 + 83 )×24 710 ×101- 710 34×3435五、应用题。
1、一台碾米机每小时可以碾稻谷207吨,5小时可以碾谷多少吨?54小时呢?2、某工厂有男职180人,女职工是男职工的95。
女职工有多少人? 求女职工有多少人就是求( )的( )是多少?所以用( )方法计算。
(按要求填空,并列式解答)3、一辆汽车每小时行驶45千米,从甲地到乙地行驶了158小时,正好到达了两地的中点。
甲乙两地全程多少千米?4、(1)一杯水重83千克,32杯重多少千克?(2)一杯水重83千克,又加了32千克,此时杯中水多少千克?5、一块长方形地的面积是15公顷,用这块地的51种小麦,31种棉花,种小麦和棉花各多少公顷?6、有四个不同的的偶数,它们的倒数的和是1,已知其中的两个数是2和4,求其余的两个数。
7、把5分别与它的倒数相加、相减、相乘、相除,再把所得的和、差、积、商相加,结果是多少?8、 110的倒数除以10,商是多少?。
