函数及图像与几何问题的参考答案

合集下载

2022-2023学年九年级上数学：二次函数的图像和性质(附答案解析)

2022-2023学年九年级上数学：二次函数的图像和性质一．选择题（共5小题）
1．将二次函数y＝x2的图象向下平移1个单位长度后，所得二次函数的表达式是（）A．y＝x2+1B．y＝x2﹣1C．y＝（x+1）2D．y＝（x﹣1）2 2．已知二次函数y＝ax2+bx+c，当﹣1≤x≤1时，总有﹣1≤y≤1，有如下几个结论：
①当b＝c＝0时，|a|≤1；
②当a＝1时，c的最大值为0；
③当x＝2时，y可以取到的最大值为7．
上述结论中，所有正确结论的序号是（）
A．①②B．①③C．②③D．①②③
3．二次函数y＝3（x+1）2﹣2的图象的顶点坐标是（）
A．（﹣1，﹣2）B．（﹣1，2）C．（1，﹣2）D．（1，2）
4．下列函数中，二次函数是（）
A．y＝﹣3x+5B．y＝x（4x﹣3）
C．y＝2（x+4）2﹣2x2D．y ＝
5．某同学将如图所示的三条水平直线m1，m2，m3的其中一条记为x轴（向右为正方向），三条竖直直线m4，m5，m6的其中一条记为y轴（向上为正方向），并在此坐标平面内画出了二次函数y＝ax2﹣2ax+1（a＜0）的图象，那么她所选择的x轴和y轴分别为直线（）
A．m1，m4B．m2，m5C．m3，m6D．m2，m4
二．填空题（共5小题）
6．已知二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如下表：
第1页（共18页）。

函数的图像和性质

学案3 函数的图像和性质一．基础自测1．（2010山东4）设()f x 为定义在R 上的奇函数，当0x ≥时，()22x f x x b =++（b 为常数），则(1)f -=（A ）-3 （B ）-1 （C ）1 (D)3解析：因为()f x 为定义在R 上的奇函数，所以f(0)=0,可求得b=-1,f(-1)=-f(1)=-2(2+2+b)=-3 答案：A 2．(2010天津南开区调研)已知ab ＝1，函数f (x )＝a x 与函数g (x )＝－log b x 的图象可能是( )解析：∵ab ＝1，∴⎩⎪⎨⎪⎧a >1，0<b <1，a x为增函数，－log b x 为增函数0<a <1，b >1，a x为减函数，－log b x 为减函数. 答案：B3. 不等式1－x 2<x ＋a 在x ∈[－1,1]上恒成立，则实数a 的取值范围是( )A ．(－∞，－2)B ．(－1，2)C ．[2，＋∞)D ．(2，＋∞) 解析：设y =1－x 2，y =x +a ，在同一直角坐标系内作出y =1－x 2的图象，再将函数y =x 的图象沿y 轴方向上、下平行移动，如右图所示，考查在x ∈[-1,1]上，使不等式1－x 2<x +a 恒成立．答案：D4．(2010·山东烟台调研)已知函数y ＝f (x )(x ∈R)满足f (x ＋2)＝f (x )，且x ∈(－1,1]时， f (x )＝|x |，则y ＝f (x )与y ＝log 7x 的交点的个数为( )A ．4B ．5C ．6D ．7解析：y ＝f (x )与y ＝log 7x 的交点即为图象的交点如图，由图象可知有6个交点．答案：C5.(2010·陕西)已知函数f (x )＝⎩⎪⎨⎪⎧2x ＋1，x <1，x 2＋ax ，x ≥1，若f (f (0))＝4a ，则实数a 等于( )A.12B.45C ．2D ．9 解析：f (x )＝⎩⎪⎨⎪⎧2x ＋1，x <1，x 2＋ax ，x ≥1.∵0<1，∴f (0)＝20＋1＝2.∵f (0)＝2≥1，∴ f (f (0))＝22＋2a ＝4a ，∴a＝2，故选C.答案：C6．2010天津10）设函数2()2()g x x x R =-∈，()4,(),()(),().g x x x g x f x g x x x g x ++<⎧=⎨-≥⎩则()f x的值域是 A ．9,0(1,)4⎡⎤-⋃+∞⎢⎥⎣⎦ B ．[0,)+∞ C ．9[,)4-+∞ D ．9,0(2,)4⎡⎤-⋃+∞⎢⎥⎣⎦解析:本题主要考查函数分类函数值域的基本求法，属于难题。

第八讲二次函数与几何图形的综合运用1(含答案)

第八讲二次函数与几何图形的运用一、知识梳理二次函数与三角形的综合运用：1、求面积及最值2、与三角形的综合运用3、与相似三角形的综合运用4、与四边形的综合运用二、例题例1：如图，已知抛物线y=﹣x 2+mx+3与x 轴交于A ，B 两点，与y 轴交于点C ，点B 的坐标为（3，0）（1）求m 的值及抛物线的顶点坐标．（2）点P 是抛物线对称轴l 上的一个动点，当PA+PC 的值最小时，求点P 的坐标．变式 1 如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0). （1）求该抛物线的解析式；（2）动点P 在x 轴上移动，当△PAE 是直角三角形时，求点P 的坐标.例2、如图，已知点A（0，2），B（2，2），C（﹣1，﹣2），抛物线F：y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P．（1）当抛物线F经过点C时，求它的表达式；（2）设点P的纵坐标为y P，求y P的最小值，此时抛物线F上有两点（x1，y1），（x2，y2），且x1＜x2≤﹣2，比较y1与y2的大小；（3）当抛物线F与线段AB有公共点时，直接写出m的取值范围．例3：在平面直角坐标系xOy中，抛物线y=ax2+bx+2过B（﹣2，6），C（2，2）两点．（1）试求抛物线的解析式；（2）记抛物线顶点为D，求△BCD的面积；（3）若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围．例4：已知二次函数y=ax2﹣2ax+c（a＞0）的图象与x轴的负半轴和正半轴分别交于A、B 两点，与y轴交于点C，它的顶点为P，直线CP与过点B且垂直于x轴的直线交于点D，且CP：PD=2：3（1）求A、B两点的坐标；（2）若tan∠PDB=，求这个二次函数的关系式．例5、如图1，二次函数y1=（x﹣2）（x﹣4）的图象与x轴交于A、B两点（点A在点B的左侧），其对称轴l与x轴交于点C，它的顶点为点D．（1）写出点D的坐标．（2）点P在对称轴l上，位于点C上方，且CP=2CD，以P为顶点的二次函数y2=ax2+bx+c （a≠0）的图象过点A．①试说明二次函数y2=ax2+bx+c（a≠0）的图象过点B；②点R在二次函数y1=（x﹣2）（x﹣4）的图象上，到x轴的距离为d，当点R的坐标为时，二次函数y2=ax2+bx+c（a≠0）的图象上有且只有三个点到x轴的距离等于2d；③如图2，已知0＜m＜2，过点M（0，m）作x轴的平行线，分别交二次函数y1=（x﹣2）（x ﹣4）、y2=ax2+bx+c（a≠0）的图象于点E、F、G、H（点E、G在对称轴l左侧），过点H 作x轴的垂线，垂足为点N，交二次函数y1=（x﹣2）（x﹣4）的图象于点Q，若△GHN∽△EHQ，求实数m的值．三、课堂练习1、如图，在Rt∠AOB的平分线ON上依次取点C，F，M，过点C作DE⊥OC，分别交OA，OB于点D，E，以FM为对角线作菱形FGMH.已知∠DFE＝∠GFH＝120°，FG＝FE.设OC＝x，图中阴影部分面积为y，则y与x之间的函数关系式是 ( )A．y＝32x2 B．y＝3x2 C．y＝23x2 D．y＝33x22、已知抛物线y=2x2+bx+c与直线y=﹣1只有一个公共点，且经过A（m﹣1，n）和B（m+3，n），过点A，B分别作x轴的垂线，垂足记为M，N，则四边形AMNB的周长为．3、直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，当OA⊥OB时，直线AB 恒过一个定点，该定点坐标为．4、如图，抛物线y=ax2+bx﹣经过点A（1，0）和点B（5，0），与y轴交于点C．（1）求抛物线的解析式；（2）以点A为圆心，作与直线BC相切的⊙A，请判断⊙A与y轴有怎样的位置关系，并说明理由；（3）在直线BC上方的抛物线上任取一点P，连接PB、PC，请问：△PBC的面积是否存在最大值？若存在，求出这个值和此时点P的坐标；若不存在，请说明理由．5、如图，在平面直角坐标系中，抛物线y=ax 2+bx+c 的顶点坐标为（2，9），与y 轴交于点A （0，5），与x 轴交于点E 、B ．（1）求二次函数y=ax 2+bx+c 的表达式；（2）过点A 作AC 平行于x 轴，交抛物线于点C ，点P 为抛物线上的一点（点P 在AC 上方），作PD 平行与y 轴交AB 于点D ，问当点P 在何位置时，四边形APCD 的面积最大？并求出最大面积；（3）若点M 在抛物线上，点N 在其对称轴上，使得以A 、E 、N 、M 为顶点的四边形是平行四边形，且AE 为其一边，求点M 、N 的坐标．六、课后作业1、已知抛物线y=ax 2﹣3x+c （a ≠0）经过点（﹣2，4），则4a+c ﹣1= ．2、a 、b 、c 是实数，点A （a+1、b ）、B （a+2，c ）在二次函数y=x 2﹣2ax+3的图象上，则b 、c 的大小关系是b c （用“＞”或“＜”号填空）3、已知二次函数n mx x y ++=2的图像经过点()1,3-P ，对称轴是经过()0,1-且平行于y轴的直线。

中考数学专项复习《二次函数图像的几何变换》练习题及答案

中考数学专项复习《二次函数图像的几何变换》练习题及答案一、单选题1．若二次函数y=mx2-（m2-3m）x+1-m的图象关于y轴对称，则m的值为（）A．0B．3C．1D．0或32．抛物线y＝（x+2）2+1可由抛物线y＝x2平移得到，下列平移正确的是（）A．先向右平移2个单位，再向上平移1个单位B．先向右平移2个单位，再向下平移1个单位C．先向左平移2个单位，再向上平移1个单位D．先向左平移2个单位，再向下平移1个单位3．将抛物线y＝﹣2（x+1）2﹣3先向右平移4个单位长度，再向上平移5个单位长度，得到的抛物线的函数表达式是（）A．y＝﹣2（x﹣5）2+8B．y＝﹣2（x﹣3）2+8C．y＝﹣2（x﹣5）2+2D．y＝﹣2（x﹣3）2+24．抛物线y=（x+2）2﹣3可以由抛物线y=x2平移得到，则下列平移过程正确的是（）A．先向左平移2个单位，再向上平移3个单位B．先向左平移2个单位，再向下平移3个单位C．先向右平移2个单位，再向下平移3个单位D．先向右平移2个单位，再向上平移3个单位5．如图，一条抛物线与x轴相交于A、B两点（点A在点B的左侧），其顶点P在线段MN上移动．若点M、N的坐标分别为（﹣1，﹣2）、（1，﹣2）点B的横坐标的最大值为3，则点A的横坐标的最小值为（）A．-3B．-1C．1D．36．在平面直角坐标系中将二次函数y=x2的图象向上平移2个单位，所得图象的解析式为（）A．y=x2﹣2B．y=x2+2C．y=（x﹣2）2D．y=（x+2）27．函数y=2x2+4x+1①；y=2x2－4x+1②的图象的位置关系是()A．②在①的上方B．②在①的下方C．②在①的左方D．②在①的右方8．将抛物线y=x2向左平移一个单位，再向上平移2个单位，得到的抛物线解析式为（）A．y=(x−1)2+2B．y=(x+1)2−2C．y=(x+1)2+2D．y=(x+2)2+1 9．在平面直角坐标系中如果抛物线y＝2x2+1不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是()A．y＝2(x－2)2+ 3B．y＝2(x－2)2－1C．y＝2(x + 2)2－1D．y＝2(x + 2)2 + 310．把抛物线y=（x﹣1）2+2向左平移1个单位，再向下平移2个单位，所得抛物线是（）A．y=x2B．y=（x﹣2）2C．y=（x﹣2）2+4D．y=x2+411．把抛物线y=x2+1向左平移3个单位，再向下平移2个单位，得到的抛物线表达式为（）A．y=（x﹣3）2+2 B．y=（x﹣3）2﹣1C．y=（x+3）2﹣1 D．y=（x﹣3）2﹣212．函数y＝ax2+bx+c的图象如图所示，那么关于x的方程ax2+bx+c－3＝0 的根情况是（）A．有两个相等的实数根B．有一个实数根C．有两个不相等的实数根D．没有实数根二、填空题13．已知将二次函数y=x2+bx+c的图象向右平移2个单位再向下平移3个单位，所得图象的解析式为y=x2﹣4x﹣5，则b=，c=．14．抛物线y=x2﹣6x+5向上平移2个单位长度，再向右平移1个单位长度后，得到的抛物线解析式是．15．把抛物线y=12x2−1先向右平移1个单位，再向下平移2个单位，得到的抛物线的解析式为.16．将二次函数y＝﹣（x﹣1）2的图象沿x轴向左平移2个单位，得到的函数表达式为．17．一抛物线和另一抛物线y＝﹣2x2的形状和开口方向完全相同，且顶点坐标是（﹣2，1），则该抛物线的解析式为.18．在平面直角坐标系中将抛物线y=x2﹣x﹣12向上（下）或左（右）平移m个单位，使平移后的抛物线恰巧经过原点，则|m|的最小值为．三、综合题19．在同一个直角坐标系中作出y＝12x2，y＝12x2－1的图象．（1）分别指出它们的开口方向、对称轴以及顶点坐标；（2）抛物线y＝12x2－1与抛物线y＝12x2有什么关系？20．如图，二次函数y=(x−1)(x−a)（a为常数）的图象的对称轴为直线x=2.（1）求a的值.（2）向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式. 21．已知二次函数y=x2﹣2mx+m2+3（m是常数）．（1）求证：不论m为何值，该函数的图象与x轴没有公共点；（2）把该函数的图象沿y轴向下平移多少个单位长度后，得到的函数的图象与x轴只有一个公共点？22．如图①，抛物线y=−x2+bx+c与x轴交于两点A，B(4，0)（点A位于点B的左侧），与y轴交于点C(0，4)，拋物线的对称轴l与x轴交于点N，长为2的线段PQ（点P位于点Q的上方）在x轴上方的抛物线对称轴上运动．（1）求抛物线的关系式；（2）在线段PQ运动过程中当PC+PA的值最小时，求此时点P的坐标；（3）如图②过点P作PM⊥y轴于点M，当△CPM和△QBN相似时，求点Q的坐标．23．已知抛物线y＝x2＋bx＋c经过点（﹣2，1），它的对称轴为直线x＝﹣1（1）求抛物线的表达式和顶点坐标.（2）如图，已知点A（P，t）（P＞0）在（1）中的抛物线上，将该抛物线向右平移若干个单位后得到抛物线l，点A在抛物线l上的对应点为点B（t，t），若抛物线l恰好经过点C（2，0），求P，t 的值.24．如图，抛物线y=x2﹣3x+k与x轴交于A、B两点，与y轴交于点C（0，﹣4）．（1）k=；（2）点A的坐标为，B的坐标为；（3）设抛物线y=x2﹣3x+k的顶点为M，求四边形ABMC的面积．参考答案1．【答案】B2．【答案】C3．【答案】D4．【答案】B5．【答案】A6．【答案】B7．【答案】D8．【答案】C9．【答案】C10．【答案】A11．【答案】C12．【答案】A13．【答案】0；-614．【答案】y=（x﹣4）2﹣315．【答案】y=12(x−1)2−316．【答案】y＝﹣(x+1)2 17．【答案】y＝﹣2（x+2）2+1 18．【答案】319．【答案】（1）解：如图所示：抛物线y＝12x2开口向上，对称轴为y轴，顶点坐标(0，0)；抛物线y＝12x2－1开口向上，对称轴为y轴，顶点坐标(0，－1)（2）解：抛物线y＝12x2－1可由抛物线y＝12x2向下平移1个单位长度得到20．【答案】（1）解：y=(x−1)(x−a)=x2−(1+a)x+a. ∵图象的对称轴为直线x=2∴a+12=2∴a =3 .（2）解：∵a =3∴二次函数的表达式为 y =x 2−4x +3 ∴抛物线向下平移3个单位后经过原点∴平移后图象所对应的二次函数的表达式为 y =x 2−4x .21．【答案】（1）证明：∵△=（﹣2m ）2﹣4×1×（m 2+3）=4m 2﹣4m 2﹣12=﹣12＜0∴方程x 2﹣2mx+m 2+3=0没有实数解即不论m 为何值，该函数的图象与x 轴没有公共点（2）解：y=x 2﹣2mx+m 2+3=（x ﹣m ）2+3把函数y=（x ﹣m ）2+3的图象沿y 轴向下平移3个单位长度后，得到函数y=（x ﹣m ）2的图象，它的顶点坐标是（m ，0）因此，这个函数的图象与x 轴只有一个公共点所以，把函数y=x 2﹣2mx+m 2+3的图象沿y 轴向下平移3个单位长度后，得到的函数的图象与x 轴只有一个公共点22．【答案】（1）解：∵y =−x 2+bx +c 过B(4，0)，C(0，4)∴0=−16+4b +c ∴b =3 c =4∴抛物线的关系式为y =−x 2+3x +4；（2）解：∵A 点关于对称轴l 的对称点是B ，连接CB 交对称轴l 于点P ，连接PB 由对称性可知 PA =PB ∴PC +PA =PC +PB ≥CB当C 、P 、B 三点在一条直线上时，PC +PA 有最小值 ∵B(4，0) C(0，4)设直线BC 的解析式为y =kx +b ∴{4k +b =0b =4 解得{k =−1b =4 ∴y =−x +4∵由在y =−x 2+3x +4得抛物线对称轴为直线x =−3−2=32 ∴y =−32+4=52∴P(32，52)；（3）解：如图：由在y =−x 2+3x +4得抛物线对称轴为直线x =−3−2=32 设Q(32，t)(t >0)，则P(32，t +2) M(0，t +2) N(32，0)∵B(4，0) C(0，4)；∴BN =52QN =t PM =32 CM =|t −2|∵∠CMP =∠QNB =90°∴△CPM 和△QBN 相似，只需CM QN =PM BN 或CM BN =PMQN ①当CM QN =PM BN 时，|t−2|t =3252 解得t =54或t =5 ∴Q(32，54)或(32，5)；②当CM BN =PM QN 时，|t−2|52=32t 解得t =2+√192或t =2−√192（舍去） ∴Q(32，2+√192)综上所述，Q 的坐标是(32，54)或(32，5)或(32，2+√192)．23．【答案】（1）解：y ＝x 2＋bx ＋c 经过点（﹣2，1）对称轴为直线x ＝﹣1，即 −b2a=−1 ∴b =2∴y =x 2+2x +c将点（﹣2，1）代入得： 1=4−4+c 解得： c =1 ∴y =x 2+2x +1∵y =x 2+2x +1=(x +1)2∴y ≥0 恒成立，当 x =−1 时取得最小值， y =0 ∴顶点坐标为： (−1，0) ；（2）解：∵y 向右平移若干单位与l 重合，且l 过点（2，0） ∴平移距离为 2−(−1)=3 ，且A （P ，t ）平移到B （t ，t ）∴t =p +3 ，即 p =t −3∴A （ t −3 ，t ）代入 y =(x +1)2 得： t =(t −3+1)2 ，即 t 2−5t +4=0 解得： t 1=1 t 2=4∴p =t −3=1−3=−2 或 p =t −3=4−3=1 ∵P ＞0∴p =−2 (舍去) ∴p =1，t =4 .24．【答案】（1）k=﹣4（2）（﹣1，0）；（4，0）（3）解：∵y=x 2﹣3x ﹣4= (x −32)2−254∴M(32，−254)设抛物线的对称轴与x 轴交于N ，如图所示：则四边形ABMC 的面积=S △ACN +S △NCM +S △NMB = 12×AN ×OC +12×NM ×ON +12×NB ×NM = 12×52×4+12×254×32+12×52×254 = 352∴四边形ABMC 的面积是 352．。

二次函数图像的性质与解析

二次函数图像的性质与解析一、二次函数的定义与标准形式1.二次函数的定义：一般地，形如y=ax^2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数。

2.二次函数的标准形式：y=a(x-h)2+k，其中顶点式y=a(x-h)2+k的图像为抛物线，a为抛物线的开口方向和大小，h、k为顶点坐标。

二、二次函数图像的性质1.开口方向：由a的符号决定，a>0时，开口向上；a<0时，开口向下。

2.对称性：二次函数图像关于y轴对称，即若点(x,y)在图像上，则点(-x,y)也在图像上。

3.顶点：二次函数图像的顶点为抛物线的最高点或最低点，顶点式y=a(x-h)^2+k中，(h,k)为顶点坐标。

4.轴：二次函数图像与x轴的交点为方程ax^2+bx+c=0的根，与y轴的交点为c/a。

5.增减性：当a>0时，二次函数图像在顶点左侧单调递减，在顶点右侧单调递增；当a<0时，二次函数图像在顶点左侧单调递增，在顶点右侧单调递减。

三、二次函数图像的解析1.求顶点：根据顶点式y=a(x-h)^2+k，直接得出顶点坐标为(h,k)。

2.求对称轴：对称轴为x=h。

3.求开口大小：开口大小由a的绝对值决定，绝对值越大，开口越大。

4.求与坐标轴的交点：与x轴的交点为方程ax^2+bx+c=0的根，与y轴的交点为c/a。

5.判断增减性：根据a的符号，判断二次函数图像在顶点两侧的单调性。

四、二次函数图像的应用1.实际问题：利用二次函数图像解决实际问题，如抛物线与坐标轴的交点问题、最值问题等。

2.几何问题：利用二次函数图像研究几何图形的性质，如求解三角形面积、距离等问题。

3.物理问题：利用二次函数图像研究物理现象，如抛物线运动、振动等。

五、二次函数图像的变换1.横向变换：对二次函数y=ax2+bx+c进行横向变换，如向左平移h个单位，得到y=a(x+h)2+k；向右平移h个单位，得到y=a(x-h)^2+k。

高中数学常用问题总结归纳

高中数学常用问题总结归纳在高中数学学习过程中，我们常常会遇到一些困难和难题。

本文将总结归纳高中数学常见的问题，帮助同学们更好地理解和应对这些困难。

以下是一些常见问题及解答：一、代数运算问题高中代数运算问题主要包括整式的运算、方程的解法等。

在解决整式的运算问题时，常常会碰到因式分解和配方法的困扰。

在解决方程的解法时，方程的分解、配方法及根的求解是常见的问题。

解决这些问题的关键在于理解代数运算的基本规则，熟练掌握因式分解和配方法，并且灵活运用这些规则和方法。

二、函数与图像问题函数与图像问题是高中数学中的重点内容。

常见问题包括函数的性质、图像的变换和对称性等。

在解决函数的性质问题时，需要掌握函数的定义、定义域、值域、单调性和奇偶性等基本概念。

在解决图像的变换问题时，了解平移、伸缩、翻转和旋转等变换方式，并能够根据给定的函数式进行图像的变换。

此外，对称性是函数与图像问题中的另一个重要方面，需要熟练掌握函数图像的对称性和判定方法。

三、几何问题高中几何问题包括平面几何和立体几何两个方面。

在解决平面几何问题时，常见的问题包括直线与圆的性质、相交定理、相似三角形等。

解决这些问题的关键在于几何图形的性质和定理的理解和运用。

在解决立体几何问题时，需要掌握立体图形的性质、体积和表面积的计算等。

在解决这些问题时，可以多画图、多列方程，以便更好地理解和解决问题。

四、概率与统计问题概率与统计问题是高中数学中的一块重要内容。

在解决概率问题时，常见的问题包括事件的概率计算、条件概率和独立事件等。

解决这些问题需要掌握基本的概率计算方法和公式，并能够运用它们解决实际问题。

在解决统计问题时，需要了解统计数据的收集和整理方法，以及数据的分析和解读。

同时，也需要掌握频率分布表、直方图和折线图等统计图形的绘制和解读。

总结：在高中数学学习过程中，我们会遇到各种各样的问题，但只要我们充分理解并掌握基本的数学概念和方法，灵活运用它们，就能够解决大多数的困难。

数学参考答案

高三数学参考答案一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1. 设全集{|13}U AB x x ==-≤<，(){|23}U AC B x x =<<，则集合B =（）A ．{|12}x x -≤<B ．{|12}x x -≤≤C ．{|23}x x <<D ．{|23}x x ≤< 【命题意图】本题考查集合交并补运算的意义，改编自2007版教材必修1第12页B 组第4题，属基础题. 【答案】B【解析】根据U A B =知图中阴影集合为{|23}x x <<，从而{|12}B x x =-≤≤.故选B .2. 设复数=1z i -，则3z =（）A ．22i -+B ．22i +C ．22i --【命题意图】本题考查复数乘方运算，改编自2007版教材选修2-2第116页A 组第1题（4），属基础题. 【答案】C【解析】3=z ()()()()()321112122i i i i i i -=--=--=--，故选C .3. 以长方体的顶点为顶点的三棱锥共有（）个A ．70B ．64C ．60D ．58【命题意图】本题以简单立体几何计数为背景考查排列组合及组合数的计算，源自2007版教材选修2-3第41页B 组第1题（5）题，属于基础题. 【答案】D【解析】三棱锥有4个顶点，从长方体8个顶点中任取4个点共有488765C =704321⨯⨯⨯=⨯⨯⨯种取法，排除其中四点共面的有：长方体的面6个，对角面6个，可得不同的三棱锥有70-12=58个．故选D ．4. 为加强环境保护，治理空气污染，某环保部门对辖区内一工厂产生的废气进行了监测，发现该厂产生的废气经过过滤后排放，过滤过程中废气的污染物数量(/)P mg L 与时间(h)t 的关系为0=ktP P e-．如果在前5个小时消除了10%的污染物,那么污染物减少27%需要花的时间约为（） A ．13小时 B ．15小时 C ．17小时 D ．19小时【命题意图】本题改编自2007版教材必修1第83页B 组第6题，考查指数和对数的运算、估算和数据处理能力，属于中档题. 【答案】B【解析】由已知5t h =时，00110%)90%P P P =-=（，故500ln 0.990%=5k P P e k -⇒=-．污染物减少27%即30000127%)73%0.7290.9P P P P P =-=≈=（，由ln 0.93ln 0.95550000.9=()(0.9)15tt t P P e P eP t h ==⇒=故选B.5. 已知tan 2α=，则sin()sin()44ππαα-+=（） A ．310-B ．310C ．35-D ．35【命题意图】本题考查三角函数求值，三角恒等变换，属于中档题. 【答案】B【解析】由22111tan 3sin()sin()cos 2()44221tan 10ππααααα--+=-=-⋅=+，故选B.6.大摆锤是一种大型游乐设备（如图），游客坐在圆形的座舱中，面向外，通常大摆锤以压肩作为安全束缚，配以安全带作为二次保险，座舱旋转的同时，悬挂座舱的主轴在电机的驱动下做单摆运动．假设小明坐在点A 处，“大摆锤”启动后，主轴OB 在平面α内绕点O 左右摆动，平面α与水平地面垂直，OB 摆动的过程中，点A 在平面β内绕点B 作圆周运动，并且始终保持OB β⊥，B β∈. 设4OB AB =，在“大摆锤”启动后，下列结论错误的是（）A ．点A 在某个定球面上运动；B ．β与水平地面所成锐角记为θ，直线OB 与水平地面所成角记为δ，则θδ+为定值；C ．可能在某个时刻，//AB α；D ．直线OA 与平面α所成角的正弦值的最大值为17．【命题意图】本题主要考查以实际问题为背景的立体几何问题，侧重考查直观想象的核心素养，属中档题．【答案】C【解析】因为点A 在平面β内绕点B 作圆周运动，并且始终保持OB β⊥，所以22OA OB AB =+又因为,OB AB 为定值，所以OA 也是定值，所以点A 在某个定球面上运动，故A 正确；作出简图如下，OB l ⊥，所以2πδθ+=，故B 正确.因为B α∈，所以不可能有//AB α，故C 不正确；设AB a ，则4OB a =，2217OA AB OB a =+=，当AB α⊥时，直线OA 与平面α所成角最大；此时直线OA 与平面α所成角的正弦值为171717a=，故D 正确；故选C .7. 已知点P 是边长为1的正方形ABCD 所在平面上一点，满足()0PA PB PC PD ⋅++=，则||PD 的最小值是（） ABCD【命题意图】本题考查解析法研究平面几何问题，向量数量积的运算，圆外一点与圆上的点的距离最值问题，属中档题．【答案】A【解析】建立如图所示的平面直角坐标系，则(0,0),(1,0),(1,1),(0,1)A B C D ．设(,)P x y ，则(,),(1,),PA x y PB x y =--=--(1,1),(,1)(23,23)PC x y PD x y PB PC PD x y =--=--⇒++=--，∴由已知得：()(23)()(23)0x x y y --+--=，即22211()()(333x y -+-=，∴点P在以11(,)33M为圆心，半径为3r =的圆上．又||PD 表示圆上的点到原点P的距离，∴min ||||33PD DM r =-==．故选A ．8. 已知函数22,(2)()(2),(2)x x f x x x -≤⎧=⎨->⎩ 若函数()(2)()y f x f x m m R =+--∈恰有2个零点，则m 的取值范围是( )A ．(2,)+∞B ．7(,2)4C ．(0,2) D ．(,2)-∞【命题意图】本题考查求分段函数解析式，利用图像研究函数零点，考查等价转化思想，数形结合思想，属中档偏难题. 【答案】A【解析】由22,(2)()(2),(2)x x f x x x -≤⎧=⎨->⎩得2,(0)(2),(0)x x f x x x ≥⎧-=⎨<⎩，所以222,(0)()(2)2,(02)34,(2)x x x y f x f x x x x x ⎧-+<⎪=+-=≤≤⎨⎪-+>⎩，所以函数()(2)y f x f x m =+--恰有2个零点等价于函数y m =与函数()(2)y f x f x =+-的图象有2个公共点，由图象可知2m >．故选A .二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得3分.9.已知圆O 的半径为定长r ，A 是圆O 所在平面内一个定点，P 是圆上任意一点，线段AP 的垂直平分线l 和直线OP 相交于点Q ．当点P 在圆上运动时，下列判断正确的是( ) A. 当点A 在圆O 内（不与圆心重合）时，点Q 的轨迹是椭圆； B. 点Q 的轨迹可能是一个定点；C. 当点A 在圆O 外时，点Q 的轨迹是双曲线的一支；D. 点Q 的轨迹不可能是抛物线．【命题意图】本题主要考查圆锥曲线的定义，侧重考查数学抽象的核心素养，源自2007版教材选修2-1第49页A 组第7题. 【答案】ABD 【解析】对A,如图1，连接QA ,由已知得|QA |＝|QP |.所以|QO |＋|QA |＝|QO |＋|QP |＝|OP |＝r .又因为点A 在圆内，所以|OA |＜|OP |，根据椭圆的定义，点Q 的轨迹是以O ，A 为焦点，r 为长轴长的椭圆.图1 图2 图3 对B ，如图2，当点A 在圆上时，点Q 与圆心重合，轨迹为定点；对C ，如图3，连接QA ,由已知得|QA |＝|QP |.所以||QA |-|QO ||＝||QP |-|QO ||＝|OP |＝r .又因为点A 在圆外，所以|OA |>|OP |，根据双曲线的定义，点Q 的轨迹是以O ，A 为焦点，r 为实轴长的双曲线.对D,由于当点A 与圆心O 重合时，点Q 的轨迹为圆，综合A,B,C 可知点Q 的轨迹不可能为抛物线. 故选ABD .10.2020年3月15日，某市物价部门对5家商场的某商品一天的销售量及其价格进行调查,5家商场的售价x （元）和销售量y （件）之间的一组数据如表所示：按公式计算，y 与x 的回归直线方程是： 3.2y x a =-+，相关系数0.986r =，则下列说法正确的有( )A ．变量,x y 线性负相关且相关性较强；B ．40a =；C ．当8.5x =时,y 的估计值为12.8；D ．相应于点(10.5,6)的残差约为0.4．【命题意图】本题考查线性回归方程的性质与实际意义，需要注意回归方程过样本中心点，属于基础题．【答案】ABC 【解析】对A ，由表可知y 随x 增大而减少，可认为变量,x y 线性负相关，且相关性强，故A 正确. 对B ,价格平均()199.51010.511105x =++++=,销售量()1111086585y =++++=. 故回归直线恒过定点(10,8)，故8 3.21040a a =-⨯+⇒=，故B 正确. 对C , 当8.5x =时, 3.28.54012.8y =-⨯+=，故C 正确.对D , 相应于点(10,8)的残差约为6(3.210.540)0.4e =--⨯+=-，故D 不正确.故选ABC11. 已知函数()sin cos f x x x ωω=+的最小正周期是π，则下列判断正确的有（）.A ．函数()f x 的图象可由函数2y x =的图象向左平移4π个单位得到； B ．函数()f x 在区间5,88ππ⎡⎤⎢⎥⎣⎦上是减函数；C ．函数()f x 的图象关于点,08π⎛⎫-⎪⎝⎭对称； D ．函数()f x 取得最大值时x 的取值集合为{|+}8，x x k k Z ππ=∈．【命题意图】本题考查正弦函数的周期性、单调性、图象的对称性，函数sin()y A x ωϕ=+的图象变换规律，属于基础题．【答案】BCD【解析】())4f x x π=+．对A ，函数()f x 的图象可由函数2y x =的图象向左平移8π个单位得到，结论不正确．对B ，当5[,]88x ππ∈时，32[,]422x πππ+∈，则()f x 在5[,]88ππ上是减函数，结论正确．对C ，因为f(-8π)=0，得到函数()f x 图象的一个对称中心为(,0)8π-，结论正确．对D ，因为sin(2)122()4428x x k x k k Z ππππππ+=⇒+=+⇒=+∈，结论正确．故选BCD ．12．下列说法正确的是( )A ．若0a b <<，则“1a b +=”是“22log log 2a b +<-”的充要条件；B ．*32n N ,(n 2)(3)n n n ++∀∈+>+；C ．22(0,),sin 241x x x xπ∃∈>+； D ．ABC ∆中，若C ∠为钝角，则()()cos sin cos cos A B >．【命题意图】本题以不等式为载体考查常用逻辑用语，不等式大小比较，导数应用等综合知识，属中档偏难题。

2023年九年级数学下册中考数学综合培优测试卷：一次函数图像与几何变换【含答案】

2023年九年级数学下册中考数学综合培优测试卷：一次函数图像与几何变换一、单选题1．在平面直角坐标系中，把直线y=3x 向左平移2个单位长度，平移后的直线解析式是（）A ．y=3x+2B ．y=3x-2C ．y=3x+6D ．y=3x-62．若一次函数y=2x-3的图象平移后经过点(3，1)，则下列叙述正确的是( )A ．沿x 轴向右平移3个单位长度B ．沿x 轴向右平移1个单位长度C ．沿x 轴向左平移3个单位长度D ．沿x 轴向左平移1个单位长度3．在平面直角坐标系中，将直线沿y 轴向下平移6个单位后，得到一条新的直线，该直y =−32x +3线与x 轴的交点坐标是（）A ．B ．C ．D ．(0，3)(−2，0)(4，0)(6，0)4．已知直线向下平移2个单位长度后得到直线，且直线与直线关于l 1：y =kx +3l 2l 2l 3：y =−x +1y 轴对称，则k 的值为（）.A ．B ．1C ．2D ．3−15．在平面直角坐标系中，将函数的图象向上平移6个单位长度，则平移后的图象与x 轴的y =3x 交点坐标为（） A ．(2,0)B ．(-2,0)C ．(6,0)D ．(-6,0)6．把直线y=-x+1向上平移3个单位长度后得到的直线的解析式为（）A ．y=-x+4B ．C ．y=x+4D ．y=x-27．将直线沿x 轴向左平移3个单位得到直线L ，则直线L 的解析式是（）y =2x +5A ．y ＝2x ＋2B ．y ＝2x ＋8C ．y ＝2x －1D ．y ＝2x ＋118．对于一次函数y ＝﹣2x+4，下列结论错误的是( )A ．函数的图象不经过第三象限B ．函数的图象与x 轴的交点坐标是(2，0)C ．函数的图象向下平移4个单位长度得y ＝﹣2x 的图象D ．若两点A(x 1，y 1)，B(x 2，y 2)在该函数图象上，且x 1＜x 2，则y 1＜y 29．将一次函数y ＝﹣3x 的图象沿y 轴向下平移4个单位长度后，所得图象的函数表达式为（）A ．y ＝﹣3（x ﹣4）B ．y ＝﹣3x +4C ．y ＝﹣3（x +4）D ．y ＝﹣3x ﹣410．在平面直角坐标系中，将直线先关于轴作轴对称变换，再将所得直线关于y =−3x +4x y 轴作轴对称变换，则经两次变换后所得直线的表达式是（）A ．B ．C ．D ．y =4x−3y =−4x +3y =3x +4y =−3x−411．将直线向上平移2个单位长度，则平移后的直线所对应的函数解析式为（）y =−2x +3A ．B ．C ．D ．y =−2x +1y =−4x +5y =−2x +5y =−4x +112．将直线向上平移5个单位长度后得到直线，则下列关于直线的说y =x +1y =kx +b y =kx +b 法错误的是（）A ．函数图象经过第一、二、三象限B ．函数图象与轴的交点在轴的正半轴x xC ．点在函数图象上(−2，4)D ．随的增大而增大y x 二、填空题13．直线 +3的图像是由正比例函数　　图像向（填上或下）平移 y =3x 个单位得到或由正比例函数图像向（填左或右）平移个单位得到可以得到的一条直线14．直线沿轴平移3个单位，则平移后直线与轴的交点坐标为　　.y =2x−1y y 15．在平面直角坐标系中，把直线y=2x 向左平移1个单位长度，平移后的直线解析式是．16．将正比例函数y=﹣2x 的图象沿y 轴向上平移5个单位，则平移后所得图象的解析式是　．17．如图，在平面直角坐标系中，A （1，0），B （3，0），点C 在第一象限，∠ABC=90°，AC=25，直线l 的关系式为： .将△ABC 沿x 轴向左平移，当点C 落在直线l 上时，线段AC 扫y =−x−3过的面积为　　平方单位.18．已知直线与直线关于y 轴对称，当时，，当y 1=ax +b(a ≠0)y 2=kx +5(k ≠0)x >−52y 1>0时，，则直线．x >52y 2<0y 1=三、综合题19．如图，直线与轴、轴交于点、，直线与轴l 1:y =2x +1x y D A l 2:y =mx +4x y 轴分别交于点、，两直线相交于点．C B P(1,b)（1）求，的值； b m （2）求的值；S △PDC −S △PAB （3）垂直于轴的直线与直线，分别交于点，，若线段的长为x x =a l 1l 2M N MN 2，求的值．a 20．如图，直线y ＝kx ＋4的图象与y 轴交于点A ，与x 轴交于点B （2，0），直线AF 交x 轴负半轴于点F ，且OF ＝2OA ．（1）求出k 的值为，直线AF 的解析式为；（2）若将直线AB 沿y 轴向下平移，平移后的直线恰好经过C （﹣3，0），与y 轴相交于点D ，且直线CD 与直线AF 交于点E ，求点E 的坐标．21．如图，一次函数的图象与反比例函数（为常数且）的图象相交于y =x +5y =kx k k ≠0 ，两点.A(−1，m)B（1）求反比例函数的表达式；（2）将一次函数的图象沿轴向下平移个单位，使平移后的图象与反y =x +5y b (b >0)比例函数的图象有且只有一个交点，求的值.y =kx b 22．已知反比例函数与正比例函数相交于 .y 1=kx y 2=x A(2，2)（1）求值.k （2）画出反比例函数的图象.（3）当时，直接写出的范围？y 1>y 2x （4）根据图象，解不等式 .kx <x−323．背景知识：已知两直线，，若，则m ：y 1=k 1x +b 1n ：y 2=k 2x +b 2(k 1k 2≠0)m ⊥n ；若，则 .k 1k 2=−1m//n k 1=k 2应用：在平面直线坐标系中，直线交x 轴于点C ，交y 轴于点D ，若 xoy l 1：y =x−1l 2⊥l 1于点，交y 轴于点A ，交x 轴于点B.P(2，1)（1）求直线的表达式； l 2（2）求的面积；△ABC （3）若将直线向下平移个单位，得到新的直线，交y 轴于点E ，交直线于点F ，l 1q l 3l 2使得，求的值.S △AEF =16q 24．已知：如图1，在平面直角坐标系中，一次函数y ＝ x+3交x 轴于点A ，交y 轴于点B ，点C34是点A 关于y 轴对称的点，过点C 作y 轴平行的射线CD ，交直线AB 与点D ，点P 是射线CD 上的一个动点．（1）求点A ，B 的坐标．（2）如图2，将△ACP 沿着AP 翻折，当点C 的对应点C′落在直线AB 上时，求点P 的坐标．（3）若直线OP 与直线AD 有交点，不妨设交点为Q(不与点D 重合)，连接CQ ，是否存在点P ，使得S △CPQ ＝2S △DPQ ，若存在，请求出对应的点Q 坐标；若不存在，请说明理由．答案解析部分1．【答案】C 2．【答案】B 3．【答案】B 4．【答案】B 5．【答案】B 6．【答案】A 7．【答案】D 8．【答案】D 9．【答案】D 10．【答案】D 11．【答案】C 12．【答案】B13．【答案】y=3x ；上；3；y=3x ；左；114．【答案】（0，2）或（0，）−415．【答案】y=2x+216．【答案】y ＝－2x+517．【答案】4018．【答案】或2x +55+2x19．【答案】（1）解：∵点在直线上，∴ ，P(1,b)l 1:y =2x +1b =2×1+1=3∵ 在直线上，∴ ，∴P(1,3)l 2:y =mx +43=m +4m =−1（2）解：∵直线与轴、轴交于点、，l 2:y =−x +4x y D A ∴ ，，A(0,1)D(−12,0)∵直线与轴、轴分别交于点、，l 2:y =−x +4x y C B ∴ ，，B(0,4)C(4,0)∴S △PDC −S △PAB =12DC ⋅y P −12AB ⋅x P =12×(12+4)×3−12×(4−1)×1=214（3）解：设直线与直线，分别交于点，， x =a l 1l 2M N 当时，；当时，，x =a y M =2a +1x =a y N =4−a ∵ ，∴ ，解得或，MN =2|2a +1−(4−a)|=2a =13a =53所以的值为或 a 135320．【答案】（1）-2；y ＝+412x （2）解：∵直线AB 沿y 轴向下平移，平移后的直线恰好经过C （﹣3，0）， ∴设直线DC 的解析式为y ＝﹣2x+d ，把C （﹣3，0）代入得d ＝﹣6，∴直线DC 的解析式为y ＝﹣2x﹣6．解得，{y =−2x−6y =12x +4{x =−4y =2∴E （﹣4，2）．21．【答案】（1）解：由题意，将点代入一次函数得： A(−1，m)y =x +5m =−1+5=4∴A(−1，4)将点代入得：，解得 A(−1，4)y =k x k−1=4k =−4则反比例函数的表达式为；y =−4x （2）解：将一次函数的图象沿轴向下平移个单位得到的一次函数的解析式为 y =x +5y b y =x +5−b 联立{y =x +5−by =−4x 整理得： x 2+(5−b)x +4=0一次函数的图象与反比例函数的图象有且只有一个交点∵y =x +5−b y =−4x 关于x 的一元二次方程只有一个实数根∴x 2+(5−b)x +4=0 此方程的根的判别式 ∴Δ=(5−b)2−4×4=0解得 b 1=1，b 2=9则b 的值为1或9.22．【答案】（1）解：∵反比例函数y 1= 与正比例函数y 2=x 相交于A （2，2）.kx ∴k=2×2=4（2）解：描出点（1，4），（2，2），（4，1），用平滑的曲线连接，画出反比例函数的图象如图，（3）解：由图象可知，当0＜x＜2和x＜-2时，y1＞y2.（4）解：观察图象，直线y=x向下平移3个单位，与反比例函数的交点为（4，1）和（-1，-4），∴不等式＜x-3的解集为：-1＜x ＜0和x ＞4.kx 23．【答案】（1）解：由，得，l 1：y =x−1k 1=1 ，，∵l 2⊥l 1∴k 2⋅k 1=−1，∴k 2=−1设，把代入解析式得：b=3，l 2：y =−x +b P(2，1) ；∴l 2：y =−x +3（2）解：由图象可得：，与x 轴交于点B 、C ，令y=0，则有 ∵l 2：y =−x +3l 1：y =x−1∴B(3，0)，C(1，0)，又与y 轴交于点A ，令x=0，则有，∵l 2：y =−x +3∴A(0，3) OA=3，BC=2，；∴∴S △ABC =12BC ⋅OA =3（3）解：将直线向下平移个单位，得到新的直线，∵l 1q l 3 ，令x=0则，，∴l 3：y =x−1−q y =−1−q ∴E(0，−1−q) ，∴AE =3−(−1−q)=4+q 交直线于点F ，解得，∵l 3l 2∴{y =−x +3y =x−1−q {x =4+q 2y =2−q 2 ，，∵S △AEF =12AE ⋅F x =16∴12×(4+q)⋅4+q 2=16解得（不符题意，舍去）.q 1=4，q 2=−12 .∴q =424．【答案】（1）解：令x=0，则y=3，∴B （0，3），令y=0，则 x+3=0，34∴x=﹣4，∴A （﹣4，0）；（2）解：∵点C 是点A 关于y 轴对称的点， ∴C （4，0），∵CD ⊥x 轴，∴x=4时，y=6，∴D （4，6），∴AC=8，CD=6，AD=10，由折叠知，AC'=AC=8，∴C'D=AD﹣AC'=2，设PC=a ，∴PC'=a ，DP=6﹣a ，在Rt △DC'P 中，a2+4=（6﹣a ）2，∴a= ，83∴P （4，）；83（3）解：设P （4，m ）， ∴CP=m ，DP=|m﹣6|，∵S △CPQ =2S △DPQ ，∴CP=2PD ，∴2|m﹣6|=m ，∴m=4或m=12，∴P （4，4）或P （4，12），∵直线AB 的解析式为y= x+3①，34当P （4，4）时，直线OP 的解析式为y=x ②，联立①②解得，x=12，y=12，∴Q （12，12），当P （4，12）时，直线OP 解析式为y=3x ③，联立①③解得，x= ，y=4，43∴Q （，4），43。

一次函数与几何图形综合题含答案

一次函数与几何图形综合专题讲座思想方法小结： 1函数方法．函数方法就是用运动、变化的观点来分析题中的数量关系,抽象、升华为函数的模型,进而解决有关问题的方法．函数的实质是研究两个变量之间的对应关系,灵活运用函数方法可以解决许多数学问题．2数形结合法．数形结合法是指将数与形结合,分析、研究、解决问题的一种思想方法,数形结合法在解决与函数有关的问题时,能起到事半功倍的作用．知识规律小结：1常数k ,b 对直线y =kx +bk ≠0位置的影响． ①当b ＞0时,直线与y 轴的正半轴相交；当b =0时,直线经过原点；当b ﹤0时,直线与y 轴的负半轴相交． ②当k ,b 异号时,即－kb＞0时,直线与x 轴正半轴相交；当b =0时,即－k b=0时,直线经过原点；当k ,b 同号时,即－kb﹤0时,直线与x 轴负半轴相交．③当k ＞O ,b ＞O 时,图象经过第一、二、三象限；当k ＞0,b =0时,图象经过第一、三象限；当b ＞O ,b ＜O 时,图象经过第一、三、四象限；当k ﹤O ,b ＞0时,图象经过第一、二、四象限；当k ﹤O ,b =0时,图象经过第二、四象限；当b ＜O ,b ＜O 时,图象经过第二、三、四象限． 2直线y =kx +bk ≠0与直线y =kxk ≠0的位置关系．直线y =kx +bk ≠0平行于直线y =kxk ≠0当b ＞0时,把直线y =kx 向上平移b 个单位,可得直线y =kx +b ；当b ﹤O 时,把直线y =kx 向下平移|b |个单位,可得直线y =kx +b ． 3直线b 1=k 1x +b 1与直线y 2=k 2x +b 2k 1≠0 ,k 2≠0的位置关系．①k 1≠k 2⇔y 1与y 2相交； ②⎩⎨⎧=≠2121b b k k ⇔y 1与y 2相交于y 轴上同一点0,b 1或0,b 2；③⎩⎨⎧≠=2121,b b k k ⇔y 1与y 2平行；④⎩⎨⎧==2121,b b k k ⇔y 1与y 2重合.例题精讲：1、直线y =－2x +2与x 轴、y 轴交于A 、B 两点,C 在y 轴的负半轴上,且OC =OB(1) 求AC(2) 在OA 的延长线上任取一点P ,作PQ ⊥BP ,交直线AC于Q ,试探究BP 与PQ 的数量关系,并证明你的结论;(3) 在2的前提下,作PM ⊥AC 于M ,BP 交AC 于N ,下面两个结论：①MQ +AC /PM 的值不变；②MQ －AC /PM 的值不变,期中只有一个正确结论,请选择并加以证明;2．本题满分12分如图①所示,直线L ：5y mx m =+与x 轴负半轴、y 轴正半轴分别交于A 、xxB 两点;1当OA =OB 时,试确定直线L 的解析式；2在1的条件下,如图②所示,设Q 为AB 延长线上一点,作直线OQ ,过A 、B 两点分别作AM ⊥OQ 于M ,BN ⊥OQ 于N ,若AM =4,BN =3,求MN 的长;3当m 取不同的值时,点B 在y 轴正半轴上运动,分别以OB 、AB 为边,点B 为直角顶点在第一、二象限内作等腰直角△OBF 和等腰直角△ABE ,连EF 交y 轴于P 点,如图③;问：当点B 在 y 轴正半轴上运动时,试猜想PB 的长是否为定值,若是,请求出其值,若不是,说明理由;考点：一次函数综合题；直角三角形全等的判定．专题：代数几何综合题．分析：1是求直线解析式的运用,会把点的坐标转化为线段的长度；2由OA =OB 得到启发,证明∴△AMO ≌△ONB ,用对应线段相等求长度； 3通过两次全等,寻找相等线段,并进行转化,求PB 的长．解答：解：1∵直线L ：y =mx +5m ,∴A －5,0,B 0,5m ,由OA =OB 得5m =5,m =1,第2题图①第2题图②第2题图③CBAl 2l 1xyE ,过点C作CF ⊥3l 于F 分别,请画出图形并求证：BE ＋CF ＝EF 3△ABC 沿y 轴向下平移,AB 边交x 轴于点P ,过P 点的直线与AC 边的延长线相交于点Q ,与y 轴相交与点M ,且BP ＝CQ ,在△ABC 平移的过程中,①OM 为定值；②MC 为定值;在这两个结论中,有且只有一个是正确的,请找出正确的结论,并求出其值;6分考点：轴对称的性质；全等三角形的判定与性质．分析：1根据题意先求直线l1与x轴、y轴的交点A、B的坐标,再根据轴对称的性质求直线l2的上点C的坐标,用待定系数法求直线l2的解析式；2根据题意结合轴对称的性质,先证明△BEA≌△AFC,再根据全等三角形的性质,结合图形证明BE+CF=EF；3首先过Q点作QH⊥y轴于H,证明△QCH≌△PBO,然后根据全等三角形的性质和△QHM≌△POM,从而得HM=OM,根据线段的和差进行计算OM的值．解答：解：1∵直线l1与x轴、y轴分别交于A、B两点,∴A－3,0,B0,3,∵直线l2与直线l1关于x轴对称,∴C0,－3∴直线l2的解析式为：y=－x－3；2如图1．答：BE+CF=EF．∵直线l2与直线l1关于x轴对称,∴AB=BC,∠EBA=∠FAC,∵BE⊥l3,CF⊥l3∴∠BEA=∠AFC=90°∴△BEA≌△AFC∴BE=AF,EA=FC,∴BE+CF=AF+EA=EF；3①对,OM=3过Q点作QH⊥y轴于H,直线l2与直线l1关于x轴对称∵∠POB=∠QHC=90°,BP=CQ,又AB=AC,∴∠ABO=∠ACB=∠HCQ,则△QCH≌△PBOAAS,∴QH=PO=OB=CH∴△QHM≌△POM∴HM=OM∴OM =BC －OB +CM =BC －CH +CM =BC －OM ∴OM =21BC =3．点评：轴对称的性质：对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等．4.如图,在平面直角坐标系中,Aa ,0,B 0,b ,且a 、b 满足.1求直线AB 的解析式；2若点M 为直线y =mx 上一点,且△ABM 是以AB 为底的等腰直角三角形,求m 值； 3过A 点的直线交y 轴于负半轴于P ,N 点的横坐标为－1,过N 点的直线交AP 于点M ,试证明的值为定值．考点：一次函数综合题；二次根式的性质与化简；一次函数图象上点的坐标特征；待定系数法求正比例函数解析式；全等三角形的判定与性质；等腰直角三角形．专题：计算题．分析：1求出a 、b 的值得到A 、B 的坐标,设直线AB 的解析式是y =kx +b ,代入得到方程组,求出即可；2当BM ⊥BA ,且BM =BA 时,过M 作MN ⊥Y 轴于N ,证△BMN ≌△ABOAAS ,求出M 的坐标即可；②当AM ⊥BA ,且AM =BA 时,过M 作MN ⊥X 轴于N ,同法求出M 的坐标；③当AM ⊥BM ,且AM =BM 时,过M 作MN ⊥X 轴于N ,MH ⊥Y 轴于H ,证△BHM ≌△AMN ,求出M 的坐标即可．3设NM 与x 轴的交点为H ,分别过M 、H 作x 轴的垂线垂足为G ,HD 交MP 于D 点,求出H 、G 的坐标,证△AMG ≌△ADH ,△AMG ≌△ADH ≌△DPC ≌△NPC ,推出PN =PD =AD =AM 代入即可求出答案．解答：解：1要使b =有意义,必须a －22=0,4-b =0, ∴a =2,b =4, ∴A 2,0,B 0,4,设直线AB 的解析式是y =kx +b , 代入得：0=2k +b ,4=b , 解得：k =－2,b =4,∴函数解析式为：y =－2x +4, 答：直线AB 的解析式是y =－2x +4． 2如图2,分三种情况：①如图1当BM ⊥BA ,且BM =BA 时,过M 作MN ⊥Y 轴于N , △BMN ≌△ABOAAS ,MN =OB =4,BN =OA =2,∴ON =2+4=6, ∴M 的坐标为4,6 , 代入y =mx 得：m =23, ②如图2当AM ⊥BA ,且AM =BA 时,过M 作MN ⊥X 轴于N ,△BOA ≌△ANMAAS ,同理求出M 的坐标为6,2,m =31,③当AM ⊥BM ,且AM =BM 时,过M 作MN ⊥X 轴于N ,MH ⊥Y 轴于H ,则△BHM ≌△AMN , ∴MN =MH ,设Mx ,x 代入y =mx 得：x =mx ,2∴m =1, 答：m 的值是23或31或1． 3解：如图3,结论2是正确的且定值为2,设NM 与x 轴的交点为H ,分别过M 、H 作x 轴的垂线垂足为G ,HD 交MP 于D 点, 由y =2k x －2k与x 轴交于H 点, ∴H 1,0, 由y =2k x －2k与y =kx －2k 交于M 点, ∴M 3,K , 而A 2,0,∴A 为HG 的中点, ∴△AMG ≌△ADHASA ,又因为N 点的横坐标为－1,且在y =2k x －2k上, ∴可得N 的纵坐标为－K ,同理P 的纵坐标为－2K , ∴ND 平行于x 轴且N 、D 的横坐标分别为－1、1 ∴N 与D 关于y 轴对称,∵△AMG ≌△ADH ≌△DPC ≌△NPC , ∴PN =PD =AD =AM , ∴AMPN-PM =2．点评：本题主要考查对一次函数图象上点的坐标特征,等腰直角三角形性质,用待定系数法求正比例函数的解析式,全等三角形的性质和判定,二次根式的性质等知识点的理解和掌握,综合运用这些性质进行推理和计算是解此题的关键．5.如图,直线AB ：y =－x －b 分别与x 、y 轴交于A 6,0、B 两点,过点B 的直线交x 轴负半轴于C ,且OB ：OC=3：1;1求直线BC 的解析式：2直线EF ：y =kx －kk ≠0交AB 于E ,交BC 于点F ,交x 轴于D ,是否存在这样的直线EF ,使得S △EBD =S △FBD 若存在,求出k 的值；若不存在,说明理由3如图,P 为A 点右侧x 轴上的一动点,以P 为直角顶点,BP 为腰在第一象限内作等腰直角△BPQ ,连接QA 并延长交ｙ轴于点K ,当P 点运动时,K 点的位置是否发现变化若不变,请求出它的坐标；如果变化,请说明理由;考点：一次函数综合题；一次函数的定义；正比例函数的图象；待定系数法求一次函数解析式．专题：计算题．分析：代入点的坐标求出解析式y =3x +6,利用坐标相等求出k 的值,用三角形全等的相等关系求出点的坐标．解答：解：1由已知：0=－6－b ,∴b =－6,∴AB ：y =－x +6． ∴B 0,6 ∴OB =6∵OB ：OC =3：1,OC =3OB=2, ∴C －2,0设BC 的解析式是Y =ax +c ,代入得；6=0•a +c , 0=－2a +c , 解得：a =3, c =6, ∴BC ：y =3x +6．直线BC 的解析式是：y =3x +6；2过E 、F 分别作EM ⊥x 轴,FN ⊥x 轴,则∠EMD =∠FND =90°． ∵S △EBD =S △FBD , ∴DE =DF ．又∵∠NDF =∠EDM , ∴△NFD ≌△EDM , ∴FN =ME ．联立y =kx －k , y =－x +6 得y E =1k 5k, 联立y =kx －k ,y =3x +6得y F =3-k 9k． ∵FN =－y F ,ME =y E , ∴1k 5k =3-k 9k-． ∵k ≠0,∴5k －3=－9k +1, ∴k =73； 3不变化K 0,－6．过Q 作QH ⊥x 轴于H , ∵△BPQ 是等腰直角三角形, ∴∠BPQ =90°,PB =PQ , ∵∠BOA =∠QHA =90°, ∴∠BPO =∠PQH , ∴△BOP ≌△HPQ , ∴PH =BO ,OP =QH , ∴PH +PO =BO +QH , 即OA +AH =BO +QH , 又OA =OB , ∴AH =QH ,∴△AHQ 是等腰直角三角形, ∴∠QAH =45°, ∴∠OAK =45°,∴△AOK 为等腰直角三角形, ∴OK =OA =6, ∴K 0,－6．点评：此题是一个综合运用的题,关键是正确求解析式和灵活运用解析式去解．6. 如图,直线AB 交X 轴负半轴于Bm ,0,交Y 轴负半轴于A 0,m ,OC ⊥AB 于C －2,－2; （1）求m 的值；-4m 2CG OG GB ,,45OAOB GOB G =∴===∴∆∆∆∴︒=∠∴∆∴=都是等腰直角三角形为等腰直角三角形的垂线，垂足为作过OCB CGO CGB CBO AOB （2）直线AD 交OC 于D ,交X 轴于E ,过B 作BF ⊥AD于F ,若OD =OE ,求AEBF 的值； 21BF 2BF BH BF AE BF 2BH BF BH AE BH ASA AOE BOH 90AOE BOH AO BO EAO HBO AOE BOH )(BF ASA AFH AFB )(AF AF 90AFH AFB AFH AFB FEBADC )(OED FEB ODEOED ODOE FAH HBO ===∴=+==∴∆≅∆∴⎪⎩⎪⎨⎧︒=∠=∠=∠=∠∆∆=∴∆≅∆∴⎪⎩⎪⎨⎧∠=∠=︒=∠=∠∆∆∠=∠∴∠=∠∴∠=∠∴∠=∠∠=∠∠=∠∴=∠=∠BFHF FAH BAF FAHCAD CADHBO ODE ADC 等）（全等三角形对应边相）（（已知）（已证）中，和在全等三角形对应边相等）（已证（公共边）中和在对顶角相等，（同角的余角相等）（3）如图,P 为x 轴上B 点左侧任一点,以AP 为边作等腰直角△APM ,其中PA =PM ,直线MB 交y 轴于Q ,当P 在x 轴上运动时,线段OQ 长是否发生变化若不变,求其值；若变化,说明理由;7.在平面直角坐标系中,一次函数y=ax+b的图像过点B－1,,与x轴交于点A4,0,与y轴交于点C,与直线y=kx交于点P,且PO=PA1求a+b的值；2求k 的值；3D 为PC 上一点,DF ⊥x 轴于点F ,交OP 于点E ,若DE=2EF ,求D 点坐标. 考点：一次函数与二元一次方程组．专题：计算题；数形结合；待定系数法．分析：1根据题意知,一次函数y =ax +b 的图象过点B －1, 25和点A 4,0,把A 、B 代入求值即可； 2设Px ,y ,根据PO =PA ,列出方程,并与y =kx 组成方程组,解方程组；3设点Dx ,－ 21x +2,因为点E 在直线y = 21x 上,所以Ex ,21x ,Fx ,0,再根据等量关系DE =2EF 列方程求解．解答：解：1根据题意得：25=－a +b 0=4a +b解方程组得：a =21, b =2 ∴a +b =－21+2=23,即a +b =23； 2设Px ,y ,则点P 即在一次函数y =ax +b 上,又在直线y =kx 上,由1得：一次函数y =ax +b 的解析式是y =－21x +2, 又∵PO =PA ,∴x 2+y 2=4－x 2+y 2 y =kxy =2x +2, 解方程组得：x =2,y =1,k =21, ∴k 的值是21；3设点Dx ,－21x +2,则Ex ,21x ,Fx ,0, ∵DE =2EF ,∴－21x +2－21x =2×21x , 解得：x =1,则－21x +2=－21×1+2=23, ∴D 1,23．点评：本题要求利用图象求解各问题,要认真体会点的坐标,一次函数与一元一次方程组之间的内在联系．8. 在直角坐标系中,B 、A 分别在x ,y 轴上,B 的坐标为3,0,∠ABO =30°,AC 平分∠OAB 交x 轴于C ；（1）求C 的坐标；解：∵∠AOB =90° ∠ABO =30°∴∠OAB =30°又 ∵ AC 是∠OAB 的角平分线∴∠OAC =∠CAB =30°∵OB =3∴OA =3OC =1 即 C 1,0（2）若D 为AB 中点,∠EDF =60°,证明：CE +CF =OC证明：取CB 中点H ,连CD ,DH∵ AO =3 CO =1 ∴AC =2又∵D ,H 分别是AB ,CD 中点∴DH =AC 21 AB =23 ∵ DB =21AB =3 BC =2 ∠ABC =30° ∴ BC =2 CD =2 ∠CDB =60°CD =1=DH∵ ∠EOF =∠EDC +∠CDF =60 ° ∠CDB =∠CDF +∠FDH =60°∴∠EDC =∠FDH∵AC =BC =2∴CD ⊥AB ADC =90°∵∠CBA =30°∴∠ECD =60°∵HD =HB =1∴∠DHF =60°在△DCE 和 △DHF 中∠EDC =∠FDH∠DCE =∠DHFDC =DH∴△DCE ≌ △DHFAAS∴CE =HF∴CH =CF +FH =CF +CE =1 OC =1∴CH =OC∴OC =CE +CF（3）若D 为AB 上一点,以D 作△DEC ,使DC =DE ,∠EDC =120°,连BE ,试问∠EBC 的度数是否发生变化；若不变,请求值;解：不变 ∠EBC =60°设DB 与CE 交与点GDC =DE ∠EDC =120°∴∠DEC =∠DCE =30°在△DGC 和△ DCB 中∠CDG =∠BDC∠DCG =∠DBC =30∴△DGC ∽ △DCB∴DG DC =DCDB DC =DE∴DG DE =DE DB 在EDG 和BDE 中DG DE =DEDB ∠EDG =∠BDE∴△EDG ∽ △BDE∴∠DEG =∠DBE =30°∴∠EBD =∠DBE +∠DBC =60°9、如图,直线AB 交x 轴正半轴于点Aa ,0,交y 轴正半轴于点B 0, b ,且a 、b 满足4 a + |4－b |=01求A 、B 两点的坐标；2D 为OA 的中点,连接BD ,过点O 作OE ⊥BD 于F ,交AB 于E ,求证∠BDO =∠EDA ；3如图,P 为x 轴上A 点右侧任意一点,以BP 为边作等腰Rt △PBM ,其中PB =PM ,直线MA 交y轴于点Q ,当点P 在x 轴上运动时,线段OQ的长是否发生变化若不变,求其值；若变化,求线段OQ 的取值范围. 考点：全等三角形的判定与性质；非负数的性质：绝对值；非负数的性质：算术平方根．专题：证明题；探究型．分析：①首先根据已知条件和非负数的性质得到关于a 、b 的方程,解方程组即可求出a ,b 的值,也就能写出A ,B 的坐标； A BO D EFyxA B O MP Qx y②作出∠AOB 的平分线,通过证△BOG ≌△OAE 得到其对应角相等解决问题；③过M 作x 轴的垂线,通过证明△PBO ≌△MPN 得出MN =AN ,转化到等腰直角三角形中去就很好解决了．解答：解：①∵4 a +|4－b |=0∴a =4,b =4,∴A 4,0,B 0,4；2作∠AOB 的角平分线,交BD 于G ,∴∠BOG =∠OAE =45°,OB =OA ,∠OBG =∠AOE =90°－∠BOF ,∴△BOG ≌△OAE ,∴OG =AE ．∵∠GOD =∠A =45°,OD =AD ,∴△GOD ≌△EDA ．∴∠GDO =∠ADE ．3过M 作MN ⊥x 轴,垂足为N ．∵∠BPM =90°,∴∠BPO +∠MPN =90°．∵∠AOB =∠MNP =90°,∴∠BPO =∠PMN ,∠PBO =∠MPN ．∵BP =MP ,∴△PBO ≌△MPN ,MN =OP ,PN =AO =BO ,OP =OA +AP =PN +AP =AN ,∴MN =AN ,∠MAN =45°．∵∠BAO =45°,∴∠BAO +∠OAQ =90°∴△BAQ 是等腰直角三角形．∴OB =OQ =4．∴无论P 点怎么动OQ 的长不变．点评：1考查的是根式和绝对值的性质． 2考查的是全等三角形的判定和性质．3本题灵活考查的是全等三角形的判定与性质,还有特殊三角形的性质．10、如图,平面直角坐标系中,点A 、B 分别在x 、y 轴上,点B 的坐标为0,1,∠BAO =30°．1求AB 的长度；2以AB 为一边作等边△ABE ,作OA 的垂直平分线MN 交AB 的垂线AD 于点D ．求证：BD =OE ．D E N M BO x y AD EB O xy F A3在2的条件下,连结DE 交AB 于F ．求证：F 为DE 的中点．考点：全等三角形的判定与性质；线段垂直平分线的性质；等边三角形的性质；含30度角的直角三角形．专题：计算题；证明题．分析：1直接运用直角三角形30°角的性质即可．2连接OD ,易证△ADO 为等边三角形,再证△ABD ≌△AEO 即可．3作EH ⊥AB 于H ,先证△ABO ≌△AEH ,得AO =EH ,再证△AFD ≌△EFH 即可．解答：1解：∵在Rt △ABO 中,∠BAO =30°,∴AB =2BO =2；2证明：连接OD ,∵△ABE 为等边三角形,∴AB =AE ,∠EAB =60°,∵∠BAO =30°,作OA 的垂直平分线MN 交AB 的垂线AD 于点D ,∴∠DAO =60°．∴∠EAO =∠NAB又∵DO =DA ,∴△ADO 为等边三角形．∴DA =AO ．在△ABD 与△AEO 中,∵AB =AE ,∠EAO =∠NAB ,DA =AO∴△ABD ≌△AEO ．∴BD =OE ．3证明：作EH ⊥AB 于H ．∵AE =BE ,∴AH =21AB ,∵BO =21AB ,∴AH =BO ,在Rt △AEH 与Rt △BAO 中,AH =BO ,AE =AB∴Rt △AEH ≌Rt △BAO ,∴EH =AO =AD ．又∵∠EHF =∠DAF =90°,在△HFE 与△AFD 中,∠EHF =∠DAF ,∠EFH =∠DFA ,EH =AD∴△HFE ≌△AFD ,∴EF =DF ．∴F 为DE 的中点．点评：本题主要考查全等三角形与等边三角形的巧妙结合,来证明角相等和线段相等．11.如图,直线y =3x +1分别与坐标轴交于A 、B 两点,在y 轴的负半轴上截取OC =OB .（1）求直线AC 的解析式；解：∵ 直线y =31x +1分别与坐标轴交于A 、B 两点∴ 可得点A 坐标为－3,0,点B 坐标为0,1∵ OC =OB∴ 可得点C 坐标为0,－1设直线AC 的解析式为y =kx +b将A －3,0,C 0,－1代入解析式－3k +b =0且b =－1可得k =－31,b =－1 ∴ 直线AC 的解析式为y =31x －1 （2）在x 轴上取一点D －1,0,过点D 做AB 的垂线,垂足为E ,交AC 于点F ,交y 轴于点G ,求F 点的坐标；解：∵ GE ⊥AB∴k k 1EG AB ⋅=- ∴ 131k ==3GE --设直线GE 的解析式为'y=-3x+b将点D 坐标－1,0代入,得'y=-3b 0⨯(-1)+= ∴ 'b 3=-∴ 直线GE 的解析式为y =－3x －3联立y =31x －1与y =－3x －3,可求出34x =-, 将其代入方程可得y =34-,∴ F 点的坐标为34-,34-（3）过点B 作AC 的平行线BM ,过点O 作直线y =kxk ＞0,分别交直线AC 、BM 于点H 、I ,试求ABBI AH +的值; 解：过点O 作AC 的平行线ON 交AB 于点N∵BM //AC ∴OIOB OH OC =∵OB =OC∴OI =OH∴O 为IH 的中点∵BM //AC∴=NBOI NA OH∵ OI =OH∴ NB =NA∴ N 为AB 中点∴ ON 是四边形ABIH 的中位线∴ AH +BI =2ON∵ N 是AB 的中点,∆AOB 是直角三角形∴ AB =2ON 直接三角形斜边的中线等于斜边的一半∴ AH +BI =AB∴ABBI AH +=1 12.如图,直线AB ：y =－x －b 分别与x 、y 轴交于A 6,0、B 两点,过点B 的直线交x 轴负半轴于C ,且OB ：OC =3：1.（1）求直线BC 的解析式；解：1因为直线AB ：y =－x －b 过点A 6,0.带入解析式就可以得到 b =－6即直线AB ：y =－x +6∵B 为直线AB 与y 轴的交点∴点 B 0,6∵OB ：OC =3：1∴OC =2 点 C －2,0已知直线上的两点 B 、C ;设直线的解析式为y =kx +m带入B 、C 的坐标;可以算出k =3 ,m =6所以BC 的解析式为：y =3x +6（2）直线EF ：y =kx －kk ≠0交AB 于E ,交BC 于点F ,交x 轴于D ,是否存在这样的直线EF ,使得S △EBD =S △FBD 若存在,求出k 的值；若不存在,说明理由2 假设存在满足题中条件的k 值因为直线EF : y =kx －kk ≠0交x 轴于点D ;所以D 点坐标为1,0在图中标出点D ,且过点D 做一直线,相交与直线AB ,BC 分别与点E ,F 然后观察△EBD 和△FBD则 S △EBD = 21DE ×h S △FBD =21DF ×h 两个三角形的高其实是一样的要使这两个三角形面积相等,只要满足DE =DF 就可以了∵点E 在直线AB 上,∴设点E 的坐标为p ,－p +6∵点F 在直线BC 上,∴设点F 的坐标为q ,3q +6而上面我们已经得到点D 的坐标为1,0点E 、F 又关于点D 对称,所以我们就可以得到两个等式,即：p +q /2=1－p +6+3q +6/2=0这样就可以求得：p =29,q =－25 点E 的坐标即为29,23,点F 的坐标即为－25,－23 把点E 代入直线EF 的解析式,得到k =73 所以存在k ,且k =73 （3）如图,P 为A 点右侧x 轴上的一动点,以P 为直角顶点,BP 为腰在第一象限内作等腰直角△BPQ ,连接QA 并延长交y 轴于点K ,当P 点运动时,K 点的位置是否发生变化若不变,请求出它的坐标；如果变化,请说明理由;3 K 点的位置不发生变化理由：首先假设直线QA 的解析式为y =ax +b ,点P 的坐标为p ,0过点Q 作直线QH 垂直于x 轴,交点为H这样图中就可以形成两个三角形,分别是△BOP 和△PHQ ,且两个三角形都是直角三角形;∵△BPQ 为等腰直角三角形,直角顶点为P∴BP =PQ ,∠BPO +∠QPH =180º—90º=90º又∵在直角三角形中,∴∠QPH +∠PQH =90º∴根据上面两个等式,我们可以得到∠BPO =∠PQH且PB=QP所以在△BOP和△PHQ中∠BOP=∠PHQ∠BPO=∠PQHPB=QP∴△BOP≌△PHQAAS∴OP=HQ=p OB=HP=6 全等三角形的对应边相等∴点Q的坐标为p+6,p然后将点A和点Q的坐标代入直线QA的解析式：y=ax+b中,得到：a=1,b=－6也就是说a,b为固定值,并不随点Pp,0的改变而改变这样直线QA：y=x－6的延长线交于Y轴的K点也不会随点P的变化而变化了;求得点K的坐标为0,－6实战练习：1.已知,如图,直线AB：y=－x+8与x轴、y轴分别相交于点B、A,过点B作直线AB的垂线交y轴于点D.（1）求直线BD的解析式；（2）若点C是x轴负半轴上的任意一点,过点C作AC的垂线与BD相交于点E,请你判断：线段AC与CE的大小关系并证明你的判断；（3）若点G为第二象限内任一点,连结EG,过点A作AF⊥FG于F,连结CF,当点C在x轴的负半轴上运动时,∠CFE的度数是否发生变化若不变,请求出∠CFE的度数；若变化,请求出其变化范围.2.直线y=x+2与x、y轴交于A、B两点,C为AB的中点.（1）求C的坐标；（2）如图,M为x轴正半轴上一点,N为OB上一点,若BN+OM=MN,求∠NCM的度数；（3）P为过B点的直线上一点,PD⊥x轴于D,PD=PB,E为直线BP上一点,F为y轴负半轴上一点,且DE=DF,试探究BF－BE的值的情况.3.如图,一次函数y=ax－b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于B0,－4且OA=AB,△OAB的面积为6.（1）求两函数的解析式；（2）若M2,0,直线BM与AO交于P,求P点的坐标；（3）在x轴上是否存在一点E,使S△ABE=5,若存在,求E点的坐标；若不存在,请说明理由;。

2022年华东师大版八年级数学下册第十七章函数及其图像综合测试练习题(精选含解析)

八年级数学下册第十七章函数及其图像综合测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、甲、乙两地相距s 千来，汽车从甲地匀速行驶到乙地，行驶的时间t （小时）关于行驶速度v （千米时）的函数图像是（）A ．B ．C ．D ．2、下列函数中，表示y 是x 的反比例函数的是（）A ．y =B ．a y x =C ．21y x =D ．13y x =3、把函数y ＝x 的图象向上平移2个单位，下列各点在平移后的函数图象上的是（）A ．（2，2）B ．（2，3）C ．（2，4）D ．（2，5）4、火车匀速通过隧道时，火车在隧道内的长度y （米）与火车行驶时间x （秒）之间的关系用图象描述如图所示，有下列结论：①火车的速度为30米/秒；②火车的长度为120米；③火车整体都在隧道内的时间为35秒；④隧道长度为1200米．其中正确的结论是（）A ．①②③B ．①②④C ．③④D ．①③④5、如图，点A 在双曲线k y x=上，AB x ⊥轴于B ，3AOB S =△，则k 的值为（）A ．不能确定B ．3C ．18D ．66、如图，Rt AOB Rt CDA ≌，且点A 、B 的坐标分别为(1,0),(0,2)B -，则OD 长是（）A ．3-B ．5C ．4D ．37、如图1，在Rt ABC 中，90C ∠=︒，点D 是BC 的中点，动点P 从点C 出发沿CA AB -运动到点B ，设点P 的运动路程为x ，PCD 的面积为y ，y 与x 的函数图象如图2所示，则AB 的长为（）．A ．10B ．12C ．D ．8、下列函数中，属于正比例函数的是（）A ．22y x =+B ．21y x =-+C ．1y x = D ．5x y = 9、在平面直角坐标系中，点()8,15-所在的象限是（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限10、已知点()14,y -，()22,y 都在直线21y x =-+上，则1y 、2y 大小关系是（）A ．12y y <B ．12y y =C ．12y y >D ．不能计较第Ⅱ卷（非选择题 70分）二、填空题（10小题，每小题4分，共计40分）1、在平面直角坐标系中，如果一个点的横、纵坐标均为整数，那么我们称这个点是格点．若格点M （a ﹣2，a +1）在第二象限，则a 的值为 _____．2、下列函数：①y kx =；②23y x =；③2(1)y x x x =--；④21y x =+；⑤22y x =-．其中一定是一次函数的有____________．（只是填写序号）3、观察图象可知：当k ＞0时，直线y ＝kx ＋b 从左向右______；当k＜0时，直线y＝kx＋b从左向右______．由此可知，一次函数y＝kx＋b（k，b是常数，k≠0）具有如下性质：当k＞0时，y随x的增大而______；当k＜0时，y随x的增大而______．4、函数y＝－7x的图象在______象限内，从左向右______，y随x的增大而______．函数y＝7x的图象在______象限内，从左向右______，y随x的增大而______．5、如图，已知△P1OA1，△P2A1A2，△P3A2A3…△PnAn﹣1An都是等腰直角三角形，点P1、P2、P3…Pn都在函数y＝4x（x＞0）的图象上，斜边OA1、A1A2、A2A3…An﹣1An都在x轴上．则点A2021的坐标为____．6、在平面内画两条互相垂直、原点重合的数轴，组成_______．水平的数轴称为x轴或______，取向______方向为正方向；竖直的数轴称为y轴或______，取向______方向为正方向．两坐标轴的交点为平面直角坐标系的______，一般用______来表示．7、在弹性限度内，弹簧的长度y（厘米）是所挂物体质量x（千克）的一次函数．一根弹簧不挂物体时长14.5厘米；当所挂物体的质量为3千克时，弹簧长16厘米．请写出y与x之间的关系式，并求当所挂物体的质量为4千克时弹簧的长度．解：设y ＝kx ＋b （k ≠0）由题意得：14.5＝b ，16＝3k ＋b ，解得：b ＝___，k ＝___．所以在弹性限度内，y =___，当x ＝4时，y ＝0.5×4＋14.5＝___（厘米）．即物体的质量为4千克时，弹簧长度为16.5厘米．8、解决含有多个变量的问题时，可以分析这些变量之间的关系，从中选取一个取值能影响其他变量的值的变量作为_______，然后根据问题的条件寻求可以反映实际问题的函数，以此作为解决问题的数学模型．9、如图，大、小两个正方形的中心均与平面直角坐标系的原点O 重合，边分别与坐标轴平行．反比例函数y ＝k x （k ≠0）的图象，与大正方形的一边交于点A （32，4），且经过小正方形的顶点B ．求图中阴影部分的面积为 _____．10、自行车运动员在长为10000 m 的路段上进行骑车训练，行驶全程所用时间为t s ，行驶的平均速度为v m/s ，则vt ＝______，用t 表示v 的函数表达式为_______；y 与x 的乘积为－2，用x 表示y 的函数表达式为______．以上两个函数表达式都具有________的形式，其中________是常数．具有________的形式．三、解答题（5小题，每小题6分，共计30分）1、请根据学习“一次函数”时积累的经验和方研究函数2y x =-+的图象和性质，并解决问题．（1）填空：①当x ＝0时，2y x =-+= ；②当x ＞0时，2y x =-+= ；③当x ＜0时，2y x =-+= ；（2）在平面直角坐标系中作出函数2y x =-+的图象；（3）观察函数图象，写出关于这个函数的两条结论；（4）进一步探究函数图象发现：①函数图象与x 轴有个交点，方程20x -+=有个解； ②方程22x -+=有个解；③若关于x 的方程2x a -+=无解，则a 的取值范围是．2、如图，在平面直角坐标系中，点B ，C ，D 的坐标分别是什么？3、如图分别是函数y＝k1x，y＝k2x，y＝k3x，y＝k4x的图象．(1)k1k2，k3k4（填“＞”或“＜”）；(2)用不等号将k1，k2，k3，k4及0依次连接起来．4、如图1，一次函数y＝43x+4的图象与x轴、y轴分别交于点A、B．(1)则点A的坐标为_______，点B的坐标为______；(2)如图2，点P为y轴上的动点，以点P为圆心，PB长为半径画弧，与BA的延长线交于点E，连接PE，已知PB＝PE，求证：∠BPE＝2∠OAB；(3)在（2）的条件下，如图3，连接PA，以PA为腰作等腰三角形PAQ，其中PA＝PQ，∠APQ＝2∠OAB．连接OQ．①则图中（不添加其他辅助线）与∠EPA相等的角有______；（都写出来）②试求线段OQ长的最小值．5、某通讯公司推出①②两种收费方式供用户选择，其中一种有月租费，另一种没有月租费，且两种收费方式的通话时间x（分钟）与收费y（元）的关系如图所示：(1)分别求出①②两种方案的收费y（元）与通话时间x（分钟）之间的函数关系式．(2)当x值为多少时两种方案收费相等．(3)选择哪种收费方案更合算？-参考答案-一、单选题1、B【解析】【分析】直接根据题意得出函数关系式，进而得出函数图象．解：由题意可得：t=sv，是反比例函数，故只有选项B符合题意．故选：B．【点睛】此题主要考查了反比例函数的应用，正确得出函数关系式是解题关键．2、D【解析】略3、C【解析】【分析】由函数“上加下减”的原则解题．【详解】解：由“上加下减”的原则可知，将直线y＝x的图象向上平移2个单位所得直线的解析式为：y＝x+2，当x＝2时，y＝2+2＝4，所以在平移后的函数图象上的是（2，4），故选：C．【点睛】本题考查函数图象的平移，一次函数图象的性质等知识，是基础考点，掌握相关知识是解题关键．4、D【分析】根据函数的图象即可确定在BC 段，所用的时间是5秒，路程是150米，则速度是30米/秒，进而即可确定其它答案．【详解】解：在BC 段，所用的时间是5秒，路程是150米，则速度是30米/秒．故①正确；火车的长度是150米，故②错误；整个火车都在隧道内的时间是：45-5-5=35秒，故③正确；隧道长是：45×30-150=1200（米），故④正确．故选：D ．【点睛】本题主要考查了用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．5、D【解析】【分析】根据反比例函数k 的几何意义直接求解即可【详解】解：∵3AOB S =△ ∴=32k 函数图象经过一、三象限0k ∴>6k ∴=故选D【点睛】本题考查了反比例函数0k y k x=≠（）中比例系数k 的几何意义：过反比例函数图象上任意一点分别作x 轴、y 轴的垂线，则垂线与坐标轴所围成的矩形的面积为k ．6、D【解析】【分析】利用全等三角形的性质证明即可．【详解】解：∵A （-1，0），B （0，2），∴OA =1，OB =2，∵△AOB ≌△CDA ，∴OB =AD =2，∴OD =AD +AO =2+1=3，故选D ．【点睛】本题考查全等三角形的性质，解题的关键是掌握全等三角形的性质，属于中考常考题型．7、D【解析】【分析】由图像可知，当08x ≤≤时，y 与x 的函关系为：y =x ，当x =8时，y =8，即P 与A 重合时，PCD ∆的面积为8，据此求出CD ，BC ，再根据勾股定理求出AB 即可P ．【详解】解：如图2，当08x ≤≤时，设y =kx ，将（3，3）代入得，k =1，()08y x x ∴=≤≤ ，当P 与A 重合时，即：PC =AC =8，由图像可知，把x =8代入y =x ，y =8，8PCD S ∆∴=,1882DC ∴⨯=， 2DC ∴=, D 是BC 的中点，24BC CD ==在Rt ABC ∆中，AB故选：D ．【点睛】本题考查了动点问题的函数图象，数形结合并熟练掌握三角形的面积计算公式与勾股定理是解题的关键．8、D【分析】根据正比例函数的定义逐个判断即可．【详解】解：A ．是二次函数，不是正比例函数，故本选项不符合题意；B ．是一次函数，但不是正比例函数，故本选项不符合题意；C ．是反比例函数，不是正比例函数，故本选项不符合题意；D ．是正比例函数，故本选项符合题意；故选：D ．【点睛】本题考查了正比例函数的定义，能熟记正比例函数的定义是解此题的关键，注意：形如y ＝kx ＋b （k 、b 为常数，k ≠0）的函数，叫一次函数，当b ＝0时，函数也叫正比例函数．9、D【解析】【分析】根据第四象限内横坐标大于零，纵坐标小于零，可得答案．【详解】解：点()8,15-所在的象限是第四象限，故选：D ．【点睛】本题考查了点的坐标，熟记各象限内点的坐标特征是解题关键．10、C【分析】根据一次函数的增减性解答．【详解】解：∵直线21y x =-+，k =-2<0，∴y 随着x 的增大而减小，∵点()14,y -，()22,y 都在直线21y x =-+上，-4<2，∴12y y >，故选：C ．【点睛】此题考查了一次函数的增减性：当k >0时，y 随x 的增大而增大；当k <0时，y 随x 的增大而减小，熟记性质是解题的关键．二、填空题1、0或1##1或0【解析】【分析】根据点M 在第二象限，求出a 的取值范围，再由格点定义得到整数a 的值．【详解】解：∵点M （a ﹣2，a +1）在第二象限，∴a -2<0，a +1>0，∴-1<a <2，∵点M 为格点，∴a 为整数，即a 的值为0或1，故答案为：0或1．【点睛】此题考查了象限内点的坐标特点，解不等式组，解题的关键是熟记直角坐标系中各象限内点的坐标特征．2、②③⑤【解析】【分析】根据一次函数的定义条件解答即可．【详解】解：①y ＝kx 当k ＝0时原式不是一次函数； ②23y x =是一次函数；③由于2(1)y x x x =--＝x ，则2(1)y x x x =--是一次函数；④y ＝x 2＋1自变量次数不为1，故不是一次函数；⑤y ＝22−x 是一次函数．故答案为：②③⑤．【点睛】本题主要考查了一次函数的定义，一次函数y ＝kx ＋b 的定义条件是：k 、b 为常数，k ≠0，自变量次数为1．3、上升下降增大减小【解析】略4、第二、四象限下降减少第一、三象限上升增大【解析】略5、（0）【解析】【分析】首先根据等腰直角三角形的性质，知点P1的横、纵坐标相等，再结合双曲线的解析式得到点P1的坐标是（2，2），则根据等腰三角形的三线合一求得点A1的坐标；同样根据等腰直角三角形的性质、点A1的坐标和双曲线的解析式求得A2点的坐标；根据A1、A2点的坐标特征即可推而广之．【详解】解：可设点P1（x，y），根据等腰直角三角形的性质可得：x=y，又∵y=4x，则x2=4，∴x=±2（负值舍去），再根据等腰三角形的三线合一，得A1的坐标是（4，0），设点P2的坐标是（4+y，y），又∵y=4x，则y（4+y）=4，即y2+4y-4=0解得，y1y2∵y＞0，∴y，再根据等腰三角形的三线合一，得A2的坐标是（0）；An点的坐标是（0）．可以再进一步求得点A故点A2021的坐标为（0）．故答案是：（0）．【点睛】本题考查了反比例函数的综合应用，解决此题的关键是要根据等腰直角三角形的性质以及反比例函数的解析式进行求解．6、平面直角坐标系横轴右纵轴上原点O【解析】略x+ 16.57、 14.5 0.5 0.514.5【解析】略8、自变量【解析】略9、40【解析】【分析】根据待定系数法求出k即可得到反比例函数的解析式；利用反比例函数系数k的几何意义求出小正方形的面积，再求出大正方形在第一象限的顶点坐标，得到大正方形的面积，根据图中阴影部分的面积=大正方形的面积-小正方形的面积即可求出结果．【详解】解：反比例函数k y x=的图象经过点3(,4)2A ， 4623k ∴=⨯=， ∴反比例函数的解析式为6y x=；小正方形的中心与平面直角坐标系的原点O 重合，边分别与坐标轴平行，∴设B 点的坐标为(,)m m ，反比例函数6y x =的图象经过B 点， 6m m ∴=， 26m ∴=，∴小正方形的面积为2424m =，大正方形的中心与平面直角坐标系的原点O 重合，边分别与坐标轴平行，且3(,4)2A ，∴大正方形在第一象限的顶点坐标为(4,4)，∴大正方形的面积为24464⨯=，∴图中阴影部分的面积=大正方形的面积-小正方形的面积642440=-=．【点睛】本题主要考查了待定系数法求反比例函数的解析式，反比例函数系数k 的几何意义，正方形的性质，熟练掌握反比例函数系数k 的几何意义是解决问题的关键．10、 10000 10000v t = 2y x -= 分式分子 (0)k y k x=≠ 【解析】略三、解答题1、（1）2；-x +2，x +2；（2）见解析；（3）函数图象关于y 轴对称；当x =0时，y 有最大值2；（4）①2 2；②1；③2a >．【解析】【分析】（1）利用绝对值的意义，分别代入计算，即可得到答案；（2）结合（1）的结论，画出分段函数的图像即可；（3）结合函数图像，归纳出函数的性质即可；（4）结合函数图像，分别进行计算，即可得到答案；【详解】解：（1）①当x ＝0时，22y x =-+=；②当x ＞0时，22y x x =-+=-+；③当x ＜0时，22y x x =-+=+；故答案为：2；-x +2；x +2；（2）函数y ＝-|x |+2的图象，如图所示：（3）函数图象关于y 轴对称；当x =0时，y 有最大值2．（答案不唯一）（4）①函数图象与x 轴有2个交点，方程20x -+=有2个解； ②方程22x -+=有1个解；③若关于x 的方程2x a -+=无解，则a 的取值范围是2a >．故答案为：2；2；1；2a >．【点睛】本题考查了一次函数的图像和性质，绝对值的意义，解题的关键是熟练掌握题意，正确的画出图像．2、B （-2，3），C （4，-3），D （-1，-4）【解析】略3、 (1)＜，＜(2)k 1＜k 2＜0＜k 3＜k 4【解析】略4、 (1)（-3，0）；（0，4）(2)证明见解析(3)①∠QPO ，∠BAQ ；②线段OQ 长的最小值为125 【解析】【分析】（1）根据题意令x ＝0，y ＝0求一次函数与坐标轴的交点；（2）由题意可知与∠EPA相等的角有∠QPO，∠BAQ．利用三角形内角和定理解决问题；（3）根据题意可知如图3中，连接BQ交x轴于T．证明△APE≌△QPB（SAS），推出∠AEP＝∠QBP，再证明OA＝OT，推出直线BT的解析式为为：443y x=+，推出点Q在直线y＝﹣43x+4上运动，再根据垂线段最短，即可解决问题．(1)解：在y＝43x+4中，令y＝0，得0＝43x+4，解得x＝﹣3，∴A（﹣3，0），在y＝43x+4中，令x＝0，得y＝4，∴B（0，4）；故答案为：（﹣3，0），（0，4）．(2)证明：如图2中，设∠ABO＝α，则∠OAB＝90°﹣α，∵PB＝PE，∴∠PBE＝∠PEB＝α，∴∠BPE＝180°﹣∠PBE﹣∠PEB＝180°﹣2α＝2（90°﹣α），∴∠BPE＝2∠OAB．(3)解：①结论：∠QPO，∠BAQ理由：如图3中，∵∠APQ＝∠BPE＝2∠OAB，∵∠BPE＝2∠OAB，∴∠APQ＝∠BPE．∴∠APQ﹣∠APB＝∠BPE﹣∠APB．∴∠QPO＝∠EPA．又∵PE＝PB，AP＝PQ∴∠PEB＝∠PBE＝∠PAQ＝∠AQP．∴∠BAQ＝180°﹣∠EAQ＝180°﹣∠APQ＝∠EPA．∴与∠EPA相等的角有∠QPO，∠BAQ．故答案为：∠QPO，∠BAQ．②如图3中，连接BQ交x轴于T．∵AP＝PQ，PE＝PB，∠APQ＝∠BPE，∴∠APE＝∠QPB，在△APE和△QPB中，PA PQAPE QPBPE PB=⎧⎪∠=∠⎨⎪=⎩，∴△APE≌△QPB（SAS），∴∠AEP＝∠QBP，∵∠AEP＝∠EBP，∴∠ABO＝∠QBP，∵∠ABO+∠BAO＝90°，∠OBT+∠OTB＝90°，∴∠BAO＝∠BTO，∴BA＝BT，∵BO⊥AT，∴OA＝OT，∴直线BT的解析式为为：443y x=+，∴点Q在直线y＝﹣43x+4上运动，∵B（0，4），T（3，0）．∴BT＝5．当OQ⊥BT时，OQ最小．∵S△BOT＝12×3×4＝12×5×OQ．∴OQ＝125．∴线段OQ长的最小值为125．【点睛】本题属于一次函数综合题，考查一次函数图象与坐标轴的交点问题、全等三角形的判定和性质、等腰三角形的性质、锐角三角函数及最短距离等知识，正确寻找全等三角形是解题的关键．5、(1)①：y=0.1x+30；②：y=0.2x(2)当x值为300时两种方案收费相等(3)当0＜x＜300时，选择②种方案；当x=300时，两种方案一样；当x＞300时，选择①种方案．【解析】【分析】（1）根据函数图象中的数据，用待定系数法可以分别求得①②两种方案的收费y（元）与通话时间x（分钟）之间的函数关系式；（2）令（1）中的两个函数值相等，即可求出当x 值为多少时两种方案收费相等；（3）根据（2）中的结果和函数图象，可以写出当x 何值时，选择哪种收费方案更合算．(1)解：设①种方案的收费y （元）与通话时间x （分钟）之间的函数关系式是y =kx +b ，∵点(0，30)，(500，80)在此函数图象上，∴3050080b k b =⎧⎨+=⎩，解得0.130k b =⎧⎨=⎩，即①种方案的收费y （元）与通话时间x （分钟）之间的函数关系式是y =0.1x +30；设②种方案的收费y （元）与通话时间x （分钟）之间的函数关系式是y =ax ，∵点(500，100)在此函数图象上，∴100=500a ，得a =0.2，即②种方案的收费y （元）与通话时间x （分钟）之间的函数关系式是y =0.2x ；(2)解：令0.1x +30=0.2x ，解得x =300，答：当x 值为300时两种方案收费相等；(3)解：由（2）中的结果和图象可得，当0＜x＜300时，选择②种方案；当x=300时，两种方案一样；当x＞300时，选择①种方案．【点睛】本题考查一次函数的应用，解答本题的关键是明确题意，求出相应的函数解析式，利用数形结合的思想解答．。

中考数学《二次函数图像的几何变换》专项练习题及答案

中考数学《二次函数图像的几何变换》专项练习题及答案一、单选题1．在平面直角坐标系中，将抛物线y=x2﹣4先向右平移两个单位，再向上平移两个单位，得到的抛物线的解析式是（）A．y=（x+2）2+2B．y=（x﹣2）2﹣2C．y=（x﹣2）2+2D．y=（x+2）2﹣22．将抛物线影响y=-x2向左平移2个单位后，得到的抛物线的解析式是（）A．y=-（x+2）2B．y=-x2+2C．y=-（x-2）2D．y=-x2-23．若将抛物线y=5x2先向右平移2个单位，再向下平移3个单位，可得到新的抛物线是（）A．y=5(x+2)2+3B．y=5(x−2)2+3C．y=5(x+2)2−3D．y=5(x−2)2−34．在平面直角坐标系内，将抛物线y=(x+2)2−3经过两次平移后，得到的新抛物线为y=(x−1)2−4.下列对这一平移过程描述正确的是（）A．先向右平移3个单位长度，再向下平移1个单位长度B．先向左平移3个单位长度，再向下平移1个单位长度C．先向右平移3个单位长度，再向上平移1个单位长度D．先向左平移3个单位长度，再向下平移1个单位长度5．下列平移中，不能使二次函数y=2x2+4x−6经过原点的是（）A．向左平移1个单位B．向右平移3个单位C．向上平移6个单位D．向上平移8个单位6．二次函数y＝x2－1的图象可由下列哪个函数图象向右平移2个单位，向下平移2个单位得到（）A．y=(x−2)2+1B．y=(x+2)2+1C．y=(x−2)2−3D．y=(x+2)2+37．如图，在直角坐标系中，O为坐标原点，点A（4，0），以OA为对角线作正方形ABOC，若将抛物线y= 12x2沿射线OC平移得到新抛物线y= 12（x-m）2+k（m＞0）．则当新抛物线与正方形的边AB有公共点时，m的值一定是（）A．2，6，8B．0<m≤6C．0<m≤8 D．0<m≤2 或6 ≤ m≤88．将抛物线y＝3x2的图象先向右平移2个单位，再向上平移5个单位后，得到的抛物线解析式是（）A．y＝3（x﹣2）2﹣5B．y＝3（x﹣2）2+5C．y＝3（x+2）2﹣5D．y＝3（x+2）2+59．在平面直角坐标系中，对于二次函数y=(x−2)2+1，下列说法中错误的是（）A．y的最小值为1B．图象顶点坐标为（2，1），对称轴为直线x=2C．当x<2时，y的值随x值的增大而增大，当x≥2时，y的值随x值的增大而减小D．它的图象可以由y=x2的图象向右平移2个单位长度，再向上平移1个单位长度得到10．抛物线y＝12x2向左平移1个单位，再向上平移2个单位后，所得抛物线的表达式是（）A．y＝12（x+1）2﹣2B．y＝12（x﹣1）2+2C．y＝12（x﹣1）2﹣2D．y＝12（x+1）2+211．将二次函数y=x2的图象如何平移可得到y=x2+4x+3的图象（）A．向右平移2个单位，向上平移一个单位B．向右平移2个单位，向下平移一个单位C．向左平移2个单位，向下平移一个单位D．向左平移2个单位，向上平移一个单位12．把抛物线y=(x+2)2向下平移2个单位长度，再向右平移1个单位长度，所得抛物线是（）A．y=(x+2)2+2B．y=(x+1)2−2C．y=x2+2D．y=x2−2二、填空题13．将抛物线y=﹣x2先向下平移2个单位，再向右平移3个单位后所得抛物线的解析式为．14．抛物线y=-x2-2x+3可由抛物线y=ax2平移得到，则a的值是。

2023学年北师大版八年级数学上学期压轴题专题09 一次函数与几何图形综合问题的五种类型含解析

专题09 一次函数与几何图形综合问题的五种类型类型一、面积问题例1．在平面直角坐标系xOy 中，已知直线AB 与x 轴交于A 点（2，0）与y 轴交于点B （0，1）．（1）求直线AB 的解析式；（2）点M （-1，y 1），N （3，y 2）在直线AB 上，比较y 1与y 2的大小. （3）若x 轴上有一点C ，且S △ABC =2，求点C 的坐标【变式训练1】已知一次函数12y kx =+的图象与x 轴交于点(2,0)B -，与正比例函数2y mx =的图象交于点(1,)A a ．（1）分别求k ，m 的值；（2）点C 为x 轴上一动点，如果ABC 的面积是6，请求出点C 的坐标．【变式训练2】如图，在正方形ABCD 中，4AB =，点P 为线段DC 上的一个动点．设DP x =，由点,,,A B C P 首尾顺次相接形成图形的面积为y ．（1）求y 关于x 的函数表达式及x 的取值范围；（2）设（1）中函数图象的两个端点分别为M N 、，且P 为第一象限内位于直线MN 右侧的一个动点，若MNP △正好构成一个等腰直角三角形，请求出满足条件的P 点坐标；（3）在（2）的条件下，若l 为经过(1,0)-且垂直于x 轴的直线，Q 为l 上的一个动点，使得MNQNMPS S=，请直接写出符合条件的点Q 的坐标．【变式训练3】如图，已知直线1:3l y x =+与过点A （3，0）的直线2l 交于点C （1，m ），且与x 轴交于点B ，与y 轴交于点D ．（1）求直线2l 的解析式；（2）若点D 关于x 轴的对称点为P ，求△PBC 的面积．类型二、一次函数与平行四边形例1.如图，在平面直角坐标系中，直线AB 与x ，y 轴分别交于点(4,0)A ，(0,3)B ，点C 是直线554y x =-+上的一个动点，连接BC ．（1）求直线AB 的函数解析式；（2）如图1，若//BC x 轴，求点C 到直线AB 的距离；（3）如图2，点(1,0)E ，点D 是直线AB 上的动点，试探索点C ，D 在运动过程中，是否存在以B ，C ，D ，E 为顶点的四边形是平行四边形，若存在，请直接写出点C ，D 的坐标；若不存在，请说明理由．【变式训练1】一次函数y = kx+1（k ≠ 0）的图象过点P （-3，2），与x 轴交于点A ，与y 轴交于点B ．（1）求k 的值及点A 、B 的坐标；（2）已知点C （-1，0），若以A ，B ，C ，D 为顶点的四边形是平行四边形，请直接写出所有符合条件的点D 的坐标．【变式训练2】平面直角坐标系xOy 中，直线1l ：2y x b =+与直线2l ：12y x =交于点()2,P m ．（1）求m ，b 的值；（2）直线()0x n n =≠与直线1l ，2l 分别交于M ，N 两点，当MN ＝3时，若以M ，N ，P ，Q 为顶点的四边形是平行四边形，请直接写出点Q 的坐标．类型三、一次函数与等腰三角形例1．一次函数的图像与x 轴、y 轴分别交于点A 0），B （0，1），以AB 为边在第一象限内做等边△ABC ．（1）线段AB 的长是，△BAO ＝ °，点C 的坐标是；（2）如果在第二象限内有一点P （a ，1），试用含a 的代数式表示四边形ABPO 的面积．（3）在y 轴上存在点M ，使△MAB 为等腰三角形，请直接写出点M 的坐标．【变式训练1】如图一，已知直线l ：6y x =-+与x 轴交于点A ，与y 轴交于点B ，直线m 与v 轴交于点(0,2)C -，与直线l 交于点(,1)D t ．（1）求直线m 的解析式；（2）如图二，点P 在直线l 上且在y 轴左侧，过点P 作//PQ y 轴交直线m 于点Q ，交x 轴于点G ，当2PCG QCG S S ∆∆=，求出P ，Q 两点的坐标；（3）将直线l ：6y x =-+向左平移12个单位得到直线n 交x 轴于E 点，点F 是点C 关于原点对称点．过点F 作直线//k x 轴．点M 在直线k 上，写出以点C ，E ，M ，为顶点且CE 为腰的等腰三角形，并把求其中一个点M 的坐标的过程写出来．【变式训练2】在如图的平面直角坐标系中，直线n 过点A （0，﹣2），且与直线l 交于点B （3，2），直线l 与y 轴交于点C ．（1）求直线n 的函数表达式；（2）若△ABC 的面积为9，求点C 的坐标；（3）若△ABC 是等腰三角形，求直线l 的函数表达式．【变式训练3】如图，直线1:l y ax a =-，1l 与x 轴交于点B ，直线2l 经过点(4,0)A ，直线1l ，2l 交于点(2,3)C -．（1）a =______；点B 的坐标为______．（2）求直线2l 的解析表达式；（3）求ABC 的面积；（4）在直线2l 上存在异于点C 的另一点P ，使得ABP △为等腰三角形，请直接写出P 点的横坐标？类型四、一次函数与直角三角形例1.如图，在平面直角坐标系中，函数y ＝－x ＋2的图象与x 轴，y 轴分别交于点A ，B ，与函数y ＝13x ＋b 的图象交于点C （－2，m ）．（1）求m 和b 的值；（2）函数y ＝－x ＋b 的图象与x 轴交于点D ，点E 从点D 出发沿DA 向，以每秒2个单位长度匀速运动到点M （到A 停止运动），设点E 的运动时间为t 秒． ①当ΔACE 的面积为12时，求t 的值；②在点E 运动过程中，是否存在t 的值，使ΔACE 为直角三角形？若存在，请求出t 的值；若不存在，请说明理由．【变式训练1】如图1，在菱形ABCD 中，60ABC ∠=︒，对角线AC BD 、交于点,O P 从B 点出发，沿B DC →→方向匀速运动，P 点运动速度为1cm/s ．图2是点P 运动时，APC △的面积2()cm y 随P 点运动时间()s x变化的函数图像．（1）AB =_______cm,a =_____；（2）P 点在BD 上运动时，x 为何值时，四边形ADCP ；（3）在P 点运动过程中，是否存在某一时刻使得APB △为直角三角形，若存在，求x 的值；若不存在，请说明理由．【变式训练2】在平面直角坐标系xOy 中，将直线2y x =向下平移2个单位后，与一次函数132y x =-+的图象相交于点A ．（1）将直线2y x =向下平移2个单位后对应的解析式为；（2）求点A 的坐标；（3）若P 是x 轴上一点，且满足△OAP 是等腰直角三角形，直接写出点P 的坐标．类型五、最值问题例1．如图，将直线34y x=-向上平移后经过点()4,3A，分别交x轴y轴于点B、C．（1）求直线BC的函数表达式；（2）点P为直线BC上一动点，连接OP．问：线段OP的长是否存在最小值？若存在，求出线段OP的最小值，若不存在，请说明理由．【变式训练1】如图，四边形OABC是张放在平面直角坐标系中的正方形纸片，点O与坐标原点重合，点A在x轴正半轴上，点C在y轴正半轴上，5OC=，点E在边BC上．（1）若点N的坐标为(3,0)，过点N且平行于y轴的直线MN与EB交于点M，将纸片沿直线OE折叠，顶点C恰好落在MN上，并与MN上的点G重合．①求点G、点E的坐标；②若直线:l y mx n=+平行于直线OE，且与长方形ABMN有公共点，请直接写出n的取值范围．（2）若点E为BC上的一动点，点C关于直线OE的对称点为G，连接BG，请求出线段BG的最小值．专题09 一次函数与几何图形综合问题的五种类型类型一、面积问题例1．在平面直角坐标系xOy 中，已知直线AB 与x 轴交于A 点（2，0）与y 轴交于点B （0，1）．（1）求直线AB 的解析式；（2）点M （-1，y 1），N （3，y 2）在直线AB 上，比较y 1与y 2的大小. （3）若x 轴上有一点C ，且S △ABC =2，求点C 的坐标【答案】（1）112y x =-+；（2）y 1＞y 2；（3）()6,0C 或()2,0-．【解析】（1）解：设直线AB 的解析式为y kx b =+△A （2，0）B （0,1），△201k b b +=⎧⎨=⎩，解得：k =12-，b =12△直线AB 的解析式为112y x =-+ （2）△y ＝﹣12x +1中k ＝﹣12＜0，△y 值随x 值的增大而减小， △﹣1＜3，△y 1＞y 2；（3）△x 轴上有一点C ，设点C （x ，0），△AC ＝|2﹣x |， △S △ABC ＝2，△12×|2﹣x |×1＝2，△x ＝﹣2或x ＝6， △C （﹣2，0）或C （6，0）．故答案为：（1）112y x =-+；（2）y 1＞y 2；（3）()6,0C 或()2,0-．【变式训练1】已知一次函数12y kx =+的图象与x 轴交于点(2,0)B -，与正比例函数2y mx =的图象交于点(1,)A a ．（1）分别求k ，m 的值；（2）点C 为x 轴上一动点，如果ABC 的面积是6，请求出点C 的坐标．【答案】（1）1k =，3m =；（2）点C 的坐标为(2,0)或(6,0)- 【解析】（1）一次函数1=2y kx +的图象与x 轴交于点2,0B -（），220k ∴-+=1k ∴=12y x ∴=+一次函数12y x =+的图象与正比例函数2y mx =的图象交于点(1,)A a ，12a ∴=+，a m =，3m ∴=；（2）设点C 的坐标为(,0)n ，过点A 作AD x ⊥轴，垂足为点D ．ABC 的面积是6，162BC AD ∴⋅=，1|(2)|362n ∴--⨯=，2n ∴=或6n =-∴点C 的坐标为(2,0)或(6,0)-，或过点A 作AD x ⊥轴，垂足为点D ．ABC 的面积是6，162BC AD ∴⋅=，1362BC ∴⨯=，4BC ∴=，点B 的坐标为(2,0)-，∴点C 的坐标为(2)0，或(60)-，．【变式训练2】如图，在正方形ABCD 中，4AB =，点P 为线段DC 上的一个动点．设DP x =，由点,,,A B C P 首尾顺次相接形成图形的面积为y ．（1）求y 关于x 的函数表达式及x 的取值范围；（2）设（1）中函数图象的两个端点分别为M N 、，且P 为第一象限内位于直线MN 右侧的一个动点，若MNP △正好构成一个等腰直角三角形，请求出满足条件的P 点坐标；（3）在（2）的条件下，若l 为经过(1,0)-且垂直于x 轴的直线，Q 为l 上的一个动点，使得MNQNMPS S=，请直接写出符合条件的点Q 的坐标．【答案】（1）y =-2x +16，0＜x ＜4；（2）（12，12）或（8，20）或（6，14）；（3）（-1，-2）或（-1，8）或（-1，38）或（-1，28）【解析】（1）由线段的和差，得PC =（4-x ），由梯形的面积公式，得y =-2x +16， △四边形ABCD 是正方形，△AB =CD =4，△x 的取值范围是0＜x ＜4；（2）设P 点坐标是（a ，b ），M （0，16），N （4，8），以MN 为边，在MN 右侧做正方形，MNAB ，正方形中心为H ，则易知A ，B ，H 即为所求P 的坐标；示意图如下求得A （12，12），B （8，20），O （6，14），故P 点可能的坐标为（12，12）或（8，20）或（6，14）；（3）由S △MNQ =S △NMP ，设Q （-1，m ），QN 所在直线方程为y =kx +b ，把Q 和N 代入方程，求得b =845m +，则可求S △NMP =12|16-b |×[4-（-1）]=|36-2m |当P 为（12，12）时，S △MNQ =40，△|36-2m |=40；解得m =-2或38，当P （8，20），同理解得m =-2或38，当P （8，20），有S △MNQ =20，解得m =8或28，综上，符合条件的Q 的坐标为（-1，-2）或（-1，8）或（-1，38）或（-1，28）．【变式训练3】如图，已知直线1:3l y x =+与过点A （3，0）的直线2l 交于点C （1，m ），且与x 轴交于点B ，与y 轴交于点D ．（1）求直线2l 的解析式；（2）若点D 关于x 轴的对称点为P ，求△PBC 的面积．【答案】（1）-26y x =+；（2）12．【解析】（1）把(1,)C m 代入y ＝x ＋3，得1＋3＝m ，△m ＝4，△(1,4)C设2l 的解析式为：y ＝kx ＋b （k ≠0），将点A ,C 的坐标代入，则430k b k b +=⎧⎨+=⎩ 解得26k b =-⎧⎨=⎩，△2l 的解析式为：-26y x =+（2）当y ＝0时，30x += ，△3x =-，△(3,0)B -，当x =0时，y =3，△(0,3)D ，△点P 、D 关于x 轴对称，△(0,3)P - ,如图，连接BP ,PC ,设PC 与x 轴的交点为Q ，设直线PC 的解析式为(0)y kx b k =+≠，将点(1,4),(0,3)C P -代入：43k b b +=⎧⎨=-⎩，解得73k b =⎧⎨=-⎩，△直线PC 的解析式为：73y x =-，令y =0，解得37x =， △BPCBQP BQCSSS=+1122c BQ OP BQ y =+1124()712227c BQ OP y =+=⨯⨯=．类型二、一次函数与平行四边形例1.如图，在平面直角坐标系中，直线AB 与x ，y 轴分别交于点(4,0)A ，(0,3)B ，点C 是直线554y x =-+上的一个动点，连接BC ．（1）求直线AB 的函数解析式；（2）如图1，若//BC x 轴，求点C 到直线AB 的距离；（3）如图2，点(1,0)E ，点D 是直线AB 上的动点，试探索点C ，D 在运动过程中，是否存在以B ，C ，D ，E 为顶点的四边形是平行四边形，若存在，请直接写出点C ，D 的坐标；若不存在，请说明理由．【答案】（1）334y x =-+；（2）2425；（3）17(2，45)8-、15(2-，69)8或1(2-，45)8、1(2，21)8或17(2，45)8-、15(2，21)8- 【解析】（1）设直线AB 的表达式为y kx b =+，则304b k b =⎧⎨=+⎩，解得343k b ⎧=-⎪⎨⎪=⎩，故AB 的表达式为334y x =-+；（2）//BC x 轴，故点C 的纵坐标为3，当3y =时，即5534y x =-+=，解得85x =，即点C 的坐标为8(5，3)，则85BC =；由点A 、B的坐标得，5AB ==，过点C 作CH AB ⊥于点H ，在△ABC 中，S △ABC =1122BC OB AB CH ⨯⨯=⨯⨯，即18135252CH ⨯⨯=⨯⨯，解得：2425CH =，即点C 到直线AB 的距离为2425；（3）设点C 、D 的坐标分别为5(,5)4m m -+、3(,3)4n n -+，当EB 是对角线时，由中点坐标公式得：01m n +=+且53305344m n +=-+-+，解得172152m n ⎧=⎪⎪⎨⎪=-⎪⎩，故点C 、D 的坐标分别为17(2，45)8-、15(2-，69)8；当EC 是对角线时，同理可得：1m n +=且5353344m n -+=-++，解得，1212m n ⎧=-⎪⎪⎨⎪=⎪⎩故点C 、D 的坐标分别为1(2-，45)8、1(2，21)8；当ED 是对角线时，同理可得：1n m +=且35035344n m -+=-++，解得152172m n ⎧=⎪⎪⎨⎪=⎪⎩，故点C 、D 的坐标分别为17(2，45)8-、15(2，21)8-．综上，点C 、D 的坐标分别为17(2，45)8-、15(2-，69)8或1(2-，45)8、1(2，21)8或17(2，45)8-、15(2，21)8-．【变式训练1】一次函数y = kx+1（k ≠ 0）的图象过点P （-3，2），与x 轴交于点A ，与y 轴交于点B ．（1）求k 的值及点A 、B 的坐标；（2）已知点C （-1，0），若以A ，B ，C ，D 为顶点的四边形是平行四边形，请直接写出所有符合条件的点D 的坐标．【答案】（1）13k =-，与x 轴交于点A （3，0），与y 轴交于点B （0，1）；（2）D （4，1）或D （2，-1）或D （-4，1）．【解析】（1）将P （-3，2）代入()10y kx k =+≠，得：13k =-函数表达式：113y x =-+，令y =0，x =3，令x =0，y =1，△与x 轴交于点A （3，0），与y 轴交于点B （0，1）；（2）分三种情况：①BC 为对角线时，点D 的坐标为（-4，1）；②AB 为对角线时，点D 的坐标为（4，1），③AC 为对角线时，点D 的坐标为（2，-1）．综上所述，点D 的坐标是（4，1）或（-4，1）或（2，-1）．【变式训练2】平面直角坐标系xOy 中，直线1l ：2y x b =+与直线2l ：12y x =交于点()2,P m ．（1）求m ，b 的值；（2）直线()0x n n =≠与直线1l ，2l 分别交于M ，N 两点，当MN ＝3时，若以M ，N ，P ，Q 为顶点的四边形是平行四边形，请直接写出点Q 的坐标．【答案】（1）13m b ==-,；（2）点Q 的坐标为()2,4，()2,2-或()6,6 【解析】（1）△直线1l ：2y x b =+与直线2l ：12y x =交于点()2,P m ，△4122m b m =+⎧⎪⎨=⨯⎪⎩，△1 3.m b ==-，（2）依题意可得直线1l ：23y x =-，△直线1l 与y 轴的交点为（0，-3） △直线()0x n n =≠与直线1l ，2l 分别交于M ，N 两点， MN ＝3， △M ，N 不是y 轴上的点，设M （x ，2x -3），则N （x ，12x ）由MN ＝3，得（2x -3）-12x =3，解得x =4，△M （4，5），则N （4，2） △以M ，N ，P ，Q 为顶点的四边形是平行四边形，①当MN 为四边形MPNQ 的对角线时，MN 的中点坐标为（4，3.5）故()2,1P 、Q 关于（4，3.5）对称，△点Q 的坐标为()6,6，②当MN 为四边形MNQP 的一边时，MN =PQ =3，且PQ 与y 轴平行，故点Q 的坐标为()2,4或()2,2- 综上，点Q 的坐标为()2,4，()2,2-或()6,6．类型三、一次函数与等腰三角形例1．一次函数的图像与x 轴、y 轴分别交于点A0），B （0，1），以AB 为边在第一象限内做等边△ABC ．（1）线段AB 的长是，△BAO ＝ °，点C 的坐标是；（2）如果在第二象限内有一点P （a ，1），试用含a 的代数式表示四边形ABPO 的面积．（3）在y 轴上存在点M ，使△MAB 为等腰三角形，请直接写出点M 的坐标．【答案】（1）2，30，C2）；（22a-；（3）（0，-1）或（0，3）【解析】（1）(3A ，0)，(0,1)B ，在Rt AOB ∆中，2AB =，2OB =AB ，可30BAO ∴∠=︒，以AB 为边在第一象限内做等边ABC ∆，60ACB ∠=︒∴，AB AC =，90OAC ∴∠=︒，C ∴2)，故答案为2，30，C 2)；（2）四边形ABPO 的面积BAO =∆的面积OBP +∆的面积1111()222a a =+⨯⨯-=；（3）2AB =，30BAO ∠=︒，60OBA ∴∠=︒，①当AB BM =时，2BM =，(0,1)M -或(0,3)M ；②当AB AM =时，ABM ∆是等边三角形，M ∴与B 关于x 轴对称，(0,1)M ∴-； ③当BM AM =时，ABM ∆是等边三角形，M ∴与B 关于x 轴对称，(0,1)M ∴-；综上所述：MAB ∆为等腰三角形时，M 点坐标为(0,1)-或(0,3)．【变式训练1】如图一，已知直线l ：6y x =-+与x 轴交于点A ，与y 轴交于点B ，直线m 与v 轴交于点(0,2)C -，与直线l 交于点(,1)D t ．（1）求直线m 的解析式；（2）如图二，点P 在直线l 上且在y 轴左侧，过点P 作//PQ y 轴交直线m 于点Q ，交x 轴于点G ，当2PCG QCG S S ∆∆=，求出P ，Q 两点的坐标；（3）将直线l ：6y x =-+向左平移12个单位得到直线n 交x 轴于E 点，点F 是点C 关于原点对称点．过点F 作直线//k x 轴．点M 在直线k 上，写出以点C ，E ，M ，为顶点且CE 为腰的等腰三角形，并把求其中一个点M 的坐标的过程写出来．【答案】（1）直线m 的解析式为325y x =-；（2）P 点的坐标为（-10，16），Q 点坐标为（-10，-8）；（3）当CE 为腰时，点M 的坐标为：M （2）或M （-2）或M （0，2）．过程见解析．【解析】（1）△D （t ，1）在直线l ：y =-x +6上，△1=-t +6，△t =5，△D （5，1），设直线m 的解析式为y =kx +b ，将点C ，D 代入得，512k b b +=⎧⎨=-⎩，解得，352k b ⎧=⎪⎨⎪=-⎩，所以，直线m 的解析式为325y x =-；（2）设P （a ，6-a ），△点P 在x 轴的左侧，△0a < △PQ △轴，G （a ，0），Q （a ，325a -），如图，点P 、Q 在x 轴两侧，△S △PCG =12PG •（-a ），S △QCG =12GQ •(-a )且S △PCG =2S △QCG ， △PG =2QG ，△6-a =2（2-35a ），解得：a =-10， △66(10)16a -=--=，332(10)2855a -=⨯--=-△P 点的坐标为（-10，16），Q 点坐标为（-10，-8）；（3）对于直线l ：y =-x +6，当x =0时，y =6；当y =0时，x =6．△A （6，0），B （0，6），△将直线l ：y =-x +6向左平移12个单位得直线n 交x 轴于点E ，点F 是点C 关于原点的对称点．点C （0，-2）， △E （-6，0），F （0，2），如图，△将直线l ：y =-x +6向左平移12个单位得直线n ，△直线n ：y =-x -6，又△F （0，2）△k 的解析式为：y =2，设M （a ，2），则MCME，CE ，当△MCE 为等腰三角形，且CE 为腰，有：①CE =MCa =a =-M （2）．M （-2）， ②ME =CE解得，a =0或a =-12（此时三点共线，不构成三角形，舍去），即M （0，2），综上，当CE 为腰时，点M 的坐标为：M （2）或M （-2）或M （0，2）．【变式训练2】在如图的平面直角坐标系中，直线n 过点A （0，﹣2），且与直线l 交于点B （3，2），直线l 与y 轴交于点C ．（1）求直线n 的函数表达式；（2）若△ABC 的面积为9，求点C 的坐标；（3）若△ABC 是等腰三角形，求直线l 的函数表达式．【答案】（1）y ＝43x ﹣2；（2）C （0，4）或（0，﹣8）；（3）直线l 的解析式为：y ＝﹣13x +3或y ＝3x ﹣7或y ＝﹣43x +6或y ＝724x +98 【解析】（1）设直线n 的解析式为：y ＝kx +b ，△直线n ：y ＝kx +b 过点A （0，﹣2）、点B （3，2），△232b k b =-⎧⎨+=⎩ ，解得：432k b ⎧=⎪⎨⎪=-⎩ ，△直线n 的函数表达式为：y ＝43x ﹣2；（2）△△ABC 的面积为9，△9＝12•AC •3，△AC ＝6， △OA ＝2，△OC ＝6﹣2＝4或OC ＝6+2＝8，△C （0，4）或（0，﹣8）；（3）分四种情况：①如图1，当AB ＝AC 时，△A （0，﹣2），B （3，2），△AB 22(22)＝5，△AC ＝5，△OA ＝2，△OC ＝3，△C （0，3），设直线l 的解析式为：y ＝mx +n ，把B （3，2）和C （0，3）代入得：323m n n +=⎧⎨=⎩ ，解得：133m n ⎧=-⎪⎨⎪=⎩ ，△直线l 的函数表达式为：y ＝13-x +3； ②如图2，AB ＝AC ＝5，△C （0，﹣7），同理可得直线l 的解析式为：y ＝3x ﹣7； ③如图3，AB ＝BC ，过点B 作BD △y 轴于点D ，△CD ＝AD ＝4，△C （0，6），同理可得直线l 的解析式为：y ＝43-x +6； ④如图4，AC ＝BC ，过点B 作BD △y轴于D ，设AC ＝a ，则BC ＝a ，CD ＝4﹣a ，根据勾股定理得：BD 2+CD 2＝BC 2，△32+（4﹣a ）2＝a 2，解得：a ＝258， △OC ＝258﹣2＝98 ，△C （0，98），同理可得直线l 的解析式为：y ＝724x +98；综上，直线l 的解析式为：y ＝13-x +3或y ＝3x ﹣7或y ＝43-x +6或y ＝724x +98．【变式训练3】如图，直线1:l y ax a =-，1l 与x 轴交于点B ，直线2l 经过点(4,0)A ，直线1l ，2l 交于点(2,3)C -．（1）a =______；点B 的坐标为______．（2）求直线2l 的解析表达式；（3）求ABC 的面积；（4）在直线2l 上存在异于点C 的另一点P ，使得ABP △为等腰三角形，请直接写出P 点的横坐标？【答案】（1）3a =-，()10B ,；（2）362y x =-；（3）92；（4）52，2813【解析】（1）△直线1:l y ax a =-经过点(2,3)C -，32a a ∴-=-，解得：3a =-；即直线1:l y ax a =-的解析式为33y x =-+；当y =0时，-3x +3=0，解得1x =，则()10B ,；故答案为：-3，（1,0）；（2）设直线2l 的解析式为:y kx b =+， △经过点()4,0A 和点(2,3)C -，△0432k b k b=+⎧⎨-=+⎩，解得：32k ，6b =-．△直线2l 的解析式为：362y x =-；（3）设ABC 的面积的面积为ABC S ；则413AB =-=，ABC 的高为3，则193322ABCS=⨯⨯=；（4）存在，设点P 的坐标为（x ，362x ），分三种情况： ①当AP=BP 时，点P 在线段AB 的垂直平分线上，△A （4,0），B （1,0），△点P 的横坐标为：41522+=； ②当AP=AB =3时，过点P 作PH △x 轴于点H ，△222PH AH AP +=，△2223(6)(4)32x x -+-=，解得x③当AB=BP =3时，作PM △x 轴于点M ， △222PM BM BP +=，△2223(6)(1)32x x -+-=，解得x =2813或x =4（舍去）；综上，符合条件的P 点的横坐标是52，2813，5213± 类型四、一次函数与直角三角形例1.如图，在平面直角坐标系中，函数y ＝－x ＋2的图象与x 轴，y 轴分别交于点A ，B ，与函数y ＝13x ＋b 的图象交于点C （－2，m ）．（1）求m 和b 的值；（2）函数y ＝－x ＋b 的图象与x 轴交于点D ，点E 从点D 出发沿DA 向，以每秒2个单位长度匀速运动到点M （到A 停止运动），设点E 的运动时间为t 秒． ①当ΔACE 的面积为12时，求t 的值；②在点E 运动过程中，是否存在t 的值，使ΔACE 为直角三角形？若存在，请求出t 的值；若不存在，请说明理由．【答案】（1）m =4，b =143；（2）①t =5；②t ＝4或t ＝6 【解析】（1）△点C （−2，m ）在直线y ＝−x ＋2上， △m ＝−（−2）＋2＝2＋2＝4，△点C （−2，4）， △函数y ＝13x ＋b 的图象过点C （−2，4），△4＝13×（−2）＋b ，得b =143，即m 的值是4，b 的值是143；（2）①△函数y ＝−x ＋2的图象与x 轴，y 轴分别交于点A ，B ，△点A （2，0），点B （0，2）， △函数y ＝13x ＋143的图象与x 轴交于点D ，△点D 的坐标为（−14，0），△AD ＝16， △△ACE 的面积为12，△(16−2t )×4÷2＝12，解得，t ＝5．即当△ACE 的面积为12时，t 的值是5； ②当t ＝4或t ＝6时，△ACE 是直角三角形，理由：当△ACE ＝90°时，AC △CE ， △点A （2，0），点B （0，2），点C （−2，4），点D （−14，0），△OA ＝OB ，AC ＝，△△BAO ＝45°，△△CAE ＝45°，△△CEA ＝45°，△CA ＝CE ＝，△AE ＝8， △AE ＝16−2t ，△8＝16−2t ，解得，t ＝4；当△CEA ＝90°时，△AC ＝，△CAE ＝45°，△AE ＝4， △AE ＝16−2t ，△4＝16−2t ，解得，t ＝6；由上可得，当t ＝4或t ＝6时，△ACE 是直角三角形．【变式训练1】如图1，在菱形ABCD 中，60ABC ∠=︒，对角线AC BD 、交于点,O P 从B 点出发，沿B DC →→方向匀速运动，P 点运动速度为1cm/s ．图2是点P 运动时，APC △的面积2()cm y 随P 点运动时间()s x变化的函数图像．（1）AB =_______cm,a =_____；（2）P 点在BD 上运动时，x 为何值时，四边形ADCP；（3）在P 点运动过程中，是否存在某一时刻使得APB △为直角三角形，若存在，求x 的值；若不存在，请说明理由．【答案】（1）2；（2；（3或1【解析】（1）在菱形ABCD 中，60ABC ∠=︒，则ABC ∆、ACD ∆为全等的两个等边三角形，设ABC ∆的边长为a，则其面积为24a ，由图2知，当点P 在点A 时，y ABC =∆的面积2=，解得2a =（负值已舍去），即菱形的边长为2，则2()AB cm =，由题意知，点P 与点O 重合时，对于图2的a 所在的位置，则1AO =，故a BO ====2（2）由（1）知点P 在BO 段运动时，对于图2第一段直线，而该直线过点、0)，设其对应的函数表达式为y kx t =+，则0t t ⎧=⎪+=，解得1k t =-⎧⎪⎨=⎪⎩，故该段函数的表达式为=-+y x ，当点P 在BD 上运动时，四边形ADCP，则点P 只能在BO 上，则四边形ADCP 的面积ACD S y ∆=+=x x =；（3）存在，理由：由（1）知，菱形的边长为2，则BP =1AO =，过点A 作AP DC ''⊥于点P ''交BD 于点P '，ABC ∆、ACD ∆均为等边三角形，则30PAP DAP ∠'=∠''=︒，①当点P 和点O 重合时，APB ∠为直角，则x BP ==②当BAP ∠'为直角时，则同理可得：PP '=x BP PP =+'=；③当BAP ∠''为直角时，则112x BD DP AD =+''=+=，综上，x 或1．【变式训练2】在平面直角坐标系xOy 中，将直线2y x =向下平移2个单位后，与一次函数132y x =-+的图象相交于点A ．（1）将直线2y x =向下平移2个单位后对应的解析式为；（2）求点A 的坐标；（3）若P 是x 轴上一点，且满足△OAP 是等腰直角三角形，直接写出点P 的坐标．【答案】（1）22y x =-；（2）（2，2）；（3）（2，0）或（4，0）．【解析】（1）根据题意，得22y x =-；故答案为：22y x =-．（2）由题意得：22132y x y x =-⎧⎪⎨=-+⎪⎩，解得：22x y =⎧⎨=⎩，△点A 的坐标为（2，2）；（3）如图所示，△P 是x 轴上一点，且满足△OAP 是等腰直角三角形，当OA =OP 时，P 点坐标为（4，0），当OP =AP 时，P 点坐标为（2，0），综上，P 点的坐标为：（2，0）或（4，0）．类型五、最值问题例1．如图，将直线34y x =-向上平移后经过点()4,3A ，分别交x 轴y 轴于点B 、C ．（1）求直线BC 的函数表达式；（2）点P 为直线BC 上一动点，连接OP ．问：线段OP 的长是否存在最小值？若存在，求出线段OP 的最小值，若不存在，请说明理由．【答案】（1）364y x =-+；（2）存在，线段OP 的最小值为4.8．【解析】（1）设平移后的直线BC 的解析式为34y x b =-+，代入()4,3A 得3344b =-⨯+，解得6b = △直线BC 的解析式为364y x =-+；（2）存在，理由如下：令x =0，得y =6，△C （0，6），故OC =6令y =0，得x =8，△B （8，0）故OB =8△BC 10= △OP △BC 时，线段OP 最小， △S △ABC =12BO CO ⨯=12BC OP ⨯，△OP = 4.8BO COBC⨯=，即线段OP 的最小值为4.8．【变式训练1】如图，四边形OABC 是张放在平面直角坐标系中的正方形纸片，点O 与坐标原点重合，点A 在x 轴正半轴上，点C 在y 轴正半轴上，5OC =，点E 在边BC 上．（1）若点N 的坐标为(3,0)，过点N 且平行于y 轴的直线MN 与EB 交于点M ，将纸片沿直线OE 折叠，顶点C 恰好落在MN 上，并与MN 上的点G 重合． ①求点G 、点E 的坐标；②若直线:l y mx n =+平行于直线OE ，且与长方形ABMN 有公共点，请直接写出n 的取值范围．（2）若点E 为BC 上的一动点，点C 关于直线OE 的对称点为G ，连接BG ，请求出线段BG 的最小值．【答案】（1）①G （3，4），E （53，5）；②-15≤n ≤-4；（2）5【解析】（1）由折叠的性质可知，OG =OC =5，由勾股定理得，GN 4=， △点G 的坐标为（3，4）；设CE =x ，则EM =3-x ，由折叠的性质可知：EG =CE =x ， △GN =4，△GM =5-4=1，在Rt △EMG 中，222EG EM MG =+，即()22231x x =-+，解得：x =53， △点E 的坐标为（53，5）；设OE所在直线的解析式为：y=kx，则53k=5，解得，k=3，△OE所在直线的解析式为：y=3x，△直线l：y=mx+n平行于直线OE，△m=3，即直线l的解析式为y=3x+n，当直线l经过点M（3，5）时，5=3×3+n，解得，n=-4，当直线l经过点A（5，0）时，0=3×5+n，解得，n=-15，△直线l与长方形ABMN有公共点时，-15≤n≤-4；（3）连接OB，OG，△OC=BC=5，△OCB=90°，△BC OC=△点C关于直线OE的对称点为点G，△OC=OG=5，△BG≥OB-OG，△当O、B、G三点共线时，BG取得最小值，△BG的最小值为5．。

中考数学狙击重难点系列专题26----双反比例函数图像与几何图形综合(含答案)

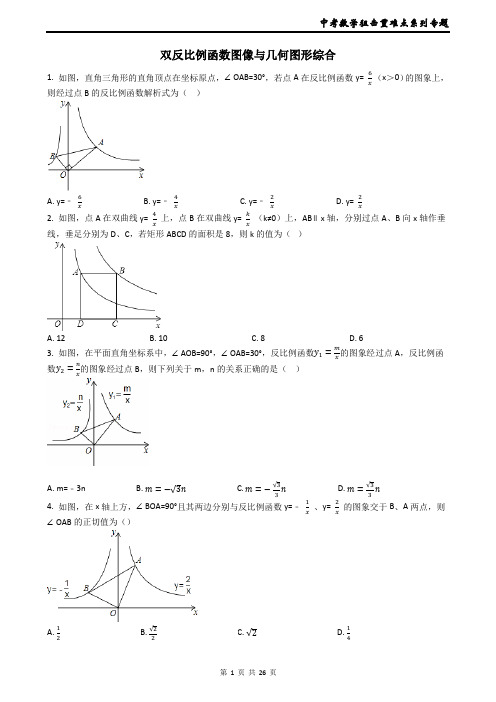
双反比例函数图像与几何图形综合1. 如图，直角三角形的直角顶点在坐标原点，∠OAB=30°，若点A在反比例函数y= （x＞0）的图象上，则经过点B的反比例函数解析式为（）A. y=﹣B. y=﹣C. y=﹣D. y=2. 如图，点A在双曲线y= 上，点B在双曲线y= （k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是8，则k的值为（）A. 12B. 10C. 8D. 63. 如图，在平面直角坐标系中，∠AOB=90°，∠OAB=30°，反比例函数的图象经过点A，反比例函数的图象经过点B，则下列关于m，n的关系正确的是（）A. m=﹣3nB.C.D.4. 如图，在x轴上方，∠BOA=90°且其两边分别与反比例函数y=﹣、y= 的图象交于B、A两点，则∠OAB的正切值为（）A. B. C. D.5. 如图，∠AOB=90°，且OA，OB分别与反比例函数y= （x＞0）、y=﹣（x＜0）的图象交于A，B 两点，则tan∠OAB的值是（）A. B. C. 1 D.6. 如图，A，B两点在反比例函数y= 的图象上，C、D两点在反比例函数y= 的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC=2，BD=3，EF= ，则k2﹣k1=（）A. 4B.C.D. 67. 如图，点是反比例函数（是常数，）上的一个动点，过点作轴、轴的平行线交反比例函数（为常数，）于点、．当点的横坐标逐渐增大时，三角形的面积( )A. 先变大再变小B. 先变小再变大C. 不变D. 无法判断8. 如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数y＝−和y＝的图象交于A点和B点，若C为x轴上任意一点，连接AC，BC，则△ABC的面积为（）A. 3B. 4C. 5D. 69. 如图，点A在反比例函数(x>0)的图象上，点B在反比例函数的图象上，AB⊥x 轴于点M，且AM：MB=1：2，则k的值为（）A. 3B. ﹣6C. 2D. 610. 如图，已知点A 、B分别在反比例函数（），-（）的图象上，且OA⊥OB ，则的值为（）A. B. 2 C. D. 411. 如图，直线l⊥x轴于点P，且与反比例函数y1= （x＞0）及y2= （x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k1﹣k2的值为（）A. 2B. 3C. 4D. ﹣412. 如图，在平面直角坐标系中，已知直线（）分别交反比例函数和在第一象限的图象于点，，过点作轴于点，交的图象于点，连结．若BDO是等腰直角三角形，则的值是________．13. 如图，在平面直角坐标系中，有一宽度为1的长方形纸带，平行于y轴，在x轴的正半轴上移动，交x轴的正半轴于点A、D，两边分别交函数y1＝（x＞0）与y2＝（x＞0）的图像于B、F和E、C，若四边形ABCD是矩形，则A点的坐标为________．14. 如图，是反比例函数和（＜）在第一象限的图象，直线AB∥x轴，并分别交两条曲线于A、B两点，若，则的值为________。

专题一第二讲函数的图像与性质

数，则f(x)＝f(|x|)，利用这个性质，可以避免一些分
类讨论，有利于灵活利用函数单调性．
对函数的考查灵活多变，但也在追求创新.2011年湖南卷第8题就体现了这一点，从定义运算的形式给出函数的解析式．
(2011· 天津高考)对实数 a 和 b，定义运算“⊗”：a⊗b＝
a，a－b≤1， b，a－b＞1.
答案：A
8．(2011·辽宁模拟 )已知函数f(x)是奇函数，且在(－∞，＋∞)上为增函数，若x，y满足等式f(x2－2x)＋f(y) ＝0，则2x＋y的最大值是 ( )
A．0
C．4
B．1
D．12
解析：∵f(x)是奇函数，且在R上为增函数， ∴f(x2－2x)＝－f(y)＝f(－y)．
∴x2－2x＝－y.
∴2x＋y＝4x－x2＝－(x－2)2＋4≤4. 答案：C
[悟方法
触类旁通]
1．求单调区间应注意：(1)勿忘定义域；(2)在多个单调
区间之间不一定能添加符号“∪”和“或”；(3)单
调区间应该用区间表示，不能用集合或不等式表示． 2．若奇函数y＝f(x)在x＝0处有定义，则f(0)＝0，灵活使用这一结论可以简化运算过程；若函数f(x)是偶函
[解 ]
(1)设 x∈(0,1]，则－x∈[－1,0)，
1 f(－x)＝－2ax＋x2. ∵f(x)是奇函数，∴f(－x)＝－f(x)． 1 ∴f(x)＝2ax－x2，x∈(0,1]．
1 2 (2)f′(x)＝2a＋x3＝2a＋x3.
1 1 ∵a>－1，x∈(0,1]，x3≥1，a＋x3＞0. ∴f′(x)>0.∴f(x)在区间(0,1]上是单调递增的．
答案：D
x2－9 1．(2011· 盐城模拟)函数 f(x)＝的定义域为____________． log2x－1

二次函数与几何图形结合题及答案

1.如图，抛物线21y x =-与x 轴交于A 、B 两点，与y 轴交于点C ．〔1〕求A 、B 、C 三点的坐标;〔2〕过点A 作AP ∥CB 交抛物线于点P ，求四边形ACBP 的面积;解：〔1〕令0y =，得210x -= 解得1x =± 令0x =，得1y =-∴A (1,0)-B (1,0)C (0,1)-……………………3分〔2〕∵O A =O B =O C =1∴∠BAC =∠AC O=∠BC O=45∵A P ∥CB ， ∴∠P AB =45过点P 作P E ⊥x 轴于E ，那么∆A P E 为等腰直角三角形令O E =a ，那么P E =1a +∴P (,1)a a +∵点P 在抛物线21y x =-上 ∴211a a +=- 解得12a =，21a =-〔不合题意，舍去〕∴P E =3……………………………………………………………………………5分∴四边形ACB P 的面积S =12AB •O C +12AB •P E =112123422⨯⨯+⨯⨯=………………………………6分2.如图,在平面直角坐标系中，△ABC 是直角三角形,∠ACB =90,AC =BC ,OA =1，OC =4，抛物线2y x bx c =++经过A ，B 两点，抛物线的顶点为D ．〔1〕求b ,c 的值；〔2〕点E 是直角三角形ABC 斜边AB 上一动点(点A 、B 除外)，过点E 作x 轴的垂线交抛物线于点F ，当线段EF 的长度最大时，求点E 的坐标；〔3〕在〔2〕的条件下：①求以点Ｅ、Ｂ、Ｆ、Ｄ为顶点的四边形的面积；②在抛物线上是否存在一点P ，使△EFP 是以EF 为直角边的直角三角形? 假设存在，求出所有点P 的坐标；假设不存在，说明理由.解：〔1〕由得：A 〔-1，0〕 B 〔4，5〕…………………1分∵二次函数2y x bx c =++的图像经过点A 〔-1，0〕B(4,5)∴101645b c b c -+=⎧⎨++=⎩…………………………………………………2分解得：b=-2 c=-3…………………………………………………3分〔2〕如２６题图：∵直线AB 经过点A 〔-1，0〕 B(4,5)∴直线AB 的解析式为：y=x+1……………………………………4分∵二次函数223y x x =--∴设点E(t ， t+1),那么F 〔t ，223t t --〕………………………5分∴EF= 2(1)(23)t t t +---………………………………………6分=2325()24t --+ ∴当32t =时，EF 的最大值=254 ∴点E 的坐标为〔32，52〕………………………………7分〔3〕①如２６题图：顺次连接点E 、B 、F 、D 得四边形ＥＢＦＤ．可求出点F 的坐标〔32，154-〕,点D 的坐标为〔1，-4〕 S EBFD 四边行 = SBEF + S DEF =12531253(4)(1)242242⨯-+⨯- =758………………………………………………10分 ②如２６题备用图：ⅰ)过点E 作a ⊥EF 交抛物线于点P,设点P(m ,223m m --)那么有：25232m m --= 解得:1226m =－,2226m += ∴12265(,)2p －, 22265(,)2p + ⅱ〕过点F 作b ⊥EF 交抛物线于3P ，设3P 〔n ，223n n --〕那么有：215423n n --=- 解得：112n = ，232n =〔与点F 重合，舍去〕 ∴3P 11524（，－）综上所述：所有点P 的坐标：12265(,)22p －，22265(,)22p +3P 〔11524（，－）. 能使△EFP 组成以EF 为直角边的直角三角形．…………………………………… 13分3.如图,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点，与y 轴交于点P ，顶点为C 〔1，－2〕. 〔1〕求此函数的关系式；〔2〕作点C 关于x 轴的对称点D ，顺次连接A 、C 、B 、D.假设在抛物线上存在点E ，使直线PE 将四边形ABCD 分成面积相等的两个四边形，求点E 的坐标；〔1〕∵c bx x y ++=2的顶点为C 〔1，－2〕， ∴2)1(2--=x y ，122--=x x y ． ……………2分２６题备用图〔2〕设直线PE 对应的函数关系式为b kx y +=由题意，四边形ACBD 是菱形.故直线PE 必过菱形ACBD 的对称中心M ． ………3分由P (0，－1)，M 〔1，0〕，得⎩⎨⎧=+-=01b k b ．从而1-=x y ， …5分设E (x ，1-x )，代入122--=x x y ，得1212--=-x x x ．解之得01=x ，32=x ，根据题意，得点E (3，2) …………………………………7分．4如图，抛物线)0(2≠++=a c bx ax y 的顶点坐标为Q ()1,2-，且与y 轴交于点C ()3,0，与x 轴交于A 、B 两点〔点A 在点B 的右侧〕，点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动〔点P 与A 不重合〕，过点P 作PD ∥y 轴，交AC 于点D ．(1)求该抛物线的函数关系式；(2)当△ADP 是直角三角形时，求点P 的坐标；(3)在问题(2)的结论下，假设点E 在x 轴上，点F 在抛物线上，问是否存在以A 、P 、E 、F 为顶点的平行四边形？假设存在，求点F 的坐标；假设不存在，请说明理由．解：〔1〕∵抛物线的顶点为Q 〔2，－1〕∴设()122--=x a y将C 〔0，3〕代入上式，得()12032--=a1=a ∴()122--=x y ，即342+-=x x y …〔3分〕〔2〕分两种情况：①当点P 1为直角顶点时,点P 1与点B 重合(如图)令y =0, 得0342=+-x x 解之得11=x , 32=x∵点A 在点B 的右边, ∴B(1,0), A(3,0)∴P 1(1,0) 〔5分〕②解:当点A 为△APD 2的直角顶点是(如图)∵OA=OC, ∠AOC= 90, ∴∠OAD 2=45当∠D 2AP 2= 90时, ∠OAP 2= 45, ∴AO 平分∠D 2AP 2- .又∵P 2D 2∥y 轴, ∴P 2D 2⊥AO, ∴P 2、D 2关于x 轴对称设直线AC 的函数关系式为b kx y +=将A(3,0), C(0,3)代入上式得 ⎩⎨⎧=+=bb k 330, ∴⎩⎨⎧=-=31b k ∴3+-=x y ……………〔7分〕 ∵D 2在3+-=x y 上, P 2在342+-=x x y 上,∴设D 2(x ,3+-x ), P 2(x ,342+-x x )∴(3+-x )+(342+-x x )=0 0652=+-x x , ∴21=x , 32=x (舍)∴当x =2时, 342+-=x x y =32422+⨯-=－1 ∴P 2的坐标为P 2(2,－1)(即为抛物线顶点)∴P 点坐标为P 1(1,0), P 2(2,－1) …………………………………………………〔9分〕(3)解: 由题(2)知,当点P 的坐标为P 1(1,0)时,不能构成平行四边形……………………〔10分〕当点P 的坐标为P 2(2,－1)(即顶点Q)时,平移直线AP(如图)交x 轴于点E,交抛物线于点F.当AP=FE 时,四边形PAFE 是平行四边形∵P(2,－1), ∴可令F(x ,1)∴1342=+-x x 解之得: 221-=x , 222+=x ∴F 点有两点, 即F 1(22-,1), F 2(22+,1) ……………〔13分〕3. 〔2021，25，10分〕如图，抛物线212y x x a =-+与x 轴交于A ，B 两点，与y 轴交于点C ，其顶点在直线y =－2x 上.(1)求a 的值；(2)求A ,B 两点的坐标; (3)以AC ,CB 为一组邻边作□ABCD ,那么点D 关于x 轴的对称点D ´是否在该抛物线上?请说明理由.考点：二次函数综合题。

中考数学考点12反比例函数的图像与性质及实际应用总复习(解析版)

反比例函数的图像与性质及实际应用【命题趋势】在中考中.反比例函数的图像与性质常以选择题和填空形式考查；反比例函数解析式主要在反比例函数综合题中与一次函数、几何图形结合考查。

【中考考查重点】一、结合具体情境体会反比例函数的意义.能根据已知条件确定反比例函数的表达式；二、能画出反比例函数的图像.根据图像和表达式探索并理解k＞0和k＜0时.图像的变化情况；三、结合具体情境体会反比例函数的意义四、能用反比例函数解决简单实际问题考点一：反比例函数的概念一般地.形如.叫做反比例函数.自变量x的取值概念范围是≠0的一切实数【提分要点】反比例函数图像上的点的横纵坐标之积是定值k1．（2021秋•南召县期末）下列函数是y关于x的反比例函数的是（）A．y＝B．y＝C．y＝﹣D．y＝﹣【答案】C【解答】解：A、不是y关于x的反比例函数.故此选项不合题意；B、不是y关于x的反比例函数.故此选项不合题意；C、是y关于x的反比例函数.故此选项符合题意；D、不是y关于x的反比例函数.是正比例函数.故此选项不合题意；故选C2．（2021•门头沟区一模）在物理实验室实验中.为了研究杠杆的平衡条件.设计了如下实验.如图.铁架台左侧钩码的个数与位置都不变.在保证杠杆水平平衡的条件下.右侧采取变动钩码数量即改变力F.或调整钩码位置即改变力臂L.确保杠杆水平平衡.则力F与力臂L满足的函数关系是（）A ．正比例函数关系B ．反比例函数关系C ．一次函数关系D ．二次函数关系【答案】B【解答】解：∵确保杠杆水平平衡.∴力F 与力臂L 满足的函数关系是反比例函数关系. 故选：B ．3．（2021秋•越秀区校级期末）函数y ＝（m ﹣1）x |m |﹣2是反比例函数.则m的值为．【答案】-1【解答】解：由题意得：|m |﹣2＝﹣1且.m ﹣1≠0；解得m ＝±1.又m ≠1； ∴m ＝﹣1．故填m ＝﹣1．考点二：反比例函数的图像与性质概念kk ＞0k ＜0图像所在象限一、三二、四增减性在每个象限内.y 随x 的增大而减少在每个象限内.y 随x 的增大而增大图像特征图像无限接近于坐标轴.但不与坐标轴相交；关于直线y=±x 成轴对称；关于原点成中心对称4．（2021秋•南开区期末）若反比例函数y＝的图象在其所在的每一象限内.y随x 的增大而减小.则k的取值范围是（）A．k＜﹣2B．k＞﹣2C．k＜2D．k＞2【答案】B【解答】解：∵反比例比例函数y＝的图象在其每一象限内.y随x的增大而减小.∴k+2＞0.解得k＞﹣2．故选：B．5．（2021秋•揭阳期末）点（x1.y1）、（x2.y2）、（x3.y3）在反比例函数y＝﹣的图象上.且x1＜0＜x2＜x3.则有（）A．y1＜y2＜y3B．y2＜y3＜y1C．y1＜y3＜y2D．y3＜y2＜y1【答案】B【解答】解：∵k＜0.∴函数图象在二.四象限.由x1＜0＜x2＜x3可知.横坐标为x1的点在第二象限.横坐标为x2.x3的点在第四象限．∵第四象限内点的纵坐标总小于第二象限内点的纵坐标.∴y1最大.在第二象限内.y随x的增大而增大.∴y2＜y3＜y1．故选：B．6．（2020秋•浦东新区校级期末）已知函数y＝kx.y随x的增大而减小.另有函数.两个函数在同一平面直角坐标系内的大致图象可能是（）A．B．C．D．【答案】B【解答】解：∵函数y＝kx中y随x的增大而减小.∴k＜0.且函数的图象经过第二、四象限.∴函数的反比例系数大于零.∴反比例函数图象经过第一、三象限.故选：B．7．（2020秋•孝义市期末）近视眼镜的度数y（度）与镜片焦距x（米）之间具有如图所示的反比例函数关系.若要配制一副度数小于400度的近视眼镜.则镜片焦距x的取值范围是（）A．0米＜x＜0.25米B．x＞0.25米C．0米＜x＜0.2米D．x＞0.2米【答案】B【解答】解：根据题意.近视眼镜的度数y（度）与镜片焦距x（米）成反比例.设y＝.∵点（0.5.200）在此函数的图象上.∴k＝0.5×200＝100.∴y＝（x＞0）.∵y＜400.∴＜400.∵x＞0.∴400x＞100.∴x＞0.25.即镜片焦距x的取值范围是x＞0.25米.故选：B．考点三：反比例函数系数k的几何意义8．（2021秋•铁西区期末）如图.A是反比例函数y＝的图象上一点.过点A作AB⊥y 轴于点B.点C在x轴上.且S△ABC＝2.则k的值为（）A．4B．﹣4C．﹣2D．2【答案】B【解答】解：设点A的坐标为（x.y）.∵点A在第二象限.∴x＜0.y＞0.∴S△ABC＝AB•OB＝|x|•|y|＝﹣xy＝2.K的几何意义在反比例函数上任取一点P(x.y),过这个点分别作x轴.y轴的垂线PM、PN.于坐标轴围成的矩形PMON的面积S=PM·PN===k基本图形面积基本图形面积∴xy＝﹣4.∵A是反比例函数y＝的图象上一点.∴k＝xy＝﹣4.故选：B．9．（2021•铜仁市）如图.矩形ABOC的顶点A在反比例函数y＝的图象上.矩形ABOC 的面积为3.则k＝．【答案】3【解答】解：∵矩形ABOC的面积为3.∴|k|＝3.又∵k＞0.∴k＝3.故答案为：3．考点四：反比例函数解析式的确定待定系数法1.设所求反比例函数解析式为：2.找出反比例函数图像上一点P（a,b）.并将其代入解析式得k=ab；3.确定反比例函数解析式利用k得几何意义题中已知面积时.考虑利用k得几何意义.由面积得.再综合图像所在象限判段k得正负.从而得出k的值.代入解析式即可10．（2021秋•房山区期末）若反比例函数的图象经过点（3.﹣2）.则该反比例函数的表达式为（）A．y＝B．y＝﹣C．y＝D．y＝﹣【答案】B【解答】解：设反比例函数的解析式为y＝（k≠0）.函数的图象经过点（3.﹣2）.∴﹣2＝.得k＝﹣6.∴反比例函数解析式为y＝﹣．故选：B．11．（2021秋•泰山区期中）如果等腰三角形的面积为6.底边长为x.底边上的高为y.则y与x的函数关系式为（）A．y＝B．y＝C．y＝D．y＝【答案】A【解答】解：∵等腰三角形的面积为6.底边长为x.底边上的高为y.∴xy＝6.∴y与x的函数关系式为：y＝．故选：A．12．（2021•江西模拟）小明学习了物理中的杠杆平衡原理发现：阻力×阻力臂＝动力×动力臂．现已知某一杠杆的阻力和阻力臂分别为2400N和1m.则动力F（单位：N）关于动力臂l（单位：m）的函数图象大致是（）A．B．C．D．【答案】A【解答】】解：∵阻力×阻力臂＝动力×动力臂.已知阻力和阻力臂分别是2400N和1m.∴动力F（单位：N）关于动力臂l（单位：m）的函数解析式为：2400×1＝Fl.则F＝.是反比例函数.A选项符合.故选：A．1．（2021秋•隆回县期中）下面的函数是反比例函数的是（）A．y＝B．y＝C．y＝D．y＝【答案】C【解答】解：A．y不是关于x的反比例函数.故本选项不符合题意；B．y是x的是正比例函数.不是反比例函数.故本选项不符合题意；C．y是关于x的反比例函数.故本选项符合题意；D．y不是关于x的反比例函数.故本选项不符合题意；故选：C．2．（2021秋•大东区期末）如果反比例函数的图象经过点P（﹣3.﹣1）.那么这个反比例函数的表达式为（）A．y＝B．y＝﹣C．y＝x D．y＝﹣x【答案】A【解答】解：设反比例函数解析式为y＝（k≠0）.∵函数经过点P（﹣3.﹣1）.∴﹣1＝.解得k＝3．∴反比例函数解析式为y＝．故选：A．3．（2021春•海淀区校级月考）某物体对地面的压力为定值.物体对地面的压强p（Pa）与受力面积S（m2）之间的函数关系如图所示.这一函数表达式为（）A．B．C．D．【答案】B【解答】解：观察图象易知p与S之间的是反比例函数关系.设p＝.由于A（20.10）在此函数的图象上.∴k＝20×10＝200.∴p＝．故选：B．4．（2020秋•瓜州县期末）如图.在某温度不变的条件下.通过一次又一次地对气缸顶部的活塞加压.测出每一次加压后气缸内气体的体积V（mL）与气体对气缸壁产生的压强p（kPa）的关系可以用如图所示的反比例函数图象进行表示.下列说法错误的是（）A．气压p与体积V表达式为p＝.则k＞0B．当气压p＝70时.体积V的取值范围为70＜V＜80C．当体积V变为原来的时.对应的气压p变为原来的D．当60≤V≤100时.气压p随着体积V的增大而减小【答案】B【解答】解：当V＝60时.p＝100.则pV＝6000.A．气压p与体积V表达式为p＝.则k＞0.故不符合题意；B．当p＝70时.V＝＞80.故符合题意；C．当体积V变为原来的时.对应的气压p变为原来的.不符合题意；D．当60≤V≤100时.气压p随着体积V的增大而减小.不符合题意；故选：B．5．（2020秋•东莞市校级期末）已知点（3.y1）.（﹣2.y2）.（2.y3）都在反比例函数的图象上.那么y1.y2与y3的大小关系是（）A．y3＜y1＜y2B．y3＜y2＜y1C．y1＜y2＜y3D．y1＜y3＜y2【答案】A【解答】解：∵k＝﹣6＜0.∴图象位于第二、四象限.在每一象限内.y随x的增大而增大.∴y2＞0.y3＜y1＜0.∴y3＜y1＜y2.故选：A．6．（2021秋•西湖区期中）已知y1和y2均是以x为自变量的函数.当x＝m时.函数值分别是M1和M2.若存在实数m.使得M1+M2＝1.则称函数y1和y2具有性质P．以下函数y1和y2不具有性质P的是（）A．y1＝x2+2x和y2＝﹣x﹣1B．y1＝x2+2x和y2＝﹣x+1C．y1＝﹣和y2＝﹣x﹣1D．y1＝﹣和y2＝﹣x+1【答案】D【解答】解：A．令y1+y2＝1.则x2+2x﹣x﹣1＝1.整理得.x2+x﹣2＝0.解得x＝﹣2或x ＝1.即函数y1和y2具有性质P.不符合题意；B．令y1+y2＝1.则x2+2x﹣x+1＝1.整理得.x2+x＝0.解得x＝0或x＝﹣1.即函数y1和y2具有性质P.不符合题意；C．令y1+y2＝1.则﹣﹣x﹣1＝1.整理得.x2+2x+1＝0.解得x1＝x2＝﹣1.即函数y1和y2具有性质P.不符合题意；D．令y1+y2＝1.则﹣﹣x+1＝1.整理得.x2+1＝0.方程无解.即函数y1和y2不具有性质P.符合题意；故选：D．7．（2021秋•会宁县期末）如图.A.B是反比例函数的图象上关于原点对称的两点.BC ∥x轴.AC∥y轴.若△ABC的面积为6.则k的值是．【答案】3【解答】解：∵反比例函数的图象在一、三象限.∴k＞0.∵BC∥x轴.AC∥y轴.∴S△AOD＝S△BOE＝k.∵反比例函数及正比例函数的图象关于原点对称.∴A、B两点关于原点对称.∴S矩形OECD＝2S△AOD＝k.∴S△ABC＝S△AOD+S△BOE+S矩形OECD＝2k＝6.解得k＝3．故答案为：3．8．（2021春•沙坪坝区校级期末）已知函数y＝（m﹣1）是反比例函数.则m的值为．【答案】-1【解答】解：根据题意m2﹣2＝﹣1.∴m＝±1.又m﹣1≠0.m≠1.所以m＝﹣1．故答案为：﹣1．1．（2018•柳州）已知反比例函数的解析式为y＝.则a的取值范围是（）A．a≠2B．a≠﹣2C．a≠±2D．a＝±2【答案】C【解答】解：根据反比例函数解析式中k是常数.不能等于0.由题意可得：|a|﹣2≠0.解得：a≠±2.故选：C．2．（2020•上海）已知反比例函数的图象经过点（2.﹣4）.那么这个反比例函数的解析式是（）A．y＝B．y＝﹣C．y＝D．y＝﹣【答案】D【解答】解：设反比例函数解析式为y＝.将（2.﹣4）代入.得：﹣4＝.解得k＝﹣8.所以这个反比例函数解析式为y＝﹣.故选：D．3．（2021•黔西南州）对于反比例函数y＝.下列说法错误的是（）A．图象经过点（1.﹣5）B．图象位于第二、第四象限C．当x＜0时.y随x的增大而减小D．当x＞0时.y随x的增大而增大【答案】C【解答】解：∵反比例函数y＝.∴当x＝1时.y＝﹣＝﹣5.故选项A不符合题意；k＝﹣5.故该函数图象位于第二、四象限.故选项B不符合题意；当x＜0.y随x的增大而增大.故选项C符合题意；当x＞0时.y随x的增大而增大.故选项D不符合题意；故选：C．4．（2021•济南）反比例函数y＝（k≠0）图象的两个分支分别位于第一、三象限.则一次函数y＝kx﹣k的图象大致是（）A．B．C．D．【答案】D【解答】解：∵反比例函数y＝（k≠0）图象的两个分支分别位于第一、三象限.∴k＞0.∴﹣k＜0.∴一次函数y＝kx﹣k的图象图象经过第一、三、四象限.故选：D．5．（2021•宜昌）某气球内充满了一定质量m的气体.当温度不变时.气球内气体的气压p（单位：kPa）是气体体积V（单位：m3）的反比例函数：p＝.能够反映两个变量p和V函数关系的图象是（）A．B．C．D．【答案】B【解答】解：∵气球内气体的气压p（单位：kPa）是气体体积V（单位：m3）的反比例函数：p＝（V.p都大于零）.∴能够反映两个变量p和V函数关系的图象是：．故选：B．6．（2021•沈阳）如图.平面直角坐标系中.O是坐标原点.点A是反比例函数y＝（k≠0）图象上的一点.过点A分别作AM⊥x轴于点M.AN⊥y轴于点N．若四边形AMON 的面积为12.则k的值是．【答案】-12【解答】解：∵四边形AMON的面积为12.∴|k|＝12.∵反比例函数图象在二四象限.∴k＜0.∴k＝﹣12.故答案为：﹣12．7．（2021•阜新）已知点A（x1.y1）.B（x2.y2）都在反比例函数y＝﹣的图象上.且x1＜0＜x2.则y1.y2的关系一定成立的是（）A．y1＞y2B．y1＜y2C．y1+y2＝0D．y1﹣y2＝0【答案】A【解答】解：∵反比例函数y＝﹣中k＝﹣1＜0.∴函数图象的两个分支分别位于二、四象限.且在每一象限内.y随x的增大而增大．∵x1＜0＜x2.∴A在第二象限.B在第四象限.∴y1＞0.y2＜0.∴y1＞y2．故选：A．8．（2020•大庆）已知正比例函数y＝k1x和反比例函数y＝.在同一平面直角坐标系下的图象如图所示.其中符合k1•k2＞0的是（）A．①②B．①④C．②③D．③④【答案】B【解答】解：①中k1＞0.k2＞0.故k1•k2＞0.故①符合题意；②中k1＜0.k2＞0.故k1•k2＜0.故②不符合题意；③中k1＞0.k2＜0.故k1•k2＜0.故③不符合题意；④中k1＜0.k2＜0.故k1•k2＞0.故④符合题意；故选：B．9．（2021•自贡）已知蓄电池的电压为定值.使用蓄电池时.电流I（单位：A）与电阻R （单位：Ω）是反比例函数关系.它的图象如图所示．下列说法正确的是（）A．函数解析式为I＝B．蓄电池的电压是18VC．当I≤10A时.R≥3.6ΩD．当R＝6Ω时.I＝4A【答案】C【解答】解：设I＝.∵图象过（4.9）.∴k＝36.∴I＝.∴蓄电池的电压是36V．∴A.B均错误；当I＝10时.R＝3.6.由图象知：当I≤10A时.R≥3.6Ω.∴C正确.符合题意；当R＝6时.I＝6.∴D错误.故选：C．10．（2020•河北）如图是8个台阶的示意图.每个台阶的高和宽分别是1和2.每个台阶凸出的角的顶点记作T m（m为1～8的整数）．函数y＝（x＜0）的图象为曲线L．（1）若L过点T1.则k＝；（2）若L过点T4.则它必定还过另一点T m.则m＝；（3）若曲线L使得T1～T8这些点分布在它的两侧.每侧各4个点.则k的整数值有个．【答案】（1）-16 （2）5 （3）7【解答】解：（1）∵每个台阶的高和宽分别是1和2.∴T1（﹣16.1）.T2（﹣14.2）.T3（﹣12.3）.T4（﹣10.4）.T5（﹣8.5）.T6（﹣6.6）.T7（﹣4.7）.T8（﹣2.8）.∵L过点T1.∴k＝﹣16×1＝﹣16.故答案为：﹣16；（2）∵L过点T4.∴k＝﹣10×4＝﹣40.∴反比例函数解析式为：y＝﹣.当x＝﹣8时.y＝5.∴T5在反比例函数图象上.∴m＝5.故答案为：5；（3）若曲线L过点T1（﹣16.1）.T8（﹣2.8）时.k＝﹣16.若曲线L过点T2（﹣14.2）.T7（﹣4.7）时.k＝﹣14×2＝﹣28.若曲线L过点T3（﹣12.3）.T6（﹣6.6）时.k＝﹣12×3＝﹣36.若曲线L过点T4（﹣10.4）.T5（﹣8.5）时.k＝﹣40.∵曲线L使得T1～T8这些点分布在它的两侧.每侧各4个点.∴﹣36＜k＜﹣28.∴整数k＝﹣35.﹣34.﹣33.﹣32.﹣31.﹣30.﹣29共7个.故答案为：7．1．（2021•抚顺模拟）下列函数中.y是x的反比例函数的是（）A．B．C．D．【答案】B【解答】解：A、是正比例函数.不是反比例函数.故此选项不合题意；B、是反比例函数.故此选项符合题意；C、不是反比例函数.故此选项不合题意；D、不是反比例函数.故此选项不合题意；故选：B．2．（2021•卧龙区二模）已知反比例函数.在下列结论中.不正确的是（）A．图象必经过点（﹣1.﹣2）B．图象在第一、三象限C．若x＜﹣1.则y＜﹣2D．点A（x1.y1）.B（x2.y2）图象上的两点.且x1＜0＜x2.则y1＜y2【答案】C【解答】解：A．反比例函数.图象必经过点（﹣1.﹣2）.原说法正确.故此选项不合题意；B．反比例函数.图象在第一、三象限.原说法正确.故此选项不合题意；C．若x＜﹣1.则y＞﹣2.原说法错误.故此选项符合题意；D．点A（x1.y1）.B（x2.y2）图象上的两点.且x1＜0＜x2.则y1＜y2.原说法正确.故此选项不合题意；故选：C．3．（2021•富阳区二模）已知反比例函数y＝.当﹣2＜x＜﹣1.则下列结论正确的是（）A．﹣3＜y＜0B．﹣2＜y＜﹣1C．﹣10＜y＜﹣5D．y＞﹣10【答案】C【解答】解：∵k＝10.且﹣2＜x＜﹣1.∴在第三象限内.y随x的增大而减小.当x＝﹣2时.y＝﹣5.当x＝﹣1时.y＝﹣10.∴﹣10＜y＜﹣5.故选：C．4．（2021•武陟县模拟）某气球内充满了一定质量的气体.当温度不变时.气球内气体的气压P（kpa）是气体体积V（m3）的反比例函数其图象如图所示.当气体体积为1m3时.气压为（）kPa．A．150B．120C．96D．84【答案】C【解答】解：设P＝.由题意知120＝.所以k＝96.故P＝.当V＝1m3时.P＝＝96（kPa）；故选：C．5．（2021•云岩区模拟）阿基米德说：“给我一个支点.我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识﹣﹣杠杆原理.即“阻力×阻力臂＝动力×动力臂”．若已知某一杠杆的阻力和阻力臂分别为1200N和0.5m.则这一杠杆的动力F和动力臂l之间的函数图象大致是（）A．B．C．D．【答案】A【解答】解：∵阻力×阻力臂＝动力×动力臂．小伟欲用撬棍撬动一块石头.已知阻力和阻力臂分别是1200N和0.5m.∴动力F（单位：N）关于动力臂l（单位：m）的函数解析式为：1200×0.5＝Fl.则F＝.是反比例函数.A选项符合.故选：A．6．（2021•昆明模拟）如图.点P在双曲线第一象限的图象上.P A⊥x轴于点A.则△OP A的面积为（）A．2B．3C．4D．6【答案】B【解答】解：∵P A⊥x轴于点A.∴S△AOP＝|k|＝＝3.故选：B．7．（2021•乐陵市一模）为预防新冠病毒.某学校每周末用药熏消毒法对教室进行消毒.已知药物释放过程中.教室内每立方米空气中含药量y（mg）与时间t（h）成正比例；药物释放完毕后.y与t成反比例.如图所示．根据图象信息.下列选项错误的是（）A．药物释放过程需要小时B．药物释放过程中.y与t的函数表达式是y＝tC．空气中含药量大于等于0.5mg/m3的时间为hD．若当空气中含药量降低到0.25mg/m3以下时对身体无害.那么从消毒开始.至少需要经过4.5小时学生才能进入教室【答案】D【解答】解：设正比例函数解析式是y＝kt.反比例函数解析式是y＝.把点（3.）代入反比例函数的解析式.得：＝.解得：m＝.当y＝1时.代入上式得t＝.把t＝时.y＝1代入正比例函数的解析式是y＝kt.得：k＝.∴正比例函数解析式是y＝t.A．由图象知.y＝1时.t＝.即药物释放过程需要小时.故A不符合题意；B．药物释放过程中.y与t成正比例.函数表达式是y＝t.故B不符合题意；C．把y＝0.5mg/m3分别代入y＝t和y＝得.0.5＝t1和0.5＝.解得：t1＝和t2＝3.∴t2﹣t1＝.∴空气中含药量大于等于0.5mg/m3的时间为h；故C不符合题意；＜0.25.解得t＞6.所以至少需要经过6小时后.学生才能进入教室.故D符合题意.故选：D．8．（2021•山西模拟）已知.A（﹣3.n）.C（3n﹣6.2）是反比例函数y＝（x＜0）图象上的两点.则反比例函数的解析式为．【答案】y＝﹣【解答】解：∵A（﹣3.n）.C（3n﹣6.2）是反比例函数y＝（x＜0）图象上的两点.∴n＝.2＝.即m＝﹣3n.m＝2（3n﹣6）.消去m得：﹣3n＝2（3n﹣6）.解得：n＝.把n＝代入得：m＝﹣4.故答案为：y＝﹣．9．（2021•雁塔区校级模拟）已知同一象限内的两点A（3.n）.B（n﹣4.n+3）均在反比例函数y＝的图象上.则该反比例函数关系式为．【答案】y＝【解答】解：∵同一象限内的两点A（3.n）.B（n﹣4.n+3）均在反比例函数y＝的图象上.∴k＝3n＝（n﹣4）（n+3）.解得n＝6或n＝﹣2.∵n＝﹣2时.A（3.﹣2）.B（﹣6.1）.∴A、B不在同一象限.故n＝﹣2舍去.∵k＝3n＝18.∴y＝.故答案为y＝．10．（2021•昭通模拟）若函数y＝是关于x的反比例函数.则a满足的条件是．【答案】a≠﹣3【解答】解：由题可得.a+3≠0.解得a≠﹣3.故答案为：a≠﹣3．。

高二数学三角函数的图象与性质试题答案及解析

高二数学三角函数的图象与性质试题答案及解析1.已知，x，y R．（1）若，求的最小值；（2）设，求的取值范围．【答案】（1）；（2）。

【解析】（1）利用“乘1法”（即任何数乘以1等于其本身）把变形为，然后，利用基本不等式求最值。

（2）利用转化与化归思想，利用把中的二元转化为一元，既得，这是一个关于的二次函数，即问题转化为二次函数给定区间上的最值问题，注意对称轴与给定区间的关系。

试题解析：（1）．当且仅当，时等号成立． 8分（2）由，得．由，，得．，当时，；当时，．所以，的取值范围是． 16分【考点】（1）转化与化归思想的应用；（2）利用基本不等式求最值，注意条件：一正、二定、三相等，（3）与三角函数有关的二次函数给定区间上的最值问题，注意对称轴与给定区间的关系。

2.已知函数(其中,,)的部分图象如图所示,则函数的解析式是 .【答案】.【解析】由图像，得,；代入得，令，得，所以函数的解析式为.【考点】三角函数的图像与性质.3.函数（其中，）的图象如图所示，为了得到的图象，只需将的图象（）A．向右平移个单位长度B．向左平移个单位长度C．向右平移个单位长度D．向左平移个单位长度【答案】C【解析】由函数图象可知，，即，所以，又过，代入得，因为，所以，即有，从而，此时为了得到的图象，只需将的图象向右平移个单位长度，故选择C.【考点】三角函数的图象、性质及图象变换.4.若对可导函数，当时恒有，若已知是一锐角三角形的两个内角，且，记则下列不等式正确的是（）A．B．C．D．【答案】C【解析】由于当时恒有，所以，故知函数Ｆ(x)在[0，1]上是减函数；又因为已知是一锐角三角形的两个内角，且，所以，因此有，故选C．【考点】１．函数的导数；２．三角函数的性质．5.已知函数满足，其图像与直线y=0的某两个交点的横坐标分别为、,的最小值为，则（）.A．B．C．D．【答案】D【解析】函数满足，即是奇函数，，即；因为其图像与直线y=0的某两个交点的横坐标分别为、,的最小值为，所以,即，.【考点】三角函数的图像与性质.6.将函数y＝cos2x的图象向右平移个单位长度，再将所得图象的所有点的横坐标伸长到原来的2倍（纵坐标不变），得到的函数解析式为（）.A．y＝sinx B．y＝－cos4x C．y＝sin4x D．y＝cosx【答案】A.【解析】.【考点】函数图像的平移伸缩变换，诱导公式.7.函数的图象沿x轴向左平移个单位后，得到一个偶函数的图象，则φ的一个可能的值为（）.A．B．C．D．【答案】A.【解析】可知，即，而此函数为偶函数，则令，得，取，得，故选A.（此题也可由选项分别代入表达式进行排除.）【考点】图像的平移，偶函数的概念，诱导公式.8.函数的一个单调递增区间为 ( )A．B．C．D．【答案】D【解析】由余弦函数的图象：知应选D．【考点】余弦函数的单调性9.函数f（x）＝Asin（ωx＋）（ω＞0）的图像与x轴交点的横坐标构成一个公差为的等差数列，要得到函数g（x）＝Acosωx的图象，只需将f（x）的图像（）A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位【答案】A【解析】由题设知,又因为,而，所以所以，=，因为所以，要得到的图象，只需将的图象向左平移个单位.故选A.【考点】1、三解函数的图象与性质；2、三角函数的图象变换；3、诱导公式.10.下列函数中，最小正周期为π的偶函数是（）A．B．C．y=sin2x+cos2x D．y=【答案】D【解析】，是最小正周期为π的奇函数；，，是最小正周期为的偶函数；,，最小正周期为，非奇非偶函数．,则函数是最小正周期为π的偶函数．【考点】1．诱导公式；2．函数的奇偶性；3．函数的周期．11.函数的最小正周期是（）A．B．C．D．【答案】D【解析】,所以最小正期为．【考点】1．函数的周期；2．倍角公式．12.函数的值域为（）A．B．C．D．【答案】B【解析】【考点】三角函数化简及性质点评：三角函数化简时常会用到关系式，其中由共同决定，结合的范围是求出值域13.函数（，，是常数，，）的部分图象如下图所示，则的值是【答案】【解析】依题意，,所以，令，则，故，所以.【考点】由y="A" sin（ωx+φ）的部分图象确定其解析式．点评：本题主要考查由函数y="A" sin（ωx+∅）的部分图象求函数的解析式，属于中档题．14.函数在点处的切线方程是( )A．B．C．D．【答案】D【解析】因为，所以，切线的斜率为－2，切线方程为，故选D。

一次函数与几何专题

求解一次函数图像上的特殊点
零点
一次函数图像与x轴的交点称为零点，可以通过解方程y = 0来求解。
极值点
一次函数图像在最高点或者最低点的纵坐标称为极值点，它对应着最大或最小的函数值。
特殊点
特殊点包括截距点、平行于y轴的直线和平行于x轴的直线。它们都有特定的纵坐标和横坐标。
如何找到一次函数的解析式
解一次方程的应用
日常生活
一次方程的应用非常广泛，比如我们可以用它来解决购物时的打折问题，或者计算出行的时间和距离关系。
建筑工程
一次方程在建筑工程中也有很多应用，比如计算建筑物的斜坡高度、角度等。
金融领域
一次方程在金融领域的应用十分重要，比如计算投资回报率、利息等。
一次函数在实际问题中应用
斜率为0表示一条水平线。 • 截距表示在数轴上的纵坐标。
平面直角坐标系中的直线方程
一般式
直线的一般式方程为Ax + By = C，其中A、B、 C为常数。这种形式的方程可以表示各种倾斜程度和位置的直线。
斜截式
直线的斜截式方程为y = mx + b，其中m为斜率， b为截距。这种形式方便计算和理解，适用于大多数情况。
1
已知斜截式方程
2
如果已知一次函数的斜截式方程y = mx + b，直接读取出斜率和截距的值。
已知点
如果已知一次函数上的两个点，可以使用两点间连线斜率的公式和任意一个点的坐标来求解出斜率和截距的值。
交通规划
一次函数可以用于交通规划，比如预测交通拥堵情况以及制定道路改进方案。
物业管理
物业管理中，一次函数可以用于预测房租涨跌趋势或物业维修费用的估计。
生产计划