山东省济宁一中2011届高三第一次模拟测试数学试题(理科)

合集下载

济宁市2011年高中阶段学校招生考试数学试题及答案(word版)

☆绝密级试卷类型A济宁市二○一一年高中阶段学校招生考试数学试题注意事项：1.本试题分第Ⅰ卷和第Ⅱ卷两部分，共10页.第Ⅰ卷2页为选择题，30分；第Ⅱ卷8页为非选择题，70分；共100分.考试时间为120分钟.2.答第Ⅰ卷前务必将自己的姓名、考号、考试科目涂写在答题卡上. 每题选出答案后，都必须用2B 铅笔把答题卡上对应题目的答案标号(ABCD)涂黑，如需改动，必须先用橡皮擦干净，再改涂其他答案.3.答第Ⅱ卷时，将密封线内的项目填写清楚，并将座号填写在第8页右侧，用钢笔或圆珠笔直接答在试卷上.考试结束，试题和答题卡一并收回.第Ｉ卷(选择题共30分)一、选择题（下列各题的四个选项中，只有一顶符合题意，每小题3分，共30分） 1. 计算－1－2的结果是A. -1B.1C.－3D.3 2. 下列等式成立的是A.532a a a =+ B.a a a =-23C .632a a a =∙ D.632)(a a = 3. 如果一个等腰三角形的两边长分别是5 cm ，6 cm ，那么此三角形的周长是A. 15 cmB. 16 cmC. 17 cmD. 16 cm 或17 cm 4. 下列计算正确的是A 5=B ．2=C.= D ．2= 5. 已知关于x 方程02=++a bx x 有一个根是)0(≠-a a ，则a-b 的值为A ．-1B ．0C ．1D ．2 6.已知//AE BD ，∠1=120o，∠2=40o，则∠C 的度数是A.10 ºB.20 ºC.30 ºD.40 º7.在2x □2xy □2y 的空格□中，分别填上“+”或“﹣”，在所得的代数式中，能构成完全平方式的概率是A. 1B.34 C. 12 D. 148..已知二次函数2y ax bx c =++中，其函数y 与自变量x 之间的部分对应值如下表所示：x… 0 1 2 3 4 … y…4114…点A （1x ，1y ）、B （2x ，2y ）在函数的图象上，则当112x <<，234x <<时，1y 与2y 的大小关系正确的是A ．12y y >B ．12y y < C. 1y ≥2yD ．1y ≤2y9. 如图，△ABC 的周长为30cm ，把△ABC 的边AC 对折，使顶点A 和C 重合，折痕交BC 边于点D ，交AC 边于点E ，AE =4 cm ，连接AD ，则△ABD 的周长是 A ．22cm B. 20cm C. 18cm D. 15cm 10. 如图，是某几何体的三视图及相关数据，则下面判断正确是 A. a ＞c B. b ＞c C. a 2+4b 2=c 2D. a 2+b 2=c 2第9☆绝密级试卷类型A济宁市二○一一年高中阶段学校招生考试数学试题第Ⅱ卷(非选择题共70分)二、填空题(每小题3分，共15分；只要求填写最后结果)11. 反比例函数xmy1-=的图象在第一、三象限，则m的取值范围是 .12. 将二次函数245y x x=-+化为2()y x h k=-+的形式，则y= ．13. 如图，在Rt△ABC中，∠C＝90º，∠A＝60º，BC＝4 cm，以点C为圆心，以3 cm的长为半径作圆，则⊙C与AB的位置关系是．14. 如图，观察每一个图中黑色正六边形的排列规律，则第10个图中黑色正六边形有个．15. 如图，等边三角形ABC中，D、E分别为AB、BC边上的两动点，且总使AD BE=，AE与CD交于点F，AG CD⊥于点G，则=AFFG.第1个图第2个图第3个图…DCAFBEG三、解答题（共55分，解答应写出文字说明、证明过程或推演步骤） 16．（5分）计算：22()a b ab b a a a--÷- 17．（5分）如图，在平行四边形ABCD 中，对角线AC 、BD 相交于点O ，过点O 作直线EF ⊥BD ，分别交AD 、BC 于点E 和F. 求证：四边形BEDF 是菱形.18．（6分）日本福岛出现核电站事故后，我国国家海洋局高度关注事态发展，紧急调集海上巡逻的海检船，在相关海域进行现场监测与海水采样，针对核泄漏在极端情况下对海洋环境的影响及时开展分析评估.如图，上午9时，海检船位于A处，观测到某港口城市P位于海检船的北偏西67.5°方向，海检船以21海里/时的速度向正北方向行驶，下午2时海检船到达B 处，这时观测到城市P位于海检船的南偏西36.9°方向，求此时海检船所在B处与城市P 的距离？(参考数据：331212 sin36.9,tan36.9,sin67.5,tan67.554135≈≈≈≈)19．（6分）某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人（不设弃权票），选出了票数最多的出甲、乙、丙三人.投票结果统计如图一：其次，对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示：图二是某同学根据上表绘制的一个不完整的条形图。

济宁一中届模拟检测一理科数学试题目

济宁一中届模拟检测一理科数学试题目济宁一中2011届第一次模拟测试数学（理）试题 2011.3一、选择题（本题共12小题，每题5分，共60分） 1.计算：=--+ii i 21)1)(2(2（A ）2 （B ）2- （C ）2i（D ）2i -2.已知a 、b 为直线，α、β为平面．在下列四个命题中， ① 若a ⊥α，b ⊥α，则a ∥b ； ② 若 a ∥α，b ∥α，则a ∥b ；③ 若a ⊥α，a ⊥β，则α∥β； ④ 若α∥b ，β∥b ，则α∥β．正确命题的个数是 (A) 1 (B) 3(C) 2 (D) 0 3.已知函数()()01f x x ≤≤的图象的一段圆弧（如图所示）1201x x<<<则（A ）1212()()f x f x x x < （B ）1212()()f x f x x x =（C ）1212()()f x f x x x > （D ）前三个判断都不正确4.将4名司机和8名售票员分配到四辆公共汽车上，每辆车上分别有1名司机和2名售票员，则可能的分配方案种数是 (A)4444242628A A CC C (B)44242628A A A A(C)44242628A CC C(D)242628C C C5.有下列四个命题:1p :若0a b ⋅=，则一定有a b ⊥; 2p : ∃x 、y ∈R, sin(x-y)=sinx-siny; 3p : (0,1)(1,)a ∀∈+∞，函数12()1xf x a-=+都恒过定点⎪⎭⎫⎝⎛2,21; 4p :方程220xy Dx Ey F ++++=表示圆的充要条件是2240D E F +-≥.其中假命题的是(A)1p ,4p (B)2p ,4p （C ）1p ,3p(D) 2p ,4p6.定义在R 上的偶函数f (x )在[)∞+,0上递增，0)31(=f ，则满足)(log 81x f ＞0的x 的取值范围是(A)()∞+,0 (B)()∞+⎪⎭⎫ ⎝⎛,221,0 (C)⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛2,2181,0 (D) ⎪⎭⎫ ⎝⎛21,07．右图的矩形，长为5，宽为2，在矩形内随机地撒300颗黄豆，数得落在阴影部分的黄豆数为138颗，则我们可以估计出阴影部分的面积约(A)523 (B)521（C ）519 (D)5168.将一张坐标纸折叠一次，使点(10，0)与(－6，8)重合，则与点(－4，2)重合的点是（A ） (4，－2) （B ） (4，－3) （C ） (3， 23) （D ） (3，－1) 9.平面上有四个互异的点A 、B 、C 、D ，满足(AB－BC )·(AD －CD )＝0，则三角形ABC 是（A ）直角三角形（B ）等腰三角形（C ）等腰直角三角形（D ）等边三角形10.已知函数f (x )的图象过点(0，－5)，它的导数'()f x ＝4x 3－4x ，则当f (x )取得最大值－5时，x 的值应为(A) －1 (B) 0 (C) 1 (D) ±111.要测量底部不能到达的电视塔AB 的高度,在CA点测得塔顶A 的仰角是45°,在D 点测得塔顶A 的仰角是30°,并测得水平面上的∠BCD =120°,CD =40m,则电视塔的高度为(A)102m (B)20m （C ）203m (D)40m12.已知函数f(x)＝x9x3m ⋅-+m+1对x ∈(0，∞+)的图象恒在x 轴上方，则m 的取值范围是（A ） 2－22＜m ＜2+22 （B ） m ＜2 （C）m＜2+22（D ） m ≥2+22二、填空题（本题共4小题，每题4分，共16分）13．观察下列各式9－1=8，16－4=12，25－9=16，36－16=20…，这些等式反映了自然数间的某种规律，设n 表示自然数，用关于n 的等式表示为 .14. 如图，正六边形ABCDEF 的两个顶点A 、D 为椭圆的两个焦点，其余4个顶点在椭圆上，则该椭圆的离心率为____________________.ADFECB15.一辆列车沿直线轨道前进，从刹车开始到停车这段时间内，测的刹车后t 秒内列车前进的距离为2270.45S t t =-米，则列车刹车后秒车停下来，期间列车前进了米．16.执行右边的程序框图,输出的T 为( )三、解答题（本题共6小题，共74分） 17． ( 本题满分12分 ) 已知函数否是？f x x x x x()cos sin cos sin =--442（1）求f x ()的最小正周期；（2）若x ∈⎡⎣⎢⎤⎦⎥02，π，求f x ()的最大值，最小值．18. ( 本题满分12分 )某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是13,遇到红灯时停留的时间都是2min. (1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;(2)求这名学生在上学路上因遇到红灯停留的总时间ξ的分布列及期望.19.( 本题满分12分 )已知)0(3,2)(,≥x x f x 成等差数列.又数列,3,)0}({1=>a a a n n 中此数列的前n 项的和S n (+∈N n )对所有大于1的正整数n 都有)(1-=n nS f S . (1)求数列}{na 的第n+1项;(2)若nn n a a b 1,11+是的等比中项,且T n 为{b n }的前n 项和,求T n.20. ( 本题满分12分 )如图，已知直角梯形ABCD 的上底2BC =，1//,2BC AD BC AD =，CD AD ⊥，平面PDC ⊥平面ABCD ，PCD∆是边长为2的等边三角形。

数学_2011年山东省某校高考数学一模试卷(理科)_(含答案)

2011年山东省某校高考数学一模试卷（理科）一、选择题（共12小题，每小题5分，满分60分） 1. 设全集为R ，集合A ={x|1x ≤1}，则∁R A =( )A {x|0≤x <1}B {x|0<x ≤1}C {x|0<x <1}D {x|x ≥1或x <0} 2. (1+2i2−i )2011=( )A 1B −1C iD −i3. 某程序框图如图所示，该程序运行后输出的k 的值是( )A 4B 5C 6D 74. 已知sinθ=45，sinθ−cosθ>1，则sin2θ=( ) A −2425 B −1225 C −45 D 24255. 定义在R 上的偶函数f(x)在[0, +∞)上递增，f(13)=0，则满足f(log 18x)>0x 的取值范围是（）A (0,12)∪(2,+∞) B (0, +∞) C (0,18)∪(12,2) D (0,12)6. 公差不为零的等差数列{a n }中，a 2，a 3，a 6成等比数列，则其公比q 为（） A 1 B 2 C 3 D 47. 某教师一天上3个班级的课，每班开1节，如果一天共9节课，上午5节、下午4节，并且教师不能连上3节课（第5节和第6节不算连上），那么这位教师一天的课表的所有排法有（）A 474种B 77种C 462种D 79种8. 已知向量a →=(x −1,2)，b →=(4,y)，若a →⊥b →，则9x +3y 的最小值为（） A 2√3 B 6 C 12 D 3√29. 一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积是（） A 12π B 4√3π C 3π D 12√3π 10. 已知双曲线x 2−y 22=1的焦点为F 1、F 2，点M 在双曲线上且MF 1→⋅MF 2→=0，则点M 到x轴的距离为（） A 43B 53C2√33D √311. 点P 是曲线x 2−y −2ln √x =0上任意一点，则点P 到直线4x +4y +1=0的最小距离是（）A √22(1−ln2) B √22(1+ln2) C √22(12+ln2) D 12(1+ln2)12. 设实数x ，y 满足约束条件{x −y −2≤0x +2y −5≥0y ≤2，则u =2xyx 2+y 2的取值范围是（）A [310，1) B [12，1] C [310，12] D [35，1]二、填空题（共4小题，每小题4分，满分16分）13. 已知(ax −√x)9的展开式中x 3的系数为9，则常数a 的值为________．14. 已知数列{a n }满足a 1=23，且对任意的正整数m ，n 都有a m+n =a m ⋅a n ，若数列{a n }的前n 项和为S n ，则S n =________．15. 不等式|x −1|<1表示的平面区域落在抛物线y 2=4x 内的图形的面积是________． 16. 下列命题中：（1）α=2kπ+π3(k ∈Z)是tanα=√3的充分不必要条件；（2）函数f(x)=|2cosx −1|的最小正周期是π；（3）△ABC 中，若cosAcosB >sinAsinB ，则△ABC 为钝角三角形；（4）若a +b =0，则函数y =asinx −bcosx 的图象的一条对称轴方程为x =π4；其中是真命题的为________．三、解答题（共6小题，满分74分）17. 已知函数f(x)=sin2x +acos 2x （a ∈R ，a 为常数），且π4是函数y =f(x)的零点．（1）求a 的值，并求函数f(x)的最小正周期；（2）若x ∈[0, π2]，求函数f(x)的值域，并写出f(x)取得最大值时x 的值．18. 某考生参加2011年大学自主招生考试，面试时从两道数学题，一道物理题，一道化学题中任选两道回答，该考生答对每一道数学题、物理题、化学题的概率依次为0.9，0.8，0.7，（1）求该考生恰好抽到两道数学题并都答对的概率；（2）求该考生在这次面试中答对试题个数X 的分布列和数学期望．19. 如图，四棱锥P −ABCD 中，AB ⊥AD ，CD ⊥AD ，PA ⊥底面ABCD ，PA =AD =CD =2AB =2，M 为PC 的中点．（1）求证：BM // 平面PAD ；（2）在平面PAD 内找一点N ，使MN ⊥平面PBD ，并求直线PC 与平面PBD 所成角的正弦值．20. 已知抛物线方程C:y 2=2px(p >0)，点F 为其焦点，点N(3, 1)在抛物线C 的内部，设点M 是抛物线C 上的任意一点，|MF →|+|MN →|的最小值为4．（1）求抛物线C 的方程；（2）过点F 作直线l 与抛物线C 交于不同两点A 、B ，与y 轴交于点P ，且PF →=λ1FA →=λ2FB →，试判断λ1+λ2是否为定值？若是定值，求出该定值并证明；若不是定值，请说明理由． 21. 已知数列{a n }中，a 1=2，a n −a n−1−2n =0(n ≥2, n ∈N)．（1）写出a 2、a 3的值（只写结果）并求出数列{a n }的通项公式；（2）设b n =1a n+1+1a n+2+1a n+3+⋯+1a 2n，若对任意的正整数n ，当m ∈[−1, 1]时，不等式t 2−2mt +16>b n 恒成立，求实数t 的取值范围．22. 已知向量p →=(a −3,x)，q →=(x +a,x)，f(x)=p →⋅q →，且m ，n 是方程f(x)=0的两个实根，（1）设g(a)=m 3+n 3+a 3，求g(a)的最小值；（2）若不等式lnx −bx <x 2在x ∈[1, +∞)上恒成立，求实数b 的取值范围；（3）对于（1）中的函数y =g(a)，给定函数ℎ(x)=c(xlnx −x 3)，(c <0)，若对任意的x 0∈[2, 3]，总存在x 1∈[1, 2]，使得g(x 0)=ℎ(x 1)，求实数c 的取值范围．2011年山东省某校高考数学一模试卷（理科）答案1. A2. D3. A4. A5. A6. C7. A8. B9. C10. C11. B12. D13. 114. 2−2n+13n15. 16√2316. （1）（3）（4）17. 解：（1）由于π4是函数y=f(x)的零点，即x=π4是方程f(x)=0的解，从而f(π4)=sinπ2+acos2π4=0，则1+12a=0，解得a=−2．所以f(x)=sin2x−2cos2x=sin2x−cos2x−1，则f(x)=√2sin(2x−π4)−1，所以函数f(x)的最小正周期为π．（2）由x∈[0, π2]，得2x−π4∈[−π4, 3π4]，则sin(2x−π4)∈[−√22, 1]，则−1≤√2sin(2x−π4)≤√2，−2≤√2sin(2x−π4)−1≤√2−1，∴ 值域为[−2, √2−1]．当2x−π4=2kπ+π2(k∈Z)，即x=kπ+38π时，f(x)有最大值，又x∈[0, π2]，故k =0时，x =38π，f(x)有最大值√2−1．18. 解：（1）该考生恰好抽到两道数学题并都答对的概率P =C 22C 42×0.9×0.9=0.135（2）X 的可能取值为0，1，2P(x =0)=0.1×0.1+0.2×0.3+2(0.1×0.3+0.1×0.2)C 42=17600P(x =2)=0.9×0.9+0.8×0.7+2(0.9×0.7+0.9×0.8)C 42=407600 P(x =1)=1−17600−407600=176600E(X)=20=1.65 19. 证明：（1）取PD 的中点E ，连接EM ，EA ，则EM // AB ，且EM =AB 所以四边形ABME 为平行四边形，所以BM // AE又AE ⊂平面PAD ，BM 不在平面PAD 内，∴ BM // 平面PAD ；解：（2）以A 为原点，AB ，AD ，AP 分别为x ，y ，z 轴，建立空间直角坐标系则B(1, 0, 0)，C(2, 2, 0)，D(0, 2, 0)，P(0, 0, 2)，M(1, 1, 1)，E(0, 1, 1)假设存在满足题意的点，则在平面PAD 内，设N(0, y, z)MN →=(−1,Y −1,Z −1)，PB →=(1,0,−2)，DB →=(1,−2,0){MN →⋅DB →=0˙，得y =12，z =12，所以N =(0,12，12)，即N 是AE 的中点，此时MN ⊥平面PBD ，设直线PC 与平面PBD 所成的角为θ，易得PC →=(2,2,−2)，MN →=(−1,−12,−12) 设PC →与MN →的夹角为α，则cosα=|PC →||MN →|˙=−√23，sinθ=−cosα=√23故直线PC 与平面PBD 所成角的正弦值为√2320. 解：（1）准线方程为l ：x =−p2，点M 到l 的距离设为d ，由抛物线定义，|MF →|+|MN →|=d +|MN →|≥3+p2=4，p =2，所以y 2=4x ．（2）设A(x 1, y 1)，B(x 2, y 2)，F(1, 0)由题意知直线l 的斜率k 存在且不等于0，设l:y =k(x −1)，则P(0, −k)，由PF →=λ1FA →=λ2FB →知(1, k)=λ1(x 1−1, y 1)=λ2(x 2−1, y 2)∴ k =λ1y 1=λ2y 2∵ k ≠0，∴ λ1=k y 1，λ2=ky 2，λ1+λ2=k ×y 1+y 2y 1y 2，将y =k(x −1)代入y 2=4x 得y 2−4k y −4=0，y 1+y 2=4k，y 1⋅y 2=−4∴y 1+y 2y 1y 2=−4k×14=−1k，∴ λ1+λ2=k ×(−1k)=−1为定值．21. 解：（1）∵ a 1=2，a n −a n−1−2n =0(n ≥2, n ∈N)∴ a 2=6，a 3=12当n ≥2时，a n −a n−1=2n ，a n−1−a n−2=2(n −1)，…，a 3−a 2=2×3，a 2−a 1=2×2，∴ a n −a 1=2[n +(n −1)+...+3+2]， ∴ a n =2[n +(n −1)+⋯+3+2+1]=2n(n+1)2=n(n +1)当n =1时，a 1=1×(1+1)=2也满足上式， ∴ 数列{a n }的通项公式为a n =n(n +1) （2）b n =1a n+1+1a n+2++1a 2n=1(n+1)(n+2)+1(n+2)(n+3)++12n(2n+1)=1(n+1)−1(n+2)+1(n+2)−1(n+3)++12n −1(2n+1)=1(n+1)−1(2n+1)=n2n 2+3n+1=1(2n+1n)+3令f(x)=2x +1x (x ≥1)，则f′(x)=2−1x 2，当x ≥1时，f ′(x)>0恒成立 ∴ f(x)在x ∈[1, +∞)上是增函数，故当x =1时，f(x)min =f(1)=3 即当n =1时，(b n )max =16要使对任意的正整数n ，当m ∈[−1, 1]时，不等式t 2−2mt +16>b n 恒成立，则须使t 2−2mt +16>(b n )max =16，即t 2−2mt >0，对∀m ∈[−1, 1]恒成立，∴ {t 2−2t >0t 2+2t >0，解得，t >2或t <−2，∴ 实数t 的取值范围为(−∞, −2)∪(2, +∞) 22. 解：（1）f(x)=x 2+(a −3)x +a 2−3a 有两个实根，所以△≥0，解得a ∈[−1, 3] 由题意{m +n =3−amn =a 2−3ag(a)=m 3+n 3+a 3=(m +n)[(m +n)2−3mn]+a 3=3a 3−9a 2+27，a ∈[−1, 3] g′(a)=9a(a −2)=0，解得a =0或2 g(0)=g(3)=27，g(−1)=g(2)=15 所以最小值为15．（2）若不等式lnx −bx <x 2在x ∈[1,+√∞)上恒成立，即x 2−lnx +bx >0恒成立，解得b>x(lnx−x2)令ℎ(x)=x(lnx−x2)，x∈[1, +∞)则ℎ′(x)=1+lnx−3x2，x∈[1, +∞)−6x，x∈[1, +∞)则ℎ′′(x)=1x∵ ℎ′′(x)=1−6x<0在[1, +∞)恒成立x∴ ℎ′(x)=1+lnx−3x2，在区间[1, +∞)为减函数则ℎ′(x)≤ℎ′(1)=−2<0恒成立∴ ℎ(x)=x(lnx−x2)在区间[1, +∞)递减则ℎ(x)≤ℎ(1)=−1故b>−1（3）由（1）得对任意的x0∈[2, 3]，g(x0)∈[15, 27]由（2）得函数ℎ(x)=c(xlnx−x3)，(c<0)，在区间[1, 2]单调递增则ℎ(1)=−c≤ℎ(x)≤ℎ(2)=c(2ln2−8)若对任意的x0∈[2, 3]，总存在x1∈[1, 2]，使得g(x0)=ℎ(x1)，则−c≤15且c(2ln2−8)≥27解得：−15≤c≤272ln2−8。

山东省济宁一中2011届高三下学期4月模拟测试(数学)

济宁一中2011届高三年级模拟考试数学试题2011.4第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设A 、B 是两个非空集合，定义运算A ×B ＝{x |x ∈A ∪B ，且x ∉A ∩B }，已知A ＝{x |y ＝2x －x 2}，B ＝{y |y ＝2x，x ＞0}，则A ×B ＝( )A ．∪(2，＋∞) B． D ．2．命题“对任意的x ∈R，x 3－x 2＋1≤0”的否定是( )A ．不存在x ∈R，x 3－x 2＋1≤0B ．存在x ∈R，x 3－x 2＋1≤0C ．存在x ∈R，x 3－x 2＋1>0D ．对任意的x ∈R，x 3－x 2＋1>03．已知函数f (x )＝⎩⎪⎨⎪⎧(3a －2)x ＋6a －1(x <1)，a x(x ≥1)，在(－∞，＋∞)上单调递减，那么实数a的取值范围是( )A ．(0,1)B ．(0，23)C ．[38，23)D ．[38，1)4.若复数2(R,12a ia i i -∈+为虚数单位)是纯虚数，则实数a 的值为A.4B. 4-C.1D. 1-5.已知在等比数列{}n a 中,1346510,4a a a a +=+=,则等比数列{}n a 的公比q 的值为A.14B.12C.2D. 86.若函数)(log )(b x x f a +=的大致图象如右图，其中b a ,（0a >且1a ≠）为常数，则函数b a x g x+=)(的大致图象是A B C D7．某计算机程序每运行一次都随机出现一个五位的二进制数A =A 的各位数中，)5,4,3,2(,11==k a a k出现0的概率为31，出现1的概率为32．记54321a a aaa ++++=ξ，当程序运行一次时，ξ的数学期望E ξ= A ．827 B ．1681 C ．113 D ．65818．已知圆C:()()()22240x a y a -+-=>及直线:30l x y -+=，当直线l C 被截得弦长为a 等于 AB ．2-C 1D 19．双曲线221mx y +=的虚轴长是实轴长的2倍，则m 等于 A ．14-B ．4-C ． 4D ．1410．设x ，y 满足约束条件⎪⎩⎪⎨⎧≥≥≥-≤--,0,0,0,023y x y x y x 若目标函数)0,0(>>+=b a by ax z 的最大值1，则b a 11+的最小值为（）A ．625B ．38C ．311D ．411．已知函数1|)(|,]1,0[,44)(2>∈-=x f x x ax x x f 的不等式关于时的解集为空集，则满足条件的实数a 的取值范围是（）A ．⎥⎦⎤ ⎝⎛∞-43,B ．),43(+∞C ．}43{D ．[)+∞,112．（理）从6名学生中选4人分别从事A 、B 、C 、D 四项不同的工作，若甲、乙两人不能从事A 工作，则不同的选派方案共有（）A ．280B ．240C ．180D ．96（文）．若函数f (x )＝x 3－3x ＋a 有3个不同的零点，则实数a 的取值范围是( ) A ．B ．(－2,2)C ．(－∞，－1)D ．(1，＋∞)二、填空题：本大题共4小题，每小题4分，共16分。

(2011济宁一模)山东省济宁市2011届高三第一次模拟考试word试题部分(数学理)

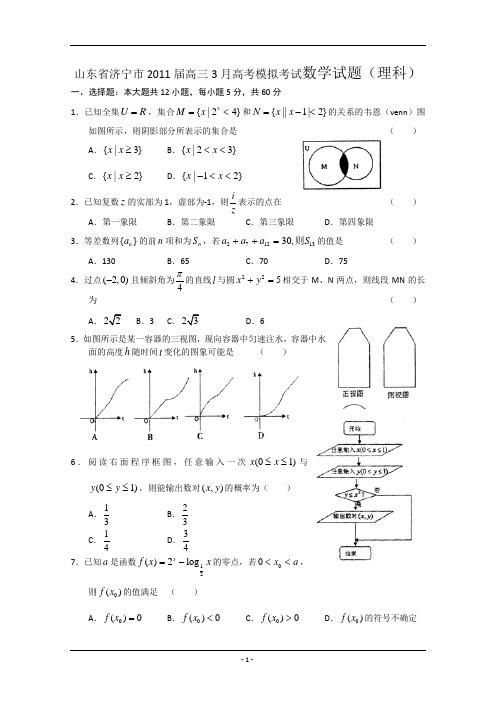
山东省济宁市2011届高三3月高考模拟考试数学试题（理科）一、选择题：本大题共12小题，每小题5分，共60分1．已知全集U R =，集合{|24}x M x =<和{||1|2}N x x =-<的关系的韦恩（venn ）图如图所示，则阴影部分所表示的集合是（）A ．{|3}x x ≥B ．{|23}x x <<C ．{|2}x x ≥D ．{|12}x x -<<2．已知复数z 的实部为1，虚部为-1，则iz表示的点在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．等差数列{}n a 的前n 项和为n S ，若27121330,a a a S ++=则的值是（）A ．130B ．65C ．70D ．754．过点(2,0)-且倾斜角为4π的直线l 与圆225x y +=相交于M 、N 两点，则线段MN 的长为（）A ．22B ．3C ．23D ．65．如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h 随时间t 变化的图象可能是（）6．阅读右面程序框图，任意输入一次(01)x x ≤≤与(01)y y ≤≤，则能输出数对(,)x y 的概率为（）A ．13 B ．23 C ．14 D ．347．已知a 是函数12()2log xf x x =-的零点，若00x a <<，则0()f x 的值满足（）A ．0()0f x =B ．0()0f x <C ．0()0f x >D ．0()f x 的符号不确定8．已知函数()cos()(0,0,0)f x A x A ωϕωϕπ=+>><<为奇函数，该函数的部分图象如图所示，EFG ∆是边长为2的等边三角形，则(1)f 的值为（）A ．32-B ．62-C ．3D ．3-9已知函数2010()sin x f x x e x =++，令1213()(),()(),(n n f x f x f x f x f x f x f x f x +''''==== ，则2011()f x =（）A ．sin xx e +B ．cos xx e +C ．sin xx e -+D ．cos xx e -+10．已知1:0,:420x x x p q m x-≤+-≤，若p q 是的充分条件，则实数m 取值范围是（）A ．22m >+B ．22m ≤+C ．2m ≥D ．6m ≥11．已知抛物线22(0)y px p =>上一点(1,)(0)M m m >到其焦点的距离为5，双曲线221x y a-=的左顶点为A ，若双曲线的一条渐近线与直线AM 平行，则实数a 的值是（）A ．125B ．19C ．15D ．1312．给定两个长度为1的平面向量OA OB和，它们的夹角为90︒，如图所示，点C 在以O 为圆心的圆弧AB 上运动，若CO xOA yOB =+，其中,x y R ∈，则x y +的最大值是（）A ．1B ．2C ．3D ．2二、填空题：本大题共4小题，每小题4分，共16分。

2011届山东省济宁一中高三模拟测试(基本能力)

济宁一中2011届高三年级模拟考试基本能力试题2011.04本试卷分第I卷和第II卷两部分，共12页，满分100分。

考试用时100分钟。

请将1-70题选择题答案填涂在答题卡上，填空及71－74题答案写在答题纸上，答在试卷上的题目无效。

第Ⅰ卷（共30分）一、一个民族想要站在科学的最高峰，就一刻也不能没有理论思维。

1.毛泽东在《七律·人民解放军占领南京》一诗中写道：“宜将剩勇追穷寇，不可沽名学霸王”。

这句诗借用西楚霸王（项羽）本可以凭优势兵力消灭刘邦，却怕落下“不义”之名而丧失机会的典故，告诫人们“宜将剩勇追穷寇”的道理。

这一典故给我们的哲学启示是A.世界上一切事物都是变化发展的B.主观和客观是具体的历史的统一C.当量的积累达到一定程度时，就应不失时机促成事物的飞跃与发展D.发挥主观能动性必须以尊重客观规律为基础2.用网络搜索引擎查询“遗传与变异”的定义，下列查询结果中最为可靠的应该是①在“百度百科”中找到的②在“百度文库”中找到的③在“人民教育出版社”网站中找到的④在“中国国家数字图书馆”中找到的A.①②B.①③C.③④D.②④3.子路问君子，子曰：“修己以敬。

”曰：“如斯而己乎？”曰：“修己以安人。

”曰：“如斯而己乎？”曰：“修己以安百姓……”子路与孔子的对话揭示了君子的三重境界：修养自己严肃认真做事；修养自己使别人安乐；修养自己使百姓安乐。

现代国家公务员同样需要“修己”，若以孔子“修已”思想衡量，应该①守责而不失范②为民而不为己③尚公而不趋利④让权而不谋权A.①②③B.②③④C.①②④D.①③④4.人造金属电池可提供相当于常规电池10倍的电力，不需要维修，充电次数可达1000次以上，使用寿命比铅蓄电池长4～5倍，而且不会污染环境。

它给我们的哲学启示是A.人的意识具有能动作用，可以改变规律B.人具有主观能动性，可以随意创造新的事物C.人们可以根据客观条件，创造出自然界原本没有的事物D.人可以改变自然界的客观性，从而创造新的事物5.意境不是意和境的简单相加，而是意和境和谐，并在此基础上生出“景外之意”、“象外之象”、“韵外之致”。

山东省济宁一中2011届高三第一次模拟测试语文

山东省济宁一中2011届高三第一次模拟测试语文试题说明：1．本试卷分第I卷和第II卷。

满分150分。

答题时间150分钟。

2．请将第I卷题目的答案选出后用2B铅笔涂在答题卡对应题目的代号上；第II卷用黑色签字笔将正确答案答在答题纸对应的位置上，答在试卷上作废。

禁止使用涂改液及胶带纸。

第Ⅰ卷（选择题共36分）一、（15分，每小题3分）1．下列各组词语中加点的字，读音都不相同的一组是（）（3分）A．创伤／重创敌军投奔／奔走相告蒙骗／蒙混过关B．别扭／别开生面旋风／旋转乾坤专横／横行霸道C．谙熟／黯然失色缜密／半嗔半笑炮烙／刨根问底D．渲染／煊赫一时罢黜／相形见绌辑录／缉拿归案2．下列词语中没有错别字的一组是: （）A．缉拿摒弃大材小用风声鹤戾，草木皆兵B．勘探荒废砰然心动金玉其外，败絮其中C．通牒暮蔼偃仰啸歌桃李不言，下自成蹊D．联袂返聘向隅而泣己所不欲，勿施于人3．下列各句中，加点词语使用正确的一项是（）A．我市数百名公安干警倾巢出动．．．．，经过数夜蹲守，终于抓获了这起枪杀案的犯罪嫌疑人。

B．他是一位乐于助人的青年，只是因为欠缺某种能力，以致有时有劲使不上，感到爱．莫能助．．．。

C．本来这是一篇不错的文章，让你们改来改去，反而改得不三不四．．．．。

D．初中毕业时你送我的那只钢笔，样子虽不太好看，但很好使，这么多年来我敝帚自．．．珍．，一直保存着。

4．下面各句中，没有语病的一项是（）A．在当今这个竞争异常激烈的时代里，任何一个企业家都不可能永远经历着辉煌而不面对挫折：遇到挫折并不可怕，可怕的是能否从失败的阴影中走出来。

B．火灾原因认定书认定引起本次火灾的原因是由于青岛拓昆工程机件有限公司车间北门外电闸短路打火引燃车间造成的。

C．专家指出，城市的数量增多、规模扩大和人口增加，使我国城市生活垃圾产生量持续增加，许多城市已经出现了不同程度的“垃圾围城”的局面。

D．交通建设质量问题不仅仅是一个经济、技术问题，而是关系到国家财产、人民生活及生命安全，是带头国计民生的重大问题。

山东济宁一中2011届高三第三次质量检测数学理

济宁市第一中学2011届高三年级第三次质量检测数学试题（理）第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案涂在答题卡上）1．已知全集，集合和的关系的韦恩图（venn）如图所示，则阴影部分所表示的集合是（）A． B．C． D．2．已知,是虚数单位，则在复平面中复数对应的点在（）A．第一象限 B．第二象限C．第三象限 D．第四象限3．函数的最小值为（）A． B． C． D．4．亲爱的同学们，我们济宁一中西校区的大门蔚为壮观，有个学生想搞清楚门洞拱顶到其正上方点的距离，他站在地面处，利用皮尺量得米，利用测角仪测得仰角°，测得仰角后通过计算得到，则的距离为（）A．米 B．米C．米 D．米5．函数的零点个数为（）A．1个 B．2个 C．3个 D．4个6．下列命题错误的是（）A．对于等比数列而言，若，则有B．点为函数的一个对称中心C．若，向量与向量的夹角为°，则在向量上的投影为D．“”的充要条件是“或（）”7．在中，若有，则的形状是（）A．锐角三角形 B．直角三角形C．钝角三角形 D．直角三角形或锐角三角形8．已知O是平面上的一个定点,A、B、C是平面上不共线的三个点,动点P满足, ,则动点P的轨迹一定通过△ABC的（）A．垂心 B．重心 C．外心 D．内心9．在下表中，每格上填一个数字后，使得每一横行成等差数列，每一纵列成等比数列，则的值为（）A．1 B．2 C．3 D．410．设函数在定义域内可导,的图象如图所示,则导函数可能为（）11．函数为奇函数，该函数的部分图像如右图所表示，、分别为最高点与最低点，并且两点间的距离为，则该函数的一条对称轴为（）A． B．C． D．12．已知，若对任意，存在，使得，则实数的取值范围是（）A． B．C． D．第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题4分，共16分，请把答案填在答题纸的相应位置）13．关于函数，在下列四个命题中：①的最小正周期是；②是偶函数；③的图像可以由的图像向左平移个单位长度得到；④若，，则以上命题正确的是_____________________________（填上所有正确命题的序号）14．很难想象城市污水不经过处理我们的生活会变成什么样。

山东省济宁市第一中学西校高一数学理测试题含解析

山东省济宁市第一中学西校高一数学理测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 函数的图象过定点A．（1，2）B．（2，1）C．（-2，1）D．（-1，1）参考答案：D2. 已知集合M＝｛(x,y)|x+y=2｝,N={(x,y)|x－y=4},那么集合M∩N为( )A.x=3,y=－1B.(3，－1)C.｛3，－1｝D.｛(3，－1)｝参考答案：D3. 函数的值域为，则实数的取值范围是（）A． B. C. D.参考答案：B4. 已知，则角所在的象限是A．第一象限B．第二象限C．第三象限D．第四象限参考答案：A略5. 已知数列{ }对任意的p，q∈N*满足且 =6，那么等于（）A． 165 B． 33 C． 30 D． 21参考答案：C略6. 下列函数中，在（0，+）上为增函数的是（）A. B.C. D.参考答案：C7. 设则=（）....参考答案：A8. 若a=20.5，b=logπ3，c=log2，则有（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．b＞c＞a参考答案：A【考点】4M：对数值大小的比较．【分析】利用对数和指数函数的单调性即可得出．【解答】解：∵a=20.5＞20=1，0＜b=logπ3＜logππ=1，＜log21=0．∴a＞b＞c．故选：A．9. 若为平面内任一点，且满足，则一定是A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．等边三角形参考答案：A略10. 已知，满足：，，，则-------( ) A． B． C．3D．10参考答案：B略二、填空题:本大题共7小题,每小题4分,共28分11. 某三棱锥的三视图如右图所示，则该三棱锥的最长棱的棱长为参考答案：12. 在△ABC中，若（a+b+c）（c+b﹣a）=3bc，则A= ．参考答案：60°【考点】余弦定理．【分析】已知等式左边利用平方差公式化简，再利用完全平方公式展开，整理得到关系式，利用余弦定理表示出cosA，将得出的关系式代入求出cosA的值，即可确定出A的度数．【解答】解：已知等式整理得：（a+b+c）（c+b﹣a）=（b+c）2﹣a2=b2+c2﹣a2+2bc=3bc，即b2+c2﹣a2=bc，∴cosA===，∵A为三角形内角，∴A=60°．故答案为：60°13. 当时，不等式恒成立，则实数的取值范围是__________．参考答案：(1,2]设，，在同一坐标系中作出它们的图象，如图所示：若时，不等式恒成立，则，解得，即实数的取值范围是(1,2]．14. 斜率为3且与圆相切的直线方程为____________.参考答案：或略15. 当0 < θ <时，p= sin θ + csc θ和q= tan θ + cot θ的大小关系是。

山东省济宁一中2011届高三第一次质量检测(数学理)

济宁市第一中学2011届高三教学质量第一次检测数学（理科）试题一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知函数()21f x x x =+-，集合(){}|M x x f x ==，(){}|N y y f x ==，则（）A ．M N =B ．M N ÝC ．MN =∅D ．M N Þ 2．命题2:,560p x R x x ∃∈-+<，则（）A ．2:,560p x R x x ⌝∃∈-+≥ B ．2:,560p x R x x ⌝∀∈-+<C ．2:,560p x R x x ⌝∀∈-+>D ．2:,560p x R x x ⌝∀∈-+≥3．已知函数()()32212f x ax a x =+-+，若1x =-是()y f x =的一个极值点，则a 的值为（）A ．2-B ．2C ．27D ．4 4．命题“若,p q ⌝则”是真命题，则下列命题一定是真命题的是（）A ．若,p q 则B ．若,p q ⌝则C ．若,q p ⌝则D ．若,q p ⌝⌝则5．将函数()lg 1y x =-的图像进行变换,使所得函数的图像与函数lg y x =的图像关于y 轴对称,这种变换是（）A ．向左平移1个单位B ．向右平移1个单位C ．向上平移1个单位D ．向下平移1个单位 6．若1122a a -<,则a 的取值范围是（）A ．1a ≥B ．0a >C ．01a <<D ．01a ≤≤7．若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“同族函数”,那么函数解析式为2y x =,值域为{}1,4的“同族函数”共有（） A ． 7个 B ． 8个C ． 9个D ． 10个8．设()f x 是定义在R 上以6为周期的函数,函数()f x 在()0,3上单调递减,且()y f x =的图像关于直线3x =对称,则下面结论中正确的是（）A ． ()()()1.5 3.5 6.5f f f <<B ． ()()()3.5 1.5 6.5f f f <<C ． ()()()6.5 3.5 1.5f f f <<D ． ()()()1.5 6.5 3.5f f f << 9．()203sin x x dx π+⎰是（）A ．2318π+ B ．2314π+ C ． 2314π- D ．2318π- 10．曲线313y x x =+在点41,3⎛⎫⎪⎝⎭处的切线与坐标轴围成的三角形的面积为（）A ．19B ．29C ．13D ．2311．给出下列四个命题，其中为真命题的为（）①“,x R ∃∈使得213x x +>”的否定是“,x R ∀∈都有213x x +≤”;②“2m =-”是“直线()210m x my +++=与直线()()2230m x m y -++-=相互垂直” 的必要不充分条件;③设圆()2222040x y Dx Ey F D E F ++++=+->与坐标轴有四个交点，分别为()()()()1212,0,,0,0,,0,A x B x C y D y ，则12120x x y y -=；④函数()sin f x x x =-的零点个数有3个． A ．①④B ．②④C ． ①③D ．②③12．设定义域为R 的函数()lg 1,10, 1x x f x x ⎧-≠⎪=⎨=⎪⎩,则关于x 的方程()()20f x bf x c ++=有7个不同实数解的充要条件（）A ． 00b c <>且B ．00b c ><且C ．00b c <=且D ．00b c ≥=且二、填空题：本大题共4小题，每小题4分，共16分．13．已知命题p ：231x ->，命题q ：()212log 50x x +-<，则p q ⌝⌝是的 _条件(填充分不必要条件、必要不充分条件、充要条件)． 14．若对于任意[]1,1a ∈-,函数()()2442f x x a x a =+-+-的值恒大于零,则x 的取值范围是________． 15．已知命题:,p x R ∃∈使tan 1x =，命题2:320q x x -+<的解集是{}|12x x <<，下列结论：①命题“p q ∧”是真命题；②命题“p q ∧⌝”是假命题；③命题“p q ⌝∨”是真命题；④命题“p q ⌝∨⌝”是假命题；其中正确的为______．（只填序号即可）16．已知函数()x f 的导函数为()x f '，且满足()()2'232xf x x f +=，则()=5'f ．三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤17．（满分12分）已知函数()32log f x x =+，[]1,9x ∈，若函数()()()22g x f x f x =+⎡⎤⎣⎦（I ）求函数()g x 的定义域；（Ⅱ）求函数()g x 的值域．18．（满分12分）已知a 是实数，函数2()()f x x x a =-．（Ⅰ）若(1)3f '=，求a 的值及曲线()y f x =在点(1,(1))f 处的切线方程；（Ⅱ）求()f x 在区间[]2,0上的最大值．19．（满分12分）设命题()2:431p x -≤;命题()()2:2110q x a x a a -+++≤,若⌝p是⌝q 的必要不充分条件，求实数a 的取值范围． 20．（满分12分）设某物体一天中的温度T 是时间t 的函数，已知32()(0)T t at bt ct d a =+++≠，其中温度的单位是℃，时间的单位是小时．中午12:00相应的0t =，中午12:00以后相应的t 取正数，中午12:00以前相应的t 取负数（如早上8：00相应的t =-4，下午16：00相应的t =4）．若测得该物体在早上8:00的温度为8℃，中午12:00的温度为60℃，下午13:00的温度为58℃，且已知该物体的温度早上8:00与下午16:00有相同的变化率．（I ）求该物体的温度T 关于时间t 的函数关系式；（II ）该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高？最高温度是多少？21．（满分12分）对于函数()f x ,若()f x x =,则称x 为()f x 的“不动点”；若()f f x x=⎡⎤⎣⎦则称x 为()f x 的“稳定点”函数()f x 的“不动点”和“稳定点”的集合分别记为A 和B ,即(){}|A x f x x ==,(){}|B x f f x x ==⎡⎤⎣⎦． (Ⅰ) 求证:A B ⊆；(Ⅱ)若()()21,f x ax a x R =-∈,且A B =≠∅,求实数a 的取值范围．22．（满分14分）已知函数()b f x ax c x=++(),,a b c 是常数是奇函数且满足()512f =,()1724f =． (Ⅰ)求a 、b 、c 的值；(Ⅱ)是判断函数()f x 在10,2⎛⎫⎪⎝⎭上的单调性并说明理由；(Ⅲ)试求函数()f x 在()0,+∞上的最小值．参考答案一、选择题 DDBCA,CCBAA,CC二、填空题 13．充分不必要；14．3x >或1x <；15．①②③④；16．6 三、解答题17．解：(1)函数()()()22g x f x f x=+⎡⎤⎣⎦满足21919x x ≤≤⎧⎨≤≤⎩，…………………………2分解得13x ≤≤，即函数()()()22g x f x f x =+⎡⎤⎣⎦的定义域为[]1,3………………4分(2)[]1,3x ∈,[]3log 0,1x ∴∈………………………………………………………5分()()()22g x f x f x =+⎡⎤⎣⎦()22332log 2log x x =+++ 233log 6log 6x x =++()23log 33x =+-…………………………………………9分当3log 0x =时, ()min 6g x =,当3log 1x =时, ()max 13g x =,………………11分即函数()g x 的值域为[]6,13．………………………………………………………12分18．（Ⅰ）()232f x x ax '=-，由'(1)3f =易得a =0，从而可得曲线()y f x =在(1,(1))f 处的切线方程为320.x y --= …………………………………………………………4分（Ⅱ）先求出可能的极值点x 1=0，x 2=23a ，再讨论极值点与区间[0,2]端点的位置关系．令'()0f x =，得1220,3ax x ==．当20,3a≤即0a ≤时，()f x 在[0,2]上单调递增， max ()(2)84f x f a ==-；…6分当22,3a≥即3a ≥时，()f x 在[0,2]上单调递减， max ()(0)0f x f ==；……8分当202,3a <<即03a <<时，()f x 在2[0,]3a 上单调递减，在2[,2]3a上单调递增，函数f (x )（0≤ x ≤2)的最大值只可能在x =0或x =2处取到，因为f (0)=0，f (2)=8－4a ，令f (2) ≥ f (0)，得a ≤ 2，所以max 84,02;()0,2 3.a a f x a -<≤⎧=⎨<<⎩…………11分综上，max84,2;()0, 2.a a f x a -≤⎧=⎨>⎩……………………………………………………12分 19．解:由p 得1431x -≤-≤,所以112x ≤≤,．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分由q 得1a x a ≤≤+,．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分又因p ⌝是q ⌝的必要非充分条件,所以p 是q 的充分非必要条件，．．．．．．．．．．．．．．8分所以1211a a ⎧≤⎪⎨⎪+>⎩或1211a a ⎧<⎪⎨⎪+≥⎩,解得102a ≤≤．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分 20．（满分12分）解：(1) 因为232T at bt c '=++,而()()44T T ''-=, 故488488a b c a b c ++=-+,∴ ()()()106004641648315860488488a T d b T a b c d c T a b c d d a b c a b c=⎧==⎧⎪⎪=-=-+-+=⎪⎪⇒⎨⎨=-=+++=⎪⎪⎪⎪=++=-+⎩⎩ ． ∴()3360(1212)T t t t t =-+-≤≤．……………………………………………6分(2) 233T t '=-, 由 ()011T t t t '==-=得或当t 在]2,2[-上变化时，()()T t T t '与的变化情况如下表:由上表知当62)(21取到最大值时或t T t t =-=，答:在上午11：00与下午14：00，该物体温度最高，最高温度是62℃．．．．．．．．．．．．．12分 21． (1)证明:当A φ=显然成立，当A φ≠时，对0x A ∀∈,有()00f x x =成立,所以()()000f f x f x x ==⎡⎤⎣⎦,即0x B ∈,所以A B ⊆．．．．．．．．．．．．．．．．．．．．．．．．．．4分 (2)由()f f x x =⎡⎤⎣⎦得()221a ax x -=,即3422210a x a x a x -+--=又因A=B ,所以342221a x a x a x -+--可分解为()()22211ax x a x ax a --+-+并且方程2210a x ax a +-+=与210ax x --=有相同的根或无实根．．．．．．．．．．．．8分当0a =时,{}1A B ==-,显然成立,当0a ≠时, 由2210a x ax a +-+=得2110ax x a++-=,显然不可能与方程210ax x --=有相同的根,所以11410a a ⎛⎫--<⎪⎝⎭,解得34a <又方程210ax x --=有实根,所以140a +≥,解得14a ≥- 所以1344a -≤<且0a ≠ 综上所述, 1344a -≤<．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分．22．解：(1)函数()f x 是奇函数,∴()()0f x f x -+=,即 0bb axc ax c x x--++++=,0c ∴=．由()512f =,()1724f =,得52a b +=,17224b a +=,解得12,2a b ==． ∴12,,02a b c ===．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分 (2)由(1)得,()122f x x x =+, ()'2122f x x =-,当10,2x ⎛⎫∈ ⎪⎝⎭时,21022x <<,则2122x >．∴()'0f x <,函数()f x 在10,2⎛⎫⎪⎝⎭上为减函数．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分(3)由()'21202f x x =-=,0x >,得12x =．当12x >时,2122x <,∴()'0f x >,即函数()f x 在1,2⎛⎫+∞ ⎪⎝⎭上为增函数．又由(2)知12x =处是函数的最小值点, 即函数()f x 在()0,+∞上的最小值为122f ⎛⎫= ⎪⎝⎭．．．．．．．．．．．．．．．．．．．14分。

高三数学第一次模拟考试理济宁市一模,含解析新人教A版

济宁市高三模拟考试数学(理工类)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部份，满分l50分，考试时间120分钟。

考试结束后，将本试卷和答题卡一并交回．注意事项：1．答第I 卷前，考生务必将自己的姓名，考号填写在答题卡上2．选择题答案利用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案的标号，非选择题答案利用0．5毫米的黑色中性(签字)笔或碳素笔书写，字体工整，笔迹清楚．参考公式：若是事件A 、B 互斥，那么P(A+B)=P(A)+P(B)．若是事件A 、B 独立，那么P(A·B)=P(A)·P(B)．第I 卷(选择题共60分)一、选择题：本大题共l2小题．每小题5分。

共60分．在每小题给出的四个选项中。

只有一项是符合题目要求的． 1．复数2=()1ii z -，则复数1z +在复平面上对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【答案】D【解析】221z=()122i i i ii==---，所以1112z i +=-，对应点位1(1,)2-，选D.2．已知全集U=R ，集合A={2(+1)y |y ln x ,x R =∈}，集合B={21x ||x |-≤}，则如图所示的阴影部份表示的集合是A ．{01>3x |x x ≤<或}B ．{|0<1x x ≤}C ．{|>3x x }D ．{|13x x ≤≤} 【答案】A【解析】2A={(+1)}0y|y ln x ,x R {y y }=∈=≥，{13}B x x =≤≤，图中阴影部份为集合()U AB ,所以{1>3}UB x x x =<或,所以(){01>3}U A B x x x =≤<或，选A.3．下列命题中正确的有①设有一个回归方程y =2—3x ，变量x 增加一个单位时，y 平均增加3个单位；②命题P ：“2000,--1>0x R x x ∃∈”的否定⌝P ：“,102x R x -x-∀∈≤”；③设随机变量X 服从正态散布N(0，1)，若P(X>1)=p ，则P(-1<X<0)=12-p ； ④在一个2×2列联表中，由计算得k 2=6．679，则有99％的把握确认这两个变量间有关系． A ．1个 B ．2个 C ．3个 D ．4个本题可以参考独立性查验临界值表【答案】C【解析】①变量x 增加一个单位时，y 平均减少3个单位，所以错误。

山东济宁一中高三第一次反馈练习——数学

山东省济宁一中2008—2009学年度高三第一次反馈练习数学试题说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分。

考试时间120分钟。

第Ⅰ卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一个选项是符合题目要求的。

） 1．已知U 是全集，M 、N 是U 的两个子集，若φ≠⋂≠⋃N M U N M ,，则下列选项中正确的是（）A ．N M C U =B ．M NC U =C ．φ=⋂)()(N C M C U UD ．U N C M C U U ≠⋃)()(2．函数)13lg(13)(2++-=x xx x f 的定义域是（）A ．⎪⎭⎫ ⎝⎛-∞-31,B ．⎪⎭⎫⎝⎛-31,31 C ．⎪⎭⎫⎝⎛-1,31 D ．),31(+∞-3．设⎩⎨⎧<>-=)0(1)0(1)(x x x f 则)(2)()()(b a b a f b a b a ≠-⋅--+的值为（）A ．aB ．bC ．a 、b 中较小的数D ．a 、b 中较大的数4．若),()(3R x x x f ∈=则函数)(x f -在其定义域上是（）A ．单调递减的偶函数B ．单调递减的奇函数C ．单调递增的偶函数D ．单调递增的奇函数 5．函数xx g x x f -=+=122)(log 1)(与在同一直角坐标系下的图象大致是（）6．若b a e xxx f <<=,ln )(，则（）A ．)()(b f a f >B ．)()(b f a f =C ．)()(b f a f <D ．1)()(>⋅b f a f 7．若)1,0(∈x ，则下列结论正确的是（）A ．x x xlg 221>> B ．21lg 2x x x>> C ．x x xlg 221>> D ．xx x 2lg 21>>8．函数22)(23+--=x x x x f 的零点个数为（）A ．0B ．1C ．2D ．39．已知函数)1(2-=x f y 的定义域是[]3,3-，则函数)(x f y =的定义域是（）A ．]2,2[-B ．[0，2]C ．[-1，2]D ．[]3,3-10．已知)(x f 是R 上的增函数，若)1()1()(x f x f x F +--=，则)(x F 的R 上的（）A ．增函数B ．减函数C ．先减后增的函数D ．先增后减的函数11．对于实数x ，符号[x ]表示不超过x 的最大整数，例如2]08.1[,3][-=-=π，定义函数][}{x x x -=，则下列命题中正确的是（）A ．函数}{x 的最大值为1B ．函数21}{)(-=x x G 有且仅有一个零点 C ．函数}{x 是周期函数D ．函数}{x 是增函数12．在股票买卖过程中，经常用到两种曲线，一种是即时价格曲线)(x f y =（实线表示）。

山东省济宁一中高三下学期模拟测试(理综)

山东省济宁一中2011届高三下学期4月模拟测试（理科综合）2011.4本试卷分第I卷和第II卷两部分，共10页。

满分240分。

考试用时150分钟。

答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在试卷和答题卡规定的位置。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（必做，共88分）注意事项：1．第Ⅰ卷共22小题，每小题4分，共88分。

2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用像皮擦干净后，再选涂其他答案标中与。

不涂在答题卡上，只答在试卷上不得分。

以下数据可供答题时参考：相对原子质量：H 1 O16 S 32 Fe 56一、选择题（本题包括15小题，每小题只有一个选项符合题意）1、乙酰胆碱是一种兴奋类神经递质，其主要功能是把信息从神经细胞传递到肌肉细胞，一旦信号通过，立即发生乙酰胆碱→胆碱+乙酸，分解后的胆碱在Na-协同下运入细胞重新合成乙酰胆碱。

关于该反应的相关叙述不正确的是（）A.突触小泡中的乙酰胆碱，以外排的形式进入组织液中B.可以防止递质长时间起作用C.胆碱被运入细胞可再次利用D.胆碱进入细胞的方式为协助扩散2、如果人体吞噬细胞不能正确地识别病原体和自身正常细胞，人体正常细胞就会被吞噬和破坏，使人患病。

下列有关说法不正确的是（）A.吞噬细胞可以识别病原体，但是不能特异性识别B.正常人体中吞噬细胞没有与自身正常细胞表面抗原特异性结合的受体C.如果人体的正常细胞被吞噬细胞吞噬和破坏，属于免疫缺陷病D.吞噬细胞在特异性免疫与非特异性免疫中均发挥重要作用3、下列与实验有关的说法，不正确的是（）A.叶绿体色素的提取和分离实验中，可用50%酒精代替丙酮作有机溶剂提取色素B.制取细胞膜、血红蛋白的提取和分离均以哺乳动物成熟的红细胞作为实验材料C.在用显微镜观察已处于视野中央的细胞时，若想放大细胞进一步观察，可以直接转动转换器换高倍物镜D.在探究植物生长调节剂对扦插枝条生根作用的实验中，插条的生根数是因变量4、右图表示某哺乳动物体内正在进行分裂的一个细胞,下列有关叙述正确的是( )A．该细胞存在于动物的各器官组织中B．该细胞在分裂间期发生过基因突变C．该细胞在图示分裂过程中染色体数目最多时为8条D．该细胞有2个染色体组，分裂产生的成熟生殖细胞的基因型有两种5、已知a、b、c、d是某细菌DNA片段上的4个基因，右图中W表示野生型，①②③分别表示三种缺失不同基因的突变体，虚线表示所缺失的基因。

山东省济宁市高三数学1月期末模拟理新人教A版

金乡一中2012—2013学年高三1月考前模拟数学（理）一.选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.若集合M ={y |y =2x,x ∈R },集合S ={x |y =lg(x −1)}, 则下列各式中正确的是（）A .M ∪S=MB .M ∪S=SC .M=SD .M∩S=∅ 2.设i 是虚数单位,则复数(1−i)−2i等于（）A ．0B ．2C ．4iD ．−4i3.如图2，正三棱柱111ABC A B C -的主视图（又称正视图）是边长为４的正方形，则此正三棱柱的侧视图（又称左视图）的面积为( )A ．． C ．．164.若βα,是两个不同的平面，下列四个条件：①存在一条直线a ，βα⊥⊥a a ,；②存在一个平面γ，βγαγ⊥⊥，；③存在两条平行直线a b a b a ,,,,βα⊂⊂∥,b β∥α；④存在两条异面直线,,,α⊂a b a a b ,β⊂∥,b β∥α．那么可以是α∥β的充分条件有（） A ．4个 B ．3个 C ．2个 D ．1个5.设函数32sin ()tan 3f x x x θθ=+，其中θ∈⎣⎢⎡⎦⎥⎤0，5π12，则导数)1(f '的取值范围是（）A ．[－2,2]B ．[2，3]C ．[3，2]D ．[2，2]6.数列{}n a 满足111,n n a a r a r +==⋅+（*,n r ∈∈N R 且0r ≠），则“1r =”是“数列{}n a 成等差数列”的（）A.充分不必要条件B. 必要不充分条件C.充分必要条件D. 既不充分也不必要条件7. 用数字0,1,2,3组成数字可以重复的四位数, 其中有且只有一个数字出现两次的四位数的个数为（）A. 144B.120C. 108D.728. 椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ，若椭圆C 上恰好有6个不同的点P ，使得12F F P ∆为等腰三角形，则椭圆C 的离心率的取值范围是（）A.12(,)33B.1(,1)2C. 2(,1)3D.111(,)(,1)3229．过双曲线M:2221y x b-=的左顶点A 作斜率为1的直线l ,若l 与双曲线M 的两条渐近线分别相交于B、C,且|AB|=|BC|,则双曲线M的离心率是 ( )9.如图，在等腰直角ABO∆中，设,,1,OA a OB b OA OB C====为AB上靠近点A的四等分点，过C作AB的垂线l，设P为垂线上任一点，,OP p=则()p b a∙-=（）A.21- B.21C.23- D .2310.若三棱锥S ABC-的所有顶点都在球O的球面上，SA⊥平面ABC，SA=1AB=，2AC=，60BAC∠=︒，则球O的表面积为（）A．64π B．16π C．12π D．4π11. 将甲、乙、丙、丁、戊共五位同学分别保送到北大、上海交大和浙大3所大学，若每所大学至少保送1人，且甲不能被保送到北大，则不同的保送方案共有（）种.A．114 B．150 C．72 D．10012.定义域为R的偶函数)(xf满足对x R∀∈，有)1()()2(fxfxf-=+，且当]3,2[∈x时，18122)(2-+-=xxxf，若函数)1|(|log)(+-=xxfya在),0(+∞上至少有三个零点，则a的取值范围是（）A．)22,0( B．)33,0( C．)55,0( D．)66,0(二．填空题：本大题共4小题，每小题5分，共20分。

山东省济宁一中2011届高三第一次模拟测试数学试题(理科)

济宁市2011年高中阶段学校招生考试数学试题及答案(word版)

济宁一中届模拟检测一理科数学试题目

数学_2011年山东省某校高考数学一模试卷(理科)_(含答案)

山东省济宁一中2011届高三下学期4月模拟测试(数学)

(2011济宁一模)山东省济宁市2011届高三第一次模拟考试word试题部分(数学理)

2011届山东省济宁一中高三模拟测试(基本能力)

山东省济宁一中2011届高三第一次模拟测试语文

山东济宁一中2011届高三第三次质量检测 数学理

山东省济宁市第一中学西校高一数学理测试题含解析

山东省济宁一中2011届高三第一次质量检测(数学理)

高三数学第一次模拟考试理济宁市一模,含解析新人教A版

山东济宁一中高三第一次反馈练习——数学

山东省济宁一中高三下学期模拟测试(理综)

山东省济宁市高三数学1月期末模拟 理 新人教A版

山东济宁一中2011届高三第三次质量检测数学理

山东省济宁市高三数学1月期末模拟理新人教A版