一下期末试卷

合集下载

2023-2024学年北京市朝阳区高一下学期期末考试数学试卷+答案解析

2023-2024学年北京市朝阳区高一下学期期末考试数学试卷一、单选题：本题共10小题，每小题5分，共50分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.若复数z满足，则()A. B. C. D.2.已知向量，，则()A. B. C.3 D.53.如图，八面体的每个面都是正三角形，并且4个顶点A，B，C，D在同一平面内，若四边形ABCD是边长为2的正方形，则这个八面体的表面积为()A.8B.16C.D.4.已知m，n是平面外的两条不同的直线，若，则“”是“”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.在中，，，，则()A. B. C. D.6.李华统计了他爸爸2024年5月的手机通话明细清单，发现他爸爸该月共通话60次，他按每次通话时间长短进行分组每组为左闭右开的区间，画出了如图所示的频率分布直方图．则每次通话时长不低于5分钟且小于15分钟的次数为()A.18B.21C.24D.277.已知向量，不共线，，，若与同向，则实数t的值为()A. B. C.3 D.或38.近年来，我国国民经济运行总体稳定，延续回升向好态势．下图是我国2023年4月到2023年12月规模以上工业增加值同比增长速度以下简称增速统计图．注：规模以上工业指年主营业务收入2000万元及以上的工业企业．下列说法正确的是()A.4月，5月，6月这三个月增速的方差比4月，5月，6月，7月这四个月增速的方差大B.4月，5月，6月这三个月增速的平均数比4月，5月，6月，7月这四个月增速的平均数小C.连续三个月增速的方差最大的是9月，10月，11月这三个月D.连续三个月增速的平均数最大的是9月，10月，11月这三个月9.在梯形ABCD中，，，，，，则与夹角的余弦值为()A. B. C. D.10.已知，，若动点P，Q与点A，M共面，且满足，，则的最大值为()A.0B.C.1D.2二、填空题：本题共6小题，每小题5分，共30分。

2023-2024学年宁夏石嘴山市平罗中学高一下学期期末考试语文试卷

2023-2024学年宁夏石嘴山市平罗中学高一下学期期末考试语文试卷阅读下面的文字，完成各题。

材料一：从“哈尔滨”的雪花到上海的“繁花”，从泉州的簪花到三亚的浪花，文旅的热度贯穿了过去一年，持续到春节，促成了“热辣滚烫”的消费潮流。

如何延续这股热潮？文旅行业需在高质量发展模式的引领下转换动能，用科技创新提升效益效率，以此推动传统文旅向数字文旅迈进，形成新质生产力。

王宁委员建议：“要突破演出空间限制，将表演艺术与旅游业、会展业、娱乐业等有机结合，打造沉浸式、互动式的演出项目。

多层次开发与表演艺术相关联的衍生产品，把新业态、新产品、新样式与新消费有机融合，培育新的消费热点、亮点和增长点。

”“演出+旅游”的实景演艺在各景区快速“蔓延”，受到游客们的青睐。

安庭委员建议，鼓励和引导社会资本参与演艺新空间的内容创作生产和运营管理；支持各地充分利用工业遗址、老旧厂房、商场、写字楼等，为演出企业提供更多的创作和演出空间。

（摘自《文旅热潮涌动，如何接住这“泼天富贵”？》，有删改）材料二：当“国潮”成为年轻人追逐的热点，传统文艺团体依托新技术和新的传播方式也找到了“新舞台”。

2023年，文艺院团仅通过抖音平台就为观众带来了6800场团体直播演出，场均观众12671人次，相当于每天有18场大型文艺演出在抖音直播上进行。

传统文艺团体通过直播找到了新的观众、获得了更多的收入，也为传承文化、传播艺术带来了新的渠道。

这些丰富多元且优质的直播内容，也满足了用户的内容消费需求。

延边歌舞团声乐部部长、国家一级演员黄梅花所说：“网络空间也需要专业的艺术表现，通过我们的演出能让更多观众接触、了解艺术，我觉得所有的付出都值得。

”吴文科表示，线上演出是网络时代文艺传播的必然结果。

“比如，观众在现场欣赏文艺演出所获得的视听感受，不可能被线上个性化个体式体验完全替代，而剧场表演所呈现出的舞台艺术，其节目体量之宏大性、审美感知之庄重性，尤其是完整的节目欣赏所带来的精神思想之丰富性，是线上演出无法替代的，但后者为前者的传承与发扬开了个好头。

一年级下册数学期末考试试卷(9套

（）个
苏教版小学数学一年级下册期末试题
学校班级姓名
全卷等级
命题人：山东省肥城市边院镇海子小学冯圣文
- — —高速公路
（1）看谁算的又对又快。（29分）
27 + 14 = 72–19 = 43 +30 =
59 + 5 = 70 + 8 = 6 + 28 =
5 + 34 = 63–5 = 24 + 60 =
1．个位是9的数有（）：
（1）39（）（2）93（）
（3）29（）（4）69（）
2．比75大，比79小的数有（）：
（1）57（）（2）75（）
（3）77（）（4）87（）
3．小红买一支铅笔要付8角，下列付法哪种对？
（1）付3张2角和2张1角。（）
（2）付8张1角。（）
（3）付1张3角和1张5角。（）
□有（）个
2．根据统计表填一填。
（1）（）的个数最少。（2）（）和（）的个数一样多。
五、走进生活，解决问题。（30分）
1．填表。
（6分）
2．（5分）
= （页）
3．
（6分）
4．树上原来有多少个桃？（5分）
= （个）
5．（8分）
（1）比便宜多少钱？（3分）
= （） = （）
（2）买了1个，找回18元。她付了多少元？（3分）
______________________________
010～2011学年度第二学期期末学业水平调查
小学一年级数学试题
（卷面总分：100分；答卷时间：50分钟）
一、直接写出得数。（每题1分，共30分）
11－2= 13－5 = 24－8 = 41－6=

上海市松江二中2023-2024学年高一下学期期末考试数学试卷【含答案】

松江二中2023学年第二学期期末考试高一数学考生注意：1.试卷满分150分，考试时间120分钟.2.本考试分设试卷和答题纸.试卷包括三部分，第一部分为填空题，第二部分为选择题，第三部分为解答题.3.答题前，务必在答题纸上填写考号、姓名、班级.作答必须涂或写在答题纸上，在试卷上作答一律不得分.一、填空题（本大题共有12题，第1-6题每题4分，第7-12题每题5分，共54分）考生应在答题纸的相应位置直接填写结果.1．已知两条相交直线a ，b ，且a//平面α，则b 与α的位置关系是.2．复数z 满足()3i 5i z -=（i 为虚数单位），则z =.3．设平面向量()sin ,1a θ= ，(cos b θ= ，若a ，b不能组成平面上的一个基底，则tan θ=．4．如图，O A B '''△是水平放置的OAB 的斜二测直观图，若3O A ''=，4OB '=，则OAB 的面积为.5．若正数x ，y 满足24xy y +=，则x y的最大值为.6．已知10π,sin cos 2ααα<<+=，则cos sin αα-的值为．7．如图，某体育公园广场放置着一块高为3米的大屏幕滚动播放各项体育赛事，大屏幕下端离地面高度3.5米，若小明同学的眼睛离地面高度1.5米，则为了获得最佳视野（最佳视野指看到大屏幕的上下夹角最大），小明应在距离大屏幕所在的平面米处观看?（精确到0.1米）.8．空间给定不共面的A 、B 、C 、D 四个点，如果这四个点到平面α的距离都相等，那么这样的平面α的个数是.9．已知二面角l αβ--的大小为60°，点P ，Q 分别在α，β上且PQ l ⊥，若点P 到β的距3Q 到α3PQ 两点之间的距离为.10．设定义在R 上的函数()f x 满足()()21f x f x =+，且当[)1,0x ∈-时，()()1f x x x =-+.若对任意[),x λ∈+∞，不等式()34f x ≤恒成立，则实数λ的最小值是.11．关于x 的实系数方程2450x x -+=和220x mx m ++=有四个不同的根，若这四个根在复平面上对应的点共圆，则m 的取值范围是.12．已知单位向量,a b 夹角为锐角，对t R ∈，a t b -⋅ 的取值范围是3[)2+∞，若向量c 满足(2)()0c a c b -⋅-=，则c r 的最小值为．二、选择题（本大题共有4题，第13、14题每题4分，第15、16题每题5分，共18分）每题有且只有一个正确答案，考生应在答题纸的相应位置上，将所选答案的代号涂黑.13．在下列判断两个平面α与β平行的四个命题中，其中假命题的是（）A ．α，β都垂直于直线l ，那么αβ∥B ．α，β都平行于平面γ，那么αβ∥C ．α，β都垂直于平面γ，那么αβ∥D ．如果l ，m 是两条异面直线，且l α∥，m α ，l β ，m β ，那么αβ∥14．已知a ,b 是平面内两个非零向量，那么“a ∥b”是“存在0λ≠，使得a b a b λλ+=+ ”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件15．如图所示，在正方体1111ABCD A B C D -中，M 是棱1AA 上一点，若平面1MBD 与棱1CC 交于点N ，则下列说法中正确的是（）A ．存在平面1MBND 与直线1BB 垂直B ．四边形1MBND 可能是正方形C ．不存在平面1MBND 与直线11A C 平行D ．任意平面1MBND 与平面1ACB 垂直16．已知函数()()5sin 2θf x x =-，πθ0,2⎛⎤∈ ⎥⎝⎦，[]0,5πx ∈，若函数()()3F x f x =-的所有零点依次记为123,,,,n x x x x ⋅⋅⋅，且1231n n x x x x x -<<<⋅⋅⋅<<，*n ∈N 若12321832222π2n n n x x x x x x --+++⋅⋅⋅+++=，则θ=（）A ．π9B ．π6C ．π4D ．π12三、解答题（本大题共有5题，满分78分）解答下列各题必须在答题纸的相应位置写出必要的步骤.17．在正方体1111ABCD A B C D -中，E 是11B C 的中点.（1）求异面直线AE 与1BC 所成的角的大小；（2）求直线AC 与平面11ABC D 所成的角的大小.18．已知向量()()()()()3,1,1,1,,4,,,,OA OB OC m OD x y m x y =-=-==∈R．(1)若,,A B C 三点共线，求m 的值；(2)若四边形ABCD 为矩形，求2x y +的值．19．在ABC 中，内角,,A B C 的对边分别为,,,tan tana b c b A b B +=(1)求角B ；(2)茬D 是边AC 上的点，且33,AD DC A ABD ∠∠θ====，求sin θ的值.20．如图，已知四面体ABCD 中，AB ⊥平面BCD ，BC CD ⊥.(1)求证：AC CD ⊥；(2)若在此四面体中任取两条棱作为一组（(),a b 和(),b a 视为同一组），则它们互相垂直的组数记为1a ；任取两个面作为一组（(),αβ和(),βα视为同一组），则它们互相垂直的组数记为2a ；任取一个面和不在此面上的一条棱作为一组（(),a α和(),a α视为同一组），则它们互相垂直的组数记为3a ，试求123a a a ++的值；(3)《九章算术》中将四个面都是直角三角形的四面体称为“鳖臑”.若此“鳖臑”中，1CD =，1AB BC ==，有一根彩带经过平面ABC 与平面ACD ，且彩带的两个端点分别固定在点B和点D 处，求彩带的最小长度.21．对于分别定义在1D ，2D 上的函数()f x ，()g x 以及实数k ，若存在11x D ∈，22x D ∈使得()()12f x g x k -=，则称函数()f x 与()g x 具有关系()M k .(1)若()cos f x x =，[]0,πx ∈；()sin g x x =，[]0,πx ∈，判断()f x 与()g x 是否具有关系()2M -，并说明理由；(2)若()2sin f x x =与()22cos sin 1g x x x =+-具有关系()M k ，求k 的取值范围；(3)已知0a >，()h x 为定义在R 上的奇函数，且满足：①在[]0,2a 上，当且仅当2ax =时，()h x 取得最大值1；②对任意x ∈R ，有()()h a x h a x +=--.判断()()sin 2πf x x h x =+与()()cos 2πg x h x x =-是否具有关系()4M ，并说明理由.1．b//平面α或b 与平面α相交【分析】画出图形不难看出直线b 与平面α的位置关系，平行或相交.【详解】由题意画出图形，当,a b 所在平面与平面α平行时，b 与平面α平行，当,a b 所在平面与平面α相交时，b 与平面α相交.故答案为:b//平面a 或b 与平面α相交.【点睛】本题考查空间中直线与平面之间的位置关系，考查空间想象能力，是基础题.2．102【分析】直接利用复数代数形式的乘除运算化简，然后利用复数模的公式计算即可.【详解】因为复数z 满足()3i 5i z -=，所以()()()5i 3i 5i 515i 13i 3i 3i 3i 1022z +-+====-+--+，所以2z =，故答案为：1023．3【分析】利用基底的定义可得//a b，再利用共线向量的坐标表示求解即得.【详解】由a ，b不能组成平面上的一个基底，得//a b ，而()sin ,1a θ= ，(cos b θ= ，cos θθ=，所以sin tan cos 3θθθ==.4．12【分析】根据斜二测画法，将直观图还原可知原三角形为直角三角形，求出两直角边的长度，即可得出答案.【详解】如图，根据斜二测画法，将直观图还原后，得到的AOB 为直角三角形，且两条直角边4OB O B ''==，26OA O A ''==，所以，OAB 的面积为1S 46122=⨯⨯=.故答案为：12.5．2【分析】根据24xy y +=得出240x y =->，得出102y <<，242x y y y -=，根据y 的范围求出x y的范围即可.【详解】24xy y +=，24x y ∴+=，240x y =->，所以12y >，即102y <<，222421212211x y y y y y y ⎡⎤⎛⎫⎛⎫-==--=---⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，根据二次函数的性质可知1y =时，上式取得最大值2.故答案为：2.6．72【分析】根据同角关系中的平方关系进行解答，注意2sin cos 0αα<涉及的函数值正负与角终边所在象限联系，结合0πα<<，进一步缩小角的范围，进而在开方运算时得出正确的符号.【详解】由已知得()21sin cos 4αα+=，即32sin cos 4αα=-，∴()2cos sin 12sin cos αααα-=-74=，由2sin cos 0αα<，且0πα<<，∴π2απ<<，∴cos sin 0αα-<，∴7cos sin αα-=故答案为：77．3.2【分析】作CD AB ⊥于D ，设CD t =，根据两角差的正切公式，结合不等式求tan ACB ∠的最大值，并确定对应的t 即可.【详解】如图：作CD AB ⊥于D ，设()0CD t t =>，则5tan ACD t∠=，2tan BCD t ∠=.所以()tan tan ACB ACD BCD ∠=∠-∠tan tan 1tan tan ACD BCD ACD BCD ∠-∠=+∠⋅∠52521t t t t -=+⋅2310t t =+310t t=+≤=t “=”）3.16≈，故 3.2t ≈（米），故答案为：3.28．7【分析】分平面α的两边分别有1个点，3个点和两边各有2个点讨论即可.【详解】因为,,,A B C D 四点不共面，所以,,,A B C D 可以看作是四面体的顶点，取四面体ABCD 各棱的中点为,,,,,E F G H M N .如图：当,,,A B C D 四个点在平面α的一侧有1个点，另一侧有3个点，且它们到平面α的距离相等，这样的平面有平面EFN ，平面EMH ，平面FMG ，平面NGH ，共4个；当,,,A B C D 四个点分别在平面α的两侧各有两个点，且它们到平面α的距离相等，这样的平面有平面EMGN ，平面EHGF ，平面MFNH ，共3个.所以满足条件的平面α共7个.故答案为：79【分析】作PD l ⊥于D ，连接QD ，则l ⊥平面PQD ，所以PDQ ∠即为二面角l αβ--的平面角，作PM β⊥于M ，则M 在QD 上，作QN α⊥于N ，则N 在PD 上，在PQD △内求PQ 即可.【详解】如图：作PD l ⊥于D ，连接QD ，又因为PQ l ⊥，,PQ PD ⊂平面PQD ，PQ PD P ⋂=，所以l ⊥平面PQD .所以PDQ ∠即为二面角l αβ--的平面角，故60PDQ ∠=︒.作PM β⊥于M ，则M 在QD 上，作QN α⊥于N ，则N 在PD 上.在R t PMD 中，PM =PM QD ⊥，60PDQ ∠=︒，所以2PD =；在R t QND 中，2QN =，QN PD ⊥，60PDQ ∠=︒，所以1QD =.由余弦定理：2222cos 60PQ DQ DP DP DQ =+-⋅⋅︒11421232=+-⨯⨯⨯=，所以PQ =.10．94-## 2.25-【分析】由题意，根据给定的函数解析式，结合等式关系，拓展其他区间的函数解析式，利用二次函数的性质，可得答案.【详解】()()21f x f x =+ ，且当[)1,0x ∈-时，()()2111324144f x x x x ⎛⎫=-++≤≤ ⎪⎝⎭=-+恒成立，∴()()()1112f x f x f x =-≤-，易知当0x >时，则()1324f x f ⎛⎫<-≤ ⎪⎝⎭恒成立，当[)2,1x ∈--，即[)11,0x +∈-时，()()()()2311321*********f x f x x x x ⎛⎫=+=-+++=-++≤≤⎡⎤ ⎪⎣⎦⎝⎭恒成立，当[)3,2x ∈--，即[)21,0x +∈-时，()()()()()25214242214112f x f x f x x x x ⎛⎫=+=+=-+++=-++≤⎡⎤ ⎪⎣⎦⎝⎭，不满足()34f x ≤恒成立，解不等式2534124x ⎛⎫-++≤ ⎪⎝⎭，251216x ⎛⎫+≥ ⎪⎝⎭，在[)3,2x ∈--上的解集为1193,,244⎡⎤⎡⎫----⎪⎢⎥⎢⎣⎦⎣⎭ ，综上所述，当9,4x ⎡⎫∈-+∞⎪⎢⎣⎭时，()34f x ≤恒成立，∴实数λ的最小值为94-.故答案为：94-.11．(01){1}⋃-，【分析】解出方程2450x x -+=，可得其对应的点,A B ，对于方程220x mx m ++=，讨论其∆，进一步分析计算即可.【详解】因为2450x x -+=的解为2i x ==±，设所对应的两点分别为,A B ，则(2),1A ，(21,)B -，设220x mx m ++=的解所对应的两点分别为C ，D ，记为(1C x ,12)(y D x ，,2)y ，当Δ0<，即01m <<时，因为,A B 关于x 轴对称，且C ，D ，关于x 轴对称，显然四点共圆；当0∆>，即1m >或0m <时，此时(1C x ,20),(D x ,0)，且122x x m +=-，故此圆的圆心为(,0)m -，半径12||2x x r -==又圆心1O 到A 的距离1O A r ==，解得1m =-，综上：()0,1{1}m ∈⋃-,故答案为：()0,1{1}⋃-.12．2【分析】根据a t b -⋅ 的最小值可求出,a b 的夹角为60θ=︒，然后根据已知设(1,0)a = ，1(2b = ，(,)c x y = ，条件(2)()0c a c b -⋅-= 可转化为点(,)C x y 在一个圆上，而结论就是求这个圆的点到原点距离的最小值．【详解】向量,a b 夹角为θ，由题意2a tb - 的取值范围是3[,)4+∞，因为a t b -⋅≥ 222324a ta b t b -⋅+≥ ，即2312cos 4t t θ+-≥，得212cos 04t t θ-+≥，因为212cos 4t t θ-+的最小值为0，所以24cos 10θ∆=-=，解得1cos 2θ=±，因为θ为锐角，所以1cos 2θ=，所以60θ=︒，不妨设(1,0)a = ，13(,)22b = ，(,)c x y = ，1313(2)()(2,)(,)(2)()()02222c a c b x y x y x x y y -⋅-=-⋅--=--+-= ，整理得2253()()444x y -+=，因此点(,)C x y 在以5(4M它到原点距离的最小值为OM ．即c r的最小值为732．故答案为：2【点睛】关键点点睛：本题考查平面向量数量积的应用，它把向量的数量积与平面上点与圆的位置关系联系在一起，是一道难题．解题的关键是首先对已知条件进行转化，如条件对t R ∈，a t b -⋅ 的取值范围是[,)2+∞，可转化为1cos 2θ=，这样向量,a b 的关系就确定了，下面为了已知(2)()0c a c b -⋅-=的明确化，设出向量坐标，从而由已知条件可得c 的坐标的关系，进而可求得答案，考查数学转化思想13．C【分析】根据线面垂直的性质判断A ；根据面面平行的概念判断B ；根据特例判断C ；根据线面平行，判断面面平行判断D.【详解】根据垂直于同一条直线的两个平面互相平行，可知A 正确；根据平行于同一个平面的两个平面互相平行，可知B 正确；根据墙角模型可知，垂直于同一个平面的两个平面未必平行，故C 错误；作l l '∥，且,l m '相交，则,l m '可确定平面γ，因为l l αα⇒' ，m α ，所以γα∥，同理γβ∥，故αβ∥，故D 正确.故选：C 14．C【分析】根据向量的模长关系以及共线，即可结合必要不充分条件进行判断.【详解】若a ∥b ，则则存在唯一的实数μ≠0，使得a b μ=，故a b b b b λμλμλ+=+=+，而()a b b b b λμλλμ+=+=+ ，存在λ使得λμλμ+=+成立，所以“a ∥b”是“存在0λ≠，使得a b a b λλ+=+ ”的充分条件，若0λ≠且a b a b λλ+=+ ，则a 与b λ 方向相同,故此时a ∥b，所以“a ∥b”是“存在0λ≠，使得”a b a b λλ+=+ 的必要条件，故a ∥b”是“存在0λ≠，使得|”a b a b λλ+=+ 的充分必要条件，故选:C 15．D【分析】根据正方体的性质判断A ，根据面面平行的性质得到四边形1MBND 是平行四边形，再由11A D BM ⊥，即可判断B ，当M 为1AA 的中点时N 为1CC 的中点，即可判断C ，建立空间直角坐标系，利用向量法说明D.【详解】对于A ：在正方体1111ABCD A B C D -中1BB ⊥平面1111D C B A ，显然平面1MBND 与平面1111D C B A 不平行，故直线1BB 不可能垂直平面1MBND ，故A 错误；对于B ：在正方体1111ABCD A B C D -中，M 是棱1AA 上一点，平面1MBD 与棱1CC 交于点N ，由平面11//BCC B 平面11ADD A ，并且1,,,B M N D 四点共面，平面11BCC B 平面1BND M BN =，平面11ADD A 平面11BND M MD =，∴1//MD BN ，同理可证1//ND MB ，故四边形1MBND 是平行四边形，在正方体1111ABCD A B C D -中，由几何知识得，11A D ⊥平面11ABB A ，∵BM ⊂平面11ABB A ，∴11A D BM ⊥，若1MBND 是正方形，有1MD BM ⊥，此时M 与1A 重合时，但显然四边形11A BCD 不是正方形，故B 错误；对于C ：当M 为1AA 的中点时，N 为1CC 的中点，所以11//A M C N 且11=A M C N ，所以11A MNC 为平行四边形，所以11//A C NM ，11A C ⊄平面1MBND ，MN ⊂平面1MBND ，所以11//A C 平面1MBND ，故C 错误；对于D ：设正方体边长为2，建立空间直角坐标系如下图所示，由几何知识得，()()()()()112,0,0,2,2,0,0,2,0,2,2,2,0,0,2A B C B D ,∴()()()112,2,2,2,2,0,0,2,2D B AC AB =-=-=,∵1110D B AC D B AB ⋅=⋅=，∴111,D B AC D B AB ⊥⊥，∵1AC AB A ⋂=，AC ⊂平面1ACB ，1AB ⊂平面1ACB ，∴1D B ⊥平面1ACB ，∵1D B ⊂平面1MBND ，∴任意平面1MBND 与平面1ACB 垂直，故D 正确.故选：D 16．A【分析】先明确函数在[]0,5π上对称轴的条数，再根据1239,,,,x x x x L 的对称性，和1238983π2222x x x x x +++++=，可求θ的值.【详解】由π2θπ2x k -=+⇒ππθ,Z 422k x k =++∈，为函数()f x 的对称轴.又函数()f x 的最小正周期为2ππ2T ==，且πθ0,2⎛⎤∈ ⎥⎝⎦，[]0,5πx ∈，所以当0k =时，可得函数()f x 的第一条对称轴为πθ42x =+，当9k =时，π9πθ19πθ5π42242x =++=+≤.所以函数()f x 在[]0,5π有9条对称轴.根据正弦函数的图象和性质可知，函数()()5sin 2θf x x =-与3y =的交点有9个，其横坐标分别为：1239,,,,x x x x L ，且1239x x x x <<<< ，且12,x x 关于πθ42x =+对称，所以12x x +=πθ242⎛⎫+ ⎪⎝⎭；23,x x 关于3πθ42x =+对称，所以23+=x x 3πθ242⎛⎫+ ⎪⎝⎭；……89,x x 关于17πθ42x =+对称，所以89x x +=17πθ242⎛⎫+⎪⎝⎭.所以12389222x x x x x +++++ 81π9θ2=+83π2=⇒πθ9=.故选：A【点睛】关键点点睛：本题的关键点就是方程()3f x =的根与对称轴的对称关系，利用对称关系和对称轴方程，表示出12389222x x x x x +++++ 即可求解.17．（1）4π（2）6π【分析】（1）由11//AD BC 得出1,AE BC 所成的角为1D AE ∠，利用余弦定理得出异面直线AE 与1BC 所成的角；（2）先证明1B C ⊥平面11ABC D ，从而得出CAO ∠为直线AC 与平面11ABC D 所成的角，再由直角三角形边角关系得出所求角.【详解】（1）11//AD BC ，1,AE BC ∴所成的角为1D AE∠连接1D E ，设2AB =，则2212222AD =+=，2221223AE =++=221215D E =+=，18952cos 22223D AE +-∠==⨯⨯ 异面直线夹角的范围为0,2π⎛⎤⎥⎝⎦，14D AE π∴∠=即异面直线AE 与1BC 所成的角为4π（2）连接1B C 交1BC 于点O ，连接AO四边形11BCC B 为正方形，11BC B C∴⊥又AB ⊥平面11BCC B ，1B C ⊂平面11BCC B 1BC AB ∴⊥1AB BC B =Q I 1B C ∴⊥平面11ABC D 即CAO ∠为直线AC 与平面11ABC D 所成的角设2AB =，则222222222,1216AC AO =+==++=63cos 222CAO ∴∠==又直线与平面所成角的范围为0,2π⎡⎤⎢⎥⎣⎦，6CAO π∴∠=即直线AC 与平面11ABC D 所成的角为6π18．(1)9m =-(2)25x y +=【分析】（1）由()()()3,1,1,1,,4OA OB OC m =-=-=，由,,A B C 三点共线，可得9m =-.（2）由()()()()4,2,,41,11,5,AB BC OC OB m m =-=-=--=-，()()(),,4,4CD OD OC x y m x m y =-=-=-- ，若四边形ABCD 为矩形，求解1,62x y =-=．即可得到结果.【详解】（1）因为()()()3,1,1,1,,4OA OB OC m =-=-=，所以()()()1,13,14,2AB OB OA =-=---=- ，()()(),43,13,3AC OC OA m m =-=--=+．又,,A B C 三点共线，所以ABAC ，所以()()43230m ⨯--+=，解得9m =-．（2）由()()()()4,2,,41,11,5,AB BC OC OB m m =-=-=--=-()()(),,4,4CD OD OC x y m x m y =-=-=--，若四边形ABCD 为矩形，则AB BC ⊥．即()41100AB BC m ⋅=--= ，解得72m =．由AB CD =- ，得74,242,x m x y ⎧-=-=-⎪⎨⎪-=⎩解得1,62x y =-=．所以25x y +=．19．(1)π6B =；【分析】（1）把给定等式切化弦，利用正弦定理边化角，再利用三角恒等变换求解作答.（2）根据给定条件，求出BD ，在ABC 和BDC 中分别利用正弦定理、余弦定理列式，求解作答.【详解】（1）在ABC中，由tan tan b A b B +=sin sin cos cos A B A B +=，由正弦定理得：sin()cos cos A B A B +=，而sin()sin(π)sin A B C C +=-=，即有sin cos cos C A B =，又()0,πC ∈，即sin 0C ≠，cos B B =，有tan B =，又(0,π)B ∈，所以π6B =.（2）因为D 是AC 边上的点，且33,AD DC A ABD ∠∠θ====，于是2,3,1,4BDC AD BD DC AC ∠θ=====，如图，在ABC 中，由正弦定理得：sin sin BC ACABCθ∠=，即4sin 8sin πsin 6BC θθ==，在BDC 中，由余弦定理得：2222cos2106cos2BC BD CD BD CD θθ=+-⋅=-，则有2264sin 106(12sin )θθ=--，整理得252sin 4θ=，解得：21sin 13θ=，而π(0,)2θ∈，所以13sin 13θ=.20．(1)证明见解析(2)1022+【分析】（1）由线面垂直得到AB CD ⊥，结合BC CD ⊥得到线面垂直，进而证明出线线垂直；（2）根据线线垂直、线面垂直以及面面垂直分析求解即可；（3）将平面ABC 与平面ACD 沿AC 展开成平面图形，则BD 即为所求，从而利用余弦定理求出答案即可.【详解】（1）因为AB ⊥平面BCD ，,,BC BD CD ⊂平面BCD ，则,,AB BC AB BD AB CD ⊥⊥⊥，又BC CD ⊥，AB BC B ⋂=，,AB BC ⊂平面ABC ，所以CD ⊥平面ABC ，因为AC ⊂平面ABC ，所以AC CD ⊥.（2）由（1）可知：,,AB BC AB BD AB CD ⊥⊥⊥，AC CD ⊥，且CD ⊥平面ABC ，BC ⊂平面ABC ，则CD BC ⊥，且其余各棱均不垂直，可得15a =；由AB ⊥平面BCD ，且AB ⊂平面ABC ，AB ⊂平面ABD ，可得平面ABC ⊥平面BCD ，平面ABD ⊥平面BCD ，同理：由CD ⊥平面ABC 可得：平面ACD ⊥平面ABC ，且其余各面均不垂直，可得23a =；由AB ⊥平面BCD ，CD ⊥平面ABC ，且其余各线面均不垂直，可得32a =；综上所述：12310a a a ++=.（3）将平面ABC 与平面ACD 沿AC 展开成如图2所示的平面图形，连接BD ，所以彩带的最小长度为图2平面图中BD 的长，.由（1）知=90ACD ∠︒，在图1中，因为AB ⊥平面BCD ，BC ⊂平面BCD ，所以AB BC ⊥，又因为1AB BC CD ===，所以45ACB ∠=︒，故在图2中，135BCD ∠=︒，所以在图2中，在BCD △中，由余弦定理得BD ===21．(1)()f x 与()g x 具有关系()2M -，理由见解析(2)25,48k ⎡⎤∈-⎢⎥⎣⎦；(3)不具有关系()4M ，理由见解析【分析】（1）根据三角函数的性质可得()ππ22f g ⎛⎫-=- ⎪⎝⎭，结合新定义即可下结论；（2）根据三角函数与二次函数的性质可得()[]2,2f x ∈-、()92,8g x ⎡⎤∈-⎢⎥⎣⎦，则()()1225,48f x g x ⎡⎤-∈-⎡⎤⎣⎦⎢⎥⎣⎦，结合新定义即可求解；（3）根据函数的对称性和周期性求出()h x 、sin 2πx 、cos 2πx 的值域.当()11h x =、1sin 2π1x =时，有()()111sin 2π2f x x h x =+=；当()21h x =-、2cos 2π1x =时，有()()222cos 2π2g x h x x =-=-，进而()()1122sin 2πcos 2π4x h x x h x ++-<，结合新定义即可下结论.【详解】（1）()f x 与()g x 具有关系()2M -，理由如下：当[]0,πx ∈时，()[]cos 1,1f x x =∈-，()[]sin 0,1g x x =∈，当1πx =，()()π1f x f ==-，当2π2x =时，()π12g x g ⎛⎫== ⎪⎝⎭，此时()ππ22f g ⎛⎫-=- ⎪⎝⎭，则()f x 与()g x 具有关系()2M -；（2）()[]2sin 2,2f x x =∈-，()222192cos sin 1cos 2sin 12sin sin 2sin 48g x x x x x x x x ⎛⎫=+-=+=-+=--+ ⎪⎝⎭，因为[]sin 1,1x ∈-，则当sin 1x =-时，21921248⎛⎫---+=- ⎪⎝⎭，则()92,8g x ⎡⎤∈-⎢⎣⎦，所以()()1225,48f x g x ⎡⎤-∈-⎡⎤⎣⎦⎢⎥⎣⎦，则25,48k ⎡⎤∈-⎢⎥⎣⎦；（3）不具有()4M 关系，理由如下：因为在[]0,2a 上，当且仅当2ax =时，()h x 取得最大值1；又()f x 为定义在R 上的奇函数，故在[]2,0a -上，当且仅当2ax =-时，()f x 取得最小值-1，由对任意x ∈R ，有()()0h a x h a x ++-=，所以()y f x =关于点(),0a 对称，又()()()h a x h a x h x a +-==--，所以()h x 的周期为2a ，故()h x 的值域为[]1,1-，[]sin 2π1,1x ∈-，[]cos 2π1,1x ∈-，当()11h x =时，122a x n =+，Z n ∈；1sin 2π1x =时，114x k =+，Z k ∈，若1224a na k +=+，则4182k a n +=+，,Z k n ∈，此时有()()111sin 2π2f x x h x =+=；当()21h x =-时，222a x ma =-+，m ∈Z ；2cos 2π1x =时，2x t =，Z t ∈，若22a ma t -+=，则241t a m =-，,Z t m ∈时，有()()222cos 2π2g x h x x =-=-；由于4128241k t a n m +=≠+-，所以()()1122sin 2πcos 2π4x h x x h x ++-<，故不存在1R x ∈，2R x ∈，使得()()1222sin 2πcos 2π4x f x x f x ++-=，所以()()sin 2πf x x h x =+与()()cos 2πg x h x x =-不具有关系()4M .【点睛】方法点睛：学生在理解相关新概念、新法则(公式)之后，运用学过的知识，结合已掌握的技能，通过推理、运算等解决问题.在新环境下研究“旧”性质.主要是将新性质应用在“旧”性质上，创造性地证明更新的性质，落脚点仍然是三角函数的图象与性质.。

湖北省武汉2023-2024学年高一下学期期末考试数学试卷含答案

武汉2023-2024学年度下学期期末考试高一数学试卷（答案在最后）命题教师：考试时间：2024年7月1日考试时长：120分钟试卷满分：150分一、选择题：本题共8小题，每题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若复数z 满足(2i)3i z +=-，则z =（）A.1i +B.1i- C.1i-+ D.1i--【答案】A 【解析】【分析】先利用复数的除法运算法则化简得到复数z ，再根据共轭复数的概念即可求解.【详解】因为(2i)3i z +=-，所以3i (3i)(2i)1i 2i 41z ---===-++，所以1i z =+.故选：A2.△ABC 中，60A =︒，BC =AC =C 的大小为（）A.75︒B.45︒C.135︒D.45︒或135︒【答案】A 【解析】【分析】利用正弦定理可得sin B =45B = ，由三角形内角和即可求解.【详解】由正弦定理可得sin sin BC AC A B=,故32sin 2B ==,由于60A =︒，故0120B ︒︒<<,故45B = ，18075C A B =--= ,故选：A3.已知数据1x ，2x ，L ，9x 的方差为25，则数据131x +，231x +，L ，931x +的标准差为（）A.25B.75C.15D.【答案】C 【解析】【分析】根据方差的性质求出新数据的方差，进而计算标准差即可.【详解】因为数据1x ，2x ，L ，9x 的方差为25，所以另一组数据131x +，231x +，L ，931x +的方差为2325225⨯=，15=.故选：C4.在正方形ABCD 中，M 是BC 的中点．若AC AM BD λμ=+，则λμ+的值为（）A.43B.53C.158D.2【答案】B 【解析】【分析】建立平面直角坐标系，利用向量的坐标运算求解作答.【详解】在正方形ABCD 中，以点A 为原点，直线AB ，AD 分别为x ，y 轴建立平面直角坐标系，如图，令||2AB =，则(2,0),(2,2),(0,2),(2,1)B C D M ，(2,2),(2,1),(2,2)AC AM BD ===-，(22,2)AM BD λμλμλμ+=-+ ，因AC AM BD λμ=+ ，于是得22222λμλμ-=⎧⎨+=⎩，解得41,33λμ==，53λμ+=所以λμ+的值为53.故选：B5.正三棱柱111ABC A B C -的底面边长为2D 为BC 中点，则三棱锥11A B DC -的体积为A.3B.32C.1D.32【答案】C 【解析】【详解】试题分析：如下图所示，连接AD ，因为ABC ∆是正三角形，且D 为BC 中点，则AD BC ⊥，又因为1BB ⊥面ABC ，故1BB AD ⊥，且1BB BC B ⋂=，所以AD ⊥面11BCC B ，所以AD 是三棱锥11A B DC -的高，所以11111133133A B DC B DC V S AD -∆=⋅==．考点：1、直线和平面垂直的判断和性质；2、三棱锥体积．6.在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若cos cos sin sin()sin B C AA C b c C ⎛⎫++= ⎪⎝⎭，3B π=，则a c +的取值范围是（）A.332⎛⎝ B.332⎛⎝ C.332⎣ D.332⎡⎢⎣【答案】A 【解析】【分析】利用三角恒等变换及正弦定理将cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭进行化简，可求出b 的值，再利用边化角将a c +化成角，然后利用辅助角公式及角的范围即可得到答案.【详解】由题知cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭，3B π=∴cos cos sin sin sin B C AB bc C ⎛⎫+=⎪⎝⎭即cos cos 3sin B C Ab c C+=由正弦定理化简得∴sin cos cos 3sin 3A cB bC C ⋅+⋅==∴23sin sin cos cos sin 3AC B C B +=∴23sin sin()sin 3AB C A +==∴2b =3B π=∴1sin sin sin a b cA B C===∴23sin sin sin sin()sin cos )3226a c A C A A A A A ππ+=+=+-=+=+ 203A π<<∴5666A πππ<+<∴)26A π<+≤即2a c <+≤故选：A .【点睛】方法点睛：边角互化的方法（1）边化角：利用正弦定理2sin sin sin a b cr A B C===（r 为ABC 外接圆半径）得2sin a r A =，2sin b r B =，2sin c r C =；（2）角化边：①利用正弦定理：sin 2aA r=，sin 2b B r =，sin 2c C r=②利用余弦定理：222cos 2b c a A bc+-=7.设O 为△ABC 的外心，若2AO AB AC =+，则sin BAC ∠的值为（）A.4B.4C.4-D.4【答案】D 【解析】【分析】设ABC 的外接圆半径为R ，由已知条件可得,2AC BO = ，所以12AC R =，且//AC BO ，取AC的中点M ，连接OM 可得π2BOM ∠=，计算cos sin BOC MOC ∠=-∠的值，再由余弦定理求出BC ，在ABC 中，由正弦定理即可求解.【详解】设ABC 的外接圆半径为R ，因为2AO AB AC =+ ,2AC AO AB BO =-=，所以1122AC BO R ==，且//AC BO ，取AC 的中点M ，连接OM ，则OM AC ⊥，因为//AC BO ，所以OM BO ⊥，即π2BOM ∠=，所以11π124cos cos sin 24AC RMC BOC MOC MOC OC OB R ⎛⎫∠=+∠=-∠=-=-=-=- ⎪⎝⎭,在BOC中由余弦定理可得：2BC R ===，在ABC中，由正弦定理得：2sin 224RBCBAC RR ∠===.故选：D8.高为8的圆台内有一个半径为2的球1O ，球心1O 在圆台的轴上，球1O 与圆台的上底面、侧面都相切.圆台内可再放入一个半径为3的球2O ，使得球2O 与球1O 、圆台的下底面及侧面都只有一个公共点.除球2O ，圆台内最多还能放入半径为3的球的个数是（）A.1 B.2C.3D.4【答案】B 【解析】【详解】作过2O 的圆台的轴截面，如图1.再作过2O 与圆台的轴垂直的截面，过截面与圆台的轴交于圆O .由图1.易求得24OO =.图1这个问题等价于：在以O 为圆心、4为半径的圆上，除2O 外最多还可放几个点，使以这些点及2O 为圆心、3为半径的圆彼此至多有一个公共点.由图2，3sin45sin sin604θ︒<=︒，有4560θ︒<<︒.图2所以，最多还可以放入36013122θ︒⎡⎤-=-=⎢⎣⎦个点，满足上述要求.因此，圆台内最多还可以放入半径为3的球2个.二、多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.已知某地区有小学生120000人，初中生75000人，高中生55000人，当地教育部门为了了解本地区中小学生的近视率，按小学生、初中生、高中生进行分层抽样，抽取一个容量为2000的样本，得到小学生，初中生，高中生的近视率分别为30%，70%，80%.下列说法中正确的有（）A.从高中生中抽取了460人B.每名学生被抽到的概率为1125C.估计该地区中小学生总体的平均近视率为60%D.估计高中学生的近视人数约为44000【答案】BD 【解析】【分析】根据分层抽样、古典概型、频率公式等知识对选项进行分析，从而确定正确选项.【详解】高中生抽取5500020004401200007500055000⨯=++人，A 选项错误.每名学生被抽到的概率为200011200007500055000125=++，B 选项正确.学生总人数为1200007500055000250000++=，估计该地区中小学生总体的平均近视率为1200007500055000132.50.30.70.80.53250000250000250000250⨯+⨯+⨯==，C 选项错误.高中学生近视人数约为550000.844000⨯=人，D 选项正确.故选：BD10.G 是ABC 的重心，2,4,120,AB AC CAB P ∠=== 是ABC 所在平面内的一点，则下列结论正确的是（）A.0GA GB GC ++= B.AB 在AC上的投影向量等于12- AC .C.3AG =D.()AP BP CP ⋅+ 的最小值为32-【答案】ACD 【解析】【分析】根据向量的线性运算，并结合重心的性质，即可判断A ，根据投影向量的定义，判断B ；根据向量数量积公式，以及重心的性质，判断C ；根据向量数量积的运算率，结合图形转化，即可判断D.【详解】A.以,GB GC 为邻边作平行四边形GBDC ，,GD BC 交于点O ，O 是BC 的中点，因为G 是ABC 的重心，所以,,A G O 三点共线，且2AG GO =，所以2GB GC GD GO +== ，2GA AG GO =-=- ，所以0GA GB GC ++=，故A 正确；B.AB 在AC 上的投影向量等于1cos1204AC AB AC AC ⨯=-，故B 错误；C.如图，因为()12AO AB AC =+ ，所以()222124AO AB AC AB AC =++⋅,即211416224342AO ⎛⎫=+-⨯⨯⨯= ⎪⎝⎭，即3AO = 因为点G 是ABC 的重心，22333AG AO ==，故C 正确；D.取BC 的中点O ，连结,PO PA ，取AO 中点M ，则2PA PO PM += ，()12AO AB AC =+，()()2221124816344AO AB AB AC AC =+⋅+=⨯-+= ,则()()()()221224AP BP CP PA PB PC PA PO PA PO PA PO ⎡⎤⋅+=⋅+=⋅=⨯+--⎢⎥⎣⎦，222132222PM OA PM =-=- ,显然当,P M 重合时，20PM = ，()AP BP CP ⋅+ 取最小值32-，故D 正确.故选：ACD【点睛】关键点点睛：本题的关键是对于重心性质的应用，以及向量的转化.11.如图，在棱长为2的正方体1111ABCD A B C D -中，O 为正方体的中心，M 为1DD 的中点，F 为侧面正方形11AA D D 内一动点，且满足1B F ∥平面1BC M ，则（）A.三棱锥1D DCB -的外接球表面积为12πB.动点F 的轨迹的线段为22C.三棱锥1F BC M -的体积为43D.若过A ，M ，1C 三点作正方体的截面Ω，Q 为截面Ω上一点，则线段1AQ 长度的取值范围为45,225⎡⎢⎣⎦【答案】AC 【解析】【分析】选项A ：三棱锥1D DCB -的外接球即为正方体的外接球，结合正方体的外接球分析；选项B ：分别取1AA ，11A D 的中点H ，G ，连接1B G ，GH ，1HB ，1AD ；证明平面1B GH ∥平面1BC M ，从而得到点F 的轨迹为线段GH ；选项C ：根据选项B 可得出GH ∥平面1BC M ，从而得到点F 到平面1BC M 的距离为H 到平面1BC M 的距离，再结合线面垂直及等体积法，利用四棱锥的体积求解所求三棱锥的体积；选项D ：设N 为1BB 的中点，从而根据面面平行的性质定理可得到截面Ω即为面1AMC N ，从而线段1AQ 长度的最大值为线段11A C 的长，最小值为四棱锥11A AMC N -以1A 为顶点的高.【详解】对于A ：由题意可知：三棱锥1D DCB -的外接球即为正方体的外接球，可知正方体的外接球的半径3R =所以三棱锥1D DCB -的外接球表面积为24π12πR =，故A 正确；对于B ：如图分别取1AA ，11A D 的中点H ，G ，连接1B G ，GH ，1HB ，1AD ．由正方体的性质可得11B H C M ∥，且1B H ⊂平面1B GH ，1C M ⊄平面1B GH ，所以1C M //平面1B GH ，同理可得：1BC //平面1B GH ，且111BC C M C ⋂=，11,BC C M ⊂平面1BC M ，所以平面1B GH ∥平面1BC M ，而1B F ∥平面1BC M ，所以1B F ⊂平面1B GH ，所以点F 的轨迹为线段GH ，其长度为12222⨯=，故B 错误；对于C ：由选项B 可知，点F 的轨迹为线段GH ，因为GH ∥平面1BC M ，则点F 到平面1BC M 的距离为H 到平面1BC M 的距离，过点B 作1BP B H ⊥，因为11B C ⊥平面11ABB A ，BP ⊂平面11ABB A ，所以11B C BP ⊥，又1111⋂=B C B H B ，111,B C B H ⊂平面11B C MH ，所以BP ⊥平面11B C MH ，所以1111111111114252232335F BC M H BC M B C MH B B C MH B C MHV V V V S BP ----====⨯=⨯⨯⨯⨯，故C 正确；对于D ：如图，设平面Ω与平面11AA B B 交于AN ，N 在1BB 上，因为截面Ω⋂平面11AA D D AM =，平面11AA D D ∥平面11BB C C ，所以1AM C N ∥，同理可证1AN C M ∥，所以截面1AMC N 为平行四边形，所以点N 为1BB 的中点，在四棱锥11A AMC N -中，侧棱11A C 最长，且11A C =设棱锥11A AMC N -的高为h ，因为1AM C M ==1AMC N 为菱形，所以1AMC 的边1AC ，又1AC =则112AMC S =⨯=△1111111142223323C AA M AA M V SD C -=⋅=⨯⨯⨯⨯=△，所以1111114333A AMC AMC C AA M V S h V --=⋅===△，解得3h =.综上，可知1AQ 长度的取值范围是,3⎡⎢⎣，故D 错误.故选：AC【点睛】关键点睛：由面面平行的性质得到动点的轨迹，再由锥体的体积公式即可判断C ，D 选项关键是找到临界点，求出临界值.三、填空题：本小题共3小题，每小题5分，共15分.12.已知复数()221i i()z m m m =-++⋅∈R 表示纯虚数，则m =________．【答案】1-【解析】【分析】根据2i 1=-和复数的分类要求得出参数值；【详解】因为复数()()2221ii=11i()z m m mm m =-++⋅-+-⋅∈R 表示纯虚数，所以210,10,m m ⎧-=⎨-≠⎩解得1m =-，故答案为：1-.13.定义集合(){},02024,03,,Z |A x y x y x y =≤≤≤≤∈，则从A 中任选一个元素()00,x y ，它满足00124x y -+-<的概率是________．【答案】42025【解析】【分析】利用列举法求解符合条件的()00,x y ，即可利用古典概型的概率公式求解.【详解】当0y =时，02024,Z x x ≤≤∈，有2025种选择，当1,2,3y =时，02024,Z x x ≤≤∈，分别有2025种选择，因此从A 中任选一个元素()00,x y ，共有202548100⨯=种选择，若00y =，则022y -=，此时由00124x y -+-<得012x -<，此时0x 可取0，1，2，若01y =或3，则021y -=，此时由00124x y -+-<得013x -<，此时0x 可取0，1，2，3，若02y =，则020y -=，此时由00124x y -+-<得014x -<，此时0x 可取0，1，2，3，4，综上可得满足00124x y -+-<的共有342516+⨯+=种情况，故概率为16481002025=故答案为：4202514.在ABC 和AEF △中，B 是EF的中点，1,6,AB EF BC CA ====，若2AB AE AC AF ⋅+⋅= ，则EF 与BC的夹角的余弦值等于__________.【答案】23【解析】【分析】【详解】由题意有：()()2AB AE AC AF AB AB BE AC AB BF ⋅+⋅=⋅++⋅+=,即22AB AB BE AC AB AC BF +⋅+⋅+⋅= ，而21AB =，据此可得：11,AC AB BE BF ⋅=⨯-=- ，即()112,2BF AC AB BF BC +⋅--=∴⋅= ，设EF 与BC 的夹角为θ，则2cos 2,cos 3BF BC θθ⨯⨯=∴= .四、解答题：本小题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.某学校为了解本校历史、物理方向学生的学业水平模拟测试数学成绩情况，分别从物理方向的学生中随机抽取60人的成绩得到样本甲，从历史方向的学生中随机抽取n 人的成绩得到样本乙，根据两个样本数据分别得到如下直方图：已知乙样本中数据在[70,80)的有10个．（1）求n 和乙样本直方图中a 的值；（2）试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的第75百位数（同一组中的数据用该组区间中点值为代表）；（3）采用分层抽样的方法从甲样本数据中分数在[60,70)和[70,80)的学生中抽取6人，并从这6人中任取2人，求这两人分数都在[70,80)中的概率．【答案】（1）50n =，0.018a =；（2）物理方向的学生本次模拟测试数学成绩的平均值为81.5，历史方向的学生本次模拟测试数学成绩的第75百位数为88.25；（3）25【解析】【分析】（1）由频率分布直方图得乙样本中数据在[70,80)的频率为0.2，这个组学生有10人，由此能求出n ，由乙样本数据直方图能求出a ；（2）利用甲、乙样本数据频率分布直方图能估计估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的第75百位数；（3）由频率分布直方图可知从分数在[60,70)和[70,80)的学生中分别抽取2人和4人，将从分数在[60,70)中抽取的2名学生分别记为1A ，2A ，从分数在[70,80)中抽取的4名学生分别记为1b ，2b ，3b ，4b ，利用列举法能求出这两人分数都在[70,80)中的概率．【小问1详解】解：由直方图可知，乙样本中数据在[70,80)的频率为0.020100.20⨯=，则100.20n=，解得50n =；由乙样本数据直方图可知，(0.0060.0160.0200.040)101a ++++⨯=，解得0.018a =；【小问2详解】解：甲样本数据的平均值估计值为(550.005650.010750.020850.045950.020)1081.5⨯+⨯+⨯+⨯+⨯⨯=，乙样本数据直方图中前3组的频率之和为(0.0060.0160.02)100.420.75++⨯=<，前4组的频率之和为(0.0060.0160.020.04)100.820.75+++⨯=>，所以乙样本数据的第75百位数在第4组，设第75百位数为x ，(80)0.040.420.75x -⨯+=，解得88.25x =，所以乙样本数据的第75百位数为88.25，即物理方向的学生本次模拟测试数学成绩的平均值为81.5，历史方向的学生本次模拟测试数学成绩的第75百位数为88.25；【小问3详解】解：由频率分布直方图可知从分数在[60,70)和[70,80)的学生中分别抽取2人和4人，将从分数在[60,70)中抽取的2名学生分别记为1A ，2A ，从分数在[70,80)中抽取的4名学生分别记为1b ，2b ，3b ，4b ，则从这6人中随机抽取2人的基本事件有：12(,)A A ，11(,)A b ，12(,)A b ，13(,)A b ，14(,)A b ，21(,)A b ，22(,)A b ，23(,)A b ，24(,)A b ，12()b b ,，13(,)b b ，14(,)b b ，23(,)b b ，24(,)b b ，34(,)b b 共15个，所抽取的两人分数都在[70,80)中的基本事件有6个，即这两人分数都在[70,80)中的概率为62155=．16.（建立空间直角坐标系答题不得分）如图，在四棱锥11A BCC B -中，平面ABC ⊥平面11BCC B ，△ABC 是正三角形，四边形11BCC B 是正方形，D 是AC 的中点．（1）求证：1//AB 平面1BDC ；（2）求直线BC 和平面1BDC 所成角的正弦值的大小．【答案】（1）证明见解析（2）55【解析】【分析】（1）连接1B C ，交1BC 于点O ，连接OD ，由中位线的性质，可知1//OD AB ，再由线面平行的判定定理，得证；（2）过点C 作1CE C D ⊥于点E ，连接BE ，可证CE ⊥平面1BDC ，从而知CBE ∠即为所求，再结合等面积法与三角函数的定义，得解．【小问1详解】连接1B C ，交1BC 于点O ，连接OD ，则O 为1B C 的中点，因为D 是AC 的中点，所以1//OD AB ，又OD ⊂平面1BDC ，1AB ⊄平面1BDC ，所以1AB ∥平面1BDC ．【小问2详解】过点C 作1CE C D ⊥于点E ，连接BE ，因为四边形11BCC B 是正方形，所以1BC CC ⊥，又平面ABC⊥平面11BCC B ，1CC ⊂平面11BCC B ，平面ABC ⋂平面11BCC B BC =，所以1CC ⊥平面ABC ，因为BD ⊂平面ABC ，所以1CC BD ⊥，因为ABC 是正三角形，且D 是AC 的中点，所以BD AC ⊥，又1CC AC C =I ，1,⊂CC AC 平面1ACC ，所以BD ⊥平面1ACC ，因为CE ⊂平面1ACC ，所以BD CE ⊥，又1C D BD D =I ，1,C D BD ⊂平面1BDC ，所以CE ⊥平面1BDC ，所以CBE ∠就是直线BC 和平面1BDC 所成角，设2BC =，在1Rt DCC 中，11CE DC CD CC ⋅=⋅，所以5CE ==，在Rt BCE 中，5sin 25CE CBE BC ∠===.17.甲、乙两人进行乒乓球对抗赛，每局依次轮流发球，连续赢2个球者获胜，且比赛结束，通过分析甲、乙过去比赛的数据知，甲发球甲赢的概率为23，乙发球甲赢的概率为25，不同球的结果互不影响，已知某局甲先发球.（1）求该局打4个球甲赢的概率；（2）求该局打5个球结束的概率.【答案】（1）875（2）44675【解析】【分析】（1）先设甲发球甲赢为事件A ，乙发球甲赢为事件B ，然后分析这4个球的发球者及输赢者，即可得到所求事件的构成，利用相互独立事件的概率计算公式即可求解；（2）先将所求事件分成甲赢与乙赢这两个互斥事件，再分析各事件的构成，利用互斥事件和相互独立事件的概率计算公式即可求得概率.【小问1详解】设甲发球甲赢为事件A ，乙发球甲赢为事件B ，该局打4个球甲赢为事件C ，由题知，2()3P A =，2()5P B =，则C ABAB =，所以23228()()()(()()353575P C P ABAB P A P B P A P B ===⨯⨯⨯=，所以该局打4个球甲赢的概率为875.【小问2详解】设该局打5个球结束时甲赢为事件D ，乙赢为事件E ，打5个球结束为事件F ，易知D ，E 为互斥事件，D ABABA =，E ABABA =，F D E =⋃，所以()()()()()()()P D P ABABA P A P B P A P B P A ==2222281135353675⎛⎫⎛⎫=-⨯⨯-⨯⨯= ⎪ ⎪⎝⎭⎝⎭，()()()()()()()P E P ABABA P A P B P A P B P A ==2222241113535375⎛⎫⎛⎫⎛⎫=⨯-⨯⨯-⨯-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以8444()()()()67575675P F P D E P D P E =⋃=+=+=，所以该局打5个球结束的概率为44675.18.在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，22cos a c b C -=.（1）求B ；（2）若点D 为边BC 的中点，点E ，F 分别在边AB ，AC （包括顶点）上，π6EDF ∠=，2b c ==.设BDE α∠=，将DEF 的面积S 表示为α的函数，并求S 的取值范围.【答案】（1）π3（2）3ππ,π328sin 23S αα=≤≤⎛⎫- ⎪⎝⎭，3,84S ⎡∈⎢⎣⎦【解析】【分析】（1）由题干及余弦定理可得222a c b ac +-=，再根据余弦定理即可求解；（2）由题可得ABC 为等边三角形，ππ32α≤≤，在BDE 与CDF 中，分别由正弦定理求出DE ，DF ，根据三角形面积公式可得3ππ,2ππ3216sin sin 36S ααα=≤≤⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，由三角恒等变换及正弦函数的图象与性质即可求解.【小问1详解】因为22cos a c b C -=，所以222222222a b c a b c a c b ab a +-+--=⋅=，即222a cb ac +-=，所以2221cos 222a cb ac B ac ac +-===.因为()0,πB ∈，所以π3B =.【小问2详解】由π3B=及2b c==可知ABC为等边三角形.又因为π6EDF∠=，BDEα∠=，所以ππ32α≤≤.在BDE中，2π3BEDα∠=-，由正弦定理可得sin sinDE BDB BED∠=，即32π2sin3DEα=⎛⎫-⎪⎝⎭.在CDF中，π6CFDα∠=-，由正弦定理可得sin sinDF CDC CFD∠=，即π2sin6DFα=⎛⎫-⎪⎝⎭.所以31π3ππsin,2ππ2ππ8632 sin sin16sin sin3636Sααααα=⨯⨯=≤≤⎛⎫⎛⎫⎛⎫⎛⎫----⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.因为2ππ11sin sin cos sin sin cos362222αααααα⎛⎫⎛⎫⎛⎫⎛⎫--=+-⎪⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭2213313sin cos cos sin sin2cos224444αααααα=-+=-1πsin223α⎛⎫=-⎪⎝⎭，因为ππ32α≤≤，所以ππ2π2,333α⎡⎤-∈⎢⎥⎣⎦，所以π3sin2,132α⎤⎛⎫-∈⎥⎪⎝⎭⎣⎦，所以1π1sin2,2342α⎤⎛⎫-∈⎥⎪⎝⎭⎣⎦.所以2ππ16sin sin36αα⎛⎫⎛⎫⎡⎤--∈⎪ ⎪⎣⎦⎝⎭⎝⎭，所以33,2ππ8416sin sin36αα⎡∈⎢⎛⎫⎛⎫⎣⎦--⎪ ⎪⎝⎭⎝⎭，所以333,2ππ8416sin sin36Sαα⎡=∈⎢⎛⎫⎛⎫⎣⎦--⎪ ⎪⎝⎭⎝⎭.所以S 的取值范围为3,84⎡⎢⎣⎦.19.（建立空间直角坐标系答题不得分）如图，在三棱柱ADP BCQ -中，侧面ABCD 为矩形．（1）若PD⊥面ABCD ，22PD AD CD ==，2NC PN =，求证：DN BN ⊥；（2）若二面角Q BC D --的大小为θ，π2π,43θ⎡⎤∈⎢⎥⎣⎦，且2cos 2AD AB θ=⋅，设直线BD 和平面QCB 所成角为α，求sin α的最大值．【答案】（1）证明见解析（2）12-【解析】【分析】（1）问题转化为证明DN⊥平面BCP ，即证明ND BC ⊥和DN PC ⊥，ND BC ⊥转化为证明BC ⊥平面PQCD ，而ND BC ⊥则只需证明PDN PCD△△（2）作出二面角Q BC D --的平面角以及直线BD 与平面QCB 所成的角，列出sin α的表达式，最后把问题转化为函数最值问题.【小问1详解】因为PD⊥平面ABCD ，BC ⊂平面ABCD ，所以PD BC ⊥，又CD BC ⊥，PD CD D ⋂=，,PD CD ⊂平面PCD ，所以BC ⊥平面PQCD ，又ND ⊂平面PQCD ，所以ND BC ⊥，在Rt PCD 中，2PD ==，则CD =3PC =，所以2NC =，1PN =，由PN PDND PC=，DPN CPD ∠=∠，所以PDN PCD △△，所以DN PC ⊥，又因为ND BC ⊥，PC BC C ⋂=，,PC BC ⊂平面BCP ，所以DN⊥平面BCP ，又因为BN ⊂平面BCP ，所以DN BN ⊥.【小问2详解】在平面QBC 中，过点C 作CF BC ⊥，因为ABCD 为矩形，所以BC CD ⊥，所以DCF ∠为二面角Q BC D --的平面角，且DCF θ∠=，又⋂=CF CD C ，,CD CF ⊂平面CDF ，所以BC ⊥平面CDF ，在平面CDF 中，过点D 作DG FC ⊥，垂足为G ，连接BG ，因为BC ⊥平面CDF ，DG ⊂平面CDF ，所以DG BC ⊥，又BC FC C ⋂=，,BC FC ⊂平面BCQ ，所以DG ⊥平面BCQ ，所以DBG ∠为直线BD 与平面QCB 所成的角，即DBG α∠=，sin DG DC θ=，又因为2cos 2AD AB θ=⋅，所以222sin 32cos 14cos 2DGBDAB AD αθθ===+++π2π,43θ⎡⎤∈⎢⎥⎣⎦可得12cos ,22θ⎡∈-⎢⎣⎦，21cos 0,2θ⎡⎤∈⎢⎥⎣⎦，设32cos t θ=+，2,32t ⎤∈+⎥⎦，则23cos 2t θ-=，()2223sin 1cos 14t θθ-=-=-，所以()2222563125651sin 14222t t t t α⎛⎫-++ ⎪--+⎝⎭=-=≤=，当且仅当25t =时等号，所以sin α51-.【点睛】关键点点睛：本题的关键是作出二面角Q BC D --的平面角以及直线BD 与平面QCB 所成的角，然后写出sin α的表达式，最后求函数最值问题利用了换元法和基本不等式.。

苏州小学一年级下期末试卷

苏州小学一年级下期末试卷一、汉字书写（每题2分，共10分）1. 请正确书写“春天”。

2. 写出“快乐”的反义词。

3. “学习”的第二个字是什么？4. “朋友”两个字的拼音是什么？5. 请写出“我们”的同音字。

二、词语填空（每题2分，共10分）1. 小明的______是红色的。

2. 我喜欢吃______。

3. 老师在______上写字。

4. 放学后，我们一起去______。

5. 春天，______开得很漂亮。

三、句子理解（每题2分，共10分）1. “小明在公园里放风筝。

”这句话告诉我们小明在哪里？2. “春天来了，花儿都开了。

”这句话描述的是什么季节？3. “小猫爱吃鱼。

”这句话告诉我们小猫喜欢吃什么？4. “老师表扬了我。

”这句话中，谁表扬了说话的人？5. “我们一起去动物园玩。

”这句话中，谁和说话的人一起去？四、阅读理解（每题5分，共20分）阅读下面的短文，回答问题。

春天到了，小草从土里钻了出来，小花也露出了笑脸。

小明和小红一起去公园玩，他们看到了许多美丽的花，还看到了小燕子在天空中飞来飞去。

小明说：“春天真美啊！”小红也说：“是啊，我喜欢春天。

”1. 小草和小花在哪个季节出现？2. 小明和小红去公园做了什么？3. 小明和小红看到了什么动物？4. 小明和小红对春天的感觉是什么？五、数学计算（每题5分，共30分）1. 5 + 7 = ?2. 12 - 4 = ?3. 8 × 3 = ?4. 24 ÷ 4 = ?5. 9 + 9 = ?6. 15 - 9 = ?六、逻辑推理（每题5分，共10分）1. 如果今天是星期一，那么后天是星期几？2. 小华有3个苹果，他给了小明2个，自己还剩下几个？七、常识判断（每题5分，共10分）1. 一年有几个季节？2. 我们通常在哪个季节穿棉衣？八、看图写话（共10分）观察下面的图片，写一段不少于30字的描述。

[图片描述：一个小男孩在公园里放风筝，天空中有几只小鸟在飞，草地上有几朵小花开放。

浙江省温州市瑞安市2023-2024学年一年级语文(下)学期期末试卷(含答案)

2023-2024学年浙江省温州市瑞安市一年级（下）期末语文试卷第一部分：积累运用（65分）1．（3分）请你为期末黑板报书写一个有趣的标题吧。

读万卷书，行万里路。

2．（14分）我会读一读，根据拼音写出正确的字。

ㅤㅤ这是阳光灿烂的shíjié。

我和小huǒbàn到xiāng jiān 游wán ，那里niǎo yǔhuāxiāng，小鱼在hé里huān kuài地游来游去。

3．（2分）“泉眼无声惜细流，树阴照水爱晴柔”的作者是（）A．杨万里B．白居易C．李白4．（2分）比赛成绩马上要出来了，小明内心真是（）A．竹篮子打水一一场空B．芝麻开花一节节高C．十五个吊桶打水一七上八下5．（2分）《咕咚》这个故事告诉我们（）A．只要互相帮助，就一定能解决问题。

B．在没有弄明白事情真相的情况下，要原地不动。

C．做事情要独立思考，不要随意听从别人的意见。

6．（11分）我会填一填，根据要求写一写。

（1）“家”共有笔，第6笔是。

（2）“医”共有笔，笔顺是（3）舞蹈跳了又跳故事游戏（4）（荡）来（荡）去来去来去（5）粽子又黏又甜玉米桃子 7．（4分）黑板报上出现了一则通知，快来补充完整吧！通知ㅤㅤ明天晚上六点，请家长朋友们在本班教室参加家长会，记得准时参加。

李老师6月24日①时间： ③参加人：家长朋友们⑤通知时间： ②地点：本班教室④事情： ⑥通知人： 8．（8分）我会读句子，把句子中空缺的字和标点符号补上。

吗呢吧呀（1）我们正忙着搬东西 □（2）亲爱的乌鸦，您的孩子好 □（3）请你帮我捉害虫 □（4）燕子为什么飞得这么低 □9．（8分）糟糕！黑板上出现词语搭配混乱的情况，你能重新连一连吗？（1）踢皮球拍毽子搭音乐听积木（2）壮观的升旗仪式洁白的荷叶圆圆的雪莲美丽的天山10．（6分）请你把黑板报上的气球送回到词语中吧！座条只一桥一鱼一鸟本棵架一飞机一大树一书11．（5分）黑板报上的句子还可以“换花样”呢！请你照样子，仿写句子。

小学数学一年级下册期末考试试卷可打印(三套)

北师大版一年级数学下册期末试卷（一）班级：姓名：成绩：一、口算（10分，每题0.5分）。

65－12＝27＋11＝61＋29＝92－42＝12＋80＝33＋57＝75－20＝35－11＝28＋52＝96－16＝38＋22＝47－11＝36＋54＝70－25＝35－14＝40＋30＝81＋15＝69－50＝84－14＝96－80＝二、填空（23分，每空1分）。

1、一个数从右边起，第一位是（）位，第二位是（）位，第三位是（）位；56的个位上是（），十位上是（）。

2、100里面有（）个十，100里面有（）个一；78里面有（）个十和（）个一。

3、1米＝（）厘米，也可以写成：1m＝（）cm；4、在（）里填上“m”或“cm”。

衣柜高2（）黄瓜长20（）房子高5（）毛巾长1（）橡皮长4（）大树高3（）5、量一量。

（）cm（）cm（）cm6、在（）填上“＜”、“＞”或“＝”。

54＋38（）38＋5443－26（）42－2669－47（）69－46伍元拾元1角5角1元1元5角储钱罐1元1元1元1元1元1元5角5角5角5角5角1角1角5角1元1角拾元拾元伍元拾元1角伍元三、统计图，涂一涂，算一算（17分）。

小明的储钱罐有这么多的钱：1、涂一涂。

（5分）2、算一算，小明一共有（）元（）角。

（2分）3、（10分）12元8角25元3角23元6角11元5角①买一共需要多少钱？列式：；②买，付了50元，找回多少钱？列式：；；③小明现在的钱可以买哪些小动物？可以买：；④买可以怎样付钱？答：；四、竖式计算。

（20分，一步计算2分，两步计算4分）35＋29＝51－24＝66－19＝45＋55＝14＋35＋46＝91－29－67＝25＋35－49＝五、看图提出“三个”数学问题并列式解答。

（6分，每空1分）兔比马多8只马有45只鱼比兔少3只你的数学问题：①；列式：；②；列式：；③；列式：；六、想一想，连一连。

（4分）七、应用题。

（20分）1、三个同学跳绳。

各地区一年级语文期末试卷五套(含答案),可直接下载打印!

人教版小学一年级语文期末考试试卷一题号一二三四五六七八九十十一总分得分一、写xi ě 出ch ū 与y ǔ 韵y ùn 母m ǔ 读d ú 音y īn 相xi ān ɡ 同t ón ɡ 的de 整zh ěn ɡ 体t ǐ 认r èn 读d ú 音y īn 节ji é。

（7分） ü i u üe ing ün ie in二、看k àn图t ú，写xi ě 出ch ū 相xi ān ɡ 应y ìn ɡ 的de 汉h àn字z ì。

（8分）三、按àn 要y āo 求qi ú填ti án 空k òn ɡ。

（8分）1.“口”加一笔变成 “木”加一笔变成2.“天”减一笔变成 “子”减一笔变成3.“问”的第一笔是，共笔。

4.“西”的第三笔是，第五笔是。

yu四、将jiānɡ汉hàn字zì与yǔ其qí正zhènɡ确què读dú音yīn连lián起qǐ来lái。

（6分）妈影会弯国校最yǐng huì mā xiao zuì wān guó五、照zhào样yànɡ子zi，填tián一yi填tián。

（9分）1.一（群）鸭子一（）猫一（）牛一（）苹果一（）伞一（）书 2.日月小土田力（明）（）（）3.二人（从）双木（）三人（）六、拼pīn一yi拼pīn，写xiě一yi写xiě。

（11分）bǐ sài lì zhèng zǎo chen nǐ hǎo赛晨kāi xīn tóu fɑ hē shuǐ huǒ chē发喝车七、看k àn 图t ú，在z ài 句j ù 中zh ōn ɡ 填ti án 入r ù 一y í 对du ì 反f ǎn 义y ì 词c í。

山东省济南市莱芜区2023-2024学年一年级语文(下)学期期末试卷(含答案)

2023-2024学年山东省济南市莱芜区一年级（下）期末语文试卷一、我会读写。

1．拼一拼，写一写。

shēn tǐtīng shuōzhāo hu jīn qiūshíjiéchūn fēng xīng kōng gùxiāng huān shēng xiào yǔ2．给加点的字选择正确读音打“√”。

（1）一听到音乐（lèyuè）响起，我就快乐（lèyuè）地跳起舞来。

（2）我觉（juéjiào）得好累，得（děi dé）上床睡觉（juéjiào）了。

（3）小红不（búbu bù）小心把小明的铅笔捧断了，难过地说：“对不（búbu bù）起，我不（búbu b ù）是故意的。

”3．我会选择合适的字组成词语（填序号）A.冰B.冻C.冷D.凉雹汗土快A.浇B.洒C.洗D.泡水茶车花4．选择同音字填空组词。

进近座坐处下步位5．选择合适的字填空组词。

支朵包首一豆子一儿歌一白云一铅笔6．课文内容填空。

（填序号）①歌台②凉伞③摇篮④停机坪荷叶是小水珠的，小蜻蜓的，小青蛙的，小鱼儿的。

7．规范书写。

（1）“晴”字用音序查字法查字典，应先查大写字母，读音是。

第七笔是，它的偏旁是，带有“日”字旁的字大多和有关。

（2）“居”和“造”都是结构，但是这两个字的笔顺规则却不一样。

“居”书写时要先后；“造”书写时要先后。

8．加偏旁，变新字，再组词。

例：元园（公园）完（完成）火（）（）主（）（）9．写出下列字的反义词。

早—— 是—— 前—— 粗—— 10．照例子仿写词句。

（1）例：走来走去（2）例：雪白雪白的棉花雪白雪白的雪白雪白的（3）例：小鸭子游泳。

小鸭子在河里游泳。

江西省宜春市宜春中学 2023-2024学年下学期高一期末考试语文试卷

江西省宜春中学2023—2024学年度下学期高一期末试卷语文学科注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，只收答题卡。

一、现代文阅读（34分）（一）现代文阅读Ⅰ（本题共5小题，18分）阅读下面的文字，完成1～5题。

《红楼梦》是艺术，艺术需要美。

因此，《红楼梦》研究也应研究它的艺术美，揭示它的审美价值。

“红学”和美学相通。

文学作品，是内容和形式的有机统一。

《红楼梦》的内容和形式都极复杂，对它做“内在”的研究，领域广阔，方法多样，并不只限于美学一途。

社会学的、心理学的、语言学的研究，可以多方面地进行，从不同角度揭示《红楼梦》的价值和意义，方法不同，目的则一。

然而，要能真正揭示它的审美价值和艺术价值，就不能不借助于美学上的研究。

说起对《红楼梦》做美学的探讨，常被人误解为只是谈论一下艺术形式、表现手法。

其实不然。

对《红楼梦》的美学研究，当然要探索它的艺术形式之美，然而并不仅限于此，更重要的是要研究它的艺术内容之美，进而了解它的内容和形式是如何统一的，达到了怎样的完美程度。

《红楼梦》的艺术形式是美的，语言、文笔都很优美，令人惊叹。

对于《红楼梦》的完美的形式结构，我们研究得还很不够，应尝试用多种方法进行研究，甚至不妨借鉴结构主义的某些方法。

当然，对《红楼梦》艺术形式的研究，不能脱离它的艺术内容孤立进行。

形式只有相对独立性，艺术的形式结构归根到底还是由艺术内容决定的。

结构主义的根本错误在于不顾内容而孤立研究形式，把艺术文学归结为只是形式。

结构主义不顾内容，但在研究文学的形式方面，却并非一无是处，如果不是搬用而是借鉴，“红学”也应吸取一些方法用来分析《红楼梦》的形式结构。

比较文艺学所特别重视的比较方法，也值得“红学”一试，如果能把《红楼梦》和西方小说做些比较，找出异同，这将使《红楼梦》研究提高一步。

人教版小学一年级下册语文期末测试卷及参考答案)

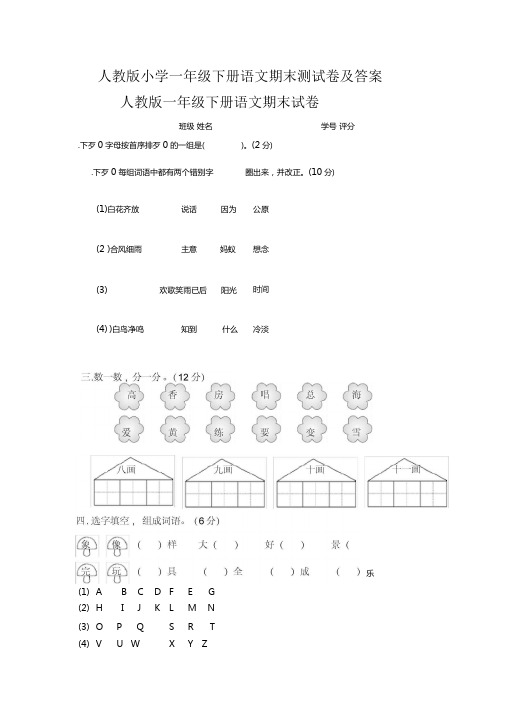
人教版小学一年级下册语文期末测试卷及答案人教版一年级下册语文期末试卷班级姓名学号评分.下歹0字母按首序排歹0的一组是()。

(2分)(1) A B C D F E G(2) H I JK LM N (3) O PQSRT(4) VU WX Y Z.下歹0每组词语中都有两个错别字圈出来，并改正。

(10分)(1)白花齐放说话因为 (2 )合风细雨主意妈蚁 (3)欢歌笑雨已后阳光(4) )白鸟净鸣知到什么 (5)公原想念时间冷淡乐美丽的长城一Z A Z A马儿可口的校园电脑甜蜜的水果一辆辆飞机雄伟的笑容一匹匹自行车六.写出带点词的反义词。

（6分）例：楼房有低有（高）1.手指有短有（)2.跑步有慢有（）。

3.道路有近有（）。

4.衣服有旧有（）。

5.灯光有暗有 ___________ 。

6.味道有甜有（1。

七.照样子，写一写。

（14分）1.表示颜色的词：如黄澄澄2.AABB的词：如快快乐乐3.表小动作的词：如踢足球4.改写句子：如王二小把敌人带进了八路军的埋伏圈。

舌攵人被王二小带讲了八路军的理伏圈。

同学们把教室打扫得了丁净净。

八.将题目和诗句用线连起来。

（12分）《所见》远看山有色歌声振林橄《小池》牧童骑黄牛处处闻啼鸟《画》草长京二月天近听水无声《静夜思》小荷才露尖尖角低头思故乡《村居》举头望明月拂堤杨柳醉春烟九. 读一读，给它们调整一下顺序。

（把序号写在括号内）（4分）（）棉花姑娘请燕子,啄木鸟,宵蛙帮它捉害虫。

（）棉花姑娘生病了，叶子上长了许多酎虫。

（）棉花姑娘病好了 ,长出了碧绿碧绿的叶子,吐出了雪白雪白的棉花。

（）七星瓢虫给棉花姑娘治好了病。

+ .短文阅读。

（15分）（一）春天来了春天来了，桃花红了，梨花白了 ,迎（y in 。

春花黄了，柳树绿了，燕子从南方飞回来了，宵蛙醒了，这一切的变化真奇妙啊！1.写出表示颜色的词语：（）（）（）（）（4分）2. 写了哪些植物，请用“一一”在句子中画出来。

人教版一年级数学下册期末检测试卷5份

人教版一年级数学下册期末试卷（全卷满分：100分，考试时间:70分钟）亲爱的同学们：经过一期的努力耕耘，我们共同播下了希望的种子。

今天，就让我们满怀信心收获累累果实吧！你准备好了吗？一、快乐天空。

1.由7个十和9个一组成的数是（），一个一个的数，与它相邻的两个数是（）和（）。

2．7元=（）角 36角=（）元（）角9角-4角=（）角 3角+5元6角=（）元（）3．一张和3张合起来是（）元（）角4. 百位十位个位这个数写作（），读作（），比它小3的数是（）。

5.一个数是24，另一个数是50，和是（）；减数是8，被减数是68，差是（）。

6．找规律，接着画，接着写。

（1）（2）16 14 12 8 6 2 0二、开心选择：a在正确答案的里画“√”1．下面的数中，和80最近的数是：2.100比（）大的多。

3.小花买橡皮用去6角，她付给营业员1元，应该找多少钱？1元6角 4角4.用做一个，4的对面是：5.妈妈买了3盒巧克力，每盒8块一共多少块（）。

18（）形最多，（）最少；黑色图形比白色图形少（）个，共有（）图形。

四、轻松计算。

60+5= 39-9= 22=5= 48-6= 55=20=56-8= 63+7= 100-90= 74-60= 8+54=60+（）=87 （）+7=61 （）-20=1669-（）=9 76-（20+40）= 90-70+38=43-（3+7）= 88-（）=40 （）+26=38五、一起购物。

个数10元 36元10元8元1、小汽车比轮船贵多少元？2、最少要花多少钱，才能买到两样东西？3、你还能提出什么数学问题?要解答哟！六、我会解读。

1.女孩比男孩多写了多少个字？我写了40个字。

我写了57个字。

2.这本书一共有多少页？这本书我已经看了68页，还有7页没看。

3.有24颗珠子，5颗穿一串，能穿几串？还剩几颗？4.两人一共折了多少只小猫？5.水果店运进56箱苹果。

水果店还剩多少箱水果？人教版小学数学下册期末质量检测一年级数学试题时间：80分钟等级：一、填一填。

一下语文期末情境性试卷

一、阅读理解（每题5分，共25分）阅读以下材料，完成题目。

【材料一】春天，万物复苏。

小草从土里探出头来，柳树发芽了，小鸟在枝头欢快地唱着歌。

小明和小红相约去公园赏花。

【材料二】公园里花儿繁多，有红的、黄的、紫的，五彩斑斓，美丽极了。

小明和小红一边欣赏，一边拍照留念。

【材料三】小明和小红在公园里遇到了一位老奶奶，她正在摘花。

小明和小红上前劝阻：“奶奶，花儿是大自然的馈赠，我们应该爱护它们，不能随意摘取。

”【材料四】老奶奶听了小明和小红的话，点了点头，表示理解。

她感谢他们的提醒，并表示以后不会再摘花了。

1. 请根据材料一，概括春天的主要特征。

（2分）2. 请根据材料二，描述公园里花儿的特点。

（3分）3. 请根据材料三，分析小明和小红的行为。

（3分）4. 请根据材料四，说明老奶奶的行为变化及其原因。

（3分）二、口语交际（每题10分，共20分）1. 请以“环保小卫士”为主题，准备一段5分钟的演讲稿，阐述你对环保的看法和行动。

（10分）2. 请根据以下情景，进行角色扮演，完成对话。

（10分）情景：小明在公交车上遇到了一位老年人，主动让座。

三、写作（每题20分，共40分）1. 请以“我心中的英雄”为题，写一篇不少于300字的作文，描述你心中的英雄及其事迹。

（20分）2. 请根据以下材料，写一篇不少于200字的作文，题目自拟。

材料：一场突如其来的暴雨袭击了我国南方某城市，导致街道积水严重，交通瘫痪。

在这次抗洪救灾中，许多志愿者和救援人员不畏艰险，奋力救援，确保了人民群众的生命财产安全。

四、综合运用（每题10分，共20分）1. 请根据以下成语，写出相应的词语。

（5分）（1）兴高采烈（2）小心翼翼2. 请根据以下诗句，填写缺失的字。

（5分）山重水复疑无路，______。

答案：一、1. 春天的主要特征：万物复苏，草木发芽，花开鸟鸣。

2. 公园里花儿的特点：花儿繁多，色彩斑斓，美丽极了。

3. 小明和小红的行为：劝阻老奶奶不要摘花，爱护大自然。