10组合博弈入门
博弈方法(10原则)

把握正确的博弈方法一、主动性原则用自己的主动进出,把现货交易风险(盈亏)控制在自己的眼皮地下。
实现了现货盈亏由“自己说了算”。
二、微分化原则把赢利、亏损和持仓的时间都微分化,特别是亏损,都控制在价差的几元钱之内。
持仓时间最长的就几个小时,最短的就2~3分钟。
果断进出,决不以任何理由长时间拖延持有亏损的单子。
例如,枸杞价从644涨到648仅跳动4个价位(也就是涨了4分钱)逾越枸杞的交易手续费,就要准备平仓。
三、独立性原则一笔现货交易,只是这一笔的,无论它是亏是赢,都与下一笔的交易毫不相关。
不能因为上一笔交易的盈亏或进出价格的高低,而影响到下一笔交易的果断进出。
四、客观性原则做当日短线,最不能容忍的就是头脑中事先就“主观”地认定了当日行情涨(或是跌),主观地认定今天只能做多或只能做空,这是短线炒手不能有的错误思维。
正确的做法是不管基本面如何、消息面如何、主力如何、价格是太高还是太低、持单是赢是亏、技术指标是否背离等等,对这些都要统统不与理睬!只能一心一意客观地“紧紧地跟随”当时盘面(眼前的价格动摇情况)做单。
五、盈亏相当原则盈亏相当指由于我微分化交易,因此我每一笔交易的赚和赔的金额大体都会是相等的,之所以能赚钱,靠“概率”来取胜的假定我每一笔赚钱和每一笔赔钱是一样多,而我当天共交易了100次,其中有70次是赚的 30次是赔的,那么我这一天就是赚了,每天只算总账的盈亏。
当然你最好能力争把每一笔交易的亏损数控制在上一笔交易的盈利数之内就更好了。
换一句话说,就是假如你上一笔交易赚了20元,那么你这一笔的交易最大亏损就只能是20元,还没有亏损到20元,就应该提前止损了。
六、停止交易原则也可能你今天一上来现货就交易的很不顺手,老是亏,连着几笔都是亏。
那么当你亏到某个数时,一到这个数,就坚决平仓关机走人,立即停止今天的任何交易。
这个原则就可以帮助你绝对不会出现一天中连续的大赔。
七、亏损时不加仓不加量原则许多人在持有了亏损单的时候,不是采取立即“主动”退出的原则,而是用资金去“死扛”并且还不断的加码。
博弈论基础教程教学设计

博弈论基础教程教学设计介绍博弈论是现代数学的重要分支之一,在社会科学和经济学中有着广泛应用。
博弈论是对战争、政治、经济和生物学等领域的分析和研究提供数学模型的一种数学理论。
本文旨在为博弈论基础教程教学设计提供参考,帮助教师更好地提高学生的学习效果和兴趣。
教材选择针对初学者,推荐使用《博弈论入门》这本书作为教材,它可以为学生提供一个循序渐进的博弈论教学体系。
教学内容主要包括博弈论中的基本概念和原理,以及常用方法和应用技巧。
在教学过程中,为了帮助学生理解和更好地掌握知识,可以通过问题练习等方式进行辅助教学。
教学内容基本概念博弈论中的基本概念包括博弈模型、策略、收益等概念。
学生需要了解这些概念的意义,并能正确运用概念进行博弈论问题的解决。
基本原理博弈论中的基本原理包括博弈的完备性原理、最小化原理、最大化原理等。
这些原理是博弈论研究的基础,学生需要理解并掌握这些原理,以便应用到实际博弈中。
常用方法博弈论中包含许多重要的方法,如纳什均衡、支配策略、迭代删除等。
学生需要理解这些方法的意义和适用范围,并能够正确应用到博弈问题中。
应用技巧博弈论在现实中有着广泛的应用,如在经济学中用来分析产业结构、竞争策略,用来解决博弈双方的合作与冲突问题,在生态学、生物学、计算机科学中也有着重要的应用。
学生需要了解这些应用,并能理解和应用博弈论相关的技巧。
教学方式讲授教师通过讲授来介绍博弈论的基本知识和概念,讲授内容可以结合教材和一些其他的参考资料,便于学生更好地理解和掌握相关的知识。
课堂互动学生在课堂上可以参与课堂互动和讨论,通过案例或问题分析来帮助学生更好地掌握博弈论知识。
实践操作学生需要根据讲授内容,进行实践操作,通过实际性问题和练习来更好地掌握博弈论知识并加深对概念和原理的理解。
作业教师可以布置一些作业来检测学生对博弈论知识的掌握情况,同时也可以为学生提供练习和巩固知识的机会。
总结本文围绕博弈论基础教程教学设计提供了一些参考意见,教师可以根据实际情况进行调整和补充。
博弈论题目总结(三)——组合游戏进阶

博弈论题⽬总结(三)——组合游戏进阶第⼆波题⽬⼤多都是sg组合游戏的基本变形,是对游戏规则的⼩改动。
容易提取出SG函数的模型,且SG函数的规律也⽐较简单⽽本⽂的题⽬需要较多的模型转化思想但博弈论的精髓还是打表翻硬币游戏⼀条直线上有很多硬币,有的正⾯朝上,有的反⾯朝上,每次可以翻⼀些硬币,但最右边的硬币必须由正变反,不能操作者输翻硬币可能会有奇奇怪怪的要求,⼀次翻好⼏个,⼀次翻连续的⼏个结论:正⾯朝上的⽯⼦之间互不影响,设正⾯朝上是1,反⾯朝上是0,那么SG(0101001)=SG(01)^SG(0001)^SG(0000001)证明见论⽂树形删边游戏SG(u)=xor{SG(v)+1}证明见jzh神犇的论⽂POJ 3710 Christmas Game环怎么处理啊?⼀个奇环可以分成等长的两条链,SG函数值为0,其他后继状态的SG函数值均>1,故奇环的SG函数值为1⼀个偶环只能分成异奇偶的两条链,SG函数值均>0,故奇环的SG函数值为0tarjan边双缩点搞⼀下就⾏了1 #include <cmath>2 #include <cstdio>3 #include <cstring>4 #include <algorithm>5#define N1 1056#define M1 5057#define ll long long8#define dd double9using namespace std;10const dd eps=1e-7;1112 template <typename _T> void read(_T &ret)13 {14 ret=0; _T fh=1; char c=getchar();15while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }16while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }17 ret=ret*fh;18 }19struct Edge{20int to[M1*2],nxt[M1*2],val[M1*2],head[N1],cte;21void ae(int u,int v,int w)22 {23 cte++; to[cte]=v; nxt[cte]=head[u];24 head[u]=cte; val[cte]=w;25 }26 }e,E;2728int T,n,m;29int low[N1],dfn[N1],use[N1],stk[N1],dad[N1],sum[N1],tim,num,tp;30void tarjan(int x,int fa)31 {32int j,v;33 low[x]=dfn[x]=++tim; stk[++tp]=x; use[x]=1;34for(j=e.head[x];j;j=e.nxt[j])35 {36 v=e.to[j]; if(e.val[j]==fa) continue;37if(!dfn[v]){38 tarjan(v,e.val[j]);39 low[x]=min(low[x],low[v]);40 }else if(use[x]){41 low[x]=min(low[x],dfn[v]);42 }43 }44if(low[x]==dfn[x])45 {46 num++;47while(stk[tp]!=x){ use[stk[tp]]=0; dad[stk[tp]]=num; sum[num]++; tp--; }48 use[x]=0; dad[x]=num; sum[num]++; tp--;49 }50 }5152void rebuild()53 {54int i,j,v;55for(i=1;i<=n;i++)56 {57for(j=e.head[i];j;j=e.nxt[j])58 {59 v=e.to[j];60if(dad[i]!=dad[v])61 E.ae(dad[i],dad[v],0);62 }63 }64 }6566int sg[N1],de;67void dfs(int x,int fa)68 {69int j,v;70for(j=E.head[x];j;j=E.nxt[j])71 {72 v=E.to[j]; if(v==fa) continue;73 dfs(v,x); sg[x]^=sg[v]+1;74 }75if(sum[x]>1 && (sum[x]&1)) sg[x]^=1;76 }7778void init()79 {80 memset(sg,0,sizeof(sg)); memset(low,0,sizeof(low));81 memset(sum,0,sizeof(sum)); memset(dfn,0,sizeof(dfn));82 memset(dad,0,sizeof(dad)); memset(use,0,sizeof(use));83 memset(&e,0,sizeof(e)); memset(&E,0,sizeof(E));84 tim=0; tp=0; num=0;85 }8687int N;88int main()89 {90int i,j,x,y;91while(scanf("%d",&N)!=EOF) {9293int ans=0;94while(N--)95 {96 init(); read(n); read(m);97for(i=1;i<=m;i++)98 {99 read(x); read(y); e.ae(x,y,i); e.ae(y,x,i);100 }101for(i=1;i<=n;i++) if(!dfn[i]) tarjan(i,-1);102 rebuild();103 dfs(dad[1],-1);104 ans^=sg[dad[1]];105 }106if(ans) puts("Sally"); else puts("Harry");107108 }109return0;110 }View CodeK倍动态减法游戏现在有⼀堆⽯⼦,两个⼈轮流取,后⼿取的⽯⼦数不能超过先⼿取的K倍,第⼀个⼈不能⼀下⼦把⽯⼦都取完,取最后⼀个⽯⼦的⼈赢,问谁能赢在探究“K倍动态减法游戏前”,先研究⼀下2倍动态减法游戏,即fibonacci博弈2倍动态减法游戏结论:当剩余⽯⼦数是斐波那契数时,先⼿必败简单证明如下⽯⼦数为2,3时,显然先⼿必败。
简单的组合博弈游戏

好运!该死的英语四级!
Problem Description 大学英语四级考试就要来临了, Kiki和Cici 在紧张的复习 之余喜欢打牌放松。“升级”?“斗地主”?那多俗啊! 作为计算机学院的学生,Kiki和Cici打牌的时候可没忘记专 业,她们打牌的规则是这样的:
1:如果轮到对方抓牌时只剩3张牌,对果轮到对方抓牌时还剩3*k张牌,对手不管取多少,剩 下的牌数是3*x+1或者3*x+2。轮到你时,你又可以构造一个 3的倍数。 所以无论哪种情况,当你留给对手为3*k的时候, 你是必胜的。
题目说Kiki先抓牌,那么当牌数为3的倍数时,Kiki就输了。 否则Kiki就能利用先手优势将留给对方的牌数变成3的倍数, 就必胜。
必败点;
下面我们证明这3个性质。
性质1:所有自然数都会出现在一个必败点中,且仅会出 现在一个必败点中;
证明:m(k)是前面没有出现过的最小自然数,自然与前k-1 个必败点中的数字都不同;m(k)>m(k-1),否则违背m(k-1) 的选择原则;n(k)=m(k)+k>m(k-1)+(k-1)=n(k-1)>m(k-1),因 此n(k)比以往出现的任何数都大,即也没有出现过。又由 于m(k)的选择原则,所有自然数都会出现在某个必败点中。 性质1证毕。
简单的组合博弈游戏
组合博弈游戏应满足以下性质:
1. 有两个游戏者。
2. 有一个可能的游戏状态集。这个状态集通常是有限的。
3. 游戏规则指定了在任何状态下双方的可能的走步和对应的后继状态 集。如果在任意状态下双方的走步集合是相同的,那么说游戏是公平 的(impartial) ,否则是不公平的(partizan) 。象棋是不公平的,因为每 个人只能移动自己的子。
游戏及惩罚

游戏一:坐气球。
每个小组三个人上来参加,两个人吹气球,一个在椅子上坐暴。
坐暴10个气球,按用时多少算胜负。
游戏二:纸杯传水。
每个组出5个人站成一列,每人嘴上叼一只纸杯,然后从前往后传水,不能用手,全凭嘴和头的动作,在规定时间内按传到最后的水的多少算胜负。
游戏三:顶橘子每个组两个同学上来参加,奖橘子顶在头上,不能用手扶,然后按主持人安排做动作,比如跨凳子,向后转,坐下起立,相互之间除了接触外也允许使用吓唬等手段,按坚持的时间长短算胜负。
这里说几个很high的惩罚方法。
1。
学广告。
大家都看过脑白金的广告吧,就让他学里面的动画人物的动作,哈哈。
当然还有很多搞笑的广告,自己找吧。
2。
表演例如让他选择“装白痴,装纯情,装gay”,不管装哪个,都很好看,呵呵。
3。
朗读准备好一段很搞笑的文字,比如那一段“我是一头猪,。
”呵呵,让他大声读出来,里面还可以要求动作。
4。
吻桌子(柱子)被罚者要亲吻指定的一个桌子5下,这时最好有照相机伺候,呵呵,出来的照片肯定很精彩!挺不错的,给大家推荐一个小游戏吧!满好玩的。
游戏名称:团队合作,张弛有道▲游戏目的:通过这个游戏,让大家认识到团队合作的重要性。
一个团队若想成功必须运用恰当的方法,而这个方法不仅包括要善于利用有效资源,还要求学会倾听他人的意见,以沟通寻求彼此间的默契。
▲游戏规则:游戏开始时,将大麻绳围在各自腰间位置,所有队员带上眼罩,在2分钟内将绳索围成指定的图形(如正方形、长方形、平行四边形、梯形、菱形、三角形),在这过程中,参加队员不能手拖手,只能通过大麻绳互相维系,最后围出图形的队伍将绳索不变形的平放置地上让大家看图形是否形似,最快围出图形且图形形似的队伍胜出。
游戏以组为单位分别进行,抽签决定游戏顺序的先后和所要摆的图形。
按游戏完成的形似和时间评出一至六名,最形似且时间最短的为第一名,其次的为第二名,以此类推。
第一名得6分,第二名得5分,以此类推,第六名得1分。
▲游戏细则:所需要设备:眼罩10个、大绳索一条、秒表1个、口哨一个。
博弈入门课程大纲第一节

博弈入门课程大纲
第一节
1 游戏1
1.1 博弈标准形式
对手
α β
α 我 β
1.2 博弈论的组成要素:策略、参与人、收益
1.3 优势策略与劣势策略
1.4博弈分析方法1:不要选择严格劣势策略。
1.5 博弈分析方法2:如果自己没有劣势策略,要分析别人的收益,要考虑别人会怎么做,并以此为基础,做出自己的决策。
换位思考,考虑一下别的处境,别人的优势策略和劣势策略。
2 游戏2选数字
2.2 正规的博弈论:
参与人,i,j
策略(strategy ) 某个人的策略si ,用大写的Si 表示某个人所有的策略Si 集合,Si={0,1,2,..100}
用小写s 表示所有人某一次的策略组合s=(si,sj,sk,….sn )。
举例{25,5,60} Strategy profile
收益(payoff ,utility )
第i 个人的收益。
ui(si,sj,…,sn),是因为它的收益取决于所有人的策略 Ui(s)
引入一个符号 s-i 表示除了i 以外,其它所有人的策略。
2.3博弈分析方法4:不要选择弱劣势策略。
70,70 100,60
60,100 80,80。
(HDUACM2010版_10)组合博弈入门共39页

08.01.2020
5
基本思路?
请陈述自己的观点
08.01.2020
6
第一部分
简单取子游戏 (组合游戏的一种)
08.01.2020
7
什么是组合游戏——
(1) 有两个玩家;
(2) 游戏的操作状态是一个有限的集合(比如: 限定大小的棋盘);
08.01.2020
15
08.01.2020
16
初步分析
(0, 0, 0) (0, 0, x) (0, 1, 1) (0, k, k) (14, 35, 46)
P-position N-position P-position P-position ???
08.01.2020
ACM程序设计
杭州电子科技大学 刘春英
今天,
你 了吗?
08.01.2020
2
每周一星(9):
Hugo
08.01.2020
3
第十讲
组合博弈入门
(Simple Game Theory)
08.01.2020
4
导引游戏
(1) 玩家:2人; (2) 道具:23张扑克牌; (3) 规则:
12
实战练习… kiki's game
08.01.2020
13
第二部分
Nim游戏
08.01.2020
14
Nim游戏简介
(1) 有两个玩家; (2) 有三堆扑克牌(比如:可以分别是
5,7,9张); (3) 游戏双方轮流操作; (4) 玩家的每次操作是选择其中某一堆牌,
组合博弈理论

博弈论(一):Nim游戏 (1)博弈论(二):Sprague-Grundy函数 (4)Game theory初步 (7)寻找必败态——一类博弈问题的快速解法 (14)博弈论(一):Nim游戏重点结论:对于一个Nim游戏的局面(a1,a2,...,an),它是P-position当且仅当a1^a2^...^an=0,其中^表示位异或(xor)运算。
Nim游戏是博弈论中最经典的模型(之一?),它又有着十分简单的规则和无比优美的结论,由这个游戏开始了解博弈论恐怕是最合适不过了。
Nim游戏是组合游戏(Combinatorial Games)的一种,准确来说,属于“Impartial Combinatorial Games”(以下简称ICG)。
满足以下条件的游戏是ICG(可能不太严谨):1、有两名选手;2、两名选手交替对游戏进行移动(move),每次一步,选手可以在(一般而言)有限的合法移动集合中任选一种进行移动;3、对于游戏的任何一种可能的局面,合法的移动集合只取决于这个局面本身,不取决于轮到哪名选手操作、以前的任何操作、骰子的点数或者其它什么因素;4、如果轮到某名选手移动,且这个局面的合法的移动集合为空(也就是说此时无法进行移动),则这名选手负。
根据这个定义,很多日常的游戏并非ICG。
例如象棋就不满足条件3,因为红方只能移动红子,黑方只能移动黑子,合法的移动集合取决于轮到哪名选手操作。
通常的Nim游戏的定义是这样的:有若干堆石子,每堆石子的数量都是有限的,合法的移动是“选择一堆石子并拿走若干颗(不能不拿)”,如果轮到某个人时所有的石子堆都已经被拿空了,则判负(因为他此刻没有任何合法的移动)。
这游戏看上去有点复杂,先从简单情况开始研究吧。
如果轮到你的时候,只剩下一堆石子,那么此时的必胜策略肯定是把这堆石子全部拿完一颗也不给对手剩,然后对手就输了。
如果剩下两堆不相等的石子,必胜策略是通过取多的一堆的石子将两堆石子变得相等,以后如果对手在某一堆里拿若干颗,你就可以在另一堆中拿同样多的颗数,直至胜利。
10个中选2个的选法

10个中选2个的选法
(原创实用版)
目录
1.组合公式的概述
2.组合公式的计算方法
3.组合公式的应用实例
正文
一、组合公式的概述
组合公式,是概率论中的一个重要概念,用于计算从一定数量的元素中选取一定数量元素的组合数量。
组合公式可以广泛应用于各种实际问题中,如在团队选拔、商品组合等场景中,都有着重要的应用价值。
二、组合公式的计算方法
组合公式的计算方法,通常被称为“组合数公式”,它的计算公式为:C(n,m) = n!/(m!(n-m)!),其中 n 表示元素总数,m 表示选取元素的数量,"!"表示阶乘。
例如,从 5 个元素中选取 2 个元素的组合数量,可以用如下公式进行计算:C(5,2) = 5!/(2!(5-2)!) = 10。
三、组合公式的应用实例
组合公式在实际生活中的应用非常广泛,下面我们通过一个实例来进行说明。
假设有一个考试团队,共有 5 名成员,现在需要从这 5 名成员中选取 2 名成员参加考试,那么如何确定选取的成员呢?这里就可以使用组合公式来计算。
首先,我们把 5 名成员看作是 5 个元素,然后根据组合公式,计算
从这 5 个元素中选取 2 个元素的组合数量,即 C(5,2) = 10。
这意味着,从 5 名成员中选取 2 名成员参加考试,一共有 10 种可能的组合方式。
然后,我们可以通过随机抽取的方式,从这 10 种组合中选取 2 名成员参加考试。
这样,就可以保证每个成员都有公平的机会参加考试。
以上就是组合公式的概述、计算方法和应用实例。
《博弈论入门》课件
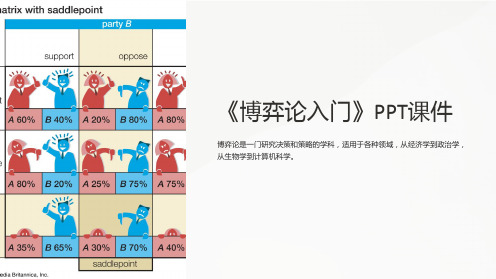
博弈论的研究方法与工具
了解博弈论的研究方法和工具对于深入理解和应用博弈论至关重要。
博弈论中的常见概念与术语
学习博弈论需要了解一些常见的概念和术语,例如博弈矩阵、纳什均衡、最 优策略等。
博弈论的经典案例分析
通过分析博弈论的经典案例,我们可以更好地理解和应用博弈论的原理。
博弈论在实际决策中的应用
实际决策中经常涉及到多个参与者的利益博弈,博弈论可以帮助我们找到最优决策策略。
总结与展望
通用于实 际生活和决策中。
《博弈论入门》PPT课件
博弈论是一门研究决策和策略的学科,适用于各种领域,从经济学到政治学, 从生物学到计算机科学。
博弈论基础知识介绍
在这一部分中,我们将探讨博弈论的基本概念和原理,包括博弈模型、策略 和解的概念。
博弈论的应用领域
博弈论在现实生活中有许多应用,包括经济学、政治学、社会学、生物学、 医学等领域。
趣味拓展小游戏

第一个游戏: 方寸大乱游戏规则:每组派5个人参加。
要求是各组派出的5个人全都要站在工作人员事先画好的圆圈内。
如果手脚是离地的可以超出圆圈的范围。
(注:每次站立10秒才算完成)第二个游戏: 七手八脚游戏规则:每组派出5人参加。
要求是抬脚和用手着地,例如主持人说“一手二脚”即一组里一只手着地和二只脚离地,而且要在10秒内完成(旁观的人可以提示),时间到了后,不可以再动,否则就算动作失败。
第三个游戏:武林秘诀游戏规则:各组排成一纵列,评分员将事先准备好的人体图象给队中的第一个人观看,然后第一个人只能用语言将看到的人体动作表达给第二个人(传递中前面的人不可以做任何动作或表情等提示下一个人做动作,否则就算动作失败),以此类推,传到最后一个人,最后一个人就要将动作做出来。
完成动作后要保持10秒才算成功。
时间限制:各组的总的完成时间要在10分钟内。
当有一组完成后,其他的各组要在两分钟内完成,每超10秒减1分。
加上上楼说的就多几个了祝你成功!呵呵,希望对你有帮助.要求游戏小组在规定的时间内在两把椅子之间建立起一座能承受一枚鸡蛋的纸质桥梁。
目的培养和锻炼创造力和团队精神资源时间:30分钟游戏时间加10分钟总结时间参与人数:6人或更多,三至五个人分为一组材料:每个小组25张A4纸每个小组一把剪刀每个小组一枚鸡蛋每个小组两把椅子空间/地点/房间布置结实的地板说明1) 将参与者分成小组,说明参与人员有15分钟时间用手中的纸在两把椅子间建立一座桥,尽可能地长,而桥梁必须能在其三分之一处能撑得住鸡蛋。
此桥必须不能接触地板,必须两侧完全为椅子所支撑(没有中间支撑)。
(5分钟)2)小组有10分钟时间进行规划和讨论。
在第5分钟和第8分钟时提醒他们。
10分钟之后,取走他们所有的纸,换成新纸(或换成其他颜色的纸),让他们继续练习(10分钟)3)小组现在有15分钟建桥。
不提醒时间,严格限制结束时间(这也是学习到的内容之一)。
在此期间,可以把正在建成的桥梁用相机照下来。
(lecture_11)组合博弈入门

定理一也适用于更多堆的情况~ 定理一也适用于更多堆的情况~
2011-3-15
19
定理一的证明…… 定理一的证明
2011-3-15
20
思考(1): 思考( ):
有了定理一, 有了定理一,如果判断某个游戏 的先手是输还是赢? 的先手是输还是赢?
2011-3-15
21
思考(2): 思考( ):
对于必胜点, 对于必胜点,如何判断有几种可 行的操作方案? 行的操作方案?
2011-3-15 27
Use of the Sprague-Grundy Function:
P-positions: Positions x for which g(x) = 0 N-positions: Positions x for which g(x) > 0
2011-3-15
28
Exercise:
35
课后练习
2008《 Programming》Exercise(12)_ )_博弈入门 2008《ACM Programming》Exercise(12)_博弈入门 1517 A Multiplication Game 1079 Calendar Game 2147 kiki's game 1404 Digital Deletions 1536 S-Nim 1729 Stone Game 1730 Northcott Game 1760 A New Tetris Game 1809 A New Tetris Game(2) 1524 A Chess Game
2011-3-15 25
Example about graph game:
5,7,9
……
2,0,0 1,0,0 0,1,0 0,0,0
简单的组合博弈游戏

1 2
保护未成年人
游戏应设置合适的年龄限制,避免对未成年人造 成不良影响。
公平竞争
游戏应遵循公平、公正的原则,防止作弊和欺诈 行为。
3
弘扬正能量
游戏内容应传递积极向上的价值观,避免传播不 良信息。
感谢观看
THANKS
错误三
忽视长远的战略规划,只关注短期利益。纠 正方法:制定长期战略目标,并适时调整自 己的战术和策略。
05
游戏中的心理学应用
玩家心理预期
预期形成
玩家在游戏过程中会根据经验和当前局面形成对结果的预期,这 种预期会影响玩家的决策。
预期管理
通过调整游戏规则、难度和奖励机制,可以影响玩家的预期,进而 影响游戏结果。
02
游戏规的元素,达成游戏设定的 目标,如获得最高分数或击败对手。
游戏元素
游戏通常包含多种元素,如数字、符号、道具等, 每种元素都有不同的功能和效果。
游戏流程
玩家需要在限定的时间内或步数内,通过选择和 组合不同的元素,达成游戏目标。
基础策略介绍
合理利用资源
特点
组合博弈游戏通常具有明确的游戏规 则、策略性强、需要玩家进行思考和 决策,同时结果往往具有不确定性。
游戏历史与发展
历史
组合博弈游戏的历史可以追溯到古代,如中国的围棋、象棋等。随着时间的推 移,人们不断创造出新的组合博弈游戏,丰富了游戏的种类和玩法。
发展
组合博弈游戏的发展与数学、心理学等学科密切相关。现代组合博弈游戏在理 论和实践方面都取得了很大的进展,成为数学、计算机科学等领域的重要研究 对象。
在游戏中,资源通常是有限的。 玩家需要根据游戏目标和当前情 况,合理分配资源和选择策略。
优先处理紧急任务
组合博弈入门ppt课件

威佐夫博奕(Wythoff Game)
有两堆各若干个物品,两个人轮流从某 一堆或同时从两堆中取同样多的物品,规 定每次至少取一个,多者不限,最后取光 者得胜。
威佐夫博奕(Wythoff Game)
这种情况下是颇为复杂的。我们用 (ak,bk)(ak ≤ bk ,k=0,1,2,…,n)表示 两堆物品的数量并称其为局势,如果甲面 对(0,0),那么甲已经输了,这种局势我 们称为奇异局势。前几个奇异局势是:(0, 0)、(1,2)、(3,5)、(4,7)、(6, 10)、(8,13)、(9,15)、(11,18)、 (12,20)。。可以看出,a0=b0=0,ak是未在 前面出现过的最小自然数,而 bk= ak + k
SG函数性质
所有的terminal position所对应的顶点, 也就是没有出边的顶点,其SG值为0,因为 它的后继集合是空集。然后对于一个g(x)=0 的顶点x,它的所有后继y都满足g(y)!=0。对 于一个g(x)!=0的顶点,必定存在一个后继y 满足g(y)=0。
那么当g(x)=0时的点其实就是必败点, 否则为必胜点。
威佐夫博奕(Wythoff Game)
假设面对的局势是(a,b),若 b = a,则同时 从两堆中取走 a 个物体,就变为了奇异局势(0, 0);如果a = ak ,b > bk,那么,取走b – bk个物 体,即变为奇异局势;如果 a = ak , b < bk ,则同 时从两堆中拿走 ak – a[b – ak])个物体,变为奇异 局势( a[b – ak] , a[b – ak]+ b – ak);如果a > ak , b= ak + k,则从第一堆中拿走多余的数量a – ak 即 可;如果a < ak ,b= ak + k,分两种情况,第一种, a=aj (j < k),从第二堆里面拿走 b – bj 即可;第 二种,a=bj (j < k),从第二堆里面拿走 b – aj 即 可。
10选4组合计算方法

10选4组合计算方法
哇塞,今天咱们来聊聊“10 选 4 组合计算方法”呀!
先来说说具体步骤哈。
首先呢,你要从 10 个元素中选出 4 个。
这就像是从一个大宝藏里挑出四颗最闪亮的宝石!计算的时候呢,根据组合数公式C(n,k)=n!/(k!(n-k)!),这里 n 就是 10,k 就是 4。
然后代入公式去计算,可得结果。
但要注意啦,计算过程中可别粗心大意算错呀!而且要搞清楚每个符号的含义,别张冠李戴咯!
再讲讲这过程中的安全性和稳定性。
就好比盖房子,基础得打牢呀!只要按照正确的步骤和方法来,那结果就是稳稳当当的。
不会出现一会儿一个样的情况,让人心里踏实着呢!
那它都有啥应用场景和优势呢?嘿,这可多了去了!比如在抽奖活动中,从一堆奖品中选出几个幸运儿,这不就是 10 选 4 嘛。
优势就是简单直接呀,能快速得出结果,而且公平公正,谁也没法挑毛病!还有在数据分析中,从大量数据里挑选出关键的几个进行分析,多高效呀!
来看看实际案例哈。
比如说学校组织一场比赛,有 10 个队伍参赛,要选出 4 个进入决赛。
用这个 10 选 4 组合计算方法,就能轻松确定各种可能的组合情况,然后根据实际情况选出最合适的 4 个队伍。
这样的应用效果多棒呀!
哎呀呀,“10 选 4 组合计算方法”就是这么好用,能解决好多实际问题,大家可得学会咯!。
博弈论组合赋权公式讲解

博弈论组合赋权公式讲解博弈论中的组合赋权公式,听起来好像是个特别高深莫测的东西,但实际上它并没有那么可怕。
让我来给您好好讲讲。
咱先来说说啥是组合赋权。
简单来讲,就是把不同的权重计算方法组合在一起,得到一个更全面、更准确的权重结果。
这就好比您做饭,要把各种调料按照一定的比例搭配,才能做出美味的菜肴。
比如说,您有两种给某个因素定权重的方法,方法 A 和方法 B。
单独用 A 可能不太全面,单独用 B 可能有偏差,那咋办?这时候组合赋权公式就派上用场啦。
那这组合赋权公式到底长啥样呢?咱就拿一个常见的公式来说吧,假设 W 是最终的组合权重,W1 是方法 A 得到的权重,W2 是方法 B得到的权重,α 和β 是两个系数,用来调整两种方法的重要程度。
那公式就是:W = α×W1 + β×W2 。
这看起来好像也不简单,是吧?但咱举个例子您就明白了。
就说选班长这事儿。
咱们有两个评选标准,一个是学习成绩,一个是组织能力。
老师用两种方法分别给这两个因素定了权重。
方法 A 觉得学习成绩的权重是 0.6,组织能力的权重是 0.4;方法 B 觉得学习成绩的权重是 0.7,组织能力的权重是 0.3 。
那这时候老师想综合考虑这两种方法,觉得方法 A 占 0.4 的重要程度,方法 B 占 0.6 的重要程度。
那咱们就按照组合赋权公式来算算。
先算学习成绩的最终权重:0.4×0.6 + 0.6×0.7 = 0.24 + 0.42 = 0.66 。
再算组织能力的最终权重:0.4×0.4 + 0.6×0.3 = 0.16 + 0.18 = 0.34 。
您看,通过这个组合赋权,咱们就得到了一个更综合、更合理的权重结果,选班长的时候就能更公平、更科学啦。
再比如说,公司要给员工发奖金,得评估员工的工作绩效。
有个评估方法是看完成的任务量,另一个评估方法是看任务的质量。
这时候用组合赋权公式,就能综合考虑这两个方面,给员工一个公正的奖金分配。
组合博弈入门ppt课件-文档资料

蔡尚真 Tel:609787
什么是组合游戏——
(1) 有两个玩家; (2) 游戏的操作状态是一个有限的集合(比如: 限定大小的棋盘); (3) 游戏双方轮流操作; (4) 双方的每次操作必须符合游戏规定; (5) 当一方不能将游戏继续进行的时候,游戏 结束,同时,对方为获胜方; (6) 无论如何操作,游戏总能在有限次操作后 结束;
必败(必胜)点属性
(1) 所有终结点是必败点(P点); (2) 从任何必胜点(N点)操作,至少有 一种方法可以进入必败点(P点); (3)无论如何操作, 从必败点(P点)都 只能进入必胜点(N点).
练习:
能取的集合 S = {1, 3, 4}
x : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14… Pos: P N P N N N N P N P N N N N P…
多堆或多子游戏
SG+尼姆博奕
各堆各自用SG,再用尼姆博弈 hdu1848
//使用求解SG来求解 #include <iostream> using namespace std; int aaa[1000000]; const int MAX=1010; int a[21],SG[MAX]; void get2() { int i; a[0]=1; a[1]=2; for(i=2;i<20;i++) { a[i]=a[i-1]+a[i-2]; } } int getSG(int n) { int i; int m; if (n==0) { return 0; } bool mex[MAX]={0}; for(i=0;;i++) { m=n-a[i]; if (m<0) { break; } if (SG[m]==-1) { SG[m]=getSG(m); } mex[SG[m]]=true; } for (i=0;;i++) { if (!mex[i]) { break;
小学生集体游戏

小学生集体游戏各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢集体活动小游戏游戏一:坐气球。
每个小组三个人上来参加,两个人吹气球,一个在椅子上坐暴。
坐暴10个气球,按用时多少算胜负。
游戏二:纸杯传水。
每个组出5个人站成一列,每人嘴上叼一只纸杯,然后从前往后传水,不能用手,全凭嘴和头的动作,在规定时间内按传到最后的水的多少算胜负。
游戏三:顶橘子每个组两个同学上来参加,奖橘子顶在头上,不能用手扶,然后按主持人安排做动作,比如跨凳子,向后转,坐下起立,相互之间除了接触外也允许使用吓唬等手段,按坚持的时间长短算胜负。
这是几个比较有意思的,其他的象心有灵犀,抢凳子,击鼓传花就不用多说了吧。
另一个要热闹的关键是惩罚措施,每个游戏获胜的领奖品,最后两名则要接受惩罚。
可以将惩罚措施写成一堆纸条,让受罚者抓阄。
这里说几个很high 的惩罚方法。
1。
学广告。
大家都看过脑白金的广告吧,就让他学里面的动画人物的动作,哈哈。
当然还有很多搞笑的广告,自己找吧。
2。
表演例如让他选择“装白痴,装纯情,装gay”,不管装哪个,都很好看,呵呵。
3。
朗读准备好一段很搞笑的文字,比如那一段“我是一头猪。
”呵呵,让他大声读出来,里面还可以要求动作。
4。
吻桌子被罚者要亲吻指定的一个桌子5下,这时最好有照相机伺候,呵呵,出来的照片肯定很精彩!挺不错的,给大家推荐一个小游戏吧!满好玩的。
游戏名称:团队合作,张弛有道▲游戏目的:通过这个游戏,让大家认识到团队合作的重要性。
一个团队若想成功必须运用恰当的方法,而这个方法不仅包括要善于利用有效资源,还要求学会倾听他人的意见,以沟通寻求彼此间的默契。
▲游戏规则:游戏开始时,将大麻绳围在各自腰间位置,所有队员带上眼罩,在2分钟内将绳索围成指定的图形,在这过程中,参加队员不能手拖手,只能通过大麻绳互相维系,最后围出图形的队伍将绳索不变形的平放置地上让大家看图形是否形似,最快围出图形且图形形似的队伍胜出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定理一也适用于更多堆的情况~ 定理一也适用于更多堆的情况~
2012-3-3
19
定理一的证明…… 定理一的证明
2012-3-3
20
思考(1): 思考( ):
有了定理一, 有了定理一,如何判断某个游戏 的先手是输还是赢? 的先手是输还是赢?
2012-3-3
21
Hale Waihona Puke 思考(2): 思考( ):
对于必胜点, 对于必胜点,如何判断有几种可 行的操作方案? 行的操作方案?
2012-3-3 15
2012-3-3
16
初步分析
(0, 0, 0) (0, 0, x) (0, 1, 1) (0, k, k) (14, 35, 46)
2012-3-3
P-position N-position P-position P-position ???
17
引入概念:Nim引入概念:Nim-Sum
2012-3-3
33
Applications:
Sums of three Subtraction Games. In the first game: m = 3 and the pile has 9 chips. In the second: m = 5 and the pile has 10 chips. In the third: m = 7 and the pile has 14c hips. g(9, 10, 14) =?
游戏双方轮流取牌; 游戏双方轮流取牌; 每人每次仅限于取1 张或3张牌; 每人每次仅限于取1张、2张或3张牌; 扑克牌取光,则游戏结束; 扑克牌取光,则游戏结束; 最后取牌的一方为胜者。 最后取牌的一方为胜者。
2012-3-3
5
基本思路? 基本思路?
请陈述自己的观点
2012-3-3
6
第一部分
简单取子游戏 组合游戏的一种) (组合游戏的一种)
2012-3-3
int main() { int n,i,m,t,s; while(scanf("%d",&k),k) { for(i=0;i<k;i++) scanf("%d",&a[i]); sort(a,a+k); memset(f,-1,sizeof(f)); f[0]=0; scanf("%d",&n); while(n--) { scanf("%d",&m); s=0; while(m--) { scanf("%d",&t); if(f[t]==-1) f[t]=mex(t); s=s^f[t]; } if(s==0) printf("L"); else printf("W"); } printf("\n"); } }
2012-3-3
32
Theorem 2.
If gi is the Sprague-Grundy function of Gi , i = 1, . . . , n, then G = G1 +· · · + Gn has Sprague-Grundy function g(x1, . . . , xn) = g1(x1)⊕· · ·⊕gn(xn).
What is the SG-value of the subtraction game with subtraction set S = {1, 2, 3}?
x 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14. . . g(x) 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2. . .
2012-3-3 25
Example about graph game:
5,7,9
……
2,0,0 1,0,0 0,1,0 0,0,0
2012-3-3 26
0,0,1
The Sprague-Grundy Function.
Definition: The Sprague-Grundy function of a graph, (X,F), is a function, g, defined on X and taking non-negative integer values, such that g(x) =min{n ≥ 0 : n<>g(y) for y ∈ F(x)}. (1) In words, g(x) the smallest non-negative integer not found among the Sprague-Grundy values of the followers of x. g(x) =mex{g(y) : y ∈ F(x)}. (2)
定义: 定义: 假设 (xm · · · x0)2 和(ym · · · y0)2 的 nim-sum是(zm · · · z0)2,则我们表示成 是 则我们表示成 (xm · · · x0)2 ⊕ (ym · · · y0)2 = (zm · · · z0)2, 这里,zk = xk + yk (mod 2)(k=0…m). 这里
2012-3-3 27
Use of the Sprague-Grundy Function:
P-positions: Positions x for which g(x) = 0 N-positions: Positions x for which g(x) > 0
2012-3-3
28
Exercise:
2012-3-3
7
什么是组合游戏—— 什么是组合游戏
(1) 有两个玩家; (2) 游戏的操作状态是一个有限的集合(比如: 限定大小的棋盘); (3) 游戏双方轮流操作; (4) 双方的每次操作必须符合游戏规定; (5) 当一方不能将游戏继续进行的时候,游戏 结束,同时,对方为获胜方; (6) 无论如何操作,游戏总能在有限次操作后 结束;
2012-3-3
10
取子游戏算法实现—— 取子游戏算法实现
1:将所有终结位置标记为必败点 将所有终结位置标记为必败点( 步骤1:将所有终结位置标记为必败点(P点); 步骤2: 将所有一步操作能进入必败点( 步骤2: 将所有一步操作能进入必败点(P点)的 位置标记为必胜点(N点) 位置标记为必胜点( 步骤3: 3:如果从某个点开始的所有一步操作都只能 步骤3:如果从某个点开始的所有一步操作都只能 进入必胜点( 进入必胜点(N点) ,则将该点标记为必败点 ( P点 ) ; 步骤4: 如果在步骤3未能找到新的必败( 步骤4: 如果在步骤3未能找到新的必败(P点), 则算法终止;否则,返回到步骤2 则算法终止;否则,返回到步骤2。
2012-3-3 8
概念:必败点和必胜点(P点 N点 概念:必败点和必胜点(P点 & N点) (P
必败点(P点 必败点(P点) :前一个选手(Previous (P P player)将取胜的位置称为必败点。
必胜点(N点 必胜点(N点) :下一个选手(Next (N player)将取胜的位置称为必胜点。
2012-3-3 29
Question:
What can the S-G value describe?
2012-3-3
30
Part 4:
Sums of Combinatorial Games
2012-3-3
31
What
is so-called ——
“Sums of Combinatorial Games”?
2012-3-3 11
课内练习: 课内练习:
Subtraction Games: subtraction set S = {1, 3, 4} x : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14… Pos: P N P N N N N P N P N N N N P…
2012-3-3
(1) Player I moves first, starting at x0. (2) Players alternate moves. (3) At position x, the player whose turn it is to move chooses a position y ∈ F(x). (4) The player who is confronted with a terminal position at his turn, and thus cannot move, loses.
2012-3-3
22
实例分析(HDOJ_1850) 实例分析 Being a Good Boy in Spring Festival
2012-3-3
23
第三部分
Graph Games & SpragueSprague-Grundy Function
2012-3-3
24
What is the graph game ?
2012-3-3 34
附:参考源码(HDOJ-1536)
#include<stdio.h> #include<string.h> #include<algorithm> using namespace std; int k,a[100],f[10001]; int mex(int p) { int i,t; bool g[101]={0}; for(i=0;i<k;i++) { t=p-a[i]; if(t<0) break; if(f[t]==-1) f[t]=mex(t); g[f[t]]=1; } for(i=0;;i++) { if(!g[i]) return i; } }
