2016中考复习4

合集下载

中考数学专题复习第4章三角形第13讲全等三角形及其性质

第13讲（全等）三角形及其性质☞【基础知识归纳】☜☞归纳1.三角形中的三条主要线段⑴三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做角平分线⑵在三角形中，连接一个顶点和它对边的中点的线段叫做中线⑶从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高（简称高）☞归纳2.三角形的中位线三角形的中位线平行于第三边，并且等于第三边的一半．☞归纳3.三角形的三边关系定理及推论三角形三边关系：任意两边之和大于第三边；任意两边之差小于第三边．☞归纳4.三角形的内角和定理及推论⑴三角形内角和：三角形三内角之和等于180°．⑵三角形外角的性质：①三角形的一个外角大于任何一个和它不相邻的内角；②三角形的一个外角等于与它不相邻的两内角之和．☞归纳5.三角形的分类①按边分：三角形分为不等边三角形和等腰三角形②按角分：三角形分为锐角三角形，直角三角形，钝角三角形 .☞归纳6.全等三角形⑴能够完全重合的两个图形就是全等图形；能够完全重合的两个三角形就是全等三角形⑵全等三角形的对应边相等，对应角相等．⑶全等三角形的对应线段(对应边上的中线、对应边上的高、对应角的平分线)相等⑷全等三角形的周长相等，面积相等☞归纳7.三角形全等的判定定理：①边边边定理：（可简写成SSS）②边角边定理：（可简写成SAS）③角边角定理：（可简写成ASA）④角角边定理：（可简写成AAS）⑤直角三角形全等的判定：（斜边、直角边定理）（可简写成 HL）☞【常考题型剖析】☜☺题型一、三角形的边和角【例1】（2016岳阳）下列长度的三根小木棒能构成三角形的是（）A.2cm，3cm，5cmB.7cm，4cm，2cmC.3cm，4cm，8cmD.3cm，3cm，4cm【答案】D【分析】选项A，因为2+3=5，所以不能构成三角形，错误；选项B，因为2+4＜6，所以不能构成三角形，错误；选项C，因为3+4＜8，所以不能构成三角形，错误；选项D，因为3+3＞4，所以能构成三角形，正确．【例2】(2015滨州)在△ABC中，∠A:∠B:∠C=3:4:5，则∠C等于（）A.45°B.60°C.75°D.90°【答案】C【分析】三角形的内角和是180°，因为∠A:∠B:∠C=3:4:5，所以∠C=180°=75°【举一反三】1.( 2016河池) 下列长度的三条线段不能组成三角形的是（）A. 5，5，10B. 4，5，6C. 4，4，4D. 3，4，5【答案】A【分析】选项A，因为5+5=10，所以不能构成三角形，错误；选项B，因为4+5>6，所以能构成三角形，正确；选项C，因为4+4>4，所以能构成三角形，正确；选项D，因为3+4＞5，所以能构成三角形，正确．2.( 2016邵阳) 如图，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（）A. AC＞BCB. AC=BCC.∠A＞∠ABCD.∠A=∠ABC【答案】A【分析】∵AD=BD，∴∠A=∠ABD，∴∠ABC＞∠A，所以C选项和D选项错误；∴AC＞BC，所以A选项正确；B选项错误．3.(2015柳州) 如图，图中∠1的大小等于（）。

(新人教版)广东中山2016中考复习复习课件：第4讲修改病句(语文)

宾语残缺我们要响应 “ 保护缺宾语，应在句地球”。末补上“的号召”
病句类型主谓搭配不当
例句他那崇高的革命品质，经常浮现在我的脑海中。
修改说明 “品质”不能 “浮现”，可改为“他那伟大的革命形象”
搭配不当（换）
动宾搭配不当
国家免除农业税后，将“进步”改成农民的种地热情有 “提高” 了明显进步。
病句示例
辨析技巧
修改方式
两个报社的记者昨天数量词作修饰成分时，后面应把“两个”调到采访了局长。紧跟两个名词时则会出现歧 “记者”前义现象。“两个”是修饰 “报社”还是修饰“记者”？有歧义。经过班主任的再三教句首出现介词，如：“随着、应去掉“经过”或育，使我明白了许多在……上、在……里、 “使” 道理。从……中、当……时、通过、经过、由于”等，要查是否滥用介词导致缺主语。看了《大决战》这部出现了“使、让、令、把、缺主语，去掉“使” 影片，使我受到了很被”等词语，可能会出现主好的教育。语残缺、语序不当的语病。
修改说明把“有没有”删掉或在“实现” 前加上“能否” 改“不管”为 “尽管”，或改 “极端”为“怎样”
病句类型主客颠倒
例句
修改说明
数学对我不感兴趣。应改为“我对数学”
语序不当（调）
谓语语序不当
我们要正确贯彻和深刻理解江泽民同志关于教育问题的讲话精神。夜深人静，想起今天一连串发生的事情，我怎么也睡不着。
病句类型
表意不明 (调或删）
例句
会议室里，几个学校的领导正在研究文艺汇演的事。
修改说明
将“几个”调至 “领导”前，消除歧义
重复啰嗦（删）
听完小王的介绍，我在心里真是由衷 “ 在心里 ” 和 “ 由地感谢杨宁。衷”语意重复，应删去“在心里”

2016年中考化学金属的活动性顺序专题复习

B点后溶液的颜色为蓝色 D点对应纵坐标为6.4
该200 g溶液中的CuCl2 质量分数为6.75% 取DE两点间的剩余固体加入盐酸，均有气泡产生
目录
上一
下一
二、填空题
11. （2010河南改编）X、Y、Z是三种金属固体，将X和Y浸入稀硫 Y溶解并产生氢气，X无变化；将X和Z浸入硝酸银溶液中，X表面有出而Z无变化。（1）判断X、Y、Z和银四种金属的活动性由强到弱的顺序______ ________________。（2）具体确定一种X后，写出X与硝酸银溶液反应的化学方程式_ ______________________。
答案
目录
上一
下一
【解析】
根据金属活动性顺序和所给试剂可以设计出的方案有：①Al、稀盐酸，②Al、 CuCl2 溶液，③ Cu、AlCl3 溶液， A错误；①③ 方案都没用到CuCl2溶液，B错误；②③方案都只选用两种试剂实现实验目的，C正确； AlCl3溶液中加入Cu不能反应，但是得出Al和Cu的金属活动性强弱，D错误。
目录
上一
下一
三、简答题
19. （2015烟台）不锈钢材料中含有的金属铬（Cr）能提高钢的化性和耐腐蚀性。为了解金属铬与常见金属铝、铜在金属活动性中的相对位置关系，小娟与小涛进行了如下探究活动。【猜想和假设】根据所学知识，猜想三种金属在金属活动顺序相对位置关系：猜想一：Cr Al Cu 猜想二：Al Cr Cu 猜想三：________________ 【实验和探究】（ 1）小娟的实验：取大小相同的铝、铬、铜三属片（用砂纸打磨光亮）
目录
上一
下一
7. （2015焦作模拟）向AgNO3和Mg(NO3)2的混合溶液中加质量的Al和Fe的混合粉末，充分反应后过滤，得到滤渣色滤液。关于该滤渣和滤液有下列四种说法： ①向滤渣中加入稀盐酸，可能有气泡产生； ②向滤液中加入稀盐酸，一定有沉淀产生； ③滤渣中一定含有Ag； ④滤液中一定含有Fe(NO3)2和Mg(NO3)2，一定不含AgNO3，有Al(NO3)3。以上说法正确的个数为（ C ） A. 0个 B. 1个 C. 2个 D. 3个

2016春中考政治(教科版八年级上册)复习(考点梳理)：第四单元一念之差与一步之遥(word版)

第四单元一念之差与一步之遥考试说明要求了解一般违法与犯罪的区别，知道不良行为、严重不良行为可能发展为违法犯罪，自觉抵制“黄、赌、毒”和“法轮功”邪教等不良诱惑。

错误！未找到引用源。

第八课一念之差错误！未找到引用源。

考点1 青少年为什么易受不良诱惑的影响？ (1)青少年好奇心强，缺乏辨别力和自控力，缺乏主见，容易盲目从众。

(2)社会上某些消极因素的影响。

(3)不良诱惑能暂时满足人的某些低级需要。

错误！未找到引用源。

考点2 “黄、赌、毒”和邪教“法轮功”等不良诱惑对青少年健康成长分别有哪些危害？(1)“黄毒”的危害：青少年一旦涉“黄”，轻者会精神萎靡、纪律涣散、不思进取，重者极易诱发性犯罪及与之相关的暴力犯罪和经济犯罪。

(2)赌博的危害：赌博是一种不正当的娱乐，容易形成贪婪、好逸恶劳、尔虞我诈、投机取巧等不良品质。

青少年染上赌瘾后，会严重影响学习和生活，甚至走上违法犯罪的道路。

(3)吸毒的危害：毒品的危害性极大，人一旦吸毒，就是踏上了人生的不归途。

它不仅会危害个人的健康和发展，也会给家庭和社会的安定造成极大的危害。

(4)“法轮功”的危害：“法轮功”是反社会、反人类、反科学的邪教，具有极大的欺骗性。

它可以使人丧失正常的思维和理智，甚至失去人性。

它已造成一些家庭妻离子散、家破人亡，破坏了社会安定。

错误！未找到引用源。

考点3 青少年怎样才能拒绝不良诱惑？ (1)要明辨是非，客观认识不良诱惑的危害，理智拒绝。

(2)把时间和精力放在学习和健康的娱乐上，远离产生不良现象的场所。

(3)学会控制自己的欲望和冲动。

特别是在没人监督的时候，约束自己的行为，克制自己的冲动和欲望，不做自己想做而不应该做的事情。

(4)遵守道德规范、法律法规和校纪校规等。

一念之差和一步之遥一念之差一步之遥危险的诱惑：不良诱惑种种及其危害拒绝诱惑：学会抵制不良诱惑千里之堤，溃于蚁穴防微杜渐错误！未找到引用源。

2016中考语文复习：《红楼梦》常考知识点

2016中考语文复习：《红楼梦》常考知识点
2016年中考语文复习：《红楼梦》常考知识点，更多2016中考模拟试题、2016中考备考经验、2016中考备考资料等信息，请及时关注2016年
中考语文复习：四大名着常考知识点汇总
《四大名着》是中、高考常考的内容，也是教育部门要求阅读的书籍，所
以对《四大名着》一定要有一定的重视，但是因为原着太多，看起来可能会
吃力。

责任心爆棚的小编为大家整理了《四大名着》中红楼梦部分常考知识点，只要记住这些考试就够了!
《红楼梦》积累知识点汇总
1、金陵十二钗指的是：(林黛玉、薛宝钗、王熙凤、贾元春、贾迎春、贾
探春、贾惜春、贾巧姐、李纨、史湘云、秦可卿、妙玉)。

2、《红楼梦》中，有“小宝钗”、“小黛玉”之称的两个人分别是(袭人)、(晴雯)。

。

2016年语文中考复习专题4 句子的仿写与修辞

专题4┃ 句子的仿写与修辞
7．［2013·安顺］仿照下面的句子，自选景物写一句话。花从春走过，留下缕缕花香；叶从夏走过，留下片片阴凉； ____________________________________________________ 示例：风从秋走过，留下阵阵金浪。 (格式正确，语句通顺即可) 8．［2013·乐山］仿照例句写一句话。例句：无论是高深莫测的星空，还是不值一提的灰尘，都是大自然精巧绝伦的艺术品。示例一：无论是烟波浩渺的太湖，还是清澈见底的漓江， __________________________________________________ 都是大自然慷慨大方的馈赠品。示例二：无论是济世兴邦 ________________________________________________ 的梦想，还是瑰丽无比的幻想，都是青年人勇往直前的助 ______________________________________________ 推剂。示例三：无论是振奋人心的成功，还是灰心丧气的失败，都是人生不可或缺的必修课。
[解析] 内容相关，运用排比修辞，语意连贯，无病句即可。
专题4┃ 句子的仿写与修辞
[温馨提示] 本考点常考的题型有： 1．考查修辞方法及其作用，如例二。 2．考查句式仿写能力。句子的仿写与修辞常见题型有选择题、填空题、综合题等。仿写题型主要有套用型仿写、续写型仿写、嵌入型仿写、修辞型仿写、改写型仿写等。
专题4┃ 句子的仿写与修辞
3．［2013·北京］对下面这首小诗修辞方法作用的分析，有误的一项是( ) 给友人不站起来才不会倒下更何况我们要去浪迹天涯跌倒是一次纪念纪念是一朵温馨的花寻找管什么日月星辰跋涉分什么春秋冬夏我们就这样携着手走呵走呵你说看到大海的时候你会纵情欢笑是呵是呵我们的笑直上云霞专题4┃ 句子的仿写与修辞

2015-2016学年中考科学一轮基础复习第4课时用显微镜观察细胞能力提升训练

第二篇生命科学第4课时用显微镜观察细胞1．王刚同学在显微镜下观察到一些细胞，他判断为植物细胞。

因为他观察到了( B )A ．细胞壁和细胞膜B ．细胞壁和液泡C ．细胞质和细胞核D ．细胞膜和细胞质【解析】植物细胞具有细胞壁、液泡和叶绿体，而动物细胞没有。

2．[2014·聊城]下列各实验中，如图41所示的两种实验仪器都需要的是 ( B )A ．观察种子的结构B ．观察叶片的结构C ．观察青霉菌D ．观察蚯蚓3．[2015·滨州]李亮同学在实验室里发现一张标签脱落的永久装片，他借助显微镜观察到如图42所示的图像，该装片属于( B ) A ．植物细胞B ．动物细胞C ．病毒D ．细菌【解析】该细胞有细胞核，却没有叶绿体、液泡、细胞壁等。

病毒不具有细胞结构，细菌没有成形的细胞核。

4．[2014·广东]观察洋葱表皮细胞时视野中出现如图43所示的现象，则最可能出错的步骤是 ( C )A ．取材B ．展平C ．盖片D ．染色【解析】视野中出现气泡是由于盖盖玻片时操作不当引起的。

5．[2014·昆明]制作人的口腔上皮细胞临时装片的操作步骤有：①取口腔上皮细胞；②滴生理盐水；③擦拭玻片；④稀碘液染色；⑤盖上盖玻片。

正确的操作顺序是图4-1图4-2图4-3( D )A．①②③④⑤B．③②①④⑤C．②①③⑤④D．③②①⑤④6．[2015·娄底]如图44所示为用显微镜观察植物细胞临时装片的两个视野，要把视野中的物像从甲图转为乙图，下列操作步骤正确的排序是 ( C )甲乙图44①转动细准焦螺旋②调节光圈③移动装片④转动转换器A．③→①→②→④ B．④→③→②→①C．③→④→②→① D．③→①→④→②【解析】根据分析可知，首先要移动玻片把物像移动到视野中央即③，因为高倍镜的视野窄，虽然在低倍镜下能看到物像，但如果偏离视野中央的话，换上高倍镜，物像可能就不在视野中了；低倍镜换高倍镜是通过转动转换器来完成的即④；当换上高倍镜后，由于视野变窄，透光量少，视野就会变得很暗，需要调节光圈或反光镜使视野变得亮一些即②；换上高倍物镜后物像只是有点模糊，一般转动细准焦螺旋就能使物像更加清晰即①。

2016年中考专项复习——阅读题型解题思路汇总

2016年中考专项复习——阅读题型解题思路汇总一、概括类题型（一）记叙类文章中的概括题型1、概括情节这种题型有三种情况：一是主人公明确，事件单一，这样的情节概括只要按照“主人公+原因+事件”的公式来概括即可。

答题思路：首先，先找到故事的主人公——人物或其他事物。

这是正确答题的关键。

可以关注两个细节来判定主人公：一是文章线索，二是文章标题。

其次是判断事件——也就是文章主要讲了一件什么事情，或者围绕主人公发生了一件什么事情。

把这两个要素都寻找完毕后，就可以在文中寻找原因。

二是主人公不明确，出现多个主语，这样的情节概括就要按照“起因+经过+结果”的公式来概括。

首先明确每一个小分句都应该有相应的主语，并且注意陈述角度的变化。

同时，概括的小情节要按照一定的关系进行组合。

三是结出提示性答案，补充完整情节的题型。

例：依照示例，概括选文主要写了哪几件事情？示例：能力遭怀疑、、答：参观受感悟改志诉恩师答题思路：这样的题型一定要充分利用所给的答案示例，首先我们先明确一下答案示例的作用：一是帮助我们划分情节，二是给答案的结构提供了示例。

做此类题时要先结合示例划分出全文的层次，明确情节的范围，然后按照答案示例的结构及字数等要求进行概括。

2、概括人物特点以记人为主的文章在概括人物特点时一定注意：人物特点分外在特点和内在特点，概括时要全面。

外在特点主要指人物的外在特征（身材、容貌、特别之处）及职业等，内在特点主要指人物的思想、品质、性格、爱好等。

答题思路：首先，细读文章，边读边圈画出有关人物的词语、句子，同时要注意与人物有关的事件；其次，对所圈画出的词语句子进行分类组合，即按内外特点进行区分，把重复的内容进行整合，结合事件进行总结；最后，组织整理出符合题目要求的答案。

注意：如果碰到题目含有“结合文章内容进行分析”或“简析”等要求时，答案一定要结合原文中的语句或事件进行概括。

如“由文章中的哪件事，可以看出他是一个什么样的人”。

2016中考复习四边形综合题

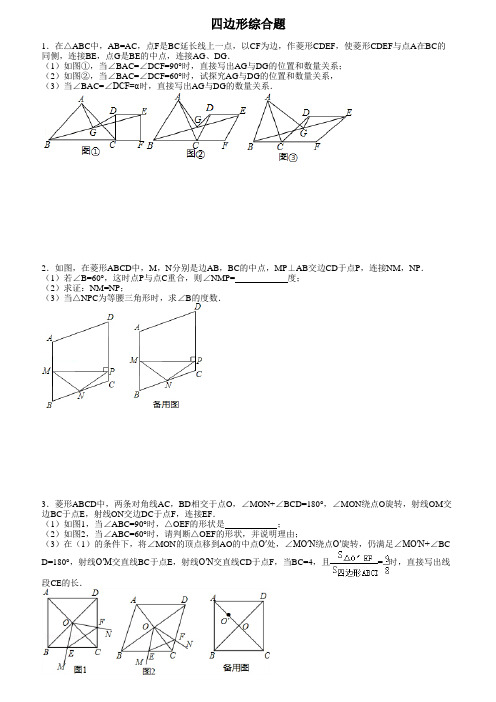
四边形综合题1．在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．（1）如图①，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；（2）如图②，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系，（3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系．2．如图，在菱形ABCD中，M，N分别是边AB，BC的中点，MP⊥AB交边CD于点P，连接NM，NP．（1）若∠B=60°，这时点P与点C重合，则∠NMP= 度；（2）求证：NM=NP；（3）当△NPC为等腰三角形时，求∠B的度数．3．菱形ABCD中，两条对角线AC，BD相交于点O，∠MON+∠BCD=180°，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF．（1）如图1，当∠ABC=90°时，△OEF的形状是；（2）如图2，当∠ABC=60°时，请判断△OEF的形状，并说明理由；（3）在（1）的条件下，将∠MON的顶点移到AO的中点O′处，∠MO′N绕点O′旋转，仍满足∠MO′N+∠BC D=180°，射线O′M交直线BC于点E，射线O′N交直线CD于点F，当BC=4，且=时，直接写出线段CE的长．4．如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP 并延长AP交CD于F点，（1）求证：四边形AECF为平行四边形；（2）若△AEP是等边三角形，连结BP，求证：△APB≌△EPC；（3）若矩形ABCD的边AB=6，BC=4，求△CPF的面积．5．如图，P为正方形ABCD的边BC上一动点（P与B、C不重合），连接AP，过点B作BQ⊥AP交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交BA的延长线于点M．（1）试探究AP与BQ的数量关系，并证明你的结论；（2）当AB=3，BP=2PC，求QM的长；（3）当BP=m，PC=n时，求AM的长．6．如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K ，点O是线段BK的中点．（1）求证：△ADP≌△ECP；（2）若BP=n•PK，试求出n的值；（3）作BM丄AE于点M，作KN丄AE于点N，连结MO、NO，如图2所示，请证明△MON是等腰三角形，并直接写出∠MON的度数．7．在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN=90°．（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°＜α＜45°）．①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；②如图2，在旋转过程中，当∠DOM=15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD=3BP时，猜想此时PE 与PF的数量关系，并给出证明；当BD=m•BP时，请直接写出PE与PF的数量关系．8．在正方形ABCD中，BD是一条对角线，点P在射线CD上（与点C、D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QH⊥BD于H，连接AH，PH．（1）若点P在线段CD上，如图1．①依题意补全图1；②判断AH与PH的数量关系与位置关系并加以证明；（2）若点P在线段CD的延长线上，且∠AHQ=152°，正方形ABCD的边长为1，请写出求DP长的思路．（可以不写出计算结果）9．如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．（1）如图①，当α=90°时，DE，DF，AD之间满足的数量关系是；（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=AD，请给出证明；（3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．10．如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时针旋转90°，得到线段CQ，连接BP ，DQ．（1）如图a，求证：△BCP≌△DCQ；（2）如图，延长BP交直线DQ于点E．①如图b，求证：BE⊥DQ；②如图c，若△BCP为等边三角形，判断△DEP的形状，并说明理由．11．已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PF，设运动时间为t （s）（0＜t＜8）．解答下列问题：（1）当t为何值时，四边形APFD是平行四边形？（2）设四边形APFE的面积为y（cm2），求y与t之间的函数关系式；（3）是否存在某一时刻t，使S四边形APFE：S菱形ABCD=17：40？若存在，求出t的值，并求出此时P，E两点间的距离；若不存在，请说明理由．12．已知菱形ABCD的边长为1，∠ADC=60°，等边△AEF两边分别交DC、CB于点E、F．（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点，求证：菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心；（2）若点E、F始终分别在边DC、CB上移动，记等边△AEF的外心为P．①猜想验证：如图2，猜想△AEF 的外心P落在哪一直线上，并加以证明；②拓展运用：如图3，当E、F分别是边DC、CB的中点时，过点P任作一直线，分别交DA边于点M，BC边于点G，DC边的延长线于点N，请你直接写出的值．13．已知：在四边形ABCD中，AD∥BC，∠BAC=∠D，点E、F分别在BC、CD上，且∠AEF=∠ACD．（1）如图1，若AB=BC=AC，求证：AE=EF；（2）如图2，若AB=BC，（1）中的结论是否仍然成立？证明你的结论；（3）如图3，若AB=kBC，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出AE与EF之间的数量关系，并证明．14．正方形ABCD的边长为4cm，点E在边AB上，将线段AE绕点E顺时针旋转α°（0＜α＜90）得线段EF，以E F为边在EF右侧作正方形EFGH；（1）如图①，分别连接线段AF、FH、AH，AH交EF于点I；①求证∠FAH的度数是一个常数；②求证：2AE2=AH•IH．（2）如图②，若α=60，点E为AB的中点，在直线AG上是否存在一点J，使△EBJ的周长最小？若存在，求出△EBJ的最小周长；若不存在，说明理由．（3）如图③，若α=45，点E从A出发，按1cm/s的速度沿AB方向运动，直至点C落在GH上停止运动，设点E 的运动时间为t（t＞0），正方形EFGH与正方形ABCD重叠部分的面积为S，请用含t的代数式表示S．15．请你认真阅读下面的小探究系列，完成所提出的问题．（1）初步探究：如图（1），点E、F分别在正方形ABCD边AB、AD上，DE⊥CF于点P，小芳看到该图后，发现DE=CF，这是因为∠EDA和∠FCD都是∠EDC的余角，就会由ASA判定得出△ADE≌△DCF．（2）类比发现：小芳进一步思考，如果四边形ABCD是矩形，如图（2），且DE⊥CF于点P，她发现，请你替她完成证明；（3）拓展延伸：如图（3），若四边形ABCD是平行四边形，试探究：当∠B与∠EPC满足什么关系时，使得成立？并证明你的结论．16．如图1，在矩形ABCD中，点E为矩形的边CD上任意一点，点P为线段AE的中点，连接BP并延长交边AD 于点F，点M为边CD上一点，连接FM，且∠DMF=∠ABF．（1）若AD=2，DE=1，求AP的长；（2）求证：PB=PF+FM；（3）若矩形ABCD改为□ABCD，如图2，（2）中的结论成立吗？若成立，请证明；不成立，说明理由．17．在菱形ABCD和正三角形BGF中，∠ABC=60°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，猜想PG与PC的关系，并证明．（提示：延长GP交CD于点E）（2）如图2，当点F在AB的延长线上时，线段PC、PG还满足（1）中的结论吗？写出你的猜想，并给与证明；（3）如图3，当点F在CB的延长线上时，线段PC、PG又有怎样的关系，直接写出你猜想．18．问题情境：小彬、小颖和小明对一道教学问题进行研究．已知，如图1，正方形ABCD中，对角线AC，BD相交于点O，点E是线段OC上一点，过点A作BE的垂线，交线段OB于点G，垂足为点F，易知：OG=OE．变式探究：分析完图1之后，小彬和小颖分别对此进行了研究，并提出了下面两个问题，请回答：（1）小彬：如图2，将图1中的点E改为线段OC延长线上的一点，过点A作BE垂线，交OB的延长线于点G，垂足为点F．求证：OG=OE．（2）小颖：如图3，将图中的“正方形ABCD”改为“菱形ABCD”，且∠ABC=60°，其余条件不变，试求的值．拓展延伸：（3）小明解决完上述问题后，又提出了如下问题：如图4，将图3中的“∠ABC=60°”改为“∠ABC=α”，并且点E，G分别在OC，OB的延长线上，其余条件不变，直接用含“α”的式子表示的值．19．已知矩形ABCD，AB=4，BD=2．现有另一个与矩形ABCD相似矩形EFGH，相似比为2：1．最初矩形E FGH的GH边放置在∠BCD的平分线处（如图1），现将矩形EFGH沿着FG作一条直线l，再连接AH、BH、DH、BE，设BC与EH的交点为M，CD与GH的交点为N（若没有交点则不计），回答下列问题．（1）如图1，当矩形ABCD矩形EFGH都不动时，求出矩形ABCD与矩形EFGH重合部分三角形的面积．（2）如图2，现矩形ABCD不动，矩形EFGH沿直线l开始出发，以1m/s的速度移动．设移动时间为t，矩形A BCD与矩形EFGH重合部分的面积为S，求出S关于t的函数关系式，并写出相应的取值范围，并且求出当t为多少时，S为最大值？（3）如图3，矩形ABCD仍然不动，矩形EFGH运动一段时间后停止在某一个点，并且此时△CEH为等腰三角形，这时，在△AHC中，AH=HC成立吗？请说明理由，并求出此时S和t的值．20．在菱形ABCD中，∠A=60°，以D为顶点作等边三角形DEF，连接EC，点N、P分别为EC、BC的中点，连接NP（1）如图1，若点E在DP上，EF与CD交于点M，连接MN，CE=3，求MN的长；（2）如图2，若M为EF中点，求证：MN=PN；（3）如图3，若四边形ABCD为平行四边形，且∠A=∠DBC≠60°，以D为顶点作三角形DEF，满足DE=DF且∠EDF=∠ABD，M、N、P仍分别为EF、EC、BC的中点，请探究∠ABD与∠MNP的和是否为一个定值，并证明你的结论．21．已知矩形ABCD的一条边AD=8，E是BC边上的一点，将矩形ABCD沿折痕AE折叠，使得顶点B落在CD 边上的点P处，PC=4（如图1）．（1）求AB的长；（2）擦去折痕AE，连结PB，设M是线段PA的一个动点（点M与点P、A不重合）．N是AB沿长线上的一个动点，并且满足PM=BN．过点M作MH⊥PB，垂足为H，连结MN交PB于点F（如图2）．①若M是PA的中点，求MH的长；②试问当点M、N在移动过程中，线段FH的长度是否发生变化？若变化，说明理由；若不变，求出线段FH的长度．22．如图1，▱ABCD中，AE⊥BC于E，AE=AD，EG⊥AB于G，延长GE、DC交于点F，连接AF．（1）若BE=2EC，AB=，求AD的长；（2）求证：EG=BG+FC；（3）如图2，若AF=5，EF=2，点M是线段AG上的一个动点，连接ME，将△GME沿ME翻折得△G′ME，连接DG′，试求当DG′取得最小值时GM的长．23．如图，正方形ABCD的对角线相交于点O，∠CAB的平分线分别交BD，BC于点E，F，作BH⊥AF于点H ，分别交AC，CD于点G，P，连接GE，GF．（1）求证：△OAE≌△OBG；（2）试问：四边形BFGE是否为菱形？若是，请证明；若不是，请说明理由；（3）试求：的值（结果保留根号）．24．在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1，旋转角为θ（0°＜θ＜90°），连接AC1、BD1，AC1与BD1交于点P．（1）如图1，若四边形ABCD是正方形．①求证：△AOC1≌△BOD1．②请直接写出AC1与BD1的位置关系．（2）如图2，若四边形ABCD是菱形，AC=5，BD=7，设AC1=kBD1．判断AC1与BD1的位置关系，说明理由，并求出k的值．（3）如图3，若四边形ABCD是平行四边形，AC=5，BD=10，连接DD1，设AC1=kBD1．请直接写出k的值和AC12+（kDD1）2的值．25．已知，如图1，矩形ABCD中，AD=6，DC=8，矩形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB ，CD，DA上，AH=2，连接CF．（1）如图2，当四边形EFGH为正方形时，求CF的长和△FCG的面积；（2）如图1，设AE=x，三角形FCG的面积=y，求与x之间的函数关系式与y的最大值；（3）当△CGF是直角三角形时，求x和y值．26．如图，点E是矩形ABCD的边BC的中点，连接DE交AC于点F．（1）如图①，求证：AF=2CF；（2）如图②，作DG⊥AC于G，试探究：当AB与AD满足什么关系时，使得AG=CF成立？并证明你的结论；（3）如图③，以DE为斜边在矩形ABCD内部作等腰Rt△DEM，交对角线BD于N，连接AM，若AB=AD，请直接写出的值．27．数学课上，张老师出示了问题1：如图1，四边形ABCD是正方形，BC=2，对角线交点记作O，点E是边BC延长线上一点．联结OE交CD边于F，设CE=x，CF=y，求y关于x的函数解析式及其定义域．（1）经过思考，小明认为可以通过添加辅助线﹣﹣过点O作OM⊥BC，垂足为M求解．你认为这个想法可行吗？请写出问题1的答案及相应的推导过程；（2）如果将问题1中的条件“四边形ABCD是正方形，BC=2”改为“四边形ABCD是平行四边形，BC=3，CD=2，”其余条件不变（如图2），请直接写出条件改变后的函数解析式；（3）如果将问题1中的条件“四边形ABCD是正方形，BC=2”进一步改为：“四边形ABCD是梯形，AD∥BC，BC=4，CD=3，AD=2”其余条件不变（如图3），请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程．28．如图，在正方形ABCD中，E、F分别是BC、DC上的两点，若EF=BE+DF．（1）求证：∠EAF=45°；（2）作∠EFC的平分线FG交AE的延长线于G，连接CG，如图2．求证：BC﹣CF=CG；（3）若F是DC的中点，AB=4，如图3，求EG的长．29．已知四边形ABCD中，E，F分别是AB，AD边上的点，DE与CF交于点G．（1）如图1，若四边形ABCD是矩形，且DE⊥CF．则DE•CD CF•AD（填“＜”或“=”或“＞”）；（2）如图2，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，使得DE•CD=CF•AD 成立？并证明你的结论；（3）如图3，若BA=BC=3，DA=DC=4，∠BAD=90°，DE⊥CF．则的值为．30．如图1，在菱形ABCD中，对角线AC与BD相交于点O，AB=13，BD=24，在菱形ABCD的外部以AB为边作等边三角形ABE．点F是对角线BD上一动点（点F不与点B、D重合），将线段AF绕点A顺时针方向旋转60°得到线段AM，连接FM．（1）求AO的长；（2）如图2，当点F在线段BO上，且点M，F，C三点在同一条直线上时，求证：∠ACM=30°；（3）连接EM，若△AEM的面积为40，请画出图形，并直接写出△AFM的周长答案1．在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．（1）如图①，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；（2）如图②，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系，（3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系．【分析】（1）延长DG与BC交于H，连接AH、AD，通过证得△BGH≌△EGD求得BH=ED，HG=DG，得出BH=DC，然后证得△ABH≌△ACD，得出∠BAH=∠CAD，AH=AD，进而求得∠HAD=90°，即可求得AG ⊥GD，AG=GD；（2）延长DG与BC交于H，连接AH、AD，通过证得△BGH≌△EGD求得BH=ED，HG=DG，得出BH=DC，然后证得△ABH≌△ACD，得出∠BAH=∠CAD，AH=AD，进而求得△HAD是等边三角形，即可证得AG⊥GD，AG=DG；（3）延长DG与BC交于H，连接AH、AD，通过证得△BGH≌△EGD求得BH=ED，HG=DG，得出BH=DC，然后证得△ABH≌△ACD，得出∠BAH=∠CAD，AH=AD，进而求得△HAD是等腰三角形，即可证得DG= AGtan．2．如图，在菱形ABCD中，M，N分别是边AB，BC的中点，MP⊥AB交边CD于点P，连接NM，NP．（1）若∠B=60°，这时点P与点C重合，则∠NMP= 30 度；（2）求证：NM=NP；（3）当△NPC为等腰三角形时，求∠B的度数．【分析】（1）根据直角三角形的中线等于斜边上的一半，即可得解；（2）延长MN交DC的延长线于点E，证明△MNB≌△ENC，进而得解；（3）NC和PN不可能相等，所以只需分PN=PC和PC=NC两种情况进行讨论即可．①若PN=PC，则∠PNC=∠NCP=2x°，在△PNC中，2x+2x+x=180，解得：x=36，∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°，②若PC=NC，则∠PNC=∠NPC=x°，在△PNC中，2x+x+x=180，解得：x=45，∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°．3．菱形ABCD中，两条对角线AC，BD相交于点O，∠MON+∠BCD=180°，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF．（1）如图1，当∠ABC=90°时，△OEF的形状是等腰直角三角形；（2）如图2，当∠ABC=60°时，请判断△OEF的形状，并说明理由；（3）在（1）的条件下，将∠MON的顶点移到AO的中点O′处，∠MO′N绕点O′旋转，仍满足∠MO′N+∠BC D=180°，射线O′M交直线BC于点E，射线O′N交直线CD于点F，当BC=4，且=时，直接写出线段CE的长．【分析】（1）先求得四边形ABCD是正方形，然后根据正方形的性质可得∠EBO=∠FCO=45°，OB=OC，再根据同角的余角相等可得∠BOE=∠COF，然后利用“角边角”证明△BOE和△COF全等，根据全等三角形对应边相等即可得证；（2）过O点作OG⊥BC于G，作OH⊥CD于H，根据菱形的性质可得CA平分∠BCD，∠ABC+BCD=180°，求得OG=OH，∠BCD=180°﹣60°=120°，从而求得∠GOH=∠EOF=60°，再根据等量减等量可得∠EOG=∠FOH ，然后利用“角边角”证明△EOG和△FOH全等，根据全等三角形对应边相等即可得证；（3）过O点作OG⊥BC于G，作OH⊥CD于H，先求得四边形O′GCH是正方形，从而求得GC=O′G=3，∠GO′H=90°，然后利用“角边角”证明△EO′G和△FO′H全等，根据全等三角形对应边相等即可证得△O′EF是等腰直角三角形，根据已知求得等腰直角三角形的直角边O′E的长，然后根据勾股定理求得EG，即可求得CE的长．4．如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP 并延长AP交CD于F点，（1）求证：四边形AECF为平行四边形；（2）若△AEP是等边三角形，连结BP，求证：△APB≌△EPC；（3）若矩形ABCD的边AB=6，BC=4，求△CPF的面积．【分析】（1）由折叠的性质得到BE=PE，EC与PB垂直，根据E为AB中点，得到AE=EB=PE，利用三角形内一边上的中线等于这条边的一半的三角形为直角三角形，得到∠APB为90°，进而得到AF与EC平行，再由A E与FC平行，利用两对边平行的四边形为平行四边形即可得证；（2）根据三角形AEP为等边三角形，得到三条边相等，三内角相等，再由折叠的性质及邻补角定义得到一对角相等，根据同角的余角相等得到一对角相等，再由AP=EB，利用AAS即可得证；（3）过P作PM⊥CD，在直角三角形EBC中，利用勾股定理求出EC的长，利用面积法求出BQ的长，根据BP =2BQ求出BP的长，在直角三角形ABP中，利用勾股定理求出AP的长，根据AF﹣AP求出PF的长，由PM与A D平行，得到三角形PMF与三角形ADF相似，由相似得比例求出PM的长，再由FC=AE=3，求出三角形CPF面积即可．5．如图，P为正方形ABCD的边BC上一动点（P与B、C不重合），连接AP，过点B作BQ⊥AP交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交BA的延长线于点M．（1）试探究AP与BQ的数量关系，并证明你的结论；（2）当AB=3，BP=2PC，求QM的长；（3）当BP=m，PC=n时，求AM的长．【分析】（1）要证AP=BQ，只需证△PBA≌△QCB即可；（2）过点Q作QH⊥AB于H，如图．易得QH=BC=AB=3，BP=2，PC=1，然后运用勾股定理可求得AP（即B Q）=，BH=2．易得DC∥AB，从而有∠CQB=∠QBA．由折叠可得∠C′QB=∠CQB，即可得到∠QBA=∠C′QB，即可得到MQ=MB．设QM=x，则有MB=x，MH=x﹣2．在Rt△MHQ中运用勾股定理就可解决问题；（3）过点Q作QH⊥AB于H，如图，同（2）的方法求出QM的长，就可得到AM的长．6．如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K ，点O是线段BK的中点．（1）求证：△ADP≌△ECP；（2）若BP=n•PK，试求出n的值；（3）作BM丄AE于点M，作KN丄AE于点N，连结MO、NO，如图2所示，请证明△MON是等腰三角形，并直接写出∠MON的度数．【分析】（1）根据菱形的性质得到AD∥BC，根据平行线的性质得到对应角相等，根据全等三角形的判定定理证明结论；（2）作PI∥CE交DE于I，根据点P是CD的中点证明CE=2PI，BE=4PI，根据相似三角形的性质证明结论；（3）作OG⊥AE于G，根据平行线等分线段定理得到MG=NG，又OG⊥MN，证明△MON是等腰三角形，根据直角三角形的性质和锐角三角函数求出∠MON的度数．7．在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN=90°．（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°＜α＜45°）．①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；②如图2，在旋转过程中，当∠DOM=15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD=3BP时，猜想此时PE 与PF的数量关系，并给出证明；当BD=m•BP时，请直接写出PE与PF的数量关系．【分析】（1）根据正方形的性质和角平分线的性质解答即可；（2）①根据正方形的性质和旋转的性质证明△FOA≌△EOD，得到答案；②作OG⊥AB于G，根据余弦的概念求出OF的长，根据勾股定理求值即可；③过点P作HP⊥BD交AB于点H，根据相似三角形的判定和性质求出PE与PF的数量关系，根据解答结果总结规律得到当BD=m•BP时，PE与PF的数量关系．8．在正方形ABCD中，BD是一条对角线，点P在射线CD上（与点C、D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QH⊥BD于H，连接AH，PH．（1）若点P在线段CD上，如图1．①依题意补全图1；②判断AH与PH的数量关系与位置关系并加以证明；（2）若点P在线段CD的延长线上，且∠AHQ=152°，正方形ABCD的边长为1，请写出求DP长的思路．（可以不写出计算结果）【分析】（1）①根据题意画出图形即可；②连接CH，先根据正方形的性质得出△DHQ是等腰直角三角形，再由SAS定理得出△HDP≌△HQC，故PH =CH，∠HPC=∠HCP，由正方形的性质即可得出结论；（2）根据四边形ABCD是正方形，QH⊥BD可知△DHQ是等腰直角三角形，再由平移的性质得出PD=CQ．作HR⊥PC于点R，由∠AHQ=152°，可得出∠AHB及∠DAH的度数，设DP=x，则DR=HR=RQ，由锐角三角函数的定义即可得出结论．9．如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．（1）如图①，当α=90°时，DE，DF，AD之间满足的数量关系是DE+DF=AD ；（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=AD，请给出证明；（3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．【分析】（1）利用正方形的性质得出角与线段的关系，易证得△APE≌△DPF，可得出AE=DF，即可得出结论DE+DF=AD，（2）取AD的中点M，连接PM，利用菱形的性质，可得出△MDP是等边三角形，易证△MPE≌△FPD，得出ME=DF，由DE+ME=AD，即可得出DE+DF=AD，（3）①当点E落在AD上时，DE+DF=AD，②当点E落在AD的延长线上时，DF﹣DE=AD．10．如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时针旋转90°，得到线段CQ，连接BP ，DQ．（1）如图a，求证：△BCP≌△DCQ；（2）如图，延长BP交直线DQ于点E．①如图b，求证：BE⊥DQ；②如图c，若△BCP为等边三角形，判断△DEP的形状，并说明理由．【分析】（1）根据旋转的性质证明∠BCP=∠DCQ，得到△BCP≌△DCQ；（2）①根据全等的性质和对顶角相等即可得到答案；②根据等边三角形的性质和旋转的性质求出∠EPD=45°，∠EDP=45°，判断△DEP的形状．11．已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PF，设运动时间为t （s）（0＜t＜8）．解答下列问题：（1）当t为何值时，四边形APFD是平行四边形？（2）设四边形APFE的面积为y（cm2），求y与t之间的函数关系式；（3）是否存在某一时刻t，使S四边形APFE：S菱形ABCD=17：40？若存在，求出t的值，并求出此时P，E两点间的距离；若不存在，请说明理由．【分析】（1）由四边形ABCD是菱形，OA=AC，OB=BD．在Rt△AOB中，运用勾股定理求出AB=10．再由△DFQ∽△DCO．得出=．求出DF．由AP=DF．求出t．（2）过点C作CG⊥AB于点G，由S菱形ABCD=AB•CG=AC•BD，求出CG．据S梯形APFD=（AP+DF）•CG．S△EFD=EF•QD．得出y与t之间的函数关系式；（3）过点C作CG⊥AB于点G，由S菱形ABCD=AB•CG，求出CG，由S四边形APFE：S菱形ABCD=17：40，求出t，再由△PBN∽△ABO，求得PN，BN，据线段关系求出EM，PM再由勾股定理求出PE．12．已知菱形ABCD的边长为1，∠ADC=60°，等边△AEF两边分别交DC、CB于点E、F．（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点，求证：菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心；（2）若点E、F始终分别在边DC、CB上移动，记等边△AEF的外心为P．①猜想验证：如图2，猜想△AEF 的外心P落在哪一直线上，并加以证明；②拓展运用：如图3，当E、F分别是边DC、CB的中点时，过点P任作一直线，分别交DA边于点M，BC边于点G，DC边的延长线于点N，请你直接写出的值．【分析】（1）连接OE、0F，由四边形ABCD是菱形，得出AC⊥BD，BD平分∠ADC，AD=DC=BC，又由E 、F分别为DC、CB中点，证得0E=OF=OA，则可得点O即为△AEF的外心；。

2020年山东省济宁市青岛版(2016)中考信息技术选择题判断题总复习4【word精校精析版】

2020年山东省济宁市青岛版（2016）中考信息技术选择题判断题总复习4一、选择题1. 聊城动物园微信发布消息，6月1日当天，所有儿童可免费参观动物园。

雯雯6月3日去游园，没有享受到优惠。

这反映了信息的（）。

A. 依附性B. 真伪性C. 时效性D. 共享性【答案】C【解析】【详解】本题考查的知识点是信息及其特征。

信息的基本特征是：载体依附性、真伪性、时效性、共享性。

动物园6月1日当天所有儿童可免费参观动物园。

6月3日去游园，错过了时间，所以享受不到优惠。

反映了信息据有时间效应，体现了信息的时效性。

故正确答案为C选项。

2. QQ是同学们常用的网络交流工具，以下做法我们不提倡的是（）。

A. 在QQ空间发布对别人的恶意评价B. 加入班级QQ群，方便交流C. 在QQ群里聊天，沟通日常学习动态信息D. 做作业遇到困难时，通过QQ向老师和同学请教【答案】A【解析】【详解】本题考查的知识点是即时通讯工具QQ的应用。

网络文明，人人有责。

在QQ空间发布对别人的恶意评价，是不文明不道德的行为。

故正确答案为A选项。

3. 列关于Windows系统中文件名的说法中，正确的是（）。

A. 文件可以没有主文件名B. 给文件命名时不能用汉字与英文字母组合C. 同一磁盘上不允许有重名的文件或文件夹D. 给文件命名时主文件名与扩展名用“.”隔开【答案】D【解析】【详解】本题考查的知识点是Windows系统文件命名。

Windows系统中文件名包括主名和扩展名组成，中间用“.”隔开，主名可以是中文、英文或中英文混用。

同一个文件夹内不允许有重名的文件或文件夹。

故正确答案为D选项。

4. 计算机断电后，信息会全部丢失，再次通电信息也不能恢复的存储器是（）。

A. U 盘B. RAMC. ROMD. 硬盘【答案】B【解析】【详解】本题考查的是存储器相关知识。

随机存取存储器(random access memory ，RAM)又称作“随机存储器”，是与CPU 直接交换数据的内部存储器，也叫主存(内存)。

2016春中考政治(教科版八年级下册)复习(考点梳理)：第四单元劳动创造世界(word版)

第四单元劳动创造世界考试说明要求1．理解劳动的意义，理解“劳动是人类生存和发展的需要”的道理，尊重劳动者。

2．树立珍惜劳动成果、节约资源的意识，养成文明消费的习惯。

错误！未找到引用源。

第九课人类的需要错误！未找到引用源。

考点1 如何理解“劳动”？(劳动对人类及人类社会有什么重要意义？)(1)劳动创造了人类，创造了世界，创造了文明；(2)劳动，促进人的成长与发展，丰富人的精神世界；(3)劳动，是美好生活的源泉，是人类生存和发展的第一需要。

错误！未找到引用源。

考点2 为什么说物质文明是人类赖以生存的基础？(1)物质文明是人类在劳动实践中所创造的物质财富。

(2)人们要生存，首先必须满足吃、喝、住、穿等物质需求，然后才能谈得上从事政治、科学、艺术、宗教等精神活动。

只有解决了必要的生活资料问题，才可能进行文化艺术和科学技术研究等精神活动。

所以，物质文明是人类赖以生存的基础。

错误！未找到引用源。

考点3 为什么说劳动创造了精神文明？(1)劳动不仅创造了物质财富，也创造了精神财富。

劳动是精神财富取之不尽，用之不竭的源泉。

(2)很多精神文明成果，起初都是在人们进行物质生产劳动过程中产生和发展的。

(3)在劳动过程中，人类不断地探索和积累丰富的知识和经验，创造了宝贵的科学、技术和文化成果。

(4)当脑力劳动从体力劳动中分离出来，当精神财富的生产从物质财富的生产中独立出来，就出现了专门从事精神劳动的思想家、科学家、艺术家等脑力劳动者，他们辛勤地创造着文化、科学、技术、艺术等丰富的精神财富。

错误！未找到引用源。

考点4 如何理解劳动促进人的成长与发展？(1)劳动不断地提高着人类自身的生理素质和心理素质，促进着人类的成长与发展。

(2)通过劳动工具的发明和使用，人类延伸了身体的某些器官的功能，加强了在自然界谋生和发展的能力。

(3)劳动是培养和发展人的道德品质、提高人的精神境界的重要途径。

2016中考总复习物质的物理属性(复习)

考点一物质的物理属性
一、物质的物理属性（一）、硬度物质的软硬程度叫做物质的硬度 1、定义： 2、比较物质硬度的方法：划痕法 (二)、物质的物理属性有哪些？
颜色、状态、气味、熔点、沸点、密度、硬度、透明度(性)、导电性、导热性、弹性、磁性、（柔）韧性、延展性、(范性)
延展性：物质易被加工成各种形状的性质 (三)、给物质进行分类的依据：物质的各种属性.
例1、下列不属于物质的物理属性的是 ( C ) A.状态 B.密度 C．质量 D.弹性例2、玻璃店里用的玻璃刀选用的材料可能是（ B ） A．玻璃 B.金刚石 C.铁器 D.竹签
例 3 ．将下列问题中主要利用了物质的哪些物理属性填在每个题目后面的横线上。
⑴为了欣赏茶叶的颜色和形状，用透明的玻璃杯泡茶。是利用了玻璃杯的 _________ 透明度比较好这个属性；
40 30 20 10
测金属块的体积
1.在量筒内放入适量的水并记下水的体积为V1 2.用细线系着金属块轻轻地放入量筒内水中并记下其总体积为V2
V2 V1
体积表达式： V石 = V2 － V1
排液法：固体的体积等于排开液体的体积
考点四：密度
★ 常考点二
密度
1．定义：某种物质组成的物体的质量与它的体积之 m 比叫做这种物质的密度，定义公式 ρ＝ V ． 2．单位：密度的国际主单位是 Kg/m3 ，实验室常用 3 3 3 3 单位是 g/cm ；二者的关系是 1 kg/m =10 g/cm ． 3．密度是物质的特性之一，不同物质的密度一般是不同的，同种物质的密度一般是相同的，它不随质量和体积改变而改变，即ρ取决于m/V的值，不是由m或V某一个物理量来决定的．
⑵玻璃刀头部装上一粒金刚石, 是利用了金刚石的________ 比较大这个属性；硬度 ⑶用铜做电线的线芯，用塑料或橡胶包在电线的外层。是利用了铜的 ________ 导电性比较好这个属性；

2016年中考名著复习——《四世同堂》

2016年中考名著复习——《四世同堂》老舍著中国现代长篇小说一、作家、作品简介老舍（1899-1966）：原名舒庆春，字舍予。

满族，北京人（正红旗）。

中国现代小说家、著名作家，杰出的语言大师，新中国第一位获得“人民艺术家”称号的作家。

老舍的一生，总是忘我地工作，他是文艺界当之无愧的“劳动模范”。

《四世同堂》是中国作家老舍创作的一部百万字的小说。

这是一部表现抗战北平沦陷区普通民众生活与抗战的长篇小说，全书共三部。

该书以北平小羊圈胡同为背景，通过复杂的矛盾纠葛，以胡同内的祁家为主，钱家、冠家以及其他居民为辅，刻画了当时社会各阶层众多普通人的形象；反抗与顺从的选择，国家与个人的选择种种艰难的选择纷繁地交织在一起，深刻地展示了普通人在大时代历史进程中所走过的艰难曲折的道路。

1949年曾在美国出版节译本，书名为《黄色风暴》，被誉为“好评最多的小说之一，也是美国同一时期所出版的最优秀的小说之一”。

二、分部介绍序号内容梗概第一部《惶惑》故事发生在抗战时期北平沦陷时期，北平小羊圈胡同里祁老人渴望圆满的度过80大寿，然而日本人突然打进来，使表面本来和睦的胡同变得风云四起。

钱家二少爷与日本人同归于尽，冠家人为取得日本人信任而告发钱家，钱默吟被迫下狱，钱家大少爷和钱夫人病死，祁瑞全在大哥的帮助下逃出城外开始抗战。

冠家最终在靠出卖女儿色相的帮助下取得了妓女所所长的职位。

瑞丰在妻子的帮助下进入教育局担任科长，不顾瑞宣的反对变相为日本人做事服务。

一边在敌人的一番拷打之后，钱老人神志不清的出狱，在胡同邻居的帮助下逐渐恢复神智，钱家儿媳产下一子。

在经历家破人亡的打击后，钱老人逐渐认清日本人的面目，独自一人在北平城内开始进行抗战。

第二部《偷生》在日本人的不断倾轧下，北平人逐渐开始缺煤缺粮，胡同里除了冠家人其余人的生活都变得越发贫乏，日本人也开始了对学校的思想控制，瑞宣不满，向学校辞职进了英国使馆工作。

由于日本人内部的势力更迭，瑞丰被新一波的势力推下科长之位，蓝东阳则成了新民会的干部，胖菊子见势改嫁给蓝东阳，瑞丰变得一无所有灰溜溜的回到五号院。

2016中考复习.植物的光合作用与呼吸作用

受光照，B培养皿遮光处理。一段时间后，观察到A培养皿中产生气泡，其中的气体能使带火星的木条复燃；B、C培养皿中未产生气泡。
第6页，共22页。
结合所学知识，分析判断下列叙述，其中不正确的是（）
B
A．培养皿A中气泡内的气体是氧气
B．培养皿B中无气泡产生是因为缺乏二氧化碳
C．通过比较A、C培养皿中的现象，可知光合作用的场所是叶绿体
“研究光照强度对植物光合作用速度的影响”，设计如下图乙实验装置。此装置的优点在于，可通过控制灯泡功率的大小或调节试管与灯泡的距离，来改变光照的强弱。试回答下列问题：
第17页，共22页。
（1）光照强度为B点时，水藻吸收二氧化碳量为0，水
藻是否进行了光合作用？
。是
（2）单位时间内，水藻释放氧气量应大于（大于、小于或等于）其光合作用产生的氧气量。
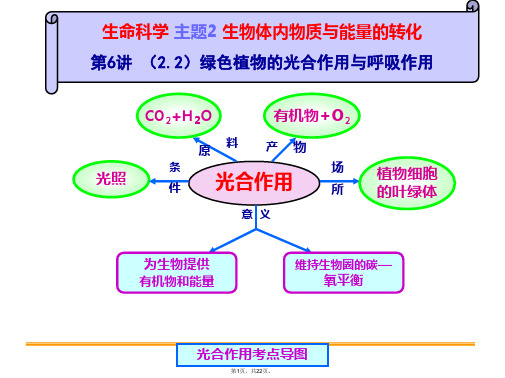
生命科学主题2 生物体内物质与能量的转化第6讲（2.2）绿色植物的光合作用与呼吸作用
光照
CO2+H2O
有机物+O2
原料
产物
条
场
件光为生物提供有机物和能量
维持生物圈的碳— 氧平衡
光合作用考点导图
第1页，共22页。
生生命命科科学学主题2 生物体内主物题质2与生能物量体的内转物化第6讲（2.2）绿质色与植能物量的的光转合化作用与呼吸作用
B．B点时植物的叶不进行光合作用
C．CD段植物的叶只进行光合作用，不进行呼吸作用 D．B点过后，植物的叶的光合作用强于呼吸作用
第15页，共22页。
【解析】AB段释放出的氧气量为负值，说明此时呼吸作用消耗的氧气超过光合作用释放出的氧气，即呼吸作用的强度大于光合作用的强度，B点释放出

2016年中考语文读背清单教材知识梳理复习课件(打包5份)4

深渊(yuān)
奢侈(shē)
崖(yá )
逡巡(qūn)
飞窜(cuà n)
《组歌》(节选)
彻夜不寐(mè i) 翱翔(á o) 憔悴(qiá o cuì )
璀璨(cuǐ càn)
天穹(qiónɡ) 馈赠(kuì )
纤细(xiān)
执拗(niù ) 心扉(fēi)
长吁短叹(xū)
千山万壑(hè ) 镶嵌(xiānɡ qiàn)
枸杞(ɡǒu qǐ) 挑剔(tiāo ti) 橄榄(ɡǎn lǎn) 《俗世奇人》发蔫(niān) 褒贬(bāo) 吃荤(hūn)
发怵(chù ) 嘉奖(jiā) 秫米(shú )
《与朱元思书》缥碧(piǎo) 泠泠(línɡ) 横柯(kē)
经纶(lú n)
轩邈(xuān miǎo) 《五柳先生传》
干涸(hé )
吞噬(shì )
水泵(bènɡ)
裸露(luǒ)
远眺(tià o)
庇护(bì )
崩塌(tā)
《旅鼠之谜》
滑稽(jī) 媲美(pì ) 幼崽(zǎi) 苔藓(xiǎn) 迷惘(wǎnɡ) 啮齿(niè ) 笃信(dǔ) 挑衅(xì n) 收敛(liǎn) 徘徊(pá i huá i) 小心翼翼(yì )
③高尔基(1868—1936)，前苏联无产阶级作家，现实主义文学的奠基人。主要作品有长篇小说《母亲》和自传体三部曲《童年》《在人间》《我的大学》等。《海燕》是高尔基在1901年3月写的“幻想曲”《春天的旋律》的结尾部分，原题为“海燕之歌”。
④沈从文(1902—1988)，现代作家、历史文物研究家。《云南的歌会》选
携(xié )
蔌(sù )
酒洌(liè )
觥筹(ɡōnɡ)

2016中考复习4

中考数学专题复习第4章三角形第13讲全等三角形及其性质

(新人教版)广东中山2016中考复习复习课件：第4讲修改病句(语文)

2016年中考化学金属的活动性顺序专题复习

2016春中考政治(教科版八年级上册)复习(考点梳理)：第四单元一念之差与一步之遥(word版)

2016中考语文复习：《红楼梦》常考知识点

2016年语文中考复习专题4 句子的仿写与修辞

2015-2016学年中考科学一轮基础复习 第4课时 用显微镜观察细胞能力提升训练

2016年中考专项复习——阅读题型解题思路汇总

2016中考复习四边形综合题

2020年山东省济宁市青岛版(2016)中考信息技术选择题判断题总复习4【word精校精析版】

2016春中考政治(教科版八年级下册)复习(考点梳理)：第四单元劳动创造世界(word版)

2016中考总复习物质的物理属性(复习)

2016年中考名著复习——《四世同堂》

2016中考复习.植物的光合作用与呼吸作用

2016年中考语文读背清单教材知识梳理复习课件(打包5份)4

2015-2016学年中考科学一轮基础复习第4课时用显微镜观察细胞能力提升训练