8.4.2 玻尔的氢原子理论

合集下载

玻尔的氢原子理论

玻尔的氢原⼦理论§4. 玻尔的氢原⼦理论⼀玻尔(1885-1962)丹麦物理学家尼尔斯·玻尔，⽣于丹麦哥本哈根的⼀个富裕知识分⼦家庭，⽗亲是哥本哈根⼤学⽣理学教授。

1903年进⼊哥本哈根⼤学数学和⾃然科学系，⼤学⼆年级时他热中于研究⽔的表⾯张⼒问题，并在丹麦皇家科学院的有奖征⽂中容获⾦质奖章，1909年获硕⼠学位，1911年以论⽂《⾦属电⼦论的研究》获博⼠学位。

1911年9⽉，他到英国剑桥卡⽂迪什实验室进修，据说他第⼀次与导师J.J.汤姆孙见⾯时，就把他论⽂中批评汤姆孙的段落当⾯指出，使导师很不⾼兴，因⽽给以冷遇。

1912年3⽉转到了曼彻斯特随卢瑟福⼯作，这成了他⼀⽣的重要转折点。

玻尔在卢瑟福实验室⼯作期间（约4个⽉），正值卢瑟福发表有核原⼦理论，并组织对这⼀理论进⾏检验。

玻尔参加了α粒⼦散射实验⼯作，因此清楚这⼀理论所⾯临的困难。

但玻尔坚信卢瑟福有核原⼦模型的正确性，认为“只有量⼦假说是摆脱困难的唯⼀出路”。

1913年提出著名的玻尔原⼦理论。

1916年任哥本哈根⼤学教授，1921年起⼀直领导着该校为他建⽴的理论物理研究所，直到去世。

玻尔于1916年、1927年分别提出对应原理和互补原理，1936年提出原⼦核的液滴核模型，1939年创⽴核裂变理论，预⾔铀的⾃⾝裂变。

曾参加第⼀颗原⼦弹的制造。

1922年因对原⼦结构和原⼦辐射的研究⽽获得诺贝尔物理学奖。

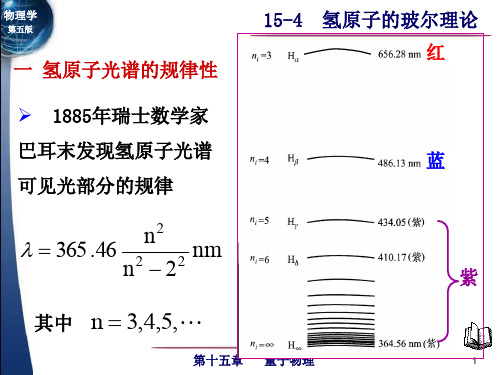
⼆玻尔的氢原⼦理论1．汉森的拜访1912年7⽉回到哥本哈根，1913年初，玻尔的好友、光谱学家汉森(H.M.Hansen)在拜访玻尔时问到原⼦结构和光谱学中的谱线有什么关系？并向玻尔详细介绍了巴尔末的发现，以及谁也⽆法对巴尔末公式作出解释。

2．斯塔克的启⽰1913年2⽉玻尔注意到德国物理学家斯塔克(J.Stark)在《原⼦动⼒学原理》⼀书中的⼀段话：“⼀个光谱的全部谱线是由单独⼀个电⼦造成的，是在这个电⼦从⼀个（⼏乎）完全分离的状态逐次向势能最⼩的状态跃迁过程中辐射出来的。

氢原子的能级与光谱.

氢原子的能级与光谱·爱因斯坦1905年提出光量子的概念后，不受名人重视，甚至到1913年德国最著名的四位物理学家(包括普朗克)还把爱因斯坦的光量子概念说成是“迷失了方向”。

可是，当时年仅28岁的玻尔，却创造性地把量子概念用到了当时人们持怀疑的卢瑟福原子结构模型，解释了近30年的光谱之谜。

§1 氢原子的能级与光谱一、玻尔的氢原子理论(一)玻尔的基本假设1.定态假设：原子只可能处于一系列不连续的能量状态E1, E2, E3,…。

处于这些状态的原子是稳定的，电子虽作加速运动，但不辐射电磁波。

2.频率条件：原子从某一定态跃迁至另一定态时，则发射(或吸收)光子，其频率满足玻尔在此把普朗克常数引入了原子领域。

(二)玻尔的氢原子理论 1.电子在原子核电场中的运动(1)基本情况：核不动；圆轨道；非相对论。

(2) 用经典力学规律计算电子绕核的运动·电子受力：·能量：得f f = - 14πε0 ( )Ze 2r 21 ε0 ( ) Ze2 r = m ( )υ2r1 2E = m υ2 - 1 4πε0 ( ) Ze2 r E = -Ze 28πε0r2.轨道角动量量子化条件玻尔假定：在所有圆轨道中，只有电子的角动量满足下式的轨道才是可能的。

玻尔引进了角动量的量子化。

3.轨道和速度 ·r n = n 2r 1 ,(玻尔半径) r 1= 0.529 Å· υn= υ1/n ，4πε0h 2 r 1 = ( me 2 )( ) 1 Z 4πε0hυ1 = Ze 2)可见, 随n↑⇒r n↑，υn↓4.能级---能量量子化将r n代入前面E式中，有n = 1,2,3,…)R：里德伯常数(见后)基态能量：E1= -13.6 eV可见，随n↑⇒E n↑，∆E n↓*玻尔的理论是半经典的量子论：对于电子绕核的运动，用经典理论处理；对于电子轨道半径，则用量子条件处理。

波尔的氢原子理论.ppt

电磁能，从而: E , r 这样电子将会在10-9s时间内落入
核内，正负电荷中和，原子宣告崩溃(塌缩)。但现实世界原子是稳定的。
(2). 原子线状光谱问题:按经典电动力学,原子发光的频率= 电子轨道运动的频率,r连续减小,f连续增大,原子发出连续光谱。但事实是：原子光谱是分立线状光谱
二、玻尔假设
玻尔深信量子化这一新概念，特别是当它看到巴耳末氢光谱公式后，原子内部结构全然呈现在他的想象中。
玻尔的氢原子理论，可分三部分
1、定态假设
原子内部存在一系列离散的具有确定能量的稳定状态——定态。电子在这些定态上运动，其量子化的能量守恒，电子不会辐射能量，这称为玻尔的定态假设
量子化能级的出现是原子稳定性的基石，因为能级之间是禁区。
势能的一半:
E

1 2
mv2

Ze2
4 0r

1 2
Ze2
4 0r

1 2
Ep
(1)、原子总能量 E 1 Ze2 , (r , E )
2 4 0r
(2)、电子轨道运动的频率:
2、经典理论的困难
ve
Z
f
2r 2
4 0mr3
(1).原子稳定性问题:卢瑟福将行星模型用于原子世界，电子绕核运动，电子带-e电荷，轨道加速运动会向外辐射
1、电子在原子核的库仑场中的运动
卢瑟福将行星模型用于原子世界，电子绕核作圆周运动(设原子核不动)
向心力：m
v2 r

Ze2
4 r 2
动能Ek

1 mv2 2

1 2
Ze2
4 0r
设：r

时势能为0，原子系统势能为E p

玻尔的氢原子理论

玻尔的氢原子理论
为此,J.汤姆孙在1904年提出了原子结构的枣糕式模型.该模型认为，原子可以看作一个球体，原子的正电荷和质量均匀分布在球内，电子则一颗一颗地镶嵌其中.1909年，J.汤姆孙的学生卢瑟福为了验证原子结构的枣糕式模型，完成了著名的α粒子散射实验.实验发现α粒子在轰击金箔时，绝大多数α粒子都穿透金箔，方向也几乎不变，但是大约有1/8 000的α粒子会发生大角度偏转，即被反弹回来.这样的实验结果是枣糕式模型根本无法解释的，因为如果说金箔中的金原子都是枣糕式的结构，那么整个金箔上各点的性质应该近乎均匀，α粒子轰击上去，要么全部透射过去，要么全部反弹回来，而不可能是一些穿透过去，一些反弹回来.
玻尔的氢原子理论
二、原子结构模型
1897年，J.汤姆孙发现了电子.在此之前，原子被认为是物质结构的最小单元，是不可分的，可是电子的发现却表明原子中包含带负电的电子.那么，原子中必然还有带正电的部分，这就说明原子是可分的，是有内部结构的.执着的科学家就会继续追问：原子的内部结构是什么样的？简洁的里德伯光谱公式是不是氢原子内部结构的外在表现？
玻尔的氢原子理论
三、玻尔的三点基本假设
为了解决原子结构有核模型的稳定性和氢原子光谱的分立性问题，玻尔提出以下三个假设：
（1）定态假设.原子中的电子绕着原子核做圆周运动，但是只能沿着一系列特定的轨道运动，而不能够任意转动，当电子在这些轨道运动时，不向外辐射电磁波，原子系统处于稳定状态，具有一定的能量.不同的轨道，具有不同的能量，按照从小到大的顺序记为E1、E2、E3等.
玻尔的氢原子理论
可是这个模型却遭到很多物理学家的质疑.因为按照当时的物理理论（包括经典力学、经典电磁理论及热力学统计物理），这样一个模型是根本不可能的，原因有以下两个：

高二物理竞赛波尔的氢原子理论PPT(课件)

中间的谱线
n
n
氢原子的第一玻尔速度：
1903 Planck 能量量子化; 1905 Einstein光量子理论。电子定态轨道角动量满足量子化条件：电子定态轨道角动量满足量子化条件：
n ∞,r ∞,E 0 电离能：将一个基态电子电离需要的最少能量。轨道半径rn∝n2，|En|∝1/n2
En
1 2
mev2
r 为保证定态假设中能量取不连续值，必须取不连续值，如何做到？
把基态氢原子的电子移到无穷远时所需要的能量，即氢原子的电离能。
电子定态轨道角动量满足量子化条件：
Ze2
4 0 r 2
Ze
氢原子的第一玻尔速度：
电子定态轨道角动量满足量子化条件：
2
原子体系的能量： 1 Ze 1 Ze 电子只能在一系列大小一定、彼此分立的轨道上绕核运动，且不辐射电磁波，能量稳定。2
轨道半径rn∝n2，|En|∝1/n2 电子只能在一系列大小一定、彼此分立的轨道上绕核运
玻若尔定基义本氢假原设子(的19基1态3年能) 量为0，则动，且不辐射电磁波，能量稳定。
为保证定态假设中能量取不连续值，必须取不连续值，如何做到？
两边同乘：
轨道半径rn∝n2，|En|∝1/n2
电子轨道r 和能量E 都是分立的 for his services in the investigation of the structure of atoms and of the radiation emanating from them
自氢原子能级图
由
态 n
E / eV
0
激 n4 发 n3
0.85 1.51
态
n2
3.4

氢原子的玻尔理论

电子在原子中可以在一些特定的圆轨道上运动而不辐射电磁波，这时，原子处于稳定状态，简称定态.
与定态相应的能量分别为 E1，E2… ， E1 < E2< E3
是对经典概念的修改！
E1+ E3
第十五章量子物理
24
物理学
第五版 (2)量子化条件
15-4 氢原子的玻尔理论
引入角动量量子化的概念 L mvr n h 2π
第十五章量子物理
2
物理学
第五版
紫外可见光
红外
15-4 氢原子的玻尔理论
莱曼系

1

R(112

1 n2
)
,
巴尔末系

1

R(
1 22

1 n2
)
,
n 2,3, n 3,4,
帕邢系

1

R(312

1 n2
),
n 4,5,
布拉开系

1

R(
1 42

1 n2
)
,
玻尔理论对氢原子光谱的解释
En

me4
8
2 0
h
2

1 n2
h Ei E f

1c Nhomakorabea
me4
8
2 0
h3c
(
1 n2f

1 ni2
)
,
ni n f

里德伯常量
R

me4
8 02 h3c

1.0973731107

波尔的氢原子理论

5
2 卢瑟福的核式模型
卢瑟福1871年8月13日出生在新西兰，1894年大学毕业，1895年到英国剑桥大学学习，成为 J.J. 汤姆孙的研究生。1908年卢瑟福荣获诺贝尔化学奖，同年在曼切斯特大学任教，继续指导他的学生进行粒子散射的实验研究。
卢瑟福的α粒子散射验证了核式模型。
19-1 波尔的氢原子理论
量子物理起源于对原子物理的研究，人们从高能粒子的散射实验和原子光谱中获得原子内部信息。
3
4
一玻尔理论的实验基础
1 汤姆逊葡萄干面包模型
1903年，汤姆孙提出原子结构模型：原子里面带正电的部分均匀地分布在整个原子球体中，而带负电的电子镶嵌在带正电的球体之中。带正电的球体与带负电的电子二者电量相等，故原子不显电性。
5 6 普芳德（Pfund）系
区域紫外可见可见红外红外
此后又发现碱金属也有类似的规律。
日期 1906年 1880年 1908年 1922年 1924年
3 里兹并合原理
~ T(m α) T(n β)
R
光谱项： T(m) (m )2
R
T (n) (n )2 10
三经典电磁理论遇到的困难
6
粒子散射
4 2
H
e
,
q 2e, 原子量为4，m 7500me
粒子束射向金箔：
-
(1) 多数 0
+
（2）少数较大
1 / 8000被反射，
（3）极少数，反弹
大部分透过。
7
1911年，卢瑟福提出原子的 “有核结构模型”
原子的核式模型
原子由原子核和核外电子构成，原子核带正电荷，占据整个原子的极小一部分空间，而电子带负电，绕着原子核转动，如同行星绕太阳转动一样。

波尔的氢原子理论

19
发射光谱和吸收光谱
1 发射光谱：原子受激后又自动“退激”而自发发出的辐射。
2 吸收光谱：在连续光谱照射下，原子吸收光子，明亮背景上出现了若干暗线。
激发态
能级图
基态 20
六玻尔理论的成功及局限
1 成功 -- 1922年获诺贝尔奖 (1)定态能级假设与原子的稳定性；(2)能级间跃迁的频率条件。 (3)能较好地解释氢原子光谱和类氢原子光谱。 2 局限性 (1)用经典理论推出电子有固定轨道、确定的空间坐标和速度 (2)人为引进量子条件，限制电子运动 (3)只能解释H及类H原子，也解释不了原子的精细结构。
1 n2 )
k=n-1
2(n 1) me 4
n2 (n 1)2 8 02h3
当n很大时：
rn
0h2n2 me 2
n2r1
En
me 4
8 02h2
1 n2
E1 n2
n 1,2,3,
nk
2 n3
me 4 8ε02h3
me 4 4ε02h3n3
23
当n很大时：
nk
2 n3
me 4
8
5 6 普芳德（Pfund）系
区域紫外可见可见红外红外
此后又发现碱金属也有类似的规律。
日期 1906年 1880年 1908年 1922年 1924年
3 里兹并合原理
~ T(m α) T(n β)
R
光谱项： T(m) (m )2
R
T (n) (n )2 10
三经典电磁理论遇到的困难
1 汤姆逊葡萄干面包模型
1903年，汤姆孙提出原子结构模型：原子里面带正电的部分均匀地分布在整个原子球体中，而带负电的电子镶嵌在带正电的球体之中。带正电的球体与带负电的电子二者电量相等，故原子不显电性。

氢原子的玻尔理论波粒二象性

式中:
R =1.096776×107m−1 为里德伯常量
m=1， 2， 3， 4，… n=m+1， m+2， m+3，…
σ
=
1 λ
=
R⎜⎛ ⎝
1 m2
−
1 n2
⎟⎞ ⎠
--里德伯方程
式中: m=1， 2， 3， 4，… n=m+1， m+2， m+3，…
赖曼系(m=1)
σ
=
R⎜⎛ ⎝
1 12
−
1 n2
激发态能级
En
=
E1 n2
=
13.6 − n2
eV
当 n → ∞ 时，
原子被电离，电子不受原子核束缚。
电离能：把电子从氢原子玻尔轨道移到无穷远所需能量。
∆E = E∞ − E1 = 13.6eV
(3) 氢原子光谱
(3) 氢原子光谱
En
=
−
1 n2
( mee4 8ε 0 2 h2
)
=
E1 n2
(n = 1,2,3,⋯)
Hα
Hβ
Hγ
6562.8Å 4861.3Å 4340.5Å
Hδ 4101.7Å
巴尔末（Balmer）找到的经验公式：
λ
=
B
n2 n2 −
4
⋯(1)
B = 3645.6Å（经验常数） n =3、4、5...
波数
σ
=
1 λ
=
R( 1 22
−
1 n2
)⋯(2)
----巴尔末公式（可见光区）
R =1.096776×107m−1 为里德伯常量
（2）承认电子在有心力场中运动，角动量守恒。但是玻尔硬加了一个角动量量子化条件。

8.4.2 玻尔的氢原子理论

1 2
m
v
n
2
e2
8 0rn
En
me4
8
2 0
h
2
1 n2
En
E1 n2
基态能量:
n 1时,
E1 13 6eV
n 1, 2 , 3 , 这种量子化的能量称为能级
4、氢原子光谱的理论解释
kn
En
h
Ek
1 me4
En
n2
8
2 0
h
2
ν~kn
me4
8
2 0
h
3c
(1 k2
1) n2
RH
则发射或吸收光子的频率为：
kn
En Ek h
称为玻尔的频率条件
玻尔的氢原子理论
Ek
玻尔的氢原子理论
2、氢原子轨道半径的计算由量子化条件及牛顿定律：
n=4 v
m n=3
mvr n h , 角动量量子化
e2
40r 2
2 2
mv r
,库仑力=向心力
n=2 n=1 r
r1 4r1
rn
n2
0h2 me2
在这些轨道上运动的电子不辐射（或吸收）能量而处于稳定状态，称为定态。
相应的轨道称为定态轨道与定态相应的能量（能级）分别为： E1，E2 ，E3 …
E1 < E2 < E3 < …
玻尔的氢原子理论
E1 E2 E3
玻尔的氢原子理论
一、玻尔的氢原子理论
1、玻尔的氢原子理论
2)角动量量子化条件假设
在定态轨道上运动的电子，其角动量只能取 h / (2 的整数倍，即
v
m

2.3 玻尔的氢原子理论

谢谢
大学物理——量子物理
玻尔的氢原子理论
卢瑟福的“核式模型”
原子核
电子
σ
1 λ
R
1 m2
1 n2
Tm பைடு நூலகம்n
里兹组合
无法解释原子稳定性、以及原子线状光谱！
1913年，玻尔在卢瑟福的核结构模型的基础上，把量子化概念应用到原子系统，结合里兹组合，提出氢原子理论。
一、玻尔的氢原子理论
解释原子稳定性
—— 定态假设
解释原子的分立光谱 —— 跃迁假设
定量分析原子光谱 —— 角动量量子化假设
1. 定态假设
原子系统只能处在一系列不连续的能量状态，在这些状态中，虽然电子绕核运动作加速运动，但不辐射也不吸收电磁波，这些状态称为原子系统的稳定状态，简称定态。
相应的不连续能量分别为 E1，E2 能量确定,定态能级原子结构稳定能量稳定，运动轨迹稳定
一、玻尔的氢原子理论
解释原子的分立光谱 —— 跃迁假设
2. 跃迁条件（频率条件）
原子能量的任何变化，包括发射或吸收电磁辐射，
都只能以在两个定态之间以跃迁的方式进行。
原子在两定态之间跃迁：En< Em 时
辐射电磁波：
hν En Em
Em
●
En
吸收电磁波：
Em
En hν Em
●
En
定态能级不连续，能级差值不连续，辐射（吸收）
电磁波频率不连续——线性分立光谱
一、玻尔的氢原子理论
定量分析原子光谱 —— 角动量量子化假设
3. 轨道角动量量子化假设
定态与电子绕核运动的一系列分立圆周轨道相对应，
电子轨道角动量只能是（h/2）的整数倍，即

玻尔的氢原子理论

氢原子光谱
赖曼系，紫外区巴尔末系，可见光区帕邢系，红外区布拉开系，红外区普丰德系，红外区哈弗莱系，红外区其他元素的光谱也有类似的规律性。原子光谱线系的规律性深刻地反映了原子内部的规律性
2. 玻尔的氢原子理论
（1）定态假设原子系统只能处在
一系列不连续的能量状态，在这些
状态中，电子虽然作加速运动，但
● 玻尔理论仍然以经典理论为基础，定态假设又和经典理论相抵触。
● 量子化条件的引进没有适当的理论解释。 ● 对谱线的强度、宽度、偏振等无法处理。
氢原子光谱
例题15-6 在气体放电管中,用能量为12.5eV的电子通过碰撞使氢原子激发,问受激发的原子向低能级跃迁时,能发射那些波长的光谱线?
解：设氢原子全部吸收电子的能量后最高能激发到第n
轨道上绕转的频率。
解按玻尔频率公式有
当很大时绕转频率为
玻尔的氢原子理论
绕转频率为
可见的值和很大时
的值相同。
在量子数很大的情况下，量子理论得到与经典理论一致的结果，这是一个普遍原则，称为对应原理。
玻尔的氢原子理论
绕转频率为
可见的值和很大时
的值相同。
在量子数很大的情况下，量子理论得到与经典理论一致的结果，这是一个普遍原则，称为对应原理。
ห้องสมุดไป่ตู้
并不辐射电磁波，这些状态称为原
子的稳定状态（简称定态），相应
的能量分别为
。
玻尔
（2）频率条件当原子从一个能量为的定态跃迁到另一能量为的定态时，就要发射或吸收一个频率为的光子。
玻尔频率公式
玻尔的氢原子理论
（3）量子化条件在电子绕核作圆周运动中，其稳定状态必须满足电子的角动量等于的整数倍的条件。

第二章玻尔氢原子理论

第二章原子的能级和辐射一、学习要点：1.氢原子光谱：线状谱、五个线系（记住名称、顺序）、广义巴尔末公式)11(~22nm R -=ν、光谱项()2nR n T =、并合原则：)()(~n T m T -=ν 2.玻尔氢原子理论：(1)玻尔三条基本假设的实验基础和内容（记熟）(2)圆轨道理论（会推导）：氢原子中假设原子核静止，电子绕核作匀速率圆周运动02200202220A 529,04,Z Z 4≈===e m a n a n e m r e e n πεπε;13714,Z Z 40202≈===c e n c n e c e n πεααπευ； ()n hcT n hc R n e m E e n --=-=∞22224220Z 2Z )41( πε，n ＝１.2.3……(3)实验验证：（a ）氢原子五个线系的形成)11(Z ~,)4(222232042n m R c h e m R e -==∞∞νπεπ (会推导）非量子化轨道跃迁 )(212n E E mv h -+=∞ν （b ）夫－赫实验：装置、.结果及分析；原子的电离电势、激发电势3.类氢离子（+++Li ,He ,正电子偶素.-μ原子等） (1) He +光谱:毕克林系的发现、波数公式、与氢原子巴耳末系的异同等(2)理论处理（会推导）：计及原子核的运动，电子和原子核绕共同质心作匀速率圆周运动e e m M m M +⋅=μ, 正负电荷中心之距Ze n r n 22204μπε =. 能量2242202Z )41(n e E n μπε-=，里德伯常数变化Mm R R e A +=∞11 重氢（氘）的发现4.椭圆轨道理论索末菲量子化条件q q n h n pdq ,⎰=为整数a n nb n e m a n e m E n p e n ϕϕϕπεπε==-==,Z 4,2Z )41(,2220224220 ，n n n ,,3,2,1;,3,2,1 ==ϕn 一定，n E 一定，长半轴一定，有n 个短半轴，有n 个椭圆轨道（状态），即n E 为n 度简并。

8.4.2 玻尔的氢原子理论

玻尔的氢原子理论

氢原子的能级与光谱.

波尔的氢原子理论.ppt

玻尔的氢原子理论

高二物理竞赛波尔的氢原子理论PPT(课件)

氢原子的玻尔理论

波尔的氢原子理论

波尔的氢原子理论

氢原子的玻尔理论 波粒二象性

8.4.2 玻尔的氢原子理论

2.3 玻尔的氢原子理论

玻尔的氢原子理论

第二章 玻尔氢原子理论

氢原子的玻尔理论波粒二象性

第二章玻尔氢原子理论