时间序列试题
金融时间序列分析英文试题(芝加哥大学) (1)

Graduate School of Business,University of ChicagoBusiness41202,Spring Quarter2008,Mr.Ruey S.TsaySolutions to MidtermProblem A:(30pts)Answer briefly the following questions.Each question has two points.1.Describe two methods for choosing a time series model.Answer:Any two of(a)Information criteria such as AIC or BIC,(b)Out-of-sample forecasts,and(c)ACF and PACF of the series.2.Describe two applications of volatility infinance.Answer:Any two of(a)derivative(option)pricing,(b)risk management,(c)portfolio selection or asset allocation.3.Give two applications of seasonal time series models infinance.Answer:(a)Earnings forecasts and(b)weather-related derivative pricing or risk man-agement.4.Describe two weaknesses of the ARCH models in modelling stock volatility.Answer:Any two of(a)symmetric response to past positive and negative shocks,(b)restrictive,(c)Not adaptive,and(d)provides no explanation about the source ofvolatility clustering.5.Give two empirical characteristics of daily stock returns.Answer:any two of(a)heavy tails,(b)non-Gaussian distribution,(c)volatility clus-tering.6.The daily simple returns of Stock A for the last week were0.02,0.01,-0.005,-0.01,and0.025,respectively.What is the weekly log return of the stock last week?What is theweekly simple return of the stock last week?Answer:Weekly log return is0.03938;weekly simple return is0.04017.7.Suppose the closing price of Stock B for the past three trading days were$100,$120,and$100,respectively.What is the arithmetic mean of the simple return of the stock for the past three days?What is the geometric average of the simple return of the stockfor the past three days? Answer:Arithmetic mean=12120−100100+100−120120=0.017.and the geometric mean is120×100−1=0.8.Consider the AR(1)model r t=0.02+0.8r t−1+a t,where the shock a t is normally distrib-uted with mean zero and variance1.What are the variance and lag-1autocorrelation function of r t?Answer:Var(r t)=11−0.82=2.78and the lag-1ACF is0.8.19.For problems6and7,suppose the daily return r t,in percentages,of Stock A followsthe model r t=1.0+a t+0.3a t−1,where a t=σt t withσ2t =1.0+0.4a2t−1and t beingstandard normal.What is the unconditional variance of a t?What is the variance of r t?Answer:Var(a t)=11−0.4=1.67.Var(r t)=(1+0.32)σ2a=1.82.10.Suppose that a n=3.0,what is the1-step ahead forecast for r n+1at the forecast originn?What is the1-step ahead volatility forecast of r t at the forecast origin n?Answer:r n(1)=1+0.3a n=1.9,andσ2n (1)=1+0.4a2n=4.6.11.Consider the simple AR(1)model r t=100+0.8r t−1+a t,where a t is normally distributedwith mean zero and variance10.Is the r t series mean-reverting?If yes,what is the half-life of the series?Answer:Yes,r t series is mean-reverting.The half-life is ln(0.5)/ln(0.8)=3.11.12.Describe two test statistics for testing the ARCH effect of an asset return series.Writedown the associated null hypotheses.Answer:(a)The Ljung-Box statistic Q(m)of the squared shocks,i.e.a2t .The nullhypothesis is H o:ρ1=ρ2=···=ρm=0,whereρi is the lag-i ACF of a2t .(b)TheEngle F-test for the regression a2t =β0+β1a2t−1+···+βm a2t−m+e t.The null hypothesisis H o:β1=β2=···=βm=0.13.Consider the following two IGARCH(1,1)models for percentage log returns:Model A:σ2t =1.0+0.1a2t−1+0.9σ2t−1Model B:σ2t =0.1a2t−1+0.9σ2t−1.Suppose thatσ2100=20and a100=−2.0.What are the3-step ahead volatility forecastsfor Models A and B?Answer:For model A:3-step ahead volatility forecast isσ2100(3)=2+(1.0+0.1×(−2.0)2+0.9×20)=21.4.For model B,the3-step ahead volatility forecast isσ2100(3)=0.1(−2.0)2+0.9×20=18.4.14.Consider the following two models for the log price of an asset:Model A:p t=p t−1+a tModel B:p t=0.00001+p t−1+a twhere the shock a t is normally distributed with mean zero and varianceσ2>0.Suppose further that p100=5.Let p n( )be the -step ahead forecast at the forecast origin n.What are the point forecasts p100( )for both models as →∞?Answer:For model A,p100( )=5for all .For model B,p100( )converges to infinity as →∞.215.Suppose that we have T =1000daily log returns for the Decile 1portfolio.Supposefurther that the sample autocorrelation at lag-12is ˆρ12=0.15.Test the hypothesis H o :ρ12=0against the alternative hypothesis H a :ρ12=pute the test statistic and draw your conclusion.Answer :t =0.151/√1000=√1000×0.15=4.74,which is highly significant.Thus,the lag-12ACF is not zero.Problem B .(20pts)It is well-known in economics that growth rate of the domestic gross product (GDP)is negatively correlated with the change in unemployment rate.Consider the U.S.quarterly real GDP and unemployment rate from the first quarter of 1948to the first quarter of 2008.Let dgdp t be the growth rate of the GDP,i.e.dgdp t =ln(GDP t )−ln(GDP t −1),and dun t be the change in unempolyment rate,i.e.dun t =U t −U t −1with U t being the civilian unemployment rate.The data were seasonally adjusted and obtained from the Federal Reserve Bank at St.Louis.The sample size after the differencing is e the attached R output to answer the following questions.1.(5points)Write down the fitted linear regression model with dgdp t and dun t representing the dependent and independent variable,respectively,including residual standard error.What is the R 2of the linear regression?Is the fitted model adequate?Why?Answer :The fitted linear regression isdgdp t =0.017−0.017dun t +e t ,ˆσe =0.0088.The R 2is 0.37.The model is not adequate because the Q (m )statistics of the residuals show that the residuals have serial correlations,i.e.Q (12)=219.4with p-value close to zero.2.(5points)To take care of the serial correlations in the residuals,a linear regression model with time-series errors is built for the two variables.Write down the fitted model,including the residual variance.Answer :The fitted linear regression model with time-series errors is(1−0.21B −0.12B 2)(1−0.86B 4)(dgdp t −0.017+0.018dun t )=(1−0.72B 4)a t ,ˆσ2a =6.01×10−5.3.(2points)Is the model in Question 2adequate?Why?Answer :Yes,the model is adequate.The Q (m )statistics of the residuals fail to indicate the existence of any serial correlations.We have Q (12)=17.53with p-value 0.13.4.(4points)Based on the fitted model in Question 2,is the growth rate of GDP negatively correlated with the change in unempolyment rate?Why?Answer :Yes,the growth rate of GDP is negatively related to the change in unemploy-ment rate.The estimated coefficient is −0.018which is highly significant,because it standard error 0.0014is small,resulting in a large t -ratio.35.(4points)To check the predictive power of the model,it was re-estimated using thefirst236data points.This re-fitted model is used to produce1-step to4-step ahead forecasts at the forecast origin t=236.The actual value of the GDP growth rates are also given.Construct the1-step ahead95%interval forecast of the model.Is the actual growth rate in the forecasting interval?Answer:The95%interval forecast is0.012±1.96×0.0077,i.e.[−0.0031,0.027].The actual value is0.0159,which is in the interval.Problem C.(16pts)Consider the quarterly earnings per share of the Microsoft stock from thefirst quarter of1992to thefirst quarter of2008.The data were obtained from First Call. To take the log transformation,we add0.5to all data points.The R output is attached. Let x t=ln(y t+0.5)be the transformed earnings,where y t is the actual earnings per share.1.(5points)Write down thefitted model for x t,including the variance of the residuals.Answer:Thefitted model is(1−B)r t=(1−0.70B+0.39B2)(1+0.39B4)a t,ˆσ2a=0.0016, where r t=ln(x t+0.5)with x t being the earnings per share.2.(2points)Is there any significant serial correlation in the residuals of thefitted model?Why?Answer:No,the Q(m)statistics of the residuals give Q(12)=9.65with p-value0.65.3.(4points)Let T=65be the forecast origin,where T is the sample size.Based on thefitted model,and,for simplicity,use the relationship y t=exp(x t)−0.5,what are the 1-step and2-step ahead forecasts of earnings per share for the Microsoft stock?Answer:The1-step and2-step earnings forecasts are0.56and0.54,respectively.4.(2points)Test the null hypothesis H o:θ4=0vs H a:θ4=0.What is the test statistic?Draw your conclusion.Answer:The test statistic is t=0.39120.1442=2.71with two-sided p-value0.0067.Thus,the seasonal MA coefficientθ4is significantly different from zero.5.(3points)Consider the regular(i.e.,non-seasonal)part of the MA model.Is it invertible?Why?Answer:Yes,it is invertible,because the polynomial1−0.6953x+0.3889x2has roots0.89±1.33i so that the absolute value of the roots(Mod in R)is1.6,which is greaterthan1.[If you compute the roots of x2−0.6953x+0.3889,the the absolute value of the roots is less than1.]Problem D.(34pts)Consider the daily log returns of the Starbucks stock,in percentages, from January1993to December2007.The relevant R output is attached.Answer the following questions.41.(2points)Is the mean log return significant different from zero?Why?Answer:No,the basic statistics show the95%confidence interval of the mean is [−0.0103,0.1624],which contains zero.2.(2points)Is there any serial correlation in the log return series?Why?Answer:Yes,the Q(m)statistics show Q(15)=38.39with p-value0.0008.3.(2points)An MA model is used to handle the mean equation,which appears to beadequate.Is there any ARCH effect in the return series?Why?Answer:Yes,because the Q(m)statistics of the squared residuals show Q(15)=112.61 with p-value close to zero.4.(6points)A GARCH(1,1)model with Student-t distribution is used for the volatilityequation.Write down thefitted model,including the degrees of freedom of the Student-t innovations and mean equation.Answer:Thefitted model isr t=0.037+a t−0.043a t−1−0.048a t−2,a t=σt t, ∼t5.27.σ2 t =0.012+0.026a2t−1+0.973σ2t−1.5.(4points)Since the constant term of the GARCH(1,1)model is not significantly differentfrom zero at the1%level,an IGARCH(1,1)model is used.Write down thefitted IGARCH(1,1)model,including the mean equation.Answer:Thefitted IGARCH(1,1)model isr t=0.077+a t−0.029a t−1−0.044a t−2,a t=σt t, t∼N(0,1).σ2 t =0.022a2t−1+0.978σ2t−1.6.(3points)Is the IGARCH(1,1)model adequate?Why?What is the3-step aheadvolatility forecast with the last data point as the forecast origin?Answer:Yes,the Q(m)statistics for the standardized residuals give Q(10)=1.77, Q(15)=10.79,and Q(20)=18.66.The p-values of these statistics are all greater than0.05.In addition,the Q(m)statistics of the squared standardized residuals also havelarge p-values.The3-step ahead volatility forecast is √3.779=1.94.7.(5points)A GJR(or TGARCH)model with Student-t distribution is alsofitted to thelog return series.Write down thefitted model,including the mean equation and all parameters.Answer:Thwfitted GJR model isr t=0.032+a t−0.043a t−1−0.048a t−2,a t=σt t, t∼t5.31.σ2 t =0.015+(0.021+0.017N t−1)a2t−1+0.970σ2t−1,where N t−1=0if a t−1≥0and=1,otherwise.58.(2points)Is the fitted GJR (or TGARCH)model adequate?Why?Answer :Yes,the Q (m )statistics of the standardized residuals and those of the squred standardized residuals all have large p-values.9.(2points)Among the GARCH(1,1),IGARCH(1,1)and GJR(1,1)models,which one is preferred?Why?Answer :The GJR(1,1)model because it has the smallest AIC value.10.(2points)Is the leverage effect of the GJR model significant?Why?Answer :Yes,the t -ratio of the leverage parameter is 2.01,which is significant at the 5%level.11.(4points)To better understand the leverage effect,use the fitted GJR to calculate theratio σ2t (a t −1=−5.10)σ2t(a t −1=5.10),assuming σ2t −1=7.5.Answer :σ2t (a t −1=−5.10)σ2t (a t −1=5.10)=0.0154+0.0379×(−5.10)2+0.97×7.50.0154+0.0208×(5.10)2+0.97×7.5=1.057.6。
[财经类试卷]统计从业资格统计基础知识与统计实务(时间序列)模拟试卷2及答案与解析
![[财经类试卷]统计从业资格统计基础知识与统计实务(时间序列)模拟试卷2及答案与解析](https://img.taocdn.com/s3/m/63c32f6ce45c3b3567ec8bd6.png)
6【正确答案】D
【试题解析】当时间序列中所包含的总量指标都是反映社会经济现象在某一瞬间上所达到的水平时,这种总量指标时间序列就称为时点序列。2011~2015年某银行的年末存款余额是时点序列,可根据间隔时间相等的间断时点序列的计算方法计算各年平均存款余额,此方法为首末折半法(简单序时平均法)。
【知识模块】时间序列
2【正确答案】A
【试题解析】这是时期相等的平均指标时间序列,可直接采用简单算术平均法来计算,所以,二季度该网站的月平均员工人数= =80(人)。
【知识模块】时间序列
3【正确答案】A
【试题解析】这属于根据间隔相等的间断时点序列求序时平均数,因此应采用“首末折半法”,用公式表示如下: 代入数据即得A项。
(A)甲;丙
(B)乙;丙
(C)甲;乙
(D)乙;丁
7累计增长量等于相应的各个逐期增长量( )。
(A)之差
(B)之商
(C)之和
(D)之积
8已知前五年的平均增长速度10%,后五年的平均增长速度为8%,求这10年的平均增长速度,下列计算方法正确的是( )。
9环比增长速度是( )。
(A)报告期观察值与前一时期观察值之比减1
【知识模块】时间序列
4【正确答案】C
【试题解析】A项是时期序列序时平均数的计算公式;B项是间隔相等的间断时点序列的序时平均数的计算公式;D项是分组资料的连续时点序列序时平均数的计算公式。
【知识模块】时间序列
5【正确答案】D
【试题解析】A项是由时期序列计算序时平均数的计算公式;C项是由间隔不等的间断时点序列计算序时平均数的计算公式。
【知识模块】时间序列
20【正确答案】B,C
【试题解析】逐期增长量与累计增长量的关系是:①逐期增长量之和等于累计增长量,即(a1-a0)+(a2-a1)+(a3-a2)+…+(an-an-1)=an-a0;②相邻的累计增长量两两相减之差值为逐期增长量,即(an-a0)-(an-1-a0)=an-an-1。
时间序列分析试题(卷)与答案解析

时间序列分析试卷1一、 填空题(每小题2分,共计20分)1. ARMA(p, q)模型_________________________________,其中模型参数为____________________。
2. 设时间序列{}t X ,则其一阶差分为_________________________。
3. 设ARMA (2, 1):1210.50.40.3t t t t t X X X εε---=++-则所对应的特征方程为_______________________。
4. 对于一阶自回归模型AR(1): 110t t t X X φε-=++,其特征根为_________,平稳域是_______________________。
5. 设ARMA(2, 1):1210.50.1t t t t t X X aX εε---=++-,当a 满足_________时,模型平稳。
6. 对于一阶自回归模型MA(1):10.3t t t X εε-=-,其自相关函数为______________________。
7. 对于二阶自回归模型AR(2):120.50.2t t t t X X X ε--=++则模型所满足的Yule-Walker 方程是______________________。
8. 设时间序列{}t X 为来自ARMA(p,q)模型:1111t t p t p t t q t q X X X φφεθεθε----=++++++则预测方差为___________________。
9. 对于时间序列{}t X ,如果___________________,则()~t X I d 。
10. 设时间序列{}t X 为来自GARCH(p ,q)模型,则其模型结构可写为_____________。
二、(10分)设时间序列{}t X 来自()2,1ARMA 过程,满足()()210.510.4ttB B X B ε-+=+,其中{}t ε是白噪声序列,并且()()2t t 0,E Var εεσ==。
统计基础知识与统计实务:时间序列试题预测(题库版)

统计基础知识与统计实务:时间序列试题预测(题库版)1、判断题发展水平是计算其他动态分析指标的基础,它只能用总量指标来表示。
()正确答案:错2、多选时期数列的特点有()。
A.数列中的各个指标值不能相加B.数列中的(江南博哥)各个指标值可以相加C.每个指标值的大小与时间长短无关D.每个指标值的大小与时期长短有关E.每个指标值通过连续不断登记取得正确答案:B, D, E参考解析:时期数列的特点主要有:①数列中每个指标数值可以相加,其和表示现象在更长时期内的发展总量;②数列中每个指标数值的大小与其时期长短有直接联系。
一般地,时期愈长,指标数值就愈大,反之就愈小;③数列中的每个指标数值,通常是通过连续不断地登记而取得的。
AC两项属于时点数列的特点。
3、单选?2007年到2013年某国社会经济发展基本资料如下,利用以上所给资料,完成下列题目:计算上述平均发展速度时使用的方法是()。
A.水平法B.累计法C.叠加法D.换算法正确答案:A4、单选设(甲)代表时期数列;(乙)代表时点数列;(丙)代表加权算术平均数;(丁)代表“首尾折半法”序时平均数。
现已知2005~2009年某银行的年末存款余额,要求计算各年平均存款余额,则该数列属于____,应采用的计算方法是____。
()A.甲;丙B.乙;丙C.甲;乙D.乙;丁正确答案:D参考解析:当时间数列中所包含的总量指标都是反映社会经济现象在某一瞬间上所达到的水平时,这种总量指标时间数列就称为时点数列。
2005~2009年某银行的年末存款余额是时点数列,可根据间隔时间相等的间断时点序列的计算方法计算各年平均存款余额,此方法为首尾折半法(简单序时平均法)。
5、单选设(甲)代表时期序列;(乙)代表时点序列;(丙)代表加权算术平均数;(丁)代表"首末折半法"序时平均数。
现已知2010~2014年某银行的年末存款余额,要求计算各年平均存款余额,则该序列属于__________,应采用的计算方法是_________。
时间序列分析试题

第九章 时间序列分析一、单项选择题1、乘法模型是分析时间序列最常用的理论模型。
这种模型将时间序列按构成分解为( ) 等四种成分,各种成分之间( ),要测定某种成分的变动,只须从原时间序列中( )。
A. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;除去其他影响成分的变动D.长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;除去其他影响成分的变动答案:C2、加法模型是分析时间序列的一种理论模型。
这种模型将时间序列按构成分解为( )等四种成分,各种成分之间( ),要测定某种成分的变动,只须从原时间序列中( )。
A. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;除去其他影响成分的变动D.. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;除去其他影响成分的变动答案:B3、利用最小二乘法求解趋势方程最基本的数学要求是( )。
A.∑=-任意值2)ˆ(t Y Y B. ∑=-min )ˆ(2t Y Y C. ∑=-max )ˆ(2t Y Y D. 0)ˆ(2∑=-t Y Y 答案:B4、从下列趋势方程t Y t86.0125ˆ-=可以得出( )。
A. 时间每增加一个单位,Y 增加0.86个单位B. 时间每增加一个单位,Y 减少0.86个单位C. 时间每增加一个单位,Y 平均增加0.86个单位D. 时间每增加一个单位,Y 平均减少0.86个单位答案:D.5、时间序列中的发展水平( )。
《统计学考研题库》【章节题库+名校考研真题+模拟试题】时间序列分析【圣才出品】

第13章时间序列分析和预测一、单项选择题1.五月份的商品销售额为60万元,该月的季节指数为120%,则消除季节因素影响后,该月的商品销售额为()万元。
[对外经济贸易大学2015研]A.72B.50C.60D.51.2【答案】B【解析】消除季节因素影响后的商品销售额=该月商品实际销售额/该月季节指数=60/120%=50(万元)。
2.毛衣销售量时间数列分析中,如果第3季的季节指数大于100%,表明该季毛衣销售量()。
[四川大学2013研]A.不受季节影响B.受季节因素影响C.属于旺季D.属于淡季【答案】C【解析】季节指数=同季的平均数/历年各季总的平均数。
故若季节指数大于100%,表示该季度的销售量超过平均水平,故为销售旺季。
3.如果时间序列的逐期观察值按几何级数递增或递减,则适合的预测模型是()。
[四川大学2013研]A.移动平均模型B.线性模型C.指数模型D.抛物线模型【答案】C【解析】时间序列的观察值按几何级数变化,说明变化幅度很大,并非线性变化情况,适合用指数模型进行拟合。
4.时间数列分析中,移动平均法只能用于修匀的数列是()。
[四川大学2013研] A.时期数数列B.时点数数列C.空间数列D.静态数列【答案】A【解析】移动平均法适用于近期预测。
当产品需求既不快速增长也不快速下降,且不存在季节性因素时,移动平均法能有效地消除预测中的随机波动,因此可以用于修匀时期数列。
5.不存在趋势的序列称为()。
A.平稳序列B.周期性序列C.季节性序列D.非平稳序列【答案】A【解析】时间序列可以分为平稳序列和非平稳序列两大类。
其中平稳序列是指基本上不存在趋势的序列;非平稳序列是指包含趋势、季节性或周期性的序列,它可能只含有其中一种成分,也可能是几种成分的组合。
6.时间序列在长时期内呈现出来的某种持续向上或持续下降的变动称为()。
A.趋势B.季节性C.周期性D.随机性【答案】A【解析】趋势是指时间序列在长期内呈现出来的某种持续上升或持续下降的变动,也称长期趋势;时间序列中的趋势可以是线性的,也可以是非线性的。
第五章-时间序列练习试题

28.计算序时平均数的方法有( )。
a、简单算术平均法b、加权算术平均法c、简单序时平均法d、加权序时平均法
29.当时间序列中的指标数值存在负数时,不易采用水平法计算平均发展速度,因为计算结果( )。
a、可能为负数b、必须为负数c、可能为虚数d、等于零、
15.说明现象在较长时期内发展的总速度的数值是()。
a、环比发展速度b、平均发展速度c、定基增长速度d、定基发展速度
16.某地区2003-2007年年底生猪存栏头数在2002的基础上分别增加20、30、40、30和50万头,则5年间平均生猪增长量()。
a、10万头b、34万头c、6万头d、13万头
17.已知环比增长速度为8.12%、3.42%、2.91%、5.13%,则定基增长速度为()。
5.时点序列的每一项指标值反映现象在某一段时期达到的水平。
6.时点序列的每一项指标数值的大小和它在时间间隔上的长短没有直接关系。
a、发展速度与1之差
b、扣除基数之后的发展速度
c、报告期比基期水平增长的相对程度
d、报告期比基期水平之差同基期水平之比
12.定基增长速度等于()。
a、累计增长量除以基期水平b、环比增长速度的连乘积
c、环比发展速度的连乘积减1d、定基发展速度减1
13.水平法计算的平均发展速度是一种()。
a、算术平均数b、几何平均数c、序时平均数d、动态平均数
26.编制时间序列应遵循的原则包括( )。
a、指标数值所属的总体范围应该一致b、指标的经济涵义应该相同
c、指标数值的计算方法应该一致d、指标数值的计算价格应该一致
27.时点序列的特点主要有( )。
a、数列中每个指标数值不能相加b、数列中每个指标数值可以相加
2022年初级统计基础知识章节试题及答案之第五章时间序列分析含答案

2022年初级统计基础知识章节试题及答案之第五章时间序列分析含答案2022年初级统计基础学问章节试题及答案之第五章时光序列分析含答案第五章时光序列分析一、单项挑选题1.构成时光数列的两个基本要素是(C) (2022年1月)A.主词和宾词B.变量和次数C.现象所属的时光及其统计指标数值D.时光和次数2.某地区历年诞生人口数是一个(B) (2022年10月)A.时期数列B.时点数列C.分配数列D.平均数数列3.某商场销售洗衣机,2022年共销售6000台,年底库存50台,这两个指标是( C ) (2022年10)A.时期指标B.时点指标C.前者是时期指标,后者是时点指标D.前者是时点指标,后者是时期指标4.累计增长量( A ) (2022年10)A.等于逐期增长量之和B.等于逐期增长量之积C.等于逐期增长量之差D.与逐期增长量没有关系5.某企业银行存款余额4月初为80万元,5月初为150万元,6月初为210万元,7月初为160万元,则该企业其次季度的平均存款余额为( C )(2022年10)A.140万元B.150万元C.160万元D.170万元6.下列指标中属于时点指标的是( A ) (2022年10)A.商品库存量B.商品销售量C.平均每人销售额D.商品销售额7.时光数列中,各项指标数值可以相加的是( A ) (2022年10)A.时期数列B.相对数时光数列C.平均数时光数列D.时点数列8.时期数列中各项指标数值( A )(2022年1月)A.可以相加B.不行以相加C.绝大部分可以相加D.绝大部分不行以相加10.某校同学人数2022年比2022年增长了8%,2022年比2022年增长了15%,2022年比2022年增长了18%,则2022-2022年同学人数共增长了( D )(2022年10月)A.8%+15%+18%B.8%×15%×18%C.(108%+115%+118%)-1D.108%×115%×118%-1二、多项挑选题1.将不同时期的进展水平加以平均而得到的平均数称为(ABD) (2022年1月)A.序时平均数B.动态平均数C.静态平均数D.平均进展水平E.普通平均数2.定基进展速度和环比进展速度的关系是(BD) (2022年10月)A.相邻两个环比进展速度之商等于相应的定基进展速度B.环比进展速度的连乘积等于定基进展速度C.定基进展速度的连乘积等于环比进展速度D.相邻两个定基进展速度之商等于相应的环比进展速度E.以上都对3.常用的测定与分析长久趋势的办法有( ABC ) (2022年1月)A.时距扩大法B.移动平均法C.最小平办法D.几何平均法E.首末折半法4.时点数列的特点有( BCD ) (2022年10)A.数列中各个指标数值可以相加B.数列中各个指标数值不具有可加性C.指标数值是通过一次记下取得的D.指标数值的大小与时期长短没有直接的联系E.指标数值是通过延续不断的记下取得的5.增长1%的肯定值等于( AC )(2022年1)A.增强一个百分点所增强的肯定量B.增强一个百分点所增强的相对量C.前期水平除以100D.后期水平乘以1%E.环比增长量除以100再除以环比进展速度6.计算平均进展速度常用的办法有( AC )(2022年10)A.几何平均法(水平法)B.调和平均法C.方程式法(累计法)D.容易算术平均法E.加权算术平均法7.增长速度( ADE )(2022年1月)A.等于增长量与基期水平之比B.逐期增长量与报告期水平之比C.累计增长量与前一期水平之比D.等于进展速度-1E.包括环比增长速度和定基增长速度8.序时平均数是( CE )(2022年10月)A.反映总体各单位标志值的普通水平B.按照同一时期标志总量和单位总量计算C.说明某一现象的数值在不同时光上的普通水平D.由变量数列计算E.由动态数列计算三、推断题1.职工人数、产量、产值、商品库存额、工资总额指标都属于时点指标。
(整理)时间序列分析试题

B.大于100%表示各月(季)水平比全期平均水平高,现象处于旺季
C.小于100%表示各月(季)水平比全期水平低,现象处于淡季
D.小于100%表示各月(季)水平比全期平均水平低,现象处于淡季
E.等于100%表示无季节变化
答案:BD.E
12、循环变动指数C%()。
3月
4月
5月
6月
7月
月初应收账款余额
(万元)
690
850
930
915
890
968
1020
则该企业2005年上半年平均每个月的应收账款余额为()。
A.
B.
C.
D.
答案:A
10、采用几何平均法计算平均发展速度时,侧重于考察()。
A.现象的全期水平,它要求实际各期水平等于各期计算水平
B.现象全期水平的总和,它要求实际各期水平之和等于各期计算水平之和
答案:A
14、元宵的销售一般在“元宵节”前后达到旺季,1月份、2月份的季节指数将()。
A.小于100% B.大于100%
C.等于100% D.大于1200%
答案:B
15、空调的销售量一般在夏季前后最多,其主要原因是空调的供求(),可以通过计算()来测定夏季期间空调的销售量高出平时的幅度。
A.受气候变化的影响;循环指数
答案:D.
17、当时间序列的二级增长量大体相同时,适宜拟合()。
A.抛物线B.指数曲线
C.直线D.对数曲线
答案:A
18、国家统计局2005年2月28日公告,经初步核算,2004年我国的国内生产总值按可比价格计算比上年增长9.5%。这个指标是一个()。
时间序列练习题

时间序列练习题时间序列分析是一种用于研究以时间为顺序的数据变动规律的方法。
它可以帮助我们理解和预测未来的趋势,对于决策和规划具有重要的意义。
本文将通过一些时间序列练习题,帮助读者更好地理解和应用时间序列分析。
练习题一:季度销售数据分析某公司的销售数据按照季度记录如下:季度销售额Q1 100Q2 200Q3 300Q4 400请你根据这些数据,进行以下的分析和预测:1. 绘制季度销售额的时间序列图。
2. 计算季度销售额的平均值。
3. 判断季度销售额是否存在趋势性,并进行趋势线的拟合。
4. 判断季度销售额是否存在季节性,如果存在,请进行季节性分解。
5. 使用你认为最适合的模型进行未来一年季度销售额的预测,并给出预测结果。
练习题二:月度股票收益率分析某股票连续12个月的收益率数据如下:月份收益率1 0.032 0.053 -0.024 0.025 -0.016 0.047 -0.038 0.019 0.0210 -0.0511 0.0112 0.03请你根据这些数据,进行以下的分析和预测:1. 绘制月度股票收益率的时间序列图。
2. 计算月度收益率的平均值和标准差。
3. 判断股票收益率是否存在趋势性,并进行趋势线的拟合。
4. 判断股票收益率是否存在季节性,如果存在,请进行季节性分解。
5. 使用你认为最适合的模型进行未来三个月股票收益率的预测,并给出预测结果。
练习题三:年度气温分析某城市过去10年(2011年至2020年)的年度平均气温数据如下:年份平均气温(摄氏度)2011 192012 212013 202014 182015 172016 182017 202018 222019 232020 21请你根据这些数据,进行以下的分析和预测:1. 绘制年度平均气温的时间序列图。
2. 计算年度平均气温的平均值、中位数和极差。
3. 判断气温是否存在趋势性,并进行趋势线的拟合。
4. 判断气温是否存在季节性,如果存在,请进行季节性分解。
南开大学时间序列分析往年期末试题考题
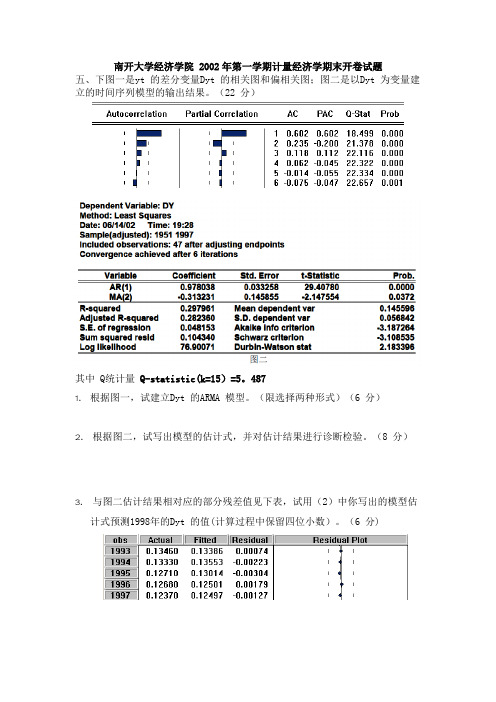
南开大学经济学院 2002年第一学期计量经济学期末开卷试题五、下图一是yt 的差分变量Dyt 的相关图和偏相关图;图二是以Dyt 为变量建立的时间序列模型的输出结果。
(22 分)其中 Q统计量Q-statistic(k=15)=5。
4871.根据图一,试建立Dyt 的ARMA 模型。
(限选择两种形式)(6 分)2.根据图二,试写出模型的估计式,并对估计结果进行诊断检验。
(8 分)3.与图二估计结果相对应的部分残差值见下表,试用(2)中你写出的模型估计式预测1998年的Dyt 的值(计算过程中保留四位小数)。
(6 分)五、(6 分,8 分,6 分)1.由图一的偏相关图和相关图的特点,可知原序列可能是ARIMA(1,1,1);ARIMA(1,1,2)等过程。
2.模型的估计式为:△yt=0.978038△yt—1+ut—0。
313231ut-2 。
此结果可取,因为所有系数都通过了t 检验,并且Q 值非常小(5。
487),远小于Q 检验的临界值χ20.05(15-1-2)=21。
3.利用yt=0。
978038△yt-1+ut-0。
313231ut-2 ,可得:Δy⌢1998 = 0.9780Δy1997 — 0.3132u⌢1996 =0.9780×0.1237-0。
3132×(—0。
0013)=0。
1214。
y⌢1998 = y1997 + Δy⌢1998 =12。
3626+0。
1214=12.48402004年计量经济学试题五、(20 分)图1 是我国1978 年-1999 年的城镇居民消费水平取对数后(记为LPI)的差分变量DLPI 相关图和偏相关图;图2 是以DLPI 为变量建立的时间序列模型的输出结果。
其中Q 统计量Q-statistic(k=12)=11.7351.根据图1,建立DLPI 的ARMA 模型.(限选两种形式)(6 分)2.根据图2,试写出模型的估计式,并对估计结果进行诊断检验.(8 分)3.与图2 估计结果相对应的部分残差值见下表,试用2 中你写出的估计模型预测2000 年DLPI 的值(计算过程保留四位小数)。
时间序列分析试题

2.设时间序列{X t}满足 ARMA(2,1)
(1 − B + 0.5B2 ) Xt = (1 + 0.4B)εt ,
(1)试分析序列{X t}的平稳性,(2)计算前 3 个 Green 函数 G0 、 G1 、 G2 。
(1)此时特征方程为: λ2 − λ + 0.5 = 0 ,特征根满足| λ1,2 |= 2 2 < 1,序列{Xt}平稳。
试给出其特征方程。
X t = 0.5X t −1 + 0.4 X t−2 + εt − 0.3εt−1 ,
λ2 − 0.5λ − 0.4 = 0 。
(4)给出一阶自回归模型 AR(1)
的特征跟和平稳域。
X t = 10 + φX t−1 + εt
特征根为 λ = φ ,平稳域为| φ |< 1。
(5)对于 ARMA(2,1)
5.设时间序列{X t}满足 ARMA(1,1)
X t = 0.5X t −1 + εt − 0.25εt −1 ,
其中 εt ~ WN (0,σ 2 ) ,(1)试求 ρ (1) ;(2)证明{Xt}的自相关系数满足 ρ2 = 0.5ρ1 。
∞
∞
∞
∑ ∑ ∑ 此时 X t = Gkεt −k ,所以 Gkεt−k = 0.5 ε Gk t−1−k + εt − 0.25εt−1 ,比较两端系数有:
X t = εt − 0.3εt−1
γ
(0)
=
EX
2 t
=
E (ε t
−
0.3ε t −1 )(ε t
−
0.3ε t −1 )
=
0.91σ
时间序列作业试题及答案

第六章动态数列-、判斷题若将某地区社会商品库存额按时间先后顺序排列,此种动态数二、1.列属于时期数列。
()定基发展速度反映了现象在一定时期内发展的总速度,环比发三、2.展速度反映了现象比前一期的增长程度。
()平均增长速度不是根据各期环比增长速度直接求得的,而是根四、3.据平均发展速度计算的。
()•用水平法计算的平均发展速度只取决于最初发展水平和最末发五、4展水平,与中间各期发展水平无关。
()平均发展速度是环比发展速度的平均数,也是一种序时平均六、5.数。
()1> X 2、X 3、J 4、V 5. Vo七、单项选择题•根据时期数列计算序时平均数应采用()。
八、1几何平均法 B.加权算术平均法C.简单九、 A.算术平均法 D.首末折半法十、2•下列数列中哪一个属于动态数列()。
十-、 A.学生按学习成绩分组形成的数列 B.工业企业按地区分组形成的数列十二、 C.职工按工资水平高低排列形成的数列 D.出口额按时间先后顺序排列形成的数列十三、3.已知某企业1月、2月、3月、4月的平均职工人数分别为190人、195人、193人和201人。
则该企业一季度的平均职工人数的计算方法为()。
十四、心(190+195+193+201)4B.190+195 + 1933十五.(190/2)+195+193 + (201/2) 、[190/2)+195+193+(201/2)C・D・ ---------------------------------4-1 44.说明现象在较长时期内发展的总速度的指标是()。
A、环比发展速度 B.平均发展速度 C.定基发展速度 D.环比增长速度5•已知各期环比增长速度为2%、5%、8%和7%,则相应的定基增长速度的计算方法为()。
A.(102%X105%X108%X107%) -100%B.102%X105%X108%X107%C.2%X5%X8%X7%D.(2%X5%X8%X7%) -100%6•定基增长速度与环比增长速度的关系是()。
10-11上学期时间序列分析A卷及答案
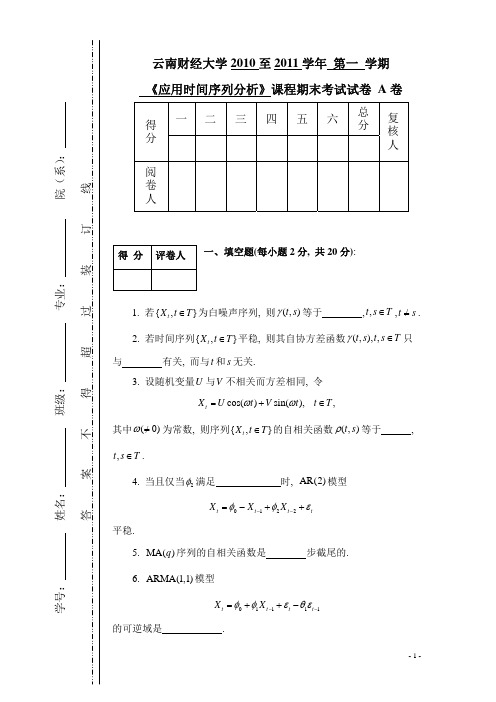
1. 若 { X t , t T } 为白噪声序列, 则 (t , s) 等于 0 , t , s T , t s. 2. 若时间序列 { X t , t T } 平稳, 则其自协方差函数 (t , s ), t , s T 只与 t s 有关, 而
ˆ (l ) 的均方误差为 的 MA(q) 序列, 则已知 X t , X t 1 , X t 2 , 时, X t l 的最佳线性预测 X t
2 (1 12 l21 ) , l 1, , q .
二、选择题(每小题 2 分, 共 20 分):
1. 对于正态序列来说, 其严平稳性与(宽)平稳性是 a a.等价的, b.不等价的.
1.试求模型的传递形式. 2.试求模型的逆转形式. 3.试求满足模型的 ARMA(1,1) 序列 { X t , t 0, 1, 2,} 的均值和自协方差函数.
-3-
-4-
得 分
评卷人
四、计算题(每小题 5 分, 共 15 分) 设 { X t , t 0, 1, 2,} 是满足 AR(2) 模型
.
2. 为了度量序列中两个随机变量之间真实的相关程度, 应该使用 b . a.自相关函数, b.偏相关函数. .
3. 平稳序列的偏相关函数 p 步截尾是其为 AR( p) 序列的 b a.充分条件, 4. 若一序列严平稳, 则其 a.一定, b b.充要条件.
是(宽)平稳的.
b.不一定. .
5. 满足平稳 ARMA 模型的 ARMA 序列有 a a.一个, b.无穷多个. .
中, 用白噪声序列 { t , t 0, 1, 2,} 线性地表示 ARMA( p, q) 序列称为模型的 a
河南大学统计学专业大二2019-2020时间序列分析测试题

河南大学统计学专业大二2019-2020时间序列分析测试题一、单选题1. 我国国内生产总值2018年为900309亿元,2019年为990865亿元,则国内生产总值2019年环比发展速度为多少? [单选题] *A、10.05%B、90.86%C、110.06(正确答案)D、9.14%答案解析:正确答案:C本题考核环比发展速度=报告期水平/基期水平=990865/900309*100%=110.06%2. 以下关于统计的说法中,错误的是()。
[单选题] *A、统计学是关于收集、整理、分析数据和从数据中得出结论的科学B、描述统计和推断统计的作用是能分开发挥统计作用的(正确答案)C、参数估计是利用样本信息推断总体特征D、描述统计的内容包括如何用图表或数学方法对数据进行整理和展示答案解析:本题考查统计学。
描述统计和推断统计可以一起发挥作用。
3. 下列统计处理中,属于推断统计的是()。
[单选题] *A、利用抽样调查数据估计城镇居民人均消费支出水平(正确答案)B、利用统计图表展示GDP的变化C、利用增长率描述人均可支配收入的基本走势D、利用统计表描述公司员工年龄分布答案解析:本题考查推断统计。
推断统计是研究如何利用样本数据来推断总体特征的统计学方法,其内容包括参数估计和假设检验两大类。
参数估计是利用样本信息推断总体特征;假设检验是利用样本信息判断对总体的假设是否成立。
选项A属于参数估计。
4. 某厂连续性生产电脑,为检验产品的质量,按每隔2小时取下20分钟生产的电脑,并做全部产品检验,这是属于()。
[单选题] *A、简单随机抽样B、等距抽样(正确答案)C、分层抽样D、整群抽样、答案解析:本题考查等距抽样。
最简单的系统抽样是等距抽样,即将总体N个单位按直线排列,根据样本量n确定抽取间隔,即抽样=N/n≈k,k为最接近N/n的一个整数。
在1~k范围内随机抽取一个整数i,令位于i位置上的单位为起始单位,往后每间隔K抽取一个单位,直至抽满n。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间序列试题Question 3令,则一阶自回归AR(1)模型变为 Y,X,100ttX,25,0.75X,e,Y,0.75Y,ett,1ttt,1t下面我们考虑一阶自回归AR(1)模型Y,0.75Y,ett,1t(a)(Autocorrelation function,缩写ACF)是信号处理,时间序列分析中常用的数学工具,反映了同一随机过程序列在不同时刻的取值之间的相关程度。
自相关函数在不同的领域,定义不完全等效。
在某些领域,自相关函数等同于自协方差(autocovariance)。
很显然,和 XYtt均为宽平稳过程,而且他们的自相关函数相同,根据宽平稳过程的性质E(Y),0t将两边取方差得, Y,0.75Y,ett,1t2 var(Y),0.75var(Y),var(e),2E(Ye)tt,1tt,1t2 ,0.75var(Y),1t即有对任何 t116 var() Y,,t2710.75,自相关系数(函数)(ACF)为E[(Y,E(Y))(Y,E(Y))]7ttt,kt,k R(k),,E(YY)tt,k16var(Y)var(Y)tt,k 7,[E(0.75YY),E(Ye)]tt,k,1tt,k 16,0.75R(k,1)kk解此方程 R(k),0.75R(k,1),0.75R(0),0.75偏自相关函数(PACF)是指除掉和之间的变量,的影响之YYY,Y?,Ytt,kt,1t,2t,k,1后,和之间的的相关性。
它的一般理论如下,假设,而且与YYE(Y),0tt,kt存在线性关系 Y,Y,?,Yt,1t,2t,kY,,Y,,Y,?,,Y,etk1t,1k2t,2kkt,kt这里为和之间的偏自相关系数。
显然本题目,则偏自相关函,YYY,0.75Y,ekktt,1ttt,k数为0.75,k,1, ,,,kk0,k,1,2T(b)设观察到过程的个实现值,过程的均值的估计,方差的估计及样Y,,t 本自相关系数(SACF)的分别定义为,T,k1,T(y,y)(y,y),tt,kTT,12,121t,ˆ;; y,Tys,T(y,y)R(k),,,tt2s,1,1tt 不妨取白噪声序列为正态白噪声序列,满足,在R软件里取{e}E(e),0,var(e),1ttt50个正态白噪声序列,程序如下: (e,e,?,e)1250>e<-rnorm(50)>e[1] 0.39372962 0.71923504 -0.39633835 0.68734734 0.54495849 -0.03610098 [7] -0.27175537 -0.84724024 1.60362191 1.49819806 -0.89744771 -0.96023499 [13] 1.02345914 0.13897881 -1.42689179 -0.32911015 -0.86611004 -1.00205736 [19] -0.79152793 -0.25384272 -1.200419231.03559849 0.98336315 0.05913430 [25] 0.51604205 1.16218379 -0.79195970 -0.84559260 1.36948942 -0.74758639 [31] -0.54921996 -0.30438707 -1.38690726 -0.52675643 1.07236980 0.31788469 [37] 0.58385993 1.152759880.30538474 0.24037567 -0.92704866 -0.80439131 [43] 2.18074163 1.46075418 0.89336542 0.51008431 2.20940357 -1.49037097 [49] 0.19150916 1.21045063根据,假定,运用R计算出的50个实现值,程序如下: {Y}Y,0.75Y,eY,0tt,1t0t> y<-numeric(length(e))> for (i in 1:50){if(i==1) y[i]<-e[i]}> for (i in 1:50){if (i>=2) y[i]<-0.75*y[i-1]+e[i]}> y[1] 0.393729617 1.014532255 0.364560838 0.960767967 1.265534465 [6] 0.913049869 0.413032029 -0.537466222 1.200522242 2.398589743 [11]0.901494599 -0.284114045 0.810373605 0.746759018 -0.866822523 [16] -0.979227042 -1.600530326 -2.202455108 -2.443369258 -2.086369666 [21] -2.765196478 -1.038298869 0.204638996 0.212613550 0.675502215 [26]1.668810455 0.459648139 -0.500856496 0.993847046 -0.002201101 [31] -0.550870791 -0.717540162 -1.925062381 -1.970553217 -0.405545117 [36]0.013725857 0.594154320 1.598375622 1.504166453 1.368500510 [41]0.099326723 -0.729896271 1.633319431 2.685743757 2.907673240 [46]2.690839243 4.227532999 1.680278779 1.451718243 2.299239310( 图1)SACF具体计算值如下 {R(k),k,0,1,2,?,49}>acf49<-numeric(49)> for (i in 1:49){acf49[i]<-sum((y[1:(50-i)]-mean(y))*(y[(i+1):50]-mean(y)))/(50*var(y))}> acf49[1] 0.733683389 0.516809284 0.436207072 0.243297111 0.075330264[6] 0.036727219 -0.011547759 -0.057582356 -0.024796823 -0.080722612 [11] -0.100487574 -0.037563011 -0.025046003 -0.026552867 -0.010089835 [16] -0.036281883 -0.061887255 -0.046860741 -0.071001290 -0.037538022 [21] -0.020328441 -0.111100541 -0.177312251 -0.200207745 -0.252854974 [26] -0.313359841 -0.309119984 -0.334793004 -0.301049560 -0.214871967 [31] -0.188408240 -0.149026470 -0.014959839 0.060032630 0.041107316 [36] 0.067483577 0.076208127 0.048752599 0.043185351 0.069998325 [41]0.062579193 0.046706145 0.050803559 0.037785997 0.043039007 [46]0.017998498 0.006166831 0.011127531 0.000321865 > acf50<-c(1,acf49) #即为片相关系数向量 (R(0),R(1),R(2),?,R(49))作图(n=50 ,Compare between ACF and SACF)> acf(y,col="red",lag.max=49,main = paste("Compare between ACF and SACF"),ylab="Value of ACF and SACF",xlab="Sample numbers is 50") > x<-c(0:49)> z<-0.75^x> lines(x,z,col="blue")( 图2)作图(n=50 ,Compare between PACF and SPACF)>pacf(y, main = paste(”Compare between PACF andSPACF”), ,ylab="Value of PACFand SPACF",xlab="Sample numbers is 50")>points(0.75,col="red")( 图3)从图2、图3可以看出,当滞后时间较短时,样本值和理论值较接近;当滞后时间较长时,样本值和理论值接近程度不显著。
(c)再取白噪声序列为正态白噪声序列,满足,在R软件{e}E(e),0,var(e),1ttt里取200个正态白噪声序列,程序如下: (e,e,?,e)12200>e<-rnorm(200)根据,假定,运用R计算出的200个实现值,程序如下: {Y}Y,0.75Y,eY,0tt,1t0t> y<-numeric(length(e))> for (i in 1:200){if(i= =1) y[i]<-e[i]} > for (i in 1:200){if (i>=2) y[i]<-0.75*y[i-1]+e[i]}( 图4)SACF具体计算值如下 {R(k),k,0,1,2,?,199}> acf199<-numeric(199)> for (i in 1:199){acf199[i]<-sum((y[1:(200-i)]-mean(y))*(y[(i+1):200]-mean(y)))/(200*var(y))}> acf200<-c(1,acf199)> acf200[1] 1.000000e+00 7.758073e-01 5.574310e-01 3.311680e-01 1.886535e-01[6] 9.893317e-02 6.372159e-02 5.130536e-02 2.869364e-02 -5.535271e-03[11] -6.756406e-02 -1.142857e-01 -1.150994e-01 -8.787237e-02 -5.261252e-02[16] -9.385960e-03 3.017781e-02 7.596401e-02 7.992528e-02 7.807371e-02[21] 7.292218e-02 9.078867e-02 1.070801e-01 8.434350e-02 5.010436e-02[26] 1.742476e-02 1.945792e-02 1.048923e-02 -4.380773e-02 -8.797972e-02[31] -1.141760e-01 -1.475487e-01 -1.882862e-01 -2.107467e-01 -2.279081e-01[36] -2.252218e-01 -2.164270e-01 -1.723217e-01 -1.516489e-01 -1.681924e-01[41] -1.804549e-01 -1.747615e-01 -1.495940e-01 -1.009271e-01 -7.364093e-02[46] -3.298211e-02 -1.417416e-02 2.238403e-02 3.162570e-02 -1.005532e-02[51] -8.967466e-02 -1.298268e-01 -1.485095e-01 -1.350147e-01 -9.857382e-02[56] -4.133492e-02 -1.321048e-02 1.414220e-02 3.738493e-028.285461e-02[61] 1.156862e-01 1.067544e-01 7.230109e-02 3.681177e-02 3.962752e-02[66] 5.787546e-02 3.253175e-02 3.625911e-02 1.544400e-02 1.275714e-02[71] -1.176494e-02 -9.838586e-03 -1.101901e-02 3.438036e-035.454736e-02[76] 9.853935e-02 1.176660e-01 9.063484e-02 8.578439e-02 6.196339e-02[81] 7.491873e-02 1.160443e-01 1.633834e-01 1.806092e-01 1.826588e-01[86] 1.478318e-01 1.205957e-01 6.053857e-02 4.069482e-02 3.832105e-02[91] 4.896761e-02 8.403540e-02 6.501103e-02 2.826300e-02 -1.634707e-02[96] -4.859304e-02 -9.780107e-02 -1.131117e-01 -1.179720e-01 -1.136121e-01 [101] -8.818896e-02 -4.614997e-02 1.084094e-02 7.058121e-02 7.671701e-02 [106] 3.839257e-02 6.483374e-03 -1.997023e-02 -7.759336e-03 -2.125648e-02 [111] -2.471079e-02 -2.999527e-02 -9.818586e-03 1.525473e-02 1.515131e-02 [116] 2.294252e-023.033874e-02 3.137203e-02 1.640767e-02 -6.060163e-03 [121] -2.315985e-02 -4.957008e-02 -7.980755e-02 -1.224426e-01 -1.439007e-01 [126] -1.536572e-01 -1.421728e-01 -1.416751e-01 -1.258753e-01 -7.909291e-02 [131] -3.484736e-02 -4.026233e-031.191162e-022.934825e-02 4.029209e-02 [136]3.170143e-02 1.585109e-02 -4.264769e-03 -3.400631e-035.514384e-03 [141] 1.669093e-02 1.737104e-02 1.207235e-02 -2.902226e-03 -4.162889e-02[146] -8.011810e-02 -1.006647e-01 -9.426404e-02 -7.201321e-02 -4.630009e-02 [151] -1.528971e-03 2.686995e-02 9.682925e-03 -2.813871e-02 -6.419090e-02 [156] -6.824336e-02 -4.577853e-02 -1.382091e-02 1.733518e-02 3.893352e-02 [161]5.945456e-02 4.568102e-02 5.563281e-026.073108e-027.889157e-02 [166] 7.785204e-02 7.402996e-02 5.634031e-02 3.439770e-02 1.586113e-02 [171] -2.116466e-02 -4.213059e-02 -7.350258e-02 -7.913785e-02 -8.800214e-02 [176] -6.814747e-02 -5.525504e-02 -1.213153e-02 1.252033e-02 2.270181e-02 [181] 1.439457e-02 1.317173e-02 1.079476e-02 4.562766e-03 -3.866208e-03 [186] -1.282684e-02 -1.509225e-02 -2.576496e-02 -3.485833e-02 -4.435910e-02 [191] -4.238782e-02 -4.659117e-02 -4.229174e-02 -3.522812e-02 -1.960786e-02 [196] -8.436343e-03 -2.446954e-03 -7.713967e-04 -7.165413e-05 9.560934e-04#即为自相关系数向量 (R(0),R(1),R(2),?,R(200))作图(n=50 ,Compare between ACF and SACF)> acf(y,col="red",lag.max=199,main = paste("Compare between ACF and SACF"),ylab="Value of ACF and SACF",xlab="Sample numbers is 200") > x<-c(0:199)> z<-0.75^x> lines(x,z,col="blue")( 图5)作图(n=200 ,Compare between PACF and SPACF)>pacf(y, main = paste(”Compare between PACF andSPACF”), ,ylab="Value of PACFand SPACF",xlab="Sample numbers is 200")>points(0.75,col="red")(图6)随着样本实现值越多(特别是滞后较短的情形下),样本值与理论值拟合程度越好。
