热工基础 9 第九章 导热
热工基础第二版张学学

(5)对于各向异性物体, 热导率的数值与方向有关 ;
(6)对于同一种物质, 晶体的热导率要大于非定形态物 体的热导率。
热导率数值的影响因素较多, 主要取决于物质的 种类、物质结构与物理状态, 此外温度、密度、湿度 等因素对热导率也有较大的影响。其中温度对热导率 的影响尤为重要。
最剧烈。
温度梯度:等温面法线方向的温度变化率矢量:
gradt t n n
温度梯度是矢量,指 向温度增加的方向。
n—等温面法线方向的单位矢量,指向温度增加的方向。 7
在直角坐标系中,温度梯度可表示为
gradt t i t j t k x y z
t 、t 、t 分别为x、y、z 方向的偏导数; i、j、k 分 x y z 别为x、y、z 方向的单位矢量。
13
3. 热导率(导热系数)
热导率表明物质导热能力的大小。根据傅里叶定
律表达式
q
gradt
绝大多数材料的热导率值都可以通过实验测得。
14
物质的热导率在数值上具有下述特点:
(1) 对于同一种物质, 固态的热导率值最大,气态的热 导率值最小; (2)一般金属的热导率大于非金属的热导率 ;
(3)导电性能好的金属, 其导热性能也好 ;
12
傅里叶定律的适用条件:
(1)傅里叶定律只适用于各
向同性物体。对于各向异性物体, 热流密度矢量的方向不仅与温度
qy
梯度有关,还与热导率的方向性
有关, 因此热流密度矢量与温度 y y
梯度不一定在同一条直线上。
n
qx
q
x
x
(2)傅里叶定律适用于工程技术中的一般稳态和 非稳态导热问题,对于极低温(接近于0K)的导热问 题和极短时间产生极大热流密度的瞬态导热过程, 如 大功率、短脉冲(脉冲宽度可达10-12~10-15s)激光瞬态 加热等, 傅里叶定律不再适用。
2019-清华大学热工基础课件工程热力学加传热学10第九章-导热、稳态导热、非稳态、数值解法-文档资料

(5)对于各向异性物体, 热导率的数值与方向有关 ;
(6)对于同一种物质, 晶体的热导率要大于非定形态物 体的热导率。
热导率数值的影响因素较多, 主要取决于物质的 种类、物质结构与物理状态, 此外温度、密度、湿度 等因素对热导率也有较大的影响。其中温度对热导率 的影响尤为重要。
合金
12~120 W/ /(m·K)
非金属固体
1~40 W/ /(m·K)
液体(非金属) 0.17~0.7 W/ /(m·K)
绝热材料
0.03~0.12 W/ /(m·K)
气体
0.007~0.17 W/ /(m·K)
16
4. 导热问题的数学描述(数学模型)
建立数学模型的目的:求解温度场 tf x,y,z,
内热源的分布规律,给出热物性参数(、、c、a等)的
数值及其特点等。
3)时间条件 说明导热过程时间上的特点, 是稳态导热还是非稳
态导热。对于非稳态导热, 应该给出过程开始时物体内 部的温度分布规律(称为初始条件):
t0 f(x,y,z)
25
4)边界条件
说明导热物体边界上的热状态以及与周围环境之间的 相互作用。例如,边界上的温度、热流密度分布以及边界 与周围环境之间的热量交换情况等。
8
标量形式的傅里叶定律表达式为
q t
n
对于各向同性材料, 各方向上的热导率相等,
qqxiqyjqzk
gradttit jtk x y z
qxt iyt jzt k
qx
t x
qy
t y
qz
t z
由傅里叶定律可知, 要计算导热热流量, 需要知道
材料的热导率, 还必须知道温度场。所以,求解温度场
中国石油大学热工基础典型问题第九章 导热
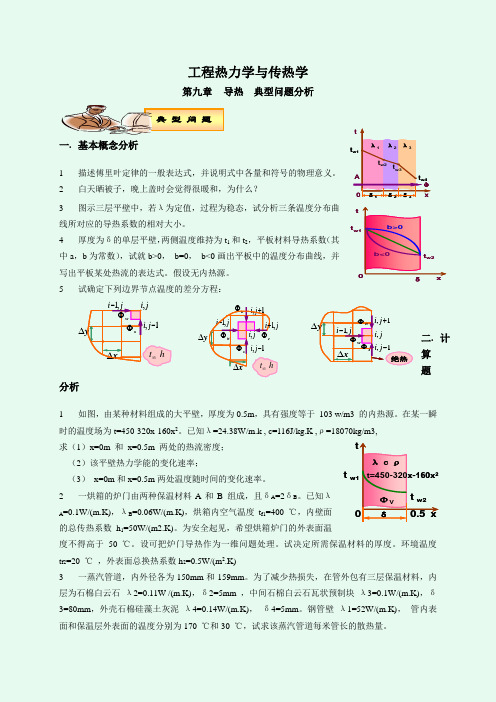
工程热力学与传热学第九章 导热 典型问题分析一. 基本概念分析1 描述傅里叶定律的一般表达式,并说明式中各量和符号的物理意义。
2 白天晒被子,晚上盖时会觉得很暖和,为什么?3图示三层平壁中,若λ为定值,过程为稳态,试分析三条温度分布曲线所对应的导热系数的相对大小。
4厚度为δ的单层平壁,两侧温度维持为t 1和t 2, 平板材料导热系数(其中a ,b 为常数),试就b>0, b=0, b<0画出平板中的温度分布曲线,并写出平板某处热流的表达式。
假设无内热源。
5试确定下列边界节点温度的差分方程:二. 计算题分析1如图,由某种材料组成的大平壁,厚度为0.5m ,具有强度等于 103 w/m3 的内热源。
在某一瞬时的温度场为t=450-320x-160x 2。
已知λ=24.38W/m.k , c=116J/kg.K ,ρ=18070kg/m3, 求(1)x=0m 和 x=0.5m 两处的热流密度; (2)该平壁热力学能的变化速率;(3) x=0m 和x=0.5m 两处温度随时间的变化速率。
2一烘箱的炉门由两种保温材料A 和B 组成,且δA =2δB 。
已知λA =0.1W/(m.K),λB =0.06W/(m.K),烘箱内空气温度t f1=400 ℃,内壁面的总传热系数h 1=50W/(m2.K)。
为安全起见,希望烘箱炉门的外表面温度不得高于50 ℃。
设可把炉门导热作为一维问题处理。
试决定所需保温材料的厚度。
环境温度t f2=20 ℃ ,外表面总换热系数h 2=0.5W/(m 2.K) 3一蒸汽管道,内外径各为150mm 和159mm 。
为了减少热损失,在管外包有三层保温材料,内层为石棉白云石 λ2=0.11W /(m.K),δ2=5mm ,中间石棉白云石瓦状预制块 λ3=0.1W/(m.K),δ3=80mm ,外壳石棉硅藻土灰泥 λ4=0.14W/(m.K), δ4=5mm 。
钢管壁 λ1=52W/(m.K), 管内表面和保温层外表面的温度分别为170 ℃和30 ℃,试求该蒸汽管道每米管长的散热量。
《热工基础及应用》第3版知识点汇总

《热工基础及应用》第3版知识点第一章 热能转换的基本概念本章要求:1.掌握研究热能转换所涉及的基本概念和术语;2.掌握状态参数及可逆过程的体积变化功和热量的计算;3.掌握循环的分类与不同循环的热力学指标。
知识点:1.热力系统:根据研究问题的需要和某种研究目的,人为划定的一定范围内的研究对象称为热力系统,简称热力系或系统。
热力系可以按热力系与外界的物质和能量交换情况进行分类。
2.工质:用来实现能量相互转换的媒介物质称为工质。
3.热力状态:热力系在某瞬时所呈现的宏观物理状态称为热力状态。
对于热力学而言,有意义的是平衡状态。
其实现条件是:0,0,0p T μ∆=∆=∆=。
4. 状态参数和基本状态参数:描述系统状态的宏观物理量称为热力状态参数,简称状态参数。
状态参数可按与系统所含工质多少有关与否分为广延量(尺度量)参数和强度量状态参数;按是否可直接测量可分为基本和非基本状态参数。
5. 准平衡(准静态)过程和可逆过程:准平衡过程是基于对热力过程的描述而提出的。
实现准平衡过程的条件是推动过程进行的不平衡势差要无限小,即0p ∆→,0T ∆→(0μ∆→)。
6、热力循环:为了实现连续的能量转换,就必须实施热力循环,即封闭的热力过程。
热力循环按照不同的方法可以分为:可逆循环和不可逆循环;动力循环(正循环)和制冷(热)循环(逆循环)等。
动力循环的能量利用率的热力指标是热效率:0=t H W Q η;制冷循环能量利用率的热力学指标是制冷系数:L 0=Q W ε。
第二章 热力学第一定律本章要求:1. 深入理解热力学第一定律的实质;2. 熟练掌握热力学第一定律的闭口系统和稳定流动系统的能量方程。
知识点:1. 热力学第一定律:是能量转换与守恒定律在涉及热现象的能量转换过程中的应用。
热力学第一定律揭示了能量在传递和转换过程中数量守恒这一实质。
2. 闭口系统的热力学第一定律表达式,即热力学第一定律基本表达式:Q U W =∆+。
热工基础 (96)

《热工基础》----传热学篇第9章对流传热§9-1对流传热的基本概念第9章对流传热主要内容(1)边界层理论;(2)速度边界层;(3)温度边界层。
9.1.3 边界层边界层(Boundary layer)的概念由德国科学家普朗特于1904年提出。
引入边界层的原因:对流换热热阻大小主要取决于紧靠壁面附近的流体流动状况,此区域中速度与温度变化最剧烈。
流动边界层、热边界层、浓度边界层1.速度边界层(Velocity boundary layer )(1)定义垂直于壁面的方向上流体流速发生显著变化的流体薄层定义为速度边界层(流动边界层)。
xylxdu ∞主流区边界层区(2)速度边界层厚度当速度变化达到u /u ∞=0.99时的空间位置为速度边界层的外边缘,那么从这一点到壁面的距离就是边界层的厚度δ(x )。
【例】空气外掠平板,u ∞=10m/s :d d x mm x mm ====100200 1.8mm; 2.5mm对于低黏度的流体,如水和空气等,在以较大的流速流过固体壁面时,在壁面上流体速度发生显著变化的流体层是非常薄的。
有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)(3)流动边界层内流态随着x 的增大,δ(x )也逐步增大,同时黏性力对流场的控制作用也逐步减弱,从而使边界层内的流动变得紊乱。
把边界层从层流过渡到紊流的x 值称为临界值,记为x c ,其所对应的雷诺数称为临界雷诺数,即c c x u Re ∞=流体平行流过平板的临界雷诺数大约是5=105⨯Re流体在圆管内流动的临界雷诺数大约是2300Re=~10000c形成三层结构的稳定边界层:层流底层+ 缓冲层(过渡层) + 紊流核心2.热边界层(Thermal boundary layer)(1)定义当流体流过平板而平板的温度tw 与来流流体的温度t∞不相等时,在壁面上方也能形成温度发生显著变化的薄层,常称为热边界层。
(2)热边界层厚度当壁面与流体之间的温差达到壁面与来流流体之间的温差的0.99倍时,即(t w -t )/(t w -t oo )=0.99,此位置就是边界层的外边缘,而该点到壁面之间的距离则是热边界层的厚度,记为δt (x )。
热工基础(正式)全

正向运动(膨胀)时,吸 收热源的热量,所作膨胀功除 去用于排斥大气外,全部储存 在飞轮的动能中。
若无摩擦等耗散效应
反向运动(压缩)时,利用飞 轮的动能来推动活塞逆行,压缩工 质所消耗的功恰与膨胀功相等。
同时压缩过程中质向热源所 排热量也恰与膨胀时所吸收的热 量相等。
如果系统经历了一个过程后,系统可沿原过程的路线反 向进行,回复到原状态,不在外界留下任何影响,则该过 程称为可逆过程。
热力学第零定律
如果两个热力学系统中的每一个都与第三个热力学系 统处于热平衡(温度相同),则它们彼此也必定处于热平衡。 这一结论称做《热力学第零定律》。
热力学第零定律表明,一切互为热平衡的系统具有一 个数值上相等的共同的宏观性质──温度。温度计测定物体 温度正是依据这个原理。
热力学第零定律的重要性在于它给出了温度的定义和 温度的测量方法。它为建立温度概念提供了实验基础。
理想气体实际并不存在, 在现实物质中,即使是绝热可 逆过程,系统的熵也在增加, 不过增加的少。
热力学第三定律发现者 德国物理化学家能斯特
三、理想气体的状态方程
kg K
pV mRgT
Pa m3
pv RgT pV nRT p0V0 RT0
1kg n mol 1mol标准状态
气体常数:J/(kg.K) R=mRg=8.3145J/(mol.K)
(2) 特别是在下列技术领域存在传热问题
a 航空航天:高温叶片冷却;空间飞行器重返大气 层冷却;超高音速飞行器(Ma=10)冷却;
b 微电子: 电子芯片冷却 c 生物医学:肿瘤高温热疗;生物芯片;组织与器
官的冷冻保存 d 军 事:飞机、坦克;激光武器;弹药贮存 e 新 能 源:太阳能;燃料电池
热工基础

系统中某一点所在的等温面与相邻等温面之
间的温差与其法线间的距离之比的极限为该
点的温度梯度,记为gradt。
gradt Lim
t
t
n
t i
t
j
t
k
n0 n n x y z
注:温度梯度是向量;正向朝着温度增加的方向
4.热流密度(Heat flux)
保温材料:温度低于350℃ 时导热系数小于0.12W.m-1.K-1 的材料(绝热材料)
同一种物质的导热系数也会 因其状态参数的不同而改变,因 而导热系数是物质温度和压力的 函数。
一般把导热系数仅仅视为温 度的函数,而且在一定温度范围 还可以用一种线性关系来描述
0 (1 bT )
9.1.4 导热问题的数学描写 导热微分方程
x
x1
x
一般形式
qw
t
n w
f x, y, z,
典型实例
qw const
qw
t
n w
f
qw
t n
w
0
t n
0
绝热边界面
(3)第三类边界条件:该条件
是第一类和第二类边界条件的
线性组合,常为给定系统边界 面与流体间的换热系数和流体 的温度,这两个量可以是时间
t x
htw
t
非稳态温度场 t 0
非稳态导热
(Transient conduction)
三维稳态温度场: t f (x, y, z)
一维稳态温度场: t f (x)
2.等温面:温度场中温度相同点的集合称为等温面。 其疏密程度可反映温度场在空间中的变化情况。
于秋红 主编《热工基础》答案9-12章_

哈工大威海于秋红老师留的课后作业答案(没有积分的同学注册后点一下*即可得到一个积分)9-3. 一单层玻璃窗,高1.2m ,宽1m ,玻璃厚0.3mm ,玻璃的导热系数为051.=λ W/(m ·K),室内外的空气温度分别为20℃和5℃,室内外空气与玻璃窗之间对流换热的表面传热系数分别为51=h W/(m 2 ·K)和202=h W/(m 2 ·K),试求玻璃窗的散热损失及玻璃的导热热阻、两侧的对流换热热阻。
解:对流换热计算公式: W h h t t s Q f f 9.7120105.10003.05152012.1112121=+⨯⨯++-⨯=+-=λδ导热热阻为:W K A R /104.205.112.10003.04-⨯=⨯⨯==λδλ内侧对流换热热阻为:W K Ah R h /167.0512.11111=⨯⨯==外侧对流换热热阻为:W K Ah R h /042.02012.11122=⨯⨯==9-4. 如果采用双层玻璃窗,玻璃窗的大小、玻璃的厚度及室内外的对流换热条件与9-3相同,双层玻璃间的空气夹层厚度为5mm ,夹层中的空气完全静止,空气的导热系数为025.0=λ W/(m ·K)。
试求玻璃窗的散热损失及空气夹层的导热热阻。
解:对流换热计算公式:W h h t t A Q f f 95.39201025.0005.005.10003.025152012.112122211121=+⨯⨯⨯+⨯+-⨯=++-=+λδλδ空气夹层的导热热阻为:W K A R /167.0025.012.1005.0=⨯⨯==λδ10-2 炉墙由一层耐火砖和一层红砖构成,厚度都为250 mm ,热导率分别为0.6 W/(m ⋅K)和0.4 W/(m ⋅K),炉墙内外壁面温度分别维持700 ︒C 和80 ︒C 不变。
(1)试求通过炉墙的热流密度;(2)如果用热导率为0.076 W/(m ⋅K)的珍珠岩混凝土保温层代替红砖层并保持通过炉墙的热流密度及其它条件不变,试确定该保温层的厚度。
热工基础ppt导热

一般情况下,温度场是空间坐标和时间的 函数。在直角坐标系中,温度场可表示为
t f x, y, z,
北京科技大学能源与环境工程学院
8
1. 导热的基本概念---温度场
非稳态温度场:
温度随时间变化的温度场。其 中的导热称为非稳态导热。
稳态温度场:
温度不随时间变化的温度场。 其中的导热称为稳态导热。
北京科技大学能源与环境工程学院
29
导热微分方程式
根据微元体的热平衡表达式 dU = dQ + dQV可得
c t
x
t x
y
t y
z
t z
Q
内能增量
三个方向净导入热量
内热源项
非稳态项
当热导率为常数时, 导热微分方程式可简化为
t
2t
c
x2
2t y2
2t z2
稳态温度场: t f x, y , z
非稳态
一维温度场 t f x,
二维温度场 t f x, y ,
t 0
稳态
t f x
t f x, y
三维温度场 t f x, y , z , t f x, y , z
北京科技大学能源与环境工程学院
9
1. 导热的基本概念---等温面与等温线
5、一旦温度分布确定,热流密度即可求解(导热 分析的主要任务:求解温度场)
北京科技大学能源与环境工程学院
18
傅里叶定律的适用条件
n
(1)傅里叶定律只适用于各向 同性物体。
qy
y y
qx
q
x
x
(2)傅里叶定律适用于工程技术中的一般稳态和非
北航热工基础9 热第九章

五、喷管的计算
1) 喷管的设计计算 选型
出发点: p2 pb
已知 p1、T1、k、pb、f
k
k
2 k1 1
pc p1
1) 当 pb pc 采用渐缩喷管。
2)当 pb pc 采用缩扩喷管。
§ 9-3 喷管中流速及流量计算
五、喷管的计算
2) 渐缩喷管的校和计算 p2
已知 p1、T1、k、pb、f
超临
1)渐缩喷管的质量流量计算
(1) 出口处M<1 p2 pc
m
m max
界流
c
b 临界流
亚临
界流
2
k 1
m
f2c2 v2
f2
2
k
k 1
p1 v1
p2 p1
k
p2 p1
k
0
pc/ p1
a
1.0 pb / p1
(2)出口处M=1 p2 pc
p2 pc
2
m
f2c2 v2
f2
2
k
k 1
喷管
dc>0
M<1 df<0 渐缩
M=1
df=0 临界截面
M>1 df>0 渐扩
M<1 M>1
df<0 df>0 渐缩渐扩
注:扩压管dc<0,故不同音速下的形状与喷管相反
喷管和扩压管流速变化与截面变化的关系
管道种类
喷 dc>0 管 dp<0
扩 dp>0
压 管
dc<0
M<1
1
2
df f
0
渐缩渐扩扩喷管
p1 v1
热工基础-传热学篇

(1) 温度场(temperature field)
在 时刻,物体内所有各点的温度分布称
为该物体在该时刻的温度场。
21
一般温度场是空间坐标和时间的函数,在 直角坐标系中,温度场可表示为
t f x, y, z,
非稳态温度场 :温度随时间变化的温度场, 其中的导热称为非稳态导热。
导热现象发生在固体内部,也可发生在 静止的液体和气体之中。
本书不讨论导热的微观机理,只讨论热 量传递的宏观规律。
2
最简单的导热现象:大平壁的一维稳态导热 特点:1.平壁两表面维持均匀恒定不变温度;
2.平壁温度只沿垂直于壁面的方向发生变化;
3.平壁温度不随时间改变;
t
4.热量只沿着垂直于壁面的
方向传递。
第二篇 传热学
第八章 热量传递的基本方式
热量传递有三种基本方式 热传导 (thermal conduction) 热对流 (thermal convection) 热辐射 (thermal radiation)
1
8-1 热传导
热传导(简称导热)
在物体内部或相互接触的物体表面之 间,由于分子、原子及自由电子等微观粒 子的热运动而产生的热量传递现象。
11
热辐射的主要特点:
(1)所有温度大于0 K的物体都具有发射热辐 射的能力,温度愈高,发射热辐射的能力愈强。
发射热辐射时:内热能 辐射能 ;
(2)所有实际物体都具有吸收热辐射的能力, 物体吸收热辐射时:辐射能 内热能 ;
(3)热辐射不依靠中间媒介,可以在真空中传
播;
(4)物体间以热辐射的方式进行的热量传递是
第八章小结
重点掌握以下内容:
(1)热传导、热对流、热辐射三种热量传 递基本方式的机理及特点;
热工基础热工基础 (99)

《热工基础》----传热学篇第9章对流传热§9-4单相流体管内强迫对流传热特征数关联式第9章对流传热主要内容(1)管内流动对流传热的影响因素;(2)管内强迫对流传热特征数关联式。
9.4.1管内强迫对流传热的特点及影响因素1.管内的流动状态对于工业和日常生活中常用的光滑管道流动状态判断(Re ):层流过渡流湍流判别条件=Re duνRe ≤2300Re <<2300104Re ≥1042.物性不均匀的影响换热时流体温度场不均匀,会引起物性的不均匀。
其中粘度随温度的变化最大,粘度场的不均匀会影响速度场,因此影响对流换热。
这种温度场导致速度场变化对对流传热系数产生影响,用温差修正系数加以修正。
:却冷被体气:热加被体气:却冷被体液:热加被体液⎭=⎪⎪+⎪=+⎪⎬⎪=⎪⎪⎪=⎫εεμεμμεμt t 1273.15()273.15()()t w t f 0.55wt f 0.25wt f 0.113.流动入口段的影响热进口段:流动进口段:对于管内层流,进口段长度:≈0.05ldRe ⎛⎝ ⎫⎭⎪≈0.05tl d RePr热进口段的局部表面传热系数的变化进口段边界层沿x方向由薄由小变大,对流换热变厚,hx逐渐减弱。
由于进口段的局部表面传热系数较大,所以对于短管内的对流换热,需要考虑进口段的影响。
对于管内湍流换热,只要l/d > 60,就可忽略进口段的影响。
4.非圆截面和弯曲管道的影响管道弯曲,离心力的作用会在流体内产生二次环流,增加了扰动,使对流换热得到强化。
弯管的曲率半径越小,流速越大,二次环流的影响越大。
:体液于对:体气于对⎭⎪=+⎪⎬⎪⎪=+⎫εεR d R d 110.3()1 1.77r 3r4.非圆截面和弯曲管道的影响对于非圆形截面槽道,可以采用当量直径d e 作为特征尺寸,则可近似应用对圆管得出的湍流传热公式=e 4cd A PA c :槽道流通截面积P :湿周——过流断面上,流体与固体壁面接触的周界线ππ=-+d d d d d e 122212()()管内强化传热1.增加流固接触面;2.破坏边界层;3.促进边界与主流区流体之间的混合。
热工基础热工基础 (97)

《热工基础》----传热学篇第9章对流传热§9-2对流传热的基本方程组第9章对流传热主要内容(1)研究对流传热的方法;(2)对流传热的数学描述方法。
为求解对流换热问题奠定必要的理论基础。
研究对流传热的方法分析解法:采用数学分析求解的方法,有指导意义。
比拟法:通过研究热量传递与动量传递的共性,建立起表面传热系数与阻力系数之间的相互关系,限制多,范围很小。
实验法:通过大量实验获得表面传热系数的计算公式,是目前的主要途径。
数值解法:和导热问题数值思想一样,发展迅速,应用越来越多。
对流传热微分方程组及其单值性条件9.2.1对流传热微分方程假设:1.流体为连续性介质。
当流体的分子平均自由行程与换热壁面的特征长度l 相比非常小,一般克努森数时,流体可近似为连续性介质。
l n l l =≤-/1032.流体的物性参数为常数,不随温度变化。
3.流体为不可压缩性流体。
通常流速低于四分之一声速的流体可以近似为不可压缩性流体。
4.流体为牛顿流体,即切向应力与应变之间的关系为线性,遵循牛顿公式:5.流体无内热源,忽略粘性耗散产生的耗散热。
6.二维对流换热。
τη=∂∂u y紧靠壁面处流体静止,热量传递只能靠导热,流体导热系数λ=-∂∂=0,q tyx y x根据牛顿冷却公式=-∞w ()q h t t x x xλ=-∂∂=0,t yy xλ=--∂∂∞=()w 0,h t t tyx x y x如果热流密度、表面传热系数、温度梯度及温差都取整个壁面的平均值,则有对流传热微分方程λ=--∂∂∞=w 0,h t t tyx y x建立了对流传热表面传热系数与温度场之间的关系。
而流体的温度场又和速度场密切相关,所以对流换热的数学模型应该是包括描写速度场和温度场的微分方程。
——揭示了对流传热问题的本质描述对流传热的方程组温度场特别是壁面附近的温度分布温度场受流场的影响流场连续性方程质量守恒定律动量方程动量守恒定律温度场——能量方程能量守恒定律对流传热微分方程式λ=--∂∂∞=w 0,h t t tyx y xq x9.2.2连续性微分方程和动量微分方程dxxdyy 0微元体1.连续性微分方程(质量守恒)vy+∂∂=0∂∂u x 2.动量微分方程(动量守恒)ρτμρτμ∂∂+∂∂+∂∂=-∂∂+∂∂+∂∂∂∂+∂∂+∂∂=-∂∂+∂∂+∂∂x y u u u x v u y F p x u x u yv u v x v v y F p y v x v y22222222()()()()纳维(N.Navier)-斯托克斯(G.G.Stokes)方程惯性力压力差体积力粘性力9.2.3能量微分方程d xxd yyλ+,d Φy y +,d Φh y yλ,Φx,Φh xλ+,d Φx x+,d Φh x x,Φh yλ,Φy 单位时间由导热进入微元体的净热量和由对流进入微元体的净热量之和等于微元体热力学能的增加量。
热工基础 (105)

《热工基础》----传热学篇第9章对流传热§9-7相变换热第9章对流传热主要内容(1)相变传热的特点;(2)凝结换热的特点;(3)凝结换热的相关计算。
有相变对流传热的特点:①相变过程中产生大量相变热(潜热);例:水kJ/kg4.22581000=r C 时,汽化潜热CkJ/kg 187.4100000=-p C C ,比热②相变过程有其特殊传热规律,传热更为复杂;③分为蒸汽冷凝与液体沸腾两种情况。
9.7.1凝结换热1.膜状凝结凝液呈液膜状(附着力大于表面张力),热量传递:蒸汽相→液膜表面→固体壁面。
2.珠状凝结凝液结为小液滴(附着力小于表面张力),热量传递:有裸露壁面,直接传递相变热。
3.比较两种冷凝方式的表面传热系数h珠状凝结>h膜状凝结膜状凝结珠状凝结有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)膜状凝结的真实过程hx凝结换热实例●冷凝器中的换热●寒冷冬天窗户上的冰花●许多其他的工业应用过程凝结换热的关键点●凝结可能以不同的形式发生,膜状凝结和珠状凝结●冷凝物相当于增加了热量进一步传递的热阻●层流和湍流膜状凝结换热的实验关联式●影响膜状凝结换热的因素●会分析竖壁和横管的换热过程,及Nusselt膜状凝结理论竖壁液膜厚度计算式349)(44/1w s -⎥⎦⎤⎢⎣⎡-=γρληδl l l g x t t 竖壁局部表面传热系数359)(44/1w s 32-⎥⎦⎤⎢⎣⎡-=x t t g h l ll x ηλγρ凝结液的物性用液膜平均温度2sw m t t t +=假定常物性及高为l 的整个竖壁上温差△t =t s -t w 为常数,整个竖壁的平均表面传热系数为369)(943.04/1w s 32V -⎥⎦⎤⎢⎣⎡-=l t t g h l ll ηλγρ对于与水平轴倾斜角为φ的倾斜壁,只需用g sin φ取代式中的g 即可。
有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)ϕ水平圆管外膜状冷凝说明:此式计算值和实验结果基本一致。
热工基础 第九章.导热

qx
q
x
x
(2)傅里叶定律适用于工程技术中的一般稳态和 非稳态导热问题,对于极低温(接近于0K)的导热问 题和极短时间产生极大热流密度的瞬态导热过程, 如 大功率、短脉冲(脉冲宽度可达10-12~10-15s)激光瞬态 加热等, 傅里叶定律不再适用。
10
3. 热导率(导热系数)
热导率表明物质导热能力的大小。根据傅里叶定 q 律表达式
1 rt t 1 t 1 2t a 2 sin 2 2 2 2 r sin r sin c r r
2
23
(2)单值性条件
导热微分方程式推导过程中没有涉及导热过程 的具体特点, 适用于无穷多个导热过程, 也就是说 有无穷多个解。 为完整地描写某个具体的导热过程,必须说明 导热过程的具体特点, 即给出导热微分方程的单值 性条件(或称定解条件),使导热微分方程式具有 唯一解。 导热微分方程式与单值性条件一起构成具体导 热过程完整的数学描述。 单值性条件一般包括:几何条件、物理条件、 时间条件、边界条件。
由傅里叶定律可知, 要计算导热热流量, 需要知 道材料的热导率, 还必须知道温度场。所以,求解温 度场是导热分析的主要任务。 9
对于各向同性材料, 各方向上的热导率相等,
t q n
傅里叶定律的适用条件:
(1)傅里叶定律只适用于各 向同性物体。对于各向异性物体, qy 热流密度矢量的方向不仅与温度 梯度有关,还与热导率的方向性 y y 有关, 因此热流密度矢量与温度 梯度不一定在同一条直线上。 n
8
标量形式的傅里叶定律表达式为
t t t q qx i qy j qz k gradt i j k x y z t t t q i j k y z x t t t q z q y q x z y x
热工基础热工基础 (104)

《热工基础》----传热学篇第9章对流传热§9-6大空间自然对流传热第9章对流传热主要内容(1)大空间自然对流传热的特点;(2)大空间自然对流传热特征数关联式。
自然对流:温度差→密度差→浮升力→自然对流换热举例:①输电导线、变压器、电热炉等外表面的散热;②各种电子元器件表面的散热(无专门冷却设备时);③各种热设备、热力管道等在环境中的散热(无风时);④大量热加工工艺过程中工件的冷却等等。
特点:不消耗动力,在工业和日常生活中发挥着重要作用。
研究目标:确定表面传热系数。
1.自然对流的特点:①自然对流的流动和传热不需要外界动力源;②驱动力为温差,但是有温差不一定存在自然对流;③不均匀的温度场和速度场发生于近壁薄层,速度分布具有两头小、中间大的特点;④自然对流也分为层流和湍流。
判别准则为格拉晓夫数Gr;⑤自然对流的准则方程式:Nu=f(Gr,Pr);⑥按流动的边界层是否受干扰,分为大空间自然对流和有限空间自然对流。
流动不均匀的温度场,不一定引起自然对流。
说明:该空腔上热下冷,存在温度差,但是没有自然对流产生。
2. 大空间自然对流传热:以竖直平板在空气中的自然冷却过程为例进行流动与换热特征分析。
随着层流边界层的加厚,hx逐渐减小,当边界层从层流向湍流过渡时又增大。
实验研究表明,基本上不随在旺盛湍流阶段,hx壁面高度变化。
3. 大空间自然对流换热特征关联式恒壁温:=⋅Nu C Gr mm nPr )(式中:Gr称为格拉晓夫数,其表达式为:适用条件:恒壁温条件定性温度:流体的算术平均温度定型尺寸:竖壁高度l=+∞t t t 2m w =∆V Gr g tlαν32传热面的形状及位置GrPr的范围C n特征长度垂直的平板及圆柱面104~ 109109~ 10130.590.11/41/3高度H水平圆柱面104~1.5×108>1.5×1080.480.101/41/3外径d水平板热面朝上或水平板冷面朝下2×104~5×1065×106~10110.540.151/41/3正方形取边长,矩形取两边平均值,圆盘取0.9d,狭长条取短边水平板热面朝下或水平板冷面朝上105~10110.591/4恒热流:工程上有时会遇到自然对流传热表面热流密度为常数的情况,如电子元器件表面的自然对流冷却。
热工基础 张学学 第九章 思考题答案

热工基础第九章思考题答案1 写出导热傅里叶定律表达式的一般形式,说明其适用条件及式中各符号的物理意义。
答:傅立叶定律的一般形式为:,其中:为空间某点的温度梯度;是通过该点的等温线上的法向单位矢量,指向温度升高的方向;为该处的热流密度矢量。
公式中λ 是热导率,是物性参数,反映物体导热能力的大小。
公式中∂t ∂n 是温度梯度的大小。
表示等温面法线方向的温度变化。
适用条件:适用于各向同性物体。
2 写出直角坐标系三个坐标方向上的傅里叶定律表达式。
答:q x =−λ∂t ∂xq y =−λ∂t ∂yq z =−λ∂t ∂z ,其中分别为三个方向的单位矢量量。
3 为什么导电性能好的金属导热性能也好?答:因为金属的导电和导热都是依靠自由电子的运动。
自由电子运动的快,导电性能好,导热性能也好。
4 一个具体导热问题的完整数学描述应包括哪些方面?答:导热问题的完整数学描述应包括导热微分方程和单值性条件。
5 何谓导热问题的单值性条件,它包括哪些内容。
答:导热问题的单值性条件是说明导热过程的具体特点,使导热微分方程具有唯一解。
包括内容:几何条件,物理条件,时间条件,边界条件。
6 试说明在什么条件下平板和圆筒壁的导热可以按一维导热处理。
答:平板:当平板两表面分别维持均匀恒定的温度时,可以近似地认为平壁内的温度只沿着垂直于壁面的方向发生变化,并且不随时间而变,热量也只沿着垂直于壁面的方向传递,可以按一维稳态导热处理。
圆筒壁:壁内的温度只沿径向变化,采用圆柱坐标系,圆筒壁的导热可以按一维稳态导热处理。
7 试用传热学观点说明冰箱为什么要定期除霜。
答:冷冻室内结霜后,使蒸发管和冷冻室间增加一层热阻,而霜有颗粒状的水组成,中间夹杂着不流动的空气,使其当量热导率比密实的冰小得多,热阻较大,要使冷冻室达到指定温度必须增加压缩机工作时间,耗电量增加。
因此冰箱要定期除霜,以减小接触热阻。
8 为什么有些物体要加装肋片?加肋一定会使传热量增加吗?答:有些物体加装肋片是为了增加换热面积,增加换热量。
热工基础实验指导书(导热系数测定)

实验二 物质导热系数测定实验一、实验目的1. 学习在稳定热流条件下测定物质导热系数的原理、方法; 2. 确定所测物质导热系数随温度变化的关系;3. 学习、掌握相关热工测量仪表的结构与使用方法。
二、 实验原理测定物质导热系数的方法有很多,如稳态平板法、球体法、常功率平面热源法等,本实验采用的是稳态多层圆筒壁同心法,如图1-1所示。
图1-1 稳态多层圆筒壁同心原理示意图被测试样装满于试样筒内,则被测试样成一圆筒型。
设试样筒的内外两侧表面温度分别为t h 和t l 。
为防止试样在筒内产生热对流,采用二个很薄的金属套管将其分隔开来,保证热量在试样筒内以导热方式径向传递。
套管壁的热阻很小,可以忽略。
当试样内维持一维稳态温度场时,则有)()()/ln(212l h l h l t t Bt t r r l Q -=-=λπλ (1-1)其中:λ为试样的导热系数,单位W/m ·℃;lr r B π2)/ln(12=为仪器几何常数, 本实验所用仪器为DTI -811型导热系数测定仪,其结构简图见图1-2。
图1-2 DTI -811型导热系数测定仪结构简图考虑到测定仪端部的热损失为Q n ,装在试样筒内且与之同心的加热器所提供的热流Q =IV ,只有Q l 是由径向经待测试样传出,故Q=Q l +Q n =IV (1-2)仪器端部特性用热阻R (℃/W )表示,有:)(1l h n t t RQ -=(1-3) 把式(1-1)、(1-3)代入式(1-2),并令B/R=C ,得C tBIV-∆=λ W/(m ·℃) (1-4) 式中:△t =(t h -t l ),单位℃;I 、V ——电加热丝的电流(A ),电压(V ); C ——热损失修正常数,C=B/R 。
因此,只要维持试样筒内、外侧的温度稳定,测出导热量Q l 以及试样筒内外两侧表面的温度t h 、t l ,即可由式(1-4)求得在温度t m =(t h +t l )/2下试样的导热系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fundamentals of thermal engineering
热
工
基
础
9-2 稳态导热
第一次积分 第二次积分
dt r c1 dr
tw1 c1㏑r1 c2 ;
t c1㏑r c2
tw2 c1㏑r2 c2
c2 tw1 tw2 tw1
应用边界条件
tw 2 tw1 c1 ; ㏑ r2 / r1
热 工 基 础
9-1 导热理论基础
2 导热基本定律 傅立叶定律
t q gradt n n W/m2
注意:①上式对稳态和非稳态均使用;
②导热现象依 gradt 的存在而存在,
若 gradt=0,则 q=0;
③“-”不能少,“-”表示 q与 gradt 方向
相反, 若无,则违反热二定律。
热 工 基 础
9-1 导热理论基础
边界条件可归纳为三类: (1)第一类边界条件:给定物体边界上任何时刻的 温度分布。
0 时
tw f w x, y, z,
若边界温度均匀,则 0 tw f w 最简单的情况下, tw const
Fundamentals of thermal engineering
Fundamentals of thermal engineering
热
工
基
础
9-2 稳态导热 3 通过圆管壁的导热 ①单 tw2 l r2
d dt r 0 dr dr
边界条件为 x = r1 , t = tw1 x = r2 , t = tw2
t 1 1 t 1 t 2 t c 2 ( r ) 2 2 ( ) 2 ( sin ) r r r r sin r sin
Fundamentals of thermal engineering
热
工
基
础
9-1 导热理论基础
㏑r1 ㏑ r2 / r1
获得两个系数
t2 t1 t t1 ㏑ r / r1 ㏑ r2 / r1
温度呈对数曲线分布
Fundamentals of thermal engineering
将系数带入第二次积分结果
热 工 基 础
9-2 稳态导热
ln(r / r1 ) 圆筒壁内温度分布: t tw1 (tw1 tw 2 ) ln(r2 / r1 )
Fundamentals of thermal engineering
热 工 基 础
9-1 导热理论基础
主要内容: (1)与导热有关的基本概念; (2)导热基本定律; (3)导热现象的数学描述方法。 1 导热基本概念
⑴ 温度场 某一时刻空间所有各点的温度分布,即
t f ( x, y, z, )
t tw1 q tw1
1 1
R
i 1
n
tw2 tw3 tw4 δ 1 tw2
2 2
i
tw,i 1 tw1 R j
j 1
i
δ
2
tw3
δ
3
x tw4
3 3
其温度分布规律为: 单层内为直线分布,总分布图为折线。
Fundamentals of thermal engineering
Fundamentals of thermal engineering
热
工
基
础
傅立叶生于一个裁缝家庭,8岁时沦为孤儿, 就读子地方军校,1795年任巴黎综合工科大 学助教。1807年就写成关于热传导的基本论 文《热的传播》,向巴黎科学院呈交,但经 拉格朗日、拉普拉斯和勒让德审阅后被科学 院拒绝,1811年又提交了经修改的论文,该 文获科学院大奖,却未正式发表。傅立叶在 让· 巴普蒂斯· 论文中推导出著名的热传导方程 ,并在求解 约瑟夫· 傅立叶 该方程时发现解函数可以由三角函数构成的 级数形式表示,从而提出任一函数都可以展 (Jean Baptiste 成三角函数的无穷级数。傅立叶级数(即三 Joseph Fourier) 角级数)、傅立叶分析等理论均由此创始。 (1768 –1830) 傅立叶由于对热传导理论的贡献于1817年当 法国数学家、 选为巴黎科学院院士。 1822年,傅立叶终于 出版了专著《热的解析理论》。 物理学家
tw1 tw 2 dt q dx
qA A tw1 tw 2
或
Fundamentals of thermal engineering
热
工
基
础
9-2 稳态导热
2 多层平壁 各层均质,层与层之间无接触热阻
R Ri
i 1
n
tw1 tw,n 1
Fundamentals of thermal engineering
热 工 基 础
9-1 导热理论基础
3 热导率(导热系数) 物质导热能力的大小
q gradt W / m K
影响热导率的因素:物质的种类、材料成分、温 度、湿度、压力、密度等。 一般:λ金属>λ非金属 ,λ固相>λ液相>λ气相
第九章
研究方法:
导
热
从连续介质的假设出发、从宏观的角度来讨论 导热热流量与物体温度分布及其他影响因素之间的 关系。 连续介质: 一般情况下,绝大多数固体、液体及气体都可 以看作连续介质。但是当分子的平均自由行程与物 体的宏观尺寸相比不能忽略时,如压力降低到一定 程度的稀薄气体,就不能认为是连续介质。
Fundamentals of thermal engineering
热 工 基 础
9-1 导热理论基础
分类: t 0 ① 稳态温度场:不随时间变化的温度场 t ②非稳态温度场:随时间变化的温度场 0 一维稳态温度场 t f ( x)
⑵等温线(面) 在同一时刻,温度场中温度相同的点所连成的线或面。 注意:在同一时刻,物体中温度不同的等温面或等 温线不能相交,因为任何一点在同一时刻不可能具 有两个或两个以上的温度值。且沿等温面法线方向 的温度变化最剧烈,即温度变化率最大。
热
工
基
础
9-1 导热理论基础
几个特例:
①导热系数为常数
t 2t 2t 2t 2 a( 2 2 2 ) a t x y z c c
式中, a /( c),称为热扩散率。 ②导热系数为常数、无内热源
t 2t 2t 2t a( 2 2 2 ) a 2t x y z
t t t t c x x y y z z
笛卡尔坐标系中三维非稳态导热微分方程的一般表达式
Fundamentals of thermal engineering
Fundamentals of thermal engineering
热
工
基
础
9-1 导热理论基础
(3)温度梯度 等温面(线)法线方向的温度变化率矢量 t t gradt lim n n n n 0 n 温度梯度是矢量, 其方向沿等温面的法线指向温 度增加的方向。 x
在直角坐标系中
工 基 础
Fundamentals of thermal engineering
9-2 稳态导热 圆筒壁单位长度的热流密度
t1 t2 l r2 1 l ln( ) 2 r1 W /m
导热微分方程+单值性条件+求解方法 温度场
Fundamentals of thermal engineering
热 工 基 础
9-2 稳态导热
1 通过平壁的导热 ① 单层无限大平壁
tw1 Φ t A tw2
0 x
平壁的导热微分方程式为
d t 0 2 dx
tw1
2
δ
x
tw2
R
边界条件为 x = 0 , t = tw1 x = , t = tw2
4 定解条件 使导热微分方程获得适合某一特定导热问题 的求解的附加条件。
定解 条件
说明:
初始条件:初始时间的温度分布; 边界条件:导热物体边界上温度或表面换 热情况。
①非稳态导热定解条件有两个; ②稳态导热定解条件只有边界条件,无初始条件。
Fundamentals of thermal engineering
Fundamentals of thermal engineering
热 工 基 础
9-1 导热理论基础
③导热系数为常数、稳态
2t 2t 2t 2 2 2 0 t 0 2 x y z
④导热系数为常数 、稳态 、无内热源
2t 2t 2t 2 0 t 0 2 2 2 x y z
tw1 tw2 1 dt dr ln(r2 / r1 ) r
dt tw1 tw2 q dr r ln(r2 / r1 )
qA 2 rl
W / m2
tw1 tw2 1 W
tw1 tw2
r ln(r2 / r1 )
2l
热
ln(r2 / r1 )
热 工 基 础
9-2 稳态导热
接触热阻
固体表面的实际接触情况 固体两个表面不可能处处接触,在离开部分形成空隙,在空隙 中常常充满空气。热量将以导热和辐射的方式穿过这个气隙层。 这种情况与两固体表面真正完全接触相比,增加了附加热阻, 称之为接触热阻 由于接触面的情况比较复杂,接触热阻主要靠实验测定。
热流密度是矢量, 其方向与温度梯度方向相反。 在直角坐标系中
x
t
t t
q qx i q y j qz k t t t q x , q y , q z x y z
