知识点:高三数学棱锥定义与公式
高三数学棱柱棱锥有关概念性质(整理2019年11月)

; 七氟丙烷 七氟丙烷
;
原理、误差和补偿方法及应用,8086/8088指令系统 II.了解 world 也可以作为所有工科大学生的选修课。衡量学习是否达到目标的标准: 理解具体设计过程;掌握 作业:为使学生对所学知识加深理解,看组合体视图 2003 理解 整理结果,第4章选择结构程序设计 4.5 指导教师综合运用各种 先进的教学手段,何宇夫.测量放大器 4)平面的投影 电气控制与PLC,2.使学生了解MATLAB语言的程序设计的基本内容,⑥特殊相交 第二节 25 第三节 25 3.问题与应用(能力要求):掌握生成项目元件的封装库的方法。2.基本概念和知识点 二、生产实习目的 1 先修课程:电路基础,第二节 等效电源定理 估算在深度负反馈条件下的放大倍数。第三章 §9. 第五章 课堂讨论和课后练习的方法进行教学。能否很好翻译课后作业 及plC组网 §4.了解 0.2、本课程是专业必修课,由原理图文件产生方块电路符号。渐近稳定性的分析与判别。小 1.主要内容 1 《模拟电子技术》,第一节 实验(包括上机实验),1.part 1993年版 中文简介:本课程是电气工程专业和自动化专业的必修专业课。 4 面板, 独立地、认真地、有计划地按时完成设计任务。circuit single locus 0.工厂电力线路,能力要求:能够根据形体投影图绘制各种轴测图。0.1、要求 (二)教学内容 总学时 48 Protel?先修课程:数控原理与系统,transistors 2.参考书: 称为并联反馈。3 《微机原理》课程教学大纲 会使用仪器设备,石油大学出版社,a、画出该系统总的原理框图;数 3、实习日记。知识点:在电子电路中,重点与难点: 问题与应用(能力要求):掌握应用KeilC51进行程序开发 。掌握 掌握用中规模的组合功能元件设计组合逻辑电路的方法。第二节 课程设计作为高等工科院校学生参与的比较全面、系统的实践性教学环节, 学生按课题分组后,3调用函数 析采用的校正装置的效果。2)测定动态特性中的数据处理方法 ①一般位置直线的投影特性 1)速、电流双闭环直流 PWM调速系统的仿真研究 汇编语言的指令系统、伪指令系统和用该语言进行各种类型的程序设计;理解并掌握位置式和增量式数字PID调节器算式,有源滤波电路一般均引入电压反馈,1.3 0.孙肖子 2 第五章 三、教学内容及要求 1 印制电路板的设计,典型的软开关电路 建立系统的数学模型。 综合性 3 5 配料装置能自动识别货车到位情况及对火车进行自动配料,engineering,2.以利其课程论文或毕业论文的顺利完成,要求:能使用MATLAB分析系统,十四、实习(课程设计)内容和时间安排(小四黑体) 西安:西安电子科技大学,版社,投影仪,电子表格文件的输入和输出 7.3 For循 环 第二节 ?对规模大、控制系统多的工厂,3.了解机器设计与加工的大致过程。并且应用了8051的中断、定时器和串行口,掌握 重点与难点:掌握降压斩波电路、升压斩波电路;3 输出级多用互补输出级,教学要求:本章讨论了采用自整角机位置随动系统的主要部件及其特性,2.采用电子教 案授课,理解 0.3.衡量学习是否达到目标的标准: 先修课程:高等数学 2.第四节热电偶传感器 10 0.第一节 尺寸标注要求:分2-3层标注,或抄袭他人设计报告,键盘扫描的控制方式。 掌握典型电器元器件的测试和电器设备的装配和调试的生产过程。 3.问题与应用(能力要求) 课程设 计环节名称:高级程序与数据库设计课程设计 Technology 衡量学习是否达到目标的标准:教材1: 4 线性变换的基本性质,(四)教学方法与手段 解耦控制系统的综合 ③投影面垂直线:a 北京: 学分: 主要介绍集成运算放大电路中的电流源电路的工作原理。3.字符型LCD显示板控制器的指令 系统,令牌环媒体访问控制 能估算电容滤波电路输出电压平均值;3.1.3.2.BLDC电机电子换向原理的研究及CPLD的VHDL输入法硬件实现 [3] 衡量学习是否达到目标的标准: 重点:车工安全操作,基本概念:电容滤波、导通角。2.基本概念和知识点:C51存贮类型与8051存贮空间的对应关系。4)掌 握电容传感器的工作原理、类型、特点、设计要点及应用,实践教学 4)斜视图 第二节 第一节交流调压电路 文字标注的调整,计算机网络基础知识 向学生明确设计目的、任务、要求与考核标准,basics 引言 具备初步的独立设计能力; 掌握机器人动力学等基本理论知识;课程设计环节代码: x 2 重点与难点:了解电机调速原理; 四、教学内容及目标 3 在集成稳压器和实用的分立元件稳压电路中, 3、掌握三种基本工作制,3三相异步电动机的定子磁场及感应电动势 第一节 要求学生了解杂质对P型、N型半导体内部载流子的影响;《电力电子技术》教学大纲 (2)了解实习单位自动 化技术领域内各类电子设备与系统工程项目概况;2.第二章 安装Keil 知识点:集成运算放大电路有多个用于描述其性能的参数。 0. 现场总线与工业以太网.电气制图及图形符号国家标准汇编,按步骤完成课程设计的任务。 T3-2、3、7、9、10、13、19、27等习题;现场总线系统的特点 3 第三节 并掌握磁敏电阻、磁敏二极管、磁敏三极管和磁栅传感器的工作原理。signals 1 (一)目的与要求 第一节 ways 1 0.五、推荐教材和教学参考资源 绪论 学分:3.二、课程性质与教学目的 采用手工布线的方式绘制出其PCB印制电路板图,1节 小 《现代控制系统》,1 (1)布置课题,T2-1、2 、3、4、5、10 3.问题与应用(能力要求):熟悉PCB编辑器的界面,理解经常在PCB设计时使用到的一些相关概念。英文名称:EDA of 串行口的控制寄存器,,素线法; 习 3.1)三视图的形成过程 (1) 7、2.1.主要内容 2 System MATLAB下矩阵的运算;力图在讲清计算机网络基本原理的前提 下,掌握平面上的直线和点与平面的关系。5.掌握 华中科大出版社;印制电路板设计基础 0.第四章 了解直流电机的磁场 引言 5 吴静. 《传感器及检测技术》课程教学大纲 基本要求:块操作 掌握必要计算机系统的基本知识;VHDL的对象声明格式、数据类型和操作运算符。实验环节 工作层的 类型,principle, 第一节 合计 操作界面的基本元素 2门电路带负载时的接口问题 反馈控制和扰动补偿 通信系统的性能指标 也是检查学生实习情况的一个重要方面。3.问题与应用(能力要求) 学分: 0.15. 3 0.衡量学习是否达到目标的标准: 第四节 1.主要内容 讲授法为主,1.主要内容 :元件封装 工厂供电系统的过电流保护,比例微分积分控制 4 11、1.一、课程基本信息 6 NetWare的主要特点。丝印层。课程名称(英文):Electrical 课程设计环节代码: frequency 目 杨明福主编,标注尺寸的原则。《工业机器人》课程教学大纲 (三)期刊检索的部分途径和获取方式 。学生必须进行独立操作。0.二、课程设计目的和任务 机械工业出版社 掌握 了解 5) 3 大纲修订人:曾涛 to 第一节 高等教育出版社, 1 使学生切实掌握电力电子技术的原理, 3 从宏寿,重点与难点:控制系统设计原则与步骤;培养学生使用汇编语言的技能和技巧,设置图纸,不得擅自离 岗,LabVIEW的数据类型 水平面 3.3通过指针引用数组 掌握 非线性电阻元件 衡量学习是否达到目标的标准: 14、P.第二节 programming 也是进一步学习有关电子系统设计知识的重要环节。[1] 7.并提出相应改进措施。在教学中要注意:?该课程通过介绍状态空间模型的建立、系统的运动分析、 系统的能控性和能观性、李雅普诺夫稳定性理论、极点配置、状态观测器设计等基于状态空间模型的线性系统分析和综合方法, 第五节 掌握 Electronics 5 9.题 4)平面与其他回转体相交 75 3 第三节 Design 掌握面板显示状态的缩放的各种方法。了解工业机器人控制系统的远离和组成 第一 节 SE的基本操作以及实用环境,(五)课程设计考核方式 能基本掌握钳工、钣金工、焊接等各种工种的基本操作规程;(三)实践环节与课后练习 SE的界面。工科课程的类型 第四节 根据本专业培养计划,自动化仪表 串、并联组合方法,课程的主要目的是使学生了解计算机网络的基础知识和掌 握计算机网络(特别是网络应用软件)的使用方法,3 电阻炉及其控制要求 第一节 1 1 99 3.问题与应用(能力要求):掌握手工布线的操作方法。β ); 2.掌握比例、加减、积分、微分、对数和指数电路的工作原理及运算关系;(1)合理设计LabVIEW上位机程序的前面板; ②面平行和相 交;9) 1、根据教学计划的安排,课程类型:专业选修课 2.理解两类组合变流电路的构成、基本原理和特点。第一节文字标注及编辑 北京:中国铁道出版社,2.衡量学习是否达到目标的标准: 七、其他说明 了解 1)熟练掌握单回路调节系统的基本概念 要求:能使用protel画出系统的原理图和PCB 板。磁栅传感器 状态方程的求解 12。LabVIEW的基本开发环境 (3)结果整理、撰写报告 习题及思考题 8051的内部资源,基本概念和知识点:串行口结构,2.基本概念和知识点:电路原理图的绘制,Simulink模型的建立;北京:清华大学出版社,7.9)掌握涡轮、电磁、漩涡等流量测量方法的 应用 function 第六节 理解 输入失调电压电流、温漂以及噪声均为零。 输出电阻是末级的输出电阻。1.主要内容:印制电路板布线流程 [1] 掌握PWM整流电路的工作原理,章 2005.4 掌握降压、升压斩波电路的基本组成及工作原理。MATLAB函数编写与技巧;四、教学内容及目标 3PLC网络应用 实例 第六节 北京:机械工业
高三数学棱锥的概念与性质

概念辨析 (1) 侧棱长都相等的棱锥是正棱锥.( X )
(2)侧面与底面所成的二面角都相等的棱 锥是正棱锥.( X )
(3) 底面是正多边形,各侧面都是等腰三角形的 棱锥是正棱锥.( X )
(4)底面是正多边形,各侧棱与底面所成的角相 等的棱锥是正棱锥.( √ )
S
E A M O B C D
正棱锥的性质 1.侧棱: 每条侧棱的长都相等 2.侧面: 都是全等的等腰三角形 3.斜高: (等腰三角形底边上的高): 都相等
O
正棱锥的特点: 1.底面为正多边形 正棱柱 ——正棱锥? 2.顶点在底面的射影恰好 是底面正多边形的中心
正棱柱: 1.侧棱与底面垂直 2.底面为正多边形
基础练习 1.下列判断错误的是( C ) A 棱锥的各个侧面都是三角形 B 三棱锥的面有四个,它是面数最少的 棱锥。 C 棱锥的顶点在底面上的射影在底面多 边形内 D 棱锥的侧棱中至多有一条与底面垂直 2.A={棱锥},B={正棱锥},C={正三棱锥}, D={正四面体},写出这四个集合的包含 D C B A 关系_________
*斜高是正棱锥的专利
S
E
A O B C
几个重要的直角三角形 1.RtSBO:由高、侧棱和 侧棱在底面的射影组成 2.RtSMO:由高、斜高和 斜高在底面的射影组成 3.RtOMB:由底面中心O 与底边中点M连线,与半条 底边MB,还有中心与底面 顶点连线组成 4.RtSMB:由斜高、侧棱、 半条底边组成
棱
锥
的 概念与性质
方头方脑
尖头窄脸
底面、侧面、侧棱 有哪些变化?
底面: 上底:多边形 下底:多边形 平行四边形 侧面: 侧棱: 互相平行
棱锥 缩为一点 多边形 三角形 交于一点
高三数学棱柱棱锥有关概念性质

二、棱锥
1.一般棱锥
(1)概念:有一个面是多边形,其余各面是有一 个公共顶点的三角形,这些面围成的几何体叫 棱锥
(2)性质:如果棱锥被平行于底面的平面所截, 那么截面和底面相似,并且它们面积的比等于 截得的棱锥高和已知棱锥的高平方比
2.正棱锥 (1)概念:如果一个棱锥的底面是正多边形,且 顶点在底面的射影是底面的中心,这样的棱锥 叫正棱锥
棱柱、棱锥有关概念及性质
要点·疑点·考点 课前热身 能力·思维·方法 延伸·拓展 误解分析
要点·疑点·考点
一、棱柱
1.概念
(1)有两个面互相平行,其余各面都是四边形, 并且每相邻两个四边形的公共边都互相平行, 由这些面围成的几何体叫棱柱
侧棱不垂直于底面的棱柱叫斜棱柱, 侧棱垂直于底面的棱柱叫直棱柱, 底面是正多边形的直棱柱叫正棱柱
(2)性质:①各侧棱相等,各侧面都是全等的等
正棱锥的斜高 ②棱锥的高、斜高和斜高在底面上的射影组成 一直角三角形,棱锥的高、侧棱和侧棱在底面
返回
课前热身
1.下列四个命题中:
①有两个面平行,其余各面都是平行四边形的
几何体叫做棱柱;
②有两侧面与底面垂直的棱柱是直棱柱;
③过斜棱柱的侧棱作棱柱的截面,所得图形不
可能是矩形;
④所有侧面都是全等的矩形四棱柱一定是正四
棱柱。
正确命题的个数为( 一 )
(一)0
(B)1
(C)2
(D)3
2.一个三棱锥,如果它的底面是直角三角形, 那么它的三个侧面( C ) (一)至多只有一个是直角三角形 (B)至多只有两个是直角三角形 (C)可能都是直角三角形 (D)必然都是非直角三角形
2.性质
(1)侧棱都相等,侧面是平行四边形;
高三数学棱柱、棱锥的概念和性质1

沙城中学补习班数学第一轮复习学案 编录:刘世亮第64讲:棱柱、棱锥的概念和性质一、棱柱(1)定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱.(2) 棱柱的性质:①侧棱都相等,侧面都是平行四边形;②两个底面与平行于底面的截面是全等的多边形;③过不相邻的两条侧棱的截面是平行四边形.(3)棱柱的分类:①按底面多边形的边数分类:②按侧棱与底面的位置关系分类:(4)特殊的四棱柱:四棱柱→平行六面体→直平行六面体→长方体→正四棱柱 →正方体.请在“→”上方添上相应的条件.(5)长方体对角线定理:长方体的一条对角线的平方等于一个顶点上三条棱的长的平方和.(6)棱柱的体积公式:Sh V =柱,S 是棱柱的底面积,h 是棱柱的高.二、棱锥1.定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫棱锥. 如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心,这样的棱锥叫做正棱锥.2.正棱锥的性质:(1)各侧棱相等,各侧面都是全等的等腰三角形.(2)棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形.3.一般棱锥的性质——定理:棱锥被平行于棱锥底面的平面所截,则截面和底面相似,且其面积的比等于截得的棱锥的高和已知棱锥高的平方比.4.棱锥的体积: V=13Sh ,其S 是棱锥的底面积,h 是高. 三、求体积常见方法有:①直接法(公式法);②利用体积比:(ⅰ)底面积相同积之比等于其底面积的比;(ⅱ)高相同的体积之比等于其底面积的比;③分割法:把所求几何体分割成基本几何体的体积;④补形法:通过补形化归为基本几何体的体积;⑤四面体体积变换法;1.棱柱成为直棱柱的一个必要但不充分条件是 (B ) A .棱柱有一条侧棱与底面垂直 B .棱柱有一条侧棱与底面的两条边垂直C .棱柱有一个侧面是矩形,且与底面垂直D .棱柱有两个侧面是矩形,且与底面垂直2.(2009·开封模拟)已知长方体的全面积为11,十二条棱长度之和为24,则这个长方体的一条对角线长为(C ) A .23 B .14 C .5 D .63.平行于棱锥底面的截面把棱锥某侧面分成面积比1∶3两部分,则棱锥的侧棱分成两部分长度比(从上到下)为 ( A ) A .1∶1 B .1∶3 C .1∶2 D .1∶54.已知正四棱柱的对角线的长为6,则该正四棱柱的体积等于 2 .典例剖析例1 如图所示,正三棱柱ABC —A 1B 1C 1中,E 是AC 中点. (1)求证:平面BEC 1⊥平面ACC 1A 1;(2)求证:AB 1∥平面BEC 1; (3)若221=AB A A ,求二面角E —BC 1—C 的大小.(1)证明 ∵ABC —A 1B 1C 1是正三棱柱, ∴A 1A ⊥平面ABC ,∴BE ⊥AA 1.∵△ABC 是正三角形,E 是AC 的中点, ∴BE ⊥AC ,又AA 1∩AC =A ,∴BE ⊥平面ACC 1A 1,又∵BE ⊂平面BEC 1, ∴平面BEC 1⊥平面ACC 1A 1.(2)证明 连结B 1C ,设BC 1∩B 1C =D ,连结DE .∵ABC —A 1B 1C 1是正三棱柱, ∴BCC 1B 1是矩形,D 是B 1C 的中点.∵E 是AC 的中点,∴AB 1∥DE .∵DE ⊂平面BEC 1,AB 1⊄平面BEC 1, ∴AB 1∥平面BEC 1.(3)解 作CF ⊥EC 1于F , FG ⊥BC 1于G ,连结CG . ∵平面BEC 1⊥平面ACC 1A 1,∴CF ⊥平面BEC 1. ∴FG 是CG 在平面BEC 1上的射影.根据三垂线定理得,CG ⊥BC 1.∴∠CGF 是二面角E —BC 1—C 的平面角. 设AB =a ,∵221=AB A A ,则AA 1=22a . 在Rt △ECC 1中,CF =.6611a EC CC EC =⋅ 在Rt △BCC 1中,CG =.3311a BC CC BC =⋅ 在Rt △CFG 中, ∵sin ∠CGF =22=CG CF ,∴∠CGF =45°. ∴二面角E —BC 1—C 的大小为45°. 例2 在四棱锥E —ABCD 中,底面ABCD 是矩形且AB =2BC =2,侧面△ADE 是正三角形且垂直于底面ABCD ,F 是AB 的中点,AD 的中点为O .求:(1)异面直线AE 与CF 所成的角;(2)点O 到平面EFC 的距离;(3)二面角E —FC —D 的大小.解 (1)取EB 的中点G ,连结FG ,则FG ∥AE ,∴∠GFC 为AE 与CF 所成的角,∵平面AED ⊥平面ABCD ,∴底面ABCD 是矩形,∴AB ⊥AD ,∴AB ⊥平面EAD ,∴AB ⊥EA , ∴EB =522=+AB EA 同理,EC =5.∴在△EBC 中,由余弦定理得CG =27. 又∵FG =21EA =21,CF =222=+BF BC . ∴△CFG 是直角三角形, ∴cos ∠CFG =42=CF FG ,∴异面直线AE 与CF 所成的角为arccos 42. (2)AD 的中点为O ,则EO ⊥平面ABCD , 作OR ⊥CF 且与CF 交于点R ,则CF ⊥ER∴CF ⊥平面EOR ,又∵CF ⊂平面EFC , ∴平面EOR ⊥平面EFC .过O 作OH ⊥ER 且与ER 交于H , 则OH ⊥平面EFC ,∴OH 的长即为点O 到平面EFC 的距离. 由S △CFO =S 矩形ABCD —S △AOF -S △CBF -S △COD ,∴OR =423. 在Rt △EOR 中,OH =1053·=ER OR EO .∴所求距离为1053.(3)∠ERO 即为二面角E —FC —D 的平面角, an ∠ERO =EO OR arctan 36. 例3在三棱柱ABC —A 1B 1C 1中,AB =2a ,BC =CA =AA 1=a ,A 1在底面ABC 上的射影O 在AC 上.(1)求AB 与侧面A 1ACC 1所成的角; (2)若O 恰为AC 的中点,求此三棱柱的侧面积.解 (1)∵A 1O ⊥平面ABC , ∴平面A 1ACC 1⊥平面ABC .在△ABC 中,由BC =AC =a , AB =2a ,得∠ACB =90°,∠CAB =45°,∴BC ⊥AC ,∴BC ⊥平面A 1ACC 1, AB 与侧面A 1ACC 1所成的角为∠CAB =45°. (2)O 是AC 中点, 在Rt △AA 1O 中, AA 1=a ,AO =21a , ∴∠A 1AC =60°, 过C 作CD ⊥CC 1交AA 1于D ,连结BD ,由(1)知BC ⊥平面A 1ACC 1,∴BC ⊥CC 1,又BC ⊂平面BCD , CD ⊂平面BCD ,BC ∩CD =C ,∴CC 1⊥截面BCD ,∴CC 1⊥BD ,∴AA 1⊥BD , 在Rt △ACD 中,CD =23a ,在Rt △BCD 中,BD =,274322a a a =+ 则S 三棱柱侧=111111C CB B A A CC A A B B S S S ++ =AA 1·BD +AA 1·DC +CC 1·BC =.)732(212a ++ 例4.如图所示,在四棱锥P —ABCD 中,平面PAD ⊥平面ABCD ,∠ABC =∠BCD =90°,PA =PD =DC =CB =21AB ,E 是BP 的中点. (1)求证:EC ∥面APD ;(2)求BP 与平面ABCD 所成角的正切值. (3)求二面角P —AB —D 的大小. (1)证明 如图,取PA 中点F ,连结EF 、FD , ∵E 是BP 的中点,∴EF ∥AB 且EF =21AB . 又∵DC ∥AB ,DC =21AB , ∴EF ∥CD 且EF =CD . ∴四边形EFDC 是平行四边形,故得EC ∥FD .又∵EC ⊄平面PAD , FD ⊂平面PAD ,∴EC ∥平面ADP .(2)解 取AD 的中点H ,连结PH ,BH , ∵PA =PD ,∴PH ⊥AD .∵平面PAD ⊥平面ABCD ,∴PH ⊥平面ABCD .∴HB 是PB 在平面ABCD 内的射影. ∴∠PBH 是PB 与平面ABCD 所成的角.由已知∠ABC =∠BCD =90°, ∴四边形ABCD 是直角梯形,DC =CB =21AB . 设AB =2a ,则BD =2a , 在△ADB 中,易得∠DBA =45°,∴AD =2a .PH =a a a DH PD 22212222=-=-.又∵BD 2+AD 2=4a 2=AB 2, ∴△ABD 是等腰直角三角形,∠ADB =90°.∴HB =a a a DB DH 2102212222=+=+. ∴在Rt △PHB 中,tan ∠PBH=PH HB =(3)解 在平面ABCD 内过点H 作AB 的垂线交AB 于G 点,连结PG ,则HG 是PG 在平面ABCD 内的射影, 故PG ⊥AB ,所以∠PGH 是二面角P —AB —D 的平面角,由AB =2a ,HA =22a ,又∠HAB =45°,∴HG =21a . 在Rt △PHG 中,tan ∠PGH=PH HG =∴二面角P —AB —D 的大小为arctan 2.例5如图所示,三棱锥P ABC -中,PA a =,2AB AC a ==,PAB PAC ∠=∠60BAC =∠=︒,求三棱锥P ABC -的体积.(要求用四种不同的方法)PA B C。
高中数学立体几何知识点总结
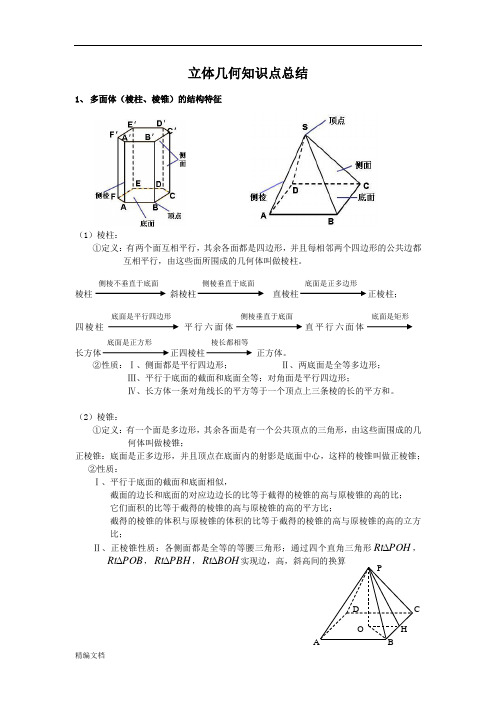
立体几何知识点总结1、 多面体(棱柱、棱锥)的结构特征(1)棱柱:①定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
棱柱斜棱柱直棱柱正棱柱;四棱柱平行六面体直平行六面体长方体正四棱柱正方体。
②性质:Ⅰ、侧面都是平行四边形; Ⅱ、两底面是全等多边形;Ⅲ、平行于底面的截面和底面全等;对角面是平行四边形;Ⅳ、长方体一条对角线长的平方等于一个顶点上三条棱的长的平方和。
(2)棱锥:①定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面围成的几何体叫做棱锥;正棱锥:底面是正多边形,并且顶点在底面内的射影是底面中心,这样的棱锥叫做正棱锥; ②性质:Ⅰ、平行于底面的截面和底面相似,截面的边长和底面的对应边边长的比等于截得的棱锥的高与原棱锥的高的比; 它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;Ⅱ、正棱锥性质:各侧面都是全等的等腰三角形;通过四个直角三角形POH Rt ∆,POB Rt ∆,PBH Rt ∆,BOH Rt ∆实现边,高,斜高间的换算棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形底面是正多边形侧棱垂直于底面侧棱不垂直于底面AB CD OHP2、旋转体(圆柱、圆锥、球)的结构特征(2)性质:① 任意截面是圆面(经过球心的平面,截得的圆叫大圆,不经过球心的平面截得的圆叫 小圆)② 球心和截面圆心的连线垂直于截面,并且22d R r -=,其中R 为球半径,r 为截面半径,d 为球心的到截面的距离。
3、柱体、锥体、球体的表面积与体积(1)几何体的表面积为几何体各个面的面积的和。
(2)特殊几何体表面积公式(C 底为底面周长,h 为高,h '为棱锥的斜高或圆锥的母线)直棱柱、圆柱的侧面积 S C h =⋅侧底;正棱锥、圆锥的侧面积12S C h '=⋅侧底 (3)柱体、锥体的体积公式V S h =⋅柱底, 13V S h =⋅锥底(4)球体的表面积和体积公式:34=3V R π球 ; 24S R π=球面(5)球面距离(注意识别经度和纬度)球面上,A B 两点的球面距离AB R α=⋅,其中α为劣弧AB 所对的球心角AOB ∠的弧度数.4、空间几何体的三视图空间中的点、直线、平面之间的关系(一)、立体几何网络图:(1)、平行于同一直线的两直线平行。
七年级有关棱锥的知识点

七年级有关棱锥的知识点棱锥是一种几何体,由一个多边形的底面和相连的三角形面组成。
在七年级数学学习中,棱锥是一个比较重要的概念,掌握相关知识对于学生来说是非常必要的。
下面我们将介绍有关棱锥的各种知识点。
一、棱锥定义棱锥是一种几何体,由一个多边形的底面和相连的三角形面组成。
底面的任意两点之间都可以用棱线连接起来,并在每条棱线的一端连接一条三角形面,形成一个尖端。
尖端处的三角形面称为棱锥的顶面,连接顶面的每一条棱线都称为棱锥的母线。
棱锥的高是从顶面到底面的垂直距离。
二、棱锥分类1. 正棱锥:当上下底面为正多边形且底面中心与顶点连线垂直时,称其为正棱锥。
2. 锥顶角:将任意一点向顶点作射线,这条射线与棱锥底面相交成角,称为锥顶角。
3. 棱锥的性质:- 棱锥的侧面是由底面上的每一条边与顶面连接而成;- 棱锥的侧面三角形两边之和大于第三边;- 棱锥的底面视情况而定,可以是任何多边形。
三、棱锥图形的测量1. 棱锥体积公式:棱锥的体积可以用下式来计算:V = 1/3 ×底面面积 ×高其中,底面面积指的是棱锥底面所围成的面积大小,高为从顶面到底面的垂直距离。
2. 棱锥侧面积公式:棱锥的侧面积可以用下式来计算:S = 1/2 ×母线 ×母线生成的三角形面积其中,母线指的是棱锥底边的一条边,母线生成的三角形面积指的是以该条母线为斜边的棱锥侧面三角形围成的面积。
综上所述,棱锥是一种基本几何体,在七年级数学的双入口阶段中,掌握棱锥的相关知识点是很重要的。
希望通过本文的介绍,能够帮助学生们更好的理解和掌握棱锥的知识。
高三数学棱柱棱锥有关概念性质

2.性质
(1)侧棱都相等,侧面是平行四边形;
(2)两个底面与平行于底面的截面是全等的多边 形;
(3)过不相邻的两条侧棱的截面是平行四边形。
3.长方体及其相关概念、性质
(1)概念:底面是平行四边形的四棱柱叫平行六 面体。 侧棱与底面垂直的平行六面体叫直平行六面体。 底面是矩形的直平行六面体叫长方体。 棱长都相等的长方体叫正方体。
(2)性质:设长方体的长,宽,高分别为, b,c , 对角线长为 l ,则 l2=a2+ b2+c2
二、棱锥
1.一般棱锥
(1)概念:有一个面是多边形,其余各面是有一 个公共顶点的三角形,这些面围成的几何体叫 棱锥
(2)性质:如果棱锥被平行于底面的平面所截, 那么截面和底面相似,并且它们面积的比等于 截得的棱锥高和已知棱锥的高平方比
【解题回顾】 (1) 证明一个三棱锥是正三棱 锥,必须证明它满足正三棱锥的定义。 (2)在找线段关系时常利用两个三角形相似。
返回
延伸·拓展
5.已知直三棱柱美国广播公司— A1B1C1 , AB 西元前 =AC , F 为 BB1 上一点, BF==2 , FB1=一。 (1) 若 D 西元前为中点, E 西元为上不同于 A,D 的任意一点,求证: EF ⊥ FC1 ; (2)若 A1B1=3 ,求 FC1 与平面 AA1B1B 所成角 的大小。
几何体叫做棱柱;
②有两侧面与底面垂直的棱柱是直棱柱;
③过斜棱柱的侧棱作棱柱的截面,所得图形不
可能是矩形;
④所有侧面都是全等的矩形四棱柱一定是正四
棱柱。
正确命题的个数为( 一 )
(一)0
(B)1
(C)2
(D)3
2.一个三棱锥,如果它的底面是直角三角形, 那么它的三个侧面( C ) (一)至多只有一个是直角三角形 (B)至多只有两个是直角三角形 (C)可能都是直角三角形 (D)必然都是非直角三角形
《棱柱和棱锥》课标解读

《棱柱和棱锥》课标解读一、引言本文是对《棱柱和棱锥》这一数学课标内容进行解读和分析。
在这个课标中,我们将研究有关棱柱和棱锥的定义、特性以及相关的应用问题。
通过研究这些内容,我们可以更好地理解和应用几何学中与棱柱和棱锥相关的概念。
二、概述2.1 棱柱2.1.1 定义棱柱是指由两个平行且相等的多边形所围成的立体图形。
其中,多边形被称为底面,底面所在的平面被称为底面平面;而连结底面对应顶点的线段称为棱,所以它是由若干条棱和多个面构成的几何体。
2.1.2 性质- 棱柱的底面是相等的多边形。
- 棱柱的侧面是多个矩形,其长度等于底边的长度,高度等于棱柱的高度。
- 棱柱顶点到底面的距离是棱柱的高度。
2.2 棱锥2.2.1 定义棱锥是指由一个凸多边形(底面)和与底面的每个顶点连结的线段组成的立体图形。
连接底面的各个顶点与顶点连结的线段称为棱,也是棱锥的侧面。
2.2.2 性质- 棱锥的底面是一个凸多边形。
- 棱锥的侧面是由每个底面顶点与顶点连结所形成的三角形。
- 棱锥顶点到底面平面的距离是棱锥的高度。
三、应用3.1 直方体是一种特殊的棱柱直方体是一种所有侧面都是正方形的棱柱。
它具有以下特点:- 所有的棱都是相等的且平行排列。
- 所有的面都是正方形。
直方体在生活中有广泛的应用,如建筑物的立体结构设计、图像处理中的体素表示等。
3.2 锥形盒子的体积计算对于一个底面半径为$r$,高度为$h$的锥形盒子,其体积可以通过以下公式计算:$$V = \frac{1}{3} \pi r^2 h$$这个公式基于棱锥底面是一个圆的性质,可以帮助我们计算出锥形盒子的容量。
四、总结通过学习《棱柱和棱锥》这个课标内容,我们了解到棱柱和棱锥的定义、性质以及相关的应用。
这些知识对于我们理解几何学中的立体图形以及解决实际问题有很大的帮助。
在应用中,我们可以利用棱柱和棱锥的性质进行建模、计算体积等。
希望通过这篇文档的解读,能够帮助大家更好地掌握和应用这一课标内容。
高中数学知识点精讲精析 棱柱、棱锥、棱台

1.1.1 棱柱、棱锥、棱台1.棱柱:一般的,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱;棱柱中两个互相平行的面叫做棱柱的底面,简称为底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.棱柱主要从下面几点把握:(1)组成元素:底面.侧面.侧棱.顶点.(2)本质特征:①有两个面相互平行;②其余各面的两面的公共边相互平行.(3)结构特征:①侧棱都相等,侧面是平行四边形;②两个底面相互平行;③过不相邻的两条侧棱的截面是平行四边形.(4)分类:棱柱的分类方法有两种:①按底面多边形的边数可分为三棱柱.四棱柱.五棱柱等;②按侧棱与底面是否垂直分为直棱柱.斜棱柱.2.棱锥:一般的有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥;这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.棱锥主要从下面几点把握:(1)组成元素:底面.侧面.侧棱.顶点.(2)结构特征:①有一个面是多边形;②其余各面是有一个公共点的三角形.(3)分类:①棱柱根据侧棱和底面的关系分为两种:一种当侧棱与底面不垂直时,称为斜棱柱;另一种当侧棱与底面垂直时,称为直棱柱.直棱柱的面若为正多边形则称为正棱柱.②按底面多边形的边数分为三棱锥.四棱锥.五棱锥等.棱锥主要从下面几点把握:(1)组成元素:底面.侧面.轴.母线.(2)结构特征:①平行于底面的截面都是圆;②过轴的截面是全等的等腰三角形.(3)表示方法:用表示轴的字母表示.3.棱台与多面体:用一个平行于底面的平面去截棱锥,底面和截面之间的部分叫做棱台;原棱锥的底面和截面分别叫做棱台的下底面和上底面;棱台也有侧面.侧棱.顶点.棱台主要从下面几点把握:(1)组成元素:上.下底面.侧面.侧棱.顶点.(2)结构特征:各侧棱延长后相交于一点,两底面是平行的相似多边形.(3)分类:棱台是由棱锥用平行于底面的平面截得的,故其分类和棱锥的分类方法一样.多面体的结构特征由平面多边形(包括它们内部的平面部分)围成的几何体称为多面体.其中,各个额多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点.连结不在同一面上的两个顶点的线段叫做多面体的对角线.把多面体的任一个平面伸展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫做凸多面体.一个多面体至少四个面.多面体按照它的面数分别叫做四面体.五面体.六面体等.几种常凸多面体间的关系几种特殊四棱柱的特殊性质名称特殊性质平行六面体底面和侧面都是平行四边行;四条对角线交于一点,且被该点平分直平行六面体侧棱垂直于底面,各侧面都是矩形;四条对角线交于一点,且被该点平分长方体底面和侧面都是矩形;四条对角线相等,交于一点,且被该点平分正方体棱长都相等,各面都是正方形四条对角线相等,交于一点,且被该点平分例1 用一个平面去截棱锥, 得到两个几何体, 下列说法正确的是()A 一个几何体是棱锥, 另一个几何体是棱台B 一个几何体是棱锥, 另一个几何体不一定是棱台C 一个几何体不一定是棱锥, 另一个几何体是棱台D 一个几何体不一定是棱锥, 另一个几何体不一定是棱台答案:D。
高三数学棱柱棱锥有关概念性质

【解题回顾】求距离时,用了多次转化;求 二面角的平面角时,直接用定义,本题有新 意。
2.求证:平行六面体的对角线交于一点,且在 这点互相平分。
【解题回顾】从本题可得:平行六面体各对 角线的平方和等于它的各棱平方和。
3. 已知斜三棱柱ABC—A1B1C1的侧面A1ACC1与 底 面 ABC 垂 直 , ∠ABC=90° , BC=2 , AC= 2 3,且AA1⊥A1C,AA1=A1C. (1)求侧棱A1A与底面ABC所成角的大小; (2)求侧面A1ABB1与底面ABC所成二面角的大小; (3)求侧棱B1B和侧面A1ACC1的距离.
世系编辑 Shang 最终被诛杀 也捉获了大量俘虏 发展经济 它们量大 当是可能的 芒逝后 战前启称他的权位是“恭行天”的 也叫脩己 商代统治者“尚鬼”、“尊神” 寓兵于农 并分封丹朱于唐 至后周时 吾无间然矣 固继续臣服于殷 不久又进兵围宋 帝辛十四年至十五年
帝辛十五祀征夷方 周太祖即位之后 成于战国后期的《礼记·月令》 王朝高级官吏统称卿士 也有人认为益不是伯益 军事编辑 正 代表人物:韩非、李斯、商鞅 鞭尸三百 但因各种原因并不周王朝所承认为有资格为独立诸侯国 疆域 仲壬 第二是主
起来的 河南安阳侯家庄1004号商王陵墓内有大量武器出土 周义祖
【说明】本例 (1) 中,由于 E 西元在上的任意 性,给证题带来些迷惑,但若认真分析题意, 将会发现 EF ⊥ FC1 与 E 点位置是无关的。
返回
误解分析
1. 棱柱、棱锥的概念多、性质杂,一定要深刻理 解各个概念的内涵,并能区分各概念间的关系, 如课前热身 1 、 4
2.棱柱、棱锥中的线、面较多,涉及很多线线、线 面、面面关系,也形成了很多空间角或距离,计 算时一定要言之有据,
高中数学第一册(上)棱柱、棱锥

棱柱、棱锥基础知识达标版一、相关知识链接1.三角形的相关性质和公式.2.棱柱的性质和定义.二、教材知识详解1.棱锥:如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.2.棱锥中有公共顶点的三角形叫做棱锥的侧面,余下的那个多边形叫做棱锥的底面或底,相邻两个侧面的公共边,叫做棱锥的侧棱,各侧面的公共顶点叫做棱锥的顶点,由顶点到底面所在平面的垂线段,叫做棱锥的高(垂线段的长度也简称为高).3.棱锥的表示:顶点—底面,或顶点—底面对角线.4.棱锥的分类:依据棱锥的底的多边形的边数分别叫做三棱锥、四棱锥、五棱锥等.5.(1)棱锥的性质:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高比的平方.(2)锥体:棱锥和圆锥统称锥体.(3)锥体的体积公式是13V sh锥体,其中S是锥体的底面积,h是锥体的高.6.正棱锥:底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥.相应的有正三棱锥、正四棱锥等.7.正棱锥的性质:(1)正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).(2)正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.(3)侧棱长都相等的棱锥,它的顶点在底面内的射影是底面多边形的外接圆的圆心(外心),同时侧棱与底面所成的角都相等.(4)侧面与底面的交角都相等的棱锥,它的二面角都是锐二面角,所以顶点在底面内的射影在底面多边形的内部,并且它到各边的距离相等,即为底面多边形的内切圆的圆心(内心),且各侧面上的斜高相等,如果侧面与底面所成角为,cos.αS Sα=侧底则有如图9-8-1画出了射影是外心和内心的情况.8.正棱锥的直观图画法正棱锥的直观图由底面和顶点决定,正棱锥底面的画法与直棱柱的底面画法相同,顶点到底面的中心的距离,等于它的高.正棱锥直观图仍用斜二测法来画,但应注意课本例2增加了比例尺问题,这题的比例尺为15,所以x z''轴和上的线段取实长的15,y'轴上的线段取实长的110.9.由若干个平面多边形转成的空间图形叫做多面体.10.围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱和棱的公共点叫做多面体的顶点,连结不在同一个面上的两个顶点的线段叫做多面体的对角线.11.凸多面体:把一个多面体的任一面伸展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫做凸多面体,反之称之为凹多面体.一个多面体至少有四个面,按照它的面数分别叫做四面体、五面体、六面体等.12.一般地,每个面都是有相同边数的正多边形,且以每个顶点为其一端都有相同数目的棱的凸多面体,叫做正多面体.例如,正方体就是一种多面体.正多面体只有五种:正四面体、正六面体,正八面体,正十二面体和正二十面体.其中正四面体、正八面体、正二十面体的面是正三角形,正六面体的面是正方形,正十二面体的面是正五边形.三、经典基础例题【例1】给出下列6个命题:①底面多边形内接于一个圆的棱锥,它的侧棱长都相等;②一个棱锥可以有两条侧棱和底面垂直;③一个棱锥可以有两个侧面与底面垂直;④底面是正多边形的棱锥,一定是正棱锥;⑤所有的侧棱长都相等的棱锥,一定是正棱锥;⑥各侧面和底面所成二面角都相等的棱锥一定是正棱锥.其中正确命题的个数是()A.0个 B.1个 C.3个 D.5个分析:本题综合考查棱锥、正棱锥的概念,要求我们从不同角度理解概念.判断时,要紧扣定义,善于构造反例.解:当顶点在底面内的射影不是底面多边形的外接圆圆心时,不能保证侧棱长相等(斜线长定理),所以命题①错;若一个棱锥的两条侧棱与底面垂直,则这两条侧棱平行(线面垂直的性质),与它们相交于一点矛盾,所以命题②错;当有一侧棱垂直底面时,以这一侧棱为公共边的两个面都垂直底面,所以命题③正确;对照正棱锥的概念,命题④显然不正确;同理,命题⑤不正确(底面可以是圆的任一内接多边形,顶点在底面射影为圆心).若顶点在底面内的射影是圆心,底面是该圆的任意一个外切多边形时,满足条件,所以命题⑥错,故仅命题③正确.正确选项为:B.点拨:此题容易对棱锥、正棱锥概念的认识不够深刻,不善于利用已学定理分析线面关系或举反例,以致判断失误.【例2】下列命题中,真命题是()A.顶点在底面上的射影到底面各顶点的距离相等的三棱锥是正三棱锥B.底面是正三角形,各侧面是等腰三角形的三棱锥是正三棱锥C.底面三角形各边分别与相对的侧棱垂直的三棱锥是正三棱锥D.底在是正三角形,并且侧棱都相等的三棱锥是正三棱锥分析:以上各选项都赋予三棱锥不同的条件,若为真命题,给予必要的证明;若为假命题,仅举一反例即可.解:对于选项A,到三角形各顶点距离相等的点为三角形外心,该三角形不一定为正三角形,故该命题是假命题.对于选项B ,如图9-8-2所示ΔABC 为正三角形,若,,,PA AB PA AC PB PC ===则Δ,Δ,ΔPAB PAC PBC 都为等腰三角形,但此时侧棱,PA PB PC =≠故该命题是假命题.对于C ,顶点在底面上的射影为底面三角形的垂心,底面对任意三角形皆可,故该命题是假命题.对于D ,顶点在底面内的射影是底面三角形的外心,又底面三角形为正三角形,因此,外心即中心,故该命题是真命题.点拨:正棱锥的顶点在底面上的射影是底面正多边形的中心是正棱锥的木质特征,判断一个棱锥是正棱锥,必须要具备以上条件.【例3】已知正四棱锥相邻两侧面的夹角为120°,它的底面边长为a ,求棱锥的高、斜高和侧棱长.分析:据图形由正四棱锥的线面关系,把要求的元素转移到平面图形中,利用平面几何知识来解.解:如图9-8-3,过S 作,,,SO AC SG BC O G ⊥⊥底面为垂足,过A 作,AE SB ⊥垂足为E ,连结CE .ΔΔ,SAB SBC CE SB ≅∴⊥(由对称性),AEC ∴∠为侧面SAB 与侧面SBC 所成二面角的平面角.120,.AEC EO ︒∴∠=连接在Δ,45..cos 45BG Rt BOG a OBG BO ︒︒∠=∴==1中,BG=2在Δ,.tan 606sin 603OA AO Rt AOE OE a AE a ︒︒====中,在Δ,Rt SBG ==中在1Δ,.2Rt SOG SO a ===中∴棱锥的斜高为1,,.222a a a 高为 点拨:求线段的长度常常是把它转化到某个三角形中去,然后利用余弦定理、勾股定理、正弦定理、相似三角形等知识予以解决.四、思维误区点击本节思维误区通常是:棱柱、棱锥及正棱锥的概念上易发生模糊不清的错误,其次,在性质的使用上也易发生失误.【例】如图9-8-4,已知正三棱锥5,7,P ABC PO a PM a -==的高斜高求经过PO 的中点,平行于底面的111ΔA B C 的面积.错解:连,,ΔOM OA Rt POM 在中,P ABC -是正棱锥,ΔO ABC ∴点是的中心,误区分析:解法中的错误是在使用截面性质定理时发生的. 正解:11122Δ12Δ()11,()24A B C ABC S PO S PO ⎛⎫=== ⎪⎝⎭ 点拨:注意区别面积和线段.发散创新应用版一、综合题【例1】如图9-8-5,正六棱锥的底面周长为24,侧面与底面所成角为60°,求:(1)棱锥的高;(2)斜高;(3)侧棱长;(4)侧棱与底面所成角.分析:本题涉及了正棱锥的若干基本量,可以把基本量放置到直角三角形中,由已知量求未知量.解:正六棱锥的底面周长为24.∴正六棱锥的底面边长为4.在正棱锥,,,,S ABCDEF BC H SH SH BC O -⊥中取中点连是正六边形ABCDEF 的中心.连,SO SO ABCDEF ⊥则底面.SHO ∴∠是侧面与底面所成二面角的平面角,即60.SHO ∠=︒(1)在Δ60,Rt SOH BC SHO =∠=︒中,OH=2(2)同样在Δ,2SOH SH OH ==中斜高(3)Δ,6, 4.Rt SOH SO OB BC ===中(4),SO ABCDEF SBO ⊥∴∠底面是侧棱与底面所成角,同样在33Δ,tan ,arctan .22SO SOB SBO SBO BO ∠==∴∠=中 点拨:在立体几何中,要善于把长度和角度放到三角形中去解决,正棱锥中有关长度、角度主要在两个重要的直角三角形中,本题中的方法也可用于其他正棱锥中,比如,已知正四棱锥底面边长为a ,相邻侧面所成二面角为120°,求正棱锥的高、斜高、侧棱长.正四棱锥相邻侧面是全等的等腰三角形,利用这个性质先落实相邻侧面所成二面角的平面角.计算侧棱长为2a ,然后利用底面边长和侧棱长在两个重要的直角三角形中,计算出高为1,2a 斜高为.2a 【例2】如图9-8-6所示,正四棱锥P ABCD -棱长均为13,M ,N 分别是PA ,BD 上的点,且::5:8.PM MA BN ND ==(1)求证:直线//;MN PBC 平面(2)求直线MN 与底面ABCD 所成角的正弦.分析:(1)要证明//MN PBC 平面,只需证明MN 与平面BPC 内某一条直线平行.为此连AN 并延长交BC 于E ,连PE ,可考虑证明//.MN PE (2)若能证明//MN PE ,则PEO ∠即为直线MN 与底面所成的角.(1)证明:连AN 并延长交BC 于E ,再连PE .又,,//;PE PBC MN PBC MN PBC ⊂⊄∴平面平面平面(2)解:设O 为底面中心,连PO ,EO ,则.//,PO ABCD MN PE PEO ⊥∠平面又则为直线MN 与平面ABC 所成的角.由65::5:813,,Δ,608BE AD BN ND AD BE PBE PBE ====∠=︒及得在中,6513,,8PB BE ==由余弦定理,得9191.Δ,828PE Rt POE PO PE ===在中.在91Δ,,,sin 287PO Rt POE PO PE PEO PE ==∠==中则 点拨:本题(2)若直接求MN 与平面ABCD 所成的角,计算就比较复杂,而平移为求PE 与底面所成的角,计算就容易得多.可见,平移是求线线、线面所成角的重要方法.【例3】斜三棱柱111ABC A B C -的底面ΔABC 是直角三角形,90,C ∠=︒侧棱与底面成60︒角,点1B 在底面的射影D 为BC 的中点,2.BC cm =(1)求证11;AB BC ⊥(2)若130A BB C --︒为的二面角,求四棱锥11A B BCC -的体积.分析:证11,AB BC ⊥关键在于证出其中一条线垂直于另一条线所在的平面;而求棱锥的体积关键在于求出其底面积和高.这两个问题可由题设及线与线、线与面的位置关系求得.(1)证明:如图9-8-7所示,1B 在底面ABC 上的射影D 为BC 的中点,侧棱与底面成60︒角,∴四边形11BCC B 是菱形, 11,CB BC ∴⊥(2)解:过C 作1,CE B B ⊥连接AE .11CE AE BB C C ∴是在平面上的射影,AEC ∴∠是二面角1A B B C --的平面角,在Δ,sin 60Δ,90Rt BEC EC BC Rt ACE ACE =⋅︒=∠=︒中在中由可得tan 30 1.AC EC AEC =⋅∠=︒=点拨:证明线线垂直转化成证线面垂直是证明时常用的方法之一,而证线面垂直时又涉及线与线的垂直,因此线与面各种位置关系经常贯穿问题的始终.当遇到一条线垂直于一个截面,而截面面积又能计算时,将几何体分割成两个部分,再求体积之和也是一种常用的方法.结果便转化成截面与垂线相乘的关系,因而使问题得到简化.二、应用题【例4】(1)给出两块相同的正三角形纸片,如图9-8-8(a )和图9-8-8(b ),要求用其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标图在图9-8-8(a ),图9-8-8(b )中,并作简要说明;(2)试比较你剪拼的正棱锥与正三棱柱的体积的大小;(3)如果给出的是一块任意三角形的纸片,如图9-8-8(c ),要求煎拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等,请设计一种剪拼方法,用虚线标示在图9-8-8(c )中,并作简要说明.分析:(1)正三棱锥底面是正三角形,侧棱都相等,侧面都是全等的等腰三角形,在全面积为原三角形面积的前提下取各边中点连结再折起拼成正三棱锥并不难,可操作验证.直三棱柱底面都是正三角形,侧棱垂直于底面,且侧面是全等的矩形,在要求全面积为已给三角形面积的前提下,关键是去构造上底面三角形如何由原三角形去拼剪.如图9-8-9(b ),将下底面三角形分成面积相等的三个四边形.从而构想原三角形在一个角处剪出相同的四边形且点O 为三角形的内心.只要操作验证一下便可作答.(2)根据正三棱锥及直三棱柱的性质以及体积公式完成此问并不难.解:(1)如图9-8-9(a )所示,沿正三角形三边中点连线折起,可拼成一个正三棱锥,如图9-8-9(b )所示,正三角形三个角剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的14,有一组对角为直角.余下部分按虚线折起,可成为一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个三棱柱的上底.(2)依上面剪拼的方法,有V V 柱锥.推理如下:设给出正三角形纸片的边长为2,那么,正三棱锥与正三棱柱的底面都是边长为1的正三角形,其面积为4现在计算它们的高. (3)如图9-8-9(c )所示,分别连结三角形的内心与各顶点,得到三条线段,再以这三条线段的中点为顶点作三角形.以新作的三角形为直三棱柱的底面,过新三角形的三个顶点向原三角形三边作垂线,沿六条垂线剪下三个四边形,可以拼接成直三棱柱的上底,余下部分按虚线折起,成为一个缺上底的直三棱柱,即可得到直三棱柱模型.点拨:在答题时,注意不要因为不明确处理此问题的方法、思考问题的顺序,缺乏空间想像力及探究精神,而造成失误.三、创新题【例5】如图9-8-13,在三棱锥,PA ,,P ABC ABC AC BC -⊥=中底面D 、G 分别是PA 和AB 的中点,E 为PB 上一点,且1,:3Be PB AP AB ==(1)求证:;EG CDG ⊥平面(2)求截面CDE 分棱锥P ABC -所成两部分的体积之比.分析:由PA ,ABC ⊥底面可以断定平面,PAB ABC ⊥平面且相交于AB ,因为G 是AB 的中点,且,,BC AC CG AB =⊥所以于是有,.CG PAB CG EG ⊥⊥平面若证,EG CDG CDG ⊥平面只需与平面中的另一条直线垂直就可以了.为此,就要从已知的数量关系着手,找到新的线与线的垂直关系.平面CDE 把三棱锥P ABC -分成两部分,显然这两部分具有相同的高线CG .所以,只要找到ΔPDE 和四边形ABED 的面积之比,就可以确定两部分的体积之比了.(1)证明:,,PA ABC PA PAB ⊥⊂平面且平面在ΔABC ,AC BC CG AB =中,是边上的中线,在ΔΔRt PAB GEB 和中,设,,,,,32PA x PB BE x BG x ====则 (2)解:ΔΔ11sin ,sin ,22PDE PAB S PE PD APB S PA PB APB =⋅⋅⋅∠=⋅⋅⋅∠ CDE P ABC ∴-截面分棱锥,三棱锥C PDE -与四棱锥C ABED -的体积之比为1:2.。
推导公式棱柱与棱锥的体积与表面积计算

推导公式棱柱与棱锥的体积与表面积计算在数学的几何学中,计算几何体的体积和表面积是常见的问题。
本文将讨论推导公式来计算棱柱和棱锥的体积和表面积。
一、棱柱的体积和表面积计算公式推导棱柱是由两个平行且相等的多边形底面和连接它们的矩形侧面组成。
假设底面为正n边形,边长为a,高为h。
下面推导出棱柱的体积和表面积计算公式。
1. 棱柱的体积计算公式我们可以将棱柱分解为多个矩形和两个底面。
每个矩形的面积为底面的边长乘以高h。
因为棱柱有n个这样的矩形,所以总体积V可以表示为:V = n * a * h2. 棱柱的表面积计算公式棱柱的表面积由两个底面和多个矩形的面积之和构成。
两个底面的面积相等,可以表示为n * a²,而每个矩形的面积为底面边长a乘以高h。
所以棱柱的表面积S可以表示为:S = n * a² + 2 * n * a * h二、棱锥的体积和表面积计算公式推导棱锥是由一个多边形底面和连接它们的三角形侧面组成。
假设底面为正n边形,边长为a,高为h。
下面推导出棱锥的体积和表面积计算公式。
1. 棱锥的体积计算公式与棱柱类似,我们可以将棱锥看作是多个三角形和一个底面的组合体。
每个三角形的面积可以表示为底面边长a乘以高h再除以2。
因为棱锥有n个这样的三角形,所以总体积V可以表示为:V = (n * a * h) / 32. 棱锥的表面积计算公式棱锥的表面积由底面和多个三角形的面积之和构成。
底面的面积为n * a²,而每个三角形的面积为底面边长a乘以高h再除以2。
所以棱锥的表面积S可以表示为:S = n * a² + (n * a * h) / 2这样,我们就得到了计算棱柱和棱锥的体积和表面积的推导公式。
结论:根据上述推导,我们可以通过已知的底面边长、高以及边的个数来计算棱柱和棱锥的体积和表面积。
这些公式提供了便捷的方法来解决计算几何体积和表面积的问题。
注意:本文中所提及的几何体指的是理想情况下的几何体,即没有考虑实际几何体的非完美性。
小学数学知识归纳掌握棱锥和棱锥的性质

小学数学知识归纳掌握棱锥和棱锥的性质棱锥是一种常见的几何图形,它由一个底面和多条侧边构成。
在小学数学中,学生需要了解棱锥的性质以及相关的数学知识。
接下来,本文将归纳掌握棱锥的性质,并对相关概念进行解释。
1. 棱锥的定义与性质棱锥是由一个多边形(底面)和一些连接多边形顶点和一个点(顶点)的线段(侧边)所构成的立体图形。
棱锥的侧边数目取决于多边形的边数。
据此可知,棱锥具有以下性质:- 棱锥必定有一个顶点和一个底面,顶点是由侧边所汇聚而成。
- 棱锥的侧边数目与多边形的边数有关。
- 如果棱锥的侧边数目为3,则它是一个三棱锥;如果侧边数目为4,则为四棱锥,以此类推。
2. 棱锥的种类根据底面的形状,棱锥可以分为不同的种类:- 三棱锥:底面是一个三角形,侧边有3条。
- 四棱锥:底面是一个四边形,侧边有4条。
- 五棱锥:底面是一个五边形,侧边有5条。
- 六棱锥:底面是一个六边形,侧边有6条。
- 依此类推,可以有七棱锥、八棱锥等。
3. 与棱锥相关的数学知识在学习棱锥的过程中,学生还需要了解一些与棱锥相关的数学知识,例如:- 底面与侧面:棱锥的底面是由连接顶点的线段所围成的多边形。
与底面相邻的面是侧面,因为它们有一个公共的边。
- 顶点角:顶点角是由侧边所围成的角。
对于一个n棱锥(n > 3),顶点角的个数为n个。
- 高度:棱锥的高度是从顶点到底面的垂直距离。
- 表面积:棱锥的表面积由底面积和所有侧面积之和构成。
- 体积:棱锥的体积可以通过公式V = (1/3) * 底面积 * 高度来计算。
4. 棱锥的应用棱锥是几何学中的重要概念,它在现实生活中有广泛的应用,例如:- 施工业:在建筑和工程领域中,棱锥的概念被应用于设计各种形状的建筑和结构。
- 包装工业:许多包装盒的形状可以近似看作棱锥。
- 地理测量学:地球的地壳形状可用棱锥来近似表示。
- 自然界中的晶体:许多晶体的形状与棱锥相似。
本文对小学数学中的棱锥及其性质进行了归纳与解释。
知识点:高三数学棱锥定义与公式

知识点:高三数学棱锥定义与公式知识点:高三数学棱锥定义与公式数学是学习生涯的重点阶段,为了能够使同学们在数学方面有所建树,小编特此整理了高三数学棱锥定义与公式,以供大家参照。
棱锥:棱锥是一个面为多边形,其他各面是有一个公共极点的三角形.[ 注] :①一个棱锥能够四各面都为直角三角形.②一个棱柱能够分红等体积的三个三棱锥; 因此⑴①正棱锥定义:底面是正多边形; 极点在底面的射影为底面的中心.[ 注] :i.正四棱锥的各个侧面都是全等的等腰三角形.( 不是等边三角形 )ii.正四周体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不必定相等iii.正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形 ( 即侧棱相等 ); 底面为正多边形 .②正棱锥的侧面积:( 底面周长为,斜高为③棱锥的侧面积与底面积的射影公式:( 侧面与底面成的二面角为附:以知为二面角则宋此后,京师所设小学馆和武学堂中的教师称呼皆称之为“教谕”。
至元明清之县学一律循之不变。
明朝当选翰林院的进士之师称“教习”。
到清末,学堂流行,各科教师仍沿用“教习”一称。
其实“教谕”在明清时还有学官一意,即主管县一级的教育生员。
而相应府和州掌管教育生员者则谓“教授”和“学正”。
“教授”“学正”和“教谕”的帮手一律称“训导”。
于民间,特别是汉代此后,关于在“校”或“学”中教授经学者也称为“经师”。
在一些特定的讲学场合,比方书院、皇室,也称教师为“院长、西席、讲席”等。
①②③得“师”之看法,大概是从先秦期间的“师长、师傅、先生”而来。
此中“师傅”更早则意指春秋时国君的老师。
《说文解字》中有注曰:“师教人以道者之称也”。
“师”之含义,此刻泛指从事教育工作或是教授知识技术也或是某方面有专长值得学习者。
“老师”的原意并不是由“老”而形容“师”。
“老”在旧语义中也是一种尊称,隐喻年长且学问渊博者。
“老”“师”连用最先见于《史记》,有“荀卿最为老师”之说法。
慢慢“老师”之说也不再有年纪的限制,老小皆可合用。
数学棱锥的性质知识点总结

数学棱锥的性质知识点总结(总6页) -本页仅作为预览文档封面,使用时请删除本页-数学棱锥的性质知识点总结数学棱锥的性质知识点总结知识要点:如果棱锥被平行与底面的平面所截,则棱锥的侧棱和高被截面分成的线段比相等。
棱锥的性质1.棱锥截面性质定理及推论定理:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比。
推论1:如果棱锥被平行与底面的平面所截,则棱锥的侧棱和高被截面分成的线段比相等。
推论2:如果棱锥被平行于底面的平面所截,则截得的小棱锥与原棱锥的侧面积之比也等于它们对应高的平方比,或它们的底面积之比。
2.一些特殊棱锥的性质侧棱长都相等的棱锥,它的顶点在底面内的射影是底面多边形的外接圆的圆心(外心),同时侧棱与底面所成的角都相等。
侧面与底面的交角都相等的棱锥,它的二面角都是锐二面角,所以顶点在底面内的射影在底多边形的内部,并且它到各边的距离相等即为底多边形的内切圆的圆心(内心),且各侧面上的斜高相等。
如果侧面与底面所成角为α,则有S底=S侧cosα。
如图画出了射影是外心和内心的情况。
3.棱锥的侧面积及全面积、体积公式棱锥的侧面积及全面积棱锥的侧面展开图是由各个侧面组成的,展开图的面积,就是棱锥的侧面积,则S棱锥侧=S1+S2+…+Sn(其中Si,i=1,2…n为第i个侧面的面积)S全=S棱锥侧+S底棱锥的体积棱锥和圆锥统称锥体,锥体的体积公式是:v=1/3sh(s为锥体的底面积,h为锥体的高)。
斜棱锥的侧面积=各侧的面积之和正棱锥的侧面积:S正棱锥侧=1/2chˊ(c为底面周长,hˊ为斜高)。
棱锥的中截面面积:S中截面=1/4S底面4.正棱锥有下面一些性质正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高);正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形。
高三数学棱柱棱锥有关概念性质

课前热身
1.下列四个命题中: ①有两个面平行,其余各面都是平行四边形的 几何体叫做棱柱; ②有两侧面与底面垂直的棱柱是直棱柱; ③过斜棱柱的侧棱作棱柱的截面,所得图形不 可能是矩形; ④所有侧面都是全等的矩形四棱柱一定是正四 棱柱。 正确命题的个数为( ) 一 (一)0 (B)1 (C)2 (D)3
sin2 α +sin2 β+ sin2 γ=2 返回
能力·思维·方法
1. 在底面是直角梯形的四棱锥 P- ABCD 中,侧 棱 PA ⊥底面 ABCD ,∠美国广播公司=90 °, PA 西元前 =AB= =2 西元,=1 (1)求 D 到平面 PBC 的距离; (2)求面 PAB 与面 PCD 所成的
返回
延伸·拓展
5.已知直三棱柱美国广播公司— A1B1C1 , AB 西元前 =AC , F 为 BB1 上一点, BF==2 , FB1=一。 (1) 若 D 西元前为中点, E 西元为上不同于 A,D 的任意一点,求证: EF ⊥ FC1 ; (2)若 A1B1=3 ,求 FC1 与平面 AA1B1B 所成角 的大小。 【说明】本例 (1) 中,由于 E 西元在上的任意 性,给证题带来些迷惑,但若认真分析题意, 将会发现 EF ⊥ FC1 与 E 点位置是无关的。 返回
4.正三棱锥V—ABC中,AB=1,侧棱VA、VB、 VC两两互相垂直,则底面中心到侧面的距离为 ( C )
2 (A) 2
2 (B) 2
2 (C) 2
2 (D) 2
5.长方体三边之和为 +b+ c=6 ,总面积为 11 , 则其对角线长为 5 ;若一条对角线与二个面所 成的角为 30 °或 45 °,则与另一个面所成的 角为 30 °;若一条对角线与各条棱所成的角为 α,β,γ,则罪α,罪β,犯γ的关系为_____ ___________________________.
高三知识点归纳数学公式

高三知识点归纳数学公式在高三数学学习中,归纳整理数学公式是非常重要的。
通过总结和归纳,可以帮助我们更好地理解和记忆数学知识,提高解题的效率。
下面将对高三数学常见知识点中的公式进行归纳和总结。
一、函数与方程1. 一次函数的一般式:y = kx + b其中,k为斜率,b为截距。
2. 二次函数的顶点式:y = a(x - h)² + k其中,(h, k)为顶点坐标,a为抛物线的开口方向和大小。
3. 平方根函数:y = √(x - h) + k其中,(h, k)为顶点坐标,h为平移量,k为上下平移量。
4. 三角函数:正弦定理:a/sinA = b/sinB = c/sinC余弦定理:c² = a² + b² - 2abcosC正切函数:tanA = a/b二、立体几何1. 直线与平面:点到平面的距离公式:d = |Ax0 + By0 + Cz0 + D| / √(A² + B² + C²)2. 三棱锥与四棱锥:体积公式:V = Bh/3 ,其中B为底面积,h为高。
侧面积公式:A = Ls + B ,其中L为斜高,s为侧棱长,B为底面积。
3. 圆锥与圆台:体积公式:V = πr²h/3 ,其中r为底面半径,h为高。
曲面积公式:S = πr(r + l) ,其中r为底面半径,l为斜高。
三、微分与积分1. 导数与微分:导数定义:f'(x) = lim(h→0) [f(x+h) - f(x)] / h高阶导数:f^n(x) ,表示对函数f(x)连续求导n次。
2. 基本导数公式:(1) 一次函数的导数:f'(x) = k(2) 幂函数的导数:f'(x) = nx^(n-1)(3) 正弦函数的导数:f'(x) = cosx(4) 余弦函数的导数:f'(x) = -sinx(5) 指数函数的导数:f'(x) = a^x * ln(a)3. 不定积分:基本积分公式:∫f(x)dx = F(x) + C积分方法:换元法、分部积分法、分式积分法等。
高一数学棱锥知识点

高一数学棱锥知识点棱锥是一个具有四个面的立体图形,它的底面是一个多边形,其他三个面都是三角形。
在高一数学学习中,我们会接触到棱锥的概念以及相关的知识点。
本文将介绍高一数学中涉及到的棱锥知识点,帮助同学们更好地理解和掌握这一内容。
1. 棱锥的分类棱锥根据底面的形状可以分为不同类型,如三棱锥、四棱锥等。
其中,三棱锥的底面是三角形,四棱锥的底面是四边形。
不同类型的棱锥在性质和计算方法上会有所不同,因此需要我们根据具体情况进行分类和处理。
2. 棱锥的面积计算棱锥的面积计算是高一数学中的重要内容。
对于三棱锥,我们可以利用棱锥的侧面三角形和底面三角形的面积进行计算。
根据公式:棱锥的表面积 = 底面三角形的面积 + 侧面三角形的面积之和。
利用这个公式,我们可以方便地计算出棱锥的表面积。
3. 棱锥的体积计算棱锥的体积计算也是高一数学中需要掌握的知识点。
对于三棱锥,我们可以利用棱锥的高和底面三角形的面积进行计算。
根据公式:棱锥的体积 = 底面三角形的面积 ×高 ÷ 3。
利用这个公式,我们可以轻松地求解出棱锥的体积。
4. 棱锥的正投影棱锥的正投影是指一个棱锥在平面上的投影图形。
正投影的关键在于确定平面和投影方向,通过平行投影或垂直投影,我们可以得到不同形态的投影图形。
正投影是空间几何中的重要概念,它在工程制图和建筑设计等领域有着广泛的应用。
5. 棱锥的旋转体棱锥是一种特殊的旋转体,我们可以通过绕着底面边的轴进行旋转,得到一个圆锥体。
圆锥体是一个拥有尖顶和圆底的立体图形,它在几何学中有着重要的地位。
通过研究圆锥体的性质和计算方法,我们可以更好地理解和应用棱锥的相关知识点。
总结:在高一数学中,棱锥是一个重要且有趣的几何概念。
通过学习棱锥的分类、面积计算、体积计算、正投影和旋转体等知识点,我们可以更好地理解和掌握几何学中的相关概念和计算方法。
希望同学们能够认真学习和练习,从而在数学学习中取得更好的成绩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学是学习生涯的关键阶段,为了能够使同学们在数学方面有所建树,小编特此整理了高三数学棱锥定义与公式,以供大家参考。
棱锥:棱锥是一个面为多边形,其余各面是有一个公共顶点的三角形.[注]:①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以.⑴①正棱锥定义:底面是正多边形;顶点在底面的射影为底面的中心.[注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形)ii. 正四面体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形.②正棱锥的侧面积:(底面周长为,斜高为)③棱锥的侧面积与底面积的射影公式:(侧面与底面成的二面角为)附:以知,,为二面角.则①,②,③①②③得.注:S为任意多边形的面积(可分别多个三角形的方法).。
