非对称密码体制
对称密码体制和非对称密码体制

对称密码体制和⾮对称密码体制⼀、对称加密 (Symmetric Key Encryption)对称加密是最快速、最简单的⼀种加密⽅式,加密(encryption)与解密(decryption)⽤的是同样的密钥(secret key)。
对称加密有很多种算法,由于它效率很⾼,所以被⼴泛使⽤在很多加密协议的核⼼当中。
⾃1977年美国颁布DES(Data Encryption Standard)密码算法作为美国数据加密标准以来,对称密码体制迅速发展,得到了世界各国的关注和普遍应⽤。
对称密码体制从⼯作⽅式上可以分为分组加密和序列密码两⼤类。
对称加密算法的优点:算法公开、计算量⼩、加密速度快、加密效率⾼。
对称加密算法的缺点:交易双⽅都使⽤同样钥匙,安全性得不到保证。
此外,每对⽤户每次使⽤对称加密算法时,都需要使⽤其他⼈不知道的惟⼀钥匙,这会使得发收信双⽅所拥有的钥匙数量呈⼏何级数增长,密钥管理成为⽤户的负担。
对称加密算法在分布式⽹络系统上使⽤较为困难,主要是因为密钥管理困难,使⽤成本较⾼。
⽽与公开密钥加密算法⽐起来,对称加密算法能够提供加密和认证却缺乏了签名功能,使得使⽤范围有所缩⼩。
对称加密通常使⽤的是相对较⼩的密钥,⼀般⼩于256 bit。
因为密钥越⼤,加密越强,但加密与解密的过程越慢。
如果你只⽤1 bit来做这个密钥,那⿊客们可以先试着⽤0来解密,不⾏的话就再⽤1解;但如果你的密钥有1 MB⼤,⿊客们可能永远也⽆法破解,但加密和解密的过程要花费很长的时间。
密钥的⼤⼩既要照顾到安全性,也要照顾到效率,是⼀个trade-off。
分组密码:也叫块加密(block cyphers),⼀次加密明⽂中的⼀个块。
是将明⽂按⼀定的位长分组,明⽂组经过加密运算得到密⽂组,密⽂组经过解密运算(加密运算的逆运算),还原成明⽂组,有 ECB、CBC、CFB、OFB 四种⼯作模式。
序列密码:也叫流加密(stream cyphers),⼀次加密明⽂中的⼀个位。
《网络安全》第5-6讲(2.4)

2.4 公钥(非对称)密码体制
2.4.2 公钥密码体制的原理
公钥密码体制的基本数学方法和基本原理如下所述。 2.用于构造公钥密码的常用单向函数 1)多项式求根 有限域GF(p)上的一个多项式
f ( x) ( x anmod p
当给定多项式的系数和x、p以后,利用Honer算法,最多进行 n次乘法,n-1次加法,就可以求得y的值。但已知多项式的系数a 和y、p以后,要求x,就需要对高次方程求根,至少要进行不小 于n2(lbp)2的整数次乘法,当n、p很大时很难求解。
定n以后求p、q的问题称为RSA问题。求n=p×q分解问题有以下几种形式:
(1)分解整数n为p、q; (2)给定整数M、C,求d使得Cd≡M mod n; (3)给定整数k、C,求M使得Mk≡C mod n; (4)给定整数x、C,决定是否存在y使得x≡y2mod n(二次剩余问题)。
遵义师范学院
给定x求y是容易的,但是当p很大时,从x=logby中要计算x是非常困难 的。如b=2,p=2100,给定x求y,只需作100次乘法,利用高速计算机可 在0.1ms内完成。而给定y求x,所需计算量为1600年。可见,有限域 GF(p)中的指数函数f(x)=bx是一个单向函数。
x=logby
遵义师范学院
遵义师范学院
2.4 公钥(非对称)密码体制
2.4.1 公钥密码体制的基本概念 3.电子签证机关
电子签证机关(即CA)是负责颁发数字证书的权威机构。CA自 身拥有密钥对,可以使用私钥完成对其他证书的数字签名,同时也拥 有一个对外开放的证书(内含公钥)。网上的公众用户通过验证CA的 数字签名建立信任,任何人都可以得到CA的证书(含公钥),用以验 证它所签发的其他证书。如果用户想建立自己的证书,首先要向CA提 出申请证书的请求。在CA判明申请者的身份后,便为他分配一个密钥 对,并且CA将申请者的公钥与身份信息绑在一起,在为之完成数字签 名后,便形成证书发给那个用户(申请者)。如果一个用户想鉴别数 字证书是否为假冒的,可以用证书发证机构CA的公钥对该证书上的数 字签名进行验证,数字签名验证的过程是使用CA公钥解密的过程,验 证通过的证书就被认为是有效的。CA在公开密码体系中非常重要,负 责签发证书以及证书和密钥的管理等必要工作。CA相当于网上公安机 构,专门发放、验证电子身份证。
非对称密码体制课件

• 解决了对称密码的诸多局限性
2020/11/18
非对称密码体制
4
非对称密码基本概念:非对称密码体制
明文
加密器 EK
PK
密钥产生器
密文
解密器 DK
SK
明文
• 密钥—(PK, SK) • PK:俗称公钥(Public Key),通常公钥是公开的,可以被任何实 体通过有效渠道获取; • SK:俗称私钥(Secret Key),通常私钥是保密的,不能被任何实 体通过非法渠道获取;
2020/11/18
非对称密码体制
3
非对称密码基本概念:非对称密码的提出
• 对称密码的局限性 • 密钥管理的困难性问题 • 陌生人间的保密通信问题 • 数字签名问题
非对称密码(1976年由W. Diffie和M. Hellman提出)与对称密码的几点 区别:
• 双钥——双钥密码、公钥密码
• 基于数学函数,而非替换和换位
2020/11/18
非对称密码体制
6
非对称密码基本概念:非对称密码的算法组成
密钥生成KG( ) • 根据输入的安全参数 ,输出公钥和私钥对(PK, SK)
• 加密E( ) • 根据输入的公钥和消息,输出密文。
• 解密D( ) • 根据输入的解密私钥和密文,算法输出消息或输出表示密文不合法的特殊符号“?”
明文
加密器 EK
K
密文
解密器 DK
K
明文
密钥产生器
• 密钥管理:若N个人相互保密通信,每人必须拥有(N-1)个私钥,N很 大时,需要保存的私钥很多。如何解决?
• 可信中心分发:共需要发N*(N-1)/2个私钥:例如N =1000时, 999 *1000/2 = 499500
信息安全导论(4-3 密码基础-非对称密码)

37
RSA算法的安全性 RSA算法的安全性
RSA的安全性是基于分解大整数困难的假定 的安全性是基于分解大整数困难的假定 的安全性是基于分解大整数困难
如果RSA的模数 被成功地分解为 ×q,则 的模数n被成功地分解为 如果 的模数 被成功地分解为p× , 获得φ(n)=(p-1)(q-1),从而攻击者能够从 获得 , 公钥e解出 解出d, 公钥 解出 ,即d≡e-1 mod φ(n),攻击成 ≡ , 功.
由私钥及其他密码信息容易计算出公开密钥 由公钥及算法描述, 由公钥及算法描述,计算私钥是困难的
因此, 因此,公钥可以发布给其他人
6
非对称加密示意图
注意
注意
7
公钥密码的核心是使用一种特殊的函 数——单项陷门函数,从一个方向求值 单项陷门函数, 单项陷门函数 是容易的, 是容易的,但逆向计算很困难 定义: 是一个函数 是一个函数, 定义:设f是一个函数,如果对于任意给 定的x,计算y,使得y=f(x)是容易计算 定的 ,计算 ,使得 是容易计算 但对于任意给定的y,计算x是难解 的,但对于任意给定的 ,计算 是难解 即求f的逆函数是难解的 则称f是 的逆函数是难解的, 的,即求 的逆函数是难解的,则称 是 一个单向函数 一个单向函数
31
RSA中的计算问题
32
RSA中的计算问题
33
前例
则1=96-5×19=5*(-19)=5*77 mod96 = - × 5×77=1 mod96 × = 下为77 则5的乘法逆元在 mod96下为 的乘法逆元在 下为
34
例
35
36
验证: × = 验证:17×17=289=3×96+1=1 mod96 = × + =
38
非对称加密算法(RSA、DSA、ECC、DH)

⾮对称加密算法(RSA、DSA、ECC、DH)⾮对称加密算法 (RSA、DSA、ECC、DH)1.1 概念⾮对称加密需要两个密钥:公钥 (publickey) 和私钥 (privatekey)。
公钥和私钥是⼀对,如果⽤公钥对数据加密,那么只能⽤对应的私钥解密。
如果⽤私钥对数据加密,只能⽤对应的公钥进⾏解密。
因为加密和解密⽤的是不同的密钥,所以称为⾮对称加密。
⾮对称加密算法的保密性好,它消除了最终⽤户交换密钥的需要。
但是加解密速度要远远慢于对称加密,在某些极端情况下,甚⾄能⽐对称加密慢上1000倍。
1.2 特点算法强度复杂、安全性依赖于算法与密钥但是由于其算法复杂,⽽使得加密解密速度没有对称加密解密的速度快。
对称密码体制中只有⼀种密钥,并且是⾮公开的,如果要解密就得让对⽅知道密钥。
所以保证其安全性就是保证密钥的安全,⽽⾮对称密钥体制有两种密钥,其中⼀个是公开的,这样就可以不需要像对称密码那样传输对⽅的密钥了。
这样安全性就⼤了很多。
1.3 ⼯作原理(1) A 要向 B 发送信息,A 和 B 都要产⽣⼀对⽤于加密和解密的公钥和私钥。
(2) A 的私钥保密,A 的公钥告诉 B;B 的私钥保密,B 的公钥告诉 A。
(3) A 要给 B 发送信息时,A ⽤ B 的公钥加密信息,因为 A 知道 B 的公钥。
(4) A 将这个消息发给 B (已经⽤ B 的公钥加密消息)。
(5) B 收到这个消息后,B ⽤⾃⼰的私钥解密 A 的消息。
其他所有收到这个报⽂的⼈都⽆法解密,因为只有 B 才有 B 的私钥。
1.4 主要算法RSA、Elgamal、背包算法、Rabin、D-H、ECC (椭圆曲线加密算法)。
使⽤最⼴泛的是 RSA 算法,Elgamal 是另⼀种常⽤的⾮对称加密算法。
1.5 应⽤场景(1) 信息加密收信者是唯⼀能够解开加密信息的⼈,因此收信者⼿⾥的必须是私钥。
发信者⼿⾥的是公钥,其它⼈知道公钥没有关系,因为其它⼈发来的信息对收信者没有意义。
什么是公钥密码体制

什么是公钥密码体制
公钥密码体制也称非对称密码体制或者双钥密码体制,是基于数学函数(如单向陷门函数)而不是基于置换和代换的工具。
公钥密码算法的最大特点是采用两个相关密钥将加密和解密能力分开,其中一个是公开的,称为公钥,用于加密;其中一个是为用户专用的,是保密的,称为私钥,用于解密。
公钥密码体制是为了解决对称密码体制中最难解决的2个问题而提出的:
1.密钥分配问题:在对称密码中,接受方和发送方使用相同密钥。
一般情况下该密钥
通过加密信道进行传输。
但是加密信道可能会被攻击者攻击。
2.数字签名问题:如果使用对称加密来进行数字签名,那么在对密钥进行管理和分发
时带来被攻击者攻击的问题。
在公钥密码体制中存在2个密钥:公钥,私钥。
公钥和加密算法是公开的,公钥用于加密数据;私钥是保密的,用于解密。
以上内容仅供参考,如需获取更多详细信息,建议查阅公钥密码体制相关的资料或咨询数学领域专业人士。
非对称密码体制-第四章网络09

11
4.2.1 RSA算法 算法
2、加密过程 、 的公钥: (1)在公钥库中查得用户 的公钥:PU={e, n}; )在公钥库中查得用户U的公钥 ; 使得0≤mi<n,i=1, (2)将明文分组 )将明文分组m=m1m2…mr,使得 , , 2,… ,r; , ; (3)对明文分组 i作加密变换: )对明文分组m 作加密变换: ci=E(mi) ≡ mie mod n, i=1,2,… ,r n, i=1,2, 传送给用户U。 (4)将密文 1 c2…cr传送给用户 。 )将密文c 3、解密过程 、 (1)先对每组密文做解密变换: )先对每组密文做解密变换: mi=D(ci) ≡cid mod n (2)合并分组得到明文 )合并分组得到明文m=m1m2…mr。
12
图4-3 RSA算法 算法
选取大素数p和q 令n=p*q,计算φ(n)
随机选取整数e 由e*d≡1(mod φ(n))计算d
将(n,e)作为公钥公开 将(p,q,d)作为私钥保密
用公钥加密 ci=E(mi)≡(mie mod n)
用私钥解密 mi=D(ci)≡(cid mod n)
13
【例4-1】选择素数: p=47 和 q=71,求出RSA 】选择素数: ,ห้องสมุดไป่ตู้出 算法的公钥和私钥。 算法的公钥和私钥。
2
4.1 公钥密码体制的基本概念
Diffie和Hellmna于1976年在《密码学的新方向》中 和 年在《 于 年在 密码学的新方向》 首次提出了公钥密码的观点, 首次提出了公钥密码的观点,即为每个用户分配两 个相互匹配又相互独立的密钥,其中: 匹配又相互独立的密钥 个相互匹配又相互独立的密钥,其中: 一个密钥被公开,称为公开密钥(公钥), ),用于 一个密钥被公开,称为公开密钥(公钥),用于 加密, 加密, 另一个密钥被保密,称为私有密钥(私钥), ),用 另一个密钥被保密,称为私有密钥(私钥),用 解密。 于解密。 所有用户的公钥均登记在类似电话号码簿的密钥本 当要给用户A发送加密信息时 发送加密信息时, 上。当要给用户 发送加密信息时,需要在密码本上 查找A用户的公钥 然后加密信息,并发给用户A。 用户的公钥, 查找 用户的公钥,然后加密信息,并发给用户 。 用户A接收到密文之后 接收到密文之后, 用户 接收到密文之后,用自己的私钥进行解密即可 得到明文。 得到明文。 1977年由 年由Rivest(李维斯特)、 )、Shamir(沙米尔) 年由 (李维斯特)、 (沙米尔) 和Adleman(埃德曼)共同提出了第一个公钥密码 (埃德曼) 算法( 密码体制), 算法(即RSA密码体制),是公钥密码中最优秀的 密码体制),是公钥密码中最优秀的 加密算法,被誉为密码学发展史上的里程碑之一。 里程碑之一 加密算法,被誉为密码学发展史上的里程碑之一。 此后, 此后,人们基于不同的计算问题提出了大量的公钥 密码算法。 密码算法。
2非对称加密实验
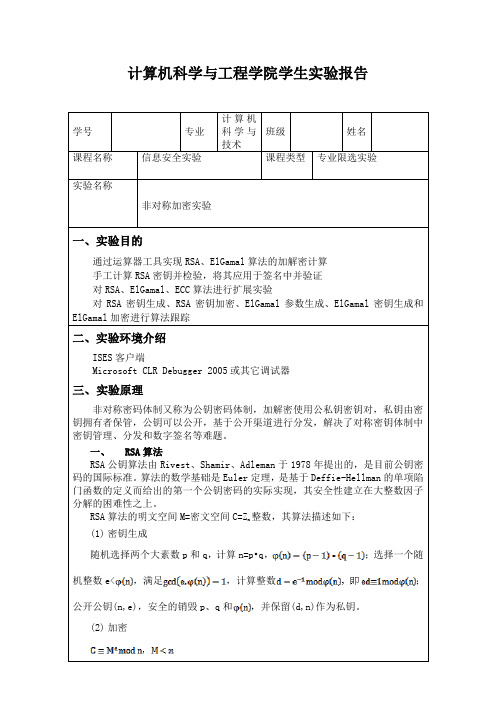
(6)解密
清除明文文本框中的内容,点击“解密”按钮对密文进行解密,明文默认以十六进制形式显示在明文文本框中,如图1.1.720所示;可选择以文本形式查看明文。
(二)扩展实验
(1)在扩展实验中点击“ELGAMAL扩展实验”按钮,进入ELGAMAL扩展实验窗体。
(1)点击“扩展实验”框中的“RSA计算”按钮,进入RSA计算窗体。
输入报文信息,点击“计算MD5值”生成报文信息的信息摘要,选择p、q值,计算n、φ(n)、e和d并输入相应的文本框中,点击“检验”按钮对计算的各个参数值进行检验。
检验无误后,根据上述计算得到的RSA私钥,计算报文MD5值即报文摘要的前8位的签名值,并输入相应的文本框;点击“生成签名并检验”按钮,检验签名输入是否正确并自动生成消息摘要前8位的签名值并显示,
标准方法可选择公钥加密/私钥解密形式和公钥加密/私钥解密形式进行加解密,此处以公钥加密/私钥解密形式进行加解密,公钥加密/私钥解密可参照完成;注意在一次加解密过程中不要重新生成密钥对。
点击“公钥加密”按钮使用生成的公钥对明文进行加密,密文以十六进制显示在密文文本框中;清除明文文本框中的内容,点击“私钥解密”按钮对密文进行解密,明文默认以文本形式显示在明文文本框中,如图1.1.72所示;可选择以16进制查看明文。
具体步骤可参照古典密码实验中实验步骤二。
三、ECC
(一)扩展实验
(1)在扩展实验中点击“ECC扩展实验”按钮,进入ECC扩展实验窗体。
(2)确定合适的椭圆曲线,获取该曲线的基础解点集。首先,在主窗口的椭圆曲线组合框内的相应文本框中,输入素数p,以及椭圆曲线的2个系数a和b;然后,点击“测试曲线”,得到该椭圆曲线的基础解点集。
精品课件-应用密码学-第5章 非对称密码(3)

2020/11/19
15
1155
图5-1 y2≡x3+x+6所表示的曲线 图5-4 y2≡x3+x+6 (mod 11)所表示的曲线
通过比较y2≡x3+x+6在平面的曲线(见图5-1所示)和y2≡x3+x+6 ( mod 11) 在平面上的点(如图5-4所示),直观感觉没有太多的联系。
P +Q+ R1=O。则P+Q =- R1=R,如图5-2。
2020/11/19
2020/11/219020/11/
图5-2 R=P+Q示意图 2020/11/19
8
8 88
点P的倍点定义为:过P点做椭圆曲线的切线,设与椭圆曲线交于R1, 则 P+P+ R1=O, 故2P=- R1=R。如图5-3。
2020/11/19
5
5 55
本章的介绍以第一种椭圆曲线为主,如图5-1是y2≡x3+x+6所表示的曲线,该图 可以用matlab实现。显然该曲线关于x轴对称。
图5-1 y2≡x3+x+6所表示的 曲线
2020/11/19
2020/11/219020/11/
2020/11/19
6
6 66
2.椭圆曲线的加法
2020/11/19
2020/11/19
2020/11/19
20
2200
- ④ 计算点:(x1,y1)=kP - ⑤ 计算点:(x2,y2)=kQ,如果x2=0,则返回第③步 - ⑥ 计算:c=mx2 - ⑦ 传送加密数据(x1,y1,c)给B
(4)解密过程
当实体B解密从A收到的密文(x1,y1,c)时,执行步骤:
密码学6 非对称密码体制

6.3.4 计算方法及其程序实现 1. 如何计算模逆元 要在已知e、m的情况下,求d,使得 e*d=1(mod m) 也即找整数k,使得e*d+mk=1 这相当于求解d、k都是未知数的二元一 次不定方程 e*d+mk=1的最小整数解
2. 扩展Euclid算法 输入:正整数a、b 输出:GCD(a,b)及满足ax+by=GCD(a,b)的整 数x、y 例如:设a=21、b=15,则GCD(a,b)=3,x=-2、 y=3 算法步骤描述: 1) 置x1=1,x2=0,y1=0,y2=1 2) 计算q=a / b,r=a % b 3) 若r=0,则GCD(a,b)=b,x=x2,y=y2,算法 结束;否则做下步 4) 依次令a=b,b=r,t=x2,x2=x1-qx2,x1=t, t=y2,y2=y1-qy2,y1=t,然后转2)
6.1.3 单向陷门函数 公钥密码体制必须设计一个满足下列条件的函数f: 1. 正向易算性──由消息x和密钥pk 容易计算y=fpk(x) 2. 反向不可算性──在不知道密钥sk的情况下,由 任意的y倒过来计算x =f-1sk(y)都是不可行的 3. 陷门依赖性──如果给定另一密钥sk,则f-1(y)是 可以计算的, sk 与pk配对,相当于陷门。 满足1、2的函数称为单向函数 满足1、2、3的函数被称为带陷门的单向函数
《信息安全技术》
第六章 非对称密码体制
6.1 概述
6.1.1 对称密码体制的缺陷 1. 密钥的安全传递比较困难 2. n个用户多点通信所需密钥数为n(n-1)/2个 3. 难以提供对主动攻击的抗击 6.1.2 公钥(非对称)密码体制的基本思想 Whitfield Diffie和Martin Hellman在1976年 首先提出:用公开的密钥(公钥)加密,用与之 对应的不公开的密钥(私钥)解密。 公钥密码体制提出的标志性文献──密码学 的新方向: W.Diffie and M.E.Hellman, New Directions in Cryptography, IEEE Transaction on Information Theory, V.IT-22.No.6, Nov 1976, PP.644-654
第九章密码技术9-1简述对称密钥密码体制、非对称密钥密码体制的

第九章密码技术9-1 简述对称密钥密码体制、非对称密钥密码体制的第九章密码技术与压缩技术9-1 简述对称密钥密码体制、非对称密钥密码体制的加密原理和各自的特点。
对称密码体制的加密方式可分为:(1)序列密码,。
它的主要原理是:通过有限状态机制产生性能优良的伪随机序列,使用该序列加密信息流,得到密文序列。
(2)分组密码。
分组密码的工作方式是将明文分成固定长度的组,用同一密钥和算法对每一块加密,输出也是固定长度的密文。
其主要特点:加解密双方在加解密过程中要使用完全相同或本质上等同的密钥。
非对称密钥密码体制的加密原理:在加密过程中,密钥被分解为一对。
这对密钥中的任何一把都可作为公开密钥通过非保密方式向他人公开,用于对信息的加密;而另一把则作为则私有密钥进行保存,用于对加密信息的解密。
其特点有:具有较强的保密功能,还克服了密钥发布的问题,并具有鉴别功能。
9-2 为什么说混合加密体制是保证网络上传输信息的安全的一种较好的可行方法,混合加密体制采用公开密钥密码技术在通信双方之间建立连接,包括双方的认证过程以及密钥的交换(传送秘密密钥),在连接建立以后,双有可以使用对称加密技术对实际传输的数据进行加密解密。
这样既解决了密钥分发的困难,又解决了加、解密的速度和效率问题,是目前解决网络上传输信息安全的一种较好的可行方法。
9-3 简述链路加密、节点加密和端对端加密等三种加密方式的特点。
链路加密方式只对通信链路中的数据加密,而不对网络节点内的数据加密。
使用链路加密装置能为链路上的所有报文提供传输服务:即经过一台节点机的所有网络信息传输均需加、解密,每一个经过的节点都必须有加密装置,以便解密、加密报文。
节点加密方式在中间节点里装有用于加、解密的保护装置,即由这个装置来完成一个密钥向另一个密钥的变换。
除了在保护装置里,即使在节点内也不会出现明文。
端对端方式由发送方加密的数据在没有到达最终目的地——接受节点之前不被解密。
加密、解密只是在源节点和目的节点进行。
密码学

1.密码体制分类:1)对称密码体制(密钥必须完全保密、加密与解密密钥相同,或可由其中一个很容易推出另一个,又称秘密密钥、单钥、传统密码体制,包括分组密码和序列密码)优点:加解密速度较快,有很高的数据吞吐率;使用的密钥相对较短;密文的长度与明文长度相同;缺点:密钥分发需要安全通道;密钥量大,难于管理;难以解决不可否认问题。
2)非对称密码体制(使用两个密钥,一个是对外公开的公钥,一个是必须保密的私钥,不能由公钥推出私钥,又称双钥或公开密钥密码体制)优点:密钥的分发相对容易;密钥管理简单;可以有效地实现数字签名。
缺点:与对称密码体制相比,非对称密码体制加解密速度较慢;同等安全强度下,非对称密码体制要求的密钥位数要多一些;密文的长度往往大于明文长度。
2.AES与DES对比:1)相似处:二者的圈(轮)函数都是由3层构成:非线性层、线性混合层、子密钥异或,只是顺序不同;AES的子密钥异或对应于DES中S盒之前的子密钥异或;AES的列混合运算的目的是让不同的字节相互影响,而DES中F函数的输出与左边一半数据相加也有类似的效果;AES的非线性运算是字节代换,对应于DES中唯一的非线性运算S盒;行移位运算保证了每一行的字节不仅仅影响其它行对应的字节,而且影响其他行所有的字节,这与DES中置换P相似。
2)不同之处:AES的密钥长度(128位192位256位)是可变的,而DES的密钥长度固定为56位;DES是面向比特的运算,AES是面向字节的运算;AES的加密运算和解密运算不一致,因而加密器不能同时用作解密器,DES 则无此限制。
3.Hash函数:也称散列、哈希、杂凑函数等,是一个从消息空间到像空间的不可逆映射;可将任意长度的输入经过变换得到固定长度的输出;是一种具有压缩特性的单向函数。
性质:1)H可应用于任意长度的消息2)H产生定长的输出3)对任意给定的消息x,计算H(x)较容易,用硬件和软件均可实现4)单向性5)抗弱碰撞性6)抗强碰撞性应用:数字签名;生成程序或者文档的数字指纹;用于安全传输和存储口令特点:1)输入数字串与输出数字串具有唯一的对应关系;输入数字串中2)任何变化会导致输出数字串也发生变化;从输出数字串不能够反求出输入数字串。
第5章 非对称密码(1)

2019/8/6
2019/8/6 2019/8/6
2019/8/6
1199
1199
5.1.2 非对称密码体制的设计准则
现在应用的非对称密码体制,其安全是指的计算上是安全的。 以著名的RSA算法所基于的大数分解难题为例,它假定n是两个大素数p 和q的乘积。现在一般认为,p和q的长度都是512比特左右,则n的长度是 1024比特左右。以人们现有的计算能力,在知道n的情况下,在短时间内是 不能分解n的,也就是说,这在计算上是安全的。从理论上讲,如果有足够 的计算能力,是可以分解n的。但如果分解n的时间超过了消息的保密期,或 者投入的物力超过了消息本身的价值,对消息保密的目的就达到了。
第一种方式从时间和代价上来看,都难以符合需要。在非对称密码体制 产生前,对于很多不是很重要的信息,用得较多的解决办法就是第二种方式 ,但效率是比较低的。
2019/8/6
2019/8/6
2019/8/6
3
33
2019/8/6
2019/8/6 2019/8/6
2019/8/6
444
44
5.3.1 非对称密码体制的原理
序列密码都属于对称密码体制。两个用户在用对称密码体制进行保密通信时,必须
要有一个双方共享的加密密钥。那么,如何才能让两个不在同一个地方的用户安全
地拥有共享密钥呢?
我们可能想到的方式包括:
(1)派一个人来把密钥从一方送到另外一方;
(2)通过邮件或快递传递密钥;
(3)电子邮件、电话或电报等方式传递等等。
2019/8/6
2019/8/6
2019/8/6
11
111111
2002年:Ronald L. Rivest,Adi Shamir,Leonard M. Adleman 公钥密码 学(RSA加密算法)
非对称密码体制

非对称密码体制
非对称密码体制的基本概念 非对称密码体制的原理 RSA算法 RSA算法中的计算问题 RSA算法的安全性 非对称密码体制的应用
非对称密码体制的基本概念
非对称密码(公钥密码)与所有以前的密码方法的不同点
基于的基本思想不同 密钥的使用方式不同
公钥密码算法的密钥具有如下特点
是加密密钥与解密密钥是本质上不同的 是大多数公钥密码算法的加密密钥和解密密钥具有互换的性质,即两者是相对的
网络信息安全技术
非对称密码体制
非对称密码体制(Asymmetric CryptoSystem),也称为公钥密码体制(Public Key Cryptosystem),是现代密码学的重要组成部 分。公钥密码的思想在1976年由Diffie和Hellman在 其《密码学新方向》一文中提出。Rivest、Shamir 和Adleman在1978年提出了首个非对称密码体制, 即著名的RSA公钥密码体制。非对称密码体制的发明 是现代密码的具有里程碑意义的重要事件,它的出现 标志着现代密码学的创立。
可以通过加密算法生成密文:
C EPKB (M )
接收方B使用私有密钥容易通过解密算法对密文进行解密,以恢复原来的明文
从公开密钥PKB推出私有密钥SKB,在计算上是不可行的
非对称密码体制的原理
定义 单向陷门函数满足下列条件的函数f:D→V
1)对于任意给定的x∈D,计算y=f(x)是容易的。 2)对于几乎所有任意给定y∈V,计算x∈D使得y=f(x),
RSA算法中的计算问题
即计算(m)cmod N是RSA非对称密码 体制中的主要运算,其计算可以由 c-1次的模乘来实现,然而当比较
(m)c mod N 的有大效时计,算这问不题是一个好的算法,因为
非对称密码体制

ElGamal加密算法
E密lG钥a对ma产l算生法办既法能用于数据加密也能用于数字签名 的 非首对先称选择加一密个算素法数p,两个随机正整数, g 和x,g, x < p,
E计lG算amya=l算gx法m的od安p全,性则依其赖公于钥计为算y,有g 限和域p;上x离是散私对钥数;这g和一p 难可题由。一组用户共享。
Hash算法 摘要1 +时间
加了时 间后的 新摘要
数字 时间戳
用DTS机构的私钥加密
DTS机构
网络安全与电子商务
网络安全与电子商务
非对称密码体制
非对称密码体制
非对称密码体制的特点 非对称密码体制的原理 非对称加密算法
非对称密码体制的应用模型
非对称密码体制的产生和特点
由Diffie 和Hellman 于1976年首次提出了用于对称密钥交换的公钥算法。 1977年Rivest, Shamir & Adleman 提出了著名的RSA公钥算法。 非对称密码体制的特点
ElG美am国a的l加DS密S(过Dig程ital Signature Standard)中的DSA(Digital
S设ig被na加tu密re A信lg息or为ithMm,)算首法先是选经择E一lG个am随al机算数法k演,变k<而p-来1,。计
密钥算对C1产=gk生m办od法p,C2=ykM mod p。
因此,使用非对称加密,明文信息必须转化成足够大的数 才能保证私钥的不可破译。
明文信息
二进制字符串 10进制大数
DOG
010001000100 111101000111
446743
RSA加密算法
择钥大私的钥质对数p的和生q,成并、得加到密n=p以*q及。数(由字于签p名和q。非常大,所以由n几
《非对称密码体制》课件

使用扩展欧几里得算法,计算d, 满足d*e % phi(n) = 1。
2. 计算n
计算n=p*q。
4. 选择公钥
选择一个与phi(n)互质的整数e。
6. 完成
完成后,公钥由n和e组成,私钥由d组成。
RSA算法的解密过程
1. 加密数据
使用公钥(n, e)加密消息M,产生密文C。
2. 计算明文
1
1. 选择素数
选择一个素数q, 以及一个大素数p = kq + 1, 保护q。
2
2. 选取g值
选择一个能提供一个循环群的数g(1 <= g <= p-1)。
3
3. 计算x,y
任意选择一个512位的长整数k,然后计算x = g^k mod p, y = (hash(M) + x*a)/k mod q, hash(M)为M的哈希值。
使用私钥d,计算出原始消息M。M = Cd (mod n)
3. 完成
接收方使用私钥d,根据公式计算出M。
RSA算法的安全性分析
RSA算法显然会受到攻击,但我们认为这个算法还是安全的。攻击者可以使用因子分解算法来破解RSA 算法,但是这需要一个非常长的时间。对于RSA算法安全保护的加强,一般使用扩展和混淆技术。
非对称密码的优势
提高了数据传输的安全性, 避免了密钥管理的麻烦。
小提示
有时候也会将它们结合使 用,来发挥它们的优势。
典型的非对称密码算法
目前最流行的非对称密码算法有:RSA算法、DSA算法、ECC算法等。下图是其概述:
RSA算法
使用65000位的密钥。在加密 时使用一个公钥,但需要一个 私钥才能进行解密。
非对称密码体制
非对称密码体制

非对称钥不等于解 密密钥,且无法从任意一个密钥推导出另一个密钥, 这样就大大加强了信息保护的力度,而且基于密钥 对的原理很容易实现数字签名和电子信封。 非对称加密算法中比较典型的是RSA算法,此外 还有背包密码算法、椭圆曲线算法、EIGamal算法等。 下面主要介绍最常用的RSA算法。
在采用公钥体制的情况下A向B传输数据的过
程,如下图所示:
使用两个密钥的加密和解密
非对称密码体制
1.1 非对称密码体制的实现过程
与对称密码技术相比较,利用非对称密码技 术进行安全通信,有以下优点: 通信双方事先不需要通过保密信道交换密钥。 密钥持有量大大减少。 非对称密码技术还提供了对称密码技术无法或很 难提供的服务。
(5)将明文P(假设P是个小于r的整数)加密为密文
C,计
算公式为:C = Pe mod r(e为幂次方)
(6)将密文C解密为明文P,计算公式为:
P = Cd mod r(d为幂次方)
非对称密码体制
1.3 对称密码体制与非对称密码体制的比较
对称密码体制是应用较早的密码体制,技术成熟。 在对称密码体制中,使用的密钥只有一个,发收信双方 都使用此密钥对数据进行加密和解密,这要求解密方事 先必须知道加密密钥。对称密码体制的特点是算法公开、 计算量小、加密速度快、加密效率高。不足之处是交易 双方都使用同样密钥,安全性得不到保证。密钥管理成 为了用户的负担。对称密码体制在分布式网络系统上使 用较为困难,主要是因为密钥管理困难,使用成本较高。
非对称密码体制
1.2 RSA算法
RSA算法是第一个既能用于数据加密又能 用于数字签名的算法,是由美国麻省理工学院 的Rivest、Shamir和Adleman在1978年提出的。
两种密码体制的对比表

1.用同一个算法加解密,而密钥有一对:一个用于加密,一个用于解密
2.发送和接收方每个拥有一对相互匹配的密钥中的一个
安全
条件
1.密钥必须保密
2.如果不掌握其他信息,要想解密报文是不可能或不现实的
)
3.知道所用的算法加上密文样本不足以破解密钥
1.两个密钥中的一个必须保密
2.如果不掌握其他信息,要想解密报文是不可能或不现实的
3.知道所用的算法加上一个密钥和密文样本,不足以破解另一个密钥
主要பைடு நூலகம்
发展
阶段
1977年DES正式成为ANSI标准;
80年代出现“过渡性”的“post DES”算法,如3DES, IDEA,RCx,CAST等;
90年代进一步成熟如Rijndael,RC6, MARS,Twofish, Serpent等算法出现;
对比项
对称密码体制
非对称密码体制(公钥密码体制)
安全性
安全性仅仅基于密钥的保密,而与公开的算法无关
安全性基于:1.密钥的长度(≥1024);2.破密计算工作量(数学中NP-完全问题的计算困难性)
数学
基础
一种明文和密文间的、用替代和置换交替的方式构造的可逆映射函数
基于数学上的单向陷门函数
》
运行
条件
1.加密和解密用同一个密钥和同一个算法
(均通过增加轮数和密钥长度改进算法;针对被加密数据采用分组或流秘密方式加密)
三类公钥算法均基于对单向陷门函数的设计,算法复杂。
RSA:基于大整数分解难题(IFP,The Integer Factorization Problem)
ElGamal、Diffie-Hellman:有限域上的乘法群上的离散对数计算难题(DLP,The Discrete Logarithm Problem)
密码体制的概念

密码体制的概念密码体制的概念密码体制是计算机系统中用于保护信息安全的重要机制。
它通过使用密码算法和密码策略来确保数据的机密性、完整性和可用性。
在密码体制中,密码算法用于加密和解密数据,密码策略用于确定密码的复杂度和使用规则。
密码算法密码算法是密码体制的核心组成部分,它用于对需要保护的数据进行加密和解密操作。
密码算法通常分为对称加密算法和非对称加密算法两类。
1. 对称加密算法对称加密算法使用相同的密钥进行加密和解密操作。
常见的对称加密算法有DES、AES等。
对称加密算法具有加密速度快、适用于大数据量加密的优点,但密钥的传递和管理需要保证安全性。
2. 非对称加密算法非对称加密算法使用一对密钥,分为公钥和私钥。
公钥用于加密数据,私钥用于解密数据。
常见的非对称加密算法有RSA、Diffie-Hellman等。
非对称加密算法具有密钥传递方便和身份验证的优点,但加密和解密的速度较慢。
密码策略密码策略是指规定密码的使用规则和复杂度要求,以增加密码的安全性。
合理的密码策略能够有效防止密码被猜测和暴力破解。
1. 密码复杂度要求密码复杂度要求包括密码长度、字符类型和组合要求。
较长且包含大写字母、小写字母、数字和特殊符号的密码更难被猜测和暴力破解。
2. 密码更新和限制密码更新和限制是指规定密码的有效期和限制密码的历史使用,防止密码长时间使用和密码的重复使用。
3. 用户身份验证用户身份验证是密码策略中的重要环节,通常包括单因素身份验证和多因素身份验证。
多因素身份验证通过结合使用多个身份验证要素,例如密码、指纹、声纹等,提高身份验证的安全性。
密码体制的应用密码体制广泛应用于各种计算机系统和网络通信中,保护数据的安全性和隐私。
例如,在互联网中,密码体制用于保护网上银行、电子商务和个人账户的安全。
在企业内部,密码体制用于保护敏感信息和重要业务数据的机密性和完整性。
密码体制也逐渐应用于移动设备、物联网和云计算等新兴领域,为人们提供更安全、便捷的数字化服务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非对称密码体制学习要点:1.非对称密码体制的概念、思想和工作方式2.Diffie-Hellman密钥交换算法3.RSA 算法4.EIgamal公钥算法5.ECC算法背景在拥有大量用户的通信网络,若想让两两用户都能进行保密通信,即要求(1)任意一对用户共享一个会话密钥(2)不同的用户对共享的会话密钥不相同2个对于密钥分配中心,N个用户则需要分配CN会话密钥,大量的数据存储和分配是一件很麻烦的事,在计算机网络环境下显的尤为突出。
另外传统密码不易实现数字签名,也进一步限制了其发展。
一、概述问题的提出—对称密码体制的缺陷:•密钥管理困难–传统密钥管理两两分别用一对密钥时,则n 个用户需要C( n, 2)= n( n-1)/ 2 个密钥,当用户量增大时密钥空间急剧增大。
如:–n= 100 时C( 100,2)= 4,995–n= 5000 时C( 5000,2)= 12,497,500•密钥分配问题•数字签名的问题–传统加密算法无法实现抗抵赖的需求,当主体A收到主体B的电子文挡(电子数据)时,无法向第三方证明此电子文档确实来源于B。
起源•公钥密码又称为双钥密码和非对称密码,是1976年由Diffie和Hellman在其“密码学新方向”一文中提出的,见划时代的文献:W.Diffie and M.E.Hellman, New Directrionsin Cryptography, IEEE Transaction on Information Theory, V.IT-22.No.6, Nov 1976, PP.644-654•RSA公钥算法是由Rivest,Shamir和Adleman在1978年提出来的, 见Communitions of the ACM. Vol.21.No.2. Feb. 1978, PP.120-126公钥密码体制的基本概念•由私钥及其他密码信息容易计算出公开密钥(a polynomial time (P-time) problem)•由公钥及算法描述,计算私钥是难的(an NP-time problem)•因此,公钥可以发布给其他人(wishing to communicate securely with its owner )•密钥分配问题(the key distribution problem )基本思想和要求•涉及到各方:发送方、接收方、攻击者•涉及到数据:公钥、私钥、明文、密文•公钥算法的条件:–产生一对密钥是计算可行的–已知公钥和明文,产生密文是计算可行的–接收方利用私钥来解密密文是计算可行的–对于攻击者,利用公钥来推断私钥是计算不可行的–已知公钥和密文,恢复明文是计算不可行的–(可选)加密和解密的顺序可交换密码学的起源和发展三个阶段:•1949年之前密码学是一门艺术•1949~1975年密码学成为科学•1976年以后密码学的新方向——公钥密码学公钥密码算法应满足以下要求:①接收方B 产生密钥对(公开钥PK B 和秘密钥SK B )在计算上是容易的。
②发方A 用收方的公开钥对消息m 加密以产生密文C ,即在计算上是容易的。
③收方B 用自己的秘密钥对C 解密,即在计算上是容易的。
公钥密码算法应满足的要求[].B PKC E m =[]B SK mD C =④敌手由B 的公开钥PK B 求秘密钥SK B 在计算上是不可行的。
⑤敌手由密文C 和B 的公开钥PK B 恢复明文m 在计算上是不可行的。
⑥加、解密次序可换,即其中最后一条虽然非常有用,但不是对所有的算法都作要求。
公钥密码算法应满足的要求[()][()]B B B B PK SK SK PK E D m D E m =公钥密码算法应满足的要求以上要求的本质之处在于要求一个陷门单向函数。
单向函数是两个集合X、Y之间的一个映射,使得Y 中每一元素y都有惟一的一个原像x∈X,且由x易于计算它的像y,由y计算它的原像x是不可行的。
这里所说的易于计算是指函数值能在其输入长度的多项式时间内求出,即如果输入长n比特,则求函数值的计算时间是n a的某个倍数,其中a是一固定的常数。
这时称求函数值的算法属于多项式类P,否则就是不可行的。
例如,函数的输入是n比特,如果求函数值所用的时间是2n的某个倍数,则认为求函数值是不可行的。
公钥密码系统特点:采用了一对密钥——加密密钥和解密密钥(且从解密密钥推出加密密钥是不可行的),一个可以公开(称之为公钥),另一个为用户专用(私钥)。
数学原理:公钥密码系统是基于陷门单向函数的概念。
对比单向函数:单向函数易于计算但求逆困难的函数;陷门单向函数:在不知道陷门信息情况下求逆困难,在知道陷门信息时易于求逆的函数。
陷门单向函数单向陷门函数是满足下列条件的函数f:(1) 给定x,计算y=f k(x)是容易的;(2) 给定y, 计算x 使x= f k-1(y)是不可行的。
(3) 存在k,已知k时,对给定的任何y,若相应的x-1(x)是容易的。
存在,则计算x 使fk单向陷门函数说明仅满足(1)、(2)两条的称为单向函数;第(3)条称为陷门性,k 称为陷门信息当用陷门函数f 作为加密函数时,可将f 公开,这相当于公开加密密钥,此时加密密钥便称为公开密钥,记为PKf 函数的设计者将k 保密,用作解密密钥,此时k 称为秘密钥匙,记为SK 。
由于设计者拥有SK ,他自然可以解出 单向陷门函数的第(2)条性质表明窃听者由截获的密文y = f (x )推测x 是不可行的.1().k x f y −=Joy 公钥环Ted Alice MikeJoy 明文输入加密算法,如解密算法明文输出Bob 公钥环Ted BobMike(3) 密钥交换:通信双方交换会话密钥,以加密通信双方后续连接所传输的信息。
每次逻辑连接使用一把新的会话密钥,用完就丢弃。
•公钥密码基于的数学难题:–背包问题;–大整数分解问题(The Integer Factorization Problem, RSA体制);–离散对数问题;–Diffie-Hellman问题。
–离散对数问题:–有限域的乘法群上的离散对数问题(The Discrete Logarithm Problem, ELGamal体制)–定义在有限域的椭圆曲线上的离散对数问题(The Elliptic Curve Discrete LogarithmProblem,类比的ELGamal体制)。
二、Diffie-Hellman密钥交换算法Diffie和Hellman在其里程碑意义的文章中,虽然给出了密码的思想,但是没有给出真正意义上的公钥密码实例,也既没能找出一个真正带陷门的单向函数然而,他们给出单向函数的实例,并且基于此提出Diffie-Hellman密钥交换算法D-H密钥交换协议背景密钥分配•人工手动分配密钥: 问题–效率低–成本高–每个用户要存储与所有用户通信的密钥–安全性差•机器自动分配密钥: 要求–任何两个用户能独立计算他们之间的秘密密钥–传输量小–存储量小–任何一个(或多个)用户不能计算出其他用户之间的秘密密钥二、Diffie-Hellman密钥交换Diffie-Hellman算法Diffie-Hellman算法是第一个公开密钥算法,发明于1976年。
Diffie-Hellman算法能够用于密钥分配,但不能用于加密或解密信息。
安全性:在于在有限域上计算离散对数非常困难。
Diffie-Hellman密钥交换算法的原理 基于有限域中计算离散对数的困难性问题之上:设F为有限域,g∈F是F的乘法群F*=F\{0}=<g>,并且对任意正整数x,计算g x是容易的;但是已知g 和y 求x 使y= g x mod n计算上几乎不可能的,称指数x 为以g为底模n 的离散对数。
如果Alice和Bob在不安全的信道上交换密钥,步骤:(1) Alice和Bob协商一个大素数n及n的本原根g,g和n可以公开;(2) Alice秘密产生一个随机数x,X=g x mod n,然后把X发送给Bob;(3) Bob秘密产生一个随机数y,Y= g y mod n,然后把Y发送给Alice;(4) Alice计算k=Y x mod n;(5) Bob计算k'=X y mod n。
k和k'是恒等的,因为k = Y x mod n=(g y)x mod n=(g x)y mod n= X y mod n= k'线路上的搭线窃听者只能得到g、n、X和Y的值,除非能计算离散对数恢复出x和y,否则就无法得到k (秘密密钥)。
Diffie-Hellman密钥交換的过程•n 与g 为公开值•双方各选一个较大的数x与y •计算出『秘密密钥』:g xy mod n例子:●二者协商后决定采用素数n=353及其本原根g=3。
●Alice 选择随机数x=97,计算X=397mod 353=40,并发送40 给Bob 。
●Bob 选择随机数y=233,计算Y=3233mod 353=248,并发送248 给Alice 。
●Alice 计算:k=Y x mod n =24897mod 353=160。
●Bob 计算:k'=X y mod n =40233mod 353=160。
即为共享秘密密钥。
mod xyk k g n′==造成中间人攻击的原因是Diffie-Hellman密钥交换不认证对方,利用数字签名可以挫败中间人攻击。
防止中間人攻击认证的Diffie-Hellman參數认证的Diffie-Hellman密钥交换通过数字签名和公钥证书相互认证可以挫败中间人攻击:(1)双方各自拥有公钥/私钥对和公开密钥证书:(2) Alice产生随机数x并发送给Bob。
(3) Bob产生随机数y并计算出共享秘密密钥k, 对x、y签名并用k加密签名;加密的签名和y一起发送给Alice。
(4) Alice计算出k,用k解密Bob的消息并验证Bob的签名。
验证后对x、y签名并用k加密签名后发送给Bob。
(5) Bob解密消息并验证Alice的签名。
Carol。
