2013年湖北省普通高校招生阳光招生问答12
2013年普通高等学校招生全国统一考试(湖北卷)

2013年普通高等学校招生全国统一考试(湖北卷)第二部分:词汇知识运用(共两节,满分30分)第一节:多项选择(共10小题;每小题1分,满分10分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
例:To make members of a team perform better, the trainer first of all has to knowtheir ___________ and weaknesses.A. strengthsB. benefitsC. techniquesD. values答案:A21. Poetry written from the ___________ of the urban youth tends to reveal their anxiety over a lack of sense of belonging.A. perspectiveB. priorityC. participationD. privilege解析:该题考查名词的意义。
句意:透视城市青年的诗倾向于揭示他们的焦虑在于缺乏归属感。
perspective“透视”;priority“优先,优先权”;participation“参加,参与”;privilege “特权,优惠”。
答案:A22. Carbon dioxide, which makes a ___________ between us and the sun, prevents heat from getting out of the atmosphere easily, so the earth is becoming warmer.A. differenceB. comparisonC. connectionD. barrier解析:该题考查动词和名词的固定搭配。
句意:在人类和太阳之间起重要作用的二氧化碳,防止热很轻松从大气中失去,因此地球正在变暖。
2013年普通高等学校招生全国统一考试(湖北卷)

2013年普通高等学校招生全国统一考试湖北卷(理工类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.在复平面内,复数z =2i1+i(i 为虚数单位)的共轭复数对应的点位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限2.已知全集为R ,集合A =⎩⎨⎧x ⎪⎪⎝⎛⎭⎫12x≤1,B ={x |x 2-6x +8≤0},则A ∩∁R B =( )A .{x |x ≤0}B .{x |2≤x ≤4}C .{x |0≤x <2或x >4}D .{x |0<x ≤2或x ≥4}3.在一次跳伞训练中,甲、乙两位学员各跳一次.设命题p 是“甲降落在指定范围”,q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为( )A .(綈p )∨(綈q ) B. p ∨(綈q )C. (綈p )∧(綈q ) D .p ∨q4.将函数y =3cos x +sin x (x ∈R)的图象向左平移m (m >0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( ) A.π12 B.π6 C.π3 D.5π65.已知0<θ<π4,则双曲线C 1:x 2cos 2θ-y 2sin 2θ=1与C 2:y 2sin 2θ-x 2sin 2θtan 2θ=1的( )A .实轴长相等B .虚轴长相等C .焦距相等D .离心率相等6.已知点A (-1,1),B (1,2),C (-2,-1),D (3,4),则向量AB →在CD →方向上的投影为( )A.322B.3152C .-322D .-31527.一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度v (t )=7-3t +251+t(t 的单位:s ,v 的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( ) A .1+25ln 5 B .8+25ln113C .4+25ln 5D .4+50ln 28.一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V 1,V 2,V 3,V 4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( )A .V 1<V 2<V 4<V 3B .V 1<V 3<V 2<V 4C .V 2<V 1<V 3<V 4D .V 2<V 3<V 1<V 49.如图,将一个各面都凃了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X ,则X 的均值E (X )=( ) A.126125 B.65 C.168125 D.7510.已知a 为常数,函数f (x )=x (ln x -ax )有两个极值点x 1,x 2(x 1<x 2),则( )A .f (x 1)>0,f (x 2)>-12B .f (x 1)<0,f (x 2)<-12C .f (x 1)>0,f (x 2)<-12D .f (x 1)<0,f (x 2)>-12第Ⅱ卷二、填空题(本大题共6小题,考生共需作答5小题,每小题5分,共25分.把答案填在题中横线上)(一)必考题(11~14题)11.从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示. (1)直方图中x 的值为________;(2)在这些用户中,用电量落在区间[100,250]内的户数为________.12.阅读如图所示的程序框图,运行相应的程序,输出的结果i =________.13.设x ,y ,z ∈R ,且满足:x 2+y 2+z 2=1,x +2y +3z =14,则x +y +z =________. 14.古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,…,第n 个三角形数为n (n +1)2=12n 2+12n .记第n 个k 边形数为N (n ,k )(k ≥3),以下列出了部分k 边形数中第n 个数的表达式: 三角形数 N (n ,3)=12n 2+12n ,正方形数 N (n ,4)=n 2, 五边形数 N (n ,5)=32n 2-12n ,六边形数 N (n ,6)=2n 2-n , ……可以推测N (n ,k )的表达式,由此计算N (10,24)=________.(二)选考题(请考生在第15、16两题中任选一题作答,如果全选,则按第15题作答结果计分)15.(选修4-1:几何证明选讲)如图,圆O 上一点C 在直径AB 上的射影为D ,点D 在半径OC 上的射影为E ,若AB =3AD ,则CEEO的值为________. 16.(选修4-4:坐标系与参数方程)在直角坐标系xOy 中,椭圆C 的参数方程为⎩⎪⎨⎪⎧x =a cos φ,y =b sin φ(φ为参数,a >b >0).在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,直线l 与圆O 的极坐标方程分别为ρsin ⎝⎛⎭⎫θ+π4=22m (m 为非零常数)与ρ=b .若直线l 经过椭圆C 的焦点,且与圆O 相切,则椭圆C 的离心率为________. 三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c ,已知cos 2A -3cos(B +C )=1. (1)求角A 的大小;(2)若△ABC 的面积S =53,b =5,求sin B sin C 的值.18.(本小题满分12分)已知等比数列{a n }满足:|a 2-a 3|=10,a 1a 2a 3=125.(1)求数列{a n }的通项公式.(2)是否存在正整数m ,使得1a 1+1a 2+…+1a m ≥1?若存在,求m 的最小值;若不存在,说明理由.19.(本小题满分12分)如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,直线PC ⊥平面ABC ,E ,F 分别是PA ,PC 的中点. (1)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明.(2)设(1)中的直线l 与圆O 的另一个交点为D ,且点Q 满足DQ →=12CP →.记直线PQ 与平面ABC 所成的角为θ,异面直线PQ 与EF 所成的角为α,二面角E -l -C 的大小为β,求证:sin θ=sin αsin β.20.(本小题满分12分)假设每天从甲地去乙地的旅客人数X 是服从正态分布N (800,502)的随机变量.记一天中从甲地去乙地的旅客人数不超过900的概率为p 0. (1)求p 0的值;(参考数据:若X ~N (μ,σ2),有P (μ-σ<X ≤μ+σ)=0.682 6,P (μ-2σ<X ≤μ+2σ)=0.954 4,P (μ-3σ<X ≤μ+3σ)=0.997 4)(2)某客运公司用A ,B 两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次.A ,B 两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1 600元/辆和2 400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B 型车不多于A 型车7辆.若每天要以不小于p 0的概率运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A 型车、B 型车各多少辆?21.(本小题满分13分)如图,已知椭圆C 1与C 2的中心在坐标原点O ,长轴均为MN 且在x 轴上,短轴长分别为2m ,2n (m >n ),过原点且不与x 轴重合的直线l 与C 1,C 2的四个交点按纵坐标从大到小依次为A ,B ,C ,D .记λ=mn ,△BDM 和△ABN 的面积分别为S 1和S 2.(1)当直线l 与y 轴重合时,若S 1=λS 2,求λ的值;(2)当λ变化时,是否存在与坐标轴不重合的直线l ,使得S 1=λS 2?并说明理由. 22.(本小题满分14分)设n 是正整数,r 为正有理数.(1)求函数f (x )=(1+x )r +1-(r +1)x -1(x >-1)的最小值.(2)证明:n r +1-(n -1)r +1r +1<n r <(n +1)r +1-n r +1r +1.(3)设x ∈R ,记[x ]为不小于x 的最小整数,例如[2]=2,[π]=4,⎣⎡⎦⎤-32=-1. 令S =381+382+383+…+3125,求[S ]的值. (参考数据:8043≈344.7,8143≈350.5,12443≈618.3, 12643≈631.7)湖北卷(理工类)1.解析:先化简复数z ,再写出其共轭复数,然后根据其实部和虚部作出判断.z =2i 1+i =2i (1-i )(1+i )(1-i )=1+i ,所以z -=1-i ,故复数z 的共轭复数对应的点位于第四象限. 答案:D2.解析:先化简集合A ,B ,再借助数轴进行集合的交集运算.A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪⎝ ⎛⎭⎪⎫12x ≤1={x |x ≥0},B ={x |x 2-6x +8≤0}={x |2≤x ≤4},所以∁R B ={x |x <2或x >4},于是A ∩∁R B ={x |0≤x <2或x >4}. 答案:C3.解析:根据逻辑联结词“或”“且”“非”的含义判断.依题意得綈p :“甲没有降落在指定范围”,綈q :“乙没有降落在指定范围”,因此“至少有一位学员没有降落在指定范围”可表示为(綈p )∨(綈q ). 答案:A4.解析:先将函数解析式化简,再写出平移后的解析式,然后根据函数为偶函数得到m 的表达式,求得m 的最小值.由于y =3cos x +sin x =2cos ⎝⎛⎭⎪⎫x -π6,向左平移m (m >0)个单位长度后得到函数y =2cos ⎝ ⎛⎭⎪⎫x +m -π6的图象.由于该图象关于y 轴对称,所以m -π6=k π(k ∈Z ,m >0),于是m =k π+π6(k ∈Z ,m >0),故当k =0时,m 取得最小值π6.答案:B5.解析:先根据θ的范围,确定双曲线方程的类型,判断焦点所在的坐标轴,然后分析双曲线C 1和C 2的实轴长、虚轴长、焦距、离心率是否相等.双曲线C 1的焦点在x 轴上,a =cos θ,b =sin θ,c =1,因此离心率e 1=1cos θ;双曲线C 2的焦点在y 轴上,由于0<θ<π4,所以a =sin θ,b =sin θtan θ,c =sin 2θ+sin 2θtan 2θ,因此离心率e 2=sin 2θ+sin 2θtan 2θsin θ=sin θ1+tan 2θsin θ=1cos θ.故两条双曲线的实轴长、虚轴长、焦距都不相等,离心率相等. 答案:D6.解析:首先求出AB →,CD →的坐标,然后根据投影的定义进行计算.由已知得AB →=(2,1),CD →=(5,5),因此AB →在CD →方向上的投影为AB →·CD →|CD →|=1552=322.答案:A7.解析:首先求出速度等于0时的时刻,从而得到汽车行驶的时间,然后利用定积分求出汽车行驶的距离.由v (t )=7-3t +251+t =0,可得t =4⎝ ⎛⎭⎪⎫t =-83舍去,因此汽车从刹车到停止一共行驶了4 s ,此期间行驶的距离为⎠⎛04v(t)d t =⎠⎛04⎝⎛⎭⎪⎫7-3t +251+t d t =⎪⎪⎪⎣⎢⎡⎦⎥⎤7t -32t 2+25ln (t +1)4=4+25ln 5.答案:C8.解析:先根据三视图判断四个几何体的形状,再结合所给数据计算各个几何体的体积,最后做出比较.由三视图可知,四个几何体自上而下依次是:圆台、圆柱、正方体、棱台,其体积分别为V 1=13×1×(π+2π+4π)=73π,V 2=π×12×2=2π,V 3=23=8,V 4=13×1×(4+8+16)=283,于是有V 2<V 1<V 3<V 4. 答案:C9.解析:先求出随机变量X 的分布列,然后利用均值的计算公式求得E(X).依题意得X 的取值可能为0,1,2,3,且P(X =0)=32125=27125,P(X =1)=9×6125=54125,P(X =2)=3×12125=36125,P(X =3)=8125.故E(X)=0×27125+1×54125+2×36125+3×8125=65. 答案:B10.解析:由已知得f′(x)=0有两个正实数根x 1,x 2(x 1<x 2),从而f′(x)的图象与x 轴有两个交点,即f ′(x)的极大值大于0,得到x 1,x 2的取值范围,然后将x 1,x 2代入f(x)的解析式,比较f(x 1)与f(x 2)的大小.f ′(x)=ln x +1-2ax(x>0),依题意ln x +1-2ax =0有两个正实数根x 1,x 2(x 1<x 2).设g(x)=ln x +1-2ax ,则g′(x)=1x -2a ,显然当a ≤0时不合题意,必有a>0.令g′(x)=0,得x =12a ,于是g(x)在⎝ ⎛⎭⎪⎫0,12a 上是增函数,在⎝ ⎛⎭⎪⎫12a ,+∞上是减函数,所以g(x)在x =12a 处取得极大值,所以f′⎝ ⎛⎭⎪⎫12a =ln 12a >0,即12a >1,0<a<12,且应有x 1<12a <x 2. 于是f(x 1)=x 1ln x 1-ax 21=x 1(2ax 1-1)-ax 21=ax 21-x 1=x 1(ax 1-1)<0.又x∈⎝ ⎛⎭⎪⎫12a ,x 2时,f ′(x)>0,x ∈(x 2,+∞)时,f ′(x)<0,所以x 2是f(x)的极大值点,所以f(x 2)>f(1)=-a>-12.答案:D11.解析:(1)根据频率分布直方图中各个小矩形的面积之和等于1,可求出x 的值;(2)求出月用电量落在[100,250)内的频率,即可求得月用电量在[100,250)内的户数. (1)由于(0.002 4+0.003 6+0.006 0+x +0.002 4+0.001 2)×50=1,解得x =0.004 4.(2)数据落在[100,250)内的频率是(0.003 6+0.006 0+0.004 4)×50=0.7,所以月用电量在[100,250)内的户数为100×0.7=70. 答案:(1)0.004 4 (2)7012.解析:按照程序框图的执行流程分析循环过程,得到输出结果.程序框图的执行流程及中间结果如下:第一步:a =10,i =1,a ≠4,a 不是奇数,a =102=5,i =2;第二步:a≠4,a 是奇数,a =3×5+1=16,i =3;第三步:a≠4,a 不是奇数,a =162=8,i =4;第四步:a≠4,a 不是奇数,a =82=4,i =5;第五步,a =4,这时跳出循环,输出i =5.答案:513.解析:先利用柯西不等式求出x +2y +3z 的最值,再结合题目条件得到x +2y +3z 的值,然后根据等号成立的条件求出x ,y ,z 的值,从而求得x +y +z 的值. 由柯西不等式可得(x 2+y 2+z 2)(12+22+32)≥(x +2y +3z)2,即(x +2y +3z)2≤14,因此x +2y +3z ≤14.因为x +2y +3z =14,所以x =y 2=z 3,解得x =1414,y =147,z=31414,于是x +y +z =3147.答案:314714.解析:先根据给出的几个结论,推测出当k 为偶数时,N(n ,k)的表达式,然后再将n=10,k =24代入,计算N(10,24)的值.由N(n ,4)=n 2,N(n ,6)=2n 2-n ,…,可以推测:当k 为偶数时,N(n ,k)=⎝ ⎛⎭⎪⎫k 2-1n2-⎝ ⎛⎭⎪⎫k 2-2n ,于是N(n ,24)=11n 2-10n ,故N(10,24)=11×102-10×10=1 000. 答案:1 00015.解析:设出圆的半径,利用相交弦定理求出CD 的长,再利用射影定理求EO 和CE 的长,从而得到比值.设圆O 的直径AB =2R ,则AD =2R 3,DO =R 3,DB =4R3.由相交弦定理,得CD 2=AD·DB ,所以CD =223R. 在Rt △CDO 中,CO =R ,由射影定理可得EO =DO 2CO =R 9,于是CE =R -R 3=8R 9,故CEEO =8.答案:816.解析:先将参数方程与极坐标方程化为普通方程,再根据直线过焦点、直线与圆相切建立关于椭圆方程中a ,b ,c 的等式,再结合a 2=b 2+c 2求得离心率. 由已知可得椭圆标准方程为x 2a 2+y2b2=1(a>b>0).由ρsin ⎝⎛⎭⎪⎫θ+π4=22m 可得ρsin θ+ρcos θ=m ,即直线的普通方程为x +y =m.又圆的普通方程为x 2+y 2=b 2,不妨设直线l 经过椭圆C 的右焦点(c ,0),则得c =m.又因为直线l 与圆O 相切,所以|m|2=b ,因此c =2b ,即c 2=2(a 2-c 2).整理,得c 2a 2=23,故椭圆C 的离心率为e =63. 答案:6317.解:(1)由cos 2A -3cos (B +C)=1,得2cos 2A +3cos A -2=0,即(2cos A -1)(cos A +2)=0. 解得cos A =12或cos A =-2(舍去).因为0<A<π,所以A =π3.(2)由S =12bc sin A =12bc ·32=34bc =53,得bc =20.又b =5,所以c =4.由余弦定理,得a 2=b 2+c 2-2bc cos A =25+16-20=21,故a =21. 又由正弦定理,得sin B sin C =b a sin A ·c a sin A =bc a 2·sin 2A =2021×34=57.18.解:(1)设等比数列{a n }的公比为q ,则由已知可得⎩⎪⎨⎪⎧a 31q 3=125,|a 1q -a 1q 2|=10,解得⎩⎪⎨⎪⎧a 1=53,q =3,或⎩⎪⎨⎪⎧a 1=-5,q =-1. 故a n =53·3n -1,或a n =-5·(-1)n -1.(2)若a n =53·3n -1,则1a n =35·⎝ ⎛⎭⎪⎫13n -1,故数列⎩⎨⎧⎭⎬⎫1a n 是首项为35,公比为13的等比数列.从而∑n =1m1a n =35·⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫13m 1-13=910·⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫13m <910<1.若a n =(-5)·(-1)n -1,则1a n =-15(-1)n -1,故数列⎩⎨⎧⎭⎬⎫1a n 是首项为-15,公比为-1的等比数列,从而∑n =1m1a n=⎩⎪⎨⎪⎧-15,m =2k -1(k∈N +)0,m =2k ,(k ∈N +),故∑n =1m 1a n <1. 综上,对任何正整数m ,总有∑n =1m1a n<1.故不存在正整数m ,使得1a 1+1a 2+…+1a m≥1成立.19.(1)解:直线l ∥平面PAC .证明如下:连接EF ,因为E ,F 分别是PA ,PC 的中点,所以EF ∥AC . 又EF ⊄平面ABC ,且AC ⊂平面ABC ,所以EF ∥平面ABC .而EF ⊂平面BEF ,且平面BEF ∩平面ABC =l ,所以EF ∥l .因为l ⊄平面PAC ,EF ⊂平面PAC ,所以直线l ∥平面PAC .(2)证法一(综合法):如图(1),连接BD ,由(1)可知交线l 即为直线BD ,且l ∥AC . 因为AB 是⊙O 的直径,所以AC ⊥BC ,于是l ⊥BC . 已知PC ⊥平面ABC ,而l ⊂平面ABC ,所以PC ⊥l . 而PC ∩BC =C ,所以l ⊥平面PBC .连接BE ,BE ,因为BF ⊂平面PBC ,所以l ⊥BF . 故∠CBF 就是二面角E -l -C 的平面角,即∠CBF =β. 由DQ →=12CP →,作DQ ∥CP ,且DQ =12CP .连接PQ ,DF ,因为F 是CP 的中点,CP =2PF ,所以DQ =PF ,从而四边形DQPF 是平行四边形,PQ ∥FD .连接CD ,因为PC ⊥平面ABC , 所以CD 是FD 在平面ABC 内的射影.故∠CDF 就是直线PQ 与平面ABC 所成的角,即∠CDF =θ. 又BD ⊥平面PBC ,所以BD ⊥BF ,所以∠BDF 为锐角.故∠BDF 为异面直线PQ 与EF 所成的角,即∠BDF =α,于是在Rt △DCF ,Rt △FBD ,Rt △BCF 中,分别可得 sin θ=CF DF ,sin α=BF DF ,sin β=CF BF, 从而sin αsin β=BF DF ·CF BF =CFDF=sin θ,即sin θ=sin αsin β.证法二(向量法):如图(2),由DQ →=12CP →,作DQ ∥CP ,且DQ =12CP .连接PQ ,EF ,BE ,BF ,BD .由(1)可知交线l 即为直线BD .以点C 为原点,向量CA →,CB →,CP →所在直线分别为x ,y ,z 轴,建立如图(2)所示的空间直角坐标系,设CA =a ,CB =b ,CP =2c ,则有C (0,0,0),A (a ,0,0),B (0,b ,0),P (0,0,2c ),Q (a ,b ,c ),E ⎝ ⎛⎭⎪⎫12a ,0,c ,F (0,0,c ).于是FE →=⎝ ⎛⎭⎪⎫12a ,0,0,QP →=(-a ,-b ,c ),BF →=(0,-b ,c ),所以cos α=|FE →·QP →||EF →||QP →|=a a 2+b 2+c 2,从而sin α=1-cos 2α=b 2+c 2a 2+b 2+c 2.取平面ABC 的一个法向量为m =(0,0,1), 可得sin θ=|m ·QP →||m |·|QP →|=ca 2+b 2+c 2. 设平面BEF 的一个法向量为n =(x ,y ,z ).由⎩⎪⎨⎪⎧n ·FE →=0,n ·BF →=0,可得⎩⎪⎨⎪⎧12ax =0,-by +cz =0取n =(0,c ,b ).于是|cos β|=|m ·n ||m ||n |=bb 2+c2,从而sin β=1-cos 2β=c b 2+c 2.故sin αsin β=b 2+c 2a 2+b 2+c 2·c b 2+c 2=ca 2+b 2+c 2=sin θ,即sin θ=sin αsin β.20.解:(1)由于随机变量X 服从正态分布N (800,502),故有μ=800,σ=50,P (700<X ≤900)=0.954 4.由正态分布的对称性,可得p 0=P (X ≤900)=P (X ≤800)+P (800<X ≤900)=12+12P (700<X ≤900)=0.977 2. (2)设A 型、B 型车辆的数量分别为x ,y ,则相应的营运成本为1 600x +2 400y .依题意,x ,y ,还需满足x +y ≤21,y ≤x +7,P (X ≤36x +60y )≥p 0.由(1)知,p 0=P (X ≤900),故P (X ≤36x +60y )≥p 0等价于36x +60y ≥900.于是问题等价于求满足约束条件⎩⎪⎨⎪⎧x +y ≤21,y ≤x +7,36x +60y ≥900,x ,y ≥0,x ,y ∈N ,且使目标函数z =1 600x +2 400y 达到最小的x ,y .作可行域如图所示,可行域的三个顶点坐标分别为P (5,12),Q (7,14),R (15,6). 由图可知,当直线z =1 600x +2 400y 经过可行域的点P 时,直线z =1 600x +2 400y 在y 轴上截距z2 400最小,即z 取得最小值.故应配备A 型车5辆、B 型车12辆. 21.解:依题意可设椭圆C 1和C 2的方程分别为C 1:x 2a 2+y 2m 2=1,C 2:x 2a 2+y 2n 2=1,其中a >m >n >0,λ=m n>1.(1)方法一:如图(1),若直线l 与y 轴重合,即直线l 的方程为x =0,则S 1=12|BD ||OM |=12a |BD |,S 2=12|AB |·|ON |=12a |AB |,所以S 1S 2=|BD ||AB |. 在C 1和C 2的方程中分别令x =0,可得y A =m ,y B =n ,y D =-m ,于是|BD ||AB |=|y B -y D ||y A -y B |=m +n m -n =λ+1λ-1. 若S 1S 2=λ,则λ+1λ-1=λ,化简,得λ2-2λ-1=0. 由λ>1,可解得λ=2+1.故当直线l 与y 轴重合时,若S 1=λS 2,则λ=2+1. 方法二:如图(1),若直线l 与y 轴重合,则|BD |=|OB |+|OD |=m +n ; |AB |=|OA |-|OB |=m -n ;S 1=12|BD ||OM |=12a |BD |,S 2=12|AB ||ON |=12a |AB |.所以S 1S 2=|BD ||AB |=m +n m -n =λ+1λ-1.若S 1S 2=λ,则λ+1λ-1=λ,化简,得λ2-2λ-1=0. 由λ>1,可解得λ=2+1.故当直线l 与y 轴重合时,若S 1=λS 2,则λ=2+1.(2)方法一:如图(2),若存在与坐标轴不重合的直线l ,使得S 1=λS 2,根据对称性,不妨设直线l :y =kx (k >0),点M (-a ,0),N (a ,0)到直线l 的距离分别为d 1,d 2,则d 1=|-ak -0|1+k2=ak1+k2,d 2=|ak -0|1+k 2=ak 1+k 2,所以d 1=d 2.又S 1=12|BD |d 1, S 2=12|AB |d 2,所以S 1S 2=|BD ||AB |=λ,即|BD |=λ|AB |.由对称性可知|AB |=|CD |,所以|BC |=|BD |-|AB |=(λ-1)|AB |, |AD |=|BD |+|AB |=(λ+1)|AB |, 于是|AD ||BC |=λ+1λ-1.①将l 的方程分别与C 1,C 2的方程联立,可求得x A =am a 2k 2+m 2,x B=ana 2k 2+n 2. 根据对称性可知x C =-x B ,x D =-x A ,于是 |AD ||BC |=1+k 2|x A -x D |1+k 2|x B -x C |=2x A 2x B =m na 2k 2+n 2a 2k 2+m 2.②从而由①和②式可得a 2k 2+n 2a 2k 2+m 2=λ+1λ(λ-1).③ 令t =λ+1λ(λ-1),则由m >n ,可得t ≠1,于是由③可解得k 2=n 2(λ2t 2-1)a 2(1-t 2).因为k ≠0,所以k 2>0.于是③式关于k 有解,当且仅当n 2(λ2t 2-1)a 2(1-t 2)>0,等价于(t 2-1)⎝⎛⎭⎪⎫t 2-1λ2<0. 由λ>1,可解得1λ<t <1,即1λ<λ+1λ(λ-1)<1.由λ>1,解得λ>1+ 2.所以当1<λ≤1+2时,不存在与坐标轴不重合的直线l ,使得S 1=λS 2; 当λ>1+2时,存在与坐标轴不重合的直线l ,使得S 1=λS 2.方法二:如图(2),若存在与坐标轴不重合的直线l ,使得S 1=λS 2,根据对称性,不妨设直线l :y =kx (k >0),点M (-a ,0),N (a ,0)到直线l 的距离分别为d 1,d 2,则d 1=|-ak -0|1+k 2=ak 1+k 2,d 2=|ak -0|1+k 2=ak 1+k 2,所以d 1=d 2.又S 1=12|BD |d 1, S 2=12|AB |d 2,所以S 1S 2=|BD ||AB |=λ.因为|BD ||AB |=1+k 2|x B -x D |1+k 2|x A -x B |=x A +x B x A -x B=λ,所以x A x B =λ+1λ-1. 由点A (x A ,kx A ),B (x B ,kx B )分别在C 1,C 2上,可得x 2A a 2+k 2x 2A m 2=1,x 2B a 2+k 2x 2Bn2=1,两式相减可得x 2A -x 2B a 2+k 2(x 2A -λ2x 2B )m 2=0.(*) 依题意得x A >x B >0,所以x 2A >x 2B .所以由(*)式可得k 2=m 2(x 2A -x 2B )a 2(λ2x 2B -x 2A ). 因为k 2>0,所以由m 2(x 2A -x 2B )a 2(λ2x 2B -x 2A )>0,可解得1<x A x B<λ. 从而1<λ+1λ-1<λ,解得λ>1+2,所以当1<λ≤1+2时,不存在与坐标轴不重合的直线l ,使得S 1=λS 2; 当λ>1+2时,存在与坐标轴不重合的直线l ,使得S 1=λS 2.22.(1)解:因为f ′(x )=(r +1)(1+x )r -(r +1)=(r +1)[(1+x )r-1],令f ′(x )=0,解得x =0.当-1<x <0时,f ′(x )<0, 所以f (x )在(-1,0)内是减函数;当x >0时,f ′(x )>0,所以f (x )在(0,+∞)内是增函数. 故函数f (x )在x =0处取得最小值f (0)=0.(2)证明:由(1),知当x ∈(-1,+∞)时,f (x )≥f (0)=0,即(1+x )r +1≥1+(r +1)x ,当且仅当x =0时等号成立,故当x >-1且x ≠0时,有(1+x )r +1>1+(r +1)x .①故①中,令x =1n(这时x >-1且x ≠0),得⎝ ⎛⎭⎪⎫1+1n r +1>1+r +1n. 上式两边同乘nr +1,得(n +1)r +1>nr +1+n r(r +1),即n r<(n +1)r +1-n r +1r +1.②当n >1时,在①中,令x =-1n (这时x >-1且x ≠0),类似可得n r>n r +1-(n -1)r +1r +1.③且当n =1时,③也成立.综合②③,得n r +1-(n -1)r +1r +1<n r <(n +1)r +1-n r +1r +1.④(3)解:在④中,令r =13,n 分别取值81,82,83,…,125,得34(8143-8043)<381<34(8243-8143),34(8243-8143)<382<34(8343-8243), 34(8343-8243)<383<34(8443-8343), …,34(12543-12443)<3125<34(12643-12543). 将以上各式相加并整理,得34(12543-8043)<S <34(12643-8143), 代入数据计算,可得34(12543-8043)≈210.2,3 4()12643-8143≈210.9.由[S]的定义,得[S]=211.。
2013年普通高等学校招生全国统一考试英语试题(湖北卷)

2013年普通高等学校招生全国统一考试(湖北卷)英语试题答案解析本试题卷共16页,81题。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用统一提供的2B铅笔将答题卡上试卷类型A后的方框涂黑。
2. 选择题的作答:每小题选出答案后,用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3. 完成句子和短文写作题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4. 考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
第一部分:听力(共两节,满分30分)做题时,先将答案划在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £ 19.15.B. £ 9.15.C. £ 9.18.答案:B1. Why doesn’t John go to school today?A. It’s the weekend.B. He’s too tired for school.C. His school is closed down.2. What will the man do tomorrow morning?A. Give Frank a bath.B. Cook Frank a meal.C. Take Frank to a vet.3. What is the male speaker?A. A student.B. A president.C. A professor.4. What does the man mean?A. The door is unlocked.B. He is not the one to blame.C. Somebody has just left the lab.5. On which floor is the woman’s apartment?A. The second.B. The fourth.C. The sixth.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
2013年全国高考英语试题及答案-湖北卷

2013年普通高等学校招生全国统一考试(湖北卷)英语本试题卷满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用统一提供的2B铅笔将答题卡上试卷类型A后的方框涂黑。
2.选择题的作答:每小题选出答案后,用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3.完成句子和短文写作题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
第一部分:听力(共两节,满分30分)做题时,先将答案划在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£ 19.15.B.£ 9.15.C.£ 9.18.答案:B1.Why doesn’t John go to school today?A.It’s the weekend.B.He’s too tired for school.C.His school is closed down.2.What will the man do tomorrow morning?A.Give Frank a bath.B.Cook Frank a meal.C.Take Frank to a vet.3.What is the male speaker?A.A student.B.A president.C.A professor.4.What does the man mean?A.The door is unlocked.B.He is not the one to blame.C.Somebody has just left the lab.5.On which floor is the woman’s apartment?A.The second.B.The fourth.C.The sixth.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
2013年普通高等学校招生全国统一考试湖北卷

2013年普通高等学校招生全国统一考试(湖北卷)数 学(文史类)一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集{1,2,3,4,5}U =,集合{1,2}A =,{2,3,4}B =,则U B A =ðA .{2}B .{3,4}C .{1,4,5}D .{2,3,4,5}2.已知π04θ<<,则双曲线1C :22221sin cos x y θθ-=与2C :22221cos sin y x θθ-=的 A .实轴长相等 B .虚轴长相等C .离心率相等D .焦距相等3.在一次跳伞训练中,甲、乙两位学员各跳一次.设命题p 是“甲降落在指定范围”,q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为 A .()p ⌝∨()q ⌝B .p ∨()q ⌝C .()p ⌝∧()q ⌝D .p ∨q4.四名同学根据各自的样本数据研究变量,x y 之间的相关关系,并求得回归直线方程,分 别得到以下四个结论:① y 与x 负相关且 2.347 6.423y x =-; ② y 与x 负相关且 3.476 5.648y x =-+; ③ y 与x 正相关且 5.4378.493y x =+; ④ y 与x 正相关且 4.326 4.578y x =--. 其中一定不正确...的结论的序号是 A .①② B .②③C .③④D . ①④5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶. 与以上事件吻合得最好的图象是6.将函数sin ()y x x x +∈R 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是A .π12B .π6C .π3D .5π67.已知点(1,1)A -、(1,2)B 、(2,1)C --、(3,4)D ,则向量AB 在CD 方向上的投影为ABC. D. 8.x 为实数,[]x 表示不超过x 的最大整数,则函数()[]f x x x =-在R 上为 A .奇函数B .偶函数C .增函数D . 周期函数9.某旅行社租用A 、B 两种型号的客车安排900名客人旅行,A 、B 两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B 型车不多于A 型车7辆.则租金最少为 A .31200元B .36000元C .36800元D .38400元10.已知函数()(ln )f x x x ax =-有两个极值点,则实数a 的取值范围是A .(,0)-∞B .1(0,)2C .(0,1)D .(0,)+∞二、填空题:本大题共7小题,每小题5分,共35分.请将答案填在答题卡对应题号.......的位置上. 答错位置,书写不清,模棱两可均不得分.11.i 为虚数单位,设复数1z ,2z 在复平面内对应的点关于原点对称,若123i z =-,则2z = . 12.某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4则(Ⅰ)平均命中环数为 ; (Ⅱ)命中环数的标准差为 .13.阅读如图所示的程序框图,运行相应的程序. 若输入m 的值为2, 则输出的结果i = .14.已知圆O :225x y +=,直线l :cos sin 1x y θθ+=(π02θ<<).设圆O 上到直线l 的距离等于1的点第13题图的个数为k ,则k = .15.在区间[2,4]-上随机地取一个数x ,若x 满足||x m ≤的概率为56,则m = . 16.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸. 若盆中积水深九寸,则平地降雨量是 寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)17.在平面直角坐标系中,若点(,)P x y 的坐标x ,y 均为整数,则称点P 为格点. 若一个多边形的顶点全是格点,则称该多边形为格点多边形. 格点多边形的面积记为S ,其内部的格点数记为N ,边界上的格点数记为L . 例如图中△ABC 是格点三角形,对应的1S =,0N =,4L =. (Ⅰ)图中格点四边形DEFG 对应的,,S N L 分别是 ;(Ⅱ)已知格点多边形的面积可表示为S aN bL c =++,其中a ,b ,c 为常数. 若某格点多边形对应的71N =,18L =, 则S = (用数值作答).三、解答题:本大题共5小题,共65分.解答应写出文字说明、证明过程或演算步骤. 18.(本小题满分12分)在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c . 已知cos23cos()1A B C -+=.(Ⅰ)求角A 的大小; (Ⅱ)若△ABC 的面积S =5b =,求sin sin B C 的值.19.(本小题满分13分)已知n S 是等比数列{}n a 的前n 项和,4S ,2S ,3S 成等差数列,且23418a a a ++=-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)是否存在正整数n ,使得2013n S ≥?若存在,求出符合条件的所有n 的集合;若不存在,说明理由.20.(本小题满分13分)如图,某地质队自水平地面A ,B ,C 三处垂直向地下钻探,自A 点向下钻到A 1处发现矿藏,再继续下钻到A 2处后下面已无矿,从而得到在A 处正下方的矿层厚度为121A A d =.同样可得在B ,C 处正下方的矿层厚度分别为122B B d =,123C C d =,且123d d d <<. 过AB ,AC 的中点M ,N 且与直线2AA 平行的平面截多面体111222A B C A B C -所得的截面DEFG 为该多面体的一个中截面,其面积记为S 中. (Ⅰ)证明:中截面DEFG 是梯形;(Ⅱ)在△ABC 中,记BC a =,BC 边上的高为h ,面积为S . 在估测三角形ABC 区域内正下方的矿藏储量(即多面体111222A B C A B C -的体积V )时,可用近似公式V S h =⋅估中来估算. 已知1231()3V d d d S =++,试判断V 估与V 的大小关系,并加以证明.21.(本小题满分13分)设0a >,0b >,已知函数()1ax bf x x +=+. (Ⅰ)当a b ≠时,讨论函数()f x 的单调性;(Ⅱ)当0x >时,称()f x 为a 、b 关于x 的加权平均数.(i )判断(1)f, f ,()bf a是否成等比数列,并证明()b f f a ≤; (ii )a 、b 的几何平均数记为G . 称2aba b+为a 、b 的调和平均数,记为H . 若()H f x G ≤≤,求x 的取值范围.第20题图22.(本小题满分14分)如图,已知椭圆1C 与2C 的中心在坐标原点O ,长轴均为MN 且在x 轴上,短轴长分别 为2m ,2()n m n >,过原点且不与x 轴重合的直线l 与1C ,2C 的四个交点按纵坐标从 大到小依次为A ,B ,C ,D .记mnλ=,△BDM 和△ABN 的面积分别为1S 和2S . (Ⅰ)当直线l 与y 轴重合时,若12S S λ=,求λ的值;(Ⅱ)当λ变化时,是否存在与坐标轴不重合的直线l ,使得12S S λ=?并说明理由.第22题图2013年普通高等学校招生全国统一考试(湖北卷)数学(文史类)试题参考答案一、选择题:1.B U BA =ð}.4,3{}5,4,3{}4,3,2{= 2.D 在双曲线1C :22221sin cos x y θθ-=与2C :22221cos sin y x θθ-=中,都有1cos sin 222=+=θθc ,即焦距相等3.A 因为p 是“甲降落在指定范围”,q 是“乙降落在指定范围”,则p -是“没有降落在指定范围”,q -是“乙没有降落在指定范围”,所以命题“至少有一位学员没有降落在指定范围”可表示为()p ⌝∨()q ⌝ . 4.D 在○1中,y 与x 不是负相关;○1一定不正确;同理○4也一定不正确.5.C 可以将小明骑车上学的行程分为三段,第一段是匀速行驶,运动方程是一次函数,即小明距学校的距离是他骑行时间的一次函数,所对应的函数图象是一条直线段,由此可以判断A 是错误的;第二段因交通拥堵停留了一段时间,这段时间内小明距学校的距离没有改变,即小明距学校的距离是行驶时间的常值函数,所对应的函数图象是平行于x 轴的一条线段,由此可以排除D ;第三段小明为了赶时间加快速度行驶,即小明在第三段的行驶速度大于第一段的行驶速度,所以第三段所对应的函数图象不与第一段的平行,从而排除B. 故选C.6.B因为sin ()y x x x =+∈R 可化为)6cos(2π-=x y (x ∈R ),将它向左平移π6个单位得x x y cos 26)6(cos 2=⎥⎦⎤⎢⎣⎡-+=ππ,其图像关于y 轴对称.7.A AB =(2,1),CD =(5,5),则向量AB 在向量CD 方向上的射影为22325515255)5,5()1,2(cos 22=⨯+⨯=+⋅==θ. 8.D 函数()[]f x x x =-表示实数x 的小数部分,有)(][]1[1)1(x f x x x x x f =-=+-+=+ ,所以函数()[]f x x x =-是以1为周期的周期函数.9.C 根据已知,设需要A 型车x 辆,B 型车y 辆,则根据题设,有⎪⎪⎩⎪⎪⎨⎧=+>>≤-≤+,9006036,0,0,7,21y x y x x y y x 画出可行域,求出三个顶点的坐标分别为A(7,14),B(5,12),C(15,6),目标函数(租金)为y x k 24001600+=,如图所示.将点B 的坐标代入其中,即得租金的最小值为:3680012240051600=⨯+⨯=k (元).10.B ax x x f 21ln )('-+=,由()(ln )f x x x ax =-由两个极值点,得0)('=x f 有两个不等的实数解,即12ln -=ax x 有两个实数解,从而直线12-=ax y 与曲线x y ln =有两个交点. 过点(0,-1)作x y ln =的切线,设切点为(x 0,y 0),则切线的斜率01x k =,切线方程为11-=x x y . 切点在切线上,则0100=-=x x y ,又切点在曲线x y ln =上,则10ln 00=⇒=x x ,即切点为(1,0).切线方程为1-=x y . 再由直线12-=ax y 与曲线x y ln =有两个交点.,知直线12-=ax y 位于两直线0=y 和1-=x y 之间,如图所示,其斜率2a 满足:0<2a <1,解得0<a <21.二、填空题:11. 23i -+ 复数123i z =-在复平面内的对应点Z 1(2,-3),它关于原点的对称点Z 2为(-2,3),所对应的复数为322+-=z i. 12. (Ⅰ)7 (Ⅱ)2 (Ⅰ)7()747109459787101=+++++++++; (Ⅱ)2 []222222)74(2)75()77(3)78()79(2)710(101-+-+-+-+-+-=s =21040=. 13. 4 初始值m =2,A =1,B=1,i =0,第一次执行程序,得 i=1,A=2,B=1,因为A <B 不成立,则第二次执行程序,得i=2,A =2×2=4,B =1×2=2,还是A <B 不成立,第三次执行程序,得 i=3,A=4×2=8,B=2×3=6,仍是A<B 不成立,第四次执行程序,得i =4,A =8×2=16,B =×4=24,有A <B 成立,输出i=4. 14. 4 这圆的圆心在原点,半径为5,圆心到直线l 的距离为1sin cos 122=+θθ,所以圆O 上到直线l的距离等于1的点有4个,如图A 、B 、C 、D 所示.15. 3 因为区间[2,4]-的长度为6,不等式||x m ≤的解区间为[-m ,m ] ,其区间长度为2m. 那么在区间[2,4]-上随机地取一个数x ,要使x 满足||x m ≤的概率为56,m 将区间 [2,4]-分为[-2,m]和[m ,4] ,且两区间的长度比为5:1,所以m =3.16. 3 如图示天池盆的半轴截面,那么盆中积水的体积为()ππ19631061069322⨯=⨯++⨯=V (立方寸),盆口面积S =196π(平方寸),所以,平地降雨量为=⨯)(寸寸23196)(19633(寸).17. (Ⅰ)3, 1, 6 (Ⅱ)79(Ⅰ)3, 1, 6 S=S △DFG +S △DEF =1+2=3 ,N=1,L =6;(Ⅱ)79 根据题设△ABC 是格点三角形,对应的1S =,0N =,4L =,有 14=+c b , ○1 由(Ⅰ)有36=++c b a , ○2再由格点△DEF 中,S=2,N=0,L=6,得26=+c b , ○3 联立○1○2○3,解得.1,1,21=-==a cb 所以当71N =,18L =时, S =791182171=-⨯+. 三、解答题:18.(Ⅰ)由cos23cos()1A B C -+=,得22cos 3cos 20A A +-=, 即(2cos 1)(cos 2)0A A -+=,解得1cos 2A = 或cos 2A =-(舍去). 因为0πA <<,所以π3A =.(Ⅱ)由11sin 22S bc A bc ====得20bc =. 又5b =,知4c =.由余弦定理得2222cos 25162021,a b c bc A =+-=+-=故a =又由正弦定理得222035sin sin sin sin sin 2147b c bc B C A A A a a a =⋅==⨯=.19. (Ⅰ)设数列{}n a 的公比为q ,则10a ≠,0q ≠. 由题意得 2432234,18,S S S S a a a -=-⎧⎨++=-⎩ 即23211121,(1)18,a q a q a q a q q q ⎧--=⎪⎨++=-⎪⎩ 解得13,2.a q =⎧⎨=-⎩故数列{}n a 的通项公式为13(2)n n a -=-.(Ⅱ)由(Ⅰ)有 3[1(2)]1(2)1(2)n n n S ⋅--==----. 若存在n ,使得2013n S ≥,则1(2)2013n --≥,即(2)2012.n -≤- 当n 为偶数时,(2)0n ->, 上式不成立;当n 为奇数时,(2)22012n n -=-≤-,即22012n ≥,则11n ≥.综上,存在符合条件的正整数n ,且所有这样的n 的集合为{21,,5}n n k k k =+∈≥N . 20. (Ⅰ)依题意12A A ⊥平面ABC ,12B B ⊥平面ABC ,12C C ⊥平面ABC ,所以A 1A 2∥B 1B 2∥C 1C 2. 又121A A d =,122B B d =,123C C d =,且123d d d << . 因此四边形1221A A B B 、1221A A C C 均是梯形.由2AA ∥平面MEFN ,2AA ⊂平面22AA B B ,且平面22AA B B 平面MEFN ME =,可得AA 2∥ME ,即A 1A 2∥DE . 同理可证A 1A 2∥FG ,所以DE ∥FG .又M 、N 分别为AB 、AC 的中点,则D 、E 、F 、G 分别为11A B 、22A B 、22A C 、11AC 的中点, 即DE 、FG 分别为梯形1221A A B B 、1221A A C C 的中位线.因此 12121211()()22DE A A B B d d =+=+,12121311()()22FG A A C C d d =+=+,而123d d d <<,故DE FG <,所以中截面DEFG 是梯形. (Ⅱ)V V <估. 证明如下:由12A A ⊥平面ABC ,MN ⊂平面ABC ,可得12A A MN ⊥. 而EM ∥A 1A 2,所以EM MN ⊥,同理可得FN MN ⊥. 由MN 是△ABC 的中位线,可得1122MN BC a ==即为梯形DEFG 的高, 因此13121231()(2)22228DEFG d d d d a a S S d d d ++==+⋅=++中梯形, 即123(2)8ahV S h d d d =⋅=++估中. 又12S ah =,所以1231231()()36ahV d d d S d d d =++=++.于是1231232131()(2)[()()]6824ah ah ahV V d d d d d d d d d d -=++-++=-+-估.由123d d d <<,得210d d ->,310d d ->,故V V <估.21. (Ⅰ)()f x 的定义域为(,1)(1,)-∞--+∞,22(1)()()(1)(1)a x ax b a bf x x x +-+-'==++.当a b >时,()0f x '>,函数()f x 在(,1)-∞-,(1,)-+∞上单调递增; 当a b <时,()0f x '<,函数()f x 在(,1)-∞-,(1,)-+∞上单调递减. (Ⅱ)(i )计算得(1)02a b f +=>,2()0b abf a a b=>+,0f =.故22(1)()[2b a b ab f f ab f a a b +=⋅==+, 即2(1)())]b f f f a =. ①所以(1),()bf f f a成等比数列.因2a b+≥(1)f f ≥.由①得()b f f a ≤. (ii )由(i )知()bf H a =,f G =.故由()H f x G ≤≤,得()()b f f x f a ≤≤. ②当a b =时,()()b f f x f a a ===.这时,x 的取值范围为(0,)+∞; 当a b >时,01ba<<,从而b a <()f x 在(0,)+∞上单调递增与②式,得bx a≤≤x的取值范围为,b a ⎡⎢⎣; 当a b <时,1ba>,从而b a >()f x 在(0,)+∞上单调递减与②式,bx a ≤,即x的取值范围为b a ⎤⎥⎦. 22. 依题意可设椭圆1C 和2C 的方程分别为1C :22221x y a m +=,2C :22221x y a n+=. 其中0a m n >>>, 1.m n λ=>(Ⅰ)解法1:如图1,若直线l 与y 轴重合,即直线l 的方程为0x =,则 111||||||22S BD OM a BD =⋅=,211||||||22S AB ON a AB =⋅=,所以12||||S BD S AB =. 在C 1和C 2的方程中分别令0x =,可得A y m =,B y n =,D y m =-, 于是||||1||||1B D A B y y BD m n AB y y m n λλ-++===---. 若12S S λ=,则11λλλ+=-,化简得2210λλ--=. 由1λ>,可解得1λ=. 故当直线l 与y 轴重合时,若12S S λ=,则1λ=.解法2:如图1,若直线l 与y 轴重合,则||||||BD OB OD m n =+=+,||||||AB OA OB m n =-=-;111||||||22S BD OM a BD =⋅=,211||||||22S AB ON a AB =⋅=. 所以12||1||1S BD m n S AB m n λλ++===--.若12S S λ=,则11λλλ+=-,化简得2210λλ--=. 由1λ>,可解得1λ=. 故当直线l 与y 轴重合时,若12S S λ=,则1λ=.(Ⅱ)解法1:如图2,若存在与坐标轴不重合的直线l ,使得12S S λ=. 根据对称性, 不妨设直线l :(0)y kx k =>,点(,0)M a -,(,0)N a 到直线l 的距离分别为1d ,2d ,则因为1d ==,2d ==12d d =.又111||2S BD d =,221||2S AB d =,所以12||||S BD S AB λ==,即||||BD AB λ=. 由对称性可知||||AB CD =,所以||||||(1)||BC BD AB AB λ=-=-, ||||||(1)||AD BD AB AB λ=+=+,于是||1||1AD BC λλ+=-. ① 将l 的方程分别与C 1,C 2的方程联立,可求得A x =B x =.根据对称性可知C B x x =-,D A x x =-,于是2||||2A B x AD BC x == ② 从而由①和②式可得1(1)λλλ+-. ③令1(1)t λλλ+=-,则由m n >,可得1t ≠,于是由③可解得222222(1)(1)n t k a t λ-=-.因为0k ≠,所以20k >. 于是③式关于k 有解,当且仅当22222(1)0(1)n t a t λ->-,第22题解答图1第22题解答图2等价于2221(1)()0t t λ--<. 由1λ>,可解得11t λ<<,即111(1)λλλλ+<<-,由1λ>,解得1λ>当11λ<≤+l ,使得12S S λ=;当1λ>l 使得12S S λ=. 解法2:如图2,若存在与坐标轴不重合的直线l ,使得12S S λ=. 根据对称性, 不妨设直线l :(0)y kx k =>,点(,0)M a -,(,0)N a 到直线l 的距离分别为1d ,2d ,则因为1d ==,2d ==12d d =.又111||2S BD d =,221||2S AB d =,所以12||||S BD S AB λ==.因为||||A B A Bx x BD AB x x λ+==-,所以11A B x x λλ+=-. 由点(,)A A A x kx ,(,)B B B x kx 分别在C 1,C 2上,可得222221A A x k x a m +=,222221B B x k x a n +=,两式相减可得22222222()0A B A B x x k x x a mλ--+=, 依题意0A B x x >>,所以22AB x x >. 所以由上式解得22222222()()A B B A m x x k a x x λ-=-. 因为20k >,所以由2222222()0()A B B A m x x a x x λ->-,可解得1ABx x λ<<.从而111λλλ+<<-,解得1λ>当11λ<≤+l ,使得12S S λ=;当1λ>l 使得12S S λ=.。
2013年湖北高考理科综合试题及答案解析版

2013年普通高等学校招生全国统一考试理科综合能力测试(新课标I卷)可能用到的相对原子质量:H 1 C 12 N 14 O 16 Mg24 S 32 K39 Mn55第Ⅰ卷一、选择题:本卷共13小题。
每小题6分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
1.关于蛋白质生物合成的叙述,正确的是()A.一种tRNA可以携带多种氨基酸B.DNA聚合酶是在细胞核中合成的C.反密码子是位于mRNA上相邻的三个碱基D.线粒体中的DNA能控制某些蛋白质的合成2.关于同一个体中细胞有丝分裂和减数第一次分裂的叙述,正确的是()A.两者前期染色体数目相同,染色体行为和DNA分子数目不同B.两者中期染色体数目不同,染色体行为和DNA分子数目相同C.两者后期染色体行为和数目不同,DNA分子数目相同D.两者后期染色体行为和数目相同,DNA分子数目不同3.关于植物细胞主动运输方式吸收所需矿质元素离子的叙述,正确的是()A.吸收不同矿质元素离子的速率都相同B.低温不影响矿质元素离子的吸收速率C.主动运输矿质元素离子的过程只发生在活细胞中D.叶肉细胞不能以主动运输的方式吸收矿质元素离子4.示意图甲、乙、丙、丁为某实验动物感染HIV后的情况()A.从图甲可以看出,HIV感染过程中存在逆转录现象B.从图乙可以看出,HIV侵入后机体能产生体液免疫C.从图丙可以推测,HIV可能对实验药物a敏感D.从图丁可以看出,HIV对试验药物b敏感5.某农场面积为140hm2,农场丰富的植物资源为黑线姬鼠提供了很好的生存条件,鼠大量繁殖吸引鹰来捕食,某研究小组采用标志重捕法来研究黑线姬鼠的种群密度,第一次捕获100只,标记后全部放掉,第二次捕获280只,发现其中有两只带有标记,下列叙述错误..的是()A.鹰的迁入率增加会影响黑线姬鼠的种群密度B.该农场黑线姬鼠的种群密度约为100只/hm2C.黑线姬鼠种群数量下降说明农场群落的丰富度下降D.植物→鼠→鹰这条食物链,第三营养级含能量少6.若用玉米为实验材料,验证孟德尔分离定律,下列因素对得出正确实验结论,影响最小的是()A.所选实验材料是否为纯合子B.所选相对性状的显隐性是否易于区分C.所选相对性状是否受一对等位基因控制D.是否严格遵守实验操作流程和统计分析方法7.化学无处不在,下列与化学有关的说法不正确的是A.侯氏制碱法的工艺过程中应用了物质溶解度的差异B.可用蘸浓盐酸的棉棒检验输送氨气的管道是否漏气C.碘是人体必需微量元素,所以要多吃富含高碘酸的食物D.黑火药由硫黄、硝石、木炭三种物质按一定比例混合制成8.香叶醇是合成玫瑰香油的主要原料,其结构简式如下:下列有关香叶醉的叙述正确的是A.香叶醇的分子式为C10H18OB.不能使溴的四氯化碳溶液褪色C.不能使酸性高锰酸钾溶液褪色D.能发生加成反应不能发生取代反应9.短周期元素W、X、Y、Z的原子序数依次增大,其简单离子都能破坏水的电离平衡的是A. W2-、X+B. X+、 Y3+C. Y3+、 Z2-D. X+、 Z2-10.银质器皿日久表面会逐渐变黑,这是生成了Ag2S的缘故.根据电化学原理可进行如下处理:在铝质容器中加入食盐溶液,再将变黑的银器漫入该溶液中,一段时间后发现黑色会褪去。
2013年湖北高考英语试题及答案word版

2013年普通高等学校招生全国统一考试(湖北卷)英语本试题卷共16页,81题。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用统一提供的2B铅笔将答题卡上试卷类型A后的方框涂黑。
2. 选择题的作答:每小题选出答案后,用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3. 完成句子和短文写作题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4. 考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
第一部分:听力(共两节,满分30分)做题时,先将答案划在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £ 19.15.B. £ 9.15.C. £ 9.18.答案:B1. Why doesn’t John go to school today?A. It’s the weekend.B. He’s too tired for school.C. His school is closed down.2. What will the man do tomorrow morning?A. Give Frank a bath.B. Cook Frank a meal.C. Take Frank to a vet.3. What is the male speaker?A. A student.B. A president.C. A professor.4. What does the man mean?A. The door is unlocked.B. He is not the one to blame.C. Somebody has just left the lab.5. On which floor is the woman’s apartment?A. The second.B. The fourth.C. The sixth.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
2013年普通高等学校招生全国统一考试(答案)

2013年普通高等学校招生全国统一考试(课标全国卷Ⅱ)一、选择题1.C 由题意得M∩N={-2,-1,0}.选C.2.C 21+i =2(1-i)2=|1-i|=2.选C.3.B 由约束条件得可行域(如图),当直线2x-3y-z=0过点A(3,4)时,z min=2×3-3×4=-6.故选B.4.B 由正弦定理bsin B =csin C及已知条件得c=22.又sin A=sin(B+C)=12×22+32×22=2+64,从而S△ABC=12bcsin A=12×2×22×2+64=3+1.故选B.5.D 在Rt△PF2F1中,令|PF2|=1,因为∠PF1F2=30°,所以|PF1|=2,|F1F2|=3.所以e=2c2a =|F1F2||PF1|+|P F2|=33.故选D.6.A cos2 α+π4=1+cos2α+π22=1-sin2α2=16.选A.评析本题考查了三角函数的化简求值,考查了降幂公式、诱导公式的应用.7.B 由框图知循环情况为:T=1,S=1,k=2;T=12,S=1+12,k=3;T=12×3,S=1+12+12×3,k=4;T=12×3×4,S=1+12+12×3+12×3×4,k=5>4,故输出S.选B.8.D∵3<2<3,1<2<5,3>2,∴log33<log32<log33,log51<log52<log55,log23>log22,∴12<a<1,0<b<12,c>1,∴c>a>b.故选D.9.A 在空间直角坐标系中,易知O(0,0,0),A(1,0,1),B(1,1,0),C(0,1,1)恰为单位正方体的四个顶点.因此该几何体以zOx平面为投影面所得的正视图为A.评析 本题考查了三视图和直观图,考查了空间想象能力.把几何体补成正方体是求解的关键.10.C 设直线AB 与抛物线的准线x=-1交于点C.分别过A,B 作AA 1垂直准线于A 1,BB 1垂直准线于B 1.由抛物线的定义可设|BF|=|BB 1|=t,|AF|=|AA 1|=3t.由三角形的相似得|BC ||AB |=|BC |4t=12,∴|BC|=2t,∴∠B 1CB=π6,∴直线的倾斜角α=π3或23π.又F(1,0),∴直线AB 的方程为y= 3(x-1)或y=- 3(x-1).故选C.11.C 由三次函数的值域为R 知, f(x)=0必有解,A 项正确;因为f(x)=x 3+ax 2+bx+c 的图象可由曲线y=x 3平移得到,所以y=f(x)的图象是中心对称图形,B 项正确;若y=f(x)有极值点,则其导数y=f '(x)必有2个零点,设为x 1,x 2(x 1<x 2),则有f '(x)=3x 2+2ax+b=3(x-x 1)(x-x 2),所以f(x)在(-∞,x 1)上递增,在(x 1,x 2)上递减,在(x 2,+∞)上递增,则x 2为极小值点,所以C 项错误,D 项正确.选C.评析 本题考查了三次函数的图象和性质,考查了利用导数研究函数的单调性和极值.掌握基本初等函数的图象和性质是解题关键.12.D 由2x(x-a)<1得a>x-12,令f(x)=x-12,即a>f(x)有解,则a>f(x)min ,又y=f(x)在(0,+∞)上递增,所以f(x)>f(0)=-1,所以a>-1,选D.评析 本题考查了函数的值域与最值的求法,考查了分离参变量的方法,熟悉基本初等函数的单调性是解题关键. 二、填空题 13.答案 0.2解析 任取两个不同的数的情况有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10种,其中和为5的有2种,所以所求概率为210=0.2. 14.答案 2解析解法一:AE·BD= AD+12AB·(AD-AB)=AD2-12AB2+0=22-12×22=2.解法二:以A为原点建立平面直角坐标系(如图).则A(0,0),B(2,0),C(2,2),D(0,2),E(1,2).∴AE=(1,2),BD=(-2,2).从而AE·BD=(1,2)·(-2,2)=1×(-2)+2×2=2.评析本题考查了向量的基本运算.向量的运算可以利用运算法则也可以利用坐标运算.15.答案24π解析设底面中心为E,则|AE|=12|AC|=62,∵体积V=13×|AB|2×|OE|=|OE|=322,∴|OA|2=|AE|2+|OE|2=6.从而以|OA|为半径的球的表面积S=4π·|OA|2=24π.评析本题考查了正四棱锥和球,考查了表面积和体积,考查了空间想象能力和运算求解能力.计算错误是失分的主要原因.16.答案56π解析令y=f(x)=cos(2x+φ),将其图象向右平移π2个单位后得f x-π2=cos2 x-π2+φ =cos(2x+φ-π)=sin(2x+φ-π)+π2=sin2x+φ-π2的图象,因为其与y=sin2x+π3的图象重合,所以φ-π2=π3+2kπ(k∈Z),所以φ=2kπ+56π(k∈Z),又-π≤φ<π,所以φ=56π.三、解答题17.解析(Ⅰ)设{a n}的公差为d.由题意得,a112=a1a13,即(a1+10d)2=a1(a1+12d).于是d(2a1+25d)=0.又a1=25,所以d=0(舍去)或d=-2.故a n=-2n+27.(Ⅱ)令S n=a1+a4+a7+…+a3n-2.由(Ⅰ)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列.从而S n=n2(a1+a3n-2)=n2(-6n+56)=-3n2+28n.18.解析(Ⅰ)证明:连结AC 1交A1C于点F,则F为AC1中点.又D是AB中点,连结DF,则BC1∥DF.因为DF⊂平面A1CD,BC1⊄平面A1CD,所以BC1∥平面A1CD.(Ⅱ)因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD.由于AC=CB,D为AB的中点,所以CD⊥AB.又AA1∩AB=A,于是CD⊥平面ABB1A1.由AA1=AC=CB=2,AB=22得∠ACB=90°,CD=,A1D=,DE=1E=3,故A1D2+DE2=A1E2,即DE⊥A1D.所以VC-A1DE =13×12×6×3×2=1.评析本题考查了三棱柱的性质,考查了直线与平面平行的判定和体积的计算,考查了空间想象能力和运算求解能力.正确地选择方法和规范化解题至关重要.19.解析(Ⅰ)当X∈[100,130)时,T=500X-300(130-X)=800X-39 000.当X∈[130,150]时,T=500×130=65 000.所以T=800X-39000, 100≤X<130, 65000,130≤X≤150.(Ⅱ)由(Ⅰ)知利润T不少于57 000元当且仅当120≤X≤150.由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T 不少于57 000元的概率的估计值为0.7.20.解析 (Ⅰ)设P(x,y),圆P 的半径为r. 由题设得y 2+2=r 2,x 2+3=r 2.从而y 2+2=x 2+3. 故P 点的轨迹方程为y 2-x 2=1. (Ⅱ)设P(x 0,y 0),由已知得00 2= 22. 又P 在双曲线y 2-x 2=1上,从而得|x 0-y 0|=1,y 02-x 02=1.由 x 0-y 0=1,y 02-x 02=1得 x 0=0,y 0=-1.此时,圆P 的半径r= 3.由 x 0-y 0=-1,y 02-x 02=1得 x 0=0,y 0=1.此时,圆P 的半径r= 3.故圆P 的方程为x 2+(y-1)2=3或x 2+(y+1)2=3. 21.解析 (Ⅰ)f(x)的定义域为(-∞,+∞), f '(x)=-e -xx(x-2).①当x∈(-∞,0)或x∈(2,+∞)时, f '(x)<0; 当x∈(0,2)时, f '(x)>0.所以f(x)在(-∞,0),(2,+∞)上单调递减,在(0,2)上单调递增.故当x=0时, f(x)取得极小值,极小值为f(0)=0;当x=2时, f(x)取得极大值,极大值为f(2)=4e -2.(Ⅱ)设切点为(t, f(t)),则l 的方程为 y=f '(t)(x-t)+f(t). 所以l 在x 轴上的截距为 m(t)=t-f (t )f '(t )=t+t t -2=t-2+2t -2+3.由已知和①得t∈(-∞,0)∪(2,+∞).令h(x)=x+2x (x≠0),则当x∈(0,+∞)时,h(x)的取值范围为[2 x∈(-∞,-2)时,h(x)的取值范围是(-∞,-3).所以当t∈(-∞,0)∪(2,+∞)时,m(t)的取值范围是(-∞,0)∪[2 +3,+∞). 综上,l 在x 轴上的截距的取值范围是(-∞,0)∪[2 2+3,+∞).评析本题考查了导数的应用,均值定理求最值,考查了综合解题的能力,正确地求导是解题的关键.22.解析(Ⅰ)证明:因为CD为△ABC外接圆的切线,所以∠DCB=∠A,由题设知BCFA =DCEA,故△CDB∽△AEF,所以∠DBC=∠EFA.因为B,E,F,C四点共圆,所以∠CFE=∠DBC,故∠EFA=∠CFE=90°.所以∠CBA=90°,因此CA是△ABC外接圆的直径.(Ⅱ)连结CE,因为∠CBE=90°,所以过B,E,F,C四点的圆的直径为CE,由DB=BE,有CE=DC,又BC2=DB·BA=2DB2,所以CA2=4DB2+BC2=6DB2.而DC2=DB·DA=3DB2,故过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为12.23.解析(Ⅰ)依题意有P(2cos α,2sin α),Q(2cos 2α,2sin 2α),因此M(cos α+cos 2α,sin α+sin 2α).M的轨迹的参数方程为x=cosα+cos2α,y=sinα+sin2α(α为参数,0<α<2π).(Ⅱ)M点到坐标原点的距离d= x2+y2=α<2π). 当α=π时,d=0,故M的轨迹过坐标原点.24.证明(Ⅰ)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca得a2+b2+c2≥ab+bc+ca.由题设得(a+b+c)2=1,即a2+b2+c2+2ab+2bc+2ca=1.所以3(ab+bc+ca)≤1,即ab+bc+ca≤13.(Ⅱ)因为a 2b +b≥2a,b2c+c≥2b,c2a+a≥2c,故a 2b +b2c+c2a+(a+b+c)≥2(a+b+c),即a 2b +b2c+c2a≥a+b+c.所以a 2b +b2c+c2a≥1.。
2013年高考英语湖北卷-答案

2013年普通高等学校招生全国统一考试(湖北卷)英语答案解析第一部分:听力第一节1.【答案】A【解析】原文:Text 1W: Wake up, John. It’s time for school.M: No school today! Oh, I’m so tired. I will not get up yet.W: No school? Why?M: It’s Saturday!2.【答案】C【解析】原文:Text 2W: Did you feed Frank today?M: Yes, I did. I also gave him a bath.3.【答案】A【解析】原文:Text 3W: Have you heard? Our president is starting a new program.M: Oh, really? How would it benefit us?W: The program requires professors to take on students in their research projects. Then, we’ll have more chance of gathering research experience.4.【答案】B【解析】原文:Text 4W: Dear me! Somebody's been leaving the lab door unlocked.M: Don’t look at me!5.【答案】C【解析】原文:Text 5W: Hello, Max. Come in, please.M: Gosh, I’m finally here. I’m nearly worn out. My apartment is only on the second floor.W: Well, I wish my apartment were four floors lower, like yours.第二节6.【答案】C7.【答案】A【解析】原文:Text 6W: Sorry about the wait. I’m Doctor Green.M: How do you do?W: Hi. I see that you’re experiencing some back pain.M: Yes, I am. My doctor’s away on vacation. He always gives me this to reduce my pain, but I’ve run out of my pills.I wonder if, uh, you might be able to give me some.W: You really should have a thorough checkup, but you’re the most polite patient I’ve seen all week, so I’ll break the rule for you.8.【答案】A9.【答案】B【解析】原文:Text 7M: Hello?W: Mr. Anderson?M: Yes?W: This is Temporary Jobs Agency. You called us several weeks ago about a job position.M: Uh-huh…W: We have a two-day job for you if you’re still available. It’s a fundraising party at Grand Hotel.M: Absolutely, yes.W: They need you there at 12:30 tomorrow. If you don’t drive, they’ll pick you up at 11at the City Hall.M: I’ll drive there myself. Thank you very much!10.【答案】B11.【答案】C12.【答案】B【解析】原文:Text 8M: Have you decided how much you’re going to ask for your flat, ma’am?W: Not yet. Oh, I’m totally at a loss where to start.M: Well, you need to consider several factors, like the size, location, condition…um, how big is your flat?W: Two bedrooms.M: That’s not very big. Is it downtown?W: Yes. It’s just a block away from the Finance Center.M: Well, that certainly adds to its value. Is it in good shape?W: It was built in the 90s, but we’ve just had it redecorated.M: You also need to consider the prices of other flats in the neighbourhood.W: Sure, sure.M: Can you decide on the offer price now?W: Um…probably not. I’d better talk with my husband first. Thanks for the information, though. I'll contact you when we have decided.13.【答案】A14.【答案】B15.【答案】A16.【答案】C【解析】原文:Text 9M: Oh, I hope Alexander likes this. It’s a bit of risk serving fish and shrimps to a guest who comes to visit us for the first time. Maybe I should also prepare a steak.W: Yeah. It’s not a bad idea.Alexander is the new director of my department, and I don’t know much about his preference. He came from another department of the company early this year.M: I’ve never met him before, but I’ve heard a lot about him from you in the past few days. It seems that he’s a very good boss, with rich business experience.W: Absolutely. He’s the one who comes to save the department.M: Really? Why do you say so?W: Well, you know, last year, when the economy was not good, our profit was far from satisfying. The company even thought about closing down this department.M: So, what about the situation this year?W: Alexander introduced a brand new system for sales and management, and it’s quite effective and efficient. The profit has even doubled in the last month.M: Wow, that’s fantastic! I cannot wait to meet him for dinner.17.【答案】B18.【答案】A19.【答案】C20.【答案】C【解析】原文:Text 10The coming next program is “One-Man Show” by David Mellor. The guy David Mellor needs no introduction. He’s so famous, not only because of his talent, but because of his looks—neither pretty nor ugly, but strange, especially his face. It’s like a flat board.On the board, eyes, nose, mouth, and ears are all in their places, but each of them possesses easily recognized characteristics. Take eyes, for example. When they’re open, what you can see are two very narrow lines. And nose?A little bit raised and shaped like a badminton bat. And his mouth is, well, let me say this way: each corner could reach the ear. As the saying goes, “Smile from ear to ear” or “Wear a big smile.” But our guy never smiles. Actually, he doesn’t know how to smile, not to say laugh. His full and very black moustache covers his upper lip. Whenever he wants to start a speech, he bites his lips for a while. During his talk, he clears his throat from time to time. Although he pretends to be gentle , he may make you feel very tense and worried.Before I invite him onto the stage, one thing I should warn you of: listen to his talk; don’t watch his face or his show. Ladies and gentlemen, now Mr. David Mello.第二部分词汇知识运用第一节多项选择21.【答案】A【解析】perspective观点、看法;priority优先权;participation参加、参与;privilege特权,此处是指城市年轻人的观点(看法),所以选A。
2013年高考自主招生热点问答

高考自主招生热点问答2013自主招生的加分政策是什么?答:通常大学将在笔试成绩的基础上,综合考虑面试成绩,确定最终认定结果。
被认定的自主招生候选人,一般将给予5-30分的优惠。
如果自主招生候选人在享有优惠政策后,高考成绩达到报考大学同类科目在当地的统招录取分数线即予以录取。
同时,对于部分在选拔取得优秀成绩的考生,如果高考总分达到报考大学同类科目在当地的统招录取分数线,高考录取后可在专业选择上享受一定的分数优惠。
对于表现特别突出、在某些领域表现出特殊潜能的考生,经专门考核认定,报学校招生领导小组讨论同意,其优惠幅度不受30分限制。
哪些证书可以获得加分?答:可加分的条件包括:1、高中或中职阶段受到市级以上(含市级)表彰的三好学生;2、高中或中职阶段获得市级青少年科技创新一等奖;3、被评为高中或中职市级优秀学生的应届毕业生4、被评为市级优秀学生干部的应届毕业生。
如果报名确认当日考生不能出示证书原件,初试不予加分;如考生进入复试,可在复试时携带证书原件和复印件,作为面试评分参考。
2013自主招生与普通高考陆续的新生入学后待遇是否相同?答:高校自主招生时国家授权高校独立组织考试录取的一种方式,纳入国家的招生计划,只是入学的方式与普通高考录取不同。
参加自主招生录取的新生,在学费标准、培养模式和学历文凭等方面与参加普通高考录取的考生享受同等待遇。
2013考生被认定为自主招生资格或提前录取后,还要做哪些事情?答:一般还需要与高校签订预录协议,完成相关信息的采集和确认工作,如提供高考报名的考生号等信息2013年艺术特长生、高水平运动员、体育特长生选拔和自主招生选拔是什么关系?答:艺术特长生、高水平运动员选拔主要是为了选拔在文艺、体育方面有突出才能的学生,其政策依据、选拔办法、优惠幅度都与自主招生有所不同。
其招生简章也将另行发布。
在笔试中,对测试科目和成绩要求也有所区别。
比如,2011年清华大学具有乒乓球、武术、击剑、网球、手球、棒球、羽毛球、象棋、围棋、国际象棋、桥牌特长的学生单独开辟了通道。
湖北省2013年普通高校招生第二批本科录取院校理工文史一志愿投档线
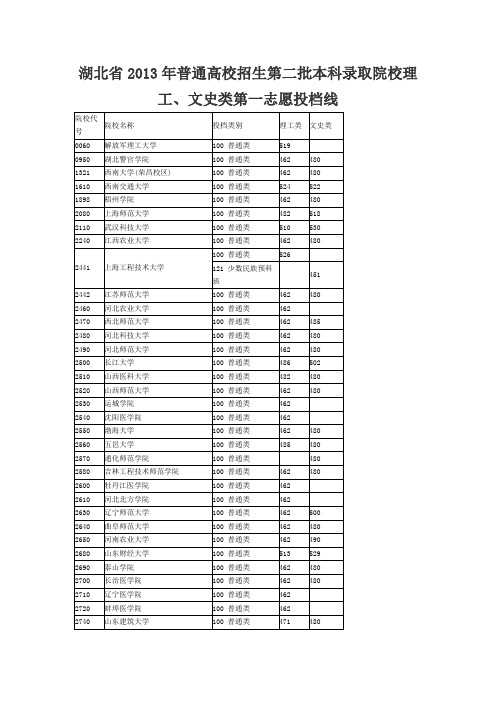
482
4280
南京工程学院
100普通类
507
480
4290
内蒙古工业大学
100普通类
462
4300
西北政法大学
100普通类
508
505
4310
天津城建大学
100普通类
472
4320
天津职业技术师范大学
100普通类
462
480
4330
湖北工程学院
100普通类
466
480
4340
嘉兴学院
100普通类
479
4210
安徽财经大学
100普通类
501
507
4220
山西财经大学
100普通类
479
480
4230
河南工业大学
100普通类
462
495
4240
武汉轻工大学
100普通类
495
505
4260
北京物资学院
100普通类
505
487
4270
湖北文理学院
100普通类(面向全省)
472
485
100普通类(面向襄阳市)
462
2740
山东建筑大学
100普通类
471
480
2750
贵州师范大学
100普通类
462
480
2760
聊城大学
100普通类
462
480
2770
青岛农业大学
100普通类
467
502
2780
四川理工学院
100普通类
462
480
2790
2013年高考湖北卷(文)
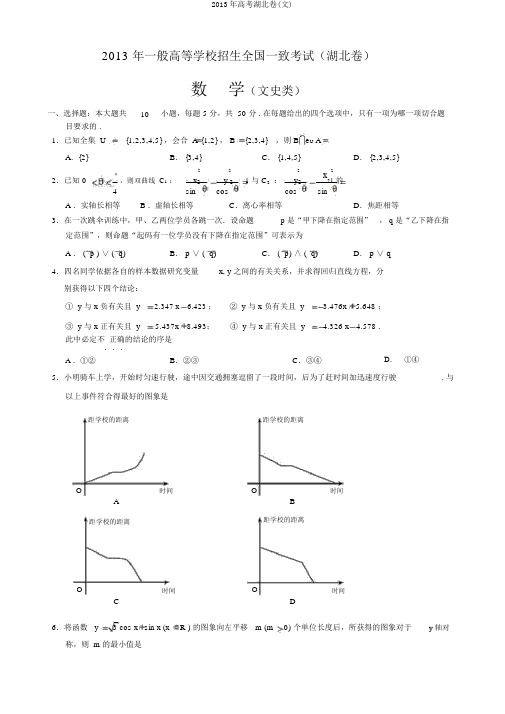
2013 年一般高等学校招生全国一致考试(湖北卷)数学(文史类)一、选择题:本大题共10小题,每题 5 分,共 50 分 . 在每题给出的四个选项中,只有一项为哪一项切合题目要求的 .1.已知全集 U{1,2,3,4,5} ,会合 A {1,2} , B{2,3,4} ,则 B e U AA .{2}B . {3,4}C . {1,4,5}D . {2,3,4,5}22222.已知 0π,则双曲线 C 1 :x 2 y 2 1与 C 2 :y 2 x21 的4sincoscossinA .实轴长相等B .虚轴长相等C .离心率相等D .焦距相等3.在一次跳伞训练中,甲、乙两位学员各跳一次.设命题 p 是“甲下降在指定范围” , q 是“乙下降在指定范围”,则命题“起码有一位学员没有下降在指定范围”可表示为A . ( p ) ∨ ( q)B . p ∨ ( q)C . ( p) ∧ ( q)D . p ∨ q4.四名同学依据各自的样本数据研究变量x, y 之间的有关关系,并求得回归直线方程,分别获得以下四个结论:① y 与 x 负有关且 y2.347 x 6.423 ; ② y 与 x 负有关且 y3.476x 5.648 ; ③ y 与 x 正有关且 y5.437x 8.493;④ y 与 x 正有关且 y4.326 x 4.578 .此中必定不 正确的结论的序是... A .①②B .②③C .③④D . ①④5.小明骑车上学,开始时匀速行驶,途中因交通拥塞逗留了一段时间,后为了赶时间加迅速度行驶. 与以上事件符合得最好的图象是距学校的距离距学校的距离O时间O时间AB距学校的距离距学校的距离O时间O时间CD6.将函数 y 3 cos x sin x (xR ) 的图象向左平移 m (m 0) 个单位长度后,所获得的图象对于 y 轴对称,则 m 的最小值是A . πB .πC .πD .5π126 367.已知点 A( 1,1) 、 B(1, 2) 、 C( 2,1) 、 D (3, 4) ,则向量 AB 在 CD 方向上的投影为32 3 15 3 2 3 15A .B . 2C .2D .228. x 为实数, [ x] 表示不超出 x 的最大整数,则函数f ( x) x[ x] 在 R 上为A .奇函数B .偶函数C .增函数D . 周期函数9. 某旅游社租用 A 、 B 两种型的客车安排 900 名客人旅游,A 、B 两种车辆的载客量分别为36 人和 60人,租金分别为1600 元 /辆和 2400 元 /辆,旅游社要求租车总数不超出21 辆,且 B 型车不多于 A 型车7 辆.则租金最少为A .31200 元B . 36000 元C . 36800 元D . 38400 元10.已知函数 f (x)x(ln x ax) 有两个极值点,则实数a 的取值范围是A . (, 0)B . (0,1C . (0, 1)D . (0,))2二、填空题:本大题共 7 小题,每题5 分,共 35 分.请将答案填在答题卡对应题 的地点上 . 答错地点,......书写不清,含糊其词均不得分 .11. i 为虚数单位,设复数z 1 , z 2 在复平面内对应的点对于原点对称,若 z 1 2 3i ,则 z 2.12.某学员在一次射击测试中射靶10 次,命中环数以下: 7, 8,7, 9, 5, 4, 9, 10, 7, 4则(Ⅰ)均匀命中环数为; (Ⅱ)命中环数的标准差为.13.阅读以下图的程序框图,运转相应的程序. 若输入 m 的值为2, 则输出的结果 i.开始输入 mA 1,B 1, i 0i i 1A A mBB iA否B ?是 输出 i结束 第 13题图22,直线 l : x cos ysinπ1 的点14.已知圆 O : xy 51( 0).设圆 O 上到直线 l 的距离等于2的个数为 k ,则 k.15.在区间 [ 2,4] 上随机地取一个数x,若 x 知足 | x |m 的概率为5,则 m.616.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸. 若盆中积水深九寸,则平川降雨量是寸.(注:①平川降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)17.在平面直角坐标系中,若点P(x, y)的坐标x ,y 均为整数,则称点P 为格点.若一个多边形的极点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S ,其内部的格点数记为N ,界限上的格点数记为L .比如图中△ABC 是格点三角形,对应的S 1,N0,L 4 .(Ⅰ)图中格点四边形DEFG对应的S, N, L 分别是;(Ⅱ)已知格点多边形的面积可表示为S aN bL c ,此中a, b, c为常数 .若某格点多边形对应的N 71, L 18,则S(用数值作答).三、解答题:本大题共 5 小题,共65 分.解答应写出文字说明、证明过程或演算步骤.18.(本小题满分12 分)在△ ABC 中,角 A , B ,C 对应的边分别是 a ,b, c . 已知 cos2 A 3cos( B C ) 1 .(Ⅰ)求角 A 的大小;(Ⅱ)若△ABC 的面积 S 5 3 , b 5 ,求 sin B sin C 的值 .19.(本小题满分13 分)已知S n是等比数列{ a n} 的前n 项和,S4, S2, S3成等差数列,且a2a3a418 .(Ⅰ)求数列{ a n} 的通项公式;(Ⅱ)能否存在正整数n ,使得S n2013 ?若存在,求出切合条件的全部n 的会合;若不存在,说明理由.20.(本小题满分13 分)如图,某地质队自水平川面 A,B,C 三处垂直向地下钻探,自 A 点向下钻到 A1处发现矿藏,再持续下钻到A2处后下边已无矿,进而获得在 A 处正下方的矿层厚度为 A1 A2 d1.相同可得在 B,C 处正下方的矿层厚度分别为 B1 B2d2, C1C2 d3,且 d1 d 2 d3 . 过AB, AC 的中点M, N 且与直线 AA2平行的平面截多面体 ABC1A B C2所得的截面 DEFG 为该多面体的一此中截面,其面积记为S .1 12 2中(Ⅰ)证明:中截面DEFG 是梯形;(Ⅱ)在△ ABC 中,记BC a,BC 边上的高为h,面积为S . 在估测三角形ABC地区内正下方的矿藏储量(即多面体 A1B1C1 A2B2C2的体积V)时,可用近似公式 V估S中 h 来估算 . 已知1(d1 d 2 d 3)S ,试判断 V估与 V 的大小关系,并加以证明 .V3第20题图21.(本小题满分13 分)设 a0 , b0 ,已知函数 f ( x)ax b .x 1(Ⅰ)当a b 时,议论函数 f (x) 的单一性;(Ⅱ)当x0 时,称 f ( x)为a、 b 对于x 的加权均匀数.( i )判断f (1) , f (b ) ,a f (b ) 能否成等比数列,并证明af (b )af (b )a;( ii ) a 、b的几何均匀数记为G.称2ab为 a 、b的调解均匀数,记为H .若H f (x)G ,求x a b的取值范围 .22.(本小题满分 14 分)如图,已知椭圆C1与 C2的中心在座标原点O,长轴均为MN且在 x 轴上,短轴长分别为 2m ,2n (m n) ,过原点且不与x 轴重合的直线l与 C1, C2的四个交点按纵坐标从大到小挨次为A,B, C, D .记m,△ BDM 和△ ABN 的面积分别为S1和S2. n(Ⅰ)当直线 l 与 y 轴重合时,若S1S2,求的值;(Ⅱ)当变化时,能否存在与坐标轴不重合的直线l,使得 S1S2?并说明原因.yABM O N xCD第 22题图2013 年一般高等学校招生全国一致考试(湖北卷)数学(文史类)试题参照答案一、选择题:1. B2.D3.A4.D5. C6. B7. A8.D9. C10.B二、填空题:11. 2 3i12.(Ⅰ) 7 (Ⅱ) 2 13. 414. 415. 316. 317.(Ⅰ) 3, 1, 6(Ⅱ) 79三、解答题:18.(Ⅰ)由 cos2 A 3cos( B C)22 0 ,1 ,得 2cos A 3cos A即 (2cos A1)(cos A2) 0 ,解得 cos A 1 或 cosA2 (舍去) .2由于 0Aπ,所以 A π.3(Ⅱ)由 S1133 5 3, 得 bc20 . 又 b5,知 c 4.bc sin Abc2bc22 4由余弦定理得 a 2b 2c 2 2bc cos A 25 1620 21, 故 a21 .b sin Acbc 2A20 3 5 又由正弦定理得sin B sin Csin Aa 2 sin 214 .aa719. (Ⅰ)设数列 { a n } 的公比为 q ,则 a 1 0 , q0 . 由题意得S 2 S 4 S 3 S 2 , a 1 q 2 a 1 q 3 a 1 q 2 ,a 2 a 3 a 4 即a 1 q(1 qq 2 )18,18,解得a 1 3,q2.故数列 { a n } 的通项公式为a n 3( 2) n 1 .(Ⅱ)由(Ⅰ)有S n3[1(2) n ]1(2)n .1(2)若存在 n ,使得 S n2013 ,则 1(2) n2013 ,即 ( 2)n2012.当 n 为偶数时, (2) n0 ,上式不建立;当 n 为奇数时, (2)n2n2012 ,即 2n2012 ,则n11.综上,存在切合条件的正整数n ,且全部这样的 n 的会合为 { n n2k1, k N , k 5} .20.(Ⅰ)依题意A1 A2平面 ABC ,B1B2平面 ABC ,C1C2平面 ABC ,所以 A1A2∥ B1B2∥C1C2. 又 A1 A2d1, B1 B2d2, C1C2d3,且 d1 d 2 d3 .所以四边形 A1 A2 B2 B1、 A1 A2 C2 C1均是梯形 .由 AA2∥平面MEFN, AA2平面 AA2 B2 B ,且平面 AA2 B2 B 平面MEFN ME ,可得 AA2∥ ME,即 A1A2∥DE . 同理可证 A1A2∥ FG,所以 DE ∥ FG.又M 、N分别为 AB、AC的中点,则 D 、 E 、 F 、G分别为A1B1、A2B2、A2C2、 A1C1的中点,即 DE 、FG分别为梯形A1A2B2B1、A1A2C2C1的中位线.所以 DE 1( A1A2B1B2 )1d2 ), FG11(d1d3 ) ,(d1( A1 A2 C1C2 )2222而 d1d2d3,故DE FG ,所以中截面 DEFG 是梯形.(Ⅱ) V估 V. 证明以下:由 A1A2平面 ABC , MN平面 ABC ,可得A1A2MN .而 EM∥ A1A2,所以EM MN ,同理可得 FN MN .由 MN 是△ ABC 的中位线,可得MN11即为梯形 DEFG 的高,BC a22所以 S中 S梯形DEFG 1d1d2d1 d 3 a a(2 d1 d 2d3 ) ,(22)822即 V估S中h ah(2d1d2d3 ) . 81,所以 V 1d 2d3 )Sahd2d3 ) .又 S ah(d1(d1 236于是 V V估ahd 2ahd 2 d 3 )ahd1) (d 3d1 )] .( d1 d 3 )8(2 d1[( d 2624由 d1d2d3,得 d2d10 , d3d10,故V估V .21. (Ⅰ) f ( x) 当 a当 af (x) 的定义域为 (, 1) ( 1,) ,a(x 1) ( ax b)a b( x 2( x 2 .1) 1)b 时, f (x) 0 ,函数 f ( x) 在 (, 1),( 1, ) 上单一递加;b 时, f (x)0 ,函数 f ( x) 在 ( , 1),( 1,) 上单一递减 .(Ⅱ)( i )计算得 f (1)a b 0 , f ( b) 2ab0 , f ( b )ab0 .2 aa ba 故 f (1) f ( b) a b 2ab ab [ f (b)] 2 , 即a 2 ab af (1) f ( b)[ f (b)] 2 .①aa所以 f (1), f (b), f ( b) 成等比数列 .aa因 a bab ,即 f (1)f (bb f ( b2) . 由①得 f ( ) ) .aaa( ii )由( i )知 f ( b)H , f (bf (x) G ,得) G.故由 Ha af ( b)f ( ) f ( b ) .②axa当 a b 时, f ( b)f (x)f ( b) a .aa 这时, x 的取值范围为 (0, ) ;当 a b 时, 0 b 1,进而b b ,由 f ( x) 在 (0, ) 上单一递加与②式,aaa得bx b,即 x 的取值范围为b , b ;aaaa当 a b 时,b1 ,进而 b b ,由 f (x) 在 (0, ) 上单一递减与②式,aaa得 b x b,即 x 的取值范围为b , b.aaa a22. 依题意可设椭圆C 1 和 C 2 的方程分别为C 1 :x 2y 21, C 2 : x 2y 2m22 2 2 1 . 此中 a m n 0, 1.a m a n n(Ⅰ) 解法 1:如图 1,若直线 l 与 y 轴重合,即直线 l 的方程为 x 0 ,则111a | BD | ,21 1 ,所以S 1|BD|. S|BD| |OM | 2S|AB| |ON | a | AB |S 2 |AB|222在 C 1 和 C 2 的方程中分别令 x 0 ,可得 y Am , y B n , y Dm ,于是 |BD || y By D |m n1 .| AB | | y A y B | m n 1若 S 1,则1,化简得21 0 . 由1,可解得21 .S21 2故当直线 l 与 y 轴重合时,若S 1 S 2 ,则 2 1 .解法 2:如图 1,若直线 l 与 y 轴重合,则| BD | | OB | | OD | m n , | AB | | OA | | OB | m n ;S 11|BD| |OM | 11 1a | AB | .2 a | BD |, S 22 |AB| |ON|22所以 S 1 |BD | mn1 .S 2 |AB| m n1若S 1,则1 ,化简得2210 . 由1,可解得21 .S 21故当直线 l 与 y 轴重合时,若1 2,则2 1 .SSy yAA BBMN xMxOON CCDD第 22 题解答图 1第 22 题解答图 2(Ⅱ) 解法 1:如图 2,若存在与坐标轴不重合的直线 l ,使得 S 1S 2 . 依据对称性,不如设直线 l : ykx (k0) ,点 M ( a, 0) , N ( a, 0) 到直线 l 的距离分别为 d 1 , d 2 ,则由于 d 1|ak0 |ak , d 2| ak 0 | ak ,所以 d 1d 2 .1 k21 k21 k21 k 2又 S 11| BD | d 11 S 1 |BD | ,即 |BD ||AB |.2 , S 2| AB | d 2 ,所以S 2|AB |2由对称性可知 | AB | |CD|,所以 |BC ||BD ||AB| (1)| AB |,|AD| |BD|| AB| ( 1) | AB |,于是|AD|1 .①|BC|1将 l 的方程分别与 C 1, C 2 的方程联立,可求得 x Aam, x Ban2 .a 2 k 22 2k 2nma依据对称性可知 x C x B , x Dx A ,于是| AD|2 x D | 2 x Am a 2 k2n21 k | x A|BC|2x C | 2 x Bn a 2k 2m 2 .②1 k | x B进而由①和②式可得a 2 k 2 n 21③a 2 k 2m 2(.1)令 t( 1,则由 m n ,可得 t1,于是由③可解得k 2n 2 ( 2t 2 1) .1)a 2 (1 t 2 )由于 k 0 ,所以 k 20 . 于是③式对于 k 有解,当且仅当n 2 ( 2t 2 1) 0 ,a 2 (1 t 2 )等价于 21)(t 210 . 由1,可解得 1t 1 ,(t2 )即1( 1 1 ,由 1,解得12 ,所以1)当 1 12 时,不存在与坐标轴不重合的直线 l ,使得 S 1S 2 ;当12 时,存在与坐标轴不重合的直线l 使得 S 1S 2.解法 2:如图 2,若存在与坐标轴不重合的直线l ,使得 S 1S 2 . 依据对称性,不如设直线 l : ykx (k 0) ,点 M ( a, 0) , N ( a, 0) 到直线 l 的距离分别为| ak 0 |ak, d 2| ak 0 |由于 d 11 1 k 21 k 2k 2 又 S 11 , S 21| AB | d 2 ,所以S 1 | BD | d 1 2 S 22d 1 , d 2 ,则ak ,所以 d 1 d 2 .1 k2 |BD | .|AB |由于 |BD |1 k2 | x Bx D | x Ax Bx A1.2,所以|AB|x B | x Ax Bx B11 k | x A由点 ( , kx A ) ,, C 上,可得A x A B(xB , kx B ) 分别在C 1 2x A 2 k 2 x A 2 x B 2 k 2 x B 2 1 ,两式相减可得 x A 2 x B 2 k 2 (x A 2 2 x B 2 ),a 2 m 2 1, a 2n 2 a 2 m 2222m 2 ( x 2 x2 )依题意 x Ax B0 ,所以 x Ax B. 所以由上式解得k22A2B2.( xxaB)A2m 2 ( x2 x 2 )x由于 k0 ,所以由AB0 ,可解得 1A .a 2( 2x2x2 )xB A B进而 11,解得12 ,所以1当 112 时,不存在与坐标轴不重合的直线l ,使得 S 1S 2 ;当12 时,存在与坐标轴不重合的直线 l 使得 S 1 S 2 .。
2013阳光高考填报志愿常见问题-7页精选文档

2013阳光高考填报志愿常见问题原编者按:为帮助2013届高考考生及家长做好填报志愿工作,我们梳理了往年考生家长提问较多的问题,在此作答,供参考。
1 如何为志愿填报做好充分的准备工作?一是搜集院校资料,了解招生政策,熟悉有关规定,了解院校招生章程;二是查询有关院校、专业近几年在各批录取分数和录取考生的位次情况;三是了解今年在本省市招生的学校、专业、人数;四是了解自己平时成绩、模拟成绩在全省、市的位次;五是了解本人体检结果,填报需要避开所限的学校、专业。
2 如何减少志愿填报的撞车现象?一是考生应量体裁衣,根据自己平时成绩、模拟成绩的位次,对照往年各学校专业录取分数情况、位次情况;二是注意填报时留有余地,并注意体检结果避开限报专业;三是特别注意有的学校招生“大小年”现象,详细分析近年录取资料;四是注意预报志愿后,考区、中学反馈的信息,如果出现扎堆现象,需要调整所报志愿。
3 如何避免高分低录甚至落榜?应坚持以下原则:1、实事求是,找准自己的位置;2、所填志愿拉开档次;3、冷门与热门学校专业相结合;4、省内与省外院校相结合;5、避开体检结果所限学校、专业;6、各批次学校志愿、专业志愿填满,尽量服从专业调剂。
4 录取批次是如何划分的?教育部《2010年普通高等学校招生工作规定》中规定:“各省级招委会要根据本地区招生工作的实际,合理安排高校录取批次。
同一高校同一学历层次的招生计划原则上应安排在同一批次录取;如确有必要,经高校与有关省级招办协商一致,可以将同一高校的不同专业安排在属于同一学历层次的不同批次录取;但同一学校、同一专业、同一学历层次的全部招生计划,在同一省(区、市)须安排在同一批次录取,并执行经有关部门批准的相同学费标准。
高校中外合作办学专业,应与本校在同一地区招生的其他专业安排在同一批次录取。
高校被安排的录取批次与上一年度有变化的,省级招办应事先与高校协商一致后,再向社会公布。
”根据教育部有关规定,各省市招委会从有利于高校选拔人才,有利于兼顾考生利益的出发点,一般大致分为以下几个批次:本科提前批:具有特殊要求的院校专业。
湖北省2013年高校招生第一批本科录取院校平行志愿投档线
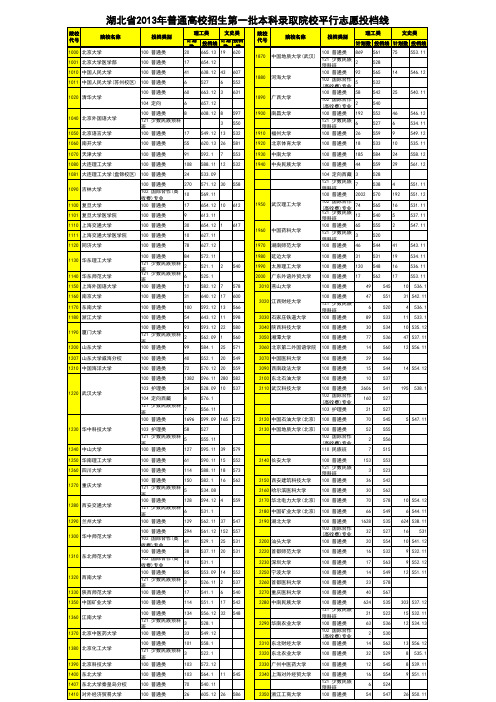
院校 代号 院校名称 投档类别 100 普通类 100 普通类 100 普通类 理工类 文史类 1000 北京大学 1001 北京大学医学部 1010 中国人民大学 计划 投档线 计划 投档 数 数 线 20 665.13 19 620 17 41 6 60 6 8 654.12 638.12 43 527 6 607 552 631 1890 1900 广西大学 南昌大学 1880 河海大学 院校 代号 1870 院校名称 投档类别 100 普通类 869 理工类 文史类 计划数 投档线 计划数 投档线 中国地质大学(武汉) 561 528 565 532 542 540 552 527 559 533 584 559 528 538 570 565 540 555 520 544 531 548 562 49 47 6 89 30 77 14 29 15 10 2606 160 21 70 52 2 7 153 3 36 30 70 66 1628 32 20 16 17 14 23 40 624 21 63 2 14 32 12 16 6 54 545 551 520 533 534 536 560 566 544 537 541 527 527 545 555 556 515 553 523 542 562 578 549 535 527 554 532 563 549 578 567 535 522 536 530 562 529 545 554 524 547 26 550.11 13 556.12 8 535.1 303 537.12 15 532.11 12 534.13 10 554.12 6 544.11 624 538.11 16 531 5 547.11 195 538.1 14 554.12 41 19 16 17 10 543.11 534.11 536.11 553.11 536.1 4 192 16 5 2 551.11 551.12 531.11 537.11 547.11 46 6 9 10 24 29 546.12 534.11 549.12 535.11 558.12 561.12 25 540.11 14 546.12 75 553.11 121 少数民族 2 预科班 100 普通类 92 102 国际合作 5 (高收费)专业 100 普通类 58 102 国际合作 2 (高收费)专业 100 普通类 192 121 少数民族 6 预科班 100 普通类 26 100 普通类 100 普通类 100 普通类 18 185 44
2013年普通高校招生统一考试湖北卷语文试题及参考答案(word)

2013年普通高等学校招生全国统一考试语文(湖北卷)一、语文基础知识(共15分,共5小题,每小题3分)1.下列各组词语中,加点字的注音全都正确的一组是()A.踹.(chuài)水竞.(jìnɡ)赛蘸(zhàn)酒擂.(léi)鼓助威B.跋涉.(shè)陡.(dǒu)峭攀登.(dēnɡ)餐霜饮雪.(xi ě)C.善.(shàn)良谦逊.(sùn)璞(pú)玉不事雕琢(zhu ó)D.荆棘.(jí)飘泊.(bó)青苔.(tāi)红漆.(qī)雕花2.下列各组词语中,没有错别字的一组是()A.彷徨愁怨寂寥静默凄婉惆伥B.顾盼精捍步履稳健风神潇洒C.睿智禀赋崇高品质趋善避恶D.辩难商榷典藉满架旁稽博采3.依次填入下列横线处的词语,最恰当的一组是()①宋人画雪常不用铅粉,把背景用墨衬黑,一层层,留出山头的白,树梢的白,甚至花蕾上的白,虚实映衬,意境悠远。
②因为睡不着,打开窗帘,遥望夜空,满天,斜月晶莹,薄雾似轻纱漫卷,。
我思念那个小山村,那个让我魂牵梦绕的地方!A.而是点染星汉如梦如幻B.总是浸染星云如诗如画C.却是绘染星光诗意盎然D.只是渲染星斗诗意朦胧4.下列各项中,没有语病的一项是()A.《美丽中国》以歌舞为主,融入京剧演唱、茶艺表演、少林武术等元素,加上奇幻的灯光,震撼的音响,一幅美丽中国的大写意,声光舞影流溢着浓郁的中国情。
B.梦在前方,路在脚下,青年要坚定信念,珍惜韶华,在追求中国梦的道路上放飞青春,以青春之我建设“青春之国家”!C.从汶川到芦山,地震确实有能量剥夺太多本该鲜活滋润的生命,但地震却没有能量剥夺站立在废墟上的那些生命依然坚强。
D.网友们纷纷撰写微博,围绕着“追星”的话题,或幽默,或自嘲,或“假正经”一番,捧腹之后,总有一种耐人寻味留在心中。
5.下列有关文学常识的表述,有错误的一项是()A.《论语》中有不少有关为人处世的格言警句。
湖北省2013年高职院校单独招生考试宣传问答

湖北省2013年高职院校单独招生考试宣传问答1.什么是高职院校单独招生考试?高职院校单独招生考试,简称“高职单招”,是普通高校招生考试制度改革的一个重要组成部分,是教育部授权部分高职院校独立组织考试录取的一种方式,即高职院校根据自身专业教学需要设置考试科目,自行命题、考试、评价、组织技能考核和面试,自主划定录取标准,自主录取。
高职单招一般于普通高校招生统一考试前完成录取,被高职单招录取的考生,将不能参加普通高校招生的其他任何形式的录取,单招学生入校后与统招学生待遇相同。
2013年我省高职单招院校为国家示范性高职院校建设计划的示范院校、国家骨干高职院校立项建设单位的院校和省级示范高职院校。
生源范围为我省符合普通高校招生报考条件的中职毕业生和高中毕业生。
高职单招计划纳入招生学校当年国家核定的本校招生计划总数内。
考试录取工作接受省招办的指导、协调和监督。
2.2013年有哪几所高职院校进行面向中职毕业生开展高职单招?答:2013年,我省开展单招的有武汉职业技术学院、武汉船舶职业技术学院、武汉铁路职业技术学院、湖北职业技术学院等4所国家级示范性高职院校,黄冈职业技术学院、襄樊职业技术学院、十堰职业技术学院、武汉软件工程职业学院、鄂州职业大学等5所骨干高职建设单位,以及恩施职业技术学院、武汉交通职业学院、湖北交通职业技术学院、湖北三峡职业技术学院、湖北城市建设职业技术学院等5所省级示范高职院校。
各高校面向中职毕业生单招的专业及拟招生人数如下:招生学校招生专业拟招生人数武汉职业技术学院空中乘务40旅游管理(酒店管理)40高分子材料加工技术100服装设计(服装工程与CAD)50武汉船舶职业技术学院供热通风与空调工程技术100酒店管理100焊接技术及自动化50汽车技术服务与营销50武汉铁路职业技术学院物流管理100高速铁路工程及维护技术100湖北职业技术学院物流管理100酒店管理100助产100黄冈职业技术学院植物类100动物类100汽车检测与维修技术100襄阳职业技术学院特殊教育100动物类100植物类100汽车检测与维修技术100十堰职业技术学院汽车检测与维修技术100旅游管理100应用化工技术100武汉软件工程职业学院软件技术100激光加工技术90应用化工技术80模具设计与制造50鄂州职业大学药学50物流管理50恩施职业技术学院畜牧兽医50旅游管理50武汉交通职业学院船舶工程技术50湖北交通职业技术学院高等级公路维护与管理50湖北三峡职业技术学院旅游管理50湖北城市建设职业技术学院建筑设计技术503.中职毕业生如何报名参加高职单招?答:凡具有我省常住户口、符合高考报名条件的中职等职业学校(含中等专业学校、职业高中、技工学校)应届、往届毕业生均可报名参加高职单招。
2013阳光高考填报志愿常见问题

2013阳光高考填报志愿常见问题作者:来源:《云南教育·视界》2013年第06期原编者按:为帮助2013届高考考生及家长做好填报志愿工作,我们梳理了往年考生家长提问较多的问题,在此作答,供参考。
1 如何为志愿填报做好充分的准备工作?一是搜集院校资料,了解招生政策,熟悉有关规定,了解院校招生章程;二是查询有关院校、专业近几年在各批录取分数和录取考生的位次情况;三是了解今年在本省市招生的学校、专业、人数;四是了解自己平时成绩、模拟成绩在全省、市的位次;五是了解本人体检结果,填报需要避开所限的学校、专业。
2 如何减少志愿填报的撞车现象?一是考生应量体裁衣,根据自己平时成绩、模拟成绩的位次,对照往年各学校专业录取分数情况、位次情况;二是注意填报时留有余地,并注意体检结果避开限报专业;三是特别注意有的学校招生“大小年”现象,详细分析近年录取资料;四是注意预报志愿后,考区、中学反馈的信息,如果出现扎堆现象,需要调整所报志愿。
3 如何避免高分低录甚至落榜?应坚持以下原则:1、实事求是,找准自己的位置;2、所填志愿拉开档次;3、冷门与热门学校专业相结合;4、省内与省外院校相结合;5、避开体检结果所限学校、专业;6、各批次学校志愿、专业志愿填满,尽量服从专业调剂。
4 录取批次是如何划分的?教育部《2010年普通高等学校招生工作规定》中规定:“各省级招委会要根据本地区招生工作的实际,合理安排高校录取批次。
同一高校同一学历层次的招生计划原则上应安排在同一批次录取;如确有必要,经高校与有关省级招办协商一致,可以将同一高校的不同专业安排在属于同一学历层次的不同批次录取;但同一学校、同一专业、同一学历层次的全部招生计划,在同一省(区、市)须安排在同一批次录取,并执行经有关部门批准的相同学费标准。
高校中外合作办学专业,应与本校在同一地区招生的其他专业安排在同一批次录取。
高校被安排的录取批次与上一年度有变化的,省级招办应事先与高校协商一致后,再向社会公布。
