圆柱绕流圆球扰流阻力系数
5 圆柱阻力系数

在这个例子中我们仅仅想确定圆柱体的阻力 系数,不需要考虑相应的 3D 的效应。因此 为了减少计算机资源的耗费, 我们将在这个例 子中进行 2D 的计算。
b 8 教程
5-5
第五章 圆柱阻力系数
定义一个 2D 平面流动
1. 2. 在 b 分析树,展开 Input Data 图标。 右击 Computational Domain 图标并且选择 Edit Definition 。Computational Domain 对 话框出现。 点击 Boundary Condition 页。 在 2D plane flow 列表选择 XY-Plane Flow (因为 Z-axis 是圆柱的轴线 ) 。在 Computational Domain 的 Z min 和 Z max 处自动定义为 Symmetry 边界 条件。
点击 Next。 5. 因为在这个项目中以水作为流体,打开 Liquids 文件夹并且双击 Water 项。
点击 Next。
b 8 教程
5-3
第五章 圆柱阻力系数
6.
在 Wall Conditions 对话框你可以定义 应用到与流体相接触壁面的默认壁面条 件。
在 这 个 项 目 中 , 我 们 保 持 默 认 的 Adiabatic wall 设置 ,假设所有的模型壁面都是绝热的 并且壁面的粗糙度为 0。 点击 Next。 对于 External 问题, 诸如这个例子中的圆柱体, Initial and Ambient Conditions 对 话框 会要 求你 定义 稳定 自由 流体 的环 境流 动条 件。 因此 你要 定义 Computational Domain 内的初始条件和 Computational Domain 上的边界条件。这个环境条件是 工程热力学参数(默认情况下静压和温度),流速,湍流参数。 在这个项目中我们在默认的热力学参数条件下进行分析 (即在一个标准大气压下 ),此 外根据雷诺数设定入口流体( X 向)的速度。 为 了 方 便 起 见 我 们 可 以 通 过 使 用 Dependency 框以雷诺数定义入口流体的流 速。 7. 点击 Velocity in X direction 区域。 Dependency 按钮被激活。 点击 Dependency。Dependency 对话框出现。
不同形状物体的阻力系数1

已知: 设边界层内速度分布为
u(y)Usin2y
U
上式中y为垂直坐标,δ为边界层名义厚度。
y y
求: (1)位移厚度δ* ;(2)动量厚度θ.(均用δ表示) 解:按速度分布式,u(0) = 0 ,u(δ)=U ,符合边界层流动特点。
(1) 按位移厚度的定义
* ( 1 - u ) d y ( 1 - s i n y ) d y ( y 2 c o sy ) 2 0 . 3 6 3
C4.5.2 平板湍流边界层
将光滑圆管湍流的结果移植到光滑平板上,速度分布用1/7指 数式,壁面切应力采用布拉修斯公式。取δ=R=d/2,由无压强 梯度平板边界层动量积分方程可得(与层流边界层对照)
湍流边界层
层流边界层
边界层厚度
壁面摩擦系数 摩擦阻力系数
0 .3 8 2
x 5 Rex
x45
0.0593 C f 5 Rex
dp U dU
dx
dx
②第二式右边得到简化(x方向二阶偏导数消失),有利于数值
计算。利用该方程就可计算壁切应力和流动阻力,具有里程碑 式意义。
C4.3.2 布拉修斯平板边界层精确解
布拉修斯利用相似性解法,引入无量纲坐标:
y y U
x
用无量纲流函数 f 表示速度分量u, v, 如
f ' u
c4不可压缩粘性流体外流c41引言c4不可压缩粘性流体外流流动特点流动特点ns方程ns方程研究方法研究方法解析法解析法自由湍流射流自由湍流射流大气边界层大气边界层交通工具交通工具动量积分方程动量积分方程壁面流动壁面流动数值法数值法建筑物绕流建筑物绕流阻力问题阻力问题动力响应动力响应生态环境生态环境边界层分离边界层分离形状阻力形状阻力边界层边界层速度分布速度分布摩擦阻力摩擦阻力尾流区尾流区形状阻力形状阻力边界层方程边界层方程摩擦阻力摩擦阻力c42边界层概念例1
流体力学Fluent报告材料——圆柱绕流

亚临界雷诺数下串列双圆柱与方柱绕流的数值模拟摘要:本文运用Fluent软件中的RNG k-ε模型对亚临界雷诺数下二维串列圆柱和方柱绕流问题进展了数值研究,通过结果比照,分析了雷诺数、柱体形状对柱体绕流阻力、升力以与涡脱频率的影响。
一般而言,Re数越大,方柱的阻力越大,圆柱体如此不然;而Re越大,两种柱体的升力均越大。
相对于圆柱,同种条件下,方柱受到的阻力要大;相反地,方柱涡脱落频率要小。
Re越大,串列柱体的Sr数越接近于单圆柱体的Sr数。
关键字:圆柱绕流、升力系数、阻力系数、斯特劳哈尔数在工程实践中,如航空、航天、航海、体育运动、风工程与地面交通等广泛的实际领域中,绕流研究在工程实际中具有重大的意义。
当流体流过圆柱时, 由于漩涡脱落,在圆柱体上产生交变作用力。
这种作用力引起柱体的振动与材料的疲劳,损坏结构,后果严重。
因此,近些年来,众多专家和学者对于圆柱绕流问题进展过细致的研究,特别是圆柱所受阻力、升力和涡脱落以与涡致振动问题。
沈立龙等[1]基于RNG k⁃ε模型,采用有限体积法研究了亚临界雷诺数下二维圆柱和方柱绕流数值模拟,得到了圆柱和方柱绕流阻力系数C d与Strouhal 数随雷诺数的变化规律。
姚熊亮等[2]采用计算流体软件CFX中LES模型计算了二维不可压缩均匀流中孤立圆柱与串列双圆柱的水动力特性。
使用非结构化网格六面体单元和有限体积法对二维N- S方程进展求解。
他们着重研究了高雷诺数时串列双圆柱在不同间距比时的压力分布、阻力、升力与Sr数随Re数的变化趋势。
费宝玲等[3]用FLUENT软件对串列圆柱绕流进展了二维模拟,他们选取间距比L/D(L 为两圆柱中心间的距离,D为圆柱直径)2、3、4共3个间距进展了数值分析。
计算均在Re = 200 的非定常条件下进展。
计算了圆柱的升阻力系数、尾涡脱落频率等描述绕流问题的主要参量,分析了不同间距对圆柱间相互作用和尾流特征的影响。
圆柱绕流的一个重要特征是流动形态取决于雷诺数。
流体力学Fluent报告——圆柱绕流

亚临界雷诺数下串列双圆柱与方柱绕流的数值模拟摘要:本文运用Fluent软件中的RNG k-ε模型对亚临界雷诺数下二维串列圆柱和方柱绕流问题进行了数值研究,通过结果对比,分析了雷诺数、柱体形状对柱体绕流阻力、升力以及涡脱频率的影响。
一般而言,Re数越大,方柱的阻力越大,圆柱体则不然;而Re越大,两种柱体的升力均越大。
相对于圆柱,同种条件下,方柱受到的阻力要大;相反地,方柱涡脱落频率要小。
Re越大,串列柱体的Sr数越接近于单圆柱体的Sr数。
关键字:圆柱绕流、升力系数、阻力系数、斯特劳哈尔数在工程实践中,如航空、航天、航海、体育运动、风工程及地面交通等广泛的实际领域中,绕流研究在工程实际中具有重大的意义。
当流体流过圆柱时 , 由于漩涡脱落,在圆柱体上产生交变作用力。
这种作用力引起柱体的振动及材料的疲劳,损坏结构,后果严重。
因此,近些年来,众多专家和学者对于圆柱绕流问题进行过细致的研究,特别是圆柱所受阻力、升力和涡脱落以及涡致振动问题。
立龙等[1]基于RNG k⁃ε模型,采用有限体积法研究了亚临界雷诺数下二维圆柱和方柱绕流数值模拟,得到了圆柱和方柱绕流阻力系数C与 Strouhal 数d随雷诺数的变化规律。
熊亮等[2]采用计算流体软件CFX中LES模型计算了二维不可压缩均匀流中孤立圆柱及串列双圆柱的水动力特性。
使用非结构化网格六面体单元和有限体积法对二维N- S方程进行求解。
他们着重研究了高雷诺数时串列双圆柱在不同间距比时的压力分布、阻力、升力及Sr数随Re数的变化趋势。
费宝玲等[3]用FLUENT软件对串列圆柱绕流进行了二维模拟,他们选取间距比L/D(L为两圆柱中心间的距离,D为圆柱直径)2、3、4共3个间距进行了数值分析。
计算均在 Re = 200 的非定常条件下进行。
计算了圆柱的升阻力系数、尾涡脱落频率等描述绕流问题的主要参量,分析了不同间距对圆柱间相互作用和尾流特征的影响。
圆柱绕流的一个重要特征是流动形态取决于雷诺数。
流体力学Fluent报告——圆柱绕流

亚临界雷诺数下串列双圆柱与方柱绕流的数值模拟摘要:本文运用Fluent软件中的RNGk-ε模型对亚临界雷诺数下二维串列圆柱和方柱绕流问题进行了数值研究,通过结果对比,分析了雷诺数、柱体形状对柱体绕流阻力、升力以及涡脱频率的影响。
一般而言,Re数越大,方柱的阻力越大,圆柱体则不然;而Re越大,两种柱体的升力均越大。
相对于圆柱,同种条件下,方柱受到的阻力要大;相反地,方柱涡脱落频率要小。
Re越大,串列柱体的Sr数越接近于单圆柱体的Sr数。
关键字:圆柱绕流、升力系数、阻力系数、斯特劳哈尔数在工程实践中,如航空、航天、航海、体育运动、风工程及地面交通等广泛的实际领域中,绕流研究在工程实际中具有重大的意义。
当流体流过圆柱时, 由于漩涡脱落,在圆柱体上产生交变作用力。
这种作用力引起柱体的振动及材料的疲劳,损坏结构,后果严重。
因此,近些年来,众多专家和学者对于圆柱绕流问题进行过细致的研究,特别是圆柱所受阻力、升力和涡脱落以及涡致振动问题。
沈立龙等[1]基于RNG k⁃ε模型,采用有限体积法研究了亚临界雷诺数下二维圆柱和方柱绕流数值模拟,得到了圆柱和方柱绕流阻力系数C与Stroduhal 数随雷诺数的变化规律。
姚熊亮等[2]采用计算流体软件CFX中LES模型计算了二维不可压缩均匀流中孤立圆柱及串列双圆柱的水动力特性。
使用非结构化网格六面体单元和有限体积法对二维N-S方程进行求解。
他们着重研究了高雷诺数时串列双圆柱在不同间距比时的压力分布、阻力、升力及Sr数随Re数的变化趋势。
费宝玲等[3]用FLUENT软件对串列圆柱绕流进行了二维模拟,他们选取间距比L/D(L为两圆柱中心间的距离,D为圆柱直径)2、3、4共3个间距进行了数值分析。
计算均在Re= 200的非定常条件下进行。
计算了圆柱的升阻力系数、尾涡脱落频率等描述绕流问题的主要参量,分析了不同间距对圆柱间相互作用和尾流特征的影响。
圆柱绕流的一个重要特征是流动形态取决于雷诺数。
圆柱绕流阻力系数

圆柱绕流阻力系数
圆柱绕流阻力系数是描述圆柱绕流阻力大小的无量纲参数,一般用Cd表示。
它的计算公式如下:
Cd = (Fd / (0.5 * ρ * U^2 * A))
其中,Cd表示圆柱绕流阻力系数,Fd表示圆柱所受的绕流阻力,ρ表示流体的密度,U 表示流体速度,A表示圆柱的参考面积。
在圆柱绕流中,圆柱所受的绕流阻力主要由两个部分组成:湍流阻力和压差阻力。
湍流阻力主要与流体粘性有关,而压差阻力则主要与流体速度和圆柱形状有关。
圆柱绕流阻力系数通常取决于流体的雷诺数(Re),即流体惯性力与粘性力的比值。
在低雷诺数下,湍流阻力相对较小,而压差阻力相对较大,因此圆柱绕流阻力系数较大。
而在高雷诺数下,湍流阻力相对较大,压差阻力相对较小,因此圆柱绕流阻力系数较小。
第五章 圆柱阻力系数

圆柱阻力系数EFD.V5 可以用于研究物体周围的流动和确定由于流动所造成物体上的升力和牵引阻力。
在这个例子中我们利用 EFD.V5 确定一个浸没在均匀流体中的圆柱体阻力系数。
这个圆柱的轴线与流体流向垂直。
在雷诺数 1、1000、105 三种情况下进行计算,R e UD ρμ=,D 圆柱的直径, U 流体的速度,ρ 是密度,μ 是动力粘度。
圆柱体的阻力系数如下式定义:212DD F C U DL ρ=此处 D F 是沿流动方向上作用在圆柱体直径D 和长度L 上总的力。
这个仿真的目的是通过 EFD.V5 来获取圆柱体阻力系数并且与 Ref.1 中的实验数据进行比较。
复制 Tutorial 2 - Drag Coefficient 文件夹到你的工作目录,此外由于 EFD.V5 在运行时会对其输入的数据进行存储,所以必须确保文件处于非只读状态。
运行 EFD.V5。
创建一个新的EFD.V5 product。
点击Insert, Existing Component并且点击模型树的根目录项。
在File Selection对话框,浏览Tutorial 2 - Drag Coefficient\cylinder 0.01m文件夹找到Cylinder0.01m.CATPart 组件并且点击Open。
并且以EFD.CATProduct文件名进行保存。
这个Cylinder分析是了一个典型的EFD.V5 External分析。
外部流体分析主要是处理流体在物体上流过的问题,诸如流体经过飞行器,汽车,建筑等。
对于外部分析远场才是计算域的边界。
你可以在EFD.V5 项目中求解一个既有内部分析又包括外部分析的流动问题(例如,流体掠过和通过一个建筑)。
如果分析的问题同时包括了内部和外部分析,则你必须定义分析的类型为外部。
首先创建一个新的EFD.V5 项目。
创建项目1. 点击Insert, Wizard。
这个项目向导会指导你一步一步完成整个项目的特性定义。
圆柱绕流阻力测定(压力分布法)
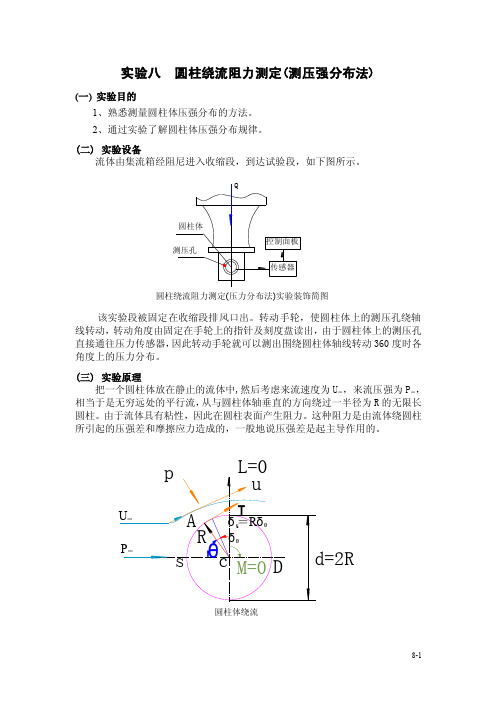
实验八圆柱绕流阻力测定(测压强分布法)(一)实验目的1、熟悉测量圆柱体压强分布的方法。
2、通过实验了解圆柱体压强分布规律。
(二)实验设备流体由集流箱经阻尼进入收缩段,到达试验段,如下图所示。
线转动,转动角度由固定在手轮上的指针及刻度盘读出,由于圆柱体上的测压孔直接通往压力传感器,因此转动手轮就可以测出围绕圆柱体轴线转动360度时各角度上的压力分布。
(三)实验原理把一个圆柱体放在静止的流体中,然后考虑来流速度为U∞,来流压强为P∞,相当于是无穷远处的平行流,从与圆柱体轴垂直的方向绕过一半径为R的无限长圆柱。
由于流体具有粘性,因此在圆柱表面产生阻力。
这种阻力是由流体绕圆柱所引起的压强差和摩擦应力造成的,一般地说压强差是起主导作用的。
圆柱体上取某一微元面积dA ,在单位长度上由压强差P 和摩擦切应力τ引起的微元阻力为:()S D P δθτθδsin cos +=θθδδδ2d R S ==绕整个封闭曲线积分得到()dSP D ⎰+=θτθsin cos以无量纲形势表示,dS U U P dS U P d U D ⎰⎰⎪⎪⎪⎪⎭⎫ ⎝⎛++=∞∞∞∞∞θρτθρρρsin 21cos 2121212222或()dS C C d C f P D ⎰+=θθsin cos 1其中221∞∞-=U P P C P ρ为压强系数,221∞=U C f ρτ为表面摩擦系数由于τ造成的阻力很小可以忽略不计,则θθd d C d C P D ⎰⎪⎭⎫⎝⎛=2cos 1 θθπd C C P D ⎰=20cos 21因此,只要测出圆柱体不同角度的P 值就可以确定阻力系数C D ,从而求得流体所受到的阻力:DD C U d F 22∞=ρ应该注意到,来流的动压强:∞∞-=P P U 0221ρ式中P 0为滞止压强,即θ=0时的压强。
因此,压力系数又可表示为:∞∞--=P P P P C P 0式中P 为圆柱上各测点的压强。
圆柱绕流圆球扰流阻力系数

C4.7.2 圆柱绕流与卡门涡街分析钝体绕流阻力的典型例子是圆柱绕流1.圆柱表面压强系数分布无粘性流体绕流圆柱时的流线图如图C4.7.1中虚线所示。
A 、B 点为前后驻点,C 、D 点为最小压强点。
AC 段为顺压梯度区,CB 段为逆压梯度区。
压强系数分布如下图对称的a 线所示。
实际流体绕流圆柱时,由于有后部发生流动分离,圆柱后表面上的压强分布与无粘性流动有很大差别。
后部压强不能恢复到与前部相同的水平,大多保持负值(表压)。
(圆柱后部流场显示)实验测得的圆柱表面压强系数如图C4.7.1中b 、c 线所示,两条线分别代表不同Re 数时的数值。
b 为边界层保持层流时发生分离的情况,分离点约在 = 80°左右;c 为边界层转捩为湍流后发生分离的情况,分离点约在 =120°左右。
(高尔夫球尾部分离)从图中可看到后部的压强均不能恢复到前部的水平。
沿圆柱面积分的压强合力,即压差阻力,以b 线最大,以c 线最小。
从图中还可发现,在尾流分离区内,压强大致是均匀分布,因此沿圆柱表面的压强分布应如图B3.6.3所示。
图C4.7.12.阻力系数随R e 数的变化用量纲分析法分析二维圆柱体绕流阻力F D 与相关物理量ρ、V 、d 、μ的关系,可得(C4.7.13)上式表明圆柱绕流阻力系数由流动Re 数(ρVd /μ)唯一确定。
图C4.7.2为二维光滑圆柱体绕流的C D -Re 关系曲线。
根据阻力与速度的关系及阻力系数变化特点,可将曲线分为6个区域,并画出与5个典型Re 数对应的圆柱尾流结构图案(图C4.7.3)。
θθ图C4.7.2(1)Re<<1,称为低雷诺数流动或蠕动流。
几乎无流动分离,流动图案上下游对称(a)。
阻力以摩擦阻力为主,且与速度一次方成比例。
(2)1≤Re≤500,有流动分离。
当Re=10,圆柱后部有一对驻涡(b)。
当Re 〉100时从圆柱后部交替释放出旋涡,组成卡门涡街(c)。
阻力由摩擦阻力和压差阻力两部分组成,且大致与速度的1.5次方成比例。
圆柱形弹丸绕流流场数值分析

Ξ圆柱形弹丸绕流流场数值分析3鞠玉涛,周长省(南京理工大学机械学院,江苏南京210094)[摘要]用数值模拟方法研究圆柱形弹丸绕流流场特性,出发方程为雷诺平增多的N2S方程,湍流模型为k2Ε两方程模型,数值格式为二阶迎风格式,得到了圆柱形弹丸在亚、跨和超音速下的绕流流场结构和阻力系数,并在此基础上给出了圆柱形弹丸头部阻力系数近似解析计算公式,与数值计算方法结果对比证明:其计算精度可以满足工程设计的要求。
[关键词]数值模拟;纳维2斯托克斯方程;弹丸;空气动力学[中图分类号]TJ011 [文献标识码]A1 引 言子母战斗部是提高弹箭威力的重要技术措施,其中,母弹开仓抛散及子弹丸弹道计算与分析等是子母战斗部设计中的关键技术,子弹丸的空气动力特性计算与分析是子弹丸弹道的前提条件,因此深入研究子弹丸的空气动力特性就显得非常重要。
由于子弹丸装填空间的限制以及子弹丸结构设计的特点,目前常采用的子弹丸气动外形为圆柱形结构,而此类气动外形在传统的空气动力工程计算方法中难以给出精确的计算结果,为此采用求解可压缩N2S方程的数值模拟技术,对一种典型的圆柱形子弹丸绕流流场特性及其阻力构成进行了数值计算分析,并在数值分析的基础上,建立物理模型,给出圆柱形弹丸头部阻力系数的近似解析计算方法,为子母战斗部的设计提供理论基础。
2 控制方程及数值方法计算采用雷诺平均的二维轴对称可压缩N2S方程,假设空气为完全气体,湍流附加粘性系数由高雷诺数k2Ε两方程模型计算,控制方程见公式(1)~(6):5U t+5Ex+5Fy+H=F v is(1)U=(Θ,Θu,Θv,e)T(2) E=(Θu,Θuu+P,Θuv,(e+p)u)T(3) F=(Θv,Θvu,Θvv+P,(e+p)v)T(4)e=Θ(C v T+u2-v22)(5)H=-Θuy(1,u,v,e+P)T(6)Θ为气流密度,P为气流压力,u,v分别为x,y方向上的气流速度,e为气流总能,F v is为粘性项,其计算公式参见文献[1]。
圆柱绕流升阻力

圆柱绕流升阻力
圆柱绕流是流体力学中的经典问题,从单一的物理现象得到了广泛的应用和研究。
圆柱绕流问题中最核心的问题是圆柱的升力和阻力特性,研究这些特性在可以帮助我们更好地理解流体流动的本质,并且可以指导对圆柱绕流问题的工程应用,例如建筑设计、风力发电等领域。
在圆柱绕流问题中,当流体绕过圆柱时,会产生压力差导致圆柱的向上升力和向后阻力。
就惯性-定常流动而言,在一定条件下,圆柱上游区域的流速大于圆柱下游区域的流速,从而导致圆柱表面附着的流体下游速度降低,上游速度增加。
这种流动形式会使周期性流体涡或叫卡门涡形成和脱落,这些涡对圆柱上升力和阻力的大小和周期有着举足轻重的影响。
在各种圆柱绕流实验中,都发现了六个不同的区域,套线区、分离尾迹区、对流卡门区、无序涡区、锋锐分界区和恒定区,以及不断生成涡的现象。
上述现象都与圆柱表面的压力分布和涡的产生、演化息息相关。
关于圆柱绕流问题的研究,透过流动本身的理解可知,圆柱绕流的升力和阻力问题都是十分复杂的。
从升力来看,由于存在于锋锐分界区的压力的波动,会导致升力的高频和低频变化。
而对于阻力则与表面的气流摩擦和涡流的脱落有关,以及卡门涡尺度与泡层厚度之比的大小也会影响阻力大小的估值。
对于圆柱绕流中的升力和阻力问题,在工程应用中可以通过相应的改变了解圆柱在不同时刻的受力变化情况,从而使设计更加应用化、理性化。
例如在石油天然气钻井平台,塔筒就是圆柱形的,如果我们能够设计出更小的升力和阻力特性,就能够增加这些平台的稳定性和耐风能力,提高其危险等级。
总体来说,在圆柱绕流问题的研究中,我们对流体流动的本质有了更深层次的了解和认识,从而为圆柱绕流问题的应用领域提供了更多的理论指导和科学依据。
液体中圆柱转子旋转运动的阻力

液体中圆柱转子旋转运动的阻力转子旋转运动是一种常见的机械运动形式,它在许多工程领域中都有着广泛的应用。
在液体中进行旋转运动时,圆柱转子会受到液体的阻力。
本文将探讨液体中圆柱转子旋转运动的阻力产生原因、计算方法以及影响因素。
我们来了解一下液体中圆柱转子旋转运动的阻力产生原因。
液体的阻力是由于液体分子之间的黏性作用力所引起的。
当圆柱转子在液体中旋转时,液体分子会受到转子表面的摩擦作用,从而形成一个与转子运动方向相反的阻力。
这个阻力称为液体中圆柱转子旋转运动的阻力。
液体中圆柱转子旋转运动的阻力可以通过以下公式进行计算:F = 6πηrv其中,F表示阻力大小,η表示液体的黏性系数,r表示圆柱转子的半径,v表示圆柱转子的角速度。
这个公式描述了液体中圆柱转子旋转运动的阻力与液体黏性、转子半径和角速度之间的关系。
黏性系数越大,阻力越大;转子半径越大,阻力越大;角速度越大,阻力越大。
除了上述的计算公式外,液体中圆柱转子旋转运动的阻力还受到其他因素的影响。
首先是液体的温度,温度越高,液体的黏性系数越小,阻力也越小。
其次是液体的流动速度,流动速度越快,液体分子与转子表面的摩擦作用也越大,阻力也越大。
此外,液体的密度和转子表面的粗糙度也会对阻力产生一定的影响。
在工程应用中,液体中圆柱转子旋转运动的阻力对于设计和优化机械装置至关重要。
通过合理选择液体的黏性系数、转子的半径和角速度,可以降低阻力,提高机械装置的效率。
此外,还可以通过改变液体的温度、流动速度和转子表面的粗糙度,来控制阻力的大小。
总结起来,液体中圆柱转子旋转运动的阻力是由于液体分子之间的摩擦作用所引起的。
阻力的大小与液体的黏性、转子的半径和角速度有关,可以通过计算公式进行估算。
此外,液体的温度、流动速度和转子表面的粗糙度也会对阻力产生影响。
在工程应用中,合理选择这些因素可以降低阻力,提高机械装置的效率。
圆柱绕流阻力实验(压强分布法)

3.14 圆柱绕流阻力实验(压强分布法)一、实验目的圆柱绕流实验是研究外流问题和形状阻力的典型实验。
通过测量圆柱表面的压强分布,认识实际流体绕圆柱流动时表面压强分布规律,并与理想流体相比较,理解形状阻力产生的原因及测量、计算方法。
二、实验原理理想流体均流对二维圆柱作无环量绕流时,圆柱表面任一点的速度分量为0,2sin r V V V θθ∞== (1)式中∞V 为来流速度。
圆柱表面任一点的压强i p 与来流压强p ∞的关系满足伯努利方程2222i p V p V g g g gθρρ∞∞+=+ (2) 式中ρ为流体密度。
以压强系数P C 表达流体压强的分布 2214sin 12i P p p C V θρ∞∞−==− (3)由于压强分布沿圆柱面前后对称,压强合力为零,称为达朗贝尔佯缪。
实际流体绕圆柱流动时,由于粘性得影响压强分布前后不对称;特别是当流动达到一定雷诺数后,粘性边界层在圆柱后部发生分离,形成漩涡。
从分离点开始圆柱体后部的压强大致接近分离点压强,不能恢复到前部的压强,破坏了前后压强分布的对称性,形成压差阻力D F 。
由于圆柱表面的摩擦阻力相对于压差阻力小得多,可忽略不计,阻力系数可表为20cos 12D D P F C C d V A πθθρ∞==∫ (4)式中A 为圆柱的迎风特征面积,压强系数P C 由(3)式确定。
实验中由多管压力计分别测量i p p ∞−和212V ρ∞ ()i m i p p g h h ρ∞∞−=− (5)201()2m V k g h h ρρ∞∞=− (6) 式中i h 为测点的静压水头高,0h 来流的总压水头高,∞h 为来流的静压水头高,m ρ测压计中液体密度,k 为测压系统损失修正系数。
这样(4)式中压强系数可表为 0()i p h h C k h h ∞∞−=− (7)测定P C 后代入(4)式求出D C ,并计算圆柱阻力D F 。
三、实验设备本实验是在多功能实验台上进行的,如下图示。
流体力学Fluent报告——圆柱绕流

亚临界雷诺数下串列双圆柱与方柱绕流的数值模拟摘要:本文运用Fluent软件中的RNG k-ε模型对亚临界雷诺数下二维串列圆柱和方柱绕流问题进行了数值研究,通过结果对比,分析了雷诺数、柱体形状对柱体绕流阻力、升力以及涡脱频率的影响。
一般而言,Re数越大,方柱的阻力越大,圆柱体则不然;而Re越大,两种柱体的升力均越大。
相对于圆柱,同种条件下,方柱受到的阻力要大;相反地,方柱涡脱落频率要小。
Re越大,串列柱体的Sr数越接近于单圆柱体的Sr数。
关键字:圆柱绕流、升力系数、阻力系数、斯特劳哈尔数在工程实践中,如航空、航天、航海、体育运动、风工程及地面交通等广泛的实际领域中,绕流研究在工程实际中具有重大的意义。
当流体流过圆柱时 , 由于漩涡脱落,在圆柱体上产生交变作用力。
这种作用力引起柱体的振动及材料的疲劳,损坏结构,后果严重。
因此,近些年来,众多专家和学者对于圆柱绕流问题进行过细致的研究,特别是圆柱所受阻力、升力和涡脱落以及涡致振动问题。
立龙等[1]基于RNG k⁃ε模型,采用有限体积法研究了亚临界雷诺数下二维圆柱和方柱绕流数值模拟,得到了圆柱和方柱绕流阻力系数C与 Strouhal 数d随雷诺数的变化规律。
熊亮等[2]采用计算流体软件CFX中LES模型计算了二维不可压缩均匀流中孤立圆柱及串列双圆柱的水动力特性。
使用非结构化网格六面体单元和有限体积法对二维N- S方程进行求解。
他们着重研究了高雷诺数时串列双圆柱在不同间距比时的压力分布、阻力、升力及Sr数随Re数的变化趋势。
费宝玲等[3]用FLUENT软件对串列圆柱绕流进行了二维模拟,他们选取间距比L/D(L为两圆柱中心间的距离,D为圆柱直径)2、3、4共3个间距进行了数值分析。
计算均在 Re = 200 的非定常条件下进行。
计算了圆柱的升阻力系数、尾涡脱落频率等描述绕流问题的主要参量,分析了不同间距对圆柱间相互作用和尾流特征的影响。
圆柱绕流的一个重要特征是流动形态取决于雷诺数。
(完整版)圆柱绕流圆球扰流阻力系数

C4.7.2 圆柱绕流与卡门涡街分析钝体绕流阻力的典型例子是圆柱绕流1 •圆柱表面压强系数分布无粘性流体绕流圆柱时的流线图如图 C4.7.1中虚线所示。
A B 点为前后驻点,C D 点为最小 压强点。
AC 段为顺压梯度区,CB 段为逆压梯度区。
压强系数分布如下图对称的 a 线所示。
实际 流体绕流圆柱时,由于有后部发生流动分离,圆柱后表面上的压强分布与无粘性流动有很大差别。
后部压强不能恢复到与前部相同的水平,大多保持负值(表压)。
(圆柱后部流场显示)实验测得的圆柱表面压强系数如图 C4.7.1中b 、c 线所示,两条线分别代表不同 Re 数时 的数值。
b 为边界层保持层流时发生分离的情况,分离点约在 =80。
左右;c 为边界层转捩为 湍流后发生分离的情况,分离点约在 =120°左右。
(高尔夫球尾部分离)从图中可看到后部的压强均不能恢复到前部的水平。
沿圆柱面积分的压强合力,即压差阻力,以 b 线最大,以c 线 最小。
从图中还可发现,在尾流分离区内,压强大致是均匀分布,因此沿圆柱表面的压强分布应 如图B3.6.3所示2.阻力系数随Re 数的变化 用量纲分析法分析二维圆柱体绕流阻力F D 与相关物理量 (C4.7•13)上式表明圆柱绕流阻力系数由流动 Re 数(p V 卩)唯一确定。
图C4.7.2为二维光滑圆柱 体绕流的C D -Re 关系曲线。
根据阻力与速度的关系及阻力系数变化特点, 可将曲线分为6个区域, 并画出与5个典型Re 数对应的圆柱尾流结构图案(图 C4.7.3)。
图 C4.7.1 卩的关系,可得 d 、 6 =[車-f(^)C4.7.2(1) Re vv 1,称为低雷诺数流动或蠕动流。
几乎无流动分离,流动图案上下游对称(a )。
阻力以摩擦阻力为主,且与速度一次方成比例。
(2) K Re < 500,有流动分离。
当Re=10,圆柱后部有一对驻涡(b )。
当Re > 100时从圆柱后部交替释放出旋涡,组成卡门涡街(c )。
圆柱绕流圆球扰流阻力系数

圆柱绕流与卡门涡街分析钝体绕流阻力的典型例子是圆柱绕流1.圆柱表面压强系数分布无粘性流体绕流圆柱时的流线图如图中虚线所示。
A、B点为前后驻点,C、D点为最小压强点。
AC段为顺压梯度区,CB段为逆压梯度区。
压强系数分布如下图对称的a线所示。
实际流体绕流圆柱时,由于有后部发生流动分离,圆柱后表面上的压强分布与无粘性流动有很大差别。
后部压强不能恢复到与前部相同的水平,大多保持负值(表压)。
(圆柱后部流场显示)实验测得的圆柱表面压强系数如图中b、c线所示,两条线分别代表不同Re数时的数值。
b 为边界层保持层流时发生分离的情况,分离点约在θ= 80°左右;c为边界层转捩为湍流后发生分离的情况,分离点约在θ=120°左右。
(高尔夫球尾部分离)从图中可看到后部的压强均不能恢复到前部的水平。
沿圆柱面积分的压强合力,即压差阻力,以b线最大,以c线最小。
从图中还可发现,在尾流分离区内,压强大致是均匀分布,因此沿圆柱表面的压强分布应如图所示。
图阻力系数随R e数的变化用量纲分析法分析二维圆柱体绕流阻力F D与相关物理量ρ、V、d、μ的关系,可得上式表明圆柱绕流阻力系数由流动Re数(ρVd/μ)唯一确定。
图为二维光滑圆柱体绕流的C-Re关系曲线。
根据阻力与速度的关系及阻力系数变化特点,可将曲线分为6个区域,并画出D与5个典型Re数对应的圆柱尾流结构图案(图。
图(1)Re<<1,称为低雷诺数流动或蠕动流。
几乎无流动分离,流动图案上下游对称(a)。
阻力以摩擦阻力为主,且与速度一次方成比例。
(2)1≤Re≤500,有流动分离。
当Re=10,圆柱后部有一对驻涡(b)。
当Re 〉100时从圆柱后部交替释放出旋涡,组成卡门涡街(c)。
阻力由摩擦阻力和压差阻力两部分组成,且大致与速度的次方成比例。
(3)500≤Re〈2×105,流动分离严重,大约从Re=104起,边界层甚至从圆柱的前部就开始分离(d),涡街破裂成为湍流,形成很宽的分离区。
流体力学Fluent报告——圆柱绕流

亚临界雷诺数下串列双圆柱与方柱绕流的数值模拟摘要:本文运用Fluent软件中的RNG k-ε模型对亚临界雷诺数下二维串列圆柱和方柱绕流问题进行了数值研究,通过结果对比,分析了雷诺数、柱体形状对柱体绕流阻力、升力以及涡脱频率的影响。
一般而言,Re数越大,方柱的阻力越大,圆柱体则不然;而Re越大,两种柱体的升力均越大。
相对于圆柱,同种条件下,方柱受到的阻力要大;相反地,方柱涡脱落频率要小。
Re越大,串列柱体的Sr数越接近于单圆柱体的Sr数。
关键字:圆柱绕流、升力系数、阻力系数、斯特劳哈尔数在工程实践中,如航空、航天、航海、体育运动、风工程及地面交通等广泛的实际领域中,绕流研究在工程实际中具有重大的意义。
当流体流过圆柱时 , 由于漩涡脱落,在圆柱体上产生交变作用力。
这种作用力引起柱体的振动及材料的疲劳,损坏结构,后果严重。
因此,近些年来,众多专家和学者对于圆柱绕流问题进行过细致的研究,特别是圆柱所受阻力、升力和涡脱落以及涡致振动问题。
立龙等[1]基于RNG k⁃ε模型,采用有限体积法研究了亚临界雷诺数下二维圆柱和方柱绕流数值模拟,得到了圆柱和方柱绕流阻力系数C与 Strouhal 数d随雷诺数的变化规律。
熊亮等[2]采用计算流体软件CFX中LES模型计算了二维不可压缩均匀流中孤立圆柱及串列双圆柱的水动力特性。
使用非结构化网格六面体单元和有限体积法对二维N- S方程进行求解。
他们着重研究了高雷诺数时串列双圆柱在不同间距比时的压力分布、阻力、升力及Sr数随Re数的变化趋势。
费宝玲等[3]用FLUENT软件对串列圆柱绕流进行了二维模拟,他们选取间距比L/D(L为两圆柱中心间的距离,D为圆柱直径)2、3、4共3个间距进行了数值分析。
计算均在 Re = 200 的非定常条件下进行。
计算了圆柱的升阻力系数、尾涡脱落频率等描述绕流问题的主要参量,分析了不同间距对圆柱间相互作用和尾流特征的影响。
圆柱绕流的一个重要特征是流动形态取决于雷诺数。
08.圆柱绕流.ppt

➢ 单位宽度圆柱体所受压差阻力和圆柱的阻力系数分别为:
D
2
1
d
p cos d
d
02
2
2
0 ( p p ) cos
v2 d
2
2
0 ( p p ) cos d 1
1 v2 d
• 检验假设的理论模型是否正确; • 了解绕流物体流动的物理图案; • 提供强度设计所需载荷分布数据。
14-7
• §将压3力.2化压成无力量分纲布的压的力表系示数形方式法
Cp
p p
1 2
v2
其中 p、v分别为来流静压和来流速度。
➢ 用向量法或坐标曲线法表示压力分布
θ
14-8
• §阻力3系.3数阻力C系D 数12的定Dv2义 S与计算
理论曲线1的偏离比超临界绕流实验曲线2的偏离更大; • 亚临界绕流实验曲线3对应于发生“阻力危机”之前的层流附面层分离
( 危机CD”≈1之.2后,的分湍离流点附约面78层°分);离超(临C界D≈绕0.流3,实分验离曲点线约2对13应0°于)。发生“阻力
14-6
§3.1 压力分布的测量
• 压力分布测试是实验流体力学的基本实验方法,在基础 性和工程性实验研究中得到广泛应用。
14-4
§2.3 两种流态
发生“阻力微机”前后的两种典型流态
亚临界(Re < Rec): CD≈1.2,层流附面层分离,分离点约78 ° ; 超临界(Re > Rec): CD≈0.3,湍流附面层分离,分离点约130 °。
14-5
§2.4 压力分布曲线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C4.7.2 圆柱绕流与卡门涡街
????分析钝体绕流阻力的典型例子是圆柱绕流
1.圆柱表面压强系数分布
????无粘性流体绕流圆柱时的流线图如图C4.7.1中虚线所示。
A 、B 点为前后驻点,C 、D 点为最小压强点。
AC 段为顺压梯度区,CB 段为逆压梯度区。
压强系数分布如下图对称的a 线所示。
实际流体绕流圆柱时,由于有后部发生流动分离,圆柱后表面上的压强分布与无粘性流动有很大差别。
后部压强不能恢复到与前部相同的水平,大多保持负值(表压)。
(圆柱后部流场显示)
????实验测得的圆柱表面压强系数如图C4.7.1中b 、c 线所示,两条线分别代表不同Re 数时的数值。
b 为边界层保持层流时发生分离的情况,分离点约在 = 80°左右;c 为边界层转捩为
湍流后发生分离的情况,分离点约在 =120°左右。
(高尔夫球尾部分离)从图中可看到后部
的压强均不能恢复到前部的水平。
沿圆柱面积分的压强合力,即压差阻力,以b 线最大,以c 线最小。
从图中还可发现,在尾流分离区内,压强大致是均匀分布,因此沿圆柱表面的压强分布应如图B3.6.3所示。
图C4.7.1
2.阻力系数随R e 数的变化
????用量纲分析法分析二维圆柱体绕流阻力F D 与相关物理量ρ、V 、d 、μ的关系,可得 上式表明圆柱绕流阻力系数由流动Re 数(ρVd /μ)唯一确定。
图C4.7.2为二维光滑圆柱体绕流的C D -Re 关系曲线。
根据阻力与速度的关系及阻力系数变化特点,可将曲线分为6个区域,并画出与5个典型Re 数对应的圆柱尾流结构图案(图。
θθ
图
C4.7.2
(1)Re<<1,称为低雷诺数流动或蠕动流。
几乎无流动分离,流动图案上下游对称(a)。
阻力以摩擦阻力为主,且与速度一次方成比例。
(2)1≤Re≤500,有流动分离。
当Re=10,圆柱后部有一对驻涡(b)。
当Re 〉100时从圆柱后部交替释放出旋涡,组成卡门涡街(c)。
阻力由摩擦阻力和压差阻力两部分组成,且大致与速度的1.5次方成比例。
(3)500≤Re〈2×105,流动分离严重,大约从Re=104起,边界层甚至从圆柱的前部就开始分离(d),涡街破裂成为湍流,形成很宽的分离区。
阻力以压差阻力为主,且与速度的二次方成比例,即C D几乎不随Re数变化。
(4)2×105≤Re≤5×105,层流边界层变为湍流边界层,分离点向后推移,阻力减小,C D下跌,至Re = 5×105时,C D=0.3达最小值,此时的分离区最小(e)。
(5)5×105≤Re≤3×106,分离点又向前移,C D回升。
(6)Re>3×106,C D与Re无关,称为自模区。
3.卡门涡街
????在圆柱绕流实验中发现,大约在Re = 40起,圆柱后部的一对旋涡开始出现不稳定地摆动,如图所示,大约到Re=70起,旋涡交替地从圆柱上脱落,两边的旋涡旋转方向相反,随流而下,在圆柱后面形成有一定规则的、交叉排列的涡列,称为卡门涡街(图)。
(圆柱后部卡门涡街演示)
图C4.7.3 卡门(V.Karman, 1911)用理想流体复势理论对涡街的诱导速度,稳定性和阻力等作了分析。
指出涡街的移动速度比来流速度小得多;涡列的排列规则有多种可能,但只有在h/ l= 0.2806(h为两涡列的间距,l为同列涡中相邻涡的间距)时才相对稳定;涡街对圆柱单位长度上引起的阻力为
由于圆柱体上的涡以一定的频率交替释放,柱体表面上的压强分布也以一定的频率发生有规则的变化,使圆柱受到周期性变化的合力作用,其频率与涡的释放频率相同。
早在19世纪,捷克人斯特劳哈尔(V.Strouhal,1878)就对电线在风中发出鸣叫声作过研究,并提出计算涡释放频率f的经验公式
上式中d为圆柱直径,Re=ρUd/μ,说明Sr由Re数唯一确定,测量表明约在Re=60-5000范围内可观察到有规则的卡门涡街,并在Re=600-5000范围内Sr数几乎保持为0.21的常数。
以后是不规则的与湍流混合的尾迹,Sr数略有降低并一直保持到2×10 5 。
????卡门涡街引起的流体振动,造成声响。
除了电线的“同鸣声”外,在管式热交换器中使管束振动,发出强烈的振动噪声,锅炉发出低频噪声即属此列(锅炉热交换管束及流场显示)。
更为严重的是对绕流物周期性的压强合力可能引起共振,潜水艇潜望镜遇到这种情况,将不能正常工作,美国华盛顿州塔克马吊桥(Tacoma,1940)因设计不当,在一次暴风雨中由桥体诱发的卡门涡街在几分钟内将桥摧毁。
目前在高层建筑、大跨度桥梁设计中避免发生气流振动和破坏的研究和实验已日益引起重视。
C4.7.3 不同形状物体的阻力系数
1.圆球
圆球绕流C D-Re关系曲线如图C4.7.5所示。
在Re《1时,阻力以摩擦阻力为主,阻力系数可以计算
F
=3πμd U(C4.7.5)
D
上式称为斯托克斯圆球阻力公式。
图C4.7.5
(C4.7.6)
圆柱绕流相似,从Re >1起就出现流动分离,压差阻力加入总阻力中去。
随着Re的增加,在总阻力中,粘性阻力所占比例不断下降,至Re=1000左右只占总阻力的5% 。
在10 3< Re<3×10 5范围内阻力系数保持平稳,但比同样直径的圆柱(C D=1.2)更低(C D=0.4)。
至Re=3×10 5也出现阻力系数突然下跌现象,从0.4跌至0.1。
普朗特曾做过实验,他在圆球前部套一金属丝圈,人为地将层流边界层提前转化为湍流边界层,结果分离点从原来的θ=80°后移到θ=120°左右,使阻力系数明显下跌。
这是因为湍流边界层内速度廓线饱满,克服分离能力比层流增强的
缘故。
边界层转捩还受到表面粗糙度的影响,实验表明光滑球发生转捩的绕流雷诺数Re d = 4×10 5,而粗糙球相应的雷诺数只有?5×104。
[思考题C4.7.3]
2.流线型体
为了降低绕流物体的压差阻力,只有从减小后部逆压梯度入手,流线型体就这样应运而生。
流线型体是前部圆滑,后部平缓,形体细长(图4.7.6)。
几乎所有游得快的鱼类都是这种体形。
(鳟鱼的体形与流线形翼形比较)但由于后部加长,摩擦阻力随之加大,必须正确处理两种阻力的关系。
图4.7.6
图C4.7.7
图C4.7.7为一水滴形流线型体在风洞实验中所做的阻力测量的结果。
流线型体的厚度t和弦长l之比t/ l为阻力图中横坐标,阻力系数C D为纵坐标。
阻力图中分别绘制了摩擦阻力、压差阻力和总阻力曲线,弦长雷诺数Re l = ρvl/μ=4×10 5。
从图中可看到最小总阻力位于t/ l= 0.25 处,C D=0.06 。
当t/ l减小时(细长型)压差阻力虽然减小,但摩擦阻力上升更快,当d / l增大时(粗短型)摩擦阻力减小,但压差阻力急剧上升,两者均使总阻力增大。
将水滴形流线体与相同厚度(直径为d)的圆柱体相比,前者的最小阻力系数(C D=0.06)只有后者最小阻力系数(C D=0.3见图的1/5。
根据空气动力学理论精心设计的层流型翼型,不仅消除了分离,而且使翼面上的边界层几乎均处于层流态,可使阻力系数降低到只有水滴型流线体的十分之一。
