2312图形的旋转作图
合集下载
人教版九年级数学上册 23.1.2图形的旋转(共20张PPT)
下课!
课堂作业：课本63页6，7， 8，10，11（做在书上） 家庭作业：练习册52页
（4）
A
B
图形A逆时针旋转900形成图形B。
巩固练习
点B的对应点是_点__C__
D
线段OB的对应线段是线__段__OC
线段AB的对应线段是线__段__CD
C A
∠A的对应角是_∠__D__
∠B的对应角是_∠__C__ 旋转中心是_点__O__
· 450
O MB
旋转的角度是_4_5_0___
△AOB的边OB的中点M的对应点在哪里？
（2）改变三角形的形状，看看旋转的效果.
讨论
把图1如何旋转可以得到图2?
(1)
(2)
分析
A Oห้องสมุดไป่ตู้
AB O
图形B可以看作图形A绕O点顺时针方向 旋转 900 得到。
分析
A
AB
O
OC
图形C可以看作图形A绕O点顺时针方向
旋转 900 得到。
分析
A O
AB D OC
图形D可以看作图形A绕O点顺时针方向 旋转 900 得到。
九年级数学上册 第23章 旋转
图案的旋转
把一个图案（如图）进行旋转，选择不同的旋转中心， 不同的旋转角，会出现不同的效果.
1.旋转中心不变，改变旋转角（如图）
a
a
o
o
2.旋转角不变，改变旋转中心
o o
3. 美丽的图案是这样形成的
练习 把一个三角形进行旋转： （1）选择不同的旋转中心，不同的旋转角，看看旋转的效果
探究
已知△ABC，分别以三个顶点为旋 转中心，以不同旋转角旋转，观察各个 旋转效果。
23.1.2图形的旋转2
二、典例解析：
• 例1．如图，△ABC绕C点旋转后，顶点A的对应 点为点D，试确定顶点B•对应点的位置，以及旋 转后的三角形．
解：（1）连接CD． （2）以CB为一边作∠BCE，使得∠BCE=∠ACD． （3）在射线CE上截取CB′=CB则B′即为所求的B的对应点． （4）连接DB′则△DB′C就是△ABC绕C点旋转后的图形．
8.如图1，小明将一张矩形纸片沿对角线剪开，得到两 张三角形纸片（如图2），量得它们的斜边长为 10cm，较小锐角为30°，再将这两张三角纸片摆 成如图3的形状，使点B、C、F、D在同一条直线上， 且点C与点F重合（在图3至图6中统一用F表示）
小明在对这两张三角形纸片进行如下操作时遇 到了三个问题，请你帮助解决．
• 例2．如图，在一个10×10的正方形DEFG网格中有一个 △ABC.
• ①在网格中画出△ABC向下平移3个单位得到△A1B1C1． • ②在网格中画出△ABC绕C点逆时针方向旋转90°得到的
△A2B2C2 • ③若以EF所在的直线为x轴，ED所在的直线为y轴建立直角
坐标系，
• 写出A1、 A2两点的坐标．
5．如图，边长为2的两个互相重合的正方形纸片按 住其中一个不动，另一个绕点B顺时针旋转一个 角度，若使重叠部分的面积为，则这个旋转角为
度．
D
AE
FCB源自G6.如图，点O是等边△ABC内一点， ∠AOB=1100． ∠BOC=α将△BOC绕点C按顺时针方向 旋转600得△ADC ，连接OD．
⑴求证：是 △COD 是等边三角形；⑵当α=1500时，试判 断 △AOD 的形状，并说明理由；⑶探究：当α为多少 度时， △AOD 是等腰三角形？
⑴将图3中的△ABF沿BD向右平移到图4的位置， 使点B与点F 重合，请你求出平移的距离；
图形旋转作图课件
角动量守恒
在无外力矩作用的情况下 ，刚体的角动量是守恒的 ，这是刚体旋转的基本物 理规律之一。
陀螺仪效应
在高速旋转的刚体中，由 于科里奥利力的作用，会 产生陀螺仪效应，影响刚 体的运动轨迹。
05
图形旋转的练习与挑战
基础练习题
基础题目1
绘制一个正方形，并其绕任意一边的中点旋
旋转矩阵
表示旋转变换的数学工具 ，可以用来描述和计算图 形的旋转。
02
图形旋转的作图方法
旋转作图的步骤
选择图形
首先，你需要选择你想要旋转 的图形。这可以是任何二维图 形，如三角形、矩形、圆形等
。
确定中心点
确定图形的中心点，这是图形 旋转的固定点。
应用旋转
使用旋转工具，将图形围绕中 心点旋转到所需的角度。
图形旋转所转过的角度。
旋转的特性
图形旋转后，形状、 大小不变，只是位置 发生变化。
旋转过程中，图形上 对应点所形成的轨迹 是一个圆。
旋转不改变图形的对 称性。
旋转的分类
01
02
03
旋转变换
图形绕某一定点旋转一定 的角度，得到一个新的图 形。
旋转作图
根据给定的条件，通过旋 转变换绘制出所需的图形 。
检查阴影和光照方向
如果你在旋转三维图形时，注意阴影 和光照的方向。在旋转后，它们可能 会改变方向或位置。
测试输出
在完成旋转作图后，测试输出效果。 确保图形在打印或显示时看起来正常 。
03
图形旋转的应用实例
几何作图中的应用
基础应用领域
图形旋转是几何作图中的基础操作之一，通过旋转图形可以轻松地绘制出各种复杂 的几何图形，如圆形、椭圆、抛物线等。
上册第二十三章 图形的旋转作图-新人教版九级数学全一册精品PPT
（4）如图，点P即为所求，点P的坐标为（2，0）．
●
1. 选项与题干的关系 完全的 陈述句 组成， 所以选 项应能 够直接 回答问 题或者 将不完 全陈述 句补充 完整， 构成完 整语句 。
●
2.运用排除法，如果正确答案不能一 眼看出 ，应首 先排除 明显是 荒诞、 拙劣或 不正确 的答案 。尽可 能多排 除一些 选择项 ，就可 以提高 选对答 案而得 分的概 率。
A2B2C2，请画出△A2B2C2 的图形；
（3）线段 BB2 的长度为
.
解：（1）△A1B1C1的图形如图所示.
三级检测练
一级基础巩固练 6. 如图，正方形网格中的每个小正方形的边长都是 1，每
个小正方形的顶点叫做格点.△ABC 的三个顶点 A,B,C 都在格点上，将△ABC 绕点 A 逆时针方向旋转 90°得 到△AB′C′,在正方形网格中，画出△AB′C′，并分 别画出旋转过程中，点 B，点 C 经过的路径.
C. （0，-1）
D. （1，0）
三级拓展延伸练
10. 如图，△ABC 三个顶点的坐标分别为 A（1，1），B （4，2），C（3，4）. （1）请画出将△ABC 向左平
移 4 个单位长度后得到的图
形△A1B1C1； （2）将△ABC 绕着点（1，0）
旋转 180°，画出旋转后得
到的△A2B2C2；
●
6.获取和解读地理信息是高考四项基 本能力 之一， 也是基 础能力 要求。 近几年 的高考 地理试 题材料 阅读量 有所增 加，表 明对学 生获取 和解读 地理信 息能力 要求提 高，准 确答题 需要全 面获取 材料中 的信息 ，理解 问题情 境，进 而全面 把握设 问实质 。
●
7.高考地理选择题常以社会热点、科 研成果 为材料 设置试 题情境 ，材料 和问题 中常出 现很多 地理概 念，很 多学生 对某些 地理概 念的内 涵和外 延理解 不深入 ，相似 的地理 概念混 淆，做 选择题 时，受 错误选 项干扰 极大， 导致错 误率很 高。
●
1. 选项与题干的关系 完全的 陈述句 组成， 所以选 项应能 够直接 回答问 题或者 将不完 全陈述 句补充 完整， 构成完 整语句 。
●
2.运用排除法，如果正确答案不能一 眼看出 ，应首 先排除 明显是 荒诞、 拙劣或 不正确 的答案 。尽可 能多排 除一些 选择项 ，就可 以提高 选对答 案而得 分的概 率。
A2B2C2，请画出△A2B2C2 的图形；
（3）线段 BB2 的长度为
.
解：（1）△A1B1C1的图形如图所示.
三级检测练
一级基础巩固练 6. 如图，正方形网格中的每个小正方形的边长都是 1，每
个小正方形的顶点叫做格点.△ABC 的三个顶点 A,B,C 都在格点上，将△ABC 绕点 A 逆时针方向旋转 90°得 到△AB′C′,在正方形网格中，画出△AB′C′，并分 别画出旋转过程中，点 B，点 C 经过的路径.
C. （0，-1）
D. （1，0）
三级拓展延伸练
10. 如图，△ABC 三个顶点的坐标分别为 A（1，1），B （4，2），C（3，4）. （1）请画出将△ABC 向左平
移 4 个单位长度后得到的图
形△A1B1C1； （2）将△ABC 绕着点（1，0）
旋转 180°，画出旋转后得
到的△A2B2C2；
●
6.获取和解读地理信息是高考四项基 本能力 之一， 也是基 础能力 要求。 近几年 的高考 地理试 题材料 阅读量 有所增 加，表 明对学 生获取 和解读 地理信 息能力 要求提 高，准 确答题 需要全 面获取 材料中 的信息 ，理解 问题情 境，进 而全面 把握设 问实质 。
●
7.高考地理选择题常以社会热点、科 研成果 为材料 设置试 题情境 ，材料 和问题 中常出 现很多 地理概 念，很 多学生 对某些 地理概 念的内 涵和外 延理解 不深入 ，相似 的地理 概念混 淆，做 选择题 时，受 错误选 项干扰 极大， 导致错 误率很 高。
最新-人教版九年级上册数学 23.1.2 旋转作图 (共18张PPT)-PPT文档资料
图（1） 图（2）
总结
知1－讲
在旋转作图时，要紧扣以下三点：(1)对应点到 旋转中心的距离相等；(2)旋转的角度相等；(3)旋 转的方向相同．
知1－练
1 如图，将线段AB绕点O顺时针旋转90°得到线段 A′B′，那么A(－2，5)的对应点A′的坐标是( B ) A．(2，5) B．(5，2) C．(2，－5)
图（1） 图（2）
知1－讲
例2 如图（1），△ABC绕点O旋转，使点A旋转到点D处，画出 顺时针旋转后的三角形，并写出简要作法．
导引：抓住“关键点”A，B，C，D，旋转中心O， 旋转角∠AOD这些要素，按步骤“连——转 ——截——连”即可得出所求作的三角形．
解：作法：(1)连接OA，OB，OC，OD； (2)分别以OB，OC为边作∠BOM＝ ∠CON＝∠AOD； (3)分别在OM，ON上截取OE＝OB， OF＝OC； (4)依次连接DE，EF，FD； 即：△DEF就是所求作的三角形， 如图（2）所示．
分析：关键是确定△ADE三个顶点的对应点， 即它们旋转后的位置.
解：因为点A是旋转中心， 所以它的对应点是它本身. 正方形ABCD中，AD=AB，∠DAB=90°， 所以旋转后点D与点B重合. 设点E的对应点为点E′.因为旋转后的图形 与旋转前的图形全等，所以∠ABE′=∠ADE =90°，BE′=DE. 因此，在CB的延长线上取点E′，使BE′= DE，则△ABE′为旋转后的图形（图（2））.Leabharlann 识点 2 旋转的应用知2－导
问题
让我们一起来欣赏一下美丽的图案，体会一下旋 转的奥秘．你们猜猜旋转到底和什么有关呢？
知2－导
（1）旋转中心不变，改变旋转角（如图）．
β α
O
231图形的旋转
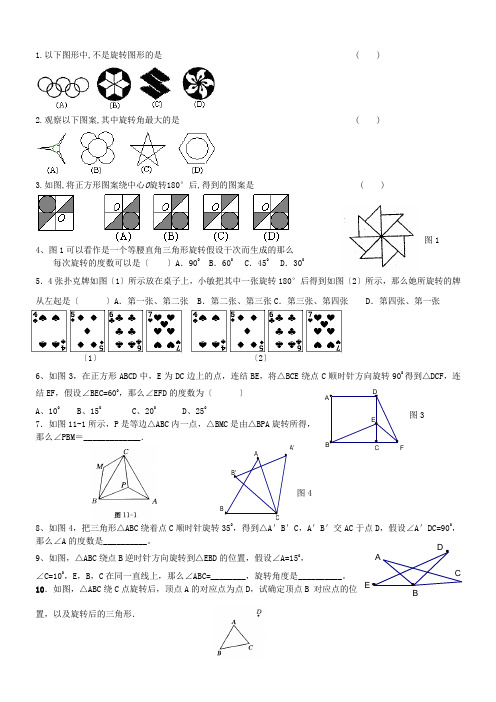
BAFDEC ABCB'A'BA CE D1.以下图形中,不是旋转图形的是 ( )2.观察以下图案,其中旋转角最大的是 ( )3.如图,将正方形图案绕中心O 旋转180°后,得到的图案是 ( )4、图1可以看作是一个等腰直角三角形旋转假设干次而生成的那么每次旋转的度数可以是〔 〕A ．900 B ．600 C ．450 D ．3005．4张扑克牌如图〔1〕所示放在桌子上，小敏把其中一张旋转180°后得到如图〔2〕所示，那么她所旋转的牌从左起是〔 〕A ．第一张、第二张 B ．第二张、第三张C ．第三张、第四张 D ．第四张、第一张〔1〕 〔2〕6、如图3，在正方形ABCD 中，E 为DC 边上的点，连结BE ，将△BCE 绕点C 顺时针方向旋转900得到△DCF ，连结EF ，假设∠BEC=600，那么∠EFD 的度数为〔 〕A 、100B 、150C 、200D 、2507．如图11-1所示，P 是等边△ABC 内一点，△BMC 是由△BPA 旋转所得， 那么∠PBM ＝_____________．8、如图4，把三角形△ABC 绕着点C 顺时针旋转350，得到△A ＇B ＇C ，A ＇B ＇交AC 于点D ，假设∠A ＇DC=900，那么∠A 的度数是__________。
9、如图，△ABC 绕点B 逆时针方向旋转到△EBD 的位置，假设∠A=150，∠C=100，E ，B ，C 在同一直线上，那么∠ABC=________，旋转角度是__________。
10．如图，△ABC 绕C 点旋转后，顶点A 的对应点为点D ，试确定顶点B•对应点的位置，以及旋转后的三角形．图1图3图411．如图，如果把钟表的指针看做三角形OAB，它绕O点按顺时针方向旋转得到△OEF，在这个旋转过程中：〔1〕旋转中心是什么？旋转角是什么？〔2〕经过旋转，点A、B分别移动到什么位置？．12．如图，四边形ABCD、四边形EFGH都是边长为1的正方形．〔1〕这个图案可以看做是哪个“根本图案〞通过旋转得到的？〔2〕请画出旋转中心和旋转角．〔3〕指出，经过旋转，点A、B、C、D分别移到什么位置？13．如图，四边形ABCD是边长为1的正方形，且DE=14，△ABF是△ADE的旋转图形．〔1〕旋转中心是哪一点？〔2〕旋转了多少度？〔3〕AF的长度是多少？〔4〕如果连结EF，那么△AEF是怎样的三角形？14．如图，如果把钟表的指针看做三角形OAB，它绕O点按顺时针方向旋转得到△OEF，在这个旋转过程中：〔1〕旋转中心是什么？旋转角是什么？〔2〕经过旋转，点A、B分别移动到什么位置？15．如图，四边形ABCD、四边形EFGH都是边长为1的正方形．〔1〕这个图案可以看做是哪个“根本图案〞通过旋转得到的？〔2〕请画出旋转中心和旋转角．〔3〕指出，经过旋转，点A、B、C、D分别移到什么位置？16．如图，K是正方形ABCD内一点，以AK为一边作正方形AKLM，使L、M•在AK的同旁，连接BK和DM，试用旋转的思想说明线段BK与DM的关系．。
23.1.2简单的旋转作图 王聪
(4)作出新图形： 沿一定的方向和角度分别作出 各关键点；
B
顺次连接各关键点；
(5)写出结论： 说明所作出的图形。
探究3：如图,ΔDEF是由△ABC绕某一中 心旋转一定的角度得到,请你找出这旋转中心 .
C D B A
E F
.
O
旋确定转中心的方法：分别作两组对应点连 线的垂直平分线，其交点为旋转中心。
A O
B
C
图形C可以看作图形B绕O点 0 顺时针方向旋转 90得到。
A O
A D
B
O
C
图形D可以看作图形C绕O点 0 顺时针方向旋转 90得到。
1、右图可以看做是一个菱形通过几次
旋转得到的？每次旋转了多少度？
2、你用“旋转”来分析图案的形 成过程时, 能完整的描述出来吗？
基本图案是:
一个菱形
旋转中心是:
A.45°
B.60°
C.90°
D.180°
图案的旋转 把一个图案（如图）进行旋转，选择不同的旋 转中心， 不同的旋转角，会出现不同的效果.
1.旋转中心不变，改变旋转角（如图）
a a
问题探究
o
o
问题探究
2.旋转角不变，改变旋转中心
o
o
问题探究
3. 美丽的图案是这样形成的
课内练习——验证
把一个三角形进行旋转：
旋转角度是:
90°
观察如图所示的图案，它可以看做是什么
“基本图案”通过怎样的旋转而得到的？
基本图案是: 四角星 两个相邻的
旋转中心是:
旋转方向是:
图案中心
顺时针
旋转角度是:
180°
做一做： 在图中，正方形ABCD与正方形EFGH 边长相等，这个图案可以看作是哪个 “基本图案”通过旋转得到的
B
顺次连接各关键点；
(5)写出结论： 说明所作出的图形。
探究3：如图,ΔDEF是由△ABC绕某一中 心旋转一定的角度得到,请你找出这旋转中心 .
C D B A
E F
.
O
旋确定转中心的方法：分别作两组对应点连 线的垂直平分线，其交点为旋转中心。
A O
B
C
图形C可以看作图形B绕O点 0 顺时针方向旋转 90得到。
A O
A D
B
O
C
图形D可以看作图形C绕O点 0 顺时针方向旋转 90得到。
1、右图可以看做是一个菱形通过几次
旋转得到的？每次旋转了多少度？
2、你用“旋转”来分析图案的形 成过程时, 能完整的描述出来吗？
基本图案是:
一个菱形
旋转中心是:
A.45°
B.60°
C.90°
D.180°
图案的旋转 把一个图案（如图）进行旋转，选择不同的旋 转中心， 不同的旋转角，会出现不同的效果.
1.旋转中心不变，改变旋转角（如图）
a a
问题探究
o
o
问题探究
2.旋转角不变，改变旋转中心
o
o
问题探究
3. 美丽的图案是这样形成的
课内练习——验证
把一个三角形进行旋转：
旋转角度是:
90°
观察如图所示的图案，它可以看做是什么
“基本图案”通过怎样的旋转而得到的？
基本图案是: 四角星 两个相邻的
旋转中心是:
旋转方向是:
图案中心
顺时针
旋转角度是:
180°
做一做： 在图中，正方形ABCD与正方形EFGH 边长相等，这个图案可以看作是哪个 “基本图案”通过旋转得到的
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
；⑤S△AOC+S△AOB=6+ 9 3 ．其中正确的结论是（）
4
A．①②③⑤
B．①②③④
C．①②③④⑤ D．①②③
举一反三：已知：如图，P为等边△ABC内一点， ∠APB=113°，∠APC=123°，试说明：以AP、BP 、CP为边长可以构成一个三角形，并确定所构成三角 形的各内角的度数．
解：将△APC绕点A顺时针旋转60°得△AQB， 则△AQB≌△APC ∴BQ=CP，AQ=AP， ∵∠1+∠3=60°， ∴△APQ是等边三角形， ∴QP=AP， ∴△QBP就是以AP，BP，CP三边为边的三角形 ， ∵∠APB=113°， ∴∠6=∠APB-∠5=53°， ∵∠AQB=∠APC=123°， ∴∠7=∠AQB-∠4=63°， ∴∠QBP=180°-∠6-∠7=64°， ∴以AP，BP，CP为边的三角形的三内角的度数 分别为64°，63°，53°．
（第二课时）
1这. 旋节转课的你定学义到：了什么知识？ 在平面内，将一个图形绕一个定点沿着某个方向
你是转这用动个什一定定点么的称方角为度旋法，转获这中样心得的，这图转形动些运的知动角称称识为为的旋旋转转？角. . 本2①、节旋旋课转转不你的改还性变图有质形：什的大么小地与形方状没，但有可解改变决定吗向；？
② 旋转前后两图形任意一对对应点与旋转中心的连 线所成的角都是旋转角，
③ 对应点到旋转中心的距离相等.
练习
1.如图，如果把钟表的指针看做四边形AOBC，它绕O点旋 转得到四边形DOEF. 在这个旋转过程中：
（1）旋转中心是什么?
旋转中心是O
（2）经过旋转，点A、B分别移动到什么位置？ 点D和点E的位置
转中心的点有 3 个
作业
1、书59页习题23.1的第1题（写本上） 2、书60页4、5、6、7、8、9（写书上） 3、全效学习44~46页
随堂练习
1.将等边△ABC绕着点A按某个方向旋转400后得到 △ADE(点B与点D是对应点)，则∠BAE的度数为_____.
动手操作
请设计一个绕一点旋转600后能与自身重合的图形.
C
O
B A
2312图形的旋转作图
B/
CC/
O
AA/
B
2、如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋 转中心.
C
A
D B
E
.O
F
旋转中心在对应点连线的垂直平分线上。
B
旋转中心应该在对 应点连线的垂直平 分线上
1.如图，如果正方形CDEF旋转后能与正 方形ABCD重合，那么图形所在的平面
M B′ A′ N B
O
A
2.⑴如图,画出△ABC绕点A按逆时针方向旋转900后的 对应三角形;
⑵如果点D是AC的中点,那么经过上述旋转后,点D旋转
到什么位置?请在图中将点D的对应点
C
D′表示出来.
B'
C' D
D'
A
B
(3)如果AD=1cm,那么点D旋转过的路径是多少?Leabharlann C' D'
C B'
D
A
B
3.如图所示的方格纸中，将△ABC向右平移8格，再以 O为旋转中心逆时针旋转900，画出旋转后的三角形.
(2)可以通过旋转变换但不能通过平移变换得到的图案是_②___⑥ (3)既可以由平移变换, 也可以由旋转变换得到的图案是_③___④_
①
②
③
④
⑤
⑥
2312图形的旋转作图
例1 ： 将A点绕O点沿顺时针方向旋转60˚.
点的旋转作法
B
A
O
B点即为所求.
2312图形的旋转作图
例2 将线段AB绕O点沿顺时针方向旋转60˚.
上可以作为旋转中心的点共有 3 个.
A
D
E
●
B
C
F
变式1（2007•潍坊）如图，两个全等的长方形ABCD与
CDEF，旋转长方形ABCD能和长方形CDEF重合，则可以
作为旋转中心的点有（ A ）
A．1个
B．2个
C．3个
D．无
数个
变式2：如图，两个有一边重合的正三角形， 那么由其中一个正三角形绕平面内某一点旋转 后能与另一个三角形重合，平面内可以作为旋
（3）旋转角是什么？ ∠AOD和∠BOE都是旋转角
（4）AO与DO的长有什么关系？BO与EO呢？ AO=DO，BO=EO （5）∠AOD与∠BOE有什么大小关系？
∠AOD=∠BOE
2、下列图形均可以由“基本图案”通过变换得到.(填序号) (1)通过平移变换但不能通过旋转变换得到的图案是__①___⑤____;
线段的旋转作法
C
A
O
D
B
则线段CD即为所求作.
2312图形的旋转作图
图形的旋转作法
例3 如图，△ABC绕C点旋转后，顶 点A得对应点为点D. 试确定顶点B对 应点的位置以及旋转后的三角形.
E
A
D 则△DEC即为所求作.
B
C
简单的旋转作图
1.已知线段AB和点O，请画出线段AB绕点O按逆时 针旋转1000后的图形.
思考：已知：如图，在△ABC中，∠BAC=1200，以BC为
边向形外作等边三角形△BCD，把△ABD绕着点D按顺
时针方向旋转600后得到△ECD，若AB=3，AC=2，求
∠BAD的度数与AD的长.
E
C A
B
D
2312
图 形 的 旋 转 作 图
（2012•十堰）如图，O是正△ABC内一点，OA=3， OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋 转60°得到线段BO′，下列结论：①△BO′A可以由 △BOC绕点B逆时针旋转60°得到；②点O与O′的距离 为4；③∠AOB=150°；④S四边形AOBO′=6+ 3 3
4
A．①②③⑤
B．①②③④
C．①②③④⑤ D．①②③
举一反三：已知：如图，P为等边△ABC内一点， ∠APB=113°，∠APC=123°，试说明：以AP、BP 、CP为边长可以构成一个三角形，并确定所构成三角 形的各内角的度数．
解：将△APC绕点A顺时针旋转60°得△AQB， 则△AQB≌△APC ∴BQ=CP，AQ=AP， ∵∠1+∠3=60°， ∴△APQ是等边三角形， ∴QP=AP， ∴△QBP就是以AP，BP，CP三边为边的三角形 ， ∵∠APB=113°， ∴∠6=∠APB-∠5=53°， ∵∠AQB=∠APC=123°， ∴∠7=∠AQB-∠4=63°， ∴∠QBP=180°-∠6-∠7=64°， ∴以AP，BP，CP为边的三角形的三内角的度数 分别为64°，63°，53°．
（第二课时）
1这. 旋节转课的你定学义到：了什么知识？ 在平面内，将一个图形绕一个定点沿着某个方向
你是转这用动个什一定定点么的称方角为度旋法，转获这中样心得的，这图转形动些运的知动角称称识为为的旋旋转转？角. . 本2①、节旋旋课转转不你的改还性变图有质形：什的大么小地与形方状没，但有可解改变决定吗向；？
② 旋转前后两图形任意一对对应点与旋转中心的连 线所成的角都是旋转角，
③ 对应点到旋转中心的距离相等.
练习
1.如图，如果把钟表的指针看做四边形AOBC，它绕O点旋 转得到四边形DOEF. 在这个旋转过程中：
（1）旋转中心是什么?
旋转中心是O
（2）经过旋转，点A、B分别移动到什么位置？ 点D和点E的位置
转中心的点有 3 个
作业
1、书59页习题23.1的第1题（写本上） 2、书60页4、5、6、7、8、9（写书上） 3、全效学习44~46页
随堂练习
1.将等边△ABC绕着点A按某个方向旋转400后得到 △ADE(点B与点D是对应点)，则∠BAE的度数为_____.
动手操作
请设计一个绕一点旋转600后能与自身重合的图形.
C
O
B A
2312图形的旋转作图
B/
CC/
O
AA/
B
2、如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋 转中心.
C
A
D B
E
.O
F
旋转中心在对应点连线的垂直平分线上。
B
旋转中心应该在对 应点连线的垂直平 分线上
1.如图，如果正方形CDEF旋转后能与正 方形ABCD重合，那么图形所在的平面
M B′ A′ N B
O
A
2.⑴如图,画出△ABC绕点A按逆时针方向旋转900后的 对应三角形;
⑵如果点D是AC的中点,那么经过上述旋转后,点D旋转
到什么位置?请在图中将点D的对应点
C
D′表示出来.
B'
C' D
D'
A
B
(3)如果AD=1cm,那么点D旋转过的路径是多少?Leabharlann C' D'
C B'
D
A
B
3.如图所示的方格纸中，将△ABC向右平移8格，再以 O为旋转中心逆时针旋转900，画出旋转后的三角形.
(2)可以通过旋转变换但不能通过平移变换得到的图案是_②___⑥ (3)既可以由平移变换, 也可以由旋转变换得到的图案是_③___④_
①
②
③
④
⑤
⑥
2312图形的旋转作图
例1 ： 将A点绕O点沿顺时针方向旋转60˚.
点的旋转作法
B
A
O
B点即为所求.
2312图形的旋转作图
例2 将线段AB绕O点沿顺时针方向旋转60˚.
上可以作为旋转中心的点共有 3 个.
A
D
E
●
B
C
F
变式1（2007•潍坊）如图，两个全等的长方形ABCD与
CDEF，旋转长方形ABCD能和长方形CDEF重合，则可以
作为旋转中心的点有（ A ）
A．1个
B．2个
C．3个
D．无
数个
变式2：如图，两个有一边重合的正三角形， 那么由其中一个正三角形绕平面内某一点旋转 后能与另一个三角形重合，平面内可以作为旋
（3）旋转角是什么？ ∠AOD和∠BOE都是旋转角
（4）AO与DO的长有什么关系？BO与EO呢？ AO=DO，BO=EO （5）∠AOD与∠BOE有什么大小关系？
∠AOD=∠BOE
2、下列图形均可以由“基本图案”通过变换得到.(填序号) (1)通过平移变换但不能通过旋转变换得到的图案是__①___⑤____;
线段的旋转作法
C
A
O
D
B
则线段CD即为所求作.
2312图形的旋转作图
图形的旋转作法
例3 如图，△ABC绕C点旋转后，顶 点A得对应点为点D. 试确定顶点B对 应点的位置以及旋转后的三角形.
E
A
D 则△DEC即为所求作.
B
C
简单的旋转作图
1.已知线段AB和点O，请画出线段AB绕点O按逆时 针旋转1000后的图形.
思考：已知：如图，在△ABC中，∠BAC=1200，以BC为
边向形外作等边三角形△BCD，把△ABD绕着点D按顺
时针方向旋转600后得到△ECD，若AB=3，AC=2，求
∠BAD的度数与AD的长.
E
C A
B
D
2312
图 形 的 旋 转 作 图
（2012•十堰）如图，O是正△ABC内一点，OA=3， OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋 转60°得到线段BO′，下列结论：①△BO′A可以由 △BOC绕点B逆时针旋转60°得到；②点O与O′的距离 为4；③∠AOB=150°；④S四边形AOBO′=6+ 3 3