山东省邹城市第七中学2015-2016学年七年级下学期期末质量检测数学试题(图片版,无答案)
山东省济宁市2015-2016学年七年级数学下册期末检测题2

山东省济宁市金乡县2015-2016学年七年级数学下学期期末质量检测试题
沁园春·雪 <毛泽东>
北国风光,千里冰封,万里雪飘。
望长城内外,惟余莽莽;
大河上下,顿失滔滔。
山舞银蛇,原驰蜡象,
欲与天公试比高。
须晴日,看红装素裹,分外妖娆。
江山如此多娇,引无数英雄竞折腰。
惜秦皇汉武,略输文采;
唐宗宋祖,稍逊风骚。
一代天骄,成吉思汗,
只识弯弓射大雕。
俱往矣,数风流人物,还看今朝。
薄雾浓云愁永昼,瑞脑消金兽。
佳节又重阳,玉枕纱厨,半夜凉初透。
东篱把酒黄昏后,有暗香盈袖。
莫道不消魂,帘卷西风,人比黄花瘦。
2015-2016学年山东省济宁市邹城八中七年级(下)期中数学模拟试卷

2015-2016学年山东省济宁市邹城八中七年级(下)期中数学模拟试卷一、选择题:1.在下列式子中,正确的是()A.=﹣B.﹣=﹣0.6C.=﹣13D.=±62.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离()A.等于4cm B.大于4cm而小于5cmC.不大于4cm D.小于4cm3.如图所示,下列说法错误的是()A.∠1和∠3是同位角B.∠1和∠5是同位角C.∠1和∠2是同旁内角D.∠5和∠6是内错角4.有下列说法中正确的说法的个数是()(1)无理数就是开方开不尽的数;(2)无理数是无限不循环小数;(3)无理数包括正无理数,零,负无理数;(4)无理数都可以用数轴上的点来表示.A.1B.2C.3D.45.在如图五幅图案中,(2)、(3)、(4)、(5)中哪一幅图案可以通过平移图案(1)得到()A..(2)B.(3)C.(4)D.(5)6.若=a﹣4,则a的取值范围是()A.a<4B.a≤4C.a>4D.a≥47.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是()A.∠3=∠A B.∠1=∠2C.∠D=∠DCE D.∠D+∠ACD=180°8.如果一个实数的平方根与它的立方根相等,则这个数是()A.0B.正实数C.0和1D.19.如图,已知AB∥CD,则∠α=()A.85°B.60°C.75°D.80°10.已知:|a|=3,=5,且|a+b|=a+b,则a﹣b的值为()A.2或8B.2或﹣8C.﹣2或8D.﹣2或﹣8 11.若点P(m,1)在第二象限内,则点Q(﹣m,0)在()A.x轴正半轴上B.x轴负半轴上C.y轴正半轴上D.y轴负半轴上12.已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数为()A.3个B.4个C.5个D.6个13.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b 的值为()A.2B.3C.4D.5二、填空题:14.如果n是的小数部分,则n=.15.把命题“等角的补角相等”改写成“如果…那么…”的形式是.16.已知=10.1,则﹣=.17.吸管吸易拉罐内的饮料时,如图所示,∠1=110°,则∠2=度.(易拉罐的上下底面互相平行)18.如图,数轴上点A表示的无理数是.19.如果点P(m+3,m﹣2)在x轴上,那么m=.三、解答题:20.计算:(1)++(2)(﹣1)﹣|﹣|21.如图,直线CD与直线AB相交于C,根据下列语句画图(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.22.如图是一只鸭子的图案,请探究下列问题:(1)写出各个顶点的坐标;(2)试计算图案覆盖的面积.23.如图,方格中有一条美丽可爱的小金鱼.(1)若方格的边长为1,则小鱼的面积为;(2)画出小鱼向左平移3格后的图形.(不要求写作图步骤和过程)24.如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠COB、∠BOF的度数.25.已知a、b满足+|b﹣|=0,解关于x的方程(a+2)x﹣b2=a﹣1.26.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?2015-2016学年山东省济宁市邹城八中七年级(下)期中数学模拟试卷参考答案与试题解析一、选择题:1.在下列式子中,正确的是()A.=﹣B.﹣=﹣0.6C.=﹣13D.=±6【分析】A、根据立方根的性质即可判定;B、根据算术平方根的定义即可判定;C根据算术平方根的性质化简即可判定;D、根据算术平方根定义即可判定.【解答】解:A,=﹣,故A选项正确;B、﹣≈﹣1.9,故B选项错误;C、=13,故C选项错误;D、=6,故D选项错误.故选:A.2.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离()A.等于4cm B.大于4cm而小于5cmC.不大于4cm D.小于4cm【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,∴点P到直线l的距离≤PC,即点P到直线l的距离不大于4.故选:C.3.如图所示,下列说法错误的是()A.∠1和∠3是同位角B.∠1和∠5是同位角C.∠1和∠2是同旁内角D.∠5和∠6是内错角【分析】根据同位角,同旁内角,内错角的定义可以得到A、C、D是正确的;∠1与∠5不是两直线被第三条直线所截得到的角,不是同位角.【解答】解:从图上可以看出∠1和∠5不存在直接联系,而其它三个选项都符合各自角的定义,正确;故选:B.4.有下列说法中正确的说法的个数是()(1)无理数就是开方开不尽的数;(2)无理数是无限不循环小数;(3)无理数包括正无理数,零,负无理数;(4)无理数都可以用数轴上的点来表示.A.1B.2C.3D.4【分析】(1)根据无理数的定义即可判定;(2)根据无理数的定义即可判定;(3)根据无理数的分类即可判定;(4)根据无理数和数轴上的点对应关系即可判定.【解答】解:(1)开方开不尽的数是无理数,但是无理数不仅仅是开方开不尽的数,故(1)说法错误;(2)无理数是无限不循环小数,故(2)说法正确;(3)0是有理数,故(3)说法错误;(4)无理数都可以用数轴上的点来表示,故(4)说法正确.故选:B.5.在如图五幅图案中,(2)、(3)、(4)、(5)中哪一幅图案可以通过平移图案(1)得到()A..(2)B.(3)C.(4)D.(5)【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.【解答】解:通过图案平移得到必须与题中已知图案完全相同,角度也必须相同,观察图形可知五幅图案中,(2)、(3)、(4)、(5)中(3)这幅图案可以通过平移图案(1)得到.故选:B.6.若=a﹣4,则a的取值范围是()A.a<4B.a≤4C.a>4D.a≥4【分析】已知等式利用二次根式性质化简,再利用绝对值的代数意义求出a的范围即可.【解答】解:∵=|a﹣4|=a﹣4,∴a﹣4≥0,即a≥4,故选:D.7.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是()A.∠3=∠A B.∠1=∠2C.∠D=∠DCE D.∠D+∠ACD=180°【分析】根据平行线的判定分别进行分析可得答案.【解答】解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;故选:B.8.如果一个实数的平方根与它的立方根相等,则这个数是()A.0B.正实数C.0和1D.1【分析】根据立方根和平方根的性质可知,只有0的立方根和它的平方根相等,解决问题.【解答】解:0的立方根和它的平方根相等都是0;1的立方根是1,平方根是±1,∴一个实数的平方根与它的立方根相等,则这个数是0.故选:A.9.如图,已知AB∥CD,则∠α=()A.85°B.60°C.75°D.80°【分析】过∠α的顶点作AB的平行线,然后根据两直线平行,同旁内角互补求出∠1,再根据两直线平行,内错角相等求出∠2,然后求解即可.【解答】解:如图,过∠α的顶点作AB的平行线EF,∵AB∥CD,∴AB∥EF∥CD,∴∠1=180°﹣120°=60°,∠2=25°,∴∠α=∠1+∠2=60°+25°=85°.故选:A.10.已知:|a|=3,=5,且|a+b|=a+b,则a﹣b的值为()A.2或8B.2或﹣8C.﹣2或8D.﹣2或﹣8【分析】利用绝对值的代数意义,以及二次根式性质求出a与b的值,即可求出a﹣b的值.【解答】解:根据题意得:a=3或﹣3,b=5或﹣5,∵|a+b|=a+b,∴a=3,b=5;a=﹣3,b=5,则a﹣b=﹣2或﹣8.故选:D.11.若点P(m,1)在第二象限内,则点Q(﹣m,0)在()A.x轴正半轴上B.x轴负半轴上C.y轴正半轴上D.y轴负半轴上【分析】根据第二象限内点的横坐标小于零,纵坐标大于零,可得不等式,根据不等式的性质,可得﹣m的取值范围,可得答案.【解答】解:由点P(m,1)在第二象限内,得m<0,﹣m>0,点Q(﹣m,0)在x轴的正半轴上,故选:A.12.已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数为()A.3个B.4个C.5个D.6个【分析】怎样选取分类的标准,才能做到点C的个数不遗不漏,按照点C所在的直线分为两种情况:当点C与点A在同一条直线上时,AC边上的高为1,AC=2,符合条件的点C有4个;当点C与点B在同一条直线上时,BC边上的高为1,BC=2,符合条件的点C有2个.【解答】解:C点所有的情况如图所示:故选:D.13.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b 的值为()A.2B.3C.4D.5【分析】直接利用平移中点的变化规律求解即可.【解答】解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A、B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.故选:A.二、填空题:14.如果n是的小数部分,则n=﹣3.【分析】先利用逼近法求出在哪两个连续的整数之间,那么两个连续整数中较小的整数是其整数部分,再进一步表示出其小数部分.【解答】解:∵3<<4,∴的整数部分为3,∴小数部分为﹣3,即n=﹣3.故答案为﹣3.15.把命题“等角的补角相等”改写成“如果…那么…”的形式是如果两个角是等角的补角,那么它们相等.【分析】命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面.【解答】解:题设为:两个角是等角的补角,结论为:相等,故写成“如果…那么…”的形式是:如果两个角是等角的补角,那么它们相等.故答案为:如果两个角是等角的补角,那么它们相等.16.已知=10.1,则﹣=﹣1.01.【分析】依据被开方数小数向左移动两位,对应的算术平方根小数点向左移动一位回答即可.【解答】解:∵=10.1,∴=1.01.∴﹣=﹣1.01.故答案为:﹣1.01.17.吸管吸易拉罐内的饮料时,如图所示,∠1=110°,则∠2=70度.(易拉罐的上下底面互相平行)【分析】本题主要利用两直线平行,同旁内角互补以及对顶角相等进行解题.【解答】解:因为易拉罐的上下底面互相平行,所以∠2与∠1的对顶角之和为180°.又因为∠1与其对顶角相等,所以∠2+∠1=180°,故∠2=180°﹣∠1=180°﹣110°=70°.18.如图,数轴上点A表示的无理数是﹣.【分析】图中正方形的边长为1,则可根据勾股定理求出正方形对角线的长度.以对角线长度为半径作圆与x轴交于点A,则OA也为圆的半径,并且等于对角线的长度.【解答】解:应用勾股定理得,正方形的对角线的长度为:,OA为圆的半径,则OA=.所以数轴上的点A表示的无理数为:﹣.故答案为:﹣.19.如果点P(m+3,m﹣2)在x轴上,那么m=2.【分析】根据x轴上的点的纵坐标等于0列式计算即可得解.【解答】解:∵点P(m+3,m﹣2)在x轴上,∴m﹣2=0,解得m=2.故答案为:2.三、解答题:20.计算:(1)++(2)(﹣1)﹣|﹣|【分析】(1)原式利用平方根、立方根定义计算即可得到结果;(2)原式利用二次根式乘法,以及绝对值的代数意义化简,计算即可得到结果.【解答】解:(1)原式=9﹣3+=6;(2)原式=2﹣﹣+=2﹣.21.如图,直线CD与直线AB相交于C,根据下列语句画图(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.【分析】(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)利用两直线平行,同旁内角互补即可解决问题.【解答】解:(1)如图所示:PQ即为所求;(2)如图所示:PR即为所求;(3)∠PQC=60°理由:∵PQ∥CD,∴∠DCB+∠PQC=180°,∵∠DCB=120°,∴∠PQC=180°﹣120°=60°.22.如图是一只鸭子的图案,请探究下列问题:(1)写出各个顶点的坐标;(2)试计算图案覆盖的面积.【分析】(1)根据各象限点的坐标特征和坐标轴上点的坐标特征写出各点坐标;(2)用长为6、宽为3的矩形的面积分别减去三个三角形的面积和一个梯形的面积进行计算.【解答】解:(1)A(﹣1,0),B(0,1),C(1,1),D(1,﹣1),E(5,1),F(4,﹣2);(2)图案覆盖的面积=6×3﹣•1•1﹣•(1+2)•2﹣•1•3﹣•2•4=9.23.如图,方格中有一条美丽可爱的小金鱼.(1)若方格的边长为1,则小鱼的面积为16;(2)画出小鱼向左平移3格后的图形.(不要求写作图步骤和过程)【分析】(1)求小鱼的面积利用长方形的面积减去周边的三角形的面积即可得到;(2)直接根据平移作图的方法作图即可.【解答】解:(1)小鱼的面积为7×6﹣×5×6﹣×2×5﹣×4×2﹣×1.5×1﹣××1﹣1﹣=16;(2)将每个关键点向左平移3个单位,连接即可.24.如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠COB、∠BOF的度数.【分析】此题利用余角和对顶角的性质,即可求出∠COB的度数,利用角平分线及补角的性质又可求出∠BOF的度数.【解答】解:∵OE⊥CD于点O,∠1=50°,∴∠AOD=90°﹣∠1=40°,∵∠BOC与∠AOD是对顶角,∴∠BOC=∠AOD=40°.∵OD平分∠AOF,∴∠DOF=∠AOD=40°,∴∠BOF=180°﹣∠BOC﹣∠DOF=180°﹣40°﹣40°=100°.25.已知a、b满足+|b﹣|=0,解关于x的方程(a+2)x﹣b2=a﹣1.【分析】根据非负数的性质列出方程求出a、b的值,代入求方程的解即可.【解答】解:∵+|b﹣|=0,∴2a+8=0,b﹣=0,解得a=﹣4,b=,∴﹣2x﹣3=﹣5,∴x=1.26.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?【分析】(1)∠1+∠2=180°而∠2+∠CDB=180°,则∠CDB=∠1,根据同位角相等,两直线平行,求得结论;(2)要说明AD与BC平行,只要说明∠BCF+∠CDA=180°即可.而根据AE∥FC 可得:∠CDA+∠DEA=180°,再据∠DAE=∠BCF就可以证得.(3)BC平分∠DBE即说明∠EBC=∠DBC是否成立.根据AE∥FC,可得:∠EBC=∠BCF,据AD∥BC得到:∠BCF=∠FAD,∠DBC=∠BAD,进而就可以证出结论.【解答】解:(1)平行;证明:∵∠2+∠CDB=180°,∠1+∠2=180°,∴∠CDB=∠1,∴AE∥FC.(2)平行,证明:∵AE∥FC,∴∠CDA+∠DAE=180°,∵∠DAE=∠BCF∴∠CDA+∠BCF=180°,∴AD∥BC.(3)平分,证明:∵AE∥FC,∴∠EBC=∠BCF,∵AD∥BC,∴∠BCF=∠FDA,∠DBC=∠BDA,又∵DA平分∠BDF,即∠FDA=∠BDA,∴∠EBC=∠DBC,∴BC平分∠DBE.。
15—16学年下学期七年级期末考试数学试题(附答案)

2015-2016学年第二学期期末联考试卷七年级数学一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如果座位表上“5列2行”记作(5,2),那么(4,3)表示()A.3列5行B.5列3行C.4列3行D.3列4行2.如果a>b,那么下列不等式中一定成立的是()A.a2>b2B.1﹣a>1﹣b C.1+a>1﹣b D.1+a>b﹣13.在下列实数中:0,,﹣3.1415,,,0.343343334…无理数有()A.1个B.2个C.3个D.4个4.下面调查中,适合采用普查的是()A.调查全国中学生心理健康现状B.调查你所在的班级同学的身高情况C.调查我市食品合格情况D.调查南京市电视台《今日生活》收视率5.若是方程kx﹣2y=2的一个解,则k等于()A.B.C.6 D.﹣6.如图,能判定EC∥AB的条件是()A.∠B=∠ACE B.∠A=∠ECD C.∠B=∠ACB D.∠A=∠ACE7.如图,在平面直角坐标系中,A(﹣3,2)、B(﹣1,0)、C(﹣1,3),将△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1,点A、B、C的对应点分别A1、B1、C1,则点A1的坐标为()A.(3,﹣3)B.(1,﹣1)C.(3,0)D.(2,﹣1)8.在平面直角坐标系中,点(﹣2,﹣2m+3)在第三象限,则m的取值范围是()A.B.C.D.9.若关于x的不等式组无解,则a的取值范围是()A.a≤3 B.a≥3 C.a<3 D.a>310.已知方程组和有相同的解,则a,b的值为()A.B.C.D.11.小明要制作一个长方形的相片框架,这个框架的长为25cm,面积不小于500cm2,则宽的长度xcm应满足的不等式组为()A.B.C.D.12.为了鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费).规定:用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费.如图是张磊家2015年9月和10月所交电费的收据,则该市规定的第一阶梯电价和第二阶梯电价分别为每度()A.0.5元、0.6元B.0. 4元、0.5元C.0.3元、0.4元D.0.6元、0.7元第6题图第7题图第12题图二、填空题:本大题共6小题,每小题3分,共18分.把答案填在题中横线上.13.的整数部分是.14.某学校为了了解八年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在25~30之间的频率为.15.已知2x﹣3y﹣1=0,请用含x的代数式表示y:.16.如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为°.17.若不等式组的解集是﹣1<x <1,则b a 212 的立方根为 . 18.如图,正方形ABCD 的顶点B 、C 都在直角坐标系的x 轴上,若点D 的坐标是(3,4),则点A 的坐标是 .第14题图 第16题图 第18题图三、解答题:本大题共6小题,共46分.解答应写出必要的文字说明、证明过程或演算步骤.19.(5分)解方程组:20.(6分)解不等式组请结合题意填空,完成本题的解答. (1)解不等式①,得 ;(2)解不等式②,得 ;(3)把不等式①和②的解集在数轴上表示出来:(4)原不等式组的解集为 .21.(7分)请根据如图所示的对话内容回答下列问题.(1)求该魔方的棱长;(2)求该长方体纸盒的长.22.(8分)已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.证明:AD∥BE.证明:∵AB∥CD(已知)∴∠4=①(②)∵∠3=∠4(已知)∴∠3=③(④)∵∠1=∠2(已知)∴∠1+∠CAF=∠2+∠CAF(等量代换)即∠BAF=∠DAC∴∠3= ⑤(等量代换)∴AD∥BE(⑥)23.(9分)某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类.在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,表)和图是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:(1)表中m=,n=;(2)在图中,将表示“自然科学”的部分补充完整;(3)若该学校打算采购一万册图书,请你估算“哲学”类图书应采购多少册较合适?(4)根据图表提供的信息,请你提出一条合理化的建议.24.(11分)在南宁市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和1台电子白板共需要2万元,购买2台电脑和1台电子白板共需要2.5万元.(1)求每台电脑、每台电子白板各多少万元?(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过32万元,但不低于30万元,请你通过计算求出有几种购买方案,哪种方案费用最低.2015-2016学年第二学期期末联考七年级数学评分细则一、选择题(本题共12小题,每小题3分,共36分)1-5 CDBBC 6-10 DBBAD 11-12 AA二、填空题(本题共6小题,每小题3分,共18分)13. 4 14. 0.4 15. y=16. 35 17. 2 18. (﹣1,4)三、解答题(本大题共6小题,共46分)注:解答题解法多样,非本细则所述的其他正确解法请阅卷老师酌情给分19. 解:,①+②×2得:7x=7,即x=1,------- 3分把x=1代入①得:y=1,------- 4分则方程组的解为------- 5分20. 解:(1)x<2,------- 1分(2)x≥﹣1,------- 3分(3)------- 5分(4)-1≤x<2.------- 6分21. 解:(1)设魔方的棱长为x cm,可得:x3=216,------- 2分解得:x=6.------- 3分(2)设该长方体纸盒的长为y cm,6y2=600,------- 5分y2=100,即y=10.------- 6分答:魔方的棱长6 cm,长方体纸盒的长为10 cm.------- 7分22. 解:①∠BAE ,------- 1分②(两直线平行,同位角相等),------- 3分③∠BAE ------- 4分④(等量代换),------- 5分⑤∠DAC ,------- 6分⑥(内错角相等,两直线平行).------- 8分23. 解:(1)m= 500 ,------- 2分n= 0.05 ;------- 3分(2)自然科学:2000×0.20=400 册如图,------- 5分(3)10000×0.05=500(册),即估算“哲学”类图书应采购500册较合适;------- 7分(4)鼓励学生多借阅哲学类的书.------- 9分24. 解:(1)设每台电脑x万元,每台电子白板y万元,根据题意得:,------- 3分解得,即每台电脑0.5万元,每台电子白板1.5万元;------- 5分(2)设需购进电脑a台,则购进电子白板(30﹣a)台,根据题意得:,------- 7分解得:13≤a≤15,∵a只能取整数,∴a=13,14,15,------- 9分∴有三种购买方案,方案1:需购进电脑13台,则购进电子白板17台,13×0.5+1.5×17=32(万元),方案2:需购进电脑14台,则购进电子白板16台,14×0.5+1.5×16=31(万元),方案3:需购进电脑15台,则购进电子白板15台,15×0.5+1.5×15=30(万元),∵30<31<32,∴购买电脑15台,电子白板15台最省钱.------- 11分。
山东省济宁市邹城八中2015-2016学年七年级(下)期中数学模拟试卷(解析版)

2015-2016学年山东省济宁市邹城八中七年级(下)期中数学模拟试卷一、选择题:1.在下列式子中,正确的是()A.=﹣B.﹣=﹣0.6 C.=﹣13 D.=±62.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离()A.等于4cm B.大于4cm而小于5cmC.不大于4cm D.小于4cm3.如图所示,下列说法错误的是()A.∠1和∠3是同位角B.∠1和∠5是同位角C.∠1和∠2是同旁内角D.∠5和∠6是内错角4.有下列说法中正确的说法的个数是()(1)无理数就是开方开不尽的数;(2)无理数是无限不循环小数;(3)无理数包括正无理数,零,负无理数;(4)无理数都可以用数轴上的点来表示.A.1 B.2 C.3 D.45.在如图五幅图案中,(2)、(3)、(4)、(5)中哪一幅图案可以通过平移图案(1)得到()A..(2)B.(3) C.(4) D.(5)6.若=a﹣4,则a的取值范围是()A.a<4 B.a≤4 C.a>4 D.a≥47.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是()A.∠3=∠4 B.∠1=∠2 C.∠D=∠DCE D.∠D+∠ACD=180°8.如果一个实数的平方根与它的立方根相等,则这个数是()A.0 B.正实数C.0和1 D.19.如图,已知AB∥CD,则∠α=()A.85°B.60°C.75°D.80°10.已知:|a|=3,=5,且|a+b|=a+b,则a﹣b的值为()A.2或8 B.2或﹣8 C.﹣2或8 D.﹣2或﹣811.若点P(m,1)在第二象限内,则点Q(﹣m,0)在()A.x轴正半轴上B.x轴负半轴上C.y轴正半轴上D.y轴负半轴上12.已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数为()A.3个B.4个C.5个D.6个13.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()A.2 B.3 C.4 D.5二、填空题:14.如果n是的小数部分,则n=.15.把命题“等角的补角相等”改写成“如果…那么…”的形式是.16.已知=10.1,则﹣=.17.吸管吸易拉罐内的饮料时,如图所示,∠1=110°,则∠2=度.(易拉罐的上下底面互相平行)18.如图,数轴上点A表示的无理数是.19.如果点P(m+3,m﹣2)在x轴上,那么m=.三、解答题:20.计算:(1)++(2)(﹣1)﹣|﹣|21.如图,直线CD与直线AB相交于C,根据下列语句画图(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.22.如图是一只鸭子的图案,请探究下列问题:(1)写出各个顶点的坐标;(2)试计算图案覆盖的面积.23.如图,方格中有一条美丽可爱的小金鱼.(1)若方格的边长为1,则小鱼的面积为;(2)画出小鱼向左平移3格后的图形.(不要求写作图步骤和过程)24.如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠COB、∠BOF的度数.25.已知a、b满足+|b﹣|=0,解关于x的方程(a+2)x﹣b2=a﹣1.26.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?2015-2016学年山东省济宁市邹城八中七年级(下)期中数学模拟试卷参考答案与试题解析一、选择题:1.在下列式子中,正确的是()A.=﹣B.﹣=﹣0.6 C.=﹣13 D.=±6【考点】立方根;算术平方根.【分析】A、根据立方根的性质即可判定;B、根据算术平方根的定义即可判定;C根据算术平方根的性质化简即可判定;D、根据算术平方根定义即可判定.【解答】解:A,=﹣,故A选项正确;B、﹣≈﹣1.9,故B选项错误;C、=13,故C选项错误;D、=6,故D选项错误.故选:A.2.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离()A.等于4cm B.大于4cm而小于5cmC.不大于4cm D.小于4cm【考点】点到直线的距离.【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,∴点P到直线l的距离≤PC,即点P到直线l的距离不大于4.故选C.3.如图所示,下列说法错误的是()A.∠1和∠3是同位角B.∠1和∠5是同位角C.∠1和∠2是同旁内角D.∠5和∠6是内错角【考点】同位角、内错角、同旁内角.【分析】根据同位角,同旁内角,内错角的定义可以得到A、C、D是正确的;∠1与∠5不是两直线被第三条直线所截得到的角,不是同位角.【解答】解:从图上可以看出∠1和∠5不存在直接联系,而其它三个选项都符合各自角的定义,正确;故选B.4.有下列说法中正确的说法的个数是()(1)无理数就是开方开不尽的数;(2)无理数是无限不循环小数;(3)无理数包括正无理数,零,负无理数;(4)无理数都可以用数轴上的点来表示.A.1 B.2 C.3 D.4【考点】无理数.【分析】(1)根据无理数的定义即可判定;(2)根据无理数的定义即可判定;(3)根据无理数的分类即可判定;(4)根据无理数和数轴上的点对应关系即可判定.【解答】解:(1)开方开不尽的数是无理数,但是无理数不仅仅是开方开不尽的数,故(1)说法错误;(2)无理数是无限不循环小数,故(2)说法正确;(3)0是有理数,故(3)说法错误;(4)无理数都可以用数轴上的点来表示,故(4)说法正确.故选:B.5.在如图五幅图案中,(2)、(3)、(4)、(5)中哪一幅图案可以通过平移图案(1)得到()A..(2)B.(3) C.(4) D.(5)【考点】生活中的平移现象.【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.【解答】解:通过图案平移得到必须与题中已知图案完全相同,角度也必须相同,观察图形可知五幅图案中,(2)、(3)、(4)、(5)中(3)这幅图案可以通过平移图案(1)得到.故选:B.6.若=a﹣4,则a的取值范围是()A.a<4 B.a≤4 C.a>4 D.a≥4【考点】二次根式的性质与化简.【分析】已知等式利用二次根式性质化简,再利用绝对值的代数意义求出a的范围即可.【解答】解:∵=|a﹣4|=a﹣4,∴a﹣4≥0,即a≥4,故选D.7.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是()A.∠3=∠4 B.∠1=∠2 C.∠D=∠DCE D.∠D+∠ACD=180°【考点】平行线的判定.【分析】根据平行线的判定分别进行分析可得答案.【解答】解:A、根据内错角相等,两直线平行可得BD∥AC,故此选项错误;B、根据内错角相等,两直线平行可得AB∥CD,故此选项正确;C、根据内错角相等,两直线平行可得BD∥AC,故此选项错误;D、根据同旁内角互补,两直线平行可得BD∥AC,故此选项错误;故选:B.8.如果一个实数的平方根与它的立方根相等,则这个数是()A.0 B.正实数C.0和1 D.1【考点】立方根;平方根.【分析】根据立方根和平方根的性质可知,只有0的立方根和它的平方根相等,解决问题.【解答】解:0的立方根和它的平方根相等都是0;1的立方根是1,平方根是±1,∴一个实数的平方根与它的立方根相等,则这个数是0.故选A.9.如图,已知AB∥CD,则∠α=()A.85°B.60°C.75°D.80°【考点】平行线的性质.【分析】过∠α的顶点作AB的平行线,然后根据两直线平行,同旁内角互补求出∠1,再根据两直线平行,内错角相等求出∠2,然后求解即可.【解答】解:如图,过∠α的顶点作AB的平行线EF,∵AB∥CD,∴AB∥EF∥CD,∴∠1=180°﹣120°=60°,∠2=25°,∴∠α=∠1+∠2=60°+25°=85°.故选A.10.已知:|a|=3,=5,且|a+b|=a+b,则a﹣b的值为()A.2或8 B.2或﹣8 C.﹣2或8 D.﹣2或﹣8【考点】实数的运算.【分析】利用绝对值的代数意义,以及二次根式性质求出a与b的值,即可求出a﹣b的值.【解答】解:根据题意得:a=3或﹣3,b=5或﹣5,∵|a+b|=a+b,∴a=3,b=5;a=﹣3,b=5,则a﹣b=﹣2或﹣8.故选D.11.若点P(m,1)在第二象限内,则点Q(﹣m,0)在()A.x轴正半轴上B.x轴负半轴上C.y轴正半轴上D.y轴负半轴上【考点】点的坐标.【分析】根据第二象限内点的横坐标小于零,纵坐标大于零,可得不等式,根据不等式的性质,可得﹣m的取值范围,可得答案.【解答】解:由点P(m,1)在第二象限内,得m<0,﹣m>0,点Q(﹣m,0)在x轴的正半轴上,故选:A.12.已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数为()A.3个B.4个C.5个D.6个【考点】三角形的面积.【分析】怎样选取分类的标准,才能做到点C的个数不遗不漏,按照点C所在的直线分为两种情况:当点C与点A在同一条直线上时,AC边上的高为1,AC=2,符合条件的点C 有4个;当点C与点B在同一条直线上时,BC边上的高为1,BC=2,符合条件的点C有2个.【解答】解:C点所有的情况如图所示:故选:D.13.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()A.2 B.3 C.4 D.5【考点】坐标与图形变化-平移.【分析】直接利用平移中点的变化规律求解即可.【解答】解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A、B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.故选:A.二、填空题:14.如果n是的小数部分,则n=﹣3.【考点】估算无理数的大小.【分析】先利用逼近法求出在哪两个连续的整数之间,那么两个连续整数中较小的整数是其整数部分,再进一步表示出其小数部分.【解答】解:∵3<<4,∴的整数部分为3,∴小数部分为﹣3,即n=﹣3.故答案为﹣3.15.把命题“等角的补角相等”改写成“如果…那么…”的形式是如果两个角是等角的补角,那么它们相等.【考点】命题与定理.【分析】命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面.【解答】解:题设为:两个角是等角的补角,结论为:相等,故写成“如果…那么…”的形式是:如果两个角是等角的补角,那么它们相等.故答案为:如果两个角是等角的补角,那么它们相等.16.已知=10.1,则﹣=﹣1.01.【考点】算术平方根.【分析】依据被开方数小数向左移动两位,对应的算术平方根小数点向左移动一位回答即可.【解答】解:∵=10.1,∴=1.01.∴﹣=﹣1.01.故答案为:﹣1.01.17.吸管吸易拉罐内的饮料时,如图所示,∠1=110°,则∠2=70度.(易拉罐的上下底面互相平行)【考点】平行线的性质;对顶角、邻补角.【分析】本题主要利用两直线平行,同旁内角互补以及对顶角相等进行解题.【解答】解:因为易拉罐的上下底面互相平行,所以∠2与∠1的对顶角之和为180°.又因为∠1与其对顶角相等,所以∠2+∠1=180°,故∠2=180°﹣∠1=180°﹣110°=70°.18.如图,数轴上点A表示的无理数是﹣.【考点】勾股定理;实数与数轴.【分析】图中正方形的边长为1,则可根据勾股定理求出正方形对角线的长度.以对角线长度为半径作圆与x轴交于点A,则OA也为圆的半径,并且等于对角线的长度.【解答】解:应用勾股定理得,正方形的对角线的长度为:,OA为圆的半径,则OA=.所以数轴上的点A表示的无理数为:﹣.故答案为:﹣.19.如果点P(m+3,m﹣2)在x轴上,那么m=2.【考点】点的坐标.【分析】根据x轴上的点的纵坐标等于0列式计算即可得解.【解答】解:∵点P(m+3,m﹣2)在x轴上,∴m﹣2=0,解得m=2.故答案为:2.三、解答题:20.计算:(1)++(2)(﹣1)﹣|﹣|【考点】实数的运算.【分析】(1)原式利用平方根、立方根定义计算即可得到结果;(2)原式利用二次根式乘法,以及绝对值的代数意义化简,计算即可得到结果.【解答】解:(1)原式=9﹣3+=6;(2)原式=2﹣﹣+=2﹣.21.如图,直线CD与直线AB相交于C,根据下列语句画图(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.【考点】作图—基本作图.【分析】(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)利用两直线平行,同旁内角互补即可解决问题.【解答】解:(1)如图所示:PQ即为所求;(2)如图所示:PR即为所求;(3)∠PQC=60°理由:∵PQ∥CD,∴∠DCB+∠PQC=180°,∵∠DCB=120°,∴∠PQC=180°﹣120°=60°.22.如图是一只鸭子的图案,请探究下列问题:(1)写出各个顶点的坐标;(2)试计算图案覆盖的面积.【考点】坐标与图形性质;三角形的面积.【分析】(1)根据各象限点的坐标特征和坐标轴上点的坐标特征写出各点坐标;(2)用长为6、宽为3的矩形的面积分别减去三个三角形的面积和一个梯形的面积进行计算.【解答】解:(1)A(﹣1,0),B(0,1),C(1,1),D(1,﹣1),E(5,1),F(4,﹣2);(2)图案覆盖的面积=6×3﹣•1•1﹣•(1+2)•2﹣•1•3﹣•2•4=9.23.如图,方格中有一条美丽可爱的小金鱼.(1)若方格的边长为1,则小鱼的面积为16;(2)画出小鱼向左平移3格后的图形.(不要求写作图步骤和过程)【考点】利用平移设计图案.【分析】(1)求小鱼的面积利用长方形的面积减去周边的三角形的面积即可得到;(2)直接根据平移作图的方法作图即可.【解答】解:(1)小鱼的面积为7×6﹣×5×6﹣×2×5﹣×4×2﹣×1.5×1﹣××1﹣1﹣=16;(2)将每个关键点向左平移3个单位,连接即可.24.如图,直线AB 、CD 相交于O ,OD 平分∠AOF ,OE ⊥CD 于点O ,∠1=50°,求∠COB 、∠BOF 的度数.【考点】垂线;角平分线的定义;余角和补角;对顶角、邻补角.【分析】此题利用余角和对顶角的性质,即可求出∠COB 的度数,利用角平分线及补角的性质又可求出∠BOF 的度数.【解答】解:∵OE ⊥CD 于点O ,∠1=50°,∴∠AOD=90°﹣∠1=40°,∵∠BOC 与∠AOD 是对顶角,∴∠BOC=∠AOD=40°.∵OD 平分∠AOF ,∴∠DOF=∠AOD=40°,∴∠BOF=180°﹣∠BOC ﹣∠DOF=180°﹣40°﹣40°=100°.25.已知a 、b 满足+|b ﹣|=0,解关于x 的方程(a+2)x ﹣b 2=a ﹣1.【考点】非负数的性质:算术平方根;非负数的性质:绝对值;解一元一次方程.【分析】根据非负数的性质列出方程求出a 、b 的值,代入求方程的解即可.【解答】解:∵+|b ﹣|=0,∴2a+8=0,b ﹣=0,解得a=﹣4,b=,∴﹣2x ﹣3=﹣5,∴x=1.26.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?【考点】平行线的判定.【分析】(1)∠1+∠2=180°而∠2+∠CDB=180°,则∠CDB=∠1,根据同位角相等,两直线平行,求得结论;(2)要说明AD与BC平行,只要说明∠BCF+∠CDA=180°即可.而根据AE∥FC可得:∠CDA+∠DEA=180°,再据∠DAE=∠BCF就可以证得.(3)BC平分∠DBE即说明∠EBC=∠DBC是否成立.根据AE∥FC,可得:∠EBC=∠BCF,据AD∥BC得到:∠BCF=∠FAD,∠DBC=∠BAD,进而就可以证出结论.【解答】解:(1)平行;证明:∵∠2+∠CDB=180°,∠1+∠2=180°,∴∠CDB=∠1,∴AE∥FC.(2)平行,证明:∵AE∥FC,∴∠CDA+∠DAE=180°,∵∠DAE=∠BCF∴∠CDA+∠BCF=180°,∴AD∥BC.(3)平分,证明:∵AE∥FC,∴∠EBC=∠BCF,∵AD∥BC,∴∠BCF=∠FDA,∠DBC=∠BDA,又∵DA平分∠BDF,即∠FDA=∠BDA,∴∠EBC=∠DBC,∴BC平分∠DBE.2016年5月12日。
山东省济宁市2015-2016学年七年级(下)期末数学试卷(解析版)

2015-2016学年山东省济宁市七年级(下)期末数学试卷一、选择题(下列各题约四个选项中,只有一项符合题意,每小题3分,共36分)1.的平方根是()A.B.C.D.2.下列调查中,适合用全面调查方式的是()A.了解某班学生“50米跑”的成绩B.了解一批灯泡的使用寿命C.了解一批袋装食品是否含有防腐剂D.了解一批炮弹的杀伤半径3.已知a<b,则下列不等式一定成立的是()A.a+5>b+5 B.﹣2a<﹣2b C.D.7a﹣7b<04.按如图的运算程序,能使输出结果为3的x,y的值是()A.x=5,y=﹣2 B.x=3,y=﹣3 C.x=﹣4,y=2 D.x=﹣3,y=﹣95.如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于()A.30°B.45°C.60°D.90°6.一个关于x的一元一次不等式组的解集在数轴上表示如图,则该不等式组的解集是()A.﹣2<x<1 B.﹣2<x≤1 C.﹣2≤x<1 D.﹣2≤x≤17.下列实数中,2π,,3.14159,﹣,,中无理数有()个.A.1 B.2 C.3 D.48.估计的值在()A.1和2之间B.2和3之间C.3和4之间D.4和5之间9.某学校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间和数据,结果如图,根据此条形图估计这一天该校学生平均课外阅读时间为()A.0.96小时 B.1.07小时 C.1.15小时 D.1.50小时10.如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为()A.向北直走700米,再向西直走100米B.向北直走100米,再向东直走700米C.向北直走300米,再向西直走400米D.向北直走400米,再向东直走300米11.为了改善住房条件,小亮的父母考察了某小区的A、B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房的面积比A套楼房的面积大24平方米,两套楼房的房价相同,第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设A套楼房的面积为x平方米,B套楼房的面积为y平方米,根据以上信息列出了下列方程组.其中正确的是()A. B.C. D.12.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是()A.(66,34)B.(67,33)C. D.(99,34)二、填空题(每小题3分,共15分)13.已知关于x,y的二元一次方程组的解互为相反数,则k的值是______.14.如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则∠ACB=______.15.一组数据:19,22,25,30,28,27,26,21,20,22,24,23,25,29,27,28,27,30,19,20,为了画频率分布直方图,先计算出最大值与最小值的差是11,如果取组距为2,应分为______组,第一组的起点定为18.5,在26.5﹣﹣28.5范围内的频数是______,频率是______.16.若a,b是实数,且+|2a﹣b+1|=0,则(b﹣a)2015等于______.17.如果不等式组的解集是0≤x<1,那么a+b的值为______.三、解答题(共8个小题,共49分)18.计算:﹣+||+.19.解不等式组,并写出它的所有非负整数解.20.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.21.解方程组:.22.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.23.为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D 四个等级,其中相应等级的里程依次为200 千米,210 千米,220千米,230 千米,获得如下不完整的统计图.根据以上信息,解答下列问题:(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?24.某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B 型号计算器,可获利润120元.(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?25.阅读下列材料:解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:解∵x﹣y=2,∴x=y+2.又∵x>1,∴y+2>1.∴y>﹣1.又∵y<0,∴﹣1<y<0.…①同理得:1<x<2.…②由①+②得﹣1+1<y+x<0+2.∴x+y的取值范围是0<x+y<2.请按照上述方法,完成下列问题:(1)已知x﹣y=3,且x>2,y<1,求(a<﹣2)x+y的取值范围;(2)已知y>1,x<﹣1,若x﹣y=a成立,求x+y的取值范围(结果用含a的式子表示).2015-2016学年山东省济宁市七年级(下)期末数学试卷参考答案与试题解析一、选择题(下列各题约四个选项中,只有一项符合题意,每小题3分,共36分)1.的平方根是()A.B. C. D.【考点】平方根.【分析】根据一个正数有两个平方根,它们互为相反数进行解答即可.【解答】解:±=±.故选:B.2.下列调查中,适合用全面调查方式的是()A.了解某班学生“50米跑”的成绩B.了解一批灯泡的使用寿命C.了解一批袋装食品是否含有防腐剂D.了解一批炮弹的杀伤半径【考点】全面调查与抽样调查.【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.【解答】解:A、人数不多,容易调查,因而适合全面调查,故选项正确;B、如果普查,所有电池都报废,这样就失去了实际意义;C、范围太广,不适合普查,故选项错误;D、如果普查,所有炮弹都报废,这样就失去了实际意义.故选A.3.已知a<b,则下列不等式一定成立的是()A.a+5>b+5 B.﹣2a<﹣2b C.D.7a﹣7b<0【考点】不等式的性质.【分析】根据不等式的性质判断即可.【解答】解:A、∵a<b,∴a+5<b+5,故本选项错误;B、∵a<b,∴﹣2a>﹣2b,故本选项错误;C、∵a<b,∴a<b,故本选项错误;D、∵a<b,∴7a<7b,∴7a﹣7b<0,故本选项正确;故选D.4.按如图的运算程序,能使输出结果为3的x,y的值是()A.x=5,y=﹣2 B.x=3,y=﹣3 C.x=﹣4,y=2 D.x=﹣3,y=﹣9【考点】代数式求值;二元一次方程的解.【分析】根据运算程序列出方程,再根据二元一次方程的解的定义对各选项分析判断利用排除法求解.【解答】解:由题意得,2x﹣y=3,A、x=5时,y=7,故A选项错误;B、x=3时,y=3,故B选项错误;C、x=﹣4时,y=﹣11,故C选项错误;D、x=﹣3时,y=﹣9,故D选项正确.故选:D.5.如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于()A.30°B.45°C.60°D.90°【考点】平行线的性质.【分析】由直角三角板的特点可得:∠C=30°,然后根据两直线平行内错角相等,即可求∠CAE的度数.【解答】解:∵∠C=30°,BC∥DE,∴∠CAE=∠C=30°.故选A.6.一个关于x的一元一次不等式组的解集在数轴上表示如图,则该不等式组的解集是()A.﹣2<x<1 B.﹣2<x≤1 C.﹣2≤x<1 D.﹣2≤x≤1【考点】在数轴上表示不等式的解集.【分析】根据不等式解集的表示方法即可判断.【解答】解:该不等式组的解集是:﹣2≤x<1.故选C.7.下列实数中,2π,,3.14159,﹣,,中无理数有()个.A.1 B.2 C.3 D.4【考点】无理数;立方根.【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【解答】解:2π,,是无理数,故选:C.8.估计的值在()A.1和2之间B.2和3之间C.3和4之间D.4和5之间【考点】估算无理数的大小.【分析】直接利用32=9,42=16得出的取值范围.【解答】解:∵32=9,42=16,∴估计在3和4之间.故选:C.9.某学校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间和数据,结果如图,根据此条形图估计这一天该校学生平均课外阅读时间为()A.0.96小时 B.1.07小时 C.1.15小时 D.1.50小时【考点】加权平均数;条形统计图.【分析】先从直方图中读出数据,再根据平均数的公式计算即可.【解答】解:50名学生平均的阅读时间为=1.07,由此可估计该校学生平均课外阅读时间也是1.07小时.故选:B.10.如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为()A.向北直走700米,再向西直走100米B.向北直走100米,再向东直走700米C.向北直走300米,再向西直走400米D.向北直走400米,再向东直走300米【考点】坐标确定位置.【分析】根据对话画出图形,进而得出从邮局出发走到晓莉家的路线.【解答】解:如图所示:从邮局出发走到晓莉家应:向北直走700米,再向西直走100米.故选:A.11.为了改善住房条件,小亮的父母考察了某小区的A、B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房的面积比A套楼房的面积大24平方米,两套楼房的房价相同,第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设A套楼房的面积为x平方米,B套楼房的面积为y平方米,根据以上信息列出了下列方程组.其中正确的是()A. B.C. D.【考点】由实际问题抽象出二元一次方程组.【分析】题中没有平均价,可设平均价为1.关键描述语是:B套楼房的面积比A套楼房的面积大24平方米;两套楼房的房价相同,即为平均价1.等量关系为:B套楼房的面积﹣A 套楼房的面积=24;0.9×1×B套楼房的面积=1.1×1×A套楼房的面积,根据等量关系可列方程组.【解答】解:设A套楼房的面积为x平方米,B套楼房的面积为y平方米,可列方程组为.故选D.12.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是()A.(66,34)B.(67,33)C. D.(99,34)【考点】坐标确定位置;规律型:点的坐标.【分析】根据走法,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,用100除以3,然后根据商和余数的情况确定出所处位置的横坐标与纵坐标即可.【解答】解:由题意得,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,∵100÷3=33余1,∴走完第100步,为第34个循环组的第1步,所处位置的横坐标为33×3+1=100,纵坐标为33×1=33,∴棋子所处位置的坐标是.故选:C.二、填空题(每小题3分,共15分)13.已知关于x,y的二元一次方程组的解互为相反数,则k的值是﹣1.【考点】二元一次方程组的解.【分析】将方程组用k表示出x,y,根据方程组的解互为相反数,得到关于k的方程,即可求出k的值.【解答】解:解方程组得:,因为关于x,y的二元一次方程组的解互为相反数,可得:2k+3﹣2﹣k=0,解得:k=﹣1.故答案为:﹣1.14.如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则∠ACB=105°.【考点】方向角.【分析】过点C作CD∥AE,从而可证明CD∥BF,然后由平行线的性质可知∠DCA=∠CAE,∠DCB=∠CBF,从而可求得∠ACB的度数.【解答】解:过点C作CD∥AE.∵CD∥AE,BF∥AE,∴CD∥BF.∵CD∥AE,∴∠DCA=∠CAE=60°,同理:∠DCB=∠CBF=45°.∴∠ACB=∠ACD+∠BCD=105°.15.一组数据:19,22,25,30,28,27,26,21,20,22,24,23,25,29,27,28,27,30,19,20,为了画频率分布直方图,先计算出最大值与最小值的差是11,如果取组距为2,应分为6组,第一组的起点定为18.5,在26.5﹣﹣28.5范围内的频数是5,频率是0.25.【考点】频数(率)分布直方图.【分析】根据频数分布直方图的制作方法,结合该组数据即可得出结论.【解答】解:∵该组数据极差为11,组距定为2,11÷2=5 (1)∴该组数据应分为6组.∵在26.5﹣﹣28.5范围内的数有:28、27、27、28、27,该组数据共20个数,∴在26.5﹣﹣28.5范围内的频数为5,频率为=0.25.故答案为:6;5;0.25.16.若a,b是实数,且+|2a﹣b+1|=0,则(b﹣a)2015等于﹣1.【考点】解二元一次方程组;非负数的性质:绝对值;非负数的性质:算术平方根.【分析】利用非负数的性质列出方程组,求出方程组的解得到a与b的值,代入原式计算即可得到结果.【解答】解:∵a,b是实数,且+|2a﹣b+1|=0,∴,解得:a=﹣2,b=﹣3,则原式=(﹣3+2)2015=(﹣1)2015=﹣1,故答案为:﹣117.如果不等式组的解集是0≤x<1,那么a+b的值为1.【考点】解一元一次不等式组.【分析】先用含有a、b的代数式把每个不等式的解集表示出来,然后根据已告知的解集,进行比对,得到两个方程,解方程求出a、b.【解答】解:由得:x≥4﹣2a由2x﹣b<3得:故原不等式组的解集为:4﹣2a≤又因为0≤x<1所以有:4﹣2a=0,解得:a=2,b=﹣1于是a+b=1.故答案为:1.三、解答题(共8个小题,共49分)18.计算:﹣+||+.【考点】实数的运算.【分析】原式第一项利用算术平方根定义计算,第二项利用立方根定义计算,第三项利用绝对值的代数意义化简,最后一项利用二次根式性质化简即可得到结果.【解答】解:原式=7﹣3+﹣1+=+.19.解不等式组,并写出它的所有非负整数解.【考点】解一元一次不等式组;一元一次不等式组的整数解.【分析】分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,即可确定出所有非负整数解.【解答】解:,由①得:x≥﹣2;由②得:x<,∴不等式组的解集为﹣2≤x<,则不等式组的所有非负整数解为:0,1,2,3.20.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.【考点】平行线的性质.【分析】由平行线的性质得到∠ABC=∠1=65°,∠ABD+∠BDC=180°,由BC平分∠ABD,得到∠ABD=2∠ABC=130°,于是得到结论.【解答】解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,∵BC平分∠ABD,∴∠ABD=2∠ABC=130°,∴∠BDC=180°﹣∠ABD=50°,∴∠2=∠BDC=50°.21.解方程组:.【考点】解二元一次方程组.【分析】方程组利用加减消元法求出解即可.【解答】解:,①+②得:﹣m=22,即m=﹣22,把m=﹣22代入①得:b=77,则方程组的解为.22.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.【考点】坐标确定位置.【分析】此题答案不唯一,建立的直角坐标系的原点不一样,答案不一样.【解答】解:以南门的位置作为原点建立直角坐标系,则动物们的位置分别表示为:南门(0,0),马(﹣3,﹣3);两栖动物(4,1);飞禽(3,4);狮子(﹣4,5).23.为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D 四个等级,其中相应等级的里程依次为200 千米,210 千米,220千米,230 千米,获得如下不完整的统计图.根据以上信息,解答下列问题:(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?【考点】条形统计图;用样本估计总体;扇形统计图.【分析】(1)根据统计图中的数据可以求得这次被抽检的电动汽车的数量,从而可以求得A 等级的电动车的数量,进而可以将条形统计图补充完整;(2)根据统计图中的数据可以得到这种电动汽车一次充电后行驶的平均里程数.【解答】解:(1)这次被抽检的电动汽车共有:30÷30%=100(辆),等级为A的电动车有:100﹣30﹣40﹣20=10(辆),补全的统计图如右图所示,(2)这种电动汽车一次充电后行驶的平均里程数为:=217(千米),即这种电动汽车一次充电后行驶的平均里程数为217千米.24.某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B 型号计算器,可获利润120元.(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?【考点】一元一次不等式的应用;二元一次方程组的应用.【分析】(1)首先设A种型号计算器的销售价格是x元,A种型号计算器的销售价格是y 元,根据题意可等量关系:①5台A型号和1台B型号计算器,可获利润76元;②销售6台A型号和3台B型号计算器,可获利润120元,根据等量关系列出方程组,再解即可;(2)根据题意表示出所用成本,进而得出不等式求出即可.【解答】解:(1)设A种型号计算器的销售价格是x元,B种型号计算器的销售价格是y 元,由题意得:,解得:;答:A种型号计算器的销售价格是42元,B种型号计算器的销售价格是56元;(2)设购进A型计算器a台,则购进B台计算器:(70﹣a)台,则30a+40(70﹣a)≤2500,解得:a≥30,答:最少需要购进A型号的计算器30台.25.阅读下列材料:解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:解∵x﹣y=2,∴x=y+2.又∵x>1,∴y+2>1.∴y>﹣1.又∵y<0,∴﹣1<y<0.…①同理得:1<x<2.…②由①+②得﹣1+1<y+x<0+2.∴x+y的取值范围是0<x+y<2.请按照上述方法,完成下列问题:(1)已知x﹣y=3,且x>2,y<1,求(a<﹣2)x+y的取值范围;(2)已知y>1,x<﹣1,若x﹣y=a成立,求x+y的取值范围(结果用含a的式子表示).【考点】一元一次不等式组的应用.【分析】(1)先求出y的取值范围,同理得出x的取值范围,即可得出结果;(2)先求出y的取值范围,同理得出x的取值范围,即可得出结果.【解答】解:(1)∵x﹣y=3,∴x=y+3.又∵x>2,∴y+3>2∴y>﹣1.又∵y<1∴﹣1<y<1.同理得:2<x<4,由①+②得:﹣1+2<y+x<1+4.∴x+y的取值范围是:1<x+y<5.(2)∵x﹣y=a,∴x=y+a.又∵x<﹣1,∴y+a<﹣1.∴y<﹣a﹣1.又∵y>1,a<﹣2,∴1<y<﹣a﹣1.同理得:a+1<x<﹣1.由①+②得:1+a+1<y+x<﹣a﹣1+(﹣1).∴x+y的取值范围是:a+2<x+y<﹣a﹣2.2016年10月4日。
山东省济宁市邹城市七年级数学下学期期中试题(含解析)

山东省济宁市邹城市2015-2016学年七年级数学下学期期中试题一、选择题1.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个C.3个D.4个2.如图所示,下列各组角的位置,判断错误的是()A.∠C和∠CFG是同旁内角B.∠CGF和∠AFG是内错角C.∠BGF和∠A是同旁内角D.∠BGF和∠AFD是同位角3.如图,E点是AD延长线上一点,下列条件中,不能判定直线BC∥AD的是()A.∠3=∠4B.∠C=∠CDEC.∠1=∠2D.∠C+∠ADC=180°4.如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有()A.1个B.2个C.3个D.4个5.规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3.按此规定[]的值为()A.3B.4C.5D.66.如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为()A.2B.4C.8D.167.已知+|b+1|=0,那么(a+b)2007的值为()A.﹣32007B.32007C.1D.﹣18.有一个数值转换器,原理如下:当输入的x为64时,输出的y是()A.8B. C. D.9.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的大小是()A.150°B.130°C.140°D.120°10.如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为()A. B.1﹣C. D.2﹣二、填空题11.的算术平方根为.12.如图是一把剪刀,其中∠1=40°,则∠2= .13.已知a、b满足+=b,则a+b的值为.14.如图,已知BO平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长是.15.若点A(2,a)关于x轴的对称点是B(b,﹣3),则ab的值是.16.如图,一张宽度相等的纸条,折叠后,若∠ABC=120°,则∠1的度数为.17.﹣27的立方根与的算术平方根的和.18.如图a,ABCD是长方形纸带(AD∥BC),∠DEF=19°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是;如果按照这样的方式再继续折叠下去,直到不能折叠为止,那么先后一共折叠的次数是.三、解答题19.(2016春•邹城市期中)计算题:.20.(2014春•静宁县校级期末)已知:如图,∠B=∠ADE,∠EDC=∠GFB,GF⊥AB.求证:CD⊥AB.21.(2016春•邹城市期中)在平面直角坐标系中,O为坐标原点,A(﹣2,3),B(2,2).(1)画出三角形OAB;(2)求三角形OAB的面积;(3)若三角形OAB中任意一点P(x1,y1)经平移后对应点为P1(x1+4,y1﹣3),请画出三角形OAB平移后得到的三角形O1A1B1,并写出点O1,A1,B的坐标.22.(2016春•邹城市期中)在一副三角板ABC和DEF中.(1)当AB∥CD,如图①,求∠DCB的度数.(2)当CD与CB重合时,如图②,判定DE与AC的位置关系,并说明理由.(3)如图③,当∠DCB等于多少度时,AB∥EC?23.(2002•河北)图形的操作过程:在图①中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分);在图②中,将折线A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影;(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:S1= ,S2= ,S3= .(3)联想与探索:如图④在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少并说明你的猜想是正确的.24.(2016春•自贡期末)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.(1)求点C,D的坐标;(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标.(3)若点P在直线BD上运动,连接PC,PO.①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.2015-2016学年山东省济宁市邹城市七年级(下)期中数学试卷参考答案与试题解析一、选择题1.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个C.3个D.4个【考点】对顶角、邻补角.【专题】应用题.【分析】一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.据此作答即可.【解答】解:只有丙图中的两个角是对顶角,故选:A.【点评】本题考查了对顶角的概念,解题的关键是掌握对顶角的概念.2.如图所示,下列各组角的位置,判断错误的是()A.∠C和∠CFG是同旁内角B.∠CGF和∠AFG是内错角C.∠BGF和∠A是同旁内角D.∠BGF和∠AF D是同位角【考点】同位角、内错角、同旁内角.【分析】本题要根据内错角、同位角以及同旁内角的定义来判断.【解答】解:A、在截线的同侧,并且在被截线之间的两个角是同旁内角,∠C和∠CFG符合同旁内角的定义,正确;B、在截线的两侧,并且在被截线之间的两个角是内错角,∠CGF和∠AFG符合内错角的定义,正确;C、在截线的同侧,并且在被截线的之间的两个角是同旁内角,∠BGF和∠A不符合同旁内角的定义,错误;D、在截线的同侧,并且在被截线的同一方的两个角是同位角,∠BGF和∠AFD符合同位角的定义,正确.故选C.【点评】本题考查了同位角、内错角、同旁内角,对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.3.如图,E点是AD延长线上一点,下列条件中,不能判定直线BC∥AD的是()A.∠3=∠4B.∠C=∠CDEC.∠1=∠2D.∠C+∠ADC=180°【考点】平行线的判定.【分析】分别利用同旁内角互补两直线平行,内错角相等两直线平行得出答案即可.【解答】解:A、∵∠3+∠4,∴BC∥AD,本选项不合题意;B、∵∠C=∠CDE,∴BC∥AD,本选项不合题意;C、∵∠1=∠2,∴AB∥CD,本选项符合题意;D、∵∠C+∠ADC=180°,∴AD∥BC,本选项不符合题意.故选:C.【点评】此题考查了平行线的判定,平行线的判定方法有:同位角相等两直线平行;内错角相等两直线平行;同旁内角互补两直线平行,熟练掌握平行线的判定是解本题的关键.4.如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有()A.1个B.2个C.3个D.4个【考点】平行线的判定.【分析】直接利用邻补角的定义,结合对顶角的性质以及平行线的判定方法分析得出答案.【解答】解:①由∠1=∠2=70°,无法得出AB∥CD,故此选项错误;②∵∠1=70°,∴∠2=70°,∵∠5=∠2=70°,∴AB∥CD,故此选项正确;③由∠3=110°,无法得出AB∥CD,故此选项错误;④∵∠1=70°,∴∠2=70°,∵∠4=110°,∴∠5=70°,∴∠5=∠2=70°,∴AB∥CD,故此选项正确;∴其中正确的有2个.【点评】此题主要考查了平行线的判定以及邻补角的定义和对顶角的性质,正确把握平行线的判定方法是解题关键.5.规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3.按此规定[]的值为()A.3B.4C.5D.6【考点】估算无理数的大小.【专题】新定义.【分析】先求出+1的范围,再根据范围求出即可.【解答】解:∵3<<4,∴4<+1<5,∴[+1]=4,故选B.【点评】本题考查了估算无理数的大小的应用,关键是求出+1的范围.6.如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为()A.2B.4C.8D.16【考点】平移的性质.【分析】首先根据平移的性质,可得BC=CE;然后根据两个三角形的高相等时,面积和底成正比,可得△ACE的面积等于△ABC的面积,据此解答即可.【解答】解:∵将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,∴BC=CE,∴△ACE的面积等于△ABC的面积,又∵△ABC的面积为2,∴△ACE的面积为2.【点评】(1)此题主要考查了平移的性质和应用,要熟练掌握,解答此题的关键是要明确:①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.②新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.(2)此题还考查了三角形的面积的求法,要熟练掌握,解答此题的关键是要明确:两个三角形的高相等时,面积和底成正比.7.已知+|b+1|=0,那么(a+b)2007的值为()A.﹣32007B.32007C.1D.﹣1【考点】非负数的性质:算术平方根;非负数的性质:绝对值.【分析】根据非负数的性质列式计算出a、b的值,根据乘方法则计算即可.【解答】解:由题意得,a+2=0,b+1=0,解得,a=﹣2,b=﹣1,则(a+b)2007=(﹣3)2007=﹣32007,故选:A.【点评】本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.8.有一个数值转换器,原理如下:当输入的x为64时,输出的y是()A.8B. C. D.【考点】算术平方根.【专题】图表型.【分析】把64按给出的程序逐步计算即可.【解答】解:由题中所给的程序可知:把64取算术平方根,结果为8,因为8是有理数,所以再取算术平方根,结果为为无理数,故y=.故选B.【点评】此类题目比较简单,解答此类题目的关键是弄清题目中所给的运算程序.9.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的大小是()A.150°B.130°C.140°D.120°【考点】平行线的性质.【专题】应用题.【分析】首先过B作BE∥AM,根据AM∥CN,可得AM∥BE∥CN,进而得到∠A=∠1,∠2+∠C=180°,然后可求出∠C的度数.【解答】解:过B作BE∥AM,∵AM∥CN,∴AM∥BE∥CN,∴∠A=∠1,∠2+∠C=180°,∵∠A=120°,∴∠1=120°,∵∠ABC=150°,∴∠2=150°﹣120°=30°,∴∠C=180°﹣30°=150°.故选A.【点评】此题主要考查了平行线性质,关键是掌握两直线平行,同旁内角互补;两直线平行,内错角相等.10.如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为()A. B.1﹣C. D.2﹣【考点】实数与数轴.【分析】设点C表示的数是x,再根据中点坐标公式即可得出x的值.【解答】解:设点C表示的数是x,∵数轴上表示1、的对应点分别为点A、点B,点A是BC的中点,∴=1,解得x=2﹣.故选D.【点评】本题考查的是实数与数轴,熟知数轴上的点与实数是一一对应关系是解答此题的关键.二、填空题11.的算术平方根为.【考点】算术平方根.【专题】计算题.【分析】首先根据算术平方根的定义计算先=2,再求2的算术平方根即可.【解答】解:∵ =2,∴的算术平方根为.故答案为:.【点评】此题考查了算术平方根的定义,解题的关键是知道=2,实际上这个题是求2的算术平方根.注意这里的双重概念.12.如图是一把剪刀,其中∠1=40°,则∠2=40°.【考点】对顶角、邻补角.【专题】应用题.【分析】剪刀即对顶角的一个应用类型,根据对顶角相等解答.【解答】解:∵∠1和∠2是对顶角,∴∠2=∠1,(对顶角相等)又∵∠1=40°,∴∠2=40°(等量代换).【点评】本题考查对顶角的定义和性质,需要熟练记忆.13.已知a、b满足+=b,则a+b的值为2014 .【考点】二次根式有意义的条件.【分析】直接利用二次根式的定义求出a的值,进而得出b的值,即可得出答案.【解答】解:∵ +=b,∴a﹣2014=0,解得:a=2014,故b=0,则a+b=2014.故答案为:2014.【点评】此题主要考查了二次根式有意义的条件,正确求出a的值是解题关键.14.如图,已知BO平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长是30 .【考点】等腰三角形的判定与性质;平行线的性质.【专题】计算题.【分析】根据BO平分∠CBA,CO平分∠ACB,且MN∥BC,可得出MO=MC,NO=NB,所以三角形AMN的周长是AB+AC.【解答】解:∵BO平分∠CBA,CO平分∠ACB,∴∠NBO=∠OBC,∠OCM=∠OCB,∵MN∥BC,∴∠NOB=∠OBC,∠MOC=∠OCB,∴∠NBO=∠NOB,∠MOC=∠MCO,∴MO=MC,NO=NB,∵AB=12,AC=18,∴△AMN的周长=AM+MN+AN=AB+AC=12+18=30.故答案为30.【点评】本题考查了等腰三角形的判定和性质以及平行线的性质,是基础知识要熟练掌握.15.若点A(2,a)关于x轴的对称点是B(b,﹣3),则ab的值是 6 .【考点】关于x轴、y轴对称的点的坐标.【专题】应用题.【分析】根据关于x轴对称的点,横坐标相同,纵坐标互为相反数得出a,b的值,从而得出ab.【解答】解:∵点A(2,a)关于x轴的对称点是B(b,﹣3),∴a=3,b=2,∴ab=6.故答案为6.【点评】本题主要考查了关于x轴对称的点,横坐标相同,纵坐标互为相反数,比较简单.16.如图,一张宽度相等的纸条,折叠后,若∠ABC=120°,则∠1的度数为60°.【考点】平行线的性质;翻折变换(折叠问题).【分析】利用平行线的性质和翻折变换的性质即可求得.【解答】解:∵∠ABC=120°,纸条的上下对边是平行的,∴∠BCD=∠ABC=120°;∵是折叠得到的∠1,∴∠1=0.5×120°=60°.故答案为:60°.【点评】本题考查平行线的性质,关键是根据知识点:两直线平行,内错角相等解答.17.﹣27的立方根与的算术平方根的和0 .【考点】实数的运算.【专题】计算题.【分析】利用立方根及算术平方根的定义计算即可得到结果.【解答】解:﹣27的立方根为﹣3, =9,9的算术平方根为3,则﹣27的立方根与的算术平方根的和为0,故答案为:0【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.18.如图a,ABCD是长方形纸带(AD∥BC),∠DEF=19°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是123°;如果按照这样的方式再继续折叠下去,直到不能折叠为止,那么先后一共折叠的次数是8 .【考点】翻折变换(折叠问题).【分析】根据两条直线平行,内错角相等,则∠BFE=∠DEF=18°,根据平角定义,则∠EFC=162°(图a),进一步求得∠BFC=162°﹣18°=144°(图b),进而求得∠CFE=144°﹣18°=126°(图c),依此类推,当角度小于19°时,就不能折叠了,即可求出折叠次数,注意折叠次数从图b是第一次折叠.【解答】解:∵AD∥BC,∠DEF=19°,∴∠BFE=∠DEF=19°,∴∠EFC=161°(图a),∴∠BFC=161°﹣19°=142°(图b),(1次)∴∠CFE=142°﹣19°=123°(图c).(2次)依此类推:123°﹣19°=104° (3次)104°﹣19°=85° (4次)85°﹣19°=66° (5次)66°﹣19°=47° (6次)47°﹣19°=28° (7次)28°﹣19°=9°.(8次)故答案为:123°;8.【点评】此题主要考查了翻折变换的性质,根据折叠能够发现相等的角进而求出是解题关键.三、解答题19.(2016春•邹城市期中)计算题:.【考点】实数的运算.【分析】分别进行乘方、二次根式的化简、开立方、绝对值等运算,然后按照实数的运算法则计算即可.【解答】解:原式=3﹣+0.5+4﹣6=1.【点评】本题考查了实数的运算,涉及了乘方、二次根式的化简、开立方、绝对值等知识点,属于基础题.20.(2014春•静宁县校级期末)已知:如图,∠B=∠ADE,∠EDC=∠GFB,GF⊥AB.求证:CD⊥AB.【考点】平行线的判定与性质.【专题】证明题.【分析】根据平行线判定推出DE∥BC推出∠DCF=∠GFB,推出CD∥GF,即可得出答案.【解答】证明:∵∠B=∠ADE,∴DE∥BC,∴∠EDC=∠DCF,∵∠EDC=∠GFB,∴∠DCF=∠GFB,∴CD∥GF,∴∠CDG=∠FGB,∵GF⊥AB∴∠CDG=∠FGB=90°,∴CD⊥AB.【点评】本题考查了平行线性质和判定的应用,主要考查学生的推理能力.21.(2016春•邹城市期中)在平面直角坐标系中,O为坐标原点,A(﹣2,3),B(2,2).(1)画出三角形OAB;(2)求三角形OAB的面积;(3)若三角形OAB中任意一点P(x1,y1)经平移后对应点为P1(x1+4,y1﹣3),请画出三角形OAB平移后得到的三角形O1A1B1,并写出点O1,A1,B的坐标.【考点】作图-平移变换.【分析】(1)直接利用A,B点坐标,在坐标系中标出得出答案;(2)直接利用三角形面积求法得出答案;(3)直接利用平移的性质得出对应点位置进而得出答案.【解答】解:(1)如图所示:△OAB即为所求;(2)S△OAB=12﹣×1×4﹣×2×3﹣×2×2=5;(3)如图所示:△O1A1B1,即为所求,O1(4,﹣3),A1(2,0),B1(6,﹣1).【点评】此题主要考查了平移变换以及三角形面积,正确得出对应点位置是解题关键.22.(2016春•邹城市期中)在一副三角板ABC和DEF中.(1)当AB∥CD,如图①,求∠DCB的度数.(2)当CD与CB重合时,如图②,判定DE与AC的位置关系,并说明理由.(3)如图③,当∠DCB等于多少度时,AB∥EC?【考点】平行线的判定与性质.【分析】(1)根据“两直线平行,内错角相等”结合三角板角的特点即可得出结论;(2)根据三角板角的特点可得出DE⊥CD,AC⊥BC,再根据“垂直于同一直线的两直线平行”即可得出结论;(3)根据“两直线平行,内错角相等”即可得出∠ABC=∠BCE,再根据三角板角的特点通过角的计算即可得出结论.【解答】解:(1)∵AB∥CD,∴∠DCB=∠ABC=30°.(2)DE∥AC.理由如下:∵∠CDE=∠ACB=90°,∴DE⊥CD,AC⊥BC,∵CD与CB重合,∴DE⊥BC,AC⊥BC,∴DE∥AC.(3)∵AB∥EC,∴∠ABC=∠BCE=30°,又∵∠DCE=45°,∴∠DCB=∠DCE﹣∠BCE=15°.故当∠DCB等于15度时,AB∥EC.【点评】本题考查了平行线的判定与性质,解题的关键是:(1)找出∠DCB=∠ABC;(2)找出DE⊥BC,AC⊥BC;(3)找出∠ABC=∠BCE.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.23.(2002•河北)图形的操作过程:在图①中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分);在图②中,将折线A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影;(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:S1= ab﹣b ,S2= ab﹣b ,S3= ab﹣b .(3)联想与探索:如图④在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少并说明你的猜想是正确的.【考点】一元二次方程的应用.【专题】几何图形问题.【分析】将矩形中空白部分相对平移,正好组成一个新的矩形,这些矩形的宽(竖直方向的边长均为b)不变,长都是减少了1个单位(水平方向的边长均为a﹣1).所以空白部分的面积是b(a﹣1)=ab﹣b.【解答】解:(1)如答图.(2)ab﹣b;ab﹣b;ab﹣b(3)猜想:依据前面的有关计算,可以猜想草地的面积仍然是ab﹣b.方案:(1)将“小路”沿着左右两个边界“剪去”;(2)将左侧的草地向右平移一个单位;(3)得到一个新矩形,如答图,理由:在新得到的矩形中,其纵向宽仍然是b,而水平方向的长变成了(a﹣1),所以草地的面积就是b(a﹣1)=ab﹣b.【点评】解题关键在于运用平移原理.24.(2016春•自贡期末)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.(1)求点C,D的坐标;(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标.(3)若点P在直线BD上运动,连接PC,PO.①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.【考点】坐标与图形性质;三角形的面积.【专题】计算题.【分析】(1)根据点的平移规律易得点C,D的坐标;(2)先计算出S平行四边形ABOC=8,设M坐标为(0,m),根据三角形面积公式得×4×|m|=8,解得m=±4,于是可得M点的坐标为(0,4)或(0,﹣4);(3)①先计算出S梯形OCDB=7,再讨论:当点P运动到点B时,S△BOC的最小值=3,则可判断S△CDP+S△BOP <4,当点P运动到点D时,S△BOC的最大值=4,于是可判断S△CDP+S△BOP>3,所以3<S△CDP+S△BOP<4;②分类讨论:当点P在BD上,如图1,作P E∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO﹣∠EPC=∠BOP ﹣∠DCP,于是∠BOP﹣∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.【解答】解:(1)由平移可知:C(0,2),D(4,2);(2)∵AB=4,CO=2,∴S平行四边形ABOC=AB•CO=4×2=8,设M坐标为(0,m),∴×4×|m|=8,解得m=±4∴M点的坐标为(0,4)或(0,﹣4);(3)①S梯形OCDB=×(3+4)×2=7,当点P运动到点B时,S△BOC最小,S△BOC的最小值=×3×2=3,S△CDP+S△BOP<4,当点P运动到点D时,S△BOC最大,S△BOC的最大值=×4×2=4,S△CDP+S△BOP>3,所以3<S△CDP+S△BOP<4;②当点P在BD上,如图1,作PE∥CD,∵CD∥AB,∴CD∥PE∥AB,∴∠DCP=∠EPC,∠BOP=∠EPO,∴∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;当点P在线段BD的延长线上时,如图2,作PE∥CD,∵CD∥AB,∴CD∥PE∥AB,∴∠DCP=∠EPC,∠BOP=∠EPO,∴∠EPO﹣∠EPC=∠BOP﹣∠DCP,∴∠BOP﹣∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.【点评】本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查三角形面积公式和平行线的性质.。
邹城试卷数学七年级下册

一、选择题(每题3分,共30分)1. 下列各数中,正数是()A. -2.5B. -1.5C. 0D. 1.52. 下列代数式中,是单项式的是()A. a + bB. 3a^2bC. 2a + 3b + 4D. a^2 + b^2 - c^23. 若a=2,b=-3,则表达式a^2 - b^2的值是()A. 5B. -5C. 1D. -14. 下列图形中,是轴对称图形的是()A. 矩形B. 平行四边形C. 梯形D. 三角形5. 一个长方形的长是8cm,宽是5cm,它的面积是()A. 20cm^2B. 40cm^2C. 48cm^2D. 80cm^26. 下列方程中,解为x=3的是()A. 2x + 1 = 7B. 3x - 2 = 7C. 4x + 3 = 7D. 5x - 4 = 77. 下列函数中,y是x的一次函数的是()A. y = x^2 + 1B. y = 2x + 3C. y = x^3 + 2xD. y = 3x^2 - 48. 若m + n = 5,m - n = 1,则m和n的值分别是()A. m = 3,n = 2B. m = 2,n = 3C. m = 4,n = 1D. m = 1,n = 49. 下列三角形中,是直角三角形的是()A. 两条边长分别为3cm和4cmB. 两条边长分别为5cm和12cmC. 两条边长分别为6cm和8cmD. 两条边长分别为7cm和24cm10. 若一个等腰三角形的底边长为10cm,腰长为8cm,则这个三角形的面积是()A. 40cm^2B. 45cm^2C. 50cm^2D. 55cm^2二、填空题(每题3分,共30分)11. 3的平方根是______,它的立方是______。
12. 若a=2,b=-3,则表达式2a^2 + 3b的值是______。
13. 一个等腰三角形的底边长为6cm,腰长为8cm,则这个三角形的周长是______cm。
14. 若y = 3x - 4,当x=2时,y的值是______。
济宁市邹城七年级下期中数学试卷及答案
2016-2017学年山东省济宁市邹城七年级(下)期中数学试卷一、选择题(每题3分)请把答案填在表格内1.16的算术平方根是()A.16 B.4 C.﹣4 D.±42.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个C.3个D.4个3.下列说法中,不正确的是()A.10的立方根是B.﹣2是4的一个平方根C.的平方根是D.0.01的算术平方根是0.14.如图,下列条件:①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,能判断直线l 1∥l2的有()A.1个B.2个C.3个D.4个5.如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()A.115°B.125°C.155°D.165°6.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于()A.20°B.30°C.35°D.40°7.若a2=4,b3=27且ab<0,则a﹣b的值为()A.﹣2 B.±5 C.5 D.﹣58.如果点A(a、b)在第三象限,则点B(﹣a+1,3b﹣5)关于原点的对称点是()A.第一象限B.第二象限C.第三象限D.第四象限9.在实数:3.14159,,1.010010001,4.21,π,中,无理数有()A.1个B.2个C.3个D.4个10.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为()A.(2,2)B.(3,2)C.(3,3)D.(2,3)11.如图,在下列四组条件中,能得到AB∥CD的是()A.∠ABD=∠BDC B.∠3=∠4C.∠BAD+∠ABC=180°D.∠1=∠212.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为()A.48 B.96 C.84 D.42二、填空(每题3分)13.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是.14.直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2= .15.已知a,b为两个连续的整数,且a<b,则a+b= .16.已知点P在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P .17.如果P(a+b,ab)在第二象限,那么点Q(a,﹣b)在第象限.18.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG=度.三、解答题:19.求下列等式中x的值:(1)2x2﹣=0(2)(x+4)3=125.20.已知2a﹣1的平方根是±3,11a+b﹣1的立方根是4,求a+2b的平方根.21.如图是小明所在学校的平面示意图,请你以教学楼为坐标原点建立平面直角坐标系,描述学校其它建筑物的位置.22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.(1)直接写出图中∠AOC的对顶角:,∠EOB的邻补角:(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.23.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:(1)过E作直线CD,使CD∥AB;(2)过E作直线EF,使EF⊥AB,垂足为F;(3)请判断直线CD与EF的位置关系,并说明理由.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.25.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)(1)A′、B′两点的坐标分别为A′、B′;(2)作出△ABC平移之后的图形△A′B′C′;(3)求△A′B′C′的面积.2016-2017学年山东省济宁市邹城七年级(下)期中数学试卷参考答案与试题解析一、选择题(每题3分)请把答案填在表格内1.16的算术平方根是()A.16 B.4 C.﹣4 D.±4【考点】22:算术平方根.【分析】根据算术平方根的概念即可求出答案.【解答】解:∵42=16,∴16的算术平方根是4,故选(B)2.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个C.3个D.4个【考点】J2:对顶角、邻补角.【分析】一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.据此作答即可.【解答】解:只有丙图中的两个角是对顶角,故选:A.3.下列说法中,不正确的是()A.10的立方根是 B.﹣2是4的一个平方根C.的平方根是D.0.01的算术平方根是0.1【考点】24:立方根;21:平方根;22:算术平方根.【分析】根据立方根,平方根的定义,即可解答.【解答】解:A.10的立方根是,正确;B.﹣2是4的一个平方根,正确;C.的平方根是±,故错误;D. 0.01的算术平方根是0.1,正确;故选C.4.如图,下列条件:①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,能判断直线l 1∥l2的有()A.1个B.2个C.3个D.4个【考点】J9:平行线的判定.【分析】利用平行线的判定方法判断即可得到结果.【解答】解:∵∠1=∠3,∴l1∥l2;∵∠4=∠5,∴l1∥l2;∵∠2+∠4=180°,∴l1∥l2,则能判断直线l1∥l2的有3个.故选C5.如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()A.115°B.125°C.155°D.165°【考点】JA:平行线的性质.【分析】如图,过点D作c∥a.由平行线的性质进行解题.【解答】解:如图,过点D作c∥a.则∠1=∠CDB=25°.又a∥b,DE⊥b,∴b∥c,DE⊥c,∴∠2=∠CDB+90°=115°.故选:A.6.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于()A.20°B.30°C.35°D.40°【考点】J2:对顶角、邻补角;IJ:角平分线的定义.【分析】根据角平分线定义求出∠AOC=∠EOC=35°,根据对顶角的定义即可求出∠BOD的度数.【解答】解:∵OA平分∠EOC,∠EOC=70°,∴∠AOC=∠EOC=35°,∴∠BOD=∠AOC=35°.故选:C.7.若a2=4,b3=27且ab<0,则a﹣b的值为()A.﹣2 B.±5 C.5 D.﹣5【考点】1E:有理数的乘方.【分析】根据有理数的乘方求出a、b,再根据异号得负判断出a的值,然后代入代数式进行计算即可得解.【解答】解:∵a2=4,b3=27,∴a=±2,b=3,∵ab<0,∴a=﹣2,∴a﹣b=﹣2﹣3=﹣5.故选D.8.如果点A(a、b)在第三象限,则点B(﹣a+1,3b﹣5)关于原点的对称点是()A.第一象限B.第二象限C.第三象限D.第四象限【考点】R6:关于原点对称的点的坐标.【分析】此题首先明确两个点关于原点对称,则横、纵坐标都是互为相反数;然后能够根据点所在的位置判断点的坐标符号,根据坐标符号得到字母的取值范围.【解答】解:∵点B(﹣a+1,3b﹣5)关于原点的对称点是(a﹣1,5﹣3b).又∵点A在第三象限即a<0,b<0.∴a﹣1<0,5﹣3b>0,∴(a﹣1,5﹣3b)是第三象限的点.故选B.9.在实数:3.14159,,1.010010001,4.21,π,中,无理数有()A .1个B .2个C .3个D .4个 【考点】26:无理数.【分析】根据无理数的定义,可得答案. 【解答】解:π是无理数, 故选:A .10.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为( ) A .(2,2) B .(3,2) C .(3,3) D .(2,3) 【考点】D5:坐标与图形性质;LB :矩形的性质.【分析】本题可在画出图后,根据矩形的性质,得知第四个顶点的横坐标应为3,纵坐标应为2.【解答】解:如图可知第四个顶点为:即:(3,2). 故选:B .11.如图,在下列四组条件中,能得到AB ∥CD 的是( )A .∠ABD=∠BDCB .∠3=∠4C .∠BAD+∠ABC=180°D .∠1=∠2 【考点】J9:平行线的判定.【分析】根据平行线的判定定理对各选项进行逐一判断即可. 【解答】解:A 、若∠ABD=∠BDC ,则AB ∥CD ,故本选项正确; B 、若∠3=∠4,则AD ∥BC ,故本选项错误;C 、若∠BAD+∠ABC=180°,则AD ∥BC ,故本选项错误; D 、若∠1=∠2,则AD ∥BC ,故本选项错误; 故选A .12.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B 到C 的方向平移到△DEF 的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )A .48B .96C .84D .42 【考点】Q2:平移的性质.【分析】根据平移的性质得出BE=6,DE=AB=10,则OE=6,则阴影部分面积=S 四边形ODFC =S 梯形ABEO ,根据梯形的面积公式即可求解.【解答】解:由平移的性质知,BE=6,DE=AB=10, ∴OE=DE ﹣DO=10﹣4=6,∴S 四边形ODFC =S 梯形ABEO =(AB+OE )•BE=(10+6)×6=48. 故选:A .二、填空(每题3分)13.如图,计划把河水引到水池A 中,先作AB ⊥CD ,垂足为B ,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是 连接直线外一点与直线上所有点的连线中,垂线段最短 .【考点】J4:垂线段最短.【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.【解答】解:根据垂线段定理,连接直线外一点与直线上所有点的连线中,垂线段最短,∴沿AB开渠,能使所开的渠道最短.故答案为:连接直线外一点与直线上所有点的连线中,垂线段最短.14.直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2= 40°.【考点】JA:平行线的性质;K7:三角形内角和定理.【分析】根据两直线平行,同位角相等可得∠3=∠1,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠4,然后根据对顶角相等解答.【解答】解:∵l1∥l2,∴∠3=∠1=85°,∴∠4=∠3﹣45°=85°﹣45°=40°,∴∠2=∠4=40°.故答案为:40°.15.已知a,b为两个连续的整数,且a<b,则a+b= 10 .【考点】2B:估算无理数的大小.【分析】根据无理数的性质,得出接近无理数的整数,即可得出a,b的值,即可得出答案.【解答】解:∵a<b,a、b为两个连续的整数,∴<<,∴a=4,b=5,∴a+b=10.故答案为:10.16.已知点P在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P (3,﹣2).【考点】D1:点的坐标.【分析】根据第二象限内点的横坐标是负数,纵坐标是正数写出即可.【解答】解:点P(3,﹣2).故答案为:(3,﹣2)答案不唯一.17.如果P(a+b,ab)在第二象限,那么点Q(a,﹣b)在第二象限.【考点】D1:点的坐标.【分析】应先判断出所求的点的横纵坐标的符号,进而判断其所在的象限.【解答】解:∵P(a+b,ab)在第二象限,∴a+b<0,ab>0,∴a,b都是负号,∴a<0,﹣b>0,∴点Q(a,﹣b)在第二象限.故填:二.18.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG=55 度.【考点】IK:角的计算.【分析】根据题意∠B′OG=∠BOG,根据平角和角平分线的定义即可求得.【解答】解:由题意可得∠B′OG=∠BOG,则∠B′OG=÷2=55°.故答案为55.三、解答题:19.求下列等式中x的值:(1)2x2﹣=0(2)(x+4)3=125.【考点】24:立方根;21:平方根.【分析】(1)直接开平方法解方程即可;(2)直接开立方解方程即可.【解答】解:(1)2x2﹣=0x=±0.5(2)(x+4)3=125x=120.已知2a﹣1的平方根是±3,11a+b﹣1的立方根是4,求a+2b的平方根.【考点】21:平方根;24:立方根.【分析】根据已知得出2a﹣1=9,11a+b﹣1=64,求出a=5,b=10,求出a+2b的值,最后求出a+2b的平方根即可.【解答】解:∵2a﹣1的平方根是±3,11a+b﹣1的立方根是4,∴2a﹣1=9,11a+b﹣1=64,∴a=5,b=10,∴a+2b=25,即a+2b的平方根是±5.21.如图是小明所在学校的平面示意图,请你以教学楼为坐标原点建立平面直角坐标系,描述学校其它建筑物的位置.【考点】D3:坐标确定位置.【分析】根据题意建立平面直角坐标系进而得出各点坐标即可.【解答】解:如图所示:实验楼(﹣2,2),行政楼(﹣2,﹣2),大门(0,﹣4),食堂(3,4),图书馆(4,﹣2).22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.(1)直接写出图中∠AOC的对顶角:∠BOD ,∠EOB的邻补角:∠AOE(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.【考点】J2:对顶角、邻补角.【分析】(1)根据对顶角和邻补角的定义直接写出即可;(2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.【解答】解:(1)∠AOC的对顶角是∠BOD,∠EOB的邻补角是∠AOE,故答案为:∠BOD,∠AOE;(2)∵∠AOC=70°,∴∠BOD=∠AOC=70°,∵∠BOE:∠EOD=2:3,∴∠BOE=×70°=28°,∴∠AOE=180°﹣28°=152°.∴∠AOE的度数为152°.23.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:(1)过E作直线CD,使CD∥AB;(2)过E作直线EF,使EF⊥AB,垂足为F;(3)请判断直线CD与EF的位置关系,并说明理由.【考点】N3:作图—复杂作图.【分析】(1)根据题意直接作出CD∥AB;(2)过点E利用三角尺作出EF⊥AB;(3)利用平行线的性质,进而得出直线CD与EF的位置关系.【解答】解:(1)、(2)如图所示:(3)CD⊥EF.理由:∵CD∥AB,∴∠CEF=∠EFB,∵EF⊥AB,∴∠EFB=90°,∴∠CEF=90°,∴CD⊥EF.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.【考点】J9:平行线的判定.【分析】首先利用平行线的性质以及角平分线的性质得到满足关于AD∥BC的条件,内错角∠2和∠E相等,得出结论.【解答】证明:∵AE平分∠BAD,∴∠1=∠2,∵AB∥CD,∠CFE=∠E,∴∠1=∠CFE=∠E,∴∠2=∠E,∴AD∥BC.25.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)(1)A′、B′两点的坐标分别为A′(3,5)、B′(1,2);(2)作出△ABC平移之后的图形△A′B′C′;(3)求△A′B′C′的面积.【考点】Q4:作图﹣平移变换.【分析】(1)由点C(﹣1,﹣3)与点C′(4,1)是对应点,得出平移规律为:向右平移5个单位,向上平移4个单位,按平移规律即可写出所求的点的坐标;(2)按平移规律作出A、B的对应点A′,B′,顺次连接A′、B′、C′,即可得到△A′B′C′;(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积即可求解.【解答】解:(1)∵△A′B′C′是△ABC平移之后得到的图象,并且C(﹣1,﹣3)的对应点C′的坐标为(4,1),∴平移前后对应点的横坐标加5,纵坐标加4,∴△ABC先向右平移5个单位,再向上平移4个单位得到△A′B′C′,∵A(﹣2,1),B(﹣4,﹣2),∴A′(3,5)、B′(1,2);(2)△A′B′C′如图所示;=4×3﹣×3×1﹣×3×2﹣×1×4(3)S△A′B′C′=12﹣1.5﹣3﹣2=5.5.故答案为(3,5),(1,2).2017年5月25日11。
山东省济宁市邹城市2015-2016学年七年级下学期期中数学试卷及参考答案

山东省济宁市邹城市2015-2016学年七年级下学期期中数学试卷一、选择题1. 如图,∠1和∠2是对顶角的图形个数有( )A . 1个B . 2个C . 3个 D . 4个2. 如图所示,下列各组角的位置,判断错误的是( )A . ∠C 和∠CFG 是同旁内角B . ∠CGF 和∠AFG 是内错角C . ∠BGF 和∠A 是同旁内角D . ∠BGF 和∠AFD 是同位角3.如图,E 点是AD 延长线上一点,下列条件中,不能判定直线BC ∥AD 的是( )A . ∠3=∠4B . ∠C=∠CDEC . ∠1=∠2D . ∠C+∠ADC=180°4. 如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB ∥CD ;②若∠5=70°,则AB ∥CD ;③若∠3=110°,则AB ∥CD ;④若∠4=110°,则AB ∥CD .其中正确的有( )A . 1个B . 2个C . 3个D . 4个5. 规定用符号[m]表示一个实数m 的整数部分,例如:[ ]=0,[3.14]=3.按此规定[+1]的值为( )A . 3B . 4C . 5D . 66. 如图,将△ABC 沿射线BC 方向移动,使点B 移动到点C ,得到△DCE ,连接AE ,若△ABC 的面积为2,则△ACE 的面积为( )A . 2B . 4C . 8D . 167. 已知 +|b+1|=0,那么(a+b )的值为( )A . ﹣3B . 3C . 1D . ﹣18. 有一个数值转换器,原理如下:当输入的x 为64时,输出的y 是( )A . 8B .C .D .9. 如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A 是120°,第二次拐的角∠B 是150°,第三次拐的角是∠C ,这时的道路恰好和第一次拐弯之前的道路平行,则∠C 的大小是( )200720072007A . 150°B . 130°C . 140°D . 120°10.如图,数轴上表示1、的对应点分别为点A,点B.若点A是BC的中点,则点C所表示的数为()A .B . 1﹣ C . D . 2﹣二、填空题11. 的算术平方根为________.12. 如图是一把剪刀,其中∠1=40°,则∠2=________.13. 已知a、b满足 + =b,则a+b的值为________.14. 如图,已知BO平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长是____ ____.15. 若点A(2,a)关于x轴的对称点是B(b,﹣3),则ab的值是________.16. 如图,一张宽度相等的纸条,折叠后,若∠ABC=120°,则∠1的度数为________.17.﹣27的立方根与的算术平方根的和________.18. 如图a,ABCD是长方形纸带(AD∥BC),∠DEF=19°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是________;如果按照这样的方式再继续折叠下去,直到不能折叠为止,那么先后一共折叠的次数是_____ ___.三、解答题19. 计算题:.20. 已知:如图,∠B=∠ADE,∠EDC=∠GFB,GF⊥AB.求证:CD⊥AB.21. 在平面直角坐标系中,O 为坐标原点,A (﹣2,3),B (2,2).(1) 画出三角形OAB ;(2) 求三角形OAB 的面积;(3) 若三角形OAB 中任意一点P (x ,y )经平移后对应点为P (x +4,y﹣3),请画出三角形OAB 平移后得到的三角形O A B ,并写出点O ,A , 的坐标.22.在一副三角板ABC 和DEF 中.(1) 当AB ∥CD ,如图①,求∠DCB 的度数.(2) 当CD 与CB 重合时,如图②,判定DE 与AC 的位置关系,并说明理由.(3) 如图③,当∠DCB 等于多少度时,AB ∥EC ?23. 图形的操作过程:在图①中,将线段A A 向右平移1个单位到B B , 得到封闭图形A A B B (即阴影部分);在图②中,将折线A A A 向右平移1个单位到B B B , 得到封闭图形AA AB B B (即阴影部分).(1) 在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影;(2) 请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:S =,S =,S =.(3) 联想与探索:如图④在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少并说明你的猜想是正确的.11111111111212122112312312332112324. 如图,在平面直角坐标系中,点A ,B 的坐标分别为(﹣1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1) 求点C ,D 的坐标;(2) 若在y 轴上存在点 M ,连接MA ,MB ,使S =S ,求出点M 的坐标.(3) 若点P 在直线BD 上运动,连接PC ,PO .①若P 在线段BD 之间时(不与B ,D 重合),求S+S 的取值范围;②若P 在直线BD 上运动,请直接写出∠CPO 、∠DCP 、∠BOP 的数量关系.参考答案1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.△M A B 平行四边形A BDC △CDP △BOP16.17.18.19.20.21.22.23.24.。
济宁市邹城七年级下期中数学试卷及答案-精选

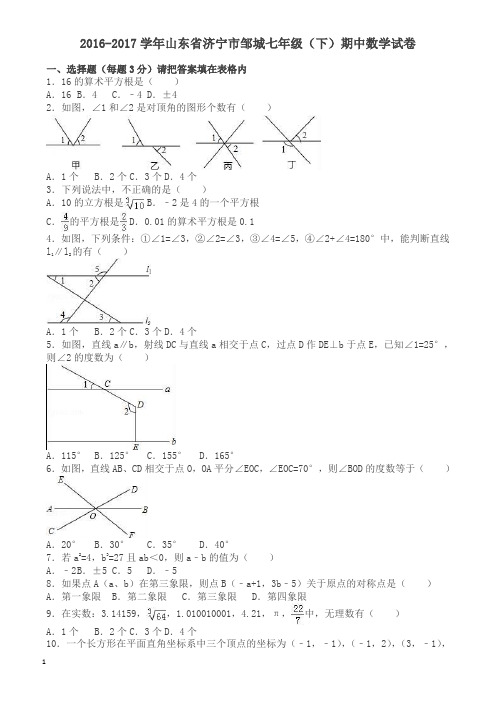
2016-2017学年山东省济宁市邹城七年级(下)期中数学试卷一、选择题(每题3分)请把答案填在表格内1.16的算术平方根是()A.16 B.4 C.﹣4 D.±42.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个C.3个D.4个3.下列说法中,不正确的是()A.10的立方根是 B.﹣2是4的一个平方根C.的平方根是 D.0.01的算术平方根是0.14.如图,下列条件:①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,能判断直线l1∥l2的有()A.1个B.2个C.3个D.4个5.如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()A.115°B.125°C.155°D.165°6.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于()A.20°B.30°C.35°D.40°7.若a2=4,b3=27且ab<0,则a﹣b的值为()A.﹣2 B.±5 C.5 D.﹣58.如果点A(a、b)在第三象限,则点B(﹣a+1,3b﹣5)关于原点的对称点是()A.第一象限B.第二象限C.第三象限D.第四象限9.在实数:3.14159,,1.010010001,4.21,π,中,无理数有()A.1个B.2个C.3个D.4个10.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为()A.(2,2)B.(3,2)C.(3,3)D.(2,3)11.如图,在下列四组条件中,能得到AB∥CD的是()A.∠ABD=∠BDC B.∠3=∠4C.∠BAD+∠ABC=180°D.∠1=∠212.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为()A.48 B.96 C.84 D.42二、填空(每题3分)13.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是.14.直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2= .15.已知a,b为两个连续的整数,且a<b,则a+b= .16.已知点P在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P .17.如果P(a+b,ab)在第二象限,那么点Q(a,﹣b)在第象限.18.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG=度.三、解答题:19.求下列等式中x的值:(1)2x2﹣=0(2)(x+4)3=125.20.已知2a﹣1的平方根是±3,11a+b﹣1的立方根是4,求a+2b的平方根.21.如图是小明所在学校的平面示意图,请你以教学楼为坐标原点建立平面直角坐标系,描述学校其它建筑物的位置.22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.(1)直接写出图中∠AOC的对顶角:,∠EOB的邻补角:(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.23.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:(1)过E作直线CD,使CD∥AB;(2)过E作直线EF,使EF⊥AB,垂足为F;(3)请判断直线CD与EF的位置关系,并说明理由.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.25.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)(1)A′、B′两点的坐标分别为A′、B′;(2)作出△ABC平移之后的图形△A′B′C′;(3)求△A′B′C′的面积.2016-2017学年山东省济宁市邹城七年级(下)期中数学试卷参考答案与试题解析一、选择题(每题3分)请把答案填在表格内1.16的算术平方根是()A.16 B.4 C.﹣4 D.±4【考点】22:算术平方根.【分析】根据算术平方根的概念即可求出答案.【解答】解:∵42=16,∴16的算术平方根是4,故选(B)2.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个C.3个D.4个【考点】J2:对顶角、邻补角.【分析】一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.据此作答即可.【解答】解:只有丙图中的两个角是对顶角,故选:A.3.下列说法中,不正确的是()A.10的立方根是 B.﹣2是4的一个平方根C.的平方根是 D.0.01的算术平方根是0.1【考点】24:立方根;21:平方根;22:算术平方根.【分析】根据立方根,平方根的定义,即可解答.【解答】解:A.10的立方根是,正确;B.﹣2是4的一个平方根,正确;C.的平方根是±,故错误;D. 0.01的算术平方根是0.1,正确;故选C.4.如图,下列条件:①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,能判断直线l1∥l2的有()A.1个B.2个C.3个D.4个【考点】J9:平行线的判定.【分析】利用平行线的判定方法判断即可得到结果.【解答】解:∵∠1=∠3,∴l1∥l2;∵∠4=∠5,∴l1∥l2;∵∠2+∠4=180°,∴l1∥l2,则能判断直线l1∥l2的有3个.故选C5.如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()A.115°B.125°C.155°D.165°【考点】JA:平行线的性质.【分析】如图,过点D作c∥a.由平行线的性质进行解题.【解答】解:如图,过点D作c∥a.则∠1=∠CDB=25°.又a∥b,DE⊥b,∴b∥c,DE⊥c,∴∠2=∠CDB+90°=115°.故选:A.6.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于()A.20°B.30°C.35°D.40°【考点】J2:对顶角、邻补角;IJ:角平分线的定义.【分析】根据角平分线定义求出∠AOC=∠EOC=35°,根据对顶角的定义即可求出∠BOD的度数.【解答】解:∵OA平分∠EOC,∠EOC=70°,∴∠AOC=∠EOC=35°,∴∠BOD=∠AOC=35°.故选:C.7.若a2=4,b3=27且ab<0,则a﹣b的值为()A.﹣2 B.±5 C.5 D.﹣5【考点】1E:有理数的乘方.【分析】根据有理数的乘方求出a、b,再根据异号得负判断出a的值,然后代入代数式进行计算即可得解.【解答】解:∵a2=4,b3=27,∴a=±2,b=3,∵ab<0,∴a=﹣2,∴a﹣b=﹣2﹣3=﹣5.故选D.8.如果点A(a、b)在第三象限,则点B(﹣a+1,3b﹣5)关于原点的对称点是()A.第一象限B.第二象限C.第三象限D.第四象限【考点】R6:关于原点对称的点的坐标.【分析】此题首先明确两个点关于原点对称,则横、纵坐标都是互为相反数;然后能够根据点所在的位置判断点的坐标符号,根据坐标符号得到字母的取值范围.【解答】解:∵点B(﹣a+1,3b﹣5)关于原点的对称点是(a﹣1,5﹣3b).又∵点A在第三象限即a<0,b<0.∴a﹣1<0,5﹣3b>0,∴(a﹣1,5﹣3b)是第三象限的点.故选B.9.在实数:3.14159,,1.010010001,4.21,π,中,无理数有()A.1个B.2个C.3个D.4个【考点】26:无理数.【分析】根据无理数的定义,可得答案.【解答】解:π是无理数,故选:A.10.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为()A.(2,2)B.(3,2)C.(3,3)D.(2,3)【考点】D5:坐标与图形性质;LB:矩形的性质.【分析】本题可在画出图后,根据矩形的性质,得知第四个顶点的横坐标应为3,纵坐标应为2.【解答】解:如图可知第四个顶点为:即:(3,2).故选:B.11.如图,在下列四组条件中,能得到AB∥CD的是()A.∠ABD=∠BDC B.∠3=∠4C.∠BAD+∠ABC=180°D.∠1=∠2【考点】J9:平行线的判定.【分析】根据平行线的判定定理对各选项进行逐一判断即可.【解答】解:A、若∠ABD=∠BDC,则AB∥CD,故本选项正确;B、若∠3=∠4,则AD∥BC,故本选项错误;C、若∠BAD+∠ABC=180°,则AD∥BC,故本选项错误;D、若∠1=∠2,则AD∥BC,故本选项错误;故选A.12.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为()A .48B .96C .84D .42 【考点】Q2:平移的性质.【分析】根据平移的性质得出BE=6,DE=AB=10,则OE=6,则阴影部分面积=S 四边形ODFC =S 梯形ABEO ,根据梯形的面积公式即可求解.【解答】解:由平移的性质知,BE=6,DE=AB=10, ∴OE=DE ﹣DO=10﹣4=6,∴S 四边形ODFC =S 梯形ABEO =(AB+OE )•BE=(10+6)×6=48.故选:A .二、填空(每题3分)13.如图,计划把河水引到水池A 中,先作AB ⊥CD ,垂足为B ,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是 连接直线外一点与直线上所有点的连线中,垂线段最短 .【考点】J4:垂线段最短.【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.【解答】解:根据垂线段定理,连接直线外一点与直线上所有点的连线中,垂线段最短, ∴沿AB 开渠,能使所开的渠道最短.故答案为:连接直线外一点与直线上所有点的连线中,垂线段最短.14.直线l 1∥l 2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2= 40° .【考点】JA :平行线的性质;K7:三角形内角和定理.【分析】根据两直线平行,同位角相等可得∠3=∠1,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠4,然后根据对顶角相等解答. 【解答】解:∵l 1∥l 2, ∴∠3=∠1=85°,∴∠4=∠3﹣45°=85°﹣45°=40°, ∴∠2=∠4=40°. 故答案为:40°.15.已知a,b为两个连续的整数,且a<b,则a+b= 10 .【考点】2B:估算无理数的大小.【分析】根据无理数的性质,得出接近无理数的整数,即可得出a,b的值,即可得出答案.【解答】解:∵a<b,a、b为两个连续的整数,∴<<,∴a=4,b=5,∴a+b=10.故答案为:10.16.已知点P在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P (3,﹣2).【考点】D1:点的坐标.【分析】根据第二象限内点的横坐标是负数,纵坐标是正数写出即可.【解答】解:点P(3,﹣2).故答案为:(3,﹣2)答案不唯一.17.如果P(a+b,ab)在第二象限,那么点Q(a,﹣b)在第二象限.【考点】D1:点的坐标.【分析】应先判断出所求的点的横纵坐标的符号,进而判断其所在的象限.【解答】解:∵P(a+b,ab)在第二象限,∴a+b<0,ab>0,∴a,b都是负号,∴a<0,﹣b>0,∴点Q(a,﹣b)在第二象限.故填:二.18.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG=55 度.【考点】IK:角的计算.【分析】根据题意∠B′OG=∠BOG,根据平角和角平分线的定义即可求得.【解答】解:由题意可得∠B′OG=∠BOG,则∠B′OG=÷2=55°.故答案为55.三、解答题:19.求下列等式中x的值:(1)2x2﹣=0(2)(x+4)3=125.【考点】24:立方根;21:平方根.【分析】(1)直接开平方法解方程即可;(2)直接开立方解方程即可.【解答】解:(1)2x2﹣=0x=±0.5(2)(x+4)3=125x=120.已知2a﹣1的平方根是±3,11a+b﹣1的立方根是4,求a+2b的平方根.【考点】21:平方根;24:立方根.【分析】根据已知得出2a﹣1=9,11a+b﹣1=64,求出a=5,b=10,求出a+2b的值,最后求出a+2b的平方根即可.【解答】解:∵2a﹣1的平方根是±3,11a+b﹣1的立方根是4,∴2a﹣1=9,11a+b﹣1=64,∴a=5,b=10,∴a+2b=25,即a+2b的平方根是±5.21.如图是小明所在学校的平面示意图,请你以教学楼为坐标原点建立平面直角坐标系,描述学校其它建筑物的位置.【考点】D3:坐标确定位置.【分析】根据题意建立平面直角坐标系进而得出各点坐标即可.【解答】解:如图所示:实验楼(﹣2,2),行政楼(﹣2,﹣2),大门(0,﹣4),食堂(3,4),图书馆(4,﹣2).22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.(1)直接写出图中∠AOC的对顶角:∠BOD ,∠EOB的邻补角:∠AOE(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.【考点】J2:对顶角、邻补角.【分析】(1)根据对顶角和邻补角的定义直接写出即可;(2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.【解答】解:(1)∠AOC的对顶角是∠BOD,∠EOB的邻补角是∠AOE,故答案为:∠BOD,∠AOE;(2)∵∠AOC=70°,∴∠BOD=∠AOC=70°,∵∠BOE:∠EOD=2:3,∴∠BOE=×70°=28°,∴∠AOE=180°﹣28°=152°.∴∠AOE的度数为152°.23.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:(1)过E作直线CD,使CD∥AB;(2)过E作直线EF,使EF⊥AB,垂足为F;(3)请判断直线CD与EF的位置关系,并说明理由.【考点】N3:作图—复杂作图.【分析】(1)根据题意直接作出CD∥AB;(2)过点E利用三角尺作出EF⊥AB;(3)利用平行线的性质,进而得出直线CD与EF的位置关系.【解答】解:(1)、(2)如图所示:(3)CD⊥EF.理由:∵CD∥AB,∴∠CEF=∠EFB,∵EF⊥AB,∴∠EFB=90°,∴∠CEF=90°,∴CD⊥EF.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.【考点】J9:平行线的判定.【分析】首先利用平行线的性质以及角平分线的性质得到满足关于AD∥BC的条件,内错角∠2和∠E相等,得出结论.【解答】证明:∵AE平分∠BAD,∴∠1=∠2,∵AB∥CD,∠CFE=∠E,∴∠1=∠CFE=∠E,∴∠2=∠E,∴AD∥BC.25.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)(1)A′、B′两点的坐标分别为A′(3,5)、B′(1,2);(2)作出△ABC平移之后的图形△A′B′C′;(3)求△A′B′C′的面积.【考点】Q4:作图﹣平移变换.【分析】(1)由点C(﹣1,﹣3)与点C′(4,1)是对应点,得出平移规律为:向右平移5个单位,向上平移4个单位,按平移规律即可写出所求的点的坐标;(2)按平移规律作出A、B的对应点A′,B′,顺次连接A′、B′、C′,即可得到△A′B′C′;(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积即可求解.【解答】解:(1)∵△A′B′C′是△ABC平移之后得到的图象,并且C(﹣1,﹣3)的对应点C′的坐标为(4,1),∴平移前后对应点的横坐标加5,纵坐标加4,∴△ABC先向右平移5个单位,再向上平移4个单位得到△A′B′C′,∵A(﹣2,1),B(﹣4,﹣2),∴A′(3,5)、B′(1,2);(2)△A′B′C′如图所示;(3)S=4×3﹣×3×1﹣×3×2﹣×1×4△A′B′C′=12﹣1.5﹣3﹣2=5.5.故答案为(3,5),(1,2).2017年5月25日。
山东省邹城市七年级数学下学期期末考试试题

山东省邹城市2015-2016学年七年级数学下学期期末考试试题2015—2016学年度第二学期期末检测七年级数学试题Λ-调色全体射生 tt. U ⅛ft ⅛⅛女生 (.Lil iM 全禅学4Oft 中的郎"孕生2. F I FIFI M 2 . <j > f ;B SPRL MU fr'Jl<fh ¾[i ∙]∖. GVtIGK. - J< tf <03"如 H H ∣J>fl ⅛列誇 J≠J1∖⅛t ∙TM - ( P H 疔的⅛A i Z I-Z 2U r ^3=Z4S. AJ "> Λ . U4 b T S f it"确的号A , H A 5ΛSJ 一 ,口分I---------19102「22 I a24 1 2S需J jtH Λ — i > ft— 3n,丄 IQ C —fiI V 『炉非检2WH >名学4民外件畀〃求疔f ;笊・tji 、护幷卉订屮旨丹台■污甘圧A 足曲t'⅛tt>r ⅛.酱n Mir A 習划卩6.为描述某地某日的气温变化常况•应制作A.折红图B.幽形图C.条形图D.豆方图7.己知x∙y耨足方SHll2xy =Z↑. WX-J^(x÷2j≡5A. 9B. 3C. 1D. -1«•己知不等式2x-a≤ O的止SfiH恰好是1・2, 3, 4. 5,那么α的取值阪田足A∙Λ>!0 B. 1O<∙MI2 C・IO≤α<12D・ 10vgMl2 9某中学现冇学生500人・计划-年后女牛在校住增加3%,勇牛衣咬牛增加4%,这样在枝学生将增加3.4%,设设校现有女生人散X和男生刚列方程为A∣x÷J = SOO w B∫x÷ ∕≡500l l<1÷4%)X + (>÷3%)∕∙ 500x(1+ 3.4%) B13%x + 4%F≈ SOOx3.4%C严y = 500∙ D fx÷∕==500,lθ+ 3%)x + d÷ 4%)J »500x(1 + 3.4%) ' (4%x ÷ 3%F ≡ SOOx 3.4%10. ⅛ιffi.动成/>在平⅛WΛΨ标系中按图中箭头所示方向运动.第1次从原点运动到点<1∙ O.第2次接着运动到点(2∙ 0).第J次接着运动到点(儿2λ∙∙∙∙∙∙.按这轉的运动規律.经过冕201£次运动后.动点P的坐标是七年氓融学试®第2页(養8頁〉二、Ia心填一填(本AA* 8个小題• *小贯3分•共24分.÷*4≡J⅛異填中的横役上•)仏■評立方根是------------ .12. A为第四飲限内一点•且点/<的坐标是方程X^y≈°的ftlA*.请你写出一个(写出一个即可)・1J.如杲2τ-7y = 5∙那久用含y的代效式表示Jt ∙ WX =M绒计痢剑一饭針据•量大ffiM B6.龄扌、備是52∙取伍1淹为10,可以分成.«1.15.如0O∙己知EflME〃/KΛAD^分ZZMQ 交HCT^ C. ZΛCn ≡140o. WZBfrJ/Ift为门.若关于*•F的一兀一次方丹纽"•的解也是二元一次方种■-3> = 6的・•[x +j = 2A»*=18.菜大型超市从牛产基堆购进一批水果•运输及销售中估汁有10%的苹果正MtKIt.苹果的进价是毎千克1・“元•商家耍话免亏本•需把咎价至少定为兀?三J耐心解一解(本人題扶7个小題•共“分•写出丈宇丸钳•证明述在戎浚算步H)19.(未題消分吕分〉计算* 2√2+√9 +<∕≡β+∣√2-^∙七年级Ii学试“鄭J贝(共N貝)21・(木题海分6分〉x+2 I解不衿式组: 3 λ,.并把其解集在数轴上表禾出来•2∣l∙x)≤5七剧4頁(Mew)22・(木分&分)⅛∣Λ FrtiWUf'U (6 M⅛l lιn VIWrtO .Clilh 如附∙M "(〃•z>1=z∣ ∙Wi I L ∕<≡ZΛ.;-«HH讣叭V KE H CD(匕知)•.∙.Z2≡ ___ ∙(乂∙∙∙ZzI = ZI (已知)•∙∙∙ AC//___ ∙(.∙. ZZ ≡__ ∙(∙∙∙ ZC = ZE (邻爪代撤)•23・(4醴獨分0窃)在平顾宜角堂标糸中,A. K. C点的*标兮别为(一5・4), (-3∙o‰ (O. Z).CO丽出三H∖KΛBC.并求三ΛJΛMΛ(的廁枳:(2)如∣U∙三〃形/IWL可以由:Ξft∣ΛM"0经过*;样的屮杠紂到?对应乳的屮林有什么变化7(3)己知点P (叫兀〉为.角彤YBC内的一点•创戊P広二角形才内的対由点严的学标为<_ •______ >•V第§更(WR<)24∙小刖在•统计”实习话动中Sfi机S合了学校若干名孕住車低対•"绘住履手机如枝現線的U袪.统计»05M作了如下的嫌计!E:家S "中*ι<r-机到学«r杏度纹计田BM SE(1)束这次的豪长PJRJi家长农不•无所谓-的人敷・开补全FB 1;(2)求图2中表示家长•无质谓” M4>Λ的度敷:七年饴触予试If M⅛< <««页)2S.(本题得分10分〉某电器超市梢件A∙ B曲种堂号的空调∙T*⅛⅛IΛ∕*IWfnl I!tn况J(1)*A∙ U型空调每台的苗价各为多少?(2)墓公司准為用不少于5万元但不趙过52万兀的金额.向该电Mifl市购买A, B 虧种主号的空Ul共I❶台•则有■几种采禺方黨?字试Je «7M (Me1>七年级数学试题参考答案 (仅供参考) 一、选择题24. 解:( 1)(6 分)家长总数: 200÷50%=400 名, 表示“无所谓”人数: 400﹣200﹣16﹣400×26%=80 名, 补全图 1(画图略); (2)( 2 分)(80÷400)×360°=72°.25. 解:(1)(5分)设 A , B 型空调每台的售价分 别为 x 万元和 y 万元,依题意得:5x 3y 3.98, .解得: x 0.46, 10x 5y 7.4 y 0.56答 :A , B 型空调每台的售价分别为 (或: A ,B 型空调每台的售价分别为0.46m 0.56(10 m ) 5.2,,解得: 4 m 6 .0.46m 0.56(10 m ) 5故共有三种购买方案:方案一: 购买 A 型空调 4 台, B 型空调 6 台; 方案二 :购买 A 型空调 5台, B 型空调 5台; 方案三:购买 A 型空调 6 台, B 型空调 4台.11. 1 ;2;15. 100 ;三、解答题12. 16.19. 解答过程略, 2. 20. 解答过程略, 2,6.21. 解答过程略,如:(1, 1 ); 13.17.1(5-7y ) ; 14. 9 ; 2 k 1 ; 18. 2.22. ( 行; 23.( 12 C 两直线平行, 2 分 ) ( 1)画三角形 ABC ( 略) , 三角形 ABC 的面积为32(4 两直线平行,同位角相等; 同错角相等 .分 ) ;画图:(略) (2 分) . 每空 1 E ; 每小题 向右平移 4 个单位,向下平移 3 个单位;横坐标增加4,纵坐标减少3; m 4 , n 3. 分) DE ; 内错角 相等,两直线平8(解答过程略) ; 0.46 万元和 0.56 万元. 4600 元和 5600 元.)2)(5 分)设购买 A 型空调 m台,则购买 B 型空调 10 m 台,依题意得:。
济宁市邹城市2015-2016学年七年级下期末数学试卷含答案解析

(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”圆心角的度数.
25.(10 分)某电器超市销售 A,B 两种型号的空调,如表是近两周的销售情
况.
销售时段
第一周
第二周
销售数量(台) A 型
5
10
B型
3
5
销售收入(万元)
3.98
7.4
(1)求 A,B 型空调每台的售价各为多少?
7.已知 x,y 满足方程组
,则 x﹣y 等于( )
A.9 B.3 C.1 D.﹣1
8.已知不等式 2x﹣a≤0 的正整数解恰好是 1,2,3,4,5,那么 a 的取值范围 是( ) A.a>10 B.10≤a≤12 C.10<a≤12 D.10≤a<12 9.某中学现有学生 500 人,计划一年后女生在校生增加 3%,男生在校生增加
(2)某公司准备用不少于 5 万元但不超过 5.2 万元的金额,向该电器超市购买
A,B 两种型号的空调共 10 台,则有哪几种采购方案?
A.∠1=∠2 B.∠3=∠4 C.∠1=∠5 D.∠3=∠5 4.a,b 是两个连续整数,若 a< <b,则 a,b 分别是( ) A.2,3 B.3,2 C.3,4 D.6,8 5.若 a>b,则下列式子正确的是( )
A.﹣5a>﹣5b B.a﹣3>b﹣3 C.4﹣a>4﹣b D. a< b
பைடு நூலகம்
6.为描述某地某日的气温变化情况,应制作( ) A.折线图 B.扇形图 C.条形图 D.直方图
2015-2016 学年山东省济宁市邹城市七年级(下)期末数学试 卷
一、选择题:每小题 3 分,共 30 分 1.要了解全校 2000 名学生课外作业负担情况,你认为以下抽样方法中比较合 理的是( ) A.调查全体男生 B.调查全体女生 C.调查七年级全体学生 D.调查各年级中的部分学生 2.若点 P(a﹣2,a)在第二象限,则 a 的取值范围是( ) A.0<a<2 B.﹣2<a<0C.a>2 D.a<0 3.如图,下列条件能判断两直线 AB,CD 平行的是( )
济宁市邹城七年级下期中数学试卷及答案-超值

2016-2017学年山东省济宁市邹城七年级(下)期中数学试卷一、选择题(每题3分)请把答案填在表格内1.16的算术平方根是()A.16 B.4 C.﹣4 D.±42.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个C.3个D.4个3.下列说法中,不正确的是()A.10的立方根是B.﹣2是4的一个平方根C.的平方根是D.0.01的算术平方根是0.14.如图,下列条件:①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,能判断直线l1∥l2的有()A.1个B.2个C.3个D.4个5.如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()A.115°B.125°C.155°D.165°6.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于()A.20°B.30°C.35°D.40°7.若a2=4,b3=27且ab<0,则a﹣b的值为()A.﹣2 B.±5 C.5 D.﹣58.如果点A(a、b)在第三象限,则点B(﹣a+1,3b﹣5)关于原点的对称点是()A.第一象限B.第二象限C.第三象限D.第四象限9.在实数:3.14159,,1.010010001,4.21,π,中,无理数有()A.1个B.2个C.3个D.4个10.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为()A.(2,2)B.(3,2)C.(3,3)D.(2,3)11.如图,在下列四组条件中,能得到AB∥CD的是()A.∠ABD=∠BDC B.∠3=∠4C.∠BAD+∠ABC=180° D.∠1=∠212.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为()A.48 B.96 C.84 D.42二、填空(每题3分)13.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是.14.直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2= .15.已知a,b为两个连续的整数,且a<b,则a+b= .16.已知点P在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P .17.如果P(a+b,ab)在第二象限,那么点Q(a,﹣b)在第象限.18.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG=度.三、解答题:19.求下列等式中x的值:(1)2x2﹣=0(2)(x+4)3=125.20.已知2a﹣1的平方根是±3,11a+b﹣1的立方根是4,求a+2b的平方根.21.如图是小明所在学校的平面示意图,请你以教学楼为坐标原点建立平面直角坐标系,描述学校其它建筑物的位置.22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.(1)直接写出图中∠AOC的对顶角:,∠EOB的邻补角:(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.23.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:(1)过E作直线CD,使CD∥AB;(2)过E作直线EF,使EF⊥AB,垂足为F;(3)请判断直线CD与EF的位置关系,并说明理由.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.25.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)(1)A′、B′两点的坐标分别为A′、B′;(2)作出△ABC平移之后的图形△A′B′C′;(3)求△A′B′C′的面积.2016-2017学年山东省济宁市邹城七年级(下)期中数学试卷参考答案与试题解析一、选择题(每题3分)请把答案填在表格内1.16的算术平方根是()A.16 B.4 C.﹣4 D.±4【考点】22:算术平方根.【分析】根据算术平方根的概念即可求出答案.【解答】解:∵42=16,∴16的算术平方根是4,故选(B)2.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个C.3个D.4个【考点】J2:对顶角、邻补角.【分析】一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.据此作答即可.【解答】解:只有丙图中的两个角是对顶角,故选:A.3.下列说法中,不正确的是()A.10的立方根是B.﹣2是4的一个平方根C.的平方根是D.0.01的算术平方根是0.1【考点】24:立方根;21:平方根;22:算术平方根.【分析】根据立方根,平方根的定义,即可解答.【解答】解:A.10的立方根是,正确;B.﹣2是4的一个平方根,正确;C.的平方根是±,故错误;D. 0.01的算术平方根是0.1,正确;故选C.4.如图,下列条件:①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,能判断直线l1∥l2的有()A.1个B.2个C.3个D.4个【考点】J9:平行线的判定.【分析】利用平行线的判定方法判断即可得到结果.【解答】解:∵∠1=∠3,∴l1∥l2;∵∠4=∠5,∴l1∥l2;∵∠2+∠4=180°,∴l1∥l2,则能判断直线l1∥l2的有3个.故选C5.如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()A.115°B.125°C.155°D.165°【考点】JA:平行线的性质.【分析】如图,过点D作c∥a.由平行线的性质进行解题.【解答】解:如图,过点D作c∥a.则∠1=∠CDB=25°.又a∥b,DE⊥b,∴b∥c,DE⊥c,∴∠2=∠CDB+90°=115°.故选:A.6.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于()A.20°B.30°C.35°D.40°【考点】J2:对顶角、邻补角;IJ:角平分线的定义.【分析】根据角平分线定义求出∠AOC=∠EOC=35°,根据对顶角的定义即可求出∠BOD的度数.【解答】解:∵OA平分∠EOC,∠EOC=70°,∴∠AOC=∠EOC=35°,∴∠BOD=∠AOC=35°.故选:C.7.若a2=4,b3=27且ab<0,则a﹣b的值为()A.﹣2 B.±5 C.5 D.﹣5【考点】1E:有理数的乘方.【分析】根据有理数的乘方求出a、b,再根据异号得负判断出a的值,然后代入代数式进行计算即可得解.【解答】解:∵a2=4,b3=27,∴a=±2,b=3,∵ab<0,∴a=﹣2,∴a﹣b=﹣2﹣3=﹣5.故选D.8.如果点A(a、b)在第三象限,则点B(﹣a+1,3b﹣5)关于原点的对称点是()A.第一象限B.第二象限C.第三象限D.第四象限【考点】R6:关于原点对称的点的坐标.【分析】此题首先明确两个点关于原点对称,则横、纵坐标都是互为相反数;然后能够根据点所在的位置判断点的坐标符号,根据坐标符号得到字母的取值范围.【解答】解:∵点B(﹣a+1,3b﹣5)关于原点的对称点是(a﹣1,5﹣3b).又∵点A在第三象限即a<0,b<0.∴a﹣1<0,5﹣3b>0,∴(a﹣1,5﹣3b)是第三象限的点.故选B.9.在实数:3.14159,,1.010010001,4.21,π,中,无理数有()A.1个B.2个C.3个D.4个【考点】26:无理数.【分析】根据无理数的定义,可得答案.【解答】解:π是无理数,故选:A.10.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为()A.(2,2)B.(3,2)C.(3,3)D.(2,3)【考点】D5:坐标与图形性质;LB:矩形的性质.【分析】本题可在画出图后,根据矩形的性质,得知第四个顶点的横坐标应为3,纵坐标应为2.【解答】解:如图可知第四个顶点为:即:(3,2). 故选:B .11.如图,在下列四组条件中,能得到AB ∥CD 的是( )A .∠ABD=∠BDCB .∠3=∠4C .∠BAD+∠ABC=180°D .∠1=∠2 【考点】J9:平行线的判定.【分析】根据平行线的判定定理对各选项进行逐一判断即可. 【解答】解:A 、若∠ABD=∠BDC ,则AB ∥CD ,故本选项正确; B 、若∠3=∠4,则AD ∥BC ,故本选项错误;C 、若∠BAD+∠ABC=180°,则AD ∥BC ,故本选项错误; D 、若∠1=∠2,则AD ∥BC ,故本选项错误; 故选A .12.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B 到C 的方向平移到△DEF 的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )A .48B .96C .84D .42 【考点】Q2:平移的性质.【分析】根据平移的性质得出BE=6,DE=AB=10,则OE=6,则阴影部分面积=S 四边形ODFC =S 梯形ABEO ,根据梯形的面积公式即可求解.【解答】解:由平移的性质知,BE=6,DE=AB=10, ∴OE=DE ﹣DO=10﹣4=6,∴S 四边形ODFC =S 梯形ABEO =(AB+OE )•BE=(10+6)×6=48.故选:A .二、填空(每题3分)13.如图,计划把河水引到水池A 中,先作AB ⊥CD ,垂足为B ,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是 连接直线外一点与直线上所有点的连线中,垂线段最短 .【考点】J4:垂线段最短.【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.【解答】解:根据垂线段定理,连接直线外一点与直线上所有点的连线中,垂线段最短,∴沿AB开渠,能使所开的渠道最短.故答案为:连接直线外一点与直线上所有点的连线中,垂线段最短.14.直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2= 40°.【考点】JA:平行线的性质;K7:三角形内角和定理.【分析】根据两直线平行,同位角相等可得∠3=∠1,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠4,然后根据对顶角相等解答.【解答】解:∵l1∥l2,∴∠3=∠1=85°,∴∠4=∠3﹣45°=85°﹣45°=40°,∴∠2=∠4=40°.故答案为:40°.15.已知a,b为两个连续的整数,且a<b,则a+b= 10 .【考点】2B:估算无理数的大小.【分析】根据无理数的性质,得出接近无理数的整数,即可得出a,b的值,即可得出答案.【解答】解:∵a<b,a、b为两个连续的整数,∴<<,∴a=4,b=5,∴a+b=10.故答案为:10.16.已知点P在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P (3,﹣2).【考点】D1:点的坐标.【分析】根据第二象限内点的横坐标是负数,纵坐标是正数写出即可.【解答】解:点P(3,﹣2).故答案为:(3,﹣2)答案不唯一.17.如果P(a+b,ab)在第二象限,那么点Q(a,﹣b)在第二象限.【考点】D1:点的坐标.【分析】应先判断出所求的点的横纵坐标的符号,进而判断其所在的象限.【解答】解:∵P(a+b,ab)在第二象限,∴a+b<0,ab>0,∴a,b都是负号,∴a<0,﹣b>0,∴点Q(a,﹣b)在第二象限.故填:二.18.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG=55 度.【考点】IK:角的计算.【分析】根据题意∠B′OG=∠BOG,根据平角和角平分线的定义即可求得.【解答】解:由题意可得∠B′OG=∠BOG,则∠B′OG=÷2=55°.故答案为55.三、解答题:19.求下列等式中x的值:(1)2x2﹣=0(2)(x+4)3=125.【考点】24:立方根;21:平方根.【分析】(1)直接开平方法解方程即可;(2)直接开立方解方程即可.【解答】解:(1)2x2﹣=0x=±0.5(2)(x+4)3=125x=120.已知2a﹣1的平方根是±3,11a+b﹣1的立方根是4,求a+2b的平方根.【考点】21:平方根;24:立方根.【分析】根据已知得出2a﹣1=9,11a+b﹣1=64,求出a=5,b=10,求出a+2b的值,最后求出a+2b的平方根即可.【解答】解:∵2a﹣1的平方根是±3,11a+b﹣1的立方根是4,∴2a﹣1=9,11a+b﹣1=64,∴a=5,b=10,∴a+2b=25,即a+2b的平方根是±5.21.如图是小明所在学校的平面示意图,请你以教学楼为坐标原点建立平面直角坐标系,描述学校其它建筑物的位置.【考点】D3:坐标确定位置.【分析】根据题意建立平面直角坐标系进而得出各点坐标即可.【解答】解:如图所示:实验楼(﹣2,2),行政楼(﹣2,﹣2),大门(0,﹣4),食堂(3,4),图书馆(4,﹣2).22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.(1)直接写出图中∠AOC的对顶角:∠BOD ,∠EOB的邻补角:∠AOE(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.【考点】J2:对顶角、邻补角.【分析】(1)根据对顶角和邻补角的定义直接写出即可;(2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.【解答】解:(1)∠AOC的对顶角是∠BOD,∠EOB的邻补角是∠AOE,故答案为:∠BOD,∠AOE;(2)∵∠AOC=70°,∴∠BOD=∠AOC=70°,∵∠BOE:∠EOD=2:3,∴∠BOE=×70°=28°,∴∠AOE=180°﹣28°=152°.∴∠AOE的度数为152°.23.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:(1)过E作直线CD,使CD∥AB;(2)过E作直线EF,使EF⊥AB,垂足为F;(3)请判断直线CD与EF的位置关系,并说明理由.【考点】N3:作图—复杂作图.【分析】(1)根据题意直接作出CD∥AB;(2)过点E利用三角尺作出EF⊥AB;(3)利用平行线的性质,进而得出直线CD与EF的位置关系.【解答】解:(1)、(2)如图所示:(3)CD⊥EF.理由:∵CD∥AB,∴∠CEF=∠EFB,∵EF⊥AB,∴∠EFB=90°,∴∠CEF=90°,∴CD⊥EF.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.【考点】J9:平行线的判定.【分析】首先利用平行线的性质以及角平分线的性质得到满足关于AD∥BC的条件,内错角∠2和∠E相等,得出结论.【解答】证明:∵AE平分∠BAD,∴∠1=∠2,∵AB∥CD,∠CFE=∠E,∴∠1=∠CFE=∠E,∴∠2=∠E,∴AD∥BC.25.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)(1)A′、B′两点的坐标分别为A′(3,5)、B′(1,2);(2)作出△ABC平移之后的图形△A′B′C′;(3)求△A′B′C′的面积.【考点】Q4:作图﹣平移变换.【分析】(1)由点C(﹣1,﹣3)与点C′(4,1)是对应点,得出平移规律为:向右平移5个单位,向上平移4个单位,按平移规律即可写出所求的点的坐标;(2)按平移规律作出A、B的对应点A′,B′,顺次连接A′、B′、C′,即可得到△A′B′C′;(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积即可求解.【解答】解:(1)∵△A′B′C′是△ABC平移之后得到的图象,并且C(﹣1,﹣3)的对应点C′的坐标为(4,1),∴平移前后对应点的横坐标加5,纵坐标加4,∴△ABC先向右平移5个单位,再向上平移4个单位得到△A′B′C′,∵A(﹣2,1),B(﹣4,﹣2),∴A′(3,5)、B′(1,2);(2)△A′B′C′如图所示;=4×3﹣×3×1﹣×3×2﹣×1×4(3)S△A′B′C′=12﹣1.5﹣3﹣2=5.5.故答案为(3,5),(1,2).2017年5月25日。
邹城期末七年级数学试卷

考试时间:120分钟满分:100分一、选择题(每题3分,共30分)1. 下列数中,不是有理数的是()A. -3B. √2C. 0.25D. 3/42. 已知 a + b = 5,a - b = 1,则 a 的值为()A. 3B. 2C. 4D. 63. 下列图形中,是轴对称图形的是()A. 正方形B. 等腰三角形C. 长方形D. 等边三角形4. 一个等腰三角形的底边长为6cm,腰长为8cm,则该三角形的面积为()A. 24cm²B. 32cm²C. 36cm²D. 40cm²5. 下列函数中,是正比例函数的是()A. y = 2x + 3B. y = 3/xC. y = 2xD. y = x² + 16. 在一次数学竞赛中,小明得了85分,比小红多15分,则小红的得分是()A. 70分B. 75分C. 80分D. 85分7. 已知等差数列 {an} 的前三项分别为 2, 5, 8,则该数列的公差是()A. 1B. 2C. 3D. 48. 下列等式中,正确的是()A. a² = aB. (a + b)² = a² + b²C. (a - b)² = a² - b²D. (a + b)² = a² + 2ab + b²9. 下列命题中,正确的是()A. 平行四边形的对角线相等B. 等腰三角形的底角相等C. 矩形的对角线互相垂直D. 直角三角形的斜边最长10. 下列函数中,是反比例函数的是()A. y = 2x + 3B. y = 3/xC. y = 2xD. y = x² + 1二、填空题(每题5分,共20分)11. 若 |x - 3| = 5,则 x 的值为_________。
12. 2a - 3b = 12,且 a = 4,则 b 的值为_________。
人教版七年级下期末数学试卷含答案解析 (4)

七年级(下)期末数学试卷一、选择题:每小题3分,共30分1.要了解全校名学生课外作业负担情况,你认为以下抽样方法中比较合理的是()A.调查全体男生B.调查全体女生C.调查七年级全体学生D.调查各年级中的部分学生2.若点P(a﹣2,a)在第二象限,则a的取值范围是()A.0<a<2 B.﹣2<a<0 C.a>2 D.a<03.如图,下列条件能判断两直线AB,CD平行的是()A.∠1=∠2 B.∠3=∠4 C.∠1=∠5 D.∠3=∠54.a,b是两个连续整数,若a<<b,则a,b分别是()A.2,3 B.3,2 C.3,4 D.6,85.若a>b,则下列式子正确的是()A.﹣5a>﹣5b B.a﹣3>b﹣3 C.4﹣a>4﹣b D.a<b6.为描述某地某日的气温变化情况,应制作()A.折线图B.扇形图C.条形图D.直方图7.已知x,y满足方程组,则x﹣y等于()A.9 B.3 C.1 D.﹣18.已知不等式2x﹣a≤0的正整数解恰好是1,2,3,4,5,那么a的取值范围是()A.a>10 B.10≤a≤12 C.10<a≤12 D.10≤a<129.某中学现有学生500人,计划一年后女生在校生增加3%,男生在校生增加4%,这样,在校学生将增加3.4%,设该校现有女生人数x和男生y,则列方程为()A.B.C.D.10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第次运动后,动点P的坐标是()A.(,0) B.(,1) C.(,2) D.(,0)二、填空题:细心填一填:每小题3分,共24分11.的立方根是.12.已知A为第四象限内一点,且点A的坐标是方程x+y=0的一组解,请你写出一个满足条件的A点坐标(写出一个即可)13.如果2x﹣7y=5,那么用含y的代数式表示x,则x=.14.统计得到一组数据,最大值时136,最小值是52,取组距为10,可以分成组.15.如图,已知直线AE∥BC,AD平分∠BAE,交BC于点C,∠BCD=140°,则∠B的度数为.16.若关于x的不等式组无解,则a的取值范围是.17.若关于x,y的二元一次方程组的解也是二元一次方程x﹣3y=6的解,则k=.18.某大型超市从生产基地购进一批水果,运输及销售中估计有10%的苹果正常损耗,苹果的进价是每千克1.8元,商家要避免亏本,需把售价至少定为元.三、耐心解一解:共46分19.计算:2+++|﹣2|20.解方程组.21.(6分)解不等式组:,并把其解集在数轴上表示出来.22.(6分)完成下面的证明(在括号中注明理由).已知:如图,BE∥CD,∠A=∠1,求证:∠C=∠E.证明:∵BE∥CD(已知),∴∠2=()又∵∠A=∠1(已知),∴AC∥(),∴∠2=(),∴∠C=∠E(等量代换)23.(6分)在平面直角坐标系中,A,B,C三点的坐标分别为(﹣5,4),(﹣3,0),(0,2).(1)画出三角形ABC,并求三角形ABC的面积;(2)如图,三角形A′B′C′可以由三角形ABC经过怎样的平移得到?对应点的坐标有什么变化?(3)已知点P(m,n)为三角形ABC内的一点,则点P在三角形A′B′C′内的对应点P′的坐标为(,)24.(8分)小明在“统计”学习活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如图的统计图.(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;(2)求图②中表示家长“无所谓”圆心角的度数.25.(10分)某电器超市销售A,B两种型号的空调,如表是近两周的销售情况.销售时段第一周第二周销售数量(台)A型510B型35销售收入(万元) 3.987.4(1)求A,B型空调每台的售价各为多少?(2)某公司准备用不少于5万元但不超过5.2万元的金额,向该电器超市购买A,B两种型号的空调共10台,则有哪几种采购方案?-学年山东省济宁市邹城市七年级(下)期末数学试卷参考答案与试题解析一、选择题:每小题3分,共30分1.要了解全校名学生课外作业负担情况,你认为以下抽样方法中比较合理的是()A.调查全体男生B.调查全体女生C.调查七年级全体学生D.调查各年级中的部分学生【考点】抽样调查的可靠性.【分析】利用抽样调查应具有全面性以及随机性,进而得出答案.【解答】解:∵要了解全校名学生课外作业负担情况,∴抽样方法中比较合理的是调查各年级中的部分学生.故选:D.【点评】此题主要考查了抽样调查的可靠性,正确把握定义是解题关键.2.若点P(a﹣2,a)在第二象限,则a的取值范围是()A.0<a<2 B.﹣2<a<0 C.a>2 D.a<0【考点】点的坐标.【分析】根据平面直角坐标系第二象限内点的坐标符号可得不等式组,再解即可.【解答】解:由题意得:,解得:0<a<2,故选:A.【点评】此题主要考查了点的坐标,关键是掌握第一象限(+,+),第二象限(﹣,+),第三象限(﹣,﹣),第四象限(+,﹣).3.如图,下列条件能判断两直线AB,CD平行的是()A.∠1=∠2 B.∠3=∠4 C.∠1=∠5 D.∠3=∠5【考点】平行线的判定.【分析】由平行线的判定方法:内错角相等,两直线平行;得出B能判断,A、C、D不能判断;即可得出结论.【解答】解:能判断直线AB∥CD的条件是∠3=∠4;理由如下:∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行);A、C、D不能判定AB∥CD;故选B.【点评】本题考查了平行线的判定方法;熟练掌握平行线的判定方法,并能进行推理论证是解决问题的关键.4.a,b是两个连续整数,若a<<b,则a,b分别是()A.2,3 B.3,2 C.3,4 D.6,8【考点】估算无理数的大小.【分析】根据,可得答案.【解答】解:根据题意,可知,可得a=2,b=3.故选:A.【点评】本题考查了估算无理数的大小,是解题关键.5.若a>b,则下列式子正确的是()A.﹣5a>﹣5b B.a﹣3>b﹣3 C.4﹣a>4﹣b D.a<b【考点】不等式的性质.【分析】看各不等式是加(减)什么数,或乘(除以)哪个数得到的,用不用变号.【解答】解:A、不等式两边都乘﹣5,不等号的方向改变,故错误;B、不等式两边都加﹣3,不等号的方向不变,正确;C、不等式两边都乘﹣1,得到﹣a<﹣b,则4﹣a<4﹣b,不等号的方向改变,故错误;D、不等式两边都乘以,不等号的方向不变,故错误;故选:B.【点评】主要考查了不等式的基本性质.不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.6.为描述某地某日的气温变化情况,应制作()A.折线图B.扇形图C.条形图D.直方图【考点】统计图的选择.【分析】根据统计图的特点进行分析可得:折线统计图表示的是事物的变化情况;扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;条形统计图能清楚地表示出每个项目的具体数目;直方图可以清楚地看出数据分布的总体态势,但是从直方图本身得不出原始的数据内容.【解答】解:根据统计图的特点,知要描述某地某日的气温变化情况,应制作折线图;故选A.【点评】此题考查了统计图的选择,根据扇形统计图、折线统计图、条形统计图和直方图各自的特点即可得出答案.7.已知x,y满足方程组,则x﹣y等于()A.9 B.3 C.1 D.﹣1【考点】解二元一次方程组.【分析】一般解法是求得方程组的解,把x,y的值代入到代数式求值,但观察方程组未知数的系数特点,把两方程分别看作整体,直接相减,即可求得x﹣y的值.【解答】解:在方程组中,①﹣②,得:x﹣y=﹣1,故选:D.【点评】此题考查解二元一次方程组,注意此题的简便方法是关键.8.已知不等式2x﹣a≤0的正整数解恰好是1,2,3,4,5,那么a的取值范围是()A.a>10 B.10≤a≤12 C.10<a≤12 D.10≤a<12【考点】一元一次不等式的整数解.【分析】先求出不等式的解集,再根据正整数解恰好是1,2,3,4,5,逆推a 的取值范围.【解答】解:解不等式2x﹣a≤0得:x≤a.根据题意得:5≤a<6,解得:10≤a<12.故选D.【点评】本题考查了一元一次不等式的整数解,解答此题要先求出不等式的解集,再根据整数解的情况确定a的取值范围.本题要求熟练掌握不等式及不等式的解法,准确的理解整数解在不等式解集中的意义,并会逆推式子中有关字母的取值范围.9.某中学现有学生500人,计划一年后女生在校生增加3%,男生在校生增加4%,这样,在校学生将增加3.4%,设该校现有女生人数x和男生y,则列方程为()A.B.C.D.【考点】由实际问题抽象出二元一次方程组.【分析】设该校现有女生x人、男生y人,根据:①现有女生人数+现有男生人数=500,②一年后男生增加的人数+一年后女生增加的人数=全校学生增加的人数,列方程组即可.【解答】解:设该校现有女生x人、男生y人,则列方程为:,故选:C.【点评】此题主要考查了二元一次方程组的应用,解题关键是弄清题意,找出合适的等量关系,列出方程组.10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是()A.(2015,0)B.(2015,1)C.(2015,2)D.(2016,0)【考点】规律型:点的坐标.【分析】设第n次到达的点为P n点,根据点的变化找出变化规律“P4n(4n,0),P4n(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,2)(n为自然数)”,由此即+1可得出结论.【解答】解:设第n次到达的点为P n点,观察,发现规律:P0(0,0),P1(1,1),P2(2,0),P3(3,2),P4(4,0),P5(5,1),…,∴P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,2)(n为自然数).∵2015=4×503+3,∴P2015点的坐标为(4×503+3,2)=(2015,2).故选C.【点评】本题考查了规律型中的点的坐标,解题的关键是找出规律“P4n(4n,0),P4n(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,2)(n为自然数)”.本题属+1于中档题,难度不大,解决该题型题目时,根据点P的变化罗列出部分点的坐标,再根据坐标的变化找出规律是关键.二、填空题:细心填一填:每小题3分,共24分11.的立方根是﹣.【考点】立方根.【分析】如果一个数x的立方等于a,那么x是a的立方根,根据此定义求解即可.【解答】解:∵(﹣)3=﹣,∴﹣的立方根根是:﹣.故答案是:﹣.【点评】此题主要考查了求一个数的立方根,解题时应先找出所要求的这个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求这个数的立方根.注意一个数的立方根与原数的性质符号相同.12.已知A为第四象限内一点,且点A的坐标是方程x+y=0的一组解,请你写出一个满足条件的A点坐标(1,﹣1)(写出一个即可)【考点】二元一次方程的解;点的坐标.【分析】由A为第四象限内一点可知其横坐标为正数,纵坐标为负数,再由点A 的坐标是方程x+y=0的一组解可知其横纵坐标互为相反数,由此两点即可得到点A坐标.【解答】解:∵点A为第四象限内一点,且点A的坐标是方程x+y=0的一组解,∴点A的坐标为(1,﹣1),故答案为:(1,﹣1).【点评】本题主要考查的是二元一次方程的解,熟记各象限内横纵坐标的符号特点是解题的关键.13.如果2x﹣7y=5,那么用含y的代数式表示x,则x=.【考点】解二元一次方程.【分析】把y看做已知数求出x即可.【解答】解:方程2x﹣7y=5,解得:x=,故答案为:【点评】此题考查了解二元一次方程,解题的关键是将y看做已知数求出x.14.统计得到一组数据,最大值时136,最小值是52,取组距为10,可以分成9组.【考点】频数(率)分布表.【分析】根据组数=(最大值﹣最小值)÷组距计算,注意小数部分要进位.【解答】解:在样本数据中最大值为136,最小值为52,它们的差是136﹣52=84,已知组距为10,由于84÷10=8.4,故可以分成9组.故答案为:9.【点评】本题考查的是组数的计算,属于基础题,掌握组数的定义:数据分成的组的个数称为组数是解题的关键,注意小数部分要进位.15.如图,已知直线AE∥BC,AD平分∠BAE,交BC于点C,∠BCD=140°,则∠B的度数为100°.【考点】平行线的性质;角平分线的定义.【分析】求出∠BCA=180°﹣∠BCD=40°,根据平行线的性质得出∠DAE=∠BCA=40°,根据角平分线定义求出∠BAE=2∠DAE=80°,根据平行线的性质得出∠B+∠BAE=180°,代入求出即可.【解答】解:∵∠BCD=140°,∴∠BCA=180°﹣∠BCD=40°,∵BC∥AE,∴∠DAE=∠BCA=40°,∵AD平分∠BAE,∴∠BAE=2∠DAE=80°,∵BC∥AE,∴∠B+∠BAE=180°,∴∠B=100°,故答案为:100°.【点评】本题考查了平行线的性质,角平分线定义的应用,能灵活运用性质进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.16.若关于x的不等式组无解,则a的取值范围是a≥﹣2.【考点】解一元一次不等式组.【分析】首先解每个不等式,然后根据不等式无解,即两个不等式的解集没有公共解即可求得.【解答】解:,解①得:x>a+3,解②得:x<1.根据题意得:a+3≥1,解得:a≥﹣2.故答案是:a≥﹣2.【点评】本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.17.若关于x,y的二元一次方程组的解也是二元一次方程x﹣3y=6的解,则k=1.【考点】二元一次方程组的解;二元一次方程的解.【分析】把k看做已知数表示出方程组的解,代入已知方程求出k的值即可.【解答】解:,①+②得:2x=6k,即x=3k,②﹣①得:2y=﹣2k,即y=﹣k,把x=3k,y=﹣k代入x﹣3y=6中得:3k+3k=6,解得:k=1,故答案为:1【点评】此题考查了二元一次方程组的解,以及二元一次方程的解,方程组的解即为能使方程组中两方程都成立的未知数的值.18.某大型超市从生产基地购进一批水果,运输及销售中估计有10%的苹果正常损耗,苹果的进价是每千克1.8元,商家要避免亏本,需把售价至少定为2元.【考点】一元一次不等式的应用.【分析】设商家把售价应该定为每千克x元,因为销售中估计有10%的苹果正常损耗,故每千克苹果损耗后的价格为x(1﹣10%),根据题意列出不等式即可.【解答】解:设商家把售价应该定为每千克x元,根据题意得:x(1﹣10%)≥1.8,解得,x≥2,故为避免亏本,商家把售价应该至少定为每千克2元.故答案为:2.【点评】本题考查一元一次不等式的应用,将现实生活中的事件与数学思想联系起来,读懂题意,根据“去掉损耗后的售价≥进价”列出不等式即可求解.三、耐心解一解:共46分19.计算:2+++|﹣2|【考点】实数的运算.【分析】原式利用算术平方根、立方根的定义,以及绝对值的代数意义化简,计算即可得到结果.【解答】解:原式=2+3﹣2+2﹣=+3.【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.20.解方程组.【考点】解二元一次方程组.【分析】方程组整理后,利用加减消元法求出解即可.【解答】解:方程组整理得:,①×2﹣②得:7x=14,即x=2,把x=2代入①得:y=6,则方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.21.解不等式组:,并把其解集在数轴上表示出来.【考点】解一元一次不等式组;在数轴上表示不等式的解集.【分析】首先分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可.【解答】解:,由①得:x<﹣,由②得:x≥﹣,不等式组的解集为:﹣≤x<﹣,在数轴上表示为:.【点评】此题主要考查了解一元一次不等式组,以及在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.22.完成下面的证明(在括号中注明理由).已知:如图,BE∥CD,∠A=∠1,求证:∠C=∠E.证明:∵BE∥CD(已知),∴∠2=∠C(两直线平行,同位角相等)又∵∠A=∠1(已知),∴AC∥DE(内错角相等,两直线平行),∴∠2=∠E(两直线平行,内错角相等),∴∠C=∠E(等量代换)【考点】平行线的性质.【分析】先根据两直线平行,得出同位角相等,再根据内错角相等,得出两直线平行,进而得出内错角相等,最后根据等量代换得出结论.【解答】证明:∵BE∥CD(已知)∴∠2=∠C(两直线平行,同位角相等)又∵∠A=∠1(已知)∴AC∥DE(内错角相等,两直线平行)∴∠2=∠E(两直线平行,内错角相等)∴∠C=∠E(等量代换)【点评】本题主要考查了平行线的性质,解题时注意区分平行线的性质与平行线的判定的区别,条件与结论不能随意颠倒位置.23.在平面直角坐标系中,A,B,C三点的坐标分别为(﹣5,4),(﹣3,0),(0,2).(1)画出三角形ABC,并求三角形ABC的面积;(2)如图,三角形A′B′C′可以由三角形ABC经过怎样的平移得到?对应点的坐标有什么变化?(3)已知点P(m,n)为三角形ABC内的一点,则点P在三角形A′B′C′内的对应点P′的坐标为(m+4,n﹣3)【考点】作图-平移变换.【分析】(1)找出点A、B、C的位置,连接AB、BC、AC可得到三角形ABC,然后依据△ABC的面积等于矩形的面积减去3个直角三角形的面积求解即可.(2)先确定出点A′的坐标,然后依据点A与点A′的位置可确定出平移的方向和距离;(3)依据平移与坐标变化的规律求解即可.【解答】解:(1)如图1所示S△ABC=S矩形AEOD﹣S△ADC﹣S△BCO﹣S△AEB=4×5﹣×5×2﹣×3×2﹣×4×2=20﹣5﹣3﹣4=8.(2)∵A(﹣5,4),A′(﹣1,1),∴点A′由点A向右平移4个单位,然后向下平移3个单位得到.∴△A′B′C′由△ABC向右平移4个单位,然后向下平移3个单位得到.(3)点P(m,n)对应点P′的坐标为(m+4,n﹣3).故答案为:(m+4,n﹣3).【点评】本题主要考查的是平移与坐标变化,掌握平移与坐标变化的规律是解题的关键.24.小明在“统计”学习活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如图的统计图.(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;(2)求图②中表示家长“无所谓”圆心角的度数.【考点】条形统计图;扇形统计图.【分析】(1)首先根据表示基本赞成的有200人,所占的百分比是50%,据此即可求得调查的总人数,然后根据百分比的意义求得表示“非常赞成”的人数,利用总人数减去其它组的人数求得家长表示“无所谓”的人数,补全直方图;(2)利用360°乘以对应的百分比求得.【解答】解:(1)这次调查的家长总数是200÷50%=400(人),家长表示“非常赞成”的人数是400×26%=104(人),则家长表示“无所谓”的人数是400﹣104﹣200﹣16=80(人).;(2)图②中表示家长“无所谓”圆心角的度数是360°×=72°.【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.25.(10分)(2016春•邹城市期末)某电器超市销售A,B两种型号的空调,如表是近两周的销售情况.销售时段第一周第二周销售数量(台)A型510B型35销售收入(万元) 3.987.4(1)求A,B型空调每台的售价各为多少?(2)某公司准备用不少于5万元但不超过5.2万元的金额,向该电器超市购买A,B两种型号的空调共10台,则有哪几种采购方案?【考点】一元一次不等式组的应用;二元一次方程组的应用.【分析】(1)设A、B两种型号空调的销售单价分别为x万元、y万元,根据5台A型号3台B型号的空调的售价为3.98万元,10台A型号5台B型号的空调的售价为37.4万元,列方程组求解即可;(2)设采购A种型号电风扇a台,则采购B种型号空调(10﹣a)台,根据不少于5万元但不超过5.2万元列不等式组求解即可.【解答】解:(1)设A、B两种型号电风扇的销售单价分别为x万元、y万元.依题意得:,解得:.答:A、B两种型号的空调的销售单价分别为4600元、5600元.(2)设采购A种型号电风扇a台,则采购B种型号电风扇(10﹣a)台.依题意得:,解得:4≤a≤6.∵a是正整数,∴a=4或a=5或a=6.∴共有三种方案:①采购A型4台,B型6台;②采购A型5台,B型5台;③采购A型6台,B型4台.【点评】本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程组和不等式求解.第21页共21页。
2015-2016人教版七年级数学下册期末考试卷及答案

2014-2015人教版七年级数学下册期末考试卷C及答案一、选择题:(本大题共10个小题,每小题3分,共30分)1.若m >-1,则下列各式中错误的...是( ) A .6m >-6 B .-5m <-5 C .m+1>0 D .1-m <22.下列各式中,正确的是( )±4 B.3.已知a >b >0,那么下列不等式组中无解..的是( )A .⎩⎨⎧-><b x a xB .⎩⎨⎧-<->b x ax C .⎩⎨⎧-<>b x a x D .⎩⎨⎧<->bx ax4.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度可能为 ( )(A) 先右转50°,后右转40° (B) 先右转50°,后左转40°(C) 先右转50°,后左转130° (D) 先右转50°,后左转50°5.解为12x y =⎧⎨=⎩的方程组是( )A.135x y x y -=⎧⎨+=⎩B.135x y x y -=-⎧⎨+=-⎩C.331x y x y -=⎧⎨-=⎩D.2335x y x y -=-⎧⎨+=⎩ 6.如图(1),在△ABC 中,∠ABC=500,∠ACB=800,BP 平分∠ABC ,CP 平分∠ACB ,则∠BPC 的大小是( )A .1000B .1100C .1150D .1200PB A(1) (2)(3)7.四条线段的长分别为3,4,5,7,则它们首尾相连可以组成不同的三角形的个数是( )A .4B .3C .2C 1A 1D .18.在各个内角都相等的多边形中,一个外角等于一个内角的12,则这个多边形的边数是( )A .5B .6C .7D .89.如图(2),△A 1B 1C 1是由△ABC 沿BC 方向平移了BC 长度的一半得到的,若△ABC 的面积为20 cm 2,则四边形A 1DCC 1的面积为( ) A .10 cm 2 B .12 c m 2 C .15 cm 2 D .17 cm 210.课间操时,小华、小军、小刚的位置如图3,小华对小刚说,如果我的位置用(•0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )A.(5,4)B.(4,5)C.(3,4)D.(4,3)二、填空题:本大题共8个小题,每小题3分,共24分,把答案直接填在答题卷的横线上. 11.49的平方根是________,算术平方根是______,-8的立方根是_____.12.不等式5x-9≤3(x+1)的解集是________. 13.如果点P(a,2)在第二象限,那么点Q(-3,a)在_______.14.如图3所示,在铁路旁边有一李庄,现要建一火车站,•为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:____________.15.从A 沿北偏东60°的方向行驶到B,再从B 沿南偏西20°的方向行驶到C,•则∠ABC=_______度.16.如图,AD ∥BC,∠D=100°,CA 平分∠BCD,则∠DAC=_______.17.给出下列正多边形:① 正三角形;② 正方形;③ 正六边形;④ 正八边形.用上述正多边形中的一种能够辅满地面的是_____________.(将所有答案的序号都填上) 18.若│x 2-25│则x=_______,y=_______.三、解答题:本大题共7个小题,共46分,解答题应写出文字说明、证明过程或演算步骤.19.解不等式组:⎪⎩⎪⎨⎧+<-≥--.21512,4)2(3x x x x ,并把解集在数轴上表示出来.20.解方程组:2313424()3(2)17x yx y x y⎧-=⎪⎨⎪--+=⎩21.如图, AD∥BC , AD平分∠EAC,你能确定∠B 与∠C的数量关系吗?请说明理由。
济宁市邹城七年级下期中数学试卷及答案-精

2016-2017学年山东省济宁市邹城七年级(下)期中数学试卷一、选择题(每题3分)请把答案填在表格内1.16的算术平方根是()A.16 B.4 C.﹣4 D.±42.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个 C.3个 D.4个3.下列说法中,不正确的是()A.10的立方根是B.﹣2是4的一个平方根C.的平方根是D.0.01的算术平方根是0.14.如图,下列条件:①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,能判断直线l 1∥l2的有()A.1个B.2个 C.3个 D.4个5.如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()A.115°B.125°C.155°D.165°6.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于()A.20°B.30°C.35°D.40°7.若a2=4,b3=27且ab<0,则a﹣b的值为()A.﹣2 B.±5 C.5 D.﹣58.如果点A(a、b)在第三象限,则点B(﹣a+1,3b﹣5)关于原点的对称点是()A .第一象限B .第二象限C .第三象限D .第四象限9.在实数:3.14159,,1.010010001,4.21,π,中,无理数有( )A .1个B .2个C .3个D .4个10.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为( ) A .(2,2) B .(3,2) C .(3,3) D .(2,3)11.如图,在下列四组条件中,能得到AB ∥CD 的是( )A .∠ABD=∠BDCB .∠3=∠4C .∠BAD+∠ABC=180°D .∠1=∠212.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B 到C 的方向平移到△DEF 的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )A .48B .96C .84D .42二、填空(每题3分)13.如图,计划把河水引到水池A 中,先作AB ⊥CD ,垂足为B ,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是 .14.直线l 1∥l 2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2= .15.已知a ,b 为两个连续的整数,且a <b ,则a+b= .16.已知点P 在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P . 17.如果P (a+b ,ab )在第二象限,那么点Q (a ,﹣b )在第 象限.18.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG= 度.三、解答题:19.求下列等式中x的值:(1)2x2﹣=0(2)(x+4)3=125.20.已知2a﹣1的平方根是±3,11a+b﹣1的立方根是4,求a+2b的平方根.21.如图是小明所在学校的平面示意图,请你以教学楼为坐标原点建立平面直角坐标系,描述学校其它建筑物的位置.22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.(1)直接写出图中∠AOC的对顶角:,∠EOB的邻补角:(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.23.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:(1)过E作直线CD,使CD∥AB;(2)过E作直线EF,使EF⊥AB,垂足为F;(3)请判断直线CD与EF的位置关系,并说明理由.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.25.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC 平移之后得到的图象,并且C的对应点C′的坐标为(4,1)(1)A′、B′两点的坐标分别为A′、B′;(2)作出△ABC平移之后的图形△A′B′C′;(3)求△A′B′C′的面积.2016-2017学年山东省济宁市邹城七年级(下)期中数学试卷参考答案与试题解析一、选择题(每题3分)请把答案填在表格内1.16的算术平方根是()A.16 B.4 C.﹣4 D.±4【考点】22:算术平方根.【分析】根据算术平方根的概念即可求出答案.【解答】解:∵42=16,∴16的算术平方根是4,故选(B)2.如图,∠1和∠2是对顶角的图形个数有()A.1个B.2个 C.3个 D.4个【考点】J2:对顶角、邻补角.【分析】一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.据此作答即可.【解答】解:只有丙图中的两个角是对顶角,故选:A.3.下列说法中,不正确的是()A.10的立方根是B.﹣2是4的一个平方根C.的平方根是D.0.01的算术平方根是0.1【考点】24:立方根;21:平方根;22:算术平方根.【分析】根据立方根,平方根的定义,即可解答.【解答】解:A.10的立方根是,正确;B.﹣2是4的一个平方根,正确;C.的平方根是±,故错误;D.0.01的算术平方根是0.1,正确;故选C.4.如图,下列条件:①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,能判断直线l 1∥l2的有()A .1个B .2个C .3个D .4个 【考点】J9:平行线的判定.【分析】利用平行线的判定方法判断即可得到结果. 【解答】解:∵∠1=∠3, ∴l 1∥l 2; ∵∠4=∠5, ∴l 1∥l 2;∵∠2+∠4=180°, ∴l 1∥l 2,则能判断直线l 1∥l 2的有3个. 故选C5.如图,直线a ∥b ,射线DC 与直线a 相交于点C ,过点D 作DE ⊥b 于点E ,已知∠1=25°,则∠2的度数为( )A .115°B .125°C .155°D .165° 【考点】JA :平行线的性质.【分析】如图,过点D 作c ∥a .由平行线的性质进行解题. 【解答】解:如图,过点D 作c ∥a . 则∠1=∠CDB=25°. 又a ∥b ,DE ⊥b , ∴b ∥c ,DE ⊥c ,∴∠2=∠CDB+90°=115°. 故选:A .6.如图,直线AB 、CD 相交于点O ,OA 平分∠EOC ,∠EOC=70°,则∠BOD 的度数等于()A.20°B.30°C.35°D.40°【考点】J2:对顶角、邻补角;IJ:角平分线的定义.【分析】根据角平分线定义求出∠AOC=∠EOC=35°,根据对顶角的定义即可求出∠BOD 的度数.【解答】解:∵OA平分∠EOC,∠EOC=70°,∴∠AOC=∠EOC=35°,∴∠BOD=∠AOC=35°.故选:C.7.若a2=4,b3=27且ab<0,则a﹣b的值为()A.﹣2 B.±5 C.5 D.﹣5【考点】1E:有理数的乘方.【分析】根据有理数的乘方求出a、b,再根据异号得负判断出a的值,然后代入代数式进行计算即可得解.【解答】解:∵a2=4,b3=27,∴a=±2,b=3,∵ab<0,∴a=﹣2,∴a﹣b=﹣2﹣3=﹣5.故选D.8.如果点A(a、b)在第三象限,则点B(﹣a+1,3b﹣5)关于原点的对称点是()A.第一象限B.第二象限C.第三象限D.第四象限【考点】R6:关于原点对称的点的坐标.【分析】此题首先明确两个点关于原点对称,则横、纵坐标都是互为相反数;然后能够根据点所在的位置判断点的坐标符号,根据坐标符号得到字母的取值范围.【解答】解:∵点B(﹣a+1,3b﹣5)关于原点的对称点是(a﹣1,5﹣3b).又∵点A在第三象限即a<0,b<0.∴a﹣1<0,5﹣3b>0,∴(a﹣1,5﹣3b)是第三象限的点.故选B.9.在实数:3.14159,,1.010010001,4.21,π,中,无理数有()A.1个B.2个 C.3个 D.4个【考点】26:无理数.【分析】根据无理数的定义,可得答案.【解答】解:π是无理数,故选:A.10.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为()A.(2,2)B.(3,2) C.(3,3) D.(2,3)【考点】D5:坐标与图形性质;LB:矩形的性质.【分析】本题可在画出图后,根据矩形的性质,得知第四个顶点的横坐标应为3,纵坐标应为2.【解答】解:如图可知第四个顶点为:即:(3,2).故选:B.11.如图,在下列四组条件中,能得到AB∥CD的是()A.∠ABD=∠BDC B.∠3=∠4C.∠BAD+∠ABC=180°D.∠1=∠2【考点】J9:平行线的判定.【分析】根据平行线的判定定理对各选项进行逐一判断即可.【解答】解:A、若∠ABD=∠BDC,则AB∥CD,故本选项正确;B、若∠3=∠4,则AD∥BC,故本选项错误;C、若∠BAD+∠ABC=180°,则AD∥BC,故本选项错误;D、若∠1=∠2,则AD∥BC,故本选项错误;故选A.12.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为()A .48B .96C .84D .42 【考点】Q2:平移的性质.【分析】根据平移的性质得出BE=6,DE=AB=10,则OE=6,则阴影部分面积=S 四边形ODFC =S 梯形ABEO ,根据梯形的面积公式即可求解.【解答】解:由平移的性质知,BE=6,DE=AB=10, ∴OE=DE ﹣DO=10﹣4=6,∴S 四边形ODFC =S 梯形ABEO =(AB+OE )•BE=(10+6)×6=48.故选:A .二、填空(每题3分)13.如图,计划把河水引到水池A 中,先作AB ⊥CD ,垂足为B ,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是 连接直线外一点与直线上所有点的连线中,垂线段最短 .【考点】J4:垂线段最短.【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.【解答】解:根据垂线段定理,连接直线外一点与直线上所有点的连线中,垂线段最短, ∴沿AB 开渠,能使所开的渠道最短.故答案为:连接直线外一点与直线上所有点的连线中,垂线段最短.14.直线l 1∥l 2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2= 40° .【考点】JA :平行线的性质;K7:三角形内角和定理.【分析】根据两直线平行,同位角相等可得∠3=∠1,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠4,然后根据对顶角相等解答. 【解答】解:∵l 1∥l 2, ∴∠3=∠1=85°,∴∠4=∠3﹣45°=85°﹣45°=40°, ∴∠2=∠4=40°.故答案为:40°.15.已知a,b为两个连续的整数,且a<b,则a+b= 10 .【考点】2B:估算无理数的大小.【分析】根据无理数的性质,得出接近无理数的整数,即可得出a,b的值,即可得出答案.【解答】解:∵a<b,a、b为两个连续的整数,∴<<,∴a=4,b=5,∴a+b=10.故答案为:10.16.已知点P在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P (3,﹣2).【考点】D1:点的坐标.【分析】根据第二象限内点的横坐标是负数,纵坐标是正数写出即可.【解答】解:点P(3,﹣2).故答案为:(3,﹣2)答案不唯一.17.如果P(a+b,ab)在第二象限,那么点Q(a,﹣b)在第二象限.【考点】D1:点的坐标.【分析】应先判断出所求的点的横纵坐标的符号,进而判断其所在的象限.【解答】解:∵P(a+b,ab)在第二象限,∴a+b<0,ab>0,∴a,b都是负号,∴a<0,﹣b>0,∴点Q(a,﹣b)在第二象限.故填:二.18.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG=55 度.【考点】IK:角的计算.【分析】根据题意∠B′OG=∠BOG,根据平角和角平分线的定义即可求得.【解答】解:由题意可得∠B′OG=∠BOG,则∠B′OG=÷2=55°.故答案为55.三、解答题:19.求下列等式中x的值:(1)2x2﹣=0(2)(x+4)3=125.【考点】24:立方根;21:平方根.【分析】(1)直接开平方法解方程即可;(2)直接开立方解方程即可.【解答】解:(1)2x2﹣=0x=±0.5(2)(x+4)3=125x=120.已知2a﹣1的平方根是±3,11a+b﹣1的立方根是4,求a+2b的平方根.【考点】21:平方根;24:立方根.【分析】根据已知得出2a﹣1=9,11a+b﹣1=64,求出a=5,b=10,求出a+2b的值,最后求出a+2b的平方根即可.【解答】解:∵2a﹣1的平方根是±3,11a+b﹣1的立方根是4,∴2a﹣1=9,11a+b﹣1=64,∴a=5,b=10,∴a+2b=25,即a+2b的平方根是±5.21.如图是小明所在学校的平面示意图,请你以教学楼为坐标原点建立平面直角坐标系,描述学校其它建筑物的位置.【考点】D3:坐标确定位置.【分析】根据题意建立平面直角坐标系进而得出各点坐标即可.【解答】解:如图所示:实验楼(﹣2,2),行政楼(﹣2,﹣2),大门(0,﹣4),食堂(3,4),图书馆(4,﹣2).22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.(1)直接写出图中∠AOC的对顶角:∠BOD ,∠EOB的邻补角:∠AOE(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.【考点】J2:对顶角、邻补角.【分析】(1)根据对顶角和邻补角的定义直接写出即可;(2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.【解答】解:(1)∠AOC的对顶角是∠BOD,∠EOB的邻补角是∠AOE,故答案为:∠BOD,∠AOE;(2)∵∠AOC=70°,∴∠BOD=∠AOC=70°,∵∠BOE:∠EOD=2:3,∴∠BOE=×70°=28°,∴∠AOE=180°﹣28°=152°.∴∠AOE的度数为152°.23.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:(1)过E作直线CD,使CD∥AB;(2)过E作直线EF,使EF⊥AB,垂足为F;(3)请判断直线CD与EF的位置关系,并说明理由.【考点】N3:作图—复杂作图.【分析】(1)根据题意直接作出CD∥AB;(2)过点E利用三角尺作出EF⊥AB;(3)利用平行线的性质,进而得出直线CD与EF的位置关系.【解答】解:(1)、(2)如图所示:(3)CD⊥EF.理由:∵CD∥AB,∴∠CEF=∠EFB,∵EF⊥AB,∴∠EFB=90°,∴∠CEF=90°,∴CD⊥EF.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.【考点】J9:平行线的判定.【分析】首先利用平行线的性质以及角平分线的性质得到满足关于AD∥BC的条件,内错角∠2和∠E相等,得出结论.【解答】证明:∵AE平分∠BAD,∴∠1=∠2,∵AB∥CD,∠CFE=∠E,∴∠1=∠CFE=∠E,∴∠2=∠E,∴AD∥BC.25.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC 平移之后得到的图象,并且C的对应点C′的坐标为(4,1)(1)A′、B′两点的坐标分别为A′(3,5)、B′(1,2);(2)作出△ABC平移之后的图形△A′B′C′;(3)求△A′B′C′的面积.【考点】Q4:作图﹣平移变换.【分析】(1)由点C(﹣1,﹣3)与点C′(4,1)是对应点,得出平移规律为:向右平移5个单位,向上平移4个单位,按平移规律即可写出所求的点的坐标;(2)按平移规律作出A、B的对应点A′,B′,顺次连接A′、B′、C′,即可得到△A′B′C′;(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积即可求解.【解答】解:(1)∵△A′B′C′是△ABC平移之后得到的图象,并且C(﹣1,﹣3)的对应点C′的坐标为(4,1),∴平移前后对应点的横坐标加5,纵坐标加4,∴△ABC先向右平移5个单位,再向上平移4个单位得到△A′B′C′,∵A(﹣2,1),B(﹣4,﹣2),∴A′(3,5)、B′(1,2);(2)△A′B′C′如图所示;(3)S=4×3﹣×3×1﹣×3×2﹣×1×4△A′B′C′=12﹣1.5﹣3﹣2=5.5.故答案为(3,5),(1,2).2017年5月25日。
