时间序列3答案
中级经济师-经济基础知识-基础练习题-第二十七章时间序列分析-三、时间序列的速度分析

中级经济师-经济基础知识-基础练习题-第二十七章时间序列分析-三、时间序列的速度分析[单选题]1.以2005年为基期,2011年和2012年我国国有农场的粮食总产量定基增长速度分别为72.1%和(江南博哥)81.3%。
2012年对2011年的环比发展速度为()。
A.5.3%B.14.1%C.105.3%D.114.1%正确答案:C参考解析:本题考查环比发展速度的计算。
定基发展速度=定基增长速度+1,且两个相邻时期定基发展速度的比率等于相应时期的环比发展速度。
所以本题中,环比发展速度=(81.3%+1)/(72.1%+1)=105.3%。
点赞(1)【环比。
比】所以164.3/137.4 结果大于1 只有D符合点赞(3)发展速度直接除,增长速度要加一点赞(0)发展速度不加一,直接不,增长速度加一后再比[单选题]4.某城市中家庭在2008年的收入为10万元,2016年的收入为36万元,以2008年为基期,则这个家庭收入的平均发展速度是()。
A.102%B.106%C.115%D.117%正确答案:D参考解析:平均发展速度是一定时期内各期环比发展速度的序时平均数,目前计算平均发展速度通常采用几何平均法。
[单选题]5.在时间序列的速度分析中,增长速度可以表示为()。
A.报告期增长量与基期水平的差B.发展水平之比C.报告期增长量与基期水平的比值D.发展速度+1正确答案:C参考解析:此题考查发展速度与增长速度。
增长速度是报告期增长量与基期水平的比值。
[单选题]6.已知某地区近三年社会消费品零售总额的环比增长速度分别为4%、6%、9%,则这时期该地区社会消费品零售总额的定基增长速度为()。
A.4%×6%×9%B.(4%×6%×9%)+1C.(104%×106%×109%)-1D.104%×106%×109%正确答案:C参考解析:此题考查发展速度与增长速度。
人大版时间序列分析基于R(第2版)习题答案
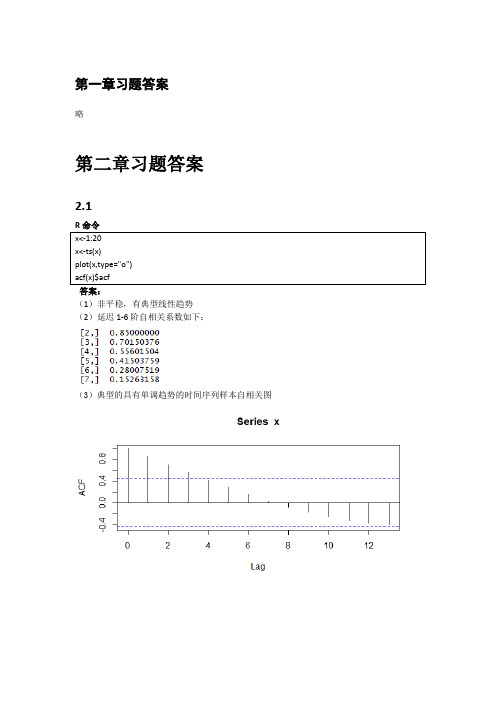
第一章习题答案略第二章习题答案2.1答案:(1)非平稳,有典型线性趋势(2)延迟1-6阶自相关系数如下:(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)1-24阶自相关系数如下(3)自相关图呈现典型的长期趋势与周期并存的特征2.3R命令答案(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列Box-Pierce testdata: rainX-squared = 0.2709, df = 3, p-value = 0.9654X-squared = 7.7505, df = 6, p-value = 0.257X-squared = 8.4681, df = 9, p-value = 0.4877X-squared = 19.914, df = 12, p-value = 0.06873X-squared = 21.803, df = 15, p-value = 0.1131X-squared = 29.445, df = 18, p-value = 0.04322.4答案:我们自定义函数,计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列Box-Pierce testdata: xX-squared = 36.592, df = 3, p-value = 5.612e-08X-squared = 84.84, df = 6, p-value = 3.331e-162.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列Box-Pierce testdata: xX-squared = 47.99, df = 3, p-value = 2.14e-10X-squared = 60.084, df = 6, p-value = 4.327e-11(2)差分序列平稳,非白噪声序列Box-Pierce testdata: yX-squared = 22.412, df = 3, p-value = 5.355e-05X-squared = 27.755, df = 6, p-value = 0.00010452.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
时间序列分析(3)

二、传递函数模型
• (2) 1阶过程的互相关函数 • 由Ezt=Eεt=0,有Eyt=0,使用Yule-Walker方程,得: γyz(0)=Eytzt=E[cd(zt-d+a1zt-d-1+…)zt+ztεt/(1-a1L)]=0 γyz(1)=Eytzt-1=E[cd(zt-d+a1zt-d-1+…)zt-1+zt-1εt/(1-a1L)]=0 ……… γyz(d)=Eytzt-d =E[cd(zt-d+a1zt-d-1+…)zt-d+zt-dεt/(1-a1L)]=cdσz2 γyz(d+1)=Eytzt-d-1 =E[cd(zt-d+a1zt-d-1+…)zt-d-1+zt-d-1εt/(1-a1L)]=cda1σz2 γyz(d+2)=Eytzt-d-2 =E[cd(zt-d+a1zt-d-1+…)zt-d-2+zt-d-2εt/(1-a1L)]=cda12σz2
一、干预分析
• (1) 一个简单的干预分析模型 • 将Enders等的劫机事件干预分析模型变换,得: (1-a1L)yt=a0+c0zt+εt 即: yt=a0/(1-a1)+c0Σa1izt-i+Σa1iεt , |a1|<1. 由此可进行脉冲响应分析: yt/zt=c0 yt+1/zt+1+yt+1/zt=c0+c0a1=c0(1+a1) yt+2/zt+2+yt+2/zt+1+yt+2/zt=c0(1+a1+a12) yt+j/zt+j+yt+j/zt+j-1+…+yt+j/zt=c0(1+a1+a12+…a1j)
时间序列王燕第二版第三章习题答案分析

17.(1)判断该序列的平稳性与纯随机性。
首先画出该序列的时序图如图1-1所示:图1-1从时序图可以看出,该序列基本上在一个数值上随机波动,故可认为该序列平稳。
再绘制序列自相关图如图1-2所示:图1-2从图1-2的序列自相关图可以看出,该序列的自相关系数一直都比较小,始终在2倍标准差范围以内,可以认为该序列自始至终都在零轴附近波动,所以认为该序列平稳。
原假设为延迟期小于或等于m期的序列值之间相互独立;备择假设为序列值之间有相关性。
当延迟期小于等于6时,p值都小于0.05,所以拒绝原假设,认为该序列为非白噪声序列。
故可以利用ARMA模型对该序列建模。
(2)如果序列平稳且非白噪声,选择适当模型拟合该序列的发展。
从图1-2可见,除了延迟1阶的偏自相关系数在2倍标准差范围之外,其他阶数的偏自相关系数都在2倍标准差范围内波动,故可以认为该序列偏自相关系数1阶截尾。
自相关图显示出非截尾的性质。
综合该序列自相关系数和偏自相关系数的性质,为拟合模型定阶为AR(1)模型。
A.A R(1)模型对于AR(1)模型,AIC=9.434581,SBC=9.468890。
对残差序列进行白噪声检验:Q统计量的P值没有大于0.05,因此认为残差序列为非白噪声序列,拒绝原假设,说明残差序列中还残留着相关信息,拟合模型不显著。
B.ARMA(1,1)模型对于ARMA(1,1)模型,AIC=9.083333,SBC=9.151950。
对残差序列进行白噪声检验:图1-3列为白噪声序列,模型信息提取比较充分。
C.AR(2)模型对于AR(2)模型,AIC=9.198930,SBC=9.268139。
对残差序列进行白噪声检验:图1-4列为白噪声序列,模型信息提取比较充分。
比较上述三个模型,见下表1:(3)利用拟合模型,预测该城市未来5年的降雪量。
用ARMA(1,1)模型可预测该城市未来5年的降雪量如下表2所示:18.(1)判断该序列的平稳性与纯随机性。
应用统计学时间序列习题及答案

计算题:34323*22562584*22582603*22602502*2250254++++++++++=a = (人计算(1)第一季度该店平均每月商品销售额(2)第一季度平均销售员人数(3)第一季度平均每个销售员的销售额 (4)第一季度平均每月每个销售员的销售额 解:(1)商品销售额为时期总量指标时间序列,4月不属一季度,该数据无用3280350300++=a = (万元)(2) 销售员人数是时点总量指标时间序列,间断间隔相等,用首尾折半法,4月初人数相当于3月末人数,这个数据有用32424045240+++=b = (人) (3)32424045240280350300+++++==平均人数一季度销售额c = (万元/人) (4)3324240452403028350300c d =+++++==平均人数一季度月平均销售额 = (万元/人)要求:(1)根据表中资料 ,计算并填制表中空白栏指标(2)计算该地财政收入的这几年的年平均发展水平、年平均增长水平(水平法)和平均增长速度(几何平均法)(3)超过平均增长速度的年份有哪些年?解:注意平均时项数的确定,写计量单位,我以下省略了单位1430%02.193*430116430%02.193*4307%02.193*4304554301)26n 0010-=-=-='-=-=∆+++=+++=a a V V n a a n a a a a n n n ((3)填全表中各年的环比增长速度,和年平均增长速度进行比较即可4. 某地1980~1990年间(以1979年为基期:a0),地区生产总值以平均 每年25%的速度增长(平均增长速度),而1991~2000年间地区生产总值以平均每年30%的速度增长(平均增长速度),2001~2012年间地区生产总值以平均每年18%的速度增长,则1980~2012年间,该地区的生产总值平均每年的增长速度是多少?(重点:正确确定时间段长短)解:注意是以1979年为基期,经过33年发展到2012年,求这段时间的平均增长速度1%118*%130*%125133121011-=-='V V5. 某地1980年的人口是120万人,1981~2000年间人口平均增长率为1.2%,之后下降到1%,按此增长率到2008年人口会达到多少?如果要求到2012年人口控制在170万以内,则2008年以后人口的增长速度应控制在什么范围内? 解:1)2(%101*%2.101*)140812*******-='==V V V a a a a ((1)分别用最小平方法的普通法和简捷法配合直线方程,并预测2010年该企业产值 (2)比较两种方法得出的结果有无异同。
第10章时间序列3季节指数法

21.6 21.2 107.1% 21.4%
21.5 21.9 108.6 21.7%
25.5
100
25.04
100
127.8
25.6%
21
二、实际预测 1、情形一:已知年度预测值,预测其它各季度值。
计算公式:某季度预测值=年度预测值×该季的季节比重 例题:已知2006年度预测值为7385吨,要求利用季节变差预测各值。
一、数据模式的分析法
1、叠加法
y
H
k
t 水平型: Y=H+S 或
y
k t
Y=H+S+C+I T
S +0
S
s>0 t
s<0
t1
t
+
t1
t
t1
趋势型: Y=T+S
Y=T+S+C+I
t
2
第一节 季节变动数据模式分析法及预测步骤
2、乘积法
y
H
S
k
k
t
t
水平季节型: Y=H×S 或 Y=H×S×C×I
y
T
S
85.8 87.3 86.3 84.7 428.3 85.7%
86.3 87.8 86.0 87.6 434.5 86.9%
102.6 103.0 102.0 100.2 511.0 102.2%
表中第一个数据来源:2150/1710.75=1.257=125.7% 其它数据同上。
12
第二节 季节指数预测法
年份
第一季度
2001
2150
2002
2192
2003
2089
应用时间序列分析 第三版 王燕 课后答案

1 1.3738
2 -0.8736
(2) | 2 | 0.3 1 , 2 1 0.8 1 , 2 1 1.4 1,模型平稳。
1 0.6
2 0.5
(3) | 2 | 0.3 1 , 2 1 0.6 1 , 2 1 1.2 1 ,模型可逆。
2、解:对于 AR(2)模型:
22 0
1 1 0 2 1 1 2 1 0.5 2 1 1 2 0 1 1 2 0.3
解得:
1 7 / 15 2 1 / 15
3、解:根据该 AR(2)模型的形式,易得: E ( xt ) 0 原模型可变为: xt 0.8xt 1 0.15xt 2 t
j
eT (3) G0 t 3 G1 t 2 G2 t 1 t 3 1 t 2 12 t 1
第二章 P34 1、 (1)因为序列具有明显的趋势,所以序列非平稳。 (2)样本自相关系数:
(k ) ˆk (0)
(x
t 1
nk
t
x )( x t k x )
t
(x
t 1
n
x) 2
1 n 1 x xt (1 2 20) 10.5 n t 1 20
(4)=17.25
(5)=12.4167
(6)=7.25
1 =0.85(0.85)
2 =0.7405(0.702)
3 =0.6214(0.556)
4 =0.4929(0.415) 5 =0.3548(0.280)
注:括号内的结果为近似公式所计算。 (3)样本自相关图: Autocorrelation Partial Correlation . |*******| . |***** | . |**** . |*** . |**. . |* . . | . . *| . . *| . | | | | | | | . |*******| . *| . | . *| . . *| . . *| . . *| . . *| . . *| . . *| . | | | | | | |
实验三平稳时间序列分析
82.9
84.7
82.9
81.5
83.4
87.7
81.879.685 Nhomakorabea877.9
89.7
85.4
86.3
80.7
83.8
90.5
84.5
82.4
86.7
83
81.8
89.3
79.3
82.7
88
79.6
87.8
83.6
79.5
83.3
88.4
86.6
84.6
79.7
86
84.2
83
84.8
83.6
82.1
81.4
85
85.8
84.2
83.5
86.5
85
80.4
85.7
86.7
86.7
82.3
86.4
82.5
82
79.5
86.7
80.5
91.7
81.6
83.9
85.6
84.8
78.4
89.9
85
86.2
83
85.4
84.4
84.5
86.2
85.6
83.2
85.7
83.5
80.1
82.2
88.6
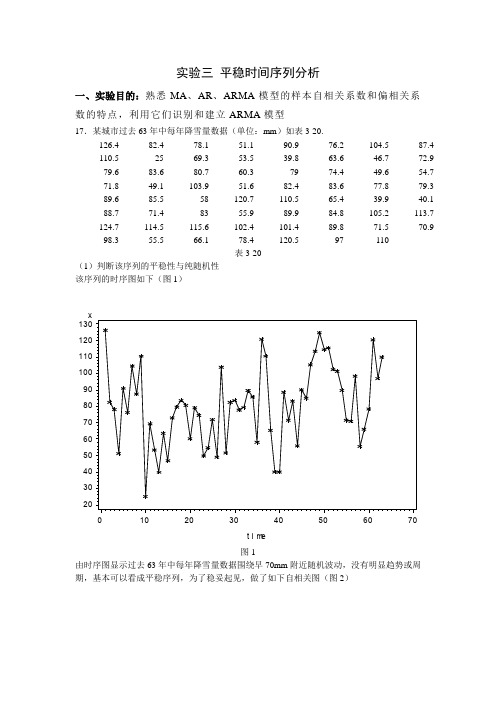
图2
自相关图显示该序列自相关系数一直都比较小,1阶开始控制在2倍的标准差范围以内,可以认为该序列自始自终都在零轴附近波动,这是随即性非常强的平稳时间序列。
纯随机性检验见下图:(图3)
图3
6阶以内P值显著小于0.05,可以认为这个拟合模型的残差序列不属于白躁声序列
(2)如果序列平稳且非白躁声,选折适当模型拟合序列的发展
《时间序列》试卷答案

《时间序列》试卷答案【篇一:时间序列分析试卷及答案3套】>一、填空题(每小题2分,共计20分)1. arma(p, q)模型_________________________________,其中模型参数为____________________。
2. 设时间序列?xt?,则其一阶差分为_________________________。
3. 设arma (2, 1):xt?0.5xt?1?0.4xt?2??t?0.3?t?1则所对应的特征方程为_______________________。
4. 对于一阶自回归模型ar(1): xt?10+?xt?1??t,其特征根为_________,平稳域是_______________________。
5. 设arma(2, 1):xt?0.5xt?1?axt?2??t?0.1?t?1,当a满足_________时,模型平稳。
6. 对于一阶自回归模型______________________。
7. 对于二阶自回归模型ar(2):xt?0.5xt?1?0.2xt?2??tma(1):xt??t?0.3?t?1,其自相关函数为则模型所满足的yule-walker方程是______________________。
8. 设时间序列?xt?为来自arma(p,q)模型:xt??1xt?1?l??pxt?p??t??1?t?1?l??q?t?q则预测方差为___________________。
9. 对于时间序列?xt?,如果___________________,则xt~i?d?。
10. 设时间序列?xt?为来自garch(p,q)模型,则其模型结构可写为_____________。
二、(10分)设时间序列?xt?来自arma?2,1?过程,满足1b0.5bx2t1?0.4bt,2其中??t?是白噪声序列,并且e??t??0,var??t。
(1)判断arma?2,1?模型的平稳性。
时间序列第2-3章习题解答

则模型的传递形式为:
=
,确定该模型的 Green 函数,使该
故该模型的 Green 函数为: 该模型可以等价表示为无穷阶 MA 模型形式为:
13. 某 ARMR(2,2)模型为: .
解因
所以
,求 . 其中
, .
14. 证明 ARMR(1,1)序列 解 方法一 因为 所以
的自相关系数为:
第 3 章 习题(王燕)
1. 已知 AR(1)模型为 解由 . 由
。求 ,
,和 。
=
=
(常均值性),有
, ,(由平稳序列的方差常性)
又
,
,故
,
所以 =
。
根据 Yule–Walker 方程,有
,
即 ,
故 =
本题也可不要推导,由相关公式和性质直接给出结果。
2. 已知某 AR(2)模型为: 求 , 的值。
1.5
样本自相关系数图
1
0.5
0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
-0.5
自相关系数如下:
延迟
1
2
3
4
5
6
7
8
自相关系数 0.5060 0.5385 0.3736 0.2907 0.2578 0.1475 0.2696 0.1862
延迟
9
10
11
12
13
14
15
16
自相关系数 0.1776 0.2584 0.2070 0.2263 0.1375 -0.0268 -0.0532 -0.1124
延迟
时间序列分析ch3习题解答12-16

1 1 , 1 ,根据 ARMA(1,1) 模型 Green 函数的递推公式得: 4 2
G0 1 , G1 1G0 1 0.5 0.25 12 , Gk 1Gk 1 1k 1G1 1k 1 , k 2
0 1
2 E (12 )
Cov( yt , yt k ) Cov( yt , yt k )
k k
ˆt (k 1) y ˆt 1 (k ) y
解: (1)成立
(2)成立
(3)成立
(4)不成立。
16. 对于 AR(1)模型: xt 1 ( xt 1 ) t ,根据 t 个历史观
E ( xt )
0 3 12 。 1 1 2 1 1 0.25
14. 证明 ARMA(1,1)序列
xt 0.5xt 1 t 0.25 t 1 ,
t ~ WN (0, 2 ) 的自相关系数为:
1, k 0 k 0.27, k 1 0.5 , k 2 k 1
j 0
G0 1 , G1 1G0 1 0.6 0.3 0.3 , Gk 1Gk 1 1k 1G1 0.3 0.6k 1 , k 2
所以该模型可以等价表示为: xt t
0.3 0.6
k k 0
t k 1
。
13. 某 ARMA(2,2)模型为: ( B) xt 3 ( B) t ,求 E ( xt ) 。其中
时间序列分析00 3.5 习 题 12. 已知 ARMA(1,1)模型为: xt 0.6 xt 1 t 0.3 t 1 ,确定该模 型的 Green 函数,使该模型可以等价表示为无穷 MA 阶模型形式。 解:由模型,知: 1 0.6,1 0.3 Green 函数为:
统计学:时间序列分析习题与答案

一、单选题1、根据季度数据测定季节比率时,各季节比率之和为()。
A.100%B.0C.400%D.1200%正确答案:C2、增长1%水平值的表达式是()。
A.报告期增长量/增长速度B.报告期发展水平/100C.基期发展水平/100D.基期发展水平/1%正确答案:C3、若报告期水平是基期水平的8倍,则我们称之为()。
A.翻了 3番B.翻了 8番C.发展速度为700%D.增长速度为800%正确答案:A4、若时间数列呈现出长时间围绕水平线的周期变化,这种现象属于()。
A.无长期趋势、有循环变动B.有长期趋势、有循环变动C.无长期趋势、无循环变动D.有长期趋势、无循环变动正确答案:B5、银行年末存款余额时间数列属于()。
A.平均指标数列B.时点数列C.时期数列D.相对指标数列正确答案:B6、某一时间数列,当时间变量t=1,2,3,...,n时,得到趋势方程为y=38+72t,那么,取t=0,2,4,6,8,...时,方程中的b将为()。
A.36B.34C.110D.144正确答案:A7、某企业2018年的产值比2014年增长了 200%,则年平均增长速度为()。
A.50%B.13.89%C.29.73%D.31.61%正确答案:D8、2010年某市年末人口为120万人,2020年年末达到153万人,则年平均增长量为()万人。
A. 3B.33C. 3.3D.30正确答案:C9、在测定长期趋势时,如果时间数列逐期增长量大体相等,则宜拟合()。
A.抛物线模型B.直线模型C.曲线模型D.指数曲线模型正确答案:B10、在测定长期趋势时,当时间数列的逐期增长速度基本不变时,宜拟合()。
A.逻辑曲线模型B.二次曲线模型C.直线模型D.指数曲线模型正确答案:D二、多选题1、编制时间数列的原则有()。
A.经济内容的一致性B.计算方法的一致性C.时间的一致性D.总体范围的一致性正确答案:A、B、C、D2、以下表述正确的有()。
时间序列分析第三章王燕第1-6题习题解答

E ( xt ) 0
;
0.7 xt 1 t ,即 xt
t
1 0.7 B
0.7i t i
i 0
所以有: Var ( xt ) (3)
0.7
i 0
2i
Var ( t )
2
1 0.7
2
2
0.51
1.96 2 ;
;
k 1 k 0.7k ,
1 1
2 2 ˆT (l )] lim Var[ xT l x l 1 12 12
.
证毕。
(3) 自相关系数 k ,由 AR(2)的递推公式,得:
1
1 0.8 16 0.695652 1 2 1 0.15 23
2 11 2 0 0.8 0.695652 0.15 1 0.406522
3 12 2 1 0.8 0.406522 0.15 0.695652 0.22087 ;
得 E ( xt ) 0 ; (2)
1 0.8, 2 0.15
1 2 2 (1 2 )(1 1 2 )(1 1 2 )
Var ( xt ) 0
1 0.15 2 1.982331 2 ; (1 0.15) (1 0.8 0.15)(1 0.8 0.15)
k 0
2 ,所以 2 0.7 0.49
(4) 因为是 AR(1)模型,偏相关系数一阶截尾,所以 22
0。
2 2. 已知某 AR(2)模型为: xt 1 xt 1 2 xt 2 t , t ~ WN (0, ) ,
时间序列分析STATA 第三课

第三课:ARMA/ARIMA建模及预测核心问题:1,前提:同方差,因此,不用考虑不同时刻变量的离散性;2,建立的是变量分布的均值模型,也就是,随机变量分布的均值所在的位置3,难点在于,时间序列数据建立模型并没有唯一性以quarterly.dta的数据来说明。
这个数据是美国的季度GDP数据,数据从1947年一季度开始,到2012年一季度结束。
研究对象,GDP,存在通货膨胀问题。
所以要用GDP平减指数(GDP Deflator)进行矫正,这里是以2005年的美元作为基准的。
所以考察变量是GDP2005,即以2005年的美元作为基准的各季度的GDP 真实值。
一,一些基本符号:D L F二,建立模型:前期准备:观察时序图相关命令:tsset, tsline/twoway从图上可以看出,GDP2005值呈线性的向右上方倾斜,第一种方法:可以用确定性分析理的方法,使用研究变量对时间变量进行回归 即:regress lrgdp date (采用的是最小二乘估计)然后对残差项进行White Noise 检验观察此图:特征大值跟大值,小值跟小值,这说明Residual 中存在着自相关信息。
肯定不是White Noise因此,从这里看出,确定性的方法比较直观,简单,但效果不好,弥补:对残差序列进行回归,建立AR 模型,这就是所谓的 残差自回归模型。
第二种方法BOX-JENKINS 方法,也就是通常所说的ARMA(p,d) /ARIMA(p,d,d)建模(采用的是最大似然估计)。
四大步骤:1、模型识别Identification :决定p 和q2、模型估计Estimation :估计εσθφμ 个),(,个)(,q p 3、模型检验Diagnostic Checking4、模型优化Parsimony1,模型识别Identification 相关命令:ac pac这个图的特征是ac值虽然在减小,但其减少类似线性,这时候就要考虑差分了,通常使用的是一阶差分和二阶差分一阶差分generate growth=lrgdp-L.lrgdp这个时候,growth就是经济增长率这张图的ac值快速减少到影音之内,说明在样本中,变量growth显现的是平稳。
2023年中级经济师经济基础考试真题及答案

2023年中级经济师经济基础考试真题及答案一、单项选择题(共70题,每题1分,每题旳备选项中,只有1个最符合题意)1、市盈率是反应企业()旳指标。
A.偿债能力B.发展能力C.营运能力D.盈利能力参照答案:D参照解析:考核第29章第3节。
精讲班讲义划线强调旳考点,冲刺班讲义内容。
盈利能力指标(利润率、净利率、收益率、盈余等)营业利润率;主营业务净利润率;资本收益率;净资产收益率;资产净利润率;一般股每股收益;市盈率;资本保值增值率2、假设某个国家2023年-2023年,GDP年均增长8%,资本存量年均增长5% ,劳动力年均增长2% ,假如资本在GDP增长中旳份额为6%,劳动力为40% ,这一时期全要素生产率增长率为( )。
A.3.0%B.4.2%C.4.0%D.7.0%参照答案:B参照解析:考核第7章经济增长与经济发展。
精讲班、冲刺班均有重点强调。
经济增长率=技术进步率+(劳动产出份额×劳动增长率)+(资本产出份额×资本增长率)即,8%=技术进步率+(40%× 2%)+(60%× 5%)技术进步率(全要素生产率)=4.2%3、某企业2023年-2023年销售收入旳年平均增长速度是27.6%,这期间对应旳年平均发展速度是()。
A.4.6%B.17.6%C.127.6%D.72.4%参照答案:C参照解析:考核第25章时间序列第3节时间序列速度分析。
精讲班、冲刺班讲义特殊强调。
平均发展速度=1+平均增长速度=1+27.6%=127.6%4、在资产负债表上,资产项目是按其流动性进行排列旳,流动性强旳项目排在前面,流动性差旳项目排在背面,下列资产项目中,排在应收账款前面旳是()。
A.固定资产B.长期投资C.存货D.货币资金参照答案:D参照解析:考核第28章第5节。
2023年真题原题。
精讲班讲义中旳原题。
冲刺班也特殊强调。
资产旳排列次序依次是:货币资金;交易性金融资产;多种债权;存货;非流动资产5、下列经济业务所产生旳现金流量中,应列入“经营活动所产生旳现金流量”项目旳是()。
第三章平稳时间序列分析-3

n
Q(ˆ )
2 t
t1
n
( xt 1 xt1 p xt p 1 t1 q tq )2 t 1
实际中最常用的参数估计方法是条件最小二乘估 计法
条件最小二乘估计
假设条件:过去未观测到的序列值为0,即
xt 0 , t 0
从而 t
(B) (B) xt
xt
t
i xt1
i 1
由时序图可见,无周期性和单调趋势,序列平稳
序列自相关图
除延迟1阶在2倍标准差外,其它都在2倍标准差范围内 波动,平稳,自相关系数1阶截尾。
所以可考虑拟合模型MA(1)
序列偏自相关图
显然,偏自相关系数拖尾。
【例3.9】 1880-1985全球气表平均温度改变值差分序列
由时序图可见,无周期性和单调趋势,序列平稳
s
t
特别当φ0=0 时,称为中心化ARMA(p,q)模型
系数多项式
引进延迟算子,中心化ARMA(p,q)模型 可简记为 (B)xt (B)t
其中p阶自回归系数多项式:
(B) 11B 2B2 pBp
q阶移动平均系数多项式:
(B) 11B 2B2 q Bq
2、平稳条件与可逆条件
ARMA(p,q)模型的平稳条件 P阶自回归系数多项式Φ(B)=0的根都在单 位圆外,即ARMA(p,q)模型的平稳性完全由 其自回归部分的平稳性决定
Pr
2 n
ˆk
2 n
0.95
Pr
2 n
ˆkk
2 n
0.95
模型定阶的经验方法:
若样本(偏)自相关系数在最初d阶明显大于2 倍标准差,后面几乎95%的值都落在2倍
标准差范围内,且衰减为小值波动的过程 很突然。这时常视为截尾,截尾阶数为d。
应用时间序列分析习题标准答案
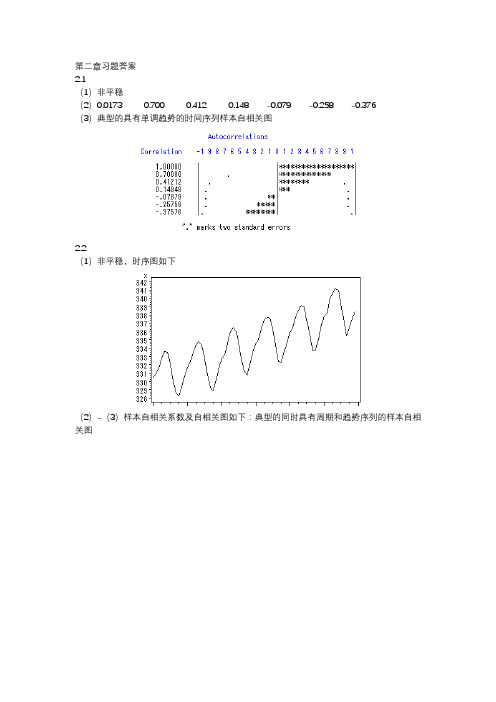
第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.0940.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.0660.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列不LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2)非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 解:1()0.7()()t t t E x E x E ε-=⋅+0)()7.01(=-t x E 0)(=t x E t t x ε=-)B 7.01(t t t B B B x εε)7.07.01()7.01(221 +++=-=-229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ022=φ3.2 解:对于AR (2)模型:⎩⎨⎧=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ 解得:⎩⎨⎧==15/115/721φφ3.3 解:根据该AR(2)模型的形式,易得:0)(=t x E原模型可变为:t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==1.98232σ⎪⎩⎪⎨⎧=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ⎪⎩⎪⎨⎧=-====015.06957.033222111φφφρφ3.4 解:原模型可变形为:t t x cB B ε=--)1(2由其平稳域判别条件知:当1||2<φ,112<+φφ且112<-φφ时,模型平稳。
第27章时间序列分析(3)
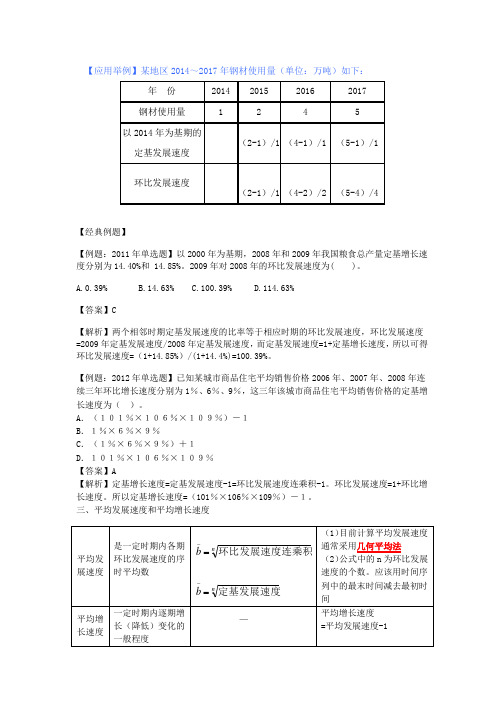
【应用举例】某地区2014~2017年钢材使用量(单位:万吨)如下:【经典例题】【例题:2011年单选题】以2000年为基期,2008年和2009年我国粮食总产量定基增长速度分别为14.40%和 14.85%。
2009年对2008年的环比发展速度为( )。
A.0.39%B.14.63%C.100.39%D.114.63%【答案】C【解析】两个相邻时期定基发展速度的比率等于相应时期的环比发展速度,环比发展速度=2009年定基发展速度/2008年定基发展速度,而定基发展速度=1+定基增长速度,所以可得环比发展速度=(1+14.85%)/(1+14.4%)=100.39%。
【例题:2012年单选题】已知某城市商品住宅平均销售价格2006年、2007年、2008年连续三年环比增长速度分别为1%、6%、9%,这三年该城市商品住宅平均销售价格的定基增长速度为()。
A.(101%×106%×109%)-1B.1%×6%×9%C.(1%×6%×9%)+1D.101%×106%×109%【答案】A【解析】定基增长速度=定基发展速度-1=环比发展速度连乘积-1。
环比发展速度=1+环比增长速度。
所以定基增长速度=(101%×106%×109%)-1。
三、平均发展速度和平均增长速度【经典例题】【例题:2016年单选题】我国2010-2015年人均国内生产总值分别为:3.1、3.6、4.0、4.3、4.7和5.2(单位:万元/人),我国2010-2015年人均国内生产总值的平均增长速度算式是( )A .B .1 3.6 4.0 4.3 4.7 5.2()5 3.13.64.0 4.3 4.7++++ C1-D .1 3.6 4.0 4.3 4.7 5.2()15 3.1 3.6 4.0 4.3 4.7++++-【答案】C【解析】 本题掌握两点:一是平均增长速度=平均发展速度-1,二是平均发展速度用几何平均法求解,开5次方。
金融时间序列分析第三版答案

金融时间序列分析第三版答案在金融时间序列分析中,时间序列分析可以从时间序列研究经济系统内所有指标之间的关系,如宏观经济变量间的相关性、金融资产价格的变动趋势和收益率曲线形态。
其中以时间序列分析为主的主要方法有()。
a.使用简单序列预测模型(如 Positive Model)。
b.运用参数估计模型预测。
一、指数序列指数是一组对某一时刻(或者一组参数)序列可能出现的趋势的函数。
指数序列通常可以分为均方指数序列和非均方指数序列。
均方指数序列主要用于对一组参数序列进行平稳性检验和估计后对平稳性进行预测。
二、股票序列股票价格的变动是时间序列规律的反映,因此对股市时间序列的研究很有必要。
股票市场上投资者一般都是追求“快进快出”,对未来作出预测,但在预测过程中仍然存在着一些不足之处。
这就要求我们对股票市场进行研究时不仅要关注其数量变化的规律,而且还要关注其时间序列特征及其他信息。
三、债券序列一般来说,一段时间内,债券价格变化趋势平稳,且变动速度比较快,这就是一段时间内较长时间内某一债券价格没有发生变动。
对于这样的序列可以采用参数估计模型来预测。
例如,利率序列和利率周期一般采用调整系数估计模型。
四、期权序列期权序列是对期权价格序列进行建模分析的一种方法。
它是利用期权产品未来收益的不确定性而建立起来的一种波动率模型。
在期权定价中,一般采用三个步骤来确定期权参数:1)时间序列信息;2)收益率曲线形态;3)期权定价模型(以参数形式表示)。
这三个步骤可以对投资组合进行动态调整,从而实现对收益率曲线形状的准确预测。
利用期权模型对收益率曲线进行建模预测所需时间通常较短,但这种方法对金融资产价格和利率存在一定周期性波动,并且难以准确地预测未来收益率趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B C C A A, A C B D D , B B D B D , B A
第六章时间序列分析
一、单项选择题
1.某地区1990—1996年排列的每年年终人口数动态数列是(b)。
A、绝对数动态数列
B、绝对数时点数列
C、相对数动态数列
D、平均数动态数列
2.某工业企业产品年生产量为20 万件,期末库存5.3万件,它们(c)。
A、是时期指标
B、是时点指标
C、前者是时期指标,后者是时点指标
D、前者是时点指标,后者是时期指标
3.间隔相等的不连续时点数列计算序时平均数的公式为(c )。
4.某地区连续4 年的经济增长率分别为8.5%,9%,8%,9.4%,则该地区经济的年平均增长率为( a)。
5.某工业企业生产的产品单位成本从2005年到2007年的平均发展速度为98%,说说明该产品单位成本( a)。
A、平均每年降低2%
B、平均每年降低1%
C、2007 年是2005 年的98%
D、2007年比2005年降低98%
6.根据近几年数据计算所的,某种商品第二季度销售量季节比率为1.7,表明该商品第二季度销售( a)。
A、处于旺季
B、处于淡季
C、增长了70%
D、增长了170%
7.对于包含四个构成因素(T,S,C,I)的时间序列,以原数列各项数值除以移动平均值(其平均项数与季节周期长度相等)后所得比率(c )。
A、只包含趋势因素
B、只包含不规则因素
C、消除了趋势和循环因素
D、消除了趋势和不规则因素
8.当时间序列的长期趋势近似于水平趋势时,测定季节变动时(b )。
A、要考虑长期趋势的影响
B、可不考虑长期趋势的影响
C、不能直接用原始资料平均法
D、剔除长期趋势的影响
9.在对时间序列作季节变动分析时,所计算的季节比率是( d)。
A、某一年月或季平均数相对于本年度序列平均水平变动的程度
B、某一年月或季平均数相对于整个序列平均水平变动的程度
C、各年同期(月或季)平均数相对于某一年水平变动的程度
D、各年同期(月或季)平均数相对于整个序列平均水平变动的程度
10.企业5月份计划要求销售收入比上月增长8%。
实际增长12%,超计划完成程度为( d)。
A.103.70%B.50%C.150%D.3.7%
11. 在时间数列的预测方法中,在作趋势外推时,若要配合指数曲线,所依据的样本资料的
特点是(b )。
A.定基发展速度大致相等B.环比发展速度大致相等
C.逐期增长量大致接近一个常数D.二级增长量大致接近一个常数
12.如果某商店销数额的逐期增长量每年都相等,则其各年的环比增长速度是( b)。
A.年年增长B.年年下降C.年年不变D.无法确定
13. 某种产品单位成本计划规定比基期下降3%,实际比基期下降3.5%,单位成本计划完成程度相对指标为( d)。
A.116.7% B.100.5% C.85.7% D.99.5%
14.发展速度的计算方法为(b )。
A.报告期水平与基期水平之差B.报告期水平和基期水平相比
C.增长量与基期水平之差D.增长量与基期水平相比
15.计算平均发展速度,实际上只与数列的(d)有关。
A.最初水平B.最末水平C.中间各期水平D.最初水平和最末水平
16、下列动态指标中,不可以取负值的指标有(b )。
A、增长量
B、平均发展速度
C、增长速度
D、平均增长速度
17、某省2001年一2005 年按年排列的每人分摊粮食数量的时间数列是( a )。
A.绝对数的时期数列B.绝对数的时点数列
C.相对数时间数列D.平均数时间数列
二、填空题
1.时间序列按其所排列指标的表现形式不同,可分为绝对指标时间序列、相对指标时间序列和___________。
2.求间隔相等的间断的时点数列的序时平均数,其计算公式为()
3.只有当时间序列没有明显的_______时,用简单平均法进行季节因素分析才比较适宜。
4.__________适用于对存在明显的长期趋势的时间序列进行季节因素分析。
5.用乘法模型测定时间数列中的季节变动,各月的季节变动之和应等于_______。
6.水平法平均发展速度仅受_________和________的影响,而不受__________的影响7.某企业9 月份计划要求成本降低5%,实际降低8%,则计划完成程度为()。
8、环比发展速度与定基发展速度之间的关系是________;增长速度与发展速度之间的关系
是________;平均发展速度与定基发展速度的的关系是________。
9、某高新技术开发区现有人口11 万,有8 家医院(其病床数合计为700 床),则该开发区
的每万人的病床数为63.636。
这个指标属于________。
10、时间序列分析的目的是______________________________________。
11、时间序列的影响因素包括______________________________________。
三.判断题
1.移动平均的平均项数越大,则它对数列的平滑休匀作用越强。
()
2.季节比率说明的是各季节相对差异。
()
3.运用季节指数进行预测时的假设前提是预测年份的季节性变化形态基本保持不变()4.循环变动与季节变动相同,都属于周期为一年的变动。
()
5.无论是月度数据、季度数据或年度数据都可以清楚地观察出季节变动。
()
6.时间序列的长期趋势如果拟合为抛物线曲线 ,这说明现象变动的变化率在较长时期中是不断变化的。
()
7.要通过移动平均法消除季节变动,则移动平均数N 应和季节周期长度一致。
()8.移动平均的项数越大,其结果会使序列数据的逐期增长量变得更大。
()
9、所研究现象的一次差(原数列的逐期增长量)大致相同,在作趋势分析时,要配合抛物
线曲线。
()
10、累积增长量等于逐期增长量之和。
()
答案
一、B C C A A A C B D D B B D B D B A
二、平均指标时间序列;;长期趋势;趋势剔除法;1200%;
最初水平,最末水平,中间水平;96.8%;环比发展速度的连乘积等于定基发展速度、增长速度等于发展速度-1、平均发展速度等与定基发展速度开方;平均指标;分析过去,认识规律,预测未来;长期趋势、季节变动、循环变动、不规则变动。
三、√√√××;√√××√。
