2017七年级数学三角形的角平分线.doc

合集下载

专题07 角的平分线性质(专题测试)(解析版)

专题07 角的平分线性质专题测试学校:___________姓名：___________班级：___________考号：___________一、选择题（共12小题，每题4分，共计48分）1．（2018春榆林市期末）如图，AD 是ABC V 的角平分线，DF AB ⊥，垂足为F ，DE DG =，ADG V 和AED V 的面积分别为60和35，则EDF V 的面积为( )A.25B.5.5C.7.5D.12.5【答案】D【详解】如图，过点D 作DH AC ⊥于H ，AD Q 是ABC V的角平分线，DF AB ⊥， DF DH ∴=，在Rt ADF V 和Rt ADH V 中，AD AD DF DH=⎧⎨=⎩， Rt ADF V ∴≌()Rt ADH HL V ，Rt ADF Rt ADH S S ∴=V V ，在Rt DEF V 和Rt DGH V 中，DE DG DF DH =⎧⎨=⎩Rt DEF ∴V ≌()Rt DGH HL V ，Rt DEF Rt DGH S S ∴=V V ，ADG QV 和AED V 的面积分别为60和35，Rt DEF Rt DGH 35S 60S ∴+=-V V ，Rt DEF S ∴V =12.5，故选D ．【名师点睛】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记掌握相关性质、正确添加辅助线构造出全等三角形是解题的关键．2．（2018春天津市期中）如图，△ABC 的三边AB ，BC ，CA 长分别是20，30，40，其三条角平分线将△ABC 分为三个三角形，则S △ABO ：S △BCO ：S △CAO 等于（）A ．1：1：1B ．1：2：3C ．2：3：4D ．3：4：5【答案】C【详解】本题主要考查三角形的角平分线。

三角形三条角平分线的交点为三角形的内心，即本题中O 点为△ABC 的内心，则O 点到△ABC 三边的距离相等，设距离为r ，有S △ABO = 12×AB×r，S △BCO = 12×BC×r，S △CAO = 12×CA×r，所以S △ABO :S △BCO :S △CAO =AB:BC:CA=20:30:40=2:3:4.故答案选C.【名师点睛】本题考查的知识点是三角形的角平分线中线和高，解题的关键是熟练的掌握三角形的角平分线中线和高.3．（2017春商丘市期中）如图，△ABC 中，AD 为△ABC 的角平分线，BE 为△ABC 的高，∠C=70°，∠ABC=48°，那么∠3是（）A ．59°B ．60°C ．56°D ．22°【答案】A【详解】在△ABC 中，∠C =70°,∠ABC =48°，则∠CAB =62°，又AD 为△ABC 的角平分线，∠1=∠2=62°÷2=31°又在△AEF 中，BE 为△ABC 的高∴∠EFA =90°−∠1=59°∴∠3=∠EFA =59°4．（2018出南阳市期末）如图，∠AOB 是平角，∠AOC=50°，∠BOD =60°，OM 平分∠BOD ，ON 平分∠AOC ，则∠MON 的度数是（）A.135°B.155°C.125°D.145°【答案】C【详解】解：∵∠AOC+∠COD+∠BOD=180°，∴∠COD=180°-∠AOC-∠COD=70°，∵OM 、ON 分别是∠AOC 、∠BOD 的平分线，∴∠MOC=12∠AOC=25°，∠DON=12∠BOD=30°，∴∠MON=∠MOC+∠COD+∠DON=125°，故选：C ．【名师点睛】本题考查角度计算，解题的关键是熟练利用角分线的性质，本题属于基础题型．5．（2018春徐州市期末）如图,在Rt △ABC 中,∠C=90°,∠A=30°,BD 是∠ABC 的平分线,AD=20,则BC 的长是 ( )A.20 C.30 D.10 【答案】D【详解】在Rt △ABC 中由于∠A=30°,因此∠ABC=60°；因为BD 是∠ABC 的角平分中线,所以∠ABD=∠DBC=30°,因此三角形ADB 为等腰三角形,BD=AD=20在直角三角形DCB 中,DC=12BD 根据勾股定理,BD²=DC²+BC²=(12BD)²+BC²,所以BC=10故选：D【名师点睛】本题考核知识点：角平分线、等腰三角形、直角三角形.解题关键点：熟记直角三角形性质、等腰三角形性质.6．（2018春信阳市期末）如图，在▱ABCD 中，已知AD 15cm =，AB 10cm =，AE 平分BAD ∠交BC 于点E ，则CE 长是( )A.8cmB.5cmC.9cmD.4cm【答案】B【详解】解：Q四边形ABCD是平行四边形，AD BC，∴==，//AD BC cm15∠交BC于点E，AEQ平分BAD∴∠=∠，DAE EABQ，//AD BC∴∠=∠，DAE AEB∴∠=∠，EAB AEB∴==，10AB BE cm()∴=-=-=．EC BC BE cm15105故选：B．【名师点睛】=是解题关键．此题主要考查了平行四边形的性质以及角平分线的定义，正确得出AB BE7．（2018春商丘市期末）如图，已知点O在直线AB上，∠COE=90°，OD平分∠AOE，∠COD=25°，则∠BOD的度数为（）A．100° B．115° C．65° D．130°【答案】B【解析】∵∠COE=90°，∠COD=25°，∴∠DOE=90°﹣25°=65°，∵OD平分∠AOE，∴∠AOD=∠DOE=65°，∴∠BOD=180°﹣∠AOD=115°，故选：B．8．（2018春芜湖市期末）如图，在△ABC中，∠ABC和∠ACB的平分线相交于点F，过F作DE∥BC，交AB 于点D，交AC于点E．若BD=4，DE=7，则线段EC的长为（）A.3B.4C.3.5D.2【答案】A【详解】∵∠ABC和∠ACB的平分线相交于点F，∴∠DBF=∠FBC，∠ECF=∠BCF，∵DF∥BC，交AB于点D，交AC于点E．∴∠DFB=∠DBF，∠CFE=∠BCF，∴BD=DF=4，FE=CE，∴CE=DE-DF=7-4=3．故选A．【名师点睛】此题主要考查学生对等腰三角形的判定与性质平行线段性质的理解和掌握，关键利用两直线平行内错角相等．9．（2018春石家庄市期末）如图，直线AB、CD相交于点O，OE平分∠AOD，若∠BOC＝70°，则∠COE的度数是（）A．110°B．120°C．135°D．145°【答案】D【详解】∵∠BOC＝70°，∴∠AOD＝∠BOC＝70°．∴∠AOC＝180°﹣70°＝110°，∵OE平分∠AOD，∴∠AOE＝12∠AOD＝12×70°＝35°．∴∠COE＝∠AOC+∠AOE＝110°+35°＝145°，故选：D．【名师点睛】此题考查角的计算，角的平分线是中考命题的热点，常与其他几何知识综合考查．10．（2018春西安市期末）如图，AB∥CD，BC平分∠ABD，∠1=50°，则∠2的度数是（）A．50o B．60o C．70o D．80o【答案】D【详解】∵AB∥CD∴∠ABC=∠1=50°，∠ABD+∠BDC=180°，∵BC平分∠ABD，∴∠ABD=2∠ABC=100°，∴∠BDC=180°-∠ABD=80°，∴∠2=∠BDC=80°．故选：D．【名师点睛】本题考查的是平行，熟练掌握平行的性质和角平分线的性质是解题的关键.11．（2018春恩施市期末）长方形如图折叠，D点折叠到D′的位置，已知∠D′FC＝40°，则∠EFC＝（）A.120°B.110°C.105°D.115°【答案】B【详解】根据翻折不变性得出，∠DFE=∠EFD′，∵∠D′FC=40°，∠DFE+∠EFD′+∠D′FC=180°，∴2∠EFD′=180°-40°=140°，∴∠EFD′=70°，∴∠EFC=∠EFD′+∠D′FC=70°+40°=110°．故选：B．【名师点睛】此题考查了角的计算和翻折变化，掌握长方形的性质和翻折不变性是解题的关键．12．（2019春周口市期末）已知∠BOC＝60°，OF平分∠BOC.若AO⊥BO，OE平分∠AOC，则∠EOF的度数是( )A．45°B．15°C．30°或60°D．45°或15°【答案】A【详解】如图1，由AO⊥BO，得∠AOB＝90°，由角的和差，得∠AOC＝∠AOB＋∠BOC＝150°，∵OE平分∠AOC，OF平分∠BOC，∴∠COE＝12∠AOC＝12×150°＝75°，∠COF＝12∠BOC＝12×60°＝30°，由角的和差，得∠EOF＝∠COE－∠COF＝75°－30°＝45°；如图2，由AO ⊥BO ，得∠AOB ＝90°，由角的和差，得∠AOC ＝∠AOB －∠BOC ＝30°，∵OE 平分∠AOC ，OF 平分∠BOC ，∴∠COE ＝12∠AOC ＝12×30°＝15°，∠COF ＝12∠BOC ＝12×60°＝30°，由角的和差，得∠EOF ＝∠COE ＋∠COF ＝15°＋30°＝45°，故选A.【名师点睛】本题考查了垂线，利用了垂线的定义，角平分线的定义，角的和差，正确地进行分类讨论、准确画出图形是解题的关键.二、填空题（共5小题，每小题4分，共计20分）13．（2018春常州市期中）如图，在△ABC 中，AF 平分∠BAC ，AC 的垂直平分线交BC 于点E ，∠B=70°，∠FAE=19°，则∠C=______度．【答案】24【详解】∵DE 是AC 的垂直平分线,∴EA=EC ，∠EAC=∠C,∴∠FAC=∠FAE+∠EAC=19°+∠EAC ，∵AF 平分∠BAC ，∴∠FAB=∠FAC.在△ABC中,∠B+∠C+∠BAC=180°所以70°+∠C+2∠FAC=180°，∴70°+∠EAC+2×(19°+∠EAC)=180° ，∴∠C=∠EAC=24°，故本题正确答案为24.【名师点睛】本题主要考查角平分线和垂直平分线的性质、三角形内角和等于180度的应用、角的概念及其计算. 14．（2016春西安市期末）如图，AE是△ABC的角平分线，AD⊥BC于点D，若∠BAC=130°，∠C=30°，则∠DAE的度数是__________.【答案】5°【详解】∵AD⊥BC，∠C=30°，∴∠CAD=90°-30°=60°，∵AE是△ABC的角平分线，∠BAC=130°，∴∠CAE=12∠BAC=12×130°=65°，∴∠DAE=∠CAE-∠CAD=65°-60°=5°．故答案为：5°．【名师点睛】本题考查了三角形的内角和定理，三角形的角平分线，高线的定义，准确识图，找出各角度之间的关系并求出度数是解题的关键．15．（2017春扬州市期末）如图，AB、CD相交于点O，OE是∠AOC的平分线，∠BOD＝70°，∠EOF＝65°，则∠AOF的度数为______°．【答案】30°【解析】∵∠AOC 与∠BOD 是对顶角，∠BOD=70°，∴∠AOC=70°，∵OE 平分∠AOC ，∴∠AOE=12∠AOC=35°， ∴∠AOF=∠EOF-∠AOE=65°-35°=30°，故答案为：30°.16．（2018春德州市期中）如图，AD 是△ABC 中∠BAC 的平分线，DE ⊥AB 于点E ，S △ABC =7，DE=2，AB=4，则AC 的长是______．【答案】3．【解析】解：如图，过点D 作DF ⊥AC 于F ．∵AD 是△ABC 中∠BAC 的角平分线，DE ⊥AB ，∴DE=DF ．由图可知，S △ABC =S △ABD +S △ACD ，∴12×4×2+12×AC×2=7，解得：AC=3．故答案为：3．17．（2018春广安市期末）如图所示，在ABC V 中，90C o ∠=，BE 平分ABC ∠，ED AB ⊥于D ，若6AC cm =，则AE DE +=________．【答案】6cm【详解】∵BE 平分∠ABC ，ED ⊥AB ，∠C=90°，∴DE=CE ，∴AE+DE=AE+CE=AC=6cm ．故答案为：6cm．【名师点睛】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．三、解答题（共4小题，每小题8分，共计32分）18．（2018春河源市期末）如图，AC、BD相交于点O，∠A=∠ABC，∠DBC=∠D，BD平分∠ABC，点E在BC 的延长线上。

(新课标)华东师大版七年级数学下册《三角形的角平分线、中线和高》同步训练及解析

2017-2018学年（新课标）华东师大版七年级下册9.1.2三角形的角平分线，中线和高线一．选择题（共8小题）1．小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解．”小华根据小明的提示作出的图形正确的是（）A．B．C．D．2．在△ABC所在的平面内存在一点P，它到A、B、C三点的距离都相等，那么点P一定是（）A．△ABC三边中垂线的交点B．△ABC三边上高线的交点C．△ABC三内角平分线的交点D．△ABC一条中位线的中点3．已知BD是△ABC的中线，AB=4，AC=3，BD=5，则△ABD的周长为（）A． 12 B．10.5 C．10 D．8.54．三角形的下列四种线段中一定能将三角形分成面积相等的两部分的是（）A．角平分线B．中位线C．高D．中线5．如图，AD是△ABC的中线，已知△ABD比△ACD的周长大6 cm，则AB与AC的差为（）A． 2cm B．3cm C．6cm D．12cm6．下列说法正确的是（）①三角形的三条中线都在三角形内部；②三角形的三条角平分线都在三角形内部；③三角形三条高都在三角形的内部．A．①②③B．①②C．②③D．①③7．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）A．锐角三角形B．钝角三角形C．直角三角形D．不能确定8．下列说法错误的是（）A．三角形的中线、高、角平分线都是线段B．任意三角形内角和都是180°C．三角形按角可分为锐角三角形、直角三角形和等腰三角形D．直角三角形两锐角互余二．填空题（共6小题）9．在△ABC中，AD为BC边的中线，若△ABD与△ADC的周长差为3，AB=8，10．如图，在△ABC中，BE是边AC上的中线，已知AB=4cm，AC=3cm，BE=5cm，则△ABC的周长是_________ cm．11．在△ABC中，已知AD是角平分线，∠B=50°，∠C=70°，∠BAD=_________ °．12．如图，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm，则△ABD 与△ACD的周长之差为_________ cm．13．如图，在△ABC中，AC⊥BC，CD⊥AB于点D．则图中共有_________ 个直角三角形．14．AD为△ABC的高，AB=AC，△ABC的周长为20cm，△ACD的周长为14cm，则AD= _________ ．三．解答题（共6小题）15．在△ABC中，BD是AC边上的中线，已知AB=6cm，△ABD的周长与△CBD 的周长的差1cm，求边BC的长．16．如图，已知：AD是△ABC的角平分线，CE是△ABC的高，∠BAC=60°，∠BCE=40°，求∠ADB的度数．17．如图，已知△ABC的周长为21cm，AB=6cm，BC边上中线AD=5cm，△ABD 周长为15cm，求AC长．18．如图，在△ABC中，∠B=60°，∠C=20°，AD为△ABC的高，AE为角平分线（1）求∠EAD的度数；（2）寻找∠DAE与∠B、∠C的关系并说明理由．19．如图，已知△ABC的高AD，角平分线AE，∠B=26°，∠ACD=56°，求∠AED的度数．20．如图，△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠EAD=5°，∠B=50°，求∠C的度数．9.1.2三角形的角平分线，中线和高线参考答案与试题解析一．选择题（共8小题）1．小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解．”小华根据小明的提示作出的图形正确的是（）A．B．C．D．考点：三角形的角平分线、中线和高；三角形的面积．菁优网版权所有分析：由三角形的三边为4，9，12，可知该三角形为钝角三角形，其最长边上的高在三角形内部，即过最长边所对的角的顶点，作对边的垂线，垂足在最长边上．解答：解：∵42+92=97＜122，∴三角形为钝角三角形，∴最长边上的高是过最长边所对的角的顶点，作对边的垂线，垂足在最长边上．故选：C．点评：本题考查了三角形高的画法．当三角形为锐角三角形时，三条高在三角形内部；当三角形是直角三角形时，两条高是三角形的直角边，一条高在三角形内部；当三角形为钝角三角形时，两条高在三角形外部，一条高在内部．2.在△ABC所在的平面内存在一点P，它到A、B、C三点的距离都相等，那么点P一定是（）A．△ABC三边中垂线的交点B．△ABC三边上高线的交点C．△ABC三内角平分线的交点D．△ABC一条中位线的中点考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据已知，作出图形，已知△ABC内一点P，PA=PB=PC，如图所示，作辅助线PM、PN、PK分别垂直三角形的三边AC、BC、AB，可证得点P是三角形的外心．问题可求．解答：解：如图所示，PA=PB=PC，作PM⊥AC于点M，则∠PMA=∠PMC=90°，在两直角三角形中，∵PM=PM，PA=PC，∴△APM≌△CPM，∴AM=MC；同理可证得：AK=BK，BN=CN，∴点P是△ABC三边中垂线的交点．故选A．点评：解答本题的关键是熟练掌握三角形的内心（三边垂直平分线的交点）和外心（三条角平分线的交点）；垂心是三条高的交点．3．已知BD是△ABC的中线，AB=4，AC=3，BD=5，则△ABD的周长为（）A． 12 B．10.5 C．10 D．8.5考点：三角形的角平分线、中线和高．菁优网版权所有分析：先由BD是△ABC的中线，得出AD=AC=1.5，再根据三角形周长的定义得出△ABD的周长=AB+BD+AD，将数值代入计算即可求解．解答：解：∵BD是△ABC的中线，∴AD=AC=1.5，∴△ABD的周长=AB+BD+AD=4+5+1.5=10.5．故选B．点评：本题考查了三角形的中线与周长，比较简单，根据中线的定义得出AD=AC=1.5是解题的关键．4．三角形的下列四种线段中一定能将三角形分成面积相等的两部分的是（）A．角平分线B．中位线C．高D．中线考点：三角形的角平分线、中线和高．菁优网版权所有分析：三角形的角平分线与中线重合时才能将三角形分成面积相等的两部分，三角形的中位线将三角形分成面积为1：3，三角形的高只有与中线重合时才能将三角形分成面积相等的两部分，三角形的中线将三角形的一条边平均分成2部分，以这2部分分别为底，分别求新三角形的面积，面积相等．解答：解：（1）三角形的角平分线把三角形分成两部分，这两部分的面积比分情况而定；（2）三角形的中位线把三角形分成两部分，这两部分的面积经计算得：三角形面积为梯形面积的；（3）三角形的高把三角形分成两部分，这两部分的面积比分情况而定；（4）三角形的中线AD把三角形分成两部分，△ABD的面积为•BD•AE，△ACD面积为•CD•AE；因为AD为中线，所以D为BC中点，所以BD=CD，所以△ABD的面积等于△ACD的面积．∴三角形的中线把三角形分成面积相等的两部分．故选D．点评：考查中线，高，中位线，角平分线的定义，及中线，高，中位线在实5．如图，AD是△ABC的中线，已知△ABD比△ACD的周长大6 cm，则AB与AC的差为（）A． 2cm B．3cm C．6cm D．12cm考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据三角形的周长和中线的定义求AB与AC的差．解答：解：∵AD是△ABC的中线，∴BD=DC．∴△ABD比△ACD的周长大6 cm，即AB与AC的差为6cm．故选C．点评：三角形的中线即三角形的一个顶点与对边中点所连接的线段．6．下列说法正确的是（）①三角形的三条中线都在三角形内部；②三角形的三条角平分线都在三角形内部；③三角形三条高都在三角形的内部．A．①②③B．①②C．②③D．①③考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据三角形的三条中线都在三角形内部；三角形的三条角平分线都在三角形内部；三角形三条高可以在内部，也可以在外部，直角三角形有两条高在解答：解：①、②正确；而对于三角形三条高：锐角三角形的三条高在三角形的内部；直角三角形有两条高在边上；钝角三角形有两条高在外部，故③错误．故选B．点评：考查了三角形的三条中线，三条角平分线，三条高的位置．三角形的三条中线都在三角形内部；三角形的三条角平分线都在三角形内部；三角形三条高可以在内部，也可以在外部，直角三角形有两条高在边上．7．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）A．锐角三角形B．钝角三角形C．直角三角形D．不能确定考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据三角形的高的特点对选项进行一一分析，即可得出答案．解答：解：A、锐角三角形，三条高线交点在三角形内，故错误；B、钝角三角形，三条高线不会交于一个顶点，故错误；C、直角三角形的直角所在的顶点正好是三条高线的交点，可以得出这个三角形是直角三角形，故正确；D、能确定C正确，故错误．故选：C．点评：此题主要考查了三角形的高，用到的知识点是钝角三角形的三条高所在的直线的交点在三角形的外部；锐角三角形的三条高所在的直线的交点在三角形的内部；直角三角形的三条高所在的直线的交点是三角形的直角顶点．8．下列说法错误的是（）A．三角形的中线、高、角平分线都是线段B．任意三角形内角和都是180°C．三角形按角可分为锐角三角形、直角三角形和等腰三角形D．直角三角形两锐角互余考点：三角形的角平分线、中线和高；三角形内角和定理；直角三角形的性质．菁优网版权所有专题：推理填空题．分析：根据三角形的中线高角平分线定义即可判断A；由三角形内角和定理能判断B；由直角三角形的分类能判断C；根据直角三角形的性质能判断D．解答：解：A、三角形的中线高角平分线都是线段，故本选项错误；B、根据三角形的内角和定理，三角形的内角和等于180°，故本选项错误；C、因为三角形按角分为直角三角形和斜三角形（锐角三角形、钝角三角形），故本选项正确；D、直角三角形两锐角互余，故本选项错误；故选C．点评：本题考查了三角形的角平分线、中线、高，三角形的内角和定理，直角三角形的性质等知识点，熟练理解和掌握这些知识是解此题的关键．二．填空题（共6小题）9．在△ABC中，AD为BC边的中线，若△ABD与△ADC的周长差为3，AB=8，则AC= 5 ．考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据三角形的中线的定义可得BD=CD，然后求出△ABD与△ADC的周长差AB与AC的差，然后代入数据计算即可得解．解答：解：∵AD为BC边的中线，∴BD=CD，∴△ABD与△ADC的周长差=（AB+AD+BD）﹣（AC+AD+CD）=AB﹣AC，∵△ABD与△ADC的周长差为3，AB=8，∴8﹣AC=3，解得AC=5．故答案为：5．点评：本题考查了三角形的中线，熟记概念并求出两个三角形的周长的差等于两边长的差是解题的关键．10．如图，在△ABC中，BE是边AC上的中线，已知AB=4cm，AC=3cm，BE=5cm，则△ABC的周长是cm．考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据三角形的中线定理：AB2+BC2=2（BE2+AE2），来求出BC的长度，然后再来求△ABC的周长．解答：解：∵在△ABC中，BE是边AC上的中线，∴AB2+BC2=2（BE2+AE2），AE=AC，∵AB=4cm，AC=3cm，BE=5cm，∴BC=（cm），∴AB+BC+AC=（cm），即△ABC的周长是cm．点评：本题主要考查了三角形的中线定理．11．在△ABC中，已知AD是角平分线，∠B=50°，∠C=70°，∠BAD= 30 °．考点：三角形的角平分线、中线和高．菁优网版权所有分析：要求∠BAD的度数，只要求得∠BAC的度数即可，可根据三角形的内角和，利用180°减去另外两个角的度数可得答案．解答：解：△ABC中，∠B=50°，∠C=70°，∴∠BAC=180°﹣∠B﹣∠C，=180°﹣50°﹣70°，=60°，∴∠BAD=∠BAC=×60°=30°．故填30．点评：本题考查了三角形的角平分线、中线和高的相关知识；利用三角形的内角和求得∠BAC的度数是正确解答本题的关键．12．如图，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm，则△ABD 与△ACD的周长之差为 2 cm．考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据三角形的周长的计算方法得到，△ABD的周长和△ADC的周长的差就是AB与AC的差．解答：解：∵AD是△ABC中BC边上的中线，∴BD=DC=BC，∴△ABD和△ADC的周长的差=（AB+BC+AD）﹣（AC+BC+AD）=AB﹣AC=5﹣3故答案为：2．点评：本题考查三角形的中线的定义以及周长的计算方法，难度适中．在三角形中，连接一个顶点和它对边的中点的线段，叫做这个三角形的中线．三角形的周长即三角形的三边和，C=a+b+c．13．如图，在△ABC中，AC⊥BC，CD⊥AB于点D．则图中共有 3 个直角三角形．考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据直角三角形的定义，解答出即可．解答：解：∵AC⊥BC，CD⊥AB，∴∠ACB=∠ADC=∠BDC=90°，∴直角三角形有：△ACB，△ADC，△BDC．故答案为：3．点评：本题主要考查了直角三角形的定义，有一个角是直角的三角形是直角三角形．14．AD为△ABC的高，AB=AC，△ABC的周长为20cm，△ACD的周长为14cm，则AD= 4cm ．考点：三角形的角平分线、中线和高．菁优网版权所有分析：如图，由于AD为△ABC的高，AB=AC，那么D为BC中点，而△ABC的周长为20cm，由此可以求出AC+CD的值，而△ACD的周长为14cm，由此就可以求出AD的长度．解答：解：如图，∵AD为△ABC的高，AB=AC，∴D为BC中点，而△ABC的周长为20cm，∴AC+CD=×20=10cm，而△ACD的周长=AC+CD+AD=14cm，∴AD=4cm．故答案为：4cm．点评：此题主要考查了等腰三角形的底边上中线的性质，也利用了三角形的周长公式，然后求出所求线段的长度．三．解答题（共6小题）15．在△ABC中，BD是AC边上的中线，已知AB=6cm，△ABD的周长与△CBD 的周长的差1cm，求边BC的长．考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据三角形的中线得出AD=CD，根据三角形的周长求出即可．解答：解：∵BD是△ABC的中线，∴△ABD和△BCD的周长的差是：（AB+BD+AD）﹣（BC+BD+CD）=AB﹣BC=1cm．又∵AB=6cm，∴BC=1cm．点评：本题主要考查对三角形的中线的理解和掌握，能正确地进行计算是解此题的关键．16．如图，已知：AD是△ABC的角平分线，CE是△ABC的高，∠BAC=60°，∠BCE=40°，求∠ADB的度数．考点：三角形的角平分线、中线和高；三角形内角和定理．菁优网版权所有分析：根据AD是△ABC的角平分线，∠BAC=60°，得出∠BAD=30°，再利用CE是△ABC的高，∠BCE=40°，得出∠B的度数，进而得出∠ADB的度数．解答：解：∵AD是△ABC的角平分线，∠BAC=60°，∴∠DAC=∠BAD=30°，∵CE是△ABC的高，∠BCE=40°，∴∠ADB=180°﹣∠B﹣∠BAD=180°﹣30°﹣50°=100°．点评：此题主要考查了角平分线的性质以及高线的性质和三角形内角和定理，根据已知得出∠B的度数是解题关键．17．如图，已知△ABC的周长为21cm，AB=6cm，BC边上中线AD=5cm，△ABD 周长为15cm，求AC长．考点：三角形的角平分线、中线和高．菁优网版权所有分析：先根据△ABD周长为15cm，AB=6cm，AD=5cm，由周长的定义可求BD的长，再根据中线的定义可求BC的长，由△ABC的周长为21cm，即可求出AC长．解答：解：∵AB=6cm，AD=5cm，△ABD周长为15cm，∴BD=15﹣6﹣5=4cm，∵AD是BC边上的中线，∴BC=8cm，∵△ABC的周长为21cm，∴AC=21﹣6﹣8=7cm．故AC长为7cm．点评：考查了三角形的周长和中线，本题的关键是由周长和中线的定义得到BC的长，题目难度中等．18．如图，在△ABC中，∠B=60°，∠C=20°，AD为△ABC的高，AE为角平分线（1）求∠EAD的度数；（2）寻找∠DAE与∠B、∠C的关系并说明理由．考点：三角形的角平分线、中线和高；三角形内角和定理．菁优网版权所有分析：（1）根据三角形的内角和定理首先求得∠BAC，然后利用角平分线的定义求得∠BAE，再在直角△BAD中求得∠BAD的度数，根据∠EAD=∠EAB ﹣∠BAD即可求得；（2）根据三角形的内角和定理，以及角平分线的定义用∠B与∠C表示出∠EAB，在直角△ABD中，利用∠B表示出∠BAD，根据∠EAD=∠EAB﹣∠BAD即可求得．解答：解：（1）∵在△ABC中，∠BAC=180°﹣∠C﹣∠B=180°﹣20°﹣60°=100°，又∵AE为角平分线，∴∠EAB=∠BAC=50°，在直角△ABD中，∠BAD=90°﹣∠B=90°﹣60°=30°，∴∠EAD=∠EAB﹣∠BAD=50°﹣30°=20°；（2）根据（1）可以得到：∠EAB=∠BAC=（180°﹣∠B﹣∠C）∠BAD=90°﹣∠B，则∠EAD=∠EAB﹣∠BAD=（180°﹣∠B﹣∠C）﹣（90°﹣∠B）=（∠B﹣∠C）．点评：本题考查了角平分线的定义，以及三及三角形的内角和定理，正确用∠B与∠C表示出∠EAB是关键．19．如图，已知△ABC的高AD，角平分线AE，∠B=26°，∠ACD=56°，求∠AED的度数．考点：三角形的角平分线、中线和高．菁优网版权所有分析：由三角形的一个外角等于与它不相邻的两个内角和知，∠BAC=∠ACD﹣∠B，∠AEC=∠B+∠BAE，而AD平分∠BAC，故可求得∠AEC的度数．解答：解：∵∠B=26°，∠ACD=56°∴∠BAC=30°∵AE平分∠BAC∴∠BAE=15°∴∠AED=∠B+∠BAE=41°．点评：本题利用了三角形内角与外角的关系和角平分线的性质求解．20．如图，△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠EAD=5°，∠B=50°，求∠C的度数．考点：三角形的角平分线、中线和高．菁优网版权所有分析：根据直角三角形两锐角互余求出∠AED，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE，然后根据角平分线的定义求出∠BAC，再利用三角形的内角和定理列式计算即可得解．解答：解：∵AD是BC边上的高，∠EAD=5°，∴∠AED=85°，∵∠B=50°，∴∠BAE=∠AED﹣∠B=85°﹣50°=35°，∵AE是∠BAC的角平分线，∴∠BAC=2∠BAE=70°，∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°．点评：本题考查了三角形的角平分线、中线和高，主要利用了直角三角形两锐角互余，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，熟记各性质并准确识图是解题的关键．。

第2讲角平分线综合(word版)

2 角平分线综合知识目标模块一双垂型例1、例2、例3难度：★★★模块二截长全等型例4、例5难度：★★★模块三延长构等腰型例6难度：★★★模块四平行等腰型例7难度：★★模块一双垂型知识导航已知点Q是∠MON平分线上的一点．⑴如图①，若已有QE⊥OM，则常可以作QF⊥ON，可以得到．(2)如图②，过点Q分别作QE⊥OM，QF⊥ON，可以得到．题型一基本双垂型例1(2016年汉阳区八上期中24题第(1)(2)问)⑴问题解决：如图，在四边形ABCD中，∠BAD＝α，∠BCD＝180°－α，BD平分∠ABC．①如图1，若α＝90°，根据教材中一个重要性质直接可得AD＝CD，这个性质是；②在图2中，求证：AD＝CD；图1 图2如图，己知∠BAC的平分线与BC的垂直平分线PQ相交于点P，PM丄AC，PN丄AB，垂足分别为M、N，AB＝3，AC＝7，求CM的长度．题型二内心（旁心）的应用(1)证明：三角形的三条角平分线交于一点；(2)证明：三角形的一条内角平分线与其不相邻的两外角平分线交于一点．练习已知：四边形ABCD中，对角线BD平分∠ABC，∠ACB＝72°，∠ABC＝60°，并且∠BAD＋∠CAD＝180°，那么∠BDC的度数为．例3(2015年武汉二中八上期中）如图，△ABC中，点D是BC上一点，已知∠DAC＝30°，∠DAB＝75°，CE平分∠ACB交AB于点E，连接DE，则∠DEC＝_________．(2016年武昌区八上期中笫10题)如图，在△ABC中，点M、N是∠ABC和∠ACB的三等分线的交点，若∠A＝60°，求∠BMN的度数．真题演练(2016年武汉二中八上期中第23题第(1)(2)问)如图，在△ABC中，BD平分∠ABC交AC于点D，∠A－∠C＝36°．(1)如图1，点E为BD延长线上一点，EH丄AC于点H，求∠E的度数；(2)如图2，CP平分∠ACB的外角交BD延长线于点P，连AP，点F是BC延长线上一点，PF＝P A，若∠DPC＝a，求∠PFC的度数（用含a的式子表示)．图1 图2模块二截长全等型知识导航已知点Q是∠MON平分线上一点，若点E是射线OM上任意一点，可以在ON上截取OF＝OE，连接QF，构造△OQF≌OQE．例4(2016年江汉区八上期中)如图，在△ABC中，∠B＝60°，AD、CE分別是∠BAC、∠BCA的平分线，AD、CE相交于点F．求证：①AC＝AE＋CD；②FE＝FD．如图，已知四边形ABCD中，∠A＋∠C＝I80°，BD平分∠ABC．求证：DC＝AD．例5(2016年江岸区八上期中第9题)如图，△ABC中，CE平分∠ACB的外角，D为CE上一点，若BC＝a，AC＝b，DB＝m，AD＝n，求m －a，与b－n的大小关系．练习如图，D是△ABC的外角∠CAE平分线AP上一点，求证：DC＋DB＞AB＋AC．模块三延长相交构等腰型知识导航已知点Q是∠MON平分线上的一点．若EQ⊥OQ于点Q，可以延长EQ艾ON于点F，从而得到等腰三角形，Q是底边EF的中点，OQ为等腰△EOF的“三线合一”例6(2016年汉阳区八上期中）△ABC 中，AB ＝AC ，∠BAC ＝90°，若D 为线段BC 上一点，∠EDB＝12∠ACB ，BE ⊥DE ，垂足为E ，DE 交AB 于F ．(1)如图，当D 与C 点重合时，探究BE 、DF 的数量关系；(2)如图，当D 不与C 重合时，线段BE 与DF 的数量关系是否发生变化，变化．证明你的结论．练习(2016-2017学年度二中广雅八上月考改编) 等腰Rt △ABC ，∠ACB ＝90°，AC ＝BC ，D 为AB 上一点，AD ＝AC ，且BE ⊥CD 于E ，CH ⊥AB 于点H ． (1)求∠BCD 的度数；(2)求CDBE的值．拓展如图，BE 、CF 分别为△ABC 的两个外角平分线，过A 作从AE 丄BE 此于点E ，作AF 丄CF 于点F ，作AD ⊥BC 于点D ，已知AB ＋AC ＝8，AD ＝3，求S △ABE ＋S △ACF 的值．BD AEF模块四平行等腰型知识导航已知OQ 是∠MON 的角平分线，点D 为边MO 上一点． ①过D 作DE ∥ON 交OQ 于点E ，則可构造出等腰△DOE ；②过D 作DF //OQ 交ON 的反向延长线于点F ，则可构出等腰△DOF ．NED MQ ONDMQOF例7(2014年江岸区八上期中)如图所示，在△ABC 中，∠ABC 和∠ACB 的平分线交于点O ，过点O 作EF ∥BC 交AB 于E ，交AC 于F ，若AB ＝10，AC ＝8，求△AEF 的周长．ACBOEF拓展如图，△ABC 中，AB ＝AC ，AD 、CD 分别是△ABC 两个外角的平分线．求证：AB ＝AD ．DF AB E总结归纳角平分线常见辅助线1．单垂或双垂型N MEO QFNMEO Q F2．截长全等型NMEFO QNMEF OQ3．延长等腰型NM EF O Q4．平行等腰型NED MQ ONDMQOF第二讲本讲课后作业A 基础刚刚1．如图，∠DAE ＝∠ADE ＝15°，DE ∥AB ，DF ⊥AB ，若AE ＝8，则DF ＝( )． A ．5 B ．4 C ．3 D ．2FD BA E C2．如图所示，BD 是∠ABC 的角平分线，AB ＝BC ，点P 在BD 上，PM ⊥AD ，PN ⊥CD ，垂足分别为M 、N ．求证：P ＝PN ．CA D F BP M N3．(2014年江岸区八上期中)如图，在四边形ABCD中，BE、CF分别平分∠ABC、∠BCD，BE、CF相交于点O，BE交CD于E，CF 交AB于F．(1)试写出∠A，∠D，∠BOC的数量关系，然后证明．(2)若∠A＋∠D＝240°，求证：OE＝OF．BDAEOF4．已知点P是∠BAC平分线上上一点，AC＞AB，求证：AC－AB>PC－PB．D CABP5．如图，已知四边形ABCD中，CA平分∠BCD，BC＞CD，AB＝AD，求证：∠B＋∠D＝180°．BDC A6．如图，在△ABC中，BD、CD分别平分∠ABC和∠ACB，ED∥AB，FD//AC，如果BC＝6，求△DEF 的周长．BA DFB综合训练7．如图，△ABC三条角平分线交于O点且三边AB、BC、CA长分別为4、5、6，O到AC的距离为2，则S△ABC＝．BCO8．(2016年武汉外校八上期中第23题）如图，等腰直角△ABC 中，AC ＝BC ，∠ACB ＝90°，∠A 、∠C 的平分线交于点P ． (1)求证：AB ＝CP ＋BC ；(2)若∠A 的外角平分线以及∠C 的平分线交于点P ，(1)中结论是否仍成立？请画出图形，写出结论，并说明理由．BAP BA。

角平分线四大模型总结+习题+解析（最全版）

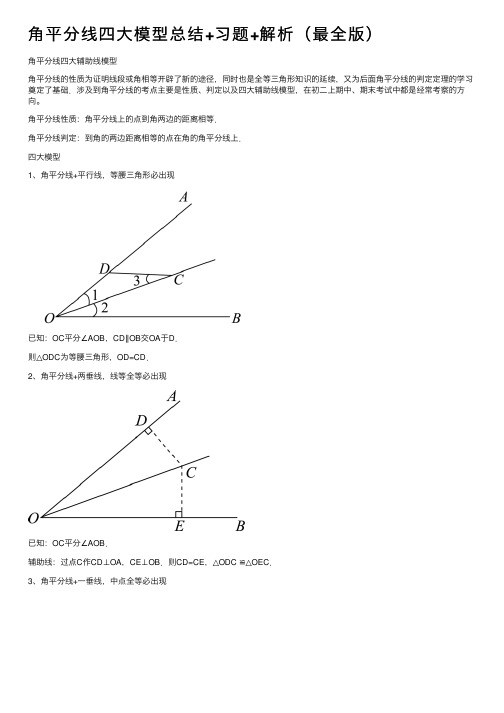
⾓平分线四⼤模型总结+习题+解析（最全版）⾓平分线四⼤辅助线模型⾓平分线的性质为证明线段或⾓相等开辟了新的途径，同时也是全等三⾓形知识的延续，⼜为后⾯⾓平分线的判定定理的学习奠定了基础．涉及到⾓平分线的考点主要是性质、判定以及四⼤辅助线模型，在初⼆上期中、期末考试中都是经常考察的⽅向。

⾓平分线性质：⾓平分线上的点到⾓两边的距离相等．⾓平分线判定：到⾓的两边距离相等的点在⾓的⾓平分线上．四⼤模型1、⾓平分线+平⾏线，等腰三⾓形必出现已知：OC平分∠AOB，CD∥OB交OA于D．则△ODC为等腰三⾓形，OD=CD．2、⾓平分线+两垂线，线等全等必出现已知：OC平分∠AOB．辅助线：过点C作CD⊥OA，CE⊥OB．则CD=CE，△ODC ≌△OEC．3、⾓平分线+⼀垂线，中点全等必出现已知：OC平分∠AOB，DC垂直OC于点C．辅助线：延长DC交OB于点E．则C是DE的中点，△ODC ≌△OEC．4、⾓平分线+截长补短线，对称全等必出现已知：OC平分∠AOB,截取OE=OD，连接CD、CE．则△ODC和△OCE关于OC对称，即△ODC ≌△OEC．【核⼼考点⼀】⾓平分线的性质与判定1．（2016?张家界模拟）如图，OP 平分MON ∠，PA ON ⊥于点A ，点Q 是射线OM 上⼀个动点，若3PA =，则PQ 的最⼩值为( )A B ．2C ．3D ．2．（2016秋?抚宁县期末）如图，在ABC ?中，AD 是它的⾓平分线，8AB cm =，6AC cm =，则:(ABD ACD S S ??= )A ．3:4B ．4:3C ．16:9D ．9:163．（2017春?崇仁县校级⽉考）如图，在ABC ?中，90ACB ∠=?，BE 平分ABC ∠，DE AB ⊥于点D ，如果3AC cm =，那么AE DE +等于( )A ．2cmB ．3cmC ．4cmD ．5cm4．（2018春?⼤东区期中）如图，在Rt ABC ?中，90C ∠=?，BD 是⾓平分线，若CD m =，2AB n =，则ABD ?的⾯积是( )A ．mnB ．5mnC ．7mnD ．6mn5．（2019秋?樊城区期末）⼩明同学在学习了全等三⾓形的相关知识后发现，只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线．如图：⼀把直尺压住射线OB ，另⼀把直尺压住射线OA 并且与第⼀把直尺交于点P ，⼩明说：“射线OP 就是BOA ∠的⾓平分线．”他这样做的依据是( )A ．⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B ．⾓平分线上的点到这个⾓两边的距离相等C ．三⾓形三条⾓平分线的交点到三条边的距离相等D ．以上均不正确6．（2019秋?梁平区期末）如图，若BD AE ⊥于B ，DC AF ⊥于C ，且DB DC =，40BAC ∠=?，130ADG ∠=?，则DGF ∠=．7．（2018春?开江县期末）如图，在Rt ABC ?中，90C ∠=?，以顶点A 为圆⼼，适当长为半径画弧，分别交AB 、AC 于点M 、N ，再分别以点M 、N 为圆⼼，⼤于12MN 的长为半径画弧，两弧交于点P ，射线AP 交边BC 于点D ．下列说法错误的是( ) A ．CAD BAD ∠=∠B ．若2CD =，则点D 到AB 的距离为2C ．若30B ∠=?，则CDA CAB ∠=∠D ．2ABD ACD S S ??=8．（2014秋?西城区校级期中）如图，点E 是AOB ∠的平分线上⼀点，EC OA ⊥，ED OB ⊥，垂⾜分别是C ，D ．下列结论中正确的有( )（1）ED EC =；（2）OD OC =；（3）ECD EDC ∠=∠；（4）EO 平分DEC ∠；（5）OE CD ⊥；（6）直线OE 是线段CD 的垂直平分线．A ．3个B ．4个C ．5个D ．6个9．（2019春?杜尔伯特县期末）如图：在ABC ?中，90C ∠=?，AD 是BAC ∠的平分线，DE AB ⊥于E ，F 在AC 上，BD DF =，证明：（1）CF EB =．（2）2AB AF EB =+．10．（2019秋?垦利区期中）如图，ABC⊥⊥且平分BC，DE AB中，AD平分BAC∠，DG BC于E，DF AC⊥于F．（1）判断BE与CF的数量关系，并说明理由；（2）如果8AB=，6AC=，求AE、BE的长．11．（2017秋?遂宁期末）某地区要在区域S内（即COD∠内部）建⼀个超市M，如图所⽰，按照要求，超市M到两个新建的居民⼩区A，B的距离相等，到两条公路OC，OD的距离也相等．这个超市应该建在何处？（要求：尺规作图，不写作法，保留作图痕迹）【核⼼考点⼆】⾓平分线+⾓两边垂线12．（2019秋?肥城市期末）如图，//AB CD ，BP 和CP 分别平分ABC ∠和DCB ∠，AD 过点P ，且与AB 垂直，垂⾜为A ，交CD 于D ，若8AD =，则点P 到BC 的距离是．13．（2015?湖州）如图，已知在ABC ?中，CD 是AB 边上的⾼线，BE 平分ABC ∠，交CD 于点E ，5BC =，2DE =，则BCE ?的⾯积等于( )A ．10B ．7C ．5D ．414．（2010秋?涵江区期末）如图所⽰，在Rt ABC ?中，90C ∠=?，BC AC =，AD 平分BAC ∠交BC 于D ，求证：AB AC CD =+．15．（2012秋?蓬江区校级期末）如图，已知90∠=∠=?，M是BC的中点，DM平分B C∠．求证：ADC（1）AM平分DAB∠；（2）DM AM⊥．16．（2016秋?西城区校级期中）已知：如图，12∠=∠，P为BN上的⼀点，PF BC⊥于F，=，PA PC（1）求证：180∠+∠=?；PCB BAP（2）线段BF、线段BC、线段AB之间有何数量关系？写出你的猜想及证明思路．【核⼼考点三】⾓平分线+垂线17．（2017秋?和平区校级⽉考）如图．在ABC ?中，BE 是⾓平分线，AD BE ⊥，垂⾜为D ，求证：21C ∠=∠+∠．18．（2013秋?昌平区期末）已知：如图，在ABC ?中，AD 平分BAC ∠，CD AD ⊥于点D ，DCB B ∠=∠，若10AC =，6AD=，求AB 的长．19．如图所⽰，ABC ?中，ACB ABC ∠>∠，AE 平分BAC ∠，CD AE ⊥于D ，求证：ACD B ∠>∠．20．已知：如图，在ABC ?中，3ABC C ∠=∠，12∠=∠，BE AE ⊥．求证：2AC AB BE -=．21．（2019秋?下陆区期中）如图，BD 是ABC ∠的⾓平分线，AD BD ⊥，垂⾜为D ，20DAC ∠=?，38C ∠=?，则BAD ∠=．22．（2019秋?曲⾩市校级⽉考）如图，在ABC ?中，AB AC =，90BAC ∠=?，BD 平分ABC ∠交AC 于D ，过C 作CE BD ⊥交BD 延长线于E ．求证：12CE BD =．23．（2019?沂源县⼀模）（1）如图（a）所⽰，BD、CE分别是ABC的外⾓平分线，过点A作AD BD⊥，AE CE⊥，垂⾜分别为D、E，连接DE，求证：1() 2DE AB BC AC=++；（2）如图（b）所⽰，BD、CE分别是ABC的内⾓平分线，其他条件不变，DE与ABC三边有怎样的数量关系？并证明这个数量关系；（3）如图（c）所⽰，BD为ABC的内⾓平分线，CE为ABC的外⾓平分线，其他条件不变，DE与ABC三边⼜有怎样的数量关系？并证明这个数量关系．24．（2017秋?夏⾢县期中）如图，在ABC ?中，ABC ∠、ACB ∠的平分线相交于F ，过F 作//DE BC ，交AB 于D ，交AC 于E ，那么下列结论：①BDF ?、CEF ?都是等腰三⾓形；②DE DB CE =+；③AD DE AE AB AC ++=+；④BF CF =．正确的有．25．（2019秋?垦利区期末）如图，平⾏四边形ABCD 中，3AB cm =，5BC cm =；，BE 平分ABC ∠，交AD 于点E ，交CD 延长线于点F ，则DE DF +的长度为．26．（2010秋?海淀区期末）如图，BD 是ABC ?的⾓平分线，//DE BC ，DE 交AB 于E ，若AB BC =，则下列结论中错误的是( )A ．BD AC ⊥B ．A EDA ∠=∠C ．2AD BC =D ．BE ED =27．如图，若BD 、CD 分别平分ABC ∠和ACB ∠，过D 作//DE AB 交BC 于E ，作//DF AC 交BC 于F ，求证：BC 的长等于DEF ?的周长．28．（2018秋?邳州市期中）如图，在四边形ABCD中，对⾓线AC平分BAD >，∠，AB AD 下列结论正确的是()A．AB AD CB CD->-B．AB AD CB CD-=-C．AB AD CB CD-<-D．AB AD-与CB CD-的⼤⼩关系不确定29．（2012?⿇城市校级模拟）在ABC∠的外⾓平分线，P是AD上的任意中，AD是BAC⼀点，试⽐较PB PC+与AB AC+的⼤⼩，并说明理由．30．（2018秋?万州区期中）已知：如图，在四边形ABCD中，AC平分BAD ∠，CE AB⊥于=+．E，且180B D∠+∠=?，求证：AE AD BE31．（2017秋?海淀区期中）如图，已知AD是BAC∠=?，C=+，31的⾓平分线，AC AB BD 求B∠的度数．32．（2019秋?平⼭县期中）如图，90∠=?，OM平分AOB∠，将直⾓三⾓板的顶点PAOB在射线OM上移动，两直⾓边分别与OA、OB相交于点C、D，问PC与PD相等吗？试说明理由．33．（2016秋?丰宁县期中）如图，在ABC ?中，100A ∠=?，40ABC ∠=?，BD 是ABC ∠的平分线，延长BD ⾄E ，使DE AD =．求证：BC AB CE =+．34．（2018秋?丰城市期中）在ABC ?中，2ACB B ∠=∠，（1）如图1，当90C ∠=?，AD 为BAC ∠的⾓平分线时，在AB 上截取AE AC =，连接DE ，求证：AB AC CD =+；（2）如图2，当90C ∠≠?，AD 为BAC ∠的⾓平分线时，线段AB 、AC 、CD ⼜有怎样的数量关系？请直接写出你的结论，不需要证明；（3）如图3，当AD 为ABC ?的外⾓平分线时，线段AB 、AC 、CD ⼜有怎样的数量关系？请写出你的猜想，并说明理由．35．（2019春?利津县期末）如图，在ABC∠平分线，AD的垂直平分线分中，AD是BAC别交AB、BC延长线于F、E．求证：（1）EAD EDA∠=∠；（2）//DF AC；（3）EAC B∠=∠．36．（2014?西城区⼆模）在ABC>，AD平分BAC∠交BC于点∠为锐⾓，AB AC，BACD．（1）如图1，若ABC是等腰直⾓三⾓形，直接写出线段AC，CD，AB之间的数量关系；（2）BC的垂直平分线交AD延长线于点E，交BC于点F．①如图2，若60∠=?，判断AC，CE，AB之间有怎样的数量关系并加以证明；ABE②如图3，若AC AB+，求BAC∠的度数．⾓平分线四⼤辅助线模型--解析⼀．⾓平分线的性质与判定（共11⼩题）1．（2016?张家界模拟）如图，OP 平分MON ∠，PA ON ⊥于点A ，点Q 是射线OM 上⼀个动点，若3PA =，则PQ 的最⼩值为( )A B ．2C ．3D ．【分析】⾸先过点P 作PB OM ⊥于B ，由OP 平分MON ∠，PA ON ⊥，3PA =，根据⾓平分线的性质，即可求得PB 的值，⼜由垂线段最短，可求得PQ 的最⼩值．【解答】解：过点P 作PB OM ⊥于B ， OP 平分MON ∠，PA ON ⊥，3PA =，3PB PA ∴==，PQ ∴的最⼩值为3．故选：C ．2．（2016秋?抚宁县期末）如图，在ABC ?中，AD 是它的⾓平分线，8AB cm =，6AC cm =，则:(ABD ACD S S ??= )A ．3:4B ．4:3C ．16:9D ．9:16【分析】利⽤⾓平分线的性质，可得出ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼相等，估计三⾓形的⾯积公式，即可得出ABD ?与ACD ?的⾯积之⽐等于对应边之⽐．【解答】解：AD 是ABC ?的⾓平分线，∴设ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼分别为1h ，2h ，12h h ∴=，ABD ∴?与ACD ?的⾯积之⽐:8:64:3AB AC ===，故选：B ．3．（2017春?崇仁县校级⽉考）如图，在ABC ?中，90ACB ∠=?，BE 平分ABC ∠，DE AB ⊥于点D ，如果3AC cm =，那么AE DE +等于( )A ．2cmB ．3cmC ．4cmD ．5cm【分析】根据⾓平分线的性质得到ED EC =，计算即可．【解答】解：BE 平分ABC ∠，DE AB ⊥，90ACB ∠=?， ED EC ∴=，3AE DE AE EC AC cm ∴+=+==，故选：B ．4．（2018春?⼤东区期中）如图，在Rt ABC ?中，90C ∠=?，BD 是⾓平分线，若CD m =，2AB n =，则ABD ?的⾯积是( )A ．mnB ．5mnC ．7mnD ．6mn【分析】过点D 作DE AB ⊥于E ，根据⾓平分线上的点到⾓的两边距离相等可得DE CD =，然后根据三⾓形的⾯积公式即可得到结论．【解答】解：如图，过点D 作DE AB ⊥于E ，BD 是ABC ∠的平分线，90C ∠=?，DE CD m ∴==，ABD ∴?的⾯积122n m mn =??=，故选：A．5．（2019秋?樊城区期末）⼩明同学在学习了全等三⾓形的相关知识后发现，只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线．如图：⼀把直尺压住射线OB，另⼀把直尺压住射线OA并且与第⼀把直尺交于点P，⼩明说：“射线OP就是BOA∠的⾓平分线．”他这样做的依据是()A．⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B．⾓平分线上的点到这个⾓两边的距离相等C．三⾓形三条⾓平分线的交点到三条边的距离相等D．以上均不正确【分析】过两把直尺的交点C作CE AO=，再根据⾓⊥，CF BO⊥，根据题意可得CE CF的内部到⾓的两边的距离相等的点在这个⾓的平分线上可得OP平分AOB∠；【解答】解：（1）如图所⽰：过两把直尺的交点P作PE AO⊥，⊥，PF BO两把完全相同的长⽅形直尺，PE PF∴=，∠（⾓的内部到⾓的两边的距离相等的点在这个⾓的平分线上），OP∴平分AOB故选：A．。

2017七年级下册数学第一单元知识点汇总

2017七年级下册数学第一单元知识点汇总2017七年级下册数学第一单元知识点汇总（浙教版）认识三角形一、三角形的基本概念：、三角形的概念：由不在同一条直线上的三条线段首尾顺次相接所组成的图形。

三角形AB记作：△AB。

2、相关概念：三角形的边：组成三角形的三条线段。

记作：AB、A、B。

三角形的内角：每两条边所组成的角。

记作：∠A、∠B、∠3、三角形的分类：二、三角形三边关系：、三角形任何两边的和大于第三边。

几何语言：若a、b、为△AB的三边，则a+b>,a+>b,b+>a想一想：这个在实际解题中该怎样应用?2、三边关系也可表述为：三角形任何两边的差都小于第三边。

三、三角形的内角和定理：三角形三个内角的和等于1800。

几何语言：△AB中，∠A+∠B+∠=1800。

四、三角形的三线：问题1、如何作三角形的高线、角平分线、中线?问题2、三角形的高线、角平分线、中线各有多少条，它们的交点在什么位置?问题3、三角形的中线有什么应用?三角形的角平分线和中线从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的角平分线三角形三个角平分线的交点叫做内心角平分线的性质角平分线上的一点到角的两边距离相等2角的内部到角的两边距离相等的点在角的平分线上三角形顶点到其内角的角平分线交对边的点连的一条线段,叫三角形的角平分线三角形的角平分线不是角的平分线：一个是线段,一个是射线三角形角平分线有个有趣的性质：三角形AB中角A的平分线为AD,则AB:A=BD:D 三角形的三条角平分线相交于一点,该点为三角形的内心,且内心到三条边的距离相等3角平分线是到角两边距离相等的所有点的集合中线连接一个顶点与它对边中点的线段,叫做三角形的中线中线的交点为重心,重心分中线2：1 中线:三角形中,连结一个顶点和它所对边的中点的连线段叫做三角形的中线中线也是线段,一个三角形有3条中线在一个角为30°直角三角形中60°角所对应的边上的中线为斜边的一半在一个三角形中,其一短边为斜边的一半,且这个三角形为30°的直角三角行,那么,60°角所对的边上的中线在此三角形中有三个等量三角形的高已知面积和底边长求高回想三角形的面积公式。

核心考点03 三角形有关概念与性质(原卷版)

核心考点03 三角形有关概念与性质目录考点一：三角形考点二：三角形的角平分线、中线和高考点三：三角形的面积考点四：三角形的稳定性考点五：三角形三边关系考点六：三角形内角和定理考点七：三角形的外角性质一．三角形（1）三角形的概念：由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形．组成三角形的线段叫做三角形的边．相邻两边的公共端点叫做三角形的顶点．相邻两边组成的角叫做三角形的内角，简称三角形的角．（2）按边的相等关系分类：不等边三角形和等腰三角形（底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形）．（3）三角形的主要线段：角平分线、中线、高．（4）三角形具有稳定性．二．三角形的角平分线、中线和高（1）从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高．（2）三角形一个内角的平分线与这个内角的对边交于一点，则这个内角的顶点与所交的点间的线段叫做三角形的角平分线．（3）三角形一边的中点与此边所对顶点的连线叫做三角形的中线．（4）三角形有三条中线，有三条高线，有三条角平分线，它们都是线段．（5）锐角三角形的三条高在三角形内部，相交于三角形内一点，直角三角形有两条高与直角边重合，另一条高在三角形内部，它们的交点是直角顶点；钝角三角形有两条高在三角形外部，一条高在三角形内部，三条高所在直线相交于三角形外一点．三．三角形的面积（1）三角形的面积等于底边长与高线乘积的一半，即S＝×底×高．△（2）三角形的中线将三角形分成面积相等的两部分．四．三角形的稳定性当三角形三边的长度确定后，三角形的形状和大小就能唯一确定下来，故三角形具有稳定性．这一特性主要应用在实际生活中．五．三角形三边关系（1）三角形三边关系定理：三角形两边之和大于第三边．（2）在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．（3）三角形的两边差小于第三边．（4）在涉及三角形的边长或周长的计算时，注意最后要用三边关系去检验，这是一个隐藏的定时炸弹，容易忽略．六．三角形内角和定理（1）三角形内角的概念：三角形内角是三角形三边的夹角．每个三角形都有三个内角，且每个内角均大于0°且小于180°．（2）三角形内角和定理：三角形内角和是180°．（3）三角形内角和定理的证明证明方法，不唯一，但其思路都是设法将三角形的三个内角移到一起，组合成一个平角．在转化中借助平行线．（4）三角形内角和定理的应用主要用在求三角形中角的度数．①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．七．三角形的外角性质（1）三角形外角的定义：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．三角形共有六个外角，其中有公共顶点的两个相等，因此共有三对．（2）三角形的外角性质：①三角形的外角和为360°．②三角形的一个外角等于和它不相邻的两个内角的和．③三角形的一个外角大于和它不相邻的任何一个内角．（3）若研究的角比较多，要设法利用三角形的外角性质②将它们转化到一个三角形中去．（4）探究角度之间的不等关系，多用外角的性质③，先从最大角开始，观察它是哪个三角形的外角．一．三角形（共1小题）1．（2018春•浦东新区期末）设M 表示直角三角形，N 表示等腰三角形，P 表示等边三角形，Q 表示等腰直角三角形．下列四个图中，能正确表示它们之间关系的是（）A ．B ．C ．D ．二．三角形的角平分线、中线和高（共5小题）2．（2021春•浦东新区期中）三角形的角平分线、中线、高都是（）A ．直线B ．线段C ．射线D ．以上都不对3．（2022春•静安区期中）下列判断错误的是（）A ．三角形的三条高的交点在三角形内B ．三角形的三条中线交于三角形内一点C ．直角三角形的三条高的交点在直角顶点D ．三角形的三条角平分线交于三角形内一点4．（2021春•徐汇区校级期中）下列说法中正确的是（）A ．三角形的三条高交于一点B ．有公共顶点且相等的两个角是对顶角C ．两条直线被第三条直线所截，所得的内错角相等D ．两条平行线被第三条直线所截，一组同旁内角的角平分线互相垂直5．（2021春•青浦区期中）直角三角形的三条高的交点在．6．（2021春•上海期中）在三角形的三条高中，位于三角形外的可能条数是条．三．三角形的面积（共10小题）7．（2021春•崇明区期末）如图，已知a ∥b ，点A 、E 在直线a 上，点B 、C 在直线b 上，且BD ＝2BC，则考点精讲下列说法中正确的是（）A ．S △BDE ＞2S △ABCB ．S △BDE ＜2S △ABC C ．S △BDE ＝2S △ABCD ．无法确定8．（2022春•杨浦区校级期末）如图，直线AB ∥CD ，点E 、N 位于直线AB 上，点F 、M 、G 位于直线CD 上，且EN ：FG ＝1：2，若△EMN 的面积为5，则△EFG 的面积为．9．（2022春•杨浦区校级期中）如图，AD ∥BC ，AC 、BD 交于点E ，BF ＝FC ，其中面积相等的三角形有对．10．（2022春•闵行区校级期中）如图：已知a ∥b ，AD ＝3，BC ＝5，S △AOD ＝2.25，S △AOB ＝3.75，则S △BOC ＝．11．（2022春•宝山区校级月考）如图，已知直线a ∥b ，点A 、B 在直线a 上，点C 、D 在直线b 上，如果△ABC 的面积和△BCD 的面积之比为2：3，那么AB ：CD 的值为．12．（2021春•徐汇区校级期中）如图，AD ∥BC ，AC 、BD 交于点E ，三角形ABE 的面积等于4，三角形CBE 的面积等于5，那么三角形DBC 的面积等于．13．（2021春•杨浦区期末）如图，在△ABC 中，AB ＝AD ＝DC ，AE ⊥BD ，如果△ABC 的面积是12，那么△ABE 的面积是．14．（2021春•松江区期中）如图，已知点B 在线段CF 上，AB ∥CD ，AD ∥BC ，DF 交AB 于点E ，联结AF 、CE ，S △BCE ：S △AEF 的比值为．15．（2021春•浦东新区期中）如图，在四边形BCEF 中，BF ∥AD ∥CE ，S △ABC ＝3，则△DEF 的面积是．16．（2021春•静安区校级期末）如图，在△ABC 中，∠C ＝90°，BC ＝8cm ，AC ＝6cm ，点E 是BC 的中点，动点P 从A 点出发，先以每秒2cm 的速度沿A →C 运动，然后以1cm /s 的速度沿C →B 运动．若设点P运动的时间是t 秒，那么当t ＝，△APE 的面积等于6．四．三角形的稳定性（共1小题）17．（2017秋•兴隆台区校级月考）木工师傅在做完门框后，为防止变形常常像图中那样钉上两条斜拉的木板条（即图中AB、CD两个木条），这样做根据的数学道理是．五．三角形三边关系（共5小题）18．（2021春•浦东新区月考）已知三角形的两边长分别为4和9，则下列数据中，能作为第三边长的是（）A．2B．3C．4D．919．（2022春•杨浦区校级期末）下列长度的三根木棒，不能构成三角形框架的是（）A．7cm，5cm，10cm B．8cm，6cm，4cmC．10cm，10cm，5cm D．5cm，5cm，10cm20．（2022春•普陀区校级期末）已知三角形中两条边的长分别为2和7，则第三边a的取值范围是．21．（2022春•徐汇区校级期末）三角形的三边分别为5，1﹣a，9，则a的取值范围为．22．（2022春•徐汇区校级期末）周长为30，各边互不相等且都是整数的三角形共有个．六．三角形内角和定理（共8小题）23．（2022春•杨浦区校级期中）在△ABC中，如果∠A+∠B＝135°，且∠B＝2∠C，那么△ABC是三角形．24．（2022春•上海期末）直角三角形中两锐角平分线所交成的角的度数是（）A．45°B．135°C．45°或135°D．都不对25．（2020春•虹口区期末）如果一个三角形的三个内角的度数之比为1：2：3，那么这个三角形中最大的一个内角等于度．26．（2021春•徐汇区校级期末）如图，△ABC中，∠B＝40°，∠C＝30°，点D为边BC上一点，将△ADC 沿直线AD折叠后，点C落到点E处，∠BAE＝30°，则∠DAC的度数为．27．（2022春•嘉定区校级期末）在△ABC中，∠B＝∠C，点D在BC边上，∠BAD＝50°（如图1）．（1）若E在△ABC的AC边上，且∠ADE＝∠B，求∠EDC的度数；（2）若∠B＝30°，E在△ABC的AC边上，△ADE是等腰三角形，求∠EDC的度数；（简写主要解答过程即可）；（3）若AD将△ABC分割成的两个三角形中有一个是等腰三角形，求∠B的度数．（直接写出答案）．28．（2022春•上海期末）在△ABC中，AB＝AC，∠1＝∠ABC，∠2＝∠ACB，BD与CE相交于点O，如图，∠BOC的大小与∠A的大小有什么关系？若∠1＝∠ABC，∠2＝∠ACB，则∠BOC与∠A大小关系如何？若∠1＝∠ABC ，∠2＝∠ACB ，则∠BOC 与∠A 大小关系如何？29．（2022春•杨浦区校级期中）如图1，已知等腰△ABC 中，∠A ＝∠C ＝30°，动点D 在AB 的平行线l 上，联结AD ．（1）如图2，若∠B ＝∠ADC ，说明AD ∥BC 的理由；（2）如图3，当∠CDA ＝∠DAB 时，△ACD 是什么三角形？为什么？（3）过点A 作l 的垂线，垂足为H ，若∠ADH ＝60°，求∠DAC 的度数．30．（2022春•宝山区校级月考）已知：如图，△ABC ．求证：∠A +∠B +∠ACB ＝180°．证明：如图，作BC 延长线CD ，过点C 作CE ∥AB ．因为CE ∥AB （已知），所以∠1＝（）∠2＝（）因为∠1+∠2+∠ACB＝180°（）所以∠A+∠B+∠C＝180°（）七．三角形的外角性质（共8小题）31．（2021春•浦东新区期末）将一副三角板如图摆放，斜边AB与直角边DE相交于点F，则∠BFE ＝．32．（2021春•浦东新区期中）如图，E为△ABC的BC边上一点，点D在BA的延长线上，DE交AC于点F，∠B＝46°，∠C＝30°，∠EFC＝70°，则∠D＝．33．（2021春•宝山区校级期中）如图，在△ABC中，∠B＝25°，∠BAC＝31°，过点A作BC边上的高，交BC的延长线于点D，CE平分∠ACD，交AD于点E．求：（1）∠ACD的度数；（2）∠AEC的度数．34．（2022春•杨浦区校级期末）如图，已知在△ABC中，∠A＝（3x+10）°，∠B＝（2x）°，∠ACD是△ABC的一个外角，且∠ACD＝（6x−10）°，求∠A的度数．35．（2021春•浦东新区期末）如图，已知∠BAC＝70°，D为△ABC的边BC上的一点，且∠CAD＝∠C，∠ADB＝60°．求∠B的度数．36．（2021春•静安区校级期末）△ABC中，∠A、∠B、∠C的外角的度数之比是2：3：4，求∠A的度数．37．（2020春•杨浦区期末）如图，已知点D为△ABC的边BC延长线上一点，DF⊥AB于点F，交AC于点E，∠A＝35°，∠D＝42°，求∠ACD的度数．解：因为DF⊥AB（已知），所以∠DFB ＝90°（垂直的意义）．因为∠DFB +∠B +∠D ＝180°（），又∠D ＝42°，所以∠B ＝ °（等式性质）．因为∠ACD ＝∠A +∠B （），又∠A ＝35°，∠B ＝ °，所以∠ACD ＝ °（等式性质）．38．（2018春•浦东新区期末）阅读、填空并将说理过程补充完整：如图，已知点D 、E 分别在△ABC 的边AB 、AC 上，且∠AED ＝∠B ，延长DE 与BC 的延长线交于点F ，∠BAC 和∠BFD 的角平分线交于点G ．那么AG 与FG 的位置关系如何？为什么？解：AG ⊥FG ．将AG 、DF 的交点记为点P ，延长AG 交BC 于点Q ．因为AG 、FG 分别平分∠BAC 和∠BFD （已知）所以∠BAG ＝，（角平分线定义）又因为∠FPQ ＝ +∠AED ，＝ +∠B（三角形的一个外角等于与它不相邻的两个内角的和）∠AED ＝∠B （已知）所以∠FPQ ＝（等式性质）（请完成以下说理过程）一、单选题1．（2022春·上海静安·七年级统考期中）下列判断错误的是（）巩固提升A．三角形的三条高的交点在三角形内B．三角形的三条中线交于三角形内一点C．直角三角形的三条高的交点在直角顶点D．三角形的三条角平分线交于三角形内一点2．（2022春·上海·七年级专题练习）已知三条线段长分别为2cm、4cm、a cm，若这三条线段首尾顺次相接能围成一个三角形，那么a的取值可以是()A．7B．4C．2D．13．（2019春·七年级课时练习）如图所示，一扇窗户打开后，用窗钩AB即可固定，这里所用的几何原理是（）A．两点之间线段最短B．垂线段最短．C．两定确定一条直线D．三角形具有稳定性4．（2019春·七年级课时练习）如图，三角形的个数是（）A．4个B．3个C．2个D．1个5．（2022春·上海·七年级专题练习）三角形的角平分线、中线和高都是()A．直线B．线段C．射线D．以上答案都不对6．（2022春·上海·七年级专题练习）如图，已知△ABC中，BD、CE分别是边AC、AB上的高，BD与CE 交于O点，如果设∠BAC＝n°，那么用含n的代数式表示∠BOC的度数是（）A ．45°+n °B ．90°﹣n °C ．90°+n °D ．180°﹣n °7．（2021春·上海·七年级上海市第二初级中学校考期中）下列说法中正确的是（）A ．三角形的三条高交于一点B ．有公共顶点且相等的两个角是对顶角C ．两条直线被第三条直线所截，所得的内错角相等D ．两条平行线被第三条直线所截，一组同旁内角的角平分线互相垂直二、填空题8．（2022春·上海闵行·七年级上海市实验学校西校校考阶段练习）在ABC V 中，已知A B C =+∠∠∠，那么ABC V 的形状________．9．（2022春·上海·七年级专题练习）已知△ABC ，a ＝6，b ＝10，则第三边c 的取值范围是_____．10．（2022春·上海·七年级专题练习）在ABC V 中，20A Ð=°，=60B Ð°，100C Ð=°，那么ABC V 是______三角形．（填“锐角”、“钝角”或“直角” ）11．（2022春·上海·七年级专题练习）如图，在Rt △ABC 中，∠ABC ＝90°，BD 是斜边AC 上的高．如果∠1＝54°，那么∠C ＝_____度．12．（2022春·上海杨浦·七年级校考期末）如图，BA CE ^于A 点，过A 点作DF //BC ，若135EAF Ð=°，则B Ð=______．13．（2022春·上海·七年级专题练习）一个四边形纸片ABCD ，∠B ＝∠D ，把纸片按如图所示折叠，使点B 落在AD 边上的B ′点，AE 是折痕，若∠C ＝86°，那么∠AEB ＝__°．14．（2022春·上海宝山·七年级校考阶段练习）如图所示，在Rt ABC △中，=90°C Ð，=30A Ð°，BD 是角平分线，则=BDC Ð________°．15．（2022春·上海闵行·七年级校考阶段练习）如图，在ABC V 中，AH 是边BC 上的高，且:2:1BH CH =，如果2ACH S =△，那么ABC S =V _____．16．（2022春·七年级单元测试）现有四根木棒，长度分别为4cm 、6cm 、8cm 、10cm ，从中任取三根木棒，能组成三角形的个数为_____个．17．（2022春·上海·七年级专题练习）已知AB CD ∥，60ACD Ð=°，:2:3BAE CAE ÐÐ=，4FCD FCE Ð=Ð，若78AEC Ð=°，则AFC Ð=____________．18．（2022春·上海闵行·七年级上海市七宝中学校考期中）如图，1:2:31:3:6ÐÐÐ=，则4Ð=___________．19．（2022春·上海·七年级校考期中）如图，AD BC ∥，AC 、BD 交于点E ，BF FC =，其中面积相等的三角形有______对．三、解答题20．（2022秋·上海闵行·七年级校考期末）已知三角形纸片ABC （如图），将纸片折叠，使点A 与点C 重合，折痕分别与边AC 、BC 交于点D 、E ，点B 关于直线DE 的对称点为点F ．(1)画出直线DE 和点F ；(2)连接EF 、FC ，如果48FEC Ð=°，求DEC Ð的度数；(3)连接AE 、BD 、DF ，如果25BE EC =，且DEF V 的面积为4，求ABC V 的面积．21．（2022春·上海·七年级专题练习）如图，已知AB //CD ，∠1＋3＝90°，BC 、CF 分别平分∠ABF 和∠BFE ，试说明AB //EF 的理由．解：∵AB //CD （已知），∴∠1＝∠2（）．∵∠1＋∠3＝90°（已知），∴∠2＋∠3＝90°（）．即∠BCF ＝90°．∵　＝180°（三角形内角和等于180°），∴ ＝90°（等式性质）．∵BC 、CF 分别平分∠ABF 和∠BFE （已知），∴ （）．∴∠ABF ＋∠BFE ＝180°（）．∴AB //FE （）．22．（2022春·上海·七年级校考期末）根据要求作图并写好结论：(1)画三角形ABC ，使得AB 的长度等于5厘米，40A Ð=°，50C Ð=°；(2)在三角形ABC 中，作出B Ð的角平分线BN ；(3)在三角形ABC 中，作出BC 边上中线AM ．23．（2021春·上海·七年级校考期中）如图，按下列要求画图并解答（不要求写画法，只写出结论）．(1)过点A 画BC 的平行线AD ；(2)画出△ABC 的边BC 上的高AH ；(3)在直线AD 上能否找一个点E （点E 不与点A 重合）使得△EBC 的面积与△ABC 的面积相等，如果能找到，请画出△EBC （画出一个三角形即可）．24．（2022春·上海·七年级期中）如图，直线AC BD ∥，连接AB ，直线,AC BD 及线段AB 把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分，当动点P 落在某个部分时，连接,PA PB ，构成,,PAC APB PBD ÐÐÐ三个角．（提示：有公共端点的两条重合射线所组成的角是0°角）(1)当动点P 落在第①部分时，求证：APB PAC PBD Ð=Ð+Ð；(2)当动点P 落在第②部分时，APB PAC PBD Ð=Ð+Ð是否成立？请说明理由．(3)当动点P 在第③部分时，全面探究,,PAC APB PBD ÐÐÐ之间的关系，并写出动点P 的具体位置和相应的结论．选择其中一种结论加以证明．25．（2021春·上海·七年级校考期中）如图1，1A BC Ð、1A CM Ð的角平分线2BA 、2CA 相交于点2A ，(1)如果164A Ð=°，那么2A Ð的度数是多少，试说明理由并完成填空；(2)如图2，164A Ð=°，如果2A BC Ð、2A CM Ð的角平分线3BA 、3CA 相交于点3A ，请直接写出3A Ð度数；(3)如图2，重复上述过程，1n A BC -Ð、1n A CM -Ð的角平分线n BA 、n CA 相交于点n A 得到n A Ð，设1A q Ð=°，请用q 表示n A Ð的度数（直接写出答案）解：（1）结论：2Ð=A ______度．说理如下：因为2BA 、2CA 平分1A BC Ð和1A CM Ð（已知），所以121A BC Ð=Ð，122A CM Ð=Ð（角平分线的意义）．因为111A CM A BC A Ð=Ð+Ð，221A Ð=Ð+Ð（）（完成以下说理过程）26．（2022春·上海·七年级专题练习）如图1，∠A 1BC 、∠A 1CM 的角平分线BA 2、CA 2相交于点A 2，(1)如果∠A1＝68°，那么∠A2的度数是多少，试说明理由；解：（1）结论：∠A2＝度．说理如下：因为BA2、CA2平分∠A1BC和∠A1CM（已知），所以∠A1BC＝2∠1，∠A1CM＝2∠2（）．因为∠A1CM＝∠A1BC+∠ ，∠2＝∠1+∠ （），（完成以下说理过程）(2)如图2，如果∠A2BC、∠A2CM的角平分线BA3、CA3相交于点A3，请直接写出∠A3的度数；(3)如图2，重复上述过程，∠An﹣1BC、∠An﹣1CM的角平分线BAn、CAn相交于点An得到∠An，设∠A1＝θ，请用θ表示∠An（直接写出答案）27．（2022春·上海·七年级校考期中）如图1，有一块三角形菜地，若从顶点A修一条小路交BC于点D，小路正好将菜地分成面积相等的两部分．(1)画出D点的位置并说明理由．(2)假设在菜地中有一点E（如图2所示），BC上是否存在点F，使折线AEF将三角形ABC的面积分为面积相等的两部分．若存在，请画出F点的位置．28．（2022春·上海·七年级专题练习）如图，由16个相同的小正方形组成的一个大正方形ABCD，其中点A 、点E 、点F 均在图中的格点上（即图中小正方形的顶点）．(1)三角形AEF 的面积（即图中阴影部分的面积）占整个大正方形ABCD 面积的；（填“几分之几”）(2)如果三角形AEF 的面积是28平方厘米，那么图中每个小正方形的面积是平方厘米；(3)如备用图，若点G 也在图中的格点上，且三角形AFG 的面积是大正方形ABCD 面积的18，那么符合要求的点G 有个．29．（2022春·上海·七年级专题练习）已知：如图所示，ABC V 中，D 、E 分别在边AC 、AB 上，CD =3AD ，BE ：AE =3：2，求DF ：FB 的值．。

3 角的平分线的性质第1课时角的平分线的性质

易错点：运用角的平分线的性质时，常因忽略“到角两边的距离”而导致错误 10．如图，在△ABC中，BD平分∠ABC，交AC于点D，BC边上有一点E，连接DE，则AD与DE的关系为( D) A．AD＞DE B．AD＝DE C．AD＜DE D．无法确定
11．如图，AD是△ABC中∠BAC的平分线，DE⊥AB交AB于点E， DF⊥AC交AC于点F.若S△ABC＝7，DE＝2，AB＝4，则AC＝( B ) A．4 B．3 C．6 D．5
上海 2006 高考理科状元-武亦文
武亦文格致中学理科班学生班级职务：学习委员高考志愿：复旦经济高考成绩：语文127分数学142分英语144分
物理145分综合27分总分585分
“一分也不能少”
“我坚持做好每天的预习、复习，每天放学回家看半小时报纸，晚上10： 30休息，感觉很轻松地度过了三年高中学习。”当得知自己的高考成绩后，格致中学的武亦文遗憾地说道，“平时模拟考试时，自己总有一门满分，这次高考却没有出现，
7．如图，在△ABC中，∠C＝90°，AD平分∠BAC，交BC于点D，已知AB＝10 cm，CD＝3 cm，则△ABD的面积为______1_5_c_m．2
8．如图，△ABC的三边AB，BC，CA的长分别为40，50，60，
其三条角平分线交于点 O ，则 S△ABO∶S△BCO∶S△CAO ＝ _____4_∶__5_∶__6___．
9．如图，在△ABC中，AD平分∠BAC，点D是BC的中点， DE⊥AB于点E，DF⊥AC于点F，求证：∠B＝∠C. 解：∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴DE＝DF，在 Rt△BDE 和 Rt△CDF 中， DE ＝ DF ， BD ＝ CD ， ∴Rt△BDE≌Rt△CDF(HL)，∴∠B＝∠C

《角平分线的性质》

2023-11-06contents •角平分线的性质的基本概念•角平分线的性质的应用•角平分线的性质的证明方法•角平分线的性质的实践应用•总结与展望•参考文献目录01角平分线的性质的基本概念定义从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线。

记法$\overset{\frown}{AB}$表示角平分线，简记为“ABfrown”或“frownAB”。

角平分线的定义语言描述一般地，我们用“$\overset{\frown}{AB}$”表示从一个角的顶点引出的把这个角分成两个相等的角的射线。

符号表示$\overset{\frown}{AB}$或简记为“ABfrown”或“frownAB”。

角平分线的表示方法•定理：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线。

角平分线上的点到这个角的两边的距离相等。

角平分线的性质定理02角平分线的性质的应用利用角平分线的性质证明等腰三角形总结词角平分线性质是等腰三角形证明中的重要工具。

详细描述利用角平分线的性质，可以证明等腰三角形的两个底角相等，从而得出等腰三角形的性质。

这是因为在角平分线上，从顶角到两边分角线上的点到两边的距离相等，所以两边的三角形内角和相等，从而得出两个底角相等。

总结词角平分线性质也是证明平行四边形的重要工具。

要点一要点二详细描述在平行四边形ABCD中，AC和BD是对角线，O是AC的中点。

利用角平分线的性质，可以证明三角形ABO和三角形CBO全等，从而得出三角形ABO是等腰三角形。

因为等腰三角形的底边上的中线也是高，所以可以得出ABO是等腰三角形的高，从而得出AB和BC平行且相等，证明了平行四边形的性质。

利用角平分线的性质证明平行四边形•总结词：角平分线性质还可以用于证明三角形内角和定理。

•详细描述：在三角形ABC中，AD是角平分线。

利用角平分线的性质，可以证明三角形ABD和三角形ACD全等，从而得出三角形ABD和ACD的面积相等。

监利县第七中学七年级数学下册第四章三角形1认识三角形第3课时三角形的中线与角平分线教案新版北师大版

第3课时三角形的中线与角平分线【知识与技能】1。

通过观察、画、折等实践操作、想像、推理、交流等过程,认识三角形的角平分线、中线;2.会画出任意三角形的角平分线、中线，通过画图、折纸了解三角形的三条三条角平分线、三条中线会交于一点。

【过程与方法】通过画、折等实践操作活动过程,开展学生的空间观念,推理能力及创新精神.学会用数学知识解决实际问题，开展应用和自主探究意识，并培养学生的动手实践能力。

【情感态度】通过对问题的解决，使学生有成就感，培养学生的合作精神，树立学好数学的信心。

【教学重点】认识三角形的中线、角平分线.【教学难点】三角形的中线、角平分线的应用。

一、情景导入,初步认知用铅笔可以支起一张均匀的三角形卡片，你知道怎样确定这个点的位置吗？【教学说明】数学来源于生活、通过问题情境，激发学生好奇心和强烈的求知欲，让学生在生动具体的情境中学习数学。

二、思考探究，获取新知探究1:三角形的中线如图，△ABC中,有一条红色线段，一端点在顶点A处，另一端点从点B沿着BC边移动到点C，观察移动过程中形成的无数条线段〔AD、AE、AF、AG……〕中,有没有特殊位置的线段？你认为有哪些特殊位置？[生甲］我观察到,有一条线段的端点是BC 的中点。

［生乙］在这些线段中，有一条线段平分∠BAC,即是∠BAC 的平分线。

［生丙］还有一条线段垂直边BC 。

［师］很好，同学们通过观察，找到了具有特殊位置的线段，这三条线段是三角形的重要线段，它们分别是三角形的中线、角平分线和高线.我们先来认识三角形的中线。

1。

在三角形中，连接一个顶点与它对边的中点的线段，叫做这个三角形的中线。

如图,点E 是BC 的中点，线段AE 是△ABC 的中线2。

由定义可知:如果AE 是△ABC 的中线，那么有：BE=EC=21BC 。

3。

在一个三角形中，有几条中线呢？它们的位置关系又如何呢？同学们来画一画,议一议。

〔1〕在纸上画一个锐角三角形，并画出它的所有中线,它们有怎样的位置关系？〔2〕钝角三角形和直角三角形的中线有几条，它们也有同样的位置关系吗？折一折,画一画，并与同伴交流.【归纳结论】一个三角形的中线共有三条，它们存在于三角形的内部，并且三条中线相交于一点.我们把这一点叫做重心。

中考数学专题17 三角形与多边形(知识点串讲)(原卷版)

专题17 三角形与多边形考点总结【思维导图】【知识要点】知识点一三角形的概念三角形的概念：由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。

三角形特性（1）三角形有三条线段（2）三条线段不在同一直线上三角形是封闭图形（3）首尾顺次相接三角形用符号“Δ”表示，顶点是A、B、C的三角形记作“ΔABC”，读作“三角形ABC”。

三角形按边分类：等腰三角形：有两条边相等的三角形叫做等腰三角形，其中相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰与底边的夹角叫做底角。

等边三角形：底边与腰相等的等腰三角形叫做等边三角形，即三边都相等。

三角形三边的关系（重点）（1）三角形的任意两边之和大于第三边。

三角形的任意两边之差小于第三边。

（这两个条件满足其中一个即可）用数学表达式表达就是：记三角形三边长分别是a，b，c，则a＋b＞c或c－b＜a。

（2）已知三角形两边的长度分别为a，b，求第三边长度的范围：|a－b|＜c＜a＋b考查题型一三角形的三边关系1．（2018·湖南中考真题）下列长度的三条线段，能组成三角形的是（）A．4cm，5cm，9cm B．8cm，8cm，15cm C．5cm，5cm，10cm D．6cm，7cm，14cm 2．（2018·湖南中考真题）已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）A．1 B．2 C．8 D．113．（2018·贵州中考真题）已知一个三角形的两边长分别为8和2，则这个三角形的第三边长可能是（）A．4 B．6 C．8 D．104．（2018·四川中考模拟）已知a、b、c是△ABC的三条边长，化简|a＋b－c|－|c－a－b|的结果为() A．2a＋2b－2c B．2a＋2b C．2c D．0三角形的分类：三角形按边的关系分类如下：不等边三角形三角形底和腰不相等的等腰三角形等腰三角形等边三角形三角形按角的关系分类如下：直角三角形（有一个角为直角的三角形）三角形锐角三角形（三个角都是锐角的三角形）钝角三角形（有一个角为钝角的三角形）1．（2018·湖南中考模拟）下列说法正确的是（）A．按角分类，三角形可以分为钝角三角形、锐角三角形和等腰直角三角形B．按边分类，三角形可分为等腰三角形、不等边三角形和等边三角形C．三角形的外角大于任何一个内角D．一个三角形中至少有一个内角不大于60°2．（2019·陕西中考模拟）等腰三角形两边长分别是2 cm和5 cm，则这个三角形周长是（）A．9 cm B．12 cm C．9 cm或12 cm D．14 cm三角形的稳定性➢三角形具有稳定性➢四边形及多边形不具有稳定性要使多边形具有稳定性，方法是将多边形分成多个三角形，这样多边形就具有稳定性了。

2017七年级数学三角形的角平分线.doc

2017七年级数学三角形的角平分线.doc11.3三角形的角平分线、中线和高教学任务分析教学流程安排课前准备教学过程设计分线．请同学们按照课本P144图11-11所示的步骤，折出三角形的角平分线．一个三角形，可以折出几条角平分线？请你折出一个三角形的所有的角平分线．你发现三角形的角平分线相交于一点吗？和其他同学交流，你们有什么发现？巡视指导．的角平分线的性质．三角形的三条角平分线相交于一点．三角形三条角平分线的交点在三角形内部．师生共同总结．总结角平分线的性质．请做课后练习（P16）第1题．学生解答，教师点评．强化三角形角平分线的概念．活动3 三角形的中线在三角形中，连结一个顶点与它对边的中点的线段，叫做三角形的中线（median oftriangle）．教师讲述．学习三角形中线的概念．AB CD如右图，D 是BC 的中点，线段AD 就是三角形的中线．分别画出锐角三角形、直角三角形、钝角三角形，并画出每个三角形的三条中线．你发现什么规律？学生画图，教师巡视指导．根据学生情况可分三个组，每组画一种三角形．作图体会中线的性质．三角形的三条中线相交于一点．三角形三条中线的交点在三角形内部．师生共同总结．总结三角形中线的性质．活动4 三角形的高线从三角形的一个顶点向它的对边所在的直线做垂线，顶点和垂足之间的线段叫做三角形的高线（height of triangle ），简称三角形的高．如右图，AD 就是三角形的一条高．教师讲述．学习三角形的高线的概念．请在P145图11-14的三个三角形中分别画出三角形的高．学生画图，教师巡视指导．注意指导钝角三角形的高线的作图．体会高线的性质．A BCD三条高线还相交于一点吗？．三角形的三条高所在的直线相交于一点．锐角三角形的三条高线的交点在三角形的内部；直角三角形的三条高线的交点是直角顶点；钝角三角形三条高线所在的直线的交点在三角形的外部．学生讨论后回答．师生共同总结．总结三角形的高的性质．请完成课后练习（P146）第2题．学生回答，教师点评．巩固高线的概念．活动5 回顾与反思1．三角形的角平分线是射线吗？2．三角形的中线是直线吗？3．三角形的高线是直线吗？．4．直角三角形的两条直角边也是三角形的高吗？5．三角形的角平分线、中线、高线的交点一定在三角形的内部吗？学生回答，教师点评．整理三角形的角平分线、中线、高线的概念．请做课后习题（146）第1题．学生回答，教师点评．应用角平分线、中线、高的概念．。

七年级数学下册专题第8讲三角形重点、考点知识总结及练习

=90°+ 1 ∠A， 2
即 D 90 1 A ． 2
【方法总结】
角平分线把一个角分成两个相等的角，利用倒角可得到角乊间的关系。此题可记住结论：
当 BD、CD 是三角形 ABC 的角平分线时， D 90 1 A 2
【随堂练习】 1．（2017 春•辉县市期末）如图，△ABC 中，AD 是 BC 边上的高，AE 是∠BAC 的平分线，∠EAD=5°，∠B=50°，求∠C 的度数．
专题第 8 讲三角形
知识点 1 三角形的三边关系
1、三角形三条边乊间的关系：三角形任意两边乊和大于第三边，三角形任意两边乊差小于第三边． 2、解题技巧：“当三条线段中最长的线段小于另两条线段乊和时，戒当三条线段中最短的线段大于另两条线段乊差时，即可组成三角形”
【典例】
1. 已知 a、b、c 为△ABC 的三边，化简：|a+b﹣c|﹣|a﹣b﹣c|+|a﹣b+2c|=________．【答案】3a﹣b 【解析】解：∵△ABC 的三边长分别是 a、b、c， ∴必须满足两边乊和大于第三边，则： a+b﹣c=（a+b）-c＞0， a﹣b﹣c=a-（b+c）＜0， a﹣b+c=（a+c）-b＞0（即 a﹣b+2c>0），
⊥AC 于 M，探究线段 PK、PM 不 CG 乊间的数量关系．
【解析】解：连接 AP，
∵CG⊥AB，PK⊥AB，PM⊥AC，
∴S△ABC=
1 2
AB•CG，S△ABP=
1 2
AB•PK，S△ACP=
1 2
AC•PM，
∵S△ABC=S△ABP+S△ACP，
∴ 1 AB•CG= 1 AB•PK+ 1 AC•PM，

与角平分线有关的常用结论、辅助线总结与练习(有答案)

与角平分线有关的常用结论、辅助线总结角平分线是我们常见的几何条件，合理的把角平分线和其它条件相结合可以形成新的结论。

一、总结下面我们来看一下常见的和角平分线有关结论或辅助线。

1、如图1，OP 平分∠AOB ，点D 在OA 上，DE ∥OB 交OE 于点E∵OP 平分∠AOB ∴∠DOE =∠EOB∵DE ∥OB ∴∠BOE =∠DEO ∴∠DOE =∠DEO∴OD =DE由此可知，当角平分线和与角的一边平行的直线相交后可以形成等腰三角形。

例题：（2016·四川南充）如图2，对折矩形纸片ABCD ，使AB 与DC 重合得到折痕EF ，将纸片展平；再一次折叠，使点D 落到EF 上点G 处，并使折痕经过点A ，展平纸片后∠DAG 的大小为（） A ．30° B ．45° C ．60° D ．75°分析：由题意可得：∠1=∠2，AN =MN ，∠MG A =90°，则NG =12AM ，故AN =NG ，则∠2=∠4，∵EF ∥AB ，∴∠4=∠3，∴∠1=∠2=∠3=13×90°=30°，∴∠DAG =60°．故选：C ．2、角平分线遇到垂线：如图3，OP 平分∠AOB ，点D 在OA 上，DP ⊥OP 于点P 。

遇到这种情况，我们可以作辅助线：延长DP 交OB 于点E ，∵OP 平分∠AOB∴∠DOP =∠EOP ∵DP ⊥OP ∴∠ODP =∠OEP∴OD =OE ∴DP =PE通过上述证明我们可以发现，当角平分线遇到垂线后，可以将垂线延长与角的两边相交，构成等腰三角形，同时，垂足即为等腰三角形底边中点。

例题：如图4，在直角梯形ABCD 中， AD ∥BC ，∠B =90°，E 为AB 上一点，且ED 平分∠ADC ，EC 平分∠BCD ．求证：AE =BE 分析：由已知，AD ∥BC ，ED 平分∠ADC ，EC 平分∠BCD ，可得DE ⊥EC ，延长DE 交CB 延长线于F ，有上述结论可知，E 为DF 中点，可证△ADE ≌△BFE3、从角平分线做角一边的垂线ED BAO 图1 图2E D P B AO图3 F图4 DPA如图3，OP 平分∠AOB ，PD ⊥OA 于点D 。

垂直平分线角平分线综合应用

垂直平分线角平分线综合应用一．解答题（共30小题）1．如图，已知∠BAC=90°，AD⊥BC于点D，∠1=∠2，EF∥BC交AC于点F．试说明AE=CF．2．如图，四边形ABCD中，∠B=90°，AB∥CD，M为BC边上的一点，且AM平分∠BAD，DM 平分∠ADC．求证：（1）AM⊥DM；（2）M为BC的中点．3．已知：如图，D是等腰△ABC底边BC上一点，它到两腰AB、AC的距离分别为DE、DF，当D 点在什么位置时，DE=DF？并加以证明．4．如图，∠B=∠C=90°，DE平分∠ADC，AE平分∠DAB，求证：E是BC的中点．5．如图在△ABC中∠C=90°，AC=BC，AD平分∠CAB，DE⊥AB于E，若AB=6cm，求△DEB 的周长．6．如图，AD为∠BAC的平分线，DF⊥AC于F，∠B=90°，DE=DC，试说明：BE=CF．7．如图，AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，且S△ABC=7，DE=2，AB=4，求AC的长．8．如图，∠ABC=60°，点D在AC上，ED=6，DE⊥BC，DF⊥AB，且DE=DF，求：（1）∠ABD的度数；（2）DB的长度．9．如图．已知AD∥BC，DC⊥AD，∠BAD的平分线交CD于点E，且点E是CD的中点．问：（1）点E在∠ABC的平分线上吗？（2）AD+BC与AB的大小关系怎样？请证明．10．如图，四边形ABCD中，∠B=∠C=90°，E是BC的中点，DE平分∠ADC．（1）求证：AE平分∠BAD；（2）判断AB、CD、AD之间的数量关系，并证明；（3）若AD=10，CB=8，求S△ADE．11．如图，BD平分∠ABC交AC于点D，DE⊥AB于E，DF⊥BC于F，AB=6，BC=8，若S△ABC=28，求DE的长．12．如图，在△ABC中，∠ACB=90゜，BE平分∠ABC，交AC于E，DE垂直平分AB于D，求证：BE+DE=AC．13．已知：如图，AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，BE=CF，求证：AD 是BC的中垂线．14．如图，在Rt△ABC中，∠C=90°，AB边的垂直平分线DE交BC于点E，垂足为D．求证：∠CAB=∠AED．15．如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N两点，DM与EN相交于点F．（1）若△CMN的周长为15cm，求AB的长；（2）若∠MFN=70°，求∠M的度数．16．如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．（1）若∠A=60°，∠ABD=24°，求∠ACF的度数；（2）若BC=5，BF：FD=5：3，S△BCF=10，求点D到AB的距离．17．已知：如图，在△ABC中，∠BAC=120°，若PM、QN分别垂直平分AB、AC．（1）求∠PAQ的度数；（2）如果BC=10cm，求△APQ的周长．18．电信部门要修建一座电视信号发射塔P，按照设计要求，发射塔P到两城镇A、B的距离必须相等，到两条高速公路m和n的距离也必须相等．请在图中作出发射塔P的位置．（尺规作图，不写作法，保留作图痕迹）19．如图：DE是△ABC中AC边的垂直平分线，若BC=8 米，AB=10厘米，求△EBC的周长．20．如图，△ABC中，AD是高，CE是中线，点G是CE的中点，DG⊥CE，点G为垂足．（1）说明：DC=BE；（2）若∠AEC=72°，求∠BCE的度数．21．如图所示，MP和NQ分别垂直平分AB 和AC．（1）若∠BAC=105°，求∠PAQ的度数；（2）若∠PAQ=25°，求∠BAC的度数．22．如图，在△ABC中，AB=AC，AD是BC边上的中线，AE⊥BE于点E，且BE=．求证：AB平分∠EAD．23．如图，在△ABC中，AB=AC，AD是△ABC点的中线，E是AC的中点，连接AC，DF⊥AB于F．求证：∠BDF=∠ADE．24．如图，在△ABC中，AB=AC，点D是BC的中点，AC的垂直平分线分别交AC，AD，AB于点E，O，F．（1）求证：点O在AB的垂直平分线上；（2）若∠CAD=20°，求∠BOF的度数．25．如图1，Rt△ABC中AB=AC，点D、E是线段AC上两动点，且AD=EC，AM垂直BD，垂足为M，AM的延长线交BC于点N，直线BD与直线NE相交于点F．试判断△DEF的形状，并加以证明．说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或者更换已知条件，完成你的证明．1、画出将△BAD沿BA方向平移BA长，然后顺时针旋转90°后图形；2、点K在线段BD上，且四边形AKNC为等腰梯形（AC∥KN，如图2）．附加题：如图3，若点D、E是直线AC上两动点，其他条件不变，试判断△DEF的形状，并说明理由．26．如图，以△ABC的边AB、AC为直角边向外作等腰直角△ABE和△ACD，M是BC的中点，请你探究线段DE与AM之间的关系．说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．①画出将△ACM绕某一点顺时针旋转180°后的图形；②∠BAC=90°（如图）附加题：如图，若以△ABC的边AB、AC为直角边，向内作等腰直角△ABE和△ACD，其它条件不变，试探究线段DE与AM之间的关系．27．如图，在Rt△ABC中，∠C=90°，∠A=60°，AB=12cm，若点P从B点出发以2cm/秒的速度向A点运动，点Q从A点出发以1cm/秒的速度向C点运动，设P、Q分别从B、A同时出发，运动时间为t秒．解答下列问题：（1）用含t的代数式表示线段AP，AQ的长；（2）当t为何值时△APQ是以PQ为底的等腰三角形？（3）当t为何值时PQ∥BC？28．如图，△ABC中，∠C=Rt∠，AC=8cm，BC=6cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒2cm，设运动的时间为t秒．（1）当t为何值时，CP把△ABC的周长分成相等的两部分．（2）当t为何值时，CP把△ABC的面积分成相等的两部分，并求出此时CP的长；（3）当t为何值时，△BCP为等腰三角形？29．如图，在△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点C出发，按C→B→A的路径，以2cm每秒的速度运动，设运动时间为t秒．（1）当t=1时，求△ACP的面积．（2）t为何值时，线段AP是∠CAB的平分线？（3）请利用备用图2继续探索：当t为何值时，△ACP是以AC为腰的等腰三角形？（直接写出结论）30．如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于E、F．试回答：（1）图中等腰三角形是．猜想：EF与BE、CF之间的关系是．理由：（2）如图②，若AB≠AC，图中等腰三角形是．在第（1）问中EF与BE、CF间的关系还存在吗？（3）如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．这时图中还有等腰三角形吗？EF与BE、CF关系又如何？说明你的理由．垂直平分线角平分线综合应用_2017年03月11日的初中数学组卷参考答案与试题解析一．解答题（共30小题）1．（2016•海淀区校级模拟）如图，已知∠BAC=90°，AD⊥BC于点D，∠1=∠2，EF∥BC交AC于点F．试说明AE=CF．【分析】作EH⊥AB于H，作FG⊥BC于G，根据角平分线的性质可得EH=ED，再证ED=FG，则EH=FG，通过证明△AEH≌△CFG即可．【解答】解：作EH⊥AB于H，作FG⊥BC于G，∵∠1=∠2，AD⊥BC，∴EH=ED（角平分线的性质）∵EF∥BC，AD⊥BC，FG⊥BC，∴四边形EFGD是矩形，∴ED=FG，∴EH=FG，∵∠BAD+∠CAD=90°，∠C+∠CAD=90°，∴∠BAD=∠C，又∵∠AHE=∠FGC=90°，∴△AEH≌△CFG（AAS）∴AE=CF．【点评】本题考查了角平分线的性质；综合利用了角平分线的性质、同角的余角相等、全等三角形的判定等知识点．2．（2016秋•宁江区期末）如图，四边形ABCD中，∠B=90°，AB∥CD，M为BC边上的一点，且AM平分∠BAD，DM平分∠ADC．求证：（1）AM⊥DM；（2）M为BC的中点．【分析】（1）根据平行线的性质得到∠BAD+∠ADC=180°，根据角平分线的定义得到∠MAD+∠ADM=90°，根据垂直的定义得到答案；（2）作NM⊥AD，根据角平分线的性质得到BM=MN，MN=CM，等量代换得到答案．【解答】解：（1）∵AB∥CD，∴∠BAD+∠ADC=180°，∵AM平分∠BAD，DM平分∠ADC，∴2∠MAD+2∠ADM=180°，∴∠MAD+∠ADM=90°，∴∠AMD=90°，即AM⊥DM；（2）作NM⊥AD交AD于N，∵∠B=90°，AB∥CD，∴BM⊥AB，CM⊥CD，∵AM平分∠BAD，DM平分∠ADC，∴BM=MN，MN=CM，∴BM=CM，即M为BC的中点．【点评】本题考查的是角平分线的性质，掌握平行线的性质和角的平分线上的点到角的两边的距离相等是解题的关键．3．（2016春•XX校级期末）已知：如图，D是等腰△ABC底边BC上一点，它到两腰AB、AC的距离分别为DE、DF，当D点在什么位置时，DE=DF？并加以证明．【分析】当D为AB的中点时，AD为等腰三角形底边上的中线，根据等腰三角形的“三线合一”可知AD为∠A的平分线，又DE⊥AB，DF⊥AC，根据角平分线的性质可证DE=DF．【解答】解：当D为BC的中点时，DE=DF．理由：∵AD为等腰三角形底边上的中线，∴AD平分∠BAC，又∵DE⊥AB，DF⊥AC，∴DE=DF．【点评】本题考查了等腰三角形的性质，角平分线性质．关键是运用等腰三角形的“三线合一”解题．4．（2016春•沭阳县期末）如图，∠B=∠C=90°，DE平分∠ADC，AE平分∠DAB，求证：E是BC 的中点．【分析】过点E作EF⊥AD，根据角平分线上的点到角的两边距离相等即刻得到结论．【解答】证明：过点E作EF⊥AD于F，∵∠B=∠C=90°，∴CD⊥BC，AB⊥BC，∵DE平分∠ADC，AE平分∠DAB，∴CE=DF，EF=BE，∴CE=BE，∴E是BC的中点．【点评】本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质并作出辅助线是解题的关键．5．（2016春•潜江校级期中）如图在△ABC中∠C=90°，AC=BC，AD平分∠CAB，DE⊥AB于E，若AB=6cm，求△DEB的周长．【分析】利用角平分线的性质求得AE=AC，CD=DE，然后利用线段中的等长来计算△DEB的周长．【解答】解：∵∠C=90°，AD平分∠CAB，交BC于D，DE⊥AB于E，∴AC=AE，CD=DE，AC=BC，∴∠B=45°，∴BE=DE，∴△DEB的周长=BE+DE+BD=BE+AC=AB=6cm．【点评】本题考查了三角形的全等的性质；解题的关键是利用角平分线的性质求得AE=AC，CD=DE，要学会进行线段的等效转移．6．（2016秋•监利县校级期中）如图，AD为∠BAC的平分线，DF⊥AC于F，∠B=90°，DE=DC，试说明：BE=CF．【分析】先由角平分线的性质就可以得出DB=DF，再证明△BDE≌△FDC就可以求出结论．【解答】解：∵∠B=90°，∴BD⊥AB．∵AD为∠BAC的平分线，且DF⊥AC，∴DB=DF．在Rt△BDE和Rt△FDC中，，∴Rt△BDE≌Rt△FDC（HL），∴BE=CF．【点评】本题考查了角平分线的性质的运用，全等三角形的判定与性质的运用，解答时证明三角形全等是关键．7．（2016秋•红安县期中）如图，AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，且S△ABC=7，DE=2，AB=4，求AC的长．【分析】根据角平分线性质求出DF，根据三角形面积公式求出△ABD的面积，求出△ADC面积，即可求出答案．【解答】解：∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC于点F，∴DE=DF=2，∵S△ADB=AB×DE=×4×2=4，∵△ABC的面积为7，∴△ADC的面积为7﹣4=3，∴AC×DF=3，∴AC×2=3，∴AC=3．【点评】本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．8．（2016春•XX市校级期中）如图，∠ABC=60°，点D在AC上，ED=6，DE⊥BC，DF⊥AB，且DE=DF，求：（1）∠ABD的度数；（2）DB的长度．【分析】（1）根据DE⊥BC，DF⊥AB，且DE=DF，即可得出点D在∠ABC的角平分线上，由∠ABC=60°，即可得出∠ABD=30°；（2）根据在直角三角形中，含30°角的直角边等于斜边的一半，即可得出DB的长．【解答】解：（1）∵DE⊥BC，DF⊥AB，且DE=DF，∴DB平分∠ABC，即∠ABD=∠ABC=×60°=30°；（2）在直角三角形BFD中，∵∠DBC=∠ABC=×60°=30°，∴DE=5，∴BD=2DE=12．【点评】本题考查了角平分线的性质以及含30度角的直角三角形的性质，在直角三角形中，含30°角的直角边等于斜边的一半．9．（2016秋•XX区校级月考）如图．已知AD∥BC，DC⊥AD，∠BAD的平分线交CD于点E，且点E是CD的中点．问：（1）点E在∠ABC的平分线上吗？（2）AD+BC与AB的大小关系怎样？请证明．【分析】（1）连结BE，作EH⊥AB于H，如图，利用角平分线的性质得ED=EH，而ED=EC，则EC=EH，然后根据角平分线的判定方法即可得到BE平分∠ABC；（2）利用“HL”可证明Rt△ADE≌Rt△AHE得到AD=AH，同样可证明Rt△BCE≌Rt△BHE得到BC=BH，于是有AD+BC=AH+BH=AB．【解答】解：（1）连结BE，作EH⊥AB于H，如图，∵AE平分∠BAD，ED⊥AD，EH⊥AB，∴ED=EH，∵点E是CD的中点，∴ED=EC，∴EC=EH，而AD∥BC，DC⊥AD，∴EC⊥BC，∴BE平分∠ABC，即点E在∠ABC的平分线上；（2）AD+BC=AB．理由如下：在Rt△ADE和Rt△AHE中，∴Rt△ADE≌Rt△AHE，∴AD=AH，同样可证明Rt△BCE≌Rt△BHE，∴BC=BH，∴AD+BC=AH+BH=AB．【点评】本题考查了角平分线：角的平分线上的点到角的两边的距离相等；到角的两边的距离相等的点在这个角的角平分线上．也考查了全等三角形的判定与性质．10．（2016秋•XX区月考）如图，四边形ABCD中，∠B=∠C=90°，E是BC的中点，DE平分∠ADC．（1）求证：AE平分∠BAD；（2）判断AB、CD、AD之间的数量关系，并证明；（3）若AD=10，CB=8，求S△ADE．【分析】（1）过点E作EF⊥DA于点F，首先根据角的平分线上的点到角的两边的距离相等可得CE=EF，根据等量代换可得BE=EF，再根据角平分线的判定可得AE平分∠BAD；（2）首先证明Rt△DFE和Rt△DCE可得DC=DF，同理可得AF=AB，再由AD=AF+DF利用等量代换可得结论；（3）根据角平分线的性质可得EF=CE，再利用三角形的面积公式可得答案．【解答】（1）证明：过点E作EF⊥DA于点F，∵∠C=90°，DE平分∠ADC，∴CE=EF，∵E是BC的中点，∴BE=CE，∴BE=EF，又∵∠B=90°，EF⊥AD，∴AE平分∠BAD．（2）证明：AD=CD+AD，∵∠C=∠DFE=90°，∴在Rt△DFE和Rt△DCE中，∴Rt△DFE和Rt△DCE（HL），∴DC=DF，同理AF=AB，∵AD=AF+DF，∴AD=CD+AD；（3）解：∵CB=8，E是BC的中点，∴CE=4，∴EF=4，∵AD=10，∴S△ADE=10×4×=20．【点评】此题主要考查了角平分线的性质和判定，以及全等三角形的性质和判定，关键是掌握角平分线的性质和判定定理．11．（2016秋•黄冈校级月考）如图，BD平分∠ABC交AC于点D，DE⊥AB于E，DF⊥BC于F，AB=6，BC=8，若S△ABC=28，求DE的长．【分析】根据角平分线性质得出DE=DF，根据三角形的面积公式得出关于DE的方程，求出即可．【解答】解：∵BD平分∠ABC交AC于点D，DE⊥AB，DF⊥BC，∴DE=DF，∵S△ABC=28，AB=6，BC=8，∴×6×DE+×8×DF=28，∴DE=DF=4．【点评】本题考查了角平分线定义的应用，能根据角平分线性质得出DE=DF是解此题的关键．12．（2016•历下区一模）如图，在△ABC中，∠ACB=90゜，BE平分∠ABC，交AC于E，DE垂直平分AB于D，求证：BE+DE=AC．【分析】根据角平分线性质得出CE=DE，根据线段垂直平分线性质得出AE=BE，代入AC=AE+CE求出即可．【解答】证明：∵∠ACB=90°，∴AC⊥BC，∵ED⊥AB，BE平分∠ABC，∴CE=DE，∵DE垂直平分AB，∴AE=BE，∵AC=AE+CE，∴BE+DE=AC．【点评】本题考查了角平分线性质和线段垂直平分线性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．13．（2016•萧山区二模）已知：如图，AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，BE=CF，求证：AD是BC的中垂线．【分析】由AD是△ABC的角平分线，DE⊥AB，DF⊥AC，根据角平分线的性质，可得DE=DF，∠BED=∠CFD=90°，继而证得Rt△BED≌Rt△CFD，则可得∠B=∠C，证得AB=AC，然后由三线合一，证得AD是BC的中垂线．【解答】证明：∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，∴DE=DF，∠BED=∠CFD=90°，在Rt△BED和Rt△CFD中，，∴Rt△BED≌Rt△CFD（SAS），∴∠B=∠C，∴AB=AC，∵AD是△ABC的角平分线，∴AD是BC的中垂线．【点评】此题考查了等腰三角形的性质与判定以及全等三角形的判定与性质．注意掌握三线合一性质的应用．14．（2016•怀柔区一模）如图，在Rt△ABC中，∠C=90°，AB边的垂直平分线DE交BC于点E，垂足为D．求证：∠CAB=∠AED．【分析】根据线段垂直平分线的性质得出AE=BE，再由直角三角形的性质即可得出结论．【解答】证明：∵DE是线段AB的垂直平分线，∴AE=BE，∠ADE=90°，∴∠EAB=∠B．在Rt△ABC中，∵∠C=90°，∴∠CAB+∠B=90°．在Rt△ADE中，∵∠ADE=90°，∴∠AED+∠EAB=90°，∴∠CAB=∠AED．【点评】本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．15．（2016秋•农安县期末）如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N 两点，DM与EN相交于点F．（1）若△CMN的周长为15cm，求AB的长；（2）若∠MFN=70°，求∠M的度数．【分析】（1）根据线段垂直平分线上的点到线段两端点的距离相等可得AM=CM，BN=，然后求出△CMN的周长=AB；（2）根据三角形的内角和定理列式求出∠MNF+∠NMF，再求出∠A+∠B，根据等边对等角可得∠A=∠ACM，∠B=∠B，然后利用三角形的内角和定理列式计算即可得解．【解答】解：（1）∵DM、EN分别垂直平分AC和BC，∴AM=CM，BN=，∴△CMN的周长=CM+MN+=AM+MN+BN=AB，∵△CMN的周长为15cm，∴AB=15cm；（2）∵∠MFN=70°，∴∠MNF+∠NMF=180°﹣70°=110°，∵∠AMD=∠NMF，∠BNE=∠MNF，∴∠AMD+∠BNE=∠MNF+∠NMF=110°，∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣110°=70°，∵AM=CM，BN=，∴∠A=∠ACM，∠B=∠B，∴∠M=180°﹣2（∠A+∠B）=180°﹣2×70°=40°．【点评】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等边对等角的性质，三角形的内角和定理，（2）整体思想的利用是解题的关键．16．（2016春•雁塔区校级期末）如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．（1）若∠A=60°，∠ABD=24°，求∠ACF的度数；（2）若BC=5，BF：FD=5：3，S△BCF=10，求点D到AB的距离．【分析】（1）根据线段垂直平分线的性质得到FB=FC，根据角平分线的定义得到∠CBA=48°，根据三角形内角和定理计算即可；（2）根据三角形的面积公式求出DG，根据角平分线的性质解答即可．【解答】解：（1）∵BD平分∠ABC，∴∠CBA=2∠CBD=2∠ABD=48°，∴∠ACB=180°﹣60°﹣48°=72°，∵EF是BC的中垂线，∴FB=FC，∴∠FCB=∠FBC=24°，∴∠ACF=72°﹣24°=48°；（2）作DG⊥BC于G，DH⊥AB于H，∵BD平分∠ABC，DG⊥BC，DH⊥AB，∴DH=DG，∵BF：FD=5：3，S△BCF=10，∴S△DCF=6，∴S△BCD=16，∴DG=，∴DH=DG=，即点D到AB的距离为．【点评】本题考查的是线段垂直平分线的性质、角平分线的性质，掌握段的垂直平分线上的点到线段的两个端点的距离相等、角的平分线上的点到角的两边的距离相等是今天的关键．17．（2016春•东明县期中）已知：如图，在△ABC中，∠BAC=120°，若PM、QN分别垂直平分AB、AC．（1）求∠PAQ的度数；（2）如果BC=10cm，求△APQ的周长．【分析】（1）根据线段垂直平分线上的点到线段两端点的距离相等可得PA=PB，再根据等边对等角的性质可得∠PAB=∠B，同理求出∠QAC=∠C，然后根据三角形的内角和定理求出∠B+∠C=60°，然后进行计算即可得解；（2）求出△APQ的周长=BC，然后代入数据即可得解．【解答】解：（1）∵PM垂直平分AB，∴PA=PB，∴∠PAB=∠B，同理，QA=QC，∴∠QAC=∠C，∵∠BAC=120°，∴∠B+∠C=180°﹣120°=60°，∴∠PAQ=∠BAC﹣（∠PAB+∠QAC）=∠BAC﹣（∠B+∠C）=120°﹣60°=60°；（2）由（1）可知：PA=PB，QA=QC，∴PA+PQ+QA=PB+PQ+QC=BC=10cm，即△APQ的周长为10cm．【点评】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等边对等角的性质，熟记性质熟记解题的关键．18．（2016秋•西市区校级期中）电信部门要修建一座电视信号发射塔P，按照设计要求，发射塔P到两城镇A、B的距离必须相等，到两条高速公路m和n的距离也必须相等．请在图中作出发射塔P的位置．（尺规作图，不写作法，保留作图痕迹）【分析】根据题意，P点既在线段AB的垂直平分线上，又在两条公路所夹角的平分线上．故两线交点即为发射塔P的位置．【解答】解：设两条公路相交于O点．P为线段AB的垂直平分线与∠MON的平分线交点或是与∠QON的平分线交点即为发射塔的位置．如图，满足条件的点有两个，即P、P′．【点评】此题考查了线段的垂直平分线和角的平分线的性质，属基本作图题．19．（2016秋•鹤庆县校级期中）如图：DE是△ABC中AC边的垂直平分线，若BC=8 米，AB=10厘米，求△EBC的周长．【分析】根据线段垂直平分线的性质得到EA=EC，根据三角形的周长公式计算即可．【解答】解：∵DE是△ABC中AC边的垂直平分线，∴EA=EC，∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+AB=18cm，答：△EBC的周长为18cm．【点评】本题考查的是线段垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．20．（2016秋•盐都区期中）如图，△ABC中，AD是高，CE是中线，点G是CE的中点，DG⊥CE，点G为垂足．（1）说明：DC=BE；（2）若∠AEC=72°，求∠BCE的度数．【分析】（1）由G是CE的中点，DG⊥CE得到DG是CE的垂直平分线，根据线段垂直平分线的性质得到DE=DC，由DE是Rt△ADB的斜边AB上的中线，根据直角三角形斜边上的中线等于斜边的一半得到DE=BE=AB，即可得到DC=BE；（2）由DE=DC得到∠DEC=∠BCE，由DE=BE得到∠B=∠EDB，根据三角形外角性质得到∠EDB=∠DEC+∠BCE=2∠BCE，则∠B=2∠BCE，由此根据外角的性质来求∠BCE的度数．【解答】解：（1）如图，∵G是CE的中点，DG⊥CE，∴DG是CE的垂直平分线，∴DE=DC，∵AD是高，CE是中线，∴DE是Rt△ADB的斜边AB上的中线，∴DE=BE=AB，∴DC=BE；（2）∵DE=DC，∴∠DEC=∠BCE，∴∠EDB=∠DEC+∠BCE=2∠BCE，∵DE=BE，∴∠B=∠EDB，∴∠B=2∠BCE，∴∠AEC=3∠BCE=72°，则∠BCE=24°．【点评】本题考查了线段垂直平分线的性质：线段垂直平分线上的点到线段两端点的距离相等．也考查了直角三角形斜边上的中线性质．21．（2016秋•和平区期中）如图所示，MP和NQ分别垂直平分AB 和AC．（1）若∠BAC=105°，求∠PAQ的度数；（2）若∠PAQ=25°，求∠BAC的度数．【分析】（1）先根据三角形内角和等于180°求出∠ABP+∠ACQ=75°，再根据线段垂直平分线的性质∠PAB=∠ABP，∠QAC=∠ACQ，所以∠PAB+∠QAC=75°，便不难求出∠PAQ的度数为30°；（2）根据线段垂直平分线的性质，得AP=BP，AQ=CQ，则∠B=∠BAP，∠C=∠CAQ，则∠APQ=2∠B，∠AQP=2∠C；根据三角形的内角和定理，得∠APQ+∠AQP=180°﹣∠PAQ=150°，则∠B+∠C=75°，进而求解．【解答】解：（1）∵∠BAC=105°，∴∠ABP+∠ACQ=180°﹣105°=75°，∵MP、NQ分别垂直平分AB和AC，∴PB=PA，QC=QA．∴∠PAB=∠ABP，∠QAC=∠ACQ，∴∠PAB+∠QAC=∠ABP+∠ACQ=75°，∴∠PAQ=105°﹣75°=30°；（2）∵MP和NQ分别垂直平分AB和AC，∴AP=BP，AQ=CQ，∴∠B=∠BAP，∠C=∠CAQ，∴∠APQ=2∠B，∠AQP=2∠C．∵∠PAQ=25°，∴∠APQ+∠AQP=180°﹣∠PAQ=155°，∴∠B+∠C=77.5°．∴∠BAC=∠B+∠C+∠PAQ=77.5°+25°=102.5°．【点评】此题综合运用了线段垂直平分线的性质、等腰三角形的性质以及三角形的外角的性质．22．（2016•西城区一模）如图，在△ABC中，AB=AC，AD是BC边上的中线，AE⊥BE于点E，且BE=．求证：AB平分∠EAD．【分析】根据等腰三角形的性质得到BD=BC，AD⊥BC根据角平分线的判定定理即可得到结论．．【解答】证明：∵AB=AC，AD是BC边上的中线，∴BD=BC，AD⊥BC，∵BE=BC，∴BD=BE，∵AE⊥BE，∴AB平分∠EAD．【点评】本题考查了等腰三角形的性质，角平分线的性质，熟练掌握等腰三角形的性质是解题的关键．23．（2016•黄冈模拟）如图，在△ABC中，AB=AC，AD是△ABC点的中线，E是AC的中点，连接AC，DF⊥AB于F．求证：∠BDF=∠ADE．【分析】根据等腰三角形的性质得到∠BAD=∠CAD，∠ADB=∠ADC=90°，根据等腰三角形的判定定理得到∠CAD=∠ADE．根据余角的性质得到∠BAD=∠BDF，等量代换即可得到结论．【解答】证明：∵AB=AC，AD是△ABC点的中线，∴∠BAD=∠CAD，∠ADB=∠ADC=90°，∵E是AC的中点，∴DE=AE=EC，∴∠CAD=∠ADE．在Rt△ABD中，∠ADB=90°，∴∠B+∠BAD=90°．∵DF⊥AB，∴∠B+∠BDF=90°，∴∠BAD=∠BDF，∴∠BDF=∠CAD，∴∠BDF=∠ADE．【点评】本题考查了等腰直角三角形的性质，余角的性质，熟练掌握等腰三角形的性质是解题的关键．24．（2016春•XX校级期末）如图，在△ABC中，AB=AC，点D是BC的中点，AC的垂直平分线分别交AC，AD，AB于点E，O，F．（1）求证：点O在AB的垂直平分线上；（2）若∠CAD=20°，求∠BOF的度数．【分析】（1）根据等腰三角形的性质可得AD⊥BC，根据垂直平分线的性质可得BO=AO，依此即可证明点O在AB的垂直平分线上；（2）根据等腰三角形的性质可得∠BAD=∠CAD=20°，∠CAB=40°，再根据垂直的定义，等腰三角形的性质和角的和差故选即可得到∠BOF的度数．【解答】（1）证明：∵AB=AC，点D是BC的中点，∴AD⊥BC，∵AD是BC的垂直平分线，∴BO=CO，∵OE是AC的垂直平分线，∴AO=CO，∴BO=AO，∴点O在AB的垂直平分线上；（2）解：∵AB=AC，点D是BC的中点，∴AD平分∠BAC，∵∠CAD=20°，∴∠BAD=∠CAD=20°，∠CAB=40°，∵OE⊥AC，∴∠EFA=90°﹣40°=50°，∵AO=CO，∴∠OBA=∠BAD=20°，∴∠BOF=∠EFA﹣∠OBA=50°﹣20°=30°．【点评】考查了等腰三角形的性质，线段垂直平分线的性质，关键是熟练掌握等腰三角形三线合一的性质．25．（2006•XX）如图1，Rt△ABC中AB=AC，点D、E是线段AC上两动点，且AD=EC，AM垂直BD，垂足为M，AM的延长线交BC于点N，直线BD与直线NE相交于点F．试判断△DEF的形状，并加以证明．说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或者更换已知条件，完成你的证明．1、画出将△BAD沿BA方向平移BA长，然后顺时针旋转90°后图形；2、点K在线段BD上，且四边形AKNC为等腰梯形（AC∥KN，如图2）．附加题：如图3，若点D、E是直线AC上两动点，其他条件不变，试判断△DEF的形状，并说明理由．【分析】（1）要证DF=EF，就要证出∠FDE=∠FED，也就是∠BDA=∠NEC，观察这两个角，不能直接用角的大小关系或全等来得出相等，那么可通过构建全等三角形来得出一个和两个分别相等的中间值，以此来证出两角相等，那么可过C作CP⊥AC，那么我们可通过证三角形ABD和APC全等来得出∠ADB=∠ACP，通过证三角形CPN和CEN全等来得出∠MEC=∠NPC．先看第一对三角形，已知的条件有AB=AD，一组直角，而∠ABD和∠PAC都是∠ADB的余角，因此∠ABD=∠PAD，那么两三角形就全等，可得出AC=PC=CE，∠ADB=∠NPC，又知道了∠NCE=∠P=45°，一条公共边，那么后面的一对三角形也全等，就能得出∠ADB=∠MEC=∠NPC，也就能得出∠FDE=∠FED了由此可得证．（2）解题思路和（1）一样，也是先证三角形ABD和APC全等，后证三角形CPN和CEN全等，来得出结论．【解答】解：△DEF是等腰三角形证明：如图，过点C作CP⊥AC，交AN延长线于点P∵Rt△ABC中AB=AC∴∠BAC=90°，∠ACB=45°∴∠P=∠ACB，∠BAD=∠ACP∵AM⊥BD∴∠ABD+∠BAM=∠BAM+∠CAP=90°∴∠ABD=∠CAP∴△BAD≌△ACP∴AD=CP，∠ADB=∠P∵AD=CE∴CE=CP∵=∴△CPN≌△CEN∴∠P=∠CEN∴∠CEN=∠ADB∴∠FDE=∠FED∴△DEF是等腰三角形．附加题：△DEF为等腰三角形证明：过点C作CP⊥AC，交AM的延长线于点P ∵Rt△ABC中AB=AC∴∠BAC=90°，∠ACB=45°∴∠P=∠ACB=∠E∵AM⊥BD∴∠ABD+∠BAM=∠BAM+∠CAP=90°∴∠ABD=∠CAP∴△BAD≌△ACP∴AD=CP，∠D=∠P∵AD=EC，CE=CP又∵=∴△CPN≌△CEN∴∠P=∠E∴∠D=∠E∴△DEF为等腰三角形．【点评】本题主要考查了等腰三角形的判定和全等三角形的判定与性质；通过已知和所求条件正确的构建出全等三角形是解题的关键．26．（2006•西岗区）如图，以△ABC的边AB、AC为直角边向外作等腰直角△ABE和△ACD，M是BC的中点，请你探究线段DE与AM之间的关系．说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．①画出将△ACM绕某一点顺时针旋转180°后的图形；②∠BAC=90°（如图）附加题：如图，若以△ABC的边AB、AC为直角边，向内作等腰直角△ABE和△ACD，其它条件不变，试探究线段DE与AM之间的关系．【分析】（1）分三种情况讨论，当∠BAC=90°，易得△ABC≌△AED；根据直角三角形的性质，可得ED=2AM；进而可以在∠BAC＞90°与∠BAC＜90°时，比较可得有ED=2AM的结论；（2）根据（1）的结论，选取②易得答案．【解答】解：（1）分三种情况；当∠BAC=90°，M是BC的中点∴AM=BM=MC=∠EAD=∠BAC=90°，AE=AB，AC=AD∴△ABC≌△AED∴ED=BC∴ED=2AM当∠BAC＞90°，易得ED=2AM当∠BAC＜90°，易得ED=2AM（2）已知（1）的结论，若∠BAC=90°，可得ED=2AM附加：结合上题可得：2AM=DE延长CA到F使AF=AC，连接BF易证△ABF≌△ADE∴BF=DE∵2AM=BF∴2AM=DE．【点评】本题为探究性题目，要求学生能全面考查可能出现的情况，并依次求出其中的关系．27．（2012•XX模拟）如图，在Rt△ABC中，∠C=90°，∠A=60°，AB=12cm，若点P从B点出发以2cm/秒的速度向A点运动，点Q从A点出发以1cm/秒的速度向C点运动，设P、Q分别从B、A同时出发，运动时间为t秒．解答下列问题：（1）用含t的代数式表示线段AP，AQ的长；（2）当t为何值时△APQ是以PQ为底的等腰三角形？（3）当t为何值时PQ∥BC？【分析】（1）由题意，可知∠B=30°，AC=6cm．BP=2t，AP=AB﹣BP，AQ=t．（2）若△APQ是以PQ为底的等腰三角形，则有AP=AQ，即12﹣2t=t，求出t即可．（3）若PQ∥BC，则有AQ：AC=AP：AB．从而问题可求．【解答】解：（1）∵Rt△ABC中，∠C=90°，∠A=60°，∴∠B=30°．又∵AB=12cm，∴AC=6cm，BP=2t，AP=AB﹣BP=12﹣2t，AQ=t．（2）∵△APQ是以PQ为底的等腰三角形，∴AP=AQ，即12﹣2t=t，解得t=4，即当t=4秒时△APQ是等腰三角形．（3）∵当AQ：AC=AP：AB时，有PQ∥BC，∴t：6=（12﹣2t）：12，解得t=3．即当t=3秒时，PQ∥BC．【点评】此题考查等腰三角形的判定和直角三角形的性质等知识点的综合应用能力．28．（2015秋•XX校级期中）如图，△ABC中，∠C=Rt∠，AC=8cm，BC=6cm，若动点P从点C 开始，按C→A→B→C的路径运动，且速度为每秒2cm，设运动的时间为t秒．（1）当t为何值时，CP把△ABC的周长分成相等的两部分．（2）当t为何值时，CP把△ABC的面积分成相等的两部分，并求出此时CP的长；（3）当t为何值时，△BCP为等腰三角形？【分析】（1）先由勾股定理求出△ABC的斜边AB=10cm，则△ABC的周长为24cm，所以当CP把△ABC的周长分成相等的两部分时，点P在AB上，此时CA+AP=BP+BC=12cm，再根据时间=路程÷速度即可求解；（2）根据中线的性质可知，点P在AB中点时，CP把△ABC的面积分成相等的两部分，进而求解即可；（3）△BCP为等腰三角形时，分三种情况进行讨论：①CP=CB；②BC=BP；③PB=PC．【解答】解：（1）△ABC中，∵∠C=Rt∠，AC=8cm，BC=6cm，∴AB=10cm，∴△ABC的周长=8+6+10=24cm，∴当CP把△ABC的周长分成相等的两部分时，点P在AB上，此时CA+AP=BP+BC=12cm，∴t=12÷2=6（秒）；（2）当点P在AB中点时，CP把△ABC的面积分成相等的两部分，此时CA+AP=8+5=13（cm），。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

11.3三角形的角平分线、中线和高
教学任务分析
教学流程安排
课前准备
教学过程设计
分线．请同学们按照课本P144图11-11所示的步骤，折出三角形的角平分线．
一个三角形，可以折出几条角平分线？请你折出一个三角形的所有的角平分线．
你发现三角形的角平分线相交于一点吗？和其他同学交流，你们有什么发现？巡视指导．的角平分线
的性质．
三角形的三条角平分线相交于一点．
三角形三条角平分线的交点在三角形内部．师生共同总结．总结角平分
线的性质．
请做课后练习（P16）第1题．学生解答，教师点
评．强化三角形角平分线的概念．
活动3 三角形的中线
在三角形中，连结一个顶点与它对边的中点的线段，
叫做三角形的中线
（median of
triangle）．教师讲述．学习三角形
中线的概
念．
A
B C
D
如右图，D 是BC 的中点，线段AD 就是三角形的中线．
分别画出锐角三角形、直角三角形、钝角三角形，并画出每个三角形的三条中线．你发现什么规律？
学生画图，教师巡视指导．根据学生情况可分三个组，每组画一种三角形．
作图体会中线的性质．
三角形的三条中线相交于一点．三角形三条中线的交点在三角形内部．
师生共同总结．
总结三角形中线的性质．活动4 三角形的高线从三角形的一个顶点向它的对边所在的直线做垂线，顶
点和垂足之间的线段叫做三角形的高线（height of triangle ），简称三角形的高．
如右图，AD 就是三角形的一条高．
教师讲述．
学习三角形的高线的概念．请在P145图11-14的三个三角形中分别画出三角形的高．
学生画图，教师巡视指导．
注意指导钝角三角形的高线的作图．
体会高线的性质．
A
B C D
三条高线还相交于一点吗？．
三角形的三条高所在的直线相交于一点．
锐角三角形的三条高线的交点在三角形的内部；直角三角形的三条高线的交点是直角顶点；钝角三角形三条高线所在的直线的交点在三角形的外部．学生讨论后回答．
师生共同总结．
总结三角形
的高的性
质．
请完成课后练习（P146）第2题．学生回答，教师点
评．巩固高线的概念．
活动5 回顾与反思
1．三角形的角平分线是射线吗？2．三角形的中线是直线吗？3．三角形的高线是直线吗？．4．直角三角形的两条直角边也是三角形的高吗？
5．三角形的角平分线、中线、高线的交点一定在三角形的内部吗？学生回答，教师点
评．
整理三角形
的角平分
线、中线、
高线的概
念．
请做课后习题（146）第1题．学生回答，教师点
评．应用角平分线、中线、高的概念．。

2017七年级数学三角形的角平分线.doc

专题07 角的平分线性质(专题测试)(解析版)

(新课标)华东师大版七年级数学下册《三角形的角平分线、中线和高》同步训练及解析

第2讲 角平分线综合(word版)

角平分线四大模型总结+习题+解析（最全版）

2017七年级下册数学第一单元知识点汇总

核心考点03 三角形有关概念与性质(原卷版)

3 角的平分线的性质 第1课时 角的平分线的性质

最新中考数学专题-三角形全等与角平分线,垂直平分线

《角平分线的性质》

监利县第七中学七年级数学下册第四章三角形1认识三角形第3课时三角形的中线与角平分线教案新版北师大版

中考数学 专题17 三角形与多边形(知识点串讲)(原卷版)

2017七年级数学三角形的角平分线.doc

七年级数学下册专题第8讲三角形重点、考点知识总结及练习

与角平分线有关的常用结论、辅助线总结与练习(有答案)

垂直平分线角平分线综合应用

第2讲角平分线综合(word版)

3 角的平分线的性质第1课时角的平分线的性质

中考数学专题17 三角形与多边形(知识点串讲)(原卷版)