P_1非协调四边形元解Stokes问题的多重网格算法
【国家自然科学基金】_多重网格方法_基金支持热词逐年推荐_【万方软件创新助手】_20140731
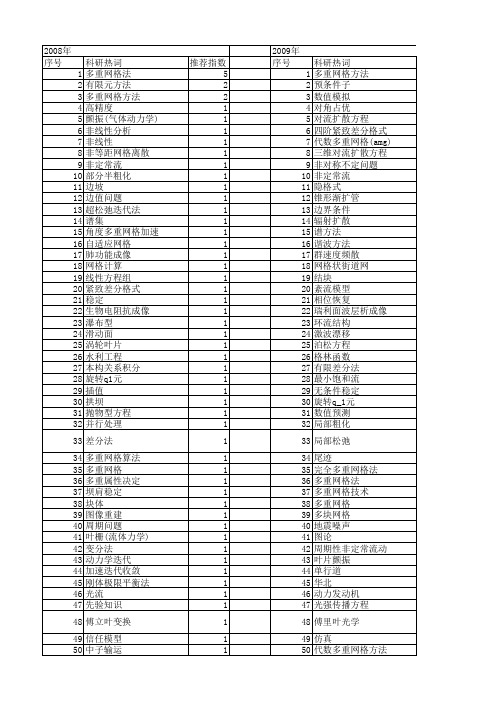
1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64
共轭梯度法 全机增升装置构形 光催化制氢 侧流状态 代数滑移模型 代数多重网格方法 代数多重网格 三维电阻率数值模拟 三维双调和方程 navier-stokes方程 dlr型k-ε 紊流模型 cfd
科研热词 多重网格方法 预条件子 数值模拟 对角占优 对流扩散方程 四阶紧致差分格式 代数多重网格(amgபைடு நூலகம் 三维对流扩散方程 非对称不定问题 非定常流 隐格式 锥形渐扩管 边界条件 辐射扩散 谱方法 谐波方法 群速度频散 网格状街道网 结块 紊流模型 相位恢复 瑞利面波层析成像 环流结构 激波漂移 泊松方程 格林函数 有限差分法 最小饱和流 无条件稳定 旋转q_1元 数值预测 局部粗化 局部松弛 尾迹 完全多重网格法 多重网格法 多重网格技术 多重网格 多块网格 地震噪声 图论 周期性非定常流动 叶片颤振 单行道 华北 动力发动机 光强传播方程 傅里叶光学 仿真 代数多重网格方法 互相关 二阶精度隐格式
53 lyusternik-wagner外推加速 54 fpk方程 55 fourier级数
1 1 1
53 54 55 56 57 58 59 60 61 62
二维三温方程 中国近海 三维数值模拟 一般网格步长 一体化分析 newton-krvlov(nk) navier-stokes方程 mortar元 lrc-amg gmres
无界区域Stokes问题基于自然边界归化的区域分解法

无界区域Stokes问题基于自然边界归化的区域分解法随着科技的不断发展,数学在许多领域的应用也越来越广泛。
其中,Stokes问题是流体力学中一个重要的数学模型,用于描述粘性流体的运动。
然而,该问题在无界区域上的求解一直是一个具有挑战性的难题。
为了解决这个问题,研究人员提出了基于自然边界归化的区域分解法。
在传统的有界区域中,Stokes问题可以通过有限元方法等数值方法进行求解。
然而,在无界区域中,问题的无穷远处边界条件的处理成为了一个困扰研究者的难题。
自然边界归化的思想在这里起到了关键的作用。
自然边界归化是一种将无界区域转化为有界区域的方法,通过引入一个人工边界,将无界区域的边界条件转化为有界区域上的边界条件。
这样一来,就可以利用传统的数值方法进行求解。
在基于自然边界归化的区域分解法中,将无界区域分割成一个核心区域和一个外边界区域。
核心区域是一个有界区域,可以通过传统的有限元方法进行求解;外边界区域则通过自然边界归化的方式进行处理。
具体而言,基于自然边界归化的区域分解法可以分为以下几个步骤:首先,选择一个合适的有界区域作为核心区域,并给出与无界区域的边界条件相对应的边界条件。
然后,将无界区域分割成核心区域和外边界区域,并利用自然边界归化的方法将无界区域的边界条件转化为有界区域上的边界条件。
接下来,利用传统的有限元方法在核心区域上求解Stokes问题。
最后,通过外边界区域上的边界条件,确定无界区域的解。
基于自然边界归化的区域分解法在解决无界区域Stokes问题方面具有很大的潜力。
它不仅可以简化问题的求解过程,还可以提高求解的精度和效率。
此外,该方法还可以应用于其他无界区域上的数学模型的求解,具有广泛的应用前景。
总之,基于自然边界归化的区域分解法为无界区域Stokes问题的求解提供了一种新的思路和方法。
通过将无界区域转化为有界区域,利用传统的数值方法进行求解,可以克服无界区域求解的困难,为相关领域的研究和应用带来了新的机遇。
用于非定常Stokes问题的一个新的低阶四边形单元变网格格式

VK ∈ J , 义 R— K 的 可 逆 变 换 F 定 如 下 :
得 到 了理 想 的 最优 误 差估 计 .
关 键 词 : tk s问题 ; 意 四边 形 单 元 ;非 协调 元 ;变 网格 So e 任 中 图 分 类 号 : 4、 1 O 2 1 2 文献标识码 : A 文 章 编 号 :1 7 —9 7 ( 0 7 0 0 0 — 7 1 4 6 2 0 ) 2— 0 1 0 6
利用 有限 元方 法 求 解依 赖 于 时 间 的偏 微 分 方
程 问题 , 般 的做 法 是 对 空 间域 采 用 有 限 元 方 法 , 一
1 单 元构 造
设 nCR 是 z — 平 面 上 的 一 个 凸 多 边 形 区 域 , 界为 a J 边 n. 是 n 的一 个 凸 四 边 形 剖 分 族 . 设 K ∈ J , 4 顶 点 坐 标 分 别 是 M z , ) 一 1 其 个 ( , ,
( , 1 , 。 1 1 , ( 1 1 . 的 四 条 边 分 1 一 ) ( , ) ~ ,) 别 记作 2 一 M — z 2 —l , 一 M , 。 R : /, 一 2= —J , 2 / g, —
Md M
网格 简单 , 刚度矩 阵带 宽 小 ,计 算 经 济 等优 点 ,本
, 1
i
的次 数低 、 能较 好 的 逼 近求 解 区域 边 界 等 优 越性 . 通过 引入变 网格思 想 ( 1 2 3 等 ) 见[ , ,] 并将 它 用 于非 定 常 So e tk s问题 , 由于该 单 元 不含 协 调 部分 , 差 误
非定常Navier-Stokes方程的一种非协调有限元投影稳定化方法

非定常Navier-Stokes方程的一种非协调有限元投影稳定化方法张莉;王彦朝;宋卫平【摘要】基于标准的L2投影算子,对非定常Navier-Stokes方程提出了一种非协调有限元投影稳定化方法.这种非协调有限元方法的速度/压力空间采用非协调有限元NCPt-P1.该方法不仅绕开了inf-sup条件对等阶元的束缚,也克服了高雷诺数下对流占优引起的振荡.同时,结合外推公式,将非线性问题转化为线性格式进行处理,从而减少了计算量.最后给出了详细的稳定性分析和误差分析.%In this paper,we propose a new stabilized nonconforming finite element method based on L2 projection for the Navier-Stokes equations with high Reynolds number.This nonconforming method use the lowest equal-order pair of mixed finite elements (i.e.,NCP1-P1).The scheme not only avoids the requirement caused by the inf-sup condition but also overcomes the convection domination caused by the high Reynolds number.We transform the nonlinear problem into a linear problem using the Extrapolation formula to simplify the computation.The stability and error analysis of this method are given in detail【期刊名称】《四川师范大学学报(自然科学版)》【年(卷),期】2017(040)004【总页数】7页(P435-441)【关键词】Navier-Stokes方程;L2投影;高雷诺数;外推公式【作者】张莉;王彦朝;宋卫平【作者单位】四川师范大学数学与软件科学学院,四川成都610066;四川师范大学数学与软件科学学院,四川成都610066;四川中电启明星信息技术有限公司,四川成都610041【正文语种】中文【中图分类】O241.82有限元方法[1]已经成为计算流体问题Stokes方程和不可压缩Navier-Stokes方程的一种重要而有力的工具.特别地,混合有限元方法[2]备受欢迎.然而混合有限元方法的研究面临2个方面的问题:1) 要求有限元空间必须满足inf-sup条件即稳定性条件.遗憾的是工程上计算方便的等阶有限元空间不满足inf-sup条件;2) 当方程呈现对流占优时,其有限元解会出现震荡.为了克服上述困难,采用稳定化技巧的混合有限元方法应运而生.目前常用的稳定化方法主要是基于残差的稳定化方法[3-4]和基于非残差的稳定化方法[5-10].又因为基于非残差的稳定化方法不需要计算二阶导数,使得稳定化格式简单而受到更多的关注.低阶元和等阶元在工程计算中的应用非常广泛,P. B. Bochev等[11]、Li J.[12]以及C. R. Dohrman等[13]分别对Stokes问题的低阶元和一般等阶元(P1-P1,Q1-Q1)的压力投影稳定化方法给出了详细的理论分析.Li J.等[14]和He Y.等[15]又把压力投影稳定化方法推广应用到Navier-Stokes方程,并给出了详细的理论分析和数值算例,其中,文献[14]对于瞬态的Navier-Stokes方程基于高斯积分提出了一种压力投影稳定化方法,有限元空间是采用的最低阶的等阶元.该方法虽然成功地绕开了inf-sup条件的限制,但是当雷诺数很大时,方程的解仍然可能出现不稳定性.随后,文献[16]对瞬态的Navier-Stokes方程提出了一种新的全离散粘性稳定化方法.这个方法不仅绕开了inf-sup条件的限制,同时克服了高雷诺数下对流占优引起的解的不稳定性,并且在时间计算上,每次只用进行线性计算,从而提高了计算效率.另一方面,不可压缩流体的非协调有限元相对于协调有限元方法更加简单,单元自由度较少,并且满足局部守恒条件,从而受到更多的关注和应用.在计算的过程中,变量之间的关联仅在相邻边的中点,所形成的方程未知数较少,进而更加有利于并行计算.文献[12,14]对Stokes方程和Navier-Stokes方程提出了一类局部稳定的协调有限元方法.其速度-压力有限元空间是P1-P1元,基于高斯积分构建稳定项,得到的新的有限元格式是稳定的,成功地绕开了inf-sup条件对等阶有限元的约束.随后文献[17]又将此稳定化方法推广应用到非协调元上计算Stokes方程,其速度-压力有限元空间是非协调元NCP1-P1元,并给出了详细的理论分析和数值算例.相对于一般的非协调元Crouzeix-Raviart(C-R)元,NCP1-P1元虽然不满足inf-sup条件,但是计算更加精确.这类局部稳定的有限元方法[12,14,17]比传统的混合有限元方法更加简单、有效且不依赖于稳定化参数.受以上讨论的启发,本文针对非定常的Navier-Stokes方程,建立了一种既能克服对流占优所引起的震荡,又能绕开inf-sup条件限制的非协调有限元稳定化方法.特别地,本文所给的投影不需要将速度或压力投影到异网格上进行计算,利用外推公式将非线性格式转换为线性格式,从而大大地减少了计算量,提高计算效率.本文考虑如下非定常Naiver-Stokes方程其中,Ω⊂R2为多边形区域,其边界Γ=∂Ω满足Lipschitz连续性,且Q=[0,T]×Ω,T>0.u(x,t)∈R2为速度,p(x,t)∈R为压力,f(x,t)∈R2为体力,λ=Re-1为粘性系数,Re为雷诺数,T>0为最终时间,,引入记号:(·,·)和‖·‖0,分别表示空间L2(Ω)(或L2(Ω)2)的内积和范数,((u,v))=(u,表示和X空间的内积和范数.在空间中,|·|1=‖·‖0与‖·‖1是等价的,因此统一用‖·‖1表示|·|1和‖·‖1.问题(1)的等价变分格式为:求(u,p)∈X×M,t∈[0,T],对∀(v,q)∈X×M,满足关系其中且a1(u;v,w)有如下性质:对区域Ω进行正则三角形剖分,记为单元Kj的直径,为Γk的中点,[u]=u|Γjk-u|Γkj表示跳量.定义其中Pn(K)为单元K上所有次数小于等于n的多项式集合.本文考虑如下的速度和压力的有限元空间:Xh=NCP1,Mh=P1,其中其中P1(Kj)表示单元Kj上所有次数小于等于1的多项式集合.由定义不难得到空间NCP1满足相容性条件:和下列性质[17]:对于任意的(u,p)∈X×M,存在(Πu,Πp)∈Xh×Mh使得对于任意的(u,p)∈(H2(Ω)∩X)×(H1(Ω)∩M),存在(Πu,Πp)∈Xh×Mh使得其中‖|为能量范数.基于高斯积分引入稳定项Gh(·,·):其中g(x)dx表示单元Kj上的Gauss积分的近似,且当多项式次数i=1,2时,等于Gauss积分.另外,g(x)=p(x)q(x)是次数小于等于2次的多项式.进而,定义ρh:L2(Ω)→W0为标准的L2投影,其中W0表示单元Kj上的分片常数函数集合,满足如下性质[17-18]:记定理 2.1[17-18] 存在与h、λ、k无关的正常β,对任意的(uh,ph),(vh,qh)∈Xh×Mh,使得记和分别是un、zn、τn和qn的空间逼近.引入如下稳定项来克服高雷诺数下对流占优引起的震荡:其中,α为稳定化参数,πl-1:L2(Ω)→(Pl-1(τh))2是标准的全局或局部L2投影,且满足性质为了便于表述,引入如下记号和引理:定义 2.1 对∀(u,p),(v,q)∈X×M,有根据文献[10],有下列稳定性结论:引理 2.1 对于任意的ph∈Mh,存在常数β1满足:其中Gh(ph,ph)=‖.用类似于文献[7,10]的方法可以得到如下定理:定理 2.2 对任意(uh,ph)∈Xh×Mh,有其中常数β2与h和α无关.由此,得到(1)式的一个新的有限元稳定格式:对∀(vh,qh)∈Xh×Mh和所有n≥1,使得其中k>0是给定一个时间步长,)∈Xh×Mh为已经求解出来的值,是一个外推公式,.当n=0时,令.下面将详细证明格式(5)是稳定的,并且误差精度能达到O(h2+(k)4).3.1 稳定性为了推导过程中的形式简单,记.定理 3.1 格式(5)是稳定的,即对任意的h,k,n>0满足证明在(5)式的第一个式子中,取,由可得将上式两边同时对n从0到N-1求和,可得(6)式.证毕.3.2 误差估计定义 3.1 对任意(v,q)∈X×M,(vh,qh)∈Xh×Mh,令投影算子(Ph,Qh):X×M→Xh×Mh满足如下关系:其中引理 3.1[17-18] 投影算子(Ph,Qh)满足如下性质:对∀v,q∈X×M,则对∀v,q∈(H2(Ω)∩X)×(H1(Ω)∩M),则定理 3.2 设u∈L∞(0,T;Hm+1(Ω))∩L∞(0,T;L∞(Ω))∩C0(0,T;H1(Ω)),u∈L∞(0,T;L∞(Ω)),ut∈L2(0,T;Hm+1(Ω))∩L∞(0,T;L2(Ω)),utt∈L2(0,T;H1(Ω)),uttt∈L2(0,T;L2(Ω)),ptt∈L2(0,T;L2(Ω)),f∈L2(0,T;H-1(Ω)),并且是方程(5)的解,则存在一个与h、k、λ无关的常数c=c(Ω,u,p,T,f)>0,对∀n∈{0,1,…,N-1}使得证明在(2)式中,取,可得(8)式减去(5)式可得令对ξ=e,η,φh,σ,ζ,τh,定义.从(9)式中加上并减去可得其中在(12)式中令,则可得由Cauchy-Schwartz不等式和Young不等式易得其中接下来估计I1、I2、I3.对I1由Young不等式得在)中加上并减去,由三角不等式和,再由Young不等式得由E[·,·]的定义和u的正则性及逆不等式得将(19)和(20)式代入(18)式,则有下面考虑I3的估计.由三角不等式、Young不等式以及u的正则性有最后考虑)|,其中线性项的估计由Young不等式和泰勒公式可得其中θ1,θ2,θ3∈(0,1).对于中的非线性项,用泰勒公式、Young不等式以及u的正则性假设可得其中θ5,θ6∈(0,1).于是将(17)、(21)、(22)、(25)式代入(15)式,并取ε=1/20,可得将(26)式从1到n相加,并乘以2k可得当n=0时,取=0,(14)~(27)式的证明中只有三线性项的估计有所不同.事实上,注意到只需要将(21)式的最后一行估计中取η-1=e-1=0即可.因此有由u和p的正则性假设,三角不等式和Gronwall不等式,并综合(27)和(28)式可得(7)式.证毕.本文对非定常Navier-Stokes方程提出了一种非协调有限元投影稳定化方法.速度/压力空间采用非协调有限元NCP1-P1,基本L2投影算子构建速度和压力稳定项,由此构造的有限元方法不仅绕开了inf-sup条件对等阶元的束缚,同时也克服了高雷诺数下对流占优引起的振荡.文中给出了详细的稳定性分析和误差分析,由误差估计可以得到误差精度达到了O(h2+k4).文中结合外推公式,将非线性问题转化为线性格式进行处理,从而减少了计算量提高了计算效率.【相关文献】[1] GIRAULT V, RAVIART P A. Finite element approximation of the Navier-Stokes equations[C]//Lecture Notes in Math,749. Berlin:Springer-Verlag,1974.[2] BREZZI F, FORTIN M. Mixed and Hybrid Finite Element Methods[M]. Berlin:Springer-Verlag,1991.[3] ZHOU T, FENG M. A least squares Petrov-Galerkin finite element method for the stationary Navier-Stokes equations[J]. Math Comput,1993,60(202):531-543.[4] DOUGLAS J, WANG J. An absolutely stabilized finite element method for the Stokes problem[J]. Math Comput,1989,52(186):495-508.[5] BECKER R, BRAACK M. A finite element pressure gradient stabilization for the Stokes equations based on local projections[J]. Calcolo,2001,38(4):173-99.[6] CODINA R. Analysis of a stabilized finite element approximation of the Oseen equations using orthogonal subscales[J]. Appl Numer Math,2008,58(3):264-283.[7] BURMAN E. Pressure projection stabilizations for Galerkin approximations of Stokes’ and Darcy’s problem[J]. Numer Meth PDE,2008,24(1):127-143.[8] FENG M, BAI Y, HE Y, et al. A new stabilized subgrid eddy viscosity method based on pressure projection and extrapolated trapezoidal rule for the transient Navier-Stokesequations[J]. J Comput Math,2011,29(4):415-440.[9] QIN Y, FENG M, LUO K, et al. Local projection stabilized finite element method for Navier-Stokes equations[J]. Appl Math Mech,2010,31(5):651-664.[10] 覃燕梅,冯民富,尹蕾. Navier-Stokes方程的一种等阶稳定化亏量校正有限元法[J]. 计算数学,2010,32(1):1-14.[11] BOCHEV P B, DOHRMAN C R, GUNZBURGER M D. Stabilization of low-order mixed finite elements for the stokes equations[J]. SIAM J Numer Anal,2006,44(1):82-101. [12] LI J, HE Y. A stabilized finite element method based on two local Gauss integrations for the Stokes equations[J]. J Comput Appl Math,2008,214:58-65.[13] DOHRMAN C R, BOCHEV P B. A stabilized finite element method for the stokes problem based on polynomial pressure projections[J]. Inter J Numer MethFluids,2004,46(2):183-201.[14] LI J, HE Y, CHEN Z. A new stabilized finite element method for the transient Navier-Stokes equations[J]. Comput Meth Appl Mech Engine,2007,197(1/2/3/4):22-35.[15] HE Y, LI J. A stabilized finite element method based on local polynomial pressure projection for the stationary Navier-Stokes equations[J]. Appl NumerMath,2008,58(10):1503-1514.[16] 覃燕梅,冯民富,周天孝. 瞬态Navier-Stokes方程的一种新的全离散粘性稳定化方法[J]. 应用数学与力学,2009,30(7):783-798.[17] LI J, CHEN Z. A new local stabilized nonconforming finite element method for the Stokes equations[J]. Computing,2008,82(2/3):157-170.[18] JING F, SU J, ZHANG X, et al. Characteristic stabilized nonconforming finite Element method for the unsteady incompressible Navier-Stokes equations[J]. Chin J Engine Math,2014,315:764-778.2010 MSC:49J20; 49K20; 65M12; 65M60。
二维非定常4-Laplacian问题的多重网格规约时间并行解法器

二维非定常4-Laplacian问题的多重网格规约时间并行解法器岳孝强;刘一寅;瞿创成【摘要】未来计算性能的提升依赖的是更高的并发度,而不再是更快的时钟频率,这将致使传统的时间步进算法成为数值模拟非定常问题的一个瓶颈.该文实验性地探究求解二维非定常4-Laplacian问题的具有高并发度的并行解法器,其中全离散格式为向后Euler格式和双线性矩形元,时间并行策略为通信器和进程分组下基于完全近似格式的多重网格规约时间算法.数值对比实验表明:基于F-FCF松弛、细/粗时间网格层的粗化因子为16/4的MGRIT算法具有更高的并发度,相对文献[Falgout,et al.SIAM J Sci Comput,2017,39:S298-S322]中的最优MGRIT解法器,它可提速2.4倍.【期刊名称】《湘潭大学学报:自然科学版》【年(卷),期】2019(000)001【总页数】6页(P49-54)【关键词】非定常4-Laplacian问题;非线性;多重网格规约;时间并行度【作者】岳孝强;刘一寅;瞿创成【作者单位】[1]湘潭大学数学与计算科学学院,湖南湘潭411105;[1]湘潭大学数学与计算科学学院,湖南湘潭411105;[1]湘潭大学数学与计算科学学院,湖南湘潭411105;【正文语种】中文【中图分类】O241.8计算科学领域将面临的一个挑战是:必须通过提高并发度来获得更快的数值计算速度,这是因为时钟速率不再提升而CPU核数却急剧增加.对发展型偏微分方程组(PDEs)而言,通过扩大空间分辨率来提升数值逼近性时,同样要求时间分辨率有类似或更大的倍增.传统的时间步进算法仅在空间维度上进行并行化,它将逐步成为长时间积分数值模拟的一个巨大瓶颈,同时可能造成计算机资源的浪费.虽然并行求解多个时间步的想法并不直观,但这是可行的,相关研究工作可追溯至1964年[1]和1967年[2].文献[3]给出时间并行算法的综述.目前,Lions等提出的parareal算法[4]和Falgout等提出的多重网格规约时间(multigrid-reduction-in-time,MGRIT)算法[5]是两个研究热点.值得一提的是,parareal算法可视为一种两水平的完全近似格式(full approximation scheme,FAS)[6]或两水平的MGRIT算法[5].虽然parareal算法在算法上是最优的,但是它的并发度受限于(大规模的)粗网格层的串行向前求解,并且多水平的parareal算法的可扩展性不佳[5].MGRIT算法克服了这些缺点,且对已有代码的破坏性很小,从而受到学者们的广泛关注[7-10].另外,文献[11]和[10]分别给出了一致、非一致时间剖分下求解整数阶、空间分数阶线性PDEs问题的两水平MGRIT算法的严格收敛性估计,文献[12]考虑的是多水平MGRIT算法的收敛框架.目前,关于求解非线性问题的MGRIT算法的研究工作较少.文献[13]针对二维非定常4-Laplacian问题进行个案研究,注重考虑的是内存开销、初值的改进和空间粗化等,但限于时间粗化因子m=4以及FCF松弛(图1).该文的数值实验平台是XBraid(parallel time integration with multigrid)[14],这是MGRIT算法的一个开源软件包,其优点是它不关心具体的空间离散,而仅在时间维度上实施并行化操作,并且它与传统的时间步进算法能够收敛到相同的数值解.本文同样基于XBraid软件包,通过对时间粗化因子m的不同取值、三种松弛模式(F松弛、FCF松弛、F-FCF松弛)进行数值比对实验,目的是给出一种求解二维非定常4-Laplacian问题的具有更高并发度的并行解法器.1 预备知识1.1 模型问题及弱形式考虑二维非定常4-Laplacian方程[15-16]ut(x,y,t)-·(|u(x,y,t)|2u(x,y,t))=f(x,y,t), (x,y)∈Ω⊂R2, t∈(0,T],(1)定解条件为(2)方程(1)常用于对土壤侵蚀与运输[17]、图像处理(如去噪、分割、修复)[18]等进行建模,其弱形式为〈ut,v〉-〈|u|2u,v〉=〈f,v〉+〈φ,v〉∂Ω, ∀v∈W1,4(Ω),对时间域[0,T]进行一致网格剖分,记剖分步长为δt.此时问题(1)~(2)的向后Euler 格式为:求uk+1∈W1,4(Ω),满足Ψ(uk+1)(v)=gk(v), ∀v∈W1,4(Ω), k=0,…,T/δt-1,(3)其中Ψ(u)(v)=〈u,v〉+δt〈|u|2u,v〉, gk(v)=〈uk+δtfk+1,v〉+〈δtφk+1,v〉∂Ω.假定每个fk均是Lipschitz的,u0∈W1,4(Ω)且·(|u0|2u0)∈L2(Ω),此时对每个k,非线性问题(3)具有唯一解[19];并且该结论对W1,4(Ω)的任意有限维子空间Vh同样成立,即求满足∀vh∈Vh, k=0,…,T/δt-1.(4)利用Newton法处理(4)中的非线性项,为此定义w方向的Frechet导数Ψ′(u)(v)[w]=〈w,v〉+δt〈[|u|2+2(u)(u)T]w,v〉,此时Newton迭代可写为其中δui,h是(5)的唯一解.对线性问题(5),采用并行有限元软件包MFEM[20]中的双线性矩形元进行空间离散,由此得到原问题(1)~(2)的完全离散格式.1.2 基于FAS的非线性MGRIT算法如图3所示,算法1给出基于FAS的两水平MGRIT算法,多水平情形只需递归调用Step 5即可,层间访问的方式通常采用标准的V循环(图2).另外,算法1中的Bc指的是原问题(1)在粗时间网格下的重新离散,Rxy和Pxy分别为空间上的限制和插值函数.算法1 基于FAS的两水平MGRIT(A, u, g)算法Step 1 在时间网格上,令第mi号节点为第i号C点,其余为F点.Step 2 对A(u)=g进行F或FCF或F-FCF松弛.Step 3 限制细网格近似值和残量到粗网格上:uc,i=umi, rc,i=gmi-[A(u)]mi. Step 4 若进行空间粗化,则令uc,i=Rxy(uc,i), rc,i=Rxy(rc,i).Step 5 求解粗问题:Bc(vc)=Bc(uc)+rc.Step 6 计算粗网格误差近似值:ec=vc-uc.Step 7 若进行空间粗化,则令ec,i=Pxy(ec,i).Step 8 校正C点处的数值:umi=umi+emi.Step 9 若已收敛,则更新F点处的数值:对A(u)=g进行F松弛;否则转Step 2. 图3 算法1Fig.3 Algorithm comparison2 数值实验及分析本节的数值实验平台:湘潭大学的64位Linux集群,每个计算结点拥有16颗2.6 GHz的Intel Xeon核,20.0 MB的高速缓冲存储器和128.0 GB内存;相关软件包版本:MFEM 3.4[20],METIS 4.0.3[21],HYPRE 2.15.1[22],XBraid 2.3.0[14];编译优化参数:-O2,其他编译参数取默认值.所考虑的4-Laplacian问题:空间求解域Ω=(0,1)×(0,1),终止时刻T=4,方程(1)中的强制函数f(x,y,t)与方程(2)中的边值φ(x,y,t)、初值u0(x,y)均由真解算得.本节仅考虑强可扩展性实验,上述4-Laplacian问题的时空离散网格规模为642×16 384,且空间维度上的进程数nps=4.例1 测试时间粗化因子m对单次MGRIT运行时间的影响.基于文献[13]的测试,Solve 14的运行时间最少.为此,针对Solve 14关于时间粗化因子m进行4种进程数下的对比数值实验,数值结果见表1.其中npt为时间维度上的进程数,m=16(4)表示最细时间网格层采用16作为粗化因子,其他时间网格层则取为4.表1 不同时间粗化因子下Solver 14的运行时间Tab.1 Runtimes for Solver 14 as functions of the coarseningfactorm=2m=4m=8m=16m=32m=16(4)npt=16581 s370 s243 s249 s364s189 snpt=32302 s196 s121 s124 s168 s96 snpt=64172 s108 s77 s81 s104s63 snpt=128100 s62 s48 s51 s60 s39 s如表1所示:(1) 不论npt取何值,当m=16(4)时,基于FCF松弛、V循环的MGRIT算法的运行时间最少;(2) 相对于m=4的情形(文献[13]的默认值),最经济的取法(即m=16(4))可平均加速1.9倍.具体的解释基于两点:(1) 时间粗化因子越大(时间网格层数越少),FCF松弛的并行效果越好,且整体的并行通信越少;(2) 粗时间网格的尺寸越大,其非线性时间步进解法器的开销越大.综合来看,当m=16(4)时,达到并行效果与并行通信的一个更好的平衡.例2 测试松弛模式(F、FCF、F-FCF)对单次MGRIT运行时间的影响,其中F-FCF表示最细时间网格选用F松弛,其他时间网格层则选用FCF松弛.同样地,针对Solve 14进行4种进程数下的对比数值实验,数值结果如表2所示,其中最后三列的时间粗化因子m=16(4).表2 不同松弛模式下Solver 14的运行时间Tab.2 Runtimes for Solver 14 as functions of the relaxation patternFCF,m=4FFCFF-FCFnpt=16370 s323 s189 s155 snpt=32196 s167 s96 s78 snpt=64108 s113 s63 s49 snpt=12862 s69s39 s31 s如表2所示:(1) 不论npt取何值,F-FCF松弛对应的运行时间最少;(2) 相对FCF、m=4的情形(文献[13]的默认值),基于F-FCF、m=16(4)的MGRIT算法可平均加速2.4倍.参考文献【相关文献】[1] Nievergelt J. Parallel methods for integrating ordinary differential equations[J]. Comm ACM, 1964, 7: 731-733.[2] Miranker W, Liniger W. Parallel methods for the numerical integration of ordinary differential equations[J]. Math Comput, 1967, 21: 303-320.[3] Gander M. 50 years of time parallel time integration[J]. Contrib Math Comput Sci, 2015, 9: 69-114.[4] Lions J, Maday Y, Turinicl G. Resolution d'EDP par un schema en temps parareel[J]. C R Acad Sci Paris Serie I Math, 2001, 332: 661-668.[5] Falgout R, Friedhoff S, Kolev T Z, et al. Parallel time integration with multigrid[J]. SIAM J Sci Comput, 2014, 36: C635-C661.[6] Gander M, Vandewalle S. Analysis of the parareal time-parallel time-integration method[J]. SIAM J Sci Comput, 2007, 29: 556-578.[7] Hessenthaler A, Nordsletten D, Rohrle O, et al. Convergence of the multigrid reduction in time algorithm for the linear elasticity equations[J]. Numer Linear Algebra Appl, 2018, 25: e2155.[8] Gander M, Kwok F, Zhang H. Multigrid interpretations of the parareal algorithm leading to an overlapping variant and MGRIT[J]. Comput Vis Sci, 2018, 19: 59-74.[9] Günther S, Gauger N R, Schroder J B. A non-intrusive parallel-in-time approach for simultaneous optimization with unsteady PDEs[J]. Optimization Methods and Software,2018:1-16.[10] Yue X, Shu S, Xu X, et al. Parallel-in-time multigrid for space-time finite element approximations of two-dimensional space-fractional diffusion equations[J]. Revised, 2018.[11] Dobrev V, Kolev T Z, Petersson N, et al. Two-level convergence theory for multigrid reduction in time (MGRIT)[J]. SIAM J Sci Comput, 2017, 39: S501-S527.[12] Hessenthaler A, Southworth B, Nordsletten D,et al. Multilevel convergence analysis of multigrid-reduction-in-time[DB]. arXiv: 1812.11508.[13] Falgout R, Manteuffel T, O'neill B, et al. Multigrid reduction in time for nonlinear parabolic problems: a case study[J]. SIAM J Sci Comput, 2017, 39: S298-S322.[14] Günther S, Gauger N, Schroder J. A non-intrusive parallel-in-time adjoint solver with the XBraid library[J].Computing and Visualization in Science, 2018, 19: 85-95.[15] Lindqvist P. Notes on the p-Laplace equation [M].2nd ed. Tech Report, University of Jyvaskyla, 2017.[16] Zhou G, Huang Y, Feng C. Preconditioned hybrid conjugate gradient algorithm for p-Laplacian[J]. Int J Numer Anal Model, 2005, 2: 123-130.[17] Bjorn B, Rowlett J. Mathematical models for erosion and the optimal transportationof sediment[J]. Int J Nonlinear Sci Numer Simul, 2013(14):323-337.[18] Elmoataz A, Toutain M, Tenbrinck D. On the p-Laplacian and ∞-Laplacian on graphs with applications in image and data processing[J]. SIAM J Imaging Sci, 2015, 8: 2412-2451.[19] Wei D. Existence, uniqueness, and numerical analysis of solutions of a quasilinear parabolic problem[J]. SIAM J Numer Anal, 1992, 29: 484-497.[20] Shiraiwa S, Wright J, Bonoli P,et al. RF wave simulation for cold edge plasmas using the MFEM library[J].22 Topical Conference on Radio-Frequency Power in Plasmas, 2017, 157: 03048.[21] Karypis G, Kumar V. A fast and high quality multilevel scheme for partitioning irregular graphs[J].SIAM J Sci Comput, 1999, 20: 359-392.[22] Henson V, Yang U. BoomerAMG: A parallel algebraic multigrid solver and preconditioner[J].Appl Numer Math, 2002, 41: 155-177.[23] De sterck H, Yang U, Heys J. Reducing complexity in parallel algebraic multigrid preconditioners[J]. SIAM J Matrix Anal Appl, 2006, 27: 1019-1039.[24] Yang U. On long-range interpolation operators for aggressive coarsening[J]. Numer Linear Algebra Appl, 2010, 17: 453-472.。
有限元基本理论及工程应用:第六章 非协调单元

( 2
j
)
l, j
)
i 1
j 1
(6-2-1)
在穿过单元边界时也可能有有限跳跃量。故φi、ψl 所张成的有限元空间Sh 仅是 L2 的一个子空间(函数自身平方可积)。不是H1(协调单元的有限元空间)
的子空间(一阶导数平方可积)。基函数ψl,j-1、ψl,j 仅在第 j 号单元内的非零,
且
l, j1 (1 2 ), l, j (1 2 ) (6-2-2)
(3)协调性分析
y,v
沿单元的一边,例如节点1、
3
v2
u2
4
e
2
η 3
2所在的边,η =-1。u,v是
4
M
v1
ξ
ê
ξ的二次函数,完全被u1, v1,α1,
1
u1
1
Mˆ
2
和u2, v2,α3 所决定。但由于不 0
x,u
(ξ,-1)
同单元的α1~α4 彼此独立,故不
图 6-3
能保证单元之间位移的协调性。
m
m
Ph Vej Wej WS (6-1-2)
j 1
j 1
WS4
为各边界外力在位移 4
Niui、 Nivi 上做的功之和
i 1
i 1
不计算边界力在内自由度上的功!
有限元解:
由 方程组:
h P
0 ,
h P
0 (i 1 ~ n);
ui
vi
h P
0 ( j 1 ~ m) (l 1 ~ 4)
能否保证收敛到真实解 ?
平面应力问题为例。设节点总数为n,单元总数为m。则总的自由度可区分为:
节点自由度 ui , vi (i 1 ~ n)
Stokes问题的非协调有限元分析

高 校 应 用 数 学 学 报
第2 卷第4 5 期
文 个 地 取 苎 常_ 字区. 还 到 间3 ) {∈2)~ x 0 翌 C, 的 方 不 数式 别.文 用 空 ( =q L ; d=} 中兰 量在 同 不 同 厢作 的 不 ( 厶q
、
(.) 21的变分形式为: P ∈V ×M满足 求(,)
^
bh)一 LhvdyV∈ q M, h, =K dhd ,∈h (吼 ∑ qi , V fx
∈ …
( ) / ・dyV ∈ =∑ r x, . , d 厂
定义l l =(^ , ) . n( ) 根据混合元理论【j 2 如果0(. 】 h.) .) ,和 (. ,分别满足(3 2 ) 2 ) ., .和(4
明 单元 对 速度 和压 力 都 有 二 阶收 敛 精度 .
§ tks j 2 So el题和有 限元方 法 I  ̄
设 是有 界多边形区域, 考虑定常So e l题 : tk sJ b
tA 蚵, , l gp = 在 -4 r- , m f i
’
=
0 ,
an.
・
其中 =( , )是 , u U T 流速,是压力, >0 12 p 为粘性系 厂 , ,T 力密度. 数, =( , )是外 12
本文采用f的记号.・) 9 】 (・ ,表示 ( 内积,明 ( ) 日 ) 是通常 Sbl  ̄I, 。 ) ( ) 及( ( ) 。 oo v ' 其模 e N
摘
要:构造 了两个非协调有限元, tks 对S o e问题满足 离散B B条件 , — 单元对速度和压
力具 有 二 阶 收敛 性 , 值 实验 验 证 了理 论 分析 结 果 . 数
Stokes问题各向异性网格Q2-P1混合元超收敛分析

() 3
{ fd = I qpgz 0 t.d ) c ̄qy ;
V v V h h ,
v
.
显然 X oC( () X塌()则 () P 础 Q ) ' Q : 2 的有限元离散形式为:
0t = /V Vdd.b . =~/ d v:g ( =/, ( I ' ) Q vzy (q v ) t 2qi dd √Q f v r ,, ) ,(
为 了简 单起见 ,设 是 边 界 同坐 标轴 平行 的 凸多 边 形 区域 . 是 一族均 匀矩 形剖 分 ,即 要 求 所 有 行 z ~轴 的 ^ 相同 ,所 有 行 一轴 的 7 相 同 ,不妨设 h . 兰h . 2 VK ∈T 1 h 三h , h
^ 1 h
h: 皿 h 是 一 个与 h无关 的正 常数 .但是 ,从 理 论分 析和 实 际 应 用 的观 点来 说 ,如 此 假 Kc 设 在很 大 程度上 限 制 了有 限 元方 法 的应 用 范 围 ,同时 对 有些 定 义 在 窄边 区域 的 问题 ,如 果用 正 则 性剖 分 , 算 量将 非常 大 ;另 一方 面有 些 问题 的解 呈各 向异 性 ,器 沿某 个方 向解 变化 非常 计 p 剧 烈,而 沿另外方 向解 变 化平 缓 ,这 时采 用各 向异性单 元 剖分 ,求 解 的 效果 会更 好 .本文 基 于
性 【 .但 这 些研 究 都是 基 于 对 剖 分 的 正 则 性 条 件 或拟 一 致 假 设 【. 2 一j 5 即满 足 h / K c 或 j K P ,
h h c ∈ , 中 / K 其 V
^ ∈ 』h
分别是 一 般 单元 的最 大直 径和最 大 内切 圆直径 , h= …a K m xh
关于定常navier-stokes方程非协调有限元三种迭代方法的研究

第 37 卷 暋 第 6 期 暋 暋 暋 暋 暋 暋 暋 暋 暋 暋 暋 暋 暋 暋 暋 陕 西 科 技 大 学 学 报 暋 暋 暋 暋 暋 暋 暋 暋 暋 暋 暋Vol.37 No.6
定常的Navier-Stokes方程非奇解支的最小二乘二重网格有限元法

( 1 1)
u -, )(,v (,w) ∑ 8( Ⅷ vW 一 hi0+hih h h qdw r d + K 一
() 1
△ v + x V v +V q , 3 / Wh U H hu H h h - ' ̄ + ^
. .
弓I 52 h (hq) , h(hT ) 理 .Vv = v,h ∈x hVz= Z,h ∈ 1
[、 ] 2 [ 相比, ]3 可以节省很 多计算量和计算 时间。 关键词 : ai - t e 方程 ; e 0 _ a ri 最小二乘二重网格有限元法 ; N v rS ks e o PtvGl k r. e n 误差估计 ; 非奇解 ; 算子
1预备知识 设, QCR (= ,) 凸多边形 区域 , 虑下 . nn 23 是 考 述 N v rSoe 方 程 : ai - t s e k
A( , ) ( , ) b uu, - P dv + u w = a u w + ( ; w) ( ,iw) (,i ) (, = , rdv 一fw)O u () 2
ug ,) f h ∑8 f 3 w u w u W + , ) K , A h V h rⅧ h (w + (- + ' +
维普资讯
文J 』 i 化 教 育
科
定常 的 airSo e 方 非奇 解支 的最 N ve— tk s 程 小 二乘 二重 网格 有 限元法
孔 令 霞 t 冯 民富
( 、 尔滨商业大学基础科 学学院, 1哈 黑龙江 哈 尔滨 10 2 2 四川大学数 学学院, 508 、 四川 成都 60 6 ) 10 4
摘 要: 文献[ 中给 出了定常的 N m rSoe 方程 的 P t v G l k 1 ] ae t s — k e o— a ri 小二乘二重 网格有 限元法。 r e n最 现在此基础之上对 N v rSoe 方程 具有 ai - t s e k
【江苏省自然科学基金】_计算误差_期刊发文热词逐年推荐_20140816
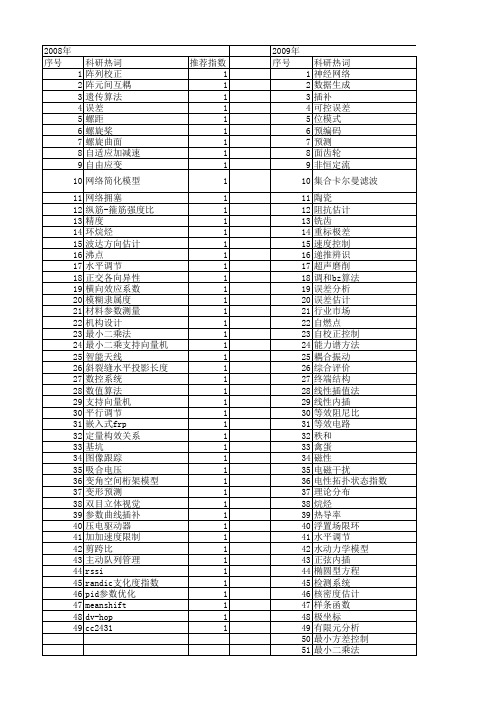
科研热词 神经网络 数据生成 插补 可控误差 位模式 预编码 预测 面齿轮 非恒定流 集合卡尔曼滤波 陶瓷 阻抗估计 铣齿 重标极差 速度控制 递推辨识 超声磨削 调和bz算法 误差分析 误差估计 行业市场 自燃点 自校正控制 能力谱方法 耦合振动 综合评价 终端结构 线性插值法 线性内插 等效阻尼比 等效电路 秩和 禽蛋 磁性 电磁干扰 电性拓扑状态指数 理论分布 烷烃 热导率 浮置场限环 水平调节 水动力学模型 正弦内插 椭圆型方程 检测系统 核密度估计 样条函数 极坐标 有限元分析 最小方差控制 最小二乘法 数控
1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65
动态面控制 初始几何 刚度预测 分子形状指数 光纤 光学断层成像 位置感知 中空纤维膜 stokes问题 rssi p_1非协调四边形元 lbb条件 gps
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
非结构网格上二维可压缩Navier—Stokes方程的并行算法

DU A N Z h i - j i a n, MA- me i
( S c h o o l o f M a t h e ma t i c s a n d I n f o r ma t i o n , X i a n y a n g N o ma r l U n i v e r s i t y , X i a n y a n g 7 1 2 0 0 0 , P . R . C . )
段治 健 , 马欣 荣 , 秦梦 梅
( 成阳师范 学院数 学与信 息科 学学院, 陕西 摘 成阳 7 1 2 0 0 0 )
要: 为 了提 高 N a v i e r — S t o k e s方程 的求解效率 , 在 分布式环境下 , 提 出了基 于区域分解算法的并行求解算法. 首先 , 通
Ab s t r a c t : Ef ic f i e n t p a r a l l e l a l g o i r t h m b a s e d d o ma i n d e c o mp o s i t i o n me t h o d o n d i s t i r b u t e d — me mo r y mu l t i — c o mp u t e r s w a s p r o p o s e d t o s o l v e N a v i e r ・ S t o k e s e q u a t i o n s o n u n s t r u c t u r e d g r i d s i n o r d e r t o a c c e l e r a t e t h e e ic f i e n c y . F i r s t l y, mu l t i l e v e l k - wa y p a r t i t i o n i n g a l g o r i t h m w a s u s e d t o h a n d l e me s h e s p r o p e r l y a n d s a v e e a c h p a t r i t i o n me s h i n d i v i d u a l l y . S e c o n d l y , t h e d a t a o f i n n e r b o u n d a r y
Q1 rot非协调元二网格法

[] 2 中通过广义 分片检验 和 FEM 检验证明了用 —— Q0 r元来求解一般 的二 阶椭 圆边值 问题 能获得 收 ‘
敛 的结 果 。林 群 在 [ ] 给 出 Q 元 的 特 征 值 误 3 中 差展 开 式 。杨 一都 在文 [ ] 4 中 给 出了 特 征 值 问 题 非 协 调 有 限 元 的 2网 格
V0. 6. . 1 2 No 3
Au 2 g. 008
文 章 编 号 :04 5 0 2 0 ) 3— 0 8 4 10 15 7 ( 0 8 0 04 —0
Q0 r 非协调元二 网格法
任善静 , 杨一都
( 州师范大学 数学与计算机科学学院 , 贵 贵州 贵阳 5 0 0 ) 5 0 1
收 稿 日期 :0 7—1 2 20 2— 0
基 金项 目: 国家 自然科 学基金资助 .N : 710 ) ( O 1 603 0
作者简 介 : 任善静 ( 9 2一) 女 , 18 , 在读硕 士研究生 , 研究方 向: 限元 。 有
48
维普资讯
文献标识码 : A
中 图 分 类 号 :2 2 04
Q ee n wog i to lme tt -rdmeh d R N S a -n , N i u E h nj g YA G Y — i d
( col f te a c n o p t c ne G i o om l nvri , uyn , u hu5 0 0 , hn ) S ho o h m t s dC m ue S i c ,uz uN r a U i s t G i g G i o 50 1C ia Ma i a r e h e y a z
第 3期
=
任善静 , 杨一都 : 非协调元- N格 法 Q -
Stokes问题的一个非协调有限元逼近

第2卷 6
第 2期
广 西师 范 大学 学 报 : 自然 科学 版
Jun l f u n x Noma Unvri : trl ce c dt n o ra a g i r l ies y Nau a S i eE io oG t n i
‘ 2
显然 口 ・ ・ 满足强制性 ]即 : ( , ) , 存在常数 a , >O 满足 以 ≥ l l V ∈ V, (,) 口 6 (・, 满 足 BB条 件 即 , 在 常数 p o满 足 ・) — ¨, 存 > ,
删
() 3
ifs p n u M
。 。
I , +b 一( v ∈M f比 ) 6( ,) o , V , (g): , ) E 。 口 ( v 比, g
其 中 , 一( ( ), —L ( , ( ,) ( uV v ,(,) 日3 )。 3 )a u =v V , )bvg 一一 ( ,i 。 gdv )
上对XY 、 的次数分别不超过 J 、的多项式空1。 9 本文还用到空1:3 一{E 。 ; qx O。 9 L( ) q L( I d = }文中的 )
c在不 同 的地方 取 不 同的 常数 , 中不 作 区别 。 文 式() 1 的变 分形 式 为 : ( , ) , ) 足 求 比 声 ∈( 满
流体力学 中的 So e 问题是标准 的混合 问题 , tk s 速度与压力同时计算 。关于该问题有限元求解 的文章 很 多 [ 分 析 的难 点 在于 单 元必 须满 足 离散 的 B b g aBezh] 卜 , a uk —rzi 。 [ 条件 ( 称 BB条 件 ) 简 — 。文献 [- -] 2 中提 出
f (h, +b(h h 一 ( ,^, V E V , a U , ) hP, ) h ' ^ P , ') , h
几个高精度单元的分析和Stokes问题的二阶格式

摘要本文主要介绍两个方面的问题:一是对用双参数有限元法构造的几个重要的高精度单元进行分析,得到了一些非常有用的结论。
二是针对StokeS问题构造了一个三角形Hermite型二阶格式,它具有结构简单自由度小等优点。
关键词:双参数高精度元构造分析Stokes问题三角形Hermite型二阶格式。
AbstraetInthispaper,wefocusonthestudyoftwoproblems.firstly,weanalyzeseveralimportanthighaccuracyelementsproposedbyusingdoublesetparametermethod,andgetsomeveryusefullconclusions.Secondly,weconstructanewtriangularHermiteTypewithformulationformixedstokesequastionswithorderO(b2):ThisformulationhastheadvantagesofsimplestructureandfewerdegreesoffreedomKeyWords:,Doublesetparameter,highaccuracyelement,structureanalyze,Stokesequations,triangleHermitetypeformulation.3刖吾有限元方法是当今数学物理、计算数学、科学与工程计算的非常有效的手段。
对于常规有限元来说,一般有两个困难,~个是从构造简单,总体自由度少因而计算量少出发,一般节点参数取为对称的单元顶点函数值和导数值,但难以保证函数值及一阶导数值在单元边界上的平均连续,如Zienkiewicz元,ACM元等,另一个是为了保证收敛性,有些单元如Veubeke元取边上外法线导数平均值及中点函数值作为节点参数,但这时总体的自由度增加,给计算代来很大的不便。
定常stokes方程的五参数四边形有限元法

定常stokes方程的五参数四边形有限元法定常Stokes方程的五参数四边形有限元法是现代流体力学中的一个重要研究课题。
它的出现填补了有限元分析中对于Stokes方程的研究,促进了现代流体力学理论的发展。
本文重点介绍了定常Stokes方程的五参数四边形有限元法,包括定常Stokes方程、五参数四边形有限元形式及其能量守恒、网格收敛性、系数收敛性等基本内容。
Stokes方程是一组三维非线性液体流动方程,可表述为:(-μu)+p=fu=0其中,u=(u,v,w)为流体速度,p为压强,μ为粘度,f是外力,称为Stokes方程。
Stokes方程是流体力学的基础,可用于描述液体非牛顿流动的特征,是现代流体力学研究的重要组成部分。
五参数四边形有限元是一种基于网格的有限元方法,它特别适用于处理坐标变换的复杂流体流动问题。
五参数四边形有限元求解Stokes方程的核心思想是:将流体流动网格四边形区域分割成五个参数空间,在每个参数空间中分别采用有限元法求解Stokes方程,最终将每个参数空间的解进行综合,得到整个流体流动的全局解,从而实现整个流体力学问题的数值求解。
五参数四边形有限元求解Stokes方程的一个重要特征是能量守恒。
这是由均匀空间网格和四边形形式简化Stokes方程得到的,它满足物理定律,具备良好的能量守恒性。
另外,五参数四边形有限元求解Stokes方程还具有网格收敛性和系数收敛性。
通过这种有限元形式,可以在网格上获得对Stokes 方程求解结果的较高精度,从而使求解过程更加精确,可以更加准确的描述流体动力学的物理机制。
在实际应用中,定常Stokes方程的五参数四边形有限元法有着广泛的应用,如 Stokes流、Boussinesq流、Lamm-Oseen旋流、Kepps-Stokes流、湍流等。
它具有计算精度高、实现技术简单等优点,能够很好地描述复杂流动场。
综上所述,定常Stokes方程的五参数四边形有限元法是现代流体力学理论的重要研究内容,它的出现填补了有限元求解Stokes方程的空白,使得液体流动的研究取得了更大的进展。
定常stokes方程的五参数四边形有限元法

定常stokes方程的五参数四边形有限元法Stokes方程是一种十分重要的流体动力学模型,它是由几何形状和斯托克斯流体力学中的参数组成,用来描述流体的可压缩性、黏滞性和压强等特性。
它是由英国数学家史蒂文斯托克斯(1831-1922)提出的,它建立在完全流动假设和一维平衡守恒定律的基础上,可以描述实际流体中流体动力的现象。
定常Stokes方程可以用来描述低速无涡流的流体动力学,括单位无量纲恒定的流体,可以用来描述实际流体中流体动力的现象。
它可以用多维和时变形式表示,它的数学形式如下:u = fp1/μ2u = g其中,u为速度向量,ρ为密度,μ为粘性摩擦系数,f为力密度,p为压强,g为重力密度。
有限元法,是建立正交有限元,采用局部坐标系,将定常Stokes 方程中的变量进行有限元离散,从而得到相应的有限元方程组的一种数值解法。
其中,四边形有限元法是一种表面有限元方法,该方法是采用三角形四边形模型在各个面上进行离散运算,以求取流体动力学量和局部参数,并绘制坐标系统用于获取求解结果。
二、实现五参数四边形有限元法在实现五参数四边形有限元法时,首先需要能够求解定常Stokes 方程,然后使用三角形有限元方法将它们转换成表面有限元方法。
该方法需要定义五个不同的参数,具体而言,需要定义:(1)流体的密度ρ。
(2)流体的粘性摩擦系数μ。
(3)流动力学量的力密度f。
(4)流体的压力p(5)流体的重力密度g这五个参数作为输入,然后设定离散元素,并在各个离散元素上采用有限元法,然后绘制坐标系,计算定常Stokes方程对应的局部参数,最终,完成五参数四边形有限元法,一致性求解流体力学参数。
三、五参数四边形有限元法的应用五参数四边形有限元法的应用非常广泛,主要用于计算实际流体中的流体动力学参数,其中包括液体管道、水力机械、热交换器等水力学设备以及海洋、大气、湖泊等实际液体流体中的流体动力学参数,它能够准确描述流体的特性,实现较高的分析效率和较低的计算成本,能够提高计算精度和提供更多的计算结果,在计算实际液体流体中流体动力学参数时可以取得较大的成效。
P1非协调四边形元解Stokes问题的多重网格算法

P1非协调四边形元解Stokes问题的多重网格算法黄萍;王琛玮;杨巨玲;徐丹丹【期刊名称】《南京师大学报(自然科学版)》【年(卷),期】2012(035)001【摘要】研究了用P1-Q0元(其中(P)1表示P1非协调四边形元)解Stokes问题的多重网格算法.由于P1- Q0元不满足LBB条件,因此其不能直接用来求解Stokes 问题.本文基于曾提出的一种(P)1-Q0元解Stokes问题的非协调混合有限元稳定化逼近方法,提出了W循环多重网格方法,证明了该方法的最优收敛性.最后给出的数值算例验证了该理论结果.%In this paper, we study the multigrid method of P1 -Q0 elements (where P, denotes P, nonconforming quadrilateral finite element) for solving Stokes problem. Since P1- Q0 elements violate the LBB condition, they can not be used for solving Stokes problem directly. Recently, we proposed a stabilized method of P1-Q0 elements for solving Stokes problem. Based on this stabilized method, we propose a. W - cycle multigrid method, and show the optimal convergence of W - cycle multigrid method with a sufficiently large number of smoothing steps. Finally, numerical experiments are presented to confirm our theoretical results.【总页数】11页(P1-11)【作者】黄萍;王琛玮;杨巨玲;徐丹丹【作者单位】中国人民解放军理工大学理学院,江苏南京211101;南京师范大学数学科学学院,江苏南京210046;中国人民解放军理工大学理学院,江苏南京211101;南京师范大学数学科学学院,江苏南京210046;南京师范大学数学科学学院,江苏南京210046;中国人民解放军理工大学理学院,江苏南京211101【正文语种】中文【中图分类】O241【相关文献】1.Mortar型非协调四边形元多重网格方法 [J], 王锋;徐为2.P1非协调Mortar元的V循环多重网格方法 [J], 张磊;杨敏3.3维Stokes问题的一种非协调-协调有限元法 [J], 张敏;罗鲲;张世全4.解Oseen方程的P1非协调四边形单元的涡旋粘性法 [J], 左芳芳;孔花;刘程熙5.Stokes问题低阶非协调混合元的改进加罚算法(英文) [J], 石东洋;唐启立因版权原因,仅展示原文概要,查看原文内容请购买。
二维图形的四边形有限元网格划分

第10卷第1期2003年2月塑性工程学报JOURNA L OF P LASTICITY E NGI NEERI NGV ol 110 N o 11Feb 1 2003二维图形的四边形有限元网格划分(北京机电研究所,北京 100083) 刘晓飞 金泉林摘 要:本文介绍了一种对二维图形进行四边形有限元网格划分的算法,算法的关键在于边界网格单元的生成及处理,以使其能够与原始图形边界相吻合,同时具有较规则的网格形状。
关键词:有限元;四边形网格中图分类号:TG 30 文献标识码:A 文章编号:100722012(2003)0120009204收稿日期:20022012151 引 言在有限元锻压数值模拟计算程序中,对物体进行有限元网格划分是一个关键步骤。
对于二维问题(平面变形问题或轴对称变形问题),有限元网格可分为三角形单元网格和四边形单元网格两种,由于四边形单元网格不管在逼近离散域方面,还是在网格质量方面,以及在计算精度方面都较三角形单元优越,因此二维问题普遍采用四边形单元网格。
进行网格划分包含在两个过程,一是数值模拟计算前对物体进行的初始网格划分;二是在数值模拟计算中,由于物体变形导致部分网格形状畸变而进行的自动网格重划分,从而重新获得规则的网格以继续进行计算。
网格重划分过程涉及到新旧网格之间的节点、单元变量的插值计算和数据转换,因此频繁的网格重划分必然导致计算精度的下降,同时增加了计算时间。
所以,如何获得较规则的单元网格,以便有效的减少网格重划分的次数,使模拟计算过程连贯进行,是四边形单元网格划分算法中的关键之一;同时,单元网格中的边界网格还起着描述物体外形轮廓的作用,它们不但要具有较好的网格形状,而且也要和原始物体的边界轮廓相吻合,否则会造成物体外形失真及体积变化,影响计算结果;当物体的某些局部几何尺寸很小时,则也需要划分相当尺寸的网格才能将它描述精确,如果整个物体都划分为和此网格一样大小的均匀网格,那么网格单元数目将非常多,这将大大增加计算时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[ 关键词 ] P 非协调 四边形元 ,t e . So s问题 , k 多重 网格算法 , 定化方法 稳
[ 中图分类号 ]0 4 [ 2 1 文献标志码 ]A [ 文章编号 ]0 1 6 6 2 1 ) 100 —l 10 - 1 ( 02 O -0 11 4
尸 1非协调 四边 形元解 So e 问题的 多重网格算法 tks
黄 萍 , 琛 玮 杨 巨玲 徐 丹 丹 王 , ,
(. 1 中国人 民解放军理T大学理学院 ,江苏 南京 2 10 ) 11 1
( . 京 师范 大学 数 学 科 学 学 院 ,江 苏 南 京 2 0 4 ) 2南 10 6
f H 。’ 一 V= :, p
,
:
【 Biblioteka l 0 f:, 在 F上,
不 能 直接用 来求解 Soe 问题 l ] tks 2 .我们 在 文 [ ]中利用 标 志 P 一Q 元 L B条 件不 足 的那一项 , 正与 ’ 8 。 。 B 修
me t r r s ne o c n r o rt e rt a e u t. n sa e p e e td t o f m u o ei lr s l i h c s
Ke r s Pl o c n o mi g q a r ae a nt lme t tk sp o lm ,mu ir t o y wo d : n o f r n u d i tr l i ee n ,So e rb e n l i f e h g i meh d,sa i z d meh d d tb l e t o i
第 0 2年 3月 2 5卷 第 1 3 1 期
・
南京师大学报 ( 自然科学版 )
V0 . 5 No. 13 1
Ma 2 2 r, 01
J U N L O A J G N R LU I E ST N trl c n e d i ) O R A FN N I O MA N V R IY( aua S i c io N e E tn
A Mut id Meh do n o fr n a rltr l ii lme t l gr to f No c no migQu d i ea nt E e n i P1 a F e
f r So v ng St ke o e o l i o s Pr bl m
So e r b e tk sp o lm.B s d o h ssa i z d meh d a e n t i tb l e to ,w r p s —c ce mu ird meh d,a d s o h p i lc n i epo oea W y l h g i t o n h w teo t ma o — v re c f W —c ce mu ir t o t u ce t a g u e fs o h n tp . F n l eg n eo y l h g i me h d wi a s f in l lr e n mb ro mo t i g se s ia l d h i y y,n me ia x e — u r le p f c i
[ 摘要 ] 研究 了用 户, 。元 ( 中 p 表示 P 非 协调 四边 形元 ) Soe 问题 的多重 网格算 法.南于 P 一Q 其 。 解 tks 一Q,
元不 满足 L B条件 ,因此其 不能直接用来求解 Soe 问题. B t s k 本文基 于曾提 出的一种 P 一Q 元解 Soe 问题 的 tks 非协 调混合有限元稳定化逼近方法 , 提出了 循环 多重网格方法 , 明了 该方法 的最优收敛性. 证 最后 给 m的数
A s atI ip pr w t y h u i i me o f —Q lm ns( hr P eo s l ocn r n udi bt c : t s ae, e u em hg d t doPl 0 e et w ee l nt n of mi q ar r n h sd t r h e d eP n o g —
lea f i l et o li tkspolm.SneP 一Q l ns ia h B o d i ,te a o b a rl n ee m n)fr ov gS e rbe t t e i s n o ic 1 o e t vo t teL Bcn io hycnnt e e me le tn ue r o igSoe rbe i cl.R cnl,w rpsdas b i dm to fP —Q lm nsf ov g sdf l n t spolm dr t osv k e y eet y epooe t iz ehdo l 0e et o sli a le e r n
Hu n ig , a g Ch n i Y n uig , n a a g Pn W n e we , a g J l Xu Da d n n
( .ntueo c ne P A U i rt f c neadT c nl y aj g2 11 C ia 1 Istt f i c , L nv syo S i c n eh oo ,N ni 1 0 , hn ) i Se ei e g n 1 ( . col fM te t a Sine ,N nigN r l iesy N mig20 4 ,C ia 2 Sh o o ahmacl cecs aj oma Un ri , a n 10 6 hn ) i n v t
