鲍威尔法编程-powell法编程 c语言编程 c++6.0
c语言pow用法 -回复

c语言pow用法-回复C语言的pow函数是用于计算一个数的幂运算的,它的用法非常简单,只需要提供底数和指数两个参数即可。
下面将一步一步地解释pow函数的用法和原理。
1. 引言在数学中,求幂运算是非常常见的计算操作。
例如,我们可以使用2的3次幂表示为2^3,即2乘以自身3次,即2 * 2 * 2 = 8。
在编程中,我们经常需要对一个数进行幂运算,这个时候C语言的pow函数就非常有用。
2. pow函数的原型和参数pow函数的原型如下所示:double pow(double x, double y);通过传递两个参数x和y,pow函数将计算x的y次幂的结果,并将结果以double类型的数据返回。
其中,x为底数,y为指数。
3. pow函数的用法示例下面通过几个示例来说明pow函数的用法:c#include <stdio.h>#include <math.h>int main() {double result;示例1:计算2的3次幂result = pow(2, 3);printf("2的3次幂:lf\n", result);示例2:计算3的平方根result = pow(3, 0.5);printf("3的平方根:lf\n", result);示例3:计算2的-2次幂result = pow(2, -2);printf("2的-2次幂:lf\n", result);return 0;}在上面的示例中,我们首先包含了`<stdio.h>`和`<math.h>`这两个头文件,然后定义了一个double类型的变量result用于存储pow函数的返回值。
在示例1中,我们使用pow函数计算了2的3次幂,并将结果打印出来。
由于2的3次幂等于8,因此打印的结果为8.000000。
在示例2中,我们使用pow函数计算了3的平方根,并将结果打印出来。
优化设计鲍威尔法程序c语言

if(f1<=f2)
for(i=1;i<n;i++)
x0[i]=x1[i];
else
for(i=1;i<n;i++)
x0[i]=x2[i];
}
else
{
for(i=r;i<n;i++)
for(j=0;j<n;j++)
s[i][j]=s[i+1][j];
f1=f2;
for(i=0;i<n;i++)
x2[i]=x3[i];
f2=f3;
} /*搜索方向为正向*/
for(i=0;i<n;i++) /*计算第三试点*/
x3[i]=x2[i]+h*s[i];
f3=f(x3);
while(f3<f2) /*判断是否未完成搜索*/
{ /*未完成,继续搜索*/
h=2*h;
for(i=0;i<n;i++)
sum+=(b[i]-a[i])*(b[i]-a[i]);
}while(sqrt(sum)>flag*0.1);
for(i=0;i<n;i++)
x[i]=(float)0.5*(b[i]+a[i]);
}
/*鲍威尔法子程序*/
voiflag,float a[],float b[],float x[])
for(i=0;i<n;i++)
x1[i]=x2[i];
f1=f2;
for(i=0;i<n;i++)
powell法matlab

powell法matlab
Powell方法是一种用于无约束优化问题的数值优化算法。
它是由Michael J.D. Powell于1964年提出的,是一种直接搜索方法,不需要计算目标函数的梯度。
在MATLAB中,可以使用内置的fminunc函数来实现Powell方法进行优化。
首先,你需要定义一个目标函数,这个函数是你想要优化的目标,比如最小化或最大化的函数。
然后,你可以使用fminunc函数来调用Powell方法进行优化。
fminunc函数的基本语法如下:
matlab.
[x,fval,exitflag,output] = fminunc(fun,x0,options)。
其中,fun是你定义的目标函数,x0是优化的初始点,options 是优化选项。
在fun中,你需要输入目标函数的表达式,并确保它能够接受输入x,并返回一个标量作为目标函数值。
在使用Powell方法时,你需要特别注意初始点的选择,因为初始点的选择可能会影响最终的优化结果。
另外,你也可以通过调整
options来设置一些优化参数,比如迭代次数、容许误差等。
除了使用MATLAB内置的fminunc函数,你还可以自己实现Powell方法的算法,这需要一定的数值计算和优化算法的知识。
你可以参考相关的优化算法书籍或者论文来了解Powell方法的具体实现细节。
总之,Powell方法是一种常用的无约束优化算法,在MATLAB 中可以通过fminunc函数来实现。
希望这些信息对你有所帮助,如果你有其他关于Powell方法或MATLAB优化的问题,也欢迎继续提问。
鲍威尔法编程-powell法编程 c语言编程 c++6.0

for(i=0;i<N;i++)
{
printf("请输入初始点x[%d]=",i);
scanf("%f",&xo[i]);
}
printf("请输入迭代精度Ef,Ex=");
scanf("%f,%f",&c,&d);
printf("请输入步长T=");
scanf("%f",&t);
{
{
for(j=0;j<N;j++)
s[j]=ss[i][j];
}
fmin=ywyh(xooo,t,s,z);
for(j=0;j<N;j++)
x[j]=z[j];
fi[i]=fmin;
for(j=0;j<N;j++)
xooo[j]=x[j];
}
for(i=0;i<N;i++)
{
s[i]=x[i]-xoo[i];xe[i]=2*x[i]-xoo[i];
int i,j=0;
a=0;b=t;
f[0]=gs(x);
for(i=0;i<N;i++)
z[i]=x[i]+b*s[i];
f[1]=gs(z);
if(f[1]<f[0])
{
do
{t=2*t;b=b+t;f[0]=f[1];
for(i=0;i<N;i++)
z[i]=x[i]+b*s[i];
f[1]=gs(z);
819韦尔奇-鲍威尔算法

韦尔奇-鲍威尔算法Welsh–Powell Algorithm
决定一个图的色数是一个难题(准确地讲,它是一个NP完全问题),目前尚不存在有效的方法
因此在对图进行点着色时常采用近似算法——尽管不能得到最优结果,但是算法的执行却是快捷有效的。
下面将介绍韦尔奇-鲍威尔(Welch-Powell)点着色算法:
韦尔奇-鲍威尔算法Welch-Powell (G)
输入:图G
输出:图G 的一个点着色方案
1. 将图中顶点按度数不增的方式排成一个序列
2. 使用一种新颜色对序列中的第一个顶点进行着色,并且按照序列次序,对与已着色顶点不邻接的每一顶点着同样的颜色,直至序列末尾。
然后从序列中去掉已着色的顶点得到一个新的序列
3. 对新序列重复步骤2直至得到空序列
acgbdef cgbef
gbe
e
c
a
g d
f
b
e
要说明的是,韦尔奇-鲍威尔算法并不总能得到最少颜色数目的染色方案。
韦尔奇-鲍威
尔算法共使
用四种颜色
1
3
5
7 2 4 6 8
韦尔奇-鲍威
尔算法共使
用两种颜色
1
2
3
4 5 6 7 8
E nd。
c语言pow的用法

c语言pow的用法C语言中的pow函数是一个常用的数学函数,用于计算一个数的指数。
这个函数在标准库<math.h>中定义,因此在使用它之前,你需要确保你的C语言环境中包含了<math.h>头文件。
一、pow函数的定义和使用------------------C语言的pow函数用于计算e的x次幂,即`e^x`,其中e是一个数学常数,约等于2.71828。
函数原型通常如下:```cdouble pow(double x, double y);```这里的x和y都是double类型的数值。
函数返回的结果是一个double类型的值,表示x的y次幂。
你可以这样在代码中使用它:```c#include <stdio.h>#include <math.h>int main() {double base = 2.0;double exponent = 3.0;double result = pow(base, exponent);printf("Result: %f\n", result); // 输出结果会是8.0,因为2的3次方等于8return 0;}```二、pow函数的精度和效率--------------pow函数在计算指数时,会使用高精度算法来实现,以保证结果的精确度。
这意味着对于大的指数值,pow函数可能会需要比较多的计算资源。
但是,对于大多数实际应用来说,pow函数已经足够精确和高效。
三、其他用法和注意事项------------除了计算指数之外,pow函数还可以用于其他数学运算中,例如开方、对数等。
在使用pow函数时,需要注意以下几点:1. 如果x是一个负数,那么pow函数的结果可能没有意义。
在实际应用中,你应该确保x是一个非负数。
2. pow函数的结果是一个double类型的数据,它可能包含小数部分。
如果你需要一个整数结果,你可以使用强制类型转换来得到一个整数。
优化设计-(Powell)法+鲍威尔修正算法

1)任选初始点X(0)=X0(1) ,给定迭代收敛精度 1 , 2 。 取初始基本方向组为单位坐标向量系,即Si(1)=ei ( i = 1, 2, … , n ), 并置迭代轮次k=1。
2)从X0(k)出发,依次沿Si(k) ( i = 1, 2, … , n ) 作一维 搜索,得n个极小点Xi(k) ( i = 1, 2, … , n ),构造新的搜 索方向 S(k) = Xn(k) -X0(k) ,并沿此方向进行一维搜索得 极小点Xn+1(k) 。 3)判断迭代终止条件 || Xn+1(k) – X0(k) ||≤ 1 ? 或 | f (Xn+1(k) ) – f (X0(k) ) |≤ 2 | f (Xn+1(k) ) | ? 若满足,则终止迭代并输出最优解: X * = Xn+1(k) 和 f * = f (X * )
依此进行下去,直到获得满足迭代收敛精度要求的 近似极小点为止。 根据这一原理构造的迭代算法称为鲍威尔基本 算法。 x2
S(1) S2(1) X3 (1) X2 (1) X2
* X (2)
S(2)
X1 (2) S1(1)
()
X0
(1)
X1
x1
2.3.3鲍威尔基本算法的缺点 鲍威尔基本算法仅具有理论意义,不要说对于 一般的函数,就是对于二次函数,它也可能失效。 因为在迭代过程中的 n个搜索方向有时会变成线性相
X0(k+1) = Xn+1(k) Si(k+1) ( i = 1, 2, … , n ) 即 { S1(k), …, Sm-1(k), S(k), Sm+1(k), …, Sn(k)} 并置 k k+1 ,返回第2)步。
鲍威尔法概述及算例求解

根据这一原理构造的迭代算法称为鲍威尔基 本算法。
(二)鲍威尔法的缺陷
鲍威尔基本算法不可能对每一个都起作用,因为在迭代 过程中的n个搜索方向有时会变成线性相关的,而不能形 成共轭方向,导致随后的迭代搜索在降维(退化)的空间 中进行,可能求不到极小点,故而进行改进。
(三)鲍威尔修正算法
为了避免这种“退化”现象的发生,鲍威尔对这一算法 进行了修正。即在每一轮产生新的搜索方向 后,首先 判断原搜索方向组是否可以直接用下一轮迭代的方向组, 若可以,即用。否则,还要进一步判断原搜索方向组中哪 个方向上的函数值下降量最大,然后再用新搜索方向替换 这个下降量最大的搜索方向,以保证逐次生成共轭方向, 即每一轮迭代的搜索方向组线性无关。
一 共轭方向的概念与共轭向量的性质
(一)共轭方向 设A为n阶实对称正定矩阵,若有两个n维向量 和 能满足 A =0 则称向量 与 对矩阵A共轭,共轭向量的 方向称为共轭方向。
(二)共轭向量的性质 设A为n×n阶实对称正定矩阵, (i=1,2,…n) 是关于A的n个互相共轭的非零向量,对于正 定二次函数f(收敛到极小点 = 沿n元二次正定函数的n个共轭方向进行n次 一维搜索就可达到目标函数的极小点。
其中: —第k起始点函数值 — k轮方向组一维搜索终点函数值 — 对 的映射点函数值 — 第k轮方向组沿诸方向一维搜索所得的各 函数下降量中最大者,其对应的方向即是
鲍威尔修正算法的判别条件
(四)鲍威尔法的计算步骤
(1)给定初始点 和计算精度 ,即取初始方向组为n 个单位坐标向量。 (2)沿 各方向进行一轮n次一维搜索 即: minf( +a )= f( + ) 得到: = 这一步相当于最优步长的坐标轮换法。 (3)经计算求出共轭方向和映射点分别为 = (4)计算k轮中相邻两点目标函数值的下降量,并求出下 降量最大者及其相应的方向
鲍威尔法

鲍威尔法二级斜齿轮减速器的优化设计姓名:王剑锋学号:109011159班级:机制096班一、基本原理前已述及,对于n维无约束最优化问题,采用原始共轭方向法在产生n个共轭方向时,有可能是线性相关或接近线性相关的,如遇这种情况,会导致在降维空间寻优使迭代计算不能收敛到真正最优点而失败。
鲍威尔在1964年提出了对上述原始共轭方向法的改进方法—鲍威尔共轭方向法。
这个改进方法与原始共轭方向法的关键区别是在构成第k + 1环基本方向组时,不再总是不管好坏一律去掉前一环的第一个方向,并再将前一环的新生方向补于最后,而是首先判断前一环的基本方向组是否需要更换;如需更换,还要进一步判断前一环原基本方向组中沿某一个方向作一维搜索函数值下降量最大,去掉该方向再将新生方向补入最后构成第k+1环的基本方向组以避免线性相关并最接近共轭。
判别前一环基本方向组是否需要更换的依据,则按导出的下列两个条件式。
(1)(2)是否得到满足来进行处理,式中各符号的涵义可参阅图5-13(P62)说明如下——k环起始点的函数值;——k环沿基本方向组依次一维搜索后的终点的函数值;——对的映射点的函数值,;——k环基本方向组中沿诸方向一维搜索所得各目标函数值下降量中之最大者,对应方向。
若条件式(1)或(2)中至少有一个成立,则第k +1环的基本方向组仍用原来第k环的基本方向组。
k十1环的初始点应选取、两点中函数值小者,亦即当时,取;时,取。
若式(1)及式(2)均不成立,则去掉原来第k环基本方向组中函数值下降量最大的方向,再将第k环所产生的新生方向补入k+1环基本方向组的最后,即以构成第k+l环的基本方向组。
k+1环的初始点应取第k环中沿方向一维搜索的极小点,亦即取。
图2显示了二维正定二次函数用鲍威尔共轭方向法求极小点的搜索路线,其几何意义亦完全可推广到n维正定二次函数。
二、迭代过程及算法框图鲍威尔共轭方向法的具体迭代步骤如下:(1)给定初始点,迭代精度,维数n,。
c语言pow函数

c语言pow函数pow函数是C语言提供的一个数学库函数,用于计算一个数的指定次幂。
函数原型:double pow(double x, double y);参数说明:-x:基数,即要进行指数运算的数-y:指数,即要进行指数运算的次数返回值:x的y次幂,即pow(x, y)pow函数的头文件为"math.h",在使用该函数前需要引入该头文件。
pow函数在C语言中的使用非常广泛,常见于科学计算、数据分析、统计学等领域。
它具有很高的灵活性,可以处理各种大小的数值,并且支持浮点数运算。
使用pow函数可以方便地进行幂运算,无需编写复杂的指数计算代码,提高了程序开发的效率。
下面是pow函数的详细解释及使用示例:1.整数幂运算pow函数可以计算整数幂的结果,如2的3次方(2^3):```c#include <stdio.h>#include <math.h>int maidouble result = pow(2, 3);printf("2的3次方为:%lf\n", result);return 0;```2.小数幂运算pow函数也支持小数幂的运算,如2的0.5次方(√2):```c#include <stdio.h>#include <math.h>int maidouble result = pow(2, 0.5);printf("2的0.5次方为:%lf\n", result);return 0;```3.负数幂运算pow函数可以计算负数幂的结果,如2的-2次方(1/2^2):```c#include <stdio.h>#include <math.h>int maidouble result = pow(2, -2);printf("2的负2次方为:%lf\n", result);return 0;```4.异常处理pow函数返回一个double类型的值,因此可以处理非常大或非常小的数值,并且可以进行溢出检测。
004第四章Powell法

例4-2 74页
上述基本算法仅具有理论意义 :
3.改进的鲍威尔方法
在改进的算法中首先判断原向量组是否需要替换。 如果需要替换,还要进一步判断原向量组中 哪个向量最坏,然后再用新产生的向量替换这个 最坏的向量,以保证逐次生成共轭方向。
3.改进的鲍威尔方法
为此,要解决两个关键问题:
(1)dk+1是否较好?是否应该进入新的方向组? 即方向组是否进行更新?
0 1 2 2 x d d x 此轮基本方向组为 3 , 3 ,起始点为 0 = ,先 1 0 d 后沿 d 3 , 3 方向,进行一维搜索,得
4 x , 2
2 1
4 x 2
2 2
4 x , 2
2 1
4 x 2
2 2
检验终止条件
x22 x02 0
3.96 x 1.9
1 2
f 2 f ( x1 ) 7.996 2
• (2)第2轮迭代计算
3.96 x 1.9
1 2
f 2 f ( x1 ) 7.996 2
构成新的方向
3.96 3.8 0.16 d x x 1.94 1.7 0.24
1.共轭方向
(d 0 )T Gd 1 0 (d 0 )T 2 f ( x)d 1 0
就是使d1直指极小点x* , d1所必须满足的条件 。
两个向量 d 和d1称为G的共轭向量,或称
d 和d 对G是共轭方向。
0 1
0
共轭方向的性质
性质1 性质2 性质3 若非零向量系d0,d1,d2,…,dm-1是对G共轭, 在n维空间中互相共轭的非零向量的个数 从任意初始点出发,顺次沿n个G的共轭方 则这m个向量是线性无关的。
十一、Powell算法(鲍威尔算法)原理以及实现

⼗⼀、Powell算法(鲍威尔算法)原理以及实现⼀、介绍 Powell算法是图像配准⾥⾯的常⽤的加速算法,可以加快搜索速度,⽽且对于低维函数的效果很好,所以本篇博客主要是为了介绍Powell算法的原理以及实现。
由于⽹上已经有了对于Powell算法的讲解,所以我只是把链接放出来(我觉得⾃⼰⽬前还没有这个讲解的能⼒),⼤家⾃⼰去了解。
放在这⾥主要也是为了节省⼤家搜索的时间。
(都是我⾟⾟苦苦搜出来的^-^)。
⼆、预备知识 了解⼀维搜索算法:进退法,消去法,黄⾦分割法 阅读以下博客:三、鲍威尔算法 具体原理阅读这⾥: 参考博客: 原理与例⼦(⼀个例⼦的计算过程):四、matlab代码实现⼀个简单函数的求解 代码来源: 这个代码的程序与思路很是简洁,我觉得写得很好。
原⽂代码放在这⾥: ⽂件:MyPowell.m function MyPowell()syms x1 x2 x3 a;f=10*(x1+x2-5)^4+(x1-x2+x3)^2 +(x2+x3)^6;error=10^(-3);D=eye(3);x0=[000]';for k=1:1:10^6MaxLength=0;x00=x0;m=0;if k==1,s=D;endfor i=1:3x=x0+a*s(:,i);ff=subs(f,{x1,x2,x3},{x(1),x(2),x(3)});t=Divide(ff,a); %调⽤了进退法分割区间aa=OneDemensionslSearch(ff,a,t); %调⽤了0.618法进⾏⼀维搜索 xx=x0+aa*s(:,i);fx0=subs(f,{x1,x2,x3},{x0(1),x0(2),x0(3)});fxx=subs(f,{x1,x2,x3},{xx(1),xx(2),xx(3)});length=fx0-fxx;if length>MaxLength,MaxLength=length;m=m+1;endx0=xx;endss=x0-x00;ReflectX=2*x0-x00;f1=subs(f,{x1,x2,x3},{x00(1),x00(2),x00(3)});f2=subs(f,{x1,x2,x3},{x0(1),x0(2),x0(3)});f3=subs(f,{x1,x2,x3},{ReflectX(1),ReflectX(2),ReflectX(3)});if f3<f1&&(f1+f3-2*f2)*(f1-f2-MaxLength)^2<0.5*MaxLength*(f1-f3)^2x=x0+a*ss;ff=subs(f,{x1,x2,x3},{x(1),x(2),x(3)});t=Divide(ff,a);aa=OneDemensionslSearch(ff,a,t);x0=x0+aa*ss;for j=m:(3-1),s(:,j)=s(:,j+1);ends(:,3)=ss;elseif f2>f3, x0=ReflectX;endendif norm(x00-x0)<error,break;endk;x0;endopx=x0;val=subs(f,{x1,x2,x3},{opx(1),opx(2),opx(3)});disp('最优点:');opx'disp('最优化值:');valdisp('迭代次数:');k ⽂件 Divide.m :%对任意⼀个⼀维函数函数进⾏区间分割,使其出现“⾼—低—⾼”的型式function output=Divide(f,x,m,n)if nargin<4,n=1e-6;endif nargin<3,m=0;endstep=n;t0=m;ft0=subs(f,{x},{t0});t1=t0+step;ft1=subs(f,{x},{t1});if ft0>=ft1t2=t1+step;ft2=subs(f,{x},{t2});while ft1>ft2t0=t1;%ft0=ft1;t1=t2;ft1=ft2;step=2*step;t2=t1+step;ft2=subs(f,{x},{t2});endelsestep=-step;t=t0;t0=t1;t1=t;ft=ft0;%ft0=ft1;ft1=ft;t2=t1+step;ft2=subs(f,{x},{t2});while ft1>ft2t0=t1;%ft0=ft1;t1=t2;ft1=ft2;step=2*step;t2=t1+step;ft2=subs(f,{x},{t2});endendoutput=[t0,t2];View Code ⽂件:OneDemensionslSearch.mfunction output=OneDemensionslSearch(f,x,s,r)if nargin<4,r=1e-6;enda=s(1);b=s(2);a1=a+0.382*(b-a);fa1=subs(f,{x},{a1});a2=a+0.618*(b-a);fa2=subs(f,{x},{a2});while abs((b-a)/b)>r && abs((fa2-fa1)/fa2)>rif fa1<fa2b=a2;a2=a1;fa2=fa1;a1=a+0.382*(b-a);fa1=subs(f,{x},{a1});elsea=a1;a1=a2;fa1=fa2;a2=a+0.618*(b-a);fa2=subs(f,{x},{a2});endendop=(a+b)/2;%fop=subs(f,{x},{op});output=op;View Code 全部放到同⼀个⼯程⽬录⾥⾯,设置为当前⽬录,然后输⼊Powell即可运⾏得到结果。
matlab鲍威尔法求二元二次函数的极小值

matlab鲍威尔法求二元二次函数的极小值鲍威尔法(Powell's method)是一种用于求解无约束优化问题的迭代算法。
在MATLAB中,你可以使用内建函数,比如fminunc 或fminsearch,或者手动实现鲍威尔法来求解二元二次函数的极小值。
不过,MATLAB并没有直接提供鲍威尔法的内建函数,因此你需要自己实现它。
下面是一个简化的鲍威尔法实现,用于求解二元二次函数的极小值。
假设我们的二元二次函数是f(x, y) = ax^2 + bxy + cy^2 + dx + ey + f。
matlabfunction [xmin, fmin] = powell_method(func, x0, tol, max_iter) % func: 目标函数句柄% x0: 初始点% tol: 收敛容忍度% max_iter: 最大迭代次数n = length(x0); % 变量的维数x = x0;B = eye(n); % 初始基矩阵为单位矩阵for k = 1:max_iter% 在当前基方向上进行一维搜索for i = 1:n% 定义搜索方向d = B(:, i);% 一维线搜索确定步长alpha = linesearch(func, x, d);% 更新当前点x_new = x + alpha * d;% 检查收敛性if norm(x_new - x) < tolreturnend% 更新xx = x_new;% 更新基矩阵B(:, n) = x_new - x;B = B(:, 1:n-1);end% 使用QR分解更新基矩阵[Q, R] = qr(B);B = Q(:, 1:n);endxmin = x;fmin = func(x);endfunction alpha = linesearch(func, x, d)% 简单的线搜索实现(这里假设函数是凸的)alpha = 0.1; % 初始步长c1 = 1e-4; % 足够小的正数while func(x + alpha * d) > func(x) + c1 * alpha * d' * grad(func, x)alpha = alpha / 2;endendfunction g = grad(func, x)% 计算梯度(这里需要func的梯度信息)% 对于二次函数ax^2 + bxy + cy^2 + dx + ey + f% 梯度是[2ax + by + d, bx + 2cy + e]'% 这里只是一个示例,你需要根据实际的func来计算梯度% 假设a = 1;b = 2;c = 1;d = -4;e = -6;g = [2*a*x(1) + b*x(2) + d; b*x(1) + 2*c*x(2) + e];end% 示例:求解函数f(x, y) = x^2 + 2xy + y^2 - 4x - 6y 的极小值func = @(x) x(1)^2 + 2*x(1)*x(2) + x(2)^2 - 4*x(1) - 6*x(2);x0 = [0; 0]; % 初始点tol = 1e-6; % 容忍度max_iter = 1000; % 最大迭代次数% 调用鲍威尔法[xmin, fmin] = powell_method(func, x0, tol, max_iter);% 显示结果disp(['极小值点:', mat2str(xmin)]);disp(['函数极小值:', num2str(fmin)]);请注意,上面的代码片段中有几个地方需要特别注意:grad 函数需要根据你的目标函数来计算梯度。
鲍威尔方法

机械优化设计中的鲍威尔方法鲍威尔(Powell )法是直接利用函数值来构造共轭方向的一种方法。
对函数 f(x)=21x 2Gx+b T +c 的极小化问题,基本思想是:在不用导数的前提下,在迭代中逐次构造G 的共轭方向。
鲍威尔算法的基本思想: 性质一:同心椭圆簇; 性质二:平行切点的连线必 经过椭圆簇中心;性质三:椭圆中心即为极小点。
一.共轭方向的生成如图1,设x k ,x k+1为从不同点出发,沿同一方向dj 进行一维搜索而到的两个极小点。
根据梯度和等值面相垂直的性质, dj 和 xk, xk+1两点处的梯度g k ,g k+1之间存在关系: (d j )T g k =0 (d j )T g k+1=0:另一方面,对于上述二次函数,其xk, xk+1两点处的梯度可表示为:g k =Gx k +b g k+1=Gx k+1+b :因而有(d j )T (g k+1-g k )=(d j )T G(x k+1-x k )=0,取d k =x k+1-x k 这说明只要沿d j 方向分别对函作两次一维搜索,得到两个极小点x k和x k+1,那么这两点的连线所给出的方向d k就是与d j一起对G 共轭的方向。
一.基本算法1)任选一初始点x 0,再选两个线性无关的向量,如坐标轴单位向量e 1=[1,0]T 和e 2=[0,1]T 作为初始搜索方向。
12)从x 0出发,顺次沿e 1, e 2作一维搜索,得x 10,x 20点,两点连线得一新方向 d 1=x 20-x 0。
用 d 1代替e 1形成两个线性无关向量d 1 ,e 2 ,作为下一轮迭代的搜索方向。
再 x 20出发,沿d 1作一维搜索得点 x 01,作为下一轮迭代的初始点。
3)从x 1出发,顺次沿,e 2。
d 1 作一维搜索,4)得到点x 11,x 21,两点连线得一新方 向:d 2=x 21-x 11。
4)沿d 2d2作一维搜索得点.x 2 ,即是二维问题的极小点x* 。
c语言pow用法

c语言pow用法C语言pow函数用法详解在C语言中,pow函数是一个非常常用的数学函数之一。
它可以用来计算一个数的幂,并返回结果。
这个函数非常有用,无论是在数学问题的解决中,还是在编程中,都可以使用pow函数帮助我们完成一系列复杂的计算。
在本文中,我将为您深入探讨pow函数的用法,希望对您有所帮助。
首先,让我们简要了解pow函数的基本用法。
pow函数的声明如下:cdouble pow(double base, double exponent);pow函数接受两个参数,base和exponent,分别代表底数和指数。
该函数将返回base的exponent次幂的值。
需要注意的是,pow函数的返回值是一个double类型,也就是一个双精度浮点数。
这是因为指数可能是一个小数,而底数和指数的计算结果可能是一个浮点数。
考虑以下例子:c#include <stdio.h>#include <math.h>int main () {double result;计算2的3次幂result = pow(2, 3);printf( "2^3 = %.2f\n", result );计算4的平方根result = pow(4, 0.5);printf( "√4 = %.2f\n", result );return 0;}上述例子中,pow函数被用来计算2的3次幂和4的平方根。
输出的结果将分别是8和2。
接下来,让我们详细了解pow函数的用法。
1. 计算整数幂pow函数可以用来计算整数次幂。
例如,要计算2的3次幂,可以将2作为底数,3作为指数传递给pow函数,如下所示:cresult = pow(2, 3);这将返回8。
pow函数可以处理任何整数作为指数,无论是正数还是负数。
2. 计算小数幂pow函数不仅可以计算整数幂,还可以计算小数幂。
例如,要计算4的平方根,可以将4作为底数,0.5作为指数传递给pow函数:cresult = pow(4, 0.5);这将返回2,因为4的平方根就是2。
鲍威尔法C语言

鲍威尔法C语言鲍威尔法C语言程序#include <stdio.h>#include <math.h>#define m 10 /*数组长度m >= 维数n */float f(float x[]);void mjtf(int n,float x0[],float h,float s[],float a[],float b[]);void mhjfgf(int n,float a[],float b[],float flag,float x[]);void mbwef(int n,float x0[],float h,float flag,float a[],floatb[],float x[]);float f(float x[]){float result;result=60-10*x[0]-4*x[1]+x[0]*x[0]+x[1]*x[1]-x[0]*x[1];return result; }/*多维进退法子程序*/void mjtf(int n,float x0[],float h,float s[],float a[],float b[]) {int i;float x1[m],x2[m],x3[m],f1,f2,f3;for(i=0;i<n;i++) /*计算初始两试点*/{x1[i]=x0[i];x2[i]=x0[i]+h*s[i];}f1=f(x1);f2=f(x2);if(f2>=f1) /*判断搜索方向*/{ /*搜索方向为反向,转身*/h=(-1)*h;for(i=0;i<n;i++)x3[i]=x1[i];f3=f1;for(i=0;i<n;i++)x1[i]=x2[i];f1=f2;for(i=0;i<n;i++)x2[i]=x3[i];f2=f3;} /*搜索方向为正向*/for(i=0;i<n;i++) /*计算第三试点*/x3[i]=x2[i]+h*s[i];f3=f(x3);while(f3<f2) /*判断是否未完成搜索*/ { /*未完成,继续搜索*/h=2*h;for(i=0;i<n;i++)x1[i]=x2[i];f1=f2;for(i=0;i<n;i++)x2[i]=x3[i];f2=f3;for(i=0;i<n;i++)x3[i]=x2[i]+h*s[i];f3=f(x3);} /*已完成*/for(i=0;i<n;i++) /*输出初始搜索区间*/{if(x1[i]<x3[i]){a[i]=x1[i]; b[i]=x3[i];}else{a[i]=x3[i];b[i]=x1[i];}}}/*多维黄金分割法子程序*/void mhjfgf(int n,float a[],float b[],float flag,float x[]){int i;float x1[m],x2[m],f1,f2,sum;for(i=0;i<n;i++) /*计算初始两试点*/ x1[i]=b[i]-(float)0.618*(b[i]-a[i]); f1=f(x1);for(i=0;i<n;i++)x2[i]=a[i]+(float)0.618*(b[i]-a[i]); f2=f(x2);do{if(f1<=f2) /*判断消去区间*/{ /*消去右*/for(i=0;i<n;i++){mjtf(n,x1,h,s[i],a,b);mhjfgf(n,a,b,flag,x1);fn[i]=f(x0)-f(x1);}for(i=0;i<n;i++)x2[i]=2*x1[i]-x0[i];for(i=1;i<n;i++)if(fn[0]<fn[i]){fn[0]=fn[i];r=i;}elser=0;f0=f(x0);f1=f(x1);f2=f(x2);if(f2>=f0||(f0-2*f1+f2)*(f0-f1-fn[0])*(f0-f1-fn[0])>=0.5*fn[0]*(f0-f2)*(f0-f2)){sum=0;for(i=0;i<n;i++)sum+=(x1[i]-x0[i])*(x1[i]-x0[i]);if(f1<=f2) for(i=1;i<n;i++)x0[i]=x1[i];elsefor(i=1;i<n;i++)x0[i]=x2[i];}else{ for(i=r;i<n;i++)for(j=0;j<n;j++)s[i][j]=s[i+1][j];for(i=0;i<n;i++)s[n][i]=x1[i]-x0[i];mjtf(n,x1,h,s[n],a,b);mhjfgf(n,a,b,flag,x1);sum=0; for(i=0;i<n;i++)sum+=(x1[i]-x0[i])*(x1[i]-x0[i]); for(i=0;i<n;i++)x0[i]=x1[i];}if(sqrt(sum)<=flag) break;elsek+=1;}for(i=0;i<n;i++)x[i]=x1[i];}/*鲍威尔法主程序*/void main(){int i,n;float h,flag,x0[m],a[m],b[m],x[m]; printf("\n<鲍威尔法>\n");printf("请输入维数:\n");scanf("%d",&n);printf("请输入初始点:");for(i=0;i<n;i++){printf("\nx0[%d]=",i);scanf("%f",&x0[i]);}printf("\n请输入初始步长:\n"); scanf("%f",&h);printf("\n请输入精度:\n");scanf("%f",&flag);mbwef(n,x0,h,flag,a,b,x);printf("\n极小点坐标为:\n");for(i=0;i<n;i++)printf("x[%d]=%f\n",i,x[i]);printf("\n极小值为:\n%f\n",f(x)); }。
鲍威尔法实验报告
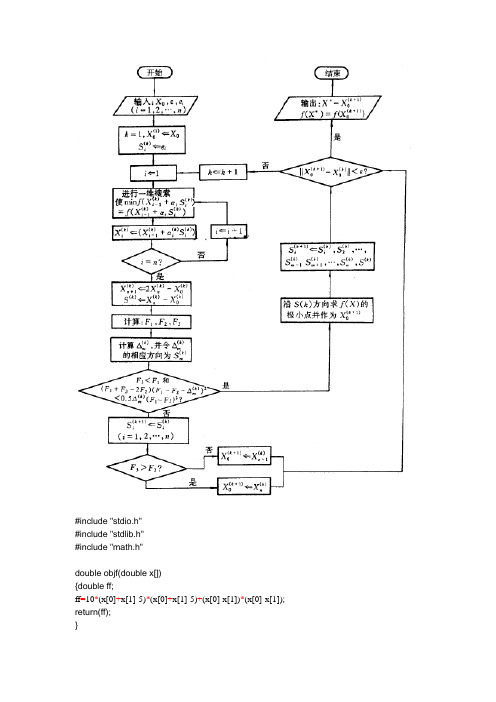
#include "stdio.h"#include "stdlib.h"#include "math.h"double objf(double x[]){double ff;ff=10*(x[0]+x[1]-5)*(x[0]+x[1]-5)+(x[0]-x[1])*(x[0]-x[1]); return(ff);}void jtf(double x0[],double h0,double s[],int n,double a[],double b[]) {int i;double *x[3],h,f1,f2,f3;for(i=0;i<3;i++)x[i]=(double *)malloc(n*sizeof(double));h=h0;for(i=0;i<n;i++)*(x[0]+i)=x0[i];f1=objf(x[0]);for(i=0;i<n;i++)*(x[1]+i)=*(x[0]+i)+h*s[i];f2=objf(x[1]);if(f2>=f1){h=-h0;for(i=0;i<n;i++)*(x[2]+i)=*(x[0]+i);f3=f1;for(i=0;i<n;i++){*(x[0]+i)=*(x[1]+i);*(x[1]+i)=*(x[2]+i);}f1=f2;f2=f3;}for(;;){h=2*h;for(i=0;i<n;i++)*(x[2]+i)=*(x[1]+i)+h*s[i];f3=objf(x[2]);if(f2<f3) break;else{ for(i=0;i<n;i++){*(x[0]+i)=*(x[1]+i);*(x[1]+i)=*(x[2]+i);}f1=f2;f2=f3;}}if(h<0)for(i=0;i<n;i++){a[i]=*(x[2]+i);b[i]=*(x[0]+i);}elsefor(i=0;i<n;i++){a[i]=*(x[0]+i);b[i]=*(x[2]+i);}for(i=0;i<3;i++)free(x[i]);}double gold(double a[],double b[],double eps,int n,double xx[]) {int i;double f1,f2,*x[2],ff,q,w;for(i=0;i<2;i++)x[i]=(double *)malloc(n*sizeof(double));for(i=0;i<n;i++){*(x[0]+i)=a[i]+0.618*(b[i]-a[i]);*(x[1]+i)=a[i]+0.382*(b[i]-a[i]);}f1=objf(x[0]);f2=objf(x[1]);do{if(f1>f2){for(i=0;i<n;i++){b[i]=*(x[0]+i);*(x[0]+i)=*(x[1]+i);}f1=f2;for(i=0;i<n;i++)*(x[1]+i)=a[i]+0.382*(b[i]-a[i]);f2=objf(x[1]);}else{ for(i=0;i<n;i++){a[i]=*(x[1]+i);*(x[1]+i)=*(x[0]+i);}f2=f1;for(i=0;i<n;i++)*(x[0]+i)=a[i]+0.618*(b[i]-a[i]);f1=objf(x[0]);}q=0;for(i=0;i<n;i++)q=q+(b[i]-a[i])*(b[i]-a[i]);w=sqrt(q);}while(w>eps);for(i=0;i<n;i++)xx[i]=0.5*(a[i]+b[i]);ff=objf(xx);for(i=0;i<2;i++)free(x[i]);return(ff);}double oneoptim(double x0[],double s[],double h0,double epsg,int n,double x[]) {double *a,*b,ff;a=(double *)malloc(n*sizeof(double));b=(double *)malloc(n*sizeof(double));jtf(x0,h0,s,n,a,b);ff=gold(a,b,epsg,n,x);free(a);free(b);return (ff);}double powell(double p[],double h0,double eps,double epsg,int n,double x[]) {int i,j,m;double *xx[4],*ss,*s;double f,f0,f1,f2,f3,fx,dlt,df,sdx,q,d;ss=(double *)malloc(n*(n+1)*sizeof(double));s=(double *)malloc(n*sizeof(double));for(i=0;i<n;i++){for(j=0;j<=n;j++)*(ss+i*(n+1)+j)=0;*(ss+i*(n+1)+i)=1;}for(i=0;i<4;i++)xx[i]=(double *)malloc(n*sizeof(double));for(i=0;i<n;i++)*(xx[0]+i)=p[i];for(;;){for(i=0;i<n;i++){*(xx[1]+i)=*(xx[0]+i);x[i]=*(xx[1]+i);}f0=f1=objf(x);dlt=-1;for(j=0;j<n;j++){for(i=0;i<n;i++){*(xx[0]+i)=x[i];*(s+i)=*(ss+i*(n+1)+j);}f=oneoptim(xx[0],s,h0,epsg,n,x); df=f0-f;if(df>dlt){dlt=df;m=j;}}sdx=0;for(i=0;i<n;i++)sdx=sdx+fabs(x[i]-(*(xx[1]+i)));if(sdx<eps){free(ss);free(s);for(i=0;i<4;i++)free(xx[i]);return(f);}for(i=0;i<n;i++)*(xx[2]+i)=x[i];f2=f;for(i=0;i<n;i++){*(xx[3]+i)=2*(*(xx[2]+i)-(*(xx[1]+i))); x[i]=*(xx[3]+i);}fx=objf(x);f3=fx;q=(f1-2*f2+f3)*(f1-f2-dlt)*(f1-f2-dlt); d=0.5*dlt*(f1-f3)*(f1-f3);if((f3<f1)||(q<d)){if(f2<=f3)for(i=0;i<n;i++)*(xx[0]+i)=*(xx[2]+i);elsefor(i=0;i<n;i++)*(xx[0]+i)=*(xx[3]+i);}else{for(i=0;i<n;i++){*(ss+(i+1)*(n+1))=x[i]-(*(xx[1]+i));*(s+i)=*(ss+(i+1)*(n+1));}f=oneoptim(xx[0],s,h0,epsg,n,x);for(i=0;i<n;i++)*(xx[0]+i)=x[i];for(j=m+1;j<=n;j++)for(i=0;i<n;i++)*(ss+i*(n+1)+j-1)=*(ss+i*(n+1)+j);}}}void main(){double p[]={1,2};double ff,x[2];ff=powell(p,0.3,0.001,0.0001,2,x);printf("x[0]=%f,x[1]=%f,ff=%f\n",x[0],x[1],ff); getchar();}。
鲍威尔法编程-powell法编程c语言编程c++6.0.doc

数字信号处理实验讲义前言 (2)实验一MA TLAB简介 (3)实验二用FFT实现信号的谱分析 (5)实验三IIR数字巴特沃思滤波器的设计 (8)实验四FIR数字滤波器的设计 (9)前言信号处理与计算机的应用紧密结合。
目前广泛应用的MA TLAB工具软件包,以其强大的分析、开发及扩展功能为信号处理提供了强有力的支持。
在数字信号处理实验中,我们主要应用MA TLAB的信号处理工具箱及其灵活、便捷的编程工具,通过上机实验,帮助学生学习、掌握和应用MA TLAB软件对信号处理所学的内容加以分析、计算,加深对信号处理基本算法的理解。
实验一 MATLAB 简介实验目的1.熟悉MA TLAB 软件的使用方法; 2.MA TLAB 的绘图功能;3.用MA TLAB 语句实现信号的描述及变换。
实验原理1.在MA TLAB 下编辑和运行程序在MA TLAB 中,对于简单问题可以在命令窗(command windows )直接输入命令,得到结果;对于比较复杂的问题则可以将多个命令放在一个脚本文件中,这个脚本文件是以m 为扩展名的,所以称之为M 文件。
用M 文件进行程序的编辑和运行步骤如下:(1)打开MA TLAB ,进入其基本界面;(2)在菜单栏的File 项中选择新建一个M 文件;(3)在M 文件编辑窗口编写程序;(4)完成之后,可以在编辑窗口利用Debug 工具调试运行程序,在命令窗口查看输出结果;也可以将此文件保存在某个目录中,在MA TLAB 的基本窗口中的File 项中选择Run The Script ,然后选择你所要运行的脚本文件及其路径,即可得出结果;也可以将此文件保存在当前目录中,在MA TLAB 命令窗口,“>>”提示符后直接输入文件名。
2.MA TLAB 的绘图功能plot(x,y) 基本绘图函数,绘制 x 和y 之间的坐标图。
figure(n ) 开设一个图形窗口nsubplot(m,n,N) 分割图形窗口的MA TLAB 函数,用于在一个窗口中显示多个图形,将图形窗口分为m 行n 列,在第N 个窗口内绘制图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
for(i=0;i<N;i++)
xooo[i]=xo[i];
for(i=0;i<N;i++)
for(j=0;j<N;j++)
{
if(i==j)
ss[i][j]=1;
else
ss[i][j]=0;
}
do
{
for(i=0;i<N;i++)
xoo[i]=xooo[i];
k=k+1;
for(i=0;i<N;i++)
{
{
for(j=0;j<N;j++)
s[j]=ss[i][j];
}
fmin=ywyh(xooo,t,s,z);
for(j=0;j<N;j++)
x[j]=z[j];
fi[i]=fmin;
for(j=0;j<N;j++)
xooo[j]=x[j];
}
for(i=0;i<N;i++)
{
s[i]=x[i]-xoo[i];xe[i]=2*x[i]-xoo[i];
//f=1.5*z[0]*z[0]+0.5*z[1]*z[1]-z[0]*z[1]-2*z[0];
return(f);
}
float ywyh(float x[N],float t,float s[N],float z[N])
{
float q=0.618,e,A[N],f[2],a,b,c=0.1,d=0.1;
{
fmin=ywyh(xooo,t,s,z);f[1]=fmin;
for(j=0;j<N;j++)
x[j]=z[j];
for(i=0;i<N-1;i++)
{
if(i<m)
{
for(j=0;j<N;j++)
ss[i][j]=ss[i][j];
}
else
{
for(j=0;j<N;j++)
ss[i][j]=ss[i+1][j];
if(f[0]>f[1])
a=b-t;
else break;}
while(f[0]>f[1]);
}
else
{
t=0-t;
do
{a=a+t;f[1]=f[0];
for(i=0;i<N;i++)
z[i]=x[i]+a*s[i];
f[0]=gs(z);
if(f[1]>f[0])
{
b=a-t;t=2*t;
}
else break;}
while(f[1]>f[0]);
}
do
{
j=j+1;
A[0]=b-q*(b-a);
for(i=0;i<N;i++)
z[i]=x[i]+A[0]*s[i];
f[0]=gs(z);
A[1]=a+q*(b-a);
for(i=0;i<N;i++)
z[i]=x[i]+A[1]*s[i];
df=(f[0]-f[1])/f[1];
else
df=0-(f[0]-f[1])/f[1];
if(xoo[0]-x[0]>0)
dx=xoo[0]-x[0];
else
dx=x[0]-xoo[0];
for(i=1;i<N;i++)
{
if(xoo[i]-x[i]>0)
dxl=xoo[i]-x[i];
else
}
}
for(i=0;i<N;i++)
ss[N-1][i]=s[i];
ks=ks+1;
}
else
{
if(fmin>f[2])
{
for(i=0;i<N;i++)
x[i]=xe[i];
f[1]=f[2];fmin=f[2];
}
else ;
}
for(i=0;i<N;i++)
xooo[i]=x[i];
if((f[0]-f[1])/f[1]>0)
int i,j,k,ks,m;
for(i=0;i<N;i++)
{
printf("请输入初始点x[%d]=",i);
scanf("%f",&xo[i]);
}
printf("请输入迭代精度Ef,Ex=");
scanf("%f,%f",&c,&d);
printf("请输入步长T=");
scanf("%f",&t);
}
f[0]=gs(xoo);f[1]=fmin;f[2]=gs(xe);fio=f[0];
dm=fio-fi[0];m=0;
for(i=0;i<N-1;i++)
{
dml=fi[i]-fi[i+1];
if(dm<dml)
{dm=dml;m=i+1;}
else ;
}
if((f[0]+f[2]-2*f[1])*(f[0]-f[1]-dm)*(f[0]-f[1]-dm)<0.5*dm*(f[0]-f[2])*(f[0]-f[2])&&f[2]<f[0])
f[1]=gs(z);
do
{
if(f[0]>f[1])
{
a=A[0];A[0]=A[1];f[0]=f[1];
A[1]=a+q*(b-a);
for(i=0;i<N;i++)
z[i]=x[i]+A[1]*s[i];
f[1]=gs(z);
j=j+1;
if(j>50)
break;
}
else
{
b=A[1];A[1]=A[0];f[1]=f[0];
printf("\n搜索累计次数k=%d\n",k);
printf("\n替换方向累计次数ks=%d\n",ks);
}
dxl=x[i]-xoo[i];
if(dx<dxl)
dx=dxl;
else ;
}
}
while(dx>c||df>d);
for(i=0;i<N;i++)
z[i]=x[i];
for(i=0;i<N;i++)
printf("\n最优点坐标x[%i]=%f\n",i,z[i]);
printf("\n最优函数值f(x)=%f\n",fmin);
int i,j=0;
a=0;b=t;
f[0]=gs(x);
for(i=0;i<N;i++)
z[i]=x[i]+b*s[i];
f[1]=gs(z);
if(f[1]<f[0])
{
do
{t=2*t;b=b+t;f[0]=f[1];
for(i=0;i<N;i++)
z[i]=x[i]+b*s[i];
f[1]=gs(z);
}while(e>d);
if(f[0]<f[1])
{
for(i=0;i<N;i++)
z[i]=x[i]+A[0]*s[i];
return(f[0]);
}
else
{
for(i=0;i<N;i++)
z[i]=x[i]+A[1]*s[i];
return(f[1]);
}
}
void main()
{
float xo[N],ss[N][N],z[N],c,d,t,fmin,xooo[N], xoo[N],fi[N],s[N],x[N],xe[N],f[N],fio,dm,dml,df,dx,dxl;
if((A[1]-A[0])/A[0]>0)
e=(A[1]-A[0])/A[0];
else
e=0-(A[1]-A[0])/A[0];
if(e<=d)
break;
else
{
a=A[0];b=A[1];
}
if((A[1]-A[0])/A[0]>0)
e=(A[1]-A[0])/A[0];
else
e=0-(A[1]-A[0])/A[0];
#include <stdio.h>
#define N 2
float gs(float z[N])
{
float f;
//f=10*(z[0]+z[1]-5)*(z[0]+z[1]-5)+(z[0]-z[1])*(z[0]-z[1]);
f=4+4.5*z[0]-4*z[1]+z[0]*z[0]+2*z[1]*z[1]-2*z[0]*z[1]+z[0]*z[0]*z[0]*z[0]-2*z[0]*z[0]*z[1];
A[0]=b-q*(b-a);
for(i=0;i<N;i++)
z[i]=x[i]+A[0]*s[i];
