拓扑学基础(林金坤编)思维导图
思维导图拓扑图与甘特图
思维导图拓扑图与甘特图2014-10-17Dr.2珍立拍你想要知道科学方法的实质,不要去听一个科学家对你说些什么,而要仔细看他在做什么。
——爱因斯坦思维导图(MindMap)思维导图又叫心智图,是表达发散性思维的有效的图形思维工具,它有利于人脑的扩散思维的展开。
思维导图运用图文并重的技巧,把各级主题的关系用相互隶属与相关的层级图表现出来,把主题关键词与图像、颜色等建立记忆链接。
放射性思考是人类大脑的自然思考方式,每一种进入大脑的资料,不论是感觉、记忆或是想法,都可以成为一个思考中心,并由此中心向外发散出成千上万的关节点,每一个关节点代表与中心主题的一个连结,而每一个连结又可以成为另一个中心主题,再向外发散出成千上万的关节点,呈现出放射性立体结构,而这些关节的连结可以视为记忆,也就是每个人的超级数据库。
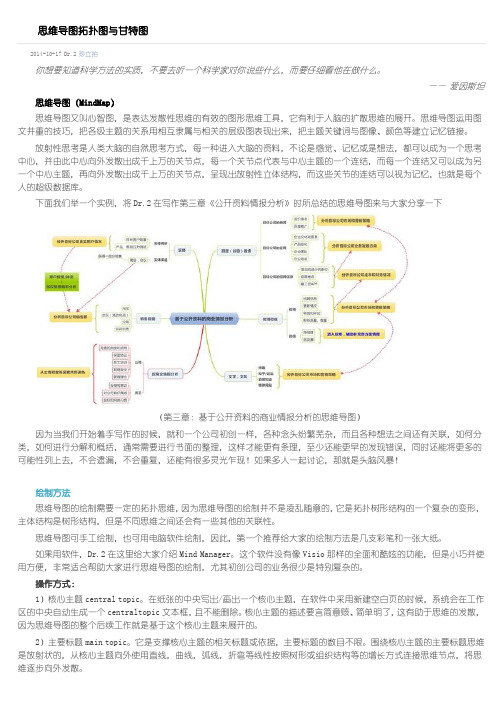
下面我们举一个实例,将Dr.2在写作第三章《公开资料情报分析》时所总结的思维导图来与大家分享一下(第三章:基于公开资料的商业情报分析的思维导图)因为当我们开始着手写作的时候,就和一个公司初创一样,各种念头纷繁芜杂,而且各种想法之间还有关联,如何分类,如何进行分解和概括,通常需要进行书面的整理,这样才能更有条理,至少还能更早的发现错误,同时还能将更多的可能性列上去,不会遗漏,不会重复,还能有很多灵光乍现!如果多人一起讨论,那就是头脑风暴!绘制方法思维导图的绘制需要一定的拓扑思维,因为思维导图的绘制并不是凌乱随意的,它是拓扑树形结构的一个复杂的变形,主体结构是树形结构,但是不同思维之间还会有一些其他的关联性。
思维导图可手工绘制,也可用电脑软件绘制,因此,第一个推荐给大家的绘制方法是几支彩笔和一张大纸。
如果用软件,Dr.2在这里给大家介绍Mind Manager。
这个软件没有像Visio那样的全面和酷炫的功能,但是小巧并使用方便,非常适合帮助大家进行思维导图的绘制,尤其初创公司的业务很少是特别复杂的。
操作方式:1)核心主题central topic。
点集拓扑学(第一章1.1)

1736年欧拉 解决七桥问题
哥尼斯堡 七桥问题 四色问题 Euler示性数
1976年9月四
Mö bius带
色问题得到解决
Department of Mathematics
哥尼斯堡七桥问题
哥尼斯堡是东普鲁士的首都,普莱格尔河横贯其中。 十八世纪在这条河上建有七座桥,将河中间的两个岛和河
岸联结起来。人们闲暇时经常在这上边散步
一天有人提出:能不能每座桥 都只走一遍,最后又回到原来的
位置。
这个问题看起来很简单, 有很有趣的问题吸引了大家. 很多人在尝试各种各样的走法,但谁也没有做到。看
来要得到一个明确理想的答案还不那么容易
Department of Mathematics
1736年,有人带着这个问题找到了当时的大数学家 欧拉,欧拉经过一番思考,很快就用一种独特的方法给出
了解答。
他把两座小岛和河的两岸分别看作四个点, 而把七座桥看 作这四个点之间的连线。那么这个问题就简化成,能不能用一 笔就把这个图形画出来。 经过进一步的分析,欧拉得出结论——不可能每座桥都走一 遍,最后回到原来的位置。并且给出了所有能够一笔画出来的 图形所应具有的条件。这是拓扑学的“先声”。
Department of Mathematics
和数学知识,能对实际问题进行分析、归纳、
提炼和解决,提高他们的数学素养。
Department of Mathematics
教学目标
掌握拓扑空间、度量空间和连续映射的定义、例子、
性质。掌握连通性,可数性,分离性,紧性等拓扑性质。 掌握几个重要的拓扑性质的可积性、可商性和遗传性。
教学要点
拓扑空间、度量空间和连续映射的定义、例子、性 质。连通性,可数性,分离性,紧性等拓扑性质。几个重
思维导图拓扑图与甘特图

思维导图拓扑图与甘特图2014-10-17Dr.2珍立拍你想要知道科学方法的实质,不要去听一个科学家对你说些什么,而要仔细看他在做什么。
——爱因斯坦思维导图(MindMap)思维导图又叫心智图,是表达发散性思维的有效的图形思维工具,它有利于人脑的扩散思维的展开。
思维导图运用图文并重的技巧,把各级主题的关系用相互隶属与相关的层级图表现出来,把主题关键词与图像、颜色等建立记忆链接。
放射性思考是人类大脑的自然思考方式,每一种进入大脑的资料,不论是感觉、记忆或是想法,都可以成为一个思考中心,并由此中心向外发散出成千上万的关节点,每一个关节点代表与中心主题的一个连结,而每一个连结又可以成为另一个中心主题,再向外发散出成千上万的关节点,呈现出放射性立体结构,而这些关节的连结可以视为记忆,也就是每个人的超级数据库。
下面我们举一个实例,将Dr.2在写作第三章《公开资料情报分析》时所总结的思维导图来与大家分享一下(第三章:基于公开资料的商业情报分析的思维导图)因为当我们开始着手写作的时候,就和一个公司初创一样,各种念头纷繁芜杂,而且各种想法之间还有关联,如何分类,如何进行分解和概括,通常需要进行书面的整理,这样才能更有条理,至少还能更早的发现错误,同时还能将更多的可能性列上去,不会遗漏,不会重复,还能有很多灵光乍现!如果多人一起讨论,那就是头脑风暴!绘制方法思维导图的绘制需要一定的拓扑思维,因为思维导图的绘制并不是凌乱随意的,它是拓扑树形结构的一个复杂的变形,主体结构是树形结构,但是不同思维之间还会有一些其他的关联性。
思维导图可手工绘制,也可用电脑软件绘制,因此,第一个推荐给大家的绘制方法是几支彩笔和一张大纸。
如果用软件,Dr.2在这里给大家介绍MindManager。
这个软件没有像Visio那样的全面和酷炫的功能,但是小巧并使用方便,非常适合帮助大家进行思维导图的绘制,尤其初创公司的业务很少是特别复杂的。
操作方式:1)核心主题centraltopic。
拓扑学的基本概念与定理

拓扑学的基本概念与定理拓扑学是数学的一个分支,研究的是空间之间的关系和性质。
它关注的不是度量和距离,而是关系和连续性。
本文将介绍拓扑学的基本概念和定理,并探讨它们在数学和实际应用中的重要性。
一、拓扑学的基本概念在深入讨论拓扑学的定理之前,我们首先需要了解一些基本概念。
1.点、集合和空间拓扑学的研究对象首先是点和集合。
点是一个抽象的概念,可以表示空间中的一个位置。
而集合则是由点组成的,是一组对象的聚集体。
拓扑学研究的是集合之间的关系。
在拓扑学中,我们将集合和它的子集看作是一个空间。
一个空间可以是有限的,也可以是无限的。
拓扑学的研究对象可以是一维、二维或更高维的空间。
2.邻域和开集在拓扑学中,邻域是一个重要的概念。
对于点x来说,它的邻域包含了离x足够近的点。
邻域可以是一个点,也可以是一个集合。
与邻域相关的概念是开集。
若一个集合的每一个点都有一个邻域包含于该集合内部,则该集合称为开集。
开集是拓扑学中的基本概念,它可以帮助我们定义距离、连续性以及其他重要的性质。
3.拓扑空间将开集作为基本概念,我们可以定义拓扑空间。
一个拓扑空间是一个集合,它满足以下三个条件:(1)空集和整个集合都是开集;(2)有限个开集的交集仍然是开集;(3)任意多个开集的并集仍然是开集。
拓扑空间中的开集定义了点与集合之间的关系,它可以帮助我们描述空间的连续性和分离性质。
二、拓扑学的基本定理在拓扑学中,有一些基本的定理对于研究空间之间的关系非常重要。
1.连通性连通性是一个拓扑空间的基本性质。
一个拓扑空间是连通的,当且仅当它不能表示为两个非空开集的不交并。
连通性可以帮助我们判断一个空间是否是一片连续的整体。
例如,欧几里得空间中的线段是连通的,而两个不相交的线段则是非连通的。
2.紧致性紧致性是另一个拓扑空间的重要性质。
一个拓扑空间是紧致的,当且仅当它的每个开覆盖都存在有限子覆盖。
紧致性可以理解为一个空间的有限性质。
例如,欧几里得平面上的闭合和有界的集合是紧致的。
拓扑学基础

第一章 拓扑空间及其相关概念
拓扑空间的概念产生于对实直线,欧氏空间以及这些空间上的 连续函数的研究,它是欧氏空间的一种推广.本章介绍拓扑空间的概 念,给出与拓扑空间相关的一些重要的拓扑概念的定义,以及它们的 性质.
满足 (1) 对于 x, y ∈ , ( x, y ) ≥0; (2) 对于 x, y ∈ , ( x, y ) =0 当且仅当 x = y ; (3) 对于 x, y ∈ , ( x, y ) = ( y, x ); (4) 对于 x, y , ∈ , ( x, y )+ ( y, z ) ≥ ( , )(称为 三角不等式),
§1.4 一些重要的拓扑概念
1. 邻域,邻域系 定义 设( X ,Τ )是拓扑空间, a ∈ M ⊂ X ,若存在 G ∈Τ ,使得 a ∈G ⊂ M ,
则称集合 M 为点 a 的邻域.对于 x ∈ X ,点 x 的所有邻域构成的集族称 为点 x 的邻域系,记作 N x .一点的邻域不一定是开集,但开集是它的每 一点的邻域,并称开集为它的点的开邻域.
( ,ε). 定理 1 设( , )是度量空间,则集族 B ={ ( , )| ∈ , >0}
是集合 上的一个拓扑的基,称这个拓扑为由集合 上的度量 诱
5
导的拓扑,记作Τ ,也称为度量拓扑. 设( , )是度量空间, Τ 表示由度量 诱导的集合 上的拓
扑,因此( ,Τ )为拓扑空间,并约定:在称度量空间( , )为拓扑 空间时,指的是拓扑空间( ,Τ ).
则称 是集合 上的度量, ( x, y )称为 与 y 之间的距离,( , ) 称为度量空间, 称为度量空间( , )的基础集.在不致引起混淆 时,简称 为度量空间.
第一章、拓扑学基础

第一章、拓扑学基础1.1拓扑空间概念拓扑空间是一个二元组(S, O),这里S是给定集合,O是由S的一些子集构成的集类,其元素称为开集,并满足如下开集公理:T1 ∅, S∈O(即,∅, S是开集);T2 若U1,U2∈O,则U1⋂U2∈O(即,O对有限交封闭);T3 开集的任意并集还是开集(即,O对任意并封闭)。
註记满足上述开集公理的O,也称为集合S上的拓扑,(S, O)为相应的拓扑空间,也记为S。
例子实数集合ℝ上的标准拓扑:开集定义为若干个开区间的并集。
不难验证:这里定义的开集满足开集公理。
只需说明:两个开区间的交集为空集或开区间。
例子离散拓扑与平凡拓扑对给定的集合S,定义下列两个拓扑:(S,O1): O1由S的所有子集构成,它是S上的拓扑(最大拓扑)。
(S,O2): O2={∅,S},它是S上的拓扑(最小拓扑)。
练习给出实数集合ℝ上三种不同的拓扑空间结构。
练习设S是一个集合,O由∅,S及S的某个固定子集A的所有子集构成。
验证O是S上的拓扑。
从而,(S,O)是一个拓扑空间。
概念设(S, O)是拓扑空间,称A⊂S是闭集,如果S\A是开集。
拓扑空间S的所有闭集构成集合,记为C。
命题拓扑空间S中的闭集满足闭集公理C1 ∅, S∈C;C2 若A1,A2∈C,则A1⋃A2∈C(即,C对有限并封闭);C3 闭集的任意交集还是闭集(即,C对任意交封闭)。
证明:利用下列等式可证。
S\(A1⋃A2)=(S\A1)⋂(S\A2),S\(B ii。
i)=(S\B i)註记开集公理与闭集公理是等价的:若S中的某些子集指定为闭集,并满足闭集公理。
则S是拓扑空间,其开集由闭集的余集所构成。
概念对拓扑空间S,点u∈S的开邻域是指包含u的开集U;子集A⊂S的开邻域是指包含A的开子集;一个点(或子集)的邻域是一个子集,它包含该点(或该子集)的一个开邻域。
例子对拓扑空间ℝ,U=(-1,1)是0的开邻域;W=[-1,1]是0的邻域。
拓扑学的基本概念-定义说明解析

拓扑学的基本概念-概述说明以及解释1.引言1.1 概述拓扑学是数学中的一个分支,研究的是空间中的形状、连通性和变化性质。
它主要关注的是不同空间对象之间的关系,而不考虑其具体的度量尺寸或几何特征。
拓扑学起源于18世纪,经过数学家们的不断探索和研究,逐渐形成了一套完整的理论体系。
在拓扑学中,我们关注的是空间对象之间的相互关系,而不关心它们的形状如何变化或者具体的度量尺寸。
例如,我们可以将两个球看作是相同的,因为它们都具有一个孔,而不关心它们的大小或者表面的形状。
这种抽象的思维方式使得拓扑学成为解决很多实际问题的强大工具,例如网络连通性分析、形状识别等。
拓扑学的基本概念包括拓扑空间、拓扑结构、连通性等。
拓扑空间是指一个具有拓扑结构的集合,通过给定的一组开集来定义集合中元素的关系。
拓扑结构则是用来描述集合中元素之间的邻近性和连通性的规则。
而连通性则是指一个空间对象是否是连通的,即是否可以通过一条连续的路径将其所有点连接起来。
拓扑学作为一门基础学科,在多个领域都有广泛的应用。
例如,在计算机科学中,拓扑学被用来描述网络中节点之间的连通性和通信路径;在物理学中,拓扑学被用来研究物质的相变性质;在生物学中,拓扑学被用来研究DNA的结构和蛋白质的折叠等。
这些应用领域的发展与拓扑学的基本概念密不可分。
本文将从拓扑学的起源、基本概念、拓扑空间与拓扑结构以及拓扑学的应用领域等方面进行介绍。
通过对这些内容的系统阐述和分析,旨在帮助读者更好地理解拓扑学的基本概念和应用,以及其在解决实际问题中的重要性。
接下来的章节将详细介绍这些内容,以期能够为读者提供一个全面而深入的拓扑学知识框架。
1.2 文章结构文章结构部分的内容可以根据以下方式进行编写:文章结构部分:本篇文章将按照以下结构组织和介绍拓扑学的基本概念:1. 引言:首先,我们将概述本文的主题和目的,为读者提供一个整体的概览。
接着,我们将介绍文章的结构,明确每个部分的内容和安排。
拓扑学

x, y X , xRy 和 yRx不能同时成立,则称关系R为非 对称的; 如果 R R R ,即对于任何 x, y, z X ,如果 xRy, yRz,则 xRz ,则称关系R是传递的.
(3)由于 z S R(A) 当且仅当存在 x A 使得 xS Rz, 当且仅当存在 x A 使得 (存在 y Y 使得 xRy, ySz ), 当且仅当存在 y R(A) 使得 ySA . (4)设 y R(A) R(B) ,即 y R( A), yR(B) . 因此存在 x A ,使得 xRy . 此时假设 x B,由于 xRy,因此 y R(B) ,这与 yR(B) 矛盾,因此 xB, 因此存在 x A B, xRy ,因此 y R(A B),R(A) R(B) R(A B).
D {x | x A 而且(x B或x C)}
E ,{x | (x A 而且x B)或x C}
F {x | x A 而且(x B xC)}
, ,
§1.2 关系,等价关系
❖ 重点:熟悉关系像,逆关系,复合关系和 等价关系的性质
❖ 难点:对命题演算知识的欠缺将影响性质 证明的严谨性
定义1.2.1 设X,Y是两个集合,如果 R X Y,即R是X 与Y的笛卡尔积 X Y的一个子集,则称R是从X到Y的 一个关系. 定义1.2.2 设R是从集合X到集合Y的一个关系,即
8. 设A,B,C,D是全集X的子集,试判断下列命题的正确性.若正确,给出证明, 若不正确,给出反例.
① A (A B) B
② A (B A) A B
③ A (B ) (A C) ⑤ (A B) (A B) A,(A B) (A B)
定义1.1.2 给定集合A,B,由A与B的全部元素
构成的集合叫做A与B的并集,记作 A B. 用描述法表示是: A B {x | x A, 或x B}
基础拓扑学笔记

0
可以定义 wi 为全集
i 1
( A B x | x A, x B
yA B yA yB
0
z wi 不存在,所以定义全集合理)
i1
在这样的定义下,条件 1 可以省去,其可由 2、3 导出
对 X ,t , X 是拓扑,称为平凡拓扑
例: X , s 2X ( X 的所有子集),称为离散拓扑
设C 2X 是拓扑空间 X 的子集族,称C 是 X 的一个 覆盖,若 C X ,若C 的每个成员都是开(闭)集,
CC
称C 为开(闭)覆盖
定理 1.2:粘接定理
n
f : X Y , X Ai , Ai 闭, f |Ai 连续,则 f 连
i 1
续
证明:只要证明 Y 的每个闭集的原像是闭集
设 B 是 Y 的闭集,则
n
n
f 1 B
f 1 B Ai
f 1 Ai
B
i 1
i 1
2.3 同胚映射 定义 1.8:X ,Y 同胚是指存在 f : X Y 满足:1) f
连续 2)一一对应 3)逆映射 f 1 也连续
在同胚映射下,开集映为开集,闭集映为闭集
例:a,b,c, d 的线性映射
例: 0,1,0, 同胚( ln x )
的闭包 A A A x | x邻域W,W A
命题 1.4:若拓扑空间 X 的子集 A 与 B 互为余集,则
A 与 B 互为余集 命题: A 是闭集
证明: y A 存在邻域U y A ,即Uy X A
X A X A
1.3 拓扑空间中的几个基本概念
推论: A X X A , B X X B
证明: A B A A B A
拓扑学的基础理论

拓扑学是数学的一个分支,研究的是空间的性质和变换,而不关注空间的度量。
它的基础理论是对空间中的点、集合和其它相关的概念进行抽象和研究。
拓扑学的基础理论主要包括空间、拓扑性质、连通性、紧性和基本拓扑空间等概念。
首先,空间是拓扑学的基本对象,也是研究的主要对象。
空间可以是一维、二维或者高维的,可以是有限的或者无限的。
例如,欧几里得空间是我们熟知的三维空间,可以用三维坐标系来描述。
除了欧几里得空间,还有很多其他种类的空间,如球面、环面、莫比乌斯带等。
空间可以通过集合和点集的方式定义,即把点集作为空间的元素,通过某种关系进行描述和研究。
拓扑性质是指关于空间的性质,例如开集、闭集、邻域、极限点、聚点等。
在拓扑学中,这些性质是通过对点集的集合运算和相容性要求来定义的。
例如,开集是指一个集合以它的每个点为中心都包含了其他点的一个集合。
闭集是指一个集合包含了它的边界上的每个点。
这些性质是拓扑学研究的基础,用于描述和区分不同的空间。
连通性是描述空间中的连接性质的概念。
拓扑学中的连通性与我们日常生活中的“连通”概念有所不同。
在拓扑学中,连通性指的是一个集合内的点之间可以通过一条连续的曲线相互连通。
例如,当一个集合不能被一条曲线分成两部分时,我们称之为连通集。
连通性的研究在网络、地理学和物理学等领域具有广泛的应用。
紧性是拓扑学中一个重要的概念,描述的是集合的紧致性质。
一个紧集是一个有限的集合,它的开覆盖可以找到有限个子集合来覆盖整个集合。
例如,在一维空间中,闭区间是紧集,而开区间则不是紧集。
紧性在分析学、拓扑学和几何学等领域中有着广泛的应用,是研究和刻画空间的重要工具。
基本拓扑空间是拓扑学中的基本概念,它是一类具有特殊性质的空间。
基本拓扑空间是指一个集合与一组子集的结构,这组子集称为拓扑,满足一定的公理。
例如,开区间是定义了一种拓扑结构的基本拓扑空间。
基本拓扑空间的研究有助于我们理解空间中的性质和变换。
拓扑学的基础理论为我们提供了一种新的分析和描述空间的方式。
图形拓扑关系的构建.ppt

1.若地图平面上反映一定意义的零维图形的附近没有其它图形 与之联系,则称这个零维图形为独立点(Point)。如水井
2.若在某个有一定意义的零维图形附近还存在另外有意义的 零维图形与之联系,则称这个零维图形为结点(Node)。
计算导出耗时的那部分拓扑关系用显式表示;其余的用 隐式表示。
例子:显示表示,美国人口统计局的双重独立地图编码。
e4
e1 e3 e2
e6
双重独立地图编码(DIME)
e5
e7
e8 e10
e9 e11
1.地图网络编码 2.结点坐标文件 3.拓扑结构文件
结点号 X坐标 Y坐标
1
X1
Y1
2
X2
Y2
3
X3
Y3
拓扑关系介绍
1.1 拓扑的来源 1.2 为什么要研究地图上的拓扑关系 1.3 建立拓扑关系的基本概念 1.4 基本的拓扑关系 1.5 拓扑关系的表示 1.6 Arc/Info中拓扑关系的构建
1.1 拓扑的来源
1.拓扑的来源
“拓扑(Topology)”一次来自希腊文,它的原意是“ 形状的研究”。拓扑学时几何学的一个分支,它研究在拓扑 变换下能够保持不变的几何属性——拓扑属性。
按照右图建立的环与内点 的包含关系是纯几何上,也就 是多对多的几何包含关系。
拓扑结构需要确定一对一的点环关系,就是一个内点就要代 表一个多边形。所以需要找出环是属于某一内点所代表的多边形 的。即是建立多边形与轮廓的关联关系。
环号与内点的圈定关系2
Ⅰ
Ⅱ
Ⅲ
ⅦⅥ Ⅳ
Ⅷ
Ⅴ
Ⅸ
Ⅹ
Topology-拓扑学基础

Topology -拓扑拓扑学学基础一.拓扑空间与连续性 §1.拓扑空间1.1定义:设X 是一非空集合,X 的一个子集族τ称为X 的一个拓扑,如果它满足: (1)X Φ,包含在τ中;(2)τ中任意多个成员的并仍在τ中; (3)τ中有限个成员的交集仍在τ中。
X 和τ一起称为拓扑空间,记作:(X τ,),称τ中的成员为拜年空间的开集。
(3′)τ中任意两个成员的并仍在τ中。
这是一个等价条件。
离散拓扑离散拓扑:X 上X 2构成X 上的拓扑。
最大最大最大((精细精细))的拓扑。
平凡拓扑平凡拓扑:由X,Φ{}构成的拓扑。
最小最小最小的拓扑。
当X 含有多于一个元素时,X 上可以有许多不同的拓扑。
如:X ={a,b,c},则{,,{}},{,,{,}},{,,{}{,}}X a X a b X a a b ΦΦΦ都是X 上的拓扑,但{,,{},{}}X a b Φ不是,因不满足(2)。
例1:X 是无穷集合,{X c f A A τ=Φ∪是的有限子集}{}τf 则不难验证是一个拓扑,称为余有限拓扑余有限拓扑余有限拓扑。
例2:X 是一个可数无限集合。
{X cc A A τ=Φ∪是的可数子集}{},则c τ是X 的拓扑,称为余可数拓扑余可数拓扑余可数拓扑。
例3:R 是实数集,{e U U τ=是若干开区间的并},若干可以是无限、有限或零,因此,e τΦ∈,e τ是R 上的拓扑,称为R 上的欧氏拓扑上的欧氏拓扑,记作:1(,)e E R τ= 以上五个拓扑的关系:,,,fc f e c e ττττττ<<不能比较大小。
1.2度量空间集合X 上的一个度量d 是一个映射d: X X R ×→,满足 (1)正定性:(,)0,,(,)0,d x x x X d x y when x y =∀∈>≠(2)对称性:(,)(,)d x y d y x =(3)三角不等式:(,)(,)(,)d x z d x y d y z ≤+集合X 上规定度量d 后称为度量空间,记为:(,)X d ,如:(,)nnE R d = 度量空间(,)X d 中,0,0x X ε∈>,00(,){(,)}B x x X d x x εε=∈< 称为以0x 为心,ε为半径的球形邻域。
第一章、拓扑学基础

第一章、拓扑学基础1.1拓扑空间概念拓扑空间是一个二元组(S, O),这里S是给定集合,O是由S的一些子集构成的集类,其元素称为开集,并满足如下开集公理:T1 ∅, S∈O(即,∅, S是开集);T2 若U1,U2∈O,则U1⋂U2∈O(即,O对有限交封闭);T3 开集的任意并集还是开集(即,O对任意并封闭)。
註记满足上述开集公理的O,也称为集合S上的拓扑,(S, O)为相应的拓扑空间,也记为S。
例子实数集合ℝ上的标准拓扑:开集定义为若干个开区间的并集。
不难验证:这里定义的开集满足开集公理。
只需说明:两个开区间的交集为空集或开区间。
例子离散拓扑与平凡拓扑对给定的集合S,定义下列两个拓扑:(S,O1): O1由S的所有子集构成,它是S上的拓扑(最大拓扑)。
(S,O2): O2={∅,S},它是S上的拓扑(最小拓扑)。
练习给出实数集合ℝ上三种不同的拓扑空间结构。
练习设S是一个集合,O由∅,S及S的某个固定子集A的所有子集构成。
验证O是S上的拓扑。
从而,(S,O)是一个拓扑空间。
概念设(S, O)是拓扑空间,称A⊂S是闭集,如果S\A是开集。
拓扑空间S的所有闭集构成集合,记为C。
命题拓扑空间S中的闭集满足闭集公理C1 ∅, S∈C;C2 若A1,A2∈C,则A1⋃A2∈C(即,C对有限并封闭);C3 闭集的任意交集还是闭集(即,C对任意交封闭)。
证明:利用下列等式可证。
S\(A1⋃A2)=(S\A1)⋂(S\A2),S\(B ii。
i)=(S\B i)註记开集公理与闭集公理是等价的:若S中的某些子集指定为闭集,并满足闭集公理。
则S是拓扑空间,其开集由闭集的余集所构成。
概念对拓扑空间S,点u∈S的开邻域是指包含u的开集U;子集A⊂S的开邻域是指包含A的开子集;一个点(或子集)的邻域是一个子集,它包含该点(或该子集)的一个开邻域。
例子对拓扑空间ℝ,U=(-1,1)是0的开邻域;W=[-1,1]是0的邻域。
拓扑关系介绍

按环记录中的关键字,可将该环上各弧段坐标数据读出,对 所有内点匹配,便能确定环与各内点的包含关系。
环号与内点的圈定关系1
Ⅵ
Ⅱ
2
Ⅶ
Ⅸ5 4
Ⅷ
Ⅲ Ⅳ Ⅴ
3Ⅹ 6
1Ⅰ
从图中可以看出:一个多边 形可能有一个或多个环,但是一 个多边形只有一个内点(数字化 的时候输入)。所以,环与内点 的拓扑关系可能是一对一或多对 一的关系。
1.7 拓扑关系是空间数据处理
拓扑关系的建立属于空间数据处理的内容。 空间数据获取有各种不同的方法,但无论哪种方法获取
的数据都可能存在这样或者那样的问题和误差,如数字化错 误、数据格式不一致、比例尺或投影不统一、数据冗余等。
因此:只有通过空间数据的处理才能使空间数据符合 GIS数据库的要求,才能实现GIS的各种功能。
空间数据处理的主要内容包括:图形编辑、自动拓扑、 坐标变换、数据压缩、结构转换、数据内插等。
建立多边形拓扑
2.1 弧段的组织 2.2 结点的匹配 2.3 检查多边形是否闭合 2.4 建立多边形
2.1 弧段的组织
边(弧段)的组织:把弧段按一定顺序存储,如X坐标 或者Y坐标的顺序,便于检索和查找,然后按顺序编号。
b
a
找最靠右边的弧段可以通过计
算弧段的方向和夹角来实现。
2.4.1 基本常识(3)
3.多边形面积的计算
设构成多边形的坐标串为(Xi,Yi)(i=1,2,3,…n),
则多边形的面积可以用如下公式求出: SA
1 2
n i 1
yi1 yi
xi1 xi
正
n
S 12 y y x x S
左右多边形表
弧线 e1 e2 e3 e4 e5 e6 e7 e8 e9 e10
点集拓扑学拓扑知识点

第4章 连通性重要知识点本章讨论拓扑空间的几种拓扑不变性质,包括连通性,局部连通性和弧连通性,并且涉及某些简单的应用.这些拓扑不变性质的研究也使我们能够区别一些互不同胚的空间. §4.1 连通空间本节重点: 掌握连通与不连通的定义.掌握如何证明一个集合的连通与否?掌握连通性的拓扑不变性、有限可积性、可商性。
我们先通过直观的方式考察一个例子.在实数空间R 中的两个区间(0,l )和[1,2),尽管它们互不相交,但它们的并(0,1)U [l ,2)=(0,2)却是一个“整体”;而另外两个区间(0,1)和(1,2),它们的并(0,1)U (1,2)是明显的两个“部分”.产生上述不同情形的原因在于,对于前一种情形,区间(0,l )有一个凝聚点1在[1,2)中;而对于后一种情形,两个区间中的任何一个都没有凝聚点在另一个中.我们通过以下的定义,用术语来区别这两种情形.定义4.1.1设A 和B 是拓扑空间X 中的两个子集.如果∅=⋂⋃⋂)()(A B B A则称子集A 和B 是隔离的.明显地,定义中的条件等价于∅=⋂B A 和 ∅=⋂A B 同时成立,也就是说,A 与B 无交并且其中的任何一个不包含另一个的任何凝聚点.应用这一术语我们就可以说,在实数空间R 中,子集(0,1)和(1,2)是隔离的,而子集(0,l )和[1,2) 不是隔离的.又例如,易见,平庸空间中任何两个非空子集都不是隔离的,而在离散空间中任何两个无交的子集都是隔离的.定义4.1.2 设X 是一个拓扑空间.如果X 中有两个非空的隔离子集A 和B 使得X=A ∪B ,则称X 是一个不连通空间;否则,则称X 是一个连通空间.显然,包含着多于两个点的离散空间是不连通空间,而任何平庸空间都是连通空间. 定理4.1.1设X 是一个拓扑空间.则下列条件等价:(l )X 是一个不连通空间;(2)X 中存在着两个非空的闭子集A 和B 使得A ∩B=∅ 和 A ∪B = X 成立;(3) X 中存在着两个非空的开子集A 和B 使得A ∩B=∅ 和 A ∪B = X 成立;(4)X 中存在着一个既开又闭的非空真子集.证明(l )蕴涵(2): 设(1)成立.令A 和B 是X 中的两个非空的隔离子集使得 A ∪B =X ,显然 A ∩B=∅,并且这时我们有B B B A B B A B X B B =⋂⋃⋂=⋃⋂=⋂=)()()(因此B 是X 中的一个闭子集;同理A 也是一个X 中的一个闭子集.这证明了集合A 和B 满足条件(2)中的要求.(2)蕴涵(3).如果X 的子集A 和B 满足条件(2)中的要求,所以A 、B 为闭集,则由于这时有A =B /和B=A ',因此A 、B 也是开集,所以A 和B 也满足条件(3)中的要求.(3)蕴涵(4).如果X 的子集A 和B 满足条件(3)中的要求,所以A 、B 是开集,则由A =B '和B=A ' 易见A 和B 都是X 中的闭集,因此A 、B 是X 中既开又闭的真(∵A 、B ≠∅,A ∪B=X ,∴A 、B ≠X )子集,所以条件(4)成立.(4)蕴涵(l ).设X 中有一个既开又闭的非空真子集A .令B=A '.则A 和B 都是X 中的非空的闭子集,它们是无交的并且使得A ∪B=X .易见两个无交的闭子集必定是隔离的(因为闭集的闭包仍为自己).因此(l )成立.例4. 1.1 有理数集Q 作为实数空间R 的子空间是一个不连通空间.这是因为对于任何一个无理数r ∈R-Q ,集合(-∞,r )∩Q =(-∞,r]∩Q 是子空间Q 中的一个既开又闭的非空真子集.定理4.1.2 实数空间R 是一个连通空间.证明 我们用反证法来证明这个定理.假设实数空间R 是不连通空间.则根据定理4.1.1,在R 中有两个非空闭集A 和B 使得A ∩B=∅ 和 A ∪B = R 成立.任意选取a ∈A 和b ∈B ,不失一般性可设a <b .令A ~=A ∩[a,b],和B ~=B ∩[a,b].于是A ~和B ~是R 中的两个非空闭集分别包含a 和b ,并且使得A ~∩B ~=∅和A ~∪B ~=[a ,b]成立.集合A ~有上界b ,故有上确界,设为b ~.由于A ~是一个闭集,所以b ~∈A ~,并且因此可见b ~<b ,因为b ~=b 将导致b ∈A ~∩B ~,而这与A ~∩B ~=∅矛盾.因此(b ~,b]⊂B ~.由于B ~是一个闭集,所以b ~∈B ~.这又导致b ~∈A ~∩B ~,也与A ~∩B ~=∅矛盾.定义4.1.3设Y 是拓扑空间X 的一个子集.如果Y 作为X 的子空间是一个连通空间,则称Y 是X 的一个连通子集;否则,称Y 是X 的一个不连通子集.拓扑空间X 的子集Y 是否是连通的,按照定义只与子空间Y 的拓扑有关(即Y 的连通与否与X 的连通与否没有关系.).因此,如果X Z Y ⊂⊂,则Y 是X 的连通子集当且仅当Y 是Z 的连通子集.这一点后面要经常用到.定理4.1.3 设Y 是拓扑空间X 的一个子集,A ,B ⊂Y .则A 和B 是子空间Y 中的隔离子集当且仅当它们是拓扑空间X 中的隔离子集.因此,Y 是X 的一个不连通子集当且仅当存在Y 中的两个非空隔离子集A 和B 使得A ∪B =Y(定义)当且仅当存在X 中的两个非空隔离子集A 和B 使得A ∪B =Y .证明 因为 ))(())(())()(())()(()))((()))((())(())((A B C B A C A Y B C B Y A C A Y B C B Y A C A B C B A C X X X X X X Y Y ⋂⋃⋂=⋂⋂⋃⋂⋂=⋂⋂⋃⋂⋂=⋂⋃⋂因此根据隔离子集的定义可见定理成立.定理4.1.4 设Y 是拓扑空间X 中的一个连通子集.如果X 中有隔离子集A 和B 使得 Y ⊂A U B ,则或者 Y ⊂A ,或者 Y ⊂B .证明 如果A 和B 是X 中的隔离子集使得Y ⊂AUB ,则∅=⋂⋃⋂⋂=⋂⋂⋃⋂⋂⊂⋂⋂⋂⋃⋂⋂⋂)()(()()())(())((A B B A Y A Y B B Y A Y A Y B Y B Y A 这说明A ∩Y 和B ∩Y 也是隔离子集.然而(A ∩Y )∪(B ∩Y )=(A ∪B )∩Y =Y因此根据定理4.1.3,集合A ∩Y 和B ∩Y 中必有一个是空集.如果 A ∩Y=∅,据上式立即可见 Y ⊂B ,如果 B ∩Y = ∅,同理可见Y ⊂A .定理4.1.5设Y 是拓扑空间X 的一个连通子集,Z ⊂X 满足条件Y Z Y ⊂⊂.则 Z 也是X 的一个连通子集.证明 假设Z 是X 中的一个不连通子集.根据定理4.1.3,在 X 中有非空隔离子集A 和B 使得Z=A ∪B .因此 Y ⊂AUB .由于Y 是连通的,根据定理4.1.4,或者Y ⊂A ,∅=⋂=⇒∅=⋂⊂⋂⇒⊂⊂B Z B B A B Z A Y Z Θ或者Y ⊂B,同理,∅=A 。
ppt拓扑学起源

拓扑学概貌之连续变换
拓扑学概貌 七桥问题 四色问题 庞加莱猜想 课程内容与学 时安排 参考文献
连续变换就是你可以捏、拉一个东西,但不能将其 扯破,也不能把原先不在一起的两个点粘在一起。 比如,对于26个(大写)英文字母,一些拓扑学家 就认为可将其分成3类 : 类 第一类:A,D,O,P,O,R; 第二类:C,E,F,G,H,l,J,K,L,M,N,S,T,U,V,W,X,Y,Z; 第三类: B; 第一类在连续变换下都可以变成 O,第二类则都可 变成 I 。
拓扑学概貌 七桥问题 四色问题 庞加莱猜想 课程内容与学 时安排 参考文献
七桥问题之问题的提出与解决
拓扑学概貌 七桥问题 四色问题 庞加莱猜想 课程内容与学 时安排 参考文献
问是 否可能 从这四 块陆地 中任一块出发 ,恰好 通过每 是 座桥一次,再回到起点? 欧拉于1736年研究并解决了此问题,他把问题归结为图 的“一笔画”问题,证明上述走法是不可能的。他不仅解 决了这个问题,且给出了连通图可以一笔画的重要条件 是它们的奇顶点(通过此点弧的条数是奇数)的个数 为0或2。
庞加莱猜想之之七个“千禧难题”之一
拓扑学概貌 七桥问题 四色问题 庞加莱猜想 课程内容与学 时安排 参考文献
2000年5月24日,美国克莱数学研究所的科学顾问委员会 把庞加莱猜想列为七个“千禧难题”(又称世界七大数学 难题)之一,这七道问题被研究所认为是“重要的经典问 题,经许多年仍未解决。”克雷数学研究所的董事会决定 建立七百万美元的大奖基金,每个“千年大奖问题”的解 决都可获得百万美元的奖励。 另外六个“千年大奖问题”分别是:NP完全问题,霍奇猜 想,黎曼假设,杨-米尔斯理论,纳维-斯托克斯方 程,BSD猜想。 提出这个猜想,庞加莱一度认为自己已经证明了它。但 没过多久,证明中的错误就被暴露了出来。于是,拓扑 学家们开始了证明它的努力。
数学拓扑结构

数学拓扑结构一、拓扑基本概念拓扑学是研究几何图形在连续变形下保持不变的性质的一门学科。
这种变形可以理解为橡皮变换,即图形可以伸缩、扭曲,但不能割断或粘合。
拓扑学作为数学的一门分支,主要研究的是图形在拓扑变换下的不变性。
二、拓扑空间定义拓扑空间是一个集合,它保留了足够的信息来表示图形的几何特性。
更具体地说,一个拓扑空间是一个满足邻域公理的集合,也就是任何一点都有一个开邻域和一个闭邻域。
在拓扑空间中,可以定义开集、闭集、连续映射等基本概念。
三、连续性概念连续性是拓扑学中的一个基本概念,它描述了一个函数在某点的极限值与函数值的关系。
如果一个函数在某点的极限值等于该点的函数值,那么这个函数在这个点上就是连续的。
反之,如果在该点上函数的极限值不等于该点的函数值,那么这个函数在这个点上就是间断的。
四、分离性公理分离性公理是用来判断一个空间是否为豪斯道夫空间的准则。
如果一个空间满足分离性公理,那么这个空间就是一个豪斯道夫空间。
分离性公理包括两个部分:第一分离性公理和第二分离性公理。
第一分离性公理要求空间中的任意两个不同的点都可以被两个不相交的开集分离;第二分离性公理要求空间中的任意两个不同的点都可以被一个闭集和一个开集分离。
五、紧致性概念紧致性是拓扑学中的一个重要概念,它描述了一个空间中点的集合是否有一个有限的开覆盖。
如果一个集合有一个有限的开覆盖,那么这个集合就是紧致的。
在实数空间中,闭区间[a, b]就是一个紧致集合的例子。
紧致性在许多数学问题中都有应用,例如在微积分和实分析中用来证明一些重要的定理。
六、连通性概念连通性是用来描述一个空间中点的一个集合是否可以被分成两个互不相交的非空开集的并集的属性。
如果一个集合可以被分成两个互不相交的非空开集的并集,那么这个集合就是非连通的;否则,这个集合就是连通的。
连通性的概念在代数拓扑和微分拓扑中有广泛的应用。
七、维数理论维数理论是研究空间的维数与空间性质之间的关系的一门学科。
