2018年湖南省普通高中学业水平考试数学试题
(完整版)2018年湖南省普通高中学业水平考试数学试题(20200814150428)
2018年湖南省普通高中学业水平考试本试题卷包括选择题、填空题和解答题三部分,时量 120分钟 满分100分一、选择题:本大题共 10小题,每小题4分,共40分•在每小题给出的四个选项中,只有 一项是符合题目要求的5. 已知函数y = f (x ) ( x [ 1,5])的图象如图A • [ 1,1]B . [1,3]C • [3,5]D • [ 1,5]6. 已知a >b , c >d ,则下列不等式恒成立的是A . a+c >b + dB . a+d>b+cC . a-c>b-dD . a-b>c-d机密★启用前1.下列几何体中为圆柱的是 ()3所示,则f (x )的单调递减区间为(7.为了得到函数y cos(x4)的图象象只需将 y cosx 的图象向左平移()1 A •丄个单位长度2 1C •丄个单位长度4B .—个单位长度2二、 填空题;本大题共 5小题,每小题4分,共20分, 11. 直线y x 3在y 轴上的截距为 ___________________ 。
12. ______________________ 比较大小:sin25 sin23 (填、”或 N ” 13.已知集合 A 1,2 , B 1,x .若 A 「|B2,则 x= _______ 。
14•某工厂甲、乙两个车间生产了同一种产品,数量分别为 60件、40件,现用分层抽样方法抽取一个容量为 n 的样本进行质量检测,已知从甲车间抽取了 6件产品,则n =。
x 215•设x , y 满足不等等式组y 2 ,贝U z = 2x — y 的最小值为 __________ 。
x y 2三、 解答题:本大题共 5小题,共40分,解答应写出文字说明、证明过程或演步 16. (本小题满分6分)函数 f(x) log 2(x1)的零点为(1 A .-Bi C .乜D . 122210.过点M (:2, 1)作圆 C : (x1)2 y 22的切线, 则切线条数为()A . 0B . 1C . 2D . 3在△ ABC 中, 已知 A = 30 ° B = 45 9.AC = •. 2,贝U BC =( )O4个单位长度7. 为了得到函数y cos(x 4)的图象象只需将y cosx的图象向左平移( )1已知函数f (x) x (x 0)x(1 )求f (1)的值(2)判断函数f (x)的奇偶性,并说明理由.(2)设函数f (x) 2,求f (x)的值域,17. (本小题满分8分)某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的 取100名学生对食堂用餐的满意度进行评分. 根据学生对食堂用餐满意度的评分,得到如图4所示的率分布直方图, (1) 求顺率分布直方图中 a 的值(2) 规定:学生对食堂用餐满意度的评分不低于80分为满意”试估计该校在食堂用 餐的3000名学生中 满意”的人数。
湖南省普通高中2018年学业水平考试数学试题

2018年湖南省普通高中学业水平考试数学本试题卷包括选择题、填空题和解答题三部分,时量120分钟 满分100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.下列几何体中为圆柱的是2.执行如图1所示的程序框图,若输入x 的值为10,则输出y 的值为 A .10 B .15 C .25 D .353.从1,2,3,4,5这五个数中任取一个数,则取到的数为偶数的概率是A .45 B .35 C .25 D .154.如图2所示,在平行四边形ABCD 中中,AB AD += A .AC B .CA C .BD D .DB5.已知函数y =f (x )([1,5]x ∈-)的图象如图3所示,则f (x )的单调递减区间为 A .[1,1]- B .[1,3] C .[3,5] D .[1,5]- 6.已知a >b ,c >d ,则下列不等式恒成立的是 A .a +c >b +d B .a +d >b +c C .a -c >b -d D .a -b >c-d 7.为了得到函数cos()4y x π=+的图象象只需将cos y x =的图象向左平移A .12个单位长度 B .2π个单位长度C .14个单位长度 D .4π个单位长度 8.函数(1)2()log x f x -=的零点为A .4B .3C .2D .1 9.在△ABC 中,已知A =30°,B =45°,AC,则BC =A .12BCD .110.过点M (2,1)作圆C :22(1)2x y -+=的切线,则切线条数为 A .0 B .1 C .2 D .3二、填空题;本大题共5小题,每小题4分,共20分, 11.直线3y x =+在y 轴上的截距为_____________。
12.比较大小:sin25°_______sin23°(填“>”或“<”) 13.已知集合{}{}1,2,1,A B x ==-.若{}2AB =,则x =______。
2018年湖南省普通高中学业水平考试试卷

2018年湖南省普通高中学业水平考试试卷一、选择题(本题包括16小题,每题3分,共48分。
每小题只有一个选项符合题意) 1.发现万有引力定律的科学家是A .爱因斯坦B .卡文迪许C .开普勒D .牛顿 2.下列物理量属于矢量的是A .质量B .功C .重力势能D .力 3.列车员说“火车9点20分到站,停车10分。
”在这句话中 A .“9点20分”是指时刻,“10分”是指时间间隔 B .“9点20分”是指时间,“10分”是指时刻 C .“9点20分”与“10分”均指时刻 D .“9点20分”与“10分”均指时间间隔4.将一个物体从地球送到月球上,该物体在地球上的惯性与在月球上的惯性相比 A .在月球上惯性大 B .在地球上惯性大 C .惯性一样大 D .大小关系无法确定5.有两个共点力,其中一个力的大小是3N ,另一个力的大小是4N ,这两个力的合力的最大值为A .1NB .5NC .7ND .12N6.一位同学从操场中心A 点出发,先向北走了6m 到达C 点,然后向东走了8m 到达B 点,可以算出A 、B 两点间的距离为10m ,如图所示。
则该同学的位移大小和路程分别是 A .10m ,14m B .14m ,10m C .10m ,10m D .14m ,14m7.在同一平直公路上有A 、B 两辆汽车,它们的v-t 图象分别为a 、b ,如图所示,a 线平行于时间轴,b 线为过原点的倾斜直线,根据图象可知A .A 车静止,B 车做匀速直线运动B .A 车静止,B 车做匀加速直线运动C .A 车做匀速直线运动,B 车做匀加速直线运动D .A 车做匀速直线运动,B 车做匀速直线运动8.下列关于质点的说法正确的是A .研究跳水运动员在空中的翻转动作时,运动员可当做质点B .研究航天器绕地球运动的运行轨道时,航天器可当做质点C .研究地球自转时,地球可当做质点D .研究火车车轮的转动时,车轮可当做质点9.开普勒第二定律告诉我们:对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等面积。
2018年湖南省高中数学学业水平考试仿真试卷Word版含解析

2018年湖南省高中数学学业水平考试仿真试卷一、选择题(共10小题,每小题4分,满分40分)1.已知集合M={0,1},集合N满足M∪N={0,1},则集合N共有()个.A.1 B.2 C.3 D.42.直线x+2y+2=0与直线2x+y﹣2=0的交点坐标是()A.(2,﹣2)B.(﹣2,2)C.(﹣2,1)D.(3,﹣4)3.不等式2x+y﹣3≤0表示的平面区域(用阴影表示)是()A.B.C. D.4.已知cosα=﹣,α是第三象限的角,则sinα=()A.﹣B.C.﹣D.5.已知函数f(x)=a x(a>0,a≠1)在[1,2]上的最大值和最小值的和为6,则a=()A.2 B.3 C.4 D.56.在△ABC中,a=b,A=120°,则B的大小为()A.30°B.45°C.60°D.90°7.一支田径队有男运动员49人,女运动员35人,用分层抽样的方法从全体运动员中抽出一个容量为24的样本,则应从男运动员中抽出的人数为()A.10 B.12 C.14 D.168.已知tanα=2,则tan(α﹣)=()A.B.C.D.﹣39.圆x2+y2=1与圆(x+1)2+(y+4)2=16的位置关系是()A.相外切B.相内切C.相交D.相离10.如图,圆O内有一个内接三角形ABC,且直径AB=2,∠ABC=45°,在圆O内随机撒一粒黄豆,则它落在三角形ABC内(阴影部分)的概率是()A.B.C.D.二、填空题(共5小题,每小题4分,满分20分)11.不等式x2﹣5x≤0的解集是.转化为十进制的数为.12.把二进制数10011(2)13.已知函数f(x)=Asinωx(A>0,ω>0)的图象如图所示,则A,ω的值分别是.14.已知函数f(x)=4﹣logx,x∈[2,8],则f(x)的值域是.215.点P是直线x+y﹣2=0上的动点,点Q是圆x2+y2=1上的动点,则线段PQ长的最小值为.三、解答题(共5小题,满分40分)16.如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:(1)某同学不小心把茎叶图中的一个数字弄污了,看不清了,在如图所示的茎叶图中用m表示,若甲运动员成绩的中位数是33,求m的值;(2)估计乙运动员在这次季后赛比赛中得分落在[20,40]内的概率.17.已知向量=(sinx,1),=(2cosx,3),x∈R.(1)当=λ时,求实数λ和tanx的值;(2)设函数f(x)=•,求f(x)的最小正周期和单调递减区间.18.如图,在三棱锥P﹣ABC中,平面PAB⊥平面ABC,△PAB是等边三角形,AC⊥BC,且AC=BC=2,O、D分别是AB,PB的中点.(1)求证:PA∥平面COD;(2)求三棱锥P﹣ABC的体积.19.已知函数f(x)=2+的图象经过点(2,3),a为常数.(1)求a的值和函数f(x)的定义域;(2)用函数单调性定义证明f(x)在(a,+∞)上是减函数.20.已知数列{an }的各项均为正数,其前n项和为Sn,且an2+an=2Sn,n∈N*.(1)求a1及an;(2)求满足Sn>210时n的最小值;(3)令bn=4,证明:对一切正整数n,都有+++…+<.2018年湖南省高中数学学业水平考试仿真试卷参考答案与试题解析一、选择题(共10小题,每小题4分,满分40分)1.已知集合M={0,1},集合N满足M∪N={0,1},则集合N共有()个.A.1 B.2 C.3 D.4【考点】19:集合的相等.【分析】根据集合的包含关系求出集合N的个数即可.【解答】解:M={0,1},集合N满足M∪N={0,1},则N⊆M,故N=∅,{0},{1},{0,1}共4种可能,故选:D.2.直线x+2y+2=0与直线2x+y﹣2=0的交点坐标是()A.(2,﹣2)B.(﹣2,2)C.(﹣2,1)D.(3,﹣4)【考点】IM:两条直线的交点坐标.【分析】根据题意,联立两直线的方程,解可得x、y的值,即可得交点坐标,即可得答案.【解答】解:根据题意,联立,解可得,即直线x+2y+2=0与直线2x+y﹣2=0的交点坐标是(2,﹣2);故选:A.3.不等式2x+y﹣3≤0表示的平面区域(用阴影表示)是()A.B.C. D.【考点】7B:二元一次不等式(组)与平面区域.【分析】作出不等式对应直线的图象,然后取特殊点代入不等式,判断不等式是否成立后得二元一次不等式表示的平面区域.【解答】解:画出不等式2x+y﹣3≤0对应的函数2x+y﹣3=0的图象,取点(0,0),把该点的坐标代入不等式2x+y﹣3≤0成立,说明不等式2x+y﹣3≤0示的平面区域与点(0,0)同侧,所以不等式2x+y﹣3≤0表示的平面区域在直线2x+y﹣3=0的右下方,并含直线.故选B.4.已知cosα=﹣,α是第三象限的角,则sinα=()A.﹣B.C.﹣D.【考点】GH:同角三角函数基本关系的运用.【分析】利用同角三角函数的基本关系、以及三角函数在各个象限中的符号,求得sinα的值.【解答】解:∵cosα=﹣,α是第三象限的角,则sinα=﹣=﹣,故选:C.5.已知函数f(x)=a x(a>0,a≠1)在[1,2]上的最大值和最小值的和为6,则a=()A.2 B.3 C.4 D.5【考点】49:指数函数的图象与性质.【分析】根据指数函数的单调性在定义域是要么递增,要么递减,即看求解.【解答】解:根据指数函数的性质:当x=1时,f(x)取得最大值,那么x=2取得最小值,或者x=1时,f(x)取得最小值,那么x=2取得最大值.∴a+a2=6.∵a>0,a≠1,∴a=2.故选:A.6.在△ABC中,a=b,A=120°,则B的大小为()A.30°B.45°C.60°D.90°【考点】HP:正弦定理.【分析】由已知利用正弦定理,特殊角的三角函数值可求sinB=,结合B的范围即可得解B 的值.【解答】解:∵a=b,A=120°,∴由正弦定理,可得:sinB=,又∵B∈(0°,60°),∴B=30°.故选:A.7.一支田径队有男运动员49人,女运动员35人,用分层抽样的方法从全体运动员中抽出一个容量为24的样本,则应从男运动员中抽出的人数为()A.10 B.12 C.14 D.16【考点】B3:分层抽样方法.【分析】先求出每个个体被抽到的概率,再用男运动员的人数乘以此概率,即得所求.【解答】解:每个个体被抽到的概率等于=,则应从男运动员中抽出的人数为49×=14,故选:C8.已知tanα=2,则tan(α﹣)=()A.B.C.D.﹣3【考点】GR:两角和与差的正切函数.【分析】由题意直接利用两角差的正切公式,求得要求式子的值.【解答】解:∵tanα=2,则tan(α﹣)==,故选:B.9.圆x2+y2=1与圆(x+1)2+(y+4)2=16的位置关系是()A.相外切B.相内切C.相交D.相离【考点】JA:圆与圆的位置关系及其判定.【分析】求出两个圆的圆心与半径,通过圆心距与半径的关系判断选项即可.【解答】解:圆x2+y2=1的圆心(0,0)半径为1;圆(x+1)2+(y+4)2=16的圆心(﹣1,﹣4),半径为4,圆心距为: =,半径和为5,半径差为:3,(3,5).所以两个圆的位置关系是相交.故选:C.10.如图,圆O内有一个内接三角形ABC,且直径AB=2,∠ABC=45°,在圆O内随机撒一粒黄豆,则它落在三角形ABC内(阴影部分)的概率是()A.B.C.D.【考点】CF:几何概型.【分析】根据题意,计算圆O的面积S圆和△ABC的面积S△ABC,求它们的面积比即可.【解答】解:圆O的直径AB=2,半径为1,所以圆的面积为S圆=π•12=π;△ABC的面积为S△ABC=•2•1=1,在圆O内随机撒一粒黄豆,它落在△ABC内(阴影部分)的概率是P==.故选:D.二、填空题(共5小题,每小题4分,满分20分)11.不等式x2﹣5x≤0的解集是{x|0≤x≤5} .【考点】74:一元二次不等式的解法.【分析】把不等式x2﹣5x≤0化为x(x﹣5)≤0,求出解集即可.【解答】解:不等式x2﹣5x≤0可化为x(x﹣5)≤0,解得0≤x≤5,∴不等式的解集是{x|0≤x≤5}.故答案为:{x|0≤x≤5}.12.把二进制数10011(2)转化为十进制的数为19 .【考点】WC:mod的完全同余系和简化剩余系.【分析】本题的考查点为二进制与十进制数之间的转换,只要我们根据二进制转换为十进制方法逐位进行转换,即可得到答案.=1+1×2+1×24=19【解答】解:10011(2)故答案为:1913.已知函数f(x)=Asinωx(A>0,ω>0)的图象如图所示,则A,ω的值分别是3,2 .【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】根据图象信息即可求出A,ω的值.【解答】解:根据图象,可知最高点为3,最低点﹣3,∴A=3.从图可以看出周期T=π,即=π,∴ω=2.故答案为:3,2.x,x∈[2,8],则f(x)的值域是[1,3] .14.已知函数f(x)=4﹣log2【考点】34:函数的值域.【分析】由x∈[2,8]上结合对数函数的单调性,即可求出函数的值域.【解答】解:∵函数f(x)=4﹣logx在x∈[2,8]时单调递减,22=3,∴当x=2时函数取最大值4﹣log28=1,当x=8时函数取最小值4﹣log2∴函数f(x)的值域为[1,3],故答案为:[1,3].15.点P是直线x+y﹣2=0上的动点,点Q是圆x2+y2=1上的动点,则线段PQ长的最小值为.【考点】J9:直线与圆的位置关系.【分析】求圆心到直线的距离减去半径可得最小值.【解答】解:圆心(0,0)到直线x+y﹣2=0的距离d==.再由d﹣r=﹣1,知最小距离为1.故答案为:.三、解答题(共5小题,满分40分)16.如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:(1)某同学不小心把茎叶图中的一个数字弄污了,看不清了,在如图所示的茎叶图中用m表示,若甲运动员成绩的中位数是33,求m的值;(2)估计乙运动员在这次季后赛比赛中得分落在[20,40]内的概率.【考点】CC:列举法计算基本事件数及事件发生的概率;BA:茎叶图.【分析】(1)由茎叶图性质利用中位数定义列出方程,求出m.(2)由篮球运动员乙的季后赛10场得分中有5场得分在区间[20,40]内,能估计乙运动员在一场季后赛比赛中得分落在[20,40]内的概率.【解答】解:(1)由茎叶图性质得:中位数为: =33,解得m=4.(2)∵篮球运动员乙的季后赛10场得分中有5场得分在区间[20,40]内,∴可以估计乙运动员在一场季后赛比赛中得分落在[20,40]内的概率为.17.已知向量=(sinx,1),=(2cosx,3),x∈R.(1)当=λ时,求实数λ和tanx的值;(2)设函数f(x)=•,求f(x)的最小正周期和单调递减区间.【考点】GL:三角函数中的恒等变换应用;9R:平面向量数量积的运算.【分析】(1)根据向量的运算性质,向量相等即可求解.(2)根据函数f(x)=•,求出f(x)的解析式,即可求出f(x)的最小正周期和单调递减区间.【解答】解:(1)向量=(sinx,1),=(2cosx,3),x∈R.当=λ时,可得∴,即tanx=.(2)函数f(x)=•,∴f(x)=2sinxcosx+3=sin2x+3.∴f(x)的最小正周期T=.∵f(x)单调递减.则,k∈Z,得:≤x≤.∴f(x)的单调递减区间为[,],k∈Z.18.如图,在三棱锥P﹣ABC中,平面PAB⊥平面ABC,△PAB是等边三角形,AC⊥BC,且AC=BC=2,O、D分别是AB,PB的中点.(1)求证:PA∥平面COD;(2)求三棱锥P﹣ABC的体积.【考点】LF:棱柱、棱锥、棱台的体积;LS:直线与平面平行的判定.【分析】(1)由O、D分别是AB,PB的中点,得OD∥AP,即可得PA∥平面COD.(2)连接OP,得OP⊥面ABC,且OP=.即可得三棱锥P﹣ABC的体积V==.【解答】解:(1)∵O、D分别是AB,PB的中点,∴OD∥AP又PA⊄平面COD,OD⊂平面COD∴PA∥平面COD.(2)连接OP,由△PAB是等边三角形,则OP⊥AB又∵平面PAB⊥平面ABC,∴OP⊥面ABC,且OP=.∴三棱锥P﹣ABC的体积V==.19.已知函数f(x)=2+的图象经过点(2,3),a为常数.(1)求a的值和函数f(x)的定义域;(2)用函数单调性定义证明f(x)在(a,+∞)上是减函数.【考点】3E:函数单调性的判断与证明;33:函数的定义域及其求法.【分析】(1)把点(2,3)代入函数解析式求出a的值;根据f(x)的解析式,求出它的定义域;(2)用单调性定义证明f(x)在(1,+∞)上是减函数即可.【解答】解:(1)函数f(x)=2+的图象经过点(2,3),∴2+=3,解得a=1;∴f(x)=2+,且x﹣1≠0,则x≠1,∴函数f(x)的定义域为{x|x≠1};(2)用函数单调性定义证明f(x)在(1,+∞)上是减函数如下;设1<x1<x2,则f (x 1)﹣f (x 2)=(2+)﹣(2+)=,∵1<x 1<x 2,∴x 2﹣x 1>0,x 1﹣1>0,x 2﹣1>0, ∴f (x 1)>f (x 2),∴f (x )在(1,+∞)上是减函数.20.已知数列{a n }的各项均为正数,其前n 项和为S n ,且a n 2+a n =2S n ,n ∈N *. (1)求a 1及a n ;(2)求满足S n >210时n 的最小值;(3)令b n =4,证明:对一切正整数n ,都有+++…+<.【考点】8K :数列与不等式的综合;8E :数列的求和.【分析】(1)当n=1时,,由此能求出a 1=1,由a n 2+a n =2S n ,得,从而(a n +a n ﹣1)(a n ﹣a n ﹣1﹣1)=0,进而数列{a n }是首项和公差都为1的等差数列,由此能求出a n =n .(2)求出S n =,由此能求出满足S n >210时n 的最小值.(3)由题意得,从而数列{}是首项和公比都是的等比数列,由此能证明对一切正整数n ,都有+++…+<.【解答】解:(1)∵数列{a n }的各项均为正数,其前n 项和为S n ,且a n 2+a n =2S n ,n ∈N *.∴当n=1时,,且a 1>0,解得a 1=1,∵a n 2+a n =2S n ,①,∴,②①﹣②,得:,整理,得:(a n +a n ﹣1)(a n ﹣a n ﹣1﹣1)=0, ∵a n >0,∴a n ﹣a n ﹣1=1,∴数列{a n }是首项和公差都为1的等差数列, ∴a n =n .(2)∵数列{a n }是首项和公差都为1的等差数列,a n =n .∴S=,n∵S>210,∴,n整理,得n2+n﹣420>0,解得n>20(n<﹣21舍),∴满足S>210时n的最小值是21.n证明:(3)由题意得,则,∴数列{}是首项和公比都是的等比数列,∴+++…+==.故对一切正整数n,都有+++…+<.。
湖南省2018年普通高中高二年级学业水平考试模拟试卷(附中版)数学(理)试题Word版含答案

湖南省2018年普通高中年级学业水平考试模拟试卷高二数学(理)试题注意事项:1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2.必须在答题卡上答题,在草稿纸、试题卷上答题无效; 3.答题时,请考生注意各大题题号后面的答题提示; 4.请勿折叠答题卡,保证字体工整、笔迹清晰、卡面清洁。
一、选择题:本大题共15小题,每小题3分,共45分.1.已知全集U ={1,2,3,4,5,6},集合A ={}1, 3, 4,6,B ={}2, 4, 5,6,则A ∩∁U B 等于A.{}1, 3B.{}2, 5C.{}4 D .2.函数f (x )=sin ⎝ ⎛⎭⎪⎫π4-x 的一个单调增区间为 A.⎝⎛⎭⎪⎫3π4,7π4 B.⎝ ⎛⎭⎪⎫-π4,3π4 C.⎝ ⎛⎭⎪⎫-π2,π2 D.⎝⎛⎭⎪⎫-3π4,π4 3.如图是某几何体的三视图,则该几何体的体积为 A .9π+42 B .36π+18 C.92π+12 D.92π+18 4.已知直线l 1:()m +2x -()m -2y +2=0,直线l 2:3x +my -1=0,且l 1⊥l 2,则m 等于A .-1 B. 6或-1 C. -6 D. -6或15.已知{}a n 是等比数列,前n 项和为S n ,a 2=2,a 5=14,则S 5=A.132 B.314 C.334 D.10186.已知向量a =(1,k ),b =(2,1),若a 与b 的夹角大小为90°,则实数k 的值为 A .-12 B.12C .-2D .27.设变量x ,y 满足约束条件⎩⎨⎧x +2y -5≤0x -y -2≤0x ≥0,则目标函数z =2x +3y +1的最大值为A .11B .10C .9D .8.58.根据表格中的数据,可以判定方程e x -x -2=0的一个根所在的区间为A.(-1,0) B .(09.已知偶函数f (x )在区间}=________. 三、解答题:本大题共5小题,共40分. 21.(本小题满分6分)已知函数f (x )=log 21+x1-x ,x ∈(-1,1).(Ⅰ)判断f (x )的奇偶性,并证明;(Ⅱ)判断f (x )在(-1,1)上的单调性,并证明.一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为b,c.(Ⅰ)若直线l:x+y-5=0,求点P(b,c)恰好在直线l上的概率;(Ⅱ)若方程x2-bx-c=0至少有一个根属于集合{1,2,3,4},就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.23.(本小题满分8分)如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥底面ABCD,M为SA的中点,N为CD 的中点.(Ⅰ)证明:平面SBD⊥平面SAC.(Ⅱ)证明:直线MN∥平面SBC.已知数列{a n}满足a1=2,a n+1=a n+2,其中n∈N*. (Ⅰ)写出a2,a3及a n;(Ⅱ)记数列{a n}的前n项和为S n,设T n=1S1+1S2+…+1Sn,试判断T n与1的关系;(Ⅲ)对于(Ⅱ)中S n,不等式S n·S n-1+4S n-λ(n+1)S n-1≥0对任意的大于1的整数n恒成立,求实数λ的取值范围.25.(本小题满分10分)已知直线x+y-2=0被圆C:x2+y2=r2所截得的弦长为8.(Ⅰ)求圆C的方程;(Ⅱ)若直线l与圆C切于点P,当直线l与x轴正半轴、y轴正半轴围成的三角形面积最小时,求点P的坐标.附加题:(附加题不记入总分) 1.(本小题满分12分)已知定点A (0,1),B (0,-1),C (1,0).动点P 满足:AP →·BP →=k |PC →|2. (Ⅰ)求动点P 的轨迹方程,并说明方程表示的曲线类型; (Ⅱ)当k =2时,求|2AP →+BP →|的最大、最小值.2.(本小题满分12分)已知数列{}a n ,{}b n 都是单调递增数列,若将这两个数列的项按由小到大的顺序排成一列(相同的项视为一项),则得到一个新数列{}c n .(Ⅰ)设数列{}a n 、{}b n 分别为等差、等比数列,若a 1=b 1=1,a 2=b 3,a 6=b 5,求c 20; (Ⅱ)设{}a n 的首项为1,各项为正整数,b n =3n ,若新数列{}c n 是等差数列,求数列{}c n 的前n 项和S n ;(Ⅲ)设b n =q n -1(q 是不小于2的正整数),c 1=b 1,是否存在等差数列{}a n ,使得对任意的n ∈N *,在b n 与b n +1之间数列{}a n 的项数总是b n ?若存在,请给出一个满足题意的等差数列{}a n ;若不存在,请说明理由.湖南省2018年普通高中高二年级学业水平考试模拟试卷数学(理)试题参考答案一、选择题:本大题共15小题,每小题3分,共45分.13.D 【解析】因为40800=120,故各层中依次抽取的人数分别是16020=8,32020=16,20020=10,12020=6.14.B 【解析】由题意知,x=8.2+8.6+10.0+11.3+11.95=10,y=6.2+7.5+8.0+8.5+9.85=8,∴=8-0.76×10=0.4,∴当x=15时,=0.76×15+0.4=11.8(万元).二、填空题:本大题共5小题,每小题3分,共15分.16.12017.318.π3【解析】由已知,sin α=437,sin(α+β)=5314,可求cos β=cos=12,所以β=π3.19.221 320.-5三、解答题:本大题共5小题,共40分.21.【解析】(Ⅰ)证明:f(-x)=log21+(-x)1-(-x)=log21-x1+x=log 2⎝ ⎛⎭⎪⎫1+x 1-x -1=-log 21+x 1-x =-f (x ),又x ∈(-1,1),所以函数f (x )是奇函数.(3分) (Ⅱ)设-1<x 1<x 2<1,f (x 2)-f (x 1)=log 21+x 21-x 2-log 21+x 11-x 1=log 2(1-x 1)(1+x 2)(1+x 1)(1-x 2)因为1-x 1>1-x 2>0;1+x 2>1+x 1>0 所以(1-x 1)(1+x 2)(1+x 1)(1-x 2)>1,所以log 2(1-x 1)(1+x 2)(1+x 1)(1-x 2)>0所以函数f (x )=log 21+x1-x在(-1,1)上是增函数.(6分) 22.【解析】(Ⅰ)因为是投掷两次,因此基本事件(b ,c )为(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个,(1分)当b +c =5时,(b ,c )的所有取值为(1,4),(2,3),(3,2),(4,1),(2分) 所以所求概率为P 1=416=14.(3分)(Ⅱ)①若方程一根为x =1,则1-b -c =0,即b +c =1,不成立. ②若方程一根为x =2,则4-2b -c =0,即2b +c =4,所以⎩⎨⎧b =1,c =2.③若方程一根为x =3,则9-3b -c =0,即3b +c =9,所以⎩⎨⎧b =2,c =3.④若方程一根为x =4,则16-4b -c =0,即4b +c =16,所以⎩⎨⎧b =3,c =4.由①②③④知,(b ,c )的所有可能取值为(1,2),(2,3),(3,4), 所以方程为“漂亮方程”的概率为P 2=316.(8分) 23.【解析】证明:(Ⅰ)∵底面ABCD 是菱形, ∴BD ⊥AC ,∵SA ⊥底面ABCD ,∴BD ⊥SA ,∵SA 与AC 交于A, ∴BD ⊥平面SAC ,∵BD 平面SBD ,∴平面SBD ⊥平面SAC .(4分) (Ⅱ)取SB 中点E ,连接ME ,CE, ∵M 为SA 中点,∴ME ∥AB 且ME =12AB ,又∵ABCD 是菱形,N 为CD 的中点, ∴CN ∥AB 且CN =12CD =12AB ,∴CN ∥EM ,且CN =EM,∴四边形CNME 是平行四边形, ∴MN ∥CE ,又MN 平面SBC, CE 平面SBC ,∴直线MN ∥平面SBC .(8分) 24.【解析】(Ⅰ) 依题可得a 2=a 1+2=4,a 3=a 2+2=6, 依题可得{a n }是公差为2的等差数列,∴a n =2n .(2分) (Ⅱ) ∵ S n =n (n +1),∴1S n =1n (n +1)=1n -1n +1,∴T n =⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1=1-1n +1<1.(5分)(Ⅲ)依题可得n (n +1)·(n -1)n +4n (n +1)-λ(n +1)(n -1)n ≥0, 即(n -1)n +4-λ(n -1)≥0,即λ≤n +4n -1对大于1的整数n 恒成立,又n +4n -1=n -1+4n -1+1≥5, 当且仅当n =3时,n +4n -1取最小值5, 所以λ的取值范围是(-∞,5].(8分) 25.【解析】(Ⅰ)因为圆C 的圆心到直线x +y -2=0的距离为d =|0+0-2|12+12=2,(1分)所以r 2=d 2+(82)2=(2)2+42=18.(2分)所以圆C 的方程为x 2+y 2=18.(3分)(Ⅱ)设直线l 与圆C 切于点P (x 0,y 0)(x 0>0,y 0>0),则x 20+y 20=18.(4分)因为k OP =y 0x 0,所以圆的切线的斜率为-x 0y 0.则切线方程为y -y 0=-x 0y 0(x -x 0),即x 0x +y 0y =18.(5分)则直线l 与x 轴正半轴的交点坐标为⎝ ⎛⎭⎪⎫18x 0,0,与y 轴正半轴的交点坐标为⎝ ⎛⎭⎪⎫0,18y 0.所以围成的三角形面积为S =12×18x 0×18y 0=162x 0y 0.因为18=x 20+y 20≥2x 0y 0,所以x 0y 0≤9.当且仅当x 0=y 0=3时,等号成立.(8分) 因为x 0>0,y 0>0,所以1x 0y 0≥19, 所以S =162x 0y 0≥1629=18. 所以当x 0=y 0=3时,S 取得最小值18.所以所求切点P 的坐标为(3,3).(10分) 附加题:(附加题不记入总分)1.【解析】(Ⅰ)设动点坐标为P (x ,y ),则=(x ,y -1),=(x ,y +1),=(1-x ,-y ).因为·=k ||2,所以x 2+y 2-1=k ,(1-k )x 2+(1-k )y 2+2kx -k -1=0. 若k =1,则方程为x =1,表示过点(1,0)且平行于y 轴的直线.若k ≠1,则方程化为⎝ ⎛⎭⎪⎫x +k 1-k 2+y 2=⎝ ⎛⎭⎪⎫11-k 2,表示以⎝ ⎛⎭⎪⎫k k -1,0为圆心,以1|1-k | 为半径的圆.(Ⅱ)当k =2时,方程化为(x -2)2+y 2=1, 因为2+=(3x ,3y -1), 所以|2+|=9x 2+9y 2-6y +1.又x 2+y 2=4x -3,所以|2+|=36x -6y -26.因为(x -2)2+y 2=1,所以令x =2+cos θ,y =sin θ, 则36x -6y -26=637cos(θ+φ)+46∈.所以|2+|的最大值为46+637=3+37, 最小值为46-637=37-3.2.【解析】(Ⅰ)设等差数列{}a n 的公差为d ,等比数列{}b n 的公比为q ,由题意得,⎩⎨⎧1+d =q21+5d =q4,解得d =0或3,因数列{}a n ,{}b n 单调递增, 所以d >0,q >1,所以d =3,q =2,所以a n =3n -2,b n =2n -1. 因为b 1=a 1,b 3=a 2,b 5=a 6,b 7>a 20,所以c 20=a 17=49. (Ⅱ)设等差数列{}c n 的公差为d ,又a 1=1,且b n =3n , 所以c 1=1,所以c n =dn +1-d . 因为b 1=3是{}c n 中的项, 所以设b 1=c n ,即d (n -1)=2. 当n ≥4时,解得d =2n -1<1,不满足各项为正整数; 当b 1=c 3=3时,d =1,此时c n =n ,只需取a n =n ,而等比数列{}b n 的项都是等差数列{}a n 中的项,所以S n =12n (n +1);当b 1=c 2=3时,d =2,此时c n =2n -1,只需取a n =2n -1,由3n=2m -1,得m =3n +12,3n 是奇数,3n +1 是正偶数,m 有正整数解,所以等比数列{}b n 的项都是等差数列{}a n 中的项,所以S n =n 2. 综上所述,数列{}c n 的前n 项和S n =12n (n +1)或S n =n 2.(Ⅲ)存在等差数列{}a n ,只需首项a 1∈(1,q ),公差d =q -1. 下证b n 与b n +1之间数列{}a n 的项数为b n .即证对任意正整数n ,都有⎩⎨⎧b n <ab 1+b 2+…+b n -1+1b n +1>ab 1+b 2+…+b n ,即⎩⎨⎧b n <a 1+q +q 2+…+qn -2+1b n +1>a 1+q +q 2+…+qn -1成立. 由b n -a 1+q +q 2+…+qn -2+1=q n -1-a 1-(1+q +q 2+…+q n -2)(q -1)=1-a 1<0,b n +1-a 1+q +q 2+…+qn -1=q n -a 1-(1+q +q 2+…+q n -2+q n -1-1)(q -1)=q -a 1>0. 所以首项a 1∈(1,q ),公差d =q -1的等差数列{}a n 符合题意.。
湖南数学学考真题(2009-2018)

2018年湖南省普通高中学业水平考试数学试卷一、选择题:本大题共10小题,每小题4分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知等差数列{n a }的前3项分别为2、4、6,则数列{n a }的第4项为A .7B .8C .10D .122.如图是一个几何体的三视图,则该几何体为A .球B .圆柱C .圆台D .圆锥 3.函数)2)(1()(+-=x x x f 的零点个数是A .0B .1C .2D .34.已知集合}2,0,1{-=A ,}3,{x =B ,若}2{=B A ,则x 的值为 A .3 B .2 C .0 D .-15.已知直线1l :12+=x y ,2l :52+=x y ,则直线1l 与2l 的位置关系是 A .重合 B .垂直 C .相交但不垂直 D .平行6.下列坐标对应的点中,落在不等式01<-+y x 表示的平面区域内的是A .(0,0)B .(2,4)C .(-1,4)D .(1,8) 7.某班有50名同学,将其编为1、2、3、…、50号,并按编号从小到大平均分成5组.现用系统抽样方法,从该班抽取5名同学进行某项调查,若第1组抽取的学生编号为3,第2组抽取的学生编号为13,则第4组抽取的学生编号为 A .14 B .23 C .33 D .438.如图,D 为等腰三角形ABC 底边AB 的中点,则下列等式恒成立的是A .0=⋅B .0=⋅C .0=⋅D .0=⋅9.将函数x y sin =的图象向左平移3π个单位长度,得到的图象对应的函数解析式为A .)3sin(π+=x yB .)3sin(π-=x yC .)32sin(π+=x yD .)32sin(π-=x y 10.如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机模拟的方法可以(第2题图)俯视图(第8题图)CABD估计图中阴影部分的面积为A .32B .54C .56D .34二、填空题:本大题共5小题,每小题4分,满分20分. 11.比较大小:5log 2 3log 2 (填“>”或“<”). 12.已知圆4)(22=+-y a x 的圆心坐标为)0,3(,则实数=a .13.某程序框图如图所示,若输入的c b a ,,值分别为3,4,5,则输出的y 值为 .14.已知角α的终边与单位圆的交点坐标为(23,21),则αcos = .15.如图,A ,B 两点在河的两岸,为了测量A 、B 之间的距离,测量者在A 的同侧选定一点C ,测出A 、C 之间的距离是100米,∠BAC=105º,∠ACB=45º,则A 、B 两点之间的距离为 米.三、解答题:本大题共5小题,满分40分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分6分)已知函数)(x f y =(]6,2[-∈x )的图象如图.根据图象写出: (1)函数)(x f y =的最大值; (2)使1)(=x f 的x 值. 17.(本小题满分8分)一批食品,每袋的标准重量是50g ,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:g ),并得到其茎叶图(如图).(第13题图)(第15题图) (第16题图)(1)求这10袋食品重量的众数,并估计这批食品实际重量的平均数;(2)若某袋食品的实际重量小于或等于47g ,则视为不合格产品,试估计这批食品重量的合格率.18.(本小题满分8分)如图,在四棱柱ABCD-A 1B 1C 1D 1中,D 1D ⊥底面ABCD ,底面ABCD 是正方形,且AB=1,D 1D=2.(1)求直线D 1B 与平面ABCD 所成角的大小; (2)求证:AC ⊥平面BB 1D 1D .19.(本小题满分8分)已知向量a =(x sin ,1),b =(x cos ,1),∈x R . (1)当4π=x 时,求向量a + b 的坐标;(2)若函数=)(x f |a + b |2m +为奇函数,求实数m 的值.4 5 6 6 95 0 0 0 1 1 2(第17题图) (第18题图)A B CD A 1 B 1C 1D 120.(本小题满分10分)已知数列{n a }的前n 项和为a S n n +=2(a 为常数,∈n N *). (1)求1a ,2a ,3a ;(2)若数列{n a }为等比数列,求常数a 的值及n a ;(3)对于(2)中的n a ,记34)(112-⋅-⋅=++n n a a n f λλ,若0)(<n f 对任意的正整数n 恒成立,求实数λ的取值范围.2018年湖南省普通高中学业水平考试数学试卷参考答案二、填空题(每小题4分,满分20分) 11.>; 12. 3; 13.4; 14. 21; 15. 2100. 三、解答题(满分40分)16.解:(1)由图象可知,函数)(x f y =的最大值为2; …………………3分(2)由图象可知,使1)(=x f 的x 值为-1或5. ……………6分 17.解:(1)这10袋食品重量的众数为50(g ), ………………2分 因为这10袋食品重量的平均数为491052515150505049464645=+++++++++(g ), 所以可以估计这批食品实际重量的平均数为49(g ); ……………4分 (2)因为这10袋食品中实际重量小于或等于47g 的有3袋,所以可以估计这批食品重量的不合格率为103,故可以估计这批食品重量的合格率为107. 8分 18.(1)解:因为D 1D ⊥面ABCD ,所以BD 为直线B D 1在平面ABCD 内的射影,所以∠D 1BD 为直线D 1B 与平面ABCD 所成的角, …………………2分又因为AB=1,所以BD=2,在Rt △D 1DB 中,1tan 11==∠BDDD BD D , 所以∠D 1BD=45º,所以直线D 1B 与平面ABCD 所成的角为45º; 4分 (2)证明:因为D 1D ⊥面ABCD ,AC 在平面ABCD 内,所以D 1D ⊥AC , 又底面ABCD 为正方形,所以AC ⊥BD , …………………6分 因为BD 与D 1D 是平面BB 1D 1D 内的两条相交直线,所以AC ⊥平面BB 1D 1D . …………………………8分 19.解:(1)因为a =(x sin ,1),b =(x cos ,1),4π=x ,所以a + b )2,2()2,cos (sin =+=x x ; …………………4分 (2)因为a + b )2,cos (sin x x +=,所以m x m x x x f ++=+++=52sin 4)cos (sin )(2, ……………6分 因为)(x f 为奇函数,所以)()(x f x f -=-,即m x m x ---=++-52sin 5)2sin(,解得5-=m . ……………8分 注:由)(x f 为奇函数,得0)0(=f ,解得5-=m 同样给分.20.解:(1)211+==a S a , ……………………1分 由212a a S +=,得22=a , ……………………2分由3213a a a S ++=,得43=a ; …………………3分 (2)因为21+=a a ,当2≥n 时,112--=-=n n n n S S a ,又{n a }为等比数列,所以11=a ,即12=+a ,得1-=a , …………5分 故12-=n n a ; …………………………………6分 (3)因为12-=n n a ,所以3242)(2-⋅-⋅=n n n f λλ, ………………7分 令n t 2=,则2≥t ,34)2(34)(22---=-⋅-⋅=λλλλt t t n f , 设34)2()(2---=λλt t g ,当0=λ时,03)(<-=n f 恒成立, …………………8分当0>λ时,34)2()(2---=λλt t g 对应的点在开口向上的抛物线上,所以0)(<n f 不可能恒成立, ……………9分当0<λ时,34)2()(2---=λλt t g 在2≥t 时有最大值34--λ,所以要使0)(<n f 对任意的正整数n 恒成立,只需034<--λ,即43->λ,此时043<<-λ,综上实数λ的取值范围为043≤<-λ. …………………………10分说明:解答题如有其它解法,酌情给分.2017年湖南省普通高中学业水平考试数学(真题)本试卷包括选择题、填空题和解答题三部分,共4页,时量120分钟,满分100分。
高三数学-2018年普通高等学校招生全国统一考试(湖南卷

绝密★启用前2018年普通高等学校招生全国统一考试(湖南卷)数学(文史类)注意事项:1.答题前,考生务必将自己的姓名、准考证号写在答题卡和该试题卷的封面上,并认真核对条形码上的姓名、准考证号和科目。
2.考生作答时,选择题和非选择题均须作在答题卡上,在草稿纸和本试卷上答题无效。
考生在答题卡上按如下要求答题:(1)选择题部分请用2B铅笔把应题目的答案标号所在方框涂黑,修改时用橡皮擦干净,不留痕迹。
(2)非选择题部分(包括填空题和解答题)请按题号用0.5毫米黑色墨水签字笔书写,否则作答无效。
(3)保持字体工整、笔迹清晰、卡面清洁、不折叠。
3.考试结束后,将本试题卷和答题卡一并交回。
4. 本试卷共5页。
如缺页,考生须声明,否则后果自负。
本试题卷他选择题和非选择题(包括填空题和解答题)两部分. 选择题部分1至2页. 非选择题部分3至5页. 时量120分钟. 满分150分. 参考公式: 如果事件A 、B 互斥,那么()()()P A B P A P B +=+ 如果事件A 、B 相互独立,那么)()()(B P A P AB P ⋅=如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率是()(1)k k n kn n P k C P P -=-球的体积公式 343V R π=,球的表面积公式24S R π=,其中R 表示球的半径一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.函数x y 2log=的定义域是A .(0,1]B . (0,+∞) C. (1,+∞) D . [1,+∞)2.已知向量),2,1(),,2(==b t a 若1t t =时,a∥b ;2t t =时,b a ⊥,则A .1,421-=-=t tB . 1,421=-=t t C. 1,421-==t t D . 1,421==t t3. 若5)1(-ax 的展开式中3x 的系数是80,则实数a 的值是A .-2B . 22 C. 34 D . 24.过半径为12的球O 表面上一点A 作球O 的截面,若OA 与该截面所成的角是60°则该截面的面积是A .πB . 2π C. 3π D . π325.“a =1”是“函数ax x f -=)(在区间[1,+∞)上为增函数”的A .充分不必要条件B . 必要不充分条件C. 充要条件 D . 既不充分也不必要条件6.在数字1,2,3与符号+,-五个元素的所有全排列中,任意两个数字都不相邻的全排列个数是A .6B . 12 C. 18 D . 24 7.圆0104422=---+y x yx 上的点到直线014=-+y x 的最大距离与最小距离的差是A .36B . 18 C. 26 D . 258.设点P 是函数x x f ωsin )(=的图象C 的一个对称中心,若点P 到图象C 的对称轴上的距离的最小值4π,则)(x f 的最小正周期是A .2πB . π C.2π D .4π9.过双曲线M :2221y x b-=的左顶点A 作斜率为1的直线l ,若l 与双曲线M 的两条渐近线分别相交于点B 、C ,且BCAB =,则双曲线M 的离心率是A .25 B . 310 C.5D .1010. 如图1:OM ∥AB ,点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内(不含边界).且OBy OA x OP +=,则实数对(x ,y )可以是A .)43,41(B . )32,32(-C. )43,41(-D . )57,51(-二.填空题:本大题共5小题,每小题4分,共20分,把答案填在答题卡中....对应题号的横上.11. 若数列{}n a 满足:1.2,111===+n a a a n n ,2,3….则=+++n a a a 21 .12. 某高校有甲、乙两个数学建模兴趣班. 其中甲班有40人,乙班50人.现分析两个班的A一次考试成绩,算得甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是 分.13. 已知⎪⎩⎪⎨⎧≤--≤+-≥022011y x y x x 则22yx +的最小值是 .14. 过三棱柱 ABC -A 1B 1C 1 的任意两条棱的中点作直线,其中与平面ABB 1A 1平行的直线共有 条. 15. 若)4sin(3)4sin()(ππ-++=x x a x f 是偶函数,则a = .三.解答题:本大题共6小题,共80分. 解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)已知),,0(,1cos )cos()22sin(sin 3πθθθπθπθ∈=⋅+--求θ的值.17.(本小题满分12分) 某安全生产监督部门对5家小型煤矿进行安全检查(简称安检). 若安检不合格,则必须整改. 若整改后经复查仍不合格,则强制关闭. 设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5,整改后安检合格的概率是0.8,计算(结果精确到0.01):(Ⅰ)恰好有两家煤矿必须整改的概率; (Ⅱ)某煤矿不被关闭的概率; (Ⅲ)至少关闭一家煤矿的概率.18.(本小题满分14分) 如图2,已知两个正四棱锥P -ABCD 与Q -ABCD 的高都是2,AB =4.(Ⅰ)证明PQ ⊥平面ABCD ;(Ⅱ)求异面直线AQ 与PB 所成的角; (Ⅲ)求点P 到平面QAD 的距离.Q B C P AD图219.(本小题满分14分) 已知函数axaxx f 313)(23-+-=.(I)讨论函数)(x f 的单调性;(Ⅱ)若曲线)(x f y =上两点A 、B 处的切线都与y 轴垂直,且线段AB 与x 轴有公共点,求实数a 的取值范围.20.(本小题满分14分) 在m (m ≥2)个不同数的排列P 1P 2…P n 中,若1≤i <j ≤m 时P i >P j (即前面某数大于后面某数),则称P i 与P j 构成一个逆序. 一个排列的全部逆序的总数称为该排列的逆序数. 记排列321)1()1( -+n n n 的逆序数为a n ,如排列21的逆序数11=a ,排列321的逆序数23a =.排列4321的逆序数36a =(Ⅰ)求a 4、a 5,并写出a n 的表达式; (Ⅱ)令nn n n na a a ab 11+++=,证明32221+<++<n b b b nn ,n =1,2,….21.(本小题满分14分)已知椭圆C 1:13422=+yx,抛物线C 2:)0(2)(2>=-p px m y ,且C 1、C 2的公共弦AB过椭圆C 1的右焦点.(Ⅰ)当x AB ⊥轴时,求p 、m 的值,并判断抛物线C 2的焦点是否在直线AB 上;(Ⅱ)若34=p 且抛物线C 2的焦点在直线AB 上,求m 的值及直线AB 的方程.参考答案1-10:DCDAABCBDC 11.12-n, 12. 85, 13. 5 ,14. 6 ,15. -3 .16.解:由已知条件得1cos cos 2cos sin 3=⋅--θθθθ.即sin2sin 32=-θθ. 解得0sin 23sin==θθ或.由0<θ<π知23sin=θ,从而323πθπθ==或.17.解:(Ⅰ)每家煤矿必须整改的概率是1-0.5,且每家煤矿是否整改是相互独立的. 所以恰好有两家煤矿必须整改的概率是31.01655.0)5.01(32251==⨯-⨯=C P .(Ⅱ)解法一 某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格,所以该煤矿被关闭的概率是1.0)8.01()5.01(2=-⨯-=P ,从而煤矿不被关闭的概率是0.90. 解法二 某煤矿不被关闭包括两种情况:(i )该煤矿第一次安检合格;(ii )该煤矿第一次安检不合格,但整改后合格.所以该煤矿不被关闭的概率是90.08.0)5.01(5.02=⨯-+=P .(Ⅲ)由题设(Ⅱ)可知,每家煤矿不被关闭的概率是0.9,且每家煤矿是否被关闭是相互独立的,所以到少关闭一家煤矿的概率是41.09.0153=-=P .18.解法一 (Ⅰ)连结AC 、BD ,设OBD AC= .由P -ABCD 与Q -ABCD 都是正四棱锥,所以PO ⊥平面ABCD ,QO ⊥平面ABCD . 从而P 、O 、Q 三点在一条直线上,所以PQ ⊥平面ABCD . (Ⅱ)由题设知,ABCD 是正方形,所以AC ⊥BD . 由(Ⅰ),PQ ⊥平面ABCD . 故可分别以直线CA 、DB 、QP 为x 轴、y 轴、z 轴建立空间直角坐标系(如图),由题设条件,相关各点的坐标分别是P (0,0,2),A (22,0,0),Q (0,0,-2),B (0,22,0).所以)2,0,22(--=AQ )2,22,0(-=PB于是3132324,cos=⨯=>=<PB AQ .从而异面直线AQ 与PB 所成的角是31arccos.(Ⅲ)由(Ⅱ),点D 的坐标是(0,-22,0),)0,22,22(--=AD,)4,0,0(-=PQ,设),,(z y x n=是平面QAD 的一个法向量,由 ⎪⎩⎪⎨⎧=⋅=⋅00AD n AQ n 得⎪⎩⎪⎨⎧=+=+02y x z x .取x =1,得)2,1,1(--=n.所以点P 到平面QAD的距离22==d.解法二 (Ⅰ)取AD 的中点,连结PM ,QM . 因为P -ABCD 与Q -ABCD 都是正四棱锥, 所以AD ⊥PM ,AD ⊥QM . 从而AD ⊥平面PQM . 又⊂PQ 平面PQM ,所以PQ ⊥AD .同理PQ ⊥AB ,所以PQ ⊥平面ABCD .(Ⅱ)连结AC 、BD 设O BD AC = ,由PQ ⊥平面ABCD 及正四棱锥的性质可知O 在PQ 上,从而P 、A 、Q 、C 四点共面.因为OA =OC ,OP =OQ ,所以P AQC 为平行四边形,AQ ∥PC .从而∠BPC (或其补角)是异面直线AQ 与PB 所成的角.因为322)22(2222=+=+==OPOCPC PB,所以31323221612122cos222=⨯⨯-+=⋅-∠PCPB BCPCPBBPC +=.从而异面直线AQ 与PB 所成的角是31arccos .(Ⅲ)连结OM ,则PQAB OM21221===.所以∠PMQ =90°,即PM ⊥MQ .由(Ⅰ)知AD ⊥PM ,所以PM ⊥平面QAD . 从而PM 的长是点P 到平面QAD 的距离. 在直角△PMO 中,22222222=+=+=OMPOPM.即点P 到平面QAD 的距离是22.19.(Ⅰ)由题设知)2(363)(,02ax ax x axx f a-=-='≠.QBCPADOM令ax x x f 2,00)(21==='得.当(i )a >0时, 若)0,(-∞∈x ,则0)(>'x f ,所以)(x f 在区间(,0)-∞上是增函数;若)2,0(a x ∈,则)(<'x f ,所以)(x f 在区间)2,0(a 上是减函数;若),2(+∞∈a x ,则)(>'x f ,所以)(x f 在区间),2(+∞a 上是增函数;(i i )当a <0时, 若)2,(a x -∞∈,则)(<'x f ,所以)(x f 在区间)2,(a-∞上是减函数;若)2,0(a x ∈,则0)(<'x f ,所以)(x f 在区间)2,0(a上是减函数; 若)0,2(a x ∈,则0)(>'x f ,所以)(x f 在区间)0,2(a上是增函数;若),0(+∞∈x ,则0)(<'x f ,所以)(x f 在区间),0(+∞上是减函数.(Ⅱ)由(Ⅰ)的讨论及题设知,曲线)(x f y =上的两点A 、B 的纵坐标为函数的极值,且函数)(x f y=在ax x2,0==处分别是取得极值af 31)0(-=,134)2(2+--=aaaf .因为线段AB 与x 轴有公共点,所以0)2()0(≤⋅af f . 即0)31)(134(2≤-+--aaa.所以)4)(3)(1(2≤--+aa a a .故0,0)4)(3)(1(≠≤--+a a a a 且.解得 -1≤a <0或3≤a ≤4.即所求实数a 的取值范围是[-1,0)∪[3,4].20.(本小题满分14分)(Ⅰ)由已知得15,1054==a a ,2)1(12)1(+=+++-+=n n n n a n .(Ⅱ)因为,2,1,22222211==+⋅+>+++=+=++n nn n n nn n n a a a a b nn n n n,所以nb b b n 221>+++ .又因为 ,2,1,222222=+-+=+++=n n n nn n n b n ,所以)]211()4121()3111[(2221+-++-+-+=+++n n n b b b n=32221232+<+-+-+n n n n .综上,,2,1,32221=+<++<n n b b b nn .21.(本小题满分14分)(Ⅰ)当AB ⊥x 轴时,点A 、B 关于x 轴对称,所以m =0,直线AB 的方程为x =1,从而点A 的坐标为(1,23)或(1,-23).因为点A 在抛物线上,所以p249=,即89=p.此时C 2的焦点坐标为(169,0),该焦点不在直线AB 上.(Ⅱ)解法一 当C 2的焦点在AB 上时,由(Ⅰ)知直线AB 的斜率存在,设直线AB的方程为)1(-=x k y .由⎪⎩⎪⎨⎧=+-=134)1(22y x x k y 消去y 得01248)43(2222=-+-+kx kx k . ……①设A 、B 的坐标分别为(x 1,y 1), (x 2,y 2), 则x 1,x 2是方程①的两根,x 1+x 2=22438kk+.因为AB 既是过C 1的右焦点的弦,又是过C 2所以)(214)212()212(2121x x x x AB +-=-+-=,且34)2()2(212121++=++=+++=x x p x x p x p x AB .从而)(214342121x x x x +-=++.所以91621=+x x ,即91643822=+kk.解得6,62±==k k 即. 因为C 2的焦点),32(m F '在直线)1(-=x k y上,所以km31-=.即3636-==m m 或.当36=m 时,直线AB 的方程为)1(6--=x y; 当36-=m时,直线AB 的方程为)1(6-=x y.解法二 当C 2的焦点在AB 时,由(Ⅰ)知直线AB 的斜率存在,设直线AB 的方程 为)1(-=x k y .由⎪⎩⎪⎨⎧-==-)1(38)(2x k y x m y 消去y 得xm k kx38)(2=--. ……①因为C 2的焦点),32(m F '在直线)1(-=x k y上,所以)132(-=k m ,即km31-=.代入①有xk kx38)32(2=-.即094)2(342222=++-k x kxk. ……②设A 、B 的坐标分别为(x 1,y 1), (x 2,y 2), 则x 1,x 2是方程②的两根,x 1+x 2=223)2(4kk+.由⎪⎩⎪⎨⎧=+-=134)1(22y x x k y 消去y 得01248)43(2222=-+-+kx kx k . ……③由于x 1,x 2也是方程③的两根,所以x 1+x 2=22438kk+.从而223)2(4k k+=22438kk+. 解得6,62±==k k 即.因为C 2的焦点),32(m F '在直线)1(-=x k y上,所以km 31-=.即3636-==m m 或.当36=m 时,直线AB 的方程为)1(6--=x y; 当36-=m时,直线AB 的方程为)1(6-=x y.解法三 设A 、B 的坐标分别为(x 1,y 1), (x 2,y 2), 因为AB 既过C 1的右焦点)0,1(F ,又是过C 2的焦点),32(m F ', 所以)212()212()2()2(212121x x p x x p x p x AB -+-=++=+++=.即916)4(3221=-=+p x x . ……①由(Ⅰ)知21x x ≠,于是直线AB 的斜率mm x x y y k313201212=--=--=, ……②且直线AB 的方程是)1(3--=x m y ,所以32)2(32121m x x m y y =-+-=+. ……③又因为⎪⎩⎪⎨⎧=+=+1243124322222121y x y x ,所以0)(4)(312122121=--⋅+++x x y y y y x x . ……④将①、②、③代入④得322=m ,即3636-==m m或.当36=m时,直线AB 的方程为)1(6--=x y;当36-=m时,直线AB 的方程为)1(6-=x y.。
2018年湖南省普通高中学业水平考试数学试卷Word版含答案

2018年湖南省普通高中学业水平考试数学试卷一、选择题:本大题共10小题,每小题4分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知等差数列{n a }的前3项分别为2、4、6,则数列{n a }的第4项为A .7B .8C .10D .12 2.如图是一个几何体的三视图,则该几何体为A .球B .圆柱C .圆台D .圆锥 3.函数)2)(1()(+-=x x x f 的零点个数是A .0B .1C .2D .34.已知集合}2,0,1{-=A ,}3,{x =B ,若}2{=B A ,则x 的值为 A .3 B .2 C .0 D .-15.已知直线1l :12+=x y ,2l :52+=x y ,则直线1l 与2l 的位置关系是 A .重合 B .垂直 C .相交但不垂直 D .平行6.下列坐标对应的点中,落在不等式01<-+y x 表示的平面区域内的是A .(0,0)B .(2,4)C .(-1,4)D .(1,8)7.某班有50名同学,将其编为1、2、3、…、50号,并按编号从小到大平均分成5组.现用系统抽样方法,从该班抽取5名同学进行某项调查,若第1组抽取的学生编号为3,第2组抽取的学生编号为13,则第4组抽取的学生编号为A .14B .23C .33D .438.如图,D 为等腰三角形ABC 底边AB 的中点,则下列等式恒成立的是A .0=⋅CB CA B .0=⋅AB CDC .0=⋅CD CA D .0=⋅CB CD9.将函数x y sin =的图象向左平移3π个单位长度,得到的图象对应的函数解析式为A .)3sin(π+=x yB .)3sin(π-=x y(第2题图)俯视图(第8题图)CABDC .)32sin(π+=x y D .)32sin(π-=x y 10.如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机模拟的方法可以估计图中阴影部分的面积为A .32B .54C .56D .34二、填空题:本大题共5小题,每小题4分,满分20分. 11.比较大小:5log 2 3log 2 (填“>”或“<”).12.已知圆4)(22=+-y a x 的圆心坐标为)0,3(,则实数=a .13.某程序框图如图所示,若输入的c b a ,,值分别为3,4,5,则输出的y 值为 . 14.已知角α的终边与单位圆的交点坐标为(23,21),则αcos = . 15.如图,A ,B 两点在河的两岸,为了测量A 、B 之间的距离,测量者在A 的同侧选定一点C ,测出A 、C 之间的距离是100米,∠BAC=105º,∠ACB=45º,则A 、B 两点之间的距离为 米.三、解答题:本大题共5小题,满分40分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分6分)已知函数)(x f y =(]6,2[-∈x )的图象如图.根据图象写出: (1)函数)(x f y =的最大值; (2)使1)(=x f 的x 值.(第10题图)(第13题图)(第15题图)(第16题图)一批食品,每袋的标准重量是50g,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:g),并得到其茎叶图(如图).(1)求这10袋食品重量的众数,并估计这批食品实际重量的平均数;(2)若某袋食品的实际重量小于或等于47g,则视为不合格产品,试估计这批食品重量的合格率.18.(本小题满分8分)如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=2.(1)求直线D1B与平面ABCD所成角的大小;(2)求证:AC⊥平面BB1D1D.4 5 6 6 95 0 0 0 1 1 2(第17题图)(第18题图)A BCDA1B1C1D1已知向量a =(x sin ,1),b =(x cos ,1),∈x R . (1)当4π=x 时,求向量a + b 的坐标;(2)若函数=)(x f |a + b |2m +为奇函数,求实数m 的值. 20.(本小题满分10分)已知数列{n a }的前n 项和为a S n n +=2(a 为常数,∈n N *). (1)求1a ,2a ,3a ;(2)若数列{n a }为等比数列,求常数a 的值及n a ;(3)对于(2)中的n a ,记34)(112-⋅-⋅=++n n a a n f λλ,若0)(<n f 对任意的正整数n 恒成立,求实数λ的取值范围.2018年湖南省普通高中学业水平考试数学试卷参考答案二、填空题(每小题4分,满分20分) 11.>; 12. 3; 13.4; 14. 21; 15. 2100. 三、解答题(满分40分)16.解:(1)由图象可知,函数)(x f y =的最大值为2; …………………3分(2)由图象可知,使1)(=x f 的x 值为-1或5. ……………6分 17.解:(1)这10袋食品重量的众数为50(g ), ………………2分 因为这10袋食品重量的平均数为491052515150505049464645=+++++++++(g ), 所以可以估计这批食品实际重量的平均数为49(g ); ……………4分(2)因为这10袋食品中实际重量小于或等于47g 的有3袋,所以可以估计这批食品重量的不合格率为103,故可以估计这批食品重量的合格率为107. 8分 18.(1)解:因为D 1D ⊥面ABCD ,所以BD 为直线B D 1在平面ABCD 内的射影,所以∠D 1BD 为直线D 1B 与平面ABCD 所成的角, …………………2分又因为AB=1,所以BD=2,在Rt △D 1DB 中,1tan 11==∠BDDD BD D , 所以∠D 1BD=45º,所以直线D 1B 与平面ABCD 所成的角为45º; 4分 (2)证明:因为D 1D ⊥面ABCD ,AC 在平面ABCD 内,所以D 1D ⊥AC , 又底面ABCD 为正方形,所以AC ⊥BD , …………………6分 因为BD 与D 1D 是平面BB 1D 1D 内的两条相交直线,所以AC ⊥平面BB 1D 1D . …………………………8分 19.解:(1)因为a =(x sin ,1),b =(x cos ,1),4π=x ,所以a + b )2,2()2,cos (sin =+=x x ; …………………4分 (2)因为a + b )2,cos (sin x x +=,所以m x m x x x f ++=+++=52sin 4)cos (sin )(2, ……………6分因为)(x f 为奇函数,所以)()(x f x f -=-,即m x m x ---=++-52sin 5)2sin(,解得5-=m . ……………8分 注:由)(x f 为奇函数,得0)0(=f ,解得5-=m 同样给分.20.解:(1)211+==a S a , ……………………1分由212a a S +=,得22=a , ……………………2分 由3213a a a S ++=,得43=a ; …………………3分 (2)因为21+=a a ,当2≥n 时,112--=-=n n n n S S a ,又{n a }为等比数列,所以11=a ,即12=+a ,得1-=a , …………5分 故12-=n n a ; …………………………………6分 (3)因为12-=n n a ,所以3242)(2-⋅-⋅=n n n f λλ, ………………7分 令n t 2=,则2≥t ,34)2(34)(22---=-⋅-⋅=λλλλt t t n f , 设34)2()(2---=λλt t g ,当0=λ时,03)(<-=n f 恒成立, …………………8分当0>λ时,34)2()(2---=λλt t g 对应的点在开口向上的抛物线上,所以0)(<n f 不可能恒成立, ……………9分当0<λ时,34)2()(2---=λλt t g 在2≥t 时有最大值34--λ,所以要使0)(<n f 对任意的正整数n 恒成立,只需034<--λ,即43->λ,此时043<<-λ,综上实数λ的取值范围为043≤<-λ. …………………………10分说明:解答题如有其它解法,酌情给分.。
2018年湖南省普通高中学业水平考试仿真试卷数学(二)参考答案

2018年湖南省高中学业水平仿真模拟试卷(二)数 学本试卷包括选择题和非选择题两部分,共4页。
时量120分钟,满分100分。
一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.已知等比数列{a n }的前3项分别为1、-2、4,则数列{a n }的第4项为 A .-6B .8C .-8D .6解:∵q =-2,∴a 4=a 3q =-8,选C2.下列坐标对应的点中,落在不等式x -2y +1<0表示的平面区域内的是 A .(0,0)B .(4,2)C .(4,-1)D .(-1,4)解:∵-1-2×4+1=-8<0,∴选D3.已知集合A={-1,0,13,1},集合N 为自然数集,则A ∩N=A .{-1,0,1}B .{-1,1}C .{0,1}D .{0,13,1}解:A ∩N={0,1},选C 4.2tan π3的值为A .1B . 2C . 3D . 6解:原式=2⋅3=6,选D5.已知向量a =(1,2),b =(x ,-1),若b ∥(a +b ),则实数x 的值为A .-2B .2C .-12D .12解:由b ∥(a +b ),知1)1(211-=-+-=+x x ,∴21-=x ,选C6.已知一个几何体的三视图如图所示,则该几何体可以是 A .正方体 B .圆柱C .三棱柱D .球解:选A7.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知a =4,c =5,sinC=1,则b 的值为 A .1B .2C .3D .6解:由勾股定理知b =3,选C8.下列关于函数f (x )=tan x 的结论正确的是 A .是偶函数 B .关于x =π2对称 C .f (π3)= 3D .f (π4)=22解:选C9.过点P(-1,3)且与圆(x -2)2+(y +1)2=25相切的直线方程为A .3x -4y +15=0B .4x +3y -5=0C .4x -3y -15=0D .3x +4y -5=0解:因为点P 在已知圆上,所以过点P 的切线方程为(-1-2)(x-2)+(3+1)(y+1)=25,选A10.函数⎩⎨⎧>+-≤-+=0,ln 20,32)(2x x x x x x f 的零点个数为A .1B .2C .3D .4解:画出草图,即知选B二、填空题:本大题共5小题,每小题4分,共20分。
2018湖南省普通高中学业水平考试数学试题
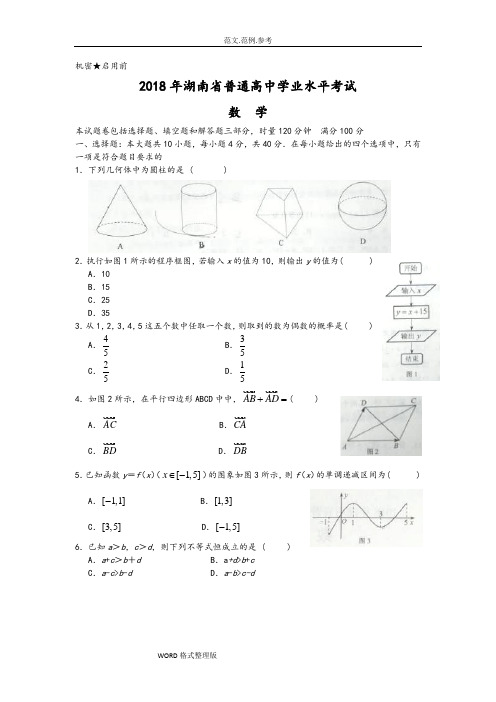
机密★启用前2018年湖南省普通高中学业水平考试数 学本试题卷包括选择题、填空题和解答题三部分,时量120分钟 满分100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.下列几何体中为圆柱的是 ( )2.执行如图1所示的程序框图,若输入x 的值为10,则输出y 的值为( ) A .10 B .15 C .25 D .35 3.从1,2,3,4,5这五个数中任取一个数,则取到的数为偶数的概率是( )A .45 B .35 C .25 D .154.如图2所示,在平行四边形ABCD 中中,AB AD +=u u u r u u u r( )A .AC u u u rB .CA u u u rC .BD u u u r D .DB u u u r5.已知函数y =f (x )([1,5]x ∈-)的图象如图3所示,则f (x )的单调递减区间为( ) A .[1,1]- B .[1,3] C .[3,5] D .[1,5]-6.已知a >b ,c >d ,则下列不等式恒成立的是 ( ) A .a +c >b +d B .a +d >b +c C .a -c >b -d D .a -b >c-d7.为了得到函数cos()4y x π=+的图象象只需将cos y x =的图象向左平移 ( )A .12个单位长度 B .2π个单位长度 C .14个单位长度 D .4π个单位长度8.函数)1(log )(2-=x x f 的零点为( )A .4B .3C .2D .19.在△ABC 中,已知A =30°,B =45°,AC,则BC =( )A .12B.2 C.2 D .110.过点M (2,1)作圆C :22(1)2x y -+=的切线,则切线条数为( ) A .0 B .1 C .2 D .3二、填空题;本大题共5小题,每小题4分,共20分, 11.直线3y x =+在y 轴上的截距为_____________。
湖南省普通高中学业水平考试真题清晰

湖南省普通高中学业水平考试真题清晰TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-2018年湖南省普通高中学业水平考试真题本试题卷包括选择题、填空题和解答题三部分,共4页.时量120分钟,满分100分一、选择题:本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列几何体中为圆柱的是 ( )2.执行如图1所示的程序框图,若输入x 的值为10,则输出y 的值为 ( )3.从1,2,3,4,5这五个数中任取一个数,则取到的数为偶数的概率是( ) A.54 B.53C.52D.514.如图2所示,在平行四边形ABCD 中,=+AD AB ( ) A.B.C.D.5.已知函数()x f y =([]5,1-∈x )的图象如图3所示,则()x f 的单调减区间为( )A.[]1,1-B.[]3,1C.[]5,3 D .[]5,1-6.已知d c b a >>,,则下列不等式恒成立的是 ( ) A.d b c a +>+ B.c b d a +>+ C.d b c a ->-D.d c b a ->-7.为了得到函数⎪⎭⎫⎝⎛+=4cos πx y 的图象,只需将x y cos =的图象向左平移( )A.21个单位长度 B.2π个单位长度 C.41个单位长度 D.4π个单位长度8.函数()()1log 2-=x x f 的零点为( )C.2D.19.在ABC ∆中,已知︒=︒=45,30B A ,2=AC ,则=BC ( ) A.21B.22 C.2310.过点()1,2M 作圆C :()2122=+-y x 的切线,则切线条数为 ( )C.2二、填空题:本大题共5小题,每小题4分,共20分。
11.直线3+=x y 在y 轴上的截距为________.12.比较大小:︒25sin ___︒23sin (填“>”或“<”). 13.已知集合{}2,1=A ,{}x B ,1-=,若{}2=B A ,则=x ________. 14.某工厂甲、乙两个车间生产了同一种产品,数量分别是60件、40件,现用分层抽样的方法抽取一个容量为n 的样本进行质量检测,已知从甲车间抽取6件产品,则=n ________.15.设y x ,满足不等式组⎪⎩⎪⎨⎧≥+≤≤222y x y x ,则y x z -=2的最小值为________.三、解答题:本大题共5小题,共40分。
湖南省2018年(长郡中学)普通高中学业水平模拟考试(三)数学试题(PDF版,含答案)

数学试题卷% 长郡版& 第$ 共 % 页& ! 页%
本小题满分3分 ! 3 ! 已知数列' 的通项公式* % * # 0) 0 0() & ! 0( 0( % & 求* ! * #! /# % & 若* 的第!项和第#项! 求数列' 的通项公式+ # * + + #! / 分别是等比数列' 0( 0( 0!
# +" ## ," 4 "( "( ' 8 % $ 若*( 则 & ! $ + ( ' 8 % , ( 9 6 $ : ' 8 %
!
-" 5 6 7 # "( -" *# , + #
# ) # ." 4 ) 4 "(
+" + *# , #
," , *# + #
." , + * # #
已知函数- 的图象与 # 轴的两个相邻交点的距离等于 ! ' ! # ( 7 ; < #)槡 $ 5 6 7 # &' 若将函数"( 的图象向左平移 个单位得到函数"( 的图象 则在下列区 # # - . % 0 间中使"( 是减函数的是 # . 1 ," -"' # %# % $ 二 填空题 本大题共/小题 每小题%分 满分# '分! +" ) ' $
本小题满分3分 ! 1 !
# % 5 6 7 ? @ < ) 7 ; < & 已知-% ( & 5 6 7 ) ! # % & 求-% 的最大值# ! &
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
★启用前
2018年省普通高中学业水平考试
数学
本试题卷包括选择题、填空题和解答题三部分,时量120分钟满分100分
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.下列几何体中为圆柱的是 ( )
2.执行如图1所示的程序框图,若输入x的值为10,则输出y的值为( ) A.10
B.15
C.25
D.35
3.从1,2,3,4,5这五个数中任取一个数,则取到的数为偶数的概率是( )
A.4
5
B.
3
5
C.2
5
D.
1
5
4.如图2所示,在平行四边形ABCD中中,AB AD
+=( )
A.AC B.CA
C.BD D.DB
5.已知函数y=f(x)([1,5]
x∈-)的图象如图3所示,则f(x)的单调递减区间为( ) A.[1,1]
- B.[1,3]
C.[3,5] D.[1,5]
-
6.已知a>b,c>d,则下列不等式恒成立的是 ( )
A.a+c>b+d B.a+d>b+c
C.a-c>b-d D.a-b>c-d
7.为了得到函数cos()4
y x π
=+的图象象只需将cos y x =的图象向左平移 ( )
A .
12个单位长度 B .2π
个单位长度 C .14个单位长度 D .4
π
个单位长度
8.函数)1(log )(2-=x x f 的零点为( )
A .4
B .3
C .2
D .1
9.在△ABC 中,已知A =30°,B =45°,AC
,则BC =( )
A .
1
2
B
.2 C
.2 D .1
10.过点M (2,1)作圆C :2
2
(1)2x y -+=的切线,则切线条数为( ) A .0 B .1 C .2 D .3
二、填空题;本大题共5小题,每小题4分,共20分, 11.直线3y x =+在y 轴上的截距为_____________。
12.比较大小:sin25°_______sin23°(填“>”或“<”) 13.已知集合{}{}1,2,1,A B x ==-.若{}2A
B =,则x =______。
14.某工厂甲、乙两个车间生产了同一种产品,数量分别为60件、40件,现用分层抽样方法抽取一个容量为n 的样本进行质量检测,已知从甲车间抽取了6件产品,则n =_____。
15.设x ,y 满足不等等式组⎪⎩
⎪
⎨⎧≥+≤≤222y x y x ,则z =2x -y 的最小值为________。
三、解答题:本大题共5小题,共40分,解答应写出文字说明、证明过程或演步 16.(本小题满分6分)
已知函数1
()(0)f x x x x
=+≠ (1)求(1)f 的值
(2)判断函数()f x 的奇偶性,并说明理由.
某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食堂用餐的满意度进行评分.根据学生对食堂用餐满意度的评分,得到如图4所示的率分布直方图, (1)求顺率分布直方图中a 的值
(2)规定:学生对食堂用餐满意度的评分不低于80分为“满意”,试估计该校在食堂
用餐的3000名学生中“满意”的人数。
18.(本小题满分8分)
已知向量22
(sin ,cos ),(
,)22
a x x
b == (1)若a b =,求tan x 的值
(2)设函数()2f x a b =⋅+,求()f x 的值域,
如图5所示,四棱锥P -ABCD 的底面是边长为2的正方形、PA ⊥底面ABCD . (1)求证:CD ⊥平面PAD ; (2)若E 为PD 的中点,三棱锥C -ADE 的体积为2
3
,求四棱锥P -ABCD 的侧面积
20.(本小题满分10分)
在等差数列{}n a 中,已知1231,5a a a =+=。
(1)求n a
(2)设2n a
n n b a =⋅,求数列{}n b 的前n 项和n T
(3)对于(2)中的n T ,设21
2
2n n n a T c +-=,求数列{}n c 中的最大项。
参考答案
二、填空题
11.3 12.> 13.2 14. .10 15.2- 三、解答题 16. 解:(1)f (1)=2 (2)定义域为(,0)
(0,)-∞+∞,11
()()()f x x x f x x x
-=-+
=-+=-- 所以()f x 为奇函数。
17.解(1)由频率分布直方图的矩形面积和为1可知:
(0.0400.0300.0150.005)101a ++++⨯=
所以0.010a =
(2)样本中不低于80分的频率为(0.0400.030)100.7+⨯=
由样本估计总体可得3000名学生中不低于80分的频率为约为0.7,所以满意的人数
为0.730002100⨯=。
故该校在校食堂用餐的3000名学生中“满意”的人数约为2100人。
18.解:(1)a b =则sin cos 2
x x ==
所以sin tan 1cos x
x x
=
=
(2)2()2cos 2sin()2224
f x a b x x x π=⋅+=++=++ 因为sin()[1,1]4
x π
+∈-,所以()f x 的值域为[1,3]。
