2017年广东省深圳市龙岗区七年级下学期数学期末试卷与解析答案
【3套打包】深圳龙岗中学最新七年级下册数学期末考试试题(含答案)

最新七年级(下)期末考试数学试题【含答案】一、选择题(本大题共6小题,每小题3分,共18分) 1、下列实数是无理数的是( )A 、-1B 、0C 、3.14D 、 5 2、如图,能判断AB ∥CD 的条件是( )A 、∠1=∠2B 、∠3=∠4C 、∠1+∠3=180°D 、∠3+∠4=180° 3、下列结论正确的是( )A 、-(-6)2 =-6B 、(- 3 )2=9C 、(-16)2 =±16D 、-(-1625 )2=16254、已知二元一次方程3x +y =0的一个解是⎩⎨⎧x =ay =b,其中a ≠0,那么( )A 、b a >0B 、b a =0C 、ba <0 D 、以上都不对5、下列说法错误的是( )A 、不等式x -3>2的解是x >5B 、不等式x <3的整数解有无数个C 、x =0是不等式2x <3的一个解D 、不等式x +3<3的整数解是0 6、如图,矩形BCDE 的各边分别平等于x 轴或y 轴,物体甲 和物体乙分别由点A (2,0)同时出发,沿矩形BCDE 的边 作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动, 物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体 运动后第26次相遇地点的坐标是( )A 、(2,0)B 、(-1,-1)C 、(-2,1)D 、(-1,1) 二、填空题(本大题共8小题,每小题3分,共24分) 7、1的平方根是 。
8、一个二元一次方程的一个解是⎩⎨⎧x =2y =-1,则这个方程可以是 。
(只要求写出一个)9、如图,在△ABC 中,∠A =90°,点D 在AC 边上,DE ∥BC , 若∠1=155°,则的度数∠B 为 。
10、某次足球比赛的记分规则如下:胜一场得3分,平一场得1分,负一场是0分。
某队踢了14场,其中负5场,共得19分。
若设胜了x 场,平了y 场, 则可列出方程组: 。
深圳市龙岗区2017-2018学年七年级下学期数学期末考试试卷(北师大版)

深圳市2017-2018学年第二学期龙岗区期末调研测试卷七年级 数学第一部分(选择题,共36分)一、选择题(本题共有12小题,每小题3分,共36分。
)1.下列运算正确的是( )A 、()523x x = B 、632x x x =⋅ C 、 23x x x =÷ D 、 ()y x y x 422=2.下面有4个汽车标志图案,其中••是不轴对称图形的是( )3.0.000043米用科学记数法表示,正确的是( )A 、4103.4-⨯ B 、5103.4-⨯ C 、6103.4-⨯ D 、51043-⨯ 4.如图1,直线a ∥b ,直线c 分别于a 、b 相交,∠1=50º,则∠2的度数为( ) A 、150º B 、130º C 、100º D 、50º5.如图2,已知B 、E 、C 、F 在同一直线上,BE=CF ,AB ∥DE ,则下列条件中,••能不判断△ABC ≌△DEF 是的( )A 、AB=DEB 、∠A=∠DC 、AC ∥DFD 、AC=DF6.下列各幅图像中,可以大致反映成熟的苹果从树上掉下来的过程中(即落地前),速度随时间变化情况的是( )7.小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图3所示的统计图,则符合这一结果的实验可能是( )A .掷一枚质地均匀的硬币,正面朝上的概率B .从一个装有2个白球和1个红球(球除了颜色外,完全相同)的不透明袋子中任意摸出一球,摸到红球的概率C .从一幅去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率D .任意买一张电影票,座位号是2的倍数的概率8.如图4,BP 是∠MBN 的平分线,D 是BP 上一点,AD ⊥BN 于点A ,AD=3,C 是BM 上的一点,BC=5,则△BCD 的面积为( ) A 、7.5 B 、8 C 、10 D 、159.如一个三角形有两条边长分别为2和8,且周长为奇数,则第三条边的长度为( ) A 、7 B 、9 C 、17或19 D 、7或910.如图,过△ABC 的顶点A ,作BC 边上的高,以下作法正确的是( )11.一只小狗在如图5的方砖上走来走去,最终停在阴影方砖上的概率是( ) A .154 B .31 C .51 D .152 12.已知y x =-22,则()()x y y x x 201712017---的值为( ) A .2 B .0 C .-2 D .1第二部分(非选择题,共64分)二、填空题(每小题3分,共12分.). 13.计算:()()33-+x x =_________________。
广东省深圳市七年级初一第二学期期末数学试卷(有答案详解)

广东省深圳市七年级第二学期期末数学试卷一、选择题(本题有12小题,每题3分,共36分)1.如图所示的是四个物理实验工具的简图,从左到右依次是小车、弹簧、钩码、三极管,其中是轴对称图形的是()A.小车B.弹簧C.钩码D.三极管2.据外汇局网站5月16日消息:国家外汇管理局统计数据显示,2016年4月,银行结售汇逆差1534亿元人民币,其中“1534亿”用科学记数法表示为()A.1.534×103B.1.534×1011C.15.34×108D.1534×1083.下列计算正确是()A.a3+a2=a5 B.a8÷a4=a2C.(a4)2=a8D.(﹣a)3(﹣a)2=a54.下列算式中正确的是()A.3a3÷2a=B.﹣0.00010=(﹣9999)0C.3.14×10﹣3=0.000314 D.5.下列语句中错误的是()A.数字0也是单项式B.单项式﹣a的系数与次数都是1C.xy是二次单项式D.﹣的系数是﹣6.如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=45°,那么∠1的度数为()A.45°B.35°C.25°D.15°7.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是()A.(SAS)B.(SSS)C.(ASA)D.(AAS)8.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.9.若等腰三角形的周长为26cm,一边为11cm,则腰长为()A.11 cm B.7.5 cmC.11 cm或7.5 cm D.以上都不对10.如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是()A.5m B.15m C.25m D.30m11.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DE=2,AC=3,则△ADC的面积是()A.3 B.4 C.5 D.612.某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是()A.当旅游人数为50时,则门票价格为70元/人B.当旅游人数为50或者100的时,门票价格都是70元/人C.两个班级都是40名学生,则两个班联合起来购票比分别购票要便宜D.当人数增多时,虽然门票价格越来越低,但是购票总费用会越来越高二、填空题(本题有4小题,每题3分,共12分)13.5m2n(2n+3m﹣n2)的计算结果是次多项式.14.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用a、b的代数式表示).15.若a+b=3,ab=2,则a2+b2=.16.如图,有一枚质地均匀的正十二面体形状的骰子,其中1个面标有“0”,1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,其余的面标有“5”,将这枚骰子掷出后:①”6”朝上的概率是0;②“5”朝上的概率最大;③“0”朝上的概率和“1”朝上的概率一样大;④“4”朝上的概率是.以上说法正确的有.(填序号)三、解答题(本大题有7题,其中17题15分,18题6分,19题8分,20题7分,21题6分,22题4分,23题6分,共52分)17.(1)计算:(2x2y)3÷6x3y2(2)用简便方法计算:1232﹣122×124.(3)先化简,再求值:x(x﹣3y)+(2x+y)(2x﹣y)﹣(2x﹣y)(x﹣y),其中x=﹣2,.18.观察设计(1)观察如图的①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;(2)借助如图之⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与如图的①~④的图案不能重合)19.如图,已知,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.请完成证明过程.20.如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?21.将长为40cm,宽为15cm的长方形白纸,按如图所示的方法粘合起来,粘合部分宽为5cm.(1)根据如图,将表格补充完整.(2)设x张白纸粘合后的总长度为ycm,则y与x之间的关系式是什么?(3)你认为多少张白纸粘合起来总长度可能为2016cm吗?为什么?22.先阅读理解下面的例题,再按要求解答下列问题.求代数式y2+4y+8的最小值.解:y2+4y+8=y2+4y+4+4=(y+2)2+4∵(y+2)2≥0,∴(y+2)2+4≥4∴y2+4y+8的最小值是4.(1)求代数式m2+m+1的最小值;(2)求代数式4﹣x2+2x的最大值.23.如图①②,点E、F分别是线段AB、线段CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)线段AD和线段BC有怎样的数量关系?请说明理由;(2)当DG⊥GC时,试判断直线AD和直线BC的位置关系,并说明理由.广东省深圳市七年级第二学期期末数学试卷一、选择题(本题有12小题,每题3分,共36分)1.如图所示的是四个物理实验工具的简图,从左到右依次是小车、弹簧、钩码、三极管,其中是轴对称图形的是()A.小车B.弹簧C.钩码D.三极管【考点】轴对称图形.【分析】根据轴对称图形的概念对各选项分析判断即可得解.【解答】解:A、是轴对称图形,故本选项正确;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误.故选A.2.据外汇局网站5月16日消息:国家外汇管理局统计数据显示,2016年4月,银行结售汇逆差1534亿元人民币,其中“1534亿”用科学记数法表示为()A.1.534×103B.1.534×1011C.15.34×108D.1534×108【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于1534亿有12位,所以可以确定n=12﹣1=11.【解答】解:1534亿=1543 0000 0000=1.534×1011,故选:B.3.下列计算正确是()A.a3+a2=a5 B.a8÷a4=a2C.(a4)2=a8D.(﹣a)3(﹣a)2=a5【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.【分析】直接利用同底数幂的乘除运算法则以及合并同类项法则和幂的乘方运算法则分别化简求出答案.【解答】解:A、a3+a2无法计算,故此选项错误;B、a8÷a4=a4,故此选项错误;C、(a4)2=a8,正确;D、(﹣a)3(﹣a)2=﹣a5,故此选项错误;故选:C.4.下列算式中正确的是()A.3a3÷2a=B.﹣0.00010=(﹣9999)0C.3.14×10﹣3=0.000314 D.【考点】整式的除法;零指数幂;负整数指数幂.【分析】分别利用整式的除法运算法则以及零指数幂的性质和负整数指数的幂的性质分别化简求出答案.【解答】解:A、3a3÷2a=a2,故此选项错误;B、﹣0.00010=﹣1,(﹣9999)0=1,故此选项错误;C、3.14×10﹣3=0.00314,故此选项错误;D、(﹣)﹣2=9,正确.故选:D.5.下列语句中错误的是()A.数字0也是单项式B.单项式﹣a的系数与次数都是1C.xy是二次单项式D.﹣的系数是﹣【考点】单项式.【分析】根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.单独一个数字也是单项式.【解答】解:单独的一个数字也是单项式,故A正确;单项式﹣a的系数应是﹣1,次数是1,故B错误;xy的次数是2,符合单项式的定义,故C正确;﹣的系数是﹣,故D正确.故选B.6.如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=45°,那么∠1的度数为()A.45°B.35°C.25°D.15°【考点】平行线的性质.【分析】如图,利用平行线的性质可得到∠2=∠3,再由直角三角形的性质可求得∠1.【解答】解:如图,由题意可知BD∥CE,∴∠3=∠2=45°,∵∠A=30°,∠ACB=90°,∴∠ABC=60°,∴∠1=60°﹣∠3=15°,故选D.7.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是()A.(SAS)B.(SSS)C.(ASA)D.(AAS)【考点】作图—基本作图;全等三角形的判定与性质.【分析】我们可以通过其作图的步骤来进行分析,作图时满足了三条边对应相等,于是我们可以判定是运用SSS,答案可得.【解答】解:作图的步骤:①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;②任意作一点O′,作射线O′A′,以O′为圆心,OC长为半径画弧,交O′A′于点C′;③以C′为圆心,CD长为半径画弧,交前弧于点D′;④过点D′作射线O′B′.所以∠A′O′B′就是与∠AOB相等的角;作图完毕.在△OCD与△O′C′D′,,∴△OCD≌△O′C′D′(SSS),∴∠A′O′B′=∠AOB,显然运用的判定方法是SSS.故选:B.8.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.【考点】三角形的角平分线、中线和高.【分析】根据三角形高线的定义:过三角形的顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.【解答】解:为△ABC中BC边上的高的是A选项.故选A.9.若等腰三角形的周长为26cm,一边为11cm,则腰长为()A.11 cm B.7.5 cmC.11 cm或7.5 cm D.以上都不对【考点】等腰三角形的性质;三角形三边关系.【分析】题中给出了周长和一边长,而没有指明这边是否为腰长,则应该分两种情况进行分析求解.【解答】解:①当11cm为腰长时,则腰长为11cm,底边=26﹣11﹣11=4cm,因为11+4>11,所以能构成三角形;②当11cm为底边时,则腰长=(26﹣11)÷2=7.5cm,因为7.5+7.5>11,所以能构成三角形.故选C.10.如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是()A.5m B.15m C.25m D.30m【考点】三角形三边关系.【分析】根据三角形的三边关系定理得到5<AB<25,根据AB的范围判断即可.【解答】解:连接AB,根据三角形的三边关系定理得:15﹣10<AB<15+10,即:5<AB<25,则AB的值在5和25之间.故选B.11.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DE=2,AC=3,则△ADC的面积是()A.3 B.4 C.5 D.6【考点】角平分线的性质.【分析】过点D作DF⊥AC于F,根据角平分线上的点到角的两边距离相等可得DE=DF,再根据(1)中所求S△ACD=3列出方程求解即可.【解答】解:如图,过点D作DF⊥AC于F,∵AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,∴DE=DF=2.=AC•DF=×3×2=3,∴S△ACD故选A.12.某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是()A.当旅游人数为50时,则门票价格为70元/人B.当旅游人数为50或者100的时,门票价格都是70元/人C.两个班级都是40名学生,则两个班联合起来购票比分别购票要便宜D.当人数增多时,虽然门票价格越来越低,但是购票总费用会越来越高【考点】函数的图象.【分析】根据景点门票价格情况图容易得出选项A、B、D错误,选项C正确;即可得出结论.【解答】解:根据题意得:当旅游人数不超过50人时,则门票价格为80元/人;当旅游人数为50﹣100时,门票价格都是70元/人;若两个班级都是40名学生,则两个班联合起来购票为70元/人,比分别购票要便宜;∵99×70>101×60,∴当人数增多时,虽然门票价格越来越低,但是购票总费用也不会越来越高;∴选项A、B、D错误,选项C正确;故选:C.二、填空题(本题有4小题,每题3分,共12分)13.5m2n(2n+3m﹣n2)的计算结果是五次多项式.【考点】单项式乘多项式;多项式.【分析】原式利用单项式乘以多项式法则计算即可得到结果.【解答】解:5m2n(2n+3m﹣n2)=10m2n2+15m3n﹣5m2n3,则计算结果是五次多项式,故答案为:五14.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是ab(用a、b的代数式表示).【考点】平方差公式的几何背景.【分析】利用大正方形的面积减去4个小正方形的面积即可求解.【解答】解:设大正方形的边长为x1,小正方形的边长为x2,由图①和②列出方程组得,解得,②的大正方形中未被小正方形覆盖部分的面积=()2﹣4×()2=ab.故答案为:ab.15.若a+b=3,ab=2,则a2+b2=5.【考点】完全平方公式.【分析】根据a2+b2=(a+b)2﹣2ab,代入计算即可.【解答】解:∵a+b=3,ab=2,∴a2+b2=(a+b)2﹣2ab=9﹣4=5.故答案为:5.16.如图,有一枚质地均匀的正十二面体形状的骰子,其中1个面标有“0”,1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,其余的面标有“5”,将这枚骰子掷出后:①”6”朝上的概率是0;②“5”朝上的概率最大;③“0”朝上的概率和“1”朝上的概率一样大;④“4”朝上的概率是.以上说法正确的有①③④.(填序号)【考点】概率的意义.【分析】正十二面每个面向上的机会相同,因而根据概率公式解答即可.【解答】解:没有6的面,所以①”6”朝上的概率是0,正确;②“5”朝上的概率=概率小,故②错误;③“0”朝上的概率=和“1”朝上的概率=一样大,正确;④“4”朝上的概率是.正确;故答案为:①③④三、解答题(本大题有7题,其中17题15分,18题6分,19题8分,20题7分,21题6分,22题4分,23题6分,共52分)17.(1)计算:(2x2y)3÷6x3y2(2)用简便方法计算:1232﹣122×124.(3)先化简,再求值:x(x﹣3y)+(2x+y)(2x﹣y)﹣(2x﹣y)(x﹣y),其中x=﹣2,.【考点】整式的混合运算—化简求值.【分析】(1)原式利用幂的乘方与积的乘方运算法则计算即可得到结果;(2)原式变形后,利用平方差公式计算即可得到结果;(3)原式利用单项式乘以多项式,平方差公式计算得到结果,将x与y的值代入计算即可求出值.【解答】解:(1)原式=8x6y3÷6x3y2=x3y;(2)原式=1232﹣×=1232﹣1232+1=1;(3)原式=x2﹣3xy+4x2﹣y2﹣2x2+2xy+xy﹣y2=3x2﹣2y2,当x=﹣2,y=﹣时,原式=12﹣=11.18.观察设计(1)观察如图的①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;(2)借助如图之⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与如图的①~④的图案不能重合)【考点】利用轴对称设计图案.【分析】(1)利用已知图形的特征分别得出其共同的特征;(2)利用(1)所写的特征画出符合题意的图形即可.【解答】解:(1)答案不唯一,例如,所给的四个图案具有的共同特征可以是:①都是轴对称图形;②面积都等于四个小正方形的面积之和;③都是直线型图案;④图案中不含钝角等等.只要写出两个即可.(2)答案不唯一,只要设计的图案同时具有所给出的两个共同特征,均正确,例如,同时具备特征①、②的部分图案如图:19.如图,已知,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.请完成证明过程.【考点】平行线的判定与性质.【分析】求出∠1=∠3,求出∠2=∠3,根据平行线的判定得出AB∥CD,根据平行线的性质得出∠A+∠ADC=180°,∠C+∠ABC=180°,即可得出答案.【解答】证明:∵BE、DF分别平分∠ABC、∠ADC,∴∠1=∠ABC,∠3=∠ADC(角平分线的定义),∵∠ABC=∠ADC,∴∠1=∠3(等量的代换),∵∠1=∠2,∴∠2=∠3(等量代换),∴AB∥DC(内错角相等,两直线平行),∴∠A+∠ADC=180°,∠C+∠ABC=180°(两直线平行,同旁内角互补)∴∠A=∠C(等量代换).20.如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?【考点】全等三角形的判定与性质.【分析】先求出AF=CE,再由平行线的性质得出∠A=∠C,由AAS证明△ADF≌△CBE,得出对应边相等即可.【解答】解:AD=BC,理由如下:∵AE=CF,∴AF=CE,∵AD∥BC,∴∠A=∠C,在△ADF和△CBE中,,∴△ADF≌△CBE(AAS),∴AD=BC.21.将长为40cm,宽为15cm的长方形白纸,按如图所示的方法粘合起来,粘合部分宽为5cm.(1)根据如图,将表格补充完整.(2)设x张白纸粘合后的总长度为ycm,则y与x之间的关系式是什么?(3)你认为多少张白纸粘合起来总长度可能为2016cm吗?为什么?【考点】函数关系式;函数值.【分析】(1)根据题意找出白纸张数跟纸条长度之间的关系,然后求解填空即可;(2)x张白纸黏合,需黏合(x﹣1)次,重叠5(x﹣1)cm,所以总长可以表示出来;(3)解当y=2016时得到的方程,若x为自变量取值范围内的值则能,反之不能.【解答】解:(1)75,180;(2)根据题意和所给图形可得出:y=40x﹣5(x﹣1)=35x+5.(3)不能.把y=2016代入y=35x+5,解得,不是整数,所以不能.22.先阅读理解下面的例题,再按要求解答下列问题.求代数式y2+4y+8的最小值.解:y2+4y+8=y2+4y+4+4=(y+2)2+4∵(y+2)2≥0,∴(y+2)2+4≥4∴y2+4y+8的最小值是4.(1)求代数式m2+m+1的最小值;(2)求代数式4﹣x2+2x的最大值.【考点】配方法的应用.【分析】(1)利用配方法把原式变形,根据非负数的性质解答;(2)利用配方法把原式变形,根据非负数的性质解答即可.【解答】解:(1)m2+m+1==,所以m2+m+1的最小值是(2)4﹣x2+2x=﹣x2+2x﹣1+5=﹣(x﹣1)2+5≤5所以4﹣x2+2x的最大值是5.23.如图①②,点E、F分别是线段AB、线段CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)线段AD和线段BC有怎样的数量关系?请说明理由;(2)当DG⊥GC时,试判断直线AD和直线BC的位置关系,并说明理由.【考点】全等三角形的判定与性质.【分析】(1)由GF垂直平分DC,可得GD=GC,同理可得,GA=GB,又由∠AGD=∠BGC,即可证得△ADG≌△BCG(SAS),继而证得结论;(2)首先延长AD,与CG相交于点O、与BC的延长线相交于点Q,由(1)可证得∠ADG=∠BCG,继而可求得∠Q的度数,【解答】解:(1)AD=BC.理由:∵GF垂直平分DC,∴GD=GC同理,GA=GB,在△ADG和△BCG中,,∴△ADG≌△BCG(SAS),∴AD=BC;(2)AD⊥BC.理由:延长AD,与CG相交于点O、与BC的延长线相交于点Q.∵△ADG≌△BCG,∴∠ADG=∠BCG,则∠GDO=∠QCO,∴∠QDC+∠QCD=∠DQC+∠DCG+∠QCG=∠QDC+∠GDQ+∠DCG=∠CDG+∠DCG,∵DG⊥GC,∴∠QDC+∠QCD=∠CDG+∠DCG=90°,∴∠Q=90°,∴AD⊥BC.第21页(共21页)。
【最新】广东省深圳市龙岗区七年级数学下学期期末质量监测试题答案北师大版

1 广东省深圳市龙岗区2017-2018学年七年级数学下学期期末质量监测试题答案一、选择题(本题共有12小题,每小题3分,共36分.)分.)1 2 3 4 5 6 7 8 9 10 11 12 ADDCABADBACB二、填空题(每小题3分,共12分)分) 13. x x 22- 14.1415.16 16. 3cm 三、解答题(本题共7小题,共52分.)分.)17.(1)17.(1)原原式=9x 4y 2÷(6x 2y) ………………………………………2分=……………………………………………………4分(2) (2) 原式原式原式=1+4-=1+4-=1+4-1…………………………………………………21…………………………………………………2分=4………………………………………………………4分(3) (3)原式原式原式=a =a 22+4a+4-3(a 22-1)+2a 22+2a………………………………1分= a 2+4a+4-3a 2+3+2a 2+2a…………………………………2分=6a+7……………………………………………………3分 当a=-5时,原式时,原式=-30+7=-=-30+7=-=-30+7=-23……………………………423……………………………4分1818.(.(.(66分)填空:把下面的推理过程补充完整,并在括号内注明理由.分)填空:把下面的推理过程补充完整,并在括号内注明理由. 如图,已知∠如图,已知∠A=A=A=∠∠F ,∠,∠C=C=C=∠∠D ,试说明BD BD∥∥CE CE.. 解:∵∠解:∵∠A=A=A=∠∠F (F (已知已知已知) )∴DF DF∥∥AC ( AC ( 内错角相等,内错角相等,两直线平行两直线平行) ) ∴∠∴∠D=D=D=∠∠ 1 ( 1 (两直线平行,内错角相等两直线平行,内错角相等两直线平行,内错角相等) )∵∠∵∠C=C=C=∠∠D(D(已知已知已知) ) ∴∠∴∠1=1=1=∠∠ C ( C (等量代换等量代换等量代换 ) )∴BD BD∥∥CE(CE(同位角相等,两直线平行同位角相等,两直线平行同位角相等,两直线平行))(每空1分)分)EDB CAF1BD FACE2 19.19.解:解:解:AE AE AE==CE.理由如下:…………………………………理由如下:…………………………………11分 ∵AB AB∥∥CF CF ∴∠∴∠∴∠A A =∠=∠ACF ACF ACF …………………………………2…………………………………2分 在△在△ADE ADE 与△与△CFE CFE 中∠∠A =∠=∠ACF ACF ACF(已证)(已证)(已证) ∠∠AED AED=∠=∠=∠CEF CEF CEF(对顶角相等)(对顶角相等)(对顶角相等) DE DE==FE FE(已知)(已知)(已知)∴△∴△AED AED AED≌△≌△≌△CEF(AAS)CEF(AAS)CEF(AAS)………………………………………5………………………………………5分∴AE AE=CE ……………………………………………………=CE ……………………………………………………=CE ……………………………………………………66分(其他方法正确也给满分)分(其他方法正确也给满分)20. 20. 解:(解:(解:(11)①甲,甲,)①甲,甲,22;(每空1分,共3分)分)(2)甲在4﹣7时的生产速度最快,…………………………………4分∵,∴他在这段时间内每小时生产零件10个.……………………个.……………………66分21. 21. ((1)6……………………………………………………………………………3分……3分 (2)如图,画出一种即给分.………………………………………………………6分)如图,画出一种即给分.………………………………………………………6分22.22.解:(解:(解:(11)证明:∵∠)证明:∵∠1=1=1=∠∠2, ∴∠∴∠1+1+1+∠∠MAC=MAC=∠∠2+∠NAC NAC,,∴∠∴∠BAC=BAC=BAC=∠∠DAE DAE,………………………1,………………………1分 在△在△ABC ABC 和△和△ADE ADE 中,中,,∴△∴△ABC ABC ABC≌△≌△≌△ADE ADE ADE((SAS SAS);…………………………………………4);…………………………………………4分(2)图中与∠)图中与∠11、∠、∠22相等的角有∠相等的角有∠MFD MFD 和∠和∠NFC NFC NFC.…………………6.…………………6分(写出一个给1分)分)23.23.((1)α+β=γ…………………………………………1分 过点P 作FG FG∥∥l 1,∴∠,∴∠CPG=CPG=CPG=∠∠β……………………2分3 ∵l 1∥l 2,FG FG∥∥l 1∴FG FG∥∥l 2, ∴∠∴∠GPD=GPD=GPD=∠∠α……………………………………………………………………………………33分 ∵∠γ=∠CPG+CPG+∠∠DPG∴∠γ=∠α+∠β……………………………………………………………………………………44分 (2)当AP=3时,时,ACP ACP ACP≌△≌△≌△BPD BPD BPD,,理由如下:……………………………………………理由如下:……………………………………………55分 ∵AP =3,AB=9AP =3,AB=9,, ∴PB=AC=6,BD=A P=3 ∵AC AC⊥⊥MN MN,∴∠CAP=90°,∴∠CAP=90°,∴∠CAP=90° ∵l 1∥l 2 ∴∠∴∠CAP+CAP+CAP+∠PBD=180°∠PBD=180°∠PBD=180°∴∠∴∠CAP=CAP=CAP=∠PBD=90°…………………………………6∠PBD=90°…………………………………6分 在△在△AEP AEP 与△与△BPD BPD 中 PB=AC ∠∠CAP=CAP=∠∠PBD BD=AP∴△∴△CAP CAP CAP≌△≌△≌△PBD PBD (SAS SAS)……………………………7)……………………………7分 (3)3)PC PC PC==PD PD,………………………………………8,………………………………………8分 PC PC⊥PD…………………………………………………9⊥PD…………………………………………………9分 ∵△∵△CAP CAP CAP≌△≌△≌△PBD PBD ∴PC PC==PD, PD, ∠∠ACP=ACP=∠∠BPD ∵∠∵∠ACP+ACP+ACP+∠ACP=90°∠ACP=90°∠ACP=90° ∴∠∴∠BPD+BPD+BPD+∠ACP=90°∠ACP=90°∠ACP=90° ∴∠∴∠CPD=180CPD=180CPD=180°°-9-90°0°0°=9=9=90°0°0°∴P C ⊥PD PD………………………………………………10………………………………………………10分20XX—019学年度第一学期生物教研组工作计划指导思想以新一轮课程改革为抓手,更新教育理念,积极推进教学改革。
深圳龙岗建文中学人教版(七年级)初一下册数学期末测试题及答案

深圳龙岗建文中学人教版(七年级)初一下册数学期末测试题及答案一、选择题1.下列运算中,正确的是( )A .(ab 2)2=a 2b 4B .a 2+a 2=2a 4C .a 2•a 3=a 6D .a 6÷a 3=a 22.已知∠1与∠2是同位角,则( )A .∠1=∠2B .∠1>∠2C .∠1<∠2D .以上都有可能3.下列等式从左到右的变形属于因式分解的是( )A .a 2﹣2a+1=(a ﹣1)2B .a (a+1)(a ﹣1)=a 3﹣aC .6x 2y 3=2x 2•3y 3D .211()x x x x+=+ 4.如图所示的四个图形中,∠1和∠2不是同位角的是( )A .B .C .D .5.下列四个等式从左到右的变形是因式分解的是 ( )A .22()()a b a b a b +-=-B .2()ab a a b a -=-C .25(1)5x x x x +-=+-D .21()x x x x x+=+ 6.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,试利用上述规律判断算式:3+32+33+34+…+32020结果的末位数字是( )A .0B .1C .3D .77.科学家发现2019﹣nCoV 冠状肺炎病毒颗粒的平均直径约为0.00000012m .数据0.00000012用科学记数法表示为( )A .1.2×107B .0.12×10﹣6C .1.2×10﹣7D .1.2×10﹣8 8.下列运算正确的是( ) A .a 2·a 3=a 6B .a 5+a 3=a 8C .(a 3)2=a 5D .a 5÷a 5=1 9.若一个多边形的每个内角都等于与它相邻外角的2倍,则它的边数为( ) A .4B .5C .6D .8 10.△ABC 是直角三角形,则下列选项一定错误的是( )A .∠A -∠B=∠CB .∠A=60°,∠B=40°C .∠A+∠B=∠CD .∠A :∠B :∠C=1:1:2 二、填空题11.分解因式:m 2﹣9=_____.12.已知一个多边形的内角和与外角和的差是1260°,则这个多边形边数是 .13.若 a m =6 , a n =2 ,则 a m−n =________14.已知()4432234464a b a a b a b ab b +=++++,则()4a b -=__________. 15.若29x kx -+是完全平方式,则k =_____.16.计算:x (x ﹣2)=_____17.已知21x y =⎧⎨=⎩是方程2x ﹣y +k =0的解,则k 的值是_____. 18.如图,将长方形纸片ABCD 沿着EF ,折叠后,点D ,C 分别落在点D ,C '的位置,ED '的延长线交BC 于点G .若∠1=64°,则∠2等于_____度.19.已知代数式2x-3y 的值为5,则-4x+6y=______.20.已知x 2a +y b ﹣1=3是关于x 、y 的二元一次方程,则ab =_____. 三、解答题21.先化简,再求值:()()()()2212112,x x x x x --+---其中2230x x --=.22.如图,网格中每个小正方形边长为1,△ABC 的顶点都在格点上.将△ABC 向左平移2格,再向上平移3格,得到△A ′B ′C ′.(1)请在图中画出平移后的△A ′B ′C ′;(2)画出平移后的△A ′B ′C ′的中线B ′D ′(3)若连接BB ′,CC ′,则这两条线段的关系是________(4)△ABC 在整个平移过程中线段AB 扫过的面积为________(5)若△ABC 与△ABE 面积相等,则图中满足条件且异于点C 的格点E 共有______个 (注:格点指网格线的交点)23.如图1是一个长为 4a ,宽为 b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).(1)图2中的阴影部分的面积为 ;(2)观察图2请你写出 ()2a b +,()2a b -,ab 之间的等量关系是 ;(3)根据(2)中的结论,若 6x y +=,114x y ⋅=,则 x y -= ; (4)实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式()()2222252a b a b a ab b ++=++.在图形上把每一部分的面积标写清楚. 24.解方程或不等式(组)(1)24231x y x y +=⎧⎨-=⎩(2)2151132x x -+-≥ (3)312(2)15233x x x x +<+⎧⎪⎨-≤+⎪⎩ 25.当,m n 都是实数,且满足28m n =+,就称点21,2n P m +⎛⎫- ⎪⎝⎭为“爱心点”. (1)判断点()5,3A 、()4,8B 哪个点为“爱心点”,并说明理由;(2)若点(),4A a -、()4,B b 是“爱心点”,请判断A 、B 两点的中点C 在第几象限?并说明理由;(3)已知P 、Q 为有理数,且关于x 、y 的方程组333x y qx y q ⎧+=+⎪⎨-=-⎪⎩解为坐标的点(),B x y 是“爱心点”,求p 、q 的值.26.先化简,再求值(x-2)2+2(x+2)(x-4)-(x-3)(x+3);其中x=1.27.如图,在方格纸内将ABC ∆水平向右平移4个单位得到'''A B C ∆.(1)补全'''A B C ∆,利用网格点和直尺画图;(2)图中AC 与''A C 的位置关系是: ;(3)画出ABC ∆中AB 边上的中线CE ;(4)平移过程中,线段AC 扫过的面积是: .28.启秀中学初一年级组计划将m本书奖励给本次期中考试中取得优异成绩的n名同学,如果每人分4本,那么还剩下78本;如果每人分8本,那么最后一人分得的书不足8本,但不少于4本.最终,年级组讨论后决定,给n名同学每人发6本书,那么将剩余多少本书?【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【解析】【分析】直接利用积的乘方运算法则以及合并同类项法则和同底数幂的乘除运算法则分别分析得出答案.【详解】解:A、(ab2)2=a2b4,故此选项正确;B、a2+a2=2a2,故此选项错误;C、a2•a3=a5,故此选项错误;D、a6÷a3=a3,故此选项错误;故选:A.【点睛】此题主要考查了积的乘方运算以及合并同类项和同底数幂的乘除运算,正确掌握运算法则是解题关键.2.D解析:D【分析】根据同位角的定义和平行线的性质判断即可.解:∵只有两直线平行时,同位角才可能相等,∴当没有限定“两直线平行”时,已知∠1与∠2是同位角可以得出∠1=∠2或∠1>∠2或∠1<∠2,三种情况都有可能.故选:D.【点睛】本题考查了同位角的定义和平行线的性质,正确理解同位角的定义是解此题的关键,“两直线平行”这个前提条件易遗漏.3.A解析:A【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【详解】A、是因式分解,故A正确;B、是整式的乘法运算,故B错误;C、是单项式的变形,故C错误;D、没把一个多项式转化成几个整式积的形式,故D错误;故选:A.【点睛】本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式.4.C解析:C【分析】根据同位角的定义,逐一判断选项,即可得到答案.【详解】A. ∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角,不符合题意;B. ∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角,不符合题意;C. ∠1与∠2分别是四条直线中的两对直线的夹角,不符合同位角的定义,故它们不是同位角,符合题意;D. ∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角,不符合题意.故选C.【点睛】本题主要考查同位角的定义,掌握同位角的定义:“两条直线被第三条直线所截,在两条直线的同侧,在第三条直线的同旁的两个角,叫做同位角”,是解题的关键.5.B解析:B根据因式分解的概念:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,即可求解.【详解】解:根据因式分解的概念,A 选项属于整式的乘法,错误;B 选项符合因式分解的概念,正确;C 选项不符合因式分解的概念,错误;D 选项因式分解错误,应为2(1)x x x x +=+,错误.故选B .【点睛】本题目考查因式分解的概念,难度不大,熟练区分因式分解与整数乘法的关系是解题的关键.6.A解析:A【分析】观察所给等式发现规律末位数字为:3,9,7,1,3,9,7,…,每4个数一组循环,进而可得算式:3+32+33+34+…+32020结果的末位数字.【详解】解:观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,…,发现规律:末位数字为:3,9,7,1,3,9,7,…,每4个数一组循环,所以2020÷4=505,而3+9+7+1=20,20×505=10100.所以算式:3+32+33+34+…+32020结果的末位数字是0.故选:A .【点睛】本题考查了规律型-数字的变化类,解决本题的关键是根据数字的变化寻找规律.7.C解析:C【分析】用科学计数法将0.00000012表示为a×10-n 即可.【详解】解:0.00000012=1.2×10﹣7,故选:C .【点睛】本题考查用科学计数法表示较小的数,绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 8.D解析:D【分析】通过幂的运算公式进行计算即可得到结果.【详解】A .23235a a a a +==,故A 错误;B .538a a a +≠,故B 错误; C .()23326a a a ⨯==,故C 错误; D .5501a a a ÷==,故D 正确;故选:D .【点睛】本题主要考查了整式乘除中的幂的运算性质,准确运用公式是解题的关键.9.C解析:C【分析】设出外角的度数,表示出内角的度数,根据一个内角与它相邻的外角互补列出方程,解方程得到答案.【详解】解:设外角为x ,则相邻的内角为2x ,由题意得,2180x x +=︒,解得,60x =︒,多边形的边数为:360606÷︒=,故选:C .【点睛】本题考查的是多边形内、外角的知识,理解一个多边形的一个内角与它相邻外角互补是解题的关键.10.B解析:B【分析】根据三角形内角和定理得出∠A +∠B +∠C =180°,和选项求出∠C (或∠B 或∠A )的度数,再判断即可.【详解】解:A 、∵∠A ﹣∠B =∠C ,∴∠A =∠B +∠C ,∵∠A+∠B+∠C=180°,∴2∠A=180°,∴∠A=90°,∴△ABC是直角三角形,故A选项是正确的;B、∵∠A=60°,∠B=40°,∴∠C=180°﹣∠A﹣∠B=180°﹣60°﹣40°=80°,∴△ABC是锐角三角形,故B选项是错误的;C、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴2∠C=180°,∴∠C=90°,∴△ABC是直角三角形,故C选项是正确的;D、∵∠A:∠B:∠C=1:1:2,∴∠A+∠B=∠C,∵∠A+∠B+∠C=180°,∴2∠C=180°,∴∠C=90°,∴△ABC是直角三角形,故D选项是正确的;故选:B.【点睛】本题考查了三角形的内角和定理的应用,主要考查学生的推理能力和辨析能力.二、填空题11.(m+3)(m﹣3)【分析】通过观察发现式子可以写成平方差的形式,故用平方差公式分解,a2﹣b2=(a+b)(a﹣b).【详解】解:m2﹣9=m2﹣32=(m+3)(m﹣3).故答案为解析:(m+3)(m﹣3)【分析】通过观察发现式子可以写成平方差的形式,故用平方差公式分解,a2﹣b2=(a+b)(a﹣b).【详解】=m 2﹣32=(m +3)(m ﹣3).故答案为:(m +3)(m ﹣3).【点睛】此题考查的是因式分解,掌握利用平方差公式因式分解是解决此题的关键.12.12【解析】试题解析:根据题意,得(n-2)•180-360=1260,解得:n=11.那么这个多边形是十一边形.考点:多边形内角与外角.解析:12【解析】试题解析:根据题意,得(n-2)•180-360=1260,解得:n=11.那么这个多边形是十一边形.考点:多边形内角与外角.13.3【解析】.故答案为3.解析:3【解析】623m n m n a a a -=÷=÷=.故答案为3.14.a4-4a3b+6a2b2-4ab3+b4【分析】原式变形后,利用(a+b )4=a4+4a3b+6a2b2+4ab3+b4,即可得到(a-b )4的结果.【详解】解:根据题意得:(a-b )4=解析:a 4-4a 3b+6a 2b 2-4ab 3+b 4【分析】原式变形后,利用(a+b )4=a 4+4a 3b+6a 2b 2+4ab 3+b 4,即可得到(a-b )4的结果.解:根据题意得:(a-b )4=[a+(-b )]4=a 4-4a 3b+6a 2b 2-4ab 3+b 4,故答案为:a 4-4a 3b+6a 2b 2-4ab 3+b 4【点睛】此题考查了完全平方公式,熟练掌握公式是解本题的关键.15.【分析】根据两数的平方和加上或减去两数积的2倍,等于两数和或差的平方,即可求出的值 .【详解】解:∵是完全平方式,即.故答案为:.【点睛】此题考查了完全平方式, 熟练掌握完全平方公式解析:6±【分析】根据两数的平方和加上或减去两数积的2倍,等于两数和或差的平方,即可求出k 的值 .【详解】解:∵29x kx -+是完全平方式,即()2293x kx x -+=± 236k ∴=±⨯=±.故答案为:6±.【点睛】此题考查了完全平方式, 熟练掌握完全平方公式的结构特点是解本题的关键16.x2﹣2x【分析】根据单项式乘多项式法则即可求出答案.【详解】解:原式=x2﹣2x故答案为:x2﹣2x .【点睛】此题考查的是整式的运算,掌握单项式乘多项式法则是解决此题的关键. 解析:x 2﹣2x【分析】根据单项式乘多项式法则即可求出答案.【详解】解:原式=x 2﹣2x故答案为:x2﹣2x.【点睛】此题考查的是整式的运算,掌握单项式乘多项式法则是解决此题的关键.17.-3【分析】把x与y的值代入方程计算即可求出k的值.【详解】解:把代入方程得:4﹣1+k=0,解得:k=﹣3,则k的值是﹣3.故答案为:﹣3.【点睛】此题考查的是根据二元一次方程的解析:-3【分析】把x与y的值代入方程计算即可求出k的值.【详解】解:把21xy=⎧⎨=⎩代入方程得:4﹣1+k=0,解得:k=﹣3,则k的值是﹣3.故答案为:﹣3.【点睛】此题考查的是根据二元一次方程的解,求方程中的参数,掌握二元一次方程解的定义是解决此题的关键.18.128【分析】由ADBC,∠1=64°,根据两直线平行,内错角相等,可求得∠DEF的度数,然后由折叠的性质,可得∠FEG的度数,进而再利用两直线平行内错角相等得到∠2的度数.【详解】解:∵A解析:128【分析】由AD//BC,∠1=64°,根据两直线平行,内错角相等,可求得∠DEF的度数,然后由折叠的性质,可得∠FEG的度数,进而再利用两直线平行内错角相等得到∠2的度数.【详解】解:∵AD//BC,∠1=64°,∴∠DEF=∠1=64°,由折叠的性质可得∠FEG=∠DEF=64°,∴∠2=∠1+∠EFG=64°+64°=128°.故答案为:128.【点睛】本题主要考察两直线平行的性质、折叠的性质以及矩形的性质,重点在于利用已知条件找到角度之间的关系.19.-10【分析】原式前两项提取-2变形后,将已知代数式的值代入计算即可求出值.【详解】解:∵2x-3y=5,∴原式=-2(2x-3y)=-2×5=-10.故答案为:-10.【点睛】本题解析:-10【分析】原式前两项提取-2变形后,将已知代数式的值代入计算即可求出值.【详解】解:∵2x-3y=5,∴原式=-2(2x-3y)=-2×5=-10.故答案为:-10.【点睛】本题考查了代数式求值,熟练掌握运算法则是解题的关键.20.1【分析】根据题意可知该式是二元一次方程组,所以x、y的指数均为1,这样就可以分别求出a、b的值,代入计算即可.【详解】解:∵是关于x、y的二元一次方程,所以x、y的指数均为1∴2a=1,解析:1【分析】根据题意可知该式是二元一次方程组,所以x、y的指数均为1,这样就可以分别求出a、b 的值,代入计算即可.【详解】解:∵2a b-1x +y =3是关于x 、y 的二元一次方程,所以x 、y 的指数均为1∴2a =1,b-1=1,解得a =12,b =2, 则ab =122⨯=1, 故答案为:1.【点睛】该题考查了二元一次方程的定义,即含有两个未知量,且未知量的指数为1,将其代数式进行求解,即可求出答案.三、解答题21.6【解析】试题分析:先根据乘法公式和单项式乘以多项式的法则计算化简,根据化简的结果,将2230x x --=变形后整体代入计算即可.试题解析:原式=()()222441212x x x x x -+---- 222441222x x x x x =-+-+-+223x x =-+∵2230x x --=,∴223x x -=,∴原式=3+3=6.22.(1)画图见解析;(2)画图见解析;(3)平行且相等;(4)12;(5)9【分析】(1)利用网格特点和平移的性质分别画出点A 、B 、C 的对应点A′、B′、C′即可得到△A′B′C′;(2)找出线段A′C′的中点E′,连接B′E′;(3)根据平移的性质求解;(4)由于线段AB 扫过的部分为平行四边形,则根据平行四边形的面积公式可求解. (5)根据同底等高面积相等可知共有9个点.【详解】(1)△A ′B ′C ′如图所示;(2)B ′D ′如图所示;(3)BB′∥CC′,BB′=CC′;(4)线段AB 扫过的面积=4×3=12;(5)有9个点.【点睛】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.23.(1)2()b a -;(2)22()()4a b a b ab +=-+;(3)±5;(4)详见解析 【分析】(1)表示出阴影部分正方形的边长,然后根据正方形的面积公式列式即可;(2)根据大正方形的面积减去小正方形的面积等于四个小长方形的面积列式即可; (3)将(x -y )2变形为(x +y )2—4xy ,再代入求值即可;(4)由已知的恒等式,画出相应的图形,如图所示.【详解】解:(1)阴影部分为一个正方形,其边长为b -a ,∴其面积为:2()b a -,故答案为:2()b a -;(2)大正方形面积为:()2a b +小正方形面积为:2()b a -=2()a b -, 四周四个长方形的面积为:4ab ,∴22()()4a b a b ab +=-+,故答案为:22()()4a b a b ab +=-+;(3)由(2)知,22()()4x y x y xy +=-+, ∴22()()4x y x y xy -=+-, ∴2()4x y x y xy -=±+-2116454-⨯=±, 故答案为:±5;(4)符合等式()()2222252a b a b a ab b ++=++的图形如图所示,【点睛】本题考查了完全平方公式的几何背景,此类题目关键在于同一个图形的面积用两种不同的方法表示.24.(1)21x y =⎧⎨=⎩;(2)1x ≤-;(3)13x -≤< 【分析】(1)根据加减消元法解答;(2)根据解一元一次不等式的方法解答即可;(3)先分别解两个不等式,再取其解集的公共部分即得结果.【详解】解:(1)对24231x y x y +=⎧⎨-=⎩①②, ①×2,得248x y +=③,③-②,得7y =7,解得:y =1,把y =1代入①,得x +2=4,解得:x =2,∴原方程组的解为:21x y =⎧⎨=⎩; (2)不等式两边同乘以6,得()()2216351x x --≥+,去括号,得426153x x --≥+,移项、合并同类项,得1111x -≥,不等式两边同除以﹣1,得1x ≤-;(3)对()312215233x x x x ⎧+<+⎪⎨-≤+⎪⎩①②, 解不等式①,得x <3,解不等式②,得1x ≥-,∴原不等式组的解集为13x -≤<.【点睛】本题考查了二元一次方程组、一元一次不等式和一元一次不等式组的解法,属于基本题型,熟练掌握解二元一次方程组和一元一次不等式的方法是关键.25.(1)()5,3A 为爱心点,理由见解析;(2)第四象限,理由见解析;(3)0p =,q =23- 【分析】(1)分别把A 、B 点坐标,代入(m ﹣1,22n +)中,求出m 和n 的值,然后代入2m =8+n 检验等号是否成立即可;(2)把点A (a ,﹣4)、B (4,b )各自代入(m ﹣1,22n +)中,分别用a 、b 表示出m 、n ,再代入2m =8+n 中可求出a 、b 的值,则可得A 和B 点的坐标,再根据中点坐标公式即可求出C 点坐标,然后即可判断点C 所在象限;(3)解方程组,用q 和p 表示x 和y ,然后代入2m =8+n 可得关于p 和q 的等式,再根据p ,q 为有理数,即可求出p 、q 的值.【详解】解:(1)A 点为“爱心点”,理由如下:当A (5,3)时,m ﹣1=5,22n +=3, 解得:m =6,n =4,则2m =12,8+n =12,所以2m =8+n ,所以A (5,3)是“爱心点”;当B (4,8)时,m ﹣1=4,22n +=8, 解得:m =5,n =14,显然2m ≠8+n ,所以B 点不是“爱心点”;(2)A 、B 两点的中点C 在第四象限,理由如下:∵点A (a ,﹣4)是“爱心点”,∴m ﹣1=a ,22n +=﹣4, 解得:m =a +1,n =﹣10. 代入2m =8+n ,得2(a +1)=8﹣10,解得:a =﹣2,所以A 点坐标为(﹣2,﹣4);∵点B (4,b )是“爱心点”,同理可得m =5,n =2b ﹣2,代入2m =8+n ,得:10=8+2b ﹣2,解得:b =2.所以点B 坐标为(4,2).∴A 、B 两点的中点C 坐标为(2442,22-+-+),即(1,﹣1),在第四象限.(3)解关于x,y的方程组3x y qx y q⎧+=+⎪⎨-=-⎪⎩,得:2x qy q⎧=-⎪⎨=⎪⎩.∵点B(x,y)是“爱心点”,∴m﹣1﹣q,22n+=2q,解得:m﹣q+1,n=4q﹣2.代入2m=8+n,得:﹣2q+2=8+4q﹣2,整理得﹣6q=4.∵p,q为有理数,若使p﹣6q结果为有理数4,则P=0,所以﹣6q=4,解得:q=﹣23.所以P=0,q=﹣23.【点睛】本题是新定义题型,以“爱心点”为载体,主要考查了解二元一次方程组、中点坐标公式等知识以及阅读理解能力和迁移运用能力,正确理解题意、熟练掌握二元一次方程组的解法是关键.26.2x2-8x-3;-9.【解析】【分析】根据整式的乘法运算法则即可化简求值.【详解】解:原式=x2-4x+4+2(x2-2x-8)-(x2-9)=x2-4x+4+2x2-4x-16-x2+9=2x2-8x-3当x=1时,原式=2-8-3=-9【点睛】此题主要考查整式的化简求值,解题的关键是熟知整式的运算法则.27.(1)图见详解;(2)平行且相等;(3)图见详解;(4)28.【分析】(1)根据图形平移的性质画出△A B C'''即可;(2)根据平移的性质可得出AC与A C''的关系;(3)先取AB的中点E,再连接CE即可;(4)线段AC扫过的面积为平行四边形AA C C''的面积,根据平行四边形的底为4,高为7,可得线段AC扫过的面积.【详解】解:(1)如图所示,△A B C'''即为所求;(2)由平移的性质可得,AC与A C''的关系是平行且相等;故答案为:平行且相等;(3)如图所示,线段CE即为所求;(4)如图所示,连接AA',CC',则线段AC扫过的面积为平行四边形AA C C''的面积,由图可得,线段AC扫过的面积4728=⨯=.故答案为:28.【点睛】本题主要考查了利用平移变换进行作图,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.28.38本【分析】先表示书的总量,利用不等关系列不等式组,求不等式组的正整数解即可得到答案.【详解】解:由题意得:4788(1)8 4788(1)4n nn n+--⎧⎨+--≥⎩<①②由①得:12 n>19由②得:1202 n≤∴不等式组的解集是:11 1922≤<n20n为正整数,20,n∴=478158, m n∴=+= 15820638.∴-⨯=答:剩下38本书.【点睛】本题考查的是不等式组的应用,掌握利用不等关系列不等式组是解题的关键.。
深圳龙岗街道南联学校初中部七年级下册数学期末试卷测试与练习(word解析版)

深圳龙岗街道南联学校初中部七年级下册数学期末试卷测试与练习(word 解析版)一、解答题1.如图,直线HD //GE ,点A 在直线HD 上,点C 在直线GE 上,点B 在直线HD 、GE 之间,∠DAB =120°.(1)如图1,若∠BCG =40°,求∠ABC 的度数;(2)如图2,AF 平分∠HAB ,BC 平分∠FCG ,∠BCG =20°,比较∠B ,∠F 的大小; (3)如图3,点P 是线段AB 上一点,PN 平分∠APC ,CN 平分∠PCE ,探究∠HAP 和∠N 的数量关系,并说明理由.2.如图,直线//PQ MN ,一副直角三角板,ABC DEF ∆∆中,90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=.(1)若DEF ∆如图1摆放,当ED 平分PEF ∠时,证明:FD 平分EFM ∠.(2)若,ABC DEF ∆∆如图2摆放时,则PDE ∠=(3)若图2中ABC ∆固定,将DEF ∆沿着AC 方向平移,边DF 与直线PQ 相交于点G ,作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H (如图3),求GHF ∠的度数.(4)若图2中DEF ∆的周长35,5cm AF cm =,现将ABC ∆固定,将DEF ∆沿着CA 方向平移至点F 与A 重合,平移后的得到''D E A ∆,点D E 、的对应点分别是''D E 、,请直接写出四边形'DEAD 的周长.(5)若图2中DEF ∆固定,(如图4)将ABC ∆绕点A 顺时针旋转,1分钟转半圈,旋转至AC 与直线AN 首次重合的过程中,当线段BC 与DEF ∆的一条边平行时,请直接写出旋转的时间.3.问题情境:(1)如图1,//AB CD ,128PAB ∠=︒,119PCD ∠=︒.求APC ∠度数.小颖同学的解题思路是:如图2,过点P 作//PE AB ,请你接着完成解答. 问题迁移:(2)如图3,//AD BC ,点P 在射线OM 上运动,当点P 在A 、B 两点之间运动时,ADP α∠=∠,PCE β∠=∠.试判断CPD ∠、α∠、β∠之间有何数量关系?(提示:过点P 作//PF AD ),请说明理由;(3)在(2)的条件下,如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你猜想CPD ∠、α∠、β∠之间的数量关系并证明.4.已知:如图(1)直线AB、CD被直线MN所截,∠1=∠2.(1)求证:AB//CD;(2)如图(2),点E在AB,CD之间的直线MN上,P、Q分别在直线AB、CD上,连接PE、EQ,PF平分∠BPE,QF平分∠EQD,则∠PEQ和∠PFQ之间有什么数量关系,请直接写出你的结论;(3)如图(3),在(2)的条件下,过P点作PH//EQ交CD于点H,连接PQ,若PQ平分∠EPH,∠QPF:∠EQF=1:5,求∠PHQ的度数.5.已知AB∥CD,∠ABE与∠CDE的角分线相交于点F.(1)如图1,若BM、DM分别是∠ABF和∠CDF的角平分线,且∠BED=100°,求∠M的度数;(2)如图2,若∠ABM=13∠ABF,∠CDM=13∠CDF,∠BED=α°,求∠M的度数;(3)若∠ABM=1n∠ABF,∠CDM=1n∠CDF,请直接写出∠M与∠BED之间的数量关系二、解答题6.已知:直线1l∥2l,A为直线1l上的一个定点,过点A的直线交2l于点B,点C在线段BA的延长线上.D,E为直线2l上的两个动点,点D在点E的左侧,连接AD,AE,满足∠AED=∠DAE.点M在2l上,且在点B的左侧.(1)如图1,若∠BAD=25°,∠AED=50°,直接写出 ABM的度数;(2)射线AF为∠CAD的角平分线.① 如图2,当点D 在点B 右侧时,用等式表示∠EAF 与∠ABD 之间的数量关系,并证明; ② 当点D 与点B 不重合,且∠ABM +∠EAF =150°时,直接写出∠EAF 的度数 .7.如图1,//AB CD ,E 是AB 、CD 之间的一点.(1)判定BAE ∠,CDE ∠与AED ∠之间的数量关系,并证明你的结论;(2)如图2,若BAE ∠、CDE ∠的两条平分线交于点F .直接写出AFD ∠与AED ∠之间的数量关系;(3)将图2中的射线DC 沿DE 翻折交AF 于点G 得图3,若AGD ∠的余角等于2E ∠的补角,求BAE ∠的大小.8.已知,如图①,∠BAD =50°,点C 为射线AD 上一点(不与A 重合),连接BC . (1)[问题提出]如图②,AB ∥CE ,∠BCD =73 °,则:∠B = .(2)[类比探究]在图①中,探究∠BAD 、∠B 和∠BCD 之间有怎样的数量关系?并用平行....线的性质....说明理由. (3)[拓展延伸]如图③,在射线BC 上取一点O ,过O 点作直线MN 使MN ∥AD ,BE 平分∠ABC 交AD 于E 点,OF 平分∠BON 交AD 于F 点,//OG BE 交AD 于G 点,当C 点沿着射线AD 方向运动时,∠FOG 的度数是否会变化?若变化,请说明理由;若不变,请求出这个不变的值.9.已知//a b ,直角ABC 的边与直线a 分别相交于O 、G 两点,与直线b 分别交于E 、F 点,90ACB ∠=.(1)将直角ABC 如图1位置摆放,如果46AOG ∠=,则CEF ∠=______; (2)将直角ABC 如图2位置摆放,N 为AC 上一点,180NEF CEF ︒∠+∠=,请写出NEF ∠与AOG ∠之间的等量关系,并说明理由.(3)将直角ABC 如图3位置摆放,若140GOC ∠=,延长AC 交直线b 于点Q ,点P 是射线GF 上一动点,探究POQ ∠,OPQ ∠与PQF ∠的数量关系,请直接写出结论. 10.综合与探究综合与实践课上,同学们以“一个含30角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线a ,b ,且//a b ,三角形ABC 是直角三角形,90BCA ∠=︒,30BAC ∠=︒,60ABC ∠=︒操作发现:(1)如图1.148∠=︒,求2∠的度数;(2)如图2.创新小组的同学把直线a 向上平移,并把2∠的位置改变,发现21120∠-∠=︒,请说明理由. 实践探究:(3)填密小组在创新小组发现的结论的基础上,将图2中的图形继续变化得到图3,AC 平分BAM ∠,此时发现1∠与2∠又存在新的数量关系,请写出1∠与2∠的数量关系并说明理由.三、解答题11.在△ABC 中,∠BAC =90°,点D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED ,边AE 交BC 于点F .(1)如图①,当AE ⊥BC 时,写出图中所有与∠B 相等的角: ;所有与∠C 相等的角: .(2)若∠C -∠B =50°,∠BAD =x °(0<x ≤45) . ① 求∠B 的度数;②是否存在这样的x 的值,使得△DEF 中有两个角相等.若存在,并求x 的值;若不存在,请说明理由.12.小明在学习过程中,对教材中的一个有趣问题做如下探究:(习题回顾)已知:如图1,在ABC 中,90ACB ∠=︒,AE 是角平分线,CD 是高,AE 、CD 相交于点F .求证:CFE CEF ∠=∠;(变式思考)如图2,在ABC 中,90ACB ∠=︒,CD 是AB 边上的高,若ABC 的外角BAG ∠的平分线交CD 的延长线于点F ,其反向延长线与BC 边的延长线交于点E ,则CFE ∠与CEF ∠还相等吗?说明理由;(探究延伸)如图3,在ABC 中,AB 上存在一点D ,使得ACD B ∠=∠,BAC ∠的平分线AE 交CD 于点F .ABC 的外角BAG ∠的平分线所在直线MN 与BC 的延长线交于点M .直接写出M ∠与CFE ∠的数量关系.13.如图①,将一副直角三角板放在同一条直线AB 上,其中∠ONM =30°,∠OCD =45°.(1)将图①中的三角板OMN 沿BA 的方向平移至图②的位置,MN 与CD 相交于点E ,求∠CEN 的度数;(2)将图①中的三角板OMN 绕点O 按逆时针方向旋转,使∠BON =30°,如图③,MN与CD相交于点E,求∠CEN的度数;(3)将图①中的三角板OMN绕点O按每秒30°的速度按逆时针方向旋转一周,在旋转的过程中,在第____________秒时,直线MN恰好与直线CD垂直.(直接写出结果)14.(1)如图1所示,△ABC中,∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F;①若∠B=90°则∠F=;②若∠B=a,求∠F的度数(用a表示);(2)如图2所示,若点G是CB延长线上任意一动点,连接AG,∠AGB与∠GAB的角平分线交于点H,随着点G的运动,∠F+∠H的值是否变化?若变化,请说明理由;若不变,请求出其值.15.如图,已知直线a∥b,∠ABC=100°,BD平分∠ABC交直线a于点D,线段EF在线段AB的左侧,线段EF沿射线AD的方向平移,在平移的过程中BD所在的直线与EF所在的直线交于点P.问∠1的度数与∠EPB的度数又怎样的关系?(特殊化)(1)当∠1=40°,交点P在直线a、直线b之间,求∠EPB的度数;(2)当∠1=70°,求∠EPB的度数;(一般化)(3)当∠1=n°,求∠EPB的度数(直接用含n的代数式表示).【参考答案】一、解答题1.(1)∠ABC=100°;(2)∠ABC>∠AFC;(3)∠N=90°﹣∠HAP;理由见解析.【分析】(1)过点B作BMHD,则HDGEBM,根据平行线的性质求得∠ABM与∠CBM,便可求得最后∠HAP;理由见解解析:(1)∠ABC=100°;(2)∠ABC>∠AFC;(3)∠N=90°﹣12析.【分析】(1)过点B作BM//HD,则HD//GE//BM,根据平行线的性质求得∠ABM与∠CBM,便可求得最后结果;(2)过B作BP//HD//GE,过F作FQ//HD//GE,由平行线的性质得,∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,由角平分线的性质和已知角的度数分别求得∠HAF,∠FCG,最后便可求得结果;(3)过P作PK//HD//GE,先由平行线的性质证明∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,再根据角平分线求得∠NPC与∠PCN,由后由三角形内角和定理便可求得结果.【详解】解:(1)过点B作BM//HD,则HD//GE//BM,如图1,∴∠ABM=180°﹣∠DAB,∠CBM=∠BCG,∵∠DAB=120°,∠BCG=40°,∴∠ABM=60°,∠CBM=40°,∴∠ABC=∠ABM+∠CBM=100°;(2)过B作BP//HD//GE,过F作FQ//HD//GE,如图2,∴∠ABP=∠HAB,∠CBP=∠BCG,∠AFQ=∠HAF,∠CFQ=∠FCG,∴∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,∵∠DAB=120°,∴∠HAB=180°﹣∠DAB=60°,∵AF平分∠HAB,BC平分∠FCG,∠BCG=20°,∴∠HAF=30°,∠FCG=40°,∴∠ABC=60°+20°=80°,∠AFC=30°+40°=70°,∴∠ABC>∠AFC;(3)过P作PK//HD//GE,如图3,∴∠APK=∠HAP,∠CPK=∠PCG,∴∠APC=∠HAP+∠PCG,∵PN平分∠APC,∴∠NPC=12∠HAP+12∠PCG,∵∠PCE=180°﹣∠PCG,CN平分∠PCE,∴∠PCN=90°﹣12∠PCG,∵∠N+∠NPC+∠PCN=180°,∴∠N=180°﹣12∠HAP﹣12∠PCG﹣90°+12∠PCG=90°﹣12∠HAP,即:∠N=90°﹣12∠HAP.【点睛】本题考查了角平分线的定义,平行线性质和判定:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用,理清各角度之间的关系是解题的关键,也是本题的难点.2.(1)见详解;(2)15°;(3)67.5°;(4)45cm;(5)10s或30s或40s 【分析】(1)运用角平分线定义及平行线性质即可证得结论;(2)如图2,过点E作EK∥MN,利用平行线性解析:(1)见详解;(2)15°;(3)67.5°;(4)45cm;(5)10s或30s或40s【分析】(1)运用角平分线定义及平行线性质即可证得结论;(2)如图2,过点E作EK∥MN,利用平行线性质即可求得答案;(3)如图3,分别过点F、H作FL∥MN,HR∥PQ,运用平行线性质和角平分线定义即可得出答案;(4)根据平移性质可得D′A=DF,DD′=EE′=AF=5cm,再结合DE+EF+DF=35cm,可得出答案;(5)设旋转时间为t秒,由题意旋转速度为1分钟转半圈,即每秒转3°,分三种情况:①当BC∥DE时,②当BC∥EF时,③当BC∥DF时,分别求出旋转角度后,列方程求解即可.【详解】(1)如图1,在△DEF中,∠EDF=90°,∠DFE=30°,∠DEF=60°,∵ED平分∠PEF,∴∠PEF=2∠PED=2∠DEF=2×60°=120°,∵PQ∥MN,∴∠MFE=180°−∠PEF=180°−120°=60°,∴∠MFD=∠MFE−∠DFE=60°−30°=30°,∴∠MFD=∠DFE,∴FD平分∠EFM;(2)如图2,过点E作EK∥MN,∵∠BAC=45°,∴∠KEA=∠BAC=45°,∵PQ∥MN,EK∥MN,∴PQ∥EK,∴∠PDE=∠DEK=∠DEF−∠KEA,又∵∠DEF=60°.∴∠PDE=60°−45°=15°,故答案为:15°;(3)如图3,分别过点F、H作FL∥MN,HR∥PQ,∴∠LFA=∠BAC=45°,∠RHG=∠QGH,∵FL∥MN,HR∥PQ,PQ∥MN,∴FL∥PQ∥HR,∴∠QGF+∠GFL=180°,∠RHF=∠HFL=∠HFA−∠LFA,∵∠FGQ和∠GFA的角平分线GH、FH相交于点H,∴∠QGH=12∠FGQ,∠HFA=12∠GFA,∵∠DFE=30°,∴∠GFA=180°−∠DFE=150°,∴∠HFA=12∠GFA=75°,∴∠RHF=∠HFL=∠HFA−∠LFA=75°−45°=30°,∴∠GFL=∠GFA−∠LFA=150°−45°=105°,∴∠RHG=∠QGH=12∠FGQ=12(180°−105°)=37.5°,∴∠GHF=∠RHG+∠RHF=37.5°+30°=67.5°;(4)如图4,∵将△DEF沿着CA方向平移至点F与A重合,平移后的得到△D′E′A,∴D′A=DF,DD′=EE′=AF=5cm,∵DE+EF+DF=35cm,∴DE+EF+D′A+AF+DD′=35+10=45(cm),即四边形DEAD′的周长为45cm;(5)设旋转时间为t秒,由题意旋转速度为1分钟转半圈,即每秒转3°,分三种情况:BC∥DE时,如图5,此时AC∥DF,∴∠CAE=∠DFE=30°,∴3t=30,解得:t=10;BC∥EF时,如图6,∵BC∥EF,∴∠BAE=∠B=45°,∴∠BAM=∠BAE+∠EAM=45°+45°=90°,∴3t=90,解得:t=30;BC∥DF时,如图7,延长BC交MN于K,延长DF交MN于R,∵∠DRM=∠EAM+∠DFE=45°+30°=75°,∴∠BKA=∠DRM=75°,∵∠ACK=180°−∠ACB=90°,∴∠CAK=90°−∠BKA=15°,∴∠CAE=180°−∠EAM−∠CAK=180°−45°−15°=120°,∴3t=120,解得:t =40,综上所述,△ABC 绕点A 顺时针旋转的时间为10s 或30s 或40s 时,线段BC 与△DEF 的一条边平行.【点睛】本题主要考查了平行线性质及判定,角平分线定义,平移的性质等,添加辅助线,利用平行线性质是解题关键.3.(1)见解析;(2),理由见解析;(3)①当在延长线时(点不与点重合),;②当在之间时(点不与点,重合),.理由见解析【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC= 解析:(1)见解析;(2)180CPD αβ∠=∠+︒-∠,理由见解析;(3)①当P 在BA 延长线时(点P 不与点A 重合),180CPD βα∠=︒-∠-∠;②当P 在BO 之间时(点P 不与点B ,O 重合),180CPD αβ∠=∠-︒+∠.理由见解析【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC =113°;(2)过过P 作//PF AD 交CD 于F ,,推出////AD PF BC ,根据平行线的性质得出180BCP ,即可得出答案;(3)画出图形(分两种情况:①点P 在BA 的延长线上,②当P 在BO 之间时(点P 不与点B ,O 重合)),根据平行线的性质即可得出答案.【详解】解:(1)过P 作//PE AB ,//AB CD ,////PE AB CD ∴,=180APE PAB ,180CPE PCD ∠+∠=︒,128PAB ∠=︒,119PCD ∠=︒52APE ∴∠=︒,61CPE ∠=︒,5261113APC ∴∠=︒+︒=︒;(2)180CPD αβ∠=∠+︒-∠,理由如下:如图3,过P 作//PF AD 交CD 于F ,//AD BC ,////AD PF BC ∴,ADP DPF ∴∠=∠,BCP CPF ∠=∠,180BCP PCE ∠+∠=︒,PCE β∠=∠,180BCP β∴∠=︒-∠又ADP α∠=∠=180CPD DPF CPF ;(3)①当P 在BA 延长线时(点P 不与点A 重合),180CPD βα∠=︒-∠-∠; 理由:如图4,过P 作//PF AD 交CD 于F ,//AD BC ,////AD PF BC ∴,ADP DPF ∴∠=∠,BCP CPF ∠=∠,180BCP PCE ∠+∠=︒,PCE β∠=∠,180BCP β∴∠=︒-∠,又ADP α∠=∠,180CPD CPF DPF αβ∴∠=∠-∠=︒-∠-∠;②当P 在BO 之间时(点P 不与点B ,O 重合),180CPD αβ∠=∠-︒+∠.理由:如图5,过P 作//PF AD 交CD 于F ,//AD BC ,////AD PF BC ∴,ADP DPF ∴∠=∠,BCP CPF ∠=∠,180BCP PCE ∠+∠=︒,PCE β∠=∠,180BCP β∴∠=︒-∠,又ADP α∠=∠180CPD DPF CPF αβ∴∠=∠-∠=∠+∠-︒.【点睛】本题考查了平行线的性质的应用,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.4.(1)见解析;(2)∠PEQ+2∠PFQ=360°;(3)30°【分析】(1)首先证明∠1=∠3,易证得AB//CD;(2)如图2中,∠PEQ+2∠PFQ=360°.作EH//AB.理由平行线解析:(1)见解析;(2)∠PEQ+2∠PFQ=360°;(3)30°【分析】(1)首先证明∠1=∠3,易证得AB//CD;(2)如图2中,∠PEQ+2∠PFQ=360°.作EH//AB.理由平行线的性质即可证明;(3)如图3中,设∠QPF=y,∠PHQ=x.∠EPQ=z,则∠EQF=∠FQH=5y,想办法构建方程即可解决问题;【详解】(1)如图1中,∵∠2=∠3,∠1=∠2,∴∠1=∠3,∴AB//CD.(2)结论:如图2中,∠PEQ+2∠PFQ=360°.理由:作EH//AB.∵AB//CD,EH//AB,∴EH//CD,∴∠1=∠2,∠3=∠4,∴∠2+∠3=∠1+∠4,∴∠PEQ=∠1+∠4,同法可证:∠PFQ=∠BPF+∠FQD,∵∠BPE=2∠BPF,∠EQD=2∠FQD,∠1+∠BPE=180°,∠4+∠EQD=180°,∴∠1+∠4+∠EQD+∠BPE=2×180°,即∠PEQ+2(∠FQD+∠BPF)=360°,∴∠PEQ+2∠PFQ=360°.(3)如图3中,设∠QPF=y,∠PHQ=x.∠EPQ=z,则∠EQF=∠FQH=5y,∵EQ//PH,∴∠EQC=∠PHQ=x,∴x+10y=180°,∵AB//CD,∴∠BPH=∠PHQ=x,∵PF平分∠BPE,∴∠EPQ+∠FPQ=∠FPH+∠BPH,∴∠FPH=y+z﹣x,∵PQ平分∠EPH,∴Z=y+y+z﹣x,∴x=2y,∴12y=180°,∴y=15°,∴x=30°,∴∠PHQ=30°.【点睛】本题考查了平行线的判定与性质,角平分线的定义等知识.(2)中能正确作出辅助线是解题的关键;(3)中能熟练掌握相关性质,找到角度之间的关系是解题的关键.5.(1)65°;(2);(3)2n∠M+∠BED=360°【分析】(1)首先作EG∥AB,FH∥AB,连结MF,利用平行线的性质可得∠ABE+∠CDE=260°,再利用角平分线的定义得到∠ABF+解析:(1)65°;(2)3606α︒-︒;(3)2n∠M+∠BED=360°【分析】(1)首先作EG∥AB,FH∥AB,连结MF,利用平行线的性质可得∠ABE+∠CDE=260°,再利用角平分线的定义得到∠ABF+∠CDF=130°,从而得到∠BFD的度数,再根据角平分线的定义和三角形外角的性质可求∠M的度数;(2)先由已知得到∠ABE =6∠ABM ,∠CDE =6∠CDM ,由(1)得∠ABE +∠CDE =360°-∠BED ,∠M =∠ABM +∠CDM ,等量代换即可求解;(3)由(2)的方法可得到2n ∠M +∠BED =360°.【详解】解:(1)如图1,作//EG AB ,//FH AB ,连结MF ,//AB CD ,//////EG AB FH CD ∴,ABF BFH ∴∠=∠,CDF DFH ∠=∠,180ABE BEG ∠+∠=︒,180GED CDE ∠+∠=︒, 360ABE BEG GED CDE ∴∠+∠+∠+∠=︒,100BED BEG DEG ∠=∠+∠=︒,260ABE CDE ∴∠+∠=︒,ABE ∠和CDE ∠的角平分线相交于E ,130ABF CDF ∴∠+∠=︒,130BFD BFH DFH ∴∠=∠+∠=︒, BM 、DM 分别是ABF ∠和CDF ∠的角平分线,12MBF ABF ∴∠=∠,12MDF CDF ∠=∠, 65MBF MDF ∴∠+∠=︒,1306565BMD ∴∠=︒-︒=︒;(2)如图1,13ABM ABF ∠=∠,13CDM CDF ∠=∠, 3ABF ABM ∴∠=∠,3CDF CDM ∠=∠,ABE ∠与CDE ∠两个角的角平分线相交于点F ,6ABE ABM ∴∠=∠,6CDE CDM ∠=∠,66360ABM CDM BED ∴∠+∠+∠=︒,BMD ABM CDM ∠=∠+∠,6360BMD BED ∴∠+∠=︒,3606BMD α︒-︒∴∠=; (3)由(2)结论可得,22360n ABM n CDM E ∠+∠+∠=︒,M ABM CDM ∠=∠+∠, 则2360n M BED ∠+∠=︒.【点睛】本题主要考查了平行线的性质和四边形的内角和,关键在于掌握两直线平行同位角相等,内错角相等,同旁内角互补的性质.二、解答题6.(1);(2)①,见解析;②或【分析】(1)由平行线的性质可得到:,,再利用角的等量代换换算即可;(2)①设,,利用角平分线的定义和角的等量代换表示出对比即可;②分类讨论点在的左右两侧的情况,解析:(1)125︒;(2)①2ABD EAF ∠=∠,见解析;②30或110︒【分析】(1)由平行线的性质可得到:DEA EAN =∠∠,MBA BAN =∠∠,再利用角的等量代换换算即可;(2)①设EAF α∠=,AED=DAE=β∠∠,利用角平分线的定义和角的等量代换表示出ABD ∠对比即可;②分类讨论点D 在B 的左右两侧的情况,运用角的等量代换换算即可.【详解】.解:(1)设在1l 上有一点N 在点A 的右侧,如图所示:∵12//l l∴DEA EAN =∠∠,MBA BAN =∠∠∴50AED DAE EAN ==︒∠=∠∠∴255050125BAN BAD DAE EAN =++=︒+︒+︒=︒∠∠∠∠125BAM =︒∠(2)①2ABD=EAF ∠∠.证明:设EAF α∠=,AED=DAE=β∠∠.∴+=+FAD EAF DAE αβ=∠∠∠.∵AF 为CAD ∠的角平分线,∴22+2CAD FAD αβ==∠∠.∵12l l ,∴EAN=AED=β∠∠.∴2+22CAN CAD DAE EAN αβββα=--=--=∠∠∠∠.∴=22ABD CAN EAF α∠∠==∠.②当点D 在点B 右侧时,如图:由①得:2ABD EAF ∠=∠又∵180ABD ABM +=︒∠∠∴2180ABM EAF +=︒∠∠∵150ABM EAF ∠+∠︒=∴18015030EAF =︒-︒=︒∠当点D 在点B 左侧,E 在B 右侧时,如图:∵AF 为CAD ∠的角平分线 ∴12DAF CAD =∠∠ ∵12l l∴AED NAE =∠∠,CAN ABE =∠∠∵DAE AED NAE ==∠∠∠ ∴11()22DAE DAE NAE DAN =+=∠∠∠∠ ∴11()(360)22EAF DAF DAE CAD DAN CAN =+=+=︒-∠∠∠∠∠∠ 11802ABE =︒-∠ ∵180ABE ABM +=︒∠∠∴11180(180)9022EAF ABM ABM =︒-︒-=︒+∠∠∠ 又∵150EAF ABM +=︒∠∠∴1190(150)16522EAF EAF EAF =︒+⨯︒-=︒-∠∠∠ ∴110EAF =︒∠当点D 和F 在点B 左侧时,设在2l 上有一点G 在点B 的右侧如图:此时仍有12DAE DAN =∠∠,12DAF CAD =∠∠ ∴11(360)1802211180(180)9022EAF DAE DAF CAN ABG ABM ABM =+=︒-=︒-=︒-︒-=︒+∠∠∠∠∠∠∠ ∴110EAF =︒∠综合所述:30EAF ∠=︒或110︒【点睛】本题主要考查了平行线的性质,角平分线的定义,角的等量代换等,灵活运用平行线的性质和角平分线定义等量代换出角的关系是解题的关键.7.(1),见解析;(2);(3)60°【分析】(1)作EF//AB ,如图1,则EF//CD ,利用平行线的性质得∠1=∠BAE ,∠2=∠CDE ,从而得到∠BAE +∠CDE =∠AED ;(2)如图2,解析:(1)BAE CDE AED ∠+∠=∠,见解析;(2)12AFD AED ∠=∠;(3)60° 【分析】(1)作EF //AB ,如图1,则EF //CD ,利用平行线的性质得∠1=∠BAE ,∠2=∠CDE ,从而得到∠BAE +∠CDE =∠AED ;(2)如图2,由(1)的结论得∠AFD =∠BAF +∠CDF ,根据角平分线的定义得到∠BAF =12∠BAE ,∠CDF =12∠CDE ,则∠AFD =12(∠BAE +∠CDE ),加上(1)的结论得到∠AFD =12∠AED ;(3)由(1)的结论得∠AGD =∠BAF +∠CDG ,利用折叠性质得∠CDG =4∠CDF ,再利用等量代换得到∠AGD =2∠AED -32∠BAE ,加上90°-∠AGD =180°-2∠AED ,从而可计算出∠BAE 的度数.【详解】解:(1)BAE CDE AED ∠+∠=∠理由如下:作//EF AB ,如图1,//AB CD ,//EF CD ∴.1BAE ∴∠=∠,2CDE ∠=∠, BAE CDE AED ∴∠+∠=∠;(2)如图2,由(1)的结论得AFD BAF CDF ∠=∠+∠,BAE ∠、CDE ∠的两条平分线交于点F ,12BAF BAE ∴∠=∠,12CDF CDE ∠=∠, 1()2AFD BAE CDE ∴∠=∠+∠, BAE CDE AED ∠+∠=∠,12AFD AED ∴∠=∠; (3)由(1)的结论得AGD BAF CDG ∠=∠+∠,而射线DC 沿DE 翻折交AF 于点G ,4CDG CDF ∴∠=∠,11422()22AGD BAF CDF BAE CDE BAE AED BAE ∴∠=∠+∠=∠+∠=∠+∠-∠= 322AED BAE ∠-∠, 901802AGD AED ︒-∠=︒-∠,390218022AED BAE AED ∴︒-∠+∠=︒-∠, 60BAE ∴∠=︒.【点睛】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.8.(1);(2),见解析;(3)不变,【分析】(1)根据平行线的性质求出,再求出的度数,利用内错角相等可求出角的度数;(2)过点作∥,类似(1)利用平行线的性质,得出三个角的关系; (3)运用解析:(1)23︒;(2)BCD A B ∠=∠+∠,见解析;(3)不变, 25FOG ∠=︒【分析】(1)根据平行线的性质求出50A DCE ∠=∠=︒,再求出BCE ∠的度数,利用内错角相等可求出角的度数;(2)过点C 作CE ∥AB ,类似(1)利用平行线的性质,得出三个角的关系;(3)运用(2)的结论和平行线的性质、角平分线的性质,可求出FOG ∠的度数,可得结论.【详解】(1)因为CE ∥AB ,所以50A DCE ∠=∠=︒,B BCE ∠=∠因为∠BCD =73 °,所以23BCE BCD DCE ∠=∠-∠=︒,故答案为:23︒(2)BCD A B ∠=∠+∠,如图②,过点C 作CE ∥AB ,则A DCE ∠=∠,B BCE ∠=∠.因为BCD DCE BCE ∠=∠+∠,所以BCD BAD B ∠=∠+∠,(3)不变,设ABE x ∠=,因为BE 平分ABC ∠,所以CBE ABE x ∠=∠=.由(2)的结论可知BCD BAD ABC ∠=∠+∠,且50BAD ︒∠=,则:502BCD x ∠=︒+.因为MN ∥AD ,所以502BON BCD x ∠=∠=︒+,因为OF 平分BON ∠, 所以1252COF NOF BON x ∠=∠=∠=︒+. 因为OG ∥BE ,所以COG CBE x ∠=∠=,所以2525FOG COF COG x x ∠=∠-∠=+-=︒︒.【点睛】本题考查了平行线的性质和角平分线的定义,解题关键是熟练运用平行线的性质证明角相等,通过等量代换等方法得出角之间的关系.9.(1)136°;(2)∠AOG+∠NEF=90°,理由见解析;(3)当点P在GF上时,∠OPQ=140°﹣∠POQ+∠PQF;当点P在线段GF的延长线上时,140°﹣∠POQ=∠OPQ+∠PQF.解析:(1)136°;(2)∠AOG+∠NEF=90°,理由见解析;(3)当点P在GF上时,∠OPQ=140°﹣∠POQ+∠PQF;当点P在线段GF的延长线上时,140°﹣∠POQ=∠OPQ+∠PQF.【分析】(1)如图1,作CP∥a,则CP∥a∥b,根据平行线的性质可得∠AOG=∠ACP,∠BCP+∠CEF=180°,然后利用∠ACP+∠BCP=90°即可求得答案;(2)如图2,作CP∥a,则CP∥a∥b,根据平行线的性质可得∠AOG=∠ACP,∠BCP+∠CEF=180°,然后结合已知条件可得∠BCP=∠NEF,然后利用∠ACP+∠BCP=90°即可得到结论;(3)分两种情况,如图3,当点P在GF上时,过点P作PN∥OG,则NP∥OG∥EF,根据平行线的性质可推出∠OPQ=∠GOP+∠PQF,进一步可得结论;如图4,当点P在线段GF 的延长线上时,同上面方法利用平行线的性质解答即可.【详解】解:(1)如图1,作CP∥a,a b,∵//∴CP∥a∥b,∴∠AOG=∠ACP,∠BCP+∠CEF=180°,∴∠BCP=180°﹣∠CEF,∵∠ACP+∠BCP=90°,∴∠AOG+180°﹣∠CEF=90°,∵∠AOG=46°,∴∠CEF=136°,故答案为136°;(2)∠AOG+∠NEF=90°.理由如下:如图2,作CP∥a,则CP∥a∥b,∴∠AOG=∠ACP,∠BCP+∠CEF=180°,而∠NEF+∠CEF=180°,∴∠BCP=∠NEF,∵∠ACP+∠BCP=90°,∴∠AOG+∠NEF=90°;(3)如图3,当点P在GF上时,过点P作PN∥OG,∴NP∥OG∥EF,∴∠GOP=∠OPN,∠PQF=∠NPQ,∴∠OPQ=∠GOP+∠PQF,∴∠OPQ=140°﹣∠POQ+∠PQF;如图4,当点P在线段GF的延长线上时,过点P作PN∥OG,∴NP∥OG∥EF,∴∠GOP =∠OPN ,∠PQF =∠NPQ ,∵∠OPN =∠OPQ +∠QPN ,∴∠GOP =∠OPQ +∠PQF ,∴140°﹣∠POQ =∠OPQ +∠PQF .【点睛】本题考查了平行线的性质以及平行公理的推论等知识,属于常考题型,正确添加辅助线、灵活应用平行线的判定和性质是解题的关键.10.(1);(2)理由见解析;(3),理由见解析.【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠ 解析:(1)242∠=︒;(2)理由见解析;(3)12∠=∠,理由见解析.【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠DBC ,则∠ABD =∠ABC−∠DBC =60°−∠1,进而得出结论;(3)过点C 作CP ∥a ,由角平分线定义得∠CAM =∠BAC =30°,∠BAM =2∠BAC =60°,由平行线的性质得∠1=∠BAM =60°,∠PCA =∠CAM =30°,∠2=∠BCP =60°,即可得出结论.【详解】解:(1)如图1 148∠=︒,90BCA ∠=︒,3180142BCA ∴∠=︒-∠-∠=︒,//a b ,2342∴∠=∠=︒;图1(2)理由如下:如图2. 过点B 作//BD a ,图22180ABD ∴∠+∠=︒,//b BD ∴,1∴∠=∠DBC ,601ABD ABC DBC ∴∠=∠-∠=︒-∠,2601180∴∠+︒-∠=︒,21120∴∠-∠=︒;(3)12∠=∠,图3理由如下:如图3,过点C 作//CP a , AC 平分BAM ∠,30CAM BAC ∴∠=∠=︒,260BAM BAC ∠=∠=︒,又//a b ,//CP b ∴,160BAM ∠=∠=︒,30PCA CAM ∴∠=∠=︒,903060BCP BCA PCA ∴∠=∠-∠=︒-︒=︒,又//CP a ,260BCP ∴∠=∠=︒,12∠∠∴=.【点睛】本题是三角形综合题目,考查了平移的性质、直角三角形的性质、平行线的判定与性质、角平分线定义、平角的定义等知识;本题综合性强,熟练掌握平移的性质和平行线的性质是解题的关键.三、解答题11.(1)∠E 、∠CAF ;∠CDE 、∠BAF ; (2)①20°;②30【分析】(1)由翻折的性质和平行线的性质即可得与∠B 相等的角;由等角代换即可得与∠C 相等的角;(2)①由三角形内角和定理可得,解析:(1)∠E 、∠CAF ;∠CDE 、∠BAF ; (2)①20°;②30(1)由翻折的性质和平行线的性质即可得与∠B 相等的角;由等角代换即可得与∠C 相等的角;(2)①由三角形内角和定理可得90B C ∠+∠=︒,再由50C B ∠∠︒-=根据角的和差计算即可得∠C 的度数,进而得∠B 的度数.②根据翻折的性质和三角形外角及三角形内角和定理,用含x 的代数式表示出∠FDE 、∠DFE 的度数,分三种情况讨论求出符合题意的x 值即可.【详解】(1)由翻折的性质可得:∠E =∠B ,∵∠BAC =90°,AE ⊥BC ,∴∠DFE =90°,∴180°-∠BAC =180°-∠DFE =90°,即:∠B +∠C =∠E +∠FDE =90°,∴∠C =∠FDE ,∴AC ∥DE ,∴∠CAF =∠E ,∴∠CAF =∠E =∠B故与∠B 相等的角有∠CAF 和∠E ;∵∠BAC =90°,AE ⊥BC ,∴∠BAF +∠CAF =90°, ∠CFA =180°-(∠CAF +∠C )=90°∴∠BAF +∠CAF =∠CAF +∠C =90°∴∠BAF =∠C又AC ∥DE ,∴∠C =∠CDE ,∴故与∠C 相等的角有∠CDE 、∠BAF ;(2)①∵90BAC ∠=︒∴90B C ∠+∠=︒又∵50C B ∠∠︒-=,∴∠C =70°,∠B =20°;②∵∠BAD =x °, ∠B =20°则160ADB x ∠︒︒=-,20ADF x ∠︒︒=+,由翻折可知:∵160ADE ADB x ∠∠︒︒==-, 20E B ∠∠︒==,∴1402FDE x ∠︒︒=-, 202DFE x ∠︒︒=+,当∠FDE =∠DFE 时,1402202x x ︒︒︒︒-=+, 解得:30x ︒︒=;当∠FDE =∠E 时,140220x ︒︒︒-=,解得:60x ︒︒=(因为0<x ≤45,故舍去);当∠DFE =∠E 时,20220x ︒︒︒+=,解得:0x ︒=(因为0<x ≤45,故舍去);综上所述,存在这样的x 的值,使得△DEF 中有两个角相等.且30x =.【点睛】本题考查图形的翻折、三角形内角和定理、平行线的判定及其性质、三角形外角的性质、等角代换,解题的关键是熟知图形翻折的性质及综合运用所学知识.12.[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸] ∠M+∠CFE=90°,证明见解析.【分析】[习题回顾]根据同角的余角相等可证明∠B=∠ACD ,再根据三角形的外角的性质即可解析:[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸]∠M+∠CFE=90°,证明见解析.【分析】[习题回顾]根据同角的余角相等可证明∠B=∠ACD ,再根据三角形的外角的性质即可证明;[变式思考]根据角平分线的定义和对顶角相等可得∠CAE=∠DAF 、再根据直角三角形的性质和等角的余角相等即可得出CFE ∠=CEF ∠;[探究延伸]根据角平分线的定义可得∠EAN=90°,根据直角三角形两锐角互余可得∠M+∠CEF=90°,再根据三角形外角的性质可得∠CEF=∠CFE ,由此可证∠M+∠CFE=90°.【详解】[习题回顾]证明:∵∠ACB=90°,CD 是高,∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,∴∠B=∠ACD ,∵AE 是角平分线,∴∠CAF=∠DAF ,∵∠CFE=∠CAF+∠ACD ,∠CEF=∠DAF+∠B ,∴∠CEF=∠CFE ;[变式思考]相等,理由如下:证明:∵AF 为∠BAG 的角平分线,∴∠GAF=∠DAF ,∵∠CAE=∠GAF ,∴∠CAE=∠DAF ,∵CD 为AB 边上的高,∠ACB=90°,∴∠ADC=90°,∴∠ADF=∠ACE=90°,∴∠DAF+∠F=90°,∠E+∠CAE=90°,∴∠CEF=∠CFE ;[探究延伸]∠M+∠CFE=90°,证明:∵C 、A 、G 三点共线 AE 、AN 为角平分线,∴∠EAN=90°,又∵∠GAN=∠CAM ,∴∠M+∠CEF=90°,∵∠CEF=∠EAB+∠B ,∠CFE=∠EAC+∠ACD ,∠ACD=∠B ,∴∠CEF=∠CFE ,∴∠M+∠CFE=90°.【点睛】本题考查三角形的外角的性质,直角三角形两锐角互余,角平分线的有关证明,等角或同角的余角相等.在本题中用的比较多的是利用等角或同角的余角相等证明角相等和三角形一个外角等于与它不相邻的两个内角之和,理解并掌握是解决此题的关键.13.(1)105°;(2)135°;(3)5.5或11.5.【分析】(1)在△CEN中,用三角形内角和定理即可求出;(2)由∠BON=30°,∠N=30°可得MN∥CB,再根据两直线平行,同旁内角解析:(1)105°;(2)135°;(3)5.5或11.5.【分析】(1)在△CEN中,用三角形内角和定理即可求出;(2)由∠BON=30°,∠N=30°可得MN∥CB,再根据两直线平行,同旁内角互补即可求出∠CEN的度数.(3)画出图形,求出在MN⊥CD时的旋转角,再除以30°即得结果.【详解】解:(1)在△CEN中,∠CEN=180°-∠ECN-∠CNE=180°-45°-30°=105°;(2)∵∠BON=30°,∠N=30°,∴∠BON=∠N,∴MN∥CB.∴∠OCD+∠CEN=180°,∵∠OCD=45°∴∠CEN=180°-45°=135°;(3)如图,MN⊥CD时,旋转角为360°-90°-45°-60°=165°,或360°-(60°-45°)=345°,所以在第165°÷30°=5.5或345°÷30°=11.5秒时,直线MN恰好与直线CD垂直.【点睛】本题以学生熟悉的三角板为载体,考查了三角形的内角和、平行线的判定和性质、垂直的定义和旋转的性质,前两小题难度不大,难点是第(3)小题,解题的关键是画出适合题意的几何图形,弄清求旋转角的思路和方法,本题的第一种情况是将旋转角∠DOM放在四边形DOMF中,用四边形内角和求解,第二种情况是用周角减去∠DOM的度数. 14.(1)①45°;②∠F=a;(2)∠F+∠H的值不变,是定值180°.【分析】(1)①②依据AD平分∠CAE,CF平分∠ACB,可得∠CAD=∠CAE,∠ACF=∠ACB,依据∠CAE是△ABC解析:(1)①45°;②∠F=12a;(2)∠F+∠H的值不变,是定值180°.【分析】(1)①②依据AD平分∠CAE,CF平分∠ACB,可得∠CAD=12∠CAE,∠ACF=12∠ACB,依据∠CAE是△ABC的外角,可得∠B=∠CAE-∠ACB,再根据∠CAD是△ACF的外角,即可得到∠F=∠CAD-∠ACF=12∠CAE-12∠ACB=12(∠CAE-∠ACB)=12∠B;(2)由(1)可得,∠F=12∠ABC,根据角平分线的定义以及三角形内角和定理,即可得到∠H=90°+12∠ABG,进而得到∠F+∠H=90°+12∠CBG=180°.【详解】解:(1)①∵AD平分∠CAE,CF平分∠ACB,∴∠CAD=12∠CAE,∠ACF=12∠ACB,∵∠CAE是△ABC的外角,∴∠B=∠CAE﹣∠ACB,∵∠CAD是△ACF的外角,∴∠F=∠CAD﹣∠ACF=12∠CAE﹣12∠ACB=12(∠CAE﹣∠ACB)=12∠B=45°,故答案为45°;②∵AD平分∠CAE,CF平分∠ACB,∴∠CAD=12∠CAE,∠ACF=12∠ACB,∵∠CAE是△ABC的外角,∴∠B=∠CAE﹣∠ACB,∵∠CAD是△ACF的外角,∴∠F=∠CAD﹣∠ACF=12∠CAE﹣12∠ACB=12(∠CAE﹣∠ACB)=12∠B=12a;(2)由(1)可得,∠F=12∠ABC,∵∠AGB与∠GAB的角平分线交于点H,∴∠AGH=12∠AGB,∠GAH=12∠GAB,∴∠H=180°﹣(∠AGH+∠GAH)=180°﹣12(∠AGB+∠GAB)=180°﹣12(180°﹣∠ABG)=90°+12∠ABG,∴∠F+∠H=12∠ABC+90°+12∠ABG=90°+12∠CBG=180°,∴∠F+∠H的值不变,是定值180°.【点睛】本题主要考查了三角形内角和定理、三角形外角性质的综合运用,熟练运用定理是解题的关键.15.(1)∠EPB=170°;(2)①当交点P在直线b的下方时:∠EPB=20°,②当交点P在直线a,b之间时:∠EPB=160°,③当交点P在直线a的上方时:∠EPB=∠1﹣50°=20°;(3)①当解析:(1)∠EPB=170°;(2)①当交点P在直线b的下方时:∠EPB=20°,②当交点P在直线a,b之间时:∠EPB=160°,③当交点P在直线a的上方时:∠EPB=∠1﹣50°=20°;(3)①当交点P在直线a,b之间时:∠EPB=180°﹣|n°﹣50°|;②当交点P在直线a上方或直线b下方时:∠EPB=|n°﹣50°|.【分析】(1)利用外角和角平分线的性质直接可求解;(2)分三种情况讨论:①当交点P在直线b的下方时;②当交点P在直线a,b之间时;③当交点P在直线a的上方时;分别画出图形求解;(3)结合(2)的探究,分两种情况得到结论:①当交点P在直线a,b之间时;②当交点P在直线a上方或直线b下方时;【详解】解:(1)∵BD平分∠ABC,∴∠ABD=∠DBC=12∠ABC=50°,∵∠EPB是△PFB的外角,∴∠EPB=∠PFB+∠PBF=∠1+(180°﹣50°)=170°;(2)①当交点P在直线b的下方时:∠EPB=∠1﹣50°=20°;②当交点P在直线a,b之间时:∠EPB=50°+(180°﹣∠1)=160°;③当交点P在直线a的上方时:∠EPB=∠1﹣50°=20°;(3)①当交点P在直线a,b之间时:∠EPB=180°﹣|n°﹣50°|;②当交点P在直线a上方或直线b下方时:∠EPB=|n°﹣50°|;【点睛】考查知识点:平行线的性质;三角形外角性质.根据动点P的位置,分类画图,结合图形求解是解决本题的关键.数形结合思想的运用是解题的突破口.。
深圳龙岗龙岗中学七年级下册数学期末试卷

深圳龙岗龙岗中学七年级下册数学期末试卷一、选择题1.下列各式从左到右的变形中,是因式分解的是( ).A .x (a-b )=ax-bxB .x 2-1+y 2=(x-1)(x+1)+y 2C .y 2-1=(y+1)(y-1)D .ax+bx+c=x (a+b )+c2.如图,∠1=∠2,则下列结论一定成立的是( )A .AB ∥CDB .AD ∥BC C .∠B =∠D D .∠1=∠2 3.下列代数运算正确的是( ) A .x•x 6=x 6B .(x 2)3=x 6C .(x+2)2=x 2+4D .(2x )3=2x 3 4.将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )A .22()()a b a b a b +-=-B .222()a b a b -=-C .2()b a b ab b -=-D .2()ab b b a b -=-5.截止到3月26日0时,全球感染新型冠状病毒肺炎的人数已经突破380000人,“山川异域,风月同天”,携手抗“疫”,刻不容缓.将380000用科学记数法表示为( ) A .0.38×106B .3.8×106C .3.8×105D .38×104 6.计算a •a 2的结果是( )A .aB .a 2C .a 3D .a 4 7.科学家发现2019﹣nCoV 冠状肺炎病毒颗粒的平均直径约为0.00000012m .数据0.00000012用科学记数法表示为( )A .1.2×107B .0.12×10﹣6C .1.2×10﹣7D .1.2×10﹣8 8.一个三角形的两边长分别是2和4,则第三边的长可能是( ) A .1B .2C .4D .7 9.已知x a y b =⎧⎨=⎩是方程组24213x y x y -=⎧⎨+=⎩的解,则32a b -的算术平方根为( ) A .4± B .4 C .2 D .2±10.若关于x 的一元一次不等式组202x m x m -<⎧⎨+>⎩无解,则m 的取值范围是( ) A .23m ≤ B .23m < C .23m ≥ D .23m >二、填空题11.新型冠状肺炎病毒(COVID ﹣19)的粒子,其直径在120~140纳米即0.00000012米~0.00000014米之间,数据0.00000012用科学记数法可以表示为_____.12.如图,四边形ABCD 中,E 、F 、G 、H 依次是各边中点,O 是形内一点,若四边形AEOH 、四边形BFOE 、四边形CGOF 的面积分别为6、7、8,四边形DHOG 面积为______.13.分解因式:29a -=__________.14.若多项式x 2-kx +25是一个完全平方式,则k 的值是______.15.因式分解:224x x -=_________.16.如图,根据长方形中的数据,计算阴影部分的面积为______ .17.若2a x =,5b x =,那么2a b x +的值是_______ ;18.若满足方程组33221x y m x y m +=+⎧⎨-=-⎩的x 与y 互为相反数,则m 的值为_____. 19.已知关于x 的不等式3()50a b x a b -+->的解集是1x <,则关于x 的不等式4ax b >的解集为_______.20.如图,将长方形纸片ABCD 沿着EF ,折叠后,点D ,C 分别落在点D ,C '的位置,ED '的延长线交BC 于点G .若∠1=64°,则∠2等于_____度.三、解答题21.已知:如图,//AB DC ,AC 和BD 相交于点O ,E 是CD 上一点,F 是OD 上一点,且∠1=∠A .(1)求证://FE OC ;(2)若∠BFE =110°,∠A =60°,求∠B 的度数.22.如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,三角形ABC 的三个顶点均在格点上.(1)将三角形ABC 先向右平移6个单位长度,再向上平移3个单位长度,得到三角形A 1B 1C 1,画出平移后的三角形A 1B 1C 1;(2)建立适当的平面直角坐标系,使得点A 的坐标为(-4,3),并直接写出点A 1的坐标; (3)求三角形ABC 的面积.23.水果商贩老徐上水果批发市场进货,他了解到草莓的批发价格是每箱60元,苹果的批发价格是每箱40元.老徐购得草莓和苹果共60箱,刚好花费3100元.(1)问草莓、苹果各购买了多少箱?(2)老徐有甲、乙两家店铺,每出售一箱草莓或苹果,甲店分别获利15元和20元,乙店分别获利12元和16元.设老徐将购进的60箱水果分配给甲店草莓a 箱,苹果b 箱,其余均分配给乙店,由于他口碑良好,两家店都很快卖完了这批水果.①若老徐在甲店获利600元,则他在乙店获利多少元?②若老徐希望获得总利润为1000元,则a b +=?24.已知m 2,3na a ==,求①m n a +的值; ②3m-2n a 的值25.先化简,再求值:2(1)(3)(2)(2)x x x x x ---++-,其中x =﹣2.26.如图,有一块长为(3)a b +米,宽为(2)a b +米的长方形空地,计划修筑东西、南北走向的两条道路,其余进行绿化(阴影部分),已知道路宽为a 米,东西走向的道路与空地北边界相距1米,则绿化的面积是多少平方米?并求出当a =3,b =2时的绿化面积.27.阅读材料:把形如2ax bx c ++的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即222)2(a ab b a b ±+=±.例如:2224213x x x x -+=-++2(1)3x =-+是224x x -+的一种形式的配方;所以,()213x -+,2(2)x -2x +,22213224x x ⎛⎫-+ ⎪⎝⎭是224x x -+的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).请根据阅读材料解决下列问题:(1)比照上面的例子,写出249x x -+三种不同形式的配方;(2)已知22610340x y x y +-++=,求32x y -的值;(3)已知2223240a b c ab b c ++---+=,求a b c ++的值.28.启秀中学初一年级组计划将m 本书奖励给本次期中考试中取得优异成绩的n 名同学,如果每人分4本,那么还剩下78本;如果每人分8本,那么最后一人分得的书不足8本,但不少于4本.最终,年级组讨论后决定,给n 名同学每人发6本书,那么将剩余多少本书?【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】A. 是整式的乘法,故A 错误;B. 没把一个多项式转化成几个整式积,故B 错误;C. 把一个多项式转化成几个整式积,故C 正确;D. 没把一个多项式转化成几个整式积,故D 错误;故选C.2.A解析:A【解析】根据内错角相等,两直线平行即可得出结论.【详解】∵∠1=∠2,∴AB ∥DC(内错角相等,两直线平行).故选A .【点睛】考查平行线的判定定理,平行线的概念,关键在于根据图形找到被截的两直线.3.B解析:B【分析】根据同底数幂的乘法,幂的乘方,完全平方公式,积的乘方运算判断即可.【详解】A .67=x x x ,故A 选项错误;B .()32236x x x ⨯==,故B 选项正确;C .22(2)44x x x +=++,故C 选项错误;D .3333(2)28x x x =⋅=,故D 选项错误.故选B .【点睛】本题考查整式的乘法公式,熟练掌握同底数幂的乘法,幂的乘方,完全平方公式和积的乘方是解题的关键.4.A解析:A【分析】根据长方形的面积=长⨯宽,分别表示出甲乙两个图形的面积,即可得到答案.【详解】解:()()=S a b a b +-甲,()()2222==S a a b b a b a ab ab b a b -+-=-+--乙. 所以()()a b a b +-22=a b -故选A .【点睛】本题考查平方差公式,难度不大,通过计算两个图形的面积即可顺利解题.5.C解析:C【分析】科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.解:380000=3.8×105.故选:C.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.6.C解析:C【分析】根据同底数幂的乘法法则计算即可.【详解】解:a•a2=a1+2=a3.故选:C.【点睛】本题考查了幂的运算性质,准确应用同底数幂的乘法是解题的关键.7.C解析:C【分析】用科学计数法将0.00000012表示为a×10-n即可.【详解】解:0.00000012=1.2×10﹣7,故选:C.【点睛】本题考查用科学计数法表示较小的数,绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.8.C解析:C【分析】根据三角形任意两边之和大于第三边,任意两边之差小于第三边求出第三边的取值范围,即可求解..【详解】设第三边为x,由三角形三条边的关系得4-2<x<4+2,∴2<x<6,∴第三边的长可能是4.故选C.【点睛】本题考查了三角形三条边的关系,熟练掌握三角形三条边的关系是解答本题的关键.解析:B【分析】把方程组24213x y x y -=⎧⎨+=⎩的解求解出来即可得到a 、b 的值,再计算32a b -的算术平方根即可得到答案;【详解】解:24213x y x y -=⎧⎨+=⎩①② 把①式×5得:248x y -= ③,用②式-③式得:55y = ,解得:y=1,把1y = 代入①式得到:24x -= ,即:6x = ,又x a y b =⎧⎨=⎩是方程组24213x y x y -=⎧⎨+=⎩的解, 所以61a b =⎧⎨=⎩, 故3216a b -=,所以32a b -的算术平方根=16的算术平方根,4== ,故答案为:4;【点睛】本题主要考查了二元一次方程组的求解以及算术平方根的定义,掌握用消元法求解二元一次方程组的解是解题的关键;10.A解析:A【分析】分别求出各不等式的解集,再根据不等式组无解即可得出m 的取值范围.【详解】解:202x m x m -<⎧⎨+>⎩①② 解不等式①,得x<2m.解不等式②,得x>2-m.因为不等式组无解,∴2-m ≥2m.解得23 m .故选A.【点睛】本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的法则是解答此题的关键.二、填空题11.2×10﹣7【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.解析:2×10﹣7【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:0.00 000 012=1.2×10﹣7,故答案是:1.2×10﹣7.【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.12.7【分析】连接OC,OB,OA,OD,易证S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,S△OAE=S△OBE,从而有S四边形AEOH+S四边形CGOF=S四边形DHO解析:7【分析】连接OC,OB,OA,OD,易证S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,S△OAE=S△OBE,从而有S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE,由此即可求得答案.【详解】连接OC,OB,OA,OD,∵E、F、G、H依次是各边中点,∴△AOE和△BOE等底等高,∴S △OAE =S △OBE ,同理可证,S △OBF =S △OCF ,S △ODG =S △OCG ,S △ODH =S △OAH ,∴S 四边形AEOH +S 四边形CGOF =S 四边形DHOG +S 四边形BFOE ,∵S 四边形AEOH =6,S 四边形BFOE =7,S 四边形CGOF =8,∴6+8=7+S 四边形DHOG ,解得:S 四边形DHOG =7,故答案为:7.【点睛】本题考查了三角形的面积.解决本题的关键将各个四边形划分,充分利用给出的中点这个条件,证得三角形的面积相等,进而证得结论.13.【解析】试题分析:本题考查实数范围内的因式分解,因式分解的步骤为:一提公因式;二看公式.在实数范围内进行因式分解的式子的结果一般要分到出现无理数为止.先把式子写成a2-32,符合平方差公式的特点解析:()()33a a +-【解析】试题分析:本题考查实数范围内的因式分解,因式分解的步骤为:一提公因式;二看公式.在实数范围内进行因式分解的式子的结果一般要分到出现无理数为止.先把式子写成a 2-32,符合平方差公式的特点,再利用平方差公式分解因式.a 2-9=a 2-32=(a+3)(a-3).故答案为(a+3)(a-3).考点:因式分解-运用公式法.14.±10【解析】【分析】根据完全平方公式,可知-kx=±2×5•x ,求解即可.【详解】解:∵x2-kx+25是一个完全平方式,∴-kx=±2×5•x ,解得k=±10.故答案为±1解析:±10【解析】【分析】根据完全平方公式()2222a b a ab b ±=±+,可知-kx=±2×5•x ,求解即可.【详解】解:∵x 2-kx+25是一个完全平方式,∴-kx=±2×5•x ,解得k=±10.故答案为±10【点睛】本题考查了完全平方公式,熟练掌握相关公式是解题关键. 15.【分析】直接提取公因式即可.【详解】.故答案为:.【点睛】本题考查了因式分解——提取公因式法,掌握知识点是解题关键.解析:2(2)x x -【分析】直接提取公因式即可.【详解】2242(2)x x x x -=-.故答案为:2(2)x x -.【点睛】本题考查了因式分解——提取公因式法,掌握知识点是解题关键.16.104【解析】两个阴影图形可以平移组成一个长方形,长为,宽为8,故阴影部分的面积13×8=104,故答案为104.解析:104【解析】两个阴影图形可以平移组成一个长方形,长为15213-=,宽为8,故阴影部分的面积13×8=104,故答案为104.17.【分析】可从入手,联想到同底数幂的乘法以及幂的乘方的逆用;逆用幂运算法则可得到(xa)2×xb,接下来将已知条件代入求值即可.对逆用同底数幂的乘法法则,得(xa)2×xb,逆用幂的解析:【分析】可从2a b x +入手,联想到同底数幂的乘法以及幂的乘方的逆用;逆用幂运算法则可得到(x a )2×x b ,接下来将已知条件代入求值即可.【详解】对2a b x +逆用同底数幂的乘法法则,得(x a )2×x b ,逆用幂的乘方法则,得(x a )2×x b ,将2a x =、5b x =代入(x a )2× x b 中,得22×5=20,故答案为:20.【点睛】此题考查同底数幂的乘法,解题关键在于掌握运算法则.18.【分析】把m 看做已知数表示出x 与y ,代入x+y =0计算即可求出m 的值.【详解】解:,①+②得:5x =3m+2,解得:x =,把x =代入①得:y =,由x 与y 互为相反数,得到=0,去分母解析:【分析】把m 看做已知数表示出x 与y ,代入x +y =0计算即可求出m 的值.【详解】解:33221x y m x y m +=+⎧⎨-=-⎩①②, ①+②得:5x =3m +2,解得:x =325m +, 把x =325m +代入①得:y =945m -, 由x 与y 互为相反数,得到3294+55m m +-=0, 去分母得:3m +2+9﹣4m =0,解得:m =11,故答案为:11此题考查了二元一次方程组的解,以及解二元一次方程组,熟练掌握方程组的解法及相反数的性质是解本题的关键.19.【分析】根据已知不等式的解集,即可确定a,b 之间得关系以及b 的符号,从而解不等式.【详解】解:∵的解集是,∴=1,a -b<0,∴a=2b,b<0.则不等式可以化为2bx>4b.∵b<解析:2x <【分析】根据已知不等式的解集,即可确定a,b 之间得关系以及b 的符号,从而解不等式.【详解】解:∵3()50a b x a b -+->的解集是1x <,∴()53a b a b --=1,a-b<0, ∴a=2b,b<0.则不等式4ax b >可以化为2bx>4b.∵b<0.∴x<2.即关于x 的不等式4ax b >的解集为x<2.【点睛】本题考查了不等式的解法,正确确定b 的符号是关键.20.128【分析】由ADBC ,∠1=64°,根据两直线平行,内错角相等,可求得∠DEF 的度数,然后由折叠的性质,可得∠FEG 的度数,进而再利用两直线平行内错角相等得到∠2的度数.【详解】解:∵A解析:128【分析】由AD //BC ,∠1=64°,根据两直线平行,内错角相等,可求得∠DEF 的度数,然后由折叠的性质,可得∠FEG的度数,进而再利用两直线平行内错角相等得到∠2的度数.【详解】解:∵AD//BC,∠1=64°,∴∠DEF=∠1=64°,由折叠的性质可得∠FEG=∠DEF=64°,∴∠2=∠1+∠EFG=64°+64°=128°.故答案为:128.【点睛】本题主要考察两直线平行的性质、折叠的性质以及矩形的性质,重点在于利用已知条件找到角度之间的关系.三、解答题21.(1)见详解;(2)50°.【分析】(1)由//AB DC,可知∠A=∠C ,然后等量代换得到∠C=∠1,利用同位角相等两直线平行即可得证;(2)由EF与OC平行,利用两直线平行同旁内角互补得到∠BFE+∠DOC=180°,然后通过三角形内角和即可求出∠B的度数.【详解】(1)证明:∵AB∥CD,∴∠A=∠C ,又∵∠1=∠A,∴∠C=∠1,∴FE∥OC;(2)解:∵FE∥OC,∴∠BFE+∠DOC=180°,又∵∠BFE=110°,∴∠DOC=180°-110°=70°,∴∠AOB=∠DOC=70°,∵∠A=60°,∴∠B=180°-60°-70°=50°.【点睛】本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.22.(1)见解析;(2)(2,6);(3)19 2【分析】(1)利用网格特点和平移的性质画出A、B、C的对应点A1、B1、C1,从而得到△A1B1C1;(2)利用A点坐标画出直角坐标系,再写出A1坐标即可;(3)利用分割法求出坐标即可.【详解】解:(1)画出平移后的△A 1B 1C 1如下图;;(2)如上图建立平面直角坐标系,使得点A 的坐标为(-4,3),由图可知:点A 1的坐标为(2,6);(3)由(2)中的图可知:A (-4,3),B (5,-1),C (0,0),∴S △ABC =11119(45)434512222+⨯-⨯⨯-⨯⨯=. 【点睛】 本题考查了作图——平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.23.(1)草莓35箱,苹果25箱;(2)①340元,②53或52【分析】(1)抓住题中关键的已知条件,老徐购得草莓和苹果共60箱,刚好花费3100元,设未知数列方程组,求解方程即可;(2)①由题意列二元一次方程,可得到34120a b +=,列式求出他在乙店获利;②根据老徐希望获得总利润为1000元,建立关于a 、b 的二元一次方程,整理可得18034a b -=,再根据a 、b 的取值范围及a 一定是4的整数倍,即可求出结果; 【详解】 (1)解:设草莓购买了x 箱,苹果购买了y 箱,根据题意得:6060403100x y x y ⎧+=⎨+=⎩, 解得3525x y ⎧=⎨=⎩.答:草莓购买了35箱,苹果购买了25箱;(2)解:①若老徐在甲店获利600元,则1520600ab +=, 整理得:34120a b +=,他在乙店的获利为:()()12351625a b -+-,=()820434a b -+,=820-4120⨯,=340元;②根据题意得:()()1520123516251000a b a b ++-+-=, 整理得:34180ab +=, 得到18034ab -=,∵a、b 均为正整数,∴a 一定是4的倍数,∴a 可能是0,4,8…,∵035a ≤≤,025b ≤≤, ∴当且仅当a=32,b=21或a=25,b=24时34180ab +=成立, ∴322153a b +=+=或28+24=52. 故答案为340元;53或52.【点睛】本题主要考查了二元一次方程组的应用,根据题意列式是解题的关键.24.①6;②89 【解析】解:①②25.23x x +-;1-【分析】先通过整式的乘法及乘法公式对原式进行去括号,然后通过合并同类项进行计算即可化简原式,再将2x =-代入即可得解.【详解】解:原式222221343x x x x x x x =-+-++-=+-将2x =-代入,原式2(2)(2)34231=-+--=--=-.【点睛】本题主要考查了整式的混合运算,熟练掌握整式的乘法公式及合并同类项的运算方法是解决本题的关键.26.()2223a ab b ++平方米;40平方米. 【分析】(1)根据平移的原理,四块绿化面积可拼成一个长方形,其边长为原边长减去再减去道路宽为a 米,由此即可求绿化的面积的代数式;然后利用多项式乘多项式法则计算,去括号合并得到最简结果,将a 与b 的值代入计算即可求出值.【详解】解:根据题意得:22(3)(2)(2)()23a b a a b a a b a b a ab b +-+-=++=++(平方米).则绿化的面积是()2223a ab b ++平方米; 当3a =,2b =时,原式2223233240=⨯+⨯⨯+=(平方米).故当a =3,b =2时,绿化面积为40平方米.答:绿化的面积是()2223a ab b ++平方米;当a =3,b =2时,绿化面积为40平方米. 【点睛】此题考查整式的混合运算与代数式求值,掌握长方形的面积计算方法是解决问题的关键.27.(1)2249(2)5x x x -+=-+;2249(3)10x x x x -+=+-;2249(3)2x x x x -+=-+;(2)19;(3)4【分析】(1)根据材料中的三种不同形式的配方,“余项“分别是常数项、一次项、二次项,可解答;(2)将x 2+y 2-6x+10y+34配方,根据平方的非负性可得x 和y 的值,可解答;(3)通过配方后,求得a ,b ,c 的值,再代入代数式求值.【详解】解:(1)249x x -+的三种配方分别为:2249(2)5x x x -+=-+;2249(3)10x x x x -+=+-;2249(3)2x x x x -+=-+(或2222549339x x x x ⎛⎫-+=-+ ⎪⎝⎭; (2)∵x 2+y 2-6x+10y+34=x 2-6x+9+y 2+10y+25=(x-3)2+(y+5)2=0,∴x-3=0,y+5=0,∴x=3,y=-5,∴3x-2y=3×3-2×(-5)=19(3)2223240a b c ab b c ++---+=()2222134421044a ab b b bc c -++-++-+= 22213(2)(1)024a b b c ⎛⎫-+-+-= ⎪⎝⎭ ∴102a b -=,3(2)04b -=,10c -= ∴1a =,2b =,1c =,则4a b c ++=【点睛】本题考查的是配方法的应用,首先利用完全平方公式使等式变为两个非负数和一个正数的和的形式,然后利用非负数的性质解决问题.28.38本【分析】先表示书的总量,利用不等关系列不等式组,求不等式组的正整数解即可得到答案.【详解】解:由题意得:4788(1)8 4788(1)4n nn n+--⎧⎨+--≥⎩<①②由①得:12 n>19由②得:1202 n≤∴不等式组的解集是:11 1922≤<n20n为正整数,20,n∴=478158,m n∴=+=15820638.∴-⨯=答:剩下38本书.【点睛】本题考查的是不等式组的应用,掌握利用不等关系列不等式组是解题的关键.。
深圳市龙岗区七年级下册期末数学试卷及答案

深圳市龙岗区七年级下册期末数学试卷一、选择题:(请将答题卡上的正确选项涂黑,每小题3分,共36分)1.(3分)计算:3(3)a 的值为( )A .327aB .33aC .39aD .27a2.(3分)下列标志中,可以看作是轴对称图形的是( )A .B .C .D .3.(3分)下列运算正确的是( )A .2233a a -=B .369a a a =C .824a a a ÷=D .11()33-=- 4.(3分)大肠杆菌的大小为0.0005~0.003毫米,能发酵多种糖类产酸、产气,是人和动物肠道中的正常栖居菌,婴儿出生后即随哺乳进入肠道,与人终身相伴.其中0.0005毫米用科学记数法表示为( )A .30.510-⨯毫米B .45010-⨯毫米C .3510-⨯毫米D .4510-⨯毫米5.(3分)有下列长度的三条线段,其中能组成三角形的是( )A .3cm 、6cm 、10cmB .10cm 、4cm 、6cmC .3cm 、1cm 、1cmD .4cm 、6cm 、9cm6.(3分)一个不透明的袋子中只装有1个黄球和3个红球,它们除颜色外完全相同,从中随机摸出一个球.下列说法正确的是( )A .摸到黄球是不可能事件B .摸到黄球的概率是34C .摸到红球是随机事件D .摸到红球是必然事件 7.(3分)如图,下列四个条件中,能判断//DE AC 的是( )A .34∠=∠B .12∠=∠C .180EDC EFC ∠+∠=︒D .ACD AFE ∠=∠8.(3分)嘉嘉买了6支笔花了9元钱,琪琪买了同样售价的x 支笔,还买了单价为5元的三角尺两幅,用y (元)表示琪琪花的总钱数,那么y 与x 之间的关系式应该是( )A . 1.510y x =+B .510y x =+C . 1.55y x =+D .55y x =+9.(3分)如图是一个平分角的仪器,其中AB AD =,BC DC =,将点A 放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )A .SSSB .SASC .ASAD .AAS10.(3分)已知5a b +=-,4ab =-,则223a ab b -+的值是( )A .49B .37C .45D .3311.(3分)在数学课上,老师提出如下问题:老师说:“小华的作法正确”请回答:小华第二步作图中①的作法和第二步作图依据的定理或性质是②()A .①作PQ 垂直平分AB ②垂线段最短B .①作PQ 平分APB ∠②等腰三角形三线合一C .①作PQ 垂直平分AB ②中垂线性质D .①作PQ 平分AB ②等腰三角形三线合一12.已知:如图①,长方形ABCD 中,E 是边AD 上一点,且6AE cm =,8AB cm =,点P 从B 出发,沿折线BE ED DC --匀速运动,运动到点C 停止.P 的运动速度为2/cm s ,运动时间为()t s ,BPC ∆的面积为2()y cm ,y 与t 的函数关系图象如图②,则下列结论正确的有( )①7a =②10b =③当3t s =时PCD ∆为等腰三角形 ④当10t s =时,212y cm =A .1个B .2个C .3个D .4个二、填空题:(本大题共4小题,每题3分,共12分)13.(3分)一个等腰三角形的一个角为80︒,则它的顶角的度数是 .14.(3分)如图,已知AB AC =,用“SAS ”定理证明ABD ACE ∆≅∆,还需添加条件 .15.(3分)如图,在ABC ∆中,已知12180∠+∠=︒,DEF A ∠=∠,70BED ∠=︒,则ACB ∠的度数为 .16.(3分)已知长方形ABCD ,E 点和F 点分别在AB 和BC 边上,如图将BEF ∆沿着EF 折叠以后得到△B EF ',B E '与AD 相交于点M ,B F '与AD 相交于点G ,则1∠与2∠的数量关系为 .三.解答题(共7题,52分)17.(8分)计算:(1)20192011()(3.14)2π-----(2)322(2)()2ab a b ab a b a -÷++18.(6分)先化简,再求值:22(2)()()5x y x y x y y --+--,其中12x =,2y =-19.(6分)有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:(1)可能性最大和最小的事件分别是哪个?(填写序号)(2)将这些事件的序号按发生的可能性从小到大的顺序排列: .20.(8分)某公交车每月的支出费用为4000元,每月的乘车人数x (人)与每月利润(利润=收入费用-支出费用)y (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的): x (人) 5001000 1500 2000 2500 3000 ⋯ y (元)3000- 2000- 1000- 0 1000 2000 ⋯ (1)在这个变化过程中, 是自变量, 是因变量;(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.21.(7分)已知在ABC ∆与ABD ∆中,AC BD =,90C D ∠=∠=︒,AD 与BC 交于点E .(1)求证:AE BE =;(2)若3AC =,4BC =,求ACE ∆的周长.22.(7分)如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF BC交DE于点F.//求证:(1)AB是CAF∠的角平分线;(2)FAD E∠=∠.23.(10分)如图,已知正方形ABCD(四边相等,四个角都是直角),点E为边AB上异于点A、B的一动点,//EF AC,交BC于点F,点G为DA延长线上一定点,满足AG AD=,GE的延长线与DF交于点H,连接BH.(1)判断BEF∆是三角形.(2)求证:AGE CDF∆≅∆.(3)探究EHB∠是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.参考答案与试题解析一、选择题:(请将答题卡上的正确选项涂黑,每小题3分,共36分)1.(3分)计算:3(3)a 的值为( )A .327aB .33aC .39aD .27a【解答】解:33(3)27a a =故选:A .2.(3分)下列标志中,可以看作是轴对称图形的是( )A .B .C .D .【解答】解:A 、不是轴对称图形,故错误;B 、不是轴对称图形,故错误;C 、是轴对称图形,故正确;D 、不是轴对称图形,故错误.故选:C .3.(3分)下列运算正确的是( )A .2233a a -=B .369a a a =C .824a a a ÷=D .11()33-=- 【解答】解:222.32A a a a -=,故本选项不合题意;B .369a a a =,故本选项符合题意;C .826a a a ÷=,故本选项不合题意;11.()33D -=,故本选项不合题意. 故选:B .4.(3分)大肠杆菌的大小为0.0005~0.003毫米,能发酵多种糖类产酸、产气,是人和动物肠道中的正常栖居菌,婴儿出生后即随哺乳进入肠道,与人终身相伴.其中0.0005毫米用科学记数法表示为( )A .30.510-⨯毫米B .45010-⨯毫米C .3510-⨯毫米D .4510-⨯毫米 【解答】解:0.0005毫米4510-=⨯毫米,故选:D .5.(3分)有下列长度的三条线段,其中能组成三角形的是( )A .3cm 、6cm 、10cmB .10cm 、4cm 、6cmC .3cm 、1cm 、1cmD .4cm 、6cm 、9cm【解答】解:根据三角形的三边关系,得A 、3610+<,不能组成三角形,不符合题意;B 、4610+=,不能够组成三角形,不符合题意;C 、113+<,不能够组成三角形,不符合题意;D 、469+>,能够组成三角形,符合题意.故选:D .6.(3分)一个不透明的袋子中只装有1个黄球和3个红球,它们除颜色外完全相同,从中随机摸出一个球.下列说法正确的是( )A .摸到黄球是不可能事件B .摸到黄球的概率是34C .摸到红球是随机事件D .摸到红球是必然事件 【解答】解:由题意可得,摸到黄球的概率是14,故选项B 错误,摸到红球和黄球都是随机事件,故选项A 、D 错误,选项C 正确,故选:C .7.(3分)如图,下列四个条件中,能判断//DE AC 的是( )A .34∠=∠B .12∠=∠C .180EDC EFC ∠+∠=︒D .ACD AFE ∠=∠【解答】解:A 、34∠=∠,//DE AC ∴,正确;B 、12∠=∠,//EF BC ∴,错误;C 、180EDC EFC ∠+∠=︒,不能得出平行线的平行,错误;D 、ACD AFE ∠=∠,//EF BC ∴,错误;故选:A .8.(3分)嘉嘉买了6支笔花了9元钱,琪琪买了同样售价的x 支笔,还买了单价为5元的三角尺两幅,用y (元)表示琪琪花的总钱数,那么y 与x 之间的关系式应该是( )A . 1.510y x =+B .510y x =+C . 1.55y x =+D .55y x =+ 【解答】解:每支笔的价格96 1.5=÷=元/支,y ∴与x 之间的关系式为: 1.510y x =+,故选:A .9.(3分)如图是一个平分角的仪器,其中AB AD =,BC DC =,将点A 放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )A .SSSB .SASC .ASAD .AAS【解答】解:在ADC ∆和ABC ∆中,AD AB DC BC AC AC =⎧⎪=⎨⎪=⎩,()ADC ABC SSS ∴∆≅∆,DAC BAC ∴∠=∠,AC ∴就是DAB ∠的平分线.故选:A .10.(3分)已知5a b +=-,4ab =-,则223a ab b -+的值是( )A .49B .37C .45D .33【解答】解:5a b +=-,4ab =-,22223()555(4)252045a ab b a b ab ∴-+=+-=-⨯-=+=,故选:C .11.(3分)在数学课上,老师提出如下问题:老师说:“小华的作法正确”请回答:小华第二步作图中①的作法和第二步作图依据的定理或性质是②.( )A .①作PQ 垂直平分AB ②垂线段最短B .①作PQ 平分APB ∠②等腰三角形三线合一C .①作PQ 垂直平分AB ②中垂线性质D .①作PQ 平分AB ②等腰三角形三线合一【解答】解:由作法可知第一步作图是作PQ 平分APB ∠.小华第二步作图的依据是等腰三角形三线合一, 故选:B .12.已知:如图①,长方形ABCD 中,E 是边AD 上一点,且6AE cm =,8AB cm =,点P 从B 出发,沿折线BE ED DC --匀速运动,运动到点C 停止.P 的运动速度为2/cm s ,运动时间为()t s ,BPC ∆的面积为2()y cm ,y 与t 的函数关系图象如图②,则下列结论正确的有( )①7a =②10b =③当3t s =时PCD ∆为等腰三角形 ④当10t s =时,212y cm = A .1个B .2个C .3个D .4个【解答】解:当P 点运动到E 点时,BPC ∆面积最大,结合函数图象可知当5t =时,BPC ∆面积最大为40, 5210BE ∴=⨯=.在Rt ABE ∆中,利用勾股定理可得8AB =. 又1402BC AB =,所以10BC =. 则1064ED =-=.当P 点从E 点到D 点时,所用时间为422s ÷=,527a ∴=+=.故①正确;P 点运动完整个过程需要时间(1048)211t s =++÷=,即11b =,②错误;6AE cm =,8AB cm =,∴2210BE AE AB +,当3t =时,6BP =,即点P 不是BE 的中点,所以当3t s =时PCD ∆不是等腰三角形,故③错误;当10t =时,P 点运动的路程为10220cm ⨯=,此时22202PC =-=,BPC ∆面积为21102102cm⨯⨯=,④错误.∴正确的结论有①.故选:A .二、填空题:(本大题共4小题,每题3分,共12分)13.(3分)一个等腰三角形的一个角为80︒,则它的顶角的度数是 80︒或20︒ . 【解答】解:(1)当80︒角为顶角,顶角度数即为80︒; (2)当80︒为底角时,顶角18028020=︒-⨯︒=︒. 故答案为:80︒或20︒.14.(3分)如图,已知AB AC =,用“SAS ”定理证明ABD ACE ∆≅∆,还需添加条件 AD AE = .【解答】解:需添加条件是AD AE =, 在ABD ∆和ACE ∆中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ()ABD ACE SAS ∴∆≅∆,故答案为:AD AE =.15.(3分)如图,在ABC ∆中,已知12180∠+∠=︒,DEF A ∠=∠,70BED ∠=︒,则ACB ∠的度数为 70︒ .【解答】解:12180∠+∠=︒,1180DFE ∠+∠=︒,2DFE ∴∠=∠,//AB EF ∴,BDE DEF ∴∠=∠,又DEF A ∠=∠,BDE A ∴∠=∠.//DE AC ∴,70ACB BED ∴∠=∠=︒;故答案为:70︒.16.(3分)已知长方形ABCD ,E 点和F 点分别在AB 和BC 边上,如图将BEF ∆沿着EF 折叠以后得到△B EF ',B E '与AD 相交于点M ,B F '与AD 相交于点G ,则1∠与2∠的数量关系为 122∠=∠ .【解答】解:由折叠可得,90B B '∠=∠=︒,22BEB '∠=∠,180BFE BEB '∴∠+∠=︒, //AD BC , 1GFC ∴∠=∠,又180BFE GFC ∠+∠=︒,1180BFE ∴∠+∠=︒,1BEB '∴∠=∠,即221∠=∠,故答案为:122∠=∠. 三.解答题(共7题,52分) 17.(8分)计算: (1)20192011()(3.14)2π-----(2)322(2)()2ab a b ab a b a -÷++ 【解答】解:(1)原式1416=---=-;(2)原式22222222b ab a ab b a =-++=+.18.(6分)先化简,再求值:22(2)()()5x y x y x y y --+--,其中12x =,2y =- 【解答】解:原式22222445x xy y x y y =-+-+-4xy =-,当12x =,2y =-时,原式14(2)42=-⨯⨯-=.19.(6分)有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:(1)可能性最大和最小的事件分别是哪个?(填写序号)(2)将这些事件的序号按发生的可能性从小到大的顺序排列: ②<③<①<④ .【解答】解:共3红2黄1绿相等的六部分,∴①指针指向红色的概率为3162=; ②指针指向绿色的概率为16; ③指针指向黄色的概率为2163=; ④指针不指向黄色为4263=,(1)可能性最大的是④,最小的是②;(2)由题意得:②<③<①<④, 故答案为:②<③<①<④.20.(8分)某公交车每月的支出费用为4000元,每月的乘车人数x (人)与每月利润(利润=收入费用-支出费用)y (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):(1)在这个变化过程中, 每月的乘车人数x 是自变量, 是因变量; (2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损; (3)请你估计当每月乘车人数为3500人时,每月利润为多少元?(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人. 【解答】解:(1)在这个变化过程中,每月的乘车人数x 是自变量,每月的利润y 是因变量;故答案为每月的乘车人数x ,每月的利润y ;(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损; 故答案为2000;(3)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,当每月的乘车人数为2000人时,每月利润为0元,则当每月乘车人数为3500人时,每月利润为3000元;(4)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,当每月的乘车人数为2000人时,每月利润为0元,则当每月利润为5000元时,每月乘车人数为4500人, 故答案为4500.21.(7分)已知在ABC ∆与ABD ∆中,AC BD =,90C D ∠=∠=︒,AD 与BC 交于点E .(1)求证:AE BE =;(2)若3AC =,4BC =,求ACE ∆的周长.【解答】(1)证明:在ACE ∆和BDE ∆中,C D AEC BEC AC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ACE BDE AAS ∴∆≅∆,AE BE ∴=;(2)解:3AC =,4BC =, 由(1)得:AE BE =,ACE ∴∆的周长347AC AE CE AC BE CE AC BC =++=++=+=+=.22.(7分)如图,C ,D 是AB 的垂直平分线上两点,延长AC ,DB 交于点E ,//AF BC 交DE 于点F .求证:(1)AB 是CAF ∠的角平分线; (2)FAD E ∠=∠.【解答】证明:(1)点C 是AB 的垂直平分线上的点,CB CA ∴=, CBA CAB ∴∠=∠, //AF BC 交DE 于点F , BAF CBA ∴∠=∠, BAF CAB ∴∠=∠.即 AB 是CAF ∠的角平分线.(2)点D 是AB 的垂直平分线上的点,DB DA ∴=,DBA DAB ∴∠=∠,DBA E CAB ∠=∠+∠,DAB FAD BAF ∠=∠+∠,CAB BAF ∠=∠,E FAD ∴∠=∠.23.(10分)如图,已知正方形ABCD (四边相等,四个角都是直角),点E 为边AB 上异于点A 、B 的一动点,//EF AC ,交BC 于点F ,点G 为DA 延长线上一定点,满足AG AD =,GE 的延长线与DF 交于点H ,连接BH . (1)判断BEF ∆是 等腰直角 三角形. (2)求证:AGE CDF ∆≅∆.(3)探究EHB ∠是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.【解答】解:(1)BEF ∆是等腰直角三角形, 正方形ABCD 中,AB BC =,90ABC ∠=︒,ABC ∴∆是等腰直角三角形, //AC EF ,BEF ∴∆是等腰直角三角形;故答案为:等腰直角; (2)证明:如图1,ABC ∆和BEF ∆为等腰直角三角形,AB BC ∴=,BE BF =,AB BE BC BF ∴-=-,即是AE FC =,四边形ABCD 为正方形,AD CD AG ∴==,90GAE DCF ∠=∠=︒,()AGE CDF SAS ∴∆≅∆,(3)45EHB ∠=︒.如图2,在GE 上截取ME HF =,AGE CDF ∆≅∆,AEG DFC ∴∠=∠180180AEG DFC ∴-∠=-∠即是MEB HFB ∠=∠,BEF ∆为等腰直角三角形, BE BF ∴=,BE BF =,ME HF =,MEB HFB ∠=∠,()MEB HFB SAS ∴∆≅∆,MBE HBF ∴∠=∠,MB BH =,90HBF EBH ∠+∠=︒,90MBE EBH ∴∠+∠=︒即是90MBH ∠=︒M BH∴∆为等腰直角三角形,∴∠=︒.45EHB。
深圳龙岗街道世纪学校初中部七年级下册数学期末试卷测试题(Word版 含解析) (2)

深圳龙岗街道世纪学校初中部七年级下册数学期末试卷测试题(Word版含解析)一、解答题1.已知,AB∥DE,点C在AB上方,连接BC、CD.(1)如图1,求证:∠BCD+∠CDE=∠ABC;(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.2.(1)如图①,若∠B+∠D=∠E,则直线AB与CD有什么位置关系?请证明(不需要注明理由).(2)如图②中,AB//CD,又能得出什么结论?请直接写出结论.(3)如图③,已知AB//CD,则∠1+∠2+…+∠n-1+∠n的度数为.3.已知AB//CD.(1)如图1,E为AB,CD之间一点,连接BE,DE,得到∠BED.求证:∠BED=∠B+∠D;(2)如图,连接AD,BC,BF平分∠ABC,DF平分∠ADC,且BF,DF所在的直线交于点F.①如图2,当点B在点A的左侧时,若∠ABC=50°,∠ADC=60°,求∠BFD的度数.②如图3,当点B在点A的右侧时,设∠ABC=α,∠ADC=β,请你求出∠BFD的度数.(用含有α,β的式子表示)4.综合与实践课上,同学们以“一个直角三角形和两条平行线”为背景开展数学活动,如图,已知两直线,a b ,且,a b ABC //是直角三角形,90BCA ∠=︒,操作发现:(1)如图1.若148∠=︒,求2∠的度数;(2)如图2,若30,1A ∠=︒∠的度数不确定,同学们把直线a 向上平移,并把2∠的位置改变,发现21120∠-∠=︒,请说明理由.(3)如图3,若∠A =30°,AC 平分BAM ∠,此时发现1∠与2∠又存在新的数量关系,请写出1∠与2∠的数量关系并说明理由.5.如图,已知//AB CD ,CN 是BCE ∠的平分线. (1)若CM 平分BCD ∠,求MCN ∠的度数;(2)若CM 在BCD ∠的内部,且CM CN ⊥于C ,求证:CM 平分BCD ∠;(3)在(2)的条件下,过点B 作BP BQ ⊥,分别交CM 、CN 于点P 、Q ,PBQ ∠绕着B 点旋转,但与CM 、CN 始终有交点,问:BPC BQC ∠+∠的值是否发生变化?若不变,求其值;若变化,求其变化范围.二、解答题6.如图,直线//PQ MN ,一副三角板(90ABC CDE ∠=∠=︒,30ACB ∠=︒,60,45EAC DCE DEC ∠=︒∠=∠=︒)按如图①放置,其中点E 在直线PQ 上,点,B C 均在直线MN 上,且CE 平分ACN ∠.(1)求DEQ ∠的度数.(2)如图②,若将三角形ABC 绕B 点以每秒5︒的速度按逆时针方向旋转(,A C 的对应点分别为,F G ).设旋转时间为t 秒(036)t ≤≤. ①在旋转过程中,若边//BG CD ,求t 的值;②若在三角形ABC 绕B 点旋转的同时,三角形CDE 绕E 点以每秒4︒的速度按顺时针方向旋转(,C D 的对应点分别为,H K ).请直接写出当边//BG HK 时t 的值.7.已知//a b ,直角ABC 的边与直线a 分别相交于O 、G 两点,与直线b 分别交于E ,F 点,且90ACB ∠=︒.(1)将直角ABC 如图1位置摆放,如果56AOG ∠=︒,则CEF ∠=________; (2)将直角ABC 如图2位置摆放,N 为AC 上一点,180NEF CEF ∠+∠=︒,请写出NEF ∠与AOG ∠之间的等量关系,并说明理由;(3)将直角ABC 如图3位置摆放,若135GOC ∠=︒,延长AC 交直线b 于点Q ,点P 是射线GF 上一动点,探究,POQ OPQ ∠∠与PQF ∠的数量关系,请直接写出结论. 8.问题情境:如图1,AB ∥CD ,∠PAB =130°,∠PCD =120°,求∠APC 的度数. 小明的思路是:如图2,过P 作PE ∥AB ,通过平行线性质来求∠APC . (1)按小明的思路,易求得∠APC 的度数为 度;(2)如图3,AD ∥BC ,点P 在射线OM 上运动,当点P 在A 、B 两点之间运动时,∠ADP =∠α,∠BCP =∠β.试判断∠CPD 、∠α、∠β之间有何数量关系?请说明理由; (3)在(2)的条件下,如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你直接写出∠CPD 、∠α、∠β间的数量关系.9.如图1所示:点E 为BC 上一点,∠A =∠D ,AB ∥CD (1)直接写出∠ACB 与∠BED 的数量关系;(2)如图2,AB ∥CD ,BG 平分∠ABE ,BG 的反向延长线与∠EDF 的平分线交于H 点,若∠DEB 比∠GHD 大60°,求∠DEB 的度数;(3)保持(2)中所求的∠DEB 的度数不变,如图3,BM 平分∠EBK ,DN 平分∠CDE ,作BP ∥DN ,则∠PBM 的度数是否改变?若不发生变化,请求它的度数,若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角).10.(感知)如图①,//,40,130AB CD AEP PFD ︒︒∠=∠=,求EPF ∠的度数.小明想到了以下方法:解:如图①,过点P 作//PM AB ,140AEP ︒∴∠=∠=(两直线平行,内错角相等)//AB CD (已知),//∴PM CD (平行于同一条直线的两直线平行),2180PFD ︒∴∠+∠=(两直线平行,同旁内角互补). 130PFD ︒∠=(已知),218013050︒︒︒∴∠=-=(等式的性质). 12405090︒︒︒∴∠+∠=+=(等式的性质).即90EPF ︒∠=(等量代换).(探究)如图②,//AB CD ,50,120AEP PFC ︒︒∠=∠=,求EPF ∠的度数.(应用)如图③所示,在(探究)的条件下,PEA ∠的平分线和PFC ∠的平分线交于点G ,则G ∠的度数是_______________︒.三、解答题11.在ABC 中,射线AG 平分BAC ∠交BC 于点G ,点D 在BC 边上运动(不与点G 重合),过点D 作//DE AC 交AB 于点E .(1)如图1,点D 在线段CG 上运动时,DF 平分EDB ∠.①若100BAC ︒∠=,30C ︒∠=,则AFD ∠=_____;若40B ︒∠=,则AFD ∠=_____; ②试探究AFD ∠与B 之间的数量关系?请说明理由;(2)点D 在线段BG 上运动时,BDE ∠的角平分线所在直线与射线AG 交于点F .试探究AFD ∠与B 之间的数量关系,并说明理由.12.问题情境:如图1,AB ∥CD ,∠PAB=130°,∠PCD=120°.求∠APC 度数. 小明的思路是:如图2,过P 作PE ∥AB ,通过平行线性质,可得∠APC=50°+60°=110°. 问题迁移:(1)如图3,AD ∥BC ,点P 在射线OM 上运动,当点P 在A 、B 两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD 、∠α、∠β之间有何数量关系?请说明理由; (2)在(1)的条件下,如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你直接写出∠CPD 、∠α、∠β间的数量关系.13.【问题探究】如图1,DF ∥CE ,∠PCE=∠α,∠PDF=∠β,猜想∠DPC 与α、β之间有何数量关系?并说明理由; 【问题迁移】如图2,DF ∥CE ,点P 在三角板AB 边上滑动,∠PCE=∠α,∠PDF=∠β. (1)当点P 在E 、F 两点之间运动时,如果α=30°,β=40°,则∠DPC= °.(2)如果点P 在E 、F 两点外侧运动时(点P 与点A 、B 、E 、F 四点不重合),写出∠DPC 与α、β之间的数量关系,并说明理由.(图1) (图2)14.如图,△ABC 和△ADE 有公共顶点A ,∠ACB =∠AED =90°,∠BAC =45°,∠DAE =30°. (1)若DE //AB ,则∠EAC = ;(2)如图1,过AC 上一点O 作OG ⊥AC ,分别交A B 、A D 、AE 于点G 、H 、F . ①若AO =2,S △AGH =4,S △AHF =1,求线段OF 的长;②如图2,∠AFO 的平分线和∠AOF 的平分线交于点M ,∠FHD 的平分线和∠OGB 的平分线交于点N ,∠N +∠M 的度数是否发生变化?若不变,求出其度数;若改变,请说明理由.15.如图①所示,在三角形纸片ABC 中,70C ∠=︒,65B ∠=︒,将纸片的一角折叠,使点A 落在ABC 内的点A '处. (1)若140∠=︒,2∠=________.(2)如图①,若各个角度不确定,试猜想1∠,2∠,A ∠之间的数量关系,直接写出结论. ②当点A 落在四边形BCDE 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,A ∠,1∠,2∠之间又存在什么关系?请说明.(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的123456∠+∠+∠+∠+∠+∠和是________.【参考答案】一、解答题1.(1)证明见解析;(2);(3). 【分析】(1)过点作,先根据平行线的性质可得,再根据平行公理推论可得,然后根据平行线的性质可得,由此即可得证;(2)过点作,同(1)的方法,先根据平行线的性质解析:(1)证明见解析;(2)90ABC F ∠-∠=︒;(3)45︒. 【分析】(1)过点C 作CF AB ∥,先根据平行线的性质可得180ABC BCF ∠+∠=︒,再根据平行公理推论可得CF DE ,然后根据平行线的性质可得180CDE BCF BCD ∠+∠+∠=︒,由此即可得证;(2)过点C 作CG AB ∥,同(1)的方法,先根据平行线的性质得出180ABC BCG ∠+∠=︒,180F BCG BCF ∠+∠+∠=︒,从而可得ABC F BCF ∠-∠=∠,再根据垂直的定义可得90BCF ∠=︒,由此即可得出结论;(3)过点G 作GM AB ,延长FG 至点N ,先根据平行线的性质可得ABH MGH ∠=∠,MGN DFG ∠=∠,从而可得MGH MGN ABH DFG ∠-∠=∠-∠,再根据角平分线的定义、结合(2)的结论可得45MGH MGN ∠=-∠︒,然后根据角的和差、对顶角相等可得BGD CG MGH MGN F ∠-∠=∠-∠,由此即可得出答案.【详解】证明:(1)如图,过点C 作CF AB ∥,180ABC BCF ∴∠+∠=︒,AB DE , CFDE ∴,180CDE DCF ∴∠+∠=︒,即180CDE BCF BCD ∠+∠+∠=︒,CDE BCF BCD ABC BCF ∴∠+∠+∠=∠+∠, BCD CDE ABC ∴∠+∠=∠;(2)如图,过点C 作CG AB ∥,180ABC BCG ∴∠+∠=︒,AB DE , CG DE ∴,180F FCG ∴∠+∠=︒,即180F BCG BCF ∠+∠+∠=︒, F BCG BCF ABC BCG ∴∠+∠+∠=∠+∠, ABC F BCF ∴∠-∠=∠, CF BC ⊥,90BCF ∴∠=︒,90ABC F ∴∠-∠=︒;(3)如图,过点G 作GM AB ,延长FG 至点N ,ABH MGH ∴∠=∠,AB DE , GM DE ∴,MGN DFG ∴∠=∠,BH 平分ABC ∠,FN 平分CFD ∠,11,22ABH AB D C CF DFG ∴∠=∠∠∠=,由(2)可知,90ABC CFD ∠-∠=︒,411225MGH MGN ABH DFG CF B D A C ∠-∠=∠-∠∠∠-==∴︒,又BGD MGH MGDCGF DGN MGN MGD ∠=∠+∠⎧⎨∠=∠=∠+∠⎩,∴-==∠∠︒.45C∠-∠BGD GF MGNMGH【点睛】本题考查了平行线的性质、对顶角相等、角平分线的定义等知识点,熟练掌握平行线的性质是解题关键.2.(1)AB//CD,证明见解析;(2)∠E1+∠E2+…∠En=∠B+∠F1+∠F2+…∠Fn-1+∠D ;(3)(n-1)•180°【分析】(1)过点E作EF//AB,利用平行线的性质则可得出解析:(1)AB//CD,证明见解析;(2)∠E1+∠E2+…∠E n=∠B+∠F1+∠F2+…∠F n-1+∠D;(3)(n-1)•180°【分析】(1)过点E作EF//AB,利用平行线的性质则可得出∠B=∠BEF,再由已知及平行线的判定即可得出AB∥CD;(2)如图,过点E作EM∥AB,过点F作FN∥AB,过点G作GH∥AB,根据探究(1)的证明过程及方法,可推出∠E+∠G=∠B+∠F+∠D,则可由此得出规律,并得出∠E1+∠E2+…∠E n=∠B+∠F1+∠F2+…∠F n-1+∠D;(3)如图,过点M作EF∥AB,过点N作GH∥AB,则可由平行线的性质得出∠1+∠2+∠MNG =180°×2,依此即可得出此题结论.【详解】解:(1)过点E作EF//AB,∴∠B=∠BEF.∵∠BEF+∠FED=∠BED,∴∠B+∠FED=∠BED.∵∠B+∠D=∠E(已知),∴∠FED=∠D.∴CD//EF(内错角相等,两直线平行).∴AB//CD.(2)过点E作EM∥AB,过点F作FN∥AB,过点G作GH∥AB,∵AB∥CD,∴AB∥EM∥FN∥GH∥CD,∴∠B =∠BEM ,∠MEF =∠EFN ,∠NFG =∠FGH ,∠HGD =∠D ,∴∠BEF +∠FGD =∠BEM +∠MEF +∠FGH +∠HGD =∠B +∠EFN +∠NFG +∠D =∠B +∠EFG +∠D , 即∠E +∠G =∠B +∠F +∠D .由此可得:开口朝左的所有角度之和与开口朝右的所有角度之和相等, ∴∠E 1+∠E 2+…∠En =∠B +∠F 1+∠F 2+…∠F n -1+∠D . 故答案为:∠E 1+∠E 2+…∠E n =∠B +∠F 1+∠F 2+…∠F n -1+∠D . (3)如图,过点M 作EF ∥AB ,过点N 作GH ∥AB ,∴∠APM +∠PME =180°, ∵EF ∥AB ,GH ∥AB , ∴EF ∥GH ,∴∠EMN +∠MNG =180°, ∴∠1+∠2+∠MNG =180°×2,依次类推:∠1+∠2+…+∠n -1+∠n =(n -1)•180°. 故答案为:(n -1)•180°. 【点睛】本题考查了平行线的性质与判定,属于基础题,关键是过E 点作AB (或CD )的平行线,把复杂的图形化归为基本图形.3.(1)见解析;(2)55°;(3) 【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图2,过点作,当点在点的左侧时,根据,,根据平行线的性质及角平分线的定义即可求的度数; ②如图解析:(1)见解析;(2)55°;(3)1118022αβ︒-+【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图2,过点F 作//FE AB ,当点B 在点A 的左侧时,根据50ABC ∠=︒,60ADC ∠=︒,根据平行线的性质及角平分线的定义即可求BFD ∠的度数;②如图3,过点F 作//EF AB ,当点B 在点A 的右侧时,ABC α∠=,ADC β∠=,根据平行线的性质及角平分线的定义即可求出BFD ∠的度数. 【详解】解:(1)如图1,过点E 作//EF AB ,则有BEF B ∠=∠,//AB CD ,//EF CD ∴,FED D ∴∠=∠,BED BEF FED B D ∴∠=∠+∠=∠+∠;(2)①如图2,过点F 作//FE AB ,有BFE FBA ∠=∠.//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.BFE EFD FBA FDC ∴∠+∠=∠+∠.即BFD FBA FDC ∠=∠+∠, BF 平分ABC ∠,DF 平分ADC ∠, 1252FBA ABC ∴∠=∠=︒,1302FDC ADC ∠=∠=︒, 55BFD FBA FDC ∴∠=∠+∠=︒.答:BFD ∠的度数为55︒;②如图3,过点F 作//FE AB ,有180BFE FBA ∠+∠=︒.180BFE FBA ∴∠=︒-∠,//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.180BFE EFD FBA FDC ∴∠+∠=︒-∠+∠.即180BFD FBA FDC ∠=︒-∠+∠, BF 平分ABC ∠,DF 平分ADC ∠, 1122FBA ABC α∴∠=∠=,1122FDC ADC β∠=∠=, 1118018022BFD FBA FDC αβ∴∠=︒-∠+∠=︒-+. 答:BFD ∠的度数为1118022αβ︒-+. 【点睛】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质. 4.(1)42°;(2)见解析;(3)∠1=∠2,理由见解析【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD=180°解析:(1)42°;(2)见解析;(3)∠1=∠2,理由见解析【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠DBC ,则∠ABD =∠ABC -∠DBC =60°-∠1,进而得出结论;(3)过点C 作CP ∥a ,由角平分线定义得∠CAM =∠BAC =30°,∠BAM =2∠BAC =60°,由平行线的性质得∠1=∠BAM =60°,∠PCA =∠CAM =30°,∠2=∠BCP =60°,即可得出结论.【详解】解:(1)∵∠1=48°,∠BCA =90°,∴∠3=180°-∠BCA -∠1=180°-90°-48°=42°,∵a ∥b ,∴∠2=∠3=42°;(2)理由如下:过点B 作BD ∥a .如图2所示:则∠2+∠ABD =180°,∵a ∥b ,∴b ∥BD ,∴∠1=∠DBC ,∴∠ABD =∠ABC -∠DBC =60°-∠1,∴∠2+60°-∠1=180°,∴∠2-∠1=120°;(3)∠1=∠2,理由如下:过点C 作CP ∥a ,如图3所示:∵AC 平分∠BAM∴∠CAM =∠BAC =30°,∠BAM =2∠BAC =60°,又∵a ∥b ,∴CP ∥b ,∠1=∠BAM =60°,∴∠PCA =∠CAM =30°,∴∠BCP =∠BCA -∠PCA =90°-30°=60°,又∵CP ∥a ,∴∠2=∠BCP =60°,∴∠1=∠2.【点睛】本题是三角形综合题目,考查了平移的性质、直角三角形的性质、平行线的判定与性质、角平分线定义、平角的定义等知识;本题综合性强,熟练掌握平移的性质和平行线的性质是解题的关键.5.(1)90°;(2)见解析;(3)不变,180°【分析】(1)根据邻补角的定义及角平分线的定义即可得解;(2)根据垂直的定义及邻补角的定义、角平分线的定义即可得解;(3),过,分别作,,根据解析:(1)90°;(2)见解析;(3)不变,180°【分析】(1)根据邻补角的定义及角平分线的定义即可得解;(2)根据垂直的定义及邻补角的定义、角平分线的定义即可得解;(3)180BPC BQC ∠+∠=︒,过Q ,P 分别作//QG AB ,//PH AB ,根据平行线的性质及平角的定义即可得解.【详解】解(1)CN ,CM 分别平分BCE ∠和BCD ∠, 12BCN BCE ∴=∠,12BCM BCD ∠=∠, 180BCE BCD ∠+∠=︒,111()90222MCN BCN BCM BCE BCD BCE BCD ∴∠=∠+∠=∠+∠=∠+∠=︒; (2)CM CN ⊥,90MCN ∴∠=︒,即90BCN BCM ∠+∠=︒,22180BCN BCM ∴∠+∠=︒,CN 是BCE ∠的平分线,2BCE BCN ∴∠=∠,2180BCE BCM ∴∠+∠=︒,又180BCE BCD ∠+∠=︒,2BCD BCM ∴∠=∠,又CM 在BCD ∠的内部,CM ∴平分BCD ∠;(3)如图,不发生变化,180BPC BQC ∠+∠=︒,过Q ,P 分别作//QG AB ,//PH AB ,则有//////QG AB PH CD ,BQG ABQ ∴∠=∠,CQG ECQ ∠=∠,BPH FBP ∠=∠,CPH DCP ∠=∠,⊥BP BQ ,CP CQ ⊥,90PBQ PCQ ∴∠=∠=︒,180ABQ PBQ FBP ∠+∠+=︒,180ECQ PCQ DCP ∠+∠+∠=︒,180ABQ FBP ECQ DCP ∴∠+∠+∠+∠=︒,BPC BQC BPH CPH BQG CQG ∴∠+∠=∠+∠+∠+∠180ABQ FBP ECQ DCP =∠+∠+∠+∠=︒,180BPC BQC ∴∠+∠=︒不变.【点睛】此题考查了平行线的性质,熟记平行线的性质及作出合理的辅助线是解题的关键.二、解答题6.(1)60°;(2)①6s ;②s 或s【分析】(1)利用平行线的性质角平分线的定义即可解决问题.(2)①首先证明∠GBC=∠DCN=30°,由此构建方程即可解决问题.②分两种情形:如图③中,当解析:(1)60°;(2)①6s;②103s或703s【分析】(1)利用平行线的性质角平分线的定义即可解决问题.(2)①首先证明∠GBC=∠DCN=30°,由此构建方程即可解决问题.②分两种情形:如图③中,当BG∥HK时,延长KH交MN于R.根据∠GBN=∠KRN构建方程即可解决问题.如图③-1中,当BG∥HK时,延长HK交MN于R.根据∠GBN+∠KRM=180°构建方程即可解决问题.【详解】解:(1)如图①中,∵∠ACB=30°,∴∠ACN=180°-∠ACB=150°,∵CE平分∠ACN,∴∠ECN=12∠ACN=75°,∵PQ∥MN,∴∠QEC+∠ECN=180°,∴∠QEC=180°-75°=105°,∴∠DEQ=∠QEC-∠CED=105°-45°=60°.(2)①如图②中,∵BG∥CD,∴∠GBC=∠DCN,∵∠DCN=∠ECN-∠ECD=75°-45°=30°,∴∠GBC=30°,∴5t=30,∴t=6s.∴在旋转过程中,若边BG∥CD,t的值为6s.②如图③中,当BG∥HK时,延长KH交MN于R.∵BG∥KR,∴∠GBN=∠KRN,∵∠QEK=60°+4t,∠K=∠QEK+∠KRN,∴∠KRN=90°-(60°+4t)=30°-4t,∴5t=30°-4t,∴t=103s.如图③-1中,当BG∥HK时,延长HK交MN于R.∵BG∥KR,∴∠GBN+∠KRM=180°,∵∠QEK=60°+4t,∠EKR=∠PEK+∠KRM,∴∠KRM=90°-(180°-60°-4t)=4t-30°,∴5t+4t-30°=180°,∴t=703s.综上所述,满足条件的t的值为103s或703s.【点睛】本题考查几何变换综合题,考查了平行线的性质,旋转变换,角平分线的定义等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.7.(1)146°;(2)∠AOG+∠NEF=90°;(3)见解析【分析】(1)作CP//a,则CP//a//b,根据平行线的性质求解.(2)作CP//a,由平行线的性质及等量代换得∠AOG+∠N解析:(1)146°;(2)∠AOG+∠NEF=90°;(3)见解析【分析】(1)作CP//a,则CP//a//b,根据平行线的性质求解.(2)作CP//a,由平行线的性质及等量代换得∠AOG+∠NEF=∠ACP+∠PCB=90°.(3)分类讨论点P在线段GF上或线段GF延长线上两种情况,过点P作a,b的平行线求解.【详解】解:(1)如图,作CP//a,∵a//b,CP//a,∴CP//a//b,∴∠AOG=∠ACP=56°,∠BCP+∠CEF=180°,∴∠BCP=180°-∠CEF,∵∠ACP+∠BCP=90°,∴∠AOG+180°-∠CEF=90°,∴∠CEF=180°-90°+∠AOG=146°.(2)∠AOG+∠NEF=90°.理由如下:如图,作CP//a,则CP//a//b,∴∠AOG=∠ACP,∠BCP+∠CEF=180°,∵∠NEF+∠CEF=180°,∴∠BCP=∠NEF,∵∠ACP+∠BCP=90°,∴∠AOG+∠NEF=90°.(3)如图,当点P在GF上时,作PN//a,连接PQ,OP,则PN//a//b,∴∠GOP=∠OPN,∠PQF=∠NPQ,∴∠OPQ=∠OPN+∠NPQ=∠GOP+∠PQF,∵∠GOC=∠GOP+∠POQ=135°,∴∠GOP=135°-∠POQ,∴∠OPQ=135°-∠POQ+∠PQF.如图,当点P在GF延长线上时,作PN//a,连接PQ,OP,则PN//a//b,∴∠GOP=∠OPN,∠PQF=∠NPQ,∵∠OPN=∠OPQ+∠QPN,∴∠GOP=∠OPQ+∠PQF,∴135°-∠POQ=∠OPQ+∠PQF.【点睛】本题考查平行线的性质的应用,解题关键是熟练掌握平行线的性质,通过添加辅助线及分类讨论的方法求解.8.(1)110°;(2)∠CPD=∠α+∠β,见解析;(3)当P在BA延长线时,∠CPD=∠β-∠α;当P在AB延长线上时,∠CPD=∠α-∠β【分析】(1)过P作PE∥AB,通过平行线性质求∠A解析:(1)110°;(2)∠CPD=∠α+∠β,见解析;(3)当P在BA延长线时,∠CPD=∠β-∠α;当P在AB延长线上时,∠CPD=∠α-∠β【分析】(1)过P作PE∥AB,通过平行线性质求∠APC即可;(2)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(3)画出图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【详解】解:(1)过点P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠A+∠APE=180°,∠C+∠CPE=180°,∵∠PAB=130°,∠PCD=120°,∴∠APE=50°,∠CPE=60°,∴∠APC=∠APE+∠CPE=110°.故答案为110°;(2)∠CPD=∠α+∠β,理由是:如图3,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β;(3)当P在BA延长线时,∠CPD=∠β-∠α,理由是:如图4,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE-∠DPE =∠β-∠α;当P在AB延长线时,∠CPD=∠α-∠β,理由是:如图5,过P 作PE ∥AD 交CD 于E ,∵AD ∥BC ,∴AD ∥PE ∥BC ,∴∠α=∠DPE ,∠β=∠CPE ,∴∠CPD =∠DPE -∠CPE =∠α-∠β.【点睛】本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,题目是一道比较典型的题目,分类讨论是解题的关键.9.(1) ;(2) ;(3)不发生变化,理由见解析【分析】(1)如图1,延长DE 交AB 于点F ,根据平行线的性质推出;(2)如图2,过点E 作ES ∥AB ,过点H 作HT ∥AB ,根据AB ∥CD ,AB ∥E 解析:(1) +180ACB BED ∠∠=︒;(2) 100︒;(3)不发生变化,理由见解析【分析】(1)如图1,延长DE 交AB 于点F ,根据平行线的性质推出+180ACB BED ∠∠=︒;(2)如图2,过点E 作ES ∥AB ,过点H 作HT ∥AB ,根据AB ∥CD ,AB ∥ES 推出BED ABE CDE ∠=∠+∠,再根据AB ∥TH ,AB ∥CD 推出GHD THD THB ∠=∠-∠,最后根据BED ∠比BHD ∠大60︒得出BED ∠的度数;(3)如图3,过点E 作EQ ∥DN ,根据DEB CDE ABE ∠=∠+∠得出βα-的度数,根据条件再逐步求出PBM ∠的度数.【详解】(1)如答图1所示,延长DE 交AB 于点F .AB ∥CD ,所以D EFB ∠=∠,又因为A D ∠=∠,所以A EFB ∠=∠,所以AC ∥DF ,所以ACB CED ∠=∠.因为+180CED BED ∠∠=︒,所以+180ACB BED ∠∠=︒.(2)如答图2所示,过点E 作ES ∥AB ,过点H 作HT ∥AB .设ABG EBG α∠=∠=,FDH EDH β∠=∠=,因为AB ∥CD ,AB ∥ES ,所以ABE BES ∠=∠,SED CED ∠=∠,所以21802BED BES SED ABE CDE αβ∠=∠+∠=∠+∠=+︒-,因为AB ∥TH ,AB ∥CD ,所以ABG THB ∠=∠,FDH DHT ∠=∠,所以GHD THD THB βα∠=∠-∠=-,因为BED ∠比BHD ∠大60︒,所以2+1802()60αββα︒---=︒,所以40βα-=︒,所以40BHD ∠=︒,所以100BED ∠=︒(3)不发生变化如答图3所示,过点E 作EQ ∥DN .设CDN EDN α∠=∠=,EBM KBM β∠=∠=,由(2)易知DEB CDE ABE ∠=∠+∠,所以2+1802100αβ︒-=︒,所以40βα-=︒, 所以180()180DEB CDE EDN EBM PBM PBM αβ∠=∠+∠+︒-∠+∠=+︒--∠, 所以80()40PBM βα∠=︒--=︒.【点睛】本题考查了平行线的性质,求角的度数,正确作出相关的辅助线,根据条件逐步求出角度的度数是解题的关键.10.[探究] 70°;[应用] 35【分析】[探究]如图②,根据AB ∥CD ,∠AEP=50°,∠PFC=120°,即可求∠EPF 的度数.[应用]如图③所示,在[探究]的条件下,根据∠PEA 的平分线解析:[探究] 70°;[应用] 35【分析】[探究]如图②,根据AB ∥CD ,∠AEP=50°,∠PFC=120°,即可求∠EPF 的度数.[应用]如图③所示,在[探究]的条件下,根据∠PEA 的平分线和∠PFC 的平分线交于点G ,可得∠G 的度数.【详解】解:[探究]如图②,过点P 作PM ∥AB ,∴∠MPE=∠AEP=50°(两直线平行,内错角相等)∵AB ∥CD (已知),∴PM ∥CD (平行于同一条直线的两直线平行),∴∠PFC=∠MPF=120°(两直线平行,内错角相等).∴∠EPF=∠MPF-MPE=120°50°=70°(等式的性质).答:∠EPF 的度数为70°;[应用]如图③所示,∵EG 是∠PEA 的平分线,PG 是∠PFC 的平分线,∴∠AEG=12∠AEP=25°,∠GCF=12∠PFC=60°,过点G 作GM ∥AB ,∴∠MGE=∠AEG=25°(两直线平行,内错角相等)∵AB ∥CD (已知),∴GM ∥CD (平行于同一条直线的两直线平行),∴∠GFC=∠MGF=60°(两直线平行,内错角相等).∴∠G=∠MGF-MGE=60°-25°=35°.答:∠G 的度数是35°.故答案为:35.【点睛】本题考查了平行线的判定与性质、平行公理及推论,解决本题的关键是掌握平行线的判定与性质.三、解答题11.(1)①115°,110°;②,证明见解析;(2),证明见解析.【解析】【分析】(1)①根据角平分线的定义求得∠CAG=∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=解析:(1)①115°,110°;②1902AFD B ︒∠=+∠,证明见解析;(2)1902AFD B ︒∠=-∠,证明见解析. 【解析】【分析】(1)①根据角平分线的定义求得∠CAG=12∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=∠GAC=50°;由三角形的内角和定理求得∠AFD的度数即可;已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=12∠BAC,∠FDM=12∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;即可得∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12(∠BAC+∠C)=12×140°=70°;再由三角形的内角和定理可求得∠AFD=110°;②∠AFD=90°+12∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=12∠BAC,∠FDM=12∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;由此可得∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12(∠BAC+∠C)=12×(180°-∠B)=90°-12∠B;再由三角形的内角和定理可得∠AFD=90°+12∠B;(2)∠AFD=90°-12∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=12∠BAC,∠NDE=12∠EDB,即可得∠FDM=∠NDE=12∠EDB;由DE//AC,根据平行线的性质可得∠EDB=∠C,∠FMD=∠GAC;即可得到∠FDM=∠NDE=12∠C,所以∠FDM+∠FMD =12∠C+12∠BAC=12(∠BAC+∠C)=12×(180°-∠B)=90°-12∠B;再由三角形外角的性质可得∠AFD=∠FDM +∠FMD=90°-12∠B.【详解】(1)①∵AG平分∠BAC,∠BAC=100°,∴∠CAG=12∠BAC=50°;∵//DE AC,∠C=30°,∴∠EDG=∠C=30°,∠FMD=∠GAC=50°;∵DF平分∠EDB,∴∠FDM=12∠EDG=15°;∴∠AFD=180°-∠FMD-∠FDM=180°-50°-15°=115°;∵∠B=40°,∴∠BAC+∠C=180°-∠B=140°;∵AG平分∠BAC,DF平分∠EDB,∴∠CAG=12∠BAC,∠FDM=12∠EDG,∵DE//AC,∴∠EDG=∠C,∠FMD=∠GAC;∴∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12(∠BAC+∠C)=12×140°=70°;∴∠AFD=180°-(∠FDM +∠FMD)=180°-70°=110°;故答案为115°,110°;②∠AFD=90°+12∠B,理由如下:∵AG平分∠BAC,DF平分∠EDB,∴∠CAG=12∠BAC,∠FDM=12∠EDG,∵DE//AC,∴∠EDG=∠C,∠FMD=∠GAC;∴∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12(∠BAC+∠C)=12×(180°-∠B)=90°-12∠B;∴∠AFD=180°-(∠FDM +∠FMD)=180°-(90°-12∠B)=90°+12∠B;(2)∠AFD=90°-12∠B,理由如下:如图,射线ED交AG于点M,∵AG平分∠BAC,DF平分∠EDB,∴∠CAG=12∠BAC,∠NDE=12∠EDB,∴∠FDM=∠NDE=12∠EDB,∵DE//AC,∴∠EDB=∠C,∠FMD=∠GAC;∴∠FDM=∠NDE=12∠C,∴∠FDM +∠FMD =12∠C+12∠BAC=12(∠BAC+∠C)=12×(180°-∠B)=90°-12∠B;∴∠AFD=∠FDM +∠FMD=90°-12∠B.【点睛】本题考查了角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质,根据角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质确定各角之间的关系是解决问题的关键.12.(1),理由见解析;(2)当点P在B、O两点之间时,;当点P在射线AM上时,.【分析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠C解析:(1)CPDαβ∠=∠+∠,理由见解析;(2)当点P在B、O两点之间时,CPDαβ∠=∠-∠;当点P在射线AM上时,CPDβα∠=∠-∠.【分析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(2)分两种情况:①点P在A、M两点之间,②点P在B、O两点之间,分别画出图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出结论.【详解】解:(1)∠CPD=∠α+∠β,理由如下:如图,过P作PE∥AD交CD于E.∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β.(2)当点P在A、M两点之间时,∠CPD=∠β-∠α.理由:如图,过P作PE∥AD交CD于E.∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE-∠DPE=∠β-∠α;当点P在B、O两点之间时,∠CPD=∠α-∠β.理由:如图,过P作PE∥AD交CD于E.∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE-∠CPE=∠α-∠β.【点睛】本题考查了平行线的性质的运用,主要考核了学生的推理能力,解决问题的关键是作平行线构造内错角,利用平行线的性质进行推导.解题时注意:问题(2)也可以运用三角形外角性质来解决.13.∠DPC=α+β,理由见解析;(1)70 ;(2) ∠DPC=α –β,理由见解析.【解析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠C解析:∠DPC=α+β,理由见解析;(1)70 ;(2) ∠DPC=α –β,理由见解析.【解析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(2)化成图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【问题探究】解:∠DPC=α+β如图,过P作PH∥DF∵DF∥CE,∴∠PCE=∠1=α,∠PDF=∠2∵∠DPC=∠2+∠1=α+β【问题迁移】(1)70(图1)(图2)(2) 如图1,∠DPC=β -α∵DF∥CE,∴∠PCE=∠1=β,∵∠DPC=∠1-∠FDP=∠1-α.∴∠DPC=β -α如图2,∠DPC= α -β∵DF∥CE,∴∠PDF=∠1=α∵∠DPC=∠1-∠ACE=∠1-β.∴∠DPC=α - β14.(1)45°;(2)①1;②是定值,∠M+∠N=142.5°【分析】(1)利用平行线的性质求解即可.(2)①利用三角形的面积求出GH,HF,再证明AO=OG=2,可得结论.②利用角平分线的定解析:(1)45°;(2)①1;②是定值,∠M+∠N=142.5°【分析】(1)利用平行线的性质求解即可.(2)①利用三角形的面积求出GH,HF,再证明AO=OG=2,可得结论.②利用角平分线的定义求出∠M,∠N(用∠FAO表示),可得结论.【详解】解:(1)如图,∵AB∥ED∴∠E=∠EAB=90°(两直线平行,内错角相等),∵∠BAC=45°,∴∠CAE=90°-45°=45°.故答案为:45°.(2)①如图1中,∵OG⊥AC,∴∠AOG=90°,∵∠OAG=45°,∴∠OAG=∠OGA=45°,∴AO=OG=2,∵S△AHG=12•GH•AO=4,S△AHF=12•FH•AO=1,∴GH=4,FH=1,∴OF=GH-HF-OG=4-1-2=1.②结论:∠N+∠M=142.5°,度数不变.理由:如图2中,∵MF,MO分别平分∠AFO,∠AOF,∴∠M=180°-12(∠AFO+∠AOF)=180°-12(180°-∠FAO)=90°+12∠FAO,∵NH ,NG 分别平分∠DHG ,∠BGH ,∴∠N =180°-12(∠DHG +∠BGH )=180°-12(∠HAG +∠AGH +∠HAG +∠AHG )=180°-12(180°+∠HAG )=90°-12∠HAG=90°-12(30°+∠FAO +45°)=52.5°-12∠FAO ,∴∠M +∠N =142.5°.【点睛】本题考查平行线的性质,角平分线的定义,三角形内角和定理,三角形外角的性质等知识,最后一个问题的解题关键是用∠FAO 表示出∠M ,∠N . 15.(1)50°;(2)①见解析;②见解析;(3)360°.【分析】(1)根据题意,已知,,可结合三角形内角和定理和折叠变换的性质求解; (2)①先根据折叠得:∠ADE=∠A′DE ,∠AED=∠A′解析:(1)50°;(2)①见解析;②见解析;(3)360°.【分析】(1)根据题意,已知70C ∠=︒,65B ∠=︒,可结合三角形内角和定理和折叠变换的性质求解;(2)①先根据折叠得:∠ADE=∠A′DE ,∠AED=∠A′ED ,由两个平角∠AEB 和∠ADC 得:∠1+∠2等于360°与四个折叠角的差,化简得结果;②利用两次外角定理得出结论;(3)由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去(∠B'GF+∠B'FG )以及(∠C'DE+∠C'ED )和(∠A'HL+∠A'LH ),再利用三角形的内角和定理即可求解.【详解】解:(1)∵70C ∠=︒,65B ∠=︒,∴∠A′=∠A=180°-(65°+70°)=45°,∴∠A′ED+∠A′DE =180°-∠A′=135°,∴∠2=360°-(∠C+∠B+∠1+∠A′ED+∠A′DE )=360°-310°=50°;(2)①122A ∠+∠=∠,理由如下由折叠得:∠ADE=∠A′DE ,∠AED=∠A′ED ,∵∠AEB+∠ADC=360°,∴∠1+∠2=360°-∠ADE-∠A′DE -∠AED-∠A′ED=360°-2∠ADE-2∠AED ,∴∠1+∠2=2(180°-∠ADE-∠AED )=2∠A ;②221A ∠=∠+∠,理由如下:∵2∠是ADF 的一个外角∴2A AFD ∠=∠+∠.∵AFD ∠是A EF '△的一个外角∴1AFD A '∠=∠+∠又∵A A '∠=∠∴221A ∠=∠+∠(3)如图由题意知,∠1+∠2+∠3+∠4+∠5+∠6=720°-(∠B'GF+∠B'FG )-(∠C'DE+∠C'ED )-(∠A'HL+∠A'LH )=720°-(180°-∠B')-(180°-C')-(180°-A')=180°+(∠B'+∠C'+∠A')又∵∠B=∠B',∠C=∠C',∠A=∠A',∠A+∠B+∠C=180°,∴∠1+∠2+∠3+∠4+∠5+∠6=360°.【点睛】题主要考查了折叠变换、三角形、四边形内角和定理.注意折叠前后图形全等;三角形内角和为180°;四边形内角和等于360度.。
广东省深圳市龙岗区2016-2017学年七年级下学期期末数学试卷(解析版)

广东省深圳市龙岗区2016-2017学年七年级(下)期末数学试卷(解析版)一、选择题(本题共有12小题,每小题3分,共36分.)1.下列运算正确的是()A.(x3)2=x5B.x2•x3=x6C.x3÷x=x2D.(x2y)2=x4y【考点】48:同底数幂的除法;46:同底数幂的乘法;47:幂的乘方与积的乘方.【分析】根据幂的乘方,可判断A;根据同底数幂的乘法,可判断B;根据同底数幂的除法,可判断C;根据积的乘方,可判断D.【解答】解:A、幂的乘方底数不变指数相乘,故A错误;B、同底数幂的乘法底数不变指数相加,故B错误;C、同底数幂的除法底数不变指数相减,故C正确;D、积的乘方等于乘方的积,故D错误;故选:C.【点评】本题考查了同底数幂的除法,熟记法则并根据法则计算是解题关键.2.下面有4个汽车标致图案,其中不是轴对称图形的是()A. B.C.D.【考点】P3:轴对称图形.【分析】根据轴对称图形的概念结合4个汽车标志图案的形状求解.【解答】解:由轴对称图形的概念可知第1个,第2个,第3个都是轴对称图形.第4个不是轴对称图形,是中心对称图形.故选D.【点评】本题考查了轴对称图形的知识,轴对称的关键是寻找对称轴,两边图象折叠后可重合.3.0.000043米用科学记数法表示,正确的是()A.4.3×10﹣4 B.4.3×10﹣5 C.4.3×10﹣6 D.43×10﹣5【考点】1J:科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000043米用科学记数法表示4.3×10﹣5,故选:B.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.4.如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为()A.150°B.130°C.100°D.50°【考点】JA:平行线的性质.【分析】先根据两直线平行同位角相等,求出∠3的度数,然后根据邻补角的定义即可求出∠2的度数.【解答】解:如图所示,∵a∥b,∠1=50°,∴∠3=∠1=50°,∵∠2+∠3=180°,∴∠2=130°.故选B.【点评】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等,两直线平行内错角相等,两直线平行同旁内角互补.5.如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是()A.AB=DE B.∠A=∠D C.AC∥DF D.AC=DF【考点】KB:全等三角形的判定.【分析】首先根据等式的性质可得BC=EF,再根据平行线的性质可得∠A=∠DEF,再分别添加四个选项中的条件,结合全等三角形的判定定理进行分析即可.【解答】解:∵BE=CF,∴BE+EC=CF+EC,即BC=EF,∵AB∥DE,∴∠A=∠DEF,A、添加AB=DE,可利用SAS判定△ABC≌△DEF,故此选项不合题意;B、添加∠A=∠D,可利用AAS判定△ABC≌△DEF,故此选项不合题意;C、添加AC∥DF,可得∠ACB=∠F,可利用ASA判定△ABC≌△DEF,故此选项不合题意;D、添加AC=DF,不能判定△ABC≌△DEF,故此选项符合题意;故选:D.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.6.下列各幅图象中,可以大致反映成熟的苹果从树上掉下来时,速度随时间变化情况的是()A. B. C.D.【考点】E6:函数的图象.【分析】苹果下落时在下落的过程中,重力势能转化为动能,速度由0开始,随时间的增大速度越来越大.【解答】解:苹果下落时重力势能转化为动能,速度随时间的增大而变大,根据此特点可知,选项C符合题意.故选C.【点评】本题通过具体的实例考查了v﹣t图象的分析,难度不大;物理中常用坐标图来反映物理量的变化,要学会分析.7.小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是()A.掷一枚质地均匀的硬币,正面朝上的概率B.从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率C.从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率D.任意买一张电影票,座位号是2的倍数的概率【考点】X8:利用频率估计概率.【分析】根据统计图可知,试验结果在0.33附近波动,即其概率P≈0.33,计算四个选项的概率,约为0.33者即为正确答案.【解答】解:A、掷一枚硬币,出现正面朝上的概率为,故此选项错误;B、从一个装有2个白球和1个红球的不透明袋子中任意摸出一球,摸到红球的概率为≈0.33,故此选项正确;C、从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率;故此选项错误;D、任意买一张电影票,座位号是2的倍数的概率不确定,但不一定是0.33,故此选项错误.故选:B.【点评】考查了利用频率估计概率的知识,解题的关键是能够分别求得每个选项的概率,然后求解,难度不大.8.如图,BP是∠MBN的平分线,D是BP上一点,AD⊥BN于点A,AD=3,C是BM上的一点,BC=5,则△BCD的面积为()A.7.5 B.8 C.10 D.15【考点】KF:角平分线的性质.【分析】作DE⊥BC于E,根据角平分线的性质求出DE的长,根据三角形面积公式计算即可.【解答】解:作DE⊥BC于E,∵BD是∠ABC的角平分线,AD⊥AB,DE⊥BC,∴DE=DA=3,∴△BCD=×BC×DE=7.5,故选:A.【点评】本题主要考查了角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.9.若一个三角形有两条边长分别为2和8,且周长为奇数,则第三条边的长度为()A.7 B.9 C.17或19 D.7或9【考点】K6:三角形三边关系.【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于三边”,求得第三边的取值范围;再根据已知的两边和是10,即为偶数,结合周长为奇数,则第三边应是奇数,即可求解.【解答】解:根据三角形的三边关系,得第三边应大于8﹣2=6,而小于8+2=10.又因为三角形的两边长分别为2和8,且周长为奇数,所以第三边应是奇数,则第三边是7或9.故选D.【点评】考查了三角形的三边关系,关键是结合已知的两边和周长,分析出第三边应满足的条件.10.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.【考点】K2:三角形的角平分线、中线和高.【分析】根据三角形高线的定义:过三角形的顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.【解答】解:为△ABC中BC边上的高的是A选项.故选A.【点评】本题考查了三角形的角平分线、中线、高线,熟记高线的定义是解题的关键.11.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是()A.B.C.D.【考点】X5:几何概率.【分析】先求出黑色方格在整个方格中所占面积的比值,再根据其比值即可得出结论.【解答】解:∵图中共有15个方格,其中黑色方格5个,∴黑色方格在整个方格中所占面积的比值==,∴最终停在阴影方砖上的概率为.故选B.【点评】本题考查的是几何概率,熟知概率公式是解答此题的关键.12.已知x2﹣2=y,则x(x﹣2017y)﹣y(1﹣2017x)的值为()A.2 B.0 C.﹣2 D.1【考点】4J:整式的混合运算—化简求值.【分析】由题意可知x2﹣y=2,原式化简整理后整体代入即可解决问题.【解答】解:∵x2﹣2=y,∴x2﹣y=2,∴x(x﹣2017y)﹣y(1﹣2017x)=x2﹣2017xy﹣y+2017xy=x2﹣y=2,故选A.【点评】本题考查整式的化简求值、去括号、合并同类项法则等知识,解题的关键是学会整体代入求值.二、填空题(每小题3分,共12分.).13.计算:(x+3)(x﹣3)=x2﹣9.【考点】4F:平方差公式.【分析】可直接用平方差公式计算.【解答】解:(x+3)(x﹣3)=x2﹣9.【点评】本题考查了平方差公式,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.14.如图,△ABC中,∠BAC=100°,DF、EG分别是AB、AC的垂直平分线,则∠DAE等于20度.【考点】KG:线段垂直平分线的性质.【分析】图中涉及两条垂直平分线,要根据其特点,转化为关于等腰三角形的知识解答.【解答】解:∵DF、EG分别是AB、AC的垂直平分线∴(1)DA=DB,则∠B=∠DAF,设∠B=∠DAF=x度(2)EA=EC,∠C=∠EAG,设∠C=∠EAG=y度因为∠BAC=100°所以x+y+∠DAE=100°根据三角形内角和定理,x+y+x+y+∠DAE=180°解得∠DAE=20°.【点评】主要考查线段的垂直平分线的性质和等腰三角形的性质.15.某人购进一批苹果,到市场零售,已知卖出苹果数量x与售价y的关系如下表,写出用【分析】应先得到1千克苹果的售价,总售价=单价×数量,把相关数值代入即可求得相关函数关系式.【解答】解:易得1千克苹果的售价是16.2÷2=8.1元,那么x千克的苹果的售价:y=8.1x,故答案为:y=8.1x.【点评】本题考查了函数关系式,解决本题的难点是得到每千克苹果的售价,关键是得到总售价的等量关系.16.如图,等边△ABC的边长为1,AB边上有一点P,Q为BC延长线上的一点,且CQ=PA,过点P作PE⊥AC于点E,过P作PF∥BQ交AC边于点F,连接PQ交AC边于点D,则DE的长为.【考点】KD:全等三角形的判定与性质;KK:等边三角形的性质.【分析】过P作BC的平行线至AC于F,通过求证△PFD和△QCD全等,推出FD=CD,再通过证明△APF是等边三角形和PE⊥AC,推出AE=EF,即可推出AE+DC=EF+FD,可得ED=AC,即可推出ED的长度.【解答】解:∵PF∥BQ,∴∠Q=∠FPD,∵等边△ABC,∴∠APF=∠B=60°,∠AFP=∠ACB=60°,∴△APF是等边三角形,∴AP=PF,AP=CQ,∵AP=CQ,∴PF=CQ,∵在△PFD和△QCD中,,∴△PFD≌△QCD(AAS),∴FD=CD,∵PE⊥AC于E,△APF是等边三角形,∴AE=EF,∴AE+DC=EF+FD,∴ED=AC,∵AC=1,∴DE=.故答案为.【点评】本题主要考查等边三角形的判定与性质、平行线的性质、全等三角形的判定与性质,关键在于正确地作出辅助线,熟练运用相关的性质、定理,认真地进行计算.三、解答题(本题共7小题,共52分.)17.(12分)计算:(1)﹣3(x﹣2y)2(2)(2x2y)3÷6x3y2(3)先化简,再求值:(2a+1)2﹣(2a﹣1)(2a+1),其中a=﹣.【考点】4J:整式的混合运算—化简求值.【分析】(1)先根据完全平方公式进行计算,再求出即可;(2)先算乘方,再算除法即可;(3)先根据完全平方公式和平方差公式进行计算,再合并同类项,最后代入求出即可.【解答】解:(1)原式=﹣3(x2﹣4xy+4y2)=﹣3x2+12xy﹣12y2;(2)原式=8x6y3÷6x3y2=x3;(3)(2a+1)2﹣(2a﹣1)(2a+1)=4a2+4a+1﹣4a2+1=4a+2,当a=﹣时,原式=﹣3+2=﹣1.【点评】本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.18.(6分)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.【考点】KD:全等三角形的判定与性质.【分析】根据BC∥DF证得∠CBD=∠FDB,利用利用等角的补角相等证得∠ABC=∠EDF,然后根据AD=EB得到AB=ED,利用AAS证明两三角形全等即可.【解答】证明:∵AD=EB∴AD﹣BD=EB﹣BD,即AB=ED又∵BC∥DF,∴∠CBD=∠FDB∴∠ABC=∠EDF在△ABC和△EDF中,∵∴△ABC≌△EDF,∴AC=EF.【点评】本题考查了全等三角形的判定与性质,解题的关键是选择最合适的方法证明两三角形全等.19.(6分)某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:(1)机动车行驶5h后加油,途中加油24升;(2)根据图形计算,机动车在加油前的行驶中每小时耗油多少升?(3)如果加油站距目的地还有400km,车速为60km/h,要到达目的地,油箱中的油是否够用?请说明理由.【考点】E6:函数的图象.【分析】(1)图象上x=5时,对应着两个点,油量一多一少,可知此时加油多少;(2)因为x=0时,Q=42,x=5时,Q=12,所以出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,因此每小时耗油量为6L;(3)由图象知,加油后还可行驶6小时,即可行驶60×6千米,然后同400千米做比较,即可求出答案.【解答】解:(1)由图可得,机动车行驶5小时后加油为36﹣12=24;(2)∵出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,因此每小时耗油量为6L,(3)由图可知,加油后可行驶6h,故加油后行驶60×6=360km,∵400>360,∴油箱中的油不够用.【点评】此题考查一次函数的实际应用,解答本题的关键是仔细观察图象,寻找题目中所给的信息,进而解决问题,难度一般.20.(6分)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下很大时,摸到白球的频率将会接近0.60;(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;(3)试估算口袋中黑、白两种颜色的球各有多少只?【考点】X8:利用频率估计概率.【分析】(1)本题需先根据表中的数据,估计出摸到白球的频率.(2)本题根据摸到白球的频率即可求出摸到白球和黑球的概率.(3)根据口袋中黑、白两种颜色的球的概率即可求出口袋中黑、白两种颜色的球有多少只.【解答】答:(1)根据题意可得当n很大时,摸到白球的频率将会接近0.60;(2)因为当n很大时,摸到白球的频率将会接近0.60;所以摸到白球的概率是0.6;摸到黑球的概率是0.4;(3)因为摸到白球的概率是0.6,摸到黑球的概率是0.4,所以口袋中黑、白两种颜色的球有白球是30×0.6=18个,黑球是30×0.4=12个;故答案为:(1)0.60;(2)0.6,0.4;【点评】本题主要考查了如何利用频率估计概率,在解题时要注意频率和概率之间的关系.21.(6分)已知:如图,AB∥CD,∠ABE=∠DCF,请说明∠E=∠F的理由.【考点】J9:平行线的判定.【分析】根据两直线平行内错角相等可得,∠ABC=∠BCD结合已知又可知∠EBC=∠FCB,所以BE∥CF(内错角相等,两直线平行)从而证两角相等.【解答】解:∵AB∥CD(已知),∴∠ABC=∠BCD(两直线平行内错角相等),∵∠ABE=∠DCF(已知),∴∠EBC=∠FCB,∴BE∥CF(内错角相等,两直线平行),∴∠E=∠F(两直线平行内错角相等).【点评】本题主要利用平行线的性质和判定及图中角的和差关系来证明.22.(6分)在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;(1)如图1,当点F与点A重合,且∠C=50°,∠B=30°时,求∠EFD的度数;(2)如果点F在线段AE上(不与点A重合)时,如图2,∠EFD与∠C﹣∠B有怎样的数量关系?请说明理由.【考点】K7:三角形内角和定理.【分析】(1)由三角形内角和定理可得∠BAC=100°,∠CAD=40°,由角平分线的性质易得∠EAC的度数,可得∠EFD;(2)由角平分线的性质和三角形的内角和得出∠BAE=90°﹣(∠C+∠B),外角的性质得出∠AEC=90°+(∠B﹣∠C),在△EFD中,由三角形内角和定理可得∠EFD.【解答】(1)解:∵∠C=50°,∠B=30°,∴∠BAC=180°﹣50°﹣30°=100°.∵AE平分∠BAC,∴∠CAE=50°.在△ACE中∠AEC=80°,在Rt△ADE中∠EFD=90°﹣80°=10°.(2)∠EFD=(∠C﹣∠B)证明:∵AE平分∠BAC,∴∠BAE==90°﹣(∠C+∠B)∵∠AEC为△ABE的外角,∴∠AEC=∠B+90°﹣(∠C+∠B)=90°+(∠B﹣∠C)∵FD⊥BC,∴∠FDE=90°.∴∠EFD=90°﹣[90°+(∠B﹣∠C)]∴∠EFD=(∠C﹣∠B).【点评】本题主要考查了三角形的内角和定理,综合利用角平分线的性质和三角形内角和定理是解答此题的关键.23.(10分)如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠BAD=25°;点D从B向C运动时,∠BDA逐渐变小(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE 是等腰三角形.【考点】KI:等腰三角形的判定;KB:全等三角形的判定.【分析】(1)根据三角形内角和定理,将已知数值代入即可求出∠BAD,根据点D的运动方向可判定∠BDA的变化情况.(2)假设△ABD≌△DCE,利用全等三角形的对应边相等得出AB=DC=2,即可求得答案.(3)假设△ADE是等腰三角形,分为三种情况:①当AD=AE时,∠ADE=∠AED=40°,根据∠AED>∠C,得出此时不符合;②当DA=DE时,求出∠DAE=∠DEA=70°,求出∠BAC,根据三角形的内角和定理求出∠BAD,根据三角形的内角和定理求出∠BDA即可;③当EA=ED时,求出∠DAC,求出∠BAD,根据三角形的内角和定理求出∠ADB.【解答】解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;故答案为:25°;小.(2)当△ABD≌△DCE时.DC=AB,∵AB=2,∴DC=2,∴当DC等于2时,△ABD≌△DCE;(3)∵AB=AC,∴∠B=∠C=40°,①当AD=AE时,∠ADE=∠AED=40°,∵∠AED>∠C,∴此时不符合;②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,∵∠BAC=180°﹣40°﹣40°=100°,∴∠BAD=100°﹣70°=30°;∴∠BDA=180°﹣30°﹣40°=110°;③当EA=ED时,∠ADE=∠DAE=40°,∴∠BAD=100°﹣40°=60°,∴∠BDA=180°﹣60°﹣40°=80°;∴当∠ADB=110°或80°时,△ADE是等腰三角形.【点评】此题主要考查学生对等腰三角形的判定与性质,全等三角形的判定与性质,三角形外角的性质等知识点的理解和掌握,此题涉及到的知识点较多,综合性较强,但难度不大,属于基础题.。
2017-2018学年广东省深圳市龙岗区七年级(下)期末数学试卷(解析版)
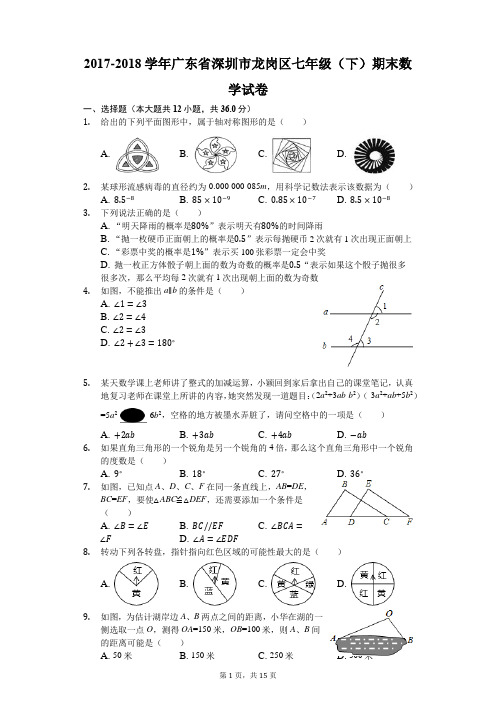
2017-2018学年广东省深圳市龙岗区七年级(下)期末数学试卷一、选择题(本大题共12小题,共36.0分)1.给出的下列平面图形中,属于轴对称图形的是()A. B. C. D.2.某球形流感病毒的直径约为0.000 000 085m,用科学记数法表示该数据为()A. B. C. D.3.下列说法正确的是()A. “明天降雨的概率是”表示明天有的时间降雨B. “抛一枚硬币正面朝上的概率是”表示每抛硬币2次就有1次出现正面朝上C. “彩票中奖的概率是”表示买100张彩票一定会中奖D. 抛一枚正方体骰子朝上面的数为奇数的概率是“表示如果这个骰子抛很多很多次,那么平均每2次就有1次出现朝上面的数为奇数4.如图,不能推出a∥b的条件是()A.B.C.D.5.某天数学课上老师讲了整式的加减运算,小颖回到家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:(2a2+3ab-b2)-(-3a2+ab+5b2)=5a2-6b2,空格的地方被墨水弄脏了,请问空格中的一项是()A. B. C. D.6.如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是()A. B. C. D.7.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是()A. B. C.D.8.转动下列各转盘,指针指向红色区域的可能性最大的是()A. B. C. D.9.如图,为估计湖岸边A、B两点之间的距离,小华在湖的一侧选取一点O,测得OA=150米,OB=100米,则A、B间的距离可能是()A. 50米B. 150米C. 250米D. 300米10.如图,直线AB,CD交于O,EO⊥AB于O,∠1与∠3的关系是()A. 互余B. 对顶角C. 互补D. 相等11.我国西部干旱缺水,在全国开展献爱心、建母亲水窖的活动,如图是某母亲水窖的横断面示意图,如果这个母亲水窖以固定的流量注水,下面能大致表示水的深度h和时间t之间的关系的图象是()A. B. C. D.12.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,则①CA平分∠BCD;②AC⊥BD;③∠ABC=∠ADC=90°;④四边形ABCD的面积为AC•BD.上述结论正确的个数是()A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共4小题,共12.0分)13.计算:x(x-2)=______14.在一个袋子中装有大小相同的4个小球,其中1个蓝色,3个红色,从袋中随机摸出个,则摸到的是蓝色小球的概率为______15.已知知xy=3,x+y=5,则x2+y2-xy=______16.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm,△ABD的周长为13cm,则AE的长为______.三、解答题(本大题共8小题,共52.0分)17.计算:计算下列各题:(1)(-3x2y)2÷(6x2y)(2)(-1)2018+(-)-2-(3.14-π)018.先化简再求值:(a+2)2-3(a+1)(a-1)+2a(a+1),其中a=-5.19.填空:把下面的推理过程补充完整,并在括号内注明理由,如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE解:∵∠A=∠F(已知)∴DF∥AC(______)∴∠D=______(______)∠C=∠D(已知)∴∠1=∠______(______)∴BD∥CE(______)20.如图,在△ABC中,D是AB上一点,DF交AC于点E,DE=FE,AB∥CF,请判断AE与CE是否相等?并说明你的理由.21.某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(小时)的函数关系如图所示.(1)根据图象填空:甲、乙中,______先完成一天的生产任务;在生产过程中,______因机器故障停止生产______小时.(2)谁在哪一段时间内的生产速度最快?求该段时间内,他每小时生产零件的个数.22.如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点的连线为边的多边形称为“格点多边形”.如图①中四边形ABCD就是一个“格点四边形”.(1)求图①中四边形ABCD的面积;(2)在图②的方格纸中画一个格点三角形,使该三角形的面积等于四边形ABCD 的面积且为轴对称图形.23.如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2.(1)求证:△ABC≌△ADE;(2)找出图中与∠1、∠2相等的角(直接写出结论,不需证明).24.如图,已知l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.(1)试探索α,β,γ之间有何数量关系?说明理由.(2)如果BD=3,AB=9,AC=6,并且AC垂直于MN,那么点P运动到什么位置时,△ACP≌△BPD说明理由.(3)在(2)的条件下,当△ACP≌△BPD时,PC与PD之间有何位置关系,说明理由.答案和解析1.【答案】A【解析】解:根据轴对称图形的概念知B、C、D都不是轴对称图形,只有A是轴对称图形.故选:A.根据轴对称图形的概念求解.本题考查轴对称图形的知识,注意掌握轴对称图形的判断方法:把某个图象沿某条直线折叠,如果图形的两部分能够重合,那么这个是轴对称图形.2.【答案】D【解析】解:0.000 000 085m,用科学记数法表示该数据为8.5×10-8.故选:D.绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.3.【答案】D【解析】解:A、应该是降雨的可能性有80%,而不是有80%的时间降雨,故A错误;B、每次试验都有随机性,2次就有1次出现正面朝上,不一定发生,故B错误;C、当购买彩票的次数不断增多时,中奖的频率逐渐稳定1%附近,故C错误;D、说法正确.故选:D.根据概率的意义作答.本题考查了概率的意义,概率只是反映事件发生的可能性的大小.4.【答案】C【解析】解:A、∵∠1和∠3为同位角,∠1=∠3,∴a∥b;故本选项正确,不符合题意;B、∵∠2和∠4为内错角,∠2=∠4,∴a∥b;故本选项正确,不符合题意;C、∵∠2与∠3是同旁内角,∴∠2=∠3,不能证明两直线平行;故本选项错误,符合题意;D、∵∠2和∠3为同位角,∠2+∠3=180°,∴a∥b.故本选项正确,不符合题意;故选:C.在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.本题考查了平行线的判定.正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.5.【答案】A【解析】解:依题意,空格中的一项是:(2a2+3ab-b2)-(-3a2+ab+5b2)-(5a2-6b2)=2a2+3ab-b2+3a2-ab-5b2-5a2+6b2=2ab.故选:A.将等式右边的已知项移到左边,再去括号,合并同类项即可.本题考查了整式的加减运算.解决此类题目的关键是运用移项的知识,同时熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.6.【答案】B【解析】解:设较小的锐角是x度,则另一角是4x度.则x+4x=90,解得:x=18°.故选:B.根据直角三角形的两个角互余即可求解.本题主要考查了直角三角形的性质,两锐角互余.7.【答案】A【解析】解:∵AB=DE,BC=EF,∴要使△ABC≌△DEF,只要满足∠B=∠E或AC=BC即可,故选:A.等三角形的判定方法SAS是指有两边对应相等,且这两边的夹角相等的两三角形全等,已知AB=DE,BC=EF,其两边的夹角是∠B和∠E,只要求出∠B=∠E即可.本题考查了对平行线的性质和全等三角形的判定的应用,注意:有两边对应相等,且这两边的夹角相等的两三角形才全等,题目比较典型,但是一道比较容易出错的题目.8.【答案】D【解析】解:红色区域面积与圆的面积之比即为指针指向红色区域的概率,观察可知红色区域面积D>C>A>B.故选:D.红色区域面积与圆的面积之比即为指针指向红色区域的概率,比较即可.考查了几何概率的计算公式,用到的知识点为:概率=相应的面积与总面积之比.9.【答案】B【解析】解:OA-OB<AB<OA+OB,则150-100<AB<150+100,即50<AB<250.则符合条件的只有B.故选:B.根据三角形的三边关系确定AB的范围,据此即可判断.本题考查了三角形三边关系定理:三角形两边之和大于第三边.已知两边确定第三边的范围时,第三边的长大于已知两边的差,且小于已知两边的和.10.【答案】A【解析】【分析】直接利用垂直的定义得出∠EOB=90°,进而得出∠1与∠3的关系.此题主要考查了垂直的定义以及互为余角的定义,正确得出∠EOB的度数是解题关键.【解答】解:∵EO⊥AB于O,∴∠EOB=90°,∴∠1+∠3=90°,则∠1与∠3的关系是互余.故选:A.11.【答案】C【解析】解:根据题意和图形的形状,可知水的最大深度h与时间t之间的关系分为两段,先快后慢.故选:C.首先看图可知,母亲水窖的下部分比上部分的体积小,故h与t的关系变为先快后慢.考查根据几何图形的性质确定函数的图象和函数图象的作图能力.要能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件,结合实际意义画出正确的图象.12.【答案】B【解析】【分析】此题考查全等三角形的判定和性质,关键是根据SSS证明△ABC与△ADC全等.证明△ABC与△ADC全等,即可解决问题.【解答】解:在△ABC与△ADC中,,∴△ABC≌△ADC(SSS),∴∠ACB=∠ACD,故①正确,∵AB=AD,BC=DC∴AC是BD的垂直平分线,即AC⊥DB,故②正确;无法判断∠ABC=∠ADC=90°,故③错误,四边形ABCD的面积=S△ADB+S△BCD=DB×OA+DB×OC=AC•BD,故④错误;故选:B.13.【答案】x2-2x【解析】解:原式=x2-2x故答案为:x2-2x根据整式的运算法则即可求出答案.本题考查整式的运算法则,解题的关键是熟练运用整式的运算法则,本题属于基础题型.14.【答案】【解析】解:∵4个小球中,有1个蓝色小球,∴P(蓝色小球)=,故答案为:.根据概率公式可得.本题主要考查概率公式,解题的关键是掌握随机事件A的概率P(A)=事件A 可能出现的结果数÷所有可能出现的结果数.15.【答案】16【解析】解:当xy=3,x+y=5时,原式=(x+y)2-3xy=25-9=16故答案为:16根据完全平方公式即可求出答案.本题考查完全平方公式,解题的关键是熟练运用完全平方公式,本题属于基础题型.16.【答案】3cm【解析】解:∵△ABC的周长为19cm,∴AB+AC+BC=19cm,∵DE是AC的垂直平分线,∴DA=DC,AE=EC,∵△ABD的周长为13cm,∴AB+BD+DA=AB+BD+DC=AB+BC=13cm,∴AC=6cm,∴AE=3cm,故答案为:3cm.根据线段的垂直平分线的性质得到DA=DC,AE=EC,根据三角形的周长公式计算即可..本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.17.【答案】解:(1)原式=9x4y2÷(6x2y)=x2y;(2)原式=1+4-1=4.【解析】(1)直接利用整式的除法运算法则计算得出答案;(2)直接利用负指数幂的性质以及零指数幂的性质分别化简得出答案.此题主要考查了整式的除法运算以及实数运算,正确化简各数是解题关键.18.【答案】解:原式=a2+4a+4-3(a2-1)+2a2+2a=a2+4a+4-3a2+3+2a2+2a=6a+7,当a=-5时,原式=-30+7=-23.【解析】先算乘法,再合并同类项,最后代入求出即可.本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.19.【答案】内错角相等,两直线平行;∠1;两直线平行,内错角相等;∠C;等量代换;同位角相等,两直线平行【解析】解:∵∠A=∠F (已知)∴DF∥AC(内错角相等,两直线平行)∴∠D=∠1(两直线平行,内错角相等)∵∠C=∠D(已知)∴∠1=∠C(等量代换)∴BD∥CE(同位角相等,两直线平行),故答案为:内错角相等,两直线平行;∠1;两直线平行,内错角相等;∠C;等量代换;同位角相等,两直线平行.由∠A=∠F依据内错角相等两直线平行知DF∥AC,据此根据平行线性质知∠D=∠1,利用等量代换得∠1=∠C,继而同位角相等两直线平行即可得证.本题主要考查平行线的判定与性质,解题的关键是掌握内错角、同位角相等,两直线平行的判定和两直线平行,内错角相等的性质.20.【答案】解:AE=CE.理由如下:∵AB∥CF,∴∠A=∠ACF在△ADE与△CFE中已证对顶角相等已知∴△AED≌△CEF(AAS)∴AE=CE.【解析】由DE=FE,AB∥CF,易证得△ADE≌△CFE,即可得AE=CE.此题考查了全等三角形的判定与性质以及平行线的性质.此题难度不大,注意掌握数形结合思想的应用.21.【答案】甲;甲;2【解析】解:(1)甲、乙中,甲先完成一天的生产任务;在生产过程中,甲因机器故障停止生产2小时故答案为:甲,甲,2;(2)甲在4-7时的生产速度最快,∵,∴他在这段时间内每小时生产零件10个.(1)根据图象不难得出结论;(2)从图上看出甲在4--7时直线斜率最大,即生产速度最快.此题考查函数图象问题,从图象中获取信息是学习函数的基本功,要结合题意熟练掌握.22.【答案】解:(1)四边形ABCD的面积为:×3×4=6;(2)如图所示:【解析】(1)直接利用对角线垂直的四边形面积求法得出答案;(2)利用等腰三角形的性质得出符合题意的答案.此题主要考查了轴对称变换以及三角形面积求法,正确得出四边形面积是解题关键.23.【答案】(1)证明:∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE,在△BAC和△DAE中,∴△ABC≌△ADE(SAS);(2)解:∵△ABC≌△ADE,∴∠B=∠D,∵∠AMB=∠DMF,∴∠1=∠MFD,∵∠MFD=∠NFC,∴∠1=∠NFC,∴与∠1、∠2相等的角有∠NFC,∠MFD.【解析】(1)根据等式的性质可得∠BAC=∠DAE,然后利用SAS判定△ABC≌△ADE;(2)利用三角形内角和定理可得∠1=∠MFD,再由对顶角相等可得∠1=∠NFC.此题主要考查了全等三角形的性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.24.【答案】解:(1)∠γ=α+∠β,理由:过点P作PF∥l1(如图1),∵l1∥l2,∴PF∥l2,∴∠α=∠DPF,∠β=∠CPF,∴∠γ=∠DPF+∠CPF=α+∠β;(2)当AP=BD=3,△ACP≌△BPD,∵l1∥l2,AC垂直于MN,∴BD⊥MN,∴∠CAP=∠PBD=90°,∵AB=9,∴PB=6,∴AC=PB,在△CAP与△PBD中,,∴△ACP≌△BPD,∴当AP=3时,△ACP≌△BPD;(3)CP⊥PD,理由:∵△ACP≌△BPD,∴∠ACP=∠DPB,∵∠ACP+∠APC=90°,∴∠APC+∠DPB=90°,∴∠CPD=90°,∴CP⊥PD.【解析】(1)过点P作PF∥l1,根据l1∥l2,可知PF∥l2,故可得出∠α=∠DPF,∠β=∠CPF,由此即可得出结论;(2)根据平行线的性质得到BD⊥MN,根据全等三角形的性质即可得到结论;(3)根据全等三角形的性质得到∠ACP=∠DPB,根据垂直的定义即可得到结论.本题考查了全等三角形的判定与性质,平行线的性质,熟练掌握全等三角形的判定与性质是解题的关键.。
2017-2018学年广东省深圳市龙岗区七年级(下)期末数学试卷

2017-2018学年广东省深圳市龙岗区七年级(下)期末数学试卷(考试时间:90分满分:100分)一、选择题(本题共有12小题,每小题3分,共36分)1.(3分)给出的下列平面图形中,属于轴对称图形的是()A.B.C.D.2.(3分)某球形流感病毒的直径约为0.000 000 085m,用科学记数法表示该数据为()A.8.5﹣8B.85×10﹣9C.0.85×10﹣7D.8.5×10﹣83.(3分)下列说法正确的是()A.“明天降雨的概率是80%”表示明天有80%的时间降雨B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上C.“彩票中奖的概率是1%”表示买100张彩票一定会中奖D.抛一枚正方体骰子朝上面的数为奇数的概率是0.5“表示如果这个骰子抛很多很多次,那么平均每2次就有1次出现朝上面的数为奇数4.(3分)如图,不能推出a∥b的条件是()A.∠1=∠3 B.∠2=∠4 C.∠2=∠3 D.∠2+∠3=180°5.(3分)某天数学课上老师讲了整式的加减运算,小颖回到家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:(2a2+3ab﹣b2)﹣(﹣3a2+ab+5b2)=5a2﹣6b2,空格的地方被墨水弄脏了,请问空格中的一项是()A.+2ab B.+3ab C.+4ab D.﹣ab6.(3分)如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是()A.9°B.18°C.27°D.36°7.(3分)如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是()A.∠B=∠E B.BC∥EF C.∠BCA=∠F D.∠A=∠EDF8.(3分)转动下列各转盘,指针指向红色区域的可能性最大的是()A.B.C.D.9.(3分)如图,为估计湖岸边A、B两点之间的距离,小华在湖的一侧选取一点O,测得OA=150米,OB =100米,则A、B间的距离可能是()A.50米B.150米C.250米D.300米10.(3分)如图,直线AB,CD交于O,EO⊥AB于O,∠1与∠3的关系是()A.互余B.对顶角C.互补D.相等11.(3分)我国西部干旱缺水,在全国开展献爱心、建母亲水窖的活动,如图是某母亲水窖的横断面示意图,如果这个母亲水窖以固定的流量注水,下面能大致表示水的深度h和时间t之间的关系的图象是()A.B.C.D.12.(3分)如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,则①CA平分∠BCD;②AC⊥BD;③∠ABC=∠ADC=90°;④四边形ABCD的面积为AC•BD.上述结论正确的个数是()A.1个B.2个C.3个D.4个二、填空题(每小题3分,共12分)13.(3分)计算:x(x﹣2)=14.(3分)在一个袋子中装有大小相同的4个小球,其中1个蓝色,3个红色,从袋中随机摸出个,则摸到的是蓝色小球的概率为15.(3分)已知知xy=3,x+y=5,则x2+y2﹣xy=16.(3分)如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm,△ABD的周长为13cm,则AE的长为.三、解答题(本题共8小题,共52分.)17.(8分)计算:计算下列各题:(1)(﹣3x2y)2÷(6x2y)(2)(﹣1)2018+(﹣)﹣2﹣(3.14﹣π)018.(4分)先化简再求值:(a+2)2﹣3(a+1)(a﹣1)+2a(a+1),其中a=﹣5.19.(6分)填空:把下面的推理过程补充完整,并在括号内注明理由,如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE解:∵∠A=∠F(已知)∴DF∥AC()∴∠D=()∠C=∠D(已知)∴∠1=∠()∴BD∥CE()20.(6分)如图,在△ABC中,D是AB上一点,DF交AC于点E,DE=FE,AB∥CF,请判断AE与CE是否相等?并说明你的理由.21.(6分)某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(小时)的函数关系如图所示.(1)根据图象填空:甲、乙中,先完成一天的生产任务;在生产过程中,因机器故障停止生产小时.(2)谁在哪一段时间内的生产速度最快?求该段时间内,他每小时生产零件的个数.22.(6分)如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点的连线为边的多边形称为“格点多边形”.如图①中四边形ABCD就是一个“格点四边形”.(1)求图①中四边形ABCD的面积;(2)在图②的方格纸中画一个格点三角形,使该三角形的面积等于四边形ABCD的面积且为轴对称图形.23.(6分)如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2.(1)求证:△ABC≌△ADE;(2)找出图中与∠1、∠2相等的角(直接写出结论,不需证明).24.(10分)如图,已知 l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.(1)试探索α,β,γ之间有何数量关系?说明理由.(2)如果BD=3,AB=9,AC=6,并且AC垂直于MN,那么点P运动到什么位置时,△ACP≌△BPD说明理由.(3)在(2)的条件下,当△ACP≌△BPD时,PC与PD之间有何位置关系,说明理由.2017-2018学年广东省深圳市龙岗区七年级(下)期末数学试卷参考答案与试题解析一、选择题(本题共有12小题,每小题3分,共36分)1.(3分)给出的下列平面图形中,属于轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念求解.【解答】解:根据轴对称图形的概念知B、C、D都不是轴对称图形,只有A是轴对称图形.故选:A.【点评】本题考查轴对称图形的知识,注意掌握轴对称图形的判断方法:把某个图象沿某条直线折叠,如果图形的两部分能够重合,那么这个是轴对称图形.2.(3分)某球形流感病毒的直径约为0.000 000 085m,用科学记数法表示该数据为()A.8.5﹣8B.85×10﹣9C.0.85×10﹣7D.8.5×10﹣8【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000 000 085m,用科学记数法表示该数据为8.5×10﹣8.故选:D.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.3.(3分)下列说法正确的是()A.“明天降雨的概率是80%”表示明天有80%的时间降雨B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上C.“彩票中奖的概率是1%”表示买100张彩票一定会中奖D.抛一枚正方体骰子朝上面的数为奇数的概率是0.5“表示如果这个骰子抛很多很多次,那么平均每2次就有1次出现朝上面的数为奇数【分析】根据概率的意义作答.【解答】解:A、应该是降雨的可能性有80%,而不是有80%的时间降雨,故A错误;B、每次试验都有随机性,2次就有1次出现正面朝上,不一定发生,故B错误;C、当购买彩票的次数不断增多时,中奖的频率逐渐稳定1%附近,故C错误;D、说法正确.故选:D.【点评】本题考查了概率的意义,概率只是反映事件发生的可能性的大小.4.(3分)如图,不能推出a∥b的条件是()A.∠1=∠3 B.∠2=∠4 C.∠2=∠3 D.∠2+∠3=180°【分析】在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.【解答】解:A、∵∠1和∠3为同位角,∠1=∠3,∴a∥b;故本选项正确,不符合题意;B、∵∠2和∠4为内错角,∠2=∠4,∴a∥b;故本选项正确,不符合题意;C、∵∠2与∠3是同旁内角,∴∠2=∠3,不能证明两直线平行;故本选项错误,符合题意;D、∵∠2和∠3为同位角,∠2+∠3=180°,∴a∥b.故本选项正确,不符合题意;故选:C.【点评】本题考查了平行线的判定.正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.5.(3分)某天数学课上老师讲了整式的加减运算,小颖回到家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:(2a2+3ab﹣b2)﹣(﹣3a2+ab+5b2)=5a2﹣6b2,空格的地方被墨水弄脏了,请问空格中的一项是()A.+2ab B.+3ab C.+4ab D.﹣ab【分析】将等式右边的已知项移到左边,再去括号,合并同类项即可.【解答】解:依题意,空格中的一项是:(2a2+3ab﹣b2)﹣(﹣3a2+ab+5b2)﹣(5a2﹣6b2)=2a2+3ab﹣b2+3a2﹣ab﹣5b2﹣5a2+6b2=2ab.故选:A.【点评】本题考查了整式的加减运算.解决此类题目的关键是运用移项的知识,同时熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.(3分)如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是()6.A.9°B.18°C.27°D.36°【分析】根据直角三角形的两个角互余即可求解.【解答】解:设较小的锐角是x度,则另一角是4x度.则x+4x=90,解得:x=18°.故选:B.【点评】本题主要考查了直角三角形的性质,两锐角互余.7.(3分)如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是()A.∠B=∠E B.BC∥EF C.∠BCA=∠F D.∠A=∠EDF【分析】等三角形的判定方法SAS是指有两边对应相等,且这两边的夹角相等的两三角形全等,已知AB=DE,BC=EF,其两边的夹角是∠B和∠E,只要求出∠B=∠E即可.【解答】解:∵AB=DE,BC=EF,∴要使△ABC≌△DEF,只要满足∠B=∠E或AC=BC即可,故选:A.【点评】本题考查了对平行线的性质和全等三角形的判定的应用,注意:有两边对应相等,且这两边的夹角相等的两三角形才全等,题目比较典型,但是一道比较容易出错的题目.8.(3分)转动下列各转盘,指针指向红色区域的可能性最大的是()A.B.C.D.【分析】红色区域面积与圆的面积之比即为指针指向红色区域的概率,比较即可.【解答】解:红色区域面积与圆的面积之比即为指针指向红色区域的概率,观察可知红色区域面积D>C>A >B.故选:D.【点评】考查了几何概率的计算公式,用到的知识点为:概率=相应的面积与总面积之比.9.(3分)如图,为估计湖岸边A、B两点之间的距离,小华在湖的一侧选取一点O,测得OA=150米,OB =100米,则A、B间的距离可能是()A.50米B.150米C.250米D.300米【分析】根据三角形的三边关系确定AB的范围,据此即可判断.【解答】解:OA﹣OB<AB<OA+OB,则150﹣100<AB<150+100,即50<AB<250.则符合条件的只有B.故选:B.【点评】本题考查了三角形三边关系定理:三角形两边之和大于第三边.已知两边确定第三边的范围时,第三边的长大于已知两边的差,且小于已知两边的和.10.(3分)如图,直线AB,CD交于O,EO⊥AB于O,∠1与∠3的关系是()A.互余B.对顶角C.互补D.相等【分析】直接利用垂直的定义得出∠EOB=90°,进而得出∠1与∠3的关系.【解答】解:∵EO⊥AB于O,∴∠EOB=90°,∴∠1+∠3=90°,则∠1与∠3的关系是互余.故选:A.【点评】此题主要考查了垂直的定义以及互为余角的定义,正确得出∠EOB的度数是解题关键.11.(3分)我国西部干旱缺水,在全国开展献爱心、建母亲水窖的活动,如图是某母亲水窖的横断面示意图,如果这个母亲水窖以固定的流量注水,下面能大致表示水的深度h和时间t之间的关系的图象是()A.B.C.D.【分析】首先看图可知,母亲水窖的下部分比上部分的体积小,故h与t的关系变为先快后慢.【解答】解:根据题意和图形的形状,可知水的最大深度h与时间t之间的关系分为两段,先快后慢.故选:C.【点评】考查根据几何图形的性质确定函数的图象和函数图象的作图能力.要能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件,结合实际意义画出正确的图象.12.(3分)如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,则①CA平分∠BCD;②AC⊥BD;③∠ABC=∠ADC=90°;④四边形ABCD的面积为AC•BD.上述结论正确的个数是()A.1个B.2个C.3个D.4个【分析】证明△ABD与△CBD全等,即可解决问题;【解答】解:在△ABD与△CBD中,,∴△ABD≌△CBD(SSS),∴∠BDA=∠BDC,故①正确,∵DA=DC,∴DO⊥AC,∴∠AOD=∠COD=90°,AO=OC,∴AC⊥DB,故②正确;无法判断∠ABC=∠ADC=90°,故③错误,四边形ABCD的面积=S△ADB+S△BCD=DB×OA+DB×OC=AC•BD,故④错误;故选:B.【点评】此题考查全等三角形的判定和性质,关键是根据SSS证明△ABD与△CBD全等.二、填空题(每小题3分,共12分)13.(3分)计算:x(x﹣2)=x2﹣2x【分析】根据整式的运算法则即可求出答案.【解答】解:原式=x2﹣2x故答案为:x2﹣2x【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算法则,本题属于基础题型.14.(3分)在一个袋子中装有大小相同的4个小球,其中1个蓝色,3个红色,从袋中随机摸出个,则摸到的是蓝色小球的概率为【分析】根据概率公式可得.【解答】解:∵4个小球中,有1个蓝色小球,∴P(蓝色小球)=,故答案为:.【点评】本题主要考查概率公式,解题的关键是掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.15.(3分)已知知xy=3,x+y=5,则x2+y2﹣xy=16【分析】根据完全平方公式即可求出答案.【解答】解:当xy=3,x+y=5时,原式=(x+y)2﹣3xy=25﹣9=16故答案为:16【点评】本题考查完全平方公式,解题的关键是熟练运用完全平方公式,本题属于基础题型.16.(3分)如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm,△ABD的周长为13cm,则AE的长为3cm .【分析】根据线段的垂直平分线的性质得到DA=DC,AE=EC,根据三角形的周长公式计算即可.【解答】解:∵△ABC的周长为19cm,∴AB+AC+BC=19cm,∵DE是AC的垂直平分线,∴DA=DC,AE=EC,∵△ABD的周长为13cm,∴AB+BD+DA=AB+BD+DC=AB+BC=13cm,∴AC=6cm,∴AE=3cm,故答案为:3cm.【点评】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.三、解答题(本题共8小题,共52分.)17.(8分)计算:计算下列各题:(1)(﹣3x2y)2÷(6x2y)(2)(﹣1)2018+(﹣)﹣2﹣(3.14﹣π)0【分析】(1)直接利用整式的除法运算法则计算得出答案;(2)直接利用负指数幂的性质以及零指数幂的性质分别化简得出答案.【解答】解:(1)原式=9x4y2÷(6x2y)=x2y;(2)原式=1+4﹣1=4.【点评】此题主要考查了整式的除法运算以及实数运算,正确化简各数是解题关键.18.(4分)先化简再求值:(a+2)2﹣3(a+1)(a﹣1)+2a(a+1),其中a=﹣5.【分析】先算乘法,再合并同类项,最后代入求出即可.【解答】解:原式=a2+4a+4﹣3(a2﹣1)+2a2+2a=a2+4a+4﹣3a2+3+2a2+2a=6a+7,当a=﹣5时,原式=﹣30+7=﹣23.【点评】本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.19.(6分)填空:把下面的推理过程补充完整,并在括号内注明理由,如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE解:∵∠A=∠F(已知)∴DF∥AC(内错角相等,两直线平行)∴∠D=∠1 (两直线平行,内错角相等)∠C=∠D(已知)∴∠1=∠∠C (等量代换)∴BD∥CE(同位角相等,两直线平行)【分析】由∠A=∠F依据内错角相等两直线平行知DF∥AC,据此根据平行线性质知∠D=∠1,利用等量代换得∠1=∠C,继而同位角相等两直线平行即可得证.【解答】解:∵∠A=∠F (已知)∴DF∥AC(内错角相等,两直线平行)∴∠D=∠1(两直线平行,内错角相等)∵∠C=∠D(已知)∴∠1=∠C(等量代换)∴BD∥CE(同位角相等,两直线平行),故答案为:内错角相等,两直线平行;∠1;两直线平行,内错角相等;∠C;等量代换;同位角相等,两直线平行.【点评】本题主要考查平行线的判定与性质,解题的关键是掌握内错角、同位角相等,两直线平行的判定和两直线平行,内错角相等的性质.20.(6分)如图,在△ABC中,D是AB上一点,DF交AC于点E,DE=FE,AB∥CF,请判断AE与CE是否相等?并说明你的理由.【分析】由DE=FE,AB∥CF,易证得△ADE≌△CFE,即可得AE=CE.【解答】解:AE=CE.理由如下:∵AB∥CF,∴∠A=∠ACF在△ADE与△CFE中∴△AED≌△CEF(AAS)∴AE=CE.【点评】此题考查了全等三角形的判定与性质以及平行线的性质.此题难度不大,注意掌握数形结合思想的应用.21.(6分)某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(小时)的函数关系如图所示.(1)根据图象填空:甲、乙中,甲先完成一天的生产任务;在生产过程中,甲因机器故障停止生产 2 小时.(2)谁在哪一段时间内的生产速度最快?求该段时间内,他每小时生产零件的个数.【分析】(1)根据图象不难得出结论;(2)从图上看出甲在4﹣﹣7时直线斜率最大,即生产速度最快.【解答】解:(1)甲、乙中,甲先完成一天的生产任务;在生产过程中,甲因机器故障停止生产2小时故答案为:甲,甲,2;(2)甲在4﹣7时的生产速度最快,∵,∴他在这段时间内每小时生产零件10个.【点评】此题考查函数图象问题,从图象中获取信息是学习函数的基本功,要结合题意熟练掌握.22.(6分)如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点的连线为边的多边形称为“格点多边形”.如图①中四边形ABCD就是一个“格点四边形”.(1)求图①中四边形ABCD的面积;(2)在图②的方格纸中画一个格点三角形,使该三角形的面积等于四边形ABCD的面积且为轴对称图形.【分析】(1)直接利用对角线垂直的四边形面积求法得出答案;(2)利用等腰三角形的性质得出符合题意的答案.【解答】解:(1)四边形ABCD的面积为:×3×4=6;(2)如图所示:【点评】此题主要考查了轴对称变换以及三角形面积求法,正确得出四边形面积是解题关键.23.(6分)如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2.(1)求证:△ABC≌△ADE;(2)找出图中与∠1、∠2相等的角(直接写出结论,不需证明).【分析】(1)根据等式的性质可得∠BAC=∠DAE,然后利用SAS判定△ABC≌△ADE;(2)利用三角形内角和定理可得∠1=∠MFD,再由对顶角相等可得∠1=∠NFC.【解答】(1)证明:∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE,在△BAC和△DAE中,∴△ABC≌△ADE(SAS);(2)解:∵△ABC≌△ADE,∴∠B=∠D,∵∠AMB=∠DMF,∴∠1=∠MFD,∵∠MFD=∠NFC,∴∠1=∠NFC,∴与∠1、∠2相等的角有∠NFC,∠MFD.【点评】此题主要考查了全等三角形的性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.24.(10分)如图,已知 l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.(1)试探索α,β,γ之间有何数量关系?说明理由.(2)如果BD=3,AB=9,AC=6,并且AC垂直于MN,那么点P运动到什么位置时,△ACP≌△BPD说明理由.(3)在(2)的条件下,当△ACP≌△BPD时,PC与PD之间有何位置关系,说明理由.【分析】(1)过点P作PF∥l1,根据l1∥l2,可知PF∥l2,故可得出∠α=∠DPF,∠β=∠CPF,由此即可得出结论;(2)根据平行线的性质得到BD⊥MN,根据全等三角形的性质即可得到结论;(3)根据全等三角形的性质得到∠ACP=∠DPB,根据垂直的定义即可得到结论.【解答】解:(1)∠γ=α+∠β,理由:过点P作PF∥l1(如图1),∵l1∥l2,∴PF∥l2,∴∠α=∠DPF,∠β=∠CPF,∴∠γ=∠DPF+∠CPF=α+∠β;(2)当AP=BD=3,△ACP≌△BPD,∵l1∥l2,AC垂直于MN,∴BD⊥MN,∴∠CAP=∠PBD=90°,∵AB=9,∴PB=6,∴AC=PB,在△CAP与△PBD中,,∴△ACP≌△BPD,∴当AP=3时,△ACP≌△BPD;(3)CP⊥PD,理由:∵△ACP≌△BPD,∴∠ACP=∠DPB,∵∠ACP+∠APC=90°,∴∠APC+∠DPB=90°,∴∠CPD=90°,∴CP⊥PD.【点评】本题考查了全等三角形的判定与性质,平行线的性质,熟练掌握全等三角形的判定与性质是解题的关键。
2017-2018学年广东省深圳市龙岗区七年级(下)期末数学试卷

2017-2018学年广东省深圳市龙岗区七年级(下)期末数学试卷一、选择题(本题共有12小题,每小题3分,共36分)1.给出的下列平面图形中,属于轴对称图形的是()A.B.C.D.2.某球形流感病毒的直径约为0.000 000 085m,用科学记数法表示该数据为()A.8.5﹣8B.85×10﹣9C.0.85×10﹣7D.8.5×10﹣83.下列说法正确的是()A.“明天降雨的概率是80%”表示明天有80%的时间降雨B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上C.“彩票中奖的概率是1%”表示买100张彩票一定会中奖D.抛一枚正方体骰子朝上面的数为奇数的概率是0.5“表示如果这个骰子抛很多很多次,那么平均每2次就有1次出现朝上面的数为奇数4.如图,不能推出a∥b的条件是()A.∠1=∠3B.∠2=∠4C.∠2=∠3D.∠2+∠3=180°5.某天数学课上老师讲了整式的加减运算,小颖回到家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:(2a2+3ab﹣b2)﹣(﹣3a2+ab+5b2)=5a2﹣6b2,空格的地方被墨水弄脏了,请问空格中的一项是()A.+2ab B.+3ab C.+4ab D.﹣ab6.如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是()A.9°B.18°C.27°D.36°7.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是()A .∠B =∠E B .BC ∥EF C .∠BCA =∠FD .∠A =∠EDF8.转动下列各转盘,指针指向红色区域的可能性最大的是( )A .B .C .D .9.如图,为估计湖岸边A 、B 两点之间的距离,小华在湖的一侧选取一点O ,测得OA =150米,OB =100米,则A 、B 间的距离可能是( )A .50米B .150米C .250米D .300米10.如图,直线AB ,CD 交于O ,EO ⊥AB 于O ,∠1与∠3的关系是( )A .互余B .对顶角C .互补D .相等11.我国西部干旱缺水,在全国开展献爱心、建母亲水窖的活动,如图是某母亲水窖的横断面示意图,如果这个母亲水窖以固定的流量注水,下面能大致表示水的深度h 和时间t 之间的关系的图象是( )A .B .C .D .12.如图,在四边形ABCD 中,AB =AD ,BC =DC ,AC 与BD 相交于点O ,则①CA 平分∠BCD ;②AC ⊥BD ;③∠ABC =∠ADC =90°;④四边形ABCD 的面积为AC •BD .上述结论正确的个数是( )A.1个B.2个C.3个D.4个二、填空题(每小题3分,共12分)13.计算:x(x﹣2)=14.在一个袋子中装有大小相同的4个小球,其中1个蓝色,3个红色,从袋中随机摸出个,则摸到的是蓝色小球的概率为15.已知知xy=3,x+y=5,则x2+y2﹣xy=16.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm,△ABD的周长为13cm,则AE的长为.三、解答题(本题共8小题,共52分.)17.(8分)计算:计算下列各题:(1)(﹣3x2y)2÷(6x2y)(2)(﹣1)2018+(﹣)﹣2﹣(3.14﹣π)018.(4分)先化简再求值:(a+2)2﹣3(a+1)(a﹣1)+2a(a+1),其中a=﹣5.19.(6分)填空:把下面的推理过程补充完整,并在括号内注明理由,如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE解:∵∠A=∠F(已知)∴DF∥AC()∴∠D=()∠C=∠D(已知)∴∠1=∠()∴BD∥CE()20.(6分)如图,在△ABC中,D是AB上一点,DF交AC于点E,DE=FE,AB∥CF,请判断AE与CE是否相等?并说明你的理由.21.(6分)某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(小时)的函数关系如图所示.(1)根据图象填空:甲、乙中,先完成一天的生产任务;在生产过程中,因机器故障停止生产小时.(2)谁在哪一段时间内的生产速度最快?求该段时间内,他每小时生产零件的个数.22.(6分)如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点的连线为边的多边形称为“格点多边形”.如图①中四边形ABCD就是一个“格点四边形”.(1)求图①中四边形ABCD的面积;(2)在图②的方格纸中画一个格点三角形,使该三角形的面积等于四边形ABCD的面积且为轴对称图形.23.(6分)如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2.(1)求证:△ABC≌△ADE;(2)找出图中与∠1、∠2相等的角(直接写出结论,不需证明).24.(10分)如图,已知l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.(1)试探索α,β,γ之间有何数量关系?说明理由.(2)如果BD=3,AB=9,AC=6,并且AC垂直于MN,那么点P运动到什么位置时,△ACP≌△BPD说明理由.(3)在(2)的条件下,当△ACP≌△BPD时,PC与PD之间有何位置关系,说明理由.2017-2018学年广东省深圳市龙岗区七年级(下)期末数学试卷参考答案与试题解析一、选择题(本题共有12小题,每小题3分,共36分)1.【解答】解:根据轴对称图形的概念知B、C、D都不是轴对称图形,只有A是轴对称图形.故选:A.2.【解答】解:0.000 000 085m,用科学记数法表示该数据为8.5×10﹣8.故选:D.3.【解答】解:A、应该是降雨的可能性有80%,而不是有80%的时间降雨,故A错误;B、每次试验都有随机性,2次就有1次出现正面朝上,不一定发生,故B错误;C、当购买彩票的次数不断增多时,中奖的频率逐渐稳定1%附近,故C错误;D、说法正确.故选:D.4.【解答】解:A、∵∠1和∠3为同位角,∠1=∠3,∴a∥b;故本选项正确,不符合题意;B、∵∠2和∠4为内错角,∠2=∠4,∴a∥b;故本选项正确,不符合题意;C、∵∠2与∠3是同旁内角,∴∠2=∠3,不能证明两直线平行;故本选项错误,符合题意;D、∵∠2和∠3为同位角,∠2+∠3=180°,∴a∥b.故本选项正确,不符合题意;故选:C.5.【解答】解:依题意,空格中的一项是:(2a2+3ab﹣b2)﹣(﹣3a2+ab+5b2)﹣(5a2﹣6b2)=2a2+3ab﹣b2+3a2﹣ab﹣5b2﹣5a2+6b2=2ab.故选:A.6.【解答】解:设较小的锐角是x度,则另一角是4x度.则x+4x=90,解得:x=18°.故选:B.7.【解答】解:∵AB=DE,BC=EF,∴要使△ABC≌△DEF,只要满足∠B=∠E或AC=BC即可,故选:A.8.【解答】解:红色区域面积与圆的面积之比即为指针指向红色区域的概率,观察可知红色区域面积D>C>A>B . 故选:D .9.【解答】解:OA ﹣OB <AB <OA +OB , 则150﹣100<AB <150+100,即50<AB <250. 则符合条件的只有B . 故选:B .10.【解答】解:∵EO ⊥AB 于O , ∴∠EOB =90°,∴∠1+∠3=90°,则∠1与∠3的关系是互余. 故选:A .11.【解答】解:根据题意和图形的形状,可知水的最大深度h 与时间t 之间的关系分为两段,先快后慢. 故选:C .12.【解答】解:在△ABC 与△ADC 中,,∴△ABC ≌△ADC (SSS ), ∴∠ACB =∠ACD ,故①正确, ∵DA =DC , ∴DO ⊥AC ,∴∠AOD =∠COD =90°,AO =OC , ∴AC ⊥DB , 故②正确;无法判断∠ABC =∠ADC =90°,故③错误,四边形ABCD 的面积=S △ADB +S △BCD =DB ×OA +DB ×OC =AC •BD , 故④错误; 故选:B .二、填空题(每小题3分,共12分)13.【解答】解:原式=x2﹣2x故答案为:x2﹣2x14.【解答】解:∵4个小球中,有1个蓝色小球,∴P(蓝色小球)=,故答案为:.15.【解答】解:当xy=3,x+y=5时,原式=(x+y)2﹣3xy=25﹣9=16故答案为:1616.【解答】解:∵△ABC的周长为19cm,∴AB+AC+BC=19cm,∵DE是AC的垂直平分线,∴DA=DC,AE=EC,∵△ABD的周长为13cm,∴AB+BD+DA=AB+BD+DC=AB+BC=13cm,∴AC=6cm,∴AE=3cm,故答案为:3cm.三、解答题(本题共8小题,共52分.)17.【解答】解:(1)原式=9x4y2÷(6x2y)=x2y;(2)原式=1+4﹣1=4.18.【解答】解:原式=a2+4a+4﹣3(a2﹣1)+2a2+2a =a2+4a+4﹣3a2+3+2a2+2a=6a+7,当a=﹣5时,原式=﹣30+7=﹣23.19.【解答】解:∵∠A=∠F(已知)∴DF∥AC(内错角相等,两直线平行)∴∠D=∠1(两直线平行,内错角相等)∵∠C=∠D(已知)∴∠1=∠C(等量代换)∴BD∥CE(同位角相等,两直线平行),故答案为:内错角相等,两直线平行;∠1;两直线平行,内错角相等;∠C;等量代换;同位角相等,两直线平行.20.【解答】解:AE=CE.理由如下:∵AB∥CF,∴∠A=∠ACF在△ADE与△CFE中∴△AED≌△CEF(AAS)∴AE=CE.21.【解答】解:(1)甲、乙中,甲先完成一天的生产任务;在生产过程中,甲因机器故障停止生产2小时故答案为:甲,甲,2;(2)甲在4﹣7时的生产速度最快,∵,∴他在这段时间内每小时生产零件10个.22.【解答】解:(1)四边形ABCD的面积为:×3×4=6;(2)如图所示:23.【解答】(1)证明:∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE,在△BAC和△DAE中,∴△ABC≌△ADE(SAS);(2)解:∵△ABC≌△ADE,∴∠B=∠D,∵∠AMB=∠DMF,∴∠1=∠MFD,∵∠MFD=∠NFC,∴∠1=∠NFC,∴与∠1、∠2相等的角有∠NFC,∠MFD.24.【解答】解:(1)∠γ=α+∠β,理由:过点P作PF∥l1(如图1),∵l1∥l2,∴PF∥l2,∴∠α=∠DPF,∠β=∠CPF,∴∠γ=∠DPF+∠CPF=α+∠β;(2)当AP=BD=3,△ACP≌△BPD,∵l1∥l2,AC垂直于MN,∴BD⊥MN,∴∠CAP=∠PBD=90°,∵AB=9,∴PB=6,∴AC=PB,∴当AP=3时,△ACP≌△BPD;(3)CP⊥PD,理由:∵△ACP≌△BPD,∴∠ACP=∠DPB,∵∠ACP+∠APC=90°,∴∠APC+∠DPB=90°,∴∠CPD=90°,∴CP⊥PD.。
深圳市龙岗区七年级下册期末数学试卷及答案

深圳市龙岗区七年级下册期末数学试卷及答案深圳市龙岗区七年级下册期末数学试卷一、选择题:(请将答题卡上的正确选项涂黑,每小题3分,共36分)1.(3分)计算:$(3a)^3$的值为()A.$27a^3$ B.$3a^3$ C.$9a^3$ D.$27a$2.(3分)下列标志中,可以看作是轴对称图形的是()A.[图1] B.[图2] C.[图3] D.[图4]3.(3分)下列运算正确的是()A.$3a^2-a^2=3$ B.$a^3a^6=a^9$ C.$a^8\diva^2=a^4$ D.$(-1)=-3$4.(3分) 0.0005毫米用科学记数法表示为()A.$0.5\times10^{-3}$毫米 B.$50\times10^{-4}$毫米C.$5\times10^{-3}$毫米 D.$5\times10^{-4}$毫米5.(3分)有下列长度的三条线段,其中能组成三角形的是()A.3cm、6cm、10cm B.10cm、4cm、6cm C.3cm、1cm、1cm D.4cm、6cm、9cm6.(3分)一个不透明的袋子中只装有1个黄球和3个红球,它们除颜色外完全相同,从中随机摸出一个球。
下列说法正确的是()A.摸到黄球是不可能事件 B。
摸到黄球的概率是$\frac{1}{4}$ C.摸到红球是随机事件 D.摸到红球是必然事件7.(3分)如图,下列四个条件中,能判断$DE//AC$的是()XXX$8.(3分)XXX买了6支笔花了9元钱,XXX买了同样售价的x支笔,还买了单价为5元的三角尺两幅,用y(元)表示琪琪花的总钱数,那么y与x之间的关系式应该是()A.$y=1.5x+10$ B.$y=5x+10$ C.$y=1.5x+5$ D.$y=5x +5$9.(3分)如图是一个平分角的仪器,其中$AB=AD$,$BC=DC$,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是()A.SSS B.XXX10.(3分)已知$a+b=-5$,$ab=-4$,则$a^2-3ab+b^2$的值是()A.49 B.37 C.45 D.3311.(3分)在数学课上,老师提出如下问题:老师说:“XXX的作法正确”请回答:XXX第二步作图中①的作法和第二步作图依据的定理或性质是②()答案不在原文中)12.已知长方形ABCD中,E是边AD上一点,且AE=6cm,AB=8cm。
2017-2018年广东省深圳市七年级(下)期末数学试卷(解析版)

2017-2018学年广东省深圳市七年级(下)期末数学试卷一、选择题1.(3分)下面有4个汽车标志图案,其中是轴对称图形的有()A.1个B.2个C.3个D.4个2.(3分)据广东省卫计委通报,5月27日广东出现首例中东呼吸综合症(MERS)疑似病例,MERS属于冠状病毒,病毒粒子成球形,直径约为140纳米(1米=1000000000纳米),用科学记数法表示为()A.1.4×1011米B.140×109米C.1.4×10﹣11米D.1.4×10﹣7米3.(3分)下列条件中,能判定两个直角三角形全等的是()A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.两条直角边对应相等4.(3分)下列运算正确的是()A.a6÷a2=a3B.a3•a3•a3=3a3C.(a3)4=a12D.(a+2b)2=a2+4b25.(3分)下列计算正确的是()A.(3x﹣y)(3x+y)=9x2﹣y2B.(x﹣9)(x+9)x2﹣9C.(x﹣y)(﹣x+y)=x2﹣y2D.(x﹣)2=x2﹣6.(3分)已知m+n=2,mn=﹣2,则(1﹣m)(1﹣n)的值为()A.﹣1B.1C.﹣3D.57.(3分)下列判断正确的个数是()(1)能够完全重合的两个图形全等;(2)两边和一角对应相等的两个三角形全等;(3)两角和一边对应相等的两个三角形全等;(4)全等三角形对应边相等.A.1个B.2个C.3个D.4个8.(3分)如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为()(1)汽车行驶时间为40分钟;(2)AB表示汽车匀速行驶;(3)在第30分钟时,汽车的速度是90千米/时;(4)第40分钟时,汽车停下来了.A.1个B.2个C.3个D.4个9.(3分)下列关于概率的描述属于“等可能性事件”的是()A.交通信号灯有“红、绿、黄”三种颜色,它们发生的概率B.掷一枚图钉,落地后钉尖“朝上”或“朝下”的概率C.小亮在沿着“直角三角形”三边的小路上散步,他出现在各边上的概率D.小明用随机抽签的方式选择以上三种答案,则A、B、C被选中的概率10.(3分)如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短11.(3分)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若CD=BD,点D到边AB的距离为6,则BC的长是()A.6B.12C.18D.2412.(3分)如图,已知AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=40°,则∠EGF的度数是()A.60°B.70°C.80°D.90°二、填空题13.(3分)若x2+mx+9是一个完全平方式,则m的值是.14.(3分)如图,有一小球在如图所示的地板上面自由滚动,则小球在地板上最终停留在黑色区域的概率为.15.(3分)如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为.16.(3分)如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=BC;(3)BD平分∠ABC;(4)AO=CO.其中正确的有(填序号).三、解答题17.计算:(1)2﹣2+()0+(﹣0.2)2014×52014(2)已知a m=3,a n=9,则a m+n=.18.先化简,再求值:[(x+2y)2﹣(3x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣,y=1.19.如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,A和C都在对称轴上.(1)△ABC以直线a为对称轴作△AB1C;(2)若∠BAC=30°,则∠BAB1=°;(3)求△ABB1的面积等于.20.“西气东输”是造福子孙后代的创世纪工程.现有两条高速公路和A、B两个城镇(如图),准备建立一个燃气中心站P,使中心站到两条公路距离相等,并且到两个城镇距离相等,请你画出中心站位置.21.一个不透明口袋中装有5个白球和6个红球,这些球除颜色外完全相同,充分搅匀后随机摸球.(1)如果先摸出一白球,将这个白球放回,再摸出一球,那么它是白球的概率是多少?(2)如果先摸出一白球,这个白球不放回,再摸出一球,那么它是白球的概率是多少?(3)如果先摸出一红球,这个红球不放回,再摸出一球,那么它是白球的概率是多少?22.如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图.(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?(2)汽车在点A的速度是多少?在点C呢?(3)司机在第28分钟开始匀速先行驶了4分钟,之后立即以减速行驶2分钟停止,请你在本图中补上从28分钟以后汽车速度与行驶时间的关系图.23.如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED证明:∵BE=FC∴BE+EF=FC+EF()即:∵AB∥CD∴∠B=∠C()∠A=∠D∠B=∠C在△ABF和△DCE中,有BF=CE∴△ABF≌△DCE()∴∠AFB=∠DEC()∴AF∥ED()24.(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD 相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?2017-2018学年广东省深圳市七年级(下)期末数学试卷参考答案与试题解析一、选择题1.(3分)下面有4个汽车标志图案,其中是轴对称图形的有()A.1个B.2个C.3个D.4个【解答】解:由轴对称图形的概念可知第1个,第2个,第3个都是轴对称图形.第4个不是轴对称图形,是中心对称图形.故是轴对称图形的有3个.故选:C.2.(3分)据广东省卫计委通报,5月27日广东出现首例中东呼吸综合症(MERS)疑似病例,MERS属于冠状病毒,病毒粒子成球形,直径约为140纳米(1米=1000000000纳米),用科学记数法表示为()A.1.4×1011米B.140×109米C.1.4×10﹣11米D.1.4×10﹣7米【解答】解:140纳米=1.4×10﹣7米,故选:D.3.(3分)下列条件中,能判定两个直角三角形全等的是()A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.两条直角边对应相等【解答】解:两直角三角形隐含一个条件是两直角相等,要判定两直角三角形全等,起码还要两个条件,故可排除A、C;而B构成了AAA,不能判定全等;D构成了SAS,可以判定两个直角三角形全等.故选:D.4.(3分)下列运算正确的是()A.a6÷a2=a3B.a3•a3•a3=3a3C.(a3)4=a12D.(a+2b)2=a2+4b2【解答】解:A、a6÷a2=a4,故A错误;B、a3•a3•a3=a9,故B错误;C、(a3)4=a12,故C正确;D、(a+2b)2=a2+4b2+4ab,故D错误.故选:C.5.(3分)下列计算正确的是()A.(3x﹣y)(3x+y)=9x2﹣y2B.(x﹣9)(x+9)x2﹣9C.(x﹣y)(﹣x+y)=x2﹣y2D.(x﹣)2=x2﹣【解答】解:A、原式=9x2﹣y2,符合题意;B、原式=x2﹣81,不符合题意;C、原式=﹣x2+2xy﹣y2,不符合题意;D、原式=x2﹣x+,不符合题意,故选:A.6.(3分)已知m+n=2,mn=﹣2,则(1﹣m)(1﹣n)的值为()A.﹣1B.1C.﹣3D.5【解答】解:∵m+n=2,mn=﹣2,∴(1﹣m)(1﹣n)=1﹣n﹣m+mn=1﹣(n+m)+mn=1﹣2﹣2=﹣3;故选:C.7.(3分)下列判断正确的个数是()(1)能够完全重合的两个图形全等;(2)两边和一角对应相等的两个三角形全等;(3)两角和一边对应相等的两个三角形全等;(4)全等三角形对应边相等.A.1个B.2个C.3个D.4个【解答】解:(1)能够完全重合的两个图形全等,正确;(2)两边和一角对应相等的两个三角形全等,必须是SAS才可以得出全等,错误;(3)两角和一边对应相等的两个三角形全等,是一角的对边或两角的夹边对应相等,正确;(4)全等三角形对应边相等,正确.所以有3个判断正确.故选:C.8.(3分)如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为()(1)汽车行驶时间为40分钟;(2)AB表示汽车匀速行驶;(3)在第30分钟时,汽车的速度是90千米/时;(4)第40分钟时,汽车停下来了.A.1个B.2个C.3个D.4个【解答】解:读图可得,在x=40时,速度为0,故(1)(4)正确;AB段,y的值相等,故速度不变,故(2)正确;x=30时,y=80,即在第30分钟时,汽车的速度是80千米/时;故(3)错误;故选:C.9.(3分)下列关于概率的描述属于“等可能性事件”的是()A.交通信号灯有“红、绿、黄”三种颜色,它们发生的概率B.掷一枚图钉,落地后钉尖“朝上”或“朝下”的概率C.小亮在沿着“直角三角形”三边的小路上散步,他出现在各边上的概率D.小明用随机抽签的方式选择以上三种答案,则A、B、C被选中的概率【解答】解:∵交通信号灯有“红、绿、黄”三种颜色,但是红黄绿灯发生的时间一般不相同,∴它们发生的概率不相同,∴它不属于“等可能性事件”,∴选项A不正确;∵图钉上下不一样,∴钉尖朝上的概率和钉尖着地的概率不相同,∴它不属于“等可能性事件”,∴选项B不正确;∵“直角三角形”三边的长度不相同,∴小亮在沿着“直角三角形”三边的小路上散步,他出现在各边上的概率不相同,∴它不属于“等可能性事件”,∴选项C不正确;∵小明用随机抽签的方式选择以上三种答案,A、B、C被选中的相同,∴它属于“等可能性事件”,∴选项D正确.故选:D.10.(3分)如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短【解答】解:构成△AOB,这里所运用的几何原理是三角形的稳定性.故选:A.11.(3分)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若CD=BD,点D到边AB的距离为6,则BC的长是()A.6B.12C.18D.24【解答】解:过D作DE⊥AB于E,∵点D到边AB的距离为6,∴DE=6,∵∠C=90°,AD平分∠BAC,DE⊥AB,∴CD=DE=6,∵CD=DB,∴DB=12,∴BC=6+12=18,故选:C.12.(3分)如图,已知AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=40°,则∠EGF的度数是()A.60°B.70°C.80°D.90°【解答】解:∵AB∥CD,∴∠BEF+∠EFG=180°,又∠EFG=40°∴∠BEF=140°;∵EG平分∠BEF,∴∠BEG=∠BEF=70°,∴∠EGF=∠BEG=70°.故选:B.二、填空题13.(3分)若x2+mx+9是一个完全平方式,则m的值是±6.【解答】解:∵x2+mx+9是一个完全平方式,∴m=±6,故答案为:±6.14.(3分)如图,有一小球在如图所示的地板上面自由滚动,则小球在地板上最终停留在黑色区域的概率为.【解答】解:∵由图可知,黑色方砖3块,共有9块方砖,∴黑色方砖在整个地板中所占的比值==,∴小球停留在黑色区域的概率是.故答案为:.15.(3分)如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为68°.【解答】解:∵长方形的对边AD∥BC,∴∠2=∠1=56°,由翻折的性质和平角的定义可得∠3=180°﹣2∠2=180°﹣2×56°=68°,∵AD∥BC,∴∠EGF=∠3=68°.故答案为:68°.16.(3分)如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=BC;(3)BD平分∠ABC;(4)AO=CO.其中正确的有(1)(2)(3)(4)(填序号).【解答】解:如图,∵直线l是四边形ABCD的对称轴,∴∠1=∠2,∠3=∠4,∵AD∥BC,∴∠2=∠3,∴∠1=∠3=∠4,∴AB∥CD,AB=BC,故(1)(2)正确;由轴对称的性质,AC⊥BD,∴BD平分∠ABC,AO=CO(等腰三角形三线合一),故(3)(4)正确.综上所述,正确的是(1)(2)(3)(4).故答案为:(1)(2)(3)(4).三、解答题17.计算:(1)2﹣2+()0+(﹣0.2)2014×52014(2)已知a m=3,a n=9,则a m+n=27.【解答】解:(1)2﹣2+()0+(﹣0.2)2014×52014=+1+(﹣0.2×5)2014=+(﹣1)2014=+1=;(2)∵a m=3,a n=9,∴a m+n=a m×a n=3×9=27,故答案为:27.18.先化简,再求值:[(x+2y)2﹣(3x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣,y=1.【解答】解:当x=﹣,y=1时,原式=(x2+4xy+4y2﹣9x2+y2﹣5y2)÷2x=(﹣8x2+4xy)÷2x=﹣4x+2y=2+2=419.如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,A和C都在对称轴上.(1)△ABC以直线a为对称轴作△AB1C;(2)若∠BAC=30°,则∠BAB1=60°;(3)求△ABB1的面积等于28.【解答】解:(1)△AB1C如图所示;(2)∠BAB1=2∠BAC=2×30°=60°;(3)△ABB1的面积=×8×7=28.故答案为:60;28.20.“西气东输”是造福子孙后代的创世纪工程.现有两条高速公路和A、B两个城镇(如图),准备建立一个燃气中心站P,使中心站到两条公路距离相等,并且到两个城镇距离相等,请你画出中心站位置.【解答】解:如图所示,.21.一个不透明口袋中装有5个白球和6个红球,这些球除颜色外完全相同,充分搅匀后随机摸球.(1)如果先摸出一白球,将这个白球放回,再摸出一球,那么它是白球的概率是多少?(2)如果先摸出一白球,这个白球不放回,再摸出一球,那么它是白球的概率是多少?(3)如果先摸出一红球,这个红球不放回,再摸出一球,那么它是白球的概率是多少?【解答】解:(1)先摸出一白球,将这个白球放回,那么第二次模球时,仍然有5个白球和6个红球,则再摸出一球,那么它是白球的概率是P=;(2)先摸出一白球,这个白球不放回,那么第二次摸球时,有4个白球和6个红球,那么它是白球的概率是P==;(3)先摸出一红球,这个红球不放回,那么第二次摸球时,有5个白球和5个红球,那么它是白球的概率是P==.22.如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图.(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?(2)汽车在点A的速度是多少?在点C呢?(3)司机在第28分钟开始匀速先行驶了4分钟,之后立即以减速行驶2分钟停止,请你在本图中补上从28分钟以后汽车速度与行驶时间的关系图.【解答】解:(1)根据图象知道:点A到点B是匀速运动、点E到点F是匀加速运动、点G到点H匀减速运动;(2)根据图象知道:汽车在点A的速度是30千米每小时,在点C的速度为0千米每小时;(3)如图所示:.23.如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED证明:∵BE=FC∴BE+EF=FC+EF(等式的性质)即:BF=CE∵AB∥CD∴∠B=∠C(两直线平行内错角相等)∠A=∠D∠B=∠C在△ABF和△DCE中,有BF=CE∴△ABF≌△DCE(AAS)∴∠AFB=∠DEC(全等三角形对应角相等)∴AF∥ED(内错角相等两直线平行)【解答】证明:∵BE=FC,∴BE+EF=FC+EF(等式的性质),即BF=CE,∵AB∥CD,∴∠B=∠C(两直线平行内错角相等),∠A=∠D,∠B=∠C,在△ABF和△DCE中,,∴△ABF≌△DCE(AAS),∴∠AFB=∠DEC(全等三角形对应角相等),∴AF∥ED(内错角相等两直线平行).故答案为:等式的性质;BF=CE;两直线平行内错角相等;AAS;全等三角形对应角相等;内错角相等两直线平行24.(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD 相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?【解答】(1)证明:∵△ABD和△ACE都是等腰直角三角形(已知)∴AB=AD,AE=AC(等腰直角三角形定义)又∵∠BAD=∠CAE=90°(已知)∴∠BAD+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAC,∴△ABE≌△ADC∴BE=DC(全等三角形的对应边相等)∠ABE=∠ADC(全等三角形的对应角相等)又∵∠BFO=∠DF A,∠ADF+∠DF A=90°(直角三角形的两个锐角互余)∴∠ABE+∠BFO=90°(等量代换)∴∠BOF=∠DAF=90,即BE⊥DC.(2)解:结论:BE=CD.理由:如图2,∵以AB、AC为边分别向外做等边△ABD和等边△ACE,∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,∴∠DAB+∠BAC=∠EAC+∠BAC,∴∠DAC=∠BAE,在△DAC和△BAE中,,∴△DAC≌△BAE(SAS),∴CD=BE,∠BEA=∠ACD,∴∠BOC=∠ECO+∠OEC=∠DCA+∠ACE+∠OEC=∠BEA+∠ACE+∠OEC=∠ACE+∠AEC=60°+60°=120°.∴∠BOC=60°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年广东省深圳市龙岗区七年级(下)期末数学试卷一、选择题(本题共有12小题,每小题3分,共36分.)1.(3分)下列运算正确的是()A.(x3)2=x5B.x2•x3=x6C.x3÷x=x2 D.(x2y)2=x4y2.(3分)下面有4个汽车标致图案,其中不是轴对称图形的是()A.B.C.D.3.(3分)0.000043米用科学记数法表示,正确的是()A.4.3×10﹣4B.4.3×10﹣5C.4.3×10﹣6D.43×10﹣54.(3分)如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为()A.150°B.130°C.100° D.50°5.(3分)如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是()A.AB=DE B.∠A=∠D C.AC∥DF D.AC=DF6.(3分)下列各幅图象中,可以大致反映成熟的苹果从树上掉下来时,速度随时间变化情况的是()A.B.C.D.7.(3分)小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是()A.掷一枚质地均匀的硬币,正面朝上的概率B.从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率C.从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率D.任意买一张电影票,座位号是2的倍数的概率8.(3分)如图,BP是∠MBN的平分线,D是BP上一点,AD⊥BN于点A,AD=3,C是BM上的一点,BC=5,则△BCD的面积为()A.7.5 B.8 C.10 D.159.(3分)若一个三角形有两条边长分别为2和8,且周长为奇数,则第三条边的长度为()A.7 B.9 C.17或19 D.7或910.(3分)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.11.(3分)一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是()A.B.C.D.12.(3分)已知x2﹣2=y,则x(x﹣2017y)﹣y(1﹣2017x)的值为()A.2 B.0 C.﹣2 D.1二、填空题(每小题3分,共12分.).13.(3分)计算:(x+3)(x﹣3)=.14.(3分)如图,△ABC中,∠BAC=100°,DF、EG分别是AB、AC的垂直平分线,则∠DAE等于度.15.(3分)某人购进一批苹果,到市场零售,已知卖出苹果数量x与售价y的关系如下表,写出用x表示y的关系式.数量x(千克)2345售价y(元)16.224.332.440.516.(3分)如图,等边△ABC的边长为1,AB边上有一点P,Q为BC延长线上的一点,且CQ=PA,过点P作PE⊥AC于点E,过P作PF∥BQ交AC边于点F,连接PQ交AC边于点D,则DE的长为.三、解答题(本题共7小题,共52分.)17.(12分)计算:(1)﹣3(x﹣2y)2(2)(2x2y)3÷6x3y2(3)先化简,再求值:(2a+1)2﹣(2a﹣1)(2a+1),其中a=﹣.18.(6分)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.19.(6分)某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:(1)机动车行驶5h后加油,途中加油升;(2)根据图形计算,机动车在加油前的行驶中每小时耗油多少升?(3)如果加油站距目的地还有400km,车速为60km/h,要到达目的地,油箱中的油是否够用?请说明理由.20.(6分)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:摸球的次数n1001502005008001000…摸到白球的次数m5896116295484601…摸到白球的频率0.580.640.580.590.6050.601…(1)请估计:当n很大时,摸到白球的频率将会接近;(2)假如你去摸一次,你摸到白球的概率是,摸到黑球的概率是;(3)试估算口袋中黑、白两种颜色的球各有多少只?21.(6分)已知:如图,AB∥CD,∠ABE=∠DCF,请说明∠E=∠F的理由.22.(6分)在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;(1)如图1,当点F与点A重合,且∠C=50°,∠B=30°时,求∠EFD的度数;(2)如果点F在线段AE上(不与点A重合)时,如图2,∠EFD与∠C﹣∠B 有怎样的数量关系?请说明理由.23.(10分)如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D 不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠BAD=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.2016-2017学年广东省深圳市龙岗区七年级(下)期末数学试卷参考答案与试题解析一、选择题(本题共有12小题,每小题3分,共36分.)1.(3分)下列运算正确的是()A.(x3)2=x5B.x2•x3=x6C.x3÷x=x2 D.(x2y)2=x4y【解答】解:A、幂的乘方底数不变指数相乘,故A错误;B、同底数幂的乘法底数不变指数相加,故B错误;C、同底数幂的除法底数不变指数相减,故C正确;D、积的乘方等于乘方的积,故D错误;故选:C.2.(3分)下面有4个汽车标致图案,其中不是轴对称图形的是()A.B.C.D.【解答】解:由轴对称图形的概念可知第1个,第2个,第3个都是轴对称图形.第4个不是轴对称图形,是中心对称图形.故选:D.3.(3分)0.000043米用科学记数法表示,正确的是()A.4.3×10﹣4B.4.3×10﹣5C.4.3×10﹣6D.43×10﹣5【解答】解:0.000043米用科学记数法表示4.3×10﹣5,故选:B.4.(3分)如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为()A.150°B.130°C.100° D.50°【解答】解:如图所示,∵a∥b,∠1=50°,∴∠3=∠1=50°,∵∠2+∠3=180°,∴∠2=130°.故选:B.5.(3分)如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是()A.AB=DE B.∠A=∠D C.AC∥DF D.AC=DF【解答】解:∵BE=CF,∴BE+EC=CF+EC,即BC=EF,∵AB∥DE,∴∠A=∠DEF,A、添加AB=DE,可利用SAS判定△ABC≌△DEF,故此选项不合题意;B、添加∠A=∠D,可利用AAS判定△ABC≌△DEF,故此选项不合题意;C、添加AC∥DF,可得∠ACB=∠F,可利用ASA判定△ABC≌△DEF,故此选项不合题意;D、添加AC=DF,不能判定△ABC≌△DEF,故此选项符合题意;故选:D.6.(3分)下列各幅图象中,可以大致反映成熟的苹果从树上掉下来时,速度随时间变化情况的是()A.B.C.D.【解答】解:苹果下落时重力势能转化为动能,速度随时间的增大而变大,根据此特点可知,选项C符合题意.故选:C.7.(3分)小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是()A.掷一枚质地均匀的硬币,正面朝上的概率B.从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率C.从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率D.任意买一张电影票,座位号是2的倍数的概率【解答】解:A、掷一枚硬币,出现正面朝上的概率为,故此选项错误;B、从一个装有2个白球和1个红球的不透明袋子中任意摸出一球,摸到红球的概率为≈0.33,故此选项正确;C、从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率;故此选项错误;D、任意买一张电影票,座位号是2的倍数的概率不确定,但不一定是0.33,故此选项错误.故选:B.8.(3分)如图,BP是∠MBN的平分线,D是BP上一点,AD⊥BN于点A,AD=3,C是BM上的一点,BC=5,则△BCD的面积为()A.7.5 B.8 C.10 D.15【解答】解:作DE⊥BC于E,∵BD是∠ABC的角平分线,AD⊥AB,DE⊥BC,∴DE=DA=3,∴△BCD=×BC×DE=7.5,故选:A.9.(3分)若一个三角形有两条边长分别为2和8,且周长为奇数,则第三条边的长度为()A.7 B.9 C.17或19 D.7或9【解答】解:根据三角形的三边关系,得第三边应大于8﹣2=6,而小于8+2=10.又因为三角形的两边长分别为2和8,且周长为奇数,所以第三边应是奇数,则第三边是7或9.故选:D.10.(3分)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.【解答】解:为△ABC中BC边上的高的是A选项.故选:A.11.(3分)一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是()A.B.C.D.【解答】解:∵图中共有15个方格,其中黑色方格5个,∴黑色方格在整个方格中所占面积的比值==,∴最终停在阴影方砖上的概率为.故选:B.12.(3分)已知x2﹣2=y,则x(x﹣2017y)﹣y(1﹣2017x)的值为()A.2 B.0 C.﹣2 D.1【解答】解:∵x2﹣2=y,∴x2﹣y=2,∴x(x﹣2017y)﹣y(1﹣2017x)=x2﹣2017xy﹣y+2017xy=x2﹣y=2,故选:A.二、填空题(每小题3分,共12分.).13.(3分)计算:(x+3)(x﹣3)=x2﹣9.【解答】解:(x+3)(x﹣3)=x2﹣9.14.(3分)如图,△ABC中,∠BAC=100°,DF、EG分别是AB、AC的垂直平分线,则∠DAE等于20度.【解答】解:∵DF、EG分别是AB、AC的垂直平分线∴(1)DA=DB,则∠B=∠DAF,设∠B=∠DAF=x度(2)EA=EC,∠C=∠EAG,设∠C=∠EAG=y度因为∠BAC=100°所以x+y+∠DAE=100°根据三角形内角和定理,x+y+x+y+∠DAE=180°解得∠DAE=20°.15.(3分)某人购进一批苹果,到市场零售,已知卖出苹果数量x与售价y的关系如下表,写出用x表示y的关系式y=8.1x.数量x(千克)2345售价y(元)16.224.332.440.5【解答】解:易得1千克苹果的售价是16.2÷2=8.1元,那么x千克的苹果的售价:y=8.1x,故答案为:y=8.1x.16.(3分)如图,等边△ABC的边长为1,AB边上有一点P,Q为BC延长线上的一点,且CQ=PA,过点P作PE⊥AC于点E,过P作PF∥BQ交AC边于点F,连接PQ交AC边于点D,则DE的长为.【解答】解:∵PF∥BQ,∴∠Q=∠FPD,∵等边△ABC,∴∠APF=∠B=60°,∠AFP=∠ACB=60°,∴△APF是等边三角形,∴AP=PF,AP=CQ,∵AP=CQ,∴PF=CQ,∵在△PFD和△QCD中,,∴△PFD≌△QCD(AAS),∴FD=CD,∵PE⊥AC于E,△APF是等边三角形,∴AE=EF,∴AE+DC=EF+FD,∴ED=AC,∵AC=1,∴DE=.故答案为.三、解答题(本题共7小题,共52分.)17.(12分)计算:(1)﹣3(x﹣2y)2(2)(2x2y)3÷6x3y2(3)先化简,再求值:(2a+1)2﹣(2a﹣1)(2a+1),其中a=﹣.【解答】解:(1)原式=﹣3(x2﹣4xy+4y2)=﹣3x2+12xy﹣12y2;(2)原式=8x6y3÷6x3y2=x3;(3)(2a+1)2﹣(2a﹣1)(2a+1)=4a2+4a+1﹣4a2+1=4a+2,当a=﹣时,原式=﹣3+2=﹣1.18.(6分)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.【解答】证明:∵AD=EB∴AD﹣BD=EB﹣BD,即AB=ED又∵BC∥DF,∴∠CBD=∠FDB∴∠ABC=∠EDF在△ABC和△EDF中,∵∴△ABC≌△EDF,∴AC=EF.19.(6分)某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:(1)机动车行驶5h后加油,途中加油24升;(2)根据图形计算,机动车在加油前的行驶中每小时耗油多少升?(3)如果加油站距目的地还有400km,车速为60km/h,要到达目的地,油箱中的油是否够用?请说明理由.【解答】解:(1)由图可得,机动车行驶5小时后加油为36﹣12=24;(2)∵出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,因此每小时耗油量为6L,(3)由图可知,加油后可行驶6h,故加油后行驶60×6=360km,∵400>360,∴油箱中的油不够用.20.(6分)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:摸球的次数n1001502005008001000…摸到白球的次数m5896116295484601…摸到白球的频率0.580.640.580.590.6050.601…(1)请估计:当n很大时,摸到白球的频率将会接近0.60;(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;(3)试估算口袋中黑、白两种颜色的球各有多少只?【解答】答:(1)根据题意可得当n很大时,摸到白球的频率将会接近0.60;(2)因为当n很大时,摸到白球的频率将会接近0.60;所以摸到白球的概率是0.6;摸到黑球的概率是0.4;(3)因为摸到白球的概率是0.6,摸到黑球的概率是0.4,所以口袋中黑、白两种颜色的球有白球是30×0.6=18个,黑球是30×0.4=12个;故答案为:(1)0.60;(2)0.6,0.4;21.(6分)已知:如图,AB∥CD,∠ABE=∠DCF,请说明∠E=∠F的理由.【解答】解:∵AB∥CD(已知),∴∠ABC=∠BCD(两直线平行内错角相等),∵∠ABE=∠DCF(已知),∴∠EBC=∠FCB,∴BE∥CF(内错角相等,两直线平行),∴∠E=∠F(两直线平行内错角相等).22.(6分)在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;(1)如图1,当点F与点A重合,且∠C=50°,∠B=30°时,求∠EFD的度数;(2)如果点F在线段AE上(不与点A重合)时,如图2,∠EFD与∠C﹣∠B 有怎样的数量关系?请说明理由.【解答】(1)解:∵∠C=50°,∠B=30°,∴∠BAC=180°﹣50°﹣30°=100°.∵AE平分∠BAC,∴∠CAE=50°.在△ACE中∠AEC=80°,在Rt△ADE中∠EFD=90°﹣80°=10°.(2)∠EFD=(∠C﹣∠B)证明:∵AE平分∠BAC,∴∠BAE==90°﹣(∠C+∠B)∵∠AEC为△ABE的外角,∴∠AEC=∠B+90°﹣(∠C+∠B)=90°+(∠B﹣∠C)∵FD⊥BC,∴∠FDE=90°.∴∠EFD=90°﹣[90°+(∠B﹣∠C)]∴∠EFD=(∠C﹣∠B).23.(10分)如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D 不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠BAD=25°;点D从B向C运动时,∠BDA逐渐变小(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.【解答】解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;故答案为:25°;小.(2)当△ABD≌△DCE时.DC=AB,∵AB=2,∴DC=2,∴当DC等于2时,△ABD≌△DCE;(3)∵AB=AC,∴∠B=∠C=40°,①当AD=AE时,∠ADE=∠AED=40°,∵∠AED>∠C,∴此时不符合;②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,∵∠BAC=180°﹣40°﹣40°=100°,∴∠BAD=100°﹣70°=30°;∴∠BDA=180°﹣30°﹣40°=110°;③当EA=ED时,∠ADE=∠DAE=40°,∴∠BAD=100°﹣40°=60°,∴∠BDA=180°﹣60°﹣40°=80°;∴当∠ADB=110°或80°时,△ADE是等腰三角形.赠送:初中数学几何模型举例【模型四】几何最值模型:图形特征:BAPl运用举例:1. △ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为AP的中点,则MF的最小值为EM FB2.如图,在边长为6的菱形ABCD中,∠BAD=60°,E为AB的中点,F为AC上一动点,则EF+BF的最小值为_________。
