《二次函数》压轴题
中考数学二次函数压轴题16道
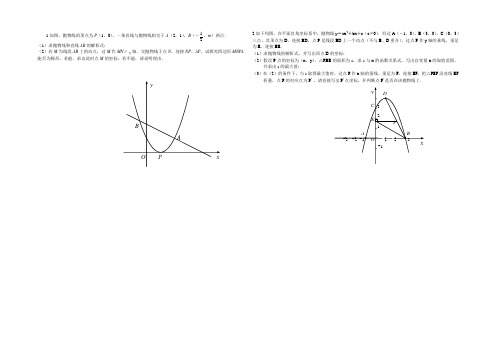
1.如图,抛物线的顶点为P (1,0),一条直线与抛物线相交于A (2,1),B (-21,m )两点.(1)求抛物线和直线AB 的解析式;(2)若M 为线段AB 上的动点,过M 作MN ∥y 轴,交抛物线于点N ,连接NP 、AP ,试探究四边形MNP A 能否为梯形,若能,求出此时点M 的坐标;若不能,请说明理由.2.如下列图,在平面直角坐标系中,抛物线y =ax2+bx +c (a ≠0).经过A (-1,0)、B (3,0)、C (0,3)三点,其顶点为D ,连接BD ,点P 是线段BD 上一个动点(不与B 、D 重合),过点P 作y 轴的垂线,垂足为E ,连接BE .(1)求抛物线的解析式,并写出顶点D 的坐标;(2)假设P 点的坐标为(x ,y ),△PBE 的面积为s ,求s 与x 的函数关系式,写出自变量x 的取值范围,并求出s 的最大值;(3)在(2)的条件下,当s 取得最大值时,过点P 作x 轴的垂线,垂足为F ,连接EF ,把△PEF 沿直线EF折叠,点P 的对应点为P ′ ,请直接写出P ′点坐标,并判断点P ′是否在该抛物线上.3.如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2-2x-8=0的两个根.(1)求这条抛物线的解析式;(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;(3)探究:若点Q是抛物线对称轴上的点,是否存有这样的点Q,使△QBC成为等腰三角形,若存有,请直接写出所有符合条件的点Q的坐标;若不存有,请说明理由.4.已知:如下列图,关于x的抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0),点B(6,0),与y 轴交于点C.(1)求出此抛物线的解析式,并写出顶点坐标;(2)在抛物线上有一点D,使四边形ABDC为等腰梯形,写出点D的坐标,并求出直线AD的解析式;(3)在(2)中的直线AD交抛物线的对称轴于点M,抛物线上有一动点P,x轴上有一动点Q.是否存有以A、M、P、Q为顶点的平行四边形?假设存有,请直接写出点Q的坐标;假设不存有,请说明理由.5.如图,矩形OABC 的两边OA 、OC 分别在x 轴和y 轴上,A (-3,0),过点C 的直线y =-2x +4与x 轴交于点D ,二次函数y =-21x2+bx +c 的图象经过B 、C 两点. (1)求B 、C 两点的坐标; (2)求二次函数的解析式;(3)若点P 是CD 的中点,求证:AP ⊥CD ;(4)在二次函数的图象上是否存有这样的点M ,使以A 、P 、C 、M 为顶点的四边形为矩形?若存有,求出点M 的坐标;若不存有,请说明理由.6.已知:抛物线y =ax2+bx +c (a ≠0)的对称轴为x =-1,与x 轴交于A 、B 两点,与y 轴交于点C ,其中A (-3,0)、C (0,-2).(1)求这条抛物线的函数表达式.(2)已知在对称轴上存有一点P ,使得△PBC 的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE ∥PC 交x 轴于点E ,连接PD 、PE .设CD 的长为m ,△PDE 的面积为S .求S 与m 之间的函数关系式.试说明S 是否存有最大值,若存有,请求出最大值;若不存有,请说明理由.7.如图,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.(1)求A、B、C三点的坐标.(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.(3)在x轴上方的抛物线上是否存有一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似?若存有,请求出M点的坐标;否则,请说明理由.8.如图,抛物线y=ax2+bx-3与x轴交于A,B两点,与y轴交于C点,且经过点(2,-3a),对称轴是直线x=1,顶点是M.(1)求抛物线对应的函数表达式;(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存有这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存有,请求出点P的坐标;若不存有,请说明理由;(3)设直线y=-x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E 三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;(4)当E是直线y=-x+3上任意一点时,(3)中的结论是否成立?(请直接写出结论)9.如图,已知抛物线y=ax2+bx+c与y轴交于点A(0,3),与x轴分别交于B(1,0)、C(5,0)两点.(1)求此抛物线的解析式;(2)若点D为线段OA的一个三等分点,求直线DC的解析式;(3)若一个动点P自OA的中点M出发,先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A.求使点P运动的总路径最短的点E、点F的坐标,并求出这个最短总路径的长.10.如图,在平面直角坐标系中,以点A(-3,0)为圆心、5为半径的圆与x轴相交于点B、C两点(点B在点C的左边),与y轴相交于D、M两点(点D在点M的下方).(1)求以直线x=-3为对称轴、且经过D、C两点的抛物线的解析式;(2)若点P是这条抛物线对称轴上的一个动点,求PC+PD的取值范围;(3)若点E为这条抛物线对称轴上的点,则在抛物线上是否存有这样的点F,使得以点B、C、E、F 为顶点的四边形是平行四边形?若存有,求出点F的坐标;若不存有,说明理由.11.如图,已知抛物线y=ax2+bx-4与直线y=x交于点A、B两点,A、B的横坐标分别为-1和4.(1)求此抛物线的解析式.(2)若平行于y轴的直线x=m(0<m<5+1)与抛物线交于点M,与直线y=x交于点N,交x轴于点P,求线段MN的长(用含m的代数式表示).(3)在(2)的条件下,连接OM、BM,是否存有m的值,使得△BOM的面积S最大?若存有,请求出m 的值,若不存有,请说明理由.12.如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.(1)求此抛物线的解析式;(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存有P点,使得以A、P、M为顶点的三角形与△OAC相似?若存有,请求出符合条件的点P的坐标;若不存有,请说明理由;(3)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.13. 如图(1),抛物线42y x x =+-与y 轴交于点A ,E (0,b )为y 轴上一动点,过点E 的直线y x b =+与抛物线交于点B 、C .b ;若不存有,说明理由.14.如图,已知抛物线212y x bx c x =++与轴交于点A (-4,0)和B (1,0)两点,与y 轴交于C 点. (1)求此抛物线的解析式;(2)设E 是线段AB 上的动点,作EF ∥AC 交BC 于F ,连接CE ,当△CEF 的面积是△BEF 面积的2倍时,求E 点的坐标;(3)若P 为抛物线上A 、C 两点间的一个动点,过P 作y 轴的平行线,交AC 于Q ,当P 点运动到什么位置时,线段PQ 的值最大,并求此时P 点的坐标.x15.如图,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点,点P 是直线BC 下方的抛物线上一动点. (1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP /C , 那么是否存有点P ,使四边形POP /C 为菱形?若存有,请求出此时点P 的坐标;若不存有,请说明理由.(3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.16.在平面直角坐标系xOy 中,抛物线2y ax bx c =++与x 轴交于A B 、两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为(30)-,,若将经过A C 、两点的直线1y kx b =+沿y 轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线2x =-.(1)求直线AC 及抛物线的函数表达式;(2)假如P 是线段AC 上一点,设ABP ∆、BPC ∆的面积分别为ABP S ∆、BPC S ∆,且:2:3ABP BPC S S ∆∆=,求点P 的坐标;(3)设Q 的半径为l ,圆心Q 在抛物线上运动,则在运动过程中是否存有Q 与坐标轴相切的情况?若存有,求出圆心Q 的坐标;若不存有,请说明理由.并探究:若设⊙Q 的半径为r ,圆心Q 在抛物线上运动,则当r 取何值时,⊙Q 与两坐轴同时相切?。
二次函数压轴题(精华版)

2016年10月26日二次函数压轴题1一.解答题〔共30小题〕1.如图,二次函数y=ax2+bx的图象经过点A〔2,4〕与B〔6,0〕.〔1〕求a,b的值;〔2〕点C是该二次函数图象上A,B两点之间的一动点,横坐标为x〔2<x<6〕,写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.2.如图,抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为〔3,0〕〔1〕求m的值与抛物线的顶点坐标.〔2〕点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.3.如图,直线y=x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为〔1,0〕.〔1〕求该抛物线的解析式;〔2〕动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标.4.如图,抛物线y=ax2+bx﹣3a经过A〔﹣1,0〕、C〔0,﹣3〕两点,与x轴交于另一点B.〔1〕求此抛物线的解析式;〔2〕点D〔m,﹣m﹣1〕在第四象限的抛物线上,求点D关于直线BC对称的点D'的坐标.〔3〕在〔2〕的条件下,连接BD,问在x轴上是否存在点P,使∠PCB=∠CBD?假如存在,请求出P点的坐标;假如不存在,请说明理由.5.如图,二次函数y=ax2+bx﹣3的图象与x轴交于B、C两点〔点B在点C的左侧〕,一次函数y=mx+n的图象经过点B和二次函数图象上另一点A,点A的坐标〔4,3〕,.〔1〕求二次函数和一次函数的解析式;〔2〕假如点P在第四象限的抛物线上,求△ABP面积S的最大值并求出此时点P的坐标;〔3〕假如点M在直线AB上,且与点A的距离是到x轴距离的倍,求点M的坐标.6.如图,抛物线y=ax2+bx+c与x轴的一个交点为A〔3,0〕,与y轴的交点为B〔0,3〕,其顶点为C,对称轴为x=1.〔1〕求抛物线的解析式;〔2〕点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标.7.点A〔2,a〕在抛物线y=x2上〔1〕求A点的坐标;〔2〕在x轴上是否存在点P,使△OAP是等腰三角形?假如存在写出P点坐标;假如不存在,说明理由.8.如图,对称轴为直线x=﹣1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中点A的坐标为〔﹣3,0〕,点C为抛物线与y轴的交点.〔1〕求函数的解析式;〔2〕假如点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;〔3〕设点Q为线段AC上的动点,作QO⊥x轴交抛物线于点D,求线段QD长度的最大值.9.如图,抛物线y=ax2+bx+c与x轴交于点A〔﹣2,0〕和点B〔6,0〕,与y轴交于点C〔0,3〕,点D是抛物线上的点,且CD∥x轴,点E是抛物线的顶点.〔1〕求抛物线的解析式;〔2〕平移该抛物线的对称轴所在直线L,当L平移到何处时,恰好将△BCD的面积分为相等的两局部?〔3〕点F在线段CD上,假如以点C,E,F为顶点的三角形与△COE相似,试求点F的坐标.10.如图,抛物线y=ax2+bx+2与x轴交于点A〔1,0〕和B〔4,0〕.〔1〕求抛物线的解析式与对称轴;〔2〕假如抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标.11.如图,抛物线y=ax2+bx+c〔a≠0〕与x轴交于点A〔﹣4,0〕,B〔1,0〕,与y轴交于点D〔0,4〕,点C〔﹣2,n〕也在此抛物线上.〔1〕求此抛物线的解析式与点C的坐标;〔2〕设BC交y轴于点E,连接AE,AC请判断△ACE的形状,并说明理由;〔3〕连接AD交BC于点F,试问:以A,B,F为顶点的三角形与△ABC相似吗?请说明理由.12.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点〔点A在点B的左侧〕,点A的坐标为〔﹣1,0〕,与y轴交于点C〔0,3〕,作直线BC.动点P在x轴上运动,过点P作PM⊥x 轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.〔1〕求抛物线的解析式和直线BC的解析式;〔2〕当点P在线段OB上运动时,求线段MN的最大值;〔3〕当点P在线段OB上运动时,假如△CMN是以MN为腰的等腰直角三角形时,求m的值;〔4〕当以C、O、M、N为顶点的四边形是平行四边形时,直接写出m的值.13.:如下列图,抛物线y=﹣x2+bx+c与x轴的两个交点分别为A〔1,0〕,B〔3,0〕.〔1〕求抛物线的解析式;〔2〕设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标;〔3〕设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小?假如存在,求出点M的坐标;假如不存在,请说明理由.14.如图,抛物线y=ax2+bx+c经过点A〔﹣3,0〕、B〔1,0〕、C〔0,3〕.〔1〕求抛物线的解析式;〔2〕假如点P为抛物线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;〔3〕设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是等腰直角三角形?假如存在,请直接写出点M的坐标;假如不存在,请说明理由.15.抛物线y=ax2+bx+c〔a≠0〕过点A〔﹣3,0〕,B〔1,0〕,C〔0,3〕三点.〔1〕求该抛物线的函数关系式;〔2〕假如抛物线的顶点为P,连接PA、AC、CP,求△PAC的面积;〔3〕过点C作y轴的垂线,交抛物线于点D,连接PD、BD,BD交AC于点E,判断四边形PCED的形状,并说明理由.16.如图,二次函数y=x2+2x+c的图象与x轴交于点A和点B〔1,0〕,以AB为边在x轴上方作正方形ABCD,动点P从点A出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,同时动点Q从点C出发,以每秒1个单位长度的速度沿CB匀速运动,当点Q到达终点B时,点P停止运动,设运动时间为t秒.连接DP,过点P作DP的垂线与y轴交于点E.〔1〕求点A的坐标;〔2〕当点P在线段AO〔点P不与A、O重合〕上运动至何处时,线段OE的长有最大值,并求出这个最大值;〔3〕在P,Q运动过程中,求当△DPE与以D,C,Q为顶点的三角形相似时t的值;〔4〕是否存在t,使△DCQ沿DQ翻折得到△DC′Q,点C′恰好落在抛物线的对称轴上?假如存在,请求出t的值;假如不存在,请说明理由.17.如图,在平面直角坐标系中,直线y=x+1与抛物线y=ax2+bx﹣3〔a≠0〕交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点〔不与点A、B 重合〕,过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.〔1〕求抛物线的解析式;〔2〕设点P的横坐标为m.①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;②连结PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积比为1:2?假如存在,直接写出m的值;假如不存在,请说明理由.18.如图,在平面直角坐标系中,矩形ABCD的三个顶点B〔1,0〕,C〔3,0〕,D〔3,4〕,以A为顶点的抛物线y=ax2+bx+c过点C,动点P从点A出发,以每秒个单位的速度沿线段AD向点D运动,运动时间为t秒,过点P作PE⊥x轴交抛物线于点M,交AC于点N.〔1〕直接写出点A的坐标,并求出抛物线的解析式;〔2〕当t为何值时,△ACM的面积最大?最大值为多少?〔3〕点Q从点C出发,以每秒1个单位的速度沿线段CD向点D运动,当t为何值时,在线段PE上存在点H,使以C,Q,N,H为顶点的四边形为菱形?19.如图,二次函数y=﹣x2﹣+3〔其中m是常数,且m>0〕的图象与x轴交于A、B〔点A位于点B的左侧〕,与y轴交于点C,作CD∥AB,点D在二次函数的图象上,连接BD,过点B作射线BE交二次函数的图象于点E,使得AB平分∠DBE.〔1〕求点C的坐标;〔2〕求证:为定值;〔3〕二次函数y=﹣x2﹣+3的顶点为F,过点C、F作直线与x轴交于点G,试说明:以GF、BD、BE的长度为三边长的三角形是什么三角形?请说明理由.20.如图1,平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为〔﹣2,0〕、〔0,﹣3〕,过点B,C的抛物线y=x2+bx+c与x轴交于点D,E〔D在E的左侧〕,直线DC与线段AB交于点F.〔1〕求抛物线y=x2+bx+c的表达式;〔2〕求点F的坐标;〔3〕如图2,设动点P从点E出发,以每秒1个单位的速度沿射线ED运动,过点P作直线DC的平行线l,过点F作x轴的平行线,交直线l于点Q.设点P的运动时间为t秒.①当点P在射线ED上运动时,四边形PQFD能否成为菱形?假如能,求出相应的t的值;假如不能,说明理由;②当0≤t≤4时,设四边形PQFD与四边形ODBC重合局部的面积为S,直接写出S与t的函数关系式以与相应的自变量t的取值围.21.如图,在平面直角坐标系中,抛物线y=ax2+bx﹣4a与直线y=﹣x+4交两坐标轴于点B,C,且与x轴交另一点A.〔1〕求抛物线的解析式;〔2〕点D〔m,m+1〕在第一象限抛物线的图象上,求点D关于直线BC对称的点D′坐标;〔3〕在〔2〕的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求△ABP的面积.22.如图,点P是直线l:y=﹣2x﹣2上的点,过点P的另一条直线m交抛物线y=x2于A,B 两点.〔1〕假如直线m的解析式为y=﹣x+2,求P,A,B三点的坐标;〔2〕假如点P的坐标为〔﹣2,2〕,当PA=PB时,求点A的坐标;〔3〕求证:对于直线l上任意一点P,在抛物线上都能找到两个不同位置的点A,使得PA=PB 成立?23.抛物线y=ax2+bx+c〔a<0〕经过点A〔﹣3,0〕、B〔1,0〕,且与y轴交于点C,设抛物线的顶点为D.〔1〕求点C、D的坐标〔用含a的式子表示〕;〔2〕当a变化时,△ACD能否为直角三角形?假如能?求出所有符合条件的a的值;假如不能,请说明理由.24.如图1,正方形ABCD的边长为1,点E在边BC上,假如∠AEF=90°,且EF交正方形的外角∠DCM的平分线CF于点F.〔1〕图1中假如点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请表示你的一个构造方案,并指出是哪两个三角形全等〔不要求证明〕;〔2〕如图2,假如点E在线段BC上滑动〔不与点B,C重合〕.①AE=EF是否一定成立?说出你的理由;②在如图2所示的直角坐标系中抛物线y=ax2+x+c经过A、D两点,当点E滑动到某处时,点F恰好落在此抛物线上,求此时点F的坐标.25.如图,抛物线y=ax2+bx+c与x轴交于A〔﹣1,0〕、B〔2,0〕两点,与y轴交于点C〔0,﹣2〕,过A、C画直线.〔1〕求二次函数的解析式;〔2〕点P在x轴正半轴上,且PA=PC,求OP的长;〔3〕假如M为线段OB上的一个动点,过点M做MN平行于y轴交抛物线于点N,当点M运动到何处时,四边形AB的面积最大?求出此时点M的坐标与四边形AB面积的最大值?26.如图,在平面直角坐标系xOy中,二次函数y=x2﹣3x的图象与x轴相交于O、A两点.〔1〕求A点和顶点C的坐标;〔2〕在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;〔3〕对于〔2〕中的点B,在直线OB下方的抛物线上是否存在点P,使得△POB的面积最大?假如存在,求出△POB的最大面积;假如不存在,请说明理由.27.如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是〔﹣1,0〕、〔0,3〕〔1〕求此抛物线对应的函数解析式;〔2〕假如点P是抛物线上位于x轴上方的一个动点,求△ABP面积的最大值;〔3〕假如过点A〔﹣1,0〕的直线AD与抛物线的对称轴和x轴围成的三角形的面积为6,求此直线的解析式.28.如图,抛物线y=﹣x2+2x+3与x轴交于点AB,与y轴交于点C,点D是抛物线的顶点,连接BC、BD.〔1〕点A的坐标是,点B的坐标是,点D的坐标是;〔2〕假如点E是x轴上一点,连接CE,且满足∠ECB=∠CBD,求点E坐标;〔3〕假如点P在x轴上且位于点B右侧,点A、Q关于点P中心对称,连接QD,且∠BDQ=45°,求点P的坐标〔请利用备用图解决问题〕29.如图〔1〕,在平面直角坐标系xOy中,▱OABC的顶点A的坐标为〔2,0〕,点C的坐标为〔2,2〕,点P在射线OA上沿OA方向以2个单位长度/s的速度向右运动,点Q在线段AB上沿AB方向以个单位长度/s的速度从点A向点B运动,设点Q运动的时间为t s〔0≤t ≤2〕,射线PQ交射线CB于点D,连接CP.〔1〕求出过O、A、B三点的抛物线的函数关系式;〔2〕当0<t<1时,求出△PAQ的面积 S与t的函数关系式,并求出当t取何值时,S有最大值;〔3〕在点P运动的过程中,∠CPD是一个定值,这个定值是;并求出当△PCD为等腰三角形时t的值;〔4〕当1≤t≤2时,线段DP的中点M运动的总路程为.30.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为〔1,0〕,点B的坐标为〔0,4〕,点E〔m,0〕是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.〔1〕求该抛物线的解析式;〔2〕当点P在直线BC上方时,请用含m的代数式表示PG的长度;〔3〕在〔2〕的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?假如存在,求出此时m的值;假如不存在,请说明理由.2016年10月26日二次函数压轴题1参考答案与试题解析一.解答题〔共30小题〕1.〔2016•〕如图,二次函数y=ax2+bx的图象经过点A〔2,4〕与B〔6,0〕.〔1〕求a,b的值;〔2〕点C是该二次函数图象上A,B两点之间的一动点,横坐标为x〔2<x<6〕,写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.【考点】待定系数法求二次函数解析式;二次函数的最值.【专题】计算题;二次函数图象与其性质.【分析】〔1〕把A与B坐标代入二次函数解析式求出a与b的值即可;〔2〕如图,过A作x轴的垂直,垂足为D〔2,0〕,连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,分别表示出三角形OAD,三角形ACD,以与三角形BCD的面积,之和即为S,确定出S关于x的函数解析式,并求出x的围,利用二次函数性质即可确定出S的最大值,以与此时x的值.【解答】解:〔1〕将A〔2,4〕与B〔6,0〕代入y=ax2+bx,得,解得:;〔2〕如图,过A作x轴的垂直,垂足为D〔2,0〕,连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,S△OAD=OD•AD=×2×4=4;S△ACD=AD•CE=×4×〔x﹣2〕=2x﹣4;S△BCD=BD•CF=×4×〔﹣x2+3x〕=﹣x2+6x,如此S=S△OAD+S△ACD+S△BCD=4+2x﹣4﹣x2+6x=﹣x2+8x,∴S关于x的函数表达式为S=﹣x2+8x〔2<x<6〕,∵S=﹣x2+8x=﹣〔x﹣4〕2+16,∴当x=4时,四边形OACB的面积S有最大值,最大值为16.【点评】此题考查了待定系数法求二次函数解析式,以与二次函数的最值,熟练掌握二次函数的性质是解此题的关键.2.〔2016•〕如图,抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为〔3,0〕〔1〕求m的值与抛物线的顶点坐标.〔2〕点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.【考点】二次函数的性质.【专题】动点型.【分析】〔1〕首先把点B的坐标为〔3,0〕代入抛物线y=﹣x2+mx+3,利用待定系数法即可求得m的值,继而求得抛物线的顶点坐标;〔2〕首先连接BC交抛物线对称轴l于点P,如此此时PA+PC的值最小,然后利用待定系数法求得直线BC的解析式,继而求得答案.【解答】解:〔1〕把点B的坐标为〔3,0〕代入抛物线y=﹣x2+mx+3得:0=﹣32+3m+3,解得:m=2,∴y=﹣x2+2x+3=﹣〔x﹣1〕2+4,∴顶点坐标为:〔1,4〕.〔2〕连接BC交抛物线对称轴l于点P,如此此时PA+PC的值最小,设直线BC的解析式为:y=kx+b,∵点C〔0,3〕,点B〔3,0〕,∴,解得:,∴直线BC的解析式为:y=﹣x+3,当x=1时,y=﹣1+3=2,∴当PA+PC的值最小时,点P的坐标为:〔1,2〕.【点评】此题考查了二次函数的性质、待定系数法求解析式以与距离最短问题.注意找到点P的位置是解此题的关键.3.〔2016•模拟〕如图,直线y=x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为〔1,0〕.〔1〕求该抛物线的解析式;〔2〕动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标.【考点】二次函数的性质.【分析】〔1〕根据直线的解析式求得点A〔0,1〕,那么把A,B坐标代入y=x2+bx+c即可求得函数解析式;〔2〕让直线解析式与抛物线的解析式结合即可求得点E的坐标.△PAE是直角三角形,应分点P为直角顶点,点A是直角顶点,点E是直角顶点三种情况探讨.【解答】解:〔1〕∵直线y=x+1与y轴交于点A,∴A〔0,1〕,∵y=x2+bx+c过〔1,0〕和〔0,1〕,如此,解得.∴抛物线的解析式为y=x2﹣x+1;〔2〕设点E的横坐标为m,如此它的纵坐标为m2﹣m+1即E点的坐标〔m,m2﹣m+1〕,又∵点E在直线y=x+1上,∴m2﹣m+1=m+1解得m1=0〔舍去〕,m2=4,∴E的坐标为〔4,3〕.〔Ⅰ〕当A为直角顶点时,过A作AP1⊥DE交x轴于P1点,设P1〔a,0〕易知D点坐标为〔﹣2,0〕,由Rt△AOD∽Rt△P1OA得=,即=,∴a=,∴P1〔,0〕.〔Ⅱ〕同理,当E为直角顶点时,过E作EP2⊥DE交x轴于P2点,由Rt△AOD∽Rt△P2ED得,=,即=,∴EP2=,∴DP2==,∴a=﹣2=,P2点坐标为〔,0〕.〔Ⅲ〕当P为直角顶点时,过E作EF⊥x轴于F,设P3〔b、0〕,由∠OPA+∠FPE=90°,得∠OPA=∠FEP,Rt△AOP∽Rt△PFE,由=得=,解得b1=3,b2=1,∴此时的点P3的坐标为〔1,0〕或〔3,0〕,综上所述,满足条件的点P的坐标为〔,0〕或〔1,0〕或〔3,0〕或〔,0〕.【点评】此题考查了待定系数法求二次函数的解析式,二次函数的性质,直线和抛物线的交点等;分类讨论的思想是解题的关键.4.〔2016•株洲模拟〕如图,抛物线y=ax2+bx﹣3a经过A〔﹣1,0〕、C〔0,﹣3〕两点,与x轴交于另一点B.〔1〕求此抛物线的解析式;〔2〕点D〔m,﹣m﹣1〕在第四象限的抛物线上,求点D关于直线BC对称的点D'的坐标.〔3〕在〔2〕的条件下,连接BD,问在x轴上是否存在点P,使∠PCB=∠CBD?假如存在,请求出P点的坐标;假如不存在,请说明理由.【考点】二次函数综合题.【分析】〔1〕将A〔﹣1,0〕、C〔0,﹣3〕两点坐标代入抛物线y=ax2+bx﹣3a中,列方程组求a、b的值即可;〔2〕将点D〔m,﹣m﹣1〕代入〔1〕中的抛物线解析式,求m的值,再根据对称性求点D 关于直线BC对称的点D'的坐标;〔3〕分两种情形①过点C作CP∥BD,交x轴于P,如此∠PCB=∠CBD,②连接BD′,过点C 作CP′∥BD′,交x轴于P′,分别求出直线CP和直线CP′的解析式即可解决问题.【解答】解:〔1〕将A〔﹣1,0〕、C〔0,﹣3〕代入抛物线y=ax2+bx﹣3a中,得,解得,∴y=x2﹣2x﹣3;〔2〕将点D〔m,﹣m﹣1〕代入y=x2﹣2x﹣3中,得m2﹣2m﹣3=﹣m﹣1,解得m=2或﹣1,∵点D〔m,﹣m﹣1〕在第四象限,∴D〔2,﹣3〕,∵直线BC解析式为y=x﹣3,∴∠BCD=∠BCO=45°,CD′=CD=2,OD′=3﹣2=1,∴点D关于直线BC对称的点D'〔0,﹣1〕;〔3〕存在.满足条件的点P有两个.①过点C作CP∥BD,交x轴于P,如此∠PCB=∠CBD,∵直线BD解析式为y=3x﹣9,∵直线CP过点C,∴直线CP的解析式为y=3x﹣3,∴点P坐标〔1,0〕,②连接BD′,过点C作CP′∥BD′,交x轴于P′,∴∠P′CB=∠D′BC,根据对称性可知∠D′BC=∠CBD,∴∠P′CB=∠CBD,∵直线BD′的解析式为y=x﹣1,∵直线CP′过点C,∴直线CP′解析式为y=x﹣3,∴P′坐标为〔9,0〕,综上所述,满足条件的点P坐标为〔1,0〕或〔9,0〕.【点评】此题考查了二次函数的综合运用.关键是由条件求抛物线解析式,根据抛物线的对称性,直线BC的特殊性求点的坐标,学会分类讨论,不能漏解.5.〔2016•东平县一模〕如图,二次函数y=ax2+bx﹣3的图象与x轴交于B、C两点〔点B 在点C的左侧〕,一次函数y=mx+n的图象经过点B和二次函数图象上另一点A,点A的坐标〔4,3〕,.〔1〕求二次函数和一次函数的解析式;〔2〕假如点P在第四象限的抛物线上,求△ABP面积S的最大值并求出此时点P的坐标;〔3〕假如点M在直线AB上,且与点A的距离是到x轴距离的倍,求点M的坐标.【考点】二次函数综合题.【分析】〔1〕过点A作AD⊥x轴于点D,如此D〔4,0〕,∠ADB=90°,在Rt△ADB中,根据正切函数的定义求出BD=6,如此B点坐标为〔﹣2,0〕,再将B,A两点的坐标代入y=ax2+bx ﹣3,运用待定系数法求出二次函数的解析式;将B,A两点的坐标代入y=mx+n,运用待定系数法求出一次函数的解析式;〔2〕根据〔1〕中求出的抛物线的解析式可设点P的坐标为〔t,t2﹣t﹣3〕,过点P作PH垂直于x轴交AB于H点,如此H〔t,t+1〕,用含t的代数式表示PH的长度,再根据S△ABP=PH•BD,求出S△ABP=﹣t2+3t+12,配方后根据二次函数的性质即可求解;〔3〕根据〔1〕中求出的直线AB的解析式可设点M的坐标为〔p,p+1〕,由点M与点A 的距离是它到x轴距离的倍,列出关于p的方程,解方程即可.【解答】解:〔1〕过点A〔4,3〕作AD⊥x轴于点D,如此D〔4,0〕,∠ADB=90°.在Rt△ADB中,∵tan∠ABD===,∴BD=6,B点坐标为〔﹣2,0〕.将B〔﹣2,0〕,A〔4,3〕代入y=ax2+bx﹣3,得,解得:,∴二次函数的解析式为y=x2﹣x﹣3;将B〔﹣2,0〕,A〔4,3〕代入y=mx+n,得,解得,∴一次函数解析式为y=x+1;〔2〕设点P的坐标为〔t,t2﹣t﹣3〕,过点P作PH垂直于x轴交AB于H点,如此H 〔t,t+1〕,∴PH=〔t+1〕﹣〔t2﹣t﹣3〕=﹣t2+t+4,∴S△ABP=S△AHP+S△BHP=PH•DM+PH•BM=PH•BD=〔﹣t2+t+4〕•6=﹣t2+3t+12=﹣〔t ﹣1〕2+,∴当t=1即P点坐标为〔1,﹣3〕时,△ABP的面积S最大,此时S△ABP=;〔3〕设点M的坐标为〔p,p+1〕,由题意,得=×|p+1|,化简整理,得p2﹣12p+20=0,解得p=2或10,当p=2时,p+1=×2+1=2;当p=10时,p+1=×10+1=6.故所求点M的坐标为〔2,2〕或〔10,6〕.【点评】此题综合考查了二次函数的图象与性质,待定系数法求函数〔二次函数和一次函数〕的解析式,三角形的面积,两点间的距离公式,平面直角坐标系的点到坐标轴的距离等重要知识点,难度不是很大.运用数形结合与方程思想是解题的关键.6.〔2016•二模〕如图,抛物线y=ax2+bx+c与x轴的一个交点为A〔3,0〕,与y轴的交点为B〔0,3〕,其顶点为C,对称轴为x=1.〔1〕求抛物线的解析式;〔2〕点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标.【考点】抛物线与x轴的交点;二次函数图象上点的坐标特征;待定系数法求二次函数解析式.【分析】〔1〕直接根据题意列出关于a、b、c的方程组,解方程组即可解决问题.〔2〕运用分类讨论的数学思想,根据等腰三角形的定义,分类讨论,数形结合,即可解决问题.【解答】解:〔1〕由题意得:,解该方程组得:a=﹣1,b=2,c=3,∴抛物线的解析式为y=﹣x2+2x+3.〔2〕由题意得:OA=3,OB=3;由勾股定理得:AB2=32+32,∴AB=3.当△ABM为等腰三角形时,①假如AB为底,∵OA=OB,∴此时点O即为所求的点M,故点M的坐标为M〔0,0〕;②假如AB为腰,以点B为圆心,以长为半径画弧,交y轴于两点,此时两点坐标为M〔0,3﹣3〕或M〔0,3+3〕,以点A为圆心,以长为半径画弧,交y轴于点〔0,﹣3〕;综上所述,当△ABM为等腰三角形时,点M的坐标分别为〔0,0〕、〔0,3﹣3〕、〔0,3+3〕、〔0,﹣3〕.【点评】该题主要考查了抛物线与x轴的交点、待定系数法求二次函数的解析式等知识点与其应用问题;解题的关键是灵活运用、大胆猜测、科学解答.7.〔2016•丹阳市校级模拟〕点A〔2,a〕在抛物线y=x2上〔1〕求A点的坐标;〔2〕在x轴上是否存在点P,使△OAP是等腰三角形?假如存在写出P点坐标;假如不存在,说明理由.【考点】二次函数综合题.【分析】〔1〕直接将A点代入解析式求出即可A点坐标即可;〔2〕分别根据以O为顶点时,以A为顶点时,以P为顶点时求出符合题意的点的坐标即可.【解答】解:〔1〕∵点A〔2,a〕在抛物线y=x2上,∴a=22=4,∴A点的坐标为:〔2,4〕;〔2〕如下列图:以O为顶点时,AO=P1O=2或AO=AP2=2∴点P坐标:〔2,0〕,〔﹣2,0〕,以A为顶点时,AO=OP,∴点P坐标:〔4,0〕;以P为顶点时,OP′=AP′,∴AE2+P′E2=P′A2,设AP′=x,如此42+〔x﹣2〕2=x2,解得:x=5,∴点P坐标:〔5,0〕,综上所述:使△OAP是等腰三角形如此P点坐标为:〔2,0〕,〔﹣2,0〕,〔4,0〕,〔5,0〕.【点评】此题主要考查了二次函数图象上点的性质以与等腰三角形的判定,利用分类讨论得出是解题关键.8.〔2016•宁津县二模〕如图,对称轴为直线x=﹣1的抛物线y=x2+bx+c与x轴相交于A,B 两点,其中点A的坐标为〔﹣3,0〕,点C为抛物线与y轴的交点.〔1〕求函数的解析式;〔2〕假如点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;〔3〕设点Q为线段AC上的动点,作QO⊥x轴交抛物线于点D,求线段QD长度的最大值.【考点】二次函数综合题.【分析】〔1〕由抛物线y=x2+bx+c的对称轴为直线x=﹣1,交x轴于A、B两点,其中A点的坐标为〔﹣3,0〕,根据二次函数的对称性,即可求得B点的坐标;〔2〕a=1时,先由对称轴为直线x=﹣1,求出b的值,再将B〔1,0〕代入,求出二次函数的解析式为y=x2+2x﹣3,得到C点坐标,然后设P点坐标为〔x,x2+2x﹣3〕,根据S△POC=4S 列出关于x的方程,解方程求出x的值,进而得到点P的坐标;△BOC〔3〕先运用待定系数法求出直线AC的解析式为y=﹣x﹣3,再设Q点坐标为〔x,﹣x﹣3〕,如此D点坐标为〔x,x2+2x﹣3〕,然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.【解答】解:〔1〕∵对称轴为直线x=﹣1的抛物线y=x2+bx+c〔a≠0〕与x轴相交于A、B两点,∴A、B两点关于直线x=﹣1对称,∵点A的坐标为〔﹣3,0〕,∴点B的坐标为〔1,0〕;〔2〕∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,∴﹣=﹣1,解得b=2.将B〔1,0〕代入y=x2+2x+c,得1+2+c=0,解得c=﹣3.如此二次函数的解析式为y=x2+2x﹣3,∴抛物线与y轴的交点C的坐标为〔0,﹣3〕,OC=3.设P点坐标为〔x,x2+2x﹣3〕,∵S△POC=4S△BOC,∴×3×|x|=4××3×1,∴|x|=4,x=±4.当x=4时,x2+2x﹣3=16+8﹣3=21;当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.∴点P的坐标为〔4,21〕或〔﹣4,5〕;〔3〕设直线AC的解析式为y=kx+t 〔k≠0〕将A〔﹣3,0〕,C〔0,﹣3〕代入,得,解得,即直线AC的解析式为y=﹣x﹣3.设Q点坐标为〔x,﹣x﹣3〕〔﹣3≤x≤0〕,如此D点坐标为〔x,x2+2x﹣3〕,QD=〔﹣x﹣3〕﹣〔x2+2x﹣3〕=﹣x2﹣3x=﹣〔x+〕2+,∴当x=﹣时,QD有最大值.【点评】此题考查了待定系数法求二次函数、一次函数的解析式,二次函数的性质以与三角形面积、线段长度问题.此题难度适中,解题的关键是运用方程思想与数形结合思想,学会构建二次函数解决最值问题,属于中考常考题型.9.〔2016•模拟〕如图,抛物线y=ax2+bx+c与x轴交于点A〔﹣2,0〕和点B〔6,0〕,与y 轴交于点C〔0,3〕,点D是抛物线上的点,且CD∥x轴,点E是抛物线的顶点.〔1〕求抛物线的解析式;〔2〕平移该抛物线的对称轴所在直线L,当L平移到何处时,恰好将△BCD的面积分为相等的两局部?〔3〕点F在线段CD上,假如以点C,E,F为顶点的三角形与△COE相似,试求点F的坐标.【考点】二次函数综合题.【分析】〔1〕利用待定系数法即可求得抛物线的解析式;〔2〕首先求得D的坐标,如此CD的长即可求得,进而求得△BCD的面积,当l平移至l1,l1与CD、BC分别交于点M、N,易证△CMN∽△BOC,求得CM和MN的关系,利用三角形的面积公式即可求解;〔3〕分成△COE∽△ECF和△COE∽△FCE两种情况,利用相似三角形的对应边的比相等即可求解.【解答】解:〔1〕根据题意得:,解得:.如此抛物线的解析式是y=﹣x2+x+3;〔2〕抛物线y=﹣x2+x+3的对称轴是x=2.∵CD∥x轴,C的坐标是〔0,3〕,∴D的坐标是〔4,3〕,∴S△BCD=CD•OC=×4×3=6.如图,当l平移至l1,l1与CD、BC分别交于点M、N.∴∠M=∠CBO,∠CMN=∠BOC=90°,∴△CMN∽△BOC,∴===2,∴CM=2MN,∴S△CMN=CM•MN=CM2.∵S△CMN=S△BCD,∴CM2=3,∴CM=2.∴当l平移到直线x=2处时,恰好将△BCD的面积分成面积相等的两局部;〔3〕设对称轴l交CD于点P,过点E作EQ⊥y轴,垂足为点Q.∵E〔2,4〕,C〔0,3〕,CD∥x轴,∴==,又∵∠EQO=∠EPC=90°,∴△EQC∽△EPC,∴∠COE=∠ECD.∵C〔0,3〕,E〔2,4〕,∴CE=,OE=2.分成两种情况:当△COE∽△ECF是,=,∴CF=,∴F的坐标是〔,3〕;当△COE∽△FCE时,=,∴CF=.∴F的坐标是〔,3〕.如此满足条件的F的坐标是〔,3〕或〔,3〕.【点评】此题考查了待定系数法求函数的解析式以与相似三角形的判定与性质,正确分成△COE∽△ECF和△COE∽△FCE两种情况进展讨论是关键.10.〔2016•模拟〕如图,抛物线y=ax2+bx+2与x轴交于点A〔1,0〕和B〔4,0〕.〔1〕求抛物线的解析式与对称轴;〔2〕假如抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标.【考点】二次函数综合题.【分析】〔1〕由点A、B的坐标利用待定系数法即可求出抛物线的解析式,再由抛物线的对称轴为x=﹣,代入数据即可得出结论;〔2〕由平行四边形的性质即可得出点C的横坐标,代入抛物线解析式中即可得出点C的坐标.【解答】解:〔1〕将点A〔1,0〕、B〔4,0〕代入y=ax2+bx+2中,得:,解得:,∴抛物线的解析式为y=.抛物线的对称轴为x=﹣=.〔2〕∵OECF是平行四边形,OE=,∴FC=,∴C点横坐标x=OE+FC=5,令y=中x=5,如此y=2,∴点C的坐标为〔5,2〕.【点评】此题考查了待定系数法求函数解析式以与平行四边形的性质,解题的关键是:〔1〕利用待定系数法求出函数解析式;〔2〕根据平行四边形找出点C的横坐标.此题属于根底题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.11.〔2016•模拟〕如图,抛物线y=ax2+bx+c〔a≠0〕与x轴交于点A〔﹣4,0〕,B〔1,0〕,与y轴交于点D〔0,4〕,点C〔﹣2,n〕也在此抛物线上.〔1〕求此抛物线的解析式与点C的坐标;〔2〕设BC交y轴于点E,连接AE,AC请判断△ACE的形状,并说明理由;〔3〕连接AD交BC于点F,试问:以A,B,F为顶点的三角形与△ABC相似吗?请说明理由.【考点】二次函数综合题.【分析】〔1〕由A、B、D三点坐标,利用待定系数法可求得抛物线解析式,把C点坐标代入解析式可求得n的值,可求得C点坐标;〔2〕把C点坐标代入抛物线解析式可求得n,可得C点坐标,利用待定系数法可求得直线BC的解析式,如此可求得E点坐标,利用勾股定理可求得AC、AE、CE的长,如此可判断△ACE的形状;〔3〕由A、D坐标可先求得直线AD解析式,联立直线BC、AD解析式可求得F点坐标,又可求得BF、BC和AB的长,由题意可知∠ABF=∠CAB,假如以A,B,F为顶点的三角形与△ABC相似只有∠BFA=∠CAB,如此判定和是否相等即可.【解答】解:〔1〕∵抛物线经过A、B、D三点,∴代入抛物线解析式可得,解得,。
二次函数压轴题(含答案)
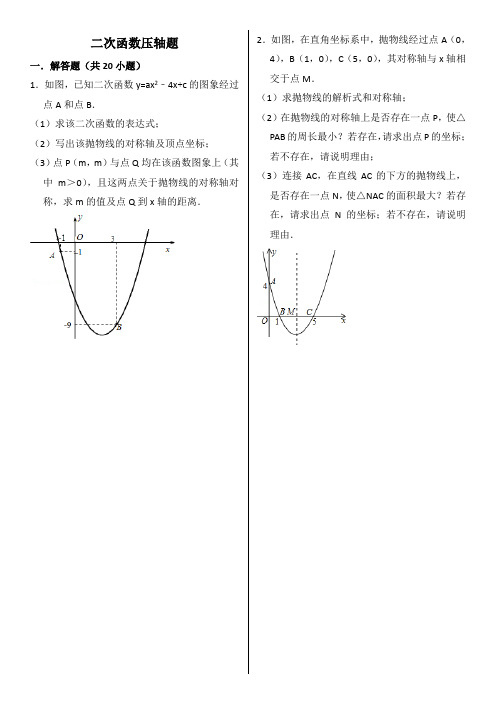
二次函数压轴题一.解答题(共20小题)1.如图,已知二次函数y=ax2﹣4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.2.如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.3.已知二次函数y=x2﹣2mx+m2﹣1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.4.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC 和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.5.如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B两点的坐标及直线AC的函数表达式;(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.6.如图,抛物线经过A(﹣1,0),B(5,0),C(0,﹣)三点.(Ⅰ)求抛物线的解析式;(Ⅱ)在抛物线的对称轴上有一点P,使PA+PC 的值最小,求点P的坐标.(Ⅲ)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y 轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.8.如图,对称轴为x=﹣1的抛物线y=ax2+bx+c (a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).(1)求点B的坐标.(2)已知a=1,C为抛物线与y轴的交点.①若点P在抛物线上,且S△POC=4S△BOC,求点P 的坐标.②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.9.如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.10.如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;(3)点M是抛物线上一点,以B,C,D,M为顶点的四边形是直角梯形,试求出点M的坐标.11.如图,直线y=x+2与抛物线y=ax2+bx+6(a ≠0)相交于A (,)和B(4,m),点P 是线段AB上异于A、B的动点,过点P作PC ⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.12.如图,在平面直角坐标系xOy中,A、B为x 轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;(3)当△BDM为直角三角形时,求m的值.13.如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.(1)点(填M或N)能到达终点;(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.14.如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).(1)求抛物线的函数表达式;(2)若点P在抛物线上,且S△AOP=4S△BOC,求点P的坐标;(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.15.如图,已知二次函数y=﹣+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.16.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.17.如图,抛物线y=﹣x2+bx+c与x轴交于点A (﹣1,0),B(5,0)两点,直线y=﹣x+3与y轴交于点C,与x轴交于点D.点P是x 轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.18.如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC 交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l在边OA(不包括O、A 两点)上平行移动,分别交x轴于点E,交CD 于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.19.如图,已知抛物线y=(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣x+b与抛物线的另一交点为D.(1)若点D的横坐标为﹣5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k 的值;(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?20.如图,抛物线y=﹣x2+bx+c与直线y=x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.(1)求抛物线的解析式;(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.二次函数压轴题参考答案一.解答题(共20小题)1.如图,已知二次函数y=ax2﹣4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.解:(1)将x=﹣1,y=﹣1;x=3,y=﹣9,分别代入y=ax2﹣4x+c得,解得,∴二次函数的表达式为y=x2﹣4x﹣6.(2)对称轴为直线x=2;顶点坐标为(2,﹣10).(3)将(m,m)代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6,解得m1=﹣1,m2=6.∵m>0,∴m1=﹣1不合题意,舍去.∴m=6,∵点P与点Q关于对称轴x=2对称,∴点Q到x轴的距离为6.2.如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.解:(1)根据已知条件可设抛物线的解析式为y=a (x﹣1)(x﹣5),把点A(0,4)代入上式得:a=,∴y=(x﹣1)(x﹣5)=x2﹣x+4=(x﹣3)2﹣,∴抛物线的对称轴是:直线x=3;(2)P点坐标为(3,).理由如下:∵点A(0,4),抛物线的对称轴是直线x=3,∴点A关于对称轴的对称点A′的坐标为(6,4)如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.设直线BA′的解析式为y=kx+b,把A′(6,4),B (1,0)代入得,解得,∴y=x ﹣,∵点P 的横坐标为3,∴y=×3﹣=, ∴P (3,).(3)在直线AC 的下方的抛物线上存在点N ,使△NAC 面积最大.设N 点的横坐标为t ,此时点N (t ,t 2﹣t +4)(0<t <5),如图2,过点N 作NG ∥y 轴交AC 于G ;作AD ⊥NG 于D ,由点A (0,4)和点C (5,0)可求出直线AC 的解析式为:y=﹣x +4,把x=t 代入得:y=﹣t +4,则G (t ,﹣t +4), 此时:NG=﹣t +4﹣(t 2﹣t +4)=﹣t 2+4t ,∵AD +CF=CO=5, ∴S △ACN =S △ANG +S △CGN=AD ×NG+NG ×CF=NG•OC=×(﹣t 2+4t )×5=﹣2t 2+10t=﹣2(t ﹣)2+,∴当t=时,△CAN 面积的最大值为,由t=,得:y=t 2﹣t +4=﹣3,∴N (,﹣3).3.已知二次函数y=x 2﹣2mx +m 2﹣1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.解:(1)∵二次函数的图象经过坐标原点O (0,0),∴代入二次函数y=x 2﹣2mx +m 2﹣1,得出:m 2﹣1=0,解得:m=±1,∴二次函数的解析式为:y=x 2﹣2x 或y=x 2+2x ; (2)∵m=2,∴二次函数y=x 2﹣2mx +m 2﹣1得:y=x 2﹣4x +3=(x ﹣2)2﹣1,∴抛物线的顶点为:D (2,﹣1), 当x=0时,y=3,∴C 点坐标为:(0,3), ∴C (0,3)、D (2,﹣1);(3)当P 、C 、D 共线时PC +PD 最短,过点D 作DE ⊥y 轴于点E , ∵PO ∥DE ,∴=,∴=,解得:PO=,∴PC +PD 最短时,P 点的坐标为:P (,0).4.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C (0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC 和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.解:(1)依题意得:,解之得:,∴抛物线解析式为y=﹣x2﹣2x+3∵对称轴为x=﹣1,且抛物线经过A(1,0),∴把B(﹣3,0)、C(0,3)分别代入直线y=mx+n,得,解之得:,∴直线y=mx+n的解析式为y=x+3;(2)设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.把x=﹣1代入直线y=x+3得,y=2,∴M(﹣1,2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2);(3)设P(﹣1,t),又∵B(﹣3,0),C(0,3),∴BC2=18,PB2=(﹣1+3)2+t2=4+t2,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,①若点B为直角顶点,则BC2+PB2=PC2即:18+4+t2=t2﹣6t+10解之得:t=﹣2;②若点C为直角顶点,则BC2+PC2=PB2即:18+t2﹣6t+10=4+t2解之得:t=4,③若点P为直角顶点,则PB2+PC2=BC2即:4+t2+t2﹣6t+10=18解之得:t1=,t2=;综上所述P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1,)或(﹣1,).5.如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B两点的坐标及直线AC的函数表达式;(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.解:(1)令y=0,解得x1=﹣1或x2=3∴A(﹣1,0)B(3,0)将C点的横坐标x=2代入y=x2﹣2x﹣3得y=﹣3∴C(2,﹣3)∴直线AC的函数解析式是y=﹣x﹣1;(2)设P点的横坐标为x(﹣1≤x≤2)则P、E的坐标分别为:P(x,﹣x﹣1)E(x,x2﹣2x﹣3)∵P点在E点的上方,PE=(﹣x﹣1)﹣(x2﹣2x ﹣3)=﹣x2+x+2=﹣(x ﹣)2+,∴当时,PE的最大值=;(3)存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+,0),F4(4﹣,0).①如图,连接C与抛物线和y轴的交点,那么CG∥x轴,此时AF=CG=2,因此F点的坐标是(﹣3,0);②如图,AF=CG=2,A点的坐标为(﹣1,0),因此F点的坐标为(1,0);③如图,此时C,G两点的纵坐标互为相反数,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1+,3),由于直线GF 的斜率与直线AC的相同,因此可设直线GF 的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+4+.因此直线GF与x 轴的交点F的坐标为(4+,0);④如图,同③可求出F的坐标为(4﹣,0).综合四种情况可得出,存在4个符合条件的F点.6.如图,抛物线经过A(﹣1,0),B(5,0),C(0,﹣)三点.(Ⅰ)求抛物线的解析式;(Ⅱ)在抛物线的对称轴上有一点P,使PA+PC 的值最小,求点P的坐标.(Ⅲ)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.解:(Ⅰ)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(﹣1,0),B(5,0),C(0,﹣)三点在抛物线上,∴,解得.∴抛物线的解析式为:y=x2﹣2x ﹣;(Ⅱ)∵抛物线的解析式为:y=x2﹣2x ﹣,∴其对称轴为直线x=﹣=﹣=2,连接BC,如图1所示,∵B(5,0),C(0,﹣),∴设直线BC的解析式为y=kx+b(k≠0),∴,解得,∴直线BC的解析式为y=x ﹣,当x=2时,y=1﹣=﹣,∴P(2,﹣);(Ⅲ)存在点N,使以A,C,M,N四点构成的四边形为平行四边形.如图2所示,①当点N在x轴下方时,∵抛物线的对称轴为直线x=2,C(0,﹣),∴N1(4,﹣);②当点N在x轴上方时,如图,过点N2作N2D⊥x轴于点D,在△AN2D与△M2CO中,∴△AN2D≌△M2CO(ASA),∴N2D=OC=,即N2点的纵坐标为.∴x2﹣2x ﹣=,解得x=2+或x=2﹣,∴N2(2+,),N3(2﹣,).综上所述,符合条件的点N的坐标为(4,﹣),(2+,)或(2﹣,).7.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y 轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.解:(1)将B、C 两点的坐标代入得,解得:;所以二次函数的表达式为:y=x2﹣2x﹣3(2)存在点P,使四边形POP′C为菱形;设P点坐标为(x,x2﹣2x﹣3),PP′交CO于E若四边形POP′C是菱形,则有PC=PO;连接PP′,则PE⊥CO于E,∵C(0,﹣3),∴CO=3,又∵OE=EC,∴OE=EC=∴y=;∴x2﹣2x﹣3=解得x1=,x2=(不合题意,舍去),∴P点的坐标为(,)(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2﹣2x﹣3),设直线BC的解析式为:y=kx+d,则,解得:∴直线BC的解析式为y=x﹣3,则Q点的坐标为(x,x﹣3);当0=x2﹣2x﹣3,解得:x1=﹣1,x2=3,∴AO=1,AB=4,S四边形ABPC=S△ABC+S△BPQ+S△CPQ=AB•OC+QP•BF +QP•OF==当时,四边形ABPC的面积最大此时P点的坐标为,四边形ABPC的面积的最大值为.8.如图,对称轴为x=﹣1的抛物线y=ax2+bx+c (a≠0)与x轴相交于A、B两点,其中点A 的坐标为(﹣3,0).(1)求点B的坐标.(2)已知a=1,C为抛物线与y轴的交点.①若点P在抛物线上,且S△POC=4S△BOC,求点P 的坐标.②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.解:(1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,∴A、B两点关于直线x=﹣1对称,∵点A的坐标为(﹣3,0),∴点B的坐标为(1,0);(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,∴=﹣1,解得b=2.将B(1,0)代入y=x2+2x+c,得1+2+c=0,解得c=﹣3.则二次函数的解析式为y=x2+2x﹣3,∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.设P点坐标为(x,x2+2x﹣3),∵S△POC=4S△BOC,∴×3×|x|=4××3×1,∴|x|=4,x=±4.当x=4时,x2+2x﹣3=16+8﹣3=21;当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.∴点P的坐标为(4,21)或(﹣4,5);②设直线AC的解析式为y=kx+t (k≠0)将A(﹣3,0),C(0,﹣3)代入,得,解得,即直线AC的解析式为y=﹣x﹣3.设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D 点坐标为(x,x2+2x﹣3),QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x +)2+,∴当x=﹣时,QD 有最大值.9.如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.解:(1)将A(1,0),B(﹣3,0)代y=﹣x2+bx+c 中得,∴.∴抛物线解析式为:y=﹣x2﹣2x+3;(2)存在.理由如下:由题知A、B两点关于抛物线的对称轴x=﹣1对称,∴直线BC与x=﹣1的交点即为Q点,此时△AQC周长最小,∵y=﹣x2﹣2x+3,∴C的坐标为:(0,3),直线BC解析式为:y=x+3,Q点坐标即为,解得,∴Q(﹣1,2);(3)存在.理由如下:设P点(x,﹣x2﹣2x+3)(﹣3<x<0),∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO ﹣,若S四边形BPCO 有最大值,则S△BPC就最大,∴S四边形BPCO=S△BPE+S直角梯形PEOC,=BE•PE +OE(PE+OC)=(x+3)(﹣x2﹣2x+3)+(﹣x)(﹣x2﹣2x+3+3)=,当x=﹣时,S四边形BPCO最大值=,∴S△BPC最大=,当x=﹣时,﹣x2﹣2x+3=,∴点P 坐标为(﹣,).10.如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;(3)点M是抛物线上一点,以B,C,D,M为顶点的四边形是直角梯形,试求出点M的坐标.解:(1)∵抛物线与y轴交于点C(0,3),∴设抛物线解析式为y=ax2+bx+3(a≠0),根据题意,得,解得,∴抛物线的解析式为y=﹣x2+2x+3.(2)存在.由y=﹣x2+2x+3得,D点坐标为(1,4),对称轴为直线x=1.①若以CD为底边,则PD=PC,设P点坐标为(x,y),根据两点间距离公式,得x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,即y=4﹣x.又P点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,解得x1=,x2=<1,应舍去,∴x=,∴y=4﹣x=,即点P 坐标为.②若以CD为一腰,∵点P在对称轴右侧的抛物线上,由抛物线对称性知,点P与点C关于直线x=1对称,此时点P坐标为(2,3).∴符合条件的点P 坐标为或(2,3).(3)由B(3,0),C(0,3),D(1,4),根据勾股定理,得CB=,CD=,BD=,∴CB2+CD2=BD2=20,∴∠BCD=90°,设对称轴交x轴于点E,过C作CM⊥DE,交抛物线于点M,垂足为F,在Rt△DCF中,∵CF=DF=1,∴∠CDF=45°,由抛物线对称性可知,∠CDM=2×45°=90°,点坐标M为(2,3),∴DM∥BC,∴四边形BCDM为直角梯形,由∠BCD=90°及题意可知,以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在.综上所述,符合条件的点M的坐标为(2,3).11.如图,直线y=x+2与抛物线y=ax2+bx+6(a ≠0)相交于A (,)和B(4,m),点P 是线段AB上异于A、B的动点,过点P作PC ⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.解:(1)∵B(4,m)在直线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx+6上,∴,解得,∴抛物线的解析式为y=2x2﹣8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n ﹣)2+,∵PC>0,∴当n=时,线段PC 最大且为.(3)∵△PAC为直角三角形,i)若点P为直角顶点,则∠APC=90°.由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;ii)若点A为直角顶点,则∠PAC=90°.如答图3﹣1,过点A (,)作AN⊥x轴于点N,则ON=,AN=.过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,∴MN=AN=,∴OM=ON+MN=+=3,∴M(3,0).设直线AM的解析式为:y=kx+b,则:,解得,∴直线AM的解析式为:y=﹣x+3 ①又抛物线的解析式为:y=2x2﹣8x+6 ②联立①②式,解得:x=3或x=(与点A重合,舍去)∴C(3,0),即点C、M点重合.当x=3时,y=x+2=5,∴P1(3,5);iii)若点C为直角顶点,则∠ACP=90°.∵y=2x2﹣8x+6=2(x﹣2)2﹣2,∴抛物线的对称轴为直线x=2.如答图3﹣2,作点A (,)关于对称轴x=2的对称点C,则点C在抛物线上,且C (,).当x=时,y=x+2=.∴P2(,).∵点P1(3,5)、P2(,)均在线段AB上,∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(,).12.如图,在平面直角坐标系xOy中,A、B为x 轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;(3)当△BDM为直角三角形时,求m的值.解:(1)y=mx2﹣2mx﹣3m=m(x﹣3)(x+1),∵m≠0,∴当y=0时,x1=﹣1,x2=3,∴A(﹣1,0),B(3,0);(2)设C1:y=ax2+bx+c,将A、B、C三点的坐标代入得:,解得,故C1:y=x2﹣x﹣.如图:过点P作PQ∥y轴,交BC于Q,由B、C的坐标可得直线BC的解析式为:y=x﹣,设P(x ,x2﹣x ﹣),则Q(x,x ﹣),PQ=x ﹣﹣(x2﹣x﹣)=﹣x2+x,S△PBC=S△PCQ+S△PBQ =PQ•OB=×(﹣x2+x)×3=﹣(x ﹣)2+,当x=时,S△PBC有最大值,Smax=,×()2﹣﹣=﹣,P(,﹣);(3)y=mx2﹣2mx﹣3m=m(x﹣1)2﹣4m,顶点M坐标(1,﹣4m),当x=0时,y=﹣3m,∴D(0,﹣3m),B(3,0),∴DM2=(0﹣1)2+(﹣3m+4m)2=m2+1,MB2=(3﹣1)2+(0+4m)2=16m2+4,BD2=(3﹣0)2+(0+3m)2=9m2+9,当△BDM为Rt△时有:DM2+BD2=MB2或DM2+MB2=BD2.①DM2+BD2=MB2时有:m2+1+9m2+9=16m2+4,解得m=﹣1(∵m<0,∴m=1舍去);②DM2+MB2=BD2时有:m2+1+16m2+4=9m2+9,解得m=﹣(m=舍去).综上,m=﹣1或﹣时,△BDM为直角三角形.13.如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.(1)点M(填M或N)能到达终点;(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.解:(1)点M.(2)经过t秒时,NB=t,OM=2t,则CN=3﹣t,AM=4﹣2t,∵A(4,0),C(0,4),∴AO=CO=4,∵∠AOC=90°,∴∠BCA=∠MAQ=45°,∴QN=CN=3﹣t∴PQ=1+t,∴S△AMQ=AM•PQ=(4﹣2t)(1+t)=﹣t2+t+2.∴S=﹣t2+t+2=﹣t2+t ﹣++2=﹣(t ﹣)2+,∵0≤t≤2∴当时,S的值最大.(3)存在.设经过t秒时,NB=t,OM=2t则CN=3﹣t,AM=4﹣2t∴∠BCA=∠MAQ=45°①若∠AQM=90°,则PQ是等腰Rt△MQA底边MA上的高∴PQ是底边MA的中线∴PQ=AP=MA∴1+t=(4﹣2t)∴t=∴点M的坐标为(1,0)②若∠QMA=90°,此时QM与QP重合∴QM=QP=MA∴1+t=4﹣2t∴t=1∴点M的坐标为(2,0).14.如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).(1)求抛物线的函数表达式;(2)若点P在抛物线上,且S△AOP=4S△BOC,求点P的坐标;(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.解:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得,解得.故该抛物线的解析式为:y=﹣x2﹣2x+3.(2)由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).∵S△AOP=4S△BOC,∴×3×|﹣x2﹣2x+3|=4××1×3.整理,得(x+1)2=0或x2+2x﹣7=0,解得x=﹣1或x=﹣1±2.则符合条件的点P的坐标为:(﹣1,4)或(﹣1+2,﹣4)或(﹣1﹣2,﹣4);(3)设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,得,解得.即直线AC的解析式为y=x+3.设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+)2+,∴当x=﹣时,QD 有最大值.15.如图,已知二次函数y=﹣+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.解:(1)把A(2,0)、B(0,﹣6)代入y=﹣+bx+c,得:解得,∴这个二次函数的解析式为y=﹣+4x﹣6.(2)∵该抛物线对称轴为直线x=﹣=4,∴点C的坐标为(4,0),∴AC=OC﹣OA=4﹣2=2,∴S△ABC =×AC×OB=×2×6=6.16.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.解:(1)在Rt△AOB中,OA=1,tan∠BAO==3,∴OB=3OA=3.∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,∴△DOC≌△AOB,∴OC=OB=3,OD=OA=1,∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).代入解析式为,解得:.∴抛物线的解析式为y=﹣x2﹣2x+3;(2)①∵抛物线的解析式为y=﹣x2﹣2x+3,∴对称轴l=﹣=﹣1,∴E点的坐标为(﹣1,0).如图,当∠CEF=90°时,PE:CE=2:1,CO:OD=3:1,此时△CEF与△COD不相似.当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP.∴,∴MP=3EM.∵P的横坐标为t,∴P(t,﹣t2﹣2t+3).∵P在第二象限,∴PM=﹣t2﹣2t+3,EM=﹣1﹣t,∴﹣t2﹣2t+3=﹣(t﹣1)(t+3),解得:t1=﹣2,t2=﹣3(因为P与C重合,所以舍去),∴t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3.∴P(﹣2,3).∴当△CEF与△COD相似时,P点的坐标为:(﹣1,4)或(﹣2,3);②设直线CD的解析式为y=kx+b,由题意,得,解得:,∴直线CD的解析式为:y=x+1.设PM与CD的交点为N,则点N的坐标为(t,t+1),∴NM=t+1.∴PN=PM﹣NM=﹣t2﹣2t+3﹣(t+1)=﹣t2﹣+2.∵S△PCD=S△PCN+S△PDN,∴S△PCD=PN•CM +PN•OM=PN(CM+OM)=PN•OC=×3(﹣t2﹣+2)=﹣(t +)2+,∴当t=﹣时,S△PCD的最大值为.17.如图,抛物线y=﹣x2+bx+c与x轴交于点A (﹣1,0),B(5,0)两点,直线y=﹣x+3与y轴交于点C,与x轴交于点D.点P是x 轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.方法一:解:(1)将点A、B坐标代入抛物线解析式,得:,解得,∴抛物线的解析式为:y=﹣x2+4x+5.(2)∵点P的横坐标为m,∴P(m,﹣m2+4m+5),E(m,﹣m+3),F(m,0).∴PE=|y P﹣y E|=|(﹣m2+4m+5)﹣(﹣m+3)|=|﹣m2+m+2|,EF=|y E﹣y F|=|(﹣m+3)﹣0|=|﹣m+3|.由题意,PE=5EF,即:|﹣m2+m+2|=5|﹣m+3|=|m+15|①若﹣m2+m+2=m+15,整理得:2m2﹣17m+26=0,解得:m=2或m=;②若﹣m2+m+2=﹣(m+15),整理得:m2﹣m﹣17=0,解得:m=或m=.由题意,m的取值范围为:﹣1<m<5,故m=、m=这两个解均舍去.∴m=2或m=.(3)假设存在.作出示意图如下:∵点E、E′关于直线PC对称,∴∠1=∠2,CE=CE′,PE=PE′.∵PE平行于y轴,∴∠1=∠3,∴∠2=∠3,∴PE=CE,∴PE=CE=PE′=CE′,即四边形PECE′是菱形.当四边形PECE′是菱形存在时,由直线CD解析式y=﹣x+3,可得OD=4,OC=3,由勾股定理得CD=5.过点E作EM∥x轴,交y轴于点M,易得△CEM ∽△CDO,∴,即,解得CE=|m|,∴PE=CE=|m|,又由(2)可知:PE=|﹣m2+m+2|∴|﹣m2+m+2|=|m|.①若﹣m2+m+2=m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣;②若﹣m2+m+2=﹣m,整理得:m2﹣6m﹣2=0,解得m1=3+,m2=3﹣.由题意,m的取值范围为:﹣1<m<5,故m=3+这个解舍去.当四边形PECE′是菱形这一条件不存在时,此时P点横坐标为0,E,C,E'三点重合与y轴上,也符合题意,∴P(0,5)综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣,),(4,5),(3﹣,2﹣3)方法二:(1)略.(2)略.(3)若E(不与C重合时)关于直线PC的对称点E′在y轴上,则直线CD与直线CE′关于PC 轴对称.∴点D关于直线PC的对称点D′也在y轴上,∴DD′⊥CP,∵y=﹣x+3,∴D(4,0),CD=5,∵OC=3,∴OD′=8或OD′=2,①当OD′=8时,D′(0,8),设P(t,﹣t2+4t+5),D(4,0),C(0,3),∵PC⊥DD′,∴K PC×K DD′=﹣1,∴,∴2t2﹣7t﹣4=0,∴t1=4,t2=﹣,②当OD′=2时,D′(0,﹣2),设P(t,﹣t2+4t+5),∵PC⊥DD′,∴K PC×K DD′=﹣1,∴=﹣1,∴t1=3+,t2=3﹣,∵点P是x轴上方的抛物线上一动点,∴﹣1<t<5,∴点P的坐标为(﹣,),(4,5),(3﹣,2﹣3).若点E与C重合时,P(0,5)也符合题意.综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣,),(4,5),(3﹣,2﹣3)18.如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC 交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l在边OA(不包括O、A 两点)上平行移动,分别交x轴于点E,交CD 于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.解:(1)∵抛物线y=ax2﹣2ax+c(a≠0)经过点A(3,0),点C(0,4),∴,解得,∴抛物线的解析式为y=﹣x2+x+4;(2)设直线AC的解析式为y=kx+b,∵A(3,0),点C(0,4),∴,解得,∴直线AC的解析式为y=﹣x+4.∵点M的横坐标为m,点M在AC上,∴M点的坐标为(m ,﹣m+4),∵点P的横坐标为m,点P在抛物线y=﹣x2+x+4上,∴点P的坐标为(m ,﹣m2+m+4),∴PM=PE﹣ME=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+4m,即PM=﹣m2+4m(0<m<3);(3)在(2)的条件下,连结PC,在CD上方的抛物线部分存在这样的点P,使得以P、C、F 为顶点的三角形和△AEM相似.理由如下:由题意,可得AE=3﹣m,EM=﹣m+4,CF=m,若以P、C、F为顶点的三角形和△AEM相似,P点在F上,PF=﹣m2+m+4﹣4=﹣m2+m.情况:①若△PFC∽△AEM,则PF:AE=FC:EM,即(﹣m2+m):(3﹣m)=m:(﹣m+4),∵m≠0且m≠3,∴m=.∵△PFC∽△AEM,∴∠PCF=∠AME,∵∠AME=∠CMF,∴∠PCF=∠CMF.在直角△CMF中,∵∠CMF+∠MCF=90°,∴∠PCF+∠MCF=90°,即∠PCM=90°,∴△PCM为直角三角形;②若△CFP∽△AEM,则CF:AE=PF:EM,即m:(3﹣m)=(﹣m2+m):(﹣m+4),∵m≠0且m≠3,∴m=1.∵△CFP∽△AEM,∴∠CPF=∠AME,∵∠AME=∠CMF,∴∠CPF=∠CMF.∴CP=CM,∴△PCM为等腰三角形.综上所述,存在这样的点P使△PFC与△AEM相。
易错压轴01 二次函数(十大易错压轴题型+举一反三+易错题通关)(解析版)

易错压轴01二次函数易错压轴一:二次函数的图象与性质例1.已知二次函数2(1)5y x =--+,当a x b ≤≤且0ab <时,y 的最小值为2a ,最大值为2b ,则a b +的值为()A .2B .12C .3D .32【答案】B【分析】本题考查了二次函数的最值问题,二次函数的增减性,由题意可得0a <,0b >,则y 的最小值为2a 为负数,最大值为2b 为正数.最大值为2b 分两种情况:①结合抛物线顶点纵坐标的取值范围,求出 2.5b =,结合图象最小值只能由x a =时求出;②结合抛物线顶点纵坐标的取值范围,图象最大值只能由x b =求出,最小值只能由x a =求出.【详解】解:二次函数2(1)5y x =--+的大致图象如下:①当01a x b <≤≤<时,当x a =时,y 取最小值,即2215()a a =--+,例2.已知Rt ABC △的直角顶点C 与原点O 重合,点A ,B 都落在抛物线24y x =上,则AB 与y 轴的交点为;若OD AB ⊥于点D ,则点D 到点()1,0的最大距离为.则24AM m =,MO m =-,BN =90MAO MOA ∠+∠=︒ ,MOA ∠MAO BON ∴∠=∠,AMO ONB ∴∽ ,AM ON MO NB ∴=,即:2244m n m n=-,1OD AB ⊥ ,14OE =,F 为OE 中点,在Rt DOE △中,1128DF OE ==,练习1.定义:把二次函数()2y a x m n =++与()2y a x m n =---(0a ≠,m 、n 是常数)称作互为“旋转函数”,如果二次函数212y x bx =+-与2214y x cx c =--+(b 、c 是常数)互为“旋转函数”,则下列选项中正确的是()A .2c =-;B .14b c =;C .当x t =时,12y y t +=-;D .不论x 取何值,120y y +=练习2.若关于x 的方程2230x kx k -+-=的一个实数根13x ≥,另一个实数根20x ≤,则关于x 的二次函数223y x kx k =-+-图象的顶点到x 轴距离h 的取值范围是.练习3.已知二次函数()(2y ax a b x b a =-++、b 是常数,0).a ≠(1)若(4)(0),M m m ->在该二次函数的图象上,当0a <时,试判断代数式a b +的正负性;(2)已知对于任意的常数a 、(0)b a ≠,二次函数的图象始终过定点P ,求证:一次函数()()2331y k x k x =++≥图象上所有的点都高于点.P 【答案】(1)a b +为正(2)见解析【分析】本题主要考查了二次函数的图象与性质,解题时要熟练掌握并能灵活运用是关1.已知二次函数()240y ax ax c a =++>图象上的两点()15,y -和()22,x y ,若12y y >,则2x 的取值范围是()A .25x >-B .22x <-C .251x -<<D .252x -<<-2.已知抛物线2y ax bx =+,当3y ≥-时,自变量x 的取值范围是2x m ≤-或2(0)x m m ≥+>,若点(),9P n 在对称轴左侧的抛物线上,则n 的取值范围是.3.已知二次函数223y x x =+-.(1)将223y x x =+-写成()2y a x h k =-+的形式,并写出它的顶点坐标;(2)当40x -<<时,直接写出函数值y 的取值范围;(3)该二次函数的图象与直线y n =有两个交点A ,B ,若6AB >,直接写出n 的取值范围.【答案】(1)()214y x =+-,顶点坐标为()1,4--(2)45y -≤<(3)5n >【分析】(1)利用完全平方公式转化为顶点式,由顶点式写出顶点坐标;易错压轴二:二次函数的图象与系数的关系例1.对于二次函数2y ax bx c =++,定义函数()()2200ax bx c x y ax bx c x ⎧++≥⎪=⎨---<⎪⎩是它的相关函数.若一次函数1y x =+与二次函数24y x x c =-+的相关函数的图象恰好两个公共点,则c 的值可能是()A.1-B.0C.1D.22例2.抛物线2y ax bx c =++的对称轴是直线=1x -,且过点(1,0),顶点位于第二象限,其部分图象如图所示,给出以下判断;①0ab >且0c <;②420a b c -+>;③80a c +>;④直线22y x =+与抛物线2y ax bx c =++两个交点的横坐标分别为12x x ,,则12125x x x x ++=-.其中结论正确的是.练习1.如图,抛物线2(0)y ax bx c a =++≠的图象与x 轴交于(2,0)-,()1,0x ,其中101x <<.有下列五个结论:①0abc >;②0a b c -+>;③20a c +>;④()(2)0a b a b -->;⑤若m ,()n m n <为关于x 的一元二次方程()1(2)10a x x x +-+=的两个根,则21m n -<+<-.其中正确结论的个数是()A .4B .3C .2D .1【答案】B【分析】本题考查了二次函数图象与各项系数的符号,根据二次函数图象判断式子的符号,一元二次方程根与系数的关系,掌握二次函数图象与性质是解题的关键,注意数形结合.根据抛物线开口方向、对称轴的位置及抛物线与y 轴交点位置,可确定a 、b 、c 的符号,练习2.如图,二次函数²y ax bx c =++的图像与x 轴交于点(30),,对称轴为直线1x =,下列结论∶①<0abc ;②420a b c -+>;③30a c +=;④抛物线上有两点11(,)M x y 和22(,)N x y ,若121x x <<,且122x x +>,则12y y >,其中正确的是.(只填写序号)【答案】①③④【分析】本题考查了二次函数图像与系数的关系,二次函数的图像与性质,根据二次函数的图像判断式子的符号,数形结合是本题最大特点.由图像的开口方向、对称轴及图像与y 轴的交点位置可分别确定a 、b 、c 的符号,从而可判定①;由抛物线的对称性可确定当1x <-时,图像位于x 轴下方,从而当2x =-时练习3.已知二次函数()2210y ax ax a =-+≠,图象经过点()1,m -,()1,n ,()3,p .(1)当2m =-时.①求二次函数的表达式;②写出一个符合条件的x 的取值范围,使得y 随x 的增大而增大;(2)若在m ,n ,p 这三个实数中,只有一个是正数,求证:13a ≤-.【答案】(1)①221y x x =-++;②1x <.(2)见解析.【分析】本题考查待定系数法求二次函数解析式及二次函数的图象和性质,熟知二次函数的图象和性质是解题的关键.(1)①利用待定系数法即可解决问题;②根据所得二次函数的图象和性质即可解决问题;(2)由这三个点在抛物线上的位置即可解决问题.【详解】(1)①当2m =-时,将点()1,2--代入函数解析式得,1.已知二次函数2y ax bx c =++(0a ≠)与x 轴的一个交点为()4,0,其对称轴为直线1x =,其部分图象如图所示,有下列5个结论:①0abc <;②240b ac -<;③930a b c ++=;④80a c +=;⑤若关于x 的方程21ax bx c ++=-有两个实数根12,x x ,且满足12x x <,则12x <-,24x >.其中正确结论的个数为()A .5B .4C .3D .22.已知二次函数2(0)y ax bx c a =++<的图象与x 轴的一个交点坐标为(1,0)-,对称轴为直线1x =,下列论中∶①0a b c -+=;②若点()()()1233,,2,,4,y y y -均在该二次函数图象上,则123y y y <<;③若m 为任意实数,则24am bm c a ++≤-;④方程210ax bx c +++=的两实数根为12,x x ,且12x x <,则121,3x x <->.正确结论的序号为.∴与x 轴的另一个交点坐标为(3,0),2(0)y ax bx c a =++<的图象向上平移一个单位长度,即为21y ax bx c =+++的图象,∴21y ax bx c =+++的图象与x 轴的两个交点一个在(1,0)-的左侧,另一个在(3,0)的右侧,∴若方程210ax bx c +++=的两实数根为12,x x ,且12x x <,则121,3x x <->,故④正确;综上可知,正确的有①③④,故答案为:①③④3.在平面直角坐标系中,设二次函数22y ax bx =++(a ,b 是常数,0a ≠).(1)若2a =时,图象经过点()11,,求二次函数的表达式.(2)写出一组a ,b 的值,使函数22y ax bx =++的图象与x 轴只有一个公共点,并求此二次函数的顶点坐标.(3)已知,二次函数22y ax bx =++的图象和直线4y ax b =+都经过点()2m ,,求证:2212a b +≥.易错压轴三:根据二次函数的对称性求函数值例1.如图,抛物线21y a x =与抛物线22y a x bx =+相交于点()1,P m -,过点P 作x 轴的平行线,与两条抛物线分别交于点M ,N ,若点M 是PN 的中点,则12a a 的值是()A .12B .2C .13D .3将()1,P m -,代入1y a x =则12a a b =-,∴()1222a a a =--,∴123a a =,∴123a a =,故选:D .例2.已知二次函数2y ax bx c =++的图像过点(1,0)A -和(0,1)C .(1)若此抛物线的对称轴是直线12x=,点C与点P关于直线12x=对称,则点P的坐标是.(2)若此抛物线的顶点在第一象限,设t a b c=++,则t的取值范围是.练习1.设二次函数24y kx kx c =-+(k ,c 为实数)的图象过点()11,A x y ,()22,B x y ,()33,C x y 三点,且3212x x x <<<,13x x =,124x x +>,下列结论正确的是()A .若0k >,则312y y y =>B .若0k >,则321y y y >>C .若0k <,则123y y y >>D .若0k <,则213y y y >>练习2.已知22x m n =++和2x m n =+时,多项式246x x ++的值相等,则当x m n =+时,多项式的值为.【答案】2【分析】本题考查了二次函数的性质,令246y x x =++,可知对称轴为直线2x =-,根据题意,求出2x m n =+=-,即可求解.【详解】解:∵()224622y x x x =++=++,练习3.自变量x 的函数值我们通常记作()f x ,()f n 表示自变量x n =时,函数()f x 的函数值,已知函数()23f x x ax =-+,其中a 为常数.(1)若2a =,求()5f 的值;(2)若存在唯一一个自变量x 的值,使得另一个函数()()g x f x =,()2g x x =+,试求满足条件的a 的值;(3)若存在实数m 且12m -<≤,使得()()223f m f m =-+,试求实数a 的取值范围.1.设函数()y f x =对一切实数不均满足(5)(5)f x f x +=-,且方程()0f x =恰好有6个不同的实根,则这6个实根的和为()A .10B .12C .18D .30【答案】D【分析】本题考查函数的零点与方程的根的关系,解题的关键是看出函数的图象关于直线5x =对称,得到函数的零点是成对出现的.根据函数()f x 满足(5)(5)f x f x +=-,可得函数的图象关于5x =对称,从而得到方程()0f x =的6个实数解中有3对,每一对的和为10,由此可得结论.【详解】解:对于任意实数,函数()f x 不均满足(5)(5)f x f x +=-∴函数的图象关于5x =对称,∴函数的零点关于5x =对称,∴方程()0f x =的根关于5x =对称,∴方程()0f x =的6个实数解中有3对,∴成对的两个根之和等于2510⨯=,6∴个实根之和是10330⨯=,故选:D .2.已知关于直线1x =对称的抛物线2y x bx c =++经过()123,A n y +,()21,B n y -两点,且点A ,B 分别位于拋物线对称轴的两侧,则位于对称轴左侧的点是(填A 或B ),若此时12y y <,则n 的取值范围是.【答案】B 10n -<</01n >>-【分析】本题考查二次函数的图象和性质.解题的关键是掌握二次函数的增减性.根据抛物线对称轴为1x =,开口向上,根据已知条件分类讨论得出点B 在对称轴的左侧;根据12y y <,进而得出不等式,解不等式即可求解.【详解】解: 抛物线2y x bx c =++关于直线1x =对称,经过()123,A n y +,()21,B n y -两点,且点A ,B 分别位于拋物线对称轴的两侧,若点A 位于对称轴左侧,则23123111n n n n +<-⎧⎪+<⎨⎪->⎩,解得412n n n <-⎧⎪<-⎨⎪>⎩,不等式组无解,不符合题意;若点B 位于对称轴左侧,则23123111n n n n +>-⎧⎪+>⎨⎪-<⎩,解得412n n n >-⎧⎪>-⎨⎪<⎩,∴不等式组的解为12n -<<;此时12y y <,()()11231n n ∴-->+-,解得:0n <,∴10n -<<,综上,12y y <时,则n 的取值范围是10n -<<,故答案为:B ,10n -<<.3.设二次函数2223y x mx m =+-+(m 为常数)的图象为f .【特例感悟】(1)当2m =,30x -≤≤时,二次函数2223y x mx m =+-+(m 为常数)的最小值是______、最大值是______;【类比探索】(2)当直线()0y m m =-<与图象f 在第一象限内交A 、B 两点(点A 在点B 的左边),A 点横坐标a ,点B 的横坐标b ,7a b =,求在a x b ≤≤范围内二次函数2223y x mx m =+-+(m 为常数)的最大值与最小值的差;【纵深拓展】(3)①不论m 为何实数时,图象f 一定会经过一个定点,求出这个定点坐标;②当02x ≤≤时,二次函数2223y x mx m =+-+(m 为常数)的最大值为9,那么图象f 的对称轴与x 轴的交点横坐标会大于0小于2吗?试说明你的理由,并指出满足条件的对称轴与定点之间的距离.【答案】(1)51-,-;(2)最大值与最小值的差为9;(3)①定点坐标为()1,4;②当02x ≤≤时,图象f 的对称轴与x 轴的交点横坐标不能大于0小于2.理由见详解,定点()1,4分别到直线=1x -、3x =的距离都是2.【分析】(1)函数的对称轴为直线2x =-,则2415y x x =+-=-,当0x =时,2411y x x =+-=-,即可求解;(2)由28273a m a m=-⎧⎨=-⎩,整理得2716480m m +-=,得到图象f 的对称轴为4x =,进而求解;(3)①222232(1)3y x mx m x m x =+-+=+-+,当1x =时,无论m 为何实数,都有4y =,即可求解;②当02m ≤-≤时,抛物线开口向上,在0x m ≤≤-时,y 随x 的增大而减小,函数在2m x -≤≤时y 随x 的增大而增大,即可求解;当对称轴为2x m =->时,函数在02x ≤≤时y 随x 的增大而减小,同理可解.本题考查的是二次函数综合运用,涉及到二次函数的图象和性质,确定函数对称轴和分类求解是解题的关键.【详解】解:(1)当2m =,30x -≤≤时,241y x x =+-,函数的对称轴为直线2x =-,则2415y x x =+-=-,当0x =时,2411y x x =+-=-,易错压轴四:二次函数的最值问题例1.已知:()2110422m a a a =--≤≤,()414n b b =≤≤,2m n +=,则下列说法中正确的是()A .n 有最大值4,最小值1B .n 有最大值3,最小值32-C .n 有最大值3,最小值1D .n 有最大值3,最小值52例2.已知二次函数()2211y ax b x =--+(a ,b 为常数且0a >),当21x -≤≤-时,y随x 的增大而增大,则ab 的最大值为.练习1.4.已知二次函数()()22y x x m =---,当0x m ≤≤时,则()A .若4m >时,函数y 有最小值24m-B .若4m >时,函数y 有最小值24mC .若4m <时,函数y 有最小值24m-D .若4m <时,函数y 有最小值24m【答案】A【分析】本题主要考查了二次函数的性质,掌握根据二次函数的性质求二次函数最值的取值范围是解题的关键.先将二次函数解析式化成顶点式,然后根据各选项m 的取值范围,确定对称轴和m 的练习2.已知抛物线1C :228=-y x ,把1C 绕点()1,0旋转180︒,得到抛物线2C ,则2C 的解析式为;在1C 和2C 构成的封闭区域内作直线l y 轴,分别交1C 和2C 与点M ,N ,则MN 的最大值为.【答案】288y x x=-+12【分析】先求出抛物线1C 的顶点为(0,8)-,与x 轴交点为(2,0)和(2,0)-,由旋转的性质可得抛物线2C 的顶点为(2,8),2C 图像上的两点(0,0)和(4,0),设二次函数的顶点式,代入(0,0)即可求出解析式;设2(,28),M m m -则2(,28)N m m m -+,可得24(1)12MN m =--+,进而可求最值;【详解】解:在228=-y x 中,令0y =得2x =或2x =-,∴抛物线1C 的顶点为(0,8)-,与x 轴交点为(2,0)和(2,0)-,将(0,8)-绕点(1,0)旋转180︒,得到抛物线2C 的顶点为(2,8);将(2,0)和(2,0)-绕点(1,0)旋转180︒,分别得到2C 图像上的点(0,0)和(4,0);设抛物线2C 的解析式为2(2)8y a x =-+,把(0,0)代入得:048,a =+,解得2a =-,∴抛物线2C 的解析式为222(2)828y x x x =--+=-+;设2(,28),M m m -则(,2N m m -2228(28)MN m m m ∴=-+--由222828x x x x -+=-可得x ∵在1C 和2C 构成的封闭区域内作直线3131,m ∴-+<<+∴当1m =时,MN 取最大值故答案为:228y x x =-+;练习3.如图,在平面直角坐标系中,二次函数2y x bx c =++的图象经过点0,4A ⎛⎫- ⎪⎝⎭,点11,4B ⎛⎫ ⎪⎝⎭.(1)求此二次函数的解析式;(2)当22x -≤≤时,求二次函数2y x bx c =++的最大值和最小值;(3)点P 为此函数图象上任意一点,其僙坐标为m ,过点P 作PQ x ∥轴,点Q 的横坐标为21m -+.已知点P 与点Q 不重合,且线段PQ 的长度随m 的增大而减小.①求m 的取值范围;②当7PQ ≤时,直接写出线段PQ 与二次函数2123y x bx c x ⎛⎫=++-≤< ⎝⎭的图象只有1个交点时m 的取值范围.m 图象只有1个交点,直线13x =关于抛物线对称轴直线4132m ∴-<<-时,PQ 当423m -≤≤-时,PQ 综上所述,423m -≤≤-PQ 与图象有2个交点,1.如图,矩形ABCD 中,42AB AD ==,,E 为边AD 上一个动点,连接BE ,取BE 的中点G ,点G 绕点E 逆时针旋转90︒得到点F ,连接CF ,则CEF △面积的最小值是()A .4B .154C .3D .114∵矩形ABCD 中,4AB =∴A GEF EHF ∠=∠=∠=∴FEH EBA ∽,EF EG =∴FE FH EHEB EA AB==,2.若点(),1p 在抛物线214y x =上过y 轴上点E 作两条相互垂直的直线与抛物线分别交于A ,B ,C ,D ,且M ,N 分别是线段AB CD ,的中点,EMN 面积的最小值为.3.设二次函数214y ax x c =-+(a ,c 是常数)的图象与x 轴有交点.(1)若图象与x 轴交于A ,B 两点的坐标分别为(10)(30),,,,求函数1y 的表达式,并写出函数图象的顶点坐标.(2)若图象与x 轴只有一个交点,且过()a c ,,求此时a ,c 的值.(3)已知1a =,若函数1y 的表达式还可以写成()()1y x m x n =--(m ,n 为常数,m n ≠且2mn =),设二次函数()()2y x m x n =---,求12y y -的最小值.【答案】(1)2143y x x =-+;()21-,(2)当2a =时,2c =;当2a =-时,2c =-(3)4-【分析】(1)将(10)(30),,,代入214y ax x c =-+,可求13a c =⎧⎨=⎩,进而可得2143y x x =-+,化成顶点式可得顶点坐标;(2)令240ax x c -+=,由图象与x 轴只有一个交点,则()2440ac ∆=--=,即4ac =,将()a c ,代入214y ax x c =-+得,34c a a c =-+,可求2a =或2a =-或0a =(舍去),然后求解作答即可;易错压轴五:二次函数的平移问题例1.若抛物线242y x x =-+-向上平移()0m m >个单位后,在14x -<<范围内与x 轴只有一个交点,则m 的取值范围是()A .2m ≥B .02m <≤C .07m <≤D .27m ≤<【答案】D 【分析】先根据函数图象平移规则“上加下减求得平移后的函数解析式,根据二次函数的性质,结合函数的图象,进而可列出不等式组求解即可.【详解】解:根据题意,平移后的抛物线的表达式为242y x x m =-+-+,∵平移后抛物线的开口向下,对称轴为直线2x =,∴要使在14x -<<范围内与x 轴只有一个交点,只需=1x -时对应图象上的点在x 轴下方,4x =时对应函数图象上的点在x 轴上或x 轴上方,如图,∴1420161620m m ---+<⎧⎨-+-+≥⎩,解得27m ≤<,故选:D .【点睛】本题考查二次函数图象的平移、二次函数与x 轴的交点问题,解答的关键是掌握二次函数的性质,以及与方程、不等式的关系.例2.如图①是杭州亚运会的徽标中的钱江潮头,可近似地看成是顶点在y 轴上的二次函数,如图②所示,已知1OC =,6AB =.当潮头以2个单位每秒的速度向x 轴正方向移动的过程中,若记潮头起始位置所在的二次函数图象与坐标轴三个交点围成的面积为ABC S ,则经过秒后,潮头所在的抛物线与坐标轴的三个交点围成的面积恰好为ABC面积的一半.练习1.已知,二次函数21(,y ax bx a b =+-是常数,且0)a ≠的图象经过()2,1,(4,3)A B ,()4,1C -三个点中的两个点,平移该函数的图象,使其顶点始终在直线1y x =-上,则平移后所得抛物线与y 轴交点的纵坐标()A .有最大值为1B .有最大值为12-C .有最小值为1D .有最小值为12-【答案】B【分析】本题考查了二次函数图象的平移,一次函数的图象和性质,待定系数法的应用;首先判断出抛物线经过点A 、C ,利用待定系数法求出抛物线解析式,根据题意设出平移后的抛物线解析式,令0x =,得到纵坐标与平移距离之间的函数关系式,进而可得答案.【详解】解:∵()2,1,(4,3)A B 在直线1y x =-上,练习2.对某一个函数给出如下定义:若存在实数0m >,对于任意的函数值,都满足m y m -≤≤,则称这个函数是有界函数....,在所有满足条件的m 中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.将函数()212,0y x x t t =-+-≤≤≥的图象向上平移t 个单位,得到的函数的边界值n 满足是9542n ≤≤时,则t 的取值范围是.练习3.已知二次函数的图像L 过点0,2⎛⎫⎪⎝⎭,顶点坐标为()1,2-.(1)求这个二次函数的表达式;(2)L 与x 轴相交于A ,B 两点(点A 在点B 左侧),求A ,B 两点坐标;(3)将L 向上平移个()0k k >单位长度,与x 轴相交于1A ,1B 两点,若点(),0K k 在线段11A B 上,求k 的取值范围.1.如图,抛物线22y x x =+与直线2y x =+交于A 、B 两点,与直线2x =交于点P ,将抛物线沿着射线AB平移P经过的路程为()A.6B.132C.254D.142.如图,抛物线2286y x x =-+-与x 轴交于点A 、B ,把抛物线在x 轴及其上方的部分记作1C ,将1C 向右平移得2C ,2C 与x 轴交于点B 、D .若直线y x m =+与1C 、2C 共有2个不同的交点,则m 的取值范围是.当1y x m =+与抛物线1C :2286y x x =-+-相切时,令21286y x x x m =-+-=+,即2276x x m -+--根据相切可知方程有两个相等的解,即27∆=-解得118m =,当2y x m =+过点()1,0A 时,即:201m =+,解得21m =-,3.在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点(1,0)A -,(5,0)B .(1)求抛物线的表达式.(2)若抛物线22y x bx c mx =++-,当2123m x m -≤≤+时,y 有最大值12,求m 的值.(3)若将抛物线2y x bx c =++平移得到新抛物线2y x bx c n =+++,当23x -<<时,新抛物线与直线1y =有且只有一个公共点,直接写出n 的取值范围.①点时,则485191251n n +-+≥⎧⎨--+≤⎩解得69n -≤≤;②当抛物线245y x x =--与直线易错压轴六:二次函数与一元二次方程例1.将抛物线223y x x =-++中x 轴上方的部分沿x 轴翻折到x 轴下方,图像的其余部分不变,得到的新图像与直线y x m =+有4个交点,则m 的取值范围是()A .5m ≤-B .2154m -≤<-C .2134m -<<-D .3m ≥-【答案】C【分析】本题考查抛物线与x 轴的交点:把求二次函数2y ax bx c =++(a 、b 、c 是常数,0a ≠)与x 轴的交点坐标问题转化为解关于x 的一元二次方程.解方程2230x x -++=得()1,0-,()3,0,再利用折叠的性质求出折叠部分的解析式为()()13y x x =+-,即()22313y x x x =---≤≤,然后求出直线y x m =+经过点()3,0时m 的值和当直线y x m =+与抛物线()22313y x x x =---≤≤有唯一公共点时m 的值,即可得解.掌握抛物线与x 轴交点坐标的求法及抛物线与直线交点坐标的求法是解题的关键.也考查了二次函数图像与几何变换.【详解】解:对抛物线223y x x =-++,当0y =时,得:2230x x -++=,解得:=1x -或3x =,∴抛物线与x 轴的交点为()1,0-、()3,0,∵将抛物线223y x x =-++中x 轴上方的部分沿x 轴翻折到x 轴下方,图像的其余部分不变,∴新图像中当13x -≤≤时,解析式为()()13y x x =+-,即2=23y x x --,如图,当直线y x m =+经过点()3,0时,此时直线y x m =+与新函数图像有3个交点,把()3,0代入直线y x m =+,解得:3m =-,将直线y x m =+向下平移时,有4个交点,例2.已知点()0,0.3A ,)B,()2,0.3C 在二次函数()20y ax bx c a =++≠的图象上,则方程20.70ax bx +-=的解为【答案】23-或3【分析】本题考查了二次函数的性质,。
二次函数压轴题专题(含答案)

二次函数压轴题专题1.如图,已知△ABC的三个顶点坐标分别为A(﹣4,0)、B(1,0)、C(﹣2,6).(1)求经过A、B、C三点的抛物线解析式;(2)设直线BC交y轴于点E,连接AE,求证:AE=CE;(3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F为顶点的三角形与△ABC相似吗?2.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A、C、D均在坐标轴上,且AB=5,sinB=.(1)求过A、C、D三点的抛物线的解析式;(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A、E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.3.如图,经过点A(0,﹣4)的抛物线y=x2+bx+c与x轴相交于B(﹣2,0),C两点,O为坐标原点.(1)求抛物线的解析式;(2)将抛物线y=x2+bx+c向上平移个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,求AM的长.参考答案,,由题意得:,=2,=2,的函数解析式可得:,,,)=,=,,=sinB=sinD=﹣﹣x x+4﹣;﹣x x+4,;=x+bx+b=x x+4,即直线x+;,))﹣(××(+.(,)时,.x2y=,即:x2+x+﹣;m=;<。
二次函数60道压轴题型专项训练(12大题型)(原卷版)—2024-2025学年九年级数学上册(浙教)

二次函数60道压轴题型专项训练(12大题型)【题型目录】压轴题型一 二次函数的图象与性质压轴题压轴题型二 二次函数与各项系数符号压轴题压轴题型三 根据二次函数的对称性求值压轴题型四 二次函数的平移压轴题压轴题型五 二次函数与坐标轴交点压轴题压轴题型六 二次函数的应用(销售、增长率等问题)压轴题型七 二次函数的应用(图形运动、拱桥、投球等问题)压轴题型八 二次函数中的存在性问题压轴题型九 二次函数与一次函数压轴题压轴题型十 二次函数的翻折问题压轴题型十一 二次函数最值问题压轴题型十二 二次函数的综合【压轴题型一 二次函数的图象与性质压轴题】1.(2024·浙江嘉兴·二模)已知直线3y x =--与抛物线2()4=--y x m 对称轴左侧部分的图象有且只有一个交点,则m 的取值范围是( )A .54m £B .54m £或74m =C .1m £D .1m £或54m =2.(2024·浙江宁波·二模)已知二次函数2y x bx c =++的图象与x 轴只有一个公共点,且当x a =和x a n =+时函数值都为m ,则m 与n 的等量关系为 .3.(2024·浙江杭州·一模)已知二次函数()()13y a x x =--的图像过点()4,m ,(),p n (1)当1m =时,求a 的值;(2)若>>0m n ,求p 的取值范围;(3)求证:0>am an +.4.(2024·浙江杭州·一模)已知二次函数2(2)3(0)y m x m =-->的图象与x 轴交于点(,0),(,0)A a B b .(1)当3a =-时,求b 的值.(2)当0a b <<时,求m 的取值范围.(3)若(1,),(1,)P a p Q b q ++两点也都在此函数图象上,求证:0p q +>.5.(2024·浙江杭州·一模)在平面直角坐标系中,点(1,)m 和(3,)n 都在二次函数2y ax bx =+(0,,¹a a b 是常数)的图象上.(1)若6==-m n ,求该二次函数的表达式和函数图象的对称轴.(2)若1a =-,m n <,求b 的取值范围.(3)已知点()()()1231,,2,,4,y y y -也都在该二次函数图象上,若0mn <且a<0,试比较123y y y ,,的大小,并说明理由.【压轴题型二 二次函数与各项系数符号压轴题】1.(23-24九年级上·浙江杭州·阶段练习)抛物线()20y ax bx c a =++¹的顶点为(12)D -,,与x 轴的一个交点A 在点(30)-,和(20)-,之间,其部分图象如图,则以下结论:①0abc <;②若方程20ax bx c m ++-=没有实数根,则2m >;③320b c +<;④图象上有两点()11,P x y 和()22,Q x y ,若12x x <且122x x +<-,则一定有12y y >;正确的是( )A .4个B .3个C .2个D .1个2.(20-21九年级上·浙江·期末)抛物线2y ax bx c =++(a ,b ,c 为常数,且0a ¹)经过点()1,0-和()0m ,;且12m <<,当1x <-时,y 随着x 的增大而减小.下列结论:①0abc >;②0a b +>③若点()13,A y -,点()23,B y 都在抛物线上,则12y y <;④()10a m b -+=;⑤若1c £-,则244b ac a -£.其中结论正确的是.3.(23-24九年级上·浙江杭州·期中)在二次函数223(0)y x tx t =-+>中.(1)若函数图象的顶点在x 轴上,求t 的值.(2)若点(,)t s 在抛物线上,令q t s =+,求证:134q £.(3)如果(2,)A m a -,()4,B b ,(,)C m a 都在这个二次函数图象上,且3a b <<,求m 的取值范围.4.(2024·云南昆明·二模)在平面直角坐标系中,抛物线()24430y mx mx m m =-+->与x 轴的交点为A ,B .(1)求抛物线的对称轴及顶点坐标;(2)若 1,m =当 3t x t +≤≤时,函数最小值为 2-,求t 的值;(3)横、纵坐标都是整数的点叫做整点.若抛物线在点 A ,B 之间的部分与线段 AB 所围成的区域内(包括边界)恰有10个整点,求m 的取值范围.5.(23-24九年级下·北京·阶段练习)已知抛物线()20y ax bx c a =++>,(1)若抛物线过点()()35m m -,,,,求抛物线的对称轴;(2)已知点()()()()0112042y x y y n -,,,,,,,在抛物线上,其中121x -<<-,若存在1x 使1y n >,试比较012y y y ,,的大小关系.【压轴题型三 根据二次函数的对称性求值】1.(2024·山东淄博·二模)二次函数2y ax bx c =++(a ,b ,c 是常数,0a ¹)的自变量x 与函数值y 的部分对应值如下表:x…2-1-012…2y ax bx c=++…tm2-2-n…且当12x =-时,与其对应的函数值0y >,有下列结论:①函数图象的顶点在第四象限内;②2-和3是关于x 的方程2ax bx c t ++=的两个根;③36m n +<-,其中正确的结论个数是( )A .0个B .1个C .2个D .3个2.(23-24九年级上·安徽芜湖·期中)已知二次函数2y ax bx c =++的图像过点(1,0)A -和(0,1)C .(1)若此抛物线的对称轴是直线12x =,点C 与点P 关于直线12x =对称,则点P 的坐标是 .(2)若此抛物线的顶点在第一象限,设t a b c =++,则t 的取值范围是 .3.(2024·云南曲靖·二模)已知抛物线²y ax bx c =++(a ,b ,c 为常数,0a ¹)(1)若20a b -=,4-+=a b c ,求此抛物线的顶点坐标;(2)在(1)的条件下,抛物线经过点()0,2,将抛物线²y ax bx c =++的图象0x <的部分向下平移h (h 为正整数)个单位长度,平移后的图象恰好与x 轴有2个交点,若点1(,)S m n y -与点2(,)Q m y 在平移后的抛物线上(点S ,Q 不重合),且点S 与点 Q 关于对称轴对称,求代数式22281244m mn n n h -+-+的值.4.(23-24九年级上·北京朝阳·期中)在平面直角坐标系xOy 中,点()1,m ,()4,n 在抛物线()20y ax bx c a =++>上.设抛物线的对称轴为直线x t =.(1)若30a b +=.比较,,m n c 的大小关系,并说明理由;(2)点()00),1(x m x ¹在抛物线上,若m c n <<,求t 及0x 的取值范围.5.(23-24九年级上·北京西城·期中)已知点()11,M x y ,()22,N x y 在抛物线()220y ax bx a =++>的图象上,设抛物线的对称轴为x t =.(1)若()2,1M -,()8,1N -,则t =_______;(2)当12x =-,223x <<时,都有122y y >>,求t 的取值范围.【压轴题型四 二次函数的平移压轴题】1.(2024·河北邯郸·二模)我们把横、纵坐标都是整数的点称为整点,如图,抛物线1C :224y x x =-++与()22:C y x m =-(m 是常数)围成的封闭区域(边界除外)内整点的个数不能是( )A .1个B .2个C .3个D .4个2.(2024·福建·模拟预测)定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC 中,点()02A ,,点()20C ,,则互异二次函数()2y x m m =--与正方形OABC 有交点时m 的最大值和最小值的差为3.(2024·广东广州·二模)在平面直角坐标系中,将过点()2,1-的抛物线211:4C y x bx =-+(b 为常数)向右平移m 个单位(0m >),再向上平移n 个单位(0n ³)得到新的抛物线2C ,其顶点为E .(1)求点E 的坐标;(用含m ,n 的式子表示)(2)若抛物线2C 与坐标轴有且只有两个公共点,求满足条件的点E 的纵坐标;(3)当1n =时,抛物线2C 与x 轴交于A 、B 两点,与y 轴交于点D ,且当02x ££时,对抛物线1C 上的任意一点P ,在抛物线2C 上总存在一点Q ,使得点P ,Q 的纵坐标相等,探究下列问题:①求m 的取值范围;②若存在一点F ,满足DF AF BF ==,求点F 的纵坐标的取值范围.4.(2024·内蒙古赤峰·二模)小爱同学学习二次函数后,对函数()21y x =--进行了探究.在经历列表、描点、连线步骤后,得到如图的函数图象.请根据函数图象,回答下列问题:(1)观察探究:①至少写出该函数的两条性质;②直接写出方程()211x --=-的解;③直接写出方程()21x a --=有四个实数根时a 的取值范围.(2)延伸思考:将函数()21y x =--的图象经过怎样的平移可得到函数()21213y x =---+的图象?写出平移过程,并直接写出当123y <£时,自变量x 的取值范围.5.(2024·山东济南·二模)已知抛物线1C :26y x mx m =--+交x 轴于点A ,B ,交y 轴于点C .(1)如图1,当点A 坐标为()30-,时,求抛物线的解析式;(2)在(1)的条件下,点D 是第二象限内抛物线上的一点,连接BD ,若BD 将四边形ABCD 平分成面积相等的两部分,求点D 的横坐标;(3)如图2,EFH V 为等边三角形,点F ,H 在x 轴上,且点E 的坐标为()06,,将抛物线1C :26y x mx m =--+向右平移m 个单位,再向下平移6m 个单位后得到新的抛物线2C ,若2C 与等边EFH V 三边恰有四个交点,求m 的取值范围.【压轴题型五 二次函数与坐标轴交点压轴题】1.(2024·浙江杭州·一模)已知抛物线2y ax bx =+与2y bx ax =+的交点为A ,与x 轴的交点分别为B ,C ,点A ,B ,C 的横坐标分别为1x ,2x ,3x ,且1230x x x ¹.若0a b +<,20a b +>,则下列说法正确的是( )A .231x x x <<B .321x x x <<C .213x x x <<D .312x x x <<2.(2023·浙江绍兴·中考真题)在平面直角坐标系xOy 中,一个图形上的点都在一边平行于x 轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数()2(2)03y x x =-££的图象(抛物线中的实线部分),它的关联矩形为矩形OABC .若二次函数()21034y x bx c x =++££图象的关联矩形恰好也是矩形OABC ,则b =.3.(23-24九年级上·浙江杭州·期中)已知抛物线()230y ax ax c a =++¹与y 轴交于点A .(1)当1a =,2c =,求该抛物线与x 轴交点坐标;(2)若1a =,点(),P m n 在二次函数抛物线23y ax ax c =++的图象上,且0n c ->,试求m 的值;(3)若点A 的坐标是()0,1,当2c c -<时,抛物线与x 轴只有一个公共点,求a 的取值范围.4.(22-23九年级上·浙江湖州·期末)在书本阅读材料中提到利用几何画板可以探索函数2y ax bx c =++的系数a ,b ,c 与图像的关系.如图1,在几何画板软件中绘制一个二次函数的图像的具体步骤如下:步骤一:在直角坐标系内的x 轴上取任意三个点A (A 不在原点),B ,C ,度量三个点的横坐标,分别记为a ,b ,c ;步骤二:绘制函数2y ax bx c =++;步骤三:任意移动A ,B ,C 三点的位置,发现抛物线的开口方向、大小、位置会发生变化.问题:如图2,将点A 移动到点()1,0-的位置.(1)若点B 移动到点()4,0-,请求出此时抛物线的对称轴;(2)在点B ,C 移动的过程中,且满足AB AC =,是否存在某一位置使得抛物线与x 轴只有一个交点,若存在,请求出此时点B 的坐标,若不存在,请说明理由.5.(22-23九年级上·浙江杭州·期末)已知二次函数2(0)y ax bx c a =++>的图象经过点(1,1)A -和(2,4)B .(1)求a ,b 满足的关系式;(2)当自变量x 的值满足12x -££时,y 随x 的增大而增大,求a 的取值范围;(3)若函数图象与x 轴无交点,求2a b +的取值范围.【压轴题型六 二次函数的应用(销售、增长率等问题)】1.(2024·天津红桥·三模)某服装店试销一种成本为每件60元的服装,规定试销期间每件服装的销售单价不低于成本,且获得的利润不得高于成本的45%.经试销发现,销售量y (件)与销售单价x (元)符合一次函数关系120y x =-+.有下列结论:①销售单价可以是90元;②该服装店销售这种服装可获得的最大利润为891元;③销售单价有两个不同的值满足该服装店销售这种服装获得的利润为500元,其中,正确结论的个数是( )A .0B .1C .2D .32.(2021·江苏连云港·中考真题)某快餐店销售A 、B 两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A 种快餐的利润,同时提高每份B 种快餐的利润.售卖时发现,在一定范围内,每份A 种快餐利润每降1元可多卖2份,每份B 种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.3.(2024·四川德阳·三模)“端午节”吃粽子是中国传统习俗,在端午节来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒定价为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x 元,日销售量为P 盒.(1)当60x =时,P 等于______;(2)当每盒售价定为多少元时,日销售利润W (元)最大?最大利润是多少?(3)小强说:“当日销售利润最大时,日销售额不是最大.”小红说:“当日销售利润不低于8000元时,每盒售价x 的范围为6080x ££.”你认为他们的说法正确吗?4.(22-23八年级下·浙江杭州·期中)某商店进购一商品,第一天每件盈利(毛利润)10元,销售500件.(1)第二、三天该商品十分畅销.销售量持续走高.在售价不变的基础上,第二、三天的销售量达到605件,求第二、三天的日平均增长率;(2)经市场调查发现,在进货价不变的情况下,若每件涨价1元,日销量将减少20件.①现要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每件应张价多少元?②现需按毛利润的10%交纳各种税费,人工费每日按销售量每件支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每件涨价应为多少?5.(2023·湖北省直辖县级单位·一模)某销售卖场对一品牌商品的销售情况进行了调查,已知该商品的进价为每件3元,每周的销售量y (件)与售价x (元/件)(x 为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:x (元/件)456y (件)1000095009000(1)求y 关于x 的函数关系式(不求自变量的取值范围);(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?(3)抗疫期间,该商场这种商品的售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠整数m 元()15m ££,捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出整数m 的值.【压轴题型七 二次函数的应用(图形运动、拱桥、投球等问题)】1.(22-23九年级上·浙江台州·期末)以初速度v (单位:m/s )从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h (单位:m )与小球的运动时间t (单位:s )之间的关系是24.9h vt t =-.现将某弹性小球从地面竖直向上抛出,初速度为9.8m/s ,经过a 秒后,将第二个相同材质的小球从地面以初速度4.9m/s 竖直上抛.若两球能在空中相遇,则a 的取值范围为( )A .34a <<B .12a <<C .324a <<D 2a <<2.(23-24九年级上·浙江湖州·期末)如图,乒乓球桌桌面是长 2.7m AB =,宽 1.5m AD =的矩形,E F ,分别是AB 和CD 的中点,在E ,F 处设置高0.15m HE =的拦网.一次运动员在AD 端发球,在P 点击打乒乓球后经过桌面O 点反弹后的运行路径近似二次项系数427a =-的抛物线的一部分.已知本次发球反弹点O 在到桌面底边AD 的距离为0.1m ,到桌面侧边AB 的距离为0.1m 处.若乒乓球沿着正前方飞行(垂直于BC ),此时球在越过拦网时正好比拦网上端GH 高0.1m ,则乒乓球落在对面的落点Q 到拦网EF 的距离为 m ;若乒乓球运行轨迹不变,飞行方向从O 点反弹后飞向对方桌面,落点Q 在距离BC 为0.2m 的Q 点处,此时QC 的长度为 m .3.(2023·浙江杭州·模拟预测)已知点(2,2)A -和点(4,)B n -在抛物线2(0)y ax a =¹上.(1)求a 的值及点B 的坐标;(2)点P 在y 轴上,且ABP V 是以AB 为直角边的三角形,求点P 的坐标;(3)将抛物线2(0)y ax a =¹向右并向下平移,记平移后点A 的对应点为A ¢,点B 的对应点为B ¢,若四边形ABB A ¢¢为正方形,求此时抛物线的表达式.4.(22-23九年级上·天津河西·期末)如图所示,在ABC V 中,90B Ð=°,5cm AB =,7cm BC =,点P 从点A 开始沿AB 边向点B 以1cm /s 的速度运动,点Q 从点B 开始沿BC 边向点C 以2cm /s 的速度运动.P 、Q 分别从A 、B 同时出发,当P 、Q 两点中有一点停止运动时,则另一点也停止运动.设运动的时间为s t .(0)t ≥(1)当t 为何值时,PQ 的长度等于5cm ;(2)求出V BPQ S 关于t 的函数解析式,计算P 、Q 出发几秒时,V BPQ S 有最大值,并求出这个最大面积?5.(23-24九年级上·浙江温州·期中)如图,抛物线2y x bx c =-++与x 轴交于点()3,0A -、()1,0B ,与y 轴交于点C .(1)求抛物线的表达式.(2)已知点D 为y 轴上一点,点D 关于直线AC 的对称点为1D .①当点1D 刚好落在第二象限的抛物线上时,求出点D 的坐标.②点P 在抛物线上(点P 不与点A 、点C 重合),连接PD ,1PD ,1DD ,是否存在点P ,使1PDD △为等腰直角三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.【压轴题型八 二次函数中的存在性问题】1.(2024·浙江宁波·一模)新定义:若一个点的横纵坐标之和为6,则称这个点为“和谐点”.若二次函数22y x x c =-+(c 为常数)在13-<<的图象上存在两个“和谐点”,则c 的取值范围是( )A .2574c <<B .2544c <<C .11c -<<D .2504c <<2.(23-24九年级上·浙江温州·期中)图1是洞头深门大桥,其桥底呈抛物线,以O 为原点,OA 所在直线为x 轴建立平面直角坐标系(如图2所示),桥面CB ∥OA ,其抛物线解析式为()218020320y x =--+,抛物线上点A 离桥面距离22AB =米,若存在一点E 使得38CE CB =,则点E 到抛物线的距离ED = 米.3.(2024·浙江宁波·模拟预测)如图,一次函数y =的图象与坐标轴交于点A 、B ,抛物线2y x bx c =++的图象经过A 、B 两点.(1)求二次函数的表达式;(2)若点P 为抛物线上一动点,在直线AB 上方是否存在点P 使PAB V 的面积最大?若存在,请求出PAB V 面积的最大值及点P 的坐标,请说明理由.4.(23-24九年级上·黑龙江伊春·期末)如图,已知抛物线22y ax x c =-+与直线y kx b =+都经过(0,3)A -、(3,0)B 两点,该抛物线的顶点为.(1)求此抛物线和直线AB 的表达式;(2)设直线AB 与该抛物线的对称轴交于点E ,在射线EB 上是否存在一点M ,过M 作x 轴的垂线交抛物线于点N ,使点M ,N ,C ,E 是平行四边形的四个顶点?若存在,直接写出点M 的坐标;若不存在,说明理由;5.(22-23九年级上·浙江温州·期中)如图,直线212y x =-+与x 轴交于点C ,与y 轴交于点B ,抛物线23103y ax x c =++经过B C ,两点,与x 轴交于另一点A ,点E 是直线BC 上方抛物线上的一动点,过E 作EF y ∥轴交x 轴于点F ,交直线BC 于点M .(1)求抛物线的解析式;(2)求线段EM 的最大值;(3)在(2)的条件下,连接AM ,点Q 是抛物线对称轴上的动点,在抛物线上是否存在点P ,使得以P Q A M ,,,为顶点的四边形为平行四边形?如果存在,请直接写出P 点坐标;如果不存在,请说明理由.【压轴题型九 二次函数与一次函数压轴题】1.(2024·浙江杭州·一模)二次函数21y x bx c =++(b ,c 是常数)过()2,0-,()0m ,两个不重合的点,一次函数2y x d =+过()0m ,和二次函数的顶点,则m 的值为( )A .﹣1B .0C .1D .22.(23-24九年级上·浙江绍兴·期末)二次函数2(,,y ax bx c a b c =++为常数,且0)ab ¹经过()()11,0,,0x ,一次函数y a x c =+经过()2,0x ,一次函数y b x c =+经过()3,0x .已知1254,1x m x m -<<-<<+,31n x n <<+,其中,m n 为整数,则m n +的值为 .3.(2024·浙江舟山·三模)已知一次函数5y x =-的图象与x 轴,y 轴分别交于点A ,B ,将点A 向左平移4个单位,得到点A ¢,且点A ¢恰好在二次函数23y ax bx =+-(a 、b 是常数,0a ¹)图象的对称轴上.(1)用含a 的代数式表示b .(2)求证:二次函数与一次函数图象交于一个定点,并求出该点的坐标.(3)若二次函数图象与线段AB 恰有一个公共点,结合函数图象,求a 的取值范围.4.(23-24九年级上·浙江宁波·期末)如图,在平面直角坐标系xOy 中,一次函数121y x =+的图象与二次函数22y x ax b =++的图象相交于A ,B 两点,点A 坐标为()1m -,,点B 坐标为()25,.(1)求m 的值以及二次函数的解析式.(2)根据图象,直接写出当1y >2y 时x 的取值范围.(3)若将二次函数向上平移t 个单位长度后,得到的图象与x 轴没有交点,求t 的取值范围.5.(2023·浙江金华·三模)如图,一次函数()00b y x b a b a=-+>>,与坐标轴交于A ,B 两点,以A 为顶点的抛物线过点B ,过点B 作y 轴的垂线交该抛物线另一点于点D ,以AB ,AD 为边构造ABCD Y ,延长BC 交抛物线于点E .(1)若2a b ==,如图1.①求该抛物线的表达式.②求点E 的坐标.(2)如图2,请问BE AB 是否为定值,若是,请求出该定值;若不是,请说明理由.【压轴题型十 二次函数的翻折问题】1.(22-23九年级上·浙江湖州·期末)抛物线223y x x =-++与y 轴交于点C ,过点C 作直线l 垂直于y 轴,将抛物线在y 轴右侧的部分沿直线l 翻折,其余部分保持不变,组成图形G ,点()1,M m y ,()21,N m y +为图形G 上两点,若12y y >,则m 的取值范围是( )A .102m £<B 1m <<C m <<D 12m <<2.(2023江苏南通·模拟预测)如图,将二次函数2y x m =-(其中0m >)的图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,形成新的图象记为1y ,另有一次函数2y x =+的图象记为2y ,若1y 与2y 恰有两个交点时,则m 的范围是 .3.(2024·浙江·模拟预测)如图,抛物线22(0)y x x m m =-++>与y 轴交于A 点,其顶点为D .直线122y x m =--分别与x 轴、y 轴交于B 、C 两点,与直线AD 相交于E 点.(1)求A 、D 的坐标(用m 的代数式表示);(2)将ACE V 沿着y 轴翻折,若点E 的对称点P 恰好落在抛物线上,求m 的值;(3)抛物线22(0)y x x m m =-++>上是否存在一点P ,使得以P 、A 、C 、E 为顶点的四边形是平行四边形?若存在,求此抛物线的解析式;若不存在,请说明理由.4.(23-24九年级上·浙江绍兴·期中)如图,在平面直角坐标系中,将二次函数223y x x =--在x 轴上方的图象沿x 轴翻折到x 轴下方,图象的其余部分不变,将这个组合的图象记为M .(1)若直线12y x n =+与图象M 恰好有3个交点.求n 的值.(2)若直线12y x n =+与图象M 恰好有2个交点.求n 的取值范围.5.(2023·浙江杭州·二模)已知二次函数2420y mx mx m m =-+-¹(),且与x 轴交于不同点M 、N .(1)若二次函数图象经过点30A (,),①求二次函数的表达式和顶点坐标;②将抛物线在05x ££之间的那部分函数图象沿直线5x =翻折,将抛物线翻折前后的这两部分合记为图象F ,若直线y kx n =+过点151C (,),且与图象F 恰有两个交点,求n 的取值范围;(2)若0m <,当4MN £时,求实数m 的取值范围.【压轴题型十一 二次函数最值问题】1.(2024·浙江温州·二模)已知二次函数222y x x -=+, 当0x t ££时,函数最大值为M ,最小值为N .若5M N =,则t 的值为 ( )A .0.5B .1.5C .3D .42.(2023·浙江杭州·模拟预测)已知二次函数()2211y ax b x =--+(a ,b 为常数且0a >),当21x -££-时,y 随x 的增大而增大,则ab 的最大值为 .3.(2024·浙江嘉兴·三模)已知二次函数 23y x bx =++的图象经过点()()()12,,,43A x n B x t C -,,.(1)求二次函数的函数表达式;(2)当 212x x -=时,①若 0nt £,求 t n -的取值范围;②设直线AB 的函数表达式为y kx m =+,求m 的最大值.4.(2024·浙江宁波·模拟预测)已知二次函数214y x bx c =-++的图象经过原点O 和点()8,0A t +,其中0t ³.(1)当0=t 时.①求y 关于x 的函数解析式;求出当x 为何值时,y 有最大值?最大值为多少?②当x a =和x b =时()a b ¹,函数值相等,求a 的值.(2)当0t >时,在08x ££范围内,y 有最大值18,求相应的t 和x 的值.5.(23-24九年级上·浙江湖州·期末)设二次函数2y ax bx c =++(a b c ,,均为常数,且0a ¹).已知函数值y 和自变量x 的部分对应取值如下表所示:x L3-2-1-01L y L n 5a -n a-4a L (1)若1a =.①求二次函数的表达式,并写出顶点坐标;②已知点()1,m y 与()23,m y -都在该二次函数图象上,且12y y ³,请求出1y 的最小值.(2)将该二次函数图象向右平移k (02k <<)个单位,若平移后的二次函数图象在20x -££的范围内有最小值为3116a -,求k 的值.【压轴题型十二 二次函数的综合】1.(22-23九年级上·浙江宁波·阶段练习)如图,抛物线218333y x x =+-与x 轴交于点A 和点B 两点,与y 轴交于点C ,D 点为抛物线上第三象限内一动点,当2180ACD ABC Ð+Ð=°时,点D 的坐标为( )A .(8,3)--B .(,)--1673C .(6,7)--D .(5,8)--2.(23-24九年级上·浙江金华·期末)定义:若x ,y 满足:24x y k =+,24y x k =+(k 为常数)且x y ¹,则称点(),M x y 为“好点”.(1)若()5,P m 是“好点”,则m .(2)在32x -<<的范围内,若二次函数23y x x c =-+的图象上至少存在一个“好点”,则c 的取值范围为 .3(2024·浙江温州·二模)在平面直角坐标系中,已知抛物线()2233y mx m x m =--+-(m 是常数,且0m ¹)经过点()2,4,且与y 轴交于点A ,其对称轴与x 轴交于点B .(1)求出二次函数的表达式.(2)垂直于y 轴的直线l 与抛物线交于点(),P a p 和(),Q b q ,与直线AB 交于点(),c n ,若a c b <<,直接写出a b c ++的取值范围.(3)当13x t =-,2x t =,33x t =+时,对应的函数值分别为1y ,2y ,3y .求证:123454y y y ++³.4.(23-24九年级下·浙江宁波·期中)如图,已知抛物线21:4C y x =,()01F ,,点()11,A x y ,()22,B x y 为抛物线上第一象限内的两点,且满足FA FB ^,以FA FB 、为边向右作矩形FAPB ,若P 点纵坐标为5.(1)求12y y +的值;(2)求12x x 的值;(3)求矩形FAPB 的面积.5.(21-22九年级上·浙江·周测)如图,在平面直角坐标系中,抛物线24y ax bx =++交y 轴于点A ,交x 轴于点()6,0B -和点()2,0C ,连接AB 、AQ 、BQ ,BQ 与y 轴交于点N .(1)求抛物线表达式;(2)点713Q æöç÷èø,,点M 在x 轴上,点E 在平面内,若BME AOM V V ≌,且四边形ANEM 是平行四边形.①求点E 的坐标;②设射线AM 与BN 相交于点P ,交BE 于点H ,将BPH V 绕点B 旋转一周,旋转后的三角形记为11BPH △,求11BP 的最小值.。
二次函数解答压轴题(共62题)(学生版)-2023年中考数学真题分项汇编(全国通用)

二次函数解答压轴题(62题)一、解答题1(2023·浙江绍兴·统考中考真题)已知二次函数y=-x2+bx+c.(1)当b=4,c=3时,①求该函数图象的顶点坐标.②当-1≤x≤3时,求y的取值范围.(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.2(2023·浙江·统考中考真题)已知点-m,0和3m,0在二次函数y=ax2+bx+3(a,b是常数,a≠0)的图像上.(1)当m=-1时,求a和b的值;(2)若二次函数的图像经过点A n,3且点A不在坐标轴上,当-2<m<-1时,求n的取值范围;(3)求证:b2+4a=0.3(2023·浙江嘉兴·统考中考真题)在二次函数y=x2-2tx+3(t>0)中,(1)若它的图象过点(2,1),则t的值为多少?(2)当0≤x≤3时,y的最小值为-2,求出t的值:(3)如果A(m-2,a),B(4,b),C(m,a)都在这个二次函数的图象上,且a<b<3,求m的取值范围.4(2023·浙江杭州·统考中考真题)设二次函数y=ax2+bx+1,(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:x⋯-10123⋯y⋯m1n1p⋯(1)若m=4,求二次函数的表达式;(2)写出一个符合条件的x的取值范围,使得y随x的增大而减小.(3)若在m、n、p这三个实数中,只有一个是正数,求a的取值范围.5(2023·湖南常德·统考中考真题)如图,二次函数的图象与x轴交于A-1,0,B5,0两点,与y轴交于点C,顶点为D.O为坐标原点,tan∠ACO=1 5.(1)求二次函数的表达式;(2)求四边形ACDB的面积;(3)P是抛物线上的一点,且在第一象限内,若∠ACO=∠PBC,求P点的坐标.6(2023·山东烟台·统考中考真题)如图,抛物线y=ax2+bx+5与x轴交于A,B两点,与y轴交于点C,AB=4.抛物线的对称轴x=3与经过点A的直线y=kx-1交于点D,与x轴交于点E.(1)求直线AD及抛物线的表达式;(2)在抛物线上是否存在点M,使得△ADM是以AD为直角边的直角三角形?若存在,求出所有点M的坐标;若不存在,请说明理由;(3)以点B为圆心,画半径为2的圆,点P为⊙B上一个动点,请求出PC+1PA的最小值.27(2023·江苏苏州·统考中考真题)如图,二次函数y=x2-6x+8的图像与x轴分别交于点A,B(点A 在点B的左侧),直线l是对称轴.点P在函数图像上,其横坐标大于4,连接PA,PB,过点P作PM⊥l,垂足为M,以点M为圆心,作半径为r的圆,PT与⊙M相切,切点为T.(1)求点A,B的坐标;(2)若以⊙M的切线长PT为边长的正方形的面积与△PAB的面积相等,且⊙M不经过点3,2,求PM长的取值范围.8(2023·山东东营·统考中考真题)如图,抛物线过点O0,0,矩形ABCD的边AB在线段,E10,0OE上(点B在点A的左侧),点C,D在抛物线上,设B t,0,当t=2时,BC=4.(1)求抛物线的函数表达式;(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形ABCD的面积时,求抛物线平移的距离.9(2023·内蒙古通辽·统考中考真题)在平面直角坐标系中,已知抛物线y=ax2+83x+c a≠0与x轴交于点A1,0和点B,与y轴交于点C0,-4.(1)求这条抛物线的函数解析式;(2)P是抛物线上一动点(不与点A,B,C重合),作PD⊥x轴,垂足为D,连接PC.①如图,若点P在第三象限,且tan∠CPD=2,求点P的坐标;②直线PD交直线BC于点E,当点E关于直线PC的对称点E 落在y轴上时,请直接写出四边形PECE 的周长.10(2023·四川自贡·统考中考真题)如图,抛物线y=-43x2+bx+4与x轴交于A(-3,0),B两点,与y轴交于点C.(1)求抛物线解析式及B,C两点坐标;(2)以A,B,C,D为顶点的四边形是平行四边形,求点D坐标;(3)该抛物线对称轴上是否存在点E,使得∠ACE=45°,若存在,求出点E的坐标;若不存在,请说明理由.11(2023·四川达州·统考中考真题)如图,抛物线y =ax 2+bx +c 过点A -1,0 ,B 3,0 ,C 0,3 .(1)求抛物线的解析式;(2)设点P 是直线BC 上方抛物线上一点,求出△PBC 的最大面积及此时点P 的坐标;(3)若点M 是抛物线对称轴上一动点,点N 为坐标平面内一点,是否存在以BC 为边,点B 、C 、M 、N 为顶点的四边形是菱形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.12(2023·四川泸州·统考中考真题)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+2x+c与坐标轴分别相交于点A,B,C0,6三点,其对称轴为x=2.(1)求该抛物线的解析式;(2)点F是该抛物线上位于第一象限的一个动点,直线AF分别与y轴,直线BC交于点D,E.①当CD=CE时,求CD的长;②若△CAD,△CDE,△CEF的面积分别为S1,S2,S3,且满足S1+S3=2S2,求点F的坐标.13(2023·全国·统考中考真题)如图,在平面直角坐标系中,抛物线y=-x2+2x+c经过点A(0,1).点P,Q在此抛物线上,其横坐标分别为m,2m(m>0),连接AP,AQ.(1)求此抛物线的解析式.(2)当点Q与此抛物线的顶点重合时,求m的值.(3)当∠PAQ的边与x轴平行时,求点P与点Q的纵坐标的差.(4)设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为h1,在点A与点Q之间部分(包括点A和点Q)的最高点与最低点的纵坐标的差为h2.当h2-h1=m时,直接写出m的值.14(2023·重庆·统考中考真题)如图,在平面直角坐标系中,抛物线y=14x2+bx+c与x轴交于点A,B,与y轴交于点C,其中B3,0,C0,-3.(1)求该抛物线的表达式;(2)点P是直线AC下方抛物线上一动点,过点P作PD⊥AC于点D,求PD的最大值及此时点P的坐标;(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F,Q为平移后的抛物线的对称轴上任意一点.写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.15(2023·四川凉山·统考中考真题)如图,已知抛物线与x轴交于A1,0两点,与y轴交于和B-5,0点C.直线y=-3x+3过抛物线的顶点P.(1)求抛物线的函数解析式;(2)若直线x=m-5<m<0与抛物线交于点E,与直线BC交于点F.①当EF取得最大值时,求m的值和EF的最大值;②当△EFC是等腰三角形时,求点E的坐标.16(2023·四川成都·统考中考真题)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+c经过点P (4,-3),与y轴交于点A(0,1),直线y=kx(k≠0)与抛物线交于B,C两点.(1)求抛物线的函数表达式;(2)若△ABP是以AB为腰的等腰三角形,求点B的坐标;(3)过点M(0,m)作y轴的垂线,交直线AB于点D,交直线AC于点E.试探究:是否存在常数m,使得OD⊥OE始终成立?若存在,求出m的值;若不存在,请说明理由.17(2023·安徽·统考中考真题)在平面直角坐标系中,点O是坐标原点,抛物线y=ax2+bx a≠0经过点A3,3,对称轴为直线x=2.(1)求a,b的值;(2)已知点B,C在抛物线上,点B的横坐标为t,点C的横坐标为t+1.过点B作x轴的垂线交直线OA于点D,过点C作x轴的垂线交直线OA于点E.(ⅰ)当0<t<2时,求△OBD与△ACE的面积之和;(ⅱ)在抛物线对称轴右侧,是否存在点B,使得以B,C,D,E为顶点的四边形的面积为32若存在,请求出点B的横坐标t的值;若不存在,请说明理由.18(2023·浙江金华·统考中考真题)如图,直线y =52x +5与x 轴,y 轴分别交于点A ,B ,抛物线的顶点P 在直线AB 上,与x 轴的交点为C ,D ,其中点C 的坐标为2,0 .直线BC 与直线PD 相交于点E .(1)如图2,若抛物线经过原点O .①求该抛物线的函数表达式;②求BEEC的值.(2)连接PC ,∠CPE 与∠BAO 能否相等?若能,求符合条件的点P 的横坐标;若不能,试说明理由.19(2023·湖南·统考中考真题)如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于C点,其中B1,0.,C0,3(1)求这个二次函数的表达式;(2)在二次函数图象上是否存在点P,使得S△PAC=S△ABC若存在,请求出P点坐标;若不存在,请说明理由;(3)点Q是对称轴l上一点,且点Q的纵坐标为a,当△QAC是锐角三角形时,求a的取值范围.20(2023·四川遂宁·统考中考真题)在平面直角坐标系中,O 为坐标原点,抛物线y =14x 2+bx +c 经过点O (0,0),对称轴过点B (2,0),直线l 过点C 2,-2 ,且垂直于y 轴.过点B 的直线l 1交抛物线于点M 、N ,交直线l 于点Q ,其中点M 、Q 在抛物线对称轴的左侧.(1)求抛物线的解析式;(2)如图1,当BM :MQ =3:5时,求点N 的坐标;(3)如图2,当点Q 恰好在y 轴上时,P 为直线l 1下方的抛物线上一动点,连接PQ 、PO ,其中PO 交l 1于点E ,设△OQE 的面积为S 1,△PQE 的面积为S 2.求S2S 1的最大值.21(2023·四川眉山·统考中考真题)在平面直角坐标系中,已知抛物线y =ax 2+bx +c 与x 轴交于点A -3,0 ,B 1,0 两点,与y 轴交于点C 0,3 ,点P 是抛物线上的一个动点.(1)求抛物线的表达式;(2)当点P 在直线AC 上方的抛物线上时,连接BP 交AC 于点D .如图1.当PDDB的值最大时,求点P 的坐标及PDDB的最大值;(3)过点P 作x 轴的垂线交直线AC 于点M ,连接PC ,将△PCM 沿直线PC 翻折,当点M 的对应点M '恰好落在y 轴上时,请直接写出此时点M 的坐标.22(2023·江西·统考中考真题)综合与实践问题提出:某兴趣小组开展综合实践活动:在Rt△ABC中,∠C=90°,D为AC上一点,CD=2,动点P 以每秒1个单位的速度从C点出发,在三角形边上沿C→B→A匀速运动,到达点A时停止,以DP为边作正方形DPEF设点P的运动时间为ts,正方形DPEF的而积为S,探究S与t的关系(1)初步感知:如图1,当点P由点C运动到点B时,①当t=1时,S=.②S关于t的函数解析式为.(2)当点P由点B运动到点A时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象请根据图象信息,求S关于t的函数解析式及线段AB的长.(3)延伸探究:若存在3个时刻t1,t2,t3(t1<t2<t3)对应的正方形DPEF的面积均相等.①t1+t2=;②当t3=4t1时,求正方形DPEF的面积.23(2023·新疆·统考中考真题)【建立模型】(1)如图1,点B 是线段CD 上的一点,AC ⊥BC ,AB ⊥BE ,ED ⊥BD ,垂足分别为C ,B ,D ,AB =BE .求证:△ACB ≌△BDE ;【类比迁移】(2)如图2,一次函数y =3x +3的图象与y 轴交于点A 、与x 轴交于点B ,将线段AB 绕点B 逆时针旋转90°得到BC 、直线AC 交x 轴于点D .①求点C 的坐标;②求直线AC 的解析式;【拓展延伸】(3)如图3,抛物线y =x 2-3x -4与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于C点,已知点Q (0,-1),连接BQ .抛物线上是否存在点M ,使得tan ∠MBQ =13,若存在,求出点M 的横坐标.24(2023·甘肃武威·统考中考真题)如图1,抛物线y=-x2+bx与x轴交于点A,与直线y=-x交于点B4,-4在y轴上.点P从点B出发,沿线段BO方向匀速运动,运动到点O时停止.,点C0,-4(1)求抛物线y=-x2+bx的表达式;(2)当BP=22时,请在图1中过点P作PD⊥OA交抛物线于点D,连接PC,OD,判断四边形OCPD 的形状,并说明理由.(3)如图2,点P从点B开始运动时,点Q从点O同时出发,以与点P相同的速度沿x轴正方向匀速运动,点P停止运动时点Q也停止运动.连接BQ,PC,求CP+BQ的最小值.25(2023·四川乐山·统考中考真题)已知x 1,y 1 ,x 2,y 2 是抛物C 1:y =-14x 2+bx (b 为常数)上的两点,当x 1+x 2=0时,总有y 1=y 2(1)求b 的值;(2)将抛物线C 1平移后得到抛物线C 2:y =-14(x -m )2+1(m >0).探究下列问题:①若抛物线C 1与抛物线C 2有一个交点,求m 的取值范围;②设抛物线C 2与x 轴交于A ,B 两点,与y 轴交于点C ,抛物线C 2的顶点为点E ,△ABC 外接圆的圆心为点F ,如果对抛物线C 1上的任意一点P ,在抛物线C 2上总存在一点Q ,使得点P 、Q 的纵坐标相等.求EF 长的取值范围.26(2023·内蒙古·统考中考真题)如图,在平面直角坐标系中,抛物线y =-x 2+3x +1交y 轴于点A ,直线y =-13x +2交抛物线于B ,C 两点(点B 在点C 的左侧),交y 轴于点D ,交x 轴于点E .(1)求点D ,E ,C 的坐标;(2)F 是线段OE 上一点OF <EF ,连接AF ,DF ,CF ,且AF 2+EF 2=21.①求证:△DFC 是直角三角形;②∠DFC 的平分线FK 交线段DC 于点K ,P 是直线BC 上方抛物线上一动点,当3tan ∠PFK =1时,求点P 的坐标.27(2023·上海·统考中考真题)在平面直角坐标系xOy中,已知直线y=34x+6与x轴交于点A,y轴交于点B,点C在线段AB上,以点C为顶点的抛物线M:y=ax2+bx+c经过点B.(1)求点A,B的坐标;(2)求b,c的值;(3)平移抛物线M至N,点C,B分别平移至点P,D,联结CD,且CD∥x轴,如果点P在x轴上,且新抛物线过点B,求抛物线N的函数解析式.28(2023·江苏扬州·统考中考真题)在平面直角坐标系xOy中,已知点A在y轴正半轴上.(1)如果四个点0,0中恰有三个点在二次函数y=ax2(a为常数,且a≠0)的图象、-1,1、1,1、0,2上.①a=;②如图1,已知菱形ABCD的顶点B、C、D在该二次函数的图象上,且AD⊥y轴,求菱形的边长;③如图2,已知正方形ABCD的顶点B、D在该二次函数的图象上,点B、D在y轴的同侧,且点B在点D的左侧,设点B、D的横坐标分别为m、n,试探究n-m是否为定值.如果是,求出这个值;如果不是,请说明理由.(2)已知正方形ABCD的顶点B、D在二次函数y=ax2(a为常数,且a>0)的图象上,点B在点D的左侧,设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式.29(2023·湖南岳阳·统考中考真题)已知抛物线Q1:y=-x2+bx+c与x轴交于A-3,0,B两点,交y 轴于点C0,3.(1)请求出抛物线Q1的表达式.(2)如图1,在y轴上有一点D0,-1,点E在抛物线Q1上,点F为坐标平面内一点,是否存在点E,F使得四边形DAEF为正方形?若存在,请求出点E,F的坐标;若不存在,请说明理由.(3)如图2,将抛物线Q1向右平移2个单位,得到抛物线Q2,抛物线Q2的顶点为K,与x轴正半轴交于点H,抛物线Q1上是否存在点P,使得∠CPK=∠CHK?若存在,请求出点P的坐标;若不存在,请说明理由.30(2023·湖南永州·统考中考真题)如图1,抛物线y =ax 2+bx +c (a ,b ,c 为常数)经过点F 0,5 ,顶点坐标为2,9 ,点P x 1,y 1 为抛物线上的动点,PH ⊥x 轴于H ,且x 1≥52.(1)求抛物线的表达式;(2)如图1,直线OP :y =y 1x 1x 交BF 于点G ,求S △BPG S △BOG的最大值;(3)如图2,四边形OBMF 为正方形,PA 交y 轴于点E ,BC 交FM 的延长线于C ,且BC ⊥BE ,PH =FC ,求点P 的横坐标.31(2023·山东枣庄·统考中考真题)如图,抛物线y=-x2+bx+c经过A(-1,0),C(0,3)两点,并交x轴于另一点B,点M是抛物线的顶点,直线AM与轴交于点D.(1)求该抛物线的表达式;(2)若点H是x轴上一动点,分别连接MH,DH,求MH+DH的最小值;(3)若点P是抛物线上一动点,问在对称轴上是否存在点Q,使得以D,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.32(2023·湖北随州·统考中考真题)如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥x轴交直线BC 于点M,交x轴于点N.(1)直接写出抛物线和直线BC的解析式;(2)如图2,连接OM,当△OCM为等腰三角形时,求m的值;(3)当P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应),若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.33(2023·四川内江·统考中考真题)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 与x 轴交于B 4,0 ,C -2,0 两点.与y 轴交于点A 0,-2 .(1)求该抛物线的函数表达式;(2)若点P 是直线AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点K ,过点P 作y 轴的平行线交x 轴于点D ,求与12PK +PD 的最大值及此时点P 的坐标;(3)在抛物线的对称轴上是否存在一点M ,使得△MAB 是以AB 为一条直角边的直角三角形:若存在,请求出点M 的坐标,若不存在,请说明理由.34(2023·湖南·统考中考真题)已知二次函数y =ax 2+bx +c a >0 .(1)若a =1,c =-1,且该二次函数的图像过点2,0 ,求b 的值;(2)如图所示,在平面直角坐标系Oxy 中,该二次函数的图像与x 轴交于点A x 1,0 ,B x 2,0 ,且x 1<0<x 2,点D 在⊙O 上且在第二象限内,点E 在x 轴正半轴上,连接DE ,且线段DE 交y 轴正半轴于点F ,∠DOF =∠DEO ,OF =32DF .①求证:DO EO=23.②当点E 在线段OB 上,且BE =1.⊙O 的半径长为线段OA 的长度的2倍,若4ac =-a 2-b 2,求2a +b 的值.35(2023·山西·统考中考真题)如图,二次函数y =-x 2+4x 的图象与x 轴的正半轴交于点A ,经过点A 的直线与该函数图象交于点B 1,3 ,与y 轴交于点C .(1)求直线AB 的函数表达式及点C 的坐标;(2)点P 是第一象限内二次函数图象上的一个动点,过点P 作直线PE ⊥x 轴于点E ,与直线AB 交于点D ,设点P 的横坐标为m .①当PD =12OC 时,求m 的值;②当点P 在直线AB 上方时,连接OP ,过点B 作BQ ⊥x 轴于点Q ,BQ 与OP 交于点F ,连接DF .设四边形FQED 的面积为S ,求S 关于m 的函数表达式,并求出S 的最大值.36(2023·湖北武汉·统考中考真题)抛物线C1:y=x2-2x-8交x轴于A,B两点(A在B的左边),交y 轴于点C.(1)直接写出A,B,C三点的坐标;(2)如图(1),作直线x=t0<t<4,分别交x轴,线段BC,抛物线C1于D,E,F三点,连接CF.若△BDE 与△CEF相似,求t的值;(3)如图(2),将抛物线C1平移得到抛物线C2,其顶点为原点.直线y=2x与抛物线C2交于O,G两点,过OG的中点H作直线MN(异于直线OG)交抛物线C2于M,N两点,直线MO与直线GN交于点P.问点P是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.37(2023·湖北宜昌·统考中考真题)如图,已知A(0,2),B(2,0).点E位于第二象限且在直线y=-2x 上,∠EOD=90°,OD=OE,连接AB,DE,AE,DB.(1)直接判断△AOB的形状:△AOB是三角形;(2)求证:△AOE≌△BOD;(3)直线EA交x轴于点C(t,0),t>2.将经过B,C两点的抛物线y1=ax2+bx-4向左平移2个单位,得到抛物线y2.①若直线EA与抛物线y1有唯一交点,求t的值;②若抛物线y2的顶点P在直线EA上,求t的值;③将抛物线y2再向下平移,2(t-1)2个单位,得到抛物线y3.若点D在抛物线y3上,求点D的坐标.38(2023·湖南郴州·统考中考真题)已知抛物线y=ax2+bx+4与x轴相交于点A1,0,与y,B4,0轴相交于点C.(1)求抛物线的表达式;(2)如图1,点P是抛物线的对称轴l上的一个动点,当△PAC的周长最小时,求PAPC的值;(3)如图2,取线段OC的中点D,在抛物线上是否存在点Q,使tan∠QDB=12若存在,求出点Q的坐标;若不存在,请说明理由.39(2023·湖北黄冈·统考中考真题)已知抛物线y =-12x 2+bx +c 与x 轴交于A ,B (4,0)两点,与y 轴交于点C (0,2),点P 为第一象限抛物线上的点,连接CA ,CB ,PB ,PC .(1)直接写出结果;b =,c =,点A 的坐标为,tan ∠ABC =;(2)如图1,当∠PCB =2∠OCA 时,求点P 的坐标;(3)如图2,点D 在y 轴负半轴上,OD =OB ,点Q 为抛物线上一点,∠QBD =90°,点E ,F 分别为△BDQ 的边DQ ,DB 上的动点,QE =DF ,记BE +QF 的最小值为m .①求m 的值;②设△PCB 的面积为S ,若S =14m 2-k ,请直接写出k 的取值范围.40(2023·湖南·统考中考真题)如图,在平面直角坐标系中,抛物线y=ax2+x+c经过点A-2,0和点B4,0,且与直线l:y=-x-1交于D、E两点(点D在点E的右侧),点M为直线l上的一动点,设点M 的横坐标为t.(1)求抛物线的解析式.(2)过点M作x轴的垂线,与拋物线交于点N.若0<t<4,求△NED面积的最大值.(3)抛物线与y轴交于点C,点R为平面直角坐标系上一点,若以B、C、M、R为顶点的四边形是菱形,请求出所有满足条件的点R的坐标.41(2023·四川·统考中考真题)如图1,在平面直角坐标系中,已知二次函数y=ax2+bx+4的图象与x 轴交于点A-2,0,B4,0,与y轴交于点C.(1)求抛物线的解析式;(2)已知E为抛物线上一点,F为抛物线对称轴l上一点,以B,E,F为顶点的三角形是等腰直角三角形,且∠BFE=90°,求出点F的坐标;(3)如图2,P为第一象限内抛物线上一点,连接AP交y轴于点M,连接BP并延长交y轴于点N,在点P运动过程中,OM+12ON是否为定值?若是,求出这个定值;若不是,请说明理由.42(2023·山东聊城·统考中考真题)如图①,抛物线y=ax2+bx-9与x轴交于点A-3,0,,B6,0与y轴交于点C,连接AC,BC.点P是x轴上任意一点.(1)求抛物线的表达式;(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;(3)如图②,当点P m,0从点A出发沿x轴向点B运动时(点P与点A,B不重合),自点P分别作PE∥BC,交AC于点E,作PD⊥BC,垂足为点D.当m为何值时,△PED面积最大,并求出最大值.43(2023·湖北荆州·统考中考真题)已知:y关于x的函数y=a-2x+b.x2+a+1(1)若函数的图象与坐标轴有两个公共点,且a=4b,则a的值是;(2)如图,若函数的图象为抛物线,与x轴有两个公共点A-2,0,B4,0,并与动直线l:x=m(0<m<4)交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为S1,△CDE 的面积为S2.①当点P为抛物线顶点时,求△PBC的面积;②探究直线l在运动过程中,S1-S2是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.44(2023·福建·统考中考真题)已知抛物线y=ax2+bx+3交x轴于A1,0,B3,0两点,M为抛物线的顶点,C,D为抛物线上不与A,B重合的相异两点,记AB中点为E,直线AD,BC的交点为P.(1)求抛物线的函数表达式;(2)若C4,3,D m,-3 4,且m<2,求证:C,D,E三点共线;(3)小明研究发现:无论C,D在抛物线上如何运动,只要C,D,E三点共线,△AMP,△MEP,△ABP中必存在面积为定值的三角形.请直接写出其中面积为定值的三角形及其面积,不必说明理由.45(2023·山东·统考中考真题)如图,直线y=-x+4交x轴于点B,交y轴于点C,对称轴为x=32的抛物线经过B,C两点,交x轴负半轴于点A.P为抛物线上一动点,点P的横坐标为m,过点P作x轴的平行线交抛物线于另一点M,作x轴的垂线PN,垂足为N,直线MN交y轴于点D.(1)求抛物线的解析式;(2)若0<m<32,当m为何值时,四边形CDNP是平行四边形?(3)若m<32,设直线MN交直线BC于点E,是否存在这样的m值,使MN=2ME?若存在,求出此时m 的值;若不存在,请说明理由.46(2023·山东·统考中考真题)已知抛物线y =-x 2+bx +c 与x 轴交于A ,B 两点,与y 轴交于点C 0,4 ,其对称轴为x =-32.(1)求抛物线的表达式;(2)如图1,点D 是线段OC 上的一动点,连接AD ,BD ,将△ABD 沿直线AD 翻折,得到△AB D ,当点B 恰好落在抛物线的对称轴上时,求点D 的坐标;(3)如图2,动点P 在直线AC 上方的抛物线上,过点P 作直线AC 的垂线,分别交直线AC ,线段BC 于点E ,F ,过点F 作FG ⊥x 轴,垂足为G ,求FG +2FP 的最大值.47(2023·辽宁大连·统考中考真题)如图,在平面直角坐标系中,抛物线C 1:y =x 2上有两点A 、B ,其中点A 的横坐标为-2,点B 的横坐标为1,抛物线C 2:y =-x 2+bx +c 过点A 、B .过A 作AC ∥x 轴交抛物线C 1另一点为点C .以AC 、12AC 长为边向上构造矩形ACDE .(1)求抛物线C 2的解析式;(2)将矩形ACDE 向左平移m 个单位,向下平移n 个单位得到矩形A C D E ,点C 的对应点C 落在抛物线C 1上.①求n 关于m 的函数关系式,并直接写出自变量m 的取值范围;②直线A E 交抛物线C 1于点P ,交抛物线C 2于点Q .当点E 为线段PQ 的中点时,求m 的值;③抛物线C 2与边E D 、A C 分别相交于点M 、N ,点M 、N 在抛物线C 2的对称轴同侧,当MN =2103时,求点C 的坐标.48(2023·湖南张家界·统考中考真题)如图,在平面直角坐标系中,已知二次函数y=ax2+bx+c的图象与x轴交于点A-2,0.点D为线段BC上的一动点. 和点B6,0两点,与y轴交于点C0,6(1)求二次函数的表达式;(2)如图1,求△AOD周长的最小值;(3)如图2,过动点D作DP∥AC交抛物线第一象限部分于点P,连接PA,PB,记△PAD与△PBD的面积和为S,当S取得最大值时,求点P的坐标,并求出此时S的最大值.49(2023·黑龙江绥化·统考中考真题)如图,抛物线y1=ax2+bx+c的图象经过A(-6,0),B(-2,0),C (0,6)三点,且一次函数y=kx+6的图象经过点B.(1)求抛物线和一次函数的解析式.(2)点E,F为平面内两点,若以E、F、B、C为顶点的四边形是正方形,且点E在点F的左侧.这样的E,F两点是否存在?如果存在,请直接写出所有满足条件的点E的坐标:如果不存在,请说明理由.(3)将抛物线y1=ax2+bx+c的图象向右平移8个单位长度得到抛物线y2,此抛物线的图象与x轴交于M,N两点(M点在N点左侧).点P是抛物线y2上的一个动点且在直线NC下方.已知点P的横坐标为PD有最大值,最大值是多少?m.过点P作PD⊥NC于点D.求m为何值时,CD+1250(2023·四川南充·统考中考真题)如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于A-1,0,B3,0两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)如图2,抛物线顶点为D,对称轴与x轴交于点E,过点K1,3的直线(直线KD除外)与抛物线交于G,H两点,直线DG,DH分别交x轴于点M,N.试探究EM⋅EN是否为定值,若是,求出该定值;若不是,说明理由.51(2023·四川宜宾·统考中考真题)如图,抛物线y=ax2+bx+c与x轴交于点A-4,0,且经、B2,0过点C-2,6.(1)求抛物线的表达式;(2)在x轴上方的抛物线上任取一点N,射线AN、BN分别与抛物线的对称轴交于点P、Q,点Q关于x轴的对称点为Q ,求△APQ 的面积;(3)点M是y轴上一动点,当∠AMC最大时,求M的坐标.52(2023·四川广安·统考中考真题)如图,二次函数y=x2+bx+c的图象交x轴于点A,B,交y轴于点C,点B的坐标为1,0,对称轴是直线x=-1,点P是x轴上一动点,PM⊥x轴,交直线AC于点M,交抛物线于点N.(1)求这个二次函数的解析式.(2)若点P在线段AO上运动(点P与点A、点O不重合),求四边形ABCN面积的最大值,并求出此时点P 的坐标.(3)若点P在x轴上运动,则在y轴上是否存在点Q,使以M、N、C、Q为顶点的四边形是菱形?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.。
中考二次函数压轴题(共23道题目)

中考二次函数压轴题(共23道题目)一.选择题(共10小题)1.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b <0,b2+8a>4ac,a<﹣1,其中结论正确的有()A.1个 B.2个 C.3个 D.4个2.如图是某二次函数的图象,将其向左平移2个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有()(1)a>0;(2)c<0;(3)2a﹣b=0;(4)a+b+c>0.A.1个 B.2个 C.3个 D.4个3.已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c >0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0;其中正确的个数为()A.1个 B.2个 C.3个 D.4个4.已知点(x1,y1)、(x2,y2)、(x3,y3)都在抛物线y=x2+bx上,x1、x2、x3为△ABC的三边,且x1<x2<x3,若对所有的正整数x1、x2、x3都满足y1<y2<y3,则b的取值范围是()A.b>﹣2 B.b>﹣3 C.b>﹣4 D.b>﹣55.如图,点A(m,n)是一次函数y=2x的图象上的任意一点,AB垂直于x轴,垂足为B,那么三角形ABO的面积S关于m的函数关系的图象大致为()A.B.CD.6.抛物线y=ax2+bx+c的图象经过原点和第一、二、三象限,那么下列结论成立的是()A.a>0,b>0,c=0 B.a>0,b<0,c=0 C.a<0,b>0,c=0 D.a<0,b<0,c=07.已知抛物线y=x2﹣(4m+1)x+2m﹣1与x轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y轴的交点在点(0,)的下方,那么m的取值范围是()A.B.C.D.全体实数8.函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A.B.C.D.9.已知抛物线y=x2+bx+c(c<0)经过点(c,0),以该抛物线与坐标轴的三个交点为顶点的三角形面积为S,则S可表示为()A.|2+b||b+1|B.c(1﹣c) C.(b+1)2D.10.下列关于函数y=(m2﹣1)x2﹣(3m﹣1)x+2的图象与坐标轴的公共点情况:①当m≠3时,有三个公共点;②m=3时,只有两个公共点;③若只有两个公共点,则m=3;④若有三个公共点,则m≠3.其中描述正确的有()个.A.一个B.两个C.三个D.四个二.填空题(共10小题)11.已知:如图,过原点的抛物线的顶点为M(﹣2,4),与x轴负半轴交于点A,对称轴与x轴交于点B,点P是抛物线上一个动点,过点P作PQ⊥MA于点Q.(1)抛物线解析式为.(2)若△MPQ与△MAB相似,则满足条件的点P的坐标为.12.将抛物线y=x2﹣2向左平移3个单位,所得抛物线的函数表达式为.13.如图所示,将矩形OABC沿AE折叠,使点O恰好落在BC上F处,以CF为边作正方形CFGH,延长BC至M,使CM=|CE﹣EO|,再以CM、CO为边作矩形CMNO.令m=,则m=;又若CO=1,CE=,Q为AE上一点且QF=,抛物线y=mx2+bx+c经过C、Q两点,则抛物线与边AB的交点坐标是.15.在平面直角坐标系中,点A、B、C的坐标分别为(0,1)、(4,2)、(2,6).如果P(x,y)是△ABC围成的区域(含边界)上的点,那么当w=xy取得最大值时,点P的坐标是.16.如图为二次函数y=ax2+bx+c的图象,在下列结论中:①ac>0;②方程ax2+bx+c=0的根是x1=﹣1,x2=5;③a+b+c<0;④当x<2时,y随着x的增大而增大.正确的结论有(请写出所有正确结论的序号).17.已知当x1=a,x2=b,x3=c时,二次函数y=x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是.18.如图,已知一动圆的圆心P在抛物线y=x2﹣3x+3上运动.若⊙P半径为1,点P的坐标为(m,n),当⊙P与x轴相交时,点P的横坐标m的取值范围是.19.如图,四边形ABCD是矩形,A、B两点在x轴的正半轴上,C、D两点在抛物线y=﹣x2+6x上.设OA=m(0<m<3),矩形ABCD的周长为l,则l与m的函数解析式为.20.若二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1),(﹣1,0),则y=a+b+c的取值范围是.三.解答题(共4小题)21.已知抛物线y=ax2﹣2x+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C,对称轴为x=1,顶点为E,直线y=﹣x+1交y轴于点D.(1)求抛物线的解析式;(2)求证:△BCE∽△BOD;(3)点P是抛物线上的一个动点,当点P运动到什么位置时,△BDP的面积等于△BOE的面积?22.如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.23.已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.(1)求抛物线的函数表达式;(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC 于点Q.①当x取何值时,线段PQ的长度取得最大值,其最大值是多少?②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.24.如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线的函数解析式;(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l 于点H,连结OP,试求△OPH的面积;②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.二次函数压轴题(共24道题目)参考答案与试题解析一.选择题(共10小题)1.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b <0,b2+8a>4ac,a<﹣1,其中结论正确的有()A.1个 B.2个 C.3个 D.4个【分析】由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.【解答】解:由抛物线的开口向下知a<0,与y轴的交点为在y轴的正半轴上,得c>0,对称轴为x=<1,∵a<0,∴2a+b<0,而抛物线与x轴有两个交点,∴b2﹣4ac>0,当x=2时,y=4a+2b+c<0,当x=1时,a+b+c=2.∵>2,∴4ac﹣b2<8a,∴b2+8a>4ac,∵①a+b+c=2,则2a+2b+2c=4,②4a+2b+c<0,③a﹣b+c<0.由①,③得到2a+2c<2,由①,②得到2a﹣c<﹣4,4a﹣2c<﹣8,上面两个相加得到6a<﹣6,∴a<﹣1.故选:D.2.如图是某二次函数的图象,将其向左平移2个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有()(1)a>0;(2)c<0;(3)2a﹣b=0;(4)a+b+c>0.A.1个 B.2个 C.3个 D.4个【分析】如图是y=ax2+bx+c的图象,根据开口方向向上知道a>0,又由与y轴的交点为在y轴的负半轴上得到c<0,由对称轴x==﹣1,可以得到2a﹣b=0,又当x=1时,可以判断a+b+c的值.由此可以判定所有结论正确与否.【解答】解:(1)∵将其向左平移2个单位后的图象的函数解析式为y=ax2+bx+c (a≠0)(如虚线部分),∴y=ax2+bx+c的对称轴为:直线x=﹣1;∵开口方向向上,∴a>0,故①正确;(2)∵与y轴的交点为在y轴的负半轴上∴c<0,故②正确;(3)∵对称轴x==﹣1,∴2a﹣b=0,故③正确;(4)当x=1时,y=a+b+c>0,故④正确.故选:D.3.已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c >0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0;其中正确的个数为()A.1个 B.2个 C.3个 D.4个【分析】由抛物线开口向上得到a大于0,再由对称轴在y轴右侧得到a与b异号,即b小于0,由抛物线与y轴交于正半轴,得到c大于0,可得出abc的符合,对于(3)作出判断;由x=1时对应的函数值小于0,将x=1代入二次函数解析式得到a+b+c小于0,(1)错误;根据对称轴在1和2之间,利用对称轴公式列出不等式,由a大于0,得到﹣2a小于0,在不等式两边同时乘以﹣2a,不等号方向改变,可得出不等式,对(2)作出判断;由x=﹣1时对应的函数值大于0,将x=﹣1代入二次函数解析式得到a﹣b+c大于0,又4a大于0,c大于0,可得出a﹣b+c+4a+c大于0,合并后得到(4)正确,综上,即可得到正确的个数.【解答】解:由图形可知:抛物线开口向上,与y轴交点在正半轴,∴a>0,b<0,c>0,即abc<0,故(3)错误;又x=1时,对应的函数值小于0,故将x=1代入得:a+b+c<0,故(1)错误;∵对称轴在1和2之间,∴1<﹣<2,又a>0,∴在不等式左右两边都乘以﹣2a得:﹣2a>b>﹣4a,故(2)正确;又x=﹣1时,对应的函数值大于0,故将x=﹣1代入得:a﹣b+c>0,又a>0,即4a>0,c>0,∴5a﹣b+2c=(a﹣b+c)+4a+c>0,故(4)错误,综上,正确的有1个,为选项(2).故选:A.4.已知点(x1,y1)、(x2,y2)、(x3,y3)都在抛物线y=x2+bx上,x1、x2、x3为△ABC的三边,且x1<x2<x3,若对所有的正整数x1、x2、x3都满足y1<y2<y3,则b的取值范围是()A.b>﹣2 B.b>﹣3 C.b>﹣4 D.b>﹣5【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,结合已知条件,可知x1、x2、x3的最小一组值是2、3、4;根据抛物线,知它与x轴的交点是(0,0)和(﹣b,0),对称轴是x=﹣.因此要满足已知条件,则其对称轴应小于2.5.【解答】解:∵x1、x2、x3为△ABC的三边,且x1<x2<x3,∴x1、x2、x3的最小一组值是2、3、4.∵抛物线y=x2+bx与x轴的交点是(0,0)和(﹣b,0),对称轴是x=﹣,∴若对所有的正整数x1、x2、x3都满足y1<y2<y3,则﹣<2.5解,得b>﹣5.故选:D.5.如图,点A(m,n)是一次函数y=2x的图象上的任意一点,AB垂直于x轴,垂足为B,那么三角形ABO的面积S关于m的函数关系的图象大致为()A.B.C.D.【分析】因为A(m,n)是一次函数y=2x的图象上的任意一点,所以n=2m.根据三角形面积公式即可得出S与m之间的函数关系,根据关系式即可解答.【解答】解:由题意可列该函数关系式:S=|m|•2|m|=m2,因为点A(m,n)是一次函数y=2x的图象上的任意一点,所以点A(m,n)在第一或三象限,又因为S>0,所以取第一、二象限内的部分.故选:D.6.抛物线y=ax2+bx+c的图象经过原点和第一、二、三象限,那么下列结论成立的是()A.a>0,b>0,c=0 B.a>0,b<0,c=0 C.a<0,b>0,c=0 D.a<0,b<0,c=0【分析】先根据图象经过象限的情况判断出a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理.【解答】解:∵抛物线经过原点,∴c=0,∵抛物线经过第一,二,三象限,可推测出抛物线开口向上,对称轴在y轴左侧∴a>0,∵对称轴在y轴左侧,∴对称轴为x=<0,又因为a>0,∴b>0.故选:A.7.已知抛物线y=x2﹣(4m+1)x+2m﹣1与x轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y轴的交点在点(0,)的下方,那么m的取值范围是()A.B.C.D.全体实数【分析】因为抛物线y=x2﹣(4m+1)x+2m﹣1与x轴有一个交点的横坐标大于2,另一个交点的横坐标小于2,且抛物线开口向上,所以令f(x)=x2﹣(4m+1)x+2m﹣1,则f(2)<0,解不等式可得m>,又因为抛物线与y轴的交点在点(0,)的下方,所以f(0)<﹣,解得m<,即可得解.【解答】解:根据题意,令f(x)=x2﹣(4m+1)x+2m﹣1,∵抛物线y=x2﹣(4m+1)x+2m﹣1与x轴有一个交点的横坐标大于2,另一个交点的横坐标小于2,且抛物线开口向上,∴f(2)<0,即4﹣2(4m+1)+2m﹣1<0,解得:m>,又∵抛物线与y轴的交点在点(0,)的下方,∴f(0)<﹣,解得:m<,综上可得:<m<,故选:A.8.函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A.B.C.D.【分析】本题可先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.【解答】解:由解析式y=﹣kx2+k可得:抛物线对称轴x=0;A、由双曲线的两支分别位于二、四象限,可得k<0,则﹣k>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上;本图象与k的取值相矛盾,故A错误;B、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象符合题意,故B正确;C、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故C错误;D、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故D错误.故选:B.9.已知抛物线y=x2+bx+c(c<0)经过点(c,0),以该抛物线与坐标轴的三个交点为顶点的三角形面积为S,则S可表示为()A.|2+b||b+1|B.c(1﹣c) C.(b+1)2D.【分析】把点(c,0)代入抛物线中,可得b、c的关系式,再设抛物线与x轴的交点分别为x1、x2,则x1、x2满足x2+bx+c=0,根据根的判别式结合两点间的距离公式可求|x1﹣x2|,那么就可得到以该抛物线与坐标轴的三个交点为顶点的三角形面积.【解答】解:∵抛物线y=x2+bx+c(c<0)经过点(c,0),∴c2+bc+c=0;∴c(c+b+1)=0;∵c<0,∴c=﹣b﹣1;设x1,x2是一元二次方程x2+bx+c=0的两根,∴x1+x2=﹣b,x1•x2=c=﹣b﹣1,∴抛物线与x轴的交点间的距离为|x1﹣x2|=====|2+b|,∴S可表示为|2+b||b+1|.故选:A.10.下列关于函数y=(m2﹣1)x2﹣(3m﹣1)x+2的图象与坐标轴的公共点情况:①当m≠3时,有三个公共点;②m=3时,只有两个公共点;③若只有两个公共点,则m=3;④若有三个公共点,则m≠3.其中描述正确的有()个.A.一个B.两个C.三个D.四个【分析】令y=0,可得出(m2﹣1)x2﹣(3m﹣1)x+2=0,得出判别式的表达式,然后根据m的取值进行判断,另外要注意m的取值决定函数是一次函数还是二次函数,不要忘了考虑一次函数的情况.【解答】解:令y=0,可得出(m2﹣1)x2﹣(3m﹣1)x+2=0,△=(3m﹣1)2﹣8(m2﹣1)=(m﹣3)2,①当m≠3,m=±1时,函数是一次函数,与坐标轴有两个交点,故错误;②当m=3时,△=0,与x轴有一个公共点,与y轴有一个公共点,总共两个,故正确;③若只有两个公共点,m=3或m=±1,故错误;④若有三个公共点,则m≠3且m≠±1,故错误;综上可得只有②正确,共个.故选:A.二.填空题(共10小题)11.已知:如图,过原点的抛物线的顶点为M(﹣2,4),与x轴负半轴交于点A,对称轴与x轴交于点B,点P是抛物线上一个动点,过点P作PQ⊥MA于点Q.(1)抛物线解析式为y=﹣x2﹣4x.(2)若△MPQ与△MAB相似,则满足条件的点P的坐标为(﹣,)、(﹣,).【分析】(1)设抛物线的解析式为:y=a(x+2)2+4,因为抛物线过原点,把(0,0)代入,求出a即可.(2)由于PQ⊥MA,即∠MQP=∠MBA=90°;所以只要满足∠PMQ=∠MAB或∠PMQ=∠AMB.①∠PMQ=∠AMB时,先找出点B关于直线MA的对称点(设为点C),显然有AC=AB=2、MC=MB=4,可根据该条件得到点C的坐标,进而求出直线MC(即直线MP)的解析式,联立抛物线的解析式即可得到点P的坐标;②∠PMQ=∠MAB时,若设直线MP与x轴的交点为D,那么△MAD必为等腰三角形,即MD=AD,根据此条件先求出点D的坐标,进而得出直线MP的解析式,联立抛物线的解析式即可得解.【解答】解:(1)∵过原点的抛物线的顶点为M(﹣2,4),∴设抛物线的解析式为:y=a(x+2)2+4,将x=0,y=0代入可得:4a+4=0,解得:a=﹣1,∴抛物线解析式为:y=﹣(x+2)2+4,即y=﹣x2﹣4x;(2)∵PQ⊥MA∴∠MQP=∠MBA=90°;若△MPQ、△MAB相似,那么需满足下面的其中一种情况:①∠PMQ=∠AMB,此时MA为∠PMB的角平分线,如图①;取点B关于直线MA的对称点C,则AC=AB=2,MC=MB=4,设点C(x,y),有:,解得(舍),∴点C的坐标为(﹣,);设直线MP的解析式:y=kx+b,代入M(﹣2,4)、(﹣,)得:,解得∴直线MP:y=x+联立抛物线的解析式,有:,解得,∴点P的坐标(﹣,);②∠PMQ=∠MAB,如右图②,此时△MAD为等腰三角形,且MD=AD,若设点D (x,0),则有:(x+4)2=(x+2)2+(0﹣4)2,解得:x=1∴点D(1,0);设直线MP的解析式:y=kx+b,代入M(﹣2,4)、D(1,0)后,有:,解得:∴直线MP:y=﹣x+联立抛物线的解析式有:,解得:,∴点P的坐标(﹣,)综上,符合条件的P点有两个,且坐标为(﹣,)、(﹣,).故答案:(1)y=﹣x2﹣4x;(2)(﹣,)、(﹣,).12.将抛物线y=x2﹣2向左平移3个单位,所得抛物线的函数表达式为y=x2+6x+7.【分析】根据二次函数图象的平移规律:左右平移,x改变:左加右减,y不变;上下平移,x不变,y改变,上加下减进行计算即可.【解答】解:根据平移规律:将抛物线y=x2﹣2向左平移3个单位得到:y=(x+3)2﹣2,y=x2+6x+7.故答案为:y=x2+6x+7.13.如图所示,将矩形OABC沿AE折叠,使点O恰好落在BC上F处,以CF为边作正方形CFGH,延长BC至M,使CM=|CE﹣EO|,再以CM、CO为边作矩形CMNO.令m=,则m=1;又若CO=1,CE=,Q为AE上一点且QF=,抛物线y=mx2+bx+c经过C、Q两点,则抛物线与边AB的交点坐标是(,).【分析】求出CM=OE﹣CE,求出四边形CFGH的面积是CO×(OE﹣CE),求出四边形CMNO的面积是(OE﹣CE)×CO,即可求出m值;求出EF值,得出EF=QF,得出等边三角形EFQ,求出EQ,求出∠CEF、∠OEA,过Q作QD⊥OE于D,求出Q坐标,代入抛物线求出抛物线的解析式,把x=代入抛物线即可求出y,即得出答案.【解答】解:∵沿AE折叠,O和F重合,∴OE=EF,∵在Rt△CEF中,EF>CE,即OE>CE,∴CM=|CE﹣EO|=OE﹣CE,=CF2=EF2﹣EC2=EO2﹣EC2=(EO+EC)(EO﹣EC)=CO×(EO﹣EC),∵S四边形CFGHS四边形CMNO=CM×CO=(OE﹣CE)×OC,∴m==1;∵CO=1,CE=,QF=,∴EF=EO==QF,C(0,1),∴sin∠EFC==,∴∠EFC=30°,∠CEF=60°,∴∠FEA=×(180°﹣60°)=60°,∵EF=QF,∴△EFQ是等边三角形,∴EQ=,过Q作QD⊥OE于D,ED=EQ=.∵由勾股定理得:DQ=,∴OD=﹣=,即Q的坐标是(,),∵抛物线过C、Q,m=1代入得:,解得:b=﹣,c=1,∴抛物线的解析式是:y=x2﹣x+1,AO=EO=,∵把x=代入抛物线得:y=,∴抛物线与AB的交点坐标是(,),故答案为:1,.14.该试题已被管理员删除15.在平面直角坐标系中,点A、B、C的坐标分别为(0,1)、(4,2)、(2,6).如果P(x,y)是△ABC围成的区域(含边界)上的点,那么当w=xy取得最大值时,点P的坐标是(,5).【分析】分别求得线段AB、线段AC、线段BC的解析式,分析每一条线段上横、纵坐标的乘积的最大值,再进一步比较.【解答】解:线段AB的解析式是y=x+1(0≤x≤4),此时w=x(x+1)=+x,则x=4时,w最大=8;线段AC的解析式是y=x+1(0≤x≤2),此时w=x(x+1)=+x,此时x=2时,w最大=12;线段BC的解析式是y=﹣2x+10(2≤x≤4),此时w=x(﹣2x+10)=﹣2x2+10x,此时x=时,w最大=12.5.综上所述,当w=xy取得最大值时,点P的坐标是(,5).16.如图为二次函数y=ax2+bx+c的图象,在下列结论中:①ac>0;②方程ax2+bx+c=0的根是x1=﹣1,x2=5;③a+b+c<0;④当x<2时,y随着x的增大而增大.正确的结论有②④(请写出所有正确结论的序号).【分析】根据抛物线的开口向下判断出a<0,再根据与y轴的交点判断出c>0,然后判断出①错误;根据与x轴的交点坐标判断出②正确;取x=1的函数值判断出③错误;先求出抛物线对称轴为直线x=2,然后根据二次函数的增减性判断出④正确.【解答】解:∵抛物线开口向下,∴a<0,∵与y轴的正半轴相交,∴c>0,∴ac<0,故①错误;∵抛物线与x轴的交点坐标为(﹣1,0),(5,0),∴方程ax2+bx+c=0的根是x1=﹣1,x2=5,故②正确;由图可知,当x=1时,函数值y>0,即a+b+c>0,故③错误;抛物线对称轴为直线x==2;当x<2时,y随着x的增大而增大,故④正确;综上所述,正确的结论是②④.故答案为:②④.17.已知当x1=a,x2=b,x3=c时,二次函数y=x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是m>﹣.【分析】根据三角形的任意两边之和大于第三边判断出a最小为2,再根据二次函数的增减性和对称性判断出对称轴在2、3之间偏向2,即小于2.5,然后列出不等式求解即可.【解答】方法一:解:∵正整数a,b,c恰好是一个三角形的三边长,且a<b<c,∴a最小是2,∵y1<y2<y3,∴﹣<2.5,解得m>﹣2.5.方法二:解:当a<b<c时,都有y1<y2<y3,即,∴,∴,∵a,b,c恰好是一个三角形的三边长,a<b<c,∴a+b<b+c,∴m>﹣(a+b),∵a,b,c为正整数,∴a,b,c的最小值分别为2、3、4,∴m>﹣(a+b)≥﹣(2+3)=﹣,∴m>﹣,故答案为:m>﹣.18.如图,已知一动圆的圆心P在抛物线y=x2﹣3x+3上运动.若⊙P半径为1,点P的坐标为(m,n),当⊙P与x轴相交时,点P的横坐标m的取值范围是3﹣<m<2或4<m<3+.【分析】由圆心P在抛物线y=x2﹣3x+3上运动,点P的坐标为(m,n),可得n=m2﹣3m+3,又由⊙P半径为1,⊙P与x轴相交,可得|m2﹣3m+3|<1,继而可求得答案.【解答】解:∵圆心P在抛物线y=x2﹣3x+3上运动,点P的坐标为(m,n),∴n=m2﹣3m+3,∵⊙P半径为1,⊙P与x轴相交,∴|n|<1,∴|m2﹣3m+3|<1,∴﹣1<m2﹣3m+3<1,解m2﹣3m+3<1,得:3﹣<m<3+,解m2﹣3m+3>﹣1,得:m<2或m>4,∴点P的横坐标m的取值范围是:3﹣<m<2或4<m<3+.故答案为:3﹣<m<2或4<m<3+.19.如图,四边形ABCD是矩形,A、B两点在x轴的正半轴上,C、D两点在抛物线y=﹣x2+6x上.设OA=m(0<m<3),矩形ABCD的周长为l,则l与m的函数解析式为l=﹣2m2+8m+12.【分析】求l与m的函数解析式就是把m当作已知量,求l,先求AD,它的长就是D点的纵坐标,再把D点纵坐标代入函数解析式求C点横坐标,C点横坐标与D点横坐标的差就是线段CD的长,用l=2(AD+CD),建立函数关系式.【解答】解:把x=m代入抛物线y=﹣x2+6x中,得AD=﹣m2+6m把y=﹣m2+6m代入抛物线y=﹣x2+6x中,得﹣m2+6m=﹣x2+6x解得x1=m,x2=6﹣m∴C的横坐标是6﹣m,故AB=6﹣m﹣m=6﹣2m∴矩形的周长是l=2(﹣m2+6m)+2(6﹣2m)即l=﹣2m2+8m+12.20.若二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1),(﹣1,0),则y=a+b+c的取值范围是0<y<2.【分析】由二次函数的解析式可知,当x=1时,所对应的函数值y=s=a+b+c.把点(0,1),(﹣1,0)代入y=ax2+bx+c,得出c=1,a﹣b+c=0,然后根据顶点在第一象限,可以画出草图并判断出a与b的符号,进而求出y=a+b+c的变化范围.【解答】解:∵二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1),(﹣1,0),∴易得:c=1,a﹣b+c=0,a<0,b>0,由a=b﹣1<0得到b<1,结合上面b>0,所以0<b<1①,由b=a+1>0得到a>﹣1,结合上面a<0,所以﹣1<a<0②,∴由①②得:﹣1<a+b<1,且c=1,得到:0<a+b+c<2,则y=a+b+c的取值范围是0<y<2.故答案为:0<y<2三.解答题(共4小题)21.已知抛物线y=ax2﹣2x+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C,对称轴为x=1,顶点为E,直线y=﹣x+1交y轴于点D.(1)求抛物线的解析式;(2)求证:△BCE∽△BOD;(3)点P是抛物线上的一个动点,当点P运动到什么位置时,△BDP的面积等于△BOE的面积?【分析】(1)在抛物线y=ax2﹣2x+c中,已知对称轴x=﹣=1,可求出a的值;再将点A的坐标代入抛物线的解析式中,可确定c的值,由此得解.(2)首先由抛物线的解析式,确定点B、C、E的坐标,由直线BD的解析式能得到点D的坐标;在求出△BCE、△BOD的三边长后,由SSS来判定这两个三角形相似.(3)△BOE的面积易得,而在(2)中求出了BD的长,由△BDP、△BOE的面积相等先求出点P到直线BD的距离,如何由这个距离求出点P的坐标?这里需要进行适当的转化;首先在y轴上取一点(可设为点M),使得点M到直线BD 的距离等于点P到直线BD的距离,通过解直角三角形先求出DM的长,由此确定点M的坐标,然后过M作平行于直线BD的直线,再联立抛物线的解析式即可确定点P的坐标.【解答】解:(1)抛物线y=ax2﹣2x+c中,对称轴x=﹣=﹣=1,∴a=1;将点A(﹣1,0)代入y=ax2﹣2x+c中,得:1+2+c=0,c=﹣3;∴抛物线的解析式:y=x2﹣2x﹣3.(2)∵抛物线的解析式:y=x2﹣2x﹣3=(x﹣1)2﹣4=(x+1)(x﹣3),∴点C(0,﹣3)、B(3,0)、E(1,﹣4);易知点D(0,1),则有:OD=1、OB=3、BD=;CE=、BC=3、BE=2;∴==,∴△BCE∽△BOD.=×BO×|y E|=×3×4=6;(3)S△BOE=×BD×h=S△BOE=6,即h=.∴S△BDP在y轴上取点M,过点M作MN1⊥BD于N1,使得MN1=h=;在Rt△MN1D中,sin∠MDN1=,且MN1=;则MD==4;∴点M(0,﹣3)或(0,5).过点M作直线l∥MN2,如右图,则直线l:y=﹣x﹣3或y=﹣x+5,联立抛物线的解析式有:或解得:、、、∴当点P的坐标为(0,﹣3)、(,﹣)、(,)、(,)时,△BDP的面积等于△BOE的面积.22.如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.【分析】(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.【解答】解:(1)∵B(4,m)在直线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx+6上,∴,解得,∴抛物线的解析式为y=2x2﹣8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n﹣)2+,∵PC>0,∴当n=时,线段PC最大且为.(3)∵△PAC为直角三角形,i)若点P为直角顶点,则∠APC=90°.由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;ii)若点A为直角顶点,则∠PAC=90°.如答图3﹣1,过点A(,)作AN⊥x轴于点N,则ON=,AN=.过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,∴MN=AN=,∴OM=ON+MN=+=3,∴M(3,0).设直线AM的解析式为:y=kx+b,则:,解得,∴直线AM的解析式为:y=﹣x+3 ①又抛物线的解析式为:y=2x2﹣8x+6 ②联立①②式,解得:x=3或x=(与点A重合,舍去)∴C(3,0),即点C、M点重合.当x=3时,y=x+2=5,∴P1(3,5);iii)若点C为直角顶点,则∠ACP=90°.∵y=2x2﹣8x+6=2(x﹣2)2﹣2,∴抛物线的对称轴为直线x=2.如答图3﹣2,作点A(,)关于对称轴x=2的对称点C,则点C在抛物线上,且C(,).当x=时,y=x+2=.2∵点P1(3,5)、P2(,)均在线段AB上,∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(,).23.已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.(1)求抛物线的函数表达式;(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC 于点Q.①当x取何值时,线段PQ的长度取得最大值,其最大值是多少?②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)已知了A,B的坐标,可用待定系数法求出函数的解析式.(2)①QP其实就是一次函数与二次函数的差,二次函数的解析式在(1)中已经求出,而一次函数可根据B,C的坐标,用待定系数法求出.那么让一次函数的解析式减去二次函数的解析式,得出的新的函数就是关于PQ,x的函数关系式,那么可根据函数的性质求出PQ的最大值以及相对应的x的取值.(3)分三种情况进行讨论:当∠QOA=90°时,Q与C重合,显然不合题意.因此这种情况不成立;当∠OAQ=90°时,P与A重合,因此P的坐标就是A的坐标;当∠OQA=90°时,如果设QP与x轴的交点为D,那么根据射影定理可得出DQ2=OD•DA.由此可得出关于x的方程即可求出x的值,然后将x代入二次函数式中即可得出P的坐标.【解答】解:(1)∵抛物线过A(3,0),B(6,0),解得:,∴所求抛物线的函数表达式是y=x2﹣x+2.(2)①∵当x=0时,y=2,∴点C的坐标为(0,2).设直线BC的函数表达式是y=kx+h.则有,解得:.∴直线BC的函数表达式是y=﹣x+2.∵0<x<6,点P、Q的横坐标相同,∴PQ=y Q﹣y P=(﹣x+2)﹣(x2﹣x+2)=﹣x2+x=﹣(x﹣3)2+1∴当x=3时,线段PQ的长度取得最大值.最大值是1.②解:当∠OAQ′=90°时,点P与点A重合,∴P(3,0)当∠Q′OA=90°时,点P与点C重合,∴x=0(不合题意)当∠OQ′A=90°时,设PQ′与x轴交于点D.∵∠OQ′D+∠AOQ′=90°,∠Q′AD+∠AQ′D=90°,∴∠OQ′D=∠Q′AD.又∵∠ODQ′=∠Q′DA=90°,∴△ODQ′∽△Q′DA.∴,即DQ′2=OD•DA.∴(﹣x+2)2=x(3﹣x),10x2﹣39x+36=0,∴x1=,x2=,∴y1=×()2﹣+2=;y2=×()2﹣+2=;∴P(,)或P(,).∴所求的点P的坐标是P(3,0)或P(,)或P(,).24.如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线的函数解析式;(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l 于点H,连结OP,试求△OPH的面积;②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)利用待定系数法求出抛物线的解析式;=S△OMH﹣S△OMP求解;(2)①如答图1,作辅助线,利用关系式S△OPH②本问涉及复杂的分类讨论,如答图2所示.由于点P可能在OC、BC、BK、AK、OA上,而等腰三角形本身又有三种情形,故讨论与计算的过程比较复杂,需要耐心细致、考虑全面.【解答】解:(1)由题意得:A(4,0),C(0,4),对称轴为x=1.设抛物线的解析式为y=ax2+bx+c,则有:,解得.∴抛物线的函数解析式为:y=﹣x2+x+4.(2)①当m=0时,直线l:y=x.∵抛物线对称轴为x=1,∴CP=1.如答图1,延长HP交y轴于点M,则△OMH、△CMP均为等腰直角三角形.∴CM=CP=1,∴OM=OC+CM=5.S△OPH=S△OMH﹣S△OMP=(OM)2﹣OM•CP=×(×5)2﹣×5×1=﹣=,∴S=.△OPH②当m=﹣3时,直线l:y=x﹣3.设直线l与x轴、y轴交于点G、点D,则G(3,0),D(0,﹣3).假设存在满足条件的点P.a)当点P在OC边上时,如答图2﹣1所示,此时点E与点O重合.设PE=a(0<a≤4),则PD=3+a,PF=PD=(3+a).过点F作FN⊥y轴于点N,则FN=PN=PF,∴EN=|PN﹣PE|=|PF﹣PE|.在Rt△EFN中,由勾股定理得:EF==.若PE=PF,则:a=(3+a),解得a=3(+1)>4,故此种情形不存在;若PF=EF,则:PF=,整理得PE=PF,即a=3+a,不成立,故此种情形不存在;若PE=EF,则:PE=,整理得PF=PE,即(3+a)=a,解得a=3.∴P1(0,3).b)当点P在BC边上时,如答图2﹣2所示,此时PE=4.若PE=PF,则点P为∠OGD的角平分线与BC的交点,有GE=GF,过点F分别作FH⊥PE于点H,FK⊥x轴于点K,∵∠OGD=135°,∴∠EPF=45°,即△PHF为等腰直角三角形,设GE=GF=t,则GK=FK=EH=t,∴PH=HF=EK=EG+GK=t+t,∴PE=PH+EH=t+t+t=4,解得t=4﹣4,则OE=3﹣t=7﹣4,∴P2(7﹣4,4)c)∵A(4,0),B(2,4),∴可求得直线AB解析式为:y=﹣2x+8;联立y=﹣2x+8与y=x﹣3,解得x=,y=.设直线BA与直线l交于点K,则K(,).当点P在线段BK上时,如答图2﹣3所示.设P(a,8﹣2a)(2≤a≤),则Q(a,a﹣3),∴PE=8﹣2a,PQ=11﹣3a,∴PF=(11﹣3a).。
50 搞定二次函数压轴100题(含详解)

搞定二次函数压轴100题1. 若二次函数y=a1x2+b1x+c1的图象记为C1,其顶点为A,二次函数y=a2x2+b2x+c2的图象记为C2,其顶点为B,且满足点A 在C2上,点B在C1上,则称这两个二次函数互为“伴侣二次函数”.(1)一个二次函数的“伴侣二次函数”有个;(2)①求二次函数y=x2+3x+2与x轴的交点;②求以上述交点为顶点的二次函数y=x2+3x+2的“伴侣二次函数”.(3)试探究a1与a2满足的数量关系.2. 已知二次函数y=x2+2bx+c(b,c为常数).(1)当b=1,c=−3时,求二次函数在−2≤x≤2上的最小值;(2)当c=3时,求二次函数在0≤x≤4上的最小值;(3)当c=4b2时,若在自变量x的值满足2b≤x≤2b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.3. 如图,已知二次函数图象的顶点坐标为(2,0),直线y=x+1与二次函数的图象交于A、B两点,其中点A在y轴上.(1)二次函数的解析式为y=;(2)证明点不在(1)中所求的二次函数的图象上;(3)若C为线段AB的中点,过C点作轴于E点,CE与二次函数的图象交于D点.①y轴上存在点K,使以K、A、D、C为顶点的四边形是平行四边形,则K点的坐标是;②二次函数的图象上是否存在点P,使得?若存在,求出P点坐标;若不存在,请说明理由.x和直线y= 4. 二次函数y=x2+px+q的顶点M是直线y=−12x+m的交点.(1)若直线y=x+m过点D(0,−3),求M点的坐标及二次函数y=x2+px+q的解析式;(2)试证明无论m取任何值,二次函数y=x2+px+q的图象与直线y=x+m总有两个不同的交点;(3)在(1)的条件下,若二次函数y=x2+px+q的图象与yx上求异于轴交于点C,与x的右交点为A,试在直线y=−12 M的点P,使P在△CMA的外接圆上.5. 已知二次函数y=−x2+bx+c+1.(1)当b=1时,求这个二次函数的对称轴方程;(2)若c=−14b2−2b,问:b为何值时,二次函数的图象与x轴相切;(3)若c=0,二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,与y轴的正半轴交于点M,以AB为直径的半圆恰好经过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别相交于点D,E,F且满足DEEF =13,求二次函数的表达式.6. 如图,已知二次函数y=−x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连接BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC 的边界),求m的取值范围;(3)点P是直线AC上的动点,若以点P,点C,点M构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).7. 已知二次函数y=−x2+bx+c的图象经过点P(0,1)与Q(2,−3).(1)求此二次函数的解析式;(2)若点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,且所得四边形ABCD恰为正方形.①求正方形的ABCD的面积;②联结PA、PD,PD交AB于点E,求证:△PAD∽△PEA.8. 如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+ 2的图象与x轴的正半轴交于点A,与y轴的正半轴交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.(1)求这个二次函数的解析式;(2)将△OAB绕点A顺时针旋转90∘后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;(3)设(2)中平移后所得二次函数图象与y轴的交点为B1,顶点为D1.点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.9. 如图,已知二次函数y=−x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连接BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).10. 已知二次函数y=mx2+nx+p图象的顶点横坐标是2,与x轴交于A(x1,0),B(x2,0),x1<0<x2,与y轴交于点C,O为坐标原点,tan∠CAO−tan∠CBO=1.(1)求证:n+4m=0;(2)求m,n的值;(3)当p>0且二次函数图象与直线y=x+3仅有一个交点时,求二次函数的最大值.11. 如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.(1)求二次函数的解析式;(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴,y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.,当x=0和x=2时,12. 已知二次函数y=(t+1)x2+2(t+2)x+32函数值相等.(1)求二次函数的表达式.(2)若一次函数y=kx+6的图象与二次函数的图象都经过点A(−3,m),求m和k的值.(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位长度后得到的图象记为G,同时将2中得到的直线y=kx+6向上平移n个单位长度.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围是多少?13. 已知二次函数y=x2−2ax−2a−6(a为常数,a≠0).(1)求证:该二次函数的图象与x轴有两个交点;(2)设该二次函数的图象与x轴交于点A(−2,0)和点B,与y轴交于点C,线段BC的垂直平分线l与x轴交于点D.①求点D的坐标;②设点P是抛物线上的一个动点,点Q是直线l上的一个动点.以点B,D,P,Q为顶点的四边形是否可能为平行四边形?若能,直接写出点Q的坐标.14. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(−1,0),B(4,0),C(0,2)三点.(1)求该二次函数的解析式;(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O 是坐标原点),求点D的坐标;(3)点P是该二次函数图象上位于一象限上的一动点,连接PA 分别交BC,y轴于点E,F,若△PEB,△CEF的面积分别为S1,S2,求S1−S2的最大值.15. 已知二次函数y=(t−4)x2−(2t−5)x+4在x=0与x=5的函数值相等.(1)求二次函数的解析式;(2)若二次函数的图象与x轴交于A,B两点(A在B左侧),与y轴交于点C,一次函数y=kx+b经过B,C两点,求一次函数的表达式;(3)在(2)的条件下,过动点D(0,m)作直线l∥x轴,其中m>−2.将二次函数图象在直线l下方的部分沿直线l向上翻折,其余部分保持不变,得到一个新图象M.若直线y=kx+b与新图象M恰有两个公共点,请直接写出m的取值范围.),A(5,0),16. 已知二次函数y=ax2+bx+c的图象经过点P(0,−52 B(1,0).(1)求该二次函数的解析式;(2)点C在该二次函数的图象上,当△ABC的面积为12时,求点C坐标;(3)在(2)的条件下,求△ABC外接圆圆心点D的坐标.17. 如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.(1)求二次函数的表达式;(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴、y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.18. 如图1,一次函数y=kx+k与二次函数y=kx2+kx(k>0)交于A,B两点,二次函数图象的顶点为P.(1)写出三条与系数k无关的一次函数与二次函数共有的结论.(2)当k为何值时,△AOP为等边三角形?(3)若一次函数y=kx+k的图象与二次函数y=kx2+2kx的图象交于点C,D,与y轴交于点F,如图2,某数学学习小组探究k=1时得出以下结论,其中正确结论的序号有.①AF=BF;②点C是BF的黄金分割点;③AFAD =√5+12;④△CFO与△ADO的面积相等.(4)在(3)中,若去掉k=1,以上正确的结论还成立吗?若成立,请选择两个加以说明.19. 如图,顶点为P(4,−4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M,N关于点P对称,连接AN,ON.(1)求该二次函数的关系式.(2)若点A的坐标是(6,−3),求△ANO的面积.(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下列问题:①证明:∠ANM=∠ONM;②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标,如果不能,请说明理由.20. 对于二次函数y=x2−3x+2和一次函数y=−2x+4,把y=t(x2−3x+2)+(1−t)(−2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E,现有点A(2,0)和抛物线E上的点B(−1,n),请完成下列任务:(1)【尝试】(1)当t=2时,抛物线y=t(x2−3x+2)+(1−t)(−2x+4)的顶点坐标为;(2)判断点A是否在抛物线E上;(3)求n的值.(2)【发现】通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,坐标为.(3)【应用】(1)二次函数y=−3x2+5x+2是二次函数y=x2−3x+2和一次函数y=−2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由;(2)以AB为边作矩形ABCD,使得其中一个顶点落在y轴上;若抛物线E经过A,B,C,D其中的三点,求出所有符合条件的t的值.与y=x2−mx−21. 已知关于x的二次函数y=x2−mx+m2+12m2+2,这两个二次函数图象中的一条与x轴交于A、B两个不同2的点.(1)试判断哪个二次函数的图象经过A、B两点(写出判断过程);(2)若A点坐标为(−1,0),求点B的坐标;(3)在(2)的条件下,设点C是抛物线上的一点,且△ABC的面积为10,直接写出点C的坐标.22. 已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(1,0)与点C(0,−3),其顶点为P.(1)求二次函数的解析式;(2)若Q为对称轴上的一点,且QC平分∠PQO,求Q点坐标;(3)当m≤x≤m+1时,y的取值范围是−4≤y≤2m,求m 的值.23. 如图,在直角坐标系中,O为原点.点A在x轴的正半轴上,点B在y轴的正半轴上,tan∠OAB=2.二次函数y=x2+mx+2的图象经过点A,B,顶点为D.(1)求这个二次函数的解析式;(2)将△OAB绕点A顺时针旋转90∘后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;(3)设(2)中平移后所得二次函数图象与y轴的交点为B1,顶点为D1.点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.24. 在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(−3,0),B(0,−3)两点,二次函数y=x2+mx+n 的图象经过点A.(1)求一次函数y=kx+b的解析式;(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;(3)当−3≤x≤0时,二次函数y=x2+mx+n的最小值为−4,求m,n的值.在x=0和x=2时25. 已知二次函数y=(t+1)x2+2(t+2)x+32的函数值相等.(1)求二次函数的解析式;(2)若一次函数y=kx+6的图象与二次函数的图象都经过点A(−3,m),求m和k的值;(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+6向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.26. 如图,在平面直角坐标系中,点A,C的坐标分别为(−1,0),(0,−√3),点B在x轴上.已知某二次函数的图象经过A,B,C 三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B,C不重合),过点P作y轴的平行线交BC于点F.(1)求该二次函数的解析式;(2)若设点P的横坐标为m,用含m的代数式表示线段PF的长;(3)求△PBC面积的最大值,并求此时点P的坐标.27. 如图,已知二次函数y=ax2+bx+c的图象经过A(−1,0),B(3,0),N(2,3)三点,且与y轴交于点C.(1)求这个二次函数的解析式,并写出顶点M及点C的坐标;(2)若直线y=kx+d经过C,M两点,且与x轴交于点D.试证明四边形CDAN是平行四边形;(3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A,B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.28. 如图,已知在平面直角坐标系xOy中,二次函数y=−x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.(1)求这个二次函数的解析式并写出其图象顶点D的坐标;(2)求∠CAD的正弦值;(3)设点P在线段DC的延长线上,且∠PAO=∠CAD,求点P 的坐标.x2+bx+c的图象29. 如图,在平面直角坐标系中,二次函数y=−14与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(−4,0).(1)求该二次函数的表达式及点C的坐标;(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.(1)求S的最大值;(2)在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.30. 已知二次函数y1=x2−2x−3及一次函数y2=x+m.(1)求该二次函数图象的顶点坐标以及它与x轴的交点坐标;(2)将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象.请你在图中画出这个新图象,并求出新图象与直线y2=x+m有三个不同公共点时m的值;(3)当0≤x≤2时,函数y=y1+y2+(m−2)x+3的图象与x轴有两个不同的公共点,求m的取值范围.31. 如图,已知二次函数y=ax2−4x+c的图象与坐标轴交于点A(−1,0)和点B(0,−5).(1)求该二次函数的解析式;(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标.32. 如图,二次函数y=ax2+bx+c的图象经过点A(−1,0),B(4,0),C(−2,−3),直线BC与y轴交于点D,E为二次函数图象上任一点.(1)求这个二次函数的表达式;(2)若点E在直线BC的上方,过点E分别作BC和y轴的垂线,交直线BC于不同的两点F,G(F在G的左侧),求△EFG的周长的最大值;(3)是否存在点E,使得△EDB是以BD为直角边的直角三角形,如果存在,求点E的坐标;如果不存在,请说明理由.x+3的图象33. 已知平面直角坐标系xOy(如图),一次函数y=34x的图象上,且MO=与y轴交于点A,点M在正比例函数y=32MA.二次函数y=x2+bx+c的图象经过点A、M.(1)求线段AM的长;(2)求这个二次函数的解析式;(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数x+3的图象上,且四边形的图象上,点D在一次函数y=34ABCD是菱形,求点C的坐标.34. 如图,二次函数y=a(x2−2mx−3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B左侧),与y轴交于点C(0,−3),点D在二次函数图象上,且CD∥AB,连接AD;过点A作射线AE交二次函数于点E,使AB 平分∠DAE.(1)当a=1时,求点D的坐标;(2)证明:无论a,m取何值,点E在同一直线上运动;(3)设该二次函数图象顶点为F,试探究:在x轴上是否存在点P,使以PF,AD,AE为边构成的三角形是以AE为斜边的直角三角形?如果存在,请用含m的代数式表示点P的横坐标;如果不存在,请说明理由.m+1(m为常数).35. 已知:二次函数y=x2−mx+34(1)若这个二次函数的图象与x轴只有一个公共点A,且A点在x轴的正半轴上.①求m的值;②四边形AOBC是正方形,且点B在y轴的负半轴上,现将这个二次函数的图象平移,使平移后的函数图象恰好经过B,C 两点,求平移后的图象对应的函数解析式;m+1的最小值(2)当0≤x≤2时,求函数y=x2−mx+34(用含m的代数式表示).36. 如图,在平面直角坐标系xOy中,将二次函数y=x2−1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.(1)求N的函数表达式;(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A,B,求PA2+PB2的最大值;(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.x2+bx+c的图象经过点A(−3,6),并与x轴37. 已知二次函数y=12交于点B(−1,0)和点C,与y轴交于点E,顶点为P,对称轴与x 轴交于点D.(1)求这个二次函数的解析式;(2)连接CP,△DCP是什么特殊形状的三角形?并加以说明;(3)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标.38. 如图,二次函数y=ax2+bx+c的图象经过点A(−1,0),B(4,0),C(−2,−3),直线BC与y轴交于点D,E为二次函数上任一点.(1)求这个二次函数的解析式;(2)若点E在直线BC的上方,过E分别作BC和y轴的垂线,交直线BC于不同的两点F,G(F在G的左侧),求△EFG周长的最大值;(3)是否存在点E,使得△EDB是以BD为直角边的直角三角形,如果存在,求点E的坐标;如果不存在,请说明理由.39. 已知关于x的二次函数y=x2+(k2−3k−4)x+2k的图象与x轴从左到右分别交于A,B两点,且这两点关于原点对称.(1)求k的值;(2)在(1)的条件下,若反比例函数y=m的图象与二次函数xy=x2+(k2−3k−4)x+2k的图象从左到右交于Q,R,S三点,且点Q的坐标为(−1,−1),点R(x R,y R),S(x S,y S)中的纵坐标y R,y S分别是一元二次方程y2+my−1=0的解,求四边形AQBS的面积S;四边形AQBS(3)在(1),(2)的条件下,在x轴下方是否存在二次函数y=x2+(k2−3k−4)x+2k图象上的点P使得S△PAB=2S△RAB,若存在,求出点P的坐标;若不存在,请说明理由.40. 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,−4).(1)求出图象与轴的交点A,B的坐标;S△MAB,若(2)在二次函数的图象上是否存在点P,使S△PAB=54存在,求出P点的坐标;若不存在,请说明理由;(3)将二次函数的图象在轴下方的部分沿轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y= x+b(b<1)与此图象有两个公共点时,的取值范围.41. 下图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,−4).(1)求出图象与x轴的交点A,B的坐标.S△MAB?若存(2)在二次函数的图象上是否存在点P,使S△PAB=54在,求出P点的坐标;若不存在,请说明理由.(3)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b 的取值范围.42. 已知二次函数y=ax2+bx+c的图象经过A(1,0),B(3,0),C(0,−3).(1)求此二次函数的解析式以及顶点D的坐标;(2)如图①,过此二次函数抛物线图象上一动点P(m,n)(0<m<3)作y轴平行线,交直线BC于点E,是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,说明理由.(3)如图②,过点A作y轴的平行线交直线BC于点F,连接DA,DB,四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点F重合时立即停止运动,求运动过程中四边形OAFC与四边形ADBF重叠部分面积S的最大值.),点F(0,1)在y轴上,43. 二次函数的顶点在原点O,经过点A(1,14直线y=−1与y轴交于点H.(1)求二次函数的解析式;(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=−1交于点M,求证:FM平分∠OFP;(3)当△FPM是等边三角形时,求P点的坐标.44. 如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A,C两点,且A(0,2),直线与x,点P是线段AC上一动点,轴的交点为B,满足sin∠ABO=√55且不与A,C两点重合,PG∥y轴交抛物线于点G.(1)求k,m和这个二次函数的解析式;(2)点E是直线BC与抛物线对称轴的交点,当△PGE∽△AOB 时,求点P的坐标;(3)若PG=21时,另外一点F在抛物线上,当S△ACF=S△ACG时,16求点F的坐标.45. 如图,△ABC是以BC为底边的等腰三角形,点A,C分别是一次x+3的图象与y轴、x轴的交点,点B在二次函数函数y=−34x2+bx+c的图象上,且该二次函数图象上存在一点D,使y=18四边形ABCD能构成平行四边形.(1)试求b,c的值,并写出该二次函数的解析式;(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:①当P运动到何处时,△APQ是直角三角形?②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?46. 如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A,B.两点,与y轴交于点C(0,−1),△ABC的面积为54(1)求该二次函数的解析式;(2)过y轴上的一点M(0,m)作y轴的垂线,若该垂线与△ABC 的外接圆有公共点,求m的取值范围;(3)在该二次函数的图象上是否存在点D,使四边形ACBD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由.47. 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).(1)求a,b的值;(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6).写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.48. 如图,三角形ABC是以BC为底边的等腰三角形,点A,C分别x+3的图象与y轴、x轴的交点,点B在二是一次函数y=−34x2+bx+c的图象上,且该二次函数图象上存在一次函数y=18点D使四边形ABCD能构成平行四边形.(1)试求b,c的值,并写出该二次函数表达式;(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:①当P运动到何处时,有PQ⊥AC?②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?49. 如图,已知二次函数y=12x2+bx+c的图象经过点A(3,6),并与x轴交于点B(1,0)和点C.(1)求二次函数的解析式及点C的坐标;(2)若D为线段AC上一点,且以D,O,C为顶点的三角形与△ABC相似,求点D的坐标;(3)设直线y=1为直线l,将该二次函数的图象在直线l下方的部分沿直线l翻折到直线l上方,图象的其余部分不变,得到一个新图象.是否存在与新图象恰有三个不同公共点且平行于AC 的直线?若存在,请求出所有符合条件的直线的解析式;若不存在,请说明理由.50. 已知二次函数y=ax2−2ax+c(a<0)的最大值为4,且抛物线过点(72,−94).点P(t,0)是x轴上的动点,抛物线与y轴的交点为C,顶点为D.(1)求该二次函数的解析式及顶点D的坐标;(2)求∣PC−PD∣的最大值及对应的点P的坐标;(3)设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a∣x∣2−2a∣x∣+c的图象只有一个公共点,求t的取值.51. 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(−2,0),点C(8,0),与y轴交于点A.(1)求二次函数y=ax2+bx+4的表达式;(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;(3)连接OM,在(2)的结论下,求OM与AC的数量关系.52. 如图,三角形ABC是以BC为底边的等腰三角形,点A,C分别x+3的图象与y轴,x轴的交点,点B在二是一次函数y=−34x2+bx+c的图象上,且该二次函数图象上存在一次函数y=18点D使四边形ABCD为平行四边形.(1)试求b,c的值,并写出该二次函数表达式;(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:①当P运动到何处时,有PQ⊥AC?②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?53. 已知关于x的二次函数y=x2+(k2−3k−4)x+2k的图象与x轴分别交于A,B两点(点A在点B左侧),且这两点关于原点对称.(1)求k的值.的图象与二次函数(2)在(1)的条件下,若反比例函数y=mxy=x2+(k2−3k−4)x+2k的图象从左到右分别交于Q,R,S三点,且点Q的坐标为(−1,−1),点R(x R,y R),S(x S,y S)的纵坐标y R,y S分别是一元二次方程y2+my−1=0的解,求四边形AQBS的面积.(3)在(1)(2)的条件下,在x轴下方的二次函数y=x2+ (k2−3k−4)x+2k的图象上是否存在点P,使得S△PAB=2S△RAB?若存在,求出点P坐标;若不存在,请说明理由.54. 如图,二次函数y=ax2−6ax+4a+3的图象与y轴交于点A,点B是x轴上一点,其坐标为(1,0),连接AB,tan∠ABO=2.(1)则点A的坐标为,a=;(2)过点A作AB的垂线与该二次函数的图象交于另一点C,求点C的坐标;(3)连接BC,过点A作直线l交线段BC于点P,设点B,点C 到l的距离分别为d1,d2,求d1+d2的最大值.55. 二次函数y=ax2+bx+4的图象与x轴交于两点A,B,与y轴交于点C,且A(−1,0),B(4,0).(1)求此二次函数的表达式.(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足,0),动点N在线段DE上运动,连接CF,为点D,点F(−76CN,FN,若以点C,D,N为顶点的三角形与△FEN相似,求点N的坐标.(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45∘,求点P的坐标.56. 在平面直角坐标系中,O为坐标原点,一次函数y=ax+b的图象与二次函数y=ax2+bx的图象交于点A,B.其中a,b均为非零实数.(1)当a=b=1时,求AB的长;(2)当a>0时,请用含a,b的代数式表示△AOB的面积;(3)当点A的横坐标小于点B的横坐标时,过点B作x轴的垂线,垂足为Bʹ.若二次函数y=ax2+bx的图象的顶点在反比例函的图象上,请用含a的代数式表示△BBʹA的面积.数y=ax57. 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(3,0),B(−1,0),C(0,−3),顶点为D.(1)求这个二次函数的解析式及顶点坐标;(2)在y轴上找一点P(点P与点C不重合),使得∠APD= 90∘,求点P坐标;(3)在(2)的条件下,将△APD沿直线AD翻折,得到△AQD,求点Q坐标.58. 已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2−4x−12=0的两个根.(1)求出该二次函数的表达式及顶点坐标;(2)如图,连接AC、BC,点P是线段OB上一个动点(点P不与点O、B重合),过点P作PQ∥AC交BC于点Q,当△CPQ的面积最大时,求点P的坐标.59. 如图,二次函数y=−x2+bx+c的图象与x轴交于点B(−3,0),与y轴交于点C(0,−3).(1)求直线BC及二次函数的解析式;(2)设抛物线的顶点为D,与x轴的另一个交点为A.点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;(3)连接CD,求∠OCA与∠OCD两角和的度数.60. 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数x刻画.y=−x2+4x刻画,斜坡可以用一次函数y=12(1)请用配方法求二次函数图象的最高点P的坐标;(2)小球的落点是A,求点A的坐标;(3)连接抛物线的最高点P与点O,A得△POA.求△POA的面积;。
中考数学二次函数-经典压轴题及详细答案

中考数学二次函数-经典压轴题及详细答案一、二次函数1.已知二次函数223y ax ax =-+的最大值为4,且该抛物线与y 轴的交点为C ,顶点为D .(1)求该二次函数的解析式及点C ,D 的坐标;(2)点(,0)P t 是x 轴上的动点,①求PC PD -的最大值及对应的点P 的坐标;②设(0,2)Q t 是y 轴上的动点,若线段PQ 与函数2||23y a x a x =-+的图像只有一个公共点,求t 的取值范围.【答案】(1)2y x 2x 3=-++,C 点坐标为(0,3),顶点D 的坐标为(1,4);(2)①最,P 的坐标为(3,0)-,②t 的取值范围为3t ≤-或332t ≤<或72t =. 【解析】【分析】(1)先利用对称轴公式x=2a 12a--=,计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;(2)根据三角形的三边关系:可知P 、C 、D 三点共线时|PC-PD|取得最大值,求出直线CD 与x 轴的交点坐标,就是此时点P 的坐标;(3)先把函数中的绝对值化去,可知22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ 过点(0,3),即点Q 与点C 重合时,两图象有一个公共点,当线段PQ 过点(3,0),即点P 与点(3,0)重合时,两函数有两个公共点,写出t 的取值;②线段PQ 与当函数y=a|x|2-2a|x|+c (x≥0)时有一个公共点时,求t 的值;③当线段PQ 过点(-3,0),即点P 与点(-3,0)重合时,线段PQ 与当函数y=a|x|2-2a|x|+c (x <0)时也有一个公共点,则当t≤-3时,都满足条件;综合以上结论,得出t 的取值.【详解】解:(1)∵2a x 12a-=-=, ∴2y ax ax 3=-+的对称轴为x 1=.∵2y ax ax 3=-+人最大值为4,∴抛物线过点()1,4.得a 2a 34-+=,解得a 1=-.∴该二次函数的解析式为2y x 2x 3=-++.C 点坐标为()0,3,顶点D 的坐标为()1,4.(2)①∵PC PD CD -≤,∴当P,C,D 三点在一条直线上时,PC PD -取得最大值.连接DC 并延长交y 轴于点P ,PC PD CD -===∴PC PD -.易得直线CD 的方程为y x 3=+.把()P t,0代入,得t 3=-.∴此时对应的点P 的坐标为()3,0-.②2y a |x |2a x 3=-+的解析式可化为22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩ 设线段PQ 所在直线的方程为y kx b =+,将()P t,0,()Q 0,2t 的坐标代入,可得线段PQ 所在直线的方程为y 2x 2t =-+.(1)当线段PQ 过点()3,0-,即点P 与点()3,0-重合时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点,此时t 3=-. ∴当t 3≤-时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. (2)当线段PQ 过点()0,3,即点Q 与点C 重合时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点,此时3t 2=. 当线段PQ 过点()3,0,即点P 与点()3,0重合时,t 3=,此时线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像有两个公共点. 所以当3t 32≤<时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. (3)将y 2x 2t =-+带入()2y x 2x 3x 0=-++≥,并整理,得2x 4x 2t 30-+-=. ()Δ1642t 3288t =--=-.令288t 0-=,解得7t 2=. ∴当7t 2=时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点.综上所述,t 的取值范围为t 3≤-或3t 32≤<或7t 2=. 【点睛】 本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.2.如图所示,抛物线2y ax bx c =++的顶点为()2,4M --,与x 轴交于A 、B 两点,且()6,0A -,与y 轴交于点C .()1求抛物线的函数解析式;()2求ABC V 的面积;()3能否在抛物线第三象限的图象上找到一点P ,使APC V 的面积最大?若能,请求出点P 的坐标;若不能,请说明理由.【答案】()1 2134y x x =+-;()212;()27334APC x S =-V 当时,有最大值,点P 的坐标是153,4P ⎛⎫-- ⎪⎝⎭. 【解析】【分析】(1)设顶点式并代入已知点()6,0A -即可;(2)令y=0,求出A 、B 和C 点坐标,运用三角形面积公式计算即可;(3)假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F ,线段PF 的长度即为两函数值之差,将APC V 的面积计算拆分为APF CPF S S +V V 即可.【详解】()1设此函数的解析式为2()y a x h k =++,∵函数图象顶点为()2,4M --,∴2(2)4y a x =+-,又∵函数图象经过点()6,0A -,∴20(62)4a =-+-解得14a =, ∴此函数的解析式为21(2)44y x =+-,即2134y x x =+-; ()2∵点C 是函数2134y x x =+-的图象与y 轴的交点, ∴点C 的坐标是()0,3-,又当0y =时,有21304y x x =+-=, 解得16x =-,22x =,∴点B 的坐标是()2,0, 则11831222ABC S AB OC =⋅=⨯⨯=V ; ()3假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F .设(),0E x ,则21,34P x x x ⎛⎫+- ⎪⎝⎭,设直线AC 的解析式为y kx b =+,∵直线AC 过点()6,0A -,()0,3C -,∴603k b b -+=⎧⎨-=⎩, 解得123k b ⎧=-⎪⎨⎪=-⎩,∴直线AC 的解析式为132y x =--, ∴点F 的坐标为1,32F x x ⎛⎫-- ⎪⎝⎭, 则221113332442PF x x x x x ⎛⎫=---+-=-- ⎪⎝⎭, ∴1122APC APF CPF S S S PF AE PF OE =+=⋅+⋅V V V2221113393276(3)22424244PF OA x x x x x ⎛⎫=⋅=--⨯=--=-++ ⎪⎝⎭, ∴当3x =-时,APC S V 有最大值274, 此时点P 的坐标是153,4P ⎛⎫-- ⎪⎝⎭. 【点睛】本题第3问中将所求三角形拆分为两个小三角形进行求解,从而将面积最大的问题转化为PF 最大进行理解.3.如图,已知抛物线2y ax bx c =++经过A (-3,0),B (1,0),C (0,3)三点,其顶点为D ,对称轴是直线l ,l 与x 轴交于点H .(1)求该抛物线的解析式;(2)若点P 是该抛物线对称轴l 上的一个动点,求△PBC 周长的最小值;(3)如图(2),若E 是线段AD 上的一个动点( E 与A 、D 不重合),过E 点作平行于y 轴的直线交抛物线于点F ,交x 轴于点G ,设点E 的横坐标为m ,△ADF 的面积为S . ①求S 与m 的函数关系式;②S 是否存在最大值?若存在,求出最大值及此时点E 的坐标; 若不存在,请说明理由.【答案】(1)2y x 2x 3=--+.(2)3210.(3)①2S m 4m 3=---.②当m=﹣2时,S 最大,最大值为1,此时点E 的坐标为(﹣2,2).【解析】【分析】(1)根据函数图象经过的三点,用待定系数法确定二次函数的解析式即可.(2)根据BC 是定值,得到当PB+PC 最小时,△PBC 的周长最小,根据点的坐标求得相应线段的长即可.(3)设点E 的横坐标为m ,表示出E (m ,2m+6),F (m ,2m 2m 3--+),最后表示出EF 的长,从而表示出S 于m 的函数关系,然后求二次函数的最值即可.【详解】解:(1)∵抛物线2y ax bx c =++经过A (-3,0),B (1,0),∴可设抛物线交点式为()()y a x 3x 1=+-.又∵抛物线2y ax bx c =++经过C (0,3),∴a 1=-.∴抛物线的解析式为:()()y x 3x 1=-+-,即2y x 2x 3=--+.(2)∵△PBC 的周长为:PB+PC+BC ,且BC 是定值.∴当PB+PC 最小时,△PBC 的周长最小.∵点A 、点B 关于对称轴I 对称,∴连接AC 交l 于点P ,即点P 为所求的点.∵AP=BP ,∴△PBC 的周长最小是:PB+PC+BC=AC+BC.∵A (-3,0),B (1,0),C (0,3),∴2,10.∴△PBC 的周长最小是:3210.(3)①∵抛物线2y x 2x 3=--+顶点D 的坐标为(﹣1,4),A (﹣3,0),∴直线AD 的解析式为y=2x+6∵点E 的横坐标为m ,∴E (m ,2m+6),F (m ,2m 2m 3--+)∴()22EF m 2m 32m 6m 4m 3=--+-+=---. ∴()22DEF AEF 1111S S S EF GH EF AG EF AH m 4m 32m 4m 32222∆∆=+=⋅⋅+⋅⋅=⋅⋅=⋅---⋅=---.∴S 与m 的函数关系式为2S m 4m 3=---.②()22S m 4m 3m 21=---=-++,∴当m=﹣2时,S 最大,最大值为1,此时点E 的坐标为(﹣2,2).4.某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间每天的定价增加x 元.求:(1)房间每天的入住量y (间)关于x (元)的函数关系式;(2)该宾馆每天的房间收费p (元)关于x (元)的函数关系式;(3)该宾馆客房部每天的利润w (元)关于x (元)的函数关系式;当每个房间的定价为每天多少元时,w 有最大值?最大值是多少?【答案】(1)y=60-10x ;(2)z=-110x 2+40x+12000;(3)w=-110x 2+42x+10800,当每个房间的定价为每天410元时,w 有最大值,且最大值是15210元.【解析】 试题分析:(1)根据题意可得房间每天的入住量=60个房间﹣每个房间每天的定价增加的钱数÷10;(2)已知每天定价增加为x 元,则每天要(200+x )元.则宾馆每天的房间收费=每天的实际定价×房间每天的入住量;(3)支出费用为20×(60﹣10x ),则利润w =(200+x )(60﹣10x )﹣20×(60﹣10x ),利用配方法化简可求最大值.试题解析:解:(1)由题意得: y =60﹣10x (2)p =(200+x )(60﹣10x )=﹣2110x +40x +12000 (3)w =(200+x )(60﹣10x )﹣20×(60﹣10x ) =﹣2110x +42x +10800 =﹣110(x ﹣210)2+15210 当x =210时,w 有最大值.此时,x +200=410,就是说,当每个房间的定价为每天410元时,w 有最大值,且最大值是15210元.点睛:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.本题主要考查的是二次函数的应用,难度一般.5.如图①,在平面直角坐标系xOy 中,抛物线y=ax 2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y 轴交于点C.(1)求抛物线的表达式;(2)如图②,用宽为4个单位长度的直尺垂直于x 轴,并沿x 轴左右平移,直尺的左右两边所在的直线与抛物线相交于P 、 Q 两点(点P 在点Q 的左侧),连接PQ ,在线段PQ 上方抛物线上有一动点D ,连接DP 、DQ.①若点P 的横坐标为12-,求△DPQ 面积的最大值,并求此时点D 的坐标; ②直尺在平移过程中,△DPQ 面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.【答案】(1)抛物线y=-x 2+2x+3;(2)①点D ( 31524,);②△PQD 面积的最大值为8【解析】分析:(1)根据点A 、B 的坐标,利用待定系数法即可求出抛物线的表达式;(2)(I )由点P 的横坐标可得出点P 、Q 的坐标,利用待定系数法可求出直线PQ 的表达式,过点D 作DE ∥y 轴交直线PQ 于点E ,设点D 的坐标为(x ,-x 2+2x+3),则点E 的坐标为(x ,-x+54),进而即可得出DE 的长度,利用三角形的面积公式可得出S △DPQ =-2x 2+6x+72,再利用二次函数的性质即可解决最值问题; (II )假设存在,设点P 的横坐标为t ,则点Q 的横坐标为4+t ,进而可得出点P 、Q 的坐标,利用待定系数法可求出直线PQ 的表达式,设点D 的坐标为(x ,-x 2+2x+3),则点E 的坐标为(x ,-2(t+1)x+t 2+4t+3),进而即可得出DE 的长度,利用三角形的面积公式可得出S △DPQ =-2x 2+4(t+2)x-2t 2-8t ,再利用二次函数的性质即可解决最值问题.详解:(1)将A (-1,0)、B (3,0)代入y=ax 2+bx+3,得:309330a b a b -+⎧⎨++⎩==,解得:12a b -⎧⎨⎩==, ∴抛物线的表达式为y=-x 2+2x+3.(2)(I )当点P 的横坐标为-12时,点Q 的横坐标为72, ∴此时点P 的坐标为(-12,74),点Q 的坐标为(72,-94). 设直线PQ 的表达式为y=mx+n ,将P(-12,74)、Q(72,-94)代入y=mx+n,得:17247924m nm n⎧-+⎪⎪⎨⎪+-⎪⎩==,解得:154mn-⎧⎪⎨⎪⎩==,∴直线PQ的表达式为y=-x+54.如图②,过点D作DE∥y轴交直线PQ于点E,设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-x+54),∴DE=-x2+2x+3-(-x+54)=-x2+3x+74,∴S△DPQ=12DE•(x Q-x P)=-2x2+6x+72=-2(x-32)2+8.∵-2<0,∴当x=32时,△DPQ的面积取最大值,最大值为8,此时点D的坐标为(32,154).(II)假设存在,设点P的横坐标为t,则点Q的横坐标为4+t,∴点P的坐标为(t,-t2+2t+3),点Q的坐标为(4+t,-(4+t)2+2(4+t)+3),利用待定系数法易知,直线PQ的表达式为y=-2(t+1)x+t2+4t+3.设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-2(t+1)x+t2+4t+3),∴DE=-x2+2x+3-[-2(t+1)x+t2+4t+3]=-x2+2(t+2)x-t2-4t,∴S△DPQ=12DE•(x Q-x P)=-2x2+4(t+2)x-2t2-8t=-2[x-(t+2)]2+8.∵-2<0,∴当x=t+2时,△DPQ的面积取最大值,最大值为8.∴假设成立,即直尺在平移过程中,△DPQ面积有最大值,面积的最大值为8.点睛:本题考查了待定系数法求二次(一次)函数解析式、二次(一次)函数图象上点的坐标特征、三角形的面积以及二次函数的最值,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数表达式;(2)(I)利用三角形的面积公式找出S△DPQ=-2x 2+6x+72;(II )利用三角形的面积公式找出S △DPQ =-2x 2+4(t+2)x-2t 2-8t .6.在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
二次函数压轴题(含答案)

面积类1.如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.(1)求抛物线的解析式.(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M 的横坐标为m,请用m的代数式表示MN的长.(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m 的值;若不存在,说明理由.考点:二次函数综合题.专题:压轴题;数形结合.分析:(1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式.(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长.(3)设MN交x轴于D,那么△BNC的面积可表示为:S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,MN的表达式在(2)中已求得,OB的长易知,由此列出关于S△BNC、m的函数关系式,根据函数的性质即可判断出△BNC是否具有最大值.解答:解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:a(0+1)(0﹣3)=3,a=﹣1;∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.(2)设直线BC的解析式为:y=kx+b,则有:,解得;故直线BC的解析式:y=﹣x+3.已知点M的横坐标为m,MN∥y,则M(m,﹣m+3)、N(m,﹣m2+2m+3);∴故MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).(3)如图;∵S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,∴S△BNC=(﹣m2+3m)•3=﹣(m﹣)2+(0<m<3);∴当m=时,△BNC的面积最大,最大值为.2.如图,抛物线的图象与x轴交于A、B两点,与y轴交于C 点,已知B点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M 点的坐标.考点:二次函数综合题..专题:压轴题;转化思想.分析:(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.(3)△MBC的面积可由S△MBC=BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.解答:解:(1)将B(4,0)代入抛物线的解析式中,得:0=16a﹣×4﹣2,即:a=;∴抛物线的解析式为:y=x2﹣x﹣2.(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);∴OA=1,OC=2,OB=4,即:OC2=OA•OB,又:OC⊥AB,∴△OAC∽△OCB,得:∠OCA=∠OBC;∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,∴△ABC为直角三角形,AB为△ABC外接圆的直径;所以该外接圆的圆心为AB的中点,且坐标为:(,0).(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=x﹣2;设直线l∥BC,则该直线的解析式可表示为:y=x+b,当直线l与抛物线只有一个交点时,可列方程:x+b=x2﹣x﹣2,即:x2﹣2x﹣2﹣b=0,且△=0;∴4﹣4×(﹣2﹣b)=0,即b=﹣4;∴直线l:y=x﹣4.所以点M即直线l和抛物线的唯一交点,有:,解得:即M(2,﹣3).过M点作MN⊥x轴于N,S△BMC=S梯形OCMN+S△MNB﹣S△OCB=×2×(2+3)+×2×3﹣×2×4=4.平行四边形类3.如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,﹣3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.(1)分别求出直线AB和这条抛物线的解析式.(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.考点:二次函数综合题;解一元二次方程-因式分解法;待定系数法求一次函数解析式;待定系数法求二次函数解析式;三角形的面积;平行四边形的判定..专题:压轴题;存在型.分析:(1)分别利用待定系数法求两函数的解析式:把A(3,0)B(0,﹣3)分别代入y=x2+mx+n 与y=kx+b,得到关于m、n的两个方程组,解方程组即可;(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),用P点的纵坐标减去M的纵坐标得到PM的长,即PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,然后根据二次函数的最值得到当t=﹣=时,PM最长为=,再利用三角形的面积公式利用S△ABM=S△BPM+S△APM计算即可;(3)由PM∥OB,根据平行四边形的判定得到当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,然后讨论:当P在第四象限:PM=OB=3,PM最长时只有,所以不可能;当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3;当P在第三象限:PM=OB=3,t2﹣3t=3,分别解一元二次方程即可得到满足条件的t的值.解答:解:(1)把A(3,0)B(0,﹣3)代入y=x2+mx+n,得解得,所以抛物线的解析式是y=x2﹣2x﹣3.设直线AB的解析式是y=kx+b,把A(3,0)B(0,﹣3)代入y=kx+b,得,解得,所以直线AB的解析式是y=x﹣3;(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),因为p在第四象限,所以PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,当t=﹣=时,二次函数的最大值,即PM最长值为=,则S△ABM=S△BPM+S△APM==.(3)存在,理由如下:∵PM∥OB,∴当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,①当P在第四象限:PM=OB=3,PM最长时只有,所以不可能有PM=3.②当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3,解得t1=,t2=(舍去),所以P点的横坐标是;③当P在第三象限:PM=OB=3,t2﹣3t=3,解得t1=(舍去),t2=,所以P 点的横坐标是.所以P点的横坐标是或.4.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B 的两条性质.考点:二次函数综合题..专题:压轴题.分析:(1)利用旋转的性质得出A′(﹣1,0),B′(0,2),再利用待定系数法求二次函数解析式即可;(2)利用S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB,再假设四边形PB′A′B的面积是△A′B′O面积的4倍,得出一元二次方程,得出P点坐标即可;(3)利用P点坐标以及B点坐标即可得出四边形PB′A′B为等腰梯形,利用等腰梯形性质得出答案即可.解答:解:(1)△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,又A(0,1),B(2,0),O(0,0),∴A′(﹣1,0),B′(0,2).方法一:设抛物线的解析式为:y=ax2+bx+c(a≠0),∵抛物线经过点A′、B′、B,∴,解得:,∴满足条件的抛物线的解析式为y=﹣x2+x+2.方法二:∵A′(﹣1,0),B′(0,2),B(2,0),设抛物线的解析式为:y=a(x+1)(x﹣2)将B′(0,2)代入得出:2=a(0+1)(0﹣2),解得:a=﹣1,故满足条件的抛物线的解析式为y=﹣(x+1)(x﹣2)=﹣x2+x+2;(2)∵P为第一象限内抛物线上的一动点,设P(x,y),则x>0,y>0,P点坐标满足y=﹣x2+x+2.连接PB,PO,PB′,∴S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB,=×1×2+×2×x+×2×y,=x+(﹣x2+x+2)+1,=﹣x2+2x+3.∵A′O=1,B′O=2,∴△A′B′O面积为:×1×2=1,假设四边形PB′A′B的面积是△A′B′O面积的4倍,则4=﹣x2+2x+3,即x2﹣2x+1=0,解得:x1=x2=1,此时y=﹣12+1+2=2,即P(1,2).∴存在点P(1,2),使四边形PB′A′B的面积是△A′B′O面积的4倍.(3)四边形PB′A′B为等腰梯形,答案不唯一,下面性质中的任意2个均可.①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)或用符号表示:①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′;②P A′=B′B;③B′P∥A′B;④B′A′=PB.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)5.如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.(1)求抛物线顶点A的坐标;(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD 的形状;(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题;分类讨论.分析:(1)先根据抛物线的解析式得出其对称轴,由此得到顶点A的横坐标,然后代入直线l的解析式中即可求出点A的坐标.(2)由A点坐标可确定抛物线的解析式,进而可得到点B的坐标.则AB、AD、BD三边的长可得,然后根据边长确定三角形的形状.(3)若以点P、A、B、D为顶点的四边形是平行四边形,应分①AB为对角线、②AD为对角线两种情况讨论,即①AD PB、②AB PD,然后结合勾股定理以及边长的等量关系列方程求出P点的坐标.解答:解:(1)∵顶点A的横坐标为x=﹣=1,且顶点A在y=x﹣5上,∴当x=1时,y=1﹣5=﹣4,∴A(1,﹣4).(2)△ABD是直角三角形.将A(1,﹣4)代入y=x2﹣2x+c,可得,1﹣2+c=﹣4,∴c=﹣3,∴y=x2﹣2x﹣3,∴B(0,﹣3)当y=0时,x2﹣2x﹣3=0,x1=﹣1,x2=3∴C(﹣1,0),D(3,0),BD2=OB2+OD2=18,AB2=(4﹣3)2+12=2,AD2=(3﹣1)2+42=20,BD2+AB2=AD2,∴∠ABD=90°,即△ABD是直角三角形.(3)存在.由题意知:直线y=x﹣5交y轴于点E(0,﹣5),交x轴于点F(5,0)∴OE=OF=5,又∵OB=OD=3∴△OEF与△OBD都是等腰直角三角形∴BD∥l,即P A∥BD则构成平行四边形只能是P ADB或P ABD,如图,过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.设P(x1,x1﹣5),则G(1,x1﹣5)则PG=|1﹣x1|,AG=|5﹣x1﹣4|=|1﹣x1|P A=BD=3由勾股定理得:(1﹣x1)2+(1﹣x1)2=18,x12﹣2x1﹣8=0,x1=﹣2或4∴P(﹣2,﹣7)或P(4,﹣1),存在点P(﹣2,﹣7)或P(4,﹣1)使以点A、B、D、P为顶点的四边形是平行四边形.周长类6.如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上.(1)求抛物线对应的函数关系式;(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S 和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)根据抛物线y=经过点B(0,4),以及顶点在直线x=上,得出b,c 即可;(2)根据菱形的性质得出C、D两点的坐标分别是(5,4)、(2,0),利用图象上点的性质得出x=5或2时,y的值即可.(3)首先设直线CD对应的函数关系式为y=kx+b,求出解析式,当x=时,求出y即可;(4)利用MN∥BD,得出△OMN∽△OBD,进而得出,得到ON=,进而表示出△PMN的面积,利用二次函数最值求出即可.解答:解:(1)∵抛物线y=经过点B(0,4)∴c=4,∵顶点在直线x=上,∴﹣=﹣=,∴b=﹣;∴所求函数关系式为;(2)在Rt△ABO中,OA=3,OB=4,∴AB=,∵四边形ABCD是菱形,∴BC=CD=DA=AB=5,∴C、D两点的坐标分别是(5,4)、(2,0),当x=5时,y=,当x=2时,y=,∴点C和点D都在所求抛物线上;(3)设CD与对称轴交于点P,则P为所求的点,设直线CD对应的函数关系式为y=kx+b,则,解得:,∴,当x=时,y=,∴P(),(4)∵MN∥BD,∴△OMN∽△OBD,∴即得ON=,设对称轴交x于点F,则(PF+OM)•OF=(+t)×,∵,S△PNF=×NF•PF=×(﹣t)×=,S=(﹣),=﹣(0<t<4),a=﹣<0∴抛物线开口向下,S存在最大值.由S△PMN=﹣t2+t=﹣(t﹣)2+,∴当t=时,S取最大值是,此时,点M的坐标为(0,).等腰三角形类7.如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过点A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.考点:二次函数综合题..专题:压轴题;分类讨论.分析:(1)首先根据OA的旋转条件确定B点位置,然后过B做x轴的垂线,通过构建直角三角形和OB的长(即OA长)确定B点的坐标.(2)已知O、A、B三点坐标,利用待定系数法求出抛物线的解析式.(3)根据(2)的抛物线解析式,可得到抛物线的对称轴,然后先设出P点的坐标,而O、B坐标已知,可先表示出△OPB三边的边长表达式,然后分①OP=OB、②OP=BP、③OB=BP 三种情况分类讨论,然后分辨是否存在符合条件的P点.解答:解:(1)如图,过B点作BC⊥x轴,垂足为C,则∠BCO=90°,∵∠AOB=120°,∴∠BOC=60°,又∵OA=OB=4,∴OC=OB=×4=2,BC=OB•sin60°=4×=2,∴点B的坐标为(﹣2,﹣2);(2)∵抛物线过原点O和点A、B,∴可设抛物线解析式为y=ax2+bx,将A(4,0),B(﹣2.﹣2)代入,得,解得,∴此抛物线的解析式为y=﹣x2+x(3)存在,如图,抛物线的对称轴是直线x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),①若OB=OP,则22+|y|2=42,解得y=±2,当y=2时,在Rt△POD中,∠PDO=90°,sin∠POD==,∴∠POD=60°,∴∠POB=∠POD+∠AOB=60°+120°=180°,即P、O、B三点在同一直线上,∴y=2不符合题意,舍去,∴点P的坐标为(2,﹣2)②若OB=PB,则42+|y+2|2=42,解得y=﹣2,故点P的坐标为(2,﹣2),③若OP=BP,则22+|y|2=42+|y+2|2,解得y=﹣2,故点P的坐标为(2,﹣2),综上所述,符合条件的点P只有一个,其坐标为(2,﹣2),8.在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(﹣1,0),如图所示:抛物线y=ax2+ax﹣2经过点B.(1)求点B的坐标;(2)求抛物线的解析式;(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)根据题意,过点B作BD⊥x轴,垂足为D;根据角的互余的关系,易得B到x、y轴的距离,即B的坐标;(2)根据抛物线过B点的坐标,可得a的值,进而可得其解析式;(3)首先假设存在,分A、C是直角顶点两种情况讨论,根据全等三角形的性质,可得答案.解答:解:(1)过点B作BD⊥x轴,垂足为D,∵∠BCD+∠ACO=90°,∠ACO+∠CAO=90°,∴∠BCD=∠CAO,(1分)又∵∠BDC=∠COA=90°,CB=AC,∴△BCD≌△CAO,(2分)∴BD=OC=1,CD=OA=2,(3分)∴点B的坐标为(﹣3,1);(4分)(2)抛物线y=ax2+ax﹣2经过点B(﹣3,1),则得到1=9a﹣3a﹣2,(5分)解得a=,所以抛物线的解析式为y=x2+x﹣2;(7分)(3)假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:①若以点C为直角顶点;则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,(8分)过点P1作P1M⊥x轴,∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,∴△MP1C≌△DBC.(10分)∴CM=CD=2,P1M=BD=1,可求得点P1(1,﹣1);(11分)②若以点A为直角顶点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,(12分)过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,(13分)∴NP2=OA=2,AN=OC=1,可求得点P2(2,1),(14分)经检验,点P1(1,﹣1)与点P2(2,1)都在抛物线y=x2+x﹣2上.(16分)9.在平面直角坐标系中,现将一块等腰直角三角板放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),如图所示,抛物线y=ax2﹣ax﹣2经过点B.(1)求点B的坐标;(2)求抛物线的解析式;(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.考点:二次函数综合题..专题:代数几何综合题;压轴题.分析:(1)首先过点B作BD⊥x轴,垂足为D,易证得△BDC≌△COA,即可得BD=OC=1,CD=OA=2,则可求得点B的坐标;(2)利用待定系数法即可求得二次函数的解析式;(3)分别从①以AC为直角边,点C为直角顶点,则延长BC至点P1使得P1C=BC,得到等腰直角三角形ACP1,过点P1作P1M⊥x轴,②若以AC为直角边,点A为直角顶点,则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形ACP2,过点P2作P2N⊥y轴,③若以AC为直角边,点A为直角顶点,则过点A作AP3⊥CA,且使得AP3=AC,得到等腰直角三角形ACP3,过点P3作P3H⊥y轴,去分析则可求得答案.解答:解:(1)过点B作BD⊥x轴,垂足为D,∵∠BCD+∠ACO=90°,∠AC0+∠OAC=90°,∴∠BCD=∠CAO,又∵∠BDC=∠COA=90°,CB=AC,∴△BDC≌△COA,∴BD=OC=1,CD=OA=2,∴点B的坐标为(3,1);(2)∵抛物线y=ax2﹣ax﹣2过点B(3,1),∴1=9a﹣3a﹣2,解得:a=,∴抛物线的解析式为y=x2﹣x﹣2;(3)假设存在点P,使得△ACP是等腰直角三角形,①若以AC为直角边,点C为直角顶点,则延长BC至点P1使得P1C=BC,得到等腰直角三角形ACP1,过点P1作P1M⊥x轴,如图(1),∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,∴△MP1C≌△DBC,∴CM=CD=2,P1M=BD=1,∴P1(﹣1,﹣1),经检验点P1在抛物线y=x2﹣x﹣2上;②若以AC为直角边,点A为直角顶点,则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形ACP2,过点P2作P2N⊥y轴,如图(2),同理可证△AP2N≌△CAO,∴NP2=OA=2,AN=OC=1,∴P2(﹣2,1),经检验P2(﹣2,1)也在抛物线y=x2﹣x﹣2上;③若以AC为直角边,点A为直角顶点,则过点A作AP3⊥CA,且使得AP3=AC,得到等腰直角三角形ACP3,过点P3作P3H⊥y轴,如图(3),同理可证△AP3H≌△CAO,∴HP3=OA=2,AH=OC=1,∴P3(2,3),经检验P3(2,3)不在抛物线y=x2﹣x﹣2上;故符合条件的点有P1(﹣1,﹣1),P2(﹣2,1)两点.综合类10.如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).(1)求直线BC与抛物线的解析式;(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.考点:二次函数综合题..专题:压轴题.分析:(1)设直线BC的解析式为y=mx+n,将B(5,0),C(0,5)两点的坐标代入,运用待定系数法即可求出直线BC的解析式;同理,将B(5,0),C(0,5)两点∑的坐标代入y=x2+bx+c,运用待定系数法即可求出抛物线的解析式;(2)MN的长是直线BC的函数值与抛物线的函数值的差,据此可得出一个关于MN的长和M点横坐标的函数关系式,根据函数的性质即可求出MN的最大值;(3)先求出△ABN的面积S2=5,则S1=6S2=30.再设平行四边形CBPQ的边BC上的高为BD,根据平行四边形的面积公式得出BD=3,过点D作直线BC的平行线,交抛物线与点P,交x轴于点E,在直线DE上截取PQ=BC,则四边形CBPQ为平行四边形.证明△EBD 为等腰直角三角形,则BE=BD=6,求出E的坐标为(﹣1,0),运用待定系数法求出直线PQ的解析式为y=﹣x﹣1,然后解方程组,即可求出点P的坐标.解答:解:(1)设直线BC的解析式为y=mx+n,将B(5,0),C(0,5)两点的坐标代入,得,解得,所以直线BC的解析式为y=﹣x+5;将B(5,0),C(0,5)两点的坐标代入y=x2+bx+c,得,解得,所以抛物线的解析式为y=x2﹣6x+5;(2)设M(x,x2﹣6x+5)(1<x<5),则N(x,﹣x+5),∵MN=(﹣x+5)﹣(x2﹣6x+5)=﹣x2+5x=﹣(x﹣)2+,∴当x=时,MN有最大值;(3)∵MN取得最大值时,x=2.5,∴﹣x+5=﹣2.5+5=2.5,即N(2.5,2.5).解方程x2﹣6x+5=0,得x=1或5,∴A(1,0),B(5,0),∴AB=5﹣1=4,∴△ABN的面积S2=×4×2.5=5,∴平行四边形CBPQ的面积S1=6S2=30.设平行四边形CBPQ的边BC上的高为BD,则BC⊥BD.∵BC=5,∴BC•BD=30,∴BD=3.过点D作直线BC的平行线,交抛物线与点P,交x轴于点E,在直线DE上截取PQ=BC,则四边形CBPQ为平行四边形.∵BC⊥BD,∠OBC=45°,∴∠EBD=45°,∴△EBD为等腰直角三角形,BE=BD=6,∵B(5,0),∴E(﹣1,0),设直线PQ的解析式为y=﹣x+t,将E(﹣1,0)代入,得1+t=0,解得t=﹣1∴直线PQ的解析式为y=﹣x﹣1.解方程组,得,,∴点P的坐标为P1(2,﹣3)(与点D重合)或P2(3,﹣4).11.如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x 轴正半轴上,且OD=OC.(1)求直线CD的解析式;(2)求抛物线的解析式;(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P 点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)利用待定系数法求出直线解析式;(2)利用待定系数法求出抛物线的解析式;(3)关键是证明△CEQ与△CDO均为等腰直角三角形;(4)如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.利用轴对称的性质、两点之间线段最短可以证明此时△PCF的周长最小.如答图③所示,利用勾股定理求出线段C′C″的长度,即△PCF周长的最小值.解答:解:(1)∵C(0,1),OD=OC,∴D点坐标为(1,0).设直线CD的解析式为y=kx+b(k≠0),将C(0,1),D(1,0)代入得:,解得:b=1,k=﹣1,∴直线CD的解析式为:y=﹣x+1.(2)设抛物线的解析式为y=a(x﹣2)2+3,将C(0,1)代入得:1=a×(﹣2)2+3,解得a=.∴y=(x﹣2)2+3=x2+2x+1.(3)证明:由题意可知,∠ECD=45°,∵OC=OD,且OC⊥OD,∴△OCD为等腰直角三角形,∠ODC=45°,∴∠ECD=∠ODC,∴CE∥x轴,则点C、E关于对称轴(直线x=2)对称,∴点E的坐标为(4,1).如答图①所示,设对称轴(直线x=2)与CE交于点M,则M(2,1),∴ME=CM=QM=2,∴△QME与△QMC均为等腰直角三角形,∴∠QEC=∠QCE=45°.又∵△OCD为等腰直角三角形,∴∠ODC=∠OCD=45°,∴∠QEC=∠QCE=∠ODC=∠OCD=45°,∴△CEQ∽△CDO.(4)存在.如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.(证明如下:不妨在线段OD上取异于点F的任一点F′,在线段QE上取异于点P的任一点P′,连接F′C″,F′P′,P′C′.由轴对称的性质可知,△P′CF′的周长=F′C″+F′P′+P′C′;而F′C″+F′P′+P′C′是点C′,C″之间的折线段,由两点之间线段最短可知:F′C″+F′P′+P′C′>C′C″,即△P′CF′的周长大于△PCE的周长.)如答图③所示,连接C′E,∵C,C′关于直线QE对称,△QCE为等腰直角三角形,∴△QC′E为等腰直角三角形,∴△CEC′为等腰直角三角形,∴点C′的坐标为(4,5);∵C,C″关于x轴对称,∴点C″的坐标为(0,﹣1).过点C′作C′N⊥y轴于点N,则NC′=4,NC″=4+1+1=6,在Rt△C′NC″中,由勾股定理得:C′C″===.综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为.12.如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.(1)求该抛物线的解析式与顶点D的坐标.(2)试判断△BCD的形状,并说明理由.(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)利用待定系数法即可求得函数的解析式;(2)利用勾股定理求得△BCD的三边的长,然后根据勾股定理的逆定理即可作出判断;(3)分p在x轴和y轴两种情况讨论,舍出P的坐标,根据相似三角形的对应边的比相等即可求解.解答:解:(1)设抛物线的解析式为y=ax2+bx+c由抛物线与y轴交于点C(0,3),可知c=3.即抛物线的解析式为y=ax2+bx+3.把点A(1,0)、点B(﹣3,0)代入,得解得a=﹣1,b=﹣2∴抛物线的解析式为y=﹣x2﹣2x+3.∵y=﹣x2﹣2x+3=﹣(x+1)2+4∴顶点D的坐标为(﹣1,4);(2)△BCD是直角三角形.理由如下:解法一:过点D分别作x轴、y轴的垂线,垂足分别为E、F.∵在Rt△BOC中,OB=3,OC=3,∴BC2=OB2+OC2=18在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1,∴CD2=DF2+CF2=2在Rt△BDE中,DE=4,BE=OB﹣OE=3﹣1=2,∴BD2=DE2+BE2=20∴BC2+CD2=BD2∴△BCD为直角三角形.解法二:过点D作DF⊥y轴于点F.在Rt△BOC中,∵OB=3,OC=3∴OB=OC∴∠OCB=45°∵在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1∴DF=CF∴∠DCF=45°∴∠BCD=180°﹣∠DCF﹣∠OCB=90°∴△BCD为直角三角形.(3)①△BCD的三边,==,又=,故当P是原点O时,△ACP∽△DBC;②当AC是直角边时,若AC与CD是对应边,设P的坐标是(0,a),则PC=3﹣a,=,即=,解得:a=﹣9,则P的坐标是(0,﹣9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;③当AC是直角边,若AC与BC是对应边时,设P的坐标是(0,b),则PC=3﹣b,则=,即=,解得:b=﹣,故P是(0,﹣)时,则△ACP∽△CBD一定成立;④当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(d,0).则AP=1﹣d,当AC与CD是对应边时,=,即=,解得:d=1﹣3,此时,两个三角形不相似;⑤当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(e,0).则AP=1﹣e,当AC与DC是对应边时,=,即=,解得:e=﹣9,符合条件.总之,符合条件的点P的坐标为:.对应练习13.如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.考点:二次函数综合题..专题:代数几何综合题;压轴题.分析:(1)利用待定系数法求二次函数解析式解答即可;(2)利用待定系数法求出直线AC的解析式,然后根据轴对称确定最短路线问题,直线AC 与对称轴的交点即为所求点D;(3)根据直线AC的解析式,设出过点E与AC平行的直线,然后与抛物线解析式联立消掉y得到关于x的一元二次方程,利用根的判别式△=0时,△ACE的面积最大,然后求出此时与AC平行的直线,然后求出点E的坐标,并求出该直线与x轴的交点F的坐标,再求出AF,再根据直线l与x轴的夹角为45°求出两直线间的距离,再求出AC间的距离,然后利用三角形的面积公式列式计算即可得解.解答:解:(1)∵抛物线y=ax2+bx+3经过点A(1,0),点C(4,3),∴,解得,所以,抛物线的解析式为y=x2﹣4x+3;(2)∵点A、B关于对称轴对称,∴点D为AC与对称轴的交点时△BCD的周长最小,设直线AC的解析式为y=kx+b(k≠0),则,解得,所以,直线AC的解析式为y=x﹣1,∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的对称轴为直线x=2,当x=2时,y=2﹣1=1,∴抛物线对称轴上存在点D(2,1),使△BCD的周长最小;(3)如图,设过点E与直线AC平行线的直线为y=x+m,联立,消掉y得,x2﹣5x+3﹣m=0,△=(﹣5)2﹣4×1×(3﹣m)=0,即m=﹣时,点E到AC的距离最大,△ACE的面积最大,此时x=,y=﹣=﹣,∴点E的坐标为(,﹣),设过点E的直线与x轴交点为F,则F(,0),∴AF=﹣1=,∵直线AC的解析式为y=x﹣1,∴∠CAB=45°,∴点F到AC的距离为×=,又∵AC==3,∴△ACE的最大面积=×3×=,此时E点坐标为(,﹣).14.如图,已知抛物线y=﹣x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).(1)求抛物线的解析式及它的对称轴方程;(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;(3)试判断△AOC与△COB是否相似?并说明理由;(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)利用待定系数法求出抛物线解析式,利用配方法或利用公式x=求出对称轴方程;(2)在抛物线解析式中,令x=0,可求出点C坐标;令y=0,可求出点B坐标.再利用待定系数法求出直线BD的解析式;(3)根据,∠AOC=∠BOC=90°,可以判定△AOC∽△COB;(4)本问为存在型问题.若△ACQ为等腰三角形,则有三种可能的情形,需要分类讨论,逐一计算,避免漏解.解答:解:(1)∵抛物线y=﹣x2+bx+4的图象经过点A(﹣2,0),∴﹣×(﹣2)2+b×(﹣2)+4=0,解得:b=,∴抛物线解析式为y=﹣x2+x+4,又∵y=﹣x2+x+4=﹣(x﹣3)2+,∴对称轴方程为:x=3.(2)在y=﹣x2+x+4中,令x=0,得y=4,∴C(0,4);令y=0,即﹣x2+x+4=0,整理得x2﹣6x﹣16=0,解得:x=8或x=﹣2,∴A(﹣2,0),B(8,0).设直线BC的解析式为y=kx+b,把B(8,0),C(0,4)的坐标分别代入解析式,得:,解得k=,b=4,∴直线BC的解析式为:y=x+4.(3)可判定△AOC∽△COB成立.理由如下:在△AOC与△COB中,∵OA=2,OC=4,OB=8,∴,又∵∠AOC=∠BOC=90°,∴△AOC∽△COB.(4)∵抛物线的对称轴方程为:x=3,可设点Q(3,t),则可求得:AC===,AQ==,CQ==.i)当AQ=CQ时,有=,25+t2=t2﹣8t+16+9,解得t=0,∴Q1(3,0);ii)当AC=AQ时,有=,t2=﹣5,此方程无实数根,∴此时△ACQ不能构成等腰三角形;iii)当AC=CQ时,有=,整理得:t2﹣8t+5=0,解得:t=4±,∴点Q坐标为:Q2(3,4+),Q3(3,4﹣).综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(3,0),Q2(3,4+),Q3(3,4﹣).15.如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx﹣2的图象过C点.(1)求抛物线的解析式;(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为相等的两部分?(3)点P是抛物线上一动点,是否存在点P,使四边形P ACB为平行四边形?若存在,求出P点坐标;若不存在,说明理由.考点:二次函数综合题..专题:压轴题.分析:如解答图所示:(1)首先构造全等三角形△AOB≌△CDA,求出点C的坐标;然后利用点C的坐标求出抛物线的解析式;(2)首先求出直线BC与AC的解析式,设直线l与BC、AC交于点E、F,则可求出EF 的表达式;根据S△CEF=S△ABC,列出方程求出直线l的解析式;(3)首先作出▱P ACB,然后证明点P在抛物线上即可.解答:解:(1)如答图1所示,过点C作CD⊥x轴于点D,则∠CAD+∠ACD=90°.∵∠OBA+∠OAB=90°,∠OAB+∠CAD=90°,∴∠OAB=∠ACD,∠OBA=∠CAD.∵在△AOB与△CDA中,∴△AOB≌△CDA(ASA).∴CD=OA=1,AD=OB=2,∴OD=OA+AD=3,∴C(3,1).∵点C(3,1)在抛物线y=x2+bx﹣2上,∴1=×9+3b﹣2,解得:b=﹣.∴抛物线的解析式为:y=x2﹣x﹣2.(2)在Rt△AOB中,OA=1,OB=2,由勾股定理得:AB=.∴S△ABC=AB2=.设直线BC的解析式为y=kx+b,∵B(0,2),C(3,1),∴,解得k=﹣,b=2,。
二次函数压轴40道

二次函数压轴题1、如图,抛物线223y x x =--+的图象与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,点D 为抛物线的顶点.(1)直接写出A 、B 、C 三点的坐标;(2)点M 为线段AB 上一点(点M 不与点A 、B 重合),过点M 作x 轴的垂线,与直线AC 交于点E ,与抛物线交于点P ,过点P 作PQ ∥AB 交抛物线于点Q ,过点Q 作QN ⊥x 轴于点N ,若点P 在点Q 左边,当矩形PMNQ 的周长最大时,求△AEM 的面积;(3)在(2)的条件下,当矩形PMNQ 的周长最大时,连接DQ ,过抛物线上一点F 作y 轴的平行线,与直线AC 交于点G (点G 在点F 的上方).若FG =,求点F 的坐标.xyPBN O MAQ CD E2、如图,抛物线2344y ax ax =++与x 轴交于点A、B(A 在B 的左侧),过点A 的直线3y kx k =+交抛物线于另一点C.(1)求抛物线的解析式;(2)连接BC,过点B 作BD⊥BC,交直线AC 于点D,若BC=5BD,求k 的值;(3)将直线3y kx k =+向上平移4个单位,平移后的直线交抛物线于E、F 两点,求△AEF 的面积的最小值.xyAOB CM D3、如图,已知抛物线223y x x =-++与x 轴交于A、B 两点(点A 在点B 的左边),与y 轴交于点C,连接BC.(1)直接写出A、B、C 三点的坐标;(2)点P 为线段BC 上的一点(不与B、C 重合),PM∥y 轴交抛物线于M,交x 轴于N,当△BCM 的面积最大时,求△BPN 的周长;(3)在(2)的条件下,在抛物线的对称轴上存在点Q,使△CNQ 为直角三角形,求点Q 的坐标.xyMCO B N A P4、如图,在平面直角坐标系中,直线1y kx =+与y 轴交于点C,与抛物线214y x =交于点A、B(点A 在点B 左侧),分别过A、B 两点作直线y=-1的垂线,垂足为E、F.(1)求证:AC=AE;(2)设△ACE、△BCF、△ECF 的面积分别为S1、S2、S3,若S1+S2S3=32,求k 的值;(3)M 为EF 的中点,连接MC 并延长交抛物线于点P,连接PA、BM.是否存在这样的点M,使△PAC 与△BMC 相似?若存在,求出所有符合条件的点M 的坐标;若不存在,请说明理由.xyBA OE FM C5、如图,抛物线1(2)()(0)y x x m m m=-+->与x 轴交于A 、B 两点(A 在B 的左侧),与y 轴交于点C ,连接AC 、BC .(1)若△ABC 为直角三角形,求m 的值;(2)在(1)的条件下,点D 是第一象限抛物线上一动点,过D 点的直线交x 轴、y 轴的正半轴于E 、F ,连接OD ,当OD 的长最小时,求△OEF 面积的最小值;(3)直线y =12x +b 经过点B ,与抛物线交于另一点G ,点P 在y 轴上,点Q 在抛物线上,以点B 、G 、P 、Q 为顶点的四边形能否成为矩形?若能,求出点P 的坐标;若不能,请说明理由.CBAxy CBAxy 备用图6、如图,抛物线2(2)4y x m x =-++的顶点C 在x 轴正半轴上,直线y =x +2与抛物线交于A 、B 两点(点A 在点B 的左侧).(1)求m 的值;(2)点P 是抛物线上一点,当△PAB 的面积是△ABC 面积的2倍时,求点P 的坐标;(3)将直线AB 向下平移t (t >0)个单位,平移后的直线与抛物线交于'A 、'B 两点('A 在'B 的左侧),当''A B C △为直角三角形时,求t 的值.A B xyCO ABxyCO 备用图7、已知抛物线2y x bx c =-++与x 轴交于点A (m -2,0)和B (2m +1,0)(点A 在点B 的左侧),与y 轴交于点C ,顶点为P ,对称轴为直线x =1.(1)求抛物线的解析式;(2)直线y =kx +2(k ≠0)与抛物线相交于不同两点M (x 1,y 1)、N (x 2,y 2)(x 1<x 2),当|x 1-x 2|最小时,求M 、N 两点的坐标;(3)若线段OB 在x 轴上移动,首尾顺次连接点O 、B 、P 、C 构成多边形的周长为L ,求L 最小值时点O 、B 移动后的坐标及L 的最小值.xyOABCP8、如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.(1)求该二次函数的解析式;(2)点G是线段AC上的动点(点G与线段AC的端点不重合),若△ABG与△ABC相似,求点G的坐标;(3)设图象M的对称轴为l,点D(m,n)(-1<m<2)是图象M上一动点,当△ACD的面积为278时,点D关于l的对称点为E,能否在图象M和l上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形.若能,求出点P的坐标;若不能,说明理由.lyB AOGDC xlyBAOGDCxHF。
2024年中考数学高频压轴题训练——二次函数压轴题(角度问题)(含答案)

2024年中考数学高频压轴题训练——二次函数压轴题(角度问题)(1)求抛物线的解析式;(2)抛物线上是否存在点,使P存在,请说明理由.(1)求该抛物线的函数表达式;(2)在直线上是否存在点,使说明理由.(3)为第一象限内抛物线上的一个动点,且在直线,垂足为,以点为圆心,,且不经过点l C P PM l ⊥M M 2PAB PT S =V M e (4.如图,已知顶点为的抛物线与x 轴交于A ,B 两点,且.(1)求点B 的坐标;(2)求二次函数的解析式;(3)作直线,问抛物线上是否存在点M ,使得,若存在,求出点M 的坐标;若不存在,请说明理由.5.如图,抛物线与x 轴交于A 、B 两点,,,与y 轴交于点C ,连接.()0,6C -()20y ax b a =+≠OC OB =()20y ax b a =+≠CB ()20y ax b a =+≠15MCB ∠=︒24y ax bx =+-()2,0A -()8,0B AC BC 、(1)求抛物线的解析式;(2)求证:;(3)点P 在抛物线上,且,求点P的坐标.6.如图,在平面直角坐标系中,已知抛物线与x 轴交于、两点,与y 轴交于点C ,连接.(1)求抛物线的解析式;(2)在对称轴上是否存在一点M ,使,若存在,请求出点M 的坐标;若不存在,请说明理由;(3)若点P 是直线下方的抛物线上的一个动点,作于点D ,当的值最大时,求此时点P 的坐标及的最大值.∠=∠ACO ABC PCB ACO ∠=∠()230y ax bx a =+-≠()3,0A ()1,0B -AC MCA MAC ∠=∠AC PD AC ⊥PD PD(1)试求抛物线的解析式;(2)点P 是直线下方抛物线上一动点,当的面积最大时,求点P 的坐标;(3)若M 是抛物线上一点,且,请直接写出点M 的坐标.BC BCP V MCB ABC ∠=∠(1)求此抛物线的解析式;(2)点E 是AC 延长线上一点,的平分线CD 交⊙于点D ,连接BD ,求点D 的坐标;(3)在(2)的条件下,抛物线上是否存在点P ,使得?如果存在,请求出点P 的坐标;如果不存在,请说明理由.9.综合与实践:如图,抛物线与x 轴交于点和点,与y 轴交于点C ,连接,点D 在抛物线上.(1)求抛物线的解析式;(2)小明探究点D 位置时发现:如图1,点D 在第一象限内的抛物线上,连接,,面积存在最大值,请帮助小明求出面积的最大值;(3)小明进一步探究点D 位置时发现:点D 在抛物线上移动,连接,存在BCE ∠O 'PDB CBD ∠=∠22y ax bx =++()1,0A -()4,0B BC BD CD BCD △BCD △CD(1)求抛物线的解析式.(2)如图1,过点D 作轴,垂足为M ,点P 在直线P 作,,求的最大值,以及此时点(3)将原抛物线沿射线方向平移个单位长度,在平移后的抛物线上存在点得,请写出所有符合条件的点G 的横坐标,并写出其中一个的求解过DM x ⊥PE AD ⊥PF DM ⊥2PE PF +CA 5245CAG ∠=︒(1)填空:___________,___________;(2)点为直线上方抛物线上一动点.①连接、,设直线交线段于点,求的最大值;②过点作于点,连接,是否存在点,使得中的,若存在,求出点的坐标;若不存在,请说明理由.(1)求抛物线的解析式;b =c =D AC BC CD BD AC E DE EBD DF AC ⊥F CD D CDF V 2DCF BAC ∠=∠D(1)求抛物线的解析式;(2)抛物线上是否存在点D ,使得?若存在,求出所有点不存在,请说明理由;(3)如图2,点E 是点B 关于抛物线对称轴的对称点,点F 是直线OB 动点,EF 与直线OB 交于点G .设和的面积分别为值.DOB OBC ∠=∠BFG V BEG V S14.如图,在平面直角坐标系中,点为坐标原点,抛物线与轴交于、两点且点,,与轴的负半轴交于点,.(1)求此抛物线的解析式;(2)在(1)的条件下,连接,点为直线下方的抛物线上的一点,过点作交于点,交直线于点,若,求点的坐标.(3)在(1)的条件下,点为该抛物线的顶点,过点作轴的平行线交抛物线于另一点,过点作于点,该抛物线对称轴右侧的抛物线上有一点,连接交于点,当时,求的度数.15.已知抛物线与轴相交于点,,与轴相交于点.O 2y x bx c =++x A B (3B 0)y C OB OC =AC P BC P PQ AC ∥AB Q BC D PD DQ =P D C x R R RH AB ⊥H M DM RH Q 2MQ RQ =MQH ∠24y ax bx =++x ()1,0A ()4,0B y C参考答案:的值最大时,此时,。
(完整版),二次函数压轴题含答案,推荐文档

∵二次函数的最小值为-4,∴ y 5 .
当 y 5 时, x 2,或x 4 .
故 P 点坐标为(-2,5)或(4,5)……………7 分
(3)如图 1,当直线 y x b(b 1) 经过 A 点时,可得 b 1.……………8 分 当直线 y x b(b 1) 经过 B 点时,可得 b 3.…………9 分
1.已知:如图一次函数 y= 1 x+1 的图象与 x 轴交于点 A,与 y 轴交于点 B;二次函数 y= 2
1 x2+bx+c 的图象与一次函数 y= 1 x+1 的图象交于 B、C 两点,与 x 轴交于 D、E 两
2
2
点且 D 点坐标为(1,0) (1)求二次函数的解析式; (2)求四边形 BDEC 的面积 S; (3)在 x 轴上是否存在点 P,使得△PBC 是以 P 为直角顶点的直角三角形?若存在,求出 所有的点 P,若不存在,请说明理由.
∴A,B 两点的坐标分别为 A(-1,0),B(3,0)………………………………4 分
(2)
在二次函数的图象上存在点 P,使 SPAB
5 4 SMAB …………………………5 分
设
p(x, y), 则 SPAB
1 2
AB
y
2
y
,又 S MAB
1 2
AB
4
8,
∴ 2 y 5 8,即y 5. 4
△OAB 是等腰直角三角形. (1)求过 A、B、C 三点的抛物线的解析式;
(2)若直线 CD∥AB 交抛物线于 D 点,求 D 点的坐标; (3)若 P 点是抛物线上的动点,且在第一象限,那么△PAB 是否有最大面积?若有, 求出此时 P 点的坐标和△PAB 的最大面积;若没有,请说明理由.
(完整word)二次函数压轴题(含答案),推荐文档

4.如图,已知抛物线 y=ax2+bx+c(a≠0)的对 称轴为直线 x=﹣1,且抛物线经过 A(1,0), C(0,3)两点,与 x 轴交于点 B. (1)若直线 y=mx+n 经过 B、C 两点,求直线 BC 和抛物线的解析式; (2)在抛物线的对称轴 x=﹣1 上找一点 M,使点 M 到点 A 的距离与到点 C 的距离之和最小,求 出点 M 的坐标; (3)设点 P 为抛物线的对称轴 x=﹣1 上的一个动 点,求使△BPC 为直角三角形的点 P 的坐标.
12.如图,在平面直角坐标系 xOy 中,A、B 为 x 轴上两点,C、D 为 y 轴上的两点,经过点 A、C、B 的抛物线的一部分 C1 与经过点 A、D、B 的抛物线的一部分 C2 组合成一条封闭 曲线,我们把这条封闭曲线成为“蛋线”.已知点 C 的坐标为(0,﹣ ),点 M 是抛物线
C2:y=mx2﹣2mx﹣3m(m<0)的顶点. (1)求 A、B 两点的坐标; (2)“蛋线”在第四象限上是否存在一点 P,使得
6.如图,抛物线经过 A(﹣1,0),B(5,0), C(0,﹣ )三点. (Ⅰ)求抛物线的解析式; (Ⅱ)在抛物线的对称轴上有一点 P,使 PA+PC
的值最小,求点 P 的坐标. (Ⅲ)点 M 为 x 轴上一动点,在抛物线上是否
存在一点 N,使以 A,C,M,N 四点构成的 四边形为平行四边形?若存在,求点 N 的坐 标;若不存在,请说明理由.
B(3,0)两点,与 y 轴交于点 C(0,3). (1)求抛物线的解析式; (2)设抛物线的顶点为 D,在其对称轴的右侧
的抛物线上是否存在点 P,使得△PDC 是等 腰三角形?若存在,求出符合条件的点 P 的 坐标;若不存在,请说明理由; (3)点 M 是抛物线上一点,以 B,C,D,M 为 顶点的四边形是直角梯形,试求出点 M 的坐 标.
二次函数压轴题集锦带答案(2024年中考真题)

二次函数压轴题集锦带答案(2024年中考真题)1.(24年安徽中考)已知物线2y x bx =-+(b 为常数)的顶点横坐标比抛物线22y x x =-+的顶点横坐标大1. (1)求b 的值;(2)点11(,)A x y 在抛物线22y x x =-+上,点11(,)B x t y h ++在抛物线2y x bx =-+上. (i)若3h t =,且10,0x t >,求h 的值; (ii)若 11x t =-,求h 的最大值.2.(24年包头中考)如图,在平面直角坐标系中,抛物线22yx bxc 与x 轴相交于()1,0A ,B 两点(点A 在点B 左侧),顶点为()2,M d ,连接AM .(1)求该抛物线的函数表达式;(2)如图1,若C 是y 轴正半轴上一点,连接,AC CM .当点C 的坐标为10,2⎛⎫ ⎪⎝⎭时,求证:ACM BAM ∠=∠;(3)如图2,连接BM ,将ABM 沿x 轴折叠,折叠后点M 落在第四象限的点M '处,过点B 的直线与线段AM '相交于点D ,与y 轴负半轴相交于点E .当87BD DE =时,3ABD S △与2M BD S '△是否相等?请说明理由.3.(24年成都中考)如图,在平面直角坐标系xOy 中,抛物线()2:230L y ax ax a a =-->与x 轴交于,A B 两点(点A 在点B 的左侧),其顶点为C ,D 是抛物线第四象限上一点. (1)求线段AB 的长(2)当1a =时,若ACD ∆的面积与ABD ∆的面积相等,求tan ABD ∠的值:(3)延长CD =交x =轴于点E =,当AD DE =时,将ADB ∆沿DE 方向平移得到A EB ''∆.将抛物线L 平移得到抛物线L ',使得点A ',B '都落在抛物线L '上.试判断抛物线L '与L 是否交于某个定点.若是,求出该定点坐标;若不是,请说明理由.4.(24年重庆中考)如图,在平面直角坐标系中,抛物线()240y ax bx a =++≠经过点()1,6-,与y 轴交于点C ,与x 轴交于A B ,两点(A 在B 的左侧),连接tan 4AC BC CBA ∠=,,.(1)求抛物线的表达式(2)点P 是射线CA 上方抛物线上的一动点,过点P 作PE x ⊥轴,垂足为E ,交AC 于点D .点M 是线段DE 上一动点,MN y ⊥轴,垂足为N ,点F 为线段BC 的中点,连接AM NF ,.当线段PD 长度取得最大值时,求AM MN NF ++的最小值(3)将该抛物线沿射线CA 方向平移,使得新抛物线经过(2)中线段PD 长度取得最大值时的点D ,且与直线AC 相交于另一点K .点Q 为新抛物线上的一个动点,当QDK ACB ∠∠=时,直接写出所有符合条件的点Q 的坐标.5.(24年浙江中考)已知二次函数2y x bx c =++(b ,c 为常数)的图象经过点(2,5)A -,对称轴为直线12x =-.(1)求二次函数的表达式(1)若点(1,7)B 向上平移2个单位长度,向左平移(0)m m >个单位长度后,恰好落在2y x bx c =++的图象上,求m 的值(3)当2≤a ≤n 时,二次函数2y x bx c =++的最大值与最小值的差为94,求n 的取值范围.6.(24年呼伦贝尔中考)如图,在平面直角坐标系中,二次函数()20y ax bx c a =++≠的图像经过原点和点()4,0A .经过点A 的直线与该二次函数图象交于点()1,3B ,与y 轴交于点C .(1)求二次函数的解析式及点C 的坐标;(2)点P 是二次函数图象上的一个动点,当点P 在直线AB 上方时,过点P 作PE x ⊥轴于点E ,与直线AB 交于点D ,设点P 的横坐标为m . ①m 为何值时线段PD 的长度最大,并求出最大值;①是否存在点P ,使得BPD △与AOC 相似.若存在,请求出点P 坐标;若不存在,请说明理由.7.(24年广州中考)已知抛物线232:621(0)G y ax ax a a a =--++>过点()1,2A x 和点()2,2B x ,直线2:l y m x n =+过点(3,1)C ,交线段AB 于点D ,记CDA 的周长为1C ,CDB △的周长为2C ,且122C C =+.(1)求抛物线G 的对称轴 (2)求m 的值(3)直线l 绕点C 以每秒3︒的速度顺时针旋转t 秒后(045)t ≤<得到直线l ',当l AB '∥时,直线l '交抛物线G 于E ,F 两点. ①求t 的值①设AEF △的面积为S ,若对于任意的0a >,均有S k ≥成立,求k 的最大值及此时抛物线G 的解析式.8.(24年绥化中考)综合与探究如图,在平面直角坐标系中,已知抛物线2y x bx c =-++与直线相交于A ,B 两点,其中点()3,4A ,()0,1B .(1)求该抛物线的函数解析式.(2)过点B 作BC x ∥轴交抛物线于点C ,连接AC ,在抛物线上是否存在点P 使1tan tan 6BCP ACB ∠=∠.若存在,请求出满足条件的所有点P 的坐标;若不存在,请说明理由.(提示:依题意补全图形,并解答)(3)将该抛物线向左平移2个单位长度得到()2111110y a x b x c a =++≠,平移后的抛物线与原抛物线相交于点D ,点E 为原抛物线对称轴上的一点,F 是平面直角坐标系内的一点,当以点B ,D ,E ,F 为顶点的四边形是菱形时,请直接写出点F 的坐标.9.(24年上海中考)在平面直角坐标系中,已知平移抛物线213y x =后得到的新抛物线经过50,3A ⎛⎫- ⎪⎝⎭和(5,0)B .(1)求平移后新抛物线的表达式(2)直线x m =(0m >)与新抛物线交于点P,与原抛物线交于点Q . ①如果PQ 小于3,求m 的取值范围①记点P 在原抛物线上的对应点为P ',如果四边形P BPQ '有一组对边平行,求点P 的坐标.10.(24年乐山中考)在平面直角坐标系xOy 中,我们称横坐标、纵坐标都为整数的点为“完美点”.抛物线222y ax ax a =-+(a 为常数且0a >)与y 轴交于点A .(1)若1a =,求抛物线的顶点坐标;(2)若线段OA (含端点)上的“完美点”个数大于3个且小于6个,求a 的取值范围;(3)若抛物线与直线y x =交于M ,N 两点,线段MN 与抛物线围成的区域(含边界)内恰有4个“完美点”,求a 的取值范围.11.(24年甘肃武威中考)如图1,抛物线()2y a x h k =-+交x 轴于O,()4,0A 两点,顶点为(2,B .点C 为OB 的中点.(1)求抛物线2()y a x h k =-+的表达式;(2)过点C 作CH OA ⊥,垂足为H,交抛物线于点E .求线段CE 的长.(3)点D 为线段OA 上一动点(O 点除外),在OC 右侧作平行四边形OCFD .①如图2,当点F 落在抛物线上时,求点F 的坐标;①如图3,连接BD ,BF ,求BD BF +的最小值.12.(24年枣庄中考)在平面直角坐标系xOy 中,点()2,3P -在二次函数()230y ax bx a =+->的图像上,记该二次函数图像的对称轴为直线x m =.(1)求m 的值(2)若点(),4Q m -在23y ax bx =+-的图像上,将该二次函数的图像向上平移5个单位长度,得到新的二次函数的图像.当04x ≤≤时,求新的二次函数的最大值与最小值的和(3)设23y ax bx =+-的图像与x 轴交点为()1,0x ,()()212,0x x x <.若2146x x <-<,求a 的取值范围.13.(24年四川广安中考)如图,抛物线223y x bx c =-++与x 轴交于A ,B 两点,与y 轴交于点C ,点A 坐标为(1,0)-,点B 坐标为(3,0).(1)求此抛物线的函数解析式.(2)点P 是直线BC 上方抛物线上一个动点,过点P 作x 轴的垂线交直线BC 于点D ,过点P 作y 轴的垂线,垂足为点E ,请探究2PD PE +是否有最大值?若有最大值,求出最大值及此时P 点的坐标;若没有最大值,请说明理由.(3)点M 为该抛物线上的点,当45∠=︒MCB 时,请直接写出所有满足条件的点M 的坐标.14.(24年四川南充中考)已知抛物线2y x bx c =-++与x 轴交于点()1,0A -,()3,0B .(1)求抛物线的解析式;(2)如图1,抛物线与y 轴交于点C ,点P 为线段OC 上一点(不与端点重合),直线PA ,PB 分别交抛物线于点E ,D ,设PAD 面积为1S ,PBE △面积为2S ,求12S S 的值; (3)如图2,点K 是抛物线对称轴与x 轴的交点,过点K 的直线(不与对称轴重合)与抛物线交于点M ,N ,过抛物线顶点G 作直线l x ∥轴,点Q 是直线l 上一动点.求QM QN +的最小值.15.(24年四川泸州中考)如图,在平面直角坐标系xOy 中,已知抛物线23y ax bx =++经过点()3,0A ,与y 轴交于点B,且关于直线1x =对称.(1)求该抛物线的解析式;(2)当1x t -≤≤时,y 的取值范围是021y t ≤≤-,求t 的值;(3)点C 是抛物线上位于第一象限的一个动点,过点C 作x 轴的垂线交直线AB 于点D,在y 轴上是否存在点E,使得以B,C,D,E 为顶点的四边形是菱形?若存在,求出该菱形的边长;若不存在,说明理由.16.(24年河北中考)如图,抛物线21:2C y ax x =-过点(4,0),顶点为Q .抛物线22211:()222C y x t t =--+-(其中t 为常数,且2t >),顶点为P .(1)直接写出a 的值和点Q 的坐标.(2)嘉嘉说:无论t 为何值,将1C 的顶点Q 向左平移2个单位长度后一定落在2C 上. 淇淇说:无论t 为何值,2C 总经过一个定点.请选择其中一人的说法进行说理.(3)当4t =时①求直线PQ 的解析式.①作直线l PQ ∥,当l 与2C 的交点到x 轴的距离恰为6时,求l 与x 轴交点的横坐标.(4)设1C 与2C 的交点A,B 的横坐标分别为,A B x x ,且A B x x <.点M 在1C 上,横坐标为()2B m m x ≤≤.点N 在2C 上,横坐标为()A n x n t ≤≤.若点M 是到直线PQ 的距离最大的点,最大距离为d ,点N 到直线PQ 的距离恰好也为d ,直接用含t 和m 的式子表示n.17.(24年武汉中考)抛物线215222y x x =+-交x 轴于A ,B 两点(A 在B 的右边),交y 轴于点C .(1)直接写出点A ,B ,C 的坐标(2)如图(1),连接AC ,BC ,过第三象限的抛物线上的点P 作直线PQ AC ∥,交y 轴于点Q .若BC 平分线段PQ ,求点P 的坐标(3)如图(2),点D 与原点O 关于点C 对称,过原点的直线EF 交抛物线于E ,F 两点(点E 在x 轴下方),线段DE 交抛物线于另一点G ,连接FG .若90EGF ∠=︒,求直线DE 的解析式.18.(24年四川德阳中考)如图,抛物线2y x x c =-+与x 轴交于点()1,0A -和点B ,与y 轴交于点C .(1)求抛物线的解析式;(2)当02x <≤时,求2y x x c =-+的函数值的取值范围;(3)将拋物线的顶点向下平移34个单位长度得到点M ,点P 为抛物线的对称轴上一动点,求PA PM +的最小值.19.(24年湖北中考)如图,二次函数23y x bx =-++交x 轴于(1,0)A -和B ,交y 轴于C .(1)求b 的值.(2)M 为函数图像上一点,满足MAB ACO ∠=∠,求M 点的横坐标.(3)将二次函数沿水平方向平移,新的图像记为L ,L 与y 轴交于点D ,记DC d =,记L 顶点横坐标为n .①求d 与n 的函数解析式.②记L 与x 轴围成的图像为,U U 与ABC ∆重合部分(不计边界)记为W ,若d 随n 增加而增加,且W 内恰有2个横坐标与纵坐标均为整数的点,直接写出n 的取值范围。
中考数学二次函数-经典压轴题附答案解析

中考数学二次函数-经典压轴题附答案解析一、二次函数1.如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.(1)求抛物线的解析式.(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.【答案】(1)y=﹣x2﹣2x+3;(2)点P(32-,154);(3)符合条件的点D的坐标为D1(0,3),D2(﹣6,﹣3),D3(﹣2,﹣7).【解析】【分析】(1)令y=0,求出点A的坐标,根据抛物线的对称轴是x=﹣1,求出点C的坐标,再根据待定系数法求出抛物线的解析式即可;(2)设点P(m,﹣m2﹣2m+3),利用抛物线与直线相交,求出点B的坐标,过点P作PF∥y 轴交直线AB于点F,利用S△ABP=S△PBF+S△PFA,用含m的式子表示出△ABP的面积,利用二次函数的最大值,即可求得点P的坐标;(3)求出点E的坐标,然后求出直线BC、直线BE、直线CE的解析式,再根据以点B、E、C、D为顶点的四边形是平行四边形,得到直线D1D2、直线D1D3、直线D2D3的解析式,即可求出交点坐标.【详解】解:(1)令y=0,可得:x﹣1=0,解得:x=1,∴点A(1,0),∵抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,∴﹣1×2﹣1=﹣3,即点C(﹣3,0),∴309330a ba b++⎧⎨-+⎩==,解得:12ab-⎧⎨-⎩=,=∴抛物线的解析式为:y=﹣x2﹣2x+3;(2)∵点P在直线AB上方的抛物线上运动,∴设点P(m,﹣m2﹣2m+3),∵抛物线与直线y=x﹣1交于A、B两点,∴2231y x xy x⎧--+⎨-⎩==,解得:1145xy-⎧⎨-⎩==,221xy=,=⎧⎨⎩∴点B(﹣4,﹣5),如图,过点P作PF∥y轴交直线AB于点F,则点F(m,m﹣1),∴PF=﹣m2﹣2m+3﹣m+1=﹣m2﹣3m+4,∴S△ABP=S△PBF+S△PFA=12(﹣m2﹣3m+4)(m+4)+12(﹣m2﹣3m+4)(1﹣m)=-52(m+32)2+1258,∴当m=32-时,P最大,∴点P(32-,154).(3)当x=﹣1时,y=﹣1﹣1=﹣2,∴点E(﹣1,﹣2),如图,直线BC的解析式为y=5x+15,直线BE的解析式为y=x﹣1,直线CE的解析式为y =﹣x﹣3,∵以点B、C、E、D为顶点的四边形是平行四边形,∴直线D1D3的解析式为y=5x+3,直线D1D2的解析式为y=x+3,直线D2D3的解析式为y=﹣x﹣9,联立533y xy x+⎧⎨+⎩==得D1(0,3),同理可得D2(﹣6,﹣3),D3(﹣2,﹣7),综上所述,符合条件的点D的坐标为D1(0,3),D2(﹣6,﹣3),D3(﹣2,﹣7).【点睛】本题考查二次函数的综合应用,解决第(2)小题中三角形面积的问题时,找到一条平行或垂直于坐标轴的边是关键;对于第(3)小题,要注意分类讨论、数形结合的运用,不要漏解.2.已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.(1)判断顶点M是否在直线y=4x+1上,并说明理由.(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(14,y1),D(34,y2)都在二次函数图象上,试比较y1与y2的大小.【答案】(1)点M在直线y=4x+1上;理由见解析;(2)x的取值范围是x<0或x>5;(3)①当0<b<12时,y1>y2,②当b=12时,y1=y2,③当12<b<45时,y1<y2.【解析】【分析】(1)根据顶点式解析式,可得顶点坐标,根据点的坐标代入函数解析式检验,可得答案;(2)根据待定系数法,可得二次函数的解析式,根据函数图象与不等式的关系:图象在下方的函数值小,可得答案;(3)根据解方程组,可得顶点M的纵坐标的范围,根据二次函数的性质,可得答案.【详解】(1)点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,∴M的坐标是(b,4b+1),把x=b代入y=4x+1,得y=4b+1,∴点M在直线y=4x+1上;(2)如图1,直线y=mx+5交y轴于点B,∴B点坐标为(0,5)又B在抛物线上,∴5=﹣(0﹣b)2+4b+1=5,解得b=2,二次函数的解析是为y=﹣(x﹣2)2+9,当y=0时,﹣(x﹣2)2+9=0,解得x1=5,x2=﹣1,∴A(5,0).由图象,得当mx+5>﹣(x﹣b)2+4b+1时,x的取值范围是x<0或x>5;(3)如图2,∵直线y=4x+1与直线AB交于点E,与y轴交于F,A(5,0),B(0,5)得直线AB的解析式为y=﹣x+5,联立EF,AB得方程组415 y xy x=+⎧⎨=-+⎩,解得45215xy⎧=⎪⎪⎨⎪=⎪⎩,∴点E(45,215),F(0,1).点M在△AOB内,1<4b+1<215,∴0<b<45.当点C,D关于抛物线的对称轴对称时,b﹣14=34﹣b,∴b=12,且二次函数图象开口向下,顶点M在直线y=4x+1上,综上:①当0<b<12时,y1>y2,②当b=12时,y1=y2,③当12<b<45时,y1<y2.【点睛】本题考查了二次函数综合题,解(1)的关键是把点的坐标代入函数解析式检验;解(2)的关键是利用函数图不等式的关系:图象在上方的函数值大;解(3)的关键是解方程组得出顶点M的纵坐标的范围,又利用了二次函数的性质:a<0时,点与对称轴的距离越小函数值越大.3.如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.(1)求抛物线的表达式;(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.(3)如图2,连接BC,PB,PC,设△PBC的面积为S.①求S关于t的函数表达式;②求P点到直线BC的距离的最大值,并求出此时点P的坐标.【答案】(1)y=﹣x2+2x+3.(2)当t=2时,点M的坐标为(1,6);当t≠2时,不存在,理由见解析;(3)y=﹣x+3;P点到直线BC的距离的最大值为28,此时点P的坐标为(32,154).【解析】【分析】(1)由点A、B的坐标,利用待定系数法即可求出抛物线的表达式;(2)连接PC,交抛物线对称轴l于点E,由点A、B的坐标可得出对称轴l为直线x=1,分t=2和t≠2两种情况考虑:当t=2时,由抛物线的对称性可得出此时存在点M,使得四边形CDPM是平行四边形,再根据点C的坐标利用平行四边形的性质可求出点P、M的坐标;当t≠2时,不存在,利用平行四边形对角线互相平分结合CE≠PE可得出此时不存在符合题意的点M;(3)①过点P作PF∥y轴,交BC于点F,由点B、C的坐标利用待定系数法可求出直线BC的解析式,根据点P的坐标可得出点F的坐标,进而可得出PF的长度,再由三角形的面积公式即可求出S关于t的函数表达式;②利用二次函数的性质找出S的最大值,利用勾股定理可求出线段BC的长度,利用面积法可求出P点到直线BC的距离的最大值,再找出此时点P的坐标即可得出结论.【详解】(1)将A(﹣1,0)、B(3,0)代入y=﹣x2+bx+c,得10930b cb c-++=⎧⎨-++=⎩,解得:23bc=⎧⎨=⎩,∴抛物线的表达式为y=﹣x2+2x+3;(2)在图1中,连接PC,交抛物线对称轴l于点E,∵抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,∴抛物线的对称轴为直线x=1,当t=2时,点C、P关于直线l对称,此时存在点M,使得四边形CDPM是平行四边形,∵抛物线的表达式为y=﹣x2+2x+3,∴点C的坐标为(0,3),点P的坐标为(2,3),∴点M的坐标为(1,6);当t≠2时,不存在,理由如下:若四边形CDPM是平行四边形,则CE=PE,∵点C的横坐标为0,点E的横坐标为0,∴点P的横坐标t=1×2﹣0=2,又∵t≠2,∴不存在;(3)①在图2中,过点P作PF∥y轴,交BC于点F.设直线BC的解析式为y=mx+n(m≠0),将B(3,0)、C(0,3)代入y=mx+n,得303m nn+=⎧⎨=⎩,解得:13mn=-⎧⎨=⎩,∴直线BC的解析式为y=﹣x+3,∵点P的坐标为(t,﹣t2+2t+3),∴点F的坐标为(t,﹣t+3),∴PF=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t,∴S=12PF•OB=﹣32t2+92t=﹣32(t﹣32)2+278;②∵﹣32<0,∴当t=32时,S取最大值,最大值为278.∵点B的坐标为(3,0),点C的坐标为(0,3),∴线段BC=2232OB OC+=,∴P点到直线BC的距离的最大值为27292832⨯=,此时点P的坐标为(32,154).【点睛】本题考查了待定系数法求一次(二次)函数解析式、平行四边形的判定与性质、三角形的面积、一次(二次)函数图象上点的坐标特征以及二次函数的性质,解题的关键是:(1)由点的坐标,利用待定系数法求出抛物线表达式;(2)分t=2和t≠2两种情况考虑;(3)①利用三角形的面积公式找出S关于t的函数表达式;②利用二次函数的性质结合面积法求出P点到直线BC的距离的最大值.4.(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=16-x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为172m.(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?【答案】(1)抛物线的函数关系式为y=16-x 2+2x+4,拱顶D 到地面OA 的距离为10 m ;(2)两排灯的水平距离最小是3.【解析】【详解】 试题分析:根据点B 和点C 在函数图象上,利用待定系数法求出b 和c 的值,从而得出函数解析式,根据解析式求出顶点坐标,得出最大值;根据题意得出车最外侧与地面OA 的交点为(2,0)(或(10,0)),然后求出当x=2或x=10时y 的值,与6进行比较大小,比6大就可以通过,比6小就不能通过;将y=8代入函数,得出x 的值,然后进行做差得出最小值.试题解析:(1)由题知点17(0,4),3,2B C ⎛⎫ ⎪⎝⎭在抛物线上 所以41719326c b c =⎧⎪⎨=-⨯++⎪⎩,解得24b c =⎧⎨=⎩,所以21246y x x =-++ 所以,当62b x a =-=时,10t y =≦ 答:21246y x x =-++,拱顶D 到地面OA 的距离为10米 (2)由题知车最外侧与地面OA 的交点为(2,0)(或(10,0)) 当x=2或x=10时,2263y =>,所以可以通过 (3)令8y =,即212486x x -++=,可得212240x x -+=,解得12623,623x x =+=-1243x x -=答:两排灯的水平距离最小是3考点:二次函数的实际应用.5.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C (0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△CDP为等腰三角形时,求点P的坐标;(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是线段EF上一动点,M(m,0)是x 轴一个动点,若∠MNC=90°,请求出m的取值范围.【答案】(1)y=﹣x2+2x+3;(2)点P的坐标为(1,2)或(2,1)或(3﹣2,23)55 4m-≤≤【解析】【分析】(1)利用待定系数法即可求得此抛物线的解析式;(2)由待定系数法即可求得直线BC的解析式,再设P(t,3﹣t),即可得D(t,﹣t2+2t+3),即可求得PD的长,然后分三种情况讨论,求点P的坐标;(3)直角三角形斜边上的中线等于斜边的一半列出关系式m=(n﹣32)2﹣54,然后根据n的取值得到最小值.【详解】解:(1)∵抛物线y=﹣x2+bx+c经过点A、B、C,A(﹣1,0),C(0,3),∴103b cc--+=⎧⎨=⎩,解得b=2,c=3.故该抛物线解析式为:y=﹣x2+2x+3.(2)令﹣x2+2x+3=0,解得x1=﹣1,x2=3,即B(3,0),设直线BC的解析式为y=kx+b′,则330bk b''=⎧⎨+=⎩,解得:k=-1,b’=3故直线BC的解析式为y=﹣x+3;∴设P (t ,3﹣t ),∴D (t ,﹣t 2+2t +3),∴PD =(﹣t 2+2t +3)﹣(3﹣t )=﹣t 2+3t ,∵OB =OC =3,∴△BOC 是等腰直角三角形,∴∠OCB =45°,当CD =PC 时,则∠CPD =∠CDP ,∵PD ∥y 轴,∴∠CPD =∠OCB =45°,∴∠CDP =45°,∴∠PCD =90°,∴直线CD 的解析式为y =x +3,解2323y x y x x =+⎧⎨=-++⎩得03x y =⎧⎨=⎩或14x y =⎧⎨=⎩ ∴D (1,4),此时P (1,2); 当CD =PD 时,则∠DCP =∠CPD =45°,∴∠CDP =90°,∴CD ∥x 轴,∴D 点的纵坐标为3,代入y =﹣x 2+2x +3得,3=﹣x 2+2x +3,解得x =0或x =2,此时P (2,1);当PC =PD 时,∵PC t , ∴=﹣t 2+3t ,解得t =0或t =3,此时P (3);综上,当△CDP 为等腰三角形时,点P 的坐标为(1,2)或(2,1)或(3) (3)如图2,由(1)y =﹣x 2+2x +3=﹣(x ﹣1)2+4,∴E (1,4),设N (1,n ),则0≤n ≤4,取CM 的中点Q (2m ,32), ∵∠MNC =90°, ∴NQ =12CM , ∴4NQ 2=CM 2,∵NQ 2=(1﹣2m )2+(n ﹣32)2, ∴4[(1﹣2m )2+(n ﹣32)2]=m 2+9, 整理得,m =(n ﹣32)2﹣54, ∵0≤n ≤4,当n =32时,m 最小值=﹣54,n =4时,m =5, 综上,m 的取值范围为:﹣54≤m ≤5.【点睛】此题考查了待定系数法求函数的解析式、平行线的性质、二次函数的最值问题、判别式的应用以及等腰直角三角形的性质等知识.此题综合性很强,难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.6.如图1,在矩形ABCD 中,DB =6,AD =3,在Rt △PEF 中,∠PEF =90°,EF =3,PF =6,△PEF (点F 和点A 重合)的边EF 和矩形的边AB 在同一直线上.现将Rt △PEF 从A 以每秒1个单位的速度向射线AB 方向匀速平移,当点F 与点B 重合时停止运动,设运动时间为t 秒,解答下列问题:(1)如图1,连接PD ,填空:PE = ,∠PFD = 度,四边形PEAD 的面积是 ;(2)如图2,当PF 经过点D 时,求△PEF 运动时间t 的值;(3)在运动的过程中,设△PEF 与△ABD 重叠部分面积为S ,请直接写出S 与t 的函数关系式及相应的t 的取值范围.【答案】(1)3009+93;(233)见解析. 【解析】 分析:(1)根据锐角三角形函数可求出角的度数,然后根据勾股定理求出PE 的长,再根据梯形的面积公式求解.(2)当PF 经过点D 时,PE ∥DA ,由EF=3,PF=6,可得∠EPD=∠ADF=30°,用三角函数计算可得3(3)根据题意,分三种情况:①当0≤t 3时,3<3时,③3≤t≤6时,根据三角形、梯形的面积的求法,求出S 与t 的函数关系式即可.详解:(1)∵在Rt △PEF 中,∠PEF=90°,EF=3,PF=6∴sin ∠P=1=2EF PF ∴∠P=30°∵PE ∥AD∴∠PAD=300, 根据勾股定理可得3所以S 四边形PEAD =12×(3+3)993+; (2)当PF 经过点D 时,PE ∥DA ,由EF=3,PF=6,得∠EPF=∠ADF=30°,在Rt △ADF 中,由AD=3,得33 ;(3)分三种情况讨论:①当0≤t 3 PF 交AD 于Q ,∵AF=t ,3t ,∴S=1233; ②3<3时,PF 交BD 于K ,作KH ⊥AB 于H ,∵AF=t ,∴3-t ,S △ABD 93, ∵∠FBK=∠FKB ,∴3,KH=KF×sin600=9-32t ,∴S=S △ABD ﹣S △FBK =239932t +③当3≤t≤33时,PE 与BD 交O ,PF 交BD 于K ,∵AF=t ,∴AE=t-3,BF=33-t, BE=33-t+3,OE=BE×tan300=9-3333t +,∴S=233233633-1224t t --++. 点睛:此题主要考查了几何变换综合题,用到的知识点有直角三角形的性质,三角函数值,三角形的面积,图形的平移等,考查了分析推理能力,分类讨论思想,数形结合思想,要熟练掌握,比较困难.7.如图,已知顶点为(0,3)C -的抛物线2(0)y ax b a =+≠与x 轴交于A ,B 两点,直线y x m =+过顶点C 和点B .(1)求m 的值;(2)求函数2(0)y ax b a =+≠的解析式;(3)抛物线上是否存在点M ,使得15MCB ∠=︒?若存在,求出点M 的坐标;若不存在,请说明理由.【答案】(1)﹣3;(2)y 13=x 2﹣3;(3)M 的坐标为(3632). 【解析】【分析】 (1)把C (0,﹣3)代入直线y =x +m 中解答即可;(2)把y =0代入直线解析式得出点B 的坐标,再利用待定系数法确定函数关系式即可; (3)分M 在BC 上方和下方两种情况进行解答即可.【详解】(1)将C (0,﹣3)代入y =x +m ,可得:m =﹣3;(2)将y =0代入y =x ﹣3得:x =3,所以点B 的坐标为(3,0),将(0,﹣3)、(3,0)代入y =ax 2+b 中,可得:390b a b =-⎧⎨+=⎩,解得:133a b ⎧=⎪⎨⎪=-⎩,所以二次函数的解析式为:y 13=x 2﹣3; (3)存在,分以下两种情况:①若M 在B 上方,设MC 交x 轴于点D ,则∠ODC =45°+15°=60°,∴OD =OC •tan30°3=设DC 为y =kx ﹣33,0),可得:k 3= 联立两个方程可得:233133y x y x ⎧=-⎪⎨=-⎪⎩, 解得:121203336x x y y ⎧=⎧=⎪⎨⎨=-=⎪⎩⎩, 所以M 1(36);②若M 在B 下方,设MC 交x 轴于点E ,则∠OEC =45°-15°=30°,∴OE =OC •tan60°=3设EC 为y =kx ﹣3,代入(30)可得:k 3= 联立两个方程可得:233133y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩,解得:12120332x x y y ⎧=⎧=⎪⎨⎨=-=-⎪⎩⎩, 所以M 23,﹣2).综上所述M 的坐标为(33,6)或(3,﹣2).【点睛】此题是一道二次函数综合题,熟练掌握待定系数法求函数解析式等知识是解题关键.8.如图,关于x 的二次函数y=x 2+bx+c 的图象与x 轴交于点A (1,0)和点B 与y 轴交于点C (0,3),抛物线的对称轴与x 轴交于点D .(1)求二次函数的表达式;(2)在y 轴上是否存在一点P ,使△PBC 为等腰三角形?若存在.请求出点P 的坐标; (3)有一个点M 从点A 出发,以每秒1个单位的速度在AB 上向点B 运动,另一个点N 从点D 与点M 同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M 到达点B 时,点M 、N 同时停止运动,问点M 、N 运动到何处时,△MNB 面积最大,试求出最大面积.【答案】(1)二次函数的表达式为:y=x 2﹣4x+3;(2)点P 的坐标为:(0,2(0,3﹣2)或(0,-3)或(0,0);(3)当点M 出发1秒到达D 点时,△MNB 面积最大,最大面积是1.此时点N 在对称轴上x 轴上方2个单位处或点N 在对称轴上x 轴下方2个单位处.【解析】【分析】(1)把A (1,0)和C (0,3)代入y=x 2+bx+c 得方程组,解方程组即可得二次函数的表达式;(2)先求出点B 的坐标,再根据勾股定理求得BC 的长,当△PBC 为等腰三角形时分三种情况进行讨论:①CP=CB ;②BP=BC ;③PB=PC ;分别根据这三种情况求出点P 的坐标; (3)设AM=t 则DN=2t ,由AB=2,得BM=2﹣t ,S △MNB=12×(2﹣t )×2t=﹣t 2+2t ,把解析式化为顶点式,根据二次函数的性质即可得△MNB 最大面积;此时点M 在D 点,点N 在对称轴上x 轴上方2个单位处或点N 在对称轴上x 轴下方2个单位处.【详解】解:(1)把A (1,0)和C (0,3)代入y=x 2+bx+c ,103b c c ++=⎧⎨=⎩解得:b=﹣4,c=3,∴二次函数的表达式为:y=x 2﹣4x+3;(2)令y=0,则x2﹣4x+3=0,解得:x=1或x=3,∴B(3,0),∴BC=32,点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图1,①当CP=CB时,PC=32,∴OP=OC+PC=3+32或OP=PC﹣OC=32﹣3∴P1(0,3+32),P2(0,3﹣32);②当PB=PC时,OP=OB=3,∴P3(0,-3);③当BP=BC时,∵OC=OB=3∴此时P与O重合,∴P4(0,0);综上所述,点P的坐标为:(0,3+32)或(0,3﹣32)或(﹣3,0)或(0,0);(3)如图2,设AM=t,由AB=2,得BM=2﹣t,则DN=2t,∴S△MNB=1×(2﹣t)×2t=﹣t2+2t=﹣(t﹣1)2+1,2当点M出发1秒到达D点时,△MNB面积最大,最大面积是1.此时点N在对称轴上x 轴上方2个单位处或点N在对称轴上x轴下方2个单位处.9.如图,已知二次函数y=ax 2+bx+c 的图象与x 轴相交于A (﹣1,0),B (3,0)两点,与y 轴相交于点C (0,﹣3).(1)求这个二次函数的表达式;(2)若P 是第四象限内这个二次函数的图象上任意一点,PH ⊥x 轴于点H ,与BC 交于点M ,连接PC .①求线段PM 的最大值;②当△PCM 是以PM 为一腰的等腰三角形时,求点P 的坐标.【答案】(1)二次函数的表达式y=x 2﹣2x ﹣3;(2)①PM 最大=94;②P (2,﹣3)或(22﹣2).【解析】【分析】(1)根据待定系数法,可得答案; (2)①根据平行于y 轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案;②根据等腰三角形的定义,可得方程,根据解方程,可得答案.【详解】(1)将A ,B ,C 代入函数解析式,得09303a b c a b c c -+=⎧⎪++=⎨⎪=-⎩,解得123a b c =⎧⎪=-⎨⎪=-⎩,这个二次函数的表达式y=x 2﹣2x ﹣3;(2)设BC 的解析式为y=kx+b ,将B ,C 的坐标代入函数解析式,得303k b b +=⎧⎨=-⎩,解得13k b =⎧⎨=-⎩, BC 的解析式为y=x ﹣3,设M (n ,n ﹣3),P (n ,n 2﹣2n ﹣3),PM=(n﹣3)﹣(n2﹣2n﹣3)=﹣n2+3n=﹣(n﹣32)2+94,当n=32时,PM最大=94;②当PM=PC时,(﹣n2+3n)2=n2+(n2﹣2n﹣3+3)2,解得n1=0(不符合题意,舍),n2=2,n2﹣2n﹣3=-3,P(2,-3);当PM=MC时,(﹣n2+3n)2=n2+(n﹣3+3)2,解得n1=0(不符合题意,舍),n2=3+2(不符合题意,舍),n3=3-2,n2﹣2n﹣3=2-42,P(3-2,2-42);综上所述:P(2,﹣3)或(3-2,2﹣42).【点睛】本题考查了二次函数的综合题,涉及到待定系数法、二次函数的最值、等腰三角形等知识,综合性较强,解题的关键是认真分析,弄清解题的思路有方法.10.(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=16-x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为172m.(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?【答案】(1)抛物线的函数关系式为y=16-x2+2x+4,拱顶D到地面OA的距离为10 m;(2)两排灯的水平距离最小是3.【解析】【详解】试题分析:根据点B 和点C 在函数图象上,利用待定系数法求出b 和c 的值,从而得出函数解析式,根据解析式求出顶点坐标,得出最大值;根据题意得出车最外侧与地面OA 的交点为(2,0)(或(10,0)),然后求出当x=2或x=10时y 的值,与6进行比较大小,比6大就可以通过,比6小就不能通过;将y=8代入函数,得出x 的值,然后进行做差得出最小值.试题解析:(1)由题知点17(0,4),3,2B C ⎛⎫ ⎪⎝⎭在抛物线上 所以41719326c b c =⎧⎪⎨=-⨯++⎪⎩,解得24b c =⎧⎨=⎩,所以21246y x x =-++ 所以,当62b x a =-=时,10t y =≦ 答:21246y x x =-++,拱顶D 到地面OA 的距离为10米 (2)由题知车最外侧与地面OA 的交点为(2,0)(或(10,0)) 当x=2或x=10时,2263y =>,所以可以通过 (3)令8y =,即212486x x -++=,可得212240x x -+=,解得1266x x =+=-12x x -=答:两排灯的水平距离最小是考点:二次函数的实际应用.11.如图所示抛物线2y ax bx c =++过点()1,0A -,点()0,3C ,且OB OC = (1)求抛物线的解析式及其对称轴;(2)点,D E 在直线1x =上的两个动点,且1DE =,点D 在点E 的上方,求四边形ACDE 的周长的最小值;(3)点P 为抛物线上一点,连接CP ,直线CP 把四边形CBPA 的面积分为3∶5两部分,求点P 的坐标.【答案】(1)2y x 2x 3=-++,对称轴为直线1x =;(2)四边形ACDE 的周长最小值为10131++;(3)12(4,5),(8,45)P P --【解析】【分析】(1)OB=OC ,则点B (3,0),则抛物线的表达式为:y=a (x+1)(x-3)=a (x 2-2x-3)=ax 2-2ax-3a ,即可求解;(2)CD+AE=A′D+DC′,则当A′、D 、C′三点共线时,CD+AE=A′D+DC′最小,周长也最小,即可求解;(3)S △PCB :S △PCA =12EB×(y C -y P ):12AE×(y C -y P )=BE :AE ,即可求解. 【详解】(1)∵OB=OC ,∴点B (3,0),则抛物线的表达式为:y=a (x+1)(x-3)=a (x 2-2x-3)=ax 2-2ax-3a ,故-3a=3,解得:a=-1,故抛物线的表达式为:y=-x 2+2x+3…①;对称轴为:直线1x =(2)ACDE 的周长=AC+DE+CD+AE ,其中AC=10、DE=1是常数,故CD+AE 最小时,周长最小,取点C 关于函数对称点C (2,3),则CD=C′D ,取点A′(-1,1),则A′D=AE ,故:CD+AE=A′D+DC′,则当A′、D 、C′三点共线时,CD+AE=A′D+DC′最小,周长也最小,四边形ACDE 的周长的最小值10101013(3)如图,设直线CP 交x 轴于点E ,直线CP 把四边形CBPA 的面积分为3:5两部分,又∵S △PCB :S △PCA =12EB×(y C -y P ):12AE×(y C -y P )=BE :AE , 则BE :AE ,=3:5或5:3,则AE=52或32, 即:点E 的坐标为(32,0)或(12,0), 将点E 、C 的坐标代入一次函数表达式:y=kx+3, 解得:k=-6或-2,故直线CP 的表达式为:y=-2x+3或y=-6x+3…② 联立①②并解得:x=4或8(不合题意值已舍去), 故点P 的坐标为(4,-5)或(8,-45). 【点睛】本题考查的是二次函数综合运用,涉及到一次函数、图象面积计算、点的对称性等,其中(1),通过确定点A′点来求最小值,是本题的难点.12.如图①,抛物线2(1)y x a x a =-++-与x 轴交于A 、B 两点(点A 位于点B 的左侧),与y 轴交于点C ,已知ABC ∆的面积为6. (1)求a 的值;(2)求ABC ∆外接圆圆心的坐标;(3)如图②,P 是抛物线上一点,点Q 为射线CA 上一点,且P 、Q 两点均在第三象限内,Q 、A 是位于直线BP 同侧的不同两点,若点P 到x 轴的距离为d ,QPB ∆的面积为2d ,且PAQ AQB ∠=∠,求点Q 的坐标.【答案】(1)-3;(2)坐标(-1,1);(3)Q ()4,1-. 【解析】 【分析】(1)利用抛物线解析式得到A 、B 、C 三点坐标,然后利用三角形面积公式列出方程解出a ;(2)利用第一问得到A 、B 、C 三点坐标,求出AC 解析式,找到AC 垂直平分线的解析式,与AB 垂直平分线解析式联立,解出x 、y 即为圆心坐标;(3)过点P 做PD ⊥x 轴,PD =d ,发现△ABP 与△QBP 的面积相等,得到A 、D 两点到PB 得距离相等,可得AQ PB ∥,求出PB 解析式,与二次函数解析式联立得到P 点坐标,又易证ABQ QPA ∆∆≌,得到BQ =AP Q 点坐标,点与点的距离列出方程,解出Q 点坐标即可 【详解】(1)解:由题意得()()1y x x a =--- 由图知:0a <所以A (,0a ),()10B ,,()0,C a - ()()112ABC S a a ∆=-⋅-=6 34()a a =-=或舍∴3a =-(2)由(1)得A (-3,0),()10B ,,()0,3C ∴直线AC 得解析式为:3y x =+AC 中点坐标为33,22⎛⎫-⎪⎝⎭ ∴AC 的垂直平分线为:y x =-又∵AB 的垂直平分线为:1x =- ∴1y x x =-⎧⎨=-⎩ 得11x y =-⎧⎨=⎩ABC ∆外接圆圆心的坐标(-1,1). (3)解:过点P 做PD ⊥x 轴 由题意得:PD =d ,∴12ABP S PD AB ∆=⋅=2d∵QPB ∆的面积为2d∴ABP BPQ S S ∆∆=,即A 、D 两点到PB 得距离相等 ∴AQ PB ∥设PB 直线解析式为;y x b =+过点(1,0)B ∴1y x =- ∴2123y x y x x =-⎧⎨=--+⎩易得45x y =-⎧⎨=⎩ 1()0x y =⎧⎨=⎩舍 所以P (-4,-5),由题意及PAQ AQB ∠=∠ 易得:ABQ QPA ∆∆≌ ∴BQ =AP 26设Q (m ,-1)(0m <) ∴()221126m -+=4m =-∴Q ()4,1-. 【点睛】本题考查二次函数综合性问题,涉及到一次函数、三角形外接圆圆心、全等三角形等知识点,第一问关键在于用a 表示出A 、B 、C 三点坐标;第二问关键在于找到AC 垂直平分线的解析式,与AB 垂直平分线解析式;第三问关键在于能够求出PB 的解析式13.如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值.【答案】(1)点A的坐标为(4,8)将A (4,8)、C(8,0)两点坐标分别代入y=ax2+bx得8=16a+4b0=64a+8b解得a=,b=4∴抛物线的解析式为:y=-x2+4x(2)①在Rt△APE和Rt△ABC中,tan∠PAE=PEAP=BCAB,即PEAP=48∴PE=AP=t.PB=8-t.∴点E的坐标为(4+t,8-t).∴点G的纵坐标为:-(4+t)2+4(4+t)=-t2+8.∴EG=-t2+8-(8-t)=-t2+t.∵-<0,∴当t=4时,线段EG最长为2.②共有三个时刻:t1=163, t2=4013,t38525.【解析】(1)根据题意即可得到点A的坐标,再由A、C两点坐标根据待定系数法即可求得抛物线的解析式;(2)①在Rt△APE和Rt△ABC中,由tan∠PAE,即可表示出点E的坐标,从而得到点G的坐标,EG的长等于点G的纵坐标减去点E的纵坐标,得到一个函数关系式,根据函数关系式的特征即可求得结果;②考虑腰和底,分情况讨论.14.如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.(1)求抛物线的函数关系式;(2)判断△ABM的形状,并说明理由;(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.【答案】(1)抛物线解析式为y=x2﹣1;(2)△ABM为直角三角形.理由见解析;(3)当m≤时,平移后的抛物线总有不动点.【解析】试题分析:(1)分别写出A、B的坐标,利用待定系数法求出抛物线的解析式即可;根据OA=OM=1,AC=BC=3,分别得到∠MAC=45°,∠BAC=45°,得到∠BAM=90°,进而得到△ABM是直角三角形;(3)根据抛物线的平以后的顶点设其解析式为,∵抛物线的不动点是抛物线与直线的交点,∴,方程总有实数根,则≥0,得到m的取值范围即可试题解析:解:(1)∵点A是直线与轴的交点,∴A点为(-1,0)∵点B在直线上,且横坐标为2,∴B点为(2,3)∵过点A、B的抛物线的顶点M在轴上,故设其解析式为:∴,解得:∴抛物线的解析式为.(2)△ABM是直角三角形,且∠BAM=90°.理由如下:作BC⊥轴于点C,∵A(-1,0)、B(2,3)∴AC=BC=3,∴∠BAC=45°;点M是抛物线的顶点,∴M点为(0,-1)∴OA=OM=1,∵∠AOM=90°∴∠MAC=45°;∴∠BAM=∠BAC+∠MAC=90°∴△ABM是直角三角形.(3)将抛物线的顶点平移至点(,),则其解析式为.∵抛物线的不动点是抛物线与直线的交点,∴化简得:∴==当时,方程总有实数根,即平移后的抛物线总有不动点∴.考点:二次函数的综合应用(待定系数法;直角三角形的判定;一元二次方程根的判别式)15.如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.(1)求此抛物线的解析式;(2)求证:AO=AM;(3)探究:①当k=0时,直线y=kx与x轴重合,求出此时的值;②试说明无论k取何值,的值都等于同一个常数.【答案】解:(1)y=x2﹣1(2)详见解析(3)详见解析【解析】【分析】(1)把点C、D的坐标代入抛物线解析式求出a、c,即可得解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级《二次函数》压轴题训练一.解答题(共30题)1.如图,已知直线y=2x+12分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的OM与直线AB相切于点D,连接PD.(1)求证:△ADM∽△AOB;(2)如果OM的半径为2,求出点M的坐标,并写出以为顶点,且过点M的抛物线的解析式;(3)在(2)的条件下,在此抛物线上是否存在点P,使得P,A,M三点为顶点的三角形与△AOB相似?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.2.如图,抛物线y=ax2+bx+c经过点A(5,0)、B(6,﹣6)和原点O,过点B的直线y=mx+n 与抛物线相交于点C(2,y).过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴,交直线DC 于点E,交x轴于点F.(1)求该抛物线的解析式;(2)求△OBC的面积;(3)是否存在这样的点P,使得以P、C、E为顶点的三角形与△OCD相似?若存在,求出点P的坐标;若不存在,请说明理由.3.如图,对称轴为直线的抛物线经过点A(6,0)和B(0,4).(1)求抛物线解析式及顶点D的坐标;(2)设点E(x,y)是抛物线上位于第四象限内一动点,将△OAE绕OA的中点旋转180°,点E落到点F的位置.求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x 的取值范围;①当四边形OEAF的面积为24时,请判断四边形OEAF的形状.②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.(3)若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,请直接写出满足条件的所有点P的坐标.4.如图,已知抛物线y=ax2﹣2ax+b与x轴交于A、B(3,0)两点,与y轴交于点C,且OC=3OA,设D为抛物线的顶点.(1)求抛物线的解析式;(2)如图(1),P为x轴上一点,若,求点P的坐标;(3)如图(2),M为抛物线上一动点,问在对称轴上是否存在点Q,使以M、D、Q为顶点的三角形与△BOD相似?若存在,求出所有符合条件的Q点的坐标;若不存在,请说明理由.5.如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C 两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).(1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;(3)已知点P是抛物线上的一个动点,点Q是对称轴l上的一动点,是否存在以P、Q、B、C为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.6.如图,抛物线y=ax2+bx+c与x轴交于A、B两点的横坐标分别是﹣1,3 (点A在点B 左侧),与y轴交于点C,抛物线的顶点M在直线y=3x﹣7上.(1)求抛物线的解析式;(2)P为线段BM上一点,过点P向x轴引垂线,垂足为Q.若点P在线段BM上运动(点P不与点B、M重合),设OQ的长为t,四边形PQAC的面积为S.求S与t之间的函数关系式及自变量t的取值范围;(3)在线段BM上是否存在点N,使△NMC为等腰三角形?若存在,请求出点N的坐标;若不存在,请说明理由.7.如图,直线L1交直线L2于y轴上一点A(0,6),交x轴上另一点C.l2交x轴于另一点B,二次函数y=ax2﹣6ax﹣16a (a>0)的图象过B、C两点,点P是线段OC上由O向C移动的动点,线段OP=t(1<t<8)(1)t为何值时,P为圆心OP为半径的圆与l1相切?(2)设抛物线对称轴与直线l1相交于M,请在x轴上求一点N.使△AMN的周长最小.(3)设点Q是AC上自C向A移动的一动点,且CQ=OP=t.若△PQC的面积为s,求S 与t的函数关系式,当△PQC为等腰三角形时,请直接写出t的值.8.如图,已知对称轴为直线x=4的抛物线交x轴于点A、B(点A在B左侧),且点B坐标为(6,0),过点B的直线交抛物线于点C(3,4).(1)写出点A坐标;(2)求抛物线解析式;(3)若点P在抛物线的BC段上,则x轴上时否存在点Q,使得以Q、B、P、C为顶点的四边形是平行四边形?若存在,请分别求出点P、Q坐标;若不存在,请说明理由;(4)若点M在线段AB上以每秒1个单位长度的速度从A向B运动,同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动,当其中一个点停止运动时,另一个点也随之停止运动.设运动时间为t秒,当t为何值,以M、N、B为顶点的三角形与△ABC相似,写出计算过程.9.已知抛物线(k是实数)与x轴有交点,将此抛物线向左平移1个单位,再向上平移4个单位,得到新的抛物线E,设抛物线E与x轴的交点为B,C,如图.(1)求抛物线E所对应的函数关系式,并求出顶点A的坐标;(2)连接AB,把AB所在的直线平移,使它经过点C,得到直线l,点P是l上一动点(与点C不重合).设以点A,B,C,P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤16时,求t的取值范围;(3)点Q是直线l上的另一个动点,以点Q为圆心,R为半径作圆Q,当R取何值时,圆Q与直线AB相切?相交?相离?直接给出结果.10.如图,抛物线y=x2﹣2mx+n+1的顶点A在x轴负半轴上,与y轴交于点B,C是抛物线上一点,且点C的横坐标为1,.(1)求抛物线的函数关系式;(2)若D是抛物线上一点,直线BD经过第一、二、四象限,且原点O到直线BD的距离为,求点D的坐标;(3)在(2)的条件下,直线BD上是否存在点P,使得以A、B、P为顶点的三角形与△AOB 相似?若存在,求出点P的坐标;若不存在,请说明理由.11.已知如图,矩形OABC的长OA=,宽OC=1,将△AOC沿AC翻折得△AFC.(1)求过A、F、C三点的抛物线解析式;(2)设(1)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标;(3)若动点P以每秒个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C 为顶点的三角形相似?12.如图,已知抛物线y=ax2+bx+c(a≠0)过点A(3,0),B(1,0),且与y轴交于点C (0,﹣3),点P是抛物线AC间上一动点,从点C沿抛物线向点A运动(点P与A、C不重合),过点P作PD∥y轴,交AC于点D.(1)求该抛物线的函数关系式;(2)当△ADP是直角三角形时,直接写出点P的坐标;(3)求线段PD的最大值,并求最大值时P点的坐标;(4)在问题(3)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.13.如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣x2+bx+c经过点A、C,与AB交于点D.(1)求抛物线的函数解析式;(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.①求S关于m的函数表达式;②当S最大时,在抛物线y=﹣x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.14.如图:抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.(1)求抛物线和直线AB的解析式;(2)点Q(x,0)是x轴上的一动点,过Q点作x轴的垂线,交抛物线于P点、交直线BA于D点,连接OD,PB,当点Q(x,0)在x轴上运动时,求PD与x之间的函数关系式;以O、B、P、D为顶点的四边形能否成为平行四边形?若能求出Q点坐标;若不能,请说明理由.(3)是否存在一点Q,使以PD为直径的圆与y轴相切?若存在,求出Q点的坐标;若不存在,请说明理由.15.已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,)三点,连接AB,过点B作BC∥x轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).(1)求抛物线的解析式;(2)记△EFA的面积为S,求S关于t的函数关系式,并求S的最大值,指出此时△EFA 的形状;(3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.16.已知抛物线y=﹣x2+3x+4交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l.在位于直线l下方的抛物线上任取一点P,过点P作直线PQ 平行于y轴交直线l于点Q.连接AP.(1)写出A,B,C三点的坐标;(2)若点P位于抛物线的对称轴的右侧:①如果以A,P,Q三点构成的三角形与△AOC相似,求出点P的坐标;②若将△APQ沿AP对折,点Q的对应点为点M.是否存在点P,使得点M落在x轴上?若存在,求出点P的坐标;若不存在,请说明理由.17.如图,抛物线y=﹣x2﹣x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(﹣3,0).(1)求直线AB的函数关系式;(2)动点E在线段OC上从原点出发以每秒一个单位的速度向C移动,过点E作EG⊥x 轴,交直线AB于点F,交抛物线于点G.设点E移动的时间为t秒,GF的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;(3)设在(2)的条件下(不考虑点E与点O、C重合的情况),连接CF,BG,当t为何值时,四边形BCFG为平行四边形?问对于所求的t值,平行四边形BCFG是否菱形?请说明理由.18.如图,抛物线y=ax2+2ax+b与直线y=x+1交于A、C两点,与y轴交于B,AB∥x轴,且S△ABC=3,D、E是直线y=x+1与坐标轴的交点,(1)求抛物线的解析式;(2)在坐标轴上找出所有的点F,使△CEF与△ABD相似,直接写出它的坐标;(3)P为x轴上一点,Q为此抛物线上一点,是否存在P,使得以A、C、P、Q为顶点的四边形是平行四边形?若存在,请求出P点的坐标;若不存在,请说明理由.19.如图,抛物线y=ax2+bx﹣3与x轴交于两点A(1,0)、B(3,0),与y轴交于点D.(1)求抛物线的解析式;(2)在抛物线是否存在一点P,使得△BDP是以BD为斜边的直角三角形,若存在,请求出点P的坐标;若不存在,请说明理由;(3)在x轴下方的抛物线上是否存在点M,过M作MN⊥x轴于点N,使以A、M、N为顶点的三角形与△BCD相似?若存在,则求出点M的坐标;若不存在,请说明理由.20.如图的平面直角坐标系中,抛物线交x轴于A、B两点(点B在点A的右侧),交y轴于点C,以OC、OB为两边作矩形OBDC,CD交抛物线于G.(1)求OC和OB的长;(2)抛物线的对称轴l在边OB(不包括O、B两点)上作平行移动,交x轴于点E,交CD于点F,交BC于点M,交抛物线于点P.设OE=m,PM=h,求h与m的函数关系式,并求出PM的最大值;(3)连接PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△BEM相似?若存在,直接求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.21.如图,在直角坐标系中,⊙M与y轴相切于点C,与x轴交于A(x1,0),B(x2,0)两点,其中x1,x2是方程x2﹣10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.(1)求过A、B、C三点的抛物线的解析式;(2)判断直线NA与⊙M的位置关系,并说明理由;(3)一动点P从点C出发,以每秒1个单位长的速度沿CM向点M运动,同时,一动点Q 从点B出发,沿射线BA以每秒4个单位长度的速度运动,当P运动到M点时,两动点同时停止运动,当时间t为何值时,以Q、O、C为顶点的三角形与△PCO相似?22.如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,D为OC的中点,直线AD交抛物线于点E(2,6),且△ABE与△ABC的面积之比为3:2.(1)求这条抛物线对应的函数关系式;(2)连接BD,试判断BD与AD的位置关系,并说明理由;(3)连接BC交直线AD于点M,在直线AD上,是否存在这样的点N(不与点M重合),使得以A、B、N为顶点的三角形与△ABM相似?若存在,请求出点N的坐标;若不存在,请说明理由.23.如图,四边形ABCD为矩形,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于点P,连接MP.已知动点运动了x秒.(1)请直接写出PN的长;(用含x的代数式表示)(2)若0秒≤x≤1秒,试求△MPA的面积S与时间x秒的函数关系式,利用函数图象,求S 的最大值.(3)若0秒≤x≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有x的对应值;若不能,试说明理由.24.如图,已知动圆A始终经过定点B(0,2),圆心A在抛物线上运动,MN为⊙A在x轴上截得的弦(点M在N左侧)(1)当A(,a)时,求a的值,并计算此时⊙A的半径与弦MN的长.(2)当⊙A的圆心A运动时,判断弦MN的长度是否发生变化?若改变,举例说明;若不变,说明理由.(3)连接BM,BN,当△OBM与△OBN相似时,计算点M的坐标.25.如图,在平面直角坐标系中,坐标轴上有A、B、C、D四个点,且OA=OC=2OD=4OB=4.(1)求经过A、D两点的直线表达式及经过A、B、C三点的抛物线的表达式.(2)E为抛物线的顶点,在直线AD上有一动P,求当S△OAP﹕S四边形AECB=1﹕7时点P的坐标.(3)点M是第一象限内的抛物线上的一个动点,过点M向x轴作垂线,垂足为N,问:是否存在点M使以O、M、N为顶点的三角形与△AOD相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.26.如图,抛物线y=﹣2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.(1)求线段AB长;(2)证明:OP=PC;(3)当点P在第一象限时,设AP长为m,△OBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;(4)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由.27.如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.(1)求点C的坐标及抛物线的解析式;(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由.28.已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x﹣2经过A、C两点,且AB=2.(1)求抛物线的解析式;(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s=,当t为何值时,s有最小值,并求出最小值.(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.29.已知:如图,一次函数y=x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=x2+bx+c的图象与一次函数y=x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)(1)求二次函数的解析式;(2)求四边形BDEC的面积S;(3)在x轴上有一动点P,从O点出发以每秒1个单位的速度沿x轴向右运动,是否存在点P使得△PBC是以P为直角顶点的直角三角形?若存在,求出点P运动的时间t的值,若不存在,请说明理由.(4)若动点P在x轴上,动点Q在射线AC上,同时从A点出发,点P沿x轴正方向以每秒2个单位的速度运动,点Q以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似,若存在,求a的值,若不存在,说明理由.30.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的关系解析式;(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;考生注意:下面的(3)、(4)、(5)题为三选一的选做题,即只能选做其中一个题目,多答时只按作答的首题评分,切记啊!(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.参考答案一.解答题(共3题)1.(1)证明:∵⊙M与直线AB相切,∴∠ADM=∠AOB=90°,又∵∠A=∠A,∴△ADM∽△AOB;(2)解:设M(0,m),由直线y=2x+12得,OA=12,OB=6,则AM=12﹣m,而DM=2,在Rt△AOB中,AB==6,∵△ADM∽△AOB,∴=,即=,解得m=2,∴M(0,2),设顶点为(,)的抛物线解析式为y=a(x﹣)2+,将M点坐标代入,得a(0﹣)2+=2,解得a=﹣2,所以,抛物线解析式为y=﹣2(x﹣)2+;(3)解:存在.△PAM中,①当顶点M为直角顶点时,M、P两点关于抛物线对称轴x=轴对称,此时MP=5,AM=12﹣2=10,AM:MP=2:1,符合题意,P(5,2);②当顶点A为直角顶点时,P点纵坐标为12,代入抛物线解析式,得﹣2(x﹣)2+=12,解得x=±,此时AP=±,AM=10,不符合题意;③当顶点P为直角顶点时,则由相似三角形的性质可知,P(n,2n+2),或P(2n,n+2),若P(n,2n+2),则2n+n=10,解得n=4,而当x=4时,y=﹣2(4﹣)2+=10,2n+2=10,符合题意,若P(2n,n+2),则n+4n=10,解得n=2,而当x=2n=4时,y=﹣2(4﹣)2+=10,n+2=4,不符合题意,所以,符合条件的P点坐标为(5,2),(4,10).2.解:(1)∵抛物线y=ax2+bx+c经过点A(5,0)、B(6,﹣6)和原点O,∴,解得,故,抛物线的函数关系式为y=﹣x2+5x;(2)∵C(2,y)在抛物线上,∴﹣22+5×2=y,解得y=6,∴C点坐标为(2,6),∵B、C在直线y=mx+n上,∴,解得,∴直线BC的解析式为y=﹣3x+12,设BC与x轴交于点G,则﹣3x+12=0,解得x=4,所以,点G的坐标为(4,0),S△OBC=S△OBG+S△OCG,=×4×|﹣6|+×4×6=12+12=24;(3)存在P,使得△OCD∽△CPE.理由如下:设P(m,n),∵∠ODC=∠E=90°,∴PE=6﹣n,CE=m﹣2,∵C点坐标为(2,6),∴CD=2,OD=6,①OD与CE是对应边时,∵△OCD∽△CPE,∴=,即=,解得,m=20﹣3n,∵(m,n)在抛物线上,∴,解得,(为点C坐标),所以,点P(,);②OD与EP是对应边时,∵△OCD∽△PCE,∴=,即=,解得,n=12﹣3m,∵(m,n)在抛物线上,∴,解得(为点C坐标),,所以,点P(6,﹣6),综上所述,P点坐标为和(6,﹣6).3.解:(1)依题意,设抛物线的解析式为:y=a(x﹣)2+h,代入A(6,0)、B(0,4)后,得:,解得∴抛物线的解析式:y=(x﹣)2﹣,顶点D(,﹣).(2)依题意,知:△OAF≌△AOE,得:OE=AF、AE=OF;∴四边形OEAF是平行四边形.∵点E(x,y)在抛物线的图象上,∴y=(x﹣)2﹣;又∵点E在第四象限,∴y<0,解得:1<x<6;S=2S△OAE=2••OA•|y E|=6•(﹣y)=﹣4(x﹣)2+25,(1<x<6).①当S=24时,﹣4(x﹣)2+25=24,解得x1=3、x2=4;1、当x=3时,E(3,﹣4),此时OE=AE,四边形OEAF为菱形;2、当x=4时,E(4,﹣4),此时OE≠AE,且∠OEA≠90°,∴四边形OEAF只是平行四边形.②假设四边形OEAF为正方形,则OE=AE,OE⊥AE,已知O(0,0)、A(6,0),则E (3,﹣3);但此时的点E不在抛物线的图象上,因此不存在符合条件的点E.(3)设平行四边形的另一顶点为Q,分两种情况讨论:①当PA为平行四边形的对角线时,另一条对角线DQ的中点为(,0),而P、A关于(,0)对称,那么点P(﹣,0);②当PA为平行四边形的边时,DQ∥PA,且PA=QD=,已知A(6,0),则P(,0)或(,0);综上,点P的坐标为(﹣,0)或(,0)或(,0).4.解:(1)由y=ax2﹣2ax+b可得抛物线对称轴为x=1,由B(3,0)可得A(﹣1,0);∵OC=3OA,∴C(0,3);依题意有:,解得;∴y=﹣x2+2x+3,(2)∵A(﹣1,0),C(0,3),∴直线AC的解析式为:y=3x+3,∵点D是抛物线的顶点,∴D(1,4),设过点D与AC平行的直线的解析式为:y=3x+b,把点D的坐标代入得:b=1,∴y=3x+1,当y=0时,x=﹣,设这个点为E(﹣,0),∴AE=.∵S△PAC=2S△DAC,∴AP=2AE=,∴P(,0)或(﹣,0).(3)存在.设M的坐标为(x,﹣x2+2x+3),①过点M作MQ⊥抛物线的对称轴于Q,∴点Q的坐标为(1,﹣x2+2x+3),∴MQ=1﹣x,DQ=4﹣(﹣x2+2x+3)=x2﹣2x+1,∵OB=3﹣1=2,OD=4,若△MDQ∽△BDO,则,即:,解得:x1=1(舍去),x2=﹣1,∴点Q的坐标为(1,0);若△MDQ∽△DBO,则,即:,解得:x3=1(舍去),x4=,∴点Q的坐标为(1,);②若∠DMQ=90°,过M作ME⊥DQ于E,若△DMQ∽△DOB,则∠MDQ=∠BDO,∠MQD=∠DBO,∴tan∠MDQ=tan∠BDO,即,∴,解得:x1=1(舍去),x2=﹣1,∴DE=x2﹣2x+1=4,∴ME=2,同理可得:EQ=1,∴QD=5,∴OQ=1,∴Q的坐标为(1,﹣1);若△DMQ∽△BOD,则∠MDQ=∠DBO,∠MQD=∠BDO,∴tan∠MDQ=tan∠DBO,即,∴,解得:x3=1(舍去),x4=,∴DE=x2﹣2x+1=,∴ME=,同理可得:EQ=1,∴QD=,OQ=4﹣=,∴Q的坐标为(1,);综上,可知Q点的坐标为:(1,0),(1,),(1,﹣1),(1,).5.解:(1)根据题意,可设抛物线的解析式为y=ax2+bx+4,根据题意,得:,解得.故抛物线的解析式为y=x2﹣x+4;(2)设⊙C与BD相切于点E,连接CE,则∠BEC=∠AOB=90°.∵A(0,4)、B(3,0)、C(8,0),∴OA=4,OB=3,OC=8,BC=5;∴AB==5,∴AB=BC.∵AB⊥BD,∴∠ABC=∠EBC+90°=∠OAB+90°,∴∠EBC=∠OAB,∴,∴△OAB≌△EBC,∴OB=EC=3.设抛物线对称轴交x轴于F.∵x=﹣=﹣=,∴F(,0),∴CF=8﹣=<3,∴对称轴l与⊙C相交;(3)由(2)知:抛物线的对称轴为x=,设Q(,y Q),已知BC=5,则有:①若BC为边,则:P(+5,y P)或(﹣5,y P),代入抛物线的解析式中,可得:P1(,)、P2(,);②若BC为对角线,则点P必在抛物线对称轴上,即此时点P是抛物线的顶点(,﹣).综上,存在符合条件的点P,坐标为(,)或(,)或(,﹣).6.解:(1)由题意可知:抛物线的对称轴为x=1.当x=1时,y=3x﹣7=﹣4,因此抛物线的顶点M的坐标为(1,﹣4).过A(﹣1,0),B(3,0)设抛物线的解析式为y=a(x﹣1)2﹣4,则有:a(3﹣1)2﹣4=0,a=1.则抛物线的解析式为:y=x2﹣2x﹣3.(2)根据(1)的抛物线可知:A(﹣1,0)、B(3,0)、C(0,﹣3);易知直线BM的解析式为y=2x﹣6;∵当x=t时,y=2t﹣6;∴PQ=6﹣2t;∴S四边形PQAC=S梯形QPCO+S△AOC=×(3+6﹣2t)×t+×3,即S四边形PQAC=﹣t2+t+(1<t<3).(3)假设存在这样的点N,使△NMC为等腰三角形.∵点N在BM上,设N点坐标为(m,2m﹣6),则CM2=12+12=2,CN2=m2+[﹣3﹣(2m﹣6)]2,或CN2=m2+[(2m﹣6)+3]2.MN2=(m﹣1)2+[4﹣(6﹣2m)]2.△NMC为等腰三角形,有以下三种可能:①若CN=CM,则m2+[(6﹣2m)﹣3]2=2,解得m1=,m2=1(舍去).则N().②若MC=MN,则(m﹣1)2+[4﹣(6﹣2m)]2=12+12.解得m=1±.∵1<m<3,∴m=1﹣舍去.∴N(1+).③若NC=NM,则m2+[3﹣(6﹣2m)]2=(m﹣1)2+[4﹣(6﹣2m)]2.解得m=2.则N(2,﹣2).故存在这样的点N,使△NMC为等腰三角形.且点N的坐标分别为:,N3(2,﹣2).7.解:(1)抛物线的解析式中,当y=0时,0=a(x2﹣6x﹣16),解得:x1=﹣2,x2=8;∴B(﹣2,0)、C(8,0).过P作PD⊥AC于D,若⊙P与直线l1相切,则PD=OP=t;易知Rt△CPD∽Rt△CAO∴=,即=解得:t=3.(2)由(1)知:抛物线的对称轴x=3;由A(0,6)、C(8,0)得:直线AC y=﹣x+6,则M(3,).△AMN中,AM长为定值,若△AMN的周长最小,那么AN+MN 的值最小;取点M关于x轴的对称点M',则M'(3,﹣);设直线AM'的解析式为:y=kx+6,则:3k+6=﹣,k=﹣∴直线AM':y=﹣x+6 当y=0时,x=;即N(,0).(3)过Q作QE⊥x轴于点E,则QE=QE=t,CE=QC=t,OE=OC﹣CE=8﹣t;∴Q(8﹣t,t).①PC=OC﹣OP=8﹣t;则S=PC•QE=×(8﹣t)×t=﹣t2+t(1<t<8).②PQ2=(8﹣t﹣t)2+(t)2=t2﹣t+64,PC2=(8﹣t)2=t2﹣16t+64,CQ2=t2;当PQ=PC时,t2﹣t+64=t2﹣16t+64,解得:t1=0(舍去),t2=;当PQ=CQ时,t2﹣t+64=t2,解得:t1=8(舍去),t2=;当PC=CQ时,t2﹣16t+64=t2,解得:t=4.∴当△PQC为等腰三角形时,t1=、t2=、t3=4.8.解:(1)设对称轴x=4交x轴于点D∴D(4,0)∵B(6,0)∴BD=2,由抛物线的对称性得:AD=2∴A(2,0);(2)设抛物线的解析式为y=a(x﹣2)(x﹣6),得4=a(3﹣2)(3﹣6)解得a=﹣,抛物线的解析式为:y=﹣x2+x﹣16(3)∵四边形PCQB为平行四边形∴PC∥QB,PC=QB∴P点的纵坐标为4∴4=﹣x2+x﹣16,解得x=3(不符合题意)或5∴P(5,4)∴PC=5﹣3=2∴QB=2∴Q(4,0)或(8,0)∴P(5,4),Q(4,0)或P(5,4),Q(8,0);(4)当运行t秒时∴BN=2t,AM=t,BM=4﹣t当△BMN∽△BAC∴∵C(3,4),B(6,0),由两点间的距离公式得BC=5∵A(2,0)∴AB=4∴,解得t=当△BNM∽△BAC时∴∴,解得t=9.解:(1)抛物线y=﹣x2+2kx﹣k2+2k﹣2(k是实数)与x轴有交点,则判别式△=(2k)2+4(﹣k2+2k﹣2)=﹣(k﹣2)2≥0,则k=2,因而抛物线的解析式是:y=﹣x2+4x﹣4,将此抛物线向左平移1个单位,再向上平移4个单位得到的抛物线是:y=﹣(x+1)2+4(x+1)﹣4+4,即:y=﹣x2+2x+3即y=﹣(x﹣1)2+4,∴顶点A坐标为(1,4);(2)令y=0,得﹣x2+2x+3=0所以B(﹣1,0),C(3,0)设直线AB的函数关系式为y=kx+b、∵A(0,4),B(﹣1,0)∴解得,∴y=2x+2∵直线l∥AB且过点C(3,0),∴直线l的函数关系式为y=2x﹣6,∵点P是l上一动点且横坐标为t,∴点P坐标为(t,2t﹣6)当P在x轴下方时(t<3),S=S△ABC+S△BCP=×4×4+×4×|2t﹣6|=20﹣4t.∵0<S≤16,∴0<20﹣4t≤16,∴1≤t<5、又t<3,∴1≤t<3当P在x轴上方时(t>3),作PM⊥x轴于M,设对称轴与x轴交点为N.则S=S梯形ANMP+S△ANB+S△PMC=[4+(2t﹣6)]•(t﹣1)+2×4﹣(t﹣3)(2t﹣6)=4t﹣4另法:∵直线l∥AB,根据等底等高的面积相等进行转化S=S△ABC+S△APC=S△ABC+S△BPC=S△ABC+S△PBC=×4×4+×4×(2t﹣6)=4t﹣4∵0<S≤16,∴0<4t﹣4≤16,∴1<t≤5.又∵t>3,∴3<t≤5.∴t的取值范围是1≤t<3或3<t≤5;(3)AB=2,过点C作CH⊥AB,H为垂足,S△ABC=×4×4=×AB×CH所以CH=,因为平行线间距离处处相等,所以点Q到直线AB的距离等于,所以当R=时相切,R时相交,R<时相离.10.解:(1)过点C作CE⊥x轴于点E,如图,∵抛物线上一点C的横坐标为1,∴C(1,n﹣2m+2),其中n﹣2m+2>0,OE=1,CE=n﹣2m+2;∵抛物线的顶点A在x轴负半轴上,∴A(m,0),△=4m2﹣4(n+1)=0,得n=m2﹣1①,其中m<0,OA=﹣m,AE=OE+OA=1﹣m,在Rt△ACE中,AC=3,∵AE2+CE2=AC2,∴(1﹣m)2+(n﹣2m+2)2=(3)2②,把①代入②得[(m﹣1)2]2+(m﹣1)2﹣90=0,∴[(m﹣1)2+10][(m﹣1)2﹣9]=0,∴(m﹣1)2﹣9=0∴m1=4,m2=﹣2,∵m<0,∴m=﹣2.把m=﹣2代入①,得n=4﹣1=3,∴抛物线的关系式为y=x2+4x+4;(2)设直线DB交x轴正半轴于点F,过点O作OM⊥DB于点M,如图,∵点O到直线DB的距离为,∴OM=,而B点坐标为(0,4),∴OB=4,∴BM==;∵OB⊥OF,OM⊥BF,∴△OBM∽△FOM,∴=,即=,∴OF=8,∴F点坐标为(8,0),设直线DB的解析式为y=kx+b,把F(8,0)、B(0,4)代入得,解得,∴直线DB的解析式为y=﹣x+4,解方程组得或,∴D点坐标为(﹣,);(3)存在.理由如下:∵OB=4,OF=8,∴BF==4,∵y=(x+2)2,∴A点坐标为(﹣2,0),∴OA=2,而OB=4,∴AB==2∴OA:OB=OB:OF,∴△OAB∽△OBF,∴∠AOB=∠OFB,∴∠ABF=∠ABO+∠OBF=∠OFB+∠OBF=90°,∴△ABF∽△AOB,此时P1在F点位置,符号要求,P1点的坐标为(8,0);当△ABP2∽△BOA时,则BP2:OA=AB:BO,即BP2:2=2:4,∴BP2=,过P2作P2H⊥x轴于H,如图,∴OH:OF=BP2:BF,即OH:8=:4,∴OH=2,把x=2代入y=﹣x+4得y=﹣×2+4=2,∴P2的坐标为(2,2);当△ABP3∽△BOA时,同样得到BP3=,∴P3A⊥OA,∴P3的横坐标为﹣2,把x=﹣2代入y=﹣x+4得y=﹣×(﹣2)+4=5,∴P3的坐标为(﹣2,6);当△ABP4∽△AOB时,则BP4:OB=AB:AO,即BP4:4=2:2,∴BP4=4,过P4作P4Q⊥y轴于Q,如图,易证得△P4QB≌△FOB,∴P4Q=8,把x=﹣8代入y=﹣x+4得y=﹣×(﹣8)+4=8,∴P4的坐标为(﹣8,8),∴满足条件的P点坐标为(﹣8,8)、(﹣2,5)、(2,2)、(8,0).11.解:(1)∵OA=,OC=1,∴tan∠OAC=.∴∠OAC=30°∠ACF=∠ACO=60°过F作FM⊥OA于M,交CB于G,则FG⊥CD.∠GCF=30°,GF=CF=OC=.CG=.∴F(,)设过A、B、C三点抛物线解析式为y=ax2+bx+c.∴c=1∴解之,得∴(2)∵由,得x1=,x2=.∴E(,0)由,得x1=0,x2=.∴D(,1).…(6分)①当DN∥EM且DN=EM时,当M在E点左侧时,M1(,0),此时N1(0,1)当M在E点右侧时,OM2=.∴M2(,0),此时N2(0,1)②当ED∥MN且ED=MN时,过D作DH⊥OA于H,M3(,0),N3(0,﹣1)(3)若以P、C、Q为顶点的三角形与△QOC相似,因∠POC=∠QCO=90°,则有CQ=OP或OC2=CQ•OP.当P、Q在y轴同侧时:由,得t=.由,得2t2﹣2t+1=0.△=4﹣8=﹣4<0,故无解.当P、Q在y轴异侧时:由,得t=3>,不合题意,舍去由,得2t2﹣2t﹣1=0.<0舍去,∴t=或12.解:(1)由题意得:,解得:.∴该抛物线的函数关系式为:y=﹣x2+4x﹣3;(2)设过A、C两点的直线解析式为:y=kx+b,∵A(3,0),C(0,﹣3),P点的坐标为:P1(1,0),P2(2,1);(3)设直线AC的解析式为y=kx+b,由题意得,解得:.∴直线AC的解析式为y=x﹣3.设P(x,﹣x2+4x﹣3)则D(x,x﹣3),PD=﹣x2+4x﹣3﹣(x﹣3)=﹣,∴PD的最大值为,P();(4)当APXF是平行四边形时,则:△APE≌△XFE,∴这两个三角形的高相等,∵P(),∴F的纵坐标为﹣,∴F.当F点与P点关于抛物线的对称轴对称时,A、P、E、F为顶点的四边形是平行四边形.F (),∴点F的坐标为:或().13.解:(1)将A、C两点坐标代入抛物线,得,解得:,∴抛物线的解析式为y=﹣x2+x+8;(2)①∵OA=8,OC=6,∴AC==10,过点Q作QE⊥BC与E点,则sin∠ACB===,∴=,∴QE=(10﹣m),∴S=•CP•QE=m×(10﹣m)=﹣m2+3m;②∵S=•CP•QE=m×(10﹣m)=﹣m2+3m=﹣(m﹣5)2+,∴当m=5时,S取最大值;在抛物线对称轴l上存在点F,使△FDQ为直角三角形,∵抛物线的解析式为y=﹣x2+x+8的对称轴为x=,D的坐标为(3,8),Q(3,4),当∠FDQ=90°时,F1(,8),当∠FQD=90°时,则F2(,4),当∠DFQ=90°时,设F(,n),则FD2+FQ2=DQ2,即+(8﹣n)2++(n﹣4)2=16,解得:n=6±,∴F3(,6+),F4(,6﹣),满足条件的点F共有四个,坐标分别为F1(,8),F2(,4),F3(,6+),F4(,6﹣).14.解:(1)设抛物线的解析式为:y1=a(x﹣1)2+4,把A(3,0)代入解析式求得a=﹣1,∴y1=﹣(x﹣1)2+4=﹣x2+2x+3,设直线AB的解析式为:y2=kx+b,由y1=﹣x2+2x+3求得B点的坐标为(0,3),把A(3,0),B(0,3)代入y2=kx+b中,解得:k=﹣1,b=3;∴直线AB的解析式为:y2=﹣x+3;(2)设存在符合条件的点Q(x,0),则P点、D点的横坐标都为x,若x Q<3,则PD=x P﹣x D=y1﹣y2=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x,当PD=OB=3时,四边形OBPD成为平行四边形﹣x2+3x=3,此方程无解,∴不存在点Q;若x Q>3,则PD=x D﹣x P=y2﹣y1=(﹣x+3)﹣(﹣x2+2x+3)=x2﹣3x,当PD=OB=3时,四边形OBPD成为平行四边形x2﹣3x=3,解得:x=,x=<0(舍去),当Q在x轴的负半轴Q′上时,如图:P′D′=(﹣x+3)﹣(﹣x2+2x+3)=x2﹣3x=OB=3,解得:x=>0(舍去),x=,∴以O、B、P、D为顶点的四边形能成为平行四边形;(3)假设存在一点Q,使以PD为直径的圆与y轴相切,①当0<x<3时,设半径r,r=PD,PD=QP﹣QD=y1﹣y2=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x,∴r=(﹣x2+3x),∴x=(﹣x2+3x),解得:x1=1,x2=0(舍去),∴Q1(1,0);①当x<0时,设半径为r,r=PD,PD=QD﹣QP=y2﹣y1=(﹣x+3)﹣(﹣x2+2x+3)=x2﹣3x,∴r=(x2﹣3x),∴﹣x=(x2﹣3x),解得:x1=1(舍去),x2=0(舍去),③当x>3时,设半径为r,r=PD,PD=QD﹣QP=y2﹣y1=(﹣x+3)﹣(﹣x2+2x+3)=x2﹣3x,∴r=(x2﹣3x),∴x=(x2﹣3x),解得:x1=5,x2=0(舍去),∴Q2(5,0);∴Q1(1,0)、Q2(5,0)时都与y轴相切.15.解:(1)根据题意得,解得:,故函数解析式为:y=;(2)过点B作BM⊥x轴于M,则BM=,OM=3,∵OA=4,∴AM=1,AB=,∵,∴∠BAM=60°,当0<t≤2时,AF=t,过点F作FH⊥x轴,∵FH=AFsin60°=,,当2<t≤4时,如图,,当0<t≤2时,当时,,∵当2<t≤4时,s<∴当t=2时,,此时AE=AF=2,又∵∠EAF=60°.∴△AEF为等边三角形.(3)当0≤t≤2时,∵若∠EFA=90°,此时∠FEA=30°,∴EA=2AF,4﹣t=2t,∴.此时E当∠FEA=90°时,此时∠EFA=30°,∴2EA=AF,∴t=2(4﹣t)∴>2,∴这种情况不存在.当2<t≤4时,有t﹣2+t=3∴t=2.5 ∴E(2.5,0),F(2.5,).16.解:(1)由题意得,y=﹣x2+3x+4=﹣(x﹣4)(x+1),故可得:A(0,4),B(4,0),C(﹣1,0),(2)过点M作x轴的垂线交l于E,交另一条直线于F,①1)若△PQA∽△AOC,则=,即=,解得:x=7;2)若△AQP∽△AOC,则=,即=,解得:x=综合1)2)可得点P均在抛物线对称轴的右侧,∴点P的坐标为,②设点Q(x,4),P(x,﹣x2+3x+4),则PQ=x2﹣3x=PM,∵△AEM∽△MFP.则有.∵ME=OA=4,AM=AQ=x,PM=PQ=x2﹣3x,∴.解得:PF=4x﹣12,∴OM=(4x﹣12)﹣x=3x﹣12,Rt△AOM中,由勾股定理得OM2+OA2=AM2,∴(3x﹣12)2+42=x2,解得x1=4,x2=5,均在抛物线对称轴的右侧,故点P的坐标为(4,0)或(5,﹣6).17.解:(1)由抛物线的解析式知:A(0,1);∵BC⊥x轴,且点C(﹣3,0)∴点B的横坐标为﹣3,将其代入抛物线的解析式中,得:﹣×9+×3+1=∴点B(﹣3,);。
