最全最新2019高考数学一轮复习知识思维导图(理科版)
高中数学知识框架思维导图(整理版)
2
2
|→
a |= (x2-x1)2+(y2-y1)2
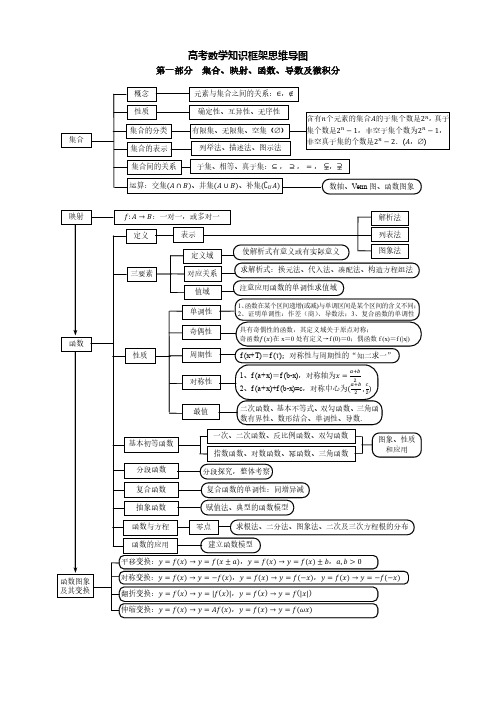
概念
模
线性运算
加、减、数乘
几何意义
平面向量基本定理:⃗ = 1 ⃗1 + 2 ⃗2 ,⃗1 、⃗2 不共线
坐标表示
平面向量
→
几何意义
数量积
⃗ ∙ ⃗⃗ =|⃗||⃗⃗|cosθ
→
→
a·b
b 在→
a 方向上的投影为|→
b |cos=——
2
离心率: = = √1 ± () .
21±co源自 抛物线 2 = 2的焦半径公式:|| = 0 + =
关于点(a,b)对称 点(2a-x ,2b-y )
点(x1,y1) ───────→
1
1
中心对称
关于点(a,b)对称 曲线 f (2a-x,2b-y)=0
曲线 f (x,y)=0 ───────→
概念
表示
通项公式、递推公式
=1 +
(−1)
2
等差数列与等比数列性质的类比
列表法
通项公式
等差数列
求和公式
等比数列
性质
an≠0,q≠0
数列
图象法
na1,q=1
n
Sn=a1(1-q )
,q≠1
1-q
常见递推类型及方法
an=a1+(n-1)d
an=am+(n-m)d
an=a1qn 1
弦长公式
|| = 2√2 − 2 .
相离、外切 = + 、相交、内切 = − 、包含.( ≥ ))
曲线与方程
轨迹方程的求法:直接法、定义法、相关点法
高考数学理科知识点框图

高考数学理科知识点框图目录第一部分集合、映射、函数、导数及微积分 (2)第二部分三角函数与平面向量 (3)第三部分数列与不等式 (4)第四部分解析几何 (5)第五部分立体几何 (6)第六部分统计与概率 (7)第一部分集合、映射、函数、导数及微积分第二部分三角函数与平面向量第三部分数列与不等式第六部分统计与概率第七部分其他部分内容的基础上礼,不但讲制度、讲规范,还要讲带着仁爱之心去执行这些规范;孔子的“仁”是在“礼”指导下的仁,是以君君、臣臣、父父、子子和等级制度为前提和目的的仁爱,不是无差别的兼爱、博爱。
练习1、阅读《论语》中的一段文字,然后回答问题。
(4分)子路曰:“卫君待子而为政,子将奚先?”子曰:“必也正名乎!”子路曰:“有是哉,子之迂也!奚其正?”子曰:“野哉,由也!君子于其所不知,盖阙如也。
名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所错手足。
故君子名之必可言也,言之必可行也。
君子于其言,无所苟而已矣。
”(13.3)1)根据子路的话可以看出子路怎样的性格?(1(2)为什么孔子那么强调“正名”的重要性?(3分)参考答案1)子路对孔子的回答不苟同,并且说孔子的观点何其迂腐,表现了他直率、淳朴的性格。
(2)孔子所处的年代,虽然周天子尚在,但礼乐已崩坏,当时的社会现实(实)已不符合西周的制度(名)。
孔子认为这些“实”的变化是不应该的,“名”和“实”混乱,社会就会引起混乱,礼乐就不能复兴,因此,他要用“名”(周礼的规定)去纠正已经改变或正在改变的“实”,“正名”,实际上是解决治国的指导思想问题。
2、阅读《论语》中的一段文字,然后回答问题。
(4分)1:颜渊问仁。
子曰:“克己复礼为仁。
一日克己复礼,天下归人焉。
为人由己,而由人乎哉?”颜渊曰:“请问其目。
”子曰:“非礼勿视,非礼勿听,非礼勿言,非礼勿动。
”颜渊曰:“回虽不敏,请事斯语矣。
”(13.3)材料2:他日,又独立,鲤趋而过庭。
2019年高考数学考前复习资料高中数学知识的框架思维导图
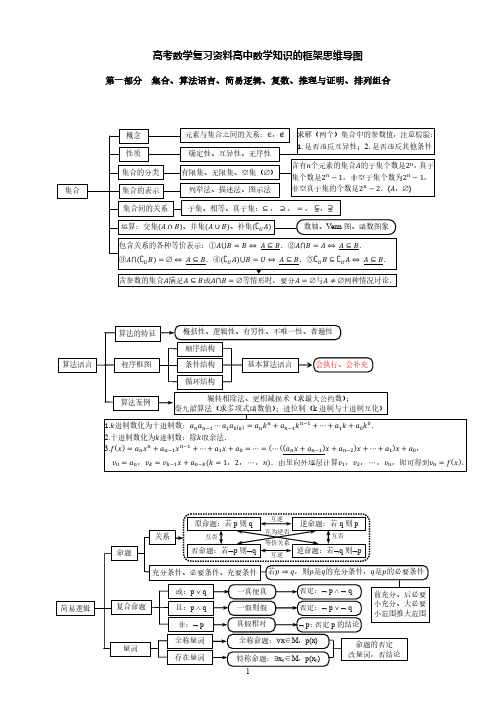
高考数学复习资料高中数学知识的框架思维导图第一部分集合、算法语言、简易逻辑、复数、推理与证明、排列组合第二部分函数、导数及微积分第三部分 三角函数与平面向量第四部分数列与不等式第五部分解析几何、坐标系与参数方程第七部分统计与概率第八部分 数学思想方法常见题型的解题规律或方法集锦1.求多面体外接球半径的常见模型:(掌握了常见模型,就不一定要画外接球与多面体的直观图) (1)截面圆的半径、大圆半径可由正弦定理r =a 2sin A求出;(2)必要时可将多面体补形为共外接球的特殊几何体. (3)多面体内切球的半径一般用等体积法求.2.同构不等式:若F (x )≥0能等价变形为f ,g (x )->f,ℎ(x )-g (x )≥ℎ(x),这种方法就称为同构不等式,简称同构法.a 2+b 2+c 2=(2R )2. ABCDB 1C 1D 1A 1abcd =R −r .OEBCDr 1 O 2O 1Ar 2Rr 13. 极点与极线的性质:关于二次曲线(圆、椭圆、双曲线、抛物线)的“四线一方程”4. 伸缩变换中椭圆与圆的对应关系5. 成立与恒成立问题,即函数有无零点,方程有解、无解,不等式成立、恒成立,求参数取值范围,一般优先考虑分离参数法:①若λ≥f(x)恒成立,则λ≥,f(x)-max;②若λ≤f(x)恒成立,则λ≤,f(x)-min;③若λ=f(x)有解,则λ∈*y|y=f(x)+;④若λ=f(x)无解,则λ∈ U*y|y=f(x)+;⑤若λ≥f(x)成立,则λ≥,f(x)-min;⑥若λ≤f(x)成立,则λ≤,f(x)-max.解决含参数问题的常用方法:⑴分离参数法;⑵分离函数法;⑶含参转化法.6. 洛必达法则,一个很实用的法则,主要用于求分式函数f (x )g(x)在x →a 时,00型或∞∞型的极限,可反复循环使用.用分离参数法(避免分类讨论)解决成立、或恒成立命题时,经常需要求在区间端点处的函数(最)值,若出现0或∞∞时,就必须用洛必达法则!7.函数凹凸性定义及性质:设f(x)在区间I 上连续,如果对I 上任意两点x 1,x 2, (1)凹函数:f (x 1+x 22)≤f (x 1)+f (x 2)2 f(x)在I 上的图形是(向上)凹的 f ′′(x )≥0(即切线的斜率递增).如图1. (2)凸函数:f (x 1+x 22)≥f (x 1)+f (x 2)2f(x)在I 上的图形是(向上)凸的 f ′′(x )≤0(即切线的斜率递减).如图2.其中的不等式又叫琴生不等式.若f(x)在x =x 0处取得极值(f ′(x 0)=0),且f ′′(x 0)>0,则f(x 0)为极小值; 若f(x)在x =x 0处取得极值(f ′(x 0)=0),且f ′′(x 0)<0,则f(x 0)为极大值.函数凹凸性的快速判断与函数单调性的快速判断方法极为类似(对数形结合时准确作图很有帮助).归纳:根据曲线、切线、单调性、凹凸性关系,可以得出以下结论 (1)对于ax ≤f(x)(x ≥0)恒成立,求实数a 的取值范围.如果f (0)=0,f ′(x )≥0(增函数),f ′′(x )≥0(凹函数),则实数a 的取值范围为a ≤f′(0). (2)对于ax ≥f(x)(x ≥0)恒成立,求实数a 的取值范围.如果f (0)=0,f ′(x )≥0(增函数),f ′′(x )≤0(凸函数),则实数a 的取值范围为a ≥f′(0).8.拉格朗日中值定理:若函数f(x)在区间(a ,b)内可导,在区间,a ,b-上连续,则∃x 0∈(a ,b),使得f ′(x 0)=f (b )−f(a)b−a.9.两个重要极限公式:⑴limx→0sinx x=1; ⑵lim x→+∞(1+1x)x =e .10.渐近线:有很多函数图象或曲线有渐近线(铅直渐近线、水平渐近线、斜渐近线),作图时就需要注意! (1)渐近线:若∃x 0∈R ,使得f (x 0)=0,则x =x 0为y =1f (x )图象的渐近线.你能作出y =1lnx,y =1sinx等函数的图象吗?高中数学中有渐近线的曲线:①y =kx,②y =x +kx(k ≠0),③y =a x ,④y =log a x ,⑤y =tan x ,⑥x 2a2−y 2b 2=1.(2)斜渐近线:对于y =f (x ),若limx→∞yx=k ,且lim x→∞(y −kx)=b ,则y =f (x )有斜渐近线y =kx +b .11.⑴如何解超越型不等式f (x )>0?所谓超越型不等式,就是不能通过等价变形,变成一元一次不等式或一元二次不等式,或变成可解的特殊的三角函数不等式.由ln x ,e x ,x α ,ax 2+bx +c ,kx +b ,kx ,sin x ,cos x 等其中几个组合成的不等式,可称为超越型不等式.一般来说,解超越型不等式,主要注意以下两个方面:①确定函数f(x)的定义域,并观察出函数f(x)的零点,常见零点有x =0,±1,±e 等; ②确定f(x)的单调性,结合①,即可求出f (x )>0的解集.⑵如何解超越型方程f (x )=0?如果在研究函数问题中出现了超越型方程f (x )=0,而通过观察又可以找到一个满足这个方程的根,那么这个根极有可能是方程的唯一根,然后要做的工作就是研究函数y =f(x)的单调性.满足f ′′(x 0)=0的实数x 0, 叫做函数f(x)的拐点.。
高考数学理科知识点框图

高考数学理科知识点框图目录第一部分集合、映射、函数、导数及微积分 (2)第二部分三角函数与平面向量 (3)第三部分数列与不等式 (4)第四部分解析几何 (5)第五部分立体几何 (6)第六部分统计与概率 (7)第一部分集合、映射、函数、导数及微积分第二部分三角函数与平面向量第三部分数列与不等式第六部分统计与概率第七部分其他部分内容的基础上礼, 不但讲制度、讲规范, 还要讲带着仁爱之心去执行这些规范;孔子的“仁”是在“礼”指导下的仁, 是以君君、臣臣、父父、子子和等级制度为前提和目的的仁爱, 不是无差别的兼爱、博爱。
练习1、阅读《论语》中的一段文字, 然后回答问题。
(4分)子路曰:“卫君待子而为政, 子将奚先?”子曰:“必也正名乎!”子路曰:“有是哉, 子之迂也!奚其正?”子曰:“野哉, 由也!君子于其所不知, 盖阙如也。
名不正, 则言不顺;言不顺, 则事不成;事不成, 则礼乐不兴;礼乐不兴, 则刑罚不中;刑罚不中, 则民无所错手足。
故君子名之必可言也, 言之必可行也。
君子于其言, 无所苟而已矣。
”(13.3)1)根据子路的话可以看出子路怎样的性格?(1(2)为什么孔子那么强调“正名”的重要性?(3分)参考答案1)子路对孔子的回答不苟同, 并且说孔子的观点何其迂腐, 表现了他直率、淳朴的性格。
(2)孔子所处的年代, 虽然周天子尚在, 但礼乐已崩坏, 当时的社会现实(实)已不符合西周的制度(名)。
孔子认为这些“实”的变化是不应该的, “名”和“实”混乱, 社会就会引起混乱, 礼乐就不能复兴, 因此, 他要用“名”(周礼的规定)去纠正已经改变或正在改变的“实”, “正名”实际上是解决治国的指导思想问题。
2、阅读《论语》中的一段文字, 然后回答问题。
(4分)材料1:颜渊问仁。
子曰:“克己复礼为仁。
一日克己复礼, 天下归人焉。
为人由己, 而由人乎哉?”颜渊曰:“请问其目。
”子曰:“非礼勿视, 非礼勿听, 非礼勿言, 非礼勿动。
高考数学理科知识点框图

高考数学理科知识点框图目录第一部分集合、映射、函数、导数及微积分 (2)第二部分三角函数与平面向量 (3)第三部分数列与不等式 (4)第四部分解析几何 (5)第五部分立体几何 (6)第六部分统计与概率 (7)第一部分集合、映射、函数、导数及微积分第二部分三角函数与平面向量第三部分数列与不等式第六部分统计与概率第七部分其他部分内容的基础上礼, 不但讲制度、讲规范, 还要讲带着仁爱之心去执行这些规范;孔子的“仁”是在“礼”指导下的仁, 是以君君、臣臣、父父、子子和等级制度为前提和目的的仁爱, 不是无差别的兼爱、博爱。
练习1、阅读《论语》中的一段文字, 然后回答问题。
(4分)子路曰:“卫君待子而为政, 子将奚先?”子曰:“必也正名乎!”子路曰:“有是哉子之迂也!奚其正?”子曰:“野哉, 由也!君子于其所不知, 盖阙如也。
名不正, 则言不顺;言不顺, 则事不成;事不成, 则礼乐不兴;礼乐不兴, 则刑罚不中;刑罚不中, 则民无所错手足。
故君子名之必可言也, 言之必可行也。
君子于其言无所苟而已矣。
”(13.3)1)根据子路的话可以看出子路怎样的性格?(1(2)为什么孔子那么强调“正名”的重要性?(3分)参考答案1)子路对孔子的回答不苟同, 并且说孔子的观点何其迂腐, 表现了他直率、淳朴的性格。
(2)孔子所处的年代, 虽然周天子尚在, 但礼乐已崩坏, 当时的社会现实(实)已不符合西周的制度(名)。
孔子认为这些“实”的变化是不应该的, “名”和“实”混乱, 社会就会引起混乱, 礼乐就不能复兴, 因此, 他要用“名”(周礼的规定)去纠正已经改变或正在改变的“实”“正名”, 实际上是解决治国的指导思想问题。
2、阅读《论语》中的一段文字, 然后回答问题。
(4分)材料1:颜渊问仁。
子曰:“克己复礼为仁。
一日克己复礼, 天下归人焉。
为人由己, 而由人乎哉?”颜渊曰:“请问其目。
”子曰:“非礼勿视, 非礼勿听, 非礼勿言, 非礼勿动。
高中数学知识框架思维导图(整理版)

柯西不等式
第四部分
位置关系
截距
解析几何
斜率公式、倾斜角的变化与斜率的变化: = tan , =
倾斜角和斜率
重合
A1B2-A2B1=0,C1B2-C2B1=0
平行
A1B2-A2B1=0,C1B2-C2B1≠0
相交
A1B2-A2B1≠0
垂直
直线的方程
z 的几何意义:
过可行域内一点(, )
向直线 = , = 作
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
对称性
y=Asin(x+)+b
化简、求值、
证明(恒等变形)
)
值域
图象
对称轴(正切函数除外)经过函数图象
的最高(或低)点且垂直 x 轴的直线,
对称中心是正余弦函数图象的零点,正
切函数的对称中心为( ,0)(k∈Z).
最值
2
①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1
2+1 −1
高三数学所有知识点思维导图

高三数学所有知识点思维导图数学是一门理论性较强的科学,它涉及到复杂的逻辑思维和抽象的概念。
为了更好地理解和掌握高三数学知识,在学习过程中,合理地组织知识点之间的联系和内在逻辑结构非常重要。
这篇文章将通过思维导图的方式,对高三数学的所有知识点进行概括总结。
一、函数与方程1. 函数的概念2. 常用函数的性质与图像a. 一次函数b. 二次函数c. 三次函数d. 高次函数e. 幂函数f. 指数函数g. 对数函数h. 三角函数3. 方程的基本概念a. 一元一次方程b. 一元二次方程c. 一元高次方程d. 二元一次方程e. 二元二次方程二、数与集合1. 实数与不等式a. 实数的性质b. 不等式的性质c. 一元一次不等式d. 一元二次不等式e. 二元一次不等式f. 二元二次不等式2. 复数与复数运算a. 复数的定义与性质b. 复数的运算c. 复数的共轭与模3. 集合与命题逻辑a. 集合的基本概念与运算b. 命题的概念与逻辑运算三、解析几何1. 平面坐标系a. 平面直角坐标系的建立与性质b. 向量的概念与运算c. 直线与方程d. 圆与方程2. 空间坐标系a. 空间直角坐标系的建立与性质b. 空间中的直线与平面c. 空间中的平面与方程四、三角函数与解三角形1. 三角函数的基本关系式a. 正弦函数与余弦函数b. 正切函数与余切函数c. 正割函数与余割函数2. 三角函数的性质与变换a. 周期性与奇偶性b. 幅角的增减关系c. 三角函数的和差化积3. 解三角形的基本概念a. 三角外角与内角b. 三角形的各种关系式c. 解三角形的方法与技巧五、数列与数学归纳法1. 数列的基本概念与性质a. 数列的定义b. 数列的通项公式与通项求和公式c. 数列的极限2. 等差数列与等比数列a. 等差数列的性质与公式b. 等差数列的求和公式c. 等比数列的性质与公式d. 等比数列的求和公式3. 数学归纳法的原理与应用a. 数学归纳法的基本思想b. 数学归纳法在证明问题中的应用六、概率与统计1. 随机事件与概率a. 随机事件的概念与性质b. 概率的定义与性质c. 概率计算与应用2. 统计方法与推理a. 统计调查与样本调查b. 描述性统计与统计推断c. 抽样分布与统计量的估计d. 假设检验与推断这篇文章通过思维导图的方式,对高三数学的所有知识点进行了系统的总结,有助于帮助学生快速理清思路,更好地掌握数学知识。
高考数学理科知识点框图

高考数学理科知识点框图目录第一部分集合、映射、函数、导数及微积分 (2)第二部分三角函数与平面向量 (3)第三部分数列与不等式 (4)第四部分解析几何 (5)第五部分立体几何 (6)第六部分统计与概率 (7)第一部分 集合、映射、函数、导数及微积分集合 映射 概念 元素、集合之间的关系运算:交、并、补 数轴、Venn 图、函数图象性质 确定性、互异性、无序性 定义 表示 解析法列表法三要素 图象法定义域 对应关系值域 性质 奇偶性 周期性对称性 单调性 定义域关于原点对称, 在x =0处有定义的奇函数→f (0)=01、函数在某个区间递增(或减)与单调区间是某个区间的含义不同;2、证明单调性:作差(商)、导数法;3、复合函数的单调性最值 二次函数、基本不等式、打钩(耐克)函数、三角函数有界性、数形结合、导数.幂函数对数函数三角函数基本初等函数 抽象函数 复合函数 赋值法、典型的函数函数与方程 二分法、图象法、二次及三次方程根的分布 零点 函数的应用 建立函数模型使解析式有意义 导数函数基本初等函数的导数 导数的概念 导数的运算法则导数的应用表示方法 换元法求解析式分段函数 几何意义、物理意义单调性 导数的正负与单调性的关系生活中的优化问题定积分与微积分 定积分与图形的计算注意应用函数的单调性求值域周期为T 的奇函数→f (T )=f (T 2)=f (0)=0复合函数的单调性:同增异减三次函数的性质、图象与应用一次、二次函数、反比例函数指数函数 图象、性质和应用平移变换对称变换 翻折变换 伸缩变换 图象及其变换 最值 极值第二部分 三角函数与平面向量角的概念 任意角的三角函数的定义 三角函数 弧度制 弧长公式、扇形面积公式 三角函数线同角三角函数的关系诱导公式和角、差角公式 二倍角公式公式的变形、逆用、“1”的替换 化简、求值、证明(恒等变形) 三角函数 的 图 象 定义域 奇偶性单调性 周期性 最值 对称轴(正切函数除外)经过函数图象的最高(或低)点且垂直x 轴的直线,对称中心是正余弦函数图象的零点, 正切函数的对称中心为(错误!, 0)(k∈Z ).正弦函数y =sin x =余弦函数y =cos x 正切函数y =tan x y =A sin(ωx +ϕ)+b ①图象可由正弦曲线经过平移、伸缩得到, 但要注意先平移后伸缩与先伸缩后平移不同;②图象也可以用五点作图法;③用整体代换求单调区间(注意ω的符号);④最小正周期T =错误!;⑤对称轴x =错误!, 对称中心为(错误!, b )(k ∈Z ). 平面向量 概念 线性运算 基本定理加、减、数乘 几何意义 坐标表示 数量积几何意义 模共线与垂直共线(平行) 垂直 值域 图象a →∥b →⇔b →=λa → ⇔ x 1y 2-x 2y 1=0 a →⊥b →⇔b →·a →=0 ⇔ x 1x 2+y 1y 2=0 解三角形 余弦定理面积 正弦定理 解的个数的讨论实际应用 S △=12ah =12ab sin C =p(p -a)(p -b)(p -c)(其中p =a +b +c2)投影 b →在a →方向上的投影为|b →|cos θ=a →·b→——|a →|设a →与b →夹角θ, 则cos θ=a →·b→——|a →|·|b →|对称性 |a →|=(x2-x1)2+(y2-y1)2夹角公式第三部分 数列与不等式概念 数列表示 等差数列与等比数列的类比 解析法:a n =f (n ) 通项公式 图象法列表法 递推公式 等差数列 通项公式 求和公式 性质判断 a n =a 1+(n -1)d a n =a 1q n -1a n +a m =a p +a r a n a m =a p a r前n 项和 S n =n(a1+an)2前n 项积(a n >0)T n =(a1an)n常见递推类型及方法 逐差累加法 逐商累积法构造等比数列{a n +q p -1} 构造等差数列 ①a n +1-a n =f (n ) ②an + 1an =f (n ) ③a n +1=pa n +q ④pa n +1a n =a n -a n +1 化为an +1qn =p q ·anqn -1+1转⑤a n + 1=pa n +q n 等比数列 a n ≠0, q ≠0 S n =⎩⎨⎧na1,q =1a1(1-qn)1-q ,q≠1公式法:应用等差、等比数列的前n 项和公式 分组求和法倒序相加法裂项求和法错位相加法常见求和方法 不等式 不等式的性质 一元二次不等式简单的线性规划 基本不等式: ab ≤a +b2 数列是特殊的函数 借助二次函数的图象 三个二次的关系可行域 目标函数 一次函数:z =ax +by z =y -bx -a :构造斜率 z =(x -a)2+(y -b)2:构造距离 应用题 几何意义:z 是直线ax +by-z =0在x 轴截距的a 倍, y 轴上截距的b 倍.最值问题 变形 和定值, 积最大;积定值, 和最小 应用时注意:一正二定三相等 2ab a +b ≤ab ≤a +b 2≤a2+b22第四部分解析几何倾斜角和斜率直线的方程位置关系直线方程的形式倾斜角的变化与斜率的变化重合平行相交垂直A1B2-A2B1=0A1B2-A2B1≠0A1A2+B1B2=0点斜式:y-y0=k(x-x0)斜截式:y=kx+b两点式:y-y1y2-y1=x-x1x2-x1截距式:xa+yb=1一般式:Ax+By+C=0注意各种形式的转化和运用范围.两直线的交点距离点到线的距离:d=| Ax0+By0+C |A2+B2,平行线间距离:d=| C1-C2 |A2+B2圆的方程圆的标准方程圆的一般方程直线与圆的位置关系两圆的位置关系相离相切相交∆<0,或d>r∆=0,或d=r∆>0,或d<r曲线与方程轨迹方程的求法:直接法、定义法、相关点法圆锥曲线椭圆双曲线抛物线定义及标准方程性质范围、对称性、顶点、焦点、长轴(实轴)、短轴(虚轴)、渐近线(双曲线)、准线(只要求抛物线)离心率对称性问题中心对称轴对称点(x1,y1) ───────→关于点(a, b)对称点(2a-x1,2b-y1) 曲线f (x,y) ───────→关于点(a, b)对称曲线f (2a-x,2b-y)⎩⎪⎨⎪⎧A·x1+x22+B·y1+y22+C=0y2-y1x2-x1·(-AB)=-1特殊对称轴x±y+C=0 直接代入法截距注意:截距可正、可负,也可为0.点(x1,y1)与点(x2,y2)关于直线Ax+By+C=0对称第五部分 立体几何点与线 空间点、 线、面的 位置关系 点在直线上点在直线外点与面 点在面内点在面外线与线 共面直线异面直线相交 平行 没有公共点只有一个公共点线与面 平行 相交有公共点没有公共点直线在平面外直线在平面内面与面 平行相交平行关系的相互转化 垂直关系的相互转化 线线 平行 线面 平行 面面平行 线线 垂直 线面 垂直 面面 垂直空间的角 异面直线所成的角 直线与平面所成的角 二面角 范围:(0︒, 90︒] 范围:[0︒, 90︒] 范围:[0︒, 180︒] 点到面的距离 直线与平面的距离 平行平面之间的距离 相互之间的转化 cos θ=|a →·b→|——|a →|·|b →|sin θ=|a →·n →|——|a →|·|n →|cos θ=n1→·n2→——|n1→|·|n2→|d =|a →·n →|——|n →|空间向量 空间直角坐标系空间的距离 空间几何体 柱体 棱柱 圆柱 正棱柱、长方体、正方体台体 棱台 圆台 锥体 棱锥 圆锥球 三棱锥、四面体、正四面体 直观图侧面积、表面积 三视图 体积长对正 高平齐宽相等第六部分统计与概率统计随机抽样抽签法随机数表法简单随机抽样系统抽样分层抽样共同特点:抽样过程中每个个体被抽到的可能性(概率)相等用样本估计总体样本频率分布估计总体总体密度曲线频率分布表和频率分布直方图茎叶图样本数字特征估计总体众数、中位数、平均数方差、标准差变量间的相关关系两个变量的线性相关散点图回归直线正态分布列联表(2×2)独立性分析概率概率的基本性质互斥事件对立事件古典概型几何概型条件概率事件的独立性用随机模拟法求概率常用的分布及期望、方差随机变量两点分布X~B(1,p)E(X)=p,D(X)=p(1-p)二项分布X~B(n,p)E(X)=np,D(X)=np(1-p)X~H(N,M,n)E(X)=nMND(X)=nMN()1-MNN-nN-1n次独立重复试验恰好发生k次的概率为P n(k)=C k n p k(1-p)n-k超几何分布若Y=aX+b,则E(Y)=aE(X)+bD(Y)=a2D(X)P(A+B)=P(A)+P(B)P( A)=1-P(A)P(A B)=P(A)·P(B)P(B | A)=错误!第七部分 其他部分内容合情推理 演绎推理 归纳类比三段论 大前提、小前提、结论两个原理 分类加法计算原理和分步乘法计算原理排列与组合 排列数:A m n =n!(n -m)!组合数:C m n =n!m!(n -m)! 性质 C mn =C n -mnC m n +1=C m n +计算原理 二项式定理 通项公式 T r +1=C r n a n -r b r首末两端“等距离”两项的二项式系数相等 C 0n +C 2n +C 4n …=C 1n +C 3n +C 5n …=2n -1C 0n +C 1n +…+C n n =2n 二项式系数性质直接证明综合法 分析法 由因导果执果索因间接证明 反证法数学归纳法 推理 证明 推理与证明 充分非必要条件、必要非充分条件、充要条件关系 条件 复合命题 或:p ∨ q且:p ∧ q非:⌝ p 猜想原命题:若p 则q 逆命题:若q则p否命题:若⌝p 则⌝q逆命题:若⌝q 则⌝p 互逆 互逆 互否 互否互为逆否 等价关系一真便真一假则假全称量词与存在量词 简易逻辑概括性、逻辑性、有穷性、不唯一性、普遍性顺序结构条件结构 循环结构命题 算法语言 算法的特征 程序框图 基本算法语言算法案例 辗转相除法、更相减损术、秦九韶算法、进位制复 数 概念 虚数、纯虚数、实部、虚部、实轴、虚轴、模、共轭复数 运算 加、减、乘、除、乘方几何意义 复数与复平面内点(向量)的对应关系、复数模的几何意义的基础上礼,不但讲制度、讲规范,还要讲带着仁爱之心去执行这些规范;孔子的“仁”是在“礼”指导下的仁,是以君君、臣臣、父父、子子和等级制度为前提和目的的仁爱,不是无差别的兼爱、博爱。
