MatLab练习册2(答案)

MATLAB作业2参考答案(2018)

MATLAB 作业二参考答案1、试求下面线性代数方程的解析解与数值解，并检验解的正确性。

2932114010110503848246303356684953X -----⎡⎤⎡⎤⎢⎥⎢⎥----⎢⎥⎢⎥=⎢⎥⎢⎥---⎢⎥⎢⎥------⎣⎦⎣⎦【求解】求出A , [A;B ] 两个矩阵的秩，可见二者相同，所以方程不是矛盾方程，应该有无穷多解。

>> A=[2,-9,3,-2,-1; 10,-1,10,5,0; 8,-2,-4,-6,3; -5,-6,-6,-8,-4]; B=[-1,-4,0; -3,-8,-4; 0,3,3; 9,-5,3]; [rank(A), rank([A B])] ans =4 4用下面的语句可以求出方程的解析解，并可以验证该解没有误差。

>> x0=null(sym(A));x_analytical=sym(A)\B; syms a; x=a*[x0 x0 x0]+x_analytical x =[ a+967/1535, a-943/1535, a-159/1535] [ -1535/1524*a, -1535/1524*a, -1535/1524*a][ -3659/1524*a-1807/1535,-3659/1524*a-257/1535,-3659/1524*a-141/1535] [ 1321/508*a+759/1535, 1321/508*a-56/1535, 1321/508*a-628/1535] [ -170/127*a-694/307, -170/127*a+719/307, -170/127*a+103/307] >> A*x-B ans =[ 0, 0, 0][ 0, 0, 0][ 0, 0, 0][ 0, 0, 0]用数值解方法也可以求出方程的解，但会存在误差，且与任意常数a 的值有关。

>> x0=null(A); x_numerical=A\B; syms a;x=a*[x0 x0 x0]+x_numerical; vpa(x,10)ans =[ .2474402553*a+.1396556436, .2474402553*a-.6840666849, .2474402553*a-.1418 420333][-.2492262414*a+.4938507789,-.2492262414*a+.7023776988e-1,-.2492262414*a+ .3853511888e-1][ -.5940839201*a, -.5940839201*a, -.5940839201*a][ .6434420813*a-.7805411315, .6434420813*a-.2178190763,.6434420813*a-.50860 89095][-.3312192394*a-1.604263460, -.3312192394*a+2.435364854,-.3312192394*a+.3867176824]>> A*x-Bans =[ 1/18014398509481984*a, 1/18014398509481984*a, 1/18014398509481984*a] [ -5/4503599627370496*a, -5/4503599627370496*a, -5/4503599627370496*a] [ -25/18014398509481984*a, -25/18014398509481984*a,-25/18014398509481984*a][ 13/18014398509481984*a, 13/18014398509481984*a, 13/18014398509481984*a]2、求解下面的联立方程，并检验得出的高精度数值解（准解析解）的精度。

matlab习题二带答案

matlab习题二带答案Matlab习题二带答案Matlab是一种强大的数值计算和科学编程软件，广泛应用于各个领域的科学研究和工程实践中。

掌握Matlab的使用对于科学家和工程师来说至关重要。

为了帮助大家更好地掌握Matlab，下面将介绍一些常见的Matlab习题，并提供相应的答案。

1. 习题一：计算平均值编写一个Matlab函数，输入一个向量，输出该向量的平均值。

答案：```matlabfunction avg = computeAverage(vector)avg = sum(vector) / length(vector);end```2. 习题二：矩阵操作编写一个Matlab函数，输入两个矩阵A和B，输出它们的乘积C。

答案：```matlabfunction C = matrixMultiplication(A, B)[m, n] = size(A);[~, p] = size(B);C = zeros(m, p);for i = 1:mfor j = 1:pfor k = 1:nC(i, j) = C(i, j) + A(i, k) * B(k, j);endendendend```3. 习题三：图像处理编写一个Matlab函数，输入一张彩色图像，输出该图像的灰度图像。

答案：```matlabfunction grayImage = convertToGray(image)grayImage = rgb2gray(image);end```4. 习题四：数据拟合给定一组数据点(x, y)，编写一个Matlab函数，拟合这些数据点为一条直线，并返回拟合直线的斜率和截距。

答案：```matlabfunction [slope, intercept] = fitLine(x, y)n = length(x);sx = sum(x);sy = sum(y);sxy = sum(x .* y);sxx = sum(x .* x);slope = (n * sxy - sx * sy) / (n * sxx - sx^2);intercept = (sy - slope * sx) / n;end```5. 习题五：数值积分编写一个Matlab函数，输入一个函数f(x)和积分区间[a, b]，输出该函数在该区间上的数值积分结果。

MATLAB程序设计与应用第二版课后题答案2(最新整理)

-0.6863 0.5621 0.4615
-0.0937 -0.6976 0.7103
D=
-0.0166
0
0
0 1.4801
0
0
0 2.5365
第四章
1.a=input('请输入一个 4 位数:');
while (a<1000|a>9999)
a=input('输入错误，请重新输入一个4位数:');
end
9
function f=factor(n,m); y=0; for k=1:n
y=y+k^m; end
10.(1)S=108 (2)x=4 12 20
y=2 4 6
1. (1) x=-10:0.1:10; y=100./(1+x.^2); plot(x,y)
第五章
(2) x=-10:0.1:10; y=1/(2*pi)*exp(-x.^2/2); plot(x,y)
第二章 3.设矩阵 A 为 A=[24 23 9 21 6;65 74 24 11 21;34 5 98 75 21;8 42 42 53 121;43 21 45 64 21]; （1） B=A(2:5,1:2:5)
B=
65 24 21 34 98 21 8 42 121 43 45 21 （2）A(7)=[] A= 24 65 34 8 43 23 5 42 21 9 24 98 42 45 21 11 75 53 64 6 21 21 121 21 （3）A+30 （4）size(A);ndims(A) （5）题目有误（6）reshape(x,3,4) （7）abs(x) （8）char(x) 4. L1 = 000010000 L2 =

matlab程序设计与应用第二版习题答案

matlab程序设计与应用第二版习题答案Matlab程序设计与应用第二版习题答案Matlab是一种强大的数学软件，广泛应用于科学计算、数据分析和工程设计等领域。

《Matlab程序设计与应用》是一本经典的教材，对于学习和掌握Matlab编程语言具有重要的意义。

本文将为大家提供《Matlab程序设计与应用第二版》中部分习题的答案，帮助读者更好地理解和应用Matlab。

第一章：Matlab基础1.1 基本操作1. a = 3; b = 4; c = sqrt(a^2 + b^2); disp(c);2. x = linspace(-pi, pi, 100); y = sin(x); plot(x, y);3. A = [1 2 3; 4 5 6; 7 8 9]; B = [9 8 7; 6 5 4; 3 2 1]; C = A + B; disp(C);1.2 控制结构1. for i = 1:10disp(i);end2. n = 0; sum = 0; while sum < 100n = n + 1;sum = sum + n;enddisp(n);3. x = 5; if x > 0disp('x is positive');elseif x < 0disp('x is negative');elsedisp('x is zero');end第二章：向量和矩阵运算2.1 向量运算1. A = [1 2 3]; B = [4 5 6]; C = A .* B; disp(C);2. A = [1 2 3]; B = [4 5 6]; C = A ./ B; disp(C);3. A = [1 2 3]; B = [4 5 6]; C = dot(A, B); disp(C);2.2 矩阵运算1. A = [1 2 3; 4 5 6]; B = [7 8; 9 10; 11 12]; C = A * B; disp(C);2. A = [1 2 3; 4 5 6]; B = [7 8; 9 10; 11 12]; C = B * A; disp(C);3. A = [1 2 3; 4 5 6]; B = [7 8; 9 10; 11 12]; C = A .* B; disp(C); 第三章：函数和脚本文件3.1 函数1. function y = myfunc(x)y = x^2 + 3*x + 2;end2. function [y1, y2] = myfunc(x1, x2)y1 = x1^2 + 3*x1 + 2;y2 = x2^2 + 3*x2 + 2;end3. function [y1, y2] = myfunc(x)y1 = x^2 + 3*x + 2;y2 = sin(x);end3.2 脚本文件1. x = linspace(0, 2*pi, 100); y = sin(x); plot(x, y);2. x = linspace(-10, 10, 100); y = x.^2 + 3*x + 2; plot(x, y);3. x = linspace(0, 2*pi, 100); y1 = sin(x); y2 = cos(x); plot(x, y1, x, y2);通过以上习题的答案，读者可以对Matlab程序设计的基本语法和常用函数有一个初步的了解。

[整理版]matlab课后习题解答第二章

第2章0000符号运算0000习题2及解答00001 说出以下四条指令产生的结果各属于哪种数据类型，是“双精度”对象，还是“符号”符号对象？00003/7+0.1; sym(3/7+0.1); sym('3/7+0.1'); vpa(sym(3/7+0.1))0000〖目的〗0000不能从显示形式判断数据类型，而必须依靠class指令。

0000〖解答〗0000c1=3/7+0.10000c2=sym(3/7+0.1)0000c3=sym('3/7+0.1')0000c4=vpa(sym(3/7+0.1))0000Cs1=class(c1)0000Cs2=class(c2)0000Cs3=class(c3)0000Cs4=class(c4) 0000c1 =00000.52860000c2 =000037/700000c3 =00000.528571428571428571428571428571430000c4 =00000.528571428571428571428571428571430000Cs1 =0000double0000Cs2 =0000sym0000Cs3 =0000sym0000Cs4 =0000sym00002 在不加专门指定的情况下，以下符号表达式中的哪一个变量被认为是自由符号变量.0000sym('sin(w*t)'),sym('a*exp(-X)'),sym('z*exp(j*th)')0000〖目的〗0000● 理解自由符号变量的确认规则。

0000〖解答〗0000symvar(sym('sin(w*t)'),1) 0 0 0 0ans = 0 0 0 0 w 0 0 0 0symvar(sym('a*exp(-X)'),1) 0 0 0 0ans = 0 0 0 0 a 0 0 0 0symvar(sym('z*exp(j*th)'),1) 0 0 0 0ans = 0 0 0 0 z 0 0 0 05求符号矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211a a a a a a a a a A 的行列式值和逆，所得结果应采用“子表达式置换”简洁化。

matelab作业2参考答案

matelab作业2参考答案Matlab作业2参考答案Matlab作业2是一项综合性的任务，要求学生运用Matlab编程语言解决一系列数学问题。

本文将为大家提供一份参考答案，帮助学生更好地理解和完成这项作业。

首先，我们将讨论作业的第一个问题，即给定一个矩阵A，求解其特征值和特征向量。

在Matlab中，可以使用eig函数来实现这一功能。

例如，假设我们有一个3×3的矩阵A，可以按照以下方式计算其特征值和特征向量：```A = [1 2 3; 4 5 6; 7 8 9];[eigenvectors, eigenvalues] = eig(A);```在上述代码中，变量eigenvectors将存储A的特征向量，而变量eigenvalues 将存储A的特征值。

通过打印这两个变量的值，我们可以得到矩阵A的特征值和特征向量。

接下来，我们将探讨作业的第二个问题，即求解线性方程组。

假设我们有一个3×3的系数矩阵A和一个3×1的常数向量b，我们需要求解方程组Ax=b。

在Matlab中，可以使用backslash运算符来求解线性方程组。

例如，假设我们有以下方程组：```A = [1 2 3; 4 5 6; 7 8 9];b = [10; 20; 30];x = A \ b;```在上述代码中，变量x将存储方程组的解。

通过打印变量x的值，我们可以得到方程组的解。

此外，作业的第三个问题要求学生使用Matlab绘制函数图像。

在Matlab中，可以使用plot函数来实现这一功能。

例如，假设我们要绘制函数y=sin(x)，其中x的取值范围为0到2π，可以按照以下方式绘制函数图像：```x = 0:0.1:2*pi;y = sin(x);plot(x, y);```在上述代码中，变量x将存储x的取值范围，变量y将存储对应的函数值。

通过调用plot函数，我们可以将函数y=sin(x)的图像绘制出来。

matlab第二版习题答案

matlab第二版习题答案Matlab是一种强大的数学软件工具，被广泛应用于科学计算、数据分析和工程设计等领域。

对于学习和掌握Matlab的人来说，习题是不可或缺的一部分。

本文将为大家提供Matlab第二版习题的答案，帮助读者更好地理解和应用Matlab。

第一章：基本操作1.1 Matlab的启动和退出启动Matlab的方法有多种，可以通过桌面图标、命令行或者启动器来打开Matlab。

退出Matlab可以直接关闭窗口或者使用命令"exit"。

1.2 Matlab的基本语法Matlab的基本语法与其他编程语言相似，包括变量的定义、运算符的使用、条件语句和循环语句等。

例如，定义一个变量x并赋值为5可以使用语句"x = 5;"。

1.3 Matlab的数据类型Matlab支持多种数据类型，包括数值型、字符型和逻辑型等。

数值型可以是整数或者浮点数，字符型用单引号或双引号表示，逻辑型只有两个值true和false。

第二章：向量和矩阵操作2.1 向量的定义和运算向量是一维数组，可以通过一对方括号来定义。

Matlab提供了丰富的向量运算函数，如加法、减法、乘法和除法等。

2.2 矩阵的定义和运算矩阵是二维数组，可以通过方括号和分号来定义。

Matlab提供了矩阵的加法、减法、乘法、转置和求逆等运算。

2.3 矩阵的索引和切片可以使用索引和切片来访问矩阵中的元素。

索引从1开始，可以使用冒号表示全部元素。

切片可以用来选择矩阵的一部分。

第三章：函数和脚本文件3.1 函数的定义和调用函数是一段独立的代码块，可以接受输入参数并返回输出结果。

在Matlab中，函数的定义以关键字"function"开头，调用函数使用函数名和参数。

3.2 脚本文件的编写和运行脚本文件是一系列Matlab语句的集合，可以保存为.m文件。

通过运行脚本文件，可以一次性执行多个语句，提高效率。

第四章：图形绘制和数据可视化4.1 图形绘制函数Matlab提供了丰富的图形绘制函数，可以绘制线图、散点图、柱状图等。

MATLAB课后习题集附标准答案

MATLAB课后习题集附标准答案第2 章 MATLAB 概论1、与其他计算机语言相比较，MA TLAB 语言突出的特点是什么？答：起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富，可扩展性强.2、MA TLAB 系统由那些部分组成？答：开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB 时，在选择组件窗口中哪些部分必须勾选，没有勾选的部分以后如何补安装？答：在安装MATLAB时，安装内容由选择组件窗口中各复选框是否被勾选来决定，可以根据自己的需要选择安装内容，但基本平台（即MATLAB选项）必须安装 . 第一次安装没有选择的内容在补安装时只需按照安装的过程进行，只是在选择组件时只勾选要补装的组件或工具箱即可. 矚慫润厲钐瘗睞枥庑赖。

4、MATLAB 操作桌面有几个窗口？如何使某个窗口脱离桌面成为独立窗口？又如何将脱离出去的窗口重新放置到桌面上？聞創沟燴鐺險爱氇谴净。

答：在MATLAB操作桌面上有五个窗口，在每个窗口的右下角有两个小按钮，一个是关闭窗口的Close 按钮，一个是可以使窗口称为独立的Undock 按钮，点击 Undock 按钮就可以使该窗口脱离桌面称为独立窗口，在独立窗口的 view 菜单中选择 Dock ，菜单项就可以将独立的窗口重新防止的桌面上.残骛楼諍锩瀨濟溆塹籟。

5、如何启动 M 文件编辑 /调试器？答：在操作桌面上选择“建立新文件”或“打开文件”操作时，M 文件编辑 /调试器将被启动 .在命令窗口中键入 edit 命令时也可以启动酽锕极額閉镇桧猪訣锥。

M 文件编辑 /调试器 .6、存储在工作空间中的数组能编辑吗？如何操作？答：存储在工作空间的数组可以通过数组编辑器进行编辑：在工作空间浏览器中双击要编辑的数组名打开数组编辑器，再选中要修改的数据单元，输入修改内容即可.彈贸摄尔霁毙攬砖卤庑。

7、命令历史窗口除了可以观察前面键入的命令外，还有什么用途？答：命令历史窗口除了用于查询以前键入的命令外，还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中 . 謀荞抟箧飆鐸怼类蒋薔。

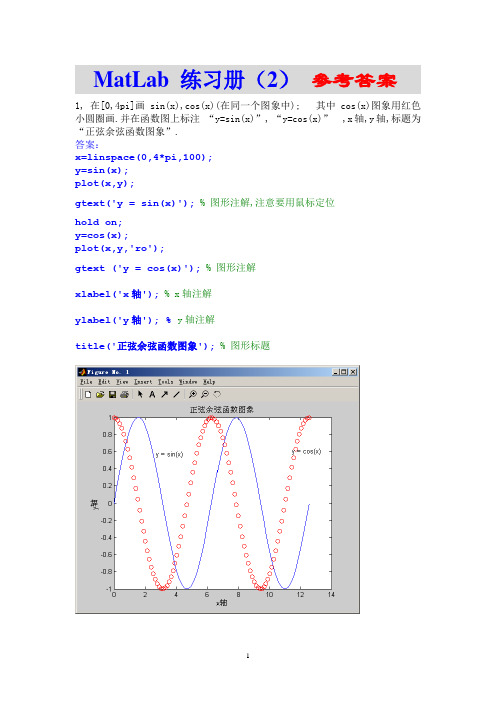
MatLab 练习册（2）参考答案1,在[0,4pi]画sin(x),cos(x)(在同一个图象中); 其中cos(x)图象用红色小圆圈画.并在函数图上标注“y=sin(x)”, “y=cos(x)” ,x轴,y轴,标题为“正弦余弦函数图象”.答案：x=linspace(0,4*pi,100);y=sin(x);plot(x,y);gtext('y = sin(x)');% 图形注解,注意要用鼠标定位hold on;y=cos(x);plot(x,y,'ro');gtext ('y = cos(x)');% 图形注解xlabel('x轴'); % x轴注解ylabel('y轴'); % y轴注解title('正弦余弦函数图象'); % 图形标题2, 画出2222)sin(y x y x z ++=所表示的三维曲面。

y x ,的取值范围是]8,8[-答案： x=-8:0.5:8;%定义自变量x 的一维刻度向量 y=x; %定义自变量y 的一维刻度向量[X,Y]=meshgrid(x,y);R=sqrt(X.^2+Y.^2); %计算中间变量22y x R +=Z=sin(R)./R; %计算相应的函数值R R z sin = mesh(X,Y,Z); %或用surf(X,Y,Z);画图3,绘制椭圆449222=++z y x 表面图,x 在[-2,2],y 在[-2,2]范围. 答案：x=-2:0.3:2;y=-2:0.3:2;[X,Y]=meshgrid(x,y);Z=sqrt(4-X.^2/9-Y.^2/4); surf(X,Y,Z);4,绘制环面:⎪⎩⎪⎨⎧=∈+=∈+=u z v vu y u v u x sin )2,0(sin )cos 1()2,0(cos )cos 1(ππ答案：u=linspace(0,2*pi,30); v=u;[U,V]=meshgrid(u,v); X=(1+cos(U)).*cos(V); Y=(1+cos(U)).*sin(V); Z=sin(U);mesh(X,Y,Z);surf(X,Y,Z);。

matlab第二版课后习题答案

matlab第二版课后习题答案
《MATLAB第二版课后习题答案》
MATLAB是一种强大的数学软件，被广泛应用于工程、科学和金融等领域。

《MATLAB第二版》是一本经典的教材，为了帮助学生更好地掌握MATLAB的使用，书中提供了大量的课后习题。

下面我们将为大家总结一些MATLAB第二版课后习题的答案，希望能对大家的学习有所帮助。

1. 第一章课后习题答案
第一章主要介绍了MATLAB的基本操作，包括变量的定义、矩阵的运算、函数的使用等。

在课后习题中，有一道题目是要求计算一个矩阵的逆矩阵。

答案是使用MATLAB中的inv函数，将原矩阵作为参数传入即可得到逆矩阵。

2. 第二章课后习题答案
第二章介绍了MATLAB中的绘图功能，包括二维和三维图形的绘制。

有一道课后习题是要求绘制一个正弦曲线和余弦曲线，并在同一张图上显示。

答案是使用MATLAB中的plot函数，分别绘制正弦曲线和余弦曲线，并使用legend函数添加图例。

3. 第三章课后习题答案
第三章介绍了MATLAB中的控制流程，包括if语句、for循环和while循环等。

有一道课后习题是要求编写一个程序，计算1到100之间所有偶数的和。

答案是使用for循环遍历1到100之间的所有数，判断是否为偶数并累加。

通过以上几个例子，我们可以看到MATLAB第二版课后习题的答案涵盖了各种基本和高级的操作，对于学习MATLAB是非常有帮助的。

希望大家在学习MATLAB的过程中能够多加练习，掌握更多的技巧和方法。

MATLAB数学实验第二版课后练习题含答案

MATLAB数学实验第二版课后练习题含答案课后练习题MATLAB数学实验第二版的课后练习题如下：第一章课后练习题1.编写MATLAB程序，计算并输出下列公式的结果：y = \\frac{1}{\\sqrt{2\\pi\\sigma^2}} e^{-\\frac{(x-\\mu)^2}{2\\sigma^2}}其中，x, $\\mu$, $\\sigma$ 分别由用户输入。

要求输出结果精确至小数点后两位。

答案如下：x=input('请输入 x 的值:');mu=input('请输入 mu 的值:');sigma=input('请输入 sigma 的值:');y=1/sqrt(2*pi*sigma^2) *exp(-(x-mu)^2/ (2*sigma^2));fprintf('y = %.2f\', y);2.编写MATLAB程序，求解下列方程的解：4x + y = 11\\\\x + 2y = 7答案如下：A= [4,1;1,2];B= [11;7];X=inv(A) *B;fprintf('x = %.2f, y = %.2f\', X(1), X(2));第二章课后练习题1.编写MATLAB程序，计算下列多项式的值：P(x) = x^4 - 2x^3 + 3x^2 - x + 1其中，x 由用户输入。

要求输出结果精确至小数点后两位。

答案如下：x=input('请输入 x 的值:');y=x^4-2*x^3+3*x^2-x+1;fprintf('P(%.2f) = %.2f\', x, y);2.编写MATLAB程序，绘制下列函数的图像：f(x) = \\begin{cases} x + 1, & x < 0 \\\\ x^2, & 0 \\leq x < 1 \\\\ 2x - 1, & x \\geq 1 \\end{cases}答案如下：x=-2:0.01:2;y1=x+1;y2=x.^2.* ((x>=0) & (x<1));y3=2*x-1;plot(x,y1,x,y2,x,y3);legend('y1 = x + 1','y2 = x^2','y3 = 2x - 1');总结本文提供了《MATLAB数学实验第二版》的部分课后练习题及其答案。

matlab课后习题答案

习题二之阳早格格创做1.怎么样明白“矩阵是MATLAB最基础的数据对于象”？问：果为背量不妨瞅成是仅有一止或者一列的矩阵，单个数据（标量）不妨瞅成是仅含一个元素的矩阵，故背量战单个数据皆不妨动做矩阵的惯例去处理.果此，矩阵是MATLAB最基础、最要害的数据对于象.2.设A战B是二个共维共大小的矩阵，问：(1)A*B战A.*B的值是可相等？问：没有相等.(2)A./B战B.\A的值是可相等？问：相等.(3)A/B战B\A的值是可相等？问：没有相等.(4)A/B战B\A所代表的数教含意是什么？问：A/B等效于B的顺左乘A矩阵，即A*inv(B)，而B\A等效于B矩阵的顺左乘A矩阵，即inv(B)*A.3.写出完毕下列支配的下令.(1)将矩阵A第2~5止中第1, 3, 5列元素赋给矩阵B.问：B=A(2:5,1:2:5); 或者B=A(2:5,[1 3 5])(2)简略矩阵A的第7号元素.问：A(7)=[](3)将矩阵A的每个元素值加30.问：A=A+30;(4)供矩阵A的大小战维数.问：size(A);ndims(A);(5)将背量t的0元素用呆板整去代替.问：t(find(t==0))=eps;(6)将含有12个元素的背量x变换成34 矩阵.问：reshape(x,3,4);(7)供一个字符串的ASCII码.问：abs(‘123’); 或者double(‘123’);(8)供一个ASCII码所对于应的字符.问：char(49);4.下列下令真止后，L1、L2、L3、L4的值分别是几？A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);问：L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0, 0]L4的值为[4, 5, 6]5.已知完毕下列支配：(1)与出A的前3止形成矩阵B，前二列形成矩阵C，左下角32⨯子矩阵形成矩阵D，B与C的乘积形成矩阵E.问：B=A(1:3,:);C=A(:,1:2);D=A(2:4,3:4);E=B*C;(2)分别供E<D、E&D、E|D、~E|~D战find(A>=10&A<25).问：E<D=010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，E&D=110111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，E|D=111111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，~E|~D=001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦find(A>=10&A<25)=[1; 5].6.当A=[34, NaN, Inf, -Inf, -pi, eps, 0]时，分解下列函数的真止截止：all(A)，any(A)，isnan(A)，isinf(A)，isfinite(A).问：all(A)的值为0any(A)的值为1isnan(A)的值为[0, 1, 0, 0, 0, 0, 0]isinf(A)的值为[0, 0, 1, 1, 0, 0, 0]isfinite(A)的值为[1, 0, 0,0, 1, 1, 1]7.用结构体矩阵去保存5名教死的基础情况数据，每名教死的数据包罗教号、姓名、博业战6门课程的结果.问：student(1).id='0001';student(1).name='Tom';student(1).major='computer';student(1).grade=[89,78,67,90,86,85];8.修坐单元矩阵B并回问有闭问题.B{1,1}=1;B{1,2}='Brenden';B{2,1}=reshape(1:9,3,3);B{2,2}={12,34,2;54,21,3;4,23,67};(1)size(B)战ndims(B)的值分别是几？问：size(B)的值为2,2.ndims(B)的值为2.(2)B(2)战B(4)的值分别是几？问：B(2)=147258369⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，B(4)=[12][34][2][54][21][3][4][23][67]⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(3)B(3)=[]战B{3}=[]真止后，B的值分别是几？问：当真止B(3)=[]后，B={1, [1, 4, 7; 2, 5, 8; 3, 6, 9], {12, 34, 2; 54, 21, 3; 4, 23, 67}}当真止B{3}=[]后，B={1,[]; [1, 4, 7; 2, 5, 8; 3, 6, 9],{12, 34, 2; 54, 21, 3; 4, 23, 67}}习题三1.写出完毕下列支配的下令.(1)修坐3阶单位矩阵A.问：A=eye(3);(2)修坐5×6随机矩阵A，其元素为[100,200]范畴内的随机整数.问：round(100+(200-100)*rand(5,6));(3)爆收均值为1，圆好为0.2的500个正态分散的随机数.问：1+sqrt(0.2)*randn(5,100);(4)爆收战A共样大小的幺矩阵.问：ones(size(A));(5)将矩阵A对于角线的元素加30.问：A+eye(size(A))*30;(6)从矩阵A提与主对于角线元素，并以那些元素形成对于角阵B.问：B=diag(diag(A));2.使用函数，真止圆阵左旋90o或者左旋90o的功能.比圆，本矩阵为A，A左旋后得到B，左旋后得到C.问：B=rot90(A);C=rot90(A,-1);3.修坐一个圆阵A，供A的顺矩阵战A的止列式的值，并考证A与A-1是互顺的.问：A=rand(3)*10;B=inv(A);C=det(A);先估计B*A，再估计A*B，由估计可知B*A=A*B，即A·A-1=A-1·A是互顺.4.供底下线性圆程组的解.问：A=[4,2,-1;3,-1,2;12,3,0];b=[2;10;8];x=inv(A)*b圆程组的解为x=6.000026.666727.3333 -⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦5.供下列矩阵的主对于角线元素、上三角阵、下三角阵、秩、范数、条件数战迹.(1)112351423052111509A-⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦(2)0.434328.9421B⎡⎤=⎢⎥-⎣⎦问：(1)与主对于角线元素：diag(A);上三角阵：triu(A)；下三角阵：tril(A);秩：rank(A);范数：norm(A,1); 或者 norm(A);或者 norm(A,inf);条件数：cond(A,1); 或者 cond(A,2); 或者 cond(A,inf)迹：trace(A);(2)【请参照(1)】.6.供矩阵A的特性值战相映的特性背量.问：[V,D]=eig(A);习题四1.从键盘输进一个4位整数，按如下准则加稀后输出.加稀准则：每位数字皆加上7，而后用战除以10的余数与代该数字；再把第一位与第三位接换，第二位与第四位接换.问：a=input('请输进4位整数：');A=[a/1000,a/100,a/10,a];A=fix(rem(A,10));A=rem(A+7,10);b=A(3)*1000+A(4)*100+A(1)*10+A(2);disp(['加稀后的值为：',num2str(b)]);2.分别用if语句战switch语句真止以下估计，其中a、b、c 的值从键盘输进.问：(1) 用if语句真止估计：a=input('请输进a的值：');b=input('请输进b的值：');c=input('请输进c的值：');x=input('请输进x的值：');y=a*x^2+b*x+c;endy=a*((sin(b))^c)+x;endy=log(abs(b+c/x));enddisp(['y=',num2str(y)]);(2) 用switch语句真止估计：a=input('请输进a的值：');b=input('请输进b的值：');c=input('请输进c的值：');x=input('请输进x的值：');switch fix(x/0.5)case {1,2}y=a*x^2+b*x+c;case num2cell(3:6)y=a*((sin(b))^c)+x;case num2cell(7:10)y=log(abs(b+c/x));enddisp(['y=',num2str(y)]);3.爆收20个二位随机整数，输出其中小于仄衡值的奇数.问：A=fix(10+89*rand(1,20));sum=0;for i=1:20sum=sum+A(i);endB=A(find(A<(sum/20)));C=B(find(rem(B,2)==0));disp(C);4. 输进20个数，供其中最大数战最小数.央供分别用循环结媾战调用MATLAB 的max 函数、min 函数去真止. 问：(1) 用循环结构真止：v_max=0;v_min=0;for i=1:20x=input(['请输进第', num2str(i), '数：']);if x>v_maxv_max=x;end;if x<v_minv_min=x;end;enddisp(['最大数为：', num2str(v_max)]);disp(['最小数为：', num2str(v_min)]);(2) 用max 函数、min 函数真止：for i=1:5A(i)=input(['请输进第', num2str(i), '数：']);enddisp(['最大数为：', num2str(max(A))]);disp(['最小数为：', num2str(min(A))]);5. 已知：236312222s =+++++，分别用循环结媾战调用MATLAB 的sum 函数供s 的值.问：(1) 用循环结构真止：s=0;for i=0:63s=s+2^i;ends(2) 调用sum函数真止：s=0:63;s=2.^s;sum(s)6.当n分别与100、1000、10000时，供下列各式的值.(1)111111(1)(ln2) 234nn+-+-++-+=(2)1111() 3574π-+-+=(3) 11111() 4166443n+++++=(4)224466(2)(2)133557(21)(21)2n nn nπ⎛⎫⨯⨯⨯⨯⎛⎫⎛⎫⎛⎫⎛⎫=⎪⎪⎪⎪ ⎪⨯⨯⨯-⨯+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭央供分别用循环结媾战背量运算（使用sum或者prod函数）去真止.问：(1) 用循环结构真止：sum=0;for k=1:100sum=sum+(-1)^(k+1)/k;endsum使用sum函数：x=[];for k=1:10000x=[x, (-1)^(k+1)/k];endsum(x)(2)用循环结构真止：sum=0;for k=1:100sum=sum+(-1)^(k+1)/(2*k-1);endsum使用sum函数：x=[];for k=1:100x=[x, (-1)^(k+1)/(2*k-1)];endsum(x)(3)用循环结构真止：sum=0;for k=1:100sum=sum+1/(4^k);endsum使用sum函数真止：x=[];for k=1:100x=[x, 1/(4^k)];endsum(x)(4)用循环结构真止：t=1;for k=1:100t=t*(((2*k)*(2*k))/((2*k-1)*(2*k+1)));endt使用prod函数真止：x=[];for k=1:100x=[x, ((2*k)*(2*k))/((2*k-1)*(2*k+1))];endprod(x)7. 编写一个函数文献，供小于任性自然数n的斐波那契（Fibnacci）数列各项.斐波那契数列定义如下：问：function x=fibnacci(n)for i=1:nif i<=2x(i)=1;elsex(i)=x(i-1)+x(i-2);endend8.编写一个函数文献，用于供二个矩阵的乘积战面乘，而后正在下令文献中调用该函数.问：函数文献myfnc.m：function [x, y]=myfnc(A, B)tryx=A*B;catchx=[];endy=A.*B;下令文献myexe.m：A=input('请输进矩阵A：');B=input('请输进矩阵B：');[x, y]=myfnc(A, B);if length(x)==0display('二矩阵的维数没有匹配，无法举止乘积运算！');disp('矩阵A 战矩阵B 的乘积为：'); xenddisp('矩阵A 战矩阵B 的面乘为：'); y9. 先用函数的递归调用定义一个函数文献供1n m i i =∑，而后调用该函数文献供100501021111k k k k k k ===++∑∑∑. 问：函数文献myfnc.m ：function sum=myfnc(n, m)if n<=1sum=1;elsesum= myfnc (n-1, m)+n^m;end正在下令窗心中调用myfnc.m 文献，估计100501021111k k k k k k ===++∑∑∑： sum=myfnc(100, 1)+myfnc(50, 2)+myfnc(10,-1) 10.写出下列步调的输出截止.① s=0;a=[12,13,14;15,16,17;18,19,20;21,22,23]; for k=afor j=1:4if rem(k(j),2)~=0s=s+k(j);endendends问：真止截止为②下令文献exe.m真止后的截止为：x =41220y=2 4 6。

matlab习题2答案

matlab习题2答案MATLAB习题2答案在MATLAB习题2中，我们学习了如何使用MATLAB编程语言解决各种数学问题和数据分析任务。

在本篇文章中，我们将探讨一些常见的习题，并给出相应的答案和解释。

第一道习题是关于矩阵运算的。

我们需要编写一个MATLAB程序，计算两个矩阵的乘积。

在MATLAB中，可以使用矩阵乘法运算符“*”来实现这个功能。

例如，如果我们有两个矩阵A和B，我们可以使用以下代码来计算它们的乘积：```matlabC = A * B;```接下来，我们需要解决一个关于插值的问题。

我们需要编写一个程序，使用插值方法来估算给定点的函数值。

在MATLAB中，可以使用interp1函数来实现这个功能。

例如，如果我们有一个已知的函数y和一组离散的点x，我们可以使用以下代码来进行插值计算：```matlabx_interp = 0:0.1:10;y_interp = interp1(x, y, x_interp, 'spline');```最后，我们需要解决一个关于数据可视化的问题。

我们需要编写一个程序，绘制给定数据的散点图和拟合曲线。

在MATLAB中，可以使用scatter和plot函数来实现这个功能。

例如，如果我们有一组数据点x和y，我们可以使用以下代码来进行数据可视化：```matlabscatter(x, y);hold on;p = polyfit(x, y, 1);y_fit = polyval(p, x);plot(x, y_fit, 'r');```通过以上习题的练习，我们可以更好地掌握MATLAB编程语言的基本语法和常用函数。

希望本篇文章对大家有所帮助，也希望大家能够在日常工作和学习中充分利用MATLAB的强大功能，提高工作效率和解决问题的能力。

（完整版）MATLAB作业2参考答案

（完整版）MATLAB作业2参考答案MATLAB 作业⼆参考答案1、试求出如下极限。

【求解】极限问题可以由下⾯语句直接求解。

>> syms x; f=(x+2)A(x+2)*(x+3)A(x+3)/(x+5F(2*x+5); limit(f,x,i nf) ans = exp(-5) >> syms x yfa=(x A 2*y+x*y A 3)/(x+y)A 3; limit(limit(fa,x,-1),y,2) ans = -6>> fc=(1-cos(xA2+yA2))*exp(xA2+yA2)/(xA2+yA2); limit(limit(fc,x,O),y,O) ans = 02、试求出下⾯函数的导数。

(1) y(x) . xsinx 、1e x , (2) atan yIn(x 2 y 2)x【求解】由求导函数diff() 可以直接得出如下结果，其中 (2)为隐函数，故需要⽤隐函数求导公式得出导数。

>> syms x;f=sqrt(x*si n( x)*sqrt(1-exp(x))); simple(diff(f)) ans =1/2/(x*s in (x)*(1-exp(x))A(1/2))A(1/2)*(si n(x)*(1-exp(x))A(1/2)+ x*cos(x)*(1-exp(x))A(1/2)-1/2*x*sin (x)/(1-exp(x))A(1/2)*exp(x)) >> syms x,y; f=ata n(y /x)_log(xA2+yA2); f1=simple(-diff(f,x)/diff(f,y)) f1 =(y+2*x)/(x-2*y)2 23、假设U cos 1 J *，试验证⼀———。

\y x y y x【求解】证明⼆者相等亦可以由⼆者之差为零来证明，故由下⾯的语句直接证明。

>> syms x y; u=acos(x/y); diff(diff(u,x),y)-diff(diff(u,y),x) ans =(1) limx (x 2)x 2(x 3)x3(x 5)2x 52..x y lim y 21(x xy 3y)3H xy2Xos2Xe2o o2xyt 2x2f2f2f4、假设 f (x, y) e dt ，试求 22 2y x x yy【求解】由下⾯的命令可以得出所需结果。

matlab教程第二章课堂练习及答案

Matlab教程第二章符号计算课堂练习1 创建符号变量有几种方法？MATLAB提供了两种创建符号变量和表达式的函数：sym和syms。

sym用于创建一个符号变量或表达式，用法如x=sym(‘x’) 及f=sym(‘x+y+z’)，syms用于创建多个符号变量，用法如syms x y z。

f=sym(‘x+y+z’)相当于syms x y zf= x+y+z2 下面三种表示方法有什么不同的含义？（1）f=3*x^2+5*x+2（2）f='3*x^2+5*x+2'（3）x=sym('x')f=3*x^2+5*x+2（1）f=3*x^2+5*x+2表示在给定x时，将3*x^2+5*x+2的数值运算结果赋值给变量f，如果没有给定x则指示错误信息。

（2）f='3*x^2+5*x+2'表示将字符串'3*x^2+5*x+2'赋值给字符变量f，没有任何计算含义，因此也不对字符串中的内容做任何分析。

（3）x=sym('x')f=3*x^2+5*x+2表示x是一个符号变量，因此算式f=3*x^2+5*x+2就具有了符号函数的意义，f也自然成为符号变量了。

3 用符号函数法求解方程a t2+b*t+c=0。

>> r=solve('a*t^2+b*t+c=0','t')[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))] [ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]4 用符号计算验证三角等式：sin(ϕ1)cos(ϕ2)-cos(ϕ1)sin(ϕ2) =sin(ϕ1-ϕ2) >> syms phi1 phi2;>> y=simple(sin(phi1)*cos(phi2)-cos(phi1)*sin(phi2)) y =sin(phi1-phi2)5 求矩阵⎥⎦⎤⎢⎣⎡=22211211a a a a A 的行列式值、逆和特征根。

matlab习题二答案

matlab习题二答案Matlab习题二答案Matlab是一种强大的数值计算和科学计算软件，广泛应用于工程、科学、金融等领域。

在学习和使用Matlab的过程中，习题是一种很好的练习和巩固知识的方式。

本文将为大家提供一些Matlab习题二的答案，希望能对大家的学习有所帮助。

1. 编写一个函数，输入一个矩阵A，输出矩阵A的转置矩阵。

```matlabfunction B = transposeMatrix(A)B = A';end```2. 编写一个函数，输入一个矩阵A，输出矩阵A的每一行的平均值。

```matlabfunction avg = rowAverage(A)avg = mean(A, 2);end```3. 编写一个函数，输入一个矩阵A和一个标量k，输出矩阵A中大于k的元素个数。

```matlabfunction count = countGreaterThanK(A, k)count = sum(A(:) > k);end```4. 编写一个函数，输入一个矩阵A和一个标量k，输出矩阵A中大于k的元素的索引。

```matlabfunction indices = findGreaterThanK(A, k)indices = find(A > k);end```5. 编写一个函数，输入一个矩阵A，输出矩阵A的每一列的方差。

```matlabfunction variances = columnVariance(A)variances = var(A);end```6. 编写一个函数，输入一个矩阵A和一个标量k，将矩阵A中小于k的元素替换为0。

```matlabfunction B = replaceLessThanK(A, k)B = A;B(A < k) = 0;end```7. 编写一个函数，输入一个矩阵A和一个标量k，将矩阵A中小于k的元素替换为k。

```matlabfunction B = replaceLessThanK(A, k)B = A;B(A < k) = k;end```8. 编写一个函数，输入一个矩阵A和一个标量k，将矩阵A中大于k的元素替换为k。

MATLAB练习题和答案

MATLAB练习题和答案MATLAB练习题和答案控制系统仿真实验Matlab部分实验结果⽬录实验⼀MATLAB基本操作 (1)实验⼆Matlab编程 (8)实验三Matlab底层图形控制 (10)实验四控制系统古典分析 (23)实验五控制系统现代分析 (28)实验六PID控制器的设计 (35)实验七系统状态空间设计 (40)实验九直流双闭环调速系统仿真 (44)实验⼀ MATLAB 基本操作1 ⽤MATLAB 可以识别的格式输⼊下⾯两个矩阵12332357135732391894A ??=??144367823355422675342189543ii B i +??+?=+?再求出它们的乘积矩阵C ，并将C 矩阵的右下⾓2×3⼦矩阵赋给D 矩阵。

赋值完成后，调⽤相应的命令查看MATLAB ⼯作空间的占⽤情况。

A=[1,2,3,3;2,3,5,7;1,3,5,7;3,2,3,9;1,8,9,4];B=[1+4i,4,3,6,7,8;2,3,3,5,5,4+2i;2,6+7i,5,3,4,2;1,8,9,5,4,3]; C=A*B;D=C(4:5,4:6); whosName Size Bytes Class AttributesA 5x4 160 doubleB 4x6 384 doublecomplexC 5x6 480 double complexD 2x3 96 double complex2 选择合适的步距绘制出下⾯的图形(,)t∈-sin(/)t，其中111t=[-1:0.1:1];y=sin(1./t);plot(t,y)3 对下⾯给出的各个矩阵求取矩阵的⾏列式、秩、特征多项式、范数、特征根、特征向量和逆矩阵。

75350 083341009103150037193......A =??-????，5765710876810957910B ??=12345678910111213141516C=，33245518118575131D --??-?=----A=[7.5,3.5,0,0;8,33,4.1,0;0,9,103,-1.5;0,0,3.7,19.3];B=[5,7,6,5;7,10,8,7;6,8,10,9;5,7,9,10];C=[1:4;5:8;9:12;13:1rtf6];D=[3,-3,-2,4;5,-5,1,8;11,8,5,-7;5,-1,-3,-1];det(A);det(B);det(C);det(D); rank(A); rank(B); rank(C); rank(D); a=poly(A); b=poly(B); c=poly(C); d=poly(D);norm(A);norm(B);norm(C);norm(D);[v,d]=eig(A,'nobalance');[v,d]=eig(B,'nobalance');[v,d]=eig(C,'nobalance');[v,d]=eig(D,'nobalance');m=inv(A);n=inv(B);p=inv(C);q=inv(D);4 求解下⾯的线性代数⽅程，并验证得出的解真正满⾜原⽅程。

精讲多练MATLAB（第二版）课后习题答案

精讲多练MATLAB（第二版）课后习题答案第1章练习题答案1-2.A=1.2 ;B=-4.6 ;C=8.0 ;D=3.5 ;E=-4.0;T=atan((2*pi*A+E/(2*pi*B*C))/D)1-3clearx=45;(sin(x*pi/180)+sqrt(35))/(72^(1/5))1-4cleara=5.67;b=7.811;exp(a+b)/log10(a+b)1-5clearx=3;y=sqrt(x)-6*(x+1/x)+(x-3.2)^2/(x+7.7)^3 1-6 clearr=15;d=2*rc=2*pi*rs=pi*r*r1-7cleara=8.5;b=14.6;c=18.4;s=(a+b+c)/2;area=sqrt(s*(s-a)*(s-b)*(s-c))第2章练习题答案2-1 c learA=[ 3 1 1;2 1 2;1 2 3];B=[1 1 -1;2 -1 0;1 -1 1];2*A+B,4*(A^2)-3*(B^2),A*B,B*A,A*B-B*A 2-2 clearA=[1/3 0 0;0 1/4 0;0 0 1/7];B=inv(inv(A)-eye(3))*62-3 clearB=[1 2 -3 -2;0 1 2 -3;0 0 1 2;0 0 0 1]; C=[1 2 0 1;0 1 2 0;0 0 1 2;0 0 0 1];A=(inv(2*eye(4)-inv(C)*B)*inv(C))'2-4 clearA=[2 -1;-1 2];B=[0 -2;-2 0];X=(1/2)*(B+2*A)2-5 clearA=[2 -3 0 2;1 5 2 1;3 -1 1 -1;4 1 2 2];B=[8;2;7;12];X=A\B2-6 A=[3 12 4 7 0 8 1];p=poly2str(A,'x')x=roots(A)2-7 A=[3 12 4 7 0 8 1];B=[1 -3 5 -15 0];[div,rest]=deconv(A,B)第三章3-1.x=sym('x');limit((cos(sqrt(x)))^(pi/x),x,0,'right')ans =exp(-1/2*pi)3-2.x=sym('x');f=sym('(3*sin(x)+x^2*cos(1/x))/((1+cos(x))*log(1+x))');limit(f,x,0)ans =3/23-3.x=sym('x');f=sym('(sqrt(4*x^2+x-1)+x+1)/sqrt(x^2+sin(x))');limit(f,x,-inf)ans =13-4.s yms x y;f=sym('(x^2+y^2)^(x^2*y^2)');limit(limit(f,x,0),y,0)ans =13-5.x=sym('x');y=sym('(tan(sqrt(x+sqrt(x+sqrt(2*x)))))^2');diff(y,x)ans=tan((x+(x+2^(1/2)*x^(1/2))^(1/2))^(1/2))*(1+tan((x+(x+2 ^(1/2)*x^(1/2 ))^(1/2))^(1/2))^2)/(x+(x+2^(1/2)*x^(1/2))^(1/2) )^(1/2)*(1+1/2/(x+2^( 1/2)*x^(1/2))^(1/2)*(1+1/2*2^(1/2)/x^(1 /2)))3-6.x=sym('x');y=sym('cos(x^2)*sin(1/x)^2');diff(y,x)ans =-2*sin(x^2)*x*sin(1/x)^2-2*cos(x^2)*sin(1/x)*cos(1/x)/x^23-7.x=sym('x');y=sym('sqrt(sin(x)-sin(x)^3)');int(y,x,0,pi)ans =4/33-8.x=sym('x');y=sym('sqrt((x+1)/(x-1))/x');int(y,x)ans=-((1+x)/(x-1))^(1/2)*(x-1)*(atan(1/(-1+x^2)^(1/2))-log(x+(-1+x^2)^(1/2)))/((1+x)*(x-1))^(1/2)3-9.dsolve('D2y+4*Dy+4*y=exp(-2*x)','x')ans =1/2*exp(-2*x)*(2*C2+2*x*C1+x^2)3-10.dsolve('x^2*Dy+x*y=y^2','y(1)=1')ans =x*exp(1/x)/(exp(1/x)+exp(1/x*t)*x-exp(1/x*t))第四章4-1.plot([1 2 4 0 5 10 11 21 3 1])4-2.t=0:pi/100:2*pi;x=cos(t);y=sin(t);plot(x,y);axis('square');4-3.R=[1 5 10 20];I=0:0.1:10;U=I'*R;plot(I,U);4-4.mon=1:12;temp=[0.2 2.3 8.7 18.5 24.6 32.1 36.8 37.1 28.3 17.8 6.4 -3.2];rainf=[4.6 3.6 2.1 2.9 3.0 2.7 2.2 2.5 4.3 3.4 2.1 3.7];plot(mon,temp,'r-p',mon,rainf,'b:s');xlabel('month');ylabel('temperature and rainfall');%title('Temperature and Rainfall Curve');%text(3,1,'rainfall');%text(9,28.3,'temperature');flag=12;while(flag)text(mon(flag),temp(flag),[num2str(mon(flag)),num2str(tem p(flag))]);text(mon(flag),rainf(flag),[num2str(mon(flag)),num2str(rainf(flag) )]);flag=flag-1;end4-5.A=[1 1 1 1 1 1 1;1 2 2 2 2 2 1;1 2 2 3 2 2 1;1 2 2 2 2 2 1;1 1 1 1 1 1 1];plot(A);4-6.x=-10:0.5:10;y=x;[X,Y]=meshgrid(x,y);Z=X.^2+Y.^2;surf(X,Y,Z);4-7.clccleartheta=(0:0.1:2)*pi;phi=(0:0.1:2)*pi;x=zeros(length(theta),length(phi));y=x;z=x;for i=1:length(theta)for j=1:length(phi)x(i,j)=2*sin(theta(i))*cos(phi(j)); y(i,j)=3*sin(theta(i))*sin(phi(j)); endz(i,:)=4*cos(theta(i));endaxis squaresubplot(2,2,1);mesh(x,y,z)title('三维')subplot(2,2,2);mesh(x,y,z)view(90,0)title('X轴视图')subplot(2,2,3);mesh(x,y,z)view(0,0)title('Y轴视图')subplot(2,2,4);mesh(x,y,z)view(0,90)title('Z轴视图')第五章5-1：clear;x=-2:0.01:2;for ii=1:401if(x(ii)<0)y(ii)=x(ii)+1;elseif (x(ii)<1)&(x(ii)>=0)y(ii)=1;elseif(x(ii)>=1)y(ii)=x(ii)^3;endendplot(x,y);5-2：function y=fenduan(x)if(x<0)y=x+1;elseif (x<1)&(x>=0)y=1;elseif(x>=1)y=x^3;end5-3：建立文件arcsin.m如下：function y=arcsin(x)if abs(x)>1disp('输入参数的绝对值必须小于1');return;endn=0;y=0;u=x;while u>epsu=(jiecheng(2*n)*x^(2*n+1))/(2^(2*n)*(jiecheng(n)^2*(2*n+1))); y=y+u;n=n+1;end建立文件jiecheng.m如下：function y=jiecheng(n)if(n<0)disp('输入参数必须为大于或等于0的整数');return;endif n==0 | n==1y=1;elsey=n*jiecheng(n-1);end5-4：建立shuliang.m文件如下：function [tu,ji]=shuliang(tou,jiao)tu=jiao/2-tou;ji=2*tou-jiao/2;在命令窗口中执行：>>[a,b]=shuliang(36,100) 5-5：for i=2:999ge=rem(i,10);shi=rem(fix(i/10),10);bai=fix(i/100);if rem((ge+shi+bai),2) & isprime(i)disp(i);endend5-6：function y=issushu(n)y=1;for ii=2:fix(n/2)if(rem(n,ii)==0)y=0;endend习题1（程序段后面的是其运行的结果）例题1.2function lt12 a=1+2*i;b=3-4*i;disp(['a+b=',num2str(a+b)]) disp(['a-b=',num2str(a-b)]) disp(['a*b=',num2str(a*b)]) disp(['a/b=',num2str(a/b)]) >> lt12 a+b=4-2i a-b=-2+6i a*b=11+2ia/b=-0.2+0.4i >>例题1.3function z=lt13x=(-3.5)*pi/180;y=6.7*pi/180;z=sin(abs(x)+abs(y))/sqrt(cos(abs(x+y))); >> lt13ans =0.1772 >>例题1.4function p1=lt14r=0.0107;n=2015-2000;p0=12.9533E8; p1=p0*(1.0+r)^n; >> lt14ans =1.5195e+009 >>例题1.5function lt15 a=1;b=2;c=3;d=sqrt(b^2-4*a*c);x1=(-b+d)/2*a;x2=(-b-d)/2*a; disp('原方程的根是：') disp(['x1=',num2str(x1)]) disp(['x2=',num2str(x2)]) >> lt15原方程的根是： x1=-1+1.4142i x2=-1-1.4142i >>。

Matlab上机练习二答案

Matlab上机练习⼆答案Matlab 上机练习⼆班级学号姓名按要求完成题⽬，并写下指令和运⾏结果。

（不需要画图）1、求??+-+-+-+-++=i 44i 93i 49i 67i 23i 57i 41i 72i 53i 84x 的共轭转置。

>> x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i]; >> x’ans =4.0000 - 8.0000i 3.0000 - 2.0000i3.0000 - 5.0000i 7.0000 + 6.0000i2.0000 + 7.0000i 9.0000 - 4.0000i1.0000 - 4.0000i 3.0000 + 9.0000i7.0000 + 5.0000i 4.0000 - 4.0000i2、计算=572396a 与??=864142b 的数组乘积。

>> a=[6 9 3;2 7 5];>> b=[2 4 1;4 6 8];>> a.*bans =12 36 38 42 403、对于B AX =，如果=753467294A ，=282637B ，求解X 。

>> A=[4 9 2;7 6 4;3 5 7];>> B=[37 26 28]’;>> X=A\BX =-0.51184.04271.33184、 -=463521a ，-=263478b ，观察a 与b 之间的六种关系运算的结果。

>> a=[1 2 3;4 5 6];>> b=[8 –7 4;3 6 2];>> a>bans =0 1 01 0 1>> a>=bans =0 1 01 0 1>> aans =1 0 10 1 0>> a<=bans =1 0 10 1 0>> a==bans =0 0 00 0 0>> a~=bans =1 1 11 1 15、[]7.0802.05--=a ，在进⾏逻辑运算时，a 相当于什么样的逻辑量。