高二第七周周练

合集下载

高二分校英语周周练试卷及答案

高二分校英语周周练试卷命题人：赵留强第Ⅰ卷第一部分:英语知识运用第一节：单项填空（共20小题，每题1分，满分20分）1. ________ the severe drought this winter, China is hoping to achieve anothergood harvest.A. In terms ofB. In favor ofC. In charge ofD. In spite of2. ____ to the doctor right away, he might have been alive.A. If he wentB. Were he goneC. Should he have goneD. Had he gone3. ______ the rain falling so frequently, it becomes more and more difficult to carryon the rescue work.A. SinceB. WithC. AsD. in that4. The professor ______ stealing his student’s ideas and publishing them made aformal public apology.A. accusing ofB. was accused ofC. charging withD. charged with5. —How do you deal with the disagreement between the company and thecustomers?—The approach ______ the problem is to meet the demand ______ by the customers.A. to solving; makingB. to solving; madeC. to solve; makingD. to solve; made6. —Do you have a minute? I’ve got so mething to tell you.—OK, you make it short.A. now thatB. if onlyC. so long asD. every time 7．They ________ have arrived at lunchtime but their flight was delayed.A．will B．can C．must D．should 8．Someone _____ his car in front of my house and it’s blocking my way．A．has parked B．parked C．was parking D．had parked 9．She _______ that she knew nothing about the crimeA. made outB. came outC. put outD. work out10. The teacher proposed that Jack ___ maths or physics instead of Englishbecause he was quick at numbers.A. must studyB. could studyC. studiedD. study11. Having _____ good grasp of computers, he is considered as _____ possibility for the job.A. a; aB. a, 不填C.不填; aD. a; the12. Had it been possible, I would have gone to visit him in the hospital. But I ____too busy at that time.A. amB. had beenC. wasD. have been13. ---Where did you get to know her?--- It was on the farm ______ we worked．A．whose B．there C．which D．where14. Because of my poor English I'm afraid I can't make myself________.A. understandB. to understandC. understandingD. understood 15．Hearing that he would have to be given another injection（注射）, the boy ______ a smile to cover up his fear．A．wear B．succeeded C．strengthened D．controlled 16．In the global financial crisis some US firms plan to________ workers by the thousand.A．lay in B．lay offC．lay down D．lay aside17. He insisted that the sky ________ clear up the following day.A．would B．should C．/ D．be18. — It is the first time I ________ pictures with my own camera.— It’s high time that you ________ a picture of me.A．had taken, took B．have taken, tookC．will take, take D．have taken, take19. You should have accomplished the program successfully, but you _____halfway.A gave upB give upC have given upD had given up20. --- My goodness! We have missed the flight.--- We _____ it, but we were caught in the traffic jam.A could have caughtB ought to catchC might catchD must have caught第二节完形填空(共20小题;每小题1.5分,满分30分)阅读下面短文,从短文后各题所给的四个选项(A、B、C和D)中,选出可以填入空白处的最佳选项。

高二语文周周练试题及答案

高二语文周周练试题及答案一、选择题（每题2分，共20分）1. 下列词语中，读音完全正确的一项是：A. 饕餮（tāo tiè）邂逅（xiè hòu）窈窕（yǎo tiǎo）B. 踌躇（chóu chú）蹉跎（cuō tuó）峥嵘（zhēng róng）C. 筵席（yán xí）蜚声（fēi shēng）逶迤（wēi yí）D. 箴言（zhēn yán）踽踽独行（jǔ jǔ dú xíng）旖旎（yǐ nǐ）2. 下列句子中，没有语病的一项是：A. 经过这次活动，使我们对传统文化有了更深刻的理解。

B. 他不仅学习优秀，而且乐于助人，深受同学们的喜爱。

C. 这本书的内容非常丰富，值得我们一读再读。

D. 由于天气原因，航班延误了，给旅客带来了不便。

3. 下列关于文学常识的表述，不正确的一项是：A. 《红楼梦》是我国古典小说的巅峰之作，作者是曹雪芹。

B. 《诗经》是我国最早的一部诗歌总集，共有305篇。

C. 鲁迅的《阿Q正传》是一篇讽刺小说，深刻揭示了当时社会的种种问题。

D. “但愿人长久，千里共婵娟”是唐代诗人杜甫的名句。

4-10. （此处省略，可根据需要添加类似题目）二、填空题（每题1分，共10分）1. “青青子衿，悠悠我心。

”出自《诗经》中的________篇。

2. 《滕王阁序》是唐代文学家________的作品。

3. “春眠不觉晓，处处闻啼鸟。

”是唐代诗人________的诗句。

4. 《水浒传》中，梁山好汉的首领是________。

5. “但愿人长久，千里共婵娟。

”出自宋代词人________的《水调歌头》。

6-10. （此处省略，可根据需要添加类似题目）三、阅读理解（共30分）阅读下面的文章，回答后面的问题。

（文章内容省略，可根据需要添加）1. 文章的中心论点是什么？请简要概括。

兴国三中高二数学周周练

兴国三中高二数学周周练（文科）命题人：黄金瑞 2012-12-18一、选择题：1、某同学由x 与y 之间的一组数据求得两个变量间的线性回归方程为y bx a =+，已知：数据x 的平均值为2，数据y 的平均值为3，则 ( )A ．回归直线必过点（2，3）B ．回归直线一定不过点（2，3）C ．点（2，3）在回归直线上方D ．点（2，3）在回归直线下方2、已知,53)(,103)(==A P AB P 则)|(A B P 等于（） A. 509 B. 21 C. 109 D. 41 3、一个口袋中有黑球和白球各5个，从中连摸两次球，每次摸一个且每次摸出后不放回，用A 表示第一次摸得白球，B 表示第二次摸得白球，则A 与B 是( )A ．互斥事件B ．不相互独立事件C ．对立事件D ．相互独立事件4、一学生通过英语听力测试的概率是21，他连续测试两次，那么其中恰好一次通过的概率是（） A. 41 B. 31 C. 21 D. 43 5、下列结论正确的是( ) ①函数关系是一种确定性关系； ②相关关系是一种非确定性关系 ③回归关系是对具有函数关系的两个变量进行统计分析的一种方法 ④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法。

A. ①② B. ①②③ C. ①②④ D. ①②③④6、在对两个变量x ，y 进行线性回归分析时，有下列步骤：①对所求出的回归直线方程作出解释； ②收集数据(i x 、i y ），1,2i =，…，n ； ③求线性回归方程； ④求未知参数； ⑤根据所搜集的数据绘制散点图如果根据可行性要求能够作出变量,x y 具有线性相关结论，则在下列操作中正确的是（）A ．①②⑤③④B ．③②④⑤①C ．②④③①⑤D ．②⑤④③①7、已知直线回归方程为2 1.5y x =-，则变量x 增加一个单位时（） A.y 平均增加1.5个单位 B.y 平均增加2个单位C.y 平均减少1.5个单位D.y 平均减少2个单位 8、某商品销售量y (件)与销售价格x (元/件)负相关，则其回归方程可能是( )A.y ^＝10x ＋170B.y ^＝ 18x ＋170C.y ^＝－18x +170D.y ^＝－10x －1709、下面的各图中，散点图与相关系数r 不符合的是（）y 2.5 t 4 4.5x 3 4 5 610、右表提供了某厂节能降耗技术改造后生产A 产品过程中记录的产量x （吨）与相应的生产能耗y （吨标准煤）的几组对应数据.根据右表提供的数据，求出y 关于x 的线性回归方程为0.70.35y x ∧=+，那么表中t 的值为A.3B.3.15C.3.5D.4.5二、填空题：11、对具有线性相关关系的变量x 和y ，由测得的一组数据已求得回归直线的斜率为6.5，且恒过(2,3)点，则这条回归直线的方程为________.12、在10个球中有6个红球，4个白球（各不相同），不放回的依次摸出2个球，在第一次摸出红球的条件下，第2次也摸出红球的概率是_________.13、甲、乙两个袋子中均装有红、白两种颜色的小球，这些小球除颜色外完全相同，其中甲袋装有4个红球、2个白球，乙袋装有1个红球、5个白球．现分别从甲、乙两袋中各随机抽取1个球，则取出的两球是红球的概率为________(答案用分数表示)14、明天上午李明要参加义务劳动，为了准时起床，他用甲、乙两个闹钟叫醒自己，假设甲闹钟准时响的概率是0.80，乙闹钟准时响的概率是0.90，则两个闹钟至少有一准时响的概率是________．三、解答题：15、调查某市出租车使用年限x 和该年支出维修费用y （万元），得到数据如下：（2）由（1）中结论预测第10年所支出的维修费用．（121()()()n i i i n i i x x y y b x x a y bx==⎧-⋅-⎪=⎪⎨-⎪⎪=-⎪⎩∑∑） 16、设进入某商场的每一位顾客购买甲种商品的概率为0.5，购买乙种商品的概率为0.6，且购买甲种商品与购买乙种商品相互独立，各顾客之间购买商品也是相互独立的。

高二数学周周练一

2023-2024学年度高二数学一、单选题A ．215【答案】D【分析】设1AC AA ==面垂直的性质可得1AA 向量法求解线线角.【详解】不妨设AC =故222AB AC BC +=，所以在直三棱柱11ABC A B -所以11,AA AC AA AB⊥⊥以A 为坐标原点建立空间直高二数学周周练一空间直角坐标系则()()10,0,2,1,0,0A B ，所以111cos ,A B AD A B AD A B = 故异面直线1A B 与AD 所成角故选：D3．最优化原理是指要求目前的最优目标的方案，这类问我们常常需要在数学模型中离的最值问题，请你利用所则M 到直线2x y --=的距A ．522B 【答案】B【分析】利用导数求得平行再利用点到直线的距离公式【详解】由函数232y =(1)(32)0x x -+=，因为0x >，可得1x =，则即平行于直线:2l x y --=D AD⋅ 所成角的余弦值为求目前存在的多种可能的方案中，选出最合理的，这类问题称之为最优化问题模型中求最大值或者最小值利用所学知识来解答：若点0的距离的最小值为（．得平行于直线离公式，即可求解x -则2023-2024学年度高二数学二、多选题2023-2024学年度高二数学6+三、填空题2023-2024学年度高二数学四、解答题15．在①只有第6项的二项式系数最大；②第4项与第8项的二项式系数相等；③所有二项式系数的和为102，这三个条件中任选一个，补充在下面（横线处）问题中，解决下面两个问题．已知230123(21)n nn x a a x a x a x a x -=+++++ （n *∈N ），若(21)n x -的展开式中，______. (1)求n 的值； (2)求2x 的系数；(3)求123||||||||n a a a a ++++ 的值．注：如果选择多个条件分别解答，则按第一个解答计分．【答案】(1)10n =； (2)2180a =； (3)1031-.【分析】（1）选择条件①，②，③，利用二项式系数的性质求出n . （2）由（1）的结论，结合二项式定理求出2a . （3）由（1）的结论，利用赋值法求出所求式子的值.【详解】（1）选择条件①，只有第6项的二项式系数最大，则(21)n x -的展开式共11项，即111n +=，所以10n =.选择条件②，第4项与第8项的二项式系数相等，则37C C n n =，解得10n =，所以10n =.选择条件③，所有二项式系数的和为102，则1022n =，解得10n =，所以10n =.（2）由（1）知，10(21)x -的展开式中2x 项为：228210C (2)(1)180x x -=，所以2180a =.2023-2024学年度高二数学(1)求点1C 到平面BCE 的距离(2)已知点M 在线段1CC CM 的长.【答案】(1)263(2)12或32【分析】选①或②，都能得（1）利用空间向量法可求出（2）设()1,1,M t ，其中方程，解之即可.【详解】（1）解：若选择又AD BE ⊥，1AA ⊂平面又AB ⊂平面11ABB A ，则若选择②，作//CF AD 交的距离；都能得到，可求出点选择则()1,1,0C 、()0,0,1E 、则()1,1,0CB =- ，(CE = 设平面BCE 的法向量为取11x =，则()1,1,2n = ，（2）解：因点M 在线段又()0,0,1E ，则(EM =又()1,1,0CB =- ，(1CC 设平面11BCC B 法向量为取21x =，可得()1,1,0m = 解得12t =或32t =，故线段17．已知()2e x xf x =-【答案】答案见解析【分析】求出函数的导数并化【详解】由题意得()2e e 21x x f x a a -'=+++1D 1,-n = 则点CC 1,1,t 0,0,=m =,0，所以，线段CM e a -+数并化简，=2023-2024学年度高二数学当0a <时，令e 0x a +=，可得()ln x a =-，当()(),ln x a ∈-∞-时，()0f x '<，()f x 在()(),ln a -∞-上单调递减；当()()ln ,x a ∈-+∞时，()0f x ¢>，()f x 在()()ln ,a -+∞上单调递增．综上所述：当0a ≥时，则()f x 在(),-∞+∞上单调递增；当0a <时，()f x 在()(),ln a -∞-上单调递减，在()()ln ,a -+∞上单调递增．18．从7名男生和5名女生中选取3人依次进行面试．(1)若参加面试的人全是女生，则有多少种不同的面试方法？(2)若参加面试的人中，恰好有1名女生，则有多少种不同的面试方法？【答案】(1)60(2)630【分析】（1）直接由排列的意义以及排列数即可解决；（2）先组合，再排列，即利用到分步乘法计数原理，结合组合数、排列数即可解决.【详解】（1）由题意从5名女生中选取3人依次进行面试，结合排列数的意义可知相当于从5名女生中选取3人依次进行排列，此时对应有35A 54360=⨯⨯=种不同的面试方法.（2）安排满足题意的面试顺序一共需要分以下两大步：一方面：由题意先抽取符合题意的组合，这里可以分为两小步：第一步从5名女生中选取1名女生；第二步从7名男生中选取312-=名男生；由分步乘法计数原理可得符合题意的组合有1257C C 521105⋅=⨯=种.另一方面：注意到3名面试者是依次进行面试的，即再对刚刚组合好的3名面试者进行一次排列，有33A 3216=⨯⨯=种排列方法.结合以上两方面且由分步乘法计数原理可知满足题意的不同的面试方法有123573C C A 1056630⋅⋅=⨯=种.19．设()821x +的第n 项系数为n a ．(1)求n a 的最大值．2023-2024学年度高二数学。

2024高二语文模拟试卷答案及解析

高二语文模拟试卷一、选择题（每题3分，共18分）1. 下列词语中加点的字，读音全都正确的一组是（）A. 邂逅（xiè）赦免（shè）鞭笞（chī）长歌当哭（dàng）B. 踯躅（zhízhú）踌躇（chóu chú）怆然（chuàng）忸怩不安（niǔní）C. 拗口（ǎo）踌躇（zhōu chú）隽永（juàn）毛骨悚然（gǒng）D. 歃血（shà）毗邻（pí）喋血（xiě）桀骜不驯（ào）2. 下列各句中，加点成语使用恰当的一项是（）A. 当我来到昔日荒芜的小山村，看到眼前绿树成荫、花果飘香的景象时，我简直不相信自己的眼睛。

B. 为了迎接这次检查，城管人员在大街小巷到处张贴标语，弄得满城风雨，惹来市民的纷纷议论。

C. 这座图书馆藏书丰富，品种齐全，简直成了包罗万象的“世界之窗”。

D. 改革开放三十年来，我国的经济建设取得了举世瞩目的巨大成就，人们的生活也日新月异。

3. 下列各句中，没有语病的一句是（）A. “嫦娥一号”卫星首次月球探测的成功，对于中国人实现探月梦想的伟大进程具有里程碑式的意义。

B. 有关部门对极少数不尊重环卫工人劳动、无理取闹、甚至殴打侮辱环卫工人的事件，及时进行了批评教育和严肃处理。

C. 我们必须拿出自己的正版计算机游戏软件，否则，拿不出新软件，就难以抵制不健康的盗版软件。

D. 这所九年制寄宿学校的150多名学生是地震中伤亡最少、震后复课最早的学校。

4. 下列句子中，加点的熟语使用不恰当的一项是（）A. 小王同学性格内向，不善言辞，可一到课堂上就变得伶牙俐齿，这让老师和同学们刮目相看。

B. 小区里的张阿姨虽然年过花甲，但干起活来仍然生龙活虎，不输于年轻人。

C. 小王同学平时学习不努力，临近高考了才开夜车，这种临时抱佛脚的做法怎么能取得好成绩呢？D. 我们中学生如果缺乏创新精神，也不能妄自菲薄自己的智能，只要努力开掘，就一定能有所作为。

2023-2024学年江苏省常州市高二上学期10月阶段调研数学质量检测模拟试题(含解析)

2023-2024学年江苏省常州市高二上册10月阶段调研数学模拟试题一、单选题1．焦点在x 轴的椭圆2214x y m +=的焦距是4，则m 的值为（）A ．8B ．3C ．5或3D ．20【正确答案】A【分析】根据焦点的位置可得m 的取值范围，结合焦距可求m 的值.【详解】因为焦点在x 轴，故4m >，而焦距是42=即8m =，故选：A.2．设a ∈R ，则“1a =”是“直线20ax y +=与直线(1)20x a y +++=平行”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【正确答案】A【分析】根据两直线平行列出方程，求出：2a =-或1，验证后均符合要求，从而得到“1a =”是“直线20ax y +=与直线(1)20x a y +++=平行”的充分不必要条件.【详解】当1a =时，20x y +=与220x y ++=的斜率相等，故平行，充分性成立，若“直线20ax y +=与直线(1)20x a y +++=平行”，则满足()120a a +-=，解得：2a =-或1，经验证，：2a =-或1时，两直线不重合，故：2a =-或1，两直线平行，故必要性不成立.故选：A3．过点A （1，2）的直线在两坐标轴上的截距之和为零，则该直线方程为（）A ．x-y +1=0B ．x+y-3＝0C ．y ＝2x 或x+y-3＝0D ．y ＝2x 或x-y+1＝0【正确答案】D【分析】考虑直线是否过坐标原点，设出直线方程，分别求解出直线方程.【详解】当直线过原点时，其斜率为20210-=-，故直线方程为y ＝2x ；当直线不过原点时，设直线方程为1x y a a+=-，代入点（1，2）可得121a a +=-，解得a ＝－1，故直线方程为x-y+1＝0.综上，可知所求直线方程为y ＝2x 或x-y+1＝0，故选：D.本题主要考查直线方程的截距式以及分类讨论思想的应用，考查逻辑推理和数学运算.在利用直线方程的截距式解题时，一定要注意讨论直线的截距是否为零.4．已知直线20l x y -+=:与圆22:220C x y y m +--=相离，则实数m 的取值范围是（）A ．(),0∞-B ．1,2⎛⎫-+∞ ⎪⎝⎭C ．1,4⎛⎫-∞- ⎪⎝⎭D ．11,24⎛⎫-- ⎪⎝⎭【正确答案】D【分析】由圆心到直线的距离大于半径即可求解.【详解】由22220x y y m +--=，得()22121x y m +-=+，∵直线20l x y -+=:与圆22:220C x y y m +--=相离，∴210,m +>⎧1124m -<<-．∴实数m 的取值范围是11,24⎛⎫-- ⎪⎝⎭，故选:D ．5．我们把离心率为2的椭圆称为“最美椭圆”.已知椭圆C 为“最美椭圆”，焦点在x 轴上，且以椭圆C 上一点P 和椭圆两焦点1F 和2F 为顶点的三角形的面积最大值为4，则椭圆C 的方程为（）A ．2212x y +=B ．22142x y +=C ．22163x y +=D ．22184x y +=【正确答案】D 【分析】先由2e =得到2c =与2b =，再由12PF F S 的最大值得4bc =，进而求得28a =，24b =，故可得到椭圆C 的方程.【详解】由已知2c e a ==，得2c =，故2b a =，∵121211222PF F P P S F F y c y bc ==⨯≤ ，即()12max 4PF F S bc == ，4=，得28a =，故22142b a ==，所以椭圆C 的方程为22184x y +=.故选：D.6．如图，已知1F ，2F 分别是椭圆的左、右焦点，现以2F 为圆心作一个圆恰好经过椭圆的中心并且交椭圆于点M ，N ．若过点1F 的直线1MF 是圆2F 的切线，则椭圆的离心率为（）A1-B ．2C ．2D 【正确答案】A【分析】由切线的性质，可得2MF c =，1MF =，再结合椭圆定义122+=MF MF a ，即得解【详解】因为过点1F 的直线1MF 圆2F 的切线，2MF c =，122F F c =，所以1MF =．由椭圆定义可得122MF MF c a +=+=，可得椭圆的离心率1c e a =-．故选：A7．设m ∈R ，过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ，则PA PB ⋅的最大值是（）A ．4B ．10C ．5D【正确答案】C【分析】由题意可知两条动直线经过定点(0,0)A 、()1,3B ，且始终垂直，有PA PB ⊥，利用勾股定理求出||AB ，再利用基本不等式求得答案.【详解】由题意可知，动直线0x my +=经过定点(0,0)A ，动直线30mx y m --+=即(1)30m x y --+=，经过定点()1,3B ，因为110⨯-⨯=m m ，所以动直线0x my +=和动直线30mx y m --+=始终垂直，P 又是两条直线的交点，则有PA PB ⊥，222||||||10PA PB AB ∴+==，故22||||||||52PA PB PA PB +⋅≤=（当且仅当||||PA PB ==时取“=”)，故选：C ．8．在平面直角坐标系xOy 中，已知圆()22:29C x y -+=，,E F 是直线:2l y x =+上的两点，若对线段EF 上任意一点P ，圆C 上均存在两点,A B ，使得cos 0APB ∠≤，则线段EF 长度的最大值为（）A ．2BC ．D ．4【正确答案】C【分析】设圆的切线为PM 、PN ，由cos 0APB ∠≤得90APB ∠≥ ，即90MPN ∠≥ ，再求得PC 的取值范围，求得点P 的坐标，即可求得EF 的最大值．【详解】由题意，圆心到直线:2l y x =+的距离为3d ==<（半径）故直线l 和圆相交；当点P 在圆外时，从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时，APB ∠才是最大的角，不妨设切线为PM ，PN ，则由cos 0APB ∠≤，得90APB ∠≥ ，90MPN ∴∠≥ ；当90MPN ∠= 时，3sin sin 452MPC PC ∠===，PC ∴=设()00,2P x x +，PC ==，解得：0x =设())2,2E F，如图，EF 之间的任何一个点P ，圆C 上均存在两点,A B ，使得90APB ∠≥ ，线段EF 长度的最大值为EF ==故选：C 二、多选题9．下列说法中正确的是A ．若两条直线互相平行，那么它们的斜率相等B ．方程()()()()211211x x y y y y x x --=--能表示平面内的任何直线C ．圆22240x y x y ++-=的圆心为()1,2-5D ．若直线()2320t x y t -++=不经过第二象限，则t 的取值范围是30,2⎡⎤⎢⎥⎣⎦【正确答案】BD【分析】由两直线平行于y 轴排除A ；根据直线平行或不平行于坐标轴，可确定方程均可以表示出来，知B 正确；整理得到圆的标准方程，进而确定圆心和半径，排除C ；由直线不过第二象限可构造不等式组求得结果，知D 正确.【详解】对于A ，若两条直线均平行于y 轴，则两条直线斜率都不存在，A 错误；对于B ，若直线不平行于坐标轴，则原方程可化为112121y y x x y y x x --=--，为直线两点式方程；当直线平行于x 轴，则原方程可化为1y y =；当直线平行于y 轴，则原方程可化为1x x =；综上所述：方程()()()()211211x x y y y y x x --=--能表示平面内的任何直线，B 正确；对于C ，圆的方程可整理为()()22125x y ++-=，则圆心为()1,2-，C 错误；对于D ，若直线不经过第二象限，则23022t t -⎧-≥⎪⎪⎨⎪-≤⎪⎩，解得：302t ≤≤，D 正确.故选.BD本题考查直线和圆部分相关命题的辨析，涉及到直线方程的应用、根据直线所过象限求解参数范围、由圆的方程确定圆心和半径等知识，属于基础知识的综合考查.10．已知222212:220,:2410O x y mx y O x y x my +-+=+--+= ．则下列说法中，正确的有（）A ．若(1,1)-在1O 内，则0m B ．当1m =时，1O 与2O 共有两条公切线C ．若1O 与2O 存在公共弦，则公共弦所在直线过定点11,36⎛⎫ ⎪⎝⎭D ．m ∃∈R ，使得1O 与2O 公共弦的斜率为12【正确答案】BC【分析】根据点与圆的位置关系判断方法判断A ，通过判断圆与圆的位置关系确定1O 与2O 的公切线的条数，通过将两圆方程相减确定两圆的公共弦的方程，判断C ，D.【详解】因为222212:220,:2410O x y mx y O x y x my +-+=+--+= ，所以1O ：222()(1)1x m y m -++=+，2O ：222(1)(2)4x y m m -+-=，则1(1)O m -，，1r =2(12)O m ，，22||r m =，则0m ≠，由(11)-，在1O 内，可得221(1)220m +---<，即0m >，A 错误；当1m =时，1(11)O -，，1r 2(12)O ，，22r =，所以12||3O O =∈(22，所以两圆相交，共两条公切线，B 正确；12O O - ，得(22)(24)10m x m y -+++-=，即(24)(221)0m x y x y -+++-=，令2402210x y x y -+=⎧⎨+-=⎩，，解得1316x y ⎧=⎪⎪⎨⎪=⎪⎩，，所以定点为1136⎛⎫ ⎪⎝⎭，，C 正确；公共弦所在直线的斜率为2224m m -+，令221242m m -=+，无解，所以D 错误，故选：BC ．11．已知椭圆2222:1(0)x y C a b a b+=>>的左､右焦点分别为12,F F ，长轴长为4，点P 在椭圆C 外，点Q 在椭圆C 上，则（）A ．椭圆C的离心率的取值范围是⎛ ⎝⎭B ．当椭圆C的离心率为2时，1QF的取值范围是[2-+C ．存在点Q 使得120QF QF ⋅=D ．1211QF QF +的最小值为1【正确答案】BCD【分析】根据点)P在椭圆C 外，即可求出b 的取值范围，即可求出离心率的取值范围，从而判断A ，根据离心率求出c ，则[]1,QF a c a c ∈-+，即可判断B ，设上顶点A ，得到120AF AF <，即可判断C ，利用基本不等式判断D.【详解】解：由题意得2a =，又点)P在椭圆C 外，则22114b+>，解得b <所以椭圆C的离心率2c e a ==>，即椭圆C的离心率的取值范围是,12⎫⎪⎪⎝⎭，故A 不正确；当2e =时，c =1b ==，所以1QF 的取值范围是[],a c a c -+，即22⎡⎣，故B 正确；设椭圆的上顶点为()0,A b ，()1,0F c -，()2,0F c ，由于222212·20AF AF b c b a =-=-<，所以存在点Q 使得120QF QF ⋅= ，故C 正确；()21121212112224QF QF QF QF QF QF QF QF ⎛⎫++=++≥+= ⎪ ⎪⎝⎭，当且仅当122QF QF ==时，等号成立，又124QF QF +=，所以12111QF QF +≥，故D 正确．故选：BCD12．法国数学家加斯帕·蒙日被称为“画法几何创始人”、“微分几何之父”．他发现与椭圆相切的两条互相垂直的切线的交点的轨迹是以该椭圆中心为圆心的圆，这个圆称为该椭圆的蒙日圆．若椭圆()2222:10x y a b a bΓ+=>>的蒙日圆为2223:2C x y a +=，过C 上的动点M 作Γ的两条切线，分别与C 交于P ，Q 两点，直线PQ 交Γ于A ，B 两点，则（）A ．椭圆Γ的离心率为2B ．MPQ 面积的最大值为232aC ．M 到Γ的左焦点的距离的最小值为(2aD ．若动点D 在Γ上，将直线DA ，DB 的斜率分别记为1k ，2k ，则1212k k =-【正确答案】ABD【分析】由条件可得222a b =，由此可求椭圆Γ的离心率，由此判断A ，由条件可得PQ 为圆C 的直径，确定MPQ 面积的表达式求其最值，由此判断B ，由条件确定2MF 的表达式求其范围，由此判断C ，结合点差法判断D.【详解】依题意，过椭圆Γ的上顶点作y 轴的垂线，过椭圆Γ的右顶点作x 轴的垂线，则这两条垂线的交点在圆C 上，所以22232a b a +=，得222a b =，所以椭圆Γ的离心率2c e a ==，故A 正确；因为点M ，P ，Q 都在圆C 上，且90PMQ ∠=︒，所以PQ 为圆C 的直径，所以2PQ =，所以MPQ面积的最大值为21322PQ a ==，故B 正确；设00(,)M x y ，Γ的左焦点为(),0F c -，连接MF ，因为222212c a b a =-=，所以()222222222000000031222222MF x c y x y x c c a x a a a =++=+++=+⨯+=，又0x ≤≤，所以(222MF a ≥-，则M 到Γ的左焦点的距离的最小值为2a ，故C 不正确；由直线PQ 经过坐标原点，易得点A ，B 关于原点对称，设()11,A x y ，()22,D x y ，则()11,B x y --，12112y y k x x -=-，12212y y k x x +=+，又2211222222221212x y b b x y b b ⎧+=⎪⎪⎨⎪+=⎪⎩，所以222212122202x x y y b b --+=，所以221212122212121212y y y y y y x x x x x x --+=⋅=---+，所以1212k k =-，故D 正确故选：ABD ．椭圆的蒙日圆及其几何性质过椭圆()222210x y a b a b+=>>上任意不同两点M ，N 作椭圆的切线，若两切线垂直且相交于P ，则动点P 的轨迹为圆2222:O x y a b +=+，此圆即椭圆的蒙日圆．椭圆的蒙日圆有如下性质：性质1：PM PN ⊥．性质2：PO 平分切点弦MN ．性质3：MON S 的最大值为2ab ，MON S 的最小值为2222a ba b +．三、填空题13．已知点(1,3)A 关于直线l 的对称点为(5,1)B -，则直线l 的方程为______________________________【正确答案】340x y ++=【分析】求出线段AB 的中垂线方程即可．【详解】131513AB k -==--，其中垂线的斜率为3-，又AB 中点为(2,2)-，∴直线方程为23(2)y x -=-+，即340x y ++=．故340x y ++=．本题考查点的对称性，考查求两点的对称轴方程．掌握对称的性质即可求解．14．已知()P ,a b 为圆C ：222440x y x y +--+=上任意一点，则-12b a +的取值范围为________【正确答案】304⎡⎤⎢⎥⎣⎦，【分析】求12b a -+的取值范围表示圆上的点()P a b ，与点()21Q -，连线的斜率的取值范围，画出图形，可知当直线与圆相切时斜率取到最值，利用点到直线的距离公式计算即可.【详解】由题意，12b a -+表示圆C 上的点()P a b ，与圆外的点()21Q -，连线的斜率.把圆22:2440C x y x y +--+=化为标准式()()22121x y -+-=，圆心()12C ，，半径1r =.设过点()21Q -，的直线方程为()12y k x -=+，即210kx y k -++=.当直线210kx y k -++=与圆C 相切时，斜率k 取得最值.由222111k k k -++=+，解得0k =或34k =.所以12b a -+的取值范围为3[0]4，.故答案为.3[0]4，15．如图，设椭圆221167x y +=的左右焦点分别为12F F 、，过焦点1F 的直线交椭圆于A B 、两点，若2ABF ∆的内切圆的面积为π，设A B 、两点的坐标分别为1122(,)(,)A x y B x y 、，则12||y y -值为_____【正确答案】83【分析】由已知2ABF ∆的内切圆的面积为π得出半径1r =，从而求出2ABF ∆的面积，再由2ABF ∆面积12122y y c =-⨯，即可求出12||y y -.【详解】因为2ABF ∆的内切圆的面积为π，所以2ABF ∆的内切圆半径1r =，2ABF ∆面积()2211282S AB AF BF a =⨯⨯++==所以2ABF ∆面积121211223822y y c y y =-⨯=-⨯⨯=，所以128||3y y -=故答案为83本题主要考查了椭圆的定义，三角形内切圆的性质，三角形的面积公式，属于中档题.16．把椭圆2212516x y +=的长轴AB 分成2018等份，过每个等分点作x 轴的垂线交椭圆的上半部分于2017个点，F 是椭圆的一个焦点，则这2017个点到F 的距离之和为______.【正确答案】10085【分析】若设过2017等分点作x 轴的垂线交椭圆的上半部分于2017个点分别为12320162017,,,,,P P P P P ⋅⋅⋅，由椭圆的定义与椭圆的对称性，得到1201722016100810102PF P F P F P F P F P F a +=+=⋅⋅⋅=+=，结合1009P F a =和题中的数据，可得答案.【详解】解：由题意可知5a =，若设过2017等分点作x 轴的垂线交椭圆的上半部分于2017个点分别为12320162017,,,,,P P P P P ⋅⋅⋅，F 是椭圆的一个焦点，设椭圆的另一个焦点为'F ，则根据椭圆的对称性，得'12017112PF P F PF PF a +=+=，同理'22016222P F P F P F P F a +=+=，……，'10081010100810082P F P F P F P F a +=+=，又因为1009P F a ==，所以12320162017210082017=20175=10085PF P F P F P F P F a a a +++⋅⋅⋅++=⨯+=⨯故10085此题考查了椭圆的标准方程、椭圆的定义与简单几何性质等知识，属于中档题.四、解答题17．已知圆C 的圆心在x 轴上，且经过点1,0,()(,2)1A B -.（1）求圆C 的标准方程；（2）过点(0,2)P 的直线l 与圆C 相交于,M N 两点，且||MN =l 的方程.【正确答案】（1）22(1)4x y -+=（2）0x =或3480x y +-=【分析】（1）根据题意，设AB 的中点为D ，求出D 的坐标，求出直线CD 的斜率，由直线的点斜式方程分析可得答案，设圆C 的标准方程为222()x a y r -+=，由圆心的位置分析可得a 的值，进而计算可得r 的值，据此分析可得答案；（2）设F 为MN 的中点，结合直线与圆的位置关系，分直线l 的斜率是否存在两种情况讨论，综合即可得答案.【详解】解：（1）设AB 的中点为D ，则(0,1)D ，由圆的性质得CD AB ⊥，所以1CD AB K K ⨯=-，得1CD K =-，所以线段AB 的垂直平分线方程是1y x =-+，设圆C 的标准方程为222()x a y r -+=，其中(,0)C a ，半径为()0r r >，由圆的性质，圆心(,0)C a 在直线CD 上，化简得1a =，所以圆心()1,0C ，||2r CA ==，所以圆C 的标准方程为22(1)4x y -+=；（2）由（1）设F 为MN 中点，则CF l ⊥，得||||FM FN =圆心C 到直线l 的距离||1d CF ===，当直线l 的斜率不存在时，l 的方程0x =，此时||1CF =，符合题意；当直线l 的斜率存在时，设l 的方程2y kx =+，即20kx y -+=，由题意得d =，解得34k =-；故直线l 的方程为324y x =-+，即3480x y +-=；综上直线l 的方程为0x =或3480x y +-=.本题考查直线与圆的位置关系，涉及直线与圆方程的综合应用，属于基础题.18．已知ABC 的顶点()5,1A ，边AB 上的中线CM 所在直线方程为250x y --=，边AC 上的高BH 所在直线方程为250x y --=，（1）求顶点C 的坐标；（2）求ABC 的面积．【正确答案】（1）()4,3C ；（2）8.【分析】（1）首先设(),C m n ，根据题意得到125250n m m n -⎧=-⎪-⎨⎪--=⎩，再解方程组即可.（2）首先设(),B a b ，得到51,22a b M ++⎛⎫ ⎪⎝⎭，从而得到15502250b a a b +⎧+--=⎪⎨⎪--=⎩，解方程得到()1,3B --，再求出BC 和点A 到直线BC 的距离，即可得到答案.【详解】（1）设(),C m n ，因为直线AC 与直线BH 垂直，且C 点在直线250x y --=上，所以125250n m m n -⎧=-⎪-⎨⎪--=⎩，解得43m n =⎧⎨=⎩，故()4,3C .（2）设(),B a b 由题知：51,22a b M ++⎛⎫ ⎪⎝⎭，所以15502250b a a b +⎧+--=⎪⎨⎪--=⎩，解得13a b =-⎧⎨=-⎩，即()1,3B --.336415BC k +==+，直线()6:345BC y x -=-，即.6590x y --=BC ==点A 到直线BC的距离d所以182ABC S == .本题主要考查直线的方程，同时考查点到直线的距离公式，属于中档题.19．圆1C ：222280x y x y +++-=与2C ：22210240x y x y +-+-=相交于A 、B 两点.(1)求圆心在直线y ＝－x 上，且经过A 、B 两点的圆的方程；(2)求经过A 、B 两点且面积最小的圆的方程.【正确答案】(1)226680x y x y ++-+=(2)()()22215x y ++-=【分析】（1）首先设圆系方程()2222210240228x y x y x y x y λ+++-+-+-=+（λ为常数），根据圆心在直线y x =-上，求λ，即可求得圆的方程；（2）面积最小的圆，就是以线段AB 为直径的圆，求出该圆的圆心和半径可得圆的方程.【详解】（1）因为圆2C 的圆心25(1,)C -不在直线y x =-上，所以所求圆不是圆2C ，故可设经过A 、B 两点的圆的方程为()2222210240228x y x y x y x y λ+++-+-+-=+（λ为常数），即22222108240111x y x λλλλλλ-+++++-=+++,则圆心坐标为115,11λλλλ---⎛⎫ ⎪++⎝⎭；又圆心在直线y ＝－x 上，故115011λλλλ---+=++，解得12λ=-，故所求方程为226680x y x y ++-+=.（2）因为圆1C 的圆心1(1,1)C --，半径1r ，圆2C 的圆心25(1,)C -，半径2r =，所以直线12C C 的方程为115111y x ++=-++，即230x y ++=，由题意可知以线段AB 为直径的圆的面积最小，由两个圆的方程相减可得直线AB 的方程为240x y -+=，联立230240x y x y ++=⎧⎨-+=⎩，解得21x y =-⎧⎨=⎩，则所求圆的圆心为(2,1)-，圆心1(1,1)C --到直线:240AB x y -+=的距离d ==所以||AB ===故面积最小的圆的方程为()()22215x y ++-=.20．如图，已知C 的圆心在原点，且与直线30x y ++=相切.点P 在直线8x =上，过点P 引C的两条切线PA 、PB ，切点为A 、B .(1)求四边形OAPB 面积的最小值；(2)求证：直线AB 过定点.【正确答案】(1)5；(2)证明见解析.【分析】（1）连接OA ，OB ，求出圆C 的方程和2OAPB OAP S S =!=（2）求出以OP 为直径的圆的方程，再求出两圆的公共弦方程即得证.【详解】（1）解：依题意得：圆心（0，0）到直线x +3y=0的距离d ＝r ，∴5r d ===，∴圆C 的方程为x2+y2165=.如图，连接OA ，OB ，∵PA ，PB 是圆C 的两条切线，∴OA ⊥AP ，OB ⊥BP ，∴112||||22OAPB OAP S S OA PA ==⋅=⨯!=∴当PO 取最小值为8时，min ()OAPB S =（2）证明：由①得，A ，B 在以OP 为直径的圆上，设点P 的坐标为（8，b ），R b ∈，则线段OP 的中点坐标为（4，2b ），∴以OP 为直径的圆方程为222(4)()1624b b x y -+-=+，即x2+y2﹣8x ﹣by ＝0.∵AB 为两圆的公共弦，∴由222216580x y x y x by ⎧+=⎪⎨⎪+--=⎩得直线AB 的方程为8x by +=165，b ∈R ，即8（x 25-）+by ＝0，则直线AB 恒过定点（25，0）.21．已知动圆M 经过定点1(1,0)F -，且与圆222:(1)8F x y -+=相内切．(1)求动圆圆心M 的轨迹C 的方程；(2)设点T 在2x =上，过点T 的两条直线分别交轨迹C 于A ，B 和P ，Q 两点，且TA TB TP TQ ⋅=⋅，求直线AB 的斜率和直线PQ 的斜率之和．【正确答案】(1)2212x y +=(2)0【分析】（1）设动圆圆心(),M x y ，半径为r ，利用椭圆的定义可得到动圆圆心M 的轨迹方程.（2）设出AB 直线方程和PQ 直线方程，分别与椭圆方程联立，写出韦达定理，利用弦长公式表示出TA TB TP TQ ⋅=⋅，即可得到斜率之和.【详解】（1）设动圆圆心(),M x y ，半径为r ，由题意得：12MF r MF r⎧=⎪⎨=-⎪⎩得12122MF MF F F +=>=．所以圆心M 的轨迹是以1F ，2F为焦点的椭圆，且1a cb ===故轨迹C 方程为2212x y +=．（2）设(2,)T t ，11(,)A x y ，22(,)B x y ，AB 直线方程为1(2)y t k x -=-，33(,)P x y ，44(,)Q x y ，PQ 直线方程为2(2)y t k x -=-，()221122x y y t k x ⎧+=⎪⎨⎪-=-⎩联立相消得2221111(21)4(2)2(2)20k x k t k x t k ++-+--=，()2111221211221842122221k k t x x k t k x x k ⎧-+=⎪+⎪⎨--⎪=⎪+⎩()22121212222121t TA TB x x k k +⋅--=++同理()2222222121t TP TQ k k +⋅=++，又TA TB TP TQ ⋅=⋅，2222121222121102121k k k k k k ++=⇒-=++，又12k k ≠，120k k +=．22．在平面直角坐标系xoy 中，已知圆22:4O x y +=，椭圆22:14x C y +=，A 为椭圆的右顶点，过原点O 且异于坐标轴的直线与椭圆C 交于,B C 两点，直线AB 与圆O 的另一个交点为P ，直线AC 与圆O 的另一个交为Q ，设直线,AB AC 的斜率分别为12,k k，（1）求椭圆的离心率；（2）求12k k 的值；（3）求证：AB AC AP AQ+为定值.【正确答案】（1（2）14-；（3）证明见解析.【分析】（1）根据椭圆离心率的公式直接求解即可；（2）设()00,B x y ，则()00,C x y --，然后根据两点间的斜率公式表示出12k k ，进一步化简整理即可求出结果；（3）分别将直线,AB AC 与椭圆联立，依次表示出点,,,B C P Q 的横坐标，然后根据线段的比与横坐标的关系转换为关于12,k k 的关系，进一步化简即可求出结果.【详解】（1）2c e a ==；（2）设()00,B x y ，则()00,C x y --，220014x y +=，因此()22200011444x y x =-=-，且()2,0A ，所以200012200012244y y y k k x x x =⋅==--+-；（3）设直线()1:2AB y k x =-，联立()()122222111221416164014y k x k x k x k x y ⎧=-⎪⇒+-+-=⎨+=⎪⎩，则221122111648221414B B k k x x k k --=⇒=++联立()()22221111222144404y k x k x k x k x y ⎧=-⇒+-+-=⎨+=⎩，则221122114422211P P k k x x k k --=⇒=++而21212814C k x k -=+,设直线()2:2AC y k x =-，联立()()222222222221416164014y k x k x k x k x y ⎧=-⎪⇒+-+-=⎨+=⎪⎩，则22212221222321116Q k k x k k --==++,22112211221122118228222214142223222221116C B P Q k k AB AC x x k k k k AP AQ x x k k ------+++=+=+------++()()()()222211112222111151411165205144414414414k k k k k k k k ++++=+===++++,解决直线与椭圆的综合问题时，要注意：（1）注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；（2）强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．。

【试卷】高二英语周练(十)

2023－2024学年第二学期高二英语周练（10）第一节阅读理解（共7小题；每小题35分，满分35分）San Francisco Fire Engine ToursRunning: February 1st through April 30thThis delicious tour goes through the city on its way to Treasure Island where we will stop at the famous Winery SF. Here you can enjoy 4 pours of some of the best wine San Francisco has to offer.(Included in tickets price)Departing from the Cannery: Tour times upon request.Duration(时长): 2 hours Price: $90Back to the Fifties TourRunning: August 16th through August 31stThis tour transports you back in time to one of San Francisco’s most fantastic periods, the 1950s! Enjoy fun history as we take you through San Francisco for a free taste of ice cream.Departing from the Cannery: 5:00 pm and 7:30 pmDuration: 2 hours Price: $90Spooky Halloween TourRunning: October 10th through October 31stJoin us for a ride through the historical Presidio district. Authentic fire gear(服装) is provided for your warmth as our entertainers take you to some of the most thrilling parts of San Francisco.Departing from the Cannery: 6:30 pm and 8:30 pmDuration: 1 hour and 30 minutes Price: Available upon requestHoliday Lights TourRunning: December 6th through December 23rdThis attractive tour takes you to some of San Francisco’s most cheerful holiday scenes. Authentic fire gear is provided for your warmth as you get into the holiday spirit.Departing from the Cannery: 7:00 pm and 9:00 pmDuration: 1 hour and 30 minutesAdvance reservations required.21. Which of the tours is available in March?A. San Francisco Winery Tour.B. Back to the Fifties Tour.C. Spooky Hallowen Tour.D. Holiday Lights Tour.22. What can tourists do on Back to the Fifties Tours?A. Go to Treasure Island.B. Enjoy the holiday scenes.C. Have free ice cream.D. Visit the Presidio district.23. What are tourists required to do to go on Holiday Lights Tour?A. Take some drinks.B. Set off early in the morning.C. Wear warm clothes.D. Make reservations in advance.CJaguar Land Rover has released new technology designed to constantly monitor drivers and passengers in order to adjust settings to match their mood（情绪）. The carmaker has tested a special system which uses a camera to film drivers to monitor their facial expressions.If the system detects (探测)a driver who is stressed, it can automatically turn on calming mood lighting. The car could respond to a driver who was tired by lowering the car’s temperature, or by beginning to play a specific playlist of music. The carmaker has also developed headrest cameras to monitor the facial expressions of passengers. If the cameras detect sleepiness, then the car can automatically dim (使变暗) the passenger lighting to help people go to sleep. Jaguar Land Rover said that the system also uses artificial intelligence to learn people’s preferences, so that it could automatically adjust a car’s settings based on their previous interactions with the car.Dr Steve Iley, Jaguar Land Rover chief medical officer, said, “As we move towards a self-driving future, the focus for us remains as much on the driver as it ever has.”“By considering the overall behavior of drivers, and using much of what we’ve learned from the advances in research around personal well-being over the last 10 or 15 years, we can make sure our customers remain comfortable, involved and alert behind the wheel in all driving situations, even motorway journeys.”The system is still being developed and is not yet available in cars, Jaguar Land Rover said.In 2015, the company released a similar system which monitors drivers to detect signs of sleepiness. The system is now in use in Jaguar cars, and alerts drivers when they become too sleepy.28. What is Jaguar Land Rover’s new invention?A. An automatically adjusted headrest.B. An intelligent alarm system.C. A mood-detection system.D. A self-driving car.29. How is Paragraph 2 developed?A. By giving examples.B. By making comparisons.C. By following time order.D. By analyzing cause and effect.30. What does Dr St eve Iley think about the new invention?A. It is customer-friendly.B. It is environmentally friendly.C. It fails to meet drivers’ need.D. It should focus greatly on passengers.31. What is the present situation of the new invention?A. It has already been banned.B. It is doubted by customers.C. It still needs to be improved.D. It is widely used in Jaguar cars.第二节七选五（共5小题；每小题5分，满分25分）Stress-eating happens when you’re not hungry and eating more than necessary to be full. Often, we’re piling on the junk food. As a result, gaining weight, illnesses and low self-confidence can all occur due to stress-eating. 36 __________ Here are some tips.ExerciseWhen you feel like reaching for a snack when you know you’re not hungry, try to change that energy into exercising. 37 __________ Not only will the sunshine and exercise make you feel good and lessen feelings of pain and stress, you’ll also have some time to think about what’s behind your urge to eat. Exercise can help you get clear and find a solution to your problem.Write Down Your FeelingsWhen stress is kicking in and you’re reaching for junk food, stop and reach for a journal, your phone or computer instead. Open up a writing space and begin to examine what is causing your stress. Think of ways you can address your problem head on. Write out what it is you want to say. 38___________ If not, drink some more water and a handful of blueberries and keep writing.Discover New Hobbies39___________ Starting a fun and enjoyable hobby can help you manage stress and hardships in other areas of life, giving you more energy and a renewed sense of hope when it’s time to deal with those problems. Before you know it, you’ll be having more fun, enjoying life more and better equipped to handle stress in a healthy way. 40 ___________A. Give it a shot and try something new.B. Explore what you love to do and do it often.C. But how can we stop stress-eating right now?D. Get up from your desk and take a walk outside.E. You can listen to music or do sports to relax yourself.F. By the time you finish, your unhealthy desires should be gone.G. Take some time on Sunday and plan out what you’re going to do for the week.第三节（共15小题；每小题１分，满分１5分）Anytime I travel on my bicycle across the country, I’m always amazed by how kind people can be to strangers.One night, my friends and I were camping in a town in Missouri. There was a severe storm and we were getting 41________. A complete stranger came by to 42________ us that there were tornadoes (龙卷风) heading our way. The stranger invited us to his home. We were surprised by his 43________ for our safety. Later we learned that there had been a lightening strike near the place where we had camped and several cattle had been 44________.Fortunately, we spent the night in a nice dry home. We were 45________ given the opportunity to take a shower. The next morning we had breakfast with the family and 46________ contact information. In a way we felt like the family had become a part of our journey. This was one of the most heartwarming 47________ of my life because this family had nothing to 48________ by being so kind to us. We were 49________ not the type they would usually 50________, but they treated us with respect and kindness. The kindness of a stranger always 51________ my faith in humanity. Whatever the person 52________ always comes with no strings attached（不附带任何条件）and that’s the most 53________ part.That family 54________ us so much that during the rest of the trip, we 55________ others out every chance we got. We even bought food with our busking(街头卖艺) tips for the homeless. It’s always heartwarming when giving feels as good as receiving.41.A.annoyed B.impatient C.excited D.nervous42.A.warn B.show C.convince D.guarantee43.A.demand B.concern C.desire D.responsibility44.A.drowned B.deserted C.killed D.trapped45.A.even B.merely C.often D.simply46.A.submitted B.exchanged C.checked D.updated47.A.experiences B.messages C.traditions ments48.A.fear B.order C.gain D.offer49.A.especially B.officially C.occasionally D.definitely50.A.ask about plain about C.agree with D.associate with51.A.reveals B.shakes C.strengthens D.shapes52.A.states B.wishes C.saves D.gives53.A.impressive B.practical C.satisfactory D.evident54.A.funded B.inspired C.owed D.delighted55.A.drove B.sought C.helped D.pointed第四节（共10小题；每小题2.5分，满分25分）Dunhuang, an oasis(绿洲) in the Taklamakan Desert, used to be a major stop along the Silk Road, but is now mainly a fascinating tourist destination.Those interested 56__________ Dunhuang’s colorful history will be attracted by the Mogao Caves, one of the city’s main attractions. The entrance to each cave 57_______________(block) by a locked door, which can only be opened by expert guides. Behind these doors are caves of all 58__________ (size)—from very small to absolutely huge. The caves contain thousands of priceless manuscripts （手稿）and silk paintings, which, upon their discovery, drew much 59__________(attend) to the area. Also, there are few things as special as walking across the desert oasis at sunrise. 60_______________ (catch) this incredible scene, you must rise early. It’s bitterly cold. But as the sun rises atop the golden dunes(沙丘) and paints a 61__________(true) picturesque scene, all your efforts pay off. Sunset is a popular time for a camel ride. Get off the camels 62__________ walk up a rather steep（陡峭的）dune overlooking Crescent Lake. From this position, 63__________(regard) as the best one, the incredible sunset is awe-inspiring.No trip to Dunhuang is complete without visiting the Dunhuang Museum, 64__________ it’s possible to put all of the city’s historical sites into proper historical context. The museum is expansive, 65_______________ (contain) many original artworks. Here, you are bound to be amazed by Dunhuang’s rich culture.2023－2024学年第二学期高二英语周练（10）二、阅读理解【文章大意】本文是一篇应用文，主要介绍了美国旧金山的四个旅游活动和路线。

地理周周练精选试题

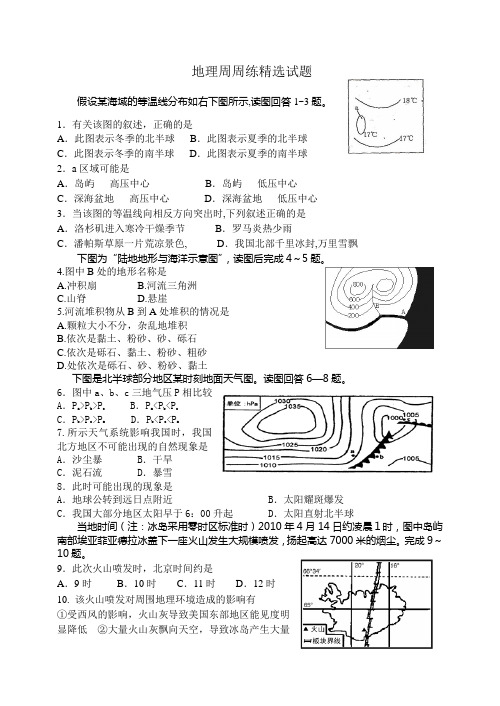
地理周周练精选试题假设某海域的等温线分布如右下图所示,读图回答1~3题。

1．有关该图的叙述，正确的是A．此图表示冬季的北半球B．此图表示夏季的北半球C．此图表示冬季的南半球D．此图表示夏季的南半球2．a区域可能是A．岛屿高压中心B．岛屿低压中心C．深海盆地高压中心D．深海盆地低压中心3．当该图的等温线向相反方向突出时,下列叙述正确的是A．洛杉矶进入寒冷干燥季节B．罗马炎热少雨C．潘帕斯草原一片荒凉景色, D．我国北部千里冰封,万里雪飘下图为“陆地地形与海洋示意图”，读图后完成4～5题。

4.图中B处的地形名称是A.冲积扇B.河流三角洲C.山脊D.悬崖5.河流堆积物从B到A处堆积的情况是A.颗粒大小不分，杂乱地堆积B.依次是黏土、粉砂、砂、砾石C.依次是砾石、黏土、粉砂、粗砂D.处依次是砾石、砂、粉砂、黏土下图是北半球部分地区某时刻地面天气图。

读图回答6—8题。

6．图中a、b、c三地气压P相比较A．P a>P b>P c B．P a<P b<P cC．P b>P c>P a D．P b<P c<P a7.所示天气系统影响我国时，我国北方地区不可能出现的自然现象是A．沙尘暴 B．干旱C．泥石流 D．暴雪8．此时可能出现的现象是A．地球公转到远日点附近 B．太阳耀斑爆发C．我国大部分地区太阳早于6：00升起 D．太阳直射北半球当地时间（注：冰岛采用零时区标准时）2010年4月14日约凌晨１时，图中岛屿南部埃亚菲亚德拉冰盖下一座火山发生大规模喷发，扬起高达7000米的烟尘。

完成9～10题。

9．此次火山喷发时，北京时间约是A．9时B．10时C．11时D．12时10. 该火山喷发对周围地理环境造成的影响有①受西风的影响，火山灰导致美国东部地区能见度明显降低②大量火山灰飘向天空，导致冰岛产生大量降水③火山喷发使周边区域冰雪急速消融④飘浮在大气中的火山灰会削弱到达地面的太阳辐射A．①②B．②③C．③④D．①④读“我国某区域略图”,完成11～12题。

高二中国地理复习题中国的疆域、行政区划、人口、民族、地形3

高二中国地理周周练试题（一）（中国的行政区划、地形、气候、河流湖泊）班级 ____________ 姓名 ________________ 学号 ________________选择题（以下各题均只有一个正确答案，请将正确答案写在后面的括号中）1.有关我国地理位置的叙述，正确的是（）A.位于东半球，跨南北半球B. 大部分位于热带地区，纬度较低C.领土最北端在黑龙江与乌苏里江主航道中心线的相交处D.西部深入亚欧大陆内部，东临太平洋，是一个海陆兼备的国家 2 .下列省区中既临渤海，又临黄海的是（） A.河北、江苏 B.辽宁、山东 C.北京、天津D.吉林、辽宁3 .当黑龙江还是冰天雪地时，海南岛却是农忙时节，造成这种差异的原因是（） A.我国跨经度大 B.我国跨纬度大 C.离海远近不同 D.地形起伏大4 .下列各组国家中，与我国云南省相邻的一组是（） A.蒙古、俄罗斯 B.越南、老挝 C.尼泊尔、印度 D.阿富汗、巴基斯坦5 .我国下列省级行政区中，有两个简称的是（） A.湖北、湖南 B.西藏、台湾 C.山西、吉林 D.四川、云南6 .与我国隔海相望的一组国家是（） A.印度、文莱、菲律宾 C.日本、朝鲜、印度尼西亚7 .下列海域属于我国内海的是（） A.渤海、黄海 B.黄海、东海海峡8 .下列叙述中，因我国人口数量过多而带来的负面影响是（） A.劳动力短缺 B.兵源不足 C.人口老龄化严重 D.住房紧张，就业困难9 .下列属于我国三级行政区划的是（）A.省、自治区、直辖市C.省、特别行政区、直辖市治乡10 .下列有关我国各民族的地区分布状况的描述，正确的是（） A.汉族全部分布在东部B.少数民族全部分布在西部C.我国民族总的分布趋势是大杂居、小聚居 B.马来西亚、朝鲜、韩国D.文莱、菲律宾、日本 C.南海、东海 D.渤海、琼州B.省、县、乡D.自治州、自治县、自D.各民族均匀分布11.横亘在高原与盆地之间的界山是（12.位于地势第二级阶梯，内有丘陵分布，并且没有绿洲的盆地是（） A.塔里木盆地 B.柴达木盆地 C.四川盆地 D.准噶尔盆地14 .分布在第三级阶梯上的主要地形是（ A.丘陵和平原 B.丘陵和盆地高原15 .位于地势第三阶梯，海拔在50米以下，临黄海和东海的地形区是（） A 东北平原 B 华北平原 C 长江中下游平原 D 江南丘陵。

高二地理周周练

高二地理周周练（7）一、单项选择题（每题15 分，每题 4 分，共 60 分）以下列图表示巴西某棉花产区降水量的季节变化。

读图完成1～3题。

1．该棉花产区的天气种类是（）降水量（ mm ）A．热带雨林天气B．地中海天气320生长远 /种植期种植期C．热带草原天气 D ．亚热带季风气候生长远 /现蕾期2．该棉花产区最可能位于（）240A．亚马孙平原B．东部沿海平原开花期 / 坐果期C．巴西高原D．南部沿海平原1503．该地区天气特色对棉花生产的有利影吐絮期80响是（）采摘期A．全年高温，蒸发旺盛B．风调雨顺，不受旱涝灾害影响01234567891011 12月份C．采摘期正当盛夏，光热充足，利于采摘 D ．生长远高温多雨，利于棉花生长读世界某地区简图，回答4～6题。

4．以下有关图中城市天气特色的表达，正确的选项是（）A．夏季酷热，冬季平易B．夏季凉爽，冬季寒冷C．夏季降水多，冬季降水少D．冬夏季降水季节分配均匀5．决定哥伦比亚河水坝修筑密度的主要影响因素是（）A．技术水平B．水能储蓄量C．能源需求量D．工业结构6.有色金属冶炼工业是西雅图的主导工业，其发展的优势条件有（）①凑近原料产地②动力充足③交通便利④劳动力充足且廉价A．①②③B．①③④C．②③④D．①②④以下列图表示近 8年来中国对美国投资总数分布。

读图完成7～ 8题。

7．中国对美国投资主要分布在（）A．太平洋及北冰洋沿岸地区B．太平洋沿岸地区C．五大湖及大西洋沿岸地区D．墨西哥湾沿岸地区8．影响中国企业到美国投资家电制造业的主要影响因素是（）A．矿产与技术B．政策与市场C．能源与交通D．土地与劳动力自 20 世纪 60 年代，甲国开始在周边乙国边境的地区成立边境工业区，吸引乙国的企业来此投资建厂，并从乙国进口原料和零部件，加工、组装成品后再销往乙国。

目前，这些边境工业区已发展成规模不等的工业中心（见图3）。

据此完成9～ 11 题。

110°100°30°N9．据图文资料推断，与乙国对照，甲国A．劳动力价格较低B．技术水平较高C．花销市场较广D．资本较雄厚10．影响甲国边境工业区区位选择的主导因素是A．廉价劳动力B．交通运输C．研发能力D．环境质量11．甲国边境工业区的发展，提高了A．乙国的劳动生产率B．甲国的环境质量C．乙国的就业率D．甲国的城镇化水平自 2011 年 7 月始，泰国发生了连续 3 个多月的洪涝灾害，多个全球有名 IT 企业在泰国成立的硬盘生产厂家在此灾害中受到不同样程度损毁，以致当年硬盘价格上涨。

高二化学《乙醛醛类》周周练

时遁市安宁阳光实验学校东华实验中学下期高二化学《乙醛醛类》周周练一、选择题。

1．(CH3)2CHCH2OH是某有机物加氢还原的产物，原有机物可能是（）A．(CH3)2CHCHOB．CH3(CH2)2CHO2．居室空气污染的主要来源之一是人们使用的装饰材料、胶合板、内墙涂料会释放出一种刺激性气味气体，该气体是（）A．甲烷 B．氨气 C．甲醛 D．二氧化硫3．甲醛与单烯烃的混合物含氧的质量分数为x，则其含碳的质量分数为（）A ．B ．C ． D．无法确定4．有一系列有机化合物按以下顺序排列：CH3CH=CHCHO，CH3CH=CHCH=CHCHO，CH3(CH=CH)3CHO，……在该系列有机物中，分子中碳元素的质量分数的最大值最接近于（）A．95.6% B．92.3% C．85.7% D．75.0%5．甲醛在一定条件下发生如下反应：2HCHO + NaOH（浓）→ HCOONa + CH3OH，在此反应中，甲醛发生的变化是（）A．仅被氧化 B．仅被还原C．既被氧化，又被还原 D．既未被氧化，也未被还原6．某饱和一元醇和一元醛的混合物共3g，跟足量的银氨溶液完全反应后，可还原出16.2gAg，下列说法正确的是（）A．一定是甲醛B．可能是乙醛C．混合物中二者的质量比是1:3 D．不可能有此种醛7．下列反应中，有机物被还原的是 ( )A.乙醛的银镜反应B.乙醛制乙醇C.乙醇制乙醛D.乙醇制乙烯8．有乙醛蒸气与乙炔的混合气体aL,当其完全燃烧时, 消耗相同状况下氧气的体积为（）A.2aLB.2.5aLC.3aLD.条件不足无法计算9．已知柠檬醛的结构简式为，根据所学知识判断下列说法不正确的是（）A．它可使酸性高锰酸钾溶液褪色 B．能发生银镜反应C．与乙醛互为同系物 D．被催化加氢的最后产物是C10H22O10．丁基有4 种形式, 不试写, 试推断化学式为C5H10O的醛有（）A.2种B.3种C.4种D.5种11．甲醛、乙醛、丙醛组成的混合物中，若氢的质量分数为9%，则氧的质量分数为（）A.16%B.37%C.48%D.无法计算12．有饱和一元醛发生银镜反应时, 生成21.6g银，再将等质量的醛完全燃烧，生成CO2为13.44L(状况)，则该醛是（）A.丙醛B.丁醛C.3—甲基丁醛D.己醛13.香料茉莉酮是一种人工合成的有机化合物，其结构简式如图：下列关于茉莉酮的说法正确的是（）A.该有机物的化学式为C11H16OB.1 mol该有机物与H2充分反应，消耗H2 4 molC.该有机物属于不饱和酮类物质，不能发生银镜反应D.该有机物能发生加成反应，但不能发生氧化反应14.下列各组混合物总物质的量不变时，各组分以任意比混合后，充分燃烧消耗O2的量不变的是（）A.乙烯、乙醇、乙醛B.乙炔、乙醛、乙二醇C.甲醇、甲醚、甲醛D.乙烷、甘油、乙醇15．已知柠檬醛的结构简式为：根据已有知识判断下说法不正确的是（）A．它能使酸性KMnO4溶液褪色B．它可与银氨溶液反应生成银镜C．它可使溴水褪色D．它被催化加氢的最后产物的分子式为C10H20O16．下列试剂中不能用于检验有机化合物中醛基的是（）A．银氨溶液 B．硝酸银溶液C．新制的氢氧化铜 D．溴水17．下列反应中有机物被还原的是（）．A．乙醛发生银镜反应 B．乙醛转化为乙醇C．乙醛制乙酸 D．乙醇转化为乙醛18．下列物质与H2加成后，生成物为3-甲基-2-丁醇的是（）．19．某烃的衍生物2.9 g，与足量的银氨溶液反应，析出10.8 g银，则该物质为（）。

高二英语(上)周周练答案教程文件

高二英语(上)周周练答案高二（上）英语周周练答案A篇 21-24 AADB B篇 25．B 26．B 27．DC篇 28．B 29．C 30．A 31．BD篇 32．B 33．C 34．A 35．D七选五 36．C 37．F 38．A 39．E 40．D41-45BCADC 46-50CDABC 51-55CABCD 56-60BACBA语法填空参考答案：61．worse 62．problems 63．asleep 64．surprising65．unhappy 66．following 67．Using 68．it 69．to go 70．before改错51. ..., our class have a ... have → had52. ... celebrations to welcoming ... welcoming → welcome53. ... teachers or students. or → and54. ... an wonderful opportunity ... an → a55. ... meet new friends ... new → old56. ... photos for the school, ... for → of57. ... put them up ... 去掉them58. ... at the photo ... photo → photos59. ... would popular ... popular前加be60. ... the days when ... when → that或去掉whenHi Worried,I'm sorry to know that you're having such a bad time at the moment. The truth is that everyone will have one of those periods when things seem to go wrong, so you don't have to worry much. The important thing is to learn to control your temper so that you m ay not do or say anything you’ll regret. Here are three useful tips:For a start, talk to someone you trust about how you feel. This is a good way of letting your anger out without hurting others or yourself. Besides the first mentioned, going outdoors and playing team games with your friends will be effective ways to get rid of anger as well .Last but not least, remain optimistic about your future. Such a positive attitude towards life can be helpful in keeping up your spirits.I hope you'll soon feel calmer and carry on as normal.Yours,Jamie。

高二数学周测试卷(含答案解析)

（1）求证；
（2）求二面角的平面角的余弦值。(理科做）
求点F到平面ABE的距离。（文科做）
21.已知椭圆的，离心率为，是其焦点，点在椭圆上。
（Ⅰ）若，且的面积等于。求椭圆的方程；
（Ⅱ）直线交椭圆于另一点，分别过点作直线的垂线，交轴于点，
当取最小值时，求直线的斜率。
22.已知函数
（1）曲线在点处的切线方程为，求的值；
（2）当时，，试求的取值范围。
参考答案及评分标准
一、选择题:共12小题，每小题5分，共60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
B
B
A
A
D
A
A
D
B
C
D
C
1.选B.【解析】∵ ，，∴ ，故选B.
2.选B.【解析】∵ ，对应的点为在第二象限，故选B.
……………………………………5分
（Ⅱ）
函数的图象为：
当时，，依题意，，则
∴ 的取值范围是 …………………………………………………………10分
18.（Ⅰ）∵ 由正弦定理得
∴
即，易知，且，
上式两边除以 ,得 ……………………………………6分
（Ⅱ）∵ ,∴ ，
由，又，，得
而
∴ …12分
19．（12分）
二、填空题共4小题，每小题5分，共20分.
13.填 .【解析】如图可知的最小值是．
14.填 .【解析】由题意得四面体是底面边长为的正三角形，侧棱垂直底面，且，，，则外接球球心在过底面中心垂直于底面的垂线上，且到底面的距离等于的一半，∴

2019-2020年高二上学期语文测试题(周考)含答案

山东省德州市陵城一中2016-2017学年高二上学期2019-2020年高二上学期语文测试题（周考）含答案一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1~3题。

元宵节舞鱼龙灯的习俗在我国历史悠久。

在我国古代文献、神话传说和民间故事中，均可以找到关于鱼灯的记载。

东汉张衡《西京赋》中有关于鱼化龙、龙化鱼的记载，两千多年前，在西汉京都长安，鱼灯、龙灯及鱼龙文艺已盛极一时。

南朝梁元帝萧绎《对灯赋》中也有“本知龙灯应无偶，复讶鱼灯有旧名”，对元宵夜抢眼夺目的龙灯、鱼灯称赞有加。

宋朝词人辛弃疾在《青玉案·元夕》“凤箫声动，玉壶光转，一夜鱼龙舞”中生动再现了通宵达旦舞鱼龙灯的盛况，体现了鱼龙舞在花灯表演中所担负的重要角色。

那么，究竟什么是鱼龙舞呢?鱼龙舞是鱼灯和龙灯混合表演的舞蹈。

鱼龙舞成为古代节日文化重要的表演习俗，源于古人的崇鲤观念。

这一观念可以追溯至六千年前西安半坡仰韶文化出土的彩陶上生动的鱼纹。

人们在从事日常的捕鱼生产中，把有关鲤鱼无法解释的自然现象加以神化，将鲤鱼视为神鱼加以膜拜，并发展到以鱼为图腾的原始巫术舞蹈。

这种发轫于巫术的舞蹈对后世鱼龙舞的形成产生了较大的影响。

元宵节表演的鱼龙舞总给人鱼龙相随，鱼龙混杂的印象。

宋代《埤雅·释鱼》记载：“俗说鱼跃龙门，过而为龙，唯鲤或然。

”《本草纲目》称：“鲤为诸鱼之长，形状可爱，能神变，常飞跃江湖。

”清代《辛氏三秦记》记载：“江海大鱼薄集龙门下，数千，不得上。

上则为龙，不上者为鱼，故云曝鲤龙门。

”唐朝大诗人李白专门为鲤鱼跳龙门写了—首诗：“黄河三尺鲤，本在孟津居，点额不成龙，归来伴凡鱼。

”按照民间传说，凡跳过龙门的鲤鱼即可变成龙，即与《西京赋》中“鱼化龙”的说法相吻合；没有跳过龙门的鲤鱼“归来伴凡鱼”。

也有记载显示，“归来伴凡鱼”的既不是原来的鲤鱼，又不是飞过龙门的飞龙，而是在“鱼化龙”中变异而成的鳌鱼。

鳌鱼保持了龙头、龙角、龙须，其身上却布满鱼鳞，保留鱼尾。

北京市2023-2024学年高二上学期阶段练习数学试题含解析

北京市2023—2024学年第一学期阶段练习高二数学（答案在最后）2023.10班级__________姓名__________学号__________本试卷共3页，共150分.考试时长120分钟.考生务必将答案写在答题纸上，在试卷上作答无效.一、选择题：本大题共12道小题，每小题4分，共48分.在每小题给出的四个选项中，只有一项符合题目的要求.把正确答案涂写在答题卡上相应的位置．．．．．．．．．．．．．．．．．.1.已知点()2,1,0A 和点()0,3,4B -，则向量AB =（）A.()2,4,4-- B.()2,4,4- C.()2,2,4-- D.()2,2,4-【答案】A 【解析】【分析】根据向量的坐标的定义，即可求解.【详解】由()2,1,0A 和点()0,3,4B -，所以()2,4,4AB =--.故选：A2.设,,i j k 是两两不共线的向量，且向量24a i j k =-++ ，32b i j k =-- ，则23a b -=（）A.1125i j k-+B.1125i j k --+C.111011i j k -++D.111011i j k-- 【答案】C 【解析】【分析】根据向量基底运算法则直接计算即可.【详解】因为24a i j k =-++ ，32b i j k =--，所以()()23224332111011a b i j k i j k i j k -=-++---=-++ .故选：C3.点M (3,-2,1)关于yOz 平面对称的点的坐标是A.(-3,2,1) B.(-3,2,-1)C.(3,2,-1)D.(-3,-2,1)【答案】D 【解析】【分析】根据空间直角坐标系对称点的坐标特点即可得到结果.【详解】点M (3,-2,1)关于平面yOz 的对称点坐标为(-3,-2,1).所以本题答案为D.【点睛】本题考查空间直角坐标系，注意仔细审题，属基础题.4.已知(1,0,1),(1,1,2)a b =--= ，则向量a 在b方向上的投影数量为（）A.3-B.2-C.2-D.62【答案】B 【解析】【分析】代入向量投影的计算公式即可求出结果.【详解】向量a 在b方向上的投影数量为cos ,2a b a b a a b a a b b -⨯+⨯+-⨯⋅⋅⋅=⋅==-⋅，故选：B.5.与向量(1,AB =-共线的单位向量是（）A.112,,222⎛⎫- ⎪ ⎪⎝⎭B.112,,222⎛⎫- ⎪ ⎪⎝⎭和11,,222⎛⎫-- ⎪ ⎪⎝⎭C.11,,222⎛⎫-- ⎪ ⎪⎝⎭D.112,,222⎛⎫ ⎪ ⎪⎝⎭和112,,222⎛⎫--- ⎪ ⎪⎝⎭【答案】B 【解析】【分析】设与向量(1,AB =- 共线的单位向量为a，则B a A λ= ，再根据1a = 求出λ，即可得解.【详解】设与向量(1,AB =- 共线的单位向量为a，则(),A a B λλλ=-= ，所以1a =，解得12λ=±，所以112,,222a ⎛⎫- ⎪⎝=⎪⎭ 或112,,222a ⎛⎫--= ⎪ ⎪⎝⎭.故选：B6.已知向量()1,1,0a =r，()1,1,0b =- ，若()()a b a b λμ+⊥+ ，则（）A.1λμ+= B.1λμ+=- C.1λμ= D.1λμ=-【答案】D 【解析】【分析】首先表示出a b λ+，a b μ+ ，依题意可得()()0a b a b λμ+⋅+= ，由数量积的坐标表示计算可得.【详解】因为()1,1,0a =r，()1,1,0b =- ，所以()1,1,0a b λλλ+=+- ，()1,1,0a b μμμ+=+- ，因为()()a b a b λμ+⊥+ ，所以()()0a b a b λμ+⋅+=，即()()()()11110λμλμ+++--=，所以1λμ=-.故选：D7.如图，空间四边形OABC 中，OA a = ，OB b = ，OC c =.点M 在OA 上，且2OM MA =，N 为BC 的中点，则MN =（）A.121232a b c -+B.132212a b c-+-r r rC.211322a b c-++ D.121232a b c +- 【答案】C 【解析】【分析】根据空间向量的加减和数乘运算直接求解即可.【详解】22,3OM MA OM OA =∴= ，N Q 为BC 的中点，()12ON OB OC ∴=+,()1221123322MN ON OM OB OC OA a b c =-=+-=-++ .故选：C.8.已知平面α⊥平面β，l αβ= ．下列结论中正确的是（）A.若直线m ⊥平面α，则//m βB.若平面γ⊥平面α，则//γβC.若直线m ⊥直线l ，则m β⊥D.若平面γ⊥直线l ，则γβ⊥【答案】D 【解析】【分析】A ，利用线面平行的判定定理；B ，面面垂直没有传递性；C ，利用面面垂直的性质定理；D ，利用面面垂直的判定定理；【详解】A ，若m α⊥，αβ⊥，则//m β或m β⊂，故A 错误；B ，若γα⊥，αβ⊥，则//γβ或γ与β相交，故B 错误；C ，若m l ⊥，αβ⊥，l αβ= ，必须m α⊂，利用面面垂直的性质定理可知m β⊥，故C 错误；D ，若l γ⊥，l αβ= ，即l β⊂，利用面面垂直的判定定理知γβ⊥，故D 正确；故选：D.【点睛】关键点点睛：本题主要考查空间直线，平面直线的位置关系的判断，熟练掌握平行和垂直位置关系的判定和性质是解题的关键，属于基础题.9.如图，在三棱锥A BCD -中，,,DA DB DC 两两垂直，且2DB DC ==，点E 为BC 中点，若直线AE 与CD 所成的角为60︒，则三棱锥A BCD -的体积等于（）A.23B.43C.2D.3【答案】D【解析】【分析】由题意可证AD ⊥平面DBC ，取BD 的中点F ，连接EF ，则AEF ∠为直线AE 与CD 所成的角，利用余弦定理求出AD ，根据三棱锥体积公式即可求得体积．【详解】如图，∵2DB DC ==，点E 为BC 的中点，∴DE BC ⊥，DE =∵DA ，DB ，DC 两两垂直，DB DC D = ，∴AD ⊥平面DBC ，取BD 的中点F ，连接EF ，∴AEF ∠为直线AE 与CD 所成的角，且1EF =，由题意可知，60AEF ∠=︒，设AD x =，连接AF ，则222212AF x AE x =+=+，，在AEF △中，由余弦定理，得222cos 2AE EF AF AEF AE EF +-∠=⋅，即2212=x =AD =∴三棱锥A BCD -的体积11122223323BCD V S AD =⋅=⨯⨯⨯=．故选：D ．10.如图，在长方体1111ABCD A B C D -中，1222AAAB BC ===，点B 到平面1ACD 的距离为（）A.69B.13C.23D.63【答案】C 【解析】【分析】将点B 到平面1ACD 距离转化为三棱锥1B ACD -的高，然后利用等体积的方法求距离即可.【详解】由题意得点B 到平面1ACD 距离为三棱锥1B ACD -的高，设点B 到平面1ACD 距离为d ，取AC 中点O ，连接1OD ，因为1111ABCD A B C D -为长方体，所以11AD CD =，所以1OD AC ⊥，221215AD =+=112AC =+=，()221232522OD ⎛⎫=-= ⎪ ⎪⎝⎭，所以11B ACD D ABC V V --=，113211211232232d ⨯=⨯⨯⨯⨯，解得23d =.故选：C.11.日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为（）A.20°B.40°C.50°D.90°【答案】B 【解析】【分析】画出过球心和晷针所确定的平面截地球和晷面的截面图，根据面面平行的性质定理和线面垂直的定义判定有关截线的关系，根据点A 处的纬度，计算出晷针与点A 处的水平面所成角.【详解】画出截面图如下图所示，其中CD 是赤道所在平面的截线；l 是点A 处的水平面的截线，依题意可知OA l ⊥；AB 是晷针所在直线.m 是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直，根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥..由于40,//AOC m CD ∠=︒，所以40OAG AOC ∠=∠=︒，由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与点A 处的水平面所成角为40BAE ∠=︒.故选：B【点睛】本小题主要考查中国古代数学文化，考查球体有关计算，涉及平面平行，线面垂直的性质，属于中档题.12.已知ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC +的最小值是()A.2-B.32-C.43-D.1-【答案】B 【解析】【分析】根据条件建立坐标系，求出点的坐标，利用坐标法结合向量数量积的公式进行计算即可．【详解】建立如图所示的坐标系，以BC 中点为坐标原点，则A ，(1,0)B -，(1,0)C ，设(,)P x y ，则()PA x y =-- ，(1,)PB x y =--- ，(1,)PC x y =--，则22223()222[(]4PA PB PC x y x y +=-+=+--∴当0x =，2y =时，取得最小值332(42⨯-=-，故选：B ．二、填空题：本大题共6小题，共30分.把答案填在答题纸中相应的横线上.13.设a ，b 为单位向量，且1a b += ，则a b ⋅= ____________.【答案】12-##0.5-【解析】【分析】由向量的数量积及运算律计算可得解.【详解】由题意得1a b == ，又1a b +=，21a b ∴+= 即()21a b+= ，整理得2221a a b b +⋅+= ，代入1a b == ，得12a b ⋅=- .故答案为：12-.14.若空间三点()4,1,3A ，()2,5,1B -，(),4,4C m 共线，则实数m =____________.【答案】5【解析】【分析】根据三点共线，转化为向量共线，即可求解.【详解】()2,6,2AB =--- ，()4,3,1AC m =-，由空间三点共线，则//AB AC ，即AC AB λ=，所以423612m λλλ-=-⎧⎪=-⎨⎪=-⎩，得12λ=-，5m =.故答案为：515.已知长方体1111ABCD A B C D -中，4AB BC ==，12CC =，则平面11A BC 与平面ABCD 所成的角的余弦值为____________.【答案】3【解析】【分析】建立空间直角坐标系，利用空间向量法计算可得.【详解】如图以D 为坐标原点，DA 为x 轴，DC 为y 轴，1DD 为z轴，建立空间直角坐标系，则()14,0,2A ，()4,4,0B ，()10,4,2C ，∴()10,4,2A B =-，()114,4,0A C =- ，设平面11A BC 的一个法向量为(),,m x y z=，则111420440A B m y z A C m x y ⎧⋅=-=⎪⎨⋅=-+=⎪⎩ ，取2z =，则()1,1,2m = ，平面ABCD 的一个法向量为()0,0,1n =，设平面11A BC 与平面ABCD 所成的角为θ，则平面11A BC 与平面ABCD所成角的余弦值||6cos ||||3m n m n θ⋅===⋅．故答案为：3．16.如图，在棱长都为1的平行六面体1111ABCD A B C D -中，AB ，AD ，1AA两两夹角均为π3，则1AC BD ⋅=____________；请选择该平行六面体的三个顶点，使得经过这三个顶点的平面与直线1AC 垂直.这三个顶点可以是____________.【答案】①.0②.点1,,A B D 或点11,,C B D （填出其中一组即可）【解析】【分析】（1）以向量AB ，AD ，1AA为基底分别表达出向量1AC uuu r 和BD ，展开即可解决；（2）由上一问可知10AC BD ⋅=，用上一问同样的方法可以证明出110AC A D ⋅= ，这样就证明了平面1A BD 与直线1AC 垂直.【详解】（1）令1a AA = ，b AB = ，c AD =，则1a b c === ，π,,,3a b a c b c === ，则有BD AD AB c b =-=- ，111AC AC CC AB AD AA b c a =+=++=++ ，故221()()AC BD c b c b a c b c a c b c b a b⋅=-⋅++=+⋅+⋅-⋅--⋅2211111111111111111111022222222=+⨯⨯+⨯⨯-⨯⨯--⨯⨯=+--=；（2）令1a AA = ，b AB = ，c AD =，则1a b c === ，π,,,3a b a c b c === 则有11A D AD AA c a =-=- ，111AC AC CC AB AD AA b c a =+=++=++ ，故2211()()AC A D c a c b a c b c a c a c a b a⋅=-⋅++=+⋅+⋅-⋅-⋅- 2211111111111111111111022222222=+⨯⨯+⨯⨯-⨯⨯-⨯⨯-=+--=，故11AC A D ⊥ ，即11AC A D ⊥，又由（1）知1AC BD ⊥，1A D BD D ⋂=，1,A D BD ⊂平面1A BD ，故直线1AC ⊥平面1A BD ；同理可证直线1AC ⊥平面11B D C .故答案为：0；点1,,A B D 或点11,,C B D 17.如图，长方体1111ABCD A B C D -中，1AB =，2BC =，13AA=，E 为BC 的中点，点P 在线段1D E 上.点P 到直线1CC 的距离的最小值为____________.【答案】2【解析】【分析】设点P 在平面ABCD 上的射影为P '，则题意所求距离最小值即为P C '长度的最小值，且P C DE '⊥时P C '的长度最小，利用三角形面积相等关系即可求解.【详解】由题意知，点P 到直线1CC 的距离即为点P 在平面ABCD 上的射影到点C 的距离.设点P 在平面ABCD 上的射影为P '，显然点P 到直线1CC 的距离的最小值为P C '长度的最小值，当P C DE '⊥时，P C '的长度最小，此时11111222DCE S DC CE =⋅=⨯⨯=，12DCE S DE CP ''=⋅= ，所以122CP '=，解得2CP '=，即点P 到直线1CC 的距离的最小值为2.故答案为：2.18.在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+ ，其中[0,1]λ∈，[0,1]μ∈，则下列说法中，正确的有_________（请填入所有正确说法的序号）①当1λ=时，1AB P △的周长为定值②当1μ=时，三棱锥1P A BC -的体积为定值③当12λ=时，有且仅有一个点P ，使得1A P BP ⊥④当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P 【答案】②④【解析】【分析】①结合1λ=得到P 在线段1CC 上，结合图形可知不同位置下周长不同；②由线面平行得到点到平面距离不变，故体积为定值；③结合图形得到不同位置下有1A P BP ⊥，判断出③错误；④结合图形得到有唯一的点P ，使得线面垂直.【详解】由题意得：1BP BC BB λμ=+ ，[0,1]λ∈，[0,1]μ∈，所以P 为正方形11BCC B 内一点，①，当1λ=时，1BP BC BB μ=+ ，即1CP BB μ= ，[0,1]μ∈，所以P 在线段1CC 上，所以1AB P △周长为11AB AP B P ++，如图1所示，当点P 在12,P P 处时，111122B P AP B P AP +≠+，故①错误；②，如图2，当1μ=时，即1BP BC BB λ=+ ，即1B P BC λ= ，[0,1]λ∈，所以P 在11B C 上，1113P A BC A BC V S h -=⋅ ，因为11B C ∥BC ，11B C ⊄平面1A BC ，BC ⊂平面1A BC ，所以点P 到平面1A BC 距离不变，即h 不变，故②正确；③，当12λ=时，即112BP BC BB μ=+ ，如图3，M 为11B C 中点，N 为BC 的中点，P 是MN 上一动点，易知当0μ=时，点P 与点N 重合时，由于△ABC 为等边三角形，N 为BC 中点，所以AN ⊥BC ，又1AA ⊥BC ，1AA AN A = ，所以BN ⊥平面1ANMA ，因为1A P ⊂平面1ANMA ，则1BP A P ⊥，当1μ=时，点P 与点M 重合时，可证明出1A M ⊥平面11BCC B ，而BM ⊂平面11BCC B ，则1A M BM ⊥，即1A P BP ⊥，故③错误；④，当12μ=时，即112BP BC BB λ=+ ，如图4所示，D 为1BB 的中点，E 为1CC 的中点，则P 为DE 上一动点，易知11A B AB ⊥，若1A B ⊥平面1AB P ，只需11A B B P ⊥即可，取11B C 的中点F ，连接1,A F BF ，又因为1A F ⊥平面11BCC B ，所以11A F B P ⊥，若11A B B P ⊥，只需1B P ⊥平面1A FB ，即1B P BF ⊥即可，如图5，易知当且仅当点P 与点E 重合时，1B P BF ⊥故只有一个点P 符合要求，使得1A B ⊥平面1AB P ，故④正确.故选：②④【点睛】立体几何的压轴题，通常情况下要画出图形，利用线面平行，线面垂直及特殊点，特殊值进行排除选项，或者用等体积法进行转化等思路进行解决.三、解答题：本大题共5小题，共72分.解答应写出必要的文字说明、证明过程或演算步骤.19.已知向量()236a m = ,,，()1,0,2= b ，()()132R c m =∈ ,,（1）求()a b c ⋅- 的值；（2）求cos b c ,；（3）求a b - 的最小值.【答案】（1）6-（2）104（3）【解析】【分析】（1）根据空间向量的减法运算法则和数量积运算公式直接计算；（2）根据空间向量夹角公式直接计算即可；（3）根据条件写出模的表达式，再直接求最小值即可.【小问1详解】因为()1,0,2= b，()2c = ，所以()0,b c -= ，又因为()6a m = ,，所以()(6a b c ⋅-==- .【小问2详解】因为()1,0,2= b，()2c = ，所以cos 4b c b c b c⋅=== ,.【小问3详解】因为()6a m = ,，()1,0,2= b ，所以()a b m -=- ，所以()(()2222214128a b m m -=-++=-+ ，当1m =时，2a b - 取得最小值28，则a b -最小值为.20.如图，在直三棱柱111ABC A B C -中，90ACB ∠=︒，12AC CB CC ===，E 是AB 中点.（1）求直线1AC 与直线1B E 所成角的余弦值；（2）求直线11A C 与平面1ACE 所成角的正弦值.【答案】（1）36（2）33【解析】【分析】（1）利用空间向量的方法求异面直线所成角即可；（2）利用空间向量的方法求线面角即可.【小问1详解】如图，以C 为原点，分别以1,,CA CB CC 为,,x y z轴建立空间直角坐标系，()12,0,2A ，()0,0,0C ，()10,2,2B ，()1,1,0E ，()12,0,2A C =--uuu r ，()11,1,2B E =--uuu r ，()()1111112,0,21,1,23cos ,6404114AC B E AC B E AC B E ⋅--⋅--===++⨯++uuu r uuu r uuu r uuu r uuu r uuu r ，所以直线1AC 与直线1B E 所成角的余弦值为36.【小问2详解】()10,0,2C ，()112,0,0AC =- ，()1,1,0CE = ，设平面1A CE 的法向量为(),,m x y z = ，则12200m A C x z m CE x y ⎧⋅=--=⎪⎨⋅=+=⎪⎩ ，令1x =，则1y =-，1z =-，所以()1,1,1m =-- ，111111cos ,3m AC m AC m AC ⋅===u r uuu u r u r uuu u r u r uuu u r ，所以直线11A C 与平面1A CE 所成角的正弦值为33.21.如图，PA ⊥平面ABC ，ABBC ⊥，22AB PA BC ===，M 为PB 的中点.（1）求证：AM ⊥平面PBC ；（2）求二面角A PCB --的余弦值.【答案】（1）证明见解析（2）10【解析】【分析】（1）首先证明BC ⊥平面PAB ，即可得到AM BC ⊥，再由AM PB ⊥，即可得证；（2）在平面ABC 内，作//Az BC ，则AP ，AB ，Az 两两互相垂直，建立空间直角坐标系A xyz -．利用向量法能求出二面角A PC B --的余弦值．【小问1详解】因为PA ⊥平面ABC ，BC ⊂平面ABC ，所以PA BC ⊥．因为BC AB ⊥，PA AB A = ，,PA AB ⊂平面PAB ，所以BC ⊥平面PAB ，AM ⊂平面PAB ，所以AM BC ⊥．因为PA AB =，M 为PB 的中点，所以AM PB ⊥，BC PB B = ，,BC PB ⊂平面PBC ，所以AM ⊥平面PBC ．【小问2详解】如图，在平面ABC 内，作//Az BC ，则AP ，AB ，Az 两两互相垂直，建立空间直角坐标系A xyz -．则()0,0,0A ，()2,0,0P ，()0,2,0B ，()0,2,1C ，()1,1,0M ．所以()2,0,0AP = ，()0,2,1AC = ，()1,1,0AM = ，设平面APC 的法向量为(),,n x y z =r，则2020n AP x n AC y z ⎧⋅==⎪⎨⋅=+=⎪⎩ ，令1y =，得()0,1,2n =- ，由（1）可知()1,1,0AM = 为平面BPC 的法向量，设二面角A PC B --的平面角为α，由图可知二面角A PC B --为锐角，则cos n AM n AM α⋅== A PC B --的余弦值为1010．22.如图，在四棱锥P ABCD -中，底面ABCD 为菱形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，3BAD π∠=，E 是线段AD 的中点，连结BE.（1）求证：BE PA ⊥；（2）在线段PB 上是否存在点F ，使得//EF 平面PCD ？若存在，求出PF PB的值；若不存在，说明理由.【答案】（1）证明见解析（2）12，理由见解析【解析】【分析】（1）根据菱形和等边三角形的性质得到BE AD ⊥，根据面面垂直的性质定理得到BE ⊥平面PAD ，最后根据线面垂直的性质证明即可；（2）根据中位线和平行四边形的性质得到EF DH ∥，然后根据线面平行的判定定理即可得到EF ∥平面PCD .【小问1详解】连接BD ，因为四边形ABCD 为菱形，π3BAD ∠=，所以三角形ABD 为等边三角形，因为E 为AD 中点，所以BE AD ⊥，因为平面PAD ⊥平面ABCD ，平面PAD ⋂平面ABCD AD =，BE ⊂平面ABCD ，所以BE ⊥平面PAD ，因为PA ⊂平面PAD ，所以BE PA ⊥.【小问2详解】当点F 为PB 中点，即12PF PB =时，EF ∥平面PCD ，理由如下：取PB 中点F ，PD 中点H ，连接EF ，FH ，DH ，因为,F H 分别为,PB PD 中点，所以FH BC ∥，12FH BC =，因为四边形ABCD 为菱形，E 为AD 中点，所以ED BC FH ∥∥，12ED BC FH ==，所以四边形EFHD 为平行四边形，EF DH ∥，因为EF ⊄平面PCD ，DH ⊂平面PCD ，所以EF ∥平面PCD .23.已知集合{}128X x x x = ，，，是集合{20072008200920222023}S = ，，，，，的一个含有8个元素的子集.（1）当{20072008201120132017201920222023}X =，，，，，，，时，设(18)i j x x X i j ∈≤≤，，，（i ）写出方程2i j x x -=的解()i j x x ，；（ii ）若方程(0)i j x x k k -=>至少有三组不同的解，写出k 的所有可能取值；（2）证明：对任意一个X ，存在正整数k ，使得方程()18i j x k i x j -=≤≤，至少有三组不同的解.【答案】（1）答案见详解（2）证明见详解【解析】【分析】（1）(i)根据两数之差为2进行解答即可；(ii)由题两数的差均为正，利用列举法解答；（2）利用反证法进行证明．【小问1详解】(i)方程2i j x x -=的解为：()2013,2011，()2019,2017，(ii)以下规定两数的差均为正，则：列出集合X 的从小到大8个数中相邻两数的差：1，3，2，4，2，3，1；中间隔一数的两数差(即上一列差数中相邻两数和)：4，5，6，6，5，4；中间相隔二数的两数差：6，9，8，9，6；中间相隔三数的两数差：10，11，11，10；中间相隔四数的两数差：12，14，12；中间相隔五数的两数差：15，15；中间相隔六数的两数差：16．这28个差数中，只有4出现3次、6出现4次，其余都不超过2次，所以k 的可能取值有4，6．【小问2详解】证明：不妨设12820072023x x x ≤<<<≤ ，记()11,2,,7i i i a x x i +=-= ，()21,2,,6i i i b x x i +=-= ，共13个差数，假设不存在满足条件的k ，则这13个数中至多两个1，两个2，两个3，两个4，两个5，两个6，则()()()1271262126749a a a b b b +++++++≥++++= ，又()()127126a a a b b b +++++++ ()()818721x x x x x x =-++--()()817222161446x x x x =-+-≤⨯+=，这与上式矛盾.所以假设错误，原命题成立.。

2021年高二上学期语文周练试题01 Word版含答案

2021年高二上学期语文周练试题01 Word版含答案一、基础知识题1．填入空缺处恰当的一组词语是（）①我才见她虑及母校前途，至于泣下。

②她，刘和珍君，那时是前往的。

③真的猛士，将更而前行。

④中外的杀人者却昂起头来。

A．黯然欣然奋然居然 B．黯然奋然欣然居然C．茫然欣然奋然居然 D．茫然奋然欣然居然2．下列词语中，加点的字读音全都正确的一组是（）A．赍．（jī）发央浼．（miǎn）睇．（dì）眄空穴．（xué）来风B．熨．（yù）帖友谊．（yì）解剖．（pōu）床笫．（zǐ）之私C．躯壳．（ké）岑．（cén）寂挨．（ái）打为虎作伥．（ch āng）D．拱券．（xuàn）泠．（líng）然烜．（xuǎn）赫如椽．（zhu àn）大笔3．依次填入下列各句横线处的成语，最恰当的一组是（）①无锡的梅园，面临太湖，以梅饰山，以山饰梅，。

②苏轼也擅长书法，他取法颜真卿，但能，与蔡襄、黄庭坚、米芾并称宋代四大家。

③这本侦破小说，构思新颖，，值得一看。

④电影中有几处看来是闲笔，实际上却是之处。

A．别具一格、不落窠臼、匠心独运、独树一帜 B．独树一帜、别具一格、匠心独运、不落窠臼C．匠心独运、不落窠臼、独树一帜、别具一格 D．别具一格、独树一帜、不落窠臼、匠心独运4．为上联“心平浪静，秋月芙蓉湘水碧”选择下联，最合适的一项是（）（3分）A．志远天高，春风杨柳麓山青 B．情深海阔，夏日荷花潇江红C．气壮山威，鲲鹏展翼楚云飞 D．身正才卓，冬雪松竹衡岳高5．填入下面一段文字中横线处的语句，与上文衔接最恰当的一项是（3分）我曾多次来过西安，我也曾多次感觉到过，而且说出来过：西安是一块宝地。

在这里，中国古代文化仿佛阳光空气一般，弥漫城中。

唐代著名诗人的那些名篇名句，很多都与西安有牵连。

谁看到灞桥、渭水等等的名字不会立即神往盛唐呢？谁走过丈八沟、乐游原这样的地方不会立即想到杜甫、李商隐的名篇呢？。

高三一轮复习第七次数学周练习

高三下学期第七周数学周测试题一．选择题（共8小题，每小题5分）1．已知集合A＝{x|y＝}，B＝{x∈R|a≤x≤a+l}，若A∩B＝∅，则实数a的取值范围为（）A．[﹣3，2]B．（﹣∞，﹣3）∪（2，+∞）C．[﹣2，1]D．（﹣∞，﹣3]∪[2，+∞）2．当1＜m＜2时，复数（3+i）+m（2﹣i）在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．第24届冬季奥林匹克运动会，将于2022年2月在北京和张家口举行，北京冬奥会会徽以汉字“冬”为灵感来源，运用中国书法的艺术形态，将厚重的东方文化底蕴与国际化的现代风格融为一体，呈现出新时代的中国新形象、新梦想．会徽图形上半部分展现滑冰运动员的造型，下半部分表现滑雪运动员的英姿．中间舞动的线条流畅且充满韵律，代表举办地起伏的山峦、赛场、冰雪滑道和节日飘舞的丝带，下部为奥运五环，不仅象征五大洲的团结，而且强调所有参赛运动员应以公正、坦诚的运动员精神在比赛场上相见．其中奥运五环的大小和间距按以下比例（如图）：若圆半径均为12，则相邻圆圆心水平距离为26，两排圆圆心垂直距离为11，设五个圆的圆心分别为O1，O2，O3，O4，O5，若双曲线C以O1，O3为焦点、以直线O2O4为一条渐近线，则C的离心率为（）A．B．C．D．4．已知m，n，s，t∈R*，m+n＝4，+＝9，其中m，n是常数，且s+t的最小值是，点M（m，n）是曲线﹣＝1的一条弦AB的中点，则弦AB所在直线方程为（）A．x﹣4y+6＝0B．4x﹣y﹣6＝0C．4x+y﹣10＝0D．x+4y﹣10＝0 5．已知0.5a＝5b＝3，则（）A．ab＜0＜a+b B．ab＜a+b＜0C．a+b＜ab＜0D．a+b＜0＜ab6．如图所示，△ABC的面积为，其中AB＝2，∠ABC＝60°，AD为BC边上的高，M为AD的中点，若，则λ+2μ的值为（）A．B．C．D．7．单位正四面体的外接球内接的最大正三角形边长为（）A．B．C．D．8．已知函数在（0，1）内恰有3个极值点和4个零点，则实数ω的取值范围是（）A．B．C．D．二．多选题（共4小题）（多选）9．已知函数f（x）＝|sin x||cos x|，则下列说法正确的是（）A．f（x）的图象关于直线对称B．f（x）的周期为C．（π，0）是f（x）的一个对称中心D．f（x）在区间上单调递增（多选）10．下列选项中正确的是（）A．若平面向量，满足，则的最大值是5B．在△ABC中，AC＝3，AB＝1，O是△ABC的外心，则的值为4C．函数f（x）＝tan（2x﹣）的图象的对称中心坐标为，k∈Z D．已知P为△ABC内任意一点，若，则点P为△ABC的垂心（多选）11．已知数列{a n}的前n项和为S n，a1＝1，S n+1＝S n+2a n+1，数列的前n项和为T n，n∈N*，则下列选项正确的是（）A．数列{a n+1}是等比数列B．数列{a n+1}是等差数列C．数列{a n}的通项公式为D．T n＞1（多选）12．如图，抛物线C：y2＝4x的焦点为F，过点F的直线与抛物线C交于M，N 两点，过点M，N分别作准线l的垂线，垂足分别为M1，N1，准线l与x轴的交点为F1，则（）A．直线F1N与抛物线C必相切B．C．|F1M|•|F1N|＝|F1F|•|MN|D．|FM1|•|FN1|＝|FF1F|•|M1N1|三．填空题（共4小题，每小题5分）13．已知数列{a n}满足a1＝a5＝0，|a n+1﹣a n|＝2，则{a n}前5项和的最大值为．14．《九章算术》中的“商功“篇主要讲述了以立体几何为主的各种形体体积的计算，其中堑堵是指底面为直角三角形的直棱柱．如图，在堑堵ABC﹣A1B1C1中，M是A1C1的中点，AB＝2AA1＝2AC，，，若，则x+y+z ＝．15．已知函数f（x）＝在区间（a，a+）上存在极值，则实数a的取值范围是．16．过抛物线y2＝2px（p＞0）焦点F的直线与抛物线的交于点A，B，O是坐标原点，且满足，S△AOB＝，则p＝（）A．2B．C．4D．高三下学期第七周数学周测试题参考答案与试题解析一．选择题（共8小题）1．已知集合A＝{x|y＝}，B＝{x∈R|a≤x≤a+l}，若A∩B＝∅，则实数a的取值范围为（）A．[﹣3，2]B．（﹣∞，﹣3）∪（2，+∞）C．[﹣2，1]D．（﹣∞，﹣3]∪[2，+∞）【分析】可求出A＝{x|﹣2≤x≤2}，然后根据A∩B＝∅可得出a的范围．【解答】解：A＝{x|4﹣x2≥0}＝{x|﹣2≤x≤2}，B＝{x|a≤x≤a+1}，且A∩B＝∅，∴a＞2或a+1＜﹣2，∴a＜﹣3或a＞2，∴a的取值范围为（﹣∞，﹣3）∪（2，+∞）．故选：B．【点评】本题考查了一元二次不等式的解法，交集和子集的定义，交集的运算，考查了计算能力，属于基础题．2．当1＜m＜2时，复数（3+i）+m（2﹣i）在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据已知条件，结合复数的四则运算，以及复数的几何意义，即可求解．【解答】解：（3+i）+m（2﹣i）＝3+2m+（1﹣m）i，∵1＜m＜2，∴3+2m＞0，1﹣m＜0，∴复数（3+i）+m（2﹣i）在复平面内对应的点（3+2m，1﹣m）位于第四象限．故选：D．【点评】本题主要考查复数的四则运算，以及复数的几何意义，属于基础题．3．第24届冬季奥林匹克运动会，将于2022年2月在北京和张家口举行，北京冬奥会会徽以汉字“冬”为灵感来源，运用中国书法的艺术形态，将厚重的东方文化底蕴与国际化的现代风格融为一体，呈现出新时代的中国新形象、新梦想．会徽图形上半部分展现滑冰运动员的造型，下半部分表现滑雪运动员的英姿．中间舞动的线条流畅且充满韵律，代表举办地起伏的山峦、赛场、冰雪滑道和节日飘舞的丝带，下部为奥运五环，不仅象征五大洲的团结，而且强调所有参赛运动员应以公正、坦诚的运动员精神在比赛场上相见．其中奥运五环的大小和间距按以下比例（如图）：若圆半径均为12，则相邻圆圆心水平距离为26，两排圆圆心垂直距离为11，设五个圆的圆心分别为O1，O2，O3，O4，O5，若双曲线C以O1，O3为焦点、以直线O2O4为一条渐近线，则C的离心率为（）A．B．C．D．【分析】建立平面直角坐标系，可得双曲线的渐近线方程，由O4（﹣13，﹣11）在渐近线上，可得a，b的关系，即可求得离心率．【解答】解：如图建立平面直角坐标系，依题意，可得双曲线的渐近线方程为，由O4（﹣13，﹣11）在渐近线上，可得﹣11＝•（−13）即可得，则双曲线C的离心率为＝．故选：B．【点评】本题考查了双曲线的渐近线、离心率，属于中档题．4．已知m，n，s，t∈R*，m+n＝4，+＝9，其中m，n是常数，且s+t的最小值是，点M（m，n）是曲线﹣＝1的一条弦AB的中点，则弦AB所在直线方程为（）A．x﹣4y+6＝0B．4x﹣y﹣6＝0C．4x+y﹣10＝0D．x+4y﹣10＝0【分析】由已知求出s+t取得最小值时m，n满足的条件，再结合m+n＝4求出m，n，再用点差法求出直线的斜率，从而得直线方程．【解答】解：∵，当且仅当，即取等号，∴，又m+n＝4，又m，n为正数，∴可解得，设弦两端点分别为（x1，y1），（x2，y2），则，两式相减得，∵x1+x2＝4，y1+y2＝4，∴，∴直线方程为，即x﹣4y+6＝0．故选：A．【点评】本题考查了直线与双曲线的综合运用，属于中档题．5．已知0.5a＝5b＝3，则（）A．ab＜0＜a+b B．ab＜a+b＜0C．a+b＜ab＜0D．a+b＜0＜ab 【分析】化简得a＝log0.53＜0，b＝log53＞0，从而可得ab＜0，化简＝+，从而比较大小．【解答】解：∵0.5a＝5b＝3，∴a＝log0.53＜0，b＝log53＞0，∴ab＜0，＝+＝log35+log30.5＝log32.5，又∴0＜log32.5＜1，∴0＜＜1，∴ab＜a+b＜0，故选：B．【点评】本题考查了指数式与对数式的互化及对数的运算，属于基础题．6．如图所示，△ABC的面积为，其中AB＝2，∠ABC＝60°，AD为BC边上的高，M为AD的中点，若，则λ+2μ的值为（）A．B．C．D．【分析】根据三角形的面积公式可求得BC，再根据AD为BC边上的高，求出BD，从而可得出点D的位置，再根据平面向量的线性运算将用表示，再根据平面向量基本定理求出λ，μ，即可得解．【解答】解：，所以BC＝3，因为AD为BC边上的高，所以，因为M为AD的中点，所以＝，又因为，所以，所以．故选：C．【点评】本题考查平面向量的基本定理，考查学生的运算能力，属于中档题．7．单位正四面体的外接球内接的最大正三角形边长为（）A．B．C．D．【分析】由题意首先求得外接球半径，然后计算外接球内接的最大正三角形边长即可．【解答】解：如图为单位正四面体A﹣BCD．过点A作面BCD的垂线交面于点E，F为外接球球心，则E为△BCD的中心，，∴．不妨设AF＝R．在Rt△BEF中，由勾股定理，得．即，解得．∴最大正三角形的边长为．故选：C．【点评】本题主要考查球与多面体的切接问题，空间想象能力的培养等知识，属于基础题．8．已知函数在（0，1）内恰有3个极值点和4个零点，则实数ω的取值范围是（）A．B．C．D．【分析】由第4个正零点小于1，第4个正极值点大于等于1可解．【解答】解：，因为x∈（0，1），所以，又f（x）在（0，1）内恰有3个极值点和4个零点，所以，解得，所以实数ω的取值范围是．故选：A．【点评】本题考查了根据函数的零点和极值点求参数的取值范围，考查了转化思想，属中档题．二．多选题（共4小题）（多选）9．已知函数f（x）＝|sin x||cos x|，则下列说法正确的是（）A．f（x）的图象关于直线对称B．f（x）的周期为C．（π，0）是f（x）的一个对称中心D．f（x）在区间上单调递增【分析】化简函数f（x），根据函数的单调性与对称性和周期性，判断选项中的命题是否正确即可．【解答】解：函数f（x）＝|sin x||cos x|＝|sin x cos x|＝|sin2x|，画出函数图象，如图所示；所以f（x）的对称轴是x＝，k∈Z；所以x＝是f（x）图象的对称轴，A正确；f（x）的最小正周期是，B正确；f（x）是偶函数，没有对称中心，C错误；x∈[，]时，2x∈[，π]，sin2x≥0，所以f（x）＝|sin2x|是单调减函数，D错误．故选：AB．【点评】本题考查了三角函数的图象与性质的应用问题，也考查了命题真假的判断问题，是基础题．（多选）10．下列选项中正确的是（）A．若平面向量，满足，则的最大值是5B．在△ABC中，AC＝3，AB＝1，O是△ABC的外心，则的值为4C．函数f（x）＝tan（2x﹣）的图象的对称中心坐标为，k∈ZD．已知P为△ABC内任意一点，若，则点P为△ABC的垂心【分析】对A选项，根据平面向量数量积的定义与性质，函数思想即可求解；对B选项，根据三角形外心的性质，向量的线性运算及向量数量积的几何定义即可求解；对C选项，根据正切函数的图象性质即可求解；对D选项，根据向量数量积的性质，三角形垂心的概念即可求解．【解答】解：对A选项，∵，∴＝＝＝＝≤＝5，∴的最大值是5，∴A选项正确；对B选项，∵在△ABC中，AC＝3，AB＝1，O是△ABC的外心，∴＝＝＝＝4，∴B选项正确；对C选项，令，可得x＝，k∈Z，∴f（x）＝tan（2x﹣）的图象的对称中心坐标为（，0），k∈Z，∴C选项错误；对D选项，∵，∴，∴，∴PB⊥CA，同理P A⊥BC，PC⊥AB，∴点P为△ABC的垂心，∴D选项正确．故选：ABD．【点评】本题考查平面向量数量积的定义与性质，函数思想，三角形外心的性质，正切函数的图象性质，三角形垂心的概念，属中档题．（多选）11．已知数列{a n}的前n项和为S n，a1＝1，S n+1＝S n+2a n+1，数列的前n项和为T n，n∈N*，则下列选项正确的是（）A．数列{a n+1}是等比数列B．数列{a n+1}是等差数列C．数列{a n}的通项公式为D．T n＞1【分析】由a n+1＝S n+1﹣S n＝2a n+1可得，，可判断A，B的正误，再求出a n，可判断C的正误，利用裂项相消法求T n，可判断D的正误．【解答】解：因为S n+1＝S n+2a n+1，所以a n+1＝S n+1﹣S n＝2a n+1，a n+1+1＝2a n+2，即，且a1+1＝2，所以数列{a n+1}是首项为2，公比为2的等比数列，故A正确，B错误；所以，即，故C正确；因为，所以，故D错误；故选：AC．【点评】本题考查了等比数列的判断和裂项相消求和，属于中档题．（多选）12．如图，抛物线C：y2＝4x的焦点为F，过点F的直线与抛物线C交于M，N 两点，过点M，N分别作准线l的垂线，垂足分别为M1，N1，准线l与x轴的交点为F1，则（）A．直线F1N与抛物线C必相切B．C．|F1M|•|F1N|＝|F1F|•|MN|D．|FM1|•|FN1|＝|FF1F|•|M1N1|【分析】选项A，联列方程，整理成y的一元二次方程，用判别式判定是否恒为零即可；选项B，由•＝4m2≥0知，选项B正确；选项C，计算得|F1F||MN|＝8m2+8，|F1M||F1N|＝4m2+8，两式不恒等，故C不正确；选项D，先计算•，从而得⊥，由等面积法知选项D正确．【解答】解：由已知F（1，0），F1（﹣1，0），设过点F的直线方程为：x＝my+1，设点M（my1+1，y1），N（my2+1，y2），则M1（﹣1，y1），N1（﹣1，y2），F1（﹣1，0），由，得y2﹣4my﹣4＝0，所以y1+y2＝4m，y1y2＝﹣4，选项A：直线F1N的方程为y＝（x+1），联立方程组得：，所以y2﹣4[（m+）y﹣1]＝0，Δ＝16（m+）2﹣16不恒为零，故选项A不正确；选项B：由题得＝（my1+2，y1），＝（my2+2，y2），而•＝m2y1y2+2m（y1+y2）+4+y1y2＝4m2≥0，所以cos＜•＞＝≥0，所以∠MF1N≤，故B正确；选项C：|F1F|＝2，|MN|＝|x1+x2+2|＝|m（y1+y2）+4|＝4m2+4，所以|F1F||MN|＝8m2+8；|F1M|2＝（my1+2）2+y12，|F1N|2＝（my2+2）2+y22，所以|F1M|2•|F1N|2＝[（my1+2）（my2+2）]2+y22（my1+2）2+y12（my2+2）2+y12y22＝（4m2+4）2﹣32m2+64m2+48＝16（m2+2）2，所以|F1M||F1N|＝4（m2+2）＝4m2+8，所以选项C不正确；选项D：∵＝（﹣2，y1），＝（﹣2．y2），∴•＝4+y1y2＝4﹣4＝0，∴⊥，在△M1FN1中，S＝|M1N1|•|F1F|＝|FM1||FN1|，故D正确．故选：BD．【点评】本题考查抛物线的应用，属于中档题．三．填空题（共4小题）13．已知数列{a n}满足a1＝a5＝0，|a n+1﹣a n|＝2，则{a n}前5项和的最大值为8．【分析】由题意，分类讨论，求出数列的前5项，从而得出结论．【解答】解：已知数列{a n}满足a1＝a5＝0，|a n+1﹣a n|＝2，则{a n}前5项分别为0，﹣2，0，﹣2，0；或0，﹣2，﹣4，﹣2，0；或0，2，0，2，0；或0，2，4，2，0；故当{a n}前5项分别为0，2，4，2，0 时，前5项的和最大，为0+2+4+2+0＝8，故答案为：8．【点评】本题主要考查等差数列的定义，数列求和，属于基础题．14．《九章算术》中的“商功“篇主要讲述了以立体几何为主的各种形体体积的计算，其中堑堵是指底面为直角三角形的直棱柱．如图，在堑堵ABC﹣A1B1C1中，M是A1C1的中点，AB＝2AA1＝2AC，，，若，则x+y+z＝．【分析】根据已知条件，结合空间向量的线性运算，即可求解．【解答】解：由图可知：，又因为，所以，所以，所以，所以，．故答案为：．【点评】本题主要考查空间向量的线性运算，属于基础题．15．已知函数f（x）＝在区间（a，a+）上存在极值，则实数a的取值范围是（，1）．【分析】求函数f（x）的导数，利用f′（x）＝0求出极值点，再结合题意列出不等式求解集即可．【解答】解：因为函数f（x）＝，x＞0，所以f′（x）＝﹣，令f′（x）＝0，解得x＝1，当f′（x）＞0，即0＜x＜1，函数单调递增，当f′（x）＜0，即x＞1，函数单调递减，所以1是函数的极值点，又因为函数f（x）在区间（a，a+）（a＞0）上存在极值，所以a＜1＜a+，解得＜a＜1，所以实数a的取值范围是（，1）．故答案为：（，1）．【点评】本题主要考查了利用导数研究函数的单调性和极值的应用问题，也考查了运算求解能力，是中档题．16．过抛物线y2＝2px（p＞0）焦点F的直线与抛物线的交于点A，B，O是坐标原点，且满足，S△AOB＝，则p＝（）A．2B．C．4D．【分析】过A，B作抛物线准线的垂线，垂足分别为C，D，由AB＝3FB，丨AC丨＝2丨BD丨，求得丨BE丨，可得直线AB的方程，与抛物线联立方程，表示|AB|的长，进而可表示三角形的面积，根据面积求得p的值【解答】解：不妨设直线AB的斜率k＞0，过A，B作抛物线准线的垂线，垂足分别为C，D，过B作BE⊥AC于E，由AB＝3FB，∴＝2，丨丨＝2丨丨，即丨AC丨＝2丨BD丨，∴E为AC的中点，即丨AE丨＝丨AB丨，∴丨BE丨＝＝丨AB丨，由S△OAB＝S OAF+S OBF＝丨BE丨•丨OF丨＝p丨AB丨，S△OAB＝丨AB丨，∴由丨AE丨＝丨AB丨，则直线AB斜率为k AB＝±2，直线AB的方程y＝2（x ﹣1），，整理得：8x2﹣10px﹣8p2＝0，则x1+x2＝，则丨AB丨＝x1+x2+p＝+p，∴S△OAB＝（+p），∴（+p）＝，解得p＝2．【点评】本题考查抛物线的标准方程，直线与抛物线的位置关系，考查韦达定理，抛物线的焦点弦公式，考查计算能力，属中档题．。

人教版语文高二上学期期中试卷及解答参考(2024-2025学年)

2024-2025学年人教版语文高二上学期期中模拟试卷(答案在后面)一、现代文阅读Ⅰ（18分）阅读下面的文章，完成1-5题。

《秋日的私语》作者：李华秋天，总是给人以无限的遐想。

在这样的季节里，每一处风景都仿佛被赋予了生命，每一片落叶都有它的故事。

我漫步在这片金黄的世界里，脚下的树叶沙沙作响，像是大地与天空之间的私语。

远处，山峦层叠，色彩斑斓；近处，溪流潺潺，清澈见底。

这一切的一切，都在诉说着秋的故事。

记得小时候，我和小伙伴们最喜欢的就是秋天。

那时候，我们会一起到田野间奔跑，追逐着彼此的身影，在那广阔的天地间尽情嬉戏。

而每当夕阳西下时，我们便围坐在一块大石头旁，听村里的老人讲述那些关于秋天的故事。

那时的快乐是如此纯粹，以至于多年后回忆起来，心中依旧暖洋洋的。

随着年龄的增长，对于秋天的感受也逐渐变得复杂起来。

它不再仅仅是收获的季节，更是一段思考的时间。

每当这个时候，我都会静下心来，回顾过去一年里所经历的事情，计划着未来。

也许是因为天气转凉的缘故吧，人们似乎变得更加敏感细腻起来，更加容易陷入深深的沉思之中。

今年的秋天特别不同寻常。

因为疫情的关系，许多活动都被取消了，人们的生活方式发生了很大改变。

但即便如此，大自然依然按照自己的节奏前进着，给予我们无尽的安慰和希望。

我相信只要我们团结一心，就没有克服不了的困难。

正如这美好的秋季一般，虽然短暂但却充满了生机与活力。

题目设置：1.文章开头提到“每一处风景都仿佛被赋予了生命”，这句话表达了作者怎样的情感？（4分）A. 对自然美景的赞叹B. 对生活变化的感慨C. 对童年记忆的怀念D. 对未来的憧憬2.根据文章内容，“我和小伙伴们”最喜爱秋天的原因是什么？（4分）A. 可以欣赏美丽的秋景B. 能够自由地玩耍C. 听长辈讲故事D. 享受丰收的乐趣3.成长之后，作者对秋天有了哪些新的理解？（6分）A. 秋天只是个收获的季节B. 秋天成为了一段反思过往展望未来的时间C. 秋天让人心情低落D. 秋天意味着结束4.本文最后一段提到了什么特殊背景？这段话想要传达给读者的主要信息是什么？（6分）A. 疫情导致活动减少；强调人类面对挑战时应保持乐观B. 自然界的不可预测性；鼓励人们珍惜眼前的美好C. 社会变革的影响；提醒大家要适应环境的变化D. 季节更替的规律；说明时间流逝的重要性5.请结合全文，简述你从这篇文章中学到了什么。

高二周考一

周周练（M1B5）I．单项选择（共10小题；每小题1分，满分10分）1. ---Where would you like to go, the cinema or the theatre?------It ________to me. A. makes many differences B. makes no differenceC. makes some differencesD. makes not a difference2. All ____of goods for daily use are available in the shopping mall.A. kindB. varietyC. varietiesD. various3. Students’ attitudes towards this matter _____greatly because of their different backgrounds.A. differedB. referredC. changedD. ranged4. You can’t imag ine what difficulty that deserted cat will have ____through the frozen winter.A. livedB. livingC. to liveD. been living5．It rained heavily in Shannxi in September,2011,_______serious flooding in several areas.A. causedB. causingC. to causeD. having caused6.Mary prepared for the computer test carefully so that she could be sure of passing it at her first ____. A. attempt B. desire C. purpose D. intention7. The two girls are so alike that strangers find ___difficult to tell one from the other.A. itB. themC. herD. that8．You can write to me ________ the school address or use my usual email address.A．to B．in C．on D．at9．There is a difference ________ ten degrees ________ temperature between the day and the night.A．in；from B．of；than C．of；in D．in；than10．The policeman’s ________ traffic directions made a ll the drivers quite ________.A．confused；confused B．confusing；confusingC．confusing；confused D．confused；confusingⅡ：完形填空（共20小题；每小题1.5分，满分30分）．阅读下面短文，掌握其大意，然后从36－55各题所给的四个选项（A、B、C和D）中选出最佳选项。

高二刷题练习册

高二刷题练习册一、选择题1. 根据题目所给的函数 $ f(x) = 2x^2 - 3x + 1 $，求导数$ f'(x) $ 的值。

A. $ 4x - 3 $B. $ 2x - 3 $C. $ 4x^2 - 3x $D. $ 2x^2 - 3 $2. 英语句子 "The boy is playing with his toys." 中，"playing" 是什么词性？A. 名词B. 动词C. 形容词D. 副词3. 根据题目所给的化学方程式 $ 2H_2 + O_2 \rightarrow 2H_2O $，下列哪个选项表示的是反应物和生成物的摩尔比例？A. 1:1:1B. 2:1:2C. 1:2:2D. 2:1:14. 在历史事件中，"The Renaissance" 通常指的是什么？A. 文艺复兴B. 工业革命C. 启蒙运动D. 法国大革命5. 根据题目所给的物理定律 $ F = ma $，其中 $ F $ 代表力，$ m $ 代表质量，$ a $ 代表加速度。

如果 $ m = 2 $ 千克，$ a = 3 $ 米/秒²，求 $ F $ 的值。

A. 6 牛顿B. 9 牛顿C. 12 牛顿D. 15 牛顿二、填空题6. 根据题目所给的数学公式 $ A = \pi r^2 $，如果圆的半径$ r = 5 $ 厘米，那么圆的面积 $ A $ 是 ________ 平方厘米。

7. 英语中，"The sun rises in the ________." 正确的填空词是________。

8. 化学中，元素周期表的第 ________ 族元素通常具有金属特性。

9. 历史中，"The Cold War" 是指第二次世界大战后，以 ________和 ________ 为首的两个阵营之间的政治和军事对峙。