Quark Cluster Model Study of Isospin-Two Dibaryons
多种群混沌映射麻雀优化算法

多种群混沌映射麻雀优化算法下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts,other materials and so on, want to know different data formats and writing methods, please pay attention!多种群混沌映射麻雀优化算法,是一种基于混沌映射和麻雀行为的智能优化算法,能够有效地应用于解决复杂的优化问题。
莱维飞行、混沌映射和自适应t分布 蜣螂算法

莱维飞行、混沌映射和自适应t分布是蜣螂算法中的三个重要概念。
莱维飞行是一种随机过程,描述了在随机游走过程中,每一步的长度和方向都遵循某种概率分布。
在蜣螂算法中,莱维飞行用于模拟蜣螂在搜寻食物时所走的路径,通过不断随机游走,可以寻找更好的食物来源。
混沌映射是一种非线性动力学系统中的映射关系,具有对初值敏感的特点。
在蜣螂算法中,混沌映射用于模拟蜣螂在移动过程中的行为,使得蜣螂能够根据当前环境进行灵活的移动和决策。
自适应t分布是一种概率分布函数,用于描述在复杂系统中数据的分布情况。
在蜣螂算法中,自适应t分布用于描述蜣螂在不同环境下的行为特征,帮助蜣螂更好地适应环境变化。
蜣螂算法是一种模拟自然界中蜣螂行为的优化算法,通过模拟蜣螂的移动、搜寻和合作等行为,可以解决许多优化问题。
莱维飞行、混沌映射和自适应t分布是蜣螂算法中的三个关键技术,它们共同作用,使得蜣螂算法具有很好的全局优化能力。
Quarks——介绍夸克的英文资料
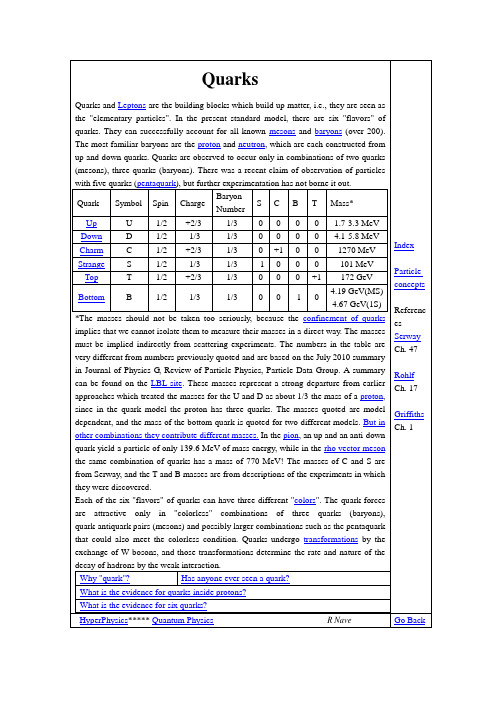
QuarksQuarks and Leptons are the building blocks which build up matter, i.e., they are seen as the "elementary particles". In the present standard model, there are six "flavors" of quarks. They can successfully account for all known mesons and baryons (over 200). The most familiar baryons are the proton and neutron, which are each constructed from up and down quarks. Quarks are observed to occur only in combinations of two quarks (mesons), three quarks (baryons). There was a recent claim of observation of particles with five quarks (pentaquark), but further experimentation has not borne it out.Quark Symbol Spin Charge BaryonNumberS C B T Mass*Up U 1/2 +2/3 1/3 0 0 0 0 1.7-3.3 MeV Down D 1/2 -1/3 1/3 0 0 0 0 4.1-5.8 MeV Charm C 1/2 +2/3 1/3 0 +1 0 0 1270 MeV Strange S 1/2 -1/3 1/3 -1 0 0 0 101 MeV Top T 1/2 +2/3 1/3 0 0 0 +1 172 GeVBottom B 1/2 -1/3 1/3 0 0 -1 0 4.19 GeV(MS) 4.67 GeV(1S)*The masses should not be taken too seriously, because the confinement of quarks implies that we cannot isolate them to measure their masses in a direct way. The masses must be implied indirectly from scattering experiments. The numbers in the table are very different from numbers previously quoted and are based on the July 2010 summary in Journal of Physics G, Review of Particle Physics, Particle Data Group. A summary can be found on the LBL site. These masses represent a strong departure from earlier approaches which treated the masses for the U and D as about 1/3 the mass of a proton, since in the quark model the proton has three quarks. The masses quoted are model dependent, and the mass of the bottom quark is quoted for two different models. But in other combinations they contribute different masses. In the pion, an up and an anti-down quark yield a particle of only 139.6 MeV of mass energy, while in the rho vector meson the same combination of quarks has a mass of 770 MeV! The masses of C and S are from Serway, and the T and B masses are from descriptions of the experiments in which they were discovered.Each of the six "flavors" of quarks can have three different "colors". The quark forces are attractive only in "colorless" combinations of three quarks (baryons), quark-antiquark pairs (mesons) and possibly larger combinations such as the pentaquark that could also meet the colorless condition. Quarks undergo transformations by the exchange of W bosons, and those transformations determine the rate and nature of the decay of hadrons by the weak interaction.Why "quark"?Has anyone ever seen a quark?What is the evidence for quarks inside protons?What is the evidence for six quarks?IndexParticle conceptsReferenc es Serway Ch. 47Rohlf Ch. 17Griffiths Ch. 1HyperPhysics***** Quantum Physics R Nave Go BackWhy "Quark"?The name "quark" was taken by Murray Gell-Mann from the book "Finnegan's Wake"by James Joyce. The line "Three quarks for Muster Mark..." appears in the fancifulbook. Gell-Mann received the 1969 Nobel Prize for his work in classifying elementary particles.IndexParticleconceptsHyperPhysics ***** Quantum PhysicsR Nave Go BackUp and Down QuarksThe up and down quarks are the most common and least massive quarks, being the constituents of protons and neutrons and thus of most ordinary matter.The fact that the free neutron decaysand nuclei decay by beta decay in processes likeis thought to be the result of a more fundamental quark processTable of quark propertiesIndexParticle conceptsHyperPhysics ***** Quantum PhysicsR Nave Go BackThe Strange QuarkIn 1947 during a study of cosmic ray interactions, a product of a proton collision with a nucleus was found to live for much longer time than expected: 10-10 seconds instead ofthe expected 10-23 seconds! This particle was named the lambda particle (Λ0) and the property which caused it to live so long was dubbed "strangeness" and that name stuck to be the name of one of the quarks from which the lambda particle is constructed. The lambda is a baryon which is made up of three quarks: an up, a down and a strange quark.The shorter lifetime of 10-23seconds was expected because the lambda as a baryon participates in the strong interaction, and that usually leads to such very short lifetimes. The long observed lifetime helped develop a new conservation law for such decays called the "conservation of strangeness". The presence of a strange quark in a particle is denoted by a quantum number S=-1. Particle decay by the strong or electromagnetic interactions preserve the strangeness quantum number. The decay process for the lambda particle must violate that rule, since there is no lighter particle which contains a strange quark - so the strange quark must be transformed to another quark in theprocess. That can only occur by the weak interaction, and that leads to a much longer lifetime. The decay processes show that strangeness is not conserved:The quark transformations necessary to accomplish these decay processes can be visualized with the help of Feynmann diagrams.The omega-minus, a baryon composed of three strange quarks, is a classicexample of the need for the property called "color" in describing particles.Since quarks are fermions with spin 1/2, they must obey the Pauliexclusion principle and cannot exist in identical states. So with threestrange quarks, the property which distinguishes them must be capable ofat least three distinct values.Conservation of strangeness is not in fact an independent conservation law, but can be viewed as a combination of the conservation of charge, isospin, and baryon number. It is often expressed in terms of hypercharge Y, defined by:Isospin and either hypercharge or strangeness are the quantum numbers often used to draw particle diagrams for the hadrons.Table of quark properties IndexParticle conceptsHyperPhysics***** Quantum Physics R Nave Go BackThe Charm QuarkIn 1974 a meson called the J/Psi particle was discovered. With a mass of 3100 MeV,over three times that of the proton, this particle was the first example of another quark, called the charm quark. The J/Psi is made up of a charm-anticharm quark pair.The lightest meson which contains a charm quark is the D meson. It provides interesting examples of decay since the charm quark must be transformed into a strange quark by the weak interaction in order for it to decay.One baryon with a charm quark is a called a lambda with symbol Λ+c . It has a composition udc and a mass of 2281 MeV/c2.Table of quark properties IndexParticle conceptsHyperPhysics***** Quantum Physics R Nave Go BackThe Top QuarkConvincing evidence for the observation of the top quark was reported by Fermilab's Tevatron facility in April 1995. The evidence was found in the collision products of 0.9 TeV protons with equally energetic antiprotons in the proton-antiproton collider. The evidence involved analysis of trillions of 1.8 TeV proton-antiproton collisions. The Collider Detector Facility group had found 56 top candidates over a predicted background of 23 and the D0 group found 17 events over a predicted background of 3.8. The value for the top quark mass from the combined data of the two groups after the completion of the run was 174.3 +/- 5.1 GeV. This is over 180 times the mass of a proton and about twice the mass of the next heaviest fundamental particle, the Z0 vector boson at about 93 GeV.The interaction is envisioned as follows: IndexParticle concept sReferen ce Ladbur yD-ZeroTable of quark propertiesHyperPhysics***** Quantum Physics R Nave Go BackConfinement of QuarksHow can one be so confident of the quark model when no one has ever seen an isolated quark? There are good reasons for the lack of direct observation. Apparently the color force does not drop off with distance like the other observed forces. It is postutated that it may actually increase with distance at the rate of about 1 GeV per fermi. A free quark is not observed because by the time the separation is on an observable scale, the energy is far above the pair production energy for quark-antiquark pairs. For the U and D quarks the masses are 10s of MeV so pair production would occur for distances much less thana fermi. You would expect a lot of mesons (quark-antiquark pairs) in very high energy collision experiments and that is what is observed.Basically, you can't see an isolated quark because the color force does not let them go, and the energy required to separate them produces quark-antiquark pairs long before they are far enough apart to observe separately.One kind of visualization of quark confinement is called the "bag model". One visualizes the quarks as contained in an elastic bag which allows the quarks to move freely around, as long as you don't try to pull them further apart. But if you try to pull a quark out, the bag stretches and resists.Another way of looking at quark confinement is expressed by Rohlf. "When we try to pull a quark out of a proton, for example by striking the quark with another energetic particle, the quark experiences a potential energy barrier from the strong interaction that increases with distance." As the example of alpha decay demonstrates, having a barrier higher than the particle energy does not prevent the escape of the particle - quantum mechanical tunneling gives a finite probability for a 6 MeV alpha particle to get through a 30 MeV high energy barrier. But the energy barrier for the alpha particle is thin enough for tunneling to be effective. In the case of the barrier facing the quark, the energy barrier does not drop off with distance, but in fact increases.Evidence for quarks in deep inelastic scattering IndexParticle conceptsReferenc eRohlf Sec 6-6HyperPhysics***** Quantum Physics R Nave Go Back The Bottom QuarkIn 1977, an experimental group at Fermilab led by Leon Lederman discovered a new resonance at 9.4 GeV/c^2 which was interpreted as a bottom-antibottom quark pair and called the Upsilon meson. From this experiment, the mass of the bottom quark is implied to be about 5 GeV/c^2. The reaction being studied waswhere N was a copper or platinum nucleus. The spectrometer had a muon-pair mass resolution of about 2%, which allowed them to measure an excess of events at 9.4 GeV/c^2. This resonance has been subsequently studied at other accelerators with a detailed investigation of the bound states of the bottom-antibottom meson.Table of quark properties IndexParticle conceptsReferenc eRohlf Ch. 17HyperPhysics***** Quantum Physics R Nave Go Back。
KSC

Abstract—We propose a parameter-free kernel spectral clustering model for large scale complex networks. The kerne spectral clustering (KSC) method works by creating a model on a subgraph of the complex network. The model requires a kernel function which can have parameters and the number of communities k has be detected in the large scale network. We exploit the structure of the projections in the eigenspace to automatically identify the number of clusters. We use the concept of entropy and balanced clusters for this purpose. We show the effectiveness of the proposed approach by comparing the cluster memberships w.r.t. several large scale community detection techniques like Louvain, Infomap and Bigclam methods. We conducted experiments on several synthetic networks of varying size and mixing parameter along with large scale real world experiments to show the efficiency of the proposed approach.摘要:我们提出一个在大规模复杂网络中的无参数核谱聚类模型。
具有禁忌搜索策略的混沌粒子群算法研究

具有禁忌搜索策略的混沌粒子群算法研究混沌粒子群算法(Chaos Particle Swarm Optimization,简称CPSO)作为一种基于粒子群算法(Particle Swarm Optimization,简称PSO)的优化算法,在解决复杂多元非线性优化问题方面具有较强的适应性和效果。
然而,在某些情况下,传统的PSO算法在搜索的过程中存在着“早熟收敛”和“易陷入局部最优”等问题。
为了克服这些问题,研究者提出了各种改进的PSO算法,并在此基础上发展了禁忌搜索策略与混沌算法相结合的混沌粒子群算法(Chaos Particle Swarm Optimization with Taboo Search Strategy,简称CPSO-TS)。
本文将着重研究CPSO-TS算法的原理和应用,并进一步探讨其在优化问题中的效果。
首先,我们来介绍一下CPSO-TS算法的原理。
CPSO-TS算法是将混沌算法与禁忌搜索策略融合到PSO中,以提高搜索的效率和质量。
具体来说,混沌算法通过引入混沌序列,增加了算法在搜索过程中的随机性,避免了PSO算法陷入局部最优解的问题。
而禁忌搜索策略则通过维护一个禁忌表,记录已经搜索过的解,避免算法在搜索过程中重复搜索相同的解,从而增加了搜索空间的广度。
CPSO-TS算法的主要步骤包括初始化、计算适应度、更新个体最优解、更新群体最优解、更新速度和位置等。
在初始化阶段,粒子的初始位置和速度通过随机产生或者根据已知信息确定。
通过计算适应度值,确定个体最优解和群体最优解,并根据这些最优解以一定的权重更新速度和位置。
在更新速度和位置的过程中,引入了混沌序列和禁忌搜索策略。
具体来说,通过引入混沌序列,增加了算法的随机性,使得算法能够跳出局部最优解,进行全局搜索。
而禁忌搜索策略则通过维护禁忌表,避免算法搜索相同的解,从而增加了搜索空间的广度。
CPSO-TS算法在实际应用中具有广泛的应用价值。
混沌麻雀搜索优化算法

混沌麻雀搜索优化算法一、本文概述随着和计算智能的快速发展,优化算法在众多领域,如机器学习、数据挖掘、模式识别、控制工程等,都发挥着越来越重要的作用。
近年来,群体智能优化算法因其强大的全局搜索能力和鲁棒性受到了广泛关注。
其中,麻雀搜索算法(Sparrow Search Algorithm, SSA)作为一种新兴的群体智能优化算法,凭借其独特的搜索机制和高效的求解能力,在众多优化问题中展现出良好的应用前景。
然而,传统的麻雀搜索算法在面对复杂多变的问题时,仍存在一定的局限性,如易陷入局部最优、搜索精度与速度之间的矛盾等。
为了解决这些问题,本文提出了一种混沌麻雀搜索优化算法(Chaotic Sparrow Search Optimization Algorithm, CSSOA)。
该算法将混沌理论引入麻雀搜索算法中,通过对搜索过程中的种群初始化、搜索策略、位置更新等环节进行改进,有效提高了算法的搜索效率和全局优化能力。
本文首先简要介绍了麻雀搜索算法的基本原理和研究现状,然后详细阐述了混沌麻雀搜索优化算法的设计思路、实现方法以及性能评估。
通过与其他群体智能优化算法的比较,验证了CSSOA在解决多模态函数优化问题、约束优化问题以及工程实际问题中的有效性和优越性。
对混沌麻雀搜索优化算法的未来研究方向和应用前景进行了展望。
本文旨在为相关领域的研究人员和实践者提供一种新型的群体智能优化算法,并为解决复杂优化问题提供新的思路和方法。
二、混沌理论基础混沌理论,起源于20世纪60年代,是一种研究非线性动态系统行为的科学。
混沌现象普遍存在于自然界中,如天气变化、股市波动、生态系统等。
混沌理论的核心在于揭示看似无序、随机的现象背后隐藏的有序性和规律性。
混沌系统具有对初始条件的敏感性,即微小的初始差异可能导致系统行为的巨大变化,这种现象被称为“蝴蝶效应”。
混沌麻雀搜索优化算法(CMSOA)借鉴了混沌理论的核心思想,将其应用于优化问题的求解过程。
DS2208数字扫描器产品参考指南说明书

-05 Rev. A
6/2018
Rev. B Software Updates Added: - New Feedback email address. - Grid Matrix parameters - Febraban parameter - USB HID POS (formerly known as Microsoft UWP USB) - Product ID (PID) Type - Product ID (PID) Value - ECLevel
-06 Rev. A
10/2018 - Added Grid Matrix sample bar code. - Moved 123Scan chapter.
-07 Rev. A
11/2019
Added: - SITA and ARINC parameters. - IBM-485 Specification Version.
No part of this publication may be reproduced or used in any form, or by any electrical or mechanical means, without permission in writing from Zebra. This includes electronic or mechanical means, such as photocopying, recording, or information storage and retrieval systems. The material in this manual is subject to change without notice.
磁场背景下有限温度NJL模型的手征性质

磁场背景下有限温度NJL模型的手征性质陈建兴;陈圆圆;王丽;候金鑫【摘要】研究有限温度时均匀磁场背景下NJL模型的手征性质,计算不同磁场强度时有限温度和化学势下的手征凝聚和相图.利用玻色子化方法,得到具有辅助玻色子场的NJL模型拉格朗日密度,以此研究超出平均场近似的情形.通过使用最优化微扰论(OPT)方法,在微扰展开到一阶时,计入了部分高阶效应.计算结果表明,相变的性质与该模型在平均场近似下定性一致.相变线上存在两种不同类型的相变:在高温低化学势下是平滑的过渡,在低温高化学势下是一阶相变,相变存在临界终点(CEP).磁场增强会加剧手征对称性破缺,具有磁催化作用.随着磁场增强,CEP向相图的左上方移动,即对应的临界温度升高而临界化学势降低.【期刊名称】《辽宁师范大学学报(自然科学版)》【年(卷),期】2018(041)002【总页数】8页(P179-186)【关键词】NJL模型;磁场背景;手征相变;OPT方法;超出平均场近似【作者】陈建兴;陈圆圆;王丽;候金鑫【作者单位】辽宁师范大学物理与电子技术学院,辽宁大连 116029;辽宁师范大学物理与电子技术学院,辽宁大连 116029;辽宁师范大学物理与电子技术学院,辽宁大连 116029;辽宁师范大学物理与电子技术学院,辽宁大连 116029【正文语种】中文【中图分类】O572.33强相互作用物质在非零温度或化学势下的性质是粒子物理学的重要前沿课题之一.运行中的相对论重离子碰撞实验[1-2]在非中心碰撞过程中会产生较强的磁场,因此研究磁场对强相互作用物质性质的影响[3-4]具有很强的现实意义.作为强相互作用的基本理论的量子色动力学(QCD),在高能区能够进行可靠的微扰计算,然而在低能区,由于QCD的非微扰性质,处理起来非常困难.为解决此问题,人们采用了各种较为有效的方法,如格点模拟方法、有效模型方法等.无论在零温情况下还是在有限温度情况下,这些方法都被广泛应用于处理强相互作用的低能区问题[5-9].采用各种有效模型,如NJL模型[10]、线性Sigma模型[11-13]等,对理解强相互作用的相结构是非常有帮助的.在从第一原理出发的格点模拟处理低温高密度区的强相互作用面临严重困难[14-15] 的情况下,有效模型方法的重要性更为突出.在量子场论框架下,用微扰方法处理有限温度问题会因出现红外发散而变得更复杂.为得到可靠的计算结果,人们通常使用各种重新求和方案[16-18].笔者采用的最优化微扰论就是其中的一种,它本质上是一种变分方法,近年来该方法成为处理零温和有限温度问题[18-19] 的重要技术手段之一.由于NJL模型中的四夸克相互作用处理起来比较困难,人们往往采用平均场近似.事实上,目前为止,很多采用NJL类模型(指具有基本的NJL模型结构,但拉格朗日密度包含的作用有差异,甚至包含描述禁闭作用PNJL模型等)研究强相互作用的相结构时,采用的是该近似[20-23].这样做的优点是简化了运算,不足之处在于忽略了夸克场的涨落.Pinto等作者采用两味道NJL模型在超出平均场近似的水平研究了强相互作用物质的相结构[24],本文将在此基础上进一步研究磁场的引入对相结构的影响.1 拉格朗日密度考虑NJL模型[25]的拉格朗日密度具有如下形式:(1)这可以说是最简单的NJL模型.事实上,现在常用的NJL模型不仅包括式(1)中的标量、赝标量相互作用,还包括矢量、赝矢量相互作用.本文采用具有两个味道的NJL模型,即夸克场ψ=(u,d)T的情形.式(1)中=rμ∂μ,m0为夸克的流质量,G是相互作用强度.m0=0时该模型具有SU(2)V×SU(2)A×U(1)V×U(1)A对称性,这是两味道QCD具有的对称性.NJL模型通常采用平均场近似进行研究,原因是式(1)中的四费米子相互作用直接处理起来较为困难.在平均场近似下,该模型简化为(2)此时,夸克的质量发生了变化,定义组分夸克质量为(3)式(3)就是NJL模型的质量间隙方程.NJL模型的拉氏量式(1)含有2个参数,即耦合常数G和流夸克质量m0.由于该模型是不可重整化的,所以在实际计算中,人们常常把正规化过程中的动量截断Λ也作为模型的一部分来处理.因此,需考虑3个待定参数:m0,G和Λ.它们可以用零温下的π介子质量、π介子衰变常数和标量真空凝聚加以确定.为讨论超出平均场的近似,一个重要的方法是引入辅助玻色子场,把NJL模型的拉氏量进行玻色子化.其出发点是式(1)对应的生成泛函(4)玻色子化后,生成泛函可以重新写为(5)因此,含有辅助场σ和的等效拉氏量为(6)需要指出的是辅助场σ和不是动力学场.事实上,利用欧拉-拉格朗日方程可得(7)因此,式(7)只是两个约束方程,不含有场随时间变化的情况,所以σ场和场不是真正的动力学场.引入夸克的同位旋化学势μf,由于SU(2)同位旋对称性,取μu=μd=μ,式(6)相应变为(8)为了描述磁场的效应,对式(8)作代换∂μ→Dμ=∂μ+iqAμ,于是有(9)这里考虑到系统处于经典的外磁场中,因电磁场Aμ是外场,所以式(9)不含它的动能项.在目前阶段,人们通常讨论匀强磁场的情况.不失一般性,假设磁场沿z轴方向,取Aμ=(0,0,Bx,0),此时,B=×A=Bek,ek为z方向的单位矢量.磁场的加入会改变带电粒子的能谱情况.对于带电为q,自旋为的费米子,磁场下的能谱可表示为[20](10)而简并度变成2 OPT方法及零温度下的有效势以方程(6)为例来讨论OPT方法在NJL模型上的实现.暂时不考虑化学势和磁场的影响是因为这两种效应可以用简单的代换得到.只讨论零温的情况,这对确定NJL 模型的参数是必要的,相关的表达式通过代换很容易推广到具有磁场背景的情形. OPT方法本质上是一种变分方法.其主要特征是在原来的拉格朗日密度中加上并减去质量项而相互作用项均乘以一个δ,用以标记微扰阶数.此时的拉格朗日密度可以记为δ.当δ=0时,δ退化成无相互作用的自由场的拉格朗日密度;当δ=1时,δ就回到原始的拉格朗日密度.因此,在以δ为标志做完到确定阶k的微扰后,需取δ=1.设P为某物理量,微扰计算到k阶的结果记作P(k),则通常使用最不敏感条件(11)确定变分参数η的值.这种做法的优点在于,可以通过较低阶的微扰计算包含体系的部分高阶效应.另一个优点是,由于改变的是质量项,所以不会影响理论的可重整性.从方程(6)出发,(12)式(12)中,除第一项外,其余各项均为相互作用项.下面计算展开到一阶的有效势密度Veff.计算可根据有效势的表达式(13)进行.式中:等号右侧的第一项Vc为经典的有效势;第二项为有效势的单圈部分,D为自由传播子;第三项为更高阶的有效势,其下标1PI表示只取单粒不可约图.根据式(13),使用费曼图技术,可得展开到δ一阶的有效势为(14)对式(14)进一步化简,可得(15)令(16)(17)(18)则式(15)可以写成更为紧致的形式:(19)式(19)已经取δ=1.由最优化方案(11)可得(20)利用Veff可以求得使Veff为最小值的真空夸克凝聚,要求有(21)(22)式(21)正好是质量间隙方程,由它可以给出夸克凝聚的表达式:(23)3 有限温度及磁场下的有效势在第2节讨论了零温无磁场情况下的有效势.有限温度T≠0下的结果,可以通过对积分公式I1、I2、I3,即式(16)~式(18)做合适的代换得到.标准代换方法是改变积分测度的表达式:(24)式(24)的代换方法是一般性的.对于玻色子,ωn=2nπT,对于费米子,ωn=(2n+1)πT, n取全部整数.于是在T≠0时,I1、I2、I3的表达式变成(25)(26)(27)上面3个公式中,代表合适的有效质量.在费米子情形下,对n求和后,有(28)(29)(30)加入沿z方向的匀强磁场后,粒子的能谱和简并情况都发生变化.对于费米子,式(25)~式(27)中的ωn应改为(31)且积分测度也发生变化,(32)于是,对于有限温度且存在磁场的情形,积分公式I1、I2、I3应分别换成和(33)(34)(35)其中,上标B表示磁场,f表示夸克的味道,且(36)注意变分参数η出现在能量的表达式ωk中.因为u,d夸克具有不同的电荷,所以加入磁场后拉格朗日密度(9)不再像(6)那样具有SU(2)对称性.因此,有效势表达式中的因子Nf应该写为对不同味道进行求和的形式(37)于是均匀磁场背景下的有效势表达式为(38)根据最优化方案可得(39)与方程(20)具有类似的形式.由于所以匀强磁场下夸克凝聚满足方程(40)4 数值计算结果与讨论为考察磁场下NJL模型的手征性质,需首先确定模型的3个参数:流夸克质量m0、耦合常数G、正规化参数Λ,具体方法见文献[24].在采用三维动量截断方案时,取π介子的质量为mπ=135 MeV,衰变常数fπ=92.4 MeV,夸克标量凝聚可得到模型中各参数的值: m=4.8 MeV,G=4.86×10-6MeV-2,Λ=640 MeV.图1 不同磁场强度下手征相变线及CEP的位置Fig.1 Chiral phase transition lines and location of CEPs at different magnetic strengths不同磁场强度下的相变曲线见图1.其中,无磁场时的相变线对应图中的实线,和时的相变线分别用点线和虚线表示.每条相变线的下方是手征破缺相区域,而上方则是手征恢复相区域.从图1可知,每条相变线上都存在两种不同的相变类型:实心圆点左侧的相变线是二阶相变(准确地说是平滑过渡)的相变线,右侧的相变线是一阶相变线,因此实心点是两种不同相变线的交界点,即临界终点(CEP).从图中可以看出,随着磁场强度的增大,CEP向左上方移动,即向临界温度升高而临界化学势降低的方向移动.在图1中,CEP的坐标分别为(0.348 GeV,0.019 GeV)、(0.329 GeV,0.062 GeV)、(0.294 GeV,0.089 GeV).当化学势为0时,随磁场强度的增大,相变的临界温度升高.因此,磁场的加入使手征破缺相增强,这表明磁场对手征对称性破缺存在催化作用.本文的结果在定性上与NJL模型在平均场近似下的结论是相同的,这说明对于NJL模型而言,平均场近似可以较好地定性描述手征相变.图1中的小实心圆点标记了时,在平均场近似下CEP的位置.此时,CEP位于(0.313 GeV,0.073 GeV),与超出平均场近似的情况相比,CEP向左上方移动,化学势降低了0.016 GeV,而温度上升了0.011 GeV.因此,超出平均场近似对CEP位置的影响是比较显著的.由于模型中流夸克的质量不为0(因手征对称性存在明显破坏),所以相变本身是不完全的,表现为CEP左侧的相变线并不对应严格的二阶相变,而仅仅为平滑过渡.图2 μ=0.1 G eV时不同磁场强度下组分夸克质量随温度变化的情况Fig.2 The constituent mass verifies with temperature at μ=0.1 GeV图2给出了当化学势μ=0.1 GeV时,磁场强度分别为实线(虚线)时组分夸克质量随温度的变化情况.组分夸克的质量行为等价的就是相变序参数——标量夸克凝聚的行为,因此该图从另一方面显示了模型手征相变的情况.从图中可以明显看到此时的相变是平滑过渡,且当磁场强度增大时组分夸克的质量增大,表明手征破缺程度更高.由于这里的相变是平滑过渡,所以必须给出合理定义(赝)临界温度的方法.取相变曲线上两个拐点处温度的平均值作为相变的(赝)临界温度(常用的另外一种定义方法是取相变曲线最陡处对应的温度),可以看到手征恢复温度随磁场增强而升高.5 结论采用的NJL模型是讨论QCD低能性质和热性质的重要场论模型之一,研究均匀磁场背景下的手征相变,给出了相图.本文的工作采取两个味道的简单的NJL模型,但在做近似处理时超出了平均场近似,并且采用了最优化微扰论方法.发现每条相变线都存在两种不同类别的相变:平滑过渡和一阶相变,磁场会加剧手征对称性破缺.随磁场强度的增大,CEP向左上方移动,即对应的临界温度升高而临界化学势降低.参考文献:[1] FOKA P, JANIK M A.An overview of experimental results from ultra-relativistic heavy-ion collisions at the CERN LHC:bulk properties and dynamical evolution[J].Reviews in Physics,2016,1:154-171.[2] LUO X F, XU N.Search for the QCD critical point with fluctuations of conserved quantities in relativistic heavy-ion collisions at RHIC:An overview [J].Nucl Sci Tech,2017,28(8):3-42.[3] RECHENBERGER S.Magnetic-field induced critical endpoint [J].Phys Rev D,2017,95:054013.[4] COSTA P.Influence of the vector interaction and an external magnetic field on the isentropes near the chiral critical end point[J].Phys RevD,2016,93:114035.[5] CHANDRASEKHARAN S, JIANG F J.Phase-diagram of two-color lattice QCD in the chiral limit[J].Phys Rev D,2006,74:014506.[6] KAWAMOTO N, MIURA K, OHNISHI A,et al.Phase diagram at finite temperature and quark density in the strong coupling limit of lattice QCD for color SU(3)[J].Phys Rev D,2007,75:014502.[7] TAWFIK A N, DIAB A M.SU(3) Polyakov linear-sigma model:Conductivity and viscous properties of QCD matter in thermal medium[J].Int J Mod Phys A,2016,31(34):1650175.[8] LIU H,XU J, CHEN L W,et al.Isospin properties of quark matter from a 3-flavor NJL model[J].Phys Rev D,2016,94:065032.[9] 陈建兴,林艳英,吴雨晴,等.有限温度下夸克介子模型的有效势[J].辽宁师范大学学报(自然科学版),2015,38(1):29-35.[10] RUGGIERI M.On the critical end point of the QCD and the NJL model phase diagrams[J].Nuovo Cim,2009,32(3/4):77-80.[11] TAWFIK A N.SU(3) Polyakov linear sigma-model in an external magnetic field[J].Phys Rev C,2014,90:015204.[12] HERBST T K,PAWLOWSKI J M,SCHAEFER B J.The phase structure of the Polyakov-quark-meson model beyond mean field [J].Phys LettB,2011,696:58-67.[13] 陈建兴,丁俊玲,陈丽丽,等.磁场下U(2)× U(2)线性σ模型的手征相变[J].辽宁师范大学学报(自然科学版),2014,37(2):171-179.[14] BRAGUTA V V,ILGENFRITZ E M, KOTOV A Y,et al.Study of the phase diagram of dense two-color QCD within lattice simulation[J].Phys RevD,2016,94:114510.[15] BORNYAKOV V G, BOYDA D L,GOY V A, et al.New approach to canonical partition functions computation in Nf=2 lattice QCD at finite baryon density[J].Phys Rev D,2017,95:094506.[16] PILAFTSIS A,TERESI D.Symmetry improved CJT effective action[J].Nucl Phys B,2013,874:594-619.[17] ANDERSEN J O,HAQUE N,MUSTAFA M G,et al.Three-loop hard-thermal-loop perturbation theory thermodynamics at finite temperature and finite baryonic and isospin chemical potential[J].Phys RevD,2016,93:054045.[18] KNEUR J L,PINTO M B.Renormalization group optimized perturbation theory at finite temperatures[J].Phys Rev D,2015,92:116008.[19] CHIKU S.Optimized perturbation theory at finite temperature:two-loop analysis[J].Prog Theor Phys,2000,104:1129-1150.[20] GATTO R,RUGGIERI M.Dressed Polyakov loop and phase diagram of hot quark matter under magnetic field[J].Phys Rev D,2010,82:054027. [21] AVANCINI S S,MENEZES D P,PROVIDENCIA C.Finite temperature quarkmatter under strong magnetic fields[J].Phys Rev C,2011,83:065805. [22] INAGAKI T,KIMURA D,MURATA T.Four-fermion interaction model in a constant magnetic field at finite temperature and chemicalpotential[J].Prog of Theo Phys,2004,111(3):371-386.[23] AVANCINI S S,MENEZES D P,PINTO M B.The QCD critical end point under strong magnetic fields[J].Phys Rev D,2012,85:091901.[24] KNEUR J L,PINTO M B, RAMOS R O.Thermodynamics and phase structure of the two-flavor nambu-jona-lasinio model beyond large-Nc[J].Phys Rev C,2010,81:065205.[25] NAMBU Y, JONA-LASINIO G.Dynamical model of elementary particles based on an analogy with superconductivity[J].Phys Rev,1961,122(1):345-358.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a rXiv:n ucl-t h /95912v15Sep1995FNUSAL -1/95Quark Cluster Model Study of Isospin-Two Dibaryons A.Valcarce (1),H.Garcilazo (2)and F.Fern´a ndez (1)(1)Grupo de F´ısica Nuclear Universidad de Salamanca,E-37008Salamanca,Spain (2)Escuela Superior de F´ısica y Matem´a ticas Instituto Polit´e cnico Nacional,Edificio 9,07738M´e xico D.F.,Mexico Abstract Based on a quark cluster model for the non-strange sector that reproduces reasonably well the nucleon-nucleon system and the excitation of the ∆iso-bar,we generate a nucleon-∆interaction and present the predictions for the several isospin two channels.The only attractive channels are 0+and 0−,but not attractive enough to generate a resonance.If a resonance is artificially generated and is required to have the observed experimental mass,then our model predicts a width that agrees with the experimental result.I.INTRODUCTIONThe possibility that a resonance may exist in theπNN system with J P=0−has been the subject of great discussion recently[1–3].A0−resonance in the isospin-0channel was proposed in Ref.[1]in order to explain a peculiar behavior of the pionic double charge exchange cross section in several nuclei from14C to48Ca.However,it was pointed out in Ref.[2]that according to the calculations of Ref.[4],a0−resonance with isospin zero is not possible and that most likely the resonance must have isospin two.The motivation of this work is to present the predictions of a quark-model based interaction about possible resonances in the isospin two sector.While the isospin one channel has been extensively studied,the isospin two is less well-known.However,there have been several works in the literature where the possibility of a bound state or a resonance in theπNN system with isospin two has been studied. Gale and Duck[5]studied this problem in the framework of the non-relativistic Faddeev equations,using a model of a rank-one separable potential for theπ-nucleon interaction in the P33channel without including the important nucleon-nucleon interaction.Their study did not support the existence ofπNN bound states,not even when they included relativistic kinematics in the Faddeev equations.They predicted a broad resonance at an energy about 350MeV above the NN threshold.In subsequent works by Ueda[6]and Kalbermann and Eisenberg[7]the system was investigated using the Heitler-London-Pauli variational method in a nonrelativistic approach.These authors,like in Ref.[5],did notfind such bound states. However,the possible existence of a quasibound system was not ruled out.Lately,there were a series of papers by Garcilazo et al.[2,4,8]based on the relativistic Faddeev equations including bothπ-nucleon and nucleon-nucleon interactions.They used separable potentials for theπ-nucleon and nucleon-nucleon subsystems with J≤2which werefitted to the phase shifts up to350MeV.They found that bound state solutions are possible when a sufficiently short-rangedπ-nucleon interaction is assumed.At the same time,they showed that the most likely configuration to have a bound state or a resonanceis that with angular momentum and parity quantum numbers J P=2−.There have been other calculations about the same problem.Arenh¨o vel[9]predicted a bound state with the quantum numbers2+and isospin two,making use of a nucleon-∆interaction mediated by the exchange of theπandρmesons(see also ref.[10]).Our aim in this work is to present the predictions based on a quark dynamical model. This model is able to describe correctly the nucleon-nucleon system as well as the deuteron. As it is based only on interactions between quarks its generalization to the nucleon-∆system is straightforward and it does not mean the inclusion of any new parameter.Therefore,it is our goal to use the nucleon-∆interaction generated by this quark model to analyze the possibility of the existence of a bound state or a resonance in the isospin-2sector in all the nucleon-∆channels with angular momentum J≤2.In Section II we will briefly describe the quark model.In Section III we will review our formalism.In Section IV we will present and discuss our results.Finally,in Section V we will summarize our conclusions.II.THE MODEL OF INTERACTIONThe constituent quark model for the nucleon-nucleon(NN)interaction developed during the last decade[11]has been recently extended in a serie of papers[12,13]by introducing a scalar meson(theσ-meson)exchange between quarks and not between the nucleons as done previously.In this work,theσ-meson parameters are related to those of the pion exchange and to the constituent quark mass through chiral symmetry requirements.This model has been successfully applied to the description of the NN scattering phase shifts[12]and the static and electromagnetic properties of the deuteron[13].At the same time it has been used to the description of processes that take place with the excitation of a∆isobar[14] and to study the pure nucleon-∆interaction[15].The model has been introduced in Refs.[12,13].The ingredients of the quark-quark interaction are the confining potential(CON),the one-gluon exchange(OGE),the one-pionexchange (OPE)and the one-sigma exchange (OSE).The explicit form of these interactions is given by (See Refs.[12,13]for details.),V CON ( r ij )=−a c λi · λj r 2ij ,(1)V OGE ( r ij )=1r ij −π3 σi · σj δ( r ij )−33αch Λ2m 3πY (Λr ij ) σi· σj +H (m πr ij)−Λ3m 2πΛ2m σY (Λrij ).(4)The main advantage of this model comes from the fact that it works with a single qq -meson vertex.Therefore,its parameters (coupling constants,cut-offmasses,...)are independent of the baryon to which the quarks are coupled,the difference among them being generated by SU(2)scaling.This makes the generalization of the NN interaction to any other non-strange baryonic system straightforward.Moreover,as explained in Refs.[12,13]the parameters associated with the scalar field are related to those of the pion exchange and the constituent quark mass through:g 2σNN /4π=36αch m 2q /m 2π,Λσ=Λπand m 2σ=(2m q )2+m 2π.Once the quark-quark interaction is chosen,an effective nucleon-∆potential can be obtained in the Born-Oppenheimer approximation,as the expectation value of the energy of the six-quark system minus the self-energies of the two clusters,which can be computed as the energy of the six-quark system when the two quark clusters do not interactV N ∆(L S T )→N ∆(L ′S ′T )(R )=ξL ′S ′T L S T (R )−ξL ′S ′T L S T (∞),(5)whereξL ′S ′T L S T (R )= ΨL ′S ′T N ∆(R )| 6i<j =1V qq (r ij )|ΨL S T N ∆(R )ΨL ′S ′T N ∆(R )|ΨL ′S ′T N ∆(R )of the nucleon-∆relative distance.We have neglected the non-local terms of the potential, however,for the qualitative analysis we are interested in,the Born-Oppenheimer approxi-mation is known to provide good results[16].The parameters of the model are summarized in Table I.III.RESULTSIn order to determine the nature(attractive or repulsive)of a given nucleon-∆(N∆) channel,we willfirst calculate the Fredholm determinant of that channel as a function of energy assuming a stable delta and nonrelativistic kinematics.That means,we will use the Lippmann-Schwinger equationT ij(q,q0)=V ij(q,q0)+ k ∞0q′2dq′V ik(q,q′)G0(E,q′)T kj(q′,q0),(7) where the two-body propagator is1G0(E,q)=.(9)m N+m∆The energy and on-shell momentum are related asE=q20/2η,(10) and we will restrict ourselves to the region E≤0.If we replace the integration in Eq.(7)by a numerical quadrature,the integral equations take the formT ij(q n,q0)=V ij(q n,q0)+ k m w m q2m V ik(q n,q m)G0(E,q m)T kj(q m,q0),(11) where q m and w m are the abscissas and weights of the quadrature(we use a40-point Gauss quadrature[17]).Eq.(11)gives rise to the set of inhomogeneous linear equationsk m M ik nm(E)T kj(q m,q0)=V ij(q n,q0),(12) withM ik nm(E)=δikδnm−w m q2m V ik(q n,q m)G0(E,q m).(13) If a bound state exists at an energy E B,the determinant of the matrix M ik nm(E B)(the Fredholm determinant)must vanish,i.e.,M ik nm(E B) =0.(14) Even if there is no bound state,the Fredholm determinant is a very useful tool to determine the nature of a given channel.If the Fredholm determinant is larger than one that means that channel is repulsive.If the Fredholm determinant is less than one that means the channel is attractive.Finally,if the Fredholm determinant passes through zero that means there is a N∆bound state at that energy.We show in Fig.1the Fredholm determinant of the N∆channels with J≤2and parity+or−as functions of energy(the channel2+is not shown since it is overwhelmingly repulsive).As seen from thisfigure,only the channels 0+and0−are attractive.Previous calculations of the isospin-2channels have been based in the three-body for-malism of theπNN system[4,5].In these works[4,5],the possibility of resonances was investigated by calculating the Fredholm determinant of the various channels for energies below theπNN threshold.We show in Table II the comparison of our results for the nature of the six states with those obtained in Refs.[4]and[5].The difference observed between the predictions of the three-body models is due to the fact that in Ref.[5]the nucleon-nucleon interaction was neglected.As seen from this table,the results of the three-body calculations and our calculation agree with each other in the case of the0−,1+,and2+channels.The three-body models predict a resonance in the2−channel while our result is that this channel is repulsive.Both three-body calculations predict a large attraction in the0−channel which is in agreement with our model since we have found that this channel is the most attractiveone.In order to determine whether a resonance exists in either the0−or0+channels,it is necessary to calculate the N∆amplitudes for E>0.Since we are looking for possible resonances which decay into a pion and two nucleons, only those channels which are attractive or have a N∆bound state are good resonance candidates.In order to investigate whether a given attractive channel possesses a resonance, we will calculate Argand diagrams between a stable and an unstable particle for the various N∆states,using the formalism of ref.[10].In this case,however,we will use relativistic kinematics and will include the width of the delta.That means,instead of the propagator (8)we will use[10]G0(S,q)=2m∆S(m2N+q2).(16)The width of the∆is taken to be[10]Γ∆(s,q)=2m2N+q2s,(17)where p0is the pion-nucleon relative momentum given byp0= [s−(m N+mπ)2][s−(m N−mπ)2]resonance or it is simply an effect of the channel coupling,we disconnected the5P2wave. The resulting Argand diagrams show a weakly attractive behavior,similar to that of the0+ and0−channels.This shows that indeed the resonance-like behavior observed in Fig.4is due simply to channel coupling.As stated before,the possibility that a resonance may exist in the0−channel has been the subject of great discussion recently[1–3].A0−resonance in the isospin-0channel was proposed in Ref.[1].However,it was pointed out in Ref.[2]that most likely the resonance must have isospin two.The proposed resonance[1–3]has a mass of2065MeV and a very small width of0.51MeV.It is therefore very interesting to investigate whether a model like the one used in this work could predict a resonance with the known features of this resonance,and particularly with such a tiny width.In order to do this,we have artificially varied the mass of theσmeson such as to increase the amount of attraction(the coupling constant of theσisfixed by chiral symmetry).We found that if mσ<375MeV a resonance appears in the0−channel.We show in Table III the mass and width of this resonance for several values of mσ.As it can be observed from this table,the width of the resonance drops dramatically when its mass approaches theπNN threshold(2017MeV).This result can be understood from simple angular momentum barrier considerations.If we call q and L to the relative momentum and relative orbital angular momentum between a nucleon and theπ-nucleon pair,respectively,then since L=1the width of the resonance will be proportional to q2L+1=q3,so that it will drop very fast as one approaches theπNN threshold since there q→0.As shown in Table III,when the mass of the sigma is taken as mσ=234MeV the mass of the resonance has the experimental value2064.4MeV and a width of0.6MeV,which is in very good agreement with the value of the width extracted by Bilger and Clement[1]. This change in the mass of the sigma generates additional attraction in the other channels, giving rise in some cases to resonances.However,all of them lie above the0−resonance, which shows that the0−channel is the most attractive one.Therefore,the sharp peak seen in the double charge exchange reactions could be justified as a nucleon-∆resonance in theisospin2channel,without resorting to exotic decay channels.We have generated artificially the additional attraction needed to produce the0−res-onance by varying the mass of the sigma meson.In principle,however,a possible source of this lacking of attraction within the quark cluster model could be the inclusion of the non-local terms of the nucleon-∆interaction and the contribution of the∆−∆channels. Both of these effects have been neglected in the present study.IV.CONCLUSIONSWe have studied the nucleon-∆system in the isospin-2channels within the quark cluster model of the baryon-baryon interaction.We have found that this model with standard parameters derived from nucleon-nucleon scattering is unable to generate any resonance with J≤2.However,we found that the0−channel is the most attractive one.We have varied freely the mass of the sigma meson in order to generate a resonance in this channel. When the mass of the0−resonance reaches the value of2065MeV,its width is equal to0.6 MeV.This very narrow width is in very good agreement with the width extracted in Refs. [1–3].ACKNOWLEDGMENTSH.G.thanks the Nuclear Physics Group at the University of Salamanca for their kind hospitality.This work has been partially funded by Direcci´o n General de Investigaci´o n Cient´ıfica y T´e cnica(DGICYT)under the Contract No.PB91-0119-C02and by COFAA-IPN(Mexico).REFERENCES[1]R.Bilger,H.A.Clement,and M.G.Schepkin,Phys.Rev.Lett.71,42(1993).[2]H.Garcilazo and L.Mathelitsch,Phys.Rev.Lett.72,2971(1994).[3]R.Bilger,H.A.Clement,and M.G.Schepkin,Phys.Rev.Lett.72,2972(1994).[4]H.Garcilazo and L.Mathelitsch,Phys.Rev.C34,1425(1986).[5]W.A.Gale and I.M.Duck,Nucl.Phys.B8,109(1968).[6]T.Ueda,Phys.Lett.B74,123(1978).[7]G.Kalbermann and J.M.Eisenberg,J.Phys.G5,35(1977).[8]H.Garcilazo,Phys.Rev.C31,257(1985).[9]H.Arenh¨o vel,Nucl.Phys.A247,473(1975).[10]H.Garcilazo and M.T.Pe˜n a,Phys.Rev.C44,2311(1991).[11]A.Faessler,F.Fern´a ndez,G.L¨u beck,and K.Shimizu,Phys.Lett.B112,201(1982).M.Oka and K.Yazaki,Prog.Theor.Phys.66,556,572(1980).[12]F.Fern´a ndez,A.Valcarce,U.Straub,and A.Faessler,Jour.of Phys.G19,2013(1993).[13]A.Valcarce,A.Buchmann,F.Fern´a ndez,and A.Faessler,Phys.Rev.C50,2246(1994).[14]F.Fern´a ndez,A.Valcarce,P.Gonz´a lez,and V.Vento,Phys.Lett.B287,35(1992);Nucl.Phys.A567,741(1994).[15]A.Valcarce,Ph.D.Thesis,University of Salamanca,(1993).A.Valcarce,F.Fern´a ndez,H.Garcilazo,M.T.Pe˜n a,and P.U.Sauer,Phys.Rev.C49,1799(1994).[16]M.Oka and K.Yazaki,in Quarks and Nuclei,International Review of Nuclear Physics,edited by W.Weise(World Scientific,Singapore,1984),Vol.1.[17]M.Abramowitz and I.A.Stegun,Handbook of Mathematical Functions(Dover,NewYork,1972).FIG.1.Fredholm determinat of the nucleon-∆channels with J≤2as a function of the non-relativistic energy E.FIG.2.Phase shift of the0+nucleon-∆channel as a function of the invariant mass W=S1/2.FIG.3.Phase shift of the0−nucleon-∆channel as a function of the invariant mass W=S1/2.FIG.4.Argand diagrams of the diagonal amplitudes of the3P2,5P2and3F2nucleon-∆partial waves.The dots correspond to the energies2.12to2.44GeV.TABLE I.Quark model parameters.m q(MeV)313b(fm)0.50+Repulsive Attractive Attractive 0−Attractive Very attractive Attractive 1+Repulsive Repulsive Repulsive 1−Repulsive Attractive Repulsive 2+Repulsive Repulsive Very repulsive 2−Very attractive Very attractive RepulsiveTABLE III.Dependence of the mass and width of the0−resonance on the mass of the sigma.mσ(MeV)M Res(MeV)ΓRes(MeV)This figure "fig1-1.png" is available in "png" format from: /ps/nucl-th/9509012v1This figure "fig2-1.png" is available in "png" format from: /ps/nucl-th/9509012v1This figure "fig1-2.png" is available in "png" format from: /ps/nucl-th/9509012v1This figure "fig2-2.png" is available in "png" format from: /ps/nucl-th/9509012v1This figure "fig1-3.png" is available in "png" format from: /ps/nucl-th/9509012v1。
