7.6锐角三角函数的简单应用(1)
76锐角三角函数应用.docx

学习目标:1. 经历探索实际问题的求解过程,进一步体会三角函数在解决问题过程屮的应用。
2. 能把实际问题转化为数学问题,能进行有关三角函数的计算并能对结果的实际意义进行说明。
3. 正确理解“旋转角、仰角、俯角、视线、方位角”从而正确理解实际问题,解决实际问题。
重点: 灵活应川“锐角三角函数、勾股定理”解直角三角形 难点: 发现、构造可解的直角三角形和盂解的直介三用形 重要概念:畀垂线视线 —水平线I视线解题要领:构造肓角三角形,解决实际问题。
问题引入:长为90 CM 的单摆AB 旋转30°后,最低点B 升高了多少?典型例题 例1・ 国庆长假,小明和同学一•起到游乐场游玩,游乐场人型摩犬轮的半径为20米,旋转-周需要12分钟。
小明乘坐最底部的车厢(离地而约0.5米)开始一周的观光。
(1) 2分钟后,小明离地面的高度是多少(精确到0.1米)?(2) 摩天轮启动多长时间后,小明和地面的高度将首次达到9m ?(提示cos55° =0.575)(3) 小明将有多长时间连续保持在离地面9 m 以上的高度?Z1是俯角,Z2仰角把实际问题抽象为儿何问题,画岀儿何图形, 明确己知量和未知量, 通过添加适为辅助线, 旋转角:ZAOB北例2・升国旗时,某同学站在离旗杆底部20m 处行注目礼,当国旗升至旗杆端时,该同学 视线的仰角恰为40。
,若双眼离地IS 1.5m,则旗杆高度为多少m? (sin40° =0.64, tan40° =0.84)例3・某商场为缓解我市“停车难"问题,拟建造地下停车库,图6是该地下停车库坡道入口 的设计示意图,其中,丄BD, ZBAD = 18°, C 在BD 上,BC=0.5m.根据规定,地下停 车库坡道入口上方耍张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD 的长就是所限制的高度,而小壳认为丿应该以CE 的长作为限制的高度•小明和小亮谁说的对? 请你判断并计算出正确的结果・(结果精确至U 0.1m )参考数据:sinl8° =0.31, cos 18° =0.95,3. 水平地面上的甲、乙两楼的距离为30米,从「卩楼顶部测得乙楼顶部的仰角为30。
§7.6 锐角三角函数的简单应用(1)

§7.6 锐角三角函数的简单应用(1)学习目标:(1)会把现实生活中较简单的实际问题转化成直角三角形的问题,在解决实际问题的过程中体会三角函数的意义,会通过作高构造直角三角形。
(2)会用计算器求任意锐角的三角函数值以及知道三角函数值求对应的的锐角 学习重点及难点:将实际问题转化成数学问题,画出相应的图形,使用恰当的三角函数解直角三角形。
学习过程:一、用计算器求下列各值(精确到0.01)sin75°=________ ,cos36°=________,tan23°13′=________,cos51.34°=__________。
cos_____°=0.25 , tan _____°=2 , sin_______°=0.76, 32s i n ______=︒二、引入:小明和小丽开心地玩跷跷板,当小丽用力将4m 长的跷跷板的一端压下并碰到地面,此时另一端离地面1.5m.你能求出此时跷跷板与地面的夹角吗?(精确到0.1°)三、例1:如图,奇奇乘坐登山缆车的吊箱经过点A 到达点B ,走过了200m 。
在这段路程中缆车行驶的路线与水平面的夹角为30°,你知道缆车垂直上升的距离是多少吗?追问:当奇奇要乘缆车继续从点B 到达比点B 高200m 的点C ,如果这段路程缆车的行驶路线与水平面的夹角为60°,缆车行进速度为1m/s ,奇奇需要多长时间能到达目的地?例2:如图,是一个实际问题抽象的几何模型,已知A 、B 之间的距离为300m ,求点M 到直线AB 的距离(精确到整数).(参考数据: 3 ≈ 1.7, 2 ≈ 1.4)A B 30°200 200 C 住宅小区 45° 30° M B A四、练习:1、若河岸的两边平行,河宽为900米,一只船由河岸的A处沿直线方向开往对岸的B处,AB与河岸的夹角是60°,船的速度为5米/秒,则船从A到B处约需时间________分钟。
九年级(下)数学教案:锐角三角函数的简单应用(全3课时)
主备人用案人授课时间年月日总第课时课题7.6锐角三角函数的简单应用(1)课型新授教学目标1.进一步掌握解直角三角形的方法,比较熟练的应用解直角三角形的知识解决与仰角、2.俯角有关的实际问题,培养学生把实际问题转化为数学问题的能力。
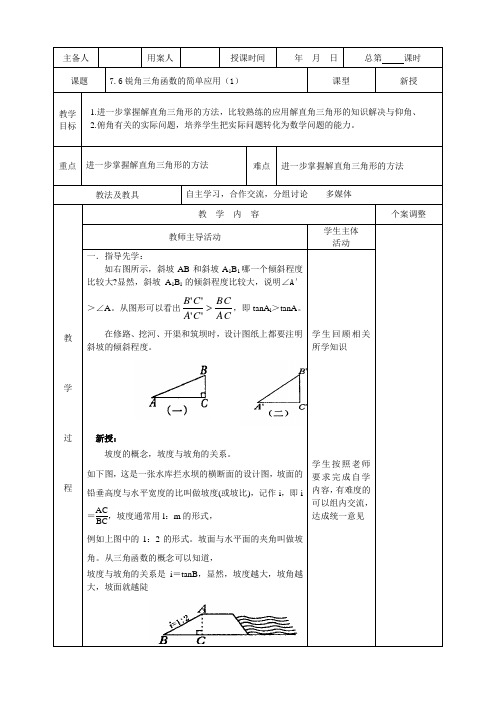
重点进一步掌握解直角三角形的方法难点进一步掌握解直角三角形的方法教法及教具自主学习,合作交流,分组讨论多媒体教学过程教学内容个案调整教师主导活动学生主体活动一.指导先学:如右图所示,斜坡AB和斜坡A1B1哪一个倾斜程度比较大?显然,斜坡A1B l的倾斜程度比较大,说明∠A′>∠A。
从图形可以看出ACBCCACB'''',即tanA l>tanA。
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度。
新授:坡度的概念,坡度与坡角的关系。
如下图,这是一张水库拦水坝的横断面的设计图,坡面的铅垂高度与水平宽度的比叫做坡度(或坡比),记作i,即i=ACBC,坡度通常用l:m的形式,例如上图中的1:2的形式。
坡面与水平面的夹角叫做坡角。
从三角函数的概念可以知道,坡度与坡角的关系是i=tanB,显然,坡度越大,坡角越大,坡面就越陡学生回顾相关所学知识学生按照老师要求完成自学内容,有难度的可以组内交流,达成统一意见教学过程教学内容个案调整教师主导活动学生主体活动四.检测巩固:如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角。
和坝底宽AD。
(i=CE:ED,单位米,结果保留根号)2.如图,单摆的摆长AB为90cm,当它摆动到∠BAB'的位置时,∠BAB'=30°。
问这时摆球B'较最低点B升高了多少?五.小结反思:通过本节课的学习,你有何收获?你还存在什么疑惑?学生独立完成,有难度的可以组内交流,教师巡视,指导学生分组讨论交流,总结归纳,教师补充板书设计7.6锐角三角函数的简单应用(1)坡度的概念,坡度与坡角的关系。
坡面的铅垂高度与水平宽度的比叫做坡度(或坡比),记作i,即i=ACBC,坡度通常用l:m的形式,坡度与坡角的关系是i=tanB,显然,坡度越大,坡角越大,坡面就越陡布置作业补充习题教学札记教学过程教学内容个案调整教师主导活动学生主体活动1、摩天轮启动多长时间后,小明离地面的高度将首次到达10m?2、小明将有多长时间连续保持在离地面20m以上的空中?三.释疑拓展:如图,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离(精确到l米)。
7.6锐角三角函数的简单应用第1课(沭阳县怀文中学)

初 三 数 学( 7.6锐角三角函数的简单应用第1课)教学目标:通过具体的一些实例,能将实际问题中的数量关系,归结为直角三角形中元素之间的关系。
教学过程:一、自主探究1.在△ABC 中,∠C=90°,∠A=45°,则BC :AC :AB = .2.在△ABC 中,∠C=90°(1)已知∠A=30°,BC=8cm ,求AB 与AC 的长;(2)已知∠A=60°,AC=3cm ,求AB 与BC 的长.二、自主合作解:拓展1.摩天轮启动多长时间后,小明离地面的高度将首次到达10m ?2.小明将有多长时间连续保持在离地面20m 以上的空中? 三、自主展示1.如图,单摆的摆长为90cm,当它摆动到AC 的位置时,∠CAB =15°,问这时摆球C 较最低点B 升高了多少?2.已知跷跷板长4m,当跷跷板的一端碰到的地面时,另一端离地面2m,求此时跷跷板与地面的夹角?3.如图,东西两炮台A 、B 相距2000米,同时发现入侵敌舰C ,炮台A 测得敌舰C 在它的南偏东30°的方向,炮台B 测得敌舰C 在它的正南方,试求敌舰与两炮台的距离(结果保留根号).四、自主拓展3.4.九年级三班小亮同学学习了“测量物体高度”一节课后,他为了测得右图所放风筝的高度,进行了如下操作:(1)在放风筝的点A 处安置测倾器,测得风筝C 的仰角60CBD =︒∠;(2)根据手中剩余线的长度求出风筝线BC 的长度为70米; (3)量出测倾器的高度 1.5AB =米. 根据测量数据,计算出风筝的高度CE 约为 米.(精确到0.11.73)5.如图,某河道要建造一座公路桥,要求桥面离地面高度AC 为3米,引桥的坡角ABC ∠为30°,则引桥的水平距离BC 的长是_________米(结果保留根号) 6.A DB EC 60° 第4题图A B C 第5题图第六题图。
锐角三角函数的简单运用

锐角三角函数的计算方法包括直接计算、利用三角恒等式化简、利用同角关系式化简等。 掌握这些计算方法是解决三角函数问题的基本技能。
对未来学习锐角三角函数的建议
01
深入理解概念
在学习锐角三角函数的过程中,要深入理解其概念,掌握其性质和定理,
这样才能更好地运用它们解决实际问题。
02 03
利用三角函数求长度
在直角三角形中,已知角度和一边长度,可以利用正弦、余弦、正切等三角函数 求出另一边的长度。
利用三角函Байду номын сангаас求距离
在平面几何问题中,可以利用三角函数求两点之间的距离,或者点到直线的距离 。
判断三角形形状问题
利用三角函数判断三角形形状
通过比较三角形的三个内角的三角函数值,可以判断三角形是锐角三角形、直角三角形还是钝角三角 形。
正弦函数的性质
01
02
03
定义域
正弦函数在第一象限和第 二象限有定义,即角度范 围在0到180度之间。
值域
正弦函数的值域为[-1,1], 表示角度的正弦值永远不 会超过1或小于-1。
单调性
正弦函数在第一象限和第 二象限内是单调递增的, 随着角度的增加,正弦值 也会增加。
余弦函数的性质
定义域
余弦函数在第一象限和第 四象限有定义,即角度范 围在0到180度之间。
锐角三角函数的 简单运用
目录
• 引言 • 锐角三角函数的性质 • 锐角三角函数的计算方法 • 锐角三角函数在几何问题中的应
用 • 锐角三角函数在实际问题中的应
用 • 总结与展望
01
引言
锐角三角函数的定义
锐角三角函数是三角函数中的一种, 主要研究锐角的角度与其边长之间的 关系。常见的锐角三角函数有正弦、 余弦和正切。
初三数学锐角三角函数的简单应用知识点

初三数学锐角三角函数的简单应用知识点
初三数学锐角三角函数的简单应用知识点
读书使学生认识丰富多彩的世界,获取信息和知识,拓展视野。
接下来小编为大家精心准备了锐角三角函数的简单应用知识点,希望大家喜欢!
学习重点难点:
重点:进一步用解直角三角形的.知识解决与仰角、俯角、方位角有关的实际问题.
难点:灵活运用三角函数解决实际问题.
【温故知新】
1.如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B 点、C点的仰角分别为60°和45°,则广告牌的高度BC为_____________米(结果保留根号).
2.如图,一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度?
变式如图,飞机沿水平方向(A,B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB 的距离MN.飞机能够测量的数据有俯角和飞行距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个求距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.。
7.6用锐角三角函数解决问题(仰角、俯角问题)

7.6 锐角三角函数的简单应用——仰角、俯角问题一、画一画 根据题意,画出仰角或俯角(1)人看气球 (2)在飞机上看地面控制中心二、实际问题问题1: “小机灵”在飞行高度为180米的飞机A 上看到上海浦东国际机场地面指挥中心B 的俯角为30°,求此时飞机A 在地面上的投影点C 离B 点的水平距离。
(结果保留根号)变式:“小机灵”在离中国馆AB 120米的C 处,用高为1米的测角仪测得中国馆的最高处A的仰角为30°,已知测角仪CD 垂直于地面,求中国馆AB 的高。
(结果保留根号)AB问题2:在南浦大桥AB 的上方有一只热气球停在P 点处,此时热气球离桥面的高度为1200米,“小机灵”在大桥的两端A 、B 分别测得热气球的仰角为27°、40°,求南浦大桥的AB 。
参考数据:sin27°≈0.5,cos27°≈0.9, tan27°≈0.5,sin40°≈0.6, cos40°≈0.8,tan40°≈0.8PB A人的眼睛 P · 0· A · 地面控制中心 B · A ·B · D C变式1:已知南浦大桥的主桥AB长900米,热气球由西向东飞行,一段时间后到达C处,此时“小机灵”在大桥两端A、B分别测得热气球的仰角为30°、45°,求此时热气球距桥面的高度。
(结果保留根号)CB A变式2:热气球继续向东飞行至D处,此时“小机灵”在大桥两端A、B分别测得热气球的仰角为40°、27°,已知主桥AB的长为900米,求此时热气球距桥面的高度。
参考数据:sin27°≈0.5,cos27°≈0.9,tan27°≈0.5,sin40°≈0.6,cos40°≈0.8,tan40°≈0.8DB A三、数学活动室思考:1、如何测量得到旗杆的高度?(图1 )2、怎样从地面测量小山的高度呢?(图2 )仪器:卷尺,高度为h的测角仪;要求:画出图形,测得的角用α、β等表示,测得的长度用a、b、c等表示。
锐角三角函数的简单应用课件

在建筑施工过程中,锐角三角函数可 以用于测量角度、高度等参数,以确 保施工的准确性和安全性。
航海问题
航向计算
在航海中,锐角三角函数可以用于计算船只的航向、风向等参数,以确保航行 的安全和准确。
距离计算
通过锐角三角函数,可以计算出船只之间的距离,以及船只与目的地之间的距 离。
物理问题
力的合成与分解
tan(60°)=√3
02
锐角三角函数的应用场景
测量问题
计算角度
在测量问题中,锐角三角函数可 以用于计算角度,例如在测量地 形、建筑物的角度等。
距离测量
通过锐角三角函数,可以计算出 两点之间的距离,例如在地图测 量、卫星定位等领域。
建筑问题
结构设计
在建筑设计过程中,锐角三角函数可 以用于计算建筑物的角度、高度等参 数,以确保建筑物的稳定性和美观性 。
设计斜坡的长度
总结词
利用三角函数优化斜坡长度
详细描述
在设计斜坡时,我们可以利用三角函数来优化斜坡的长度。首先,确定斜坡的角度和起点、终点的位 置,然后利用三角函数计算斜坡的长度。这样可以确保斜坡的长度符合设计要求,并且能够满足车辆 和行人的通行需求。
计算太阳的角度
总结词
利用三角函数确定太阳位置
VS
角度,值域为R。
特殊角的三角函数值
0°
sin(0°)=0,cos(0°)=1 ,tan(0°)=0
30°
sin(30°)=1/2, cos(30°)=√3/2,
tan(30°)=1/√3
45°
sin(45°)=cos(45°)=√2/ 2,tan(45°)=1
60°
sin(60°)=√3/2, cos(60°)=1/2,
锐角三角函数应用题的方法与技巧

锐角三角函数应用题的方法与技巧
x
《锐角三角函数应用题的方法与技巧》
一、总体思路
1、识别出三角形所涉及的三角函数,并确定三角函数的参数:根据题干里面提供的线段、角度等长度或角度来初步判断三角形的形状,并由此来计算出三个角度和三条边。
2、判断题目的性质:根据题目要求,判断出是求边长还是求角度。
3、解答:
(1)求边长:利用相应的三角函数关系(正弦定理、余弦定理、正切定理等),求出答案;
(2)求角度:利用相应的三角函数关系,求出角度的三角函数值,再用反三角函数求出角度。
二、技巧总结
1、画图法:根据题干中提供的信息,画出准确的三角形图形,便于计算和判断。
2、直角三角形快速求角度:根据对边比斜边的特点,找出角度所对应的三角函数值,再用反三角函数计算出角度。
3、正弦定理、余弦定理:正弦定理可用于计算夹角的一边的长度,余弦定理可用于求另一边的长度。
4、正切定理:正切定理可以用于求夹角的角度大小。
5、各种三角函数的关系:在计算三个角度的大小时,可以利用三个角度的和为180°;在计算三条边的长度时,可以利用三条边之和的性质。
九年级数学下册 第7章 锐角三角形 7.6 锐角三角函数的简单应用作业设计 (新版)苏科版

7.6 锐角三角函数的简单应用的值是________1、如图,已知AB是⊙O的直径,弦CD⊥AB,AC=22,BC=1,那么sin ABD2、一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)3、如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD 方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:≈1.414,≈1.732)4、如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);(2)求海轮在B处时与灯塔C的距离(结果保留整数).(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)5.如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取≈1.73,结果保留整数)6.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为m(结果保留根号)7.如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:)8.如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)参考答案221.2.解:如图,过点C作CD⊥AB交AB延长线于D.在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,∴CD=AC=40海里.在Rt△CBD中,∵∠CDB=90°,∠CBD=90°﹣37°=53°,∴BC=≈=50(海里),∴海警船到大事故船C处所需的时间大约为:50÷40=(小时).3. 解:∵∠CBD=∠A+∠ACB,∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°,∴∠A=∠ACB,∴BC=AB=10(米).在直角△BCD中,CD=BC•sin∠CBD=10×=5≈5×1.732=8.7(米).答:这棵树CD的高度为8.7米.4.解:(1)C作AB的垂线,设垂足为D,根据题意可得:∠1=∠2=42°,∠3=∠4=55°,设CD的长为x海里,在Rt△ACD中,tan42°=,则AD=x•tan42°,在Rt△BCD中,tan55°=,则BD=x•tan55°,∵AB=80,∴AD+BD=80,∴x•tan42°+x•tan55°=80,解得:x≈34.4,答:海轮在航行过程中与灯塔C的最短距离是34.4海里;(2)在Rt△BCD中,cos55°=,∴BC=≈60海里,答:海轮在B处时与灯塔C的距离是60海里.5. 解:∵∠BDE=30°,∠BCE=60°,∴∠CBD=60°﹣∠BDE=30°=∠BDE,∴BC=CD=10米,在Rt△BCE中,sin60°=,即=,∴BE=5,AB=BE+AE=5+1≈10米.答:旗杆AB的高度大约是10米.6. 解:作CE⊥AB于点E,在Rt△BCE中,BE=CD=5m,CE==5m,在Rt△ACE中,AE=CE•tan45°=5m,AB=BE+AE=(5+5)m.故答案为:(5+5).7. 解:在Rt△DEB中,DE=BE•tan45°=2.7米,在Rt△CEB中,CE=BE•tan30°=0.9米,则CD=DE﹣CE=2.7﹣0.9≈1.2米.故塑像CD的高度大约为1.2米.8 解:设梯子的长为xm.在Rt△ABO中,cos∠ABO=,∴OB=AB•cos∠ABO=x•cos60°=x.在Rt△CDO中,cos∠CDO=,∴OD=CD•cos∠CDO=x•cos51°18′≈0.625x.∵BD=OD﹣OB,∴0.625x﹣x=1,解得x=8.故梯子的长是8米.。
7.6锐角三角函数的简单应用(1)课件坡度

例2:
.如图,水坝的横截面是梯形ABCD,迎水坡BC 的坡角 为30°,背水坡AD的坡度 i 为1:1.2, 坝顶宽DC=2.5米,坝高4.5米. (tan 40 ° ≈ 5/6) 求:(1)背水坡AD的坡角 3 1.732 (2)坝底宽AB的长。
D
C
A
E
F
B
思考:在上题中,为了提高堤坝的 防洪能力,市防汛指挥部 决定加固堤坝,要求坝顶CD加宽0.5米,背水坡AD的坡度 改为1:1.4,已知堤坝的总长度为5㎞, 求完成该项工程所需的土方(精确到0.1米3)
C A
D
如图,有一段斜坡BC长为10米,坡角 ∠CBD=30°,为方便残疾人的轮椅车通行, 现准备把坡角降为5°。求斜坡新起点A与原 起点B的距离 (结果精确到0.1米)
C
C
°
5°
B
30°
D
A
(第20题)
B
D
练习1:
如图,某拦河坝截面的原设计方案为AH//BC,
:
坡角 ABC 60 ,坝顶到坝脚的距离AB=6m. 为了提高拦河坝的安全性,现将坡角改为45
如图,沿水库拦水坝的背水坡将坝面 加宽两米,坡度由原来的1:2改成 1:2.5,已知原背水坡长BD=13.4米, 求: (1)原背水坡的坡角 和加宽后 的背水坡的坡角 ;
(2)加宽后水坝的横截面面积增 加了多少?(精确到0.01)
2.0
C 1:2.5 1:2 D
A B
E F
说能出你这节课的收获 和体验让大家与你分享
由此,点A 需向右平移至点D ,请你计算AD的长 ADHBEFC
练习2:
如图是沿水库拦河坝的背水坡,将坡顶 加宽2米,坡度由原来的1:2改为1:2.5,已 知坝高6米,坝长50米. 求(1)加宽部分横断面AFEB的面积; (2)完成这一工程需要多少土方?
锐角三角函数的简单应用

7.6锐角三角函数的简单应用(1)学习目标:进一步掌握解直角三角形的方法,比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题,培养学生把实际问题转化为数学问题的能力. 学习重点:解决与仰角、俯角有关的实际问题. 学习过程 一、概念学习仰角、俯角的定义如右图,从下往上看,视线与水平线的夹角叫仰角,从上往下看,视线与水平线的夹角叫做俯角.右图中的∠2就是仰角,∠1就是俯角. 二、例题讲解例1、为了测量停留在空中的气球的高度,小明先站在地面上某点观测气球,测得仰角为30°,然后他向气球方向前进了50m ,此时观测气球,测得仰角为45°.若小明的眼睛离地面1.6m ,小明如何计算气球的高度呢(精确到0.01m )解:例2、(09年广东深圳、山东东营)如图,斜坡AC 的坡度(坡比)为1:3,AC =10米.坡顶有一旗杆BC ,旗杆顶端B 点与A 点有一条彩带AB 相连,AB =14米.试求旗杆BC 的高度.例3、(09年湖南娄底)在学习实践科学发展观的活动中,某单位在如图所示的办公楼迎ABC D街的墙面上垂挂一长为30米的宣传条幅AE ,张明同学站在离办公楼的地面C 处测得条幅顶端A 的仰角为50°,测得条幅底端E 的仰角为30°. 问张明同学是在离该单位办公楼水平距离多远的地方进行测量?(精确到整数米)(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20,sin30°=0.50,cos30°≈0.87,tan30°≈0.58)三、课后练习 A 级:1、(09年广西柳州)如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为︒60,看这栋高楼底部的俯角为︒30,热气球与高楼的水平距离为66 m ,这栋高楼有多高?(结果精确到0.1 m ,参考数据:73.13≈)2、(09年湖北仙桃)如图所示,小华同学在距离某建筑物6米的点A 处测得广告牌B 点、C 点的仰角分别为52°和35°,则广告牌的高度BC 为__________米(精确到0.1C AB米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)3、(09年山东济南)九年级三班小亮同学学习了“测量物体高度”一节课后,他为了测得右图所放风筝的高度,进行了如下操作: (1)在放风筝的点A 处安置测倾器,测得风筝C 的仰角60CBD =︒∠;(2)根据手中剩余线的长度出风筝线BC 的长度为70米; (3)量出测倾器的高度 1.5AB =米.根据测量数据,计算出风筝的高度CE 约为 米.(精确到0.11.73) B 级:4、(09年内蒙包头)如图,线段AB DC 、分别表示甲、乙两建筑物的高,AB BC DC BC ⊥,⊥,从B 点测得D 点的仰角α为60°从A 点测得D 点的仰角β为30°,已知甲建筑物高36AB =米.1.414 1.732)(1)求乙建筑物的高DC ;(2)求甲、乙两建筑物之间的距离BC (结果精确到0.01米).5、(09年安徽芜湖)如图,一艘核潜艇在海面下500米A 点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B 点处测得俯角为60°正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度?(精确到米,参考(第2题图)αβD乙CBA 甲AD B EC60° (第3题图)1.4141.7322.236)C 级:6、(09年山东济宁)坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋(公元1112年),为砖彻八角形十三层楼阁式建筑.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量太子灵踪塔的高度,携带的测量工具有:测角仪、皮尺、小镜子.(1)小华利用测角仪和皮尺测量塔高.图1为小华测量塔高的示意图.她先在塔前的平地上选择一点A ,用测角仪测出看塔顶()M 的仰角α=35°,在点A 和塔之间选择一点B ,测出看塔顶()M 的仰角β=45°,然后用皮尺量出A 、B 两点间的距离为18.6m ,量出自身的高度为1.6m .请你利用上述数据帮助小华计算出塔的高度(tan35°≈0.7,结果保留整数).(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影NP 的长为m a (如图2),你能否利用这一数据设计一个测量方案?如果能,请回答下列问题: ①在你设计的测量方案中,选用的测量工具是: ; ②要计算出塔的高,你还需要测量哪些数据? .7.6 锐角三角函数的简单应用(2)学习目标:能利用解直角三角形的知识,解决与方向角有关的实际问题,进一步培养学生把实际问题转化为数学问题的能力. 学习重点:方向角的问题B A N Mα β D 图1 P N M图 230°60°B AD C海面学习过程: 一、例题解析: 例1、(09年四川眉山)海船以5海里/小时的速度向正东方向行驶,在A 处看见灯塔B 在海船的北偏东60°方向,2小时后船行驶到C 处,发现此时灯塔B 在海船的北偏西45°方向,求此时灯塔B 到C 处的距离.例2、(09年江苏)如图,在航线l 的两侧分别有观测点A 和B ,点A 到航线l 的距离为2km ,点B 位于点A 北偏东60°方向且与A 相距10km 处.现有一轮船从位于点B 南偏西76°方向的C 处,正沿该航线自西向东航行,5min 后该轮船行至点A 的正北方向的D 处. (1)求观测点B 到航线l 的距离;(2)求该轮船航行的速度(结果精确到0.1km/h ).1.73,sin760.97°≈,cos760.24°≈,tan76 4.01°≈)例3、(09年湖北黄冈)如图,在海面上生产了一股强台风,台风中心(记为点M )位于海滨城市(记作点A )的南偏西15°,距离为B )正西方向72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由.(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?A二、课后练习:A级:1、(09年湖南怀化)如图,小明从A地沿北偏东30方向走到B地,再从B地向正南方向走200m到C地,此时小明离A地m.B级:2、(09年广东湛江)如图,某军港有一雷达站P,军舰M停泊在雷达站P的南偏东60°方向36海里处,另一艘军舰N位于军舰M的正西方向,与雷达站P相距(1)军舰N在雷达站P的什么方向?(2)两军舰M N、的距离.(结果保留根号)3、(09年湖北十堰)如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).1.4141.732)C级:4、如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M 的南偏东60°方向上有一点A,以A为圆心、500m为半径的圆形区域为居民区.取MN 上的另一点B,测得BA的方向为南偏东75°.已知MB=400m,通过计算回答,如果不改变方向,输水管道是否会穿过居民区.。
7.6锐角三角函数的简单应用(1)

tan 25°≈ 0.47 西 tan 55°≈ 1.43
B C
A
E D 南
F
练习1:A、B两镇相距60km,小山C在A镇的 北偏东60°方向,在B镇的北偏西30°方向.经 探测,发现小山C周围20km的圆形区域内储有 大量煤炭,有关部门规定,该区域内禁止建房 修路.现计划修筑连接A、B两镇的一条笔直的 公路,试分析这条公路是否会经过该区域?
C
C
°
5°
B
30°
D
A
(第20题)
B
D
OHale Waihona Puke 2.小明将有多长时间连续保持在 离地面10m以上的空中? D B A C
1.单摆的摆长AB为90cm,当它摆动到 AB’的位置时, ∠BAB’=11°,问这时摆球B’ 较最低点B升高了多少(精确到1cm)?
sin11 0.191 cos11 0.982 tan11 0.194
B’
仰角、俯角问题中的基本图形
C
A
B C
D
A
D
B
练习:为改善楼梯的安全性能,准备将楼梯的 倾斜角由60°调整为45 °.已知调整后的楼 梯比原来多占地4米,求楼梯的高度. D
A
B
C
请你试一试: 升国旗时,某同学站在离旗杆底部24m处行 注目礼,当国旗升至旗杆顶端时,该同学视线的 仰角恰为30°,若双眼离地面1.5m,求旗杆的高 度.
D.80cos 20m
2、如图是一个拦水大坝的横断面图,AD∥BC, 斜坡AB=10m,大坝高为8m, (1)则斜坡AB的坡度
iAB ____.
(2)如果坡度 iAB 1: 3,则坡角 B ____ . (3)如果坡度 iAB 1: 2, AB 8m ,则大坝高度为___.
九年级数学锐角三角函数的简单应用1

§7.6锐角三角函数的简单应用⑴主备:李维明班级________姓名____________一.学习目标:1.能把实际问题抽象为几何问题,借助直角三角形、锐角三角函数把已知量与未知量联系在一起解决实际问题;2. 比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题,培养学生把实际问题转化为数学问题的能力.二.学习重点难点:重点:应用解直角三角形的知识解决与仰角、俯角有关的实际问题.难点:灵活运用三角函数解决实际问题.三.教学过程【温故知新】1.(10辽宁丹东市)如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m.(即小颖的眼睛距地面的距离),那么这棵树高是.第1题第2题第3题2.(11浙江义乌)右图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是52m,则乘电梯从点B到点C 上升的高度h是m.3.(11广东茂名)如图,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B ,并测得它的俯角为45°,则船与观测者之间的水平距离BC=米.在这题中出现了俯角,那什么是俯角?我们如何给它定义呢?这个就是我们今天学习的内容.1.概念学习:仰角、俯角的定义如右图,从下往上看,视线与水平线的夹角叫仰角,从上往下看,视线与水平线的夹角叫做俯角.【例题解析】例1.如图,小明欲利用测角仪测量树的高度.已知他离树的水平距离BC为10m,测角仪的高度CD为1.5m,测得树顶A的仰角为33°.求树的高度AB.(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)Ⅰ.动点观测某人在A点观察塔顶C的仰角,前进100米后再次观测塔顶C的仰角,数据如下列各图所示,试求塔的高度.100m100m100m例1.如图,在一次数学课外实践活动中,要求测教学楼的高度AB.小CD,测得教学楼顶端A的仰角为30°,Array到达E,又测得教学楼顶端A的仰角为60°.求A BC D4560变式1:(10湖北鄂州)如图,一艘舰艇在海面下500米A 点处测得俯角为30°前下方的海底C 处有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B 点处测得俯角为60°前下方的海底C 处有黑匣子信号发出,求海底黑匣子C 点距离海面的深度(结果保留根号).变式2(11江苏宿迁)如图,为了测量某建筑物CD 的高度,先在地面上用测角仪自A 处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m ,此时自B 处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m ,请你计算出该建筑物的高度.(取3=1.732,结果精确到1m )变式3(10 天津)永乐桥摩天轮是天津市的标志性景观之一.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C 处测得摩天轮的最高点A 的仰角为45︒,再往摩天轮的方向前进50 m 至D 处,测得最高点A 的仰角为60︒.求该兴趣小组测得的摩天轮的高度AB (3≈1.732,结果保留整数).B A 1.545︒30︒100变式4(11山东德州)某兴趣小组用高为1.2米的仪器测量建筑物CD 的高度.如示意图,由距CD 一定距离的A 处用仪器观察建筑物顶部D 的仰角为β,在A 和C 之间选一点B ,由B 处用仪器观察建筑物顶部D 的仰角为α.测得A ,B 之间的距离为4米,tan α=1.6,tan β=1.2,试求建筑物CD 的高度.Ⅱ.动点观测例2.如图,某高速公路建设中需要确定隧道AB 的长度.已知在离地面1500m 高度C 处的飞机上,测量人员测得正前方A 、B 两点处的俯角分别为60°和45°.求隧道AB 的长.(参考数据:3=1.73)A C DB E F GC A B45° 30° F E P BA变式1(10广西柳州)如图,从热气球P 上测得两建筑物A 、B 的底部的俯角分别为45°和30°,如果A 、B 两建筑物的距离为90m ,P 点在地面上的正投影恰好落在线段AB 上,求热气球P 的高度.(结果精确到0.01m ,参考数据:2≈1.414,3≈1.732)变式2(10湖北襄樊)如图,热气球的探测器显示,从热气球A 看一栋大楼顶部B 的俯角为30°,看这栋大楼底部C 的俯角为60°,热气球A 的高度为240米,求这栋大楼的高度.变式3(10 云南昆明)热气球的探测器显示,从热气球A 处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,A 处与高楼的水平距离为60m ,这栋高楼有多高?(结果精确到0.1m ,参考数据:2≈1.414,3≈1.732)。
锐角三角函数应用(1)

E
B C
某居民小区有一朝向为正南方向的居民楼, b 该居民楼的一楼是高6米的小区超市,超市以上是居 民住房.在该楼的前面要盖一栋高20米的新楼.当冬季 正午的阳光与水平线的夹角为30°时.问:若新楼的 影子恰好落在超市1米高的窗台处,两楼应相距多少 D 米?
太阳光 30°
A
住 宅 楼
新 楼
F B
E
定 义
斜边
注意:三角函数的定义,必须在直角三角形中. B
∠A的对边
斜边
sinA
∠A的对边
cosA tanA
∠A的邻边 斜边
A ∠A的邻边
C
∠A的对边 ∠A的邻边
1.锐角A的正弦、余弦、和正切统称∠A的三角函数
2.∠A的取值范围是什么?sinA ,cosA与tanA的取值范围又如何?
1.互余两角三角函数关系: 0-A) 1.SinA=cos(90
b
A
1.两锐角之间的关系:
∠A+∠B=900
解 直 角 三 角 形
2.三边之间的关系:
c
B
a
A
a +b =c
2
2
2
b
C
sinA=
cosA= 3.边角之间 的关系
a
c b c
a b
tanA=
特殊角的三角函数值表
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
300 450 600
1 2 2 2 3 2
A
住 宅 楼
新 楼
B
C
某居民小区有一朝向为正南方向的居民楼, 该居民楼的一楼是高6米的小区超市,超市以上是居 民住房.在该楼的前面要盖一栋高20米的新楼.当冬季 正午的阳光与水平线的夹角为30°时. 问:(3)若新楼的影子恰好落在超市1米高的窗台处, D 两楼应相距多少米?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学教学案7.6锐角三角函数的简单应用(1)班级____姓名_____ 教学目标:
通过具体的一些实例,能将实际问题中的数量关系,归结为直角三角形中元素之间的关系。
教学重点、难点:
通过具体的一些实例,能将实际问题中的数量关系,归结为直角三角形中元素之间的关系。
教学过程:
一、复习巩固:
1、在△ABC 中,∠C=90°,∠A=45°,则BC :AC :AB = 。
2、在△ABC 中,∠C=90°。
(1)已知∠A=30°,BC=8cm ,求AB 与AC 的长;
(2)已知∠A=60°,AC=3cm ,求AB 与BC 的长。
二、例题学习:
例1、如图,东西两炮台A 、B 相距2000米,同时发现入侵敌舰C ,炮台A 测得敌舰C 在它的南偏东30°的方向,炮台B 测得敌舰C 在它的正南方,试求敌舰与两炮台的距离。
例2:“五一”节,小明和同学一起到游乐场游玩,游乐场的大型摩天轮的半径为20m ,旋转1周需要12min 。
小明乘坐最底部的车厢(离地面约0.5m )开始1周的观光,2min 后小 明离地面的高度是多少
分析:如图,小明开始在车厢点B ,经过2min 后到了点C ,点C 离地面的高度就是小明离地面的高度,其实就是DA 的长度
DA= AE -
解:
拓展延伸:
1、摩天轮启动多长时间后,小明离地面的高度将首次到达(20.5310 )m ?
2、小明将有多长时间连续保持在离地面30.5m以上的空中?
例3、某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为30°时.
问:(1)超市以上的居民住房采光是否有影响,为什么?
(2)若要使超市采光不受影响,两楼应相距多少米?
(3)若新楼的影子恰好落在超市1米高的窗台处,两楼应相距多少米?
三、课堂练习
A'的位置时,∠BA B'=30°。
问这时摆1、如图,单摆的摆长AB为90cm,当它摆动到B
球B'较最低B升高了多少?
2、已知跷跷板长4m,当跷跷板的一端碰到地面时,另一端离地面2m.求此时跷跷板与地面的夹角。
