The introduction of game theory (lecture notes 9)
第七章 博奕论(Game Theory教材课程

max
是
u1
即该博奕的纳什均衡解
max u 2
maxu1 maxu2
U1 Uq12
q2
6q2 6q1
2q1 2q2
0 0
的解,
求解上述方程组:
q 1 * q 2 * 2 , Q 4 u 1 1 , u 2 4 , u 1 u 2 8
标志着博奕论的初步形成。 50年代,合作博奕发展到鼎盛阶段,非合作博奕开始出现 纳什和夏普里的讨价还价模型, 塔克的“囚徒困境” 60年代以后,selten,Haysany,Krops,Wilseen
“信誉问题模型” (动态不完全信息博弈) 最近十多年,博弈论几乎贯穿了整个微观经济学,产业组
织理论和企业制度理论,并扩展到宏观经济学,环境、劳动、 福利经济学等领域。
新厂商的市场进入问题
B
打入
A
打击
(0,10)
和平共处
(-2,3)
(5,5)
6.博奕进程的信息
完美信息博奕:在动态博奕中,博弈方对博弈的进程, 即次此行为前各博奕方的行为完全了解
非完美信息博弈:
完全信息博弈:博奕各方完全了解所有博奕方各种策 略组合下得益情况 非完全信息博弈:
7.2.2博弈的主要分类
1 3、赢得(利益):参加博奕各方从博奕中所获得的 利
益 支付矩阵,博弈树
零和博奕:各博奕方赢得的代数和为零 非零和博奕:各博奕方赢得的代数和不为零
4.均衡:所有博奕方的最优策略的组合
博奕分析的目的是使用博奕规则决定均衡
5.得益的信息
完全信息博奕:博奕各方完全了解所有博奕方各种策略 组合下得益情况的博奕,如囚徒困境和田忌赛马。
7。3 完全信息静态博奕——纳什均衡
game theory11 博弈论 英文

/100
16
Review
WPBE
Poker Game
Summary
Simple Poker Game – Normal Form
Summary
WPBE 1
WPBE 1 is (U,A) and p=0, 1-p=1
• P1 behaves optimally given action of P2
• P2 behaves optimally given his beliefs and P1’s action • P2’s beliefs are consistent with P1’s actions
q < 1/2
and
q < 1/2
O 2,4 A q
R p
U 1-p F A 1-q q F 1-q
3,0
1,1
4,1
/100
0,0
11
Review
WPBE
Poker Game
Summary
WPBE 3
WPBE 3 is (O,F) and p = ½; q < 1/2
•
• •
P1 behaves optimally given action of P2
•
Why is bluffing needed?
• no other strategy works
/100 15
Review
WPBE
Poker Game
Summary
Simple Poker Game
• What is the equilibrium in this game?
• information set => no backward induction • find normal-form game (Bayesian game) • how many strategies do players have? • P1 – 4 strategies (FF, FR, RF, RR) • P2 – 2 strategies (F, C)
Theintroductionofgametheorylecturenotes4

The Bargaining Problem
• The “Bargaining Problem” arises in economic situations where there are gains from trade, for example, when a buyer values an item more than a seller. The question is how to divide the gains, for example, what price should be charged?
• Players move sequentially, making alternating offers. • Examples:
– A Seller and a Buyer bargain over the price of a house. – A Labor Union and Firm bargain over wages & benefits. – Two countries, e.g. China and U.S.A bargain over the terms of a
• Bargaining problems arise when the size of the market is small and there are no obvious price standards because the good is unique, e.g. a house at a particular location. A custom contract to erect a building, etc.
movie star doesn’t get the work and the film company doesn’t get the movie star. • The disagreement value is know by some other terms, e.g. the best alternative to negotiated agreement “BATNA.” • By gains from trade we mean that M>a+b.
Kockesen L., Game Theory Lecture Notes

Introduction
1.1 W HAT IS G AME T HEORY ?
We, humans, cannot survive without interacting with other humans, and ironically, it sometimes seems that we have survived despite those interactions. Production and exchange require cooperation between individuals at some level but the same interactions may also lead to disastrous confrontations. Human history is as much a history of fights and wars as it is a history of successful cooperation. Many human interactions carry the potentials of cooperation and harmony as well as conflict and disaster. Examples are abound: relationships among couples, siblings, countries, management and labor unions, neighbors, students and professors, and so on. One can argue that the increasingly complex technologies, institutions, and cultural norms that have existed in human societies have been there in order to facilitate and regulate these interactions. For example, internet technology greatly facilitates buyer-seller transactions, but also complicates them further by increasing opportunities for cheating and fraud. Workers and managers have usually opposing interests when it comes to wages and working conditions, and labor unions as well as labor law provide channels and rules through which any potential conflict between them can be addressed. Similarly, several cultural and religious norms, such as altruism or reciprocity, bring some order to potentially dangerous interactions between individuals. All these norms and institutions constantly evolve as the nature of the underlying interactions keep changing. In this sense, understanding human behavior in its social and institutional context requires a proper understanding of human interaction. Economics, sociology, psychology, and political science are all devoted to studying human behavior in different realms of social life. However, in many instances they treat individuals in isolation, for convenience if not for anything else. In other words, they assume that to understand 1
游戏理论概括英文作文

游戏理论概括英文作文英文:Game theory is a branch of applied mathematics and economics that studies strategic interactions between rational decision-makers. It provides a framework for analyzing and understanding how individuals, firms, and governments make decisions in competitive situations. The central concept of game theory is the "game," which is a formal model of a strategic interaction between two or more players. Each player in the game has a set of possible strategies, and the outcome of the game depends on the strategies chosen by all players.One of the most famous games in game theory is the prisoner's dilemma, which illustrates the concept of Nash equilibrium, named after the mathematician John Nash. In the prisoner's dilemma, two suspects are arrested and placed in separate cells. They are given the option to cooperate with each other by remaining silent, or to betrayeach other by confessing. The outcome of their decision depends on the choices made by both suspects. The Nash equilibrium in this game occurs when both suspects choose to betray each other, even though they would be better off if they both remained silent. This example demonstrates how rational individuals may not always make the best decisions when they are in a competitive situation.Another important concept in game theory is the notion of a dominant strategy, which is a strategy that always provides the best outcome for a player, regardless of the strategies chosen by other players. For example, in the game of rock-paper-scissors, if one player always chooses "rock" regardless of the other player's choice, they have a dominant strategy. Understanding dominant strategies can help players make optimal decisions in competitive games.Game theory has applications in various fields, including economics, political science, biology, and computer science. For example, it is used to analyze voting behavior in elections, to model the behavior of firms in oligopoly markets, and to study the evolution ofcooperation in biological systems. In computer science, game theory is used to design algorithms for multi-agent systems and to analyze the behavior of autonomous agents.In conclusion, game theory provides a powerful framework for analyzing strategic interactions and understanding the behavior of rational decision-makers in competitive situations. By studying game theory, we cangain insights into a wide range of phenomena in the social and natural sciences.中文:博弈论是应用数学和经济学的一个分支,研究理性决策者之间的战略互动。
英语第一章阅读 game theory 原文及翻译

The essence of a game is the interdependence of player strategies. There are two distinct types of strategic interdependence: sequential and simultaneous. In the former the players move in sequence, each aware of the others’ previous actions. In the latter the players act at the same time, each ignorant of the others’ actions.
Game theory was pioneered by Princeton mathematician john von Neumann. In the early years the emphasis was on games of pure conflict (zero-sum games). Other games were considered in a cooperative form. That is, the participants were supposed to choose and implement their actions jointly. Recent research has focused on games that are neither zero sum nor purely cooperative. In these games the players choose their actions separately, but their links to others involve elements of both competition and cooperation.
1 Introduction of game theory

+
To lead or not to lead48
after the first four races in the 1983 America’s Cup finals, Liberty led 3-1 in a best-of-seven series. On the morning of the fifth race, ‘’cases of champagne had been delivered to Liberty’s dock. The wives of the crew were ready to celebrate their husbands.
+
Some illustrations-pick a number 48
I have picked a number between 1 and 100, and your goal is to guess the number. If you guess correctly on the first try, I will pay you $100, and If you fail, I will give you five guesses, and after each wrong guess, I will also tell you if you are too high or too low. Of course, there is a bigger reward for getting the right answer quickly. Thus the possible reward might be $80, $60, $40, $20, $0.
+
an introduction to game theory pdf

an introduction to game theory pdfGame theory is the study of strategic decision-making in situations where the outcome of one person's actions depends on the actions of others.It is a field of mathematics and economics that aims to understand how rational actors behave in competitive or cooperative situations.The basic idea of game theory is to model a situation as a game,where each player has a set of possible actions and a payoff associated with each action.The payoff depends on the actions of all players,and the goal of each player is to maximize their own payoff. Game theory analyzes these games to determine the optimal strategies for each player and the likely outcome of the game.There are two main types of games in game theory: zero-sum games and non-zero-sum games.In zero-sum games,the total payoff to all players is constant,so one player's gain is necessarily another player's loss.In non-zero-sum games,the total payoff can increase or decrease,and players can cooperate to achieve a better outcome for all.Game theory has applications in a wide range of fields, including economics,politics,psychology,and biology. It can be used to analyze phenomena such as oligopoly, auctions,voting,and animal behavior.Game theory has also been used to develop strategies for negotiation, conflict resolution,and decision-making under uncertainty.In summary,game theory is a framework for analyzing strategic interactions between rational actors.By modeling situations as games and analyzing the optimal strategies for each player,game theory provides insights into how people and organizations behave in complex situations.。
Theintroductionofgametheorylecturenotes11

Example 1: Prisoner’s Dileห้องสมุดไป่ตู้ma Again.
• Recall the Prisoner’s Dilemma game from last week, where player 1’s preferences depend on whether player 2 is nice or selfish.
– Talk is cheap: “Yeah, right”; “whatever”; “I could care less” are common. – The more credible signals involve costly actions, e.g. a college diploma,
C 1
D
2 CD 4,4 0,6
6,0 2,2
Player 2: Selfish
2 CD
C 1
D
6,6 2,4 4,2 0,0
Player 2: Nice
• Suppose the player 2 can costlessly signal to player 1 her action choice before Player 1 gets to choose. The signal is nonbinding, “cheap talk.” Player 1 observes this signal before making his own move, but still does not know what type of player 2 he is facing, selfish or nice.
gametheory2博弈论英文精品PPT课件

Review
Elimination
Nash Equilibrium
Summary
Games
Course topics:
• Games of complete and perfect information • Static Games (Nash Equilibrium) • Dynamic Games (Backward Induction)
6 / 43
Review
Elimination
Nash Equilibrium
Summary
Games
• Consider the following game:
• Two players • Each player chooses between two actions: A and B • Payoff for all outcomes is in the table below:
1
2
A
B
your ID keyword
A 50,50 0,200
B 200,0 80,80
1
2
A
B
A 50,50 0,200
B 200,0 80,80
7 / 43
Review
Elimination
Nash Equilibrium
Summary
Games
• Game Participation:
• you can win up to 200 CZK • send SMS with your action • phone numbers + IDs will be strictly protected • participant will be matched randomly in pairs, one pair will be
Game Theory Introduction

7
In this course we focus on Non-cooperative games:
◦ These games relate to situations where the players compete with each other and can neither enter into binding agreements (contracts) nor negotiate ◦ Players make decisions independently
8
In this lecture we focus on one-short games
◦ These games relate to situations where the players interact with each other only once
E.g. Two firms make a one-short decision about their prices in a particular market
13
A firm has a dominant strategy when
it has one action that WORKS BEST
(that maximises its payoff) NO MATTER what its rival does.
14
Firm B Advertise
Advertise
• Game theory is used to study how individuals and firms make their decisions when they need to take into account the actions of others. • The theory retains the assumptions of traditional microeconomics (of self interest and maximising behaviour).
01 An introduction of game theory解析

微观经济学的基石
1980 1981
劳伦斯-罗-克莱因 詹姆士-托宾
经济体制模型 金融市场分析
1995 1996
罗伯特-卢卡斯 威廉-维克瑞
理性预期与宏观经济 信息经济学
1982
1983 1984 1985 1986
乔治-斯蒂格勒
罗拉尔-德布鲁 理查德-约翰-斯通 弗兰科-莫迪利安尼 詹姆斯-布坎南
1
-7000 -10000 -16000 -10000 运输路线扩展形
博弈方的能力和理性
完全理性和有限理性
完全理性:有完美的分析判断能力和不会犯选择 行为的错误 有限理性:博弈方的判断选择能力有缺陷
个体理性和集体理性
个体理性:一个体利益最大为目标
集体理性:追求集体利益最大化 合作博弈:允许存在有约束力协议的博弈
1989 1990 1991 1992
特里夫-哈维默因 哈里-马科维茨、威廉-夏 普和默顿-米勒 罗纳德-考斯因 贝克尔
现代经济计量学指导原则 金融经济 经济制度结构和函数中交易费 用和产权 人类行为的分析
2004 2005 2006 2007
ห้องสมุดไป่ตู้
1993
罗伯特-福格尔和道格拉 斯-诺斯
经济理论和定量方法
什么是博弈?
下棋 game—— “下棋”、“玩牌”,赌博和其他许多智力游 戏在内的对抗性游戏、对抗性体育竞赛 “赌博式”实验:
请10个志愿者来参加,每人出赌资10元。 出资者在字条上写一个数字,该数字是0-100之间任何一
个整数。只有一个人是赢家。
游戏规则:谁写的数字最接近平均数的一半,谁就是赢家。
非合作博弈:不允许存在有约束力协议的博弈
第三节博弈论(GameTheory)

第三节博弈论(Game Theory)在国际关系的研究过程中,我们时常会运用到博弈论这样一个工具。
博弈论在英语中称之为“Game Theory”。
很多人会认为这是一种所谓的游戏理论,其实不然,我们不能把Games 与Fun 同论,而应该将博弈论称之为是一种“Strategic interaction”(策略性互动)。
“博弈”一词现如今在我们的生活中出现的已经很频繁,我们经常会听说各种类型的国家间博弈(如:中美博弈),“博弈论”已经深刻的影响了世界局势和地区局势的发展。
在iChange创设的危机联动体系中,博弈论将得到充分利用,代表也将有机会运用博弈论的知识来解决iChange 核心学术委员会设计的危机。
在这一节中,我将对博弈论进行一个初步的介绍与讨论,代表们可以从这一节中了解到博弈论的相关历史以及一些经典案例的剖析。
(请注意:博弈论的应用范围非常广泛,涵盖数学、经济学、生物学、计算机科学、国际关系、政治学及军事战略等多种学科,对博弈论案例的一些深入分析有时需要运用到高等数学知识,在本节中我们不会涉及较多的数学概念,仅会通过一些基本的数学分析和逻辑推理来方便理解将要讨论的经典博弈案例。
)3.1 从“叙利亚局势”到“零和博弈”在先前关于现实主义理论的讨论中,我们对国家间博弈已经有了初步的了解,那就是国家是有目的的行为体,他们总为了实现自己利益的最大化而选择对自己最有利的战略,其次,政治结果不仅仅只取决于一个国家的战略选择还取决于其他国家的战略选择,多种选择的互相作用,或者策略性互动会产生不同的结果。
因此,国家行为体在选择战略前会预判他国的战略。
在这样的条件下,让我们用一个简单的模型分析一下发生在2013年叙利亚局势1:叙利亚危机从2011年发展至今已经将进入第四个年头。
叙利亚危机从叙利亚政府军屠杀平民和儿童再到使用化学武器而骤然升级,以2013年8月底美国欲对叙利亚动武达到最为紧张的状态,同年9月中旬,叙利亚阿萨德政府以愿意向国际社会交出化学武器并同意立即加入《禁止化学武器公约》的态度而使得局势趋向缓和。
博弈论介绍 Introduction of Game Theory

但是,尽管政府当时无力制止这种事 情,公众也不必担心彩电价格会上涨。 这是因为,“彩电厂商自律联盟”只不 过是一种“囚徒困境”,彩电价格不会 上涨。在高峰会议之后不到二周,国内 彩电价格不是上涨而是一路下跌。这是 因为厂商们都有这样一种心态:无论其 他厂商是否降价,我自己降价是 有利于自己的市场份额扩 大的。
Binmore教授与其同事(特别是牛津大学的 Paul Klemperer教授)一道提出了一种相当别 致的拍卖机制设计——盎格鲁-荷兰式拍卖。 这实际上是一种融合了开放的英国式拍卖与 密封的荷兰式拍卖的优点的三阶段混合型拍 卖机制,它保留了英国式拍卖通过动态竞价 揭示私人信息的优势,同时借助密封拍卖特 有的不确定性增加对新进入者的吸引力。但 是,这种在经济学理论上具有潜在优势的新 机制的实际表现究竟如何呢?为了低成本地 检验这种新机制的绩效,同时也为了说服英 国电讯部门的官员们采纳这种复杂的机制, Binmore教授所领导的拍卖设计团队决定借助 实验经济学的方法,并且邀请官员们亲身参 与拍卖实验。
2、为什么要成立WTO? 为什么要成立WTO? WTO
英国3G 牌照拍卖案例 现执教于英国伦敦大学学院(UCL)的著名 博弈论大师、英国第三代(3G)移动通讯频 谱牌照拍卖市场设计团队的领导者Kenneth Binmore 教授 教授,接受英国政府的咨询委托并了 解了英国2G频谱市场的竞争格局以后,他和 同事们很快就意识到了拷贝美国联邦通讯委 员会(FCC)的英式拍卖机制的潜在危险性。 当时,英国2G拍卖市场有4个在位的电讯运营 商,正好与英国政府决定发放的牌照数量相 等。在这样的背景下,采用纯粹的英式拍卖 机制将无法吸引潜在的新运营商参与拍卖, 其结局很可能是由4个在位运营商按照低价瓜 分未来的3G移动通讯市场。
博弈论-Game Theory
4.Understand the application of game theory in economics, management, computer science and other disciplines through group cooperation and topical discussion.
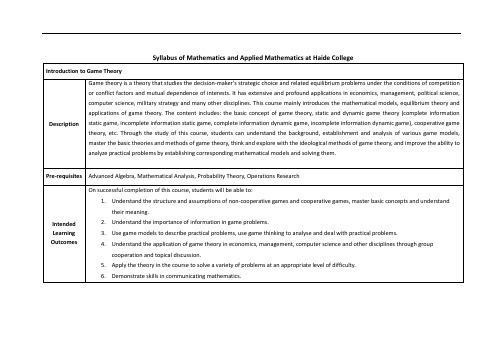
5.Apply the theory in the course to solve a variety of problems at an appropriate level of difficulty.
6.Demonstrate skills in communicating mathematics.
Pre-requisites
Advanced Algebra, Mathematical Analysis, Probability Theory, Operations Research
Intended Learning Outcomes
On successful completion of this course, students will be able to:
Syllabus ofMathematics and Applied Mathematicsat Haide College
Introduction to Game Theory
Description
Game theory is a theory that studies the decision-maker's strategic choice and related equilibrium problems under the conditions of competition or conflict factors and mutual dependence of interests. It has extensive and profound applications in economics, management, political science, computer science, military strategy and many other disciplines. This course mainly introduces the mathematical models, equilibrium theory and applications of game theory. The content includes: the basic concept of game theory, static and dynamic game theory (complete information static game, incomplete information static game, complete information dynamic game, incomplete information dynamic game), cooperative game theory, etc. Through the study of this course, students can understand the background, establishment and analysis of various game models, master the basic theories and methods of game theory, think and explore with the ideological methods of game theory, and improve the ability to analyze practical problems by establishing corresponding mathematical models and solving them.
博弈论的数学原理

博弈论的数学原理Game theory is a branch of mathematics that deals with the study of strategic decision making. It is used in various fields such as economics, political science, biology, and computer science. 博弈论是数学的一个分支,专门研究战略决策。
它被应用于经济学、政治科学、生物学和计算机科学等多个领域。
One of the fundamental concepts in game theory is the idea of a "game" as a set of players, strategies, and payoffs. Players are the participants in the game, each with their own set of possible actions. Strategies are the choices that players make, based on their goals and expectations. Payoffs are the outcomes of the game, which depend on the choices made by the players. 博弈论的一个基本概念是将“博弈”看作一个包含玩家、策略和回报的集合。
玩家是游戏的参与者,每个玩家都有一系列可能的行动。
策略是玩家根据自己的目标和期望所做出的选择。
回报是游戏的结果,取决于玩家的选择。
Game theory also considers the concept of Nash equilibrium, which occurs when each player's strategy is the best response to the strategies chosen by the other players. In other words, no player canbenefit by changing their strategy if the strategies of the other players remain unchanged. 博弈论还考虑了纳什均衡的概念,即当每个玩家的策略都是对其他玩家选择策略的最佳应对时出现。
game theory6 博弈论 英文

Introduction to Game Theory
Lecture 6
Disclaimer: this presentation is only a supporting material and is not sufficient to master the topics covered during the lecture. Study of relevant books is strongly recommended.
-3,-1 0,2
NE: (IN,A) (OUT,F) -amic Games
Centipede Game
Ultimatum Game
Summary
Subgame Perfect NE
• solves the problem with not sensible predictions • is found using Backward Induction
8 / 27
Review
Dynamic Games
Centipede Game
Ultimatum Game
Summary
• Another example:
4 / 27
Review
Dynamic Games
Centipede Game
Ultimatum Game
Summary
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Finitely Repeated Games
• Writingபைடு நூலகம்down the strategy space for repeated games is difficult, even if the game is repeated just 2 rounds. • Finite Repetition of a Game with a Unique Equilibrium
– Two types of repeated games: – Finitely repeated: the game is played for a finite and known number of rounds, for example, 2 rounds. – Infinitely or Indefinitely repeated: the game has no predetermined length; players act as though it will be played indefinitely, or it ends only with some probability
Repeated Games
Repeated Games
• With the exception of our discussion of bargaining, we have examined the effect of repetition on strategic behavior in games. • If a game is played repeatedly, players may behave differently than if the game is a one-shot game. (e.g. borrow friend’s car versus rent-a-car).
– Fortunately, we may be able to determine how to play a finitely repeated game by looking at the equilibrium or equilibrium in the one-shot or “stage game” version of the game. – For example, consider a 2x2 game with a unique equilibrium, e.g. the Prisoner’s Dilemma – Does the equilibrium change if this game is played just 2 rounds?
Finitely Repeated Games
• A repeated game is a special kind of game (in extensive or strategic form) where the same one-shot “stage” game is played over and over again. • A finitely repeated game is one in which the game is played a fixed and known number of times. • If the stage game has a unique Nash equilibrium, this equilibrium is the unique subgame perfect equilibrium of the finitely repeated game. • If the stage game has multiple equilibria, then there are many subgame perfect equilibria of the finitely repeated game. Some of these involve the play of strategies that are collectively more profitable for players than the oneshot stage game Nash equilibria.
Finitely Repeated Games
• A Game with a Unique Equilibrium Played Finitely Many Times Always Has the Same Subgame Perfect Equilibrium Outcome
– To see this, apply backward induction to the finitely repeated game to obtain the subgame perfect Nash equilibrium (spne). – In the last round, round 2, both players know that the game will not continue further. They will therefore both play their dominant strategy of Confess. – Knowing the results of round 2 are Confess, Confess, there are no benefits to playing Don’t Confess in round 1. Hence, both players play Confess in round 1 as well. – As long as there is a known, finite end, there will be no change in the equilibrium outcome of a game with a unique equilibrium. Also true for zero or constant sum games.
